ANSYS网格划分浅谈
ANSYS自由网格与映射网格解析

ANSYS自由网格与映射网格解析ANSYS软件平台提供了自由网格划分(Free)和映射网格划分(Mapped)两种策略。
自由网格划分用于空间自由曲面和复杂实体,采用三角形、四边形、四面体进行划分,通过网格数量、边长及曲率来控制网格的质量。
而映射划分则是用于曲线、曲面、实体的网格划分方法,可使用三角形、四边形、四面体、五面体和六面体进行划分,通过指定单元边长、网格数量等参数对网格进行严格控制。
映射划分只用于规则的几何图素,对于裁剪曲面或者空间自由曲面等复杂几何体则难以控制。
在进行一般的网格控制之前,用户应该考虑好,是使用自由网格划分还是映射网格划分。
自由网格划分对于单元没有特殊的限制,也没有指定的分布模式,而映射网格划分则不但对单元形状有所控制,而且对单元排布模式也有要求。
两者划分结果的差别如图2.52所示。
2.7.1 自由网格划分自由网格划分是自动化程度最高的网格划分技术之一,它可以在面上(平面、曲面)自动生成三角形或四边形网格,在体上自动生成四面体网格。
通常情况下,可利用ANSYS的智能尺寸控制技术(SMARTSIZE命令)来自动控制网格的大小和疏密分布,也可人工设置网格的大小(AESIZE、LESIZE、KESIZE、ESIZE等系列命令)并控制疏密分布,以及选择分网算法等(MOPT命令)。
对于复杂几何模型而言,这种分网方法省时省力,但缺点是单元数量通常会很大,计算效率降低。
同时,由于这种方法对于三维复杂模型只能生成四面体单元,为了获得较好的计算精度,建议采用二次四面体单元(92号体单元SOLID92)。
如果选用的是六面体单元,则此方法自动将六面体单元退化为阶次一致的四面体单元,因此,最好不要选用线性的六面体单元(没有中间节点,比如45号单元),因为该单元退化后为线性的四面体单元,具有过刚的刚度,计算精度较差;如果选用二次的六面体单元(比如95号单元),由于其是退化形式,节点数与其六面体原型单元一致,只是有多个节点在同一位置而已,因此,可以利用TCHG命令将模型中的退化形式的四面体单元变化为非退化的四面体单元,减少每个单元的节点数量,提高求解效率。
ANSYS网格划分方式总结

(1) 网格划分概念:实体模型是无法直接用来进行有限元计算得,故需对它进行网格划分以生成有限元模型。
有限元模型是实际结构和物质的数学表示方式。
在ANSYS中,能够用单元来对实体模型进行划分,以产生有限元模型,那个进程称作实体模型的网格化。
本质上对实体模型进行网格划分也确实是用一个个单元将实体模型划分成众多子区域。
这些子区域(单元),是有属性的,也确实是前面设置的单元属性。
另外也能够直接利用单元和节点生成有限元模型。
实体模型进行网格划分确实是用一个个单元将实体模型划分成众多子区域(单元)。
(2)什么缘故我选用plane55那个四边形单元后,仍能够把实体模型划分成三角形区域集合???答案:ansys为面模型的划分只提供三角形单元和四边形单元,为体单元只提供四面体单元和六面体单元。
不管你选择的单元是多少个节点,只若是2D单元,确信组成一个四边形或是三角形,绝对没有五、六边形等特殊形状。
网格划分也确实是用所选单元将实体模型划分成众多三角形单元和四边形子区域。
见下面的plane77/78/55都是节点数量大于4的,但都是通过各类插值或是归并的方式形成一个四边形或三角形。
因此不管你选择什么单元,只若是对面的划分,meshtool上的划分类型设置就只有tri和quad两种选择。
若是那个单元只组成三角形,例如plane35,那么不管你在meshtool上划分设置时tri 仍是quad,划分出的结果都是三角形。
因此在选用plane55单元,而划分的是采纳tri划分时,就会把两个点归并为一个点。
如上图的plane55,下面是plane单元的节点组成,可见每一个单元上都有两个节点标号相同,说明两个节点是重合的。
一样在采纳plane77 单元,进行tri划分时,会有三个节点重合。
那个地址再也不一一列出。
(3)如何利用在线帮忙:点击对话框中的help,例如你想了解plane35的相关属性,你能够点击上右图中的help,亦能够,点击help—>help topic弹出下面的对话康,点击索引按钮,输入你想查询的关键词。
ANSYSWorkbenchMesh网格划分(自己总结)

ANSYSWorkbenchMesh网格划分(自己总结)Workbench Mesh网格划分分析步骤网格划分工具平台就是为ANSYS软件的不同物理场和求解器提供相应的网格文件,Workbench中集成了很多网格划分软件/应用程序,有ICEM CFD,TGrid,CFX,GAMBIT,ANSYS Prep/Post等。
网格文件有两类:①有限元分析的结构网格:结构动力学分析,电磁场仿真,显示动力学分析;②计算流体力学分析的网格:用于ANSYS CFX,ANSYS FLUENT,Polyflow;这两类网格的具体要求如下:结构网格:①细化网格来捕捉关心部位的梯度,例如温度、应变能、应力能、位移等;②大部分可划分为四面体网格,但六面体单元仍然是首选;③有些显示有限元求解器需要六面体网格;④结构网格的四面体单元通常是二阶的;CFD网格:①细化网格来捕捉关心的梯度,例如速度、压力、温度等;②于是流体分析,网格的质量和平滑度对结果的精确度至关重要,这导致较大的网格数量,经常数百万的单元;③大部分可划分为四面体网格,但六面体单元仍然是首选,流体分析中,同样的求解精度,六面体节点数少于四面体网格的一半。
④CFD网格的四面体单元通常是一阶的一般而言,针对不同分析类型有不同的网格划分要求:①结构分析:使用高阶单元划分较为粗糙的网格;②CFD:好的,平滑过渡的网格,边界层转化;③显示动力学分析:需要均匀尺寸的网格;物理选项实体单元默认中结点关联中心缺省值Coarse Coarse Medium Coarse 平滑度过渡 Mechanical CFD Electromagnetic Explicit Kept Dropped Kept Dropped Medium Medium Medium Fine Fast Slow Fast Slow 注:上面的几项分别对应Advanced中的Element Midside Nodes,以及Sizeing中的Relevance Center,Smoothing,Transition。
ansys复杂几何模型的系列网格划分

二、 映射网格划分
映射网格划分是对规整模型的一种规整网格划分方法,其原始概念是:对于面,只能是四边形面,网格划分数需在对边上保持一致,形成的单元全部为四边形;对于体,只能是六面体,对应线和面的网格划分数保持一致;形成的单元全部为六面体。在ANSYS中,这些条件有了很大的放宽,包括:
1 面可以是三角形、四边形、或其它任意多边形。对于四边以上的多边形,必须用LCCAT命令将某些边联成一条边,以使得对于网格划分而言,仍然是三角形或四边形;或者用AMAP命令定义3到4个顶点(程序自动将两个顶点之间的所有线段联成一条)来进行映射划分。
复杂几何模型的系列网格划分
众所周知,对于有限元分析来说,网格划分是其中最关键的一个步骤,网格划分的好坏直接影响到解算的精度和速度。在ANSYS中,大家知道,网格划分有三、划分网格。在这里,我们仅对网格划分这个步骤所涉及到的一些问题,尤其是与复杂模型相关的一些问题作简要阐述。
子结构(也称超单元)也是一种解决大型问题的有效手段,并且在ANSYS中,超单元可以用于诸如各种非线性以及装配件之间的接触分析等,有效地降低大型模型的求解规模。
巧妙地利用结构的对称性对实际工作也大有帮助,对于常规的结构和载荷都是轴对称或平面对称的问题,毫无疑问应该利用其对称性,对于一些特殊情况,也可以加以利用,比如:如果结构轴对称而载荷非轴对称,则可用ANSYS专门用于处理此类问题的25、83和61号单元;对于由多个部件构成装配件,如果其每个零件都满足平面对称性,但各对称平面又不是同一个的情况下,则可用多个对称面来处理模型(或至少可用此方法来减少建模工作量:各零件只需处理一半的模型然后拷贝或映射即可生成总体模型)。
2 面上对边的网格划分数可以不同,但有一些限制条件。
3 面上可以形成全三角形的映射网格。
ANSYS网格划分浅谈

ANSYS网格划分浅谈在本学期,我们学习了CAX这门课程。
通过对这一门课程8周的学习使我对本模块的认识和了解有了一种新的看法。
在老师的认真教育和带领下把我们引入了一个新的领域。
在CAX这个领域中包括CAD CAM CAE CAPP等的各项技术,这些技术都是将理论知识和计算机辅助集合在一起的新兴工业工程技术,是要将理论和实践的学科。
在下面我主要将我这段学习期间对于ANSYS软件的学习中关于有限元网格划分的一些认识和经验做个报告总结。
1、ANSYS网格划分简述ANSYS软件是融结构、流体、电场、磁场、声场分析于一体的大型通用有限元分析软件。
由世界上最大的有限元分析软件公司之一的美国ANSYS开发,它能与多数CAD软件接口,实现数据的共享和交换,如Pro/Engineer, NASTRAN, Alogor, I-DEAS, AutoCAD等,是现代产品设计中的高级CAD工具之一。
ANSYS有限元网格划分是进行数值模拟分析至关重要的一步,它直接影响着后续数值计算分析结果的精确性。
在划分网格前,用户首先需要对模型中将要用到的单元属性进行定义。
在ANSYS中,大家知道,网格划分有三个步骤:定义单元属性(包括实常数)、在几何模型上定义网格属性、划分网格。
单元属性主要包括:单元类型、实常数、材料常数。
典型的实常数包括:厚度、横截面面积、高度、梁的惯性矩等。
材料属性包括:弹性模量、泊松比、密度、热膨胀系数等。
ANSYS网格划分的指导思想是首先进行总体模型规划,包括物理模型的构造、单元类型的选择、网格密度的确定等多方面的内容。
在网格划分和初步求解时,做到先简单后复杂,先粗后精,2D单元和3D单元合理搭配使用。
为提高求解的效率要充分利用重复与对称等特征,由于工程结构一般具有重复对称或轴对称、镜象对称等特点,采用子结构或对称模型可以提高求解的效率和精度。
利用轴对称或子结构时要注意场合,在进行模态分析、屈曲分析整体求解时,则应采用整体模型,同时选择合理的起点并设置合理的坐标系,可以提高求解的精度和效率,例如,轴对称场合多采用柱坐标系。
ansys如何划分网格

自由划分网格( 自由划分网格(Free meshing)和映射网格划分(Mapped )和映射网格划分( meshing)。 )。 • 自由划分网格主要用于划分边界形状不规则的区域,它 自由划分网格主要用于划分边界形状不规则的区域, 生成的网格相互之间呈不规则的排列。 生成的网格相互之间呈不规则的排列。常用于复杂形状 的边界选择自由划分网格。 的边界选择自由划分网格。自由网格缺点是分析精度不 够高。 够高。 • 映射网格划分用于单元形状有限制,并要符合一定的网 映射网格划分用于单元形状有限制, 格模式。映射面网格只包含四边形或三角形单元, 格模式。映射面网格只包含四边形或三角形单元,映射 体网格只包含六面体单元。 体网格只包含六面体单元。映射网格的特点是具有规则 的形状,单元明显地成行排列。 的形状,单元明显地成行排列。
January 30, 2001 Inventory #001441 11-2
多媒体教程
划分网格专题讲座 划分网格专题讲座 划分网格专题讲座 划分网格专题讲座 划分网格专题讲座 划分网格专题讲座 划分网格专题讲座 划分网格专题讲座 划分网格专题讲座 划分网格专题讲座 划分网格专题讲座 划分网格专题讲座 划分网格专题讲座 划分网格专题讲座 ANSYS 划分网格专题讲座 ANSYS 划分网格专题讲座
• 映射网格划分要求面或者体有规则的形状,即必须满足一定的准则。 映射网格划分要求面或者体有规则的形状,即必须满足一定的准则。 同时SmartSizing不支持映射网格划分。 不支持映射网格划分。 同时 不支持映射网格划分 • 面映射网格包括全部是四边形单元或者全部是三角形单元。面接受映 面映射网格包括全部是四边形单元或者全部是三角形单元。 射网格划分,必须满足以下条件: 射网格划分,必须满足以下条件: • ① 该面必须是三条边或四条边。 该面必须是三条边或四条边。 • ② 如果是四条边,对边必须划分为相同数目的单元,或者是划分一 如果是四条边,对边必须划分为相同数目的单元, 过渡型网格。 过渡型网格。 • ③ 如果是三条边,则各边设置的单元划分数必须为偶数且相等,否 如果是三条边,则各边设置的单元划分数必须为偶数且相等, 软件会自动决定单元划分数。 则ANSYS软件会自动决定单元划分数。 软件会自动决定单元划分数 • ④ 网格划分必须设置为映射网格。 网格划分必须设置为映射网格。 • 如果一个面多于四条边,则不能直接用映射网格划分,但可以使某些 如果一个面多于四条边,则不能直接用映射网格划分, 线相连接,使总线数减小到4条之后再用映射网格划分 条之后再用映射网格划分。 线相连接,使总线数减小到 条之后再用映射网格划分。
ANSYS网格划分详细介绍

ANSYS网格划分详细介绍众所周知,对于有限元分析来说,网格划分是其中最关键的一个步骤,网格划分的好坏直接影响到解算的精度和速度。
在ANSYS中,大家知道,网格划分有三个步骤:定义单元属性(包括实常数)、在几何模型上定义网格属性、划分网格。
在这里,我们仅对网格划分这个步骤所涉及到的一些问题,尤其是与复杂模型相关的一些问题作简要阐述。
一、自由网格划分自由网格划分是自动化程度最高的网格划分技术之一,它在面上(平面、曲面)可以自动生成三角形或四边形网格,在体上自动生成四面体网格。
通常情况下,可利用ANSYS 的智能尺寸控制技术(SMARTSIZE命令)来自动控制网格的大小和疏密分布,也可进行人工设置网格的大小(AESIZE、LESIZE、KESIZE、ESIZE等系列命令)并控制疏密分布以及选择分网算法等(MOPT命令)。
对于复杂几何模型而言,这种分网方法省时省力,但缺点是单元数量通常会很大,计算效率降低。
同时,由于这种方法对于三维复杂模型只能生成四面体单元,为了获得较好的计算精度,建议采用二次四面体单元(92号单元)。
如果选用的是六面体单元,则此方法自动将六面体单元退化为阶次一致的四面体单元,因此,最好不要选用线性的六面体单元(没有中间节点,比如45号单元),因为该单元退化后为线性的四面体单元,具有过刚的刚度,计算精度较差;如果选用二次的六面体单元(比如95号单元),由于其是退化形式,节点数与其六面体原型单元一致,只是有多个节点在同一位置而已,因此,可以利用TCHG命令将模型中的退化形式的四面体单元变化为非退化的四面体单元,减少每个单元的节点数量,提高求解效率。
在有些情况下,必须要用六面体单元的退化形式来进行自由网格划分,比如,在进行混合网格划分(后面详述)时,只有用六面体单元才能形成金字塔过渡单元。
对于计算流体力学和考虑集肤效应的电磁场分析而言,自由网格划分中的层网格功能(由LESIZE命令的LAYER1和LAYER2域控制)是非常有用的。
ANSYS的建模方法和网格划分

ANSYS的建模方法和网格划分ANSYS是一种广泛应用于工程领域的数值分析软件,它的建模方法和网格划分是进行仿真分析的关键步骤。
本文将介绍的基本原理和常用技术。
一、建模方法1.1 几何建模在ANSYS中,几何建模是将实际物体转化为计算机能够识别和处理的几何外形,是进行仿真分析的基础。
几何建模可以通过直接绘制几何外形、导入CAD模型或利用几何操作进行创建。
直接绘制几何外形是最简易的建模方法,可以通过ANSYS的几何绘制工具直接绘制点、线、面、体等几何外形。
这种方法适用于几何外形较简易的状况。
导入CAD模型是将已有的CAD文件导入到ANSYS中进行分析。
导入的CAD文件可以是各种格式,如IGES、STEP、SAT等。
通过导入CAD模型,可以便利地利用已有的CAD设计进行分析。
几何操作是通过几何操作工具进行模型的创建和修改。
几何操作工具包括旋转、缩放、挤压、倒角等操作。
利用几何操作可以对模型进行分外灵活的设计和修改。
1.2 材料属性定义在进行仿真分析前,需要定义材料的物理性质和力学性能。
在ANSYS中,可以通过在建模环境中定义材料属性的方法进行。
定义材料属性包括确定材料的密度、弹性模量、泊松比、热膨胀系数等物理性质。
这些属性对于仿真分析的准确性和可靠性起到重要作用。
定义材料的力学性能包括确定材料的材料模型和本构干系,如线弹性、非线弹性、塑性、强化塑性等。
这些性能可以依据实际需要进行选择和确定。
1.3 界面条件设置界面条件设置是定义与外部环境或其他系统之间的边界条件和加载条件。
在ANSYS中,可以通过多种方式进行界面条件设置。
界面条件设置包括确定材料与外界的热传导、流体传输、气固反应、接触等边界条件。
这些条件对于模拟实际工程问题的边界反应至关重要。
加载条件设置包括定义外加力、固定边界、压力加载、温度加载等力学和热力加载条件。
通过加载条件设置,可以模拟实际工程中的载荷和边界约束。
二、网格划分网格划分是ANSYS进行仿真分析的关键步骤。
ANSYS网格划分技巧

【分享】复杂几何模型的系列网格划分技术众所周知,对于有限元分析来说,网格划分是其中最关键的一个步骤,网格划分的好坏直接影响到解算的精度和速度。
在ANSYS中,大家知道,网格划分有三个步骤:定义单元属性(包括实常数)、在几何模型上定义网格属性、划分网格。
在这里,我们仅对网格划分这个步骤所涉及到的一些问题,尤其是与复杂模型相关的一些问题作简要阐述。
一、自由网格划分自由网格划分是自动化程度最高的网格划分技术之一,它在面上(平面、曲面)可以自动生成三角形或四边形网格,在体上自动生成四面体网格。
通常情况下,可利用ANS YS的智能尺寸控制技术(SMARTS IZE命令)来自动控制网格的大小和疏密分布,也可进行人工设置网格的大小(AESIZE、LESIZE、KESIZE、ESIZE等系列命令)并控制疏密分布以及选择分网算法等(MOPT命令)。
对于复杂几何模型而言,这种分网方法省时省力,但缺点是单元数量通常会很大,计算效率降低。
同时,由于这种方法对于三维复杂模型只能生成四面体单元,为了获得较好的计算精度,建议采用二次四面体单元(92号单元)。
如果选用的是六面体单元,则此方法自动将六面体单元退化为阶次一致的四面体单元,因此,最好不要选用线性的六面体单元(没有中间节点,比如45号单元),因为该单元退化后为线性的四面体单元,具有过刚的刚度,计算精度较差;如果选用二次的六面体单元(比如95号单元),由于其是退化形式,节点数与其六面体原型单元一致,只是有多个节点在同一位置而已,因此,可以利用TC HG命令将模型中的退化形式的四面体单元变化为非退化的四面体单元,减少每个单元的节点数量,提高求解效率。
在有些情况下,必须要用六面体单元的退化形式来进行自由网格划分,比如,在进行混合网格划分(后面详述)时,只有用六面体单元才能形成金字塔过渡单元。
ANSYSworkbench网格划分初学者整理by-syy
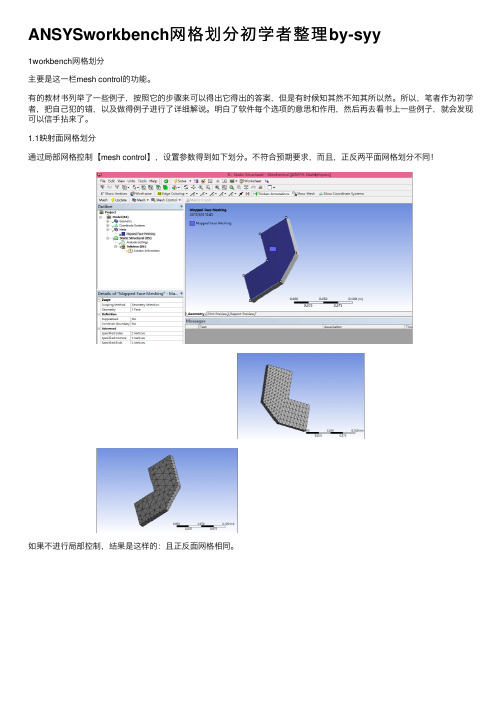
ANSYSworkbench⽹格划分初学者整理by-syy1workbench⽹格划分主要是这⼀栏mesh control的功能。
有的教材书列举了⼀些例⼦,按照它的步骤来可以得出它得出的答案,但是有时候知其然不知其所以然。
所以,笔者作为初学者,把⾃⼰犯的错,以及做得例⼦进⾏了详细解说。
明⽩了软件每个选项的意思和作⽤,然后再去看书上⼀些例⼦,就会发现可以信⼿拈来了。
1.1映射⾯⽹格划分通过局部⽹格控制【mesh control】,设置参数得到如下划分。
不符合预期要求,⽽且,正反两平⾯⽹格划分不同!如果不进⾏局部控制,结果是这样的:且正反⾯⽹格相同。
要使正反⾯都相同必须两⾯都设置局部控制:其中sides、corners、ends的设置将决定该⾯上⽹格的划分。
如下设置三点side:其余四点为end得到:正反⼀样。
另⼀种设置⽅式:⼀个side,内陷的那个是corner,其余五个是end得到结果:这些点的设置是什么意思?1.2Sizing通过选择“体”(注意直接选容易选成了⾯),然后开始body sizing中的sphere of influence上图根据实际实体⼤⼩设置sphere radius(半径)和element size很重要。
Element size如果⼤了,则body sizing设置与否都⽆作⽤。
这个的意思是,将包括在球体内的实体以element size⼤⼩来细分。
结果:1.3建⽴局部坐标这个累死了。
到处找资料也没有说得清楚的!!⾸先,教程是这样说的:Apply那⾥怎么选中这个局部坐标系的原点?⼀定要记得先选geometry selection!!然后取点局部坐标系有什么⽤呢?在⽹格细分⾥这么⽤:虽然结果奇奇怪怪的,但⾄少也说明了,在这两个地⽅,⽹格确实分的很细!其实不⽤建⽴局部坐标也可以。
在geometry那⼀栏不要选中整个体,选择某个点,得到vertax sizing就可以设置了!1.4⽹格偏置Bias type的功能从以下两张对⽐图就可以看出来!上图⽤了参数2的偏置,下图没⽤,特别注意behivor:hard的作⽤。
Ansys网格划分浅析

Ansys网格划分浅析摘要:合适的网格划分对ansys有限元分析结果有至关重要的作用。
本文就如何划分网格展开一系列讨论,对网格划分的步骤和方法进行论述和比较。
最终说明网格划分综合应用和技巧。
关键词:ansys 网格划分有限元引言:ansys有限元分析软件是世界上最大的有限元分析软件公司之一的美国ansys公司研发的产品,主要用于结构,流体,电场,磁场和声场等物理场独立或耦合分析,功能强大应用广泛,是一个便于学习和使用的优秀有限元分析程序。
[1]随着有限元理论和计算机硬件的发展,ansys作为一款功能强大的有限元分析软件在土木工程领域特别是结构分析过程中有广泛应用。
网格划分是ansys分析过程中必不可少的步骤,对分析结果的好坏影响很大。
因此对有限元网格划分技术的研究是非常必要的。
1 ansys网格划分步骤创建几何模型后,得到分析目标的几何模型。
然而几何模型不能用于计算分析,必须将其划分网格生成单元,节点从而得到有限元分析模型。
2 ansys网格划分方法传统的网格划分方法主要有自由网格划分,映射网格划分和扫略网格划分。
自由网格划分一般对单元形状没有限制,对规则或不规则的模型都可以进行网格划分。
自由网格划分是自动化程度最高的网格划分技术之一。
[2]通常情况下,能通过ansys的智能尺寸控制技术来自动控制网格大小和疏密程度,也可以人工设置网格。
自由网格划分虽然省时省力,但缺点是单元数量通常会很大,计算效率会降低。
映射网格划分是一种半自动的网格生成方法。
这种方法的缺点是必须将需要划分的区域先划分为所要求的简单区域,这是一个复杂的过程,需要的时间和精力较多,而且各个映射之间的网格密度相互影响很大。
对于3D几何体,还可以采用扫略网格划分。
扫略网格划分就是从源面(如边界面)网格扫略整个体生成体单元。
[3]通常情况下,对于复杂几何实体,经过简单切分处理就能自动形成规则六面体网格。
它比映射网格划分更加灵活。
从以上方法可以看出每一种划分方式都各有利弊,在实际的操作中,为了提高计算精度和减少计算时间,我们可以尝试以上方法的混合使用。
ANSYS有限元分析中的网格划分

ANSYS有限元分析中的网格划分有限元分析中的网格划分好坏直接关系到模型计算的准确性。
本文简述了网格划分应用的基本理论,并以ANSYS限元分析中的网格划分为实例对象,详细讲述了网格划分基本理论及其在工程中的实际应用,具有一定的指导意义。
作者: 张洪才关键字: CAE ANSYS 网格划分有限元1 引言ANSYS有限元网格划分是进行数值模拟分析至关重要的一步,它直接影响着后续数值计算分析结果的精确性。
网格划分涉及单元的形状及其拓扑类型、单元类型、网格生成器的选择、网格的密度、单元的编号以及几何体素。
从几何表达上讲,梁和杆是相同的,从物理和数值求解上讲则是有区别的。
同理,平面应力和平面应变情况设计的单元求解方程也不相同。
在有限元数值求解中,单元的等效节点力、刚度矩阵、质量矩阵等均用数值积分生成,连续体单元以及壳、板、梁单元的面内均采用高斯(Gauss)积分,而壳、板、梁单元的厚度方向采用辛普生(Simpson)积分。
辛普生积分点的间隔是一定的,沿厚度分成奇数积分点。
由于不同单元的刚度矩阵不同,采用数值积分的求解方式不同,因此实际应用中,一定要采用合理的单元来模拟求解。
2 ANSYS网格划分的指导思想ANSYS网格划分的指导思想是首先进行总体模型规划,包括物理模型的构造、单元类型的选择、网格密度的确定等多方面的内容。
在网格划分和初步求解时,做到先简单后复杂,先粗后精,2D单元和3D单元合理搭配使用。
为提高求解的效率要充分利用重复与对称等特征,由于工程结构一般具有重复对称或轴对称、镜象对称等特点,采用子结构或对称模型可以提高求解的效率和精度。
利用轴对称或子结构时要注意场合,如在进行模态分析、屈曲分析整体求解时,则应采用整体模型,同时选择合理的起点并设置合理的坐标系,可以提高求解的精度和效率,例如,轴对称场合多采用柱坐标系。
有限元分析的精度和效率与单元的密度和几何形状有着密切的关系,按照相应的误差准则和网格疏密程度,避免网格的畸形。
ANSYS网格划分要点

ANSYS网格划分要点ANSYS网格划分要点在划分网格前,用户首先需要对模型中将要用到的单元属性进行定义。
单元属性主要包括:单元类型、实常数、材料常数。
典型的实常数包括:厚度、横截面面积、高度、梁的惯性矩等。
材料属性包括:弹性模量、泊松比、密度、热膨胀系数等。
ANSYS为用户提供了两种网格划分类型:自由和映射所谓“自由”,体现在没有特定的准则,对单元形状无限制,生成的单元不规则,基本适用于所有的模型。
自由网格生成的内部节点位置比较随意,用户无法控制。
操作方式是打开Mesh Tool工具条上的Free选项。
所用单元形状依赖于是格划分。
对于面,自由网格可以只由四边形单元组成,也可以只由三角形单元组成,或两者混合。
对于体,自由网格一般限制为四面体单元。
映射网格划分要求面或体形状满足一定规则,且映射面网格只包括三角形单元或四边形单元,映射体网格只包括六面体单元,它生成的单元形状比较规则,适用于形状规则的面和体。
对于映射网格划分,生成的单元尺寸依赖于当前DSIZE、ESIZE、KESIZE、LESIZE和ASIZE的设置。
Smartsize不能用于映射网格划分。
当使用硬点时,不支持映射网格划分。
面映射网格划分:包括全部是四边形单元或者全部是三角形单元。
此面必须由3或4条线围成,在对边上必须有相等的单元划分数。
如果此面由3条线围成,则三条边上的单元划分数必须相等且必须是偶数。
对边网格数之差相等,或者一对对边网格数相等,另一对网格数之差为偶数,也可以进行映射网格划分。
如果一个面由多于4条的线围成,则它不能直接采用映射网格进行划分,然而,为了将总的线数减少到4,其中的某些线可以被加起来(add)或连接起来(concatenated,一种进行网格划分时的操作)。
代替进行连接操作(concatenation),可以用拾取一个面的3个或4个角点来进行面映射网格划分,这种简化的映射网格划分方法将两个关键点之间的多条线内部连接起来。
Ansys_workbench网格划分相关

Ansys_workbench网格划分相关Mesh 网格划分方法—四面体(Patch Conforming和Patch Independent)、扫掠、自动、多区、CFX划分1.四面体网格优点—适用于任意体、快速自动生成、关键区域使用曲度和近似尺寸功能细化网格、可使用边界层膨胀细化实体边界。
缺点—在近似网格密度下,单元和节点数高于六面体网格、不可能使网格在一个方向排列、由于几何和单元性能的非均质性,不适用于薄实体或环形体常用参数—最小和最大尺寸、面和体的尺寸、Advanced尺寸功能、增长比(Growth—对CFD逐渐变化,避免突变)、平滑(smooth—有助于获得更加均匀尺寸的网格)、统计学(Statistics)、Mesh MetricsPathch Conforming—默认考虑几何面和体生成表面网格,会考虑小的边和面,然后基于TGRID Tetra算法由表面网格生成体网格。
作用—多体部件可混合使用Patch Conforming四面体和扫掠方法共同生成网格,可联合Pinch Control 功能有助于移除短边,基于最小尺寸具有内在网格缺陷Patch Independent—基于ICEM CFD T etra算法,先生成体网格并映射到表面产生表面网格。
如果没有载荷或命名,就不考虑面和边界(顶点和边),此法容许质量差的CAD几何。
作用—可修补碎面、短边、差的面差数,如果面上没有载荷或者命名,就不考虑面和边了,直接将网格跟其它面作一体划。
如果有命名则要单独划分该区域网格体膨胀—直接选择要膨胀的面,就可使面向内径向生成边界层面膨胀—选择要膨胀的面,在选择面的边,就可以向面内膨胀2.扫掠网格体须是可扫掠的、膨胀可产生纯六面体或棱柱网格,手动设置源和目标面,通常一对一,薄壁模型(Src/Trg选择Manual Thin)可自动划分多个面,在厚度方向上划分多个单元。
3.自动化分网格—应该划分成四面体,其与扫掠取决于体是否可扫掠,同一部件的体有一致网格,可程序化控制膨胀4.多区扫掠网格划分—基于ICEM CFD六面体模块,多区划分完后,可给多区添加膨胀5.CFX网格—使用四面体和棱柱网格对循环对称或旋转对称几何划分网格,不考虑网格尺寸或没有网格应用尺寸可使用CFX网格全局网格控制1.Physics Preference 物理设置包括力学(Mechanical)、CFD、电磁(Electromagnetic)、显示(Explicit)分析2.结构分析—使用哪个高阶单元划分较为粗糙的网格。
ANSYS有限元网格划分浅析

ANSYS有限元网格划分浅析有限元分析作为现代工程设计领域中不行或缺的工具,旨在通过对复杂结构进行数值模拟,猜测其力学行为和性能。
而有限元网格划分作为有限元分析的前提条件,直接影响着分析结果的准确性和计算效率。
本文将对ANSYS有限元网格划分的原理和技巧进行浅析,并探讨其在工程设计中的应用。
一、有限元网格划分的基本原理有限元网格划分是将连续物体离散化成有限个离散单元,构建有限元模型的过程。
其原理主要涉及两个方面:几何划分和节点生成。
1.1 几何划分几何划分是将实际结构划分为有限单元的过程,主要包括自动划分和手动划分两种方式。
自动几何划分是ANSYS通过对实际结构进行自动网格划分的功能,依据用户指定的几何参数进行自适应划分,最大程度地保持结构的准确外形。
这种划分方法具有快速、高效的优点,特殊适用于复杂结构的网格划分。
手动几何划分是由用户通过手动操作构建网格划分,使用ANSYS提供的几何划分工具进行几何实体的划分和组合,依据结构外形和特点进行网格划分的方式。
这种划分方法需要用户具备一定的几何划分技巧和阅历,能够对结构进行合理的划分。
1.2 节点生成节点生成是指依据坐标系和几何划分,自动生成有限元网格中的节点坐标。
在划分完成后,节点将依据有限元单元的外形和尺寸进行生成。
节点生成过程中主要包括节点编号、坐标值和自由度的定义。
节点编号是为每个节点赐予唯一的标识,便利在后续分析中进行节点相关的计算;坐标值是节点在几何坐标系中的坐标值,用于描述节点在空间中的详尽位置;自由度的定义是为节点定义相应的位移或位移的导数,用于后续求解分析中的节点位移计算。
二、ANSYS有限元网格划分的技巧2.1 网格密度的控制网格密度是指网格单元数目与结构体积之比,其决定了有限元模型对结构细部行为的描述能力。
合理控制网格密度能够提高分析结果的准确性和计算效率。
一般来说,细节丰富的区域应接受较小的网格单元,而结构较简易的区域可以接受较大的网格单元。
基于ANSYS软件的有限元法网格划分技术浅析

关键 词 :N有 限 单 元 法 分 析 软 件 , 以进 行 结 NY 可
构线性分析和热分析 , 以及对流体 、 电力 、 电磁场及碰撞等领域 的分析 。 广泛应用于机 械 、 电机 、 土木 、 电子及航空等领域。它将 有限元分析 、 计算机图形学和优化技术相结合 , 已成为解决现代 工 程学 问题 的有 力 工具 。 随着数值分析方法 的逐步完善和计算机运算速度 的飞速发 展, 整个计算 系统用于求解运算 的时间越来越少 , 而数据准备 和 运算结果 的表现问题却 日益突 出。划分网格是建立有 限元模 型 的一个重要环节 ,也是利用 A S S软件进行各种分析的基础 , NY 它要求考虑的问题较 多, 需要 的工作量大 , 对不 同的模型对象所 采 用 的方 法 也 不 一样 。重 要 的 是 网 格划 分 的 准确 度 和 精 度 对 后 处 理及 分 析 结 果将 产 生 直 接 影 响 。 因此 , 有 限元 网格 划分 的技 对 术研究成为必要 。本文结合工程实例, 就如何合理地进行 网格划 分 作一 浅 析 。 2 有 限 单 元 法 的基 本 思 想 有 限单元法 是处 理复杂工程 问题 的一种数 值计算方法 , 它 将 一个 形状 复杂的连续体分解成 为有 限个 形状 简单 的单元 , 通 过 离 散 化 , 求 解 连 续 体 应 力 、 变 、 度 等 问 题 转 换 为 求 解 有 把 应 温 限个 单 元 的 问题 。在 工 程 或 物 理 问题 的数 学 模 型 ( 本 变 量 、 基 基 本方程 、 求解域和边界条件 ) 确定 以后 , 限元法作 为对其进行 有 分析 的数值计算方法 的基本思想可简单概括为如下 3 : 点 21 一个表示结构或连续体 的求解 域离散为若 干个子域 .将 ( 单元 )并通过他们边界上的节点相互 连接为一个组合体。 , 22 .用每个单 元内所假设的近似 函数来分 片表 示全求解 域 内待 求 解 的未 知 场 变 量 。 而每 个 单 元 内的 近 似 函 数 由未 知 场 函 数( 或其导数 ) 在单元各个节点上 的数值和与其对应的插值函数 来 表 达 。 由于 在 联 结 相邻 单 元 的节 点 上 ,场 函 数 具 有 相 同 的 数 值, 因而 将 它们 作 为数 值 求 解 的 基本 未 知量 。这 样 一 来 , 解 原 求 待求场函数 的无穷多 自由度 问题转换为求解场函数节点值的有 限 自由度 问 题 。 23通过和原 问题数学模 型( . 例如基本方程 、 边界条件等 ) 等 效的变分原理或加权余量法 , 建立求解基本未知量( 场函数节 点
ANSYS网格划分详细介绍

ANSYS网格划分详细介绍ANSYS网格划分详细介绍众所周知,对于有限元分析来说,网格划分是其中最关键的一个步骤,网格划分的好坏直接影响到解算的精度和速度。
在ANSYS中,大家知道,网格划分有三个步骤:定义单元属性(包括实常数)、在几何模型上定义网格属性、划分网格。
在这里,我们仅对网格划分这个步骤所涉及到的一些问题,尤其是与复杂模型相关的一些问题作简要阐述。
一、自由网格划分自由网格划分是自动化程度最高的网格划分技术之一,它在面上(平面、曲面)可以自动生成三角形或四边形网格,在体上自动生成四面体网格。
通常情况下,可利用ANSYS 的智能尺寸控制技术(SMARTSIZE命令)来自动控制网格的大小和疏密分布,也可进行人工设置网格的大小(AESIZE、LESIZE、KESIZE、ESIZE等系列命令)并控制疏密分布以及选择分网算法等(MOPT命令)。
对于复杂几何模型而言,这种分网方法省时省力,但缺点是单元数量通常会很大,计算效率降低。
同时,由于这种方法对于三维复杂模型只能生成四面体单元,为了获得较好的计算精度,建议采用二次四面体单元(92号单元)。
如果选用的是六面体单元,则此方法自动将六面体单元退化为阶次一致的四面体单元,因此,最好不要选用线性的六面体单元(没有中间节点,比如45号单元),因为该单元退化后为线性的四面体单元,具有过刚的刚度,计算精度较差;如果选用二次的六面体单元(比如95号单元),由于其是退化形式,节点数与其六面体原型单元一致,只是有多个节点在同一位置而已,因此,可以利用TCHG命令将模型中的退化形式的四面体单元变化为非退化的四面体单元,减少每个单元的节点数量,提高求解效率。
在有些情况下,必须要用六面体单元的退化形式来进行自由网格划分,比如,在进行混合网格划分(后面详述)时,只有用六面体单元才能形成金字塔过渡单元。
对于计算流体力学和考虑集肤效应的电磁场分析而言,自由网格划分中的层网格功能(由LESIZE命令的LAYER1和LAYER2域控制)是非常有用的。
ANSYS-网格划分方法总结

(1) 网格划分定义:实体模型是无法直接用来进行有限元计算得,故需对它进行网格划分以生成有限元模型。
有限元模型是实际结构和物质的数学表示方法。
在ANSYS中,可以用单元来对实体模型进行划分,以产生有限元模型,这个过程称作实体模型的网格化。
本质上对实体模型进行网格划分也就是用一个个单元将实体模型划分成众多子区域。
这些子区域(单元),是有属性的,也就是前面设置的单元属性。
另外也可以直接利用单元和节点生成有限元模型。
实体模型进行网格划分就是用一个个单元将实体模型划分成众多子区域(单元)。
(2)为什么我选用plane55这个四边形单元后,仍可以把实体模型划分成三角形区域集合???答案:ansys为面模型的划分只提供三角形单元和四边形单元,为体单元只提供四面体单元和六面体单元。
不管你选择的单元是多少个节点,只要是2D单元,肯定构成一个四边形或者是三角形,绝对没有五、六边形等特殊形状。
网格划分也就是用所选单元将实体模型划分成众多三角形单元和四边形子区域。
见下面的plane77/78/55都是节点数目大于4的,但都是通过各种插值或者是合并的方式形成一个四边形或者三角形。
所以不管你选择什么单元,只要是对面的划分,meshtool上的划分类型设置就只有tri和quad两种选择。
如果这个单元只构成三角形,例如plane35,则无论你在meshtool上划分设置时tri 还是quad,划分出的结果都是三角形。
所以在选用plane55单元,而划分的是采用tri划分时,就会把两个点合并为一个点。
如上图的plane55,下面是plane单元的节点组成,可见每一个单元上都有两个节点标号相同,表明两个节点是重合的。
同样在采用plane77 单元,进行tri划分时,会有三个节点重合。
这里不再一一列出。
(3)如何使用在线帮助:点击对话框中的help,例如你想了解plane35的相关属性,你可以点击上右图中的help,亦可以,点击help—>help topic弹出下面的对话康,点击索引按钮,输入你想查询的关键词。
浅谈ANSOFT_MAXWELL网格剖分

仅作探讨,欢迎拍砖!曾经看到师兄一篇大作,将ANSYS和ANSOFT做过南慕容北乔峰的类比,真是崇拜得五体投地,一塌糊涂,屁滚尿流,接二连三,不三不四。
个人比较欣赏乔峰大侠,遂,改投ANSOFT门下。
想当年ANSYS的APDL用得忒熟无比,想想就此放弃,于心不忍,于是重操APDL。
近日,在论坛上看到有人对MAXWELL的网格剖分大发牢骚,甚至还恶言相向,GG我实在看不下去了,于是有此文。
就从网格剖分谈开去。
开篇之前,对比下面两幅图。
图1ANSYS映射网格剖分(APDL如下)/clear/filname,joe_yan,1/prep7et,1,solid117block,0,10,0,10,0,10mshkey,1mshape,0,3Daesize,all,1vmesh,allsave图2ANSOFT MAXWELL网格剖分(自适应剖分)对比图1、2明眼人一看就知道显然是图1的网格划分优良。
于是乎,俗人皆言:“MAXWELL 网格剖分垃圾~~!!”掌嘴!!我要说。
先声明,本人不是MAXWELL的死忠!个人更偏向于ANSYS的APDL,一看到那黑乎乎一块的经典界面,我就澎湃。
即便如此,本人还是坚持MAXWELL的网格剖分很强大。
MAXWELL有两种网格剖分形式,其一,如上图2所示的自适应剖分;其二,手动剖分。
其中手动剖分又分为二,其一,选择剖分;其二,内部剖分。
其中,选择剖分又分为二,其一,基于长度;其二,基于表层深度。
为何一个网格剖分要纠结如斯?我要说,因为MAXWELL 人性化。
比如说,为何手动剖分又要分为表层剖分和内部剖分,因为,表层剖分主要是针对集肤效应而言,大家都知道,集肤效应主要集中在导磁体表面,可是如何做到从内到外将网格剖分从疏到密的剖分呢?我们可以采用MAXWELL提供的表层剖分功能。
至此有人又要叫嚣了:“诶,你看,明明ANSYS网格剖分要比ANSOFT网格剖分来的均匀而细致。
”我要说,对!!爸特!!!针对不同分析,网格也呈现出不一样的规律性。
ANSYS网格划分总结大全

有限元分析中的网格划分好坏直接关系到模型计算的准确性。
本文简述了网格划分应用的基本理论,并以ANSYS限元分析中的网格划分为实例对象,详细讲述了网格划分基本理论及其在工程中的实际应用,具有一定的指导意义。
1 引言ANSYS有限元网格划分是进行数值模拟分析至关重要的一步,它直接影响着后续数值计算分析结果的精确性。
网格划分涉及单元的形状及其拓扑类型、单元类型、网格生成器的选择、网格的密度、单元的编号以及几何体素。
从几何表达上讲,梁和杆是相同的,从物理和数值求解上讲则是有区别的。
同理,平面应力和平面应变情况设计的单元求解方程也不相同。
在有限元数值求解中,单元的等效节点力、刚度矩阵、质量矩阵等均用数值积分生成,连续体单元以及壳、板、梁单元的面内均采用高斯(Gauss)积分,而壳、板、梁单元的厚度方向采用辛普生(Simpson)积分。
辛普生积分点的间隔是一定的,沿厚度分成奇数积分点。
由于不同单元的刚度矩阵不同,采用数值积分的求解方式不同,因此实际应用中,一定要采用合理的单元来模拟求解。
2 ANSYS网格划分的指导思想ANSYS网格划分的指导思想是首先进行总体模型规划,包括物理模型的构造、单元类型的选择、网格密度的确定等多方面的内容。
在网格划分和初步求解时,做到先简单后复杂,先粗后精,2D单元和3D单元合理搭配使用。
为提高求解的效率要充分利用重复与对称等特征,由于工程结构一般具有重复对称或轴对称、镜象对称等特点,采用子结构或对称模型可以提高求解的效率和精度。
利用轴对称或子结构时要注意场合,如在进行模态分析、屈曲分析整体求解时,则应采用整体模型,同时选择合理的起点并设置合理的坐标系,可以提高求解的精度和效率,例如,轴对称场合多采用柱坐标系。
有限元分析的精度和效率与单元的密度和几何形状有着密切的关系,按照相应的误差准则和网格疏密程度,避免网格的畸形。
在网格重划分过程中常采用曲率控制、单元尺寸与数量控制、穿透控制等控制准则。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
ANSYS网格划分浅谈在本学期,我们学习了CAX这门课程。
通过对这一门课程8周的学习使我对本模块的认识和了解有了一种新的看法。
在老师的认真教育和带领下把我们引入了一个新的领域。
在CAX这个领域中包括CAD CAM CAE CAPP等的各项技术,这些技术都是将理论知识和计算机辅助集合在一起的新兴工业工程技术,是要将理论和实践的学科。
在下面我主要将我这段学习期间对于ANSYS软件的学习中关于有限元网格划分的一些认识和经验做个报告总结。
1、ANSYS网格划分简述ANSYS软件是融结构、流体、电场、磁场、声场分析于一体的大型通用有限元分析软件。
由世界上最大的有限元分析软件公司之一的美国ANSYS开发,它能与多数CAD软件接口,实现数据的共享和交换,如Pro/Engineer, NASTRAN, Alogor, I-DEAS, AutoCAD等,是现代产品设计中的高级CAD工具之一。
ANSYS有限元网格划分是进行数值模拟分析至关重要的一步,它直接影响着后续数值计算分析结果的精确性。
在划分网格前,用户首先需要对模型中将要用到的单元属性进行定义。
在ANSYS中,大家知道,网格划分有三个步骤:定义单元属性(包括实常数)、在几何模型上定义网格属性、划分网格。
单元属性主要包括:单元类型、实常数、材料常数。
典型的实常数包括:厚度、横截面面积、高度、梁的惯性矩等。
材料属性包括:弹性模量、泊松比、密度、热膨胀系数等。
ANSYS网格划分的指导思想是首先进行总体模型规划,包括物理模型的构造、单元类型的选择、网格密度的确定等多方面的内容。
在网格划分和初步求解时,做到先简单后复杂,先粗后精,2D单元和3D单元合理搭配使用。
为提高求解的效率要充分利用重复与对称等特征,由于工程结构一般具有重复对称或轴对称、镜象对称等特点,采用子结构或对称模型可以提高求解的效率和精度。
利用轴对称或子结构时要注意场合,在进行模态分析、屈曲分析整体求解时,则应采用整体模型,同时选择合理的起点并设置合理的坐标系,可以提高求解的精度和效率,例如,轴对称场合多采用柱坐标系。
有限元分析的精度和效率与单元的密度和几何形状有着密切的关系,按照相应的误差准则和网格疏密程度,避免网格的畸形。
在网格重划分过程中常采用曲率控制、单元尺寸与数量控制、穿透控制等控制准则。
在选用单元时要注意剪力自锁、沙漏和网格扭曲、不可压缩材料的体积自锁等问题。
ANSYS软件平台提供了网格映射划分和自由适应划分的策略。
映射划分用于曲线、曲面、实体的网格划分方法,可使用三角形、四边形、四面体、五面体和六面体,通过指定单元边长、网格数量等参数对网格进行严格控制,映射划分只用于规则的几何图素,对于裁剪曲面或者空间自由曲面等复杂几何体则难以控制。
自由网格划分用于空间自由曲面和复杂实体,采用三角形、四边形、四面体进行划分,采用网格数量、边长及曲率来控制网格的质量。
2、ANSYS网格划分基本原则网格划分涉及单元的形状及其拓扑类型、单元类型、网格生成器的选择、网格的密度、单元的编号以及几何体素。
从几何表达上讲,梁和杆是相同的,从物理和数值求解上讲则是有区别的。
同理,平面应力和平面应变情况设计的单元求解方程也不相同。
在有限元数值求解中,单元的等效节点力、刚度矩阵、质量矩阵等均用数值积分生成,连续体单元以及壳、板、梁单元的面内均采用高斯(Gauss)积分,而壳、板、梁单元的厚度方向采用辛普生(Simpson)积分。
辛普生积分点的间隔是一定的,沿厚度分成奇数积分点。
由于不同单元的刚度矩阵不同,采用数值积分的求解方式不同,因此实际应用中,一定要采用合理的单元来模拟求解。
2.1 网格数量网格数量的多少将影响计算结果的精度和计算规模的大小。
一般来讲,网格数量增加,计算精度会有所提高,但同时计算规模也会增加,所以在确定网格数量时应权衡两个因数综合考虑。
当网格数量增加到一定程度后,再继续增加网格时精度提高甚微,而计算时间却有大幅度增加。
所以应注意增加网格的经济性。
实际应用时可以比较两种网格划分的计算结果,如果两次计算结果相差较大,可以继续增加网格,相反则停止计算。
在决定网格数量时应考虑分析数据的类型。
在静力分析时,如果仅仅是计算结构的变形,网格数量可以少一些。
如果需要计算应力,则在精度要求相同的情况下应取相对较多的网格。
同样在响应计算中,计算应力响应所取的网格数应比计算位移响应多。
在计算结构固有动力特性时,若仅仅是计算少数低阶模态,可以选择较少的网格,如果计算的模态阶次较高,则应选择较多的网格。
在热分析中,结构内部的温度梯度不大,不需要大量的内部单元,这时可划分较少的网格。
2.2 网格疏密网格疏密是指在结构不同部位采用大小不同的网格,这是为了适应计算数据的分布特点。
在计算数据变化梯度较大的部位(如应力集中处),为了较好地反映数据变化规律,需要采用比较密集的网格。
而在计算数据变化梯度较小的部位,为减小模型规模,则应划分相对稀疏的网格。
这样,整个结构便表现出疏密不同的网格划分形式。
下面通过实例给出网格疏密对计算精度的影响。
网格数量应增加到结构的关键部位,在次要部位增加网格是不必要的,也是不经济的。
划分疏密不同的网格主要用于应力分析(包括静应力和动应力),而计算固有特性时则趋于采用较均匀的钢格形式。
这是因为固有频率和振型主要取决于结构质量分布和刚度分布,不存在类似应力集中的现象,采用均匀网格可使结构刚度矩阵和质量矩阵的元素不致相差太大,可减小数值计算误差。
同样,在结构温度场计算中也趋于采用均匀网格。
2.3 单元阶次许多单元都具有线性、二次和三次等形式,其中二次和三次形式的单元称为高阶单元。
选用高阶单元可提高计算精度,因为高阶单元的曲线或曲面边界能够更好地逼近结构的曲线和曲面边界,且高次插值函数可更高精度地逼近复杂场函数,所以当结构形状不规则、应力分布或变形很复杂时可以选用高阶单元。
但高阶单元的节点数较多,在网格数量相同的情况下由高阶单元组成的模型规模要大得多,因此在使用时应权衡考虑计算精度和时间。
增加网格数量和单元阶次都可以提高计算精度。
因此在精度一定的情况下,用高阶单元离散结构时应选择适当的网格数量,太多的网格并不能明显提高计算精度,反而会使计算时间大大增加。
为了兼顾计算精度和计算量,同一结构可以采用不同阶次的单元,即精度要求高的重要部位用高阶单元,精度要求低的次要部位用低阶单元。
不同阶次单元之间或采用特殊的过渡单元连接,或采用多点约束等式连接。
2.4 网格质量网格质量是指网格几何形状的合理性。
质量好坏将影响计算精度。
质量太差的网格甚至会中止计算。
直观上看,网格各边或各个内角相差不大、网格面不过分扭曲、边节点位于边界等份点附近的网格质量较好。
网格质量可用细长比、锥度比、内角、翘曲量、拉伸值、边节点位置偏差等指标度量。
单元的质量和数量对求解结果和求解过程影响较大,如果结构单元全部由等边三角形、正方形、正四面体、立方六面体等单元构成,则求解精度可接近实际值,但由于这种理想情况在实际工程结构中很难做到。
因此根据模型的不同特征,设计不同形状种类的网格,有助于改善网格的质量和求解精度。
单元质量评价一般可采用以下几个指标:(1)单元的边长比、面积比或体积比以正三角形、正四面体、正六面体为参考基准。
理想单元的边长比为1,可接受单元的边长比的范围线性单元长宽比小于3,二次单元小于10。
对于同形态的单元,线性单元对边长比的敏感性较高阶单元高,非线性比线性分析更敏感。
(2)扭曲度:单元面内的扭转和面外的翘曲程度。
(3)疏密过渡:网格的疏密主要表现为应力梯度方向和横向过渡情况,应力集中的情况应妥善处理,而对于分析影响较小的局部特征应分析其情况,如外圆角的影响比内圆角的影响小的多。
(4)节点编号排布:节点编号对于求解过程中的总体刚度矩阵的元素分布、分析耗时、内存及空间有一定的影响。
合理的节点、单元编号有助于利用刚度矩阵对称、带状分布、稀疏矩阵等方法提高求解效率,同时要注意消除重复的节点和单元。
2.5 位移协调性位移协调是指单元上的力和力矩能够通过节点传递相邻单元。
为保证位移协调,一个单元的节点必须同时也是相邻单元的节点,而不应是内点或边界点。
相邻单元的共有节点具有相同的自由度性质。
否则,单元之间须用多点约束等式或约束单元进行约束处理。
3、ANSYS 网格划分的几种方法在ANSYS中,网格划分有三个步骤:定义单元属性(包括实常数)、在几何模型上定义网格属性、划分网格。
3.1、自由网格划分自由网格划分是自动化程度最高的网格划分技术之一,它在面上(平面、曲面)可以自动生成三角形或四边形网格,在体上自动生成四面体网格。
通常情况下,可利用ANSYS的智能尺寸控制技术(SMARTSIZE命令)来自动控制网格的大小和疏密分布,也可进行人工设置网格的大小(AESIZE、LESIZE、 KESIZE、ESIZE 等系列命令)并控制疏密分布以及选择分网算法等(MOPT命令)。
对于复杂几何模型而言,这种分网方法省时省力,但缺点是单元数量通常会很大,计算效率降低。
同时,由于这种方法对于三维复杂模型只能生成四面体单元,为了获得较好的计算精度,建议采用二次四面体单元。
如果选用的是六面体单元,则此方法自动将六面体单元退化为阶次一致的四面体单元,因此,最好不要选用线性的六面体单元,因为该单元退化后为线性的四面体单元,具有过刚的刚度,计算精度较差;如果选用二次的六面体单元,由于其是退化形式,节点数与其六面体原型单元一致,只是有多个节点在同一位置而已,因此,可以利用TCHG命令将模型中的退化形式的四面体单元变化为非退化的四面体单元,减少每个单元的节点数量,提高求解效率。
3.2、映射网格划分映射网格划分是对规整模型的一种规整网格划分方法,其原始概念是:对于面,只能是四边形面,网格划分数需在对边上保持一致,形成的单元全部为四边形;对于体,只能是六面体,对应线和面的网格划分数保持一致;形成的单元全部为六面体。
在ANSYS中,这些条件有了很大的放宽,包括:面可以是三角形、四边形、或其它任意多边形。
对于四边以上的多边形,必须用LCCAT命令将某些边联成一条边,以使得对于网格划分而言,仍然是三角形或四边形;或者用AMAP 命令定义3到4个顶点(程序自动将两个顶点之间的所有线段联成一条)来进行映射划分。
如果一个面要进行映射网格划分的话,这个面必须满足以下几个条件:(1)、这个面只能由三条或四条边组成或者是个实心圆面。
(2)、这个面的相对边必须划分成同样的等份。
(3)、如果这个面是三角形的话,那么三条边也必须使用相等的等份进行划分。
(4)、网格划分值必须被设置成mapped(通过MSHKEY)。
这个值导致所有网格划分都使用三角形或四边形,具体取决于其单元类型或者单元的形状属性值。
