实验三 薄壁圆筒弯扭组合主应力测定
薄壁圆管弯扭组合变形应变测定实验

图2
图3
图4
图5
1
四.实验内容及方法
1.指定点的主应力大小和方向的测定 受弯扭组合变形作用的薄壁圆管其表面各点处于平面应力状态,用应变花测出三个方
向的线应变, 然后运用应变-应力换算关系求出主应力的大小和方向。由于本实验用的是 45 应变花,若测得应变ε-45、ε0、ε45,则主应力大小的计算公式为
(N)
读数应变
∆P
(N)
弯矩
M
εMd
(με)
∆εMd
(με)
扭矩
Mn
εnd
∆εnd
(με)
(με)
剪力 Q
εQd
(με)
∆εQd
(με)
Δε d均 (με)
应力 σ
( ) MN m2
σM
τn
τQ
4
七.思考题
1.测定由弯矩、剪力、扭矩所引起的应变,还有哪些接线方法,请画出测量电桥的接
法。
2.本实验中能否用二轴 45 应变花替代三轴 45 应变花来确定主应力的大小和方向?
为什么?
表3
被测点
主应力
A
B
C
D
( ) σ MN
1
m2
( ) σ MN
3
m2
φ0 (度)
表1 读数应变
载荷 P ∆P
(N) (N)
应变仪测量通道上,重复步骤 3、4、5。
8.将薄壁圆管上A、C两点-45 、45 方向的应变片按图 5(c)全桥测量接线方法接至
应变仪测量通道上,重复步骤 3、4、5。
六.实验结果的处理
1.计算 A、B、C、D 四点的主应力大小和方向。
2.计算Ⅰ-Ⅰ截面上分别由弯矩、剪力、扭矩所引起的应力。
薄壁圆筒弯扭组合主应力测定

实验三薄壁圆筒弯扭组合主应力测定一、试验目的1.测定薄壁圆筒弯扭组合变形时指定点的主应力和主方向,并与理论计算值比较。
2.学习用应变花测定构件某点主应力和主方向的方法。
二、设备和仪器1、多功能力学实验台2、YE2538A 程控静态应变仪三、试样薄壁圆筒(见图)左端固定,籍固定在圆筒右端的水平杆加载。
在截面I-I 处粘贴有应变片m、n、a、b、c、d、e 和f,在截面II-II 处粘贴有应变片g 和h,其中应变片m 和n 粘贴于圆筒最高点和最低点,其方位均沿圆柱面母线。
其余各应变片粘贴的位置如图11-1a 和图11-1b 所示,它们的方位均与圆周线成45°或-45°角,展开图如图(11-1c)所示。
圆筒用不锈钢1Cr18Ni9Ti 制造,材料弹性模量E = 202 Gpa ,泊松比μ=0.28 ,圆筒外径D=40mm,内径d=36.40mm。
在图中的k 是三轴应变花,它的三个敏感栅与圆筒母线的夹角分别是0°、60°和120°(见图)。
四、实验原理据平面应变分析理论知,若某点任意三个方向的线应变已知,就能计算出该点的主应变和主方向,从而计算出主应力。
因此测量某点的主应力和主方向时,必须在测点布置三枚应变片。
通常将三个敏感栅粘贴在同一基底上,称为应变花。
常用的应变花有两种:一种是三敏感栅轴线互成120°角(如图13-1 所示),称等角应变花。
另一种是两敏感栅轴线互相垂直,另一敏感栅轴线在它们的分角线上,称直角应变花。
我们采用的是前者。
由应变分析和应力分析理论知,测得ε0 o、ε60 o 和ε120 o 后,可按下列公式计算主应力和主方向:五、实验步骤1.将弯扭组合实验装置旋转到位(有锥销定位)并固定,将加载用附件安装好。
2.力传感器接线、设置参数。
载荷限值设置350N3.将应变花的三个敏感栅分别接入所选通道(通常0°、60°、120°三敏感栅依次选1、2、3 通道),按多点1/4 桥公共补偿法接线。
薄壁圆筒在弯曲和扭转组合变形下的主应力测试实验

薄壁圆筒在弯曲和扭转组合变形下的主应力测试实验
实验目的: (1)了解在弯曲和扭转组合变形情况下的测试方法
(2)测定薄壁圆筒试件在弯曲和扭转组合受力情况下,试件表面某
点的正应力,并与理论值比较。
实验仪器: XL3418材料力学多功能试验台;测力仪;静力电阻应变仪。
实验原理: 薄壁圆筒受弯曲和扭转组合作用,使圆筒的m 点处于平面应力状态如图1所示。
在m 点单元体上有弯矩引起来的正应力x σ,和由扭矩引起来的剪应力n τ。
主应力是一对拉应力1σ和一对压应力3σ。
理论值计算:
132x σσσ=±
022n
x
tg τασ-=
x z M
W σ= 4
3132z D d W D π⎡⎤⎛⎫=-⎢⎥ ⎪⎝⎭⎢⎥⎣⎦ M P L =∆⋅
n T
T
W τ= 43116T D d W D π⎡⎤⎛⎫=-⎢⎥ ⎪⎝⎭⎢⎥⎣⎦
T P a =∆⋅
实验值计算:
°
°
145453()2(1)E εεσσμ-+=- °°°°°45-450045-45()2(2)
tg εεαεεε-=
--
图1 圆筒m 点的应力状况。
薄壁圆筒弯扭组合实验中弯曲切应力的测量

\: : :
j
~
初始 荷载
每 缴 荷 裁
5 N 0
20 0 N
图 1 b 截面 示意 图 ()
图 2 应变 花布 置及编 号
最终荷载(等级加载) 4
80 5 N
①课题来源 : 深圳 大 学 实 验 室 与 设 备 管 理 研 究 基 金 资 金 助 项 目 。
中国科 教创新 导刊 C i d c t n In v t n H r l hn E u a i n o a l e ad a o o
为 了 更 好 地 培 养 工 科 专 业 学 生 的 实 践 能 力 与 创 新 精 神 , 校 对 实 验 教 学 内 我 容 进 行 了 改 革 , 幅 度 的 增 加 了 “ 索 大 探
性 、 计 性 和 综 合 性 ” 验 项 目在 实 验 教 设 实
1 薄壁 圆筒弯 扭组合 实验设备
分 别 代 表 与 扭 矩 对 应 当载 荷 增 量 =2 0 时 , ( 4 计 0N 按 式 ) 算 出 的 岛 =1 . e , 按 等 量 逐 级 加 载 方 8 # 而 2 法在 实验 装置上测 得一组实验 数据如表 2
所示 。 实 验 数 据 的 线 性 关 系 很 好 平 均 增 量 为
3 实验 误差分析
经 过 仔 细 分 析 研 究 , 们 认 为 造 成 实 我 验 较 大 误 差 的 原 因 是 应 变 计 技 术 原 因 所
图 1( 圆筒弯 扭组 合 实验 装置 图 a) 表 1 实验参 数
圆筒 内径 3 .rm 56 a
圆 筒外 径
臂 度
4 mm 4l
其 中心 位 置 的影 响和 敏 感 棚 横 向效 应 的 影
3-7 薄壁圆筒受内压、弯、扭组合载荷时

图 1-8 应变花
图 3-22 应变花
轴线互成 120°角(如图 3-22 所示),称等角应变花。另一种是两敏感栅轴线互相垂直,
另一敏感栅轴线在它们的分角线上,称 45 度应变花。我们采用的是前者。由应变分析和应
力分析理论知,测得 0 、 60 和 120 后,可按以下公式计算主应力和主方向。
主应力
圆筒用不锈钢 1Cr18Ni9Ti 制造,材料弹性模量 E 202GPa ,泊松比 0.28 ,圆筒
外径 D=40mm,内径 d=36.40mm。
支架 放气栓 注油接头
k
h
270
260
250
ⅡⅠ am
240
fb
300
gd e
nc
Ⅱ
Ⅰ 水平线
水平线
(a)
Ⅱ-Ⅱ
Ⅰ-Ⅰ
a
mb 45o
F
h
gf
eo
45
12
E(0 60 120 3(1 )
)
2E 3(1 )
(0 60 )2 (60 120 )2 ( 120 0 )2
(3-29)
主方向
tan
20
3( 60 120 ) 2 0 60 120
(3-30)
五、实验要求与数据处理
内力素测定。
各内力和内压应分别测定。将事先拟定的接桥方案交老师检查,以检查正确与否及方
aPT
aT aFS
a
a
aM =aP N
+
aM
aPT
a
薄壁圆管弯扭组合变形测定实验报告数据

薄壁圆管弯扭组合变形测定实验报告数据薄壁圆管弯扭组合变形测定实验被广泛应用于管件的研究与开发。
组合变形可以有效的预测管件组合连接的性能、寿命以及机械特性,是非常重要的。
本文针对薄壁圆管弯扭组合变形的测定实验进行了报告,主要详细介绍了实际测试参数以及激活试验的步骤与测试数据,并且对测试结果进行了分析。
首先,说明实际进行测试的薄壁圆管弯扭组合参数,主要包括外径为20mm、壁厚为2mm的圆管,外面覆盖紧固件。
紧固件包括M20×2.5螺旋紧固件和M20×3.5普通螺栓。
实验中弯曲圆管以一定的频率和扭曲力使其变形,以模拟实际服役过程中的变形。
接着,介绍实验的步骤与测试数据。
测试开始前,圆管的径向和轴向变形记录在表1中。
实验共分为两个步骤:步骤一进行弯曲变形,步骤二进行扭曲变形。
在弯曲变形的实验中,测试频率为1.5Hz,载荷范围为0.4~0.6N,变形量从0~5度逐步增加,每次增加1度,循环7次,变形量从5~-5度,每次减少1度,循环7次,最终累计变形量为50度,每次变形变形量都得到记录,详细记录见表2。
在扭曲变形的实验中,测试频率为1.5Hz,载荷范围为0.4~0.6N,变形量从0~45度逐步增加,每次增加5度,循环9次,变形量从45~-45度,每次减少5度,循环9次,最终累计变形量为90度,每次变形变形量都得到记录,详细记录见表3。
最后,对薄壁圆管弯扭组合变形测试结果进行分析。
分析以薄壁圆管变形量和比重曲率为主要指标,记录在表4中,可以看出薄壁圆管变形量在弯曲测试中最大值到达了19度,在扭曲测试中最大值到达了39度;而比重曲率也随之变化,其最大值达到了0.000632。
根据结果,可以得出薄壁圆管在变形受力过程中,曲率变化是连续的,变形量变化也是有序的,比重曲率也有一定的变化,说明管件在变形受力过程中,能够得到较好的适应性,管件的结构强度也可以较好的满足实际应用的需求。
总的来说,本文对薄壁圆管弯扭组合变形测定实验进行了报告,在实验中,使用了M20×2.5螺旋紧固件和M20×3.5普通螺栓,变形量最大达到了19度和39度,比重曲率最大达到了0.000632。
主应力的测量

b
γ xy εx −εy
(3-2)
a
对于各向同性材料,主应变 ε 1 、 ε 3 和主应力
p
a = 250
D=55
d D
σ 1 、 σ 3 方向一致。应用广义胡克定律,即可确定主应力为:
b = 260
d=51
σ1 =
E (ε 1 + µε 3 ) 1− µ 2
σ3 =
E (ε 3 + µε 1 ) (3-3) 1− µ 2
0 0 0 0 0
0
(3-5)
将式(3-25)代入式(3-2) ,可得主应变和主方向为:
ε 1 ε − 45 + ε 45 2 (ε − 45 − ε 0 ) 2 + (ε 45 − ε 0 ) 2 ± = ε3 2 2
0 0 0 0 0 0
tan 2a o =
ε 45 − ε − 45 2ε 0 − ε − 45 − ε 45
弯扭组合变形的主应力测定
一、实验目的 (1)测定薄壁圆筒表面上一点的主应力。 (2)测定薄壁圆筒所受的弯矩和扭矩。 (3)掌握通过桥路的不同连接方案消扭测弯、消弯测扭的方法。 二、实验设备 (1)多功能组合实验台 (2)静态数字电阻应变仪 (3)游标卡尺和钢尺 三、实验原理和方法 1.测定主应力大小和方向 薄壁圆筒弯扭组合变形受力简图,截面为被测位置,由应力状态理论分析可知,薄壁圆筒表 面上的 A 、B 点处于平面应力状态。 若再被测位置 x 、y 平面内, 沿 x 、y 方向的线应变 ε x 、
T=
Eε n π ( D 4 − d 4 ) (1 + µ ) 16 D
(1)测量试件尺寸、加力臂的长度和测点距力臂的距离。 (2)将薄壁圆筒上的应变片按不同测试要求接入电阻应变仪组成不同的测量电桥,并调整 好所用仪器设备。完成以下两项参数的测定: ①主应力大小、方向测定:将 A 、 B 两点的应变片按半桥接线,并按公共温度补偿法组成 测量线路,进行半桥测量。 ②测定弯矩 M 、扭矩 T :根据上述接法组桥,或自行设计组桥方案。 (3)实验加载。用均匀慢速加载至初荷载 Fo ,记录各点应变仪的初读数,然后分级等增量 加载,每增加一级荷载,依次记录各点应变片的应变读数,直至最终荷载。每项实验至少重 复两次。 (4)完成一项测试后,重新组桥测试,重复步骤(2)和(3) 。 (5)完成全部实验后,卸除载荷,关闭电源,拆线整理仪器设备,清理现场。 注意: 注意:实验装置中, 实验装置中,圆筒的管壁很薄, 圆筒的管壁很薄,为避免损坏装置, 为避免损坏装置,注意切勿超载, 注意切勿超载,不能用力扳动圆 筒的自由端和力臂。 筒的自由端和力臂 。 五、实 验 结 果 处 理 (1)根据所测应变值计算主应力 σ 1 和 σ 3 及主应力方向 a o ,并与理论值进行比较,计算 相对误差。 (2)根据各种组桥方式测出的应变,计算出弯矩和扭矩。并与理论值比较,计算相对误差 值。 (3)分析误差产生的主要原因。 (4)按规定写出实验报告。
薄壁圆筒内力素及主应力测定实验

薄壁圆筒内力素及主应力测定实验摘要:关键词:桥、内力、弯矩、扭矩实验值与理论值存在误差的原因主要是由于实验过程中的累积误差及实际实验条件与理想环境不一致所致,另外应变花的布置位置和布置方向有偏差对实验结果也有一定的影响。
摘要:在实际测量过程中,电阻应变片的贴片位置、栅长大小以及横向效应均会对测量的精确度产生影响。
该文从以上3个方面对《材料力学》课程的电测综合性实验——圆筒的弯扭组合实验中,利用全桥接法测量弯曲切应变的误差原因进行了全面分析,指出测量误差主要是由于电阻应变花的敏感栅中心偏离中性轴所致。
关键词:弯扭组合;弯曲切应变;电阻应变花;测量误差。
电阻应变测量技术(简称电测法)是用电阻应变片测量构件表面的应变,根据应力与应变之间的关系,确定构件表面应力状态的一种实验应力分析方法,具有电阻应变片的尺寸小、重量轻、安装方便、一般不会干扰构件的应力状态、测量灵敏度与精度高等优点,是工程实验应力分析中应用最广泛和最有效的手段之一。
在教学过程中我们发现,主应力、与弯矩对应的正应变以及与扭矩对应的扭转切应变的测量结果均与理论值接近,误差很小,而与剪力对应的弯曲切应变的测量结果与理论值相比误差较大,高达58%左右。
圆筒的弯扭组合实验装置如图1所示,圆筒的外径D=40 am,内径d=34 mm,圆筒的材料为铝合金,其E=70 GPa,移=0.33。
I—I横截面处的外表面中性轴上的A、c点和上下边缘的B、D点作为测量点,在每个测量点粘贴1个450一3直角应变花。
圆筒在测量点位置的展开图以及各敏感栅的编号如图2所示,其中每个应变花中间的敏感栅沿圆筒的轴线方向。
为了观察实验数据的线性情况,实验采用等量逐级加载方式,载荷增量为△F=100N。
与剪力对应的弯曲切应变利用A、C两点的450和一450 4个敏感栅(即敏感栅1、3、7、9)组成如图3所示的全桥电路进行测量,该桥路可消除扭转切应变而仅保留弯曲切应变,且扩大了输出值,提高了实验的测量精度。
薄壁圆管弯扭组合变形测定实验报告数据

薄壁圆管弯扭组合变形测定实验报告数据随着发展,薄壁圆管已经成为多个领域的重要元件,并可用于满足许多不同的需求。
以薄壁圆管为研究对象的变形实验的结果,可以深入了解圆管的变形特性,为薄壁圆管应用和研究作出科学可靠的贡献。
本文研究薄壁圆管弯扭组合变形测定实验。
实验准备实验准备包括选择正确的圆管,准备测试条件,准备测试仪器,以及安装测试仪器。
研究圆管的钢材为45#,表面阳极氧化处理。
圆管的外径为(50,60,70,80)mm,壁厚分别为(2,3,4)mm。
为了准确测量圆管弯扭变形,我们使用三轴张计测试仪器,安装在圆管上。
实验过程实验过程主要包括:首先设置实验条件(包括规定的外径、壁厚、弯曲角度等),将圆管垂直固定在实验台上,然后控制电动千分尺在给定的偏转角度范围内轻轻地弯曲圆管,并使用三轴张力计测量圆管的弯曲角度。
实验分别在温度20°C、 30°C和40°C下进行,每种温度下进行3次实验,对每种实验条件重复3次,以准确测定圆管在各种温度和角度条件下的变形情况。
实验结果实验结果表明:随着温度的升高,圆管的弯曲角度也随之增加,最大角度可达26°。
薄壁圆管的变形角度与外径、壁厚以及弯曲角度密切相关,当外径和壁厚不变时,圆管的变形角度越大,变形角度越大。
此外,圆管弯曲变形也与材料本身的性能有关,钢材的强度越高,圆管的变形角度越小。
结论薄壁圆管的弯扭变形实验表明:外径、壁厚与圆管弯曲角度的变化有直接的关系;随着温度的升高,圆管的变形角度增大;另外,材料性能也会影响圆管的变形性能,钢材强度越高,圆管变形角度越小。
本实验为薄壁圆管的研究开发和实际应用提供了科学可靠的参考,也为更深入相关研究提供了依据。
薄壁圆筒在弯扭组合变形主应力测定报告

薄壁圆筒在弯扭组合变形主应力测定报告一、概述薄壁圆筒是工程中常见的一种结构形式,其在使用过程中受到的弯曲和扭转载荷往往同时存在,因此对其在弯扭组合变形条件下的主应力进行准确测定具有重要意义。
本报告旨在对薄壁圆筒在弯扭组合变形下的主应力进行测定,并提供权威的数据支持。
二、实验目的1.对薄壁圆筒在弯曲和扭转载荷下的主应力进行测定;2.掌握薄壁圆筒在弯扭组合变形条件下的变形规律;3.提供准确可靠的数据支持,为工程设计提供参考依据。
三、实验原理在弯曲和扭转载荷共同作用下,薄壁圆筒内部会产生主应力和主剪应力。
其主应力由弯曲应力和扭转应力共同决定,根据相关理论原理,可以通过测定薄壁圆筒表面的变形情况,推导出其在弯扭组合变形条件下的主应力。
四、实验装置和材料1.薄壁圆筒实验样品;2.应变仪;3.扭转载荷施加装置;4.弯曲载荷施加装置;5.数据采集系统;6.相关辅助工具;7.其他必要的辅助材料。
五、实验步骤1.准备薄壁圆筒样品,清洁表面并固定在实验台上;2.根据实验要求,施加弯曲载荷,并记录薄壁圆筒的变形情况;3.根据实验要求,施加扭转载荷,并记录薄壁圆筒的变形情况;4.利用应变仪等装置对薄壁圆筒表面的应变变化进行实时监测和记录;5.根据采集的数据,推导出薄壁圆筒在弯扭组合变形条件下的主应力。
六、实验数据处理和分析1.根据实验采集的数据,绘制出薄壁圆筒在不同弯曲和扭转载荷下的主应力变化曲线;2.对数据进行详细分析和比对,得出薄壁圆筒在不同载荷情况下的主应力范围;3.分析实验中存在的误差和不确定性,并提出相应的修正方案;4.对实验结果进行合理的解释和结论。
七、实验结果与结论1.根据实验数据处理和分析,得出薄壁圆筒在弯扭组合变形条件下的主应力范围为△σ;2.对实验结果进行科学的解释和结论,明确指出实验的可靠性和局限性;3.在结论部分提出对后续研究和工程应用的建议和展望。
八、实验总结1.总结全文工作,重点强调实验的意义和价值;2.对实验中存在的问题和不足进行梳理和反思;3.为未来相关研究和工程设计提供经验和借鉴。
弯扭组合变形实验(主应力)

弯扭组合变形实验——主应力的测定一、实验目的1.测量薄壁圆管在弯曲和扭转组合变形下,其表面一点的主应力大小及方位。
2.掌握用电阻应变花测量某一点主应力大小及方位的方法。
3.将测点主应力值与该点主应力的理论值进行分析比较。
二、预习思考要点1.试分析本实验装置是如何使薄壁圆管产生弯曲和扭转组合变形的。
2.薄壁圆管在弯扭组合变形下其横截面上有几种内力?哪几种?有几种应力?哪几种?3.薄壁圆管在弯扭组合变形下其表面一点处于什么应力状态?在主应力方位未知的情况下,确定该点的应力状态需求解几个未知量?哪几个?三、实验装置及仪器1.弯扭组合变形实验装置如图1-29所示,装置上的薄壁圆管一端固定,另一端自由。
在自由端装有与圆管轴线垂直的加力杆,该杆呈水平状态。
载荷F作用于加力杆的自由端。
此时,薄壁圆管发生弯曲和扭转的组合变形。
在距圆管自由端为L1的横截面的上、下表面B和D处各贴有一个45°应变花(或60°应变花)如图1-29。
设圆管的外径为D,内径为d,载荷作用点至圆管轴线的距离为L2。
图1-29 簿壁圆管主应力测量装置2.静态电阻应变仪。
3.游标卡尺、钢尺等。
四、实验原理理论分析表明,薄壁圆管发生弯扭组合变形时,其表面各点均处于平面应力状态,如图1-29所示的I-I 截面的上表面B 点和下表面D 点的应力状态分别如图1-30所示。
(a ) (b )图1-30 簿壁圆管上、下表面点的应力状态由应力状态理论可知,对于平面应力状态问题,要用实验方法测定某一点的主应力大小及方位,一般只要测得该点一对正交方向的应变分量εx 、εy 及γxy 即可。
用实验手段测定线应变ε较为容易,但角应变γxy 的测定却困难得多,而由平面应力状态下一点的应变分析可知平面上某点处的坐标应 变分量εx 、εy 及γxy 与该点处任一指定方向α的线应变εα有下列关系:αγαεαεεα2sin 21sin cos 22xy y x ++= (1-55)从理论上说可以测定过该点任意三个不同方向上的线应变εα、εβ、εγ,建立三个如式1-55那样的独立方程,解此方程组即可完全地、唯一地确定εx 、εy 、γxy ,但因方程中出现了三角函数,为了解算简便,在实验测试中,生产厂家已将三个应变片互相夹一特殊角,组合在同一基底上组成应变花,本实验采用互成45°的直角应变花,布设方式如图1-31所示。
弯扭组合变形的主应力测定-2010年秋

tan 2α 0 = −2τ n / σ M
D点
⎛ −σ M ⎞ σ1 − σ M 2 = ± ⎜ ⎟ + (− τ n ) σ3 2 ⎝ 2 ⎠
2
tan 2α 0 = −2(− τ n ) / (− σ M )
2、分析产生误差的主要原因。 相对误差 = 七、数据处理 附表 1 圆筒的尺寸和有关参数 a = 250 mm 弹性模量 E = 71 GPa L = 300 mm 泊 松 比 μ = 0.32 D = 40 mm 内 径 d = 34 mm 附表 2 数据表格 应 变载荷 100N 200N 300N 400N 平均值 实验值 理论值 0°应变计 ε0 Δε0 45°应变计 ε45 Δε45 -45°应变计 ε-45 Δε-45 实验值 − 理论值 × 100% 理论值
y c b
y
αc
a
+45D
αb αa
o
x
−45D
o
x
图1
图2
⎧ε a = ε x cos 2 α a + ε y sin 2 α a − γ xy sin α a cos α a ⎪ ⎪ 2 2 ⎨ε b = ε x cos α b + ε y sin α b − γ xy sin α b cos α b ⎪ 2 2 ⎪ ⎩ε c = ε x cos α c + ε y sin α c − γ xy sin α c cos α c
⎧ε x = ε 0D ⎪ ⎨ε y = ε 45D − ε 0D + ε −45D ⎪ ⎩γ xy = ε −45D − ε 45D
主应变公式为
(2)
⎧ε1 ε x + ε y 1 2 (ε x − ε y )2 + γ xy ± ⎨ = 2 2 ⎩ε 3
薄壁圆筒的弯扭组合变形实验

1薄壁圆筒的弯扭组合变形实验一、试验目的1.测定薄壁圆筒弯扭组合变形时指定点的主应力和主方向,并与理论计算值进行比较。
2.测定薄壁圆筒弯扭组合变形时指定截面上的弯矩、扭矩和剪力引起的应力,并与理论值比较。
3. 学习布片原则、应变成份分析和各种组桥方法。
二、设备和仪器1. 力学试验台。
2. 静态应变仪。
3. 辅助工具和量具。
三、试样与试验装置薄壁圆筒试样(见图5.1a )左端固定,籍固定在圆筒右端的水平杆加载。
圆筒用不锈钢1C r 18N i 9T i 或其它钢材制成,材料弹性模量E 和泊松比µ为己知,或由试验者自行测定,圆筒外径D ,内径d 。
四、试验原理1. 指定点的主应力和主方向测定弯扭组合变形任一截面(如I-I 截面)上b 点的应力状态如图5.1(b)所示,相应其它各测点的应力状态见图 5.1(d)。
根据理论分析可知:弯曲正应力WM M =σ,式中:M=Fl I-I,()143απ−=D W ,D d /=α;薄壁圆筒扭转切应力PT W T=τ,式中:T=Fh ,()16143p απ−=D W ;弯曲切应力Q QF 0 F R tτπ=,()40d D R +=,()2d D t −=;由此可求得相应点的主应力1`2`3σσσ及主方向0α的理论值如何由实验来测定任一截面的主应力和主方向呢?据平面应变分析理论知,若某点任意三个方向的线应变已知,就能计算出该点的主应变和主方向,从而计算出该点的主应力和主方向。
因此测量某点的主应力和主方向时,必须在测点布置三枚应变片,工程中常用应变花 测定。
常见的应变花有45o 应变花和等角应变花等。
在图5.1a 中的I-I 截面的b 、d (或a 、c ),即采用了45o 应变花进行测量,其展示图如图5.61(c)所示。
2采用单臂(多点)半桥公共温度补偿测量法,等量逐级加载。
在每一载荷作用下,分别测得b 、d (或a 、c )两点沿-45o 、0o 、和45o 方向的应变值o o o ``45045εεε−和后,将测量结果记录在实验报告中。
试验三薄壁圆筒在弯扭组合变形下主应力测定

4.根据加载方案,调整好实验加载装置。 5.加载。均匀缓慢加载至初载荷 P0,记下各点应变的初始读数;然后分级等增量加载,每增加一级 载荷,依次记录各点电阻应变片的应变值,直到最终载荷。实验至少重复两次。 6.作完实验后,卸掉载荷,关闭电源,整理好所用仪器设备,清理实 验现场,将所用仪器设备复原,实验资料交指导教师检查签字。 7.实验装置中,圆筒的管壁很薄,为避免损坏装置,注意切勿超载, 不能用力扳动圆筒的自由端和力臂。 附表 1 (试件相关数据) 圆筒的尺寸和有关参数 计算长度 外 内 载荷 (N) 电 阻 应 变 仪 读 数 45° 径 径 L= D= a= P △P ε △ ε 平均值 0 ε △ ε 平均值 ε -45° △ ε 平均值 八、实验结果处理 1.主应力及方向 m 或 mˊ点实测值主应力及方向计算: 70 40 d = 35 mm mm mm mm 70 140 70 210 70 280 70 350 70 420 弹性模量 E = 210 泊 松 比 μ = 0.26 电阻应变片灵敏系数 K= 2.06 GPa 附表 2(实验数 据)m 点三个方向 线应变
σx =
τn =
式中
M WZ
Mn WT
M — 弯矩,M = P·L Mn — 扭矩,Mn = P·a Wz — 抗弯截面模量,对空心圆筒: WZ =
πD 3
d [1 − ( ) 4 ] 32 D d [1 − ( ) 4 ] D 16
WT — 抗扭截面模量,对空心圆筒: WT = W 由二向应力状态分析可得到主应力及其方向
tg 2a 0 = (ε 45° − ε − 45° ) /(2ε 0° − ε − 45° − ε 45° )
六、实验方案设计: a:半桥接法单臂工作,温度互补 b:半桥接法邻臂工作,温度互补 c:全桥接法对臂工作,温度互补 d:半桥接法双臂工作,温度互补 七、实验步骤: 1.设计好本实验所需的各类数据表格 2.测量试件尺寸、加力臂的长度和测点距力臂的距离,确定试件有关参数。附表 1 将薄壁圆筒上的应变片按不同测试要求接到仪器上,组成不同的测量电桥。调整好仪器,检查整个测试系 统是否处于正常工作状态。 3.加载方案。先选取适当的初载荷 P0(一般取 P0 =10%Pmax 左右) ,估算 Pmax(该实验载荷范围 Pmax ≤700N) ,分 4~6 级加载。
弯扭组合变形时的应力测定 工程力学实验报告

弯扭组合变形时的应力测定一、 实验目的1.用电测法测定平面应力状态下的主应力大小及其方向,并与理论值进行比较。
2.测定弯扭组合变形杆件中的弯矩和扭矩分别引起的应变,并确定内力分量弯矩和扭矩的实验值。
3.进一步掌握电测法和应变仪的使用。
了解半桥单臂,半桥双臂和全桥的接线方法。
二、 实验仪器1.弯扭组合实验装置。
2.电阻应变仪。
三、 实验原理和方法弯扭组合变形实验装置示,见指导书中图。
Ⅰ-Ⅰ截面为被测位置,取其前、后、上、下的A 、B 、C 、D 为被测的四个点,其应力状态见下左图(截面Ⅰ-Ⅰ的展开图)。
每点处按-450、0、+450方向粘贴一片450的应变花,将截面Ⅰ-Ⅰ展开如下右图所示。
四、实验内容和方法1.确定主应力大小及方向:弯扭组合变形薄壁圆管表面上的点处于平面应力状态,用应变花测出三个方向的线应变后,可算出主应变的大小和方向,再应用广义胡克定律即可求出主应力的大小和方向。
主应力()()()⎥⎦⎤⎢⎣⎡-+--±++-=︒+︒-︒+︒-24502045454522.121211εεεεμεεμμσE主方向 ()()0454*******tan εεεεεεα----=︒-︒+︒-︒+A,B,C,D 点应力状(a) 截面Ⅰ-BD A CRR R 5 RBD A CRR tR i RB D AC R 9 R 3 R 1R 7(d )扭矩(c )主应力(b )弯矩式中:045-ε、0ε、045+ε分别表示与管轴线成045-ε、0ε、045+ε方向的线应变 2. 单一内力分量或该内力分量引起的应变测定: (1)弯矩M 及其所引起的应变测定(a )弯矩引起正应变的测定:用B 、D 两测点轴线方向的应变片组成半桥双臂测量线路, B 、D 两处由于弯矩引起的正应变: 2dsM εε= 式中:ds ε为应变仪的读数应变;M ε是由弯矩引起的轴线方向的应变(b )弯矩试验值的计算:2EWEW M ds M ε=ε= W ——薄壁圆管横截面的抗弯截面模量(2)扭矩T 及其所引起剪应变的测定:(a )扭矩引起应变的测定: 用A 、C 两测点沿±45°方向的四片应变组成全桥测量线路,可测得扭矩引起的主应变的实验值为:41dsεε=(b )扭矩T 试验值的计算: ()p ds W ET εμ+=14 W p ——薄壁圆管的抗扭截面模量3.被测截面的内力分量及测点的应力分量的理论计算值: 弯矩理论值:M =FL 扭矩理论值:T =Fb 弯曲正应力理论值: z M FLW W σ==扭转剪应力理论值: p pT Fb W W τ== 主应力: 222.1)2(2τσσσ+±=主方向: στα22tan 0-=五、实验步骤1.打开弯扭组合实验装置。
薄壁圆管弯扭组合变形测定实验报告数据

薄壁圆管弯扭组合变形测定实验报告数据薄壁圆管弯扭组合变形测定实验是为了测量材料的弯曲和扭转变形量来决定材料的变形性能的实验。
变形性能是一种材料性能指标,它可以定量衡量材料在一定外力作用下的变形特性。
薄壁圆管弯扭组合变形测定实验也可以用于优化设计和改进过程,从而提高产品的质量。
本文报告主要是就圆管弯扭组合变形过程中材料的应变和变形程度,采用特定参数进行实验,得出实验结果,对结果进行分析,进而对弯扭组合变形特性进行定量评价。
第二部分:实验原理薄壁圆管弯扭组合变形测定实验的实验原理基于几何变形理论,该理论表明在弯曲和扭转过程中,材料的变形量和应变分别与圆管半径、安装位置和弯曲和扭转角度有关,当然还有材料的性质也会影响材料的变形量。
因此,实验是使用特定参数,具体来说,用直径为50mm的钢圆管板材作为试件,安装在固定的机架上,以水平位置为0°,分别采用单弯或单扭操作,以10°为间隔,记录实验参数和测量数据,从而得到材料的变形量和应变数据。
第三部分:实验结果根据上述实验参数,我们进行了实验测量,并得到了以下结果。
表1:钢圆管材料在弯曲和扭转过程中变形量、应变数据|度(°) |曲变形量(mm) |转变形量(mm) |曲应变(10-3)|转应变(10-3) || --- | --- | --- | --- | --- || 0 | 0.00 | 0.00 | 0.00 | 0.00 || 10 | 0.23 | 0.30 | 7.19 | 27.50 || 20 | 0.47 | 0.60 | 14.38 | 54.99 || 30 | 0.68 | 0.90 | 21.57 | 82.48 || 40 | 0.94 | 1.20 | 28.76 | 109.97 || 50 | 1.19 | 1.50 | 35.95 | 137.46 || 60 | 1.45 | 1.80 | 43.13 | 164.95 |第四部分:实验分析从表1的实验数据可以看出,圆管材料的弯曲变形量随着实验角度的增加而逐渐增加,扭转变形量也随着实验角度的增加而逐渐增大,弯曲应变随着实验角度的增加而逐渐增加,而扭转应变也随着实验角度的增加而逐渐增大。
弯扭组合变形主应力的测定
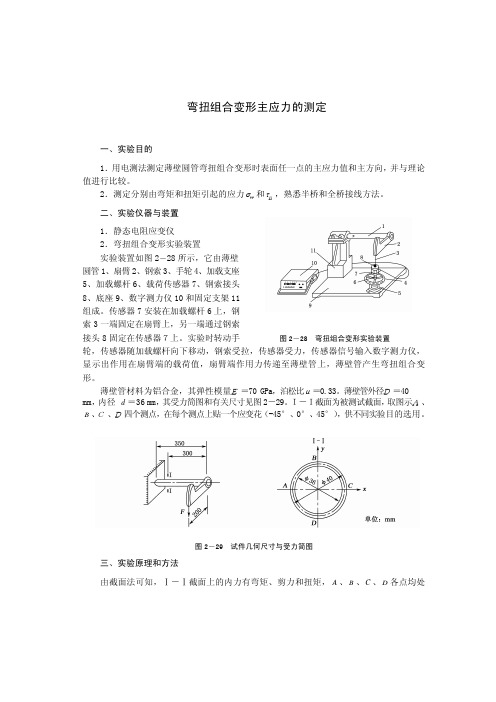
弯扭组合变形主应力的测定 一、实验目的1.用电测法测定薄壁圆管弯扭组合变形时表面任一点的主应力值和主方向,并与理论值进行比较。
2.测定分别由弯矩和扭矩引起的应力σ和nτ,熟悉半桥和全桥接线方法。
w二、实验仪器与装置 1.静态电阻应变仪 2.弯扭组合变形实验装置 实验装置如图2-28所示,它由薄壁圆管1、扇臂2、钢索3、手轮4、加载支座5、加载螺杆6、载荷传感器7、钢索接头8、底座9、数字测力仪10和固定支架11组成。
传感器7安装在加载螺杆6上,钢索3一端固定在扇臂上,另一端通过钢索接头8固定在传感器7上。
实验时转动手 图2-28 弯扭组合变形实验装置轮,传感器随加载螺杆向下移动,钢索受拉,传感器受力,传感器信号输入数字测力仪,显示出作用在扇臂端的载荷值,扇臂端作用力传递至薄壁管上,薄壁管产生弯扭组合变形。
薄壁管材料为铝合金,其弹性模量E=70 GPa,泊松比μ=0.33。
薄壁管外径D=40 mm,内径 d=36 mm,其受力简图和有关尺寸见图2-29。
I-I截面为被测试截面,取图示A、B、C、D四个测点,在每个测点上贴一个应变花(-45°、0°、45°),供不同实验目的选用。
图2-29 试件几何尺寸与受力简图三、实验原理和方法由截面法可知,Ⅰ-Ⅰ截面上的内力有弯矩、剪力和扭矩,A、B、C、D各点均处于平面应力状态。
用电测法测试时,按其主应力方向是已知还是未知,而采用不同的贴片形式。
1.主应力方向已知 主应力的方向就是主应变方向。
只要沿两个主应力方向各贴一个电阻片,即可测出该点的两个主应变I ε和II ε,进而由广义虎克定律计算出主应力: σⅠ=2μ−1E(εⅠ+μεⅡ),σⅡ2μ−=1E(εⅡ+μεⅠ) (2 - 14) 2.主应力方向未知 由于主应力方向未知,故主应变方向亦未知。
由材料力学中应变分析可知,某一点的三个应变分量yxεε、和xyr,可由任意三个方向的正应变ϕαθεεε、、确定。
