竖壁自然对流的数值模拟
自然对流影响结冰的数值模拟及实验研究

如 图 2假设 r 向流动速度 为 u z 向流动速 度为 , , 方 ,方 控制方 程l如 下 9 j
收 稿 日期 : 1-52 2 00—8 0
作者简介 : 刘仍通 (94 , , 18 一)男 硕士研究生 , 研究方 向为冰蓄冷及数值传热学。
Hale Waihona Puke 第5 期 刘仍通 , : 等 自然对流影响结冰 的数值模拟及实验研究
冰 蓄冷 系统就 是利用 了低 谷期 的电在夜 间满负荷 开启 制冷机 组 , 由蓄 冷设备 将 冷量 以冰 的形 式 蓄 并 存 起来 , 白天用 电高峰期将 冷量释放 出来承担 空调负 荷 。冰 蓄冷系统 包括动态 蓄冰 和静态蓄 冰 , 中静 在 其 态 蓄冰包括 盘管式 和冰球式 蓄冰 。许多 学者对 盘管式 蓄冰进行 了实验 和理论研 究 。由于有 自然对 流和水 的过冷现象 的存在 , 加上蓄冰 过程是 一个相变 过程 , 再 随着时 间的推移相 变界 面一直在变 化 。因此 蓄冰过 程是 一个很 复杂 的传热 问题 。通常在处 理浮力驱 动时 引人 B us e os ns i q假设 。然 而 , 于 非 B us eq流体 对 os ns i
自然 对 流 影 响 结 冰 的 数 值 模 拟 及 实验 研 究
刘仍 通 , 潘 阳
( 华东交通大学 土木建筑学院 , 江西 南昌 30 1) 303
摘 要 : 了 了解在 结冰 过 程 中水 的 自然 对 流对 蓄 冰 桶 内温 度分 布 的 影 响 以及 水的 实 际的 流 动 情 况 , 用数 值 模 拟 软 件 对 竖 为 利 直铜管结冰过程进行 了研 究, 通过 实验对数值模拟得 出的温度分布进行 了验证 。从数值模 拟计算得 出: 靠近 管壁 的底 角出 现 了和 主流 区流 动 相反 的漩 涡 , 随 着 时 间 的推 移 漩 涡 不 断 向上 移 动 ; 向 温 度 分布 出现 了翻 转 现 象 , 向 温 差很 小 ; 密 且 纵 径 且 度翻转现 象对冰层的轮廓有影响 , 使得冰层 出现倒锥形。 关 键 词: 自然 对 流 ; 冰 ; 差 ; 值 模拟 结 温 数 中 图分 类 号 :39 05 文 献 标 识码 : A
5-5-自然对流
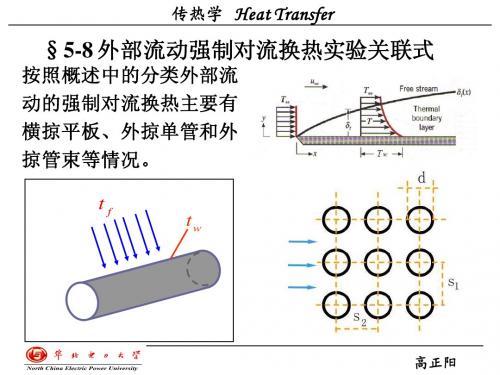
管束的排列方式有顺排和叉排两种形式。叉排中的 流动扰动比顺排时要剧烈,因此换热也较强。此外, 管束的间距s1和s2及管排数也影响换热强度。
顺排 叉排
最小截面
高正阳
传热学 Heat Transfer
2. 平均表面传热系数 h 计算的关联式
Nu C Re
m
式中C、m 之值见教材表,上式主要用于气体,因此Pr 数的影响归到了系数 C 中。
2 2
高正阳
传热学 Heat Transfer
三、大空间自然对流换热的实验关联式
自然对流换热分类:
大空间 有限空间
常用的关联式: Nu C (Gr Pr)
n
Gr
g v tl
2
3
Ra Gr Pr
高பைடு நூலகம்阳
传热学 Heat Transfer
t w t
t w t
水平大平板上下不同的自然对流状态示意图
Nu C Re Pr
n 1/ 3
式中C、n 之值见教材表5-5 定性温度取
tr 1 2
t
w
tf
特征长度取管外径d
特征流速取来流速度
u
对于高温气流冲刷的管子,若 壁温过高,可能发生爆管现象, 在管子的那一点易发生?
高正阳
传热学 Heat Transfer
二、外掠管束换热实验关联式
1. 流动和换热的特征
高正阳
传热学 Heat Transfer
1. 在对流温差大小相同的情况下,在夏季与冬季, 屋顶天花板内侧的对流换热是否相同?为什么? 2. 在地球上设计的一个自然对流换热实验装置,是 否同样可以在宇宙飞船上进行实验?
高正阳
地面结构热试验自然对流换热数值研究

第43卷第6期STRUCTURE & ENVIRONMENT ENGINEERING V ol.43,No.6 地面结构热试验自然对流换热数值研究王伟何振威黄敏胡由宏王智勇刘永清(北京强度环境研究所,北京100076)摘要:基于ANSYS CFX,发展了一种自然对流换热数值仿真计算方法。
应用该方法对地面热试验中的自然对流换热进行了数值研1究。
分别给出了大空间自然对流、平板型热试验真实工况下的换热热流密度大小,并将其与大空间自然对流工程经验公式计算结果、地面试验结果进行对比。
结果表明,数值仿真结果具有一定的合理性和准确性,可作为地面热试验自然对流损失项补偿的依据,从而提高地面热试验的准确度和有效性。
关键词:热试验;自然对流换热;数值研究;ANSYS CFX中图分类号:V416.4 文献标识码:A 文章编号:1006-3919(2016)06-0038-06Numerical Research on the natural convection heat transfer ofthermal test under ground conditionsWANG Wei HE Zhenwei HUANG Min HU Youhong WANG Zhiyong LIUYongqing(Beijing Institute of Structure and Environment Engineering, Beijing 100076, China)Abstract:In order to investigate the natural convection heat transfer in themal test under ground conditions,a numerial method was developed based on ANSYS CFX. With this method, the heat flux of hot wall ininfinite space as well as in the real case of plat thermal test was received, which was proved to be correctafter contrast with the result of engineering formula and test result. By applying the achievement, the validity and precision of thermal test under ground conditions can be increased.Key words:thermal test; natural convection heat transfer; numerical research; ANSYS CFX0 引言不依靠外力推动,由流体自身温度场的不均匀性所引起的流动称为自然对流[1]。
竖壁贴附射流空气池的数值模拟_刘艳鹏

第25卷第1期2007年1月西安航空技术高等专科学校学报Journal of Xi 'an Aerotechnical CollegeVol .25No .1Jan .2007收稿日期:2006-11-25基金项目:国家自然科学基金资助项目:多元通风模式分析及设计原理研究(50278075)。
作者简介:刘艳鹏(1978-),女,河南省南阳市人,在读硕士研究生。
竖壁贴附射流空气池的数值模拟刘艳鹏1,张如春2,刘 靖3(1.西安建筑科技大学环境与市政工程学院,陕西西安710055;2.江西省建筑设计研究总院,江西南昌330046;3.广西电力工程建设公司,广西南宁530022)摘 要:以verhoff 经验公式为基础[1],建立竖壁贴附射流送风的数值计算模型,对于不同工况进行模拟计算,然后将模拟计算结果的速度场与verhoff 经验公式进行对比分析。
通过研究表明,当顶棚送风口距侧墙的垂直距离比较小时,竖壁贴附送风可以依靠侧墙的贴附效应在房间下部产生空气池现象,形成和置换通风类似的气流组织。
关键词:竖壁贴附射流;置换通风;数值模拟;贴附效应中图分类号:T U834.25 文献标识码:A 文章编号:1008-9233(2007)01-0023-031 引言近年来,随着人们对室内空气质量的日益重视,置换通风[2]与传统的混合通风相比,作为一种空气品质高、热舒适性好、耗能少的送风方式,开始受到广泛的重视,并成为当前研究的热点之一,在工业、民用和公共建筑中开始得到越来越多的应用。
竖壁贴附送风本质上是介于混合通风和置换通风之间的一种气流组织形式;由其形成的室内诸参数场虽然与置换通风存在一定的差别,但当送风口距侧墙的垂直距离比较近、侧墙的贴附效应(Coanda Effect )很强的时候,送风射流可以将新鲜空气尽可能的下送至地面,并产生和置换通风相似的空气池(Air Lake )现象,此时两者的气流组织参数场将具有很大的相似性;在一些空间不大、布置底部侧送风口不方便的场合,可以考虑采用竖壁贴附送风的方式来获得优于混合通风、近似于置换通风的气流组织效果;竖壁贴附送风与置换通风的相似性会随着送风口距侧墙垂直距离的增加而迅速减弱,室内流场也将快速向混合通风转变;而送风风速的改变对竖壁贴附送风气流组织效果的影响却并不明显。
自然对流换热

大空间自然对流换热:周围没有其它物体阻碍换热面上边界层 形成和发展的自然对流换热。
有限空间自然对流换热:否则称为有限空间自然对流换热 。
1大空间自然对流换热
边界层:层流→紊流。
转变点取决于温差和流体 的性质 Gr Pr>109 流态为紊流 边界层内速度分布:
y 0和y 处,均为零
y= 1 处具有最大流速
形成厚 15 mm 的竖直空气夹层。试计算通过空气夹层的自然
对流换热量。
解 定性温度 tm (tw1 tw2 ) / 2 (100 40) / 2 70℃,据此查附录得,空气物性
1.029 kg/m3 , 20.02106 m2/s , 0.0296 W/(m 1m/
4
(
h
)1/
9
Gr Pr 2 105 ~ 1.1107 时,
Num
0.073(Gr
Pr
)1m/
3
(
h
)1/
9
(5-32)
(5-33) (5-34)
以上各式的适用范围为: Pr 0.5 ~ 2 h / 11 ~ 42
准则的定,性温度 : tm (tw1 tw2 ) / 2
例 5-8 温度分别为 100℃和 40℃,面积均为0.50.5 m2 的两竖壁,
)1/
9
0.197
(1.002
104
)1m/
4
(
0.015 0.5
)1/
9
1.335
Num 1.335 0.0296 2.63 W/(m2 K)
0.015
自然对流换热量为
Q Ft 2.63(0.50.5)(100 40) 39.5 W
作业
1. 4.
多孔泡沫金属中等温竖壁面空气自然对流传热的积分解

隙率 0 9 . 、孔 密度 5P I 多 孔 泡 沫 铝 后 其 强 化 倍 数 达 9以 上 ,但 孔 隙 率 、孔 密 度 增 大 时 , 流 体 边 界 层 厚 度 增 长 P 的
过 快 ,会 使 得 传 热 恶 化 。
关 键 词 :多 孔 泡 沫 金 属 ;局 部 热 平 衡 ; 自然 对 流 ;竖 壁 面 ;边 界 层 积 分 解
所 选的参数范 围内 (L 孑 隙率 0 9 . 5 . ~0 9 ,孔 密 度 5 4 P I,孔 隙 率 越 大 、P I 大 ,边 界 层 也 越 厚 ;空 气 流 速 ~ 0 P) P越
很ቤተ መጻሕፍቲ ባይዱ快 达 到 最 大 值 ,且 此 后 的速 度 峰 值 几 乎 维 持 不 变 ; 自然 对 流 传 热 的 强 化 效 果 非 常 明 显 ,相 比 光 壁 面 ,加 入 孔
W EN i , LI Zhe u n 2。 LIJu i n Je U ng a g xa g ( le f En r y,Na jn i est f c n lg Colge eg o n i g Unv r i o Teh oo y,Na jn 1 0 9 y n i g 2 0 0 ,Jin s a g u,C ia hn
Jii e c h lC mp n t mie a iiy, J ln 1 2 0 , J ln, C ia) lnFu lAlo o o a y wi Li td Liblt h ii 3 1 1 ii hn
Absr c :The c ve ton h a r ns e orna u a l ta t on c i e tt a f r f t r lfow far o e n i o h r a e tc ls r a e e o i v ra s t e m lv r ia u f c mbe e dd d wih p o e a o m st or tc ly s ud e sng bo t or usm t lf a wa he e i a l t i d u i und r —a e h o y a o a he m a qu lb i m a y l y rt e r nd l c lt r le ii r u as s umpton i .The c ns r a i n e ua i s we e smplfe n l zng t e o d r o a niud f e c e m o e v to q ton r i ii d by a a y i h r e fm g t e o a h t r a t n o ve b u i i e a i n nd he s l d y sng nt gr to m e ho .I wa s wn ha t de l p f l d t d t s ho t t he veo o fui bo d r —a r un a y l ye t c e s wih hikn s t m e a f a t I o m wa m uc f s e ha t t f l i v ri a s f c be a e f dit r nc s s h a t r t n ha o p a n e tc I ur a e c us o s u ba e
高瑞利数下封闭腔内自然对流的数值模拟

高瑞利数下封闭腔内自然对流的数值模拟阳祥;陶文铨【摘要】为了推广应用高瑞利数下的自然对流换热技术,有必要对自然对流流动与换热特性进行深入研究.采用不引入人工扰动的直接数值模拟方法,对发生在高宽比为4的封闭腔内的自然对流流动与换热进行了研究,分析了平均温度、平均主流速度、涡量和局部努塞尔数的分布特性.研究结果表明:从静止等温流体初始条件出发,不引入任何人工扰动自然对流可以顺利发展到湍流,节约了计算资源;即便瑞利数等于1010,自然对流的平均温度、平均主流速度、涡量和局部努赛尔数分布都具有边界层型流动和换热的特征;在普朗特数为0.71~500的范围,当封闭腔内自然对流换热出现湍流换热特征时,局部瑞利数处于107~108量级.【期刊名称】《西安交通大学学报》【年(卷),期】2014(048)005【总页数】5页(P27-31)【关键词】封闭腔;湍流;自然对流;直接数值模拟【作者】阳祥;陶文铨【作者单位】国家核电技术有限公司北京研发中心,100190,北京;西安交通大学能源与动力工程学院,710049,西安【正文语种】中文【中图分类】TK124竖直封闭腔内的自然对流是传热与流动学科中的一个经典问题,有很多工程应用背景,如核反应堆中的换热、放射性废料的冷却、房间通风、太阳能集热器和电子器件冷却等。
竖直壁面存在温差的封闭腔内沿高温、低温竖直壁面会分别形成上升流动和下降流动,并且在腔内形成回流,高瑞利数Ra流动会形成层流、过渡和湍流区域。
Tian和Karayiannis对弱湍流自然对流进行了实验研究,首次发表了加热封闭腔内温度等值线分布和速度矢量分布的实验结果[1-2]。
Giel等对几种高宽比的封闭腔内自然对流传热(高Ra)进行了试验研究,测量了速度和温度的平均值和脉动值分布,并进一步获得了脉动速度和温度的频谱图;在分析试验结果的基础上他们认为高宽比大于等于4的封闭腔内发生湍流自然对流时展向的尺寸大小对流动和换热影响很小[3]。
气液并流垂直液膜流动的数值模拟_许松林

张力和壁面黏附作用产生的源项.
1) 气-液界面剪切力和表面张力
为了简化模型,多数研究者专注于具有光滑相界
面的稳定的液膜流动,并忽略气相剪切力的影响,本
文的模型同时考虑了气相剪切力和表面张力的影响
以及液膜界面的分子黏度,液膜表面的切向和法向力
平衡方程为
2014 年 12 月
许松林等:气液并流垂直液膜流动的数值模拟
·1041·
⎧⎪eijnjti = 0 ⎨⎪⎩− p + 2μeijnjti
=
σ( 1 R1
+
1 R2
)
(5)
式中:eij 为应变率张量;nj 为自由界面的单位法向量;
ti 为自由界面的单位切向量;p 为压力;μ 为流体黏 度;R1 和 R 2 为界面的半径曲率;σ 为表面张力. 曲率 项由 Fluent 根据每个单元格的体积分布梯度计算.
究[1-5]表明,液膜中的动量、热量和质量传递受液膜的 特性影响很大,尤其是气-液界面的波动,液膜表面小 振幅的波有利于液膜的传热和传质.虽然经历了近 半个世纪的研究,尚未获得可普遍接受的关于界面波 在气-液及液-固边界对液膜中动量、热量和质量传递 影响的机理.但是波动液膜的传热和传质受到波动
收稿日期:2013-12-15;修回日期:2014-01-16. 基金项目:国家自然科学基金资助项目(20976118,21176170). 作者简介:许松林(1966— ),男,博士,副研究员. 通讯作者:许松林,slxu@. 网络出版时间:2014-03-24. 网络出版地址:/kcms/doi/10.11784/tdxbz201312038.html.
竖直管内降液膜流动在工业过程设备中经常遇 到,如制冷设备、降膜蒸发器、塔顶冷凝器和湿壁吸 收器等,其中往往同时发生传热和传质现象.在工业 使用范围内竖直管内的降液膜形成时,并流或逆流的 气相会对液膜的表面产生剪切力,导致液膜表面形成 振 幅 不 一 的 波 .近 年 来 的 大 量 理 论 和 实 验 测 试 研
自然对流换热.x

平板的B、m见表 (6-11)
(6-44) (6-43)
四、有限空间自然对流换热的实验关联式
1、准则方程一般形式
Nu
c Gr
Pr n
H
m
这里: Gr
gV t 3
ν2
Nu h
特征长度:
定性温度:
,
tm
tw1
tw2 2
V
1 273 tm
t tw1 tw2
2、实验关联式
(1)竖空气夹层(常壁温)
•薄层内的速度分布则有两 tw 头小中间大的特点。
•壁面处由于粘性作用速度 x 为零,在薄层外缘,由于温
边界层速度分布曲线 边界层温度分布曲线
t∞
度已均匀,速度也等于零。
•在 偏 近 热 壁 处 速 度 有 一 个
峰值
0
y
这种流体速度变化的区域相对于流体沿着平板上升
方向(图中的x方向)的尺度是很薄的,因而可以称
格拉晓夫数Gr。
自然对流的流动特征
热竖壁为例:
温度和速度分布 温度不均 → 密度不均 → 速度分布
(1)不均匀的温度场只是在壁面附近的 薄层内。
(2)速度场先增大后减小,与温度场的 边界层基本重合。
(3) 流动状态也有层流和湍流之分。 (4) 局部表面传热系数的变化如图所
示。
hx ~ x
二、 自然对流传热的控制方程
ν2
3
——格拉晓夫准则
(6-34)
V——体积膨胀系数(
K 1), 理想气体有 V
1 T
定性温度:tm
tw
t 2
H 竖壁或竖圆柱的高度
特征长度:l d 水平放置圆柱(横圆柱)的外径
l 水平壁的长度
C类-徐体冰-竖缝式鱼道水流结构的数值模拟[1]
![C类-徐体冰-竖缝式鱼道水流结构的数值模拟[1]](https://img.taocdn.com/s3/m/37df92826529647d272852d9.png)
2009年11月水 利 学 报SHUILI XUEBAO 第40卷 第11期收稿日期:2009-07-02作者简介:徐体兵(1983-),男,安徽岳西人,硕士生,主要从事水工水力学研究。
E -mail:tibingxu@ 文章编号:0559-9350(2009)11-1386-06竖缝式鱼道水流结构的数值模拟徐体兵,孙双科(中国水利水电科学研究院水力学研究所,北京 100038)摘要:对竖缝式鱼道的水流结构进行了数值模拟计算,系统研究了鱼道水池长宽比和隔板墩头布置体型对水池内水流流态的影响。
研究表明,鱼道水池长宽比是影响竖缝式鱼道水流结构的主要控制因素,长宽比在8 8~10 5 8的范围内,可以获得较好的流态。
研究还表明,隔板是否设置墩头对水流结构的影响有限,从避免漂浮物滞留与防止泥沙淤积角度看,在实际的鱼道工程中可考虑不设隔板墩头。
关键词:竖缝式鱼道;数值模拟;水流流场;隔板墩头中图分类号:TV133文献标识码:A1 问题的提出竖缝式鱼道是一种结构简单、过鱼效率较高的鱼道布置形式[1],目前在国际上十分流行,加拿大、美国、日本等鱼道技术先进国家都较多采用了竖缝式鱼道[2-3],我国近年来兴建的上庄鱼道、老龙口鱼道、长洲鱼道等也采用了这种布置方式[4-8]。
对于竖缝式鱼道的水力特性与设计方法,国外学者进行了较多的研究。
加拿大阿尔伯特大学的Rajaratnam 与S W u 等[9-12]对竖缝式鱼道的流场结构进行了试验研究,发现当鱼道各级水池的长宽比为L B =10 8时可以获得较稳定的流态[9-12];法国的Larinier[13]研究了竖缝式鱼道的消能效率,认为各级水池内的单位体积消能率宜小于200W/m 3;Barton [14]、Fujihara [15]、Stephan [16]等则先后对竖缝式鱼道的水力特性进行了数值模拟计算。
从目前国内外已有的研究成果看,仍缺乏对竖缝式鱼道细部结构的系统研究。
竖环形夹层内自然对流换热的实验研究及数值计算

竖环形夹层内自然对流换热的实验研究及数值计算现如今,全球能源需求不断增长,能源的合理利用已成为全球热议的话题。
随着科技的发展,换热技术的运用越来越普遍。
换热器具有传热效率高、能耗低的优点,广泛应用于食品、医药、石油化工、电力、冶金、汽车等行业。
竖环形夹层换热器是一种新型的换热器,它由一个夹层和多个竖环形介质组成,在某些特殊工况下,具有良好的换热性能和热效率。
因此,竖环形夹层换热器在现代工业中有着重要的作用。
1.2究目的竖环形夹层换热器的换热性能和热效率依赖于内部介质的自然对流换热,因此,研究竖环形夹层内自然对流换热的实验研究和数值计算,可以更好地了解换热器的工作性能,从而为设计提供有效的依据。
本文的研究目的是通过实验研究探究竖环形夹层换热器内自然对流换热的特征,并基于数值模拟,分析不同参数对热性能的影响机理,为竖环形夹层换热器的设计与优化提供有效的理论支持。
第二部分验研究2.1究设备实验采用自制的竖环形夹层换热器,其外形如图1所示,包括水流导管、热源导管两个部分。
热源导管的长度为2.5 m,直径为38 mm,采用SUS316材质制成。
水流导管的长度为2.5 m,直径为38 mm,采用SUS316不锈钢材质制成。
夹层以0.3 mm石墨衬底,覆盖石墨层的厚度为1.2 mm,夹层内径为38 mm,夹层外径为45 mm。
热源温度为70,水流温度为50左右。
2.2验方法本实验采用的是一种基于流压损失的试验方法,在恒定的加热量、水流量和热源温度下,测量换热器内介质进出口的温度,并根据压降-流量关系,绘制出换热器内介质进出口温度随流量变化的趋势图,从而得到各种流量、温度和压降等性能指标。
第三部分值计算3.1仿真数据准备3.1.1仿真模型本文采用COMSOL Multiphysics热仿真软件,建立竖环形夹层换热器的三维热仿真模型,分别考虑竖环形介质的热属性和流体流动特性。
3.1.2仿真参数仿真结果的准确性取决于仿真参数的准确性。
竖壁液膜温度分布数值模拟和红外抑制效果

Ab s t r a c t : F o r t h e p ur p o s e o f wa r s h i p i n f r a r e d s t e a l t h,a n a n a l y t i c a l r e s e a r c h o n a me t h o d o f s u bc o o l i n g f a l l i n g l i q — u i d il f ms f l o wi n g o v e r a p l a t e o f s hi p i n t o t h e i n f r a r e d s t e a l t h wa s c o n d uc t e d. Th e mo d e l s o f t h e l a mi n a r f l o w a n d t h e h e a t t r a ns f e r o f t h e s u bc o o l i n g i f l ms we r e e s t a b l i s h e d. A s t e a d y t wo d i me n s i o na l c o n v e c t i o n he a t t r a n s f e r p r o b l e m wa s
Ap p l i c a t i o n o f l i q u i d il f m o n s h i p s u r f a c e i n t e mp e r a t u r e d i s t r i bu t i o n a n d i n f r a r e d s u p p r e s s i o n e fe c t i v e
s o l v e d b y a p p l y i n g w a y s a n d s k i l l s f o r w o r k i n g o u t o n e - d i me n s i o n u n s t e a d y s t a t e h e a t c o n d u c t i o n p r o b l e m a n d u s i n g v o l u me o f l f u i d me t h o d c o mp u t a t i o n a l l y . Nu me r i c a l r e s u l t s o f t e mp e r a t u r e d i s t r i b u t i o n o f s u b c o o l i n g f a l l i n g l i q u i d
基于FLuent热对流边界的水平和竖直长圆管自然对流换规律和程序实现

水平长圆管自然对流换热计算1 圆筒稳态导热热阻R=12πλln(r2r1)式中:λ:管道材料导热系数,W/m∙K−1。
2 格拉晓夫数和瑞利数(Grashof Number and Rayleigh Number)在外部驱动(如强制对流)的情况下,该流动的性质由雷诺数表征,雷诺数描述了惯性力和粘性力的比。
但是,对于自然对流等内部驱动的流动,速度尺度最初是未知的。
在这种情况下,用格拉晓夫数表征流动状态。
格拉晓夫数描述了流体中的粘性扩散和和内部驱动力(浮力)之比。
像雷诺数一样,格拉晓夫数需要定义特征长度,流体的物性和密度差。
在通用情况下,格拉晓夫数通过下式定义:Gr L=gρ(ρext−ρs)L32式中:g:重力加速度,m/s2;ρ:流体的密度,kg/m3;ρext:自由流密度,kg/m3;ρs:壁面流体的密度,kg/m3;L:特征长度,m;μ:流体的动力粘度,kg/(m∙s)。
上式可以适用于任何密度可以变化的流体,流体的密度可以不仅仅取决于流体的密度。
可以适用于湿空气,其密度取决于湿空气的温度和蒸汽浓度。
当流体的密度仅由温度决定时,格拉晓夫数通过下式定义:Gr L=gαp(T s−T ext)L3(μ/ρ)2式中:g:重力加速度,m/s2;αp:流体的体积膨胀系数,1/K;T s:壁面流体的温度,K;T ext:自由流温度,K;L:特征长度,m;μ:流体的动力粘度,kg/(m∙s);ρ:流体的密度,kg/m3。
通常,流体的体积膨胀系数由下式给出:αp=−1ρ(ðρðT)p对于理想气体:αp=1当格拉晓夫数到达109时,流动状态从湍流转换为层流,格拉晓夫数大于109时流动状态为湍流。
瑞利数是流动状态的另一个指标。
瑞利数和格拉晓夫数相似,除了瑞利数会考虑热扩散率:Ra=Pr∙Gr。
当瑞利数较小时,流体域内热传递中热传导占主导地位(详情参见热传递的三种方式)。
在这种情况下,换热系数与热对流无关,相反,把流体视为静止状态更准确。
自然对流与强制对流及计算实例

天然对流与强迫对流及盘算实例热设计是电子装备开辟中必不成少的环节.本连载从热设计的基本——传热着手,介绍根本的热设计办法.前面介绍的热传导具有清除个别内温差的后果.上篇绍的热对流,则具有下降平均温度的后果.下面就经由过程具体的盘算来分离解释天然对流与强迫对流的情形.起首,天然对流的传热系数可以表述为公式(2).热流量=天然对传播热系数×物体概况积×(概况温度-流体温度) (2)许多文献中都记录了盘算传热系数的公式,可以把流体的特征值带入公式中进行盘算,可以实用于所有流体.但每次盘算的时刻,都必须代入五个特征值.是以,公式(3)事先代入了空气的特征值,简化了公式.天然对传播热系数h=2 .51C(⊿T/L)0.25(W/m2K) (3)2.51是代入空气的特征值后求得的系数.假如是向水中散热,2.51须要换成水的特征值.公式(3)消失了C.L.⊿T三个参数.C和L从表1中选择.例如,发烧板竖立和横躺时,四周空气的流淌各不雷同.对传播热系数也会随之改变,系数C就负责接收这一差别.代表长度L与C是成对界说的.盘算代表长度的公式因物体外形而异,是以,在盘算的时刻,须要从表1中选择类似的外形.须要留意的是,暗示大小的L位于分母.这就暗示物体越小,对传播热系数越大.⊿T是指公式(2)中的(概况温度-流体温度).温差变大后,传热系数也会变大.物体与空气之间的温差越大,紧邻物体那部分空气的升温越大.是以,风速加快后,传热系数也会变大.公式(3)叫做“半理论半试验公式”.第二篇中介绍的热传导公式可以或许经由过程求解微分方程的方法求出,但天然对流与气流有关,没有完整实用的理论公式.能树立理论公式的,只有产生的气流较简略的平板垂直放置的情形.因为在这种情形下,理论上的温度鸿沟线的厚度可以盘算出来.但是,假如发烧板程度放置,气流就会变得庞杂,盘算的难度也会增长.这种情形下,就要依据原始的理论公式,经由过程试验求出系数.也就是说,在公式(3)中,理论盘算得出的数值0.25可以直接套用,C的值则要经由过程试验求出.天然对传播热系数无法大幅改变图4:天然对传播热系数无法大幅改变物体沿流淌偏向的尺寸越小,单位面积的散热量越大.天然对流的传热系数随斜率和面的曲率变更,但变更的幅度不大.而强迫空冷可以经由过程进步风速和湍流化,大幅改变传热系数.外形和设置装备摆设对于天然对流的传热系数会产生多大的影响(图4)?举例来说,平面的传热系数h等于2.51×0.56×((Ts-Ta)/H)0.25,而圆筒面的传热系数h等于2.51×0.55×((Ts-T<a)/H)0.25.平面为0.56,圆筒面为0.55,不同只有2%阁下,由此可见,平面与圆筒面的传热系数不同不大.这就意味着当发烧板竖直时,下概况的传热才能会越来越差,而上概况的传热才能根本不变.产生竖直后,下概况只受到沿竖直面的向量成分的浮力.也就是说,下概况的浮力变弱.假设垂直时的传热系数为hv,竖直时的传热系数为hθ,物体沿垂直偏向竖直角度θ,此时,下概况的传热系数大致为:hθ=hv.(cosθ)0.25 (4)(θ在0~60度阁下的规模内时公式成立)假如竖直45度,传热系数将缩小8%阁下.由此可知,即使竖直发烧板,传热系数也没有太大变更.但一旦接近程度,传热系数就会急剧下降.经由过程上面的介绍,大家应当已经明确,进步天然对传播热系数其实难度颇大.但物体越小,对传播热系数越大.比方说,我们可以采取把散热器翅片朋分成几个部分的办法.在翅片截断的地方,热鸿沟层将重置,起到阻拦鸿沟层变厚的感化,借此可以进步对传播热系数.但如许做会削减翅片的概况积,总的散热才能依旧变更不大.强迫对传播热系数的简略单纯盘算公式接下来看看强迫对流的传热系数.装配电扇的强迫对流的公式如下. 热流量=强迫对传播热系数×物体概况积×(概况温度-流体温度) (5)强迫对传播热系数的盘算也有许多种公式(图5).图5:强迫对流热传导的简略单纯盘算公式强迫对流时,盘算热流量应用与强迫对流对应的传热系数.依据流体的流淌是在层流区域照样在湍流区域,盘算应用的传热系数均不合.强迫对流时,一旦进步风速,状况也会在途中随之改变.比方说,即等于在没有风的房间里,喷鼻烟的烟雾也是一开端径直向上,在途中四处飘散.径直向上的地方是层流,飘散的地方是湍流.在层流区,喷鼻烟烟雾中颗粒物是单向流淌.而在湍流区,颗粒物会到处乱飞,跟着时光的推移,烟雾的外形将产生改变.湍流长短定常流,流向会随时光改变.印刷电路板周边的空气也一样,最初为层流,半途改变成湍流.从散热的角度来看,湍流更有利于散热.因为在湍流中,热空气与冷空气将互相混杂,冷空气会得到接近壁面的机遇,加倍轻易传热.也就是说,湍流化可以或许下降温度.尤其是对于低流速和水冷式,湍流化十分有用.但湍流化也会导致流体阻力增大,这回增长电扇和水泵的负荷.强迫形成湍流化的肇端点时,可以采取在流体的通道中设置崛起物(湍流促进器)的方法.在强迫空冷的散热器中,可以看到这种设置崛起的例子(注4).(注4)天然对流也消失湍流,但在电子产品的热设计中,可以以为根本不消失天然湍流化.但温度达到500~600℃的高温后,因为浮力加强,所以也会消失湍流化.遏制流淌的力与促进流淌的力,二者的均衡决议着湍流的肇端点.遏制流淌的力是粘性力,在壁面邻近的感化较强,而促进流淌的力则是惯性力或浮力.粘性力强,则流淌受到遏制.因为气流之间会互相束缚.例如,在细缝和接近壁面的地方,粘性力较强.同样,翅片与翅片之间的距离越窄,粘性力越强,也就很难产生湍流化.而惯性力由速度产生,只要进步速度,惯性力就会随之增大. 仍以喷鼻烟的烟雾为例,在烟雾开端流淌时,热源上部的空气迟缓上升,产生流淌的区域也十分狭小.但跟着流淌的进行,四周的静止流体也被带动,流淌的区域不竭扩展.是以,粘性力会下降.而在浮力的加快感化下,空气的流速不竭加快.因而产生了湍流化.依据层流和湍流的不合,强迫对流的传热系数公式消失相当大的不同.起首是层流的公式.层流平均传热系数hm=3.86√(V/L) (6)个中参加了空气的特征值,3.86与天然对流公式(3)中的2.51寄义雷同.湍流相干公式是试验性公式,系数和指数都有变更.湍流平均传热系数hm=6×(V/L0.25)0.8 (7)要想简略进行断定的话,无妨把两个系数都盘算出来,选择传热系数大的一方.下面,让我们应用上面介绍的常识,定量研讨对流的散热才能. 【演习1】平板的放置方法与散热才能假设有一块长200mm.宽100mm(疏忽厚度),温度保持在40℃的平板(图6),平板的温度平均,并且没有热辐射,下列放置方法的散热才能有多大不同?图6:【演习1】平板的放置方法与散热才能思虑纵长200mm×横宽100mm(疏忽厚度)的平板的升温保持在40K(℃)时,图中3种模式的散热才能.假设平板的温度平均,且没有热辐射.(a)垂直放置(以100mm的短边为高)(b)垂直放置(以200mm的长边为高)(c)程度放置须请求的数值是热流量,相当于散热量,这就必须起首求出传热系数,须要应用公式(3).(a)和(b)是垂直放置,C值应用平板垂直放置时的数值.因为升温固定在40K(℃),所以⊿T为40(注5).至此,所稀有值已经完好,可以盘算出传热系数.(注5)温度必须要多次盘算,比较麻烦.假如不知道温度,就求不出传热系数,是以,最初先假设温度为30℃,盘算出h.把成果代入公式进行盘算,得到的温度一般不等于30℃,此时要应用得出的数值从新盘算.经由重复盘算,逐渐逼近精确数值.(a)以100mm的短边为高的垂直平板传热系数 h概况积S=0.1×0.2×2=0.04m2散热量W=0.04×6.29×40=10.1W(b)以200mm的长边为高的垂直平板传热系数 h=概况积S=0.1×0.2×2=0.04m2散热量W=0.04×5.29×40=8.5W由上述盘算可知,(b)的散热量比(a)低15%阁下.但盘算的前提是平板的温度完整平均,也就是导热系数无穷大,假如是印刷电路板,散热量上的不同还会更大.倘使导热才能差,平板上侧与下侧之间将会消失温差.纵向放置的话,上侧与下侧的温差会更大,最高温度将消失相当大的不同.程度放置时,平板上侧与下侧的传热系数不合,盘算比较庞杂.上侧的C值为0.52,下侧为0.26,刚好是上侧的一半.是以,下侧的散热量也是上侧的一半.这种情形须要分离盘算上侧和下侧的散热量,然后相加.(c)程度放置平板代表长度 L=(0.1×0.2×2)/(0.1+0.2)=0.133m上概况对传播热系数 h=5.43 W/m2K上概况概况积S=0.1×0.2=0.02m2上概况散热量W=0.02×5.43×40=4.34W下概况对传播热系数 h=2.72 W/m2K下概况概况积S=0.1×0.2=0.02m2下概况散热量W=0.02×2.72×40=2.17W总散热量 W=4.34+2.17=6.51W这采取的是热盘算中经常应用的盘算每个面的发烧量,然后相加的办法.【演习2】大空间产生热对流,小空间产生热传导接下来看一下在200mm×200mm×20mm的平整机壳中装配180mm×180mm×1mm的电路板(发烧功率5W)的情形(图7). 图7:【演习2】空间大为热对流,空间小为热传导思虑在尺寸为200mm×200mm×20mm的机壳内装配180mm×180mm×1mm的印刷电路板(发烧功率为5W)时,图中3种情形下的散热才能.假设没有热辐射.大家可以将其算作是加热器.关于电路板的装配地位,下面哪种是精确的?别的,这里假设热辐射可以疏忽.(a)电路板设置在上部(距离机壳顶面1mm)时温度最低(b)电路板设置在中部(距离机壳顶面7.5mm)时温度最低(c)电路板设置鄙人部(距离机壳顶面15mm)时温度最低这个标题中有一点要留意,那就是空间狭小.空气无法流淌时,产生的是热传导,空间够大时产生的是热对流.划分的界线值随状况和发烧量而变,大致为几毫米.假如小于该界线值,空气将无法流淌,大于该界线值空气就可以流淌.定性地来说,只要距离足够,空气就能轮回,从而带走热能,使部件释放的热传到机壳顶面并发散出去,由此起到降温的感化.上面提到,当距离很小时产生的是热传导.热传导的热阻等于空气层的厚度/(传热面积×空气的导热系数),是以(a)的情形下, 热阻(1mm)=0.001/(0.18×0.18×0.03)=1.03K/W;(b)的情形下,热阻(7.5㎜)=0.0075/(0.18×0.18×0.03)=7.7K/W,比(a)的热阻大许多.而在(c)的情形下,距离达到15mm,可以以为能充分产生对流.此时,对流的热阻增长到两个(电路板概况→空气,空气→机壳顶面).按照传热系数为10W/m2K盘算,电路板到空气的对流热阻=1/(电路板概况积×天然对传播热系数(程度))空气到机壳的对流热阻=1/(机壳概况积×天然对传播热系数(程度))热阻(15mm)=1/(0.18×0.18×10)+1/(0.2×0.2×10)由此可知,(a)的情形下热阻最小.温度最低.估量(b)的温度最高,原因是根本没有产生流淌.传热系数单靠手工盘算很可贵到精确成果,是以,笔者试着应用热流体解析模仿进行周详盘算,得到了这三种情形下电路板的温度.成果为,当情形温度为35℃时,(a)距离1mm时,电路板温度为56℃(b)距离7.5mm时,电路板温度为72.5℃(c)距离15mm时,电路板温度为59.6℃这就意味着必须要防止温度最高的(b)的情形.5~7mm阁下的距离难以产生对流,进行热传导时消失空气层过厚的问题,很难散热,是最好要避开的距离.装配部件的时刻很轻易产生这么大的裂缝,在这种情形下,无妨直接让电路板与机壳接触,经由过程热传导散热.。
竖壁降膜流动特性与稳定性的数值研究

图 1 物理模 型及 边界条件
图 2 液膜结构特性 参数示意图
本 保持 恒定 , 且波长规则 , 出 现 了准 稳 态 的类 正 弦
波; 在 下游 0 . 4 m到 0 . 7 m位 置 处 , 每 隔 5~ 6个 波 形, 较 为规则 地 出现 波 长加 长 , 振 幅增 大 的波 动 ; 在 下游 0 . 7~ 0 . 9 m处 , 水 膜 表 面 波 动振 幅 继 续 增 大 , 波动虽 然变 得不 规则 , 同 时也 呈 现 出较 为 明显 的类
物理 模 型如 图 1所示 , 温 度 为 的水 膜 以一 定 的初 始速 度 沿竖 直恒 温 ( )固壁 向下 流 动 , 水 膜
从图中可见 , 降膜主要 由和固壁相连的表 面波基部
底层 ( 基 液膜 ) 及 其 上 的表面 波组成 。
外侧是温度为 , 压力为大气压的静止空气 。计算
摘 要 : 采 用流体体 积法 ( V O F ) 对 于 高雷诺数 竖壁 降膜 流场进 行 了数值 模拟 , 分析 了液膜速 度分 布 、
平均讨论 了波动特性对于降膜传质
及 稳定性 的影响 。计算结 果表 明, 随着流 动 向下 游发展 , 平均 液膜 厚度 先是迅 速 减 小, 然后 减 小速 度 趋缓 ; 波动振 幅和 波长随着流动 距 离的增加 持 续增 大 , 这将 导 致 波动传 质能 力增 强 , 同时也使得 基 液
膜 厚度不 断减 小, 液膜 的稳 定性 变差。采 用 V O F方 法的模 拟 结果 与 高速 摄 影 实验数 据符 合 良好 , 说
明V O F方 法准确描述 了绝 大部 分液膜 流动特性 , 在 总体上对 于竖壁 降膜 流场进 行 了准确的预测 。
纵向涡强化竖直平板自然对流换热的数值模拟

12 数值模 型 .
1 2 1 湍 流 模 型 与 辐 射 模 型 . .
本研 究选 用 改进 的 , 湍流 模型 中 的 K C N c 一 E HE 模 型来 对纵 向 涡发 生 器强 化 自然 对 流 换 热 进 行 模
关键词 : 纵向涡;自然对流; 强化换热 ; 数值模拟 中图分类号 : K14 T 2 文献标识码 : A
利 用纵 向涡 发生器 产生 的纵 向涡 旋使 贴近壁 面
1 数 值 模 拟
1 1 物理模 型 .
模 型包 括封 闭房 间和实 验 面 , 闭房 间为 5n× 封 i 3n× . i(n 长 , 6 r 宽 a
为 30 0 mm, 竖直 放 置 在 房 间 内. 向涡 发 生 器 对 由 纵
的流体速度改变 , 导致热边界层分离和流场不稳定 或湍流度加强 , 可使传热强化. 向涡强化换热效果 纵 与纵 向 涡 发 生 器 的几 何 结 构 、 小 、 量 、 诺 数 大 数 雷
( e及 发 生 器 间 的距 离 相对 于传 热 壁 面 的位 置 等 R) 因素 有关 , 目前 已有 不少 学者通 过 实验 、 数值模 拟及 理论 分析 等手 段对 纵 向涡强化 换热 进行 了研 究 ¨ 引. Fn ¨对 有 限空 间 内直 角 三 角 翼 发 生 器 对产 生 eg等 纵 向涡 强化竖 直平 板 自然对 流换 热 的影 响作 了实验 性研 究 , 龙靖 安 等 提 出 对 多排 纵 向涡 发生 器 采 取 错 列布 置 时 , 提高竖 直 发热板 的平 均换热 系数 . 可
维普资讯
l6 1
竖壁自然对流的数值模拟

, 这个依赖关系从图 2可以反映出来, 且它
可以从表 1 给出的 b 值来确定。
3 结束语
文中对竖壁自然对流层流换 热进行了数值模 拟, 得到的量纲一的温度、 速度和其它物理量的变化 规律 , 与理论分析相符。该模拟结果进一步表现了 对流换热的特点。随着 Pr 的增大, 速度边界层的厚 度变化不大, 但热边界层的厚度迅速减小, 壁面处温 度梯度的绝对值增大, 换热增强。自然对流不消耗 动力 , 对自然对流的研究 , 可使其在工业和日常生活 中发挥重要作用。 参考文献 :
Abstract : T he attempt to investigate the feature of natural heat convect io n invo lv es transform in g con tro l equations in boundary layer in to approx i m ate equations . Based on th ism ethod , approx i m ate equations becom e five ordin ary d ifferentia l equat io ns by in troduc ing indirect variab les. Adoptin g MATLAB fo r nu m erical si m u lation o f th e approx i m a te so lu tio ns renders possible not on ly the featu re of distribu tio n o f tem perature and ve loc ity in boundary layer o f la m in ar flow, but a lso the chang ing rules of other quantit ie s o f physics. K ey w ords: natural convection; vertical p late ; boundary layer ; num erica l si m ulat io ns
竖壁对流换热系数计算模型的探讨

竖壁对流换热系数计算模型的探讨
孙志礼;闫明;李国权
【期刊名称】《东北大学学报(自然科学版)》
【年(卷),期】2005(026)005
【摘要】根据流体边界层理论,研究了高普朗特数常物性不可压缩流体在重力作用下,沿竖直壁面无初速度加速流动过程中速度边界层和热边界层的形成规律,给出了速度边界层和热边界层的厚度函数.据此,研究了该模型下对流换热系数的计算方法,推导出计算公式.在短距离流动中,该模型的速度边界层和热边界层较流体外掠水平板模型厚,换热较弱,因此对流系数较小.工程实际中的许多换热问题都可以简化成流体在重力作用下沿竖直平板流动模型.把该模型下得到的对流系数公式应用于飞机附件机匣的传热计算中,得到了比较精确的结果.
【总页数】4页(P484-487)
【作者】孙志礼;闫明;李国权
【作者单位】东北大学,机械工程与自动化学院,辽宁,沈阳,110004;东北大学,机械工程与自动化学院,辽宁,沈阳,110004;沈阳发动机设计研究所,辽宁,沈阳,110015【正文语种】中文
【中图分类】TK124
【相关文献】
1.RC框架-内填带竖缝剪力墙结构的滞回性能及计算模型研究 [J], 肖魁;张其林
2.在语言转换中构建竖式计算模型——以“两、三位数乘一位数”为例 [J], 卢清
荣
3.不等温壁竖平板层流自然对流换热问题探讨 [J], 侯秦;孙筱云;裘国红
4.巷壁与风流间对流换热系数计算及敏感性分析 [J], 高佳南;吴奉亮
5.致密微孔壁复合冷却对流换热系数研究 [J], 陈焱;吉洪湖;胡娅萍
因版权原因,仅展示原文概要,查看原文内容请购买。
中小Gr数下竖壁自然对流传热特性

中小Gr数下竖壁自然对流传热特性
范铭;高鹰
【期刊名称】《东南大学学报:自然科学版》
【年(卷),期】1998(028)001
【摘要】对求解竖壁自然对流过程中所作的两个近似假设αp/αγ=0和α^2u/αx^2=0进行了理论分析,提出了新的近似假设αp/αγ=μα^2/αγ^2,它保证了自然对流控制方程简化形式在边界上与NS方程的一致性,将竖壁地流控制方程的适用范围拓展到中小Gr数,进而求得其传热特性,其理论解结果与实验结果更为一体。
【总页数】7页(P68-74)
【作者】范铭;高鹰
【作者单位】东南大学动力工程系;东南大学动力工程系
【正文语种】中文
【中图分类】TK124
【相关文献】
1.高雷诺数竖壁降膜流动特性的数值研究 [J], 刘玉峰;童一峻;任海刚;张群
2.竖壁自储水式蒸馏器空腔自然对流换热及产水特性 [J], 谢果;郑宏飞;熊建银
3.多孔泡沫金属中等温竖壁面空气自然对流传热的积分解 [J], 文杰;刘振广;李菊香
4.封闭空腔内耦合的自然对流传热两个竖直导热壁的影响 [J], 夏吉良;辛明道
5.高Rayleigh数条件下竖圆环夹层内自然对流换热的实验研究 [J], 魏琪;杨世铭
因版权原因,仅展示原文概要,查看原文内容请购买。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
[ 3]
1 物理方程及其简化
1 1 控制方程和边界条件 竖直壁面的自然对流换热如图 1 所示, 图中 g 是重力加速度 , T 、 分别 是主流的 温度和密 度,
,在
此借助 MATLAB 手段, 通过数值计算的方法对竖壁
基金项目 : 甘肃省自然科学科研基金重点资 助项目 ( 3ZS051 A 25 030 , 3ZS 042 B25 049 ) ; 兰州 交通大学 科研基金 ( DX S 07 0028, DX S 07 00289) 作者简介 : 李 珍 ( 1979 - ) , 女 , 河北省唐山人 , 硕士 , 研究方向 : 计算流体力学 , E m ai: l heb l izh en @ 163. com。
!
相应的边界条件为 : y 1 ( 0 ) = 0 , y2 ( 0 ) = 0 , y2 ( ! ∀ )∀0 , y4 ( 0 ) = 1 , y 4 ( !∀ ) ∀ 0 , 其中, y 1 为修正 流函数, y 2 为速度, y 4 为温度。
; 是运动黏度 ; a 是热扩散率; 是流体的 T -T 密度 ; p 0 是标准大气压; v 是垂直于主流方向的流速。 边界条件为 : y = 0 , u= v= 0 , T = TW = 常数; y ∀ u∀ 0 , T∀ T 。
1 4
时的两个边界条 件必须
由 != 0时的相应边界条件代替。可以设定 y 3 ( 0 ) = df d T = a, y 5 ( 0 ) = = b。通过给 a, b 一 2 ! = 0 d! ! = 0 d! 个试探值 , 从而获得 a, b 的值, 如表 1 。对于某些普 朗特常数 , 认为积分限无限大 , 所以对结果必须进行 实验以确定 ! 值
第 1期
李
பைடு நூலகம்
珍, 等 : 竖壁自然对流的数值模拟 以简化为具有如下形式的两个常微分方程 df df df * f 2-2 +T = 0 , 3+ 3 d! d! d! dT d T P rf = 0 , 2 + 3 d! d!
* 2 * * 3 2 2 [ 4]
59 : ( 4) ( 5)
TW 是壁面温度 , T 是流体的温度, u 是主流方向的流 速。运用数量级分析
[ 1] [ 2] 李世武 , 熊莉 芳 . 封闭 方腔 自然对 流换 热的 研究 [ J] . 工业加 热 , 2007, 36( 3) : 10- 13 . 孙 亮 , 孙一峰 , 孙德军 , 等 . 水平自然热对流 中流量和热通量 的研究 [ J] . 水动力学研究与进展 , 2006, 21( 2) : 252- 258 . [ 3] [ 4] 杨世铭 , 陶文铨 . 传热学 [ M ]. 北京 : 高等教育出版社 , 2006. 郭宽良 , 孔祥谦 , 陈善年 . 计 算传热学 [ M ] . 合肥 : 中 国科学技 术大学出版社 , 1988 . [ 5] [ 6] [ 7] [ 8] 杨强生 . 对流传热与传质 [ M ]. 北京 : 高等教育出版社 , 1985. EDW ARD B M. A n engineer s gu ide to MA TLA B [ M ] . 北京 : 电 子工业出版社 . 2002 . 张 奕 , 郭恩震 . 传热学 [ M ]. 南京 : 东南大学出版社 , 2004. 葛新石 , 王义方 , 郭宽良 . 传热的 基本原 理 [ M ]. 合肥 : 安徽教 育出版社 , 1985 .
分方程表示。含有新变量的微分方程如下: dy 1 dy 2 dy 3 dy 4 2 = y 2, = y 3, = 2y 2 - 3y 1 y 3 - y 4, = d! d! d! d! y 5, 方程中, 是流体的体积膨胀系数, 1 = 1 T
p
0
dy 5 = - 3P ry 1 y 5。 d!
[ 4]
: != 0 , f= 0 , df = 0 和 d!
df * ∀ 0和 T ∀ 0 。 d! df df , y 3 = 2, d! d!
2
1 3 最终求解方程及边界条件 引入下面的中间变量: y 1 = f, y 2 =
*
y4 = T , y5 =
*
d T , 可以将上述系统用五个一阶常微 d!
第 18 卷
第 1期
2008 年 1 月
黑 龙 江 科 技 学 院 学 报 Journal of H e ilo ng jiang Institute o f Sc ie nce& T echno lo gy
Vo. l 18 N o . 1 Jan . 2008
文章编号 : 1671 - 0118( 2008) 01 - 0058- 03
0 980 9 0 674 2 0 418 6
- 0 085 2 - 0 504 8 - 1 167 4
60
黑
龙
江
科
技
学
院
学
报
第 18 卷
在速度差 , 否则会由于黏滞摩擦而引起主流运动 , 因 而该处的速度也要为 0 。可见, 在接近热壁的中 间处速度有一个峰值 , 其速度分布曲线为图 2 所示 的单峰形曲线 ; y 3 曲线反映了 y 2 曲线变化的快慢, 即反映出边界层内流体的速度变化率 , 故其在边界 层外界其值也为 0 ; y 4 为边界层内的温度分布曲线, 壁面附近温度变化较快, 离表面较远处温度变化较 慢。在贴壁处 , 流体温度等于壁面温度 TW , 在离开 壁面的方向上逐步降低。在边界层外温度不均匀作 用消 失 , 流 体 温 度 恢 复为 远 离 表 面 的 主 流 温 度 [ 3] T ; y 5 为温度梯度曲线 , 温度梯度是普朗特数 P r 的函数
[ 6]
[ 5]
, !
。文中对于 P r = 0 01 , 积分限为
0< ! < !m ax = 20 , 如图 2a。对于 P r = 0 72 和 10 ,积 分限为 0< ! < !m ax = 5 , 如图 2b、 2c 。对于三个不同 的普朗特数, 各未知量曲线图见图 2。
表 1 y3 ( 0)和 y5 ( 0)的计算结果 T ab le 1 Calcu lation resu lts of y3 ( 0 ) and y5 ( 0)
[ 3]
的方法 , 常物性、 无内热源、
不可压缩牛顿流体沿竖直壁面的二维稳态对流换热 的微分方程组可简化为: u v + = 0 , x y u u u + v = g (T - T ) + x y u T T T +v = a 2。 x y y
2 2
( 1) u 2, y ( 2) ( 3)
*
式中 , P r 是普朗特常数, 式中的 f 和 T 都只是 ! 的 函数。 该系统的边界条件为 T = 1 ; !∀ ,
Num erical simulations of natural convection from vertical plate
L I Zhen , C H U Yandong , LI X ia nf eng , ZHANG J ian gang
1, 2 1 1 1
( 1. D epa rt m ent ofM a the m atics and P hys ics , L anzhou Jiaotong U n iversity , L anzhou 730070, China ; 2. Depart m ent of Basic T each ing , T angshan Co llege , T ang shan 063000, Ch ina)
[ 4]
,
2 数值解及结果分析
求解这些方程, ! ∀
2 *
1 2 相似方程和边界条件 实践表明 , 竖壁自然对流边界层中的局部速度 分布是相似的, 它的局 部温度分布也 是相似的 。 根据这个条件, 利用量纲一的参数相似变换后 , 把竖 壁自然对流换热 的控制方 程即偏微 分方程 ( 1 ) ~ ( 3) 转化为常微分方程 , 从而使得数值求解简单化。 y G rx 为得到相似解, 引入相似变量 ! = x 4
竖壁自然对流的数值模拟
李
摘
珍 ,
1 , 2
褚衍东 ,
1
李险峰 ,
1
张建刚
1
( 1. 兰州交通大学 数理学院 , 兰州 730070 ;
2 . 唐山学院 基础教学部 , 河北 唐山 063000)
要 : 为了研究竖壁自然对流换热的特点 , 将边界层的控制方程转化为相似方程 。 在此基
础上, 进一步采用引入中间变量的方法, 将相似方程转化为五个常微分方程 。运用 MATLAB 对相 似解进行数值模拟, 获得了层流边界层内速度和温度的分布特点 , 同时 , 得到了与其相关的其它物 理量的变化规律 。 关键词 : 自然对流 ; 竖壁 ; 边界层 ; 数值模拟 中图分类号 : TK124 文献标识码: A
0 引
言
自然对流层流换热进行了数值模拟研究 , 并且从传 热学的角度对所得曲线图进行分析 , 得出了层流边 界层内速度和温度及相关物理量的变化规律, 其结 果与理论分析相吻合。
自然对流在工业上和日常生活中有着广泛的应 用 , 自然对流换热问题也是数值传热学研究的经典 课题之一。目前 , 已经有许多人针对此问题从不同 [ 1- 2] 角度做出充分的研究 。笔者对竖壁自然对流层 流换热问题作了进一步的研究 , 对于竖壁自然对流 边界层方程的分析解已由 E. P ohlhausen 给出
Abstract : T he attempt to investigate the feature of natural heat convect io n invo lv es transform in g con tro l equations in boundary layer in to approx i m ate equations . Based on th ism ethod , approx i m ate equations becom e five ordin ary d ifferentia l equat io ns by in troduc ing indirect variab les. Adoptin g MATLAB fo r nu m erical si m u lation o f th e approx i m a te so lu tio ns renders possible not on ly the featu re of distribu tio n o f tem perature and ve loc ity in boundary layer o f la m in ar flow, but a lso the chang ing rules of other quantit ie s o f physics. K ey w ords: natural convection; vertical p late ; boundary layer ; num erica l si m ulat io ns
