自考高等数学公式大全
专升本高数公式大全

专升本高数公式大全1.二次函数的图像方程:f(x)=a(x-h)²+k2.平面直角坐标方程:Ax+By+C=03.二次曲线方程:Ax² + By² + Cxy + Dx + Ey + F = 04.圆的标准方程:(x-a)²+(y-b)²=r²5.椭圆的标准方程:(x-a)²/b²+(y-b)²/a²=16.双曲线的标准方程:(x-a)²/b²-(y-b)²/a²=17.抛物线的标准方程:(x-a)²=4p(y-b)8.三角函数的正余弦和差公式:(1) sin(A ± B)= sinAcosB ± cosAsinB(2) cos(A ± B) = cosAcosB ∓ sinAsinB(3) tan(A ± B) = (tanA ± tanB) / (1 ∓ tanAtanB)9.三角函数的倍角公式:(1) sin2A = 2sinAcosA(2) cos2A = cos²A - sin²A(3) tan2A = (2tanA) / (1 - tan²A)10.三角函数的半角公式:(1) sin(A/2) = ±√[(1 - cosA) / 2](2) c os(A/2) = ±√[(1 + cosA) / 2](3) tan(A/2) = ±√[(1 - cosA) / (1 + cosA)]注:±的选取根据A的象限确定。
11.三角方程的化简公式:(1) sin²x + cos²x = 1(2) 1 + tan²x = sec²x(3) 1 + cot²x = csc²x12.导数的基本公式:(1) (cf(x))' = cf'(x)(2)(f(x)±g(x))'=f'(x)±g'(x)(3)(f(x)g(x))'=f'(x)g(x)+f(x)g'(x)(4)(f(x)/g(x))'=[f'(x)g(x)-f(x)g'(x)]/[g(x)]²(5)(f(g(x)))'=f'(g(x))g'(x)(6)(f(x)⋅g(x)⋅h(x))'=f'(x)g(x)h(x)+f(x)g'(x)h(x)+f(x)g(x)h'( x)13.微分的基本公式:(1) dy = f'(x)dx(2) dy = dx/g'(y)(3) dy = p(x)dx + q(x)dx² + r(x)f'(x)14.积分的基本公式:(1) ∫cf(x)dx = c∫f(x)dx(2) ∫[f(x) ± g(x)]dx = ∫f(x)dx ± ∫g(x)dx(3) ∫f'(x)dx = f(x) + C(4) ∫f'(g(x))g'(x)dx = f(g(x)) + C15.牛顿-莱布尼兹公式:∫[a, b]f(x)dx = F(b) - F(a)注:其中F(x)为f(x)的一个原函数。
自考高等数学全部公式

自考高等数学全部公式为了简化回答,我将提供一些常用的高等数学公式。
由于高等数学的内容非常广泛,无法一一列举所有的公式。
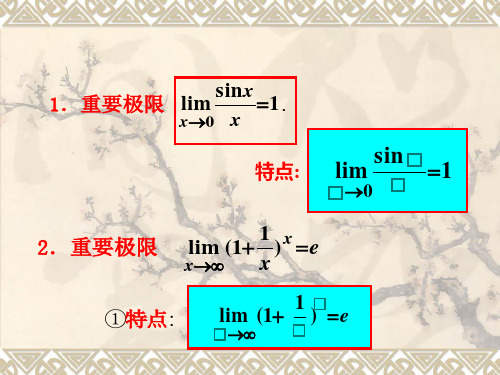
以下是一些常见的高等数学公式分类,并附上一些例子:1.极限公式:- 孙子定理:$\lim_{x \to 0} \frac{\sin x}{x} = 1$- 自然对数的极限:$\lim_{x \to \infty} (1 + \frac{1}{x})^x = e$2.导数公式:-基本导数公式:- $\frac{d}{dx} (a) = 0$ 其中 a 是常数- $\frac{d}{dx} (x^n) = nx^{n-1}$ 其中 n 是常数- $\frac{d}{dx} (e^x) = e^{x}$- $\frac{d}{dx} (\ln x) = \frac{1}{x}$-导数的四则运算规则:- $\frac{d}{dx} (u + v) = \frac{du}{dx} + \frac{dv}{dx}$- $\frac{d}{dx} (uv) = u\frac{dv}{dx}+v\frac{du}{dx}$- $\frac{d}{dx} (\frac{u}{v})= \frac{v\frac{du}{dx}-u\frac{dv}{dx}}{v^2}$- 链式法则:$\frac{dy}{dx} = \frac{dy}{du}\frac{du}{dx}$3.积分公式:-不定积分公式:- $\int (a) dx = ax + C$ 其中 a 是常数,C 是常数- $\int (x^n) dx = \frac{x^{n+1}}{n+1} + C$ 其中 n 是非零常数,C 是常数- $\int (e^x) dx = e^x + C$ 其中 C 是常数- $\int \frac{1}{x} dx = \ln ,x, + C$ 其中 C 是常数-定积分公式:- $\int_{a}^{b} f(x) dx = F(b) - F(a)$ 其中 F(x) 是 f(x) 的原函数4.级数公式:-等比数列的和:$\sum_{n=0}^{\infty} ar^n = \frac{a}{1-r}$ 其中 a 是首项,r 是公比- 幂级数:$\sum_{n=0}^{\infty} c_n(x-a)^n$ 其中 $c_n$ 是常数系数,a 是中心点5.微分方程公式:- 一阶线性常微分方程:$\frac{dy}{dx} + p(x)y = q(x)$- 二阶齐次线性常微分方程:$\frac{d^2 y}{dx^2} +p(x)\frac{dy}{dx} + q(x)y=0$以上只是高等数学中的一小部分公式,还有很多其他公式如三角函数的和差化积、积化和差等。
自考高等数学公式大全

自考高等数学公式大全(总4页)-CAL-FENGHAI.-(YICAI)-Company One1-CAL-本页仅作为文档封面,使用请直接删除《高等数学(工本)》公式第一章 空间解析几何与向量代数1. 空间两点间的距离公式21221221221)()()(z z y y x x p p -+-+-=2. 向量的投影3. 数量积与向量积: 向量的数量积公式:设},,{},,,{z y x z y x b b b a a a ==.2︒⊥的充要条件是:0=⋅向量的数量积公式:.3︒//的充要条件是0=⨯4. 空间的曲面和曲线以及空间中平面与直线平面方程公式: ),,(o o o o z y x M },,{C B A =点法式:0)()()(=-+-+-o o o z z C y y B x x A直线方程公式: },,{n m l S = ,),,(o o o o z y x M点向式:nz z m y y l x x o o o -=-=- 5. 二次曲面 第二章 多元函数微分学6. 多元函数的基本概念,偏导数和全微分偏导数公式:.2︒设),(),,(),,(y x v y x u v u f z ψϕ===.3︒设0),,(=z y x F FzFy y z Fz Fx x z -=∂∂-=∂∂ 全微分公式:设),,(y x f z =dy yz dx x z dz ∂∂+∂∂=7. 复合函数与隐函数的偏导数8. 偏导数的应用:二元函数极值9. 高阶导数第三章 重积分10. 二重积分计算公式:.1︒⎰⎰=DkA kd σ(A 为D 的面积) 11. 三重积分计算公式:.1︒利用直角坐标系计算,Ω为⎪⎩⎪⎨⎧≤≤≤≤≤≤b x a x y y x y y x z z y x z )()(),(),(2121 .2︒利用柱面坐标计算:Ω为⎪⎩⎪⎨⎧===z y r y r x ϑϑsin cos.3︒利用球面坐标计算:Ω为⎪⎩⎪⎨⎧===ϕϕϑϕϑcos sin sin sin cos r y r y r x12. 重积分的应用公式:.1︒曲顶柱体的体积:⎰⎰=Ddxdy y x f V ,),(曲面),(:y x f z =∑.2︒设V 为Ω的体积:⎰⎰⎰Ω=dv V.3︒设∑为曲面),(y x f z =曲面的面积为σd f f S Dy x ⎰⎰++=221第四章 曲线积分与曲面积分13. 对弧长的曲线积分 (1)若L :b x a x f y ≤≤=),(,则⎰⎰+=ba L dx x x x f dl y x f )(1)](,[),(2ϕϕ(2)若L :βαψϕ≤≤⎩⎨⎧==t t y t x ,)()( 则⎰⎰'+'=βαψϕψϕdx t t t t f dl y x f L )()()](),([),(22(3)当1),(=y x f 时,曲线L 由B 的弧长为⎰=Ldl S 。
专升本高数公式大全

导数公式:基本积分表:三角函数的有理式积分:222212211cos 12sin u dudx x tg u u u x u u x +==+-=+=, , , 一些初等函数: 两个重要极限:ax x aa a ctgx x x tgx x x x ctgx x tgx a x x ln 1)(log ln )(csc )(csc sec )(sec csc )(sec )(22='='⋅-='⋅='-='='222211)(11)(11)(arccos 11)(arcsin x arcctgx x arctgx x x x x +-='+='--='-='⎰⎰⎰⎰⎰⎰⎰⎰⎰⎰+±+=±+=+=+=+-=⋅+=⋅+-==+==Ca x x a x dx C shx chxdx C chx shxdx Ca a dx a Cx ctgxdx x Cx dx tgx x Cctgx xdx x dx C tgx xdx x dx xx)ln(ln csc csc sec sec csc sin sec cos 22222222C axx a dx C x a xa a x a dx C a x ax a a x dx C a xarctg a x a dx Cctgx x xdx C tgx x xdx Cx ctgxdx C x tgxdx +=-+-+=-++-=-+=++-=++=+=+-=⎰⎰⎰⎰⎰⎰⎰⎰arcsin ln 21ln 211csc ln csc sec ln sec sin ln cos ln 22222222⎰⎰⎰⎰⎰++-=-+-+--=-+++++=+-===-Cax a x a x dx x a Ca x x a a x x dx a x Ca x x a a x x dx a x I nn xdx xdx I n n nn arcsin 22ln 22)ln(221cos sin 2222222222222222222222ππ三角函数公式: ·诱导公式:·和差角公式: ·和差化积公式:2sin2sin 2cos cos 2cos2cos 2cos cos 2sin2cos 2sin sin 2cos2sin2sin sin βαβαβαβαβαβαβαβαβαβαβαβα-+=--+=+-+=--+=+αββαβαβαβαβαβαβαβαβαβαβαctg ctg ctg ctg ctg tg tg tg tg tg ±⋅=±⋅±=±=±±=±1)(1)(sin sin cos cos )cos(sin cos cos sin )sin( xxarthx x x archx x x arshx e e e e chx shx thx e e chx e e shx x x xx xx xx -+=-+±=++=+-==+=-=----11ln21)1ln(1ln(:2:2:22)双曲正切双曲余弦双曲正弦...590457182818284.2)11(lim 1sin lim 0==+=∞→→e xxx x x x·倍角公式:·半角公式:ααααααααααααααααααcos 1sin sin cos 1cos 1cos 12cos 1sin sin cos 1cos 1cos 122cos 12cos 2cos 12sin -=+=-+±=+=-=+-±=+±=-±=ctg tg·正弦定理:R CcB b A a 2sin sin sin === ·余弦定理:C ab b a c cos 2222-+=·反三角函数性质:arcctgx arctgx x x -=-=2arccos 2arcsin ππ高阶导数公式——莱布尼兹(Leibniz )公式:)()()()2()1()(0)()()(!)1()1(!2)1()(n k k n n n n nk k k n k n n uv v u k k n n n v u n n v nu v u v u C uv +++--++''-+'+==---=-∑中值定理与导数应用:拉格朗日中值定理。
自考高等数学全部公式
变限求导公式
(1) [ f (t )dt ] f ( x) ;
a x
(2) [
b x
f (t )dt ] f ( x) ;
(3) [
(4) [
(5) [
(x)
a b
f (t )dt ] f [ ( x )] ( x ) ;
g( x)
f ( t )dt ] f [ g( x )] g( x ) ;
自由项 f ( x )
e x pm ( x )
方程 y ay by f ( x ) 的特解 y
(1) 不是特征根
(2) 是单特征根
y Qm ( x )e x
y x Qm ( x )e x
y x 2 Qm ( x )e x
(3) 是二重特征根
(1) α iβ 不是特征根
e
x
y ex [Ql ( x )cosx Rl ( x )sinx ]
y xex [Ql ( x )cosx
[ Pm ( x )cos x
Pn ( x )sin x ]
(2) α iβ 是特征根
Rl ( x )sinx] 其中lmax{ ,n} m
f ( x0 x ) f ( x0 ) f ( x ) f ( x0 ) y f ( x ) lim lim lim x 0 x x 0 x x0 x x x0
基本初等函数和常数的求导公式
(1)(c ) 0 ;
(2) ( x ) x 1 ;
1 1 x2 dx arcsinx C ;
(4)d(arctanx )
1 1 x 1
2
dx;
(5)d(arcsinx )
自考高等数学公式

高等数学公式大全1.导数公式:
2.两个重要极限:
3.倍角公式:; ;
4.空间解析几何和向量代数:
5.
6., 三点式
7.
8.多元函数微分法及应用
9.
10.微分法在几何上的应用:
(1)
(2)
11.方向导数与梯度:
12.多元函数的极值:
13.重积分及其应用:
14.柱面坐标和球面坐标:
15.曲线积分:
16.曲面积分:
(3)高斯公式:注意侧向!
17.常数项级数:
18.级数审敛法:
,满足
比较判别法的极限形式:
19.绝对收敛与条件收敛:
20.幂级数:
21.一些函数展开成幂级数:
;
22.傅立叶级数:
23.微分方程的相关概念:(1)
一阶线性微分方程:, 通解
全微分方程:
(2)二阶常系数齐次线性微分方程:
其特解:
大题目:1.求直线或平面;2.隐函数求导或求全微分dz;3。
复合函数求导;4.梯度或方向导数;5.交换积分次序;6.直(或极)角坐标系二重积分;7.两类曲线积分各一题,注意是否用格林公式或积分与路径无关;9两类曲面积分各一题,注意是否用高斯公式;11.一阶线性微分方程求解;12.收敛半径收敛区间;13.傅里叶级数an或bn;14.求空间曲面面积;15.函数的展开;16。
曲面的切平面、法线或曲线的切线、法平面;17.三重积分(直角、柱或球);18.判别级数敛散性(比较、根值或比值)或判别条件收敛还是绝对收敛。
山东专升本必备高等数学公式大全

山东专升本权威网络教育培训机构-金名网校1山东专升本金名网校网络教育培训机构高等数学公式·平方关系:sin 2α+cos 2α=1tan 2α+1=sec 2αcot 2α+1=csc 2α积的关系:sinα=tanα·cosαcosα=cotα·sinαtanα=sinα·secαcotα=cosα·cscαsecα=tanα·cscαcscα=secα·cotα·倒数关系:tanα·cotα=1sinα·cscα=1cosα·secα=1·倍角公式:sin(2α)=2sinα·cosα=aa cot tan 2+cos(2α)=cos 2α-sin 2α=2cos 2α-1=1-2sin 2αtan(2α)==)(2tan^1tan 2a a -·降幂公式sin 2α=2)2cos(1a -cos 2α=2)2cos(1a +tan 2α=)2cos(1)2cos(1a a +-两角和与差的三角函数:cos(α+β)=cosα·cosβ-sinα·sinβcos(α-β)=cosα·cosβ+sinα·sinβsin(α±β)=sinα·cosβ±cosα·sinβtan(α+β)=(tanα+tanβ)/(1-tanα·tanβ).·积化和差公式:sinα·cosβ=21[sin(α+β)+sin(α-β)]cosα·sinβ=21[sin(α+β)-sin(α-β)]cosα·cosβ=21[cos(α+β)+cos(α-β)]sinα·sinβ=-21[cos(α+β)-cos(α-β)]半角公式αααααααααααcos 1sin sin cos 1cos 1cos 122cos 12cos 2cos 12sin -=+=-+±=+±=-±=ctg ·和差化积公式:sinα+sinβ=2sin[(α+β)/2]cos[(α-β)/2]sinα-sinβ=2cos[(α+β)/2]sin[(α-β)/2]cosα+cosβ=2cos[(α+β)/2]cos[(α-β)/2]cosα-cosβ=-2sin[(α+β)/2]sin[(α-β)/2]山东专升本权威网络教育培训机构-金名网校2·推导公式tanα+cotα=a2sin 2tanα-cotα=-2cot2α1+cos2α=2cos 2α1-cos2α=2sin 2α1+sinα=(2sin a +2cos a )2三角函数的角度换算公式一:sin (2kπ+α)=sinαcos (2kπ+α)=cosαtan (2kπ+α)=tanαcot (2kπ+α)=cotα公式四:sin (π-α)=sinαcos (π-α)=-cosαtan (π-α)=-tanαcot (π-α)=-cotα公式六:sin (π/2+α)=cosαcos (π/2+α)=-sinαtan (π/2+α)=-cotαcot (π/2+α)=-tanαsin (π/2-α)=cosαcos (π/2-α)=sinαtan (π/2-α)=cotα公式二:sin (π+α)=-sinαcos (π+α)=-cosαtan (π+α)=tanαcot (π+α)=cotα公式三:sin (-α)=-sinαcos (-α)=cosαtan (-α)=-tanαcot (-α)=-cotα公式五:sin (2π-α)=-sinαcos (2π-α)=cosαtan (2π-α)=-tanαcot (2π-α)=-cotαsin (3π/2+α)=-cosαcos (3π/2+α)=sinαtan (3π/2+α)=-cotαcot (3π/2+α)=-tanαsin (3π/2-α)=-cosαcos (3π/2-α)=-sinαtan (3π/2-α)=cotαcot (3π/2-α)=tanαcot(π/2-α)=tanα平常针对不同条件的常用的两个公式sin²α+cos²α=1tan*αotα=1对数函数对数公式及性质换底公式:loga M=logbM/logbA(b>0且b≠1)对数与指数之间的关系当a>0且a≠1时,a x=N x=㏒aN(3)自然对数:lnb=logebln1=0lne=1单调性:a>1时,在定义域上为单调增函数,并且上凸;0<1时,在定义域上为单调减函数,并且下凹。
高等数学必背公式大全

高等数学必背公式大全1、勾股定理:a2+b2=c22、椭圆方程:(x-x0)2/a2+(y-y0)2/b2=13、两点公式:,P1P2,=√((x2-x1)2+(y2-y1)2)4、双曲线方程:a2(x2/b2)-(y2/c2)=15、圆的方程:(x-x0)2+(y-y0)2=r26、三角形公式:a2+b2=c27、直线方程:y = kx + b (斜率k和截距b)8、斜率定理:m1*m2=-1/K29、余弦定理:a2 = b2 + c2 - 2bc*cosA10、正弦定理:a * sinA = b * sinB = c * sinC11、贝塞尔曲线方程:(x-x0)4+(y-y0)4=r412、三角函数公式:sin2A + cos2A = 113、极坐标方程:r = a * e(acosθ + bsinθ)14、反正弦定理:y = arcsin(x/a) + c15、偏微分公式:dy/dx = (dy/du) * (du/dx)16、平面四边形公式:a2+b2=c2+d217、反余弦定理:y = arccos(x/a) + c18、三角形面积公式:S = 1/2 * a * b * sinC19、多边形内角和公式:(n-2)*π=∑(内角弧度)20、抛物线公式:y=ax2+bx+c21、多项式求导公式:f'(x) = an-1 * xn-1 + an-2 * xn-2 + …… + a1 * x + a022、函数变换公式:f(x+h) = f(x) + hf'(x)23、矩阵乘法公式:(AB)ij = ∑k=1n(Aik*Bkj)24、求和公式:∑(a1+an)*n/225、模除法:a / b = a mod b + b * (a div b)26、几何平均数公式:(a1*a2*a3*……*an)^(1/n)27、距离公式:L=(x2-x1)^2+(y2-y1)^228、几何中点公式:(x1+x2)/2,(y1+y2)/229、坐标转换公式:x = x0 + (x-x0)cosα - (y-y0)sinα。
专升本数学公式汇总

小数加减法(一)
6.45+4.29=10.74 6.45-4.29=2.16
6.45 6.45
+ 4.29- 4.29
10.742.16
六、习题精选
计算竞技场
1、口算:
3.4+0.57.5+2.18.5-2.5
9.9-7.78.6-2.55.9+3.6
5.6-2.43.8-1.6
2、计算下列各题并且验算
教学重点
1、小数加、减法的笔算方法以及小数加减混合运算。
2、能根据数据特点正确应用加法的运算定律进行小数的简便计算。
教学难点
1、理解小数点对齐,即数位对齐的道理。
2、灵活选用方法使混合运算简便。
3、感受解题策略的多样化和灵活性。
教学准备
课本、课件。
教学过程
教学内容
学生活动
补充、总结
一、复习旧知,引出新知。
成绩面前不炫耀,永远保持着踏踏实实,平平常常的生活态度和格调。以成熟,豁达,自信,睿智处世做事。就ᅳ定会拥有属于自己的一片广阔的天地。
6.456.45
+ 4.29- 4.29
10.742.16
(2)师:大家同意这样写竖式吗?
(3)比较整数加减法和小数加减法异同:计算方法上都是一位对着一位减是一样的,不同之处在于小数点,盖住小数点就是大家熟悉的整数减法了。
(4)小结:从这两个算式我们看出小数加减法和整数是相似的,只是要多小数点。
(5)计算:1.25+0.45 4.38-1.28
得数的小数部分末尾出现什么了?像这样的情况你知道还可以怎么写吗?根据是什么?
(6)小结:当小数加减法得数的小数部分末尾出现0的时候,我们要对结果进行化简,向横式汇报的时候就写最简结果就可以了,这也是我们数学简洁美的一种体现。
成人高考高数必考公式

成人高考高数必考公式
1.函数相关公式:
-基本初等函数(加减乘除、幂函数、指数函数、对数函数、三角函数、反三角函数等)的性质和公式;
-基本函数的导数公式(如幂函数的导数、指数函数和对数函数的导数、三角函数的导数等);
-基本函数的积分公式(如幂函数的积分、指数函数和对数函数的积分、三角函数的积分等);
-复合函数的求导公式(链式法则)。
2.极限公式:
- 基本初等函数的极限(如无穷小量的定义、极限的四则运算法则、lnx、ex、sinx、cosx等函数的极限等);
-极限运算的性质(如极限的唯一性、有界性、保号性、夹逼定理等);
-数列极限的相关公式和性质(如比较定理、夹逼定理等)。
3.导数和微分公式:
-导数的定义、性质和基本公式(如函数和导函数的关系、四则运算法则、常数函数、幂函数、指数函数、对数函数等导数的公式);
-高阶导数的定义与求法;
-隐函数和参数方程的求导公式;
-微分的定义和微分公式(如微分的四则运算法则、复合函数的微分等)。
4.积分公式与定积分:
-不定积分和定积分的定义和性质;
-基本的定积分公式(如幂函数的定积分、三角函数的定积分、指数函数和对数函数的定积分、反常积分等);
-牛顿-莱布尼茨公式(积分的几何、物理、微分方程等应用)。
5.一阶微分方程和二阶线性微分方程的基本解法:
-一阶微分方程的分离变量法、齐次方程法、一阶线性非齐次方程法等;
-二阶线性微分方程的常系数齐次方程解法、常系数非齐次方程通解公式等。
高等数学各章重要公式及知识点归总

第一章 函数类1. y=x 1,x ≠0 →y=□1,□≠0 (-∞,0)∪(0,+∞)类2.y=2n x ,x ≥0 →y=2n □,□≥0 [0,+∞)反函数(一一对应)1. 函数的定义域对应着反函数的值域 函数的值域对应着反函数的定义域2. 若f (x )过(a ,b ),f -1(x )过(b ,a )3. f (x )和f -1(x )的图像关于y=x 对称4.Sinx sin[arcsinx]=x →arcsinx arcsin[sinx]=xEg.f[f -1(3)]=3基本初等函数幂函数:y=x u ,u 取任意的实数 共同点(1,1)偶函数:图像关于y 轴对称 y=x 2 指数函数(变化最快):y=a x ,a >0且a ≠12共同点(0,1)对数函数:y=log a x ,a >0且a ≠1 y=a x →log a y=x →y=log a x1.a >1 (若a=e ≈2.71 →y=log e x=lnx ) 2.0<a <1共同点(1,0)y=e x 反函数是 y=log e x=lnx反sinx :ππcosx :[2k π-π,2k π] k ∈z ,增函数 [2k π,2k π+π] k ∈z ,减函数tanx:单调增区间:z k k π2πk π2π-∈++),(cotx:→1.奇函数:sinx,tanx,cotx原点对称偶函数:cosx y=x对称2.有界函数:sinx,cosx 有界是根据值域定的3.周期函数:sinx,cosx→T=2πtanx,cotx→T=πtanx·cotx=1 sin0=0Sin2x=2sinxcosxCos2x=cos2x-sin2x=2cos2x-1=1-2sin2x2.特殊角度→函数值反三角函数:arcsinx,arccosx,arctanx,arccotx arcsinx:arccox:arctanx :arccotx:→1.奇函数:arcsinx ,arctanx2.有界函数:arcsinx ,arccosx ,arctanx ,arccotxarcsin1=2π arcsin 23=3π arctan1=4π arctan 3=3π定义域: -1≤x ≤1复合函数:y=f (u),u=g (x ) , y=f[g(x)] Z ⊂D复合1.y=u 2,u=sinx →y=sin 2x2.y=u 3,u=cosv ,v=2x+3→y=cos 3(2x+3) 条件:3.y=arccosu ,u=x 2+3→y=arccos (x 2+3)×初等函数:由基本的初等函数经过有限次的四则运算及复合得到的函数 复合函数的分解:1.由内到外,分解的每一步必须为基本初等型 2.遇到四则运算或基本初等型则停止 e x ,x ≥0 分段函数:f (x )=X+1,x <0取整函数:设x 为任一实数,不超过x 的最大整数称为x 的整数部分,记作:[x] Eg: [1.5]=1 [2.8]=2 [4.5]=4 [e]=2 [π]=3[-1.5]=-2 [-2.8]=-3 [-4.5]=-5 x-1<[x]≤x 隐函数:x+y=2,sinx+cosy=3参数方程: x=sint x=t 2+2→y 与x →y 与xy=cost y=3t引入参数,导致y 与x 有联系幂指函数:y=u (x )v (x )→1.lny=lnu (x )v (x )=v (x )lnu (x )2.)()()()(x lnu x v x lnu e ey x v ==,恒等变形函数的性质:必须在所给的定义域内单调性,有界性,周期性,奇偶性1.常见的有界函数:sinx,cosx,arcsinx,arccosx,arctanx,arccotx2.有界函数的运算:有界+有界=有界有界-有界=有界有界×有界=有界无穷大量±有界一定>0+∞+有界=+∞-∞+有界=-∞周期函数:sinx→T=2πcosx→T=2πtanx→T=πcotx→T=π奇偶性:1.偶函数:图像关于y轴对称,f(x0)=f(-x0)2.奇函数:图像关于原点对称,f(x0)=-f(-x0)常见的奇函数:sinx,tanx,cotx,arcsinx,arctanx,x n(n为奇数)常见的偶函数:cosx,x n(n为偶数),|x|常熟C C,C≠0→偶函数0,可奇可偶奇偶运算规则:偶偶:+ - ×÷是偶函数→x2,1-x2,x2(1-x)2,1+x2,,cosx1=secx奇奇:+ - 是奇函数x+x3×÷是偶函数x×x=x2x·sinx sin4x=sinx·sinx·sinx·sinx 1+x21+x2 1-x2奇偶:×÷是奇函数x×x2=x3+ - 可奇,可偶,非奇非偶极限等差数列: 1,2,3,4,……,n ,…… 公差d=1,通项x n =n=1+(n-1)×1通项x n =x 1+(n-1)d →等差数列:首项x 1,公差d前n 项和,(求和公式):2nxn +x1)(等比数列:2,22,23,24,……,2n 公比q=2,x n =2n =2·2n-1 X n =x 1·q n-1 →等比数列:首项x 1(x 1≠0),公比q (q ≠1)前n 项和公式:s n 特殊数列前n 项和:1.2n 1n n 4321k z n 1k )(+=+⋯⋯++++== 2.=+=+⋯⋯+++==21)n-2n (11)-2n 5311-2k z n 1k ()(n 2 3.1k z n =k 2=12+22+32+……+n 2=61-2n 1n n ))((+ 4.1k z =∞k 3=13+23+33+……+n 3=]2n 1n [)(+ 2 5.1n 1-n 131-2121-111n n 12?11?11k k 1z n 1k ++⋯⋯++=++⋯⋯++=+=)()(=1n 1-1+ =1n n + 数列极限的定义:若不存在常数a ,则极限不存在,或x n 发散1-q几何含义:当n>N 时,所有的点x n 都落在(a-ε,a+ε)内,只有有限个(至多只有N 个)在其外数列的性质:极限存在的充要条件:左极限=右极限1.唯一性2.有界性:|x n -a|<ξ3.保号性:∀ξ>0,∃n >N ,使得|x n -a|<ξ 若a >0,n >N 时,x n >0 若a <0,n >N 时,x n <0 去心领域:只考虑点a 邻近的点,不考虑点a ,即考虑点集(a-δ,a )∪(a ,a+δ),称这个点集为点a 的去心邻域函数的极限性质:1.函数极限的唯一性:若A =∞→→)(x f lim x x0x ,则极限必唯一2.函数极限的局部有界性3.函数极限的局部保号性:若A =→)(x f lim x0xA >0,0<|x-x 0|<δ,f (x )>0A <0,0<|x-x 0|<δ,f (x )<0无穷小(无穷小量)与无穷大常数的极限永远是本身关系:1.∞=→)(x f lim x0x →0x f 1limx0x =→)(互为倒数关系2.0x f 0x f lim x0x ≠=→)(且)(→∞=→)(x f 1limx0x01=∞ ∞=01总结:极限不存在的三种情形 1.limf (x )=∞ 2.左极限≠右极限3.没有确定的函数值极限值区间内波动]1,1[sinx lim x -=∞→方法一:000=⨯=⨯有界)无穷小量(即无穷小量有界函数 方法二:四则运算:(极限存在,则可以拆) 1.lim[f (x )±g (x )]=limf (x )±limg (x )=A ±B 2.lim[f (x )·g (x )]=limf (x )·limg (x )=A ·B 3.)()()()()(0x lim g x lim f x g x f lim≠==B BA 4.limC ·f (x )=C ·limf (x )=C ·A C 是常数 5.lim[f(x)]n =limf (x )·limf (x )……=A n总结:x →x 0时,x 0在初等函数定义域内,可直接将值代入求极限 方法三:消0因子法(0)方法四:抓大头思想(∞∞) 方法五:利用分子有理化求极限 方法六:先求和再求极限 方法七:先求积再求极限方法八:利用夹逼准则求极限(找两边) 极限存在准则:1.夹逼准则(1)x n ≤y n ≤z n ,且a zn lim a xn lim n n ==∞→∞→,→a yn lim n =∞→(2)g (x )≤f (x )≤h (x ),且A A ==)(,)(x lim h x lim g →A =)(x limf2.单调有界数列必有极限→{x n }单调增且有上届→则{x n }必有极限 数列是以点的形式→{x n }单调减且有下届→则{x n }有极限 方法九:利用两个重要极限求极限0·∞ 谁简单就把谁往下放 ① 1□□sin lim 1x sinx lim0□0x =→=→→1.sin □和分母中的□必须保持一致 → 12xsin2xlim 0x =→2.□→00·∞→∞⨯=⨯→001000 →01⨯∞=∞⨯∞→∞∞②e x 1limx1x =+→)( ①∞1 e x11limxx =+∞→)( ②1+形式→e □1lim 0□□1=+→时)(e n 11lim nn =+∞→)( ③互为倒数总结:若今后遇到∞1型①若)()](1[lim x g x f + 为∞1,则原式=)()(x g x limf e②若)(x g )]([lim x f 为∞1,则原式=)(x g ]1)([lim e ⨯-x f方法十:利用等价无穷小求极限 → 无穷小的比较→型→0,∞,c (c ≠0) 常用的等价无穷小的公式:前提条件 : □→0Sin □~□ , tan □~□ , arcsin □~□ , arctan □~□注意1.因子:只有乘除关系,等价必须是因子 2.非0因子直接代入方法十一:利用左右极限求极限左极限:0-0x x x x x f lim -0<),(→ 右极限:+→+00x x x x x f lim 0<),(极限存在的充要条件:若A A =→→=+→→→)()()(x f lim x f lim x f lim 0-0x x x x x x左极限=右极限极限不存在:1.limf (x )=∞2.左极限≠右极限3.没有确定的函数值极限值区间内波动]1,1[sinx lim x -=∞→注意:分段函数分界点要分左右极限 已知极限求反参数幂指函数方法处理:连续与间断→极限的应用设f (x )在x 0的邻域内又定义,如果)()(0x x x f x f lim 0=→,则称f (x )在x 0处连续。
(完整版)专升本高数公式大全

高等数学公式求导公式表:()0C '= (C 为常数); 1()x x ααα-'=(α为实数); ()ln (0,1)x x a a aa a '=>≠; ()x x e e '=;1(log )(0,1)ln x a a a x a'=>≠; 1(ln )x x '=;(sin )cos x x '=;(cos )sin x x '=-;12(tan )sec 2cos x x x'==; (sec )sec tan x x x '=⋅;12(cot )csc 2sin x x x'=-=-; (csc )csc cot x x x '=-⋅;(arcsin )x ';(arccos )x ';1(arctan )21x x '=+; 1(arccot )21x x '=-+.基本积分表:d k x kx C=+⎰ (k 为常数).特别地,当0k =时,0d x C=⎰.11d 1x x x C ααα+=++⎰ (1)α≠- 1d ln ||x x Cx =+⎰ d ln x xa a x Ca =+⎰ (0,1)a a >≠. d x x e x e C =+⎰.sin d cos x x x C=-+⎰. cos d sin x x x C=+⎰.22d sec d tan cos xx x x C x==+⎰⎰. 22d csc d cot sin xx x x C x==-+⎰⎰. sec tan d sec x x x x C =+⎰.csc cot d csc x x x x C =-+⎰.arcsinx x C=+arccos x C'=-+.21d arctan1x x Cx=++⎰cotarc x C'=-+.tan d ln cosx x x C=-+⎰.cot d ln sinx x x C=+⎰.sec d ln sec tanx x x x C=++⎰.csc d ln csc cotx x x x C=-+⎰.2211d arctanxx Ca x a a=++⎰.2211d ln2x ax Cx a a x a-=+-+⎰.arcsin(0)xx C aa=+>.lnx x C=+.21arcsin22a xx Ca=+.31sec d sec tan ln sec tan2x x x x x x C⎡⎤=+++⎣⎦⎰三角函数的有理式积分:2222212sin cos tan1121u u x du x x u dxu u u-====+++, , , 一些初等函数:()(0,1)log(0,1)sin,cos,tan,cot,sec,cscarcsin,arccos,arctan,arccotxay xy a a ay x a ay x y x y x y x y x y xy x y x y x y xμμ==>≠=>≠==========幂函数:为实数指数函数:对数函数:三角函数:反三角函数::2:2:x xx xx xx xe eshxe echxshx e ethxchx e e-----=+=-==+双曲正弦双曲余弦双曲正切ln(ln(11ln21arshx x archx x xarthx x==±++=-两个重要极限:sin lim 1x x x =→ ()11lim 1lim 10x xx ex x x ⎛⎫+=+= ⎪→∞→⎝⎭等价无穷小量替换当0x →时,~sin ~tan ~arcsin ~arctan x x x x x~ln(1)~x +1xe -,121cos ~2x x -,2~sin 2~tan 2x x x11~2x三角函数公式:·诱导公式:·和差角公式: ·和差化积公式:2sin2sin 2cos cos 2cos2cos 2cos cos 2sin2cos 2sin sin 2cos2sin2sin sin βαβαβαβαβαβαβαβαβαβαβαβα-+=--+=+-+=--+=+sin()sin cos cos sin cos()cos cos sin sin tan tan tan()1tan tan cot cot 1cot()cot cot αβαβαβαβαβαβαβαβαβαβαββα±=±±=±±=⋅⋅±=±·倍角公式:·半角公式:sin cos 221cos sin 1cos sin tancot 2sin 1cos 2sin 1cos αααααααααααα==-+======+- ·正弦定理:R CcB b A a 2sin sin sin === ·余弦定理:C ab b a c cos 2222-+=·反三角函数性质:arcsin arccos arctan cot 22x x x arc x ππ=-=- 高阶导数公式——莱布尼兹(Leibniz )公式:)()()()2()1()(0)()()(!)1()1(!2)1()(n k k n n n n nk k k n k n n uv v u k k n n n v u n n v nu v u v u C uv +++--++''-+'+==---=-∑中值定理与导数应用:()0()()()()()()()()()()F()f f b f a f b a f b f a f F b F a F x x ξξξξ'='-=-'-='-=罗尔中值定理:拉格朗日中值定理:柯西中值定理:当时,柯西中值定理就是拉格朗日中值定理。
专升本高数公式大全

专升本高数公式大全1.初等函数的性质- 一次函数的表达式:y = kx + b,其中k为斜率,b为截距。
- 二次函数的表达式:y = ax² + bx + c,其中a、b、c为常数。
-绝对值函数的表达式:y=,x。
2.导数与微分的基本公式- 函数极限的定义:lim(x→a) f(x) = L。
- 导数的定义:f'(x) = lim(Δx→0) [f(x+Δx) - f(x)] / Δx。
-基本导数公式:- (1) 若f(x) = xⁿ,则f'(x) = nxⁿ⁻¹。
-(2)若f(x)=eˣ,则f'(x)=eˣ。
- (3) 若f(x) = sin(x),则f'(x) = cos(x)。
- (4) 若f(x) = cos(x),则f'(x) = -sin(x)。
- (5) 若f(x) = ln(x),则f'(x) = 1/x。
3.极限的基本性质-极限的四则运算:- (1) 若lim(x→a) f(x) = A,lim(x→a) g(x) = B,则lim(x→a) [f(x)±g(x)] = A±B。
- (2) 若lim(x→a) f(x) = A,lim(x→a) g(x) = B,则lim(x→a) [f(x)g(x)] = AB。
- (3) 若lim(x→a) f(x) = A,lim(x→a) g(x) = B(B≠0),则lim(x→a) [f(x)/g(x)] = A/B。
- (4) 若lim(x→a) f(x) = A,则lim(x→a) [c·f(x)] = c·A。
4.函数的极值与最值-函数的极值:设f(x)在x₀处有定义,称f(x)在x₀处有极小值,如果存在εₒ>0,使得当0<,x-x₀,<εₒ时,恒有f(x)≥f(x₀)。
-函数的最值:设f(x)在区间I上有定义,x₀∈I,如果对于任意x∈I,恒有f(x)≥f(x₀),则称f(x)在x₀处有最小值。
成人高考专升本——高等数学函数基本公式

高等数学函数基本公式1. 基本初等函数求导公式函数的和、差、积、商的求导法则 设)(x u u =,)(x v v =都可导,则反函数求导法则若函数)(y x ϕ=在某区间y I 内可导、单调且0)(≠'y ϕ,则它的反函数)(x f y =在对应区间xI 内也可导,且)(1)(y x f ϕ'=' 或 dy dx dx dy 1=复合函数求导法则设)(u f y =,而)(x u ϕ=且)(u f 及)(x ϕ都可导,则复合函数)]([x f y ϕ=的导数为dy dy du dx du dx =或()()y f u x ϕ'''=2. 双曲函数与反双曲函数的导数.双曲函数与反双曲函数都是初等函数,它们的导数都可以用前面的求导公式和求导法则求出.可以推出下表列出的公式:三、基本初等函数的微分公式与微分运算法则 从函数的微分表达式:d ()d y f x x '=可以看出,要计算函数的微分,只要计算函数的导数,再乘以自变量的微分.因此,可得如下的微分公式和微分运算法则. 1. 基本初等函数的微分公式由基本初等函数的导数公式,可以直接写出基本初等函数的微分公式.为了便于对照,列表于下:2.函数和、差、积、商的微分法则由于函数和、差、积、商的求导法则,可推得相应的微分法则.为了便于对照,列成下表(表中)(),(xvvxuu==都可导).现在我们仅证明乘积的微分法则.3. 复合函数的微分法则(一阶微分形式的不变性)一阶微分形式不变性:设f是可微函数,)(ufy=,则无论u是自变量,或是另一个变量x的可微函数,都同样有d()dy f u u'=.4.例题例3)12sin(+=xy,求d y.例42ln(1e)xy=+,求d y.例513e cosxy x-=,求d y.例6在下列等式左端的括号中填入适当的函数,使等式成立.(1)()d d x x=;(2)()d cos d t tω=.。
高等数学公式大全(完整版)

高等数学公式导数公式:基本积分表:三角函数的有理式积分:222212211cos 12sin u dudx x tg u u u x u u x +==+-=+=, , , ax x a a a ctgx x x tgx x x x ctgx x tgx a x x ln 1)(log ln )(csc )(csc sec )(sec csc )(sec )(22='='⋅-='⋅='-='='222211)(11)(11)(arccos 11)(arcsin x arcctgx x arctgx x x x x +-='+='--='-='⎰⎰⎰⎰⎰⎰⎰⎰⎰⎰+±+=±+=+=+=+-=⋅+=⋅+-==+==Ca x x a x dx C shx chxdx C chx shxdx Ca a dx a Cx ctgxdx x C x dx tgx x Cctgx xdx x dx C tgx xdx x dx xx)ln(ln csc csc sec sec csc sin sec cos 22222222C axx a dx C x a xa a x a dx C a x ax a a x dx C a xarctg a x a dx Cctgx x xdx C tgx x xdx Cx ctgxdx C x tgxdx +=-+-+=-++-=-+=++-=++=+=+-=⎰⎰⎰⎰⎰⎰⎰⎰arcsin ln 21ln 211csc ln csc sec ln sec sin ln cos ln 22222222⎰⎰⎰⎰⎰++-=-+-+--=-+++++=+-===-Cax a x a x dx x a Ca x x a a x x dx a x Ca x x a a x x dx a x I nn xdx xdx I n n nn arcsin 22ln 22)ln(221cos sin 2222222222222222222222ππ一些初等函数: 两个重要极限:三角函数公式: ·诱导公式:函数 角A sincos tg ctg -α -sinα cosα -tgα -ctgα 90°-α cosα sinαctgαtgα 90°+α cosα -sinα -ctgα -tgα 180°-α sinα-cosα -tgα-ctgα 180°+α -sinα -cosα tgα ctgα 270°-α -cosα -sinα ctgα tgα 270°+α -cosα sinα -ctgα -tgα360°-α -sinα cosα -tgα -ctgα 360°+αsinαcosαtgαctgα·和差角公式: ·和差化积公式:2sin2sin 2cos cos 2cos2cos 2cos cos 2sin2cos 2sin sin 2cos2sin2sin sin βαβαβαβαβαβαβαβαβαβαβαβα-+=--+=+-+=--+=+αββαβαβαβαβαβαβαβαβαβαβαctg ctg ctg ctg ctg tg tg tg tg tg ±⋅=±⋅±=±=±±=±1)(1)(sin sin cos cos )cos(sin cos cos sin )sin(μμμxxarthx x x archx x x arshx e e e e chx shx thx e e chx e e shx x x xx xx xx -+=-+±=++=+-==+=-=----11ln21)1ln(1ln(:2:2:22)双曲正切双曲余弦双曲正弦...590457182818284.2)11(lim 1sin lim0==+=∞→→e xxxx x x·倍角公式:·半角公式:ααααααααααααααααααcos 1sin sin cos 1cos 1cos 12cos 1sin sin cos 1cos 1cos 122cos 12cos 2cos 12sin -=+=-+±=+=-=+-±=+±=-±=ctg tg·正弦定理:R CcB b A a 2sin sin sin === ·余弦定理:C ab b a c cos 2222-+=·反三角函数性质:arcctgx arctgx x x -=-=2arccos 2arcsin ππ高阶导数公式——莱布尼兹(Leibniz )公式:)()()()2()1()(0)()()(!)1()1(!2)1()(n k k n n n n nk k k n k n n uv v u k k n n n v u n n v nu v u v u C uv +++--++''-+'+==---=-∑ΛΛΛ中值定理与导数应用:拉格朗日中值定理。
专升本高数-重要公式

高等数学重要公式1.初等函数函数名称函数的记号函数的图形函数的性质指数函数a):不论x为何值,y总为正数;b):当x=0时,y=1.对数函数a):其图形总位于y轴右侧,并过(1,0)点b):当a>1时,在区间(0,1)的值为负;在区间(-,+∞)的值为正;在定义域内单调增.幂函数a为任意实数这里只画出部分函数图形的一部分。
令a=m/na):当m为偶数n为奇数时,y是偶函数;b):当m,n都是奇数时,y是奇函数;c):当m奇n偶时,y在(-∞,0)无意义.三角函数(正弦函数)这里只写出了正弦函数a):正弦函数是以2π为周期的周期函数b):正弦函数是奇函数且反三角函数(反正弦函数)这里只写出了反正弦函数a):由于此函数为多值函数,因此我们此函数值限制在[-π/2,π/2]上,并称其为反正弦函数的主值.2.双曲函数函数的名称函数的表达式函数的图形函数的性质双曲正弦a):其定义域为:(-∞,+∞);b):是奇函数;c):在定义域内是单调增双曲余弦a):其定义域为:(-∞,+∞);b):是偶函数;c):其图像过点(0,1);双曲正切a):其定义域为:(-∞,+∞);b):是奇函数;c):其图形夹在水平直线y=1及y=-1之间;在定域内单调增;3.双曲函数的和差公式4.反双曲函数反双曲正弦函数其定义域为:(-∞,+∞);反双曲余弦函数其定义域为:[1,+∞);反双曲正切函数其定义域为:(-1,+1);5.函数极限的运算规则6.两个重要极限7.函数的四则运算求导法则8.复合函数的求导法则,其中u为中间变量9.反函数求导法则10.基本初等函数的微分公式导数公式微分公式11.微分运算法则函数和、差、积、商的求导法则函数和、差、积、商的微分法则不定积分的运算法则12.不定积分的求法换元法13.分部积分法14.定积分运算法则15.牛顿-莱布尼兹公式16.定积分的公式换元公式17.分部积分法27.不同坐标系下的积分方法:直角坐标系下的积分方法极坐标系中的积分方法极点O在(σ)的外部,区域(σ)用不等式表示为R1(θ)≤ρ≤R2(θ),α≤θ≤β,则积分公式如下:极点O在(σ)的内部,区域(σ)的边界方程为ρ=R(θ),0≤θ≤2π,则积分公式如下:极点O在(σ)的边界上,边界方程为ρ=R(θ),θ1≤θ≤θ2,则积分公式如下:。
专升本高等数学常用公式

专升本高等数学常用公式高等数学是大学本科阶段的核心课程之一,其中常用的公式有很多。
下面是高等数学常用公式的一个简要总结。
由于篇幅限制,无法给出所有的公式,但会涵盖主要的内容。
微分学常用公式:1. 极限的定义:对于函数f(x),若lim(x->a)f(x)=L,则称函数f(x)在点a处的极限为L,记作lim(x->a)f(x)=L。
2. 导数定义:如果函数f(x)在点x0处有极限lim(h->0)[f(x0+h)-f(x0)]/h存在,则称函数f(x)在x0处可导,导数为f'(x0),即f'(x0)=lim(h->0)[f(x0+h)-f(x0)]/h。
3.基本导数公式:-常函数导数:(c)'=0,其中c为常数。
- 幂函数导数:(x^n)' = nx^(n-1),其中n为正整数。
-指数函数导数:(e^x)'=e^x。
- 对数函数导数:(lnx)' = 1/x。
-三角函数导数:* (sinx)' = cosx。
* (cosx)' = -sinx。
* (tanx)' = sec^2x。
* (cotx)' = -csc^2x。
* (arcsinx)' = 1/√(1-x^2)。
* (arccosx)' = -1/√(1-x^2)。
* (arctanx)' = 1/(1+x^2)。
* (arccotx)' = -1/(1+x^2)。
-复合函数导数:*(f(g(x)))'=f'(g(x))*g'(x),其中f(x)和g(x)都可导。
积分学常用公式:1.不定积分公式:-基本初等函数积分:* ∫(c)dx = cx,其中c为常数。
* ∫(x^n)dx = (x^(n+1))/(n+1),其中n不等于-1* ∫(e^x)dx = e^x。
* ∫(lnx)dx = xlnx - x,其中x>0。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
《高等数学(工本)》公式第一章 空间解析几何与向量代数1. 空间两点间的距离公式21221221221)()()(z z y y x x p p -+-+-=2. 向量的投影3. 数量积与向量积:向量的数量积公式:设},,{},,,{z y x z y x b b b a a a == .1︒z z y y x x b a b a b a b a ++=⋅ .2︒⊥的充要条件是:0=⋅.3︒b a =∧)cos(向量的数量积公式:.1︒k b a b a j b a b a i b a b a b b b a a a kj ib a x y y x z x x z y z z y zy xz y x)()()(-+-+-==⨯.2︒=ϕsin.3︒//的充要条件是0=⨯4. 空间的曲面和曲线以及空间中平面与直线平面方程公式: ),,(o o o o z y x M },,{C B A =点法式:0)()()(=-+-+-o o o z z C y y B x x A直线方程公式: },,{n m l S = ,),,(o o o o z y x M 点向式:nz z m y y l x x oo o -=-=-5. 二次曲面第二章 多元函数微分学6. 多元函数的基本概念,偏导数和全微分偏导数公式:.1︒),(),,(),,(y x v y x u v u f z ψϕ===x vv z x u u z x z ∂∂∂∂+∂∂∂∂=∂∂ yv v z y u u z y z ∂∂∂∂+∂∂∂∂=∂∂ .2︒设),(),,(),,(y x v y x u v u f z ψϕ===dxdvv z dx du u z dx dz ∂∂+∂∂=.3︒设0),,(=z y x FFzFyy z FzFx x z -=∂∂-=∂∂ 全微分公式:设),,(y x f z =dy yz dx x z dz ∂∂+∂∂= 7. 复合函数与隐函数的偏导数 8. 偏导数的应用:二元函数极值 9. 高阶导数第三章 重积分10. 二重积分计算公式:.1︒⎰⎰=D kA kd σ(A 为D 的面积).2︒⎰⎰⎰⎰⎰⎰==)()()()(1212),(),(),(y y cdDx x badx y x f dy dy y x f dx d y x f ϕϕϕϕσ.3︒⎰⎰⎰⎰=Drdr r r f d d y x f )()(12)sin ,cos (),(θϕθϕβαϑϑϑσ11. 三重积分计算公式:.1︒利用直角坐标系计算,Ω为⎪⎩⎪⎨⎧≤≤≤≤≤≤b x a x y y x y y x z z y x z )()(),(),(2121⎰⎰⎰⎰⎰⎰=Ω),(),()()(2121),,(),,(y x z y x z x y x y badz z y x f dy dx d z y x f σ.2︒利用柱面坐标计算:Ω为⎪⎩⎪⎨⎧===z y r y r x ϑϑsin cos⎰⎰⎰⎰⎰⎰=Ω),(),()()(212121),sin ,cos (),,(ϑϑϑϑϑϑϑϑr z r z r r dz z r r f rdr dx dv z y x f.3︒利用球面坐标计算:Ω为⎪⎩⎪⎨⎧===ϕϕϑϕϑcos sin sin sin cos r y r y r x⎰⎰⎰Ωdv z y x f ),,(⎰⎰⎰=),(),(2)()(2121sin )cos ,sin sin ,sin cos (ϑϕϑϕϑϕϑϕβαϕϕϕϑϕϑϕϑr r dr r r r r f d d12. 重积分的应用公式:.1︒曲顶柱体的体积:⎰⎰=Ddxdy y x f V ,),(曲面),(:y x f z =∑.2︒设V 为Ω的体积:⎰⎰⎰Ω=dv V.3︒设∑为曲面),(y x f z =曲面的面积为σd f f S Dy x ⎰⎰++=221第四章 曲线积分与曲面积分13. 对弧长的曲线积分(1)若L :b x a x f y ≤≤=),(,则⎰⎰+=baLdx x x x f dl y x f )(1)](,[),(2ϕϕ(2)若L :βαψϕ≤≤⎩⎨⎧==t t y t x ,)()(则⎰⎰'+'=βαψϕψϕdx t t t t f dl y x f L)()()](),([),(22(3)当1),(=y x f 时,曲线L 由B 的弧长为⎰=Ldl S 。
14. 对坐标的曲线积分(1)终点起点)()()(:)](,[),(b B a A x y L dx x x P dx y x P AB baL ABϕϕ==⎰⎰(2)[]终点起点)()()()(:)]()(),(),(βαψϕϕψϕβαB A t y t x L dt t t t P dx y x P AB L AB ⎩⎨⎧=='=⎰⎰15. 格林公式及其应用 格林公式:Qdy Pdx dxdy y Px Q LD+=∂∂-∂∂⎰⎰⎰)(其中L 是沿正向取的闭区域的边界曲线。
16. 姻亲的种类(P66) 17. 对面积的曲面积分⎰⎰⎰⎰++=∑Dxyy x dxdy z z y x z y x f ds z y x f 221)],(,,[),,( ∑=),(:y x z z18. 对坐标的曲面积分⎰⎰⎰⎰±=∑Dxy dxdy y x z y x R dxdy z y x R )],(,,[),,( 下侧取负号上侧取正号∑=),(:y x z z第五章 常微分方程19. 微分方程基本概念 20. 三类一阶微分方程(1)一阶线性微分方程:)()(x Q y x p y =+'通解])([)()(C dx e x Q ey dx x p dxx p +=⎰⎰⎰-(2)二阶常系数线性齐次微分方程公式:0=+'+''qy y p y 特征方程:02=++q pr r.1︒21r r ≠实根:通解为x r x r e c e c y 2121+=.2︒21r r =实根:通解为xr e c c y 1)(21+=.3︒i r βα±=21,:通解为)sin cos (21x c c e y xββα+=(3) 二阶常系数线性非齐次微分方程公式:ax m e x P qy y p y )(=+'+''通解为*y y y += y 为对应齐次方程的通解x m k e x Q x y α)(*= *y 为所求方程的一个特解0=k :a 不是特征方程的根 1=k :a 是特征方程的单根2=k :a 是特征方程的重根第六章 无穷级数21. 数项级数的基本概念以及基本性质22 22. 数项级数的审敛法审敛准则公式:.1︒比值判别法:⎪⎪⎪⎩⎪⎪⎪⎨⎧=∞><=∑∑∑∞=∞=∞=+∞→不定级数发散级数收敛级数1111,1),(1,1limn n n n n n nn n u u u q u u.2︒比较判别法:1)设n n v u ≤,而∑∞=1n nv收敛,则∑∞=1n nu收敛。
2)设n n v u ≥,而∑∞=1n nv发散,则∑∞=1n nu发散。
23. 幂级数以及函数的幂级数展开式幂级数的收敛半径和收敛区间 公式:.1︒收敛半径1lim +∞→=n nn a a R.2︒收敛区间:1)[-R,R] 2)[-R,R ) 3)(-R ,R]设发散,右边开收敛,右边闭∑∞==1:n nn R a R x发散,左边开收敛,左边闭)(∑∞=--=1:n nn R a R x.3︒R x x R x x R x x R x x x x a n n n -=-=-+==--∑∞=00001)令( 幂级数的展开式公式:.1︒+∞<<∞-+++++=x n x x x e nxΛΛ!!212.2︒+∞<<∞--+-=x x x x x x Λ!7!5!3sin 753.3︒+∞<<∞--+-=x x x x x Λ!6!4!21cos 642.4︒11432)1ln(432≤<--+-=+x x x x x x Λ.5︒1111132<<-+++=-x x x x xΛ。
