二次函数中的几何最值问题
解题秘诀二次函数最值的4种解法

解题秘诀二次函数最值的4种解法二次函数是高中数学中的一个重要知识点,掌握了解题的秘诀和方法,就可以更好地解决与二次函数相关的各种问题。
本文将介绍四种解法来求解二次函数的最值问题。
一、二次函数的最值根据导数解法要求解二次函数的最值,可以通过求导数的方法来解决。
具体步骤如下:1. 将二次函数表示为一般式:f(x) = ax^2 + bx + c。
2. 对函数进行求导,得到导函数:f'(x) = 2ax + b。
3.导函数表示了二次函数的斜率,要求函数的最值,就是要求导函数为零点时的x值。
4. 解方程2ax + b = 0,求得x = -b / 2a。
5.将求得的x值代入二次函数,计算得到对应的y值。
6.x和y的值就是二次函数的最值。
二、二次函数的最值根据顶点法解法顶点法也是求解二次函数的最值的一种方法,具体步骤如下:1. 将二次函数表示为一般式:f(x) = ax^2 + bx + c。
2.求出二次函数的顶点坐标,顶点的x值为-x/2a。
3.将求得的x值代入二次函数,计算得到对应的y值。
4.x和y的值就是二次函数的最值。
三、二次函数的最值根据平移法解法平移法是一种通过平移变换求解二次函数最值的方法,具体步骤如下:1. 将二次函数表示为一般式:f(x) = ax^2 + bx + c。
2.将二次函数表示为顶点形式:f(x)=a(x-h)^2+k,其中(h,k)为顶点坐标。
3.根据函数的几何性质,二次函数的最值就是顶点的纵坐标k。
四、二次函数的最值根据因式分解解法因式分解是一种求解二次函数最值的常用方法,具体步骤如下:1. 将二次函数表示为一般式:f(x) = ax^2 + bx + c。
2.将二次函数进行因式分解:f(x)=a(x-x1)(x-x2),其中x1和x2为二次函数的两个零点。
3.根据函数的几何性质,二次函数的最值为x轴与二次函数的拐点处的纵坐标。
通过以上四种解法,我们可以灵活地解决二次函数的最值问题。
二次函数求几何最值

二次函数求几何最值类型1:勾股定理【例题1】如图,在△ABC 中,∠ACB =90°,AC =3,CB =5,点D 是CB 边上的一个动点,将线段AD 绕着点D 顺时针旋转90°,得到线段DE ,连接BE ,则线段BE 的最小值为____________..(提示:一线三垂直全等+线段最值,,过点E 作EF ⊥BC 于点F ,则DF =AC =3,EF =CD ,设CD =EF =x ,则FB =5-3-x =2-x ,在Rt △EFB 中,BE 2=x 2+(2-x )2=2(x -1)2+2≥2) 【例题2】如图,C 是线段AB 上一动点,△ACD 、△CBE 都是等边三角形,M 、N 分别是CD 、BE 的中点,若AB =4,则线段MN 的最小值为___________.(提示:连接CN ,则∠ECN =30°,∴∠MCN =90°,设AC =2x ,则BC =4-2x ,∴CM=x ,CN-x ),∴MN 2=x 2+3(2-x )2=4(x -32)2+3≥3)类型2:全等三角形【例题3】如图,D 为等边△ABC 边BC 上的一动点,AB =2,以AD 为边在AD 的右侧作等边△ADE ,则△CDE 的面积最大值为___________..(提示:手拉手全等,法1,二次函数求最值,过点D 作DG ⊥CE 的延长线于点G ,易证△ABD ≌△ACE (SAS ),∴BD =CE ,设BD =x ,则CE =x ,CD =2-x ,∴DG(2-x ),∴S △CDE =12·x(2-x )(x -1)2;法2ABD ≌△ACE (SAS ),∴S 四边形ADCEE =S △ADC AD ⊥BC 时,△ADECDE )【例题4】如图,在△ABC 中,AB =AC =5,BC =,D 为边AB 上一动点(B 除外),以CD 为一边作正方形CDEF ,连接BE ,则△BDE 面积的最大值为___________.ABCDEFED CBAABCD EM NNMED CBAFEDCBA【答案】8.(提示:弦图+12345模型,AH,∴tan∠ABH=12,∴CN=4,BN=8,设BD=x,则DN=8-x,∴EN=8-x,∴S△BDE=12x(8-x)=-12(x-4)2+8≤8)【例题5】如图,在Rt△ABC中,∠ABC=90°,点D为AC的中点,点E为边AB上的一点,连接DE,将线段DE绕点D逆时针旋转90°得到线段DF,连接EF、BF.若AB=6,BC=8,则当△BEF的面积最大时,BF的长为___________..(提示:一线三垂直全等,AG=GB=3,GD=HF=4,设AE=x,则EG=DH=3-x,EB=6-x,∴GH=x+1,∴S△BEF=12(6-x)(x+1)=-12(x-52)2+498≤498,当x=52时,BI=GH=7 2,∵IF=4-3=1,∴BF)类型3:相似三角形【例题6】如图,梯形ABCD中,AD∥BC,AB=AD=CD=6,∠ABC=60°,E、F分别是AD、CD上的动点,且∠BEF=120°,则DF的最大值为____________.【答案】32.(提示:一线三等角相似,设AE=x,DF=y,则ED=6-x,∵△ABE∽△DEF,∴66x=xy,化简得y=-16(x-3)2+32≤32)AB CDEFNMHEBDAFCAB CDEFIHGFEDCBAFE DCBA【例题7】如图,在边长为6的菱形ABCD 中,AC 为其对角线,∠ABC =60°,点M 、N 分别是边BC 、CD 上的动点,且MB =NC ,连接AM 、AN 、MN ,MN 交AC 于点P ,则点P 到直线CD 的距离的最大值为___________..(提示:一线三等角相似,问题转化为求CP 的最小值,设BM =x ,则MC =6-x ,∵△ABM ∽△MCP ,∴66x -=x CP ,∴CP =16x (6-x )=-16(x -3)2+32≤32)【例题8】如图,正方形ABCD 的边长是4,P 为BC 上的动点,连接P A ,过点P 作PQ ⊥P A 交CD 于点Q ,连接AQ ,则AQ 的最小值为____________.【答案】5.(提示:一线三直角相似,设BP =x ,则PC =4-x ,∴QC =(4)4x x -,∴DQ =4-(4)4x x-=14(x -2)2+3≥3,∴当BP =2时,DQ 有最小值3,此时AQ 有最小值5)【例题9】如图,在Rt △ABC 中,∠ACB =90°,∠BAC =30°,AC =4,点D 是边AC 上一动点,连接BD ,以BD 为斜边作Rt △BDE ,使∠BDE =30°,∠BED =90°,连接CE ,则△CDE 面积的最大值为__________..(提示:手拉手相似,△BAD ∽△BCE ,∴∠BCE =∠A =30°,过点E 作EM ⊥AC ,交AC 的延长线于点M ,设CM =x ,则CE =2x ,EM,CD =4-4x ,)NMPDCB A A BCDPQ ABCE【例题10】如图,在△ABC 中,D 为AC 边上的动点,过点D 分别作DE ∥BC 交AB 于点E ,DF ∥AB 交BC 于点F ,已知△ABC 的面积为1,则四边形BEDF 面积的最大值为____________.【答案】12.(提示:设数法+A 字相似,设AG =1,BC =2,则BF =x ,则ED =x ,FC =2-x ,∵ED ∥BC ,∴AH =12x ,∴HG =1-12x ,∴S 梯形BEDF =12(x +x )(1-12x )=-12(x -1)2+12≤12)类型4:转化问题【例题11】如图,正方形ABCD 的边长为2,E 为AD 边上一动点,连接BE 、CE ,以CE 为边向右侧作正方形CEFG .(1)若BE,则正方形CEFG 的面积为___________; (2)连接DF 、DG ,则△DFG 面积的最小值为___________.【答案】(1)5;(2)1.5.(提示:转化法,(1)当BE时,AE =ED =1,∴CE;(2)设ED =x ,则CE 2=x 2+22,∴S △DFG =12S □ECGF -S △EDC =12(x 2+22)-12×2x =12(x -1)2+32≥32)ABC DEFHGF EDCBAABCDEFG。
二次函数动点及最值问题
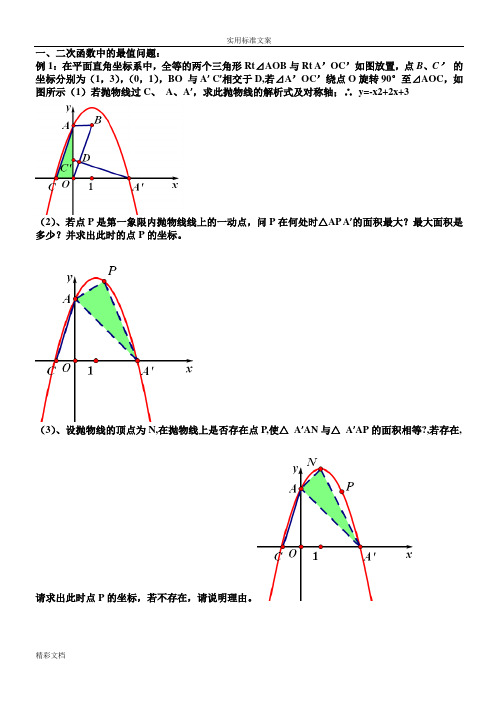
一、二次函数中的最值问题:例1:在平面直角坐标系中,全等的两个三角形Rt⊿AOB与Rt A’OC’如图放置,点B、C’的坐标分别为(1,3),(0,1),BO 与A’ C’相交于D,若⊿A’OC’绕点O旋转90°至⊿AOC,如图所示(1)若抛物线过C、A、A’,求此抛物线的解析式及对称轴;∴y=-x2+2x+3(2)、若点P是第一象限内抛物线线上的一动点,问P在何处时△AP A’的面积最大?最大面积是多少?并求出此时的点P的坐标。
(3)、设抛物线的顶点为N,在抛物线上是否存在点P,使△A’AN与△A’AP的面积相等?,若存在,请求出此时点P的坐标,若不存在,请说明理由。
例2、(2012攀枝花)如图,在平面直角坐标系xOy中,四边形ABCD是菱形,顶点A.C.D均在坐标轴上,且AB=5,sinB=.(1)求过A.C.D三点的抛物线的解析式;(2)记直线AB的解析式为y1=mx+n,(1)中抛物线的解析式为y2=ax2+bx+c,求当y1<y2时,自变量x的取值范围;(3)设直线AB与(1)中抛物线的另一个交点为E,P点为抛物线上A.E两点之间的一个动点,当P点在何处时,△PAE的面积最大?并求出面积的最大值.解答:解:(1)∵四边形ABCD是菱形,∴AB=AD=CD=BC=5,sinB=sinD=;Rt△OCD中,OC=CD•sinD=4,OD=3;OA=AD﹣OD=2,即:A(﹣2,0)、B(﹣5,4)、C(0,4)、D(3,0);设抛物线的解析式为:y=a(x+2)(x﹣3),得:2×(﹣3)a=4,a=﹣;∴抛物线:y=﹣x2+x+4.(2)由A(﹣2,0)、B(﹣5,4)得直线AB:y1=﹣x﹣;由(1)得:y2=﹣x2+x+4,则:,解得:,;由图可知:当y1<y2时,﹣2<x<5.(3)∵S△APE=AE•h,∴当P到直线AB的距离最远时,S△ABC最大;若设直线L∥AB,则直线L与抛物线有且只有一个交点时,该交点为点P;设直线L:y=﹣x+b,当直线L与抛物线有且只有一个交点时,﹣x+b=﹣x2+x+4,且△=0;求得:b=,即直线L:y=﹣x+;可得点P(,).由(2)得:E(5,﹣),则直线PE:y=﹣x+9;新课标第一网则点F(,0),AF=OA+OF=;∴△PAE的最大值:S△PAE=S△PAF+S△AEF=××(+)=.综上所述,当P(,)时,△PAE的面积最大,为.针对训练:1、(2013宜宾)如图,抛物线y1=x2﹣1交x轴的正半轴于点A,交y轴于点B,将此抛物线向右平移4个单位得抛物线y2,两条抛物线相交于点C.(1)请直接写出抛物线y2的解析式;(2)若点P是x轴上一动点,且满足∠CPA=∠OBA,求出所有满足条件的P点坐标;(3)在第四象限内抛物线y2上,是否存在点Q,使得△QOC中OC边上的高h有最大值?若存在,请求出点Q的坐标及h的最大值;若不存在,请说明理由.解答:解:(1)抛物线y1=x﹣1向右平移4个单位的顶点坐标为(4,﹣1),所以,抛物线y2的解析式为y2=(x﹣4)2﹣1;(2)x=0时,y=﹣1,y=0时,x2﹣1=0,解得x1=1,x2=﹣1,所以,点A(1,0),B(0,﹣1),∴∠OBA=45°,联立,解得,∴点C的坐标为(2,3),∵∠CPA=∠OBA,∴点P在点A的左边时,坐标为(﹣1,0),在点A的右边时,坐标为(5,0),所以,点P的坐标为(﹣1,0)或(5,0);(3)存在.∵点C(2,3),∴直线OC的解析式为y=x,设与OC平行的直线y=x+b,联立,消掉y得,2x2﹣19x+30﹣2b=0,当△=0,方程有两个相等的实数根时,△QOC中OC边上的高h有最大值,此时x1=x2=×(﹣)=,此时y=(﹣4)2﹣1=﹣,∴存在第四象限的点Q(,﹣),使得△QOC中OC边上的高h有最大值,此时△=192﹣4×2×(30﹣2b)=0,解得b=﹣,∴过点Q与OC平行的直线解析式为y=x﹣,令y=0,则x﹣=0,解得x=,设直线与x轴的交点为E,则E(,0),过点C作CD⊥x轴于D,根据勾股定理,OC==,则sin ∠COD==, 解得h 最大=×=.2、如图,抛物线)0(2232≠--=a x ax y 的图象与x 轴交于A 、B 两点,与y 轴交于C 点,已知B 点坐标为()0,4.(1)求抛物线的解析式;(2)试探究ABC ∆的外接圆的圆心位置,并求出圆心坐标;(3)若点M 是线段BC 下方的抛物线上一点,求MBC ∆的面积的最大值,并类型一、最值问题:类型一、最值问题:(2013•泸州)如图,在直角坐标系中,点A 的坐标为(﹣2,0),点B 的坐标为(1,﹣),已知抛物线y=ax 2+bx+c (a ≠0)经过三点A 、B 、O (O 为原点).(1)求抛物线的解析式;(2)在该抛物线的对称轴上,是否存在点C ,使△BOC 的周长最小?若存在,求出点C 的坐标;若不存在,请说明理由;(3)如果点P 是该抛物线上x 轴上方的一个动点,那么△PAB 是否有最大面积?若有,求出此时P 点的坐标及△PAB 的最大面积;若没有,请说明理由.(注意:本题中的结果均保留根号)),﹣﹣(+,解得:﹣,﹣,﹣﹣x(PE(+y)﹣y)﹣((y+(﹣x+x x+()﹣的面积最大,最大值为××,,类型二、探索三角形的存在性。
怎样求解二次函数中的几何最值问题

数学篇解题指南几何图形与二次函数的综合题难度一般较大.在解答此类问题时,同学们要认真观察、分析图形的结构特征,充分挖掘几何图形的性质,再利用二次函数的性质求解.下面笔者就以二次函数中线段最值问题与图形面积最值问题的常见解法举例说明.一、二次函数中的线段最值问题常见的二次函数中的线段最值问题有:(1)求某条线段的最值;(2)求几条线段的和的最小值或差的最大值.这类问题侧重于考查二次函数与直线的位置关系、二次函数的性质、平面几何图形的性质.解答此类问题,通常需根据直线与二次函数的位置关系,利用二次函数的对称性转换点或线段的位置,构造出三角形、平行四边形、三点共线的情况等,从而运用三角形、平四边形的性质,以及一些平面几何定理,如“两点间线段最短”“两边之差小于第三边”,求得最值.例1在平面直角坐标系中,抛物线y =ax 2+bx +c 经过A (-2,-4),O (0,0),B(2,0)三点.(1)求抛物线y =ax 2+bx +c 的解析式;(2)若点M 是该抛物线对称轴上的一点,求AM +OM 的最小值.分析:题目(1)是一个求二次函数解析式的简单问题,只要把三个点代入解析式,组成方程组求解即可;(2)是在(1)求解出的二次函数解析式的基础上,求对称轴上一点到两个固定点的距离和问题,即“求AM +OM 的最小值”.准确画出二次函数的图象,如图1所示,利用二次函数的对称性以及对称轴的相关知识,可以得出OM =BM ,从而将AM +OM 转化为当A 、B 、M 三点共线时,两线段和最小.解:(1)把A (-2,-4),O (0,0),B (2,0)三点的坐标代入y =ax 2+bx +c 中,得方程组的解为,a =-12,b =1,c =0,所以抛物线的解析式为y =-12x 2+x ;(2)由y =-12x 2+x =-12(x -1)2+12,可得抛物线的对称轴为x =1,并且对称轴垂直平分线段OB ,∵点M 是抛物线对称轴上的一点,∴OM =BM ,∴OM +AM =BM +AM ,连接AB 交直线x =1于M 点,此时OM +AM 最小.过点A 作AN ⊥x 轴于点N ,在Rt△ABN 中,AB =AB 2+BN 2=42+42=42,因此OM +AM 的最小值为42.评注:二次函数的图象具有对称性,点M 是对称轴上的一点,利用此性质可以得到OM =BM ,这样便将“OM +AM ”转化为“BM +AM ”,进一步转化为求AM +BM 最小值问题,然后利用“两点之间线段最短”的原理求解即可.二、二次函数中图形面积的最值问题二次函数中图形面积的最值问题往往是二次函数线段最值问题的升华.求解此类问题时往往需要将不规则或复杂的图形通过“分割法”或“补形法”转化为规则的图形,然后利用规则图形的面积公式来求解.一般地,怎样求解二次函数中的几何最值问题南京师范大学盐城实验学校程梦书x y 图119数学篇解题指南二次函数中图形面积的最值问题往往通过“转化”思想,化为“线段(和)”最值问题.此外,经过割补后所求区域的面积,可通过不同区域的面积相加或相减来求得.例2已知抛物线经过点A (-1,0)、B (3,0)、C(0,3).(1)求抛物线的解析式;(2)点M 是线段BC 上的点(不与B ,C 重合),过M 作MN //y 轴交抛物线于N ,若点M 的横坐标为m ,请用m 的代数式表示MN 的长;(3)在(2)的条件下,连接NB 、NC ,是否存在m ,使△BNC 的面积最大?若存在,求m 的值;若不存在,说明理由.分析:(1)求二次函数解析式比较容易,直接将三点坐标代入组成方程组即可.(2)中点M 虽是动点,但坐标可以用二次函数的解析式表示出来,随后表示出点N 的坐标,即可表示MN 的长.(3)△BNC 面积直接求解比较困难,利用转化思想化为S △MNC +S △MNB .利用面积公式,将“面积”最值问题转化为“线段”最值问题来求解.(如图2所示).解:(1)∵抛物线过点A (-1,0)、B (3,0),∴设抛物线的解析式为:y =a (x +1)(x -3),又∵抛物线过点C (0,3),∴a (0+1)(0-3)=3,解得a =-1,所以,抛物线的解析式为:y =-(x +1)(x -3)=-x 2+2x +3;(2)设直线BC 的解析式为y =kx +b ,则有:故直线BC 的解析式为:y =-x +3,已知点M 的横坐标为m ,则M (m ,-m +3)、N (m ,-m 2+2m +3),∴MN =|(-m 2+2m +3)-(-m +3)|=|-m 2+3m |,∵点M 在B 、C 之间,∴点N 高于点M ,∴0<m <3,∴MN =|-m 2+3m |=-m 2+3m 即MN =-m 2+3m (0<m <3);(3)存在,S △BNC =S △MNC +S △MNB ,∵MN //y 轴,∴延长NM 交x 轴于点D ,∴点C 到MN 的距离为OD ,∴S △MNC =12MN ×OD ,S △MNB =12MN ×DB ,S △BNC =S △MNC +S △MNB =12MN (OD +DB )=12MN ×OB ,∴当|MN |最大时,△BNC 的面积最大,MN =-m 2+3m =-(m -32)2+94,当m =32时,MN 有最大值为94,所以当m =32时,S △BNC 的面积最大,故△BNC 的面积最大值为12×94×3=278.评注:求解二次函数的最值问题时,一定要准确绘制出函数的图象,特别是开口方向、与x 轴的交点、与y 轴的交点、对称轴.否则,可能得到错解或无解.利用二次函数求最值需要注意:当二次函数的开口向下时,在顶点处取得最大值;当二次函数的开口向上时,在顶点处取得最小值.二次函数中的几何最值问题往往涉及“线段和最小”或“图形面积最大”等问题.同学们应掌握二次函数的图象和性质,将最值图2。
中考二次函数中的几何最值问题(二)

A''二次函数中的几何最值问题(二)模型一.如图,在平面上有两个定点A 、B ,MN 为定直线上移动的长度一定的线段,若要使四边形AMNB 的周长最小,试确定MN 的位置。
作法:作A 点关于直线的对称点A‘,再将A’向平行于定直线的方向(B 侧)平移一个MN 的长度到A’’,连接A’’B 和直线的交点即为N 点,M 点亦随之确定。
例1. 已知:如图1,直线1y x =--分别交x 轴、y 轴于A 、E 两点,抛物线249y x bx c=-++经过点A ,且过点()5,0B ,与y 轴交于点C ,点D 为抛物线的顶点,连接BC 。
(1)求抛物线的解析式及顶点D 的坐标;(2)如图2,若在直线BC 上方的抛物线上有一点F ,当BCF ∆的面积最大时,有一线段MN=2(点M 在点N 的左侧)在直线AE 上移动,首尾顺次连接点F 、M 、N 、B 构成四边形FMNB ,请求出四边形FMNB 的周长最小时点M 的横坐标;NM A迁移练习1.如图1,已知抛物线343832--=x x y 与轴交于和两点(点在点的左侧)与轴相交于点,顶点为. (1)求出点的坐标;(2)如图1,若线段在x 轴上移动,且点移动后的对应点为.首尾顺次连接点、、、构成四边形,请求出四边形的周长最小值.x A B A B y C D ,,A B D OB ,O B ','O B 'O 'B D C ''OBDC ''OBDC模型二. 如图,平面上有2条定直线l ,m,A 、B 为直线两侧的2个定点,点M 为直线l 上的动点,点N 为直线m 上的动点,要使得AN+BM+MN 的长度最小,试确定M 、N 的位置.作法:作A 点关于直线l 的对称点A’,B 点关于直线m 的对称点B’,连接A’B’与直线l,m 的交点即为M 、N.需要注意的是:模型中的两条定直线不一定是平行的。
《实际问题与二次函数》(几何图形最值)

2023-11-08CATALOGUE目录•引言•二次函数基本概念•几何图形与二次函数•二次函数最值概念•几何图形最值问题求解•实际问题最值应用案例01引言几何图形最值问题是数学中的一个经典问题,它涉及到图形的形状、大小和位置的最优化。
在实际生活中,几何图形最值问题也有广泛的应用,例如建筑设计、城市规划、物理研究等。
课程背景介绍1课程目标23理解几何图形最值的基本概念和解决方法。
学习如何运用数学方法和计算机技术求解几何图形最值问题。
掌握常见的几何图形最值问题的建模和求解技巧。
课程大纲1. 几何图形最值的基本概念最值的定义和性质几何图形的参数化课程大纲2. 求解方法与技术问题的数学建模微积分方法课程大纲010203线性代数方法数值计算方法计算机模拟技术3. 常见的几何图形最值问题直线段的最短长度圆形的最大面积课程大纲课程大纲椭圆形的最小周长立体图形的最大体积 4. 应用案例分析010302课程大纲02城市规划中的最值问题03物理研究中的最值问题02二次函数基本概念当轴动区间定时,二次函数的最值出现在对称轴上。
具体地,如果对称轴为x=-b/2a,那么当x=-b/2a时,二次函数取得最小值y=c-b^2/4a。
当轴定区间动时,二次函数的最值出现在区间的端点或对称轴上。
具体地,如果对称轴为x=-b/2a,那么当x=-b/2a时,二次函数取得最小值y=c-b^2/4a;当x取区间端点时,二次函数取得最大值。
当轴动区间动时,二次函数的最值出现在区间的端点、对称轴或二者重合处。
具体地,如果对称轴为x=-b/2a,那么当x=-b/2a时,二次函数取得最小值y=c-b^2/4a;当x取区间端点时,二次函数取得最大值。
03几何图形与二次函数矩形与二次函数在几何图形中最值问题中有着密切的联系。
详细描述在矩形中,长和宽可以看作是二次函数图像的两个根,而面积则可看作是二次函数的顶点。
因此,矩形的最值问题可以通过二次函数来求解。
二次函数与几何的动点及最值、存在性问题(解析版)

二次函数与几何的动点及最值、存在性问题目录题型01平行y轴动线段最大值与最小值问题题型02抛物线上的点到某一直线的距离问题题型03已知点关于直线对称点问题题型04特殊角度存在性问题题型05将军饮马模型解决存在性问题题型06二次函数中面积存在性问题题型07二次函数中等腰三角形存在性问题题型08二次函数中直角三角形存在性问题题型09二次函数中全等三角形存在性问题题型10二次函数中相似三角形存在性问题题型11二次函数中平行四边形存在性问题题型12二次函数中矩形存在性问题题型13二次函数中菱形存在性问题题型14二次函数中正方形存在性问题二次函数常见存在性问题:(1)等线段问题:将动点坐标用函数解析式以“一母式”的结构表示出来,再利用点到点或点到直线的距离公式列出方程或方程组,然后解出参数的值,即可以将线段表示出来.【说明】在平面直角坐标系中该点在某一函数图像上,设该点的横坐标为m,则可用含m字母的函数解析式来表示该点的纵坐标,简称“设横表纵”或“一母式”.(2)平行y轴动线段最大值与最小值问题:将动点坐标用函数解析式以“一母式”的结构表示出来,再用纵坐标的较大值减去较小值,再利用二次函数的性质求出动线段的最大值或最小值.(3)求已知点关于直线对称点问题:先求出直线解析式,再利用两直线垂直的性质(两直线垂直,斜率之积等于-1)求出已知点所在直线的斜率及解析式,最后用中点坐标公式即可求出对称点的坐标.(4)“抛物线上是否存在一点,使其到某一直线的距离为最值”的问题:常常利用直线方程与二次函数解析式联立方程组,求出切点坐标,运用点到直线的距离公式进行求解.(5)二次函数与一次函数、特殊图形、旋转及特殊角度综合:图形或一次函数与x 轴的角度特殊化,利用与角度有关知识点求解函数图像上的点,结合动点的活动范围,求已知点与动点是否构成新的特殊图形.2.二次函数与三角形综合(1)将军饮马问题:本考点主要分为两类:①在定直线上是否存在点到两定点的距离之和最小;②三角形周长最小或最大的问题,主要运用的就是二次函数具有对称性.(2)不规则三角形面积最大或最小值问题:利用割补法将不规则三角形分割成两个或以上的三角形或四边形,在利用“一母式”将动点坐标表示出来,作线段差,用线段差来表示三角形的底或高,用面积公式求出各部分面积,各部分面积之和就是所求三角形的面积.将三角形的面积用二次函数的结构表示出来,再利用二次函数的性质求出面积的最值及动点坐标.(3)与等腰三角形、直角三角形的综合问题:对于此类问题,我们可以利用两圆一线或两线一圆的基本模型来进行计算.问题分情况找点画图解法等腰三角形已知点A ,B 和直线l ,在l 上求点P ,使△PAB 为等腰三角形以AB为腰分别以点A ,B 为圆心,以AB 长为半径画圆,与已知直线的交点P 1,P 2,P 4,P 5即为所求分别表示出点A ,B ,P 的坐标,再表示出线段AB ,BP ,AP 的长度,由①AB =AP ;②AB =BP ;③BP =AP 列方程解出坐标以AB 为底作线段AB 的垂直平分线,与已知直线的交点P 3即为所求分别表示出点A ,B ,P 的坐标,再表示出线段AB ,BP ,AP 的长度,由①AB =AP ;②AB =BP ;③BP =AP 列方程解出坐标问题分情况找点画图解法直角三角形已知点A ,B 和直线l ,在l 上求点P ,使△PAB 为直角三角形以AB为直角边分别过点A ,B 作AB 的垂线,与已知直线的交点P 1,P 4即为所求分别表示出点A ,B ,P 的坐标,再表示出线段AB ,BP ,AP 的长度,由①AB 2=BP 2+AP 2;②BP 2=AB 2+AP 2;③AP 2=AB 2+BP 2列方程解出坐标以AB 为斜边以AB 的中点Q 为圆心,QA 为半径作圆,与已知直线的交点P 2,P 3即为所求注:其他常见解题思路有:①作垂直,构造“三垂直”模型,利用相似列比例关系得方程求解;②平移垂线法:若以AB 为直角边,且AB 的一条垂线的解析式易求(通常为过原点O 与AB 垂直的直线),可将这条直线分别平移至过点A 或点B 得到相应解析式,再联立方程求解.(4)与全等三角形、相似三角形的综合问题:在没有指定对应点的情况下,理论上有六种情况需要讨论,但在实际情况中,通常不会超过四种,要注意边角关系,积极分类讨论来进行计算.情况一探究三角形相似的存在性问题的一般思路:解答三角形相似的存在性问题时,要具备分类讨论思想及数形结合思想,要先找出三角形相似的分类标准,一般涉及动态问题要以静制动,动中求静,具体如下:①假设结论成立,分情况讨论.探究三角形相似时,往往没有明确指出两个三角形的对应点(尤其是以文字形式出现求证两个三角形相似的题目),或者涉及动点问题,因动点问题中点的位置的不确定,此时应考虑不同的对应关系,分情况讨论;②确定分类标准.在分类时,先要找出分类的标准,看两个相似三角形是否有对应相等的角,若有,找出对应相等的角后,再根据其他角进行分类讨论来确定相似三角形成立的条件;若没有,则分别按三种角对应来分类讨论;③建立关系式,并计算.由相似三角形列出相应的比例式,将比例式中的线段用所设点的坐标表示出来(其长度多借助勾股定理运算),整理可得一元一次方程或者一元二次方程,解方程可得字母的值,再通过计算得出相应的点的坐标.情况二探究全等三角形的存在性问题的思路与探究相似三角形的存在性问题类似,但是除了要找角相等外,还至少要找一组对应边相等.3.二次函数与四边形的综合问题特殊四边形的探究问题解题步骤如下:①先假设结论成立;②设出点坐标,求边长;③建立关系式,并计算.若四边形的四个顶点位置已确定,则直接利用四边形边的性质进行计算;若四边形的四个顶点位置不确定,需分情况讨论:a.探究平行四边形:①以已知边为平行四边形的某条边,画出所有的符合条件的图形后,利用平行四边形的对边相等进行计算;②以已知边为平行四边形的对角线,画出所有的符合条件的图形后,利用平行四边形对角线互相平分的性质进行计算;③若平行四边形的各顶点位置不确定,需分情况讨论,常以已知的一边作为一边或对角线分情况讨论.b.探究菱形:①已知三个定点去求未知点坐标;②已知两个定点去求未知点坐标,一般会用到菱形的对角线互相垂直平分、四边相等的性质列关系式.c.探究正方形:利用正方形对角线互相垂直平分且相等的性质进行计算,一般是分别计算出两条对角线的长度,令其相等,得到方程再求解.d.探究矩形:利用矩形对边相等、对角线相等列等量关系式求解;或根据邻边垂直,利用勾股定理列关系式求解.题型01平行y轴动线段最大值与最小值问题1(2023·广东东莞·一模)如图,抛物线y=x2+bx+c与x轴交于A、B两点,与y轴交于点C,OA=OC =3,顶点为D.(1)求此函数的关系式;(2)在AC 下方的抛物线上有一点N ,过点N 作直线l ∥y 轴,交AC 与点M ,当点N 坐标为多少时,线段MN 的长度最大?最大是多少?(3)在对称轴上有一点K ,在抛物线上有一点L ,若使A ,B ,K ,L 为顶点形成平行四边形,求出K ,L 点的坐标.(4)在y 轴上是否存在一点E ,使△ADE 为直角三角形,若存在,直接写出点E 的坐标;若不存在,说明理由.【答案】(1)y =x 2+2x -3(2)当N 的坐标为-32,-154 ,MN 有最大值94(3)K -1,4 ,L -1,-4 或K -1,12 ,L -5,12 或K -1,12 ,L 3,12(4)存在,点E 的坐标为0,32 或0,-72或0,-1 或0,-3【分析】(1)由OA =OC =3求得A -3,0 ,C 0,-3 ,再分别代入抛物线解析式y =x 2+bx +c ,得到以b ,c 为未知数的二元一次方程组,求出b ,c 的值即可;(2)求出直线AC 的解析式,再设出M 、N 的坐标,把MN 表示成二次函数,配方即可;(3)根据平行四边形的性质,以AB 为边,以AB 为对角线,分类讨论即可;(4)设出E 的坐标,分别表示出△ADE 的平分,再分每一条都可能为斜边,分类讨论即可.【详解】(1)∵抛物线y =x 2+bx +c 经过点A ,点C ,且OA =OC =3,∴A -3,0 ,C 0,-3 ,∴将其分别代入抛物线解析式,得c =-39-3b +c =0,解得b =2c =-3 .故此抛物线的函数表达式为:y =x 2+2x -3;(2)设直线AC 的解析式为y =kx +t ,将A -3,0 ,C 0,-3 代入,得t =-3-3k +t =0 ,解得k =-1t =-3 ,∴直线AC 的解析式为y =-x -3,设N 的坐标为n ,n 2+2n -3 ,则M n ,-n -3 ,∴MN =-n -3-n 2+2n -3 =-n 2-3n =-n +32 +94,∵-1<0,∴当n =-32时,MN 有最大值,为94,把n =-32代入抛物线得,N 的坐标为-32,-154,当N 的坐标为-32,-154 ,MN 有最大值94;(3)①当以AB 为对角线时,根据平行四边形对角线互相平分,∴KL 必过-1,0 ,∴L 必在抛物线上的顶点D 处,∵y =x 2+2x -3=x +1 2-4,∴K -1,4 ,L -1,-4②当以AB 为边时,AB =KL =4,∵K 在对称轴上x =-1,∴L 的横坐标为3或-5,代入抛物线得L -5,12 或L 3,12 ,此时K 都为-1,12 ,综上,K -1,4 ,L -1,-4 或K -1,12 ,L -5,12 或K -1,12 ,L 3,12 ;(4)存在,由y =x 2+2x -3=x +1 2-4,得抛物线顶点坐标为D -1,-4 ∵A -3,0 ,∴AD 2=-3+1 2+0+4 2=20,设E 0,m ,则AE 2=-3-0 2+0-m 2=9+m 2,DE 2=-1-0 2+-4-m 2=17+m 2+8m ,①AE 为斜边,由AE 2=AD 2+DE 2得:9+m 2=20+17+m 2+8m ,解得:m =-72,②DE 为斜边,由DE 2=AD 2+AE 2得:9+m 2+20=17+m 2+8m ,解得:m =32,③AD 为斜边,由AD 2=ED 2+AE 2得:20=17+m 2+8m +9+m 2,解得:m =-1或-3,∴点E 的坐标为0,32 或0,-72或0,-1 或0,-3 .【点睛】本题主要考查待定系数法求二次函数解析式,二次函数图象与性质,平行四边形的判定与性质以及勾股定理等知识,会运用待定系数法列方程组,两点间距离公式求MN 的长,由平行四边形的性质判定边相等,运用勾股定理列方程.2(2023·河南南阳·统考一模)如图,抛物线与x 轴相交于点A 、B (点A 在点B 的左侧),与y 轴的交于点C 0,-4 ,点P 是第三象限内抛物线上的一个动点,设点P 的横坐标为m ,过点P 作直线PD ⊥x 轴于点D ,作直线AC 交PD 于点E .已知抛物线的顶点P 坐标为-3,-254.(1)求抛物线的解析式;(2)求点A 、B 的坐标和直线AC 的解析式;(3)求当线段CP =CE 时m 的值;(4)连接BC ,过点P 作直线l ∥BC 交y 轴于点F ,试探究:在点P 运动过程中是否存在m ,使得CE =DF ,若存在直接写出m 的值;若不存在,请说明理由.【答案】(1)y =14x 2+32x -4(2)A -8,0 ,B 2,0 ,y =-12x -4(3)-4(4)存在,m =2-25或m =-4【分析】(1)运用待定系数法即可求得抛物线的解析式;(2)令y =0,解方程即可求得点A 、B 的坐标,再运用待定系数法即可求得直线AC 的解析式;(3)过点C 作CF ⊥PE 于点F ,根据等腰三角形的性质可得点F 是PE 的中点,设P m ,14m 2+32m -4 ,则E m ,-12m -4 ,可得F m ,18m 2+12m -4 ,再由点F 与点C 的纵坐标相同建立方程求解即可;(4)过C 作CH ⊥PD 于H ,设P m ,14m 2+32m -4 ,由PF ∥BC ,可得直线PF 解析式为y =2x +14m 2-12m -4,进而可得OF =14m 2-12m -4 ,再证得Rt △CHE ≅Rt △DOF HL ,得出∠HCE =∠FDO ,进而推出∠FDO =∠CAO ,即tan ∠FDO =tan ∠CAO ,据此建立方程求解即可.【详解】(1)解:∵抛物线的顶点坐标为-3,-254∴设抛物线的解析式为y =a x +3 2-254,把点C 0,-4 代入,得:-4=9a -254,解得:a =14,∴y =14x +3 2-254=14x 2+32x -4,∴该抛物线的解析式为y =14x 2+32x -4.(2)解:令y =0,得14x 2+32x -4=0,解得:x 1=-8,x 2=2,∴A -8,0 ,B 2,0 ,,设直线AC 的解析式为y =kx +b ,则-8k +b =0b =-4 ,解得:k =-12b =-4 ,∴直线AC 的解析式为y =-12x -4.(3)解:如图,过点C 作CF ⊥PE 于点F ,∵CP =CE ,∴EF =PF ,即点F 是PE 的中点,设P m ,14m 2+32m -4 ,则E m ,-12m -4 ,∴F m ,18m 2+12m -4 ,∵PE ∥y 轴,CF ⊥PE ,∴CF ∥x 轴,∴18m 2+12m -4=-4,解得:m =-4或m =0(不符合题意,舍去),∴m =-4.(4)解:存在m ,使得CE =DF ,理由如下:如图:过C 作CH ⊥PD 于H ,设P m,14m2+32m-4,由B2,0,C0,-4,由待定系数法可得直线BC解析式为y=2x-4,根据PF∥BC,设直线PF解析式为y=2x+c,将P m,14m2+32m-4代入得:1 4m2+32m-4=2m+c,∴c=14m2-12m-4,∴直线PF解析式为y=2x+14m2-12m-4,令x=0得y=14m2-12m-4,∴F0,14m2-12m-4,∴OF=14m2-12m-4,∵∠CHD=∠PDO=∠COD=90°,∴四边形CODH是矩形,∴CH=OD,∵CE=DF,∴Rt△CHE≅Rt△DOF HL,∴∠HCE=∠FDO,∵∠HCE=∠CAO,∴∠FDO=∠CAO,∴tan∠FDO=tan∠CAO,∴OF OD =OCOA,即14m2-12m-4-m=48=12,∴1 4m2-12m-4=-12m或14m2-12m-4=12m,解得:m=-4或m=4或m=2-25或m=2+25,∵P在第三象限,∴m=2-25或m=-4.【点睛】本题属于二次函数综合题,主要考查了待定系数法求函数解析式、二次函数综合应用、等腰三角形性质、矩形判定及性质、相似三角形判定及性质、解直角三角形等知识点,解题的关键是用含m的代数式表示相关点坐标和相关线段的长度.3(2023·山东聊城·统考三模)抛物线y=-x2+bx+c与x轴交于点A3,0,与y轴交于点C0,3,点P 为抛物线上的动点.(2)若P 为直线AC 上方抛物线上的动点,作PH ∥x 轴交直线AC 于点H ,求PH 的最大值;(3)点N 为抛物线对称轴上的动点,是否存在点N ,使直线AC 垂直平分线段PN ?若存在,请直接写出点N 的纵坐标;若不存在,请说明理由.【答案】(1)b =2,c =3(2)PH 取得最大值为94(3)存在,2-2或2+2【分析】(1)将坐标代入解析式,构建方程求解;(2)设PH 交y 轴于点M ,P m ,-m 2+2m +3 ,则PM =m ;待定系数法确定直线AC 的解析式为y =-x +3,从而确定PH =m -m 2-2m =-m 2+3m =-m -32 2+94,解得PH 最大值为94;(3)如图,设PN 与AC 交于点G ,可设直线PN 的解析式为y =x +p ,设点N (1,n ),求得y =x +(n -1);联立y =-x +3y =x +(n -1) ,解得x =-n 2+2y =n 2+1,所以点P 的横坐标为2×-n 2+2 -1=-n +3,纵坐标为2×n2+1 -n =2,由二次函数解析式构建方程-(-n +3)2+2(-n +3)+3=2,解得n =2±2;【详解】(1)∵抛物线y =-x 2+bx +c 与x 轴交于点A 3,0 ,与y 轴交于点C 0,3 ,∴-9+3b +c =0c =3,解得:b =2c =3 ,∴b =2,c =3;(2)设PH 交y 轴于点M ,P m ,-m 2+2m +3 ,∴PM =m ,∵PH ∥x 轴,∴点H 的纵坐标为-m 2+2m +3,设直线AC 的解析式为y =kx +n ,∴3k +n =0n =3 ,解得:k =-1n =3 ,∴直线AC 的解析式为y =-x +3.∴-m 2+2m +3=-x +3,∴x =m 2-2m ,∴H m 2-2m ,-m 2+2m +3 ,∴PH =m -m 2-2m =-m 2+3m =-m -322+94,∴当m =32时,PH 取得最大值为94(3)存在点N ,使直线AC 垂直平分线段PN ,点N 的纵坐标为2-2或2+2如图,设PN 与AC 交于点G ,∵AC 垂直平分PN ,直线AC 的解析式为y =-x +3∴可设直线PN 的解析式为y =x +p 设点N (1,n ),则n =1+p ∴p =n -1,∴y =x +(n -1)联立y =-x +3y =x +(n -1) ,解得x =-n 2+2y =n 2+1∴点P 的横坐标为2×-n 2+2 -1=-n +3,纵坐标为2×n 2+1 -n =2∴-(-n +3)2+2(-n +3)+3=2,解得n =2±2∴点N 的纵坐标为2-2或2+2.【点睛】本题考查利用二次函数解析式及点坐标求待定参数、待定系数法确定函数解析式、二次函数极值及其它二次函数综合问题,利用直线间的位置关系、点线间的位置关系,融合方程的知识求解坐标是解题的关键.题型02抛物线上的点到某一直线的距离问题1(2023·广东梅州·统考二模)探究求新:已知抛物线G 1:y =14x 2+3x -2,将抛物线G 1平移可得到抛物线G 2:y =14x 2.(1)求抛物线G 1平移得到抛物线G 2的平移路径;(2)设T 0,t ,直线l :y =-t ,是否存在这样的t ,使得抛物线G 2上任意一点到T 的距离等于到直线l 的距离?若存在,求出t 的值;若不存在,试说明理由;(3)设H 0,1 ,Q 1,8 ,M 为抛物线G 2上一动点,试求QM +MH 的最小值.参考公式:若点M x 1,y 1 ,N x 2,y 2 为平面上两点,则有MN =x 1-x 22+y 1-y 2 2.【答案】(1)将G 1向左平移-6个单位,向上平移11个单位(2)存在,1(3)9【分析】(1)设G 1向左平移a 个单位,向上平移b 个单位得到函数G 2,列方程组即可求解;(2)设P x 0,x 204为抛物线G 2上的一点,根据题意列方程即可;(3)点H 坐标与(2)中t =1时的T 点重合,过点M 作MA ⊥l ,垂足为A ,如图所示,则有MH =MA ,当且仅当Q ,M ,A 三点共线时QM +MA 取得最小值.【详解】(1).解:设G 1向左平移a 个单位,向上平移b 个单位得到函数G 2,由平移法则可知14(x +a )2+3(x +a )-2+b =14x 2,整理可得14x 2+3+12a x +14a 2+3a -2+b =14x 2,可得方程组3+12a =014a 2+3a -2+b =0,解得a =-6b =11 ;∴平移路径为将G 1向左平移-6个单位,向上平移11个单位;(2)解:存在这样的t ,且t =1时满足条件,设P x 0,x 204为抛物线G 2上的一点,则点P 到直线l 的距离为x 204+t ,点P 到点T 距离为(x 0-0)2+x 204-t2,联立可得:x 204+t =(x 0-0)2+x 204-t2,两边同时平方合并同类项后可得x 20-x 20t =0解得:t =1;(3)解:点H 坐标与(2)中t =1时的T 点重合,作直线l :y =-1,过点M 作MA ⊥直线l ,垂足为A ,如图所示,则有MH =MA ,此时QM +MH =QM +MA ,当且仅当Q ,M ,A 三点共线时QM +MA 取得最小值即QM +MA =QA =8-(-1)=9∴QM +MH 的最小值为9;【点睛】本题考查二次函数综合题,涉及到线段最小值、平移性质等,灵活运用所学知识是关键.2(2023·湖北宜昌·统考一模)如图,已知:点P 是直线l :y =x -2上的一动点,其横坐标为m (m 是常数),点M 是抛物线C :y =x 2+2mx -2m +2的顶点.(1)求点M 的坐标;(用含m 的式子表示)(2)当点P 在直线l 运动时,抛物线C 始终经过一个定点N ,求点N 的坐标,并判断点N 是否是点M 的最高位置?(3)当点P 在直线l 运动时,点M 也随之运动,此时直线l 与抛物线C 有两个交点A ,B (A ,B 可以重合),A ,B 两点到y 轴的距离之和为d .①求m 的取值范围;②求d 的最小值.【答案】(1)M -m ,-m 2-2m +2(2)N (1,3),点N 是点M 的最高位置(3)①m ≤-52或m ≥32;②d 取得最小值为2【分析】(1)将抛物线解析式写成顶点式即可求解;(2)根据解析式含有m 项的系数为0,得出当x =1时,y =3,即N (1,3),根据二次函数的性质得出-m 2-2m +2=-m +1 2+3的最大值为3,即可得出点N 是点M 的最高位置;(3)①根据直线与抛物线有交点,联立方程,根据一元二次方程根的判别式大于等于0,求得m 的范围,即可求解;②设A ,B 的坐标分别为x 1,y 1 ,x 2,y 2 ,其中x 1<x 2,由①可知x 1,x 2是方程x 2+2mx -x -2m +4=0的两根,根据x 1+x 2=-2m +1,分情况讨论,求得d 是m 的一次函数,进而根据一次函数的性质即可求解.【详解】(1)解:y =x 2+2mx -2m +2=x +m 2-m 2-2m +2,∴顶点M -m ,-m 2-2m +2 ,(2)解:∵y =x 2+2mx -2m +2=x 2+2+2m x -1 ,∴当x =1时,y =3,抛物线C 始终经过一个定点1,3 ,即N (1,3);∵M -m ,-m 2-2m +2 ,-m 2-2m +2=-m +1 2+3,∴M 的纵坐标最大值为3,∴点N 是点M 的最高位置;(3)解:①联立y =x -2y =x 2+2mx -2m +2 ,得x 2+2mx -x -2m +4=0,∵直线l 与抛物线C 有两个交点A ,B (A ,B 可以重合),∴Δ=b 2-4ac =2m -1 2-4-2m +4 ,=4m 2+4m -15≥0,∵4m 2+4m -15=0,解得m 1=-52,m 2=32,∴当4m 2+4m -15≥0时,m ≤-52或m ≥32,②设A ,B 的坐标分别为x 1,y 1 ,x 2,y 2 ,其中x 1<x 2,由①可知x 1,x 2是方程x 2+2mx -x -2m +4=0的两根,∴x1+x 2=-2m +1,当m =-3时,如图所示,y A =0,当-3≤m ≤-52时,y 1≥0,y 2≥0,则d =x 1+x 2 =-2m +1 ,∵-2<0,∴当m =-52时,d 取得最小值为-2×-52 +1=5+1=6,当m ≥32时,d =-x 1+x 2 =--2m +1 =2m -1,∴当m =32时,d 取得最小值为2×32-1=2,综上所述,d 取得最小值为2.【点睛】本题考查了二次函数的性质,一元二次方程与二次函数的关系,熟练掌握二次函数的性质是解题的关键.3(2023·云南楚雄·统考一模)抛物线y =x 2-2x -3交x 轴于A ,B 两点(A 在B 的左边),C 是第一象限抛物线上一点,直线AC 交y 轴于点P .(1)直接写出A ,B 两点的坐标;(2)如图①,当OP =OA 时,在抛物线上存在点D (异于点B ),使B ,D 两点到AC 的距离相等,求出所有满足条件的点D 的横坐标;(3)如图②,直线BP 交抛物线于另一点E ,连接CE 交y 轴于点F ,点C 的横坐标为m ,求FP OP 的值(用含m 的式子表示).【答案】(1)A (-1,0),B (3,0)(2)0或3-41或3+41(3)13m 【分析】(1)令y =0,解方程可得结论;(2)分两种情形:①若点D 在AC 的下方时,过点B 作AC 的平行线与抛物线交点即为D 1.②若点D 在AC 的上方时,点D 1关于点P 的对称点G (0,5),过点G 作AC 的平行线交抛物线于点D 2,D 3,D 2,D 3符合条件.构建方程组分别求解即可;(3)设E 点的横坐标为n ,过点P 的直线的解析式为y =kx +b ,由y =kx +b y =x 2-2x -3 ,可得x 2-(2+k )x -3-b =0,设x 1,x 2是方程x 2-(2+k )x -3-b =0的两根,则x 1x 2=-3-b ,推出x A ⋅x C =x B ⋅x E =-3-b 可得n =-1-b 3,设直线CE 的解析式为y =px +q ,同法可得mn =-3-q 推出q =-mn -3,推出q =-(3+b )-1-b 3 -3=13b 2+2b ,推出OF =13b 2+b ,可得结论.【详解】(1)解:令y =0,得x 2-2x -3=0,解得:x =3或-1,∴A (-1,0),B (3,0);(2)∵OP =OA =1,∴P (0,1),∴直线AC 的解析式为y =x +1.①若点D 在AC 的下方时,过点B 作AC 的平行线与抛物线交点即为D 1.∵B (3,0),BD 1∥AC ,∴直线BD 1的解析式为y =x -3,由y =x -3y =x 2-2x -3,解得x =3y =0 或x =0y =-3 ,∴D 1(0,-3),∴D 1的横坐标为0.②若点D 在AC 的上方时,点D 1关于点P 的对称点G (0,5),过点G 作AC 的平行线l 交抛物线于点D 2,D 3,D 2,D 3符合条件.直线l 的解析式为y =x +5,由y =x +5y =x 2-2x -3 ,可得x 2-3x -8=0,解得:x =3-412或3+412,∴D 2,D 3的横坐标为3-412,3+412,综上所述,满足条件的点D 的横坐标为0,3-412,3+412.(3)设E 点的横坐标为n ,过点P 的直线的解析式为y =kx +b ,由y =kx +b y =x 2-2x -3,可得x 2-(2+k )x -3-b =0,设x 1,x 2是方程x 2-(2+k )x -3-b =0的两根,则x 1x 2=-3-b ,∴x A ⋅x C =x B ⋅x E =-3-b∵x A =-1,∴x C =3+b ,∴m =3+b ,∵x B =3,∴x E =-1-b 3,∴n =-1-b 3,设直线CE 的解析式为y =px +q ,同法可得mn =-3-q∴q =-mn -3,∴q =-(3+b )-1-b 3 -3=13b 2+2b ,∴OF =13b 2+2b ,∴FP OP=13b +1=13(m -3)+1=13m .【点睛】本题属于二次函数综合题,考查了二次函数的性质,一次函数的性质,一元二次方程的根与系数的关系等知识,解题的关键是学会构建一次函数,构建方程组确定交点坐标,学会利用参数解决问题,属于中考压轴题.题型03已知点关于直线对称点问题1(2023·辽宁阜新·统考中考真题)如图,在平面直角坐标系中,二次函数y =-x 2+bx -c 的图象与x 轴交于点A (-3,0)和点B (1,0),与y 轴交于点C .(1)求这个二次函数的表达式.(2)如图1,二次函数图象的对称轴与直线AC :y =x +3交于点D ,若点M 是直线AC 上方抛物线上的一个动点,求△MCD 面积的最大值.(3)如图2,点P 是直线AC 上的一个动点,过点P 的直线l 与BC 平行,则在直线l 上是否存在点Q ,使点B 与点P 关于直线CQ 对称?若存在,请直接写出点Q 的坐标;若不存在,请说明理由.【答案】(1)y =-x 2-2x +3;(2)S △MCD 最大=98;(3)Q 1-5,-5 或1+5,5 .【分析】(1)根据抛物线的交点式直接得出结果;(2)作MQ ⊥AC 于Q ,作ME ⊥AB 于F ,交AC 于E ,先求出抛物线的对称轴,进而求得C ,D 坐标及CD 的长,从而得出过M 的直线y =x +m 与抛物线相切时,△MCD 的面积最大,根据x +m =-x 2-2x +3的△=0求得m 的值,进而求得M 的坐标,进一步求得CD 上的高MQ 的值,进一步得出结果;(3)分两种情形:当点P 在线段AC 上时,连接BP ,交CQ 于R ,设P (t ,t +3),根据CP =CB 求得t 的值,可推出四边形BCPQ 是平行四边形,进而求得Q 点坐标;当点P 在AC 的延长线上时,同样方法得出结果.【详解】(1)解:由题意得,y =-(x +3)(x -1)=-x 2-2x +3;(2)解:如图1,作MQ ⊥AC 于Q ,作ME ⊥AB 于F ,交AC 于E ,∵OA =OC =3,∠AOC =90°,∴∠CAO =∠ACO =45°,∴∠MEQ =∠AEF =90°-∠CAO =45°,抛物线的对称轴是直线:x =-3+12=-1,∴y =x +3=-1+3=2,∴D (1,2),∵C (0,3),∴CD =2,故只需△MCD 的边CD 上的高最大时,△MCD 的面积最大,设过点M 与AC 平行的直线的解析式为:y =x +m ,当直线y =x +m 与抛物线相切时,△MCD 的面积最大,由x +m =-x 2-2x +3得,x 2+3x +(m -3)=0,由△=0得,32-4(m -3)=0得,m -3=94,∴x 2+3x +94=0,∴x 1=x 2=-32,∴y =--32 2-2×-32 +3=154,y =x +3=-32+3=32,∴ME =154-32=94,∴MQ =ME ⋅sin ∠MEQ =ME ⋅sin45°=94×22=928,∴S △MCD 最大=12×2×928=98;(3)解:如图2,当点P 在线段AC 上时,连接BP ,交CQ 于R ,∵点B 和点Q 关于CQ 对称,∴CP =CB ,设P (t ,t +3),由CP 2=CB 2得,2t 2=10,∴t 1=-5,t 2=5(舍去),∴P -5,3-5 ,∵PQ ∥BC ,∴CR =BR =1,∴CR =QR ,∴四边形BCPQ 是平行四边形,∵1+(-5)-0=1-5,0+(3-5)-3=-5,∴Q 1-5,-5 ;如图3,当点P 在AC 的延长线上时,由上可知:P 5,3+5 ,同理可得:Q 1+5,5 ,综上所述:Q 1-5,-5 或1+5,5 .【点睛】本题考查了二次函数及其图象的性质,一元二次方程的解法,平行四边形的判定和性质,轴对称的性质等知识,解决问题的关键是分类讨论.2(2023·四川甘孜·统考中考真题)已知抛物线y =x 2+bx +c 与x 轴相交于A -1,0 ,B 两点,与y 轴相交于点C 0,-3 .(1)求b ,c 的值;(2)P 为第一象限抛物线上一点,△PBC 的面积与△ABC 的面积相等,求直线AP 的解析式;(3)在(2)的条件下,设E 是直线BC 上一点,点P 关于AE 的对称点为点P ,试探究,是否存在满足条件的点E ,使得点P 恰好落在直线BC 上,如果存在,求出点P 的坐标;如果不存在,请说明理由.【答案】(1)b =-2,c =-3.(2)y =x +1(3)存在,点P 的坐标为1+21,-2+21 或1-21,-2-21【分析】(1)由待定系数法即可求解;(2)S △PBC =S △ABC 得到AP ∥BC ,即可求解;(3)由题意的:∠AEP =∠AEP ,P E =PE ,即可求解.【详解】(1)由题意,得1-b +c =0,c =-3.∴b =-2,c =-3.(2)由(1)得抛物线的解析式为y =x 2-2x -3.令y =0,则x 2-2x -3=0,得x 1=-1,x 2=3.∴B 点的坐标为3,0 .∵S △PBC =S △ABC ,∴AP ∥BC .∵B 3,0,C 0,-3 ,∵AP∥BC,∴可设直线AP的解析式为y=x+m.∵A(-1,0)在直线AP上,∴0=-1+m.∴m=1.∴直线AP的解析式为y=x+1.(3)设P点坐标为m,n.∵点P在直线y=x+1和抛物线y=x2-2x-3上,∴n=m+1,n=m2-2m-3.∴m+1=m2-2m-3.解得m1=4,m2=-1(舍去).∴点P的坐标为4,5.由翻折,得∠AEP=∠AEP ,P E=PE.∵AP∥BC,∴∠PAE=∠AEP '.∴∠PAE=∠PEA.∴PE=PA=4+12=52.2+5-0设点E的坐标为t,t-3,则PE2=t-42.2+t-3-52=52∴t=6±21.当t=6+21时,点E的坐标为6+21,3+21.设P (s,s-3),由P E=AP,P E=PE=52得:s-6-212,2=522+s-3-3-21解得:s=1+21,则点P 的坐标为1+21,-2+21.当t=6-21时,同理可得,点P 的坐标为1-21,-2-21.综上所述,点P 的坐标为1+21,-2+21.或1-21,-2-21【点睛】本题是二次函数的综合题,主要考查了用待定系数法求一次函数、二次函数的解析式,二次函数的性质,此题题型较好,综合性比较强,用的数学思想是分类讨论和数形结合的思想.3(2023·江苏连云港·连云港市新海实验中学校考二模)如图,“爱心”图案是由抛物线y=-x2+m的一部分及其关于直线y=-x的对称图形组成,点E、F是“爱心”图案与其对称轴的两个交点,点A、B、C、D是该图案与坐标轴的交点,且点D的坐标为6,0.(1)求m 的值及AC 的长;(2)求EF 的长;(3)若点P 是该图案上的一动点,点P 、点Q 关于直线y =-x 对称,连接PQ ,求PQ 的最大值及此时Q 点的坐标.【答案】(1)m =6,AC =6+6(2)52(3)2542,Q -234,-12【分析】(1)用待定系数法求得m 与抛物线的解析式,再求出抛物线与坐标轴的交点坐标,进而求得A 的坐标,根据对称性质求得B ,C 的坐标,即可求得结果;(2)将抛物线的解析式与直线EF 的解析式联立方程组进行求解,得到E ,F 的坐标,即可求得结果;(3)设P (m ,-m 2+6),则Q (m 2-6,-m ),可得PQ =2×m -12 2-252 ,即求m -12 2-252的最值,根据二次函数的最值,即可得到m 的值,即可求得.【详解】(1)把D 6,0 代入y =-x 2+m 得0=-6+m解得m =6∴抛物线的解析式为:y =-x 2+6∴A 0,6根据对称性可得B -6,0 ,C 0,-6∴AC =AO +OC =6+6(2)联立y =-x y =-x 2+6解得x =3y =-3 或x =-2y =2 ∴E -2,2 ,F 3,-3∴EF =-2-3 2+2+3 2=52(3)设P (m ,-m 2+6),则Q (m 2-6,-m )∴PQ =m -m 2-6 2+-m 2+6--m 2整理得PQ =2×m -12 2-254 ∵m -12 2≥0∴当m -12 2=0时,即m =12时,m -12 2-254 有最大值为254∴PQ 的最大值为2542∴12 2-6=-234故Q -234,-12【点睛】本题考查二次函数综合应用,涉及待定系数法求函数解析式,两点间的距离公式,求抛物线与一次函数的交点坐标,二次函数的最值等知识,解题的关键是掌握关于直线y =-x 对称的点坐标的关系.题型04特殊角度存在性问题1(2023·山西忻州·统考模拟预测)如图,抛物线y =18x 2+34x -2与x 轴交于A ,B 两点,与y 轴交于点C .P 是直线AC 下方抛物线上一个动点,过点P 作直线l ∥BC ,交AC 于点D ,过点P 作PE ⊥x 轴,垂足为E ,PE 交AC 于点F .(1)直接写出A ,B ,C 三点的坐标,并求出直线AC 的函数表达式;(2)当线段PF 取最大值时,求△DPF 的面积;(3)试探究在拋物线的对称轴上是否存在点Q ,使得∠CAQ =45°?若存在,请直接写出点Q 的坐标;若不存在,请说明理由.【答案】(1)A -8,0 ,B 2,0 ,C 0,-2 .y =-14x -2(2)85(3)存在,-3,3 或-3,-253【分析】(1)对于直线y =18x 2+34x -2,当x =0时,y =-2,即点C 0,-2 ,令18x 2+34x -2=0,则x =2或-8,则点A ,B 的坐标分别为-8,0 ,2,0 即求出三个点的坐标,设直线AC 的表达式为y =kx +b ,利用待定系数法求解即可;(2)设点P 的横坐标为m ,则P m ,18m 2+34m -2 ,F m ,-14m -2 ,表示出PF =-18m 2-m ,求出PF max =2,再表示出点D 到直线PF 的距离d =85,利用S △DPF =12⋅PF ⋅d 进行求解即可;(3)由抛物线的表达式知,其对称轴为x =-3,当点Q 在x 轴上方时,设抛物线的对称轴交x 轴于点N ,交AC 于H ,故点Q 作QT ⊥AC 于点T ,在△AQH 中,∠CAQ =45°,tan ∠QHA =4,用解直角三角形的方法求出QH =174,即可求出Q 点坐标,当点Q Q 在x 轴上方时,直线AQ 的表达式为y =35x +8 ,当∠CAQ =45°时,AQ ⊥AQ ,即可求解.【详解】(1)解:对于抛物线y =18x 2+34x -2,当x =0时,y =-2,即点C 0,-2 ,令18x 2+34x -2=0,则x =2或-8,则点A ,B 的坐标分别为-8,0 ,2,0 ,即点A ,B ,C 三点的坐标分别为-8,0 ,2,0 ,0,-2 ,设直线AC 的表达式为y =kx +b ,则-8k +b =0b =-2 ,解得k =-14b =-2 ,∴直线AC 的函数表达式为y =-14x -2;(2)设点P 的横坐标为m ,则P m ,18m 2+34m -2 ,F m ,-14m -2 ,PF =-14m -2 -18m 2+34m -2 =-18m 2-m ,当m =--12×-18 =-4时,PF 最大,PF max =-18×(-4)2--4 =2,此时,P -4,-3 ,由B 2,0 ,C 0,-2 ,可得直线BC 的函数表达式为y =x -2,设直线l 的函数表达式为y =x +p ,将P -4,-3 代入可得p =1,∴直线l 的函数表达式为y =x +1,由y =-14x -2y =x +1 ,解得x =-125y =-75,∴D -125,-75 ,点D 到直线PF 的距离d =-125--4 =85,∴S △DPF =12⋅PF ⋅d =12×2×85=85.(3)存在,理由:由抛物线的表达式知,其对称轴为x =-3,当点Q 在x 轴上方时,如下图:设抛物线的对称轴交x 轴于点N ,交AC 于H ,故点Q 作QT ⊥AC 于点T ,则∠ACO =∠QHA ,则tan ∠ACO =tan ∠QHA =4,当x =3时,y =-14x -2=-54,则点H -3,-54 ,由点A ,H 的坐标得,AH =5174,在△AQH 中,∠CAQ =45°,tan ∠QHA =4,设TH =x ,则QT =4x ,则QH =17x ,则AH =AT +TH =5x =5174,则x =174,则QH =17x =174,则174-54=3,则点Q -3,3 ;当点Q Q 在x 轴上方时,直线AQ 的表达式为y =35x +8 ,当∠CAQ =45°时,AQ ⊥AQ ,则直线AQ 的表达式为y =-53x +8 ,当x =-3时,y =-5x +8 =-25,。
二次函数最值问题及解题技巧(个人整理)

二次函数最值问题及解题技巧(个人整理)一、二次函数线段最值问题1、平行于x轴的线段最值问题1)首先表示出线段两个端点的坐标2)用右侧端点的横坐标减去左侧端点的横坐标3)得到一个线段长关于自变量的二次函数4)将其化为顶点式,并根据a的正负及自变量的取值范围判断最值2、平行于y轴的线段最值问题1)首先表示出线段两个端点的坐标2)用上面端点的纵坐标减去下面端点的纵坐标3)得到一个线段长关于自变量的二次函数解析式4)将其化为顶点式,并根据a的正负及自变量的取值范围判断最值3、既不平行于x轴,又不平行于y轴的线段最值问题1)以此线段为斜边构造一个直角三角形,并使此直角三角形的两条直角边分别平行于x轴、y轴2)根据线段两个端点的坐标表示出直角顶点坐标3)根据“上减下,右减左”分别表示出两直角边长4)根据勾股定理表示出斜边的平方(即两直角边的平方和)5)得到一个斜边的平方关于自变量的二次函数6)将其化为顶点式,并根据a的正负及自变量的取值规模判断最值7)根据所求得的斜边平方的最值求出斜边的最值即可2、二次函数周长最值问题1、矩形周长最值问题1)一般会给出一点落在抛物线上,从这点向两坐标轴引垂线构成一个矩形,求其周长最值2)可先设此点坐标,点p到x轴、y轴的距离和再乘以2,即为周长3)将其化为顶点式,并根据a的正负及自变量的取值范围判断最值2、利用两点之间线段最短求三角形周长最值1)首先判断图形中那些边是定值,哪些边是变量2)使用二次函数轴对称性及两点之间线段最短找到两条变革的边,并求其和的最小值3)周长最小值即为两条变革的边的和最小值加上不变的边长3、二次函数面积最值问题1、规则图形面积最值问题(这里规则图形指三角形必有一边平行于坐标轴,四边形必有一组对边平行于坐标轴)1)首先表示出所需的边长及高2)使用求面积公式表示出面积3)得到一个面积关于自变量的二次函数4)将其化为顶点式,并根据a的正负及自变量的取值规模判断最值2、不划定规矩图形面积最值问题1)支解。
高中数学中的二次函数与最值问题

高中数学中的二次函数与最值问题二次函数是高中数学中的重要内容之一,其与最值问题的关系更是难以忽视。
本文将系统地介绍二次函数的定义、性质以及如何利用二次函数求解最值问题。
一、二次函数的定义与性质二次函数是形如y=ax^2+bx+c的函数,其中a、b和c是实数且a不等于0。
二次函数的图像通常是一个抛物线,可以是开口向上或开口向下的形态。
以下是二次函数的一些重要性质:1. 零点:二次函数的零点是其对应的抛物线与x轴相交的点,即使得函数值为0的x值。
零点的求解可以通过因式分解、配方法或求根公式来实现。
2. 頂点坐标:二次函数的顶点是抛物线的最高点(当a小于0时)或最低点(当a大于0时)。
顶点的x坐标可以通过公式x=-b/2a来计算,y坐标则可将x值代入二次函数中得到。
3. 对称轴:二次函数的对称轴是通过抛物线的顶点并平行于y轴的线。
对称轴的方程形式为x=-b/2a。
4. 单调性:当a大于0时,抛物线开口向上,函数值随x的增大而增大;当a小于0时,抛物线开口向下,函数值随x的增大而减小。
二、二次函数求解最值问题的方法在实际问题中,我们常常需要求解二次函数的最大值或最小值。
这些问题可能涉及到经济、物理、几何等领域。
以下是求解二次函数最值问题的常用方法:1. 完成平方:通过将二次函数表示成平方项的和来求解最值问题。
对于一般形式的二次函数,可以通过配方法来实现。
例如,对于函数y=ax^2+bx+c,可以通过将x^2+bx视为一个完全平方进行变形,从而得到最小值或最大值。
2. 求导数:利用导数的性质,求解二次函数的导数,并找到导数为0的点。
这些点即为原函数的最值点。
求导数的方法可以通过一阶导数、二阶导数等进行,具体视题目要求而定。
3. 利用顶点坐标:如果已知二次函数的顶点坐标,则直接取顶点的y值即为函数的最值。
4. 利用最值问题的性质:根据二次函数的几何特性,当a大于0时,函数有最小值;当a小于0时,函数有最大值。
二次函数中的几何最值问题

二次函数的基本性质
对称性
二次函数的图像关于垂直于 x 轴的直线 x=-b/2a 对称。
增减性
当 a>0 时,二次函数是开口向上的抛物线,函数单调递增;当 a<0 时,二次函数是开口向下 的抛物线,函数单调递减。
最值
二次函数有一个最值点,通常用完全平方式求得。
几何最值问题的概念解析
在平面直角坐标系中,如何求一些特定几何形状的最大或最小值?这就是几 何最值问题。
几何最值问题的实际应用
1 建筑设计
建筑物的结构设计,如何在保证结构安全的前提下尽可能节省材料成本。
2 矿山开采
矿床的几何特征分析,如何在最短时间内挖掘出最大的矿石。
3 制造工艺
生产过程中的工艺设计,如何在保证产品质量的前提下尽可能节约原材料和能源。
总结和展望
几何最值问题是数学中的一个重要分支,具有广泛的应用前景。希望大家在学习中发现其重要性,并能用它来 解决实际问题。
解决几何最值问题的方法
完成平方
将二次项化为完全平方,从而得出最值点坐标。
利用导数
求导数,得出极值点,再求函数值得出最值。
几何最值问题的例题分析
求最大体积
已知一个金字塔底边长为 6 米,高为 8 米,求它的 最大体积。
求最小周长
已知一个底边长为 8 米的直角三角形,且其中一个 锐角为 30 度,求它的最小周长。
二次函数中的几何最值问 题
在学习二次函数时,我们会遇到许多几何最值问题。了解这些问题的定义、 解决方法和实际应用,可以帮助我们更好地理解二次函数和几何学。
二次函数的定义与图像
定义
由一般式 y=ax²+bx+c (a≠0)所表示的函数称为二次 函数。
二次函数中几何的最值问题完整版

二次函数中几何的最值问题Document serial number【NL89WT-NY98YT-NC8CB-NNUUT-NUT108】二次函数中几何的最值问题一、解答题1、如图,在平面直角坐标系中,△ABC的三个顶点坐标分别为A(-2,0)、B (6,0)、C(0,-2),抛物线y=a+bx+c(a≠0)经过A、B、C三点。
(1)求直线AC的解析式;(2)求此抛物线的解析式;(3)若抛物线的顶点为D,试探究在直线AC上是否存在一点P,使得△BPD的周长最小,若存在,求出P点的坐标;若不存在,请说明理由。
2、如图,已知抛物线y=-+mx+3与x轴交于A,B两点,与y轴交于点C,点B 的坐标为(3,0)。
(1)求m的值及抛物线的顶点坐标;(2)点P是抛物线对称轴l上的一个动点,当PA+PC的值最小时,求点P的坐标。
3、如图,二次函数y=a+bx的图象经过点A(2,4)与B(6,0).(1)求a,b的值;(2)点C是该二次函数图象上A,B两点之间的一动点,横坐标为x(2<x<6),写出四边形OACB的面积S关于点C的横坐标x的函数表达式,并求S的最大值。
4、如图,抛物线y=+bx+c(a、b、c为常数,a≠0)经过点A(﹣1,0),B (5,﹣6),C(6,0).(1)求抛物线的解析式;(2)如图,在直线AB下方的抛物线上是否存在点P使四边形PACB的面积最大若存在,请求出点P的坐标;若不存在,请说明理由;(3)若点Q为抛物线的对称轴上的一个动点,试指出△QAB为等腰三角形的点Q 一共有几个并请求出其中某一个点Q的坐标.5、如图,长方形OABC的OA边在x轴的正半轴上,OC在y轴的正半轴上,抛物线y=+bx经过点B(1,4)和点E(3,0)两点.(1)求抛物线的解析式;(2)若点D在线段OC上,且BD⊥DE,BD=DE,求D点的坐标;(3)在条件(2)下,在抛物线的对称轴上找一点M,使得△BDM的周长为最小,并求△BDM周长的最小值及此时点M的坐标;(4)在条件(2)下,从B点到E点这段抛物线的图象上,是否存在一个点P,使得△PAD的面积最大若存在,请求出△PAD面积的最大值及此时P点的坐标;若不存在,请说明理由.6、如图,抛物线y=-3x+与x轴相交于A、B两点,与y轴相交于点C,点D是直线BC下方抛物线上一点,过点D作y轴的平行线,与直线BC相交于点E(1)求直线BC的解析式;(2)当线段DE的长度最大时,求点D的坐标。
二次函数中几何的最值问题

二次函数中几何的最值问题一、解答题1、如图,在平面直角坐标系中,△ABC的三个顶点坐标分别为A(-2,0)、B (6,0)、C(0,-2),抛物线y=a+bx+c(a≠0)经过A、B、C三点。
(1)求直线AC的解析式;(2)求此抛物线的解析式;(3)若抛物线的顶点为D,试探究在直线AC上是否存在一点P,使得△BPD的周长最小,若存在,求出P点的坐标;若不存在,请说明理由。
2、如图,已知抛物线y=-+mx+3与x轴交于A,B两点,与y轴交于点C,点B的坐标为(3,0)。
(1)求m的值及抛物线的顶点坐标;(2)点P是抛物线对称轴l上的一个动点,当PA+PC的值最小时,求点P的坐标。
3、如图,二次函数y=a+bx的图象经过点A(2,4)与B(6,0).(1)求a,b的值;(2)点C是该二次函数图象上A,B两点之间的一动点,横坐标为x(2<x<6),写出四边形OACB的面积S关于点C的横坐标x的函数表达式,并求S的最大值。
4、如图,抛物线y=+bx+c(a、b、c为常数,a≠0)经过点A(﹣1,0),B(5,﹣6),C(6,0).(1)求抛物线的解析式;(2)如图,在直线AB下方的抛物线上是否存在点P使四边形PACB的面积最大?若存在,请求出点P的坐标;若不存在,请说明理由;(3)若点Q为抛物线的对称轴上的一个动点,试指出△QAB为等腰三角形的点Q一共有几个?并请求出其中某一个点Q的坐标.5、如图,长方形OABC的OA边在x轴的正半轴上,OC在y轴的正半轴上,抛物线y=+bx经过点B(1,4)和点E(3,0)两点.(1)求抛物线的解析式;(2)若点D在线段OC上,且BD⊥DE,BD=DE,求D点的坐标;(3)在条件(2)下,在抛物线的对称轴上找一点M,使得△BDM的周长为最小,并求△BDM周长的最小值及此时点M的坐标;(4)在条件(2)下,从B点到E点这段抛物线的图象上,是否存在一个点P,使得△PAD的面积最大?若存在,请求出△PAD面积的最大值及此时P点的坐标;若不存在,请说明理由.6、如图,抛物线y=-3x+与x轴相交于A、B两点,与y轴相交于点C,点D是直线BC下方抛物线上一点,过点D作y轴的平行线,与直线BC相交于点E (1)求直线BC的解析式;(2)当线段DE的长度最大时,求点D的坐标。
二次函数背景下的几何问题——线段最值问题

二次函数背景下的几何问题——线段最值问题线段最值问题是在二次函数背景下的一种几何问题,主要是求解一个线段的最大值或最小值。
这个问题可以通过二次函数的图像和相关的数学理论来解决。
在解决这类问题时,我们可以利用二次函数的性质和相关的数学技巧来找到线段的最值点,从而得出最值。
首先,我们来回顾一下二次函数的一般形式:f(x) = ax^2 + bx+ c,其中a、b、c都是常数且a不等于0。
根据二次函数的图像特点,我们知道它是一个抛物线,可以是开口向上(a>0)或开口向下(a<0)的。
对于线段最值问题,我们通常要确定线段的端点,然后找出其中的最大值或最小值点。
这可以通过以下步骤来完成:1.确定二次函数的图像形状:根据二次函数的参数a的值,确定抛物线是开口向上还是开口向下。
2.确定线段的端点:线段的端点可以是给定的数值,也可以通过求解二次函数的解来确定。
根据二次函数的性质,它的两个解(也就是x的值)对应着抛物线与x轴的交点,即抛物线的顶点和x轴的两个交点。
3.求解最值点:对于线段的最大值点,我们需要找到抛物线的顶点,并通过计算确定它的y坐标值。
通过二次函数的解析式,我们可以知道抛物线的顶点坐标是(-b/2a, f(-b/2a))。
同样的,对于线段的最小值点,我们也可以通过类似的方法来解决。
4.判断最值点是否在线段上:在找到最值点之后,我们需要判断它是否在给定的线段上。
这可以通过将最值点的x坐标值与线段的端点的x坐标值进行比较来实现。
如果最值点的x坐标值位于线段的端点之间,则最值点就在线段上。
通过以上步骤,我们可以很容易地求解线段的最值问题。
当然,在实际应用中,可能会碰到更复杂的情况,例如线段与其他二次函数曲线的交点等。
但是,通过理解二次函数的性质和运用相关的数学知识,我们可以应对这些情况并解决问题。
总结而言,线段最值问题是在二次函数背景下的一种几何问题,通过确定二次函数的图像形状、线段的端点、求解最值点和判断最值点是否在线段上,我们可以解决线段的最值问题。
二次函数背景下的几何问题——线段最值问题

二次函数背景下的几何问题——线段最值问题一、【教学内容分析】二次函数是一次函数和反比例函数的继续和发展,是初中数学学习的重点和难点,也为以后更高层次函数的学习奠定了基础.以二次函数为背景的试题常受命题者的青睐,它能够全面考察学生的数形结合能力与计算能力,同时它也是学生学习高中数学知识所必备的.而此命题一般不会用以纯函数的形式出现,而是结合几何图形或点的运动使几何图形发生变化,从而让代数与几何有机结合起来. 二次函数背景下的线段最值问题是利用重要的几何结论(如两点之间线段最短、垂线段最短、三角形两边之和大于第三边、两边之差小于第三边等)及二次函数的性质求最值.这类问题大多是“将军饮马”模型的变式应用,试题通过考查点在直线上运动时与它相关线段的最值情况,不但能了解学生综合运用数学知识的能力,而且还能通过学生对“动”与“定”之间的关系的思考,深入了解学生在图形的运动变化中探索几何元素之间位置关系和数量关系的能力和识别能力,体现新课程对学生几何探索活动过程、合情推理能力的要求.二【疑难点分析】培养学生能正确运用将军饮马等几何模型、函数模型,解决二次函数背景下的线段最值问题.三、【教学目标】(1)掌握利用基本事实——两点之间线段最短、三角形的三边关系构建几何模型,解决因动点产生的二次函数背景下的线段最值问题.(2)根据问题构建函数模型,解决因动点产生的二次函数背景下的线段最值问题.四、【教学重难点】重点:能运用几何模型和函数模型解决因动点产生的二次函数背景下的线段最值问题.难点:提高学生运用二次函数知识与几何知识解决数学综合题的能力.五、【教学媒体】PPT 课件、微课、导学练六、【教法】讲练结合法、问题教学法七、【学法】小组合作交流法、自主探究法、观察发现法八、【教学流程框图】教学过程设计:教学内容(一)微课助手,忆旧知播放微课视频短片,让学生回顾下数学史上著名的“将军饮马”问题(二)重点难点,细解读1、模型一:如图 1,点 P 在直线 l 上运动,找出一点 p 使得PA+PB 取最小值.观察模型并回答以下两个问题:教学策略让学生通过观察模型一,总结出模型一的特点和所运用的方法.设计意图通过回顾“将军饮马”问题,烘托问题情境,利用微课吸引学生的注意力,在历史经典中唤起学生的兴趣,激发学生探究问题的欲望,让学生回忆起旧知.为了落实好下面的模型应用,把知识背景归纳成一般化的数学模型. 在温故中实现引新,为展开模型应值时,求点 P 的坐标 (1)该模型有什么特征?(2)基本解法是什么?特征:定点 A 、B 同侧,P 为动点; 原理:两点之间,线段最短; 思想:转化(化同侧为异侧);方法:轴对称法.模型运用:(2016•漳州)已知:如图,A (-1,0),B (3,0),C(0,3),抛物线经过点 A 、B 、C , 抛物线的顶点为 D .(1) 求抛物线的解析式和抛物线的顶点 D ;(2) 点 P 在对称轴上,PA+PC取最小 .解题思路分析:(1)利用两点式或者一般式求抛物线的解析式;通过小组讨论,再请学生代表解析.教师给予点评,并板演解答过程.用提供知识、方法及经验的支持.二次函数类的压轴题第一问通常为求点坐标、解析式,本小问要求学生能够熟练地掌握待定系数法求函数解析式或利用函数解析式求点坐标,相对较简单,通过第一小问的解答增进学生解压轴题的信心. 同时在具体的实例中学习把知识迁移应用并体会“将军饮马”问题中蕴含的数学本 质.利用对称思想(2)步骤:板书解题过程:(2)解:连接 BC,与对称轴的点即为点 P,如图所示,点 P为所求,则可得 P 的横坐标为1.设直线BC 的解析式为y=kx+b(k≠0),将点 B(3,0)、C(0,3)代入y=kx+b(k≠0),可得:⎧3k +b = 0 ⎧k = -1⎨,解得:⎨⎩b = 3 ⎩b = 3则直线 BC 的表达式为:y = -x + 3 .当x =1时,y =-1+3 = 2 .∴当点 P 的坐标为(1,2)时,PA+PC 取最小值.让学生独立思考,通过类比上一把复杂的问题简单化.变式 1:已知:如图,A(-1,0),B (3,0),C(0,3),抛物线经过点 A、B、C.点 P 在对称轴上.(1)求抛物线的解析式和抛物线的顶点 D;(2)△PAC周长最小时,求点P 的坐标.解题思路分析:由于AC 为定值,要使△PAC周长最小,则此问题转化成在对称轴上找一点 P,使得PA+PC 最小即可.2、模型二:在直线 l 上,找出一点P,使|PA-PB|的值最大.观察模型并回答以下两个问题:(1)该模型有什么特征?还能利用对称轴的知识去解决?(2)小组成员间每人找一点 P,进行比较,你有什么发现?(3)这个模型的基本解法是什么?题,规范书写解题过程.再与学生强调此类型题解题步骤:(1)找对称点;(2)连线并求直线解析式;(3)求点坐标.这一环节问题一个接着一个,形成了问题串,具有挑战性,能极大引起学生的思考,教师在这一环节中要善于运用语言不断鼓励学生.引导学生得出这一模型的基本解法:使A、B、P 三点共线,原理是:三角形两边之差小于第三边.经历画图-观察-说理等活动,得出作图原理,将该问题归类建模,熟悉并理解该几何模型,培养学生的逻辑思维能力.对于问题教师要给学生足够的时间进行讨论、交流,让学生对图象进行细致的观察、类比、分析、及时检测学生对所学知识的掌握情况,加深对这一模型的理解 .基本解法:使A、B、P 三点共线;基本原理:三角形两边之差小于第三边;基本思想:转化(化折为直).变式 2:已知:如图,A(-1,0),B (3,0),C(0,3),抛物线经过点 A、B、C.点 P 在对称轴上.(1)求抛物线的解析式和抛物线的顶点 D;(2)|PA-PC|最大,求点 P 的坐标.解题思路分析:交流,同时鼓励学生尽可能多的从图象中获取信息,以小组的形式对信息进行分析、综合、概括、归纳,形成知识系统.教师鼓励学生先独立完成,然后共同交流,总结知识,提炼方法.(2)解:连接直线 AC 交对称轴于点P,如图所示,点P 为所求,则可得P 的横坐标为1. 设直线AC 的解析式为y =kx +b(k ≠ 0),将点A ( -1,0 )、 C (0,3 )代入y=kx+b(k≠0),可得:⎧-k +b = 0 ⎧k = 3⎨,解得:⎨⎩b = 3 ⎩b = 3则直线 AC 的表达式为:y = 3x + 3.当x =1时,y = 3 +3 = 6 .∴当点 P 的坐标为(1,6)时,|PA-PC|最取大值.模型三:如图,在平面直角坐标系中如何表示线段 AB 的长度. 对于这个探究,教师利用微课进行讲解,组织学生先观看微课。
二次函数中几何图形周长的最值问题题型与解法

做法:
1.作A点关于对称轴的对称点对称点B
2.链接CB与对称轴的交点就是我们做 要求的G点的位置
G
3.连接AG
G 4.此时的△ACH的周长最小
(2)在直线BC上是否存在点H,使得△ACH的周长最小,若存在,
求出△GAC的周长最小值,并求出点G的坐标;若不存在,请说明
理由。
做法:
M
1.作A点关于直线BD的对
(1)求A、B、C的坐标;
(2)点M为线段AB上一点(点M不与点A、B重合)
,过点M作x轴的垂线,与直线AC交于点E,与抛物
线交于点P,过点P作PQ∥AB交抛物线于点Q,过
F
点Q作QN⊥x轴于点N.若点P在点Q左边,当矩形
PQMN的周长最大时,求△AEM的面积;
做法:
1.过D点作对称轴,与PQ相交于点F
2. 根据我市现目前考试题型来看,该部分是个重点,也是个难点, 很大一部分学生对该部分望而生畏,几乎不敢动笔,分析了一下, 其主要原因有两点:其一,因为此题涉及的解题过程比较繁杂, 再加上思路不清晰,会花大量的时间思考,所以这部分学生就选 择放弃了;另外的,还有部分学生是压根就不会做这类题,对解 决该题没有思路,没有参考方向,所以根本不看这题。
④任意角的非直角三角形周长最大值的求法 例:(2)如图,在平面直角坐标系中,抛物线y=﹣x2﹣2x+3与轴交于A、B两点,与y轴 交于点C,点D为抛物线的顶点. (1)求直线AC的解析式,并直接写出D点的坐标. (2)如图1,在直线AC的上方抛物线上有一动点P,过P点作PQ垂直于x轴交AC于点Q, PM∥BD交AC于点M.求△PQM周长最大值; 做法:
2.C矩形 PQNM=2(PQ+PM)=2(2DF+PM)
二次函数中几何图形周长的最值问题题型及解法

2. 根据我市现目前考试题型来看,该部分是个重点,也是个难点, 很大一部分学生对该部分望而生畏,几乎不敢动笔,分析了一下, 其主要原因有两点:其一,因为此题涉及的解题过程比较繁杂, 再加上思路不清晰,会花大量的时间思考,所以这部分学生就选 择放弃了;另外的,还有部分学生是压根就不会做这类题,对解 决该题没有思路,没有参考方向,所以根本不看这题。
C(0,﹣3).如图,在直线BD和直线BC上是否分别存在点M、N,使得
△AMN的周长最小?若存在,请求出△AMN周长最小值以及M、N的坐标;
若不存在,请说明理由。
A1
做法:
E M
1.作A点关于直线BD的对称点对称点A1,与BD相交于点E 2.作A点关于直线BC的对称点对称点A2,与BD相交于点F
N F
做法:
1.作A点关于对称轴的对称点对称点B
2.链接CB与对称轴的交点就是我们做 要求的G点的位置
G
3.连接AG
G 4.此时的△ACH的周长最小
(2)在直线BC上是否存在点H,使得△ACH的周长最小,若存在,
求出△GAC的周长最小值,并求出点G的坐标;若不存在,请说明
理由。
做法:
M
1.作A点关于直线BD的对
第二部分 基本题型及解法
例题
1. 一个动点在抛物线上求三角形周长的最大值 45°角的直角三角形周长最大值的求法 例1:(1)已知:抛物线y=ax2+bx+c(a≠0)经过点A(1,0),
B(3,0),C(0,﹣3).如图,点P是直线BC上方抛物线上一动
点.过点P作PE平行y轴交BC于点E,作PF垂直BC交BC于点F,是否 存在点P,使△PEF的周长最大?若存在,求出△PEF周长最大值,并
二次函数中几何图形周长的最值问题题型及解法

谢 谢!
教育是行善的智慧 无忧是无畏的行者
2. 根据我市现目前考试题型来看,该部分是个重点,也是个难点, 很大一部分学生对该部分望而生畏,几乎不敢动笔,分析了一下, 其主要原因有两点:其一,因为此题涉及的解题过程比较繁杂, 再加上思路不清晰,会花大量的时间思考,所以这部分学生就选 择放弃了;另外的,还有部分学生是压根就不会做这类题,对解 决该题没有思路,没有参考方向,所以根本不看这题。
做法: 1.作A点关于直线OM的对称点对称点A1
A1
2.作A点关于直线OM的对称点对称点A2
3.链接A1A2与OM,ON相交于点P,Q,
P
此时的交点就是我们做要找的吃草和喝
水的位置
4.连接AP,AQ
Q A2
4.此时走的路程最短
例4:已知:抛物线y=ax2+bx+c(a≠0)经过点A(1,0),B(3,0),
C(0,﹣3).如图,若点C关于点B的对称点为点E,是否存在x轴上的点
M,y轴上的点N,使得四边形DNME的周长最小?若存在,请求出M、N
点的坐标,并求出DNME的周长最小值;若不存在,请说明理由。
E
做法:
D’
1.作E点关于X轴的对称点对称点E’
2.作D点关于y轴的对称点对称点D’
NM
3.链接D’E’与x轴,y轴相交于点M,N,此时的交点就是 我们做要找的点的位置
做法:
1.过D点作对称轴,与PQ相交于点F
2.C矩形 PQNM=2(PQ+PM)=2(2DF+PM)
3. 一个动点在一条直线上求三角形周长最小值
初中复习方略数学微专题四 二次函数中几何图形线段、周长、面积的最值

抛物线对称轴为直线 x=- 2
=1,
2×(-1)
3k+c=0
设直线 AC 的解析式为 y=kx+c,将 A(3,0),C(0,3)代入,得:
,
c=3
k=-1
解得:
,
c=3
∴直线 AC 的解析式为 y=-x+3,∴P(1,2);
(3)存在.设 P(1,t),①以 AC 为边时,如图 2,∵四边形 ACPQ 是菱形, ∴CP=CA, ∴12+(3-t)2=32+32,解得:t=3± 17 , ∴P1(1,3- 17 ),P2(1,3+ 17 ), ∴Q1(4,- 17 ),Q2(4, 17 ),
1.(2021·天津中考)已知抛物线 y=ax2-2ax+c(a,c 为常数,a≠0)经过点 C(0,- 1),顶点为 D. (1)当 a=1 时,求该抛物线的顶点坐标; (2)当 a>0 时,点 E(0,1+a),若 DE=2 2 DC,求该抛物线的解析式; (3)当 a<-1 时,点 F(0,1-a),过点 C 作直线 l 平行于 x 轴,M(m,0)是 x 轴上 的动点,N(m+3,-1)是直线 l 上的动点.当 a 为何值时,FM+DN 的最小值为 2 10 ,并求此时点 M,N 的坐标.
(2021·常德中考)如图,在平面直角坐标系 xOy 中,平行四边形 ABCD 的 AB 边与 y 轴交于 E 点,F 是 AD 的中点,B、C、D 的坐标分别为(-2,0),(8,0),(13, 10). (1)求过 B、E、C 三点的抛物线的解析式; (2)试判断抛物线的顶点是否在直线 EF 上; (3)设过 F 作与 AB 平行的直线交 y 轴于 Q,M 是线段 EQ 之间的动点,射线 BM 与抛物线交于另一点 P,当△PBQ 的面积最大时,求 P 的坐标.
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
对称 + 对称
典型 例题
(4)如图,M为 x 轴上一动点, 求 CM
1 MB 的最小值. 2
特征:(一动两定点) (1)求两条线段之和最短; (2)其中有一条为几分之 几的线段
M
Q
解决方法:
构造角 + 垂线
典型 例题
解决方法:
对称 + 垂线
C
Q
M
课堂 小结
2个原理,2种手段,1种思想
3. 求几何最值有哪些常见方法呢? (1)轴对称; (2)平移;
典型 例题
(1)填空:点A、B、C、D、P 的坐标分别为:
y
(0, 3)
C
D (1, 4) P (2, 3)
(-1, A 0)
O
(3, 0)
B
x
典型 例题
(2)如图,M为y轴上一动点, 求BM+DM最小值.
D'
y C
M M
D (1,4)
P′
特征:(两动两定点) (1)求三条线段之和最短; (2)有一条固定线段(固 定线段两端点为动点)
解决方法: 利用作“平移”将其转化为 一条线段求之。
变式 训练
变式:如图,M为 y 轴上一动点, N为抛物线对称轴上一动点,
求 PM+MN+NA的最小值.
P
特征:(两动两定点) (1)求三条线段之和最短; (2)无固定线段
特征:(一动两定点) 求两条线段之和最短;
解决方法: 利用作“对称”将其转化为 一条线段求之。
A O
B
(3,0)x
变式 训练
E
特征:(两动两定点) (1)求三条线段之和最短; (2)有一条固定线段(固 定线段两端点为定点
解决方法: 利用作“对称”将其转化为 一条线段求之。
典型 例题
(3)如图,M为 y轴上一动点, N为抛物线对称轴上一动点, 且MN⊥ y轴,求 PM+MN+NA的最小值.
二次函数中的几何最值
知识 要点
1. 在学过的几何中,有哪些与线段最值相关的定理? 1. 所有两点的连线中,线段最短。 2. 直线外一点与直线上各点连接的线段中,垂线段最短。 2. 如图,已知线段AB,点C 为平面内任一点,比较大小
AC+BC AB
A
B
若求两条(或多条)线 段之和最短时,常将其 转化为一条线段求之。
2个原理: (1)两点之间,线段最短;(2)垂线段最短。
2种手段: (1)轴对称; (2)平移。
一种思想: 转化的思想
