2017海南高考数学试题
海南省2017年高考文科数学试题及答案(Word)

海南省2017年高考文科数学试题及答案(word 版)(考试时间:120分钟 试卷满分:150分)一、选择题:本题共12小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的。
1. 设集合{}{}123234A B ==,,, ,,, 则=ABA. {}123,4,,B. {}123,, C 。
{}234,, D. {}134,, 2。
(1+i )(2+i)=A. 1-i B 。
1+3i C 。
3+i D 。
3+3i 3。
函数()fx =πsin (2x+)3的最小正周期为A 。
4π B. 2π C 。
π D 。
2π4. 设非零向量a ,b 满足+=-b b a a 则A 。
a ⊥bB 。
=b aC 。
a ∥b D. >b a5。
若a >1,则双曲线x y a=222-1的离心率的取值范围是A 。
2+∞(,) B. 22(,) C 。
2(1,) D 。
12(,)6. 如图,网格纸上小正方形的边长为1,粗实线画出的 是某几何体的三视图,该几何体由一平面将一圆柱截 去一部分后所得,则该几何体的体积为A 。
90πB 。
63πC 。
42πD 。
36π7。
设x 、y 满足约束条件2+330233030x y x y y -≤⎧⎪-+≥⎨⎪+≥⎩。
则2z x y =+ 的最小值是A. -15 B 。
-9 C. 1 D. 9 8. 函数2()ln(28)f x x x =-- 的单调递增区间是A.(—∞,-2) B 。
(—∞,—1) C 。
(1, +∞) D. (4, +∞) 9。
甲、乙、丙、丁四位同学一起去向老师询问成语竞赛的成绩,老师说,你们四人中有2位优秀,2位良好,我现在给甲看乙、丙的成绩,给乙看丙的成绩,给丁看甲的成绩,看后甲对大家说:我还是不知道我的成绩,根据以上信息,则 A. 乙可以知道两人的成绩B. 丁可能知道两人的成绩C 。
2017年海南省高考文科数学试题及答案

海南省2017年高考文科数学试题及答案(word 版)(考试时间:120分钟 试卷满分:150分)一、选择题:本题共12小题,每小题5分,共60分。
在每小题给出的四个选项中,只有一项是符合题目要求的。
1. 设集合{}{}123234A B ==,,, ,,, 则=ABA. {}123,4,,B. {}123,,C. {}234,,D. {}134,, 2.(1+i )(2+i )=A. 1-iB. 1+3iC. 3+iD. 3+3i 3. 函数()fx =πsin (2x+)3的最小正周期为A. 4πB. 2πC. πD. 2π4. 设非零向量a ,b 满足+=-b b a a 则A. a ⊥bB. =b aC. a ∥bD. >b a5. 若a >1,则双曲线x y a=222-1的离心率的取值范围是A. 2∞(,)B. 22(,)C. 2(1,)D. 12(,)6. 如图,网格纸上小正方形的边长为1,粗实线画出的 是某几何体的三视图,该几何体由一平面将一圆柱截 去一部分后所得,则该几何体的体积为A. 90πB.63πC.42πD.36π7. 设x 、y 满足约束条件2+330233030x y x y y -≤⎧⎪-+≥⎨⎪+≥⎩。
则2z x y =+ 的最小值是A. -15B.-9C. 1D. 9 8. 函数2()ln(28)f x x x =-- 的单调递增区间是A.(-∞,-2)B. (-∞,-1)C.(1, +∞)D. (4, +∞)9. 甲、乙、丙、丁四位同学一起去向老师询问成语竞赛的成绩,老师说,你们四人中有2位优秀,2位良好,我现在给甲看乙、丙的成绩,给乙看丙的成绩,给丁看甲的成绩,看后甲对大家说:我还是不知道我的成绩,根据以上信息,则 A. 乙可以知道两人的成绩 B. 丁可能知道两人的成绩C. 乙、丁可以知道对方的成绩D. 乙、丁可以知道自己的成绩10. 执行右面的程序框图,如果输入的a = -1,则输出的S=A. 2B. 3C. 4D. 511. 从分别写有1,2,3,4,5的5张卡片中随机抽取1张,放回后再随机抽取1张,则抽得的第一张卡片上的数大于第二张卡片上 的数的概率为A.110 B. 15 C. 310D. 2512. 过抛物线C:y 2=4x 的焦点F ,且斜率为3的直线交C 于点M (M 在x 轴上方),l 为C 的准线,点N 在l 上且MN ⊥l,则M 到直线NF 的距离为A. 5B. 22C. 23D. 33 二、填空题,本题共4小题,每小题5分,共20分. 13. 函数()cos sin =2+fx x x 的最大值为 .14. 已知函数()f x 是定义在R 上的奇函数,当x ()-,0∈∞时,()322=+f x x x ,则()2=f15. 长方体的长、宽、高分别为3,2,1,其顶点都在球O 的球面上,则球O 的表面积为 16. △ABC 的内角A,B,C 的对边分别为a,b,c,若2b cosB=a cosC+c cosA,则B=三、解答题:共70分。
[高考数学] 2017年海南省高考文科数学试题及答案
![[高考数学] 2017年海南省高考文科数学试题及答案](https://img.taocdn.com/s3/m/dadb94ef0408763231126edb6f1aff00bed570df.png)
海南省2017年高考文科数学试题及答案(word 版)(考试时间:120分钟 试卷满分:150分)一、选择题:本题共12小题,每小题5分,共60分。
在每小题给出的四个选项中,只有一项是符合题目要求的。
1. 设集合{}{}123234A B ==,,, ,,,则=A BA.{}123,4,, B. {}123,, C. {}234,, D. {}134,,2.(1+i )(2+i )=A. 1-iB. 1+3iC. 3+iD. 3+3i3. 函数()fx =πsin (2x+)3的最小正周期为A. 4πB. 2πC. πD. 2π4. 设非零向量a ,b 满足+=-b b a a 则A. a ⊥bB. =ba C. a ∥b D.>ba5. 若a >1,则双曲线x y a =222-1的离心率的取值范围是A. 2+∞(,)B. 22(,)C. 2(1,)D. 12(,)6. 如图,网格纸上小正方形的边长为1,粗实线画出的 是某几何体的三视图,该几何体由一平面将一圆柱截 去一部分后所得,则该几何体的体积为A. 90πB.63πC.42πD.36π7. 设x 、y 满足约束条件2+330233030x y x y y -≤⎧⎪-+≥⎨⎪+≥⎩。
则2z x y =+ 的最小值是A. -15B.-9C. 1D. 98. 函数2()ln(28)f x x x=--的单调递增区间是A.(-∞,-2)B. (-∞,-1)C.(1, +∞)D. (4, +∞)9. 甲、乙、丙、丁四位同学一起去向老师询问成语竞赛的成绩,老师说,你们四人中有2位优秀,2位良好,我现在给甲看乙、丙的成绩,给乙看丙的成绩,给丁看甲的成绩,看后甲对大家说:我还是不知道我的成绩,根据以上信息,则A. 乙可以知道两人的成绩B. 丁可能知道两人的成绩C. 乙、丁可以知道对方的成绩D. 乙、丁可以知道自己的成绩10. 执行右面的程序框图,如果输入的a = -1,则输出的S=A. 2B. 3C. 4D. 511. 从分别写有1,2,3,4,5的5张卡片中随机抽取1张,放回后再随机抽取1张,则抽得的第一张卡片上的数大于第二张卡片上的数的概率为A.110 B.15 C.310 D.2512. 过抛物线C:y2=4x的焦点F,且斜率为3的直线交C于点M(M在x轴上方),l为C的准线,点N在l上且MN⊥l,则M到直线NF的距离为A. 5B. 22C. 23D. 33二、填空题,本题共4小题,每小题5分,共20分.13. 函数()cos sin=2+f x x x的最大值为 .14. 已知函数()f x是定义在R上的奇函数,当x()-,0∈∞时,()322=+f x x x,则()2= f15. 长方体的长、宽、高分别为3,2,1,其顶点都在球O的球面上,则球O的表面积为16. △ABC的内角A,B,C的对边分别为a,b,c,若2b cosB=a cosC+c cosA,则B=三、解答题:共70分。
17年高考数学真题高考题(3套)

2017年普通高等学校招生全国统一考试全国Ⅰ(文数)一、选择题:本大题共12小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的.1.(2017·全国Ⅰ卷,文1)已知集合A={x|x<2},B={x|3-2x>0},则( A )(A)A∩B=(x|x<错误!未找到引用源。
)(B)A∩B=(C)A∪B=(x|x<错误!未找到引用源。
)(D)A∪B=R解析:B={x|3-2x>0}=(x|x<错误!未找到引用源。
),A∩B=(x|x<错误!未找到引用源。
),故选A.2.(2017·全国Ⅰ卷,文2)为评估一种农作物的种植效果,选了n块地作试验田.这n块地的亩产量(单位:kg)分别为x1,x2,…,xn,下面给出的指标中可以用来评估这种农作物亩产量稳定程度的是( B )(A)x1,x2,…,xn的平均数(B)x1,x2,…,xn的标准差(C)x1,x2,…,xn的最大值(D)x1,x2,…,xn的中位数解析:标准差衡量样本的稳定程度,故选B.3.(2017·全国Ⅰ卷,文3)下列各式的运算结果为纯虚数的是( C )(A)i(1+i)2(B)i2(1-i)(C)(1+i)2(D)i(1+i)解析:(1+i)2=2i,故选C.4.(2017·全国Ⅰ卷,文4)如图,正方形ABCD内的图形来自中国古代的太极图.正方形内切圆中的黑色部分和白色部分关于正方形的中心成中心对称.在正方形内随机取一点,则此点取自黑色部分的概率是( B )(A)错误!未找到引用源。
(B)错误!未找到引用源。
(C)错误!未找到引用源。
(D)错误!未找到引用源。
解析:不妨设正方形的边长为2,则正方形的面积为4,圆的半径为1,圆的面积为πr2=π.黑色部分的面积为圆面积的错误!未找到引用源。
,即为错误!未找到引用源。
,所以点取自黑色部分的概率是错误!未找到引用源。
2017年全国统一高考数学试卷(文科)(新课标ⅰ)(含解析版)

2017年全国统一高考数学试卷(文科)(新课标Ⅰ)一、选择题:本大题共12小题,每小题5分,共60分。
在每小题给出的四个选项中,只有一项是符合题目要求的。
1.(5分)已知集合A={x|x<2},B={x|3﹣2x>0},则( )A.A∩B={x|x<}B.A∩B=∅C.A∪B={x|x<}D.A∪B=R2.(5分)为评估一种农作物的种植效果,选了n块地作试验田.这n块地的亩产量(单位:kg)分别是x1,x2,…,x n,下面给出的指标中可以用来评估这种农作物亩产量稳定程度的是( )A.x1,x2,…,x n的平均数B.x1,x2,…,x n的标准差C.x1,x2,…,x n的最大值D.x1,x2,…,x n的中位数3.(5分)下列各式的运算结果为纯虚数的是( )A.i(1+i)2B.i2(1﹣i)C.(1+i)2D.i(1+i)4.(5分)如图,正方形ABCD内的图形来自中国古代的太极图.正方形内切圆中的黑色部分和白色部分关于正方形的中心成中心对称.在正方形内随机取一点,则此点取自黑色部分的概率是( )A.B.C.D.5.(5分)已知F是双曲线C:x2﹣=1的右焦点,P是C上一点,且PF与x 轴垂直,点A的坐标是(1,3),则△APF的面积为( )A.B.C.D.6.(5分)如图,在下列四个正方体中,A,B为正方体的两个顶点,M,N,Q为所在棱的中点,则在这四个正方体中,直线AB与平面MNQ不平行的是( )A.B.C.D.7.(5分)设x,y满足约束条件,则z=x+y的最大值为( )A.0B.1C.2D.38.(5分)函数y=的部分图象大致为( )A.B.C.D.9.(5分)已知函数f(x)=lnx+ln(2﹣x),则( )A.f(x)在(0,2)单调递增B.f(x)在(0,2)单调递减C.y=f(x)的图象关于直线x=1对称D.y=f(x)的图象关于点(1,0)对称10.(5分)如图程序框图是为了求出满足3n﹣2n>1000的最小偶数n,那么在和两个空白框中,可以分别填入( )A.A>1000和n=n+1B.A>1000和n=n+2C.A≤1000和n=n+1D.A≤1000和n=n+211.(5分)△ABC的内角A,B,C的对边分别为a,b,c,已知sinB+sinA(sinC﹣cosC)=0,a=2,c=,则C=( )A.B.C.D.12.(5分)设A,B是椭圆C:+=1长轴的两个端点,若C上存在点M满足∠AMB=120°,则m的取值范围是( )A.(0,1]∪[9,+∞)B.(0,]∪[9,+∞)C.(0,1]∪[4,+∞)D.(0,]∪[4,+∞)二、填空题:本题共4小题,每小题5分,共20分。
海南高考2017数学真题

海南高考2017数学真题
2017年,海南的高考数学试题备受关注,考生们紧张备战。
本文将对海南高考2017年数学真题进行分析和讨论,帮助考生更好地理解和准备考试。
首先,我们来看一道典型的选择题。
题目如下:
已知等差数列$\{a_n\}$的前四项依次为2,$a$,$b$,7,且
$a+b=12$,则$b$的值为()
A. 4
B.10
C.5
D.9
这道题主要考察考生对等差数列的性质和运用能力。
根据题目中的条件可列出方程$a+b=12$,又根据等差数列的性质有$a+5=7$,解方程可以得到$a=5,b=7$,所以答案为C.5。
接下来是一道解答题:
已知函数$f(x)=2^x$,$g(x)=\log_2x$,$h(x)=f(g(x))$,求$h(x)$的定义域。
这道题考察了考生对函数复合的理解和运用。
首先根据已知条件$h(x)=f(g(x))$,代入函数,得$h(x)=2^{\log_2x}=x$。
由于对数函数的定义域为正实数,所以$h(x)$的定义域也为正实数。
以上是对海南高考2017年数学真题中的两道题目的解析,希望能对考生有所帮助。
祝愿所有参加高考的考生都能取得优异的成绩,前程似锦!。
2017海南高考数学试题

2017年普通高等学校招生全国统一考试(海南)理科数学一、选择题:本题共12小题,每小题5分,共60分。
在每小题给出的四个选项 中,只有一项是符合题目要求的。
1.1()1 iA . 1 2iB . 1 -2i2. 设集合丄八1,2,4 1,三=1 A . 〈1,-3?B . 〈1,01C . 〈1,3?D . 〈1,513. 我国古代数学名著《算法统宗》中有如下问题: “远望巍巍塔七层,红光点点 倍加增,共灯三百八十一,请问尖头几盏灯?”意思是:一座 7层塔共挂了 381 盏灯,且相邻两层中的下一层灯数是上一层灯数的 2倍,则塔的顶层共有灯() A . 1盏 B . 3盏 C . 5盏 D . 9盏4. 如图,网格纸上小正方形的边长为 1,学科&网粗实线画出的是某几何体的三 视图,该几何体由一平面将一圆柱截去一部分所得,则该几何体的体积为() A . 90二 B . 63二 C . 42二 D . 362x 3y-3 乞 05. 设x ,y 满足约束条件 2x-3y ,3_0,则 2x y 的最小值是()y 3_0A . -15B . -9C . 1D . 96. 安排3名志愿者完成4项工作,每人至少完成1项,每项工作由1人完成,则 不同的安排方式共有()A . 12 种B . 18 种C . 24 种D . 36 种7•甲、乙、丙、丁四位同学一起去问老师询问成语竞赛的成绩.老师说:你们四 人中有2位优秀,2位良好,我现在给甲看乙、丙的成绩,给乙看丙的成绩,给 丁看甲的成绩.看后甲对大家说:我还是不知道我的成绩.根据以上信息,则() A .乙可以知道四人的成绩 B . 丁可以知道四人的成绩C .乙、丁可以知道对方的成绩D .乙、丁可以知道自己的成绩C . 2 i=08.执行右面的程序框图,如果输入的a = T,则输出的S =()A . 2B . 3C . 4D . 5面直线厶3与三C i 所成角的余弦值为()12. 已知 ABC 是边长为2的等边三角形,P 为平面ABC 内一点,则PA (PB PC) 的最X 2 y 29若双曲线 C: — 2 =1 ( a 0 , b 0)a b截得的弦长为2,则C 的离心率为()2 o的一条渐近线被圆 X - 2 y^4所C . 、22.310.已知直三棱柱二「沁-二己。
2017年高考真题——理数(海南卷)含答案

绝密★启用前2017年普通高等学校招生全国统一考试理科数学本试卷5页,23小题,满分150分。
考试用时120分钟。
注意事项:1.答卷前,考生务必将自己的姓名、考生号、考场号和座位号填写在答题卡上。
用2B铅笔将试卷类型(B)填涂在答题卡相应位置上.将条形码横贴在答题卡右上角“条形码粘贴处”。
2.作答选择题时,选出每小题答案后,用2B铅笔在答题卡上对应题目选项的答案信息点涂黑;如需要改动,用橡皮擦干净后,再选涂其他答案。
答案不能答在试卷上.3.非选择题必须用黑色字迹的钢笔或签字笔作答,答案必须写在答题卡各题目指定区域内相应位置上;如需改动,先划掉原来的答案,然后再写上新答案;不准使用铅笔和涂改液.不按以上要求作答无效。
4.考生必须保证答题卡的整洁。
考试结束后,将试卷和答题卡一并交回。
一、选择题:本题共12小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的.1.已知集合A={x|x〈1},B={x|31x },则A .{|0}AB x x =< B .A B =RC .{|1}AB x x =>D .AB =∅2.如图,正方形ABCD 内的图形来自中国古代的太极图。
正方形内切圆中的黑色部分和白色部分关于正方形的中心成中心对称.在正方形内随机取一点,则此点取自黑色部分的概率是A .14B .π8C .12D .π43.设有下面四个命题1p :若复数z 满足1z∈R ,则z ∈R ;2p :若复数z 满足2z ∈R ,则z ∈R ;3p :若复数12,z z 满足12z z ∈R ,则12z z =; 4p :若复数z ∈R ,则z ∈R .其中的真命题为A .13,p p B .14,p p C .23,p p D .24,p p4.记nS 为等差数列{}na 的前n 项和.若4524aa +=,648S =,则{}n a 的公差为A .1B .2C .4D .8 5.函数()f x 在(,)-∞+∞单调递减,且为奇函数.若(11)f =-,则满足21()1x f --≤≤的x 的取值范围是A .[2,2]-B .[1,1]-C .[0,4]D .[1,3] 6.621(1)(1)x x++展开式中2x 的系数为 A .15 B .20 C .30 D .357.某多面体的三视图如图所示,其中正视图和左视图都由正方形和等腰直角三角形组成,正方形的边长为2,俯视图为等腰直角三角形.该多面体的各个面中有若干个是梯形,这些梯形的面积之和为A .10B .12C .14D .168.右面程序框图是为了求出满足3n −2n >1000的最小偶数n ,那么在和两个空白框中,可以分别填入A.A〉1 000和n=n+1B.A〉1 000和n=n+2C.A≤1 000和n=n+1D.A≤1 000和n=n+2),则下面结论正确的是9.已知曲线C1:y=cos x,C2:y=sin (2x+2π3A.把C1上各点的横坐标伸长到原来的2倍,纵坐标不变,再把得到个单位长度,得到曲线C2的曲线向右平移π6B.把C1上各点的横坐标伸长到原来的2倍,纵坐标不变,再把得到个单位长度,得到曲线C2的曲线向左平移π12C.把C1上各点的横坐标缩短到原来的1倍,纵坐标不变,再把得2个单位长度,得到曲线C2到的曲线向右平移π6倍,纵坐标不变,再把得到D.把C1上各点的横坐标缩短到原来的12的曲线向左平移π个单位长度,得到曲线C21210.已知F为抛物线C:y2=4x的焦点,过F作两条互相垂直的直线l 1,l 2,直线l 1与C 交于A 、B 两点,直线l 2与C 交于D 、E 两点,则|AB |+|DE |的最小值为A .16B .14C .12D .10 11.设xyz 为正数,且235xy z ==,则A .2x 〈3y <5zB .5z <2x 〈3yC .3y <5z 〈2xD .3y 〈2x <5z12.几位大学生响应国家的创业号召,开发了一款应用软件.为激发大家学习数学的兴趣,他们推出了“解数学题获取软件激活码”的活动。
2017年海南省高考数学试卷与解析word(理科)(全国新课标Ⅱ)

2017年海南省高考数学试卷(理科)(全国新课标Ⅱ)一、选择题:本题共12小题,每小题5分,共60分。
在每小题给出的四个选项中,只有一项是符合题目要求的。
1.(5分)=()A.1+2i B.1﹣2i C.2+i D.2﹣i2.(5分)设集合A={1,2,4},B={x|x2﹣4x+m=0}.若A∩B={1},则B=()A.{1,﹣3}B.{1,0}C.{1,3}D.{1,5}3.(5分)我国古代数学名著《算法统宗》中有如下问题:“远望巍巍塔七层,红光点点倍加增,共灯三百八十一,请问尖头几盏灯?”意思是:一座7层塔共挂了381盏灯,且相邻两层中的下一层灯数是上一层灯数的2倍,则塔的顶层共有灯()A.1盏 B.3盏 C.5盏 D.9盏4.(5分)如图,网格纸上小正方形的边长为1,粗实线画出的是某几何体的三视图,该几何体由一平面将一圆柱截去一部分后所得,则该几何体的体积为()A.90πB.63πC.42πD.36π5.(5分)设x,y满足约束条件,则z=2x+y的最小值是()A.﹣15 B.﹣9 C.1 D.96.(5分)安排3名志愿者完成4项工作,每人至少完成1项,每项工作由1人完成,则不同的安排方式共有()A.12种B.18种C.24种D.36种7.(5分)甲、乙、丙、丁四位同学一起去问老师询问成语竞赛的成绩.老师说:你们四人中有2位优秀,2位良好,我现在给甲看乙、丙的成绩,给乙看丙的成绩,给丁看甲的成绩.看后甲对大家说:我还是不知道我的成绩.根据以上信息,则()A.乙可以知道四人的成绩B.丁可以知道四人的成绩C.乙、丁可以知道对方的成绩D.乙、丁可以知道自己的成绩8.(5分)执行如图的程序框图,如果输入的a=﹣1,则输出的S=()A.2 B.3 C.4 D.59.(5分)若双曲线C:﹣=1(a>0,b>0)的一条渐近线被圆(x﹣2)2+y2=4所截得的弦长为2,则C的离心率为()A.2 B.C.D.10.(5分)已知直三棱柱ABC﹣A1B1C1中,∠ABC=120°,AB=2,BC=CC1=1,则异面直线AB1与BC1所成角的余弦值为()A.B.C.D.11.(5分)若x=﹣2是函数f(x)=(x2+ax﹣1)e x﹣1的极值点,则f(x)的极小值为()A.﹣1 B.﹣2e﹣3C.5e﹣3 D.112.(5分)已知△ABC是边长为2的等边三角形,P为平面ABC内一点,则•(+)的最小值是()A.﹣2 B.﹣ C.﹣ D.﹣1二、填空题:本题共4小题,每小题5分,共20分。
2017年普通高等学校招生全国统一考试 理数(海南卷)word版(含答案) (7)

2017年普通高等学校招生全国统一考试理科数学一、选择题:本题共12小题,每小题5分,共60分。
在每小题给出的四个选项中,只有一项是符合题目要求的。
1.( ) A . B . C . D . 2.设集合,.若,则( ) A . B . C . D . 3.我国古代数学名著《算法统宗》中有如下问题:“远望巍巍塔七层,红光点点倍加增,共灯三百八十一,请问尖头几盏灯?”意思是:一座7层塔共挂了381盏灯,且相邻两层中的下一层灯数是上一层灯数的2倍,则塔的顶层共有灯( ) A .1盏 B .3盏 C .5盏 D .9盏4.如图,网格纸上小正方形的边长为1,粗实线画出的是某几何体的三视图,该几何体由一平面将一圆柱截去一部分所得,则该几何体的体积为( )A .B .C .D .5.设,满足约束条件,则的最小值是( )A .B .C .D .6.安排3名志愿者完成4项工作,每人至少完成1项,每项工作由1人完成,则不同的安排方式共有( )A .12种B .18种C .24种D .36种7.甲、乙、丙、丁四位同学一起去问老师询问成语竞赛的成绩.老师说:你们四人中有2位优秀,2位良好,我现在给甲看乙、丙的成绩,给乙看丙的成绩,给丁看甲的成绩.看后甲对大家说:我还是不知道我的成绩.根据以上信息,则( ) A .乙可以知道四人的成绩 B .丁可以知道四人的成绩C .乙、丁可以知道对方的成绩D .乙、丁可以知道自己的成绩 8.执行右面的程序框图,如果输入的,则输出的( )A .2B .3C .4D .531ii+=+12i +12i -2i +2i -{}1,2,4A ={}240x x x m B =-+={}1A B =B ={}1,3-{}1,0{}1,3{}1,590π63π42π36πx y 2330233030x y x y y +-≤⎧⎪-+≥⎨⎪+≥⎩2z x y =+15-9-191a =-S =9.若双曲线(,)的一条渐近线被圆所截得的弦长为2,则的离心率为( )A .2 BCD 10.已知直三棱柱中,,,,则异面直线与所成角的余弦值为( ) A .BC D 11.若是函数的极值点,则的极小值为( ) A. B. C. D.112.已知是边长为2的等边三角形,P 为平面ABC 内一点,则的最小值是( ) A. B. C. D. 二、填空题:本题共4小题,每小题5分,共20分。
2017年海南省高考数学试卷(理科)(全国新课标ⅱ)

2017年海南省高考数学试卷(理科)(全国新课标Ⅱ)一、选择题:本题共 小题,每小题 分,共 分。
在每小题给出的四个选项中,只有一项是符合题目要求的。
.( 分) (). . ﹣ . . ﹣.( 分)设集合 , , , ﹣ .若 ∩ ,则 (). ,﹣ . , . , . ,.( 分)我国古代数学名著《算法统宗》中有如下问题: 远望巍巍塔七层,红光点点倍加增,共灯三百八十一,请问尖头几盏灯? 意思是:一座 层塔共挂了 盏灯,且相邻两层中的下一层灯数是上一层灯数的 倍,则塔的顶层共有灯(). 盏 . 盏 . 盏 . 盏.( 分)如图,网格纸上小正方形的边长为 ,粗实线画出的是某几何体的三视图,该几何体由一平面将一圆柱截去一部分后所得,则该几何体的体积为(). . . ..( 分)设 , 满足约束条件,则 的最小值是().﹣ .﹣ . ..( 分)安排 名志愿者完成 项工作,每人至少完成 项,每项工作由 人完成,则不同的安排方式共有(). 种 . 种 . 种 . 种.( 分)甲、乙、丙、丁四位同学一起去问老师询问成语竞赛的成绩.老师说:你们四人中有 位优秀, 位良好,我现在给甲看乙、丙的成绩,给乙看丙的成绩,给丁看甲的成绩.看后甲对大家说:我还是不知道我的成绩.根据以上信息,则().乙可以知道四人的成绩 .丁可以知道四人的成绩.乙、丁可以知道对方的成绩 .乙、丁可以知道自己的成绩.( 分)执行如图的程序框图,如果输入的 ﹣ ,则输出的 (). . . ..( 分)若双曲线 :﹣ ( > , > )的一条渐近线被圆( ﹣ ) 所截得的弦长为 ,则 的离心率为( ). . . ..( 分)已知直三棱柱 ﹣ 中,∠ , , ,则异面直线 与 所成角的余弦值为( )A .B .C .D .11.(5分)若x=﹣2是函数f (x )=(x 2+ax ﹣1)e x ﹣1的极值点,则f (x )的极小值为( )A .﹣1B .﹣2e ﹣3C .5e ﹣3D .112.(5分)已知△ABC 是边长为2的等边三角形,P 为平面ABC 内一点,则•(+)的最小值是( )A.﹣2 B.﹣C.﹣D.﹣1二、填空题:本题共4小题,每小题5分,共20分。
2017年理科数学海南省高考真题含答案

绝密★启用前2017年普通高等学校招生全国统一考试理科数学注意事项:1.答题前,考生先将自己的姓名、准考证号填写清楚,将条形码准确粘贴在条形码区域内。
2.选择题必须使用2B 铅笔填涂;非选择题必须使用0.5毫米黑色字迹的签字笔书写,字体工整,笔迹清楚3.请按照题号顺序在答题卡各题目的答题区域内作答,超出答题区域书写的答案无效;在草稿纸、试卷上答题无效4.作图可先使用铅笔画出,确定后必须用黑色字迹的签字笔描黑。
5.保持卡面清洁,不要折叠、不要弄破、弄皱,不准使用涂改液、修正带、刮纸刀一、选择题:本题共12小题,每小题5分,共60分。
在每小题给出的四个选项中,只有一项是符合题目要求的。
1.31ii+=+( ) A .12i + B .12i - C .2i + D .2i -2.设集合{}1,2,4A =,{}240x x x m B =-+=.若{}1AB =,则B =( )A .{}1,3-B .{}1,0C .{}1,3D .{}1,53.我国古代数学名著《算法统宗》中有如下问题:“远望巍巍塔七层,红光点点倍加增,共灯三百八十一,请问尖头几盏灯?”意思是:一座7层塔共挂了381盏灯,且相邻两层中的下一层灯数是上一层灯数的2倍,则塔的顶层共有灯( )A .1盏B .3盏C .5盏D .9盏4.如图,网格纸上小正方形的边长为1,学 科&网粗实线画出的是某几何体的三视图,该几何体由一平面将一圆柱截去一部分所得,则该几何体的体积为( )A .90πB .63πC .42πD .36π5.设x ,y 满足约束条件2330233030x y x y y +-≤⎧⎪-+≥⎨⎪+≥⎩,则2z x y =+的最小值是( )A .15-B .9-C .1D .96.安排3名志愿者完成4项工作,每人至少完成1项,每项工作由1人完成,则不同的安排方式共有( ) A .12种 B .18种 C .24种 D .36种7.甲、乙、丙、丁四位同学一起去向老师询问成语竞赛的成绩.老师说:你们四人中有2位优秀,2位良好,我现在给甲看乙、丙的成绩,给乙看丙的成绩,学 科&网给丁看甲的成绩.看后甲对大家说:我还是不知道我的成绩.根据以上信息,则( )A .乙可以知道四人的成绩B .丁可以知道四人的成绩C .乙、丁可以知道对方的成绩D .乙、丁可以知道自己的成绩 8.执行右面的程序框图,如果输入的1a =-,则输出的S =( )A .2B .3C .4D .59.若双曲线C:22221x y a b-=(0a >,0b >)的一条渐近线被圆()2224x y -+=所截得的弦长为2,则C的离心率为( )A .2 BCD10.已知直三棱柱111C C AB -A B 中,C 120∠AB =,2AB =,1C CC 1B ==,则异面直线1AB 与1C B 所成角的余弦值为( ) A.2 B.5 C.5D.3 11.若2x =-是函数21`()(1)x f x x ax e-=+-的极值点,则()f x 的极小值为( )A.1-B.32e -- C.35e - D.112.已知ABC ∆是边长为2的等边三角形,P 为平面ABC 内一点,则()PA PB PC ⋅+的最小值是( ) A.2- B.32-C. 43- D.1- 二、填空题:本题共4小题,每小题5分,共20分。
2017海南高考数学试题(K12教育文档)

2017海南高考数学试题(word版可编辑修改)编辑整理:尊敬的读者朋友们:这里是精品文档编辑中心,本文档内容是由我和我的同事精心编辑整理后发布的,发布之前我们对文中内容进行仔细校对,但是难免会有疏漏的地方,但是任然希望(2017海南高考数学试题(word 版可编辑修改))的内容能够给您的工作和学习带来便利。
同时也真诚的希望收到您的建议和反馈,这将是我们进步的源泉,前进的动力。
本文可编辑可修改,如果觉得对您有帮助请收藏以便随时查阅,最后祝您生活愉快业绩进步,以下为2017海南高考数学试题(word版可编辑修改)的全部内容。
2017年普通高等学校招生全国统一考试(海南)理科数学一、选择题:本题共12小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的。
1.31ii+=+( ) A .12i + B .12i - C .2i + D .2i - 2。
设集合{}1,2,4A =,{}240x x x m B =-+=.若{}1A B =,则B =( ) A .{}1,3- B .{}1,0 C .{}1,3 D .{}1,53。
我国古代数学名著《算法统宗》中有如下问题:“远望巍巍塔七层,红光点点倍加增,共灯三百八十一,请问尖头几盏灯?"意思是:一座7层塔共挂了381盏灯,且相邻两层中的下一层灯数是上一层灯数的2倍,则塔的顶层共有灯( ) A .1盏 B .3盏 C .5盏 D .9盏4。
如图,网格纸上小正方形的边长为1,学科&网粗实线画出的是某几何体的三视图,该几何体由一平面将一圆柱截去一部分所得,则该几何体的体积为( ) A .90π B .63π C .42π D .36π5.设x ,y 满足约束条件2330233030x y x y y +-≤⎧⎪-+≥⎨⎪+≥⎩,则2z x y =+的最小值是( )A .15-B .9-C .1D .96。
安排3名志愿者完成4项工作,每人至少完成1项,每项工作由1人完成,则不同的安排方式共有( )A .12种B .18种C .24种D .36种7。
2017高考数学真题及答案

2017高考数学真题及答案2017年的高考数学试题被认为是一道很有代表性的试题,涵盖了广泛的知识点,考查了学生对数学知识的全面掌握和灵活运用能力。
下面将对2017年高考数学试题进行全面的解析,帮助同学们更好地理解和掌握这些题目的解题方法。
一、选择题部分1.已知函数f(x)=2x^2 - 4x + 2,则f(1)的值为多少?A. -1B. 0C. 1D. 2这是一道简单的函数取值题,只需要将x=1代入函数f(x)中即可得到f(1)的值,计算得f(1)=2*1^2 - 4*1 + 2 = 0,所以答案为B. 0。
2.若x^2 + 2ax + 3a^2 > 0对一切实数x成立,则a的取值范围是?A. a > 0B. a < 0C. a ≠ 0D. a = 0这是一道关于二次函数的判别式的题目,当二次函数的判别式小于0时,函数图像不与x轴相交,即函数的值始终大于0。
由判别式Δ = 4a^2 - 4*3*a^2 > 0可得a^2 > 3a^2,解得a < 0,所以答案为B. a < 0。
二、填空题部分1.在平面直角坐标系中,过点A(3,4),且与两坐标轴的夹角等于直角的直线方程是y = 4/3x,即为B的表达式。
这题考察了直线的方程,过点A(3,4)且与两坐标轴的夹角等于直角的直线斜率为tan45°=1,带入点A的横纵坐标可以得到直线方程为y = 1x,即为B的表达式。
2.方程2sin(x - π/6) = √3的根的个数为填写的数。
这是一道关于三角函数的方程题,将方程转换为sin(x - π/6) = √3/2,根据sin函数的性质可知0 < √3/2 < 1,所以方程有两个根,即为2。
三、解答题部分1.若a+b=3,a^2 + b^2 = 9,则a^3 + b^3的值为多少?这是一道代数题,需要用到(a+b)^3 = a^3 + b^3 + 3ab(a+b)的代数公式。
2017年全国统一高考真题数学试卷(理科)(新课标ⅲ)(含答案及解析)
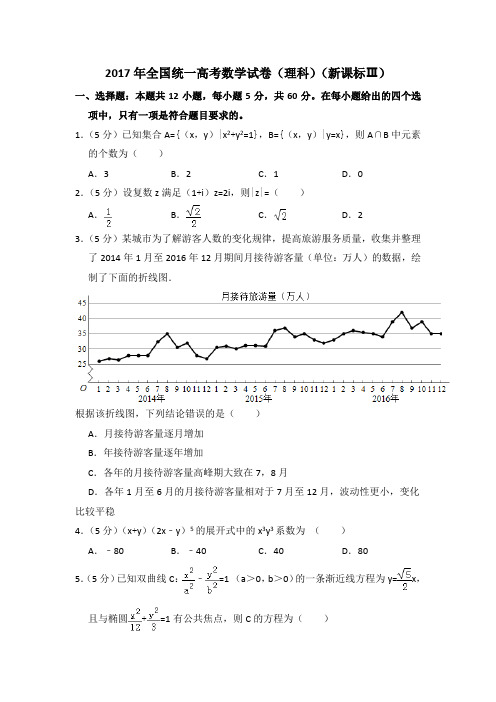
2017年全国统一高考数学试卷(理科)(新课标Ⅲ)一、选择题:本题共12小题,每小题5分,共60分。
在每小题给出的四个选项中,只有一项是符合题目要求的。
1.(5分)已知集合A={(x,y)|x2+y2=1},B={(x,y)|y=x},则A∩B中元素的个数为()A.3B.2C.1D.02.(5分)设复数z满足(1+i)z=2i,则|z|=()A.B.C.D.23.(5分)某城市为了解游客人数的变化规律,提高旅游服务质量,收集并整理了2014年1月至2016年12月期间月接待游客量(单位:万人)的数据,绘制了下面的折线图.根据该折线图,下列结论错误的是()A.月接待游客量逐月增加B.年接待游客量逐年增加C.各年的月接待游客量高峰期大致在7,8月D.各年1月至6月的月接待游客量相对于7月至12月,波动性更小,变化比较平稳4.(5分)(x+y)(2x﹣y)5的展开式中的x3y3系数为()A.﹣80B.﹣40C.40D.805.(5分)已知双曲线C:﹣=1 (a>0,b>0)的一条渐近线方程为y=x,且与椭圆+=1有公共焦点,则C的方程为()A.﹣=1B.﹣=1C.﹣=1D.﹣=1 6.(5分)设函数f(x)=cos(x+),则下列结论错误的是()A.f(x)的一个周期为﹣2πB.y=f(x)的图象关于直线x=对称C.f(x+π)的一个零点为x=D.f(x)在(,π)单调递减7.(5分)执行如图的程序框图,为使输出S的值小于91,则输入的正整数N 的最小值为()A.5B.4C.3D.28.(5分)已知圆柱的高为1,它的两个底面的圆周在直径为2的同一个球的球面上,则该圆柱的体积为()A.πB.C.D.9.(5分)等差数列{a n}的首项为1,公差不为0.若a2,a3,a6成等比数列,则{a n}前6项的和为()A.﹣24B.﹣3C.3D.810.(5分)已知椭圆C:=1(a>b>0)的左、右顶点分别为A1,A2,且以线段A1A2为直径的圆与直线bx﹣ay+2ab=0相切,则C的离心率为()A.B.C.D.11.(5分)已知函数f(x)=x2﹣2x+a(e x﹣1+e﹣x+1)有唯一零点,则a=()A.﹣B.C.D.112.(5分)在矩形ABCD中,AB=1,AD=2,动点P在以点C为圆心且与BD相切的圆上.若=λ+μ,则λ+μ的最大值为()A.3B.2C.D.2二、填空题:本题共4小题,每小题5分,共20分。
2017海南省高考试题

2017海南省高考试题海南省高考是每年年末海南省举行的选拔高中毕业生进入大学的考试,非常重要。
下面将为大家介绍2017年海南省高考试题的内容和难度。
一、数学选择题(共40道题,每题2分,共80分)本次高考数学选择题难度适中,涵盖了多个知识点。
题目以应用题为主,要求考生掌握数学知识的实际应用能力。
例如:1.设ABCD为平面上的一个四边形,满足AB=BC=CD=DA,若∠ADC=105°,则∠BAC的度数为:A.30°B.45°C.60°D.75°2.新东方出版社订购了2100本初三数学教材,并根据参考价格计算了金额。
根据折扣规则:第1到第1000本按每本8折,第1001到第2000本按9折,第2001本及以后按九五折。
则出版社订购数学教材的总金额是:A.193200元B.191100元C.195000元D.192090元二、语文阅读题(共20道题,每题3分,共60分)语文阅读题主要考查考生对文言文和现代文的理解能力以及对文章整体意义的把握。
例如:阅读下面一则新年贺词,完成1~3题。
我们是充满憧憬和希望的一代年轻人。
我们热爱生活,热爱春天,热爱和平。
我们正是祖国的花朵,是祖国的未来和希望。
1.全文共由多少部分组成?A.2部分B.3部分C.4部分D.5部分2.充满憧憬和希望的是谁?A.祖国B.年轻人C.春天D.和平3.文中用了哪个词来形容我们?A.年轻B.充满憧憬和希望C.热爱D.祖国三、英语阅读理解题(共20道题,每题3分,共60分)英语阅读理解题要求考生理解短文内容,包括主旨、细节、推测等。
例如:阅读下列短文,回答题目。
Magic Show in TownCome to the magical world of illusion! Enjoy a great magic show performed by the famous magician, David Copperfield. With his amazing tricks, you will feel like you've entered a different reality.Date: June 15thTime: 7:30 PMLocation: City TheaterTickets: Available at the box office or onlinePrice: ¥100 per ticketDon't miss this incredible event! Bring your friends and family for a night full of excitement and wonder.4. When is the magic show taking place?A. June 5thB. June 15thC. May 15thD. May 5th5. How can you purchase tickets?A. Only at the box officeB. Only onlineC. Either at the box office or onlineD. By calling a toll-free number以上仅为部分题目的内容示例,由于篇幅限制无法一一列举完整试题。
2017数学高考试题答案

2017数学高考试题答案一、选择题1. 根据题目所给的函数f(x) = 2x^3 - 3x^2 - 12x + 5,求f(2)的值。
解析:将x=2代入函数f(x)中,得到f(2) = 2*(2)^3 - 3*(2)^2 - 12*2 + 5 = 16 - 12 - 24 + 5 = -15。
2. 题目描述了一个等差数列的前五项和为50,首项为a1,公差为d。
求该等差数列的前三项和。
解析:设等差数列的前n项和为Sn,根据等差数列前n项和的公式Sn = n/2 * (2*a1 + (n-1)*d),代入n=5, Sn=50得到:50 = 5/2 *(2*a1 + 4*d)。
化简得:a1 + 2*d = 20。
现在我们需要求前三项和,即S3 = 3/2 * (2*a1 + 2*d)。
由于我们已经知道a1 + 2*d = 20,所以S3 = 3/2 * 20 = 30。
3. 题目要求解不等式3x - 2 > 7x - 6,并表示解集。
解析:将不等式3x - 2 > 7x - 6化简,首先将7x移到左边得到4x < 4,然后除以4得到x < 1。
所以解集为x < 1。
4. 题目描述了一个圆的半径为5,圆心位于坐标轴上,求圆上一点到圆心的最大距离。
解析:圆的方程为(x - h)^2 + (y - k)^2 = r^2,其中(h, k)是圆心坐标,r是半径。
由于圆心位于坐标轴上,所以h和k中有一个为0。
不妨设h=0,k不为0(因为如果k=0,则圆心就在x轴上)。
圆上一点到圆心的最大距离就是圆的直径,所以最大距离为2r = 2*5 = 10。
5. 题目要求解方程2x^2 - 5x + 3 = 0的根。
解析:这是一个二次方程,我们可以使用求根公式x = [-b ±sqrt(b^2 - 4ac)] / (2a)来解。
将a=2, b=-5, c=3代入公式,得到x = [5 ± sqrt((-5)^2 - 4*2*3)] / (2*2) = [5 ± sqrt(25 - 24)] / 4 = [5 ± sqrt(1)] / 4。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
2017年普通高等学校招生全国统一考试(海南)
理科数学
一、选择题:本题共12小题,每小题5分,共60分。
在每小题给出的四个选项中,只有一项是符合题目要求的。
1.31i i
+=+( ) A .12i + B .12i - C .2i + D .2i - 2.设集合{}1,2,4A =,{}
240x x x m B =-+=.若{}1A B =,则B =( ) A .{}1,3- B .{}1,0 C .{}1,3 D .{}1,5 3.我国古代数学名著《算法统宗》中有如下问题:“远望巍巍塔七层,红光点点倍加增,共灯三百八十一,请问尖头几盏灯?”意思是:一座7层塔共挂了381盏灯,且相邻两层中的下一层灯数是上一层灯数的2倍,则塔的顶层共有灯( ) A .1盏 B .3盏 C .5盏 D .9盏 4.如图,网格纸上小正方形的边长为1,学科&网粗实线画出的是某几何体的三视图,该几何体由一平面将一圆柱截去一部分所得,则该几何体的体积为( ) A .90π B .63π C .42π D .36π
5.设x ,y 满足约束条件2330233030x y x y y +-≤⎧⎪
-+≥⎨⎪+≥⎩,则2z x y =+的最小值是( )
A .15-
B .9-
C .1
D .9
6.安排3名志愿者完成4项工作,每人至少完成1项,每项工作由1人完成,则不同的安排方式共有( )
A .12种
B .18种
C .24种
D .36种 7.甲、乙、丙、丁四位同学一起去问老师询问成语竞赛的成绩.老师说:你们四人中有2位优秀,2位良好,我现在给甲看乙、丙的成绩,给乙看丙的成绩,给丁看甲的成绩.看后甲对大家说:我还是不知道我的成绩.根据以上信息,则( ) A .乙可以知道四人的成绩 B .丁可以知道四人的成绩 C .乙、丁可以知道对方的成绩 D .乙、丁可以知道自己的成绩 8.执行右面的程序框图,如果输入的1a =-,则输出的S =( )
A .2
B .3
C .4
D .5
9.若双曲线C:22221x y a b
-=(0a >,0b >)的一条渐近线被圆()2
224x y -+=所
截得的弦长为2,则C 的离心率为( )
A .2 B
C
D
.
3
10.已知直三棱柱111C C AB -A B 中,C 120∠AB =,2AB =,1C CC 1B ==,则异面直线1AB 与1C B 所成角的余弦值为( ) A
.
2 B
.5 C
.5
D
.3 11.若2x =-是函数21`()(1)x f x x ax e -=+-的极值点,则()f x 的极小值为( ) A.1- B.32e -- C.35e - D.1 12.已知ABC ∆是边长为2的等边三角形,P 为平面ABC 内一点,则()PA PB PC ⋅+的最小值是( )
A.2-
B.32-
C. 4
3
- D.1-
二、填空题:本题共4小题,每小题5分,共20分。
13.一批产品的二等品率为0.02,从这批产品中每次随机取一件,有放回地抽取100次,X 表示抽到的二等品件数,则D X = .
14.函数(
)23sin 4f x x x =-(0,2x π⎡⎤
∈⎢⎥⎣⎦
)的最大值是 .
15.等差数列{}n a 的前n 项和为n S ,33a =,410S =,则11
n
k k
S ==∑
. 16.已知F 是抛物线C:28y x =的焦点,M 是C 上一点,F M 的延长线交y 轴于点
N .若M 为F N 的中点,则F N = .
三、解答题:共70分。
解答应写出文字说明、解答过程或演算步骤。
第17~21
题为必做题,每个试题考生都必须作答。
第22、23题为选考题,考生根据要求作答。
(一)必考题:共60分。
17.(12分)
ABC ∆的内角,,A B C 的对边分别为,,a b c ,已知2sin()8sin 2
B
A C +=.
(1)求cos B
(2)若6a c += , ABC ∆面积为2,求.b
18.(12分)
淡水养殖场进行某水产品的新、旧网箱养殖方法的产量对比,收获时各随机抽取
(
养殖法的箱产量不低于50kg,估计A 的概率;
K 2=n(ad−bc)2
(
a+b )(c+d )(a+c )(b+d)
19.(12分)
如图,四棱锥P-ABCD 中,侧面PAD 为等比三角形且垂直于底面三角形BCD ,
01
,90,2
AB BC AD BAD ABC ==
∠=∠= E (1)证明:直线//CE 平面PAB (2)点M 在棱PC 上,且直线BM 与底面
ABCD 所成锐角为0
45 ,求二面角M-AB-D
20. (12分)
设O 为坐标原点,动点M 在椭圆C :2
212
x y +=上,过M 做x 轴的垂线,垂足为N ,点P 满足2NP NM =
.
(1) 求点P 的轨迹方程;
(2) 设点Q 在直线x=-3上,且1OP PQ ⋅=.证明:过点P 且垂直于OQ 的直线l 过C 的左焦点F. 21.(12分)
已知函数3
()ln ,f x ax ax x x =--且()0f x ≥. (1)求a ;
(2)证明:()f x 存在唯一的极大值点0x ,且2
30()2e
f x --<<.
(二)选考题:共10分。
请考生在第22、23题中任选一题作答。
如果多做,按所做的第一题计分。
22.[选修4-4:坐标系与参数方程](10分)
在直角坐标系xoy 中,以坐标原点为极点,x 轴的正半轴为极轴建立极坐标系,曲线1C 的极坐标方程为cos 4ρθ=.
(1)M 为曲线1C 上的动点,点P 在线段OM 上,且满足16OM OP ⋅=,求点P 的轨迹2C 的直角坐标方程;
(2)设点A 的极坐标为(2,
)3
π
,点B 在曲线2C 上,求OAB ∆面积的最大值.
23.[选修4-5:不等式选讲](10分) 已知3
3
0,0,2a b a b >>+=,证明: (1)5
5()()4a b a b ++≥; (2)2a b +≤.。
