结构化学习题解析
结构化学习题、详解、答案

第一章 量子力学基础题 解1.1. 给出黑体辐射频率分布函数),(T R ν的单位。
解: 黑体辐射的频率分布函数),(T R ν表示黑体辐射的频率分布,ννd ),(T R 表示在温度T 单位时间内由单位黑体表面积上所发射的频率在νννd ~+间的辐射能量。
121s m J s )(---⋅⋅=νR2m J )(-⋅=νRs m w s m sJm J 2-22⋅⋅=⋅⋅=⋅-- 式中w 是功率.1.2. 分别计算红光λ=600 nm 和X 射线λ=100 pm 的1个光子的能量、动量和质量。
解:λνc=,νh E =,λhp =,2ch m ν=(1) 波长1λ=600 nm 的红光,813419119310m s 6.62610J s 3.31310J 60010mE h ν----⨯⋅==⨯⋅⨯=⨯⨯ 12793411s m kg 10104.1m10600s J 10626.6----⋅⋅⨯=⨯⋅⨯==λhp 19361128123.31310J 3.68110kg (310m s )h m c ν---⨯===⨯⨯⋅ (2)X 射线2λ=100 pm8134152212310m s 6.62610J s 1.98810J 10010mE h ν----⨯⋅==⨯⋅⨯=⨯⨯ 124123422s m kg 10626.6m10100s J 10626.6----⋅⋅⨯=⨯⋅⨯==λhp 15322228121.98810J2.20910kg (310m s )h m c ν---⨯===⨯⨯⋅ 1.3. 计算波长λ=400nm 的光照射到金属铯上所产生的光电子的初速度。
已知铯的临阈波长为600nm解:根据W h T -=ν其中,201, 2e Tm W h υν== 2012e m h h υνν=-51 6.03010(m s )υ-====⨯⋅1.4. 氢原子光谱中巴尔麦系中波长最长的一条谱线的波数、波长和频率各是多少?波长最短的一条呢?解:氢原子光谱中巴尔麦系谱线的波数可表达为4, 3, )121(~~22=-=n n R ν其中5-11.09710cm ,R=⨯ 称为Rydberg 常数。
结构化学习题解答解析

习题选解第一章1.1 E = 1.988⨯10-18Jp = 6.626⨯10-27kg ⋅m ⋅s -1 1.2 h = 6.442⨯10-34J ⋅s w = 5.869⨯10-19J ν0 = 9.11⨯1014s -1 1.4 光子能量21.24eV ;电子动能 5.481eV 1.5 70.8pm1.9 (1)1/4;(2)2.63⨯10-5;(3)2/l ;(4)01.10 3个,E 1 = h 2/(8ml 2);E 2 = 4h 2/(8ml 2);E 3 = 9h 2/(8ml 2) 1.13 301.5 nm 1.16 0.14 nm 1.17 86.2nm1.20 (1)无,l /2;(2)无,0;(3)有,2224n h l ;(4)有,2228n h ml 1.21 (1)是,能量无确定值,22513h E mL =;(2) 是,能量无确定值,2297104h E mL = 1.22 (1) 2222k E mr =,i k φψ, k =0, ±1, ±2, …;(2) 136pm 1.23 (1) h 2/(8ml 2);(2) l /2,2/l ;(3)01.24 n x =3, n y =1, n z =2;n x =3, n y =2, n z =1;n x =2, n y =1, n z =3;n x =2, n y =3, n z =1;n x =1, n y =2, n z =3;n x =1, n y =3, n z =2 1.25 (1)不是,x →∞时,ψ→∞不满足平方可积;(2)不是,x →-∞时,ψ→∞不满足平方可积;(3)不是,在x =0处一阶微商不连续;(4)不是,ψ不满足平方可积;(5) 不是,ψ不满足平方可积,在x =0处一阶微商不连续;(6) 是 1.27 11πsin 42π2n n -;n =3;1/4;说明当n →∞时,一维势箱中运动的粒子,其概率分布与经典力学相同 1.28 (1)1ψ=;(2) ψ=(3) i m φψ=;(4) 0/r a ψ-=1.29 (1)是;(2) 是;(3) 不是;(4) 是;(5) 不是1.31 (1) 是d/d x 和d 2/d x 2的本征函数,本征值分别为a 、a 2(2) 不是d/d x 和d 2/d x 2的本征函数(3) 不是d/d x 的本征函数,是d 2/d x 2的本征函数,本征值为-a 2 (4) 不是d/d x 的本征函数,是d 2/d x 2的本征函数,本征值为-a 2 (5) 不是d/d x 和d 2/d x 2的本征函数 (6) 不是d/d x 和d 2/d x 2的本征函数1.34 无确定值,2258h E ml =1.351.36 (a /2, a /4, a /2),(a /2, 3a /4, a /2);y = a /2 1.37 (1) 是;(2) 是;(3) 不是;(1) 不是 1.38 |p |=nh /2l第二章 2.1 3a 0/2 2.5 22.6 (1) ()22212349R C C C ⎡⎤-++⎣⎦;(2)21C ;;(4)1;(5) 2223()C C - ;(6)0 2.14 (1) -3.4eV ;(2) ;(3)0;(4)r /a 0(5)(6)2.15 (1);(2) n =2, l =1, m =0;(3) E =-3.4eV ,|M | =0,M z = 02.16 (1) 1111(1)(1)(1)(1)(2)(2)(1)(2)s s s s αψβΦαψβ=;(2) E = -78.6eV2.17 (1) 112112112(1)(1)(1)(1)(3)(3)(2)(2)(2)(2)(3)(3)(3)(3)(3)(3)(3)(3)s s s s s s s s s αψβψαΦαψβψααψβψα=或112112112(1)(1)(1)(1)(3)(3)(2)(2)(2)(2)(3)(3)(3)(3)(3)(3)(3)(3)s s s s s s s s sαψβψβΦαψβψβαψβψβ=; (2) E = -204.03eV2.18 (1) 3P 0;(2) 3P 2;(3) 4S 3/2;(4) 6S 5/2;(5) 3F 2;(6) 3F 4;(7) 4F 3/2;(8) 4F 9/2;(9) 5D 4 2.19 (1) 1S(1S 0);(2) 2P(2P 3/2 2P 1/2);(3) 1S(1S 0), 3P(3P 2, 3P 1, 3P 0), 1D(1D 2);(4) 1S(1S 0), 3P(3P 2, 3P 1, 3P 0), 1D(1D 2), 3F(3F 4, 3F 3, 3F 2), 1G(1G 4); (5) 1P(1P 1),3P(3P 2, 3P 1, 3P 0);(6)1S(1S 0), 3S(3S 1), 1P(1P 1),3P(3P 2, 3P 1, 3P 0), 1D(1D 2), 3D(3D 3, 3D 2, 3D 1) 2.21 第一种2.22 未成对电子数:2l +1 基支项:2212l l S ++2.24 (1) 4S 、2D 、2P(2) 4D 、4P 、4S 、2D(2)、2P(2)、2S(2) (3) 4P 、2D 、2P 、2S(4) 4P 、4D 、4F 、2S 、2P(2)、2D(3)、2F(2)、2G (5)1S 3P 1D 1S 1S 3P 1D 3P 3P 5D, 5P,5S, 3D, 3P, 3S, 1D, 1P, 1S3F, 3D,3P1D 1D 3F, 3D, 3P 1G,1F, 1D, 1P,1S3 F 3F 5G, 5F , 5D, 3G, 3F , 3D, 1G, 1F , 1D 3H, 3G, 3F, 3D,3P1G 1G 3H, 3G, 3F 1I, 1H, 1G,1F,1D2.25 I 1= 11.46eV2.26 (1)5;(2)15;(3)4;(4)45;(5)675;(6)1350 ;;(4) 2, 1, 0, -1, -2;(5)5 2.29 (1)A, C ;(2)A, B ;(3)B, C 2.31 2个节面2.32 (1))122z s s p ψψψψ=++;(2) 无,<E>=-6.8eV ,1/3; (3) 3 ,2/3; (4) 有,0,0第三章3.7 (1)OF :(1σ)2(2σ)2(3σ)2(4σ)2(5σ)2(1π)4(2π)3,一个σ键,一个三电子π键,键级3/2,顺磁性(2)NO :(1σ)2(2σ)2(3σ)2(4σ)2(1π)4 (5σ)2(2π)1,1σ,1π,一个三电子π键,键级5/2,顺磁性 (3)CO :(1σ)2(2σ)2(3σ)2(4σ)2(1π)4 (5σ)2,一个σ键,二个π键,键级3,反磁性(4)CN :(1σ)2(2σ)2(3σ)2(4σ)2(1π)4 (5σ)1,一个单电子σ键,二个π键,键级5/2,顺磁性 (5)HF :(1σ)2(2σ)2(3σ)2(1π)4,一个σ键,键级1,反磁性3.8 (1) O 2:2*22*2222*1*1112222222s s s s pz px py px py σσσσσππππ;O 2+:2*22*2222*111222222s s s s pz px py px σσσσσπππ;O 2-:2*22*2222*2*1112222222s s s s pz px py px py σσσσσππππ;键级:O 2+ > O 2 > O 2-;键长:O 2+ < O 2 < O 2- (2) OF :(1σ)2(2σ)2(3σ)2(4σ)2(5σ)2(1π)4(2π)3;OF +:(1σ)2(2σ)2(3σ)2(4σ)2(5σ)2(1π)4(2π)2;OF -:(1σ)2(2σ)2(3σ)2(4σ)2(5σ)2(1π)4(2π)4;键级:OF + > OF > OF -;键长:OF + < OF < OF -3.10 (1)得电子变为AB -型负离子后比原来中性分子键能大的分子:C 2,CN(2)失电子变为AB +型正离子后比原来中性分子键能大的分子:O 2,F 2,NO 3.12 p x -d xy (否);p y -d yz (π);d x 2-y 2-d x 2-y 2(δ);d z 2-d z 2(σ);p x -p x (π) 3.13原子轨道3s 3p z 3p x 3p y 3d z 23d zx 3d yz 3d xy 3d x 2-y 2沿z 轴对称类型(节面数) 0 0 1 10 1 1 2 2 有14对轨道对符合对称性匹配:原子轨道对 3s -3s 3s -3p z 3s -3d z 2 3p z -3p z 3p z -3d z 23d z 2-3d z 2 3p x -3p x 分子轨道类型 σ σ σ σσσπ原子轨道对 3p x -3d xz 3p y -3p y 3p y -3d yz 3d xz -3d xz 3d yz -3d yz 3d xy -3d xy 3d x 2-y 2-3d x 2-y 2分子轨道类型 π π π ππδδ3.14 (1) E I <E 1<E 2<E II ;(2) 222112/()a a a +;(3) 222112/()b b b +;(4) ψI 含φ1(A)原子轨道的成份多一些,ψII 含φ2(B)原子轨道的成份多一些;(5) 这个化学键的电子云会偏向A 原子3.15 1122x s p ψψ=+;21263x y s p p ψψψψ=-+;312662x y z s p p p ψψψψψ=--+;412662x y z s p p p ψψψψψ=---3.17 (1)0.73;(2)0.71;(3)0.683.23 NF :1σ22σ23σ24σ25σ21π42π2,键级:2,顺磁性;NF +:1σ22σ23σ24σ25σ21π42π1,键级:2.5,顺磁性;NF -:1σ22σ23σ24σ25σ21π42π3,键级:1.5,顺磁性第四章4.1 (1)π34,(2)π78,(3) π78,(4) π88,(5) π910,(6) π78,(7) π34,(8) π34,(9)无,(10) π1414,(11) π44,(12) π34(2个),(13) π34(2个),(14) π34(2个),(15)无,(16) π34(2个),(17) π34,(18) π46,(19) π46,(20)π46,(21) π344.6 (1) 1E α=,E 2 = α,3E α=;(2) ()112312φψψ=++)213φψψ-()312312φψψ=-+; (3) -0.828β;(4) C C C0.51.00.7074.8 (1) E 1=α+2β,E 2=E 3=α-β(2) 环丙烯正离子、自由基和负离子的离域能分别为-2β、-β和0(3) )1123φψψψ++,)21232φψψψ=--,)323φψψ=-(4) 4.11 (1) 2个π34,(2) E 1=α+2β, E 2=α+β,E 3=α-β(3) α+2βα+βα-β(4) 离域能为-1.528β 4.14 6α+5.656β第六章6.2 存在对称中心i : C 2h C 4h C 6h D 2h D 4h D 6h D 3d D 5d S 2 S 6存在垂直于主轴的镜面σh :C 2h C 3h C 4h C 5h C 6h D 2h D 3h D 4h D 5h D 6h S 3 S 5 6.3(1) CO —C ∞v ,CO 2—D ∞h ,NO 2+—D ∞h ,乙炔—D ∞h ,H 2S —C 2v ,NH 3—C 3v ,CH 3Cl —C 3v ,HOCl —C s ,H 2O 2—C 2,NO 2—C 2v ,CH 4—T d ,SF 6—O h(2) 重叠式乙烷—D 3h ,交叉式乙烷—D 3d ,椅式环己烷—D 3d ,船式环己烷—C 2v ,丙二烯—D 2d ,CHCl 2Br —C s ,CH 2=C=CCl 2—C 2v ,CHCl=C=CHCl —C 2,CH 3-CCl 3(交叉式)—C 3v , CH 3-CCl 3(重叠式)—C 3v(3) 顺式(重叠式)二茂铁—D 5h ,反式(交叉式)二茂铁—D 5d ,[Co(NH 2–CH 2–CH 2–NH 2)3]3+—D 3,1,3,5,7四甲基–环辛四烯—S 4(4) [PtCl 4]2-—D 4h ,HCHO —C 2v ,顺式二氯乙烯—C 2v ,反式二氯乙烯—C 2h ,CH 2=CCl 2—C 2v ,苯分子—D 6h ,萘分子—D 2h ,对二氯苯—D 2h ,邻二氯苯—C 2v ,间二氯苯—C 2v , BCl 3—D 3h ,[CO 3]2-—D 3h6.4B N B N B N H H H H H HD 3h ,B B BNH 2NH 2H 2ND 3hFH HFHHC 2h , H FF HHH C 2h, HHHHFFC2h ,CC FC 2h ,6.5 (1)D 2h (2)D 2d (3)D 26.6 (1) 去掉2个球有以下3种情况:2vvd (2) 去掉3个球有以下3种情况:s s 3v6.7⑴正三角形D 3h ⑵正方形 D 4h ⑶正六边形D 6h ⑷长方形 D 2h ⑸中国国旗上的一个五角星 D 5h ⑹正三棱锥 C 3v ⑺正三棱柱D 3h ⑻正四棱锥C 4v ⑼正四棱柱 D 4h ⑽双正四棱锥D 4h ⑾正六棱柱D 6h ⑿正四面体T d ⒀正八面体 O h⒁正六面体(即立方体)O h⒂圆锥体C ∞v ⒃园柱体D ∞h6.8 XX XXXXXXXX XXX XXX X XXXXXXX XXXXXX XXX XX Y XXY XYXYYXX YC s C 2D 2dC 2vC i C 1C 2hC s C sC 2vD 2hC 2hC 2hC 4v C 2C 2v第七章 7.1点阵点数目1 1 1 1每个点阵点代表的内容 白1、黑2白1、黑1白1、黑1白3 黑球和白球的数目 白1、黑2白1、黑1白1、黑1白37.7(1)0,0,0; 1/2,1/2,0; 1/2,0,1/2; 0,1/2,1/2; 1/4,1/4,1/4; 1/4,3/4,3/4; 3/4,1/4,3/4; 3/4,3/4,1/4;(2)154.5pm 7.8 (右图)7.9 d 110=233.8pm ;d 220=143.2pm7.10 201pm7.11 (100)与(010):90°;(100)与(001):90°;(100)与(210):26.56°7.14 (1)C 2v ,正交;(2) C 2h ,单斜;(3)D 2h ,正交;(4) D 4h ,四方; (5)D 6h ,六方;(6)C 3v ,三方;(7)C 3i ,三方(8)C 3h ,六方;(9)D 3h ,六方; (10)S 4,四方;(11)C s ,单斜;(12) O h ,立方;(13)T d ,立方; (14) D 2d ,四方;(15)O ,立方;(16) C 6h ,六方;(17) D 3,三方; (18) T ,立方;(19) D 3d 三方;(20)T h ,立方 7.157.17(100)(010)(120)(230)第八章8.1 28.0748.2 21.453gcm-3r=138.7pm8.3 a=b=328pm,c=536pm;3.187gcm-38.4 r =185.8pm,0.967gcm-3,d=303pm8.8 a=352.4pm,8.908gcm-3,r=124.6pm8.14 r=146pm8.17 CaS:正负离子配位数皆为6,正八面体,A1,晶体结构型式为cF;CsBr:正负离子配位数皆为8,立方体,立方简单,晶体结构型式为cP8.18 (2) 154pm;(3) 1.53gcm-3;(4) 274pm8.20 cF;分数坐标:0,0,0; 1/2,1/2,0; 1/2,0,1/2; 0,1/2,1/2;80.99%8.22 (1)Ti4+:000;Ba2+:1/2,1/2,1/2;O2-:0,0,1/2; 0,1/2,0; 1/2,0,0(2) BaTiO3 (3)cP(4)与Ba2+离子配位的O2-负离子数为12;与Ti4+离子配位的O2-负离子数为6(6) A1第九章9.2 cF,a=359pm9.5 (1) a=415.8pm;(2) x = 0.92,(NiO)76(Ni2O3)8;(3) A1,正八面体空隙,92%;(4) 294pm9.8 (1) 21.45gcm-3,r = 186.7pm;(2)有两个,分别来自200和4009.9 (1)19.356gcm-3;(2) 共有7对粉末线,衍射指标依次为(110), (200), (211), (220), (310), (222) (321) 9.10 (1) r = 128pm;(2) 仅有(200)和(400)的衍射峰;(3) (200)与(400)衍射峰对应的2L值分别为50.4mm和116.8mm9.11 (1) a=565.9pm;(2)cF;(3)n = 49.12 (1) r=137.0pm;(2)2级9.16 106.6pm9.17 141.9pm9.18 k1/k2=1.7149.19 11MHz9.26 λ1,λ3,λ5由HCl产生,HCl核间距129pm;λ2,λ4,λ6由HBr产生,HBr核间距143pm9.28 131pm;477.7Nm−19.30 64.32⨯1012s−1;1.5547⨯10−14s;1859.7 Nm−1;12.83kJ;3.859cm−1附录III 模型实习实习一、分子的对称性目的:1. 掌握寻找分子中独立对称元素、判断分子点群的方法;2. 根据分子所属点群判断分子有无偶极矩3. 根据分子所属点群判断分子有无旋光性。
结构化学习题解答6

(c)
Cl Pt O NH2 H O H NH2
Cl NH2
O
H H
Cl Pt Cl
O
NH2
该化合物无σ—π配键。
[6.15] 硅胶干燥剂中常加入 CoCl (蓝色),吸水 2 后变为粉红色,试用配位场理论解释其原因。
[ 解 ] : Co2+ 为 d7 构型。在无水 CoCl2 中, Co2+ 受配体 Cl-的作用d轨道能级发生分裂,7个d电子按电子排 布三原则填充在分裂后的轨道上。当电子发生 d—d 跃迁时,吸收波长为 650~750nm 的红光,因而显示 蓝色。但CoCl2吸水后,变为[Co(H2O)6]Cl2,即由相 对较强的配体H2O取代了相对较弱的配体Cl-,引起 d轨道分裂能变大,使电子发生d—d跃迁时吸收的能 量增大,即吸收光的波长缩短(蓝移)。 [Co(H2O)6]Cl2 吸收波长为 490~500nm 的蓝光,因而 呈粉红色。
a1g e2g
处在高能级轨道a1g*上的电子易失去,所以Co(C5H5) 2易被氧 化成为Co(C5H5) 2+ 。
[6.12] 用Jahn-Teller效应说明下列配位离子中哪些会发生变形。 (a) N i(H2O)62+ (b) CuCl42(c)CuCl64(d)Ti(H2O)63+ (e)Cr(H2O)62+ (f) MnCl64[解]: Jahn-Teller效应的大意是:在对称的非线型配合物中, 若出现简并态,则该配合物是不稳定的。此时它必然会发 生变形,使其中一个轨道能级降低,消除简并,获得额外 的稳定化能。对过渡金属配合物来说,产生Jahn-Teller效 应的根源是中心原子d电子分布的不对称性。 对于六配位的配合物,d电子的构型为d0 , d5(HS)和d10 时,其电子分布是球对称的,最稳定的几何构型是正八面 体。d电子的构型为d3 ,d6(LS) 和d8时,其分布是八面体 对称,配合物也呈正八面体构型。 若d电子分布不对称,则配合物将发生畸变,产生长键 和短键之别。若d电子分布的不对称性涉及到能级较高eg* 的轨道,则畸变程度大;若d电子分布的不对称性只涉及 到能级较低的t2g轨道,则畸变程度较小。具体情况是:
结构化学习题集剖析

结构化学习题集习题1:1.1 某同步加速器,可把质子加速至具有100×109eV的动能,试问此时质子速度多大?1.2 计算波长为600nm(红光),550nm(黄光),400nm(蓝光)和200nm(紫光)光子的能量。
1.3 在黑体辐射中,对一个电热容器加热到不同温度,从一个针孔辐射出不同波长的极大值,试从其推导Planck常数的数值:T/℃1000 1500 2000 2500 3000 3500l max/nm 2181 1600 1240 1035 878 7631.4 计算下列粒子的德布洛意波长(1) 动能为100eV的电子;(2) 动能为10eV的中子;(3) 速度为1000m/s的氢原子.1.5 质量0.004kg子弹以500ms-1速度运动,原子中的电子以1000ms-1速度运动,试估计它们位置的不确定度, 证明子弹有确定的运动轨道, 可用经典力学处理, 而电子运动需量子力学处理。
1.6 用测不准原理说明普通光学光栅(间隙约10-6m)观察不到10000V电压加速的电子衍射。
1.7 小球的质量为2mg,重心位置可准确到2μm,在确定小球运动速度时,讨论测不准关系有否实际意义?1.8 判断下列算符是否是线性\厄米算符:(1)(2)(3)x1+x2(4)1.9 下列函数是否是的本征函数?若是,求其本征值:(1)exp(ikx)(2)coskx (3)k (4)kx1.10 氢原子1s态本征函数为(a0为玻尔半径),试求1s态归一化波函数。
1.11 已知一维谐振子的本征函数为其中a n和α都是常数,证明n=0与n=1时两个本征函数正交。
1.12 若是算符的本征函数(B为常数), 试求α值,并求其本征值。
1.13 计算Poisson 方括,1.14 证明Poisson 方括的下列性质:(1)(2)1.15 角动量算符定义为:, ,证明: (1) (2)1.16 在什么条件下?1.17 设体系处于状态中,角动量和M Z有无定值。
结构化学练习题集与答案解析

结构化学练习题集与答案解析结构化学练习题一、填空题试卷中可能用到的常数:电子质量(9.110×10-31kg ), 真空光速(2.998×108m.s -1), 电子电荷(-1.602×10-19C ),Planck 常量(6.626×10-34J.s ), Bohr 半径(5.29×10-11m ), Bohr 磁子(9.274×10-24J.T -1), Avogadro 常数(6.022×1023mol -1)1. 导致"量子"概念引入的三个著名实验分别是___, ________ 和__________.2. 测不准关系_____________________。
3. 氢原子光谱实验中,波尔提出原子存在于具有确定能量的(),此时原子不辐射能量,从()向()跃迁才发射或吸收能量;光电效应实验中入射光的频率越大,则()越大。
4. 按照晶体部结构的周期性,划分出一个个大小和形状完全一样的平行六面体,以代表晶体结构的基本重复单位,叫。
程中,a 称为力学量算符A的。
5. 方6. 如果某一微观体系有多种可能状态,则由它们线性组合所得的状态也是体系的可能状态,这叫做原理。
7. 将多电子原子中的其它所有电子对某一个电子的排斥作用看成是球对称的,是只与径向有关的力场,这就是近似。
8. 原子单位中,长度的单位是一个Bohr 半径,质量的单位是一个电子的静止质量,而能量的单位为。
9. He + 离子的薛定谔方程为()。
ψψa A =?10. 钠的电子组态为1s22s22p63s1,写出光谱项______,光谱支项__________。
11. 给出下列分子所属点群:吡啶_______,BF3______,NO3-_______,二茂铁_____________。
12. 在C2+,NO,H2+,He2+,等分子中,存在单电子σ键的是________,存在三电子σ键的是__________,存在单电子π键的是________,存在三电子π键的是_____________。
结构化学习题解答

3. 证明Slater行列式波函数
1 1sα (1) 1sα ( 2) ψ (q1 , q 2 ) = (1) 2! 2 sα (1) 2 sα ( 2)
是氦原子忽略电子相互作用的 Schrödinger 方程的解,并求其能量 本征值。 解1:
ψ (1,2) =
1 2
[1s(1)α (1)2 s( 2)α ( 2) − 2 s(1)α (1)1s( 2)α ( 2)]
q→∞ q→∞
d * * d * = ∫ ψi ψ dx = ∫ ψ ( − i ) ψ dx 分部积分公式: dx dx −∞ −∞ ∫ vdu = uv − ∫ udv ∞ d ˆ xψ )* dx = ∫ψ [( − i )ψ ] dx = ∫ ψ ( p dx −∞ 证毕
∞ * −∞
∞
∂ ∂ ∂ ∂ =− {[ x , ] + [ x , ]} ∂x ∂x ∂x 2m ∂x
2
∂ ∂ 2 2 ∂ ≠0 {( −1) ( −1)} = + =− 2m ∂x ∂x m ∂x
ˆ 的本征态ψ (q ),则体系的坐标q 因此,若体系处于其能量算符 H
无确定值。
7. 设粒子在一维箱中运动,其状态由波函数
∑
习题二 1. 比较H的2s电子、He+的2s电子和He的2s电子的能量大小。 2. 求Li原子的第一电离能I1,并写出基态Li原子的Slater行列式波函 数。 3. 证明Slater行列式波函数
1 1sα (1) 1sα ( 2) ψ (q1 , q 2 ) = (1) 2! 2 sα (1) 2 sα ( 2)
* ˆ ψ ψ ψ = p dx ∫ x ∫ ( − i * −∞ ∞
d )ψdx = − i ∫ ψ *dψ dx
大学结构化学真题答案解析

大学结构化学真题答案解析导言:结构化学是大学化学课程中的重要部分,它涉及到分子的构建,反应机理的理解以及材料的性质与应用等方面。
对于学习者来说,理解和掌握结构化学的知识点是至关重要的。
在学习过程中,很多学生都会遇到真题解析不清楚的问题。
本文将通过对大学结构化学真题的解析,帮助读者更好地理解和掌握这门学科。
一、选择题解析1. 在一定条件下,甲醛(HCHO)可以发生以下反应:2 HCHO(l) → CH2O2(l)该反应属于()。
A. 加成反应B. 氧化反应C. 脱羧反应D. 氧杂环化反应解析:该反应涉及到甲醛的氧化,生成新的化合物CH2O2。
根据氧化反应的定义,选择B. 氧化反应。
2. 以下化合物对臭氧有类似的反应,其共同特点是()。
A. 含有共轭体系B. 有多个官能团C. 具有高电负性D. 具有轻的原子解析:臭氧(O3)是一种强氧化剂,能够与共轭体系的化合物发生反应。
根据题目中的提示,选择A. 含有共轭体系。
3. 在刚果红试验中,加热含有过氧化氢(H2O2)和硫酸铁(II)(FeSO4)的溶液会产生酶催化的氧气。
以下反应不属于该试验中产生氧气的反应的是()。
A. 2H2O2(aq) + 2FeSO4(aq) → O2(g) + 2H2O(l) + 2FeSO4(aq)B. H2O2(aq) + 2FeSO4(aq) → O2(g) + 2H2O(l) + SO4(aq)C. 2H2O2(aq) + 2FeSO4(aq) → O2(g) + H2O(l) + 2FeSO4(aq)D. 2H2O2(aq) + 2FeSO4(aq) → O2(g) + H2O(l) + S O4(aq)解析:根据反应物和产物的配比关系,可以推导出正确的反应式。
根据题目中的提示,选择B. H2O2(aq) + 2FeSO4(aq) → O2(g) +2H2O(l) + SO4(aq)。
二、填空题解析1. 比色法测定镍含量的原理是利用()与镍离子生成有色化合物。
结构化学第一二章习题解答

(A) n2
(B) 2(l+1)
(C) 2l+1
(D) n-1
(E) n-l-1
6. 试写出 He 原子基态的 Slater 行列式波函数。
基态 He 原子的 Slater 行列式波函数为
1
21 1 ss2 1α α1 2
1s1β1 1s2β2
7. 写出 He 原子的薛定谔方程.
9. 基态Ni原子可能的电子组态为:(a)[Ar]3d84s2; (b)[Ar]3d94s1,由光谱实验确定其能量最低的光谱支项为3F4。 试 判断它是哪种组态。
(a) Leabharlann 2 1 0 12 03F4
m s 1 ,S 1 ; m L 3 ,L 3 ; L S 4
a0
a a0 2
1
x2
a
1
xsin2nxa
a
a
sin2nx
dx
a
a 2 0 2n
a 0 2n 0
a 2
粒子的平均位置在势箱的中央,说明它在势箱左、右两个半
边出现的几率各为0.5,即 n 2 图形对势箱中心点是对称的。
计算:(a) 粒子坐标的平均值; (b) 粒子动量的平均值。
[解]:(a)由于 xnxcnx 无本征值,
只能求粒子坐标的平均值:
x0an *xx nxdx
a 0
2 a
s
innx
a
x
2 a
sinnaxdx
2 a xsin2 nxdx 2 a x1cos2nxdx
根据态M叠加2 原理1和正交0 归 一3化条2件2
结构化学习题解答

组态 a: m s 1 ,S 1 ;m L 3 ,L 3 ;L S 4 。因此,能量最
低的光谱支项为3F4,与光谱实验结果相同。
组态 b: m s 1 ,S 1 ,m L 2 ,L 2 ;L S 3 。因此,能量最
低的光谱支项为3D3,与光谱实验结果不同。
子组态的“电子—空位”关系,(2p)5组态与(2p)1组态具
有相同的谱项。因此,本问题转化为推求(2p)1组态的光
谱项和光谱支项。这里只有一个电子,S= ½ , L=1 ,故
光谱项为2P。又 J113或 J111 ,
22
22
因此有两个光谱支项: 2 P3 和 2 P1
2
2
对C原子激发态(1s)2(2s)2(2p)1(3p)1,只考虑组态(2p)1(3p)1即可。 2P和3P电子是不等价电子,因而(2p)1(3p)1组态不受Pauli原理限 制,可按下述步骤推求其谱项:由
2s和2p三个电子层皆充满电子,它们对整个原子的轨道
角动量和自旋角动量均无贡献。Na原子的轨道角动量和
自旋角动量仅由3s电子决定;L= 0,S = 1/2 ,故光谱项为
2S;J只能为1/2 ,故光谱支项为
S2 1/ 2
F原子的基组态为(1s)2(2s)2(2p)5。与上述理由相同,该组
态的光谱项和光谱支项只决定于(2p)5组态。根据等价电
(c)由于 p xnxcnx,p x 无本征值.可按下式计算 的p x平均值。
p l xp xdx
x
n
xn
0
l
2 sin nx ih d
2 sin nx dx
0l
l 2 dx l
l
ih
结构化学习题讲解

A. E h c
B.
E
h2 2m2
C.
E
e
12.25
2
D.A,B,C 都可以
3. 已 经 适 应 黑 暗 的 人 眼 感 觉 510nm 的 光 的 绝 对 阈 值 在 眼 角 膜 表 面 处 为
11003.5×10-17J。它对应的光子数是(
)
A. 9×
D. 27×108
5. 根据测不准关系,试说明具有动能为 50eV 的电子通过周期为 10-6m 的光栅能否产
生衍射现象? 6. 计算德布罗意波长为 70.8pm 的电子所具有的动能。
7.
下列哪些函数是
d2 dx 2
和
d dx
的共同的本征函数:(1)
e x ,(2)
e2x ,(3)
5sinx,(4)
sinx+cosx,(5)x3。求出本征函数的本征值。
量为_________;它有_____个径向节面,_____个角度节面。 3. 已知氢原子的某一状态波函数为:
n,l,m r, ,
1 26
a0
3 / 2 r er / 2a0 .
a0
2
3 cos
则此状态角度分布的节面数为____ ,径向节面为_____个。处于该状态时,氢原 子的能量为________eV,其角动量的绝对值为|M|=______,此状态角动量在 z 方向 的分量为______,此状态的 n,l,m 值分别为____________。 4. 已知某一个原子轨道有两个径向节面、一个角度节面,该轨道是_____轨道。 5. 氢原子的一个主量子数为 n=4 的状态有____个简并态。 6. 氦原子的 3dxy 状态的能量为________eV,轨道角动量为______,轨道角动量在磁 场方向的分量为______;它有____个径向节面,____个角度节面。
结构化学第九章习题解析
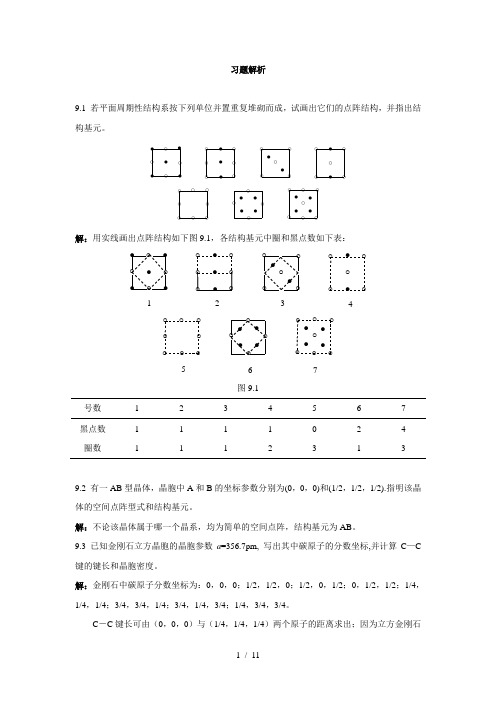
习题解析9.1 若平面周期性结构系按下列单位并置重复堆砌而成,试画出它们的点阵结构,并指出结构基元。
●●●●●●●●●●●●●●●●●●●●○○○○○○○○○○○○○○○○○○○○○○○○○○○○○○○○○○○○○○○解:用实线画出点阵结构如下图9.1,各结构基元中圈和黑点数如下表:●●●●●●●●●●●●●●●●●●●●○○○○○○○○○○○○○○○○○○○○○○○○○○○○○○○○○○○○○○○1234567图9.1号数 1 2 3 4 5 6 7黑点数 1 1 1 1 0 2 4 圈数 1 1 1 2 3 1 39.2 有一AB型晶体,晶胞中A和B的坐标参数分别为(0,0,0)和(1/2,1/2,1/2).指明该晶体的空间点阵型式和结构基元。
解:不论该晶体属于哪一个晶系,均为简单的空间点阵,结构基元为AB。
9.3 已知金刚石立方晶胞的晶胞参数a=356.7pm, 写出其中碳原子的分数坐标,并计算C—C 键的键长和晶胞密度。
解:金刚石中碳原子分数坐标为:0,0,0;1/2,1/2,0;1/2,0,1/2;0,1/2,1/2;1/4,1/4,1/4;3/4,3/4,1/4;3/4,1/4,3/4;1/4,3/4,3/4。
C-C键长可由(0,0,0)与(1/4,1/4,1/4)两个原子的距离求出;因为立方金刚石a=b=c =356.7pmr c-c=×356.7pm = 154.4pm 密度D =ZM/N A V=-1-10323-1812.0g mol (356.710cm)(6.022 10mol )⨯⋅⨯⨯⨯ = 3.51 g·cm -39.4 立方晶系的金属钨的粉末衍射线指标如下:110,200,211,220,310,222,321,400,试问:(a)钨晶体属于什么点阵形式?(b)X-射线波长为154.4pm, 220衍射角为43.62°,计算晶胞参数。
结构化学习题解答2(北大)

0
0
1 3 32a 0
2 r a0
e
2
r a0
d 0 d 1 3 dr dr 32a 0
解之得:
r a 0
e
r 1 r a0 re 2 0 5 a0 32a 0
dr sin d d
0 0
4 a0 27 3 4 a 0 216
1 a0 2
因为 r 的增大而单调下降,所以不能用令一阶导数为0 2 的方法求其最大值离核的距离。分析 1s 的表达式可见, =0
2 1s 随着
27 (c) e 3 a 0
2 1s
e
2
r a0
cos2
由式可见,若r相同,则当θ=00或θ=1800时ρ最大(亦 可令 ),以ρ0表示,即: sin 0, 0 0 或180 0
r 0 r , 0 ,180 a 0 将 0 对r微分并使之为0,有:
试问下列问题: (a) 原子轨道能E=? (b) 轨道角动量|M|=?轨道磁距|μ|=? (c) 轨道角动量M和Z轴的夹角是多少度? (d) 列出计算电子离核平均距离的公式(不必计算出 具体 的数值)。 (e) 节面的个数、位置和形状怎样? (f) 几率密度极大值的位置在何处? (g) 画出径向分布图。
I 2 E He
2 2 13 .595 eV 2 1
54 .38eV
(b)从原子的电离能的定义出发,按下述步骤求He原子基 态的能量:
He ( g ) He g e He g He
结构化学习题解答

结构化学习题解答《物质结构》第三章习题1、试述正八面体场、正四面体场、正方形场中,中心离子d轨道的分裂方式。
2、试根据晶体场理论说明直线形配合物MX2中(以分子轴为z轴),中心原子的d轨道如何分裂,并给出这些轨道的能量高低顺序。
3*、试根据晶体场理论说明三角双锥配合物中,中心原子的d轨道如何分裂,并给出这些轨道的能量高低顺序。
4、简述分裂能?与中心离子与配体的关系。
5、配体CN-,NH3,H2O,X-在络光谱化学序列中的顺序就是( )(A) X-< CN--< NH3 < H2O (B) CN-< NH3< X- < H2O(C) X-< H2O < NH3 < CN-(D) H2O < X- < NH3 < CN-6、在下列每对络合物中,哪一个有较大的?O,并给出解释。
①[Fe(H2O)6]2+ 与[Fe(H2O)6]3+②(b)[CoCl6]4-与[CoCl4]2-③[CoCl6]3-与[CoF6]3-④[Fe(CN)6]4- 与[Os(CN)6]4-7、下列配合物离子中, 分裂能最大的就是( )(A)[Co(NH3)6]2+(B)[Co(NH3)6]3+(C)[Co(H2O)6]3+(D)[Rh(NH3)6]3+8、下列配位离子中,?O值最大的就是( )(A) [CoCl6]4-(B) [CoCl4]2-(C) [CoCl6]3-(D) [CoF6]3-9、以下结论就是否正确?“凡就是在弱场配体作用下,中心离子d 电子一定取高自旋态;凡就是在强场配体作用下,中心离子d电子一定取低自旋态。
”10、试写出d6金属离子在八面体场中的电子排布与未成对电子数(分强场与弱场两种情况)。
11、下列络合物哪些就是高自旋的( )(A) [Co(NH3)6]3+(B) [Co(NH3)6]2+(C) [Co(CN)6]4-(D) [Co(H2O)6]3+12、按配位场理论,正八面体场中无高低自旋态之分的组态就是( )(A) d3 (B) d4(C) d5(D) d6(E) d713、试判断下列配位离子为高自旋构型还就是低自旋构型, 并写出d电子的排布。
结构化学期末复习-问答题全解

问答题 ( 附答案 )1. 2 分为什么处在第一激发态的He 原子会出现三重态发射光谱?2. 5 分下列休克尔分子轨道中哪个是归一化的?若不是归一化的,请给出归一化系数。
(原子轨道ϕϕϕ321,,是已归一化的)a. ()ϕϕ21121+=ψ b. ()ϕϕϕ3212241+-=ψ 3. 5 分一质量为m 的粒子,在区间[a ,b ]运动,处于状态x ψ1=,试将ψ归一化。
4. 5 分试写出在价键理论中描述 H 2 运动状态的、符合 Pauli 原理的波函数, 并区分其单态和三重态。
5. 5 分对一个运动速率v<<c 的自由粒子,有人作了如下推导 :mv v E v h hp mv 21=====νλ A B C D E结果得出211=的结论。
问错在何处? 说明理由。
6. 5 分电子具有波动性,为什么电子显像管中电子却能正确地进行扫描? (假设显像管中电子的加速电压为1000?V)7. 5 分θθcos 3cos 53-是否是算符)d d sin cos d d (ˆ222θθθθF +-= 的本征函数,若是,本征值是多少?8. 5 分对在边长为L 的三维立方箱中的11个电子,请画出其基态电子排布图,并指出多重态数目。
9. 5 分对在二维方势箱中的9个电子,画出其基态电子排布图。
*. 5 分 (3231)11. 2 分假定ψ1和ψ2是对应于能量E 的简并态波函数,证明ψ=c 1ψ1+ c 2ψ2同样也是对应于能量E 的波函数。
12. 2 分He +中处于x p 2ψ的电子,其角动量在x ,y ,z 方向上的分量是否具有确定值?若有,其值是多少?若没有,其平均值是多少?13. 2 分氢原子中z p 2ψ状态的电子,其角动量在x ,y 方向上的分量是否有确定值?若有,其值是多少?若没有,其平均值是多少?14. 2 分写出中心力场近似下的单电子薛定谔方程。
15. 2 分氢原子2p x 态电子云的角度分布图(Y p x2)2如下,在半径为r 的虚线表示的球面上,有a ,b ,c ,d 四点,指出何处电子出现的概率密度最大?何处电子出现的概率密度最小?(见附图)16. 2 分氢原子p 2ψ状态的R 2(r )-r 图如下,指出在任一给定方向上,图中所标四点,当r 为何处时电子出现概率密度最大,何处最小? (见附图)17. 2 分如果一个电子的状态不用量子数n ,l ,m ,m s 来描述,而用n ,l ,j ,m j 描述,试证明一定n 值的状态数目仍是2n 2个。
结构化学课后习题答案

结构化学课后习题答案结构化化学课后习题答案一、化学键与分子结构1. 选择题a) 正确答案:D解析:选择题中,选项D提到了共价键的形成是通过电子的共享,符合共价键的定义。
b) 正确答案:B解析:选择题中,选项B提到了离子键的形成是通过电子的转移,符合离子键的定义。
c) 正确答案:C解析:选择题中,选项C提到了金属键的形成是通过金属原子之间的电子云重叠,符合金属键的定义。
d) 正确答案:A解析:选择题中,选项A提到了氢键的形成是通过氢原子与高电负性原子之间的吸引力,符合氢键的定义。
2. 填空题a) 正确答案:共价键解析:填空题中,根据问题描述,两个非金属原子之间的键称为共价键。
b) 正确答案:离子键解析:填空题中,根据问题描述,一个金属原子将电子转移到一个非金属原子上形成的键称为离子键。
c) 正确答案:金属键解析:填空题中,根据问题描述,金属原子之间的电子云重叠形成的键称为金属键。
d) 正确答案:氢键解析:填空题中,根据问题描述,氢原子与高电负性原子之间的吸引力形成的键称为氢键。
二、有机化学1. 选择题a) 正确答案:C解析:选择题中,选项C提到了烷烃是由碳和氢组成的,符合烷烃的定义。
b) 正确答案:D解析:选择题中,选项D提到了烯烃是由含有一个或多个双键的碳原子组成的,符合烯烃的定义。
c) 正确答案:B解析:选择题中,选项B提到了炔烃是由含有一个或多个三键的碳原子组成的,符合炔烃的定义。
d) 正确答案:A解析:选择题中,选项A提到了芳香烃是由芳香环结构组成的,符合芳香烃的定义。
2. 填空题a) 正确答案:醇解析:填空题中,根据问题描述,含有羟基(-OH)的有机化合物称为醇。
b) 正确答案:醚解析:填空题中,根据问题描述,含有氧原子连接两个碳原子的有机化合物称为醚。
c) 正确答案:酮解析:填空题中,根据问题描述,含有羰基(C=O)的有机化合物称为酮。
d) 正确答案:酯解析:填空题中,根据问题描述,含有羧基(-COO)的有机化合物称为酯。
《结构化学》(1-5章)习题解析

目录第一章--------------------------------------------------------------------------------------------------1 第二章-------------------------------------------------------------------------------------------------14 第三章-------------------------------------------------------------------------------------------------30 第四章-------------------------------------------------------------------------------------------------42 第五章-------------------------------------------------------------------------------------------------48第一章习题1001 首先提出能量量子化假定的科学家是:---------------------------( )(A) Einstein (B) Bohr (C) Schrodinger (D) Planck 1002 光波粒二象性的关系式为_______________________________________。
1003 德布罗意关系式为____________________;宏观物体的λ值比微观物体的λ值_______________。
1004 在电子衍射实验中,│ψ│2对一个电子来说,代表___________________。
1005 求德布罗意波长为0.1 nm 的电子的动量和动能。
结构化学课后习题及答案
01.量子力学基础知识【1.1】将锂在火焰上燃烧,放出红光,波长λ=670.8nm ,这是Li 原子由电子组态 (1s)2(2p)1→(1s)2(2s)1跃迁时产生的,试计算该红光的频率、波数以及以k J·mol -1为单位的能量。
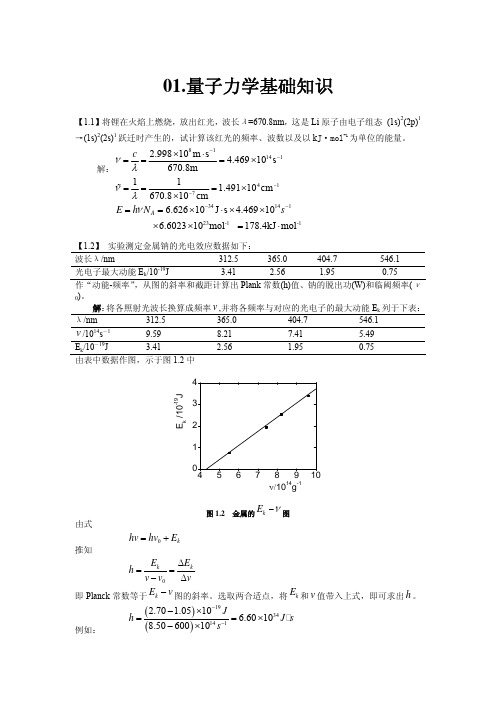
解:811412.99810m s 4.46910s 670.8m cνλ−−×⋅===× 41711 1.49110cm 670.810cm νλ−−===××%3414123-1 -16.62610J s 4.46910 6.602310mol 178.4kJ mol A E h N sν−−==×⋅××××=⋅【1.2】 实验测定金属钠的光电效应数据如下:波长λ/nm 312.5 365.0 404.7 546.1 光电子最大动能E k /10-19J 3.41 2.56 1.95 0.75 作“动能-频率”,从图的斜率和截距计算出Plank 常数(h)值、钠的脱出功(W)和临阈频率(ν0)。
解:将各照射光波长换算成频率,并将各频率与对应的光电子的最大动能E k 列于下表:v λ/nm 312.5 365.0 404.7 546.1v /1014s -19.59 8.21 7.41 5.49E k /10-19J 3.41 2.56 1.95 0.75 由表中数据作图,示于图1.2中E k /10-19Jν/1014g-1图1.2 金属的kE ν−图由式 0k hv hv E =+推知0k kE E h v v v Δ==−Δ即Planck 常数等于图的斜率。
选取两合适点,将和v 值带入上式,即可求出h 。
例如: k E −v k E ()()19341412.708.50 1.0510 6.601060010J h J s s −−−×==×−×图中直线与横坐标的交点所代表的即金属的临界频率,由图可知,。
结构化学试题合辑(附解析)-化学-材料科学-中国科技大学-共558页

(e)C2H2;(f)CH3OH;(g)ND3;(h)OCS;(i)P4;(j)PCl3;(k)PCl5; (l)BB12Cl2-12;(m)UF6;(n)Ar。 10. 给出下列者的点群:(a) FeF63-; (b) IF6; (c) CH2=C=CH2; (d) 立方烷C8H8;
(e)C6H5Cr(CO)3; (f) B2H6; (g) XeF4; (h) F2O; (i) 螺旋状戊烷。 11.二茂铁C5H5FeC5H5结构是一个铁原子夹心式地位于两个平行的正五边形中间。
11.忽略电子的自旋轨道相互作用,但考虑电子的自旋状态,试确定主量子数是 n 的氢原子
电子能级的简并度。
12.在求解氢原子电子的 Schrödinger 方程时,曾忽略了万有引力的作用。质子和电子在万 有引力作用下的势能为
V ′ = GMμ r 其中万有引力常数 G =6.67×10-8 cm3.g-1.s-1。试计算V ′ 所引起的电子能量的修正值。 13.试比较能量算符 Hˆ 和 Hˆ + Cˆ 的本征值和本征函数。其中 Cˆ 为任一常数 c 所对应的算符。
2. 考虑相对论效应,则以速度υ 运动的粒子的动能为
T = μ0c2 1−υ 2 c2 − μ0c2
其中
μ0
为粒子的静止质量。试证明当υ
<<
c
时,
T
≈
1 2
结构化学习题解答7北大

3
75.4 37.7 0.347 2.67×3=8 220 0.04675
4
90.4 45.2 0.503 3.59×3=11 311 0.04573
5
95.6 47.8 0.549 3.92×3=12 222 0.04575
6 117.4 58.7 0.730 5.21×3=16 400 0.04562
2θ/(0) 27.3 31.8 45.5 53.9 56.6 66.3 75.5
d/pm 326.7 281.4 199.4 170.1 162.6 141.0 125.9
I/I0 18 100 80
5
21 20 20
按这组d-I/I0值查表,得知它为NaCl晶体。
[7.27] 金 属 铝 属 立 方 晶 系 , 用 Cu Ka 射 线 摄 取 333 衍 射 , θ=81017ˊ,由此计算晶胞参数。
代入有关数据,得:
d 224
[( 22 1.0482
22 1.2922
42 )
1
]1/ 2Leabharlann 2.4552 106 pm2
[(3.642 2.396 2.655)
1
]1 / 2
106 pm2
339.2 pm
sin 1 ( 154.2 pm )
2 339.2 pm 13.14
(c)S8分子属于点群D4d,独立的对称元素有:I8,4C2,4σd。
[7.31] 已知NaCl晶体立方晶胞参数a=563.94pm实验测得衍射 111的衍射角θ=5.100,求实验所用X射线的波长。 [解]:
d hkl a /(h 2 k 2 l 2 )1/ 2
563.94 pm / 3
325.59 pm
结构化学基础习题解析

结构化学基础习题解析
本文旨在介绍结构化学的基础习题及其解析,以提高读者对结构化学的理解和应用。
结构化学是一种分析物质的结构的科学,它融合了物理化学、生物化学和化学物理学等学科,是物理、化学和生物研究的重要基础。
结构化学的基本概念是研究物质的结构,其中包括物质的大小、结构、形状及其相互作用。
在结构化学中,研究人员可以使用分子模型和物理量子化学来研究物质的结构和性质,从而推断出发生的化学反应的机理。
结构化学的基础习题主要包括物质的独特性质、分子模型和晶格结构。
首先,物质的独特性质是由其原子组成、结构和配位数等决定的。
研究人员可以利用原子的性质和能量,结合分子模型和物理量子化学,以解释原子的特定性状。
其次,分子模型是一种理解物质结构的技术,包括用不同颜色表示原子、用箱线表示分子结构、计算分子中各原子间的距离,以及计算分子的总能量等。
最后,晶格结构是指物质的晶体构造,即原子、分子和离子之间的特定排列结构,它可以帮助研究人员了解物质的构型特性和性质。
此外,结构化学关注的还有化学反应的机理和过程,以及各种物质的结构变化与物性之间的关系。
研究人员可以利用结构信息,如原子组成、分子模型和晶格结构,解释某一特定物质的特性和行为,从而利用这些信息推断出发生的化学反应机理。
总之,结构化学的基础习题包括独特性质、分子模型和晶格结构,
以及化学反应的机理等内容,是了解物质的结构和性质的基础。
结构化学的基础习题可以帮助读者更合理地使用结构化学来解释物质的结构、性质和行为,从而推断出发生的化学反应的机理,同时提高读者的结构化学知识。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
第一章 量子力学基础知识一. 填空题1. 经典物理学无法解释的代表性实验有__________、___________和____________。
2. 联系实物微粒的波动性和微粒性的两个重要公式分别是___________________和______________________。
3. 德布罗意关系式为________________;宏观物体的λ值比微观物体的λ值________。
4. 1927年戴维逊和革未的电子衍射实验证明了实物粒子也具有波动性。
欲使电子射线产生的衍射环纹与Cu 的K α线(波长为154 pm 的单色X 射线)产生的衍射环纹相同, 电子的能量应为________________J 。
5. 对于立方势箱中的粒子,在22815ma h E <的能量范围内有____个态,有___个能级。
6. 在边长为a 的立方势箱中运动的粒子,其能级2243ma h E =的简并度是______, 22827mah E =的简并度是_______。
7. 质量为m 的粒子被局限在边长为a 的立方箱中运动。
波函数ψ211(x ,y ,z )=_________________________;当粒子处于状态ψ211时,概率密度最大处坐标是___________;若体系的能量为2247ma h , 其简并度是_______________。
二. 选择题1. 若用电子束与中子束分别作衍射实验,得到大小相同的环纹,则说明二者( )A . 动量相同B . 动能相同C . 质量相同2. 任一自由的实物粒子,其波长为λ,今欲求其能量,须用下列哪个公式 ( )A .λc h E =B . 222λm h E =C .225.12⎪⎭⎫ ⎝⎛=λ e E D .A ,B ,C 都可以 3. 已经适应黑暗的人眼感觉510nm 的光的绝对阈值在眼角膜表面处为11003.5×10-17J 。
它对应的光子数是( )A . 9×104B . 90C . 270D . 27×108 4. 微粒在间隔为1eV 的二能级之间跃迁所产生的光谱线的波数v~应为( )cm -1 (已知1eV=1.602×10-19J)A . 4032B . 8065C . 16130D . 20165. 在量子力学中,描述微观粒子运动状态的量是( )A .坐标和动量B .坐标和动量的不确定量C .波函数ψD .Schrödinger 方程6. 下列函数中属于品优函数的是( )A .()x e x =ψB .()x x =ψC .()2x e x -=ψD .()21x x -=ψ 7. 波函数归一化的表达式是( )A .02=⎰τψdB .12>⎰τψdC .12=⎰τψdD .12<⎰τψd 8. 若c 为任意常数,则与ψ描述体系同一状态的波函数是( )A .ψ*B .ψ*ψC .c ψ*D .c*ψ 9.代表粒子在空间某点附近出现几率大小的数学表达式是( ) A .ψ B .ψ* C .ψψ* D .ψψ*d τ 10.粒子处于定态意味着( ) A .粒子处于概率最大的状态 B .粒子处于势能为零的状态 C .粒子的力学量平均值及概率密度分布都与时间无关的状态 D .粒子处于静止状态 11.对原算符而言,本征函数的线性组合具有下列性质中的( ) A .是原算符的本征函数 B .不是原算符的本征函数 C .不一定是原算符的本征函数 D .无法确定是否是原算符的本征函数 12.对于厄米算符, 下面哪种说法是对的( ) A . 厄米算符中必然不包含虚数 B . 厄米算符的本征值必定是实数 C . 厄米算符的本征函数中必然不包含虚数 13.对于算符Ĝ的非本征态ψ,下面哪种说法是对的( ) A .不可能测量其本征值g B .不可能测量其平均值〈g 〉 C .本征值与平均值均可测量,且二者相等 14.所有内在性质完全相同,无法用物理测量的方法进行分辨的微观粒子称为( ) A .基本粒子 B .全同粒子 C .场量子 D .费米子 15.设ψ不是能量算符Ĥ的本征函数,则当体系处于ψ所描述的状态时,对于能量E 的一次测量 ( ) A .不可能得到能量算符的本征值 B .必定得到能量算符的本征值之一 C .可能得到能量算符的本征值之一 D .无有任何意义 16. Pauli 原理的正确叙述为( )A .电子体系的空间波函数对于交换电子必须是反对称的B .原子中每个电子的运动状态必须用四个量子数来描述C .同一原子中不可能有四个量子数完全相同的两个电子D .每个自旋-轨道最多只能容纳自旋方向相反的两个电子17. 已知一维谐振子的势能表达式为221kx V =,则该体系的定态薛定锷方程为( ) A .ψψE kx m =⎥⎦⎤⎢⎣⎡+∇222212 B .ψψE kx m =⎥⎦⎤⎢⎣⎡-∇222212 C .ψψE kx m =⎥⎦⎤⎢⎣⎡-∇-222212 D .ψψE kx m =⎥⎦⎤⎢⎣⎡+∇-222212 18. 在长l =1 nm 的一维势箱中运动的He 原子,其de Broglie 波长的最大值是( )A .0.5 nmB .1 nmC .1.5 nmD .2.0 nmE .2.5 nm19. 若K d =⎰τψ2,利用下列哪个常数乘ψ可以使之归一化( )A . KB . K 2C .K /1 20. 算符2222ˆdx d p x -=作用于函数()l x n l x πψsin 2=的结果是ψ(x )乘以常数,该常数是( )A .ħ2B .-ħ2C .n 2ħ2D .2224l h n 21. 描述全同粒子体系状态的完全波函数对于交换其中任意两个粒子的坐标必须是( )A .对称的B .反对称的C .非对称的D .对称或反对称的22. 在关于一维势箱中运动粒子的ψx 和2x ψ的下列说法中,不正确的是 ( )A .ψx 为粒子运动的状态函数B .2x ψ表示粒子出现的概率随x 的变化情况C .ψx 可以大于或小于零,2x ψ无正、负之分D .当∞→x n 时,2x ψ图像中的峰会多而密集,连成一片,表明粒子在0<x <a 内各处出现的概率相同23. 处于状态()a x n x πψsin =的一维势箱中的粒子,出现在4a x =处的概率是( ) A .224=⎪⎭⎫ ⎝⎛=a P ψ B .2122=⎪⎭⎫ ⎝⎛=a P ψ C .a a a P 142=⎪⎭⎫ ⎝⎛=ψ D .a a a P 1422=⎥⎦⎤⎢⎣⎡⎪⎭⎫ ⎝⎛=ψ E .题目提法不妥,以上四个答案都不对 24. 立方势箱中的粒子,具有22812ma h E =的状态量子数,n x n y n z 是( ) A .211 B .231 C .222 D .21325. 一个在一维势箱中运动的粒子,其能量随着量子数n 的增大( ),其能级差 E n +1-E n随着势箱长度的增大( )A .越来越小B .越来越大C .不变26. 下列算符中不属于线性算符的是( )A .dx dB .2∇C .用常数乘D .E .积分27. 在长l =1 nm 的一维势箱中运动的He 原子, 其零点能约为( )A .16.5×10-24JB .9.5×10-7 JC .1.9×10-6 JD .8.3×10-24J28. 在一立方势箱中,势箱宽度为l , 粒子质量为m ,2247mlh E ≤的能级数和状态数分别是( )A .5,11B .6,17C .6,6D .5,14E .6,14三. 证明与计算题1. 用透射电子显微镜摄取某化合物的选区电子衍射图,加速电压为200kV ,计算电子加速后运动时的波长。
2. 欲使中子的德布罗意波长达到154pm ,则它们的动能和动量各应是多少3. “根据测不准原理,任一微观粒子的动量都不能精确测定,因而只能求其平均值”。
这种说法对否?为什么?4. 计算下列粒子的德布罗意波长,并说明这些粒子是否能被观察到波动性。
(1). 弹丸的质量为10g ,直径为1cm ,运动速率为106m·s -1;(2). 电子质量为9.10⨯10-28g ,直径为2.80⨯10-13cm ,运动速率为106m·s -1;(3). 氢原子质量为1.6⨯10-24g ,直径约为7⨯10-9cm ,运动速率为103m·s -1,若加速到106m·s -1,结果如何?5. 根据测不准关系,试说明具有动能为50eV 的电子通过周期为10-6m 的光栅能否产生衍射现象?6. 计算德布罗意波长为70.8pm 的电子所具有的动能。
7. 下列哪些函数是22dx d 和dxd 的共同的本征函数:(1) xe ,(2) x e 2,(3) 5sinx ,(4) sin x +cos x ,(5)x 3。
求出本征函数的本征值。
8. (1).2ax xe -=ψ是算符⎪⎪⎭⎫ ⎝⎛-22224x a dx d 的本征函数,求其本征值; (2). ix Ne -=ψ是算符x pˆ的本征函数,求其本征值。
9. θθcos 3cos 53-是否是算符⎪⎪⎭⎫ ⎝⎛+-=θθθθF d d sin cos d d ˆ222 的本征函数,若是,本征值是多少?10. 已知一维势箱粒子的归一化波函数为() 3,2,1,sin 2==n lx n l x πψ 试比较一维势箱粒子基态(n =1)和第一激发态(n =2)在0.4l ~0.6l 区间内出现的几率。
11. 函数()lx l l x l x ππψsin 232sin 22+=是否是一维势箱中粒子的一种可能的状态?如果是,其能量有没有确定值?如有,其值是多少?如果没有确定值,其平均值是多少?12. 作为近似, 苯可以视为边长为0.28 nm 的二维方势箱, 若把苯中π电子看作在此二维势箱中运动的粒子, 试计算苯中成键电子从基态跃迁到第一激发态的波长。
13. 已知一维势箱的两个波函数分别为:⎪⎭⎫ ⎝⎛=⎪⎭⎫ ⎝⎛=l x l l x l πψπψ2sin 2,sin 221,请证明这两个波函数是相互正交的。
14. 试计算长度为a 的一维势箱中的粒子从n =2跃迁到n =3的能级时,德布罗意长的变化。
15. 一个在一维势箱中运动的电子,其最低跃迁频率是2.0⨯1014s -1,求一维势箱的长度。
第二章 原子的结构和性质一. 填空题1. 氢原子中电子的一个状态为:φθπψ2sin sin 281123202/300a Zre a Zr a Z -⎪⎪⎭⎫ ⎝⎛⎪⎪⎭⎫ ⎝⎛=,则量子数n 为____,l 为____,m 为____,轨道名称为____。
