计算方法分段线性_三次样条插值
S(xi 0) S(xi 0) 不包括端点a, b
上述二式共给出了4n-2个条件,而待定系数有4n
个,因此还需要2个条件才能确定S(x)。
x0 x1 x2 x3 x4 x5
x6 x
通常在区间端点 a x 0, b x n上各加一个条件,
S(x),S' (x),S' ' (x)
在a, b 上连续)
三次样条函数插值
则称S(x)为三次样条插值函数。
比线性插值要求严 苛得多！
y
y=f(x) (黑色)
y=S(x) （蓝色）
x0
xi
xi+1
xn
x
问题：这个S(x)是三次样条插值函数吗？
回答：不是。 原因： 1）在每个区间内都是3次多项式； 2）在小区区间端点xi处连续并且：f(xi)=S(xi) ； 3）S”(x)在xi 点不连续，即不光滑。
x 0
1 f(0) 1
x 1
0 0
f(1)
1 x
x 2
x 2
1
在[1,2]上，
S(x)
x 1
2 2
f(1)
x 1 f(2) 21
1 2
(x
2)
1 (x 5
1)
3 x4 10 5
在[2,3]上，
S(x)
x 2
3 3
f(2)
1 2
,
f(5)
148 17576
max | f(x) S(x) | 2 h2 1 h2 1
a x b
8
4
4
综上可得 max | f(x) S(x) |
2 h2
1
a x b
8
4
y
y=S(x)：分段线性函数
y
1 1 x2
1 23 45 x
现象：在[0, 1]上逼近效果最差，在其 它区间，逐渐变好。
满足自然边界条件的三次样条插值函数称为自然 样条插值函数。
• 这样，由上给定的任一种边界条件加上插值条 件和连接条件，则得出4n个方程，可以唯一确 定4n个系数。
• 从而得到三次样条插值函数S(x)在各个子区间 xi , xi+1上的表达式S(xi）(i=1,2,…,)。
• 但是，这种做法当n较大时，计算工作量很大， 不便于实际应用。
能产生多 少个方程？
2）要求 S(x),S' (x),S' ' (x) 在整个插值区间a, b
上连续，因此在连接点 x1, … , x n1 上连续。
满足条件： 1）插值条件(n+1个节点)
S(xi ) f(x i ), i 0,1, … , n
2）连接条件(3n-3个节点) S(xi 0) S(xi 0)
0x
1
设 | f(4)(x) | 1, x (0,1)
则3次插值多项式的误差
|
R(x)
||
f(4)(ξ) (x 4!
x0 )(x
x1)(x
x2 )(x
x3 )
|
41！| (x x0 )(x x1)(x x2 )(x x3 ) |
41！
1 3
1 3
2 3
1
• 希望找到一种方便计算机计算简单的构造方法 -显式方法。
2.5.2 三次样条插值函数的求法
记：
S(xi )
f(x i )
yi;
Si (x)
Mi 1
(xi x)3 6hi
hi xi xi1
计算方法 (Numerical Analysis)
第3次 分段线性插值与三次样条插值
内容
1. 高次插值的龙格现象 2. 分段线性插值与误差估计 3. 三次样条插值与误差估计
高次插值的龙格现象
2.4.1 高次插值的龙格现象
插值多项式余项公式
R(x)
f(n1)(ξ) (x (n 1)!
x x2 x3 x2
f(x3 )
2 3 60
x
33 2
2
将各小区间的线性插值函数连接在一起，得
2 1x 3
30
2
2
S(x)
3 2x2 23
30
2
3
2
3 60
x
33 2
2
30 x 45 45 x 60 60 x 90
因此，次数太高的高次插值多项式往往并不实用， 因为节点数增加时，计算量增大了，但插值函数 的精度未必能够提高。称为龙格现象。
Home
分段线性插值与误差估计
为克服龙格现象，可以采用分段插值的方法：
• 将插值区间分成若干个小的区间，在每 个小区间进行线性插值，
• 然后相互连接，用连接相邻节点的折线 逼近被插函数
Home
三次样条插值与误差估计
2.5.1 三次样条函数
在船体、飞机等外形曲线的设计中,不仅要求曲 线连续,而且要有二阶光滑度,即有连续的二阶导 数。
要求分段插值函数在整个区间上具有连续的二 阶导数。
因此有必要寻求一种新的插值方法,这就是样条 函数插值法
样条函 数来历
定义5.4 . 设函数f(x)定义在区间a, b上，在给定
x0 )(x
x1)
(x
xn )，
ξ (a, b)
例：设函数f(x)定义在区间[0, 1]上 ，并且满足 |f(4) (x)|<1，xϵ[0, 1]。在4个插值节点 x0=0, x1=1/3, x2=2/3, x3=1, 对f(x)进行插值得多项式P3(x)，估计误差。
下面讨论误差的情况：
|
f(x)
S(x)
||
f(ξ) 2！
(x
-
xk )(x
-
xk 1)
|
记
g(x)
(x - xk )(x - xk1), 解g(x)
0，得x*
xk
xk1， 2
得知x*是g(x)的极值点，将x*代入g(x)：
g(x* )
(x *
- xk )(x*
- xk1)
1 2
(x k 1
考察函数
f(x)
1 1 x2
,
5 x 5
右图给出了 P5 (x )
y P10(x)
和 P10(x ) 的图像,当n
f(x)
增大时,Pn(x ) 在两端
会发生激烈的振荡，
称为龙格现象。
P5(x)
-5
0
5x
该现象表明：在大范围内使用高次插值,逼近的 效果往往是不理想的。
另外，从舍入误差来看，高次插值误差的传播也 较为严重，一个节点上产生的舍入误差会在计算 中不断放大，并传播到其它节点上。
x4 5-4
f(5)
1 17
(x
5)
1 (x 26
4)
9 x 31 442 221
将这些分段线性函数拼接在一起，得：
S(x)
x 2
1，x
[0,1]
S(x) 3 x 4 , x [1,2]
10
5
S(x)
1 10
x
2 5
,
x
[2,3]
S(x) 7 x 19 , x [3,4]
2 648
0.0031
但是当区间[a, b]比较大的时候，误差可能很大。
影响误差的因素：一般地说
• 插值节点的个数：插值节点越多，即使用高 次插值，误差越小
• f(x)的高阶导数绝对值：越小，误差越小
适当提高插值多项式的次数，有可能提高 计算结果的准确程度，但并非次数越高越 好。
当插值节点增多时，也不能绝对保证非节 点处的插值精度得到改善，有时反而误差 更大。
S1(x)
x xk
xk1 xk1
f(x k )
x xk xk1 xk
f(x k1)
(xk x xk1)
在几何上就是用折线替代曲线,如图所示。
y
y=f(x)
y=p(x)
x0 x1
x2
xn x
例2.19 已知f(x)在四个节点上的函数表如下：
xi
30 45 60 90
f(x)
S(x)
|
M2 2
max
xk xxk 1
|
(x
-
xk )(x
-
xk1)
|
max | f(x) S(x) | M2 h2
a x b
8
其中：
M2
max | f(x) |, a x b
h mkax(xk1 - xk )
证明： 当x [xk , xk1]时，
Si(x) ai0 ai1x ai2x2 ai3x3 i 0,1,...n, 1
分析：待定系数：ai 0, ai 1, ai 2, ai 3 ，n个子区间，要
确 定S(x)，需要确定4n个待定系数。
已知： 1）要求 S( xi )= f ( xi ), i = 0, 1,…, n
Matlab实验报告六(三次样条与分段线性插值)范文
本题是给出粗略等分点让你插入更多点用双线性插值法来作出更清晰的山区地貌图。
2.问题求解
x=0:400:2800;
y=0:400:2400;
z=[1430 1450 1470 1320 1280 1200 1080 940;
1450 1480 1500 1550 1510 1430 1300 1200;
2.分段线性插值与计算量与n无关;n越大，误差越小.
3.三次样条插值比分段线性插值更光滑。
4.‘linear’：分段线性插值；‘spline’：三次样条值。
【实验环境】
MatlabR2010b
二、实验内容
问题1对函数 ，x[-5,5]，分别用分段线性插值和三次样条插值作插值（其中插值节点不少于20），并分别作出每种插值方法的误差曲线.
本次实验因为是我们课本没有的内容，心理上给了我很大的压力，幸好我们还能根据老师的课件以及例题去掌握这次实验所需要的各种插值法，但结果还好，两道题都做出来了。
plot(x,y,'*',x1,yl,'r',x1,y2,'b')
y0=1./(1+x1.^2);
y3=yl-y0;
y4=ys-y0;
holdon
plot(x1,y3,'y',x1,y4,'g')
3.结果
4误。
问题2山区地貌图在某山区（平面区域（0，2800）（0，2400）内，单位：米）测得一些地点的高程（单位：米）如表1，试作出该山区的地貌图.
1.分析问题
本题先取出少量的插值节点并作出图形，再用分段线性插值法和三次样条插值法做出更精确的图形，最后在作出误差曲线。
三次样条插值
0)
s(xn 0) s(xn 0)
三弯矩插值法
x xi,
x i+1
s”(x) M i , M i+1
记Mi = s″(xi), f(xi)= yi ,考虑它在任一区间[xi, xi+1]上的形式. 根据三次样条的定义可知 , s(x)的二阶导数 s ″(x)在每一个子区
间[xi, xi+1] ( i=0,1,2,,n-1)上都是线性函数.
2 6
M
i
)(xi1
xi
)
(1)
同理在[xi1, xi ]上讨论得
s(xi )
yi xi
yi1 xi1
(
2 6
M
i
1 6 M i1)(xi
xi1)
(2)
因为s( x)连续，所以（1）（2）即
yi1 yi xi1 xi
1 ( 6 M i1
2 6
M i )(xi1
xi )
yi xi
yi1 xi1
(2) (n 1)内节点处连续及光滑性条件：
s(x s( x
j j
0) 0)
s(x j 0) s(x j 0)
j
1,2,...,n
1
s(x j 0) s(x j 0)
对于待定系数a j ,bj , c j .d j j 1,2,...n,即4n个未知系数，
而插值条件为4n 2个，还缺两个，因此须给出两个 条件称为边界条件，有以下三类：
——分段三次插值多项式
分段插值存在着一个缺点,就是会导致插值函数在子区间的端点 (衔接处)不光滑,即导数不连续。
实际应用中，如机翼设计、船体放样等往往要求有二阶光滑度， 即二阶连续导数。早期工程师制图时，把富有弹性的细长木条 （所谓样条SPLINE ）用压铁固定在样点上，其它地方让其自 由弯曲，然后画下曲线（称为样条曲线），它实际上是由分段 多项式光滑连接而成，在样点上要求二阶连续可导。
计算方法大作业1 克服Runge现象
x3
x2
x
1
S1 ( x)
-0.34685
0.2086
0.073964
0.038462
S2 (x)
S (xi 0 ) S x(i 0 )
S
'
(xi
0) S
xi' (
0 )i
S
'
'
x(i
0)S
xi' ' (
0)
1 ,n2, . . . , 1
（1）
这里共有了 3n-3 个条件，再加上条件（2）中的 n+1 个插值条件，共有 4n-2 个条件，
因此还需要 2 个方程才能确定 S (x) .通常可在区间[a, b]的端点 a x0,b xn 上各加一个边
dn1
1
2
Mn
dn
（6）
2 1
2
2
2
1 M1 d1
M2
d2
n 1
2
n
1
M
n
1
dn1
n
n 2 M n dn
由式（1）内点拼接条件，可得
i M i1 2M i i M i1 d j i 1, 2,..., n 1
（3） （4）
其中
i
hi 1 hi1
, hi
i
hi hi 1
Matlab实验报告六(三次样条与分段线性插值)
实验名称插值与拟合
所属课程数学软件与实验
实验类型综合型实验
专业信息与计算科学
班级
学号
姓名
指导教师
一、实验概述
【实验目的】
学会在matlab环境下使用几种不同的插值法和拟合两种方法构造函数依据已经知道的某些特殊点来推测实际问题中需要知道但又不便于测量出来的量。
【实验原理】
1.z=interp2(x0,y0,z0,x,y,’method’): 要求x0,y0单调；x, y可取为矩阵, 或x取行向量, y取为列向量, x,y的值分别不能超出x0,y0的范围。
2.分段线性插值与计算量与n无关;n越大, 误差越小.
3.三次样条插值比分段线性插值更光滑。
4.‘linear’ : 分段线性插值；‘spline’ : 三次样条
二、实验内容
问题1 对函数, x([-5,5], 分别用分段线性插值和三次样条插值作插值（其中插值节点不少于20）, 并分别作出每种插值方法的误差曲线.
1180 1320 1450 1420 1400 1300 700 900];
mesh(x,y,z)
xi=0:20:2800;
yi=0:20:2400;
zi=interp2(x,y,z,xi',yi,'cubic');
mesh(xi,yi,zi)
3.结果
4.结论及分析
通过实验,结果正确,分析无误。
三、实验小结
1270 1500 1200 1100 1350 1450 1200 1150
1230 1390 1500 1500 1400 900 1100 1060
1180 1320 1450 1420 1400 1300 700 900
数值分析三次样条插值
0
2
1
n1
1
n2
2 n1
M d 0
MM dd n2 M d 2
1 1 2 2
n1 n1 n n
di f xi2, xi1, xi
华长生制作
7
2、 三弯矩构造法
三次样条插值函数 S( x) 可以有多种表达式，有时用二阶导数
值S( xi) Mi (i 0,1,, n)
Mi
xi
表示时，使用更方便。 在力学上解释
为细M梁i 在 S处( x的) 弯矩，并且得到的弯矩与相邻两个弯矩有关，故
称用由于表S(示x)在区间的算[x法i , x为i三1](弯i 矩0,算1,法,。n 1) 上是三次多项式，
hn
n1 3
Mn
f
x0 , x1 f
xn1, xn
其中
0
h1 h1h n
1
0 ,
hn , 0 hnh0
d1
6(
f
[
x
,
0
x1]
f
x[ , n1
x
n])(h1
h
n)
1
.
可解出 M i (i 0,1,, n) ，方程组的矩阵形式为
2
hi
min hi
,M4
max x[a,b]
f (4) (x)
1in
华长生制作
16
精品课件！
精品课件！
可见S(x), S(x)和S(x)在[a,b]上一致收敛到f (x), f (x)和f (x)
数值计算方法(三次样条插值)
(1 ) 输入插值点 u ;
( 2 ) 对于 j 1 , 2 ,..., n 做
如果
u
x
则计算
j
A1, A2 , B1, B 2;
v A 1 f j 1 A 2 f j B 1 f j 1 B 2 f j;
s( xn 0) s( xn 0)
精品
三次样条插值
用三弯矩阵构造三次条样插值函数
（1）s( x j ) f ( x j ) ( j 0,1,2,... n); (2) 在每个小区间 [ x j1, x j ]( j 1,2,..., n)上 s( x)是不超过
三次多项式； (3) 在开区间（ a, b）上 s( x)有连续的二阶导数 ,
则称 s( x)为区间 [a, b]对应于划分 的三次样条函数。 精品
y j1
x x j1 x j x j1
yj
y j1 (x x j1)(y j y j1) /(x j x j1)
精品
分段线性插值
算法： 1 .输入 x i , y i ( i 0 ,1 ,..., n ) 2 .按 k 1 , 2 ,..., m 做
(1) 输入插值点 u
(2) 对于 j 1,2,..., n 做
如果
u
x
则
j
精品
分段线性插值
1 0 v y j 1 ( u x j 1 )( y j y j 1 ) /( x j x j 1 )
2 0 输出 u , v
分段插值函数
I1 ( x )
I(x)
I2(x)
I
n
计算方法分段线性_三次样条插值
计算方法分段线性_三次样条插值分段线性和三次样条插值是两种常用的插值方法，在数值分析和插值问题中广泛使用。
1.分段线性插值分段线性插值是一种简单直观的插值方法，将插值区间划分为若干个子区间，在每个子区间上用线性函数进行插值。
假设给定的插值节点有n+1 个，节点为 (x0, y0), (x1, y1), ..., (xn, yn)，并且满足 x0 <x1 < ... < xn。
则对于任意 xx 使得 x 在 [xi, xi+1] 之间，可以通过线性插值得到其函数值 yy，即：yy = yi + (xx - xi) * (yi+1 - yi) / (xi+1 - xi)分段线性插值方法简单易懂，适用于一些较简单的插值问题。
但是由于插值函数在节点之间是线性的，可能不能准确地反映出数据的特征，因此不适用于一些需要高精度的插值问题。
三次样条插值是一种更复杂、更精确的插值方法，将插值区间划分为若干个子区间，在每个子区间上用三次多项式进行插值。
三次样条插值方法的基本思想是找到一组三次多项式，满足在每个子区间内插值点的函数值和一阶导数值相等，并且两个相邻多项式在节点处的二阶导数值也相等。
具体的求解步骤如下：(1) 假设有 n+1 个插值节点 (x0, y0), (x1, y1), ..., (xn, yn)，构造 n 个三次多项式，即每个多项式在 [xi, xi+1] 之间插值。
(2) 对每个子区间内的多项式进行插值，设第 i 个子区间的多项式为 Si(x) = ai + bi(x-xi) + ci(x-xi)^2 + di(x-xi)^3、将插值节点的函数值和一阶导数值代入多项式中，可以得到 n 个线性方程，利用这 n 个线性方程可以求解出 n 个子区间的系数。
(3)由于n个子区间的多项式必须在节点处一阶导数值相等，因此再设立n-1个方程，利用这些方程可以求解出n-1个子区间的二阶导数值。
(4)将求解得到的系数和二阶导数值代入每个子区间的多项式中，得到完整的三次样条插值函数。
三次样条插值算法详解
三次样条插值算法要求数据点数量较多，且在某些情况下可能存在数值不稳定性，如数据 点过多或数据点分布不均等情况。此外，该算法对于离散数据点的拟合效果可能不如其他 插值方法。
对未来研究的展望
01
02
03
改进算法稳定性
针对数值不稳定性问题， 未来研究可以探索改进算 法的数值稳定性，提高算 法的鲁棒性。
3
数据转换
对数据进行必要的转换，如标准化、归一化等， 以适应算法需求。
构建插值函数
确定插值节点
根据数据点确定插值节点，确保插值函数在节点处连续且光滑。
构造插值多项式
根据节点和数据点，构造三次多项式作为插值函数。
确定边界条件
根据实际情况确定插值函数的边界条件，如周期性、对称性等。
求解插值函数
求解线性方程组
06
结论
三次样条插值算法总结
适用性
三次样条插值算法适用于各种连续、光滑、可微的分段函数插值问题，尤其在处理具有复 杂变化趋势的数据时表现出色。
优点
该算法能够保证插值函数在分段连接处连续且具有二阶导数，从而在插值过程中保持数据 的平滑性和连续性。此外，三次样条插值算法具有简单、易实现的特点，且计算效率较高 。
根据数据点的数量和分布，合理分段，确保 拟合的精度和连续性。
求解线性方程组
使用高效的方法求解线性方程组，如高斯消 元法或迭代法。
结果输出
输出拟合得到的插值函数，以及相关的误差 分析和图表。
03
三次样条插值算法步骤
数据准备
1 2
数据收集
收集需要插值的原始数据点，确保数据准确可靠。
数据清洗
对数据进行预处理，如去除异常值、缺失值处理 等。
几种常用的插值方法
几种常用的插值方法数学系信息与计算科学1班平指导老师：唐振先摘要:插值在诸如机械加工等工程技术和数据处理等科学研究中有许多直接的应用,在很多领域都要用插值的办法找出表格和中间值,插值还是数值积分微分方程数值解等数值计算的基础。
本文归纳了几种常用的插值方法,并简单分析了其各自的优缺点。
关键词:任意阶多项式插值,分段多项式插值。
引言:所谓插值,通俗地说就是在若干以知的函数值之间插入一些未知函数值,而插值函数的类型最简单的选取是代数多项式。
用多项式建立插值函数的方法主要用两种：一种是任意阶的插值多项式,它主要有三种基本的插值公式：单项式,拉格朗日和牛顿插值；另一种是分段多项式插值,它有Hermite和spine插值和分段线性插值。
一．任意阶多项式插值：1.用单项式基本插值公式进行多项式插值：多项式插值是求通过几个已知数据点的那个n-1阶多项式,即P n-1(X)=A1+A2X+…A n X n-1,它是一个单项式基本函数X0,X1…X n-1的集合来定义多项式,由已知n个点（X,Y）构成的集合,可以使多项式通过没数据点,并为n个未知系数Ai写出n个方程,这n个方程组成的方程组的系数矩阵为Vandermonde 矩阵。
虽然这个过程直观易懂,但它都不是建立插值多项式最好的办法,因为Vandermonde方程组有可能是病态的,这样会导致单项式系数不确定。
另外,单项式中的各项可能在大小上有很大的差异,这就导致了多项式计算中的舍入误差。
2.拉格朗日基本插值公式进行插值：先构造一组插值函数L i （x ）=011011()()()()()()()()i i n i i i i i i n x x x x x x x x x x x x x x x x -+-+--------，其中i=0，…n.容易看出n 次多项式L i （x ）满足L i （x ）=1，（i=j ）；L i （x ）=0，（i ≠j ），其中i=0，1…n ，令L i （x ）=0()ni i i y l x =∑这就是拉格朗日插值多项式。
插值算法——精选推荐
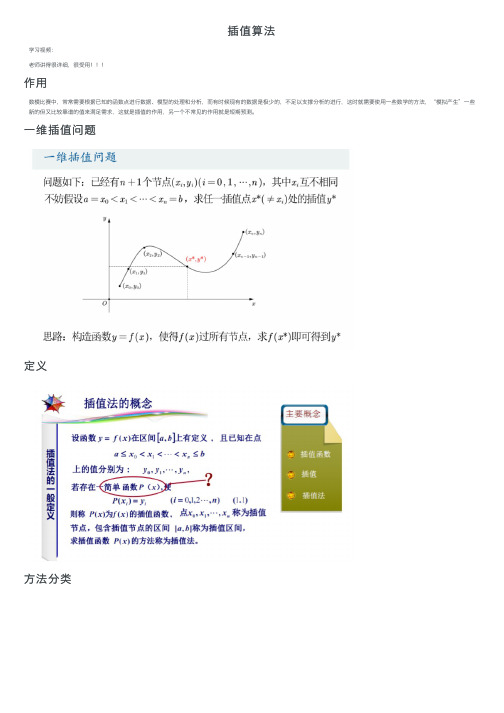
插值算法学习视频：⽼师讲得很详细，很受⽤！！！作⽤数模⽐赛中，常常需要根据已知的函数点进⾏数据、模型的处理和分析，⽽有时候现有的数据是极少的，不⾜以⽀撑分析的进⾏，这时就需要使⽤⼀些数学的⽅法，“模拟产⽣”⼀些新的但⼜⽐较靠谱的值来满⾜需求，这就是插值的作⽤，另⼀个不常见的作⽤就是短期预测。
⼀维插值问题定义⽅法分类本⽂重点介绍数学建模常⽤的两种⽅法：三次样条插值和分段三次埃尔⽶特插值插值多项式原理拉格朗⽇插值法⽅法主要有拉格朗⽇插值法，具体不介绍，它会出现龙波现象（在两端处波动极⼤,产⽣明显的震荡）。
但觉得可以出⼀个ACM题。
分段线性插值插值多项式次数⾼精度未必显著提⾼插值多项式次数越⾼摄⼊误差可能显著增⼤如何提⾼插值精度呢采⽤分段低次插值是⼀种办法概念⽜顿插值法评价与拉格朗⽇插值法相⽐，⽜顿插 值法的计算过程具有继承性。
（⽜顿插值法每次插值只和前n项 的值有关，这样每次只要在原来 的函数上添加新的项，就能够产 ⽣新的函数） 但是⽜顿插值也存在龙格现象的 问题。
致命缺点上⾯讲的两种插值仅仅要求插值多项式在插值节点处与被插函数有相等的函数值，⽽这种插值多项式却不能全⾯反映被插值函数的性态。
然⽽在许多实际问题中，不仅要求插值函数与被插值函数在所有节点处有相同的函数值，它也需要在⼀个或全部节点上插值多项式与被插函数有相同的低阶甚⾄⾼阶的导数值。
对于这些情况，拉格朗⽇插值和⽜顿插值都不能满⾜埃尔⽶特(Hermite)插值概念保持播值曲线在节点处有切线（光滑），使插值函数和被插函数的密和程度更好。
不但要求在节点上的函数值相等，⽽且还要求对应的导数值也相等,甚⾄要求 ⾼阶导数也相等，满⾜这种要求的插值多项式就是埃尔⽶特插值多项式。
缺点与改进直接使⽤Hermite插值得到的多项式次数较⾼，也存在着龙格现象， 因此在实际应⽤中，往往使⽤分段三次Hermite插值多项式(PCHIP)。
Matlab有内置的函数（实现过程已经帮我们封装好了，会调⽤就⾏了）： p = pchip(x,y,new_x)x是已知的样本点的横坐标;y是已知的样本点的纵坐标;new_x是要插⼊处对应的横坐标三次样条插值Matlab有内置的函数： p = spline(x,y,new_x)x是已知的样本点的横坐标;y是已知的样本点的纵坐标;new_x是要插⼊处对应的横坐标代码% 分段三次埃尔⽶特插值x = -pi:pi; y = sin(x);new_x = -pi:0.1:pi;p = pchip(x,y,new_x);figure(1); % 在同⼀个脚本⽂件⾥⾯，要想画多个图，需要给每个图编号，否则只会显⽰最后⼀个图哦~plot(x, y, 'o', new_x, p, 'r-')% plot函数⽤法:% plot(x1,y1,x2,y2)% 线⽅式： - 实线 :点线 -. 虚点线 - - 波折线% 点⽅式： . 圆点 +加号 * 星号 x x形 o ⼩圆% 颜⾊： y黄； r红； g绿； b蓝； w⽩； k⿊； m紫； c青% 三次样条插值和分段三次埃尔⽶特插值的对⽐x = -pi:pi;y = sin(x);new_x = -pi:0.1:pi;p1 = pchip(x,y,new_x); %分段三次埃尔⽶特插值p2 = spline(x,y,new_x); %三次样条插值figure(2);plot(x,y,'o',new_x,p1,'r-',new_x,p2,'b-')legend('样本点','三次埃尔⽶特插值','三次样条插值','Location','SouthEast') %标注显⽰在东南⽅向% 说明：% LEGEND(string1,string2,string3, …)% 分别将字符串1、字符串2、字符串3……标注到图中，每个字符串对应的图标为画图时的图标。