关于举办第十届高中数学夏令营暨
丘成桐中学生数学夏令营好吗

丘成桐中学生数学夏令营好吗
丘成桐中学生数学夏令营好不好?如果你是一个对数学有兴趣
的学生,那么这个夏令营对你来说肯定是非常好的选择。
首先,丘成桐中学生数学夏令营是由国际著名数学家丘成桐教授亲自领导的,这意味着你将有机会接受顶尖数学家的指导和教育,深入了解数学的本质和精髓。
其次,夏令营的课程设置非常丰富,包括数学思维、数学分析、代数学和几何学等多个领域,内容涵盖了初中到高中各个年级的数学知识点和技能。
此外,夏令营还会组织各种有趣的活动和交流,让你认识来自不同地区和学校的同龄人,并且在互相竞争和合作中不断提升自己的数学水平和能力。
总之,丘成桐中学生数学夏令营是一个非常好的学术交流平台,可以让你在短时间内学到更多的数学知识和技能,同时还有机会结交志同道合的朋友,拓宽自己的眼界和视野。
- 1 -。
第11届陈省身全国高中数学夏令营

第11届陈省身全国高中数学夏令营陈省身全国高中数学夏令营,在《中等数学》编辑部的支持下,已经连续举办了十届,全国中学生数学冬令营赛前集训也已成功举办了十次,广受参与者的好评,成绩斐然。
为帮助广大学子备战2021年全国高中数学联赛,将于2021年7月在天津市分别举办以下活动:(1) 第十一届陈省身全国高中数学夏令营(简称“数学夏令营”)以全国高中数学联赛大纲规定的内容为重点,讲解知识要点,释疑学习难点,透析联赛考试重点,精讲方法技巧,为中学生的数学学习排疑解难。
(2) 2021年数学奥林匹克教练员培训班(简称“培训班”)由陈省身数学周组织委员会制订教学计划。
凡认真参加学习、考试合格的学员,将颁发“陈省身杯数学奥林匹克教练员证书”。
现将有关事宜通知如下:活动时间:2021年7月18日全天报到,7月19日至7月28日授课。
一、二、授课教师:数学竞赛专家(《中等数学》编委)三、活动对象:数学夏令营针对高中学生,培训班针对中学教师四、培训费用:数学夏令营4800元/人,培训班3800元/人(含证书工本费),食宿费用自理。
五、报名方式:可以学校为单位统一由带队老师发送邮件向联系人报名,同时也接纳个人 报名。
请与组委会人员联系后填写报名表,于2021年7月1日前将报名表发送至邮箱cijhh@,并缴纳全额学费,汇款时请备注学生姓名,并电话或微信通告知组委会人员。
六、联系方式:李老师131****3520(微信)王老师185****2290(微信)七、咨询地址:天津市和平区建设路78号科学会堂301室“陈省身数学周”组织委员会天津市和平区英才培训学校有限公司2021年5月中等数学数学竞赛的必胜宝典天津师范大学、天津市数学学会主办■针对性强:全国专门从事数学竞赛辅导、指导的刊物■权威性高:与权威机构联合主办,全国著名奥赛专家亲自撰稿■资料齐全:囊括各地及多国竞赛试题,荟萃参赛经验、技巧■栏目多样:数学活动课程讲座、命题与解题、学生习作、竞赛之窗、课外训练等《中等数学》每年12期,每月12曰出版,大16开48觅,每期定价8元,邮发代号:6-75地址:天津市河西区吴家窑大街57号增1号电话:022 -23540118 158****1163。
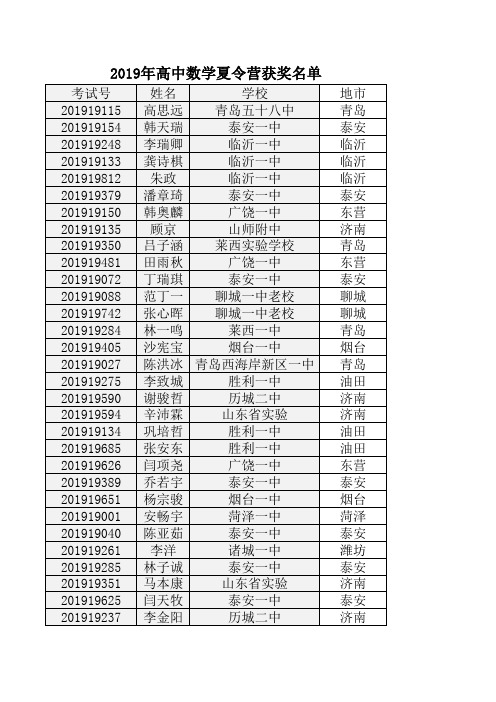
2019年高中数学夏令营获奖名单
赵奕杰
历城二中
胡玉帅
临邑一中
解文浩
五莲一中
李青天
广饶一中
宋佳昕 济宁孔子国际学校
谭金生
烟台二中
王圣远 烟台开发区高级中学
王仝
东平高级中学
王子豪
泰安一中
吴明轩
郓城一中
袁朔星 烟台开发区高级中学
张瑞哲
山东省实验
张阳
山师附中
赵嘉宁
日照一中
邹清源
威海二中
董保国
庆云一中
郝钰涵
禹城一中
焦方亮
临沂一中
刘福龙
城阳一中
201919779 201919176 201919206 201919247 201919426 201919470 201919527 201919532 201919555 201919569 201919676 201919729 201919747 201919768 201919817 201919077 201919160 201919202 201919292 201919323 201919520 201919062 201919209 201919353 201919371 201919382 201919384 201919414 201919425 201919447 201919498 201919559 201919579 201919605
潍坊 青岛 临沂 枣庄 济南 临沂 济南 青岛 临沂 东营 济南 临沂 东营 烟台 济南 枣庄 临沂 临沂 德州 青岛 济南 济南 菏泽 烟台 烟台 济南 东营 济南 枣庄 青岛 青岛 临沂 泰安 烟台
201919637 201919005 201919172 201919295 201919409 201919652 201919686 201919778 201919108 201919751 201919002 201919238 201919322 201919505 201919576 201919121 201919141 201919318 201919418 201919509 201919538 201919561 201919774 201919663 201919026 201919074 201919102 201919152 201919531 201919698 201919785 201919117 201919213 201919217
有关夏令营活动方案6篇

有关夏令营活动方案6篇夏令营活动方案篇1夏令营宗旨和目的:培养兴趣、发展特长、弥补差弱一、艺术实践路线选择湖南湘西凤凰古镇二、艺术实践设计思想培养学生画、看、听、行、说、写等方面综合能力三、艺术实践设计形式以学生美术专业课程形式设计,以学生走进社会走进自然为训练途径,以各景点和活动场所为校外课堂。
四、代收费用每人850元(含往返交通费、导游费、餐饮费、住宿费、各景点门票费、照相费)五、湖南湘西凤凰古镇实践活动内容及时间安排第一天:参加活动的全体学员于12:30在画中颜画室集合,进行安全知识学习,下午13:00从黄冈出发,15:30到达武汉火车站(2159次武昌17:08分发车,06:10分怀化站下),在火车上组织学员进行团队交流活动。
晚上住火车上。
第二天:火车早上6:10抵达湖南怀化站,学员进早餐,8点乘汽车去凤凰古镇,10点半到达目的,安排住宿。
中午在宿舍休息,整理内务,进中餐。
下午在凤凰古镇写生.(沈从文故居北门城楼回龙阁吊脚楼)晚上赏古镇夜景,品古镇小吃,在沱江旁放“许愿船”.第三天:上午继续在凤凰古镇写生,参观当地的民族工艺品(苗族银饰,苗族刺绣,苗族剪纸,蜡染,扎染,纸扎.织花带,木雕)请民族工艺扎染大师,讲解印染工艺。
中午进餐,午休一小时.下午坐沱江泛舟到桃花岛,沿途进行做画.第四天:游黄丝桥古城景区在离县城25公里处的苗区,有一座完整的石头城。
第五天:前往富有民族特色的山江苗人谷,了解苗人当地的生活环境和习性,进行风景、人物作画.晚上和苗族居民一起进行篝火晚会.第六天:参观文人沈从文故居.下午出发准备从凤凰坐车到吉首,傍晚做火车回武汉第七天:早上到达武汉,坐汽车回到黄冈.校外课堂:1、看:了解湘西历史和文化,了解少数民族生活,民族工艺,民族艺术特点。
2、画:特色建筑,民族人物、服饰,风景名胜。
3、行:积极主动参与团队活动,团结友爱,互相帮助,自己动手,生活自理。
4、照:用相机拍下风景名胜,拍下同学们集体活动欢乐和幸福的照片。
浙江省A9协作体2025届2024年8月高三年级八月暑期返校联考数学试卷答案

浙江省A9协作体暑假返校联考高三数学参考答案一、单选题:本题共8小题,每小题5分,共40分,在每小题给出的四个选项中,只有一项是符合题目要求的。
1.答案:A.【解析】因为A={x|x>0},B={x|0≤x≤1},所以,A∩B={x|D<x≤1},故选A.所以Z =1+2i ,2.答案: C.【解析】因为=F √F +2²=√5,故选C .3.答案:D.【解析】因为(2a-b)⊥a ,所以(2a-b)a=0,则(2a-b)a=3×1+(4-m)×2=0,所故选D .4.答案, B.【解析】因为所以故选B5.答案:A.【解析】因为函数y=2²-a-在区间(1.+z)上单调递增,所以y=x²-ax+1在(1.+z)上单调递增,则即a ≤2,故选A .6.答案:B.【解析】画出函数在同一坐标系内画出图象,图象在区间[-π,π]因为,所以以1。
上有三个不同的交点。
即方程有三个不同的根.故选B.7.答案:C.【解析】设圆柱的底面半径为r,高为h,由则h =2-2r ,所以V=πr²h=2πr²(1-r),因为V(r)=-2π(3r²-2r),令V (r)=0,则所以故选C .8.答案: D.【解析】由f(8)=1逆推得,f (8)=1→f (7)=2→f (6)=4→f (5)=8→f (4)=16→f (3)=32→f (2)=64→f (1)=128;f (8)=1→f (7)=2→f (6)=4→f (5)=8→f (4)=16→f (3)=32→f (2)=64→f (I )=21:f (8)=1→f (7)=2→f (6)=4→f (5)=8→f (4)=16→f (3)=5→f (2)=10→f (d )=20;f(8)=1→f(7)=2→f(6)=4→f(5)=8→ʃ(4)=16→f(3)=5→f(2)=10→f(1)=3;f(8)=1→f(7)=2→f(6)=4→f(5)=1→f(4)=2→f(3)=4→f(2)=8→f(d)=16;f(8)=1→f(7)=2→f(6)=4→f(5)=1→ʃ(4)=2→f(3)=4→f(2)=1→f(I)=2.所以,f(4)≤16.故选D.二、多选题:本题共3小题,每题6分,共18分,在每小题给出的四个选项中,有多项是符合题目要求,全部选对得6分,部分选对分别记0分、2分、4分或0分、3分,有选错的得0分。
夏令营教授推荐信11篇

夏令营教授推荐信11篇夏令营教授推荐信1尊敬的__大学的领导:你们好!很高兴能以这样的方式向你们推荐我最优秀的学生张爽,作为班主任,把优秀的学生推荐给优秀的大学是我义不容辞的责任。
希望我的这封推荐信能够帮你们更多更好的了解张爽同学,同时也能够使张爽同学进入北京大学的夏令营得到锻炼。
张爽同学是以河间市中考第一的成绩进入我班的。
当时他刚刚进入高中,踌躇满志,意气风发,高中生活把他打造成了意志坚强、底蕴深厚、成熟内敛、热爱生活,有爱心、同情心、上进心,具备优秀的思维品格、超强的学习能力的优秀高中生。
她热爱生活,富有爱心。
我认为,一个优秀人才,首先应是热爱生活的,对生活和未来充满希望、信心和勇气,张爽同学就是这样。
他富有爱心,曾为失学的同学竭尽全力,为遭遇不幸的同学无私捐助,多次参与班级、学校组织的爱心活动。
作为班里的数学课代表,学习委员,她长期耐心的帮助学习较差的几个同学,不惜耽误自己的学习时间,使这几个同学的成绩有较大的提高。
她自主学习能力很强,除了学好日常各门功课外,利用很多业余时间参加了生物、物理、英语、作文竞赛,曾获得全国中学生语文能力大赛二等奖,迎奥运作文大赛二等奖,中学生英语能力竞赛二等奖,希望杯数学竞赛一等奖。
她热爱读书,读文学、读历史、读哲学,不断的从中西先贤那里汲取智慧和思想,这在今天的理科生中实属罕见,因为博览,所以全面。
因为勤奋,所以突出,她多次被评为年级学习之星,校园学习之星,多次获得学校一等奖学金。
该同学有着年轻人的热情和朝气,有着广泛的爱好和兴趣。
演讲比赛,她显示出主持人的睿智和风采,博得阵阵掌声;文艺汇演,动听的英文歌曲,让同学们啧啧称赞;吉他弹奏,绘画,更显出她的才气。
我相信,有全面的素质和扎实的功底,加上大学的.宽松环境,张爽同学必将具有良好的发展前景。
因此,我完全有理由相信他将成为优秀乃至杰出人才,并郑重向贵校推荐,希望贵校给他以机会,让她参加北京大学的夏令营活动。
夏令营活动策划方案

夏令营活动策划方案夏令营活动策划方案 1一、夏令营介绍夏令营活动通过全方位,立体化,直观性的夏令营交流活动,使学生快乐、收获、健康。
通过多元训练提升营员的思想品德教育等各方面的综合素质:通过组织丰富多彩的益智游戏,强调对营员体能和技能的训练,锻炼营员动手、动脑能力;培养营员坚强、独立自主的品质和良好的团队合作意识;引导营员树立敢面对困难和战胜困难的自信心;帮助营员戒除不良行为,矫正心理偏差,架起父母和子女心灵沟通的金桥。
内容丰富的活动,进一步丰富营员生活的同时,能让每个营员在活动中都有所收益。
通过拓展训练,营员不断磨练战胜困难的毅力,在克服心理惰性的同时认识自身潜能,增强自信心。
同时增进对集体的参与意识与责任心,改善人际关系,学会关心,更为融洽地参与群体合作,提高团队合作精神。
学会欣赏、关注和爱护大自然,启发想象力与创造力,提高解决问题的能力,从而更进一步的促进学生的全面发展。
“在这里,平凡的孩子将变得优秀,优秀的孩子将成为精英”,让他们收获一个有汗水,有泪水,有快乐,有思想的假期。
二、夏令营特色名师授课,求知健心形式多样多元技能三、夏令营主题健康运动阳光未来四、夏令营活动基地东街口营地五、承、主办单位主办单位: ____承办单位:____六、参加对象和名额5--12岁之间的小朋友七、营员条件1、对夏令营活动感兴趣的2、有一定纪律性家长支持的八、活动时间7月初—8月底(具体时间待定)九、相关事项收费元/人证书:在活动结束之后为营员颁发训练营结业证书。
膳食:专业配餐,实行分餐制。
赠送物品:营服一套,营帽及胸牌,教师、营员通讯录,全体师生合影夏令营活动策划方案 2一、夏令营目的暑假为期两个月,为了丰富学生假期生活,增长学生知识,锻炼学生才干,发展学生个性,让孩子在漫长的暑期有一个释放身心、开心学习、拓展视野、发展特长的新天地,我校充分利用优质师资资源,积极创设活动载体,组织同学们开展暑期夏令营活动,以精心设计的文化课程、特长课程,结合校外活动,让学生在夏令营活动中健康快乐学有所获。
高中夏令营活动方案

高中夏令营活动方案夏令营是让学生度过一个充实而有趣的暑假的好机会,也是学生们展现才能和锻炼自己的平台。
为了提供一份完善的高中夏令营活动方案,以下是一个详细的计划。
一、活动目标该夏令营的目标是通过学习、互动和体验,帮助学生全面发展他们的技能和兴趣,加强他们的交流能力和团队合作,培养他们的领导才能。
二、活动时间和地点1. 时间:夏季学校假期,持续为期两周。
2. 地点:选择安全、有足够活动空间的校园或度假村。
三、活动内容1. 学术课程为了提高学生的学习能力和挑战他们的思维,我们将提供以下学术课程:- 数学:提供数学竞赛、数论和几何等课程,鼓励学生解决复杂的数学问题。
- 科学:开设实验室课程,让学生亲自进行实验和研究,培养他们的科学精神。
- 文学:组织读书讨论会和写作比赛,激发学生的文学创造力和表达能力。
2. 手工艺和技能培训为了培养学生的动手能力和创造力,我们将提供以下手工艺和技能培训:- 绘画和雕塑:举办艺术工作坊,教授学生绘画和雕塑技巧,展示他们的艺术天赋。
- 音乐和舞蹈:组织音乐和舞蹈课程,培养学生的音乐才能和表演技巧。
- 烹饪和餐饮:开设烹饪班,学生可以学习烹饪技巧和餐饮管理知识,培养他们的厨艺。
3. 团队合作和领导力培养为了提高学生的团队合作和领导能力,我们将提供以下活动:- 团队游戏和挑战:组织各种团队游戏和挑战,让学生通过合作解决问题。
- 演讲和辩论:组织演讲和辩论比赛,锻炼学生的演讲技巧和逻辑思维能力。
- 社区服务项目:安排学生参与社区服务活动,培养他们的社会责任感和领导才能。
四、活动安排1. 每天安排5-6个小时的课程和活动,包括学术课程、手工艺和技能培训、团队合作和领导力培养。
2. 设计休息时间,确保学生有足够的休息和放松。
3. 安排文化交流活动,让学生了解不同文化背景的人并促进他们之间的交流和理解。
五、活动费用1. 活动费用包括住宿、膳食、课程和活动费用。
2. 提供奖学金计划,确保每个学生都有机会参加夏令营活动。
内部控制审计评价实施办法1.doc

内部控制审计评价实施办法1 内部控制审计评价实施办法第一章总则第一条:为了加强XXXX公司(以下简称公司)的内部控制,促使公司内部各项管理制度化、程序化、规范化,保证公司的经营活动高效有序进行,保护国有资产的安全与完整,确保实现公司的经营目标,依据《公司审计制度》第四条的规定,制定本办法。
第二条:本办法所称内部控制,是指公司内部为实现经营目标,保护资产完整,保证对国家法律法规的遵循,提高经济运行的效率及效果,而采取的各种措施和程序。
第三条:公司依据审计署关于《内部审计工作的规定》,对内部控制实行审计监督。
公司直属各部门、各单位管理职能的健全性、合规性、有效性及控股子公司内部控制的有效性,依照公司《审计制度》接受审计监督。
公司审计机构(以下简称审计机构)依照公司各项管理制度和各部门、各单位的工作职责对内部控制实施情况进行审计监督。
第四条:审计机构依据相关制度在职权范围内对公司各部门、各单位及控股子公司的内部控制实施情况作出审计评价。
第二章内部控制审计评价的内容第五条:审计机构对货币资金内部控制实施情况审计评价的内容有:(一)、出纳和会计的职责是否严格分离,库存现金是否严格遵守金融部门规定的限额。
现金日记帐是否序时登记,现金是否按规定的范围内使用;(二)、是否设有“小金库”有无白条抵库现象,会计主管是否定期审核现金日级帐;(三)、银行帐户的开设是否符合有关规定,银行存款日记帐是否按银行帐户分别设置;(四)、银行存款日记帐是否逐笔序时登记,是否定期编制银行存款余额调节表;(五)、是否制定了货币资金管理办法,重大开支项目是否建立“双签”制;(六)、银行帐户是否存在对外出租、出借的情况。
第六条:审计机构对存货内部控制实施情况审计评价的内容有:(一)、物资处、工具处、生产部等物资主管部门是否制定了完整的物资管理办法;(二)、仓储部门在收到原材料、工具、外购外协件时,是否对其数量进行验点,并同收货报告单进行核对;(三)、生产单位在领用原材料、工具、外购外协件时,物资、生产部门是否严格按定额发放,对超定额发放或领用有无追责制;(四)、物资主管部门是否存在库存物资超储积压、损坏、变质、长期滞呆等情况,对待报废的物资是否及时申请报废处理;(五)、生产单位对未消耗的原材料、工具、外购外协件等物资,是否按机台结存管理,是否月按编报原材料结存表,原材料成本核算是否真实准确,;(六)、物资主管部门对库存物资是否定期进行盘点,帐与帐、帐与实物是否相符。
北大数学夏令营获奖名单公示

北大数学夏令营获奖名单公示
摘要:
1.引言
2.北大数学夏令营的基本信息
3.获奖名单的公示时间和方式
4.获奖学生的优秀表现
5.北大数学夏令营的意义和影响
6.结束语
正文:
北大数学夏令营获奖名单公示
近日,北京大学数学科学学院公示了2022 年数学夏令营获奖名单。
本次夏令营吸引了全国各地众多优秀高中生参加,旨在选拔和培养数学拔尖人才。
经过激烈的竞争和严格的选拔,共有50 名学生脱颖而出,获得了奖项。
2022 年北大数学夏令营自7 月初开营,持续了两周时间。
在这期间,学生们接受了来自国内外知名数学专家的授课,课程涵盖了数学分析、高等代数、概率论与数理统计等多个领域。
此外,学生们还参加了丰富的课外活动,如小组讨论、数学建模竞赛等。
获奖名单的公示时间为8 月1 日至8 月7 日,公示方式包括在北大数学科学学院官方网站上发布以及通过邮件通知获奖学生。
所有获奖学生都将获得一定程度的奖学金资助,用于支持他们在未来学术道路上持续发展。
本次夏令营的获奖学生表现优异,他们在各个课程和活动中都展示出了扎
实的数学功底和出色的学术能力。
在接下来的学习生涯中,他们将继续努力,为我国数学事业的发展贡献力量。
北大数学夏令营作为选拔和培养数学人才的重要平台,对于激发学生对数学的兴趣、提高学生数学素养、培养数学拔尖人才具有重要的意义。
希望获奖的学生能够珍惜这次荣誉,继续努力,为我国数学事业的繁荣做出更大的贡献。
至此,2022 年北大数学夏令营圆满落幕。
2024年浙江高中数学夏令营测试题参考答案

2024年浙江数学夏令营测试题参考答案(本试卷共20道填空题,每题5分,总分满分100分)1. 已知集合A ={x|y =√x −2},B ={x|x 2−9x +8≤0},则A ∩B = 。
答案 {x ∣2≤x ≤8}2. 设x,y ∈R ,且√2−siny=2√3−3cosy=1,则cos (x −y )= 。
答案 233. 已知复数z 1,z 2满足|z 1|=|z 2|=1,|z 1+z 2|=√3,则|z 1−2z 2|= 。
答案 √34. 已知点M (1,2),过点N (−2,0)的直线与抛物线y 2=4x 相切于A ,则△MAN 为面积的最大值为 。
【答案】4+3√25. 实数x,y 满足x 2+(y −2)2≤1,则√3y √x 2+y 2的取值范围为 。
答案 [1,2] 【解】√3y √x 2+y 2=√x 2+2√3xy+3y 2x 2+y 2=y 2+√3xyx 2+y 2令t =x y 则√3y√x 2+y 2=√1+2√3t+1t 2+1, 考虑圆面x 2+(y −2)2≤1上的点与原点连线的斜率,可知t =xy ∈[−√33,√33] 所以,原式∈[1,2]当(x,y )=(√32,32)时原式=2 当(x,y )=(−√32,32)时原式=1。
注:最大值也可由柯西不等式直接得到:(x 2+y 2)(1+3)≥(x +√3y)2则√3y√x 2+y 2≤2.6. 已知a k =122k−1+122k−1+1(k ∈N ∗)。
若存在m ∈N ∗,当n ≥m 时恒有∑a k n k=1>20232024,则m 的最小值为 。
答案 4解析 22k−1=(22k−1)2−1, 所以a k =122k −1+122k−1+1=22k−122k −1=(22k−1+1)−1(22k−1−1)(22k−1+1)=122k−1−1−122k−1,所以∑a k n k=1=1−122n−1,由∑a k n k=1>20232024可得22n−1>2024,即22n>2025,即2n ≥11,所以n ≥4,即m 的最小值为4.7. 设点P 是△ABC 的外心,且CP ⃗⃗⃗⃗⃗ =λCA ⃗⃗⃗⃗⃗ +μCB ⃗⃗⃗⃗⃗ ,3λ+4μ=2(λ,μ∈R,λ≠0)。
高中数学竞赛详细流程

高中数学竞赛详细流程
1、初赛。
在每年四月份,高一时自愿报名,高二下学期的3、4月份参加县级初试,在学校报名,学校会动员的,每个县有一定的名额;
2、夏令营训练。
通过初试的同学于高二暑假参加省级比赛,会去某个承办比赛的大学参加夏令营,时间大约会有十天,每天上下午各请一个著名教师或大学教授来讲奥数,夏令营期间还会有一场模拟考试,结果对比赛结果没有影响;
3、省级选拔赛。
夏令营最后一天是省级选拔赛,会有两张卷子,每张各150分,考试时间在两小时左右,中间有休息时间;比赛结果在高三开学的时候出来;
4、省级复试。
晋级的人参加省里的复试,前几名会被保送清华、北大、复旦等名校,还会从中选几人参加国家集训队,每天都会进行考试,不合格的人会被淘汰,最后剩下的人去参加国际奥赛。
2010高中数学夏令营获奖名单

三等奖
胜利一中 潍坊一中 德州一中 莒南一中 夏津一中 胜利一中 聊城一中 青岛五十八中 山师附中 德州一中 胜利一中 济宁一中 昌乐二中 淄博四中
青岛二中 学校 淄博四中
潍坊四中 临沂一中 省实验
杨勐譞 张国军 张建鑫 张杰 张康 张庆 张彤 张文浩 张宇阳 张占磊 赵嘉栋 赵兴红 周浩 朱琳
省实验 历城二中 齐河一中 省实验 莘县实验高中 聊城一中 淄博四中
夏津一中 胶州一中 省实验 省实验 泰西中学 青岛二中 淄博四中
历城二中 烟台二中 山师附中 青岛二中 烟台一中 淄博四中
巩正一 谷珍妮 侯梦昱 黄子腾 姜庆远 姜荣健 李春尧
李建宇 李秋瑞 李睿 李适然 李潇 李雅沁 李悦
李钊 李宗锟 刘春媛 刘嘉平 刘明祖 刘佩增
邹昊源 姓名 白宗磊
蔡言义 陈考杰 崔春婧文
博兴二中 青岛二中 诸城实验
省实验 省实验 寿光现代中学
临沂一中 历城二中 济南外国语
淄博七中 高密一中 省实验中学 省实验 莒南一中 东营一中 省实验 省实验 胶州一中 德州一中 省实验
崔磊 崔正言 邸校东
丁洋 董川泓 方跃财 丰迪生
富豪 公维康
郭寿杰 郭鑫 何玉有 胡大鹏 胡梦娇 黄显铧 姜兴 靳可欣 荆飞 荆昭辉 康子一
章丘四中 省实验 德州一中 胜利一中 胜利一中 潍坊一中 历城二中 潍坊一中 莱芜一中 临朐一中
青岛二中 繁华中学
历城二中 青岛二中 聊城一中 山师附中 临沂一中 淄博四中
日照一中西校 广饶一中
孙跃 孙昭颖 滕亚函 王安邦 王博 王聪 王梦洁 王明玥 王鹏 王仕伟
王守恺 王亚梁
王勇帅 王真 夏新会 徐传祝 许柏宁 许文彬
浙江省数学会

浙江省数学会,英文名称:Zhejiang Mathematical Society;英文缩写:ZMS。
浙江省数学会成立于1951年。
本学会是浙江省数学科学工作者自愿组成并依法登记的学术性、公益性、非营利性的法人社会团体,是发展我省数学科学事业的主要社会力量。
学会业务主管单位是浙江省科学技术协会;在业务上接受中国数学会指导;挂靠单位是浙江大学。
学会的宗旨是团结全省广大数学工作者,为促进数学科学和数学教育的发展,繁荣我省的科教事业,促进科学技术水平的提高和科学技术人才的成长,为加速实现我国社会主义现代化作出贡献。
学会大力发挥学术交流主渠道作用,积极开展各项学术活动,包括与国内外数学界的交流,使学术交流成为推动自主创新的活水源头。
学会十分重视与高等院校,特别是与挂靠单位浙江大学的密切合作,联合开展高层次、高水准的学术研究和学术交流活动,有效地增强了学会的活力和凝聚力。
学会充分发挥各专业委员会的作用,开展丰富多彩的活动。
学会竭诚为会员服务,积极创造条件,营造良好的学术氛围,在教学、科研等方面热心为广大会员搭建学习、交流、提高的平台。
积极为国家悉心培养人才、发现举荐人才、吸引凝聚人才作贡献。
学会积极开展高职院校和中学的数学学科的学术交流活动。
职业教育数学专业委员会坚持每年举办学术报告会和优秀论文评选活动,组织力量编写出版高职数学教材等,对高职院校数学教学的改革和教学质量的提升起到了很好的作用。
中学数学教育专业委员会和普及工作委员会每年联合举办一、两次由省、市教研室数学教研员及部分中学骨干数学教师参加的中学数学研讨会。
研讨中学数学教育的改革与创新;研讨中学数学基础教育与高观点下的课堂教学;研讨数学竞赛以及新课程背景下高中数学特长生的培养,等等。
内容充实,形式新颖,注重理论联系实际。
学会还经常组织高校著名教授、专家到中学为教师或学生作专题讲座,或参与有关地区数学骨干教师的专业培训活动,为广大中学教师介绍当今数学科学的发展情况及有关前沿信息;交流教学、科研等方面的心得等。
三十年教师梦 一辈子育人心——记兰州一中教师崔兴旺

高中数学联赛 中 , 带班 级 2 中 2 进 , 所 6人 4 在业 务上强人一筹 , 能做一 名合 的甘 肃 省 代 表 队 的 集 训 工 作 及 带 队 参 才
人 获 奖 , 中特 等 奖 1 , 等 奖 7人 , 格 的 教 师 。 其 人一
赛 ;第 1 “ 6届全 国青少年信息学 ( 计算
有 三 个 :必须 有 1 的教 学 经验 和一 5年
更是身体力行 。除正常的教学工作外 ,
崔 兴 旺 老 师对 所 教 学 科 具 有 系统 、 他还 积极参与 每年的数学 奥林 匹克活
定积累 , 必须在教书育人 中有 突出的表 坚实的基础理论素养和专业知识 , 熟练 动 。 “ 国小学生数学奥林匹克” 如 全 甘肃 现, 必须在数学教育 的改革发展 中要有 掌握 教育学 、 心理 学和教学 法的基础理 赛区的组织 、 评卷工作 ;甘肃省小学生 “
突 出 的 贡献 。
论 知识 , 积 极参 加甘 肃 省 中 小 学 教 师 数学冬令 营” 并 的命题 、 组织 、 卷工作 ; 评
他 曾担任 兰州一 中五届高 中数学 继续教育学 习, 断提 高 自己。他长期 “ 国 小 学 生 数 学 奥 林 匹 克 夏 令 营 ” 不 全 的 实验班 的班主任 , 一直担任数学竞赛辅 自费订 阅 5种 以上的数学期刊 , 注并 甘肃省代 表队 的选 拔 、 训 , 关 培 受省数 学
导 工作 。 带 的 班 多 次 被评 为学 校 优 秀 掌握本学科教育教学发 展动态 , 他 为了使 会委派 多次率 队参 加全 国中小学数 学
班集体 , 高考成绩和数学竞赛成绩都非 教学 效果更好 ,对其他 学科 的相关 知 奥林 匹克 , 并获得好成绩 ;全国初中数 “
教育部办公厅关于举办第十届全国中学生运动会科学论文报告会暨第五届中国学校体育科学大会的通知

教育部办公厅关于举办第十届全国中学生运动会科学论文报告会暨第五届中国学校体育科学大会的通知文章属性•【制定机关】教育部•【公布日期】2008.06.02•【文号】教体艺厅函[2008]16号•【施行日期】2008.06.02•【效力等级】部门规范性文件•【时效性】现行有效•【主题分类】体育正文教育部办公厅关于举办第十届全国中学生运动会科学论文报告会暨第五届中国学校体育科学大会的通知(2008年6月2日教体艺厅函〔2008〕16号)各省、自治区、直辖市教育厅(教委),新疆生产建设兵团教育局:根据《教育部国家体育总局共青团中央关于举办中华人民共和国第十届中学生运动会的通知》精神,第十届全国中学生运动会科学论文报告会定于2009年8月在湖南省长沙市举行。
经商中国教育学会、中国高等教育学会,第十届全国中学生运动会科报会与第五届学校体育科学大会合并举行。
现将举办会议的有关事宜通知如下:一、指导思想以党的十七大精神为指导,以科学发展观为统领,全面贯彻落实《中共中央国务院关于加强青少年体育增强青少年体质的意见》(中发〔2007〕7号),进一步推动全国亿万学生阳光体育运动的广泛开展,不断提高学生体质健康水平,促进广大学生身心全面发展。
本届科报会的主题是:阳光体育、健康成长。
二、征文原则以《第十届全国中学生运动会科学论文报告会暨第五届中国学校体育科学大会选题指南》(附后)的内容范畴为主,撰写时注重掌握以下原则:1.重点突出。
论文应以研究贯彻落实中央7号文件、保证学生每天锻炼一小时、开展阳光体育运动、提高体育课教学质量等方面的内容为重点。
2.方法科学。
论文研究应正确运用定性研究与定量研究相结合、理论探索与实验研究相结合、总结历史和研究现实与把握未来相结合的方法,努力体现论文的科学性、实用性和时代性。
3.行文规范。
论文应主题鲜明、论据充分、内容充实、格式规范、结构严谨、文字与图表清晰。
4.字数适宜。
每篇论文不超过5000字,并提供不超过600字的论文摘要,每篇论文署名作者不超过5人。
大连市第一中学大事记

大连市第一中学大事记大连市第一中学大事记一九五二年:1、八月二十五日举行建校典礼2、大连第二高级中学与第六初级中学合并成立大连市第一所完全中学,定名为大连中学,冷冉(市教育局中教科科长)兼任校长。
一九五三年1、初中首届毕业生200人4个班。
2、高中市内走读生转第一高中就读。
3、来校插班学习,成为设有二处宿舍的住宿中学。
4、4月大连中学附设业余中学开学。
一九五四年1、高中首届毕业生六个班270名,其中华侨25名,留苏预备生8名。
2、于冶青(旅顺中学校长)来校担任校长。
一九五五年1、9月开设综合技术教育课。
2、和苏联在大连新办中学建立联系,组织观摩,苏联教师上课。
一九五六年1、三月八日同原西岗区朱德路小学合并。
2、改校名为“旅大市大连第一中学”。
3、教育部长董纯才、教育厅长肖文来校视察。
4、学校建立民进支部。
一九五八年1、学生大搞勤工俭学,创建校办工厂。
2、与苏联库叶岛萨哈林斯克中学建立关系,交流学生作品。
一九五九年1、获全国“先进单位”称号。
一九六O年1、自然灾害,学生大搞小秋收活动。
一九六二年1、建校十年大庆。
3、中小学分离,小学部分在原学生宿舍成立大同小学。
4、工厂停产。
一九六四年1、由薛殿琛为教练,带校足球队去青岛参加全国少年足球赛。
2、王明泰为教练的射击队获市射击比赛冠军。
一九六五年1、参加省少年足球表演赛获全胜。
2、射击比赛再获冠军。
一九六六年1、“文化大革命”开始,高考制度被取消,全校停课“闹革命”。
2、工作组进驻学校。
3、成立以付玉敏为主任的文革筹委会。
一九六七年1、学校教师,学生纷纷成立战斗队,进行大串联。
2、军宣队进驻学校。
主任吴玉栋。
一九六八年1、十月动员1963年、1964年、1965年入校的初高中六届毕业生,下乡到丹东市岫岩县黄花甸公社、朝阳公社接受贫下中农的再教育。
2、十月新入学的学生复课闹革命。
3、第一批工宣队进驻学校(石灰石矿厂)。
一九六九年1、九月开始整党。
2、第二批工宣队进驻(大麻厂)。
江苏省南通市如皋中学2024届高三创新实验班夏令营数学试题(含解析)

2024届江苏省如皋中学高三创新实验班夏令营试题数学一、选择题(本题共8小题,每小题5分,共40分.)1.已知集合{}21x A x =>,{}2log 0B x x =<,则AC B =A.()0,1 B.(]0,1 C.()1,+∞ D.[)1,+∞2.已知复数1z ,2z 在复平面内对应的点分别为()1,1-,()0,1,则12z z 的共轭复数为()A.1i +B.1i -+C.1i-- D.1i-3.向量()()1,2,1,0a b ==-,则b 在a上的投影向量是()A .55-B.C.1255⎛⎫-- ⎪⎝⎭,D.1255⎛⎫ ⎪⎝⎭,4.声音的等级()f x (单位:Db )与声音强度x (单位:2W /m )满足()1210lg110xf x -=⨯.火箭发射时,声音的等级约为160dB ;一般噪音时,声音的等级约为90dB ,那么火箭发射时的声音强度约为一般噪音时声音强度的()A.510倍B.610倍C.710倍D.810倍5.已知F 为双曲线22:145x y C -=的左焦点,P 为其右支上一点,点()0,6A -,则APF 周长的最小值为()A.4+B.4+C.6+D.6+6.已知()00,P x y 是:40l x y -+=上一点,过点P 作圆22:5O x y +=的两条切线,切点分别为,A B ,当直线AB 与l 平行时,AB =()A.B.2C.2D.47.正项等比数列{}n a 的公比为q ,前n 项和为n S ,则“1q >”是“2021202320222S S S +>”的()A.充分不必要条件B.必要不充分条件C.充要条件D.既不充分也不必要条件8.已知sin sin 12αβ-=-,1cos cos 2αβ-=,则()cos αβ-=A. B.12-C.12D.32二、选择题:本题共4小题,每小题5分,共20分.9.下列统计量中,能度量样本12,,,n x x x 的离散程度的是()A.样本12,,,n x x x 的标准差B.样本12,,,n x x x 的中位数C.样本12,,,n x x x 的极差D.样本12,,,n x x x 的平均数10.中国传统文化中很多内容体现了数学的“对称美”,如图所示的太极图是由黑白两个鱼形纹组成的图案,俗称阴阳鱼,太极图展现了一种相互转化,相对统一的和谐美,定义:圆O 的圆心在原点,若函数的图像将圆O 的周长和面积同时等分成两部分,则这个函数称为圆O 的一个“太极函数”,则()A .对于圆O ,其“太极函数”有1个B.函数()()()2200x x x f x x x x ⎧-≥⎪=⎨--<⎪⎩是圆O 的一个“太极函数”C.函数()33f x x x =-不是圆O 的“太极函数”D.函数())lnf x x =+是圆O 的一个“太极函数”11.定义在R 上的函数()f x 满足()()()f x y f x f y +=+,当0x <时,()0f x >,则()f x 满足()A.()00f = B.()y f x =是奇函数C.()f x 在[],m n 上有最大值()f n D.()10f x ->的解集为(),1∞-12.已知异面直线a 与直线b 所成角为60 ,平面α与平面β的夹角为80 ,直线a 与平面α所成的角为15 ,点P 为平面αβ、外一定点,则下列结论正确的是()A.过点P 且与直线a b 、所成角均为30 的直线有3条B.过点P 且与平面αβ、所成角都是30 的直线有4条C.过点P 作与平面α成55 角的直线,可以作无数条D.过点P 作与平面α成55 角,且与直线a 成60 的直线,可以作3条三、填空题:本题共4小题,每小题5分,共20分.13.将6个相同的小球放入4个编号为1,2,3,4的盒子中,,恰有1个空盒子,则放法有___________种.14.已知棱台的上、下底面面积分别为4,16,高为3,则棱台的体积为________.15.已知函数5π()sin cos(),(0)6f x x x ωωω=++>在[0,π]上的值域为[,1]2-,则ω的取值范围为_________.16.已知椭圆()222210x y a b a b+=>>的左焦点为F ,过点F 且倾斜角为45°的直线l 与椭圆交于A ,B 两点(点B 在x 轴上方),且2FB AF =,则椭圆的离心率为___________.四、解答题:本题共6小题,共70分.解答应写出文字说明、证明过程或演算步骤.17.已知函数()ln ()R f x x a x a =-∈(1)求()f x 的极值;(2)若()1f x ≥,求a 的值,并证明:()2.x f x x e >-18.ABC 的内角A ,B ,C 的对边分别为a ,b ,c ,且()sin sin sin b c B c C a A ++=.(1)求角A ;(2)求22sin sin B C +的最小值.19.如图,在正四棱柱1111ABCD A B C D -中,1222AA AB BC ===,M 是棱1CC上任意一点.(1)求证:AM BD ⊥;(2)若M 是棱1CC 的中点,求异面直线AM 与BC 所成角的余弦值.20.已知数列{}n a 中,11a =,()12N 2nn na a n a ++=∈+.(1)求234,,a a a 的值,并猜想数列{}n a 的通项公式;(2)证明数列1n a ⎧⎫⎨⎬⎩⎭是等差数列.21.现代排球赛为5局3胜制,每局25分,决胜局15分.前4局比赛中,一队只有赢得至少25分,并领先对方2分时,才胜1局.在第5局比赛中先获得15分并领先对方2分的一方获胜.在一个回合中,赢的球队获得1分,输的球队不得分,且下一回合的发球权属于获胜方.经过统计,甲、乙两支球队在每一个回合中输赢的情况如下:当甲队拥有发球权时,甲队获胜的概率为23;当乙队拥有发球权时,甲队获胜的概率为12.(1)假设在第1局比赛开始之初,甲队拥有发球权,求甲队在前3个回合中恰好获得2分的概率;(2)当两支球队比拼到第5局时,两支球队至少要进行15个回合,设甲队在第i 个回合拥有发球权的概率为i P .假设在第5局由乙队先开球,求在第15个回合中甲队开球的概率,并判断在此回合中甲、乙两队开球的概率的大小.22.已知双曲线C :()222210,0x y a b a b-=>>的虚轴长为4,直线20x y -=为双曲线C 的一条渐近线.(1)求双曲线C 的标准方程;(2)记双曲线C 的左、右顶点分别为A ,B ,斜率为正的直线l 过点()2,0T ,交双曲线C 于点M ,N (点M 在第一象限),直线MA 交y 轴于点P ,直线NB 交y 轴于点Q ,记PAT 面积为1S ,QBT △面积为2S ,求证:12S S 为定值.2024届江苏省如皋中学高三创新实验班夏令营试题数学一、选择题(本题共8小题,每小题5分,共40分.在每小题给出的四个选项中,只有一项是符合题目要求的.)1.已知集合{}21x A x =>,{}2log 0B x x =<,则A CB =A.()0,1 B.(]0,1 C.()1,+∞ D.[)1,+∞【答案】D 【解析】【分析】通过解指数和对数不等式求得集合A,B ,再利用补集的定义直接求解即可.【详解】{}{}{}{}2210log 001x A x x x B x x x x =>=>=<=<<,,则{}1A C Bx x =≥故选D.【点睛】本题主要考查了指数与对数不等式的求解及集合补集的运算,属于基础题.2.已知复数1z ,2z 在复平面内对应的点分别为()1,1-,()0,1,则12z z 的共轭复数为()A.1i+ B.1i-+ C.1i-- D.1i-【答案】B 【解析】【分析】根据题意11z i =-,2z i =,121z z i z ==--,再计算共轭复数得到答案.【详解】复数1z ,2z 在复平面内对应的点分别为()1,1-,()0,1,故11zi =-,2z i =,()122111i i z i z i z i i ---====---,故1z i =-+.故选:B .【点睛】本题考查了复数的除法,共轭复数,复数对应的点,意在考查学生对于复数知识的综合应用.3.向量()()1,2,1,0a b ==-,则b 在a上的投影向量是()A.5-B.5C.1255⎛⎫-- ⎪⎝⎭, D.1255⎛⎫⎪⎝⎭,【答案】C 【解析】【分析】利用投影向量的定义求解.【详解】解:因为向量()()1,2,1,0a b ==-,所以b 在a 上的投影向量是212,5155a b a a a⎛⎫⋅⋅=--- ⎪=⎝⎭,故选:C 4.声音的等级()f x (单位:Db )与声音强度x (单位:2W /m )满足()1210lg110xf x -=⨯.火箭发射时,声音的等级约为160dB ;一般噪音时,声音的等级约为90dB ,那么火箭发射时的声音强度约为一般噪音时声音强度的()A.510倍B.610倍C.710倍D.810倍【答案】C 【解析】【分析】根据声音的等级()f x (单位:Db )与声音强度x (单位:2W /m )满足()1210lg110x f x -=⨯.分别求得火箭发射时和一般噪音时的声音强度求解.【详解】解:因为火箭发射时,声音的等级约为160dB ,所以11210lg160110x -=⨯,解得4110x =;因为一般噪音时,声音的等级约为90dB ,所以21210lg 90110x -=⨯,解得3210x -=,;所以火箭发射时的声音强度约为一般噪音时声音强度的71210x x =倍,故选:C 5.已知F 为双曲线22:145x y C -=的左焦点,P 为其右支上一点,点()0,6A -,则APF 周长的最小值为()A.4+ B.4+ C.6+ D.6+【答案】B 【解析】【分析】设双曲线的右焦点为M ,由双曲线方程可求出a ,b ,c 的值,利用双曲线的定义以及三点共线即可求出APF 的周长的最小值.【详解】设双曲线的右焦点为M ,由双曲线的方程可得:224,5ab ==,则2,3a bc ===,所以(3,0),(3,0)F M -,且||||24PF PM a -==,所以||||4PF PM =+,APF 的周长为||||||||||4|PA PF AF PA PM AF ++=+++∣444PA PM AM =++++++,当且仅当M ,P ,A 三点共线时取等号,则APF 周长的最小值为4+B .6.已知()00,P x y 是:40l x y -+=上一点,过点P 作圆22:5O x y +=的两条切线,切点分别为,A B ,当直线AB 与l 平行时,AB =()A.B.2C.302D.4【答案】C 【解析】【分析】根据给定条件,利用圆的切线的性质,结合面积法求解作答.【详解】连接,,OA OB OP ,由,PA PB 切圆O 于,A B 知,,,OA PA OB PB OP AB ⊥⊥⊥,因为直线AB 与l 平行,则OP l ⊥,||OP =,而圆O于是||PA ==,由四边形OAPB 面积2OPA S S = ,得11||||2||||22AB OP OA AP =⨯,所以2||||||||2OA AP AB OP ===.故选:C7.正项等比数列{}n a 的公比为q ,前n 项和为n S ,则“1q >”是“2021202320222S S S +>”的()A.充分不必要条件B.必要不充分条件C.充要条件D.既不充分也不必要条件【答案】C 解析】【分析】根据给定条件,利用数列前n 项和的意义,正项等比数列的意义,结合充分条件、必要条件的定义判断作答.【详解】依题意,2021202320222023202220222022201232022S S S S S S S a a +⇔>>->⇔-,而{}n a 是公比为q 的正项等比数列,因此20232022202220221a a a q a q >⇔>⇔>,所以“1q>”是“2021202320222S S S +>”的充要条件.故选:C8.已知sin sin 12αβ-=-,1cos cos 2αβ-=,则()cos αβ-=A.B.12-C.12D.2【答案】D 【解析】【详解】由已知可得22227sin sin -2sin sin 4{2sin sin +2cos cos 1cos cos 2cos cos 4αβαβαβαβαβαβ+=-⇒=+-=()cos -=2αβ⇒,故选D.二、选择题:本题共4小题,每小题5分,共20分.在每小题给出的选项中,有多项符合题目要求.全部选对的得5分,部分选对的得2分,有选错的得0分.9.下列统计量中,能度量样本12,,,n x x x 的离散程度的是()A.样本12,,,n x x x 的标准差B.样本12,,,n x x x 的中位数C.样本12,,,n x x x 的极差D.样本12,,,n x x x 的平均数【答案】AC 【解析】【分析】考查所给的选项哪些是考查数据的离散程度,哪些是考查数据的集中趋势即可确定正确选项.【详解】由标准差的定义可知,标准差考查的是数据的离散程度;由中位数的定义可知,中位数考查的是数据的集中趋势;由极差的定义可知,极差考查的是数据的离散程度;由平均数的定义可知,平均数考查的是数据的集中趋势;故选:AC.10.中国传统文化中很多内容体现了数学的“对称美”,如图所示的太极图是由黑白两个鱼形纹组成的图案,俗称阴阳鱼,太极图展现了一种相互转化,相对统一的和谐美,定义:圆O 的圆心在原点,若函数的图像将圆O 的周长和面积同时等分成两部分,则这个函数称为圆O 的一个“太极函数”,则()A.对于圆O ,其“太极函数”有1个B.函数()()()2200x x x f x x x x ⎧-≥⎪=⎨--<⎪⎩是圆O 的一个“太极函数”C.函数()33f x x x =-不是圆O 的“太极函数”D.函数())lnf x x=是圆O 的一个“太极函数”【答案】BD 【解析】【分析】根据题意,只需判断所给函数的奇偶性即可得答案.【详解】解:对于A 选项,圆O ,其“太极函数”不止1个,故错误;对于B 选项,由于函数()()()2200x x x f x x x x ⎧-≥⎪=⎨--<⎪⎩,当0x ≥时,()()2f x x x f x -=-+=-,当0x <时,()()2f x x x f x +-==-,故()()()2200x x x f x x x x ⎧-≥⎪=⎨--<⎪⎩为奇函数,故根据对称性可知函数()()()2200x x x f x x x x ⎧-≥⎪=⎨--<⎪⎩为圆O 的一个“太极函数”,故正确;对于C 选项,函数定义域为R ,()()33f x x x f x -=-+=-,也是奇函数,故为圆O 的一个“太极函数”,故错误;对于D 选项,函数定义域为R ,()))()lnln ln x x f x f x ⎛⎫=-==-=--,故为奇函数,故函数())lnf x x=+是圆O 的一个“太极函数”,故正确.故选:BD11.定义在R 上的函数()f x 满足()()()f x y f x f y +=+,当0x <时,()0f x >,则()f x 满足()A.()00f = B.()y f x =是奇函数C.()f x 在[],m n 上有最大值()f n D.()10f x ->的解集为(),1∞-【答案】ABD 【解析】【分析】利用赋值法可判断A 选项的正误;利用函数奇偶性的定义可判断B 选项的正误;利用函数单调性的定义可判断C 选项的正误;利用函数()f x 的单调性解不等式()10f x ->,可判断D 选项的正误.【详解】对于A 选项,令0x y ==,可得()()020f f =,解得()00f =,A 对;对于B 选项,函数()y f x =的定义域为R ,令y x =-,可得()()()00f x f x f +-==,则()()f x f x -=-,故函数()y f x =是奇函数,B 对;对于C 选项,任取1x 、2x R ∈且12x x <,则()120f x x ->,即()()()()()1212120f x x f x f x f x f x -=+-=->,所以()()12f x f x >,所以,函数()f x 为R 上的减函数,所以,()f x 在[],m n 上有最大值()f m ,C 错;对于D 选项,由于()f x 为R 上的减函数,由()()100f x f ->=,可得10x -<,解得1x <,D 对.故选:ABD.12.已知异面直线a 与直线b 所成角为60 ,平面α与平面β的夹角为80 ,直线a 与平面α所成的角为15 ,点P 为平面αβ、外一定点,则下列结论正确的是()A.过点P 且与直线a b 、所成角均为30 的直线有3条B.过点P 且与平面αβ、所成角都是30 的直线有4条C.过点P 作与平面α成55 角的直线,可以作无数条D.过点P 作与平面α成55 角,且与直线a 成60 的直线,可以作3条【答案】BC 【解析】【分析】利用异面直线所成角的定义判断A ;利用线面角的意义判断B ;利用圆锥母线与底面所成角的意义判断BD 作答.【详解】因为异面直线a 与直线b 所成角为60 ,显然过点P 分别与直线,a b 平行的直线,a b ''的夹角为60 ,在直线,a b ''确定的平面内过点P 与,a b ''都成30 角的直线只有1条,所以过点P 与直线,a b 所成角均为30 的直线只有1条,A 错误;因为平面α与平面β的夹角为80,则过点P 与平面,αβ所成角都是80402=和18080502-= 的直线各有一条,m n ,若过点P 与平面,αβ所成角都是30 ,则在直线m 的两侧各有一条,在直线n 的两侧各有一条,因此共224⨯=条,B 正确;以P 为顶点,母线与底面成55 角的圆锥底面所在平面为α,满足点P 在α外,且过点P 的直线与平面α成55 角,如图,圆锥每条母线与平面α都成55 角,因此可以作无数条,C 正确;过点P 作//PZ a ,交平面α于点Z ,过点Z 及圆锥底面圆心O 的直线与圆锥底面圆交于点12,Q Q ,显然121270,40,110Q PQ ZPQ ZPQ ∠=∠=∠= ,设Q 为圆锥底面圆周上任意一点,于是40110ZPQ ≤∠≤,因此圆锥母线中与直线PZ 成60 的直线有2条,即与直线a 成60 的直线有2条,D 错误.故选:BC【点睛】方法点睛:该题考查立体几何综合应用,属于难题,关于角度的方法有:(1)异面直线所成角:平移异面直线至有交点,则异面直线所成角即为平移后相交直线所成角;(2)线面角:过线上一点做面的垂线,连接垂足及线与面的交点形成线段,则线与该线段所成角即为线面角;(3)面面角:过面面交线上一点在两个面中分别做交线的垂线,则两垂线的夹角即为面面角.三、填空题:本题共4小题,每小题5分,共20分.13.将6个相同的小球放入4个编号为1,2,3,4的盒子中,,恰有1个空盒子,则放法有___________种.【答案】40【解析】【分析】放置方法:6个球放入3个盒子,按球的个数分成三种情况:(1,2,3),(2,2,2),(1,1,3),第一步选空盒子,然后把放入三个盒子.【详解】第一步选空盒子,第二步6个球放入3个盒子,按球的个数分成三种情况:(1,2,3),(2,2,2),(1,1,3)进行放置,方法数为:131433C (A 1C )40++=.故答案为:40.14.已知棱台的上、下底面面积分别为4,16,高为3,则棱台的体积为________.【答案】28【解析】【分析】直接利用棱台的体积公式,求出棱台的体积.【详解】11()(416)32833VS S h '=++=⨯+⨯=故答案为:28.【点睛】本题考查棱台的体积,考查计算能力,是基础题.15.已知函数5π()sin cos(),(0)6f x x x ωωω=++>在[0,π]上的值域为[,1]2-,则ω的取值范围为_________.【答案】55[,]63【解析】【分析】根据给定条件,化简函数()f x ,再利用正弦函数性质结合已知值域,列式求解作答.【详解】依题意,1π()sin cos sin()223f x x x x ωωω=-=-,由[0,π],0x ω∈>,得ππππ333x ωω-≤-≤-,函数sin y x =在ππ[,32-上单调递增,函数值集合为[,1]2-,在π4π[,]23上单调递减,函数值集合为[,1]2-,因为函数()f x 在[0,π]上的值域为[,1]2-,则有ππ4ππ233ω≤-≤,解得5563ω≤≤,所以ω的取值范围为55[,63.故答案为:55[,]6316.已知椭圆()222210x y a b a b+=>>的左焦点为F ,过点F 且倾斜角为45°的直线l 与椭圆交于A ,B 两点(点B 在x 轴上方),且2FB AF = ,则椭圆的离心率为___________.【答案】23【解析】【分析】利用椭圆焦点坐标,求解直线方程,利用且112F B AF =转化求解椭圆的离心率即可.【详解】解:设(),0,0Fc c ->,由题意知,l 的斜率为tan 451︒=,则直线方程为y x c =+,设()()1122,,,A x y B x y ,联立直线和椭圆的方程得22221y x c x y ab =+⎧⎪⎨+=⎪⎩,整理得22222222()20a b y cb y c b a b +-+-=,则212222cb y y a b +=+,22221222c b a b y y a b -=+,且112F B AF = ,可得212y y =-,则21222cb y a b -=+,222221222c b a b y a b --=+,所以222222222222()cb c b a b a b a b --=++,可得2292c a =,所以3c e a==故答案为:23.【点睛】关键点睛:本题的关键是由向量的关系得两点的纵坐标的关系,结合韦达定理进行求解.四、解答题:本题共6小题,共70分.解答应写出文字说明、证明过程或演算步骤.17.已知函数()ln ()R f x x a x a =-∈(1)求()f x 的极值;(2)若()1f x ≥,求a 的值,并证明:()2.x f x x e >-【答案】(1)当0a ≤时,()f x 无极值;当0a >时,()f x 的极小值为()ln f a a a a =-,无极大值;(2)1,证明见解析.【解析】【分析】(1)先求导函数,再对参数进行分类讨论,即可求出极值.(2)由(1)得,()ln 1f x x x =-≥,即ln 1x x ≤-,故要证()2x f x x e >-,只要证21xx e -<,构造函数,求导即可求解.【详解】解:(1)()1(0)a x af x x x x-∴=-=>'①当0a ≤时,()0f x '>,()f x 在(0,)+∞上单调递增.()f x ∴在()0,∞+上无极值.②当0a >时,令()0f x '>得x a >;令()0f x '<得0x a <<.()f x ∴在(0,)a 上单调递减,在(,)a +∞上单调递增.()f x ∴的极小值为()ln f a a a a =-,无极大值.综上,当0a ≤时,()f x 无极值;当0a >时,()f x 的极小值为()ln f a a a a =-,无极大值.(2)由(1)可知,①当0a ≤时,()f x 在(0,)+∞上单调递增,而(1)1f =,∴当(0,1)x ∈时,()1f x <,即()1f x ≥不恒成立.②当0a >时,()f x 在(0,)a 上单调递减,在(,)a +∞上单调递增.min ()()ln 1.f x f a a a a ∴==-≥令()ln (0)g a a a a a =->,则()1(ln 1)ln .g a a a '=-+=-当(0,1)a ∈时,()0g a '>,()g a 在(0,1)上单调递增;当(1,)∈+∞a 时,()0g a '<,()g a 在(1,)+∞上单调递减.()(1) 1.g a g ∴≤=1.a ∴=设()()2ln (0)x x h x f x x e x x e x =-+=--+>,下面证明()0.h x > 当1a =时,()ln 1f x x x =-≥,即ln 1.x x ≤-ln 21,x x x ∴+≤-∴只要证21(*).x x e -<令()21,0x q x e x x =-+>,则'() 2.x q x e =-∴当(0,ln 2)x ∈时,'()0q x <,()q x 在(0,ln 2)上单调递减;当(ln 2,)x ∈+∞时,'()0q x >,()q x 在(ln 2,)+∞上单调递增.3()(ln 2)3ln 4ln ln 40.q x q e ∴≥=-=->(*)∴式成立,即()2x f x x e >-成立.18.ABC 的内角A ,B ,C 的对边分别为a ,b ,c ,且()sin sin sin b c B c C a A ++=.(1)求角A ;(2)求22sin sin B C+的最小值.【答案】(1)2π3A =;(2)12.【解析】【分析】(1)根据()sin sin sin b c B c C a A ++=,利用正弦定理得到222b c a bc +-=-,再利用余弦定理求解;(2)根据π3B C+=,利用三角恒等变换,将问题转化为221πsin sin 1sin 226B C B ⎛⎫+=-+ ⎪⎝⎭,利用正弦函数的性质求解.【详解】(1)因为()sin sin sin b c B c C a A ++=,由正弦定理得()22b c b c a ++=,即222b c a bc +-=-,由余弦定理得2221cos 22b c a A bc +-==-,因为()0,πA ∈,所以2π3A =.(2)因为π3B C +=,所以2221cos π21cos 23sin sin 32π2B B B B ⎛⎫-- ⎪-⎝⎭+-⎛⎫ ⎝+⎪⎭=111π1cos2sin21sin 222226B B B ⎛⎫⎛⎫=-+=-+ ⎪ ⎪ ⎪⎝⎭⎝⎭,因为π0,3B ⎛⎫∈ ⎪⎝⎭,所以π52,666Bππ⎛⎫+∈ ⎪⎝⎭,则π1sin 2(,1]62B ⎛⎫+∈ ⎪⎝⎭,所以1π11sin 2262B ⎛⎫-+≥ ⎪⎝⎭,当且仅当π6B =时等号成立,所以22sin sin B C +的最小值为12.19.如图,在正四棱柱1111ABCD A B C D -中,1222AA AB BC ===,M 是棱1CC 上任意一点.(1)求证:AM BD ⊥;(2)若M 是棱1CC 的中点,求异面直线AM 与BC 所成角的余弦值.【答案】(1)证明过程见解析(2)3【解析】【分析】(1)建立空间直角坐标系,利用空间向量证明线线垂直;(2)在第一问的基础上,利用空间向量求解异面直角的夹角余弦值.【小问1详解】证明:以A 为原点,AB ,AD ,1AA 所在直线分别为x 轴,y 轴,z 轴,建立空间直角坐标系,因为1222AA AB BC ===,所以()()()()0,0,0,1,0,0,0,1,0,1,1,A B D M m ,02m ≤≤,()()1,1,,1,1,0AM m BD ==-,()()1,1,1,1,0110AM BD m ⋅=⋅-=-+=,所以AM BD ⊥;【小问2详解】M 是棱1CC 的中点,故()()1,1,0,1,1,1C M ,则()()1,1,1,0,1,0AM BC ==,设异面直线AM 与BC 所成角的大小为θ,则cos cos ,3AM BC AM BC AM BCθ⋅====⋅,故异面直线AM 与BC 所成角的余弦值为3.20.已知数列{}n a 中,11a =,()12N 2nn na a n a ++=∈+.(1)求234,,a a a 的值,并猜想数列{}n a 的通项公式;(2)证明数列1n a ⎧⎫⎨⎬⎩⎭是等差数列.【答案】(1)234212,,325aa a ===,21n a n =+;(2)证明见解析.【解析】【分析】(1)根据给定的递推公式,分别令1,2,3n=,即可求解234,,a a a 的值,猜想得出数列的通项公式.(2)将给定的递推公式两边取倒数,再利用等差数列的定义推理作答.【小问1详解】在数列{}n a 中,11a =,122nn na a a +=+,令1n=,得1212222213a a a ===++;令2n =,得2322122a a a ==+;令3n =,得3432225a a a ==+;所以234212,,325aa a ===,猜想数列{}n a 的通项公式为21n a n =+.【小问2详解】由12()N 2n n na a n a ++=∈+,11a =,得0n a ≠,1211122n n n n a a a a ++==+,即11112n n a a +-=,所以数列1{}n a 是以111a =为首项,12为公差的是等差数列.21.现代排球赛为5局3胜制,每局25分,决胜局15分.前4局比赛中,一队只有赢得至少25分,并领先对方2分时,才胜1局.在第5局比赛中先获得15分并领先对方2分的一方获胜.在一个回合中,赢的球队获得1分,输的球队不得分,且下一回合的发球权属于获胜方.经过统计,甲、乙两支球队在每一个回合中输赢的情况如下:当甲队拥有发球权时,甲队获胜的概率为23;当乙队拥有发球权时,甲队获胜的概率为12.(1)假设在第1局比赛开始之初,甲队拥有发球权,求甲队在前3个回合中恰好获得2分的概率;(2)当两支球队比拼到第5局时,两支球队至少要进行15个回合,设甲队在第i 个回合拥有发球权的概率为i P.假设在第5局由乙队先开球,求在第15个回合中甲队开球的概率,并判断在此回合中甲、乙两队开球的概率的大小.【答案】(1)1027(2)1514331556P =-⨯,甲队开球的概率大于乙队开球的概率.【解析】【分析】(1)甲队在前3个回合中恰好获得2分,分为3种情况,依次求出对应的概率,即可求解;(2)根据已知条件,结合等比数列的性质,以及全概率公式,即可求解.【小问1详解】在前3个回合中甲队恰好获得2分对应的胜负情况如下:胜胜负,胜负胜,负胜胜,共3种情况,对应的概率分别为1221433327P =⨯⨯=,221113329P =⨯⨯=,311213239P =⨯⨯=,所以甲队在前3个回合中恰好获得2分的概率41110279927P =++=;【小问2详解】根据全概率公式得12111(1)3262i i i i P P P P +=+-=+,即1313565i i P P +⎛⎫-=- ⎪⎝⎭,易知10P =,所以35i P ⎧⎫-⎨⎬⎩⎭是以35-为首项,16为公比的等比数列,所以1331556i i P -=-⨯,故1514331556P =-⨯,因为14151414113166021056106P --=-⨯=>⨯,所以1512P >,而在每一个回合中,甲、乙两队开球的概率之和为1,从而可得在此回合中甲队开球的概率大于乙队开球的概率.【点睛】方法点睛:甲队在第i 个回合拥有发球权的概率为i P,由全概率公式得12111(1)3262i i i i P P P P +=+-=+,问题转化为数列的递推公式,通过构造等比数列,求出通项.22.已知双曲线C :()222210,0x y a b a b-=>>的虚轴长为4,直线20x y -=为双曲线C 的一条渐近线.(1)求双曲线C 的标准方程;(2)记双曲线C 的左、右顶点分别为A ,B ,斜率为正的直线l 过点()2,0T ,交双曲线C 于点M ,N (点M 在第一象限),直线MA 交y 轴于点P ,直线NB 交y 轴于点Q ,记PAT 面积为1S ,QBT △面积为2S ,求证:12S S 为定值.【答案】(1)2214y x -=;(2)证明见解析.【解析】【分析】(1)根据渐近线方程以及虚轴长度可知,a b ,然后可知方程(2)假设直线方程2x ny =+,并与双曲线方程联立,可得关于y 的二次方程,紧接着使用韦达定理,分别求得,P Q 坐标并表示出12S S ,简单计算即可.【详解】解:(1)由题意可得,因为一条渐近线方程为2y x =,所以2ba=,解得1a =,则双曲线的方程为2214y x -=;(2)证明:可得()1,0A -,()10B ,,设直线l :2x ny =+,()11,M x y ,()22,N x y ,联立22142y x x ny ⎧-=⎪⎨⎪=+⎩,整理可得()224116120n y ny -++=,可得1221641n y y n +=--,1221241y y n =-,即有()121234nyy y y =-+,设直线MA :11(1)1y y x x =++,可得110,1y P x ⎛⎫⎪+⎝⎭,设直线NB:22(1)1y y x x =--,可得220,1y Q x ⎛⎫⎪-⎝⎭,又3AT =,1BT =,所以()()1121122122311331y y ny x S S y ny y x ++==+-()()12112112212234333334y y y ny y y ny y y y y y -+++==+-++12123339y y y y -=-+1=.【点睛】方法点睛:解决直线与圆锥曲线的一般方法(1)假设直线方程;(2)联立方程:(3)使用韦达定理;(4)根据条件计算.。
【收藏】除了清北,还有哪些大学举行夏令营、学科营?(不完全汇总)

【收藏】除了清北,还有哪些大学举行夏令营、学科营?(不完全汇总)天科学堂王老师整理汇总2015年举行过夏令营或学科营的大学,想要报考自招的同学们,还不赶紧收藏!厦大、中国科学院、中国地质、南京大学、中石油、西北农林科技、北航、北中医、南开、天津、上交、中国海洋大学,么有一个你心动的吗?厦门大学2015年中学生化学夏令营招生简章一、活动时间:现面向全国高中拟招收10-15名优秀营员,此次夏令营将于7月17-21日在厦门大学进行,即日起受理报名申请。
二、申请资格1. 高二年级学生,2016年应届毕业生。
2. 高中期间总评成绩排名在年级前10%之内,化学成绩优秀。
自主招生在线3. 对化学、化工领域的科学研究有着浓厚的兴趣,具有潜在的科研能力。
4. 英语水平良好三、活动内容结合厦门大学化学化工学科特点,夏令营将安排学科介绍、实验室参观、与科研一线的优秀师生交流、与参加国家拔尖学生培养计划的本科生座谈等活动。
厦门大学2015年中学生物理学夏令营招生简章招生对象:热爱物理、综合素质优秀、数理化成绩突出、身心健康、有志于报考物理学专业的高二理科学生(参加2016年高考)。
夏令营安排1、2015年7月17日报到,营期为2014年7月18日至21日。
2、活动内容:开营仪式(全校各学院(研究院)中学生和大学生夏令营营员参加)、学科导航、科普报告、面试考察、参观活动、交流互动等。
3、我系将在夏令营中选拔优秀营员,并给予表彰。
中国科学院大学“2015年中学生科学夏令营”营员来源:2015年计划在浙江、辽宁、山东、河南、湖南、云南、北京、江苏、陕西、四川、湖北等11个省市招募营员(高二学生)共330名,其中每个省市30名。
招募方式全部为中学校长推荐。
(所在中学是否具有校荐资格请咨询分省招生组)时间:7月25-31日,为期7天(7月25日报到,7月31日离营)。
活动内容:夏令营将安排丰富多彩的活动,充分考虑听(院士专家科普报告)、看(重点研究所、实验室)、做(动手实验)、玩(文体活动)、演(联谊晚会)、写(总结报告)、比(比赛奖励)等形式。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
关于举办第十届高中数学夏令营暨
第三十一期中学数学讲习班第一次通知
为了培养中学生的数学兴趣,开发智力潜能,提高参加高考以及数学竞赛的应试能力和竞赛成绩,拓展个性才能的空间,提高中学数学奥林匹克教练水平,中国科学技术大学数学科学学院今年暑假在中国科学技术大学举办第十届高中数学夏令营暨第三十一期中学数学(教练员)讲习班。
中国科学技术大学党委副书记叶向东教授、安徽省数学会秘书长陈发来教授任本届夏令营营长。
中国科学技术大学数学科学学院在校本部举办过九届全国中学生数学夏令营,连续举办了30期暑期中学数学讲习班,已有500余所中学的教师和学生参加过夏令营和讲习班。
本期讲习班由陈永高(南京师范大学)、余红兵(苏州大学)、李建泉(天津师范大学) 、陈计(宁波大学)、陈发来(中国科学技术大学)、李思敏(中国科学技术大学)、王建伟(中国科学技术大学)、王新茂(中国科学技术大学)等专家主讲(主讲教师以第二次通知为准)。
主讲专家具有丰富的数学授课及竞赛培训经验,历年来他们严谨生动的讲解受到讲习班师生的欢迎和好评。
现将本次活动的有关事宜通知如下:
一.参加人员
各省市高中学生和数学教师,请携带学生证和教师资格证。
二.活动时间和地点
2016年7月24日报到,7月25日-7月30日上课。
报到地点:安徽省合肥市金寨路96号中国科学技术大学东区五教一楼5104教室,时间::2016年7月24日8:00 -18.00。
三.培训内容
1.本次培训分为普通班、高级班。
普通班注重高中数学基础,提高数学兴趣与修养,增强理解问题、解决问题的能力,为学员提高高考成绩打下基础(建议高一学生参加);高级班在高中数学的基础上进一步提高解题技巧,开拓数学视野,提高数学竞赛的应试能力(建议高二或已经全部学习完成高中数学知识成绩突出的高一学生参加),同时培养数学竞赛教练员。
2.邀请国内著名数学家做数学科普知识及近代前沿数学知识讲座。
四.关于教练员证
1.凡参加本期讲习班学习,经考核合格的教师将授予中国数学奥林匹克二级教练员证书。
申请者需带两张二寸彩色照片。
2.凡申报一级教练员证书的老师,必须是已获得二级教练员证书者,同时又必须是培养过获得全国联赛一等奖选手,或联赛二等奖并在国内外正式刊物上发表过有关数学竞赛研究论文者,申报者请携证书及证明原件,报到时验原件,收复印件。
教练员申报表在附后的网页中下载,自行打印填写,加盖单位公章,报到时需提交。
五.关于报名
为了便于安排食宿、教室、以及掌握办班规模等,请各位务于2016年5月25日前将报名表填好发送下面信箱。
我们将根据报名情况于6月15日前后发第二次通知。
报名时一律预交报名费100元,开班后统一结算。
本次通知、第二次通知和教练员申报表请在中国科学技术大学数学科学学院主页资源中心-文档下载:
/new/bencandy.php?fid=47&id=1032
六.活动费用
学员除食宿、差旅费用由所在单位按有关规定报销外,每位参加的教师交注册费1000元,高中学生交注册费900元。
以学校为单位参加学生人数(老师不计)每超过20人,免1人注册费,最多免2人注册费。
七.关于食宿
就餐地点在科大学生餐厅,我们协助办理饭卡。
因届时周边住宿房源紧张,欢迎学员提前自行预订科大附近的旅馆。
如需会务组预订住宿,请在报名表中务必填上住宿的选择,以便订房。
天庭商务酒店标准间:168元/天;城市之家标间:160元/天。
(以上为参考价格,旅馆价格以报到时公布的价格为准。
)
报名表和报名费请寄:
230026 安徽省合肥市中国科学技术大学数学科学学院李晶晶收
Email:kdsx@
联系人咨询电话:黄学俊(63601007 ) 李晶晶(63600206)
乘车路线:合肥南站: 108
合肥火车站:乘1,129,10路车到科大东区站;
从火车站打的约20元;
其他线路:乘126,148,705,901,108,118,121,158路车到科大东区站。
安徽省数学会中国科学技术大学
数学科学学院2016年4月25日2016年4月25日
报名表回执
此通知可自行复印、传阅。
凡此通知发往市、县教委的,请转往下属有关中学,谢谢!
(单位公章)2016年月日。
