10进制到进制转换表
十进制数与十六进制数的转换方法

一,十进制转换十六进制若十进制数23785转为十六进制,则用23785/16=1486余9,1486/16=92余……14,92/16=5余………….12,5/16=0余……………..5,十六进制中,10对应为a、11对应为b、。
、15对应为f,再将余数倒写为5ce9,则十进制23785=十六进制5ce9二,十六进制转换十进制十六进制数的第0位的权值为16的0次方,第1位的权值为16的1次方,第2位的权值为16的2次方……所以,在第N(N从0开始)位上,如果是是数 X (X 大于等于0,并且X小于等于 15,即:F)表示的大小为 X * 16的N次方。
假设有一个十六进数 2AF5, 那么如何换算成10进制呢?用竖式计算: 2AF5换算成10进制:第0位: 5 * 16^0 = 5第1位: F * 16^1 = 240第2位: A * 16^2 = 2560第3位: 2 * 16^3 = 8192直接计算就是:5 * 16^0 + F * 16^1 + A * 16^2 + 2 * 16^3 = 10997三,二进制的1101转化成十进制1101(2)=1*2^0+0*2^1+1*2^2+1*2^3=1+0+4+8=13 转化成十进制要从右到左用二进制的每个数去乘以2的相应次方不过次方要从0开始十进制转二进制四,二进制转八进制在把二进制数转换为八进制表示形式时,对每三位二进制位进行分组,应该从小数点所在位置分别向左向右划分,若整数部分倍数不是3的倍数,可以在最高位前面补若干个0;对小数部分,当其位数不是的倍数时,在最低位后补若干个0.然后从左到右把每组的八进制码依次写出,即得转换结果.你算一下就知道了啊比如110=2^2+2+0=6五,二进制转十六进制要将二进制转为16进制,只需将二进制的位数由右向左每四位一个单位分隔,分的不够的前边补零,用四位数的二进制数来代表一个16进制。
转换表如下,括号内为十六进制0000(0)0001(1)0010(2)0011(3)0100(4)0101(5)0110(6)0111(7)1000(8)1001(9)1010(A)1011(B)1100(C)1101(D)1110(E)1111(F)十六进制为AB。
很完整的2、8、10、16进制转换方法

比如 00000000 00000000 00000000 00000101 是 5的 原码。
生活中其实很多地方的计数方法都多少有点不同进制的影子。
比如我们最常用的10进制,其实起源于人有10个指头。如果我们的祖先始终没有摆脱手脚不分的境况,我想我们现在一定是在使用20进制。
至于二进制……没有袜子称为0只袜子,有一只袜子称为1只袜子,但若有两袜子,则我们常说的是:1双袜子。
生活中还有:七进制,比如星期。十六进制,比如小时或“一打”,六十进制,比如分钟或角度……
6.2.5 十六进制数转换成十进制数
2进制,用两个阿拉伯数字:0、1;
8进制,用八个阿拉伯数字:0、1、2、3、4、5、6、7;
10进制,用十个阿拉伯数字:0到9;
16进制,用十六个阿拉伯数字……等等,阿拉伯人或说是印度人,只发明了10个数字啊?
16进制就是逢16进1,但我们只有0~9这十个数字,所以我们用A,B,C,D,E,F这五个字母来分别表示10,11,12,13,14,15。字母不区分大小写。
我们找到问号字符(?)的ASCII值是63,那么我们可以把它转换为八进值:77,然后用 ‘\77′来表示’?'。由于是八进制,所以本应写成 ‘\077′,但因为C,C++规定不允许使用斜杠加10进制数来表示字符,所以这里的0可以不写。
事实上我们很少在实际编程中非要用转义符加八进制数来表示一个字符,所以,6.2.4小节的内容,大家仅仅了解就行。
0000 = 0 + 0 + 0 + 0 = 0 0
二进制数要转换为十六进制,就是以4位一段,分别转换为十六进制。
如(上行为二制数,下面为对应的十六进制):
数制转换 二进制 八进制 十进制 十六进制之间的数制转换

1.计算机中的数制:
3.1十进制转换为二进制:整数部分用除2取余法,小数部分用
乘2取整法;
例如:78.6875
3.2二进制转换为十进制:按权展开求和
例如:1001110.1011
1001110.1011=1*26+0*25+0*24+1*23+1*22+1*21+0*20+1*2-1+0
*2-2+1*2-3+1*2-4=64+8+4+2+0.5+0.125+0.0625=78.6875
3.3二进制转换为八进制
将二进制数从小数点开始,整数部分从右向左3位一组,小
数部分从左向右3位一组,不足三位用0补充;
3.4八进制转换为二进制
每一位八进制数分别转换为3位二进制数即可;
3.5二进制转换为十六进制
将二进制数从小数点开始,整数部分从右向左4位一组,小数部分从左向右4位一组,不足三位用0补充;
3.6十六进制转换为二进制
将每一位十六进制数分别转换为4位二进制数;
3.7书写规则:
二进制100B (100)2
八进制100O (100)8
十进制100D (100)10
十六进制100H (100)16
FrontPage 2003
1.窗口组成:
2.菜单栏,工具栏,格式栏,任务窗格,状态栏,标记栏,网页标签,视图模式(设计视图,拆分视图,代码视图,预览视图)
3.创建新网页:
4.保存网页
5.打开网页
6.关闭网页
7.网页编辑
1)文本的输入和格式化
2)图片的输入和编辑
3)表格的插入和编辑
4)超链接的插入和编辑
5)框架网页的插入和编辑
8.。
进制的使用及转换

十六进制(英文名称:Hexadecimal),是计算机中数据的一种表示方法。
同我们日常生活中的表示法不一样。
它由0-9,A-F组成,字母不区分大小写。
与10进制的对应关系是:0-9对应0-9;A-F对应10-15;N进制的数可以用0~(N-1)的数表示,超过9的用字母A-F。
基本简介: 十六进制(英文名称:Hexadecimal),是计算机中数据的一种表示方法。
同我们日常生活中的表示法不一样。
它由0-9,A-F组成,字母不区分大小写。
与10进制的对应关系是:0-9对应0-9;A-F 对应10-15;N进制的数可以用0~(N-1)的数表示,超过9的用字母A-F。
表示方法: 十六进制照样采用位置计数法,位权是16为底的幂。
对于n位整数,m位小数的十六进制数用加权系数的形式表示如下:举例说明转换二进制转换十进制二进制数第0位的权值是2的0次方,第1位的权值是2的1次方……所以,设有一个二进制数:0,转换为10进制为:356用横式计算: 0×2+0×2+1×2+0×2+0×2+1×2+1×2+0×2+1×2=3560乘以多少都是0,所以我们也可以直接跳过值为0的位:1×2+1×2+1×2+1×2=3564+32+64+256 =356八进制转换十进制八进制就是逢8进1。
八进制数采用 0~7这八数来表达一个数。
八进制数第0位的权值为8的0次方,第1位权值为8的1次方,第2位权值为8的2次方……所以,设有一个八进制数:1507,转换为十进制为:839,具体方法如下:可以用横式直接计算: 7×8+0×8+5×8+1×8=839也可以用竖式表示: 第0位7×8^0=7第1位0×8^1=0第2位5×8^2=320第3位1×8^3=512十六进制转换十进制16进制就是逢16进1,但我们只有0~9这十个数字,所以我们用A,B,C,D,E,F这六个字母来分别表示10,11,12,13,14,15。
二进制、十进制、八进制、十六进制四种进制之间相互的转换

二进制、十进制、八进制、十六进制四种进制之间相互的转换一.在计算机应用中,二进制使用后缀b表示;十进制使用后缀d表示八制使用后缀Q表示,十六制使用后缀H表示。
二.二进制,十六进制与十进制的计算转换1.二进制转换为十进制计算公式:二进制数据X位数字乘以2的X-1次方的积的总和例:10101011b=( )d相应的十进制值即为:27 +25+23+21+20=128+32+8+2+1=1712.十六进制转换十进制计算公式:二进制数据X位数字乘以16的X-1次方的积的总和(与二进制转换十制进同理的,将底数换为16)注意:在十六进制中,10-15依次用A,B,C,D,E,F表示例:1F3E H=()d计算:1*16的3次方+15*16的2次方+3*16的1次方+14*16的0次方=1*4096+15*256+3*16+14=7998三.十进制与二进制,十六制的计算转换1.十进制转换为二进制十进制数据数字除以2的余数的逆序组合例:404d=( )b2|404余02|202余02|101余02|50余12|25余02|12余12|6余02|3余12|1计算结果便是:1101010002.十进制转换十六进制。
与上面同理,注意的是10以上的数字用字母表示,除数是16十六进制与二进制的转换,建议通过十进制来进行中转。
带小数点的十进制转换为二进制时同理,小数店后的数位指数为负指数===================================================================== =================关于“进制之间的转换”问题的分析指导在计算机文化一书中,在其中一个章节里面详细介绍了进制之间的转换,而且在考试中进制转换也占了一定的比例,虽然分数不是很多,但是因为平时大家接触的不多,并且有点繁复,所以很多学员在做这种题目,要么选择猜答案,要么选择放弃。
笔者觉得只要掌握了方法,其实这些题目也很简单的,下面我就对进制的转换进行具体的分析和讲解,以供大家参考。
计算机各进制换算

一:十进制数转换成二进制数。
随便拿出一个十进制数“39”,(假如你今天买书用了39元)先来把这个39转换成2进制数。
商余数步数39/2= 19 1第一步19/2= 9 1 (这里的19是第一步运算结果的商)第二步9/2= 4 1 (这里的9是第二步运算结果的商)第三步4/2= 2 0 (这里的4是第三步运算结果的商)第四步2/2= 1 0 (这里的2是第四步运算结果的商)第五步1/2= 0 1 (这里的1是第五步运算结果的商)第六步那么十进制数39转换成2进制数就是100111. 既39(10)=100111(2)解析一:1. 当要求把一个10进制数转换成2进制数的时候,就用那个数一直除以2得到商和余数。
2. 用上一步运算结果的商在来除以2,再来得到商和余数。
3. 就这样,一直用上一步的商来除以2,得到商和余数!那么什么时候停止呢?4. 请看上述运算图,第六步的运算过程是用1除以2.得到的商是0,余数是1. 那么请你记住,记好了啊共2点。
A: 当运算到商为“0”的时候,就不用运算了。
B:1/2的商为“0”余数为“1”。
这个你要死记住,答案并不是0.5!答案就是商为“0”余数为“1”。
你不用去思考为什么,记好了就行了!5. 在上述图中你会清晰的看到每一步运算结果的余数,你倒着把它们写下来就是“100111”了。
那么这个就是结果了。
6. 在上述图中符号“/”代表“除以”。
二:十进制数转换成八进制数。
随便拿出一个十进制数“358”,(假如你今天买彩票中了358元)。
358是我们现实生活中所用10进制表达出来的一个数值,转换成八进制数十多少?商余数步数358/8= 44 6第一步44/8= 5 4 (这里的44是第一步运算结果的商)第二步5/8= 0 5 (这里的5是第二步运算结果的商)第三步那么十进制数358转换成8进制数就是546。
既358(10)=546(8)解析二: 1.没什么好说的啦,10进制数转换成2进制数和10进制数转换成8进制数的唯一不一样的地方就是除数变了,除数由“2” 变成了“8”。
十进制数转换为其他进制数

十进制数转换为其他进制数的方法为了使问题简化,首先我们讨论只有整数部分的数的转换。
假设我们要将一个十进制数4009转化成一个16进制数,也就是要将4009表示成(k2k1k)16(这里,k2、k1、k是0~15之间的整数。
我们假设需要用3位16进制数表示)。
则根据16进制数的定义:4009 = k2×162+k1×161+k×160 = k2×162+k1×16+k=(k2×16+k1)×16+k从上面的式子我们看出,k0是4009被16除之后的余数。
因为(k2×16+k1)×16是可以被16整除的,且商数为k2×16+k1。
如果将此商数再次用16去除,则得到的余数是k1,商数为k2。
这向我们指出了求k、k1、k2的方法如下:(1)先用16除4009,得到的商为250,余数为9。
则k=9;(2)再用上一步的商250除以16,得到的商为15,余数为10。
则k1=10;k2=15。
根据表2-1,k1用16进制符号A表示,k2用16进制符号F表示。
则有:4009 =(FA9)16如果我们将上述计算过程用称为“长除法”的算式表示出来,会更加清晰:16|4009 余数16|250……………9 K16|15……………10 K10……………15 K2在上述算式中,每次我们将得到的余数写在右边,将商写在下面,这样就可以一直除下去。
如此先后得到的余数,就是从低位到高位排列的16进制数各位的数码。
这种方法显然可以推广到更大的数的转化。
例2-1:将整数6890转换为16进制数。
算式为:16|6890 余数16|430 …………………10 k16|26 …………………14 k116|1 …………………10 k20 …………………1 k3则:6890 =(1AEA)16注意,在上面用长除法作数制转换时,我们一直要将除法进行到商为0止。
十转二进制简便方法

十转二进制简便方法一、了解二进制数1.1 什么是二进制数二进制数由0和1两个数字组成,是计算机中最基本的数字系统。
1.2 二进制数与十进制数的对应关系计算机中所有数字最终都要转换成二进制数进行处理。
十进制数与二进制数之间存在一个对应关系,可以通过一种简便的方法进行转换。
二、十转二进制简便方法2.1 方法一:除2取余法除2取余法是最常用、最简单的方法,可以将十进制数转换为二进制数。
具体步骤如下: 1. 将十进制数除以2,得到商和余数。
2. 再将商除以2,得到新的商和余数。
3. 重复以上步骤,直到商为0为止。
4. 逆序排列所得的余数,即为对应的二进制数。
例如,将十进制数23转换为二进制数:23 ÷ 2 = 11 (1)11 ÷ 2 = 5 (1)5 ÷ 2 = 2 (1)2 ÷ 2 = 1 01 ÷ 2 = 0 (1)将余数逆序排列,得到二进制数10111,即23的二进制表示为10111。
2.2 方法二:位运算法在计算机中,可以使用位运算法快速将一个十进制数转换为二进制数。
具体步骤如下: 1. 将十进制数转换为二进制数。
2. 使用位运算符”<<“不断左移。
例如,将十进制数23转换为二进制数:23 = 10111 (二进制)23 << 1 = 101110 (左移一位)23 << 2 = 1011100 (左移两位)23 << 3 = 10111000 (左移三位)通过位运算法,可以快速得到23的二进制表示10111000。
2.3 方法三:查表法在一些特定场景下,可以通过查表法将十进制数快速转换为二进制数。
具体步骤如下: 1. 准备一个十进制数与二进制数对应的表格。
2. 查找对应的二进制数。
例如,将十进制数23转换为二进制数,可以使用如下对应表格:十进制二进制0 00001 00012 00103 00114 01005 01016 01107 01118 10009 100110 101011 101112 110013 110114 111015 1111通过查表法,可以快速得到23的二进制表示10111。
10进制转其他进制的方法

10进制转其他进制的方法在数字系统中,我们通常使用10个数字来表示所有的数字,从0到9、这种系统被称为十进制系统。
然而,有时我们需要将数字转换为其他进制,如二进制、八进制或十六进制。
下面是几种常见的将十进制转换为其他进制的方法:一、二进制转换方法:将十进制数字转换为二进制数字的方法是通过除2取余法。
以下是一个将十进制数字转换为二进制数字的例子:例子:将十进制数字27转换为二进制数字。
步骤1:用27除以2,并将商和余数记录下来。
27÷2=13 (1)步骤2:再用13除以2,并将商和余数记录下来。
13÷2=6 (1)步骤3:再用6除以2,并将商和余数记录下来。
6÷2=3 0步骤4:再用3除以2,并将商和余数记录下来。
3÷2=1 (1)步骤5:最后再用1除以2,并将商和余数记录下来。
1÷2=0 (1)二、八进制转换方法:将十进制数字转换为八进制数字的方法是通过除8取余法。
以下是一个将十进制数字转换为八进制数字的例子:例子:将十进制数字35转换为八进制数字。
步骤1:用35除以8,并将商和余数记录下来。
35÷8=4 (3)步骤2:再用4除以8,并将商和余数记录下来。
4÷8=0 (4)步骤3:将余数从最后一个到第一个,得到八进制数字:43所以,35的八进制表示为43三、十六进制转换方法:将十进制数字转换为十六进制数字的方法是通过除16取余法。
十六进制数字中,对于10到15分别用字母A到F表示。
以下是一个将十进制数字转换为十六进制数字的例子:例子:将十进制数字123转换为十六进制数字。
步骤1:用123除以16,并将商和余数记录下来。
123÷16=7...11(余数为11,对应十六进制中的B)步骤2:再用7除以16,并将商和余数记录下来。
7÷16=0...7(余数为7)步骤3:将余数从最后一个到第一个,得到十六进制数字:7B。
十进制二进制十三进制十六进制转化
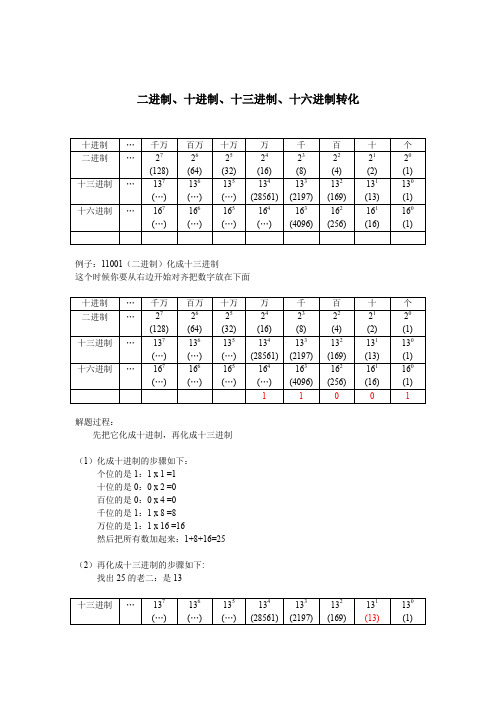
二进制、十进制、十三进制、十六进制转化十进制…千万百万十万万千百十个二进制 (27)(128)26(64)25(32)24(16)23(8)22(4)21(2)20(1)十三进制 (137)(…)136(…)135(…)134(28561)133(2197)132(169)131(13)130(1)十六进制 (167)(…)166(…)165(…)164(…)163(4096)162(256)161(16)160(1)例子:11001(二进制)化成十三进制这个时候你要从右边开始对齐把数字放在下面十进制…千万百万十万万千百十个二进制 (27)(128)26(64)25(32)24(16)23(8)22(4)21(2)20(1)十三进制 (137)(…)136(…)135(…)134(28561)133(2197)132(169)131(13)130(1)十六进制 (167)(…)166(…)165(…)164(…)163(4096)162(256)161(16)160(1)1 1 0 0 1解题过程:先把它化成十进制,再化成十三进制(1)化成十进制的步骤如下:个位的是1:1 x 1 =1十位的是0:0 x 2 =0百位的是0:0 x 4 =0千位的是1:1 x 8 =8万位的是1:1 x 16 =16然后把所有数加起来:1+8+16=25(2)再化成十三进制的步骤如下:找出25的老二:是13十三进制 (137)(…)136(…)135(…)134(28561)133(2197)132(169)131(13)130(1)用老大除以老二:25/13=1...12(余数)商是1(右边起第二个,称右2)现在余数12是老大,继续找老二这个时候只有1是符合,所以1为老二用老大除以老二:12/1=12商是12 (右边起第一个,称右1),用C表示到这里结束所以结果就是:1C余数超过9的用字母表示:10---------A11---------B12--------C(十三进制,余数小于13)进制转换的题目:1101000的十进制转换成十三进制、十六进制十进制…千万百万十万万千百十个二进制 (27)(128)26(64)25(32)24(16)23(8)22(4)21(2)20(1)十三进制 (137)(…)136(…)135(…)134(28561)133(2197)132(169)131(13)130(1)十六进制 (167)(…)166(…)165(…)164(…)163(4096)162(256)161(16)160(1)1 1 0 1 0 0 0 0解题过程:先把它化成十进制,再化成十三进制和十六进制(1)化成十进制的步骤如下:个位的是0: 1 x 1 =1十位的是0:0 x 2 =0百位的是0:0 x 4 =0千位的是0: 1 x 8 =8万位的是1: 1 x 16 =16十万位的是0:0 x 32 =0百万位的是1: 1 x 64 = 64千万位的是1: 1 x 128 -128然后把所有数加起来:1+8+16+64+128=217 (2)再把十进制化成十三进制的步骤如下:十三进制 (137)(…)136(…)135(…)134(28561)133(2197)132(169)131(13)130(1)老大217,老二169:217/169=1......48 (得数1在右3位置) 老大48,老二13:48/13=3......9 (得数3在右2位置) 老大9,老二1:9/1=9 (得数9在右1位置)所以得数就是:139(十三进制)十进制化成十三进制的步骤如下:十六进制 (167)(…)166(…)165(…)164(…)163(4096)162(256)161(16)160(1)老大217,老二16:217/16=13(用D表示)......9 (得数D在右2位置)老大9,老二1:9/1=9 (得数9在右1位置)所以结果就是:D9 (十六进制)10---------A11---------B12--------C13---------D14---------E15--------F(十六进制,余数不小于16)以此类推特别情况:跳过的用0代替。
10进制如何转换为16进制

2进制——16进制转换表
0--0000 1--0001 2--0010 3--0011 4--0100 5--0101 6--0110 7--0111 8--1000 9--1001 A--1010 B--1011 C--1100 D--1101 E--1110 F--1111
60928如何转化为0xee00?
60928/16=3808…0 3080/16=238…0 238/16=14…14(e) 14(e) 上式余数由下到上排列 →ee00 最后加上前缀0x,60928就变为十六进制0xee00(也 可以写成0XEE00)
十进制转十六进制的 第二种方法
练习
将下列十进制数转换为十六进制数: 42 18 65535
………(0x2a) ………(0x12) ……(0xffff)
十六进制整数介绍
以0X或0x为前缀,其后由0~9 的数字和A~F(或a~f)的字母组成, 无前缀0X或0x的十六进制整数是不 合法的十六进制整数
十进制转十六进制思路
直接用十进制数除以16求商取余,若余数 是0~9的数字则直接保留,若余数是10~15的 数字则依次对应转化为字母A~F(或a~f)。 之后再用上面的商除以16求商取余,以此类 推,直至最后的商变成小于16的数字,最后 再将余数由下至上排列并加上前缀0X(0x) 即可。
60928先转换为二进制在转换为十六 进制的过程
60928转换为二进制→1110 1110 0000 0000 如上,将每4位分成一组的2进制数并转换为相应的16进 制数: 1110→e 1110→e 0000→0 0000→o 每4位 加上前缀0x 所以1110 1110 0000 0000 ee00 0xee00
二、八、十、十六进制的使用及转换

二、八、十、十六进制的使用及转换十六进制(英文名称:Hexadecimal),是计算机中数据的一种表示方法。
同我们日常生活中的表示法不一样。
它由0-9,A-F组成,字母不区分大小写。
与10进制的对应关系是:0-9对应0-9;A-F对应10-15;N进制的数可以用0~(N-1)的数表示,超过9的用字母A-F。
基本简介: 十六进制(英文名称:Hexadecimal),是计算机中数据的一种表示方法。
同我们日常生活中的表示法不一样。
它由0-9,A-F组成,字母不区分大小写。
与10进制的对应关系是:0-9对应0-9;A-F对应10-15;N进制的数可以用0~(N-1)的数表示,超过9的用字母A-F。
表示方法: 十六进制照样采用位置计数法,位权是16为底的幂。
对于n位整数,m位小数的十六进制数用加权系数的形式表示如下:转换二进制转换十进制二进制数第0位的权值是2的0次方,第1位的权值是2的1次方……所以,设有一个二进制数:101100100,转换为10进制为:356用横式计算: 0×2+0×2+1×2+0×2+0×2+1×2+1×2+0×2+1×2=3560乘以多少都是0,所以我们也可以直接跳过值为0的位:1×2+1×2+1×2+1×2=3564+32+64+256 =356八进制转换十进制八进制就是逢8进1。
八进制数采用0~7这八数来表达一个数。
八进制数第0位的权值为8的0次方,第1位权值为8的1次方,第2位权值为8的2次方……所以,设有一个八进制数:1507,转换为十进制为:839,具体方法如下:可以用横式直接计算: 7×8+0×8+5×8+1×8=839也可以用竖式表示: 第0位7×8^0=7第1位0×8^1=0第2位5×8^2=320第3位1×8^3=512十六进制转换十进制16进制就是逢16进1,但我们只有0~9这十个数字,所以我们用A,B,C,D,E,F这六个字母来分别表示10,11,12,13,14,15。
2-10进制换算

10进制数转换为2进制数给你一个十进制,比如:6,如果将它转换成二进制数呢?10进制数转换成二进制数,这是一个连续除2的过程:把要转换的数,除以2,得到商和余数,将商继续除以2,直到商为0。
最后将所有余数倒序排列,得到数就是转换结果。
听起来有些糊涂?我们结合例子来说明。
比如要转换6为二进制数。
“把要转换的数,除以2,得到商和余数”。
那么:要转换的数是6, 6 ÷ 2,得到商是3,余数是0。
(不要告诉我你不会计算6÷3!)“将商继续除以2,直到商为0……”现在商是3,还不是0,所以继续除以2。
那就: 3 ÷ 2, 得到商是1,余数是1。
“将商继续除以2,直到商为0……”现在商是1,还不是0,所以继续除以2。
那就: 1 ÷ 2, 得到商是0,余数是1(拿笔纸算一下,1÷2是不是商0余1!)“将商继续除以2,直到商为0……最后将所有余数倒序排列”好极!现在商已经是0。
我们三次计算依次得到余数分别是:0、1、1,将所有余数倒序排列,那就是:110了!6转换成二进制,结果是110。
把上面的一段改成用表格来表示,则为:(在计算机中,÷用 / 来表示)如果是在考试时,我们要画这样表还是有点费时间,所更常见的换算过程是使用下图的连除:(图:1)请大家对照图,表,及文字说明,并且自已拿笔计算一遍如何将6转换为二进制数。
说了半天,我们的转换结果对吗?二进制数110是6吗?你已经学会如何将二进制数转换成10进制数了,所以请现在就计算一下110换成10进制是否就是6。
二进制数转换为十进制数二进制数第0位的权值是2的0次方,第1位的权值是2的1次方……所以,设有一个二进制数:0110 0100,转换为10进制为:下面是竖式:0110 0100 换算成十进制第0位 0 * 20 = 0第1位 0 * 21 = 0第2位 1 * 22 = 4第3位 0 * 23 = 0第4位 0 * 24 = 0第5位 1 * 25 = 32第6位 1 * 26 = 64第7位 0 * 27 = 0 +---------------------------100用横式计算为:0 * 20 + 0 * 21 + 1 * 22 + 1 * 23 + 0 * 24 + 1 * 25 + 1 * 26 + 0 * 27 = 1000乘以多少都是0,所以我们也可以直接跳过值为0的位:1 * 22 + 1 * 23 + 1 * 25 + 1 * 26 = 100孟逸轩。
计算机各进制换算

一:十进制数转换成二进制数。
随便拿出一个十进制数“39”,(假如你今天买书用了39元)先来把这个39转换成2进制数。
商余数步数39/2= 19 1第一步19/2= 9 1 (这里的19是第一步运算结果的商)第二步9/2= 4 1 (这里的9是第二步运算结果的商)第三步4/2= 2 0 (这里的4是第三步运算结果的商)第四步2/2= 1 0 (这里的2是第四步运算结果的商)第五步1/2= 0 1 (这里的1是第五步运算结果的商)第六步那么十进制数39转换成2进制数就是100111. 既39(10)=100111(2)解析一:1. 当要求把一个10进制数转换成2进制数的时候,就用那个数一直除以2得到商和余数。
2. 用上一步运算结果的商在来除以2,再来得到商和余数。
3. 就这样,一直用上一步的商来除以2,得到商和余数!那么什么时候停止呢?4. 请看上述运算图,第六步的运算过程是用1除以2.得到的商是0,余数是1. 那么请你记住,记好了啊共2点。
A: 当运算到商为“0”的时候,就不用运算了。
B:1/2的商为“0”余数为“1”。
这个你要死记住,答案并不是0.5!答案就是商为“0”余数为“1”。
你不用去思考为什么,记好了就行了!5. 在上述图中你会清晰的看到每一步运算结果的余数,你倒着把它们写下来就是“100111”了。
那么这个就是结果了。
6. 在上述图中符号“/”代表“除以”。
二:十进制数转换成八进制数。
随便拿出一个十进制数“358”,(假如你今天买彩票中了358元)。
358是我们现实生活中所用10进制表达出来的一个数值,转换成八进制数十多少?商余数步数358/8= 44 6第一步44/8= 5 4 (这里的44是第一步运算结果的商)第二步5/8= 0 5 (这里的5是第二步运算结果的商)第三步那么十进制数358转换成8进制数就是546。
既358(10)=546(8)解析二: 1.没什么好说的啦,10进制数转换成2进制数和10进制数转换成8进制数的唯一不一样的地方就是除数变了,除数由“2” 变成了“8”。
