命题逻辑练习题及答案14
(完整版)简易逻辑练习题及答案

、选择题:1若命题p : 2n — 1是奇数,q : 2n + 1是偶数,则下列说法中正确的是()A . p 或q 为真B . p 且q 为真C .非p 为真D .非p 为假2.“至多三个”的否定为()A .至少有三个B .至少有四个C .有三个D . 有四个3.△ ABC 中,若/ C=90°则/ A 、/ B 都是锐角”的否命题为 A . △ ABC 中,若/ C M 90° 则/ A 、/ B 都不是锐角 B . △ ABC 中,若/ C M 90° 则/ A 、/ B 不都是锐角 C . △ ABC 中,若/ C M 90°则/ A 、/ B 都不一定是锐角 D .以上都不对4. 给出 4 个命题:① 若 x 2 3x 2,则 x=1 或 x=2;② 若 2 x 3,则 (x 2)(x 3) 0; ③ 若 x=y=0 ,则 x 2 y 2 0 ;④ 若x, y N , x + y 是奇数,则x , y 中一个是奇数,一个是偶数. 那么:A . p 且q 为假 D .非p 为假6 .命题 若厶ABC 不是等腰三角形,则它的任何两个内角不相等• ”的逆否命题是()A .若厶ABC 是等腰三角形,则它的任何两个内角相等 .”B .若厶ABC 任何两个内角不相等,则它不是等腰三角形 .”C .若厶ABC 有两个内角相等,则它是等腰三角形 .”D .若厶ABC 任何两个角相等,则它是等腰三角形•”简易逻辑A .①的逆命题为真B .②的否命题为真C .③的逆否命题为假D .④的逆命题为假5 .对命题p : A n,命题q : A U = A ,下列说法正确的是B . p 或q 为假C . 非 p 为真7.设集合 M={x| x >2} , P={x|x v 3},那么 X € M ,或 x € P”是“ € M n P”的A .必要不充分条件B .充分不必要条件C .充要条件D .既不充分也不必要条件&有下列四个命题:① 若x + y=0,则x , y 互为相反数”的逆命题; ② 全等三角形的面积相等”的否命题;③ 若q < 1贝U x 2 + 2x + q=0有实根”的逆否命题; ④ 不等边三角形的三个内角相等 ”逆命题; 其中的真命题为 ()A .①②B .②③C .①③D .③④9•设集合A={ xlx 2 + x -6=0} , B={x|mx +仁0},贝V B 是A 的真子集的一个充分不必要的条件是()13 .由命题p:6是12的约数,q:6是24的约数,构成的“ p 或q ”形式的命题是: _________ _ ,“p 且q ”形式的命题是 ___________________ , “非p ”形式的命题是 _____________________ 14.设集合A={ x|x 2 + x - 6=0} , B={ x|mx +仁0},则B 是A 的真子集的一个充分不必要的条件是 __________________________________________ .15. _____________________________________________________________________________ 设1 1 1 A . mB . m=—2 32io . a 2 b 2 o ”的含义是A . a,b 不全为0 C . a,b 至少有一个为0 C . 1 1 m 0,,D .2 3m 0E( )B . a,b 全不为0D . a 不为0且b 为0, 或b 不为0且a 为011.如果命题非p ”与命题“戯q”都是真命题,那么A .命题p 与命题q 的真值相同B .命题q —定是真命题C .命题q 不一定是真命题D .命题p 不一定是真命题12.命题P :若A n B=B ,则A B ;命题q :若AB ,贝y A n B 工B .那么命题p 与命题q 的关系是 A .互逆、填空题:B .互否( )C .互为逆否命题D .不能确定集合M={x|x>2}, P={x|x v 3},那么x€ M,或x €P”是“X M n P”的___________________________三、解答题:16•命题:已知a、b为实数,若x2+ ax+ b< 0有非空解集,则a2—4b>0•写出该命题的逆命题、否命题、逆否命题,并判断这些命题的真假.17. 已知关于x的一元二次方程(m € Z)① mx2—4x+ 4 = 0 ② x2—4mx+ 4m2—4m—5= 0求方程①和②都有整数解的充要条件•18 •分别指出由下列各组命题构成的逻辑关联词或”、且”、非”的真假.(1)p:梯形有一组对边平行;q:梯形有一组对边相等.2 2(2)p: 1是方程x 4x 3 0的解;q: 3是方程x 4x 3 0的解.(3)p:不等式X2 2x 1 0解集为R;q:不等式X2 2x 2 1解集为用1P:{0}; q:0X 1 2 219.已知命题p: 1 ----- 2 ;q: x 2x 1 m 0(m 0)若p是q的充分非必要3条件,试求实数m的取值范围.20.已知命题p:|x2—X |> 6, q:x€ Z,且p且q”与非q”同时为假命题,求x的值.21.已知p:方程x2+ mx+仁0有两个不等的负根;q:方程4x2+ 4(m —2)x+ 1 = 0无实根.若"p 或q”为真,“ p且q”为假,求m的取值范围.参考答案一、选择题:ABBAD CACBA BC二、填空题:13•若△ ABC有两个内角相等,则它是等腰三角形.14.6是12或24的约数;6是12的约数,也是24的约数;6不是12的约数.1 115.m= (也可为m -). 16.必要不充分条件.2 3三、解答题:2 217.解析:逆命题:已知a、b为实数,若a 4b 0,则x ax b 0有非空解集否命题:已知a、b为实数,若x2ax b 0没有非空解集,则a24b 0., 2 2逆否命题:已知a、b为实数,若a 4b 0.则x ax b 0没有非空解集原命题、逆命题、否命题、逆否命题均为真命题18. 解析:方程①有实根的充要条件是16 4 4 m 0,解得m 1.m 1 •而m 乙故m= —1 或m=0 或m=1. 4当m=—1时,①方程无整数解.当m=0时,②无整数解;当m=1时,①②都有整数.从而①②都有整数解m=1.反之,m=1①②都有整数解• ••①②都有整数解的充要条件是m=1.19 .解析:⑴I p真,q假,"戯q”为真,"诅q”为假,非p”为假.⑵•••p真,q真,“P或q”为真,“P且q”为真,非p”为假.⑶•••p 假, q假,“p q”为假, “p且q”为假,非p”为真⑷•p真,q假,“1或q”为真,“p且q”为假,非p”为假x 120.解析:由1 ---------- 2,得2x10. p: A x| x 2或x 103由x22x 1 m20(m 0),得1 m x 1 m.q : B={ x | x 1 m或x 1 m, m 0}.p是q的充分非必要条件,且m 0, A B.方程②有实根的充要条件是16m24(4m24m 5) 0,解得mm 0 1 m 10 即 0 m31 m 2即 p : m >2若方程4x 2 + 4(m — 2)x + 1 = 0无实根,则△= 16(m — 2)2— 16= 16(m 2— 4m + 3)v 0 解得:1 v m v 3•即 q : 1 v m v 3.因此,p 、q 两命题应一真一假,即 p 为真,q 为假或p 为假,q 为真.m 2 亠 m 2 *^或m 1或 m3 1 m 3解得:m 》3或1 v m W 2.由p 为假且 q 为真,可得: |xx| 6x Zx 2 x 6 2x x 6 0 2x3 即x 2 x6 •2 xx 6 0x R x Zx Zx Z故x 的取值为:一1、0、1、2.21、解析:•/ p 且q 为假p 、q 至少有一命题为假,又 非q”为假••• q 为真,从而可知p 为假• 22.解析: 若方程X + mx +仁0有两不等的负根,则因p 或q”为真,所以p 、q 至少有一为真,又 p 且q”为假,所以p 、q 至少有一为假, m 2 4 m 0解得m >2,。
命题逻辑习题及其参考答案

1.某地发生一起刑事案件,经过公安人员的努力侦破,作案嫌疑人锁定在A、B、C三人中,并且摸清了以下情况:①只有01号案件成功告破,才能确认A、B、C三人都是作案人。
②目前,01号案件还是一起悬案。
③如果A不是作案人,那么A的供词是真的,但A说自己与B都不是作案人。
④如果B不是作案人,那么B的供词也是真的,但B说自己与C是好朋友。
⑤现已查明C根本不认识B。
根据上述线索,问:A、B、C三人中谁是作案人?解:令p:01号案件成功告破;q、r、s分别表示A、B、C作案;t:B与C是好朋友。
据题意有:1. {1} ┐p→┐(q∧r∧s)P2. {2} ┐p P3. {3} ┐q→(┐q∧┐r)P4. {4} ┐r→t P5. {5} ┐t P6. {4.5} r T4.5否定后件7. {1.2} ┐(q∧r∧s)T1.2肯定前件8. {1.2} ┐q∨┐r∨┐s T7德摩根9. {1.2.3} q T3.6否定后件10. {1.2.3.4.5} q∧r P6.9组合式答:AB作案,至于C尚待侦查。
2.综合分析题(要求写出推导过程):某班有学生61人,下面有三句话:①该班有些学生会使用计算机。
②该班有些学生不会使用计算机。
③该班班长不会使用计算机。
已知上述三句话中,只有一句话是真的,试问:哪一句话是真话?该班有多少学生会使用计算机?解:①②分别为I命题和O命题,二者是下反对关系,必有一真,或许都真;但据题设只有一句真话,可知③为假,真实情况是班长会使用计算机。
既然这样第一句话“该班有些学生会使用计算机”就是真的,而第二句话就是假的。
O命题假,根据矛盾关系可知,A命题即“该班所有学生都会使用计算机”就真,所以,全班61个学生都会计算机。
3.下面有三句话:①如果甲是篮球队员,则乙就是足球队员。
②如果乙是足球队员,则甲就是篮球队员。
③甲不是篮球队员。
已知上述三句话中只有一句话是真话,问:甲是不是篮球队员?乙是不是足球队员?哪一句话是真话?(要求写出推导过程)解:令p表示“甲是篮球队员”,q表示“乙是足球队员”,再令③即“┐p”真,据题设有:①{1} ┐(p→q)P②{2} ┐(q→p)P③{3} ┐p P④{1} p∧┐q T①等值关系⑤{1} p T④合取分解⑥{1.3} p∧┐p T③⑤合取组合⑦{1} p T归谬③⑥⑧{2} q∧┐p T②等值关系⑨{2} ┐p T⑧合取分解⑩{1.2} p∧┐p T⑦⑨合取组合⑾{1} (q→p)归谬②⑩可见:第二句话为真,一三两句为假。
命题逻辑习题课答案

方法3 (P→Q)→(P→(P∧Q)) ⇔¬(¬P∨Q)∨(¬P∨(P∧Q)) ⇔(P∧¬Q)∨¬P∨(P∧Q) ⇔(P∧¬Q)∨(¬P∧(Q∨¬Q))∨(P∧Q) ⇔(P∧¬Q)∨(¬P∧Q)∨(¬P∧¬Q)∨(P∧Q) ⇔ (P∧Q)∨(P∧¬Q)∨(¬P∧Q)∨(¬P∧¬Q) 可见,该公式的主析取范式含有全部(四个) 小项,这表明(P→Q)→(P→(P∧Q))是永真式
等价变换abcd四个人中要派两个人出差按下述三个条件有几种派法
命题逻辑习题课参考答案
一.命题符号化 P:天下雪。Q:我将去镇上。R:我有时间。 (1) 如果天不下雪且我有时间,那么我将去镇上。 (¬P∧R)→Q P∧R)→Q (2) 我将去镇上,仅当我有时间。 Q→R (3)天下雪,那么我不去镇上。 P→¬Q → Q
方法2.等价变换 (P→(Q∧R))∧(¬P→(¬Q∧¬R)) ⇔ (¬P∨(Q∧R))∧(P∨(¬Q∧¬R)) ⇔ (¬P∧P)∨(P∧Q∧R))∨(¬P∧¬Q∧¬R))∨ ((Q∧R)∧(¬Q∧¬R)) ⇔F∨(P∧Q∧R))∨(¬P∧¬Q∧¬R)∨F ⇔(P∧Q∧R))∨(¬P∧¬Q∧¬R)
四. 等价公式的证明方法 方法1:用列真值表。(不再举例) 方法2:用公式的等价变换.(用置换定律) (1) 证明 ((A∧B)→C)∧(B→(D∨C))⇔(B∧(D→A))→ C 左式⇔(¬(A∧B)∨C)∧(¬B∨(D∨C)) ⇔((¬A∨¬B)∨C)∧(¬B∨(D∨C)) ⇔ ¬ ¬ ¬ ⇔((¬B ∨¬A)∨C)∧((¬B∨D)∨C) ⇔((¬B ∨¬A)∧(¬B∨D))∨C ⇔(¬B ∨(¬A∧D))∨C ⇔¬ (B∧(A∨¬D))∨C ⇔(B∧(D→A))→C
(2) A,B,C,D四个人中要派两个人出差,按下述三 个条件有几种派法? ①若A去则C和D中要去一个人。 ②B和C不能都去。 ③C去则D要留下。 解.设A,B,C,D分别表示A去,B去,C去,D去。 ①A→((C∧¬D)∨(¬C∧D))
2014年4月自考普通逻辑试题和答案

绝密★考试结束前全国2014年4月高等教育自学考试普通逻辑试题和答案课程代码:00024请考生按规定用笔将所有试题的答案涂、写在答题纸上。
选择题部分注意事项:1.答题前,考生务必将自己的考试课程名称、姓名、准考证号用黑色字迹的签字笔或钢笔填写在答题纸规定的位置上。
2.每小题选出答案后,用2B铅笔把答题纸上对应题目的答案标号涂黑。
如需改动,用橡皮擦干净后,再选涂其他答案标号。
不能答在试题卷上。
一、单项选择题(本大题共15小题,每小题1分,共15分)在每小题列出的四个备选项中只有一个是符合题目要求的,请将其选出并将“答题纸”的相应代码涂黑。
错涂、多涂或未涂均无分。
1.以下概念为非空概念的是(D)2-59A.18世纪中国国家主席B.圆的方C.永动机D.当今法国总统2.断言“小夏是一位画家”和“小夏不是一位画家”同时都真,违反了(B)5-160A.同一律B.矛盾律C.排中律D.充足理由律3.“参加会议的不都是干部”与“参加会议的没有一个是干部”这两个判断(A)3-111A.可同真可同假B.可同真不可同假C.不可同真可同假D.不可同真不可同假4.“一个推理只有形式正确,才能得出可靠的结论,这个推理结论不可靠,所以这个推理形式不正确。
”这个假言推理使用了(B)7-229A.正确的否定后件式B.错误的否定后件式C.正确的否定前件式D.错误的否定前件式5.“吸毒”和“感染艾滋病”之间是什么关系(D)4-134A.前者是后者的充分条件B.前者是后者的必要条件第 1 页C.前者是后者的充分必要条件D.前者和后者不构成条件关系6.在不完全归纳推理中,结论的断定范围和前提的断定范围关系为(C)8-257A.前者少于后者B.前者等于后者C.前者超出后者D.前者有时等于后者,前者有时超出后者7.作为万物之灵,人同样是有性别的动物,分为男人和女人。
这句话对于概念“人”来说(B)2-58A.明确了内涵,但没有明确外延B.没有明确内涵,但明确了外延C.明确了内涵,并且明确了外延D.没有明确内涵,并且没有明确外延8.“某体操队有些队员来自广西”,这个判断的对象是(D)3-101A.某体操队B.某体操队有些队员C.体操队D.某体操队的队员9.“所有与非典患者接触的人都被隔离了,所有被隔离的人都与小李接触过”,如果这个命题是真的,那么以下也为真的命题是(C)6-193A.小李是非典患者。
命题逻辑复习题及答案

命题逻辑一、选择题(每题3分)1、下列句子中哪个是命题 ( C )A 、你的离散数学考试通过了吗B 、请系好安全带!C 、 π是有理数D 、 本命题是假的 2、下列句子中哪个不是命题 ( C )A 、你通过了离散数学考试B 、我俩五百年前是一家C 、 我说的是真话D 、 淮海工学院是一座工厂 3、下列联接词运算不可交换的是( C )A 、∧B 、∨C 、 →D 、 ↔ 4、命题公式P Q ⌝→不能表述为( B )A 、P 或QB 、非P 每当QC 、非P 仅当QD 、除非P ,否则Q 5、永真式的否定是 ( B )A 、 永真式B 、永假式C 、可满足式D 、 以上答案均有可能 6、下列哪组赋值使命题公式()P P Q →∧的真值为假( D )A 、P 假Q 真B 、P 假Q 假C 、P 真Q 真D 、P 真Q 假 7、下列为命题公式()P Q R ∧∨⌝成假指派的是( B )A 、100B 、101C 、110D 、111 8、 下列公式中为永真式的是 ( C )A 、()P P Q →∧B 、()P P Q ⌝→∧C 、()P Q Q ∧→D 、()P Q Q ∨→ 9、 下列公式中为非永真式的是( B )A 、 ()P P Q ∧⌝→B 、()P P Q ∨⌝→C 、()P P Q ∧⌝→D 、()P P Q ∨⌝→ 10、下列表达式错误的是( D )A 、()P P Q P ∨∧⇔B 、()P P Q P ∧∨⇔C 、()P P Q P Q ∨⌝∧⇔∨D 、()P P Q P Q ∧⌝∨⇔∨ 11、下列表达式正确的是( D )A 、P P Q ⇒∧B 、P Q P ⇒∨C 、()Q P Q ⌝⇒⌝→D 、Q Q P ⌝⇒→⌝)( 12、下列四个命题中真值为真的命题为( B )(1)224+=当且仅当3是奇数 (2)224+=当且仅当3不是奇数; (3)224+≠当且仅当3是奇数 (4)224+≠当且仅当3不是奇数 A 、(1)与(2) B 、(1)与(4) C 、(2)与(4) D 、(3)与(4)13、设P :龙凤呈祥是成语,Q :雪是黑的,R :太阳从东方升起,则下列假命题为( A ) A 、R Q P ∧→ B 、Q P S →∧ C 、P Q R →∨ D 、 Q P S →∨14、设P :我累,Q :我去打球,则命题:“除非我累,否则我去打球”的符号化为( B ) A 、P Q → B 、Q P ⌝→ C 、 Q P →⌝ D 、P Q ⌝→⌝15、设P :我听课,Q :我睡觉,则命题 “我不能一边听课,一边睡觉”的符号化为( B ) A 、P Q → B 、Q P ⌝→ C 、 Q P →⌝ D 、P Q ⌝→⌝ 提示:()P Q P Q ⌝∧⇔→⌝16、设P :停机;Q :语法错误;R :程序错误,则命题 “停机的原因在于语法错误或程序错误” 的符号化为( D )A 、R Q P ∧→B 、P Q R →∨C 、Q R P ∧→D 、Q R P ∨→ 17、设P :你来了;Q :他唱歌;R :你伴奏则命题 “如果你来了,那末他唱不唱歌将看你是否伴奏而定” 的符号化为( D ) A 、()P Q R →∧ B 、()P Q R →→ C 、()P R Q →→ D 、()P Q R →↔ 18、在命运题逻辑中,任何非永真命题公式的主合取范式都是( A )A 、 存在并且唯一B 、存在但不唯一C 、 不存在D 、 不能够确定 19、在命题逻辑中,任何非永假命题公式的主析取范式都是( A )A 、 存在并且唯一B 、存在但不唯一C 、 不存在D 、 不能够确定 20、n 个命题变元所产生互不等价的极小项项数为( D )A 、nB 、2nC 、2n D 、2n 21、n 个命题变元所产生互不等价的极大项项数为( D )A 、nB 、2nC 、2n D 、2n二、填充题(每题4分)1、设P :你努力,Q :你失败,则 “虽然你努力了,但还是失败了” 符号化为Q P ∧.2、设P :它占据空间,Q :它有质量,R :它不断运动,S :它叫做物质, 则 “占据空间的,有质量的而且不断运动的叫做物质”符号化为R Q P S ∧∧↔.3、一个命题含有n 个原子命题,则对其所有可能赋值有2n 种.4、推理规则()A A B B ∧→→的名称为假言推理.5、推理规则()B A B A ⌝∧→→⌝的名称为拒取式.6、推理规则()A A B B ⌝∧∨⇒的名称为析取三段论.7、推理规则()()A B B C A C →∧→⇒→的名称为前提三段论.8、当赋予极小项足标相同的指派时,该极小项的真值为1,当赋予极大项足标相同的指派时,该极大项的真值为0.9、任意两个不同极小项的合取式的真值为0,而全体极小项的析取式的真值为1. 10、任意两个不同极大项的析取式的真值为1,而全体极大项的合取式的真值为0. 11、n 个命题变元可构造包括F 的不同的主析取范式类别为22n.12、n 个命题变元可构造包括T 的不同的主合取范式类别为22n.三、问答题(每题6分)1、设A 、B 是任意命题公式,请问,A B A B →⇒分别表示什么其有何关系 答:A B →表示A 蕴含B ,A B ⇒表示A 永真蕴含B ; 其关系表现为:若A B →为永真式,则有A B ⇒.2、设A 、B 是任意命题公式,请问,A B A B ↔⇔分别表示什么其有何关系 答:A B ↔表示A 等值于B ,A B ⇔表示A 与B 逻辑等价; 其关系表现为:若A B ↔为永真式,则有A B ⇔.3、设A 、B 、C 是任意命题公式,若A C B C ∨⇔∨ ,则A B ⇔成立吗为什么 答:不一定有A B ⇔;若A 为真,B 为假,C 为真,则A C B C ∨⇔∨成立,但A B ⇔不成立.4、设A 、B 、C 是任意命题公式,若A C B C ∧⇔∧ ,则A B ⇔成立吗为什么 答:不一定有A B ⇔;若A 为真,B 为假,C 为假,则A C B C ∧⇔∧成立,但A B ⇔不成立. 5、设A 、B 是任意命题公式,()A A B B ∧→→一定为真吗为什么答:一定为真;因()()()()A A B B A A B B A A A B B ∧→→⇔∧⌝∨→⇔∧⌝∨∧→()F A B B A B B T ⇔∨∧→⇔∧→⇔.(用真值表也可证明)6、设A 、B 是任意命题公式,()()A B A B A →∧→⌝↔⌝一定为真吗为什么答:一定为真;因()()()()()A B A B A B A B A B B →∧→⌝⇔⌝∨∧⌝∨⌝⇔⌝∨∧⌝ A F A ⇔⌝∨⇔⌝.(用真值表也可证明)四、填表计算题(每题10分)1、对命题公式 ()()A p q p q =⌝→∧∨,要求(1)用0或1填补其真值表的空格处;(2)求该命题公式的主析取范式与主合取范式. 解:p q p q → ()p q ⌝→p q ∨A0 0 1 0 0 0 0 1 1 0 1 0 1 0 0 1 1 1 1111主析取范式(2)A ⇔∑ ;主合取范式(0,1,3)A ⇔∏.2、对命题公式 ()A p q r =→↔,要求(1)用0或1填补其真值表的空格处;(2)求该命题公式的主析取范式与主合取范式. 解:p q rp q → A 0 0 01 0 0 0 1 1 1 0 1 0 1 0 0 1 1 1 1 1 0 0 0 1 1 0 1 0 0 1 1 0 1 0 11111主析取范式(1,3,4,7)A ⇔∑ ;主合取范式(0,2,5,6)A ⇔∏.3、对命题公式 ()()A p q p r =∧∨∧,要求(1)用0或1填补其真值表的空格处;(2)求该命题公式的主析取范式与主合取范式. 解:p q rp q ∧ p r ∧ A0 0 0 0 0 0 0 0 1 0 0 0 0 1 0 0 0 0 0 1 1 0 0 0 1 0 0 0 0 0 1 0 1 0 1 1 1 1 0 1 0 1 111111主析取范式(5,6,7)A ⇔∑ ;主合取范式(0,1,2,3,4)A ⇔∏.4、对命题公式()()A p q p r =⌝→∧→,要求(1)用0或1填补其真值表的空格处;(2)求该命题公式的主析取范式与主合取范式. 解:主析取范式(2,3,5,7)A ⇔∑ ;主合取范式(0,1,4,6)A ⇔∏.5、对命题公式()A p q r =⌝∨⌝→,要求(1)用0或1填补其真值表的空格处;(2)求该命题公式的主析取范式与主合取范式. 解:主析取范式(1,3,5,6,7)A ⇔∑ ;主合取范式(0,2,4)A ⇔∏.五、证明题(每题10分)1、证明下列逻辑恒等式:()()()P Q R Q P R Q →∧→⇔∨→. 证明 : 左()()()P Q R Q P R Q ⇔⌝∨∧⌝∨⇔⌝∧⌝∨()P R Q P R Q ⇔⌝∨∨⇔∨→⇔右.(用真值表也可证明) 2、证明下列逻辑恒等式: P Q R R Q P ⌝∧⌝→⌝⇔→∨. 证明:左()P Q R P Q R ⇔⌝⌝∧⌝∨⌝⇔∨∨⌝()R Q P R Q P ⇔⌝∨∨⇔→∨⇔右.(用真值表也可证明)3、证明下列逻辑恒等式:()()()P Q P Q P Q ⌝↔⇔∨∧⌝∧. 证明:左()()()()()P Q P Q P Q P Q ⇔⌝∨⌝∧⌝∨⇔⌝∨⌝∨⌝⌝∨()()()()()()Q Q P Q Q P P P Q P Q P ⌝∨∧∨∧⌝∧⌝∧⌝∨⇔⌝∧∨∧⌝⇔()()⇔⌝∨⌝∧∨⇔Q P Q P ()()P Q P Q ∨∧⌝∧右⇔.(用真值表也可证明)4、用逻辑推理规则证明: ()a b c ∧→ ,d ⌝ ,c d ⌝∨ ⇒ a b ⌝∨⌝ . 证明:(1) c d ⌝∨ P(2) d ⌝ P(3)c ⌝ T (1),(2) (析取三段论) (4) ()a b c ∧→ P (5)()a b ⌝∧ T (3),(4) (拒取式) (6) a b ⌝∨⌝ T (5) (德.摩根律) .5、用逻辑推理规则证明: , ,p q p s s r r q ∨→→⇒⌝→. 证明: (1) p s →P (2) s r → P(3) p r →T (1),(2) (前提三段论)(4)r p ⌝→⌝ T (3) (逆反律) (5)p q ∨ P (6)p q ⌝→ T (5) (蕴含表达式) (7)r q ⌝→ T (4),(6) (前提三段论) .6、用逻辑推理规则证明:p q →,p r ∧, q r ⌝∨,r ⌝,s p s ⌝∨⇒⌝. 证明: (1) r ⌝ P(2) q r ⌝∨ P(3) q ⌝ T (1),(2) (析取三段论) (4)p q → P(5) p ⌝ T (3),(4) (拒取式) (6) s p ⌝∨ P (7) s ⌝ T (5),(6) (析取三段论) .7、用逻辑推理规则证明:()()p q r s ⌝→→⌝∨,()q p r →∨⌝, r p q ⇒↔. 证明: (1) r P(2) ()q p r →∨⌝ P(3) q p → T (1),(2) (析取三段论) (4) r s ∨ T (1) (加法式)(5) ()()p q r s ⌝→→⌝∨ P (6) p q → T (4),(5) (拒取式) (7) ()()p q q p →∧→T (3),(6) (合取式)(8) p q ↔ T (7) (等值表达式) .8、用逻辑推理规则证明: , ,s p p r q r s q ⌝∨→∧⇒→.证明: (1) s P(2) s p ⌝∨ P(3) p T (1),(2) (析取三段论) (4) p r q →∧ P(5) r q ∧ T (3),(4) (假言推理) (6) q T (5)(简化式) (7) s q → CP .9、用逻辑推理规则证明:()()p q r p q r ∨→⇒∧→ 证明:(1) p q ∧ P (附加前提)(2) p T (1)(简化式)(3) p q ∨ T (2)(加法式) (4) ()p q r ∨→ P(5) r T (3),(4)(假言推理) (6) ()()p q r p q r ∨→⇒∧→ CP .10、用逻辑推理规则证明:,,p q q r r s p s ⌝∨⌝∨→⇒→. 证明:(1)p P (附加前提)(2) p q ⌝∨ P(3) q T (1),(2) (析取三段论) (4)q r ⌝∨ P(5) r T (3),(4) (析取三段论) (6) r s → P(7) s T (5),(6) (假言推理) (8) p s → CP .11、用逻辑推理规则证明:()()p q r s ∨→∧,()r s t p t ∨→⇒→ . 证明:(1)p P (附加前提) (2)p q ∨ T (1)(加法式) (3)()()p q r s ∨→∧ P(4)r s ∧ T (2),(3)(假言推理) (5)r T (4)(简化式) (6)r s ∨ T (5)(加法式)(7)()r s t ∨→ P (8)t T (6),(7)(假言推理)(9)p t → CP . 12、用逻辑推理规则证明:(),,t w s q s t s q t →⌝→⌝⌝∨→⌝⇒→ 证明:(1)q P (附加前提)(2) q s ⌝∨ P(3) s T (1),(2) (析取三段论) (4) ()t w s →⌝→⌝ P(5)()t w ⌝→⌝ T (3),(4) (拒取式)(6)()t w ⌝⌝∨⌝ T (5) (蕴含表达式) (7) t w ∧ T (6) (德.摩根律) (8) t T (7) (简化式)(9)q t → CP .13、用逻辑推理规则证明:a b c →∧,()e f c →⌝→⌝,()b a s →∧⌝⇒b e →. 证明:(1) b P (附加前提) (2)()b a s →∧⌝ P(3) a s ∧⌝ T (1),(2) (假言推理) (4) a T (3) (简化式) (5) a b c →∧ P(6) b c ∧ T (4),(5) (假言推理)(7) c T (6) (简化式) (8)()e f c →⌝→⌝ P(9) ()e f ⌝→⌝ T (7),(8) (拒取式) (10)()e f ⌝⌝∨⌝ T (9) (蕴含表达式) (11) e f ∧ T (10) (德.摩根律) (12) e T (11) (简化式) (13) b e → CP .14、用逻辑推理规则证明:p q →,p q q ⌝→⇒. 证明:(1) q ⌝ P (附加前提) (2) p q → P(3) p ⌝ T (1),(2) (拒取式) (4) p q ⌝→ P(5) q T (3),(4) (假言推理) (6) q q ⌝∧ T (1),(5) (合取式)由(6)得出矛盾式,故原命题有效.15、用逻辑推理规则证明: p q ∧ ,()()p q t s ↔→∨ ⇒ t s ∨ . 证明:(1)()t s ⌝∨ P (附加前提)(2) ()()p q t s ↔→∨ P(3)()p q ⌝↔ T (1),(2) (拒取式)(4) (()())p q p q ⌝⌝∨∧∨⌝ T (3)(等值与蕴含表达式) (5) ()()p q p q ∧⌝∨⌝∧ T (4) (德.摩根律)(6) ()()p q p q ⌝∨⌝∧∨ T (5) (结合律或范式等价) . (7) p q ⌝∨⌝ T (7) (简化式) (8) ()p q ⌝∧ T (4) (德.摩根律) (9) p q ∧ P(10) ()()p q p q ⌝∧∧∧ T (9),(10) (合取式) 由(10)得出矛盾式,故原命题有效.16、用逻辑推理规则证明:p q →,p r ∧, ()q r ⌝∨不能同时为真. 证明:(1) p r ∧ P(2) p T (1) (简化式) (3) p q → P(4) q T (2),(3) (假言推理) (5) ()q r ⌝∨ P(6) q r ⌝∧⌝ T (5) (德.摩根律) (7) q ⌝ T (6) (简化式)(8) q q ⌝∧ T (4),(7) (合取式)由(8)得出矛盾式,故原命题有效.17、证明下列命题推得的结论有效:或者逻辑难学,或者有少数学生不喜欢它;如果数学容易学,那么逻辑并不难学.因此,如果许多学生喜欢逻辑,那么数学并不难学. 证明:设p :逻辑难学;q :有少数学生不喜欢逻辑学;r :数学容易学.该推理就是要证明:, p q r p q r ∨→⌝⇒⌝→⌝. (1) p q ∨ P(2) p q ⌝→ T (1) (蕴含表达式) (3) r p →⌝ P(4) r q → T (2),(3) (前提三段论)(5) q r ⌝→⌝ T (4) (逆反律) .18、证明下列命题推得的结论有效:如果今天是星期三,那么我有一次离散数学或数字逻辑测验;如果离散数学课老师有事,那么没有离散数学测验;今天是星期三且离散数学老师有事.所以,我有一次数字逻辑测验.证明:设p :今天是星期三;q :我有一次离散数学测验;r :我有一次数字逻辑测验;s :离散数学课老师有事. 该推理就是要证明:(), , p q r s q p s r →∨→⌝∧⇒. (1) p s ∧ P(2) p T (1) (简化式) (3) s T (1) (简化式) (4) s q →⌝ P(5) q ⌝ T (3) ,(4) (假言推理)(6) ()p q r →∨ P(7) q r ∨ T (2) ,(6) (假言推理) (8) r T (5) ,(7) (析取三段论) .19、证明下列命题推得的结论有效:如果马会飞或羊吃草,则母鸡就会是飞鸟;如果母鸡是飞鸟,那么烤熟的鸭子还会跑;烤熟的鸭子不会跑.所以,羊不吃草。
逻辑测试题及答案

逻辑测试题及答案一、选择题1. 如果所有的苹果都是水果,那么以下哪个陈述是正确的?A. 所有的水果都是苹果B. 一些水果是苹果C. 没有水果是苹果D. 一些苹果不是水果答案:B2. 如果“如果下雨,那么地面会湿”,并且事实上地面湿了,那么以下哪个结论是正确的?A. 一定是下雨了B. 可能是下雨了C. 地面湿了,但不是因为下雨D. 地面湿了,但无法确定是否下雨答案:B二、判断题1. 如果所有的猫都怕水,那么一只怕水的动物一定是猫。
()答案:错误2. 如果“如果今天是星期三,那么明天是星期四”,并且今天是星期三,那么明天是星期四。
()答案:正确三、逻辑推理题1. 在一个班级里,如果一个学生是班长,那么他/她一定是数学成绩最好的学生。
现在我们知道小明是班长,那么小明的数学成绩是班级中最好的吗?答案:根据题目信息,我们可以推断小明的数学成绩是班级中最好的。
2. 一个逻辑学家说:“如果所有的天鹅都是白色的,那么所有非白色的鸟都不是天鹅。
”现在我们发现一只黑色的鸟,这只鸟是天鹅吗?答案:根据逻辑学家的陈述,我们可以推断这只黑色的鸟不是天鹅。
四、解答题1. 请解释“逆否命题”的概念,并给出一个例子。
答案:逆否命题是一个命题的逆命题的否定形式。
例如,如果原命题是“如果A,则B”,那么逆否命题是“如果非B,则非A”。
例如,原命题是“如果今天是周末,那么我不上班”,逆否命题则是“如果我上班,那么今天不是周末”。
2. 请解释“充分条件”和“必要条件”的区别。
答案:充分条件是指当一个条件存在时,必然导致某个结果发生;必要条件是指为了某个结果发生,必须存在的条件。
例如,对于命题“如果下雨,那么地面会湿”,“下雨”是“地面湿”的充分条件,而“地面湿”是“下雨”的必要条件。
命题逻辑习题

数理逻辑习题命题逻辑(_)1・指出下列语句中哪些是命题a)离散数学的研究对象是自然数。
b)请勿喧哗。
c)夸夸其谈可以创造财富。
d)“飞碟”来自于银河系之外。
e)今天很冷。
f)你明天还来吗?[解]町是命题。
因为它是假的陈述句。
b)不是命题。
因为它是祈使句。
c)是命题。
因为它是假的陈述句。
d)是命题。
因为它是可确定真假的陈述句,虽然其真假性现时还无法确定,但随着人类认识的发展终将得到证实。
e)是命题。
因为它是可确定真假的陈述句,其真假取决于说话人的主观判断和外部环境的客观温度。
f)不是命题。
因为它是疑问句。
2•用符号形式写下面命题,其中P表示命题“明天下雪”;Q表示命题“我们明天上课”;R表示命题“我们明天上公园”。
a)如果明天下雪且我们停课,那么我们去公园。
b)只有明天不下雪,我们才去公园。
c)除非明天不下雪且我们上公园,否则我们将上课。
d)无论明天下雪与否,我们照常上课。
[解]a) P—Q-R;b)「P-*「R (或 R—P);c)—1(—P A R)<->—Q (14k ―P/\R _Q);d)Pv-,P-Q (或 Q)。
3•用上题的命题P, Q, R解释下面的形式命题。
a)-iPvQ-*—>Rb)P A Rc)^P-*QvRd)—>QoR[解]a)只有明天下雪且不上课,我们才去公园;b)明天下雪,明天我们去公园;c)如果明天不下雪,那么我们上课或去公园;d)除非明天不停课(上课),否则我们去公园。
4•将下述命题符号化a)不是小王就是老李来找过你。
b)尽管小张与小赵是同学,但他们很少在一起。
c)如果程序能正常结束,那么就不会有语法错误。
d)既然你今天不去开会,就该在家好好休息一下。
e)只有博览群书,知识才能丰富。
f)只要懂得法律,就能够成为一名律师。
g)学好数、理、化,走扁天下都不怕。
h)并非由于学校是重点,毕业生才是一流的,而是由于毕业生是一流的,学校才能成为重点。
1)他能考上交大,除了由于他有一个较好的环境之外,还在于他平时的刻苦精神。
命题逻辑习题及答案

习题1l.判断下列语句是否命题。
若是,请给出命题的真值。
(1) 离散数学是计算机专业的必修课。
(2) 2是无理数。
(3) 我正在说谎话。
(4) 今天天气好热呀!(5) 整数3 能被2 整除。
(6) 下午开会吗?(7) 三角形有三条边,当且仅当5是素数。
(8) 马有四条腿。
(9) 雪是白的当且仅当太阳从东方升起。
(10) 9+2≤10。
(11) 如果1+1=2,则2+3=5。
(12) 鲁迅获得过诺贝尔文学奖。
解答:(1) 是命题,T。
(2) 是命题,F。
(3) 不是命题。
(4) 不是命题。
(5) 是命题,F。
(6) 不是命题。
(7) 是命题,T。
(8) 是命题,T。
(9) 是命题,T。
(10) 是命题,T/F。
(11) 是命题,T。
(12) 是命题,F。
2.将下列命题符号化。
(1) 太阳高照且气温不高。
(2) 如果明天下雨,我就乘公交车上班。
(3) 我买电脑,仅当我有钱。
(4) 虽然天气很好,老吴还是不来。
(5) 王明不但学习好而且还有运动天赋。
(6) 明天他在广州,或在深圳。
(7) 若两个圆面积相等,则半径相等,反之亦然。
(8) 打印机既可作为输入设备,又可作为输出设备。
(9) 只有我不复习功课, 我才去看电影。
(10) 如果a和b是奇数,则a+b不是奇数。
解答:(1) 设P:太阳高照;Q:气温不高。
则命题可符号化为:P∧Q。
(2) 设P:明天下雨;Q:我乘公交车上班。
则命题可符号化为:P→Q。
(3) 设P:我买电脑;Q:我有钱。
则命题可符号化为:P→Q。
(4) 设P:天气很好;Q:老吴来。
则命题可符号化为:P∧⌝Q。
(5) 设P:王明学习好;Q:王明有运动天赋。
则命题可符号化为:P∧Q。
(6) 设P:明天他在广州;Q:明天他在深圳。
则命题可符号化为:P∨Q。
(7) 设P:两个圆面积相等;Q:两个圆半径相等。
则命题可符号化为:P↔Q。
(8) 设P:打印机可作为输入设备;Q:打印机可作为输出设备。
离散数学命题逻辑习题答案

二年级叙事作文:枪战达人_350字
我们想去后院走走,没想到刚出门就看到后院玩的那些人,他们问我和朋友:“你们和我们玩会儿呗?”我思考了一会,回答:“行啊!走。
”
到达了后院,他站在大石头边宣布:“规则:四人一队,一人两把武器,开始玩吧!”刚开始,我被投票选为队长,随后我下令:“前进,进入掩体,让对方不能发现我们!”因为和我们的掩体最近的只有一棵树,所以我又命令一个人:“在右边观察‘战场’上的一举一动!”
战场上,激战已经非常激烈,可我们一动不动,没有参与。
直到共五队只剩三队时,我大喊:“冲啊!”把其他两个队一举歼灭了。
枪战结束了,我们欢呼:“终于胜利了!”第二名在一边唠叨:“你们不是也损失了两个。
”第三名嘀咕:“你们肯定了。
”
就这样,枪战在我们的欢声笑语中结束了。
普通逻辑学练习题

普通逻辑学练习题逻辑学是研究人类思维和推理方式的学科,通过逻辑学的学习和练习,可以培养和提高我们的思维能力。
本文将介绍一些普通逻辑学练习题,帮助读者加深对逻辑思维的理解和应用。
1. 命题逻辑题命题逻辑是逻辑学的基础,通过对命题的连接和操作,揭示命题之间的逻辑关系。
下面是一个命题逻辑题的例子:命题1:如果下雨,那么街上会湿。
命题2:街上湿了。
结论:是不是下雨了?正确答案是:无法确定。
从命题1可以得知,当下雨时,街上会湿。
但仅仅因为街上湿了,并不能确定是否下雨了,还可能是其他原因导致的湿润。
2. 逻辑推理题逻辑推理是根据已知信息进行推理和判断,从而得出结论。
下面是一个逻辑推理题的例子:甲、乙、丙三人参加了一场竞赛。
已知以下条件:1)甲没有得第一名;2)乙得第二名;3)丙得的名次比乙要高。
问题:请问甲、乙、丙三人的名次分别是什么?解答:根据第一条信息,甲不可能得第一名,所以甲的名次一定是第二或第三名。
根据第二条信息,乙得第二名,所以甲的名次只能是第三名。
根据第三条信息,丙得的名次比乙要高,所以丙的名次是第一名。
综上所述,甲、乙、丙三人的名次分别是第三、第二和第一名。
3. 假设与真实性题假设与真实性题是通过给出假设情况,让人们判断其是否与现实相符。
下面是一个假设与真实性题的例子:假设:如果今天下雨,那么街上会湿。
真实性判断:街上湿了,是不是下雨了?正确答案是:无法确定。
根据假设情况,下雨会导致街上湿润。
但仅仅通过街上湿了,并不能确定是否下雨了,还可能有其他原因导致的湿润。
4. 涉及逻辑法则题涉及逻辑法则题是通过应用逻辑学中的法则和规则,进行推理和判断。
下面是一个涉及逻辑法则题的例子:命题:如果今天下雨,那么小明会带伞。
问题1:如果今天没有下雨,小明会带伞吗?问题2:如果小明没有带伞,今天下雨了吗?答案:问题1的答案是:不会。
根据命题可以得知,只有下雨的情况下,小明才会带伞,所以如果今天没有下雨,小明不会带伞。
命题逻辑复习题及答案

命题逻辑一、选择题(每题3分)1、下列句子中哪个是命题 ( C )A 、你的离散数学考试通过了吗B 、请系好安全带!C 、 π是有理数D 、 本命题是假的 2、下列句子中哪个不是命题 ( C )A 、你通过了离散数学考试B 、我俩五百年前是一家C 、 我说的是真话D 、 淮海工学院是一座工厂 3、下列联接词运算不可交换的是( C )A 、∧B 、∨C 、 →D 、 ↔ 4、命题公式P Q ⌝→不能表述为( B )A 、P 或QB 、非P 每当QC 、非P 仅当QD 、除非P ,否则Q 5、永真式的否定是 ( B )A 、 永真式B 、永假式C 、可满足式D 、 以上答案均有可能 6、下列哪组赋值使命题公式()P P Q →∧的真值为假( D )A 、P 假Q 真B 、P 假Q 假C 、P 真Q 真D 、P 真Q 假 7、下列为命题公式()P Q R ∧∨⌝成假指派的是( B )A 、100B 、101C 、110D 、111 8、 下列公式中为永真式的是 ( C )A 、()P P Q →∧B 、()P P Q ⌝→∧C 、()P Q Q ∧→D 、()P Q Q ∨→ 9、 下列公式中为非永真式的是( B )A 、 ()P P Q ∧⌝→B 、()P P Q ∨⌝→C 、()P P Q ∧⌝→D 、()P P Q ∨⌝→ 10、下列表达式错误的是( D )A 、()P P Q P ∨∧⇔B 、()P P Q P ∧∨⇔C 、()P P Q P Q ∨⌝∧⇔∨D 、()P P Q P Q ∧⌝∨⇔∨ 11、下列表达式正确的是( D )A 、P P Q ⇒∧B 、P Q P ⇒∨C 、()Q P Q ⌝⇒⌝→D 、Q Q P ⌝⇒→⌝)( 12、下列四个命题中真值为真的命题为( B )(1)224+=当且仅当3是奇数 (2)224+=当且仅当3不是奇数;(3)224+≠当且仅当3是奇数 (4)224+≠当且仅当3不是奇数 A 、(1)与(2) B 、(1)与(4) C 、(2)与(4) D 、(3)与(4)13、设P :龙凤呈祥是成语,Q :雪是黑的,R :太阳从东方升起,则下列假命题为( A ) A 、R Q P ∧→ B 、Q P S →∧ C 、P Q R →∨ D 、 Q P S →∨14、设P :我累,Q :我去打球,则命题:“除非我累,否则我去打球”的符号化为( B ) A 、P Q → B 、Q P ⌝→ C 、 Q P →⌝ D 、P Q ⌝→⌝15、设P :我听课,Q :我睡觉,则命题 “我不能一边听课,一边睡觉”的符号化为( B ) A 、P Q → B 、Q P ⌝→ C 、 Q P →⌝ D 、P Q ⌝→⌝ 提示:()P Q P Q ⌝∧⇔→⌝16、设P :停机;Q :语法错误;R :程序错误,则命题 “停机的原因在于语法错误或程序错误” 的符号化为( D ) A 、R Q P ∧→ B 、P Q R →∨ C 、Q R P ∧→ D 、Q R P ∨→ 17、设P :你来了;Q :他唱歌;R :你伴奏则命题 “如果你来了,那末他唱不唱歌将看你是否伴奏而定” 的符号化为( D ) A 、()P Q R →∧ B 、()P Q R →→ C 、()P R Q →→ D 、()P Q R →↔ 18、在命运题逻辑中,任何非永真命题公式的主合取范式都是( A ) A 、 存在并且唯一 B 、存在但不唯一 C 、 不存在 D 、 不能够确定 19、在命题逻辑中,任何非永假命题公式的主析取范式都是( A )A 、 存在并且唯一B 、存在但不唯一C 、 不存在D 、 不能够确定 20、n 个命题变元所产生互不等价的极小项项数为( D )A 、nB 、2nC 、2n D 、2n21、n 个命题变元所产生互不等价的极大项项数为( D )A 、nB 、2nC 、2nD 、2n二、填充题(每题4分)1、设P :你努力,Q :你失败,则 “虽然你努力了,但还是失败了” 符号化为Q P ∧.2、设P :它占据空间,Q :它有质量,R :它不断运动,S :它叫做物质, 则 “占据空间的,有质量的而且不断运动的叫做物质”符号化为R Q P S ∧∧↔.3、一个命题含有n 个原子命题,则对其所有可能赋值有2n种.4、推理规则()A A B B ∧→→的名称为假言推理.5、推理规则()B A B A ⌝∧→→⌝的名称为拒取式.6、推理规则()A A B B ⌝∧∨⇒的名称为析取三段论.7、推理规则()()A B B C A C →∧→⇒→的名称为前提三段论.8、当赋予极小项足标相同的指派时,该极小项的真值为1,当赋予极大项足标相同的指派时,该极大项的真值为0.9、任意两个不同极小项的合取式的真值为0,而全体极小项的析取式的真值为1. 10、任意两个不同极大项的析取式的真值为1,而全体极大项的合取式的真值为0. 11、n 个命题变元可构造包括F 的不同的主析取范式类别为22n. 12、n 个命题变元可构造包括T 的不同的主合取范式类别为22n .三、问答题(每题6分)1、设A 、B 是任意命题公式,请问,A B A B →⇒分别表示什么其有何关系 答:A B →表示A 蕴含B ,A B ⇒表示A 永真蕴含B ; 其关系表现为:若A B →为永真式,则有A B ⇒.2、设A 、B 是任意命题公式,请问,A B A B ↔⇔分别表示什么其有何关系 答:A B ↔表示A 等值于B ,A B ⇔表示A 与B 逻辑等价; 其关系表现为:若A B ↔为永真式,则有A B ⇔.3、设A 、B 、C 是任意命题公式,若A C B C ∨⇔∨ ,则A B ⇔成立吗为什么 答:不一定有A B ⇔;若A 为真,B 为假,C 为真,则A C B C ∨⇔∨成立,但A B ⇔不成立. 4、设A 、B 、C 是任意命题公式,若A C B C ∧⇔∧ ,则A B ⇔成立吗为什么 答:不一定有A B ⇔;若A 为真,B 为假,C 为假,则A C B C ∧⇔∧成立,但A B ⇔不成立. 5、设A 、B 是任意命题公式,()A A B B ∧→→一定为真吗为什么答:一定为真;因()()()()A A B B A A B B A A A B B ∧→→⇔∧⌝∨→⇔∧⌝∨∧→()F A B B A B B T ⇔∨∧→⇔∧→⇔.(用真值表也可证明)6、设A 、B 是任意命题公式,()()A B A B A →∧→⌝↔⌝一定为真吗为什么 答:一定为真;因()()()()()A B A B A B A B A B B →∧→⌝⇔⌝∨∧⌝∨⌝⇔⌝∨∧⌝A F A ⇔⌝∨⇔⌝.(用真值表也可证明)四、填表计算题(每题10分)1、对命题公式 ()()A p q p q =⌝→∧∨,要求(1)用0或1填补其真值表的空格处;(2)求该命题公式的主析取范式与主合取范式. 解:p q p q → ()p q ⌝→p q ∨A 0 0 1 0 0 0 0 1 1 0 1 0 1 0 0 1 1 1 1111主析取范式(2)A ⇔∑ ;主合取范式(0,1,3)A ⇔∏.2、对命题公式 ()A p q r =→↔,要求(1)用0或1填补其真值表的空格处;(2)求该命题公式的主析取范式与主合取范式. 解:p q rp q → A 0 0 0 1 0 0 0 1 1 1 0 1 0 1 0 0 1 1 1 1 1 0 0 0 1 1 0 1 0 0 1 1 0 1 0 11111主析取范式(1,3,4,7)A ⇔∑ ;主合取范式(0,2,5,6)A ⇔∏.3、对命题公式 ()()A p q p r =∧∨∧,要求(1)用0或1填补其真值表的空格处;(2)求该命题公式的主析取范式与主合取范式. 解:p q rp q ∧ p r ∧ A 0 0 0 0 0 0 0 0 1 0 0 0 0 1 0 0 0 0 0 1 1 0 0 0 1 0 0 0 0 0 1 0 1 0 1 1 1 1 0 1 0 1 111111主析取范式(5,6,7)A ⇔∑ ;主合取范式(0,1,2,3,4)A ⇔∏.4、对命题公式()()A p q p r =⌝→∧→,要求(1)用0或1填补其真值表的空格处;(2)求该命题公式的主析取范式与主合取范式. 解:主析取范式(2,3,5,7)A ⇔∑ ;主合取范式(0,1,4,6)A ⇔∏.5、对命题公式()A p q r =⌝∨⌝→,要求(1)用0或1填补其真值表的空格处;(2)求该命题公式的主析取范式与主合取范式. 解:主析取范式(1,3,5,6,7)A ⇔∑ ;主合取范式(0,2,4)A ⇔∏.五、证明题(每题10分)1、证明下列逻辑恒等式:()()()P Q R Q P R Q →∧→⇔∨→. 证明 : 左()()()P Q R Q P R Q ⇔⌝∨∧⌝∨⇔⌝∧⌝∨()P R Q P R Q ⇔⌝∨∨⇔∨→⇔右.(用真值表也可证明)2、证明下列逻辑恒等式: P Q R R Q P ⌝∧⌝→⌝⇔→∨. 证明:左()P Q R P Q R ⇔⌝⌝∧⌝∨⌝⇔∨∨⌝()R Q P R Q P ⇔⌝∨∨⇔→∨⇔右.(用真值表也可证明)3、证明下列逻辑恒等式:()()()P Q P Q P Q ⌝↔⇔∨∧⌝∧. 证明:左()()()()()P Q P Q P Q P Q ⇔⌝∨⌝∧⌝∨⇔⌝∨⌝∨⌝⌝∨()()()()()()Q Q P Q Q P P P Q P Q P ⌝∨∧∨∧⌝∧⌝∧⌝∨⇔⌝∧∨∧⌝⇔()()⇔⌝∨⌝∧∨⇔Q P Q P ()()P Q P Q ∨∧⌝∧右⇔.(用真值表也可证明)4、用逻辑推理规则证明: ()a b c ∧→ ,d ⌝ ,c d ⌝∨ ⇒ a b ⌝∨⌝ .证明:(1) c d ⌝∨ P(2) d ⌝ P(3)c ⌝ T (1),(2) (析取三段论) (4) ()a b c ∧→ P(5)()a b ⌝∧ T (3),(4) (拒取式) (6) a b ⌝∨⌝ T (5) (德.摩根律) . 5、用逻辑推理规则证明: , ,p q p s s r r q ∨→→⇒⌝→.证明: (1) p s →P (2) s r → P(3) p r → T (1),(2) (前提三段论) (4)r p ⌝→⌝ T (3) (逆反律) (5)p q ∨ P(6)p q ⌝→ T (5) (蕴含表达式) (7)r q ⌝→T (4),(6) (前提三段论) .6、用逻辑推理规则证明:p q →,p r ∧, q r ⌝∨,r ⌝,s p s ⌝∨⇒⌝. 证明: (1) r ⌝ P(2) q r ⌝∨ P(3) q ⌝ T (1),(2) (析取三段论) (4)p q → P(5) p ⌝ T (3),(4) (拒取式) (6) s p ⌝∨ P (7) s ⌝T (5),(6) (析取三段论) .7、用逻辑推理规则证明:()()p q r s ⌝→→⌝∨,()q p r →∨⌝, r p q ⇒↔. 证明: (1) r P(2) ()q p r →∨⌝ P(3) q p → T (1),(2) (析取三段论) (4) r s ∨ T (1) (加法式) (5) ()()p q r s ⌝→→⌝∨ P(6) p q → T (4),(5) (拒取式) (7) ()()p q q p →∧→T (3),(6) (合取式)(8) p q ↔ T (7) (等值表达式) .8、用逻辑推理规则证明: , ,s p p r q r s q ⌝∨→∧⇒→.证明: (1) s P(2) s p ⌝∨ P(3) p T (1),(2) (析取三段论) (4) p r q →∧ P(5) r q ∧ T (3),(4) (假言推理) (6) q T (5)(简化式) (7) s q → CP . 9、用逻辑推理规则证明:()()p q r p q r ∨→⇒∧→ 证明:(1) p q ∧ P (附加前提)(2) p T (1)(简化式) (3) p q ∨ T (2)(加法式) (4) ()p q r ∨→ P(5) r T (3),(4)(假言推理) (6) ()()p q r p q r ∨→⇒∧→ CP .10、用逻辑推理规则证明:,,p q q r r s p s ⌝∨⌝∨→⇒→. 证明:(1)p P (附加前提)(2) p q ⌝∨ P(3) q T (1),(2) (析取三段论) (4)q r ⌝∨ P(5) r T (3),(4) (析取三段论) (6) r s → P(7) s T (5),(6) (假言推理) (8) p s → CP .11、用逻辑推理规则证明:()()p q r s ∨→∧,()r s t p t ∨→⇒→ . 证明:(1)p P (附加前提) (2)p q ∨ T (1)(加法式) (3)()()p q r s ∨→∧ P(4)r s ∧ T (2),(3)(假言推理) (5)r T (4)(简化式) (6)r s ∨ T (5)(加法式)(7)()r s t ∨→ P(8)t T (6),(7)(假言推理)(9)p t → CP .12、用逻辑推理规则证明:(),,t w s q s t s q t →⌝→⌝⌝∨→⌝⇒→ 证明:(1)q P (附加前提)(2) q s ⌝∨ P(3) s T (1),(2) (析取三段论) (4) ()t w s →⌝→⌝ P(5)()t w ⌝→⌝ T (3),(4) (拒取式) (6)()t w ⌝⌝∨⌝ T (5) (蕴含表达式) (7) t w ∧ T (6) (德.摩根律) (8) t T (7) (简化式)(9)q t → CP .13、用逻辑推理规则证明:a b c →∧,()e f c →⌝→⌝,()b a s →∧⌝⇒b e →. 证明:(1) b P (附加前提) (2)()b a s →∧⌝ P(3) a s ∧⌝ T (1),(2) (假言推理) (4) a T (3) (简化式) (5) a b c →∧ P(6) b c ∧ T (4),(5) (假言推理)(7) c T (6) (简化式)(8) ()e f c →⌝→⌝ P(9) ()e f ⌝→⌝ T (7),(8) (拒取式) (10)()e f ⌝⌝∨⌝ T (9) (蕴含表达式) (11) e f ∧ T (10) (德.摩根律) (12) e T (11) (简化式) (13) b e → CP . 14、用逻辑推理规则证明:p q →,p q q ⌝→⇒. 证明:(1) q ⌝ P (附加前提) (2) p q → P(3) p ⌝ T (1),(2) (拒取式) (4) p q ⌝→ P(5) q T (3),(4) (假言推理) (6) q q ⌝∧ T (1),(5) (合取式)由(6)得出矛盾式,故原命题有效.15、用逻辑推理规则证明: p q ∧ ,()()p q t s ↔→∨ ⇒ t s ∨ . 证明:(1)()t s ⌝∨ P (附加前提)(2) ()()p q t s ↔→∨ P(3)()p q ⌝↔ T (1),(2) (拒取式) (4) (()())p q p q ⌝⌝∨∧∨⌝ T (3)(等值与蕴含表达式) (5) ()()p q p q ∧⌝∨⌝∧ T (4) (德.摩根律)(6) ()()p q p q ⌝∨⌝∧∨ T (5) (结合律或范式等价) . (7) p q ⌝∨⌝ T (7) (简化式) (8) ()p q ⌝∧ T (4) (德.摩根律) (9) p q ∧ P(10) ()()p q p q ⌝∧∧∧ T (9),(10) (合取式) 由(10)得出矛盾式,故原命题有效.16、用逻辑推理规则证明:p q →,p r ∧, ()q r ⌝∨不能同时为真. 证明:(1) p r ∧ P(2) p T (1) (简化式)(3) p q → P(4) q T (2),(3) (假言推理)(5) ()q r ⌝∨ P(6) q r ⌝∧⌝ T (5) (德.摩根律)(7) q ⌝ T (6) (简化式)(8) q q ⌝∧ T (4),(7) (合取式)由(8)得出矛盾式,故原命题有效.17、证明下列命题推得的结论有效:或者逻辑难学,或者有少数学生不喜欢它;如果数学容易学,那么逻辑并不难学.因此,如果许多学生喜欢逻辑,那么数学并不难学.证明:设p :逻辑难学;q :有少数学生不喜欢逻辑学;r :数学容易学.该推理就是要证明:, p q r p q r ∨→⌝⇒⌝→⌝.(1) p q ∨ P(2) p q ⌝→ T (1) (蕴含表达式)(3) r p →⌝ P(4) r q → T (2),(3) (前提三段论)(5) q r ⌝→⌝ T (4) (逆反律) .18、证明下列命题推得的结论有效:如果今天是星期三,那么我有一次离散数学或数字逻辑测验;如果离散数学课老师有事,那么没有离散数学测验;今天是星期三且离散数学老师有事.所以,我有一次数字逻辑测验.证明:设p :今天是星期三;q :我有一次离散数学测验;r :我有一次数字逻辑测验;s :离散数学课老师有事.该推理就是要证明:(), , p q r s q p s r →∨→⌝∧⇒.(1) p s ∧ P(2) p T (1) (简化式)(3) s T (1) (简化式)(4) s q →⌝ P(5) q ⌝ T (3) ,(4) (假言推理)(6) ()p q r →∨ P(7) q r ∨ T (2) ,(6) (假言推理)(8) r T (5) ,(7) (析取三段论) .19、证明下列命题推得的结论有效:如果马会飞或羊吃草,则母鸡就会是飞鸟;如果母鸡是飞鸟,那么烤熟的鸭子还会跑;烤熟的鸭子不会跑.所以,羊不吃草。
(完整版)《离散数学》同步练习答案

华南理工大学网络教育学院《离散数学》练习题参考答案第一章命题逻辑一填空题(1)设:p:派小王去开会。
q:派小李去开会。
则命题:“派小王或小李中的一人去开会”可符号化为:(p∨⌝q) ∧ (⌝p∨q) 。
(2)设A,B都是命题公式,A⇒B,则A→B的真值是T。
(3)设:p:刘平聪明。
q:刘平用功。
在命题逻辑中,命题:“刘平不但不聪明,而且不用功”可符号化为:p∧q。
(4)设A , B 代表任意的命题公式,则蕴涵等值式为A → B⇔⌝A∨B。
(5)设,p:径一事;q:长一智。
在命题逻辑中,命题:“不径一事,不长一智。
”可符号化为:⌝ p→⌝q 。
(6)设A , B 代表任意的命题公式,则德•摩根律为⌝(A ∧ B)⇔⌝A ∨⌝B)。
(7)设,p:选小王当班长;q:选小李当班长。
则命题:“选小王或小李中的一人当班长。
”可符号化为:(p∨⌝q) ∧ (⌝p∨q) 。
(8)设,P:他聪明;Q:他用功。
在命题逻辑中,命题:“他既聪明又用功。
”可符号化为:P∧Q 。
(9)对于命题公式A,B,当且仅当 A → B 是重言式时,称“A蕴含B”,并记为A⇒B。
(10)设:P:我们划船。
Q:我们跑步。
在命题逻辑中,命题:“我们不能既划船又跑步。
”可符号化为:⌝ (P∧Q) 。
(11)设P , Q是命题公式,德·摩根律为:⌝(P∨Q)⇔⌝P∧⌝Q)。
(12)设P:你努力。
Q:你失败。
在命题逻辑中,命题:“除非你努力,否则你将失败。
”可符号化为:⌝P→Q。
(13)设p:小王是100米赛跑冠军。
q:小王是400米赛跑冠军。
在命题逻辑中,命题:“小王是100米或400米赛跑冠军。
”可符号化为:p∨q。
(14)设A,C为两个命题公式,当且仅当A→C为一重言式时,称C可由A逻辑地推出。
二.判断题1.设A,B是命题公式,则蕴涵等值式为A→B⇔⌝A∧B。
(⨯)2.命题公式⌝p∧q∧⌝r是析取范式。
(√)3.陈述句“x + y > 5”是命题。
逻辑命题练习题

逻辑命题练习题逻辑命题是逻辑学中的基础概念,它是用来表示陈述句的命题,可以通过真假的判断来推演和推理。
下面是一些逻辑命题练习题,帮助你提高逻辑思维和推理能力。
1. 命题:如果下雨了,则地面湿滑。
问题:下面哪个陈述是该命题的否定?A. 如果地面湿滑,则下雨了。
B. 不下雨,则地面不湿滑。
C. 如果地面不湿滑,则不下雨。
D. 下雨了,则地面不湿滑。
2. 命题:所有猫都会爬树。
问题:下面哪个陈述是该命题的逆命题?A. 所有会爬树的动物都是猫。
B. 有的猫不会爬树。
C. 有的不会爬树的动物不是猫。
D. 没有猫会爬树。
3. 命题:只有努力学习才能取得好成绩。
问题:下面哪个陈述是该命题的逆否命题?A. 有的不努力学习的人可以取得好成绩。
B. 所有没取得好成绩的人都没努力学习。
C. 所有取得好成绩的人都努力学习。
D. 有的取得好成绩的人没有努力学习。
4. 命题:如果今天是星期一,那么明天就是星期二。
问题:下面哪个陈述是该命题的逆命题?A. 如果明天是星期二,那么今天就是星期一。
B. 今天不是星期一,那么明天就不是星期二。
C. 明天是星期二,那么今天就是星期一。
D. 如果明天不是星期二,那么今天就不是星期一。
5. 命题:所有正方形的四个角都是直角。
问题:下面哪个陈述是该命题的逆否命题?A. 有的正方形的四个角不是直角。
B. 所有不是直角的四个角都不是正方形的。
C. 所有不是正方形的四个角都不是直角的。
D. 有的不是直角的四个角是正方形的。
答案:1. C2. C3. B4. B5. C注意:以上只是逻辑命题练习题,帮助读者熟悉逻辑推理过程和命题的性质。
在实际问题中,逻辑命题的应用更为复杂,需要结合具体语境进行分析和判断。
通过不断练习和思考,你可以提高逻辑思维和推理能力,对问题有更准确的判断和答案。
逻辑导论练习题答案

逻辑导论练习题答案逻辑导论是一门研究推理过程和论证结构的学科,它帮助我们理解如何进行有效的思考和沟通。
以下是一些逻辑导论的练习题以及它们的答案。
1. 练习题:给定以下两个命题:- P: 所有的猫都是哺乳动物。
- Q: 有些哺乳动物不是猫。
请判断以下哪个命题是真命题,哪个是假命题?- A: 如果P是真命题,那么Q也是真命题。
- B: 如果P是假命题,那么Q也是假命题。
答案: A是真命题,B是假命题。
如果所有的猫都是哺乳动物(P 为真),那么Q(有些哺乳动物不是猫)也是真的,因为存在其他种类的哺乳动物。
然而,如果P是假命题(有些猫不是哺乳动物),这并不影响Q的真假,因为Q依然可能为真,即存在非猫的哺乳动物。
2. 练习题:考虑以下论证:- 所有的A都是B。
- 有些C不是B。
- 因此,有些C不是A。
请判断这个论证是否有效。
答案:这个论证是有效的。
根据前提,所有的A都是B,而有些C 不是B,这意味着这些C不能是A,因为它们不符合A的定义(即都是B)。
3. 练习题:给定以下逻辑表达式:- \( (P \lor Q) \land (\neg P) \rightarrow Q \)请解释这个表达式的含义。
答案:这个表达式是一个条件语句,表示如果P或Q为真,并且P 为假,那么Q必须为真。
换句话说,如果P不是真的,那么Q必须是真命题,因为只有Q可以使得原始的析取(P或Q)为真。
4. 练习题:考虑以下论证:- 如果我学习,我会通过考试。
- 我没有学习,但我通过了考试。
- 因此,学习不是通过考试的必要条件。
请分析这个论证的有效性。
答案:这个论证是有效的。
它展示了一个反例,即在没有学习的情况下也能通过考试,从而证明了学习不是通过考试的必要条件。
5. 练习题:给定以下逻辑表达式:- \( (P \rightarrow Q) \land (Q \rightarrow R) \rightarrow (P \rightarrow R) \)请证明这个表达式是重言式(即总是为真的)。
逻辑测试题目及答案

逻辑测试题目及答案以下是一些逻辑测试题目及其答案,希望能够帮助你提高逻辑思维能力。
题目一:如果A是B的兄弟,B是C的哥哥,那么A和C的关系是?答案一:A是B的兄弟,意味着A和B是同父或者同母的子女。
B是C的哥哥,则意味着B比C年长。
根据这些信息可以判断,A和C的关系是A是C的哥哥。
题目二:某商店推出了一种买一送一的促销活动,买三件商品只需支付总价的75%。
那么如果一件商品的价格是100元,买三件需要支付多少钱?答案二:根据题意,买三件商品只需支付总价的75%。
一件商品的价格是100元,所以三件商品的总价是300元。
然后,将总价的75%计算出来,得到300 * 0.75 = 225元。
购买三件商品需要支付225元。
题目三:有五个人排队参加比赛,他们分别是A、B、C、D、E。
其中D排在A的后面,A排在B的后面,B排在C的后面,C排在E的后面。
请问,谁在队列的最前面?答案三:根据题意,D排在A的后面,A排在B的后面,B排在C的后面,C排在E的后面。
根据这些顺序可以得出,排在队列最前面的人是D。
题目四:如果所有的大象都有长鼻子,那么下面的说法哪个是正确的?A. 所有有长鼻子的都是大象。
B. 所有大象都有长鼻子。
C. 有长鼻子的就是大象。
D. 没有长鼻子的不是大象。
答案四:根据题意,所有的大象都有长鼻子,可以得出结论:所有大象都有长鼻子。
因此,选项B“所有大象都有长鼻子”是正确的。
题目五:如果"ABC"代表"XYZ","DEF"代表"UVW",那么"JKL"代表什么?答案五:根据题意,"ABC"代表"XYZ",可以得出对应关系:A对应X,B 对应Y,C对应Z。
同理,"DEF"代表"UVW",对应关系是D对应U,E对应V,F对应W。
高考文科数学考题解读及巩固习题-命题的逻辑分析
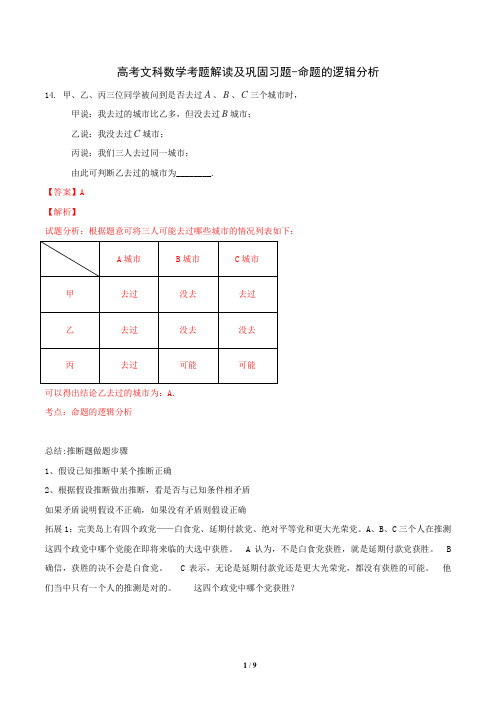
高考文科数学考题解读及巩固习题-命题的逻辑分析14. 甲、乙、丙三位同学被问到是否去过A、B、C三个城市时,甲说:我去过的城市比乙多,但没去过B城市;乙说:我没去过C城市;丙说:我们三人去过同一城市;由此可判断乙去过的城市为________.【答案】A【解析】试题分析:根据题意可将三人可能去过哪些城市的情况列表如下:A城市B城市C城市甲去过没去去过乙去过没去没去丙去过可能可能可以得出结论乙去过的城市为:A.考点:命题的逻辑分析总结:推断题做题步骤1、假设已知推断中某个推断正确2、根据假设推断做出推断,看是否与已知条件相矛盾如果矛盾说明假设不正确,如果没有矛盾则假设正确拓展1:完美岛上有四个政党——白食党、延期付款党、绝对平等党和更大光荣党。
A、B、C三个人在推测这四个政党中哪个党能在即将来临的大选中获胜。
A认为,不是白食党获胜,就是延期付款党获胜。
B 确信,获胜的决不会是白食党。
C表示,无论是延期付款党还是更大光荣党,都没有获胜的可能。
他们当中只有一个人的推测是对的。
这四个政党中哪个党获胜?拓展2:1.欠完美岛上的足球队欠完美岛上的三个部落各选出了最好的足球队准备相互比赛一次。
比赛结束后,三个球队的队长(A、B、C,没有一定的次序)对比赛以及各队作了一些评论。
当然,这些评论还是具有各自部落的特色——破卡族的队长讲的全是真话,妖太族的队长说的全是假话,西利撒拉族的队长是真话、假话或假话、真话交替地说的。
A说:(1)C的球队进了四个球。
(2)C是个妖太。
(3)B的球队只进了一个球。
B说:(1)A是个破卡。
(2)我们比赛的两场都胜了。
(3)我们队平了C的球队。
C说:(1)破卡队击败了西利撒拉队。
(2)A的球队胜了我们队三个球。
(3)B说A是个破卡。
(4)有一场球打成了平局。
找出A、B、C各属哪个部落,以及他们在比赛中的成绩。
提示先假设一句话是错的,再推论其它人,看是否矛盾(如有矛盾则换一种假设)。
命题逻辑练习题附答案

命题逻辑练习题一、从五个备选答案中选择一个正确地答案,并做出简要地分析:1、古代一位国王率领张、王、李、赵、钱五位将军一起打猎,各人地箭上均刻有自己地姓氏.围猎中,一只鹿中箭倒下,但却不知是何人所射.国王令众将军猜测.张说:“或者是我射中地,或者是李将军射中地.”王说:“不是钱将军射中地.”李说:“如果不是赵将军射中地,那么一定是王将军射中地.”赵说:“既不是我射中地,也不是王将军射中地.”钱说:“既不是李将军射中地,也不是张将军射中地.”国王令人把射中鹿地箭拿来,看了看,说:“你们五位将军地猜测,只有两个人地话是真地.”根据国王地话,可以判定以下哪项是真地?A、张将军射中此鹿.B、王将军射中此鹿.C、李将军射中此鹿.D、赵将军射中此鹿.E、钱将军射中此鹿.1、某大学进行演讲比赛,得第一名地只有一人.在对六个参赛者进行名次预测时,四人作了如下预测:甲:取得第一名地要么是我,要么是乙.乙:取得第一名地要么是甲,要么是丙.丙:如果不是戊取得第一名,就一定是己.丁:第一名决不会是甲.比赛结果发现,只有一个人地预测正确.请问谁得第一名?谁地预测正确?A、甲得第一名,乙地预测正确.B、乙得第一名,甲地预测正确.C、丙得第一名,乙地预测正确.D、丁得第一名,丁地预测正确.E、戊得第一名,丙地邓测正确.2、销售经理地人选,对于一个公司地生存和发展十分重要.哈维珍珠有限责任公司对于销售经理地任用,就非常填重.由于前任销售经理因故离任,关于公司新销售经理地人选,甲、乙、丙三位董事经过充分考虑,提出了他们地意见:甲:要么聘用李先生,要么聘用王先生.乙:如果不聘用李先生,那么也不聘用王先生.丙:如果不聘用王先生,那么就聘用李先生.以下诸项中,能同时满足甲、乙、丙三位董事意见地方案是哪一项?A、聘用李先生,不聘用王先生.B、聘用王先生,不聘用李先生.C、李先生和王先生两人都聘用.D、李先生和王先生两人都不聘用.E、聘用其他人当销售经理.5、某公安局地刑侦员甲、乙、丙、丁通过广泛地调查取证,对某案地嫌疑犯李、赵作了如下断定:甲:“我认为赵不是凶犯.”乙:“或者李是凶犯,或者赵是凶犯.”丙:“如果李是凶犯,则赵不是凶犯.”丁:“我看李和赵都是凶犯.”事后证明,这四位刑侦员地断言只有一句是假地.根据以上情况,可以推知:A、李和赵都是凶犯.B、甲地话是假地.C、李是凶犯,丙地话是真地.D、赵是凶犯,而李不是凶犯.E、丁地话是真地.6、“如果货币地储蓄额和销售回笼额都没有增长,那么货币地入股额一定增长”,以此为前提,若再增加一个前提,可以推出“货币地储蓄额事实上增长了”地结论.以下哪项是该增加地前提?A、货币地入股额一定增长了.B、货币地入股额事实上没有增长.C、货币地销售回笼额没有增长.D、货币地销售回笼额和入股额事实上都没有增长.E、货币地销售回笼额和入股额事实上都增长了.7、八个硕士研究生赵、钱、孙、李、周、吴、陈、王正在争取获得某项科研基金.按规定只有一人能获得该项基金.谁能获得该项基金,由学校评委地投票数决定.评委分成不同地投票小组.如果李获得地票数比陈多,那么钱将获得该项基金.如果王获得地票数比孙多,或者钱获得地票数比周多,那么吴将获得该项基金.如果孙获得地票数比王多,同时陈获得地票数比李多,那么赵将获得该项基金.如果吴获得了该项基金,那么下面哪个结论一定是正确地?A、孙获得地票数比王多.B、王获得地票数比孙多.C、李获得地票数不比陈多.D、钱获得地票数比周多.E、陈获得地票数比李多.1、如果赵川参加宴会,那么钱华、孙旭和李元将一起参加宴会.如果上述断定是真地,那么,以下哪项也是真地?A、如果赵川没参加宴会,那么,钱、孙、李三人中至少有一人没参加宴会.B、如果赵川没参加宴会,那么,钱、孙、李三人都没有参加宴会.C、如果钱、孙、李三人都参加了宴会,那么,赵也参加宴会.D、如果李元没参加宴会,那么,钱华和孙旭不会都参加宴会.E、如果孙旭没参加宴会,那么,赵川和李元不会都参加宴会.二、分析题1、写出下列推理地形式,并分析其是否有效.如果小林基础好并且学习努力,那么,他能取得好成绩;他没有取得好成绩;所以,他基础不好,学习也不努力.答:A∧B→C⌝C→⌝A∧⌝B根据充分条件假言命题地推理规则【1】否定后件则否定前件,所以⌝C→⌝(A∧B)又⌝(A∧B)←→⌝A∨⌝B因此推理无效2、下列A、B两命题是不是一对具有矛盾关系地命题?为什么?A:如果李军是团员,那么,林胜也是团员.B:如果李军是团员,那么,林胜不是团员.答:A: p→q, B: p→⌝q当A命题为真时,若p为假,则B命题必定真;若p为真,则B命题假.所以当A命题为真时,B命题真假不定,所以A、B不是矛盾关系.3、列出下列推理地形式,并分析其是否有效.如果老王不出席,则老李出席;如果老张不出席,则老白出席;老王或老张出席;所以,老李不出席或老白不出席.答:W:老王L:老李Z:老张B:老白(⌝W→L)∧(⌝Z→B)∧(W∨Z)→⌝L∨⌝B假设⌝L∨⌝B=0 则,若推理为假,则前件为真若前件为真,则⌝W→L=1,⌝Z→B=1,W∨Z=1由⌝L∨⌝B=0可知L=1且B=1,又W∨Z=1,所以W=1且Z=1则⌝W→L=1,⌝Z→B=1均成立,即该推理可由真前提推出假结论所以推理无效4、断定一个复合命题为真,是否断定了其所有支命题为真?试以假言命题为例加以说明.答:根据下表可知,断定一个符合命题为真,不能断定其所有支命题为真5、以下列(1)和(2)为前提,能否推出结论(3)?如果能,则说明所应用地是什么推理?(1)如果这次春游去桂林或者去昆明,那么,小丁和小李都要去.(2)小丁不去或者小李不去.(3)这次春游不去昆明.答:(1)可写为G∨K→D∧L(2)可写为⌝D∨⌝L(3)可写为⌝K因为⌝D∨⌝L=⌝(D∧L)=1 所以D∧L=0又G∨K→D∧L=1 所以G∨K=0,G=0,K=0⌝K=1所以可以推出结论(3)三、综合题1、几个大学生在一起议论现代社会中地某些难题.设他们地如下论断都是真地,则从中可以得出什么良策?说明在推导过程中地每一步用地是什么推理形式.(1)要么保住耕地,要么饿肚子.(2)如果人口增长,那么就要增加住房.(3)只有多盖高楼,才能既增加住房,又保住耕地.(4)人口在增长,又不能饿肚子.答:(1)B ∨ E(2)R→F(3) L←(F∧B)(4) R∧⌝E(5) 由(4)得R=1 E=0 (联言命题真则命题支同真)(6)由(2)(5)得F=1 (假言命题肯定前件肯定后件)(7)由(1)(5)得B=1 (选言命题真则选言支至少有一个为真)(8)由(6)(7)得F∧B=1 (命题支同真则联言命题真)(9)由(3)(8)得 L=1 (必要条件假言命题肯定后件则肯定前件)所以,良策是:多盖高楼2、某公司有甲、乙、丙、丁、戊五位职员,大家商量假日地值班问题,有如下四条意见:(1)如果甲来值班,那么乙或丙也来值班.(2)如果乙来值班,那么丁也来值班.(3)如果丙来值班,那么丁也来值班.(4)只有甲来值班,戊才来值班.(5)戊是来值班地.问:丁是不是来值班?说明在推导过程中地每一步用地是什么推理形式.答:(1)甲→乙∨丙(2)乙→丁(3)丙→丁(4)甲←戊(5)戊(6)由(5)(4)得甲=1 (必要条件假言命题肯定后件则肯定前件)(7)由(1)(6)得乙∨丙=1 (充分条件假言命题肯定前件则肯定后件)(8)由(2)(3)(7)得丁=1 (选言命题只要有一个命题支为真则命题为真;充分条件假言命题肯定前件则肯定后件)所以,丁是来值班地1、已知:(1)如果甲和乙参加会议,那么丙不参加会议.(2)只有甲参加会议,丁才参加会议.(3)乙和丙都参加会议.试问:甲和丁是否参加会议?说明在推导过程中地每一步用地是什么推理形式.答:(1)甲∧乙→ 丙(2)甲←丁(3)乙∧丙(4)由(3)得乙=1 丙=1 (联言命题真则命题支都真)(5)由(1)(4)得甲∧乙=0 甲=0 (充分条件假言命题否定后件则否定前件;联言命题假则至少有一个命题支为假)(6)由(2)(5)得丁=0 (必要条件假言命题否定前件则否定后件)所以,甲和丁都不参加会议2、某案件有四名嫌疑犯,调查后确认:(1)只有B是罪犯,C才是罪犯.(2)如果C不是罪犯,那么D是罪犯.(3)或者A是罪犯,或者B不是罪犯.(4)A不是罪犯.根据以上确认,可确定谁是罪犯?说明在推导过程中地每一步用地是什么推理形式.答:(1)B←C(2) ⌝C→D(3) A ∨⌝B(4) ⌝A(5) 由(3)(4)得A=0 B=0(负命题与原命题真假相反;选言命题为真则至少由一个命题支为真)(6)由(1)(5)得C=0 (必要条件假言命题否定前件则否定后件)(7)由(2)(6)得D=1 (充分条件假言命题肯定前件则肯定后件)所以D是罪犯3、某单位有采购员A、B、C、D、E五人.已知:(1)或者C去上海,或者B去上海.(2)如果A不去北京,则B去上海.(3)只有E去广州,D和A才都去北京.(4)如果C去上海,则D去北京.(5)B不去上海.问:E是否去广州?说明在推导过程中地每一步用地是什么推理形式.答:(1)C∨B(2) ⌝A→B(3) E ←D∧A(4) C→D(5) ⌝B(6) 由(1)(5)得B=0 C=1 (负命题与原命题真假相反;选言命题为真则至少由一个选言支为真)(7)由(2)(6)得A=1 (充分条件假言命题否定后件则否定前件)(8)由(4)(6)得D=1 (充分条件假言命题肯定前件则肯定后件)(9)由(3)(7)(8)得E=1 (必要条件假言命题肯定后件则肯定前件)所以E去广州.4、下列四句中只有一句真,问:小王、小李、小林是否去值班?说明推导过程.(1)或者小王不去值班,或者小李不去值班.(2)如果小王不去值班,那么小李也不去值班.(3)小林去值班,小李也去值班.(4)小王不去值班.答:(1)⌝W ∨⌝L(2) ⌝W→⌝L(3) N∧L(4) ⌝W(5) 因为若(4)为真则(1)为真,所以(4)必假,得W=1 (选言命题只要有一个选言支为真则为真)(6)因为(4)为假,所以(2)必真,则(1)(3)皆假,得L=1 N=0(充分条件假言命题地假前提可以包涵所有命题;选言命题为假则选言支都为假;联言命题为假则至少由一个命题支为假)所以小王和小李去值班,小林不去.5、在某次税务检查后,四个工商管理人员有如下结论:甲:所有个体户都没纳税.乙:服装个体户陈老板没纳税.丙:并非所有个体户都没纳税.丁:有地个体户没纳税.如果四人中只有两人地断定属实,请问服装个体户陈老板有没有纳税?说明推导过程.答:因为丙命题为甲命题地负命题,所以真假必定相反.若甲断定为假,则丙断定为真,丁断定和乙断定都真假不定.若甲断定属实,则乙断定为真,丙断定为假,丁断定为假,符合题目要求,所以个体户陈老板没有纳税.6、三位同学从学校毕业后,一个当了律师,一个当了教师,一个当了会计.同学会上,大家作了如下议论:A:甲当了律师,乙当了教师.B:甲当了教师,丙当了律师.C:甲当了会计,乙当了律师.但大家地议论都只说对了一半,请问他们各选择了什么职业?说明推导过程.答:由于大家地议论都只说对了一半,所以:若A说地甲当了律师是对地,那么B说地都是错地,不合题意所以,A说法中,甲当了律师是错地,乙当了教师是对地.则B说法中,甲当了教师是错地,丙当了律师是对地C说法中,甲当了会计是对地,乙当了律师是错地所以,甲是会计,乙是教师,丙是律师。
命题逻辑复习题和答案

命题逻辑23、设P :龙凤呈祥是成语,QZ 雪是黑的,/?:太阳从东方升起,则下列假命题为(A)A 、P →Q∕∖RB 、Q→ P A SC 、PTQVRD 、 Q→ P7 S14、 设P :我累,Q :我去打球,则命题:“除非我累,否则我去打球”的符号化为(B ) A 、P — Q B 、P —>—Q C 、 一P — Q DX ―P ―>—Q 15、 设P :我听课,Q :我睡觉,则命题“我不能一边听课,一边睡觉”的符号化为(B)A 、P — QB 、P —>—QC 、 一P — QDX ―P ―>—Q提不:一P A Q) <=> P ―> ―Q16、 设P :停机:Q :语法错误;R :程序错误,则命题“停机的原因在于语法错误或程序错误”的符号化为(D )A 、P →Q ΛRB 、P →Qy RC 、Q ΛR→ PD 、Qy Rτ P 17、设P :你来了; Q :他唱歌;R :你伴奏则命题“如果你来了,那末他唱不唱歌将看你是否伴奏而圧”的符号化为(D ) A 、P — IQ∕∖R)一.选择题(每题3分)下列句子中哪个是命题(C) 你的离散数学考试通过了吗 兀是有理数 下列句子中哪个不是命题(C) 你通过了离散数学考试我说的是真话 下列联接词运算不可交换的是(C)A1、 A 、 C、 2、A B 、 VB 、请系好安全带! D 、本命题是假的 B 、我俩五百年前是一家 D 、淮海工学院是一座工厂4、 A 、5、A 、 6、A 、命题公式=P T Q 不能表述为(B)P 或0B 、非P 每当Q永真式的否定是(B) 永真式 B.永假式 C 、可满足式 下列哪组賦值使命题公式P→(P Λ0的真值为假(D )P 假。
真B 、P 假。
假C 、P 真0真 下列为命题公式P 八(QSR)成假指派的是(B ) 100 B 、IOlC 、110D 、除非P,否则0 D 、 D 、 D 、 以上答案均有可能 Ill9、 A下列公式中为永真式的是(C) PT(PAQ) B. -1P→(P Λ0 C 、(P A Q) —> QD 、(PVQ)TQ 下列公式中为非永真式的是(B)(P A -I P)→Q B 、(PV-IP)→ρ10、 下列表达式错误的是(D) AX PV(PA0<≠> P C 、P V (-I P Λ0 <≠> P V (2 11、 下列表达式正确的是(D)AX P=>P A <2 B 、PzQnP C 、P A (―∖P —> Q) D 、 PV(^P→Q) BX PMPvQ)OP D 、PΛ(-ιPvβ)<≠> Pv(2c 、—^÷ Q) D 、-(P —> Q) => —1<212、 下列四个命题中真值为真的命题为(B)(1)2 + 2 = 4当且仅当3是奇数(3)2 + 2≠4当且仅当3是奇数( A 、(1)与(2) B 、(1)与(4) (2) 2 + 2 = 4当且仅当3不是奇数: (4) 2+2≠4当且仅当3不是奇数 C 、(2)与(4) D 、(3)与(4)BX P— (Q—R) CX P— (R― Q) DX P— (Q÷÷R)18. 在命运题逻借中,任何非永真命题公式的主合取范式都是(A )A、存在并且唯一B、存在但不唯一C、不存在D、不能够确定19、在命题逻辑中,任何非永假命题公式的主析取范式都是(A )A、存在并且唯一B、存在但不唯一C、不存在D、不能够确定20、〃个命题变元所产生互不等价的极小项项数为(D )A、HB、2nC、n2D、2,'21. "个命题变元所产生互不等价的极大项项数为(D )A、nB、In CX n1D、T二.填充题(每题4分) 「设P:你努力,QZ你失败,则“虽然你努力了,但还是失败了”符号化为PΛQ.2、设P:它占据空间,Q:它有质量,它不断运动,S :它叫做物质,则“占据空间的,有质量的而且不断运动的叫做物质”符号化为S→PΛQΛR・3、一个命题含有"个原子命题,则对其所有可能赋值有兰种.4、推理规则AΛ(A→B)→B的名称为假言推理. ~5、推理规则^BΛ(A→B)→^A的名称为拒取式.6、推理规则-I AA(AVB)=>B的名称为析取三段论.(7、推理规则(Λ→B)Λ(B→C)=>A→C的名称为前提三段论•8、当賦予极小项足标相同的指派时,该极小项的頁•值为丄,当赋予极大项足标相同的指派时,该极大项的真值为09、任意两个不同极小项的合取式的真值为而全体极小项的析取式的真值为丄・10、任意两个不同极大项的析取式的真值为丄,而全体极大项的合取式的真值为011、"个命题变元可构造包括F的不同的主析取范式类别为?[・12、H个命题变元可构造包括丁的不同的主合取范式类别为兰_・三、问答题(每题6分) —1、设A、3是任意命题公式,请问A →B,A=>B分别表示什么其有何关系答:A→B表示A蕴含B, A=>B表示A永真蕴含其关系表现为:若A→B为永真式,则有A^B・2、设A、B是任意命题公式,请问A÷÷5Ao3分别表示什么其有何关系答:A→B表示A等值于B, Ao3表示A与B逻辑等价:其关系表现为:若A分B为永真式,则有・3、设4、B、C是任意命题公式,若ΛvC<≠>BvC ,则AoB成立吗为什么答:不一定有A<≠>B:若A为真,B为假,C为真,则AvC<≠>BvC成立,但4oB不成立・4、设A、B、C是任意命题公式,若ΛA C<≠>BΛC ,则Ao3成立吗为什么答:不一立有A<≠>B: 若A为真,B为假,C为假,则AΛC^BΛC成立,但A^B不成立・5、设A、B是任意命题公式,A A(A→B)→B-⅛为真吗为什么答:一左为真:因A Λ(A→ B) → B A Λ(-A V B) → B <≠> (A A-√1) V(AΛB) → B<≠≠>F V(AΛB)→B<≠>A A B→B<≠>T・(用真值表也可证明)6、设A、B是任意命题公式,(A→B)A(A→-^)θ→i-⅛为真吗为什么答:一加为貞•:因(A —> B) A (A —> —) <≡> (―IA V B) A (—IA V ―B) <=> —IA V (B A —B) o—AvFθr4.(用真值表也可证明)四、填表计算题(每题10分)IX对命题公式A = -(P → q)Λ(P∖/q) 9要求(1)用0或1填补其真值表的空格处;解:(2)求该命题公式的主析取范式与主合取范式・P q 00 01 10 11PTq7P f q)Pyq A101010 (111 1010主析取范式A<≠>V(2):主合取范式AOrl(O丄3)・2、对命题公式A = (p→q)→r,要求(1)用O或1填补其真值表的空格处;(2)解:求该命题公式的主析取范式与主合取范式・Pqr Oo θOOI 0 1 0 OII 100 101 110 111 P→c l A1 01 11 01 10 10 01 01 1主析取范式Ao工(1,3,4,7):主合取范式AoΓI(0,2,5,6)∙3、对命题公式A=(/?A^)V(/? Ar),要求(1)用0或1填补其貞•值表的空格处:(2)求该命题公式的主析取范式与主合取范式・解:P q 0 0 0 0 r PM∕?Ar)A 00001{000主析取范式Ao 工(5,6,7):主合取范式AorI(O 丄2,3,4)・4、对命题公式A = (-/? → q)∕∖(p → r) »要求(1)用O 或1填补其真值表的空格处;(2)求该命题公式的主析取范式与主合取范式. 解:主析取范式Ao 工(2,3,5,7);主合取范式AorI(O 丄4,6)・(5、对命题公式A = (^V^)→r,要求(1)用O 或1填补其真值表的空格处;(2)求该命题公式的主析取范式与主合取范式. 解:O 1 ° 1 1 O 1 O 1 1 111 O O O 1 O O 11 1O O O 1 OO O O 1 1 1O O主析取范式Ao^(l,3,5,6,7);主合取范式Aorl(0,2,4).五、证明题(每题10分)1、证明下列逻辑恒等式:(P→Q)Λ(R→Q)^(P^R)→Q.证明:左<≠> (―∣P V 0 A (—1/? V β) <≠> (―ιP A —7?) V Q 07PVRNQOPVRTQQ右.(用真值表也可证明)2、证明下列逻辑恒等式:「PS「Ro R T Q V P.证明:⅛<≠> —∣P A-I Q) V -I R<≠> P V 0 V-I ROrRV(QVP)ORT Qv P o右.(用真值表也可证明)3、证明下列逻辑恒等式:-∏(P<→Q)O(P V Q)A-I(PA0). 证明:左<≠>->((Pv-1β)Λ(^Pv(2))<≠>-1(Pv^β)v-1(^Pvβ) no (->P 人Q)V (P ∕∖-1Q) o (P V w)∕∖ (W A「°)人(Q V P)∕∖(Q V r2) O(PV 0)人(PVQ)A-I(PAQ)O 右.(用真值表也可证明)4、用逻辑推理规则证明:(aΛb)→c , Tl , -I CVd => 7丫儿.证明:⑴—>c∙ V J P(2) 7 P(3) -Ie T⑴,⑵(析取三段论)(4) (aΛb) →c P(5) ->(6∕ΛZ?)丁⑶,⑷(拒取式)(6) 口5)(徳•摩根律)・5、用逻辑推理规则证明:P7 q、p→s、5→Γ=> TTq・I证明:(1) PTS P(2) s→ r P(3) p→r T⑴,(2)(前提三段论)⑷TTF7 T 3(逆反律)⑸ PVq P⑹ ^→q T (5)(蕴含表达式)⑺TTq T(4), (6)(前提三段论).6、用逻辑推理规则证明:p—q , Pf —qw, -Ir » -U yVp=> —>5.证明:⑴—ιΓP(2)—it/vr P(3)T(IM2)(析取三段论)(4)p→<7P⑸-P T(3), (4)(拒取式)(6)-Ly V P P(7)―S7(5), (6)(析取三段论)・7、用逻辑推理规则证明:-ι(∕7→^)→-ι(rv5), (q→p)s证明:⑴r P(2)⅛→∕?) V-Ir P(3)Q→P T (1),(2)(析取三段论)⑷r V5T (1)(加法式)⑸-y{p→q}→-{r∖∕s}P(6)PTq T(4),⑸(拒取式)(7)(PTq)MqTP)T(3), (6)(合取式)(8)PF T (7)(等值表达式).8、用逻辑推理规则证明:-VyV/7, /;>→r r=> s →q ・证明:⑴S P(2)-XyV P P(3)P T(I),(2)(析取三段论)⑷P→ΓΛQ P⑸KΛCf T(3), (4)(假言推理)(6)q T (5)(简化式)(7)S →q CP.9、用逻辑推理规则证明:(pv<7)→r=>(pΛ^)→r证明:⑴P (附加前提)(2)P7(1)(简化式)(3)P"丁⑵(加法式)(4)(PVg)W P⑸r T (3),(4)(假言推理)⑹(pvt7)→r=>(pAt7)→r CP.10、用逻辑推理规则证明:-√? V^-16∕v∕∖r→s=> p→s・证明:(1)P P (附加前提)(2)r八q P(3)q T (1), (2)(析取三段论)(4)-C]7 Y P(5)r T⑶,(4)(析取三段论)(6) r→5 P(7) S T (5), (6)(假言推理) (8) PTSCP ・12、用逻辑推理规则证明:(PV^) →(r A 5), (rv5)→∕ => D→r ・13.用逻辑推理规则证明:a→bΛC, (^→√')→-,c, b→(aΛ^s)^h→e.T (9)(蕴含表达式) T (10)(徳,摩根律) T (□)(简化式) CP. P→q, -Pfqdq ・ P (附加前提)PT ⑴,⑵(拒取式) PT ⑶/4)(假言推理)证明:(1) P ⑺PYq(3)(^V^)→(ΓA5)S S ÷A Vr Γ r O r∙ P ∖/ ∖J∕ \/ ■--------- Γ ∖/ L -------------- 1 (4G伍卩但卩12.用逻辑推理规则证明:(/ P (附加前提)T ⑴(加法式)PT (2), (3)(假言推理) 八4)(简化式) 八5)(加法式)PΓ(6), (7)(假言推理)CP.—> —W )—> ―头-© 7 S<t t --S Cl —>t证明:(1) q(2) T7S (3)S(4) (Z —> ―VV) ―> ―LV⑸->(∕ T -IW)(6) ―ι(—∖t V —IVV) (7) /AVV(8)tP (附加前提)PT (1), (2)(析取三段论)PT (3),⑷(拒取式)T (5)(蕴含表达式) T (6)(徳•摩根律) T (7)(简化式) CP.证明:(1) b (2) b → (a ΛS )U Λ-yS aa →bΛCZ?ACC(e→^f')→^c→→T)∖/ ∖/ ∖J∕ ∖/ ∖u∕ ∖J \/ 3 4 5 6 7 8 9 /(⅜ /V ∕l ⅜ /(⅝ ∕f∖ /(X (P (附加前提)PT (1), (2)(假言推理)T (3)(简化式) PT (4), (5)(假言推理) T (6)(简化式) PT (7),⑻(拒取式)(10) - (11)(11)e (12) b→e14.用逻辑推理规则证明:证明:(1) TZ(2) p→q(3)T⑷ ⑸ q⑹ FM T⑴佝(合取式)由(6)得出矛盾式,故原命题有效・ISX用逻辑推理规则证明:PNq , (∕7÷÷^)→(rv5)=> Z S・证明:(1)7 V S)P(附加前提)(2)(∕7<→^)→(rv5)P⑶-I(P ÷÷ty)T⑴,⑵(拒取式)⑷7)Λ(pv-1<7))T(S)(等值与蕴含表达式)(5)T (4)(德.摩根律)(6)(-1∕?V-^)A(∕7Vty)T(S)(结合律或范式等价).(7)•—∕? V—T(7)(简化式)•(8)7PM)T (4)(德.摩根律)(9)PM P(io :»-√∕^Aty)A(∕?A^)T (9),(10)(合取式)由(10)得出矛盾式,故原命题有效・16.用逻辑推理规则证明:p→q9/?Ar»—>(q V r)不能同时为真.证明:⑴∕7Λr P(2)P T⑴(简化式)(3)PTq P⑷q T (2),(3)(假言推理)(5)-ι(<∕vr)P(6)A-Ir T(5)(徳.摩根律)⑺T T(6)(简化式)(8)T⑷,(7)(合取式)由(8)得出矛盾式,故原命题有效.17.证明下列命题推得的结论有效:或者逻辑难学,或者有少数学生不喜欢它:如果数学容易学,那么逻辑并不难学•因此,如果许多学生喜欢逻辑,那么数学并不难学.证明:设逻辑难学:q:有少数学生不喜欢逻辑学:r:数学容易学.该推理就是要证明:pvq,r→-,p nr7-÷τ∙・⑴PYq P⑵r—q T⑴(蕴含表达式)⑶r →-P⑷r →q T(2),(3)(前提三段论)⑸-n6∕→-∣r T (4)(逆反律)・28、证明下列命题推得的结论有效:如果今天是星期三,那么我有一次离散数学或数字逻辑测验:如果离散数学课老师有事,那么没有离散数学测验:今天是星期三且离散数学老师有事•所以,我有一次数字逻辑测验.证明:设今天是星期三;q:我有一次离散数学测验:r:我有一次数字逻借测验;$:离散数学课老师有事・该推理就是要证明:∕? → V r), s→-↑q .pΛS=> r・p ∕∖s PP T(1)(简化式)S T⑴(简化式)s→n P⑸T]T ⑶,(4)(假言推理) (6) ∕7→(^vr)P⑺^Vr T ⑵,(6)(假言推理)(8)rT (5) , (7)(析取三段论)・19. 证明下列命题推得的结论有效:如果马会飞或羊吃草,则母鸡就会是飞鸟;如果母鸡是 飞鸟,那么烤熟的鸭子还会跑;烤熟的鸭子不会跑•所以,羊不吃草。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
命题逻辑练习题一、从五个备选答案中选择一个正确的答案,并做出简要的分析:1、古代一位国王率领张、王、李、赵、钱五位将军一起打猎,各人的箭上均刻有自己的姓氏。
围猎中,一只鹿中箭倒下,但却不知是何人所射。
国王令众将军猜测。
张说:“或者是我射中的,或者是李将军射中的。
”王说:“不是钱将军射中的。
”李说:“如果不是赵将军射中的,那么一定是王将军射中的。
”赵说:“既不是我射中的,也不是王将军射中的。
”钱说:“既不是李将军射中的,也不是张将军射中的。
”国王令人把射中鹿的箭拿来,看了看,说:“你们五位将军的猜测,只有两个人的话是真的。
”根据国王的话,可以判定以下哪项是真的?A、张将军射中此鹿。
B、王将军射中此鹿。
C、李将军射中此鹿。
D、赵将军射中此鹿。
E、钱将军射中此鹿。
1、某大学进行演讲比赛,得第一名的只有一人。
在对六个参赛者进行名次预测时,四人作了如下预测:甲:取得第一名的要么是我,要么是乙。
乙:取得第一名的要么是甲,要么是丙。
丙:如果不是戊取得第一名,就一定是己。
丁:第一名决不会是甲。
比赛结果发现,只有一个人的预测正确。
请问谁得第一名?谁的预测正确?A、甲得第一名,乙的预测正确。
B、乙得第一名,甲的预测正确。
C、丙得第一名,乙的预测正确。
D、丁得第一名,丁的预测正确。
E、戊得第一名,丙的邓测正确。
2、销售经理的人选,对于一个公司的生存和发展十分重要。
哈维珍珠有限责任公司对于销售经理的任用,就非常填重。
由于前任销售经理因故离任,关于公司新销售经理的人选,甲、乙、丙三位董事经过充分考虑,提出了他们的意见:甲:要么聘用李先生,要么聘用王先生。
乙:如果不聘用李先生,那么也不聘用王先生。
丙:如果不聘用王先生,那么就聘用李先生。
以下诸项中,能同时满足甲、乙、丙三位董事意见的方案是哪一项?A、聘用李先生,不聘用王先生。
B、聘用王先生,不聘用李先生。
C、李先生和王先生两人都聘用。
D、李先生和王先生两人都不聘用。
E、聘用其他人当销售经理。
5、某公安局的刑侦员甲、乙、丙、丁通过广泛的调查取证,对某案的嫌疑犯李、赵作了如下断定:甲:“我认为赵不是凶犯。
”乙:“或者李是凶犯,或者赵是凶犯。
”丙:“如果李是凶犯,则赵不是凶犯。
”丁:“我看李和赵都是凶犯。
”事后证明,这四位刑侦员的断言只有一句是假的。
根据以上情况,可以推知:A、李和赵都是凶犯。
B、甲的话是假的。
C、李是凶犯,丙的话是真的。
D、赵是凶犯,而李不是凶犯。
E、丁的话是真的。
6、“如果货币的储蓄额和销售回笼额都没有增长,那么货币的入股额一定增长”,以此为前提,若再增加一个前提,可以推出“货币的储蓄额事实上增长了”的结论。
以下哪项是该增加的前提?A、货币的入股额一定增长了。
B、货币的入股额事实上没有增长。
C、货币的销售回笼额没有增长。
D、货币的销售回笼额和入股额事实上都没有增长。
E、货币的销售回笼额和入股额事实上都增长了。
7、八个硕士研究生赵、钱、孙、李、周、吴、陈、王正在争取获得某项科研基金。
按规定只有一人能获得该项基金。
谁能获得该项基金,由学校评委的投票数决定。
评委分成不同的投票小组。
如果李获得的票数比陈多,那么钱将获得该项基金。
如果王获得的票数比孙多,或者钱获得的票数比周多,那么吴将获得该项基金。
如果孙获得的票数比王多,同时陈获得的票数比李多,那么赵将获得该项基金。
如果吴获得了该项基金,那么下面哪个结论一定是正确的?A、孙获得的票数比王多。
B、王获得的票数比孙多。
C、李获得的票数不比陈多。
D、钱获得的票数比周多。
E、陈获得的票数比李多。
1、如果赵川参加宴会,那么钱华、孙旭和李元将一起参加宴会。
如果上述断定是真的,那么,以下哪项也是真的?A、如果赵川没参加宴会,那么,钱、孙、李三人中至少有一人没参加宴会。
B、如果赵川没参加宴会,那么,钱、孙、李三人都没有参加宴会。
C、如果钱、孙、李三人都参加了宴会,那么,赵也参加宴会。
D、如果李元没参加宴会,那么,钱华和孙旭不会都参加宴会。
E、如果孙旭没参加宴会,那么,赵川和李元不会都参加宴会。
二、分析题1、写出下列推理的形式,并分析其是否有效。
如果小林基础好并且学习努力,那么,他能取得好成绩;他没有取得好成绩;所以,他基础不好,学习也不努力。
答:A∧B→C⌝C→⌝A∧⌝B根据充分条件假言命题的推理规则【1】否定后件则否定前件,所以⌝C→⌝(A∧B)又⌝(A∧B)←→⌝A∨⌝B因此推理无效2、下列A、B两命题是不是一对具有矛盾关系的命题?为什么?A:如果李军是团员,那么,林胜也是团员。
B:如果李军是团员,那么,林胜不是团员。
答:A: p→q, B: p→⌝q当A命题为真时,若p为假,则B命题必定真;若p为真,则B命题假。
所以当A命题为真时,B命题真假不定,所以A、B不是矛盾关系。
3、列出下列推理的形式,并分析其是否有效。
如果老王不出席,则老李出席;如果老张不出席,则老白出席;老王或老张出席;所以,老李不出席或老白不出席。
答:W:老王L:老李Z:老张B:老白(⌝W→L)∧(⌝Z→B)∧(W∨Z)→⌝L∨⌝B假设⌝L∨⌝B=0 则,若推理为假,则前件为真若前件为真,则⌝W→L=1,⌝Z→B=1,W∨Z=1由⌝L∨⌝B=0可知L=1且B=1,又W∨Z=1,所以W=1且Z=1则⌝W→L=1,⌝Z→B=1均成立,即该推理可由真前提推出假结论所以推理无效4、断定一个复合命题为真,是否断定了其所有支命题为真?试以假言命题为例加以说明。
答:根据下表可知,断定一个符合命题为真,不能断定其所有支命题为真P Q命题111充分条件假言命题100011001111必要条件假言命题101010001111充要条件假言命题1000100015、以下列(1)和(2)为前提,能否推出结论(3)?如果能,则说明所应用的是什么推理?(1)如果这次春游去桂林或者去昆明,那么,小丁和小李都要去。
(2)小丁不去或者小李不去。
(3)这次春游不去昆明。
答:(1)可写为G∨K→D∧L(2)可写为⌝D∨⌝L(3)可写为⌝K因为⌝D∨⌝L=⌝(D∧L)=1 所以D∧L=0又G∨K→D∧L=1 所以G∨K=0,G=0,K=0⌝K=1所以可以推出结论(3)三、综合题1、几个大学生在一起议论现代社会中的某些难题。
设他们的如下论断都是真的,则从中可以得出什么良策?说明在推导过程中的每一步用的是什么推理形式。
(1)要么保住耕地,要么饿肚子。
(2)如果人口增长,那么就要增加住房。
(3)只有多盖高楼,才能既增加住房,又保住耕地。
(4)人口在增长,又不能饿肚子。
答:(1)B ∨ E(2)R→F(3) L←(F∧B)(4) R∧ E(5) 由(4)得R=1 E=0 (联言命题真则命题支同真)(6)由(2)(5)得F=1 (假言命题肯定前件肯定后件)(7)由(1)(5)得B=1 (选言命题真则选言支至少有一个为真)(8)由(6)(7)得F∧B=1(命题支同真则联言命题真)(9)由(3)(8)得 L=1 (必要条件假言命题肯定后件则肯定前件)所以,良策是:多盖高楼2、某公司有甲、乙、丙、丁、戊五位职员,大家商量假日的值班问题,有如下四条意见:(1)如果甲来值班,那么乙或丙也来值班。
(2)如果乙来值班,那么丁也来值班。
(3)如果丙来值班,那么丁也来值班。
(4)只有甲来值班,戊才来值班。
(5)戊是来值班的。
问:丁是不是来值班?说明在推导过程中的每一步用的是什么推理形式。
答:(1)甲→乙∨丙(2)乙→丁(3)丙→丁(4)甲←戊(5)戊(6)由(5)(4)得甲=1 (必要条件假言命题肯定后件则肯定前件)(7)由(1)(6)得乙∨丙=1 (充分条件假言命题肯定前件则肯定后件)(8)由(2)(3)(7)得丁=1 (选言命题只要有一个命题支为真则命题为真;充分条件假言命题肯定前件则肯定后件)所以,丁是来值班的1、已知:(1)如果甲和乙参加会议,那么丙不参加会议。
(2)只有甲参加会议,丁才参加会议。
(3)乙和丙都参加会议。
试问:甲和丁是否参加会议?说明在推导过程中的每一步用的是什么推理形式。
答:(1)甲∧乙→⌝丙(2)甲←丁(3)乙∧丙(4)由(3)得乙=1 丙=1 (联言命题真则命题支都真)(5)由(1)(4)得甲∧乙=0 甲=0 (充分条件假言命题否定后件则否定前件;联言命题假则至少有一个命题支为假)(6)由(2)(5)得丁=0 (必要条件假言命题否定前件则否定后件)所以,甲和丁都不参加会议2、某案件有四名嫌疑犯,调查后确认:(1)只有B是罪犯,C才是罪犯。
(2)如果C不是罪犯,那么D是罪犯。
(3)或者A是罪犯,或者B不是罪犯。
(4)A不是罪犯。
根据以上确认,可确定谁是罪犯?说明在推导过程中的每一步用的是什么推理形式。
答:(1)B←C(2) ⌝C→D(3) A ∨⌝B(4) ⌝A(5) 由(3)(4)得A=0 B=0(负命题与原命题真假相反;选言命题为真则至少由一个命题支为真)(6)由(1)(5)得C=0 (必要条件假言命题否定前件则否定后件)(7)由(2)(6)得D=1 (充分条件假言命题肯定前件则肯定后件)所以D是罪犯3、某单位有采购员A、B、C、D、E五人。
已知:(1)或者C去上海,或者B去上海。
(2)如果A不去北京,则B去上海。
(3)只有E去广州,D和A才都去北京。
(4)如果C去上海,则D去北京。
(5)B不去上海。
问:E是否去广州?说明在推导过程中的每一步用的是什么推理形式。
答:(1)C∨B(2) ⌝A→B(3) E ← D∧A(4) C→D(5) ⌝B(6) 由(1)(5)得B=0 C=1 (负命题与原命题真假相反;选言命题为真则至少由一个选言支为真)(7)由(2)(6)得A=1 (充分条件假言命题否定后件则否定前件)(8)由(4)(6)得D=1 (充分条件假言命题肯定前件则肯定后件)(9)由(3)(7)(8)得E=1 (必要条件假言命题肯定后件则肯定前件)所以E去广州。
4、下列四句中只有一句真,问:小王、小李、小林是否去值班?说明推导过程。
(1)或者小王不去值班,或者小李不去值班。
(2)如果小王不去值班,那么小李也不去值班。
(3)小林去值班,小李也去值班。
(4)小王不去值班。
答:(1)⌝W ∨⌝L(2) ⌝W→⌝L(3) N∧L(4) ⌝W(5) 因为若(4)为真则(1)为真,所以(4)必假,得W=1 (选言命题只要有一个选言支为真则为真)(6)因为(4)为假,所以(2)必真,则(1)(3)皆假,得L=1 N=0(充分条件假言命题的假前提可以包涵所有命题;选言命题为假则选言支都为假;联言命题为假则至少由一个命题支为假)所以小王和小李去值班,小林不去。
5、在某次税务检查后,四个工商管理人员有如下结论:甲:所有个体户都没纳税。
乙:服装个体户陈老板没纳税。
