16matlab关于一个字符串向量处理问题
matlab字符运算 -回复

matlab字符运算-回复MATLAB字符运算是MATLAB软件中的一项重要功能,它使用户能够对字符进行各种操作和处理。
在本文中,我们将逐步介绍MATLAB字符运算的基本知识和常见用法。
1. 字符串的表示方法在MATLAB中,字符串可以用单引号或双引号括起来表示。
例如,'Hello'和"World"都是有效的表示字符串的方式。
需要注意的是,使用单引号或双引号的选择并不会对字符串的处理方法产生影响。
2. 字符串的连接使用加号运算符(+)可以将两个字符串连接起来,形成一个新的字符串。
例如,在命令窗口输入以下代码:str1 = 'Hello';str2 = 'World';str3 = str1 + str2;运行后,str3的值将会是'HelloWorld'。
3. 字符串的索引和切片在MATLAB中,可以使用索引(indexing)和切片(slicing)方法访问和操作字符串。
索引是指获取字符串中某个位置上字符的方法,而切片是指获取字符串中连续一段字符的方法。
要获取字符串中特定位置上的字符,可以使用方括号和索引值。
例如,要获取字符串'Hello'中的第一个字符,可以输入以下代码:str = 'Hello';char1 = str(1);运行后,char1的值将会是'H'。
要获取字符串中连续一段字符,可以使用冒号(:)进行切片。
例如,要获取字符串'Hello'中的前三个字符,可以输入以下代码:str = 'Hello';subStr = str(1:3);运行后,subStr的值将会是'Hel'。
4. 字符串的长度使用MATLAB内置函数length()可以获取字符串的长度。
以下是一个示例:str = 'Hello';len = length(str);运行后,len的值将会是5。
MATLAB程序设计与应用(刘卫国编)课后实验答案

实验一MATLAB运算基础之邯郸勺丸创作1. 先求下列表达式的值,然后显示MATLAB工作空间的使用情况并保管全部变量。
(1)0 122sin851ze =+(2)21ln( 2z x=+,其中2120.455i x+⎡⎤=⎢⎥-⎣⎦(3)0.30.330.3sin(0.3)ln, 3.0, 2.9,,2.9,3.0 22a ae e az a a--+=++=--(4)2242011122123t tz t tt t t⎧≤<⎪=-≤<⎨⎪-+≤<⎩,其中t解:M文件:z1=2*sin(85*pi/180)/(1+exp(2))x=[2 1+2*i;-.45 5];z2=1/2*log(x+sqrt(1+x^2))a=-3.0:0.1:3.0;z3=(exp(0.3.*a)-exp(-0.3.*a))./2.*sin(a+0.3)+log((0.3+a)./2)t=0:0.5:2.5;z4=(t>=0&t<1).*(t.^2)+(t>=1&t<2).*(t.^2-1)+(t>=2&t<3) .*(t.^2-2*t+1) 运算结果:z1=2*sin(85*pi/180)/(1+exp(2))x=[2 1+2*i;-.45 5];z2=1/2*log(x+sqrt(1+x^2))a=-3.0:0.1:3.0;z3=(exp(0.3.*a)-exp(-0.3.*a))./2.*sin(a+0.3)+log((0.3+a)./2)t=0:0.5:2.5;z4=(t>=0&t<1).*(t.^2)+(t>=1&t<2).*(t.^2-1)+(t>=2&t<3) .*(t.^2-2*t+1) z1 =z2 =z3 =Columns 1 through 4Columns 5 through 8Columns 9 through 12Columns 13 through 16Columns 17 through 20Columns 21 through 24Columns 25 through 28-1.8436 + 3.1416i -2.2727 + 3.1416i -2.9837 + 3.1416i -37.0245 Columns 29 through 32-3.0017 -2.3085 -1.8971 -1.5978Columns 33 through 36-1.3575 -1.1531 -0.9723 -0.8083Columns 37 through 40-0.6567 -0.5151 -0.3819 -0.2561Columns 41 through 44-0.1374 -0.0255 0.0792 0.1766Columns 45 through 480.2663 0.3478 0.4206 0.4841Columns 49 through 520.5379 0.5815 0.6145 0.6366Columns 53 through 560.6474 0.6470 0.6351 0.6119Columns 57 through 600.5777 0.5327 0.4774 0.4126Column 610.3388z4 =2. 已知:求下列表达式的值:(1) A+6*B和A-B+I(其中I为单位矩阵)(2) A*B和A.*B(3) A^3和A.^3(4) A/B及B\A(5) [A,B]和[A([1,3],:);B^2]解:M 文件:A=[12 34 -4;34 7 87;3 65 7];B=[1 3 -1;2 0 3;3 -2 7]; A+6.*BA-B+eye(3)A*BA.*BA^3A.^3A/BB\A[A,B][A([1,3],:);B^2]运算结果:A=[12 34 -4;34 7 87;3 65 7];B=[1 3 -1;2 0 3;3 -2 7];A+6.*BA-B+eye(3)A*BA.*BA^3A.^3A/BB\A[A,B][A([1,3],:);B^2]ans =18 52 -1046 7 10521 53 49ans =12 31 -332 8 840 67 1ans =68 44 62309 -72 596154 -5 241ans =12 102 468 0 2619 -130 49ans =37226 233824 48604247370 149188 60076678688 454142 118820ans =1728 39304 -6439304 343 65850327 274625 343ans =ans =ans =12 34 -4 1 3 -134 7 87 2 0 33 65 7 3 -2 7ans =12 34 -43 65 74 5 111 0 1920 -5 403. 设有矩阵A和B(1) 求它们的乘积C。
matlab简单编程21个题目及答案
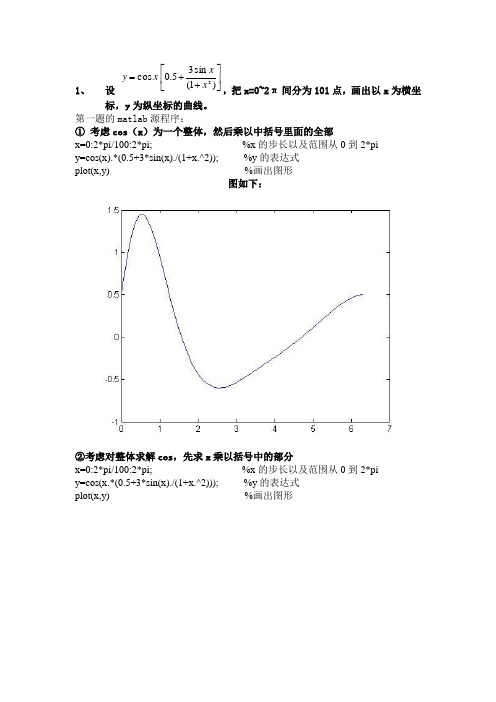
1、设⎥⎦⎤⎢⎣⎡++=)1(sin35.0cos2xxxy,把x=0~2π间分为101点,画出以x为横坐标,y为纵坐标的曲线。
第一题的matlab源程序:①考虑cos(x)为一个整体,然后乘以中括号里面的全部x=0:2*pi/100:2*pi; %x的步长以及范围从0到2*pi y=cos(x).*(0.5+3*sin(x)./(1+x.^2)); %y的表达式plot(x,y)%画出图形图如下:②考虑对整体求解cos,先求x乘以括号中的部分x=0:2*pi/100:2*pi; %x的步长以及范围从0到2*pi y=cos(x.*(0.5+3*sin(x)./(1+x.^2))); %y的表达式plot(x,y) %画出图形图如下:2、产生8×6阶的正态分布随机数矩阵R1, 求其各列的平均值和均方差。
并求该矩阵全体数的平均值和均方差。
第二题的matlab源程序如下:R1=randn(8,6) %产生正态分布随机矩阵R1 =1.0933 -0.7697 1.5442 -0.1924 1.4193 0.21571.1093 0.3714 0.0859 0.8886 0.2916 -1.1658-0.8637 -0.2256 -1.4916 -0.7648 0.1978 -1.14800.0774 1.1174 -0.7423 -1.4023 1.5877 0.1049-1.2141 -1.0891 -1.0616 -1.4224 -0.8045 0.7223-1.1135 0.0326 2.3505 0.4882 0.6966 2.5855-0.0068 0.5525 -0.6156 -0.1774 0.8351 -0.66691.5326 1.1006 0.7481 -0.1961 -0.2437 0.1873aver=(sum(R1(1:end,1:end)))./8 %产生各行的平均值aver =0.0768 0.1363 0.1022 -0.3473 0.4975 0.1044a=std(R1(1:end,1:end)) %产生各行的均方差也就是标准差a =1.0819 0.8093 1.3456 0.8233 0.8079 1.2150aver1=(sum(R1(:)))./48 %全体数的平均值aver1 =0.0950b=std(R1(:)) %全体数的均方差即标准差b =1.01033、设x=rcost+3t,y=rsint+3,分别令r=2,3,4,画出参数t=0~10区间生成的x~y 曲线。
MATLAB程序设计与应用(刘卫国编)课后实验答案

实验一 MATLAB 运算基础1. 先求下列表达式的值,然后显示MATLAB 工作空间的使用情况并保存全部变量。
(1) 0122sin851z e =+(2) 21ln(2z x =+,其中2120.455i x +⎡⎤=⎢⎥-⎣⎦ (3) 0.30.330.3sin(0.3)ln , 3.0, 2.9,,2.9,3.022a a e e a z a a --+=++=--(4) 2242011122123t t z t t t t t ⎧≤<⎪=-≤<⎨⎪-+≤<⎩,其中t =0:: 解:2. 已知:1234413134787,2033657327A B --⎡⎤⎡⎤⎢⎥⎢⎥==⎢⎥⎢⎥⎢⎥⎢⎥-⎣⎦⎣⎦求下列表达式的值:(1) A+6*B 和A-B+I (其中I 为单位矩阵)(2) A*B 和A.*B(3) A^3和A.^3(4) A/B 及B\A(5) [A,B]和[A([1,3],:);B^2]解:运算结果:3. 设有矩阵A 和B1234530166789101769,111213141502341617181920970212223242541311A B ⎡⎤⎡⎤⎢⎥⎢⎥-⎢⎥⎢⎥⎢⎥⎢⎥==-⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎣⎦⎣⎦ (1) 求它们的乘积C 。
(2) 将矩阵C 的右下角3×2子矩阵赋给D 。
(3) 查看MATLAB 工作空间的使用情况。
解:. 运算结果:4. 完成下列操作:(1) 求[100,999]之间能被21整除的数的个数。
(2) 建立一个字符串向量,删除其中的大写字母。
解:(1) 结果:(2). 建立一个字符串向量例如:ch='ABC123d4e56Fg9';则要求结果是:实验二 MATLAB 矩阵分析与处理1. 设有分块矩阵33322322E R A O S ⨯⨯⨯⨯⎡⎤=⎢⎥⎣⎦,其中E 、R 、O 、S 分别为单位矩阵、随机矩阵、零矩阵和对角阵,试通过数值计算验证22E R RS A O S +⎡⎤=⎢⎥⎣⎦。
MATLAB)课后实验答案[1]
![MATLAB)课后实验答案[1]](https://img.taocdn.com/s3/m/adaedec65727a5e9846a61d9.png)
实验一 MATLAB 运算基础1。
先求下列表达式的值,然后显示MATLAB 工作空间的使用情况并保存全部变量。
(1) 0122sin 851z e =+(2) 21ln(2z x =,其中2120.455i x +⎡⎤=⎢⎥-⎣⎦ (3) 0.30.330.3sin(0.3)ln , 3.0, 2.9,,2.9,3.022a a e e az a a --+=++=--(4) 2242011122123t t z t t t t t ⎧≤<⎪=-≤<⎨⎪-+≤<⎩,其中t =0:0.5:2.5 解:4. 完成下列操作:(1)求[100,999]之间能被21整除的数的个数. (2) 建立一个字符串向量,删除其中的大写字母。
解:(1) 结果:(2)。
建立一个字符串向量例如:ch=’ABC123d4e56Fg9';则要求结果是:实验二 MATLAB 矩阵分析与处理1. 设有分块矩阵33322322E R A O S ⨯⨯⨯⨯⎡⎤=⎢⎥⎣⎦,其中E 、R 、O 、S 分别为单位矩阵、随机矩阵、零矩阵和对角阵,试通过数值计算验证22E R RS A OS +⎡⎤=⎢⎥⎣⎦。
解: M 文件如下;5。
下面是一个线性方程组:1231112340.951110.673450.52111456x x x ⎡⎤⎢⎥⎡⎤⎡⎤⎢⎥⎢⎥⎢⎥⎢⎥=⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎣⎦⎣⎦⎢⎥⎢⎥⎣⎦ch =123d4e56g9(1) 求方程的解。
(2) 将方程右边向量元素b 3改为0。
53再求解,并比较b 3的变化和解的相对变化。
(3) 计算系数矩阵A 的条件数并分析结论。
解: M 文件如下:实验三 选择结构程序设计1. 求分段函数的值.2226035605231x x x x y x x x x x x x ⎧+-<≠-⎪=-+≤<≠≠⎨⎪--⎩且且及其他用if 语句实现,分别输出x=-5.0,—3.0,1.0,2。
2021年MATLAB)课后实验答案[1]
![2021年MATLAB)课后实验答案[1]](https://img.taocdn.com/s3/m/04d862d3eff9aef8951e06c1.png)
实验一 MATLAB运算基础欧阳光明(2021.03.07)1. 先求下列表达式的值,然后显示MATLAB工作空间的使用情况并保存全部变量。
(1)0 122sin851ze =+(2)21ln( 2z x=+,其中2120.455i x+⎡⎤=⎢⎥-⎣⎦(3)0.30.330.3sin(0.3)ln, 3.0, 2.9,,2.9,3.0 22a ae e az a a--+=++=--(4)2242011122123t tz t tt t t⎧≤<⎪=-≤<⎨⎪-+≤<⎩,其中t=0:0.5:2.5解:4. 完成下列操作:(1) 求[100,999]之间能被21整除的数的个数。
(2) 建立一个字符串向量,删除其中的大写字母。
解:(1) 结果:(2). 建立一个字符串向量 例如:ch='ABC123d4e56Fg9';则要求结果是:实验二 MATLAB 矩阵分析与处理1. 设有分块矩阵33322322E R A O S ⨯⨯⨯⨯⎡⎤=⎢⎥⎣⎦,其中E 、R 、O 、S 分别为单位矩阵、随机矩阵、零矩阵和对角阵,试通过数值计算验证22E R RS A O S +⎡⎤=⎢⎥⎣⎦。
解: M 文件如下;5. 下面是一个线性方程组:(1) 求方程的解。
(2) 将方程右边向量元素b 3改为0.53再求解,并比较b 3的变化和解的相对变化。
(3) 计算系数矩阵A 的条件数并分析结论。
解: M文件如下:实验三选择结构程序设计1. 求分段函数的值。
用if语句实现,分别输出x=-5.0,-3.0,1.0,2.0,2.5,3.0,5.0时的y值。
解:M文件如下:2. 输入一个百分制成绩,要求输出成绩等级A、B、C、D、E。
其中90分~100分为A,80分~89分为B,79分~79分为C,60分~69分为D,60分以下为E。
要求:(1) 分别用if语句和switch语句实现。
(2) 输入百分制成绩后要判断该成绩的合理性,对不合理的成绩应输出出错信息。
MATLAB程序设计及应用(第二版)课后实验答案

Matlab课后实验题答案实验一 MATLAB运算基础1. 先求下列表达式的值,然后显示MATLAB工作空间的使用情况并保存全部变量。
(1)0 122sin851ze =+(2)21ln( 2z x=+,其中2120.455i x+⎡⎤=⎢⎥-⎣⎦(3)0.30.330.3sin(0.3)ln, 3.0, 2.9,,2.9,3.0 22a ae e az a a--+=++=--(4)2242011122123t tz t tt t t⎧≤<⎪=-≤<⎨⎪-+≤<⎩,其中t=0:0.5:2.52. 已知:1234413134787,2033657327A B --⎡⎤⎡⎤⎢⎥⎢⎥==⎢⎥⎢⎥⎢⎥⎢⎥-⎣⎦⎣⎦求下列表达式的值:(1) A+6*B 和A-B+I (其中I 为单位矩阵) (2) A*B 和A.*B (3) A^3和A.^3 (4) A/B 及B\A(5) [A,B]和[A([1,3],:);B^2] 解:3. 设有矩阵A 和B123453166789101769,111213141502341617181920970212223242541311A B ⎡⎤⎡⎤⎢⎥⎢⎥-⎢⎥⎢⎥⎢⎥⎢⎥==-⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎣⎦⎣⎦(1) 求它们的乘积C 。
(2) 将矩阵C 的右下角3×2子矩阵赋给D 。
(3) 查看MATLAB 工作空间的使用情况。
4. 完成下列操作:(1) 求[100,999]之间能被21整除的数的个数。
(2) 建立一个字符串向量,删除其中的大写字母。
解:(1) 结果:(2). 建立一个字符串向量 例如:ch='ABC123d4e56Fg9';则要求结果是:实验二 MATLAB 矩阵分析与处理1. 设有分块矩阵33322322E R A O S ⨯⨯⨯⨯⎡⎤=⎢⎥⎣⎦,其中E 、R 、O 、S 分别为单位矩阵、随机矩阵、零矩阵和对角阵,试通过数值计算验证22E R RS A OS +⎡⎤=⎢⎥⎣⎦。
MATLAB)课后实验答案

实验一 MATLAB 运算基础1、 先求下列表达式得值,然后显示MATLAB 工作空间得使用情况并保存全部变量。
(1) 0122sin 851z e =+(2) 21ln(2z x =+,其中2120.455i x +⎡⎤=⎢⎥-⎣⎦ (3) 0.30.330.3sin(0.3)ln , 3.0, 2.9,,2.9,3.022a a e e a z a a --+=++=--L (4) 2242011122123t t z t t t t t ⎧≤<⎪=-≤<⎨⎪-+≤<⎩,其中t =0:0、5:2、5 解:4、 完成下列操作:(1) 求[100,999]之间能被21整除得数得个数。
(2) 建立一个字符串向量,删除其中得大写字母。
解:(1) 结果:(2)、 建立一个字符串向量 例如:ch='ABC123d4e56Fg9';则要求结果就是:实验二 MATLAB 矩阵分析与处理1、 设有分块矩阵33322322E R A O S ⨯⨯⨯⨯⎡⎤=⎢⎥⎣⎦,其中E 、R 、O 、S 分别为单位矩阵、随机矩阵、零矩阵与对角阵,试通过数值计算验证22E R RS A OS +⎡⎤=⎢⎥⎣⎦。
解: M 文件如下;5、 下面就是一个线性方程组:1231112340.951110.673450.52111456x x x ⎡⎤⎢⎥⎡⎤⎡⎤⎢⎥⎢⎥⎢⎥⎢⎥=⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎣⎦⎣⎦⎢⎥⎢⎥⎣⎦(1) 求方程得解。
(2) 将方程右边向量元素b 3改为0、53再求解,并比较b 3得变化与解得相对变化。
(3) 计算系数矩阵A 得条件数并分析结论。
解: M 文件如下:实验三 选择结构程序设计1、 求分段函数得值。
2226035605231x x x x y x x x x x x x ⎧+-<≠-⎪=-+≤<≠≠⎨⎪--⎩且且及其他用if 语句实现,分别输出x=-5、0,-3、0,1、0,2、0,2、5,3、0,5、0时得y 值。
matlab简单编程21个题目及答案

1、设⎥⎦⎤⎢⎣⎡++=)1(sin35.0cos2xxxy,把x=0~2π间分为101点,画出以x为横坐标,y为纵坐标的曲线。
第一题的matlab源程序:①考虑cos(x)为一个整体,然后乘以中括号里面的全部x=0:2*pi/100:2*pi; %x的步长以及范围从0到2*pi y=cos(x).*(0.5+3*sin(x)./(1+x.^2)); %y的表达式plot(x,y)%画出图形图如下:②考虑对整体求解cos,先求x乘以括号中的部分x=0:2*pi/100:2*pi; %x的步长以及范围从0到2*pi y=cos(x.*(0.5+3*sin(x)./(1+x.^2))); %y的表达式plot(x,y) %画出图形图如下:2、产生8×6阶的正态分布随机数矩阵R1, 求其各列的平均值和均方差。
并求该矩阵全体数的平均值和均方差。
第二题的matlab源程序如下:R1=randn(8,6) %产生正态分布随机矩阵R1 =1.0933 -0.7697 1.5442 -0.1924 1.4193 0.21571.1093 0.3714 0.0859 0.8886 0.2916 -1.1658-0.8637 -0.2256 -1.4916 -0.7648 0.1978 -1.14800.0774 1.1174 -0.7423 -1.4023 1.5877 0.1049-1.2141 -1.0891 -1.0616 -1.4224 -0.8045 0.7223-1.1135 0.0326 2.3505 0.4882 0.6966 2.5855-0.0068 0.5525 -0.6156 -0.1774 0.8351 -0.66691.5326 1.1006 0.7481 -0.1961 -0.2437 0.1873aver=(sum(R1(1:end,1:end)))./8 %产生各行的平均值aver =0.0768 0.1363 0.1022 -0.3473 0.4975 0.1044a=std(R1(1:end,1:end)) %产生各行的均方差也就是标准差a =1.0819 0.8093 1.3456 0.8233 0.8079 1.2150aver1=(sum(R1(:)))./48 %全体数的平均值aver1 =0.0950b=std(R1(:)) %全体数的均方差即标准差b =1.01033、设x=rcost+3t,y=rsint+3,分别令r=2,3,4,画出参数t=0~10区间生成的x~y 曲线。
matlab字符串函数

matlab字符串函数MATLAB 是一款广泛应用于科学计算、算法开发、数据分析和可视化的强大软件。
字符串处理是 MATLAB 中常见的任务之一。
本文将详细介绍 MATLAB 中常用的字符串函数,并提供基本示例。
1.字符串基本操作字符串是一组字符的序列,在 MATLAB 中可以使用单引号或双引号来创建字符串。
例如:```str1 = 'hello, world';str2 = "hello, world";```MATLAB 中的字符串可以使用各种运算符进行操作,比如连接字符串、重复字符串、删除字符串等。
以下是一些常见的字符串操作:- 连接字符串:使用加号运算符可以将两个字符串合并为一个字符串。
例如:```str1 = 'hello';str2 = 'world';str3 = str1 + " " + str2;% str3 = 'hello world'```- 复制字符串:使用乘法运算符可以将一个字符串重复多次。
例如:```str1 = 'hello';str2 = str1 * 3;% str2 = 'hellohellohello'- 删除字符串:使用 delete 函数可以删除一个字符串的一部分。
例如:```str1 = 'hello, world';str2 = delete(str1, 6:11);% str2 = 'hello'```2.字符串查找和替换在处理字符串时,通常需要查找一个子串或将一个子串替换为另一个字符串。
MATLAB 提供了一些函数来完成这些任务。
- 查找子串:使用 findstr 函数可以查找一个子串在另一个字符串中的位置。
例如:```str1 = 'hello, world';pos = findstr(str1, 'world');% pos = 8```- 替换子串:使用 strrep 函数可以将一个字符串中的所有出现的一个子串替换为另一个字符串。
(完整版)MATLAB)课后实验答案[1]
![(完整版)MATLAB)课后实验答案[1]](https://img.taocdn.com/s3/m/f6c08c5902d276a201292ece.png)
1 + e2 (2) z = 1 ln( x + 1 + x 2 ) ,其中 x = ⎡⎢ 2⎣-0.45 ⎦2 2 ⎪t 2 - 2t + 1 2 ≤ t <3 ⎨实验一MATLAB 运算基础1. 先求下列表达式的值,然后显示 MATLAB 工作空间的使用情况并保存全部变量。
(1) z = 2sin 8501221 + 2i ⎤5 ⎥(3) z = e 0.3a - e -0.3asin(a + 0.3) + ln 0.3 + a ,a = -3.0, - 2.9, L , 2.9, 3.03⎧t 2 0 ≤ t < 1 (4) z = ⎪t 2 - 11 ≤ t <2 ,其中 t=0:0.5:2.5 4⎩解:M 文件:z1=2*sin(85*pi/180)/(1+exp(2))x=[2 1+2*i;-.45 5];z2=1/2*log(x+sqrt(1+x^2))a=-3.0:0.1:3.0;3=(exp(0.3.*a)-exp(-0.3.*a))./2.*sin(a+0.3)+log((0.3+a)./2)t=0:0.5:2.5;z4=(t>=0&t<1).*(t.^2)+(t>=1&t<2).*(t.^2-1)+(t>=2&t<3) .*(t.^2-2*t+1)4.完成下列操作:(1)求[100,999]之间能被21整除的数的个数。
(2)建立一个字符串向量,删除其中的大写字母。
解:(1)结果:m=100:999;n=find(mod(m,21)==0);length(n)ans=43(2).建立一个字符串向量例如:ch='ABC123d4e56Fg9';则要求结果是:ch='ABC123d4e56Fg9';k=find(ch>='A'&ch<='Z');ch(k)=[]ch=⎣O2⨯3⎥,其中E、R、O、S分别为单位矩阵、随机矩阵、零矩S⎦阵和对角阵,试通过数值计算验证A=⎢⎥。
《MATLAB仿真技术》实验指导书2016附问题详解

实验项目及学时安排实验一 MATLAB环境的熟悉与基本运算 2学时实验二 MATLAB数值计算实验 2学时实验三 MATLAB数组应用实验 2学时实验四 MATLAB符号计算实验 2学时实验五 MATLAB的图形绘制实验 2学时实验六 MATLAB的程序设计实验 2学时实验七 MATLAB工具箱Simulink的应用实验 2学时实验八 MATLAB图形用户接口GUI的应用实验 2学时实验一 MATLAB环境的熟悉与基本运算一、实验目的1.熟悉MATLAB开发环境2.掌握矩阵、变量、表达式的各种基本运算二、实验基本知识1.熟悉MATLAB环境:MATLAB桌面和命令窗口、命令历史窗口、帮助信息浏览器、工作空间浏览器、文件和搜索路径浏览器。
2.掌握MATLAB常用命令3.MATLAB变量与运算符变量命名规则如下:(1)变量名可以由英语字母、数字和下划线组成(2)变量名应以英文字母开头(3)长度不大于31个(4)区分大小写MATLAB中设置了一些特殊的变量与常量,列于下表。
MATLAB运算符,通过下面几个表来说明MATLAB的各种常用运算符4.MATLAB的一维、二维数组的寻访表6 子数组访问与赋值常用的相关指令格式5.MATLAB的基本运算表7 两种运算指令形式和实质涵的异同表6.MATLAB的常用函数表8 标准数组生成函数表9 数组操作函数三、实验容1、学习使用help命令,例如在命令窗口输入help eye,然后根据帮助说明,学习使用指令eye(其它不会用的指令,依照此方法类推)2、学习使用clc、clear,观察command window、command history和workspace等窗口的变化结果。
3、初步程序的编写练习,新建M-file,保存(自己设定文件名,例如exerc1、exerc2、 exerc3……),学习使用MATLAB的基本运算符、数组寻访指令、标准数组生成函数和数组操作函数。
MATLAB)课后实验答案[1](最新整理)
](https://img.taocdn.com/s3/m/2bd1298ccf84b9d529ea7a94.png)
5. 下面是一个线性方程组:
1112340.95x ⎡⎤⎢⎥⎡⎤⎡⎤⎢⎥
实验三 选择结构程序设计
1. 求分段函数的值。
222603560523
1x x x x y x x x x x x x ⎧+-<≠-⎪=-+≤<≠≠⎨⎪--⎩
且且及其他用if 语句实现,分别输出x=-5.0,-3.0,1.0,2.0,2.5,3.0,5.0时的y 值。
解:M 文件如下:
2. 输入一个百分制成绩,要求输出成绩等级A、B、C、D、E。
其中90分~100分为A,80分~89分为B,79分~79分为C,60分~69分为D,60分以下为E。
要求:
(1) 分别用if语句和switch语句实现。
(2) 输入百分制成绩后要判断该成绩的合理性,对不合理的成绩应输出出错信息。
解:M文件如下
3. 硅谷公司员工的工资计算方法如下:
(1) 工作时数超过120小时者,超过部分加发15%。
(2) 工作时数低于60小时者,扣发700元。
(3) 其余按每小时84元计发。
试编程按输入的工号和该号员工的工时数,计算应发工资。
解:M文件下
运算结果如下;
5. 若两个连续自然数的乘积减1是素数,则称这两个边疆自然数是亲密数对,该素数是亲密素数。
例如,2×3-1=5,由于5是素数,所以2和3是亲密数,5是亲密素数。
求[2,50]区间内:
(1) 亲密数对的对数。
(2) 与上述亲密数对对应的所有亲密素数之和。
解:
M文件:。
matlab中字符串向量的定义

在Matlab中,字符串向量是一种非常重要且方便的数据类型,可以用于存储和处理文本数据。
在本文中,我将探讨字符串向量的定义、使用和相关知识,以便你能更深入地理解这个主题。
1. 字符串向量的定义在Matlab中,字符串向量可以简单地理解为由字符组成的一维数组。
要定义一个字符串向量,可以使用单引号或双引号将字符括起来,例如:```Matlabstr1 = 'hello';str2 = "world";```以上代码定义了两个字符串向量,分别为'hello'和"world"。
需要注意的是,在Matlab中,单引号和双引号都可以用来定义字符串,但是两者在处理转义字符和特殊字符时略有不同。
2. 字符串向量的基本操作在Matlab中,字符串向量可以进行基本的操作,例如连接、截取和查找等。
你可以使用加号将两个字符串连接起来,也可以使用substr函数对字符串进行截取,例如:```MatlabnewStr = [str1 str2]; % 连接操作substr = str2(1:3); % 截取操作index = strfind(str1, 'l'); % 查找操作```通过以上操作,你可以很方便地对字符串向量进行处理,实现你所需的功能。
3. 字符串向量的高级操作除了基本操作之外,Matlab还提供了丰富的函数和工具,用于对字符串向量进行高级的操作。
你可以使用regexp函数进行正则表达式匹配,使用replace函数进行替换操作,以及使用split函数进行分割操作,例如:```Matlabstr = 'apple,banana,orange';result = split(str, ','); % 分割操作```利用这些高级操作,你可以更加灵活地处理字符串向量,满足各种复杂的需求。
4. 个人观点和总结字符串向量在Matlab中是一个非常有用的数据类型,它可以方便地存储和处理文本数据,而且提供了丰富的操作和函数,供你使用。
Matlab中的字符串处理技巧与常用函数介绍

Matlab中的字符串处理技巧与常用函数介绍引言在科学计算和数据分析领域,字符串处理是一项常见且重要的任务。
字符串处理技巧的熟练使用可以帮助我们更加高效地完成科研工作。
本文将介绍Matlab中一些常用的字符串处理函数及其应用技巧,希望能对读者在日常工作中有所帮助。
一、字符串的基本操作在Matlab中,字符串是一种常用的数据类型,用于表示字符序列。
字符串的基本操作有创建、连接、拆分和替换等。
1. 字符串的创建Matlab中创建字符串的方法很多。
可以使用单引号或双引号将字符序列括起来,也可以使用字符串函数进行创建。
例如:str1 = 'Hello, world!';str2 = "Matlab is powerful!";str3 = string("I love programming!");2. 字符串的连接字符串的连接是指将两个或多个字符串合并为一个新的字符串。
在Matlab中,我们可以使用加号"+"进行字符串的连接操作。
例如:str4 = strcat(str1, " ", str2); % 使用strcat函数连接字符串str5 = str1 + " " + str2; % 使用加号连接字符串3. 字符串的拆分在字符串处理中,有时需要将一个字符串拆分成若干子串。
Matlab提供了split 函数用于字符串的拆分。
示例代码如下:s = "Hello,world,Matlab";str_array = split(s, ','); % 将字符串按逗号拆分为字符串数组4. 字符串的替换字符串的替换是指将一个字符串中的某一部分替换为另一个字符串。
在Matlab 中,我们可以使用replace函数进行字符串的替换操作。
示例代码如下:s = "Hello, world!";new_s = replace(s, "world", "Matlab"); % 将字符串中的"world"替换为"Matlab"二、字符串的查询与匹配除了基本的字符串操作外,我们在处理字符串时还常常需要进行查询与匹配操作。
MATLAB字符串

MATLAB字符串MATLAB真正强有力的地方在于它的数值处理能力。
然而,经常希望操作文本,例如把标号和标题放在图上。
在MATLAB里,文本当作特征字符串或简单地当作字符串。
6.1 字符串在MATLAB中的字符串一般是ASCII值的数值数组,它作为字符串表达式进行显示。
例如,» t=' How about this character string? 't = How about this character string?» size(t)ans = 1 32» whosName Size Elements Bytes Density Complexans 1 by 2 2 16 Full Not 1 by 32 32 256 Full No一个字符串是由单引号括起来的简单文本。
在字符串里的每个字符是数组里的一个元素,字符串的存储要求每个字符8个字节,如同MATLAB的其它变量。
因为ASCII字符只要求一个字节,故这种存储要求是浪费的,7/8所分配的存储空间无用。
然而,对字符串保持同样的数据结构简化MATLAB的内部数据结构。
所给出的字符串操作并不是MATLAB的基本特点,但这种表达是方便和可接受的。
为了了解下面字符串的ASCII表达,只需对字符串执行一些算术运算。
最简单和计算上最有效的方法是取数组的绝对值。
例如,» u=abs(t)u =Columns 1 through 1272 111 119 32 97 98 111 117 116 32 116 104Columns 13 through 24105 115 32 99 104 97 114 97 99 116 101 114Columns 25 through 3232 115 116 114 105 110 103 63» u=t+0u =Columns 1 through 1272 111 119 32 97 98 111 117 116 32 116 104Columns 13 through 24105 115 32 99 104 97 114 97 99 116 101 114Columns 25 through 3232 115 116 114 105 110 103 63在上面后一个例子里,加零到字符串也改变了它的ASCII的表示。
MATLAB第五章 字符串处理

k=
1 1 1 0 0
第七章 字符串处理
实际上,还可以采用其它的关系操作符(<、<=、>、
>=、!=),这样就可以比较两个字符串的大小关系,当然实际 确定其大小关系时采用的是其ASCII码。例如:
>> A='abcd'; B='aabe'; >>k1=A>B k1 = 0 1 1 0 >> k2=A>=B k2 = 1 1 1 0 >> k3=A<B k3 = 0 0 0 1
比较复杂的任务。例如: >> str='Example 12 made on 08/18/05'; >>k=findstr(str,'08') k= 20 >> str1=strrep(str,'18','19') str1 = Example 12 made on 08/19/05 这里将str中的日期修改为2005年08月19日。
r=sentence allwords='';
while(any(r))
[w,r]=strtok(r); allwords=strvcat(allwords,w);
end
第七章 字符串处理 这时输入
>> str1='I wish this book can be benefical to you';
>> let1=isletter(str1);
>> let2=isspace(str1); >> let3=let1| let2; >>if all(let3) disp('所有字符均为英文字母或空格') else disp('字符中包含非英文字母和空格')
Matlab编程与应用习题和一些参考答案

Matlab 上机实验一、二1.安装Matlab 软件。
2.验证所学内容和教材上的例子。
3.求下列联立方程的解⎪⎪⎩⎪⎪⎨⎧=+-+-=-+=++-=--+41025695842475412743w z y x w z x w z y x w z y x>> a=[3 4 -7 -12;5 -7 4 2;1 0 8 -5;-6 5 -2 10];>> b=[4;4;9;4];>> c=a\bc =5.22264.45701.47181.59944.设⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡------=81272956313841A ,⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡-----=793183262345B ,求C1=A*B’;C2=A’*B;C3=A.*B,并求上述所有方阵的逆阵。
>> A=[1 4 8 13;-3 6 -5 -9;2 -7 -12 -8];>> B=[5 4 3 -2;6 -2 3 -8;-1 3 -9 7];>> C1=A*B'C1 =19 -82 3012 27 3-38 54 29>> C2=A'*BC2 =-15 16 -24 3663 -17 93 -10522 6 117 -6019 46 84 -10>> C3=A.*BC3 =5 16 24 -26-18 -12 -15 72-2 -21 108 -56>> inv(C1)ans =0.0062 0.0400 -0.0106-0.0046 0.0169 0.00300.0168 0.0209 0.0150>> inv(C2)Warning: Matrix is close to singular or badly scaled.Results may be inaccurate. RCOND = 8.e-019.ans =1.0e+015 *-0.9553 -0.2391 -0.1997 0.27000.9667 0.2420 0.2021 -0.2732-0.4473 -0.1120 -0.0935 0.1264-1.1259 -0.2818 -0.2353 0.3182>> inv(C3)??? Error using ==> invMatrix must be square.5.设 ⎥⎦⎤⎢⎣⎡++=)1(sin 35.0cos 2x x x y ,把x=0~2π间分为101点,画出以x 为横坐标,y 为纵坐标的曲线。
