常见校验算法
各种校验码校验算法分析

各种校验码校验算法分析二进制数据经过传送、存取等环节会发生误码1变成0或0变成1这就有如何发现及纠正误码的问题。
所有解决此类问题的方法就是在原始数据数码位基础上增加几位校验冗余位。
一、码距一个编码系统中任意两个合法编码码字之间不同的二进数位bit数叫这两个码字的码距而整个编码系统中任意两个码字的的最小距离就是该编码系统的码距。
如图1所示的一个编码系统用三个bit来表示八个不同信息中。
在这个系统中两个码字之间不同的bit数从1到3不等但最小值为1故这个系统的码距为1。
如果任何码字中一位或多位被颠倒了结果这个码字就不能与其它有效信息区分开。
例如如果传送信息001而被误收为011因011仍是表中的合法码字接收机仍将认为011是正确的信息。
然而如果用四个二进数字来编8个码字那么在码字间的最小距离可以增加到2如图2的表中所示。
信息序号二进码字 a2 a1 a0 0 0 0 0 1 0 0 1 2 0 1 0 3 0 1 1 4 1 0 0 5 1 0 1 6 1 1 0 7 1 1 1 图 1 信息序号二进码字 a3 a2 a1 a0 0 0 0 0 0 1 1 0 0 1 2 1 0 1 0 3 0 0 1 1 4 1 1 0 0 5 0 1 0 1 6 0 1 1 0 7 1 1 1 1 图 2 注意图8-2的8个码字相互间最少有两bit 的差异。
因此如果任何信息的一个数位被颠倒就成为一个不用的码字接收机能检查出来。
例如信息是1001误收为1011接收机知道发生了一个差错因为1011不是一个码字表中没有。
然而差错不能被纠正。
假定只有一个数位是错的正确码字可以是100111110011或1010。
接收者不能确定原来到底是这4个码字中的那一个。
也可看到在这个系统中偶数个2或4差错也无法发现。
为了使一个系统能检查和纠正一个差错码间最小距离必须至少是“3”。
最小距离为3时或能纠正一个错或能检二个错但不能同时纠一个错和检二个错。
密码校验的一些规则

密码校验的一些规则摘要:1.密码校验的必要性2.密码校验的基本规则3.常见的密码校验算法4.密码校验的实际应用5.密码校验的未来发展趋势正文:在数字化时代,信息安全成为了人们日益关注的问题。
为了保护个人信息和财产安全,密码成为了最常见的一种身份验证方式。
然而,简单的密码容易被破解,因此密码校验应运而生,它可以有效提高密码的安全性。
密码校验的基本规则包括:密码长度、字符种类、大小写组合等。
一般来说,密码越长、字符种类越多,密码的强度就越高。
为了提高密码的安全性,许多网站和应用会要求用户设置包含数字、字母和特殊符号的复杂密码。
常见的密码校验算法有:MD5、SHA-1、SHA-256 等。
这些算法通过对密码进行哈希运算,将原始密码转换成固定长度的摘要,从而实现对密码的快速校验。
然而,随着计算机技术的发展,这些算法逐渐暴露出安全性不足的问题,比如被暴力破解等。
因此,更为安全的密码校验算法也在不断涌现,如bcrypt、scrypt 等。
密码校验在现实生活中的应用非常广泛,例如:网上银行、电子邮件、社交媒体等。
这些应用通常会对用户密码进行加密存储,以保护用户信息的安全。
当用户登录时,网站会通过密码校验算法对用户输入的密码进行验证,只有校验通过,用户才能成功登录。
随着人工智能、量子计算等技术的发展,密码校验面临着越来越严峻的挑战。
为了应对这些挑战,密码学研究者正在不断探索新的密码校验技术和方法,如密码哈希函数、代理重加密等。
可以预见,未来密码校验技术将会更加复杂和安全。
总之,密码校验作为保障信息安全的重要手段,已经深入到我们日常生活的方方面面。
crc32算法与示例

crc32算法与示例CRC32算法是一种常用的校验算法,它可以用来验证数据的完整性。
本文将介绍CRC32算法的原理和示例,帮助读者理解并应用这一算法。
一、CRC32算法概述CRC32算法是循环冗余校验(Cyclic Redundancy Check)的一种变种。
它通过对数据进行多项式除法运算,得到一个32位的校验值。
这个校验值可以用来验证数据在传输或存储过程中是否发生了错误。
二、CRC32算法原理CRC32算法的核心思想是将数据看成一个二进制数,然后通过除法运算得到校验值。
具体步骤如下:1.选择一个32位的生成多项式,通常取0x04C11DB7。
2.将数据看成一个二进制数,按照最高位在前的顺序排列。
3.在数据的最高位补32个0,得到一个新的二进制数。
4.用生成多项式除以这个新的二进制数,得到余数。
5.将余数作为校验值。
三、CRC32算法示例为了更好地理解CRC32算法,下面举一个简单的示例。
假设我们要发送一个包含4个字节的数据:0x01 0x02 0x03 0x04。
1.我们首先选择生成多项式0x04C11DB7。
2.将数据看成一个二进制数,按照最高位在前的顺序排列得到:00000001 00000010 00000011 00000100。
3.在数据的最高位补32个0,得到一个新的二进制数:00000000 00000000 00000000 00000001 00000000 00000010 00000011 00000100。
4.用生成多项式0x04C11DB7除以这个新的二进制数,得到余数为0x0C9F 0x9C3B。
5.将余数0x0C9F 0x9C3B作为校验值。
因此,经过CRC32算法计算,数据0x01 0x02 0x03 0x04的校验值为0x0C9F 0x9C3B。
四、CRC32算法应用举例CRC32算法广泛应用于数据传输和存储的过程中,用于验证数据的完整性。
例如,在网络传输中,发送方可以通过计算数据的CRC32值,将其附加在数据后面一起发送。
各种校验码校验算法分析

各种校验码校验算法分析二进制数据经过传送、存取等环节会发生误码1变成0或0变成1这就有如何发现及纠正误码的问题。
所有解决此类问题的方法就是在原始数据数码位基础上增加几位校验冗余位。
一、码距一个编码系统中任意两个合法编码码字之间不同的二进数位bit数叫这两个码字的码距而整个编码系统中任意两个码字的的最小距离就是该编码系统的码距。
如图1所示的一个编码系统用三个bit来表示八个不同信息中。
在这个系统中两个码字之间不同的bit数从1到3不等但最小值为1故这个系统的码距为1。
如果任何码字中一位或多位被颠倒了结果这个码字就不能与其它有效信息区分开。
例如如果传送信息001而被误收为011因011仍是表中的合法码字接收机仍将认为011是正确的信息。
然而如果用四个二进数字来编8个码字那么在码字间的最小距离可以增加到2如图2的表中所示。
信息序号二进码字 a2 a1 a0 0 0 0 0 1 0 0 1 2 0 1 0 3 0 1 1 4 1 0 0 5 1 0 1 6 1 1 0 7 1 1 1 图 1 信息序号二进码字 a3 a2 a1 a0 0 0 0 0 0 1 1 0 0 1 2 1 0 1 0 3 0 0 1 1 4 1 1 0 0 5 0 1 0 1 6 0 1 1 0 7 1 1 1 1 图 2 注意图8-2的8个码字相互间最少有两bit 的差异。
因此如果任何信息的一个数位被颠倒就成为一个不用的码字接收机能检查出来。
例如信息是1001误收为1011接收机知道发生了一个差错因为1011不是一个码字表中没有。
然而差错不能被纠正。
假定只有一个数位是错的正确码字可以是100111110011或1010。
接收者不能确定原来到底是这4个码字中的那一个。
也可看到在这个系统中偶数个2或4差错也无法发现。
为了使一个系统能检查和纠正一个差错码间最小距离必须至少是“3”。
最小距离为3时或能纠正一个错或能检二个错但不能同时纠一个错和检二个错。
数字校验算法

数字校验算法数字校验算法是一种用于验证数据完整性和准确性的数学算法。
它通过对数据进行计算和比较,确定数据是否被篡改或损坏。
数字校验算法广泛应用于计算机网络、数据传输以及存储系统等领域,保证数据的可靠性和安全性。
本文将介绍几种常见的数字校验算法及其原理。
一、奇偶校验算法奇偶校验算法是最简单的数字校验算法之一。
它通过在数据位中添加一个奇偶位来确保数据的正确性。
具体操作是在数据中添加一个位,使得数据位和奇偶位的总位数为奇数或偶数。
接收端通过计算数据位和奇偶位的总位数是否为奇数或偶数来判断数据是否正确。
如果总位数不匹配,则说明数据传输中发生了错误。
二、循环冗余校验算法循环冗余校验算法(CRC)是一种常用的数字校验算法。
它通过对数据进行多项式的除法运算来生成校验码。
发送端首先将数据和生成多项式进行除法运算,得到余数作为校验码,然后将数据和校验码一起发送。
接收端将接收到的数据和生成多项式进行除法运算,如果余数为0,则说明数据传输正确;如果余数不为0,则说明数据传输错误。
三、哈希校验算法哈希校验算法是一种基于哈希函数的数字校验算法。
它通过对数据进行哈希运算,得到一个固定长度的校验值。
发送端将数据和校验值一起发送,接收端对接收到的数据进行相同的哈希运算,并将得到的校验值与接收到的校验值进行比较。
如果两者相同,则说明数据传输正确;如果不同,则说明数据传输错误。
四、消息认证码算法消息认证码算法(MAC)是一种常用的数字校验算法。
它通过对数据进行加密和认证来确保数据的完整性和真实性。
发送端使用密钥对数据进行加密和认证,并将加密后的数据和认证标签一起发送。
接收端使用相同的密钥对接收到的数据进行解密和认证,并将得到的认证标签与接收到的认证标签进行比较。
如果两者相同,则说明数据传输正确;如果不同,则说明数据传输错误。
五、数字签名算法数字签名算法是一种常用的数字校验算法。
它通过使用私钥对数据进行加密和签名,确保数据的完整性、真实性和不可抵赖性。
CRC常见算法的C语言实现

CRC常见算法的C语言实现CRC(Cyclic Redundancy Check)是一种常见的数据校验算法,用于检测或校正以循环方式传输的数据中的错误。
CRC算法在通信、存储、校验等领域得到广泛应用。
以下是CRC常见算法的C语言实现示例。
1.CRC-8校验算法:```// CRC-8 polynomial: x^8+x^2+x+1 (0x07)unsigned char crc8(const unsigned char *data, unsigned int length)unsigned char crc = 0;for (unsigned int i = 0; i < length; i++)crc ^= data[i];for (unsigned int j = 0; j < 8; j++)if (crc & 0x80)crc = (crc << 1) ^ 0x07;elsecrc <<= 1;}}return crc;```2.CRC-16校验算法:```// CRC-16 polynomial: x^16+x^15+x^2+1 (0x8005)unsigned short crc16(const unsigned char *data, unsigned int length)unsigned short crc = 0;for (unsigned int i = 0; i < length; i++)crc ^= (unsigned short)data[i] << 8;for (unsigned int j = 0; j < 8; j++)if (crc & 0x8000)crc = (crc << 1) ^ 0x8005;elsecrc <<= 1;}}return crc;```3.CRC-32校验算法:```// CRC-32 polynomial: 0x04c11db7unsigned int crc32(const unsigned char *data, unsigned int length)unsigned int crc = 0xFFFFFFFF;for (unsigned int i = 0; i < length; i++)crc ^= data[i];for (unsigned int j = 0; j < 8; j++)if (crc & 1)elsecrc >>= 1;}}return ~crc;```以上是常见的CRC校验算法的C语言实现示例。
各种校验码校验算法分析

各种校验码校验算法分析校验码校验算法是一种用于数据传输或存储中验证数据完整性和准确性的技术,它能够检测出数据在传输或存储过程中是否发生了错误或损坏,从而确保数据的可靠性。
在实际应用中,校验码校验算法广泛应用于通信、网络传输、存储和数据处理等领域,其设计和选择对数据可靠性和安全性至关重要。
常见的校验码校验算法包括奇偶校验码、循环冗余校验码(CRC)、校验和、哈希校验码等。
下面将对这几种常见的校验码校验算法进行详细分析:1.奇偶校验码:奇偶校验码是最简单的一种校验码校验算法,它通过检测数据中的奇偶位来判断数据是否正确。
在奇偶校验中,通常规定数据中的位数为偶数个或奇数个,如果数据中出现奇数个1,则在校验位中加上1,使总的1的数量为偶数;如果数据中出现偶数个1,则在校验位中加上0,使总的1的数量仍为偶数。
在数据传输或存储中,接收方会通过比较校验位和数据位的和是否为偶数来判断数据的正确性。
奇偶校验码虽然简单易实现,但只能检测出奇数个错误位(例如一个错误的位),并不能检测出多个错误位或连续错误的情况。
因此,奇偶校验码一般用于对数据传输的基本错误进行检测。
2.循环冗余校验码(CRC):CRC是一种基于多项式除法的校验码校验算法,它通过对数据进行特定的多项式运算来计算出校验码。
接收方在收到数据后,也会对数据进行相同的多项式运算,然后比较计算出的校验码与发送方发送的校验码是否一致,从而判断数据是否正确。
CRC校验码具有较高的检错能力和容错率,能够有效地检测出多个位错误和定位错误的位置,因此广泛应用于计算机网络传输、磁盘存储、通信协议等领域。
3.校验和:校验和是一种简单的校验码校验算法,它通过对数据中所有位进行求和操作来计算出校验码。
接收方在接收到数据后,也会对数据进行相同的求和操作,然后比较计算出的校验和与发送方发送的校验和是否一致,从而判断数据是否正确。
校验和算法比较简单,计算速度较快,但只能检测出简单的错误情况,对于复杂的错误或多位错误检测能力有限。
三种常用的CRC16校验算法的C51程序的优化

}
ptr++;
count--;
}
return crc.x;
}
编译后函数crc2的代码长度为76,函数crc3的代码长度为68,变化不是太大,但是执行效率是很不一样的,具体差别见后面的表一。
优化后的查表+计算法的程序为:
unsigned int crc5(unsigned char *ptr,unsigned char len)
crc.x <<=4;
crc.c[0] ^=crch[t];
crc.c[1] ^=crcl[t];
t = (crc.c[0]>>4) ^ (*ptr & 0x0F);
crc.x <<=4;
crc.c[0] ^=crch[t];
crc ^= crc_ta[da^(*ptr/16)]; /* CRC的高4位和本字节的前半字节相加后查表*/
/*计算CRC,然后加上上一次CRC的余数 */
da = ((crc/256))/16; /* 暂存CRC的高4位 */
crc <<=4; /* CRC右移4位, 相当于CRC的低12位) */
unsigned int crc3(unsigned char *ptr,unsigned char count)
{
data unsigned char i;
union{
unsigned char c[2];
unsigned int x;
}data crc;
pData++;
}
return CRC16;
}
编译后,函数crc0的代码为68字节,加上表格占用的512字节,一共使用了580个字节的代码空间。
信息校验算法

信息校验算法
信息校验算法是一种用于检测数据完整性和准确性的技术。
常见的校验算法包括:
1. Checksum:一种简单的校验算法,通过将数据中的每个字节相加,然后取结果的最低有效字节,来检测数据是否在传输过程中发生了变化。
2. 奇偶校验:通过在数据中添加一个额外的位,使得整个数据(包括校验位)中的1的个数是偶数(偶校验)或奇数(奇校验)。
如果数据中的任何位发生变化,奇偶校验位的值也会发生变化,从而检测出错误。
3. 海明码校验:一种线性分组码,用于检测数据中的错误。
它将数据分成多个部分,并为每一部分添加冗余信息。
通过使用多个校验公式,海明码可以在多个位置检测到错误。
4. 循环冗余校验(CRC):一种用于检测错误的技术,它通过将数据视为多项式并计算其系数,然后添加一个额外的多项式作为校验码。
接收方使用相同的算法重新计算校验码,并与发送方的校验码进行比较。
如果两者匹配,则数据被认为是正确的;否则,数据被认为是有错误的。
5. 哈希算法:一种将任意大小的数据映射为固定大小散列值的算法。
常见的哈希算法包括MD系列和SHA系列。
哈希算法常用于验证数据的完整性和一致性,因为相同的输入总是产生相同的输出。
这些校验算法在不同的应用场景中都有其优势和局限性。
选择哪种算法取决于数据的性质、所需的错误检测能力以及计算和存储资源等因素。
三种常用的CRC16校验算法的C51程序的优化

};
union{
unsigned char c[2];
unsigned int x;
}data crc;
unsigned char t;
crc.x =0;
while(len!=0) {
t = (crc.c[0]>>4) ^ (*ptr >>4);
crc.c[1] ^=crcl[t];
ptr++;
len--;
}
return crc.x;
}
优化前后的代码长度分别为1ห้องสมุดไป่ตู้5字节和146字节(包括了32字节的表格空间)。
代码测试:仅代码长度变短是不够的,衡量优化后的程序一个重要的标准是看优化前后两个函数执行相同的计算量使用的时间,或者说执行的效率是否提高了。如果优化后的函数需要时间少,就说明我们优化后的函数确实提高了效率,否则就是反而降低了程序的效率,优化失败。我在 Keil C51 下编写了一个测试程序,在程序中调用了上面的六个函数,共同计算一个长度为200字节的CRC校验,并记录下每个函数使用的时间。测试方法为:使用 Keil C51 的软件仿真功能(采用带计时功能的硬件仿真器也可以),在每个函数上加上断点,记录下执行到每个断点的时间,然后前后相减就得出每个函数的执行时间。仿真时使用的单片机型号为AT89C51,晶体频率为12MHz。
三种常用的CRC16校验算法的C51程序的优化
CRC校验又称为循环冗余校验,是数据通讯中常用的一种校验算法。它可以有效的判别出数据在传输过程中是否发生了错误,从而保障了传输的数据可靠性。
CRC校验有多种方式,如:CRC8、CRC16、CRC32等等。在实际使用中,我们经常使用CRC16校验。CRC16校验也有多种,如:1005多项式、1021多项式(CRC-ITU)等。在这里我们不讨论CRC算法是怎样产生的,而是重点落在几种算法的C51程序的优化上。
计算机中的校验码

计算机中的校验码计算机中的校验码(Checksum)是一种用来验证数据完整性的方法。
在计算机通信和数据传输领域,校验码被广泛应用,可以保证数据的准确性和可靠性。
本文将介绍计算机中常见的几种校验码及其应用。
一、奇偶校验码(Parity Check)奇偶校验码是最基础、最简单的一种校验码。
它根据每个字节中二进制的1的个数来确定最高位是0还是1,从而实现数据的校验。
奇偶校验码主要用于串行数据传输中,通过校验码的比对,接收方可以判断数据是否正确。
奇偶校验码的计算方法是将每个字节中所有位的和模2,得到的余数作为校验位。
当接收方收到数据后,再次计算校验位,与接收到的校验位进行比对,如果两者相等,则数据传输正确;如果不相等,则数据传输错误。
二、循环冗余校验码(Cyclic Redundancy Check)循环冗余校验码是一种更加强大和可靠的校验码。
它利用多项式除法的原理,对数据进行多次运算,最终得到一个校验码。
在数据传输过程中,发送方将数据和对应的校验码一起发送给接收方。
接收方收到数据后,再次进行多项式除法运算,如果计算出的校验码与接收到的校验码相等,则数据传输正确;如果不相等,则数据传输错误。
循环冗余校验码广泛应用于计算机网络中,例如以太网、Wi-Fi、蓝牙等。
它可以快速检测出数据传输过程中发生的错误,并进行纠正或重传。
三、校验和(Checksum)校验和是一种常用的校验码。
它通过对数据进行累加求和,然后将得到的结果添加到数据中,形成一个校验和。
校验和的计算方法可以采用加法或者异或操作。
在传输过程中,发送方计算出校验和并将其附加在数据中一起发送给接收方。
接收方收到数据后,再次计算校验和,将结果与接收到的校验和进行比对。
如果两者相等,则数据传输正确;否则,数据传输错误。
校验和广泛应用于文件校验、数据完整性校验等方面。
与循环冗余校验码相比,校验和的计算速度较快,但其纠错能力相对较差。
四、哈希校验码(Hash Checksum)哈希校验码是一种高级的校验码算法。
常用的通信校验

常用的通信校验通信校验是指在信息传输过程中通过一定的算法对信息进行加密或校验,以确保信息的正确性、完整性和安全性。
通信校验是通信系统中非常重要的一部分,同时也是我们日常生活中经常接触到的一些术语。
下面就来介绍一下常用的通信校验。
1. 奇偶校验在计算机领域中,奇偶校验是最常用的一种校验方式。
它的原理很简单:将字节的值转换为二进制,并计算二进制数中1的个数。
如果1的数量是偶数,则在数据后面添加一个0,使其长度偶数;如果1的数量是奇数,则在数据后面添加一个1,使其长度奇数。
在接收方,再根据数据的奇偶性来检验数据是否正确。
2. CRC校验CRC 校验是一种基于差错多项式的校验方式,它主要用于数据通信和存储中的差错控制。
在发送数据时,发送端会将数据按照预定的CRC计算方式进行计算,并将计算的结果加入数据包的尾部;在接收端,接收方也采用相同的方式进行计算,并将计算出的结果与接收到的数据进行比较,从而确定数据传输的可靠性。
3. 校验和校验校验和校验是一种常见但不是很安全的校验方式,它的原理是在发送数据时,将数据进行加和运算后加入数据包的尾部;在接收方,接收方将接收到的数据进行加和运算,并将计算出的结果与接收到的校验和进行比较,以判断数据传输的可靠性。
虽然校验和校验方式简单,但是在数据长度较长时,校验和容易被伪造,因此不适用于对数据的安全性要求较高的场合。
4. MD5校验MD5(Message Digest Algorithm 5)是一种常用的数据加密和校验算法。
与前面提到的校验方式不同,MD5校验针对的不是数据的完整性,而是数据的安全性。
它主要是将数据经过一系列复杂的运算后生成一个128位的数字指纹,再将该数字指纹加入数据包中。
在数据传输过程中,接收方会对收到的数据进行MD5运算,从而判断数据在传输过程中是否被篡改。
总的来说,通信校验是保证信息传输可靠和安全的关键。
各种校验方式都有自己的特点和适用场景,应根据需求进行选择。
校验码的基础知识

校验码的基础知识校验码是一种用于验证信息完整性和准确性的技术手段。
在计算机领域,校验码常常被用于数据传输和存储过程中,确保数据的准确无误。
本文将介绍校验码的基础知识,包括校验码的定义、常见的校验码算法和应用场景等。
一、校验码的定义校验码,即校验和码,是一种通过对数据进行运算得到的一段二进制码。
它可以用于检测和校正数据传输或存储中的错误。
校验码的计算方式通常基于数据的位操作,通过对数据进行一系列的运算,得到一个固定长度的校验码值。
这个校验码值可以在数据传输或存储过程中与原始数据一起传输或存储,接收方在接收到数据后再次计算校验码,并与接收到的校验码进行比较,以验证数据的完整性和准确性。
二、常见的校验码算法1. 奇偶校验:奇偶校验是最简单的一种校验码算法,它通过统计数据中二进制位中1的个数,来判断数据中是否存在错误。
如果数据中1的个数为偶数,则校验位为0;如果数据中1的个数为奇数,则校验位为1。
奇偶校验只能检测出奇数个错误位,无法检测出偶数个错误位。
2. 校验和:校验和是一种常用的校验码算法,它通过将数据划分为若干个字节或字,并对每个字节进行加法运算,得到最终的校验和值。
接收方在接收到数据后再次计算校验和,如果计算得到的校验和与接收到的校验和一致,则数据传输正确,否则存在错误。
3. 循环冗余校验(CRC):CRC是一种广泛应用于数据传输和存储过程中的校验码算法。
它通过对数据进行多项式除法来计算校验码。
CRC算法具有良好的错误检测和纠正能力,常用于网络通信、存储系统等领域。
三、校验码的应用场景1. 数据传输:在数据传输过程中,校验码可以用于验证数据的完整性和准确性。
发送方在发送数据前计算校验码,并将校验码与数据一起发送给接收方。
接收方在接收到数据后再次计算校验码,通过比较计算得到的校验码与接收到的校验码,可以判断数据是否传输正确。
2. 数据存储:在数据存储过程中,校验码可以用于验证数据的完整性。
通过计算数据的校验码,并将校验码与数据一起存储,可以在读取数据时进行校验,以确保数据的准确无误。
校验和算法——精选推荐

校验和算法1、CRC(循环冗余码)校验和的算法为:所有各字节的和模256的余。
即各字节⼆进制算术和,不计超过256的溢出值(即只取其和的低8位数据),然后⽤0x100减去这个算数累加和,得出得值就是此⾏得校验和。
例如:(16进制数) 10 00 10 00 18 F0 9F E5 80 5F 20 B9 F0 FF 1F E5 18 F0 9F E5。
这串数据的CRC校验和为:byte checksum=10+00+10+00+18+F0+9F+E5+80+5F+20+B9+F0+FF+1F+E5+18+F0+9F+E5;checksum=0x100-checksum;(结果为0x1D);2、奇偶校验法⼤家都知道,信息是以⽐特流的⽅式传输的,类似01000001。
在传输过程中,有可能会发⽣错误,⽐如,我们存储了01000001,但是取出来却是01000000,即低位由0变成了1。
为了检测到这种错误,我们可以通过“奇偶校验”来实现。
假如,我们存储的数据是⼀个字节,8个⽐特位,那我们就可以计算每个字节⽐特位是1的个数,如果是偶数个1,那么,我们就把第九个位设为1,如果是奇数个1,那么就把第九个位设为0,这样连续9个字节⽐特位为1的位数肯定是奇数。
这中⽅法叫做“奇校验”,“偶校验”和此类似。
当然,在实际应⽤中,也可以把⼀个字节的前7位作为数据位,最后⼀个为作为校验位。
3、CRC16的算法也是求余,但还没有搞清楚,只验证了它的程序,如下word CalculateCRC16(uchar* ptr, uchar len){uchar i;word crc=0xffff; //CRC的初始值,值不同则结果也不同,看具体要求while(len--){for(i=0x80; i!=0; i>>=1){if((crc&0x8000)!=0){crc<<=1; crc^=0x1021;} //0x1021表⽰其中的CCITT值,此值可能不同else crc<<=1;if((*ptr&i)!=0)crc^=0x1021;}ptr++;}return(crc);}如上程序,如果CRC初始值为0xffff;CCITT=0x1021。
各种校验码校验算法分析

各种校验码校验算法分析校验码是一种用于验证数据完整性和准确性的算法。
在计算机科学中,常见的校验码算法包括纵向冗余校验(VRC),横向冗余校验(HRC),循环冗余校验(CRC),校验和和哈希校验等。
下面将对这些校验码算法进行分析。
VRC是一种最简单的校验码算法,它将数据位分为数据位和校验位两部分。
数据位按照一定的规则进行编码,校验位是根据数据位计算得到的。
当数据接收方收到数据后,它也会按照相同的规则计算校验位,并将计算得到的校验位与发送方传来的校验位进行比较,如果两者一致,则认为数据传输正确。
然而,VRC算法只能检测数据传输中的单比特错误,无法检测到多比特错误。
HRC是一种通过对数据进行按位求和来计算校验位的算法。
它与VRC算法类似,只是校验位的计算方法不同。
与VRC算法相比,HRC算法更加复杂,但也能检测到更多的错误。
然而,HRC算法仍然无法检测到多比特错误。
CRC是一种更为强大的校验码算法,它通过对数据进行除法运算来计算校验位。
CRC算法将数据视为二进制数,将除法运算看作一个模2整除的过程。
发送方在传输数据之前,计算数据的CRC校验位并将其附加在数据末尾。
接收方在接收数据后,也计算接收到的数据的CRC校验位,并与接收到的校验位进行比较。
如果两者一致,则认为数据传输正确。
与VRC和HRC算法相比,CRC算法具有更高的错误检测能力。
校验和是一种将数据按照一定规则进行求和来计算校验位的算法。
校验和算法将数据视为一系列数值,按照一定的规则进行求和,然后将求和结果的低位部分作为校验位。
校验和算法简单易实现,但其错误检测能力有限,无法检测到一些错误。
哈希校验是一种借助哈希函数来计算校验位的算法。
哈希函数将数据映射为一个固定长度的哈希值,该哈希值称为校验值。
发送方在发送数据之前,计算数据的哈希值并将其附加在数据末尾。
接收方在接收数据后,也计算接收到的数据的哈希值,并与接收到的校验值进行比较。
如果两者一致,则认为数据传输正确。
校验码的计算方法

校验码的计算方法校验码是指通过一定的算法对数据进行计算,以便在数据传输或存储过程中验证数据的完整性和准确性。
校验码的计算方法有多种,常见的包括奇偶校验、CRC校验、MD5校验等。
下面将分别介绍这些常见的校验码计算方法。
奇偶校验是一种简单的校验方法,适用于对数据位数进行校验。
其原理是通过统计数据中“1”的个数,如果“1”的个数为偶数,则校验位为0,如果“1”的个数为奇数,则校验位为1。
通过这种方法可以检测数据中是否存在奇数个的错误位。
奇偶校验适用于对单个字节或字符进行校验,但对于多字节或多字符的数据校验效果不佳。
CRC(Cyclic Redundancy Check)校验是一种基于多项式的校验方法,适用于对二进制数据进行校验。
CRC校验通过对数据进行多项式除法运算,得到余数作为校验码。
接收端同样对接收到的数据进行CRC校验,并将计算得到的校验码与接收到的校验码进行比对,从而验证数据的完整性。
CRC校验方法适用于数据传输过程中的错误检测,广泛应用于网络通信、存储系统等领域。
MD5(Message Digest Algorithm 5)是一种广泛应用的哈希函数,用于对任意长度的数据产生一个128位的哈希值。
MD5校验通过对数据进行哈希运算,得到固定长度的校验码。
MD5校验具有较高的安全性,不可逆性和唯一性,适用于对数据完整性和一致性进行验证。
MD5校验常用于文件完整性校验、数字签名等场景。
除了上述介绍的奇偶校验、CRC校验和MD5校验外,还有其他多种校验码的计算方法,如SHA-1、SHA-256等。
不同的校验方法适用于不同的场景,选择合适的校验方法可以提高数据的可靠性和安全性。
在实际应用中,校验码的计算方法需要根据具体的需求和场景进行选择。
在数据传输过程中,需要对数据进行校验以确保数据的完整性和准确性;在存储过程中,需要对数据进行校验以防止数据损坏或篡改。
因此,了解不同的校验码计算方法,并根据实际情况进行选择和应用,对保障数据的安全和可靠性具有重要意义。
串口常用校验算法(累加和、异或和)
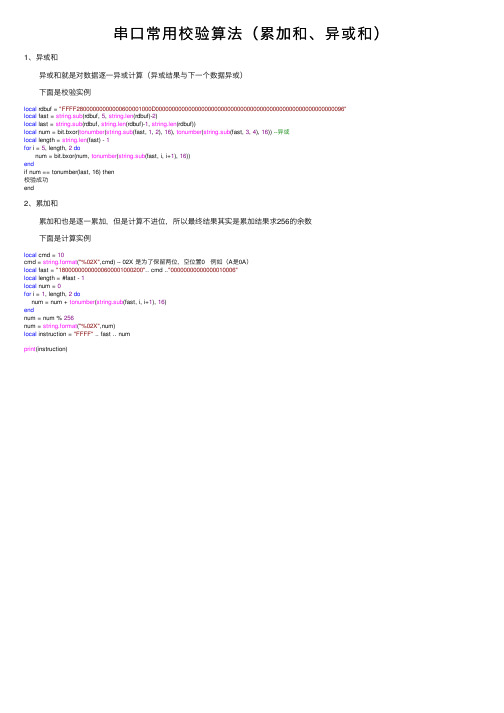
串⼝常⽤校验算法(累加和、异或和)1、异或和 异或和就是对数据逐⼀异或计算(异或结果与下⼀个数据异或) 下⾯是校验实例local rdbuf = "FFFF28000000000000600001000D0000000000000000000000000000000000000000000000000000000096"local fast = string.sub(rdbuf, 5, string.len(rdbuf)-2)local last = string.sub(rdbuf, string.len(rdbuf)-1, string.len(rdbuf))local num = bit.bxor(tonumber(string.sub(fast, 1, 2), 16), tonumber(string.sub(fast, 3, 4), 16)) --异或local length = string.len(fast) - 1for i = 5, length, 2donum = bit.bxor(num, tonumber(string.sub(fast, i, i+1), 16))endif num == tonumber(last, 16) then校验成功end2、累加和 累加和也是逐⼀累加,但是计算不进位,所以最终结果其实是累加结果求256的余数 下⾯是计算实例local cmd = 10cmd = string.format("%02X",cmd) -- 02X 是为了保留两位,空位置0 例如(A是0A)local fast = "18000000000000600001000200".. cmd .."00000000000000010006"local length = #fast - 1local num = 0for i = 1, length, 2donum = num + tonumber(string.sub(fast, i, i+1), 16)endnum = num % 256num = string.format("%02X",num)local instruction = "FFFF" .. fast .. numprint(instruction)。
校验算法——精选推荐

校验算法# 校验算法### 常见的校验算法------------------------------ LRC- BCC- CRC### LRC------------------------------ 简介- 纵向冗余校验(Longitudinal Redundancy Check,简称:LRC)是通信中常⽤的⼀种校验形式,也称LRC校验或纵向校验。
它是⼀种从纵向通道上的特定⽐特串产⽣校验⽐特的错误检测⽅法。
在⾏列格式中(如磁带),LRC经常是与VRC⼀起使⽤,这样就会为每个字符校验码。
在⼯业领域Modbus协议Ascii模式采⽤该算法。
- 具体算法如下1. 对需要校验的数据(2n个字符)两两组成⼀个16进制的数值求和。
2. 将求和结果与256求模。
3. ⽤256减去所得模值得到校验结果(另⼀种⽅法:将模值按位取反然后加1)。
- 算法举例```例如16进制数据:01 A0 7C FF 02(16进制计算) 求和:01 + A0 + 7C + FF + 02 = 21E 取模:21E % 100 = 1E 计算:100 - 1E = E2(10进制计算) 求和:01 + 160 + 124 + 255 + 02 = 542 取模:542 % 256 = 30 计算:256 - 30 = 226```### BCC------------------------------ 简介- BCC(Block Check Character/信息组校验码),因校验码是将所有数据异或得出,故俗称异或校验。
- 具体算法- 将每⼀个字节的数据(⼀般是两个16进制的字符)进⾏异或后即得到校验码。
- 算法举例```例如16进制数据:01 A0 7C FF 02计算:01 xor A0 xor 7C xor FF xor 02 = 20校验码是:20```### CRC------------------------------ 简介- CRC即循环冗余校验码(Cyclic Redundancy Check):是数据通信领域中最常⽤的⼀种查错校验码,其特征是信息字段和校验字段的长度可以任意选定。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
常见校验算法一、校验算法奇偶校验MD5校验求校验和BCC(Block Check Character/信息组校验码),好像也是常说的异或校验方法CRC(Cyclic Redundancy Check/循环冗余校验)LRC(Longitudinal Redundancy Check/纵向冗余校验)二、奇偶校验内存中最小的单位是比特,也称为“位”,位有只有两种状态分别以1和0来标示,每8个连续的比特叫做一个字节(byte)。
不带奇偶校验的内存每个字节只有8位,如果其某一位存储了错误的值,就会导致其存储的相应数据发生变化,进而导致应用程序发生错误。
而奇偶校验就是在每一字节(8位)之外又增加了一位作为错误检测位。
在某字节中存储数据之后,在其8个位上存储的数据是固定的,因为位只能有两种状态1或0,假设存储的数据用位标示为1、1、1、0、0、1、0、1,那么把每个位相加(1+1+1+0+0+1+0+1=5),结果是奇数,那么在校验位定义为1,反之为0。
当CPU读取存储的数据时,它会再次把前8位中存储的数据相加,计算结果是否与校验位相一致。
从而一定程度上能检测出内存错误,奇偶校验只能检测出错误而无法对其进行修正,同时虽然双位同时发生错误的概率相当低,但奇偶校验却无法检测出双位错误三、MD5校验MD5的全称是Message-Digest Algorithm 5,在90年代初由MIT的计算机科学实验室和RSA Data Security Inc 发明,由MD2/MD3/MD4 发展而来的。
MD5的实际应用是对一段Message(字节串)产生fingerprint(指纹),可以防止被“篡改”。
举个例子,天天安全网提供下载的MD5校验值软件WinMD5.zip,其MD5值是1e07ab3591d25583eff5129293dc98d2,但你下载该软件后计算MD5 发现其值却是81395f50b94bb4891a4ce4ffb6ccf64b,那说明该ZIP已经被他人修改过,那还用不用该软件那你可自己琢磨着看啦。
四、求校验和求校验和其实是一种或运算。
如下://--------------------------------------------------------------------------------------------------//如下是计算校验位函数// checkdata,包括起始位在内的前九位数据的校验和//--------------------------------------------------------------------------------------------------unsigned char CLU_checkdata(void){ //求校验和unsigned char checkdata=0;for(point=0;point<9,TI=1;point++){checkdata=checkdata | buffer[point];}return(checkdata);}四、BCC(Block Check Character/信息组校验符号)BCC校验其实是奇偶校验的一种,但也是经常使用并且效率较高的一种,所谓BCC校验法(block check character),就是在发送前和发送后分别把BCC以前包括ETX字符的所有字符按位异或后,按要求变换(增加或前去一个固定的值)后所得到的字符进行比较,相等即认为通信无错误,不相等则认为通信出错.非接触卡读卡器与PC机的通讯格式如下:STX(02H)+ 6个字节的卡号+VERH+VERL+EOT(04H)STX(02H)起始字节EOT(04H)结束字节6个字节的卡号为六个十六进制的ASCII字符,6个字节的传送,高字节在前,低字节在后。
例如:卡号:8 D E F 9 E传输的数据格式:38 44 45 46 39 45 (十六进制)在校验时采用目前最通用的BCC校验方式:具体的方法是:将有效的卡号接字节作异或(XOR)校验:38H (XOR)44H (XOR)45H (XOR)46H (XOR)39H(XOR)45H =03H然后将接收到的数据VERH+VERL合成一个字节数据,30H(HEX)=0,33H(HEX)=3合成数据为03H,接收到的数据与我们收到的卡号的校验数据一致,则接收到的卡号为正确卡号。
再比如现有卡号为:卡号:0 5 8 E 4 2传输的数据格式:30 35 38 45 34 32 (十六进制)在校验时采用目前最通用的BCC校验方式:具体的方法是:将有效的卡号接字节作异或(XOR)校验:30H (XOR)35H (XOR)38H (XOR)45H (XOR)34H(XOR)32H =7EH然后将接收到的数据VERH+VERL合成一个字节数据,37H(HEX)=7,45H(HEX)=E合成数据为7EH,接收到的数据与我们收到的卡号的校验数据一致,则接收到的卡号为正确卡号。
在编写程序时,可以先将所有数据都接收到计算机的内存中,然后计算BCC校验值VALUE1,再将接收的BCC值拼成一个十六进制数VALUE2,然后比较这两个值,如果相等,则接收到的卡号为合法卡号,然后按您的系统作相应的处理。
VB代码如下:Public Function bcc(a As String) As StringDim b As Integerb = 0For i = 1 To Len(a) Step 2b = b Xor ("&h" + Mid(a, i, 2))Nextb = b And &HFFIf b < 16 Thenbcc = "0" + Hex(b)Elsebcc = Hex(b)End IfEnd Function五、CRC(Cyclic Redundancy Check/循环冗余校验)CRC 校验的基本思想是利用线性编码理论,在发送端根据要传送的k位二进制码序列,以一定的规则产生一个校验用的监督码(既CRC码)r位,并附在信息后边,构成一个新的二进制码序列数共(k+r)位,最后发送出去。
在接收端,则根据信息码和CRC码之间所遵循的规则进行检验,以确定传送中是否出错。
16位的CRC码产生的规则是先将要发送的二进制序列数左移16位(既乘以)后,再除以一个多项式,最后所得到的余数既是CRC码.它是利用除法及余数的原理来作错误侦测(Error Detecting)的。
实际应用时,发送装置计算出CRC值并随数据一同发送给接收装置,接收装置对收到的数据重新计算CRC并与收到的CRC相比较,若两个CRC值不同,则说明数据通讯出现错误。
根据应用环境与习惯的不同,CRC又可分为以下几种标准:①CRC-12码;②CRC-16码;③CRC-CCITT码;④CRC-32码。
CRC-12码通常用来传送6-bit字符串。
CRC-16及CRC-CCITT码则用是来传送8-bit字符,其中CRC-16为美国采用,而CRC-CCITT为欧洲国家所采用。
CRC-32码大都被采用在一种称为Point-to-Point的同步传输中。
下面为CRC计算过程:1.设置CRC寄存器,并给其赋值FFFF(hex)。
2.将数据的第一个8-bit字符与16位CRC寄存器的低8位进行异或,并把结果存入CRC寄存器。
3.CRC寄存器向右移一位,MSB补零,移出并检查LSB。
4.如果LSB为0,重复第三步;若LSB为1,CRC寄存器与多项式码相异或。
5.重复第3与第4步直到8次移位全部完成。
此时一个8-bit数据处理完毕。
6.重复第2至第5步直到所有数据全部处理完成。
7.最终CRC寄存器的内容即为CRC值。
常用的CRC循环冗余校验标准多项式如下:CRC(16位) = X16+X15+X2+1CRC(CCITT) = X16+X12 +X5+1CRC(32位) = X32+X26+X23+X16+X12+X11+X10+X8+X7+X5+X4+X2+X+1以CRC(16位)多项式为例,其对应校验二进制位列为1 1000 0000 0000 0101。
CRC基本原理是:在K位信息码后再拼接R位的校验码,整个编码长度为N位,因此,这种编码又叫(N,K)码。
对于一个给定的(N,K)码,可以证明存在一个最高次幂为N-K=R的多项式G(x),根据G(x)可以生成K位信息的校验码,而G(x)叫做这个CRC码的生成多项式。
校验码的具体生成过程为:假设发送信息用信息多项式C(X)表示,将C(x)左移R位,则可表示成C(x)*2R,这样C(x)的右边就会空出R位,这就是校验码的位置。
通过C(x)*2R除以生成多项式G(x)得到的余数就是校验码。
几个基本概念1、多项式与二进制数码多项式和二进制数有直接对应关系:x的最高幂次对应二进制数的最高位,以下各位对应多项式的各幂次,有此幂次项对应1,无此幂次项对应0。
可以看出:x的最高幂次为R,转换成对应的二进制数有R+1位。
多项式包括生成多项式G(x)和信息多项式C(x)。
如生成多项式为G(x)=x4+x3+x+1,可转换为二进制数码11011。
而发送信息位1111,可转换为数据多项式为C(x)=x3+x2+x+1。
2、生成多项式是接受方和发送方的一个约定,也就是一个二进制数,在整个传输过程中,这个数始终保持不变。
在发送方,利用生成多项式对信息多项式做模2除生成校验码。
在接受方利用生成多项式对收到的编码多项式做模2除检测和确定错误位置。
应满足以下条件:a、生成多项式的最高位和最低位必须为1。
b、当被传送信息(CRC码)任何一位发生错误时,被生成多项式做模2除后应该使余数不为0。
c、不同位发生错误时,应该使余数不同。
d、对余数继续做模2除,应使余数循环。
将这些要求反映为数学关系是比较复杂的。
但可以从有关资料查到常用的对应于不同码制的生成多项式如图9所示:N K 码距d G(x)多项式G(x)7 4 3 x3+x+1 10117 4 3 x3+x2+1 11017 3 4 x4+x3+x2+1 111017 3 4 x4+x2+x+1 1011115 11 3 x4+x+1 1001115 7 5 x8+x7+x6+x4+1 11101000131 26 3 x5+x2+1 10010131 21 5 x10+x9+x8+x6+x5+x3+1 1110110100163 57 3 x6+x+1 100001163 51 5 x12+x10+x5+x4+x2+1 10100001101011041 1024 x16+x15+x2+1 110000000000001013、模2除(按位除)模2除做法与算术除法类似,但每一位除(减)的结果不影响其它位,即不向上一位借位。
