现代控制理论习题解答(第五章)
现代控制理论第五章答案

比较 f () 和 f * ( ) 求出反馈矩阵 G[3r 2r2]T
观测器方程为:
xˆ (AGC)xˆGybu
3r 2r2
10xˆ23rr2y10u
【习题5-11】已知系统状态空间表达式为
x 0 2 1 1 x 1 0 u
0 1
1 0 01 0
c2A1B0 1 10 2 30 11 0
1 0 10 1
d2 1
计算几个矩阵
Dc c2 1A Ad d1 2cc 21 A1 1
0 2
0 2
1 0
EDB 11
第五章主要内容:
§5—1 线性反馈控制系统的基本结构及其特性 主要知识点:
1、状态反馈、输出反馈的基本概念; 2、三种反馈控制系统的基本结构和特点; 3、闭环系统的能控性和能观性。
§ 5—2 极点配置问题
主要知识点: 1、极点配置的基本概念; 2、极点任意配置的条件; 3、极点配置的设计方法。
§5—3 系统镇定问题 主要知识点:
s 1
0
0
1
(s 1)(s 2)
1
s 1 1
(s 1)2
(s
s
1)( s
s
2)
(s 1)2
0
1
(s 1)(s 2)
【习题5-8】已知系统
1 0 0 1 0 x0 2 3x0 1u
期望的闭环特征多项式
f* () ( 2 )2 ( 3 )3 7 2 1 6 12
比较 f () 和 f * ( ) 求出反馈矩阵
现代控制理论李斌第五章课后习题

现代控制理论李斌第五章课后习题现代控制理论第五章部分习题参考答案5.1 设系统的状态⽅程为bu Ax x+= ,⽽ ?---=9432A ,??=13b 。
试确定状态反馈矩阵K ,使闭环系统的极点配置在21j ±-。
解根据题意,要求的特征多项式为52)21)(21()(2*++=++-+=λλλλλj j f设状态反馈阵[]21k k K =,则闭环系统的特征多项式为[]1212212122333()det ()det 49(113)(302414)k k f I A BK k k k k k k λλλλλλ+++??=--=?-+++=++++++⽐较)(*λf 与)(λf 各对应项的系数,可解得181011-=k ,6472=k ,所以??-=64718101K 。
5.2 已知系统的状态空间描述为cxy bu Ax x =+=⽽=0110A ,??=10b ,[]10=c 。
若采⽤状态反馈,试分析当反馈矩阵[]01-=K 时,闭环系统的能控性和能观测性。
解采⽤状态反馈后闭环系统的系统矩阵为=-=02101bK A A 能控性矩阵 []==01101b A b M c ,2=c rankM 。
能观测性矩阵==02101cA c M o ,2=o rankM 。
能控性矩阵和能观测性矩阵均满秩,故闭环系统完全能控且完全能观测。
5.3 设线性定常系统的状态空间描述为cxy bu Ax x =+=⽽ =200120001A ,=101b ,[]011=c 。
试设计⼀个状态观测器,要求将其极点配置在3-,4-,5-上。
画出状态变量图。
解根据题意,状态观测器要求的特征多项式为604712)5)(4)(3()(23*+++=+++=λλλλλλλf设误差反馈阵[]Tg g g G 321=,则观测器的特征多项式为[]--+-+-=--=21201det )(det )(332211λλλλλg g g g g g Gc A I f )424()834()5(3213212213--++++--+-++=g g g g g g g g λλλ⽐较)(*λf 与)(λf 各对应项的系数,可解得1031-=g ,1202=g ,2102=g ,所以[]TG 210120103-=。
现代控制理论课后习题答案

精心整理绪论为了帮助大家在期末复习中能更全面地掌握书中知识点,并且在以后参加考研考博考试直到工作中,为大家提供一个理论参考依据,我们11级自动化二班的同学们在王整风教授的带领下合力编写了这本《现代控制理论习题集》(刘豹第三版),希望大家好好利用这本辅助工具。
根据老师要求,本次任务分组化,责任到个人。
我们班整体分为五大组,每组负责整理一章习题,每个人的任务由组长具体分配,一个人大概分1~2道题,每个人任务虽然不算多,但也给同学们提出了要求:1.写清题号,抄题,画图(用CAD或word画)。
2.题解详略得当,老师要求的步骤必须写上。
3.遇到一题多解,要尽量写出多种方法。
本习题集贯穿全书,为大家展示了控制理论的基础、性质和控制一个动态系统的四个基本步骤,即建模、系统辨识、信号处理、综合控制输入。
我们紧贴原课本,强调运用统一、联系的方法分析处理每一道题,将各章节的知识点都有机地整合在一起,力争做到了对控制理论概念阐述明确,给每道题的解析赋予了较强的物理概念及工程背景。
在课后题中出现的本章节重难点部分,我们加上了必要的文字和图例说明,让读者感觉每一题都思路清晰,简单明了,由于我们给习题配以多种解法,更有助于发散大家的思维,做到举一反三!这本书是由11级自动化二班《现代控制理论》授课老师王整风教授全程监管,魏琳琳同学负责分组和发布任务书,由五个小组组组长李卓钰、程俊辉、林玉松、王亚楠、张宝峰负责自己章节的初步审核,然后汇总到胡玉皓同学那里,并由他做最后的总审核工作,绪论是段培龙同学和付博同学共同编写的。
本书耗时两周,在同学的共同努力下完成,是二班大家庭里又一份智慧和努力的结晶,望大家能够合理使用,如发现错误请及时通知,欢迎大家的批评指正!2014年6月2日第一章 控制系统的状态空间表达式1-1 试求图1-27系统的模拟结构图,并建立其状态空间表达式 解:系统的模拟结构图如下: 系统的状态方程如下: 令y s =)(θ,则1x y =所以,系统的状态空间表达式及输出方程表达式为1-2有电路如图1-28所示。
现代控制理论课后习题答案

现代控制理论课后习题答案第⼀章习题1.2求下列多项式矩阵()s D 和()s N 的两个不同的gcrd:()2223(),()1232s s s s s s s s s ??++== ? ?+-??D N 解:()()22232321s s s s s s s++ =++ ? ?D S N S ; ()3r 2,1,2E -:223381s s s s s s ??++ ?-- ? ???;()3r 2,3,3E :223051s s s s s ??++ ?- ? ???;()3r 1,3,2E s --:01051s s ?? ?- ? ;()3r 2,1,5E s -:01001s ?? ?;()3r 3,1,1E -:01000s ?? ? ? ???;()1r 2,3E :01000s ?? ? ? ???;()1r 1,2E :00100s ?? ?;所以⼀个gcrd 为001s ??;取任⼀单模矩阵预制相乘即可得另⼀个gcrd 。
1.9 求转移矩阵t A e (1)已知1141??=A ,根据拉⽒反变换求解转移矩阵tA e 。
(2) 已知412102113-?? ?= ? ?-??A ,根据C-H 有限项展开法求解转移矩阵t A e 。
解:(1)11()41s s s --??-= ?--??I A1110.50.50.250.2511(3)(1)(3)(1)13131()4141110.50.5(3)(1)(3)(1)(3)(1)3131s s s s s s s s s s s s s s s s s s s s s s s --+---+-+??-+-+ ? ?-=== ? ?---+ ?-+ ? ?-+-+-+-+?I A 3311330.5e 0.5e 0.25e 0.25e e ()e e 0.5e 0.5e t t t t t t tt t s ------??+-??=-= ??? ?-+?A L I A (2)由2412()12(1)(3)0113λλλλλλ--?? ?=--=--= ? ?--??A I -,得1,233,1λλ== 对1,23λ=,可以计算1,2()2rank λ=A I -,所以该特征值的⼏何重数为1。
《现代控制理论》第三版_.习题答案

1 0 0 3 1 0 5 2 1 52 7 1 5 2 70 125 3 5 7 5 0 0 1 1 B 2 ; 2 5 5
1 0 a1 0 0 1 0 1 0 0 1 a2 3 7 5
0 B 0 1
C (b0 a0bn ) (bn1 an1bn ) 2 1 0
3 1 a 或者 2 2 1 a1 0 a0
e At I At 1 22 1 33 A t A t 2! 3! t2 t4 t6 t3 t5 1 4 16 64 , 4 16 t 2! 4! 6! 3! 5! 3 5 2 4 6 t t t t t t 4 16 64 , 1 4 16 64 3! 5! 2! 4! 6!
0 0 1 B M 1 0 0 0 0 1 M2
1 0 B 1 M1 B1 M2
1 B1 M1 B1 B2 M2
0
0 0 1 0 C 0 0 0 1
1-5. 根据微分方程, 写状态方程, 画模 拟结构图。
1 a2 a2 2 a1 3 2 a a a 1 2 2 a0
1 a2 a1
1 a2
12 b1 b0
b3 b 2 b1 1 b0
凯莱哈密顿法: 1,2 2 j
0 (t ) 1 1 e1t 1 2(e 2 jt e 2 jt ) (t ) 1 2t 4 2 jt 2 jt e j ( e e ) 2 1
《现代控制理论》第3版课后习题答案
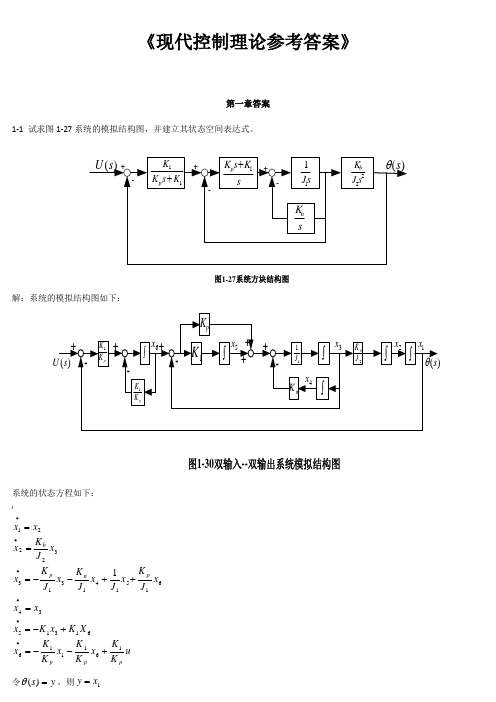
《现代控制理论参考答案》第一章答案1-1 试求图1-27系统的模拟结构图,并建立其状态空间表达式。
图1-27系统方块结构图解:系统的模拟结构图如下:图1-30双输入--双输出系统模拟结构图系统的状态方程如下: )u K K x K K x K K x X K x K x x x x J K x J x J K x J K x x J K x x x pp p p n pb1611166131534615141313322211+--=+-==++--===••••••令y s =)(θ,则1x y =所以,系统的状态空间表达式及输出方程表达式为[]⎥⎥⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎢⎢⎣⎡=⎥⎥⎥⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎢⎢⎢⎣⎡+⎥⎥⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎢⎢⎣⎡⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎣⎡-----=⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎣⎡••••••654321165432111111112654321000001000000000000010010000000000010x x x x x x y uK K x x x x x x K K K K K K J K J J K J K J K x x x x x x p p pp n p b1-2有电路如图1-28所示。
以电压)(t u 为输入量,求以电感中的电流和电容上的电压作为状态变量的状态方程,和以电阻2R 上的电压作为输出量的输出方程。
U图1-28 电路图解:由图,令32211,,x u x i x i c ===,输出量22x R y =有电路原理可知:•••+==+=++3213222231111x C x x x x R x L ux x L x R 既得22213322222131111111111x R y x C x C x x L x L R x u L x L x L R x =+-=+-=+--=•••写成矢量矩阵形式为: `[]⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡=⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎣⎡+⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡⎥⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎢⎣⎡----=⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎣⎡32121321222111321000*********x x x R y u L x x x CCL L R L L R x x x 。
《现代控制理论》第3版课后习题答案
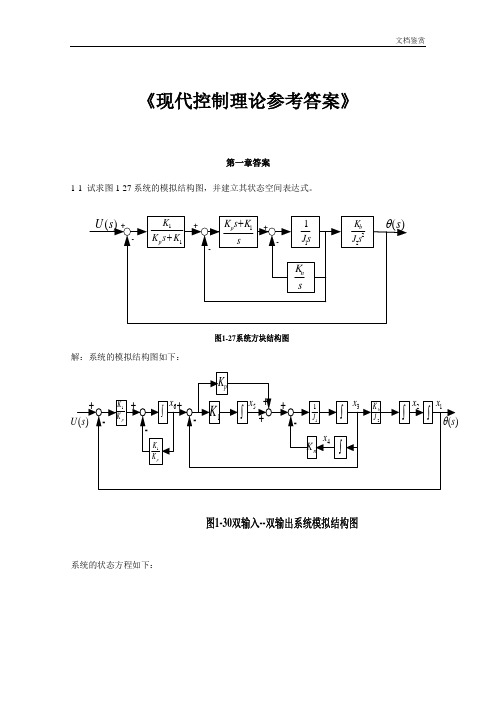
《现代控制理论参考答案》第一章答案1-1 试求图1-27系统的模拟结构图,并建立其状态空间表达式。
11K s K K p +sK s K p 1+s J 11sK n 22s J K b -++-+-)(s θ)(s U 图1-27系统方块结构图解:系统的模拟结构图如下:)(s U )(s θ---+++图1-30双输入--双输出系统模拟结构图1K pK K 1pK K 1+++pK n K ⎰⎰⎰11J ⎰2J K b ⎰⎰-1x 2x 3x 4x 5x 6x系统的状态方程如下:u K K x K K x K K x X K x K x x x x J K x J x J K x J K x x J K x x x pp p p n pb1611166131534615141313322211+--=+-==++--===••••••令y s =)(θ,则1x y =所以,系统的状态空间表达式及输出方程表达式为[]⎥⎥⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎢⎢⎣⎡=⎥⎥⎥⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎢⎢⎢⎣⎡+⎥⎥⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎢⎢⎣⎡⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎣⎡-----=⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎣⎡••••••654321165432111111112654321000001000000000000010010000000000010x x x x x x y uK K x x x x x x K K K K K K J K J J K J K J K x x x x x x p p pp npb1-2有电路如图1-28所示。
以电压)(t u 为输入量,求以电感中的电流和电容上的电压作为状态变量的状态方程,和以电阻2R 上的电压作为输出量的输出方程。
R1L1R2L2CU---------Uc ---------i1i2图1-28 电路图解:由图,令32211,,x u x i x i c ===,输出量22x R y =有电路原理可知:•••+==+=++3213222231111x C x x x x R x L ux x L x R 既得22213322222131111111111x R y x C x C x x L x L R x u L x L x L R x =+-=+-=+--=•••写成矢量矩阵形式为:[]⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡=⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎣⎡+⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡⎥⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎢⎣⎡----=⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎣⎡32121321222111321000*********x x x R y u L x x x CCL L R L L R x x x 。
《现代控制理论》第3版(刘豹唐万生)课后习题答案
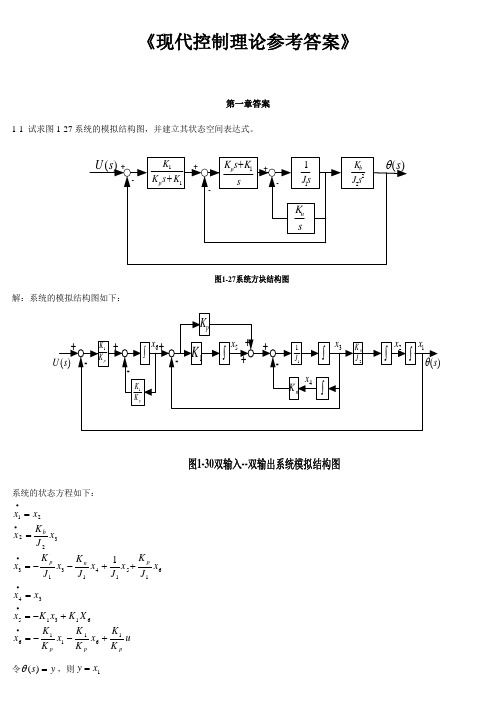
《现代控制理论参考答案》第一章答案1-1 试求图1-27系统的模拟结构图,并建立其状态空间表达式。
11K s K K p +sK s K p 1+s J 11sK n 22s J K b -++-+-)(s θ)(s U 图1-27系统方块结构图解:系统的模拟结构图如下:)(s U )(s θ---+++图1-30双输入--双输出系统模拟结构图1K pK K 1pK K 1+++pK n K ⎰⎰⎰11J ⎰2J K b ⎰⎰-1x 2x 3x 4x 5x 6x系统的状态方程如下:u K K x K K x K K x X K x K x x x x J K x J x J K x J K x x J K x x x pp p p n pb1611166131534615141313322211+--=+-==++--===∙∙∙∙∙∙令y s =)(θ,则1x y =所以,系统的状态空间表达式及输出方程表达式为[]⎥⎥⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎢⎢⎣⎡=⎥⎥⎥⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎢⎢⎢⎣⎡+⎥⎥⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎢⎢⎣⎡⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎣⎡-----=⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎣⎡∙∙∙∙∙∙654321165432111111112654321000001000000000000010010000000000010x x x x x x y uK K x x x x x x K K K K K K J K J J K J K J K x x x x x x p p pp n p b1-2有电路如图1-28所示。
以电压)(t u 为输入量,求以电感中的电流和电容上的电压作为状态变量的状态方程,和以电阻2R 上的电压作为输出量的输出方程。
R1L1R2L2CU---------Uc---------i1i2图1-28 电路图解:由图,令32211,,x u x i x i c ===,输出量22x R y =有电路原理可知:∙∙∙+==+=++3213222231111x C x x x x R x L ux x L x R 既得22213322222131111111111x R y x C x C x x L x L R x u L x L x L R x =+-=+-=+--=∙∙∙写成矢量矩阵形式为:[]⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡=⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎣⎡+⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡⎥⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎢⎣⎡----=⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎣⎡32121321222111321000*********x x x R y u L x x x CCL L R L L R x x x 。
(完整word版)《现代控制理论》第3版课后习题答案
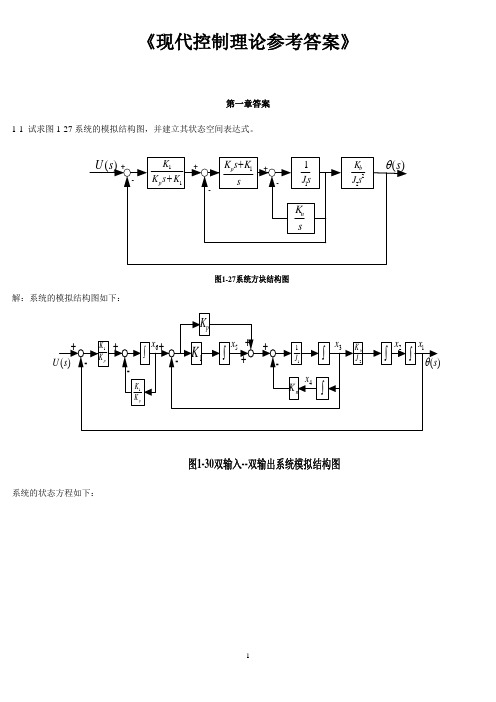
《现代控制理论参考答案》第一章答案1-1 试求图1-27系统的模拟结构图,并建立其状态空间表达式。
图1-27系统方块结构图解:系统的模拟结构图如下:图1-30双输入--双输出系统模拟结构图系统的状态方程如下:u K K x K K x K K x X K x K x x x x J K x J x J K x J K x x J K x x x pp p p n p b1611166131534615141313322211+--=+-==++--===••••••令y s =)(θ,则1x y =所以,系统的状态空间表达式及输出方程表达式为[]⎥⎥⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎢⎢⎣⎡=⎥⎥⎥⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎢⎢⎢⎣⎡+⎥⎥⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎢⎢⎣⎡⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎣⎡-----=⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎣⎡••••••654321165432111111112654321000001000000000000010010000000000010x x x x x x y uK K x x x x x x K K K K K K J K J J K J K J K x x x x x x p p pp npb1-2有电路如图1-28所示。
以电压)(t u 为输入量,求以电感中的电流和电容上的电压作为状态变量的状态方程,和以电阻2R 上的电压作为输出量的输出方程。
U图1-28 电路图解:由图,令32211,,x u x i x i c ===,输出量22x R y =有电路原理可知:•••+==+=++3213222231111x C x x x x R x L ux x L x R 既得22213322222131111111111x R y x C x C x x L x L R x u L x L x L R x =+-=+-=+--=•••写成矢量矩阵形式为:[]⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡=⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎣⎡+⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡⎥⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎢⎣⎡----=⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎣⎡32121321222111321000*********x x x R y u L x x x CCL L R L L R x x x 。
《现代控制理论》第三版 第五章.习题答案

1 0
f * ( ) ( r )( 2r ) 2 3r 2r 2
3r 比较得: G 2 2r
6
5-12 (1) 由于系统属于能观 I 型,所以能观,故 存在状态观测器, 且 rank c = 1 (2) 构造变换阵作线性变换, 设 0 0 1 0 0 1 c0 1 T 0 1 0 ,T 0 1 0 c 1 0 0 1 0 0 0 0 1 0 1 0 0 0 1 A T 1 AT 0 1 0 0 0 1 0 1 0 1 0 0 0 0 0 1 0 0
f * ( ) 3 12 2 24 40
所以 K 40 13 1 (3) K KTc 1 4 1.2 0.1
2 5-5(1) M b Ab A b 2 4 0 0 1 0 1 1 5 det M 0 RankM 3 所以系统通过状态 反馈能镇定。
型所以能观故存在状态观测器且rank可由y直接提供故只需设计二维状态观测器
第五章 作业
参考答案
5-2.解法 1: (1) 0 10 0 2 0 , M b , Ab , A b 10 110 10 100 990
rankM 3满秩 可以任意极点配置
3 12 2 24 40 解之: K 4 1.2 0.1 解法 2:(1)
《现代控制理论》第3版(刘豹-唐万生)课后习题答案
《现代控制理论参考答案》第一章答案1-1 试求图1-27系统的模拟结构图,并建立其状态空间表达式。
图1-27系统方块结构图解:系统的模拟结构图如下:图1-30双输入--双输出系统模拟结构图系统的状态方程如下:uK K x K K x K K x X K x K x x x x J K x J x J K x J K x x J K x x x p p pp n p b1611166131534615141313322211+--=+-==++--===••••••令y s =)(θ,则1x y =所以,系统的状态空间表达式及输出方程表达式为[]⎥⎥⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎢⎢⎣⎡=⎥⎥⎥⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎢⎢⎢⎣⎡+⎥⎥⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎢⎢⎣⎡⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎣⎡-----=⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎣⎡••••••654321165432111111112654321000001000000000000010010000000000010x x x x x x y uK K x x x x x x K K K K K K J K J J K J K J K x x x x x x p p pp n p b1-2有电路如图1-28所示。
以电压)(t u 为输入量,求以电感中的电流和电容上的电压作为状态变量的状态方程,和以电阻2R 上的电压作为输出量的输出方程。
L1L2U图1-28 电路图解:由图,令32211,,x u x i x i c ===,输出量22x R y =有电路原理可知:•••+==+=++3213222231111x C x x x x R x L ux x L x R 既得22213322222131111111111x R y x C x C x x L x L R x u L x L x L R x =+-=+-=+--=•••写成矢量矩阵形式为:[]⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡=⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎣⎡+⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡⎥⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎢⎣⎡----=⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎣⎡32121321222111321000*********x x x R y u L x x x CCL L R L L R x x x 。
《现代控制理论》课后习题全部答案(最完整打印版)
第一章习题答案1-1 试求图1-27系统的模拟结构图,并建立其状态空间表达式。
11K s K K p +sK s K p 1+s J 11sK n 22s J K b -++-+-)(s θ)(s U 图1-27系统方块结构图解:系统的模拟结构图如下:)(s U )(s θ---+++图1-30双输入--双输出系统模拟结构图1K pK K 1pK K 1+++pK n K ⎰⎰⎰11J ⎰2J K b ⎰⎰-1x 2x 3x 4x 5x 6x系统的状态方程如下:u K K x K K x K K x X K x K x x x x J K x J x J K x J K x x J K x x x pp p p n p b1611166131534615141313322211+--=+-==++--===∙∙∙∙∙∙阿令y s =)(θ,则1x y =所以,系统的状态空间表达式及输出方程表达式为[]⎥⎥⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎢⎢⎣⎡=⎥⎥⎥⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎢⎢⎢⎣⎡+⎥⎥⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎢⎢⎣⎡⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎣⎡-----=⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎣⎡∙∙∙∙∙∙654321165432111111112654321000001000000000000010010000000000010x x x x x x y uK K x x x x x x K K K K K K J K J J K J K J K x x x x x x p p pp npb1-2有电路如图1-28所示。
以电压)(t u 为输入量,求以电感中的电流和电容上的电压作为状态变量的状态方程,和以电阻2R 上的电压作为输出量的输出方程。
R1L1R2L2CU---------Uc---------i1i2图1-28 电路图解:由图,令32211,,x u x i x i c ===,输出量22x R y =有电路原理可知:∙∙∙+==+=++3213222231111x C x x x x R x L ux x L x R 既得22213322222131111111111x R y x C x C x x L x L R x u L x L x L R x =+-=+-=+--=∙∙∙写成矢量矩阵形式为:[]⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡=⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎣⎡+⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡⎥⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎢⎣⎡----=⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎣⎡32121321222111321000*********x x x R y u L x x x CC L L R L L R x x x 。
(完整word版)《现代控制理论》第3版课后习题答案

《现代控制理论参考答案》第一章答案1-1 试求图1-27系统的模拟结构图,并建立其状态空间表达式。
图1-27系统方块结构图解:系统的模拟结构图如下:图1-30双输入--双输出系统模拟结构图系统的状态方程如下:u K K x K K x K K x X K x K x x x x J K x J x J K x J K x x J K x x x pp p p n p b1611166131534615141313322211+--=+-==++--===••••••令y s =)(θ,则1x y =所以,系统的状态空间表达式及输出方程表达式为[]⎥⎥⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎢⎢⎣⎡=⎥⎥⎥⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎢⎢⎢⎣⎡+⎥⎥⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎢⎢⎣⎡⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎣⎡-----=⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎣⎡••••••654321165432111111112654321000001000000000000010010000000000010x x x x x x y uK K x x x x x x K K K K K K J K J J K J K J K x x x x x x p p pp npb1-2有电路如图1-28所示。
以电压)(t u 为输入量,求以电感中的电流和电容上的电压作为状态变量的状态方程,和以电阻2R 上的电压作为输出量的输出方程。
U图1-28 电路图解:由图,令32211,,x u x i x i c ===,输出量22x R y =有电路原理可知:•••+==+=++3213222231111x C x x x x R x L ux x L x R 既得22213322222131111111111x R y x C x C x x L x L R x u L x L x L R x =+-=+-=+--=•••写成矢量矩阵形式为:[]⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡=⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎣⎡+⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡⎥⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎢⎣⎡----=⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎣⎡32121321222111321000*********x x x R y u L x x x CCL L R L L R x x x 。
《现代控制理论》课后习题答案5
5.11 已知系统状态方程
⎡1 1⎤ ⎡1⎤ =⎢ x x+⎢ ⎥u ⎥ ⎣0 1⎦ ⎣1⎦
计算状态反馈增益矩阵,使得闭环极点为 −2 和 −3 ,并画出反馈系统的结构图。 答:由 A = ⎢ ⎥ , B = ⎢1⎥ ,得能控性矩阵为 ⎣0 1⎦ ⎣ ⎦
⎡1 1⎤
⎡1⎤
Γ c ( A, B ) = [ B
rankQoF ≤ rankQo
由于 S o 又可以看成为 S F 的输出反馈系统,因而有
rankQo ≤ rankQoF
由以上两式可得
rankQo = rankQoF
因此,系统 S F 完全能观测等价于 S 0 完全能观测。 5.8 采用状态反馈实现闭环极点任意配置的条件是什么? 答:采用状态反馈实现闭环极点任意配置的条件是,开环系统是能控的。 5.9 采用状态反馈实现闭环极点任意配置,其状态反馈增益矩阵 K 的行数和列数如何确 定,计算方法有几种? 答:状态反馈增益矩阵 K 的行数是输入变量的个数,列数是状态变量的个数。计算方法有: 1.直接法;2.变换法;3. 利用爱克曼公式求解。 5.10 为什么要进行极点配置?解决系统极点配置问题的思路和步骤是什么?
(λ + 3) 2 = λ 2 + 6λ + 9
⎡ −2 1 ⎤ ⎡0 ⎤ = ( A − BK ) x + Bv = ⎢ x x+ ⎢ ⎥v ⎥ ⎣ −1 −4 ⎦ ⎣1 ⎦
它的单位阶跃响应曲线为:
Step Response 0.12
0.1 System: g Rise Time (sec): 1.3 0.08
m
非奇异的矩阵 U ,使得
Γ cK [( A − BK ), B] = Γ c [ A, B]U 由此可得:若 rank(Γ c [ A, B ]) = n ,即有 n 个线性无关的列向量,则 Γ cK [( A − BK ), B ] 也有 n 个线性无关的列向量,故 rank(Γ cK [( A − BK ), B]) = n
《现代控制理论》第3版课后习题答案.
《现代控制理论参考答案》第一章答案1-1 试求图1-27系统的模拟结构图,并建立其状态空间表达式。
11K s K K p +sK s K p 1+s J 11sK n 22s J K b -++-+-)(s θ)(s U 图1-27系统方块结构图解:系统的模拟结构图如下:)(s U )(s θ---+++图1-30双输入--双输出系统模拟结构图1K pK K 1pK K 1+++pK n K ⎰⎰⎰11J ⎰2J K b ⎰⎰-1x 2x 3x 4x 5x 6x系统的状态方程如下:u K K x K K x K K x X K x K x x x x J K x J x J K x J K x x J K x x x pp p p n pb1611166131534615141313322211+--=+-==++--===∙∙∙∙∙∙令y s =)(θ,则1x y =所以,系统的状态空间表达式及输出方程表达式为[]⎥⎥⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎢⎢⎣⎡=⎥⎥⎥⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎢⎢⎢⎣⎡+⎥⎥⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎢⎢⎣⎡⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎣⎡-----=⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎣⎡∙∙∙∙∙∙654321165432111111112654321000001000000000000010010000000000010x x x x x x y uK K x x x x x x K K K K K K J K J J K J K J K x x x x x x p p pp npb1-2有电路如图1-28所示。
以电压)(t u 为输入量,求以电感中的电流和电容上的电压作为状态变量的状态方程,和以电阻2R 上的电压作为输出量的输出方程。
R1L1R2L2CU---------Uc---------i1i2图1-28 电路图解:由图,令32211,,x u x i x i c ===,输出量22x R y =有电路原理可知:∙∙∙+==+=++3213222231111x C x x x x R x L ux x L x R 既得22213322222131111111111x R y x C x C x x L x L R x u L x L x L R x =+-=+-=+--=∙∙∙写成矢量矩阵形式为:[]⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡=⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎣⎡+⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡⎥⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎢⎣⎡----=⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎣⎡32121321222111321000*********x x x R y u L x x x CCL L R L L R x x x 。
现代控制理论智慧树知到课后章节答案2023年下临沂大学

现代控制理论智慧树知到课后章节答案2023年下临沂大学临沂大学绪论单元测试1.现代控制理论的主要内容()A:最优控制B:非线性系统理论C:线性系统D:系统辨识答案:最优控制;非线性系统理论;线性系统;系统辨识2.现代控制理论运用哪些数学工具()A:微分方程B:线性代数C:几何学D:数理统计答案:微分方程;线性代数3.控制论是谁发表的()A:奈奎斯特B:劳伦斯C:维纳D:钱学森答案:维纳4.大系统和与智能控制理论和方法有哪些()A:鲁棒控制B:最优估计C:最优控制D:系统辨识答案:鲁棒控制;最优估计;最优控制;系统辨识5.下面哪个不是大系统的特点()A:规模庞大B:信息复杂且多C:运用人力多D:结构复杂答案:运用人力多6.哪个不是20世纪三大科技()A:进化论B:智能控制理论C:空间技术D:原子能技术答案:进化论7.经典控制理论形成的目的是采用各种自动调节装置来解决生产和军事中的简单控制问题。
()A:错 B:对答案:对8.自适应控制所要解决的问题也是寻求最优控制律,自适应控制所依据的数学模型由于先验知识缺少,需要在系统运行过程中去提取有关模型的信息,使模型逐渐完善。
()A:错 B:对答案:对9.非线性系统状态的运动规律和改变这些规律的可能性与实施方法,建立和揭示系统结构、参数、行为和性能之间的关系。
()A:错 B:对答案:对10.现代控制理论是建立在状态空间法基础上的一种控制理论。
()A:对 B:错答案:对第一章测试1.下面关于建模和模型说法正确的是()A:无论是何种系统,其模型均可用来提示规律或者因果关系。
B:为设计控制器为目的建立只需要简练就可以了。
C:工程系统模型建模有两种途径,一是机理建模,而是系统辨识。
D:建模实际上是通过数据,图表,数学表达式,程序,逻辑关系或者各种方式的组合表示状态变量,输入变量,输出变量,参数之间的关系。
答案:无论是何种系统,其模型均可用来提示规律或者因果关系。
;工程系统模型建模有两种途径,一是机理建模,而是系统辨识。
《现代控制理论》刘豹著(第版)课后习题答案

《现代控制理论》刘豹著(第3版)课后习题答案《现代控制理论》刘豹著(第3版)课后习题答案第一章习题答案1-1试求图1-27系统的模拟结构图,并建立其状态空间表达式。
解:系统的模拟结构图如下:系统的状态方程如下:令,则所以,系统的状态空间表达式及输出方程表达式为1-2有电路如图1-28所示。
以电压为输入量,求以电感中的电流和电容上的电压作为状态变量的状态方程,和以电阻上的电压作为输出量的输出方程。
解:由图,令,输出量有电路原理可知:既得写成矢量矩阵形式为:1-3参考例子1-3(P19).1-4两输入,,两输出,的系统,其模拟结构图如图1-30所示,试求其状态空间表达式和传递函数阵。
解:系统的状态空间表达式如下所示:1-5系统的动态特性由下列微分方程描述列写其相应的状态空间表达式,并画出相应的模拟结构图。
解:令,则有相应的模拟结构图如下:1-6(2)已知系统传递函数,试求出系统的约旦标准型的实现,并画出相应的模拟结构图解:1-7给定下列状态空间表达式‘(1)画出其模拟结构图(2)求系统的传递函数解:(2)1-8求下列矩阵的特征矢量(3)解:A的特征方程解之得:当时,解得:令得(或令,得)当时,解得:令得(或令,得)当时,解得:令得1-9将下列状态空间表达式化成约旦标准型(并联分解)(2)解:A的特征方程当时,解之得令得当时,解之得令得当时,解之得令得约旦标准型1-10已知两系统的传递函数分别为W1(s)和W2(s)试求两子系统串联联结和并联连接时,系统的传递函数阵,并讨论所得结果解:(1)串联联结(2)并联联结1-11(第3版教材)已知如图1-22所示的系统,其中子系统1、2的传递函数阵分别为求系统的闭环传递函数解:1-11(第2版教材)已知如图1-22所示的系统,其中子系统1、2的传递函数阵分别为求系统的闭环传递函数解:1-12已知差分方程为试将其用离散状态空间表达式表示,并使驱动函数u的系数b(即控制列阵)为(1)解法1:解法2:求T,使得得所以所以,状态空间表达式为第二章习题答案2-4用三种方法计算以下矩阵指数函数。
现代控制理论第5章答案

现代控制理论第五章习题答案5-1已知系统状态方程为:111001101011x x u -⎡⎤⎡⎤⎢⎥⎢⎥=+⎢⎥⎢⎥⎢⎥⎢⎥⎣⎦⎣⎦试设计一状态反馈阵使闭环系统极点配置为-1,-2,-3。
解:依题意有:2011012112M bAbA b ⎡⎤⎢⎥⎡⎤==⎣⎦⎢⎥⎢⎥⎣⎦3r a n k M =, 系统能控。
系统0(,,)A b C =∑的特征多项式为: 332(1)(1)1321I A λλλλλλ-=---+=-++则将系统写成能控标准I 型,则有010*********x x u ⎡⎤⎡⎤⎢⎥⎢⎥=+⎢⎥⎢⎥⎢⎥⎢⎥--⎣⎦⎣⎦。
引入状态反馈后,系统的状态方程为:()x A bK x bu =++ ,其中3K ⨯为1矩阵,设[]012K k k k =,则系统(,,)KA bK C =∑的特征多项式为:32210()det[()](3)(2)(1)f I A bK k k k λλλλλ=-+=+--+-+-根据给定的极点值,得到期望特征多项式为:*32()(1)(2)(3)6116f λλλλλλλ=+++=+++比较*()()f f λλ与各对应项系数,可解得:012599k k k =-=-=-,则有:[]-5-9-9K =。
5-3有系统:[]21001110x x u y x-⎡⎤⎡⎤=+⎢⎥⎢⎥-⎣⎦⎣⎦= (1) 画出模拟结构图。
(2) 若动态性能不满足要求,可否任意配置极点? (3) 若指定极点为-3,-3,求状态反馈阵。
解(1)系统模拟结构图如下:(2)系统采用状态反馈任意配置极点的充要条件是系统(,,)A b C =∑完全能控。
1110011,01011A b -⎡⎤⎡⎤⎢⎥⎢⎥==⎢⎥⎢⎥⎢⎥⎢⎥⎣⎦⎣⎦对于系统0(,,)A b C =∑有:[]0111M b Ab ⎡⎤==⎢⎥-⎣⎦2rankM =,系统能控,故若系统动态性能不满足要求,可任意配置极点。
(3)系统(,,)A b C =∑的特征多项式为:2(2)(1)32I A λλλλλ-=++=++则将系统写成能控标准I 型,则有010231x x u⎡⎤⎡⎤=+⎢⎥⎢⎥--⎣⎦⎣⎦。
《现代控制理论》习题解答 2016-5-18

2s 7 ( s 3)( s 4) 1-13 G ( s ) 1 s3
1 0 0 x 1 0 x 1-14 2 x 3 a2 0 4 a4 0 x y( z) 2( z 1) 2 1-15 u ( z ) ( z 3z 1)
10 s 26 ( s 2)( s 3)( s 4) 。 2s 10 ( s 2)( s 3)
0 x1 0 u1 y1 1 0 0 0 x2 ; 。 0 u2 y2 0 1 0 0 x3 b2 x4
x1 x2 x3 。 u ; (0 0 0 0 0 1) x4 x 5 x 6
1-04 设状态变量为 x1 i1 , x2 i2 , x3 uC ,状态方程, : x1 i1 , x2 i2 , x3 uC ,状态方程
2( s 2) ( s 1)( s 3) 并联 G ( s ) W1 ( s ) W2 ( s ) 1 s 1
2( s 3) ( s 2)( s 4) 。 s 1 s2
第二章习题解答
1 0 0 A 2-01 (1) 注意 A 0 1 0 1 0 1 2 1 0 A1t 1 1 t ,其中 A1 1 , A2 ,而 e L [( sI A1 ) ] e , 1 2 A2
1 ( s 1)( s 3) 1-18 串联 G ( s ) W2 ( s )W1 ( s ) 1 ( s 1)2 s 2 5s 7 ( s 2)( s 3)( s 4) ; 1 ( s 1)( s 2)
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
第五章 状态反馈和状态观测器3-5-1 已知系统结构图如图题3-5-1图所示。
(1)写出系统状态空间表达式;(2)试设计一个状态反馈矩阵,将闭环极点特征值配置在j 53±-上。
)(t y题3-5-1图【解】:方法一:根据系统结构直接设状态变量如题3-5-1图所示,写状态空间表达式:[]x y u x x 10112101=⎥⎦⎤⎢⎣⎡-+⎥⎦⎤⎢⎣⎡--=& 23111=⎥⎦⎤⎢⎣⎡--=c c U rank U系统能控,可以设计状态反馈阵。
设状态反馈阵为][21k k K = 状态反馈控制规律为:Kx r u -= 求希望特征多项式:34625)3()(*22++=++=s s s s f求加入反馈后的系统特征多项式:)22()3()(1212k s k k s bK A sI s f ++-++=+-=依据极点配置的定义求反馈矩阵:]1316[131634)22(6)3(21112=⎩⎨⎧==⇒⎩⎨⎧=+=+-K k k k k k 方法二:[][][]1316)346(311110)(*10211=++⎥⎦⎤⎢⎣⎡--==--I A A A f U K c方法三:(若不考虑原受控对象的结构,仅从配置极点位置的角度出发) 求系统传递函数写出能控标准型:2321)111()()(2++-=+-+=s s ss s s U s Y []xy u x x 10103210-=⎥⎦⎤⎢⎣⎡+⎥⎦⎤⎢⎣⎡--=& 求系统希望特征多项式:34625)3()(*22++=++=s s s s f求状态反馈矩阵K ~:[][][]33236234~21=--==k k K [][][][]5.05.031111010111=⎥⎦⎤⎢⎣⎡--==--Ab bP⎥⎦⎤⎢⎣⎡-=⎥⎦⎤⎢⎣⎡=105.05.011A P P P []1316~==P K K【解】:依据系统传递函数写出能控标准型ss s s s s s U s Y 2310)2)(1(10)()(23++=++= []x y u x x 0010100320100010=⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡+⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡--=&求系统希望特征多项式:464]1)1)[(2()(*232+++=+++=s s s s s s f求状态反馈矩阵:[][][]144342604321=---==k k k K 。
【解】:系统传递函数无零极点对消,所以系统既能控又能观。
可以通过状态反馈进行极点的任意配置。
另有状态反馈不改变系统的零点。
(1)由闭环传递函数得希望极点为-2,-2,-3。
受控对象传递函数:6522)3)(1)(2()2)(1()(232--+-+=++-+-=s s s s s s s s s s s G 受控对象状态空间表达式的能控标准型:[]xy u x x 112100256100010-=⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡+⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡-=& 希望特征多项式为:12167)3()2()(*232+++=++=s s s s s s f状态反馈矩阵:[][][]5211827516612321=-++==k k k K 。
结构图如图题3-5-3图1所示:题3-5-3图1(2)由闭传递函数得希望极点为-1,1,-3。
希望特征多项式为:33)3)(1)(1()(*23--+=+-+=s s s s s s s f状态反馈矩阵:[][][]143235163321=-+-+-==k k k K 。
结构图如图题3-5-3图2所示:题3-5-3图23-5-4 已知系统状态空间表达式为[]xy u x x 210011*********-=⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡+⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡---=&,试判断系统的能控性和能观性,若不完全能控,用结构分解将系统分解为能控和不能控的子系统,并讨论用状态反馈是否可以使闭环系统稳定。
【解】:判系统的能控性和能观性:[]2,2103111012=⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡---==c c rankU b A AbbU2,432321210020=⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡----=⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡=rankV CA CA C V系统不能控不能观。
按能控性进行结构分解: 取⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡--=⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡=-111011001,1100110011c c R R 分解后的状态空间表达式为:[]⎥⎦⎤⎢⎣⎡--=⎥⎦⎤⎢⎣⎡=⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡+⎥⎦⎤⎢⎣⎡⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡-----=+⎥⎦⎤⎢⎣⎡=⎥⎦⎤⎢⎣⎡--c c c c c c c c c c c c c c x x x x CR y u x x u b R x x AR R x x 211)(001100221110)()(11&&因为不能控分量对应的特征值为-1,因此对系统的稳定性无影响,所以可以通过状态反馈的方法,对能控子空间进行极点的任意配置(左半平面),从而使系统稳定。
【解】:被控对象状态空间表达式的能控标准型: 因为系统的传递函数可写成:23231)3()1()(s s s s s s s G ++=++=所以能控标准型为:[]xy u x x 011100300100010=⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡+⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡-=& 闭环后的希望特征多项式为:485)1()2()(*232+++=++=s s s s s s f状态反馈系数阵:[][][]284350804321=---==k k k K 。
闭环传递函数为:2223)2(1)1()2(14851)(+=+++=++++=s s s s s s s s s G b系统闭环传递函数出现零极点对消现象,又有原受控对象本身能控,且状态反馈不改变系统的能控性,所以该闭环系统不能观。
3-5-6 已知系统状态方程为u x x ⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡+⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡--=100130100001&,试判断系统是否可以通过状态反馈分别配置以下两组特征值:(1){-2,-2,-1};(2){-2,-2,-3}。
若能配置,求出反馈阵。
【解】:判系统的能控性:[]2,2111100002=⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡-==c c rankU b A AbbU系统不能控.按能控性分解: 取⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡-=⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡=-001010110,0110101001c c R Ru x x u b R x x AR R x x c cc c c c c c c ⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡+⎥⎦⎤⎢⎣⎡⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡--=+⎥⎦⎤⎢⎣⎡=⎥⎦⎤⎢⎣⎡--001100011030)()(11&& 不能控子空间的特征值为-1。
(1)对能控子空间进行极点配置,极点位置在-2,-2:u x x c c ⎥⎦⎤⎢⎣⎡+⎥⎦⎤⎢⎣⎡-=011130&44)2()(*22++=+=s s s s f [][])(*10121A f U k k K c -==[][]65)10014113041130(10011021=⎥⎦⎤⎢⎣⎡+⎥⎦⎤⎢⎣⎡-+⎥⎦⎤⎢⎣⎡-⎥⎦⎤⎢⎣⎡=-所以[]065=K原系统的状态反馈阵K 为:1-=c R K K[][]510001*********=⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡-⨯=K(2)因为状态反馈不能改变不能控部分的极点,而不能控部分的极点为-1,所以不能通过状态反馈将极点配置在{-2,-2,-3}。
3-5-7 已知系统状态空间表达式为[]xy u x x 01100010=⎥⎦⎤⎢⎣⎡+⎥⎦⎤⎢⎣⎡=&,试设计一个状态观测器,使状态观测器的极点为-r ,-2r ,(r>0)。
【解】:方法一:判能观性2,100100=⎥⎦⎤⎢⎣⎡=⎥⎦⎤⎢⎣⎡=rankV CA C V 。
系统能观,可以构造状态观测器。
确定观测器的希望特征多项式:2223)2)(()(*r rs s r s r s s f ++=++=确定观测矩阵[]T l l L 21=,观测器的特征多项式为:[]2122101001000)()(l s l s l l s s LC A sI s f ++=⎥⎦⎤⎢⎣⎡+⎥⎦⎤⎢⎣⎡-⎥⎦⎤⎢⎣⎡=--= )()(*s f s f =⎪⎩⎪⎨⎧==⇒22123r l r l 方法二:⎥⎦⎤⎢⎣⎡=⎥⎦⎤⎢⎣⎡=-10)(*1021V A f l l L⎥⎦⎤⎢⎣⎡=⎥⎦⎤⎢⎣⎡⎥⎦⎤⎢⎣⎡⎪⎭⎪⎬⎫⎪⎩⎪⎨⎧⎥⎦⎤⎢⎣⎡+⎥⎦⎤⎢⎣⎡+⎥⎦⎤⎢⎣⎡=-21222310001000102001030010r r r r方法三:被控对象特征多项式:20010)(s sI A sI s f =⎥⎦⎤⎢⎣⎡-=-= 确定观测器的希望特征多项式:2223)2)(()(*r rs s r s r s s f ++=++=对应于能观标准型的观测器矩阵:⎥⎥⎦⎤⎢⎢⎣⎡=⎥⎥⎦⎤⎢⎢⎣⎡--=⎥⎦⎤⎢⎣⎡--=⎥⎦⎤⎢⎣⎡=r r r r a a a a l l L 320302**22110021 对应于原系统的观测器矩阵:[]⎥⎦⎤⎢⎣⎡==⎥⎦⎤⎢⎣⎡=⎥⎦⎤⎢⎣⎡=-0110,101011101Ap p P V P o ⎥⎦⎤⎢⎣⎡=⎥⎥⎦⎤⎢⎢⎣⎡⎥⎦⎤⎢⎣⎡==2223320110r r r r L P L o 3-5-8已知系统的状态空间表达式为[]xy u x x 011102101110321=⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡+⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡------=& (1)设计一个全维观测器,将观测器的极点配置在-3,-4,-5处。
(2)设计一个降维观测器,将观测器的极点配置在-3,-4处。
(3)画出其结构图。
【解】: (1)方法一: 确定能观性:3,1053431011020=⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡----=⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡=rankV CA CA C V系统能观,可设计观测器。
求希望特征多项式:604712)5)(4)(3()(*23+++=+++=s s s s s s s f求观测器特征多项式:LC A sI s f +-=)(计算观测器系数矩阵:令)()(*s f s f =得⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡--=5.135.155.6L方法二:⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡--=⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡=⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡=-5.135.155.6100)(*10321V A f l l l L 结构图如图题3-5-8图1所示:题3-5-8图1(2)确定降维观测器的维数:m=1,n=3,则n-m= 2。
分解输出系数矩阵c ,获得线性变换矩阵T ,对原状态空间表达式进行线性变换,使各输出变量y 变成各状态变量的单值函数:[][][]01,1,0112121====c c c c C⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡=⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡-=⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡=⎥⎦⎤⎢⎣⎡=---⨯100010011,10001001110001001101112221T I c c T []1,001x y CT C ===,111110421222112111⎥⎦⎤⎢⎣⎡=⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡-------==-A AA A AT T A[]⎥⎦⎤⎢⎣⎡----=⎥⎦⎤⎢⎣⎡=--=-=1111,10,42,122211211A A A A⎥⎦⎤⎢⎣⎡==⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡==-10,2,102211B B B T B 计算线性变换后降维观测器的反馈矩阵1221⨯⎥⎦⎤⎢⎣⎡=l l L (一个输出两个状态)127)4)(3()(*2++=++=s s s s s f[]42111100)()(211222--⎥⎥⎦⎤⎢⎢⎣⎡+⎥⎦⎤⎢⎣⎡-----⎥⎦⎤⎢⎣⎡=--=l l s s A L A sI s f )22()224(21122l l s l l s -++--+= ⎥⎦⎤⎢⎣⎡-=⎥⎥⎦⎤⎢⎢⎣⎡=⇒=8333.21667.3)()(*21l l L s f s f 求降维状态观测器的状态方程(状态变量z )u y z z u B L B y A L A y L z A L A zzz⎥⎦⎤⎢⎣⎡-+⎥⎦⎤⎢⎣⎡-+⎥⎦⎤⎢⎣⎡⎥⎦⎤⎢⎣⎡-=-+-++-=⎥⎦⎤⎢⎣⎡=6667.63333.612133333.126667.66667.113333.5)()())((21121121122221&&&求降维状态观测器的输出方程(系统针对于线性变换后的状态信号⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡=321ˆˆˆˆx x x x )⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡-+=⎥⎦⎤⎢⎣⎡+=⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡y z y z y y L z y x x x 8333.21667.3ˆˆˆ21321求对应于原系统的降维状态观测器的状态信号xˆ: ⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡-+--==⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡=y z y z y z x T x x x x 8333.21667.31667.2ˆˆˆˆˆ211311绘制模拟结构图依据受控对象,降维观测器的状态方程,以及 原系统的降维观测器的输出方程:⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡-+--=⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡=y z y z y z x x xx 8333.21667.31667.2ˆˆˆˆ211321结构图如图题3-5-8图2所示:2ˆx题3-5-8图2(2)确定一个全维状态观测器,并使观测器的极点全部为-5; (3)确定一个降维状态观测器,并使观测器的极点在-5处; (4)分别画出闭环系统的结构图。
