必修三、必修五复习题一

合集下载

岳麓版必修三第五单元过关题1

岳麓版必修三第五单元过关题一、选择题（共20小题，每题2．5分，共50分）鸦片战争后，西方文化与中国传统文化碰撞交汇。

据此回答1—5题。

1、“善师四夷者，能治四夷；不善师夷者，外夷制之。

“这种思想最早出现在解析：选A 。

题干体现的是“师夷长技以制夷”的思想，最早在《海国图志》中体现出来。

故选A 项。

2、在洋务派与顽固派的“体用之争”中，两者的斗争焦点不可能包括A 、是否修建铁路、开矿山、兴电报B 、是否维护清政府的统治C 、是否在同文馆中增设天文算学馆D 、是否派遣留学生解析：选B 。

本题考查学生的比较归纳能力。

洋务派与顽固派都代表封建地主阶级，都主张维护清政府的统治，二者的分歧在于用什么手段去维护清政府的统治。

3、“不可变者，伦幻也，非法制也；圣道也，非机械也；心术也，非工艺也。

”这种说法应归属于A 、西学东渐成B 、西学中用C 、中体西用D 、西体中用解析：选C 。

本题考查学生对材料的理解分析能力。

材料强调中国传统的道德、体制是不能变的，能变的是中国的技术，是典型的中体西用思想。

4、“洋人制胜之道，专以轮船、火器为先……又本之天文度数，参以勾股算法，故能巧法其中。

”体现的观点属于A 、顽固派B 、洋务派C 、早期维新派D 、维新派解析：选B 。

本题考查学生对材料的理解分析能力。

材料中强调了西方技术的先进，说明这一派别认识到了西方技术的先进，中国技术的落后，但仅停留于物质层面，这与洋务派的观点是相符的。

5、从鸦片战争前后到期19世纪90年代，中国思想界的发展历程是A 、中体西用-----开眼看世界----维新变法B 、开眼看世界----维新变法-----中体西用C 、开眼开世界----追求民主共和-----维新变法D 、开眼看世界----中体西用------维新变法解析：选D 。

鸦片战争前后林则徐等人认识到中国的落后主张学习外国先近技术，开始开眼开世界，19世纪60年代洋务派出现后以“中体西用“为指导思想发展近代工业，洋务运动的失败让国人看到学习西方技术无法挽救中国，于是掀起了变法运动。

新人教A 必修一,必修二,必修三,必修四,必修五,选修2-1综合试题(2)

假期作业一、选择题：1．函数)4(log 3-=x y 的定义域为（）A ．RB ．),4()4,(+∞-∞C ．)4,(-∞D ． ),4(+∞ 2. 设a R ∈，则1a >是11a< 的（）（A ）充分但不必要条件（B ）必要但不充分条件（C ）充要条件（D ）既不充分也不必要条件3．s in14ºcos16º+cos14ºsin16º的值是（）A ．23 B ．21 C ．23 D ．-21 4．若集合{}{}084|,51|<+-=<-=x x B x x A ，则=B A （） A ．{}6|<x x B ．{}2|>x x C ．{}62|<<x x D ． Φ5．某电视台在娱乐频道节目播放中，每小时播放广告20分钟，那么随机打开电视机观看这个频道看到广告的概率为（） A ．12 B ．13 C ．14 D ．166．下面为一个求20个数的平均数的程序,在横线上应填充的语句为( )A.i>20B.i<20C.i>=20D.i<=207．在等比数列{}n a 中，)(0*N n a n ∈>且,16,464==a a 则数列{}n a 的公比q 是（）A ．1B ．2C ．3D ．48．已知a =),sin ,23(αb =)31,(cos α且a ∥b ，则锐角α的大小为（）A ．6π B ．3πC ．4πD ．125π9．如图所示，一个空间几何体的正视图和侧视图都是边长为2的正方形，俯视图是一个圆，那么这个几何体的体积为（） A ．2πB ．πC ．2πD ．4π 10．已知函数b x x x f +-=2)(2在区间)4,2(内有唯一零点，则b 的取值范围是（） A ． R B ．)0,(-∞ C ．),8(+∞- D ．)0,8(-11．已知x>0,设xx y 1+=，则（） A ．y ≥2 B ．y ≤2 C ．y=2 D ．不能确定12．三个数21log ,)21(,33321===c b a 的大小顺序为（）A ．a c b <<B ．c a b <<C ．b a c <<D ．a b c <<13 ．已知中心在原点的椭圆C 的右焦点为(1,0)F ,离心率等于21,则C 的方程是（）A ．14322=+y x B ．13422=+y x C ．12422=+y x D ．13422=+y x（文）设函数f （x ）=2x+lnx 则（） A ．x=12为f(x)的极大值点 B ．x=12为f(x)的极小值点 C ．x=2为 f(x)的极大值点 D ．x=2为 f(x)的极小值点二、填空题：本大题共5小题，每小题4分，共20分。

高一数学必修3、5综合试卷

高一下学期数学必修二、五综合复习试题一、选择题：（本大题共12小题，每小题5分，共60分．） 1．下列命题正确的是（）A. 经过三点确定一个平面B. 经过一条直线和一个点确定一个平面C. 三条平行直线必共面D. 两两相交且不共点的三条直线确定一个平面 2．已知A(2,4)与B(3,3)关于直线l 对称，则直线l 的方程为(A) x ＋y ＝0 (B) x －y ＝0 (C) x ＋y －6＝0 (D) x －y ＋1＝0 3．如图是由圆柱与圆锥组合而成的几何体的三视图，则该几何体的表面积为A. 20πB. 24πC. 28πD. 32π4．某圆柱的高为2，底面周长为16，其三视图如右图．圆柱表面上的点在正视图上的对应点为，圆柱表面上的点在左视图上的对应点为，则在此圆柱侧面上，从A 到B 的路径中，最短路径的长度为A. B. C. D. 25．如图，在正方体1111ABCD A B C D -中， E 为线段11A C 的中点，则异面直线DE 与1B C 所成角的大小为（）A.3π B. 4π C. 6πD. 12π6．若直线l 过点()0,A a ，斜率为1，圆224x y +=上恰有1个点到l 的距离为1，则a 的值为（）A. 32B. 32±C. 2±D. 2±7．在△ABC 中，45,2==A a ，若此三角形有两解，则b 的范围为（） A ．222<<b B ．b > 2 C ．b<2 D ．221<<b8．在△ABC 中，若sinC+sin （B ﹣A ）=sin2A ，则△ABC 的形状为（） A ．等腰三角形 B ．直角三角形C ．等腰直角三角形D ．等腰三角形或直角三角形9．设,x y 满足约束条件2330233030x y x y y +-≤⎧⎪++≥⎨⎪+≥⎩，则2z x y =+的最小值是A. B. C. D.10．如图，在下列四个正方体中，A ，B 为正方体的两个顶点，M ，N ，Q 为所在棱的中点，则在这四个正方体中，直线AB 与平面MNQ 不平行的是A. B.C. D.11．甲船在岛A 的正南方B 处，10AB =千米，甲船以每小时千米的速度向正北航行，同时乙船自出发以每小时千米的速度向北偏东的方向驶去，当甲，乙两船相距最近时，它们所航行的时间是（）A. 分钟B. 分钟C. 分钟D. 分钟 12．对于使22x x M -+≤成立的所有常数M 中，我们把M 的最小值1叫做22x x -+的上确界,若,,1a b R a b +∈+=且，则122a b--的上确界为（） A ．92 B ．92- C ．41D ．4-二、填空题（本大题共4小题，每小题5分，共20分．）13．如图，正方形''''A B C D 的边长为(0)acm a >，它是一个水平放置的平面图形的直观图，则它的原图形ABCD 的周长是__________2cm ．14．在平面直角坐标系中，经过三点（0，0），（1，1），（2，0）的圆的方程为__________． 15．已知直线(1)20k x y +++=恒过定点C ，且以C 为圆心，5为半径的圆与直线3410x y ++=17．已知圆C 的方程：224x y +=和直线l 的方程：34120x y ++=，点P 是圆C 上动点，直线l 与两坐标轴交于A 、B 两点．(1)求与圆C 相切且垂直于直线l 的直线方程； (2)求ABC ∆面积的取值范围。

高中语文必修五基础知识复习题及答案.doc

高中语文必修五基础知识复习题及答案.doc高中语文必修五基础知识复习题及答案一、本大题共 4 小题，每小题 3 分，共 12 分1、下列加点字的注音全都正确的一项是()A. 蓬蒿(g āo) 迤逦(y ǐ) 簪笏(z ān) 玷辱(di àn)B. 尴尬(g ān) 洗漱(sh ù) 毡笠(zh ān) 讥诮(xi ào)C.庇护(b ì) 央浼(mi ǎn) 降服(xi áng) 怂恿(s ǒng)D.凫水(f ú) 酒馔(zhu àn) 斜睨(n ì) 笑靥(y è)2.下列词语中没有错别字的一组是 ()A.老当益壮一愁莫展斐然成章沧海一粟B.相形见绌沐浴清化携幼入室意气用事A.李科长在办公室里来回踱着，瞻前顾后，再也想不出一点可以向上级汇报的“成果”。

B.有时书中的人物命运，引起我的沉思和联想，凝视着窗外神秘的夜空，不免出神入化。

D.一个远涉重洋、寄身美国、茕茕孑立的中国弱女子，要控告有钱有势的美国地头蛇是何等艰难 !4.下列各句中，没有语病的一句是 ()A.最后一位火炬手抵达位于伊斯坦布尔市中心的塔克希姆广场，并点燃圣火盆，这标志着伊斯坦布尔的火炬传递圆满结束。

C.几组蝴蝶展框吸引了参观者，大家都以为这是标本，看到殿框上方“仿真蝴蝶微型风筝”的标志，使大家恍然大悟。

二、本大题 22 题，每小题 2 分，共 66 分A. 小知不及大知B. 臣以险衅，夙遭闵凶C.云销雨霁，彩彻区明D.携幼入室，有酒盈樽6.下列各句中没有通假字的一项是 ()A、辩乎荣辱之境B、适百里者，宿舂粮 ;7.指出各句加点词解释有误的一项是 ()A 、复驾言兮焉求言：助词B、悟已往之不谏谏：进谏C、既自以心为形役役：奴役D、三径就荒就：接近8.选出“故”与“豫章故郡，洪都新府”的“故”意思相同的一项()A. 扶苏以数谏故，上使外将兵。

人教版高中语文必修1-5文学常识专题复习

高中语文必修1-5文学常识专题复习（一）必修一1.《烛之武退秦师》《左传》，相传为春秋末年答因史官左丘明所作。

“传”意为注释，《左传》是给儒家经典《春秋》所作的注释性文字，所以它又被称为《左氏春秋》《春秋左氏传》（简称《左传》），与《公羊传》《谷梁传》合称“春秋三传”。

《左传》是我国第一部叙事详细的编年史著作，同时也是杰出的散文巨著。

它主要记载了东周前期二百四五十年间各国政治、经济、军事、外交和文化方面的重要事件和重要人物，在一定程度上真实地反映了那个时代的风貌，是研究我国先秦历史很有价值的文献，同时又有极高的文学价值。

2.《荆轲刺秦王》《战国策》，是一部战国时代的史料汇编，也是一部重要的散文集。

作者已不可考。

最初有《国策》《国事》《短长》《事语》《长书》《修书》等名称，经汉代刘向整理编辑，始定名为《战国策》。

全书共三十三卷，分国别编辑，依次是：东周一卷，西周一卷，秦五卷，齐六卷，楚四卷，赵四卷，魏四卷，韩三卷，燕三卷，宋、卫合一卷，中山一卷。

箕踞，两脚张开，两膝微曲地坐着，形似箕，叫作“箕踞”。

这种姿势是表示傲视对方的意思。

跪，与坐不同，往往在有急事或表示谢罪之时，直身，两股也离开了脚跟。

所以前人指出跪与坐二者的区别是“跪危而坐安”。

如《史记•刺客列传》：“荆轲遂见太子，言田光已死，致光之言。

太子再拜而跪，膝行流涕。

”跪也表示对长者的尊敬。

如《史记•魏其武安侯列传》：“（田蚡）往来侍酒魏其，跪起如子侄。

”3.《鸿门宴》《史记》，是我国第一部纪传体通史，记载了从传说中的黄帝到汉我帝元狩元年（前122）三千年左右的历史。

鲁迅评其为“史家之绝唱，无韵之《离骚》”。

古代“座次”问题（1）官职：古代以右为尊。

如“位在廉颇之右”。

（朝代不同有変化）（2）车骑：以左为尊。

如信陵君屋左以待侯生：“坐定，公子从车骑，虚左。

”（3）室内：室内座位以坐西朝东的方向为最尊，其左手位为次，右手位更次，对面为最次。

（4）堂上座位：北为帝（尊），南为臣（卑）。

高中物理必修3物理全册全单元精选试卷复习练习(Word版含答案)

高中物理必修3物理全册全单元精选试卷复习练习(Word 版含答案)一、必修第3册静电场及其应用解答题易错题培优（难）1．我们可以借鉴研究静电场的方法来研究地球周围空间的引力场，如用“引力场强度”、“引力势”的概念描述引力场。

已知地球质量为M ，半径为R ，万有引力常量为G ，将地球视为均质球体，且忽略自转。

(1)类比电场强度的定义方法，写出地球引力场的“引力场强度E ”的定义式，并结合万有引力定律，推导距离地心为r （r >R ）处的引力场强度的表达式2=GM E r 引； (2)设地面处和距离地面高为h 处的引力场强度分别为E 引和'E 引，如果它们满足'0.02E E E -≤引引引，则该空间就可以近似为匀强场，也就是我们常说的重力场。

请估算地球重力场可视为匀强场的高度h （取地球半径R =6400km ）；(3)某同学查阅资料知道:地球引力场的“引力势”的表达式为=-G Mrϕ引（以无穷远处引力势为0）。

请你设定物理情景，简要叙述推导该表达式的主要步骤。

【答案】(1)引力场强度定义式FE m=引，推导见解析；(2)h =64976m ；(3)推导见解析. 【解析】【分析】【详解】(1)引力场强度定义式F E m=引 2MmF Gr = 联立得2M E Gr =引 (2)根据题意2M E GR =引 '2M E G r=引 '0.02E E E -=引引引h r R R =-=解得h =64976m(3)定义式引力势=p E mϕ引，式中p E 为某位置的引力势能把某物体从无穷远移动到某点引力做的功=0-=-p p W E E 引即=-p E W 引则当质量为m 的物体自无穷远处移动到距离地球r 处时，引力做功为W 引通过计算得0MmW Gr =引＞所以=-p MmE Gr =-M Grϕ引2．万有引力和库仑力有类似的规律，有很多可以类比的地方。

必修三和必修五期末复习训练题一(详解参考答案)

2017—2018学年（下）高一数学期末训练题（一）Array命题人: 杨凤升一、选择题：（本大题包括12小题，每小题5分，共60分，每小题给出的四个选项中，只有一项．．．．是符合题目要求的，请将正确选项填涂在答题卡上）1．若a＞b＞0，且ab=1，则下列不等式成立的是（）A．a+＜＜log2（a+b））B．＜log2（a+b）＜a+C．a+＜log2（a+b）＜D．log2（a+b））＜a+＜【解答】解：∵a＞b＞0，且ab=1，∴可取a=2，b=．则=4，==，log2（a+b）==∈（1，2），∴＜log2（a+b）＜a+．故选：B．2．传承传统文化再掀热潮，在刚刚过去的新春假期中，央视科教频道以诗词知识竞赛为主的《中国诗词大会》火爆荧屏，如图的茎叶图是两位选手在个人追逐赛中的比赛得分，则下列说法正确的是（）A．甲的平均数大于乙的平均数B．甲的中位数大于乙的中位数C．甲的方差大于乙的方差 D．甲的平均数等于乙的中位数【解答】解：由茎叶图，知：=（59+45+32+38+24+26+11+12+14）=29，=（51+43+30+34+20+25+27+28+12）=30，S2甲=[302+162+32+92+（﹣5）2+（﹣3）2+（﹣18）2+（﹣17）2+（﹣15）2]≈235.3，S2乙=[212+132+02+42+（﹣10）2+（﹣5）2+（﹣3）2+（﹣2）2+（﹣18）2]≈120.9，甲的中位数为：26，乙的中位数为：28，∴甲的方差大于乙的方差．故选：C．3．设S n为等差数列{a n}的前n项和，S8=4a3，a7=﹣2，则a9=（）A．﹣6 B．﹣4 C．﹣2 D．2【解答】解：∵S n为等差数列{a n}的前n项和，S8=4a3，a7=﹣2，∴，解得a1=10，d=﹣2，∴a9=a1+8d=10﹣16=﹣6．故选：A．4．为了研究某班学生的脚长x（单位：厘米）和身高y（单位：厘米）的关系，从该班随机抽取10名学生，根据测量数据的散点图可以看出y与x之间有线性相关关系，设其回归直线方程为=x+，已知x i=225，y i=1600，=4，该班某学生的脚长为24，据此估计其身高为（）A．160 B．163 C．166 D．170【解答】解：由线性回归方程为=4x+，则=x i=22.5，=y i=160，则数据的样本中心点（22.5，160），由回归直线方程样本中心点，则=﹣4x=160﹣4×22.5=70，∴回归直线方程为=4x+70，当x=24时，=4×24+70=166，则估计其身高为166，故选C．5．二次不等式ax2+bx+1＞0的解集为{x|﹣1＜x＜}，则ab的值为（）A．﹣5 B．5 C．﹣6 D．6【解答】解：∵不等式ax2+bx+1＞0的解集为{x|﹣1＜x＜}，∴a＜0，∴原不等式等价于﹣ax2﹣bx﹣1＜0，由韦达定理知﹣1+=﹣，﹣1×3=，∴a=﹣3，b=﹣2，∴ab=6．故选D6．两个等差数列{a n}，{b n}，记数列{a n}，{b n}的前n项的和分别为S n，T n，且=，则=（）A．B．C．D．【解答】解：分别设a n=kn，b n=k（n+1），k≠0为常数．则S6==21k，T3==9k，∴==．故选：D．7．如图，一货轮航行到M处，测得灯塔S在货轮的北偏东15°，与灯塔S相距20n mile，随后货轮按北偏西30°的方向航行30min后，又测得灯塔在货轮的东北方向，则货轮的速度为（）A．20（+）n mile/h B．20（﹣）n mile/hC．20（+）n mile/h D．20（﹣）n mile/h【解答】解：由题意知SM=20，∠NMS=45°，∴SM与正东方向的夹角为75°，MN与正东方向的夹角为，60°∴SNM=105°∴∠MSN=30°，△MNS中利用正弦定理可得，=．MN==10（）n mile，∴货轮航行的速度v==20（） n mile/h．故选：B．8．某校高二年级共有24个班，为了解该年级学生对数学的喜爱程度，将每个班编号，依次为1到24，现用系统抽样方法抽取4个班进行调查，若抽到的编号之和为52，则抽取的最小编号是（）A．2 B．3 C．4 D．5【解答】解：24个班分为4组，抽取间隔为24÷4=6．设抽到的最小编号为x，得：4x+=52，解得：x=4，故选：C．9．在平面上，过点P作直线l的垂线所得的垂足称为点P在直线l上的投影，由区域中的点在直线x+y﹣2=0上的投影构成的线段记为AB，则|AB|=（）A．2B．4 C．3D．6【解答】解：作出不等式组对应的平面区域如图：（阴影部分），区域内的点在直线x+y﹣2=0上的投影构成线段R′Q′，即SAB，而R′Q′=RQ，由得，即Q（﹣1，1）由得，即R（2，﹣2），则|AB|=|QR|===3，故选：C10.执行如图所示的程序框图，若输入的x，y∈R，那么输出的S的最大值为（）A．0 B．1 C．2 D．3【解答】解：由程序框图知：算法的功能是求可行域内，目标还是S=2x+y 的最大值，画出可行域如图：当时，S=2x+y的值最大，且最大值为2．故选：C．11.△ABC中，若，则的值为（）A．2 B．4 C．D．2【解答】解：△ABC中，∵，即+=，∴bc•cos（π﹣A）+ac•cosB=c2，∴a•cosB﹣b•cosA=c，∴a•﹣b•=，即 a2﹣b2=c2．∴=====4，故选：B．12．将正方形ABCD分割成n2（n≥2，n∈N）个全等的小正方形（图1，图2分别给出了n=2，3的情形），在每个小正方形的顶点各放置一个数，使位于正方形ABCD 的四边及平行于某边的任一直线上的数都分别依次成等差数列，若顶点A，B，C，D处的四个数互不相同且和为1，记所有顶点上的数之和为f（n），则f（4）=（）A．4 B．B6 C．D．【解答】解：根据题意可判断：使位于正方形ABCD的四边及平行于某边的任一直线上的数都分别依次成等差数列，所以每一横行上的数据的和也为等差数列，设{a n}为第n横行上的数据的和，∴a1=（D+A），a4=（B+C），∴a1+a2+a3+a4=（a1+a4）=（A+B+C+D），∵A，B，C，D处的四个数互不相同且和为1，∴×1=故选：C第Ⅱ卷（非选择题，共90分）二、填空题(本大题包括4小题，每小题5分，共20分，把正确答案填在答题卡中的横线上）13．三进制数2 012(3)化为六进制数为abc(6)，则a＋b＋c＝________.解析：2 012(3)＝2×33＋0×32＋1×31＋2×30＝59.三进制数2 012(3)化为六进制数为135(6)，∴a＋b＋c＝9.答案：914．在区间[0，5]上随机地选择一个数p，则方程x2+2px+3p﹣2=0有两个负根的概率为．【解答】解：方程x2+2px+3p﹣2=0有两个负根等价于，解关于p的不等式组可得＜p≤1或p≥2，∴所求概率P==故答案为：15．若△ABC的内角满足sinA+sinB=2sinC，则cosC的最小值是．【解答】解：由正弦定理得a+b=2c，得c=（a+b），由余弦定理得cosC====≥=，当且仅当时，取等号，故≤cosC＜1，故cosC的最小值是．故答案为：．16．已知数列{a n}、{b n}满足b n=lna n，n∈N*，其中{b n}是等差数列，且，则b1+b2+…+b1009= 2018 ．【解答】解：数列{a n}、{b n}满足b n=lna n，n∈N*，其中{b n}是等差数列，∴b n+1﹣b n=lna n+1﹣lna n=ln=常数t．∴=常数e t=q＞0，因此数列{a n}为等比数列．且，∴a1a1009=a2a1008==…．则b 1+b2+…+b1009=ln（a1a2…a1009）==lne2018=2018．故答案为：2018．三、解答题：（本大题包括6小题，共70分，解答应写出文字说明，证明过程或演算步骤）17．（本小题满分10分）某连锁经营公司所属5个零售店某月的销售额和利润额资料如下表：商店名称 A B C D E 销售额x（千万元） 3 5 6 7 9利润额y（千万元） 2 3 3 4 5 （Ⅰ）用最小二乘法计算利润额y对销售额x的回归直线方程；（Ⅱ）当销售额为4（千万元）时，估计利润额的大小．附：线性回归方程中，，．【解答】解：（Ⅰ）设回归直线的方程是：，，∴==0.5，=0.4，∴y对销售额x的回归直线方程为：=0.5x+0.4；﹣﹣﹣﹣﹣﹣（8分）（Ⅱ）当销售额为4（千万元）时，利润额为：=0.5×4+0.4=2.4（千万元）．﹣﹣﹣（12分）18．（本小题满分12分）从某学校的800名男生中随机抽取50名测量身高，被测学生身高全部介于155cm和195cm之间，将测量结果按如下方式分成八组：第一组[155，160），第二组[160，165），…，第八组[190，195]，下图是按上述分组方法得到的频率分布直方图的一部分，已知第一组与第八组人数相同，第六组的人数为4人．（Ⅰ）求第七组的频率；（Ⅱ）估计该校的800名男生的身高的中位数以及身高在180cm以上（含180cm）的人数；（Ⅲ）若从身高属于第六组和第八组的所有男生中随机抽取两名男生，求抽出的两名男生是在同一组的概率．【解答】解：（Ⅰ）第六组的频率=0.08，所以第七组的频率为1﹣0.08﹣5×（0.008×2+0.016+0.04×2+0.06）=0.06；（Ⅱ）身高在第一组[155，160）的频率为0.008×5=0.04，身高在第二组[160，165）的频率为0.016×5=0.08，身高在第三组[165，170）的频率为0.04×5=0.2，身高在第四组[170，175）的频率为0.04×5=0.2，由于0.04+0.08+0.2=0.32＜0.5，0.04+0.08+0.2+0.2=0.52＞0.5，估计这所学校的800名男生的身高的中位数为m，则170＜m＜175，由0.04+0.08+0.2+（m﹣170）×0.04=0.5得m=174.5所以可估计这所学校的800名男生的身高的中位数为174.5，由直方图得后三组频率为0.06+0.08+0.008×5=0.18，所以身高在180cm以上（含180cm）的人数为0.18×800=144人；（Ⅲ）第六组[180，185）的人数为4人，设为a，b，c，d，第八组[190，195]的人数为2人，设为A，B，则从中抽两名的情况有ab，ac，ad，bc，bd，cd，aA，bA，cA，dA，aB，bB，cB，dB，AB共15种，其中抽出的两名男生是在同一组的有ab，ac，ad，bc，bd，cd，AB共7种情况，故抽出的两名男生是在同一组的概率为．19.（本小题满分12分）已知向量=（2，1），=（x，y）．（1）若x∈{﹣1，0，1，2}，y∈{﹣1，0，1}，求向量∥的概率；（2）若x∈[﹣1，2]，y∈[﹣1，1]，求向量，的夹角是钝角的概率．【解答】解：（1）由题意知本题是一个等可能事件的概率，设“∥”为事件A，由∥，得x=2y．Ω={（﹣1，﹣1），（﹣1，0），（﹣1，1），（0，﹣1），（0，0），（0，1），（1，﹣1），（1，0），（1，1），（2，﹣1），（2，0），（2，1）}共包含12个基本事件；其中A={（0，0），（2，1）}，包含2个基本事件．则．（2）设“两个向量的夹角是钝角”为事件B，由两个向量的夹角是钝角，可得＜0，即2x+y＜0，且x≠2y．则．20．（本小题满分12分）解关于x的不等式[（m+3）x﹣1]（x+1）＞0（m∈R）．【解答】解：下面对参数m进行分类讨论：①当m=﹣3时，原不等式为x+1＞0，∴不等式的解为{x|x＜﹣1}．②当m＞﹣3时，原不等式可化为．∵，∴不等式的解为{x|x＜﹣1或．③当m＜﹣3时，原不等式可化为．∵，当﹣4＜m＜﹣3时，原不等式的解集为；当m＜﹣4时，原不等式的解集为；当m=﹣4时，原不等式无解，即解集为∅．（11分）综上述，原不等式的解集情况为：①当m＜﹣4时，解集为；②当m=﹣4时，无解，即∅；③当﹣4＜m＜﹣3时，解集为；④当m=﹣3时，解集为{x|x＜﹣1}；⑤当m＞﹣3时，解集为{x|x＜﹣1或．21.（本小题满分12分）已知a，b，c分别为△ABC三个内角A，B，C的对边，（1）求A的大小；（2）若a=7，求△ABC的周长的取值范围．【解答】解：（1）∵，∴由正弦定理可得，∴sinAcosC+sinAsinC=sin（A+C）+sinC，∴sinA﹣cosA=1，∴sin（A﹣30°）=，∴A﹣30°=30°，∴A=60°；（2）由题意，b＞0，c＞0，b+c＞a=7，∴由余弦定理49==（b+c）2﹣3bc≥（b+c）2（当且仅当b=c时取等号），∴b+c≤14，∵b+c＞7，∴7＜b+c≤14，∴△ABC的周长的取值范围为（14，21]．22．（本小题满分12分）已知数列{a n}是等差数列，a5=5，若（6﹣a1）=a2+a3，且A、B、C三点共线（O为该直线外一点）；点列（n，b n）在函数x关于y=x对称的图象上．（1）求a n和b n；（2）记数列C n=a n b n+b n（n∈N*），若{C n}的前n项和为T n，求使不等式成立的最小自然数n的值．【解答】解：（1）设数列{a n}的公差为d，则∵（6﹣a1）=a2+a3，且A、B、C三点共线，∴由三点共线的条件，可得6﹣a1=a2+a3，∴a1+d=2，∵a5=5，∴a1+4d=5，∴d=1，a1=1，∴a n=n；∵点列（n，b n）在函数x的关于y=x对称的图象上∴；（2）C n=a n b n+b n=，∴T n=，∴T n=两式相减，可得T n==∴T n=∴3﹣T n=∴等价于∴n＞6∴使不等式成立的最小自然数n的值为7．。

高考必修三专题三四五试题

必修三专题三四五试题1．（2012·上海单科卷·22）“一切传统均不再神圣。

无政府主义、自由主义、唯物主义、实验主义……以及最新的布尔什维克主义，均找到支持者。

”上述情景出现于A．戊戌变法时期 B．清末新政时期 C．辛亥革命时期 D．新文化运动时期2．（2012·全国大纲卷·16）张謇评论某人时说：“以四朝之元老，筹三省之海防，统胜兵精卒五十营，设机厂、学堂六七处，历时二十年之久，用财数千万之多……曾无一端立于可战之地，以善可和之局。

”张謇评论的是A．曾国藩 B．李鸿章 C．张之洞 D．袁世凯3．（2012·四川文综卷·21）1898年，康有为在《进呈法国革命记序》中说，“普天地杀戮变化之惨，未有若近世革命之祸酷者矣，盖自法肇之也”，“近世万国”目睹其祸，纷纷“行立宪之政，盖皆由法国革命而来。

……亦可鉴也”。

康有为的用意在于A．论证法国大革命的世界意义 B．坚定光绪帝实施变法的决心C．促使光绪帝效法法国大革命 D．阐述法国大革命的严重后果4．（2012·北京文综卷·16）下面的史料中，数字符号表示部分句读的位置。

其中句读错误的是西人立国具有本①末虽礼乐教化远逊中华②然其驯致富强具有体③用育才于学堂论政于议院国民一体上下同心务实而戒虚④谋定而后动此其体也轮船大炮洋枪水雷铁路电线⑤此其用也中国遗其体而求⑥其用无论竭蹶步趋常不相及⑦就令铁舰成行铁路四达果足恃欤A．①②⑥ B．①③⑥ C．②④⑤ D．③④⑦5．（2012·天津文综·2）戊戌变法期间，湖南《湘报》发表了《醒世歌》：“若把地球来参详，中国并不在中央，地球本来是浑圆物，谁是中央谁四旁。

”这首诗歌所表达的主要思想是A．提倡维新变法B．鼓励人们向西方学习C．宣传科学救国 D．劝导国人放弃天朝观念6．（2012·海南单科卷·15）某学者曾提及：一群志趣相投者“生育于此种‘学问饥荒’之环境中，冥思枯索，欲构成一种‘不中不西即中即西’之新学派”；由于固有之旧思想根深蒂固，所汲取的西学极为有限，其学说难免支离破碎。

高中学业水平考试数学复习题及答案【全套】

A. 2倍 B. 直线 l ，则直线 l与l 之间的距离为.
√ √ √ √ √ √ √ √ √ √ √ √ √ √ √ √ √ √ √ √ √ √ √ √ √ √ √ √ √ √
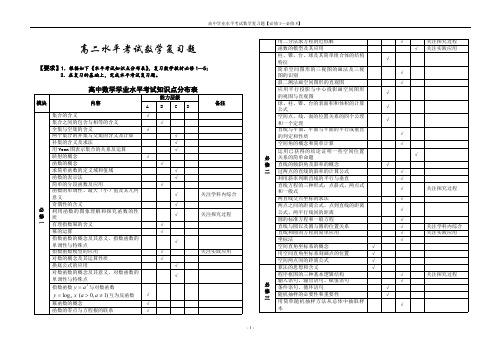
关注探究过程关注实践应用
关注探究过程
关注学科内综合关注实践应用
关注探究过程
高中学业水平考试数学复习题【必修 1—必修 5】
分层抽样和系统抽样方法列频率分布表、画频率分布直方图、频率折线图、茎叶图样本数据标准差的意义和作用合理选取样本、从样本数据中提取基本的数字特征，并能做出合理的解释用样本的频率分布估计总体分布、用样本的数字特征估计总体的数字特征随机抽样的基本方法和样本估计总体的基本思想的实际应用散点图的作法利用散点图直观认识变量之间的相关关系最小二乘法根据给出的线性回归方程系数公式建立线性回归方程概率的意义及频率和概率的区别两个互斥事件的概率加法公式及应用古典概型及其概率的计算公式、用列举法计算概率几何概型的意义任意角的概念和弧度制弧度与角度的互化任意角三角函数的定义正弦、余弦、正切函数的诱导公式正弦、余弦、正切函数的图象画法及性质的运用三角函数的周期性同角三角函数的基本关系式 y A sin x 的实际意义三角函数模型的简单应用平面向量和向量相等的含义及向量的几何表示向量加、减法的运算及其几何意义向量数乘的运算向量数乘运算的几何意义及两向量共线的含义向量的线性运算性质及其几何意义平面向量的基本定理及其意义平面向量的正交分解及其坐标表示
-2-
必修四
x
B
x 是 8的约数 ,则 A 与 B 的关系是
C. A B D.
R

A = x 5,B = x 3x 7 8 2 x则 (C B. x x 2 C. x x 5

新人教A 必修一,必修二,必修三,必修四,必修五,选修2-1综合试题

永城市高级中学数学假期作业2013-07 周秀环一、选择题1.设全集U={1,2,3,4,5,6} ,设集合P={1,2,3,4} ,Q{3,4,5},则P∩(C U Q)= （）A ．{1,2,3,4,6}B ．{1,2,3,4,5}C ．{1,2,5}D ．{1,2} 2. 下列函数中,在区间()0,+∞上为增函数的是（）A ．()ln 2y x =+B ．y =C ．12xy ⎛⎫= ⎪⎝⎭D ．1y x x=+3.121()()2x f x x =-的零点个数为（）A ．0B ．1C ．2D ．3 4. 在等差数列{a n }中,已知a 4+a 8=16,则该数列前11项和S 11= （）A ．58B ．88C ．143D ．1765.把函数y=cos2x+1的图象上所有点的横坐标伸长到原来的2倍(纵坐标不变),然后向左平移1个单位长度,再向下平移 1个单位长度,得到的图像是6.函数2sin (09)63x y x ππ⎛⎫=-≤≤⎪⎝⎭的最大值与最小值之和为（）A ．2B ．0C ．-1D ．1--7.是方程2320x x -+=的两个根,则tan()αβ+的值为（）A ．3-B ．1-C ．1D ．38.向量a =(1.cos θ)与b=(-1, 2cos θ)垂直,则cos 2θ等于A2B 12C ．0D ．-19.设a,b 是两个非零向量.（）A ．若|a+b|=|a|-|b|,则a⊥bB ．若a⊥b,则|a+b|=|a|-|b|C ．若|a+b|=|a|-|b|,则存在实数λ,使得a=λ bD ．若存在实数λ,使得a=λb,则|a+b|=|a|-|b|10．下列命题正确的是（）A ．若两条直线和同一个平面所成的角相等,则这两条直线平行B ．若一个平面内有三个点到另一个平面的距离相等,则这两个平面平行C ．若一条直线平行于两个相交平面,则这条直线与这两个平面的交线平行D ．若两个平面都垂直于第三个平面,则这两个平面平行11.我国古代数学名著《九章算术》中“开立圆术”曰:置积尺数,以十六乘之,九而一,所得开立方除之,即立圆径. “开立圆术”相当于给出了已知球的体积V ,求其直径d 的一个近似公式d ≈. 人们还用过一些类似的近似公式. 根据π =3.14159 判断,下列近似公式中最精确的一个是（）A ．d ≈B ．d ≈C ．d ≈D ．d 12.正方形ABCD 的边长为1,点E 在边AB 上,点F 在边BC 上,13AB BF ==动点P 从E 出发沿直线向F 运动,每当碰到正方形的边时反弹,反弹时反射角等于入射角,当点P 第一次碰到E 时,P 与正方形的边碰撞的次数为（） A ．8 B ．6 C ．4 D ．3二、填空题、13.已知ABC ∆得三边长成公比为,则其最大角的余弦值为_________. 14.直线y x =被圆22(2)4x y +-=截得的弦长为_____________15.设单位向量(,),(2,1)m x y b ==-。

新人教A 必修一,必修二,必修三,必修四,必修五,选修2-1综合(1)

高一暑假作业数学试题一、选择题(共12个小题，每小题5分，共60分) 1.已知命题:p x ∀∈R ，sin 1x ≤，则（）Ａ．:p x ⌝∃∈R ，sin 1x ≥ Ｂ．:p x ⌝∀∈R ，sin 1x ≥ Ｃ．:p x ⌝∃∈R ，sin 1x >Ｄ．:p x ⌝∀∈R ，sin 1x >2. “2x <”是“260x x --<”的（）Ａ．充分而不必要条件Ｂ．必要而不充分条件Ｃ．充要条件Ｄ．既不充分也不必要条件3．已知向量b a b a 与则),2,1,1(),1,2,0(--==的夹角为 ( )A.0°B.45°C.90D.180°4．已知方程221||12x y m m+=--表示焦点在y 轴上的椭圆，则m 的取值范围是（） A ．m<2 B ．1<m<2 C ．m<－1或1<m<23D ．m<－1或1<m<2 5．过双曲线的一个焦点2F 作垂直于实轴的弦PQ ，1F 是另一焦点，若∠21π=Q PF ，则双曲线的离心率e 等于（）A ．12-B ．12+C ．2D ．22+ 6. 已知的值分别为与则若μλμλλ,//),2,12,6(),2,0,1(b a b a -=+= ( )A.21,51 B.5，2C.21,51--D.-5，-27．设,x y 满足24122x y x y x y +≥⎧⎪-≥-⎨⎪-≤⎩，则z x y =+ （）（A ）有最小值2，最大值3 （B ）有最小值2，无最大值（C ）有最大值3，无最小值（D ）既无最小值，也无最大值8．在同一坐标系中，方程22221a x b y +=与20(0)ax by a b +=>>的曲线大致是（）9．当x >0时，不等式x 2－mx ＋9>0恒成立，则实数m 的取值范围是( )A ．(－∞，6)B ．(－∞，6]C ．[6，＋∞)D ．(6，＋∞)10．已知双曲线)0(122>=-mn ny m x 的离心率为2,有一个焦点恰好是抛物线x y 42=的焦点,则此双曲线的渐近线方程是 ( )A ．03=±y xB ．03=±y x C ．03=±y x D ．03=±y x11．若21,F F 是椭圆17922=+y x 的两个焦点，A 为椭圆上一点，且1245AF F ∠= ，则Δ12AF F 的面积为（）A ．7B ．27 C ．47 D ．25712．设x ，y 满足约束条件⎩⎪⎨⎪⎧3x －y －6≤0，x －y ＋2≥0，x ≥0，y ≥0，若目标函数z ＝ax ＋by (a >0，b >0)的最大值为12，则2a ＋3b 的最小值为( ) A.256B.83C.113D ．4第Ⅱ卷（共90分）二、填空题(共4个小题，每小题4分，共16分)13．对于x ∈R ，式子1kx 2＋kx ＋1恒有意义，则常数k 的取值范围是__________．14. 在平行六面体1111D C B A ABCD -中，M 为AC 与BD 的交点，若c A A b D A a B A ===11111,,，则M B 1= 。