叠加原理练习
叠加原理例题

叠加原理例题叠加原理是物理学中的一个重要概念,它在解决复杂物理问题时起着至关重要的作用。
通过叠加原理,我们可以将一个复杂的物理系统分解成若干简单的部分,分别进行分析,最后再将它们的效果叠加在一起,得到整个系统的行为。
下面,我们通过几个例题来深入理解叠加原理的应用。
例题一,弹簧振子叠加。
假设有两个弹簧振子,它们的振动方程分别为:振子A,$x_1 = A_1 \sin(\omega_1 t + \phi_1)$。
振子B,$x_2 = A_2 \sin(\omega_2 t + \phi_2)$。
其中,$A_1$和$A_2$分别为振幅,$\omega_1$和$\omega_2$分别为角频率,$\phi_1$和$\phi_2$分别为初相位。
现在将这两个振子连接起来,形成一个新的系统。
根据叠加原理,整个系统的振动方程可以表示为:$x = x_1 + x_2 = A_1 \sin(\omega_1 t + \phi_1) + A_2 \sin(\omega_2 t + \phi_2)$。
通过叠加原理,我们可以将复杂的双振子系统简化为两个单振子系统的叠加。
这样,我们就可以更容易地分析整个系统的振动特性。
例题二,电场叠加。
假设有两个点电荷,它们分别产生的电场分别为:电荷A产生的电场,$E_1 = \frac{kQ_1}{r_1^2}$。
电荷B产生的电场,$E_2 = \frac{kQ_2}{r_2^2}$。
现在将这两个点电荷放在同一空间中,根据叠加原理,整个空间中的电场可以表示为:$E = E_1 + E_2 = \frac{kQ_1}{r_1^2} + \frac{kQ_2}{r_2^2}$。
通过叠加原理,我们可以将复杂的电场分布问题简化为两个点电荷产生的电场的叠加。
这样,我们就可以更方便地计算任意位置的电场强度。
例题三,波的叠加。
假设有两个波源,它们分别产生的波动方程分别为:波源A产生的波动方程,$y_1 = A_1 \sin(kx \omega t + \phi_1)$。
叠加原理例题

叠加原理例题叠加原理是物理学中非常重要的一个原理,它在解决复杂问题时起着至关重要的作用。
通过叠加原理,我们可以将一个复杂的问题分解成若干个简单的部分,然后分别求解,最后再将它们合并在一起,得到整个问题的解。
下面,我们通过一些例题来深入理解叠加原理的应用。
例题一:一根长为L的均匀细杆,质量为m,静止放在光滑水平桌面上。
现在在离杆的一端距离为a处有一个质量为M的小物块,求杆的加速度。
解析:根据叠加原理,我们可以分别考虑杆和小物块的受力情况。
对于杆来说,它受到重力和支持力的作用,而对于小物块来说,它受到重力和杆的支持力的作用。
我们可以分别求解杆和小物块的加速度,然后将它们合并在一起得到整个系统的加速度。
首先,考虑杆的受力情况。
杆受到重力和支持力的作用,根据牛顿第二定律,杆的加速度为a1 = (Mg T)/m,其中T为支持力。
其次,考虑小物块的受力情况。
小物块受到重力和杆的支持力的作用,根据牛顿第二定律,小物块的加速度为a2 = T/M。
最后,将杆和小物块的加速度合并在一起,得到整个系统的加速度为a = a1 +a2 = (Mg T)/m + T/M。
通过这个例题,我们可以看到叠加原理的应用。
通过分别求解每个部分的问题,然后将它们合并在一起,得到整个系统的解。
这种分而治之的思想在物理学中有着广泛的应用。
例题二:一根长为L的均匀细杆,质量为m,静止放在光滑水平桌面上。
现在在离杆的一端距离为a处有一个质量为M的小物块,同时在离杆的另一端距离为b处有一个质量为m的小物块,求杆的加速度。
解析:同样地,根据叠加原理,我们可以分别考虑杆和两个小物块的受力情况。
对于杆来说,它受到重力和支持力的作用,而对于两个小物块来说,它们分别受到重力和杆的支持力的作用。
我们可以分别求解杆和两个小物块的加速度,然后将它们合并在一起得到整个系统的加速度。
首先,考虑杆的受力情况。
杆受到重力和支持力的作用,根据牛顿第二定律,杆的加速度为a1 = (Mg T)/m,其中T为支持力。
电磁场练习题电场与磁场的叠加与相互作用

电磁场练习题电场与磁场的叠加与相互作用电磁场练习题——电场与磁场的叠加与相互作用在物理学中,电磁场是电荷与电流所产生的场,由电场和磁场组成。
电磁场的相互作用以及叠加是电磁学的重要内容。
下面,我们将通过一些实例来解析电场与磁场的叠加与相互作用。
1. 实例一:平行板电容器中的带电粒子假设有一个带正电荷q的质点,位于距离一个平行板电容器距离为d的位置。
平行板电容器的两个平行的金属板分别带上正电荷和负电荷,形成了一个匀强电场。
此时,电场的电势差为ΔV,根据电场的叠加原理,带电粒子所受到的电场力为F1 = qΔV。
假设带电粒子的速度v与电场垂直,则带电粒子还受到一个宽度为d的磁场,根据磁场的叠加原理,粒子在磁场中受到的洛伦兹力为F2 = qvB。
因此,带电粒子所受到的合力为F = F1 + F2 = qΔV + qvB。
2. 实例二:电流通过直导线考虑一个长直导线,导线中有电流I,与导线平行的方向定义为x轴方向。
在导线周围产生一个以导线为轴线的环形磁场。
现在,我们再在导线周围和导线之间施加一个电场,即有一个电场E与导线方向相同。
根据磁场的叠加原理,磁场B和电场E的合力为F1 = qE。
根据电场的叠加原理,导线所带来的电场力为F2 = ILB,其中L为导线的长度,B为导线周围的磁场强度。
所以,导线受到的总合力为F = F1 + F2 = qE + ILB。
3. 实例三:异向电场和磁场中的运动粒子假设有一个粒子,同时存在电场和磁场。
电场E方向为x轴方向,磁场B方向为z轴方向。
粒子的速度v方向既不与电场方向也不与磁场方向垂直,而是与两者夹角θ。
粒子在电场中受到的电场力为F1 = qE。
粒子在磁场中受到的洛伦兹力为F2 = qvBsinθ。
所以,粒子所受到的合力为F = F1 + F2 = qE + qvBsi nθ。
当粒子在电磁场中运动时,合力将改变粒子的运动轨迹。
总结起来,电场与磁场的叠加与相互作用是电磁学中的基本概念。
实验二叠加原理实验

实验二叠加原理实验实验二叠加原理实验一、实验目的1.理解和掌握叠加原理的基本概念和应用。
2.学习使用叠加原理分析和解决实际问题。
3.培养实验操作和团队协作能力。
二、实验原理叠加原理是指多个电源共同作用在某一电阻元件上时,元件上的电压和电流是各电源单独作用时产生的电压和电流之和。
叠加原理是线性电路分析的基本原理之一,适用于所有的线性电阻电路。
三、实验步骤1.准备实验器材:电源、电阻器、电压表、电流表、开关、导线等。
2.搭建实验电路:连接电源、电阻器和电流表、电压表,确保电路连接正确无误。
3.记录实验数据:在电阻器上分别施加不同的电压,并记录相应的电压表和电流表读数。
4.分析实验数据:根据叠加原理,计算出各电源单独作用时的电压和电流,并比较实验数据与理论值是否一致。
5.讨论与总结:分析实验结果,总结叠加原理的应用和注意事项。
四、实验结果与分析1.实验数据记录2.数据分析根据叠加原理,计算出各电源单独作用时的电压和电流:在本次实验中得到了较好的验证。
3.结果讨论与总结通过本次实验,我们验证了叠加原理在电阻电路中的应用。
实验结果表明,多个电源共同作用时,电阻器上的电压和电流是各电源单独作用时产生的电压和电流之和。
在分析电路时,叠加原理可以帮助我们简化问题,提高电路分析的效率和准确性。
需要注意的是,叠加原理只适用于线性电阻电路,对于非线性电路或含有电容、电感的电路,叠加原理不适用。
此外,在实际操作中还需注意电路的安全问题,确保实验过程不会对人员和环境造成损害。
通过本次实验,我们加深了对叠加原理的理解和应用能力,为后续的电路分析和设计打下坚实基础。
叠加原理练习题及答案

叠加原理练习题及答案在学习物理的过程中,我们经常会遇到叠加原理这一概念。
叠加原理在物理学中扮演着重要的角色,因为它可以帮助我们分析和解决各种物理问题。
在本文中,我们将介绍一些叠加原理的练习题,并提供答案以供参考。
第一道题目是关于力学的。
假设有两个力,一个向右施加50N的力,另一个向左施加30N的力。
请问物体受到的合力是多少?根据叠加原理,我们可以将这两个力进行矢量相加。
由于力是矢量量,我们需要考虑其大小和方向。
向右施加的力是正方向,向左施加的力是负方向。
因此,合力为50N - 30N,即20N向右。
第二道题目涉及电路。
一个电路中有两个电池,一个电池的电动势为2V,另一个电池的电动势为3V。
两个电池的正负极分别相连,形成一个闭合电路。
请问电路中的总电动势是多少?根据叠加原理,我们可以将两个电动势相加,即2V + 3V,得出总电动势为5V。
第三道题目考察光学。
一束红光和一束绿光同时照射到一个反射镜上。
红光的波长为650nm,绿光的波长为550nm。
请问,反射镜上的光的波长是多少?根据叠加原理,我们可以将这两束光的波长进行叠加。
由于光的波长足够小,我们可以简单地将两个波长相加。
即650nm + 550nm,得出反射镜上的光的波长为1200nm,即1.2μm。
第四道题目涉及声音。
一个人同时发出两个频率为200Hz和400Hz的声音。
请问,听到的声音频率会是多少?根据叠加原理,我们可以将这两个频率进行叠加。
听到的声音频率实际上是两个声音频率的平均值。
即 (200Hz + 400Hz) / 2,得出听到的声音频率为300Hz。
以上是四个关于叠加原理的练习题及其答案。
通过这些题目,我们可以看到在物理学中,叠加原理始终都是一个重要的工具。
它可以帮助我们分析和解决各种问题,无论是力学、电路、光学还是声学。
通过理解和应用叠加原理,我们能够更好地理解物理学的基本原理,并应用于实际场景中。
练习题对于学习叠加原理来说是非常重要的。
一、波的叠加原理

图甲
图乙
二、波的干涉
定义:频率相同的两列波相遇时,使某些区
域的振动始终加强,而使另一些区域的振动
始终减弱,并且振动加强和减弱的区域互相 间隔,这种现象称为波的干涉.
a点位移是否总是最大? b点位移是否总是为零?
二、波的干涉条件
1)频率相同;…
a、b、c点是加强还是减弱? S1 S2
a b
1 2
1
2
实际波型
1
2
一、波的叠加原理
1、波传播的独立性
几列波相遇之后, 仍 然保持它们各自原有的特 征不变,并按照原来的方 向继续前进,好象没有遇 到过其他波一样互不干扰.
2、波的叠加原理
在几列波重叠的区域 里,质点振动的位移等于 这几列波单独传播时引起 的位移的矢量和.
从一条弦线的两端,各发生一如图甲所示 的横脉冲,它们均沿弦线传播,速度相 等,传播方向相反,在它们传播的过程 中,可能出现的脉冲波形是图乙中的
c
红线:波峰ຫໍສະໝຸດ 蓝线:波谷一、波的叠加原理
1、波传播的独立性 几列波相遇之后, 仍然保持它们各自 原有的特征(频率、波长、振幅、振动方向 等)不变,并按照原来的方向继续前进,好 象没有遇到过其他波一样互不干扰. 例 : a 众多说话声中,能辨别出某个人的声音.
b 乐队中各乐器演奏的独立性.
生活中的例子
波在叠加时的特点
叠加原理的验证实验(电工学实验).doc

叠加原理的验证实验(电工学实验).doc
叠加原理是电工学中非常重要的基本原理,它指出在一个线性的、稳态的电路中,每个电源单独作用时,电路中的电流、电势及功率等物理量可以按照其单独作用时的结果来计算。
换句话说,如果一个电路中有多个电源作用,那么每个电源都可以看做是单独作用的,而整个电路中电流、电势及功率等物理量的总和就是所有单独作用结果的代数和。
为了验证叠加原理的正确性,我们可以进行如下的实验:
【实验材料】:
1.电源:直流电源和交流电源各一台;
2.电阻:10欧姆、20欧姆、30欧姆、40欧姆、50欧姆、60欧姆、70欧姆、80欧姆、90欧姆、100欧姆共10个,分别编号为R1-R10;
3.万用表:VC8145A型数字台式万用表一台。
1.将直流电源连接至一个电阻上,用万用表测量该电阻上的电流和电势(电压),记录下来。
3.将两次测量所得的电流和电势相加,得到该电路中的总电流和总电势(电压)。
4.将上述实验步骤中使用的电阻换成另一个电阻,并重复步骤1-3,直至所有的电阻都被测量完毕。
1.在连接电路时要注意正确连接,以免损坏电源和电阻等器件。
2.测量电阻、电流和电势(电压)时要仔细操作,防止出现测量误差。
3.在交流电路中,要注意相位的影响,以免对测量结果产生影响。
电场磁场的叠加原理 作业练习

作业练习课程基本信息学科 物理年级 高三年级 学期 春季课题 电场磁场的叠加原理 教科书书 名:人教版教材出版社:人民教育出版社学生信息姓名 学校班级学号作业练习1.(2020·江西吉水中学、崇仁一中、南城一中三校第一次联考)一段均匀带电的半圆形细线在其圆心O 处产生的场强为E ,把细线分成等长的圆弧AB 、BC 、CD ,则圆弧BC 在圆心O 处产生的场强为( )A .E B.E 2 C.E 3 D.E42.(2019·山东济宁二模)如图所示,一个绝缘圆环,当它的14均匀带电且电荷量为+q 时,圆心O 处的电场强度大小为E 。
现使半圆ABC 均匀带电+2q ,而另一半圆ADC 均匀带电-2q ,则圆心O 处电场强度的大小和方向为( ) A .22E ,方向由O 指向D B .4E ,方向由O 指向D C .22E ,方向由O 指向B D .03.如图所示,半径为R 的大球O 被内切地挖去半径为R2的小球O ′,余下的部分均匀地带有电荷量Q 。
今在两球球心连线OO ′的延长线上,距大球球心O 的距离为r (r >R )处放置一个点电荷q ,则q 所受的力大小为(你可以不必进行复杂的计算,而是根据所学的物理知识和物理方法进行分析,从而判断解的合理性。
)( ) A.kQq 7r ⎣⎢⎡⎦⎥⎤8-4r 22r -R 2 B.kQq 7r 2⎣⎢⎡⎦⎥⎤8+4r 22r -R 2C.kQq 7r 2⎣⎢⎡⎦⎥⎤8-4r 22r -R 2D.kQq r 2⎣⎢⎡⎦⎥⎤8-4r 22r -R 24.如图所示,A 、B 、C 、D 、E 是半径为r 的圆周上等间距的五个点,在这些点上各固定一个点电荷,除A 点处的电荷量为-q 外,其余各点处的电荷量均为+q ,则圆心O 处( ) A .场强大小为kq r 2,方向沿OA 方向 B .场强大小为kq r 2,方向沿AO 方向 C .场强大小为2kqr 2,方向沿OA 方向D .场强大小为2kqr2,方向沿AO 方向5.(2019·江西南昌调研)如图所示,M 、N 和P 是以MN 为直径的半圆弧上的三点,O 为半圆弧的圆心,∠MOP =60°,在M 、N 处各有一条长直导线垂直穿过纸面,导线中通有大小相等的恒定电流,方向如图所示,这时O 点的磁感应强度大小为B 1.若将M 处长直导线移至P 处,则O 点的磁感应强度在大小为B 2,那么B 2与B 1之比为( ) A.3∶1 B.3∶2 C .1∶1 D.1∶26.(多选)(2019·名校学术联盟)正三角形ABC 的三个顶点处分别固定有水平放置的长直导线,并通以如图所示方向的恒定电流,导线中的电流大小相等,三角形中心O 点的磁感应强度大小为B O ,已知通电直导线在某点产生的磁场与通电直导线的电流大小成正比,则下列说法正确的是( )A .O 点处的磁感应强度方向竖直向下B .B 、C 处两导线电流在O 点产生的合磁场方向水平向左 C .B 处电流在O 点处产生的磁场磁感应强度大小为12B OD .将A 处电流大小减半,则O 点处的磁场磁感应强度大小为34B O参考答案1.B2.A3.C4.C5.B6.BCD。
波的叠加

波的叠加
波的叠加
创新微课
一、波的独立传播特性
你知道“风声、雨声、读书声,声声入耳”体现了波的什么性质 吗? 声波在相遇时,会保
1 持各自的频率、振幅 等运动特征,而不受 其它波的影响。
波的叠加
二、波的叠加原理
在几列波重叠的区域里,介质 的质点同时参与1 这几列波引起 的振动,质点的位移等于这几 列波单独传播时引起的位移的 矢量和。
使得所有质点的振动的位移加倍,C正确. 【答案】 BC
波的叠加
【练习】关于波的衍射和叠加,下列说法正确的是
( BDG )
A.衍射和叠加是机械波特有的现象 B.对同一列波,缝或孔、障碍物尺寸越小,衍射现象越
明显 C.只有横波才能发生衍射现象,纵波不能发生衍射现象 D.两列波相遇时能够保持各自的状态互不干扰
创新微课
波的叠加
【例题】如右图所示,沿一条直线相向传 播的两列波的振幅和波长均相等,当 它们相遇时可能出现的波形是下列选项中的( BC )
1
创新微课
波的叠加
创新微课
【解析】两列波的半个波形相遇时,B正确. 当两列波完全相遇时(即重叠在一起),由波的叠加原理可知,所
有质点振动的位移均等于每列波单独传播时引起的位移的矢量和, 1
E.由于两列波1 相遇时叠加,所以当它们分开时波的频率、
振幅都会发生变化 F.如果这两列波叠加以后使某些区域振动加强,某些区 域
振动减弱,那么这两列波发生明显衍射 G.两列波重叠的区域里,任何一点的总位移都等于两列
波分别引起的位移的矢量和
创新微课
ቤተ መጻሕፍቲ ባይዱ
同学,下节再见
电场强度 场强叠加原理
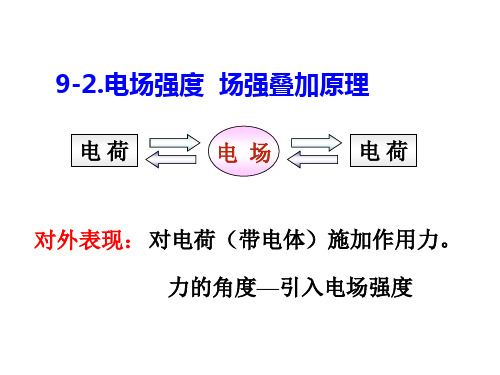
电荷
电场
电荷
对外表现: 对电荷(带电体)施加作用力。 力的角度—引入电场强度
一、电场强度
1 试验电荷 点电荷 (定位准确) 电荷足够小 (对原电场的影响小)
2 电场强度
试验电荷
Q
q0
F
场源电荷
Question:
1.将不同电荷量的2个点电荷A.B放在同一位置, 受力相同吗?
Ea
c
E
a
1、不形成闭合回线,也不中断,而是起于正电荷(或 无穷远处)、止于负电荷(或无穷远处);
2、任何两条电场线不相交。
几种典型电场的电场线分布图形 正点电荷与负点电荷的电场线
-
+
一对等量异号点电荷的电场线
-
+
一对等量正点电荷的电场线
+
+
一对不等量异号点电荷的电场线
2q
-q
带电平行板电容器的电场线 +++++++++++++
(2) 任何两条电场线不相交.
我们可以在电场中取一个垂直于电场方向
的小面元dS,通过该小面元的电场线根数与
该面元的面积的比值称为电场线密度。我们
规定电场中某点的场强的大小在数值上等于
该点的电场线密度。
dS
E
E dN dS
总结:
E
方向:切线方向
大小: E dN =电场线密度
dS
Eb
Ec
b
E dE
Qdx
Q
a 4 0 Lx 2 4 0a(a L)
P点的电场强度沿x轴负方向
电磁学复习练习题作业(答案)

第一次作业(库仑定律和电场强度叠加原理)一 选择题[ C ]1下列几个说法中哪一个是正确的?(A) 电场中某点场强的方向,就是将点电荷放在该点所受电场力的方向.(B) 在以点电荷为中心的球面上, 由该点电荷所产生的场强处处相同.(C) 场强可由q F E / 定出,其中q 为试验电荷,q 可正、可负,F 为试验电荷所受的电场力.(D) 以上说法都不正确.[ C ]2 在边长为a 的正方体中心处放置一电荷为Q 的点电荷,则正方体顶角处的电场强度的大小为: (A)2012a Q . (B) 206a Q.(C)203a Q . (D)20a Q.[ B ]3图中所示为一沿x 轴放置的“无限长”分段均匀带电直线,电荷线密度分别为+(x <0)和- (x >0),则Oxy 坐标平面上点(0,a )处的场强E为(A) 0. (B)i a 02 . (C) i a 04 . (D) j i a04 . 【提示】根据)sin (sin 4120 a E x )cos (cos 4210aE y对+ 均匀带电直线2,021对— 均匀带电直线0,221在(0,a )点的场强是4个场强的矢量和[ A ]4电荷面密度分别为+ 和- 的两块“无限大”均匀带电的平行平板,如图放置,则其周围空间各点电场强度随位置坐标x 变化的关系曲线为:(设场强方向 向右为正、向左为负)O +- x y (0, a ) O x -a a y+ -O -a +a 0/x(A)EO E -a +a 02/ x (B)OE -a +a 02/ x(C)-02/OE -a +a2/ x(D)/ 02/【提示】依据02E 及场强叠加 二.填空题5. 电荷为-5×10-9 C 的试验电荷放在电场中某点时,受到 20×10-9 N 的向下的力,则该点的电场强度大小为_____________________,方向____________.4N / C 2分 向上 1分6. 电荷均为+q 的两个点电荷分别位于x 轴上的+a 和-a 位置,如图所示.则y 轴上各点电场强度的表示式为E=j y a qy2/322042 , (j为y 方向单位矢量) ,场强最大值的位置在y =2/a7.两根相互平行的“无限长”均匀带正电直线1、2,相距为d ,其电荷线密度分别为 1和 2如图所示,则场强等于零的点与直线1的距离a 为d 211三计算题8.如图所示,一电荷面密度为 的“无限大”平面,在距离平面a 处的一点的场强大小的一半是由平面上的一个半径为R 的圆面积范围内的电荷所产生的.试求该圆半径的大小.解:电荷面密度为 的无限大均匀带电平面在任意点的场强大小为E = / (2 0) 2分以图中O 点为圆心,取半径为r →r +d r 的环形面积,其电量为d q = 2 r d r 2分它在距离平面为a 的一点处产生的场强+q +q -a+aO xy12a daR O E2/32202d ra ardrE2分则半径为R 的圆面积内的电荷在该点的场强为R r a r r a E 02/3220d 222012R a a 2分 由题意,令E = / (40),得到R =a 32分9.如图所示,真空中一长为L 的均匀带电细直杆,总电荷为q ,试求在直杆延长线上距杆的一端距离为d 的P 点的电场强度.解:设杆的左端为坐标原点O ,x 轴沿直杆方向.带电直杆的电荷线密度为 =q / L ,在x 处取一电荷元d q = d x = q d x / L ,它在P 点的场强: 204d d x d L q E204d x d L L xq 2分总场强为 Lx d L xL q E 020)(d 4- d L d q 043分 方向沿x 轴,即杆的延长线方向.10.一个细玻璃棒被弯成半径为R 的半圆形,沿其上半部分均匀分布有电荷+Q ,沿其下半部分均匀分布有电荷-Q ,如图所示.试求圆心O 处的电场强度. 解:把所有电荷都当作正电荷处理.在 处取微小电荷 d q = d l = 2Q d /它在O 处产生场强d 24d d 20220RQR q E2分按 角变化,将d E 分解成二个分量:d sin 2sin d d 202RQ E E xOd cos 2cos d d 202R Q E E y3分对各分量分别积分,积分时考虑到一半是负电荷2/2/0202d sin d sin 2R QE x =0 2分 2022/2/0202d cos d cos 2R QR Q E y2分 所以j RQ j E i E E y x2021分 第三次作业答案(高斯定理和电势2)1. 以下各种说法是否正确?(回答时需说明理由)(1)场强为零的地方,电势也一定为零。
叠加原理例题

叠加原理例题叠加原理是指当有多个力作用于物体时,物体所受的合力等于各个力的矢量和。
下面是一个例题:一个物体在水平地面上受到两个力的作用,一个力F1以角度α施加在物体上方,另一个力F2以角度β施加在物体下方。
力F1的大小为5N,角度α为30°,力F2的大小为8N,角度β为60°。
求物体所受合力的大小和方向。
解答:首先根据叠加原理,求出物体在x轴和y轴上受到的力的分量。
设物体所受合力的大小为F,夹角与x轴的夹角为θ。
物体在x轴上受到的力的分量为Fx = F1 * cos(α) + F2 * cos(β)= 5N * cos(30°) + 8N * cos(60°)= 5N * √3/2 + 8N * 1/2= 5√3/2 N + 4N物体在y轴上受到的力的分量为Fy = F1 * sin(α) - F2 * sin(β)= 5N * sin(30°) - 8N * sin(60°)= 5N * 1/2 - 8N * √3/2= 5/2 N - 4√3 N/2= (5 - 4√3)/2 N然后根据勾股定理,可以求得物体所受合力的大小:F = √(Fx^2 + Fy^2)= √((5√3/2 N + 4N)^2 + (5 - 4√3)/2 N)^2)= √(75/4 + 20√3 + 16 + 25/4 - 10√3 + 12/4)= √(53/4 + 10√3)最后,根据三角函数的性质,可以求得物体所受合力的方向:tan(θ) = Fy / Fx= ((5 - 4√3)/2 N) / (5√3/2 N + 4N)= (5 - 4√3) / (5√3 + 8)至此,我们求得物体所受合力的大小为√(53/4 + 10√3) N,方向为θ = arctan((5 - 4√3) / (5√3 + 8))。
电磁学练习题(毕奥—萨伐尔定律-(1))

磁感应强度,毕奥—萨伐尔定律、磁感应强度叠加原理1. 选择题1. 两条无限长载流导线,间距0.5厘米,电流10A ,电流方向相同,在两导线间距中点处磁场强度大小为:( )(A )0 (B )πμ02000(C )πμ04000 (D )πμ0400 答案:(A )2.通有电流J 的无限长直导线弯成如图所示的3种形状,则P 、Q 、O 各点磁感应强度的大小关系为( )A .PB >Q B >O B B .Q B >P B >O BC . Q B >O B >P BD .O B >Q B >P B 答案:D3.在一个平面内,有两条垂直交叉但相互绝缘的导线,流过每条导线的电流相等,方向如图所示。
问那个区域中有些点的磁感应强度可能为零:( )A .仅在象限1B .仅在象限2C .仅在象限1、3D .仅在象限2、4答案:D4.边长为a 的一个导体方框上通有电流I ,则此方框中心点的磁场强度( ) A .与a 无关 B .正比于2a C .正比于a D .与a 成反比答案:D5.边长为l 的正方形线圈,分别用图示两种方式通以电流I ,图中ab 、cd 与正方形共面,在这两种情况下,线圈在其中心产生的磁感应强度的大小分别为( )A .01=B ,02=B B .01=B ,lIB πμ0222=C .l I B πμ0122=,02=BD .l I B πμ0122=, lIB πμ0222= 答案:C6.载流的圆形线圈(半径1a )与正方形线圈(边长2a )通有相同的电流强度I 。
若两个线圈中心1O 、2O 处的磁感应强度大小相同,则1a :2a =( ) A .1:1 B .π2:1 C .π2:4 D .π2:8 答案:D7.如图所示,两根长直载流导线垂直纸面放置,电流A I 11=,方向垂宜纸面向外;电流A I 22=,方向垂直纸面向内。
则P 点磁感应强度B 的方向与X 抽的夹角为( )A .30°B .60°C .120°D .210°答案:A8.四条相互平行的载流长直导线电流强度均为I ,方向如图所示。
1.7 叠加原理
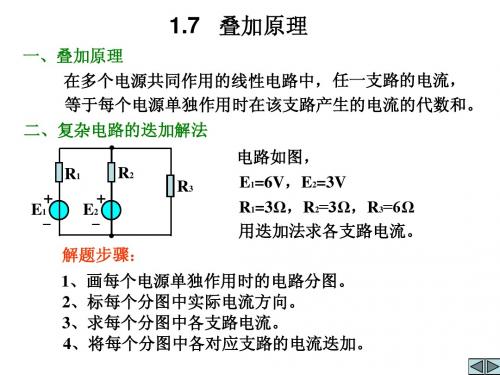
1.7 叠加原理一、叠加原理在多个电源共同作用的线性电路中,二、复杂电路的迭加解法电路如图,E 1=6V ,E 2=3V用迭加法求各支路电流。
解题步骤:1、画每个电源单独作用时的电路分图。
2、标每个分图中实际电流方向。
3、求每个分图中各支路电流。
4、将每个分图中各对应支路的电流迭加。
R 1=3Ω,R 2=3Ω,R 3=6Ω任一支路的电流,等于每个电源单独作用时在该支路产生的电流的代数和。
+-E 1R 1R 2+-E 2R 3解:原电路+I1′I 2′I 3′I 1"I 2"I 3"E 1单独作用时:I 1′I 2′I 3′E 2单独作用时:I 1"=[R 3/(R 1+R 3)]·I 2"=0.4A I 2"=E 2/(R 2+R 1//R 3)=0.6AI 3"=I 2"-I 1"=0.2A =R 1+-E 1R 2R 3-R 1R 2+E 2R 3(先求总电流I 1′)(先求总电流I 2")迭加时,注意方向I 1 =I 2 = I 2′-I 2 " = 0.2AI 3 = I 3′+ I 3 " = 0.6A=E 1/(R 1+R 2//R 3)=1.2A =0.8A =[R 3/(R 2+R 3)]·I 1′= I 1′=0.4A-I 2′I 1′-I 1 "= 0.8A三、说明1、迭加定理只适应于求线性电路中的电压、电流2、功率不可迭加,3、画电路分图时,各支路位置要保持不变。
迭加法解题举例:用迭加法求图示电路中A 点的电位U A 。
10Ω5Ω20Ω+50V -50VAU A ′+=+50V 10Ω5Ω20Ω(a)U A "5Ω10Ω20Ω-50V (b)(a)图中:(b)图中:∴+50V 单独作用-50V 单独作用U A ′=[(5//20)/(10+5//20)]•50V=100/7(v)U A " =[(10//20)/(5+10//20)](-50V )= -200/7(V)U A = -100/7 = -14.28(V)因为:P=(I 1+I 2)2 R ≠I 12·R +I 22·R。
电场叠加原理课堂练习题目

1、有一均匀带电直线,长为l ,电量为q ,求距它为r 处p 点场强。
解:如图所取坐标,把带电体分成一系列点电荷,dy 段在p 处产生场强为:)(4422020r y dyr dq dE +==πελπε )(l q =λ ① 由图知: ⎪⎩⎪⎨⎧=-=⎪⎭⎫⎝⎛--=⎪⎭⎫ ⎝⎛-==θθθθππθβd r dy rctg rtg rtg rtg y 2csc 22 代⑴中有: 2'04rdydE πελ=θπελθθππθβsin rdysin dE )cos(dE )cos(dE cos dE dE 'x 20422==-=-==θθππθβrctg rtg rtg rtg y -=⎪⎭⎫⎝⎛--=⎪⎭⎫ ⎝⎛-==22θθd csc r dy 2=,θβsin rcos r r '==∴θπεθθλ22024sin rd csc r dE x =)cos (cos rr d sin dE E x x 21004421θθπελπεθθλθθ-===⎰⎰ θβcos dE sin dE dE y =-=)sin (sin r d r cos dE E yy 12004421θθπελθπεθλθθ-===⎰⎰ 讨论:无限长均匀带电直线πθθ==210,,rE x 02πελ=⇒,0=y E . 即无限均匀带电直线,电场垂直直线,0>λ,E 背向直线;0<λ,E指向直线。
2、有一无限大均匀带电平面,电荷面密度为σ,求在平面附近任一点场强。
解:如图所取坐标,x 轴垂直带电平面,把带电平面分成一系列平行于z 轴的无限长窄条,阴影部分在p 点产生场强为(无限长均匀带电直线结果)()rdy r dE 00212πεσπελ⋅==()()220222122022cos yx xdyyx x yx dydE dE x +=+⋅+==πεσπεσθ()()⎰⎰⎰+∞∞-+∞∞-+=+==2222022yxdyx yx xdydE E x x πεσπεσ10222212εππππεσπεσ=⎥⎦⎤⎢⎣⎡⎪⎭⎫ ⎝⎛--=⋅=+∞∞--x y Ag x x 0==⎰y y dE E (由对称性可知)结论:无限大均匀带电平面产生均匀场,大小为2εσ⎩⎨⎧<>指向平面背离平面:0:0σ。
叠加原理练习

叠加原理练习
叠加原理是指在一个物理系统中,多个作用力同时存在时,它们对系统的影响可以简单地相加。
这个概念在物理学、工程学和自然科学的各个领域都有着广泛的应用。
例如,假设一个物体受到两个力的作用,一个向右的力和一个向上的力。
根据叠加原理,这两个力可以简单地相加,得出一个向上和向右的合力。
这个合力代表了这两个力对这个物体的合作用。
在物理学中,叠加原理也经常被用来计算不同光源发出的光的互相干扰。
当光线穿过一个透明介质时,它们会被散射、反射和折射,这就会形成多个光线。
这些光线会相互干扰,使得它们在最终到达物体的点时产生干涉。
利用叠加原理,我们可以计算出这些光线的干涉模式,并预测出它们在某些点的亮度和颜色。
这就是光学中的叠加原理应用,为我们提供了非常重要的工具。
除了物理学和光学,叠加原理还可以用来解决其他的问题。
例如,在声学和电学中,我们可以用叠加原理来计算不同声源和电源对系统的影响。
这些应用都需要仔细的计算和分析,但叠加原理提供了一个非常有用的框架来理解这些问题。
叠加原理一般只适用于线性系统,即那些具有恒定关系的系统。
这意味着,当我们增加一个力、光源或声源时,它们的作用是不会改变系统的本质特性的。
这使得叠加原理在许多情况下非常有用,但也需要注意它的局限性。
总之,叠加原理是一个非常有用的物理原理,在各个领域都有着广泛的应用。
它帮助我们理解复杂的系统,并预测它们的行为。
对于学习物理学和其他自然科学的人来说,掌握叠加原理是非常重要的。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
复杂直流电路专项复习
_____________叠加定理专题
一、叠加定理的内容
当线性电路中有几个电源共同作用时,各支路的电流(或电压)等于各个电源分别单独作用时在该支路产生的电流(或电压)的代数和(叠加)。
在使用叠加定理分析计算电路应注意以下几点:
(1) 叠加定理只能用于计算线性电路(即电路中的元件均为线性元件)的支路电流或电压(不能直接进行功率的叠加计算);
(2) 电压源不作用时应视为短路,电流源不作用时应视为开路;
(3) 叠加时要注意分电流(或分电压)与所求的电流(或电压)之间的参考方向,正确选取各分量的正负号。
(4)每个电源单独作用时,必须画出分图,且尽量保持原图结构不变。
(5)叠加原理只能用来求电路中的电压和电流,而不能用来计算功率。
二、应用举例
【例3-3】如图3-8(a)所示电路,已知E 1 = 17 V ,E 2 = 17 V ,R 1 = 2 Ω,R 2 = 1 Ω,R 3 = 5 Ω,试应用叠加定理求各支路电流I 1、I 2、I 3 。
(1) 当电源E 1单独作用时,将E 2视为短路,设
R 23 = R 2∥R 3 = 0.83 Ω
则 A
1A 5A
683
.217
1322
313
23
223111=+==+=
==+='I R R R 'I 'I R R R 'I R R E 'I (2) 当电源E 2单独作用时,将E 1视为短路,设
R 13 =R 1∥R 3 = 1.43 Ω
则
A
2A 5A
743
.217
23
11
323
13
113222=+==+===+=''I R R R ''I ''I R R R ''I R R E ''I
(3) 当电源E 1、E 2共同作用时(叠加),若各电流分量与原电路电流参考方向相同时,在电流分量前面选取“+”号,反之,则选取“-”号:
I 1 = I 1′- I 1″ = 1 A , I 2 = - I 2′ + I 2″ = 1 A , I 3 = I 3′ + I 3″ = 3 A
巩固练习
1、在题1图所示电路中,2A恒流源单独作用时,I=。
题1图题2图题3图
2、如题2图示电路中,已知:E=9V,I k =6mA,当电压源E单独作用时,通过RL的电流是1mA,那么当电压源E和电流源Ik共同作用时,通过电阻RL的电流I L是__________。
A、3mA
B、4mA
C、-3mA
D、-4mA
3、如题3图所示电路,试用叠加定理求电流I1和I2。
解:当12V作用时,I1’= A,I2’= A;(3分)
当4V作用时,I1’’= A, I2’’= A;(3分)
当3A作用时,I1’’’= A, I2’’’= A;(3分)
当各电源共同作用时,I1= A,I2= A。
(3分)
4、如下图所示,回答下列问题:(12分)
(1)当U S单独工作时,R4两端的功率为;(3分)
(2)当I S1单独工作时,R4两端的功率为;(3分)
(3)当I S2单独工作时,R4两端的功率为;(3分)
(4)当共同作用时,R4两端的功率为。
(3分)
5、如右图电路用叠加定理求U。
(1)、当US1单独作用时,在图(1)中求U1=
(2)、当US2单独作用时,在图(2)中求U2=
(3)、求U=
6、由叠加原理,求得题图63电路中U ab=0时的U s值为多少?
7、试用叠加定理求下图所示电路中的电压U。
补充
电路组成与转换原理
从A、B、C 节点向左看去,各节点对地的等效电阻均为2R。
