信息论_信息理论与编码_王虹_吕锋_学习指导答案【5,6章】
信息理论与编码 第二版 (吕锋 王虹 著) 人民邮电出版社 课后答案

课后答案网 您最真诚的朋友
网团队竭诚为学生服务,免费提供各门课后答案,不用积分,甚至不用注
册,旨在为广大学生提供自主学习的平台!
课后答案网:
视频教程网:
PPT 课件网:
课后答案网:
若侵犯了您的版权利益,敬请来信告知!
课后答案网 w w w .h a c k s h p .c n
课后答案网
课后答案网
课后答案网
课后答案网
课后答案网
课后答案网
课后答案网
课后答案网
课后答案网
课后答案网
课后答案网
课后答案网
课后答案网
课后答案网
课后答案网
课后答案网
课后答案网
课后答案网
课后答案网
课后答案网
课后答案网
课后答案网
课后答案网
课后答案网
课后答案网
课后答案网
课后答案网
课后答案网
课后答案网
课后答案网
课后答案网
课后答案网
课后答案网
课后答案网
课后答案网
课后答案网
课后答案网 。
信息论与编码技术第五章课后习题答案

5.4 已知信源的各个消息分别为字母 A,B,C,D,现用二进制码元对消息字母作信源编码,A:
(2) 考虑没有给予编码的信源序列出现的概率,该定长码引起的错误概率 P 是多少?
解:(1)信源序列中含有 3 个或小于 3 个“0”的各信源序列个数有:
M
=
C0 100
+
C1 100
+
C2 100
+
C3 100
=1+100+4950+161700=166750
对 M 个信源序列进行无失真的二元等长编码,必须: 2l ≥ M = 166750 = 217.35
L =4*(1/4)*1=1(码符号/信源符号)
Rt= H(X)/(t* L )=1/(1*10*10-2)=10(比特/秒)
5.5 若消息符号、对应概率分布和二进制编码如下:
消 息 符 a0
a1
a2
a3
号
pi
1/2 1/4 1/8 1/8
编码
0
10
110 111
试求:
(1) 消息符号熵; (2) 各个消息符号所需的平均二进制码个数;
5.6 某信源有 8 个符号{a1, a2 , a3,", a8} ,概率分别为 l/2,l/4,1/8,1/16,1/32,1/64,1/128,1/128,
试编成这样的码:000,001,010,011,100,101,110,111 的码。求:(1) 信源的符号熵 H(X); (2) 出现一个“1”或一个“0”的概率;(3) 这种码的编码效率;(4) 相应的香农码和费诺码;(5) 该码的 编码效率。
信息理论与编码课后答案第5章

第5章 有噪信道编码5.1 基本要求通过本章学习,了解信道编码的目的,了解译码规则对错误概率的影响,掌握两种典型的译码规则:最佳译码规则和极大似然译码规则。
掌握信息率与平均差错率的关系,掌握最小汉明距离译码规则,掌握有噪信道编码定理(香农第二定理)的基本思想,了解典型序列的概念,了解定理的证明方法,掌握线性分组码的生成和校验。
5.2 学习要点5.2.1 信道译码函数与平均差错率5.2.1.1 信道译码模型从数学角度讲,信道译码是一个变换或函数,称为译码函数,记为F 。
信道译码模型如图5.1所示。
5.2.1.2 信道译码函数信道译码函数F 是从输出符号集合B 到输入符号集合A 的映射:*()j j F b a A =∈,1,2,...j s =其含义是:将接收符号j b B ∈译为某个输入符号*j a A ∈。
译码函数又称译码规则。
5.2.1.3 平均差错率在信道输出端接收到符号j b 时,按译码规则*()j j F b a A =∈将j b 译为*j a ,若此时信道输入刚好是*j a ,则称为译码正确,否则称为译码错误。
j b 的译码正确概率是后验概率:*(|)()|j j j j P X a Y b P F b b ⎡⎤===⎣⎦ (5.1)j b 的译码错误概率:(|)()|1()|j j j j j P e b P X F b Y b P F b b ⎡⎤⎡⎤=≠==-⎣⎦⎣⎦ (5.2)平均差错率是译码错误概率的统计平均,记为e P :{}1111()(|)()1()|1(),1()|()s se j j j j j j j ssj j j j j j j P P b P e b P b P F b b P F b b P F b P b F b ====⎡⎤==-⎣⎦⎡⎤⎡⎤⎡⎤=-=-⎣⎦⎣⎦⎣⎦∑∑∑∑ (5.3)5.2.2 两种典型的译码规则两种典型的译码规则是最佳译码规则和极大似然译码规则。
信息理论与编码课后答案(吕锋王虹着)

第一章教材习题1.1.试述信息与知识、消息和信号之间的区别与联系,并举例说明。
1.2.详述钟义信先生的信息定义体系。
1.3.试查阅文献,说明信息具有哪些特征和性质?1.4.说明通信系统模型由哪几部分组成,并详细讨论每一部分的功能。
1.5.试述信息论的研究内容?第二章教材习题信源模型2.1试简述信源分类以及各种信源特点。
信息的描述2.2在非理想观察模型中,存在哪些不确定性,它们与信息有何关系?不确定性与信息2.3一副充分洗乱的牌(含52张),试问:(1)任一特定排列所给出的不确定性是多少?(2)随机抽取13张牌,13张牌的点数互不相同时的不确定性是多少?2.4同时扔出两个正常的骰子,也就是各面呈现的概率都是1/6,求:(1)“3和5同时出现”这事件的自信息量。
(2)“两个1同时出现”这事件的自信息量。
(3)两个点数的各种组合(无序对)的统计平均自信息量。
(4)两个点数之和(即2,3,…,12构成的子集)的熵。
(5)两个点数中至少有一个是1的自信息量。
2.5设在一只布袋中装有100只对人手的感觉完全相同的木球,每只上涂有1种颜色。
100只球的颜色有下列三种情况:(1)红色球和白色球各50只;(2)红色球99只,白色球1只;(3)红,黄,蓝,白色各25只。
求从布袋中随意取出一只球时,猜测其颜色所需要的信息量。
2.8大量统计表明,男性红绿色盲的发病率为7%,女性发病率为0.5%,如果你问一位男同志是否为红绿色盲,他回答“是”或“否”。
(1)这二个回答中各含多少信息量?(2)平均每个回答中含有多少信息量?(3)如果你问一位女同志,则答案中含有的平均信息量是多少?联合熵和条件熵2.9任意三个离散随机变量X 、Y 和Z ,求证:()()()()H XYZ H XY H XZ H X −≤−。
平均互信息及其性质2.11设随机变量12{,}{0,1}X x x ==和12{,}{0,1}Y y y ==的联合概率空间为11122122(,)(,)(,)(,)133818XY XY x y x y x y x y P ⎡⎤⎡⎤=⎢⎥⎢⎥⎣⎦⎣⎦定义一个新随机变量Z X Y =×(普通乘积)。
《信息论与编码》部分课后习题参考答案

P ( y1 = 0 | M 1 ) P ( y1 = 0)
因为信道为无记忆信道,所以
P( y1 = 0 | M 1 ) = P( y1 = 0 | x11 x12 = 00) = P( y1 = 0 | x11 = 0) = P(0 | 0) = p
同理,得 I ( y1 = 0 | M i ) = P ( y1 = 0 | xi1 xi 2 ) = P ( y1 = 0 | xi1 ) 输出第一个符号是 y1=0 时, 有可能是四个消息中任意一个第一个数字传送来的。 所以
第二章
2.1 同时掷两个骰子,设每个骰子各个面向上的概率都是 1/6。试求: (1)事件“2 和 6 同时出现”的自信息量; (2)事件“两个 3 同时出现”的自信息量; (3)事件“两个点数中至少有一个是 5”的自信息量; (4)两个点数之和的熵。 答: (1)事件“2 和 6 同时出现”的概率为:
《信息论与编码》
部分课后习题参考答案
1.1 怎样理解消息、信号和信息三者之间的区别与联系。 答:信号是一种载体,是消息的物理体现,它使无形的消息具体化。通信系统中传输的是 信号。 消息是信息的载体, 信息是指消息中包含的有意义的内容, 是消息中的未知成分。 1.2 信息论的研究范畴可以分成哪几种,它们之间是如何区分的? 答:信息论的研究范畴可分为三种:狭义信息论、一般信息论、广义信息论。 1.3 有同学不同意“消息中未知的成分才算是信息”的说法。他举例说,他从三岁就开始背 诵李白诗句“床前明月光,疑是地上霜。举头望明月,低头思故乡。 ” ,随着年龄的增长, 离家求学、远赴重洋,每次读到、听到这首诗都会带给他新的不同的感受,怎么能说这 些已知的诗句没有带给他任何信息呢?请从广义信心论的角度对此现象作出解释。 答:从广义信息论的角度来分析,它涉及了信息的社会性、实用性等主观因素,同时受知识 水平、文化素质的影响。这位同学在欣赏京剧时也因为主观因素而获得了享受,因此属于广 义信息论的范畴。
《信息理论与编码》,答案,考试重点(1--3章)

《信息理论与编码》,答案,考试重点(1--3章)《信息理论与编码》习题参考答案1. 信息是什么?信息与消息有什么区别和联系?答:信息是对事物存在和运动过程中的不确定性的描述。
信息就是各种消息符号所包含的具有特定意义的抽象内容,⽽消息是信息这⼀抽象内容通过语⾔、⽂字、图像和数据等的具体表现形式。
2. 语法信息、语义信息和语⽤信息的定义是什么?三者的关系是什么?答:语法信息是最基本最抽象的类型,它只是表现事物的现象⽽不考虑信息的内涵。
语义信息是对客观现象的具体描述,不对现象本⾝做出优劣判断。
语⽤信息是信息的最⾼层次。
它以语法、语义信息为基础,不仅要考虑状态和状态之间关系以及它们的含义,还要进⼀步考察这种关系及含义对于信息使⽤者的效⽤和价值。
三者之间是内涵与外延的关系。
第2章1. ⼀个布袋内放100个球,其中80个球是红⾊的,20个球是⽩⾊的,若随机摸取⼀个球,猜测其颜⾊,求平均摸取⼀次所能获得的⾃信息量?答:依据题意,这⼀随机事件的概率空间为120.80.2X x x P =其中:1x 表⽰摸出的球为红球事件,2x 表⽰摸出的球是⽩球事件。
a)如果摸出的是红球,则获得的信息量是()()11log log0.8I x p x =-=-(⽐特)b)如果摸出的是⽩球,则获得的信息量是()()22log log0.2I x p x =-=-(⽐特)c) 如果每次摸出⼀个球后⼜放回袋中,再进⾏下⼀次摸取。
则如此摸取n 次,红球出现的次数为()1np x 次,⽩球出现的次数为()2np x 次。
随机摸取n 次后总共所获得信息量为()()()()1122np x I x np x I x +d)则平均随机摸取⼀次所获得的信息量为()()()()()()()()()112211221log log 0.72 H X np x I x np x I x n p x p x p x p x =+=-+=⽐特/次2. 居住某地区的⼥孩中有25%是⼤学⽣,在⼥⼤学⽣中有75%是⾝⾼1.6⽶以上的,⽽⼥孩中⾝⾼1.6⽶以上的占总数的⼀半。
信息论与编码习题参考答案(全)

信息论与编码习题参考答案 第一章 单符号离散信源1.1同时掷一对均匀的子,试求:(1)“2和6同时出现”这一事件的自信息量; (2)“两个5同时出现”这一事件的自信息量; (3)两个点数的各种组合的熵; (4)两个点数之和的熵;(5)“两个点数中至少有一个是1”的自信息量。
解:bitP a I N n P bit P a I N n P c c N 17.536log log )(361)2(17.418log log )(362)1(36662221111616==-=∴====-=∴===⨯==样本空间:(3)信源空间:bit x H 32.436log 3662log 3615)(=⨯⨯+⨯⨯=∴ bitx H 71.3636log 366536log 3610 436log 368336log 366236log 36436log 362)(=⨯⨯+⨯+⨯+⨯⨯=∴++ (5) bit P a I N n P 17.11136log log )(3611333==-=∴==1.2如有6行、8列的棋型方格,若有两个质点A 和B ,分别以等概落入任一方格内,且它们的坐标分别为(Xa ,Ya ), (Xb ,Yb ),但A ,B 不能同时落入同一方格内。
(1) 若仅有质点A ,求A 落入任一方格的平均信息量; (2) 若已知A 已落入,求B 落入的平均信息量; (3) 若A ,B 是可辨认的,求A ,B 落入的平均信息量。
解:bita P a P a a P a I a P A i 58.548log )(log )()(H 48log )(log )(481)(:)1(481i i i i i ==-=∴=-=∴=∑=落入任一格的概率Θbitb P b P b b P b I b P A i 55.547log )(log )()(H 47log )(log )(471)(:B ,)2(481i i i i i ==-=∴=-=∴=∑=落入任一格的概率是落入任一格的情况下在已知ΘbitAB P AB P AB H AB P AB I AB P AB i i i i i i i 14.11)4748log()(log )()()(log )(471481)()3(47481=⨯=-=-=∴⨯=∑⨯=是同时落入某两格的概率1.3从大量统计资料知道,男性中红绿色盲的发病率为7%,女性发病率为0.5%.如果你问一位男士:“你是否是红绿色盲?”他的回答可能是:“是”,也可能“不是”。
信息论与编码知识梳理及课后答案共69页文档

•
46、寓形宇内复几时,曷不委心任去 留。
•
47、采菊东篱下,悠然见南山。
•
48、啸傲东轩下,聊复得此生。
•
49、勤学如春起之苗,不见其增,日 有所长 。
•
50、环堵萧然,不蔽风日;短褐穿结 ,箪瓢 屡空, 晏如也 。
谢谢你的阅读
❖ 知识就是财富 ❖ 丰富你的人生
71、既然我已经踏上这条道路,那么,任何东西都不应妨碍我沿着这条路走下去。——康德 72、家庭成为快乐的种子在外也不致成为障碍物但在旅行之际却是夜间的伴侣。——西塞罗 73、坚持意志伟大的事业需要始终不渝的精神。——伏尔泰 74、路漫漫其修道远,吾将上下而求索。——屈原 75、内外相应,言行相称。——韩非
信息论基础与编码(第五章)

信息论基础与编码(第五章)信息论基础与编码(第五章)5-1 有⼀信源,它有六种可能的输出,其概率分布如下表所⽰,表中给出了对应的六种编码12345C C C C C 、、、、和6C 。
(1)求这些码中哪些是唯⼀可译码;(2)求哪些是⾮延长码(即时码);(3)对所有唯⼀可译码求出其平均码长。
001111解:(1)1,2,3,6是唯⼀可译码; (2)1,3,6是即时码。
5-2证明若存在⼀个码长为12,,,ql l l 的唯⼀可译码,则⼀定存在具有相同码长的即时码。
证明:由定理可知若存在⼀个码长为的唯⼀可译码,则必定满⾜kraft 不等式1。
由定理4可知若码长满⾜kraft 不等式,则⼀定存在这样码长的即时码。
所以若存在码长的唯⼀可译码,则⼀定存在具有相同码长P (y=0)的即时码。
5-3设信源126126()s s s S p p p P s=?,611ii p==∑。
将此信源编码成为r 元唯⼀可译变长码(即码符号集12{,,,}r X x x x =),其对应的码长为(126,,,l l l )=(1,1,2,3,2,3),求r 值的最⼩下限。
解:要将此信源编码成为 r 元唯⼀可译变长码,其码字对应的码长(l 1 ,l 2 ,l 3, l 4,l 5, l 6)=(1,1,2,3,2,3) 必须满⾜克拉夫特不等式,即LqL L ,,2,1Λ∑=-qi l ir1≤4?LqL L ,,2,1Λ132321161≤+++++=------=-∑r r r r r r ri li所以要满⾜ 122232≤++rr r ,其中 r 是⼤于或等于1的正整数。
可见,当r=1时,不能满⾜Kraft 不等式。
当r=2, 1824222>++,不能满⾜Kraft 。
当r=3, 127262729232<=++,满⾜Kraft 。
所以,求得r 的最⼤值下限值等于3。
5-4设某城市有805门公务电话和60000门居民电话。
信息论与编码第五章习题参考答案
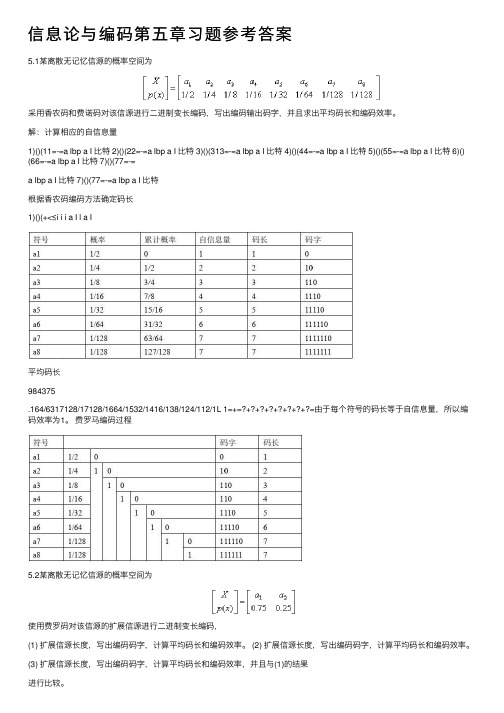
信息论与编码第五章习题参考答案5.1某离散⽆记忆信源的概率空间为采⽤⾹农码和费诺码对该信源进⾏⼆进制变长编码,写出编码输出码字,并且求出平均码长和编码效率。
解:计算相应的⾃信息量1)()(11=-=a lbp a I ⽐特 2)()(22=-=a lbp a I ⽐特 3)()(313=-=a lbp a I ⽐特 4)()(44=-=a lbp a I ⽐特 5)()(55=-=a lbp a I ⽐特 6)() (66=-=a lbp a I ⽐特 7)()(77=-=a lbp a I ⽐特 7)()(77=-=a lbp a I ⽐特根据⾹农码编码⽅法确定码长1)()(+<≤i i i a I l a I平均码长984375.164/6317128/17128/1664/1532/1416/138/124/112/1L 1=+=?+?+?+?+?+?+?+?=由于每个符号的码长等于⾃信息量,所以编码效率为1。
费罗马编码过程5.2某离散⽆记忆信源的概率空间为使⽤费罗码对该信源的扩展信源进⾏⼆进制变长编码,(1) 扩展信源长度,写出编码码字,计算平均码长和编码效率。
(2) 扩展信源长度,写出编码码字,计算平均码长和编码效率。
(3) 扩展信源长度,写出编码码字,计算平均码长和编码效率,并且与(1)的结果进⾏⽐较。
解:信息熵811.025.025.075.075.0)(=--=lb lb X H ⽐特/符号(1)平均码长11=L ⽐特/符号编码效率为%1.81X)(H 11==L η(2)平均码长为84375.0)3161316321631169(212=?+?+?+?=L ⽐特/符号编码效率%9684375.0811.0X)(H 22===L η(3)当N=4时,序列码长309.3725617256362563352569442569242562732562732256814=?+?+??+??+??+?+??+?=L平均码长827.04309.34==L %1.98827.0811.0X)(H 43===L η可见,随着信源扩展长度的增加,平均码长逐渐逼近熵,编码效率也逐渐提⾼。
信息论与编码习题答案

信息论与编码习题答案信息论与编码是通信和数据传输领域的基础学科,它涉及到信息的量化、传输和编码。
以下是一些典型的信息论与编码习题及其答案。
# 习题1:信息熵的计算问题:给定一个随机变量X,其可能的取值为{A, B, C, D},概率分别为P(A) = 0.3, P(B) = 0.25, P(C) = 0.25, P(D) = 0.2。
计算X的熵H(X)。
答案:H(X) = -∑(P(x) * log2(P(x)))= -(0.3 * log2(0.3) + 0.25 * log2(0.25) + 0.25 *log2(0.25) + 0.2 * log2(0.2))≈ 1.846# 习题2:信道容量的计算问题:考虑一个二进制信道,其中传输错误的概率为0.01。
求该信道的信道容量C。
答案:C = log2(2) * (1 - H(error))= 1 * (1 - (-0.01 * log2(0.01) - 0.99 * log2(0.99))) ≈ 0.98 nats# 习题3:编码效率的分析问题:一个编码器将4位二进制数字编码为8位二进制码字。
如果编码器使用了一种特定的编码方案,使得每个码字都具有相同的汉明距离,求这个编码方案的效率。
答案:编码效率 = 信息位数 / 总位数= 4 / 8= 0.5# 习题4:错误检测与纠正问题:给定一个(7,4)汉明码,它能够检测最多2个错误并纠正1个错误。
如果接收到的码字是1101100,请确定原始的4位信息位是什么。
答案:通过汉明码的生成矩阵和校验矩阵,我们可以计算出接收到的码字的校验位,并与接收到的码字的校验位进行比较,从而确定错误的位置并纠正。
通过计算,我们发现原始的4位信息位是0101。
# 习题5:数据压缩问题:如果一个文本文件包含10000个字符,每个字符使用8位编码,如何通过霍夫曼编码实现数据压缩?答案:首先,我们需要统计文本中每个字符的出现频率。
信息论与编码理论习题答案

资料范本本资料为word版本,可以直接编辑和打印,感谢您的下载信息论与编码理论习题答案地点:__________________时间:__________________说明:本资料适用于约定双方经过谈判,协商而共同承认,共同遵守的责任与义务,仅供参考,文档可直接下载或修改,不需要的部分可直接删除,使用时请详细阅读内容第二章信息量和熵2.2 八元编码系统,码长为3,第一个符号用于同步,每秒1000个码字,求它的信息速率。
解:同步信息均相同,不含信息,因此每个码字的信息量为 2=23=6 bit因此,信息速率为 61000=6000 bit/s2.3 掷一对无偏骰子,告诉你得到的总的点数为:(a) 7; (b) 12。
问各得到多少信息量。
解:(1) 可能的组合为 {1,6},{2,5},{3,4},{4,3},{5,2},{6,1} ==得到的信息量 ===2.585 bit(2) 可能的唯一,为 {6,6}=得到的信息量===5.17 bit2.4 经过充分洗牌后的一副扑克(52张),问:(a) 任何一种特定的排列所给出的信息量是多少?(b) 若从中抽取13张牌,所给出的点数都不相同时得到多少信息量?解:(a) =信息量===225.58 bit(b)==信息量==13.208 bit2.9 随机掷3颗骰子,X表示第一颗骰子的结果,Y表示第一和第二颗骰子的点数之和,Z表示3颗骰子的点数之和,试求、、、、。
解:令第一第二第三颗骰子的结果分别为,,,相互独立,则,,==6=2.585 bit===2(36+18+12+9+)+6=3.2744 bit=-=-[-]而=,所以= 2-=1.8955 bit或=-=+-而= ,所以=2-=1.8955 bit===2.585 bit=+=1.8955+2.585=4.4805 bit2.10 设一个系统传送10个数字,0,1,…,9。
奇数在传送过程中以0.5的概率错成另外一个奇数,其余正确接收,求收到一个数字平均得到的信息量。
(完整版)信息论第五章答案

5.1 设信源⎭⎬⎫⎩⎨⎧=⎥⎦⎤⎢⎣⎡01.01.015.017.018.019.02.0)(7654321x x x x x x x X P X (1) 求信源熵H(X); (2) 编二进制香农码;(3) 计算平均码长和编码效率。
解: (1)symbolbit x p x p X H i i i /609.2)01.0log 01.01.0log 1.015.0log 15.017.0log 17.018.0log 18.019.0log 19.02.0log 2.0()(log )()(2222222712=⨯+⨯+⨯+⨯+⨯+⨯+⨯-=-=∑=%1.8314.3609.2)()(14.301.071.0415.0317.0318.0319.032.03)(=====⨯+⨯+⨯+⨯+⨯+⨯+⨯==∑KX H R X H x p k K ii i η5.2 对信源⎭⎬⎫⎩⎨⎧=⎥⎦⎤⎢⎣⎡01.01.015.017.018.019.02.0)(7654321x x x x x x x X P X 编二进制费诺码,计算编码效率。
%2.9574.2609.2)()(74.201.041.0415.0317.0218.0319.032.02)(=====⨯+⨯+⨯+⨯+⨯+⨯+⨯==∑KX H R X H x p k K ii i η5.3 对信源⎭⎬⎫⎩⎨⎧=⎥⎦⎤⎢⎣⎡01.01.015.017.018.019.02.0)(7654321x x x x x x x X P X 编二进制和三进制哈夫曼码,计算各自的平均码长和编码效率。
解:%9.9572.2609.2)()(72.201.041.0415.0317.0318.0319.022.02)(=====⨯+⨯+⨯+⨯+⨯+⨯+⨯==∑KX H R X H x p k K ii i η%4.913log 8.1609.2log )()(8.1)01.01.015.017.018.019.0(22.01)(22=⨯====+++++⨯+⨯==∑m LK X H R X H x p k K ii i η5.4 设信源⎪⎭⎪⎬⎫⎪⎩⎪⎨⎧=⎥⎦⎤⎢⎣⎡12811281641321161814121)(87654321x x x x x x x x X P X (1) 求信源熵H(X);(2) 编二进制香农码和二进制费诺码;(3) 计算二进制香农码和二进制费诺码的平均码长和编码效率; (4) 编三进制费诺码;(5) 计算三进制费诺码的平均码长和编码效率;解: (1)symbolbit x p x p X H i i i /984.1128log 1281128log 128164log 64132log 32116log 1618log 814log 412log 21)(log )()(22222222812=⨯+⨯+⨯+⨯+⨯+⨯+⨯+⨯=-=∑==127/64 bit/symbol (2)二进制费诺码:香农编码效率:%100984.1984.1)()(64/127984.17128171281664153214161381241121)(======⨯+⨯+⨯+⨯+⨯+⨯+⨯+⨯==∑KX H R X H x p k K ii i η费诺编码效率:%100984.1984.1)()(984.17128171281664153214161381241121)(=====⨯+⨯+⨯+⨯+⨯+⨯+⨯+⨯==∑KX H R X H x p k K ii i η(5)%3.943log 328.1984.1log )()(328.14128141281364133212161281141121)(22=⨯=⋅===⨯+⨯+⨯+⨯+⨯+⨯+⨯+⨯==∑m K X H R X H x p k K ii i η5.5 设无记忆二进制信源⎭⎬⎫⎩⎨⎧=⎥⎦⎤⎢⎣⎡1.09.010)(X P X先把信源序列编成数字0,1,2,……,8,再替换成二进制变长码字,如下表所示。
信息论与编码第五章答案学习资料

信息论与编码第五章答案5.1 设信源1234567()0.20.190.180.170.150.10.01Xa a a a a a a p X ⎡⎤⎧⎫=⎨⎬⎢⎥⎣⎦⎩⎭ (1) 求信源熵H(X); (2) 编二进制香农码;(3) 计算平均码长和编码效率. 解: (1)721222222()()log ()0.2log 0.20.19log 0.190.18log 0.180.17log 0.170.15log 0.150.1log 0.10.01log 0.012.609/i i i H X p a p a bit symbol==-=-⨯-⨯-⨯-⨯-⨯-⨯-⨯=∑(2)(3)71()0.230.1930.1830.1730.1530.140.0173.141()()/ 2.609 3.14183.1%i i i K k p x H X H X K Rη===⨯+⨯+⨯+⨯+⨯+⨯+⨯====÷=∑5.2 对习题5.1的信源编二进制费诺码,计算编码效率.解:a i p(a i)编码码字k ia10.20002 a20.19100103 a30.1810113 a40.1710102 a50.15101103 a60.11011104 a70.011111145.3 对信源编二进制和三进制哈夫曼码,计算各自的平均码长和编码效率.解:二进制哈夫曼码:x i p(x i)编码码字k i s61s50.610s40.391s30.350s20.261x10.20102 x20.191112 x30.1800003 x40.1710013 x50.1500103 s10.111x60.1001104 x70.01101114三进制哈夫曼码:x i p(x i)编码码字k i s31s20.540s10.261x10.2221 x20.190002 x30.181012 x40.172022 x50.150102 x60.11112 x70.0121225.4 设信源(1) 求信源熵H(X);(2) 编二进制香农码和二进制费诺码;(3) 计算二进制香农码和二进制费诺码的平均码长和编码效率;(4) 编三进制费诺码;(5) 计算三进制费诺码的平均码长和编码效率;解:(1)(2)二进制香农码:x i p(x i)p a(x i)k i码字x10.5010x20.250.5210x30.1250.753110x40.06250.87541110x50.031250.9375511110x60.0156250.968756111110x70.00781250.98437571111110x80.00781250.992187571111111二进制费诺码:xi p(x i)编码码字k i x10.5001 x20.2510102 x30.125101103 x40.06251011104x50.0312510111105 x60.015625101111106 x70.00781251011111107 x80.0078125111111117 (3)香农编码效率:费诺编码效率:(4)x i p(x i)编码码字k i x10.5001 x20.25111 x30.12520202 x40.06251212 x50.03125202203 x60.01562512213 x70.00781252022204 x80.0078125122214 (5)5.5 设无记忆二进制信源先把信源序列编成数字0,1,2,……,8,再替换成二进制变长码字,如下表所示.(1) 验证码字的可分离性;(2) 求对应于一个数字的信源序列的平均长度;(3) 求对应于一个码字的信源序列的平均长度;(4) 计算,并计算编码效率;(5) 若用4位信源符号合起来编成二进制哈夫曼码,求它的平均码长,并计算编码效率.序列数字二元码字101000011100100131010000131011000014110000000151101000000161110000000017111100000000805.6 有二元平稳马氏链,已知p(0/0) = 0.8,p(1/1) = 0.7,求它的符号熵.用三个符号合成一个来编写二进制哈夫曼码,求新符号的平均码字长度和编码效率.5.7 对题5.6的信源进行游程编码.若“0”游程长度的截至值为16,“1”游程长度的截至值为8,求编码效率. 5.8 选择帧长N= 64(1) 对001000000000000000000000000000000100000000000000 0000000000000000遍L-D码;(2) 对100001000010110000000001001000010100100000000111 0000010000000010遍L-D码再译码;(3) 对000000000000000000000000000000000000000000000000 0000000000000000遍L-D码;(4) 对101000110101110001100011101001100001111011001010 00110101011010010遍L-D码;(5) 对上述结果进行讨论.。
信息论、编码与密码学课后复习题答案

《信息论、编码与密码学》课后习题答案第1章 信源编码1.1考虑一个信源概率为{0.30,0.25,0.20,0.15,0.10}的DMS 。
求信源熵H (X )。
解: 信源熵 ∑=-=512)(log )(k k k p p X HH(X)=-[0.30*(-1.737)+0.25*(-2)+0.2*(-2.322)+0.15*(-2.737)+0.1*(-3.322)]=[0.521+0.5+0.464+0.411+0.332] =2.228(bit)故得其信源熵H(X)为2.228bit1.2 证明一个离散信源在它的输出符号等概率的情况下其熵达到最大值。
解: 若二元离散信源的统计特性为P+Q=1 H(X)=-[P*log(P)+(1-P)*log(1-P)] 对H(X)求导求极值,由dH(X)/d(P)=0可得211101log ==-=-p ppp p可知当概率P=Q=1/2时,有信源熵)(1)(max bit X H =对于三元离散信源,当概率3/1321===P P P 时,信源熵)(585.1)(m ax bit X H =,此结论可以推广到N 元的离散信源。
1.3 证明不等式ln 1x x ≤-。
画出曲线1ln y x =和21y x =-的平面图以表明上述不等式的正确性。
证明:max ()ln 1(0)1()()01001()0()0ln 11ln 1ln 1f x x x x f x xf x x x x f x f x f x x x x x x x =-+>'=''==>∴<≤>≤=≤-≥≤-≤-令,又有时此时也即当时同理可得此时综上可得证毕绘制图形说明如下 可以很明确说明上述 不等式的正确性。
1.4 证明(;)0I X Y ≥。
在什么条件下等号成立?1111(,)(,)(,)(,)log()()n mi j i j i j n mi j i j i j i j I P x y I x y P x y P x y P x P y =====∑∑∑∑(X ;Y )=当和相互独立时等号成立。
