(完整)北师大版七年级上计算题
北师大七年级数学上册有理数计算题
北师大七年级数学上册有理数计算题以下是格式错误已经删除的段落：6+（－7）+（9）+23）－(－14)－(－13)－(＋(－33)－(－2)22以下是经过小幅度改写后的文章：一、有理数加法1.（－9）+（－13）=（－22）2.（－12）+27=153.（－28）+（－34）=（－62）4.67+（－92）=（－25）5.|5+（－3）|=26.（－5）+|―3|=（－8）7.38+（－22）+（+62）+（－78）=08.（－8）+（－10）+2+（－1）=（－17）9.（－3）+0+（+4）+（－6）=（－5）10.（－8）+47+18+（－27）=3011.（－5）+21+（－95）+29=（－50）12.（－）+（－）+（－）=（－）13.6+（－7）+（9）+2=1014.72+65+（-105）+（－28）=415.（－23）+|－63|+|－37|+（－77）=（－200）16.19+（－195）+47=（－129）17.（+18）+（－32）+（－16）+（+26）=（－4）18.（－8）+（－32）+2+（－2）+12=（－28）19.5+（－53）+4=（－44）20.5+（－34）+（－）+（－）=（－39）21.（－20）+（－5）+（－5）+（－12）=（－42）22.（－23）+（－59）+（－|－32|）+（－12）=（－126）23.72+（－5）=67二、有理数减法1.7－9=（－2）2.0－(－9)=93.（－25）－(－13)=（－12）4.（－32）－5=（－37）5.（－26）－（－12）=（－14）6.12－18=（－6）7.1－（－2）=38.（－20）－(+5)－(－5)－（－12）=（－8）9.（－23）－（－59）－（－|－32|）－（－12）=（－20）10.72－（－5）=77三、有理数乘法1.（－9）×3=（－27）2.（－13）×（－）=133.（－2）×3=（－6）4.1×（－）=（－1）5.3×（－5）＋3×（－13）=（－54）6.（－4）×（－10）×（－3）=1207.（－8）×3=（－24）四则运算是数学中最基础的运算之一，包括加减乘除四种运算。
北师大版七年级数学上册整式计算题专项练习(附答案)
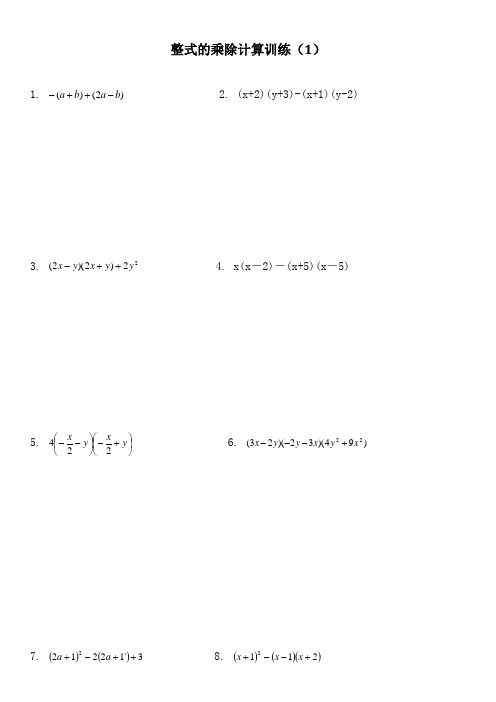
整式的乘除计算训练（1）1. )2()(b a b a -++-2. (x+2)(y+3)-(x+1)(y-2)3. 22)2)(2(y y x y x ++-4. x(x －2)－(x+5)(x －5)5. ⎪⎭⎫ ⎝⎛+-⎪⎭⎫ ⎝⎛--y x y x224 6. )94)(32)(23(22x y x y y x +---7. ()()3`122122++-+a a 8. ()()()2112+--+x x x9. (x －3y)(x+3y)－(x －3y)2 10. 23(1)(1)(21)x x x +---11. 22)23()23(y x y x --+ 12. 22)()(y x y x -+13. ×810014. 3022)2(21)x (4554---÷⎪⎭⎫⎝⎛--π-+⎪⎭⎫⎝⎛-÷⎪⎭⎫ ⎝⎛15. (1211200622332141）（）（）（）-⨯+----16—19题用乘法公式计算×1001 17.1992-18.298 19.2010200820092⨯-20.化简求值：)4)(12()12(2+-+-a a a ，其中2-=a 。
21. 化简求值2(2)2()()2(3)x y x y x y y x y +--++-,其中12,2x y =-=。
22. 5(x －1)(x +3)－2(x －5)(x －2) 23. (a －b )(a 2+ab +b 2)24. (3y+2)(y－4)－3(y－2)(y－3) 25. a(b－c)+b(c－a)+c(a－b)1y2)226. (－2mn2)2－4mn3(mn+1) 27. 3xy(－2x)3·(－428. (－x－2)(x+2) 29. 5×108·(3×102) 30. (x－3y)(x+3y)－(x－3y)2 31. (a+b－c)(a－b－c)答案1. a-2b2. 5x+y+83. 4x2+y24. -2x+255. x2-4y26. 16y4-81x47. 4a2+28. x+39. 6xy-18y2 10. -x2+4x-4 11. 24xy 12. x4-2x2y2+y413. 1 14. 10 15. 161216. 原式=(1000-1)×(1000+1) 17. 原式=(99+1)×(99-1)=1000000-1 =100×98=999999 =980018. 原式=(900-2)2 19. 原式=20092-(2009+1)(2009-1)=10000-400+4 =20092-20092+1=9604 =120.原式=6a2+3a-3，当a=2时，原式=6×(-2)2+3×(-2)-3=1521.原式=-x2+6xy，当x=2，y=12时，原式=-(-2)2+6×(-2)×12=-1022. -3x2+24x-35 23. a3-b3 24. 5y-26 25. 026. -4mn3 27. -3x4y5 28. -x2-4x-4 29. 1.5×1011230. 6xy-18y2 31. a2-2ac+c2-b22014年北师大七年级数学上册《整式及其加减》计算题专项练习一一．解答题（共12小题）1．计算题①12﹣（﹣8）+（﹣7）﹣15；②﹣12+2×（﹣5）﹣（﹣3）3÷；③（2x﹣3y）+（5x+4y）；④（5a2+2a﹣1）﹣4（3﹣8a+2a2）．2．（1）计算：4+（﹣2）2×2﹣（﹣36）÷4；（2）化简：3（3a﹣2b）﹣2（a﹣3b）．3．计算：（1）7x+4（x2﹣2）﹣2（2x2﹣x+3）；（2）4ab﹣3b2﹣[（a2+b2）﹣（a2﹣b2）]；（3）（3mn﹣5m2）﹣（3m2﹣5mn）；（4）2a+2（a+1）﹣3（a﹣1）．4．化简（1）2（2a2+9b）+3（﹣5a2﹣4b）（2）3（x3+2x2﹣1）﹣（3x3+4x2﹣2）5．（2009?柳州）先化简，再求值：3（x﹣1）﹣（x﹣5），其中x=2．6．已知x=5，y=3，求代数式3（x+y）+4（x+y）﹣6（x+y）的值．7．已知A=x2﹣3y2，B=x2﹣y2，求解2A﹣B．8．若已知M=x2+3x﹣5，N=3x2+5，并且6M=2N﹣4，求x．9．已知A=5a2﹣2ab，B=﹣4a2+4ab，求：（1）A+B；（2）2A﹣B；（3）先化简，再求值：3（A+B）﹣2（2A﹣B），其中A=﹣2，B=1．10．设a=14x﹣6，b=﹣7x+3，c=21x﹣1．（1）求a﹣（b﹣c）的值；（2）当x=时，求a﹣（b﹣c）的值．11．化简求值：已知a、b满足：|a﹣2|+（b+1）2=0，求代数式2（2a﹣3b）﹣（a﹣4b）+2（﹣3a+2b）的值．12．已知（x+1）2+|y﹣1|=0，求2（xy﹣5xy2）﹣（3xy2﹣xy）的值．2014年北师大七年级数学上册《整式及其加减》计算题专项练习一参考答案与试题解析一．解答题（共12小题）1．计算题①12﹣（﹣8）+（﹣7）﹣15；②﹣12+2×（﹣5）﹣（﹣3）3÷；③（2x﹣3y）+（5x+4y）；④（5a2+2a﹣1）﹣4（3﹣8a+2a2）．考点：整式的加减；有理数的混合运算．专题：计算题．分析：（1）直接进行有理数的加减即可得出答案．（2）先进行幂的运算，然后根据先乘除后加减的法则进行计算．（3）先去括号，然后合并同类项即可得出结果．（4）先去括号，然后合并同类项即可得出结果．解答：解：①原式=12+8﹣7﹣15=﹣2；②原式=﹣1﹣10+27÷=﹣11+81=70；③原式=2x﹣3y+5x+4y=7x+y；④原式=5a2+2a﹣1﹣12+32a﹣8a2=﹣3a2+34a﹣13．点评：本题考查了整式的加减及有理数的混合运算，属于基础题，解答本题的关键熟记去括号法则，熟练运用合并同类项的法则，这是各地中考的常考点．2．（1）计算：4+（﹣2）2×2﹣（﹣36）÷4；（2）化简：3（3a﹣2b）﹣2（a﹣3b）．考点：整式的加减；有理数的混合运算．分析：（1）按照有理数混合运算的顺序，先乘方后乘除最后算加减；（2）运用整式的加减运算顺序计算：先去括号，再合并同类项．解答：解：（1）原式=4+4×2﹣（﹣9）=4+8+9=17；（2）原式=9a﹣6b﹣2a+6b=（9﹣2）a+（﹣6+6）b=7a．点评：在混合运算中要特别注意运算顺序：先三级，后二级，再一级；熟记去括号法则：﹣﹣得+，﹣+得﹣，++得+，+﹣得﹣；及熟练运用合并同类项的法则：字母和字母的指数不变，只把系数相加减．3．计算：（1）7x+4（x2﹣2）﹣2（2x2﹣x+3）；（2）4ab﹣3b2﹣[（a2+b2）﹣（a2﹣b2）]；（3）（3mn﹣5m2）﹣（3m2﹣5mn）；（4）2a+2（a+1）﹣3（a﹣1）．考点：整式的加减．分析：（1）先去括号，再合并同类项即可；（2）先去括号，再合并同类项即可；（3）先去括号，再合并同类项即可；（4）先去括号，再合并同类项即可．解答：解：（1）7x+4（x2﹣2）﹣2（2x2﹣x+3）=7x+4x2﹣8﹣4x2+2x﹣6=9x﹣14；（2）4ab﹣3b2﹣[（a2+b2）﹣（a2﹣b2）]=4ab﹣3b2﹣[a2+b2﹣a2+b2]=4ab﹣3b2﹣2b2=4ab﹣5b2；（3）（3mn﹣5m2）﹣（3m2﹣5mn）=3mn﹣5m2﹣3m2+5mn=8mn﹣8m2；（4）2a+2（a+1）﹣3（a﹣1）=2a+2a+2﹣3a+3=a+5．点评：本题考查了整式的加减，解决此类题目的关键是熟记去括号法则，熟练运用合并同类项的法则，这是各地中考的常考点．4．化简（1）2（2a2+9b）+3（﹣5a2﹣4b）（2）3（x3+2x2﹣1）﹣（3x3+4x2﹣2）考点：整式的加减．专题：计算题．分析：（1）原式利用去括号法则去括号后，合并同类项即可得到结果；（2）原式利用去括号法则去括号后，合并同类项即可得到结果．解答：解：（1）原式=4a2+18b﹣15a2﹣12b=﹣11a2+6b；（2）原式=3x3+6x2﹣3﹣3x3﹣4x2+2=2x2﹣1．点评：此题考查了整式的加减，涉及的知识有：去括号法则，以及合并同类项法则，熟练掌握法则是解本题的关键．5．（2009?柳州）先化简，再求值：3（x﹣1）﹣（x﹣5），其中x=2．考点：整式的加减—化简求值．分析：本题应对方程去括号，合并同类项，将整式化为最简式，然后把x的值代入即可．解答：解：原式=3x﹣3﹣x+5=2x+2，当x=2时，原式=2×2+2=6．点评：本题考查了整式的化简．整式的加减运算实际上就是去括号、合并同类项，这是各地中考的常考点．6．已知x=5，y=3，求代数式3（x+y）+4（x+y）﹣6（x+y）的值．考点：整式的加减—化简求值．分析：先把x+y当作一个整体来合并同类项，再代入求出即可．解答：解：∵x=5，y=3，∴3（x+y）+4（x+y）﹣6（x+y）=x+y=5+3=8．点评：本题考查了整式的加减的应用，主要考查学生的计算能力，用了整体思想．7．已知A=x2﹣3y2，B=x2﹣y2，求解2A﹣B．考点：整式的加减．分析：直接把A、B代入式子，进一步去括号，合并得出答案即可．解答：解：2A﹣B=2（x2﹣3y2）﹣（x2﹣y2）=2x2﹣6y2﹣x2+y2=x2﹣5y2．点评：此题考查整式的加减混合运算，掌握去括号法则和运算的方法是解决问题的关键．8．若已知M=x2+3x﹣5，N=3x2+5，并且6M=2N﹣4，求x．考点：整式的加减；解一元一次方程．专题：计算题．分析：把M与N代入计算即可求出x的值．解答：解：∵M=x2+3x﹣5，N=3x2+5，∴代入得：6x2+18x﹣30=6x2+10﹣4，解得：x=2．点评：此题考查了整式的加减，熟练掌握运算法则是解本题的关键．9．已知A=5a2﹣2ab，B=﹣4a2+4ab，求：（1）A+B；（2）2A﹣B；（3）先化简，再求值：3（A+B）﹣2（2A﹣B），其中A=﹣2，B=1．考点：整式的加减；整式的加减—化简求值．专题：计算题．分析：（1）把A与B代入A+B中计算即可得到结果；（2）把A与B代入2A﹣B中计算即可得到结果；（3）原式去括号合并得到最简结果，把A与B的值代入计算即可求出值．解答：解：（1）∵A=5a2﹣2ab，B=﹣4a2+4ab，∴A+B=5a2﹣2ab﹣4a2+4ab=a2+2ab；（2）∵A=5a2﹣2ab，B=﹣4a2+4ab，∴2A﹣B=10a2﹣4ab+4a2﹣4ab=14a2﹣8ab；（3）原式=3A+3B﹣4A+2B=﹣A+5B，把A=﹣2，B=1代入得：原式=2+5=7．点评：此题考查了整式的加减，熟练掌握运算法则是解本题的关键．10．设a=14x﹣6，b=﹣7x+3，c=21x﹣1．（1）求a﹣（b﹣c）的值；（2）当x=时，求a﹣（b﹣c）的值．考点：整式的加减；代数式求值．专题：计算题．分析：（1）把a，b，c代入a﹣（b﹣c）中计算即可得到结果；（2）把x的值代入（1）的结果计算即可得到结果．解答：解：（1）把a=14x﹣6，b=﹣7x+3，c=21x﹣1代入得：a﹣（b﹣c）=a﹣b+c=14x﹣6+7x﹣3+21x﹣1=42x﹣10；（2）把x=代入得：原式=42×﹣10=﹣10=．点评：此题考查了整式的加减，以及代数式求值，熟练掌握运算法则是解本题的关键．11．化简求值：已知a、b满足：|a﹣2|+（b+1）2=0，求代数式2（2a﹣3b）﹣（a﹣4b）+2（﹣3a+2b）的值．考点：整式的加减—化简求值；非负数的性质：绝对值；非负数的性质：偶次方．专题：计算题．分析：原式去括号合并得到最简结果，利用非负数的性质求出a与b的值，代入计算即可求出值．解答：解：原式=4a﹣6b﹣a+4b﹣6a+4b=﹣3a+2b，∵|a﹣2|+（b+1）2=0，∴a=2，b=﹣1，则原式=﹣6﹣2=﹣8．点评：此题考查了整式的加减﹣化简求值，熟练掌握运算法则是解本题的关键．12．已知（x+1）2+|y﹣1|=0，求2（xy﹣5xy2）﹣（3xy2﹣xy）的值．考点：整式的加减—化简求值；非负数的性质：绝对值；非负数的性质：偶次方．分析：因为平方与绝对值都是非负数，且（x+1）2+|y﹣1|=0，所以x+1=0，y﹣1=0，解得x，y的值．再运用整式的加减运算，去括号、合并同类项，然后代入求值即可．解答：解：2（xy﹣5xy2）﹣（3xy2﹣xy）=（2xy﹣10xy2）﹣（3xy2﹣xy）=2xy﹣10xy2﹣3xy2+xy=（2xy+xy）+（﹣3xy2﹣10xy2）=3xy﹣13xy2，∵（x+1）2+|y﹣1|=0∴（x+1）=0，y﹣1=0∴x=﹣1，y=1．∴当x=﹣1，y=1时，3xy﹣13xy2=3×（﹣1）×1﹣13×（﹣1）×12=﹣3+13=10．答：2（xy﹣5xy2）﹣（3xy2﹣xy）的值为10．点评：整式的加减运算实际上就是去括号、合并同类项，这是各地中考的常考点．代入求值时要化简．。
北师大版七年级数学计算题
北师大版七年级数学计算题一、有理数运算（1 - 5题）1. 计算：(-2)+3 - (-5)- 解析：- 首先去括号，根据去括号法则，括号前是“-”号，把括号和它前面的“ - ”号去掉后，原括号里各项的符号都要改变。
所以-(-5)=5。
- 则原式=-2 + 3+5。
- 按照从左到右的顺序计算，-2+3 = 1，1 + 5=6。
2. 计算：-3×(-4)÷(-2)- 解析：- 按照从左到右的顺序进行乘除运算。
- 先计算-3×(-4)=12。
- 再计算12÷(-2)= - 6。
3. 计算：(-2)^3+(-3)×[(-4)^2 - 2]- 解析：- 先计算指数运算。
(-2)^3=-8，(-4)^2 = 16。
- 然后计算括号内的式子，(-4)^2-2 = 16 - 2=14。
- 接着计算乘法-3×14=-42。
- 最后计算加法-8+(-42)=-8 - 42=-50。
4. 计算：(1)/(2)-<=ft(-(1)/(3))+<=ft(-(1)/(4))- 解析：- 首先去括号，-<=ft(-(1)/(3))=(1)/(3)。
- 然后通分，分母2、3、4的最小公倍数是12。
- (1)/(2)=(6)/(12)，(1)/(3)=(4)/(12)，(1)/(4)=(3)/(12)。
- 原式=(6)/(12)+(4)/(12)-(3)/(12)=(6 + 4-3)/(12)=(7)/(12)。
5. 计算：0.25×(-2)^3-<=ft[4÷<=ft(-(2)/(3))^2+1]- 解析：- 先计算指数运算，(-2)^3=-8，<=ft(-(2)/(3))^2=(4)/(9)。
- 然后计算乘法0.25×(-8)=-2。
- 接着计算括号内的式子，4÷(4)/(9)=4×(9)/(4)=9，9 + 1=10。
北师大版七年级 数学上第4章基本平面图形 -- 线段计算题(含答案)
北师大版七年级数学上第4章基本平面图形 -- 线段计算题（含答案）AB=6C AB D AC BD1. 已知：线段厘米，点是的中点，点在的中点，求线段的长．AB=6AB C BC=2AB D AC2. 如图，已知线段，延长线段到，使，点是的中点．求：AC（1）的长；BD（2）的长．B C AD2:3:4M AD CD=8MC3. 如图、两点把线段分成三部分，是的中点，，求的长．C ABD BC AD=7BD=5CD4. 已知：为线段的中点，在线段上，且，，求：线段的长度．AB=20cm C AB D AC E BC DE 5. 如图，，是上任意一点，是的中点，是的中点，求线段的长．AC=6cm BC=15cm M AC CB N6. 如图，线段，线段，点是的中点，在上取一点，使得CN:NB=1:2MN，求的长．7. 如图，，两点把线段分成三部分，其比为，是的中点，B C MN MB:BC:CN =2:3:4P MN ，求的长．PC =2cm MN8. 已知，如图，点在线段上，且，，点、分别是、的中C AB AC =6cm BC =14cm M N AC BC 点．（1）求线段的长度；MN（2）在（1）中，如果，，其它条件不变，你能猜测出的长度吗？AC =acm BC =bcm MN 请说出你发现的结论，并说明理由．9. 已知、两点在数轴上表示的数为和，、均为数轴上的点，且． A B a b M N OA <OB （1）若、的位置如图所示，试化简：．A B |a|−|b|+|a +b|+|a−b|（2）如图，若，，求图中以、、、、这个点为端点的所|a|+|b|=8.9MN =3A N O M B 5有线段长度的和；（3）如图，为中点，为中点，且，，若点为数轴上一点，M AB N OA MN =2AB−15a =−3P 且，试求点所对应的数为多少？PA =23ABP10. 阅读材料：我们知道：点、在数轴上分别表示有理数、，、两点之间的距A B a b A B 离表示为，在数轴上、两点之间的距离．所以式子的几何意义是AB A B AB =|a−b||x−3|数轴上表示有理数的点与表示有理数的点之间的距离．3x 根据上述材料，解答下列问题：（1）若，则________；|x−3|=|x +1|x =（2）式子的最小值为________；|x−3|+|x +1|（3）若，求的值．|x−3|+|x +1|=7x11. 如图，是定长线段上一点，、两点分别从、出发以、的速度沿P AB C D P B 1cm/s 2cm/s 直线向左运动（在线段上，在线段上）AB C AP D BP （1）若、运动到任一时刻时，总有，请说明点在线段上的位置：C D PD =2AC P AB（2）在（1）的条件下，是直线上一点，且，求的值．Q AB AQ−BQ =PQ PQAB（3）在（1）的条件下，若、运动秒后，恰好有，此时点停止运动，点C D 5CD =12ABC D 继续运动（点在线段上），、分别是、的中点，下列结论：①的值D PB M N CD PD PM−PN 不变；②的值不变，可以说明，只有一个结论是正确的，请你找出正确的结论并求MNAB 值．12. 如图，、是线段上两点，已知，、分别为、的中点，C D AB AC:CD:DB =1:2:3M N AC DB且，求线段的长．AB =18cm MN13. （应用题）如图所示，，，是一条公路上的三个村庄，，间路程为，A B C A B 100km ，间路程为，现在，之间建一个车站，设，之间的路程为． A C 40km A B P P C xkm （1）用含的代数式表示车站到三个村庄的路程之和；x（2）若路程之和为，则车站应设在何处？102km（3）若要使车站到三个村庄的路程总和最小，问车站应设在何处？最小值是多少？14. 已知线段，，线段在直线上运动（在左侧，在左侧）． AB =12CD =6CD AB A B C D （1）、分别是线段、的中点，若，求；M N AC BD BC =4MN（2）当运动到点与点重合时，是线段延长线上一点，下列两个结论：①CD D B P AB 是定值；②是定值，请作出正确的选择，并求出其定值．PA +PB PCPA−PBPC15. 如图甲，点是线段上一点，、两点分别从、同时出发，以、的O AB C D O B 2cm/s 4cm/s 速度在直线上运动，点在线段之间，点在线段之间．AB C OA D OB（1）设、两点同时沿直线向左运动秒时，，求的值；C D AB t AC:OD =1:2OAOB（2）在（1）的条件下，若、运动秒后都停止运动，此时恰有，求C D 52OD−AC =12BD的长；CD （3）在（2）的条件下，将线段在线段上左右滑动如图乙（点在之间，点在CD AB C OA D 之间），若、分别为、的中点，试说明线段的长度总不发生变化．OB M N AC BD MN16. 线段，点是线段中点，点是线段上一点，且，是线段AB =12cm O AB C AB AC =12BCP 的中点．AC（1）求线段的长．（如图所示）OP（2）若将题目中：点是线段上一点，改为点是直线上一点，线段还可以是C AB C AB OP 多长？（画出示意图）17. 已知：如图，是定长线段上一定点，、两点分别从、出发以、1M AB C D M B 1cm/s 的速度沿直线向左运动，运动方向如箭头所示（在线段上，在线段上）3cm/s BA C AM D BM（1）若，当点、运动了，求的值．AB =10cm C D 2s AC +MD（2）若点、运动时，总有，直接填空：________．C D MD =3AC AM =AB（3）在（2）的条件下，是直线上一点，且，求的值．N AB AN−BN =MN MNAB参考答案与试题解析北师大版七上线段计算题一、 解答题 （本题共计 17 小题 ，每题 10 分 ，共计170分 ） 1.【答案】解：∵ 厘米，是的中点，AB =6C AB ∴ 厘米，AC =3∵ 点在的中点，D AC ∴ 厘米，DC =1.5∴ 厘米．BD =BC +CD =4.52.【答案】、．1833.【答案】解：设，，，AB =2x BC =3x CD =4x ∴ ，，AD =9x MD =92x则，，CD =4x =8x =2．MC =MD−CD =92x−4x =12x =12×2=14.【答案】解：∵ ，AD =7BD =5∴ AB =AD +BD =12∵ 是的中点C AB ∴AC =12AB =6∴ ．CD =AD−AC =7−6=15.【答案】．10cm6.【答案】解：∵ 是的中点，M AC ∴，MC =AM =12AC =12×6=3cm又∵ CN:NB =1:2∴，CN =13BC =13×15=5cm∴ ．MN =MC +NC =3cm +5cm =8cm 7.【答案】．MN =36cm 8.【答案】解：（1）∵ ，，AC =6cm BC =14cm 点、分别是、的中点，M N AC BC ∴ ，，MC =3cm NC =7cm ∴ ；MN =MC +NC =10cm（2）．理由是：MN =12(a +b)cm∵ ，，AC =acm BC =bcm 点、分别是、的中点，M N AC BC ∴ ，，MC =12acmNC =12bcm ∴ ．MN =MC +NC =12(a +b)cm9.【答案】所有线段长度的和为41.6（3）∵ a =−3∴ OA =3∵ 为的中点，为的中点M AB N OA ∴ ，AM =12ABAN =12OA∴ MN =AM−AN =12AB−12OA =12AB−32又MN =2AB−15∴2AB−15=12AB−32解得：AB =9∴PA =23AB =6若点在点的左边时，点在原点的左边（图略）P A P OP =9故点所对应的数为P −9若点在点的右边时，点在原点的右边（图略）P A P OP =3故点所对应的数为P 3答：所对应的数为或．P −9310.【答案】，，或．14x =92x =−5211.【答案】解：（1）根据、的运动速度知：C D BD =2PC ∵ ，PD =2AC ∴ ，即，BD +PD =2(PC +AC)PB =2AP ∴ 点在线段上的处；P AB 13（2）如图：∵ ，AQ−BQ =PQ ∴ ；AQ =PQ +BQ 又，AQ =AP +PQ ∴ ，AP =BQ ∴ ，PQ =13AB∴ ．PQAB =13当点在的延长线上时Q ′AB AQ ′−AP =PQ′所以AQ ′−B Q ′=PQ =AB所以；PQAB=1（3）②．MNAB 的值不变理由：当时，点停止运动，此时，CD =12ABC CP =5AB =30①如图，当，在点的同侧时M N PMN =PN−PM =12PD−(PD−MD)=MD−12PD =12CD−12PD =12(CD−PD)=12CP =52②如图，当，在点的异侧时M N PMN =PM +PN =MD−PD +12PD =MD−12PD =12CD−12PD =12(CD−PD)=12CP =52∴ MNAB=5230=112当点停止运动，点继续运动时，的值不变，所以，．C D MN MNAB =11212.【答案】的长为．MN 12cm13.【答案】解：（1）路程之和为；PA +PC +PB =40+x +100−(40+x)+x =(100+x)km （2），，车站在两侧处；100+x =102x =2C 2km （3）当时，，车站建在处路程和最小，路程和为．x =0x +100=100C 100km 14.【答案】解：（1）如图，∵ 、分别为线段、的中点，1M N AC BD ∴，AM =12AC =12(AB +BC)=8，DN =12BD =12(CD +BC)=5∴ ；MN =AD−AM−DN =9如图，∵ 、分别为线段、的中点，2M N AC BD ∴，AM =12AC =12(AB−BC)=4，DN =12BD =12(CD−BC)=1∴ ；MN =AD−AM−DN =12+6−4−4−1=9（2）①正确．证明：．PA +PBPC=2∵，PA +PBPC=(PC +AC)+(PC−CB)PC=2PC PC=2∴ ①是定值．PA +PBPC215.【答案】解：（1）设，则，AC =x OD =2x 又∵ ，OC =2t DB =4t ∴ ，，OA =x +2t OB =2x +4t∴ ；OA OB =12（2）设，，又，，由，得AC =x OD =2x OC =52×2=5(cm)BD =52×4=10(cm)OD−AC =12BD ，，2x−x =12×10x =5，OD =2x =2×5=10(cm)；CD =OD +OC =10+5=15(cm)（3）在（2）中有，，，，AC =5(cm)BD =10(cm)CD =15AB =AC +BD +CD =30(cm)设，，AM =CM =x BN =DN =y ∵ ，，2x +15+2y =30x +y =7.5∴ ．MN =CM +CD +DN =x +15+y =22.516.【答案】解：（1）OP =AO−AP =12AB−AP=12AB−12AC =12AB−12×13AB．=13AB =4（2）如下图所示：此时，．OP =AO +AP =12AB +AP =12AB +12AC =12AB +12AB =AB =1217.【答案】解：（1）当点、运动了时，，C D 2s CM =2cm BD =6cm∵ ，，AB =10cm CM =2cm BD =6cm∴ AC +MD =AB−CM−BD =10−2−6=2cm（2）14（3）当点在线段上时，如图N AB∵ ，又∵ AN−BN =MN AN−AM =MN ∴ ，∴ ，即．BN =AM =14AB MN =12AB MN AB =12当点在线段的延长线上时，如图N AB∵ ，又∵ AN−BN =MN AN−BN =AB ∴ ，即．综上所述MN =AB MN AB =1MN AB =12或1。
北师大版七年级数学上册《有理数混合运算》典型例题(含答案)
《有理数混合运算》典型例题例1 计算.4116531211-++- 解法一：原式.1271121912151041845653123-=-=-++-=-++-= 解法二：原式.127112521231046114116531211-=+-=-++-+--=--++--= 说明：加减混合运算时，带分数可以化为假分数，也可把带分数的整数部分与分数部分分别加减，这是因为带分数是一个整数和一个分数的和. 例如：.211211;411411--=---=- 例2 计算.414)216(⎪⎭⎫ ⎝⎛-⨯÷- 错解：原式＝（－216）÷（－1）＝216. 正解：原式.211345441)54(==⎪⎭⎫ ⎝⎛-⨯-= 分析：对这种乘除同级混合运算应遵循从左到右的运算顺序，事实上错解就错在这一点.计算：（1）⎪⎭⎫ ⎝⎛-÷⎪⎭⎫ ⎝⎛-⨯22176412； （2）15)3(4)3(23+-⨯--⨯； （3）911321321÷⎪⎭⎫ ⎝⎛-⨯-； （4）[]4)103(412÷-⨯-. 例3 计算：（1）333)1(3)2(4-÷---；（2）)311()131(23422-÷-⨯⨯--． 解 （1）333)1(3)2(4-÷---)1(27)8(4-÷---=.392712=+=（2）方法一：)311()131(23422-÷-⨯⨯-- )34()32(1216-÷-⨯--=)43(816-⨯+-= .22616-=--= 方法二：)311()131(23422-÷-⨯⨯-- )43()131(1216-⨯-⨯--= )43()124(16-⨯---= .22)93(16-=-+-=说明：在进行有理数的混合运算时，一要注意运算顺序的正确；二要注意符号的变化；三要注意在运用运算性质时不要出现错误．例4 计算：])54(17)511781851[()5(2--⨯---⨯- 分析 该题有双重括号看起来比较复杂，但只要我们按运算顺序去做都可以求出结果．在计算时我们还应考虑灵活运用运算性质来简化计算．解 ])54(17)511781851[()5(2--⨯---⨯- ]251617)511725851[()5(-⨯---⨯-= ]251651725)51[()5(----⨯-= 516171251+++= 51146=． 说明： 有理数混合运算的步骤，初学者应写得详细一些，这是避免出现错误的好办法．例5 计算：32)]52()611[()]941(531[-⨯-÷-⨯． 分析：此题运算顺序是：第一步计算)941(-和)611(-；第二步做乘法；第三步做乘方运算；第四步做除法． 解：原式32)]52(65[]9558[-⨯÷⨯= 32)31()98(-÷=)271(8164-÷= )27(8164-⨯= 364-= 3121-= 说明：由此例题可以看出，括号在确定运算顺序上的作用，所以计算题也需认真审题．。
北师大版七年级数学上册第二章 有理数及其运算 计算题专题练习题(含答案)
北师大版七年级数学上册第二章 有理数及其运算 计算题专题练习题专题(一) 有理数的加减运算1、计算：(－2)＋3＋1＋(－3)＋2＋(－4)．解：原式＝[(－2)＋2]＋[3＋(－3)]＋1＋(－4)＝0＋0＋1＋(－4)＝－3.2、计算：(＋9)－(＋10)＋(－2)－(－8)＋3.解：原式＝9－10－2＋8＋3＝(9＋8＋3)－(10＋2)＝20－12＝8.3、计算：(1)－23－35＋78－13－25＋18； 解：原式＝(－23－13)＋(－35－25)＋(78＋18) ＝－1－1＋1＝－1.(2)－479－(－315)－(＋229)＋(－615)． 解：原式＝[－479－(＋229)]＋[－(－315)＋(－615)] ＝－7－3＝－10.4、计算：|－0.75|＋(－3)－(－0.25)＋|－18|＋78. 解：原式＝0.75－3＋0.25＋18＋78＝(0.75＋0.25)＋(18＋78)－3 ＝1＋1－3＝－1.5、计算：－156＋(－523)＋2434＋312. 解：原式＝(－1－56)＋(－5－23)＋(24＋34)＋(3＋12) ＝[(－1)＋(－5)＋24＋3]＋[(－56)＋(－23)＋34＋12] ＝21＋(－14) ＝2034. 6、计算：634＋313－514－312＋123. 解：原式＝6＋34＋3＋13－5－14－3－12＋1＋23＝(6＋3－5－3＋1)＋(34＋13－14－12＋23) ＝2＋1＝3.7、计算：(1)(－7)－(＋5)＋(－4)－(－10)；解：原式＝－7－5－4＋10＝－6.(2)3.5－4.6＋3.5－2.4；解：原式＝(3.5＋3.5)＋(－2.4－4.6)＝7－7＝0.(3)－9＋6－(＋11)－(－15)；解：原式＝－9＋6－11＋15＝(－9－11)＋(6＋15)＝－20＋21＝1.(4)12＋(－23)＋45＋(－12)＋(－13)； 解：原式＝[12＋(－12)]＋[(－23)＋(－13)]＋45＝0＋(－1)＋45＝－15.(5)－478－(－512)＋(－412)－318；解：原式＝－478＋512－412－318＝(－478－318)＋(512－412) ＝－8＋1＝－7.(6)0.25＋112＋(－23)－14＋(－512)； 解：原式＝14＋112＋(－23)－14＋(－512) ＝(14－14)＋[112＋(－23)＋(－512)] ＝－1.(7)|－12|－(－2.5)－(－1)－|0－212|； 解：原式＝12＋2.5＋1－212＝(12＋1)＋(2.5－212) ＝112.(8)－205＋40034＋(－20423)＋(－112)； 解：原式＝(－205)＋400＋34＋(－204)＋(－23)＋(－1)＋(－12) ＝(400－205－204－1)＋(34－23－12)＝－10＋(－512) ＝－10512.(9)0＋1－[(－1)－(－37)－(＋5)－(－47)]＋|－4|； 解：原式＝1－[(－1)＋37－5＋47]＋4 ＝1－[(－1＋37＋47)－5]＋4 ＝10.(10)－12－16－112－120－130－142－156－172； 解：原式＝－(12＋16＋112＋120＋130＋142＋156＋172) ＝－(1－12＋12－13＋13－14＋14－15＋15－16＋16－17＋17－18＋18－19) ＝－(1－19) ＝－89.(11)1－2－3＋4＋5－6－7＋8＋…＋97－98－99＋100.解：原式＝(1－2)＋(－3＋4)＋(5－6)＋(－7＋8)＋…＋(97－98)＋(－99＋100) ＝－1＋1－1＋1－…－1＋1＝0.8、观察下列各式：12＝11×2＝1－12，16＝12×3＝12－13，112＝13×4＝13－14，…，根据规律完成下列各题．(1)19×10＝19－110； (2)计算12＋16＋112＋120＋…＋19 900的值为99100．专题(二) 有理数的混合运算1、计算：531×(－29)×(－2115)×(－412)． 解：原式＝－531×29×3115×92＝－(531×3115)×(29×92) ＝－13×1 ＝－13.2、计算：(14－16＋124)×(－48)． 解：原式＝14×(－48)－16×(－48)＋124×(－48) ＝－12＋8－2＝－6.3、计算：4×(－367)－3×(－367)－6×367. 解：原式＝－367×(4－3＋6) ＝－27.4、计算：(16－27＋23)÷(－542)． 解：原式＝(16－27＋23)×(－425) ＝16×(－425)－27×(－425)＋23×(－425) ＝－75＋125－285＝－235.5、计算：(能用简便方法的尽量用简便方法计算)(1)－0.75×(－112)÷(－214)； 解：原式＝－34×(－32)×(－49)＝－12.(2)－(3－5)×32÷(－1)3；解：原式＝－(－2)×9÷(－1)＝－2×9÷1＝－18.(3)(－1.5)×45÷(－25)×34； 解：原式＝32×45×52×34＝94.(4)－14＋16÷(－2)3×(－3－1)；解：原式＝－1＋16÷(－8)×(－4)＝－1＋8＝7.(5)(－5)÷(－127)×(－214)÷7； 解：原式＝－5×79×94×17＝－54.(6)0.7×1949＋234×(－14)＋0.7×59＋14×(－14)； 解：原式＝0.7×(1949＋59)－14×(234＋14) ＝0.7×20－14×3＝－28.(7)391314×(－14)； 解：原式＝(40－114)×(－14)＝40×(－14)－114×(－14) ＝－560＋1＝－559.(8)1318÷(－7)； 解：原式＝1318×(－17) ＝(14－78)×(－17) ＝－2＋18＝－178.(9)12.5×6.787 5×18＋1.25×678.75×0.125＋0.125×533.75×18； 解：原式＝(12.5×6.787 5＋1.25×678.75＋0.125×533.75)×18＝[125×(0.678 75＋6.787 5＋0.533 75)]×18＝125×8×18＝125.(10)(－5)－(－5)×110÷110×(－5)； 解：原式＝(－5)－(－5)×110×10×(－5)＝－5－25＝－30.(11)(－42)÷(223)2＋512×(－16)－(－0.5)2； 解：原式＝(－16)÷649－1112－14＝－94－1112－14＝－4112.(12)148÷(38－56＋14)； 解：因为(38－56＋14)÷148＝(38－56＋14)×48 ＝38×48－56×48＋14×48 ＝18－40＋12＝－10，所以148÷(38－56＋14)＝－110.(13)(－12)÷(－4)－27÷(－3)×(－13)； 解：原式＝3－9×13＝3－3＝0.(14)(－2)3－16×(38－1)＋2÷(12―14―16)． 解：原式＝－8－16×38＋16＋2÷(612－312－212) ＝－8－6＋16＋2÷112＝2＋24＝26.。
北师大版七年级上册数学 计算题训练
七年级上册数学 计算题训练 1
完成时间：______ （2） 24 +︱6－10︱－ 3 (1)2014
（3） 32 32 3 2 4
（4）
32
1 3
52
3 5
240
4
1
4
（5） 14
1
1 2
3
3 32
；
（6） (1 5 7 ) (60) 2 6 12
（2）若 3A＋6B 的值与 a 的取值无关，求 b 的值．
七年级上册数学 计算题训练 5
完成时间：______ 1、已知 A x2 ax 1，B 2bx2 4x 1 ，且多项式 2A B 的值与字母 x 的取值无关，求 a, b 的值.
2 、 如 果 代 数 式 (2x2 ax y 6)－(2bx2－3x 5y－1) 的 值 与 字 母 x 所 取 的 值 无 关 ， 试 求 代 数 式
4
2
2
4、先化简，后求值：
（1）5（3x2y－xy2）－3（－xy2＋4x2y），其中 x＝1，y＝－ 1 ． 2
（2） 1 (4a2 2a 8b) (a 2b) , 其中 a 1 ,b =2014．
4
2
七年级上册数学 计算题训练 4
完成时间：______
1、已知 (x 2)2 + y 1 ＝0，求 5x2y—[2x2y－（xy2－2x2y）－4]－2xy2 的值。 2
2、先化简，再求值
已知 a 1 (b 2)2 0,
求
2a 2
8ab
1 2
(ab
4a 2
)
1 2
ab
的值．
3、已知代数式 3a2 (4ab a2 ) 2(a2 2ab b2 ) ． （1）试说明这个代数式的值与 a 的取值无关；
(完整)北师大版七年级上计算题
七年级上计算练习1．计算（1）3+（﹣1）﹣（﹣5） （2）+（﹣3）2×（﹣）2．计算：（1）（-8）×5-40=_____； （2）（-1．2）÷（-13）-（-2）=______． 3．[(x+y)2－(x －y)2－4x 2y 2]÷(2xy)4．若22218160x x y y +++-+=，求xy的值．5．计算：﹣12+3×（﹣2）3﹣（﹣6）÷（﹣）2． 1512412246⎛⎫--⨯ ⎪⎝⎭6．计算：－20+（－14）－（－18）－137．计算题：（1）24+（-14）+（-16）+8 （2）33(2)()424-⨯÷-⨯（3）21114()(60)31215--⨯- （4）4211(10.5)[2(3)]3---⨯⨯--8．有理数混合运算（1）-32-[8÷（-2）3-1]+3÷2×12； （2）（-2）3-6÷（12-13）-36×（-12-518+56）．（3）254(7)(6)-+--+-9．解方程：（1）4(0.5)17x x ++= （2）2151136x x +--=10． 计算：（1）)9()3(15252-÷-+⎪⎭⎫⎝⎛-⨯- （2）（+16）+（-25）+（+24）+（-32）（3）)9()5()21()10(-+--+-- （4） （-4）-（-1）+（-6）÷2．11．计算：（本题共12分，每小题3分）（1）（＋3）＋（－5） －4－（－2）； （2）251×（－61）×113÷54（3）（61＋31－21）÷（－181）； （4）432)3(--÷2014)1(716-+．12．计算：（1）72÷（﹣2）3+（﹣）2×32﹣（﹣3）×4． （2）-22×7-6÷(-3)+513．计 算：（1）()2432a a a +÷ （2）|-1|-2÷+（-2）2．（3）()24335274158.0--+⎪⎭⎫ ⎝⎛+-⎪⎭⎫ ⎝⎛---14．解方程：（1）4(1)13(2)x x --=- （2）322132x x x +--=-15．计算：（1）7(2)(3)--+-. （2）5.6+（－0.9）+4.4+（－8.1）（3）1(27)(3)3-÷-⨯（4）(4) 3.12( 2.5)-⨯⨯-.（5）111()20245-++⨯ （6）888120(3)(7)(3)37(3)999-⨯-+-⨯-+⨯-16．计算：（1）（﹣21）+（﹣13）﹣（﹣25）﹣（+28） （2）﹣22﹣6÷（﹣2）×13（3）)361()436597(-÷+- （4）⎪⎭⎫ ⎝⎛÷⎥⎥⎦⎤⎢⎢⎣⎡⎪⎭⎫ ⎝⎛⨯⨯415-8.0-31-3-2142217．计算（每小题3分，共12分）（1）()()3182624----+-； （2）()()43526⨯--⨯-+； （3）)87()87()21(43-÷⎥⎦⎤⎢⎣⎡---+ （4）4211(10.5)2(3)3⎡⎤---⨯⨯--⎣⎦18．计算（1）)5()2()10(8---+-+ （2）)311(5352312-+--（3）)169(83)43(-÷⨯- （4）)1()4(40)2(1-⨯--÷+-÷（5））（）（36-43197-65⨯+ （6）192324×（－12） 19．x y yx xy y x 222223-+-20．（1）计算：（1+﹣）×（﹣24）（2）计算：﹣32﹣[﹣1+（1﹣2×）÷（﹣）]．21．计算题 （1）－32＋（—1）200116÷＋（—5）2 （2）()()()3221532⎡⎤-⨯-÷-+-⎣⎦22．计算：])3(2[61122015--⨯--23．（1）)654()8.4()612(545---+++； （2）)]95(32[)3(2-+-⨯-；（3）4231(2)(4)()(1)2-÷-⨯--； （4）41111()36234-+-+-⨯24．计算：（1）⎪⎭⎫ ⎝⎛+-⎪⎭⎫ ⎝⎛--⎪⎭⎫ ⎝⎛-+⎪⎭⎫ ⎝⎛+32354231251 （2）)61(6)3(524-÷--⨯+-（3）52412561314÷⎥⎦⎤⎢⎣⎡⨯⎪⎪⎭⎫ ⎝⎛+-- （4）123(6)()2-+--⨯-．25．（1）﹣﹣﹣（﹣）﹣（2）9.872+（﹣）+（﹣5.872）（3）（﹣）÷（﹣）； （4）（5）1.3×（﹣9.12）+（﹣7）×9.12 （6）﹣14﹣×[2﹣（﹣3）]2（7）[÷（﹣）+0.4×]×（﹣1）5 （8）[1]2÷[（1﹣）×]326．计算：（1）－4+28－（－19）+（－24）； （2）.42-3-5322÷-⨯+）（）（27．计算（1）11－18－12 + 19 （2）（－5）× （－7）+ 20÷（－4） （3）111(36)964⎛⎫+-⨯- ⎪⎝⎭（4）124×1()3-－12÷23（5）3 +12 ÷ 22×（－3）－5 （6）－21+2014×35()6-×0－（－3）28．计算（1）(3)2-244-⨯+÷（）﹣（﹣3） （2）-5+（﹣3）2﹣3.14)π-（×-212⎛⎫- ⎪⎝⎭÷20151-（）29.（本题满分18分）计算题：（1）)14(612-++-）（ （2）543+-- （3）)60()1276521(-⨯-+ （4）)8(6523)9(-÷⨯÷-（5）423592÷---⨯-）（）（ （6））（）（）（）（3212131213-⨯-+-÷-30计算：（1）（2）52﹣3×[﹣32+（﹣2）×（﹣3）]+（﹣4）331．（4分）若多项式222)25(23mx x y x +-+-的值与x 的值无关，求m 的值。
北师大版七年级数学上册整式计算题专项练习(附答案)
北师大版七年级数学上册整式计算题专项练习(附答案)1.将表达式化简：$-a-b+2a-b=-b+a$2.将表达式化简：$(x+2)(y+3)-(x+1)(y-2)=xy+3x+2y+6-xy+x-2y+2=x+3x+2+6+x-2y+2=4x-2y+10$3.将表达式化简：$(2x-y)(2x+y)+2y2=4x2-y2+2y2=4x2$4.将表达式化简：$\frac{x(x-y)}{x-2}+\frac{2y}{x-2}=\frac{x(x-y)+2y}{x-2}=\frac{x^{2}-xy+2y}{x-2}$6.将表达式化简：$(2a+1)^{2}-2(2a+1)+3=4a^{2}+8a+4-4a-2+3=4a^{2}+4a+5$8.将表达式化简：$-(x-5)(x+5)-\frac{(3x-2y)(-2y-3x)}{x+1}=\frac{-(x^{2}-25)(x+1)+(9x^{2}-12xy+4y^{2})}{x+1}=\frac{-x^{3}-10x^{2}-21x+4y^{2}}{x+1}$10.将表达式化简：$3(x+1)(x-1)-(2x-1)(x+y)2(x-y)2=3(x^{2}-1)-2x^{3}+x^{2}y+xy^{2}-2xy^{2}+2y^{3}=3x^{2}-3-2x^{3}+x^{2}y-y^{2}$15.将表达式化简：$-\frac{1}{2}-(-1)^{2006}+\frac{2^{11}\times(-3)^{432}}{2}= -\frac{1}{2}-1+2^{10}\times3^{432}=2^{10}\times3^{432}-\frac{3}{2}$20.将表达式化简：$(2a-1)^{2}+(2a-1)(a+4)=4a^{2}-4a+1+2a^{2}+7a-4=6a^{2}+3a-3$21.将表达式化简：$(x+2y)^{2}-2(x-y)(x+y)+2y(x-3y)=x^{2}+4xy+4y^{2}-2(x^{2}-y^{2})+2xy-6y^{2}=x^{2}+6xy-8y^{2}$22.将表达式化简：$5(x-1)(x+3)-2(x-5)(x-2)=5(x^{2}+2x-3)-2(x^{2}-3x+10)=3x^{2}+16x-40$23.将表达式化简：$(a-b)(a^{2}+ab+b^{2})=a^{3}-b^{3}$24.将表达式化简：$(3y+2)(y-4)-3(y-2)(y-3)=3y^{2}-5y-18$25.将表达式化简：$a(b-c)+b(c-a)+c(a-b)=ab-ac+bc-bc+ac-ab=0$26.将表达式化简：$(-2mn^{2})^{2}-4mn^{3}(mn+1)=4m^{2}n^{4}-4m^{2}n^{4}-4mn^{3}= -4mn^{3}$28.将表达式化简：$-(x+2)(x-2)=-(x^{2}-4)=-x^{2}+4$30.将表达式化简：$(x-3y)(x+3y)-(x-3y)=x^{2}-9y^{2}-x+3y$1.原式=2.原式=-400+4=9604；原式=-+1=13.原式=900×219；原式=-(2009+1)(2009-1)=2xxxxxxxxxxxx=-xxxxxxx4.原式=6a^2+3a-3，当a=2时，原式=6×(-2)^2+3×(-2)-3=24-6-3=155.原式=-x^2+6xy，当x=2，y=2时，原式=-(-2)^2+6×(-2)×2=-4-24=-286.原式=-3x^2+24x-357.原式=a^3-b3=(a-b)(a^2+ab+b^2)8.原式=5y-269.原式=6xy-18y210.原式=(a-c+b)^2-b^2=a^2-2ac+2bc+c^2-b^211.原式=15×10^912.原式=2a+2解答题：1.①原式=12-(-8)+(-7)-15=38②原式=-1+2×(-5)-(-3)÷(-1)=-1+(-10)-3=-14③原式=2x-3y+5x+4y=7x+y④原式=5a+2a^-1-4(3-8a+2a)=5a+2a^-1-12+32a-8a=34a+2a^-1-122.1) 原式=4-2×2-(-36)÷4=4-4+9=92) 原式=9a-6b-2a+6b=7a3.①原式=7x+4(x-2)-2(2x-x+3)=7x+4x-8-2x+2=9x-6②原式=4ab-3b-[(a+b)-(a-b)]=4ab-3b-a-b+a+b=4ab-3b-a③原式=3mn-5m-3m+5mn=8mn-8m④原式=2a+2(a+1)-3(a-1)=2a+2a+2-3a+3=4a+54.①原式=4a+18b-15a-12b=4a-15a+18b-12b=-11a+6b②原式=3x+6x^-1-3x-4x^-1=2x+2x^-15.原式=3(x-1)-(x-5)=3x-3-x+5=2x+26.原式=3(x+y)+4(x+y)-6(x+y)=7(x+y)=7(5+3)=567.原式=2(x-3y)-(x-y)=2x-6y-x+y=x-5y8.由6M=2N-4得M=N/3-2/3，代入M=x+3x-5和N=3x+5中得到：x+3x-5=N/3-2/3+3x-5解得x=7/69.原式=A+B=5a-2ab-4a+4ab=a先化简，再求值：3（A+B）﹣2（2A﹣B），其中A=﹣2，B=1．分析：先代入数值，再按照整式的加减运算顺序进行计算．解答：代入A=﹣2，B=1得：3（A+B）﹣2（2A﹣B）=3（﹣2+1）﹣2（2（﹣2）﹣1）=3﹣4﹣（﹣5）=9．点评：本题考查了整式的加减及代数式的化简，解答本题的关键在于熟练掌握整式的加减运算顺序及代入数值的方法．10．设a=14x﹣6，b=﹣7x+3，c=21x﹣1．1）求a﹣（b﹣c）的值；2）当x=时，求a﹣（b﹣c）的值．分析：先代入数值，再按照整式的加减运算顺序进行计算．解答：代入a=14x﹣6，b=﹣7x+3，c=21x﹣1得：1）a﹣（b﹣c）=14x﹣6﹣（﹣7x+3﹣21x+1）=14x﹣6﹣﹣7x+3﹣21x﹣1=6x﹣4；2）当x=时，a﹣（b﹣c）=6×﹣4﹣4=﹣28．点评：本题考查了整式的加减及代数式的化简，解答本题的关键在于熟练掌握整式的加减运算顺序及代入数值的方法．11．化简求值：已知a、b满足：|a﹣2|+（b+1）=0，求代数式2（2a﹣3b）﹣（a﹣4b）+2（﹣3a+2b）的值．分析：先化简|a﹣2|+（b+1）=0得a=2，b=﹣1，再代入求值．解答：代入a=2，b=﹣1得：2（2a﹣3b）﹣（a﹣4b）+2（﹣3a+2b）=2（2×2﹣3（﹣1））﹣（2﹣4（﹣1））+2（﹣3×2+2（﹣1））=4+9+6=19．点评：本题考查了整式的加减及代数式的化简，解答本题的关键在于熟练掌握绝对值的性质及代入求值的方法．12．已知（x+1）+|y﹣1|=0，求2（xy﹣5xy）﹣（3xy﹣xy）的值．分析：先解方程|x﹣1|+（y+1）=0，得x=﹣1，y=﹣2，再代入求值．解答：解方程得x=﹣1，y=﹣2，代入得：2（xy﹣5xy）﹣（3xy﹣xy）=2（﹣1×﹣2﹣5﹣1×﹣2）﹣（3﹣1×﹣2）=4﹣（3+2）=﹣1．点评：本题考查了整式的加减及代数式的化简，解答本题的关键在于熟练掌握绝对值的性质及代入求值的方法．解答：将3（x+y）+4（x+y）﹣6（x+y）化简得：(3+4-6)(x+y)=x+y=-2代入x=5，y=3，得到3（5+3）+4（5+3）﹣6（5+3）=24 所以，代数式3（x+y）+4（x+y）﹣6（x+y）的值为24.点评：本题考查了整式的加减、化简和求值，需要熟练掌握去括号、合并同类项和代入数值的方法。
七年级上册数学北师大版计算题
七年级上册数学北师大版计算题一、有理数的运算1. 加法运算- 计算：( - 3)+5- 解析：有理数加法法则为，异号两数相加，取绝对值较大的符号，并用较大的绝对值减去较小的绝对值。
| - 3|=3，|5| = 5，5>3，所以结果为正，( - 3)+5 = 5 -3=2。
2. 减法运算- 计算：4-( - 2)- 解析：减去一个数等于加上这个数的相反数。
所以4-( - 2)=4 + 2 = 6。
3. 乘法运算- 计算：( - 2)×3- 解析：两数相乘，异号得负，并把绝对值相乘。
| - 2|×|3|=2×3 = 6，所以( - 2)×3=-6。
4. 除法运算- 计算：( - 8)÷( - 2)- 解析：两数相除，同号得正，并把绝对值相除。
| - 8|÷| - 2|=8÷2 = 4，所以( - 8)÷( - 2)=4。
5. 混合运算- 计算：2×( - 3)+( - 2)^2- 解析：- 先算乘方，( - 2)^2=4。
- 再算乘法，2×( - 3)=-6。
- 最后算加法，-6 + 4=-2。
二、整式的加减1. 同类项的合并- 化简：3x+2y - 5x - y- 解析：- 首先找出同类项，3x和-5x是同类项，2y和-y是同类项。
- 合并同类项，(3x - 5x)+(2y - y)=-2x + y。
2. 整式的加减运算- 计算：(2a^2+3a - 1)-(3a^2 - 2a+4)- 解析：- 去括号，括号前是“-”号，把括号和它前面的“-”号去掉后，原括号里各项的符号都要改变。
得到2a^2+3a - 1 - 3a^2+2a - 4。
- 再合并同类项，(2a^2 - 3a^2)+(3a+2a)+(-1 - 4)=-a^2 + 5a - 5。
三、一元一次方程1. 简单方程的求解- 解方程：2x+3 = 7- 解析：- 首先进行移项，把常数项移到等号右边，得到2x=7 - 3。
北师大版七年级上册计算题汇总
计算题汇总一、有理数加减乘除混合运算（1）()()()()959149-+--+-- （2） ()3.5-+()2.3-()5.2--()8.4+-（3） (－5)×(－7)－5×（－6） （4）()⎪⎭⎫ ⎝⎛+⨯-654360 （5）753(36)964⎛⎫-+-⨯- ⎪⎝⎭； （6）（7）⎥⎦⎤⎢⎣⎡⎪⎭⎫ ⎝⎛-+-⨯-854342（8）⎥⎥⎦⎤⎢⎢⎣⎡-⎪⎭⎫ ⎝⎛-⨯-6532182（9）()[]3252-+⨯ （10）])3(2[31)5.01(122008--⨯⨯-+-（11） (－2)2－|－7|＋3－2×12⎛⎫-⎪⎝⎭（12）()()425.5232÷--⨯--（13） 18.0)35()5(124-+-⨯-÷- （14））（）（23235-÷-+--（15） ()2123358--⎪⎭⎫ ⎝⎛-÷++- （16）()()20072212343--⎪⎭⎫ ⎝⎛⨯---（17）42000223(1)(2)-+⨯---（18）15954362--+⎪⎭⎫⎝⎛-⨯-（19）()73)81()2(16132008-⨯---÷+- （20）)3(|28|)3()1(2010-÷+---⨯-二、整式的加减 1、（1） （2）（3）()()642322-++--xy x xy x （4）5x 2－2(3y 2－5x 2)＋(－4y 2＋7xy )2、化简求值（1）)3(2)52(422222ab b a b a ab b a --+-+其中1-=a ，32-=b（2）().41,2006,123132-==⎪⎭⎫⎝⎛----y x y x y x 其中（3），其中.（4）)(3)(3)22(22222222y y x x y x y x +++--，其中1-=x ，2=y（5）3326183222+-+--a a a a ,其中21=a .（6）]1)2(3[3622+---xy x y xy ,其中02132=⎪⎭⎫ ⎝⎛-++y x .（7）3(ab －5b 2＋2a 2)－(7ab ＋16a 2－25b 2)，其中|a －1|＋(b ＋1)2＝0.3、解答题（1）（5分）化简关于的代数式.当为何值时，代数式的值是常数？（2）有这样一道题：“计算的值，其中.甲同学把“错抄成但他计算的结果也是正确的，试说明理由，并求出这个结果.（3）(9分)小强和小亮在同时计算这样一道求值题：“当a ＝－3时，求整式7a 2－[5a －(4a －1)＋4a 2]－(2a 2－a ＋1)的值．”小亮正确求得结果为7，而小强在计算时，错把a ＝－3看成了a ＝3，但计算的结果却也正确，你能说明为什么吗？三、解一元一次方程1、（1）（1）5)21(43y =--y （2）3112-=-x x（3）5278x x -=+ （4）14(0.75)22x -+=（5）111(15)(7)523x x +=-- （6） 131262=--+x x （7）142312-+=-y y （8） 1676352212--=+--x x x（9）()()x x 2152831--=-- （10）0262921=---x x(11)142312-+=-y y （12） 14.04.15.03=--xx。
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
七年级上计算练习1．计算（1）3+（﹣1）﹣（﹣5） （2）+（﹣3）2×（﹣）2．计算：（1）（-8）×5-40=_____； （2）（-1．2）÷（-13）-（-2）=______． 3．[(x+y)2－(x －y)2－4x 2y 2]÷(2xy)4．若22218160x x y y +++-+=，求xy的值．5．计算：﹣12+3×（﹣2）3﹣（﹣6）÷（﹣）2． 1512412246⎛⎫--⨯ ⎪⎝⎭6．计算：－20+（－14）－（－18）－137．计算题：（1）24+（-14）+（-16）+8 （2）33(2)()424-⨯÷-⨯（3）21114()(60)31215--⨯- （4）4211(10.5)[2(3)]3---⨯⨯--8．有理数混合运算（1）-32-[8÷（-2）3-1]+3÷2×12； （2）（-2）3-6÷（12-13）-36×（-12-518+56）．（3）254(7)(6)-+--+-9．解方程：（1）4(0.5)17x x ++= （2）2151136x x +--=10． 计算：（1）)9()3(15252-÷-+⎪⎭⎫⎝⎛-⨯- （2）（+16）+（-25）+（+24）+（-32）（3）)9()5()21()10(-+--+-- （4） （-4）-（-1）+（-6）÷2．11．计算：（本题共12分，每小题3分）（1）（＋3）＋（－5） －4－（－2）； （2）251×（－61）×113÷54（3）（61＋31－21）÷（－181）； （4）432)3(--÷2014)1(716-+．12．计算：（1）72÷（﹣2）3+（﹣）2×32﹣（﹣3）×4． （2）-22×7-6÷(-3)+513．计 算：（1）()2432a a a +÷ （2）|-1|-2÷+（-2）2．（3）()24335274158.0--+⎪⎭⎫ ⎝⎛+-⎪⎭⎫ ⎝⎛---14．解方程：（1）4(1)13(2)x x --=- （2）322132x x x +--=-15．计算：（1）7(2)(3)--+-. （2）5.6+（－0.9）+4.4+（－8.1）（3）1(27)(3)3-÷-⨯（4）(4) 3.12( 2.5)-⨯⨯-.（5）111()20245-++⨯ （6）888120(3)(7)(3)37(3)999-⨯-+-⨯-+⨯-16．计算：（1）（﹣21）+（﹣13）﹣（﹣25）﹣（+28） （2）﹣22﹣6÷（﹣2）×13（3）)361()436597(-÷+- （4）⎪⎭⎫ ⎝⎛÷⎥⎥⎦⎤⎢⎢⎣⎡⎪⎭⎫ ⎝⎛⨯⨯415-8.0-31-3-2142217．计算（每小题3分，共12分）（1）()()3182624----+-； （2）()()43526⨯--⨯-+； （3）)87()87()21(43-÷⎥⎦⎤⎢⎣⎡---+ （4）4211(10.5)2(3)3⎡⎤---⨯⨯--⎣⎦18．计算（1）)5()2()10(8---+-+ （2）)311(5352312-+--（3）)169(83)43(-÷⨯- （4）)1()4(40)2(1-⨯--÷+-÷（5））（）（36-43197-65⨯+ （6）192324×（－12） 19．x y yx xy y x 222223-+-20．（1）计算：（1+﹣）×（﹣24）（2）计算：﹣32﹣[﹣1+（1﹣2×）÷（﹣）]．21．计算题 （1）－32＋（—1）200116÷＋（—5）2 （2）()()()3221532⎡⎤-⨯-÷-+-⎣⎦22．计算：])3(2[61122015--⨯--23．（1）)654()8.4()612(545---+++； （2）)]95(32[)3(2-+-⨯-；（3）4231(2)(4)()(1)2-÷-⨯--； （4）41111()36234-+-+-⨯24．计算：（1）⎪⎭⎫ ⎝⎛+-⎪⎭⎫ ⎝⎛--⎪⎭⎫ ⎝⎛-+⎪⎭⎫ ⎝⎛+32354231251 （2）)61(6)3(524-÷--⨯+-（3）52412561314÷⎥⎦⎤⎢⎣⎡⨯⎪⎪⎭⎫ ⎝⎛+-- （4）123(6)()2-+--⨯-．25．（1）﹣﹣﹣（﹣）﹣（2）9.872+（﹣）+（﹣5.872）（3）（﹣）÷（﹣）； （4）（5）1.3×（﹣9.12）+（﹣7）×9.12 （6）﹣14﹣×[2﹣（﹣3）]2（7）[÷（﹣）+0.4×]×（﹣1）5 （8）[1]2÷[（1﹣）×]326．计算：（1）－4+28－（－19）+（－24）； （2）.42-3-5322÷-⨯+）（）（27．计算（1）11－18－12 + 19 （2）（－5）× （－7）+ 20÷（－4） （3）111(36)964⎛⎫+-⨯- ⎪⎝⎭（4）124×1()3-－12÷23（5）3 +12 ÷ 22×（－3）－5 （6）－21+2014×35()6-×0－（－3）28．计算（1）(3)2-244-⨯+÷（）﹣（﹣3） （2）-5+（﹣3）2﹣3.14)π-（×-212⎛⎫- ⎪⎝⎭÷20151-（）29.（本题满分18分）计算题：（1）)14(612-++-）（ （2）543+-- （3）)60()1276521(-⨯-+ （4）)8(6523)9(-÷⨯÷-（5）423592÷---⨯-）（）（ （6））（）（）（）（3212131213-⨯-+-÷-30计算：（1）（2）52﹣3×[﹣32+（﹣2）×（﹣3）]+（﹣4）331．（4分）若多项式222)25(23mx x y x +-+-的值与x 的值无关，求m 的值。
32．计算（1）)16()7(1723-+--- （2）)1816191(36--⨯（3）])3(2[31)5.01(123--⨯⨯---（4）1003)1()4()81()2(16-+-⨯---÷33．计算：（1）12﹣（﹣15）+（﹣23） （2）3×（3）﹣23÷8﹣×（﹣2）2（4）﹣6×．34．计算．（1）－9＋6÷（－2） （2）493510⎛⎫⨯-÷ ⎪⎝⎭（3）22350(5)1--÷-- （4）32511(2)()(24)3612．35．计算：（1）206137+-+-； （2） 2228313）（）（-÷+-⨯36．计算题（每小题4分，共20分）（1）()3.5-+()2.3-()5.2--()8.4+- （2）⎪⎭⎫⎝⎛-+-127659521()36-⨯ （3）（4）()()52531144222⨯÷---+- 37．（2015秋•高密市校级月考）先化简，再求值：（1）（5a+2a 2﹣3﹣4a 3）﹣（﹣a+3a 3﹣a 2），其中a=﹣2；（2）3x 2﹣[x 2﹣2（3x ﹣x 2）]，其中x=﹣7；（3）2（x 2y+xy ）﹣3（x 2y ﹣xy ）﹣4x 2y ，其中x=1，y=﹣1．38．计算：a a -π+a <<π）（精确到0.1）．39．计算（每题3分，共12分） （1）8＋（－14）－5－（－0．25） （2）1133()33-⨯÷⨯-（3）131()(48)6412-+-⨯- （4）2211130.41235⎡⎤⎛⎫⎛⎫⨯-⨯-+÷-⎢⎥ ⎪ ⎪⎝⎭⎝⎭⎢⎥⎣⎦40．计算：（1）3(9)8---+ （2）13(1)(48)64-+⨯-（3）3116(2)()(4)8÷---⨯- （4）2211(10)3(4)2---÷⨯÷-41．计算：（本题16分）（1） 7－（－3）＋（－5）－|－8| （2）（－8）÷（－4）－（－3）3×（－123）（3）)42()72114331-⨯--（； （4）14.035)5(224-+⎪⎭⎫⎝⎛-⨯-÷-．42．阅读解题：1111212=-⨯，3121321-=⨯，4131431-=⨯， ... 计算：+⨯+⨯+⨯431321211 (200520041)⨯+=+-+-+-413131212111 (2005)120041-+ =120051-=20052004 理解以上方法的真正含义，计算： （1）111 (10111112100101)+++⨯⨯⨯（2） (200720051)531311⨯++⨯+⨯43．先化简，后求值： )4(3)3(2)1(22-+--+-x x x x ，其中.1-=x44．计算：（1）)4()5(3+-++- （2）2)2()8(3)2(-÷--⨯-（3）)60)216743(-⨯+-（（4） 2211(10)2(4)2---÷⨯+-。