8水平三因素水平表1
三因素三水平五指标

三因素三水平五指标为了全面评估和讨论主题“三因素三水平五指标”,我们将从简到繁的方式展开,并逐步深入探讨。
在文章中,我们将多次提及这个主题,并分享个人观点和理解。
让我们了解一下“三因素三水平五指标”的概念。
这个概念源自于管理学和绩效评估领域,是用来评估和衡量组织绩效和业务成功的一种方法。
下面,我们将详细介绍每个要素。
三因素指的是:目标、因素和结果。
首先是目标,它是我们要达到的预期成果或愿景。
设置明确的目标有助于组织明确自己的方向和意图。
其次是因素,它们是影响业务绩效的各种因素,包括市场环境、竞争对手、内外部资源等。
最后是结果,也就是通过评估因素对目标的影响,得出的具体业务绩效结果。
三水平则是:规定、计划和实际。
规定水平是在设定目标时,组织所预期的水平。
计划水平是根据因素的影响和分析,制定的实际可达到的水平。
实际水平是实际达到的结果与规定水平和计划水平的对比。
五指标是:效果、效率、质量、成本和创新。
效果指的是达到的结果的质量和影响力。
效率是在达到目标的过程中,所消耗的资源和时间等因素。
质量指的是所提供产品或服务的质量水平。
成本则是实现结果所需要的经济投入。
创新是指组织在业务过程中的创新能力和创新成果。
“三因素三水平五指标”方法能够全面评估和衡量组织绩效和业务成功。
它帮助组织设定明确的目标,分析和评估各种因素对目标的影响,并最终得出具体的业务绩效结果。
它也着重关注效果、效率、质量、成本和创新这五个关键指标,以全面评估组织的绩效和业务水平。
个人观点和理解方面,我认为“三因素三水平五指标”是一种非常实用和有价值的方法。
它能够帮助组织全面评估和了解自己的业务绩效,并在需要的时候进行调整和优化。
通过设定清晰的目标,组织能够更好地明确自己的方向和愿景,同时通过评估各个因素的影响,找出影响业务绩效的关键因素,有针对性地进行改进。
五个关键指标也提供了一个全面评估绩效的角度。
不仅要关注结果的效果和质量,还要考虑效率和成本的因素,以及创新能力的评估。
海氏三要素评估法

Hay group的海氏系统法Hay group的海氏系统法是美国工资设计专家Hay在1951年开发出来的,实质上是一种评分法,认为所有职位所包含的付酬因素可以抽象为三种具有普遍适用性的因素,即智能水平、解决问题能力和风险责任,他设计了三套评价量表,最后将所得分值加以综合,算出各个工作职位的相对价值。
该评估法认为,一个岗位之所以能够存在的理由是必须承担一定的责任,即该岗位的产出。
那么通过投入什么才能有相应的产出呢?即担任该岗位人员的知识和技能。
那么具备一定“知能” 的员工通过什么方式来取得产出呢?是通过在岗位中解决所面对的问题,即投入“知能”通过“解决问题”这一生产过程,来获得最终的产出“应负责任”。
体系的逻辑关系是:投入—过程—产出,即投入智能来解决问题,完成应付的责任。
海氏(Hay Group)三要素评估法海氏三要素评估法是国际上使用最广泛的一种岗位评估方法。
据统计,世界500强的企业中有1/3以上的企业岗位评估时都采用了海氏三要素评估法。
它通过三个方面对岗位的价值进行评估,并且通过较为正确的分值计算确定岗位的等级。
“三要素评估法”所指的三个要素该评估法认为,一个岗位之所以能够存在的理由是必须承担一定的责任,即该岗位的产出。
那么通过投入什么才能有相应的产出呢?即担任该岗位人员的知识和技能。
那么具备一定“知能” 的员工通过什么方式来取得产出呢?是通过在岗位中解决所面对的问题,即投入“知能”通过“解决问题”这一生产过程,来获得最终的产出“应负责任”,如下图所示:海氏评估法对所评估的岗位按照以上三个要素及相应的标准进行评估打分,得出每个岗位评估分,即岗位评估分=知能得分+解决问题得分+应负责任得分。
其中知能得分和应负责任评估分和最后得分都是绝对分,而解决问题的评估分是相对分(百分值),经过调整后为最后得分后才是绝对分。
利用海氏评估法在评估三种主要付酬因素方面不同的分数时,还必须考虑各岗位的“形状构成”,以确定该因素的权重,进而据此计算出各岗位相对价值的总分,完成岗位评价活动。
三因素三水平正交表

三因素三水平正交表三因素三水平正交表1. 引言在实验设计中,正交表是一种重要的工具,用于帮助研究人员系统地设计和分析实验。
三因素三水平正交表是一种常用的正交设计,适用于同时研究三个因素对实验结果的影响。
本文将深入介绍三因素三水平正交表的概念、应用和分析方法,并分享本人对该设计方法的观点和理解。
2. 三因素三水平正交表的概念三因素三水平正交表是一种设计矩阵,用于确定三个因素的水平组合。
这种设计方法的特点是各个水平之间相互正交,即它们之间的相互作用效应被控制在最小程度上。
正交表能够帮助研究人员实现对实验因素的均衡和有效控制,提高实验结论的可靠性和稳定性。
3. 三因素三水平正交表的应用三因素三水平正交表广泛应用于各个领域的实验研究中。
在材料科学领域,研究人员可以使用这种设计方法来研究不同材料成分、工艺参数和环境条件对材料性质的影响。
在农学领域,研究人员可以利用三因素三水平正交表来探究不同施肥方案、种植密度和灌溉水量对作物产量的影响。
在医学研究中,正交表可以用于研究药物剂量、治疗时间和患者芳龄对治疗效果的影响。
4. 三因素三水平正交表的分析方法对于三因素三水平正交表的分析,通常采用方差分析方法。
研究人员首先计算不同因素之间的平方和,并进行方差分析,以确定各个因素的显著性水平。
通过计算F值和p值,可以确定每个因素的主效应和交互效应是否显著。
研究人员根据分析结果可以得出结论,并进一步对实验因素进行优化和调整。
5. 我的观点和理解在我看来,三因素三水平正交表是一种非常有用的设计工具,可以帮助研究人员系统地研究多个因素对实验结果的影响。
通过合理设计正交表,可以减少实验中因素相互影响的干扰,更加准确地评估因素对实验结果的贡献。
正交表还可以提供实验结果的响应曲面,帮助研究人员更好地理解因素之间的关系。
总结本文深入探讨了三因素三水平正交表的概念、应用和分析方法,并分享了本人对该设计方法的观点和理解。
三因素三水平正交表是一种重要的实验设计工具,可以帮助研究人员系统地研究多个因素对实验结果的影响。
海氏(Hay Group)三要素评估法

海氏(Hay Group)三要素评估法海氏三要素评估法是国际上使用最广泛的一种岗位评估方法。
据统计,世界500强的企业中有1/3以上的企业岗位评估时都采用了海氏三要素评估法。
它通过三个方面对岗位的价值进行评估,并且通过较为正确的分值计算确定岗位的等级。
为什么用这三个要素来评估一个岗位是科学的呢?该评估法认为,一个岗位之所以能够存在的理由是必须承担一定的责任,即该岗位的产出。
那么通过投入什么才能有相应的产出呢?即担任该岗位人员的知识和技能。
那么具备一定“知能” 的员工通过什么方式来取得产出呢?是通过在岗位中解决所面对的问题,即投入“知能”通过“解决问题”这一生产过程,来获得最终的产出“应负责任”:海氏评估法对所评估的岗位按照以上三个要素及相应的标准进行评估打分,得出每个岗位评估分,即岗位评估分=知能得分+解决问题得分+应负责任得分。
其中知能得分和应负责任评估分和最后得分都是绝对分,而解决问题的评估分是相对分(百分值),经过调整后为最后得分后才是绝对分。
利用海氏评估法在评估三种主要付酬因素方面不同的分数时,还必须考虑各岗位的“形状构成”,以确定该因素的权重,进而据此计算出各岗位相对价值的总分,完成岗位评价活动。
所谓职务的“形状”主要取决于知能和解决问题的能力两因素相对于岗位责任这一因素的影响力的对比与分配。
从这个角度去观察,企业中的岗位可分为三种类型:①“上山”型。
此岗位的责任比知能与解决问题的能力重要。
如公司总裁、销售经理、负责生产的干部等。
②“平路”型。
知能和解决问题能力在此类职务中与责任并重,平分秋色。
如会计、人事等职能干部。
③“下山”型。
此类岗位的职责不及职能与解决问题能力重要。
如科研开发、市场分析干部等。
通常要由职务薪酬设计专家分析各类岗位的形状构成,并据此给知能、解决问题的能力这两因素与责任因素各自分配不同的权重,即分别向前两者与后者指派代表其重要性的一个百分数,两个百分数之和应恰为100%。
海氏(HayGroup)三要素评估法

海氏(HayGroup)三要素评估法海氏(Hay Group)三要素评估法海氏三要素评估法是国际上使用最广泛的一种岗位评估方法。
据统计,世界500强的企业中有1/3以上的企业岗位评估时都采用了海氏三要素评估法。
它通过三个方面对岗位的价值进行评估,并且通过较为正确的分值计算确定岗位的等级。
为什么用这三个要素来评估一个岗位是科学的呢,该评估法认为,一个岗位之所以能够存在的理由是必须承担一定的责任,即该岗位的产出。
那么通过投入什么才能有相应的产出呢,即担任该岗位人员的知识和技能。
那么具备一定“知能” 的员工通过什么方式来取得产出呢,是通过在岗位中解决所面对的问题,即投入“知能”通过“解决问题”这一生产过程,来获得最终的产出“应负责任”。
海氏评估法对所评估的岗位按照以上三个要素及相应的标准进行评估打分,得出每个岗位评估分,即岗位评估分=知能得分+解决问题得分+应负责任得分。
其中知能得分和应负责任评估分和最后得分都是绝对分,而解决问题的评估分是相对分(百分值),经过调整后为最后得分后才是绝对分。
利用海氏评估法在评估三种主要付酬因素方面不同的分数时,还必须考虑各岗位的“形状构成”,以确定该因素的权重,进而据此计算出各岗位相对价值的总分,完成岗位评价活动。
所谓职务的“形状”主要取决于知能和解决问题的能力两因素相对于岗位责任这一因素的影响力的对比与分配。
从这个角度去观察,企业中的岗位可分为三种类型:?“上山”型。
此岗位的责任比知能与解决问题的能力重要。
如公司总裁、销售经理、负责生产的干部等。
?“平路”型。
知能和解决问题能力在此类职务中与责任并重,平分秋色。
如会计、人事等职能干部。
? “下山”型。
此类岗位的职责不及知能与解决问题能力重要。
如科研开发、市场分析干部等。
通常要由职务薪酬设计专家分析各类岗位的形状构成,并据此给知能、解决问题的能力这两因素与责任因素各自分配不同的权重,即分别向前两者与后者指派代表其重要性的一个百分数,两个百分数之和应恰为100,。
四因素三水平(l9)正交实验方案excel表

四因素三水平(l9)正交实验方案excel表摘要:1.介绍四因素三水平正交实验方案2.解释Excel表在实验方案中的应用3.详细步骤:创建Excel表、输入数据、设置参数、分析结果4.分析结果的解释与实用性正文:在我们的实验研究中,常常需要考虑多个因素对实验结果的影响。
四因素三水平正交实验方案就是一个很好的方法,它可以同时考察四个因素在不同水平下的影响,从而帮助我们找到关键因素并优化实验方案。
在这个基础上,Excel表格的应用使得数据分析变得更加简便和高效。
首先,我们需要在Excel中创建一个表格,按照实验要求输入四因素三水平的数据。
在表格中,可以将因素名称设为列标题,水平编号设为行标题。
例如,我们可以将因素A、B、C、D分别命名为“因素A”、“因素B”、“因素C”和“因素D”。
接下来,我们需要设置Excel表格的参数。
在“数据”菜单中,点击“数据分析”,然后选择“回归”选项。
在弹出的对话框中,分别设置“因变量区域”和“自变量区域”。
在此示例中,我们可以将实验结果数据设为因变量,因素水平数据设为自变量。
设置完毕后,点击“确定”。
在分析结果中,我们可以看到每个因素对实验结果的影响程度。
Excel会自动计算各因素的F值、P值和平方和,帮助我们判断因素是否显著。
同时,还可以通过直观地观察回归系数来判断因素之间的交互作用。
根据分析结果,我们可以对实验方案进行优化,以提高实验效果。
最后,根据实验目的和实际情况,我们可以将分析结果整理成报告,为后续实验提供参考。
在撰写报告时,注意突出可读性和实用性,使得实验数据和分析结论更加易于理解和应用。
总之,通过四因素三水平正交实验方案和Excel表格的应用,我们可以高效地分析多个因素对实验结果的影响,从而为优化实验方案提供有力支持。
三水平试验方差分析

列方差分析表如下:
最佳条件的选择: 对显著因子应取最好的水平,对不显著因子的水平可以 任意选取;在实际中通常从降低成本操作方便等角度加 以选择,上面的例子中对因子A与B应选择A2B2,因子C 可以任选,譬如为节约材料可选择C1
验证试验:
对A2B2C1进行三次试验,结果为:234,240,220,平均 值为231.3. 此结果是满意的
方差分析(2): 由于这里的试验指标是产品的产量,越大越好,所以最优方案应取 各因素中yjk的最大值所对应的水平。因素A应取第1水平,因素B应 取第3水平,因素C应取第3水平。交互作用A×B也是显著的,但由 于A×B占两列,直观分析法有些困难,因此把A和B的各种组合的试 验结果对照起来分析。
从表中看出,当A取第1水平、B取第3水平时,试验结果为13.17,是 所有结果中的最大值,因此取A1B3。于是,最优方案就取A1B3C3.
QC
1 3
( 308025
273529
328329
) 303294
.3
S A Q A P 1421 .6
S B Q B P 5686 .9
S C Q C P 427 .6
9
S Q P
y
2 i
P
310519
302866 .78 7652 .2
i1
S e S S A S B S C 116 . 2
L27(313)交互列表
解:(选用正交表L27(313)
P 1 ( 100 . 64 ) 2 375 . 13 , 27
根据前面的公式作如下计算:Q A
1 9
( 36
. 73
2
30
. 70
2
33
. 21
三因素混合水平正交试验设计

三因素混合水平正交试验设计1. 什么是三因素混合水平正交试验设计?好家伙,提到“三因素混合水平正交试验设计”,听起来就像是一门深奥的科学,其实,它就像做菜一样,有点复杂,但其实也没那么吓人。
简单来说,这是一种科学的实验设计方法,主要用来研究多个因素对结果的影响。
就像你在调配一杯饮料,水、糖、柠檬三种成分的比例不同,最终的味道也会截然不同。
这里的“三因素”就是这三种成分,而“混合水平”则是指不同的比例。
正交试验就是为了找到一个最优组合,让你喝到最佳口感。
1.1 为什么要用这种设计?你可能会问,为什么不直接试一试,反正也不算难嘛?嘿,听我说,这就像我们在考试之前不复习一样,结果往往是惨不忍睹。
用正交试验设计,可以有效减少试验次数,提高效率,帮你快速找到最优解。
想象一下,如果你有八个不同的口味,而你想尝试每一种搭配,那简直是要你命啊!但如果用正交试验设计,选出几个关键的组合,快速找出最佳搭配,那就轻松多了。
1.2 具体怎么做?实施这个试验设计可不复杂,首先得确定你要研究的三个因素,比如说温度、时间和材料的配比。
然后,给每个因素设置几个水平。
比如,温度可以设为低、中、高;时间可以设为短、中、长;材料的配比可以设为少、中、多。
这样一来,咱们就有了一个清晰的试验框架。
接着,使用正交表来安排试验。
这就好比在选一场比赛的阵容,你不可能把所有的球员都上场,得挑出最有可能赢的组合。
正交表会帮你排出一个高效的试验顺序,确保每个因素的不同水平都能被试到。
2. 试验结果分析试完试验之后,结果就像一块拼图,得慢慢把它拼起来。
我们要统计每组试验的结果,然后分析哪种组合最有效。
这里就需要用到一些统计学的工具,比如方差分析。
这一步就像在做一份成绩单,看看谁是班里的“学霸”,哪个组合表现最好。
通过这种方式,我们不仅能看到结果,还能找到影响结果的关键因素。
2.1 结果可视化别忘了,把结果用图表展示出来,这样更直观。
数据就像一串串数字,光看不出啥,画成图就一目了然了。
三因素三水平正交表例题

三因素三水平正交表例题例题1:某产品的质量受A、B、C三个因素影响,每个因素有三个水平。
A因素的三个水平为A1 = 10,A2 = 20,A3 = 30;B因素的三个水平为B1 = 5,B2 = 10,B3 = 15;C因素的三个水平为C1 = 2,C2 = 4,C3 = 6。
试用正交表安排试验,找出最佳的因素水平组合以提高产品质量(以产品质量指标越大越好)。
1. 选择正交表。
- 对于三因素三水平的试验,我们可以选用L9(3⁴)正交表。
2. 表头设计。
- 将A、B、C三个因素分别安排在正交表的三列上,例如A安排在第1列,B安排在第2列,C安排在第3列。
3. 确定试验方案。
- 根据正交表L9(3⁴)的安排进行试验。
例如,第1号试验的因素水平组合为A1、B1、C1;第2号试验为A1、B2、C2;第3号试验为A1、B3、C3;第4号试验为A2、B1、C2;第5号试验为A2、B2、C3;第6号试验为A2、B3、C1;第7号试验为A3、B1、C3;第8号试验为A3、B2、C1;第9号试验为A3、B3、C2。
4. 进行试验并记录结果。
- 假设经过试验得到9个试验结果分别为y1,y2,y3,y4,y5,y6,y7,y8,y9。
5. 分析试验结果。
- 计算各因素同一水平下试验结果的平均值。
- 对于A因素:- K1A=(y1 + y2+y3)/3,K2A=(y4 + y5 + y6)/3,K3A=(y7 + y8 + y9)/3。
- 计算极差RA = max(K1A,K2A,K3A)-min(K1A,K2A,K3A)。
- 对于B因素:- K1B=(y1 + y4 + y7)/3,K2B=(y2 + y5 + y8)/3,K3B=(y3 + y6 + y9)/3。
- 计算极差RB = max(K1B,K2B,K3B)-min(K1B,K2B,K3B)。
- 对于C因素:- K1C=(y1 + y6 + y8)/3,K2C=(y2 + y4 + y9)/3,K3C=(y3 + y5 + y7)/3。
四因素三水平得均匀设计表

四因素三水平得均匀设计表1. 任务背景在实验设计中,四因素三水平设计表是一种常用的实验设计方法。
它可以帮助研究人员系统地探索和分析多个因素对实验结果的影响,并确定最优的因素组合。
本文将介绍四因素三水平得均匀设计表的基本原理、设计步骤和数据分析方法。
2. 四因素三水平设计表的基本原理四因素三水平设计表是一种全因素试验设计方法,它包括四个因素和三个水平。
每个因素都有三个水平,分别记为-1、0和+1。
因素的水平可以表示为低、中、高三个水平或者其他具体的取值。
在四因素三水平设计表中,每个因素的每个水平都与其他因素的每个水平组合一次,共有81个试验点。
这种设计表的主要目的是通过系统地变化因素的水平,观察因素对实验结果的影响,并找出最优的因素组合。
3. 四因素三水平设计表的设计步骤四因素三水平设计表的设计步骤如下:步骤1:确定因素首先,确定需要研究的四个因素。
这些因素可以是任何与实验结果相关的变量,例如温度、压力、pH值等。
步骤2:确定水平然后,确定每个因素的三个水平。
水平的选择应该与实验的实际情况相符,并且应该覆盖因素可能的变化范围。
步骤3:构建设计表接下来,根据确定的因素和水平构建设计表。
设计表应该包括所有可能的因素水平组合,并且每个组合只出现一次。
步骤4:随机化试验顺序为了避免实验结果受到试验顺序的影响,需要对设计表进行随机化处理。
随机化可以通过计算机程序或随机数表来实现。
步骤5:进行实验按照设计表中的试验顺序进行实验。
在每个试验点上,记录因素水平和实验结果。
4. 数据分析方法完成实验后,需要对实验结果进行数据分析。
常用的数据分析方法包括方差分析和回归分析。
方差分析方差分析可以用来确定各个因素对实验结果的影响是否显著。
通过计算因素之间的方差比和F值,可以判断因素的主效应和交互效应是否显著。
回归分析回归分析可以用来建立实验结果与因素之间的数学模型。
通过回归方程,可以预测在不同因素水平下的实验结果,并找到最优的因素组合。
三因素完全随机实验设计
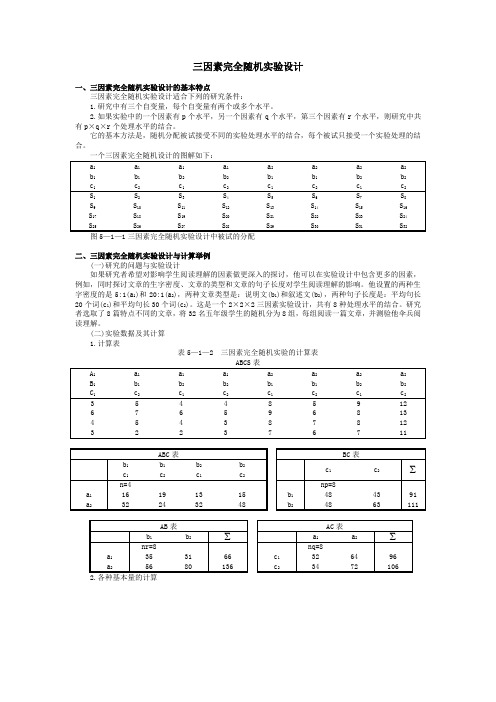
三因素完全随机实验设计一、三因素完全随机实验设计的基本特点三因素完全随机实验设计适合下列的研究条件:1.研究中有三个自变量,每个自变量有两个或多个水平。
2.如果实验中的一个因素有p 个水平,另一个因素有q 个水平,第三个因素有r 个水平,则研究中共有p ×q ×r 个处理水平的结合。
它的基本方法是,随机分配被试接受不同的实验处理水平的结合,每个被试只接受一个实验处理的结合。
二、三因素完全随机实验设计与计算举例(一)研究的问题与实验设计如果研究者希望对影响学生阅读理解的因素做更深入的探讨,他可以在实验设计中包含更多的因素,例如,同时探讨文章的生字密度、文章的类型和文章的句子长度对学生阅读理解的影响。
他设置的两种生字密度的是5:1(a 1)和20:1(a 2),两种文章类型是:说明文(b 1)和叙述文(b 2),两种句子长度是:平均句长20个词(c 1)和平均句长30个词(c 2)。
这是一个2×2×2三因素实验设计,共有8种处理水平的结合。
研究者选取了8篇特点不同的文章,将32名五年级学生的随机分为8组,每组阅读一篇文章,并测验他伞兵阅读理解。
(二)实验数据及其计算 1.计算表表5—1—2 三因素完全随机实验的计算表211111111()2222111122111136202.00(202)[]1275.125(4)(2)(2)(2)[](3)(6)1544.000()(66)[](4pqnrijkl i j k l ijklp q n rijkli j k l Y npqr pqnri j k l qnrijkl pi k l j YY YABCS Y A nqr=================++=∑∑∑∑=====+===∑∑∑∑∑∑∑∑∑∑∑∑2(136))(2)(2)(4)(2)(2)+=1428.2502221111()(91)(111)[](4)(2)(2)(4)(2)(2)p n rijkl qi j l k Y B npr ======+∑∑∑∑=1287.6252221111()(96)(106)[](4)(2)(2)(4)(2)(2)pqnijkl ri j k l Y C npq ======+∑∑∑∑=1278.2502221111()(35)(56)[](4)(2)(4)(2)nrijkl pqi l j k Y AB nr ======++∑∑∑∑=1465.2502221111()(32)(64)[](4)(2)(4)(2)qnijkl pri k j l Y AC nq======++∑∑∑∑=1432.5002221111()(48)(48)[](4)(2)(4)(2)pn ijkl qri j k l Y BC nq ======++∑∑∑∑=1303.2502221111()(16)(32)[]44nijkl pqri j k l Y ABC n======++∑∑∑∑=1506.5003.平方和分解与计算 (1)平方和的分解模式:SS 总变异=SS 处理间+SS 处理内=(SSA+SSB+SSAC+SSBC+|SSABC)+SS 单元内 (2)平方和的计算:SS 总变异=[ABCS]-[Y]=268.875 SSA=[A]-[Y]=153.125 SSB=[B]-[Y]=12.500 SSC=[C]-[Y] =3.125SSAB=[AB]-[Y]-SSA-SSB=24.500 SSAC=[AC]-[Y]-SSA-SSC=1.125 SSBC=[BC]-[Y]-SSB-SSC=12.500SSABC=[ABC]-[Y]-SSA-SSB-SSC-SSAB-SSAC-SSGBC=24.500SS单元内=SS总变异-SSA-SSB-SSC=SSAB-SSBC-SSAC-SSABC=37.5004.方差分析表及对结果的解释表5—1—3中的方差分析表明,三个和效应中,A、B两个因素的主效应是统计显著的,即文章生字密度的主效应是显著的(F(1,24)=98.00,p<.01),文章类型的主效应是显著的(F(1,24)=8.00,p<.01),文章类型的主效应是显著的(F(1,24)=8.00,p<.01)。
三因素析因实验计算表

表1:三因素析因实验ABCN计算表一、平方和的计算: ()93.5925333480022=⨯⨯⨯==∑∑∑∑npqrX G ijrk07.66893.592565942=-=-=∑∑∑∑G X SS ijrkt()90.28693.59253343342751912222=-⨯⨯++=-=∑∑∑∑∙G nqrXSSpjrkA()07.893.59253342542682782222=-⨯⨯++=-=∑∑∑∑∙G nprXSSqrki B()24.15093.59253343192152662222=-⨯⨯++=-=∑∑∑∑∙G npqXSS kij rC()G SSSSnrXSSABpqrkAB---=∑∑∑∑∙∙293.193.592590.28607.834110110114869297586667222222222=---⨯++++++++=()G SSSS nqXSSAC prkq AC---=∑∑∑∑∙∙226.893.592590.28624.15034131103859577431089563222222222=---⨯++++++++=()G SS SS npXSS B C qrki BC ---=∑∑∑∑∙∙293.693.592507.824.15034106103110637379859289222222222=---⨯++++++++=()G SS SSSSSSSSSSnX SSC BABCACABpqrkABC-------=∑∑∑∑∙∙∙274.793.592524.15007.890.28693.626.893.16396=-------=()1986396659422=-=-=∑∑∑∑∑∑∑∑∙∙∙nXXSS kijrke二、不同效应模型F 值的计算1. 固定效应模型eA A MSMS F =eB B MSMS F =eC C MSMS F =eABAB MS MSF =eBCBC MS MSF =eAC AC MSMS F =eABC ABC MSMSF =2. 随机效应模型 )(ABCABACAABACABC A A MSMS MSMSorMS MS MSMS F -+++=')(ABCABBCBABBCABC B B MSMSMSMSorMS MS MSMS F -+++=')(ABCBCACCBCACABC C C MSMSMSMSorMSMSMSMS F -+++='ABCAB AB MSMS F =ABCBC BC MSMS F =A B CAC AC MSMS F =eA B C A B C MSMSF =3. 混合效应模型(1) A 固定,B 、C 随机 )('ABCACABAACABABC A A MSMSMSMSorMSMSMSMS F -+++=BCBB MSMSF /= BC C C MS MS F /= ABCABAB MSMSF /=ABCACAC MSMSF /= e BC BC MS MS F /= e A B CA B C MS MSF /=(2) B 固定,A 、C 随机ACA A MSMSF /= )('A B CBCABBBCABABC B B MSMSMSMSorMSMSMSMS F -+++=ACC C MS MS F /= ABCABAB MSMSF /= e ACAC MS MSF /=ABCBCBC MSMSF /= e A B CA B C MS MSF /=(3)C 固定,A 、B 随机 ABAA MSMS F /= ABBB MS MS F /=)('ABCBCACCBCACABC C C MSMSMSMSorMSMSMSMS F -+++=eABAB MSMSF /=A B CAC AC MSMSF /= A B CBC BC MSMS F /= e A B CA B C MS MSF /=(4)A 、B 固定,C 随机ACAA MSMSF /=BCBB MSMS F /=e C C MS MS F /= ABC ABAB MSMS F /=eACAC MS MSF /=e BC BC MS MS F /=e A B CA B C MS MSF /=(5)A 、C 固定,B 随机 ABAA MSMSF /=eBB MS MS F /= BCCC MSMSF /=e ABAB MSMSF /=ABCAC AC MSMSF /=e BC BC MS MS F /=e A B CA B C MS MSF /=(6)B 、C 固定,A 随机eAA MSMSF /=ABBB MSMSF /=ACCC MS MS F /= e ABAB MSMSF /=eACAC MS MSF /=ABCBC BC MSMSF /=e A B CA B C MS MSF /=三、方差分析表表2:三因素析因实验的方差分析表四、SPSS 运算结果在SPSS 中执行如下操作,可以完成上述三因素析因实验设计数据的分析 1.固定效应方差分析ANALYSIS ——GENERAL LINEAR MODEL ——UNIV ARIA TE 将A 、B 、C 三个因素都定义为固定因素,得到分析结果如下:Tests of Between-Subjects Effects Dependent Variable: X88.496.301.05.)81,2(=F 56.348.201.05.)81,4(=F 65.846.401.05.)8,2(=Fa R Squared = .970 (Adjusted R Squared = .960)2.随机效应方差分析将A、B、C都定义为随机效应,得到结果如下:Tests of Between-Subjects EffectsDependent Variable: Xa MS(A * B) + MS(A * C) - MS(A * B * C)b MS(A * B) + MS(B * C) - 1.000 MS(A * B * C)c MS(A * C) + MS(B * C) - 1.000 MS(A * B * C) + 7.216E-15 MS(Error)d MS(A * B * C)e MS(Error)3.混合效应模型(1)A、B固定,C随机将A、B定义为固定因素,C定义为随机因素,得到的计算结果如下:Tests of Between-Subjects Effectsa MS(A * C)b MS(B * C)c MS(A * C) + MS(B * C) - 1.000 MS(A * B * C) + 7.327E-15 MS(Error)d MS(A * B * C)e MS(Error)(2)A固定,B、C随机Tests of Between-Subjects Effectsa MS(A * B) + MS(A * C) - MS(A * B * C)b MS(A * B) + MS(B * C) - 1.000 MS(A * B * C)c MS(A * C) + MS(B * C) - 1.000 MS(A * B * C) + 7.216E-15 MS(Error)d MS(A * B * C)e MS(Error)结论:从上面模型检验结果可以看出,A、C的主效应显著。
三因数四水平正交表

三因数四水平正交表(实用版)目录1.引言2.三因数四水平正交表的定义和构成3.三因数四水平正交表的应用4.结论正文【引言】在工程技术、质量管理以及科学研究等领域,实验设计与数据分析的方法和工具至关重要。
其中,正交表作为一种实验设计方法,能够在最少的试验次数下,获得最具代表性的数据。
本文将介绍一种常见的正交表设计方法——三因数四水平正交表。
【三因数四水平正交表的定义和构成】三因数四水平正交表,顾名思义,是由三个因素和四个水平组成的正交表。
其中,三个因素分别是 A、B、C,分别代表三个不同的变量;四个水平则是指每个因素有四个取值,即 A1、A2、A3、A4,B1、B2、B3、B4,C1、C2、C3、C4。
通过这三个因素和四个水平的组合,可以得到一个三维的四象限表格,用于指导实验过程。
【三因数四水平正交表的应用】三因数四水平正交表在实际应用中具有广泛的用途,主要体现在以下几个方面:1.优化实验设计:通过使用三因数四水平正交表,可以在最少的实验次数下,全面评估各因素和其水平对实验结果的影响,从而提高实验效率。
2.降低误差:正交表设计方法可以有效避免因实验顺序、操作者等因素引起的误差,保证实验数据的准确性。
3.数据分析:在实验过程中,通过记录各因素和其水平的组合以及对应的实验结果,可以得到一份完整的实验数据。
利用统计方法对这些数据进行分析,可以得出各因素对实验结果的影响程度,为后续的优化和决策提供有力支持。
【结论】总之,三因数四水平正交表作为一种有效的实验设计方法,可以帮助工程师和技术人员在实际工作中提高实验效率、降低误差,并为数据分析和决策提供有力依据。
