2019版同步优化探究理数练习:第八章 第七节 双曲线 Word版含解析
2019版同步优化探究文数(北师大版)练习:第八章 第七节 双曲线 Word版含解析

课时作业 A 组——基础对点练1.已知F 为双曲线C :x 2-my 2=3m (m >0)的一个焦点,则点F 到C 的一条渐近线的距离为( )A.3 B .3 C.3mD .3m解析:双曲线方程为x 23m -y 23=1,焦点F 到一条渐近线的距离为 3.选A.答案:A2.已知双曲线x 2a 2-y 23=1(a >0)的离心率为2,则a =( )A .2 B.62C.52D .1解析:因为双曲线的方程为x 2a 2-y 23=1,所以e 2=1+3a 2=4,因此a 2=1,a =1.选D.答案:D3.双曲线x 2-4y 2=-1的渐近线方程为( ) A .x ±2y =0 B .y ±2x =0 C .x ±4y =0D .y ±4x =0解析:依题意,题中的双曲线即y 214-x 2=1,因此其渐近线方程是y 214-x 2=0,即x ±2y =0,选A. 答案:A4.已知双曲线x 23-y 2=1的左、右焦点分别为F 1,F 2,点P 在双曲线上,且满足|PF 1|+|PF 2|=25,则△PF 1F 2的面积为( ) A .1 B. 3 C. 5D.12解析:在双曲线x 23-y 2=1中,a =3,b =1,c =2.不防设P 点在双曲线的右支上,则有|PF 1|-|PF 2|=2a =23,又|PF 1|+|PF 2|=25,∴|PF 1|=5+3,|PF 2|=5- 3.又|F 1F 2|=2c =4,而|PF 1|2+|PF 2|2=|F 1F 2|2,∴PF 1⊥PF 2,∴S △PF 1F 2=12×|PF 1|×|PF 2|=12×(5+3)×(5-3)=1.故选A. 答案:A5.已知双曲线C :x 2a 2-y 2b 2=1(a >0,b >0),直线l :y =2x -2.若直线l 平行于双曲线C 的一条渐近线且经过C 的一个顶点,则双曲线C 的焦点到渐近线的距离为( ) A .1 B .2 C. 5D .4解析:根据题意,双曲线C 的方程为x 2a 2-y 2b 2=1(a >0,b >0),其焦点在x 轴上,渐近线方程为y =±b a x ,又由直线l 平行于双曲线C 的一条渐近线,可知ba =2,直线l :y =2x -2与x 轴的交点坐标为(1,0),即双曲线C 的一个顶点坐标为(1,0),即a =1,则b =2a =2,故双曲线C 的焦点到渐近线的距离为2,故选B. 答案:B6.已知双曲线的焦点到渐近线的距离等于半实轴长,则该双曲线的离心率为( ) A.5+12B .2 C. 2D .2 2解析:不妨设双曲线的方程为x 2a 2-y 2b 2=1(a >0,b >0),因为焦点F (c,0)到渐近线bx -ay =0的距离为a ,所以bca 2+b 2=a ,即bc c =a ,所以b a =1,所以该双曲线的离心率e =ca=1+(b a)2=2,故选C. 答案:C7.已知双曲线C :x 2a 2-y 2b 2=1的离心率e =54,且其右焦点为F 2 (5,0),则双曲线C 的方程为( ) A.x 24-y 23=1 B.x 29-y 216=1 C.x 216-y 29=1 D.x 23-y 24=1 解析:由题意得e =1+b 2a 2=54,又右焦点为F 2(5,0),a 2+b 2=c 2,所以a 2=16,b 2=9,故双曲线C 的方程为x 216-y 29=1.答案:C8.已知双曲线x 2a 2-y 2b 2=1(a >0,b >0)的焦距为25,且双曲线的一条渐近线与直线2x +y =0垂直,则双曲线的方程为( ) A.x 24-y 2=1 B .x 2-y 24=1C.3x 220-3y 25=1 D.3x 25-3y 220=1 解析:由题意得c =5,b a =12,则a =2,b =1,所以双曲线的方程为x 24-y 2=1.答案:A9.(2018·山西八校联考)已知双曲线C :x 2a 2-y 2b 2=1(a >0,b >0)的左、右焦点分别为F 1,F 2,焦距为2c ,直线y =33(x +c )与双曲线的一个交点P 满足∠PF 2F 1=2∠PF 1F 2,则双曲线的离心率e 为( ) A. 2 B. 3 C .23+1 D.3+1解析:∵直线y =33(x +c )过左焦点F 1,且其倾斜角为30°,∴∠PF 1F 2=30°,∠PF 2F 1=60°,∴∠F 2PF 1=90°,即F 1P ⊥F 2P .∴|PF 2|=12|F 1F 2|=c ,|PF 1|=|F 1F 2|sin 60°=3c ,由双曲线的定义得2a =|PF 1|-|PF 2|=3c -c ,∴双曲线C 的离心率e =c a =c3c -c2=3+1,选D.答案:D10.已知F 1,F 2是双曲线C :x 2a 2-y 2b 2=1(a >0,b >0)的两个焦点,P 是双曲线C 上一点,若|PF 1|+|PF 2|=6a ,且△PF 1F 2最小内角的大小为30°,则双曲线C 的渐近线方程是( ) A.2x ±y =0 B .x ±2y =0 C .2x ±y =0D .x ±2y =0解析:不妨设|PF 1|>|PF 2|,则⎩⎪⎨⎪⎧|PF 1|-|PF 2|=2a ,|PF 1|+|PF 2|=6a ,所以|PF 1|=4a ,|PF 2|=2a ,且|F 1F 2|=2c ,即|PF 2|为最小边,即∠PF 1F 2=30°,则△PF 1F 2为直角三角形,所以2c =23a ,所以b =2a ,即渐近线方程为y =±2x ,故选A. 答案:A11.已知双曲线C :x 2a 2-y 2b2=1(a >0,b >0)的焦距为10,点P (2,1)在C 的一条渐近线上,则C的方程为( ) A.x 220-y 25=1 B.x 25-y 220=1 C.x 280-y 220=1 D.x 220-y 280=1 解析:依题意⎩⎪⎨⎪⎧a 2+b 2=251=b a ×2,解得⎩⎪⎨⎪⎧a 2=20b 2=5,∴双曲线C 的方程为x 220-y 25=1.答案:A12.已知双曲线过点(4,3),且渐近线方程为y =±12x ,则该双曲线的标准方程为________.解析:法一:因为双曲线过点(4,3)且渐近线方程为y =±12x ,故点(4,3)在直线y =12x 的下方.设该双曲线的标准方程为x 2a 2-y 2b 2=1(a >0,b >0),所以⎩⎨⎧42a 2-(3)2b2=1,b a =12,,解得⎩⎪⎨⎪⎧a =2,b =1,故双曲线方程为x 24-y 2=1.法二:因为双曲线的渐近线方程为y =±12x ,故可设双曲线为x 24-y 2=λ(λ≠0),又双曲线过点(4, 3),所以424-(3)2=λ,所以λ=1,故双曲线方程为 x 24-y 2=1.答案:x 24-y 2=113.双曲线Γ:y 2a 2-x 2b 2=1(a >0,b >0)的焦距为10,焦点到渐近线的距离为3,则Γ的实轴长等于________.解析:双曲线的焦点(0,5)到渐近线y =ab x ,即ax -by =0的距离为|5b |a 2+b 2=5bc=b =3,所以a =4,2a =8. 答案:814.已知双曲线C :x 2a 2-y 2b 2=1(a >0,b >0)与椭圆x 29+y 24=1有相同的焦点,且双曲线C 的渐近线方程为y =±2x ,则双曲线C 的方程为________.解析:易得椭圆的焦点为(-5,0),(5,0),∴⎩⎪⎨⎪⎧a 2+b 2=5,b a =2,∴a 2=1,b 2=4, ∴双曲线C 的方程为x 2-y 24=1.答案:x 2-y 24=115.(2018·合肥市质检)双曲线M :x 2a 2-y 2b 2=1(a >0,b >0)的左、右焦点分别为F 1,F 2,直线x=a 与双曲线M 的渐近线交于点P ,若sin ∠PF 1F 2=13,则该双曲线的离心率为________.解析:不妨设P 为直线x =a 与双曲线M 的渐近线在第一象限内的交点,则P 点坐标为(a ,b ),因为sin ∠PF 1F 2=13,所以|PF 1|=3b ,所以(a +c )2+b 2=9b 2,即9a 2+2ac -7c 2=0,7e 2-2e -9=0,又e >1,解得e =97.答案:97B 组——能力提升练1.已知F 1,F 2是双曲线C :x 2a 2-y 2b 2=1(a >0,b >0)的两个焦点,若在双曲线上存在点P 满足2|PF 1→+PF 2→|≤|F 1F 2→|,则双曲线的离心率的取值范围是( ) A .(1,2] B .(1,2] C .[2,+∞)D .[2,+∞)解析:∵2|PF 1→+PF 2→|≤|F 1F 2→|⇒4|OP →|≤2c ⇒|OP →|≤c 2,又|OP →|≥a ,∴a ≤c 2,即c ≥2a ,∴e =ca ≥2.故选D. 答案:D2.若实数k 满足0<k <9,则曲线x 225-y 29-k =1与曲线x 225-k -y 29=1的( )A .离心率相等B .虚半轴长相等C .实半轴长相等D .焦距相等解析:由0<k <9,易知两曲线均为双曲线且焦点都在x 轴上,由25+9-k =25-k +9,得两双曲线的焦距相等.答案:D3.(2018·云南五市联考)设P 为双曲线x 2-y 215=1右支上一点,M ,N 分别是圆(x +4)2+y 2=4和(x -4)2+y 2=1上的点,设|PM |-|PN |的最大值和最小值分别为m ,n ,则|m -n |=( ) A .4 B .5 C .6D .7解析:易知双曲线的两个焦点分别为F 1(-4,0),F 2(4,0),恰为两个圆的圆心,两个圆的半径分别为2,1,所以|PM |max =|PF 1|+2,|PN |min =|PF 2|-1,故|PM |-|PN |的最大值为(|PF 1|+2)-(|PF 2|-1)=(|PF 1|-|PF 2|)+3=5,同理|PM |-|PN |的最小值为(|PF 1|-2)-(|PF 2|+1)=(|PF 1|-|PF 2|)-3=-1,所以|m -n |=6,故选C. 答案:C4.(2018·江南十校联考)已知l 是双曲线C :x 22-y 24=1的一条渐近线,P 是l 上的一点,F 1,F 2分别是C 的左、右焦点,若PF 1→·PF 2→=0,则点P 到x 轴的距离为( ) A.233B. 2 C .2D.263解析:由题意知F 1(-6,0),F 2(6,0),不妨设l 的方程为y =2x ,点P (x 0,2x 0),由PF 1→·PF 2→=(-6-x 0,-2x 0)·(6-x 0,-2x 0)=3x 20-6=0,得x 0=±2,故点P 到x 轴的距离为2|x 0|=2,故选C. 答案:C5.已知双曲线x 24-y 2b 2=1(b >0),以原点为圆心,双曲线的实半轴长为半径长的圆与双曲线的两条渐近线相交于A ,B ,C ,D 四点,四边形ABCD 的面积为2b ,则双曲线的方程为( ) A.x 24-3y 24=1 B.x 24-4y 23=1 C.x 24-y 24=1 D.x 24-y 212=1 解析:根据圆和双曲线的对称性,可知四边形ABCD 为矩形.双曲线的渐近线方程为y =±b2x ,圆的方程为x 2+y 2=4,不妨设交点A 在第一象限,由y =b2x ,x 2+y 2=4得x A =44+b2,y A =2b4+b 2,故四边形ABCD 的面积为4x A y A =32b4+b 2=2b ,解得b 2=12,故所求的双曲线方程为x 24-y 212=1,选D.答案:D6.已知双曲线x 2a 2-y 2b 2=1(a >0,b >0)的左、右焦点分别为F 1、F 2,以|F 1F 2|为直径的圆与双曲线渐近线的一个交点为(3,4),则此双曲线的方程为( ) A.x 216-y 29=1 B.x 23-y 24=1 C.x 29-y 216=1 D.x 24-y 23=1 解析:因为以|F 1F 2|为直径的圆与双曲线渐近线的一个交点为(3,4),所以c =5,b a =43,又c 2=a 2+b 2,所以a =3,b =4,所以此双曲线的方程为x 29-y 216=1.答案:C7.过双曲线x 2a 2-y 2b2=1(a >0,b >0)的一个焦点F 作一条渐近线的垂线,垂足为点A ,与另一条渐近线交于点B ,若FB →=2F A →,则此双曲线的离心率为( ) A. 2 B. 3 C .2D. 5解析:不妨设B (x ,-bax ),|OB |=x 2+(-bax )2=c ,可取B (-a ,b ),由题意可知点A 为BF 的中点,所以A (c -a 2,b 2),又点A 在直线y =b a x 上,则b a ·c -a 2=b2,c =2a ,e =2.答案:C8.若直线l 1和直线l 2相交于一点,将直线l 1绕该点逆时针旋转到与l 2第一次重合时所转的角为θ,则角θ就称为l 1到l 2的角,tan θ=k 2-k 11+k 1k 2,其中k 1,k 2分别是l 1,l 2的斜率,已知双曲线E :x 2a 2-y 2b 2=1(a >0,b >0)的右焦点为F ,A 是右顶点,P 是直线x =a 2c 上的一点,e 是双曲线的离心率,直线P A 到PF 的角为θ,则tan θ的最大值为( ) A.1e B.e1+eC.e 21+eD.e 2解析:设P A ,PF 的斜率分别为k 3,k 4,由题意可知tan θ=k 4-k 31+k 3k 4,不妨设P (a 2c ,y )(y >0),则k 3=y a 2c -a ,k 4=y a 2c -c .令m =a 2c -a ,n =a2c -c ,则tan θ=y n -ym 1+y n ×y m =m -n mn y+y ,由m -n =c-a >0,得当mn y +y 取得最小值时tan θ取最大值,又y >0,m <0,n <0,所以mny +y ≥2mn ,当且仅当y =mn 时等号成立,此时tan θ=m -n2mn =c -a2(a 2c -a )(a 2c-c )=e21+e,故选C.答案:C9.(2018·淄博模拟)过双曲线x 2a 2-y 2b 2=1(a >0,b >0)的左焦点F 1,作圆x 2+y 2=a 2的切线交双曲线的右支于点P ,切点为T ,PF 1的中点M 在第一象限,则以下结论正确的是( ) A .b -a =|MO |-|MT | B .b -a >|MO |-|MT | C .b -a <|MO |-|MT | D .b -a =|MO |+|MT |解析:如图,连接OT ,则OT ⊥F 1T ,在直角三角形OTF 1中,|F 1T |=|OF 1|2-|OT |2=b ,连接PF 2,∵M 为线段F 1P 的中点,O 为F 1F 2的中点, ∴|OM |=12|PF 2|,∴|MO |-|MT |=12|PF 2|-⎝⎛⎭⎫12|PF 1|-|F 1T |=12(|PF 2|-|PF 1|)+b =12×(-2a )+b =b -a ,故选A. 答案:A10.(2018·昆明市检测)已知点F 为双曲线C :x 2a 2-y 2b 2=1(a >0,b >0)的一个焦点,以点F 为圆心的圆与C 的渐近线相切,且与C 交于A ,B 两点,若AF ⊥x 轴,则C 的离心率为________. 解析:不妨设F 为双曲线的右焦点,则F (c,0),易知双曲线的渐近线方程为y =±ba x ,则双曲线的焦点F 到渐近线的距离d =bc a 2+b2=b ,所以圆F 的半径为b .在双曲线方程中,令x=c ,得y =±b 2a ,所以A (c ,±b 2a ).因为点A 在圆F 上,所以b 2a=b ,即a =b ,所以c =a 2+b 2=2a ,所以e =ca = 2.答案: 211.双曲线x 2a 2-y 2b 2=1(a >0,b >0)上一点M (-3,4)关于一条渐近线的对称点恰为右焦点F 2,则该双曲线的标准方程为______________.解析:不妨设双曲线x 2a 2-y 2b 2=1的右焦点F 2(c,0)关于渐近线y =ba x 对称的点在双曲线上,则过焦点F 2且垂直于该渐近线的直线方程为y -0=-a b (x -c ),即y =-ab(x -c ).联立可得方程组⎩⎨⎧y =b ax ,y =-ab (x -c ),解得⎩⎨⎧x =a 2c,y =abc ,由中点坐标公式可得F 2关于渐近线对称的点的坐标为(2a 2c -c ,2abc),将其代入双曲线的方程可得(2a 2-c 2)2a 2c 2-4a 2c 2=1,化简可得c 2=5a 2,c 2=a 2+b 2=5a 2,所以b 2=4a 2.因为M (-3,4)在双曲线x 2a 2-y 2b 2=1上,所以9a 2-16b 2=1,9a 2-164a2=1,所以a 2=5,b 2=20,则该双曲线的标准方程为x 25-y 220=1.答案:x 25-y 220=112.设双曲线x 2-y 23=1的左,右焦点分别为F 1,F 2.若点P 在双曲线上,且△F 1PF 2为锐角三角形,则|PF 1|+|PF 2|的取值范围是______.解析:由题意不妨设点P 在双曲线的右支上,现考虑两种极限情况:当PF 2⊥x 轴时,|PF 1|+|PF 2|有最大值8;当∠P 为直角时,|PF 1|+|PF 2|有最小值27.因为△F 1PF 2为锐角三角形,所以|PF 1|+|PF 2|的取值范围为(27,8). 答案:(27,8)13.(2018·沈阳质量监测)已知P 是双曲线x 23-y 2=1上任意一点,过点P 分别作双曲线的两条渐近线的垂线,垂足分别为A ,B ,则P A →·PB →的值是________. 解析:设P (x 0,y 0),因为该双曲线的渐近线分别是x 3-y =0,x3+y =0,所以可取|P A |=|x 03-y 0|13+1,|PB |=|x 03+y 0|13+1,又cos ∠APB =-cos ∠AOB =-cos2∠AOx =-cos π3=-12,所以P A →·PB→=|P A →|·|PB →|·cos ∠APB =|x 203-y 20|43·(-12)=34×(-12)=-38.答案:-38。
2019版同步优化探究理数练习:第八章第七节双曲线含答案解析

课时作业A组一一基础对点练1 .已知F为双曲线C: x2—3m(m>0)的一个焦点,则点F到C的一条渐近线的距离为( )A. 3C. 3mD. 3m2 2解析:双曲线方程为3m—鲁二1,焦点F到一条渐近线的距离为,3.选A.答案:A2 22.已知双曲线拿一卷二1(a>0)的离心率为2,则a=( )CF解析:2 2因为双曲线的方程为?一3 =31,所以e2= 1 + T = 4,因此a2= 1, a = 1.选 D.a答案:3.双曲线x2—4y2=—1的渐近线方程为(A. x±y= 0C . x±!y=0 2解析:依题意,题中的双曲线即1 —x2^ 1,4B. yi2x= 0D . y±4x=因此其渐近线方程是2t —x2= 0, 即卩xi2y= 0,选A.4答案:A24 .已知双曲线倉—y2= 1的左、右焦点分别为F1, F2,点P在双曲线上,且满足|PF1| + |PF2| = 2 5, 则厶PF1F2的面积为( )A . 1 B. 3C..5D.|解析:在双曲线x3 —y2= 1中,a= .3, b= 1,c= 2.不防设P点在双曲线的右支上,则有|PF1|—|PF2| =2a = 2 3,又|PF1|+|PF2|= 2 5,A |PF1匸5+ .3, |PF2|= 5—, 3.又|F1F2| = 2c= 4,而|PF1|2A A+ |PF2|2= |F1F2^,A PF1 丄PF2,.・. SA PF1F2=|PF1|X |PF2|=十( .5+ . 3)X ( . 5—. 3)= 1•故选A.答案:A2 25.已知双曲线C :拿―b 2= 1(a>0, b>0),直线I : y =2x — 2•若直线I 平行于双曲线C 的一条渐近线且经过C 的一个顶点,则双曲线C 的焦点到渐近线的距离为D . 422b解析:根据题意,双曲线C 的方程为彩—缶=1(a>0, b>0),其焦点在x 轴上,渐近线方程为y =±bx ,又由直线I 平行于双曲线C 的一条渐近线,可知2 = 2,直线I : y = 2x — 2与x 轴的交点坐标为 a (1,0),即双曲线C 的一个顶点坐标为(1,0),即a = 1,则b = 2a = 2,故双曲线C 的焦点到渐近线 的距离为2,故选B.答案:B6.已知双曲线的焦点到渐近线的距离等于半实轴长,贝U 该双曲线的离心率为C. 2解析:不妨设双曲线的方程为 令一y}= 1(a>0, b>0),因为焦点F(c,0)到渐近线bx — ay = 0的距离 为a ,所以爲畀孑a ,即学=a ,所以b =1所以该双曲线的离心率e =a = 故选C. 答案:Cb 2 51 + 2=,又右焦点为 F 2(5,0), a2 + b 2= c 2,所以 a 2= 16, b 2 = 9,故双曲 a 4C. .57.已知双曲线 C : 2 2A ——匚=1 A.4 3 1 x 2 y C.x6—9 =1x 2 V 25孑一亩=1的离心率e = 4,且其右焦点为F 2(5,0),则双曲线C 的方程为()2 2一 V- = 1B .916_12 2=解析:由题意得e =2 2线C的方程为16-首=1.答案:C2 28.已知双曲线拿一存=1(a>0, b>0)的焦距为2 5,且双曲线的一条渐近线与直线2x+ y= 0垂直, 则双曲线的方程为()2巧-y2=1C3x! 3y C.202 B. x2-y=142 2D3X_-3y_= 15 20解析: 由题意得c= 5, b= 2,则a= 2, b= 1,所以双曲线的方程为^4 — /= 1. 答案:9. (2018山西八校联考)已知双曲线2 2C:学—狰=1(a>0, b>0)的左、右焦点分别为F1, F2,焦距为2c,直线y= c)与双曲线的()A. 2C. 2 .3+ 1解析:•••直线y= ~33(x+ c)过左焦点/ F2PF仁90° 即F i P丄F2P. •••|PF2 个交点P满足/ PF2F I = 2/PF1F2,则双曲线的离心率e为B. 3D. 3+ 1F1,且其倾斜角为30° A/ PF1F2= 30° / PF2F1 = 60° 二1匸2尸卡2|= C, |PF1|= |F I F2|S in 60°=寸3c,由双曲线的定义得2a=|PF1|—|PF2|=A/3C— c,.••双曲线 C 的离心率e=£ = 一1,选 D.a73c— c2答案:D2 210.已知F1, F2是双曲线C:拿一*= 1(a>0, b>0)的两个焦点,P是双曲线C上一点,若|PF1|+ |PF2| = 6&,且厶PF1F2最小内角的大小为30°则双曲线C的渐近线方程是( )A. 2xiy= 0 B . x±. 2y= 0C. 2x±y= 0D. x±2y= 0解析: 不妨设|PF1|>|PF2|,则|PF1|—|PF2|=2a,|PF1|+ |PF2|= 6a,所以|PF1|= 4a, |PF2| = 2a,且IF1F2匸2c,即|PF2|为最小边,即/ PF1F2= 30° 则厶PF1F2 为直角三角形,所以2c = 2.3a ,所以b = 2a ,即渐近线方程为y =±, 2x ,故选A. 答案:A•••双曲线C 的方程为20—彳=1. 答案:A42x 2 所以~4—(J3)2 =入所以入=1,故双曲线方程为才—y 2= 1. 2x13.双曲线r /—1(a>0, b>0)的焦距为10,焦点到渐近线的距离为 3,贝U r 的实轴长等解析:双曲线的焦点(0,5)到渐近线y = ;x ,即ax — by = 0的距离为.[订呼二¥= b = 3,所以a =法二:因为双曲线的渐近线方程为y = X 2 ,故可设双曲线为4y 2= X 疋0),又双曲线过点(4, 3), 11•已知双曲线 C :2 2x y 孑一1(a>0, b>0)的焦距为10,点P(2,1)在C 的一条渐近线上,则C 的方程为()2 2A x_ — y_ 1A .205x 2y 22BL5 20— 丫= 120 80解析:依题意a 2+ b 2= 251= bX 2 aa 2= 20,解得b 2二5,12 .已知双曲线过点(4 ,3), 且渐近线方程为y 二±2x ,则该双曲线的标准方程解析:法一:因为双曲线过点(4,3)且渐近线方程为y = ±2x ,故点(4,3)在直线y =*x 的下方.设 该双曲线的标准方程为a 2— £= 1(a>42 \[3 2孑— 0, b>0),所以 ab 1 b 2a = 2,,解得a = 2,故双曲线b = 1,答案:4—y 2二 1程为y =吃X ,则双曲线C 的方程为 ___________________ 解析:易得椭圆的焦点为(一5, 0), ( 5, 0),a 2 +b 2= 5,二 a 2= 1, b 2 = 4,2•••双曲线C 的方程为X 2— y 4 = 1.2答案:x 2—” 1X 2y 215. (2018合肥市质检)双曲线M :孑一看1(a>0, b>0)的左、右焦点分别为 F 1, F 2,直线x = a1与双曲线M 的渐近线交于点P ,若sin /PF 1F 2=3则该双曲线的离心率为 __________________________ . 解析:不妨设P 为直线x = a 与双曲线M 的渐近线在第一象限内的交点,贝UP 点坐标为(a , b),因为 sin / PF 1F 2 = 3,所以|PF 1|= 3b ,所以(a + c)2+ b 2= 9b 2,即 9a 2+ 2ac — 7c 2= 0,7e 2— 2e — 9=0,9又e>1,解得e = 7.B 组一一能力提升练C :字一£= 1(a>0, b>0)的两个焦点,若在双曲线上存在点 P 满足2|PF i+ PF 2|W |F i F 2|,则双曲线的离心率的取值范围是()A • (1, .2]B . (1,2] C. [,2,+x)D . [2 ,+x)—》 —》 —》 —》 —》 c —》cC解析:T 2|PF 1 + PF 2|< |F 1F 2|? 4|0P|W 2c? |OP|< ,又 |OP|> a ,: a ^., 即 卩 c > 2a,A e =—》2.2 2 a故选D. 答案:D4,2a = 8.1有相同的焦点,且双曲线C 的渐近线方1 •已知F i , F 2是双曲线14.已知双曲线C :x 2 xb>0)与椭圆9 +2 2 2 22•若实数k 满足0<k<9,则曲线25-冷=1与曲线25X Tk —y9二1的( )A •离心率相等B •虚半轴长相等C .实半轴长相等D •焦距相等解析:由0<k<9,易知两曲线均为双曲线且焦点都在 x 轴上,由25+ 9— k = 25 — k + 9,得两双 曲线的焦距相等. 答案:D3. (2018云南五市联考)设P 为双曲线x 2—£= 1右支上一点,M , N 分别是圆(x + 4)2+ y 2= 4和(x — 4)2 + y 2= 1上的点,设|PM|— |PN|的最大值和最小值分别为 m , n ,则|m — n 匸( )A . 4B . 5C . 6F 1( — 4,0), F 2(4,0),恰为两个圆的圆心,两个圆的半径分别min= |PF 2| — 1, 故 |PM|— |PN| 的最大值为(|PF 1| + 2)—(|PF 2|— 1) |PN|的最小值为(|PF 1|— 2)— (|PF 2|+ 1) = (|PF 1— |PF 2|) — 3 =—x 2 y 2曲线C : — — ; = 1的一条渐近线,P 是l 上的一点,F 1, F 2=0,则点P 到x 轴的距离为()B .V 2解析:由题意知F 1( — 6, 0), F 2( .6, 0),不妨设I 的方程为y = 2x ,点P(x 0, ,2x 0),由PF 1 PF 2 =(—.6 — X 0,— 2x 0) ( 6 — X 0,— 2x 0) = 3x o — 6 = 0,得 x °= ±. 2,故点 P 到 x 轴的距离为.2|x °| =2,故选C. 答案:Cx 2y 25.已知双曲线4 —器=1(b>0),以原点为圆心,双曲线的实半轴长为半径长的圆与双曲线的两条渐近线相交于A , B , C , D 四点,四边形ABCD 的面积为2b ,则双曲线的方程为( )解析:易知双曲线的两个焦点分别为 为 2,1,所以 |PM|max = |PF 1|+ 2,|PN=(|PF 1— |PF 2|) + 3 = 5,同理 |PM —1,所以|m — n| = 6,故选C. 答案:C4. (2018江南十校联考)已知I 是双分别是C 的左、右焦点,若PF 1 PF 2A. 3 C . 2D.2,63略34°= 1近线交于点B ,若FB = 2FA ,贝吐匕双曲线的离心率为()A. 2 C . 2c — a b b b c — a b小所以A(~2 , 2),又点A 在直线y = ax 上,则a •厂二2,c = 2a , e = 2.答案:8.若直线|1和直线12相交于一点,将直线11绕该点逆时针旋转到与12第一次重合时所转的角为9, k 2 一 k 1 x 2则角9就称为l 1到l 2的角,tan A 亓匚危,其中k 1, k 2分别是l 1, l 2的斜率,已知双曲线E :孑一2 2x y ‘ C<r — = 1解析:根据圆和双曲线的对称性,可知四边形 ABCD 为矩形•双曲线的渐近线方程为y =字,圆的方程为x 2 + y 2 = 4,不妨设交点 A 在第一象限,由y = bx,x 2 + y 2= 4得X A = /—^=2,『A = j 2,2 v 4+ b \!4+ b故四边形ABCD 的面积为4x A y A =秽:2= 2b ,解得b 2= 12,故所求的双曲线方程为》—卷=1,选D.答案:D2 26•已知双曲线拿一” 1(a>0, b>0)的左、右焦点分别为F i 、F 2,以|F I F 2|为直径的圆与双曲线渐近线的一个交点为(3,4),贝吐匕双曲线的方程为()B x ! y !_ 1 x 2y 2D — — —= 1x 2 y 2A•花- 9 二 12 2Cx_—y _ 二解析: 因为以|F I F 2|为直径的圆与双曲线渐近线的一个交点为(3,4),所以c = 5,+ b 2, 所以a = 3, b = 4,所以此双曲 2 2线的方程为x 9 —务=1.C2 27.过双曲线拿一^2= 1(a>0, b>0)的 答案: 个焦点F 作一条渐近线的垂线,垂足为点A ,与另一条渐B. 3 D. 5解析: 不妨设B(x ,—,OB|=x 2 + — ;x 2= c ,可取B( — a , b),由题意可知点A 为BF 的中占I2 2滸=1(a>0, b>0)的右焦点为F , A 是右顶点,P 是直线x =三上的一点,e 是双曲线的离心率,直 线PA 到PF 的角为9,则tan B 的最大值为() B. ;i e+eC. 2 1+ e答案:C2 -9. (2018淄博模拟)过双曲线拿一^2= 1(a>0, b>0)的左焦点F 1,作圆x 2 + / = a 2的切线交双曲线的右支于点P ,切点为T , PF i 的中点M 在第一象限,则以下结论正确的是()b — a = |M0| —|MT| b — a>|MO|— |MT|b — a = |MO| + |MT|解析:如图,连接OT ,贝U OT 丄F 1T ,在直角三角形 OTF 1;|OF 1|2—|OT|2= b ,连接 PF 2,••• M 为线段F 1P 的中点,O 为F 1F 2的中点,•••|MO| —|MT|= 2|PF 2|— 2|PF 1|— |F 1T| = 2(|PF 2|— |PF 1|)+ b =qx (— 2a) + b = b — a ,故选 A.答案:A X 2 y 210. (2018昆明市检测)已知点F 为双曲线C :孑一詁=1(a>0, b>0)的一个焦点,以点F 为圆心的A.1 e D.f解析:设PA , PF 的斜率分别为k 3, k 4, 由题意可知 tan2k 4— k 3 aak ,不妨设 P(_c , y)(y>0),则 ky . ) 人 =,k4=a^~. 令—a — c2 a m =c — a , n2a=——c ,贝U tan y —y n mm — n r ‘口 9== ,由 m — n = c — a>0,得 y y mn ' '当号+ y 取得最小值时 AlZtan 9取最大值,又y>0, m<0, *0,所以罗+ y > 2 :'mn ,当且仅当y = : mn时等号成立,此时tan m — n A ------2 mnc — a:-a - c=2 J + e ,故选 C.C . b — a<|MO|— |MT|中,|F 1T| =圆与C 的渐近线相切,且与C 交于A , B 两点,若AF 丄x 轴,则C 的离心率为 解析:不妨设F 为双曲线的右焦点,则F(c,O),易知双曲线的渐近线方程为y =,贝U 双曲线的焦点F 到渐近线的距离d = 严 尸b,所以圆F 的半径为b.在双曲线方程中,令x = c,得,寸 a 2 * * 5+ b 2ab2 _______________________________________________•因为点A 在圆F 上,所以占=b ,即a = b ,所以c= • a 2+ b 2= 2a ,所以所以A(c ,c e=_ a2.答案:22 211•双曲线拿一皆1(a>0, b>0)上一点M( — 3,4)关于一条渐近线的对称点恰为右焦点F 2, 则该双曲线的标准方程为 _____________________________ .x 2 y 2b解析:不妨设双曲线孑一生二1的右焦点F 2(C ,0)关于渐近线y = ax 对称的点在双曲线上, 则过焦点F 2且垂直于该渐近线的直线方程为y — 0二—早仪―c),a即 y = — b (x —c )-联立可得方程组b 尸a x , a尸一b x —c ,2ab )c)解析:由题意不妨设点P 在双曲线的右支上,现考虑两种极限情况:当PF 2丄X 轴时,|PF 1|+|PF 2| 有最大值8;当/ P 为直角时,|PF i |+ |PF 2|有最小值2.7因为△ F 1PF 2为锐角三角形,所以|PF i | + |PF 21的取值范围为(2 .'7,8). 答案:(2 7, 8)X 213.(2018沈阳质量监测)已知P 是双曲线—y 2= 1上任意一点,过点P 分别作双曲线的两条渐近线的垂线,垂足分别为 A ,B ,求PAPB 的值.x解析:设P (x o ,y o ),因为该双曲线的渐近线分别是 — y =0,X 0 騙+ yo1|PB| =— ,又 cos / APB = — cos / AOB = — cos2/ AOx = 2 lX0-y21 1 (—刁 | cos / APB = 3 1 =3X (—2) IIIII II II II II II I III II II In—cos 3=I II II II I 舟,所以PA PB = |P A | |P BI IIIII I I I III I I I I I I II II I II II I I I .x o , I 羽-y o ly = 0,所以可取|PA|=讨丘—,W 1x2方程为x4—y2= 1.1 1 1 12a x= c 解得「aby=石,由中点坐标公式可得F2关于渐近线对称的点的坐标为(2? —c,2 2— 2 2 2将其代入双曲线的方程可得―a_2c2 —= 1,化简可得c2= 5a2, c2= a2+ b2= 5a2,所以b2= 4a2.a c c因为M(—3, 4)在双曲线拿一£= 1上,所以事一学=1,事一着=1,所以a2= 5, b2= 20,则该2 2双曲线的标准方程为x—= 1.5 202 2答案:x一2o二112.设双曲线x2—£ = 1的左,右焦点分别为F i, F2若点P在双曲线上,且△ F1PF2为锐角三角形,则|PF i|+ |PF2|的取值范围是。
(完整版)双曲线标准方程及几何性质知识点及习题,推荐文档

9 2
,
1
的双曲线的
标准方程。
x2 【例 6】设 F1、F2 分别是双曲线 a2
y2 b2
1的左、右焦点,若双曲线上存在点 A,使
F1AF2 90 ,且︱AF1︱=3︱AF2︱,求双曲线的离心率。
练习。已知双曲线 x2 y 2 1的离心率 e 2 3 ,过 A(a,0), B(0,b) 的直线到原点的距离
5
【例 2】求虚轴长为 12,离心率为 双曲线标准方程。
4
【例 3】求焦距为 26,且经过点 M(0,12)双曲线标准方程。
练习。焦点为 0,6,且与双曲线 x2 y2 1有相同的渐近线的双曲线方程是 ( 2
)
A. x2 y 2 1
12 24
B. y 2 x2 1
12 24
C. y 2 x2 1
24 12
D. x2 y 2 1
24 12
【例 4】与双曲线 x2 y2 1有公共渐进线,且经过点 A 3, 2 3 9 16
练习。求一条渐近线方程是 3x 4 y 0 ,一个焦点是 4,0的双曲线标准方程,并求此双曲
线的离心率.
解决双曲线的性质问题,关键是找好等量关系,特别是 e、a、b、c 四者的关系,构造出
F1 、F2
分别是双曲线的左、右焦点,若| PF1 | 3 ,则| PF2 |
()
A.1 或 5
B. 6
C. 7
D. 9
11.已知双曲线
x2 a2
y2 b2
1, (a
0, b
0) 的左,右焦点分别为 F1, F2 ,点
P
在双曲线的右
支上,且| PF1 | 4 | PF2 | ,则双曲线的离心率 e 的最大值为 ( )
(精校)《双曲线》练习题经典(含答案)(可编辑修改)

∴Error!=-Error!,解得 λ=-14。∴曲线 C 的方程是 x2-Error!=1。
31.(本题满分 12 分) 已知中心在原点的双曲线 C 的右焦点为 2, 0 ,右顶点为 3, 0 。
y2 D. - =1
3
11.设 F1,F2 是双曲线 x2- =1 的两个焦点,P 是双曲线上的一点,且 3|PF1|=4|PF2|,则△
PF1F2 的面积等于( C ) A.4Error!
B.8
C.24
D.48
12.过双曲线 x2-y2=8 的左焦点 F1 有一条弦 PQ 在左支上,若|PQ|=7,F2 是双曲线的右焦点,
9λ
(2)由题设知直线 l 的方程为 y=Error!x-2,设 A(x1,y1),B(x2,y2),
联立方程组
y y2
2x x2
2, 1.
消去
y
得:(λ+2)x2-4
x+4-λ=0.
∵方程组有两解,∴λ+2≠0 且 Δ>0,
∴λ>2 或 λ〈0 且 λ≠-2,x1·x2=Error!,
A. ﹣ =1 B. ﹣ =1 C. ﹣ =1 D. ﹣ =1
17.如图,F1、F2 是双曲线
=1(a>0,b>0)的左、右焦点,过 F1 的直
线 l 与双曲线的左右两支分别交于点 A、B.若△ABF2为等边三角形,则双曲线的离心率为( B )
A.4 B. C.
D.
18.如图,已知双曲线 ﹣ =1(a>0,b>0)的左右焦点分别为 F1,F2,|F1F2|=4,P 是
30。已知 曲线 C: +x2=1.
高考数学统考一轮复习 第八章 平面解析几何 第七节 双曲线课时规范练(文,含解析)北师大版

学习资料第八章平面解析几何第七节双曲线课时规范练A组—-基础对点练1.双曲线错误!-错误!=1(0<m<3)的焦距为()A.6B.12C.36 D。
236-2m2解析:c2=36-m2+m2=36,∴c=6。
双曲线的焦距为12。
答案:B2.双曲线8kx2-ky2=8的一个焦点是(0,3),则k的值是()A.1 B.-1C.错误!D。
-错误!解析:kx2-错误!=1,焦点在y轴上,c=3,解得k=-1。
答案:B3.(2020·山东滕州月考)已知双曲线错误!-错误!=1的左、右焦点分别为F1、F2,若双曲线的左支上有一点M到右焦点F2的距离为18,N是MF2的中点,O为坐标原点,则|NO|等于()A.错误!B.1C.2 D.4解析:由双曲线x225-错误!=1,知a=5,由双曲线定义|MF2|-|MF1|=2a=10,得|MF1|=8,∴|NO|=错误!|MF1|=4。
答案:D4.(2020·湖南永州模拟)焦点是(0,±2),且与双曲线错误!-错误!=1有相同的渐近线的双曲线的方程是()A.x2-错误!=1 B.y2-错误!=1C.x2-y2=2 D。
y2-x2=2解析:由已知,双曲线焦点在y轴上,且为等轴双曲线,故选D。
答案:D5.双曲线错误!-错误!=1的渐近线方程是()A.y=±错误!x B.y=±错误!xC.y=±错误!x D。
y=±错误!x解析:双曲线错误!-错误!=1中,a=3,b=2,双曲线的渐近线方程为y=±错误!x.答案:C6.(2020·石家庄模拟)若双曲线M:x2a2-错误!=1(a>0,b>0)的左、右焦点分别是F1、F2,P为双曲线M上一点,且|PF1|=15,|PF2|=7,|F1F2|=10,则双曲线M的离心率为()A.3 B.2C。
错误!D。
错误!解析:P为双曲线M上一点,且|PF1|=15,|PF2|=7,|F1F2|=10,由双曲线的定义可得|PF1|-|PF2|=2a=8,|F1F2|=2c=10,则双曲线的离心率为:e=错误!=错误!.答案:D7.(2020·彭州模拟)设F为双曲线C:错误!-错误!=1(a>0,b>0)的右焦点,过坐标原点的直线依次与双曲线C的左、右支交于点P、Q,若|PQ|=2|QF|,∠PQF=60°,则该双曲线的离心率为()A.错误!B.1+错误!C.2+ 3 D。
2019版一轮优化探究理数(苏教版)练习:第九章 第七节 双曲线 Word版含解析

一、填空题1.已知点M (-2,0)、N (2,0),动点P 满足条件|PM |-|PN |=22,则动点P 的轨迹方程为________.解析:因为|MN |=4,22<4,所以动点P 的轨迹是以M 、N 为焦点,实轴长为22的双曲线靠近点N 的一支,即x 2-y 2=2,x ≥2.答案:x 2-y 2=2(x ≥2)2.双曲线x 24-y 212=1的焦点到渐近线的距离为________.解析:双曲线x 24-y 212=1的渐近线为y =±3x ,c =4+12=4,其焦点坐标为(±4,0),由点到直线的距离公式可得焦点到渐近线的距离为431+(±3)2=2 3.答案:2 3 3.与双曲线x 29-y 216=1有公共渐近线且经过点A (-3,23)的双曲线的方程是________.解析:由条件可设所求双曲线方程为x 29-y 216=k (k >0),将点A (-3,23)代入得k =(-3)29-(23)216=14,所以所求双曲线方程为4x 29-y 24=1.答案:4x 29-y 24=14.在平面直角坐标系xOy 中,已知△ABC 的顶点A (-5,0)和C (5,0),顶点B 在双曲线x 216-y 29=1上,则sin B |sin A -sin C |为________. 解析:由题意得a =4,b =3,c =5.A 、C 为双曲线的焦点,∴||BC |-|BA ||=8,|AC |=10.由正弦定理得sin B |sin A -sin C |=|AC |||BC |-|BA ||=108=54.答案:545.已知F 1、F 2为双曲线C :x 2-y 2=1的左、右焦点,点P 在C 上,∠F 1PF 2=60°,则|PF 1|·|PF 2|=________.解析:如图,设|PF1|=m ,|PF 2|=n .则⎩⎪⎨⎪⎧ |m -n |=2,(22)2=m 2+n 2-2mn cos ∠F 1PF 2.∴⎩⎪⎨⎪⎧m 2-2mn +n 2=4,m 2-mn +n 2=8.∴mn =4. 即|PF 1|·|PF 2|=4.答案:46.已知点F 1,F 2分别是双曲线的两个焦点,P 为该曲线上一点,若△PF 1F 2为等腰直角三角形,则该双曲线的离心率为________.解析:不妨设P 点在双曲线的右支上,则|PF 1|-|PF 2|=2a .∵△PF 1F 2是等腰直角三角形,∴只能是∠PF 2F 1=90°,∴|PF 2|=|F 1F 2|=2c ,∴|PF 1|=2a +|PF 2|=2a +2c ,∴(2a +2c )2=2·(2c )2,即c 2-2ac -a 2=0,两边同除以a 2,得e 2-2e -1=0.∵e >1,∴e =2+1. 答案:2+17.若双曲线x 2a 2-y 23=1(a >0)的离心率为2,则a 等于________.解析:由离心率公式,得a 2+3a 2=22(a >0),解得a =1.答案:18.A 、F 分别是双曲线9x 2-3y 2=1的左顶点和右焦点,P 是双曲线右支上任一点,若∠PF A =λ·∠P AF ,则λ=________.解析:特殊值法,取点P 为(23,1),得∠PF A =2∠P AF ,故λ=2.答案:29.若双曲线x 24-y 2b 2=1 (b >0) 的渐近线方程为y =±12x ,则b 等于________.解析:双曲线x 24-y 2b 2=1的渐近线方程为x 24-y 2b 2=0,即y =±b 2x (b >0),∴b =1.答案:1二、解答题10.如图所示,双曲线的中心在坐标原点,焦点在x 轴上,F1,F 2分别为左、右焦点,双曲线的左支上有一点P ,∠F 1PF 2=π3,且△PF 1F 2的面积为23,又双曲线的离心率为2,求该双曲线的方程.解析:设双曲线方程为:x 2a 2-y 2b 2=1(a >0,b >0), F 1(-c,0),F 2(c,0),P (x 0,y 0).在△PF 1F 2中,由余弦定理,得:|F 1F 2|2=|PF 1|2+|PF 2|2-2|PF 1|·|PF 2|·cos π3=(|PF 1|-|PF 2|)2+|PF 1|·|PF 2|,即4c 2=4a 2+|PF 1|·|PF 2|.又∵S △PF 1F 2=23,∴12|PF 1|·|PF 2|·sin π3=2 3.∴|PF 1|·|PF 2|=8.∴4c 2=4a 2+8,即b 2=2.又∵e =c a =2,∴a 2=23.∴双曲线的方程为:3x 22-y 22=1.11.已知双曲线x 2a 2-y 2b 2=1(a >0,b >0)的离心率e =233,直线l 过A (a,0),B (0,-b )两点,原点O 到直线l 的距离是32.(1)求双曲线的方程;(2)过点B 作直线m 交双曲线于M 、N 两点,若OM →·ON →=-23,求直线m 的方程.解析:(1)依题意,l 的方程为x a +y -b=1, 即bx -ay -ab =0,由原点O 到l 的距离为32, 得ab a 2+b 2=ab c =32, 又e =c a =233,∴b =1,a = 3.故所求双曲线方程为x 23-y 2=1.(2)显然直线m 不与x 轴垂直,设m 方程为y =kx -1,则点M 、N 坐标(x 1,y 1),(x 2,y 2)是方程组⎩⎨⎧ y =kx -1x 23-y 2=1的解,消去y ,得(1-3k 2)x 2+6kx -6=0.①依题意,1-3k 2≠0,由根与系数关系,知x 1+x 2=6k 3k 2-1,x 1x 2=63k 2-1.OM →·ON →=(x 1,y 1)·(x 2,y 2)=x 1x 2+y 1y 2=x 1x 2+(kx 1-1)(kx 2-1)=(1+k 2)x 1x 2-k (x 1+x 2)+1=6(1+k 2)3k 2-1-6k 23k 2-1+1=63k 2-1+1.又∵OM →·ON →=-23,∴63k 2-1+1=-23,k =±12,经检验知,当k =±12时,方程①有两个不相等的实数根,∴方程为y =12x -1或y =-12x -1.12.A ,B ,C 是我方三个炮兵阵地,A 在B 正东6 km ,C 在B的北偏西30°,相距4 km ,P 为敌炮阵地,某时刻A 处发现敌炮阵地的某种信号,由于B ,C 两地比A 距P 地远,因此4 s后,B ,C 才同时发现这一信号,此信号的传播速度为1 km/s ,A 若炮击P 地,求炮击的方位角.解析:如图所示,以直线BA为x轴、线段BA的中垂线为y轴建立直角坐标系,则B(-3,0),A(3,0),C(-5,23).∵|PB|=|PC|.∴点P在线段BC的垂直平分线上.∵k BC=-3,BC中点为D(-4,3),∴直线PD的方程为y-3=13(x+4).①又|PB|-|P A|=4,故P在以A、B为焦点的双曲线的右支上.设P(x,y),则双曲线方程为x24-y25=1(x≥0).②由①、②解得x=8,y=53,所以P(8,53).因此k P A=538-3= 3.故炮击的方位角为北偏东30°.。
2019版同步优化探究理数(北师大版)练习:第八章第八节曲线与方程含答案解析

x+ 3a 2 y2
即
2
12a
-4a2=1.
∴点 P 的轨迹为双曲线.故选 D.
答案: D
4.已知动点 P(x, y)与两定点 M(-1,0),N(1,0)连线的斜率之积等于常数 λ(λ≠0).则动点 P 的轨
迹 C 的方程为
.
解析: 由题设知直线 PM 与 PN 的斜率存在且均不为零,所以
整理得 x2-yλ2= 1(λ≠ 0, x≠ ±1). 即动点 P 的轨迹 C 的方程为 x2- yλ2=1(λ≠0,x≠ ±1) 答案: x2-yλ2=1(λ≠0,x≠±1)
2,所以
mn= 4,又直线
AC 与 BD 的交点
为 M,
所以
y y-m x+2= x-2 ,
y y-n x-2=x+2,
所以
4y m=x+2,
-4y n=x-2,
16y2 所以- x2-4=4,所以点
M
的轨迹方程为
x2 4+
y2=
1(y≠0). 答案: x42+y2=1(y≠0)
x2 y2 4.过椭圆 a2+b2= 1(a> b> 0)上任意一点 M 作 x 轴的垂线,垂足为 N,则线段 MN 中点的轨迹方
∵Q→P·Q→F=F→P·F→Q,
∴(0, y+1) ·(- x,2)=(x,y-1) ·(x,- 2), 即 2(y+1)=x2-2(y-1),整理得 x2=4y, ∴动点 P 的轨迹 C 的方程为 x2= 4y.
答案: A
2.已知两定点 A(-2,0), B(1,0),如果动点 P 满足 |PA|=2|PB|,则动点 P 的轨迹是 ( )
x-2 2+y2-3,
故曲线 E 的方程为 y2=6x.
(2)设直线 AB 的方程为 my=x-2,
2019版同步优化探究理数北师大版练习:第八章第七节双曲线含解析

2019版同步优化探究理数北师大版练习:第八章第七节双曲线含解析1 / 11 / 1课时作业A 组 —— 基础对点练1.已知 F 为双曲线 C :x 2-my 2= 3m(m>0)的一个焦点,则点 F 到 C 的一条渐近线的距离为 ()A. 3 B .3C. 3mD .3mx2y2分析:双曲线方程为 3m - 3 =1,焦点 F 到一条渐近线的距离为 3.选 A.答案: A22x y2.已知双曲线 a 2- 3 = 1(a>0)的离心率为 2,则 a = ()6A .2 B. 25C. 2D .1x 2 y 2232分析: 由于双曲线的方程为 a 2- 3 =1,所以 e = 1+ a 2= 4,所以 a = 1, a = 1. 选 D.答案: D2 2)3.双曲线 x -4y =- 1 的渐近线方程为 (A . x ±2y =0B .y ±2x =0C .x ±4y =0D .y ±4x =0y 2 2y 2 2分析:依题意,题中的双曲线即 1 -x =1,所以其渐近线方程是1 - x =0,即 x ±2y44= 0,选 A.答案: Ax 224.已知双曲线 3 -y =1 的左、右焦点分别为 F 1,F 2,点 P 在双曲线上,且知足 |PF 1|+|PF 2|=2 5,则△ PF 1F 2 的面积为 ( )A . 1B. 3。
(完整版)双曲线及其标准方程测试题及解析人教版

双曲线及其标准方程测试题及解析(人教版)§2.2双曲线2.2.1双曲线及其标准方程课时目标1.了解双曲线的定义、几何图形和标准方程的推导过程.2.掌握双曲线的标准方程.3.会利用双曲线的定义和标准方程解决简单的应用问题.1.双曲线的有关概念(1)双曲线的定义平面内与两个定点F1,F2的距离的差的绝对值等于常数(小于________)的点的轨迹叫做双曲线.平面内与两个定点F1,F2的距离的差的绝对值等于|F1F2|时的点的轨迹为__________________________________________.平面内与两个定点F1,F2的距离的差的绝对值大于|F1F2|时的点的轨迹__________.(2)双曲线的焦点和焦距双曲线定义中的两个定点F1、F2叫做________________,两焦点间的距离叫做________________.2.双曲线的标准方程(1)焦点在x轴上的双曲线的标准方程是________________,焦点F1__________,F2__________.(2)焦点在y轴上的双曲线的标准方程是________________________,焦点F1________,F2__________.(3)双曲线中a、b、c的关系是____________.一、选择题1.已知平面上定点F1、F2及动点M,命题甲:||MF1|-|MF2||=2a(a为常数),命题乙:M点轨迹是以F1、F2为焦点的双曲线,则甲是乙的()A.充分不必要条件B.必要不充分条件C.充要条件D.既不充分也不必要条件2.若ax2+by2=b(ab0),则这个曲线是()A.双曲线,焦点在x轴上B.双曲线,焦点在y轴上C.椭圆,焦点在x轴上D.椭圆,焦点在y轴上3.焦点分别为(-2,0),(2,0)且经过点(2,3)的双曲线的标准方程为()A.x2-y23=1B.x23-y2=1C.y2-x23=1D.x22-y22=14.双曲线x2m-y23+m=1的一个焦点为(2,0),则m的值为()A.12B.1或3C.1+22D.2-125.一动圆与两圆:x2+y2=1和x2+y2-8x+12=0都外切,则动圆圆心的轨迹为()A.抛物线B.圆C.双曲线的一支D.椭圆6.已知双曲线中心在坐标原点且一个焦点为F1(-5,0),点P位于该双曲线上,线段PF1的中点坐标为(0,2),则该双曲线的方程是()A.x24-y2=1B.x2-y24=1C.x22-y23=1D.x23-y22=1题号123456答案二、填空题7.设F1、F2是双曲线x24-y2=1的两个焦点,点P在双曲线上,且PF1→PF2→=0,则|PF1||PF2|=______. 8.已知方程x21+k-y21-k=1表示双曲线,则k的取值范围是________.9.F1、F2是双曲线x29-y216=1的两个焦点,P在双曲线上且满足|PF1||PF2|=32,则∠F1PF2=______.三、解答题10.设双曲线与椭圆x227+y236=1有相同的焦点,且与椭圆相交,一个交点A的纵坐标为4,求此双曲线的标准方程.11.在△ABC中,B(4,0)、C(-4,0),动点A满足sinB -sinC=12sinA,求动点A的轨迹方程.能力提升12.若点O和点F(-2,0)分别为双曲线x2a2-y2=1(a0)的中心和左焦点,点P为双曲线右支上的任意一点,则OP→FP→的取值范围为()A.[3-23,+∞)B.[3+23,+∞)C.[-74,+∞)D.[74,+∞)13.已知双曲线的一个焦点为F(7,0),直线y=x-1与其相交于M,N两点,MN中点的横坐标为-23,求双曲线的标准方程.1.双曲线的标准方程可以通过待定系数法求得.2.和双曲线有关的轨迹问题要按照求轨迹方程的一般步骤来解,也要和双曲线的定义相结合.3.直线和双曲线的交点问题可以转化为解方程组(设而不求),利用韦达定理,弦长公式等解决.§2.2双曲线2.2.1双曲线及其标准方程答案知识梳理1.(1)|F1F2|以F1,F2为端点的两条射线不存在(2)双曲线的焦点双曲线的焦距2.(1)x2a2-y2b2=1(a0,b0)(-c,0)(c,0)(2)y2a2-x2b2=1(a0,b0)(0,-c)(0,c)(3)c2=a2+b2作业设计1.B[根据双曲线的定义,乙⇒甲,但甲乙,只有当2a|F1F2|且a≠0时,其轨迹才是双曲线.] 2.B[原方程可化为x2ba+y2=1,因为ab0,所以ba0,所以曲线是焦点在y轴上的双曲线,故选B.]3.A[∵双曲线的焦点在x轴上,∴设双曲线方程为x2a2-y2b2=1(a0,b0).由题知c=2,∴a2+b2=4.①又点(2,3)在双曲线上,∴22a2-32b2=1.②由①②解得a2=1,b2=3,∴所求双曲线的标准方程为x2-y23=1.]4.A[∵双曲线的焦点为(2,0),在x轴上且c=2,∴m+3+m=c2=4.∴m=12.]5.C[由题意两定圆的圆心坐标为O1(0,0),O2(4,0),设动圆圆心为O,动圆半径为r,则|OO1|=r+1,|OO2|=r+2,∴|OO2|-|OO1|=1|O1O2|=4,故动圆圆心的轨迹为双曲线的一支.]6.B[设双曲线方程为x2a2-y2b2=1,因为c=5,c2=a2+b2,所以b2=5-a2,所以x2a2-y25-a2=1.由于线段PF1的中点坐标为(0,2),则P点的坐标为(5,4).代入双曲线方程得5a2-165-a2=1,解得a2=1或a2=25(舍去),所以双曲线方程为x2-y24=1.故选B.]7.2解析∵||PF1|-|PF2||=4,又PF1⊥PF2,|F1F2|=25,∴|PF1|2+|PF2|2=20,∴(|PF1|-|PF2|)2=20-2|PF1||PF2|=16,∴|PF1||PF2|=2.8.-1k1解析因为方程x21+k-y21-k=1表示双曲线,所以(1+k)(1-k)0.所以(k+1)(k-1)0.所以-1k1.9.90°解析设∠F1PF2=α,|PF1|=r1,|PF2|=r2.在△F1PF2中,由余弦定理,得(2c)2=r21+r22-2r1r2cosα,∴cosα=(r1-r2)2+2r1r2-4c22r1r2=36+64-10064=0.∴α=90°.10.解方法一设双曲线的标准方程为y2a2-x2b2=1(a0,b0),由题意知c2=36-27=9,c=3.又点A的纵坐标为4,则横坐标为±15,于是有42a2-(±15)2b2=1,a2+b2=9,解得a2=4,b2=5. 所以双曲线的标准方程为y24-x25=1.方法二将点A的纵坐标代入椭圆方程得A(±15,4),又两焦点分别为F1(0,3),F2(0,-3).所以2a=|(±15-0)2+(4+3)2-(±15-0)2+(4-3)2|=4,即a=2,b2=c2-a2=9-4=5,所以双曲线的标准方程为y24-x25=1.11.解设A点的坐标为(x,y),在△ABC中,由正弦定理,得asinA=bsinB=csinC=2R,代入sinB-sinC=12sinA,得|AC|2R-|AB|2R=12|BC|2R,又|BC|=8,所以|AC|-|AB|=4.因此A点的轨迹是以B、C为焦点的双曲线的右支(除去右顶点)且2a=4,2c=8,所以a=2,c=4,b2=12.所以A点的轨迹方程为x24-y212=1(x2).12.B[由c=2得a2+1=4,∴a2=3,∴双曲线方程为x23-y2=1.设P(x,y)(x≥3),∴OP→FP→=(x,y)(x+2,y)=x2+2x+y2=x2+2x+x23-1=43x2+2x-1(x≥3).令g(x)=43x2+2x-1(x≥3),则g(x)在[3,+∞)上单调递增.g(x)min=g(3)=3+23.OP→FP→的取值范围为[3+23,+∞).]13.解设双曲线的标准方程为x2a2-y2b2=1,且c=7,则a2+b2=7.①由MN中点的横坐标为-23知,中点坐标为-23,-53.设M(x1,y1),N(x2,y2),则由x21a2-y21b2=1,x22a2-y22b2=1,得b2(x1+x2)(x1-x2)-a2(y1+y2)(y1-y2)=0.∵x1+x2=-43y1+y2=-103,且y1-y2x1-x2=1,∴2b2=5a2.②由①,②求得a2=2,b2=5.∴所求双曲线的标准方程为x22-y25=1.。
2019版同步优化探究文数(北师大版)练习第八章 第七节 双曲线 Word版含解析

课时作业组——基础对点练.已知为双曲线:-=(>)的一个焦点,则点到的一条渐近线的距离为( )..解析:双曲线方程为-=,焦点到一条渐近线的距离为.选.答案:.已知双曲线-=(>)的离心率为,则=( )..解析:因为双曲线的方程为-=,所以=+=,因此=,=.选.答案:.双曲线-=-的渐近线方程为( ).±=.±=.±=.±=解析:依题意,题中的双曲线即-=,因此其渐近线方程是-=,即±=,选.答案:.已知双曲线-=的左、右焦点分别为,,点在双曲线上,且满足+=,则△的面积为( ).解析:在双曲线-=中,=,=,=.不防设点在双曲线的右支上,则有-==,又+=,∴=+,=-.又==,而+=,∴⊥,∴△=××=×(+)×(-)=.故选.答案:.已知双曲线:-=(>,>),直线:=-.若直线平行于双曲线的一条渐近线且经过的一个顶点,则双曲线的焦点到渐近线的距离为( )...解析:根据题意,双曲线的方程为-=(>,>),其焦点在轴上,渐近线方程为=±,又由直线平行于双曲线的一条渐近线,可知=,直线:=-与轴的交点坐标为(),即双曲线的一个顶点坐标为(),即=,则==,故双曲线的焦点到渐近线的距离为,故选.答案:.已知双曲线的焦点到渐近线的距离等于半实轴长,则该双曲线的离心率为( )..解析:不妨设双曲线的方程为-=(>,>),因为焦点()到渐近线-=的距离为,所以=,即=,所以=,所以该双曲线的离心率===,故选.答案:.已知双曲线:-=的离心率=,且其右焦点为 (),则双曲线的方程为( )-=-=-=-=解析:由题意得==,又右焦点为(),+=,所以=,=,故双曲线的方程为-=.答案:.已知双曲线-=(>,>)的焦距为,且双曲线的一条渐近线与直线+=垂直,则双曲线的方程为( ).-=-=-=-=解析:由题意得=,=,则=,=,所以双曲线的方程为-=.答案:.(·山西八校联考)已知双曲线:-=(>,>)的左、右焦点分别为,,焦距为,直线=(+)与双曲线的一个交点满足∠=∠,则双曲线的离心率为( )+.+解析:∵直线=(+)过左焦点,且其倾斜角为°,∴∠=°,∠=°,∴∠=°,即⊥.∴==,=°=,由双曲线的定义得=-=-,∴双曲线的离心率===+,选.答案:.已知,是双曲线:-=(>,>)的两个焦点,是双曲线上一点,若+=,且△最小内角的大小为°,则双曲线的渐近线方程是( ).±=±=.±=.±=解析:不妨设>,则(\\(-=,+=,))所以=,=,且=,即为最小边,即∠=°,则△为直角三角形,所以=,所以=,即渐近线方程为=±,故选.答案:.已知双曲线:-=(>,>)的焦距为,点()在的一条渐近线上,则的方程为( )-=-=-=-=解析:依题意(\\(+==()×)),解得(\\(==)),∴双曲线的方程为-=.答案:。
2019版同步优化探究理数(北师大版)练习:第八章 第六节 抛物线含答案解析

课时作业 A 组——基础对点练1.(2017·沈阳质量监测)抛物线y =4ax 2(a ≠0)的焦点坐标是( ) A .(0,a ) B .(a,0) C.⎝ ⎛⎭⎪⎫0,116a D.⎝ ⎛⎭⎪⎫116,0 解析:将y =4ax 2(a ≠0)化为标准方程得x 2=14a y (a ≠0),所以焦点坐标为⎝ ⎛⎭⎪⎫0,116a ,所以选C.答案:C2.(2017·辽宁五校联考)已知AB 是抛物线y 2=2x 的一条焦点弦,|AB |=4,则AB 中点C 的横坐标是( ) A .2 B.12 C.32D.52解析:设A (x 1,y 1),B (x 2,y 2),则|AB |=x 1+x 2+p =4,又p =1,所以x 1+x 2=3,所以点C 的横坐标是x 1+x 22=32.答案:C3.(2017·邯郸质检)设F 为抛物线y 2=2x 的焦点,A 、B 、C 为抛物线上三点,若F 为△ABC 的重心,则|F A →|+|FB →|+|FC →|的值为( ) A .1 B .2 C .3D .4解析:依题意,设点A (x 1,y 1)、B (x 2,y 2)、C (x 3,y 3),又焦点F ⎝ ⎛⎭⎪⎫12,0,x 1+x 2+x 3=3×12=32,则|F A →|+|FB →|+|FC →|=(x 1+12)+(x 2+12)+⎝ ⎛⎭⎪⎫x 3+12=(x 1+x 2+x 3)+32=32+32=3.选C.答案:C4.已知直线l :y =kx -k 与抛物线C :y 2=4x 及其准线分别交于M ,N 两点,F 为抛物线的焦点,若2FM →=MN →,则实数k 等于( ) A .±33 B .±1 C .±3D .±2解析:抛物线C :y 2=4x 的焦点F (1,0),直线l :y =kx -k 过抛物线的焦点,如图.过M 作MM ′⊥准线x =-1,垂足为M ′,由抛物线的定相等,由2FM →=义,得|MM ′|=|MF |,易知∠M ′MN 与直线l 的倾斜角MN →,得cos ∠M ′MN =|MM ′||MN |=12,则tan ∠M ′MN =±3,∴直线l的斜率k =±3,故选C. 答案:C5.已知P 为抛物线y 2=4x 上一个动点,Q 为圆x 2+(y -4)2=1上一个动点,那么点P 到点Q 的距离与点P 到抛物线的准线距离之和的最小值是( ) A .25-1 B .25-2 C.17-1D.17-2解析:由题意得圆x 2+(y -4)2=1的圆心A (0,4),半径r =1,抛物线的焦点F (1,0).由抛物线的几何性质可得:点P 到点Q 的距离与点P 到抛物线的准线距离之和的最小值是|AF |-r =1+16-1=17-1.选C. 答案:C6.(2017·沈阳质量监测)已知抛物线x 2=4y 的焦点为F ,准线为l ,P 为抛物线上一点,过P 作P A ⊥l 于点A ,当∠AFO =30°(O 为坐标原点)时,|PF |= .解析:设l 与y 轴的交点为B ,在Rt △ABF 中,∠AFB =30°,|BF |=2,所以|AB |=233,设P (x 0,y 0),则x 0=±233,代入x 2=4y 中,得y 0=13,从而|PF |=|P A |=y 0+1=43. 答案:437.(2017·云南检测)已知抛物线C 的方程为y 2=2px (p >0),⊙M 的方程为x 2+y 2+8x +12=0,如果抛物线C 的准线与⊙M 相切,那么p 的值为 .解析:将⊙M 的方程化为标准方程:(x +4)2+y 2=4,圆心坐标为(-4,0),半径r =2,又抛物线的准线方程为x =-p 2,∴|4-p2|=2,解得p =12或4. 答案:12或48.如图,过抛物线y 2=2px (p >0)的焦点F 的直线l 依次交抛物线及其准线于点A ,B ,C ,若|BC |=2|BF |,且|AF |=3,则抛物线的方程是 .解析:分别过点A 、B 作准线的垂线AE 、BD ,分别交准线于点E 、D (图略),则|BF |=|BD |,∵|BC |=2|BF |,∴|BC |=2|BD |,∴∠BCD =30°,又|AE |=|AF |=3,∴|AC |=6,即点F 是AC 的中点,根据题意得p =32,∴抛物线的方程是y 2=3x . 答案:y 2=3x9.已知抛物线y 2=4px (p >0)的焦点为F ,圆W :(x +p )2+y 2=p 2的圆心到过点F 的直线l 的距离为p .(1)求直线l 的斜率;(2)若直线l 与抛物线交于A 、B 两点,△WAB 的面积为8,求抛物线的方程.解析:(1)易知抛物线y 2=4px (p >0)的焦点为F (p,0),依题意直线l 的斜率存在且不为0,设直线l 的方程为x =my +p ,因为W (-p,0), 所以点W 到直线l 的距离为|-p -p |1+(-m )2=p ,解得m =±3,所以直线l 的斜率为±33. (2)由(1)知直线l 的方程为x =±3y +p ,由于两条直线关于x 轴对称,不妨取x =3y +p , 联立⎩⎨⎧x =3y +p ,y 2=4px ,消去x 得y 2-43py -4p 2=0,设A (x 1,y 1),B (x 2,y 2),则y 1+y 2=43p ,y 1y 2=-4p 2, 所以|AB |=1+(3)2·(43p )2+4×4p 2=16p , 因为△WAB 的面积为8,所以12p ×16p =8,得p =1, 所以抛物线的方程为y 2=4x .10.(2017·合肥质检)已知抛物线C 1:x 2=2py (p >0),O 是坐标原点,点A ,B 为抛物线C 1上异于O 点的两点,以OA 为直径的圆C 2过点B . (1)若A (-2,1),求p 的值以及圆C 2的方程; (2)求圆C 2的面积S 的最小值(用p 表示).解析:(1)∵A (-2,1)在抛物线C 1上,∴4=2p ,p =2.又圆C 2的圆心为⎝ ⎛⎭⎪⎫-1,12,半径为|OA |2=52,∴圆C 2的方程为(x +1)2+⎝ ⎛⎭⎪⎫y -122=54.(2)记A (x 1,x 212p ),B (x 2,x 222p ).则OB →=(x 2,x 222p ),AB →=(x 2-x 1,x 22-x 212p ). 由OB →·AB →=0知,x 2(x 2-x 1)+x 22(x 22-x 21)4p 2=0.∵x 2≠0,且x 1≠x 2,∴x 22+x 1·x 2=-4p 2,∴x 1=-⎝ ⎛⎭⎪⎫x 2+4p 2x 2. ∴x 21=x 22+16p 4x 22+8p 2≥216p 4+8p 2=16p 2,当且仅当x 22=16p 4x 22,即x 22=4p 2时取等号.又|OA |2=x 21+x 414p 2=14p2(x 41+4p 2·x 21),注意到x 21≥16p 2, ∴|OA |2≥14p 2(162·p 4+4p 2·16p 2)=80p 2.而S =π·|OA |24,∴S ≥20πp 2,即S 的最小值为20πp 2,当且仅当x 22=4p 2时取得.B 组——能力提升练1.已知抛物线C :y 2=mx (m >0)的焦点为F ,点A (0,-3).若射线F A 与抛物线C 相交于点M ,与其准线相交于点D ,且|FM |∶|MD |=1∶2,则点M 的纵坐标为( ) A .-13 B .-33 C .-23D .-233解析:依题意,F 点的坐标为(m4,0),设点M 在准线上的射影为K ,由抛物线的定义知|MF |=|MK |,因为|FM |∶|MD |=1∶2,所以|KD |∶|KM |=3∶1,k FD =3,k FD =0+3m 4-0=43m ,所以43m =3,解得m =4,所以直线FM 的方程为y =3(x -1),与y 2=4x 联立,解得x =3(舍去)或x =13,所以y 2=43,y =-233或y =233(舍去),故点M 的坐标为(13,-233),故选D.答案:D2.(2018·石家庄质检)已知圆C 1:x 2+(y -2)2=4,抛物线C 2:y 2=2px (p >0),C 1与C 2相交于A ,B 两点,且|AB |=855,则抛物线C 2的方程为( ) A .y 2=85x B .y 2=165x C .y 2=325xD .y 2=645x解析:由题意,知直线AB 必过原点,则设AB 的方程为y =kx (k >0),圆心C 1(0,2)到直线AB 的距离d =2k 2+1=22-(455)2=255,解得k =2(k =-2舍去).由⎩⎨⎧y =2x x 2+(y -2)2=4,可取A (0,0),B (85,165),把(85,165)代入抛物线方程,得(165)2=2p ·85,解得p =165,所以抛物线C 2的方程为y 2=325x ,故选C. 答案:C3.已知点P 在抛物线y 2=x 上,点Q 在圆(x +12)2+(y -4)2=1上,则|PQ |的最小值为( ) A.352-1 B.332-1 C .23-1D.10-1解析:设点P (y 2,y )(y ∈R),圆(x +12)2+(y -4)2=1的圆心为A (-12,4),则|P A |2=(y 2+12)2+(y -4)2=y 4+2y 2-8y +654,令t =y 4+2y 2-8y +654,则t ′=4y 3+4y -8,令m =t ′=4y 3+4y -8,则m ′=12y 2+4>0,所以m =t ′=4y 3+4y -8在R 上是增函数,因为t ′|y =1=0,所以y =1为t =y 4+2y 2-8y +654的极小值点也是最小值点,所以|P A |2=t 的最小值为454,所以|P A |的最小值为352,所以|PQ |的最小值为352-1,故选A. 答案:A4.(2018·山西八校联考)已知抛物线y 2=4x 的准线与x 轴相交于点P ,过点P 且斜率为k (k >0)的直线l 与抛物线交于A ,B 两点,F 为抛物线的焦点,若|FB |=2|F A |,则AB 的长度为 .解析:依题意知P (-1,0),F (1,0),设A (x 1,y 1),B (x 2,y 2),由|FB |=2|F A |,得x 2+1=2(x 1+1),即x 2=2x 1+1 ①,∵P (-1,0),则AB 的方程为y =kx +k ,与y 2=4x 联立,得k 2x 2+(2k 2-4)x +k 2=0,则Δ=(2k 2-4)2-4k 4>0,即k 2<1,x 1x 2=1 ②,由①②得x 1=12,则A (12,2), ∴k =2-012-(-1)=223.∴x 1+x 2=52, |AB |=(1+89)[(x 1+x 2)2-4x 1x 2]=172.答案:1725.(2018·昆明市检测)设F 为抛物线C :y 2=2px (p >0)的焦点,曲线y =kx (k >0)与C 交于点A ,直线F A 恰与曲线y =k x (k >0)相切于点A ,F A 交C 的准线于点B ,则|F A ||BA |等于 . 解析:由⎩⎪⎨⎪⎧y 2=2px ,y =kx,解得⎩⎨⎧x =k32pk ,y =32pk .由y =k x ,得y ′=-k x 2,所以k F A =32pkk32pk -p 2=-kk 234p 2k 2,化简得k =p 242,所以x =k 32pk=p 4, |F A ||AB |=|x F -x A ||x A -x B |=p 2-p 4p 4-(-p 2)=13.答案:136.(2017·唐山统考)已知抛物线y 2=2px (p >0),过点C (-2,0)的直线l 交抛物线于A 、B 两点,坐标原点为O ,OA →·OB →=12. (1)求抛物线的方程;(2)当以AB 为直径的圆与y 轴相切时,求直线l 的方程. 解析:(1)设l :x =my -2,代入y 2=2px , 得y 2-2pmy +4p =0.(*) 设A (x 1,y 1),B (x 2,y 2),则y 1+y 2=2pm ,y 1y 2=4p ,则x 1x 2=y 21y 224p 2=4.因为OA →·OB →=12,所以x 1x 2+y 1y 2=12,即4+4p =12, 得p =2,抛物线的方程为y 2=4x . (2)(1)中(*)式可化为y 2-4my +8=0, y 1+y 2=4m ,y 1y 2=8. 设AB 的中点为M ,则|AB |=2x M =x 1+x 2=m (y 1+y 2)-4=4m 2-4,① 又|AB |=1+m 2|y 1-y 2| =(1+m 2)(16m 2-32),②由①②得(1+m 2)(16m 2-32)=(4m 2-4)2, 解得m 2=3,m =±3.所以,直线l 的方程为x +3y +2=0或x -3y +2=0. 7.如图,由部分抛物线:y 2=mx +1(m >0,x ≥0)和半圆x 2+y 2=r 2(x ≤0)所组成的曲线称为“黄金抛物线C ”,若“黄金抛物线C ”经过点(3,2)和⎝ ⎛⎭⎪⎫-12,32. (1)求“黄金抛物线C ”的方程;(2)设P (0,1)和Q (0,-1),过点P 作直线l 与“黄金抛物线C ”相交于A ,P ,B 三点,问是否存在这样的直线l ,使得QP 平分∠AQB ?若存在,求出直线l 的方程;若不存在,说明理由. 解析:(1)∵“黄金抛物线C ”过点(3,2)和⎝ ⎛⎭⎪⎫-12,32,∴r 2=⎝ ⎛⎭⎪⎫-122+⎝ ⎛⎭⎪⎫322=1,4=3m +1,∴m =1.∴“黄金抛物线C ”的方程为y 2=x +1(x ≥0)和x 2+y 2=1(x ≤0).(2)假设存在这样的直线l ,使得QP 平分∠AQB ,显然直线l 的斜率存在且不为0, 设直线l :y =kx +1,联立⎩⎨⎧y =kx +1y 2=x +1,消去y ,得k 2x 2+(2k -1)x =0,∴x B =1-2kk 2,y B =1-k k ,即B ⎝ ⎛⎭⎪⎫1-2k k 2,1-k k ,∴k BQ =k 1-2k , 联立⎩⎨⎧y =kx +1x 2+y 2=1,消去y ,得(k 2+1)x 2+2kx =0,∴x A =-2kk 2+1,y A =1-k 2k 2+1,即A ⎝ ⎛⎭⎪⎫-2k k 2+1,1-k 2k 2+1,∴k AQ =-1k , ∵QP 平分∠AQB ,∴k AQ +k BQ =0, ∴k 1-2k -1k=0,解得k =-1±2, 由图形可得k =-1-2应舍去,∴k =2-1,∴存在直线l:y=(2-1)x+1,使得QP平分∠AQB.。
2019-2020学年高中数学 8.7双 曲 线同步训练 理 新人教A版.doc

2019-2020学年高中数学 8.7双 曲 线同步训练 理 新人教A 版一、选择题(每小题6分,共36分)1.已知双曲线22x a -22y b=1的一个焦点与圆x 2+y 2-2x=0线的方程为( )(A )5x 2-25y 4=1 (B )2x 5-2y 4=1 (C )2y 5-2x 4=1 (D )5y 2-25x 4=1 2.(2012·沈阳模拟)双曲线2x n-y 2=1(n >1)的两个焦点为F 1,F 2,P 在双曲线上,且满足|PF 1|+|PF 2|=PF 1F 2的面积为( ) (A)12(B)1 (C)2 (D)43.(预测题)设双曲线的一个焦点为F ,虚轴的一个端点为B ,如果直线FB 与该双曲线的一条渐近线垂直,那么此双曲线的离心率为( )(A (B(C (D4.已知双曲线2x 25-2y 9=1的左支上一点M 到右焦点F 2的距离为18,N 是线段MF 2的中点,O 是坐标原点,则|ON|等于( )(A )4 (B )2 (C )1 (D )235.(2012·武汉模拟)已知抛物线y 2=4x 的准线与双曲线222x y a-=1(a>0)交于A ,B 两点,点F 为抛物线的焦点,若△FAB 为直角三角形,则双曲线的离心率是( )(C)2(D)36.设F 1、F 2分别为双曲线22x a -22y b=1(a >0,b >0)的左、右焦点.若在双曲线右支上存在点P ,满足|PF 2|=|F 1F 2|,且F 2到直线PF 1的距离等于双曲线的实轴长,则该双曲线的渐近线方程为( ) (A )3x ±4y=0 (B )3x ±5y=0 (C )4x ±3y=0 (D )5x ±4y=0 二、填空题(每小题6分,共18分)7.(2012·杭州模拟)已知直线ax+y+2=0与双曲线x 2-2y 4=1的一条渐近线平行,则这两条平行直线之间的距离是______.8.(2012·随州模拟)P 为双曲线x 2-2y 15=1右支上一点,M 、N 分别是圆(x+4)2+y 2=4和(x-4)2+y 2=1上的点,则|PM|-|PN|的最大值为_______.9.(易错题)以下四个关于圆锥曲线的命题中:①设A 、B 为两个定点,k 为非零常数,若|PA |-|PB |=k ,则动点P 的轨迹为双曲线;②过定圆C 上一定点A 作圆的动弦AB ,O 为坐标原点,若OP =12(OA +OB ),则动点P 的轨迹为椭圆;③方程2x 2-5x+2=0的两根可分别作为椭圆和双曲线的离心率;④双曲线2x 25-2y 9=1与椭圆2x 35+y 2=1有相同的焦点.其中真命题的序号为_______(写出所有真命题的序号). 三、解答题(每小题15分,共30分)10.(2012·黄冈模拟)点P 是以F 1,F 2为焦点的双曲线E :22x a -22y b=1(a>0,b>0)上的一点,已知PF 1⊥PF 2,|PF 1|=2|PF 2|,O 为坐标原点.(1)求双曲线的离心率e ;(2)过点P 作直线分别与双曲线两渐近线相交于P 1,P 2两点,且1OP ·2OP =274-,12PP +2PP =0,求双曲线E 的方程.11.已知斜率为1的直线l 与双曲线C :22x a -22y b=1(a>0,b>0)相交于B 、D 两点,且BD 的中点为M(1,3).(1)求C 的离心率;(2)设C 的右顶点为A ,右焦点为F ,|DF|·|BF|=17,求证:过A 、B 、D 三点的圆与x 轴相切. 【探究创新】(16分)某飞船返回仓顺利返回地球后,为了及时救出航天员,地面指挥中心在返回仓预计到达的区域内安排了三个救援中心(如图1分别记为A ,B ,C ),B 地在A 地正东方向上,两地相距6 km ; C 地在B 地北偏东30°方向上,两地相距4 km ,假设P 为航天员着陆点,某一时刻A 救援中心接到从P 点发出的求救信号,经过4 s 后,B 、C 两个救援中心也同时接收到这一信号,已知该信号的传播速度为1 km/s. (1)求A 、C 两地救援中心的距离; (2)求P 相对A 的方向角;(3)试分析信号分别从P 点处和P 点的正上方Q 点(如图2,返回仓经Q 点垂直落至P 点)处发出时,A 、B 两个救援中心收到信号的时间差的变化情况(变大还是变小),并证明你的结论.答案解析1.【解析】选A.因为圆x 2+y 2-2x=0的圆心坐标为(1,0),所以双曲线中c=1,又因为双曲线的离心率为ca所以2=45,因此,双曲线方程为5x 2-25y 4=1. 2.【解析】选B.不妨设点P在双曲线的右支上,则1212PF PF PF PF ⎧-=⎪⎨+=⎪⎩∴|PF 12又∴|PF 1|2+|PF 2|2=|F 1F 2|2,∴∠F 1PF 2=90°, ∴12PF F S=121PF PF 2=1. 3.【解析】选D.因为焦点在x 轴上与焦点在y 轴上的离心率一样,所以不妨设双曲线方程为22x a -22y b=1(a>0,b>0),则双曲线的渐近线的斜率k=ba±, 一个焦点坐标为F(c,0),一个虚轴的端点为B(0,b),所以k FB =bc-,又因为直线FB 与双曲线的一条渐近线垂直,所以k ·k FB =b b ()ac -)=-1(b a-显然不符合),即b 2=ac,c 2-a 2=ac,所以,c 2-a 2-ac=0,即e 2-e-1=0,解得e=12+(负值舍去). 【变式备选】双曲线 22x a -22y b =1(a >0,b >0)的离心率为2,则2b 13a+的最小值为( )(A (B (C )2 (D )1 【解析】选A.因为双曲线的离心率为2,所以ca=2, 即c=2a ,c 2=4a 2;又因为c 2=a 2+b 2,所以a 2+b 2=4a 2,即,因此2b 13a +=23a 13a +=1a 3a +≥a=13a 时等号成立.即2b 13a +的最小值为3.4.【解析】选A.设双曲线的左焦点为F 1,由双曲线的定义知: |MF 2|-|MF 1|=10,又因为|MF 2|=18,所以|MF 1|=8, 而|ON|=12|MF 1|=4. 5.【解析】选B.由题意易知,抛物线的准线方程为x=-1,焦点为F(1,0),直线x=-1与双曲线的交点坐标为(-1),若△FAB 为直角三角形,则只能是∠AFB 为直角,△FAB 为等腰直角三角形,所以=2⇒从而可得所以双曲线的离心率e=c a 选B.6.【解析】选C.设PF 1的中点为M ,因为|PF 2|=|F 1F 2|, 所以F 2M ⊥PF 1,因为|F 2M|=2a , 在直角三角形F 1F 2M 中,|F 1,故|PF 1|=4b,根据双曲线的定义得4b-2c=2a,即2b-c=a,因为c 2=a 2+b 2,所以(2b-a)2=a 2+b 2,即3b 2-4ab=0,即3b=4a, 故双曲线的渐近线方程是y=4x 3±, 即4x ±3y=0.【变式备选】F 1,F 2是双曲线C :22x a -22y b=1(a>0,b>0)的两个焦点,P 是C 上一点,且△F 1PF 2是等腰直角三角形,则双曲线C 的离心率为( ) (A)1+(B)2(C)3(D)3【解析】选A.设双曲线C 的焦距为2c,依题设不妨令|F 1F 2|=|PF 2|,即2c=2b a,∴2c=22c a a -,即2ac=c 2-a 2,∴e 2-2e-1=0,∴e=1又∵e >1,∴7.【解析】∵双曲线方程为:x 2-2y 4=1, ∴其渐近线方程为:y=±2x, 又∵ax+y+2=0与渐近线平行, ∴a=2,∴两平行线之间的距离为8.【解析】双曲线的两个焦点F 1(-4,0)、F 2(4,0)分别为两个圆的圆心,两圆的半径分别为r 1=2,r 2=1.由题意得|PM|max =|PF 1|+2,|PN|min =|PF 2|-1,故|PM|-|PN|的最大值为(|PF 1|+2)-(|PF 2|-1)=|PF 1|-|PF 2|+3=5. 答案:5【方法技巧】圆锥曲线上的点到定点距离的和、差的最值的求法:一般不用选变量建立目标函数的方法求解,而是利用该点适合圆锥曲线的定义,将所求转化为与焦点的距离有关的最值问题,再利用数形结合法求解.9.【解析】①错误,当k >0且k <|AB|,表示以A 、B 为焦点的双曲线的一支;当k >0且k=|AB|时表示一条射线;当k >0且k >|AB|时,不表示任何图形;当k <0时,类似同上.②错误,P 是AB 中点,且P 到圆心与A 的距离的平方和为定值.故P 的轨迹应为圆.③方程两根为12和2,可以作为椭圆和双曲线的离心率,故正确.④由标准方程易求双曲线和椭圆的焦点坐标都为(0),故正确. 答案:③④10.【解析】(1)∵|PF 1|=2|PF 2|,|PF 1|-|PF 2|=2a , ∴|PF 1|=4a ,|PF 2|=2a.∵PF 1⊥PF 2,∴(4a)2+(2a)2=(2c)2,即5a 2=c 2, ∴e(2)由(1)知双曲线的方程可设为22x a -22y 4a=1,渐近线方程为y =±2x.设P 1(x 1,2x 1),P 2(x 2,-2x 2),P(x ,y), ∵1OP ·2OP =-3x 1x 2=274-⇒x 1x 2=94, ∵21PP +2PP =0⇒12122x x x 32(2x x )y 3⎧⎪⎪⎨⎪⎪⎩+=-=∵点P 在双曲线上,∴2122(2x x )9a +-2122(2x x )9a -=1, 化简得x 1x 2=29a 8,∴29a 8=94⇒a 2=2,∴双曲线方程为2x 2-2y 8=1.11.【解析】(1)由题意知,l 的方程为y =x +2.代入C 的方程,并化简,得(b 2-a 2)x 2-4a 2x -4a 2-a 2b 2=0. 设B(x 1,y 1)、D(x 2,y 2),则x 1+x 2=2224a b a -, x 1·x 2=222224a a b b a +--, ①由M(1,3)为BD 的中点知12x x 2+=1, 故12×2224a b a -=1, 即b 2=3a 2, ②故c 2a , 所以C 的离心率e =ca=2. (2)由①②知,C 的方程为:3x 2-y 2=3a 2,A(a,0),F(2a,0),x 1+x 2=2,x 1·x 2=243a 2+-<0,故不妨设x 1≤-a ,x 2≥a.|BF|1,|FD|2-a,|BF|·|FD|=(a -2x 1)(2x 2-a)=-4x 1x 2+2a(x 1+x 2)-a 2=5a 2+4a +8.又|BF|·|FD|=17,故5a 2+4a +8=17, 解得a =1或a =95-(舍去).故|BD|1-x 2|·=6.连接MA ,则由A(1,0),M(1,3)知|MA|=3, 从而|MA|=|MB|=|MD|,且MA ⊥x 轴,因此以M 为圆心,MA 为半径的圆经过A 、B 、D 三点,且在点A 处与x 轴相切. 所以过A 、B 、D 三点的圆与x 轴相切. 【探究创新】 【解析】(1)以AB 的中点为坐标原点,AB 所在直线为x 轴建立平面直角坐标系,则A(-3,0),B(3,0),C(5,,则 (km),即A、C两个救援中心的距离为km.(2)∵|PC|=|PB|,所以P在BC线段的垂直平分线上.又∵|PB|-|PA|=4,所以P在以A、B为焦点的双曲线的左支上,且|A B|=6,∴双曲线方程为2x4-2y5=1(x<0).BC的垂直平分线的方程为-7=0,联立两方程解得: x=-8.∴P(-8,∴k PA=tan∠PAB=∴∠PAB=120°,所以P点在A点的北偏西30°方向上.(3)如图,设|PQ|=h,|PB|=x,|PA|=y,∵|QB|-|QA|22=(x y)-<1, ∴|QB| -|QA|<|PB|-|PA|,∴QB1-QA1<PB1-PA1.即信号从P点的正上方Q点处发出时A、B收到信号的时间差比信号从P点处发出时A、B收到信号的时间差变小.。
2019高三数学理北师大版一轮教师用书:第8章 第7节 双

第七节双曲线[考纲传真](教师用书独具)1.了解双曲线的实际背景,了解双曲线在刻画现实世界和解决实际问题中的作用.2.了解双曲线的定义、几何图形和标准方程,知道其简单的几何性质(范围、对称性、顶点、离心率、渐近线).3.理解数形结合思想.4.了解双曲线的简单应用.(对应学生用书第144页)[基础知识填充]1.双曲线的定义(1)平面内到两定点F1,F2的距离之差的绝对值等于常数(大于零且小于|F1F2|)的点的集合叫作双曲线.这两个定点F1,F2叫作双曲线的焦点,两焦点之间的距离叫作双曲线的焦距.(2)集合P={M|||MF1|-|MF2||=2a},|F1F2|=2c,其中a,c为常数且a>0,c>0.①当2a<|F1F2|时,M点的轨迹是双曲线;②当2a=|F1F2|时,M点的轨迹是两条射线;③当2a>|F1F2|时,M点不存在.2.双曲线的标准方程和几何性质[1.三种常见双曲线方程的设法(1)若已知双曲线过两点,焦点位置不能确定,可设方程为Ax2+By2=1(AB<0).(2)当已知双曲线的渐近线方程bx±ay=0,求双曲线方程时,可设双曲线方程为b2x2-a2y2=λ(λ≠0).(3)与双曲线x2a2-y2b2=1有相同的渐近线的双曲线方程可设为x2a2-y2b2=λ(λ≠0).2.等轴双曲线实轴和虚轴等长的双曲线叫作等轴双曲线,其渐近线方程为y=±x,离心率为e= 2.[基本能力自测]1.(思考辨析)判断下列结论的正误.(正确的打“√”,错误的打“×”)(1)平面内到点F1(0,4),F2(0,-4)距离之差的绝对值等于8的点的轨迹是双曲线.()(2)方程x2m-y2n=1(mn>0)表示焦点在x轴上的双曲线.()(3)双曲线x2m2-y2n2=λ(m>0,n>0,λ≠0)的渐近线方程是x2m2-y2n2=0,即xm±yn=0.()(4)等轴双曲线的渐近线互相垂直,离心率等于 2.() [答案](1)×(2)×(3)√(4)√2.(教材改编)已知双曲线x2a2-y23=1(a>0)的离心率为2,则a=()A .2B .62C .52 D .1D [依题意,e =ca =a 2+3a =2,所以a 2+3=2a ,则a 2=1,a =1.]3.若双曲线E :x 29-y 216=1的左、右焦点分别为F 1,F 2,点P 在双曲线E 上,且|PF 1|=3,则|PF 2|等于( ) A .11 B .9 C .5 D .3B [由题意知a =3,b =4,∴c =5.由双曲线的定义||PF 1|-|PF 2||=|3-|PF 2||=2a =6,∴|PF 2|=9.]4.已知双曲线x 2a 2-y 2b 2=1(a >0,b >0)的焦距为25,且双曲线的一条渐近线与直线2x +y =0垂直,则双曲线的方程为( ) A .x 24-y 2=1 B .x 2-y 24=1C .3x 220-3y 25=1D .3x 25-3y 220=1A[由题意可得⎩⎪⎨⎪⎧b a =12,a 2+b 2=5,a >0,b >0,解得a =2,则b =1,所以双曲线的方程为x 24-y 2=1,故选A .]5.(2017·全国卷Ⅲ)双曲线x 2a 2-y 29=1(a >0)的一条渐近线方程为y =35x ,则a =________.5 [∵双曲线的标准方程为x 2a 2-y 29=1(a >0), ∴双曲线的渐近线方程为y =±3a x .又双曲线的一条渐近线方程为y =35x ,∴a =5.](对应学生用书第145页)(1)已知双曲线x 2-y 224=1的两个焦点为F 1,F 2,P 为双曲线右支上一点.若|PF 1|=43|PF 2|,则△F 1PF 2的面积为( ) A .48 B .24 C .12D .6(2)(2017·湖北武汉调研)若双曲线x 24-y 212=1的左焦点为F ,点P 是双曲线右支上的动点,A (1,4),则|PF |+|P A |的最小值是( ) A .8 B .9 C .10D .12(1)B (2)B [(1)由双曲线的定义可得 |PF 1|-|PF 2|=13|PF 2|=2a =2,解得|PF 2|=6,故|PF 1|=8,又|F 1F 2|=10, 由勾股定理可知三角形PF 1F 2为直角三角形, 因此S△PF 1F 2=12|PF 1|·|PF 2|=24.(2)由题意知,双曲线x 24-y 212=1的左焦点F 的坐标为(-4,0),设双曲线的右焦点为B ,则B (4,0),由双曲线的定义知|PF |+|P A |=4+|PB |+|P A |≥4+|AB |=4+(4-1)2+(0-4)2=4+5=9,当且仅当A ,P ,B 三点共线且P 在A ,B 之间时取等号. 所以|PF |+|P A |的最小值为9.][跟踪训练] 已知双曲线C 的离心率为2,焦点为F 1,F 2,点A 在C 上.若|F 1A |=2|F 2A |,则cos ∠AF 2F 1=( )【导学号:79140294】A .14B .13C .24D .23A [由e =ca =2得c =2a ,如图,由双曲线的定义得|F 1A |-|F 2A |=2a .又|F 1A |=2|F 2A |,故|F 1A |=4a ,|F 2A |=2a ,∴cos ∠AF 2F 1=(4a )2+(2a )2-(4a )22×4a ×2a =14.](1)(2017·全国卷Ⅲ)已知双曲线C :x 2a 2-y 2b 2=1(a >0,b >0)的一条渐近线方程为y =52x ,且与椭圆x 212+y 23=1有公共焦点,则C 的方程为( )A .x 28-y 210=1 B .x 24-y 25=1 C .x 25-y 24=1D .x 24-y 23=1(2)(2018·湖北调考)已知点A (-1,0),B (1,0)为双曲线x 2a 2-y 2b 2=1(a >0,b >0)的左、右顶点,点M 在双曲线上,△ABM 为等腰三角形,且顶角为120°,则该双曲线的标准方程为( )A .x 2-y 24=1B .x 2-y 23=1C .x 2-y 22=1D .x 2-y 2=1(1)B (2)D [(1)由y =52x 可得b a =52. ① 由椭圆x 212+y 23=1的焦点为(3,0),(-3,0), 可得a 2+b 2=9.②由①②可得a 2=4,b 2=5. 所以C 的方程为x 24-y 25=1. 故选B .(2)由题意知a =1.不妨设点M 在第一象限,则由题意有|AB |=|BM |=2,∠ABM =120°.过点M 作MN ⊥x 轴于点N ,则|BN |=1,|MN |=3,所以M (2,3),代入双曲线方程得4-3b 2=1,解得b =1,所以双曲线的方程为x 2-y 2=1,故选D .][跟踪训练] (1)已知双曲线C :x a 2-y b 2=1的离心率e =54,且其右焦点为F 2(5,0),则双曲线C 的方程为( ) A .x 24-y 23=1 B .x 29-y 216=1 C .x 216-y 29=1D .x 23-y 24=1 (2)设椭圆C 1的离心率为513,焦点在x 轴上且长轴长为26,若曲线C 2上的点到椭圆C 1的两个焦点的距离的差的绝对值等于8,则曲线C 2的标准方程为__________.(1)C (2)x 216-y 29=1 [由焦点F 2(5,0)知c =5. 又e =c a =54,得a =4,b 2=c 2-a 2=9. 所以双曲线C 的标准方程为x 216-y 29=1.(2)由题意知椭圆C 1的焦点坐标为F 1(-5,0),F 2(5,0),设曲线C 2上的一点P ,则||PF 1|-|PF 2||=8. 由双曲线的定义知:a =4,b =3.故曲线C 2的标准方程为x 242-y 232=1,即x 216-y 29=1.]◎角度1 双曲线的离心率问题(2018·长沙模拟(二))已知双曲线x 2a 2-y 2b 2=1(a >0,b >0)的渐近线与圆(x -22)2+y 2=83相切,则该双曲线的离心率为( ) A .62 B .32 C . 3D .3A [由双曲线x 2a 2-y 2b 2=1(a >0,b >0)的渐近线y =ba x ,即bx -ay =0与圆相切得|22b |b 2+a2=22b c =223,即c =3b ,则c 2=3b 2=3(c 2-a 2),化简得2c =3a ,则该双曲线的离心率为e =c a =32=62,故选A .]◎角度2 双曲线的渐近线问题(2018·合肥二检)已知双曲线x 2a 2-y 2b 2=1(a >0,b >0)的离心率为3,则该双曲线的渐近线方程为________.y =±2x [因为e =ca =3,所以c 2=a 2+b 2=3a 2,故b =2a ,则此双曲线的渐近线方程为y =±ba x =±2x .]◎角度3 双曲线性质的综合应用(2017·全国卷Ⅰ)已知F 是双曲线C :x 2-y 23=1的右焦点,P 是C 上一点,且PF 与x 轴垂直,点A 的坐标是(1,3),则△APF 的面积为( ) A .13 B .12 C .23D .32D [因为F 是双曲线C :x 2-y23=1的右焦点,所以F (2,0).因为PF ⊥x 轴,所以可设P 的坐标为(2,y P ). 因为P 是C 上一点,所以4-y 2P3=1,解得y P =±3, 所以P (2,±3),|PF |=3.又因为A (1,3),所以点A 到直线PF 的距离为1, 所以S △APF =12×|PF |×1=12×3×1=32. 故选D .][跟踪训练] (1)(2017·全国卷Ⅱ)若a >1,则双曲线x a 2-y 2=1的离心率的取值范围是( ) A .(2,+∞) B .(2,2) C .(1,2)D .(1,2)(2)(2016·全国卷Ⅰ)已知方程x 2m 2+n -y 23m 2-n =1表示双曲线,且该双曲线两焦点间的距离为4,则n 的取值范围是( )A .(-1,3)B .(-1,3)C .(0,3)D .(0,3)(3)(2017·武汉调研)双曲线C :y 2a 2-x 2b 2=1(a >0,b >0)的离心率为54,焦点到渐近线的距离为3,则C 的实轴长等于________.【导学号:79140295】(1)C (2)A (3)8 [(1)由题意得双曲线的离心率e =a 2+1a .∴e 2=a 2+1a 2=1+1a2.∵a >1,∴0<1a 2<1,∴1<1+1a 2<2, ∴1<e < 2. 故选C .(2)若双曲线的焦点在x 轴上,则⎩⎨⎧m 2+n >0,3m 2-n >0.又∵(m 2+n )+(3m 2-n )=4,∴m 2=1,∴⎩⎨⎧1+n >0,3-n >0,∴-1<n <3.若双曲线的焦点在y 轴上,则双曲线的标准方程为y 2n -3m 2-x 2-m 2-n =1,即⎩⎨⎧n -3m 2>0,-m 2-n >0,即n >3m 2且n <-m 2,此时n 不存在.故选A .(3)因为e =c a =54,所以c =54a ,设双曲线的一条渐近线方程为y =ab x ,即ax -by =0,焦点为(0,c ),所以bc a 2+b 2=b =3,所以a =c 2-b 2=2516a 2-9,所以a 2=16,即a =4,故2a =8.]。
双曲线(讲)-2019年高考数学(文)---精校解析 Word版
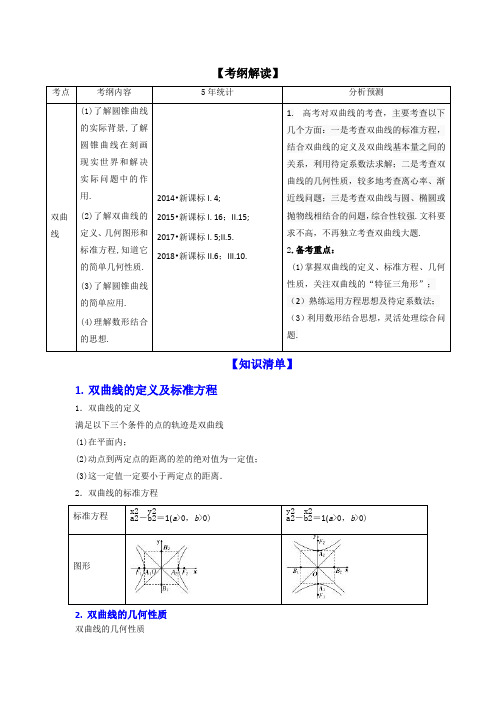
【考纲解读】【知识清单】1.双曲线的定义及标准方程1.双曲线的定义满足以下三个条件的点的轨迹是双曲线(1)在平面内;(2)动点到两定点的距离的差的绝对值为一定值;(3)这一定值一定要小于两定点的距离.2.双曲线的标准方程2.双曲线的几何性质双曲线的几何性质考点1 双曲线的定义及标准方程【1-1】【2017天津,文5】已知双曲线的左焦点为,点在双曲线的渐近线上,是边长为2的等边三角形(为原点),则双曲线的方程为()(A)(B)(C)(D)【答案】【1-2】【2018年天津卷文】已知双曲线的离心率为2,过右焦点且垂直于轴的直线与双曲线交于两点.设到双曲线的同一条渐近线的距离分别为和,且则双曲线的方程为A. B.C.D.【答案】A 【解析】设双曲线的右焦点坐标为(c >0),则,由可得:,不妨设:,双曲线的一条渐近线方程为,据此可得:,,则,则,双曲线的离心率:,据此可得:,则双曲线的方程为.本题选择A选项. 【综合点评】 1.双曲线的轨迹类型是;2.双曲线标准方程的求解方法是”待定系数法”,“先定型,后计算”.【领悟技法】1.待定系数法求双曲线方程的常用方法(1)与双曲线a2x2-b2y2=1共渐近线的可设为a2x2-b2y2=λ(λ≠0);(2)若渐近线方程为y =±a b x ,则可设为a2x2-b2y2=λ(λ≠0); (3)若过两个已知点则设为m x2+n y2=1(mn <0). 2.应用双曲线的定义需注意的问题:在双曲线的定义中要注意双曲线上的点(动点)具备的几何条件,即“到两定点(焦点)的距离之差的绝对值为一常数,且该常数必须小于两定点的距离”.若定义中的“绝对值”去掉,点的轨迹是双曲线的一支.同时注意定义的转化应用.3.求双曲线方程时一是标准形式判断;二是注意a 、b 、c 的关系易错易混.【触类旁通】【变式一】【2017天津,理5】已知双曲线的左焦点为,离心率为.若经过和两点的直线平行于双曲线的一条渐近线,则双曲线的方程为(A ) (B )(C )(D )【变式二】【2018届重庆市巴蜀中学高三9月月考】已知双曲线的左、右焦点分别为,点为异于的两点,且的中点在双曲线的左支上,点关于和的对称点分别为,则的值为( )A. 26B.C. 52D.【答案】D【解析】设MN 与双曲线的交点为点P ,由几何关系结合三角形中位线可得:,则:,点P 位于双曲线的左支,则:.本题选择D选项.【综合点评】1、在焦点三角形中,注意双曲线的定义和正弦定理、余弦定理交汇解题;2、求双曲线方程需要两个独立条件.考点2 双曲线的简单几何性质【2-1】【2018年全国卷Ⅲ文】已知双曲线的离心率为,则点到的渐近线的距离为A. B. C. D.【答案】D【2-2】【2017课标II,文5】若,则双曲线的离心率的取值范围是()A. B. C. D.【答案】C【解析】由题意,因为,所以,则,故选C.【2-3】【2017江苏,8】在平面直角坐标系中,双曲线的右准线与它的两条渐近线分别交于点,,其焦点是,则四边形的面积是 .【答案】【综合点评】1.已知渐近线方程y =mx ,若焦点位置不明确要分m =a b 或m =b a讨论,求离心率值,需要寻求的等式,求离心率取值范围,需寻求关于的不等式关系,并结合求.2.注意数形结合思想在处理渐近线夹角,离心率范围求法中的应用.【领悟技法】1.双曲线的标准方程中对a 、b 的要求只是a >0,b >0易误认为与椭圆标准方程中a ,b 的要求相同.若a >b >0,则双曲线的离心率e ∈(1,); 若a =b >0,则双曲线的离心率e =; 若0<a <b ,则双曲线的离心率e >.2.注意区分双曲线中的a ,b ,c 大小关系与椭圆a 、b 、c 关系,在椭圆中a 2=b 2+c 2,而在双曲线中c 2=a 2+b 2.3.等轴双曲线的离心率与渐近线关系双曲线为等轴双曲线⇔双曲线的离心率e =⇔双曲线的两条渐近线互相垂直(位置关系). 4.双曲线的焦点到渐近线的距离等于虚半轴长b 5.渐近线与离心率a2x2-b2y2=1(a >0,b >0)的一条渐近线的斜率为a b = a2b2= a2c2-a2=.可以看出,双曲线的渐近线和离心率的实质都表示双曲线张口的大小.【触类旁通】【变式1】【2018年浙江卷】双曲线的焦点坐标是( )A. (−,0),(,0) B. (−2,0),(2,0) C. (0,−),(0,) D. (0,−2),(0,2)【答案】B【变式2】【2018届湖南省株洲市醴陵第二中学、醴陵第四中学高三上学期期中联考】已知双曲线E:﹣=1(a>0,b>0),点F为E的左焦点,点P为E上位于第一象限内的点,P关于原点的对称点为Q,且满足|PF|=3|FQ|,若|OP|=b,则E的离心率为()A. B. C. 2 D.【答案】B【解析】由题意可知:双曲线的右焦点,由关于原点的对称点为则四边形为平行四边形则由,根据椭圆的定义在中,则,整理得则双曲线的离心率故答案选【综合点评】1、充分利用条件列关于的等式或不等式,可得离心率的取值或取值范围;2、双曲线的渐近线是与之间的比值关系,再结合,可得的关系,及离心率的关系,从这点而言,渐近线方程和离心率是有联系的.【易错试题常警惕】易错典例:已知圆,圆都内切于动圆,试求动圆圆心的轨迹方程.易错分析:忽视双曲线定义.温馨提示:双曲线的轨迹类型是.【学科素养提升之思想方法篇】数形结合百般好,隔裂分家万事休——数形结合思想我国著名数学家华罗庚曾说过:"数形结合百般好,隔裂分家万事休.""数"与"形"反映了事物两个方面的属性.我们认为,数形结合,主要指的是数与形之间的一一对应关系.数形结合就或"以数解形"即通过抽象思维与形象思维的结合,可以使复杂问题简单化,抽象问题具体化,从而起到优化解题途径的目的.数形结合的思想,其实质是将抽象的数学语言与直观的图像结合起来,关键是代数问题与图形之间的相互转化,它可以使代数问题几何化,几何问题代数化.在运用数形结合思想分析和解决问题时,要注意三点:第一要彻底明白一些概念和运算的几何意义以及曲线的代数特征,对数学题目中的条件和结论既分析其几何意义又分析其代数意义;第二是恰当设参、合理用参,建立关系,由数思形,以形想数,做好数形转化;第三是正确确定参数的取值范围.【典例】【2018年全国卷Ⅲ理】设是双曲线()的左、右焦点,是坐标原点.过作的一条渐近线的垂线,垂足为.若,则的离心率为()A. B. 2 C. D.【答案】C。
2020年同步优化探究理数(北师大版)练习:第八章第七节双曲线Word版含解析.doc

课时作业 A 组一一基础对点练1.已知F 为双曲线C : x 2— m\j z = 3m(m>0)的一个焦点,则点F 到C 的一条渐近 线的距离为()B. 3C. 3mD . 3m解析:双曲线方程为 盖—£二1,焦点F 到一条渐近线的距离为 3.选 A. 答案:A2 2x y2.已知双曲线 孑一3= 1(a>0)的离心率为2,C . 2选D. 答案:3. 双曲线x 2 — 4y 2= — 1的渐近线方程为( A. x ±y = 0 C . x ±y = 02解析:依题意,题中的双曲线即片—x 2二1,因此其渐近线方程是4=0,选 A. 答案:A24. 已知双曲线x3 — y 2= 1的左、右焦点分别为F 1, F 2,点P 在双曲线上,且满足 |PF 1|+ |PF 2| = 2 5,则△ PF 1F 2 的面积为( ) A. 1 B. 3C. .5则a =(解析:因为双曲线的方程为 号一£二1,所以=4,因此 a 2= 1, a = 1.x 2解析:在双曲线3 — y 2二1中,a = 3, b = 1, c = 2.不防设P 点在双曲线的右支 上,则有 |PF 1|—|PF 2匸2a = 2 3,又 |PF 1|+|PF 2|= 2.5,二 |PF 1 = 5+ 3, |PF 2| =5— 3•又|F 1F 2|= 2c = 4,而|PF 1『+ |PF 2|2=尸许2『,二 PF 1 丄 PF 2,A S A PF 1F 21 1=2^ |PF 1|X |PF 2| = 2X( ,5+ , 3)X ( 5— 3)= 1.故选 A. 答案:A225. 已知双曲线C :字一b 2= 1(a>0, b>0),直线l : y = 2x — 2.若直线l 平行于双曲 线C 的一条渐近线且经过C 的一个顶点,则双曲线 C 的焦点到渐近线的距离为B. 2D. 4解析:根据题意,双曲线C 的方程为$—£= 1(a>0, b>0),其焦点在x 轴上,渐 近线方程为y =£x ,又由直线I 平行于双曲线C 的一条渐近线,可知2 = 2,直a a 线I : y = 2x — 2与x 轴的交点坐标为(1,0),即双曲线C 的一个顶点坐标为(1,0), 即a = 1,则b = 2a = 2,故双曲线C 的焦点到渐近线的距离为2,故选B. 答案:B6.已知双曲线的焦点到渐近线的距离等于半实轴长,贝U 该双曲线的离心率为B. 2C. .22 2解析:不妨设双曲线的方程为拿一律=1(a>0, b>0),因为焦点F(c,0)到渐近线bx bc bc b-ay= 0的距离为a ,所以a 2+b 2 = a ,即;=a ,所以a= X 所以该双曲线的离答案:C C :拿一y 2= 1的离心率e =4,且其右焦点为F 2(5,0),则双曲线CC. ,5心率e = c=a1+ b2= 2,故选 C.a 丫7.已知双曲线c_ c_ e= a" 3c — c ■.3+ 1,选 D.的方程为()2 2 —乞=1 A. 43 1x 2y C.w —9 =1 D. 2 2x y 9 一 _16 = 2 x 2 _y_= 1 B. 3 4 1 b 2 5 1 + 孑=4’ 又右焦点为 F 2(5,0), a 2 + b 2 = c 2,所以 a 2= 16, 2 2 b 2= 9,故双曲线C 的方程为16—卷=1. 解析:由题意得e = 答案:C 2 2 8.已知双曲线拿一*= 1(a>0, b>0)的焦距为 2 5, 且双曲线的一条渐近线与直线2x + y = 0垂直,则双曲线的方程为()24 7 C 3x !疋 C.20 2 缶1 _ 3x 2 3y2 .5 20 1 B . x 2 解析: b i x 2由题意得c = 5,舌=2,则a =2, b = 1,所以双曲线的方程为"4 — y 2= 1. 答案: 2 2 9. (2018 山西八校联考)已知双曲线C :拿一討1(a>0, b>0)的左、右焦点分别 为F i , F 2,焦距为2c ,直线y = "f (x + c )与双曲线的一个交点P 满足/ PF 2F I = 2A. .2 C . 2 .3+ 1B. 3 D. 3+ 1 解析:•••直线 3 y = 3 (x + c)过左焦点F 1,且其倾斜角为 30° .Z PF 1F 2= 30°/ PF 1F 2,则双曲线的离心率e 为()1 / PF 2F 1 = 60° •••/ F 2PF 1 = 90°即卩 F 1P 丄F 2P.A |PF 2| = 2尸们2| = c,|PF 1=|F 1F 2|sin60°= 3c ,由双曲线的定义得 2a = |PF 1|—|PF 2|= 3c — c ,.••双曲线C 的离心率1线y 二1x 的下方.设该双曲线的标准方程为2 2拿一古=1(a>0, b>0),所以答案:D2 2双曲线C 的方程为2x0—倉=1. 答案:A12.已知双曲线过点(4,3),且渐近线方程为y 二gx ,则该双曲线的标准方程因为双曲线过点(4, 3)且渐近线方程为y =±x ,故点(4, .3)在直10.已知F i , F 2是双曲线C :上一点,若|PF i |+|PF 2|= 6&,且厶PF 1F 2最小内角的大小为30°则双曲线C 的 渐近线方程是() A. 2x 酉=0 B . x ± 2y = 0 C . 2x ±^= 0D . x ±2y = 0解析: 不妨设|PF i |>|PF 2|,则|PF i |—|PF 2| = 2a ,|PF |+ |PF | =所以 |PF i |= 4a , |PF 2|= 2a , 且|F i F 2|= 2c ,即|PF 2|为最小边,即/ PF i F 2= 30° 则 △ PF i F 2为直角三角形,所以2c = 2 3a ,所以b = 2a ,即渐近线方程为y =± 2 x ,故选A. 答案:A2 211.已知双曲线C :拿一*= 1(a>0, b>0)的焦距为i0,点P(2,i)在C 的一条渐近 线上,贝U C 的方程为() x 2 yA — 一匚=1 A.20 52 2C £ 一 y- = 1Bx !—/ = 1 B .5 20_1 x 2 y 2D — 一 ~^—= 1解析:依题意a 2+b 2= 25,解得a 2 = 20b 2 = 5 ,解析:法P 是双曲线C,解得a = 2,故双曲线方程为4 — y 1 2 3= 1.b = 1, 42,故可设双曲线为x 4—W= W 0),又L42L£双曲线过点(4, ©),所以4 — (Q3)2=入所以=1,故双曲线方程为"4—y 2= 1. 2答案::—/= 12 /13.双曲线r 拿一b 2= 1(a>0, b>0)的焦距为10,焦点到渐近线的距离为3,则r 的实轴长等于2 2 2 214.已知双曲线C :拿一^2= 1(a>0, b>0)与椭圆倉+眷=1有相同的焦点,且双 曲线C 的渐近线方程为y = ±x ,则双曲线C 的方程为 解析:易得椭圆的焦点为(一.5, 0), ( 5, 0),a 2 +b 2 = 5, :「2,a•••双曲线C 的方程为x 2—4=1. 答案:x 2— ; = 12 215. (2018合肥市质检)双曲线M :字一^2= 1(a>0, b>0)的左、右焦点分别为F 1,1坐标为(a , b),因为 sin /PF I F 2 = 3,所以 |PF i 匸3b ,所以(a + c)2+ b 2= 9b 2,即 9a 2 +1F 2,直线x = a 与双曲线M 的渐近线交于点P ,若sin / PF 1F 2=§,则该双曲线的 离心率为 ________________ .解析:不妨设P 为直线x = a 与双曲线M 的渐近线在第一象限内的交点,则P 点法二:因为双曲线的渐近线方程为y =解析: 双曲线的焦点(0,5)到渐近线y =b x , 即ax — b 尸0的距离为;订匕尸?b = 3, 答案:所以 a=4,2a = 8. 二 a 2= 1, b 2 = 4,2ac — 7c 2= 0,7e 2— 2e — 9= 0,又 e>1,解得 e = 9. 9答案:7B 组一一能力提升练2 21. 已知F i , F 2是双曲线C : *—1(a>0, b>0)的两个焦点,若在双曲线上存 在点P 满足2|P F 1 + P F 2|< |F 7F 2|,则双曲线的离心率的取值范围是( )A. (1, 2] B . (1,2] C . [ 2,+x )D . [2 ,+x )解析:T 2|P F 1 + P F 2|< |F 1F 2|? 4|5P|W 2c? |5P|W 号,又|O )P|> a ,二 a <号,即 c > 2a , ••• e = c >2.故选 D.a 答案:D一X 2 y 2 x 2 y 22.若实数k 满足0<k<9,贝U 曲线25— 9— k = 1与曲线25—k — 9 = 1的( )B. 虚半轴长相等C. 实半轴长相等解析:由0<k<9,易知两曲线均为双曲线且焦点都在x 轴上,由〔25+ 9— k =5 625 — k + 9,得两双曲线的焦距相等. 答案:D6 (2018云南五市联考)设P 为双曲线x 2—聶=1右支上一点,M , N 分别是圆(x + 4)2 + y 2= 4和(x — 4)2 + y 2 = 1上的点,设|PM|—|PN|的最大值和最小值分别为 m , n ,则 |m — n|=()B . 5C. 6D . 7解析:易知双曲线的两个焦点分别为F 1( — 4,0), F 2(4,0),恰为两个圆的圆心,两 个圆的半径分别为 2,1,所以 |PM|max = |PF 1|+ 2, |PN|min = |PF 2|— 1, 故 |PM|— |PN| 的最大值为(|PF 1|+ 2)— (|PF 2|— 1) = (|PF 1|— |PF 2|) + 3= 5,同理 |PM|— |PN|A .离心率相等 D .焦距相等值为(|PF i |— 2)— (|PF 2|+ 1) = (|PF I |—|PF 2|) — 3= — 1,所以 |m — n|= 6,故选 C. 答案:CX 2 y 24. (2018江南十校联考)已知I 是双曲线C :空—亍=1的一条渐近线,P 是I 上 的一点,F i , F 2分别是C 的左、右焦点,若P F i P F 2= 0,则点P 到x 轴的距离B. 2解析:由题意知F i (— 6, 0), F 2( 6, 0),不妨设I 的方程为y = 2x ,点P(x o , 2x o ), 由P F i P F 2= ( —V 6 — X o ,—V 2x o )(76 — x o ,—/2x o ) = 3x o — 6= 0,得 x o = ±.2,故点P 到x 轴的距离为2|x o |= 2,故选C. 答案:C2 25. 已知双曲线乡—治=1(b>0),以原点为圆心,双曲线的实半轴长为半径长的圆 与双曲线的两条渐近线相交于 A , B , C , D 四点,四边形ABCD 的面积为2b , 则双曲线的方程为() x 2 A.7 - 3v -_ 1 B x ! 4Y !_ 1 -4 - 1B .4 —3 - 1C x2— C.4 2 2 2—1 D x -—亠 1 4 14 12 1解析:根据圆和双曲线的对称性,可知四边形ABCD 为矩形.双曲线的渐近线方 程为y=gx ,圆的方程为x 2 + y 2= 4,不妨设交点A 在第一象限,由y =吳,x 2+宀4得2 4+ b 2, yA = 4+b 2,故四边形ABCD 的面积为4xAyA = 4+P答案:D的圆与双曲线渐近线的一个交点为(3,4),贝吐匕双曲线的方程为( )的最小A. C . 2D. 2.6 32b ,解得b 2= 12,故所求的双曲线方程为2 2x — y 4 121,选 D. 6.已知双曲线 拿一*= 1(a>0, b>0)的左、右焦点分别为 F 1、F 2,以|F 1F 21为直径x 2 y 2A ————1 A.16 92 2C x__ y_ 二 1 C.9 16—解析:因为以|F 1F 2|为直径的圆与双曲线渐近线的一个交点为(3,4),所以c = 5, £ a3,又c 2= a 2 + b 2,所以a = 3, b = 4,所以此双曲线的方程为 看—磊=1. 答案:C2 27.过双曲线拿一b ^= 1(a>0, b>0)的一个焦点F 作一条渐近线的垂线,垂足为点 A ,与另一条渐近线交于点 B ,若FB = 2FA ,则此双曲线的离心率为( )A. ,2B. .3D. 5知点A 为BF 的中点,所以A(c _2a, 2),又点A 在直线y =|x 上,则|, c = 2a , e = 2. 答案:C8. 若直线|1和直线12相交于一点,将直线11绕该点逆时针旋转到与12第一次重 k 2 k 1合时所转的角为9,则角9就称为11到12的角,tan 已―,其中k 1, k 2分别1 + K 1K 22 2是l 1, l 2的斜率,已知双曲线E :拿一活=1(a>0, b>0)的右焦点为F , A 是右顶a 2点,P 是直线x =;上的一点,e 是双曲线的离心率,直线 PA 到PF 的角为9,W则tan 9的最大值为( )B.l 1 ec ^l =2,1 + ek 4 _ k 3解析:设PA, PF 的斜率分别为也,k4,由题意可知tan 缸齐—&不妨设B x 2 y 2 1 B.3 _ 4二 1x 2 y 2 彳 D 一 — —= 14 3 1C . 2解析:不妨设B(x ,—,OB|=x 2 + — ;X 2= c ,可取B( — a , b),由题意可1 A.— e D.|y —y y y a 7 8 a 2 ny)(y>0),贝Uk 3= a 2 ,k 4 = a 2 .令 m = - — a , n =; — c ,贝U tan A — y yaa c c ▲、科、/科 a — c 1 + x 工 c c nm门,由m — n = c — a>0,得当 乎+ y 取得最小值时tan B 取最大值,又y>0, mr +y m<0, n<0,所以m y n + y >2乜而,当且仅当丫={而时等号成立,此时tan Ac — a2 2 a aa — — c c c答案:9. (2018淄博模拟)过双曲线予一治=1(a>0, b>0)的左焦点F i ,作圆的切线交双曲线的右支于点 P ,切点为T , PF i 的中点M 在第一象限,则以下结 论正确的是()b — a = |M0|— |MT| b — a>|MO|— |MT|b — a = |MO|+ |MT|解析:如图,连接OT ,贝U OT 丄F 1T ,在直角三角形 OTF 1 中,|F 1T|= ;'|OF 1|2—|OTf = b ,连接 PF 2, ••• M 为线段F 1P 的中点,O 为F 1F 2的中点,7 1 1••• |MO|— |MT|= 2|PF 2| — 2|PF 1|—|F 1T| = 2(|PF 2|—|PF 1|)+ b = a ,故选A. 答案:A8 210. (2018昆明市检测)已知点F 为双曲线C : _2 — 法1(a>0, b>0)的一个焦点,a b 以点F 为圆心的圆与C 的渐近线相切,且与C 交于A , B 两点,若AF 丄x 轴, 则C 的离心率为 _____________________ .x 2 + y 2= a 2C . b — a<|MO|— |MT|联立可得方程组 b y二a x ,a 2x =_, c 解得「 ab尸c ,由中点坐标公式可得F 2关于渐近线对称的点的坐标为(cW2ab ) c )2a 2— c 2 2 4a 2将其代入双曲线的方程可得-a —一- 了 = 1化简可得c 2= 5a 2, c 2 = a 2 + b 2=5a 2,所以b 2= 4a 2.因为M( — 3, 4)在双曲线字—討1 上,所以学—琴=1, =1,所以a 2 = 5, b 2= 20,则该双曲线的标准方程为x — £ = 1.5 20卫 16a 2 4a 2 12.设双曲线x 2 — 3 = 1的左,右焦点分别为 F 1, F 2.若点P 在双曲线上,且△解析:不妨设F 为双曲线的右焦点,则F(c,0),易知双曲线的渐近线方程为y =』 abc一x ,则双曲线的焦点F 到渐近线的距离d = 需二b ,所以圆F 的半径为b.在 b 2双曲线方程中,令x =c ,得y = ±a ,所以A(c ,a b ,即卩 a = b ,所以 c = a 2 + b 2=・ 2a ,所以 e =c , 2.aa答案:• 211. 双曲线x 2 — £= 1(a>0, b>0)上一点 M( — 3,4)关于— 「条渐近线的对称点恰为右焦点F 2,则该双曲线的标准方程为 _______________________________ • 22b解析:不妨设双曲线拿一b ^= 1的右焦点F 2(c,0)关于渐近线y =ax 对称的点在双曲线上,a 则过焦点F 2且垂直于该渐近线的直线方程为 y — 0= —b (x — c),•因为点A 在圆F 上,所以阳 a即 y =—£(x —3 8-F 1PF 2为锐角三角形,则|PF i |+ |PF 21的取值范围是 _____________ . 解析:由题意不妨设点P 在双曲线的右支上,现考虑两种极限情况:当PF 2丄x轴时,|PF 1|+ |PF 2|有最大值8;当Z P 为直角时,|PF i |+ |PF 2|有最小值2.7•因为 △ F 1PF 2为锐角三角形,所以|PF i |+ |PF 21的取值范围为(2 7, 8). 答案:(2 7, 8)213. (2018沈阳质量监测)已知P 是双曲线X — y 2= 1上任意一点,过点P 分别作 双曲线的两条渐近线的垂线,垂足分别为 A ,B ,求RAPB 的值. 解析:设P(x o , y o ),因为该双曲线的渐近线分别是x oX 0騙-y °|騙 + y o |可取 |PA|= .——-,|PB|= j —,又 cos Z APB = — cos Z AOB = — cos2Z AOx 、1+1=—cos n=- 1 所以 PA P B = |PA| |PB| •s Z APB = 20y- 2頁11)(-X3-4 ----1,所以1+ 13 8-。
(word完整版)高中数学双曲线课后习题(带答案)(2021年整理)

(word完整版)高中数学双曲线课后习题(带答案)(word版可编辑修改) 编辑整理:尊敬的读者朋友们:这里是精品文档编辑中心,本文档内容是由我和我的同事精心编辑整理后发布的,发布之前我们对文中内容进行仔细校对,但是难免会有疏漏的地方,但是任然希望((word完整版)高中数学双曲线课后习题(带答案)(word版可编辑修改))的内容能够给您的工作和学习带来便利。
同时也真诚的希望收到您的建议和反馈,这将是我们进步的源泉,前进的动力。
本文可编辑可修改,如果觉得对您有帮助请收藏以便随时查阅,最后祝您生活愉快业绩进步,以下为(word完整版)高中数学双曲线课后习题(带答案)(word版可编辑修改)的全部内容。
双曲线课后习题一、选择题(本大题共10小题,每小题5分,共50分)1.到两定点()0,31-F 、()0,32F 的距离之差的绝对值等于6的点M 的轨迹 ( )A .椭圆B .线段C .双曲线D .两条射线2.方程11122=-++ky k x 表示双曲线,则k 的取值范围是( ) A .11<<-k B .0>k C .0≥k D .1>k 或1-<k3. 双曲线14122222=--+m y m x 的焦距是( ) A .4 B .22 C .8 D .与m 有关4.已知m ,n 为两个不相等的非零实数,则方程m x -y+n=0与n x 2+my 2=mn 所表示的曲线可能是A B C D 5. 双曲线的两条准线将实轴三等分,则它的离心率为 ( ) A .23B .3C .34D .36.焦点为()6,0,且与双曲线1222=-y x 有相同的渐近线的双曲线方程是( )A .1241222=-y xB .1241222=-x yC .1122422=-x yD .1122422=-y x7.若a k <<0,双曲线12222=+--k b y k a x 与双曲线12222=-by a x 有( )A .相同的虚轴B .相同的实轴C .相同的渐近线D . 相同的焦点8.过双曲线191622=-y x 左焦点F 1的弦AB 长为6,则2ABF ∆(F 2为右焦点)的周长是( ) A .28 B .22 C .14 D .129.已知双曲线方程为1422=-y x ,过P (1,0)的直线L 与双曲线只有一个公共点,则L 条数共有 ( ) A .4条 B .3条 C .2条 D .1条 10.给出下列曲线:①4x +2y -1=0; ②x 2+y 2=3; ③1222=+y x ④1222=-y x ,其中与直线 y=-2x -3有交点的所有曲线是( )A .①③B .②④C .①②③D .②③④ 二、填空题(本题共4小题,每小题6分,共24分)11.双曲线17922=-y x 的右焦点到右准线的距离为__________________________.12.与椭圆1251622=+y x 有相同的焦点,且两准线间的距离为310的双曲线方程为____________.13.直线1+=x y 与双曲线13222=-y x 相交于B A ,两点,则AB =__________________.4.过点)1,3(-M 且被点M 平分的双曲线1422=-y x 的弦所在直线方程为 .三、解答题(本大题共6题,共76分)15.求一条渐近线方程是043=+y x ,一个焦点是()0,4的双曲线标准方程,并求此双曲线的离心率.(12分)16.双曲线()0222>=-a a y x 的两个焦点分别为21,F F ,P 为双曲线上任意一点,求证:21PF PO PF 、、成等比数列(O 为坐标原点).(12分)17.已知动点P 与双曲线x 2-y 2=1的两个焦点F 1,F 2的距离之和为定值,且cos ∠F 1PF 2的最小值为-错误!。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
课时作业A组——基础对点练1.已知F为双曲线C:x2-my2=3m(m>0)的一个焦点,则点F到C的一条渐近线的距离为()A.3B.3C.3mD.3m解析:双曲线方程为x23m-y23=1,焦点F到一条渐近线的距离为3.选A.答案:A2.已知双曲线x2a2-y23=1(a>0)的离心率为2,则a=( )A.2 B.62C.52D.1解析:因为双曲线的方程为x2a2-y23=1,所以e2=1+3a2=4,因此a2=1,a=1.选D.答案:D 3.双曲线x2-4y2=-1的渐近线方程为( )A.x±2y=0 B.y±2x=0C.x±4y=0 D.y±4x=0解析:依题意,题中的双曲线即y214-x2=1,因此其渐近线方程是y214-x2=0,即x±2y=0,选A.答案:A4.已知双曲线x2 3-y 2=1的左、右焦点分别为F 1,F 2,点P 在双曲线上,且满足|PF 1|+|PF 2|=25,则△PF 1F 2的面积为( )A .1 B.3C.5D.12解析:在双曲线x23-y 2=1中,a =3,b =1,c =2.不防设P 点在双曲线的右支上,则有|PF 1|-|PF 2|=2a =23,又|PF 1|+|PF 2|=25,∴|PF 1|=5+3,|PF 2|=5-3.又|F 1F 2|=2c =4,而|PF 1|2+|PF 2|2=|F 1F 2|2,∴PF 1⊥PF 2,∴S △PF 1F 2=12×|PF 1|×|PF 2|=12×(5+3)×(5-3)=1.故选A.答案:A5.已知双曲线C :x2a2-y2b2=1(a >0,b >0),直线l :y =2x -2.若直线l 平行于双曲线C 的一条渐近线且经过C 的一个顶点,则双曲线C 的焦点到渐近线的距离为( )A .1B .2 C.5D .4解析:根据题意,双曲线C 的方程为x2a2-y2b2=1(a >0,b >0),其焦点在x 轴上,渐近线方程为y =±b a x ,又由直线l 平行于双曲线C 的一条渐近线,可知ba =2,直线l :y =2x -2与x 轴的交点坐标为(1,0),即双曲线C 的一个顶点坐标为(1,0),即a =1,则b =2a =2,故双曲线C 的焦点到渐近线的距离为2,故选B. 答案:B6.已知双曲线的焦点到渐近线的距离等于半实轴长,则该双曲线的离心率为( )A.5+12 B .2C.2D .22解析:不妨设双曲线的方程为x2a2-y2b2=1(a >0,b >0),因为焦点F (c,0)到渐近线bx -ay =0的距离为a ,所以bc a2+b2=a ,即bcc =a ,所以ba =1,所以该双曲线的离心率e =ca= 错误!=2,故选C. 答案:C7.已知双曲线C :x2a2-y2b2=1的离心率e =54,且其右焦点为F 2(5,0),则双曲线C 的方程为( )A.x24-y23=1 B.x29-y216=1 C.x216-y29=1 D.x23-y24=1 解析:由题意得e =1+b2a2=54,又右焦点为F 2(5,0),a 2+b 2=c 2,所以a 2=16,b 2=9,故双曲线C 的方程为x216-y29=1. 答案:C 8.已知双曲线x2a2-y2b2=1(a >0,b >0)的焦距为25,且双曲线的一条渐近线与直线2x +y =0垂直,则双曲线的方程为( )A.x24-y2=1 B.x2-y24=1C.3x220-3y25=1 D.3x25-3y220=1解析:由题意得c=5,ba=12,则a=2,b=1,所以双曲线的方程为x24-y2=1.答案:A9.(2018·山西八校联考)已知双曲线C:x2a2-y2b2=1(a>0,b>0)的左、右焦点分别为F1,F2,焦距为2c,直线y=3 3(x+c)与双曲线的一个交点P满足∠PF2F1=2∠PF1F2,则双曲线的离心率e为( ) A.2B.3C.23+1 D.3+1解析:∵直线y=33(x+c)过左焦点F1,且其倾斜角为30°,∴∠PF1F2=30°,∠PF2F1=60°,∴∠F2PF1=90°,即F1P⊥F2P.∴|PF2|=12|F1F2|=c,|PF1|=|F1F2|sin 60°=3c,由双曲线的定义得2a=|PF1|-|PF2|=3c-c,∴双曲线C的离心率e=ca=c3c-c2=3+1,选D.答案:D10.已知F1,F2是双曲线C:x2a2-y2b2=1(a>0,b>0)的两个焦点,P是双曲线C上一点,若|PF1|+|PF2|=6a,且△PF1F2最小内角的大小为30°,则双曲线C的渐近线方程是( )A.2x±y=0 B.x±2y=0C .2x ±y =0D .x ±2y =0解析:不妨设|PF 1|>|PF 2|,则⎩⎪⎨⎪⎧|PF1|-|PF2|=2a ,|PF1|+|PF2|=6a ,所以|PF 1|=4a ,|PF 2|=2a ,且|F 1F 2|=2c ,即|PF 2|为最小边,即∠PF 1F 2=30°,则△PF 1F 2为直角三角形,所以2c =23a ,所以b =2a ,即渐近线方程为y =±2x ,故选A.答案:A11.已知双曲线C :x2a2-y2b2=1(a >0,b >0)的焦距为10,点P (2,1)在C 的一条渐近线上,则C 的方程为( ) A.x220-y25=1 B.x25-y220=1C.x280-y220=1 D.x220-y280=1 解析:依题意⎩⎪⎨⎪⎧a2+b2=251=ba×2,解得⎩⎪⎨⎪⎧a2=20b2=5,∴双曲线C 的方程为x220-y25=1.答案:A12.已知双曲线过点(4,3),且渐近线方程为y =±12x ,则该双曲线的标准方程为.解析:法一:因为双曲线过点(4,3)且渐近线方程为y =±12x ,故点(4,3)在直线y =12x的下方.设该双曲线的标准方程为x2a2-y2b2=1(a >0,b >0),所以错误!,解得错误!故双曲线方程为x24-y 2=1.法二:因为双曲线的渐近线方程为y =±12x ,故可设双曲线为x24-y 2=λ(λ≠0),又双曲线过点(4,3),所以424-(3)2=λ,所以λ=1,故双曲线方程为x24-y 2=1.答案:x24-y 2=113.双曲线Γ:y2a2-x2b2=1(a >0,b >0)的焦距为10,焦点到渐近线的距离为3,则Γ的实轴长等于. 解析:双曲线的焦点(0,5)到渐近线y =ab x ,即ax -by =0的距离为|5b|a2+b2=5bc =b =3,所以a =4,2a =8. 答案:814.已知双曲线C :x2a2-y2b2=1(a >0,b >0)与椭圆x29+y24=1有相同的焦点,且双曲线C 的渐近线方程为y =±2x ,则双曲线C 的方程为. 解析:易得椭圆的焦点为(-5,0),(5,0),∴⎩⎪⎨⎪⎧a2+b2=5,ba=2,∴a 2=1,b 2=4,∴双曲线C 的方程为x 2-y24=1.答案:x 2-y24=115.(2018·合肥市质检)双曲线M :x2a2-y2b2=1(a >0,b >0)的左、右焦点分别为F 1,F 2,直线x =a 与双曲线M 的渐近线交于点P ,若sin ∠PF 1F 2=13,则该双曲线的离心率为.解析:不妨设P 为直线x =a 与双曲线M 的渐近线在第一象限内的交点,则P 点坐标为(a ,b ),因为sin ∠PF 1F 2=13,所以|PF 1|=3b ,所以(a +c )2+b 2=9b 2,即9a 2+2ac -7c 2=0,7e 2-2e -9=0,又e >1,解得e =97.答案:97B 组——能力提升练1.已知F 1,F 2是双曲线C :x2a2-y2b2=1(a >0,b >0)的两个焦点,若在双曲线上存在点P 满足2|PF1→+PF2→|≤|F1F2→|,则双曲线的离心率的取值范围是( )A .(1,2]B .(1,2]C .[2,+∞)D .[2,+∞)解析:∵2|PF1→+PF2→|≤|F1F2→|⇒4|OP →|≤2c ⇒|OP →|≤c 2,又|OP →|≥a ,∴a ≤c 2,即c ≥2a ,∴e =c a ≥2.故选D. 答案:D2.若实数k 满足0<k <9,则曲线x225-y29-k =1与曲线x225-k -y29=1的( )A .离心率相等B .虚半轴长相等C .实半轴长相等D .焦距相等 解析:由0<k <9,易知两曲线均为双曲线且焦点都在x 轴上,由25+9-k =25-k +9,得两双曲线的焦距相等.答案:D3.(2018·云南五市联考)设P 为双曲线x 2-y215=1右支上一点,M ,N 分别是圆(x +4)2+y 2=4和(x -4)2+y 2=1上的点,设|PM |-|PN |的最大值和最小值分别为m ,n ,则|m -n |=( )A .4B .5C .6D .7解析:易知双曲线的两个焦点分别为F 1(-4,0),F 2(4,0),恰为两个圆的圆心,两个圆的半径分别为2,1,所以|PM |max =|PF 1|+2,|PN |min =|PF 2|-1,故|PM |-|PN |的最大值为(|PF 1|+2)-(|PF 2|-1)=(|PF 1|-|PF 2|)+3=5,同理|PM |-|PN |的最小值为(|PF 1|-2)-(|PF 2|+1)=(|PF 1|-|PF 2|)-3=-1,所以|m -n |=6,故选C.答案:C4.(2018·江南十校联考)已知l 是双曲线C :x22-y24=1的一条渐近线,P 是l 上的一点,F 1,F 2分别是C 的左、右焦点,若PF1→·PF2→=0,则点P 到x 轴的距离为( )A.233B.2C .2 D.263解析:由题意知F 1(-6,0),F 2(6,0),不妨设l 的方程为y =2x ,点P (x 0,2x 0),由PF1→·PF2→=(-6-x 0,-2x 0)·(6-x 0,-2x 0)=3x 20-6=0,得x 0=±2,故点P 到x 轴的距离为2|x 0|=2,故选C.答案:C5.已知双曲线x24-y2b2=1(b >0),以原点为圆心,双曲线的实半轴长为半径长的圆与双曲线的两条渐近线相交于A,B ,C ,D 四点,四边形ABCD 的面积为2b ,则双曲线的方程为( )A.x24-3y24=1 B.x24-4y23=1C.x24-y24=1 D.x24-y212=1解析:根据圆和双曲线的对称性,可知四边形ABCD 为矩形.双曲线的渐近线方程为y =±b2x ,圆的方程为x 2+y 2=4,不妨设交点A 在第一象限,由y =b2x ,x 2+y 2=4得x A =44+b2,y A =2b4+b2,故四边形ABCD 的面积为4x A y A =32b4+b2=2b ,解得b 2=12,故所求的双曲线方程为x24-y212=1,选D.答案:D6.已知双曲线x2a2-y2b2=1(a >0,b >0)的左、右焦点分别为F 1、F 2,以|F 1F 2|为直径的圆与双曲线渐近线的一个交点为(3,4),则此双曲线的方程为( )A.x216-y29=1 B.x23-y24=1 C.x29-y216=1 D.x24-y23=1解析:因为以|F 1F 2|为直径的圆与双曲线渐近线的一个交点为(3,4),所以c =5,b a =43,又c 2=a 2+b 2,所以a =3,b =4,所以此双曲线的方程为x29-y216=1. 答案:C7.过双曲线x2a2-y2b2=1(a >0,b >0)的一个焦点F 作一条渐近线的垂线,垂足为点A ,与另一条渐近线交于点B ,若FB →=2FA →,则此双曲线的离心率为( )A.2B.3 C .2 D.5解析:不妨设B (x ,-bax ),|OB |=错误!=c ,可取B (-a ,b ),由题意可知点A 为BF 的中点,所以A (c -a 2,b 2),又点A 在直线y =b a x 上,则b a ·c -a 2=b2,c =2a ,e =2.答案:C8.若直线l 1和直线l 2相交于一点,将直线l 1绕该点逆时针旋转到与l 2第一次重合时所转的角为θ,则角θ就称为l 1到l 2的角,tanθ=k2-k11+k1k2,其中k 1,k 2分别是l 1,l 2的斜率,已知双曲线E :x2a2-y2b2=1(a >0,b >0)的右焦点为F ,A 是右顶点,P 是直线x =a2c上的一点,e 是双曲线的离心率,直线P A 到PF 的角为θ,则tan θ的最大值为( )A.1eB.e 1+eC.e 21+e D.e2解析:设P A ,PF 的斜率分别为k 3,k 4,由题意可知tan θ=k4-k31+k3k4,不妨设P (a2c,y )(y >0),则k 3=ya2c -a ,k 4=ya2c-c .令m =a2c -a ,n =a2c-c ,则tan θ=yn-y m 1+y n ×y m =m -nmny+y,由m -n =c-a >0,得当mn y +y 取得最小值时tan θ取最大值,又y >0,m <0,n <0,所以mn y+y ≥2mn ,当且仅当y =mn 时等号成立,此时tan θ=m -n 2mn=错误!=错误!,故选C.答案:C9.(2018·淄博模拟)过双曲线x2a2-y2b2=1(a >0,b >0)的左焦点F 1,作圆x 2+y 2=a 2的切线交双曲线的右支于点P ,切点为T ,PF 1的中点M 在第一象限,则以下结论正确的是( )A .b -a =|MO |-|MT |B .b -a >|MO |-|MT |C .b -a <|MO |-|MT |D .b -a =|MO |+|MT |接OT ,则OT ⊥F 1T ,在直角三角形OTF 1中,|F 1T |=解析:如图,连|OF1|2-|OT|2=b ,连接PF 2, F 1P 的中点,O 为F 1F 2的中点,∵M 为线段∴|OM |=12|PF 2|,∴|MO |-|MT |=12|PF 2|-⎝ ⎛⎭⎪⎪⎫12|PF1|-|F1T|=12(|PF 2|-|PF 1|)+b =12×(-2a )+b =b -a ,故选A.答案:A10.(2018·昆明市检测)已知点F 为双曲线C :x2a2-y2b2=1(a >0,b >0)的一个焦点,以点F 为圆心的圆与C 的渐近线相切,且与C 交于A ,B两点,若AF ⊥x 轴,则C 的离心率为.解析:不妨设F 为双曲线的右焦点,则F (c,0),易知双曲线的渐近线方程为y =±bax ,则双曲线的焦点F 到渐近线的距离d =bc a2+b2=b ,所以圆F 的半径为b .在双曲线方程中,令x =c ,得y =±b2a ,所以A (c ,±b2a ).因为点A 在圆F 上,所以b2a=b ,即a =b ,所以c =a2+b2=2a ,所以e =ca=2.答案:211.双曲线x2a2-y2b2=1(a >0,b >0)上一点M (-3,4)关于一条渐近线的对称点恰为右焦点F 2,则该双曲线的标准方程为.解析:不妨设双曲线x2a2-y2b2=1的右焦点F 2(c,0)关于渐近线y =bax 对称的点在双曲线上,则过焦点F 2且垂直于该渐近线的直线方程为y -0=-ab (x -c ),即y =-ab(x -c ).联立可得方程组错误!解得⎩⎪⎨⎪⎧x =a2c,y =abc,由中点坐标公式可得F 2关于渐近线对称的点的坐标为(2a2c -c ,2abc),将其代入双曲线的方程可得错误!-错误!=1,化简可得c 2=5a 2,c 2=a 2+b 2=5a 2,所以b 2=4a 2.因为M (-3,4)在双曲线x2a2-y2b2=1上,所以9a2-16b2=1,9a2-164a2=1,所以a 2=5,b 2=20,则该双曲线的标准方程为x25-y220=1.答案:x25-y220=112.设双曲线x 2-y23=1的左,右焦点分别为F 1,F 2.若点P 在双曲线上,且△F 1PF 2为锐角三角形,则|PF 1|+|PF 2|的取值范围是.解析:由题意不妨设点P 在双曲线的右支上,现考虑两种极限情况:当PF 2⊥x 轴时,|PF 1|+|PF 2|有最大值8;当∠P 为直角时,|PF 1|+|PF 2|有最小值27.因为△F 1PF 2为锐角三角形,所以|PF 1|+|PF 2|的取值范围为(27,8).答案:(27,8)13.(2018·沈阳质量监测)已知P 是双曲线x23-y 2=1上任意一点,过点P 分别作双曲线的两条渐近线的垂线,垂足分别为A ,B ,求PA →·PB→的值.解析:设P (x 0,y 0),因为该双曲线的渐近线分别是x 3-y =0,x 3+y =0,所以可取|P A |=|x03-y0|13+1,|PB |=|x03+y0|13+1,又cos ∠APB =-cos ∠AOB =-cos2∠AOx =-cos π3=-12,所以PA →·PB →=|PA →|·|PB →|·cos ∠APB =|x203-y20|43·(-12)=34×(-12)=-38.。
