人教版数学六年级上册第八单元综合测试卷(附答案)

合集下载

人教版数学六年级上册第八单元测试题(含答案)

人教版数学六年级上册第八单元测试及答案一．选择题（共8小题）1．4÷11的商用循环小数表示，则小数点后面第20位数字是（）A．0B．3C．7D．62．有一列数按如下方式排列：2，4，6，8，10……x，□……那么方框里应填（）A．x+2B．2x C．y3．按规律填数：1、、、、、…，第11个数是（）A．B．C．D．4．用小棒按下面的规律摆三角形，摆n个三角形用（）根小棒．A．2n+1B．2（n﹣1）C．3+2n5．用同样长的小棒摆出如下的图形．照这样继续摆，摆第6个图形用了（）根小棒．A．20B．25C．246．2×9＝18，22×99＝2178，222×999＝221778，2222×9999＝22217778，222222×999999＝（）A．2222177778B．222221777778C．22222217777778D．22222221777777787．将一些小圆球如图摆放，第6幅图有（）个小圆球．A．30B．42C．568．4÷7的商的小数部分第30位上的数字是（）A．8B．4C．2二．填空题（共8小题）9．先观察算式，找出规律再填数．21×9＝189321×9＝28894321×9＝38889×9＝488889×9＝．×9＝．10．小亮像下面这样摆三角形，摆1个用3根小棒，摆2个用5根小棒……根据这样的条件把下表填写完整．摆1个摆2个摆3个摆4个……摆8个摆个25根3根5根根根……根11．用小棒按照如图方式摆图形：摆n个八边形需要根小棒．12．通过计算发现规律．6543﹣2345＝9876﹣5678＝7654﹣3456＝按找到的规律，再写两个算式．13．10.1÷11商的小数部分第100位上的数字是．14．（1）算一算，找规律．6+6+6＝18﹣6﹣6﹣6＝7+7+7＝21﹣7﹣7﹣7＝10+10+10＝30﹣10﹣10﹣10＝（2）根据自己发现的规律再写出两组这样的算式．15．找规律填数．①608、、610、．②1689、1699、、、．16．找规律，填一填．（1）15，10，13，8，11，，，4．（2）1，2，5，10，，，37．（3），，，，，，，…三．判断题（共5小题）17．如图，如果一个小三角形的边长为1cm，第五个图形的周长是15cm．．（判断对错）18．根据33×4＝132，333×4＝1332，3333×4＝13332，可知33333×4＝133332．（判断对错）19．下面一组有规律排列的数：60、75、90、105、120，则1415不是这组数中的数．．（判断对错）20．在数列“，，，，，，…”中，第10个数是．（判断对错）21．1除以111的商的小数部分第15位数字是0．（判断对错）四．应用题（共5小题）22．小明在学习分数除注时做了下面的3道计算题，小明发现：“一个数（0除外）除以一个分数，所得的商一定大于它本身”．①如果让你继续研究分数除法，你还想研究什么问题，请在下面写出来．②请对你提出的问题进行研究，看看能得出什么结论？23．有一列数：，，，，，，，…它的前2015个数的和是多少？24．10月1日小时姐姐带领大家去旅游，来到一块形状是等边三角形的果园，它的边长是54米，三边及内部都植满了石榴树；每颗树之间均相距6米，各个顶点上都植有一颗；小时姐姐给同学们分工，每两位同学摘一颗，正好分完．聪明的你知道小时姐姐共带了多少名同学吗？25．按下面的方式摆桌子和椅子，一张桌子可以坐4人，两张桌子可以坐6人……（1）照这种方式摆下去，10张桌子可以坐多少人？（2）n张桌子可以坐多少人？（3）坐60人需要多少张桌子？26．1、4、7、10、13、…这个数列中，有6个连续数字的和是159，那么这6个数中最小的是几？答案与解析一．选择题（共8小题）1．【分析】把4÷11的商用循环小数表示出来，看看循环节有几位小数，然后用20除以循环节的位数即可判断．【解答】解：4÷11＝0.，循环节是36两个数字；20÷2＝10，所以20位上的数是6；故选：D．【点评】此题考查学生循环节的概念，以及分析判断能力．2．【分析】2，4，6，8，10，后一个数比前一个数多2，所以□里面的前一个数加上2即可求解．【解答】解：□里面的前一个数是x，则□里面应填：x+2．故选：A．【点评】关键是根据已知的数得出前后数之间的变化关系的规律，然后再利用这个变化规律再回到问题中去解决问题；注意用字母表示数的方法．3．【分析】由题意得：分子是连续的奇数，分母是从1开始连续自然数的平方，由此得出第n个数为．【解答】解：2×11﹣1＝21112＝121．所以第11个数是．故选：A．【点评】此题考查数字的变化规律，找出数字之间的运算规律，利用规律，解决问题．4．【分析】摆一个三角形需3根小棒；摆二个三角形需5根小棒；摆三个三角形时需要7根小棒；摆四个三角形时需要9根小棒；…第一个三角形需要3根小棒，以后每增加1个三角形就需要增加2根小棒；当有n个三角形时小棒的数量就是3+2（n﹣1）＝2n+1，据此即可解答问题．【解答】解：根据题干分析可得，当有n个三角形时小棒的数量就是：3+2（n﹣1）＝3+2n﹣2＝2n+1（根）答：摆n个三角形需要2n+1根小棒．故选：A．【点评】解决本题关键是找出小棒的数量随三角形的数量变化的规律，写出通项公式，进而求解．5．【分析】图1用5根小棒摆成，图2用9根小棒摆成，图3用13根小棒摆成，仔细观察发现，每增加一个五六边形其小棒根数增加4根，所以可得第n个图形需要小棒5+4（n﹣1）＝4n+1根，据此即可解答问题．【解答】解：由图可知：图形1的小棒根数为5；图形2的小棒根数为9；图形3的小棒根数为13；…由该搭建方式可得出规律：图形标号每增加1，小棒的个数增加4，所以可以得出规律：第n个图形需要小棒5+4（n﹣1）＝4n+1根，当n＝6时，需要小棒：4×6+1＝25（根）答：摆第6个图形用了25根小棒．故选：B．【点评】本题是一道关于图形变化规律型的，关键在于通过题中图形的变化情况，通过归纳与总结找出普遍规律求解即可．6．【分析】通过分析2×9＝18；22×99＝2178；222×999＝221778；2222×9999＝22217778 可知：乘数每多几个2和9，它们的乘积中1的前面就多几个2，8前面就多几个7，据此解答即可．【解答】解：根据分析可得222222×999999＝222221777778故选：B．【点评】“式”的规律：关键是根据已知的式子或数得出前后算式或前后数之间的变化关系和规律，然后再利用这个变化规律再回到问题中去解决问题．7．【分析】从第一个图形开始分析小圆圈的个数：第一个图形中有1×2＝2个小圆球，第二个图形中有2×3＝6个小圆球，第三个图形中有3×4＝12个小圆球，第四个图形中有4×5＝20个小圆球，…第n个图形有n（n+1）个小圆球，利用规律解决问题．【解答】解：观察图形可知：第一个图形中有1×2＝2个小圆球，第二个图形中有2×3＝6个小圆球，第三个图形中有3×4＝12个小圆球，第四个图形中有4×5＝20个小圆球，…所以第六幅图有6×7＝42个小圆球．故选：B．【点评】此题主要考查了图形的规律，通过归纳与总结结合图形得出图形个数之间的规律是解决问题的关键．8．【分析】首先把4÷7化成小数，看它的循环节是几位数，再根据“周期”问题，用30除以循环节的位数，如果能整除，则是循环节的末位上的数字，如果不能整除，余数是几计算循环节的第几位上的数字．由此解答．【解答】解：4÷7＝0.7142，循环节是6位数，30÷6＝5，所以商的小数部分第30位上的数是8；故选：A．【点评】此题主要考查除法商化成小数的方法，以及根据“周期问题”判断循环小数的某一位上数字是几的方法．二．填空题（共8小题）9．【分析】通过观察可知算式的特点：第一个因数左边数位上的数字依次比右边数位上的数字多1，第二个因数为9；积最高位比第一个因数最高位上的数字小1，中间8的个数＝等号右边的数最高位上的数字﹣1，个位为9，依次写出3道题．【解答】解：根据规律可知：21×9＝189321×9＝28894321×9＝3888954321×9＝488889654321×9＝5888889．7654321×9＝68888889．故答案为：54321，654321，5888889，7654321，68888889．【点评】考查了“式”的规律，本题要求学生通过观察，分析、归纳并发现其中的规律，并应用发现的规律解决问题．10．【分析】根据图示可知：摆1个三角形需要小棒：3根；摆2个三角形需要小棒：3+2＝5（根）；摆3个三角形需要小棒：3+2＝2＝7（根）……摆n个三角形需要小棒：3+2（n﹣1）＝（2n+1）根．据此解答．【解答】解：摆1个三角形需要小棒：3根摆2个三角形需要小棒：3+2＝5（根）摆3个三角形需要小棒：3+2＝2＝7（根）……摆n个三角形需要小棒：3+2（n﹣1）＝（2n+1）根根据规律，填表如下：摆1个摆2个摆3个摆4个……摆8个摆12个3根5根7根9根……17根25根故答案为：7；9；17；12．【点评】本题主要考查数与形结合的规律，关键根据图示发现这组图形的规律，并运用规律做题．11．【分析】根据图示可知，这组图形的规律：摆1个八边形需要小棒：8根；摆2个八边形需要小棒：8+7＝15（根）；摆3个八边形需要小棒：8+7+7＝22（根）；……摆n个八边形需要小棒根数：8+7（n﹣1）＝（7n+1）根．据此解答．【解答】解：摆1个八边形需要小棒：8根摆2个八边形需要小棒：8+7＝15（根）摆3个八边形需要小棒：8+7+7＝22（根）……摆n个八边形需要小棒根数：8+7（n﹣1）＝（7n+1）根故答案为：（7n+1）．【点评】本题主要考查数与形结合的规律，关键根据图示发现规律，并运用规律做题．12．【分析】通过计算可以得出：被减数从低位到高位各数位上的数字依次加1，减数从高位到低位各数位数字依次减1，且被减数的最高位上的数字比减数的最高位数字大4．【解答】解：6543﹣2345＝41989876﹣5678＝41987654﹣3456＝4198另外两个算式：8765﹣4567＝41985432﹣1234＝4198故答案为：4198，4198，4198．【点评】仔细观察被减数和减数的特征以及差的规律，是解答此类题的关键．13．【分析】计算10.1除以11可知等于0.9181818…可以看出双数位上永远是1，第100位是双位数，据此解答即可．【解答】解：10.1÷11＝0.9181818…观察可知双数位上永远是1，第100位是双位数，所以10.1÷11商的小数部分第100位上的数字是1．故答案为：1【点评】此题主要考查了根据“周期问题”判断循环小数的某一位上数字是几的方法．14．【分析】通过计算，观察这几组算式发现共同的规律：三个一样的加数，用它们的和再减去这三个加数等于0．【解答】解：算一算，找规律．6+6+6＝1818﹣6﹣6﹣6＝07+7+7＝2121﹣7﹣7﹣7＝010+10+10＝3030﹣10﹣10﹣10＝0故答案为：18，0；21，0；30，0．【点评】解答此题的关键是观察所给出的算式，找出算式之间数与数的关系，得出规律，再根据规律解决问题．15．【分析】①观察608和610两个数，中间应该是609，发现规律是后一个数比前一个数大1，据此解答即可；②观察1689和1699两个数，发现1689+10＝1699，规律是前一个数加10等于后一个数，据此解答即可．【解答】解：①608+1＝609610+1＝611②1699+10＝17091709+10＝17191719+10＝1729故答案为：609，611；1709，1719，1729．【点评】通过观察，分析、归纳并发现其中的规律，并应用发现的规律解决问题是应该具备的基本能力．16．【分析】（1）15﹣2＝13，13﹣2＝11，10﹣2＝8，发现规律，奇数项依次减2是连续奇数，偶数项依次减2是连续偶数，据此解答即可；（2）1，1×1+1＝2，2×2+1＝5，3×3+1＝10，发现规律第n个数是（n﹣1）×（n﹣1）+1，可得第5个数是4×4+1＝17，第6个数是5×5+1＝26，据此解答即可；（3）观察前4个数，分子：1+1＝2，2+1＝3，3+1＝4，分母：5+2＝7，7+2＝9，9+2＝11，发现规律，分子依次加1，分母依次加2，4+1＝5，5+1＝6，6+1＝7；11+2＝13，13+2＝15，15+2＝17．据此解答即可．【解答】解：根据分析可知：（1）11﹣5＝66+3＝9（2）4×4+1＝175×5+1＝26（3）4+1＝55+1＝66+1＝711+2＝1313+2＝1515+2＝17故答案为：6，9；17，26；，，．【点评】通过观察，分析、归纳并发现其中的规律，并应用发现的规律解决问题是应该具备的基本能力．三．判断题（共5小题）17．【分析】依题意可知：当n＝1时，周长＝边长×3；当n＝2时，周长＝边长×4；当n＝3时，周长＝边长×5；当n＝4时，周长＝边长×6；…；当有n个三角形时，图形周长＝边长×（n+2）．【解答】解：根据题干分析可得：当有n个三角形时，图形周长＝边长×（n+2），当n＝5时，图形周长是：1×（5+2）＝7（cm），答：第五个图形的周长是7cm．故答案为：×．【点评】此题考查的知识点是图形数字的变化类问题，关键是观察分析得出三角形个数与图形周长的关系为边长×（n+2）＝周长．18．【分析】根据观察知：第2个因数都是4，其结果最高位都是1、最低位都是2、中间都是3，3的个数比第一个因数中3的个数少1，据此解答．【解答】解：33×4＝132，333×4＝1332，3333×4＝13332，可知：33333×4＝133332．故答案为：√．【点评】找出算式中各个因数的变化规律是解题的关键．19．【分析】这组数每次递增15，所以用1415减去60，看能否被15整除即，如果能整除就是，否则不是；据此解答．【解答】解：75﹣60＝15，90﹣75＝15，…，所以这组数每次递增15，（1415﹣60）÷15≈90.33，所以，1415不是这组数中的数．故答案为：√．【点评】此题考查了数列的规律，关键是求出每次递增的数．20．【分析】这组数据的分子从左到右分别是1、3、5、7…，即是从1开始相邻的奇数；分母分别是1、4、9、16…，即分别是1、2、3、4…各数的平方．因此，第10数的分子是19，分母是102，即100．也就是第10个数是．【解答】解：这个数列中从左到右分别是1、3、5、7、9、11、13、15、17、19…分母是102＝100因此，在数列“，，，，，，…”中，第10个数是．故答案为：√．【点评】解答此题的关键是找规律，可分子、分母分别找，找到规律，根据规律解答就比较容易了．21．【分析】先求出1除以111的商，看它的循环节是几位数，再根据“周期”问题，用15除以循环节的位数，如果能整除，则是循环节的末位上的数字，如果不能整除，余数是几，计算循环节的第几位上的数字．由此解答．【解答】解：1÷111＝0.009009…，循环节是009，三位，15÷3＝5，所以商的小数部分第15位数字是9．故答案为：×．【点评】此题主要考查算术中的规律，以及根据“周期问题”判断循环小数的某一位上数字是几的方法．四．应用题（共5小题）22．【分析】①观察给出的算式中除数都是真分数，都小于1，所以得到的商都是大于被除数；所以可以找一些除数是大于1的分数，再进行计算；②根据①的计算结果，得出结论．【解答】解：①问题：除数大于1时，被除数与商的大小关系是怎么样的？6÷＝6×＝44＜6；3.6÷＝3.6×＝2.72.7＜3.6；÷＝×＝＜．②根据①可得：一个数（0除外）除以一个大于1的数，商小于这个数．【点评】两个不为0的数相除，当除数大于1时，商小于被除数；当除数等于1时，商等于被除数；当除数小于1时，商大于被除数．23．【分析】此题属典型的高斯求和问题，先找出这一串数字的变化规律，再利用高斯求和的知识求得答案．【解答】解：以1为分母的数有1个，相加和S1＝1，以2为分母的数有2个，相加和S2＝+＝，以3为分母的数有3个，相加和S3＝++＝2，…以n为分母的数有n个，相加和S n＝++…+＝＝，求前2015个数的和，先确定第2015个数分母是什么，即求满足1+2+3+4…+m＝≥2015的最小整数n，易得n＝63，62×63÷2＝1953，分母为63的数有2015﹣1953＝62个，即、、、…、，则前2015个数的和是：S＝S1+S2+…S62++++…+＝（1+2+3+…62）÷2+（1+2+3+…+62）÷63＝（1+62）×62÷2÷2+（1+62）×62÷2÷63＝976.5+31＝1007.5答：它的前2015个数的和是1007.5．【点评】考查了数列中的规律，此题关键是总结出S n＝，据此即可求得结果．24．【分析】由题意可知，最外层每边是54÷6＝9（棵），每边不包括三角形顶点外9﹣2＝7（棵），最外层一共载7×3+3＝24（棵）．第二层是边长为30米的等边三角形，用同样的方法即可求出一共有多少棵．再算出第三层、第四层（一共四层）棵数，进而计算出总棵数，用总棵数乘2就是小时姐姐共带的同学数．【解答】解：如图最外层：7×3+3＝24（棵）第二层：4×3+3＝15（棵）第三层：2×3+3＝9（棵）第四层：1棵（24+15+9+1）×2＝49×2＝98（名）答：小时姐姐共带了98名同学．【点评】解答此题的关键，也是难点，是求出石榴树的总棵数．25．【分析】观察摆放的桌子，不难发现：在1张桌子坐4人的基础上，多1张桌子，多2人．由此规律即可解决问题．【解答】解：（1）n＝1时，可坐4人，可以写成2×1+2；n＝2时，可坐6人，可以写成2×2+2；n＝3时，可坐8人，可以写成2×3+2；…；所以当n＝10时，可坐2×10+2＝22（人）答：10张桌子可以坐22人；（2）根据（1）发现规律：n张桌子可坐（2n+2）人．答：n张桌子可以坐（2n+2）人；（3）2n+2＝60n＝29（张），答：坐60人需要29张桌子．【点评】主要考查了学生通过特例分析从而归纳总结出一般结论的能力．对于找规律的题目首先应找出哪些部分发生了变化，是按照什么规律变化的，通过分析找到各部分的变化规律后直接利用规律求解．26．【分析】据题意可知，这个数列是公差为3的等差数列，由此可设这6个数中最小的数为x，则后边5个数与第一个数的差分别为3，6，…15，又因为有6个连续数的和是159，据此可得等量关系式：x+（x+3）+…+（x+15）＝159，解此方程即得这6个数中最小的是多少．【解答】解：设这6个数中最小的数为x，据题意可得方程：x+（x+3）+…+（x+15）＝1596x+（3+6+…+15）＝1596x+45＝1596x＝114x＝19答：这6个数中最小的是19．【点评】根据数列的排列规律及已知条件列出等量关系式是完成本题的关键．。

人教版数学六年级上册第八单元测试(附答案)

精品数学单元测试卷一．选择题（共10小题）1．观察下面的点阵图形，根据圆点的变化，探究其规律，则第8个图形中圆点的个数为（）A．25B．26C．27D．292．按如图方式摆放桌子和椅子．当摆放8张桌子时，可以坐（）人．A．30B．32C．34D．363．下面这组图形是按照一定规律排列的，照这样的规律，第8个图形有（）个黑色小方形A．26B．24C．22D．204．观察下面的算式:5×9＝4555×99＝5445555×999＝5544455555×9999＝55544445则＝（）A．B．C．5．已知99×99＝9801，999×999＝9980019999×9999＝99980001，下一个式子是（）A．99999×99999＝999800001B．99999×99999＝9999800001C．99999×99999＝9999980001D．99999×99999＝999999800016．根据你发现的规律，算式1234567×8+7的得数是（）A．9876B．98765C．987654D．98765437．一组数据按下面顺序依次排列:1，3，2014，2，4，2012，3，5，2010，4，6，2008 (2016)数是（）A．672B．674C．670D．6768．观察已给数列，括号中应填入所缺的数为:1，1，2，3，5，8，13（），34，……A．15B．17C．21D．309．将化成小数后，小数点后第2013位上的数字是（）A．2B．4C．3D．810．0.123412341234…，小数点后第100个数字是（）A．1B．2C．3D．4二．填空题（共8小题）11．如图，下面每个图中有多少个白色小正方形和多少个灰色小正方形？（1）把下面的表格补充完整．第1个图第2个图第3个图第4个图白色12灰色810（2）照这样接着画下去，第6个图中有个自色小正方形和个灰色小正方形．（3）想一想:照这样的规律，第n个图中有个白色小正方形和个灰色小正方形．（4）照这样的规律，如果某个图中灰色小正方形有30个，那么自色小正方形有个，它是第个图．12．用小棒按照如下的方式摆图形．（1）摆一个六边形需要6根小棒，摆2个六边形需要11根小棒，摆三个六边形需要根小棒．（2）照这样摆下去:摆n个六边形需要根小棒，但n＝60时，需要根小棒．13．已知1＝12，1+3＝22，1+3+5＝32，1+3+5+7＝42那么1+3+5+7+9+11+13＝．14．观察前四个算式的规律，利用发现的规律巧算最后一题．1＝121+3＝221+3+5＝321+3+5+7＝4221+23+25+…+45+47+49＝2﹣2＝．15．按规律填1，，，，，……16．按规律继续填数:10、13、16、19、、、．18、27、36、45、、、．17．10.1÷11商的小数部分第100位上的数字是．18．找规律:、、、、、、三．判断题（共5小题）19．如图:那么第7个点阵有45个点．．（判断对错）20．44×9＝396，444×9＝3996，由此可得44444×9＝399996．（判断对错）21．在数列”，，，，，，…”中，第10个数是．（判断对错）22．一个数列为:1，2，3，1，2，3，…按这样的顺序排下去，第20个数是3．（判断对错）23．30÷11＝2.，小数点后100位上的数字是7．．（判断对错）四．应用题（共3小题）24．小明用小棒搭房子．搭2间用9根，搭3间用13根．照这样计算，如果搭10间房子，需要用多少根小棒？25．先计算前三题，再根据发现的规律直接写出其他算式的结果．1+3═＝221+3+5═＝321+3+5+7═＝…1+3+5+7+…+15═＝1+3+5+7+…+2017＝＝26．有一列数:，，，，，，，…它的前2015个数的和是多少？五．解答题（共6小题）27．将小长方体木块按如图方式进行摆放．12345…小长方体的个数露在外面的面数…28．用一根长96厘米的绳子在地上摆正方形．1234正方形个数正方形边长（厘米）2412顶点数47（1）填写上表．（2）像这样摆下去，当这根绳子摆出12个正方形时，正方形的边长是厘米；当这根绳子摆出n个正方形时，顶点数是个．29．将小正方体按图方式摆放在地上．123456…a小正方体的个数露在外面的面的个数5…30．根据各式的规律填空:1＝121+3＝221+3+5＝321+3+5+7＝42（1）1+3+5+7+9+11+13＝2．（2）从1开始，个连续奇数相加的和是202．31．数列2，3，，，……，则其中第6个数是．32．2÷11的商用简便方法记作，小数点后面第100位上的数字是答案与解析一．选择题（共10小题）1．解:由分析可图可知，第n个图的点数是（4n﹣3）个第8个图形中圆点的个数为:4×8﹣3＝32﹣3＝29答:第8个图形中圆点的个数为29．故选:D．2．解:6+4×（8﹣1）＝6+4×7＝6+28＝34（人）答:当摆放8张桌子时，可以坐34人．故选:C．3．解:第一个图形中黑色正方形有:8个；第二个图形中黑色正方形有:8+2＝10（个）；第三个图形中黑色正方形有:8+2+2＝12（个）；……第n个图形中黑色正方形有:8+（n﹣1）×2＝（2n+6）（个）．所以，第8个图形中黑色小正方形个数为:2×8+6＝16+6＝22（个）答:第8个图形有22个黑色小方形．故选:C．4．解:的积中，应该有10个4，4前面有9个5，积的最后一位数字是5．＝．故选:C．5．解:已知99×99＝9801，999×999＝998001 9999×9999＝99980001，下一个式子是: 99999×99999＝9999800001故选:B．6．解:1+9＝2+8＝3+7＝4+6＝5+5＝6+4＝7+3，算式1234567×8+7＝9876543．故选:D．7．解:根据观察发现，这组数据每3个数一组:第一个数字为从1开始的自然数排列；第二个数为从3开始的自然数排列；第3个数为从2014开始，每组减2．第2016个数包含几组:2016÷3＝672（组）所以第2016个数为:2014﹣（672﹣1）×2＝2014﹣1342＝672答:第2016个数为672．故选:A．8．解:要填的数是:8+13＝21；故选:C．9．解:＝0.4285，它每6个数字一个循环:1、4、2、8、5、7；2013÷6＝335 (3)余数是3，所以小数点后第2013位上的数字是2；故选:A．10．解:小数0.123412341234…循环节为1234，共4位数．100÷4＝25，小数点后第100个数字是4．故选:D．二．填空题（共8小题）11．解:（1）观察可知，第1个图有1个白色小正方形和8个灰色小正方形，第2个图有2个白色小正方形和10个灰色小正方形，第3个图有3个白色小正方形和12个灰色小正方形，第4个图有4个白色小正方形和14个灰色小正方形．（2）根据上题可推出第6个图中有6个自色小正方形和18个灰色小正方形；（3）第n个图中有n个白色小正方形和2n+6个灰色小正方形；（4）2n+6＝302n＝30﹣62n＝24n＝24÷2n＝12故答案为:（1）3，4，12，14；（2）6，18:；（3）n，2n+6；（4）12，12．12．解:根据题干分析可得:摆1个六边形需要6根小棒，可以写作:5×1+1＝6（根）；摆2个需要11根小棒，可以写作:5×2+1＝11（根）；摆3个需要16根小棒，可以写成:5×3+1＝16（根）；…，摆n个六边形需要（5n+1）根小棒．摆n＝60个六边形需要:5×60+1＝301（根）小棒，故答案为:16，（5n+1），301．13．解:1+3+5+7+9+11+13＝72＝49；故答案为:49．14．解:（1+3+5+7+......49）﹣（1+3+5+ (19)＝[（49+1）÷2]2﹣[（1+19）÷2]2＝252﹣102＝625﹣100＝525故答案为:25，10，525．15．解:利用规律，则组数为:1、、、、、……故答案为:；．16．解:（1）19+3＝2222+3＝2525+3＝28；（2）45+9＝5454+9＝6363+9＝72；故答案为:22，25，28；54，63，72．17．解:10.1÷11＝0.9181818…观察可知双数位上永远是1，第100位是双位数，所以10.1÷11商的小数部分第100位上的数字是1．故答案为:118．解:第一空分子是8+2＝10，分母是52＝25第二空分子是10+2＝12，分母是62＝36、、、、、、．故答案为:，．三．判断题（共5小题）19．解:1+4+6+8+10+12+14＝5555＞45所以第7个点阵有45个点的说法是错误的；故答案为:×．20．解:因为44×9＝396444×9＝3996所以44444×9＝399996．故答案为:√．21．解:这个数列中从左到右分别是1、3、5、7、9、11、13、15、17、19…分母是102＝100因此，在数列”，，，，，，…”中，第10个数是．故答案为:√．22．解:20÷3＝6（组）…2（个）每组中的第2个是2，所以第20个数是2．故答案为:×．23．解:循环节是72两个数字；100÷2＝50，说明到第100位数字出现了50个循环节，所以100位上的数字是2；所以原题错误．故答案为:×．四．应用题（共3小题）24．解:根据图示，2间房:5+4＝9（根）3间房:5+4+4＝13（根）……10间房:5+4×（10﹣1）＝41（根）答:搭10间房子，需要用41根小棒．25．解:1+3═4＝221+3+5═9＝321+3+5+7═16＝42…1+3+5+7+…+15═64＝821+3+5+7+…+2017＝1016064＝10082故答案为:4，22，9，32，16，42，64，82，1016064，10082．26．解:以1为分母的数有1个，相加和S1＝1，以2为分母的数有2个，相加和S2＝+＝，以3为分母的数有3个，相加和S3＝++＝2，…以n为分母的数有n个，相加和S n＝++…+＝＝，求前2015个数的和，先确定第2015个数分母是什么，即求满足1+2+3+4…+m＝≥2015的最小整数n，易得n＝63，62×63÷2＝1953，分母为63的数有2015﹣1953＝62个，即、、、…、，则前2015个数的和是:S＝S1+S2+…S62++++…+＝（1+2+3+…62）÷2+（1+2+3+…+62）÷63＝（1+62）×62÷2÷2+（1+62）×62÷2÷63＝976.5+31＝1007.5答:它的前2015个数的和是1007.5．五．解答题（共6小题）27．解:根据题干分析可得:1个小长方体有5个面露在外面，再增加一个长方体，2个小长方体有8个面露在外面；3个小长方体有11个面露在外面．每增加1个长方体漏在外面的面就增加3个即:n个长方体有5+（n﹣1）×3＝5+（n﹣1）×3＝5+3n﹣3＝3n+2当n＝4时，3×4+2＝14（个）当n＝5时，3×5+2＝17（个）据此完成表格如下:12345小长方体的个数58111417露在外面的面数发现:n个长方体有5+（n﹣1）×3＝3n+2个面露在外面．28．解:（1）正方形个数1234正方形边长（厘米）2412（8）（6）顶点数47（10）（13）（2）96÷12÷4＝8÷4＝2（厘米）根据所给图形顶点的个数发现规律:1个正方形，顶点个数:3+1＝4（个）2个正方形，顶点个数:3×2+1＝7（个）3个正方形，顶点个数:3×3+1＝10（个）……n个正方形，顶点个数:（3×n+1）个．答:摆12个正方形，边长为2厘米；摆n个正方形，有（3n+1）个顶点．故答案为:2；（3n+1）．29．解:根据题干分析可得，1个小正方体，露在外面的面的个数是3×1+2＝5个，2个小正方体拼在一起，露在外面的面的个数是3×2+2＝8（个）3个小正方体拼在一起，露在外面的面的个数是3×3+2＝11（个）4个小正方体拼在一起，露在外面的面的个数是3×4+2＝14（个）5个小正方体拼在一起，露在外面的面的个数是3×5+2＝17（个）6个小正方体拼在一起，露在外面的面的个数是3×6+2＝20（个）…，则a个小正方体拼在一起，露在外面的面的个数是3×a+2＝3a+2（个）故完成表格如下:小正方体的个数123456…a 露在外面的面的个数5811141720…3a+2 30．解:（1）1+3+5+7+9+11+13＝72；（2）观察图形可知，从1开始的连续奇数的和等于奇数个数的平方，所以从1开始，20个连续奇数相加的和是202．故答案为:（1）7；（2）20．31．解:这组数据的规律为:后面的数等于前面的数乘所以，第6个数为:2×＝答:其中第6个数是．故答案为:．32．解:2÷11＝0.循环节是18两个数字；100÷2＝50，说明到第100位数字出现了50个循环节，所以100位上的数字是8；故答案为:0.，8．。

2022年新人教版小学六年级数学上册第八单元学习质量检测卷(附参考答案)

2022年新人教版小学六年级数学上册第八单元学习质量检测卷时间：90分钟满分：100分班级__________姓名__________得分__________一、选择题（共8小题，满分16分，每小题2分）1．（2分）下列图形都是由一样大小的小棒按照一定规律所组成的，其中第1个图形中有1根小棒，第2个图形中有3根小棒，第3个图形中有7根小棒，第4个图形中有15根小棒，⋯按此规律排列下去，则第6个图形中有（）根小棒。

A．31B．32C．63D．642．（2分）将黑色棋子按照一定规律排列成一系列如图所示的图案，第1个图中有8枚黑棋子，第2个图中有13枚黑棋子，第3个图中有18枚黑棋子，按照此规律，第9个图中有（）枚黑棋子。

A．49B．48C．47D．463．（2分）观察图形，按此规律，第⑩个图中〇的个数有（）个。

A．55B．40C．36D．104．（2分）如图所示，用白色小正方形和黑色长方形按照下面的摆法，组成不同的长方形。

当摆5个黑色长方形时，四周需要摆（）个白色小正方形。

A．16B．20C．26D．365．（2分）如图是由同样大小的圆按一定规律排列所组成的，其中第1个图形中有4个圆，第2个图形中有8个圆，第3个图形中有14个圆，第4个图形中有22个圆……，按此规律排列下去，第20个图形中有（）个圆。

A．422B．412C．402D．3926．（2分）疫情期间，为方便全员核酸检测，某社区需要搭建如图1的单顶帐篷，需要17根钢管。

这样的帐篷按图2、图3的方式串起来搭建，则串起来搭建n顶帐篷需要（）根钢管。

A．11n+6B．11n﹣6C．17n D．17n﹣67．（2分）△◎◇口△◎◇☐△◎◇☐……这组排列共有110个图形，其中◎共有（）个。

A．26B．27C．28D．298．（2分）小明在玩一张长10厘米、宽6厘米的卡片时，意外地发现下面两种摆法，都正好从写字台的一端摆到另一端，写字台的这条边可能是（）厘米。

六年级上册数学第八单元练习卷含答案(8.数与形)新人教版

新人教版六年级上册数学第八单元练习卷含答案8.数与形一、填空1．如图所示，观察小圆圈的摆放规律，第一个图中有5个小圆圈，第二个图中有8个小圆圈，第100个图中有_____个小圆圈。

2．找规律，下列图中有大小相同的菱形，第1幅图中有1个菱形，第2幅图中有3个菱形，第3幅图中有5个菱形，则第4幅图中有____个菱形，第n幅图中有______个菱形。

1 2 3 n3．用同样大小的黑色棋子按下图所示的方式摆图形，按照这样的规律摆下去，则第n个图形需棋子_______枚（用含n的代数式表示）。

…第1个图第2个图第3个图4．观察表一，寻找规律，表二、表三、表四分别是从表一中截取的一部分，其中a、b、c的值分别为________。

表一表二表三表四5．如图①是一块瓷砖的图案，用这种瓷砖来铺设地面。

如果铺成一个2x2的正方形图案（如图②），其中完整的圆共有5个，如果铺成一个3x3的正方形图案（如图③），其中完整的圆共有13个，如果铺成一个4x4的正方形图案（如图④），其中完整的圆共有25个。

若这样铺成一个10x10的正方形图案，则其中完整的圆共有___个。

……①②③④6．如下图，用同样大小的黑、白两种颜色的棋子摆设如下图所示的正方形图案，则第n个图案需要用白色棋子______枚（用含有n的代数式表示，并写成最简形式）。

7．用火柴棒按下图中的方式搭图形，按照这种方式搭下去，搭第334个图形需___根火柴棒。

（a）（b）（c）8．将正整数按如图所示的规律排列下去，若有序实数对（n，m）表示第n排，从左到右第m个数，如(4，2)表示实数9，则表示实数17的有序实数对是_____。

1………………第一排3 2…………第二排4 5 6………第三排10 9 8 7……第四排…9.如下图，用n表示等边三角形边上的小圆圈，f (n)表示这个三角形中小圆圈的总数，那么f(n)和n的关系是________。

……10.观察下图中角的个数，计算出第50个图中有_______个角。

人教版数学六年级上册第八单元测试题(含答案)

人教版小学数学六年级上册8单元测试卷(含答案及周测培优)

第7、8单元过关检测卷一、填空。

(每空1分，共28分)1．扇形统计图用一个圆表示( )，用圆内各个扇形的大小表示( )占( )的百分之几，扇形统计图可以表示出( )与( )之间的关系。

2．要统计欣欣从6岁到12岁的身高变化情况，应选用( )统计图；要统计幸福村各种农作物种植面积占耕地总面积的百分比，应选用( )统计图；要统计某市各小学2017年秋在校学生人数，应选用( )统计图。

3．如图：☆★★△△□☆★★△△□…，第23个图形是( )，第51个图形是( )。

4．如下图，摆第1条小鱼用了( )根火柴棒，摆第2条小鱼用了( )根火柴棒，摆第3条小鱼用了( )根火柴棒，照这样摆下去，摆第5条小鱼要用( )根火柴棒。

5．找规律填数：(1)1，3，6，( )，( )。

(2)1，4，9，( )，( )。

6．如图，这是六(2)班图书角中各种图书所占百分比的不完整统计图。

(1)这个圆代表的是( )，科普书占图书总数的( )%。

(2)已知文学书有150本，那么作文书有( )本，科普书有( )本。

7．下面是六(1)班同学英语口语测试成绩的统计表和统计图，请将它们补充完整。

8．用小棒按照如下方式摆图形：(1)摆第5个图形需用( )根小棒；(2)摆第n个图形需用( )根小棒。

二、选择。

(将正确答案的字母填在括号里)(每题3分，共15分) 1．如图，六(1)班优秀的人数和六(2)班优秀的人数相比，( )。

A．同样多B．六(1)班多C．六(2)班多D．无法确定哪个班多2．在一个圆形花坛内种了三种花(如图所示)，统计图( )能准确地表示各种花的占地面积。

3．统计股票某日的走势情况，应绘制( )统计图。

A．条形B．折线C．扇形D．三种都可以4．周日早晨，张昊到离家800 m的体育馆练习羽毛球，走路用了10分钟，然后用20分钟时间练习羽毛球，练完球后跑步回家，用了5分钟。

下图中，正确描述张昊离家时间和离家距离关系的是( )。

5．A、B、C、D四人照相，2人照一张(不能重复)，A照了3张，B照了2张，C照了1张，D照了( )张。

人教版六年级数学上册第八单元数与形测试题(附答案)

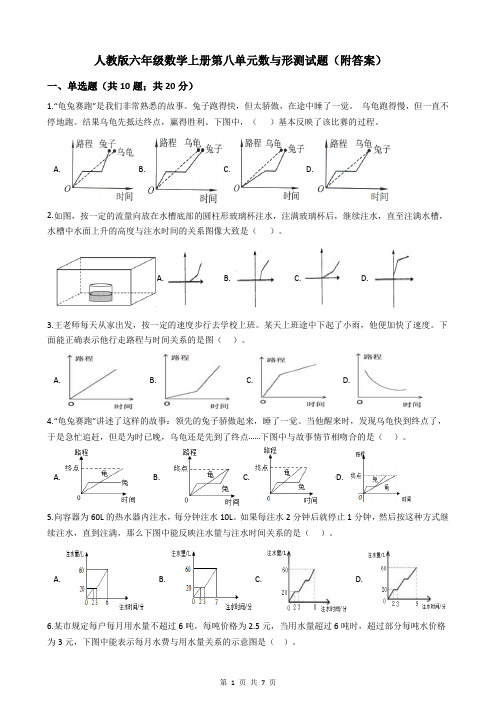
人教版六年级数学上册第八单元数与形测试题（附答案）一、单选题（共10题；共20分）1.“龟兔赛跑”是我们非常熟悉的故事。

兔子跑得快，但太骄傲，在途中睡了一觉。

乌龟跑得慢，但一直不停地跑。

结果乌龟先抵达终点，赢得胜利。

下图中，（）基本反映了该比赛的过程。

A. B. C. D.2.如图，按一定的流量向放在水槽底部的圆柱形玻璃杯注水，注满玻璃杯后，继续注水，直至注满水槽，水槽中水面上升的高度与注水时间的关系图像大致是（）。

A. B. C. D.3.王老师每天从家出发，按一定的速度步行去学校上班。

某天上班途中下起了小雨，他便加快了速度。

下面能正确表示他行走路程与时间关系的是图（）。

A. B. C. D.4.“龟兔赛跑”讲述了这样的故事：领先的兔子骄傲起来，睡了一觉。

当他醒来时，发现乌龟快到终点了，于是急忙追赶，但是为时已晚，乌龟还是先到了终点……下图中与故事情节相吻合的是（）。

A. B. C. D.5.向容器为60L的热水器内注水，每分钟注水10L。

如果每注水2分钟后就停止1分钟，然后按这种方式继续注水，直到注满，那么下图中能反映注水量与注水时间关系的是（）。

A. B. C. D.6.某市规定每户每月用水量不超过6吨，每吨价格为2.5元，当用水量超过6吨时，超过部分每吨水价格为3元，下图中能表示每月水费与用水量关系的示意图是（）。

A. B. C. D.7.珠海市规定：每年每户用气（天然气）员不超过300立方米，每立方米3.45元；当用气量超过300立方米时，超过的部分每立方米为4.15元。

下图中能正确表示每年用气费用与用气量关系的示意图是（）A. B. C.8.李芳和妈妈周日早上从家出发，乘车0.5小时，到达离家5km远的科技馆，在参观1.5小时后，乘车0.5小时返回家中。

下面四幅图中，能够描述她们这一活动行程的是（）。

A. B. C. D.9.一只兔子和一条小狗从同一地点出发，同时开始向东运动，兔子的运动距离与时间关系如图中实线部分ABCD所示，小狗的运动距离与时间关系图象如图中虚线部分AD所示。

人教版新教材小学数学6年级上册第7、8单元测试卷-1附答案

人民教育出版社（即人教版、统编版、部编版）小学数学六年级上册第七、八单元合并测验卷-1（附答案）六年级上册数学第七、八单元合并测试卷一、选择。

(将正确答案的序号填在括号里)(每题3分，共30分)1．要反映才才住院期间的体温变化情况，应选用( )统计图。

A.条形B.折线C．扇形D．复式条形2．下面是学校图书室各类图书所占百分比情况统计表，适合用( )统计图表示。

A.条形B.折线C．扇形D．以上都不对3．成成从家出发去书店买书，走了大约一半路程时，想起忘了带钱，于是立即掉头回家取钱，再出发去书店，买了几本书后回家。

下面的图( )比较准确地反映了成成这一活动行程。

A. B.C. D.4．状状、小丽(女)、李明、小芳(女)四个好朋友站成一排拍合照，要求男女间隔排列，一共有( )种站法。

A.24B.8 C．16 D．125．植树活动中，挖坑的人数占总人数的75%，抬水的人数占总人数的25%。

下面图形表示正确的是( )。

6．下面是某校六年级学生期中数学测试情况统计图，如果该校六年级共有240人，那么数学不及格的学生有( )人。

A.10B.24 C．48 D．60第6题图第7题图7．萌萌从家骑车到图书馆，先上坡后下坡，行程情况如图所示。

如果返回时上、下坡的速度仍保持不变，那么萌萌从图书馆骑车回家需要( )分钟。

A.30B.37.2 C．48 D．19.28．如图，按此规律继续画下去，第8个图形中有( )个灰色正方形。

…A.32B.28 C．25 D．249．如图，一张方桌可以坐8人(每边坐2人)，两张同样的方桌拼在一起可以坐12人……那么20张这样的方桌拼在一起可以坐( )人。

A.160B.96 C．84 D．8010．利用所学的面积计算的知识，根据下面图形的拼摆，发现( )公式成立。

A.a2＋c2＝b2B.a2＋b2＝c2 C．b2＋c2＝a2 D．以上都不对二、填空。

(除标注外，每空1分，共44分)11．找规律填数。

人教版数学六年级上册《第八单元综合检测》含答案

人教版数学六年级上学期第八单元测试考试时间：90分钟；满分：100分一．填空题（共9小题,每空2分,共30分）1．（2019•保定模拟）用长4厘米、宽3厘米的长方形学具排成如图,最上层是一个学具,以下每层多一块．排5层,得到的图形的周长是厘米；如果排300层,得到图形的周长是厘米．2．（2019春•郾城区期末）找规律填数,6.877、6.872、6.867、、、． 3．（2019春•英山县期末）在12,25,38,411,514⋯⋯这列分数中,第10个分数是 4．（2019春•成武县期末）如图,强强用小棒搭房子,照这样搭下去,搭5间房子要用根小棒；搭间房子要用61根小棒．5．（2019春•镇江期末）观察下面算式,找一找,发现规律,再填一填．143142002⨯=,143213003⨯=,143284004⨯=, 14335⨯= , 143⨯ = ⋯⋯ 6．（2019•防城港模拟）①33129+=,2(12)9+=；②33312336++=,2(123)36++=； ③33331234100+++=,2(1234)100+++=；⋯⋯通过观察发现：333333123456+++++= ．（填得数）7．（2019春•淮安期末）一列分数1121231234,,,,,,,,,1223334444中,57是其中的第个．8．（2019•江西模拟）现有一堆建筑需要清运,它第一次运走总量的12008．第二次运走余下的220081-,第三次运走余下的320083-,第四次运走余下的420086-,第五次运走余下的5200810-,依次规律继续运下去,当运走49次后,余下废料是总量的． 9．（2019春•重庆期末）找规律：21、44、69、816、、、1449二．判断题（共5小题,每空1分,共5分）10．（2019•河南模拟）摆1个正方形需要4根小棒,往后每多摆1个正方形就增加3根小棒,按这样的规律摆10个正方形,一共需要31根小棒．（）11．（2019•武侯区）⋯,第五个点阵中点的个数是14521+⨯=．（）12．（2019•湘潭）若一列数为：2,4,6,8,10,96⋯⋯,98,100,则这列数的和是2550．（）13．（2019春•绍兴期末）在数列“11,34,59,716,925,1136,⋯”中,第10个数是19100．（）14．（2019•应城市校级模拟）下面一组有规律排列的数：60、75、90、105、120,则1415不是这组数中的数．（）三．选择题（共6小题,每题2分,共12分）15．（2019春•皇姑区期末）把正方形桌子拼在一起,一张正方形桌子能坐8个人,两张正方形桌子能坐12个人,如图．如果10张桌子拼在一起能围坐()人．A．36B．40C．44D．4816．（2019春•邓州市期末）2.22,2.30,2.38,2.46,()括号里应填()A．2.22B．2.50C．2.5417．（2019•绵阳）一列数1,12,12,13,13,13,14,14,14,14⋯⋯中的第27个数是()A．16B．17C．18D．1918．（2019•长沙模拟）如图：照这样画,第12幅图有()个三角形．A．18B．20C．22D．2419．（2019•河南模拟）观察下面的点阵图形,根据圆点的变化,探究其规律,则第8个图形中圆点的个数为( )A．25B．26C．27D．2920．（2019•利州区）一组数据按下面顺序依次排列：1,3,2019,2,4,2019,3,5,2019,4,6,2008⋯第2019个数是( )A．672B．674C．670D．676四．解答题（共9小题,5分+6分+6分+6分+6分+6分+6分+6分+6分= 53分）21．观察下面的图形并填表．图形三角形四边形五边形六边形 ⋯N 边形边数分成的三角形个数22．（2019•邵阳模拟）图①是一个三角形,分别连接这个三角形三边的中点得到图②,再分别连接图②中间小三角形三边的中点,得到图③．（1）图②得到5个三角形,照这样图③得到个三角形；按上面的方法继续下去,图10能得个三角形；图n 能得到个三角形．（2）图能得到61个三角形．23．如图,一张0A 纸的面积大约是1平方米,而1A 纸的面积是0A 纸的一半,2A 纸的面积是1A 纸的一半,3A 纸的面积是2A 纸的一半,以此类推．（1）需要张4A 纸正好覆盖一张0A 纸．（2）一张1A 纸较长的边长是多少毫米？24．（2019•东莞市）观察下面的算式看看你有什么发现？ 33129+= 2(12)9+= 33312336++= 2(123)36++= 33331234100+++= 2(1234)100+++=⋯通过你的发现计算：33333123415++++⋯+= ．25．（2019•岳阳模拟）想一想,空格处应该填几？（从上到下填写）26．（2019•长沙）已知一串分数：11,12,22,13,23,33,14,24,34,44⋯（1）750是此串分数中的第多少个分数？（2）第115个分数是多少？27．（2019春•任城区期中）（1）通过计算,探索规律：215225=可写成1001225⨯⨯+；225625=可写成1002325⨯⨯+；2351225=可写成1003425⨯⨯+；2452025=可写成1004525⨯⨯+；2755625=可写成；2857225=可写成；（2）从第（1）题的结果,归纳、猜想得：2(105)n+=．（3）验证（2）中结论左右是否相等．（4）根据上面的归纳,请算出：105 2=．28．下列图案由边长相等的黑白两色正方形按一定规律拼接而成,依规律填表．黑色正方形个数1234⋯n白色正方形个数（2）当8n=时,白色正方形一共有多少个？29．（2019秋•成都校级期中）一场乒乓球比赛,16个同学参加．（1）如果采用单循环赛（每两名同学都要赛一场）,一共需要赛多少场？（2）如果采用单淘汰赛(16人分成8组进行第一轮比赛,败者淘汰．8名胜者再分成4组进行第二轮比赛,如此反复,直到决出冠军）,一共需要赛多少场？（1答案与解析一．填空题（共9小题,每空2分,共30分）1．（2019•保定模拟）用长4厘米、宽3厘米的长方形学具排成如图,最上层是一个学具,以下每层多一块．排5层,得到的图形的周长是70厘米；如果排300层,得到图形的周长是厘米．【分析】（1）根据图示可知,摆5层求图形的周长,可以用转化的方法,把图形转化为长5个4厘米,宽5个3厘米的长方形,利用长方形周长公式求其周长即可．（2）根据所给图示发现规律：排几层求周长,就可以转化为长和宽都是层数个长4厘米,宽3厘米的长方形周长的和．据此解答．【解答】解：（1）(4535)2⨯+⨯⨯=+⨯(2015)2=⨯35270=（厘米）答：这个图形的周长为70厘米．（2）(43)2300+⨯⨯=⨯⨯72300=⨯143004200=（厘米）答：排300层,得到图形的周长是4200厘米．故答案为：70；4200．【点评】本题主要考查数与形结合的规律,关键根据图示发现规律,丙运用规律做题．2．（2019春•郾城区期末）找规律填数,6.877、6.872、6.867、 6.862、、．【分析】6.877 6.8720.005-=,可得后一个数比前一个数少0.005；据此解答．-=,6.872 6.8670.005【解答】解：6.8670.005 6.862-=-=6.8620.005 6.8576.8570.005 6.852-=即6.877、6.872、6.867、6.862、6.857、6.852．故答案为：6.862、6.857、6.852．【点评】先根据给出的数据找出规律,再利用规律进行求解．3．（2019春•英山县期末）在12,25,38,411,514⋯⋯这列分数中,第10个分数是1029【分析】规律：分子是连续的自然数,分母依次增加3,据此解答即可．【解答】解：第10个分数分子是10分母是：23(101)+⨯-227=+29=即第10个分数是10 29．故答案为：10 29．【点评】数列中的规律：关键是根据已知的式子或数得出前后算式或前后数之间的变化关系和规律,然后再利用这个变化规律再回到问题中去解决问题．4．（2019春•成武县期末）如图,强强用小棒搭房子,照这样搭下去,搭5间房子要用26根小棒；搭间房子要用61根小棒．【分析】搭一间房用6根小棒,2间房用11根小棒,3间房用16根小棒,以后每增加一间房就多用5根小棒,所以搭n间房子需要(15)n+根小棒．由此解决问题．【解答】解：搭一间房用6根小棒,可以写成115+⨯；2间房用11根小棒,可以写成125+⨯；3间房用16根小棒,可以写成135+⨯；⋯所以搭n间房子需要(15)n+根小棒．当5n=时,需要小棒15526+⨯=（根),61根小棒可以搭：(611)5-÷605=÷12=（间)答：搭5间房子要用 26根小棒；搭 12间房子要用61根小棒．故答案为：26,12．【点评】主要考查了通过特例分析从而归纳总结出一般结论的能力．对于找规律的题目首先应找出哪些部分发生了变化,是按照什么规律变化的．5．（2019春•镇江期末）观察下面算式,找一找,发现规律,再填一填． 143142002⨯=,143213003⨯=,143284004⨯=,14335⨯= 5005 ,143⨯ = ⋯⋯ 【分析】1431414372100122002⨯=⨯⨯=⨯= 1432114373100123003⨯=⨯⨯=⨯= 1432814374100124004⨯=⨯⨯=⨯=规律：第前两个因数的积是14371001⨯=,然后乘第三个因数（一位因数是几）积就是几千零几,据此解答即可．【解答】解：14335143755005⨯=⨯⨯= 14342143766006⨯=⨯⨯=故答案为：5005,42,6006（答案不唯一）．【点评】解答此题的关键是观察所给出的算式,找出算式之间数与数的关系,得出规律,再根据规律解决问题． 6．（2019•防城港模拟）①33129+=,2(12)9+=； ②33312336++=,2(123)36++=；③33331234100+++=,2(1234)100+++=；⋯⋯通过观察发现：333333123456+++++= 441 ．（填得数）【分析】①33129+=,2(12)9+=； ②33312336++=,2(123)36++=；③33331234100+++=,2(1234)100+++=；⋯⋯纵观各式不难发现：左边底数由上而小分别是1、2之和；1、2、3之和；1、2、3、4之和⋯⋯；每个加数的指数都是3；右边是所有加数去掉指数的和的平方．据此即可求出333333123456+++++的和．【解答】解：333333123456+++++2(123456)=+++++221=441=即通过观察发现：333333123456441+++++=．故答案为：441．【点评】解答此题的关键是根据前三个算式找出规律,然后再根据规律解答．7．（2019春•淮安期末）一列分数1121231234,,,,,,,,,1223334444中,57是其中的第26个．【分析】观察数列发现：分母是几的分数就有几个,分子是从1开始一直到与分母相同；即分母是n分数有n个,是从1n到nn,所以先求出分母是1、2、3、4、5、6的一共有多少个,再加上5,即可求出57是第多少个．【解答】解：12345621+++++=66是第21个分数21526+=,所以57是其中的第26个．故答案为：26．【点评】关键是根据已知的数得出前后数之间的变化关系的规律,然后再利用这个变化规律再回到问题中去解决问题．8．（2019•江西模拟）现有一堆建筑需要清运,它第一次运走总量的12008．第二次运走余下的220081-,第三次运走余下的320083-,第四次运走余下的420086-,第五次运走余下的5200810-,依次规律继续运下去,当运走49次后,余下废料是总量的49 200848-．【分析】由题意,可得规律：分子代表运走的次数n,分母是2008(1)n--,因此,第49次时,分子为49,分母为2008(1)2008(491)200848n--=--=-．据此解答．【解答】解：它第一次运走总量的1 2008．第二次运走余下的2 20081-第三次运走余下的3 20083-第四次运走余下的420086-第五次运走余下的5200810-⋯⋯当运走49次后,余下废料是总量的49200848-．答：当运走49次后,余下废料是总量的49200848-．【点评】本题主要考查算术中的规律,关键运用分数的意义做题． 9．（2019春•重庆期末）找规律：21、44、69、816、 1025 、、1449【分析】这列分数的分子是从2开始的公差为2的等差递增数列,即每项加2等于它后面和它相邻的项,由此即可求出所空缺的两项的分子；211=、242=、293=⋯⋯分母是项数的平方,由此即可求出所空缺的两项的分母,进而写出所空缺的两个分数．【解答】解：第一空分子是8210+=,分母是2525= 第二空分子是10212+=,分母是2636= 21、44、69、816、1025、1236、1449．故答案为：1025,1236．【点评】解答此题的关键是根据这一数列的前几项分别找出分子、分母的变化规律,然后再根据规律解答．二．判断题（共5小题,每空1分,共5分）10．（2019•河南模拟）摆1个正方形需要4根小棒,往后每多摆1个正方形就增加3根小棒,按这样的规律摆10个正方形,一共需要31根小棒． √ ．（判断对错）【分析】摆一个正方形要小棒4根；摆两个正方形要小棒(43)+根,即7根；摆三个正方形要小棒(432)+⨯根,即10根,由此得到摆n 个正方形要小棒43(1)31n n +⨯-=+根；然后把10n =代入31n +中即可求出摆10个正方形需要的小棒数．【解答】解：摆一个正方形要小棒4根；摆两个正方形要小棒(43)+根,即7根；摆三个正方形要小棒(432)+⨯根,即10根,⋯,所以摆n 个正方形要小棒：43(1)31n n +⨯-=+（根)； 10n =,310131⨯+=（根)；答：摆10个正方形一共需要31根小棒．原题说法正确．故答案为：√．【点评】本题考查了规律型：图形的变化类：通过从一些特殊的图形变化中发现不变的因素或按规律变化的因素,然后推广到一般情况．11．（2019•武侯区）⋯,第五个点阵中点的个数是14521+⨯=．错误．（判断对错）【分析】根据题干,第一个点阵有1个点,第二个点阵上下左右各增加了一个点即有：114+⨯个点,第三个点阵上下左右各增加了2个点即有：122+⨯个点由此可得：第n 点阵的点数1(1)4n =+-⨯,由此规律即可解决判断．【解答】解：根据题干分析可得：第n 点阵的点数1(1)4n =+-⨯, 5n =时,点数个数为：1(51)417+-⨯=．所以原题说法错误．故答案为：错误．【点评】抓住题干,从特殊的例子推理得出一般的结论,由此即可解决此类问题．12．（2019•湘潭）若一列数为：2,4,6,8,10,96⋯⋯,98,100,则这列数的和是2550． √ （判断对错）【分析】求2,4,6,8,10,96⋯⋯,98,100的和即为求：246810100+++++⋯+=？50n =,根据等差数列的求和公式完成计算．【解答】解：246810100+++++⋯+ 50(2100)2⨯+=51002=2550=所以原题计算正确．故答案为：√．【点评】根据等差数列求和公式进行计算,找出等差数列的公差,首项,尾项和项数是计算的关键． 13．（2019春•绍兴期末）在数列“11,34,59,716,925,1136,⋯”中,第10个数是19100． √ （判断对错）【分析】这组数据的分子从左到右分别是1、3、5、7⋯,即是从1开始相邻的奇数；分母分别是1、4、9、16⋯,即分别是1、2、3、4⋯各数的平方．因此,第10数的分子是19,分母是210,即100．也就是第10个数是19 100．【解答】解：这个数列中从左到右分别是1、3、5、7、9、11、13、15、17、19⋯分母是210100=因此,在数列“11,34,59,716,925,1136,⋯”中,第10个数是19100．故答案为：√．【点评】解答此题的关键是找规律,可分子、分母分别找,找到规律,根据规律解答就比较容易了．14．（2019•应城市校级模拟）下面一组有规律排列的数：60、75、90、105、120,则1415不是这组数中的数．√．（判断对错）【分析】这组数每次递增15,所以用1415减去60,看能否被15整除即,如果能整除就是,否则不是；据此解答．【解答】解：756015-=,907515-=,⋯,所以这组数每次递增15,(141560)1590.33-÷≈,所以,1415不是这组数中的数．故答案为：√．【点评】此题考查了数列的规律,关键是求出每次递增的数．三．选择题（共6小题,每题2分,共12分）15．（2019春•皇姑区期末）把正方形桌子拼在一起,一张正方形桌子能坐8个人,两张正方形桌子能坐12个人,如图．如果10张桌子拼在一起能围坐()人．A．36B．40C．44D．48【分析】根据题意,1张桌子可以坐8人可以写成144⨯+人,2张桌子可以坐12人可以写成244⨯+人,3张桌子16人,可以写成34416⨯+=人,⋯,y张桌子就可以坐44y+人,由此即可解决问题．【解答】解：1张桌子可以坐8人可以写成144⨯+人,2张桌子可以坐12人可以写成244⨯+人,3张桌子16人,可以写成34416⨯+=人,⋯,则y张桌子就可以坐44y+人,当10y=时,学生总数为：410444⨯+=（人),答：如果10张桌子拼在一起能围坐44人．故选：C．【点评】此类规律题一定要注意结合图形进行分析,发现规律：每多一张桌子,多坐4人．从而得出y张桌子可以坐44y+人．16．（2019春•邓州市期末）2.22,2.30,2.38,2.46,()括号里应填()A．2.22B．2.50C．2.54【分析】2.30 2.220.08-=,2.38 2.300.08-=,2.46 2.380.08-=,规律：依次增加0.08．【解答】解：2.460.08 2.54+=故选：C．【点评】数列中的规律：关键是根据已知的式子或数得出前后算式或前后数之间的变化关系和规律,然后再利用这个变化规律再回到问题中去解决问题．17．（2019•绵阳）一列数1,12,12,13,13,13,14,14,14,14⋯⋯中的第27个数是()A．16B．17C．18D．19【分析】从这组数的分母可以得出规律,当分母数为n时,则共有n个1n,所以第27个数为1n,则123127123n n+++⋯+-<<+++⋯+,可以求出n,进而得解．【解答】解：根据规律,设第27个数为1n,则123127123n n +++⋯+-<<+++⋯+,所以7(71)7(71)2722⨯-⨯+<<；所以7n=,则第27个数是17．故选：B．【点评】通过观察,分析、归纳并发现其中的规律,并应用发现的规律解决问题是应该具备的基本能力．18．（2019•长沙模拟）如图：照这样画,第12幅图有()个三角形．A．18B．20C．22D．24【分析】根据题意,第一幅图有2个三角形,第二幅图有4个三角形,第3幅图有6个三角形,可推出第n幅图有2n个三角形,据此即可解答问题．【解答】解：根据题干分析可得,第一幅图有2个三角形,第二幅图有4个三角形,第3幅图有6个三角形,可推出第n幅图有2n个三角形,当12⨯=（个)n=时,21224答：第12幅图有24个三角形．故选：D．【点评】主要考查了学生通过特例分析从而归纳总结出一般结论的能力．对于找规律的题目首先应找出哪些部分发生了变化,是按照什么规律变化的,通过分析找到各部分的变化规律后直接利用规律求解．19．（2019•河南模拟）观察下面的点阵图形,根据圆点的变化,探究其规律,则第8个图形中圆点的个数为( )A．25B．26C．27D．29【分析】第1个图由1个点,第2个图形由5个点,第3个图形由9个点,第4个图形有13个点1⋯⋯、5、9、=⨯-、13⋯⋯很明显,是首项为1,公差为4的等差递增数列,即每项加4就是它后面和它相邻的项．1413n-个．=⨯-⋯⋯第n个图的点数是(43)=⨯-、94334423=⨯-、13443【解答】解：由分析可图可知,第n个图的点数是(43)n-个第8个图形中圆点的个数为：⨯-483=-32329=答：第8个图形中圆点的个数为29．故选：D．【点评】解答此题的关键是根据图的序数与点个数找出规律,然后再根据规律即可求出第n个图点的个数．20．（2019•利州区）一组数据按下面顺序依次排列：1,3,2019,2,4,2019,3,5,2019,4,6,2008⋯第2019个数是( )A．672B．674C．670D．676【分析】根据观察发现,这组数据每3个数一组：第一个数字为从1开始的自然数排列；第二个数为从3开始的自然数排列；第3个数为从2019开始,每组减2．先求第2019个数包含几组：20163672÷=（组),然后计算第2019个数为：2014(6721)2672--⨯=．【解答】解：根据观察发现,这组数据每3个数一组：第一个数字为从1开始的自然数排列；第二个数为从3开始的自然数排列；第3个数为从2019开始,每组减2．第2019个数包含几组：÷=（组)20163672所以第2019个数为：--⨯2014(6721)2=-20141342672=答：第2019个数为672．故选：A．【点评】本题主要根据所给数据发现其规律,并运用规律做题．四．解答题（共9小题,5分+6分+6分+6分+6分+6分+6分+6分+6分= 53分）21．观察下面的图形并填表．图形三角形四边形五边形六边形⋯N边形边数分成的三角形个数【分析】观察图形可知,多边形的边数为3时,有1个三角形,可以写成321-=个；多边形边数为4时,可以分成2个三角形,可以写成422-=个,多边形的边数为5时,可以分成3个三角形：523-=个；多边形边数为6时,可以分成4个三角形：624-=个,由此即可得出规律解决问题．【解答】解：多边形的边数为3时,有1个三角形,可以写成321-=个；多边形边数为4时,可以分成2个三角形,可以写成422-=个,多边形的边数为5时,可以分成3个三角形,可以写成523-=个；多边形边数为6时,可以分成4个三角形,可以写成624-=个；⋯多边形的边数为N时,可以分成2N-个三角形,由此可以完成表格如下：【点评】主要考查了学生通过特例分析从而归纳总结出一般结论的能力．对于找规律的题目首先应找出哪些部分发生了变化,是按照什么规律变化的,通过分析找到各部分的变化规律后直接利用规律求解．22．（2019•邵阳模拟）图①是一个三角形,分别连接这个三角形三边的中点得到图②,再分别连接图②中间小三角形三边的中点,得到图③．（1）图②得到5个三角形,照这样图③得到9个三角形；按上面的方法继续下去,图10能得个三角形；图n能得到个三角形．（2）图能得到61个三角形．【分析】可先直接通过图形写出三角形的个数；本题可分别写出1n=,2,3⋯时所对应的三角形个数,找出有关于n的代数式；找出规律解答．【解答】解：（1）图②中有5个三角形,图③中有9个三角形．依题意得：1n=时,有1个三角形；n=时,有5个三角形；2n=时,有9个三角形；3⋯所以当n nn-个三角形．=时有43图10能得410337n-个三角形；⨯-=个三角形；图n能得到43（2）假设存在正整数n,使得第n个图形中有61个三角形,根据题意得：4361n-=解得：16n=故答案为：9,37,43n-,16．【点评】此题考查了图形的变化规律,对于找规律的题目首先应找出哪些部分发生了变化,是按照什么规律变化的,找出规律,解决问题．23．如图,一张0A 纸的面积大约是1平方米,而1A 纸的面积是0A 纸的一半,2A 纸的面积是1A 纸的一半,3A 纸的面积是2A 纸的一半,以此类推．（1）需要 16 张4A 纸正好覆盖一张0A 纸．（2）一张1A 纸较长的边长是多少毫米？【分析】（1）观察题干可得：0A 纸的面积和4A 纸的面积无直接联系,需要1A 、2A 、3A 这三个中间量搭建桥梁．1张0A 纸的面积等于2张1A 纸的面积,1张1A 纸的面积等于2张2A 纸的面积,根据等量代换原理,1张0A 纸的面积等于4张2A 纸的面积,依此类推,可以找出0A 纸和4A 纸的面积关系,即10214283164A A A A A ====．（2）观察题干图形可得：1张1A 纸较长边边长等于2张3A 纸的较长边长度,1张3A 纸的较长边边长等于2张4A 边较短边长度,根据等量代换原理,1张1A 纸较长边边长等于4张4A 边较短边长度,代入数据即可．【解答】（1）根据题干分析可得：1张0A 纸的面积等于2张1A 纸的面积,1张1A 纸的面积等于2张2A 纸的面积,根据等量代换原理,1张0A 纸的面积等于224⨯=（张)2A 纸的面积；因为1张2A 纸的面积等于2张3A 纸的面积,所以1张0A 纸的面积等于428⨯=（张)3A 纸的面积；因为1张3A 纸的面积等于2张4A 纸的面积,所以1张0A 纸的面积等于8216⨯=（张)4A 纸的面积．（2）根据观察图形,由等量代换原理可得1张1A 纸较长边边长等于4张4A 边较短边长度,代入题干已知数据可得：2104840⨯=（毫米）故答案为：（1）16；（2）840【点评】主要考察学生通过观察图形捕捉有用信息,发现规律,并能够应用等量代换原理解决问题的能力． 24．（2019•东莞市）观察下面的算式看看你有什么发现？ 33129+= 2(12)9+= 33312336++= 2(123)36++= 33331234100+++= 2(1234)100+++=⋯通过你的发现计算：33333++++⋯+=14400．123415【分析】由已知算式可以看出：左边是从1开始的相邻自然数的立方的和,右边是左边各加数去掉立方后和的平方．据此即可根所这规律求出最后一个算式的计算结果．【解答】解：123415++++⋯⋯+=⨯+1678=+1128=1202=120144003333312341514400++++⋯+=．故答案为：14400．【点评】解答此题的关键是根据已知算式找出规律,然后再根据规律求出最后一题的计算结果填空．25．（2019•岳阳模拟）想一想,空格处应该填几？（从上到下填写）【分析】先找出规律,再填数．此题的规律是：右上角的数比左上角的数多2,右下角的数比左下角的数少4．【解答】解：（1）9211+=（2）8210+=+=8412故答案为：11；10,12【点评】数列中的规律：关键是根据已知的式子或数得出前后算式或前后数之间的变化关系和规律,然后再利用这个变化规律再回到问题中去解决问题．26．（2019•长沙）已知一串分数：11,12,22,13,23,33,14,24,34,44⋯（1）750是此串分数中的第多少个分数？（2）第115个分数是多少？【分析】（1）观察给出的数列知道,分母是1的分数有1个,分母是2的分数有2个,分母是3的分数有3个⋯分母是n的分数有n个,由此知道根据等差数列前n项的和(1)2n n+÷,求出1到49的和,进而求出750是此串分数中的第几个分数；（2）根据等差数列前n项的和(1)2n n+÷,先求出和为120是此串分数中的第几个分数,进而求出第115个分数是几．【解答】解：（1）49(491)2⨯+÷,49502=⨯÷,1225=,也就是说第1225个分数是49 49,往后推7个分数就是7 50,122571232+=,所以750是此串分数中的第1232个分数；（2）(1)2120n n+÷=,即(1)240n n+=,因为1516240⨯=,所以15n=,也就是说,第120个数是15 15往前推,115个分数是10 15,答：（1）750是此串分数中的第1232个分数,（2）第115个分数是1015．【点评】关键是根据给出的数列,归纳总结出规律,再根据规律解决问题．27．（2019春•任城区期中）（1）通过计算,探索规律：215225=可写成1001225⨯⨯+；225625=可写成1002325⨯⨯+；2351225=可写成1003425⨯⨯+； 2452025=可写成1004525⨯⨯+； 2755625=可写成 1007825⨯⨯+ ； 2857225=可写成；（2）从第（1）题的结果,归纳、猜想得：2(105)n += ．（3）验证（2）中结论左右是否相等．（4）根据上面的归纳,请算出：105 2= ．【分析】（1）通过观察可以看出,个位是5的平方数,得数是100⨯去掉个位上的5剩下的数⨯（去掉个位上的5剩下的数1)25++；（2）根据第（1）题的规律可得：2(105)100(1)25n n n +=⨯⨯++；（3）验证（2）中结论左右是否相等,只要把上面的结论的左边去掉括号化简看看是否等于右边即可判断；（4）把2105即10n =时,代入2(105)100(1)25n n n +=⨯⨯++即可得出结果．【解答】解：（1）2755625=可写成1007825⨯⨯+, 2857225=可写成1008925⨯⨯+；（2）100(1)25n n ⨯⨯++；（3）左边100= 2221055100n n +⨯⨯+= 210025n n ++, 右边100= 210025n n ++, 所以,左边=右边,因此结论正确；（4）10n =时,105 22100101001025=⨯+⨯+ 10000100025=++, 11025=；故答案为：1007825⨯⨯+,1008925⨯⨯+,100(1)25n n ⨯⨯++,11025．【点评】本题的关键是根据第一题得出规律：2(105)100(1)25n n n +=⨯⨯++． 28．下列图案由边长相等的黑白两色正方形按一定规律拼接而成,依规律填表．（1）（2）当8n=时,白色正方形一共有多少个？【分析】根据题意,第一个图形白色正方形为8个,第二个图形白色正方形为13个,第三个图形白色正方形为18个,后一个图形比前一个图形多5个白色正方形,则第n个图形白色正方形的个数为53n+个．【解答】解：（2）第n个图形白色正方形的个数为53n=时．n+,当853n+=⨯+583=+40343=（个)答：当8n=时,白色正方形一共有43个．【点评】主要考查了学生通过特例分析从而归纳总结出一般结论的能力．对于找规律的题目首先应找出哪些部分发生了变化,是按照什么规律变化的,通过分析找到各部分的变化规律后直接利用规律求解．29．（2019秋•成都校级期中）一场乒乓球比赛,16个同学参加．（1）如果采用单循环赛（每两名同学都要赛一场）,一共需要赛多少场？（2）如果采用单淘汰赛(16人分成8组进行第一轮比赛,败者淘汰．8名胜者再分成4组进行第二轮比赛,如此反复,直到决出冠军）,一共需要赛多少场？【分析】（1）单循环赛每名同学都要和另外的15个人赛一场,一共要赛1516240⨯=场,由于两个人之间的比赛实际是同一场比赛,去掉重复计算的情况,实际只赛了：2402120÷=场；（2）第一轮比赛要赛：1628÷=场,第四轮比赛÷=场,第二轮比赛要赛：824÷=场,第三轮比赛要赛：422要赛：221÷=场,然后把各轮的场数相加即可得出所求问题．【解答】解：（1）(161)162-⨯÷,15162=⨯÷,=（场)；120答：如果采用单循环赛一共需要赛120场．（2）第一轮比赛要赛：1628÷=（场),第二轮比赛要赛：824÷=（场),第三轮比赛要赛：422÷=（场),第四轮比赛要赛：221÷=（场),+++=（场)；842115答：如果采用单淘汰赛一共需要赛15场．【点评】本题是握手问题的综合应用,在采用单循环赛制时,如果人数比较少,可以用枚举法解答；如果人数比较多,可以用公式：(1)2n n-÷解答．。

六年级上册数学单元测试- 第八单元数学广角-数与形测试卷人教版(含解析)

2020-2021学年人教版数学六年级上学期第八单元测试卷一、选择题（共10题；共20分）1.填在下面各正方形中的四个数之间都有相同的规律，根据此规律，m的值是（）。

A. 38B. 52C. 66D. 742.某餐厅里，一张桌子可坐6人，如图所示：按照上面的规律，n张桌子能坐（）人。

A. 6n+4B. 4n+4C. 4n+2D. 6n+63.如下图，用火柴棒搭房子，搭三间用了13根。

照这样计算，搭504间用（）根火柴棒。

A. 2013B. 2015C. 20174.有一组图，它的排列规律如下图，第7个图形由（）个组成。

A. 21B. 25C. 28D. 325.根据下图的规律，可知第⑥个图中有（）个。

A. 21B. 25C. 296.甜甜按照一定的规律用小棒摆出了下边的4幅图，如果按照这个规律继续摆，第6幅图要用的小棒根数是（）A. 31根B. 45根C. 57根D. 63根7.“数形结合”是一种数学思想方法，通过数与形之间的对应关系，体现抽象思维与形象思维的结合。

下图的图形对应的算式是（）A. 14+116+164+1256+⋯=13B. 12+14+18+116+⋯=1C. 13+16+112+124+⋯=23D. 都不对8.把一些规格相同的杯子叠起来（如图），4个杯子叠起来高20厘米，6个杯子叠起来高26厘米。

n个杯子叠起来的高度可以用下面（）的关系式来表示。

A. 6n-10B. 3n+11C. 6n-4D. 3n+89.将一些小圆球如下图摆放，第六幅图有（）个小圆球。

A. 30B. 42C. 48D. 5610.根据图中的信息，第六个图案所对应的式子是( )A. 7＋1B. 62＋1C. 72＋1D. 82＋1二、判断题（共2题；共4分）11.摆1个正方形需要4根小棒，往后每多摆1个正方形就增加3根小棒，按这样的规律摆10个正方形，一共需要31根小棒．（判断对错）12.…，第五个点阵中点的个数是1+4×5=21．三、填空题（共10题；共18分）13.给某环形道种了2012棵树，如果从某一棵开始，每隔5棵树挂一盏彩灯，依次绕圈挂下去，一共挂了2012盏彩灯。

人教版六年级上册数学第7、8单元综合测试卷(含答案)

人教版六年级上册数学第7、8单元综合测试卷（含答案）一、认真审题，填一填。

(每小题4分，共20分)1．据了解，在首次火星探测任务名称征集活动中，排名前8的工程候选名称分别为“天问”“凤凰”“追梦”“朱雀”“凤翔”“腾龙”“麒麟”“火星”，如果想直观看到这8个名称在网络投票中的投票数应该选用( )统计图，如果想知道这8个名称分别占总投票数的百分比，应该选用( )统计图。

2．六年级学生在垃圾分类知识竞赛中，成绩分为A 、B 、C 三个等级，结果如右边两幅不完整的统计图。

结合两幅统计图中的信息，这次共有( )人参加竞赛活动，在扇形统计图中C 级占( )%。

3．根据算式的规律填空：16＝12－13，112＝13－14，120＝14－15，在算式172＝1 □－1○中，□＝( )，○＝( )。

4．如下图，用同样长的小木棒摆一摆，照这样摆下去，第(6)幅图需要( )根这样的小木棒。

5．“转化”是解决问题的常用策略之一，有时画图可以帮助我们找到转化的方法。

例如借助右图，可以将算式12＋14＋18＋116＋132＋164＋1128转化成：( )。

(写算式并计算出结果)二、仔细推敲，选一选。

(将正确答案的序号填在括号里)(每小题2分，共10分)1．下列说法正确的是( )。

A．条形统计图可以直观地表示部分和总量之间的关系B．折线统计图只能表示数量的多少C．扇形、折线和条形统计图都可以表示数量的变化趋势D．扇形统计图可以直观地看出部分与总量之间的关系2．近期，由于天气干冷，病毒活跃，某市进入流感高发季节。

根据疾控中心要求，张老师每天都及时收集、整理本校各班因流感请假的人数情况，以便采取应对措施。

如果要统计各年级请假人数占全校人数的百分比，选用( )统计图比较合适。

A．条形B．折线C．扇形D．都可以3．如图是某校六年级学生参加摄影、象棋、武术、十字绣四个兴趣小组人数的扇形统计图(每人必须参加且只能参加一个兴趣小组)，以下说法错误的是( )。

人教版六年级数学上册第8单元综合检测卷附答案

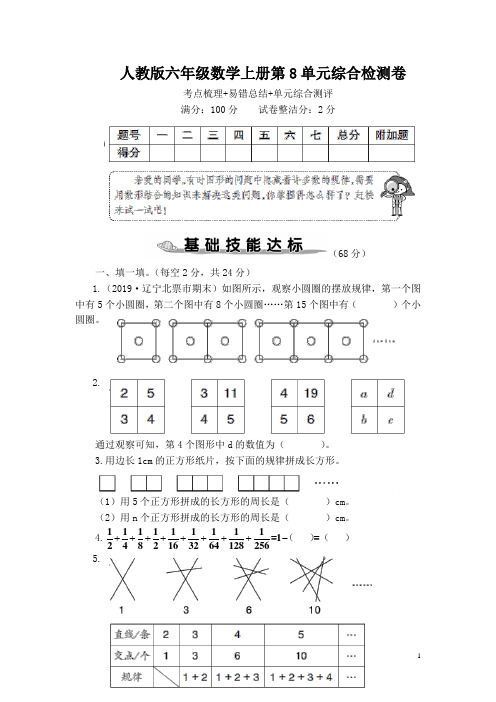
人教版六年级数学上册第8单元综合检测卷考点梳理+易错总结+单元综合测评满分：100分试卷整洁分：2分（68分）一、填一填。

（每空2分，共24分）1.（2019·辽宁北票市期末）如图所示，观察小圆圈的摆放规律，第一个图中有5个小圆圈，第二个图中有8个小圆圈……第15个图中有（）个小圆圈。

2.通过观察可知，第4个图形中d 的数值为（）。

3.用边长1cm 的正方形纸片，按下面的规律拼成长方形。

（1）用5个正方形拼成的长方形的周长是（）cm 。

（2）用n 个正方形拼成的长方形的周长是（）cm 。

4.==++++++++-11111111112482163264128256（）（）5.按照规律，第6个图形最多有（）个交点,第8个图形最多有个交点。

6.先观察下列图形的规律，再填空。

照这样排下去，第5个图形一共由（）个小三角形组成，第n个图形一共由（）个小三角形组成。

二、选一选。

（将正确答案的字母填在括号里）（18分）1.有一组图，排列规律如下图，第10个图形由( )个组成。

A.45B.55C.602.观察下列图形，则第n个图形中三角形的个数是( )个。

A.4n+4B.4n-4C.4n3.一列数1，2，2，3，3，3，4，4，4，4，…中第34个数为( )。

A.6B.7C.84.一个方阵的最外层每边有9人，这个方阵最外层一共有( )人。

A.36B.32C.285.观察下图：第1个图中有1个正方形，第2个图中共有5个正方形，第3个图中共有14个正方形，按此规律，第5个图中共有( )个正方形。

A.54B.55C.586.张芳从家出发准备去商场买东西，走到商场后，才想起没带钱包，于是回家取钱。

在返回商场的路上碰到好朋友小冬，于是两人在那里聊了一会。

后来，张芳发现时间太晚了，就没去商场，直接回家了。

( )反映了张芳的行程情况。

三、根据图形与数的规律接着画一画，填一填。

（8分）四、下面每个图中涂阴影的小正方形各有多少个？（8分）利用规律直接写一写。

2022年秋人教版数学六年级上册第八单元考试测试卷及部分答案(共五套)

2022年秋人教版数学六年级上册第八单元考试测试卷（一）一、先计算下面各题,再找出规律。

++=+++=++++=二、六(1)班有八名同学进行乒乓球比赛,如果每两名同学之间都要进行一场比赛,一共要比赛多少场?怎样推算呢?从简单的情况开始研究,运用画图法解答:……①1②1+2=3③1+2+3=6④1+2+3+4=10……三、观察图中的点阵图和相应的等式,探究其中的规律,在④和⑤后面的横线上分别写出相应的等式。

……①1=12②1+3=22③1+3+5=32④⑤……四、观察下列图形,按规律把算式补充完整。

………………①1②1+3③4+5④9+7⑤16+⑥25+⑦36+五、观察点阵中的规律,填一填。

………………①1②1+4③1+8④1+12⑤1+⑥1+⑦1+六、如图依次排列着5盏灯,用不同位置上亮灯和灭灯表示一个具体的数(亮灯用□表示,灭灯用■表示)。

请根据下面前四种状况所表示的数,完成下列问题。

写出图⑤表示的数。

在图⑥中画出亮灯和灭灯的状况。

七、把边长为1厘米的正方形纸片,按下面的规律拼成长方形:1.用5个正方形拼成的长方形的周长是多少厘米?2.用m 个正方形拼成的长方形的周长是多少厘米?八、观察点阵与算式的对应规律,并填空。

…………①1②1+4③1+4+4④1+4+4+4⑤……⑥第⑥个点阵图中有多少个点?九、如图是用棋子摆成的图案,摆第1个图案需要7枚棋子,摆第2个图案需要19枚棋子,摆第3个图案需要37枚棋子,按照这样的方式摆下去,则摆第10个图案需要多少枚棋子?…………①6+1=7②6×(1+2)+1=19③6×(1+2+3)+1=37……⑩十、用火柴棒摆出图形。

摆第1个图形要4根火柴棒。

那么摆第5个图形要多少根火柴棒?十一、在圆上画直线,用4条直线最多能将一个圆分成几块?用10条直线呢?………………①1条直线分2块②2条直线分4块③3条直线分7块④……⑩十二、用形如的正方形去框数表里的数,每次框出4个数。

人教版小学六年级数学上册第8单元《数学广角—数与形》单元测试题(含答案)共2套

人教版六年级数学上册《8.数学广角——数与形》单元测试1一、单选题(总分：25分本大题共5小题，共25分)1.(本题5分)如图，小明用3根小棒搭成一个三角形，5根小棒搭成2个三角形，找这样搭5个三角形需要（）根小棒．A.10B.11C.122.(本题5分)按图中的规律接着画下去，第（5）个图形一共有（）个这样的圆点．A.20B.21C.23D.263.(本题5分)在下图中，矩形方框内有（）个三角形A.12B.13C.16D.154.(本题5分)10张照片用图钉像如图那样钉在橱窗里一共要用多少个图钉？（）A.22B.245.(本题5分)如图，有一排间距相同但高度不等的小树，树根成一条直线，树顶也成一条直线，这两条直线成45度角，最高的小树高2.8米，最低的小树高峰1.4米，那么从左向右数第4棵树的高度是（）米．A.2.6B.2.4C.2.2D.2.0二、填空题(总分：40分本大题共8小题，共40分)6.(本题5分)填在下面三个田字格内的数有相同的规律，根据此规律，C=____7.(本题5分)如图，一个大正方形用“+”字形连续均分，所得的小正方形越来越多，依次是4个，7个，10个…第5次均分后所得的小正方形有____个．8.(本题5分)如图，摆1个三角形需要3根小棒，摆2个三角形需要5根小棒，摆3个三角形需要7根小棒…，像这样连续摆10个三角形共需要____根小棒；有37根小棒可以摆____个这样的三角形．9.(本题5分)摆一个正方形需4根小棒，摆两个正方形需7根小棒…．摆n个正方形需____根小棒．10.(本题5分)边长为1厘米的正方体，如图这样层层重叠放置，那么当重叠到第5层时，这个立体图形的表面积是____平方厘米．11.(本题5分)如图所示，原图旋转____次才会第一次出现“”．12.(本题5分)如图，淘气用小棒搭房子，他搭1个图形用了5根小棒，搭2个图形用了9根小棒…，像这样搭第n个图形要用____根小棒．13.(本题5分)第4个点阵共有____个点第5个点阵共有____个点．三、解答题(总分：35分本大题共5小题，共35分)14.(本题7分)下面每行的数字是按一定规律排列下去的，请找出规律填在方框里．15.(本题7分)如图的方式，2008根火柴棒能摆成多少个正方形？16.(本题7分)先画出第五个图形并填空．再想一想：后面的第10个方框里有____个点，第51个方框里有____个点．17.(本题7分)观察下面图中小圆圈的摆放规律，并按照这样的规律继续摆放，第15个图形中小圆圈的个数有多少个？18.(本题7分)观察各题中数的变化规律，再填数．人教版六年级数学上册《8.数学广角——数与形》单元测试2参考答案与试题解析1.【答案】：B;【解析】：解：一个三角形需要3根火柴，2个三角形需要3+2=5根火柴，3个三角形需要3+2×2=7根火柴，…5个三角形需要3+2×（5-1）=11根火柴．答：像这样摆5个同样的三角形需要11根小棒．故选：B．2.【答案】：B;【解析】：解：根据分析可得：第（5）个图形一共有圆点的个数是：1+（5-1）×5=1+20=21（个）故选：B．3.【答案】：C;【解析】：三角形的个数=图形个数×图形个数，那么第四个图形中三角形的个数就是4×4.4.【答案】：A;【解析】：解：10-1=9（张）4+9×2=22（个）故答案选：A．5.【答案】：C;【解析】：解：因为：树根成一条直线，树顶也成一条直线∠A=45°，最高的小树高2.8米，最低的小树高峰1.4米所以AC=2.8米，AB=1.4米，BC=AC-AB=1.4米又因为：这排树的间距相同所以：1.4÷7=0.2（米）0.2×4+1.4=0.8+1.4=2.2（米）答：那么从左向右数第4棵树的高度是2.2米．故选：C．6.【答案】：108;【解析】：解：根据前两个图形的规律可知：A=7，B=9，所以：C=9×（5+7）=9×12=108故答案为：108．7.【答案】：16;【解析】：解：根据题干分析可得：第1次均分后得到的小正方形是3×1+1=4个第2次均分后得到的小正方形是3×2+1=7个第3次均分后得到的小正方形是3×3+1=10个第4次均分后得到的小正方形是3×4+1=13个则第n次均分后得到的小正方形是3n+1个；那么第5次均分后得到的小正方形是3n+1=3×5+1=16（个）答：第5次均分后所得的小正方形有 16个．故答案为：16．8.【答案】：21;18;【解析】：解：结合图形，发现：搭第n个图形，需要3+2（n-1）=2n+1（根）．摆这样的10个小三角形，需要2×10+1=21根有37根小棒，可以摆2n+1=372n=37-12n=36n=18答：摆这样的10个小三角形，需要21根小棒．有37根小棒，可以摆18个这样的小三角形．故答案为：21；18．9.【答案】：3n+1;【解析】：解：第一个正方形由四根火柴摆成，以后加三根就可加一个正方形，摆n个正方形需要3n+1根小棒．故答案为：3n+1．10.【答案】：90;【解析】：解：当重叠到5层时，有1+3+6+10+15=35个正方体，表面积为：（1+2+3+4+5）×6=90（平方厘米）．答：这个立体图形的表面积是90平方厘米．故答案为：90．11.【答案】：6;【解析】：解：根据题干分析可得，第一次凸起指向右，第2次指向右下，第3次指向下，第4次指向左下，第5次指向左，则第6次就出现原图，故答案为：6．12.【答案】：1+4n;【解析】：解：搭一间房用5根小棒，可以写成1+1×4；2间房用9根小棒，可以写成1+2×4；3间房用13根小棒，可以写成1+3×4；…所以搭n间房子需要1+4n根小棒．答：搭n间房子要用1+4n根小棒．故答案为：1+4n．13.【答案】：15;18;【解析】：解：如图把每幅图中的点进行如下划分，则第一幅图中的点数为：3+1×3；第二幅图中点数为：3+2×3；第三幅图中点数为：3+3×3，…由此可得第n幅图中点数为：3+3n，当n=4时，3+3×4=15（个），当n=5时，3+3×5=18（个）；答：第4个点阵中有15个点，第5点阵中有18个点．故答案为：15；18．14.【答案】：解：如图：;【解析】：观察图形可知，每一行的第一个数和最后一个数都是1，其它的数是上面一行中的相邻的两个数的和，由此计算即可填空．15.【答案】：解：根据题干分析可得：摆n个正方形需要4+3（n-1）=3n+1根火柴棒，当3n+1=2008时，3n=2007n=669答：2008根火柴棒能摆成669个正方形．;【解析】：观察图形可知，摆一个正方形需要4根火柴棒，以后每多摆一个，需要3根火柴棒，所以摆n个正方形需要4+3（n-1）=3n+1根火柴棒，据此即可解答问题．16.【答案】：37201;【解析】：解：第五个图形有1+4×4个点，如图：因为第n个图中共有1+4（n-1）个点，所以第10个图中有1+4×（10-1）=37个点，则第51个图共有1+4×（51-1）=201个点．答：后面的第10个方框里有37个点，第51个方框里有201个点．故答案为：37；201．17.【答案】：解：根据图形分析可知：（用s表示图中小黑点的个数）n=1时，s=1；n=2时，s=3=2×1+1；n=3时，s=7=3×2+1；n=4时，s=13=4×3+1；n=5时，s=21=5×4+1；…；第n个图中小黑点的个数为n（n-1）+1．第15个图形中的小黑点个数是15×（15-1）+1=15×14+1=210+1=211．答：第15个图形中小圆圈的个数有211个．;【解析】：经过对一组图形进行分析比较，找出规律，再经过计算得出第n个图形中小黑点的个数，进一步即可求解．18.【答案】：解：13+14-9=18故答案为：;【解析】：由题意可得：每个正方形中对角上的两个数的和分别相等，如5+14=9+10、7+16=11+12，据此即可解答问题．第八单元测试卷2一、选择题。

人教版数学六年级上册第八单元测试试卷(含答案)(1)

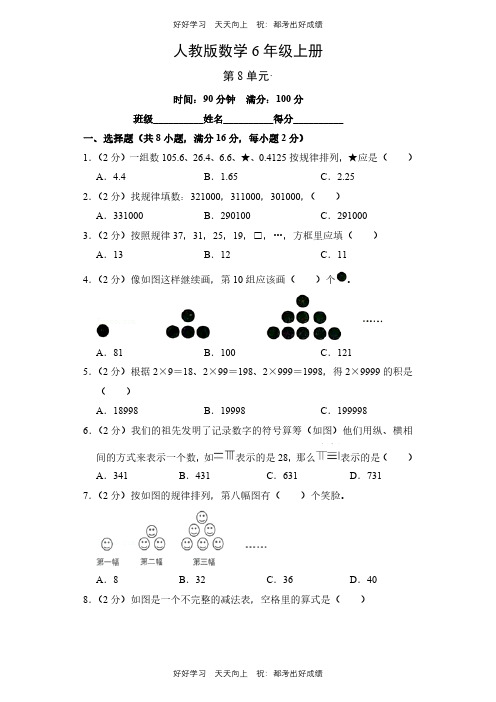
人教版数学6年级上册第8单元·时间：90分钟满分：100分班级__________姓名__________得分__________一、选择题（共8小题，满分16分，每小题2分）1．（2分）一组数105.6、26.4、6.6、★、0.4125按规律排列，★应是（）A．4.4B．1.65C．2.252．（2分）找规律填数：321000，311000，301000，（）A．331000B．290100C．2910003．（2分）按照规律37，31，25，19，□，…，方框里应填（）A．13B．12C．114．（2分）像如图这样继续画，第10组应该画（）个。

A．81B．100C．1215．（2分）根据2×9＝18、2×99＝198、2×999＝1998，得2×9999的积是（）A．18998B．19998C．1999986．（2分）我们的祖先发明了记录数字的符号算筹（如图）他们用纵、横相间的方式来表示一个数，如表示的是28，那么表示的是（）A．341B．431C．631D．731 7．（2分）按如图的规律排列，第八幅图有（）个笑脸。

A．8B．32C．36D．408．（2分）如图是一个不完整的减法表，空格里的算式是（）A．6﹣3B．7﹣3C．8﹣3二、填空题（共8小题，满分16分，每小题2分）9．（2分）如图规律排列第8幅点阵图中有个●，第n幅点阵图中有个●。

10．（2分）找规律，填合适的数。

（1）6、12、、、30、（2）64、、、40、 11．（2分）找规律，“？”代表的数是。

12．（2分）按规律填数。

3、4、、 7、、8、6、 2、 13．（2分）找规律：12345679×9＝11111111112345679×18＝22222222212345679×27＝33333333312345679×36＝ ……12345679× ＝88888888814．（2分）找规律，接着填一填，画一面。

人教版数学六年级上册《第八单元综合测试题》含答案

人教版数学六年级上学期第八单元测试一．选择题(共8小题)1．有一根1m长的木条,第一次锯掉它的,第二次锯掉余下的,第三次锯掉余下的……,第六次锯掉余下的后,这根木条还剩()A．m B．C．m2．,,,,,,这列数的每一项越来越小,越来越接近()A．5B．1C．0D．﹣13．按规律填数：18,9,4.5,2.25,1.125,(),0.28125……A．0.5625B．0.125C．0.65D．0.56354．像如图这样用小棒摆正方形,摆1个正方形需要4根小棒,摆2个正方形需要7根小棒,摆3个正方形主要10根小棒,那么摆n个正方形需要()根小棒．A．3n B．3n+1C．4n D．4n﹣15．下面第3个图形有9个等边三角形,第6个图有()个等边三角形．A．18B．21C．246．下面与1+3+5+7+9+11+7+5+3+1的结果相等的算式是()A．42B．62﹣42C．62+427．按下列算式的规律,第4个算式应该是()A．4+5+6＝15B．4+4+8＝16C．5+5+8＝188．任取一个两位数,如果是双数就除以2；如果是单数就乘3加1,得出结果后,如上反复进行,最后总能得到的结果是()A．1B．9C．7二．填空题(共8小题)9．找规律填一填：81＝9×9,882＝98×9,8883＝987×9…888885＝×9．10．用等腰梯形按下图的规律拼图形．等腰梯形的个数1234……所拼图形的周长581114……5个这样的等腰梯形拼成的图形的周长是,n个这样的等腰梯形拼成的图形的周长是；当拼成的图形的周长是92时,用了个等腰梯形．11．丁丁和当当玩用吸管摆梯形的游戏(如图),照这样摆下去,摆第10个梯形要用吸管根．12．.小军玩抛硬币的游戏,规则是：将一枚硬币抛起,落下后正面朝上就向前走8步,背面朝上就后退6步,小军一共抛了10次硬币,结果向前走了52步,有次反面朝上．13．9作为被除数,13作为除数,那么商的小数点后第200位上的数字是．14．看一看,想一想,填一填．12×8+2＝98123×8+3＝9871234×8+4＝987612345×8+＝123456×8+＝×8+＝15．下面各题中都有一个数不符合规律,把它划出来,并改正．(1)5,10,15,16,25,30．．(2)88,77,66,55,45,33．．(3)13,23,33,43,53,73．．16．有一串数：1、2、2、3、4、1、2、2、3、4、1、2、2、3、4……从左面第一个数起,第2018个数是,前60个数中共有个质数．三．判断题(共5小题)17．摆一个△用了三根小棒,摆用了6根小棒．(判断对错)18．3×4＝12,33×34＝1122,333×334＝111222根据前三题的得数,33333×33334＝11112222．(判断对错)19．2,4,8,14,22,,4420．一个数列为：1,2,3,1,2,3,…按这样的顺序排下去,第20个数是3．(判断对错)21．19.小数点后第80位上的数字是2．．(判断对错)四．应用题(共5小题)22．在计算一个数与15相乘时,有一种简便的算法﹣﹣“加半添0”法．例如,计算24×15,先用24的一半(即12)与24相加,得36；再在36的末尾添一个0,得360．你能用这种方法计算下面各题吗?26×1528×1532×1548×1523．按规律填数：20,40,60,,．24．先观察、分析下面各组小正方体的摆放情况,再填写表格．(每个小正方体的棱长都是1cm)层数12345……小正方体的个数13610……图形的表面积/cm26142436……图形的体积/cm313610……25．杨辉三角,是中国南宋数学家杨辉1261年所著的《详解九章算法》一书中出现的一种几何排列．你能计算图中的杨辉三角中一共有多少个数字吗26．斐波那契数列由十三世纪意大利数学家斐波那契发现．数列中的一系列数字常常被人们称之为神奇数、奇异数．具体数列为1,1,2,3,5,8,13,21,34,…答案与解析一．选择题(共8小题)1．【分析】这是有关分数乘法的应用题,第一次锯掉它的,还剩下原来的(1﹣)；第二次锯掉余下的,第二次还剩下第一次剩下的(1﹣)；第三次锯掉余下的,第三次还剩下第二次剩下的(1﹣)…以此类推,第六次锯掉余下的后,还剩下第五次的(1﹣),然后再进一步解答．【解答】解：1×[(1﹣)×(1﹣)×(1﹣)×…×(1﹣)]＝1×[×××…×]＝1×＝(米)答：这根木条还剩米．故选：A．【点评】此题属于分数乘法应用题,此题关键在于求出最后剩下总数的几分之几．2．【分析】分母越来越大,分数就越来越小,当分母无限大的时候,这个数就无限的接近于0．【解答】解：根据分析可得：,,,,,,这列数的每一项越来越小,越来越接近0；故选：C．【点评】本题考查的是探索规律的知识,找到题目的规律是解答本题的关键．3．【分析】18÷9＝2,9÷4.5＝2,4.5÷2.25＝2,2.5÷1.125＝2,后一个数是前一个数的一半,由此求解．【解答】解：1.125÷2＝0.5625验证：0.5625÷2＝0.28125这列数是：18,9,4.5,2.25,1.125,0.5625,0.28125．故选：A．【点评】关键是根据已知的数得出前后数之间的变化关系的规律,然后再利用这个变化规律再回到问题中去解决问题．4．【分析】根据图示发现：摆1个正方形需要4根小棒,摆2个正方形需要7根小棒,摆3个正方形主要10根小棒,……摆n个正方形需要4+(n﹣1)×3＝(3n+1)根小棒．据此解答．【解答】解：摆1个正方形需要4根小棒摆2个正方形需要7根小棒摆3个正方形主要10根小棒……摆n个正方形需要小棒：4+(n﹣1)×3＝4+3n﹣3＝(3n+1)根答：摆n个正方形需要(3n+1)根小棒．故选：B．【点评】本题考查了图形的变化类问题,主要培养学生的观察能力和总结能力．5．【分析】第一个图形有1个等边三角形,第二个有5个,第三个图形有9个…1＝4×1﹣3、5＝4×2﹣3、9＝4×3﹣3…第n个图形由(4n﹣3)等边三角形,由此即可计算出第6个图形等边三角形的个数．【解答】解：第一个图形有1个等边三角形,1＝4×1﹣3第二个有5个,5＝4×2﹣3第三个图形有9个9＝4×3﹣3…第n个图形由(4n﹣3)等边三角形第6个图形等边三形的个数为：4×6﹣3＝24﹣3＝21(个)答：第6个图形有21个等边三角形．故选：B．【点评】解答此题的关键是根据图形的序号与等边三角形个数之间的关系找出规律,然后再根据规律求出第6个图形中等边三角形的个数．6．【分析】1+3+5+7+9+11+7+5+3+1根据加法结合律分段计算,(1+3+5+7+9+11)+(7+5+3+1)＝36+16,36＝62,16＝42,这样这个算式就等于62+42．【解答】解：1+3+5+7+9+11+7+5+3+1＝(1+3+5+7+9+11)+(7+5+3+1)＝36+16＝62+42故选：C．【点评】一眼即可看出这个算式的和不可能等于42,更不可能是62﹣42,根据排除法,有可能是62+42,看能不能把这个加法算式分段计算,一段是62＝36,一段是42＝16．7．【分析】每个式子的第一个加数和第二个加数相同,比上一个算式的前两个加数都多1,第三个加数比上一个算式的第三个加数多2,据此解答即可．【解答】解：根据分析可得,第4个算式应该是：4+4+8＝16故选：B．【点评】解答此题的关键是观察所给出的算式,找出算式之间数与数的关系,得出规律,再根据规律解决问题．8．【分析】任意写出1个两位数,按照“如果是双数就除以2；如果是单数就乘3加1”,反复计算,直到结果重复出现一个数值,从而解决问题．【解答】解：当这个两位数是18时：18÷2＝99×3+1＝2828÷2＝1414÷2＝77×3+1＝2222÷2＝1111×3+1＝3434÷2＝1717×3+1＝5252÷2＝2626÷2＝1313×3+1＝4040÷2＝2020÷2＝1010÷2＝55×3+1＝1616÷2＝88÷2＝44÷2＝22÷2＝11×3+1＝44÷2＝22÷2＝1；结果是4,2,1循环出现,选项中有1,可以说最后是1．故选：A．【点评】本题是冰雹猜想,又称角谷猜想,是指：一个正整数x,如果是奇数就乘3再加1,如果是偶数就除以偶数因数2ⁿ,这样经过若干个次数,最终回到1．二．填空题(共8小题)9．【分析】根据前三道题的结果可知：乘积末尾的数字与第一个因数的末位数字之和是10,乘积中除末尾的数字其它都是8,8的个数和第一个因数的位数相同,而且第2个因数都是9,第一个因数从9开始依次减少1．【解答】解：根据分析可得：81＝9×9882＝98×98883＝987×9…888885＝98765×9故答案为：98765．【点评】抓住数字特点,找出规律,容易解决问题．10．【分析】根据图示以及所给统计表中的数据发现：1个等腰梯形的周长是：1×3+2＝5；2个等腰梯形的周长为：2×3+2＝8；3个等腰梯形的周长为：3×3+2＝11；……n个等腰梯形的周长为：3n+2．据此解答．【解答】解：1个等腰梯形的周长是：1×3+2＝52个等腰梯形的周长为：2×3+2＝83个等腰梯形的周长为：3×3+2＝11……n个等腰梯形的周长为：3n+2当n＝5时3×5+2＝15+2＝173n+2＝923n＝90n＝30答：5个这样的等腰梯形拼成的图形的周长是17,n个这样的等腰梯形拼成的图形的周长是(3n+2)；当拼成的图形的周长是92时,用了30个等腰梯形．故答案为：17；(3n+2)；30．【点评】本题考查了图形的变化类问题,主要培养学生的观察能力和总结能力．11．【分析】通过分析找到各部分的变化规律：摆1个梯形需要吸管5根；摆2个梯形需要吸管：5+4＝9(根)；摆3个梯形需要吸管：5+4+4＝13(根)……摆n个梯形需要吸管：5+4(n﹣1)＝(5n+1)根．据此解答．【解答】解：根据题干可知,摆1个梯形需要吸管5根摆2个梯形需要吸管：5+4＝9(根)摆3个梯形需要吸管：5+4+4＝13(根)……摆n个梯形需要吸管：5+4(n﹣1)＝(5n+1)根摆10个梯形需要吸管：5×10+1＝51(根)答：摆第10个梯形要用吸管51根．故答案为：51．【点评】主要考查了学生通过特例分析从而归纳总结出一般结论的能力．对于找规律的题目首先应找出哪些部分发生了变化,是按照什么规律变化的．12．【分析】设背面朝上有x次,则正面朝上则有(10﹣x)次,根据题意可得方程：(10﹣x)×15﹣6x＝52,然后解方程求出x的值,进而求出另一个量．【解答】解：设背面朝上有x次,则正面朝上则有(10﹣x)次,(10﹣x)×8﹣6x＝5280﹣8x﹣6x＝5214x＝28x＝2答：硬币背面朝上有2次．故答案为：2．【点评】解答此题的关键是：设出所求的一个量为未知数,进而用未知数表示出另一个量,然后找出数量的间的相等关系式,继而根据关系式,列出方程,解答即可．13．【分析】首先根据小数除法的计算法则,求出9÷13的商,根据商的循环节(即循环周期),然后用200除以循环节的位数,如果能整除,则第200位上的数字是循环节末位上的数字,如果不能整除,就从循环节的首位开始数,余数是几第200位上的数字就是循环节第几位上的数字,据此解答．【解答】解：9÷13＝0.9230,循环节是6位数,200÷6＝33…2,所以商的小数点后第200位上的数字是9．故答案为：9．【点评】此题解答关键是明确：9÷13的商循环节是几位数,然后用200除以循环节的位数,如果能整除,则第200位上的数字是循环节末位上的数字,如果不能整除,就从循环节的首位开始数,余数是几第200位上的数字就是循环节第几位上的数字．14．【分析】每个式子都是,一个因数乘8加一个加数＝结果；先看每个式子的因数,从上到下,位数依次加1,每个数位的数从高低,以1,2,3,4……排列,所以,最后一个式子的因数为1234567；再看加数,从上到下都是1位数,且依次加1,所以后三个式子,从上到下为5,6,7；最后看结果,从上到下,位数依次加1,没个数为从高到低,以9,8,7,6……倒叙排列,所以后三个式子的结果从上到下,98765,987654,9876543．以此作答．【解答】解：由分析可知：12345×8+5＝98765；123456×8+6＝987654；1234567×8+7＝9876543．故答案为：5,98765,6,987654,1234567,7,9876543．【点评】本题主要考查“式”的规律,需要学生具备较好的数感．15．【分析】(1)观察各数,发现除了16,其他数都是5的倍数；(2)观察各数,发现除了45,其他数都是11的倍数；(3)观察各数,前面5个数,前后两个数之差为10,只有73和53的差为20．【解答】解：(1)16是不符合规律的数,每个数等于前一个数加5,故16所在位置的数应该是15+5＝20；(2)45是不符合规律的数,每个数等于前一个数减11,故45所在位置的数应该是55﹣11＝44；(3)73是不符合规律的数,每个数等于前一个数加10,故73所在位置的数应该是53+10＝63．故答案为：20,44,63．【点评】本题主要考查数列中数的规律,需要具备较好的数感．16．【分析】观察这串数,发现循环的数是组1、2、2、3、4,共5个数．求第2018个数,用2018除以5求余数即可；求前60个数有几个质数,先求出有几组数,再乘每组数中质数的个数．【解答】解：2018÷5＝403……3,所以第2018个数就是数组中第3个数2；60÷5＝12(组)每组数中有3个质数,12×3＝36(个)答：第2018个数是2,前60个数中共有36个质数．故答案为：2,36．【点评】本题主要考查数列中的规律,需要具备良好的数感,准确找出循环的数组是本题解题的关键．三．判断题(共5小题)17．【分析】摆一个三角形用3根小棒,摆2个三角形用5根小棒,摆3个三角形用7根小棒…每增加一个三角形就会增加2根小棒,所以小棒的根数S与三角形的个数n之间的关系是：S＝3+(n﹣1)×2；由此求解．【解答】解：3+(n﹣1)×2＝3+1×2＝5所以题干的说法是错误的．故答案为：×．【点评】对于找规律的题目首先应找出哪些部分发生了变化,是按照什么规律变化的,通过分析找到各部分的变化规律后直接利用规律求解．18．【分析】根据3×4＝12,33×34＝1122,333×334＝111222,可得规律是：积的各位数字是由1和2组成,1在2的前面；因数的位数都相同,积中1和2的个数等于其中一个因数的位数；然后据此规律解答即可．【解答】解：根据分析可得：33333×33334＝1111122222；所以,原题说法错误．故答案为：×．【点评】本题关键是找到积的规律和积与因数的位数的关系,然后再利用这个规律去解答问题．19．【分析】观察给出的数知道,4﹣2＝2,8﹣4＝4,14﹣8＝6,22﹣14＝8,…,从第二个数起,每一个数是它前面的数加2、4、6、8、10、…所得,由此得出答案．【解答】解：根据分析可得,22+10＝32即2,4,8,14,22,32,44．故答案为：32．【点评】关键是根据已知的数得出前后数之间的变化关系和规律,然后再利用这个变化规律再回到问题中去解决问题．20．【分析】根据对数列的观察发现每3个一组(1,2,3),每组的排列都是一样的,找出第20个数是那组中的第几个既可以找到答案．【解答】解：20÷3＝6(组)…2(个)每组中的第2个是2,所以第20个数是2．故答案为：×．【点评】找出数字排列的规律,再找出第几个数是第几组中的第几个,就可以判断出它是几．21．【分析】一个循环小数,找出循环是从小数点后第几位开始的,循环节有几位,再求80里面有多少这样的位数,进而求解．【解答】解：19.可以看出：循环从小数点后第一位就开始了,循环节是325,共3位；80÷3＝26…2,那么第80位的数字就是2．故答案为：√．【点评】本题是把循环节看成一个整体,求出80里面有多少个这样的整体,再由余数判断数字是几．四．应用题(共5小题)22．【分析】根据巧算的方法：“加半添0”法解答即可．【解答】解：26÷2+26＝39所以26×15＝39028÷2+28＝42所以28×15＝42032÷2+32＝48所以32×15＝48048÷2+48＝72所以48×15＝720【点评】解答此题的关键是找出算式之间数与数的关系,得出规律,再根据规律解决问题．23．【分析】40﹣20＝20,60﹣40＝20,规律：依次增加20；据此解答即可．【解答】解：60+20＝8080+20＝100所以20,40,60,80,100．故答案为：80；100．【点评】通过观察,分析、归纳并发现其中的规律,并应用发现的规律解决问题是应该具备的基本能力．24．【分析】(1)从上往下数出小正方体的个数,相加即可求解；(2)观察发现,每个小正方体的面积都是1×1＝1平方厘米,第1个图形时,表面积是6×1个面的面积；第2个图形时,小正方体有6×(1+2)＝3个,而图形中的表面积＝6×3﹣4×1＝14个面的面积；第3个图形时,小正方体有6×(1+2+3)个,而图形中的表面积＝6×6﹣4×(1+2)＝24个面的面积；第4个图形时,小正方体有6×(1+2+3+4)个,而图形中的表面积＝6×10﹣4×(1+2+3)＝36个面的面积；第5个图形时,小正方体有6×(1+2++3+4+5)个,而图形中的表面积＝6×15﹣4×(1+2+3+4)＝50个面的面积；(3)从上往下数出小正方体的个数,相加即可求解,观察发现,第5个图形时,体积＝1+2+3+4+5＝15个小正方体的体积．【解答】解：层数12345……小正方体的个数1361015……图形的表面积/cm2614243650……图形的体积/cm31361015……【点评】本题主要考查不规则立体图形的表面积,找出规律是解答本题的关键．25．【分析】经过观察发现,这些数字组成的三角形是等腰三角形,两腰上的数都是1,第1行有1个数字,第2行有2个数字,第,3行有3个数字,…,一共10行,有1+2+3+4+5+6+7+8+9+10＝55(个)数字,据此解答即可．【解答】解：根据分析可知：1+2+3+4+5+6+7+8+9+10＝55(个)答：图中的杨辉三角中一共有55个数字．【点评】本题考查了数与形结合的变化规律,主要培养学生的观察能力和总结能力．26．【分析】观察数列的奇偶性发现：第1、2个数是奇数,第3个数是偶数；第4、5个数是奇数,第6个数是偶数……,每三个数看成一组,每组的前两个数是奇数,第三个数是偶数,用100除以3,求出商和余数,再根据余数进行判断,由此求解．【解答】解：100÷3＝33 (1)余数是1,所以第100个数是第34个循环的第1个数,是奇数．答：第100个数是奇数．【点评】解决这类问题关键是把重复出现的部分看成一组,根据除法的意义,求出总数量里面有多少个这样的一组,还余几,然后根据余数进行推算．。

人教版数学六年级上册第八单元综合测试卷(附答案)

人教版数学六年级上册第八单元测试题(含答案)

人教版数学六年级上册第八单元测试(附答案)

2022年新人教版小学六年级数学上册第八单元学习质量检测卷(附参考答案)

六年级上册数学第八单元练习卷含答案(8.数与形)新人教版

人教版数学六年级上册第八单元测试题(含答案)

人教版小学数学六年级上册8单元测试卷(含答案及周测培优)

人教版六年级数学上册第八单元数与形测试题(附答案)

人教版新教材小学数学6年级上册第7、8单元测试卷-1附答案

人教版数学六年级上册《第八单元综合检测》含答案

六年级上册数学单元测试- 第八单元 数学广角-数与形测试卷 人教版(含解析)

人教版六年级上册数学第7、8单元综合测试卷(含答案)

人教版六年级数学上册第8单元综合检测卷 附答案

2022年秋人教版数学六年级上册第八单元考试测试卷及部分答案(共五套)

人教版小学六年级数学上册第8单元《数学广角—数与形》单元测试题(含答案)共2套

人教版数学六年级上册第八单元测试试卷(含答案)(1)

人教版数学六年级上册《第八单元综合测试题》含答案

六年级上册数学单元测试- 第八单元数学广角-数与形测试卷人教版(含解析)

人教版六年级数学上册第8单元综合检测卷附答案