六同第三讲直线型面积计算

合集下载

六年级奥数几何;第3讲;直线型面积_三_;教师版

第三讲直线型面积（三）1. 相似模型的熟练运用；2. 燕尾定理模型的熟练运用.一、相似三角形性质(平行线分线段成比例)相交线段AD 和AE 被平行线段BC 和DE 所截，得到的三角形ABC 和ADE 形状完全相似．所谓“形状完全相似”的含义是：两个三角形的对应角相等，对应边成比例．这种关系称为“相似”，相似三角形对应边的比例关系在解几何问题的时候非常有用，要多加练习．（左边是金字塔模型，右边是沙漏模型）ADAB=AE AC=DE BC=AG AFE DAG G E D BA相似三角形面积之比等于对应边长之比的平方：22ABC ADE S AB S AD ΔΔ=. 在实际运用的时候，相似的三角形往往作为图形的一部分，有时还要经过翻转、平移等变化．二、燕尾定理：在三角形ABC 中，AD ，BE ，CF 相交于同一点O ，那么::ABO ACO S S BD DC ΔΔ=．具体关系如下：S ΔAGC :S ΔBGC =S ΔAGD :S ΔBGD =AD :DBS ΔAGB :S ΔCGB =S ΔAGF :S ΔCGF =AF :FC S ΔABG :S ΔAGC =S ΔBGE :S ΔCGE =BE :EC GFE DC B A上述定理给出了一个新的转化面积比与线段比的手段，因为ABO Δ和ACO Δ的形状很象燕子的尾巴，所以这个定理被称为燕尾定理．该定理在许多几何题目中都有着广泛的运用．板块一：相似模型【例 1】如图，已知在平行四边形ABCD 中，16AB =，10AD =，4BE =，那么FC 的长度是多少？FEDCBA【解析】图中有一个沙漏，也有金字塔，但我们用沙漏就能解决问题，因为AB 平行于CD ，所以::4:161:4BF FC BE CD ===，所以410814FC =×=+．【巩固】如图，DE 平行BC ，若:2:3AD DB =，那么:ADE ECB S S =△△________．A ED CB【解析】根据金字塔模型:::2:(23)2:5AD AB AE AC DE BC ===+=，22:2:54:25ADE ABC S S ==△△，设4ADE S =△份，则25ABC S =△份，255315BEC S =÷×=△份，所以:4:15ADE ECB S S =△△．【例 2】如图， ABC △中，DE ，FG ，BC 互相平行，AD DF FB ==，则::ADE DEGF FGCB S S S =△四边形四边形．EGF A D CB【解析】设1ADE S =△份，根据面积比等于相似比的平方，所以22::1:4ADE AFG S S AD AF ==△△，22::1:9ADE ABC S S AD AB ==△△，因此4AFG S =△份，9ABC S =△份，进而有3DEGF S =四边形份，5FGCB S =四边形份，所以::1:3:5ADE DEGF FGCB S S S =△四边形四边形【巩固】如图， ABC △中，DE ，FG ，MN ，PQ ，BC 互相平行，AD DF FM MP PB ====，则::::ADE DEGF FGNM MNQP PQCB S S S S S =△四边形四边形四边形四边形．Q E GNMF PA D CB【解析】设1ADE S =△份，22::1:4ADE AFG S S AD AF ==△△，因此4AFGS =△份，进而有3DEGF S =四边形份，同理有5FGNM S =四边形份，7MNQP S =四边形份，9PQCB S =四边形份．所以有::::1:3:5:7:9ADE DEGF FGNM MNQP PQCB S S S S S =△四边形四边形四边形四边形【总结】继续拓展，我们得到一个规律：平行线等分线段后，所分出来的图形的面积成等差数列．【例 3】已知正方形ABCD ，过C 的直线分别交AB 、AD 的延长线于点E 、F ，且10cm AE =，15cm AF =，求正方形ABCD 的边长．FAEDCB【解析】方法一：本题有两个金字塔模型，根据这两个模型有::BC AF CE EF =，::DC AE CF EF =，设正方形的边长为cm x ，所以有1BC DC CE CF AF AE EF EF +=+=，即11510x x+=，解得6x =，所以正方形的边长为6cm ．方法二：或根据一个金字塔列方程即151015x x−=，解得6x =【例 4】如图，三角形ABC 是一块锐角三角形余料，边120BC =毫米，高80AD =毫米，要把它加工成正方形零件，使正方形的一边在BC 上，其余两个顶点分别在AB 、AC 上，这个正方形零件的边长是多少？GNPAD CB【解析】观察图中有金字塔模型5个，用与已知边有关系的两个金字塔模型，所以有PN AP BC AB =，PH BPAD AB=，设正方形的边长为x 毫米，PN PHBC AD +=1AP BP AB AB+=，即112080x x +=，解得48x =，即正方形的边长为48毫米．【巩固】如图，在ABC △中，有长方形DEFG ，G 、F 在BC 上，D 、E 分别在AB 、AC 上，AH 是ABC △ 边BC 的高，交DE 于M ，:1:2DG DE =，12BC =厘米，8AH =厘米，求长方形的长和宽．E H GMFAD CB【解析】观察图中有金字塔模型5个，用与已知边有关系的两个金字塔模型，所以DE AD BC AB =，DG BDAH AB=，所以有1DE DG AD BD BC AH AB AB +=+=，设DG x =，则2DE x =，所以有21128x x +=，解得247x =，4827x =，因此长方形的长和宽分别是487厘米，247厘米．【例 5】在图中的正方形中，A ，B ，C 分别是所在边的中点，CDO +的面积是ABO +面积的几倍？ABCDO EFAB CD O【解析】连接BC ，易知OA ∥EF ，根据相似三角形性质，可知::OB OD AE AD =，且::1:2OA BE DA DE ==，所以CDO +的面积等于CBO +的面积；由1124OA BE AC ==可得3CO OA =，所以3CDO CBO ABO S S S ==+++，即CDO +的面积是ABO +面积的3倍．【例 6】图中ABCD 是边长为12cm 的正方形，从G 到正方形顶点C 、D 连成一个三角形，已知这个三角形在AB 上截得的EF 长度为4cm ，那么三角形GDC 的面积是多少？ABCD E FGNABCDE FG【解析】根据题中条件，可以直接判断出EF 与DC 平行，从而三角形GEF 与三角形GDC 相似，这样，就可以采用相似三角形性质来解决问题．做GM 垂直DC 于M ，交AB 于N ．因为EF ∥DC ，所以三角形GEF 与三角形GDC 相似，且相似比为:4:121:3EF DC ==，所以:1:3GN GM =，又因为12MN GM GN =−=，所以()18GM cm =，所以三角形GDC 的面积为()2112181082cm ××=．【例 7】如图，将一个边长为2的正方形两边长分别延长1和3，割出图中的阴影部分，求阴影部分的面积是多少？B MNE【解析】根据相似三角形的对应边成比例有：31223NF =++；12312EM =++，则59NF =，53EM =， 19512225330S ⎛⎞⎛⎞=×−×−=⎜⎟⎜⎟⎝⎠⎝⎠阴【例 8】如右图，长方形ABCD 中，16EF =，9FG =，求AG 的长．DABC EFG【解析】因为DA ∥BE ，根据相似三角形性质知DG AGGB GE=，又因为DF ∥AB ，DG FGGB GA=，所以AG FGGE GA=，即2225922515AG GE FG =⋅=×==，所以15AG =．【例 9】 (第21届迎春杯试题)如图，已知正方形ABCD 的边长为4，F 是BC 边的中点，E 是DC 边上的点，且:1:3DE EC =，AF 与BE 相交于点G ，求ABG S △GFAEDC BM GFAEDCB GFAEDCB【解析】方法一：连接AE ，延长AF ，DC 两条线交于点M ，构造出两个沙漏，所以有::1:1AB CM BF FC ==，因此4CM =，根据题意有3CE =，再根据另一个沙漏有::4:7GB GE AB EM ==，所以4432(442)471111ABG ABE S S ==××÷=+△△．方法二：连接,AE EF ，分别求4224ABF S =×÷=△，4441232247AEF S =×−×÷−×÷−=△，根据蝴蝶定理::4:7ABF AEF S S BG GE ==△△，所以4432(442)471111ABG ABE S S ==××÷=+△△．【例 10】已知长方形ABCD 的面积为70厘米，E 是AD 的中点，F 、G 是BC 边上的三等分点，求阴影EHO △的面积是多少厘米？HO DCBAABC DO H【解析】因为E 是AD 的中点，F 、G 是BC 边上的三等分点，由此可以说明如果把长方形的长分成6份的话，那么3ED AD ==份、2BF FG GC ===份，大家能在图形中找到沙漏EOD △和BOG △：有34ED BG ∶=∶，所以34OD BO =∶∶，相当于把BD 分成(34+)7份，同理也可以在图中在次找到沙漏：EHD △和BHF △也是沙漏，32ED BF =∶∶，由此可以推出：32HD BH =∶∶, 相当于把BD 分成(32+)5份，那么我们就可以把BD 分成35份(5和7的最小公倍数)其中OD 占15份，BH 占14份，HO 占6份，连接EB 则可知BED △的面积为357042÷=，在BD 为底的三角形中HO 占6份，则面积为：3563235×=(平方厘米).【例 11】已知三角形ABC 的面积为a ，:2:1AF FC =，E 是BD 的中点，且EF ∥BC ，交CD 于G ，求阴影部分的面积．D E GF【解析】已知:2:1AF FC =，且EF ∥BC ，利用相似三角形性质可知::2:3EF BC AF AC ==，所以23EF BC =，且:4:9AEF ABC S S =++．又因为E 是BD 的中点，所以EG 是三角形DBC 的中位线，那么12EG BC =，12::3:423EG EF ==，所以:1:4GF EF =，可得:1:8CFG AFE S S =++，所以:1:18CFG ABC S S =++，那么18CFG aS =+．【例 12】如图，长方形ABCD 中，E 为AD 的中点，AF 与BE 、BD 分别交于G 、H ，OE 垂直AD 于E ，交AF 于O ，已知5cm AH =，3cm HF =，求AG ．ABCDEF GHO【解析】由于AB ∥DF ，利用相似三角形性质可以得到::5:3AB DF AH HF ==，又因为E 为AD 中点，那么有:1:2OE FD =，所以3:5:10:32AB OE ==，利用相似三角形性质可以得到::10:3AG GO AB OE ==，而()()11534cm 22AO AF ==×+=，所以()10404cm 1313AG =×=．【例 13】 (2008年第十二届香港保良局小学数学世界邀请赛(队际赛))如图，ABCD 为正方形，1cm AM NB DE FC ====且2cm MN =，请问四边形PQRS 的面积为多少？SR CDAQ FPSR CAQFP【解析】 (法1)由//AB CD ，有MP PC MN DC =，所以2PC PM =，又MQ MBQC EC=，所以 12MQ QC MC ==，所以111236PQ MC MC MC =−=，所以SPQR S 占AMCF S 的16，所以121(112)63SPQR S =××++=2(cm )．(法2)如图，连结AE ，则14482ABE S Δ=××=(2cm )，而RB ER AB EF =，所以2RB ABEF EF ==，22168333ABR ABE S S ΔΔ==×=(2cm )．而1134322MBQ ANS S S ΔΔ==×××=(2cm )，因为MN MPDC PC =，所以13MP MC =，则11424233MNP S Δ=×××=(2cm )，阴影部分面积等于164233333ABR ANS MBQ MNP S S S S ΔΔΔΔ−−+=−−+=(2cm )．板块二、燕尾模型【例 14】如右图，三角形ABC 中，:4:9BD DC =，:4:3CE EA =，求:AF FB ．O F EDCBA【解析】根据燕尾定理得::4:912:27AOB AOC S S BD CD ===△△ ::3:412:16AOB BOC S S AE CE ===△△（都有AOB △的面积要统一，所以找最小公倍数）所以:27:16:AOC BOC S S AF FB ==△△【点评】本题关键是把AOB △的面积统一，这种找最小公倍数的方法，在我们用比例解题中屡见不鲜，如果能掌握它的转化本质，我们就能达到解奥数题四两拨千斤的巨大力量！【巩固】如图，:2:3BD DC =,:5:3AE CE =,则:AF BF =GF EDCBA【解析】根据燕尾定理有:2:310:15ABG ACG S S ==△△,:5:310:6ABG BCGS S ==△△,所以:15:65:2:ACG BCG S S AF BF ===△△【例 15】 (2009年第七届希望杯五年级一试试题）如图，三角形ABC 的面积是1，E 是AC 的中点，点D在BC 上，且:1:2BD DC =，AD 与BE 交于点F ．则四边形DFEC 的面积等于．FED CBA33321F E DC BAABCDEF【解析】方法一：连接CF ，根据燕尾定理，12ABF ACF S BD S DC ==△△，1ABF CBF S AES EC==△△,设1BDF S =△份，则2DCF S =△份，3ABF S =△份，3AEF EFC S S ==△△份，如图所标所以551212DCEF ABC S S ==△方法二：连接DE ，由题目条件可得到1133ABD ABC S S ==△△，11212233ADE ADC ABC S S S ==×=△△△，所以11ABD ADE S BF FE S ==△△，111111122323212DEF DEB BEC ABC S S S S =×=××=×××=△△△△，而211323CDE ABC S S =××=△△．所以则四边形DFEC 的面积等于512．【巩固】如图，三角形ABC 的面积是2200cm ，E 在AC 上，点D 在BC 上，且:3:5AE EC =,:2:3BD DC =，AD 与BE 交于点F ．则四边形DFEC 的面积等于．FED CBAF EDCBA【解析】连接CF ，根据燕尾定理，2639ABF ACF S BD S DC ===△△，36510ABF CBF S AE S EC ===△△,设6ABF S =△份，则9ACF S =△份,10BCF S =△份，5459358EFC S =×=+△份，310623CDF S =×=+△份，所以24545200(6910)(6)8(6)93(cm )88DCFE S =÷++×+=×+=【巩固】如图，E 在AC 上，D 在BC 上，且:2:3AE EC =,:1:2BD DC =，AD 与BE 交于点F ．四边形DFEC 的面积等于222cm ，则三角形ABC 的面积．A BCDE FA BCDEF 2.41.62A BC DE F 12【解析】连接CF ,根据燕尾定理，12ABF ACF S BD S DC ==△△，23ABF CBF S AE S EC ==△△, 设1BDF S =△份，则2DCF S =△份，2ABF S =△份，4AFC S =△份，24 1.623AEF S =×=+△ 份,34 2.423EFC S =×=+△份,如图所标,所以2 2.4 4.4EFDC S =+=份,2349ABC S =++=△份所以222 4.4945(cm )ABC S =÷×=△【巩固】如图，长方形ABCD 的面积是2平方厘米，2EC DE =，F 是DG 的中点．阴影部分的面积是多少平方厘米?FE D CBA33FE D CBA213【解析】设1DEF S =△份，则根据燕尾定理其他面积如图所示551212BCD S S ==△阴影平方厘米.【例 16】 ABCD 是边长为12厘米的正方形，E 、F 分别是AB 、BC 边的中点，AF 与CE 交于G ，则四边形AGCD 的面积是_________平方厘米．GFE DCGFED CA【解析】连接AC 、GB ，设1AGC S =△份，根据燕尾定理得1AGBS =△份，1BGC S =△份，则11126S =++×=正方形（）份，314ADCG S =+=份，所以22126496(cm )ADCG S =÷×=【例 17】如图，正方形ABCD 的面积是120平方厘米，E 是AB 的中点，F 是BC 的中点，四边形BGHF的面积是_____平方厘米．HGEDCB AHGEDCB A【解析】连接BH ,根据沙漏模型得:1:2BG GD =,设1BHC S =△份，根据燕尾定理2CHD S =△份，2BHD S =△份，因此122)210S =++×=正方形（份，127236BFHG S =+=，所以712010146BFHG S =÷×=(平方厘米).【例 18】如图所示，在ABC △中，:3:1BE EC =，D 是AE 的中点，那么:AF FC = ．FE D C BAFE DCB A【解析】连接CD ．由于:1:1ABD BED S S =△△，:3:4BED BCD S S =△△，所以:3:4ABD BCD S S =△△，根据燕尾定理，::3:4ABD BCD AF FC S S ==△△．【巩固】在ABC Δ中，:3:2BD DC =， :3:1AE EC =，求:OB OE =？A BCDE OABCDE O【解析】连接OC ．因为:3:2BD DC =，根据燕尾定理，::3:2AOB AOC S S BD BC ΔΔ==，即32AOB AOC S S ΔΔ=；又:3:1AE EC =，所以43AOC AOE S S ΔΔ=．则3342223AOB AOC AOE AOE S S S S ΔΔΔΔ==×=，所以::2:1AOB AOE OB OE S S ΔΔ==．【例 19】 (2008年“学而思杯”六年级数学试题)如右图，三角形ABC 中，:::3:2AF FB BD DC CE AE ===，且三角形ABC 的面积是1，则三角形ABE 的面积为______，三角形AGE 的面积为________，三角形GHI 的面积为______．I HGFEDC BAI HG FEDCBA【分析】连接AH 、BI 、CG ．由于:3:2CE AE =，所以25AE AC =，故2255ABE ABC S S ΔΔ==；根据燕尾定理，::2:3ACG ABG S S CD BD ΔΔ==，::3:2BCG ABG S S CE EA ΔΔ==，所以::4:6:9ACG ABG BCG S S S ΔΔΔ=，则419ACG S Δ=，919BCG S Δ=；那么2248551995AGE AGC S S ΔΔ==×=；同样分析可得919ACH S Δ=，则::4:9ACG ACH EG EH S S ΔΔ==，::4:19ACG ACB EG EB S S ΔΔ==，所以::4:5:10EG GH HB =，同样分析可得::10:5:4AG GI ID =，所以5521101055BIE BAE S S ΔΔ==×=，55111919519GHI BIE S S ΔΔ==×=．【巩固】(2009年第七届“走进美妙的数学花园”初赛六年级)如图，ABC Δ中2BD DA =，2CE EB =，2AF FC =，那么ABC Δ的面积是阴影三角形面积的倍．BCDFGHIIHGFDCB【分析】如图，连接AI ．根据燕尾定理，::2:1BCI ACI S S BD AD ΔΔ==，::1:2BCI ABI S S CF AF ΔΔ==，所以，::1:2:4ACI BCI ABI S S S ΔΔΔ=，那么，221247BCI ABC ABC S S S ΔΔΔ==++．同理可知ACG Δ和ABH Δ的面积也都等于ABC Δ面积的27，所以阴影三角形的面积等于ABC Δ面积的211377−×=，所以ABC Δ的面积是阴影三角形面积的7倍．【例 20】如图，三角形ABC 被分成6个三角形，已知其中4个三角形的面积，问三角形ABC 的面积是多少?35304084O FED CBA【解析】设BOF S x =△，由题意知:4:3BD DC =根据燕尾定理,得::4:3ABO ACO BDO CDO S S S S ==△△△△,所以33(84)6344ACO S x x =×+=+△，再根据::ABO BCO AOE COE S S S S =△△△△，列方程3(84):(4030)(6335):354x x ++=+−解得56x =:35(5684):(4030)AOE S =++△,所以70AOE S =△所以三角形ABC 的面积是844030355670315+++++=【巩固】(101中入学考题)一块三角形草坪前，工人王师傅正在用剪草机剪草坪．一看到小灵通，王师傅热情地打招呼，说：“小灵通，听说你很会动脑筋，我也想问问你，这块草坪我把它分成东、西、南、北四部分(如图).修剪西部、东部、南部各需10分钟、16分钟、20分钟，请你想一想修剪北部需要多少分钟？”162010y x FED BA【分析】如右图所示，将北部分分成两个三角形，并标上字母．即有(10):20:16(16):20:10x y y x +=⎧⎨+=⎩，即有5404216y x x y =+⎧⎨=+⎩，解得2024x y =⎧⎨=⎩所以修剪北部草坪需要202444+=分钟.【例 21】如右图，ABC △中，G 是AC 的中点，D 、E 、F 是BC 边上的四等分点，AD 与BG 交于M ，AF 与BG 交于N ，已知ABM △的面积比四边形FCGN 的面积大7.2平方厘米，则ABC △的面积是多少平方厘米？N M GA BCD EFNMGA BCD EF【解析】连接CM 、CN ．根据燕尾定理，::1:1ABM CBM S S AG GC ==△△，::1:3ABM ACM S S BD CD ==△△，所以15ABM ABC S S =△△；再根据燕尾定理，::1:1ABN CBN S S AG GC ==△△，所以::4:3ABN FBN CBN FBN S S S S ==△△△△，所以:4:3AN NF =，那么1422437ANG AFC S S =×=+△△，所以2515177428FCGN AFC ABC ABC S S S S ⎛⎞=−=×=⎜⎟⎝⎠△△△．根据题意，有157.2528ABCABC S S −=△△，可得336ABC S =△(平方厘米)【巩固】（2007年四中分班考试题)如图，ABC Δ中，点D 是边AC 的中点，点E 、F 是边BC 的三等分点，若ABC Δ的面积为1，那么四边形CDMF 的面积是_________．FABCDEM NF ABC DEMN【解析】由于点D 是边AC 的中点，点E 、F 是边BC 的三等分点，如果能求出BN 、NM 、MD 三段的比，那么所分成的六小块的面积都可以求出来，其中当然也包括四边形CDMF 的面积．连接CM 、CN ．根据燕尾定理，::2:1ABM ACM S S BF CF ΔΔ==，而2ACM ADM S S ΔΔ=，所以24ABM ACM ADM S S S ΔΔΔ==，那么4BM DM =，即45BM BD =．那么421453215BMF BCD BM BF S S BD BC ΔΔ=××=××=，14721530CDMF S =−=四边形．另解：得出24ABM ACM ADM S S S ΔΔΔ==后，可得111155210ADM ABD S S ΔΔ==×=，则11731030ACF ADM CDMF S S S ΔΔ=−=−=四边形．【例 22】如图，三角形ABC 的面积是1，BD DE EC ==，CF FG GA ==，三角形ABC 被分成9部分，请写出这9部分的面积各是多少?GFE D CBAN MQPGF EDCBA【解析】设BG 与AD 交于点P ，BG 与AE 交于点Q ，BF 与AD 交于点M ，BF 与AE 交于点N ．连接CP ，CQ ，CM ，CN ．根据燕尾定理，::1:2ABP CBP S S AG GC ==△△，::1:2ABP ACP S S BD CD ==△△，设1ABP S =△(份)，则1225ABC S =++=△(份)，所以15ABP S =△同理可得，27ABQ S =△,12ABN S =△,而13ABG S =△，所以2137535APQ S =−=△，1213721AQG S =−=△．同理，335BPM S =△121BDM S =△,所以1239273570PQMN S =−−=四边形，139********MNED S =−−=四边形,1151321426NFCE S =−−=四边形,1115321642GFNQ S =−−=四边形【巩固】如图，ABC Δ的面积为1，点D 、E 是BC 边的三等分点，点F 、G 是AC 边的三等分点，那么四边形JKIH 的面积是多少？K JI HABC D EF GKJI HA BCD EFG【解析】连接CK 、CI 、CJ ．根据燕尾定理，::1:2ACK ABK S S CD BD ΔΔ==，::1:2ABK CBK S S AG CG ΔΔ==，所以::1:2:4ACK ABK CBK S S S ΔΔΔ=，那么111247ACK S Δ==++，11321AGK ACK S S ΔΔ==．类似分析可得215AGI S Δ=．又::2:1ABJ CBJ S S AF CF ΔΔ==，::2:1ABJ ACJ S S BD CD ΔΔ==，可得14ACJ S Δ=．那么，111742184CGKJ S =−=．根据对称性，可知四边形CEHJ 的面积也为1784，那么四边形JKIH 周围的图形的面积之和为172161228415370CGKJ AGI ABE S S S ΔΔ×++=×++=，所以四边形JKIH 的面积为61917070−=．【例 23】如图，面积为l 的三角形ABC 中，D 、E 、F 、G 、H 、I 分别是AB 、BC 、CA 的三等分点,求阴影部分面积.IHED CBAINMQPHED CBA【解析】三角形在开会，那么就好好利用三角形中最好用的比例和燕尾定理吧！令BI 与CD 的交点为M ，AF 与CD 的交点为N ，BI 与AF 的交点为P ,BI 与CE 的交点为Q ,连接AM 、BN 、CP⑴求ADMI S 四边形：在ABC △中，根据燕尾定理，::1:2ABM CBM S S AI CI ==△△::1:2ACM CBM S S AD BD ==△△设1ABM S =△(份)，则2CBM S =△(份),1ACM S =△(份),4ABC S =△(份),所以14ABM ACM ABC S S S ==△△△，所以11312ADM ABM ABC S S S ==△△△,112AIM ABC S S =△△,所以111()12126ABC ABC ADMI S S S =+=△△四边形,同理可得另外两个顶点的四边形面积也分别是ABC △面积的16⑵求DNPQE S 五边形：在ABC △中，根据燕尾定理::1:2ABN ACN S S BF CF ==△△::1:2ACN BCN S S AD BD ==△△,所以111133721ADN ABN ABC ABC S S S S ==×=△△△△,同理121BEQ ABC S S =△△在ABC △中，根据燕尾定理::1:2ABP ACP S S BF CF ==△△,::1:2ABP CBP S S AI CI ==△△ 所以15ABP ABC S S =△△所以1111152121105ABP ADN BEP ABC ABC DNPQE S S S S S S ⎛⎞=−−=−−=⎜⎟⎝⎠△△△△△五边形同理另外两个五边形面积是ABC △面积的11105所以11113133610570S =−×−×=阴影【例 24】如图，面积为l 的三角形ABC 中，D 、E 、F 、G 、H 、I 分别是AB 、BC 、CA 的三等分点,求中心六边形面积.IGHED CBAS RI NM QPGHEDCBA【解析】设深黑色六个三角形的顶点分别为N 、R 、P 、S 、M 、Q ，连接CR在ABC △中根据燕尾定理，::.2:1ABR ACR S S BG CG ==△△,::1:2ABR CBR S S AI CI ==△△所以27ABR ABC S S =△△,同理27ACS ABC S S =△△,27CQB ABC S S =△△所以222117777RQS S =−−−=△同理17MNP S =△ 根据容斥原理，和上题结果11131777010S =+−=六边形【例 25】已知四边形ABCD ，CHFG 为正方形，:1:8S S =乙甲，a 与b 是两个正方形的边长，求:?a b =乙甲baOEDC乙甲baMGOED C 【解析】观察图形，感觉阴影部分像蝴蝶定理，但是细细分析发现用蝴蝶定理无法继续往下走，注意到题目条件中给出了两个正方形的边长，有边长就可以利用比例，再发现在连接辅助线后可以利用燕尾，那么我们就用燕尾定理来求解连接EO 、AF ，根据燕尾定理：::AOE AOF S S a b =△△，::AOF EOF S S a b =△△ 所以 22::AOE EOF S S a b =△△，作OM ⊥AE 、ON ⊥EF ， ∵AE =EF∴22::OM ON a b = ∴33::1:8S S a b ==乙甲 ∴:1:2a b =【例 26】（2009年清华附中入学测试题）如图，四边形ABCD 是矩形，E 、F 分别是AB 、BC 上的点，且13AE AB =，14CF BC =，AF 与CE 相交于G ，若矩形ABCD 的面积为120，则AEG Δ与CGF Δ的面积之和为．BEGH BE GBEG【解析】(法1)如图，过F 做CE 的平行线交AB 于H ，则::1:3EH HB CF FB ==，所以122AE EB EH ==，::2AG GF AE EH ==，即2AG GF =，所以122311033942AEG ABF ABCD S S S ΔΔ=××=××=-．且22313342EG HF EC EC ==×=，故CG GE =，则1152CGF AEG S S ΔΔ=××=．所以两三角形面积之和为10515+=．(法2)如上右图，连接AC 、BG ．根据燕尾定理，::3:1ABG ACG S S BF CF ΔΔ==，::2:1BCG ACG S S BE AE ΔΔ==，而1602ABC ABCD S S Δ==-，所以3321ABG S Δ=++，160302ABC S Δ=×=，2321BCG S Δ=++，160203ABC S Δ=×=，则1103AEGABG S S ΔΔ==，154CFG BCG S S ΔΔ==，所以两个三角形的面积之和为15．练习1. 已知ABC △中，DE 平行BC ，若:2:3AD DB =，且DBCE S 梯形比ADE S △大28.5cm ，求ABC S △．A ED CB【解析】根据金字塔模型::2:(23)2:5AD AB DE BC ==+=，22:2:54:25ADE ABC S S ==△△，设4ADE S =△份，则25ABC S =△份，25421DBCE S =−=梯形份，DBCE S 梯形比ADE S △大17份，恰好是28.5cm ，所以212.5cm ABC S =△练习2. 如图，O 是矩形一条对角线的中点，图中已经标出两个三角形的面积为3和4，那么阴影部分的一块直角三角形的面积是多少？34OFE DB34OF E DB【解析】连接OB ,面积为4的三角形占了矩形面积的14，所以431OEB S =−=△,所以:1:3OE EA =,所以:5:8CE CA =,由三角形相似可得阴影部分面积为25258()88×=．练习3. 如图，三角形PDM 的面积是8平方厘米，长方形ABCD 的长是6厘米，宽是4厘米，M 是BC的中点，则三角形APD 的面积是平方厘米．ABCDP MKN ABCDP M【解析】本题在矩形内连接三点构成一个三角形，而且其中一点是矩形某一条边的中点，一般需要通过这一点做垂线．取AD 的中点N ，连接MN ，设MN 交PD 于K ．则三角形PDM 被分成两个三角形，而且这两个三角形有公共的底边MK ，可知三角形PDM 的面积等于182MK BC ××=(平方厘米)，所以8MK=3(厘米)，那么84433NK =−=(厘米)．因为NK 是三角形APD 的中位线，所以823AP NK =×=(厘米)，所以三角形APD 的面积为186823××=(平方厘米)．练习4. 如图，已知3BD DC =，2EC AE =，BE 与CD 相交于点O ,则ABC △被分成的4部分面积各占ABC △ 面积的几分之几？OE DCBA13.54.59211213O E D CBA【解析】连接CO ,设1AEO S =△份，则其他部分的面积如图所示，所以1291830ABC S =+++=△份，所以四部分按从小到大各占ABC △面积的12 4.5139313.59,,,30306030103020+===练习5. 两条线段把三角形分为三个三角形和一个四边形，如图所示，三个三角形的面积分别是3，7，7，则阴影四边形的面积是多少？773773FEDCx+3x773FED C【解析】方法一：遇到没有标注字母的图形，我们第一步要做的就是给图形各点标注字母，方便后面的计算.再看这道题，出现两个面积相等且共底的三角形．设三角形为ABC ，BE 和CD 交于F ，则BF FE =，再连结DE ．所以三角形DEF 的面积为3.设三角形ADE 的面积为x ，则()():33:10:10x AD DB x +==+，所以15x =，四边形的面积为18．方法二：设ADF S x =△，根据燕尾定理::ABF BFC AFE EFC S S S S =△△△△,得到3AEF S x =+△，再根据向右下飞的燕子，有(37):7:3x x ++=，解得7.5x =四边形的面积为7.57.5318++=练习6. 右图的大三角形被分成5个小三角形，其中4个的面积已经标在图中，那么，阴影三角形的面积是．4321【解析】方法一：整个题目读完，我们没有发现任何与边长相关的条件，也没有任何与高或者垂直有关系的字眼，由此，我们可以推断，这道题不能依靠三角形面积公式求解.我们发现右图三角形中存在一个比例关系：()2:13:4S =+阴影，解得2S =阴影.方法二：回顾下燕尾定理，有2:41:3S +=阴影（），解得2S =阴影.练习7. (2007年香港圣公会数学竞赛)如图所示，在ABC △中，12CP CB =，13CQ CA =，BQ 与AP 相交于点X ，若ABC △的面积为6，则ABX △的面积等于．XQPABC XQPABC4411XQPCBA【解析】方法一：连接PQ ．由于12CP CB =，13CQ CA =，所以23ABQ ABC S S =++，1126BPQ BCQ ABC S S S ==+++．由蝴蝶定理知，21:::4:136ABQ BPQ ABC ABC AX XP S S S S ===++++，所以441226 2.455255ABX ABP ABC ABC S S S S ==×==×=++++．方法二：连接CX 设1CPX S =△份，根据燕尾定理标出其他部分面积，所以6(1144)4 2.4ABX S =÷+++×=△练习8. 如图，三角形ABC 的面积是1，2BD DC =，2CE AE =，AD 与BE 相交于点F ，请写出这4部分的面积各是多少?ABCDE F48621ABCDEF【解析】连接CF ，设1AEF S =△份，则其他几部分面积可以有燕尾定理标出如图所示，所以121AEF S =△,62217ABF S ==△,821BDF S =△,242217FDCE S +==。

直线图形面积计算一：利用倍数关系求解面积六年级[暑假一]

名师堂学校方法讲义之一年级：六年级日期：7月8日直线图形—利用倍数关系求面积【方法与技能】我们已经学过的直线型图形包括三角形、长方形、正方形、平行四边形、梯形、菱形等图形，一般称为基本图形或规则图形.我们的面积及周长都有相应的公式直接计算.根据图形之间长与宽、底与高的倍数关系求解图形面积是近年来各类竞赛与考试经常出现的考点。

在这类问题中，我们可以采用等分法求解，也可以用倍比法求解。

即根据等底或等高的平行四边形、三角形，它们的高（或底）的倍数关系就是面积的倍数关系，从而顺利求解。

【典型例题】例1：已知三角形ABC的面积为1，BE=2AB，BC=CD，求三角形BDE的面积？（下页图）例2：如右图，A为△CDE的DE边上中点，3BC=CD，若△ABC（阴影部分）面积为5平方厘米.求△ABD及△ACE的面积.例3：如下页右上图，在正方形ABCD中，三角形ABE的面积是8平方厘例4：如右图，已知：S△ABC=1，例5：如下图，在三角形ABC中，DC=2BD，CE=3AE，三角形ADE的面积是20平方厘米，求三角形ABC的面积。

例6：上右图所示三个小平行四边形的面积是12平方厘米、25平方厘米和42平方厘米。

那么大平行四边形的面积是多少平方厘米？例7：如下左图：已知梯形中两个三角形的面积分别是8平方厘米和12平方厘米，梯形的面积是多少平方厘米？名师课堂——关键教方法名师堂市中心校区地址：顺城街体育场路2号商业很行六楼8661966286741998AB D CE12 4225812D【应用拓展】1、如下图是由四个小长方形拼接而成的大长方形，其中三个小长方形的面积分别是24平方分米、15平方分米和25平方分米。

那么，图中阴影部分的面积是多少平方分米？2、如下左图，由九个小长方形拼接成大长方形，其中三个小长方形的面积分别时15平方米、30平方米和45平方米。

图中阴影部分的面积是多少平方米？3、如上右图，BD 、DE 、EC 的长分别是2、4、2，F 是线段AE 的中点，△ABC 的高为4，△DEF 的面积是（）。

第三讲基本直线形面积公式

正方形长方形平行四边形三角形梯形正方形的面积和长方形的面积公式是我们所熟悉的，如图：左上角是面积为16的正方形，那么它的边长是多少？你还能求出哪些线段的长度呢？24？3618在几何中，所谓直线形就是指由线段构成的图形，在日常生活中，我们最常见的直线形有以下几种：在有关直线形的计算中，计算周长和面积是最常见的两类，我们已经学过了如何计算直线形的周长，接下来我们将学习如何计算直线形的面积。

如图，有一块长方形的田地被分成了五小块，分别种了茄子、黄瓜、豆角、莴笋和苦瓜，其中茄子地的面积是16平方米，黄瓜地的面积是28平方米，豆角地的面积是32平方米，莴笋地的面积是72平方米，而且左上茄子地恰好是一个正方形，请问：剩下的苦瓜地的面积是多少？如图，有一块长方形的田地被分成了四小块，分别种了冬瓜、西瓜、南瓜和黄瓜，其中冬瓜地的面积是24平方米，西瓜地的面积是36平方米，南瓜地的面积是18平方米，而且左下角西瓜地恰好是一个正方形，请问：剩下的黄瓜地面积是多少？长宽边长正方形的面积=边长*长方形的面积=长*宽如图，平行四边形的两组对边平行且相等，我们把两组对边用不同颜色标出来为了计算平行四边形面积，我们可以把平行四边形切成两块，然后拼成一个长方形，如图：要计算平行四边形的面积，需要知道一条底，以及它所对应的高。

当然我们可以用另外一种方式把上面的平行四边形剪拼成一个长方形，如下图所示，同样得到相对于这条底的若干条高这个平行四边形的面积和拼成的长方形的面积相同，都等于长方形的长乘以宽，长方形的长和宽在平行四边形中都可以找到对应线段，在平行四边形中，这两条线段分别叫底和高。

于是我们有：如下图所示，同学们可以画出这条底对应的若干条高，并且这些高是相等的，都等于上下两条平行线间的距离。

平行四边形面积=底*高高高高底如图是由两个边长分别为4和7的正方形拼成的，请求出图中阴影部分的面积。

阴影部分是平行四边形，应该选哪条边作为底呢？相应的高是多少呢？如图，大正方形里有一个小正方形还有一个阴影平行四边形，如果大正方形的边长是20cm，小正方形的边长是8cm，那么图中阴影平行四边形的面积是多少？三角形中也有相对应的底和高。

003直线型面积

３３、一块正方形的钢板，先截去宽５分米的长方形，又截去宽８分米的长方形（如下图），面积比原来的正方形减少１８１平方分米，原正方形的边长是多少？
３４、如图１６－５，长方形ＡＢＣＤ的面积是２平方厘米，ＥＣ＝２ＤＥ，Ｆ是ＤＧ的中点．阴影部分的面积是多少平方厘米？３５、如图１６－６，已知Ｄ是ＢＣ中点，Ｅ是ＣＤ的中点，Ｆ是ＡＣ的中点．三角形ＡＢＣ由①～⑥这６部分组成，其中②比⑤多６平方厘米．那么三角形ＡＢＣ的面积是多少平方厘米？
等
于多少？
３０、人民路小学操场长 90 米，宽 45 米，改造后，长增加 10 米，宽增加 5 米。现在操场面积比原来增加多少平方米？
本站网址：ｗｗｗ．ａｏｓｈｕｗａｎｇ．ｎｅｔ答疑热线：（吕老师）１５１０１１９６５２０；１５５１０３２３９２８奥数王－帮你解决学奥数的一切问题！第 3页共4页
水木学校独家版权资料，请勿外传！
31、一个长方形，如果宽不变，长增加 6 米，那么它的面积增加 54 平方米，如果长不变，宽减少 3 米，那么它的面积减少 36 平方米，这个长方形原来的面积是多少平方米？
３２、下图是一个养禽专业户用一段长１８米的篱笆和一堵墙围成的一个长方形养鸡场，求占地面积有最大有多大。
水木学校独家版权资料，请勿外传！
２１、一张长方形纸片，把它的右上角往下折叠（如图甲），阴影部分面积
占原纸片面积的 2 ；再把左下角往上折叠（如图乙），乙图中阴影部分面 7
积占原纸片面积的＿＿＿＿＿＿＿＿＿（答案用分数表示）．
２２、设正方形的面积为ｌ，图中 E、F 分别为 AB、
AD 的中点， GC＝ 1 FC ，则阴影部分的面积 3

直线型面积

第一讲直线型面积（一）卷Ⅰ这一讲我们主要介绍的知识点：1. 三角形和平行四边形的等积变换.2. 三角形面积公式1sin 2S ab c =的变形应用及几个重要规律. 3. 勾股定理及其应用.本讲的主线是介绍并反复运用三角形面积公式1s i n 2S a b c =的变形应用及几个重要规律，灵魂在于卷Ⅱ的知识点所渗透的思想及原创题目，我相信这也会是教师上课的亮点所在。

作业相对于例题来说比较简单。

【例1】如右图，在平行四边形ABCD 中，直线CF 交AB 于E ，交DA 延长线于F ，若S △ADE=1，求△BEF的面积．分析：本题主要是让学生并会运用等底等高的两个三角形面积相等（或夹在一组平行线之间的三角形面积相等）和等量代换的思想. 连接AC.∵AB//CD ，∴S △ADE =S △ACE同理：AD//BC ，∴S △ACF =S △ABF又S △ACF =S △ACE +S △AEF ，S △ABF =S △BEF +S △AEF ∴ S △ACE =S △BEF ，即S △BEF =S △ADE =1．专题精讲教学目标F E D C B A F ED C BA[前铺] 如图所示，四边形ABCD 与AEGF 都是平行四边形，请你证明它们的面积相等．分析：本题主要是让学生了解并会运用等底等高的两个平行四边形面积相等和三角形面积等于与它等底等高的平行四边形面积的一半.证明：连接BE.（我们通过△ABE 把这两个看似无关的平行四边形联系在一起.） ∵在平行四边形ABCD 中，12ABES AB AB =⨯⨯边上的高， ∴ABEABCD 1SS 2=（也就是等积变换的重要依据③的特殊情况）同理，ABEAEGF 1SS 2=.∴平行四边形ABCD 与AEGF 面积相等.[拓展] 如图所示，正方形ABCD 的边长为8厘米，长方形EBGF 的长BG 为10厘米，那么长方形的宽为几厘米？GFEDCBAGFEDCBA GFD B AGFD CB A分析：本题主要是让学生会运用等底等高的两个平行四边形面积相等（长方形和正方形可以看作特殊的平行四边形）．三角形面积等于与它等底等高的平行四边形面积的一半. 证明：连接AG.（我们通过△ABG 把这两个长方形和正方形联系在一起）. ∵在正方形ABCD 中，G12AB S AB AB =⨯⨯边上的高， ∴ABGABCD1SS 2=（三角形面积等于与它等底等高的平行四边形面积的一半）同理，ABGEFGB 1SS 2=长. ∴正方形ABCD 与长方形EFGB 面积相等. 长方形的宽=8×8÷10=6.4（厘米）.【例2】如图，长方形ABCD 的面积是2平方厘米，EC=2DE ，F 是DG 的中点．四边形EFGC 的面积是多少平方厘米?分析：连接FC.△DBF 、△BFG 的面积相等，设为x 平方厘米;△FGC 、△DFC 的面积相等，设为y 平方厘米，那么△DEF 的面积为13y 平方厘米．BCD S =2x+2y=1，BDE S =x+13y=l×13=13，所以有x+y=0.53x+y=1⎧⎨⎩①②．解得x=0.25,y=0.25．四边形EFGC 的面积是为y+23y=53×0.25=512平方厘米．本题主要体现出代数思想在几何题中的运用，面对棘手的几何题目我们借助于这样的思想就可以迎刃而解。

直线型面积计算

直线型面积计算例1：（原例3）、已知长方形ABCD 的面积是40平方厘米，AE=5cm ，求BD 的长。

例2：（原例1）、三角形ABC 的面积为36平方分米,DC=2BD,求阴影部分的面积。

例3、如图，在三角形ABC 中，D 是BC 的中点，AE=3ED ，三角形ABC 的面积为96平方厘米，求阴影部分。

练习：如下图，已知在三角形ABC 中，BE=3AE ，CD=2AD 。

若三角形ADE 的面积为1平方厘米。

求三角形ABC 的面积。

CC例4、下图是由大、小两个正方形组成的，小正方形的边长是4厘米，大正方形边长为5厘米，求三角形ABC 的面积。

D C例5：两个相同的直角三角形如下图所示（单位：厘米）重叠在一起，求阴影部分的面积.FA例6、如下图所示，在一个等腰直角三角形中，削去一个三角形后，剩下一个上底长5厘米、下地长9厘米的等腰梯形（阴影部分）。

求这个梯形的面积。

练习：在下图所示的等腰直角三角形中，剪去一个三角形后，剩下的部分是一个直角梯形（阴影部分）。

已知梯形的面积为36平方厘米，上底为3厘米，求下底和高。

例7、在下图的直角三角形中有一个矩形，求矩形的面积。

练习：在下图中，长方形AEFD的面积是18平方厘米，BE长3厘米，求CD的长。

6====Word 行业资料分享--可编辑版本--双击可删====F ED CBA例8、在下图中，平行四边形ABCD 的边长长10厘米，直角三角形ECB 的直角边EC 长8厘米。

已知阴影部分的总面积比三角形EFG 的面积大10平方厘米，求平行四边形ABCD 的面积。

练习：在下图中，AB=8厘米，CD=4厘米，BC=6厘米，三角形AFB 比三角形EFD 的面积大18平方厘米。

求ED 的长。

AF BCDE练习巩固1、一块长方形草坪，中间有两条宽1米的走道，求植草（阴影部分）的面积。

2、在直角三角形ABC 中，AB=4cm,BC=3m,AC=5cm 。

求AC 边上的高BE 的长。

小学奥数平面直线型几何知识汇总

平面直线型几何专题吴哲孙雪艳2016年3月目录第1讲等积变形第2讲一半模型第3讲等高(等底)模型第4讲鸟头模型第5讲风筝模型第6讲蝴蝶模型第7讲沙漏模型和金字塔模型第8讲燕尾模型第1讲等积变形【知识点分析】1、定义：图形形状发生变化，面积保持不变。

比如：对称、平移、旋转等都是保持图形面积。

2、常见类型：（1）同底等高—— 两平行线间的等积变形（平行线间距离处处相等）平行线“拉点“法（A 1可以在L 1上随便拉到任何地方）112ABC A BC L //L S =S △△若，则技巧：平行线的来源A 、平行四边形(包括长方形和正方形)和梯形B 、已知平行C 、并排摆放的正方形的同方向对角线（2）等底同高ABD ACD D BC S =S △△若为中点，则A 1CBAL 2L 1BC（3）等高等底12ABC EFG BC=FG h h S =S △△若、=，则3、本质：将三角形的面积关系转化成三角形底和高等对应的线段长度关系【典型例题】例1：将任意一的三角形分割为四个面积相等的小三角形，可以怎么分？你能想到多少种？【解题点拨】图中的点为中点、三等分点或四等分点ABFG例2：如图，在梯形A B C D 中，共有八个三角形，其中面积相等的三角形共有哪几对？【解题点拨】考察平行线间的等积变形，梯形上下两个底平行以MP 为底：△MPN =△MPO 以NO 为底：△N OM=△NOP等量减等量，差相等：△MNQ =△POQ例3：正方形A B C D 和正方形C E F G ，且正方形A B C D 边长为20厘米，则图中阴影面积为多少平方厘米？【解题点拨】考察平行线间的等积变形，并排摆放的正方形的同方向对角线平行。

如图，连接CF ，则BD//CF,以CF 为底，△CFD 与△CFB 面积相等，同时减去△CFH，得到△BCH 与△DFH 面积相等，所以阴影部分面积就等于△BCD 的面积，等于20×20÷2=200平方厘米FCAFCA本题直接求阴影面积比较麻烦，利用等积变形巧妙转化方便解题。

直线图形面积计算一：利用倍数关系求解面积六年级[暑假一]

在这类问题中，我们可以采用等分法求解，也可以用倍比法求解。

即根据等底或等高的平行四边形、三角形，它们的高（或底）的倍数关系就是面积的倍数关系，从而顺利求解。

例6：上右图所示三个小平行四边形的面积是12平方厘米、25平方厘米和42平方厘米。

那么大平行四边形的面积是多少平方厘米？例7：如下左图：已知梯形中两个三角形的面积分别是8平方厘米和12平方厘米，梯形的面积是多少平方厘米？名师课堂——关键教方法名师堂市中心校区地址：顺城街体育场路2号商业很行六楼8661966286741998AB CE12 4225812D【应用拓展】1、如下图是由四个小长方形拼接而成的大长方形，其中三个小长方形的面积分别是24平方分米、15平方分米和25平方分米。

图中阴影部分的面积是多少平方米？3、如上右图，BD 、DE 、EC 的长分别是2、4、2，F 是线段AE 的中点，△ABC 的高为4，△DEF 的面积是（）。

图形复习五年级数学

直线型面积计算（1）对于三角形的面积计算，我们除了熟练运用基本的计算公式，在技巧性很强的奥数题中还要根据相应的性质和结论来解题，下面就是我们小学奥数常用的三条性质：【例 1】如图，长方形ABCD 的面积是56平方厘米，点E 、F 、G 分别是长方形ABCD 边上的中点，H 为AD 边上的任意一点，求阴影部分的面积．E BA E BA【分析】本题是等底等高的两个三角形面积相等的应用．连接BH 、CH ． ∵AE EB =， ∴S S AEH BEH = ．同理，S S BFH CFH = ，S =S CGH DGH ，∴11S S 562822==⨯=阴影长方形ABCD （平方厘米）．［铺垫］你有多少种方法将任意一个三角形分成：⑴2个面积相等的三角形； ⑵3个面积相等的三角形； ⑶4个面积相等的三角形．［分析］ ⑴如右图，D 、E 、F 分别是对应边上的中点，这样就将三角形分成了2个面积相等的三角形；CBAEA B CFCB A⑵如右图，D 、E 是BC 的三等分点，F 、G 分别是对应线段的中点；答案不唯一；①等底等高的两个三角形面积相等；②两个三角形高相等，面积比等于它们的底之比；两个三角形底相等，面积比等于它们的高之比；③夹在一组平行线之间的等积变形，如BCD ACD S S ∆∆=；反之，如果BCD ACD S S ∆∆=，则可知直线AB 平行于CD ．DC BAED A BC FC BADGDA BC⑶如下图，答案不唯一，以下仅供参考．(5)(4)(3)(2)(1)【例 2】如图，三角形ABC 的面积为1，其中3AE AB =，2BD BC =，三角形BDE 的面积是多少？EDCB AEDC B A【分析】连接CE ．∵3AE AB =，∴2BE AB =，2BCE ACB S S ∆∆=．又∵2BD BC =，∴244BDE BCE ABC S S S ∆∆∆===．【例 3】如图，三角形ABC 中，2DC BD =，3CE AE =，三角形ADE 的面积是20平方厘米，三角形ABC 的面积是多少？ECBA 【分析】 ∵3CE AE =，∴4AC AE =,4ADC ADE S S ∆∆=;又∵2DC BD =,∴32BC DC =,361202ABC ADC ADE S S S ∆∆∆===（平方厘米）．［铺垫］如图，三角形ABC 被分成了甲、乙两部分，4BD DC ==，3BE =，6AE =，甲部分面积是乙部分面积的几分之几？乙甲E CBAABCDE［分析］连接AD ．∵3BE =,6AE =，∴13BE AB =,13BDE ABD S S ∆∆=．又∵4BD DC ==,∴12ABD ABC S S ∆∆=,∴1136BDE ABD ABC S S S ∆∆∆==,∴15S S =乙甲．［拓展］如图，在三角形ABC 中，8BC =厘米，6AD =厘米，E 、F 分别为AB 和AC 的中点，那么三角形EBF 的面积是多少平方厘米？FE CAFE CA［分析］ ∵F 是AC 的中点,∴12ABF ABC S S ∆∆=，同理12BEF ABF S S ∆∆=，∴111866442BEF ABC S S ∆∆==⨯⨯⨯=（平方厘米）．【例 4】如图，已知三角形ABC 面积为1，延长AB 至D ，使BD AB =；延长BC 至E ，使2CE BC =；延长CA 至F ，使3AF AC =，求三角形DEF 的面积．F EDCB A AB CDEF【分析】本题是性质的反复使用（还可以用燕尾定理，但本讲不用这种方法，燕尾定理我们会放到五年级春季再讲）．连接AE 、CD ． ∵S 1S 1S 1ABC ABC DBC == ，， ∴S 1DBC = ．同理可得其它，最后三角形DEF 的面积18=．［拓展］如图，四边形EFGH 的面积是66平方米，EA AB =，CB BF =，DC CG =，HD DA =，求四边形ABCD 的面积．H GFED CB A A B CDEFGH［分析］连接BD .设1DCB S S = ，2DAB S S =∵CB BF =，∴2CDF CDB CDB CB BFS S S CB∆∆∆+==,又∵DC CG =,∴12CFG CDF S S S ∆∆==，同理22AEH S S ∆=， ∴2CFG AEH ABCD S S S ∆∆+=连接AC ，同理2HDG BEF ABCD S S S ∆∆+=∴5EFGH CFG AEH HDG BEF ABCD ABCD S S S S S S S ∆∆∆∆=++++=，111355ABCD EFGH S S ==（平方米）．［拓展］如图，已知长方形ADEF 的面积16，三角形ADB 的面积是3，三角形ACF 的面积是4，那么三角形ABC 的面积是多少？F CA F CA［分析］连接对角线AE ． ∵ADEF 是长方形∴12ADE AEF ADEF S S S ∆∆==∴38ADB ADE S DB DE S ∆∆==， 12ACF AEF S FC EF S ∆∆== ∴58BE DE DB DE DE -==，12CE FE CF EF EF -== ∴1515162822BEC S ∆=⨯⨯⨯=∴132ABC ADEF ADB ACF CBE S S S S S ∆∆∆∆=---= ．［拓展］如图，长方形ABCD 中，:2:3BE EC =，:1:2DF FC =，三角形DFG 的面积为2平方厘米，求长方形ABCD 的面积．ABCD EF GABCD EF G［分析］连接AE ，FE ．因为:2:3BE EC =，:1:2DF FC =，所以3111()53210DEF ABCD ABCD S S S =⨯⨯= 长方形长方形．因为12AED ABCD S S = 长方形，11::5:1210AG GF ==，所以510AGD GDF S S == ，所以12AFD S = ．因为16AFD ABCD S S = 长方形，所以长方形ABCD 的面积是72平方厘米．【例 5】（第八届小数报数学竞赛决赛试题）如下图，E 、F 分别是梯形ABCD 的下底BC 和腰CD 上的点，DF FC =，并且甲、乙、丙3个三角形面积相等．已知梯形ABCD 的面积是32平方厘米．求图中阴影部分的面积．BC【分析】因为乙、丙两个三角形面积相等，底DF FC =．所以A 到CD 的距离与E 到CD 的距离相等，即AE 与CD 平行，四边形ADCE 是平行四边形，阴影部分的面积=平行四边形ADCE 的面积的12，所以阴影部分的面积=乙的面积2⨯．从而阴影部分的面积23212.85=⨯=（平方厘米）．［拓展］如图，在平行四边形ABCD 中，BE EC =，2CF FD =．求阴影面积与空白面积的比．B［分析］因为BE EC =，2CF FD =，所以14ABE ABCD S S =四边形，16ADF ABCD S S = 四边形．因为2AD BE =，所以2AG GE =，所以11312BGE ABE ABCD S S S == 四边形，2136ABG ABE ABCD S S S == 四边形．同理可得，18ADH ABCD S S = 四边形，124DHF ABCD S S = 四边形．因为12B C D A B C D S S = 四边形，所以空白部分的面积111112()21224683ABCD ABCD S S =--++=四边形四边形，所以阴影部分的面积是13A B C D S 四边形．12:1:233=，所以阴影面积与空白面积的比是1:2．【例 6】如图所示，四边形ABCD 与AEGF 都是平行四边形，请你证明它们的面积相等．GFEB AGFEB A【分析】本题主要是让学生了解并会运用等底等高的两个平行四边形面积相等和三角形面积等于与它等底等高的平行四边形面积的一半．证明：连接BE ．（我们通过ABE 把这两个看似无关的平行四边形联系在一起．）∵在平行四边形ABCD 中，12ABE S AB AB =⨯⨯ 边上的高，∴1S S 2ABG ABCD = （也就是等积变换的重要依据③的特殊情况）．同理，1S S 2ABE AEGF = ，∴平行四边形ABCD 与AEGF 面积相等．［拓展］如图所示，正方形ABCD 的边长为8厘米，长方形EBGF 的长BG 为10厘米，那么长方形的宽为几厘米？A BGC E F DABGCEF D［分析］本题主要是让学生会运用等底等高的两个平行四边形面积相等（长方形和正方形可以看作特殊的平行四边形）．三角形面积等于与它等底等高的平行四边形面积的一半．证明：连接AG .（我们通过ABG 把这两个长方形和正方形联系在一起）．∵在正方形ABCD 中，G 12AB S AB AB =⨯⨯ 边上的高，∴1S S 2ABG ABCD = （三角形面积等于与它等底等高的平行四边形面积的一半）同理，1S S 2ABG EFGB = ．∴正方形ABCD 与长方形EFGB 面积相等. 长方形的宽8810 6.4=⨯÷=（厘米）．【例 7】如图，正方形ABCD 和正方形CEFG ，且正方形ABCD 边长为10厘米，求图中三角形BFD 的面积为多少平方厘米？HGFED C BAHG FED C BA【分析】连接CF ．∵BD ，CF 都是正方形的对角线∴45DBC FCE ∠=∠=︒，BD ∥CF ．∴BFD ∆与BCD ∆同底等高，11010502BFD BCD S S ∆∆==⨯⨯=(平方厘米) ．【例 8】（03年西城某重点中学小升初分班考题）右图是由大、小两个正方形组成的，小正方形的边长是4厘米，求三角形ABC的面积．AA【分析】这道题似乎缺少大正方形的边长这个条件，实际上本题的结果与大正方形的边长没关系．连接AD （见右上图），可以看出，三角形ABD 与三角形ACD 的底都等于小正方形的边长，高都等于大正方形的边长，所以面积相等．因为三角形AGD 是三角形ABD 与三角形ACD 的公共部分，所以去掉这个公共部分，根据差不变性质，剩下的两个部分，即三角形ABG 与三角形GCD 面积仍然相等．根据等量代换，求三角形ABC 的面积等于求三角形BCD 的面积，等于4428⨯÷=．［拓展］（小学数学夏令营五年级组试题）如图，四边形ABCD 和四边形DEFG 都是正方形，已知三角形AFH 的面积为6平方厘米，求三角形CDH 的面积．［分析］通常求三角形的面积，都是先求它的底和高．题目中没有一条线段的长度是已知的，所以我们只能通过创造等积的方法来求．直接找三角形HDC 与三角形AFH 的关系还很难，而且也没有利用“四边形ABCD 和四边形DEFG 是正方形”这一条件．我们不妨将它们都补上梯形DEFH 这一块．寻找新得到大三角形CEF 和大直角梯形DEFA 之间的关系．经过验算，可以知道它们的面积是相等的．从而得到三角形HDC 与三角形AFH 面积相等，也是6平方厘米．【例 9】如右图，在平行四边形ABCD 中，直线CF 交AB 于E ，交DA 延长线于F ，若1ADE S = ，求BEF 的面积．AB CDEFABCDEF［分析］本题主要是让学生并会运用等底等高的两个三角形面积相等（或夹在一组平行线之间的三角形面积相等）和等量代换的思想.连接AC ．∵AB ∥CD ，∴ADE ACE S S = ．同理AD ∥BC ，∴ACF ABF S S = ．又ACF ACE AEF S S S =+ ，ABF BEF AEF S S S =+ ，∴ ACE BEF S S = ，即 1BEF ADE S S == ．【例10】（小学数学奥林匹克决赛试题）右图中，ABCD 是74⨯的长方形，DEFG 是102⨯的长方形，求三角形BCO 与三角形EFO 的面积之差．【分析】直接求出三角形BCO 与三角形EFO 的面积之差，不太容易做到．如果利用差不变性质，将所求面积之差转化为另外两个图形的面积之差，而这两个图形的面积之差容易求出，那么问题就解决了．法1：连结BE （见右图）．三角形BCO 与三角形EFO 都加上三角形BEO ，则原来的问题转化为求三角形BEC 与三角形BEF 的面积之差．所求为4(107)22(107)23⨯-÷-⨯-÷=．法2：连结CF （见右图）．三角形BCO 与三角形EFO 都加上三角形CFO ，则原来的问题转化为求三角形BCF 与三角形ECF 的面积之差．所求为4(107)22(107)23⨯-÷-⨯-÷=．法3：延长BC 交GF 于H （见右图）．三角形BCO 与三角形EFO 都加上梯形COFH ，则原来的问题转化为求三角形BHF 与矩形CEFH 的面积之差．所求为(42)(107)22(107)3+⨯-÷-⨯-=．法4：延长AB ，FE 交于H （见右图）．三角形BCO 与三角形EFO都加上梯形BHEO ，则原来的问题转化为求矩形BHEC 与直角三角形BHF 的面积之差．所求为4(107)(4⨯--+⨯-÷=．【例11】如右图所示，在长方形内画出一些直线，已知边上有三块面积分别是13，35，49．那么图中阴影部分的面积是多少？OA BCDE F GOA B CDE F G O A B C DE FGH O AB CD E FGH OAB CDE FGBE【分析】三角形ABC 的面积+三角形CDE 的面积(133549)+++=长方形面积+阴影部分面积；又因为三角形ABC 的面积=三角形CDE 的面积12=长方形面积，所以可得：阴影部分面积13354997=++=．1．如图，在长方形ABCD 中，Y 是BD 的中点，Z 是DY 的中点，如果24AB =厘米，8BC =厘米，求三角形ZCY 的面积．ABC DZ Y【分析】 ∵Y 是BD 的中点，Z 是DY 的中点，∴1122ZY DB =⨯⨯，14ZCY DCB S S = ，又∵ABCD 是长方形，∴11124442ZCY DCB ABCD S S S ==⨯= (平方厘米)．2．如图，三角形ABC 中，AB 是AD 的5倍，AC 是AE 的3倍，如果三角形ADE 的面积等于1，那么三角形ABC 的面积是多少？A BCD EA BCDE【分析】连接BE .∵13AE EC = ∴13ABE ABC S S ∆∆=.又∵15AD AB =∴11515ADE ABE ABC S S S ∆∆∆==，∴1515ABC ADE S S ∆∆==.3．两个正方形组成右图所示的组合图形．已知组合图形的周长是52厘米，4DG =厘米，求阴影部分的面积．A【分析】组合图形的周长并不等于两个正方形的周长之和，因为CG 部分重合了．用组合图形的周长减去DG ，就得到大、小正方形边长之和的三倍，所以两个正方形的边长之和等于(524)316-÷=（厘米）．又由两个正方形的边长之差是4厘米，可求出大正方形边长(164)210=+÷=（厘米），小正方形边长(164)26=-÷=（厘米）．阴影部分面积410266238BDG BFG S S =+=⨯÷+⨯÷= （平方厘米）．4．在右图中，平行四边形ABCD 的边BC 长10厘米，直角三角形ECB 的直角边EC 长8厘米．已知阴影部分的总面积比三角形EFG 的面积大10平方厘米，求平行四边形ABCD 的面积．［分析］因为阴影部分比三角形EFG 的面积大10平方厘米，都加上梯形FGCB 后，根据差不变性质，所得的两个新图形的面积差不变，即平行四边行ABCD 比直角三角形ECB 的面积大10平方厘米，所以平行四边形ABCD 的面积等于10821050⨯÷+=平方厘米．5．右图中，4CA AB ==厘米，三角形ABE 比三角形CDE 的面积大2平方厘米，求CD 的长．ABCD E【分析】连结CB ．三角形DCB 的面积为44226⨯÷-=平方厘米，6243CD =⨯÷=厘米．直线型面积计算（2）在小学的学习中几何是一个很重要的部分，每一个几何图形都非常美妙，几何图形的美妙不仅来源于它的外形，更重要的是在几何模型上出现的那些美妙的规律，下面我们就一起来看看几个美妙的几何模型：模型一：任意四边形中的比例关系(“蝴蝶定理”)：S 4S 3S 2S 1O DCBA①1243::S S S S =或者1324S S S S ⨯=⨯ ②()()1243::AO OC S S S S =++蝴蝶定理为我们提供了解决不规则四边形的面积问题的一个途径．通过构造模型，一方面可以使不规则四边形的面积关系与四边形内的三角形相联系；另一方面，也可以得到与面积对应的对角线的比例关系．模型二：梯形中比例关系(“梯形蝴蝶定理”)：A BCDOba S 3S 2S 1S 4①2213::S S a b =②221324::::::S S S S a b ab ab =； ③S 的对应份数为()2a b +．梯形蝴蝶定理给我们提供了解决梯形面积与上、下底之间关系互相转换的渠道，通过构造模型，直接应用结论，往往在题目中有事半功倍的效果．模型三：相似三角形性质：GF E ABCDAB CDEF G①AD AE DE AFAB AC BC AG===； ②22:ADE ABC S S AF AG =△△：．所谓的相似三角形，就是形状相同，大小不同的三角形(只要其形状不改变，不论大小怎样改变它们都相似)，与相似三角形相关的常用的性质及定理如下：⑴相似三角形的一切对应线段的长度成比例，并且这个比例等于它们的相似比； ⑵相似三角形的面积比等于它们相似比的平方；⑶连接三角形两边中点的线段叫做三角形的中位线．三角形中位线定理：三角形的中位线长等于它所对应的底边长的一半．相似三角形模型，给我们提供了三角形之间的边与面积关系相互转化的工具．在小学奥数里，出现最多的情况是因为两条平行线而出现的相似三角形【例 9】如图，四边形被两条对角线分成4个三角形，其中三个三角形的面积已知，求：⑴三角形BGC 的面积；⑵:AG GC =？B【分析】 ⑴根据蝴蝶定理，123BGC S ⨯=⨯ ，那么6BGC S = ；⑵根据蝴蝶定理，()():12:361:3AG GC =++=．【例 10】 (2006年南京智力数学冬令营)如下图，梯形ABCD 的AB ∥CD ，对角线AC ，BD 交于O ，已知AOB 与BOC 的面积分别为25 平方厘米与35平方厘米，那么梯形ABCD 的面积是________平方厘米．3525OABCD 【分析】根据梯形蝴蝶定理，2::25:35AOB BOC S S a ab == ，可得:5:7a b =，再根据梯形蝴蝶定理，2222::5:725:49AOB DOC S S a b === ，所以49DOC S = (平方厘米)．那么梯形ABCD 的面积为25353549144+++=(平方厘米)．［铺垫］梯形ABCD 的对角线AC 与BD 交于点O ，已知梯形上底为2，且三角形ABO 的面积等于三角形BOC 面积的23，求三角形AOD 与三角形BOC 的面积之比．OA BC D ［分析］根据梯形蝴蝶定理，2::2:3AOB BOC S S ab b == ，可以求出:2:3a b =，再根据梯形蝴蝶定理，2222::2:34:9AOD BOC S S a b === ．通过利用已有几何模型，我们轻松解决了这个问题，而没有像以前一样，为了某个条件的缺乏而千辛万苦进行构造假设，所以，请同学们一定要牢记几何模型的结论．【例 11】四边形ABCD 的对角线AC 与BD 交于点O (如图所示)．如果三角形ABD 的面积等于三角形BCD 的面积的13，且2AO =，3DO =，那么CO 的长度是DO 的长度的_________倍．ABC DOH GA B C D O靠拢，从而快速解决；⑵通过画辅助线来改造不良四边形．看到题目中给出条件:1:3ABD BCD S S = ，这可以向模型一蝴蝶定理靠拢，于是得出一种解法．又观察题目中给出的已知条件是面积的关系，转化为边的关系，可以得到第二种解法，但是第二种解法需要一个中介来改造这个“不良四边形”，于是可以作AH 垂直BD 于H ，CG 垂直BD 于G ，面积比转化为高之比．再应用结论：三角形高相同，则面积之比等于底边之比，得出结果．请老师注意比较两种解法，使学生体会到蝴蝶定理的优势，从而主观上愿意掌握并使用蝴蝶定理解决问题．解法一：∵::1:3ABD BDC AO OC S S ∆∆==， ∴236OC =⨯=，∴:6:32:1OC OD ==．解法二：作AH BD ⊥于H ，CG BD ⊥于G ． ∵13ABD BCD S S ∆∆=，∴13AH CG =，∴13AOD DOC S S ∆∆=，∴13AO CO =，∴236OC =⨯=，∴:6:32:1OC OD ==．【例 12】在边长为1的正方形ABCD 中，2BE EC =，2DF FC =．求四边形ABGD 的面积．ABCDE FGABCDE FG【分析】题目要求四边形ABGD 的面积，可以发现这个四边形是个“不良四边形”，需要对它进行改造．通常在一个四边形中画辅助线，会想到画对角线，又注意到E 、F 都是三等分点，如果连接EF ，因为EF ∥BD ，则可以构造一个梯形，从而应用梯形蝴蝶定理快速求解．因为2BE EC =，2DF FC =，所以:3:1BD EF =．根据梯形蝴蝶定理可以知道，等腰梯形BDFE 四部分面积比为1:3:3:9；而等腰梯形BDFE 的面积为：111141122339⨯⨯-⨯⨯=，所以9113394BDG BDFE S S =⨯=+++ ，得11311244ABGD ADB BDG S S S =+=⨯⨯+= ．【例 13】如图，正方形ABCD 面积为1，M 是AD 边上的中点．求图中阴影部分的面积．【分析】因为M 是AD 边上的中点，所以12AM =，可得34AMCB S =梯形，由于:1:2AM BC =，根据梯形蝴蝶定理可以知道 22:::1:12:12:21:2:2:4AMG ABG MCG BCG S S S S =⨯⨯= （）（），所以阴影部分面积占梯形面积的22412249+=+++，所以341493S =⨯=阴影．【例 14】如图，在长方形ABCD 中，6AB =，2AD =，AE EF FB ==，求阴影部分的面积．DD【分析】如图，连接DE ，DE 将阴影部分的面积分为两个部分，其中三角形AED 的面积为26322⨯÷÷=．由于:1:3E F D C =，根据梯形蝴蝶定理，:3:1DEO EFO S S = ，所以34DEO DEF S S = ，而2D E F A D ES S == ，所以32 1.54D E O S =⨯= ，阴影部分的面积为2 1.5 3.5+=．相似三角形性质【例 7】在图中的正方形中，A ，B ，C 分别是所在边的中点，CDO 的面积是ABO 面积的几倍？A BCD OE FA BCD O【分析】连接BC ，易知OA ∥EF ，根据相似三角形性质，可知::OB OD AE AD =，且::1:2OA BE DA DE ==，所以CDO 的面积等于CBO 的面积；由1124OA BE AC ==可得3CO OA =，所以3CDO CBO ABO S S S == ，即CDO 的面积是ABO 面积的3倍．【例 8】如图，线段AB 与BC 垂直，已知4AD EC ==，6BD BE ==，那么图中阴影部分面积是多少？A BCDA BDA BD【分析】解法一：这个图是个对称图形，且各边长度已经给出，不妨连接这个图形的对称轴看看．作辅助线BO ，则图形关于BO 对称，有ADO CEO S S = ，DBO EBO S S = ，且:4:62:3ADO DBO S S == ．设ADO 的面积为2份，则DBO 的面积为3份，直角三角形ABE 的面积为8份．因为610230ABE S =⨯÷= ，而阴影部分的面积为4份，所以阴影部分的面积为308415÷⨯=．解法二：连接DE 、AC ．由于4AD EC ==，6BD BE ==，所以DE ∥AC ，根据相似三角形性质，可知::6:103:5DE AC BD BA ===，根据梯形蝴蝶定理，()()22:::3:35:35:59:15:15:25DOE DOA COE COA S S S S =⨯⨯= ，所以()():1515:915152515:32AD E C S S =++++=阴影梯形，即1532ADECS S =阴影梯形；又11101066=3222ADEC S =⨯⨯-⨯⨯梯形，所以151532ADEC S S ==阴影梯形．【例 9】右图中正方形的面积为1， E 、F 分别为AB 、BD 的中点，13GC FC =．求阴影部分的面积．AB EABE【分析】题中条件给出的都是比例关系，由此可以初步推断阴影部分的面积要通过比例求解，而图中出现最多的就是三角形，那么首先想到的就是利用相似三角形的性质．阴影部分为三角形，已知底边为正方形边长的一半，只要求出高，便可求出面积．可以作FH 垂直BC 于H ，GI 垂直BC 于I ．根据相似三角形性质，::1:3CI CH CG CF ==，又因为CH HB =，所以:1:6CI CB =，即():61:65:6BI BC =-=，所以115522624BGE S =⨯⨯=．【例10】如图，长方形ABCD 中，E 为AD 的中点，AF 与BE 、BD 分别交于G 、H ，OE 垂直AD 于E ，交AF 于O ，已知5AH cm =，3HF cm =，求AG ．ABC DEFGHO【分析】由于AB ∥DF ，利用相似三角形性质可以得到::5:3AB DF AH HF ==，又因为E 为AD 中点，那么有:1:2OE FD =，所以3:5:10:32AB OE ==，利用相似三角形性质可以得到::10:3AG GO AB OE ==，而()()1153422AO AF cm ==⨯+=，所以()104041313AG cm =⨯=．【例11】 ABCD 是平行四边形，面积为72平方厘米，E 、F 分别为AB 、BC 的中点，则图中阴影部分的面积为＿＿＿＿平方厘米．BB【分析】注意引导学生利用三角形的中位线定理以及平行线的相关性质．设G 、H 分别为AD 、DC 的中点，连接GH 、EF 、BD ．可得1=4AED ABCD S S 平行四边形，对角线BD 被EF 、AC 、GH 平均分成四段，又OM ∥EF ，所以23::2:344DO ED BD BD ==，()()::32:31:3OE ED ED OD ED =-=-=，所以 11117263434AEO ABCD S S =⨯=⨯⨯= 平行四边形(平方厘米)，212ADO AEO S S =⨯= (平方厘米)．同理可得6CFM S = 平方厘米，12CDM S = 平方厘米．所以 366624ABC AEO CFM S S S --=--= (平方厘米)，于是，阴影部分的面积为24121248++=(平方厘米)．练习5． (第十届华杯赛)如下图，四边形ABCD 中，对角线AC 和BD 交于O 点，已知1AO =，并且35ABD CBD =三角形的面积三角形的面积，那么OC 的长是多少？ABCDO【分析】根据蝴蝶定理，ABD AO CBD CO =三角形的面积三角形的面积，所以35AO CO =，又1AO =，所以53CO =．6．如图，梯形ABCD 中，AOB ∆、COD ∆的面积分别为1.2和2.7，求梯形ABCD 的面积．ODC BA 【分析】根据梯形蝴蝶定理，22::4:9AOB ACOD S S a b == ，所以:2:3a b =，2:::3:2AOD AOB S S ab a b a === ，31.2 1.82AOD COB S S ==⨯= ，1.2 1.8 1.82.77.5ABCD S =+++=梯形．7．已知三角形ABC 的面积为a ，:2:1AF FC =，E 是BD 的中点，且EF ∥BC ，交CD 于G ，求阴影部分的面积．【分析】已知:2:1A F F C =，且EF ∥BC ，利用相似三角形性质可知::2:3EF BC AF AC ==，所以23EF BC =，且:4:9A E F ABC S S = ．又因为E 是BD 的中点，所以EG 是三角形DBC 的中位线，那么12EG BC =，12::3:423EG EF ==，所以:1:4GF EF =，可得:1:8CFG AFE S S = ，所以:1:18CFG ABC S S = ，那么18CFG aS = ．8．在下图的正方形ABCD 中，E 是BC 边的中点，AE 与BD 相交于F 点，三角形BEF 的面积为1平方厘米，那么正方形ABCD 面积是平方厘米．A BCDEF【分析】根据相似三角形性质可知::1:2EF AF BE AD ==，所以33ABE BEF S S == (平方厘米)，那么412ABCD ABE S S == (平方厘米)．。

小学奥数-直线型面积讲义图文版

1. 熟练运用直线型面积的最基本性质——等积变形；2. 熟练掌握直线型面积的两个模型：（1）等积变形（2）鸟头模型直线型面积求解是在以三角形、长方形、正方形、梯形等一些规则图形为基础上进行的。

最基本的思想是等积变形。

一、等积变形①等底等高的两个三角形面积相等；②两个三角形高相等，面积比等于它们的底之比；两个三角形底相等，面积比等于它们的高之比；如左图12::S S a b =baS 2S 1 DC BA③夹在一组平行线之间的等积变形，如右上图ACD BCD S S =△△；反之，如果ACD BCD S S =△△，则可知直线AB 平行于CD ．④等底等高的两个平行四边形面积相等(长方形和正方形可以看作特殊的平行四边形)； ⑤三角形面积等于与它等底等高的平行四边形面积的一半；⑥两个平行四边形高相等，面积比等于它们的底之比；两个平行四边形底相等，面积比等于它们的高之比．二、鸟头定理两个三角形中有一个角相等或互补，这两个三角形叫做共角三角形．共角三角形的面积比等于对应角(相等角或互补角)两夹边的乘积之比．如图在ABC △中，,D E 分别是,AB AC 上的点如图 ⑴(或D 在BA 的延长线上，E 在AC 上)，则:():()ABC ADE S S AB AC AD AE =⨯⨯△△EDCBAEDA知识精讲教学目标第一讲直线型面积（一）板块一、等积变形【例 1】如图，长方形ABCD 的面积是56平方厘米，点E 、F 、G 分别是长方形ABCD 边上的中点，H 为AD 边上的任意一点，求阴影部分的面积．FE CBAFE C【解析】本题是等底等高的两个三角形面积相等的应用．连接BH 、CH ． ∵AE EB =，∴AEH BEH S S =△△．同理，BFH CFH S S =△△，S =S CGH DGH ，∴11562822ABCD S S ==⨯=阴影长方形(平方厘米)．【巩固】图中的E 、F 、G 分别是正方形ABCD 三条边的三等分点，如果正方形的边长是12，那么阴影部分的面积是．E GCB654321HBCG E【例 2】如图，有三个正方形的顶点D 、G 、K 恰好在同一条直线上，其中正方形GFEB 的边长为10厘米，求阴影部分的面积．KO QH G F EB A K O QH GF EBA【解析】对于这种几个正方形并排放在一起的图形，一般可以连接正方形同方向的对角线，连得的这些对角线互相都是平行的，从而可以利用面积比例模型进行面积的转化．如右图所示，连接FK 、GE 、BD ，则////BD GE FK ，根据几何五大模型中的面积比例模型，可得DGE BGE S S ∆∆=，KGE FGE S S ∆∆=，所以阴影部分的面积就等于正方形GFEB 的面积，即为210100=平方厘米．【巩固】右图是由大、小两个正方形组成的，小正方形的边长是4厘米，求三角形ABC 的面积．GAB CDGAB CDF【巩固】(2008年西城实验考题)如图，ABCD 与AEFG 均为正方形，三角形ABH 的面积为6平方厘米，图中阴影部分的面积为．BE FHBCEFH【巩固】正方形ABCD 和正方形CEFG ，且正方形ABCD 边长为10厘米，则图中阴影面积为多少平方厘米？D G HE CCEHG D【例 3】长方形ABCD 的面积为362cm ，E 、F 、G 为各边中点，H 为AD 边上任意一点，问阴影部分面积是多少？HGE【解析】解法一：寻找可利用的条件，连接BH 、HC ，如下图：H E可得：12EHB AHB S S ∆∆=、12FHB CHB S S ∆∆=、12DHG DHC S S ∆∆=，而36ABCD AHB CHB CHD S S S S ∆∆∆=++= 即11()361822EHB BHF DHG AHB CHB CHD S S S S S S ∆∆∆∆∆∆++=++=⨯=；而EHB BHF DHG EBF S S S S S ∆∆∆∆++=+阴影，11111()()36 4.522228EBF S BE BF AB BC ∆=⨯⨯=⨯⨯⨯⨯=⨯=．所以阴影部分的面积是：1818 4.513.5EBF S S ∆=-=-=阴影解法二：特殊点法．找H 的特殊点，把H 点与D 点重合，那么图形就可变成右图：GE (H )这样阴影部分的面积就是DEF ∆的面积，根据鸟头定理，则有：11111113636363613.52222222ABCD AED BEF CFD S S S S S ∆∆∆=---=-⨯⨯-⨯⨯⨯-⨯⨯=阴影．【巩固】在边长为6厘米的正方形ABCD 内任取一点P ，将正方形的一组对边二等分，另一组对边三等分，分别与P 点连接,求阴影部分面积．P CAA CPCA【例 4】 (2007首届全国资优生思维能力测试)ABCD 是边长为12的正方形，如图所示，P 是内部任意一点，4BL DM ==、5BK DN ==，那么阴影部分的面积是．PKK P【解析】（法1）特殊点法．由于P 是内部任意一点，不妨设P 点与A 点重合(如上中图)，那么阴影部分就是AMN ∆和ALK ∆．而AMN ∆的面积为(125)4214-⨯÷=，ALK ∆的面积为(124)5220-⨯÷=，所以阴影部分的面积为142034+=．（法2）寻找可以利用的条件，连接AP 、BP 、CP 、DP 可得右上图所示：则有:211127222PDC PAB ABCD S S S ∆∆+==⨯=同理可得：72PAD PBC S S ∆∆+=;而::4:121:3PDM PDC S S DM DC ∆∆===,即13PDM PDC S S ∆∆=；同理：13PBL PAB S S ∆∆=,512PND PDA S S ∆∆=,512PBK PBC S S ∆∆=;所以：15()()()()312PDM PBL PND PBK PDC PAB PDA PBC S S S S S S S S ∆∆∆∆∆∆∆∆+++=+++而()()()()PDM PBL PND PBK PNM PLK DNM BLK S S S S S S S S ∆∆∆∆∆∆∆∆+++=+++阴影面积；145102DNM BLK S S ∆∆==⨯⨯=；所以阴影部分的面积是：15()()()312PNM PLK PDC PAB PDA PBC DNM BLK S S S S S S S S ∆∆∆∆∆∆∆∆+=+++-+即为：15727210224302034312⨯+⨯-⨯=+-=．【例 5】 (2008年四中考题)如右图，AD DB =，AE EF FC ==，已知阴影部分面积为5平方厘米，ABC∆的面积是平方厘米．DADA【解析】连接CD ．根据题意可知，DEF ∆的面积为DAC ∆面积的13，DAC ∆的面积为ABC ∆面积的12，所以DEF ∆的面积为ABC ∆面积的111236⨯=．而DEF ∆的面积为5平方厘米，所以ABC ∆的面积为15306÷=(平方厘米)．【巩固】图中三角形ABC 的面积是180平方厘米，D 是BC 的中点，AD 的长是AE 长的3倍，EF 的长是BF长的3倍．那么三角形AEF 的面积是多少平方厘米？F ECBA【例 6】如图，大长方形由面积是12平方厘米、24平方厘米、36平方厘米、48平方厘米的四个小长方形组合而成．求阴影部分的面积．48cm 224cm 236cm 212cm 2MNB A12cm 236cm 224cm 248cm 2【解析】如图，将大长方形的长的长度设为1，则12112364AB ==+，24124483CD ==+，所以1113412MN =-=，阴影部分面积为211(12243648)5(cm )212+++⨯⨯=．【例 7】 (2009年第七届”希望杯”二试六年级)如图，在三角形ABC 中，已知三角形ADE 、三角形DCE 、三角形BCD 的面积分别是89，28，26．那么三角形DBE 的面积是．D【解析】根据题意可知，8928117ADCADE DCE S S S ∆∆∆=+=+=，所以::26:1172:9BDC ADC BD AD S S ∆∆===，那么::2:9DBE ADE S S BD AD ∆∆==，故222789(901)2019S =⨯=-⨯=-=．【例 8】 O 是长方形ABCD 内一点，已知OBC ∆的面积是25cm ，OAB ∆的面积是22cm ，求OBD ∆的面积是多少？POD C B【解析】由于ABCD 是长方形，所以12AOD BOC ABCD S S S ∆∆+=，而12ABD ABCD S S ∆=，所以AOD BOC ABD S S S ∆∆∆+=，则BOC OAB OBD S S S ∆∆∆=+，所以2523cm OBD BOC OAB S S S ∆∆∆=-=-=．【例 9】如右图，过平行四边形ABCD 内的一点P 作边的平行线EF 、GH ，若PBD ∆的面积为8平方分米，求平行四边形PHCF 的面积比平行四边形PGAE 的面积大多少平方分米？CEFHPCEFH P【解析】根据差不变原理，要求平行四边形PHCF 的面积与平行四边形PGAE 的面积差，相当于求平行四边形BCFE 的面积与平行四边形ABHG 的面积差．如右上图，连接CP 、AP ．由于12BCP ADP ABP BDP ADP ABCD S S S S S S ∆∆∆∆∆+=++=，所以BCP ABP BDP S S S ∆∆∆-=．而12BCP BCFE S S ∆=，12ABP ABHG S S ∆=，所以()2216BCFE ABHG BCP ABP BDP S S S S S ∆∆∆-=-==(平方分米)．【例 10】如右图，正方形ABCD 的面积是20，正三角形BPC ∆的面积是15，求阴影BPD ∆的面积．PBAOAB P【解析】连接AC 交BD 于O 点，并连接PO ．如下图所示，可得//PO DC ，所以DPO ∆与CPO ∆面积相等(同底等高)，所以有：BPO CPO BPO PDO BPD S S S S S ∆∆∆∆∆+=+=，因为1120544BOC ABCD S S ∆==⨯=，所以15510BPD S ∆=-=．【巩固】如右图，正方形ABCD 的面积是12，正三角形BPC ∆的面积是5，求阴影BPD ∆的面积．PBAOAB DP【例 11】 (2008年”华杯赛”决赛)右图中，ABCD 和CGEF 是两个正方形，AG 和CF 相交于H ，已知CH等于CF 的三分之一，三角形CHG 的面积等于6平方厘米，求五边形ABGEF 的面积．HG F E D C B AHGF ED CB A【解析】连接AC 、GF ，由于AC 与GF 平行，可知四边形ACGF 构成一个梯形．由于HCG ∆面积为6平方厘米，且CH 等于CF 的三分之一，所以CH 等于FH 的12，根据梯形蝴蝶定理或相似三角形性质，可知FHG ∆的面积为12平方厘米，AHF ∆的面积为6平方厘米，AHC ∆的面积为3平方厘米．那么正方形CGEF 的面积为()612236+⨯=平方厘米，所以其边长为6厘米．又AFC ∆的面积为639+=平方厘米，所以9263AD =⨯÷=(厘米)，即正方形ABCD 的边长为3厘米．那么，五边形ABGEF 的面积为：21369349.52++⨯=(平方厘米)．【例 12】如图，已知长方形ADEF 的面积16，三角形ADB 的面积是3，三角形ACF 的面积是4，那么三角形ABC 的面积是多少？F ED CB AF ED CB A F ED CB A【解析】方法一：连接对角线AE ． ∵ADEF 是长方形∴12ADE AEF ADEF S S S ∆∆==∴38ADB ADE S DB DE S ∆∆==， 12ACF AEF S FC EF S ∆∆== 5BE DE DB -1CE FE CF -∴1515162822BEC S ∆=⨯⨯⨯=∴132ABC ADEFADB ACF CBE S SS S S ∆∆∆∆=---=．方法二：连接BF ，由图知1628ABF S =÷=△，所以16835BEF S =--=△，又由4ACF S =△，恰好是AEF △面积的一半，所以C 是EF 的中点，因此52 2.5BCE BCF S S ==÷=△△，所以1634 2.5 6.5ABC S =---=△【例 13】 (第七届”小机灵杯”数学竞赛五年级复赛)如图所示，三角形ABC 中，D 是AB 边的中点，E 是AC边上的一点，且3AE EC =，O 为DC 与BE 的交点．若CEO ∆的面积为a 平方厘米，BDO ∆的面积为b 平方厘米．且b a -是2.5平方厘米，那么三角形ABC 的面积是平方厘米．E baOD CBA【解析】 12ABC BCD BCO S S b S ∆∆∆==+，14ABC BCE BCO S S a S ∆∆∆==+，所以112.524ABC ABC S S b a ∆∆-=-=(平方厘米)．所以 2.5410ABC S ∆=⨯=(平方厘米)．【例 14】如图，长方形ABCD 的面积是2平方厘米，2EC DE =，F 是DG 的中点．阴影部分的面积是多少平方厘米？G FD C【解析】如下图，连接FC ，DBF 、BFG 的面积相等，设为x 平方厘米;FGC 、DFC 的面积相等，设为y 平方厘米，那么DEF 的面积为13y 平方厘米．xyy x GFE DCBA221BCD S x y =+=，BDE 111S =x+y=l 333⨯=．所以有0.531x y x y +=⎧⎨+=⎩①②．比较②、①式，②式左边比①式左边多2x ，②式右边比①式右边大0.5，有20.5x =，即0.25x =,0.25y =．而阴影部分面积为2550.253312y y +=⨯=平方厘米．【例 15】 (2008年第一届”学而思杯”综合素质测评六年级2试)如图，45BC =，21AC =，ABC ∆被分成9个面积相等的小三角形，那么DI FK += ．KJIH GFE DC B A【解析】由题意可知，::2:9BAD ABC BD BC S S ∆∆==，所以2109BD BC ==，35CD BC BD =-=；又::2:5DIF DFC DI DC S S ∆∆==，所以2145DI DC ==，同样分析可得10FK =，所以141024DI FK +=+=．【巩固】（2009年清华附中入学测试题）如图，在角MON 的两边上分别有A 、C 、E 及B 、D 、F 六个点，并且OAB ∆、ABC ∆、BCD ∆、CDE ∆、DEF ∆的面积都等于1，则DCF ∆的面积等于．OBD FN【例 16】 (2009年四中入学测试题)如图，已知5CD =，7DE =，15EF =，6FG =，线段AB 将图形分成两部分，左边部分面积是38，右边部分面积是65，那么三角形ADG 的面积是．GFE DC BAABC DE FG【解析】连接AF ，BD ．根据题意可知，571527CF =++=；715628DG =++=；所以，1527BE CBF F S S ∆∆=，1227BE CBF C S S ∆∆=，2128AEG ADG S S ∆∆=，728AED ADG S S ∆∆=，于是：2115652827ADG CBF S S ∆∆+=；712382827ADG CBF S S ∆∆+=；可得40ADG S ∆=．故三角形ADG 的面积是40．【例 17】 (2008年走美六年级初赛)如图所示，长方形ABCD 内的阴影部分的面积之和为70，8AB =，15AD =，四边形EFGO 的面积为．O GFEDBA【解析】利用图形中的包含关系可以先求出三角形AOE 、DOG 和四边形EFGO 的面积之和，以及三角形AOE 和DOG 的面积之和，进而求出四边形EFGO 的面积．由于长方形ABCD 的面积为158120⨯=，所以三角形BOC 的面积为1120304⨯=，所以三角形AOE 和DOG 的面积之和为312070204⨯-=；又三角形AOE 、DOG 和四边形EFGO 的面积之和为111203024⎛⎫⨯-= ⎪⎝⎭，所以四边形EFGO 的面积为302010-=．另解：从整体上来看，四边形EFGO 的面积=三角形AFC 面积+三角形BFD 面积-白色部分的面积，而三角形AFC 面积+三角形BFD 面积为长方形面积的一半，即60，白色部分的面积等于长方形面积减去阴影部分的面积，即1207050-=，所以四边形的面积为605010-=．【巩固】(2008年”华杯赛”初赛)如图所示，矩形ABCD 的面积为24平方厘米．三角形ADM 与三角形BCN的面积之和为7.8平方厘米，则四边形PMON 的面积是平方厘米．NOMPDCBA【例 18】 (清华附中分班考试题)如图，如果长方形ABCD 的面积是56平方厘米，那么四边形MNPQ 的面积是多少平方厘米？3PD C B333D CB【解析】如图，过M 、N 、P 、Q 分别作长方形ABCD 的各边的平行线．易知交成中间的阴影正方形的边长为3厘米，面积等于9平方厘米．设MQD ∆、NAM ∆、PBN ∆、QCP ∆的面积之和为S ，四边形MNPQ的面积等于x ，则569x S x S +=⎧⎨-=⎩，解得32.5x =(平方厘米)．板块二鸟头模型【例 19】如图在ABC △中，,D E 分别是,AB AC 上的点，且:2:5AD AB =，:4:7AE AC =，16ADE S =△平方厘米，求ABC △的面积．EDCBAEDCBA【解析】连接BE ，::2:5(24):(54)ADE ABE S S AD AB ===⨯⨯△△，::4:7(45):(75)ABE ABC S S AE AC ===⨯⨯△△，所以:(24):(75)ADE ABC S S =⨯⨯△△，设8ADE S =△份，则35ABC S =△份，16ADE S =△平方厘米，所以1份是2平方厘米，35份就是70平方厘米，ABC △的面积是70平方厘米．由此我们得到一个重要的定理，共角定理：共角三角形的面积比等于对应角(相等角或互补角)两夹边的乘积之比．【巩固】如图，三角形ABC 被分成了甲(阴影部分)、乙两部分，4BD DC ==，3BE =，6AE =，乙部分面积是甲部分面积的几倍？乙甲E DCBAA BCDE甲乙【解析】连接AD ．∵3BE =，6AE =∴3AB BE =，3ABD BDE S S = 又∵4BD DC ==，∴2ABC ABD S S =，∴6ABC BDE S S =，5S S =乙甲．【例 20】如图在ABC △中，D 在BA 的延长线上，E 在AC 上，且:5:2AB AD =，:3:2AE EC =，12ADE S =△平方厘米，求ABC △的面积．EDCBA EDCBA【解析】连接BE ，::2:5(23):(53)ADE ABE S S AD AB ===⨯⨯△△[]::3:(32)(35):(32)5ABE ABC S S AE AC ==+=⨯+⨯△△，所以[]:(32):5(32)6:25ADE ABC S S =⨯⨯+=△△，设6ADE S =△份，则25ABC S =△份，12ADE S =△平方厘米，所以1份是2平方厘米，25份就是50平方厘米，ABC △的面积是50平方厘米．由此我们得到一个重要的定理，共角定理：共角三角形的面积比等于对应角(相等角或互补角)两夹边的乘积之比【例 21】如图，三角形ABC 的面积为3平方厘米，其中:2:5AB BE =，:3:2BC CD =，三角形BDE 的面积是多少？AB EC DDC EB A【解析】由于180ABC DBE ︒∠+∠=，所以可以用共角定理，设2AB =份，3BC =份，则5BE =份，325BD =+=份，由共角定理:():()(23):(55)6:25ABC BDE S S AB BC BE BD =⨯⨯=⨯⨯=△△，设6ABC S =△份，恰好是3平方厘米，所以1份是0.5平方厘米，25份就是250.512.5⨯=平方厘米，三角形BDE 的面积是12.5平方厘米【例 22】已知DEF △的面积为7平方厘米，,2,3BE CE AD BD CF AF ===，求ABC △的面积．FED CBA【解析】 :():()(11):(23)1:6BDE ABC S S BD BE BA BC =⨯⨯=⨯⨯=△△，:():()(13):(24)3:8CEF ABC S S CE CF CB CA =⨯⨯=⨯⨯=△△:():()(21):(34)1:6ADF ABC S S AD AF AB AC =⨯⨯=⨯⨯=△△设24ABC S =△份，则4BDE S =△份，4ADF S =△份，9CEF S =△份，244497DEF S =---=△份，恰好是7平方厘米，所以24ABC S =△平方厘米【例 23】如图，已知三角形ABC 面积为1，延长AB 至D ，使BD AB =；延长BC 至E ，使2CE BC =；延长CA 至F ，使3AF AC =，求三角形DEF 的面积．F EDCB AABCDEF【解析】 (法1)本题是性质的反复使用．连接AE 、CD ． ∵11ABC DBC S S =，1ABC S =， ∴S 1DBC =．同理可得其它，最后三角形DEF 的面积18=．(法2)用共角定理∵在ABC 和CFE 中，ACB ∠与FCE ∠互补， ∴111428ABC FCE S AC BC S FC CE ⋅⨯===⋅⨯．又1ABCS=，所以8FCES=．同理可得6ADFS =，3BDES=．所以186318DEFABCFCEADFBDESS SS S=+++=+++=．【例 24】如图，平行四边形ABCD ，BE AB =，2CF CB =，3GD DC =，4HA AD =，平行四边形ABCD 的面积是2，求平行四边形ABCD 与四边形EFGH 的面积比．HGAB CD EFHGA B CD EF【解析】连接AC 、BD ．根据共角定理∵在ABC △和BFE △中，ABC ∠与FBE ∠互补，∴111133ABC FBE S AB BC S BE BF ⋅⨯===⋅⨯△△．又1ABC S =△，所以3FBE S =△．同理可得8GCF S =△，15DHG S =△，8AEH S =△．所以8815+3+236EFGH AEH CFG DHG BEF ABCD S S S S S S =++++=++=△△△△．所以213618ABCD EFGH S S ==．【例 25】如图，将四边形ABCD 的四条边AB 、CB 、CD 、AD 分别延长两倍至点E 、F 、G 、H ，若四边形ABCD 的面积为5，则四边形EFGH 的面积是．A B CD E F GHA B CD EF GH【解析】连接AC 、BD ．由于2BE AB =，2BF BC =，于是4BEF ABC S S ∆∆=，同理4HDG ADC S S ∆∆=．于是444BEF HDG ABC ADC ABCD S S S S S ∆∆∆∆+=+=．再由于3AE AB =，3AH AD =，于是9AEH ABD S S ∆∆=，同理9CFG CBD S S ∆∆=．于是999AEH CFG ABD CBD ABCD S S S S S ∆∆∆∆+=+=．那么491260EFGH BEF HDG AEH CFG ABCD ABCD ABCD ABCD ABCD S S S S S S S S S S ∆∆∆∆=+++-=+-==．【例 26】如图，1ABC S =△，5BC BD =，4AC EC =，DG GS SE ==，AF FG =．求FGSS．SGF E DCBA【解析】本题题目本身很简单，但它把本讲的两个重要知识点融合到一起，既可以看作是”当两个三角形有一个角相等或互补时，这两个三角形的面积比等于夹这个角的两边长度的乘积比”的反复运用，也可以看作是找点，最妙的是其中包含了找点的3种情况．最后求得FGS S △的面积为4321115432210FGS S =⨯⨯⨯⨯=△．练习1. (第三届“华杯赛”初赛试题）一个长方形分成4个不同的三角形，绿色三角形面积占长方形面积的15%，黄色三角形面积是221cm ．问：长方形的面积是多少平方厘米？红绿黄红练习2. 如图，在平行四边形ABCD 中，EF 平行AC ，连结BE 、AE 、CF 、BF 那么与BEC 等积的三角形一共有哪几个三角形？F DECBA练习3. (97迎春杯决赛)如图，长方形ABCD 的面积是1，M 是AD 边的中点，N 在AB 边上，且2AN BN =.那么，阴影部分的面积是多少？课后练习练习4. 如图，三角形ABC 的面积是24，D 、E 和F 分别是BC 、AC 和AD 的中点．求三角形DEF 的面积．FE DCBA练习5. 如图，三角形ABC 中，AB 是AD 的5倍，AC 是AE 的3倍，如果三角形ADE 的面积等于1，那么三角形ABC 的面积是多少？E D CBA AB CD E练习6. 如图，在ABC △中，延长AB 至D ，使BD AB =，延长BC 至E ，使12CE BC =，F 是AC 的中点，若ABC △的面积是2，则DEF △的面积是多少？A BCDEF。

2013寒假 6年级第06讲直线型面积3

1. 右图的大三角形被分成 5 个小三角形，其中 4 个的面积已经标在图中，那么，阴影三角形的面积是．
2.
如图， E 在 AC 上， D 在 BC 上，且 AE : EC 2 : 3 , BD : DC 等于 22 cm2 ，则三角形 ABC 的面积．
1: 2 ， AD 与 BE 交于点 F ．四边形 DFEC 的面积
第六讲直线型面积三
知识点拨燕尾定理
在三角形 ABC 中, AD , BE , CF 相交于同一点 G ,那么 S
A F G B E C S ABG :S AGC =S BGE :S CGE =BE:EC S AGB :S CGB =S AGF :S CGF =AF:FC S AGC :S BGC =S AGD :S BGD =AD:DB
D C
G
F
A
E
B
5.
如图，在△ABC 中，△AEO 的面积是 1，△ABO 的面积是 2，△BOD 的面积是 3，则四边形 DCEO 的面积是多少？
6.
如图，
ABC 中 BD
2DA ， CE
2EB ， AF
2FC ，那么
ABC 的面积是阴影三角形面积的
A
倍．
D G F H B E I C
3
课后练习
4
3
7 7
2
课堂练习
1. 如图所示，在 △ABC 中， BE : EC
3:1 ， D 是 AE 的中点，那么 AF : FC
．
A F
D
B
2. 如图所示，在 ABC 中， CP 于．
E
C
1 CB, CQ 2
1 CA, BQ 与 AP 相交于点 X ，若 ABC 的面积为 6 ，则 ABX 的面积等 3

五年级奥数专题直线型面积计算(学生版)

学科培优数学“直线型面积计算”学生姓名授课日期教师姓名授课时长知识定位本讲讲解已经学过的几种基本平面几何图形：正方形、长方形、三角形、平行四边形、梯形等的相关面积计算方法,是几何问题中的常见常考内容。

知识梳理一、基本平面图形的计算公式【授课批注】在复习学校所学基本面积公式的同时也顺带复习周长的公式,这些知识点在具体题目中都可能用到。

二、重要模型模型一：同一三角形中,相应面积与底的正比关系：bs 2s 1即：两个三角形高相等,面积之比等于对应底边之比。

S 1︰S 2 =a ︰b ；模型一的拓展：等分点结论（“鸟头定理”）如图,三角形AED 占三角形ABC 面积的23×14=16模型二：任意四边形中的比例关系（“蝴蝶定理”） ①S 1︰S 2=S 4︰S 3 或者S 1×S 3=S 2×S 4②AO ︰OC=（S 1+S 2）︰（S 4+S 3）模型三：梯形中比例关系（“梯形蝴蝶定理”）①S 1︰S 3=a 2︰b 2 ②S 1︰S 3︰S 2︰S 4= a 2︰b 2︰ab ︰ab ; ③S 的对应份数为（a+b ）2【授课批注】因为四年级还没学过比例,所以在讲用比所表示的模型时可使用份数这个概念,学生更容易理解。

对于部分学有余力的学生可以先讲比例再直接引入上面的关系式。

【重点难点解析】1．等底或等高的三角形的面积关系2．长方形或平行四边形与同底等高三角形的面积关系 3. 三角形内不规则图形部分的面积计算【竞赛考点挖掘】1. 基本几何图形的面积计算2. 三角形中底和高与面积的关系3. 四边形对角线所分成的四个三角形的面积关系S 4S 3s 2s 1ba S 4S 3s 2s 1O DCB A例题精讲【试题来源】【题目】图中三角形ABC的面积是180平方厘米,D是BC的中点,AD的长是AE长的3倍, EF 的长是BF长的3倍．那么三角形AEF的面积是多少平方厘米?【试题来源】【题目】如图,把四边形ABCD的各边都延长2倍,得到一个新四边形EFGH如果ABCD的面积是5平方厘米,则EFGH的面积是多少平方厘米?【试题来源】【题目】图中的四边形土地的总面积是52公顷,两条对角线把它分成了4个小三角形,其中2个小三角形的面积分别是6公顷和7公顷．那么最大的一个三角形的面积是多少公顷?【试题来源】【题目】如图16-4,已知．AE=15AC,CD=14BC,BF=16AB,那么DEFABC三角形的面积三角形的面积等于多少?【试题来源】【题目】如图,长方形ABCD的面积是2平方厘米,EC=2DE,F是DG的中点．阴影部分的面积是多少平方厘米?【试题来源】【题目】如图,已知D是BC中点,E是CD的中点,F是AC的中点．三角形ABC由①～⑥这6部分组成,其中②比⑤多6平方厘米．那么三角形ABC的面积是多少平方厘米?【试题来源】【题目】左下图是一个各条边分别为5厘米、12厘米、13厘米的直角三角形．如右下图,将它的短直角边对折到斜边上去与斜边相重合,那么右下图中的阴影部分(即未被盖住的部分)的面积是多少平方厘米?习题演练【试题来源】【题目】如图,在一个梯形内有两个三角形的面积分别为10与12,已知梯形的上底长是下底长的23．那么余下阴影部分的面积是多少?【试题来源】【题目】图中ABCD是梯形,三角形ADE面积是1．8,三角形ABF的面积是9,三角形BCF的面积是27．那么阴影部分面积是多少?【试题来源】【题目】如图,梯形ABCD的上底AD长为3厘米,下底BC长为9厘米,而三角形ABO的面积为12平方厘米．则梯形ABCD的面积为多少平方厘米?【试题来源】【题目】如图,BD,CF将长方形ABCD分成4块,红色三角形面积是4平方厘米,黄色三角形面积是6平方厘米．问：绿色四边形面积是多少平方厘米?【试题来源】【题目】如图,平行四边形ABCD周长为75厘米．以BC为底时高是14厘米；以CD为底时高是16厘米．求平行四边形ABCD的面积．【试题来源】【题目】如图,一个正方形被分成4个小长方形,它们的面积分别是110平方米、15平方米、3 10平方米和25平方米．已知图中的阴影部分是正方形,那么它的面积是多少平方米?【试题来源】【题目】图中外侧的四边形是一边长为10厘米的正方形,求阴影部分的面积．【试题来源】【题目】如图,长方形被其内的一些直线划分成了若干块,已知边上有3块面积分别是13,35,49．那么图中阴影部分的面积是多少?【试题来源】【题目】在右图的△ABC中,CE=2AE,BD=3DC,已知△DEC的面积是4cm2,求△ABC的面积。

第03讲基本直线型面积公式(学生版)-三升四暑期数学奥数培优讲义

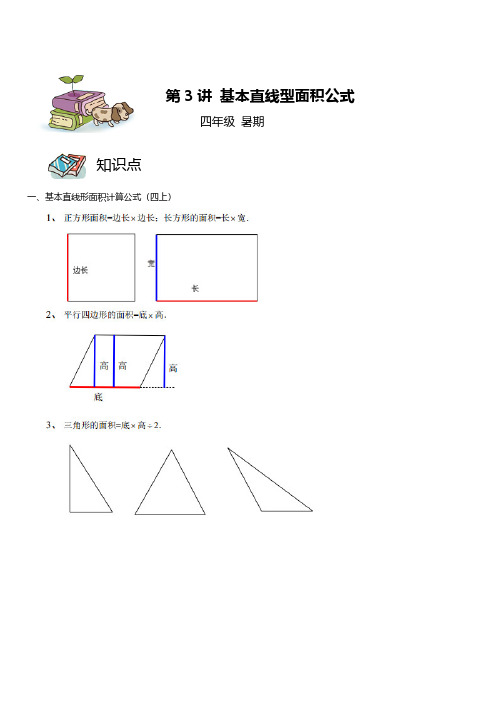
一、基本直线形面积计算公式（四上）第3讲基本直线型面积公式四年级暑期知识点熟练掌握各种图形面积公式，梯形和三角形的面积公式最后一定要除以 2.理解每个图形的高是什么，会做高.一、长方形、正方形1、如下图，有一块长方形田地被分成了五小块，分别栽种了茄子、黄瓜、豆角、莴笋和苦瓜．其中栽种茄子的面积是16平方米，栽种黄瓜的面积是28平方米，栽种豆角的面积是32平方米，栽种莴笋的面积是72平方米，而且左上角栽种茄子的田地恰好是一个正方形．请问：剩下的栽种苦瓜的田地面积是多少？课堂例题方法精讲2、（金帆四年级春季）如图有九个小长方形，其中编号为1，2，3，4，5的5个小长方形的面积分别为2，4，6，8，10平方米，求6号长方形的面积．二、三角形求面积3、如下图所示，两个正方形并排放在一起，大正方形的边长是8厘米，小正方形的边长是6厘米．请问：阴影三角形的面积是多少？4、如图，小正方形的边长为6厘米，大正方形的边长为11厘米，请问：图中阴影部分的面积？5、如图，把两个正方形拼在一起，小正方形的边长是5厘米，大正方形的边长是7厘米．请问：阴影部分的面积是多少？三、平行四边形6、下图是由两个边长分别为4和7的正方形拼成的，请求出阴影平行四边形的面积．7、如下图所示，两个边长10厘米的正方形相互错开3厘米，那么图中阴影平行四边形的面积是多少？8、图中，平行四边形的面积是24，大正方形的边长是8，小正方形的面积是________．9、如图，两个一样的长方形相互错开2厘米拼在一起，长方形的长是10厘米，宽是4厘米，请问：图中阴影平行四边形的面积是多少？四、梯形10、一个正方形和一个长方形按下图的方式排放，已知正方形的面积是49平方厘米，长方形的长为11厘米，宽为8厘米，那么阴影部分的面积是多少？11、如图，两个正方形按如图方式放在一起，小正方形的边长为3厘米，大正方形的面积是49平方厘米．请问：阴影部分的面积是多少？12、如图，ABCD是直角梯形，△AEC和△EBD都是等腰直角三角形，已知梯形高为20，那么梯形的面积是______（改自2010年4月18日考试真题）13、如图所示，平行四边形的一边长为15厘米，这条边上的高为6厘米，一条线段将此平行四边形分成了两部分，它们的面积相差18平方厘米．请问：其中梯形的上底是多少厘米？1、如图，有一块长方形田地被分成了四小块，分别栽种了冬瓜、西瓜、南瓜、黄瓜，其中冬瓜地的面积是24平方米，西瓜地的面积是36平方米，南瓜地的面积是18平方米，而且左下角西瓜地恰好是一个正方形．请问：剩下的黄瓜地的面积是多少？2、如图，大正方形里有一个小正方形还有一个阴影平行四边形．如果大正方形的边长是20厘米，小正方形的边长是8厘米．那么阴影平行四边形的面积是多少？3、右图是由两个边长分别为4和6的正方形拼成的，请求出阴影三角形的面积． 36 1824随堂练习4、如下图，大正方形的边长是8厘米，小正方形的边长是6厘米．请问：图中的阴影图形的面积是多少平方厘米？1、在下面的三角形中，以AB 为底作高，正确的是__________．课后作业2、如图，大正方形被分成三块区域．左上角的正方形面积为4，右上角的长方形面积为6，那么大正方形的面积是__________．3、下图中，大正方形的面积是64，小正方形的面积是36．那么平行四边形的面积是__________．4、下图是边长为8和6的两个正方形拼成的，根据图中所示的线段长度，阴影三角形的面积是_________.5、如图，两个正方形并排放在一起，小正方形的面积是81平方厘米，大正方形的面积是169平方厘米．那么阴影梯形的面积是___________平方厘米．6、（金帆四年级春季）如图，平行四边形ABCD的边BC长10cm，直角三角形BCE的直角边EC长8cm，已知两块阴影部分的面积和比△EFG的面积大10cm2，求CF的长．。

第三讲基本直线形面积公式

于是我们有：如下图所示，同学们可以画出这条底对应的若干条高，并且这些高是相等的，都等于上下两条平行线间的距离。

平行四边形面积=底*高高高高底如图是由两个边长分别为4和7的正方形拼成的，请求出图中阴影部分的面积。

6年级-14-直线形面积综合-难版

第13讲直线形面积综合一定综合性的直线形面积问题，重点是需要利用同底或同高的两三角形的面积相除的商等于对应高或对应底相除的商这一性质的问题，有时合理添加辅助线是解决问题的关键。

我们还会常常用到以下结论：（1）等底等高的两个三角形面积相等；（2）两个三角形高相等，面积比等于它们的底之比；两个三角形底相等，面积比等于它们的高之比；如左图12::S S a b =baS 2S 1（3）在三角形ABC 中，AD ，BE ，CF 相交于同一点O ，那么::ABO ACO S S BD DC ∆∆=．知识梳理OFE DC BA【例1】★如右图，ABFE 和CDEF 都是矩形，AB 的长是4厘米，BC 的长是3厘米，那么图中阴影部分的面积是平方厘米．A B CDE F【解析】图中阴影部分的面积等于长方形ABCD 面积的一半，即4326⨯÷=(平方厘米)．【小试牛刀】(2009年四中小升初入学测试题)如图所示，平行四边形的面积是50平方厘米，则阴影部分的面积是平方厘米．【解析】根据面积比例模型，可知图中空白三角形面积等于平行四边形面积的一半，所以阴影部分的面积也等于平行四边形面积的一半，为50225÷=平方厘米．【例2】★★如图，长方形ABCD 的面积是56平方厘米，点E 、F 、G 分别是长方形ABCD 边上的中点，H 为AD 边上的任意一点，求阴影部分的面积．典型例题E BAE BA【解析】本题是等底等高的两个三角形面积相等的应用．连接BH 、CH ． ∵AE EB =， ∴AEH BEH S S =△△．同理，BFH CFH S S =△△，S =S CGH DGH V V ， ∴11562822ABCD S S ==⨯=阴影长方形(平方厘米)．【小试牛刀】图中的E 、F 、G 分别是正方形ABCD 三条边的三等分点，如果正方形的边长是12，那么阴影部分的面积是．E GCBBCGE【解析】把另外三个三等分点标出之后，正方形的3个边就都被分成了相等的三段．把H 和这些分点以及正方形的顶点相连，把整个正方形分割成了9个形状各不相同的三角形．这9个三角形的底边分别是在正方形的3个边上，它们的长度都是正方形边长的三分之一．阴影部分被分割成了3个三角形，右边三角形的面积和第1第2个三角形相等：中间三角形的面积和第3第4个三角形相等；左边三角形的面积和第5个第6个三角形相等．因此这3个阴影三角形的面积分别是ABH 、BCH 和CDH 的三分之一，因此全部阴影的总面积就等于正方形面积的三分之一．正方形的面积是144，阴影部分的面积就是48．【例3】★★★已知图中，三角形ABC的面积为8平方厘米，AE＝ED，BD=23BC，求阴影部分的面积。

六年级数学几何图形面积计算的技巧和方法

六年级数学几何图形面积计算的技巧和方法一、熟练掌握基本图形面积公式的推导对于长方形、正方形、平行四边形、三角形以及梯形等基本几何图形的面积计算，同学们要熟练掌握其面积公式的推导过程，并能够熟练运用。

如：长方形的面积=长×宽；正方形的面积=边长×边长；平行四边形的面积=底×高；三角形的面积=底×高÷2；梯形的面积=(上底+下底)×高÷2。

这些基本图形的面积计算是同学们必须掌握的基本技能。

二、学会灵活运用组合图形在几何图形中，有很多是由两个或多个基本图形组合在一起，这种图形叫做组合图形。

在计算其面积时，同学们要学会分割法和添补法，正确地分割出基本图形，再根据图形中各个基本图形的面积公式来计算。

如果分割出的基本图形不规则，则要利用割补法把它转化成已学过的基本图形来计算。

三、掌握常用的辅助线在几何图形中，添加辅助线是解决几何问题的重要方法之一。

添辅助线的方法一般有：平行线法、变换方向法、同一法、与圆有关的辅助线法等。

在学习中要灵活运用各种辅助线，会添加辅助线是解几何题的必要技能之一。

如求梯形面积时，需要连接对角线，将梯形转化为三角形来求解；求圆的面积时，可以化曲为直，把圆转化为近似长方形或扇形来求解。

四、合理选择方法有些几何图形的面积在一般情况下需要多次分割和添补才能得出结果。

此时同学们需要尝试多种方法，从不同角度分析问题，比较不同方法的优劣，最终选择最简单的方法。

有些几何图形在特殊情况下，可以利用特殊图形（如正方形、圆等）的面积进行求解。

因此，同学们需要了解这些特殊情况下的求解方法，以提高解题效率。

五、重视单位转换在几何图形中，不同的单位需要转换成相同的单位才能进行计算。

同学们在解题时需要时刻关注单位转换，避免出现错误。

在解答完成后要认真检查自己的答案，确保单位一致。

六、总结反思解题后要总结解题规律，反思解题思路，优化解题方法，从而形成解题规律。

六同第三讲直线型面积计算.

第三讲直线型面积计算教学目标：1.掌握等量代换和割补法的性质与特点2.灵活运用这两种方法决求直线型图形的面积。

3.培养学生分析问题解决问题的能力教学重难点：割补法在求图形面积中的应用。

教学方法：讲练教学用具：讲义教学过程:一、故事导入一位农夫请了工程师、物理学家和数学家来，想用最少的篱笆围出最大的面积。

工程师用篱笆围出一个圆，宣称这是最优设计。

物理学家将篱笆拉开成一条长长的直线，认为围起半个地球总够大了。

（讲到这里，老师们可以停下来问问同学们还有更好的方法吗？让学生们各抒己见）揭晓答案，数学家好好嘲笑了他们一番。

他用很少的篱笆把自己围起来，然后说：“我现在是在外面。

”师：这个故事告诉我们想问题不能墨守成规，而要把思路发散开来。

就像我们同学从3年级开始就已经学习了长方形、正方形、梯形、三角形等图形，对于他们的面积公式肯定是熟记于心。

（这里可以带着学生复习一下面积公式：长方形S=a×b；正方形 S=a×a；梯形 S=(a+b) ×h÷2；三角形 S= a×h÷2。

另外老师可以准备一些规则以及不规则的图形卡片，引导学生发现生活中实际有很多平面图形并不是规则的图形，那么我们该如何来求它们的面积呢？这就需要一定的方法了）下面就跟着老师走进今天的数学课堂，学完今天的内容大家就会豁然开朗了！那么我们一起来学习----直线型面积计算二、新课学习例1：（原例3）、已知长方形ABCD的面积是40平方厘米，AE=5cm，求BD的长。

解析：可以很容易发现BD是三角形ABD的一条边，又因为AE为BD的高，那么在已知高的情况下如何求底边？利用公式三角形 S= a×h÷2变形得a=s×2÷h。

可以求得BD。

三角形ABD的面积：40÷2=20平方厘米BD的长：20×2÷5=8厘米小结：本题采用公式变形的方法计算出结果，称之定义法。

曲线 ,直线线及轴所围成平面区域的面积.

曲线 ,直线线及轴所围成平面区域的面积.曲线、直线、线以及轴之间的组合，可以围成各种形状的平面区域。

无论是高中数学还是大学高等数学课程中，面积计算都是一个非常重要的知识点。

在本文中，我们将会深入探讨曲线、直线、线以及轴所围成平面区域的面积的计算方法。

在高中数学中，我们学过了如何计算简单的平面图形的面积，如正方形、矩形、三角形和圆形等。

这些形状的面积计算方法都很简单，但是当遇到更加复杂的形状时，就需要运用一些更加高级的数学知识。

当曲线、直线与轴相交，它们之间所围成的区域可以被分成若干个不规则的小形状，这些小形状的面积可以通过定积分进行求解。

例如，当我们想要计算 y=x^2 与x=0, x=1 所围成的区域的面积时，我们可以通过下面的计算来求解：∫(0,1) x^2 dx = 1/3因此，这个区域的面积是 1/3。

在高等数学中，更加复杂的区域的面积可以通过计算曲线方程的积分来进行求解。

例如，当我们想要计算y=sin(x) 与 y=cos(x) 所围成的区域的面积时，我们可以通过下面的计算来求解：∫(0,π/2) [sin(x) - cos(x)] dx = 2-ln(2)因此，这个区域的面积是 2-ln(2)。

除了积分法之外，我们还可以用矩阵行列式的方法来计算曲线、直线、线以及轴所围成区域的面积。

这种方法通常适用于一些更加抽象的形状。

例如，当我们想要计算x+y=1 与 y=x^2 的交点所围成的区域的面积时，我们可以通过下面的计算来求解：|∫(0,1) x^2 dx 1/2| |1/2 0 |因此，这个区域的面积是 1/2。

还有一种方法，可以用于计算两个曲线之间的面积。

我们可以通过计算这两个曲线之间的实际距离来求解这个面积。

例如，当我们想要计算 y=x 与 y=x^2 所围成的区域的面积时，我们可以通过计算这两条曲线之间的距离来进行求解。

具体做法是，将距离函数取绝对值，然后对它求积分，得到的结果就是这两条曲线之间的面积。

1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

第三讲直线型面积计算教学目标：1.掌握等量代换和割补法的性质与特点2.灵活运用这两种方法决求直线型图形的面积。

3.培养学生分析问题解决问题的能力教学重难点：割补法在求图形面积中的应用。

教学方法：讲练教学用具：讲义教学过程:一、故事导入一位农夫请了工程师、物理学家和数学家来，想用最少的篱笆围出最大的面积。

工程师用篱笆围出一个圆，宣称这是最优设计。

物理学家将篱笆拉开成一条长长的直线，认为围起半个地球总够大了。

（讲到这里，老师们可以停下来问问同学们还有更好的方法吗？让学生们各抒己见）揭晓答案，数学家好好嘲笑了他们一番。

他用很少的篱笆把自己围起来，然后说：“我现在是在外面。

”师：这个故事告诉我们想问题不能墨守成规，而要把思路发散开来。

就像我们同学从3年级开始就已经学习了长方形、正方形、梯形、三角形等图形，对于他们的面积公式肯定是熟记于心。

（这里可以带着学生复习一下面积公式：长方形S=a×b；正方形S=a×a；梯形S=(a+b) ×h÷2；三角形S= a×h÷2。

解析：可以很容易发现BD 是三角形ABD 的一条边，又因为AE 为BD 的高，那么在已知高的情况下如何求底边？利用公式三角形 S= a ×h ÷2变形得a=s ×2÷h 。

可以求得BD 。

三角形ABD 的面积：40÷2=20平方厘米 BD 的长：20×2÷5=8厘米小结：本题采用公式变形的方法计算出结果，称之定义法。

例2：（原例1）、三角形ABC 的面积为36平方分米,DC=2BD,求阴影部分的面积。

解析：由题意DC=2BD ，可以理解成BD 被分成3份，BD 占1份，DC 占2份，又因为三角形ADC 和三角形ABD 等高，所以三角形ADC 是三角形ABD 的2倍。

36÷（1+2）×2=24平方分米过渡：来看下一个例题可不可以用这个方法呢？例3、如图，在三角形ABC 中，D 是BC 的中点，AE=3ED ，三角形ABC 的面积为96平方厘米，求阴影部分。

DC解析：D 为三角形ABC 的底边BC 的中点，BD=CD ，而且三角形ABD 和ADC 等高，所以三角形ABD 和ADC 面积相等。

也可以理解为AD 把三角形ABC 分成了面积相等的两部分，三角形ABD 占一份。

同样的，在三角形ABD 中，底边AD 上有这样的关系----AE=3ED ，说明AD 被分成了4等分，ED 占一份，AE 占3份，即三角形ABD 被分成了面积相等的4部分，三角形ABE 占3份。

SABD=96÷2=48平方厘米 48÷4×3=36平方厘米小结：通过以上两个例题，我们知道了同高三角形面积的份数关系等于底的分数关系（因为有些学生不知道比，所以老师们可以视班里学生情况总结）下面我们看下练习7练习：如下图，已知在三角形ABC 中，BE=3AE ，CD=2AD 。

若三角形ADE 的面积为1平方厘米。

求三角形ABC 的面积。

CBC解析：这一题和刚才的两题就有点区别了，题目中给出了边的份数关系和小三角形ADE 的面积。

我们要求大三角形ABC 的面积。

连接BD ，我们还是从大三角形开始分析：CD=2AD ，说明AC 被分成了3等份，CD 占2份，即三角形ABC 被分成了面积相等的3等份，三角形ABD 占一份；BE=3AE,说明AB 被分成了4等份，AE占一份，即三角形ABD的面积被分成了4等份，三角形ADE占一份。

这样我们就找到了SADE与SABC的关系。

1×（3+1）=4（平方厘米）4×（2+1）=12（平方厘米）例4、下图是由大、小两个正方形组成的，小正方形的边长是4厘米，大正方形边长为5厘米，求三角形ABC的面积。

解析：这个题目只有小正方形的边长是已知的，而三角形ABC中有一部分在小正方形中，还有一部分在大正方形中。

如果我们能通过等量代换把三角形ABC全部都转换到小正方形中就好解决了。

连接AD，显然AD∥BC,接下来怎么转化呢？我们把梯形ABCD单独拿出来讨论，发现，三角形ABD和ACD有公共的底AD，且它们的高相等（由于AD∥BC）。

所以，SABD=SACD，而这两个三角形有一个公共的部分---三角形ADF，根据我们前面讲的，等式两边都减去SADF后所得结果仍然相等，联系图形，即SABF=SCDF。

这是著名的蝶形定理中的一个性质。

然后，我们就可以把三角形ABC全部转化到小正方形中了，SABC=SBCD。

SABC=SBCD=4×4÷2=8（平方厘米）答：三角形ABC的面积为8平方厘米。

小结：这一题我们连接AD，利用两个正方形的对角线，找出一个梯形，然后再进行等量代换。

把三角形ABC中的ABF割下来补到三角形CDF中，这样就用到了我们今天要学习的第二种方法----割补法，把不能直接求的面积转化为可以求的面积。

这一题还要注意蝶形定理的运用。

例5：两个相同的直角三角形如下图所示（单位：厘米）重叠在一起，求阴影部分的面积.FA解析：先看一个简单的加减法算式13=5+8，如果等式的两边都减去3，结果还会不会相等呢？（提问）其实这里面隐含着一个很重要的性质----两个相等的量同时减去一个相同的量，所得结果仍然相等，简称同减。

现在我们来看这一题，阴影部分的面积不能直接求出，可以转化为△ABC与△DOC的面积差。

△ABC和△DEF是相同的三角形，所以S△ABC=S△DEF；从图中看出，△DOC是△ABC和△DEF的公共部分。

根据我们前面的分析，可以得出S△ABC-S△DOC =S△DEF -S△DOC，所以S阴=SOEFC。

SOEFC=（10+7）×2÷2=17（平方厘米）答：阴影部分的面积为17平方厘米。

例6、如下图所示，在一个等腰直角三角形中，削去一个三角形后，剩下一个上底长5厘米、下地长9厘米的等腰梯形（阴影部分）。

求这个梯形的面积。

解析：已知条件只给出了大、小两个直角三角形的斜边长，可是求三角形的面积需要知道直角边长，怎么办呢？能不能想办法把直角边转化为直角边呢？题目所给的三角形非常特殊，等腰直角三角形，其底角为45度。

我们将这个三角形沿着其中一条直角边旋转180度，之后得到下图：A我们发现，三角形ABC和DEF仍然是等腰直角三角形，且这两个三角形的面积可以直接得出。

然后根据我们刚才学习的等量代换的思想，可以计算出阴影部分的面积，然后再得出题目所求。

SABC=9×9÷2=40.5（平方厘米）SDEF=5×5÷2=12.5（平方厘米）S阴=40.5-12.5=28（平方厘米）S梯=28÷2=14（平方厘米）这种方法我们利用了这里特殊的45度角，除了利用补图形的办法外，还有没有别的办法呢？求三角形的面积需要知道底边长和对应边上的高，我们给这个等腰三角形作高，大家有没有什么发现呢？（引导学生，让他们学会利用等腰直角三角形特殊的45度角）如下图MN垂直于AC，三角形CNM和FHM也都是等腰直角三角形，MN=CN=AC÷2=4.5（厘米）MH=FH=CD÷2=2.5（厘米）HN=4.5-2.5=2（厘米）S梯=（5+9）×2÷2=14（平方厘米）ADM F小结：这一题我们有两种方法，都是利用了等腰直角三角形中特殊的45度角，或者是旋转补图形，或者是作高。

下面大家看练习题8练习：在下图所示的等腰直角三角形中，剪去一个三角形后，剩下的部分是一个直角梯形（阴影部分）。

已知梯形的面积为36平方厘米，上底为3厘米，求下底和高。

解析：这一题和例题的条件很相似，只是例题中平行于底边剪掉一个三角形，而本题中则平行于一条直角边剪掉一个三角形。

根据刚才的学习，大家应该对等腰直角三角形中特殊的45度角很有好感了！因为它对我们解题很有帮助。

与例题类似，我们先补图形，如下图：我们发现，三角形AOF，AEF，ABC都是等腰直角三角形。

因为题目中告诉了直角梯形的上底，即OF=OE=3，AO=3，所以三角形AEF的面积可求。

等腰梯形EFCB的面积也可求，这样就能求出三角形ABC的面积。

根据三角形的面积计算公式，可以求出BC，AD，然后再求CD，OD，即下底和高。

（3+3）×3÷2=9（平方厘米）36×2+9=81（平方厘米）BC ×AD ÷2=CD ×AD=CD ×CD=81（平方厘米） CD= AD =9（厘米） OD=9-3=6（厘米）答：下底为9厘米，高为6厘米。

例7、在下图的直角三角形中有一个矩形，求矩形的面积。

解析：求矩形的面积我们必须知道其长和宽，而题目给出的条件与所求没有任何关系，所以我们要想办法把已知条件转化为我们可以用的量。

因为题目给出的是一个直角三角形，我们给它补一个相同的直角三角形，让它变成一个矩形，如下图：GF E D C我们发现，在矩形ABCD 中，三角形ABC 和ACD 相等；在矩形AEOG 中，三角形AOG 和AOE 相等；在矩形CFOH 中，三角形COF 和COH 相等。

根据等量代换的思想，SABC-SCOH-SAOE=SACD-SCOF-SAOG ，即SBEOH=SDFOG 。

矩形DOFG 的面积可以有已知条件求出，所以得解。

SBEOH=SDFOG=4×6=24小结：在这一例中，我们利用对称的思想补图形，然后再进行等量代换，得出题目所求。

下面大家看练习题9，用类似的方法试试看。

练习：在下图中，长方形AEFD 的面积是18平方厘米，BE 长3厘米，求CD 的长。

D解析：这一题和例题非常的类似，只是把已知和求解调换了。

同样的，我们先要补图形，如图MD C BA和例题类似，在矩形ABGC 中，三角形ABC 和BGC 相等；在矩形BEFM 中，三角形BEF 和BMF 相等；在矩形CDFH 中，三角形CDF 和FHC 相等。

所以，SABC-SBEF-SCDF=SBGC-SBMF-SFHC ，即SAEFD=SGMFHSGMFH=FM ×HF=BE ×CD CD=18÷3=6(厘米)过渡：是不是所有的图形问题都可以用这种对称的思想解决呢？（提问）接下来我们看例8。

六同第三讲直线型面积计算

六年级奥数 几何;第3讲;直线型面积_三_;教师版

直线图形面积计算一：利用倍数关系求解面积六年级[暑假一]

第三讲 基本直线形面积公式

003直线型面积

直线型面积

直线型面积计算

小学奥数平面直线型几何知识汇总

直线图形面积计算一：利用倍数关系求解面积六年级[暑假一]

图形复习五年级数学

小学奥数-直线型面积讲义图文版

2013寒假 6年级 第06讲 直线型面积3

五年级奥数专题 直线型面积计算(学生版)

第03讲 基本直线型面积公式(学生版)-三升四暑期数学奥数培优讲义

第三讲 基本直线形面积公式

6年级-14-直线形面积综合-难版

六年级数学几何图形面积计算的技巧和方法

六同第三讲 直线型面积计算.

曲线 ,直线 线 及 轴所围成平面区域的面积.

六年级奥数几何;第3讲;直线型面积_三_;教师版

第三讲基本直线形面积公式

2013寒假 6年级第06讲直线型面积3

五年级奥数专题直线型面积计算(学生版)

第03讲基本直线型面积公式(学生版)-三升四暑期数学奥数培优讲义

第三讲基本直线形面积公式

六同第三讲直线型面积计算.

曲线 ,直线线及轴所围成平面区域的面积.