最新转动惯量计算公式
(完整word版)转动惯量计算公式
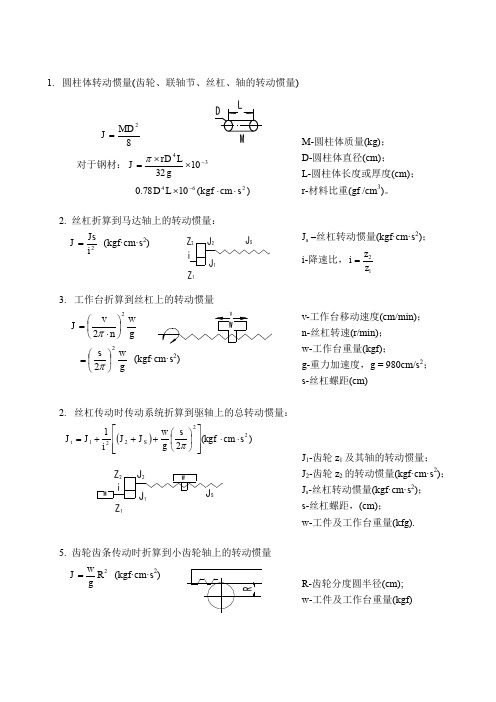
1. 圆柱体转动惯量(齿轮、联轴节、丝杠、轴的转动惯量)82MD J =对于钢材:341032-⨯⨯=gLrD J π)(1078.0264s cm kgf L D ⋅⋅⨯-M-圆柱体质量(kg); D-圆柱体直径(cm); L-圆柱体长度或厚度(cm); r-材料比重(gf /cm 3)。
2. 丝杠折算到马达轴上的转动惯量:2i Js J = (kgf·cm·s 2)J s –丝杠转动惯量(kgf·cm·s 2); i-降速比,12z z i =3. 工作台折算到丝杠上的转动惯量g w22⎪⎭⎫ ⎝⎛⋅=n v J π g w2s 2⎪⎭⎫ ⎝⎛=π (kgf·cm·s 2) v -工作台移动速度(cm/min); n-丝杠转速(r/min); w-工作台重量(kgf);g-重力加速度,g = 980cm/s 2; s-丝杠螺距(cm)2. 丝杠传动时传动系统折算到驱轴上的总转动惯量:())s cm (kgf 2g w 122221⋅⋅⎥⎥⎦⎤⎢⎢⎣⎡⎪⎭⎫ ⎝⎛+++=πs J J iJ J S tJ 1-齿轮z 1及其轴的转动惯量; J 2-齿轮z 2的转动惯量(kgf·cm·s 2); J s -丝杠转动惯量(kgf·cm·s 2); s-丝杠螺距,(cm); w-工件及工作台重量(kfg).5. 齿轮齿条传动时折算到小齿轮轴上的转动惯量2gw R J =(kgf·cm·s 2)R-齿轮分度圆半径(cm); w-工件及工作台重量(kgf)6. 齿轮齿条传动时传动系统折算到马达轴上的总转动惯量⎪⎪⎭⎫⎝⎛++=2221g w 1R J i J J tJ 1,J 2-分别为Ⅰ轴,Ⅱ轴上齿轮的转动惯量(kgf·cm·s 2);R-齿轮z 分度圆半径(cm); w-工件及工作台重量(kgf)。
最新转动惯量计算公式

12 1. 圆柱体转动惯量(齿轮、联轴节、丝杠、轴的转动惯量)3 4 582MD J =6对于钢材:341032-⨯⨯=gLrD J π7 )(1078.0264s cm kgf L D ⋅⋅⨯-89 M-圆柱体质量(kg);D-圆柱体直径(cm); 11 L-圆柱体长度或厚度(cm); 12r-材料比重(gf /cm 3)。
1314 2. 丝杠折算到马达轴上的转动惯量:152i Js J = (kgf·c1617 J s –丝杠转动惯量18 (kgf·c m·s 2);19 i-降速比,12z z i =2122gw22⎪⎭⎫ ⎝⎛⋅=n v J π 23gw2s 2⎪⎭⎫ ⎝⎛=π (kgf·c m·s 2) 2425 v -工作台移动速度(cm/min);26 n-丝杠转速(r/min); 27 w-工作台重量(kgf);28g-重力加速度,g = 980cm/s 2; 29 s-丝杠螺距(cm)3031 2. 丝杠传动时传动系统折算到驱轴上的总转动惯量:32())s cm (kgf 2g w 122221⋅⋅⎥⎥⎦⎤⎢⎢⎣⎡⎪⎭⎫ ⎝⎛+++=πs J J iJ J S t 33 3435 36 37 383940 J 1-齿轮z 1及其轴的转动惯量;41 J 2-齿轮z 2的转动惯量42 (kgf ·cm ·s 2);43J s -丝杠转动惯量(kgf ·cm ·s 2);44s-丝杠螺距,(cm); 45 w-工件及工作台重量(kfg).4647 5. 齿轮齿条传动时折算到小齿轮轴上的转动惯量482gw RJ =(kgf ·c 49 50 R-齿轮分度圆半径(cm);w-工件及工作台重量(kgf)53 5455 56 5758 6. 齿轮齿条传动时传动系统折算到马达轴上的总转动惯量59⎪⎪⎭⎫ ⎝⎛++=2221g w 1R J i J J t 6061 6263 64J 1,J 2-分别为Ⅰ轴,65Ⅱ轴上齿轮的转动惯量(kgf ·c m·s 2);66R-齿轮z 分度圆半径(cm); 67w-工件及工作台重量(kgf)。
转动惯量计算公式是什么

转动惯量计算公式是什么 转动惯量是⼤学物理中⼀个⼗分重要的知识点。
下⾯是由店铺编辑为⼤家整理的“转动惯量的定义以及计算公式”,仅供参考,欢迎⼤家阅读本⽂。
转动惯量 转动惯量(Moment of Inertia),⼜称质量惯性矩,简称惯距,是经典⼒学中物体绕轴转动时惯性的量度,常⽤⽤字⺟I或J表⽰。
转动惯量的SI单位为kg·m²。
对于⼀个质点,I=mr²,其中,m是其质量,r是质点和转轴的垂直距离。
和线性动⼒学中的质量相类似,在旋转动⼒学中,转动惯量的⾓⾊相当于物体旋转运动的惯性,可⽤于建⽴⾓动量、⾓速度、⼒矩和⾓加速度等数个量之间的关系。
对于规则物体,其转动惯量可以按照相应公式直接计算;对于外形复杂和质量分布不均的物体,转动惯量可通过实验⽅法来测定。
实验室中最常⻅的转动惯量测试⽅法为三线摆法。
转动惯量计算公式 1、对于细杆: 当回转轴过杆的中点(质⼼)并垂直于杆时I=mL²/I²;其中m是杆的质量,L是杆的⻓度。
当回转轴过杆的端点并垂直于杆时I=mL²/3;其中m是杆的质量,L是杆的⻓度。
2、对于圆柱体: 当回转轴是圆柱体轴线时I=mr²/2;其中m是圆柱体的质量,r是圆柱体的半径。
3、对于细圆环: 当回转轴通过环⼼且与环⾯垂直时,I=mR²;当回转轴通过环边缘且与环⾯垂直时,I=2mR²;I=mR²/2沿环的某⼀直径;R为其半径。
4、对于⽴⽅体: 当回转轴为其中⼼轴时,I=mL²/6;当回转轴为其棱边时I=2mL²/3;当回转轴为其体对⾓线时,I=3mL²/16;L为⽴⽅体边⻓。
5、对于实⼼球体: 当回转轴为球体的中⼼轴时,I=2mR²/5;当回转轴为球体的切线时,I=7mR²/5;R为球体半径。
转动惯量公式是什么 怎么计算

转动惯量公式是什么怎么计算
在经典力学中,转动惯量通常以I或J表示,SI单位为kg·m ²。
对于一个质点,I=mr²,其中m是其质量,r是质点和转轴的垂直距离。
转动惯量公式是什么怎么计算
1转动惯量是什么
转动惯量是刚体绕轴转动时惯性(回转物体保持其匀速圆周运动或静止的特性)的量度,用字母I或J表示。
在经典力学中,转动惯量(又称质量惯性矩,简称惯矩)通常以I或J表示,SI 单位为kg·m²。
对于一个质点,I=mr²,其中m 是其质量,r是质点和转轴的垂直距离。
转动惯量在旋转动力学中的角色相当于线性动力学中的质量,可形式地理解为一个物体对于旋转运动的惯性,用于建立角动量、角速度、力矩和角加速度等数个量之间的关系。
2质量转动惯量
其量值取决于物体的形状、质量分布及转轴的位置。
刚体的转动惯量有着重要的物理意义,在科学实验、工程技术、航
天、电力、机械、仪表等工业领域也是一个重要参量。
电磁系仪表的指示系统,因线圈的转动惯量不同,可分别用于测量微小电流(检流计)或电量(冲击电流计)。
在发动机叶片、飞轮、陀螺以及人造卫星的外形设计上,精确地测定转动惯量,都是十分必要的。
转动惯量只决定于刚体的形状、质量分布和转轴的位置,而同刚体绕轴的转动状态(如角速度的大小)无关。
形状规则的匀质刚体,其转动惯量可直接用公式计算得到。
而对于不规则刚体或非均质刚体的转动惯量,一般通过实验的方法来进行测定,因而实验方法就显得十分重要。
转动惯量应用于刚体各种运动的动力学计算中。
10种常见刚体转动惯量公式

10种常见刚体转动惯量公式
刚体转动惯量是指刚体在转动运动时所需要的转动势能。
它可以衡量刚体转动时所需要的力的大小。
常见的刚体转动惯量公式有以下10种:
1.圆柱体转动惯量公式:I=1/2mr^2
2.圆锥体转动惯量公式:I=1/3mr^2
3.球体转动惯量公式:I=2/5mr^2
4.圆筒体转动惯量公式:I=1/2mr^2
5.正方体转动惯量公式:I
6.三棱锥体转动惯量公式:I=1/3mr^2
7.六棱锥体转动惯量公式:I=1/4mr^2
8.五棱锥体转动惯量公式:I=1/5mr^2
9.四棱锥体转动惯量公式:I=1/6mr^2
10.八棱锥体转动惯量公式:I=1/8mr^2
在上述公式中,m表示刚体的质量,r表示刚体的转动半径。
转动惯量基本公式

转动惯量基本公式
常用转动惯量表达式:I=mr2。
其中m是其质量,r是质点和转轴的垂直距离。
转动惯量是刚体绕轴转动时惯性(回转物体保持其匀速圆周运动或静止的特性)的量度。
1、对于细杆:
当回转轴过杆的中点(质心)并旋转轴杆时i=ml2/i2;其中m就是杆的'质量,l就是
杆的长度。
当回转轴过杆的端点并旋转轴杆时i=ml2/3;其中m就是杆的质量,l就是杆
的长度。
2、对于圆柱体:
当回转轴就是圆柱体轴线时i=mr2/2;其中m就是圆柱体的质量,r就是圆柱体的半径。
3、对于细圆环:
当回转轴通过环心且与环面横向时,i=mr2;当回转轴通过环路边缘且与环面横向时,i=2mr2;i=mr2/2沿环的某一直径;r为其半径。
4、对于立方体:
当回转轴为其中心轴时,i=ml2/6;当回转轴为其棱边时i=2ml2/3;当回转轴为其体
对角线时,i=3ml2/16;l为立方体边长。
5、对于实心球体:
当回转轴为球体的中心轴时,i=2mr2/5;当回转轴为球体的切线时,i=7mr2/5;r为
球体半径。
常用物体的转动惯量与扭矩的计算

常用物体的转动惯量与扭矩的计算转动惯量和扭矩是物体在转动过程中的两个重要物理量。
转动惯量描述了物体绕其中一轴线旋转时对于其转动的惯性,而扭矩则描述了物体受到的力矩引起的转动效果。
下面将对常用物体的转动惯量和扭矩的计算进行说明。
1.点质量:对于一个质量为m的点质量,绕与其距离为r的轴线旋转,其转动惯量I可以通过以下公式计算:I=m*r^2其中,m为质量,r为距离。
2.刚体:对于一个刚体,在其质心坐标系下,其转动惯量Ic可以通过以下公式计算:Ic=Σ(m_i*r_i^2)其中,m_i为每个质点的质量,r_i为该质点与质心的距离,Σ表示对每个质点进行求和。
3.线状物体:对于一根长度为L,质量均匀分布的细长直杆绕与其一个端点为轴转动,其转动惯量I可以通过以下公式计算:I=(1/3)*m*L^2其中,m为质量,L为长度。
4.圆盘:对于一个质量为m,半径为R的均匀圆盘绕其垂直于盘面且通过质心的轴线转动,其转动惯量I可以通过以下公式计算:I=(1/2)*m*R^25.球体:对于一个质量为m,半径为R的均匀球体绕其直径为轴转动,其转动惯量I可以通过以下公式计算:I=(2/5)*m*R^26.圆环:对于一个质量为m,半径为R的均匀圆环绕其垂直于环面且通过质心的轴线转动,其转动惯量I可以通过以下公式计算:I=m*R^2对于扭矩的计算,扭矩τ可以通过以下公式计算:τ=rxF其中,r为力矩的作用点到轴的距离,F为作用力,x为叉乘运算符。
通常情况下,扭矩也可以简化为:τ = r * F * sinθ其中,θ为力和杆的夹角。
综上所述,对于常用物体的转动惯量和扭矩的计算,可以根据物体的形状和质量分布情况来确定相应的公式,并利用这些公式进行计算。
这些公式在物理和工程领域中有着广泛的应用。
机械设计转动惯量计算公式

1. 圆柱体转动惯量(齿轮、联轴节、丝杠、轴的转动惯量)82MD J =对于钢材:341032-⨯⨯=gLrD J π)(1078.0264s cm kgf L D ⋅⋅⨯-M-圆柱体质量(kg); D-圆柱体直径(cm); L-圆柱体长度或厚度(cm); r-材料比重(gf /cm 3)。
2. 丝杠折算到马达轴上的转动惯量:2i Js J =(kgf·c m·s 2) J s (kgf·c m·s 2); i-降速比,12z z i =3. 工作台折算到丝杠上的转动惯量gw22⎪⎭⎫ ⎝⎛⋅=n v J π g w 2s 2⎪⎭⎫ ⎝⎛=π (kgf·c m·s 2) v -工作台移动速度(cm/min); n-丝杠转速(r/min); w-工作台重量(kgf);g-重力加速度,g = 980cm/s 2; s-丝杠螺距(cm)2. 丝杠传动时传动系统折算到驱轴上的总转动惯量:())s cm (kgf 2g w 122221⋅⋅⎥⎥⎦⎤⎢⎢⎣⎡⎪⎭⎫ ⎝⎛+++=πs J J iJ J S tJ 1-齿轮z 1及其轴的转动惯量; J 2-齿轮z 2的转动惯量(kgf ·cm ·s 2);J s -丝杠转动惯量(kgf ·cm ·s 2); s-丝杠螺距,(cm); w-工件及工作台重量(kfg).5. 齿轮齿条传动时折算到小齿轮轴上的转动惯量2gw R J =(kgf ·c m·s 2)R-齿轮分度圆半径(cm); w-工件及工作台重量(kgf)6. 齿轮齿条传动时传动系统折算到马达轴上的总转动惯量⎪⎪⎭⎫⎝⎛++=2221g w 1R J i J J tJ 1,J 2-分别为Ⅰ轴,Ⅱ轴上齿轮的转动惯量(kgf ·c m·s 2);R-齿轮z 分度圆半径(cm); w-工件及工作台重量(kgf)。
转动惯量计算公式-转动惯量公式
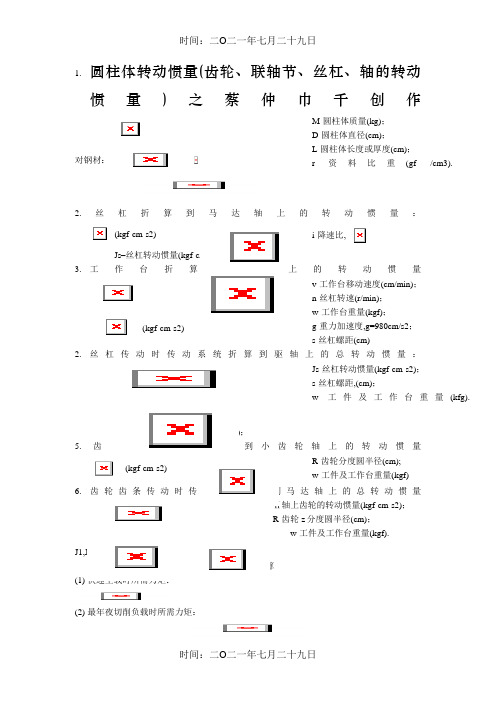
1.圆柱体转动惯量(齿轮、联轴节、丝杠、轴的转动惯量)之蔡仲巾千创作对钢材:M-圆柱体质量(kg);D-圆柱体直径(cm);L-圆柱体长度或厚度(cm);r-资料比重(gf /cm3).2.丝杠折算到马达轴上的转动惯量:(kgf·cm·s2)Js–丝杠转动惯量(kgf·cm·s2);i-降速比,3.工作台折算到丝杠上的转动惯量(kgf·cm·s2)v-工作台移动速度(cm/min);n-丝杠转速(r/min);w-工作台重量(kgf);g-重力加速度,g=980cm/s2;s-丝杠螺距(cm)2.丝杠传动时传动系统折算到驱轴上的总转动惯量:J1-齿轮z1及其轴的转动惯量;J2-齿轮z2的转动惯量(kgf·cm·s2);Js-丝杠转动惯量(kgf·cm·s2);s-丝杠螺距,(cm);w-工件及工作台重量(kfg).5. 齿轮齿条传动时折算到小齿轮轴上的转动惯量(kgf·cm·s2)R-齿轮分度圆半径(cm); w-工件及工作台重量(kgf)6. 齿轮齿条传动时传动系统折算到马达轴上的总转动惯量J1,J2-分别为Ⅰ轴,Ⅱ轴上齿轮的转动惯量(kgf·cm·s2);R-齿轮z分度圆半径(cm);w-工件及工作台重量(kgf).马达力矩计算(1) 快速空载时所需力矩:(2) 最年夜切削负载时所需力矩:(3) 快速进给时所需力矩:式中Mamax—空载启动时折算到马达轴上的加速力矩(kgf·m);Mf—折算到马达轴上的摩擦力矩(kgf·m);M0—由于丝杠预紧引起的折算到马达轴上的附加摩擦力矩(kgf·m);Mat—切削时折算到马达轴上的加速力矩(kgf·m);Mt—折算到马达轴上的切削负载力矩(kgf·m).在采纳滚动丝杠螺母传动时,Ma、Mf、M0、Mt的计算公式如下:(4) 加速力矩:(kgf·m)Jr—折算到马达轴上的总惯量;T—系统时间常数(s);n—马达转速(r/min);当n=nmax时,计算Mamaxn=nt时,计算Matnt—切削时的转速(r/min)(5) 摩擦力矩:(kgf·m)F0—导轨摩擦力(kgf);s—丝杠螺距(cm);i—齿轮降速比;η—传动链总效率;一般η=0.7~0.85.(6) 附加摩擦力矩:(kgf·m)P0—滚珠丝杠预加载荷(kg·f);s—丝杠螺距(cm);η—传动链总效率;i —齿轮降速比;η0—滚珠丝杠未预紧式的效率,计算公式见本手册第2测第425页,一般η0≥0.9.(7)切削力矩:(kgf·m)Pt—进给方向的最年夜切削力(kg·f);s—丝杠螺距(cm);η—传动链总效率;i—齿轮降速比.。
转动惯量与功率计算公式

转动惯量与功率计算公式
转动惯量的计算公式:
1.对于质点转动:转动惯量(J)与质点的质量(m)和质点离旋转轴的距
离(r)的平方成正比,即J=m*r^2
2.对于集中质量的刚体转动:假设刚体由N个质点组成,每个质点的
质量分别为m1,m2,...,mN,它们离旋转轴的距离分别为r1,r2,...,rN,则刚体的转动惯量等于所有质点的转动惯量之和,即
J=m1*r1^2+m2*r2^2+...+mN*rN^2
3. 对于连续分布质量的刚体转动:刚体可以看做由无数个质点组成,质点的质量微元为dm,质点离旋转轴的距离为r,则刚体的转动惯量可以
用积分的形式表示,即J = ∫ r^2 dm,其中积分区间为整个刚体。
计算功率的公式:
功率(P)表示单位时间内所做的功,可以用两种公式计算:
1. 对于匀速直线运动:假设物体做功的力为F,物体的速度为v,角
度为θ,则功率可以用力F和速度v的点积来计算,即P = F * v *
cosθ,其中θ为力和速度之间的夹角。
2.对于旋转运动:假设物体转动的角速度为ω,转动的力矩为τ,
则功率可以用力矩τ和角速度ω的乘积来计算,即P=τ*ω。
对于匀速直线运动和旋转运动,如果力和速度或力矩和角速度的方向
相同,则功率为正值,表示物体在做正功;如果方向相反,则功率为负值,表示物体在受到外力反作用做负功。
以上是转动惯量和功率的计算公式。
在实际应用中,这些公式可以帮助我们计算物体的转动惯量和功率,从而理解并分析物体的运动特性。
转动惯量计算

转动惯量计算
惯量是物体对转动的惯性的度量,可以通过以下公式计算:
1. 对于质点的转动惯量:
I = m * r^2
其中,I代表转动惯量,m代表质量,r代表离转轴的距离。
2. 对于刚体的转动惯量:
I = Σ(m * r^2)
其中,I代表转动惯量,Σ表示对所有质点求和,m代表质量,r代表质点离转轴的距离。
3. 对于一些常见几何形状的转动惯量,可以使用以下公式
计算:
- 球体的转动惯量:
I = (2/5) * m * r^2
- 圆柱体绕轴线的转动惯量:
I = (1/2) * m * r^2
- 薄圆环绕直径轴线的转动惯量:
I = (1/2) * m * r^2
- 均匀长方体绕轴线的转动惯量:
I = (1/12) * m * (a^2 + b^2)
其中,I代表转动惯量,m代表质量,r代表半径,a和b 代表长方体的边长。
需要注意的是,以上公式仅适用于一些简单的几何形状,对于其他复杂的形状,转动惯量的计算可能需要使用积分或其他数值方法进行近似求解。
高数转动惯量计算公式

高数转动惯量计算公式转动惯量的计算公式可以分为以下四种:1、半径(R)与质量(m)积分法:I=∫^R_0m(r^2)dr2、外接轴线与质量积分法:I=∫^L_0m(r^2)dR3、偏心率与质量积分法:I=∫E_O^E_Ae^2r^2dT4、轴距与质心距积分法:I=∫^B_Aurdr其中,转动惯量I表示转动体围绕某一轴线所需要的动能,分别用三角函数与余弦定理计算;半径R、外接轴线L分别表示转动体的中心到轴线的距离;偏心率E与质心距积分法的轴距A、B分别表示质心距离轴线的距离。
半径(R)与质量(m)积分法:用半径(R)与质量(m)积分法来计算转动惯量的公式可以表示为:I=∫^R_0m(r^2)dr即:I=∫^R_0[mz^2cos^2(θ) + ms^2sin^2(θ)] dz其中,R表示旋转体中心距离轴线的距离;m表示质量;r表示旋转物体形态时中心距离轴线距离;z表示质点到轴距离投影;θ表示投影角度。
外接轴线与质量积分法:用外接轴线与质量积分法来计算转动惯量的公式可以表示为:I=∫^L_0m(r^2)dR即:I=∫^l_0 m[(r-r_a)^2cos^2(θ) + (r+r_a)^2sin^2(θ)] dR其中,L表示外接轴线的长度;m表示质量;R表示质点到轴距离;r_a表示质心到轴距离;θ表示投影角度。
偏心率与质量积分法:用偏心率与质量积分法来计算转动惯量的公式可以表示为:I=∫E_O^E_Ae^2r^2dT即:I=∫E_O^E_A[ (dr/dT)^2 + r^2dΩ^2] dT其中,e表示偏心率;r表示质点到轴距离;E_o、E_A表示圆心角的两个极限;dr/dT表示距离抛物线的斜率;dΩ表示角速度的变化率。
轴距与质心距积分法:用轴距与质心距积分法来计算转动惯量的公式可以表示为:I=∫^B_Aurdr即:I=∫^B_A[ m(r-r_c)^2 + (r+r_c)^2] dr其中,A、B表示质心距离轴线的轴距;m表示质量;r表示旋转物体形态时中心距离轴线距离;r_c表示质心偏移的距离。
转动惯量计算公式

转动惯量计算公式
转动惯量计算公式
转动惯量是研究物体转动特性的重要参数,也是动力学中的一个重要概念。
它描述了物体在转动运动中所具有的转动惯性,物体在外力作用下所产生的转动力矩与转动角加速度成正比。
转动惯量计算公式就是用来计算物体的转动惯量的公式。
转动惯量计算公式的基本形式为:I=m*r^2,其中I表示转动惯量,m表示物体的质量,r表示物体质心到轴心的距离。
这个公式表明,物体的转动惯量与质量和物体质心到轴心的距离有关。
转动惯量的大小取决于物体的形状和尺寸,因此,对于不同的物体,其转动惯量计算公式也不尽相同。
例如,对于圆柱形物体,其转动惯量计算公式为:I=1/2*m*r^2;对于球形物体,其转动惯量计算公式为:I=2/5*m*r^2;对于扁圆形物体,其转动惯量计算公式为:I=1/12*m*(3R^2+H^2),其中R表示扁圆形物体的半径,H表示扁圆形物体的厚度。
转动惯量是物体转动特性的重要参数,它可以帮助我们研究物体的转动运动特性,从而更好地控制物体的运动。
因此,转动惯量计算公式对于物体运动的研究和控制至关重要。
刚体转动惯量公式

大学物理常用转动惯量公式
常用转动惯量表达式:I=mr。
1、转动惯量是刚体绕轴转动时惯性的量度,通常以/或J表示。
在经典力学中,转动惯量通常以/或J表示,SI 单位为kg·m。
对于一个质点,/= mr,其中m 是其质量,r 是质点和转轴的垂直距离。
2、惯性矩是衡量梁截面抵抗弯曲能力的截面几何量,而转动惯量则是物体转动时的惯性的度量。
转动惯量的计算公式可以看出,转动惯量受旋转轴的位置以及物体本身的质量大小和分布影响。
惯性矩的距离是相对于平面内的一条线,转动惯量距离是相对于对平面内一点。
而且量纲不一样,转动惯量是r^2dm=r^2*密度*dA在A 内积分,惯性矩是y^2dA在A内的积分。
刚体就不用考虑惯性矩了,因为它不变形。
3、最一般地说,转动惯量是一个张量。
这是因为对于一个三维空间中的物体来说存在无数个可选的转动轴,每个转动轴都对应着一个描述其转动惯性大小的量,这些量并不是全都互相独立的,我们可以简洁地将这些量整理成一个3×3矩阵。
对于离散系统和连续系统来说,这个矩阵的定义式是不同的。
— 1 —— 1 —。
10种常见刚体转动惯量公式

10种常见刚体转动惯量公式研究刚体的运动状态,刚体的转动惯量是非常重要的物理量之一、它描述了刚体绕其中一轴线旋转时所具有的惯性特性。
转动惯量的大小和刚体质量的分布以及轴线的位置有关。
下面将介绍十种常见的刚体转动惯量公式,并对每一种情况进行详细的说明。
1.关于轴线的质量均匀分布若沿轴线方向均匀分布有质量m的刚体,则其转动惯量公式为:I=m*r^2其中I表示转动惯量,m表示刚体的质量,r表示刚体质量均匀分布点到轴线的距离。
2.点状物体绕轴线转动对于一个点状物体质量为m,绕与通过该点的轴线转动,则其转动惯量公式为:I=m*r^2其中r表示点状物体到轴线的距离。
3.均匀细杆绕一端轴线转动若沿杆的一端作为轴线,质量为m,长度为L的均匀细杆绕该轴线转动,则其转动惯量公式为:I=(1/3)*m*L^24.空心球绕直径轴线转动对于一个质量为m,外半径为R,内半径为r的空心球绕直径轴线转动,则其转动惯量公式为:I=(2/3)*m*R^25.均质球体绕直径轴线转动对于一个均匀密度的球体,质量为m,直径为d,绕直径轴线转动,则其转动惯量公式为:I=(2/5)*m*(d/2)^26.长方体绕通过质心的轴线转动对于一个质量为m,长为L,宽为W,高为H的长方体绕通过质心的轴线转动,则其转动惯量公式为:I=(1/12)*m*(L^2+W^2)7.绕一个边的正方体绕通过质心的轴线转动对于一个边长为a,质量为m的正方体绕通过质心和垂直于一条边的轴线转动,则其转动惯量公式为:I=(1/6)*m*a^28.绕对角线的长方体转动对于一个质量为m,长为L,宽为W,高为H的长方体绕对角线转动,则其转动惯量公式为:I=(1/12)*m*(L^2+W^2+H^2)9.圆环绕垂直于轴线的直径转动对于半径为R,质量为m的环绕垂直于轴线的直径旋转,则其转动惯量公式为:I=m*R^210.圆盘绕轴线转动对于半径为R,质量为m的圆盘绕瞬心轴线转动,则其转动惯量公式为:I=(1/2)*m*R^2以上是十种常见的刚体转动惯量公式。
最全的转动惯量的计算资料

最全的转动惯量的计算资料转动惯量是描述物体的转动特性的物理量,它的计算涉及到物体的形状、质量分布以及围绕哪个轴进行转动等因素。
以下是最全的转动惯量的计算资料。
1.转动惯量的定义转动惯量(或称为角动量的惯性矩)是描述物体转动惯性大小的物理量,通常用字母I表示。
对于质量分布连续的物体,其转动惯量可以通过积分计算得到。
2.刚体的转动惯量刚体的转动惯量取决于物体的形状和围绕的轴。
对于质量分布均匀的刚体,其转动惯量可以通过以下公式计算:I=(1/2)*m*r^2其中,I是转动惯量,m是质量,r是质量到转轴的距离。
3.基本几何体的转动惯量针对常见的几何体,转动惯量的计算公式如下:-线段绕自身一端转动:I=(1/3)*m*L^2其中,I是转动惯量,m是质量,L是线段的长度。
-圆环绕轴转动:I=m*R^2其中,I是转动惯量,m是质量,R是圆环的半径。
-矩形薄片绕轴转动:I=(1/12)*m*(a^2+b^2)其中,I是转动惯量,m是质量,a和b是矩形薄片的长度和宽度。
-矩形薄棒绕轴转动:I=(1/12)*m*(L^2+B^2)其中,I是转动惯量,m是质量,L和B是矩形薄棒的长度和宽度。
-圆盘绕轴转动:I=(1/2)*m*R^2其中,I是转动惯量,m是质量,R是圆盘的半径。
-球体绕直径转动:I=(2/5)*m*R^2其中,I是转动惯量,m是质量,R是球体的半径。
4.复杂体的转动惯量对于复杂形状的物体,转动惯量的计算可能需要使用积分方法。
下面是一些常见的复杂体的转动惯量计算公式:-绕X轴或Y轴对称的物体:I = ∫(r^2 * dm)其中,I是转动惯量,r是质点到转轴的距离,dm是质点的质量微元。
-长方体绕对称轴:I=(1/12)*m*(a^2+b^2)其中,I是转动惯量,m是质量,a和b是长方体的两个相邻边的长度。
-均匀圆环绕直径转动:I=m*R^2其中,I是转动惯量,m是质量,R是圆环的半径。
-均匀圆盘绕对称轴转动:I=(1/2)*m*R^2其中,I是转动惯量,m是质量,R是圆盘的半径。
杆的转动惯量计算公式

杆的转动惯量计算公式
1. 对于绕一端转动的均质细杆(长度为L,质量为m)
- 转动惯量公式为I = (1)/(3)mL^2。
- 推导过程:
- 把细杆看作是由无数个质量元dm组成。
- 设杆的线密度λ=(m)/(L),对于距离转轴x处的质量元dm=λ dx。
- 根据转动惯量的定义I=∫ r^2dm,这里r = x(因为是绕一端转动)。
- 所以I=∫_0^Lx^2λ dx=λ∫_0^Lx^2dx。
- 又因为λ=(m)/(L),∫_0^Lx^2d x=(1)/(3)L^3。
- 则I=(1)/(3)mL^2。
2. 对于绕中心轴转动的均质细杆(长度为L,质量为m)
- 转动惯量公式为I=(1)/(12)mL^2。
- 推导过程:
- 同样把细杆看作由无数质量元组成,线密度λ=(m)/(L)。
- 对于距离中心轴x处的质量元dm = λ dx,这里x的取值范围是-(L)/(2)到(L)/(2)。
- 根据转动惯量定义I=∫ r^2dm,这里r = x。
- 所以I = 2∫_0^(L)/(2)x^2λ dx(利用对称性,只计算一半再乘以2)。
- 计算积分2λ∫_0^(L)/(2)x^2dx,因为λ=(m)/(L),
∫_0^(L)/(2)x^2dx=(1)/(24)L^3。
- 可得I=(1)/(12)mL^2。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
1. 圆柱体转动惯量(齿轮、联轴节、丝杠、轴的转动惯量)
8
2
MD J =
对于钢材:3
410
32-⨯⨯=
g
L
rD J π
)(1078.0264s cm kgf L D ⋅⋅⨯-
M-圆柱体质量(kg);
D-圆柱体直径(cm); L-圆柱体长度或厚度(cm); r-材料比重(gf /cm 3)。
2. 丝杠折算到马达轴上的转动惯量:
2i Js J = (kgf·cm·s 2)
J s –丝杠转动惯量(kgf·cm·s 2); i-降速比,1
2
z z i =
3. 工作台折算到丝杠上的转动惯量
g w
22⎪
⎭
⎫ ⎝⎛⋅=n v J π g w
2s 2
⎪
⎭⎫
⎝⎛=π (kgf·cm·s 2) v -工作台移动速度(cm/min); n-丝杠转速(r/min); w-工作台重量(kgf);
g-重力加速度,g = 980cm/s 2; s-丝杠螺距(cm)
2. 丝杠传动时传动系统折算到驱轴上的总转动惯量:
())
s cm (kgf 2g w 1
22
22
1⋅⋅⎥⎥
⎦
⎤⎢⎢⎣⎡⎪⎭⎫ ⎝⎛+++=πs J J i
J J S t
J 1-齿轮z 1及其轴的转动惯量; J 2-齿轮z 2的转动惯量(kgf·cm·s 2); J s -丝杠转动惯量(kgf·cm·s 2); s-丝杠螺距,(cm); w-工件及工作台重量(kfg).
5. 齿轮齿条传动时折算到小齿轮轴上的转动惯量
2
g
w R J =
(kgf·cm·s 2)
R-齿轮分度圆半径(cm); w-工件及工作台重量(kgf)
6. 齿轮齿条传动时传动系统折算到马达轴上的总转动惯量
⎪⎪⎭⎫
⎝⎛++=2221g w 1R J i J J t
J 1,J 2-分别为Ⅰ轴,
Ⅱ轴上齿轮的转动惯量(kgf·cm·s 2);
R-齿轮z 分度圆半径(cm); w-工件及工作台重量(kgf)。
马达力矩计算
(1) 快速空载时所需力矩:
0f amax M M M M ++= (2) 最大切削负载时所需力矩: t 0f t a M M M M M +++=
(3) 快速进给时所需力矩:
0f M M M +=
式中M amax —空载启动时折算到马达轴上的加速力矩(kgf·m);
M f —折算到马达轴上的摩擦力矩(kgf·m);
M 0—由于丝杠预紧引起的折算到马达轴上的附加摩擦力矩(kgf·m);
M at —切削时折算到马达轴上的加速力矩(kgf·m); M t —折算到马达轴上的切削负载力矩(kgf·m)。
在采用滚动丝杠螺母传动时,M a 、M f 、M 0、M t 的计算公式如下: (4) 加速力矩: 2a 106.9M -⨯=
T
n
J r (kgf·m) s T 17
1=
J r —折算到马达轴上的总惯量; T —系统时间常数(s); n —马达转速( r/min );
当 n = n max 时,计算M amax
n = n t 时,计算M at
n t —切削时的转速( r / min )
(5) 摩擦力矩:
20f 10i
2s
F M -⨯⋅⋅⋅=
ηπ(kgf·m)
F 0—导轨摩擦力(kgf); s —丝杠螺距(cm); i —齿轮降速比;
η—传动链总效率;一般η=0.7~0.85。
(6) 附加摩擦力矩:
()
22
0001012M -⨯-⋅=
ηπηi
s P (kgf·m) P 0—滚珠丝杠预加载荷(kg·f);
s —丝杠螺距(cm);
η—传动链总效率; i —齿轮降速比;
η0—滚珠丝杠未预紧式的效率,计算公式 见本手册第2测第425页,一般η0≥0.9。
(7) 切削力矩: 2t 102M -⨯⋅=
i
s
P t πη(kgf·m) P t —进给方向的最大切削力(kg· f); s —丝杠螺距(cm);
η—传动链总效率;
i —齿轮降速比。
Unit 1 Can you play the guitar?
一、单词讲解:
1、guitar n. 吉他 → play the guitar 弹吉他
⑴ guitar, drum, piano, violin 为乐器 →(名词前要加定冠词the )。
即:play the guitar, play the drums, play the piano, play the violin 。
⑵ chess 棋牌类游戏前不加定冠词the 。
→即:play chess, play cards 。
⑶ soccer, tennis, baseball, ping-pong, basketball, volleyball 等球类运动前也不加the
即:play soccer, play tennis, play baseball, play ping-pong, play basketball, play volleyball 。
2、sing v. 唱歌 → I can sing well. singer n. 歌手 3、swim v. 游泳 swimmer n. 游泳者
swimming n./G. 游泳 → swimming club / be good at swimming / help me with swimming 4、dance v. 跳舞 n. 舞蹈 dancer n. 跳舞者
dancing n./G. 跳舞 → I am good at dancing. 5、draw v. 画画 → I can’t draw well.
drawing n. 画,图画 → Her drawings are very good. I like them. 6、chess n. 国际象棋 → play chess 下国际象棋 ① 说(某种语言);说话 → speak English /Chinese ② 演讲,发言 → She wants to speak in the class meeting.
① 说某种语言的人 → an English speaker = a speaker of English
② 演讲者,发言人
8、join + 某个组织、俱乐部、社会团体、军队,党派等 “加入……(成为其中的一员)” → join the art club / join the army / join the Party / join the League
join + sb. “参加到某人的行列中,和某人一起” → Come and join us.
join (sb.) in + 活动 “加入某人的活动中,加入做…,参加某个活动(比赛) ”→ She wants to join us in the game.
n. → I’m good at English. 9、be good at + pron. → She isn’t good at it. G. → They’re good at singing.
speaker n.
7、speak v.
join in …=take part in +活动。
