期末复习习题
期末复习题
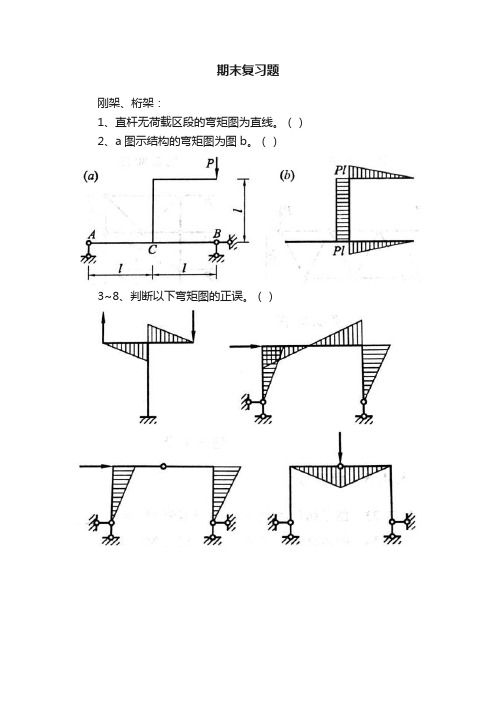
期末复习题刚架、桁架:1、直杆无荷载区段的弯矩图为直线。
()2、a图示结构的弯矩图为图b。
()3~8、判断以下弯矩图的正误。
()9~10、图示体系A(K)点处的弯矩为(),()侧受拉。
11、图示结构中截面K的剪力值为()12~13、图示结构中K截面的弯矩值为(),剪力值为()。
14. 图示刚架截面K的弯矩(以下侧受拉为正)为。
3 kN m15、图示桁架中零杆(含零支杆)个数为:()16、图示桁架中零杆(含零支杆)个数为:()17、图示桁架零杆的个数为()(A)5根;(B)6根;(C)7根;(D)8根。
18、图示桁架中的零杆为()A、DC, EC, DE, DF, EFB、DE, DF, EFC、AF, BF, DE, DF, EFD、DC, EC, AF, BFA 、CH BI DG ,,B 、BI AB BG DC DG DE ,,,,,21~23、图示桁架各杆的轴力为()。
24.图示桁架a 、b 杆轴力分别为、。
25.图示桁架中杆a、b的轴力分别为F Na=____,F Nb=____。
26、图示结构中1杆的轴力为()27、静定结构因支座移动,()A、会产生内力,但无位移B、会产生位移,但无内力C、内力和位移均不会产生D、内力和位移均会产生28、静定结构的几何特征是:()A.无多余的约束;B.几何不变体系;C.有多余的约束;D.几何不变且无多余约束。
虚功原理(静定结构位移的计算):1、形体系的虚功原理可表述为:变形体系处于平衡的必要和充分条件是,对于任何虚位移,外力所作虚功总和等于各微段上的内力在其变形上所作的虚功总和。
简单的说,即。
2、图乘法的应用条件是:①杆段是________杆段;②两个弯矩图中至少有一个是____图形。
3、在功的表达式中,凡与力对应的因子称为广义力,凡与位移对应的因子称为广义位移。
()4、在超静定结构计算中,一部分杆考虑弯曲变形,另一部分杆考虑轴向变形,则此结构为:()A.梁B.桁架;C.横梁刚度为无限大的排架;D.组合结构。
期末复习题——精选推荐

第一章电子支付概述一、单选题1.传统支付形式不包括() p2A、现金B、支票 C 、智能卡D、信用卡2.电子支付的类型不包括()p8A 、网上支付 B、电话支付 C、移动支付 D、现金3.淘宝的“支付宝”是属于以下哪一种支付类型()p8A 、充值卡支付B 、网上银行支付 C、第三方支付 D 、电话支付4.目前推广的尚未成熟的的电子支付产业的模式是()p9A 、复制PayPalB 、支付网关C 、移动支付5.银行卡网上支付的核心问题是( )p13A、银行服务B、支付信息的安全传输和身份认证C、持卡人信息的安全D、资金结算过程的安全6.支付网关的主要功能为()。
P12A、进行通信和协议转换,完成数据加密与解密B、代替银行等金融机构进行支付授权C、处理交易中的资金划拨等事宜D、为银行等金融机构申请证书7、由中央银行拥有和运行,其中主要职责是负责同城支付交易的资金清算是指()A、电子汇兑系统B、网上银行系统C、同城清算所D、全国手工联行系统二、多选题1、电子货币按流通的形态分类,可分为()A、开环型电子货币B、闭环型电子货币C、电子现金型电子货币D、信用卡型电子货币2、网络支付的条件为()A、商家系统B、客户系统C、支付网关 C、安全认证3、电子货币的功能包括()。
A、转账结算B、储蓄C、兑现D、消费贷款三、判断题1、电子支付是网上支付的更高级形式(× )2、后支付系统包括信用卡系统、电子支票系统和智能卡系统(× )3、电子支票不是数字支票(×)四、名词解释1、电子支付指电子交易的当事人,包括消费者、厂商和金融机构,使用安全电子支付手段,通过网络进行的货币支付或资金流转。
2、网络支付指电子交易的当事人,包括消费者、厂商、和金融机构,使用安全电子支付手段通过网络进行的货币支付或资金流转。
主要包括有电子货币类,电子信用卡类,电子支票类。
3支付系统(Payment System)是由提供支付清算服务的中介机构和实现支付指令传送及资金清算的专业技术手段共同组成,用以实现债权债务清偿及资金转移的一种金融安排,有时也称为清算系统(Clear System)。
数据库期末复习题(学生)

数据库原理与应用教程复习题(一)一、填空题(每空1分,共10分)1.数据库系统的核心是___ __。
2.在关系模型中,实体以及实体间的联系都是用______来表示的。
3.设关系模型R(A,B,C),F是R上的函数依赖集,F={A→B,C→B},则R的候选码为_________。
4.层次模型用“树结构”来表示数据之间的联系,网状模型用“_________” 来表示数据之间的联系。
5.SQL Server中,一个简单的数据库可以只有一个_________文件和一个日志文件。
6.聚集索引和非聚集索引的存储结构都采用____________索引结构。
7.一个事务必须具有的四个属性是原子性、一致性、__________和持久性。
8.在T-SQL中,查询表中数据时,可用___________关键字滤掉重复行。
9.调用标量函数时必须提供至少由两部分组成的名称,即________. 函数名。
10.触发器是当数据库服务器中发生数据操作语言事件时会自动执行的存储过程。
二、选择题(每小题1分,共20分)1、数据管理的发展不包括下面哪个阶段()(A)文件系统(B)数据库系统(C)人工管理(D)统一管理2、一个学生可以同时借阅多本书,一本书只能由一个学生借阅,学生和图书之间是什么样的联系()(A)一对一(B)一对多(C)多对多(D)以上全不是3、如果事务1将数据库中的A值从200改为300,事务2读A值为300,事务1又将刚才的操作撤销,A值恢复为200,那么事务2读取了“脏”数据。
这种情况是由于数据库保护中的那方面不当而引起的()(A)并发控制 (B)完整性约束(C)安全性控制(D)数据库的恢复4、在关系模型中,“元组”是指( )(A)表中的一行(B)表中的一列(C)表中的一个数据(D)表中的一个成分5、有学生、选修和课程三个关系,学生S(学号,姓名,性别….),课程C(课程号,课程名),选修SC(学号,课程号,成绩)。
小学三年级英语期末复习题(三篇)

【导语】做英语习题可能在多数⼈眼中认为是⼀种附加的负担,语⾔的学习嘛,做题感觉很奇怪,可是中国的⼤环境仍然是考试,这种政策是⼀时半会⼉都将存在的,所以有必要做题来⾯对这些考试。
以下是⽆忧考整理的《⼩学三年级英语期末复习题(三篇)》,希望帮助到您。
⼩学三年级英语期末复习题篇⼀ ⼀、连线。
将下列字母的⼤⼩写形式连起来。
U B P D V Q Y I L d v u b p I y j q i ⼆、选出不同类的单词。
1.A.mothe B.brother C.teacher 2. A.duck B.desk C.chair 3. A.plane B.pear C.peach 4. A.small B.giraffe C.short 5. A.fifteen B.twelve C.friend 6. A.bike B.grape C.bus 三、单项选择。
()1.—cats can you see? —I can see twenty.A.HowB.WhatC.How many ( )2.—I haveapple.—Me too.A.anB.aC.some ( )3.—Who’s that man?—He’s my .A.motheB. fatherC.sister ( )4. Do you like oranges?— .A.Yes,I do.B.No,I do.C.Yes,I don’t. 四、根据所给的情景选出正确的句⼦。
()1.你想知道那个男孩是谁,你应该这样问:A.Who’s this boy?B. Who’s that boy?C.Who’s that girl? ( )2.想询问别⼈⼩汽车在哪⾥,应怎样问:A.Where’s my car?B.Where’s my cat?C.This is my car. ( )3.如果有⼈对你说:“I’m sorry.”你应该怎么回答:A.Thank you.B.You’re welcome.C.it’s OK. ( )4.你想知道别⼈是来⾃哪个地⽅,应该这样问:A.Where are you from?B.How are you?C.how old are you? 五、从B栏中选择与A栏相对应的句⼦,只填编号。
《机械制图》期末考试复习题及参考答案

机械制图复习题(课程代码 352271)一、简答题1.简述平面体截交线的特点及基本作图方法。
2.试简要说明尺寸基准的概念。
如何选择尺寸基准?3.试说明剖面图标注的包括哪些内容?如何标注?4.根据所学的知识,试阐述读图和画图的相互关系。
5.简述平面体与平面体相贯线的特点及基本作图方法。
6.机械制图中剖面图的主要包括哪些种类。
7.简述在机械图样中粗实线的主要用途(至少列出五个)。
8. 根据所学的知识,试阐述组合体读图和画图的相互关系。
9.试说明机械制图中剖面图的主要包括哪些种类,并解释。
10、何谓正视方向?选择正视方向的原则有哪些?二、绘图题:1.已知三棱柱的两个投影和棱面上折线ABC的水平投影,试作棱柱的侧面投影和折线ABC 的其余两个投影。
2.根据组合体的立体图,选择其主视方向,完成其三面投影图,并标注尺寸。
注:绘图尺寸由立体图直接测量后圆整,按比例1:1绘制。
3.试在指定位置完成组合体的1-1半剖图和2-2全剖面图。
4.如图所示,已知五边形ABCDE的部分水平投影及部分正面投影, 试完成该五边形的水平和正面投影。
5.根据组合体的立体图,选择其主视方向,完成其三面投影图,并标注尺寸。
注:绘图尺寸由立体图直接测量后圆整,底板倒角半径为R5。
按比例1:1绘制。
6.读懂下列投影图,试将正面投影图绘制为全剖视图。
7.已知正五棱柱被截切后的正面投影和部分侧面投影,试完成其水平投影,并补全侧面投影。
8.根据组合体的立体图,选择其主视方向,完成其三面投影图,并标注尺寸。
注:绘图尺寸由立体图直接测量后圆整,按比例1:1绘制。
9.试读懂组合体三面投影图,并补全其三面投影图中所缺的图线。
10.已知组合体的正面和侧面水平投影,试完成其水平投影图。
11.如图所示,已知四边形ABCD的水平投影及AB、BC两边的正面投影, 试完成该四边形的正面投影和侧面投影。
12. 已知正三棱锥被截切后的正面投影和部分水平投影,试完成其侧面投影,并补全水平投影。
微分几何期末复习题

微分几何复习题一、填空题1. 向量()(,3,)r t t t a =具有固定方向,则a = 。
2. 非零向量()r t 满足(),,0r r r '''=的充要条件是 。
3. 若向量函数()r t 满足()()0r t r t '⨯=,则()r t 具有固定 。
4. 曲线()r r t =的正常点是指满足 的点.5. 曲线3()(2,,)t r t t t e =在任意点的切向量为 。
6. 曲线()(cosh ,sinh ,)r t a t a t at =在0t =点的切向量为 。
7. 曲线()(cos ,sin ,)r t a t a t bt =在0t =点的切向量为 。
8. 设曲线在P 点的切向量为α,主法向量为β,则过P 由,αβ确定的平面 是曲线在P 点的 。
9. 若0()r t 是曲线()r r t =的正则点,则曲线()r r t =在0()r t 的密切平面方程是 。
10. 曲线()r r t =在点0()r t 的单位切向量是α,则曲线在0()r t 点的法平面方程是 。
11. 一曲线的副法向量是常向量,则这曲线的挠率τ= 。
12. 曲线()r r t =在t = 1点处有2γβ=,则曲线在 t = 1对应的点处其挠率 (1)τ= 。
13. 曲线x =cos t ,y =sin t , z =t 在t =0处的切线方程是 。
14. 曲线的主法向量的正向总是指向 。
15. 空间曲线为一般螺线的充要条件是它的副法向量 。
16. 曲线()r t ={t 3-t 2-t , t 2-2t +2, 2}上的点不是正常点的是t = 。
17. 曲线()r r t =的曲率是 。
18. 曲线()r r t =的挠率是 。
19. 一般螺线的曲率和挠率的关系是 。
20. 曲率为0的曲线是 , 挠率为0的曲线是 。
21. 设有曲线2:,,t t C x e y e z t -===,当1t =时的切线方程为 。
税法期末复习题与答案

1.单项选择题(增值税)1、受托加工应税消费品的单位和个人是增值税的()。
A 、纳税人、纳税人 B 、扣缴义务人、扣缴义务人 C 、代征人、代征人 D 、担保人、担保人2、下列项目应确认收入实现计算销项税的是()。
A 、将购买的货物用于集体福利、将购买的货物用于集体福利B 、将购买的货物用于非应税项目、将购买的货物用于非应税项目C 、将购买的货物交加工单位委托加工后收回继续生产使用、将购买的货物交加工单位委托加工后收回继续生产使用D 、将购买的货物作为投资给其他单位、将购买的货物作为投资给其他单位3、纳税人发生混合销售行为,视为销售货物,一并征收增值税的适用范围是()。
A 、一切企业、单位及个人、一切企业、单位及个人 B 、国有企业、国有企业C 、非从事货物的生产、批发或零售的企业、单位及个人D 、从事货物的生产、批发或零售的企业、单位及个人、从事货物的生产、批发或零售的企业、单位及个人4、一般纳税人因销货退回或折让而退还给购买方的增值税额,应作以下处理()。
A 、 从发生销货退回或折让当期的进项税额中扣减从发生销货退回或折让当期的进项税额中扣减B 、 不予扣减,直接作为期间费用计入当期损益予扣减,直接作为期间费用计入当期损益C 、 从发生销货退回或折让当期的销项税额中扣减发生销货退回或折让当期的销项税额中扣减D 、 从发生销货退回以后期间的销项税额中扣减从发生销货退回以后期间的销项税额中扣减5、下列行为中应抵扣进项税额的是()。
A 、将外购的货物无偿赠送他人、将外购的货物无偿赠送他人B 、将外购货物用于福利部门、将外购货物用于福利部门C 、开具涂改的专用发票、开具涂改的专用发票D 、在产品被盗、在产品被盗6、下列支付的运费中不允许计算扣除进项税额的是()。
A 、销售自产小轿车支付的运输费用、销售自产小轿车支付的运输费用B 、外购气体支付的运输费用、外购气体支付的运输费用C 、外购职工福利用品的运输费用、外购职工福利用品的运输费用D 、向小规模纳税人购进农业产品的运输费用、向小规模纳税人购进农业产品的运输费用7、下列()属于视同销售行为,应计算增值税销项税额。
《中国政治制度史》期末复习综合练习题

《中国政治制度史》期末复习综合练习题一、单选题1.秦以后各朝代政治结构的共同点是( D )的统治。
A.民主制 B.世袭制 C.共和制 D.皇权专制2.中国古代社会直接实行( B )的统治。
A.共和制度 B.君主专制 C.城邦制度 D.联邦制度3.启是从暴力夺取政权的,将传统的首领选举制改为( C )。
A.君主立宪制 B.共和制 C.世袭君主制 D.民主共和制4.从夏代创建王权制度到秦统一中国建立皇帝制度,( C )一直是最高统治者的专称。
A.皇帝 B.君主 C.王 D.总统5.明朝张居正主持的赋税制度的改革是( C )。
A.租庸调制 B.两税法 C.一条鞭法 D.摊丁入亩6.古代官吏致仕的年龄是( A )岁。
A.70 B.65 C.60 D.557.明清时代中国的政体是( D )。
A、贵族君主制B、君主丞相制C、君主宰辅制D、绝对君主制8.在先秦时代占主导的官吏选任制是( A )。
A、世官世禄制B、乡举里选制C、简选制D、军功、事功选拔制9.三国魏实行的“九品中正制”属于( A )。
A.制度荐举 B.私人荐举 C.官府荐举 D.自荐10.晚清时期的国体是( C )。
A.领主封建制B. 地主封建制C.半殖民地半封建制D.封建地主和买办资产阶级性质11.秦汉时九卿中掌民族及外交事务的是( C )。
A、太仆B、廷尉C、典客D、奉常12.隋炀帝改革国家组织,增设谒者台和( A ),与御史台合称三台。
A、司隶台B、都水台C、殿内省D、少府监13.在中国历史上六部职权最大的时期是( D )A、唐朝B、宋朝C、元朝D、明朝14.清代掌管礼仪、学校、科举等事务的是( C )。
A、吏部B、户部C、礼部D、国子监15.两汉国家结构与秦代最大不同是( C )A、郡县制B、属国制C、郡国并存制D、监查制26.明代首创的国家组织是( B )A、都察院B、通政司C、大理寺D、六部17.我国出现“私学”教育是在( B )时期。
语文期末复习题

一、选择题:1.下列词语中,加点词的注音完全正确的一项是()A.点缀.(zhuì)尸骸.(hái )奖券.(juàn )饿殍.(piǎo )B.豪恸.(tòng )伫.立(zhù)蹒.跚(pán )短暂.(zhàn )C.徘徊.(huái )拙.笨(zhuō)嗥.叫(háo )皱褶.(zhě)D.遒.劲(qiú)栖.息(qī)婀娜.(nuó)颔.首(hán )2.下列词语中,有错别字的一项是()A.黝黑慰藉羞涩无影无踪B.馈赠白皙胆怯欣喜若狂C.隔模笨拙炫耀良师益友D.踌躇积攒寂寥梦寐以求3.下列句子中,加点词语运用不当的一句是()A.夏去秋来,菊花盛开,姹紫嫣红....,煞是好看。
B.他这个人太循规蹈矩....了,没有丝毫的创新精神,当今社会并不欢迎这种人。
C.各种花卉,争奇斗艳,若用国色天香....来形容,实不为过。
D.有的同志孤陋寡闻,见微知著....,他们的见解往往是片面的,甚至是错误的。
4.下列句子中,标点符号完全正确的一句是()A.老人说:“你能不能补画一张送我,作为我晚年最珍贵的收藏”?B.树的美在于姿势的清健或挺拔、苗条或婀娜,在于活力、在于精神!C.我想人是由三部分组成的:对往事的追忆;对现实的把握和对未来的憧憬。
D.我们看见一只雌鹿—当时我们是这样认为—正在涉过这条急流,它的胸部淹没在白色的水花中。
5.下列成语中,有错别字的一组是()A.百衣百顺本末倒置再接再厉B.燃眉之急忐忑不安心悦诚服C.不谙世事受益匪浅丧失殆尽D.毛骨悚然众目睽睽才疏学浅6.下列各句中,修辞手法辨析有误的一项是()A.小屋点缀了山,什么来点缀小屋呢?那是树!设问B.有时深夜,我会突然想起那些高原上的原住民,它们的魂魄,如今栖息在何处云端?拟人C.没有绿色哪有生命?没有生命哪有爱情?没有爱情哪有歌声?排比反问D.你们是否听说过有关红玫瑰的传说?反问7.填入文中横线的上的句子,与文段衔接恰当的一项是()娇生惯养是低能儿的摇篮,高山上寒土使松柏更加挺拔。
《高等数学(一)》期末复习题(答案)

《高等数学(一)》期末复习题一、选择题1. 极限)x x →∞的结果是 ( C ).(A )0 (B ) ∞ (C ) 12(D )不存在 2. 设()xxx f +-=11ln,则)(x f 是 ( A ). (A )奇函数 (B) 偶函数 (C )非奇非偶函数 (D )既奇又偶函数 3. 极限21lim sinx x x→= ( A ) . (A )0 (B) 1 (C )+∞ (D )-∞ 4. 方程3310x x -+=在区间(0,1)内( B ).(A )无实根 (B )有唯一实根 (C )有两个实根 (D )有三个实根 5. 设()()ln 1f x x =+,g (x )=x ,则当0x →时,()f x 是()g x 的( A ).(A )等价无穷小 (B) 低阶无穷小(C )高阶无穷小 (D) 同阶但非等价无穷小 6. 下列变量中,是无穷小量的为( A ).(A ))1(ln →x x (B ))0(1ln +→x x (C )cos (0)x x → (D ))2(422→--x x x 7. 极限011lim(sinsin )x x x x x→- 的结果是( C ).(A )0 (B ) 1 (C ) 1- (D )不存在8. 下列函数中满足罗尔定理条件的是( D ).(A )()2,[0,1]f x x x =-∈ (B) 3(),[0,1]f x x x =∈ (C )(),[1,1]f x x x =∈- (D)4(),[1,1]f x x x =∈-9. 函数1cos sin ++=x x y 是( C ).(A )奇函数 (B )偶函数 (C )非奇非偶函数 (D )既是奇函数又是偶函数 10. 当0→x 时, 下列是无穷小量的是( B ).(A )1+x e (B) )1ln(+x (C) )1sin(+x (D) 1+x11. 当x →∞时,下列函数中有极限的是( A ).(A )211x x +- (B) cos x (C) 1xe(D)arctan x 12. 方程310(0)x px p ++=>的实根个数是 ( B ).(A )零个 (B )一个 (C )二个 (D )三个 13.21()1dx x '=+⎰( B ).(A )211x + (B )211C x++ (C ) arctan x (D ) arctan x c + 14. 定积分()f x dx ⎰是( A ).(A )一个函数族 (B )()f x 的的一个原函数 (C )一个常数 (D )一个非负常数15.函数(ln y x =+是( A ).(A )奇函数 (B )偶函数 (C ) 非奇非偶函数 (D )既是奇函数又是偶函数 16. 设函数在区间上连续,在开区间内可导,且,则( B ).(A) (B) (C) (D) 17. 设曲线221x y e-=-,则下列选项成立的是( C ). (A) 没有渐近线 (B) 仅有铅直渐近线 (C) 既有水平渐近线又有铅直渐近线 (D) 仅有水平渐近线 18. 设是的一个原函数,则等式( D )成立.(A )(B) (C ) (D)19. 设⎰+=C x dx x xf arcsin )(,则⎰=dx x f )(1( B ). (A )C x +--32)1(43 (B )C x +--32)1(31 (C )C x +-322)1(43 (D )C x +-322)1(32()f x []0,1()0,1()0f x '>()00f <()()10f f >()10f >()()10f f <F x ()f x ()dd d x f x x F x (())()⎰='=+⎰F x x f x c()()d '=⎰F x x F x ()()d dd d xf x x f x (())()⎰=20. 数列})1({nn n-+的极限为( A ).(A )1(B) 1-(C) 0(D) 不存在21. 下列命题中正确的是( B ).(A )有界量和无穷大量的乘积仍为无穷大量(B )有界量和无穷小量的乘积仍为无穷小量 (C )两无穷大量的和仍为无穷大量 (D )两无穷大量的差为零 22. 若()()f x g x ''=,则下列式子一定成立的有( C ).(A)()()f x g x = (B)()()df x dg x =⎰⎰(C)(())(())df x dg x ''=⎰⎰(D)()()1f x g x =+ 23. 下列曲线有斜渐近线的是 ( C ).(A)sin y x x =+ (B)2sin y x x =+ (C)1siny x x =+ (D)21sin y x x=+ 24. 函数)1,0(11)(≠>+-=a a a a x x f x x ( B ).(A )是奇函数 (B )是偶函数(C )既奇函数又是偶函数 (D )是非奇非偶函数 25. 下列函数中满足罗尔定理条件的是( D ).(A )]1,0[,1)(∈-=x x x f (B)]1,0[,)(2∈=x x x f (C )()sin ,[1,1]f x x x =∈- (D)]1,1[,)(2-∈=x x x f26. 若函数221)1(xx x x f +=+,则=)(x f ( B ). (A )2x (B )22-x (C )2)1(-x (D )12-x 27. 设函数,ln )(x x x f =则下面关于)(x f 的说法正确的是( A ).(A )在(0,e 1)内单调递减 (B)在(+∞,1e)内单调递减 (C )在(0,+∞)内单调递减 (D)(0,+∞)在内单调递增28. 设1)(+=x x f ,则)1)((+x f f =( D ).(A )x (B )x + 1 (C )x + 2 (D )x + 329. 已知0)1(lim 2=--+∞→b ax x x x ,其中a ,b 是常数,则( C ).(A )1,1==b a , (B )1,1=-=b a (C )1,1-==b a (D )1,1-=-=b a 30. 下列函数在指定的变化过程中,( B )是无穷小量.(A ) (B )(C ) (D )31. 设函数(),2x xe ef x -+=则下面关于)(x f 的说法正确的是( B ) .(A )在(0,)+∞内单调递减 (B)在(,0)-∞内单调递减 (C )在(,0)-∞内单调递增 (D)在(,)-∞+∞内单调递增32. 下列函数中,在给定趋势下是无界变量且为无穷大的函数是( C ).(A ))(1sin∞→=x xx y (B )())(1∞→=-n n y n (C ))0(ln +→=x x y (D ))0(1cos 1→=x xx y33. 设⎪⎩⎪⎨⎧≤>=0,0,1sin )(x x x xx x f ,则)(x f 在0=x 处( B ). (A )连续且可导(B )连续但不可导 (C )不连续但可导(D )既不连续又不可导34. 在下列等式中,正确的是( C ).(A )()()f x dx f x '=⎰ (B) ()()df x f x =⎰(C )()()df x dx f x dx=⎰ (D)[()]()d f x dx f x =⎰ 35. 曲线x x y -=3在点(1,0)处的切线是( A ).(A )22-=x y(B )22+-=x ye 1xx ,()→∞sin ,()xxx →∞ln(),()11+→x x x xx +-→110,()(C )22+=x y(D )22--=x y36. 已知441x y =,则y ''=( B ). (A ) 3x (B )23x (C )x 6 (D ) 6 37. 若x xf =)1(,则=')(x f ( D ).(A )x 1 (B )21x (C )x 1- (D )21x-38. 下列各组函数中,是相同的函数的是( B ).(A )()()2ln 2ln f x x g x x == 和 (B )()||f x x = 和 ()g x =(C )()f x x = 和 ()2g x =(D )()||x f x x=和 ()g x =1 39. 函数()()20ln 10x f x x a x ≠=+⎨⎪=⎩ 在0x =处连续,则a =( B ).(A )0 (B )14(C )1 (D )240. 曲线ln y x x =的平行于直线10x y -+=的切线方程为( A ).(A )1y x =- (B )(1)y x =-+ (C )()()ln 11y x x =-- (D )y x = 41. 设函数()||f x x =,则函数在点0x =处( C ).(A )连续且可导 (B )连续且可微 (C )连续不可导 (D )不连续不可微 42. 设()f x 可微,则0()(2)limh f x f x h h→--=( D ).(A )()f x '- (B)1()2f x ' (C )2()f x '- (D)2()f x '43. 点0x =是函数4y x =的( D ).(A )驻点但非极值点 (B )拐点 (C )驻点且是拐点 (D )驻点且是极值点 44. 曲线1||y x =的渐近线情况是( C ). (A )只有水平渐近线 (B )只有垂直渐近线(C )既有水平渐近线又有垂直渐近线 (D )既无水平渐近线又无垂直渐近线45.211f dx x x⎛⎫' ⎪⎝⎭⎰的结果是( D ). (A )1f C x ⎛⎫-+ ⎪⎝⎭(B )1f C x ⎛⎫--+ ⎪⎝⎭(C )1f C x ⎛⎫+ ⎪⎝⎭(D )1f C x ⎛⎫-+ ⎪⎝⎭46.x x dxe e -+⎰的结果是( A ).(A )arctan x e C + (B )arctan x e C -+ (C )x x e e C --+ (D )ln()x x e e C -++47. 下列各组函数中,是相同函数的是( C ).(A) ()f x x =和()g x =()211x f x x -=-和1y x =+(C) ()f x x =和()22(sin cos )g x x x x =+ (D) ()2ln f x x =和()2ln g x x =48. 设函数()()2sin 21112111x x x f x x x x -⎧<⎪-⎪⎪==⎨⎪->⎪⎪⎩,则()1lim x f x →=( D ).(A) 0 (B) 1 (C) 2 (D)不存在49. 设函数22456x y x x -=-+,则2x =是函数的( A ).(A) 可去间断点 (B) 跳跃间断点 (C) 无穷间断点 (D) 振荡间断点 50. 设函数()y f x =在点0x 处可导,且()f x '>0, 曲线则()y f x =在点()()00,x f x 处的切线的倾斜角为( C ). (A) 0 (B)2π(C)锐角 (D)钝角 51. 曲线ln y x =上某点的切线平行于直线23y x =-,则该点坐标是( D ).(A) 12,ln2⎛⎫ ⎪⎝⎭ (B) 12,ln 2⎛⎫- ⎪⎝⎭ (C) 1,ln 22⎛⎫ ⎪⎝⎭ (D) 1,ln 22⎛⎫- ⎪⎝⎭52. 函数2x y x e -=及图象在()1,2内是( B ).(A)单调减少且是凸的 (B)单调增加且是凸的 (C)单调减少且是凹的 (D)单调增加且是凹的 53. 以下结论正确的是( C ).(A) 若0x 为函数()y f x =的驻点,则0x 必为函数()y f x =的极值点. (B) 函数()y f x =导数不存在的点,一定不是函数()y f x =的极值点. (C) 若函数()y f x =在0x 处取得极值,且()0f x '存在,则必有()0f x '=0. (D) 若函数()y f x =在0x 处连续,则()0f x '一定存在.54. 设函数22132x y x x -=-+,则1x =是函数的( A ).(A )可去间断点 (B) 跳跃间断点 (C) 无穷间断点 (D) 振荡间断点 55. 设函数()y f x =的一个原函数为12x x e ,则()f x =( A ).(A) ()121x x e - (B)12xx e - (C) ()121x x e + (D) 12xxe56. 若()()f x dx F x c =+⎰,则()sin cos xf x dx =⎰( D ).(A) ()sin F x c + (B) ()sin F x c -+ (C) ()cos F x c + (D) ()cos F x c -+57. 函数21,0e ,0xx x y x ⎧+<=⎨≥⎩在点0x =处( D ).(A )连续且可导 (B) 不连续且不可导 (C) 不连续但可导 (D) 连续但不可导 58. 函数 2)1ln(++-=x x y 的定义域是( C ).(A ) []1,2- (B ) [)1,2- (C )(]1,2- (D )()1,2- 59. 极限x x e ∞→lim 的值是( D ).(A )∞+ (B ) 0 (C )∞- (D )不存在 60. =--→211)1sin(limx x x ( C ).(A )1 (B ) 0 (C )21-(D )2161. 曲线 23-+=x x y 在点)0,1(处的切线方程是( B ).(A ) )1(2-=x y (B ))1(4-=x y (C )14-=x y (D ))1(3-=x y62. 函数, 0,0xx x y e x <⎧=⎨≥⎩在点0x =处( B ). (A )连续且可导 (B) 不连续且不可导 (C) 不连续但可导 (D) 连续但不可导 63. 下列各微分式正确的是( C ).(A ))(2x d xdx = (B ))2(sin 2cos x d xdx = (C ))5(x d dx --= (D )22)()(dx x d = 64. 设⎰+=C xdx x f 2cos 2)( ,则 =)(x f ( B ). (A )2sin x (B ) 2sin x - (C )C x +2sin (D )2sin 2x-65. 设()f x 可微,则0(2)()limh f x h f x h→+-=( D ).(A )()f x '- (B)1()2f x ' (C)2()f x '- (D)2()f x ' 66.⎰=+dx x xln 2( B ).(A )Cx x ++-22ln 212 (B )C x ++2)ln 2(21(C )C x ++ln 2ln (D )C xx++-2ln 1 67. 函数)1lg(12+++=x x y 的定义域是( B ).(A )()()+∞--,01,2 (B )()),0(0,1+∞- (C )),0()0,1(+∞- (D )),1(+∞-68. 设0tan 4()lim6sin x x f x x →+=,则0()lim x f x x→=( B ) .(A )1 (B )2 (C )6 (D )24 69. 下列各式中,极限存在的是( A ).(A ) x x cos lim 0→ (B )x x arctan lim ∞→ (C )x x sin lim ∞→ (D )x x 2lim +∞→70. =+∞→xx xx )1(lim ( D ). (A )e (B )2e (C )1 (D )e1 71. 设0sin 4()lim5sin x x f x x →+=,则0()lim x f x x→=( B ) .(A )0 (B )1 (C )5 (D )2572. 曲线x x y ln =的平行于直线01=+-y x 的切线方程是( C ).(A )x y = (B ))1)(1(ln --=x x y (C )1-=x y (D ))1(+-=x y73. 已知x x y 3sin = ,则=dy ( B ).(A )dx x x )3sin 33cos (+- (B )dx x x x )3cos 33(sin + (C )dx x x )3sin 3(cos + (D )dx x x x )3cos 3(sin + 74. 下列等式成立的是( C ).(A )⎰++=-C x dx x 111ααα (B )⎰+=C x a dx a x x ln (C )⎰+=C x xdx sin cos (D )⎰++=C xxdx 211tan 75. 极限01lim sinx x x→= ( A ) . (A ) 0 (B) 1 (C )+∞ (D) -∞ 76. 设()1cos f x x =-,()2g x x =,则当0x →时,()f x 是()g x 的( D ).(A )等价无穷小 (B) 低阶无穷小 (C ) 高阶无穷小 (D) 同阶但非等价无穷小 77. 计算⎰xdx x e x cos sin sin 的结果中正确的是( D ).(A )C e x +sin (B )C x e x +cos sin (C )C x e x +sin sin (D )C x e x +-)1(sin sin78. 5lg 1)(-=x x f 的定义域是( D ).(A )()),5(5,+∞∞- (B )()),6(6,+∞∞-(C )()),4(4,+∞∞- (D )())5,4(4, ∞- ()),6(6,5+∞79. 如果函数f (x )的定义域为[1,2],则函数f (x )+f (x 2)的定义域是( B ).(A )[1,2] (B )[1,2] (C )]2,2[- (D )]2,1[]1,2[ --80. 函数)1lg()1lg(22x x x x y -++++=( D ).(A )是奇函数,非偶函数 (B )是偶函数,非奇函数 (C )既非奇函数,又非偶函数 (D )既是奇函数,又是偶函数 81. 设()sin f x x x =,则)(x f 是( C ).(A )非奇非偶函数 (B) 奇函数 (C)偶函数 (D) 既奇又偶函数 82. 函数)10(1)(2≤≤--=x x x f 的反函数=-)(1x f( C ).(A )21x - (B )21x --(C ))01(12≤≤--x x (D ))01(12≤≤---x x 83. 下列数列收敛的是( C ).(A )1)1()(1+-=+n n n f n (B )⎪⎩⎪⎨⎧-+=为偶数为奇数n nn n n f ,11,11)((C )⎪⎩⎪⎨⎧+=为偶数为奇数n n n n n f ,11,1)( (D )⎪⎪⎩⎪⎪⎨⎧-+=为偶数为奇数n n n f nn n n ,221,221)(84. 设1111.0个n n y =,则当∞→n 时,该数列( C ).(A )收敛于0.1 (B )收敛于0.2 (C )收敛于91(D )发散 85. 下列极限存在的是( A ).(A )2)1(lim x x x x +∞→ (B )121lim -∞→x x (C )x x e 10lim → (D )x x x 1lim 2++∞→ 86. xx xx x x sin 2sin 2lim 22+-+∞→=( A ).(A )21(B )2 (C )0 (D )不存在 87. =--→1)1sin(lim 21x x x ( B ).(A )1 (B )2 (C )21(D )0 88. 下列极限中结果等于e 的是( B ).(A )xx x x x sin 0)sin 1(lim +→ (B )x xx x x sin )sin 1(lim +∞→ (C )xxx xxsin )sin 1(lim -∞→- (D )xxx xxsin 0)sin 1(lim +→89. 函数||ln 1x y =的间断点有( C )个. (A )1 (B )2 (C )3 (D )4 90. 下列结论错误的是( A ).(A )如果函数f (x )在点x =x 0处连续,则f (x )在点x =x 0处可导; (B )如果函数f (x )在点x =x 0处不连续,则f (x )在点x =x 0处不可导; (C )如果函数f (x )在点x =x 0处可导,则f (x )在点x =x 0处连续; (D )如果函数f (x )在点x =x 0处不可导,则f (x )在点x =x 0处也可能连续。
大学概率论期末复习题七套

试题(一)一、填空题1.设 A 、B 、C 是三个随机事件。
试用 A 、B 、C 分别表示事件 1)A 、B 、C 至少有一个发生 2)A 、B 、C 中恰有一个发生3)A 、B 、C 不多于一个发生2.设 A 、B 为随机事件, P (A)=0.5,P(B)=0.6,P(B A)=0.8。
则P(B )A =3.若事件A 和事件B 相互独立, P()=,A αP(B)=0.3,P(AB)=0.7,则α=4. 将C,C,E,E,I,N,S 等7个字母随机的排成一行,那末恰好排成英文单词SCIENCE 的概率为5. 甲、乙两人独立的对同一目标射击一次,其命中率分别为0.6和0.5,现已知目标被命中,则它是甲射中的概率为二、选择题1. 设A,B 为两随机事件,且B A ⊂,则下列式子正确的是 (A )P (A+B) = P (A); (B )()P(A);P AB =(C )(|A)P(B);P B = (D )(A)P B -=()P(A)P B -2. 以A 表示事件“甲种产品畅销,乙种产品滞销”,则其对立事件A 为 (A )“甲种产品滞销,乙种产品畅销”; (B )“甲、乙两种产品均畅销” (C )“甲种产品滞销”; (D )“甲种产品滞销或乙种产品畅销”。
3. 袋中有50个乒乓球,其中20个黄的,30个白的,现在两个人不放回地依次从袋中随机各取一球。
则第二人取到黄球的概率是(A )1/5 (B )2/5 (C )3/5 (D )4/5 4. 对于事件A ,B ,下列命题正确的是 (A )若A ,B 互不相容,则A 与B 也互不相容。
(B )若A ,B 相容,那么A 与B 也相容。
(C )若A ,B 互不相容,且概率都大于零,则A ,B 也相互独立。
(D )若A ,B 相互独立,那么A 与B 也相互独立。
5. 若()1P B A =,那么下列命题中正确的是(A )A B ⊂ (B )B A ⊂ (C )A B -=∅ (D )()0P A B -=三、计算题1. 10把钥匙中有3把能打开门,今任意取两把,求能打开门的概率。
马克思期末考试复习题

一、单项选择题(每小题1分,共25题) 单项选择题(每小题 分 题 1、哲学的基本问题是( ) 、哲学的基本问题是( A 物质和运动的关系问题 B 可知论和不可知论的关系问题 √ D 思维和存在的关系问题 C 理论和实践的关系问题 2、马克思主义哲学和具体科学的关系是( ) 、马克思主义哲学和具体科学的关系是( √ A 整体与局部关系 B 一般与个别关系 C 代替与被代替的关系 D 绝对和相对关系 3、下列观点属于客观唯心主义的是( ) 、下列观点属于客观唯心主义的是( A 万物皆备于我 B 存在就是被感知 √ C 生死由命,富贵在天 生死由命, D 心外无物 4、唯物主义哲学发展的三个基本历史形态是( ) 、唯物主义哲学发展的三个基本历史形态是( A 形而上学唯物主义、庸俗唯物主义、辩证唯物主义 形而上学唯物主义、庸俗唯物主义、 古代朴素唯物主义、形而上学唯物主义、 √ B 古代朴素唯物主义、形而上学唯物主义、实践唯物主义或辩证唯物主 义和历史的唯物主义 C 奴隶社会时期的唯物主义、封建社会时期的唯物主义、资本主义时期 奴隶社会时期的唯物主义、封建社会时期的唯物主义、 的唯物主义 D 机械唯物主义、形而上学唯物主义、辩证唯物主义 机械唯物主义、形而上学唯物主义、 5、划分历史唯物主义和历史唯心主义的唯一标准在于( ) 、划分历史唯物主义和历史唯心主义的唯一标准在于( A 是否承认社会的内部矛盾推动社会发展 B 是否承认社会历史是发展变化的 √ C 是否承认社会存在决定社会意识 D 是否承认社会历史发展是有规律的
4、产业资本的循环是如何实现的?
• 【答案要点】 • (1)产业资本在循环过程中要经历三个不同阶段,与次相应的是资 本依次执行三种不同的职能。 第一,购买生产资料和劳动力的阶段,产业资本执行的是货币资本的 职能。(1分) 第二,是生产资料与劳动力按比例结合在一起从事资本主义生产的阶 段,在这阶段上,生产资料与劳动者相结合生产物质财富并上生产资 本得以增殖,执行的是生产资本的职能。(1分) 第三,是售卖阶段,即商品资本向货币资本的转化阶段。产业资本执 行商品资本的职能,通过商品买卖实现商品的价值,满足人们的需要。 (1分) • (2)产业资本的运动必须具备两个基本前提条件: • 一是,产业资本的三种职能形式必须在空间上同时并存;(1分) • 二是,产业资本的三种职能形式必须保持时间上继起。(1分)
《科学与技术》期末复习重点习题

《科学与技术》期末复习重点习题《科学与技术》期末复习重点习题一、填空题1.科学发展经历了不同的时代。
16世纪是以科学家伽利略为代表的个体活动时代;17世纪是以科学家牛顿为代表的皇家学会时代;18世纪到第二次世界大战前是以科学家爱迪生的“实验工厂”为代表集体研究时代。
今天,科学已经进入了跨国建制时代。
2. 18世纪末法国启蒙思想家狄德罗指出:技术是为了某一目的共同协作组成的各种工具和规则体系。
3.20世纪80年代,我国开始引入高技术这一名词,并于1986年3月制定了《高技术研究发展计划纲要》,这一纲要简称为863计划。
4.自然选择学说的要点是变异的普遍性、繁殖过剩、生存斗争和适者生存。
5.19世纪自然科学的三大发现是细胞学说、科学进化论、能量守恒和转换定律。
6.电磁场理论揭示了电场、磁场、电磁场。
7.工业革命的标志是蒸汽机的使用.8.化工技术革命主要包括化肥工业、人工合成燃料、制药工业、安全炸药等几个方面。
9. 目前,国际上公认的并列入21世纪重点研究开发的高新技术领域包括信息技术、生物技术、新材料技术、新能源技术、空间技术和海洋技术等。
-10-14-15-2010.原子的范围是10 m ,原子核的范围是10 - 10 m ,夸克的范围10 m 。
11.原子能释放的方式是衰变、裂变和聚变反应。
12.核反应堆是进行裂变反应的专门装置,它的主要作用是能量持续不断释放。
13.核电站是利用原子核裂变反应所释放出的核能,驱动汽轮发电机组进行发电的发电厂。
14.我国第一座自行设计自主建设的核电站是秦山核电站,装机容量300 MW15.现化学发展的特点是研究层面由宏观向微观发展,研究方法由定性向定量发展,研究对象由静态向动态发展,研究结果由描述性向推理性发展。
16. 基础分析化学的任务有定性分析和定量分析。
17. 三大合成高分子材料是塑料、合成纤维和合成橡胶。
18.细胞膜具有_物质转运__、_能量转换_、__信息转换__等重要功能。
离散数学期末复习题

离散数学期末复习题第一章集合论一、判断题(1)空集是任何集合的真子集. ( 错 )(2){}φ是空集. ( 错 ) (3){}{}a a a },{∈ ( 对 ) (4)设集合{}{}{}{}AA 22,1,2,1,2,1⊆=则. ( 对 ) (5)如果B A a ⋃∉,则A a ∉或B a ∉. ( 错 )解 B A a ⋃∉则B A B A a ⋂=⋃∈,即A a ∈且B a ∈,所以A a ∉且B a ∉(6)如果A ∪.,B A B B ⊆=则 ( 对 )(7)设集合},,{321a a a A =,},,{321b b b B =,则},,,,,{332211><><><=⨯b a b a b a B A ( 错 )(8)设集合}1,0{=A ,则}1},0{,0},0{,1,,0,{><><><><=φφρ是A2到A 的关系. ( 对 )解 A 2}},1{},0{,{A φ=, =⨯A A 2}1,,0,,1},1{,0},1{,1},0{,0},0{,1,,0,{><><><><><><><><A A φφ(9)关系的复合运算满足交换律. ( 错 )(10).条件具有传递性的充分必要上的关系是集合ρρρρA = ( 错 )(11)设.~,上的传递关系也是则上的传递关系是集合A A ρρ ( 对 ) (12)集合A 上的对称关系必不是反对称的. ( 错 )(13)设21,ρρ为集合A 上的等价关系, 则21ρρ⋂也是集合A 上的等价关系( 对 )(14)设ρ是集合A 上的等价关系, 则当ρ>∈<b a ,时, ρρ][][b a = ( 对 )(15)设21,ρρ为集合 A 上的等价关系, 则 ( 错 )二、单项选择题(1)设R 为实数集合,下列集合中哪一个不是空集 ( A )A. {}R x x x ∈=-且,01|2 B .{}R x x x ∈=+且,09|2C. {}R x x x x ∈+=且,1|D. {}R x x x ∈-=且,1|2(2)设B A ,为集合,若φ=B A \,则一定有 ( C )A. φ=B B .φ≠B C. B A ⊆ D. B A ⊇(3)下列各式中不正确的是 ( C )A. φφ⊆ B .{}φφ∈ C. φφ⊂ D. {}}{,φφφ∈ (4)设{}}{,a a A =,则下列各式中错误的是 ( B )A. {}A a 2∈ B .{}A a 2⊆ C. {}A a 2}{∈ D. {}Aa 2}{⊆ (5)设{}2,1=A ,{}c b a B ,,=,{}d c C ,=,则)(C B A ⨯为 ( B ) A. {}><><c c ,2,1, B .{}><><c c ,2,,1C. {}><><2,,,1c cD. {}><><2,,1,c c(6)设{}b A ,0=,{}3,,1b B =,则B A 的恒等关系为 ( A ) A. {}><><><><3,3,,,1,1,0,0b b B .{}><><><3,3,1,1,0,0C. {}><><><3,3,,,0,0b bD. {}><><><><0,3,3,,,1,1,0b b(7)设{}c b a A ,,=上的二元关系如下,则具有传递性的为 ( D )A. {}><><><><=a b b a a c c a ,,,,,,,1ρB . {}><><=a c c a ,,,2ρC. {}><><><><=c b a b c c b a ,,,,,,,3ρD. {}><=a a ,4ρ(8)设ρ为集合A 上的等价关系,对任意A a ∈,其等价类[]ρa 为 ( B )A. 空集; B .非空集; C. 是否为空集不能确定; D. }|{A x x ∈.(9)映射的复合运算满足 ( B )A. 交换律 B .结合律 C. 幂等律 D. 分配律(10)设A ,B 是集合,则下列说法中( C )是正确的.A .A 到B 的关系都是A 到B 的映射B .A 到B 的映射都是可逆的C .A 到B 的双射都是可逆的D .B A ⊂时必不存在A 到B 的双射(11)设A 是集合,则( B )成立.A .A A #22#=B .A X X A⊆↔∈2 C .{}A2∈φ D .{}AA 2∈ (12)设A 是有限集(n A =#),则A 上既是≤又是~的关系共有(B ).A .0个B .1个C .2个D .n 个三、填空题1. 设}}2,1{,2,1{=A ,则=A2____________.填}}},2,1{,2{}},2,1{,1{},2,1{}},2,1{{},2{},1{,{2A A φ=2.设}}{,{φφ=A ,则A 2= . 填}}},{{},{,{2A A φφφ=3.设集合B A ,中元素的个数分别为5#=A ,7#=B ,且9)(#=⋃B A ,则集合B A ⋂中元素的个数=⋂)(#B A .34.设集合}4,1001|{Z x x x x A ∈≤≤=的倍数,是,}5,1001|{Z x x x x B ∈≤≤=的倍数,是,则B A 中元素的个数为 .405.设 },{b a A =, ρ 是 A2 上的包含于关系,,则有ρ= .},,},{,}{},{,},{,}{},{,,,}{,,}{,,,{><><><><><><><><><A A A b b b A a a a A b a φφφφφ6.设21,ρρ为集合 A 上的二元关系, 则=21ρρ .~1~2ρρ7.集合A 上的二元关系ρ为传递的充分必要条件是 .ρρρ⊆8. 设集合{}{}><><==0,2,2,02,1,01ρ上的关系A 及集合A 到集合{}4,2,0=B 的关系=2ρ{><b a ,|><b a ,A b a B A ∈⨯∈,且∩}=21,ρρ 则B ___________________. 填 }2,2,0,2,2,0,0,0{><><><><四、解答题1. 设 A d c b a A },,,,{=上的关系 },,,,,,,,,,,,,,,{><><><><><><><><=c d d c a b b a d d c c b b a a ρ(1)写出ρ的关系矩阵;(2)验证ρ是A 上的等价关系;(3)求出A 的各元素的等价类。
《检测技术》期末考试复习题及参考答案

检测技术复习题(课程代码392220)一、单项选择题1.按误差出现的规律分,下列误差不属于系统误差的是()A电子电路的噪声干扰产生的误差;B仪表本身材料,零件工艺上的缺陷;C测量者不良读数习惯引起的误差;D测试工作中使用仪表的方法不正确;2.下列传感器可以测量温度的是()A 应变片B AD590C 氯化锂D CCD传感器3. 下列传感器不可以测量振动的是()A 应变片 B电容传感器C SHT11D 压电传感器4.下列测量最准确的是()A 65.98±0.02mmB 0.488±0.004mmC 0.0098±0.0012mmD 1.98±0.04mm5.下列哪些指标不属于传感器的静态指标()A 精度 B灵敏度C阻尼比 D 线性度6.莫尔条纹的移动对被测位移量所起的作用是()A 调制B 放大C 细分D 降噪7.电涡流式传感器利用涡流效应将检测量的变化转换成线圈的()A 电阻变化B 电容变化C 涡流变化D 电感变化8.变压器隔离电路中赖以传递信号的途径是()A.光电耦合B.磁通耦合C.漏电耦合D.电容耦合9.光照射在某些半导体材料表面上时,半导体材料中有些电子和空穴可以从原来不导电的束缚状态变为能导电的自由状态,使半导体的导电率增加,这种现象叫()A 内光电效应B 外光电现象C 热电效应D 光生伏特效应10.下列不具有压电特性的材料是()A 石英B 钛酸钡C PVC薄膜D 霍尔片11.一般意义上的传感器包含了敏感元件和()两个组成部分。
A放大电路 B 数据采集电路C 转换电路D滤波电路12.DS18B20默认的温度分辨率是()A 0.5℃B 0.25℃C 0.125℃D 0.0625℃13.两片压电元件串联与单片相比,下列说法正确的是()A串联时输出电压不变,电荷量与单片时相同;B串联时输出电压增加一倍,电荷量与单片时相同;C 串联时电荷量时增加一倍,电容量不变;D串联时电荷量增加一倍,电容量为单片的一半;14.下列哪些指标不属于传感器的静态指标()A 精度 B灵敏度C频率响应 D 线性度15.热电阻的引线电阻对测量结果有较大影响,采用()引线方式测量精度最高。
大学数学期末考试复习题及参考答案(三套)

大学数学期末考试复习题第一章一、选择题1.下列各组函数中相等的是. …….. ……..…………………………………………………………………………………….( ) A .2ln )(,ln 2)(x x g x x f ==B .0)(,1)(x x g x f ==C .1)(,11)(2-=-⋅+=x x g x x x f D .2)(|,|)(x x g x x f ==2.下列函数中为奇函数的是. ……. …….. …………………………………………………………………………………….( ). A .)1ln()(2++=x x x f B .||)(x e x f = C .x x f cos )(= D .1sin )1()(2--=x xx x f3.极限⎪⎭⎫⎝⎛+++∞→22221lim n n n n n 的值为………………………………………………………………………..…….( ) A .0 B .1 C .21D .∞ 4.极限xxx x sin lim+∞→的值为.. …….. ……..……………………………………………………………………………...…….( )A .0B .1C .2D .∞5.当0→x 时,下列各项中与 23x 为等价无穷小的是…………………………………………………….( )A .)1(3-xe x B .x cos 1- C .x x sin tan - D .)1ln(x + 6.设12)(-=xx f ,则当0→x 时,有…………………………………………………………………………..…….( ). A .)(x f 与x 是等价无穷小 B .)(x f 与x 同阶但非等价无穷小 C .)(x f 是比x 高阶的无穷小 D .)(x f 是比x 低阶的无穷小7.函数)(x f 在点x 0可导是)(x f 在点x 0连续的____________条件. ………...………………....…..( ) A .充分不必要 B .必要不充分 C .充要 D .既不充分也不必要8.设函数⎪⎩⎪⎨⎧<≤--<≤≤≤-=01,110,21,2)(2x x x x x x x f ,则下述结论正确的是……………………………………….( )A .在0=x ,1=x 处间断B .在0=x ,1=x 处连续C .在0=x 处间断,在1=x 处连续D .在1=x 处间断,在0=x 处连续 9.极限xx x 10)1(lim -→-的值为.. …….. ……..…………………………………………………………………………………….( )A .1B .e -C .e1D .e 二、填空题10.函数ln y x =的定义域为(用区间表示) . 11. 函数xxy -+=11的定义域为(用区间表示) . 12. 已知x xx f +=1)(,则=))((x f f . 13. 函数x x y 2353+-=的反函数为 .14. =→xx x 1sin lim 20 .15. 当________=α时,αx 与x 2sin 是0→x 时的同阶无穷小.16. 设21)1(lim e kx xx =+→,则=k .17. 设1sin lim0-=→xkxx ,则=k .18. =⎪⎭⎫ ⎝⎛+++∞→11232lim x x x x .9. 设⎪⎩⎪⎨⎧≤+>=0,0,1sin )(2x x a x xx x f 在点0=x 处连续,则=a . 三、解答与证明题20. 求下列数列极限 (1)⎪⎪⎭⎫⎝⎛+⨯++⨯+⨯∞→)1(1321211lim n n n (2))12(lim +-+∞→n n n n (3)⎪⎭⎫⎝⎛++++++∞→n n n n n n n n 22221lim (4)n n n nx 10...21lim +++∞→ 21. 求下列函数极限(1)15723lim 2323+++-∞→x x x x x (2)134lim 22++∞→x x x(3)503020)12()23()32(lim ++-∞→x x x x (4)11lim 31--→x x x (5)28lim 32--→x x x (6))1311(lim 31x x x ---→ (7))1(lim x x x -++∞→ (8)xx x x ln )1(lim1-→(9)xx x sin ln lim 0→ (10)x xx 3sin 2sin lim 0→(11)30sin tan lim xx x x -→ (12)x x x 10)51(lim -→ 22. 若432lim23=-+-→x ax x x ,求a 的值. 23. 若已知411lim21=-++→x b a x x ,求a,b 值. 24. 当 a 取何值时,函数)(x f 在 x =0 处连续:(1)⎩⎨⎧≥+<=0,0,)(x x a x e x f x . (2)⎪⎩⎪⎨⎧≤+>-+=0),cos(0,11)(x x a x xx x f . 25. 证明(1)方程01423=+-x x 在区间)1,0(内至少有一个根.(2)方程x e x 3=在)1,0(内至少有一个根.第二章一、选择题1、设函数)(x f 在点0x 可导,则=-+→hx f h x f h )()2(lim000( ).(A ) )(0x f '-; (B) )(0x f '; (C) )(20x f '; (D) )(20x f '-. 2、设函数)(x f 是可导函数,且13)1()1(lim-=--→xx f f x ,则曲线)(x f y =在点))1(,1(f 处切线的斜率是 ……………………………………………( ). (A) 3; (B) 1- ; (C) 13 ; (D) 3-.3、设)()()(x a x x f ϕ-=,其中)(x ϕ在a x =处连续,则)(a f '= ………( ). (A) )(a ϕ ; (B)0; (C)a ; (D))(a a ϕ.4、若0x 为函数)(x f 的极值点,则…………………………………………( ). (A)0)(0='x f ; (B)0)(0≠'x f ; (C)0)(0='x f 或不存在; (D))(0x f '不存在.5、设)0)(1ln(≠+=a ax y ,则y ''= ( ).(A)22)1(ax a +; (B)2)1(ax a +; (C)22)1(ax a +-; (D)2)1(ax a +-. 6、由方程5ln =-y xe y 确定的隐函数)(x y y =的导数=dxdy( ). (A)1-y y xe e ; (B)y y xe e -1; (C)yy e xe -1; (D)y y e xe 1-.7、)2sin sin (lim xx x x x +∞→= ……………………………………… ( ).(A)2; (B)1; (C)3; (D)极限不存在.8、设x x y =)0(>x 则='y ( ).(A)x x ; (B) x x x ln ; (C) 1-x x ; (D))1(ln +x x x .9、曲线x y sin 1+=在点)1,0(处的切线方程是…………………………( ). (A)01=--y x (B)01=+-y x (C)01=++y x (D)01=-+y x 10.下列函数在所给区间满足罗尔定理条件的是……………………( )(A) 2(),[0,3]f x x x =∈ (B) 21(),[1,1]f x x x=∈-(C) (),[1,1]f x x x =∈-(D) ()[0,3]f x x =∈ 二、填空题11、 设x x y 2sin 2+=,则=dy .12、已知x x y n ln )3(=-,(N n n ∈≥,3),则)(n y = .13、已知过曲线24y x =-上点P 的切线平行于直线x y =,则切点P 的坐标为 . 14. 已知2)1(='f ,则=-+-→2)1()(lim31x x f x f x .15. 设x a y =(0>a 且1≠a ),则=)(n y .16. 曲线3)1(-=x y 的拐点是 . 17.设函数)(x f 在0x 处可导,则xx x f x x f x ∆∆--∆+→∆)()(lim000= .18.设⎩⎨⎧≥+<=0)(x x a x e x f x ,当a =_____时,)(x f 在x = 0处可导.19.若函数5)(23-+-=x x ax x f 在),(+∞-∞上单调递增,则a 的取值范围为 .20. 设由参数方程⎩⎨⎧-=-=)cos 1()sin (t a y t t a x (其中0>a )确定的函数为)(x y y =,则=dxdy. 三、解答与证明题21.设e x x e y +=,求y '. 22.求下列函数的二阶导数.(1) 设x e y x sin =,求y ''. (2) 设1arctan1xy x-=+,求y ''23. 求曲线21x y =在点(4,2)处的切线方程和法线方程. 24. 讨论下列函数在点0=x 处的连续性和可导性:(1) 0 0 )1ln()(⎩⎨⎧<≥+=x x x x x f , (2) 0 tan 01sin )(2⎪⎩⎪⎨⎧≤>=x x x xx x f . 25. 求由方程ln xy x y x e -=所确定的隐函数y 的导数dxdy. 26. 求极限: (1)]1)1ln(1[lim 0x x x -+→; (2)30sin tan lim xx x x -→; (3))arctan 2(lim x x x -+∞→π; (4)x x x +→0lim ;(5))1sin 1(lim 0x x x -→; (6)200sin lim xdt t xx ⎰→. 27. 设函数)(x y y =由参数方程⎩⎨⎧-=+=tt y t x arctan )1ln(2所确定,求22dx yd .28.求函数()(f x x =-. 29. 求函数32332y x x x =-++的凹凸区间、拐点. 30. 已知点)3,1(为曲线1423+++=bx ax x y 的拐点. (1) 求b a ,的值; (2)求函数1423+++=bx ax x y 的极值. 31. 设11xy x-=+,求()n y 32.设b a <<0,证明:a b ab ba a --<+ln ln 222. 33. 设0,()(0)0,x f x f ≥=连续,0'()x f x >当时,存在且'()f x 单调增加,证明:当0x >时函数()f x x 单调增加.34. 证明:当0>x 时,x x x x<+<+)1ln(1. 35. 证明:当0x >时,有1x x x e xe <-<成立.第三章一、选择题:1.下列凑微分正确的一个是 ( ) A .)2(sin cos x d xdx = ; B. )11(arctan 2xd xdx += C .)1(ln x d xdx = D. )1(12x d dx x -=2.若⎰+=,)(c x dx x f 则⎰-dx x f )32(= ( )A .2-3x+c ; B. c x +-31; C. x+c ; D. c x +-2)32(213.在以下等式中,正确的一个是 ( ) A .⎰=')()(x f dx x f B. ⎰=')(])([x f dx x f C .⎰=)(])([x f dx x f d D. ⎰='')(])([x f dx x f 4. 设x x f 3sin )(=',则⎰dx x f )(是 ( )A .cos3x ; B. cos3x+c ; C.c x +-3cos 31; D.2193sin c x c x++- 5. 若,0(),0x x x f x e x ≥⎧=⎨<⎩,则21()d f x x -=⎰( ). A. 13e -- B. 13e -+ C. 3e - D. 3e + 6. 下列定积分是负数的是( )(A )dx x ⎰20sin π(B)dx x ⎰20cos π(C)dx x ⎰ππ2sin (D)dx x ⎰ππ2cos7. 若4)12(1=+⎰dx x a,则a = ( )(A) 3 (B) 2 (C) 0 (D) 48.若⎰∞-=31dx e kx ,则k=( ) (A)31 (B)-31(C) 3 (D)-3 9.=+⎰)1(212x dt t t dx d ( ) (A )x x+12(B) 212-+x x(C) 241x x + (D) 2512x x +10.若,21)(21)(0-=⎰x f dt t f x且1)0(=f ,则=)(x f ( ) (A)2x e (B)x e 21 (C)x e 2 (D)x e 221 二、填空题: 1.x d xdx 3(arcsin ________312=-).2.⎰=+________________912dx x .3.若⎰+=,3cos )(c x dx x f 则f (x )= .4. ⎰='____________________)()(22dx x f x xf . 5. F(x ) =dt t x ⎰+223,则=')1(F _________.6. 极限020cos d limxx t t x→⎰= ;7. 23423sin 1x e xdx x x -++⎰= 8.设()f x 连续,(0)1f =,则曲线0()d xy f x x =⎰在()0,0处的切线方程是 ;三、解答题:1、2x dx 2、⎰-+322x x dx3、⎰+dx x x214、422331.1x x dx x ⎛⎫++ ⎪+⎝⎭⎰ 5、cos 2.cos sin xdx x x -⎰6、dx x x ⎰-42 7、⎰-+211xdx8、⎰xdx x arctan 29、1x ⎰10、10d e ex xx-+⎰11、10x ⎰12、22()e d xx x x --+⎰;13.40d 1cos2xx xπ+⎰;14.41x ⎰;15.1d ln x x x+∞⎰16.2203sin d limx x t t x→⎰;17.求曲线xxe y e y -==,及直线1=x 所围成的平面图形的面积.18. 求由曲线)cos 2(2θ+=a r 所围图形的面积19. 由曲线2y x =和2x y =所围成的图形绕y 轴旋转后所得旋转体体积. 20. 计算曲线)3(31x x y -=上相应于31≤≤x 的一段弧的弧长大学数学期末考试复习题参考答案第一章一、选择题1、D2、A3、C4、B5、C6、B7、A8、C9、D二、填空题10、]3,0( 11、)1,1[- 12、x x21+ 13、)23(2353≠-+=x x x y 14、0 15、1 16、2 17、-1 18、e 19、0三、解答与证明题20(1)⎪⎪⎭⎫⎝⎛+⨯++⨯+⨯∞→)1(1321211lim n n n )1113121211(lim +-++-+-=∞→n n n 1)111(lim =+-=∞→n n . (2)2111211lim12lim )12(lim=+++=+++=+-+∞→∞→∞→nn n n n n n n n n n . (3)因为 1212222222+≤++++++≤+n n n n n n n n n n n n ,而 11lim lim 2222=+=+∞→∞→n n n n n n n , 所以121lim 222=⎪⎭⎫⎝⎛++++++∞→n n n n n n nn . (4)因为n nn n n nn n n nn 101010...101010...211010=+++<+++<=,110lim 10lim 1==∞→∞→nn nn ,故1010...21lim =+++∞→n n n n n .21(1)15723lim2323+++-∞→x x x x x 33115723lim x xx x x +++-=∞→53=.(2)331341lim 134lim 2222=++=++∞→∞→xx x x x x . (3)503020)12()23()32(lim ++-∞→x x x x 503020122332lim ⎪⎭⎫ ⎝⎛+⎪⎭⎫ ⎝⎛+⎪⎭⎫ ⎝⎛-=∞→x x x x 503020)02()03()02(++-=3023⎪⎭⎫⎝⎛=. (4)11lim31--→x x x 1)1)(1(lim333231-++-=→x x x x x 3)1(lim 3321=++=→x x x .(5)12)42(lim 28lim2232=++=--→→x x x x x x . (6)112lim 131lim )1311(lim 2132131-=+++-=--++=---→→→xx x x x x x x x x x . (7))1(lim x x x -++∞→011lim=++=+∞→xx x .(8)11)1(lim ln )1(lim11=--=-→→x x x x x x x x .(9)0sin lim ln sin lnlim 00==→→xxx x x x . (10)x xx 3sin 2sin lim0→3232lim 32lim 00===→→x x x x . (11)30sin tan limx x x x -→30)cos 1(tan lim x x x x -⋅=→3202lim x x x x ⋅=→21=. (12)xx x 1)51(lim -→ xt 51-== tt t 511lim -∞→⎪⎭⎫ ⎝⎛+511lim -∞→⎥⎥⎦⎤⎢⎢⎣⎡⎪⎭⎫ ⎝⎛+=t t t 5-=e .22 解 由题意知 0)2(lim 23=+-→a x x x ,即06232=+⨯-a ,从而3-=a .23 解 因1→x 时, 012→-x , 而函数极限存在, 则)1(0→→++x b a x即 0lim 1=++→b a x x从而01=++b a (1)故原式=)1)(1)(1(1lim 11lim121a a x x x x x a a x x x ++++--=-+-+→→ aa a x x x +=++++=→141)1)(1(1lim1即41141=+a(2) 由(1)(2)解得1,0-==b a .24 解 (1)因为 a x a x f x x =+=++→→)(lim )(lim 0,1lim )(lim 0==--→→x x x e x f ,而 ,)0(a f = 故要使 )(lim 0x f x -→)(lim 0x f x +→=)0(f =,须且只须 1=a .所以当且仅当1=a 时,函数)(x f 在0=x 处连续.(2)因为 21111lim 11lim )(lim 00=++=-+=+++→→→x xx x f x x x , a x a x f x x cos )cos(lim )(lim 00=+=--→→,而 ,cos )0(a f = 故要使 )(lim 0x f x -→)(lim 0x f x +→=)0(f =, 须且只须 21cos =a ,即32ππ±=k a )(Z k ∈. 所以当且仅当32ππ±=k a )(Z k ∈时,函数)(x f 在0=x 处连续.25 证 (1)令14)(23+-=x x x f ,则)(x f 在[0,1]上连续, 且,02)1(,01)0(<-=>=f f由零点定理知,),1,0(∈∃ξ使,0)(=ξf 即01423=+-ξξ,所以方程01423=+-x x 在(0,1)内至少有一个根.(2)设x e x f x3)(-=,则)(x f 在]1,0[上连续,且03)1(,01)0(<-=>=e f f ,故由零点定理知方程在)1,0(内至少有一个根.第二章一、选择题1、C2、D3、A4、C5、C6、B7、A8、D9、B 10、D 二、填空题11、dx x x )2cos 2(2+ 12、21x -13、)415,21(- 14、1215、nx a a )(ln 16、(1,0) 17、)(20x f ' 18、1. 19、),31(+∞ 20、t tcos 1sin -.三、解答与证明题21、解:1-+='e x ex e y .22、解:(1)(sin cos )xy e x x '=+,(sin cos )(cos sin )2cos x x x y e x x e x x e x ''=++-=.(2) 2111111x y x x x '-⎛⎫'=⎪+⎝⎭-⎛⎫+ ⎪+⎝⎭()()2222(1)1(1)(1)(1)1x x x x x x -+--+=⋅+++- 22212(1)(1)x x --==++ ()1211y x -'⎡⎤''=-+⎢⎥⎣⎦()()22222121x x x x -=+⋅=+ 23、解:2121-='x y ,所以4121)4(421=='=-x x y , 所以切线方程为)4(412-=-x y ,法线方程为)4(42--=-x y . 24、解:(1)因为0)(lim 0=+→x f x ,0)(lim 0=-→x f x ,所以,0)(lim 0=→x f x .且0)0(=f ,因此,函数在0=x 处连续.10lim 0)0()(lim )0(00'=--=--=++→→+x x x f x f f x x ,10)1ln(lim 0)0()(lim )0(00'=--+=--=+-→→-x x x f x f f x x ,所以函数在0=x 处可导. (2)因为0)(lim 0=+→x f x ,0)(lim 0=-→x f x ,所以,0)(lim 0=→x f x .且0)0(=f ,因此,函数在0=x 处连续.01sin lim 001sinlim 0)0()(lim )0(0200'==--=--=+++→→→+xx x x x x f x f f x x x , 10tan lim 0)0()(lim )0(00'=--=--=--→→-x x x f x f f x x ,所以函数在0=x 处不可导.25、解:两边同时对x 求导得,11ln ()xy y x y e y xy x ''--=+,所以,1ln xyxy yye x y x xe--'=+. 26、解:(1)原式=)1ln()1ln(limx x x x x ++-→=20)1ln(lim x x x x +-→=xx x 2111lim 0+-→=)1(21lim 0x x +→=21.(2)30sin tan lim x x x x -→=30)1cos 1(sin lim xx x x -→=x x x x x cos )cos 1(sin lim 30⋅-→121lim 320⋅⋅=→x x x x =21. (3))arctan 2(lim x x x -+∞→πx x x 1)arctan 2(lim -=+∞→π22111limxx x -+-=+∞→11lim 22=+=+∞→x x x .(4)xx x +→0lim =xx xx x x eeln lim ln 00lim +→+=→,0ln lim 0=+→x x x ,所以原极限10=e .(5))1sin 1(lim 0x x x -→ x x x x x sin sin lim 0-=→20sin lim xx x x -=→x x x 2cos 1lim 0-=→2sin lim 0x x →=0=. (6)2sin lim x dt t x x ⎰→=x x x 2sin lim 0→=21.27、解:22111221dy dy tdt t dx t dx dt t -+===+,22221()12241d dy d y t dt dx dx t dx t dt t +===+. 28、解:函数定义域为),(+∞-∞.'()f x =,令'()0f x =,得驻点1=x ,1x =-为不可导点.由上表可以看出,函数在),1(),1,(+∞--∞上单调上升,函数在(1,1)-上单调下降;函数在1-=x 处取得极大值0)1(=-f ,在1=x 处取得极小值343)1(-=f , 29、解:函数定义域为),(+∞-∞.2363y x x '=-+,666(1)y x x ''=-=-,令0y ''=,得x =1.当1x >时,0y ''>;当1x <时,0y ''<,所以函数的拐点为(1,3),在(-∞,1)上是凸的;在(1,+∞)上是凹的. 30、解:(1)b ax x y ++='232,a x y 26+=''.由条件,有⎩⎨⎧+=+++=a b a 2601413,解得9,3-=-=b a .(2)149323+--=x x x y ,函数定义域为),(+∞-∞.)3)(1(3963)(2-+=--='x x x x x f ,)1(666)(-=-=''x x x f .令0)(='x f ,得稳定点 11-=x ,32=x . 又012)1(<-=-''f ,012)3(>=''f故149323+--=x x x y 在点1-=x 处取极大值,极大值为19)1(=-f , 在点3=x 处取极小值,极小值为13)3(-=f .31. 解:122111x y x x--+==-+++()2121(1)y x '=-+,()()()312121y x ''=--+()()()41212(3)1y x '''=---+…… ()n y()()1121!1nn n x +=-+32. 证明:令x x f ln )(=, 则)(x f 在],[b a 上连续,在),(b a 内可导.所以由Lagrange 中值定理知,),(b a ∈∃ξ,使)()()(ξf ab a f b f '=--,即ξ1ln ln =--a b a b .又由),(b a ∈ξ,故22211ba ab +>>ξ.. 即222ln ln ba aa b a b +>--. 33. 证明:1)令()(0)f x F x x x=>()2'()()(2)'()xf x f x F x x-=2(0)0'()[()(0)]f xf x f x f x =-- 2'()'()(0)xf x xf x xξξ-<<微分中值定理 '()'()f x f xξ-=当0x >时,'()f x 单调增加 ∴'()'(),'()'()0f f x f x f ξξ<->即故有()'()0.(0,)f x F x x>+∞即在单调增加 34. 证明:令)1ln()(u u f +=,则)(u f 在],0[x 上满足Lagrange 中值定理条件,故),0(x ∈∃ξ,使)0)(()0()(-'=-x f f x f ξ,即)0(11)01ln()1ln(-+=+-+x x ξ,即ξ+=+1)1ln(x x . 又由),0(x ∈ξ,故x xx x <+<+ξ11,即x x xx <+<+)1ln(1. 35. 证明:令()[],0,t f t e t x =∈,()t f t e =在[]0,x 应用拉格朗日中值定理 ()00,0x e e e x x ξ-=-<ξ<x e 是单调增函数,0x e e e ξ∴<<,故有1xxx e xe <-<,0x > 证毕第三章一、选择题1-5 DCBDA 6-10 CBCDC 二、填空题 1.3 2. 11arctan 33x C + 3. -3sin3x 4. 221()+C 4f x5. -2 6. -1 7. 0 8.y x =三、解答题1. 572222=557x dx x dx dx x x C --=-+⎰⎰2.2111=23(3)(1)41311ln ||43dx dx dx dx x x x x x x x Cx ⎛⎫=- ⎪+-+--+⎝⎭-=++⎰⎰⎰⎰3. 22221(1)1=ln |1|+C 1212x d x dx x x x +=+++⎰⎰ 4. 42232233113arctan .11x x dx x dx x x C x x ⎛⎫++⎛⎫=+=++ ⎪ ⎪++⎝⎭⎝⎭⎰⎰5.22cos 2cos sin (cos sin )sin cos .cos sin cos sin x x x dx dx x x dx x x C x x x x-==+=-+--⎰⎰⎰ 6.dx x x ⎰-42=c xx +--)2arccos 24(tan 227.⎰-+211xdx =cxx x +-+-211arcsin8.⎰xdx x arctan 2=c x x x x +++-)1ln(6161arctan 312239.令t x tan =,则1x ⎰=3344111cos d ln sin 21cos tt t t ππππ-=+⎰=10. 10d e ex x x -+⎰=112200e 1d de e 1e 1x x x x x =++⎰⎰1arctan(e )arctan e 4xπ==-11.10x ⎰=102⎰2121216π===⎰12. 22()e d xx x x --+⎰=22220002e d 2de 2e2e d xxx x x x x x x ----=-=-+⎰⎰⎰262e=-13.40d 1cos2x x x π+⎰=442001d d tan 2cos 2x x x x x ππ=⎰⎰ 444000111ln 2tan tan d lncos 228284x x x x x πππππ=-=+=-⎰14. 41x⎰412ln x =⎰4112x x ⎤=-⎥⎦⎰124ln 2x ⎡⎤=-⎢⎥⎣⎦⎰ 14218ln 22d x x -=-⎰8ln24=-15. ee 11d d(ln )ln(ln )ln ln e x x x x xx +∞+∞+∞===+∞⎰⎰ 16. 2222032200sin d 2sin 22(2)8=333lim lim lim x x x x t t x x x x x →→→==⎰17.如图所示,解方程组xxy e y e-⎧=⎨=⎩,得交点(0,1),所求面积为 11100()d []2x x x x A e e x e e e e---=-=+=+-⎰18.解:∵1D :⎩⎨⎧+<<<<)cos 2(200θπθa r∴12220141122[2(2cos3)]4[4(sin 3sin 6)1823212D D S S a d a a ππθθπθθθπ==+=+++=⎰19. 思路: 该平面图形绕y 轴旋转而成体积V 可看作1D :⎩⎨⎧≤≤≤≤y x y 010绕y 轴旋转而成的体积1V ,减去2D :⎩⎨⎧≤≤≤≤2010yx y 绕y 而成的立体体积2V 所得,见轴旋转图解: πππ103)()(1222121=-=-=⎰⎰dy y dy y V V V20.解:122y '==, ∴3432322(21)214)1(113123313122-=+=+=-+='+=⎰⎰⎰x x dx xx dx x x dx y s ba。
期末复习题——油田化学

中国石油大学(北京)远程教育学院《油田化学》复习题一、名词解释。
一、名词解释。
1、晶格取代:、晶格取代:2、稠化时间:、稠化时间:3、体积波及系数:、体积波及系数:4、注水调剖:、注水调剖:5、人工井壁:、人工井壁:6、双液法:、双液法:7、聚合物:、聚合物:8、表面活性剂HLB 值:值:9、渗透水化:、渗透水化:10、临界胶束浓度:、临界胶束浓度:1111、单体:、单体:、单体:1212、乳状液:、乳状液:、乳状液: 1313、缩聚反应:、缩聚反应:、缩聚反应: 1414、水泥浆减阻剂:、水泥浆减阻剂:、水泥浆减阻剂: 1515、铝氧八面体:、铝氧八面体:、铝氧八面体: 1616、晶层:、晶层:、晶层: 1717、聚合度:、聚合度:、聚合度: 1818、表面活性剂:、表面活性剂:、表面活性剂: 1919、单液法:、单液法:、单液法: 2020、冻胶:、冻胶:、冻胶: 2121、油井结蜡:、油井结蜡:、油井结蜡: 2222、流度:、流度:、流度: 2323、吸附:、吸附:、吸附: 2424、界面:、界面:、界面: 2525、出砂:、出砂:、出砂: 2626、离子交换吸附、离子交换吸附、离子交换吸附: : 2727、表面张力:、表面张力:、表面张力: 2828、硅氧四面体:、硅氧四面体:、硅氧四面体: 2929、近井地带:、近井地带:、近井地带: 3030、化学吸附:、化学吸附:、化学吸附: 3131、链节:、链节:、链节: 3232、剪切变稀:、剪切变稀:、剪切变稀: 3333、物理吸附、物理吸附、物理吸附: : 3434、剪切增稠、剪切增稠、剪切增稠: : 3535、表面:、表面:、表面:二、判断正误题。
正确的用(T )表示,错误的用(F )表示。
)表示。
1、粘土表面存在永久负电荷、可变负电荷和正电荷,其代数和为零。
( )2、水泥浆转化为水泥石需经过水化、凝结和硬化三个过程。
( )3、阳离子交换容量与粘土矿物种类和粘土分散度有关。
2023-2024学年冀教版八年级数学下册期末复习试题(一)(含答案)

2023-2024学年度下期冀教版数学八年级下册期末复习习题精选(一)(满分120分,限时100分钟)一、选择题(每小题3分,共42分)1.(2023河北保定期末)为了解某市七年级8 000名学生的身高情况,从中抽取了60名学生进行身高检查.下列判断:①这种调查方式是抽样调查;②8 000名学生是总体;③每名学生的身高是个体;④60名学生是总体的一个样本;⑤60名学生是样本容量.其中正确的判断有( )A.5个B.4个C.3个D.2个2.(2023广东深圳南山二模)剪纸艺术是中国民间艺术之一,很多剪纸作品体现了数学中的对称美.如图,蝴蝶剪纸是轴对称图形,将其放在平面直角坐标系中,如果图中点E的坐标为(m,3),其关于y轴对称的点F的坐标为(4,n),则m+n的值为( )A.-1B.0C.1D.-93.(2023陕西西安雁塔模拟)一次函数y=(-2m+1)x的图像经过(-1,y1),(2,y2)两点,且y1>y2,则m的值可以是( )A. B.0 C.1 D.-4.(2023浙江温州三模)某校九(1)班50名学生的视力频数分布直方图如图所示(每一组含前一个边界值,不含后一个边界值),若视力达到 4.8以上(含 4.8)为达标,则该班学生视力的达标率为( )A.8%B.18%C.29%D.36%5.(2023山东临沂兰陵期中)下面的三个问题中都有两个变量:①正方形的周长y与边长x;②汽车以30千米/时的速度行驶,它的行驶路程y(千米)与时间x(小时);③水箱以0.8 L/min的流量往外放水,水箱中的剩余水量y(L)与放水时间x(min).其中,变量y与变量x之间的函数关系可以利用如图所示的图像表示的是( )A.①②B.①③C.②③D.①②③6.(2023天津南开期末)已知张强家、体育场、文具店在同一直线上.给出的图像反映的过程是:张强从家跑步去体育场,在体育场锻练了若干分钟后又走到文具店去买笔,然后散步走回家.图中x(min)表示张强离开家的时间,y(km)表示张强离家的距离,则下列说法错误的是( )A.体育场离文具店1 kmB.张强在文具店停留了20 minC.张强从文具店回家的平均速度是 km/minD.当30≤x≤45时,y=7.(2023重庆忠县期末)如图,四边形ABCD是矩形,有一动点P从点B出发,沿B→C→D→A绕矩形的边匀速运动,当点P到达点A时停止运动.在点P的运动过程中,△ABP的面积S随时间t变化的函数图像大致是( )8.【新独家原创】在菱形ABCD中,AC=6,BD=8,点E为BC上一动点,则的最小值为( )A. B. C. D.9.(2023河南新乡长垣期末)随着暑假临近,某游泳馆推出了甲、乙两种消费卡,设消费次数为x,所需费用为y元,且y与x的函数关系的图像如图所示.根据图中信息判断,下列说法错误的是( )A.甲种消费卡为20元/次=10x+100B.y乙C.点B的坐标为(10,200)D.洋洋爸爸准备了240元钱用于洋洋在该游泳馆消费,选择甲种消费卡划算10.(2023上海虹口期末)在平面直角坐标系中,点A(0,6),点B(-6,0),坐标轴上有一点C,使得△ABC为等腰三角形,则这样的点C一共有( )A.5个B.6个C.7个D.8个11.(2023河南濮阳二模)如图,以矩形ABCD的顶点A为圆心,AD长为半径画弧交CB的延长线于点E,过点D作DF∥AE交BC于点F,连接AF.若AB=4,AD=5,则AF的长是( )A.2B.3C.3D.312.(2023福建福州台江模拟)“开开心心”商场2021年1~4月的销售总额如图1,其中A商品的销售额占当月销售总额的百分比如图2.根据图中信息,有以下四个结论,其中推断不合理的是( )A.1~4月该商场的销售总额为290万元B.2月份A商品的销售额为12万元C.1~4月A商品的销售额占当月销售总额的百分比最低的月份是4月D.2~4月A商品的销售额占当月销售总额的百分比与1月份相比都下降了13.【新考法】(2023河南郑州金水期末)现有一四边形ABCD,借助此四边形作平行四边形EFGH,两位同学提供了如图所示的方案,对于方案Ⅰ、Ⅱ,下列说法正确的是( )方案Ⅰ方案Ⅱ作边AB,BC,CD,AD的垂直平分线l1,l2,l3,l4,分别交AB,BC,CD,AD于点E,F,G,H,顺次连接这四点得到的四边形EFGH即为所求连接AC,BD,过四边形ABCD各顶点分别作AC,BD 的平行线EF,GH,EH,FG,这四条平行线围成的四边形EFGH即为所求A.Ⅰ可行、Ⅱ不可行B.Ⅰ不可行、Ⅱ可行C.Ⅰ、Ⅱ都可行D.Ⅰ、Ⅱ都不可行14.【一题多解】(2022贵州黔东南州中考)如图,在边长为2的等边三角形ABC的外侧作正方形ABED,过点D作DF⊥BC交CB的延长线于点F,则DF的长为( )A.2+2B.5-C.3-D.+1二、填空题(每小题4分,共12分)15.(2023北京房山期末)如图,菱形ABCD的对角线AC,BD相交于点O,点E为BC的中点,连接OE,若OE=,OA=4,则AB= ,菱形ABCD的面积是.16.【河北常考·双填空题】(2023河北石家庄桥西期末)在同一直线上,甲骑自行车,乙步行,分别由A,B两地同时向右匀速出发,当甲追上乙时,两人同时停止.下图是两人之间的距离y(km)与所经过的时间t(h)之间的函数关系图像,观察图像,出发后h甲追上乙.若乙的速度为8 km/h,则经过1.5 h甲行驶的路程为.17.(2023河北沧州献县期末)五子棋是一种两人对弈的棋类游戏,规则是:在正方形棋盘中,由黑方先行,白方后行,轮流弈子,下在棋盘横线与竖线的交叉点上,直到某一方首先在任一方向(横向、竖向或者是斜着的方向)上连成五子获胜.如图,这一部分棋盘是两个五子棋爱好者的对弈图.观察棋盘,以点O为原点,在棋盘上建立平面直角坐标系,将每个棋子看成一个点.若黑子A的坐标为(7,5),为了不让白方获胜,此时黑方应该下在坐标为的位置.三、解答题(共66分)18.[含评分细则](2023湖北武汉期中)(12分)已知点P(2a-2,a+5),解答下列各题:(1)若点P在x轴上,求出点P的坐标.(2)若点Q的坐标为(4,5),直线PQ∥y轴,求出点P的坐标.(3)若点P在第二象限,且它到x轴的距离与到y轴的距离相等,求a2 023+2 023的值.19.[含评分细则](2023广东深圳期中)(12分)自行车骑行爱好者小轩为备战中国国际自行车公开赛,积极训练.下图是他最近一次在深圳湾体育公园骑车训练时,离家的距离s(km)与所用时间t(h)之间的函数图像.请根据图像回答下列问题:(1)途中小轩共休息了h.(2)小轩第一次休息后,骑行速度恢复到第1小时的速度,请求出目的地离家的距离a是多少.(3)小轩第二次休息后返回家时,速度和到达目的地前的最快车速相同,则全程最快车速是km/h.(4)已知小轩是早上7点离开家的,请通过计算,求出小轩回到家的时间.20.[含评分细则]【新素材】(2023四川绵阳涪城模拟)(14分)青少年“心理健康”问题引起社会的广泛关注,某区为了解学生的心理健康状况,对中学初二学生进行了一次“心理健康”知识测试,随机抽取了部分学生的成绩作为样本,绘制了不完整的频率分布表和频率分布直方图(频率分布表每组含前一个边界值,不含后一个边界值).学生心理健康测试成绩频率分布表分组频数频率50~60 4 0.0860~70 14 0.2870~80 m 0.3280~90 6 0.1290~100 10 0.20合计 1.00请解答下列问题:(1)学生心理健康测试成绩频率分布表中,m= .(2)请补全学生心理健康测试成绩频数分布直方图.(3)若成绩在60分以下(不含60分)心理健康状况为不良,60分~70分(含60分)为一般,70分~90分(含70分)为良好,90分(含90分)以上为优秀,请补全学生心理健康测试成绩扇形统计图.21.[含评分细则](2023江苏无锡梁溪期末)(14分)某学校新建的初中部即将投入使用,为了改善教室空气环境,该校八年级1班班委会计划到朝阳花卉基地购买绿植,已知该基地一盆绿萝与一盆吊兰的费用之和是16元.班委会决定用80元购买绿萝,用120元购买吊兰,所购绿萝数量正好是吊兰数量的两倍.(1)分别求出每盆绿萝和每盆吊兰的价格.(2)该校八年级所有班级准备一起到该基地购买绿萝和吊兰共计120盆,其中绿萝数量不超过吊兰数量的一半,则八年级购买这两种绿植各多少盆时总费用最少?最少费用是多少元?22.[含评分细则](2023四川达州渠县期末)(14分)如图,在△ABC中,∠BAC=90°,∠B=45°,BC=10,过点A作AD∥BC,且点D在点A的右侧.点P从点A出发沿射线AD以每秒1个单位长度的速度运动,同时点Q从点C出发沿射线CB以每秒2个单位长度的速度运动,在线段QC 上取点E,使得QE=2,连接PE,设点P的运动时间为t秒.(1)若PE⊥BC,求BQ的长.(2)是否存在t值,使以A,B,E,P为顶点的四边形为平行四边形?若存在,求出t的值;若不存在,请说明理由.答案解析1.D 为了解某市七年级8 000名学生的身高情况,从中抽取了60名学生进行身高检查.①这种调查方式是抽样调查,说法正确;②8 000名学生的身高情况是总体,故原说法错误;③每名学生的身高是个体,说法正确;④60名学生身高情况是总体的一个样本,故原说法错误;⑤60是样本容量,故原说法错误.所以正确的判断有2个.故选D.2.A ∵图中点E的坐标为(m,3),其关于y轴对称的点F的坐标为(4,n),∴m=-4,n=3,∴m+n=-4+3=-1,故选A.3.C ∵-1<2,且y1>y2,∴y随x的增大而减小,∴-2m+1<0,解得m>.故选C.4.D 若视力达到4.8以上(含4.8)为达标,则该班学生视力的达标率为×100%=36%.故选D.5.A 正方形的周长y与边长x的关系式为y=4x,故①符合题意;汽车以30千米/时的速度行驶,它的行驶路程y(千米)与时间x(小时)的关系式为y=30x,故②符合题意;水箱以0.8 L/min的流量往外放水,水箱中的剩余水量y(L)与放水时间x(min)的关系式为y=水箱原来的水量-0.8x,故③不符合题意.所以变量y与变量x之间的函数关系可以用题中的图像表示的是①②.故选A.6.D A.体育场到文具店的距离为2.5-1.5=1(km),故A选项正确,不符合题意;B.张强在文具店停留了65-45=20(min),故B选项正确,不符合题意;C.张强从文具店回家的平均速度为 1.5÷(100-65)= km/min,故C选项正确,不符合题意;D.当30≤x≤45时,设y=kx+b(k≠0),则∴当30≤x≤45时,y=-,故D选项错误,符合题意.故选D.7.B 由题意可知,当点P从点B向点C运动时,S=AB·BP,△ABP的面积S与t成正比例函数关系且随时间t的增大而增大;当点P从点C向点D运动时,S=AB·BC,△ABP的面积S不随时间t的变化而变化;当点P从点D向点A运动时,S=AB·AP,△ABP的面积S是t的一次函数且随时间t的增大而减小.所以在点P的运动过程中,△ABP的面积S随时间t变化的函数图像大致是选项B的图像.故选B.8.B ∵四边形ABCD是菱形,AC=6,BD=8,∴OB=AC=3,AC⊥BD.OB是定值,要想的值最小,则OE取最小值.当OE⊥BC时,OE取最小值,由勾股定理可求得BC==5,∵BC·OE=OB·OC,∴OE=,∴.故选B.9.D 设甲对应的函数解析式为y甲=kx(k≠0),∵点(5,100)在该函数图像上,∴5k=100,解得k=20,即甲对应的函数解析式为y甲=20x,即甲种消费卡为20元/次,故选项A不符合题意;设乙对应的函数解析式为y乙=ax+b(a≠0),∵点(0,100),(20,300)在该函数图像上,∴即乙对应的函数解析式为y乙=10x+100,故选项B不符合题意;令20x=10x+100,解得x=10,20×10=200,故点B的坐标为(10,200),故选项C不符合题意;当y=240时,甲种消费卡可消费240÷20=12(次),乙种消费卡可消费的次数为(240-100)÷10=14,因为12<14,所以洋洋爸爸准备240元钱用于洋洋在该游泳馆消费,选择乙种消费卡划算,故选项D符合题意.故选D.10.C 如图,当BC=AB时,以点B为圆心、AB长为半径画圆,与坐标轴分别交于点C1、C2、C3、A.当AC=AB时,以点A为圆心、AB长为半径画圆,与坐标轴分别交于点C4、C5、C6、B.当AC=BC时,点C应该在AB的垂直平分线上,∵OA=OB,∴点O在AB的垂直平分线上.综上,这样的C点共有7个,分别是点C1、C2、C3、C4、C5、C6、O.故选C.11.A ∵四边形ABCD是矩形,∴AD∥BC,∠ABC=90°,∴∠ABE=90°,∵DF∥AE,AD∥EF,∴四边形ADFE是平行四边形,由作图得AE=AD=5,∴四边形ADFE是菱形,∴FE=AE=5,∵BE==3,∴BF=FE-BE=5-3=2,∴AF=.12.C A.1~4月该商场的销售总额为85+80+60+65=290万元,故A不符合题意;B.2月份A商品的销售额为80×15%=12万元,故B不符合题意;C.1~4月A商品的销售额占当月销售总额的百分比最低的月份是2月,故C符合题意;D.2~4月A商品的销售额占当月销售总额的百分比与1月份相比都下降了,故D不符合题意. 故选C.12.C 本题列举两种方案,从中选取可行方案,考查形式比较新颖.方案Ⅰ,如图,连接AC,∵l1,l2,l3,l4分别垂直平分AB,BC,CD,AD,∴E,F,G,H分别是AB,BC,CD,AD的中点,∴EF是△ABC的中位线,GH是△ADC的中位线,∴EF∥AC,EF=AC,GH∥AC,GH=AC,∴EF∥GH,且EF=GH,∴四边形EFGH是平行四边形,∴方案Ⅰ可行.方案Ⅱ,∵EF∥AC,GH∥AC,∴EF∥GH,∵EH∥BD,FG∥BD,∴EH∥FG,∴四边形EFGH是平行四边形,方案Ⅱ可行.故选C.14.D 解法一:如图1,延长DA,BC交于点G,∵四边形ABED是正方形,∴∠BAD=90°,AD=AB,∴∠BAG=180°-90°=90°.∵△ABC是边长为2的等边三角形,∴AB=AC=2,∠ABC=∠BAC=60°,∴∠CAG=∠BAG-∠BAC=30°,∠G=90°-∠ABC=30°,∴∠CAG=∠G,∴AC=CG=2,∴BG=BC+CG=4,∴AG=,∴DG=AD+AG=2+2.在△DFG中,DF⊥BC,∠G=30°,∴DF=×(2+2.故选D.解法二:如图2,过点E作EG⊥DF于点G,作EH⊥BC交CB的延长线于点H,则∠BHE=∠DGE=90°.∵△ABC是边长为2的等边三角形,∴AB=2,∠ABC=60°.∵四边形ABED是正方形,∴BE=DE=AB=2,∠ABE=∠BED=90°,∴∠EBH=180°-∠ABC-∠ABE=180°-60°-90°=30°,∴EH=×2=1,∴BH=.∵EG⊥DF,EH⊥BC,DF⊥BC,∴∠EGF=∠EHB=∠DFH=90°,∴四边形EGFH是矩形,∴FG=EH=1,∠BEH+∠BEG=∠GEH=90°.∵∠DEG+∠BEG=90°,∴∠BEH=∠DEG.在△BEH和△DEG中,∴△BEH≌△DEG(AAS),∴DG=BH=,∴DF=DG+FG=+1.故选D.15.2;16解析∵菱形ABCD的对角线AC与BD相交于点O,∴DO⊥CO,AC=2OA=2OC=8,∵E是BC的中点,∴OE是△CAB的中位线,∴AB=2OE=2,∴OB==2,∴BD=2OB=4,∴菱形ABCD的面积=×8×4=16.16.2;30km解析由图像可知,出发后2 h甲追上乙,A,B两地相距24 km,设甲的速度为x km/h,根据题意得2x=8×2+24,解得x=20,20×1.5=30(km).经过1.5 h甲行驶的路程为30 km.17.(3,7)或(7,3)18.解析(1)∵点P在x轴上,∴a+5=0,∴a=-5,∴2a-2=-12,∴点P的坐标为(-12,0).4分(2)∵点Q的坐标为(4,5),直线PQ∥y轴,∴2a-2=4,∴a=3,∴a+5=8,∴P(4,8).8分(3)∵点P在第二象限,且它到x轴的距离与到y轴的距离相等,∴2a-2=-(a+5),∴a=-1,此时P(-4,4)在第二象限,符合题意,∴a2 023+2 023=(-1)2 023+2 023=2 022,∴a2 023+2 023的值为2 022.12分19.解析(1)途中小轩共休息了2-1.5+4-3=1.5(h).故答案为1.5.3分(2)25+15×(3-2)=40(km).∴a=40.6分(3)全程最快车速是(25-15)÷(1.5-1)=20(km/h).故答案为20.9分(4)4+40÷20=6(h),7+6=13,∴小轩回到家的时间是13点.12分20.解析(1)由表格可得,抽取的学生数为4÷0.08=50,∴m=50×0.32=16.故答案为16.4分(2)补全的学生心理健康测试成绩频数分布直方图如图1所示.8分(3)良好率:(0.32+0.12)×100%=44%,9分优秀率:0.2×100%=20%,10分补全的学生心理健康测试成绩扇形统计图如图2所示.14分21.解析(1)设每盆绿萝x元,则每盆吊兰(16-x)元.根据题意得=2×,解得x=4.4分经检验,x=4是方程的解且符合题意.∴16-x=12.答:每盆绿萝4元,每盆吊兰12元.6分(2)设购买吊兰a盆,总费用为y元.依题意得,购买绿萝(120-a)盆,则y=12a+4(120-a)=8a+480.9分∵绿萝数量不超过吊兰数量的一半,∴120-a≤a,解得a≥80.10分对于y=8a+480,y随a的增大而增大,∴当a=80时,y取得最小值,最小值为8×80+480=1 120,12分此时120-a=40.答:购买吊兰80盆,绿萝40盆时,总费用最少,为1 120元.14分22.解析(1)如图,过A点作AM⊥BC于点M,设AC交PE于点N.∵∠BAC=90°,∠B=45°,∴∠C=45°=∠B,∴AB=AC,∴BM=CM,∴AM=BC=5,2分∵AD∥BC,∴∠PAN=∠C=45°,∵PE⊥BC,∴PE=AM=5,PE⊥AD,∴△APN和△CEN是等腰直角三角形,4分∴PN=AP=t,∴CE=NE=PE-PN=5-t,∵CE=CQ-QE=2t-2,∴5-t=2t-2,6分解得t=,∴BQ=BC-CQ=10-2×.7分(2)存在.8分若以A,B,E,P为顶点的四边形为平行四边形,则AP=BE,分两种情况:①当点E在点B的右侧时,有解得t=4.②当点E在点B的左侧时,有解得t=12.∴存在t值,使以A,B,E,P为顶点的四边形为平行四边形,此时t的值为4或12.14分。
《薪酬管理》期末复习题及参考答案

薪酬管理复习题第一章薪酬管理概述一、单项选择题(A)1.工资理论史上的第一个里程碑是A.生存工资理论B.工资基金理论C.工资差别理论D.均衡价格工资理论(A)2.工资基金理论的代表人物是A.约翰·穆勒B.亚当·斯密C.大卫·李嘉图D.约翰·贝茨·克拉克(C)3.阐释了岗位工资制度的理论依据是A.生存工资理论B.工资基金理论C.工资差别理论D.均衡价格工资理论(A)4.洛夫等经济学家发展并完善了A.效率工资理论B.制度学派工资理论C.知识资本理论D.生存工资理论(A)5.整体薪酬构成中,属于保障薪酬的是A.基本工资B.奖金C.福利D.津贴二、多项选择题(ABCDE)1.基本薪酬的特点包括A.常规性B.结构性C.等级性D.固定性E.基准性(ABCD)2.整体薪酬的理念包括A.整体理念B.客户理念C.业绩理念D.个体化理论E.效益理念(ABCDE)3.整体薪酬的构成包括A.保障薪酬B.激励薪酬C.薪酬的替代品D.薪酬的补充E.薪酬的柔性部分(BCD)4.薪酬管理的目标包括A.透明性B.有效性C.合法性D.公平性E.激励性三填空题1.报酬是指员工从企业那里得到的作为个人贡献回报的他认为有的各种东西,一般分为内在报酬和外在报酬。
1.价值2.从薪酬支付的主客体而言,薪酬支付的客体是。
2.雇员3.19世纪后期,美国经济学家约翰·贝茨·克拉克(John Bates Clark)在其著作《》中提出了边际生产力分配论。
3.财富的分配4.洛夫等经济学家发展并完善了。
4.效率工资理论5.制度学派则是从的角度研究影响工资水平的因素。
5.现实四名词解释1.薪酬:是报酬体系的一部分,是指员工从企业那里得到的各种直接和间接的经济收入,相当于经济报酬部分。
2.基本薪酬:基本薪酬又称基本工资,是指一个组织根据员工所承担或完成的工作本身或者是员工具备的完成工作的技能或能力向员工支付的稳定性报酬。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
36. 一个图中包含k个连通分量,若按深度优先 搜索方法访问所有节点,则必须调用_____次深 度优先遍历算法 A. k B. 1 C. k-1 D. k+1
37. 对于有18个元素的有序表R[1...18]进行二分 查找,则查找R[3]的比较序列的下标为 A. 1、2、3 B. 9、5、2、3 C. 9、5、3 D. 9、4、2、3
17. 广义表((),a,(a),((a)))的长度是_______,深度 是_________
18. 具有n个节点的二叉树采用二叉链存储结构, 共有_______个空指针域
19.在有n个顶点的有向图中,每个顶点的度最 大可达_______
20. 设n是偶数,试计算运行下列程序段后m的 值并给出该程序段的时间复杂度 int m =0,i,j for(i=1;i<=n;i++) for(j=2*i;j<=n;j++) m++;
38. 在下列排序算法中,_____可能出现下列情 况:在最后一趟开始之前,所有的元素都不一 定在其最终的位置上 A. 堆排序 B. 冒泡排序 C. 直接插入排序 D. 快速排序
39. 若一棵哈夫曼树的叶子节点个数为5,则该 树的总节点个数为多少?
40. 对给定的数列R={7,16,4,8,20,9,6,18,5},构造 一棵二叉排序树,求: (1)给出按中序遍历得到的数列R1 (2)给出按后序遍历得到的数列R2
54. 将整数序列{30,15,21,40,25,26,36,37}中的数 依次插入到一棵空的二叉排序树中,试构造相 应的二叉排序树,给出构造过程
55. 以数据集合{2,5,7,9,13}为权值构造一棵哈夫 曼树,并计算其带权路径长度
56. 设A、B、C、D、E这5个字母出现的频率分 别为2,5,7,9,13,要求根据这5个字母设计 Huffman编码,并画出对应的Huffman树
45. 对由n(n>=2)个权值均不同的字符构成的哈 夫曼树,关于该树的叙述中,错误的是_______ A. 该树一定是一棵完全二叉树 B. 该树中一定没有度为1的节点 C. 树中两个权值最小的节点一定是兄弟节点 D. 树中任一非叶子节点的权值一定不小于下一层 任一节点的权值
46. 已知一个长度为16的顺序表,其元素按关键 字有序排序,若采用折半查找法查找一个不存 在的元素,则比较的次数最多是 A. 4 B. 5 C. 6 D. 7
12. 以关键字序列 {265,301,751,129,937,863,742,694,76,438}为例, 给出归并排序算法的各趟排序结束时关键字序 列的状态
13. 链表不具备的特点是 A. 可随机访问任一节点 B. 插入删除不需要移动元素 C. 不必事先估计存储空间 D. 所需空间与其长度成正比
34.在以下排序算法中,_______不能保证每趟 排序至少能将一个元素放到其最终位置上 A. 快速排序 B. 希尔排序 C. 堆排序 D. 冒泡排序
35. 一个n*n的对称矩阵,如果采用压缩存储放 入内存,则容量为 A. n2 B. n2/2 C. n(n+1)/2 D. (n+1)2/2
25. 顺序队和链队的区别仅在于________不同
26. 一棵完全二叉树上有1001个节点,其中叶子 节点的个数是多少?
27. 下列说法中,不正确的是 A. 数据元素是数据的基本单位 B. 数据项是数据中不可分割的最小可标识单位 C. 数据可由若干个数据元素构成 D. 数据项可由若干个数据元素构成
48. 为实现快速排序法,待排序序列宜采用存储 方式是 A. 顺序存储 B. 散列存储 C. 链式存储 D. 索引存储
49. 将一棵有80个节点的完全二叉树按层编号, 根节点的编号为1,则对编号为40的结点x,该 节点 A. 无左、右孩子 B. 有左孩子,无右孩子 C. 有右孩子,无左孩子 D. 有左、右孩子
50. 一个10阶对称矩阵A,采用行优先顺序压缩 存储上三角元素,a00为第一个元素,其存储地 址为0,每个元素占有1个存储地址空间,则a45 的地址为________
一个10阶对称矩阵A,采用行优先顺序压缩存 储下三角元素,a00为第一个元素,其存储地址 为0,每个元素占有1个存储地址空间,则a45的 地址为________
30. 有一种排序方法,它每趟都从未排序序列中 挑选出最小元素,并将其放入已排序序列的一 端,该排序方法是_______ A. 希尔排序 B. 归并排序 C. 直接插入排序 D. 简单选择排序
31. 设高度为h(根节点为第1层)的二叉树上只有 度为0和度为2的节点,则此类二叉树中所包含 的节点数至少为 A. 2h B. 2h-1 C. 2h+1 D. h+1
7. 在一组记录的关键字为{46,79,56,38,40,84}, 利用快速排序的方法,以第1个记录为基准得到 的第一次划分结果为_________
8. 设n为3的倍数,分析以下算法的时间复杂度 void fun(int n) { int i, j, x, y; for(i=1; i<=n; i++) if(3*i<=n) for(j=3*i;j<=n;j++) { x++; y = 3*x+2; } }
51. 假定一棵二叉树的节点数为22,则它的最小 深度为_____,最大深度为_______
52. 构造n个节点的强连通图,至少有_____条弧 A. n B. n/2 C. n+1 D. n-1
53. 在一个具有n个顶点的无向图中,要连通全 部顶点至少需要_______条边 A. n B. n+1 C. n-1 D. n/2
47. 将关键字序列{7,8,30,11,18,9,14}散列存储到 散列表中,散列表的存储空间是一个下标从0开 始的一维数组,散列函数为 H(key)=(key*3)mod7,处理冲突采用线性探测 散列法,要求装填因子为0.7 (1)请画出所构造的散列表 (2) 分别计算等概率情况下,查找成功和查找 不成功的平均查找长度
41. 在一棵度为3的树中,度为3的节点个数为2, 度为2的节点个数为1,则度为0的节点个数为 ________ A. 4 B. 5 C. 6 D. 7
42. 某二叉树的先序遍历序列和后序遍历序列正 好相反,则该二叉树一定是_______ A. 空或只有一个节点 B. 完全二叉树 C. 二叉排序树 D. 高度等于其节点数
期末复习习题集
1. 数据结构在计算机内存中的表示指 A. 数据的存储结构 B. 数据结构 C. 数据的逻辑结构 D. 数据元素之间的关系
2. 串是________ A. 不少于一个字母的序列 B. 任意个字母的序列 C. 不少于一个字符的序列 D. 有限个字符的序列
3. 在n个节点的线索二叉树中,线索的数目为 A. n-1 B. n C. n+1 D. 2n
14. 一个栈的进栈序列是abcde,则栈的不可能 的输出序列是 A. edcba B. decba C. dceab D. abcde
15. 用直接插入序列对下面4个序列进行递增排 序,元素比较次数最少的是 A. 94,32,40,90,80,46,21,69 B. 32,40,21,46,69,94,90,80 C. 21,32,46,40,80,69,90,94 D. 90,69,80,46,21,32,94,40
28. 广义表((a,b,c,d))的表头是______,表尾是 _____ A. a B. ( ) C. (a,b,c,d) D. ((a,b,c,d))
29. 在对n个元素进行冒泡排序的过程中,最好 情况下的时间复杂度为 A. O(1) B. O(log2n) C. O(n2) D. O(n)
32. 无向图的邻接矩阵是一个____ A. 对称矩阵 B. 零矩阵 C. 上三角矩阵 D. 对角矩阵
33. 对线性表进行二分查找时,要求线性表必须 _______ A. 以顺序方式存储 B. 以链式方式存储 C. 以顺序方式存储且节点按关键字有序排序 D. 以链表方式存储且节点按关键字有序排序
21. 下述函数中对应的时间复杂度最小是 A. T1(n) = nlog2n+5000n B. T2(n) = n2-8000n C. T3(n) = nlog2 n 6000n D. T4(n) = 1000log2n
22. 以下各种存储结构中,最适合用做链队的链 表是 A. 带队首指针和队尾指针的循环单链表 B. 带队首指针和队尾指针的非循环单链表 C. 只带队首指针的非循环单链表 D. 只带队首指针的循环单链表
43. 有一个长度为12的有序表R[0...11],按二分 查找法对该表进行查找,在表内各元素等概率 情况下查找成功和查找失败所需的平均比较次 数是多少?
44. 已知一棵完全二叉树的第6层(设根为第一层) 有8个叶子节点,则该完全二叉树的节点个数最 多是________ A. 39 B. 52 C. 111 D. 119
4. 顺序队列在实现的时候,通常将数组看成是 一个首尾相连的环,这样做的目的是为了避免 产生______现象
5. 设有两个串p和q,其中q是p的子串,求q在p 中首次出现的位置的算法称为________
6. 对二叉排序树进行_______遍历,可以得到按 关键字从小到大排列的节点序列
23. 设二维数组A[6][10],每个数组元素占用4个 存储单元,若按行优先顺序存放的数组元素 a[3][5]的存储地址为1000,则a[0][0]的存储地址 是____ A. 872 B. 860 C. 868 D. 864
