常微分方程的Euler解法
第五章:常微分方程数值解法第一节欧拉法

常微分方程数值解法欧拉法

)
f ( xn1, yn1)
hL
y(k ) n 1
yn1
L
hL
k 1
y(0) n 1
yn1
Q
hL 1,
y (k 1) n 1
yn1 (k
)
在迭代公式中取极限,有
yn1 yn h f ( xn1, yn1 ) 因此yn(k1)的极限就是隐式方程的解
几何意义
y
设已知曲线上一点 Pn (xn , yn ),过该 点作弦线,斜率为(xn+1 , yn +1 ) 点的 方向场f(x,y)方向,若步长h充分小, 可用弦线和垂线x=xn+1的交点近似 曲线与垂线的交点。
式。隐式公式不能直接求解,一般需要用Euler显式公式
得到初值,然后用Euler隐式公式迭代求解。因此隐式公
式较显式公式计算复杂,但稳定性好
y0 n1
yn
h
y(k 1) n1
yn
h
f (xn , yn )
f
( xn1 ,
y(k) n1
)
收敛性
y (k 1) n 1
yn1
h
f
( xn1,
y(k ) n 1
如何求解
解析解法:(常微分方程理论)
只能求解极少一类常微分方程;实际中给定的问题不一 定是解析表达式,而是函数表,无法用解析解法。
数值解法: 求解所有的常微分方程
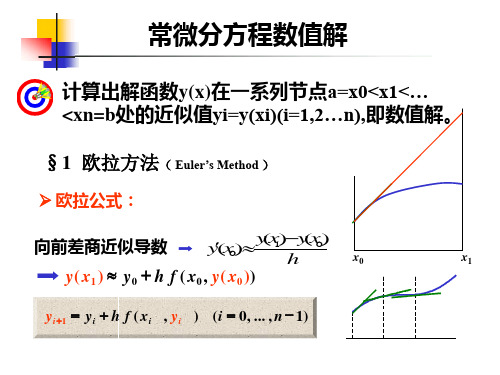
计算解函数 y(x) 在一系列节点 a = x0< x1<…< xn= b
处的近似值 yi y( xi ) (i 1, ... , n)
y(xn1) y(xn ) hy(xn ) y(xn ) yn
y(xn1) yn1 yn h f (xn , yn )
Euler法与修正的Euler法局部截断误差Range-Kutta公式

Comparison with exact results
Temperature, θ(K)
1500
1000
500
0 0
-500
-1000
-1500
Exact solution
h=120 h=240
100
200
300
400
500
Tim e, t (sec)
h=480
Figure 4. Comparison of Euler’s method with exact solution for different step sizes 5
考虑形如
k
ynk ynk 1 h i fni i0
的 k步法,称为阿当姆斯(Adams)方法. k为显0式方法, 为隐k 式0方法,通常称为阿
当姆斯显式与隐式公式,也称Adams-Bashforth公式与Adam -Monlton公式.
22
阿当姆斯显式公式
kp
公式
c p1
1 1 yn1 yn h fn
y( xn ) f ( xn , yn )
y( xn )
d dx
f
( xn ,
yn )
0.5h[f(xn,yn)+f(xn+1, yn+hf(xn, yn))]
=hy’(xn)+0.5h2y”(xn)+0.5h2y'(xn) [fy’]n+
O局 故(h部修y3n)截正+1断 的= 误Eyun差l+er:h法yy(’具xddyn(x有y+(x1x)20n–))阶+fy精0n(+.xy15度0,=hy。2y)y(,”xxn)(–xnxy)n0+=OO((hh33))
euler方法求解常微分方程matlab

euler方法求解常微分方程matlab以euler方法求解常微分方程matlab常微分方程是数学中的重要分支之一,它描述了自然界和工程中的许多现象和过程。
求解常微分方程的方法有很多,其中一种常用的方法是欧拉方法。
欧拉方法是一种数值解常微分方程的方法,它通过将微分方程转化为差分方程,从而得到近似解。
在matlab中,我们可以使用欧拉方法来求解常微分方程。
下面我们将以一个具体的例子来说明如何使用matlab来求解常微分方程。
假设我们要求解的常微分方程是一阶线性常微分方程:dy/dx = f(x, y)其中f(x, y)是已知的函数。
我们需要给定一个初始条件y(x0) = y0,其中x0和y0是已知的常数。
我们需要定义函数f(x, y)。
在matlab中,我们可以使用匿名函数来定义函数。
例如,如果我们要求解的常微分方程是dy/dx = x^2 + y,那么我们可以定义函数f(x, y)如下:f = @(x, y) x^2 + y接下来,我们需要定义初始条件x0和y0。
假设x0 = 0,y0 = 1,我们可以定义初始条件如下:x0 = 0;y0 = 1;然后,我们需要定义步长h,即每一步的增量。
步长h越小,求解的结果越精确,但计算量也会增加。
在matlab中,我们可以使用input函数来让用户输入步长h。
例如,我们可以这样定义步长h:h = input('请输入步长h:');接下来,我们需要定义求解的区间。
假设我们要求解的区间是0到1,我们可以定义区间如下:a = 0;b = 1;然后,我们需要计算步数n。
步数n可以通过区间长度除以步长h 来得到。
在matlab中,我们可以使用ceil函数来向上取整。
例如,我们可以这样计算步数n:n = ceil((b - a) / h);接下来,我们需要定义一个数组x和一个数组y,用来存储每一步的计算结果。
我们可以使用zeros函数来创建这两个数组,并将初始条件存储在数组中。
解常微分方程初值问题的euler方法的并行计算方法

解常微分方程初值问题的euler方法的并行计算方法
euler数值解常微分方程(ODE)初值问题的并行计算技术是一种在不同进程之间有效分享计算资源的方法,可以帮助快速解决ODES初值问题。
随着计算机硬件和软件的快速发展,为了满足新兴应用,并行计算技术被广泛应用于各个领域,其中也包括ODE。
euler数值解常微分方程初值问题的并行计算方法是通过将计算任务分解为一系列的小任务,然后分配给多个处理器进行求解以节省计算时间,改善计算效率。
该技术能够在大规模系统内构建强大的计算能力,能够快速有效地解决ODEs初值问题,而不需要耗费太多的计算资源。
针对ODEs初值问题,常用的并行计算技术主要有基于迭代的分布式计算和基于消息传递的分布式计算。
基于迭代的分布式计算可以有效利用多处理器,通过连续地迭代求解ODEs,从而克服时间步骤的限制,增加求解的效率。
基于消息传递的分布式计算则将原始Ode分割为数个子问题,并通过网络技术在远程计算机上进行计算,从而减少求解时间步骤,改进求解效率。
总之,euler数值解常微分方程初值问题的并行计算方法,在不同进程之间有效分享计算资源的方法,可以有效地改进ODEs求解效率,减少求解时间,为实际应用提供有效的计算方案。
解常微分方程初值问题的隐式euler方法及并行计算方法

解常微分方程初值问题的隐式euler方法及并行计算方法在现代科学技术发展的今天,为了更加有效地求解复杂的微分方程,隐式Euler方法和并行计算技术都受到了极大的关注。
在本文中,我们将探讨解微分方程初值问题的隐式Euler方法及其并行计算方法。
一、隐式Euler方法
隐式Euler方法是一种数值分析技术,用于求解一类特殊的常微分方程的解。
它的主要思路是利用Euler公式,将微分方程离散化,然后将这个微分方程用某种数值近似方法求解。
在隐式Euler方法中,当我们知道离散生成的差分方程组的当前时刻的状态值时,利用Euler公式可以求出其下一个时刻的状态值。
隐式Euler方法的主要优点在于其具有稳定性,即当生成有限差分方程组后,使用Euler公式求解可以使产生的误差更小,从而更有效地求解问题。
二、并行计算方法
随着计算机的发展,越来越多的计算机资源可以用于解决复杂的模型问题,其中最重要的就是并行计算技术。
并行计算是一种在多台计算机上同时运行的技术,其目的是将一个大的计算任务分解成多个小的计算任务,由不同的计算机同时处理。
实现并行计算的关键是合理、有序地分解任务,使得多台计算机能够更有效地实现任务。
并行计算技术和隐式Euler方法有着很好的结合,可以从计算任务的平衡性和分解粒度等方面充分发挥优势,提高隐式euler方法求
解微分方程的效率。
三、结论
本文介绍了隐式Euler方法和并行计算技术可以更有效地解决微分方程初值问题。
隐式Euler方法具有稳定性,而并行计算技术可以实现任务分解,提高求解效率。
因此,将这两种技术结合,可以大大提高复杂微分方程的求解效率。
MATLAB Euler法解常微分方程

Euler 法解常微分方程Euler 法解常微分方程算法:Step 1 分别取积分上限、积分下限、步长Step 2计算h n n +=判断b n ≤是否成立,成立转到Step 3,否则继续进行Step 4 Step 3 计算),(1n n n n y x hf y y +=+Step 4 ),(1n n n n y x hf y y +=+Euler 法解常微分方程算程序:function euler2(fun,y0,A,h)%fun--y'%y0---初值%A----x 取值范围%a----x 左区间端点值%b----x 右区间端点值%h----给定步长x=min(A);b=max(A);y=y0;while x<b-hb=y;y=y+h*feval(fun,x,b)x=x+h;end例:用Euler 法计算下列初值问题(取步长h=0.2))6.00(1)0('2≤≤⎩⎨⎧=--=x y xy y y输入:fun=inline('-y-x*y^2')euler2(fun,1,[0 0.6],0.2)得到:y =0.8000y =0.6144y =0.4613指导教师: 年 月 日改进Euelr 法解常微分方程改进Euler 法解常微分方程算法:Step 1 分别取积分上限、积分下限、步长Step 2 取一个以h 为步长,a ,b 分别为左右端点的矩阵Step 3 (1)做显性Euler 预测),(1n n i i y x hf y y +=+(2)将1+i y 带入)],(),([2h 111+++++=i i i i i i y x f y x f y y Step 4计算h n n +=判断b n ≤是否成立,成立返回Step 3,否则继续进行Step 5 Step 5 )],(),([2h 111+++++=i i i i i i y x f y x f y y 改进Euler 法解常微分方程算程序:function gaijineuler2(fun,y0,A,h)%fun--y'%y0---初值%A----x 取值范围%a----x 左区间端点值%b----x 右区间端点值%h----给定步长a=min(A);b=max(A);x=a:h:b;y(1)=y0;for i=1:length(x)-1w1=feval(fun,x(i),y(i));y(i+1)=y(i)+h*w1;w2=feval(fun,x(i+1),y(i+1));y(i+1)=y(i)+h*(w1+w2)/2;endx=x'y=y'例:用改进Euler 法计算下列初值问题(取步长h=0.25) )50(2)0('2≤≤⎩⎨⎧=-=x y xy y 输入:fun=inline('-x*y^2')gaijineuler2(fun,2,[0 5],0.25)得到:x =0.25000.50000.75001.00001.25001.50001.75002.00002.25002.50002.75003.00003.25003.50003.75004.00004.25004.50004.75005.0000y =2.00001.87501.59391.28241.00960.79320.62820.50370.40970.33790.28240.23890.20430.17650.15380.13520.11960.10660.09550.08610.0779指导教师:年月日。
欧拉方程微分方程详解

欧拉方程微分方程详解欧拉方程(Euler's equation)是一类具有特殊形式的二阶常系数线性微分方程。
它的一般形式为:ax^2 y'' + bxy' + cy = 0其中,a、b、c都是常数,且a不等于0。
欧拉方程是一种特殊的微分方程,它的解具有一定的特殊性。
下面我们将对欧拉方程的求解方法进行详细介绍。
首先,我们考虑求解形如x^m的解。
将x^m代入欧拉方程中,得到:a(m)(m-1)x^m + bm*x^m + cx^m = 0化简后得到:am(m-1)x^m + bmx^m + cx^m = 0整理得:am(m-1) + bm + c = 0这是一个关于m的二次方程,可以用求根公式来求解m的值。
当求解得到m的值时,我们就得到了一个形如x^m的解。
接下来,我们考虑求解形如x^m * ln(x)的解。
将x^m * ln(x)代入欧拉方程中,得到:a(m)(m-1)x^m * ln(x) + bmx^m * ln(x) + cx^m * ln(x) = 0将x^m分离出来,得到:x^m * [a(m)(m-1)ln(x) + bm ln(x) + c] = 0由于x不等于0,所以要使上式成立,必须有:a(m)(m-1)ln(x) + bm ln(x) + c = 0这是一个关于m的一次方程,可以用求解一次方程的方法来求解m的值。
当求解得到m的值时,我们就得到了一个形如x^m * ln(x)的解。
最后,我们考虑求解形如x^m * ln^2(x)的解。
将x^m * ln^2(x)代入欧拉方程中,得到:a(m)(m-1)x^m * ln^2(x) + bmx^m * ln^2(x) + cx^m * ln^2(x) = 0将x^m分离出来,得到:x^m * [a(m)(m-1)ln^2(x) + bm ln^2(x) + c] = 0由于x不等于0,所以要使上式成立,必须有:a(m)(m-1)ln^2(x) + bm ln^2(x) + c = 0这是一个关于m的二次方程,可以用求解二次方程的方法来求解m的值。
常微分方程数值解实验报告

常微分方程数值解实验报告学院:数学与信息科学专业:信息与计算科学:思义学号:201216524 课程:常微分方程数值解实验一:常微分方程的数值解法1、分别用Euler 法、改进的Euler 法(预报校正格式)和S —K 法求解初值问题。
(h=0.1)并与真解作比较。
⎩⎨⎧=++-=10(1y')y x y 1.1实验代码:%欧拉法function [x,y]=naeuler(dyfun,xspan,y0,h)%dyfun 是常微分方程,xspan 是x 的取值围,y0是初值,h 是步长 x=xspan(1):h:xspan(2); y(1)=y0; for n=1:length(x)-1y(n+1)=y(n)+h*feval(dyfun,x(n),y(n)); end%改进的欧拉法function [x,m,y]=naeuler2(dyfun,xspan,y0,h)%dyfun 是常微分方程,xspan 是x 的取值围,y0是初值,h 是步长。
%返回值x 为x 取值,m 为预报解,y 为校正解 x=xspan(1):h:xspan(2); y(1)=y0;m=zeros(length(x)-1,1); for n=1:length(x)-1 k1=feval(dyfun,x(n),y(n)); y(n+1)=y(n)+h*k1; m(n)=y(n+1);k2=feval(dyfun,x(n+1),y(n+1));y(n+1)=y(n)+h*(k1+k2)/2;end%四阶S—K法function [x,y]=rk(dyfun,xspan,y0,h)%dyfun是常微分方程,xspan是x的取值围,y0是初值,h是步长。
x=xspan(1):h:xspan(2);y(1)=y0;for n=1:length(x)-1k1=feval(dyfun,x(n),y(n));k2=feval(dyfun,x(n)+h/2,y(n)+(h*k1)/2);k3=feval(dyfun,x(n)+h/2,y(n)+(h*k2)/2);k4=feval(dyfun,x(n)+h,y(n)+h*k3);y(n+1)=y(n)+(h/6)*(k1+2*k2+2*k3+k4);end%主程序x=[0:0.1:1];y=exp(-x)+x;dyfun=inline('-y+x+1');[x1,y1]=naeuler(dyfun,[0,1],1,0.1);[x2,m,y2]=naeuler2(dyfun,[0,1],1,0.1);[x3,y3]=rk(dyfun,[0,1],1,0.1);plot(x,y,'r',x1,y1,'+',x2,y2,'*',x3,y3,'o');xlabel('x');ylabel('y');legend('y为真解','y1为欧拉解','y2为改进欧拉解','y3为S—K解','Location','NorthWest');1.2实验结果:x 真解y 欧拉解y1 预报值m 校正值y2 S—K解y30.0 1.0000 1.0000 1.0000 1.00000.1 1.0048 1.0000 1.0000 1.0050 1.00480.2 1.0187 1.0100 1.0145 1.0190 1.01870.3 1.0408 1.0290 1.0371 1.0412 1.04080.4 1.0703 1.0561 1.0671 1.0708 1.07030.5 1.1065 1.0905 1.1037 1.1071 1.10650.6 1.1488 1.1314 1.1464 1.1494 1.14880.7 1.1966 1.1783 1.1945 1.1972 1.19660.8 1.2493 1.2305 1.2475 1.2500 1.24930.9 1.3066 1.2874 1.3050 1.3072 1.30661.0 1.3679 1.3487 1.3665 1.3685 1.36792、选取一种理论上收敛但是不稳定的算法对问题1进行计算,并与真解作比较。
欧拉公式求解常微分方程数值解培训教材
例:用欧拉法解初值问题
y=yxy2(0x0.6)
y(0)=1
取步长 h = 0.2.计算过程保留4位小数.
解:f(x,y)=-y-xy2 , h = 0.2,由欧拉公式得
yk+ 1=yk+h(fxk,yk)=ykhky hkx yk 2 =0.2yk(4xkyk)k(=0,1,2)
故y(0.2)y1=0.2×1(4-0×1)=0.800 0 y(0.4)y2=0.2×0.8×(4-0.2×0.8)=0.614 4 y(0.6)y3=0.2×0.614 4×(4-0.4×0.4613)=0.800 0
Step 2: 将 K2 代入第1式,得到 y i+ 1 = y i+ h1 y ( x i) + 2 [ y ( x i) + p y ( h x i) + O ( h 2 )] = y i+ (1 + 2 ) h y ( x i) + 2 p 2 y h ( x i) + O ( h 3 )
f y ( x, f y ( x,
y) y)
dy dx f (x,
y)
K 2= f(x i+ p,y h i+ p1 h ) K = f(x i,y i)+ px h (x i,y fi)+ p1 h fy (x K i,y i)+ O (h 2 ) = y (x i)+ py h (x i)+ O (h 2 )
例1:用预报-校正公式求解初值问题
y
+y+
y
sinx=
y() =
取步长 h = 0.2,计算 y(1.2), y(1.4)的近似值,计算过程保
euler方法求解常微分方程

euler方法求解常微分方程
欧拉方法是一种简单而又广泛使用的数值方法,用于解决常微分方程(ODEs)。
它基于将微分方程的导数近似为有限差分,从而得到方程的近似解。
以下是欧拉方法的步骤:
1. 设定初始条件,例如 y(0) = y0。
2. 将时间轴离散化,选择固定的时间间隔 h,即每隔 h 时间计
算一次解。
3. 根据微分方程和初始条件,使用欧拉公式迭代计算 y(i+1),
其中 i 表示当前时间步数。
欧拉公式如下所示:
y(i+1) = y(i) + h*f(t(i), y(i))
其中,f(t(i), y(i)) 表示在当前时间(t(i),y(i))处的导数值。
4. 重复步骤 3 直到达到所需的时间点。
需要注意的是,由于欧拉方法做了近似,所以其精度可能不够高。
为了提高精度,可以使用其他更高级别的数值方法,例如龙格-库塔方法(Runge-Kutta methods)。
解常微分方程初值问题的隐式euler方法及并行计算方法

解常微分方程初值问题的隐式euler方法及并行计算方法解常微分方程初值问题(initialvalueproblem,IVP)在微积分数学中使用非常普遍,它能够表示许多物理和社会现象的发展趋势。
但微分方程的数值解法通常很难解决,而计算复杂度高,计算时间也长,另外,自由边界条件也很难处理。
为了解决这个问题,隐式Euler 方法(implicit Euler Method, IEM)被提出,它是一种改进的数值解法,可以有效地计算出IVP的解。
隐式Euler方法的优点在于,它可以解决较为复杂的方程,并且具有一定的收敛速度。
隐式Euler方法通常用于解决常微分方程初值问题,它可以更有效地求解IVP,而不受自由边界条件的影响,因为它可以对方程进行积分。
然而,隐式Euler方法有一个重要的缺点:它计算出的解并不能完全准确,而且其他方法也不能完全替代它。
此外,由于隐式Euler 方法只能给出局部解,所以当IVP计算范围较大时,它的计算效率也会大大降低。
为了提高隐式Euler方法的效率,并行计算方法也可以用来解决IVP问题。
并行计算是指使用多台计算机或多个CPU来处理IVP问题。
并行计算可以显著降低隐式Euler方法的计算时间,因为它可以将IVP问题分解成多个部分,分别由不同CPU来处理,因此可以协同完成IVP的求解。
隐式Euler方法和并行计算方法是两种有效的求解IVP的方法,它们分别具有自己的优点和缺点。
隐式Euler方法可以有效地求解IVP,而并行计算的优势在于它可以大大减少计算时间。
合理使用这
两种方法,能够有效地求解IVP,提高IVP的求解效率。
euler方法的原理

euler方法的原理摘要:1.Euler方法的定义和原理2.Euler方法的应用场景3.Euler方法的优缺点4.提高Euler方法收敛速度的方法5.总结正文:Euler方法是一种求解常微分方程初值问题的数值方法。
它的基本思想是将微分方程中的导数项用差分的形式表示,然后通过迭代公式逐步逼近解。
Euler方法在许多领域都有广泛的应用,如物理、工程、经济学等。
Euler方法的原理如下:对于常微分方程dy/dx = f(x, y),我们可以将其离散化为差分方程dy[n+1]/dx = f(x[n+1], y[n+1])。
在此基础上,Euler方法通过以下迭代公式求解:y[n+1] = y[n] + h * f(x[n+1], y[n])其中,h为步长,x[n+1] = x[n] + h,y[n]为当前近似解。
Euler方法的应用场景主要包括:1.求解具有连续导数的微分方程,例如物理中的运动方程、电磁学方程等。
2.分析动态系统,如力学、生物学中的模型。
3.金融领域,如利率衍生品定价、风险管理等方面的计算。
Euler方法虽然简单易实现,但也存在一定的优缺点:优点:1.概念清晰,容易理解。
2.计算速度较快,适用于大规模计算。
缺点:1.收敛速度较慢,尤其在区间端点附近。
2.对于非线性方程,收敛性不易保证。
为了提高Euler方法的收敛速度,可以采用以下方法:1.减小步长h,使离散方程更接近原方程。
2.使用复合Euler方法,即在迭代过程中用更高阶的数值方法修正Euler方法。
总之,Euler方法作为一种基本的数值方法,在实际应用中具有重要意义。
数学建模之欧拉算法(求解常微分方程)

数学建模之欧拉算法(求解常微分⽅程)⽬录数学建模之求解常微分算法常微分⽅程欧拉算法定义定义:在数学和计算机科学中,欧拉⽅法,命名⾃它的发明者莱昂哈德·欧拉,是⼀种⼀阶数值⽅法,⽤以对给定初值的常微分⽅程(即初值问题)求解。
它是⼀种解决数值常微分⽅程的最基本的⼀类显型⽅法(Explicit method )。
欧拉法是常微分⽅程的数值解法的⼀种,其基本思想是迭代。
其中分为前进的EULER 法、后退的EULER 法、改进的EULER 法。
所谓迭代,就是逐次替代,最后求出所要求的解,并达到⼀定的精度。
误差可以很容易地计算出来。
⾮线性⽅程都是所谓“解不出来”的,即使是d yd x =y 2+x 2。
对于⽤微分⽅程解决实际问题来说,数值解法是⼀个重要的⼿段。
公式推导设微分⽅程为d y d x =f (x n ,y (x n )),a ≤x ≤b y (a )=y 0差商近似导数若⽤向前差商y (x n +1)−y (x n )h 代替y ′(x n )带⼊微分⽅程d y d x =f (x n ,y (x n ))中,可得y (x n +1)−y (x n )h ≈f (x n ,y (x n ))y (x n +1)=y (x n )+hf (x n ,y (x n ))如果⽤y (x n )的近似值y n 代⼊上式右端,所得结果作为y (x n +1)得近似值,记为y n +1,则有y n +1=y n +hf (x n ,y n ),n =0,1,⋯,N −1这样,微分⽅程的近似解可以通过求解下述式⼦来获得y n +1=y n +hf (x n ,y n ),n =0,1,⋯,N −1y 0=y (a )算法缺点欧拉算法简单地取切线地端点作为起点来计算,当步数增多时,误差会因积累⽽越来越⼤。
因此,欧拉算法⼀般不⽤于实际计算。
{{Processing math: 100%。
计算方法 常微分方程初值问题数值解法 Euler公式 龙格 库塔法

第12次 常微分方程初值问题数值解法
内容
1. 常微分方程初值问题解的存在性定理 2. Euler公式 3. 梯形公式 4. 两步Euler公式 5. 欧拉法的局部截断误差 6. 改进型Euler公式 7. 龙格-库塔法 8. 算法实现
常微分方程初值问题 解的存在性定理
欧拉法的局部截断误差
9.2.4. 欧拉法的局部截断误差
衡量求解公式好坏的一个主要标准是求解公式的精 度, 因此引入局部截断误差和阶数的概念。
定义9.1 在yi准确的前提下, 即 yi y(xi)时, 用数值
方法计算yi+1的误差:
R i yi( 1 ) x y i 1
称为该数值方法计算时yi+1的局部截断误差。
通常表示成下列平均化形式
yi1的近似 y p y i hf(x i , y i )
yi1的近似 y c y i hf(x i 1 , y p )
yi1的更好 的近似
y i1
1 2
(y p
yc)
i 0, 1, 2 … , n 1
(9.12)
例9.2 用改进欧拉法解初值问题
y
y
2x y
f( y 1 ) x f,( y 2 ) x L y , 1 y 2 , y 1 ,y 2 R
则方程( 9.1 ) 在a, b上存在唯一的连续可微分的 解的解 y=y(x) 。
推论:如果函数f(x,y)对y的偏导数
f(x, y
y)
在带形
区域 R { a x b ,y - }
内有界。
两步欧拉公式的局部截断误差为:
y(i1 x )yi1O3 ()h
从而两步欧拉公式的阶数是2.推导过程省略。
常微分方程初值问题的数值解法

常微分方程初值问题的数值解法在实际应用中,对于某些微分方程,我们并不能直接给出其解析解,需要通过数值方法来求得其近似解,以便更好地理解和掌握现象的本质。
常微分方程初值问题(IVP)即为一种最常见的微分方程求解问题,其求解方法有多种,本文将对常微分方程初值问题的数值解法进行较为详细的介绍。
一、欧拉法欧拉法是最基本的一种数值解法,它采用泰勒级数展开并截断低阶项,从而获得一个差分方程近似求解。
具体来讲,设 t 为独立变量,y(t) 为函数 y 关于 t 的函数,方程为:$$y'(t) = f(t, y(t)), \qquad y(t_0) = y_0$$其中 f(t,y(t)) 为已知的函数,y(t_0) 为已知的初值。
将函数 y(t) 进行泰勒级数展开:$$y(t+h) = y(t) + hf(t, y(t)) + O(h^2)$$其中 h 表示步长,O(h^2) 表示其他高阶项。
为了使误差较小,一般取步长 h 尽可能小,于是我们可以用欧拉公式表示数值解:$$y_{n+1} = y_n + hf(t_n, y_n), \qquad y_0 = y(t_0)$$欧拉法的优点是容易理解和实现,但是由于截取低阶项且使用的单步法,所以误差较大,精度较低,在具体应用时需要慎重考虑。
二、龙格-库塔法龙格-库塔法(Runge-Kutta method)是一种多步法,比欧拉法更加精确。
龙格-库塔法的主要思想是使用不同的插值多项式来计算近似解,并且将时间步长分解,每次计算需要多次求解。
以下简要介绍二阶和四阶龙格-库塔法。
二阶龙格-库塔法将时间步长 h 分解成两步 h/2,得到近似解表达式:$$\begin{aligned} k_1 &= hf(t_n, y_n)\\ k_2 &= hf(t_n+h/2,y_n+k_1/2)\\ y_{n+1} &= y_n+k_2+O(h^3)\\ \end{aligned}$$四阶龙格-库塔法四阶龙格-库塔法是龙格-库塔法中应用最为广泛的一种方法,其需要计算的中间值较多,但是具有更高的精度。
常微分方程数值解法-欧拉方法(1)

课题报告题目:常微分方程的数值解法-欧拉方法院 (系):理学院专业:数学与信息专业指导教师:***组员:艾佳欢(组长) 邓云娜柏茜钟岩刘磊2015 年 5 月 11 日常微分方程数值解法-欧拉方法摘要:从常微分方程数值解的基本概念入手,了解最基本的数值解法--欧拉方法。
并利用欧拉方法显式隐式的特点探究如何求解微分方程,以及欧拉方法的误差分析及校正。
关键词:数值解,欧拉方法,误差,校正ABSTRACT: From the basic concept of numerical solution of ordinary differential equations, and understand the most basic numerical solution of euler method. And by using euler explicitly implicit characteristics and explore how to solve differential equations and the error analysis and correction of euler method.KEYWORDS :arithmetic solution,Euler's method,error,revise1.初值问题数值解基本概念初值问题的数值解法,是通过微分方程离散化而给出解在某些节点上的近似值。
在[]b a ,上引入节点{}),,1(,:1100n k x x h b x x x a x k k k n nk k =-==<<<=-=称为步长。
在多数情况下,采用等步长,即),1,0(,n k kh a x nab h k =+=-=。
记准确解为)(x y ,记)(k x y 的近似值为k y ,记),(k k y x f 为k f .一阶常微分方程的初值问题⎩⎨⎧=∈=')2.1()()()1.1(),())(,()(0 x y a y b a x x y x f x y , 若f 在{}〈+∞≤≤=y b x a D ,内连续,且满足Lip 条件:0≥∃L 使2121),(),(y y L y x f y x f -≤-,则初值问题的连续可微解)(x y 在],[b a 上唯一存在,称解)(x y 在节点i x 处的近似值)(i i x y y =为其数值解,该方法称为数值方法。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
毕业论文题目:常微分方程的Euler解法及其程序设计学院:数学与信息科学学院专业:数学与应用数学毕业年限: 2011年6月学生:学号:指导教师:常微分方程的Euler解法及其程序设计摘要本文总结了常微分方程的Euler解法,对各种格式给出了误差估计,设计了这些格式的计算程序.关键词常微分方程;Euler解法;误差分析;程序设计Euler Method of Ordinary Differential Equation and ItsProgrammingAbstract Euler method of ordinary differential equation is summarized,the error of each format is analyzed and its programming is designed in this paper. Keywords Ordinary differential equation; Euler method; Error analysis; Programming科学技术中常常需要求解常微分方程的定解问题,这类问题最简单的形式,即为微分方程(,)dyf x y dx= (1)的初值问题00(,),().dyf x y dx y x y ⎧=⎪⎨⎪=⎩ (2)定理 (存在与唯一性定理)如果方程(1)的右端函数(,)f x y 在闭矩形域000000:,R x a x x a y b y y b -≤≤+-≤≤+上满足如下条件:(1)在R 上连续;(2)在R 上关于变量y 满足利普希茨(Lipschitz )条件,即存在常数L ,使对于R 上任何一对点(,)x y 和(,)x y 有不等式:(,)(,)f x y f x y L y y -≤-,则初值问题(2)在区间00000x h x x h -≤≤+上存在唯一解00(),()y y x y x y ==,其中0(,)min(,),max (,)x y R bh a M f x y M∈==.根据存在与唯一性定理,只要(,)f x y 关于y 满足Lipschitz 条件(,)(,)f x y f x y L y y -≤-,即可保证其解()y y x =存在并唯一.然而解析方法只能用来求解少数较简单和典型的常微分方程,例如线性常系数微分方程等,对于变系数常微分方程的解析求解就比较困难,而一般的非线性常微分方程就更不用说,因此,在大多数情况下,实际问题中归结出来的微分方程主要靠数值解法求解.所谓数值解法,就是寻找()y x 在一系列离散节点121n n x x x x +<<<<<上的近似值121,,,,n n y y y y +.相邻两个节点的间距1n n h x x +=-称为步长,假定h为定数,节点为0,0,1,2,n x x nh n =+=.1 Euler 解法 (1)Euler 格式Euler 格式的计算公式为1(,)n n n n y y hf x y +=+ (0,1,2)n =. (3) 下面用4种方法推导公式(3) a 泰勒展开法在n x 处展开1()()n n y x y x h +=+有 '2''11()()()()2!n n n n y x y x hy x h y ξ+=++ 1()n n n x x ξ+≤≤, (4)略去余项,得'1()()()()(,())n n n n n n y x y x hy x y x hf x y x +≈+=+.用近似值n y 代替()n y x ,把上式右端所得结果记为1n y +,得1(,)n n n n y y hf x y +=+ (0,1,2)n =.b 数值差商由导数定义知'1()()()(,())n n n n n y x y x y x f x y x h+-≈=,所以1()()(,())n n n n y x y x hf x y x +≈+.用n y 代替()n y x ,把上式右端所得结果记为1n y +,即得公式(3). c 数值积分在区间[]1,n n x x +上对微分方程(1)进行积分,得11()()(,())n nx n n x y x y x f x y x dx ++=+⎰, (5)利用左矩形公式得1()()(,())n n n n y x y x hf x y x +≈+.用n y 代替()n y x ,把上式右端所得结果记为1n y +,即得公式(3). d 几何方法在Oxy 平面中,微分方程{00.'(,),()y f x y y x y ==的解()y y x =称为它的积分曲线.积分曲线上的一点(,)x y 的切线斜率等于函数(,)f x y 的值.如果按函数(,)f x y 在Oxy 平面上建立一个方向场,那么,积分曲线上的每一点的切线方向均与方向场在该点的方向一致.基于上述对微分方程解的几何解释,从初始点000(,)p x y 出发,依方向场在该 点的方向上推进到1x x =上一点1p ,然后再从1p 依方向场的方向推进到2x x =上 的一点2p .循环前进,可作出一条折线012p p p (如图1)图1一般地,设已作出该折线的极点n p ,过(,)n n n p x y 依方向场的方向再推进到111(,)n n n p x y +++,显然,两个极点n p ,1n p +的坐标有下列关系:11(,)n nn n n ny y f x y x x ++-=-,1(,)n n n n y y hf x y +=+.若初值0.y 已知,则依上式可逐步算出1000(,)y y hf x y =+, 2111(,)y y hf x y =+,1(,)n n n n y y hf x y +=+.即得Euler 格式的计算公式(3).(2)梯形格式如果用梯形公式计算(5)式右端的积分,得[]111()()(,())(,())2n n n n n n hy x y x f x y x f x y x +++≈++ (0,1,2)n =. 对于上式右端,用n y 代替()n y x ,把上式右端所得结果记为1n y +,即得梯形公式[]111(,)(,)2n n n n n n hy y f x y f x y +++=++ (0,1,2)n =. (6)梯形公式(6)是关于1n y +的隐式方程,因此称梯形法为隐式方法,而公式(3)是1n y +的显式形式,因此称欧拉法为显式方法.(3)改进的Euler 格式先用Euler 格式求得一个初步的近似值1n y +,称之为预测值,预测值1n y +的精度可能很差,再用梯形公式将它校正一次,得1n y +,这个结果称之为校正值.而这样建立的预测—校正系统通常称为改进的Euler 格式.预测 1(,)n n n n y y hf x y +=+校正 111(,)(,)2n n n n n n hy y f x y f x y +++⎡⎤=++⎣⎦ 这一计算格式亦可表示为:[]11(,)(,(,))2n n n n n n n n hy y f x y f x y hf x y ++=+++, 或表示为下列平均化形式:11(,)(,)1()2p n n n c n n p n p c y y hf x y y y hf x y y y y ++⎧⎪=+⎪⎪=+⎨⎪⎪=+⎪⎩2 误差与精度 (1)截断误差在实际计算中,即使初始值是准确的,但所得的数值解往往与初始值问题的准确解有一定的误差.用111()n n n y x y ε+++=-,表示在节点1n x +处准确解与数值解之差,称之为整体截断误差,它不仅与1n x x +=这步计算有关,而且与121,,,n n x x x --这些步计算有关.为方便估计,假定()i y i n ≤为准确的,即在()()i i y y x i n =≤的前提下估计误差111()n n n E y x y +++=-,这种误差称为局部截断误差.如果局部截断误差11(),p n E O h ++=这里h 是等距节点的步长,则称所用的数值解的方法的阶数是p ,或称该方法有p 阶精确度.显然,步长h 越小,阶数p 越高,则局部截断误差越小,计算结果的精度也越高.(2)Euler 格式是一阶方法首先,可以通过几何直观来考察Euler 格式的精度.假设()n n y y x =,即顶点n p 落在积分曲线()y y x =上,那么,按Euler 格式作出的折线1n n p p +便是()y y x =过点n p 的切线(如图2).从图形上看,这样定出的顶点1n p +显著地偏离了原来的积分曲线,可见Euler 格式是相当粗糙的.图2首先考虑Euler 格式的局部截断误差1n E +,由(4)式得'2''11()()()()2!n n n n y x y x hy x h y ξ+=++1()n n n x x ξ+≤≤. 由Euler 格式,有'1(,)()n n n n n n y y hf x y y hy x +=+=+,上面两式相减,则Euler 格式的局部截断误差显然为22111()''()''()22n n n n h h E y x y y y x ξ+++=-=≈.若令max ''()a x bM y x ≤≤=,则有221()2n M E h O h +≤=, 这表明Euler 格式是一阶方法.下面考虑Euler 格式的整体截断误差n ε. 由(3)式和(4)式,有1111()()(,())n n n n n y x y x hf x y x E ----=++,111(,)n n n n y y hf x y ---=+.两式相减得111111[(,())(,)]n n n n n n n h f x y x f x y E εε------≤+-+.由Lipschitz 条件及22i M E h ≤,有 22111(1)22n n n n M MhL h hL h εεεε---≤++=++.反复使用这个不等式,得21(1)2n n M hL h εε-≤++12222200(1)(1)(1)(1)222n ni n i M M M hL h hL h hL h hL εε--=≤++++≤≤+++∑20(1)1(1)2n nM hL hL h hLε+-=++0(1)[(1)1]2n n MhhL hL Lε=+++-. 又1(),(1)[(1)]nnhLb a L hL nh b a hL hL e -=-+=+≤,所以()()0(1)2b a L b a Ln Mh e e Lεε--≤+-. 上式表明,Euler 格式的整体截断误差由初始误差0ε和局部截断误差界22M h 决定. 又00()y x y =,所以00ε=,则()n O h ε=.这表明当0→h 时,0→n ε,也就是说当h 充分小时近似值n y 能和)(n x y 充分接近,即数值解是收敛的.综上所述,Euler 格式的整体截断误差比局部截断误差低一阶,这表明Euler 格式的精度是比较差的,为了提高精度,减小误差,可采用梯形格式. (3)梯形格式是二阶方法首先考察梯形格式的局部截断误差. 由泰勒展式,有231()()'()''()()2n n n n h y x y x hy x y x O h +=+++, (7) 21'()'()''()()n n n y x y x hy x O h +=++. (8) 由(8)式,有1'()'()''()()n n n y x y x y x O h h+-=+.将上式代入(7)式,得311()()['()'()]()2n n n n hy x y x y x y x O h ++=+++, (9)又由梯形公式(6),有 []111(,)(,)2n n n n n n hy y f x y f x y +++=++. (10)由微分中值定理,有1111111(,)(,())(,)[()]n n n n y n n n f x y f x y x f x y y x η+++++++=+-1111'()(,)[()]n y n n n y x f x y y x η++++=+-,这里η是介于1n y +与1()n y x +之间的值,将上式代入(10)式,有11111['()'()](,)[()]22n n n n y n n n h hy y y x y x f x y y x η+++++=+++-.将上式与(9)式相减,得梯形格式的局部截断误差为311111()(,)[()]()2n n y n n n hy y x f x y y x O h η+++++-=-+, 即有31111()()1(,)2n n y n y y x O h hf x η+++-=-.因此梯形方法是二阶方法.梯形方法是隐式的,可用迭代法求解,其迭代公式如下:{(0)1(1)()111(,)(,)(,)2n n n n k k n n n n n n y y hf x y h yy f x y f x y +++++=+⎡⎤=++⎣⎦ (0,1,2,)k =. 下面分析迭代过程的收敛性: 因为(1)()111111(,)(,)2k k n n n n n n h y y f x y f x y +++++++⎡⎤-=-⎣⎦, 于是有(1)()11112k k n n n n hLy y y y +++++-≤-,式中L 为(,)f x y 对y 满足Lipschitz 常数,如果h 选取充分小,使得12hL<,则当k →∞时有(1)11k n n y y +++→,这说明迭代过程是收敛的.可见,梯形格式虽提高了精度,但在应用迭代公式进行实际计算时,每迭代一次,都要重新计算函数f 的值,而迭代又要反复进行若干次,计算量很大,为减小计算量,便可采用改进的Euler 格式.3 程序设计(1)Euler 格式的算法及其程序设计 应用Euler 方法计算初值问题'(,),()y f t y y a η== a t b ≤≤的解()y t 在区间[],a b 上的N 个等距点的近似值的算法. 输入 端点,a b ; 区间等分数N; 初值η 输出 ()y t 在t 的N 个点处的近似值y1 step()/;;;h b a N t ayη←-←←2step对1,2,,,i N=做34step step-3 step(,);;y y hf t y t a ih←+←+4step输出(,)t y 5step停机例:求解初值问题 {'2/(0)1y y x yy=-=01x<<.源程序如下:# include <stdio.h># include <math.h>void main(){int i;double a,b,c,h,t,y,z;a=0;b=1;c=1;h=(b-a)/10;t=a;y=c;for(i=1;i<=10;i++){y=y+h(y-2*t/y);t=a+i*h;z=sqrt(1+2*t);printf("%f %f %f\n",t,y,z);}}运行结果如下:(2)改进的Euler 格式的算法及其程序设计应用改进的Euler 方法计算初值问题'(,),()y f t y y a η== a t b ≤≤的解()y t 在区间[],a b 上的N+1个等距点的近似值的算法.输入 端点,a b ; 区间等分数N; 初值η输出 ()y t 在t 的N+1个点处的近似值y .1step ()/;;;h b a N t a y η←-←←2step 输出(,)t y .3step 对1,2,,,i N =做45step step -4step (,);;(,);1().2p c p p c y y hf t y t a ih y y hf t y y y y ←+←+←+←+5step 输出(,)t y6step 停机下面用改进的Euler 格式计算上面的例题:求解初值问题 {'2/(0)1y y x y y =-= 01x <<. 源程序如下:# include <stdio .h># include <math .h>void main(){int i;double a,b,c,h,t,y,y1,y2,z;a=0;b=1;c=1;h=(b-a)/10;t=a;y=c;for(i=1;i<=10;i++){y1=y+h(y-2*t/y);t=a+i*h;y2=y+h(y1-2*t/y1);y=(y1+y2)/2;z=sqrt(1+2*t);printf("%f %f %f\n",t,y,z);}}运行结果如下:y和其数值从上面的运行结果可以看出,该常微分方程欧拉解法的精确解n y x很接近.由此可知,常微分方程欧拉解法对大量计算数据来说精度是很解()n高的,可以满足绝大多数工程上的要求.由于欧拉解法的稳定性和收敛性,可以通过减少h的值来进一步提高其精度.参考文献[1] 庆扬,王能超,易大义.数值计算方法[M].:华中科技大学,2006[2] 林成森.数值计算方法[M].:科学,2005[3] 信真,车刚明,欧阳洁,封建湖.计算方法[M].:西北工业大学,2000[4] 朱长青.数值计算方法及其应用[M].:科学,2006[5] 曾喆昭,文卉.数值计算[M].:清华大学,2005[6] 丽娟.常微分方程的Euler解法及其计算机实现[J].师学院学报(自然科学版),2005,24(6):11-14[7] 马燕,根耀,杜利锋,竹林.常微分方程的数值解法及其在计算机中的实现[J].大学学报(自然科学版),2000,19(2):23-25[8] 均亮,邓易冬,徐宏坤.基于C++的常微分方程欧拉解法的误差分析[J].信息技术,2007,7:92-94。
