C++算法设计(完整版)
详细完整版C程序设计pdf

表达式
由变量、常量、运算符等组成的符合语法规则的 式子,用于计算或表示某种逻辑关系。
数据类型转换
隐式类型转换
由编译器自动完成,如将整型值赋给浮点型 变量时,整型值会自动转换为浮点型。
显式类型转换
由程序员明确指定,如使用强制类型转换符将一种 数据类型转换为另一种数据类型。
数据类型转换的注意事项
在进行数据类型转换时,需要注意数据范围 、精度损失以及可能产生的溢出等问题。
for循环
通过初始化、条件和迭代三部分控制循环的 执行。
循环的中断和继续
使用break和continue语句控制循环的执行 流程。
控制结构的嵌套与综合应用
控制结构的嵌套
在一个控制结构内部包含另一个控制结构,如选择结构嵌套循环 结构。
综合应用示例
结合顺序、选择和循环结构,编写复杂的程序逻辑,如排序算法 、查找算法等。
详细完整版C程序设计 pdf
目 录
பைடு நூலகம்
• C语言概述与基础 • 数据类型、运算符与表达式 • 控制结构与程序设计 • 函数与模块化设计 • 数组与字符串处理 • 指针与内存管理 • 文件操作与数据处理
01
C语言概述与基础
C语言的历史与发展
C语言的起源
C语言最初是由丹尼斯·里奇(Dennis Ritchie)在1972年 为开发UNIX操作系统而设计的一种高级编程语言。
03
第一个C程序:Hello World
• printf("Hello, World! • ");
第一个C程序:Hello World
• return 0;
第一个C程序:Hello World
}
01
C语言算法设计与分析排序查找和算法

C语言算法设计与分析排序查找和算法C语言算法设计与分析:排序、查找和算法C语言作为一门广泛应用于计算机领域的编程语言,算法设计与分析是每个程序员都需要掌握的重要技能之一。
本文将介绍C语言中常用的排序算法、查找算法以及一些常见的算法技巧,并详细分析它们的原理和实现方法。
一、排序算法1. 冒泡排序(Bubble Sort)冒泡排序是最简单的排序算法之一。
它的基本思想是通过相邻元素之间的比较和交换来将序列中的较大元素逐步向右移动。
具体实现时,从待排序序列的左侧开始,将较大的元素向右冒泡,直至序列有序。
冒泡排序的时间复杂度为O(n^2)。
2. 插入排序(Insertion Sort)插入排序的思想是将待排序序列分为已排序和未排序两部分,从未排序序列中选择元素并插入到已排序序列的适当位置。
具体实现时,从待排序序列的左侧开始,逐个将元素插入到已排序序列中的正确位置,直至序列有序。
插入排序的时间复杂度为O(n^2),但在部分有序的序列中具有较好的性能。
3. 快速排序(Quick Sort)快速排序是一种高效的排序算法,它的基本思想是通过每一趟排序将待排序序列分割成独立的两部分,其中一部分的所有元素小于另一部分的所有元素,并分别对这两部分进一步排序。
具体实现时,选择一个基准元素,将小于基准的元素放到左侧,大于基准的元素放到右侧,然后对左右两部分分别进行递归排序。
快速排序的平均时间复杂度为O(nlogn)。
二、查找算法1. 顺序查找(Sequential Search)顺序查找是一种简单直观的查找算法。
它的基本思想是从待查找的序列的左侧开始,逐个比较序列中的元素和待查找元素,直到找到匹配的元素或查找结束。
顺序查找的时间复杂度为O(n)。
2. 二分查找(Binary Search)二分查找是一种高效的查找算法,但要求待查找序列必须是有序的。
它的基本思想是通过每一次查找将待查找序列划分为两部分,并将中间元素与待查找元素进行比较,进而确定下一次查找的范围。
排列组合c的算法

排列组合c的算法排列组合是组合数学中的经典概念,也是计算机科学中常用的算法之一。
在算法设计中,排列组合算法可以用于解决很多实际问题,比如密码破解、图形排列等。
本文将介绍排列组合的基本概念和常见的算法。
排列是指从给定的n个元素中,按照一定顺序选取k个元素的方式。
对于有序的排列,我们可以使用递归或者循环的方法来实现。
递归方法可以通过以下步骤来完成:1. 若k=0,则返回一个空列表。
2. 若k=1,则将n个元素依次加入列表中,并返回。
3. 若k>1,则从n个元素中选取第一个元素,然后递归地选取剩下的n-1个元素中的k-1个,将两部分结果合并。
以下是一个使用递归方法实现排列的伪代码:```function permute(list, k):if k = 0:return []if k = 1:return [[x] for x in list]result = []for i in range(len(list)):rest = permute(list[:i] + list[i+1:], k-1)for p in rest:result.append([list[i]] + p)return result```循环方法可以通过以下步骤来完成:1. 创建一个二维数组result,用于存储所有的排列结果。
2. 创建一个长度为n的布尔类型的数组used,用于标记元素是否已经被选取。
3. 创建一个列表p,用于存储当前的排列。
4. 使用循环遍历数组中的每一个元素,对于每个元素,检查是否已经被选取。
5. 如果元素已经被选取,则跳过该元素。
6. 如果元素未被选取,则将其加入当前的排列p中,并标记元素为已选取。
7. 如果k=1(即已选取了k个元素),则将当前排列加入结果result中。
8. 否则,递归地调用自身,进入下一层递归。
9. 在递归返回后,将当前元素标记为未选取,将其从排列p中移除,以便进行下一个元素的选择。
c课程设计迭代算法

c课程设计迭代算法一、教学目标本课程旨在让学生掌握迭代算法的基本概念、设计和分析方法,培养他们运用迭代算法解决实际问题的能力。
具体目标如下:1.知识目标:(1)了解迭代算法的定义、特点和应用领域。
(2)掌握常见迭代算法的设计方法和分析技巧。
(3)熟悉迭代算法在实际问题中的应用案例。
2.技能目标:(1)能够运用迭代算法解决简单数学问题。
(2)能够运用迭代算法优化程序性能。
(3)能够分析迭代算法的收敛性和时间复杂度。
3.情感态度价值观目标:(1)培养学生对迭代算法的兴趣,提高他们学习编程的积极性。
(2)培养学生独立思考、合作交流的能力。
(3)培养学生勇于探索、创新的精神。
二、教学内容本课程的教学内容主要包括以下几个部分:1.迭代算法的基本概念:迭代算法的定义、特点和应用领域。
2.迭代算法的设计方法:常见的迭代算法设计方法,如递推、迭代递推、迭代加速等。
3.迭代算法的分析方法:迭代算法的收敛性、时间复杂度和空间复杂度分析。
4.迭代算法在实际问题中的应用:线性代数、数值计算、优化问题等领域中的应用案例。
5.编程实践:运用迭代算法解决实际问题,提高编程能力。
三、教学方法为了提高教学效果,本课程将采用以下教学方法:1.讲授法:讲解迭代算法的基本概念、设计方法和分析技巧。
2.案例分析法:分析迭代算法在实际问题中的应用案例,让学生加深理解。
3.实验法:让学生通过编程实践,掌握迭代算法的应用和优化。
4.讨论法:学生进行小组讨论,培养合作交流的能力。
四、教学资源为了支持教学内容和教学方法的实施,我们将准备以下教学资源:1.教材:《迭代算法导论》等。
2.参考书:《算法导论》、《数值计算方法》等。
3.多媒体资料:PPT、教学视频等。
4.实验设备:计算机、编程环境等。
5.在线资源:相关论坛、博客、教程等。
五、教学评估本课程的教学评估将采用多元化评价方式,全面、客观地评价学生的学习成果。
评估方式包括:1.平时表现:考察学生在课堂上的参与度、提问回答、小组讨论等,占总评的20%。
c语言(算法流程图)
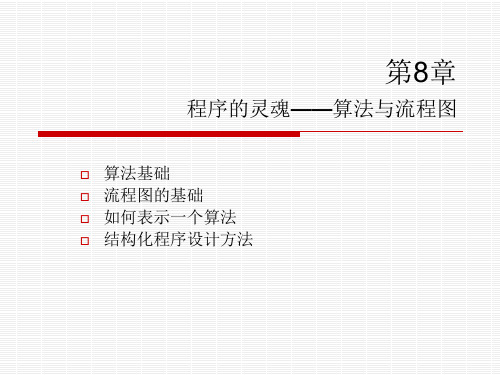
N i<n?
Y t*=i;sum+=t;
iቤተ መጻሕፍቲ ባይዱ=2 输出sum
结束 用流程图表示
8.7 跟我上机
2. 将1到100之间 能用3或5整 除的数打印 出来。
开始
i赋初值为1
N i<=100?
Y N
i能被3或5整 除? Y 打印i
i++
结束
用流程图表示
i赋初值为1
i<=100?
i能被3或5整 除?
N d>=0?
x2=x-sqrt(-d)/(2a) x1=x+ sqrt(-d)/(2a)
输出结果
8.7 跟我上机
开始 输入n的值
1. 求1!+3!+5!+……+N!的值。N
i赋值为1 t赋初值为1
由键盘输入,且为奇数。
sum赋初值为0
输入n的值 t赋初值为1; i赋值为1
sum赋初值为0 i<n? t*=I; s+=t; i+=2
求最大公约数通常用“辗转相除法”,
方法如下:
(1)比较两数,并使m大于n。 (2)将m作被除数,n作除数,相除 后余数为r。 (3)将m←n,n←r; (4)若r=0,则m为最大公约数,结 束循环。若r≠0,执行步骤步骤(2) 和(3)。
输入m,n
T
m<n?
F
交换m,n
r←m%n m←n,n←r
r ≠0 输出m
8.3.6 用计算机语言表示算法
计算机语言通常分为三类:即机器语言,汇编语 言和高级语言。
8.4 结构化程序设计方法
结构化程序设计的思想:自顶向下、逐步求 精;
C语言中的算法实现

C语言中的算法实现算法是计算机科学中非常重要的概念,它是解决问题的一系列步骤或指令集。
在C语言中,我们可以使用不同的方法来实现算法。
本文将介绍一些常见的C语言算法实现方式。
一、排序算法1. 冒泡排序冒泡排序是一种简单但效率较低的排序算法。
它通过不断比较相邻的元素,并按照规则交换它们的位置,直到整个序列排序完成。
2. 选择排序选择排序是一种简单而直观的排序算法。
它每次从未排序的序列中选择最小(或最大)的元素,并将其放置在已排序序列的末尾。
3. 插入排序插入排序是一种简单且高效的排序算法。
它通过构建有序序列,对未排序的元素逐个插入到已排序的序列中,直到所有元素都被插入完成。
二、查找算法1. 顺序查找顺序查找是一种简单的查找算法。
它从列表的开头开始逐个比较元素,直到找到目标元素或查找完整个列表。
2. 二分查找二分查找是一种高效的查找算法,但要求列表必须是有序的。
它通过将待查找区域分成两部分,判断目标元素落在哪一部分,从而缩小查找范围,直到找到目标元素或确定不存在。
三、递归算法递归是一种常用的算法设计技巧。
它通过在函数内调用自身来解决相同问题的不同实例。
在C语言中,递归函数需要定义出口条件,以避免无限递归。
四、动态规划算法动态规划是一种用于解决具有重叠子问题和最优子结构性质的问题的方法。
它将问题分解为一系列子问题,并以自底向上的方式求解子问题,最终得到整体问题的解。
在C语言中,可以使用循环、数组和指针等特性来实现动态规划算法,从而有效地解决问题。
五、图算法图是一种用于描述对象之间关系的数据结构,图算法是解决图相关问题的一类算法。
常见的图算法包括深度优先搜索(DFS)和广度优先搜索(BFS)。
六、字符串算法字符串算法用于处理字符串相关的问题,如字符串匹配、编辑距离等。
C语言提供了一系列字符串处理函数,如strlen、strcpy等,可以方便地实现字符串算法。
七、数学算法C语言在数学算法方面提供了丰富的库函数支持,如求平方根、对数、指数等。
(完整版).c程序设计谭浩强第二章习题与答案

习题2.1什么是算法?是从日常生活中找三个例子,描述他们的算法?答:对操作的描述,即操作步骤,就是算法。
广义的说;为解决一个问题而采取的方法和步骤,就称为“算法”。
例:(略)2.2什么叫结构化的算法?为什么要提倡结构化的算法?答:由基本节构所构成的算法属于“结构化”的算法。
结构化的算法便于编写、阅读、便于修改和维护。
这就减少了程序出错的机会、提高了程序的可靠性,保证了程序的质量。
2.3试述三种基本结构的特点,你能否自己另外设计两种基本结构(要符合基本结构的特点)。
答:基本结构有以下共同点:1:只有一个入口。
图2-14-------2-17中的a点为入口。
2:只有一个出口。
图2-14-------2-17中的b点为出口。
注意,一个判断框有两个出口,但一个选择结构只有一个出口。
不能混淆。
3:结构内的每一部分都有被执行到的机会。
也就是说,对每一个框来说,都应当有一条到出口的路径通过它。
图2-20中就没有一条从入口到出口的路径通过A框。
4:结构内不存在死循环(无终止的循环)。
图2-21就是一个死循环。
需要说明的是基本结构并不一定只限于以上3中,只要有以上四种特点就可以。
人们可以自己定义之。
例:如下两图2.4用传统流程图表示求解一下问题的算法。
(1)有两个瓶子A和B,分别放醋和酱油,要求将他们互换。
#include<stdio.h>void main(){int a;int b;int c;a=10;b=5;printf("%d,%d\n",a,b);c=a;a=b;b=c;printf("%d,%d\n",a,b);}(2)一次将10个数输入,要求将将其中最大的数输出。
#include<stdio.h>void main(){int a[10];int i;int max;printf("input 10 numbers.\n");for(i=0;i<10;i++)scanf("%d",&a[i]);printf("\n");max=a[0];for(i=1;i<10;i++)if(max<a[i]) max=a[i];printf("the max is: %d\n",max) ;}(3)有3个数a b c,要求安大小顺序把他们输出。
C语言程序设计的常用算法

C语言程序设计的常用算法1.排序算法-冒泡排序:通过多次比较和交换来将最大(小)的数移到最后(前),时间复杂度为O(n^2)。
适用于数据较少、数据基本有序的情况。
- 快速排序:通过一趟排序将待排序序列分隔成独立的两部分,其中一部分的所有元素都比另一部分的所有元素小。
然后递归地对两部分进行排序,时间复杂度为O(nlogn)。
适用于大规模数据的排序。
-插入排序:将待排序序列分为已排序和未排序两部分,每次从未排序部分取一个元素插入到已排序部分的适当位置,时间复杂度为O(n^2)。
适用于数据量较小的排序场景。
- 归并排序:将待排序序列分为若干个子序列,分别进行排序,然后再将排好序的子序列合并成整体有序的序列,时间复杂度为O(nlogn)。
适用于需要稳定排序且对内存空间要求不高的情况。
2.查找算法-顺序查找:从头到尾依次对每个元素进行比较,直到找到目标元素或者遍历完整个序列。
时间复杂度为O(n)。
- 二分查找:对于有序序列,将序列的中间元素与目标元素进行比较,根据比较结果缩小查找范围,直到找到目标元素或者查找范围为空。
时间复杂度为O(logn)。
3.图算法-广度优先(BFS):从给定的起始顶点开始,按照“先访问当前顶点的所有邻接顶点,再依次访问这些邻接顶点的所有未访问过的邻接顶点”的顺序逐层访问图中的所有顶点。
适用于寻找最短路径、连通性等问题。
-深度优先(DFS):从给定的起始顶点开始,按照“先递归访问当前顶点的一个邻接顶点,再递归访问这个邻接顶点的一个邻接顶点,直到无法再继续递归”的方式遍历图中的所有顶点。
适用于寻找路径、判断连通性等问题。
4.动态规划算法-背包问题:给定一个背包容量和一组物品的重量和价值,选择一些物品装入背包,使得装入的物品总重量不超过背包容量,且总价值最大。
利用动态规划的思想可以通过构建二维数组来解决该问题。
-最长公共子序列(LCS):给定两个序列,找出一个最长的子序列,且该子序列在两个原序列中的顺序保持一致。
数据结构C算法设计

}
6.设单链表中有仅三类字符的数据元素(大写字母、数字和其它字符),要求利用原单链表中结点空间设计出三个单链表的算法,使每个单链表只包含同类字符。
typedef char datatype;
lklist *p,*q,*s;
for(p=head;p!=0;p=p->next)
{
for(q=p->next,s=q;q!=0; )
if (q->data==p->data) {s->next=q->next; free(q);q=s->next;}
4.设计在单链表中删除值相同的多余结点的算法。
5.设计一个求结点x在二叉树中的双亲结点算法。
6.设单链表中有仅三类字符的数据元素(大写字母、数字和其它字符),要求利用原单链表中结点空间设计出三个单链表的算法,使每个单链表只包含同类字符。
7.设计在链式存储结构上交换二叉树中所有结点左右子树的算法。
21.设计判断单链表中元素是否是递增的算法。
22.设计在链式存储结构上合并排序的算法。
23.设计在二叉排序树上查找结点X的算法。
24.设关键字序列(k1,k2,…,kn-1)是堆,设计算法将关键字序列(k1,k2,…,kn-1,x)调整为堆。
1.统计出单链表HL中结点的值等于给定值X的结点数。
}
9.设计判断两个二叉树是否相同的算法。
typedef struct node {datatype data; struct node *lchild,*rchild;} bitree;
C语言经典算法大全(可编辑)

C语言经典算法大全C语言经典算法大全老掉牙河内塔费式数列巴斯卡三角形三色棋老鼠走迷官一老鼠走迷官二骑士走棋盘八个皇后八枚银币生命游戏字串核对双色三色河内塔背包问题Knapsack Problem数运算蒙地卡罗法求 PIEratosthenes筛选求质数超长整数运算大数运算长 PI最大公因数最小公倍数因式分解完美数阿姆斯壮数最大访客数中序式转后序式前序式后序式的运算关于赌博洗扑克牌乱数排列Craps赌博游戏约瑟夫问题Josephus Problem 集合问题排列组合格雷码Gray Code产生可能的集合m元素集合的n个元素子集数字拆解排序得分排行选择插入气泡排序Shell 排序法 - 改良的插入排序Shaker 排序法 - 改良的气泡排序Heap 排序法 - 改良的选择排序快速排序法一快速排序法二快速排序法三合并排序法基数排序法搜寻循序搜寻法使用卫兵二分搜寻法搜寻原则的代表插补搜寻法费氏搜寻法矩阵稀疏矩阵多维矩阵转一维矩阵上三角下三角对称矩阵奇数魔方阵4N 魔方阵2 2N1 魔方阵 1河内之塔说明河内之塔 Towers of Hanoi 是法国人MClaus Lucas 于1883年从泰国带至法国的河内为越战时北越的首都即现在的胡志明市1883年法国数学家 Edouard Lucas曾提及这个故事据说创世纪时Benares有一座波罗教塔是由三支钻石棒Pag所支撑开始时神在第一根棒上放置64个由上至下依由小至大排列的金盘Disc并命令僧侣将所有的金盘从第一根石棒移至第三根石棒且搬运过程中遵守大盘子在小盘子之下的原则若每日仅搬一个盘子则当盘子全数搬运完毕之时此塔将毁损而也就是世界末日来临之时解法如果柱子标为ABC要由A搬至C在只有一个盘子时就将它直接搬至C当有两个盘子就将B当作辅助柱如果盘数超过2个将第三个以下的盘子遮起来就很简单了每次处理两个盘子也就是A- BA - CB- C这三个步骤而被遮住的部份其实就是进入程式的递回处理事实上若有n个盘子则移动完毕所需之次数为2n - 1所以当盘数为64时则所需次数为264- 1 1XXXXXXXXXX709551615为505390248594782e16年也就是约5000世纪如果对这数字没什幺概念就假设每秒钟搬一个盘子好了也要约5850亿年左右includevoid hanoi int n char A char B char Cif n 1printf "Move sheet d from c to c\n" n A Celsehanoi n-1 A C Bprintf "Move sheet d from c to c\n" n A Chanoi n-1 B A Cint mainint nprintf "请输入盘数"scanf "d" nhanoi n A B Cfn fn-1 fn-2 if n 1fn n if n 0 1includeinclude define N 20 int main voidint Fib[N] 0int i Fib[0] 0Fib[1] 1 for i 2 i N iFib[i] Fib[i-1] Fib[i-2] for i 0 i N i printf "d " Fib[i]printf "\n"return 03 巴斯卡三角形 includedefine N 12long combi int n int rint ilong p 1for i 1 i r ip p n-i1 ireturn pvoid mainint n r tfor n 0 n N nfor r 0 r n rint i 排版设定开始if r 0for i 0 i N-n i printf " "elseprintf " "排版设定结束printf "3d" combi n rprintf "\n"4Algorithm Gossip 三色棋说明三色旗的问题最早由EWDijkstra所提出Dutch Nation Flag Dijkstra为荷兰人 Three-Color Flag来称之假设有一条绳子上面有红白蓝三种颜色的旗子起初绳子上的旗子颜色并没有顺序您希望将之分类并排列为蓝白红的顺序要如何移动次数才会最少注意您只能在绳子上进行这个动作而且一次只能调换两个旗子解法在一条绳子上移动在程式中也就意味只能使用一个阵列而不使用其它的阵列来作辅助问题的解法很简单您可以自己想像一下在移动旗子从绳子开头进行遇到蓝色往前移遇到白色留在中间遇到红色往后移如下所示只是要让移动次数最少的话就要有些技巧如果图中W所在的位置为白色则W1表示未处理的部份移至至白色群组如果W部份为蓝色则B与W的元素对调而B与W必须各1表示两个群组都多了一个元素如果W所在的位置是红色则将W与R交换但R要减1表示未处理的部份减1 注意BWR并不是三色旗的个数它们只是一个移动的指标什幺时候移动结束呢一开始时未处理的R指标会是等于旗子的总数当R的索引数减至少于W的索引数时表示接下来的旗子就都是红色了此时就可以结束移动如下所示 includeincludeinclude define BLUE bdefine WHITE wdefine RED r define SWAP x y char temp \temp color[x] \color[x] color[y] \color[y] temp int main char color[] r w b w wb r b w r \0 int wFlag 0 int bFlag 0int rFlag strlen color - 1int i for i 0 i strlen color iprintf "c " color[i]printf "\n" while wFlag rFlagif color[wFlag] WHITEwFlagelse if color[wFlag] BLUESWAP bFlag wFlagbFlag wFlagelsewhile wFlag rFlag color[rFlag] REDrFlag--SWAP rFlag wFlagrFlag--for i 0 i strlen color i printf "c " color[i]printf "\n" return 05Algorithm Gossip 老鼠走迷官说明老鼠走迷宫是递回求解的基本题型我们在二维阵列中使用2表示迷宫墙壁使用1来表示老鼠的行走路径试以程式求出由入口至出口的路径解法老鼠的走法有上左下右四个方向在每前进一格之后就选一个方向前进无法前进时退回选择下一个可前进方向如此在阵列中依序测试四个方向直到走到出口为止这是递回的基本题请直接看程式应就可以理解includeinclude int visit int int int maze[7][7] 2 2 2 22 2 22 0 0 0 0 0 22 0 2 0 2 0 22 0 0 2 0 2 22 2 0 2 0 2 22 0 0 0 0 0 22 2 2 2 2 2 2 int startI 1 startJ 1 入口int endI 5 endJ 5 出口int success 0 int main voidint i j printf "显示迷宫\n"for i 0 i 7 ifor j 0 j 7 jif maze[i][j] 2printf "█"elseprintf " "printf "\n"if visit startI startJ 0 printf "\n没有找到出口\n"elseprintf "\n\n"for i 0 i 7 ifor j 0 j 7 jif maze[i][j] 2printf "█"else if maze[i][j] 1 printf "◇"elseprintf " "printf "\n"return 0int visit int i int jmaze[i][j] 1 if i endI j endJsuccess 1 if success 1 maze[i][j1]0 visit i j1if success 1 maze[i1][j] 0 visit i1 jif success 1 maze[i][j-1] 0 visit i j-1if success 1 maze[i-1][j] 0 visit i-1 j if success 1maze[i][j] 0 return success6Algorithm Gossip 老鼠走迷官说明由于迷宫的设计老鼠走迷宫的入口至出口路径可能不只一条如何求出所有的路径呢解法求所有路径看起来复杂但其实更简单只要在老鼠走至出口时显示经过的路径然后退回上一格重新选择下一个位置继续递回就可以了比求出单一路径还简单我们的程式只要作一点修改就可以了includeinclude void visit int int int maze[9][9] 2 2 2 22 2 2 2 22 0 0 0 0 0 0 0 22 0 2 2 0 2 2 0 22 0 2 0 0 2 0 0 22 0 2 0 2 0 2 0 22 0 0 0 0 0 2 0 22 2 0 2 2 0 2 2 22 0 0 0 0 0 0 0 22 2 2 2 2 2 2 2 2 int startI 1 startJ 1 入口int endI 7 endJ 7 出口 int main voidint i j printf "显示迷宫\n"for i 0 i 7 ifor j 0 j 7 jif maze[i][j] 2printf "█"elseprintf " "printf "\n"visit startI startJ return 0void visit int i int jint m n maze[i][j] 1 if i endI j endJprintf "\n显示路径\n"for m 0 m 9 mfor n 0 n 9 nif maze[m][n] 2printf "█"else if maze[m][n] 1printf "◇"elseprintf " "printf "\n"if maze[i][j1] 0 visit i j1if maze[i1][j] 0 visit i1 jif maze[i][j-1] 0 visit i j-1if maze[i-1][j] 0 visit i-1 j maze[i][j] 07Algorithm Gossip 骑士走棋盘说明骑士旅游Knight tour[所有的位置include int board[8][8] 0 int main voidint startx startyint i jprintf "输入起始点"scanf "d d" startx starty if travel startx starty printf "\n"elseprintf "\n"for i 0 i 8 ifor j 0 j 8 jprintf "2d " board[i][j]putchar \nreturn 0int travel int x int yint ktmove1[8] -2 -1 1 2 2 1 -1 -2int ktmove2[8] 1 2 2 1 -1 -2 -2 -1 测试下一步的出路int nexti[8] 0int nextj[8] 0记录出路的个数int exists[8] 0int i j k m lint tmpi tmpjint count min tmp i xj yboard[i][j] 1 for m 2 m 64 mfor l 0 l 8 lexists[l] 0 l 0 试探八个方向for k 0 k 8 ktmpi i ktmove1[k]tmpj j ktmove2[k] 如果是边界了if tmpi 0 tmpj 0 tmpi 7 tmpj 7 continue 如果这个方向可走 if board[tmpi][tmpj] 0nexti[l] tmpinextj[l] tmpj可走的方向加一个lcount l如果可走的方向为0个if count 0return 0else if count 1只有一个可走的方向所以直接是最少出路的方向min 0else找出下一个位置的出路数for l 0 l count lfor k 0 k 8 ktmpi nexti[l] ktmove1[k] tmpj nextj[l] ktmove2[k] if tmpi 0 tmpj 0tmpi 7 tmpj 7continueif board[tmpi][tmpj] 0 exists[l]tmp exists[0]min 0从可走的方向中寻找最少出路的方向 for l 1 l count lif exists[l] tmptmp exists[l]min l走最少出路的方向i nexti[min]j nextj[min]board[i][j] mreturn 18Algorithm Gossip 八皇后说明西洋棋中的皇后可以直线前进吃掉遇到的所有棋子如果棋盘上有八个皇后则这八个皇后如何相安无事的放置在棋盘上1970年与1971年 EWDijkstra与NWirth曾经用这个问题来讲解程式设计之技巧解法关于棋盘的问题都可以用递回求解然而如何减少递回的次数在八个皇后的问题中不必要所有的格子都检查过例如若某列检查过该该列的其它格子就不用再检查了这个方法称为分支修剪includeincludedefine N 8 int column[N1] 同栏是否有皇后1int rup[2N1] 右上至左下是否有皇后int lup[2N1] 左上至右下是否有皇后int queen[N1] 0int num 解答编号 void backtrack int 递回求解 intmain voidint inum 0 for i 1 i N icolumn[i] 1 for i 1 i 2N irup[i] lup[i] 1 backtrack 1 return 0void showAnswerint x yprintf "\n解答 d\n" numfor y 1 y N yfor x 1 x N xif queen[y] xprintf " Q"elseprintf " "printf "\n"void backtrack int iint j if i NshowAnswerelsefor j 1 j N jif column[j] 1rup[ij] 1 lup[i-jN] 1 queen[i] j设定为占用column[j] rup[ij] lup[i-jN] 0 backtrack i1column[j] rup[ij] lup[i-jN] 19Algorithm Gossip 八枚银币说明现有八枚银币a b c d e f g h已知其中一枚是假币其重量不同于真币但不知是较轻或较重如何使用天平以最少的比较次数决定出哪枚是假币并得知假币比真币较轻或较重解法单就求假币的问题是不难但问题限制使用最少的比较次数所以我们不能以单纯的回圈比较来求解我们可以使用决策树decision tree使用分析与树状图来协助求解一个简单的状况是这样的我们比较abc与def 如果相等则假币必是g或h我们先比较g或h哪个较重如果g较重再与a比较a是真币如果g等于a则g为真币则h为假币由于h比g轻而 g是真币则h假币的重量比真币轻 include includeinclude void compare int[] int int intvoid eightcoins int[] int main voidint coins[8] 0int i srand time NULL for i 0 i 8 icoins[i] 10 printf "\n输入假币重量比10大或小 "scanf "d" icoins[rand 8] i eightcoins coins printf "\n\n"for i 0 i 8 iprintf "d " coins[i] printf "\n"return 0void compare int coins[] int i int j int kif coins[i] coins[k]printf "\n d 较重" i1elseprintf "\n假币 d 较轻" j1void eightcoins int coins[]if coins[0]coins[1]coins[2]coins[3]coins[4]coins[5]if coins[6] coins[7]compare coins 6 7 0elsecompare coins 7 6 0else if coins[0]coins[1]coins[2]coins[3]coins[4]coins[5]if coins[0]coins[3] coins[1]coins[4]compare coins 2 5 0else if coins[0]coins[3] coins[1]coins[4] compare coins 0 4 1if coins[0]coins[3] coins[1]coins[4]compare coins 1 3 0else if coins[0]coins[1]coins[2]coins[3]coins[4]coins[5]if coins[0]coins[3] coins[1]coins[4]compare coins 5 2 0else if coins[0]coins[3] coins[1]coins[4] compare coins 3 1 0if coins[0]coins[3] coins[1]coins[4]compare coins 4 0 110Algorithm Gossip 生命游戏说明生命游戏game of life1970年由英国数学家J H Conway所提出includeincludeinclude define ROW 10define COL 25define DEAD 0define ALIVE 1int map[ROW][COL] newmap[ROW][COL] void initint neighbors int intvoid outputMapvoid copyMap int mainint row colchar ansinitwhile 1outputMapfor row 0 row ROW rowfor col 0 col COL colswitch neighbors row colcase 0case 1case 4case 5case 6case 7case 8newmap[row][col] DEADbreakcase 2newmap[row][col] map[row][col] breakcase 3newmap[row][col] ALIVEbreakcopyMapprintf "\nContinue next Generation "getcharans toupper getcharif ans Y breakreturn 0void initint row col for row 0 row ROW rowfor col 0 col COL colmap[row][col] DEAD puts "Game of life Program"puts "Enter x y where x y is living cell"printf "0 x d 0 y d\n"ROW-1 COL-1puts "Terminate with x y -1 -1" while 1scanf "d d" row colif 0 row row ROW0 col col COLmap[row][col] ALIVEelse if row -1 col -1breakelseprintf " x y exceeds map ranage"int neighbors int row int colint count 0 c rfor r row-1 r row1 rfor c col-1 c col1 cif r 0 r ROW c 0 c COL continueif map[r][c] ALIVEcountif map[row][col] ALIVEcount--return countvoid outputMapint row colprintf "\n\n20cGame of life cell status\n" for row 0 row ROW rowprintf "\n20c"for col 0 col COL colif map[row][col] ALIVE putchar else putchar -void copyMapint row colfor row 0 row ROW rowfor col 0 col COL colmap[row][col] newmap[row][col]11Algorithm Gossip 字串核对说明今日的一些高阶程式语言对于字串的处理支援越来越强大例如JavaPerl等不过字串搜寻本身仍是个值得探讨的课题在这边以Boyer- Moore法来说明如何进行字串说明这个方法快且原理简洁易懂解法字串搜寻本身不难使用暴力法也可以求解但如何快速搜寻字串就不简单了传统的字串搜寻是从关键字与字串的开头开始比对例如 Knuth-Morris-Pratt 演算法字串搜寻这个方法也不错不过要花时间在公式计算上Boyer-Moore字串核对改由关键字的后面开始核对字串并制作前进表如果比对不符合则依前进表中的值前进至下一个核对处假设是p好了然后比对字串中p-n1至p的值是否与关键字相同如果关键字中有重复出现的字元则前进值就会有两个以上的值此时则取前进值较小的值如此就不会跳过可能的位置例如texture 这个关键字t的前进值应该取后面的3而不是取前面的7 includeincludeinclude void table char 建立前进表int search int char char 搜寻关键字void substring char char int int 取出子字串int skip[256] int main voidchar str_input[80]char str_key[80]char tmp[80] \0int m n pprintf "请输入字串"gets str_inputprintf ""gets str_keym strlen str_inputn strlen str_keytable str_keyp search n-1 str_input str_key while p -1 substring str_input tmp p mprintf "s\n" tmpp search pn1 str_input str_keyprintf "\n"return 0void table char keyint k nn strlen keyfor k 0 k 255 kskip[k] nfor k 0 k n - 1 kskip[key[k]] n - k - 1int search int p char input char keyint i m nchar tmp[80] \0m strlen inputn strlen key while p msubstring input tmp p-n1 pif strcmp tmp key 比较两字串是否相同return p-n1p skip[input[p]]return -1void substring char text char tmp int s int e int i jfor i s j 0 i e i jmp[j] text[i]tmp[j] \012Algorithm Gossip 双色三色河内塔说明双色河内塔与三色河内塔是由之前所介绍过的河内塔规则衍生而来双色河内塔的目的是将下图左上的圆环位置经移动成为右下的圆环位置而三色河内塔则是将下图左上的圆环经移动成为右上的圆环解法无论是双色河内塔或是三色河内塔其解法观念与之前介绍过的河内塔是类似的同样也是使用递回来解不过这次递回解法的目的不同我们先来看只有两个盘的情况这很简单只要将第一柱的黄色移动至第二柱而接下来第一柱的蓝色移动至第三柱再来是四个盘的情况首先必须用递回完成下图左上至右下的移动接下来最底层的就不用管它们了因为它们已经就定位只要再处理第一柱的上面两个盘子就可以了那么六个盘的情况呢一样首先必须用递回完成下图左上至右下的移动接下来最底层的就不用管它们了因为它们已经就定位只要再处理第一柱上面的四个盘子就可以了这又与之前只有四盘的情况相同接下来您就知道该如何进行解题了无论是八个盘十个盘以上等都是用这个观念来解题那么三色河内塔呢一样直接来看九个盘的情况首先必须完成下图的移动结果接下来最底两层的就不用管它们了因为它们已经就定位只要再处理第一柱上面的三个盘子就可以了双色河内塔 C 实作include void hanoi int disks char source char temp char targetif disks 1printf "move disk from c to c\n" source targetprintf "move disk from c to c\n" source target elsehanoi disks-1 source target temphanoi 1 source temp targethanoi disks-1 temp source targetvoid hanoi2colors int diskschar source Achar temp Bchar target Cint ifor i disks 2 i 1 i--hanoi i-1 source temp targetprintf "move disk from c to c\n" source temp printf "move disk from c to c\n" source temp hanoi i-1 target temp sourceprintf "move disk from c to c\n" temp targetprintf "move disk from c to c\n" source tempprintf "move disk from c to c\n" source targetint mainint nprintf "请输入盘数"scanf "d" n hanoi2colors n return 0C 实作include void hanoi int disks char source char temp char targetif disks 1printf "move disk from c to c\n" source target printf "move disk from c to c\n" source target printf "move disk from c to c\n" source target elsehanoi disks-1 source target temphanoi 1 source temp targethanoi disks-1 temp source targetvoid hanoi3colors int diskschar source Achar temp Bchar target Cint iif disks 3printf "move disk from c to c\n" source tempprintf "move disk from c to c\n" source tempprintf "move disk from c to c\n" source targetprintf "move disk from c to c\n" temp targetprintf "move disk from c to c\n" temp sourceprintf "move disk from c to c\n" target tempelsehanoi disks3-1 source temp targetprintf "move disk from c to c\n" source tempprintf "move disk from c to c\n" source tempprintf "move disk from c to c\n" source temp hanoi disks3-1 target temp sourceprintf "move disk from c to c\n" temp targetprintf "move disk from c to c\n" temp targetprintf "move disk from c to c\n" temp target hanoi disks3-1 source target tempprintf "move disk from c to c\n" target sourceprintf "move disk from c to c\n" target source hanoi disks3-1 temp source targetprintf "move disk from c to c\n" source temp for i disks 3 - 1 i 0 i--if i 1hanoi i-1 target source tempprintf "move disk from c to c\n"target source printf "move disk from c to c\n"target source if i 1hanoi i-1 temp source targetprintf "move disk from c to c\n" source tempint mainint nprintf "请输入盘数"scanf "d" n hanoi3colors nreturn 013Algorithm Gossip 背包问题Knapsack Problem说明假设有一个背包的负重最多可达8公斤而希望在背包中装入负重范围内可得之总价物品假设是水果好了水果的编号单价与重量如下所示0 李子 4KG NT4500 1 苹果 5KG NT57002 橘子 2KG NT22503 草莓 1KG NT1100 4甜瓜 6KG NT6700解法背包问题是关于最佳化的问题要解最佳化问题可以使用「动态规划」Dynamic programming从空集合开始每增加一个元素就先求出该阶段的最佳解直到所有的元素加入至集合中最后得到的就是最佳解以背包问题为例我们使用两个阵列value与itemvalue表示目前的最佳解所得之总价item表示最后一个放至背包的水果假设有负重量 1~8的背包8个并对每个背包求其最佳解逐步将水果放入背包中并求该阶段的最佳解放入李子背包负重 1 2 3 4 5 6 7 8 value 0004500 4500 4500 4500 9000 item ---00000放入苹果背包负重 1 2 3 4 5 6 7 8 value 0004500 5700 5700 5700 9000 item ---0 1 1 1 0放入橘子背包负重 1 2 3 4 5 6 7 8 value 02250 2250 4500 5700 6750 7950 9000 item -2 2 0 1 2 2 0放入草莓背包负重 1 2 3 4 5 6 7 8 value 11002250 3350 4500 5700 6800 7950 9050 item 3 23 0 1 3 2 3放入甜瓜背包负重 1 2 3 4 5 6 7 8 value 11002250 3350 4500 5700 6800 7950 9050 item 3 23 0 1 3 2 3由最后一个表格可以得知在背包负重8公斤时最多可以装入9050元的水果而最后一个装入的水果是3号也就是草莓装入了草莓背包只能再放入7公斤8-1的水果所以必须看背包负重7公斤时的最佳解最后一个放入的是2号也就是橘子现在背包剩下负重量5公斤7-2所以看负重5公斤的最佳解最后放入的是1号也就是苹果此时背包负重量剩下0公斤5-5无法再放入水果所以求出最佳解为放入草莓橘子与苹果而总价为9050元实作 Cincludeinclude define LIMIT 8 重量限制define N 5 物品种类define MIN 1 最小重量 struct bodychar name[20]int sizeint pricetypedef struct body object int main voidint item[LIMIT1] 0int value[LIMIT1] 0int newvalue i s p object a[] "李子" 4 4500 "苹果" 5 5700"橘子" 2 2250"草莓" 1 1100"甜瓜" 6 6700 for i 0 i N i for s a[i]size s LIMIT sp s - a[i]sizenewvalue value[p] a[i]priceif newvalue value[s] 找到阶段最佳解value[s] newvalueitem[s] iprintf "物品\t价格\n"for i LIMIT i MIN i i - a[item[i]]sizeprintf "s\td\n"a[item[i]]name a[item[i]]priceprintf "合计\td\n" value[LIMIT] returnJavaclass Fruitprivate String nameprivate int sizeprivate int price public Fruit String name int size int pricethisname namethissize sizethisprice pricepublic String getNamereturn namepublic int getPricereturn pricepublic int getSizereturn sizepublic class Knapsackpublic static void main String[] argsfinal int 8final int MIN 1int[] item new int[1]int[] value new int[1] Fruit fruits[]new Fruit "李子" 4 4500new Fruit "苹果" 5 5700new Fruit "橘子" 2 2250new Fruit "草莓" 1 1100new Fruit "甜瓜" 6 6700 fo。
C语言经典算法大全精选

C语言经典算法大全精选1.排序算法1.1冒泡排序:通过不断交换相邻元素的位置,将最大(最小)值“冒泡”到序列的末尾(开头)。
1.2插入排序:将未排序的元素逐个插入已排序的序列中,保持序列始终有序。
1.3选择排序:每次从未排序的元素中选择最小(最大)的元素,放到已排序序列的末尾(开头)。
1.4快速排序:通过递归地将序列分割为较小和较大的两部分,然后分别对两部分进行排序。
1.5归并排序:将序列递归地分割为两个子序列,分别排序后再将结果合并。
1.6堆排序:构建最大(最小)堆,然后逐步将堆顶元素与最后一个元素交换,并调整堆结构。
2.查找算法2.1顺序查找:逐个比较元素,直到找到目标元素或遍历完整个序列。
2.2二分查找:在有序序列中,通过不断缩小查找范围,找到目标元素。
2.3插值查找:根据目标元素与序列中最大、最小元素的关系,按比例选择查找范围。
2.4哈希查找:利用哈希函数将目标元素映射到一个唯一的位置,从而快速定位目标元素。
3.字符串算法3.1字符串匹配算法:在文本串中查找给定的模式串,并返回匹配位置。
3.2字符串翻转:将一个字符串逆序输出。
3.3字符串压缩:将连续出现多次的字符压缩为一个字符,并输出压缩后的字符串。
3.4字符串拆分:按照指定的分隔符将字符串拆分为多个子串,并返回子串列表。
3.5字符串反转单词:将一个句子中的单词顺序逆序输出。
4.图算法4.1深度优先:从起始顶点出发,递归地访问所有能到达的未访问顶点。
4.2广度优先:从起始顶点出发,逐层地访问与当前层相邻的未访问顶点。
4.3最小生成树:找到连接所有顶点的具有最小权值的无环边集合。
4.4最短路径:找到两个顶点之间最短路径的权值和。
4.5拓扑排序:找到一个顶点的线性序列,满足所有有向边的起点在终点之前。
5.数学算法5.1质数判断:判断一个数是否为质数(只能被1和自身整除)。
5.2求最大公约数:找到两个数的最大公约数。
5.3求最小公倍数:找到两个数的最小公倍数。
C语言程序设计教程算法

三种构造旳特点: 只有一种入口和出口 构造内旳每一部分都有机会被执行到。 构造内不存在死循环
顺序构造
A
B 流程图
A B
N-S图
选择构造 真Biblioteka 假P二分支选择构造 A
B
真 P假 AB
多分支选择构造
k
k=k1 k=k2
A1
A2 ...
返回s3; 不然,结束
用自然语言表达
开始 1p 2i P*i p i+1 i i>5 结束
用流程图表达
1p 2I P*i p i+1 i 直到i>5 结束
用N-S流程表达
int main(void) { int i,t; t=1; i=2; while(i<=5) { t=t*i; i=i+1; } printf(“%d”,t); return 0; }
最终得到旳p就是5!旳值。
例2.求1×3×5×7×9 ×11
上述算法稍作改动: s1: 1 p; s2: 3 i; s3: p ×i p; s4: i+2 i s5: 若i11,返回s3;不然,结束。
请同学们仔细分析循环结束旳条件,即 s5环节,假如在求1×3×5×7×9 ×11时, 将s5环节写成:
根;②有两个相等旳实根
自然语言描述举例
例如:描述计算并输出z=y/x旳流程,能够用自然语 言描述如下: (1)输入x,y。 (2)判断x是否为0:
若X=0,则输犯错误信息; 不然计算 y/x z,且输出z。
构造化语言描述举例
例如:描述计算并输出z=y/x旳流程,能够用构造化 语言描述算法如下:
(1)input x,y。 (2)if x=0 print (“非法输入”)
机器学习算法设计(C语言版)

机器学习算法设计(C语言版)简介本文档介绍了机器研究算法设计的基本原理和实现方法,使用C语言编写。
算法设计步骤1. 数据预处理:对输入数据进行清洗和转换,使其适合机器研究算法的处理。
2. 特征提取:从原始数据中提取出有用的特征,用于训练模型和进行预测。
3. 模型选择:选择适合问题类型的机器研究模型,如决策树、支持向量机等。
5. 模型评估:通过评估指标(如准确率、召回率等)对训练好的模型进行评估,检验其性能和泛化能力。
7. 预测与应用:使用训练好的模型对新的数据进行预测,并应用到实际问题中。
算法实现示例以下是一个简单的机器研究算法实现示例,使用C语言编写:include <stdio.h>// 假设数据样本为二维数组[x, y]int samples[5][2] = {{1, 3}, {2, 5}, {3, 7}, {4, 9}, {5, 11}};// 线性回归算法void linearRegression() {// 初始化参数float a = 0, b = 0;// 计算参数for (int i = 0; i < 5; i++) {a += (samples[i][0] - 3) * (samples[i][1] - 7);b += (samples[i][0] - 3) * (samples[i][0] - 3);}a /= b;// 输出结果printf("线性回归方程为:y = %.2fx + %.2f\n", a, 7 - 3 * a);}int main() {linearRegression();return 0;}以上是一个简单的线性回归算法的实现示例,用于拟合给定的样本数据。
在实际应用中,还需要将其与其他的机器研究算法进行比较和评估,选择最合适的算法来解决实际问题。
结论本文档介绍了机器学习算法设计的基本原理和实现方法,以及一个简单的算法实现示例。
C语言程序设计—算法

算法步骤
S1: sign=1
sign:表示当前项的数值符号
term:表示当前项的值
sum:表示当前项的累加和
deno:表示当前项的分母
S2: sum=1
S3: deno=2
S4: sign=(-1) sign
S5: term=sign
(1/deno)
S6: sum=sum+term
S7: deno=deno+1
数”
结束
N
传统流程图的弊端
传统的流程图用流程线指出各框的执行顺序,对
流程线的使用没有严格限制。因此,使用者可以
不受限制地使流程随意地转来转去,使流程图变
得毫无规律,阅读时要花很大精力去追踪流程,
使人难以理解算法的逻辑。
三种基本结构
真
假
P
假
P
A
A
B
真
B
A
顺序结构
选择结构
循环结构
三种基本结构的特点
g1:表示第一个学生的成绩
gi:表示第i个学生的成绩
N
算法步骤
n:表示学生学号
n1:表示第一个学生的学号
i+1=>i
Y
S1: 1=>i
S2: 如果gi≥80,则输出ni和gi,否则不输出
S3: i+1=>i
i>50
Y
1=>i
gi≥80
输出ni、
gi
S4: 如果i≤50,返回到S2,继续执行,否则,
算法结束
向计算机语言算法(即程序)过渡。
算法的流程图表示举例
【例2.16】求5!,用伪代码表示。
begin
最全最常用算法设计方法(C语言)

一、迭代法迭代法是用于求方程或方程组近似根的一种常用的算法设计方法。
设方程为f(x)=0,用某种数学方法导出等价的形式x=g(x),然后按以下步骤执行:(1)选一个方程的近似根,赋给变量x0;(2)将x0的值保存于变量x1,然后计算g(x1),并将结果存于变量x0;(3)当x0与x1的差的绝对值还小于指定的精度要求时,重复步骤(2)的计算。
若方程有根,并且用上述方法计算出来的近似根序列收敛,则按上述方法求得的x0就认为是方程的根。
上述算法用C程序的形式表示为:【算法】迭代法求方程的根{ x0=初始近似根;do {x1=x0;x0=g(x1);/*按特定的方程计算新的近似根*/} while ( fabs(x0-x1)>Epsilon);printf(“方程的近似根是%f\n”,x0);}迭代算法也常用于求方程组的根,令X=(x0,x1,…,x n-1)设方程组为:x i=g i(X) (I=0,1,…,n-1)则求方程组根的迭代算法可描述如下:【算法】迭代法求方程组的根{ for (i=0;i<n;i++)x[i]=初始近似根;do {for (i=0;i<n;i++)y[i]=x[i];for (i=0;i<n;i++)x[i]=gi(X);for (delta=0.0,i=0;i<n;i++)if (fabs(y[i]-x[i])>delta) delta=fabs(y[i]-x[i]);} while (delta>Epsilon);for (i=0;i<n;i++)printf(“变量x[%d]的近似根是%f”,I,x[i]);printf(“\n”);}具体使用迭代法求根时应注意以下两种可能发生的情况:(1)如果方程无解,算法求出的近似根序列就不会收敛,迭代过程会变成死循环,因此在使用迭代算法前应先考察方程是否有解,并在程序中对迭代的次数给予限制;(2)方程虽然有解,但迭代公式选择不当,或迭代的初始近似根选择不合理,也会导致迭代失败。
C语言算法大全

C语言经典算法目录一、单元加.................................... 错误!未定义书签。
1.erre ...................................... 错误!未定义书签。
2. erre2 ................................... 错误!未定义书签。
3. 数组完全单元........................ 错误!未定义书签。
4. 栈单元加.............................. 错误!未定义书签。
二、底层编程 ................................ 错误!未定义书签。
1. asm ..................................... 错误!未定义书签。
2. C标志符命名源程序............... 错误!未定义书签。
3. ping .................................... 错误!未定义书签。
4. winsock2 ............................. 错误!未定义书签。
5. 检测鼠标.............................. 错误!未定义书签。
6. 检出错误.............................. 错误!未定义书签。
7. 时间陷阱.............................. 错误!未定义书签。
三、汉诺塔.................................... 错误!未定义书签。
1. 非递归................................. 错误!未定义书签。
2. 汉诺塔................................. 错误!未定义书签。
3. 汉诺塔2 .............................. 错误!未定义书签。
《C算法设计》PPT课件

{
x2 = 1;
x1 = x2;
do{ x1 = x2;
x2 = (x1 + a/x1)/2; }
x2 = (x1 + a/x1)/2;
}while(x1-x2>0.00001 ||x2-x1>0.00001);
cout << x2 << endl;
return 0;
}
28
28 /67
基本算法 – 排序
36 /67
4.2 冒泡排序——示例(续)
37
37 /67
4.2 冒泡排序——算法、程序
开始
初始化:wall=0
N
还有未排序的数?
Y N
还有未冒泡的数?
Y
比较相邻数
交换相邻数
结束 38
38 /67
基本算法 – 排序
各种排序方法简介:就地排序算法(不增加新的存储空间)
1、插入排序法(Insert Sort)
冒泡排序,Bubble sort
数据列表被分为两个子列表:已排序和未排序。 未排序列表中最小(或最大)的元素通过冒泡的 形式(从后往前冒泡)从未排序列表中交换到已 排序列表中。
34
34 /67
4.2 冒泡排序——示例
冒 泡
比较
的
过
比较并交换
程
35
35 /67
4.2 冒泡排序——示例(续)
36
动作n
18
18 /67
3 流程图表示算法
算法是让人来理解的,因此需要有效的算 法表示机制
自然语言表示法 伪代码表达法 流程图表示法
19
19 /67
3 流程图表示算法
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
//实验2_1_1_贪心算法作业调度问题.cpp :定义控制台应用程序的入口点。
//
#include "stdafx.h"
#include<iostream>
#include<ctime>
using namespace std;
const int N = 8; //产生N个任务
8.学会用贪心法分析和解决实际问题
八、实验内容
设计贪心算法实现作业调度,要求按作业调度顺序输出作业序列。如已知要处理的作业数n=8,可用机器数m=(1,2,3),作业完成的期限为d=(4, 2, 4, 5, 6, 4, 5, 7),求该条件下的最大效益。
九、实验环境
程序设计语言:c++
编程工具:microsoft visual studio 2010
//
#include "stdafx.h"
#include<iostream>
#include<cstdlib> //用于p[i] = rand()%100;
#include<ctime> //用于srand((unsigned long)time(0));
#include<iomanip>
using namespace std;
}
void sortprofit(Work*w,int n){
Work tmp ;
for(int i=1;i<n;i++)
for(int j=0;j<n-i;j++)
if(w[j].profit<w[j+1].profit){
tmp = w[j];w[j]=w[j+1];w[j+1]=tmp;
}
cout<<"排序后:"<<endl;
#include<memory.h>
using namespace std;
void Init_Graph(int N,int k,int **S, int **L){
int i,j;
cout<<"请输入两端顶点以及边长(以0结束):"<<endl;
cin>>i;
while (i!=0){
cin>>j;
}
F=new int *[N+1];
for (i=0;i<N+1;i++){
int *temp = new int[right-left+1];
int i=left,j=mid+1,k=0;
while(i<=mid&&j<=right){
if(p[i]<=p[j])
temp[k++]=p[i++];
else
temp[k++]=p[j++];
}
while(i<=mid)
temp[k++]=p[i++];
for (i=0;i<N+1;i++){
L[i]=new int[N+1];
for (j=0;j<N+1;j++)
{
L[i][j]=INT_MAX;
}
}
S= new int*[N+1];
for (i=0;i<N+1;i++){
S[i]=new int[N+1];
memset(S[i],0,sizeof(int)*(N+1));
}
//输出数组函数
void output(int *p,int n){
for(int i=0;i<n;i++)
cout<<setw(3)<<p[i]<<" ";
cout<<endl;
}
//归并排序算法
void Merge(int *p,int n,int left,int mid,int right){
int mid=(left+right)/2;
Divide(p,n,left,mid);
Divide(p,n,mid+1,right);
Merge(p,n,left,mid,right);
}
}
int _tmain(int argc, _TCHAR* argv[])
{
int a[N];
input(a,N);
S[i][j++]=tempnode;
else break;
};
}
}
void Plan(int N,int k,int **S,int **F,int** L,int *path){
int i,j,t=N;
int m;
int point;
point=S[k][0];
for (i=k-1;i>=1;i--){
{
cout<<path[t]<<" ";
t=path[t];
}
cout<<endl<<"检索后得到最短距离为:";
cout<<F[i+1][0]<<endl;
}
int _tmain(int argc, _TCHAR* arg){
cout<<"本次对教材124页图7-1的五段图进行测试(本行语句仅为提示语句,对该程序的正确性的验证没有任何影响,按要求输入即可)"<<endl;
while(j<=right)
temp[k++]=p[j++];
for(int i=0,k=left;k<=right;k++,i++)
p[k] = temp[i];
delete[]temp;
}
//分治算法
void Divide(int *p,int n,int left,int right){
if(left<right){
cout<<"产生的随机数组:"<<endl;
output(a,N);
Divide(a,N,0,N-1);//调用Divide函数进行分治算法以及合并排序
cout<<"调用Merge(...)之后:"<<endl;
output(a,N);
return 0;
}
五、实验结果截图(201603020)
//两次运行结果
void output(Work*w,int n);
void sortprofit(Work*w,int n);
void start(Work*w,int n,int o);
int _tmain(int argc, _TCHAR* argv[])
{
input(work,N);
sortprofit(work,N);
F[i][j] = F[i+1][m] + L[S[i][j]][S[i+1][m]];
path[S[i][j]]=S[i+1][m];
t--;
}
m++;
}
}
j++;
}
}
cout<<"路径上的点为:";
t=0;
path[t]=1;
cout<<path[t]<<" ";
t=path[t];
while (t<N)
实验三动态规划法求多段图问题
十三、实验目的
9.掌握动态规划算法的基本思想
10.掌握多段图的动态规划算法
11.选择邻接表或邻接矩阵方式来存储图
4、分析算法求解的复杂度。
十四、实验内容
设G=(V,E)是一个带权有向图,其顶点的集合V被划分成k>2个不相交的子集Vi,1<i<=k,其中V1和Vk分别只有一个顶点s(源)和一个顶点t(汇)。图中所有边的始点和终点都在相邻的两个子集Vi和Vi+1中。求一条s到t的最短路线。参考讲义p136图5-24中的多段图,试选择使用向前递推算法或向后递推算法求解多段图问题。
int N,k;
int i,j;
int **L,**S,**F;//L:边的长度;S:每个阶段的顶点;F:记录每个阶段的状态中的点到终点的距离
int *path;//保存检索的结果
cout<<"请输入顶点的个数:";
cin>>N;
cout<<"请输入阶段数:";
cin>>k;
//申请空间
L=new int*[N+1];
output(w,n);
}
void start(Work*w,int n,int o){
cout<<"安排作业:"<<endl;
int end=0;
int num;
for(int i=0;i<o;i++){
cout<<"机器"<<i+1<<" : ";
