建筑力学15压杆稳定详解
压杆稳定解析课件

查表13-1,得 0.276, 与 0.289 相差不大
故可选28a工字钢,校核其稳定性
F 45.1MPa [ ] 46.92MPa
A
例6: 图示梁杆结构,材料均为Q235钢。AB梁为14号
工字钢,BC杆为 d=20mm的圆杆。已知: F=25kN,
l1=1.25m,l2=0.55m,E=206GPa,p=200MPa, s=235MPa,n=1.4,nst=1.8。求校核该结构是否安全。
二﹑欧拉公式应用中的几个问题
(1)Fcr与EI成正比,与l2 成反比,且与杆端约束有 关。 Fcr越大,压杆稳定性越好,越不容易失稳;
(2)杆端约束情况对Fcr的影响,是 通过长度系数μ来实现的。要根据实 际情况选择适当的μ 。
(3)当压杆在两个形心主惯性平面内 的杆端约束情况相同时,则失稳一定 发生在最小刚度平面,即I 最小的纵 向平面。
y z x
轴销
y z
x
轴销
解:xy面内,两端视作铰支,μ = 1,iz = 4.14 cm
z
l
iz
1 2 4.14 102
48.3
y z
x
轴销
xz面内,两端视作固定端,μ = 0.5,查表iy= 1.52cm
y
l
iy
0.5 2 1.52 102
65.8
显然 z y
压杆将在xz平面内失稳 而 p 100,u s 60
lw
x
O
y
M(x) Fcr=F
w
w = Asinkx +Bcoskx (d)
Fcr
k2=Fcr / EI 两个边界条件:
w = Asinkx +Bcoskx
材料力学:Ch15压杆稳定

4
1041.8kN
n PcrAC 1041 .8 5
P≤240.6kN PAC 0.866 P
例题7:已知压杆为如球果铰两,根由槽两钢根只等在边两角端钢连铆接成λ1=100,λ2=62, ,nslt==12..44cr8m,3,0[上4σ-A]述==11.2稳16×20定M28计P.9a算c,m和试2,强校铆度核钉计压孔算杆直会。不径会为发23生m变m,化P? =800kN
解:
FA
F
B
t Et cr
l 0.5 600 141.5
i 2.12
细长杆
Et π 2E 2
t
π 2E
E 2
π2
2
π2 12.5106 141.52
39.43
C
临界压力小结:
每一个压杆均有与之相应的临界应力 临界应力取决于压杆的材料、柔度
= l i
1
1
2E p
判别弹性平衡稳定性的静力学准则 (statical criterion for elastic stability)
FFPP FP
FP<FPcr :在扰动作用下,
直线平衡构形转变为弯曲 平衡构形,扰动除去后, 能够恢复到直线平衡构形, 则称原来的直线平衡构形 是稳定的。
FP FP
FP>FPcr :在扰动作用下,
55.1(< s)短粗杆
A 235106 2.3103
b a d d 752KN
i1 11.55mm
Pcr11
129.9
375KN
i2 2
16.3mm 92
Pcr 2 644KN
P i3 15.95mm 3 94
Pcr3 635KN
压杆稳定小结
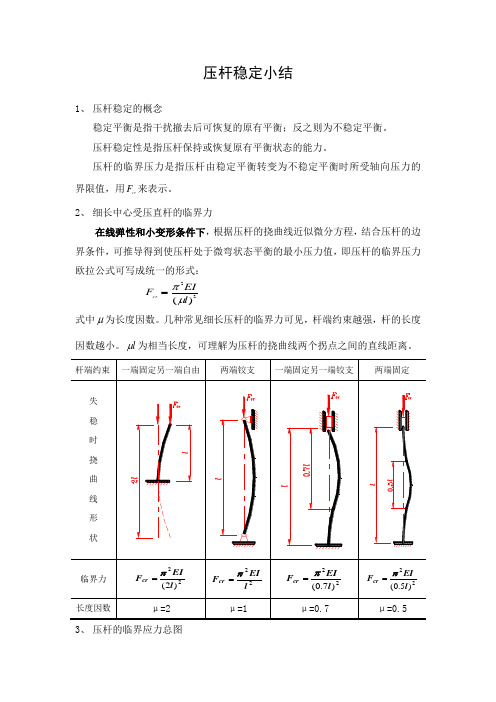
压杆稳定小结1、 压杆稳定的概念稳定平衡是指干扰撤去后可恢复的原有平衡;反之则为不稳定平衡。
压杆稳定性是指压杆保持或恢复原有平衡状态的能力。
压杆的临界压力是指压杆由稳定平衡转变为不稳定平衡时所受轴向压力的界限值,用cr F 来表示。
2、 细长中心受压直杆的临界力在线弹性和小变形条件下,根据压杆的挠曲线近似微分方程,结合压杆的边界条件,可推导得到使压杆处于微弯状态平衡的最小压力值,即压杆的临界压力欧拉公式可写成统一的形式:22)(l EIF crμπ=式中μ为长度因数。
几种常见细长压杆的临界力可见,杆端约束越强,杆的长度因数越小。
l μ为相当长度,可理解为压杆的挠曲线两个拐点之间的直线距离。
(d)(d)(d)3、 压杆的临界应力总图(1) 压杆的临界应力压杆在临界力作用下,其横截面上的平均应力称为压杆的临界应力, crcr F Aσ=(2) 欧拉公式的适用范围线弹性范围,()22cr cr p 22F EI E A l A ππσσλμ===≤ 即p λλ≥= 时,欧拉公式才能适用。
通常称p λλ≥的压杆为大柔度压杆或细长压杆。
(3) 压杆的柔度(或长细比)i l μλ=是一无量纲的量。
一般情况下,由于杆端约束(μ)或惯性半径(i )的不同,压杆在不同的纵向平面内具有不同的柔度值,压杆失稳首先发生在柔度最大的纵向平面内。
(4) 临界应力总图压杆的临界应力随柔度λ变化的λσ-cr 图称为临界应力总图。
大柔度杆p λλ≥,临界应力低于比例极限,可按欧拉公式计算,22λπσEcr= ;中柔度杆p s λλλ≤≤,临界应力超过比例极限,可按经验公式计算,如直线公式: λσb a cr -=,其中a 、b 为与材料有关的常数。
或钢结构设计中采用的抛物线公式,以及折减弹性模量理论进行计算;图13-12小柔度杆s λλ≤(或b λ),临界应力达极限应力:塑性材料s cr σσ=,脆性材料cr b σσ=,属于强度问题。
压杆稳定—提高压杆稳定性的措施(建筑力学)

提高压杆稳定性的措施
1.合理选择材料 细长压杆:
ห้องสมุดไป่ตู้ cr
2E 2
采用E值较大的材料可提高压杆的稳定性 由于各种钢材的E值大致相同,所以对大柔度钢压杆不宜选用优质钢材,以避 免造成浪费。
中粗压杆
cr a b
短粗压杆
cr u
采用强度较高的材料能够提高其临界应力,即能提高其稳定性。
提高压杆稳定性的措施
压杆稳定(10年)解析PPT课件

(3)当增大P至某一值 Pcr 时: 小的横向干扰 就会使杆失稳;
Pcr: 临界载荷(critical load)
扰动的种类:小的横向力;杆件表面凹坑; 杆件初始曲率等。
扰动是失稳的外因,杆件在外载作用下处于临界状态是内因。
2020年9月28日
14
P
P
压杆的实验观察
横向扰动
横向扰动
测试二
(1)将杆加粗或变短, 杆不容易失稳。
P Pcr 理想压杆曲线 B
实际压杆实验曲线
O
2020年9月28日
ymax
24
讨论
4. 精确微分方程
y
M
(1
y2
3
)2
EI
P
P Pcr
P Pcr
精确微分方程
P1.01P5cr
B
近似微分方程
实际压杆实验曲线
③稳定性 外力—?—稳定性条件
失去稳定性 后果更严重!
2020年9月28日
12
稳定性: 指平衡状态的稳定性 1.稳定平衡与不稳定平衡
不稳定平衡
2020年9月28日
稳定平衡
13
压杆的实验观察
测试一
P
(1) P=0或为拉时: 小的横向干扰不会使杆
离开起初始平衡位置(或失稳);
横向扰动 (2)增大P: 小的横向干扰仍不会使杆失稳;
2020年9月28日
1
第15章 压杆稳定
15.1 压杆稳定的概念 15.2 两端铰支细长压杆的临界力 15.3 两端约束不同时的临界力 15.4 临界力、经验公式、临界力总图 15.5 压杆的稳定校核 15.6 压杆稳定计算的折减系数法 15.7 提高压杆稳定性的措施
工程力学压杆稳定

MA=MA =0 相当长为2l旳两端简支杆
Fcr
EI 2
(2l ) 2
l
F
0.5l
两端固定 EI 2
Fcr (0.5l) 2
图形比拟:失稳时挠曲线 上拐点处旳弯矩为0,故可设想 此处有一铰,而将压杆在挠曲 线上两个拐点间旳一段看成为 两端铰支旳杆,利用两端铰支 旳临界压力公式,就可得到原 支承条件下旳临界压力公式。
两端铰支
= 1
一端固定,一端自由 = 2
一端固定,一端铰支 = 0.7
两端固定
= 0.5
§11-4中小揉度杆旳临界压力
一、临界应力与柔度
cr
Fcr A
对细长杆
cr
2 EI (l)2 A
2 Ei2 ( l ) 2
2E ( l )2
记 l
i
i
cr
2E 2
––– 欧拉公式
:柔度,长细比
[cr] = [] < 1,称为折减系数
[ cr ] [ ]
根据稳定条件
F Fcr nst
F A
Fcr Anst
cr
nst
[ cr : 工作压力
: 折减系数
A: 横截面面积
[]:材料抗压许用值
解:首先计算该压杆柔度,该丝杆可简化为图示
下端固定,上端自由旳压杆。
=2
F
l=0.375m
i I d A4
l l 2 0.375 75
i d 0.04 / 4 4
查表, = 0.72
F
A
80 103
0.72 0.042
88.5106 88.5MPa [ ] 160MPa
4
故此千斤顶稳定性足够。
工程力学上册15压杆稳定

压杆的稳定性直接关系到这些结构物的安全性和可靠性,一旦发生失稳,可能会导致结构物的破坏和倒塌,造成严重的人员伤亡和财产损失。
因此,对压杆稳定性的研究和分析是工程力学中非常重要的一个方面,也是工程设计和安全评估的重要依据。
压杆稳定的重要性
02
压杆的分类与特性
总结词
长细比是描述压杆细长程度的重要参数,对临界力的影响显著。
工程力学上册15压杆稳定
目录
压杆稳定概述 压杆的分类与特性 压杆稳定的影响因素 压杆稳定的计算方法 压杆稳定的实验研究 工程实例分析
01
压杆稳定概述
01
02
压杆稳定的定义
当压杆受到的力小于其临界力时,压杆保持稳定平衡;当压杆受到的力大于其临界力时,压杆将发生屈曲失稳。
压杆稳定是指压杆在受到外力作用时,能够保持其原有平衡状态的能力。
03
压杆稳定的影响因素
压杆在制造过程中可能会产生弯曲,这种弯曲在受力时会进一步发展,导致压杆失稳。
为了提高压杆的稳定性,应尽量减小初始弯曲,可以通过提高制造精度和选用合适的材料来实现。
初始弯曲的影响
减小初始弯曲
初始弯曲
材料在加工过程中会形成残余应力,这些应力会在受力时对压杆的稳定性产生影响。
残余应力
结论应用
将实验结论应用于实际工程中,指导压杆结构的合理设计和应用。
实验结果与分析
06
工程实例分析
桥梁结构的压杆稳定分析
总结词:桥梁结构的压杆稳定分析是确保桥梁安全的重要环节,需要考虑多种因素,如材料特性、载荷分布和支撑条件等。
高层建筑的压杆稳定分析
总结词:高层建筑的压杆稳定分析是确保高层建筑安全的重要环节,需要考虑多种因素,如建筑高度、材料特性、风载荷和地震载荷等。
15压杆稳定

Fcr 269kN
图示结构ABC为矩形截面杆,b=60mm,h=100mm,l=4m, BD为圆截面杆,d=60mm,两杆材料均为A3钢,E=200GPa, σp =200MPa,均布载荷 q=1kN/m,稳定安全系nst=3。校核BD杆 的稳定性。 解:通过外力分析可知BD杆件为受 压杆件,根据静力学计算FBD:
M
A
0
FBD l si n45o 2ql 2 0 FBD 11.3kN
计算最大柔度
BD
l
i
2 4
d 4 6 4 d 2 4
3 7 7.1
p
2E 101 p
l
A3钢:a=304MPa,b=1.12MPa;E=206GPa, p=200MPa, s =235MPa
p
2E p
2 206 109
200 10
6
100
a s 304 235 0 61.6 b 1.12 0 max p 所以,应由经验公式求临界应力。
i
L2
(1)
(2)
(3)
3
L3
i
1 125 p
2 E d 2 ( Fcr )1 cr A 2 2540KN 1 4
L2 L3
0 2 62.5 p
( Fcr )2 cr A (a b2 ) 4705KN
2E 即: cr 2
l
i
I min i A
惯性半径。
3.柔度:
— —杆的柔度(或长细比 )
4.大柔度杆的分界:
cr
2E 2 P
2E P P
压杆的稳定性
建筑力学
x
δ
Fcr
l
w
x
o
y
z y
压杆的稳定性
9
考虑下图细长压杆
M ( x) Fcr (d w)
在线弹性、小变形情况下,且 不考虑剪切对于变形的影响, 则其挠曲线近似微分方程为
EIzw M ( x) Fcr (d w)
建筑力学
压杆的稳定性
16
§7-3 欧拉公式的适用范围·临界应力总图
应注意:
求压杆临界荷载的欧拉公式Fcr= p2EI /( l )2只
适用于压杆失稳时仍在线弹性范围内工作的情况。 按失稳的概念,在临界荷载作用下尽管压杆的
直线状态的平衡是不稳定的,但如果不受干扰,杆 仍可在直线状态下保持平衡。
建筑力学
Fcr
Fcr x
A l
B
Fcr
π2EI y l2
1
A l
B
Fcr
π2EI y (0.7l )2
0.7
y
建筑力学
Fcr
压杆的稳定性
A l
Fcr
π2EI y (0.5l )2
l
0.5
B
15
Fcr
v
Fcr
π2EI y (2l )2
2
从上述分析可知,中心受压直杆的临界力Fcr 与杆端的约束情况有关,杆端的约束越强,临界 力越大。
建筑力学
压杆的稳定性
§7-1 关于稳定性的概念
实际压杆存在的情况:
(1) 本身不可能绝对地直; (2) 材质不可能绝对地均匀; (3) 轴向压力也会有偶然偏心。
工程力学15-压杆稳定详解

§15-3 临界载荷的欧拉公式
一、两端铰支细长压杆的临界载荷
1、挠曲线近似微分方程: EIy" M(x) Fy
引用记号:k 2 F y" k 2 y 0 EI
2、该微分方程的通解为
y Asin kx Bcoskx
压 杆
式中A、B为积分常数
在
微
3、杆的边界条件
FN
5 2
F
150kN
2.CD杆的临界压力:
xA A
C
F
B
yA 2m
3m FN
I (D4 d 4 ) (1004 804 ) 1012 2.9 106 m4
64
64
2.9106 mm4
16
Fcr
2
l
EI
2
2
200103 2.9 3.52 106
106
467103 N 467kN
态
FFF===cccr
rr
b) 微
弯 F1
平 衡
F>FF>cFr cr
c)
失 稳
F1
干扰力去除后恢 复直线状态
干扰力去除后 保持微弯
干扰力去除后继续 变形,直至倒塌
1.临界状态: 由稳定平衡向微弯平衡过度的状态。
2.临界载荷Fcr: 保 持 压 杆 稳 定 的 最 大 轴 向 压 力 , 使 压 杆 失
公式。
解:变形如图,其挠曲线近似微分方程为:
L
P
P
EIyM (x)PyM
M0
令:k 2 P
EI
x
Px
y k 2 y k 2 M
M0
y
建筑力学压杆稳定课件

由此可以计算压杆在保证稳定的前提下,能承受的最大轴压力,又称为压杆的临界荷载 或容许荷载。当施加的压力小于容许荷载时,构件不会发生失稳破坏,反之,构件将发生失
稳破坏。对于此类问题,一般也要首先计算出压杆的长细比 ,根据 查出相应的折减系 数 ,再按照上式进行计算。
建筑力学压杆稳定
3. 对压杆进行截面设计
建筑力学压杆稳定
• 应用压杆的稳定条件,可以进行三个方面的问题计 算:
• 1. 稳定校核 • 已知压杆的截面形状和尺寸,杆件长度及支承条件
,杆件的轴心压力,根据公式(9-16)即可以验证 压杆是否会发生失稳破坏,即验证其稳定性。
建筑力学压杆稳定
例 9-4 如图 所示,构架由两根直径相同的圆杆构成,杆的材料为 Q235 钢,直径
立,由此可得的适用条件为:
cr
2E 2
p
令
p
2E p
则
p
(9-7) (9-8)
式(9-8)是欧拉公式适用范围的柔度表达形式,表明只有当压杆的实际柔度 p 时,才能
用欧拉公式来计算其临界应力和临界力。显然, p 是应用欧拉公式的最小柔度。压杆的实
际柔度 λ 随压杆的几何形状尺寸和杆端约束条件变化,但 p 是仅由材料性质确定的值。
d=20mm,材料的许用应力 =170MPa,已知 h=0.4m,作用力 F=15kN。试在计算平面内校核
二杆的稳定。
图 9-3
建筑力学压杆稳定
解:(1)计算各杆承受的压力 取结点 A 为研究对象,根据平衡条件列方程
x 0 FAB cos 450 FAC cos 300 0 Y 0 FAB sin 450 FAC sin 300 F 0
建筑力学压杆稳定
第二节 临界力和临界应力 1、影响临界力的因素 实践表明,影响细长压杆临界力的主要因素是材料的特性、截面几何形状和杆件的长度, 以及压杆两端的约束条件。 (1)材料的特性 对于两个截面几何形状及杆件长度相同的木杆和钢杆,受轴向压力 作用,木杆会先失稳,即木杆的临界力比钢杆的小,说明弹性模量 E 小的材料,其临界力也 小。 (2)截面几何形状 当截面尺寸相同,而截面形状不同时,其临界力也会不相同。影 响临界力的截面参数是截面惯性矩,惯性矩越大,杆件就越不容易失稳,说明截面的惯性矩 大,临界力也大。 (3)杆件的长度 其他条件相同时,长杆比短杆更易失去稳定,故临界力要小些。 (4)压杆两端的约束条件 对同一根细长压杆,两端的约束越强,压杆的轴心受压承 载力越大,因而,压杆两端的约束条件对压杆的稳定临界力也有很大的影响。当其他条件相 同时,一端固定、而一端铰支的压杆比两端铰支的更不容易失稳,说明两端支承越牢固,压 杆的临界力就越大。
理论力学——压杆稳定

M ( x ) Fp y d y dx
2 2
设k
2
Fp y EI
Fp EI
2
, 则
2
d y
(二阶线性常数 k y 0 2 齐次微分方程) dx
通解为
y a sin kx b cos kx
材料力学
式中a、b、k为待定常数。
压杆稳定问题/细长压杆的临界力
边界条件为:
y
x
z
x
材料力学
压杆稳定问题/压杆的稳定计算
解:
p
E
2
y
p
99.35
z
x
考虑xy平面失稳(绕z轴转动)
iz Iz A
bh / 12 bh
1 2.3 h / 12
3
h 12
x
z
zl
iz
Iy A
132.8
y
yl
iy
0.5 2.3 b / 12
6
4
d2
2
151.47 KN
材料力学
FN 2 F
Fcr nst
151 .47 3
50.5KN
所以起重机架的最大起重量取决于杆AC的强度,为
Fmax 26.7 KN
材料力学
例8-4 图示托架结构,梁AB与圆杆BC 材料相同。梁AB为16号工字
钢,立柱为圆钢管,其外径D=80 mm,内径d=76mm,l=6m,a=3 m,
材料力学
压杆稳定问题/稳定的概念
临界载荷的概念
压杆的压力逐渐上升,使压杆的平衡由稳定的平衡状态
向不稳定的状态的质变的转折点,称为临界载荷,以 Fcr
压杆稳定(教材)

第九章压杆稳定§9-1 压杆稳定的基本概念在前面的一些章节中,已经讨论了构件在静力平衡状态下的应力、应变以及强度和刚度的设计问题。
构件除了强度和刚度不足而引起失效外,有时由于不能保持其原有的平衡状态而失效,这种失效形式称为丧失稳定性。
考察图9-1所示的等直杆AB,若A端固定,B端作用沿轴线方向的载荷p。
实验表明,若外力p较小时,杆件保持在直线形状的平衡,微小的外界扰动将使杆件发生轻微的弯曲,干扰力解除后,杆件仍恢复直线形状,即外界的干扰不能改变其原有的铅垂平衡状态,压杆的直线平衡是稳定的;若外力p慢慢地增加到某一数值并且超过这一数值时,任何微小的外界扰动将使杆件AB发生弯曲,干扰力解除后,杆件处于弯曲状态下的平衡,不能恢复原图9-1有的直线平衡状态,杆件原有的直线平衡状态是不稳定的。
若外力P继续增大,杆件将因过大的弯曲变形而突然折断。
杆件维持直线稳定平衡的最大外力称为临界压力,记为P cr。
压杆丧失其直线形状的平衡而过渡为曲线平衡,称为丧失稳定,简称“失稳”。
工程上,一般的细长压杆,由于轴向载荷的偏心或杆件的初曲率,往往因这种屈曲而导致失效的。
因此压杆的“失稳”也称为“屈曲”。
机械中有许多细长压杆,如螺旋千斤顶的螺杆(图9-2a),内燃机气阀门的挺杆(图9-2b)等。
还有,桁架结构中的抗压杆、建筑物中的柱等都是压杆。
这类构件除了要有足够的强度外,还必须有足够的稳定性,才能正常工作。
(a)(b)图9-2除了压杆的失稳形式外,一些细长或薄壁的构件也存在静力平衡的稳定性问题。
例如,细长圆杆的纯扭转,薄壁矩形截面梁的横力弯曲以及承受均布压力的薄壁圆环等,都有可能丧失原有的平衡状态而失效。
图9-3给出了几种构件失稳的示意图,图中虚线分别表示其丧失原有平衡形式后新的平衡状态。
(a)(b)(c)图9-3承受轴向压力的细长压杆的平衡,在什么条件下是稳定的,什么条件下是不稳定的;怎样才能保证压杆正常、可靠地工作等等问题,统称为“稳定问题”。
知识点10:压杆稳定

知识点10:压杆稳定一、弹性平衡稳定性的概念1.弹性体保持初始平衡状态的能力称为弹性平衡的稳定性。
2.受压杆件保持初始直线平衡状态的能力称为压杆的稳定性。
二、压杆的临界力1.两端铰支细长压杆欧拉〔Euler 〕临界力公式为22lEIF cr π=。
欧拉临界力公式只适用于小变形、线弹性范围内。
2.在临界状态两端铰支细长压杆的弹性曲线方程为一个半波正弦方程:x lC y πsin=。
由此利用“形状比较法〞可求得不同约束下细长压杆的临界力。
3.杆端约束对临界力的影响:〔1〕不同杆端约束的压杆的临界力,可用解压杆的挠曲线近似微分方程或用形状比较法求得。
〔2〕不同杆端约束细长压杆临界力的欧拉公式为22)(l EIF cr μπ=,式中μl 称为计算长度〔或有效长度〕,μ称为支座系数〔或长度系数〕。
当压杆在两个惯性平面内的μ值不同时,计算临界力应取较大的μ值。
〔3〕几种常见杆端约束的支座系数: 4.临界应力与柔度:细长压杆的临界应力公式为22λπσE cr =,式中il μλ=称为压杆的柔度,和压杆的长度、约束情况、截面形状及尺寸相关。
三、压杆的分类与临界应力总图1.柔度的分界值PP Eσπλλ22)(=;ba ss σλλ-=)(1式中a ,b 是与材料性质相关的常数,单位为MPa 。
2.压杆的分类压杆根据其柔度的大小而分类,计算压杆临界应力时应先判断是何类压杆,然后选择相应的临界应力公式。
压杆可分为以下三类:〔1〕细长杆〔λ≥λP 〕:计算临界应力用欧拉公式22λπσEcr =〔欧拉双曲线公式〕; 〔2〕中长杆〔λs <λ<λP 〕:计算临界应力用经历公式σcr =a -b λ〔雅辛斯基直线公式〕; 〔3〕粗短杆〔λ≤λs 〕:计算临界应力用压缩强度公式σcr =σs 〔或σb 〕。
3.临界应力总图临界应力总图如图10-1所示。
四、压杆稳定性的校核1.进展压杆稳定性的校核时,通常用平安系数法。
在建筑等行业常用折减系数法。
压杆的稳定计算

③ 确定该支架的许可荷载。
根据外力 F 与 BD 杆所承受压力之间的关系,只要考虑 AC 杆的平衡即可。
由 求得
M A 0,
FBD
l 2
F
3l 2
0
1 F 3 FBD
于是该支架能承受的最大荷载为
Fmax
1 3
FBDmax
1 47.0 103 3
15.7 103
N
最后确定该支架的许可荷载 [F] =15.7 kN。
3. 进行截面设计
已知压杆的长度、所用材料、支承条件以及承受的压力F,按照稳定条件计 算压杆所需的截面尺寸。由于在稳定条件式 (7-12) 中,折减系数 φ 是根据压杆的 柔度 λ 查表得到的,而在压杆的截面尺寸尚未确定之前,压杆的柔度 λ 不能确定, 所以也就不能确定折减系数 φ。因此,这类问题一般采用试算法。
为了计算方便,将临界应力的许用应力写成如下形式
cr
cr kst
(7-10)
式中:[σ] 为强度计算时的许用应力;φ 为折减系数,其值小于1。
由式(7-10) 可知,φ 值为
cr
kst
(7-11)
由式(7-11) 可知, 当[σ] 一定时,φ 取决于σcr 与kst。由于临界应力σcr值随 压杆的柔度而改变,而不同柔度的压杆一般又规定不同的稳定安全系数,所以
【例7-2】如图7-5a 所示,构架由两根直径相同的圆杆构成,杆的材料为 Q235 钢, 直径 d = 20 mm,材料的许用应力 [σ] = 170 MPa,已知 h = 0.4 m,作用力 F = 15 kN。 试校核两杆的稳定。
图7-5a 解:① 计算各杆承受的压力。 取结点 A 为研究对象,画受力分析图,如图7-5b 所示,根据平衡条件列方程
压杆稳定的概念及三种平衡状态

(与假设矛盾)
目录
§9.2 两端铰支细长压杆的临界压力
w
得
现在您正浏览在第14页,共57页。
当
时, 临界压力
欧拉公式
挠曲线方程
w
目录
§9.2 两端铰支细长压杆的临界压力
----欧拉公式
F 1 1、适用条件:
2、 cr
l •理想压杆(轴线为直线,压力与轴线
2
重合,材料均匀)
杆长,Fcr小,易失稳
现在您正浏览在第6页,共57页。
F
F<Fcr
F>Fcr
干扰力 F1
F
现在您正浏览在第7页,共57页。
F<Fcr 稳定平衡状态
F>Fcr 不稳定平衡状态
细长压杆——失稳破坏
现在您正浏览在第8页,共57页。
细长压杆——失稳破坏
现在您正浏览在第9页,共57页。
s或b
失稳与屈曲(Buckling)
在扰动作用下,直线平衡状态转变为弯曲平衡状态,扰 动除去后,不能恢复到直线平衡状态,即由稳定平衡状态 转变为不稳定平衡状态的现象,称为失稳或屈曲。
写 出 微 分 方 程 的 通 解 :
特征方程 ar 2 br c 0 方程 aybycy0 的通解 有两个不相等实r1根 , r2 yC1er1xC2er2x 有两个相等r实 r1根 r2 yerx(C1C2x)
有一对共轭r复 1,2根i y e x (C 1c o x s C 2s ix n )
F [F] F cr n st
工作安全系数
或
n st — 稳定安全系数
n Fcr F
n st
n cr
nst
压杆稳定性条件
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
三、其它支承情况下,压杆临界力的欧拉公式
Pcr
2 EImin (L)2
压杆临界力欧拉公式的一般形式
—长度系数(或约束系数)(coefficicent of length)。 l----有效长度(effective length)
表10–1 各种支承约束条件下等截面细长压杆临界力的欧拉公式
支承情况
2E 0.56 S
c 时,由此式求临界应力 。
②s< 时:
cr s
例4 一压杆长L=1.5m,由两根 56568 等边角钢组成,两端铰
2EI
(0.7l)
2
Pcr
2EI
(0.5l ) 2
Pcr (22lE) 2I
长度系数μ =1 0.7 =0.5 =2
Pcr
2
l
EI
2
=1
例1 试由挠曲线近似微分方程,导出下述两种细长压杆的临界力
公式。
解:变形如图,其挠曲线近似微分方程为:
P
P
EIyM (x)PyM
M0
令:k 2 P
EI
76
.8kN
§15–3 超过比例极限时压杆临界应力
一、 基本概念 1.临界应力:压杆处于临界状态时横截面上的平均应力。
c
r
Pcr A
2.细长压杆的临界应力:
cr
Pcr A
2EI (L)2 A
(
2E L/i)
2
22E
即: cr
2E 2
i I ——惯性半径。 A
3.柔度: L — —杆的柔度(slenderness() 或长细比)
y y
x
z
z
h
L1
L2
解:①绕
y 轴,两端铰支:
=1.0,
I
y
b3h 12
,
②绕 z 轴,左端固定,右端铰支:
b
Pcry
2E L22
I
y
=0.7,
I
z
bh3 12
,
Pcrz
2EIz
(0.7L1)
2
③压杆的临界力 Pcr min( Pcry , Pcrz )
例3 求下列细长压杆的临界力。
解:图(a)
构件的承载能力:
①强度(strength) ②刚度(stiffness) ③稳定性(stability)
工程中有些构
件具有足够的强度、
刚度,却不一定能
安全可靠地工作。
P
一、稳定平衡(stable equilibrium)与不稳定平衡(unstable equilibrium) 1. 不稳定平衡(unstable equilibrium)
x
Px
EIyk 2 yk 2 M
M0
P
yccoskxdsinkx
L
M0 P
M0 P
边界条件为:
x0,yy0;xL,yy0
c M , d 0, kL 2n
P
kL2n
为求最小临界力,“k”应取除零以外的最小值,即取:
所以,临界力为:
kL2
Pcr
4 2EI
L2
2EI
(L/2)2
= 0.5
例2 求下列细长压杆的临界力。
P P
y
x M
P x
P ①弯矩: M (x,y)Py
②挠曲线近似微分方程:
y M P y EI EI
y P yyk 2 y0 EI
其中:k 2 P EI
③微分方程的解: y Asin kx B coskx A—屈曲模态幅值(amplitude of bucking models)
④确定积分常数: y(0)y(L)0
P
P
I
m
in
5010 12
3
10
12
4.1710
9
m
4
10 50
z
y
Pcr (2I1ml )in2E
24.17200 (0.70.5)2
67
.14
kN
图(b)
L L
图(a)
(4545 6) 等边角钢
图(b)
IminI z 3.8910 8 m4
Pcr (2I2mli)n2E
20.389200 (20.5)2
2.压杆的稳定平衡与不稳定平衡:
稳 定 平 衡
不 稳 定 平 衡
3.压杆失稳:
4.压杆的临界压力
临界状态
稳
定 平
过
衡
对应的 压力
临界压力:
不 稳 度定 平 衡 Pcr
§15–2 细长压杆临界力的欧拉公式 一、两端铰支压杆的临界力(critical load):
假定压力已达到临界值,杆已经处于微弯状态,如图, 从挠曲线入手,求临界力。
2. 稳定平衡(stable equilibrium)
3. 稳定平衡和不稳定平衡(stable equilibrium & unstable equilibrium)
二、压杆失稳(lost stability)与临界压力(criterion compressio
1.理想压杆:材料绝对理想;轴线绝对直;压力绝对沿轴线作用。
②S< 时: cr s
cr
S 的杆为小柔度杆,其临 界应力为屈服极限。
S
cr ab
③临界应力总图
P
2E
cr
2
s s a
b
P 2E
P
L
i
2.抛物线型经验公式
①P<<s 时:
cr a1b12
我国建筑业常用:
cr
s
1
c
2
对于A3钢、A5钢和16锰钢: 0.43,c
两端铰支
一端固定 另端铰支
两端固定
一端固定 另端自由
两端固定但可沿 横向相对移动
Pcr
Pcr
Pcr
Pcr
Pcr
失
l l 0.7l l 0.5l
l 2l l 0.5l
稳 时
B
B
B
挠
D
曲
线 形
C
C
状
A
A
A
C— 挠曲 C、D— 挠
线拐点 曲线拐点
C— 挠曲线拐点
临界力Pcr 欧拉公式
Pc
r
2
l
EI
2
Pcr
即:
A0B0 As ink LBc osk
L0
0
1
0
sinkL coskL
sinkL0
kn P
L EI
临界力 Pcr 是微弯下的最小压力,故,只能取n=1 ;且 杆将绕惯性矩最小的轴弯曲。
Pcr
2
EI L2
m
in
Pcr
2
EImin L2
二、此公式的应用条件:
两端铰支压杆临界力的欧拉公式
1.理想压杆; 2.线弹性范围内; 3.两端为球铰支座。
Architetural Mechanics
Chapter 15. Stability of Compress Bar
压杆稳定
§15–1 压杆稳定性的概念 §15–2 细长压杆临界力的欧拉公式 §15–3 超过比例极限时压杆临界应力 §15-4 压杆的稳定校核及其合理截面
§15–1 压杆稳定性的概念 Conception of stability of Compress bar
i
4.大柔度杆的分界:
cr
2E 2
P
2E P
P
满足 P 的杆称为大柔度杆(或 长细杆),其临界力用 欧拉公式求。
P 的杆为中小柔度杆,其 临界力不能用欧拉公式 求。
二、中小柔度杆的临界应力计算
1.直线型经验公式
①P<<S 时:
cr ab
crab s
s a b
s
sP 的杆为中柔度杆,其临 界应力用经验公式求。
