初中数学找规律习题大全word精品
初一数学找规律练习题

初一数学找规律练习题一、数字规律1. 观察下列数列,找出规律,并写出下一个数:2, 4, 8, 16, 32, ____1, 3, 6, 10, 15, ____1, 4, 9, 16, 25, ____二、图形规律1. 观察下列图形,找出规律,并画出下一个图形:(图形:△ △△ △△△ △△△△)(图形:○□○□○□○□)3. 观察下列图形,找出规律,并画出下一个图形:(图形:□■□■■□■■■)三、数列与图形结合规律1. 观察下列数列与图形的结合,找出规律,并写出下一个数和画出对应的图形:数列:1, 2, 3, 4, 5图形:(△)(△△)(△△△)(△△△△)数列:1, 3, 6, 10, 15图形:(○)(□□)(△△△)(■■■■)四、应用题1. 小明发现一个有趣的现象,从1开始,连续几个自然数的和等于这几个自然数的个数乘以(个数加1)除以2。
请你找出这个规律,并计算1到100的和。
2. 小华在纸上画了一排正方形,每个正方形的边长分别为1cm、2cm、3cm、4cm……,请问这排正方形总面积是多少平方厘米?3. 一个数字三角形,第一行有1个数字,第二行有2个数字,以此类推,第n行有n个数字。
求这个数字三角形前10行的数字总和。
五、数表规律1 2 3 42 3 4 53 4 5 64 5 6 __1 3 6 102 5 9 143 7 12 184 __ __ __六、操作规律A → A + 1B → B + 2C → C + 3D → D + 4(初始值:A=1, B=2, C=3, D=4)A → A × 2B → B × 3C → C × 4D → D × 5(初始值:A=1, B=1, C=1, D=1)七、逻辑推理规律A > B,B > C,C > D那么 A > D 是否成立?如果 P 则 Q,如果 Q 则 R那么如果 P 则 R 是否成立?八、综合应用题1. 一个班级有50名学生,每名学生都有一个唯一的编号,编号从1到50。
(完整word版)初二数学找规律专题训练

初二数学找规律专题训练一、填空题1.课本中有这样一句话:“利用勾股定理能够作出,,线段(如图所示).”即:OA=1,过 A 作 AA1⊥OA 且 AA1=1,依据勾股定理,得 OA1=;再过 A1作 A1 A2⊥OA1且 A1A2=1,得 OA2=;以此类推,得OA2017=______ .2.3.如图,动点P在平面直角坐标系中按图中箭头所示方向运动,第1次从原点运动到点(1 12,),第次接着运动到点( 2,0),第 3 次接着运动到点( 3,2),第4 次接着运动到点(4,0),,按这样的运动规律,经过第 2017 次运动后,动点P 的坐标是 ______ .4. 正方形B C O,A B2C C,ABCC按如下图搁置,点 A 、A 、A 在直线y=x+1 上,点 C、A11122133321231 C2、 C3在x 轴上,则A n的坐标是 ______ .5. 在如下图的平面直角坐标系中,△OA1B1是边长为2 的等边三角形,作△B2A2B1成中心对称,再作△B2A3B3与△B2A2B1对于点B2成中心对称,,这样作下去,则与△OA1B1对于点 B1△B2015A2016B2016的顶点 A2016的坐标是______.第 4 题第 5 题6. 在直角坐标系中,直线y=x+2与y轴交于点A1A1B1C1O A2B2C2C1 A3B3C1C2,按如图方式作正方形、、,A 、A 、A 在直线 y=x+2 上,点 C、C 、C 在 x 轴上,图中暗影部分三角形的面积从左到右挨次记123123为 S1、S2、 S3、 S n,则 S n的值为 ______ (用含 n 的代数式表示, n 为正整数).7.在平面直角坐标系中,直线l: y=x-1 与 x 轴交于点 A1,如下图挨次作正方形 A1B1C1O、正方形 A2B2C2C1、、正方形 A n B n C n C n-1,使得点 A1、A2、 A3、在直线 l 上,点 C1、C2、C3、在 y 轴正半轴上,则点 B n的坐标是 ______ .8.察看以下图形:已知 a∥b,在第一个图中,可得∠1+∠2=180 °,则依据以上规律,∠1+ ∠2+∠P1 + +∠P n=______ 度.8.察看以下一组式的变形过程,而后回答以下问题:例1:====-1.例2:=-,=-,=-利用以上结论解答以下问题:(1)= ______(2)应用上边的结论,求以下式子的值.+++ +(3)拓展提升,求以下式子的值.+++ +.9.阅读下边的文字,解答问题.大家知道是无理数,而无理数是无穷不循环小数,所以的小数部分我们不行能所有地写出来,可是因为 1<<2,所以的整数部分为1,将减去其整数部分1,差就是小数部分-1,依据以上的内容,解答下边的问题:(1)的整数部分是 _______,小数部分是 ______;(2)1+的整数部分是_______,小数部分是 ____;(3) 若设 2+的整数部分是x,小数部分是y,求 x-y 的值。
初中数学找规律专项练习题有答案.doc

初中数学找规律专项练习题有答案2、用四舍五入法31500 取近似数,并精确到千位,用科学数法可表示.3、察下面的一列数:0, 1,2, 3, 4, 5, 6⋯你找出其中排列的律,并按此律填空.( 1)第 10 个数是,第21个数是.( 2) 40 是第个数,26是第个数.4、一按律排列的数:,,,,⋯你推断第9 个数是.5、算:__________ ;( -2 )100+( -2 )101=.6 、若, = __________.7 、大杆菌每20 分便由 1 个分裂成 2 个, 3 小后种大杆菌由 1 个分裂成 __________ 个 .8、猜数字游中,小明写出如下一数:,,,,⋯,小亮猜想出第六个数字是,根据此律,第n 个数是9、10 、若与| b+5| 的互相反数,=____ ____11 、在数制中,通常我使用的是“十位制”,即“逢十一”. 而数制方法很多,如60 位制:60 秒化 1 分, 60 分化 1 小; 24 位制: 24 小化 1 天; 7 位制: 7 天化 1 周等⋯而二位制是算机理数据的依据. 已知二位制与十位制的比如下表:十位0 1 2 3 4 5 6 ⋯制二制0 1 10 11 100 101 110 ⋯将二位制10101010 (二) 写成十位制数.12 、求,可令 S= , 2S=,因此 2S-S =,所以=. 仿照以上推理算出的是_________________.二、选择题(每空?分,共?分)13 、的是⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯【】A . 2B . 1C . 0D . 114 、已知8.62 = 73.96 ,若 x2= 0.7396 , x 的等于()A 86. 2B 862C ± 0.862D ± 86215 、算: ( - 2) 100+( - 2) 101的是()A.2 100B. - 1C. - 2D. - 210016 、算等于 ( ) .A.B.C.D.17 、已知 a、 b 互相反数, c 、 d 互倒数, m的1, p 是数到原点距离 1 的数,那么的是( ) .A.3 B . 2 C . 1 D . 018 、若,的大小关系是() .A. B . C . D .19 、察下列等式:31=3, 32=9, 33=27, 34 =81, 35=243, 36=729 , 37=2 187 ,⋯ . 解答下列: 3+32+33+34 +⋯+3 2 013的末尾数字是 ( )A.0B.1C.3D.720 、算机是将信息化成二制行理的,二制即“逢二一”. 将二制化成十制数,例如:;;. 将二制数化成十制数的果()A.8B.13C.15D.16三、简答题21 、:你能比两个数和的大小?(本 6 分)了解决个,我先把它抽象成数学,写出它的一般形式,比与的大小(n正整数),从分析n=1, n=2, n=3,⋯的情形入手,通,律,猜想出.( 1)(每空0.5 分)比各数的大小①;② 2332;③ 3443;④ 4554( 2)由( 1)猜想出与的大小关系是;(2分)( 3)由( 2)可知:.(2分)22、察下列解程:算: 1+ 5+ 52+ 53+⋯+ 524+ 525的 .解: S= 1+ 5+ 52+ 53+⋯+ 524+ 525,( 1)5S= 5+ 52+ 53+⋯+525 + 526 ( 2)( 2)-( 1),得 4S=526 - 1S=通,你一定学会了一种解决的方法,用你学到的方法算:(1) 1+ 3+ 32+ 33+⋯+ 39+ 310(2) 1+x+x2+x3+⋯+x99+x10023、探索律:察下面由※ 成的案和算式,解答:1+3=4=1+3+5=9=1+3+5+7=16=1+3+5+7+9=25=( 1) 猜想1+3+5+7+9+ ⋯ +29=;( 2) 猜想 1+3+5+7+9+ ⋯ + ( 2n-1 ) +( 2n+1)=;( 3) 用上述 律 算:(3 分)41+43+45+ ⋯⋯ +77+7924 、已知点 A 在数 上 的数是 a ,点 B 在数 上 的数是 b ,且 .将、 B 之 的距离 作,定.A( 1)的( 2)的( 3) 点P 在数 上 的数是 x ,当 ,求 x 的 ;25 、 察下列算式,你 了什么 律?( 1)根据你 的 律, 算下面算式的 ;_____ ____( 2) 用一个含的算式表示 个 律: ____ _____26 、用“☆”定 一种新运算: 于任意有理数 a 和 b , 定 a ☆ b = .如: 1☆ 3= =16.( 1)求( -2 )☆ 3 的;( 2)若 (☆ 3)☆ (-)=8 ,求a的;( 3)若 2☆x = m,☆ 3=n(其中x 有理数),比m, n 的大小.四、计算题27、算参考答案一、填空题1、.【考点】探索律(数字的化).【分析】根据已知数字化律,得出奇数之和数字个数的平方,而得出答案:∵1=12; 1+3 =22; 1+3+5=32; 1+3+5+7=42;⋯,∴∴左括号中最后一个数字是 2n- 1.∵ 2014=,∴由 2n- 1=1007 解得 n=504.∴ 1+3+5+⋯ +2014=10072 =.2、3.2 × 104;3、 9, 20; 41, 27.4、.解答:解:=,=,=,⋯第 9 个数是=,1005、-0.5,-26、07、512 .(即 29 = 512 )8、.解:∵分数的分子分是: 2 2 =4, 23 =8, 24 =16,⋯分数的分母分是: 2 2 +3=7, 23+3=11, 24+3=19,⋯∴第 n 个数是.9、± 110 、 _25__11 、 170提示:10101010(二)=1×27+0×26+1×25+0×24+1×23+0×22+1×2=128+32+8+2=170.12、二、选择题13、 B14、 C15 、 D16 、 D17 、 B18 、 B19 、 C20 、 B三、简答题21 、解:( 1) 12< 21;② 23< 32;③ 34> 43;④ 45> 54⋯⋯⋯⋯⋯⋯⋯⋯ 2 分(2)当 n=1 或 2 , n n+1<( n+1)n;当 n> 2 的整数, n n+1>( n+1)n.⋯⋯⋯ 2 分(3)>.22 、( 1);(2).23 、( 1)225 ( 2)(3) 41+43+45+ ⋯⋯ +77+79=(1+3+5+7+9+ ⋯ +79) —( 1+3+5+7+9+ ⋯ +39 )= —=120024 、( 1) 2014 ( 2 分)(2) 5 ( 2 分)(3)三种情况x < -4 无解( 2 分)-4≤ x≤ 1x= -(2分)x > 1无解25 、( 1)(2)26 、( 1)解:( -2 )☆ 3 .⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯ 1 分( 2)解:. ⋯⋯⋯⋯⋯⋯⋯⋯ 2 分解得,⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯ 3 分( 3)解:由意,,所以.所以.⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯ 5 分四、计算题27 、— 34。
(完整word版)七年级数学找规律练习题和答案

找规律练习题1 •用黑白两种颜色的正六边形地砖按如下所示的规律拼成若干个图案:第X 1=1,第二个数为X 2=3,第三个数开始依次记为 X 3, X 4,…,X n ;从第二个数开始,每个数是它相中有白色地砖 块。
2.我国著名数学家华罗庚曾说过:“数形结合百般好,隔裂分家万事非。
在一个边长为1的正方形纸版上, 形彩色纸片(n 1 规律,计算丄 2为大于1 1 1 48的整数) 1 班1 1 依次贴上面积为 1 , 1 ,2 4 。
请你用“数形结合”的思想, 8 ”如图, 1 丄的矩 2n 依数形变化的 邻两个数和的一半。
(如: X 2=^l X3 )2 (1)求第三、第四、第五个数,并写出计算过程; (2)根据(1)的结果,推测X 8= (3)探索这一列数的规律,猜想第 k 个数X k = . ( k 是大于2的整数) 4•将一张长方形的纸对折,如图所示可得到一条折痕(图中虚线) .继续对折,对折时每次折痕与上次的折痕保持平行,连 续对折三次后,可以得到 7条折痕,那么对折四次可以得到 ________________ 条折痕.如果对折n 次,可以得到 ______________ 条折 痕• 1 1 1 1 1 1 1 ■ ■ 1 4 1 | 1 1 1 1 1 111 1 1 V 1 1 1 1 1 1 1 hL1 V 1 1 a ii k i 1119 1 l> V i i I I I I l> 1 1 I l> I 1 I I I i 1 >1 1 ■ KPI ■ ・ W P a L h h F 1I 4 1 il >1 I ii ■l >l 4 I A I 第一次对折第二次对折第三友对折5.观察下面一列有规律的数 1 2 _5 _6_ 3,8,15,24,35,48 根据这个规律可知第 n 个数是(n 是正整数) 6.古希腊数学家把数 1, 3, 6, 10, 15, 21 ,……,叫做三角形数,它有一定的规律性,则第 形数的差为 _____________________ 。
初中数学找规律习题大全

1找规律专项训练一:数式问题223344aa2222,?4??48??8??3?2,,3???2?为正整数)……,若b(1.(湛江)已知a、1515bb3388a?b?则.2.(贵阳)有一列数a,a,a,a,a,…,a,其中a=5×2+1,a=5×3+2,a=5×4+3,a45122n3314=5×5+4,a=5×6+5,…,当a=2009时,n的值等于()n5A.2010 B.2009 C.401 D.334345aaa23.(沈阳)有一组单项式:a,-,,-,….观察它们构成规律,用你发现的规律写出第10个单234项式为.1234,??,,,…,那么第7个数是.4.(牡丹江)有一列数105172 233547a?ba?ba?b b?a,……,其中第10,,,个式子是5.(南充)一组按规律排列的多项式:()1910191017102110b?ba?bbaa?a?B. D .C.A.112233?1?2??2?3??3?1?(安徽)观察下列等式:6.,,……,422343 2)证明你写出的等式的正确性.n个等式;((1)猜想并写出第7.(绵阳)将正整数依次按下表规律排成四列,则根据表中的排列规律,数2009应排的位置是第行第列.第1列第2列3第列4列第?n;▲22,3,…从小到大按下面规律排列.若第4行第列的数为32,则①18.(台州)将正整数,jj ii.表示)▲(用②第,行第列的数为n321第…列列第第列第列n1312…第行22n3??2nn?1n2…第行33n3?2n?22nn2?1…第行………………二:定义运算问题22b?a?a?b???24x? 3,其法则为:),求方程(4(定西)在实数范围内定义运算“1.的解.”aaaa?a21,与它前面那个数的倒数的差,每一个数都等于,,若,2.有一列数从第二个数开始,,,1321n a 为(则)200712007?21D.B.A.C.2三:剪纸问题1.(2004年河南)如图(9),把一个正方形三次对折后沿虚线剪下则得到的图形是()2.(2004年浙江湖州)小强拿了一张正方形的纸如图(10)①,沿虚线对折一次得图②,再对折一次得图③,然后用剪刀沿图③中的虚线(虚线与底边平行)剪去一个角,再打开后的形状应是()3.(2004年浙江衢州)如图(11),将一张正方形纸片剪成四个小正方形,然后将其中的一个正方形再剪成四个小正方形,再将其中的一个正方形剪成四个小正方形,如此继续下去,……,根据以上操作方法,请你填写下表:3N 4 5 1 2 3 操作次数N ……7 10 4 正方形的个数……x A、A、AA、A、A?A?OAAA?AA?AA过点,轴的正半轴上依次截取3.(莆田)如图,在??x P、、PP、P、P0?xy?,得直角三角形轴的垂线与反比例函数的图象相交于点分别作53214532314142253124x,PAPA、AAAP、APA、AAOP、并设其面积分别为514224131243352?y x yS,、S、S、S、SS的值为则.551432P1P 2 P3PP4 5O x AAAAA5 3 4 1 2 10题图)(第(长春)用正三角形和正六边形按如图所示的规律拼图案,即从第二个图案开始,每个图案都比上一个4.的代数式n (用含n图案多一个正六边形和两个正三角形,则第个图案中正三角形的个数为. 表示)题)(第4100,用同样大小的黑色棋子按图所示的方式摆图案,按照这样的规律摆下去,第6(丹东)如图5.4枚.个图案需棋子……32图案图案1图案6图n个图中最小的三角形的个数有 6.(抚顺)观察下列图形(每幅图中最小的三角形都是全等的),请写出第....个.个图第4 第3个图第1个图第2个图题图)(第167.(哈尔滨)观察下列图形:它们是按一定规律排列的,依照此规律,第16个图形共有个★.五:对称问题、1.(伊春)在平面直角坐标系中,已知3个点的坐标分别为、. 一只电子蛙位于,A1)(11) 1,A(0,2)A(132坐标原点处,第1次电子蛙由原点跳到以为对称中心的对称点,第2次电子蛙由点跳到以为对APAP2111称中心的对称点,第3次电子蛙由点跳到以为对称中心的对称点,…,按此规律,电子蛙分别PPAP3223以、、为对称中心继续跳下去.问当电子蛙跳了2009次后,电子蛙落点的坐标是(_______ ,AAAP3122009_______).2.(2004年宁波)仔细观察下列图案,如图(12),并按规律在横线上画出合适的图形。
初中数学找规律习题大全

初中数学找规律习题大全TTA standardization office【TTA 5AB- TTAK 08- TTA 2C】找规律专项训练一:数式问题 1.(湛江)已知22223322333388+=⨯+=⨯,,244441515+=⨯,……,若288a ab b +=⨯(a 、b 为正整数)则a b += .2.(贵阳)有一列数a 1,a 2,a 3,a 4,a 5,…,a n ,其中a 1=5×2+1,a 2=5×3+2,a 3=5×4+3,a 4=5×5+4,a 5=5×6+5,…,当a n =2009时,n 的值等于( )A .2010B .2009C .401D .3343.(沈阳)有一组单项式:a 2,-a 32,a 43,-a 54,….观察它们构成规律,用你发现的规律写出第10个单项式为 .4.(牡丹江)有一列数1234251017--,,,,…,那么第7个数是 . 5.(南充)一组按规律排列的多项式:a b +,23a b -,35a b +,47a b -,……,其中第10个式子是( )A .1019a b +B .1019a b -C .1017a b -D .1021a b -6.(安徽)观察下列等式:111122⨯=-,222233⨯=-,333344⨯=-,…… (1)猜想并写出第n 个等式;(2)证明你写出的等式的正确性.7.(绵阳)将正整数依次按下表规律排成四列,则根据表中的排列规律,数2009应排的位置是第 行第 列.(台8.州)将正整数1,2,3,…从小到大按下面规律排列.若第4行第2列的数为32,则①n = ▲ ;②第i 行第j 列的数为 ▲ (用i ,j 表示).第1列 第2列 第3列 … 第n 列 第1行 … 第2行 … 第3行 … ………………二:定义运算问题1.(定西)在实数范围内定义运算“⊕”,其法则为:22a b a b ⊕=-,求方程(4⊕3)⊕24x =的解. 2.有一列数1a ,2a ,3a ,,n a ,从第二个数开始,每一个数都等于1与它前面那个数的倒数的差,若12a =,则2007a 为( ) A.2007B.2C.12D.1-三:剪纸问题1. (2004年河南)如图(9),把一个正方形三次对折后沿虚线剪下则得到的图形是( )2. (2004年浙江湖州)小强拿了一张正方形的纸如图(10)①,沿虚线对折一次得图②,再对折一次得图③,然后用剪刀沿图③中的虚线(虚线与底边平行)剪去一个角,再打开后的形状应是( )3. (2004年浙江衢州)如图(11),将一张正方形纸片剪成四个小正方形,然后将其中的一个正方形再剪成四个小正方形,再将其中的一个正方形剪成四个小正方形,如此继续下去,……,根据以上操作方法,请你填写下表:第4行 12 11 10 ……操作次数N1 2 34 5 … N …3.(莆田)如图,在x 轴的正半轴上依次112233445OA A A A A A A A A ====,截取过点12345A A A A A 、、、、分别作x 轴的垂线与反比例函数()20y x x=≠的图象相交于点12345P P P P P 、、、、,得直角三角形1112233344455OP A A P A A P A A P A A P A 2、、、、,并设其面积分别为12345S S S S S 、、、、,则5S 的值为 .4.(长春)用正三角形和正六边形按如图所示的规律拼图案,即从第二个图案开始,每个图案都比上一个图案多一个正六边形和两个正三角形,则第n 个图案中正三角形的个数为 (用含n 的代数式表示).5.(丹东)如图6,用同样大小的黑色棋子按图所示的方式摆图案,按照这样的规律摆下去,第100个图案需棋子 枚.6.(抚顺)观察下列图形(每幅图中最小..的三角形都是全等的),请写出第n 个图中最小..的三角形的个数有 个.7.(哈尔滨)观察下列图形:它们是按一定规律排列的,依照此规律,第16个图形共有 个★. 五:对称问题1.(伊春)在平面直角坐标系中,已知3个点的坐标分别为1(11)A ,、2(02)A ,、3(11)A -,. 一只电子蛙位于坐标原点处,第1次电子蛙由原点跳到以1A 为对称中心的对称点1P ,第2次电子蛙由1P 点跳到以2A 为对称中心的对称点2P ,第3次电子蛙由2P 点跳到以3A 为对称中心的对称点3P ,…,按此规律,电子蛙分别以1A 、2A 、3A 为对称中心继续跳下去.问当电子蛙跳了2009次后,电子蛙落点的坐标是2009P (_______ ,_______).2.(2004年宁波)仔细观察下列图案,如图(12),并按规律在横线上画出合适的图形。
(完整版)初中数学找规律题及其答案
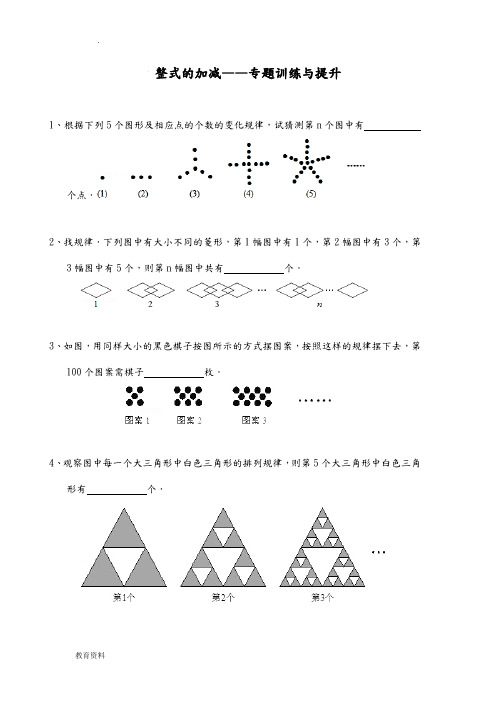
整式的加减——专题训练与提升1、根据下列5个图形及相应点的个数的变化规律,试猜测第n个图中有个点.2、找规律.下列图中有大小不同的菱形,第1幅图中有1个,第2幅图中有3个,第3幅图中有5个,则第n幅图中共有个.3、如图,用同样大小的黑色棋子按图所示的方式摆图案,按照这样的规律摆下去,第100个图案需棋子枚.4、观察图中每一个大三角形中白色三角形的排列规律,则第5个大三角形中白色三角形有个.5、观察下列图形,它们是按一定规律排列的,依照此规律,第16个图形共有个★.6、如图①,图②,图③,图④,…,是用围棋棋子按照某种规律摆成的一行“广”字,按照这种规律,第5个“广”字中的棋子个数是,第n个“广”字中的棋子个数是.7、如图1是二环三角形,可得S=∠A1+∠A2+…+∠A6=360°,下图2是二环四边形,可得S=∠A1+∠A2+…+∠A7=720°,图3是二环五边形,可得S=1080°,…聪明的同学,请你根据以上规律直接写出二环n边形(n≥3的整数)中,S= 度.(用含n的代数式表示最后结果)8、观察下列图形(每幅图中最小的三角形都是全等的),请写出第n个图中最小的三角形的个数有个.9、将一个正三角形纸片剪成四个全等的小正三角形,再将其中的一个按同样的方法剪成四个更小的正三角形,…如此继续下去,结果如下表.则a n = .(用含n的代数式表示)所剪次数正三角形个数10、用正三角形和正六边形按如图所示的规律拼图案,即从第二个图案开始,每个图案都比上一个图案多一个正六边形和两个正三角形,则第n个图案中正三角形的个数为(用含n的代数式表示).11、如图①是一块瓷砖的图案,用这种瓷砖来铺设地面.如果铺成一个2×2的正方形图案(如图②),其中完整的圆共有5个,如果铺成一个3×3的正方形图案(如图③),其中完整的圆共有13个,如果铺成一个4×4的正方形图案(如图④),其中完整的圆共有25个.若这样铺成一个10×10的正方形图案,则其中完整的圆共有个.12、根据下列图形的排列规律,第2008个图形是福娃(填写福娃名称即可).13、用火柴棒按照如图所示的方式摆图形,则第n个图形中,所需火柴棒的根数是.14、下列图案均是用长度相同的小木棒按一定的规律拼搭而成:拼搭第1个图案需4根小木棒,拼搭第2个图案需10根小木棒,…,依次规律,拼搭第8个图案需小木棒根.15、一张长方形桌子需配6把椅子,按如图方式将桌子拼在一起,那么8张桌子需配椅子把.16、下列每个图是由若干个圆点组成的形如四边形的图案,当每条边(包括顶点)上有n(n≥2个圆点时,图案的圆点数为S n.按此规律推断S n关于n的关系式为:S n= .17、如图是由火柴棒搭成的几何图案,则第n个图案中有根火柴棒.(用含n的代数式表示)18、观察下列图形的构成规律,根据此规律,第8个图形中有个圆.19、观察表一,寻找规律.表二,表三分别是从表一中选取的一部分,则a+b的值为.表一:0 1 2 3 ....表二:表三:20、如图所示的图案是由正六边形密铺而成,黑色正六边形周围第一层有六个白色正六边形,则第n 层有 个白色正六边形.1 3 5 7 ....2 5 8 11 ....3 7 11 15 .... ....................11 14 a11 13 17 b21、把边长为3的正三角形各边三等分,分割得到图①,图中含有1个边长是1的正六边形;把边长为4的正三角形各边四等分,分割得到图②,图中含有3个边长是1的正六边形;把边长为5的正三角形各边五等分,分割得到图③,图中含有6个边长是1的正六边形;…依此规律,把边长为7的正三角形各边七等分,并按同样的方法分割,得到的图形中含有个边长是1的正六边形.22、观察下列图形的排列规律(其中☆,□,●分别表示五角星、正方形、圆)●□☆●●□☆●□☆●●□☆●…若第一个图形是圆,则第2008个图形是(填名称).23、下列图中有大小不同的菱形,第1幅图中有1个菱形,第2幅图中有3个菱形,第3幅图中有5个菱形,按照图示的规律摆下去,则第n幅图中有个菱形.24、如图,观察下列图案,它们都是由边长为1cm的小正方形按一定规律拼接而成的,依此规律,则第16个图案中的小正方形有个.25、用同样大小的黑色棋子按图所示的方式摆图形,按照这样的规律摆下去,则第n个图形需棋子枚.(用含n的代数式表示)27、如图所示是一副“三角形图”,第一行有一个三角形,第二行有2个三角形,第三行有4个三角形,第四行有8个三角形,…,你是否发现三角形的排列规律,请写出第七行有个三角形.28、如图,用3根小木棒可以摆出第(1)个正三角形,加上2根木棒可以摆出第(2)个正三角形,再加上2根木棒可以摆出第(3)个正三角形…这样继续摆下去,当摆出第(n)个正三角形时,共用了木棒根.29、观察下列图形,根据变化规律推测第100个与第个图形位置相同.30、如图,用火柴棒按以下方式搭小鱼,搭1条小鱼用8根火柴棒,搭2条小鱼用14根,…,则搭n条小鱼需要根火柴棒.(用含n的代数式表示)整式的加减——专题训练与提升参考答案1.n2-n+1 2.(2n-1)3.302 4.121 5.49 6.152n+5 7.360(n-2)8.4n-19.3n+1 10.2n+2 11.181 12.欢欢13.3n+1 14.88 15.2016.4n-4 17.2n(n+1)18.65 19.37 20.6n 21.15 22.正方形23.(2n-1) 24.136 26.3n+1 27.64 28.2n+1 29.1或4 30.6n+2。
(完整word)初中数学找规律

例题:(10西城二模)一组按规律排列的整数 5, 7, 11, 19,…,第6个整数为,根据上述规律,第n 个整数为 _____________ ( n 为正整数)•••第6个整数是26 3 67,第n 个整数是2n 3 (n 为正整数).练习:1 4 9 16 1' (10怀柔二莫)按一定规律排列的一列数依次为:3,产,亍……,按此规 律排列下去,这列数中的第5个数是 ____________ ,第n 个数是 ______________________________________2、(09东城一模)按一定规律排列的一列数依次为: -…,按此规律排列下去,这列数中的第 9个数是 35 答案:12 n1n ( 1)例题:(10通州一模)某些植物发芽有这样一种规律:当年所发新芽第二年不发 芽,老芽在以后每年都发芽.发芽规律见下表(设第一年前的新芽数为 a )照这样下去,第8年老芽数与总芽数的比值为.解:第8年的老芽数是21a ,新芽数是13a ,总芽数是34a ,贝吐匕值为 •34 练习:1、( 08石景山一模)小说《达•芬奇密码》中的一个故事里出现了一串神秘排列 的数,将这串令人费解的数从小到大的顺序排列为:1,1, 2, 3, 5, 8 ,则答案: 25 n 211 , 2n 11 ] 丄 丄 丄2,3,10,15, 26这列数的第8个数是______________ .2答案:212、(09房山二模)填在下面三个田字格内的数有相同的规律,根据此规律,请填 出图4中的数字.答案:7,9,11,176((1)n 与(1)n1)例题:(09通州二模)12.观察并分析下列数据,寻找规律:0,..、36 ,3,- 2、.3,,15,— 3・.2,……那么第10个数据是 _____________ ;第n 个数据 是 ______ .•••第10个数据是3-3,第n 个数据是(1)n1.. 3n 3 . 练习:1、(10房山一模)一组按规律排列的式子: 4,%~|,■16,...(a 0),其中第a a a a 8个式子是 _____ ,第n 个式子是 ________ (n 为正整数). 答案: 64( 1)n 1 n 223 3n 1aa58112、(10门头沟二模)一组按一定规律排列的式子:一a 2,-,—-,—,…,23 4(a ^ 0),则第n 个式子是 ________ (n 为正整数)3n 1答案:(1)0-—n3、(09崇文一模)一组按规律排列的数:2, 0, 4, 0, 6, 0,…,其中第7个数 是 ________ ,第n 个数是 _________ ( n 为正整数). 答案:8,』^(n 1)57 9108例题:(08通州二模)世界上著名的莱布尼茨三角形如图所示:贝U排在第10行从左边数第3个位置上的数是_______ .•••第10行倒数第三个数是———.72 90 360练习:1、(08大兴一模)自然数按一定规律排成下表,那么第200行的第5个数是_____ .12 34 5 67 89 101113 14 1512答案:199052、如图的数字方阵中,方框所缺的数,按照适宜的规律填上(A、100B、128C、129D、130答案:C例题:(11平谷二模)如图,将连续的正整数1,2,3,4……依次标在下列三角形中,那么2011这个数在第 ____ 个三角形的 ________ 顶点处(第二空填:上,左下,右下).• 2011 这个数在第671个三角形的上顶点处.故答案为:671, 上.练习:1、(08 崇文一模)观察下列等式:31 1 2 , 32 1 8 , 33 1 26 , 34 1 80 , 35 1 242 ,…….通过观察,用你所发现的规律确 定32008 1的个位数字是 ______ . ___ 答案:32、右图为手的示意图,在各个手指间标记字母A ,B ,C, D 请你按图中箭头所指 方向(即A — B ^C T C T B ^B^d …的方式)从 A 开始 数连续的正整数1, 2, 3, 4,…,当数到12时,对应的字母是 当字母C 第201次出现时,恰好数到的数是 当字母C 第2n 1次出现时(n 为正整数),恰 好数到的数是 ____ (用含n 的代数式表示). 答案:B, 603, 6n+3例题:(09平谷一模)已知:£2£2232 34 44 4……若b x1 1 '2 2 ‘3 3'10=a +10 (a 、b 都是正整数),则a+b 的最小值是 _________ . 二a+b 的最小值是19 练习:1. ( 10密云一模)下面是按一定规律排列的一列数:第1个数: 1 1 122第2个数: 1 1 11 (1)211 1323 第3个数: 1 1 11 (1)2 1423232n 11 1L 1(“第n 个数:2n(1)3;4 ;4 5 6那么,在第10个数、第11个数、第12个数、第13个数中,最大的数是()A.第10个数B .第11个数 C.第12个数 D.第13个数答案:A例题1: (10昌平一模)观察下列图案:照这样它们是按照一定规律排列的,依照此规律,第5个图案中共有________ 个三角形,第n (n 1,且n为整数)个图案中三角形的个数为_________ (用含有n的式子表示).解答:解:第5个图案中,有6+4X4=22 (个)三角形;第n个图案中,有6+4(n-1 )=4n+2 (个)三角形.例题2. (10西城一模)在平面直角坐标系中,我们称边长为1、且顶点的横、纵坐标均为整数的正方形为单位格点正方形.如图,在菱形ABCD中,四个顶点坐标分别是(一8,0 ),(0,4 ),(8,0 ),(0,点正方形的个数是个;若菱形ABGD n的四个顶点坐标分别为(—2n,0 ),(0, n), (2n,0), (0,—n)(n 为正整数),则菱形ABnG D n能覆盖的单位格点正方形的个数为_______________________ (用含有n的式子表示).答案为:4n2-4n .—4),贝U菱形ABCD能覆盖的单位格练习:.1、(10大兴一模)如图4所示,把同样大小的黑色棋子摆放在正多边形的边上,按的规律摆下去,则第n个图形需要黑色棋子的个数是_______________第1个图形第2个图形第3个图形第4个图形(图4)答案:n(n 2)2、(08顺义二模)如图,图①,图②,图③,图④……是用围棋棋子摆成的一列图①图②图③图④具有一定规律的“山”字•则第n个“山”字中的棋子个数是______________答案:5n+23、(08丰台二模)用黑白两种颜色的正方形纸片,按黑色纸片数逐渐加1的规律拼成一列图案:请问第n个图案中有白色纸片的张数为A. 4n 3B. 3n 1C. nD. 2n 2答案:B第1个第2个第3个4、(10丰台一模)在平面直角坐标系中,横坐标、纵坐标都为整数的点称为整点•请你观察图中正方形ABCD, ABC2D2,AB3C3D3…每个正方形四条边上的整点答案:80个.的个数•按此规律推算出正方形Ao BwC o D。
完整)初中数学找规律专项练习题(有答案)

完整)初中数学找规律专项练习题(有答案)1、观察规律:1=1;1+3=4;1+3+5=9;1+3+5+7=16;…,则2+6+10+14+…+2014的值是多少?2、用四舍五入法对取近似数,并精确到千位,用科学计数法表示为多少?3、观察下面的一列数:-1,2,-3,4,-5,6…请找出其中排列的规律,并按此规律填空。
(1)第10个数是多少?第21个数是多少?(2)-40是第几个数?26是第几个数?4、一组按规律排列的数:1,3,6,10,15…请推断第9个数是多少?5、计算:(-100)+(-101)=多少?(-2)+(-2)=多少?6、若。
则等于多少?7、大肠杆菌每过20分钟便由1个分裂成2个,经过3小时后这种大肠杆菌由1个分裂成多少个?8、猜数字游戏中,XXX写出如下一组数:1,3,5,7,9…n个数是…,XXX猜想出第六个数字是多少?根据此规律,第9、10个数字分别是多少?9、若。
与|b+5|的值互为相反数,则等于多少?10、在计数制中,通常我们使用的是“十进位制”,即“逢十进一”.而计数制方法很多,如60进位制:60秒化为1分,60分化为1小时;24进位制:24小时化为1天;7进位制:7天化为1周等…而二进位制是计算机处理数据的依据.已知二进位制与十进位制的比较如下表:十进位制二进制 1 1 2 10 3 11 4 100 5 101 6 110 …… 请将二进位制xxxxxxxx(二)写成十进位制数为多少?11、为求。
值,可令S=。
则2S=。
因此所以。
仿照以上推理计算出的值是多少?二、选择题13、的值是多少?【】A.-2 B.-1 C.0 D.114、已知8.62=73.96,若x=0.7396,则x的值等于()A.86.2B.862C.±0.862D.±86215、计算:(-2)+(-2)的值是多少?A.2B.-1C.-2D.-416、计算等于多少?A. B. C. D.17、已知a、b互为相反数,c、d互为倒数,m的绝对值为1,p是数轴到原点距离为1的数,那么的值是多少?A.3 B.2 C.1 D.018、若。
找规律练习题(打印版)

找规律练习题(打印版)### 找规律练习题(打印版)#### 一、数字规律题题目1:观察下列数字序列,找出规律并填写下一个数字。
1, 3, 5, 7, __答案: 9解析:这是一个等差数列,公差为2。
题目2:观察下列数字序列,找出规律并填写下一个数字。
2, 4, 8, 16, __答案: 32解析:这是一个等比数列,公比为2。
题目3:观察下列数字序列,找出规律并填写下一个数字。
1, 0, -1, 0, 1, 0, -1, __答案: 0解析:这是一个循环数列,每三个数字循环一次。
#### 二、图形规律题题目4:观察下列图形序列,找出规律并画出下一个图形。
```●● ●● ● ●● ● ● ●_____```答案:```● ●● ● ●● ● ● ●● ● ● ● ●```解析:每行的图形数量是前一行的两倍。
题目5:观察下列图形序列,找出规律并画出下一个图形。
```●● ●● ● ● ●_____```答案:```● ● ● ● ●● ● ● ●```解析:每行图形数量与前一行相同,但图形排列方式发生变化。
#### 三、逻辑规律题题目6:观察下列逻辑序列,找出规律并填写下一个序列。
A, B, C, D, E, __答案: F解析:这是一个字母序列,按照字母表顺序排列。
题目7:观察下列逻辑序列,找出规律并填写下一个序列。
红,黄,蓝,绿,__答案:紫解析:这是一个颜色序列,按照彩虹的颜色顺序排列。
#### 四、综合规律题题目8:观察下列综合序列,找出规律并填写下一个序列。
1, 3, 5, 7, 9, __, 13答案: 11解析:这是一个等差数列,公差为2,但需要跳过10。
题目9:观察下列综合序列,找出规律并填写下一个图形。
```● ●● ● ●● ● ● ● ●_____```答案:```● ● ● ●● ● ● ●```解析:每行的图形数量与前一行相同,但图形排列方式发生变化,形成对称。
#### 五、应用规律题题目10:观察下列应用序列,找出规律并填写下一个序列。
(word版)初中数学规律题汇总(全部有解析),文档

初中数学律拓展研究“有比才有〞。
通比,可以事物的相同点和不同点,更容易找到事物的化律。
找律的目,通常按照一定的序出一系列量,要求我根据些的量找出一般律。
揭示的律,常常包含着事物的序列号。
所以,把量和序列号放在一起加以比,就比容易其中的奥秘。
初中数学考中,常出数列的找律,本文就此的解方法行探索:一、根本方法——看增幅〔一〕如增幅相等〔等差数列〕:每个数和它的前一个数行比,如增幅相等,第n个数可以表示:a1+(n-1)b,其中a数列的第一位数,b增幅,(n-1)b第一位数到第n位的增幅。
然后再化代数式a+(n-1)b。
例:4、10、16、22、28⋯⋯,求第n位数。
分析:第二位数起,每位数都比前一位数增加6,增幅都是6,所以,第n位数是:4+(n-1)6=6n-2〔二〕如增幅不相等,但是增幅以同等幅度增加〔即增幅的增幅相等,也即增幅等差数列〕。
如增幅分3、5、7、9,明增幅以同等幅度增加。
此种数列第n位的数也有一种通用求法。
根本思路是:1、求出数列的第n-1位到第n位的增幅;2、求出第1位到第第n位的增幅;3、数列的第1位数加上增幅即是第 n位数。
此解法然,但是此的通用解法,当然此也可用其它技巧,或用分析察的方法求出,方法就的多了。
〔三〕增幅不相等,但是增幅同比增加,即增幅等比数列,如:2、3、5、9,17增幅1、2、4、8.〔四〕增幅不相等,且增幅也不以同等幅度增加〔即增幅的增幅也不相等〕。
此大概没有通用解法,只用分析察的方法,但是,此包括第二的,如用分析察法,也有一些技巧。
二、根本技巧1〔一〕出序列号:找律的目,通常按照一定的序出一系列量,要求我根据些的量找出一般律。
找出的律,通常包序列号。
所以,把量和序列号放在一起加以比,就比容易其中的奥秘。
例如,察以下各式数:0,3,8,15,24,⋯⋯。
按此律写出的第100个数是10021,第n个数是n21。
解答一,可以先找一般律,然后使用个律,算出第100个数。
找规律练习题(共10篇)

找规律练习题(共10篇)找规律练习题(一): 找规律题及答案初中数学规律题解题基本方法初中数学考试中,经常出现数列的找规律题,本文就此类题的解题方法进行探索:一、基本方法——看增幅(一)如增幅相等(此实为等差数列):对每个数和它的前一个数进行比较,如增幅相等,则第n个数可以表示为:a+(n-1)b,其中a为数列的第一位数,b为增幅,(n-1)b为第一位数到第n位的总增幅.然后再简化代数式a+(n-1)b. 例:4、10、16、22、28……,求第n位数.分析:第二位数起,每位数都比前一位数增加6,增幅相都是6,所以,第n位数是:4+(n-1)×6=6n-2(二)如增幅不相等,但是,增幅以同等幅度增加(即增幅的增幅相等,也即增幅为等差数列).如增幅分别为3、5、7、9,说明增幅以同等幅度增加.此种数列第n位的数也有一种通用求法.基本思路是:1、求出数列的第n-1位到第n位的增幅;2、求出第1位到第第n位的总增幅;3、数列的第1位数加上总增幅即是第n位数.举例说明:2、5、10、17……,求第n位数.分析:数列的增幅分别为:3、5、7,增幅以同等幅度增加.那么,数列的第n-1位到第n位的增幅是:3+2×(n-2)=2n-1,总增幅为:〔3+(2n-1)〕×(n-1)÷2=(n+1)×(n-1)=n2-1所以,第n位数是:2+ n2-1= n2+1此解法虽然较烦,但是此类题的通用解法,当然此题也可用其它技巧,或用分析观察凑的方法求出,方法就简单的多了.(三)增幅不相等,但是,增幅同比增加,即增幅为等比数列,如:2、3、5、9,17增幅为1、2、4、8.(三)增幅不相等,且增幅也不以同等幅度增加(即增幅的增幅也不相等).此类题大概没有通用解法,只用分析观察的方法,但是,此类题包括第二类的题,如用分析观察法,也有一些技巧.二、基本技巧(一)标出序列号:找规律的题目,通常按照一定的顺序给出一系列量,要求我们根据这些已知的量找出一般规律.找出的规律,通常包序列号.所以,把变量和序列号放在一起加以比较,就比较容易发现其中的奥秘.例如,观察下列各式数:0,3,8,15,24,…….试按此规律写出的第100个数是 .解答这一题,可以先找一般规律,然后使用这个规律,计算出第100个数.我们把有关的量放在一起加以比较:给出的数:0,3,8,15,24,…….序列号:1,2,3, 4, 5,…….容易发现,已知数的每一项,都等于它的序列号的平方减1.因此,第n项是n2-1,第100项是1002-1.(二)公因式法:每位数分成最小公因式相乘,然后再找规律,看是不是与n2、n3,或2n、3n,或2n、3n有关.例如:1,9,25,49,(),(),的第n为(2n-1)2(三)看例题:A: 2、9、28、65.增幅是7、19、37.,增幅的增幅是12、18 答案与3有关且.即:n3+1B:2、4、8、16.增幅是2、4、8.. .答案与2的乘方有关即:2n(四)有的可对每位数同时减去第一位数,成为第二位开始的新数列,然后用(一)、(二)、(三)技巧找出每位数与位置的关系.再在找出的规律上加上第一位数,恢复到原来.例:2、5、10、17、26……,同时减去2后得到新数列:0、3、8、15、24……,序列号:1、2、3、4、5分析观察可得,新数列的第n项为:n2-1,所以题中数列的第n项为:(n2-1)+2=n2+1(五)有的可对每位数同时加上,或乘以,或除以第一位数,成为新数列,然后,在再找出规律,并恢复到原来.例:4,16,36,64,,144,196,… (第一百个数)同除以4后可得新数列:1、4、9、16…,很显然是位置数的平方.(六)同技巧(四)、(五)一样,有的可对每位数同加、或减、或乘、或除同一数(一般为1、2、3).当然,同时加、或减的可能性大一些,同时乘、或除的不太常见.(七)观察一下,能否把一个数列的奇数位置与偶数位置分开成为两个数列,再分别找规律.三、基本步骤1、先看增幅是否相等,如相等,用基本方法(一)解题.2、如不相等,综合运用技巧(一)、(二)、(三)找规律3、如不行,就运用技巧(四)、(五)、(六),变换成新数列,然后运用技巧(一)、(二)、(三)找出新数列的规律4、最后,如增幅以同等幅度增加,则用用基本方法(二)解题四、练习题例1:一道初中数学找规律题0,3,8,15,24,2,5,10,17,26,0,6,16,30,48(1)第一组有什么规律(2)第二、三组分别跟第一组有什么关系(3)取每组的第7个数,求这三个数的和2、观察下面两行数2,4,8,16,32,64, ...(1)5,7,11,19,35,67...(2)根据你发现的规律,取每行第十个数,求得他们的和.(要求写出最后的计算结果和详细解题过程.)3、白黑白黑黑白黑黑黑白黑黑黑黑白黑黑黑黑黑排列的珠子,前2023个中有几个是黑的4、 3^2-1^2=8×1 5^2-3^2=8×2 7^2-5^2=8×3 ……用含有N的代数式表示规律写出两个连续技术的平方差为888的等式五、对于数表1、先看行的规律,然后,以列为单位用数列找规律方法找规律2、看看有没有一个数是上面两数或下面两数的和或差找规律试题练习找规律试题练习找规律试题练习找规律试题练习 1.一根1m长的小棒,第一次截去它的13 ,第二次截去剩下的13 ,如此截下去,第N次后剩下的小棒的长度是()m . 2.如图,按一定的规律用牙签搭图形:① ② ③ (1)按图示的规律填表:图形标号① ② ③ …… ⑩ 牙签根数…… (2)搭第n个图形需要________________________根牙签. 3. 已知1+2+3+…+31+32+33==17×33,求1-3+2-6+3-9+4-12+…+31-93+32-96+33-99的值. 4. 如图,在的内部从引出3条射线,那么图中共有___个角;如果引出5条射线,有___个角;如果引出条射线,有_ _个角. 5. 在数1,2,3,…,50前添“+”或“-”,并求它们的和,所得结果的最小非负数是多少请列出算式解答. 6. 如果有理数a,b满足∣ab-2∣+(1-b)2=0, 求+…+的值. 7.在一单位为1cm的方格纸上,依右图所示的规律,设定点A1、A2、A3、A4…、An,连结点A1、A2、A3组成三角形,记为,连结点A2、A3、A4组成三角形,记为…,连结点An、An+1、An+2组成三角形,记为(n为正整数).请你推断,当的面积为100cm2时,n= . 8.请观察下列算式:(8分) , 则第10个算为 = ,第n个算式为 = 请计算+++…+ 9、x, -3x2,5x3,-7x4, 9x5 …… 1. (23 )N,2 2. (1)2、7、15…155 (2)(1+2+3+…+n)×3-n或 3.-2×17×33 4.略 5.0 6.20232023 8. 略 9.(-1)n ( 1-2n) xn望采纳!找规律练习题(二): 一年级找规律练习题小学的【找规律练习题】1,2,3,(),5,6,(),8.1,3,5,7,(),11,13,152,4,6,8,(),12,14,1613,12,11,10,(),8,7,6【找规律练习题】找规律练习题(三): 二年级找规律练习题第一题:1,3,5,7,9第二题:2,4,6,8,10,第三题:1,4,9,16,25,36,(第一个数1乘1,第二个数2乘2以此类推)第四题:3,6,9,12第五题:条件不全.方法很多.找规律练习题(四): 找规律练习题1,4,16,32,()第一个数是第三个数的16倍,第二个数是第四个数的8倍,所以填64. 找规律练习题(五): 初一找规律习题20道(要稍微难一点的)35 69 10 12()()()()() () () () ()35 69 10 1217 18 20 2433 34 36 40 481.观察由棱长为1的小正方体摆成的图形:如图,图1共有1个小立方体,其中一个看得见,0个看不见;如图2:共有8个小立方体,其中7个看得见,1个看不见;如图3:共有27个小立方体,其中19个看得见,8个看不见.则第6个图中,看不见的小立方体有____个.2.(1)3的平方-1=8=8乘15的平方-3的平方=16=8乘27的平方-5的平方=24=8乘39的平方-7的平方=32=8乘4.15的平方-13的平方=____=______(2)归纳猜想得(2N+1)的平方-(2N-1)的平方=________(3)计算出:111的平方-99的平方=______3.观察:28=5的平方+3 31=5的平方+653的平方=2809 09=3的平方 56的平方=3136 36=6的平方(1)归纳观察上述式子发现十位数为______的两位数的______,如果前两位是_____,后两位数是______.(2)举例验证__________________________.4.(1)通过计算比较下列各组数中两个数的大小.1的平方__2的1次方 2的3次方___3的平方 3的4次方__4的3次方,4的5次方__5的4次方,5的6次方__6的5次方.(2)从第1题的结果经过归纳,可以猜想出N的(N+1)次方和(N+1)的N次方(N 大于或等于3)的大小关系_____________(3)根据下面的归纳猜想得到一般结论,试比较下列两数的大小.1998的1999次方______1999的1998次方1.观察由棱长为1的小正方体摆成的图形:如图,图1共有1个小立方体,其中一个看得见,0个看不见;如图2:共有8个小立方体,其中7个看得见,1个看不见;如图3:共有27个小立方体,其中19个看得见,8个看不见.则第6个图中,看不见的小立方体有125____个.2.(1)3的平方-1=8=8乘15的平方-3的平方=16=8乘27的平方-5的平方=24=8乘39的平方-7的平方=32=8乘4.15的平方-13的平方=_64___=__8乘8____(2)归纳猜想得(2N+1)的平方-(2N-1)的平方=_8N_______(3)计算出:111的平方-99的平方=_400_____3.观察:28=5的平方+3 31=5的平方+653的平方=2809 09=3的平方 56的平方=3136 36=6的平方(1)归纳观察上述式子发现十位数为______的两位数的______,如果前两位是_____,后两位数是______.(2)举例验证__________________________.4.(1)通过计算比较下列各组数中两个数的大小.1的平方5的4次方,5的6次方>6的5次方.(2)从第1题的结果经过归纳,可以猜想出N的(N+1)次方和(N+1)的N次方(N 大于或等于3)的大小关系__(N+1)次方 >(N+1)的N次方(N大于或等于3)(3)根据下面的归纳猜想得到一般结论,试比较下列两数的大小.1998的1999次方>1999的1998次方好了吗希望最佳找规律练习题(六): 一年级数学找规律,填空练习题( ) 、 2、4、()、10、()( 2 ) 、 2、4、( 6 )、10、( 16 )2+2=42+4=64+6=106+10=16找规律练习题(七): 一年级找规律练习题 2,7 5 ( ) ,1 8 ( ) ( ) ,10 3 ( ) ( ),9 ( ) ( ) ( ) ,7、5、(3)、18、(9)、(10)、12、(14)3、(5)、(7)、9、(11)、(13)一年的规律题很简单的,没你写的那么复杂.一般是加二减二的.找规律练习题(八): 一年级找规律练习题 2 5 7 ( ) ,1 8 ( ) ( ) ,3 10 ( ) ( ) ,9 ( ) ( ) ( ) .2 5 7 (12 ) ,1 8 ( 9) (17 ) ,3 10 (13 ) (23 ) ,9 ( 10) ( 19)(29 ) .每一个填的数字都是前两个数的和找规律练习题(九): 找规律数学思考题50道1.输入 1 2 3 4 5输出 1 3/5 2/5 5/17 3/13则输入50时,输出的结果是多少2.n M1 22 43 74 11用n的代数式表示M3.①. -2,4,-8,16,-32,64.;②. 0,6,-6,18,-30,66.;③. -1,2,-4,8,-16,32.;⑴第①行数中有什么规律.⑵第.②,③行树分别与第①行数有什么关系.⑶取每行数中的第10个数,计算这三个数的和4.问:0,1,0,-1,0,1,0,-1,0.第2023个数字是多少5.已知:a+b=1,ab= —1,设S1=a+b,S2=a^2+b^2,S2=a^3+b^3,……SN=a^n+b^n(1)计算:S1=( ) ,S2=( ), S3=( ),S4=( )(2)试写出 SN-2,SN-1 ,SN之间的关系式(3)根据以上得出的结论,计算a^6+b^6的值6.按一定的规律排列的一列数依次为:1/2,1/3,1/10,1/15,1/26,1/35...按此规律排列下去,下列数中的第7个数是().7.找规律,再填数.0.5、75%、六分之五、0.875、( )、()已知答案是 90% 十二分之十一,[email protected]=9 [email protected]=15 [email protected]=25这些算式有什么规律9. 7/4. 10/9. ( ). 16/25. ( )10.1/11 2/10 3/9 4/8 5/7 6/6 7/5 8/4 9/3 10/2 11/1这11个分数中的乘积是( )这11个分数中,( )与( )的差最大这11个分数中,( )与( )的和最接近111. 12.5 5 2 () () 0.12815 6 2.4 () () 0.153612.第一列第2列第3列第4列第一行 1 4 5 10第二行 4 8 10 12第三行 9 12 15 14. . . .1. 81所在的行和列分别是多少2. 100所在的行和列分别是多少13.7*9=63;8*8=64;11*13=143;12*12=144;23*24=624;25*25=625用字母表示数14.5,19,13,17,21,25,29,23,. 4,7,10,13,16,19,22,25.它们中间第15对相同的数是——( )15.第一列第二列第三列第四列第一行 2第二行 4 6第三行 8 10 12第四行 14 16 18 20.根据上面的规律,说说2023所在行,列分别是什么16.-2 -1 0 10 1 2 3 44 5 6 7 8 910 11 12 13 14 15 1617 18 19 20 21 22 23 24 251)第十行所有的数字是什么2)第二十五行从左往右第26个数字是3)第三十八行有几个数字4)前十行所有数字的和17.0,—3,8,—15,24,...(),...()添第100个数18.0.5 1.5 4.5 ( ) 40.5. 括号里面填什么19.找规律:在线段AB中间插入1个点,共有3条线段;在中间插入2个点时有6条线段;在中间插入3个点时,共有10条线段,那么在中间插入N个点时,共有多少条线段20.找规律:根2/2,1/2,根6/6,根2/4,根10/10下一个是__21.5 12 21 32 得出公式第N个数22.“^”代表几次方例:2^3= 8二进制1101换算成1×2^3+1×2^2+0×2^1+1×2^0=13,按此方式,十进制数换成二进制列式为:23.对正整数n的“F”运算:①当n为奇数时,结果为3n+5 ②当n为偶数时,结果为n/2^k当n=26时 ,26 F②=13 F ① = 44 F ②=11 …………24.f(x)=x/1+x 例:f(3)=3/1+3,f(1/3)=1/3÷(1+1/3)计算f(1/2023)+f(1/2023)+f(1/2023)+……+f(1/2)+f(1)+f(1)+f(2)+f(3)+……+f( 2023)+f(2023)=25.20分之1;15分之1;14分之1;问第四个数是多少26.27,28,24,20,21,12,(),(),()27.25,28,33,40,(),(),()28.1,1,2,2,3,4,4,8,(),(),()29.47,46,23,22,11,(),(),()30.24,12,36,18,54,(),( ),( )31. 1,3,7,82,4,65,9 看看每组数有什么规律32.小明背对小亮,让小亮按下列四个步骤操作:第一步分发左、中、右三堆牌,每堆牌不少于两张,且各堆牌的张数相同;第二步从左边一堆拿出两张,放入中间一堆;第三步从右边一堆拿出一张,放入中间一堆;第四步左边一堆有几张牌,就从中间一堆拿几张牌放入左边一堆.这时,小明准确说出了中间一堆牌现有的张数.你认为中间一堆牌的张数是33.1*2*3*4+1=252*3*4*5+1=1213*4*5*6+1=361请找其规律. 34.1、2、3.求N35.2、5、10、17. 求N36. 2、9、28、65.求N 37. 2、4、8、16.求N38.观察下列等式 9-1=8,16-4=12,25-9=16,36-16=20这些等式反映了自然数间的某种规律设n表示正整数用关于n的等式表示出来这种规律39. 98.95.96.97.94.99请问后面两个数.40. 边上圆圈的个数:1.2.3.4.5小圆圈的总数:.3.6.10.15如果用N表示等边三角形边上的小圆圈数,M表示这个三角形中小圆圈的总数,求M,N之间的关系.41.1,3,8,24,2,6,15,( )42.24,18,27/2,81/8,( )43.25,32,37,47( )44.4,3,1,12,9,3,17,5( )45.86,72,63,54,45,( )46.19,4,18,3,16,1,17( )47.□▽□ □□▽ □▽□ ▽□□ ()()()48.1+2+3+……+n=()49.(1x2)/1+(2x3)/1+(3x4)/1+……+(99x100)/150.观察下列等式:39*41=40的平方-1的平方,56*64=60的平方-4的平方,83*97=90的平方-7的平方,49*52=50的平方-2的平方,65*75=70的平方-5的平方(1)请你把发现的规律用字母表现出来:mn=__________找规律练习题(十): 数字找规律题目第一排4,3,8,1第二排2,7,3,4第三排,1,1,5问好数字是多少?a.8b.2c.6d.7突然发现问题有补充,泥垢,我不想动脑了,下文自己看看吧1、看数字和自然数列的关系如:1,4,9,16,...对比1,2,3,4,.显然是a(n)=n^2.2、对比前后数字差和如:1,1,2,3,5,8,.显然是前两个之和等于第三个,a(n)=a(n-2)+a(n-1) ,(n>=3).(斐波那契数列)再如:1,2,4,7,11,16.是前一项加自然数列等于后一项.a(n)=a(n-1)+(n-1),(n>=2).再如:3,4,6,9,13.3,4,6,9,14.你看看这两个数列再往下怎么写第一个是:加自然数列;第二个是前两项相加-1.所以往下写为:3,4,6,9,13,18,24.3,4,6,9,14,22,35.3、看隔项关系如1,1,3,4,5,9,7,16.叉开看就是:1,3,5,7和1,4,9,16单数为奇数列,偶数是自然数平方.。
初中找规律练习题

初中找规律练习题一、数字规律1. 观察下列数列,找出规律,并写出下一个数:2, 4, 8, 16, 32, ____2. 找出数列中的规律,并填入适当的数字:5, 10, 15, 20, ____, 303. 根据规律,完成数列:1, 3, 6, 10, 15, ____, ____二、图形规律1. 观察下列图形,找出规律,并画出下一个图形:AABAABCBA_____2. 找出图形排列规律,并选择正确的选项:A. △□○B. □○△C. ○△□△□○ □○△ ○△□3. 根据规律,补全图形:○○● ●○○ ○●○ _____三、字母规律1. 观察下列字母序列,找出规律,并写出下一个字母: A, C, E, G, ____2. 找出字母排列规律,并填入适当的字母:B, D, F, H, ____, L3. 根据规律,完成字母序列:A, B, C, D, E, ____, ____四、混合规律1. 观察下列序列,找出规律,并写出下一个元素:1A, 2B, 3C, 4D, ____2. 找出序列中的规律,并填入适当的元素:○5, ●7, ○9, ●11, ____, ●153. 根据规律,完成序列:AB, ABC, ABCD, ____, _____五、实际应用规律1. 小明每天做10道题,连续做了5天。
请找出他第6天应该做的题目数量。
2. 一辆汽车每行驶100公里,耗油10升。
请根据这个规律,计算行驶500公里需要耗多少油。
3. 小华每天吃一个苹果,一周共吃了几个苹果?根据这个规律,计算两周共吃了多少个苹果。
六、数列推理3, 6, 9, 12, 15, ____2, 5, 10, 17, 28, ____3. 找出数列中的错误数字,并将其改正:4, 8, 12, 18, 24, 32七、图形变换规律1. 观察下列图形序列,找出规律,并画出下一个图形:■■■■■■_____2. 根据图形变换规律,选择正确的选项:A. ■□B. □■C. ■■■□ □■ ■■3. 补全下列图形序列:▲△▽ △▽▲ ▽▲△ _____八、逻辑推理规律1. 根据规律,选择正确的答案:A. 苹果B. 香蕉C. 橙子草莓菠萝 ____2. 找出逻辑关系,并填入适当的词语:春天 > 花开 > ____3. 完成下列逻辑序列:太阳 > 光照 > ____月亮 > __________ > 夜晚九、数学运算规律1. 观察下列算式,找出规律,并计算结果:2 + 4 = 6, 4 + 8 = 12, 6 + 12 = ____2. 根据规律,填写下一个算式的结果:3 × 3 = 9,4 × 4 = 16,5 × 5 = ____3. 找出算式中的规律,并计算一个算式的结果:1² + 2² = 5, 2² + 3² = 13, 3² + 4² = ____十、综合应用规律1. 一本书有200页,小明每天阅读20页,根据这个规律,计算小明阅读完整本书需要多少天。
初中数学找规律题型

初中数学找规律题型一、观察数列:1,3,7,13,21,...,按此规律,下一个数是多少?A. 31B. 32C. 33D. 34(答案:A)二、一组按规律排列的数是:2,5,10,17,26,...,根据这组数的规律,紧接着的下一个数是多少?A. 35B. 36C. 37D. 38(答案:C)三、图形规律题:第一个图形有1个正方形,第二个图形有1+2=3个正方形,第三个图形有1+2+3=6个正方形,依此类推,第五个图形有多少个正方形?A. 10B. 15C. 20D. 25(答案:B)四、数列找规律:1,11,21,31,...,按此规律,第6个数是多少?A. 51B. 60C. 61D. 62(答案:C)五、一组数列如下:2,4,8,16,32,...,按此数列的规律,第8个数是?A. 128B. 256C. 512D. 1024(答案:C)六、观察以下数列:3,7,11,15,19,...,根据这个规律,第10个数是?A. 35B. 39C. 43D. 47(答案:B)七、图形规律题:第一个图由1个三角形组成,第二个图由1+2=3个三角形组成,第三个图由1+2+3=6个三角形组成,那么第七个图由多少个三角形组成?A. 21B. 28C. 35D. 42(答案:B)八、数列规律题:1/2,1/3,1/4,1/5,1/6,...,按此规律,第10个数是?A. 1/9B. 1/10C. 1/11D. 1/12(答案:C)。
七年级找规律试题及答案

七年级找规律试题及答案
一、选择题
1. 下列数列中,哪一个是按照规律排列的?
A. 2, 4, 8, 16, 32
B. 1, 3, 5, 7, 11
C. 3, 6, 12, 24, 48
D. 2, 5, 8, 11, 14
答案:A
2. 观察下列数列,找出缺失的数字。
2, 4, 8, 16, ?
A. 32
B. 24
C. 18
D. 20
答案:A
二、填空题
3. 完成下列数列:1, 2, 4, 8, _, _, 128。
答案:16, 32
4. 找出下列数列的规律,并填写缺失的数字:3, 7, 15, 31, _, _。
答案:63, 127
三、解答题
5. 一个数列的前几项是:2, 5, 8, 11, 14, ... 请找出数列的第10
项。
答案:第10项是23。
6. 观察下列数列,找出规律并写出下一个数字:1, 4, 9, 16, 25, 36, _。
答案:49
四、应用题
7. 一个等差数列的前三项分别是2, 5, 8,求这个数列的第10项。
答案:第10项是23。
8. 一个等比数列的前三项分别是3, 6, 12,求这个数列的第5项。
答案:第5项是48。
五、思考题
9. 一个数列的前几项是:1, 2, 4, 7, 11, ... 请找出数列的第100项。
答案:第100项是2584。
10. 一个数列的前几项是:1, 1, 2, 3, 5, 8, 13, ... 请找出数列的第10项。
答案:第10项是55。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
找规律专项训练一:数式问题222 3 23 4 2 4 a2a1.(湛江)已知2 2,3 ,4 4 , ... ,若88(a 、b 为正整数)3388 1515b b贝 U a b = ________ .2. (贵阳)有一列数 a 1,a 2, a 3, a 4, a 5,…,a n ,其中 a 1 = 5X 2+ 1,a 2 = 5x 3+ 2, a 3= 5x 4+ 3, a 4=5 x 5+ 4, a 5= 5x 6 + 5,…,当 a n = 2009 时,n 的值等于()A . 2010B . 2009C . 401D . 3343453. (沈阳)有一组单项式:a 2,— ~r , a T ,—,….观察它们构成规律,用你发现的规律写出第 2 34项式为 ____________ .1 23 4 4. (牡丹江)有一列数,一,-一,一,…,那么第7个数是 ____________ .2 510 177.(绵阳)将正整数依次按下表规律排成四列,则根据表中的排列规律,数 2009应排的位置是第 ________行第 ___________ 列.8. (台州)将正整数1, 2, 3,…从小到大按下面规律排列.若第 4行第2列的数为32,则①n 二—▲_ ②第i 行第j 列的数为 ▲ (用i , j 表示).第1列 第2列第3列… 第n 列第1行12 3 …n6.(安徽)观察下列等式:1 12 23 31 1, 22, 33--, 223344A . 10 , 19a bB . 10 , 19a -bC . 10, 17a -bD .(1)猜想并写出第n 个等式;(2)证明你写出的等式的正确性. 10个单5. (南充)一组按规律排列的多项式:233547a b , a -b , a b , a - b ,,其中第10个式子是(10 , 21a- b2 2㊉”,其法则为:a ㊉b = a -b ,求方程(4㊉3) ® x = 24的解.2•有一列数a i ,a 2,a 3,…,a n ,从第二个数开始,每一个数都等于1与它前面那个数的倒数的差, 若= 2, 则 a 2007 为( )1 A. 2007B. 2C.D. -12三:剪纸问题 1.(2004年河南)如图(9),把一个正方形三次对折后沿虚线剪下则得到的图形是()2. (2004年浙江湖州)小强拿了一张正方形的纸如图(10)①,沿虚线对折一次得图②,再对折一次 得图③,然后用剪刀沿图③中的虚线(虚线与底边平行)剪去一个角,再打开后的形状应是( )□ /仝 ① ② ③ffi Cio)3.(2004年浙江衢州)如图(11),将一张正方形纸片剪成 剪成四个小正方形,再将其中的一个正方形剪成四个小正方形, 请你填写下表:2n第3行 2n ・12n 2 2n 3 3n:定义运算问题1.(定西)在实数范围内定义运算右下方折 沿虚线剪开iAH C E图 C11)操作次数N 1 2 34 5N正方形的个数4 7103.(莆田)如图,在x 轴的正半轴上依次截取 0A = AA 2= A2A 3=,过点A|、A 、A 3、A 4、A2分别作x 轴的垂线与反比例函数y x = 0的图象相交于点 R 、P 2、P 3、F 4、F 5,得直角三角形xORA 、AP 2A 2、A 2F 3A 5、A 3P 4A 4、AH RA S ,并设其面积分别为 S 、S 2、S 3、S 4、S s,则 S s 的值为 __________ .4. (长春)用正三角形和正六边形按如图所示的规律拼图案,即从第二个图案开始,每个图案都比上一个 图案多一个正六边形和两个正三角形,则第n 个图案中正三角形的个数为 ______________ (用含n 的代数式A i A 2 A 3 A A Sx(第10题图)(第 4题)5. (丹东)如图6,用同样大小的黑色棋子按图所示的方式摆图案,按照这样的规律摆下去,第100个图案需棋子 _____________ 枚.图案1 图案2图案3图66. (抚顺)观察下列图形(每幅图中最小..的三角形都是全等的),请写出第n 个图中最小.的三角形的个数有 个.第1个图第2个图第3个图(第16题图)7.(哈尔滨)观察下列图形: 五:对称问题1. (伊春)在平面直角坐标系中,已知 3个点的坐标分别为 A (1,1)、血(0,2)、A3(-1 ,). —只电子蛙位于 坐标原点处,第1次电子蛙由原点跳到以 A 为对称中心的对称点 R,第2次电子蛙由P 点跳到以A 2为对 称中心的对称点F 2,第3次电子蛙由P 2点跳到以A 为对称中心的对称点 P s ,…,按此规律,电子蛙分别 以A 、A 2、A 为对称中心继续跳下去. 问当电子蛙跳了 2009次后,电子蛙落点的坐标是 P 2009 ( _________________ ).2. (2004年宁波)仔细观察下列图案,如图(12),并按规律在横线上画出合适的图形。
出3C (D — H *X图(12)3. (2004年资阳市)分析图(14)①,②,④中阴影部分的分布规律,按此规律在图( 14)③中画出其中的阴影部分.★ ★ 會★第J 个图形 第2个图形 ★* * * * * *第3个图形 它们是按一定规律排列的,依照此规律,第★ ★ ★★★ ★ ★ ★ ★ ★ ★ ★責第4个图形 16个图形共有第4个图图(15)1我们平常用的数是十进制数,女口 2639=2O03+6X 102+3X101+9X10°,表示十进制的数要用 10个数码(又叫数字):0, 1, 2, 3, 4, 5, 6, 7, 8, 9。
在电子数字计算机中用的是二进制,只要两个数码:0和1。
如二进制中101=1 X22+0 X 21+1 X 20等于十进制的数 5, 10111=1 X 24+0疋3+ 1X22+ 1X21+ 1 X2°等于十进制中 的数23,那么二进制中的1101等于十进制的数 _________________ 。
2、从1开始,将连续的奇数相加, 和的情况有如下规律:1=1=12; 1+3=4=22 ; 1+3+5=9=32; 1+3+5+7=16=4 2 ; 1+3+5+7+9=25=5 2;…按此规律请你猜想从 1开始,将前10个奇数(即当最后一个奇数是 19时),它们的和是 ________ 。
3、小王利用计算机设计了一个计算程序,输入和输出的数据如下表:输入i 2 3 4 5输出1 22 53 104 175 26那么,当输入数据是 8时,输出的数据是( )A 、61 63 654、如下左图所示,摆第一个“小屋子”要 5枚棋子,摆第二个要' *«* •第一个“上”字" 第二个“上””字第三个“上”字和 ________ 枚棋子;(2 )第n 个“上”字需用 ___________ 枚棋子。
7、如图一串有黑有白,其排列有一定规律的珠子,被盒子遮住一部分,则这串珠子被盒子遮住的部分有/ 7\/ P\/ 72\N % 7 /r■6711枚棋子,摆第三个要17枚棋子,则摆第30个“小屋子”要枚棋子•5、如下右图是某同学在沙滩上用石子摆成的小房子,观察图形的变化规律,写出第 个小房子用了块石子。
O O O O O O O Q O O(1)D O OOQo o O oOO6、如下图是用棋子摆成的 “上”字:如果按照以上规律继续摆下去,那么通过观察,可以发现:(1)第四、第五个“上”字分别需用\ /_______ 颗.8、根据下列5个图形及相应点的个数的变化规律:猜想第 形中有 ____________ 个点。
10、观察下面的点阵图和相应的等式,探究其中的规律:(1)在④和⑤后面的横线上分别写出相应的等式;(2)通过猜想写出与第n 个点阵相对应的等式 ______________________ 。
11、 用边长为1cm 的小正方形搭成如下的塔状图形,则第n 次所搭图形的周长是 ________________ c m (用含n 的 代数式表示)。
□ fii第1次 第2次 第3次 第4次 …12、 如图,都是由边长为 1的正方体叠成的图形。
例如第(1)个图形的表面积为 6个平方单位,第(2) 个图形的表面积为18个平方单位,第(3)个图形的表面积是 36个平方单位。
依此规律。
则第(5)个 图形的表面积 ___________________ 个平方单位。
经观察可以发现:图(2)比图(1)多出2个 比图(3)多出10个“树枝”,照此规律,图(7)⑸“树枝”,图(3)比图(2)多出5个“树枝”,图(4)比图(6)多出 个“树枝”。
①仁12; ② 1+3=22;(1)6个图形有第7题图个点,第n 个图③1+3+5=32⑤ __________⑵⑷13、图(1)是一个水平摆放的小正方体木块,图( 2)、( 3)是由这样的小正方体木块叠放而成,按照这样的规律继续叠放下去,至第七个叠放的图形中,小正方体木块总数应是( )A 25B 66C 91D 120s= __________ .16、如图用火柴摆去系列图案,按这种方式摆下去,当每边摆 10根时(即n =10)时,需要的火柴棒总数为 _______ 根;14、如图是由大小相同的小立方体木块叠入而成的几何体,图⑴中有 1个立方体,图⑵中有 4个立方体,图⑶中有9个立方体,••… 按这样的规律叠放下去,15、图1是棱长为a 的小正方体,图2、图3由这样的小正方体摆放而成•按照这样的方法继续摆放,由上而下分别叫第一层、第二层、…、第 n 层,第n 层的小正方体的个数为 s .解答下列问题:图1(1)按照要求填表:n 1 2 34s136(2 )写出当n =10 时a(1)图317、用火柴棒按如图的方式搭一行三角形,搭一个三角形需 3支火柴棒,搭2个三角形需 3个三角形需7支火柴棒,照这样的规律下去,搭 n 个三角形需要 S 支火柴棒,那么用的式子是 ____________ ( n 为正整数)ZSZS7n=35支火柴棒,搭n 的式子表示S。
