小升初专项培优测评卷(十六)平面图形的认识与测量(二)(原卷版)
小学六年级数学小升初珍藏版复习资料第14讲 平面图形的认识与测量(原卷)

2022-2023学年小升初数学精讲精练专题汇编讲义第14讲平面图形的认识与测量知识点一:线和角的认识1.线段、直线、射线的特点(1)线段有两个端点,可以度量长度;射线只有一个端点,它可以向一端无限延伸,不可以度量长度;直线没有端点,它可以向两端无限延伸,不能度量长度。
(2)两点之间线段最短。
2.垂直与平行(1)同一平面内,两条直线的位置关系是平行和相交。
如果两条直线相交成直角,就说这两条直线互相垂直,其中一条直线叫作另一条直线的垂线,它们的交点叫作垂足。
过直线外一点只能画一条已知直线的垂线。
(2)平行线之间的距离处处相等;点到直线的所有连线中,垂线段最短。
3.角(1) 由一点出发的两条射线组成的图形叫角;角的大小与两边的画出的长短无关,与两边张开的大小有关。
(2)角的分类锐角直角钝角平角周角大于0。
小于90。
90。
大于90。
小于180。
180°360°知识点二:三角形的认识与测量1.三角形的认识知识精讲(1)三角形的特殊性质:三角形具有稳定性。
(2)三角形三边关系:在一个三角形中,任意两边之和大于第三边,任意两边之差小于第三边。
(3)三角形的分类:三角形按角分,分为锐角三角形、直角三角形和钝角三角形;按边分,分为特殊三角形和一般三角形。
等腰三角形和等边三角形是特殊三角形,等边三角形是特殊的等腰三角形。
(4)三角形的内角和是( 180° )2.三角形的面积两个完全一样的三角形可以拼成一个平行四边形,这个平行四边形的底就是三角形的底,所拼成平行四边形的高就是三角形的高。
每个三角形的面积是所拼成平行四边形面积的一半。
因为平行高四边形的面积=底×高,所以三角形的面积= 1底×高,用字母2ah 。
表示为: S=12知识点三:四边形的认识与测量1.四边形的认识(1)四边形的特殊性质:不稳定,易变形。
(2)平行四边形两组对边分别平行且相等,梯形只有一组对边平行。
小升初六年级数学名校冲刺精编讲义第16讲 平面图形的认识与测量(二)(学生版)

第16讲平面图形的认识与测量(二)知识点一:圆的认识1.在同圆或等圆中,所有的直径都相等,所有的半径都相等。
2.圆是轴对称图形,圆有无数条对称轴,圆的对称轴就是直径所在的直线。
知识点二:圆的周长和面积1.圆的周长(1)圆周率:圆的周长与直径的比值叫作圆周率。
圆周率用希腊字母“π”表示,它是一个无限不循环小数。
经过精密计算:π=3.1415926…在小学数学中,我们常常取圆周率的近似值3.14(2)圆的周长= 圆周率×直径或圆周率×半径×2用字母表示为:C= πd或2πr 2.圆的面积:把一个圆平均分成若干份,剪开后拼成一个近似的平行四边形,如果分的份数越多,拼成的图形越接近长方形,这个近似长方形的长等于圆周长的一半,宽等于圆的半径,由此圆的面积S= πr23.圆环的面积(1)同一个圆心的两个半径不相等的圆,它们之间的部分叫作圆环(2)面积公式: S=πR2-πr2知识点三:组合图形的面积1.求组合图形面积的方法。
(1)分割法:把阴影部分分割成几个基本图形,利用求几个基本图形面积的和求出阴影部分的面积。
(2)添补法:在阴影部分上添补一个基本图形,使其变成另一个基本图形,计算出这个基本图形的面积后减去补上的基本图形的面积,从而求出阴影部分的面积。
考点一:圆的认识和圆周率【例1】(2019•鼓楼区)操作:(1)以O点为圆心,3格长为半径,画一个半圆形.(2)画出半圆形的对称轴.(3)把半圆形向右平移8格.1.(2019秋•花都区期末)下面说法正确的是()A.所有半径都相等,所有直径都相等B.在同一个圆中,扇形的大小与这个扇形的圆心角的大小有关C.大圆的圆周率比小圆的圆周率大2.(2019秋•沧州期末)下面关于圆周率π的说法正确的是()A.π是圆的周长与这个圆的直径的比值B.π是循环小数π=D.π是圆的面积与这个圆的半径的比值C. 3.143.(2019秋•凌源市期末)关于圆的知识,下面说法不正确的是()A.圆心只决定圆的位置,不决定圆的大小B.两端都在圆上的线段叫做直径C.半径相等的两个圆的面积相等D.圆周率是圆周长和这个圆直径的比值4.(2019秋•香坊区期末)下列说法正确的是()A.用圆规画圆时.若圆规两脚间的距离是3cm,则所画圆的直接为3cmB.用4个圆心角都是90︒的扇形,一定可以拼成一个圆C.圆的半径扩大到原来的2倍,周长也扩大到原来的2倍D.小明身高1m,爸爸身高180cm,小明和爸爸身高的比是1:1805.(2019秋•西城区期末)如图所示图形中,对称轴条教最少的是() A.B.C.D.考点二:圆的周长和面积【例2】(2019•天津模拟)计算阴影部分的面积和周长.(单位:厘米)【例3】(2019•番禺区校级模拟)求如图的周长和面积.【例4】(2019秋•古丈县期末)求阴影部分的面积和周长.1.(2019•鄞州区)在一张长12厘米、宽10厘米的彩纸上画一个最大的圆,这个圆的周长是厘米,面积是平方厘米.2.(2019•福田区)已知小圆的半径是2厘米,大圆的半径是3厘米,小圆和大圆周长的比是,面积的比是.3.(2019•长沙)一张半圆形纸片周长是20.56cm,他的半径是cm,面积是2cm.4.(2019秋•中方县期末)把一个直径是5厘米的圆分成若干等份,然后把它剪开,照如图的样子拼起来,拼成的图形的周长比原来圆的周长增加厘米.5.(2019•宿迁)从一个长10分米,宽4分米的长方形木板上锯下一个最大的半圆,半圆的直径是分米,半圆的周长是分米,半圆的面积是平方分米.6.(2019•临川区)如图是三个半圆,求阴影部分的周长.7.(2019•株洲)求图形的周长.8.(2019•中山区)求图中阴影部分的周长.( 取3)9.(2019•玄武区)图中阴影部分的面积是15平方厘米,求环形的面积10.(2019•淮安)如图,长方形的面积和圆的面积相等,已知圆的半径是4厘米,求阴影部分的周长和面积.考点三:组合图形的周长和面积【例5】(2019春•新田县期末)求下列图形的周长或面积【例6】(2019秋•江南区期末)求阴影部分的周长与面积.【例7】(2019•高台县)求图阴影部分的周长和面积.1.(2019•郑州)请求出图中阴影部分的面积(单位:厘米).2.求如图中阴影部分的面积,已知圆的半径为4厘米.3.(1)求图(1)阴影部分的周长. (2)求图(2)阴影部分的面积.(3)如图(3)已知:1S 比2S 多28平方厘米,求BC 长多少厘米?4.求阴影部分的周长与面积:(单位cm )5.(2019秋•黄冈期末)求图中阴影部分的周长和面积.(单位:厘米)6.求图中阴影部分的周长和面积.(单位:厘米)7.求下列图形的周长和面积:(单位:米)8.求下面图形中阴影部分的面积.(单位:)cm (1)长方形面积245cm.(2)(3)(4)9.(2019•厦门)图中圆的周长是12.56cm,圆的面积正好等于长方形的面积,求阴影部分的面积.10.(2019•北京模拟)如图,已知4AOC=;60∠=︒,求阴影部分的面积.OC cm=,2OD cm11.(2019•东莞)求阴影部分的面积、周长.考点四:与圆有关的实际问题【例8】(2019•营山县模拟)将圆平均分成若干个小扇形,剪拼成一个近似的长方形(如图).(1)如果长方形的长是12.56厘米,圆的面积是多少?(2)如果圆的半径是10厘米,阴影部分的面积是多少?【例9】(2019•丹阳市)已知图中阴影部分的面积是220cm,环形的面积是多少平方厘米?【例10】(2019春•武城县期末)一片草地中央有一个边长为8m的正方形羊圈(如图),将一只羊用10m 长的绳子系在羊圈墙外一个角的顶点上,这只羊能吃到的草地面积是多少平方米?1.(2019•娄底模拟)一只环形玉佩的外圆半径为2厘米,比内圆半径多1.5厘米,这只环形玉佩的面积是多少平方厘米?2.(2019•江北区)滨江公园有一个圆形水池,沿着它的外沿修一圈2米宽的草坪,水池的半径是5米,那么草坪的面积是多少平方米?3.(2019•绵阳)一个长方形与一个圆的面积相等,如果长方形的长与圆的直径都是8厘米,那么长方形的宽是多少厘米?(取3.14)4.(2019•石家庄)一个圆形花坛的直径是6m,现在沿花坛的外围铺一条宽1m的石子路,若每平方米石子路面造价80元,建造这条石子路共需多少元?5.(2019秋•海安县期末)在400米的运动场上要举行400米比赛,(起点要前移多少米才恰当?)跑道每道宽1.25米,外一圈起点要比内一圈前移多少米?6.(2019•长汀县模拟)一个圆形羊圈半径6 米,如果要扩建这个羊圈,把它的直径增加2米.(1)扩建后,这个羊圈的周长是多少米?(2)扩建后,这个羊圈的面积增加了多少平方米?7.如图,一只狗用皮带系在1010的正方形狗窝的一角,皮带长为14,在狗窝外面狗能活动的范围的面积是多少?画出示意图并计算.(狗的大小忽略不计,长度单位:分米)小升初专项培优测评卷(十六)平面图形的认识与测量(二)1.(2019秋•望江县期末)如图是光明小学的运动场的示意图,阴影部分为跑道.求跑道的占地面积.2.(2019秋•达州期中)如图是一个花台的平面图,5为圆的半径(单位:)m.求这个花台的周长是多少厘米?3.(2019•郑州)求如图图形阴影部分的面积.4.(2019•石家庄)求如图阴影部分的周长和面积.5.有一个200m的环形跑道(如图所示).(1)东东沿着第二条跑道(由内向外)跑一圈,他跑了多少米?(π取3.14)(2)如果在这个跑道上进行100m赛跑,那么如何确定起跑线的位置呢?(π取3.14)6.(2019•邵阳模拟)某赛车的左、右轮子的距离为2米,因此,当车子转弯时,外侧的轮子比内侧的轮子多走了一段路.赛车跑道如图所示,当赛车车轮行走一圈时,外轮比内轮多走多少米?7.(2019•长沙模拟)如图所示为一卷紧绕成的牛皮纸,纸卷直径为20厘米,中间有一直径为6厘米的卷轴.已知纸的厚度为0.4毫米,问:这卷纸展开后大约有多少米?(保留小数点后一位)8.(2019•沈河区)如图,一只羊被一条5米长的绳子拴在木桩上.求羊活动的面积是多少?。
人教版六年级小升初数学复习资料《图形的认识和测量》知识点+练习题(含答案)

13.图形的认识与测量(一)【学习内容】平面图形的基础知识(课本96页)【学习目标】1.进一步掌握基本的平面图形的特点等知识。
2.通过比较、分类、归纳等方式理解这些平面图形之间的关系。
【学习过程】一、知识梳理1.想一想。
(1)用直尺把两点连接起来,就得到一条线段,把线段的一端无限延长,可以得到一条()线;把线段的两端无限延长,可以得到一条()线。
直线、射线和线段有什么区别?(2)从一点引出两条射线,就组成一个角。
角的大小与什么有关?请把表中的空格填写完2.分一分。
(1)根据同一个平面内两条直线的位置关系可以把下面的几组直线分成几类?①②③④⑤⑥⑦⑧⑨(2)请把下面的三角形按照特点分类,整理到表格中。
想一想,三角形还有哪些特点?3.说一说(1)根据下面四边形的关系图说一说它们各自的特点。
(2)和同学们交流一下圆有什么特点?二、课堂练习1.判断。
(1)一条直线长10米。
()(2)长方形一定是平行四边形。
()(3)小于180°的角都是钝角。
()(4)不相交的两条直线肯定是平行线。
()2.选择。
(1)等腰三角形的一个底角是45°,这个三角形是()。
A.锐角三角形B. 直角三角形C.钝角三角形(2)平行四边形有()高,梯形有()条高,三角形有()条高。
A.无数条B.一条C.三条(3)用3根小棒围成一个三角形,其中两根小棒分别长3cm和5cm,另一根应该选()。
A.2cmB.4cmC.8cm三、当堂检测1.填空。
(1)一个等腰三角形,它的顶角是72度,它的底角是()度。
(2)用圆规画一个直径4cm的圆,圆规两脚间的距离应该是()厘米。
2.画一画。
(1)如果从A、B两点各修一条小路与公路相连通,怎样修能使这两条小路最短?(2)画出下面三角形的一条高过,然后过A点作三角形BC边的平行线。
14.图形的认识与测量(二)【学习内容】平面图形的周长和面积(课本97页)【学习目标】1.引导学生回忆整理平面图形的周长和面积的意义及计算公式的推导过程,并能熟练应用公式进行计算。
第7章 平面图形的认识(二)-平行线几何模型(M模型 培优篇) 苏科版七年级数学下册基础知识讲与练

专题7.16 平行线几何模型(M 模型)(巩固培优篇)(专项练习)1.已知直线AB //CD ,EF 是截线,点M 在直线AB 、CD 之间. (1) 如图1,连接GM ,HM .求证:∠M =∠AGM +∠CHM ;(2) 如图2,在∠GHC 的角平分线上取两点M 、Q ,使得∠AGM =∠HGQ .试判断∠M 与∠GQH 之间的数量关系,并说明理由.2.阅读下面内容,并解答问题. 已知:如图1,AB CD ,直线EF 分别交AB ,CD 于点E ,F .BEF ∠的平分线与DFE ∠的平分线交于点G .(1) 求证:EG FG ⊥;(2) 填空,并从下列①、②两题中任选一题说明理由.我选择 题.①在图1的基础上,分别作BEG ∠的平分线与DFG ∠的平分线交于点M ,得到图2,则EMF ∠的度数为 .②如图3,ABCD ,直线EF 分别交AB ,CD 于点E ,F .点O 在直线AB ,CD 之间,且在直线EF 右侧,BEO ∠的平分线与DFO ∠的平分线交于点P ,则EOF ∠与EPF ∠满足的数量关系为 .3.已知直线a b ∥,直线EF 分别与直线a ,b 相交于点E ,F ,点A ,B 分别在直线a ,b 上,且在直线EF 的左侧,点P 是直线EF 上一动点(不与点E ,F 重合),设∠P AE =∠1,∠APB =∠2,∠PBF =∠3.(1) 如图1,当点P 在线段EF 上运动时,试说明∠1+∠3=∠2; (2) 当点P 在线段EF 外运动时有两种情况.①如图2写出∠1,∠2,∠3之间的关系并给出证明;②如图3所示,猜想∠1,∠2,∠3之间的关系(不要求证明).4.问题情境:如图①,直线AB CD ∥,点E ,F 分别在直线AB ,CD 上. (1) 猜想:若1130∠=︒,2150∠=︒,试猜想P ∠=______°;(2) 探究:在图①中探究1∠,2∠,P ∠之间的数量关系,并证明你的结论; (3) 拓展:将图①变为图②,若12325∠+∠=︒,75EPG ∠=︒,求PGF ∠的度数.5.如图:(1) 如图1,AB CD ∥,=45ABE ∠︒,21CDE ∠=︒,直接写出BED ∠的度数.(2) 如图2,AB CD ∥,点E 为直线AB ,CD 间的一点,BF 平分ABE ∠,DF 平分CDE ∠,写出BED ∠与F ∠之间的关系并说明理由.(3) 如图3,AB 与CD 相交于点G ,点E 为BGD ∠内一点,BF 平分ABE ∠,DF 平分CDE ∠,若60BGD ∠=︒,95BFD ∠=︒,直接写出BED ∠的度数.6.(1)已知:如图(a ),直线DE AB ∥.求证:ABC CDE BCD ∠+∠=∠; (2)如图(b ),如果点C 在AB 与ED 之外,其他条件不变,那么会有什么结果?你还能就本题作出什么新的猜想?7.如图,//AB CD ,点E 在直线AB ,CD 内部,且AE CE ⊥. (1)如图1,连接AC ,若AE 平分BAC ∠,求证:CE 平分ACD ∠; (2)如图2,点M 在线段AE 上,①若MCE ECD ∠=∠,当直角顶点E 移动时,BAE ∠与MCD ∠是否存在确定的数量关系?并说明理由;②若1MCE ECD n∠=∠(n 为正整数),当直角顶点E 移动时,BAE ∠与MCD ∠是否存在确定的数量关系?并说明理由.8.已知直线l1//l2,A是l1上的一点,B是l2上的一点,直线l3和直线l1,l2交于C和D,直线CD上有一点P.(1)如果P点在C,D之间运动时,问∠P AC,∠APB,∠PBD有怎样的数量关系?请说明理由.(2)若点P在C,D两点的外侧运动时(P点与C,D不重合),试探索∠P AC,∠APB,∠PBD之间的关系又是如何?(请直接写出答案,不需要证明)9.(1)如图,AB//CD,CF平分∠DCE,若∠DCF=30°,∠E=20°,求∠ABE的度数;(2)如图,AB//CD,∠EBF=2∠ABF,CF平分∠DCE,若∠F的2倍与∠E的补角的和为190°,求∠ABE的度数.(3)如图,P为(2)中射线BE上一点,G是CD上任一点,PQ平分∠BPG,GN//PQ,GM平分∠DGP,若∠B=30°,求∠MGN的度数.10.如图1,已知AB∥CD,∠B=30°,∠D=120°;(1)若∠E=60°,则∠F=;(2)请探索∠E与∠F之间满足的数量关系?说明理由;(3)如图2,已知EP平分∠BEF,FG平分∠EFD,反向延长FG交EP于点P,求∠P 的度数.11.如图1,AB//CD,E是AB,CD之间的一点.(1)判定∠BAE,∠CDE与∠AED之间的数量关系,并证明你的结论;(2)如图2,若∠BAE,∠CDE的角平分线交于点F,直接写出∠AFD与∠AED之间的数量关系;(3)将图2中的射线DC沿DE翻折交AF于点G得图3,若∠AGD的余角等于2∠E的补角,求∠BAE的大小.12.已知AB//CD.(1)如图1,E 为AB ,CD 之间一点,连接BE ,DE ,得到∠BED .求证:∠BED =∠B +∠D ;(2)如图,连接AD ,BC ,BF 平分∠ABC ,DF 平分∠ADC ,且BF ,DF 所在的直线交于点F .①如图2,当点B 在点A 的左侧时,若∠ABC =50°,∠ADC =60°,求∠BFD 的度数. ②如图3,当点B 在点A 的右侧时,设∠ABC =α,∠ADC =β,请你求出∠BFD 的度数.(用含有α,β的式子表示)13.已知,AB ∥CD .点M 在AB 上,点N 在CD 上.(1)如图1中,∠BME 、∠E 、∠END 的数量关系为: ;(不需要证明) 如图2中,∠BMF 、∠F 、∠FND 的数量关系为: ;(不需要证明) (2)如图3中,NE 平分∠FND ,MB 平分∠FME ,且2∠E +∠F =180°,求∠FME 的度数;(3)如图4中,∠BME =60°,EF 平分∠MEN ,NP 平分∠END ,且EQ ∥NP ,则∠FEQ 的大小是否发生变化,若变化,请说明理由,若不变化,求出∠FEQ 的度数.14.如图1,点A 、B 分别在直线GH 、MN 上,GAC NBD ∠=∠,C D ∠=∠. (1)求证://GH MN ;(提示:可延长AC 交MN 于点P 进行证明)(2)如图2,AE 平分GAC ∠,DE 平分BDC ∠,若AED GAC ∠=∠,求GAC ∠与ACD ∠之间的数量关系;(3)在(2)的条件下,如图3,BF 平分DBM ∠,点K 在射线BF 上,13KAG GAC ∠=∠,若AKB ACD ∠=∠,直接写出GAC ∠的度数.15.已知AB ∥CD ,∠ABE 的角分线与∠CDE 的角分线相交于点F .(1)如图1,若BM 、DM 分别是∠ABF 和∠CDF 的角平分线,且∠BED =100°,求∠M 的度数;(2)如图2,若∠ABM =13∠ABF ,∠CDM =13∠CDF ,∠BED =α°,求∠M 的度数;(3)若∠ABM =1n ∠ABF ,∠CDM =1n∠CDF ,请直接写出∠M 与∠BED 之间的数量关系.16.已知直线AM 、CN 和点B 在同一平面内,且AM ∥CN ,AB ⊥BC . (1)如图1,求∠A 和∠C 之间的数量关系;(2)如图2,若BD ⊥AM ,垂足为D ,求证:∠ABD =∠C ;(3)如图3,已知点D 、E 、F 都在直线AM 上,且∠ABD =∠NCB ,BF 平分∠DBC ,BE 平分∠ABD .若∠FCB +∠NCF =180°,∠BFC =3∠DBE ,请直接写出∠EBC 的度数.17.如图1,点A 在直线MN 上,点B 在直线ST 上,点C 在MN ,ST 之间,且满足MAC ACB SBC ∠+∠+∠360=︒.(1)证明://MN ST ;(2)如图2,若60ACB ∠=︒,//AD CB ,点E 在线段BC 上,连接AE ,且2DAE CBT ∠=∠,试判断CAE ∠与CAN ∠的数量关系,并说明理由;(3)如图3,若180ACB n︒∠=(n 为大于等于2的整数),点E 在线段BC 上,连接AE ,若MAE n CBT ∠=∠,则:CAE CAN ∠∠=______.18.如图1,直线AB //CD ,点P 在两平行线之间,点E 在AB 上,点F 在CD 上,连接PE ,PF .(1)若∠PEB =60°,∠PFD =50°,请求出∠EPF .(请写出必要的步骤,并说明理由) (2)如图2,若点P ,Q 在直线AB 与CD 之间时,∠1=30°,∠2=40°,∠3=70°,请求出∠4= .(不需说明理由,请直接写出答案)(3)如图3,在图1的基础上,作P 1E 平分∠PEB ,P 1F 平分∠PFD ,若设∠PEB =x °,∠PFD =y °,则∠P 1= (用含x ,y 的式子表示).若P 2E 平分∠P 1EB ,P 2F 平分∠P 1FD ,可得∠P 2;P 3E 平分∠P 2EB ,P 3F 平分∠P 2FD ,可得∠P 3…,依次平分下去,则∠Pn = .(用含x ,y 的式子表示)19.已知//AM CN ,点B 为平面内一点,AB BC ⊥于B .(1)如图1,点B 在两条平行线外,则A ∠与C ∠之间的数量关系为______; (2)点B 在两条平行线之间,过点B 作BD AM ⊥于点D . ①如图2,说明ABD C ∠=∠成立的理由;②如图3,BF 平分DBC ∠交DM 于点,F BE 平分ABD ∠交DM 于点E .若180,3FCB NCF BFC DBE ∠∠∠∠+=︒=,求EBC ∠的度数.20.如图1,MN ∥PQ ,点C 、B 分别在直线MN 、PQ 上,点A 在直线MN 、PQ 之间. (1)求证:∠CAB =∠MCA +∠PBA ;(2)如图2,CD ∥AB ,点E 在PQ 上,∠ECN =∠CAB ,求证:∠MCA =∠DCE ; (3)如图3,BF 平分∠ABP ,CG 平分∠ACN ,AF ∥CG .若∠CAB =60°,求∠AFB 的度数.21.如图,//MN GH ,点A 、B 分别在直线MN 、GH 上,点O 在直线MN 、GH 之间,若116NAO ∠=︒,144OBH ∠=︒.(1)AOB ∠= ︒;(2)如图2,点C 、D 是NAO ∠、GBO ∠角平分线上的两点,且35CDB ∠=︒,求ACD ∠ 的度数;(3)如图3,点F 是平面上的一点,连结F A 、FB ,E 是射线F A 上的一点,若MAE ∠=n OAE ∠,HBF n OBF ∠=∠,且60AFB ∠=︒,求n 的值.22.如图1,AB //CD ,点E 、F 分别在AB 、CD 上,点O 在直线AB 、CD 之间,且100EOF ∠=︒.(1)求BEO OFD ∠+∠的值;(2)如图2,直线MN 分别交BEO ∠、OFC ∠的角平分线于点M 、N ,直接写出EMN FNM ∠-∠的值;(3)如图3,EG 在AEO ∠内,AEG m OEG ∠=∠;FH 在DFO ∠内,DFH m OFH ∠=∠,直线MN 分别交EG 、FH 分别于点M 、N ,且50FMN ENM ∠-∠=︒,直接写出m 的值.23.已知//AB CD ,定点E ,F 分别在直线AB ,CD 上,在平行线AB ,CD 之间有一动点P .(1)如图1所示时,试问AEP ∠,EPF ∠,PFC ∠满足怎样的数量关系?并说明理由. (2)除了(1)的结论外,试问AEP ∠,EPF ∠,PFC ∠还可能满足怎样的数量关系?请画图并证明(3)当EPF ∠满足0180EPF ︒<∠<︒,且QE ,QF 分别平分PEB ∠和PFD ∠, ①若60EPF ∠=︒,则EQF ∠=__________°.②猜想EPF ∠与EQF ∠的数量关系.(直接写出结论)24.如图1,由线段,,,AB AM CM CD 组成的图形像英文字母M ,称为“M 形BAMCD ”.(1)如图1,M 形BAMCD 中,若//,50AB CD A C ∠+∠=︒,则M ∠=______; (2)如图2,连接M 形BAMCD 中,B D 两点,若150,B D AMC α∠+∠=︒∠=,试探求A∠与C ∠的数量关系,并说明理由;(3)如图3,在(2)的条件下,且AC 的延长线与BD 的延长线有交点,当点M 在线段BD 的延长线上从左向右移动的过程中,直接写出A ∠与C ∠所有可能的数量关系.参考答案1.(1)证明见详解(2)180GQH M ∠=︒-∠;理由见详解【分析】(1)过点M 作MN AB ∥,由AB CD ∥,可知MN AB CD ∥∥.由此可知:AGM GMN ∠=∠,CHM HMN ∠=∠,故=AGM CHM GMN HMN M ∠+∠=∠+∠∠;(2)由(1)可知=AGM CHM M ∠+∠∠.再由CHM GHM ∠=∠,∠AGM =∠HGQ ,可知 :M HGQ GHM ∠=∠+∠,利用三角形内角和是180°,可得180GQH M ∠=︒-∠.(1)解:如图:过点M 作MN AB ∥, ∴MN AB CD ∥∥,∴AGM GMN ∠=∠,CHM HMN ∠=∠, ∵M GMN HMN ∠=∠+∠, ∴=M AGM CHM ∠∠+∠.(2)解:180GQH M ∠=︒-∠,理由如下: 如图:过点M 作MN AB ∥, 由(1)知=M AGM CHM ∠∠+∠, ∵HM 平分GHC ∠, ∴CHM GHM ∠=∠, ∵∠AGM =∠HGQ , ∴M HGQ GHM ∠=∠+∠, ∵180HGQ GHM GQH ∠+∠+∠=︒, ∴180GQH M ∠=︒-∠.【点拨】本题考查了利用平行线的性质求角之间的数量关系,正确的作出辅助线是解决本题的关键,同时这也是比较常见的几何模型“猪蹄模型”的应用.2.(1)见分析(2)①45︒;②结论:2EOF EPF ∠=∠【分析】(1)利用平行线的性质解决问题即可;(2)①利用基本结论EMF BEM MFD ∠=∠+∠求解即可;②利用基本结论EOF BEO DFO ∠=∠+∠,EPF BEP DFP ∠=∠+∠,求解即可.解:(1)证明:如图,过G 作GH AB ,AB CD ,AB GH CD ∴,BEG EGH DFG FGH ∠∠∠∠∴==,,180BEF DFE ∴∠+∠=︒,EG 平分BEF ∠,FG 平分DFE ∠,12GEB BEF ∴∠=∠,12GFD DFE ∠=∠, 111()90222GEB GFD BEF DFE BEF DFE ∴∠+∠=∠+∠=∠+∠=︒, 在EFG ∆中,180GEF GFE G ∠+∠+∠=︒,90EGF GEB GFD ∴∠=∠+∠=︒,EG FG ∴⊥;(2)解:①如图2中,由题意,90BEG DFG ∠+∠=︒,EM 平分BEG ∠,MF 平分DFG ∠, 1()452BEM MFD BEG DFG ∴∠+∠=∠+∠=︒,45EMF BEM MFD ∴∠=∠+∠=︒,故答案为:45︒;②结论:2EOF EPF ∠=∠.理由:如图3中,由题意,EOF BEO DFO ∠=∠+∠,EPF BEP DFP ∠=∠+∠,PE 平分BEO ∠,PF 平分DFO ∠,2BEO BEP ∴∠=∠,2DFO DFP ∠=∠,2EOF EPF ∴∠=∠,故答案为:2EOF EPF ∠=∠.【点拨】本题考查平行线的性质和判定,角平分线的性质,垂直的定义,解题的关键是熟练掌握相关的性质.3.(1)证明见详解 (2)①312;证明见详解;②123∠=∠+∠;证明见详解【分析】(1)如图4过点P 作PC a ∥,利用平行线的传递性可知PC a b ∥∥,根据平行线的性质可知1APC ∠=∠,3BPC ∠=∠,根据等量代换就可以得出213∠=∠+∠;(2)①如图5过点P 作PC a ∥,利用平行线的传递性可知PC a b ∥∥,根据平行线的性质可知3BPC ∠=∠,1APC ∠=∠,根据等量代换就可以得出312;②如图6过点P 作PC a ∥,利用平行线的传递性可知PC a b ∥∥,根据平行线的性质可知1APC ∠=∠,3BPC ∠=∠,根据等量代换就可以得出123∠=∠+∠.(1)解:如图4所示:过点P 作PC a ∥, ∵a b ∥ ∴PC a b ∥∥∴1APC ∠=∠,3BPC ∠=∠, ∵2APC BPC ∠=∠+∠, ∴213∠=∠+∠;(2)解:①如图5过点P 作PC a ∥, ∵a b ∥ ∴PC a b ∥∥∴3BPC ∠=∠,1APC ∠=∠, ∵2BPC APC ∠=∠+∠, ∴312;②如图6过点P 作PC a ∥,∵a b ∥ ∴PC a b ∥∥∴1APC ∠=∠,3BPC ∠=∠, ∵2APC BPC ∠=∠+∠, ∴123∠=∠+∠.【点拨】本题利用“猪蹄模型”及其变式考查了利用平行线的性质求角之间的数量关系,准确的作出辅助线和找到对应的内错角是解决本题的关键.4.(1)80︒(2)36012P ∠=︒-∠-∠;证明见详解(3)140︒【分析】(1)过点P 作MN AB ∥,利用平行的性质就可以求角度,解决此问; (2)利用平行线的性质求位置角的数量关系,就可以解决此问;(3)分别过点P 、点G 作MN AB ∥、KR AB ∥,然后利用平行线的性质求位置角的数量关系即可.(1)解:如图过点P 作MN AB ∥,∵AB CD ∥, ∴AB MN CD ∥∥. ∴1180EPN ∠+∠=︒,2180FPN ∠+∠=︒.∵1130∠=︒,2150∠=︒, ∴12360EPN FPN ∠+∠+∠+∠=︒ ∴36013015080EPN FPN ∠+=︒-︒-︒=︒. ∵P EPN FPN ∠=∠+∠, ∴∠P =80°. 故答案为:80︒;(2)解:36012P ∠=︒-∠-∠,理由如下:如图过点P 作MN AB ∥,∵AB CD ∥, ∴AB MN CD ∥∥. ∴1180EPN ∠+∠=︒,2180FPN ∠+∠=︒.∴12360EPN FPN ∠+∠+∠+∠=︒ ∵EPN FPN P ∠+∠=∠,36012P ∠=︒-∠-∠.(3)如图分别过点P 、点G 作MN AB ∥、KR AB ∥∵AB CD ∥,∴AB MN KR CD ∥∥∥. ∴1180EPN ∠+∠=︒,180NPG PGR ∠+∠=︒, 2180RGF ∠+∠=︒.∴12540EPN NPG PGR RGF ∠+∠+∠+∠++∠=︒ ∵75EPG EPN NPG ∠=∠+∠=︒,PGR RGF PGF ∠+∠=∠,12325∠+∠=︒,∴12540PGF EPG ∠+∠+∠+∠=︒ ∴54032575140PGF ∠=︒-︒-︒=︒ 故答案为:140︒.【点拨】本题考查了平行线的性质定理,准确的作出辅助线和正确的计算是解决本题的关键.5.(1)∠BED =66°;(2)∠BED =2∠F ,见分析;(3)∠BED 的度数为130°.【分析】(1)首先作EF ∥AB ,根据直线AB ∥CD ,可得EF ∥CD ,所以∠ABE =∠1=45°,∠CDE=∠2=21°,据此推得∠BED=∠1+∠2=66°;(2)首先作EG∥AB,延长DE交BF于点H,利用三角形的外角性质以及角平分线的定义即可得到∠BED=2∠F;(3)延长DF交AB于点H,延长GE到I,利用三角形的外角性质以及角平分线的定义即可得到∠BED的度数为130°.解:(1)如图,作EF∥AB,,∵直线AB∥CD,∴EF∥CD,∴∠ABE=∠1=45°,∠CDE=∠2=21°,∴∠BED=∠1+∠2=66°;(2)解:∠BED=2∠F,理由是:过点E作EG∥AB,延长DE交BF于点H,∵AB∥CD,∴AB∥CD∥EG,∴∠5=∠1+∠2,∠6=∠3+∠4,又∵BF平分∠ABE,DF平分∠CDE,∴∠2=∠1,∠3=∠4,则∠5=2∠2,∠6=2∠3,∴∠BED=2(∠2+∠3) ,又∠F+∠3=∠BHD,∠BHD+∠2=∠BED,∴∠3+∠2+∠F=∠BED,综上∠BED=∠F+12∠BED,即∠BED=2∠F;(3)解:延长DF交AB于点H,延长GE到I,∵∠BGD=60°,∴∠3=∠1+∠BGD=∠1+60°,∠BFD=∠2+∠3=∠2+∠1+60°=95°,∴∠2+∠1=35°,即2(∠2+∠1) =70°,∵BF平分∠ABE,DF平分∠CDE,∴∠ABE=2∠2,∠CDE=2∠1,∴∠BEI=∠ABE +∠BGE=2∠2+∠BGE,∠DEI=∠CDE+∠DGE=2∠1+∠DGE,∴∠BED=∠BEI+∠DEI=2(∠2+∠1)+( ∠BGE+∠DGE)=70°+60°=130°,∴∠BED的度数为130°.【点拨】本题考查了平行线的判定和性质,三角形的外角性质等知识,掌握平行线的判定和性质,正确添加辅助线是解题关键.∠-∠=∠,见分析6.(1)见分析;(2)当点C在AB与ED之外时,ABC CDE BCD【分析】(1)由题意首先过点C作CF∥AB,由直线AB∥ED,可得AB∥CF∥DE,然后由两直线平行,内错角相等,即可证得∠ABC+∠CDE=∠BCD;(2)根据题意首先由两直线平行,内错角相等,可得∠ABC=∠BFD,然后根据三角形外角的性质即可证得∠ABC-∠CDE=∠BCD.解:(1)证明:过点C作CF∥AB,∵AB∥ED,∴AB∥ED∥CF,∴∠BCF=∠ABC,∠DCF=∠EDC,∴∠ABC+∠CDE=∠BCD;(2)结论:∠ABC-∠CDE=∠BCD,证明:如图:∵AB ∥ED , ∴∠ABC =∠BFD ,在△DFC 中,∠BFD =∠BCD +∠CDE , ∴∠ABC =∠BCD +∠CDE , ∴∠ABC -∠CDE =∠BCD .若点C 在直线AB 与DE 之间,猜想360ABC BCD CDE ︒∠+∠+∠=,∵AB ∥ED ∥CF ,∴180,180,ABC BCF CDE DCF ︒︒∠+∠=∠+∠=∴360ABC BCD CDE ABC BCF DCF CDE ︒∠+∠+∠=∠+∠+∠+∠=.【点拨】本题考查的是平行线的性质及三角形外角的性质,熟练掌握平行线的性质是解答本题的关键,注意掌握辅助线的作法.7.(1)见分析;(2)①∠BAE +12∠MCD =90°,理由见分析;②∠BAE +1nn +∠MCD =90°,理由见分析.【分析】(1)根据平行的性质可得∠BAC +∠DCA =180°,再根据AE CE ⊥可得∠EAC +∠ECA =90°,根据AE 平分∠BAC 可得∠BAE =∠EAC ,等量代换可得∠ECD +∠EAC =90°,继而求得∠DCE =∠ECA ;(2)①过E 作EF ∥AB ,先利用平行线的传递性得出EF ∥AB ∥CD ,再利用平行线的性质及已知条件可推得答案;②过E 作EF ∥AB ,先利用平行线的传递性得出EF ∥AB ∥CD ,再利用平行线的性质及已知条件可推得答案.(1)解:因为//AB CD , 所以∠BAC +∠DCA =180°,因为AE CE ⊥,所以∠EAC +∠ECA =90°,因为AE 平分∠BAC ,所以∠BAE =∠EAC ,所以∠BAE +∠DCE =90°,所以∠EAC +∠DCE =90°,所以∠DCE =∠ECA ,所以CE 平分∠ACD ;(2)①∠BAE 与∠MCD 存在确定的数量关系:∠BAE +12∠MCD =90°,理由如下: 过E 作EF ∥AB ,∵AB ∥CD ,∴EF ∥AB ∥CD ,∴∠BAE =∠AEF ,∠FEC =∠DCE ,∵∠E =90°,∴∠BAE +∠ECD =90°,∵∠MCE =∠ECD ,∴∠BAE +12∠MCD =90°;②∠BAE 与∠MCD 存在确定的数量关系:∠BAE +1n n +∠MCD =90°, 理由如下: 过E 作EF ∥AB ,∵AB ∥CD ,∴EF ∥AB ∥CD ,∴∠BAE =∠AEF ,∠FEC =∠DCE ,∵∠E =90°,∴∠BAE +∠ECD =90°,∵∠MCE =1n∠ECD , ∴∠BAE +1n n +∠MCD =90°. 【点拨】本题主要考查平行线的性质和角平分线的定义,解决本题的关键是要添加辅助线利用平行性质.8.(1)PAC PBD APB ∠+∠=∠;(2)当点P 在直线1l 上方时,∠-∠=∠PBD PAC APB ;当点P 在直线2l 下方时,∠-∠=∠PAC PBD APB .【分析】(1)过点P 作1//PE l ,由“平行于同一条直线的两直线平行”可得出12////PE l l ,再由“两直线平行,内错角相等”得出PAC APE ∠=∠、PBD BPE ∠=∠,再根据角与角的关系即可得出结论;(2)按点P 的两种情况分类讨论:①当点P 在直线1l 上方时;②当点P 在直线2l 下方时,同理(1)可得PAC APE ∠=∠、PBD BPE ∠=∠,再根据角与角的关系即可得出结论.解:(1)PAC PBD APB ∠+∠=∠.过点P 作1//PE l ,如图1所示.1//PE l ,12l l //,12////PE l l ∴,PAC APE ∴∠=∠,PBD BPE ∠=∠,APB APE BPE ∠=∠+∠,PAC PBD APB ∴∠+∠=∠.(2)结论:当点P 在直线1l 上方时,∠-∠=∠PBD PAC APB ;当点P 在直线2l 下方时,∠-∠=∠PAC PBD APB .①当点P 在直线1l 上方时,如图2所示.过点P 作1//PE l .1//PE l ,12l l //,12////PE l l ∴,PAC APE ∴∠=∠,PBD BPE ∠=∠,APB BPE APE ∠=∠-∠,PBD PAC APB ∴∠-∠=∠.②当点P 在直线2l 下方时,如图3所示.过点P 作1//PE l .1//PE l ,12l l //,12////PE l l ∴,PAC APE ∴∠=∠,PBD BPE ∠=∠,APB APE BPE ∠=∠-∠,PAC PBD APB ∴∠-∠=∠.【点拨】本题考查了平行线的性质以及角的计算,解题的关键是根据“两直线平行,内错角相等”找到相等的角.本题属于基础题,难度不大,解决该题型题目时,根据平行线的性质得出相等(或互补)的角是关键.9.(1)∠ABE =40°;(2)∠ABE =30°;(3)∠MGN =15°.【分析】(1)过E 作EM ∥AB ,根据平行线的判定与性质和角平分线的定义解答即可;(2)过E 作EM ∥AB ,过F 作FN ∥AB ,根据平行线的判定与性质,角平分线的定义以及解一元一次方程解答即可;(3)过P 作PL ∥AB ,根据平行线的判定与性质,三角形的内角和定理,三角形的一个外角等于与它不相邻的两个内角的和的性质,角平分线的定义解答即可.解:(1)过E 作EM ∥AB ,∵AB∥CD,∴CD∥EM∥AB,∴∠ABE=∠BEM,∠DCE=∠CEM,∵CF平分∠DCE,∴∠DCE=2∠DCF,∵∠DCF=30°,∴∠DCE=60°,∴∠CEM=60°,又∵∠CEB=20°,∴∠BEM=∠CEM﹣∠CEB=40°,∴∠ABE=40°;(2)过E作EM∥AB,过F作FN∥AB,∵∠EBF=2∠ABF,∴设∠ABF=x,∠EBF=2x,则∠ABE=3x,∵CF平分∠DCE,∴设∠DCF=∠ECF=y,则∠DCE=2y,∵AB∥CD,∴EM∥AB∥CD,∴∠DCE=∠CEM=2y,∠BEM=∠ABE=3x,∴∠CEB=∠CEM﹣∠BEM=2y﹣3x,同理∠CFB=y﹣x,∵2∠CFB+(180°﹣∠CEB)=190°,∴2(y﹣x)+180°﹣(2y﹣3x)=190°,∴x =10°,∴∠ABE =3x =30°;(3)过P 作PL ∥AB ,∵GM 平分∠DGP ,∴设∠DGM =∠PGM =y ,则∠DGP =2y ,∵PQ 平分∠BPG ,∴设∠BPQ =∠GPQ =x ,则∠BPG =2x ,∵PQ ∥GN ,∴∠PGN =∠GPQ =x ,∵AB ∥CD ,∴PL ∥AB ∥CD ,∴∠GPL =∠DGP =2y ,∠BPL =∠ABP =30°,∵∠BPL =∠GPL ﹣∠BPG ,∴30°=2y ﹣2x ,∴y ﹣x =15°,∵∠MGN =∠PGM ﹣∠PGN =y ﹣x ,∴∠MGN =15°.【点拨】此题考查平行线的判定与性质,角平分线的定义,三角形的内角和定理,解题关键在于作辅助线和掌握判定定理.10.(1)90︒ (2)30F E ∠=∠+︒,理由见分析 (3)15︒【分析】(1)如图1,分别过点E ,F 作//EM AB ,//FN AB ,根据平行线的性质得到30B BEM ∠=∠=︒,MEF EFN ∠=∠,180D DFN ∠+∠=︒,代入数据即可得到结论;(2)如图1,根据平行线的性质得到30B BEM ∠=∠=︒,MEF EFN ∠=∠,由//AB CD ,//AB FN ,得到//CD FN ,根据平行线的性质得到180D DFN ∠+∠=︒,于是得到结论;(3)如图2,过点F 作//FH EP ,设2BEF x ∠=︒,则(230)EFD x ∠=+︒,根据角平分线的定义得到12PEF BEF x ∠=∠=︒,1(15)2EFG EFD x ∠=∠=+︒,根据平行线的性质得到PEF EFH x ∠=∠=︒,P HFG ∠=∠,于是得到结论.(1)解:如图1,分别过点E ,F 作//EM AB ,//FN AB ,////EM AB FN ∴,30B BEM ∴∠=∠=︒,MEF EFN ∠=∠,又//AB CD ,//AB FN ,//CD FN ∴,180D DFN ∴∠+∠=︒,又120D ∠=︒,60DFN ∴∠=︒,30BEF MEF ∴∠=∠+︒,60EFD EFN ∠=∠+︒,60EFD MEF ∴∠=∠+︒3090EFD BEF ∴∠=∠+︒=︒;故答案为:90︒;(2)解:如图1,分别过点E ,F 作//EM AB ,//FN AB ,////EM AB FN ∴,30B BEM ∴∠=∠=︒,MEF EFN ∠=∠,又//AB CD ,//AB FN ,//CD FN ∴,180D DFN ∴∠+∠=︒,又120D ∠=︒,60DFN ∴∠=︒,30BEF MEF ∴∠=∠+︒,60EFD EFN ∠=∠+︒,60EFD MEF ∴∠=∠+︒,30EFD BEF ∴∠=∠+︒;(3)解:如图2,过点F 作//FH EP ,由(2)知,30EFD BEF ∠=∠+︒,设2BEF x ∠=︒,则(230)EFD x ∠=+︒, EP 平分BEF ∠,GF 平分EFD ∠,12PEF BEF x ∴∠=∠=︒,1(15)2EFG EFD x ∠=∠=+︒, //FH EP ,PEF EFH x ∴∠=∠=︒,P HFG ∠=∠,15HFG EFG EFH ∠=∠-∠=︒,15P ∴∠=︒.【点拨】本题考查了平行线的性质,角平分线的定义,熟练掌握平行线的性质定理是解题的关键.11.(1)BAE CDE AED ∠+∠=∠;(2)12AFD AED ∠=∠;(3)60=︒∠BAE 【分析】(1)作EF ∥AB ,如图1,则EF ∥CD ,利用平行线的性质得∠1=∠EAE ,∠2=∠CDE ,从而得到∠BAE +∠CDE =∠AED(2)如图2,由(1)的结论得∠AFD =12∠BAE ,∠CDF =12∠CDE ,则∠AFD =12(∠BAE +∠CDE ),加上(1)的结论得到∠AFD =12∠AED ;(3)由(1)的结论得∠AGD =∠BAF +∠CDG ,利用折叠性质得∠CDG =4∠CDF ,再利用等量代换得到∠AGD =2∠AED -32∠BAE ,加上90°-∠AGD =180°-2∠AED ,从而计算出∠BAE 的度数.解:(1)∠BAE +∠CDE =∠AED理由如下:作EF ∥AB ,如图1∵AB ∥CD∴EF ∥CD∴∠1=∠BAE ,∠2=∠CDE∴∠BAE +∠CDE =∠AED(2)如图2,由(1)的结论得∠AFD =∠BAF +∠CDF∵∠BAE 、∠CDE 的两条平分线交于点F∴∠BAF =12∠BAE ,∠CDF =12∠CDE∴∠AFE =12(∠BAE +∠CDE )∵∠BAE +∠CDE =∠AED∴∠AFD =12∠AED(3)由(1)的结论得∠AGD =∠BAF +∠CDG而射线DC 沿DE 翻折交AF 于点G∴∠CDG =4∠CDF∴∠AGD =∠BAF +4∠CDF =12∠BAE +2∠CDE =12∠BAE +2(∠AED -∠BAE )=2∠AED -32∠BAE ∵90°-∠AGD =180°-2∠AED∴90°-2∠AED +32∠BAE =180°-2∠AED ∴∠BAE =60°【点拨】本题考查了平行线性质:两直线平行,同位角相等;两直线平行,同旁内角互补;两直线平行,内错角相等.12.(1)见分析;(2)55°;(3)1118022αβ︒-+ 【分析】(1)根据平行线的判定定理与性质定理解答即可;(2)①如图2,过点F 作//FE AB ,当点B 在点A 的左侧时,根据50ABC ∠=︒,60ADC ∠=︒,根据平行线的性质及角平分线的定义即可求BFD ∠的度数;②如图3,过点F 作//EF AB ,当点B 在点A 的右侧时,ABC α∠=,ADC β∠=,根据平行线的性质及角平分线的定义即可求出BFD ∠的度数.解:(1)如图1,过点E 作//EF AB ,则有BEF B ∠=∠,//AB CD ,//EF CD ∴,FED D ∴∠=∠,BED BEF FED B D ∴∠=∠+∠=∠+∠;(2)①如图2,过点F 作//FE AB ,有BFE FBA ∠=∠.//AB CD ,//EF CD ∴.EFD FDC ∴∠=∠.BFE EFD FBA FDC ∴∠+∠=∠+∠.即BFD FBA FDC ∠=∠+∠, BF 平分ABC ∠,DF 平分ADC ∠,1252FBA ABC ∴∠=∠=︒,1302FDC ADC ∠=∠=︒, 55BFD FBA FDC ∴∠=∠+∠=︒.答:BFD ∠的度数为55︒;②如图3,过点F 作//FE AB ,有180BFE FBA ∠+∠=︒.180BFE FBA ∴∠=︒-∠,//AB CD ,//EF CD ∴.EFD FDC ∴∠=∠.180BFE EFD FBA FDC ∴∠+∠=︒-∠+∠.即180BFD FBA FDC ∠=︒-∠+∠, BF 平分ABC ∠,DF 平分ADC ∠,1122FBA ABC α∴∠=∠=,1122FDC ADC β∠=∠=, 1118018022BFD FBA FDC αβ∴∠=︒-∠+∠=︒-+. 答:BFD ∠的度数为1118022αβ︒-+. 【点拨】本题考查了平行线的判定与性质,解决本题的关键是熟练掌握平行线的判定与性质.13.(1)∠BME =∠MEN ﹣∠END ;∠BMF =∠MFN +∠FND ;(2)120°;(3)不变,30°【分析】(1)过E 作EH ∥AB ,易得EH ∥AB ∥CD ,根据平行线的性质可求解;过F 作FH ∥AB ,易得FH ∥AB ∥CD ,根据平行线的性质可求解;(2)根据(1)的结论及角平分线的定义可得2(∠BME+∠END)+∠BMF-∠FND=180°,可求解∠BMF=60°,进而可求解;∠BME,进而可求解.(3)根据平行线的性质及角平分线的定义可推知∠FEQ=12解:(1)过E作EH∥AB,如图1,∴∠BME=∠MEH,∵AB∥CD,∴HE∥CD,∴∠END=∠HEN,∴∠MEN=∠MEH+∠HEN=∠BME+∠END,即∠BME=∠MEN﹣∠END.如图2,过F作FH∥AB,∴∠BMF=∠MFK,∵AB∥CD,∴FH∥CD,∴∠FND=∠KFN,∴∠MFN=∠MFK﹣∠KFN=∠BMF﹣∠FND,即:∠BMF=∠MFN+∠FND.故答案为∠BME=∠MEN﹣∠END;∠BMF=∠MFN+∠FND.(2)由(1)得∠BME=∠MEN﹣∠END;∠BMF=∠MFN+∠FND.∵NE平分∠FND,MB平分∠FME,∴∠FME=∠BME+∠BMF,∠FND=∠FNE+∠END,∵2∠MEN+∠MFN=180°,∴2(∠BME +∠END )+∠BMF ﹣∠FND =180°,∴2∠BME +2∠END +∠BMF ﹣∠FND =180°,即2∠BMF +∠FND +∠BMF ﹣∠FND =180°,解得∠BMF =60°,∴∠FME =2∠BMF =120°;(3)∠FEQ 的大小没发生变化,∠FEQ =30°.由(1)知:∠MEN =∠BME +∠END ,∵EF 平分∠MEN ,NP 平分∠END ,∴∠FEN =12∠MEN =12(∠BME +∠END ),∠ENP =12∠END ,∵EQ ∥NP ,∴∠NEQ =∠ENP ,∴∠FEQ =∠FEN ﹣∠NEQ =12(∠BME +∠END )﹣12∠END =12∠BME ,∵∠BME =60°,∴∠FEQ =12×60°=30°.【点拨】本题主要考查平行线的性质及角平分线的定义,作平行线的辅助线是解题的关键.14.(1)见分析;(2)3ACD GAC ∠=∠,见分析;(3)54019⎛⎫ ⎪⎝⎭°或54023︒⎛⎫ ⎪⎝⎭. 【分析】(1)根据平行线的判定与性质求证即可;(2)根据三角形的内角和为180°和平角定义得到AQD E EAQ ∠=∠+∠,结合平行线的性质得到BDQ E EAQ ∠=∠+∠,再根据角平分线的定义证得2CDB E GAC ∠=∠+∠,结合已知即可得出结论;(3)分当K 在直线GH 下方和当K 在直线GH 上方两种情况,根据平行线性质、三角形外角性质、角平分线定义求解即可.解:(1)如图1,延长AC 交MN 于点P ,∵ACD C ∠=∠,∴//AP BD ,∴NBD NPA ∠=∠,∵GAC NBD ∠=∠,∴GAC NPA ∠=∠,∴//GH MN ;(2)延长AC 交MN 于点P ,交DE 于点Q ,∵180E EAQ AQE ∠+∠+∠=°,180AQE AQD ∠+∠=°,∴AQD E EAQ ∠=∠+∠,∵//AP BD ,∴AQD BDQ ∠=∠,∴BDQ E EAQ ∠=∠+∠,∵AE 平分GAC ∠,DE 平分BDC ∠,∴2GAC EAQ ∠=∠,2CDB BDQ ∠=∠,∴2CDB E GAC ∠=∠+∠,∵AED GAC ∠=∠,ACD CDB ∠=∠,∴23ACD GAC GAC GAC ∠=∠+∠=∠;(3)当K 在直线GH 下方时,如图,设射线BF 交GH 于I ,∵//GH MN ,∴AIB FBM ∠=∠,∵BF 平分MBD ∠, ∴1(180)2DBF FBM DBN ∠=∠=-∠°, ∴AIB DBF ∠=∠,∵AIB KAG AKB ∠+∠=∠,AKB ACD ∠=∠,∴ACD DBF KAG ∠=∠+∠,∵13KAG GAC ∠=∠,GAC NBD ∠=∠, ∴11(180)332GAC DBN ACD GAC ∠+-∠=∠=∠°, 即1190332GAC GAC GAC ∠+-∠=∠°,解得:54019GAC ⎛⎫∠= ⎪⎝⎭. 当K 在直线GH 上方时,如图,同理可证得1(180)2AIB DBN AKB KAG ∠=-∠=∠+∠°, 则有113(180)32GAC GAC GAC ∠+∠=-∠,解得:54023GAC ⎛⎫∠= ⎪⎝⎭.综上,故答案为54019⎛⎫ ⎪⎝⎭°或54023︒⎛⎫ ⎪⎝⎭. 【点拨】本题考查平行线的判定与性质、角平分线的定义、三角形的外角性质、三角形的内角和定理、平角定义、角度的运算,熟练掌握相关知识的联系与运用是解答的关键.15.(1)65°(2)3606α︒-︒(3)2n ∠M +∠BED =360° 【分析】(1)首先作EG ∥AB ,FH ∥AB ,利用平行线的性质可得∠ABE +∠CDE =260°,再利用角平分线的定义得到∠ABF +∠CDF =130°,从而得到∠BFD 的度数,再根据角平分线的定义可求∠M 的度数;(2)先由已知得到∠ABE =6∠ABM ,∠CDE =6∠CDM ,由(1)得∠ABE +∠CDE =360°-∠BED ,∠M =∠ABM +∠CDM ,等量代换即可求解;(3)先由已知得到ABF n ABM ∠=∠,CDF n CDM ∠=∠,由(2)的方法可得到2n ∠M +∠BED =360°.解:(1)如图1,作//EG AB ,//FH AB ,∵AB CD ∥,∴EG AB FH CD ∥∥∥,∴ABF BFH ∠=∠,CDF DFH ∠=∠,180ABE BEG ∠+∠=︒,180GED CDE ∠+∠=︒, ∴360ABE BEG GED CDE ∠+∠+∠+∠=︒,∵100BED BEG DEG ∠=∠+∠=︒,∴260ABE CDE ∠+∠=︒,∵ABE ∠的角平分线和CDE ∠的角平分线相交于F ,∴130ABF CDF ∠+∠=︒,∴130BFD BFH DFH ∠=∠+∠=︒,∵BM 、DM 分别是ABF ∠和CDF ∠的角平分线, ∴12MBF ABF ∠=∠,12MDF CDF ∠=∠,∴65MBF MDF ∠+∠=︒,∴1306565BMD ∠=︒-︒=︒;(2)如图2,∵13ABM ABF ∠=∠,13CDM CDF ∠=∠, ∴3ABF ABM ∠=∠,3CDF CDM ∠=∠,∵ABE ∠与CDE ∠两个角的角平分线相交于点F ,∴6ABE ABM ∠=∠,6CDE CDM ∠=∠,∴66360ABM CDM BED ∠+∠+∠=︒,∵BMD ABM CDM ∠=∠+∠,∴6360BMD BED ∠+∠=︒, ∴3606BMD α︒-︒∠=; (3)∵∠ABM =1n ∠ABF ,∠CDM =1n∠CDF , ∴ABF n ABM ∠=∠,CDF n CDM ∠=∠,∵ABE ∠与CDE ∠两个角的角平分线相交于点F ,∴2ABE n ABM ∠=∠,2CDE n CDM ∠=∠,∴22360n ABM n CDM BED ∠+∠+∠=︒,∠=∠+∠,∵M ABM CDM∴2360n M BED∠+∠=︒.【点拨】本题主要考查了平行线的性质和角平分线的计算,关键在于掌握两直线平行同位角相等,内错角相等,同旁内角互补的性质.16.(1)∠A+∠C=90°;(2)见分析;(3)∠EBC=105°.【分析】(1)通过平行线性质和直角三角形内角关系求解.(2)画辅助平行线找角的联系.(3)利用(2)的结论,结合角平分线性质求解.解:(1)如图1,∵AM∥CN,∴∠C=∠AOB,∵AB⊥BC,∴∠ABC=90°,∴∠A+∠AOB=90°,∠A+∠C=90°,故答案为:∠A+∠C=90°;(2)如图2,过点B作BG∥DM,∵BD⊥AM,∴DB⊥BG,∴∠DBG=90°,∴∠ABD+∠ABG=90°,∵AB⊥BC,∴∠CBG+∠ABG=90°,∴∠ABD=∠CBG,∵AM∥CN,∴∠C=∠CBG,∴∠ABD=∠C;(3)如图3,过点B作BG∥DM,∵AM∥CN,∴CN∥BG,∴∠CBG=∠BCN,∵BF平分∠DBC,BE平分∠ABD,∴∠DBF=∠CBF,∠DBE=∠ABE,∵∠ABD=∠NCB,∴∠ABD=∠CBG,∴∠ABF=∠GBF,设∠DBE=α,∠ABF=β,则∠ABE=α,∠ABD=2α=∠CBG,∠GBF=∠AFB=β,∠BFC=3∠DBE=3α,∵BG∥DM,∴∠DFB=∠GBF=β,∴∠AFC=∠BFC+∠DFB=3α+β,∵∠AFC+∠NCF=180°,∠FCB+∠NCF=180°,∴∠FCB=∠AFC=3α+β,△BCF中,由∠CBF+∠BFC+∠BCF=180°得:2α+β+3α+3α+β=180°,∵AB⊥BC,∴β+β+2α=90°,∴α=15°,∴∠ABE=15°,∴∠EBC=∠ABE+∠ABC=15°+90°=105°.【点拨】本题考查平行线性质,三角形内角和定理,角平分线的定义,画辅助线,找到角的关系是求解本题的关键.17.(1)见分析;(2)见分析;(3)n -1【分析】(1)连接AB ,根据已知证明∠MAB +∠SBA =180°,即可得证;(2)作CF ∥ST ,设∠CBT =α,表示出∠CAN ,∠ACF ,∠BCF ,根据AD ∥BC ,得到∠DAC =120°,求出∠CAE 即可得到结论;(3)作CF ∥ST ,设∠CBT =β,得到∠CBT =∠BCF =β,分别表示出∠CAN 和∠CAE ,即可得到比值.解:(1)如图,连接AB ,,360MAC ACB SBC ∠+∠+∠=︒,180ACB ABC BAC ∠+∠+∠=︒,180MAB SBA ∴∠+∠=︒,//MN ST ∴(2)2CAE CAN ∠=∠,理由:作//CF ST ,则////,MN CF ST 如图,设CBT α∠=,则2DAE α∠=.BCF CBT α∠=∠=,60CAN ACF α∠=∠=︒-,AD //BC ,180120DAC ACB ∠=︒-∠=︒,12012022(60)2CAE DAE CAN αα∴∠=︒-∠=︒-=︒-=∠.即2CAE CAN ∠=∠.(3)作//CF ST ,则////,MN CF ST 如图,设CBT β∠=,则MAE n β∠=.//CF ST ,CBT BCF β∴∠=∠=,180180n ACF CAN n nββ︒︒-∠=∠=-=, 1801180180(180)n CAE MAE CAN n n n n βββ︒-∠=︒-∠-∠=︒--+=︒-, 11::1n CAE CAN n n n-∠∠==-, 故答案为n 1-.【点拨】本题主要考查平行线的性质和判定,解题关键是角度的灵活转换,构建数量关系式.18.(1)110°;(2)80°;(3)()()11,22nx y x y ⎛⎫+︒+︒ ⎪⎝⎭ 【分析】(1)过点P 作PH ∥AB ∥CD ,根据平行线的性质:两直线平行,内错角相等即可证得;(2)同理依据两直线平行,内错角相等即可证得∠1+∠4=∠2+∠3,求得∠4=80°;(3)利用(1)的结论和角平分线的性质即可写出结论.解:(1)如图1,过点P 作PH ∥AB ∥CD ,∴∠1=∠EPH ,∠2=∠FPH ,而∠EPF =∠EPH +∠FPH ,∴∠EPF =∠1+∠2=110°;(2)过点P 作//PM AB ,//QN AB ,//PM AB ,1EPM ∴∠=∠,//,//,//QN AB PM AB AB CD ,//P //QN//AB M DC ∴,MPQ NQP ∴∠=∠,2NQF ∠=∠,3EPM MPQ ∠=∠+∠,4PQN NQF ∠=∠+∠,∴∠1+∠4=∠2+∠3,∵∠1=30°,∠2=40°,∠3=70°,∴∠4=80°,故答案为:80°;(3)过点P 作////PH AB CD ,1PE 平分PEB ∠,11PEB PEP ∴∠=∠,同理11DFP PFP ∠=∠, ∴111EPF PEB PFP ∠=∠+∠1122PFD BEP =+ ()12PFD BEP =+ ()12x y =+︒,同理1()()2nnyP x∠=+︒,故答案为:11() 2P x y∠=+︒,1()()2nnyP x∠=+︒.【点拨】本题考查了平行线性质的应用,解题的关键是学会添加常用辅助线,构造平行线解决问题,学会探究规律,利用规律解决问题.19.(1)∠A+∠C=90°;(2)①见分析;②105°【分析】(1)根据平行线的性质以及直角三角形的性质进行证明即可;(2)①过点B作BG∥DM,根据平行线找角的联系即可求解;②先过点B作BG∥DM,根据角平分线的定义,得出∠ABF=∠GBF,再设∠DBE=α,∠ABF=β,根据∠CBF+∠BFC+∠BCF=180°,可得2α+β+3α+3α+β=180°,根据AB⊥BC,可得β+β+2α=90°,最后解方程组即可得到∠ABE=15°,进而得出∠EBC=∠ABE+∠ABC=15°+90°=105°.解:(1)如图1,AM与BC的交点记作点O,∵AM∥CN,∴∠C=∠AOB,∵AB⊥BC,∴∠A+∠AOB=90°,∴∠A+∠C=90°;(2)①如图2,过点B作BG∥DM,∵BD⊥AM,∴DB⊥BG,∴∠DBG=90°,∴∠ABD+∠ABG=90°,∵AB⊥BC,∴∠CBG+∠ABG=90°,∴∠ABD=∠CBG,∵AM∥CN,BG∥DM,BG CN//,∴∠C=∠CBG,∠ABD=∠C;②如图3,过点B作BG∥DM,∵BF平分∠DBC,BE平分∠ABD,∴∠DBF=∠CBF,∠DBE=∠ABE,由(2)知∠ABD=∠CBG,∴∠ABF=∠GBF,设∠DBE=α,∠ABF=β,则∠ABE=α,∠ABD=2α=∠CBG,∠GBF=∠AFB=β,∠BFC=3∠DBE=3α,∴∠AFC=3α+β,∵∠AFC+∠NCF=180°,∠FCB+∠NCF=180°,∴∠FCB=∠AFC=3α+β,△BCF中,由∠CBF+∠BFC+∠BCF=180°得:2α+β+3α+3α+β=180°,∵AB⊥BC,∴β+β+2α=90°,∴α=15°,∴∠ABE=15°,∴∠EBC=∠ABE+∠ABC=15°+90°=105°.【点拨】本题主要考查了平行线的性质的运用,解决问题的关键是作平行线构造内错角,运用等角的余角(补角)相等进行推导.余角和补角计算的应用,常常与等式的性质、等量代换相关联.解题时注意方程思想的运用.20.(1)证明见分析;(2)证明见分析;(3)120°.【分析】(1)过点A作AD∥MN,根据两直线平行,内错角相等得到∠MCA=∠DAC,∠PBA=∠DAB,根据角的和差等量代换即可得解;(2)由两直线平行,同旁内角互补得到∴、∠CAB+∠ACD=180°,由邻补角定义得到∠ECM+∠ECN=180°,再等量代换即可得解;(3)由平行线的性质得到,∠F AB=120°﹣∠GCA,再由角平分线的定义及平行线的性质得到∠GCA﹣∠ABF=60°,最后根据三角形的内角和是180°即可求解.解:(1)证明:如图1,过点A作AD∥MN,∵MN∥PQ,AD∥MN,∴AD∥MN∥PQ,∴∠MCA=∠DAC,∠PBA=∠DAB,∴∠CAB=∠DAC+∠DAB=∠MCA+∠PBA,即:∠CAB=∠MCA+∠PBA;(2)如图2,∵CD∥AB,∴∠CAB+∠ACD=180°,∵∠ECM+∠ECN=180°,∵∠ECN=∠CAB∴∠ECM=∠ACD,即∠MCA+∠ACE=∠DCE+∠ACE,∴∠MCA=∠DCE;(3)∵AF∥CG,∴∠GCA+∠F AC=180°,∵∠CAB=60°即∠GCA+∠CAB+∠F AB=180°,∴∠F AB=180°﹣60°﹣∠GCA=120°﹣∠GCA,由(1)可知,∠CAB =∠MCA +∠ABP , ∵BF 平分∠ABP ,CG 平分∠ACN , ∴∠ACN =2∠GCA ,∠ABP =2∠ABF , 又∵∠MCA =180°﹣∠ACN ,∴∠CAB =180°﹣2∠GCA +2∠ABF =60°, ∴∠GCA ﹣∠ABF =60°, ∵∠AFB +∠ABF +∠F AB =180°, ∴∠AFB =180°﹣∠F AB ﹣∠FBA =180°﹣(120°﹣∠GCA )﹣∠ABF =180°﹣120°+∠GCA ﹣∠ABF =120°.【点拨】本题主要考查了平行线的性质,线段、角、相交线与平行线,准确的推导是解决本题的关键.21.(1)100;(2)75°;(3)n =3.【分析】(1)如图:过O 作OP //MN ,由MN //OP //GH 得∠NAO +∠POA =180°,∠POB +∠OBH =180°,即∠NAO +∠AOB +∠OBH =360°,即可求出∠AOB ;(2)如图:分别延长AC 、CD 交GH 于点E 、F ,先根据角平分线求得58NAC ∠=︒,再根据平行线的性质得到58CEF ∠=︒;进一步求得18DBF ∠=︒,17DFB ∠=︒,然后根据三角形外角的性质解答即可;(3)设BF 交MN 于K ,由∠NAO =116°,得∠MAO =64°,故∠MAE =641nn ︒⨯+,同理∠OBH =144°,∠HBF =n ∠OBF ,得∠FBH =1441n n ︒⨯+,从而=n BKA FBH n ∠∠=⨯︒+1441,又∠FKN =∠F +∠F AK ,得144606411n nn n ︒︒︒⨯=+⨯++,即可求n . 解:(1)如图:过O 作OP //MN , ∵MN //GHl ∴MN //OP //GH∴∠NAO +∠POA =180°,∠POB +∠OBH =180° ∴∠NAO +∠AOB +∠OBH =360° ∵∠NAO =116°,∠OBH =144° ∴∠AOB =360°-116°-144°=100°;(2)分别延长AC 、CD 交GH 于点E 、F ,∵AC 平分NAO ∠且116NAO ∠=︒, ∴58NAC ∠=︒, 又∵MN //GH , ∴58CEF ∠=︒;∵144OBH ∠=︒,36OBG ∠=︒ ∵BD 平分OBG ∠, ∴18DBF ∠=︒, 又∵,CDB ∠=︒35∴351817DFB CDB DBF ∠=∠-∠=-=︒; ∴175875ACD DFB AEF ∠=∠+∠=︒+︒=︒; (3)设FB 交MN 于K ,∵116NAO ∠=︒,则MAO ∠=︒64; ∴641nMAE n ∠=⨯︒+ ∵144OBH ∠=︒, ∴+1n FBH n ∠=⨯︒144,=n BKA FBH n ∠∠=⨯︒+1441, 在△F AK 中,64601nBKA FKA F n ∠=∠+∠=⨯︒+︒+, ∴144646011n n n n ⨯︒=⨯︒+︒++, ∴3n =.经检验:3n =是原方程的根,且符合题意.【点拨】本题主要考查平行线的性质及应用,正确作出辅助线、构造平行线、再利用平行线性质进行求解是解答本题的关键.22.(1)260BEO DFO ∠+∠=︒ ;(2)EMN FNM ∠-∠的值为40°;(3)53.【分析】(1)过点O 作OG ∥AB ,可得AB ∥OG ∥CD ,利用平行线的性质可求解; (2)过点M 作MK ∥A B ,过点N 作NH ∥CD ,由角平分线的定义可设∠BEM =∠OEM =x ,∠CFN =∠OFN =y ,由∠BEO +∠DFO =260°可求x -y =40°,进而求解;(3)设直线FK 与EG 交于点H ,FK 与AB 交于点K ,根据平行线的性质即三角形外角的性质及50FMN ENM ∠-∠=︒,可得50KFD AEG ∠-∠=︒,结合260AEG n OEG DFK n OFK BEO DFO ∠=∠=∠∠+∠=︒,,,可得11180100AEG AEG KFD KFD n n∠+∠+︒-∠-∠=︒,即可得关于n 的方程,计算可求解n 值. 解:证明:过点O 作OG ∥AB ,∵AB ∥CD , ∴AB ∥OG ∥CD ,∴180180BEO EOG DFO FOG ∠+∠=︒∠+∠=︒,, ∴360BEO EOG DFO FOG ∠+∠+∠+∠=︒, 即360BEO EOF DFO ∠+∠+∠=︒, ∵∠EOF =100°,∴∠260BEO DFO +∠=︒;(2)解:过点M 作MK ∥AB ,过点N 作NH ∥CD ,。
2020-2021学年苏科版数学七年级下册第7章《平面图形的认识(二)》培优练习(二)

2020-2021学年七年级下册第7章《平面图形的认识(二)》常考题培优练习(二)1.填写下列空格完成证明:如图,EF∥AD,∠BAC=70°,∠1=∠2,求∠AGD.解:∵EF∥AD,∴∠2=.(理由是:)∵∠1=∠2,∴∠1=∠3.(理由是:)∴∥.(理由是:)∴∠BAC+=180°.(理由是:)∵∠BAC=70°,∴∠AGD=°.2.如图,已知直线l1∥l2,且l3和l1、l2分别交于A、B两点,点P在AB上.(1)试找出∠1、∠2、∠3之间的关系并说出理由;(2)如果点P在A、B两点之间运动时,问∠1、∠2、∠3之间的关系是否发生变化?(3)如果点P在A、B两点外侧运动时,试探究∠1、∠2、∠3之间的关系(点P和A、B不重合)3.如图,将一张上、下两边平行(即AB∥CD)的纸带沿直线MN折叠,EF为折痕.(1)试说明∠1=∠2;(2)已知∠2=40°,求∠BEF的度数.4.当三角形中一个内角α是另一个内角β的两倍时,我们称此三角形为“特征三角形”,其中α称为“特征角”.(1)已知一个“特征三角形”的“特征角”为100°,求这个“特征三角形”的最小内角的度数;(2)是否存在“特征角”为120°的三角形?若存在.请举例说明;若不存在,请说明理由.5.探究与发现:如图1所示的图形,像我们常见的学习用品﹣﹣圆规.我们不妨把这样图形叫做“规形图”,(1)观察“规形图”,试探究∠BDC与∠A、∠B、∠C之间的关系,并说明理由;(2)请你直接利用以上结论,解决以下三个问题:①如图2,把一块三角尺XYZ放置在△ABC上,使三角尺的两条直角边XY、XZ恰好经过点B、C,∠A=40°,则∠ABX+∠ACX=°;②如图3,DC平分∠ADB,EC平分∠AEB,若∠DAE=40°,∠DBE=130°,求∠DCE的度数;③如图4,∠ABD,∠ACD的10等分线相交于点G1、G2…、G9,若∠BDC=133°,∠BG1C=70°,求∠A的度数.6.(1)如图①,△ABC中,点D、E在边BC上,AE平分∠BAC,AD⊥BC,∠C=40°,∠B=60°,求:①∠CAE的度数;②∠DAE的度数.(2)如图②,若把(1)中的条件“AD⊥BC”变成“F为AE延长线上一点,且FD⊥BC”,其他条件不变,求出∠DFE的度数.(3)在△ABC中,AE平分∠BAC,若F为EA延长线上一点,FD⊥BC,且∠C=α,∠B=β(β>α),试猜想∠DFE的度数(用α,β表示),请自己作出对应图形并说明理由.(1)如图1,已知AE、BE分别是∠BAO和∠ABO角的平分线,点A、B在运动的过程中,∠AEB的大小是否会发生变化?若发生变化,请说明变化的情况;若不发生变化,试求出∠AEB的大小.(2)如图2,已知AB不平行CD,AD、BC分别是∠BAP和∠ABM的角平分线,又DE、CE分别是∠ADC和∠BCD的角平分线,点A、B在运动的过程中,∠CED的大小是否会发生变化?若发生变化,请说明理由;若不发生变化,试求出其值.8.已知凸四边形ABCD中,∠A=∠C=90°.(1)如图①,若DE平分∠ADC,BF平分∠ABC的邻补角,求证:DE⊥BF;(2)如图②,若BF、DE分别平分∠ABC、∠ADC的邻补角,判断DE∥BF.(1)如图1,已知AE、BE分别是∠BAO和∠ABO角的平分线,点A、B在运动的过程中,∠AEB的大小是否会发生变化?若发生变化,请说明变化的情况;若不发生变化,试求出∠AEB的大小.(2)如图2,已知AB不平行CD,AD、BC分别是∠BAP和∠ABM的角平分线,又DE、CE分别是∠ADC和∠BCD的角平分线,点A、B在运动的过程中,∠CED的大小是否会发生变化?若发生变化,请说明理由;若不发生变化,试求出其值.(3)如图3,延长BA至G,已知∠BAO、∠OAG的角平分线与∠BOQ的角平分线及延长线相交于E、F,在△AEF中,如果有一个角是另一个角的3倍,直接写出∠ABO的度数=.10.(1)如图①,∠DCE=∠ECB=α,∠DAE=∠EAB=β,∠D=30°,∠B=40°①用α或β表示∠CNA,∠MP A,∠CNA=,∠MP A=②求∠E的大小.(2)如图②,∠BAD的平分线AE与∠BCD的平分线CE交于点E,则∠E与∠B,∠D之间是否存在某种等量关系?若存在,写出结论,说明理由;若不存在,说明理由.参考答案1.解:∵EF=AD,∴∠2=∠3,(理由是:两直线平行,同位角相等)∵∠1=∠2,∴∠1=∠3,(理由是:等量代换)∴DG∥AB(理由是:内错角相等,两直线平行)∴∠BAC+∠AGD=180°(理由是:两直线平行,同旁内角互补)∵∠BAC=70°,∴∠AGD=110°.故答案为:∠3;两直线平行,同位角相等;等量代换;DG;AB;内错角相等,两直线平行;∠AGD;两直线平行,同旁内角互补;110.2.解:(1)∠1+∠2=∠3;理由:过点P作l1的平行线,∵l1∥l2,∴l1∥l2∥PQ,∴∠1=∠4,∠2=∠5,(两直线平行,内错角相等)∵∠4+∠5=∠3,∴∠1+∠2=∠3;(2)同(1)可证:∠1+∠2=∠3;(3)∠1﹣∠2=∠3或∠2﹣∠1=∠3理由:当点P在下侧时,过点P作l1的平行线PQ,∵l1∥l2,∴l1∥l2∥PQ,∴∠2=∠4,∠1=∠3+∠4,(两直线平行,内错角相等)∴∠1﹣∠2=∠3;当点P在上侧时,同理可得:∠2﹣∠1=∠3.3.解:(1)∵AB∥CD,∴∠MEB=∠MFD,∵A′E∥C′F,∴∠MEA′=∠MFC′,∴∠MEA′﹣∠MEB=∠MFC′﹣∠MFD,即∠1=∠2;(2)由折叠知,∠C′FN==70°,∵A′E∥C′F,∴∠A′EN=∠C′FN=70°,∵∠1=∠2,∴∠BEF=70°+40°=110°.4.解:设三角形的三个内角为α、β、γ,(1)∵α=2β,且α+β+γ=180°,∴当α=100°时,β=50°,则γ=30°,∴这个“特征三角形”的最小内角的度数30°;(2)不存在.∵α=2β,且α+β+γ=180°,∴当α=120°时,β=60°,则γ=0°,此时不能构成三角形,∴不存在“特征角”为120°的三角形.5.解:(1)如图(1),连接AD并延长至点F,,根据外角的性质,可得∠BDF=∠BAD+∠B,∠CDF=∠C+∠CAD,又∵∠BDC=∠BDF+∠CDF,∠BAC=∠BAD+∠CAD,∴∠BDC=∠A+∠B+∠C;(2)①由(1),可得∠ABX+∠ACX+∠A=∠BXC,∵∠A=40°,∠BXC=90°,∴∠ABX+∠ACX=90°﹣40°=50°,故答案为:50.②由(1),可得∠DBE=∠DAE+∠ADB+∠AEB,∴∠ADB+∠AEB=∠DBE﹣∠DAE=130°﹣40°=90°,∴(∠ADB+∠AEB)=90°÷2=45°,∴∠DCE=(∠ADB+∠AEB)+∠DAE=45°+40°=85°;③∠BG1C=(∠ABD+∠ACD)+∠A,∵∠BG1C=70°,∴设∠A为x°,∵∠ABD+∠ACD=133°﹣x°∴(133﹣x)+x=70,∴13.3﹣x+x=70,解得x=63,即∠A的度数为63°.6.解:(1)如图(1).∵AD⊥BC,∴∠ADB=90°,∴∠BAD=90°﹣∠B=90°﹣60°=30°,∵∠BAC=180°﹣∠B﹣∠C=180°﹣60°﹣40°=80°,而AE平分∠BAC,∴∠BAE=∠BAC=×80°=40°,∴∠DAE=∠BAE﹣∠BAD=40°﹣30°=10°;(2)如图2中,作AH⊥BC于H.由(1)可知∠HAE=10°,∵AH∥EF,∴∠DFE=∠HAE=10°(3)结论:∠DFE=(∠B﹣∠C).理由如下:如图3中,作AH⊥BC于H,FD⊥BC于D.∵∠HAE=∠EAB﹣∠BAH,∠BAH=90°﹣∠B,∠BAE=(180°﹣∠B﹣∠C),∴∠HAE=90°﹣∠B﹣∠C﹣(90°﹣∠B)=(∠B﹣∠C),∵AH∥FD,∴∠DFE=∠HAE,∴∠DFE=(∠B﹣∠C).7.解:(1)∠AEB的大小不变.如图1,∵直线MN与直线PQ垂直相交于O,∴∠AOB=90°,∴∠OAB+∠OBA=90°,∵AE、BE分别是∠BAO和∠ABO角的平分线,∴∠BAE=∠OAB,∠ABE=∠ABO,∴∠BAE+∠ABE=(∠OAB+∠ABO)=45°,∴△ABE中,∠AEB=180°﹣45°=135°;(2)∠CED的大小不变.如图2,延长AD、BC交于点F.∵直线MN与直线PQ垂直相交于O,∴∠AOB=90°,∴∠OAB+∠OBA=90°,∴∠P AB+∠MBA=270°,∵AD、BC分别是∠BAP和∠ABM的角平分线,∴∠BAD=∠BAP,∠ABC=∠ABM,∴∠BAD+∠ABC=(∠P AB+∠ABM)=135°,∴∠F=45°,∴∠FDC+∠FCD=135°,∴∠CDA+∠DCB=225°,∵DE、CE分别是∠ADC和∠BCD的角平分线,∴∠CDE+∠DCE=112.5°,∴△CDE中,∠E=180°﹣112.5°=67.5°.8.解:(1)DE⊥BF.延长DE交BF于G,∵∠ABC+∠ADC=180°,∠ABC+∠CBM=180°,∴∠ADC=∠CBM,∵DE平分∠ADC,BF平分∠ABC外角,∴∠CDE=∠ADC,∠EBF=∠CBM,∴∠CDE=∠EBF.∵∠DEC=∠BEG,∴∠EGB=∠C=90°,∴DE⊥BF.(2)DE∥BF,连接BD,∵∠ABC+∠ADC=180°,∴∠NDC+∠MBC=180°,∵BF、DE分别平分∠ABC、∠ADC的外角,∴∠EDC+∠CBF=90°,∴∠EDC+∠CDB+∠CBD+∠FBC=180°,∴DE∥BF.9.解:(1)∠AEB的大小不变,∵直线MN与直线PQ垂直相交于O,∴∠AOB=90°,∴∠OAB+∠OBA=90°,∵AE、BE分别是∠BAO和∠ABO角的平分线,∴∠BAE=∠OAB,∠ABE=∠ABO,∴∠BAE+∠ABE=(∠OAB+∠ABO)=45°,∴∠AEB=135°;(2)∠CED的大小不变.延长AD、BC交于点F.∵直线MN与直线PQ垂直相交于O,∴∠AOB=90°,∴∠OAB+∠OBA=90°,∴∠P AB+∠MBA=270°,∵AD、BC分别是∠BAP和∠ABM的角平分线,∴∠BAD=∠BAP,∠ABC=∠ABM,∴∠BAD+∠ABC=(∠P AB+∠ABM)=135°,∴∠F=45°,∴∠FDC+∠FCD=135°,∴∠CDA+∠DCB=225°,∵DE、CE分别是∠ADC和∠BCD的角平分线,∴∠CDE+∠DCE=112.5°,∴∠E=67.5°;(3)∵∠BAO与∠BOQ的角平分线相交于E,∴∠EAO=∠BAO,∠EOQ=∠BOQ,∴∠E=∠EOQ﹣∠EAO=(∠BOQ﹣∠BAO)=∠ABO,∵AE、AF分别是∠BAO和∠OAG的角平分线,∴∠EAF=90°.在△AEF中,∵有一个角是另一个角的3倍,故有:①∠EAF=3∠E,∠E=30°,∠ABO=60°;②∠EAF=3∠F,∠E=60°,∠ABO=120°;③∠F=3∠E,∠E=22.5°,∠ABO=45°;④∠E=3∠F,∠E=67.5°,∠ABO=135°.∴∠ABO为60°或45°.故答案为:60°或45°.10.解:(1)①∠CNA=∠D+∠DCE=40°+α,∠CP A=∠B+∠BAP=30°+β,故答案为:40°+α,30°+β;②∵∠ECD=∠ECB=∠BCD,∠EAD=∠EAB=∠BAD,∵∠D+∠ECD=∠E+∠EAD,∠B+∠EAB=∠E+∠ECB,∴∠D+∠ECD+∠B+∠EAB=∠E+∠EAD+∠E+∠EC∴∠D+∠B=2∠E,∴∠E=(∠D+∠B)=35°;(2)设BC交AD于点F,∵∠BFD=∠B+∠BAD,∴∠BCD=∠BFD+∠D=∠B+∠BAD+∠D,∵CE平分∠BCD,AE平分∠BAD∴∠ECD=∠ECB=∠BCD,∠EAD=∠EAB=∠BAD,∵∠E+∠ECB=∠B+∠EAB,∴∠E=∠B+∠EAB﹣∠ECB=∠B+∠BAE﹣∠BCD=∠B+∠BAE﹣(∠B+∠BAD+∠D)=(∠B﹣∠D).。
小升初数学专题培优测试卷 平面图形的周长和面积 含答案(原卷+解析)

小升初专题培优测试卷平面图形的周长和面积一.填一填(共12小题,每空1分,共18分)1.小芳用两根同样长的铁丝分别围成一个长方形和一个正方形,长方形的长18厘米,宽12厘米,长方形的周长是厘米,正方形的面积是平方厘米.2.一个三角形的底是16厘米,高是10厘米,三角形的面积是厘米2;与它等底等高的平行四边形的面积是厘米2.3.一个三角形的面积比它等底等高的平行四边形的面积少12.5平方分米,平行四边形的面积是平方分米,三角形的面积是平方分米.4.一个直角梯形的上底是6厘米,下底是9厘米,两条腰分别是4厘米和5厘米,这个梯形的周长是,面积是.5.一个圆环,内圆周长是25.12cm,外圆半径是6cm,圆环的面积是2cm.6.一个梯形的下底是15厘米,把下底缩短5厘米后就变成一个平行四边形,且面积减少20平方厘米,原来梯形的面积是平方厘米.7.在推导圆的面积公式时,将圆等分成若干份,拼成一个近似的长方形,已知长方形的长比宽多6.42厘米,圆的面积是平方厘米.8.把一个圆沿对称轴分成两个半圆后,周长增加了12厘米.每个半圆的周长是厘米.9.一个挂钟的分针长14厘米,从中午12:00到当天下午的13:00,这根分针扫过的面积是平方厘米,分针的尖端走了厘米.10.在边长是8米的正方形花坛四周铺上一条宽是1米的彩色小路,则小路的面积是平方米.11.如图,在一个面积是20平方厘米的正方形内画一个最大的圆,圆的面积是平方厘米,继续在这个圆内画一个最大的正方形,画出的正方形的面积是平方厘米.12.如图,如果涂色部分面积是225dm,那么圆环的面积是2dm.二.选一选(共6小题,每小题1分,共6分)13.面积相等的情况下,长方形、正方形和圆相比,()的周长最短.A.长方形B.正方形C.圆14.如图,两条平行线间三个图形,()的面积最小.A.三角形B.平行四边形C.梯形14题15.等腰梯形周长是48厘米,面积是96平方厘米,高是8厘米,则腰长()A.24厘米B.12厘米C.18厘米D.36厘米16.如图,图中正方形的面积是20平方厘米,图中阴影部分的面积是()第10题第11题第12题A.25π平方厘米B.20π平方厘米C.18.75π平方厘米D.15π平方厘米17.如图中阴影部分的周长是(π取3.14)(⋯)A.25.12 B.29.12C.33.12 D.37.1218.用三张边长都是8厘米的正方形铁皮,分别按如图剪下不同规格的圆片.哪张铁皮剩下的废料多?( )A.甲铁皮剩下的废料多B.乙铁皮剩下的废料多C.丙铁皮剩下的废料多D.剩下的废料同样多三.计算题(共7小题,3+3+3+6+8+8+12=43分)19.计算下列图形的面积(单位:厘米) 20.求阴影部分的面积.21.求图中阴影部分的面积.(单位:厘米) 22.求阴影部分的周长和面积23.求各图中阴影部分的面积.(单位:)cm24.求下列图形的周长或面积25.求下列各图阴影部分的面积和周长.四.解决问题(共6小题,第27题、28题、29题每题4分,其余每题5分,共27分)28.一个长方形与一个圆的面积相等,如果长方形的长与圆的直径都是8厘米,那么长方形的宽是多少厘米?(取3.14)29.一个圆形花圃的半径是4米,花圃的外面筑了一条宽2米的环形小路.这条小路的面积是多少平方米?30.一块梯形广告牌,上底长5.4米,下底长12米,高40分米,两面喷漆,每平方米用油漆200克,共用油漆多少千克?31.(已知圆的周长和长方形的周长相等,长方形的宽是多少厘米?32.如下图,一个平行四边形被分成甲、乙两部分,甲的面积比乙大264m,甲的上底是多少米?33.如图是一块草地上残留的一段墙角,90AB=米,6BC=米,M为紧靠在BC段残墙∠=︒,10ABC外侧地面上的一个木桩,3MC=米.现木桩上栓有一只白山羊,若这只羊能吃到草的最远距离为8米,求这只羊能吃到草的区域的最大面积.(π取3.14)小升初专题培优测试卷平面图形的周长和面积参考答案与试题解析一.填一填(共12小题)1.(2020•延平区)小芳用两根同样长的铁丝分别围成一个长方形和一个正方形,长方形的长18厘米,宽12厘米,长方形的周长是厘米,正方形的面积是平方厘米.【分析】已知两根铁丝同样长,就是长方形和正方形的周长相等,首先根据长方体的周长公式求出周长,周长除以4得出正方形的边长,根据正方形的面积公式解答即可.【解答】解:(1812)230260+⨯=⨯=(厘米);÷⨯÷,(604)(604)=⨯,1515=(平方厘米);225答:长方形的周长是60厘米,正方形的面积是225平方厘米.故答案为:60,225.【点评】此题主要考查长方形、正方形的周长和面积的计算,直接根据公式解答即可,关键在于理解长方形和正方形的周长相等.2.(2020•福田区)一个三角形的底是16厘米,高是10厘米,三角形的面积是厘米2;与它等底等高的平行四边形的面积是厘米2.【分析】依据三角形的面积=底⨯高2÷,平行四边形的面积=底⨯高,则三角形的面积是与其等底等高的平行四边形面积的一半,因此与它等底等高的平行四边形的面积是三角形面积的2倍,据此求解即可.【解答】解:三角形的面积:16102⨯÷=÷1602=(厘米2)80平行四边形的面积:802160⨯=(厘米2)答:三角形的面积是80厘米2,与它等底等高的平行四边形的面积是160厘米2.故答案为:80;160.【点评】解答此题的主要依据是:三角形的面积是与其等底等高的平行四边形面积的一半.3.(2020•济南)一个三角形的面积比它等底等高的平行四边形的面积少12.5平方分米,平行四边形的面积是平方分米,三角形的面积是平方分米.【分析】根据等底等高的三角形和平行四边形面积之间的关系,三角形的面积是这个平行四边形面积的一半,由此解答即可.【解答】解:12.5225⨯=(平方分米)2512.512.5-=(平方分米)答:平行四边形的面积是25平方分米,三角形的面积是12.5平方分米. 故答案为:25,12.5.【点评】此题主要考查了等底等高的三角形和平行四边形面积之间的关系.4.(2020•栖霞区)一个直角梯形的上底是6厘米,下底是9厘米,两条腰分别是4厘米和5厘米,这个梯形的周长是 ,面积是 .【分析】梯形的周长=梯形的上下底+两腰长度,梯形的面积=(上底+下底)⨯高2÷,根据直角三角形的特征,在直角三角形中,直角边小于斜边,由此确定直角梯形的高是4厘米,把数据代入公式解答. 【解答】解:694524+++=(厘米) (69)42+⨯÷1542=⨯÷ 30=(平方厘米)答:这个梯形的周长是24厘米,面积是30平方厘米. 故答案为:24厘米,30平方厘米.【点评】此题主要考查梯形的周长公式、面积公式的灵活运用,关键是熟记公式.5.(2020秋•隆昌市期末)一个圆环,内圆周长是25.12cm ,外圆半径是6cm ,圆环的面积是 2cm . 【分析】首先求出内圆的半径,再根据环形面积公式:()22S R r π=-环形,把数据代入公式解答. 【解答】解:25.12 3.1424÷÷=(厘米)223.14(64)⨯-3.14(3616)=⨯-3.1420=⨯62.8=(平方厘米)答:圆环的面积是62.8平方厘米. 故答案为:62.8.【点评】此题主要考查环形面积公式的灵活运用,关键是熟记公式.6.(2020•丰台区)一个梯形的下底是15厘米,把下底缩短5厘米后就变成一个平行四边形,且面积减少20平方厘米,原来梯形的面积是 平方厘米.【分析】根据题意,可用15减去5计算出梯形的上底,减少的20平方厘米的面积为底为5厘米的三角形,所以可利用三角形的面积公式2h S a =÷求出三角形的高,即是梯形的高,最后再根据梯形的面积公式S =(上底+下底)⨯高2÷进行计算即可得到答案. 【解答】解:梯形的上底:15510-=(厘米)梯形的高:20258⨯÷=(厘米) 梯形的面积: (1015)82+⨯÷2582=⨯÷ 100=(平方厘米)答:原来梯形的面积是100平方厘米. 故答案为:100.【点评】解答此题的关键是根据缩短图形确定梯形的高和梯形的上底,然后再利用梯形的面积公式进行解答即可.7.(2020•贵阳)在推导圆的面积公式时,将圆等分成若干份,拼成一个近似的长方形,已知长方形的长比宽多6.42厘米,圆的面积是 平方厘米.【分析】拼成的长方形的两个长的和是圆的周长,即圆的周长的一半是长方形的长;长方形的宽是圆的半径,通过二者的关系求出圆的半径,进而求出圆的面积. 【解答】解:设圆的半径为r ,那么它的周长就是2r π,由题意得:22 6.42r r π÷-=,6.42r r π-=, (1) 6.42r π-=,6.42(3.141)r =÷-, 6.42 2.14r =÷, 3r =; 2S r π=, 23.143=⨯,3.149=⨯,28.26=(平方厘米); 故答案为:28.26.【点评】本题关键是理解拼成的长方形的长和宽分别是什么,然后根据它们的关系求出圆的半径. 8.(2020•西区)把一个圆沿对称轴分成两个半圆后,周长增加了12厘米.每个半圆的周长是 厘米. 【分析】如图所示,把一个圆沿对称轴分成两个半圆后,周长多了两个直径的长度,于是可以求出直径的长度,也就能求出圆的周长,每个半圆的周长=圆的周长的一半+直径,问题得解.【解答】解:圆的直径:1226÷=(厘米),半圆的周长:3.14626⨯÷+,18.8426=÷+,=+,9.426=(厘米);15.42答:每个半圆的周长是15.42厘米.故答案为:15.42.【点评】此题主要考查半圆的周长的计算方法,关键是明白:把一个圆沿对称轴分成两个半圆后,周长多了两个直径的长度.9.(2020秋•淮南期末)一个挂钟的分针长14厘米,从中午12:00到当天下午的13:00,这根分针扫过的面积是平方厘米,分针的尖端走了厘米.【分析】从中午12:00到当天下午的13:00,分针正好转了1圈,又因分针长14厘米,即分针所经过的圆的半径是14厘米,从而利用圆的周长公式即可求出分针走过的路程;利用圆的面积公式即可求出分针“扫过”的面积.【解答】解:2⨯3.1414=⨯3.14196=(平方厘米)615.44⨯⨯3.14142=⨯3.1428=(厘米)87.92答:分针扫过的面积是615.44平方厘米,分针的尖端走了87.92厘米.故答案为:615.44;87.92.【点评】本题通过时钟问题考查了圆的周长和面积.解答此题的关键是明白,从中午12:00到当天下午的13:00,分针正好转了1圈.10.(2020秋•高碑店市期末)在边长是8米的正方形花坛四周铺上一条宽是1米的彩色小路,则小路的面积是平方米.【分析】如图,首先判断出正方形ABCD 的边长是10(81210)+⨯=米,然后根据正方形的面积=边长⨯边长,用边长是10米的正方形的面积减去边长是8米的水池的面积,求出小路的面积是多少即可.【解答】解:如图, (812)(812)88+⨯⨯+⨯-⨯10064=- 36=(平方米)答:小路的面积是36平方米. 故答案为:36.【点评】此题主要考查了正方形的面积的求法,要熟练掌握,解答此题的关键是分别求出正方形ABCD 的面积和水池的面积各是多少.11.(2020•常熟市)如图,在一个面积是20平方厘米的正方形内画一个最大的圆,圆的面积是 平方厘米,继续在这个圆内画一个最大的正方形,画出的正方形的面积是 平方厘米.【分析】由题意可知:这个最大圆的直径应该等于大正方形的边长,据此利用圆的面积公式即可求出圆的面积;小正方形的对角线等于圆的直径,则小正方形的面积对角线的平方的2倍,据此解答即可. 【解答】解:(1)设正方形的边长为a ,圆的半径为2a, 则220a =平方厘米,圆的面积23.14()2a=⨯23.144a =⨯3.145=⨯15.7=(平方厘米);(2)因为220a =平方厘米,则小正方形的面积是20210÷=(平方厘米).答:圆的面积是15.7平方厘米,小正方形的面积是10平方厘米. 故答案为:15.7、10.【点评】解答此题的关键是明白:这个最大圆的直径应该等于大正方形的边长.12.(2020秋•江汉区期末)如图,如果涂色部分面积是225dm ,那么圆环的面积是 2dm .【分析】观察图形,设大圆的半径是R ,小圆的半径是r ,则大正方形的边长是R ,小正方形的边长是r ,所以阴影部分的面积等于2225R r -=平方分米,又因为圆环的面积22()R r π=-据此代入即可求出圆环的面积.【解答】解:根据题干分析可得:3.142578.5⨯=(平方分米)答:圆环的面积是78.5平方分米. 故答案为:78.5.【点评】解答此题的关键是明确2225R r -=平方分米,据此代入圆环的面积22()R r π=-计算即可解答. 二.选一选(共6小题)13.(2020•桐梓县模拟)面积相等的情况下,长方形、正方形和圆相比,( )的周长最短. A .长方形B .正方形C .圆【分析】周长相等时,形状越近似于圆,面积越大,反之,面积相等,形状越不接近圆,周长越大;所以长方形,正方形,圆的面积相等,他们周长大小比较的排列顺序为(从大到小):长方形,正方形,圆. 【解答】解:当长方形、正方形、圆三个图形的面积相等时,它们周长的长短关系是颠倒的,即长方形>正方形>圆,即圆的周长最短. 故选:C .【点评】考查了图形的面积及周长的比较,是一个经典题型.本题从数量上认证了面积一定,长方形的周长>正方形的周长>圆的周长.14.(2020秋•卫东区期末)如图,两条平行线间三个图形,()的面积最小.A.三角形B.平行四边形C.梯形【分析】因为夹在平行线之间的垂线段长度相等,所以三个图形的高相等,依据各自的面积公式即可推出结果;三角形面积=底⨯高2÷.÷,平行四边形面积=底⨯高,梯形面积=(上底+下底)⨯高2【解答】解:三角形的面积12÷=⨯高=⨯高26平行四边形的面积7=⨯高梯形的面积(38)=+⨯高2 5.5÷=⨯高<<5.567由此可以看出梯形的面积最小.故选:C.【点评】此题主要考查等高的图形面积大小,利用各自的面积公式即可以推算.15.(2020•福田区校级模拟)等腰梯形周长是48厘米,面积是96平方厘米,高是8厘米,则腰长() A.24厘米B.12厘米C.18厘米D.36厘米【分析】根据题干,可以利用梯形的面积公式先求出上底加下底的和是多少,再利用周长求得两腰的长度.【解答】解:根据题干可得,梯形的上底与下底的和为:962824⨯÷=(厘米),梯形的腰长为:-÷,(4824)2=÷,242=(厘米),12故选:B.【点评】此题考查了梯形的面积和周长公式的灵活应用.16.(2020秋•武侯区期末)如图,图中正方形的面积是20平方厘米,图中阴影部分的面积是()A.25π平方厘米B.20π平方厘米C .18.75π平方厘米D .15π平方厘米 【分析】阴影部分的面积34=圆的面积.因正方形的面积是20平方厘米,正方形的边长就是圆的半径,所以半径的平方就是20.据此根据圆的面积公式2S r π=解答即可.【解答】解:3204π⨯⨯ 15π=⨯15π=(平方厘米)答:阴影部分的面积是15π平方厘米.故选:D .【点评】在求不规则图形的面积时,一般要转化为求几个规则图形面积相加或相减的方法进行计算.解答此题的关键是理解圆的半径的平方等于正方形的面积.17.(2006秋•崇明县期末)如图中阴影部分的周长是(π取3.14)(⋯ )A .25.12B .29.12C .33.12D .37.12【分析】根据题意,1S 部分的内侧的周长等于以4为半径的圆的14周长,外侧的周长等于以(22)+为半径的圆的14周长,将这两部分的面积相加后再加上(22)+就是图形1S 的阴影部分的周长; 图形2S 的一侧的周长是以4为半径的圆的14周长,另一侧的周长等于以(22)+为半径的圆的14周长,将这两部分的面积相再加上(22)+就是图形2S 的阴影部分的周长,最后再将图形1S 的周长加上图形2S 的周长即可得到答案.【解答】解:1S 的周长为:113.1424 3.142(22)(22)44⨯⨯⨯+⨯⨯⨯+++ 6.28 6.284=++12.564=+16.56=2S 的周长为:112 3.144 3.1424(22)44⨯⨯⨯+⨯⨯⨯++ 6.28 6.284=++12.564=+16.56=图中阴影部分的周长为:16.5616.5633.12+=.故选:C .【点评】解答此题的关键是将1S 、2S 的两条弧看作是以4为半径的14圆的周长,然后再加上4条横边的长即可. 18.(2020•崇安区)用三张边长都是8厘米的正方形铁皮,分别按如图剪下不同规格的圆片.哪张铁皮剩下的废料多?( )A .甲铁皮剩下的废料多B .乙铁皮剩下的废料多C .丙铁皮剩下的废料多D .剩下的废料同样多【分析】①剪法甲:剩下的铁皮的面积=正方形的面积4-个小圆的面积;②剪法乙:剩下的铁皮的面积=正方形的面积1-个大圆的面积;③剪法丙:剩下的铁皮的面积=正方形的面积16-个小圆的面积;正方形的边长是8厘米,则能求出正方形的面积和圆的面积,从而求得剩下的铁皮的面积即可.【解答】解:因为正方形的边长是8厘米,则正方形的面积是:8864⨯=(平方厘米);①剪法甲:圆的半径是8222÷÷=(厘米);剩下的铁皮的面积是264 3.1424-⨯⨯6450.24=-13.76=(平方厘米);②剪法乙:圆的半径是824÷=(厘米);剩下的铁皮的面积是264 3.144-⨯6450.24=-13.76=(平方厘米);③剪法丙:圆的半径是8421÷÷=(厘米),剩下的铁皮的面积是264 3.14116-⨯⨯6450.24=-13.76=(平方厘米)所以剩下的废料同样多;答:剩下的废料一样大.故选:D .【点评】此题主要考查了正方形、圆的面积公式的应用,解答此题的关键是要弄清楚:剩下的铁皮的面积=正方形的面积-圆的面积.三.计算题(共7小题)19.(2020•山东模拟)计算下列图形的面积(单位:厘米)【分析】这个图形由一个底为14厘米,高为4.5厘米的平行四边形和一个上底为14厘米,下底为25厘米,高为4.5厘米的梯形组成.根据平行四边形形面积计算公式“S ah =”、梯形面积计算公式“()2S a b h =+÷”即可解答.【解答】解:14 4.5(1425) 4.52⨯++⨯÷14 4.539 4.52=⨯+⨯÷6387.75=+150.75=(平方厘米)答:这个图形的面积是150.75平方厘米.【点评】解答此题的关键是平行四边形面积计算公式、梯形面积计算公式的熟练运用.20.(2020•北京模拟)求阴影部分的面积.(π取3.14)【分析】通过观察图形可知,阴影部分的面积等于长方形的面积减去直径是4厘米的半圆面积再减去底和高多少4厘米的三角形的面积,根据长方形的面积公式:S ab =,圆的面积公式:2S r π=,三角形的面积公式:2S ah =÷,把数据分别代入公式解答.【解答】解:284 3.14(42)2442⨯-⨯÷÷-⨯÷32 3.14428=-⨯÷-32 6.288=--17.72=(平方厘米)答:阴影部分的面积是17.72平方厘米.【点评】解答求组合部分的面积,关键是观察分析图形是由哪几部分组成的,是求各部分的面积和、还是求各部分的面积差,再根据相应的面积公式解答.21.(2020•揭阳)求图中阴影部分的面积.(单位:厘米)【分析】阴影部分的面积=正方形的面积+半径为4厘米的圆的面积,然后根据正方形和圆形的面积公式解答即可.【解答】解:23.14444⨯+⨯50.2416=+66.24=(平方厘米)答:阴影部分的面积是66.24平方厘米.【点评】解答此题的关键是根据图,判断出阴影部分的面积是由哪些图形的面积相减所得,由此再根据相应的面积公式解答即可.22.(2020•石家庄)求如图阴影部分的周长和面积.【分析】如图所示: 阴影部分的周长3=个圆周长的一半4+厘米的直径 1.5=个圆的周长4+厘米的直径;根据圆的周长公式C d π=解答即可;沿上图割补,那么阴影的面积=直径是4厘米的半圆的面积,根据圆的面积公式:2S r π=,把数据代入公式解答即可.【解答】解:周长:3.144 1.54⨯⨯+18.844=+22.84=(厘米)面积:23.14(42)2⨯÷÷3.142=⨯6.28=(平方厘米)答:阴影部分的周长是22.84厘米,面积是6.28平方厘米.【点评】本题考查了圆与组合图形的周长和面积计算,可以根据几何图形的特征,通过转化的方法,化复杂为简单,变组合图形为基本图形的加减组合.23.(2020•郑州模拟)求各图中阴影部分的面积.(单位:)cm【分析】根据题意,(1)阴影部分的面积=直角梯形的面积-半圆的面积,代入数字计算即可;(2)将月牙形移入四分之一圆内,阴影部分的面积=长方形的面积-三角形的面积,代入数字计算即可.【解答】解:(1)21(57)42 3.14(42)2+⨯÷-⨯⨯÷ 24 6.28=-17.72=(平方厘米)(2)48442⨯-⨯÷328=-24=(平方厘米)【点评】此题重点考查应用割补法计算阴影部分的面积.24.(2020春•新田县期末)求下列图形的周长或面积【分析】(1)此图是两端部分是直径为40米的半圆,中间部分是为长为100米,宽为40米的长方形,两端的两个半圆通过平移可看作一个同直径的圆.这个图形的周长为圆周长加上长方形长的2倍;面积为圆面积加长方形面积.根据长方形面积计算公式“S ab =”、圆面积计算公式“2S r π=”、圆周长计算公式“C d π=”及半径与直径的关系“2d r =”即可解答. (2)把这个图形的下部分的阴影半圆通过旋转可以到上部分空白半圆的位置,这样阴影部分就是一个半径为4厘米的半圆.这个图形的周长就是半圆周长,即圆周长的一半加半径;面积就是圆面积的一半.根据圆面积计算公式“2S r π=”、圆周长计算公式“2C r π=”即可解答.【解答】解:(1)3.14401002⨯+⨯125.6200=+325.6=(米)2403.14()100402⨯+⨯ 23.142010040=⨯+⨯12564000=+5256=(平方米)答:这个图形的周长是325.6米,面积是5256平方米.(2)3.1442242⨯⨯÷+⨯12.568=+220.56()cm =23.1442⨯÷3.14162=⨯÷50.242=÷225.12()cm =答:这个图形的周长是20.56cm ,面积是225.12cm .【点评】解答此题的关键是对图形进行整合,然后再根据整合后相关图形的周长、面积计算公式解答.25.求下列各图阴影部分的面积和周长.【分析】(1)观察图形可知,阴影部分的面积等于长12厘米、宽6厘米的长方形的面积与直径是6厘米的34圆的面积之和,周长等于直径6厘米的圆的周长的34与两条12厘米的线段之和;据此计算即可解答;(2)阴影部分的面积等于长10厘米,宽1025÷=厘米的长方形的面积与半径是5厘米的半圆的面积之差,阴影部分的周长等于半径5厘米的半圆的周长;据此计算即可解答问题;(3)阴影部分的面积等于直径是6410+=厘米的半圆的面积减去空白处的两个小半圆的面积之差,阴影部分的周长等于直径10厘米的圆的周长;据此计算即可解答问题;(4)阴影部分的面积等于半径是325+=厘米的34圆的面积与半径是3厘米的34圆的面积之差,阴影部分的周长等于半径5厘米的圆的周长的14加上半径是3厘米的圆的周长的14,再加上两条2厘米的线段的和;据此计算即可解答问题.【解答】解:(1)23126 3.14(62)4⨯+⨯÷⨯7221.195=+93.195=(平方厘米)33.1461224⨯⨯+⨯14.1324=+38.13=(厘米)答:阴影部分的面积是93.195平方厘米,周长是38.13厘米.(2)1025÷=(厘米)2105 3.1452⨯-⨯÷5039.25=-10.75=(平方厘米)3.1410210⨯÷+15.710=+25.7=(厘米)答:阴影部分的面积是10.75平方厘米,周长是25.7厘米.(3)6410+=(厘米)2223.14(102)2 3.14(62)2 3.14(42)2⨯÷÷-⨯÷÷-⨯÷÷3.14(12.54.52)=⨯--3.146=⨯18.84=(平方厘米)3.141031.4⨯=(厘米)答:阴影部分的面积是18.84平方厘米,周长是31.4厘米.(4)325+=(厘米)22333.145 3.14344⨯⨯-⨯⨯ 58.87521.195=-37.68=(平方厘米)113.1452 3.14322244⨯⨯⨯+⨯⨯⨯+⨯ 7.85 4.714=++16.56=(厘米)答:阴影部分的面积是37.68平方厘米,周长是16.56厘米.【点评】关键是明确阴影部分的面积和周长是由哪部分我们学过的图形组成的,再利用相应的公式解答.五.解决问题(共6小题)28.(2020•绵阳)一个长方形与一个圆的面积相等,如果长方形的长与圆的直径都是8厘米,那么长方形的宽是多少厘米?(取3.14)【分析】首先根据圆的面积公式:2S r π=,求出圆的面积,再根据长方形的面积公式:S ab =,那么b S a =÷,把数据代入公式解答.【解答】解:23.14(82)⨯÷3.1416=⨯50.24=(平方厘米), 50.248 6.28÷=(厘米),答:长方形的宽是6.28厘米.【点评】此题主要考查圆的面积公式、长方形的面积公式的灵活运用,关键是熟记公式.29.(2020•萧山区模拟)一个圆形花圃的半径是4米,花圃的外面筑了一条宽2米的环形小路.这条小路的面积是多少平方米?【分析】根据环形面积=外圆面积-内圆面积,首先用花圃半径加上小路宽(2米)求出外圆半径,然后把数据代入公式解答.【解答】解:223.14[(42)4]⨯+-3.14[3616]=⨯-3.1420=⨯62.8=(平方米), 答:这条小路的面积是62.8平方米.【点评】此题主要考查环形面积公式的灵活运用,关键是熟记公式.30.(2020•萧山区模拟)一块梯形广告牌,上底长5.4米,下底长12米,高40分米,两面喷漆,每平方米用油漆200克,共用油漆多少千克?【分析】根据梯形的面积公式:()2S a b h =+÷,把数据代入公式求出广告牌两面的面积,然后用油漆的面积乘每平方米用油漆的质量即可.【解答】解:200克0.2=千克40分米4=米(5.412)4220.2+⨯÷⨯⨯17.44220.2=⨯÷⨯⨯69.60.2=⨯13.92=(千克)答:一共用油漆13.92千克.【点评】此题主要考查梯形面积公式的灵活运用,关键是熟记公式.31.(2020•天津模拟)已知圆的周长和长方形的周长相等,长方形的宽是多少厘米?【分析】首先根据圆的周长公式:C d π=,求出圆的周长,再根据长方形的周长公式:()2C a b =+⨯,那么2b C a =÷-,把数据代入公式解答.【解答】解:3.1416216⨯÷-50.24216=÷-=-25.1216=(厘米)9.12答:长方形的宽是9.12厘米.【点评】此题主要考查圆的周长公式、长方形的周长公式的灵活运用,关键是熟记公式.32.(2020•保定模拟)如下图,一个平行四边形被分成甲、乙两部分,甲的面积比乙大264m,甲的上底是多少米?【分析】观察图示可知:甲部分是梯形,乙部分是三角形,根据平行四边形的性质可知乙的底为40-甲的上底,两部分的高是16米,于是利用平行四边形的面积-三角形的面积64=,据此列出方程即可求出甲的上底.【解答】解:设甲的上底为x米,则+⨯÷--⨯÷=x x(40)162(40)16264+⨯--⨯=(40)8(40)864x xx x+⨯-⨯+=8408408864x=1664x=4答:甲的上底是4米.【点评】此题主要考查平行四边形的意义及梯形和三角形的面积公式的灵活应用.33.(2020秋•崇明区期末)如图是一块草地上残留的一段墙角,90BC=米,MAB=米,6ABC∠=︒,10为紧靠在BC段残墙外侧地面上的一个木桩,3MC=米.现木桩上栓有一只白山羊,若这只羊能吃到草的最远距离为8米,求这只羊能吃到草的区域的最大面积.(π取3.14)。
六年级小升初数学模拟培优试题测试卷(附答案解析)

六年级小升初数学模拟培优试题测试卷(附答案解析)一、选择题1.把一个直径4毫米的手表零件,画在图纸上的直径是8厘米,这幅图纸的比例尺是( ).A.1:2 B.2:1 C.1:20 D.20:12.用同样大小的正方体木块拼成一个大正方形,下面小正方体的块数不能拼成大正方体的是().A.24块B.27块C.64块3.一瓶橙汁的25是14L,这瓶橙汁有多少升?正确的算式是( ).A.25×14B.25÷14C.14÷25D.25-144.一个三角形三个内角度数的比是2:3:5,这个三角形中最大的内角是()。
A.锐角B.直角C.钝角5.用6千克棉花的17和1千克铁的67相比较,结果是()。
A.6千克棉花的17重B.1千克铁的67C.一样重D.无法比较6.观察如图,与字母B和字母F相对的面分别是()。
A.C、D B.A、E C. D 、E D.A、E 7.下面说法错误的是()。
A.39515=可以看做一个比例。
B.比例就是由比值相等的两个比组成的等式。
C.两个量的倍数关系无法转换成两个量相比的关系。
D.根据24389⨯=⨯,至少可以写出4个不同的比例。
8.如图将一个圆柱转化成一个长方体、体积()。
A.不变B.增加C.减少9.某城市限定每户每月用水量不超过6吨时,每吨价格为2元;当用水量超过6吨时,超过部分每吨水价为3元,每户每月水费y(元)与用水量x(吨)的关系是图中的()。
A.B.C.D.10.如图,按一定的流量向放在水槽底部的圆柱体玻璃杯注水,注满玻璃杯后,继续注水,直至注满水槽,水槽中水面上升的高度与注水时间的关系图象大致是()A.B.C.D.二、填空题11.124小时=_________分钟 3040立方厘米=_________立方分米十12.3():160.375()%()===。
十13.如果a÷b=c(a、b、c都是非零的自然数),那么a和b的最大公因数是(______),a和b的最小公倍数是(______)。
【小升初】小学数学《平面图形的测量专题课程》含答案
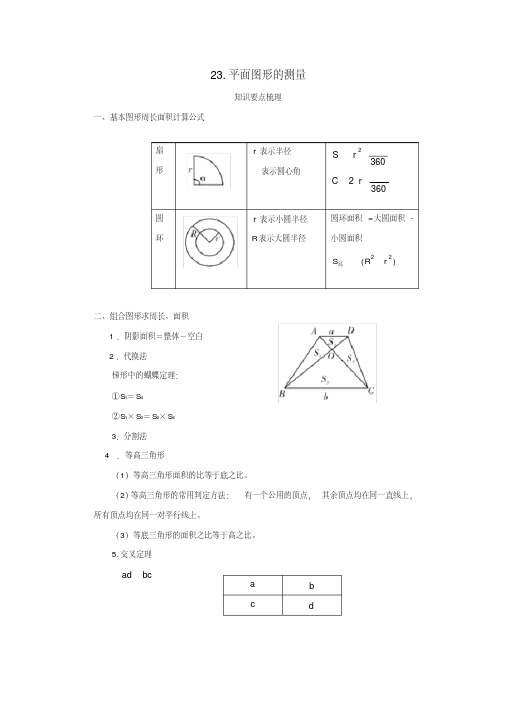
一、基本图形周长面积计算公式
知识要点梳理
扇
r 表示半径
S r2
360
形
表示圆心角
C 2r 360
圆
r 表示小圆半径
圆环面积 =大圆面积 -
环
R 表示大圆半径
小圆面积
S环
(R2 r 2 )
二、组合图形求周长、面积
1 .阴影面积=整体-空白
2 .代换法
梯形中的蝴蝶定理:
①S1= S4
小相同的小长方形,则图中阴影部分的面积是(
)。
3 .(西安高新某中入学 )某小区准备在长方形地块上种植花草,设
计图纸如图, BD、 CF 将长方形 ABCD分成四块,红色三角形面积是 8
平方厘米,黄色三角形面积是 12 平方厘米,问绿色四边形面积是(
)平方厘米。
4 .(江西某师大附中入学 )三角形 ABC的面积是 21 平方厘米,点
别等于大、小正方形的边长) ,则二者的面积相等,分别去掉公共部分(三角形
CFH),
那么剩余的部分的面积, 仍然相等, 即三角形 BCH和三角形 HFD的面积相等, 于是阴影
部分的面积就变成了大正方形的面积的一半,据此代入数据 100÷ 2=50(平方厘米)
答:三角形 BFD的面积为 50 平方厘米。
23.平图形的测量 25.12 3.12.56 3.14 0.86
二、 1.C B 2.C
三、 1. 【解析】阴影部分面积 =梯形 ABCD的面积 =(8-3
+8)
×5÷ 2=32.5
答: 阴影部分面积为 32.5 。
2. 【解析】阴影部分面积 =(16-2) ×(10-3)=98
( 米2) 答: 小草覆盖的面积是 98 平方米。
数学小学六年级小升初复习培优试卷测试卷(带答案)

数学小学六年级小升初复习培优试卷测试卷(带答案)一、选择题1.正方形的周长和它的边长()。
A.成正比例B.成反比例C.不成比例D.无法确定2.钟面上5时整,时针与分针形成的角是()。
A.钝角B.直角C.平角3.一根绳子长310米,用去了15米,还剩多少米?根据题意,正确的算式是()。
A.310×15B.310×(1-15)C.310-154.用一根小棒粘住长方形一条边,旋转一周,这个长方形转动后产生的图形是()。
A.三角形B.圆形C.圆柱5.某地区烛光晚餐中,设座位有x排,每排坐30人,则有8人无座位;每排坐31人,则空26个座位,则下列方程正确的是()A.30x-8=31x+26 B.30x-8=31x-26C.30x+8=31x+26 D.30x+8=31x-266.下图是正方体纸盒展开后的平面图,在正方体纸盒上与5号面相对的面是()。
A.1 B.2 C.37.x、y是两个变化的量,如果x3(0)=≠yy,在下面的表达中错误的是()。
A.x与y成正比例关系B.其图像是条直线C.y=3x D.若x×5,则y×58.把一个转盘平均分成9份,上面分别写有1、2、3、4、5、6、7、8、9。
任意转动转盘,指针落在某个区域的可能性,正确的表述是()。
A.奇数的可能性最大B.合数的可能性最大C.质数的可能性最大D.奇数和偶数的可能性相等9.一种电视机提价后,又降价,现价( )原价.A.高于B.低于C.等于10.把一个圆形纸片对折两次后,得到下图,然后沿虚线剪开,得到两部分,其中较大一部分展开后是()。
A.B.C.D.二、填空题11.第七次人口普查,我国人口共有1411780000人,这个数读作(______),把这个数改写成用“亿”作单位的数是(______),省略“亿”位后面的尾数约是(________)。
十12.10.01里面有(________)个0.01,119的分数单位是(________),再增加(________)个这样的单位正好是最小的质数。
人教版六年级数学小升初专题练习:图形的认识、测量、变换

(人教新课标)小升初数学模拟试题图形的认识、测量、变换班级姓名分数6.图形的认识、测量、变换一、填空。
(25分)1.在同一平面内,经过一点能画()条直线,经过两点能画()条直线。
2.从直线外一点到这条直线可以画无数条线段,其中最短的是和这条直线()的线段。
3.两条直线相交,组成了4个角。
如果其中一个角是90°,那么另外三个角各是()。
4.右图中,∠1=(),∠2=()。
5.在3点钟的时候,时针和分针组成的较小的角的度数是();在6点30分的时候,时针分针组成的较小的角的度数是()。
6.一个等腰三角形的一个底角是45°,它的顶角是(),这个三角形又叫做()三角形。
7.数一数,右图有()个长方形。
8.将一张正方形纸连续对折三次,展开后其中一份是这张纸的()。
9.四条线段的长度分别是2 cm、3 cm、5 cm、7 cm,其中长分别是()、()、()时,三条线段才能围成一个三角形。
10.连接圆心和圆上任意一点的()叫做()。
11.阳阳坐在教室的第4列第3行,用(4,3)表示;冬冬坐在教室的第3列第1行应表示为()。
12.观察物体,是从()面看到的形状,是从()面看到的形状,从左面看到的形状是()。
(请画出来)二、选择。
(10分)1.下列各选项中,右边图形和左边图形形成轴对称图形的是()。
A.B.C.D.2.三角形中最小的一个角是50°,按角分类这是一个()三角形。
A.锐角B.直角C.钝角D.不能确定3.用一根木条给一个长方形加固,若只考虑加固效果的话,采用()最好。
A. B. C. D.4.下列图形中,对称轴条数最多的是()。
A.B.C.D.5.下列形体,截面形状不可能是长方形的是()。
A.B.C.D.6.把一个平行四边形任意分割成两个梯形,这两个梯形中()是相等的。
A.高B.上底与下底的和C.周长D.面积7.用火柴棒按下图的方式搭正方形。
搭20个这样的的正方形需要()根火柴棒。
小升初专项培优测评卷(十九)立体图形的认识与测量(二)(原卷版)

小升初专项培优测评卷(十九)立体图形的认识与测量(二)考试时间:80分钟;满分:100分题号一二三四五总分得分教师寄话:静心思考,用心审题,细心检查,成功属于你!一.填一填(共12小题,每小题2分,共24分)1.(2019•茂名)一个边长3厘米的正方形,以它的一条边为轴,旋转后的图形是,这个旋转后的图形的体积是立方厘米.2.(2019•南京)有一张长方体铁皮(如图),剪下图中两个圆及一块长方形,正好可以做成一个圆柱体,这个圆柱体的底面半径为10厘米,那么圆柱的底面积是平方厘米,体积是立方厘米.3.(2019•保定模拟)(单位:)的长直角边为轴旋转一周(如图)得到几何体cm以直角三角形是,体积是3cm.4.(2019•株洲模拟)两个完全相同的圆柱能拼成一个长12厘米的圆柱,但表面积比原来减少了25.12平方厘米,原来一个圆柱体的体积是立方厘米.若将原来一个圆柱体削成一个最大的圆锥,则体积会减少立方厘米.5.(2019春•上海月考)一个直角三角形的三条边长分别是3cm、4cm和5cm,若以直角边为轴旋转一圈,旋转一圈形成的图形体积是立方厘米.( 取3.14)6.(2019春•通州区校级期末)把一个圆柱木料削成一个最大的圆锥,体积减少了24立方厘米,原来圆柱的底面积是9平方厘米,削成的圆锥的高是厘米.7.(2019春•成武县期末)底面积是230cm,高是5cm的圆锥的体积是3cm,与它等底等高的圆柱的体积是3cm.8.(2019春•环江县期中)一个圆柱和一个圆锥等底等高,如果圆柱比圆锥的体积多376dm,则圆柱的体积是3dm.dm,圆锥的体积是39.(2019春•交城县期中)如图,把一个底面半径为4cm的圆柱,拼成一个近似的长方体,长方体的表面积比圆柱增加了2cm.40cm,圆柱的高是cm,体积是310.(2019春•武穴市校级期中)一个棱长是6dm的正方体容器装满了水后,倒入一个底面积是218dm的圆锥形容器正好装满,这个圆锥的高是.11.(2019•防城港模拟)将一段底面直径和高都是10厘米的圆木沿直径切割成两个半圆柱,表面积之和比原来增加了平方厘米.12.(2019•泉州)图中一个小球的体积是立方厘米,一个大球的体积是立方厘米.二.选一选(共8小题,每小题2分,共16分)13.(2019•衡阳模拟)把一个正方体加工成一个最大的圆柱体,下面的说法正确的是() A.正方体的体积等于圆柱体的体积B.正方体的表面积等于圆柱体的表面积C.正方体的棱长等于圆柱的高D.正方体的棱长等于圆柱的底面周长的一半14.(2019春•滨海县期末)下面的三句话中,()是错误的.A.圆锥的顶点到底面圆心的距离是圆锥的高B.一个圆柱侧面展开图是正方形,这个圆柱的底面周长和高相等C.三角形的底和高成反比例15.(2019•长沙模拟)一个圆柱的侧面展开图是一个正方形,这个圆柱的高与底面半径的比值是() A.πB.2πC.r16.圆柱、圆锥、正方体和长方体的底面周长和高相等,()的体积最大.A.圆柱B.圆锥C.正方体D.长方体17.(2019•郑州模拟)把一个圆柱体沿半径和高平均切成若干份以后,重新拼插成一个近似长方体,原来圆柱体的侧面积是281.64cm.长方体的表面积比圆柱体增加()A.216cm32cm D.226cm C.224cm B.218.(2019•新罗区模拟)一个底面积是220cm的圆柱,斜着截去了一段后,剩下的图)cm.形如图.截后剩下的图形的体积是(3A.140B.180C.220D.36019.(2019•保定模拟)把一个圆柱削成一个与它等底等高的圆锥,削去的体积是90立方厘米,这个圆柱的体积是多少立方厘米?列式正确的是()A.90330÷=⨯=D.90245÷=B.9023135÷⨯=C.90327020.(2019•湘潭模拟)一个底面半径是10厘米的圆锥,它的高如果增加3厘米,它的体积将会增加()立方厘米.A.3.14B.78.5C.314D.7.85三.计算题(共3小题,6+6+8=20分)21.(2019春•吉水县期末)求如图图形的表面积.(单位:厘米)22.(2019•如东县)如图是一个直角三角形.AC边上的高是多少厘米?(请先在图中画出高,并计算)再算一算,以AC为轴旋转一周形成的立体图形的体积是多少立方厘米?23.(2019•临川区校级模拟)如图所示,某机器零件中间是一个棱长为2厘米的正方体,两边各是圆柱体的一半,求这个零件的表面积和体积.四.走进生活,解决问题(共7小题,第24题、第25题每题5分,其余每题6分,共40分)24.(2019•鄂托克旗)用塑料绳捆扎一个圆柱形的蛋糕盒(如图,单位:厘米),打结处正好是底面圆心,打结用去绳长25厘米.扎这个盒子至少用去塑料绳多少厘米?在它的整个侧面贴上商标和说明,这部分的面积是多少平方厘米?25.(2019•许昌)如图是用塑料薄膜覆盖的蔬菜大棚,长15米,横截面是一个直径2米的半圆.(1)这个大棚的种植面积是多少平方米?(2)覆盖在这个大棚上的塑料薄膜约有多少平方米?(3)大棚内的空间大约有多大?26.(2019•萧山区模拟)一个底面直径是4厘米的圆锥如图,从顶点沿着高将它切成两半后,表面积增加了24平方分米.这个圆锥的体积是多少平方厘米?27.(2019•福州)有一个高8厘米,容量为50毫升的圆形容器A,里面装满了水,现把长16厘米的圆柱B垂直放入,使B的底和A的底面接触,这时一部分水从容器中溢出,当把B从A拿走后,A中的水的高度只有6厘米,求圆柱体B的体积是多少?28.(2019•益阳模拟)一个圆柱形水桶,底面半径为20cm,里面盛有80cm深的水,现将一个底面周长为62.8cm的圆锥形铁块完全浸没在水中,水面上升了116.圆锥形铁块的高度是多少?( 取3.14)29.(2019•渝北区)一个装满水的矿泉水瓶,内直径是8厘米.小亮喝了一些,水的高度还有12厘米,把瓶盖拧紧后倒置放平无水部分高10厘米.小亮喝了多少水?30.(2019•西区)一个圆柱形木块切成四块(如图1),表面积增加48平方厘米;切成三块(如图2),表面积增加了50.24平方厘米.若削成一个最大的圆锥体(如图3),体积减少了多少立方厘米?。
小升初数学培优之 平面图形含答案

平面图形[同步巩固演练]1、已知AB=50厘米,图中各圆的周长总和是()厘米。
A、50B、100C、157D、3142、有相同周长的长方形、正方形和圆,它们的面积的大小关系是()。
A、S正方形>S长主形>S圆B、S长主形>S正方形>S圆C、S圆>S长主形>S正方形D、S圆>S 正方形>S长主形3、半径是1的半圆面的周长与面积分别是()A、5.14和1.57B、1.57和5.14C、1.57和1.57D、5.14和5.144、一张长方形纸片长5厘米,宽4厘米,在这张长方形纸片中剪一个最大的圆,这个圆的面积是( )平方厘米.A、19.625B、12.56C、50.24D、78.55、(全国小奥赛试题)有三个圆心相同的半圆,它们的直径分别为1、3、5,用线段分割成8块(如图所示)如果每块的字母代表这一块面积,并且相同的字母代表相同的面积.求A:B等于多少?6、(北京市第六届小学生迎春杯数学竞赛决赛试题)图中扇形的半径OA=OB=6厘米,角AOB等于45。
,AC垂直于点C,那么图中阴影部分的面积是多少平方厘米?(取3.14)[能力拓展平台]1、右图中直角梯形的面积是54平方厘米,求阴影部分面积。
2、(全国小奥赛试题)有八个半径为1毫米的小圆,用它们圆周的一部分连成一个花瓣圆形(如图),图中黑点是这些圆的圆心。
如果圆周率π=3.1416,那么花瓣圆形的面积是多少平方厘米?3、(第三届华杯赛决赛试题)有两个圆,它们的面积之和为1991平方厘米,小圆的周长是大圆周长的90%,问大圆的面积是多少?4、下图中阴影甲的面积比阴影乙的面积多28平方厘米,AB=40厘米,CB 垂直于AB ,求BC的长。
5、(北京市第七届迎春杯数学竞赛试题)图中,一个正方形各边都被四等分,分成十六个小正方形,图A 是一个圆,图B 是由三个半圆围成的图形,那么图A 与图B 的面积之间的关系是什么?6、(全国小奥赛试题)A 、B 两点把一个周长为1米的圆周等分成两部分(如图),蓝精灵从B 点出发在这个圆周上沿逆时针方向作跳跃运动,它每跳一步长是83米。
数学六年级小升初质量培优试题测试卷(带答案)

数学六年级小升初质量培优试题测试卷(带答案)一、选择题1.圆的半径与它的()不成比例。
A.直径B.周长C.面积2.钟面上5时整,时针与分针形成的角是()。
A.钝角B.直角C.平角3.光明村今年每百户拥有电脑96台,比去年增加了32台,今年比去年增加了百分之多少?正确的算式是().A.32÷96×100%B.32÷(96-32)×100%C.96÷32×100%4.从一张上底为4cm、下底为6cm、高为3cm的梯形上剪出一个最大的三角形,这个三角形的面积是()。
A.9cm2B.15cm2C.7.5cm2D.6cm25.如果x是一个大于0的数,那么x+79和x×79比较的结果是()。
A.x×79大B.x+79大C.无法确定6.用6个同样大的正方体拼成一个物体,从前面看是,从上面看是,从右面观察拼成的物体,看到的图形是()。
A.B.C.7.我们可以用很多种方式表达一个数,下面表达错误的是()。
A.B.C.D.8.a是奇数,b是偶数,下面结果是奇数的式子是()。
A.a+b B.2a+b C.2(a+b)9.一种商品降价10%后再提价10%这种商品的价格()A.不变B.低于原价C.高于原价10.将一些小圆球如下图摆放,第六幅图有多少个小圆球?()第一幅第二幅第三幅第四幅A.30 B.42 C.48 D.56二、填空题11.8080毫升=(______)升35时=(______)分 4.6米=(______)厘米12.9÷()=0.6=()∶20=()()=()%。
13.女生和男生的人数比是4∶5,女生的人数比男生的人数少(________)%,男生的人数比女生的人数多(________)%。
14.一个圆的半径扩大到原来的3倍,直径扩大到原来的(________)倍,周长扩大到原来的(________)倍,面积扩大到原来的(________)倍。
平面图形的认识(二)综合培优-(1)

平面图形的认识〔二〕综合培优1.假设△ABC的三边长分别为整数,周长为11,且有一边长为4,那么这个三角形的最大边长为2.如图,假设AB∥CD,那么∠A、∠E、∠D之间的关系是3.(2013.)将一副直角三角板ABC和DEF按如下图方式放置〔其中∠A=60°,∠F=45°〕,假设使点E落在边AC上,且ED∥BC,那么∠CEF=_______4.如下图,将含有30°角的三角板的直角顶点放在相互平行的两条直线其中一条上,假设∠1=35°,那么∠2的度数为5.满足以下条件的△ABC中,不是直角三角形的是〔〕.A.∠A+∠B=∠CB.∠A:∠B:∠C=2:3:1C.∠A=2∠B=3∠CD.一个外角等于和它相邻的角6.如图,两平面镜α、β的夹角为θ,入射光线AO平行于β入射到α上,经两次反射后的出射光线O′R平行于α,那么角θ等于_________度.第18题第19题7.〔1〕如图,∠ABE=142°,∠C=72°,那么∠A=________,∠ABC=________.〔2〕.一个多边形截去一个角〔不过顶点〕后,形成的多边形的角和是2520°,那么原多边形的边数是〔〕△ABC中,∠A=12∠B=13∠C,那么△ABC是_______三角形.8.〔2013.〕如图,量角器的直径与直角三角板ABC的斜边AB重合,其中量角器0刻度线的端点N与点A重合,射线CP从CA处出发沿顺时针方向以每秒3度的速度旋转,CP与量角器的半圆弧交于点E,第24秒时,点E在量角器上对应的读数是_______.9. (2013.)如图,在四边形ABCD中,点M,N分别在AB,BC上,将△BMN沿MN翻折,得△FMN,假设MF//AD,FN ∥DC,那么∠B=_______°.10.假设两个角的两边分别平行,且其中一个角比另一个角的2倍少30°,那么这两个角分别为______________.11.如图,把△ABC沿线段DE折叠,使点A落在点F处,BC∥DE,假设∠B=50°,那么∠BDF=_______°.12.光线a照射到平面镜CD上,然后在平面镜AB和CD之间来回反射,这时光线的入射角等于反射角,即∠1=∠6,∠5=∠3,∠2=∠4.假设∠1=55°,∠3=75°,那么∠2=_______度.13.如图,假设AB∥CD,BF平分∠ABE,DF平分∠CDE,∠BED=80°,那么∠BFD=_______.14.如图,AB∥CD,BE平分∠ABC,DE平分∠ADC,∠BAD=80°,试求:(1)∠EDC的度数;(2)假设∠BCD=n°,试求∠BED的度数.15.,如图,在△ABC中,∠B>∠C,AD是BC边上的高,AE平分∠BAC.(1)假设∠B=40°,∠C=30°,那么∠DAE=_______;(2)假设∠B=80°,∠C=40°,那么∠DAE=_______;(3)由(1)、(2)我能猜测出∠DAE与∠B、∠C之间的关系为______________,并说明理由.16.(1)如图,小莉画了一个角∠MON=80°,点A、B分别在射线OM、ON上移动,△AOB的角平分线AC与BD交于点P.试问:随着点A、B位置的变化,∠APB的大小是否会变化?假设保持不变,请求出∠APB的度数;假设发生变化,求出变化围.(2)聪明的小莉想出了一个画30°角的方法:①画两条相交的直线OX、OY,使∠XOY=60°,②在射线OX、OY上分别再任意取A、B点,③作∠ABY的平分线BD,BD的反向延长线交∠OAB的平分线于点C,那么∠C就是30°的角.你认为小莉的方确吗?请你说明理由.17.如图1,一个三角形的纸片ABC.点D,E分别是△ABC边上的两点.研究(1):如果沿直线DE折叠,那么∠BDA'与∠A的关系是______________,研究(2):如果折成图2的形状.猜测∠BDA',∠CEA'和∠A的关系.并说明理由;研究(3):如果折成图3的形状,猜测∠BDA',∠CEA'和∠A的关系,并说明理由.18.(2013.湘西)如图,一副分别含有30°和45°角的两个直角三角板,拼成如以下图形,假设∠C =90°,∠B =45°,∠E =30°,那么∠BFD 的度数是19.光线以如下图的角度α照射到平面镜工上,然后在平面镜I ,Ⅱ之间来回反射.假设∠α=50°,∠β=60°,那么∠γ等于20.假设用等腰直角三角板画∠AOB =45°,并将三角板沿OB 方向平移到如下图的虚线处后绕点M 逆时针方向旋转22°,那么三角板的斜边与射线OA 的夹角α为_______°.21.如图,△ABC 的外角∠ACD 的平分线CP 与角∠ABC 的平分线BP 交于点P .假设 ∠BPC =40°,那么∠CAP =_______.22.〔2013.〕当三角形中一个角α是另一个角β的两倍时,我们称此三角形为“特征三角形〞,其中a 称为“特征角〞.如果一个“特征三角形〞的“特征角〞为100°,那么这个“特征三角形〞的最小角的度数为_______. 23.如图,在△ABC 中,∠ACB =70°,∠1=∠2.求∠BPC 的度数.24.如图,小明在操场上从A 点出发,沿直线前进10米后向左转40°,•再沿直线前进10米后,又向左转40°,…,照这样走下去,他第一次回到出发地A 点时,一共走了_____米.25、如图,在△ABC 中,CD 是高,点E 、F 、G 分别在BC 、AB 、AC 上,且EF ⊥AB ,∠1=∠2,试判断DG 与BC 的位置关系,并说明理由。
小升初数学名校冲刺精编教程讲义-第16讲平面图形的认识与测量(二)(学生版)

第16讲平面图形的认识与测量(二)知识点一:圆的认识1.在同圆或等圆中,所有的直径都相等,所有的半径都相等。
2.圆是轴对称图形,圆有无数条对称轴,圆的对称轴就是直径所在的直线。
知识点二:圆的周长和面积1.圆的周长(1)圆周率:圆的周长与直径的比值叫作圆周率。
圆周率用希腊字母“π”表示,它是一个无限不循环小数。
经过精密计算:π=3.1415926…在小学数学中,我们常常取圆周率的近似值3.14(2)圆的周长= 圆周率×直径或圆周率×半径×2用字母表示为:C= πd或2πr 2.圆的面积:把一个圆平均分成若干份,剪开后拼成一个近似的平行四边形,如果分的份数越多,拼成的图形越接近长方形,这个近似长方形的长等于圆周长的一半,宽等于圆的半径,由此圆的面积S= πr23.圆环的面积(1)同一个圆心的两个半径不相等的圆,它们之间的部分叫作圆环(2)面积公式: S=πR2-πr2知识点三:组合图形的面积1.求组合图形面积的方法。
(1)分割法:把阴影部分分割成几个基本图形,利用求几个基本图形面积的和求出阴影部分的面积。
(2)添补法:在阴影部分上添补一个基本图形,使其变成另一个基本图形,计算出这个基本图形的面积后减去补上的基本图形的面积,从而求出阴影部分的面积。
考点一:圆的认识和圆周率【例1】(2019?鼓楼区)操作:(1)以O点为圆心,3格长为半径,画一个半圆形.(2)画出半圆形的对称轴.(3)把半圆形向右平移8格.1.(2019秋?花都区期末)下面说法正确的是()A.所有半径都相等,所有直径都相等B.在同一个圆中,扇形的大小与这个扇形的圆心角的大小有关C.大圆的圆周率比小圆的圆周率大2.(2019秋?沧州期末)下面关于圆周率的说法正确的是()A.是圆的周长与这个圆的直径的比值B.是循环小数C. 3.14D.是圆的面积与这个圆的半径的比值3.(2019秋?凌源市期末)关于圆的知识,下面说法不正确的是()A.圆心只决定圆的位置,不决定圆的大小B.两端都在圆上的线段叫做直径C.半径相等的两个圆的面积相等D.圆周率是圆周长和这个圆直径的比值4.(2019秋?香坊区期末)下列说法正确的是()A.用圆规画圆时.若圆规两脚间的距离是3cm,则所画圆的直接为3cmB.用4个圆心角都是90的扇形,一定可以拼成一个圆C.圆的半径扩大到原来的2倍,周长也扩大到原来的2倍D.小明身高1m,爸爸身高180cm,小明和爸爸身高的比是1:1805.(2019秋?西城区期末)如图所示图形中,对称轴条教最少的是() A.B.C.D.考点二:圆的周长和面积【例2】(2019?天津模拟)计算阴影部分的面积和周长.(单位:厘米)【例3】(2019?番禺区校级模拟)求如图的周长和面积.【例4】(2019秋?古丈县期末)求阴影部分的面积和周长.1.(2019?鄞州区)在一张长12厘米、宽10厘米的彩纸上画一个最大的圆,这个圆的周长是厘米,面积是平方厘米.2.(2019?福田区)已知小圆的半径是2厘米,大圆的半径是3厘米,小圆和大圆周长的比是,面积的比是.3.(2019?长沙)一张半圆形纸片周长是20.56cm,他的半径是cm,面积是2cm.4.(2019秋?中方县期末)把一个直径是5厘米的圆分成若干等份,然后把它剪开,照如图的样子拼起来,拼成的图形的周长比原来圆的周长增加厘米.5.(2019?宿迁)从一个长10分米,宽4分米的长方形木板上锯下一个最大的半圆,半圆的直径是分米,半圆的周长是分米,半圆的面积是平方分米.6.(2019?临川区)如图是三个半圆,求阴影部分的周长.7.(2019?株洲)求图形的周长.8.(2019?中山区)求图中阴影部分的周长.(取3)9.(2019?玄武区)图中阴影部分的面积是15平方厘米,求环形的面积10.(2019?淮安)如图,长方形的面积和圆的面积相等,已知圆的半径是4厘米,求阴影部分的周长和面积.考点三:组合图形的周长和面积【例5】(2019春?新田县期末)求下列图形的周长或面积【例6】(2019秋?江南区期末)求阴影部分的周长与面积.【例7】(2019?高台县)求图阴影部分的周长和面积.1.(2019?郑州)请求出图中阴影部分的面积(单位:厘米).2.求如图中阴影部分的面积,已知圆的半径为4厘米.3.(1)求图(1)阴影部分的周长.(2)求图(2)阴影部分的面积.(3)如图(3)已知:1S 比2S 多28平方厘米,求BC 长多少厘米?4.求阴影部分的周长与面积:(单位cm )5.(2019秋?黄冈期末)求图中阴影部分的周长和面积.(单位:厘米)6.求图中阴影部分的周长和面积.(单位:厘米)7.求下列图形的周长和面积:(单位:米)8.求下面图形中阴影部分的面积.(单位:)cm (1)长方形面积245cm.(2)(3)(4)9.(2019?厦门)图中圆的周长是12.56cm,圆的面积正好等于长方形的面积,求阴影部分的面积.OD cm;60AOC,求阴影部分的面积.OC cm,210.(2019?北京模拟)如图,已知411.(2019?东莞)求阴影部分的面积、周长.考点四:与圆有关的实际问题【例8】(2019?营山县模拟)将圆平均分成若干个小扇形,剪拼成一个近似的长方形(如图).(1)如果长方形的长是12.56厘米,圆的面积是多少?(2)如果圆的半径是10厘米,阴影部分的面积是多少?【例9】(2019?丹阳市)已知图中阴影部分的面积是220cm,环形的面积是多少平方厘米?【例10】(2019春?武城县期末)一片草地中央有一个边长为8m的正方形羊圈(如图),将一只羊用10m 长的绳子系在羊圈墙外一个角的顶点上,这只羊能吃到的草地面积是多少平方米?1.(2019?娄底模拟)一只环形玉佩的外圆半径为2厘米,比内圆半径多 1.5厘米,这只环形玉佩的面积是多少平方厘米?2.(2019?江北区)滨江公园有一个圆形水池,沿着它的外沿修一圈2米宽的草坪,水池的半径是5米,那么草坪的面积是多少平方米?3.(2019?绵阳)一个长方形与一个圆的面积相等,如果长方形的长与圆的直径都是8厘米,那么长方形的宽是多少厘米?(取 3.14)4.(2019?石家庄)一个圆形花坛的直径是6m,现在沿花坛的外围铺一条宽1m的石子路,若每平方米石子路面造价80元,建造这条石子路共需多少元?5.(2019秋?海安县期末)在400米的运动场上要举行400米比赛,(起点要前移多少米才恰当?)跑道每道宽 1.25米,外一圈起点要比内一圈前移多少米?6.(2019?长汀县模拟)一个圆形羊圈半径 6 米,如果要扩建这个羊圈,把它的直径增加2米.(1)扩建后,这个羊圈的周长是多少米?(2)扩建后,这个羊圈的面积增加了多少平方米?7.如图,一只狗用皮带系在1010的正方形狗窝的一角,皮带长为14,在狗窝外面狗能活动的范围的面积是多少?画出示意图并计算.(狗的大小忽略不计,长度单位:分米)小升初专项培优测评卷(十六)平面图形的认识与测量(二)1.(2019秋?望江县期末)如图是光明小学的运动场的示意图,阴影部分为跑道.求跑道的占地面积.m.求这个花台的周长是多少2.(2019秋?达州期中)如图是一个花台的平面图,5为圆的半径(单位:)厘米?3.(2019?郑州)求如图图形阴影部分的面积.4.(2019?石家庄)求如图阴影部分的周长和面积.5.有一个200m的环形跑道(如图所示).(1)东东沿着第二条跑道(由内向外)跑一圈,他跑了多少米?(取3.14)(2)如果在这个跑道上进行100m赛跑,那么如何确定起跑线的位置呢?(取3.14)6.(2019?邵阳模拟)某赛车的左、右轮子的距离为2米,因此,当车子转弯时,外侧的轮子比内侧的轮子多走了一段路.赛车跑道如图所示,当赛车车轮行走一圈时,外轮比内轮多走多少米?7.(2019?长沙模拟)如图所示为一卷紧绕成的牛皮纸,纸卷直径为20厘米,中间有一直径为6厘米的卷轴.已知纸的厚度为0.4毫米,问:这卷纸展开后大约有多少米?(保留小数点后一位)8.(2019?沈河区)如图,一只羊被一条5米长的绳子拴在木桩上.求羊活动的面积是多少?。
人教版六年级下册数学 小升初分班考专题:平面图形(含答案)

人教版六年级下册数学小升初分班考专题:平面图形一、单选题1.一个正方形的边长为2a米,这个正方形的面积是()平方米。
A.4a B.4a2C.8a2D.2a22.在一个梯形纸片上剪一刀,不会得到()。
A.两个三角形B.两个平行四边形C.一个三角形和一个平行四边形D.梯形3.一个三角形的两条边长分别是5 cm 和9 cm,它的周长可能是()cm。
A.9B.21C.28D.304.下图中每个小方格的面积均为1个面积单位,阴影部分的面积是()。
A.2个面积单位B.3个面积单位C.4个面积单位D.5个面积单位5.把一个长方形拉成平行四边形(边长不变),这个平行四边形和原来长方形相比()。
A.周长不变,面积变了B.周长变了,面积不变C.周长和面积都变了D.周长和面积都不变6.笑笑家到公路有三条笔直的小路,长度分别是480米、420米、350米。
其中有一条小路与公路是垂直的,这条小路的长度是()A.350米B.420米C.480米D.无法确定二、填空题7.一个等腰三角形,如果一个底角是80°,它的顶角是°;如果顶角是80°,它的一个底角是°。
8.把一个等边三角形对折,再沿折痕剪开,得到两个相同的直角三角形,其中一个直角三角形的两个锐角的度数分别是°和°。
9.一个三角形指示牌既是钝角三角形。
又是等腰三角形,它的一个内角是40°,其余两个内角分别是°和°10.一个长方形池塘的长是8米,宽是5米。
这个池塘的周长是米。
11.一个梯形的面积是42平方厘米,上底5厘米,高6厘米,下底是厘米。
12.一个长方形广场,长250米,宽150米,王叔叔每天沿着广场跑5周。
王叔叔每天跑米,合千米。
13.一个三角形,底是8米,高是60分米,面积是平方米,与它等底等高的平行四边形的面积是平方米。
14.下图是两个相同的长方形,把它们拼成一个大长方形有两种拼法。
【小升初数学】-考前专项讲练测十二《图形的认识和测量》含答案)全国通用版

小升初数学专题突破一(分类)NO.15图形的认识和测量(2)姓名班级等第一、认真想一想,填空1、在同一平面内两条直线的位置关系有()和()。
两条直线相交,如果其中一个角是90度,其余3个角都是(),这两条直线一定()。
2、通过纸上一点,能画()条直线;通过一张纸上两点,能画()条直线。
3、钟面上5时整,时针和分针组成()角,4时30分时针和分针组成()角,()时整,时针和分针组成平角,()时整或()时整,时针和分针组成直角。
4、经过1小时,钟面上分针转过的角度与时针转过的角度相差()°5. 270平方厘米=()平方分米1.04公顷=()平方米6. 一个平行四边形的底是9分米,高是底的2倍,它的面积是()平方分米。
与它等底等高的三角形的面积是()平方厘米。
7. 一个梯形上底与下底的和是15厘米,高是8.8厘米,面积是()。
8. 一个挂钟的时针长5厘米,一昼夜这根时针的尖端走了()厘米,针尖扫的面积是()平方厘米。
9. 用4个边长是2厘米的小正方形拼成一个大长方形,长方形的周长可能是( )厘米,也可能是( )厘米。
10. 在长20厘米,宽1.8分米的长方形里画一个最大的圆,圆的周长是( )面积是( )。
二、选择1. 两个( )梯形可以拼成一个长方形。
A.等底等高B.完全一样C.完全一样的直角2. 用木条钉成的长方形拉成一个平行四边形,它的高和面积( )A .都比原来大B .都比原来小C .都与原来相等3. 等腰梯形周长是48厘米,面积是96平方厘米,高是8厘米,则腰长( )。
A .24厘米B .12厘米C .18厘米D .36厘米4.属于射线的是( )A 、圆的半径B 、角的边C 、平行线D 、弧5.用一个10倍的放大镜看5°的角,这个角是( )°A 、50B 、5C 、20D 、406.在直角三角形中,∠B 是直角,∠A 是∠B 的25,那么∠C ( )° A 、60 B 、36 C 、547.如果一个三角形中最小的一个角大于45,这个三角形( ) A 、有一个直角 B 、有一个钝角 C 、另外两个角是锐角8.从12时到12时15分,分针旋转的角度是( )。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
小升初专项培优测评卷(十六)
平面图形的认识与测量(二)
考试时间:80分钟;满分:100分 题号 一 二 三 四 五 总分
得分 教师寄话:静心思考,用心审题,细心检查,成功属于你!
一.填一填(共12小题,第3题3分,其余每题2分,共25分)
1.(2019•贵阳)同一个圆中,周长与半径的比是 ,直径与半径的比值是 .
2.(2019•慈溪市)画一个周长是6.28厘米的圆,圆规两脚间的距离是 厘米,这个圆的面积是 平方厘米.
3.(2019•南安市校级模拟)在一张长6分米,宽4分米的长方形纸里面剪去一个最大的圆,这个圆 的直径是 分米,周长是 分米,面积是 平方分米.
4.(2019•福田区)已知小圆的半径是2厘米,大圆的半径是3厘米,小圆和大圆周长的比是 ,面积的比是 .
5.(2019秋•中方县期末)把一个直径是5厘米的圆分成若干等份,然后把它剪
开,照如图的样子拼起来,拼成的图形的周长比原来圆的周长增加 厘米.
6.(2019•西区)把一个圆沿对称轴分成两个半圆后,周长增加了12厘米.每个
半圆的周长是 厘米.
7.(2019•广州模拟)一个挂钟的时针长4厘米,分针长8厘米,从9:00到11:00分针的尖端“走过”了 厘米,时针“扫过”的面积是 平方厘米.(π取3.14)
8.(2019•北京模拟)一个圆的周长是31.4cm ,半径增加了2cm 后,面积增加了 %
9.(2019秋•隆昌市期末)一个圆环,内圆周长是25.12cm ,外圆半径是6cm ,圆环的面积是 2cm .
10.(2019•天津模拟)大圆半径是小圆半径的2倍,大圆面积比小圆面积多12平方厘米,小圆面积是 平方厘米.
11.(2019秋•隆昌市期末)如图,圆的周长是18.84cm ,空白部分是一个正方形.则阴影部分的面积是 2cm .
12.(2019秋•武侯区期末)如图,长方形的周长是24厘米,阴影部分的面积是 平方厘米.(π取3.14)
二.选一选(共8小题,每小题2分,共16分)
13.(2019•保定模拟)圆周率π表示( )
第11题 第12题
A .圆周长与直径的比值
B .圆周长与半径的比值
C .直径与圆周长的比值
D .半径与圆周长的比值
14.(2019秋•元江县期末)画一个周长是12.56cm 的圆,圆规两脚之间的距离是( )cm .
A .2
B .3
C .4
15.(2019•郴州模拟)一根绳子可围成一个半径是6米的圆,若用它围成一个正三角形,它的边长是( )米
A .π
B .4π
C .6π
D .12π
16.(2019•宁波模拟)小圆半径是3厘米,大圆半径是5厘米,小圆面积是大圆面积的( )
A .53
B .925
C .35
D .259
17.(2019•成都)把一个圆平均分成若干份,切拼成一个近似的长方形,长方形与圆比( )
A .周长、面积都相等
B .长方形周长大、圆面积大
C .面积都相等、长方形周长大
18.(2019•河南模拟)一个长方形和一个圆的周长相等.已知长方形的长是9分米,宽是6.7分米,圆的面积是( )
A .31.4平方分米
B .78.5平方分米
C .314平方分米
D .68.8平方分米
19.(2019•玉溪模拟)在一个边长是8厘米的正方形内画一个最大的圆,圆面积占正方形面积的( )
A .2π
B .14
C .12
D .4
π 20.(2019•揭阳)如图,一个三角形的三个顶点分别为三个半径为3厘米的圆
的圆心,则图中阴影部分的面积是( )平方厘米.
A .π
B .9π
C .4.5π
D .3π
三.计算题(共4小题,每小题6分,共24分)
21.(2019•番禺区校级模拟)求如图的周长和面积.
22.(2019•邵阳模拟)如图,正方形的边长是4厘米,求阴影部分的周长和面积.
23.(2019•怀化模拟)求出下面图形的周长和面积.(单位:厘米)( 3.14)π=
24.(2019•邵阳模拟)小圆直径6cm,大圆直径10cm,求下面阴影部分的周长和面积.
四.操作题(共2小题,每小题3分,共6分)
25.(2019•固原模拟)按要求操作与解答.
(1)画一个边长为4厘米的正方形.(2)在正方形内画一个最大的圆.
(3)假如把正方形内的圆外部分称为“阴影部分”,求阴影部分面积与圆面积的比.
26.(2019•泉州)在如图的长方形中画一个最大的半圆,并涂上阴影,再计算空白部分的面积.
五.走进生活,解决问题(共6小题,第27题4分,其余每题5分,共29分)
27.(2019•广汉市校级模拟)一只钟表的分针长8厘米,那么半小时分针针尖走过的距离是多少厘米?半小时分针扫过的面积是多少?
28.(2019•娄底模拟)一只环形玉佩的外圆半径为2厘米,比内圆半径多1.5厘米,这只环形玉佩的面积是多少平方厘米?
29.(2019秋•巩义市期末)人民公园内的圆形石桌上刻有一个中国象棋棋盘,石桌的直径是40cm.(1)棋盘的面积是多少?
(2)棋盘的面积占石桌面积的几分之几?
30.(2019•营山县模拟)将圆平均分成若干个小扇形,剪拼成一个近似的长方形(如图).
(1)如果长方形的长是12.56厘米,圆的面积是多少?
(2)如果圆的半径是10厘米,阴影部分的面积是多少?
31.(2019•武汉模拟)如图,草地上有一个长10米,宽8米的关闭着的羊圈,在羊圈的一角A用16米的绳子拴着一只羊P,则这只羊在草地上的活动范围有多大?( 取3.14)
32.(2019秋•虹口区期末)如图,某中学校园有一块长方形空地ABCD,AD的长为30米,在AD上有一段长24米的旧篱笆墙AE,现利用旧篱笆墙AE以及新购的48米长的篱笆材料围成一个面积最大的半圆形花园,但不能超出长方形ABCD的范围.
(1)若AB长为10米,求半圆形花园的面积;
(2)若AB长为15米,当围成的半圆形花园面积最大时,直径为多少米?(精确到1米)。
