2017年重庆市一诊试题
重庆2017届一诊理综2017-0117

高2017届学业质量调研抽测第一次理科综合试题(2017-0117)理科综合能力测试试题卷共16页,考试时间为150分钟,满分为300分.注意事项:1.本试卷分第卷(选择题)和第卷(非选择题)两部分.请考生把姓名、准考证号写在试卷左上角。
2.作答时,务必将答案写在答题卡上,写在本试卷和草稿纸上无效。
3.考试结束后,将本试卷答题卡和草稿纸一并交回.可能用到的相对原子质量:H1 C12 N14 O16 Na23 Al27第Ⅰ卷(选择题共126分)一、选择题:本大题共13小题,每小题6分。
在每小题给出的四个选项中,只有一项是符合题目要求的。
1.下列关于细胞结构和生理的说法,错误的是A.红细胞在清水中吸水膨胀的事实表明动物细胞能进行渗透作用B.处于质壁分离状态时植物细胞原生质层两侧的溶液浓度基本一致C.注入人体的麻醉药能经自由扩散由内环境进入突触间隙D.在抗利尿激素的作用下肾小管吸收水分的粉饰属于被动运输2.有关核糖体相关的叙述,正确的是A.氨基酸脱水缩合需要的酶不在核糖体上B.核糖体中的蛋白质和rRNA并不都是来自基因的表达C.线粒体,叶绿体内没有核糖体,不能合成自己的蛋白质D.mRNA在核糖体上翻译为氨基酸序列后,遗传信息量有所损失3.下列有关生理活动的说法,不正确的是A.生长素从根尖分生区移向伸长区,属于极性运输B.乙烯能促进果实成熟,主要产生于植物的成熟部位C. 人在安静时维持体温所需的能量主要来自肝脏等器官内细胞的有氧呼吸D. 当促甲状腺激素释放激素与甲状腺激素同时作用于垂体时将起拮抗作用4.下列叙述中无基因重组发生的是A.减数分裂时果蝇的红眼基因和长翅基因分配到同一个精子中B.格林菲思和艾弗里转化实验中的R型转化为S型C.用高茎豌豆的杂合体自交获取高茎豌豆的纯合体D.同源染色体内非姐妹染色单体间的交叉互换5.下列有关实验处理和结论,正确的是A.在光照下提取的叶绿体色素液能吸收光能,光解水和合成A TPB.用甲基绿染液能将口腔上皮细胞DNA染色,体现了细胞膜的选择透过性C.在经研磨和离心提取到的乳酸菌细胞质基质中加入葡萄糖后能产生ATPD.利用过氧化氢,新鲜的猪肝研磨液和氯化铁溶液研究酶的专一性6.据<科学>杂志报道,北大周德敏教授的团队完成了一项被赞为疫苗领域的”革命”的实验---用活体禽流感病毒制作的疫苗对感染该病毒的小鼠等接种,均迅速恢复了健康.他们的做法是调整活病毒的一个遗传密码,使其只能在实验室特定的培养物上繁殖,一旦进入接种的生物体内,其自我扶植机制就会失效.下列说法正确的是A.该疫苗的变异将引起该病毒表面抗原结构大幅度的改变B.该疫苗一旦进入内环境,将被吞噬细胞等非特异性免疫全部清除C.该病毒没有感染力,能激发小鼠建立起非特异性免疫和体液免疫D.该病毒进入小鼠的细胞,能使小鼠建立起相应的体液免疫和细胞免疫7.下列关于物质应用的说法错误的是A.玻璃容器可长期盛放各种酸B.纯碱可用于清洗油污C.浓氨水可检验氯气管道漏气D.Na2S可除去污水中的Cu2+8.苯乙烯的结构为,该物质在一定条件下能和氢气完全加成,加成产物的一溴取代物有A.4种B.5种C.6种D.7种9.N A为阿伏加德罗常数的值,下列说法正确的是A.标准状况下.22.4L的CCl4中含有的CCl4分子数为N AB.在密闭容器中充入1.5molH2和0.5molN2,充分反应后可得到NH3分子数为N AC.一定条件下,2.3gNa完全与O2反应生成3.6g产物时失去的电子数为0.1N AD.常温下,2.7gAl与足量浓度为18mol/L的浓硫酸反应时,转移的电子数为0.3 N A10.下图所示实验中,能够达到目的的是A B C D验证:化学能转化为电能验证:非金属性Cl>C>Si验证:铁发生析氢腐蚀验证:温度对平衡移动的影响11.下列说法中不正确的是A.醛能发生银镜反应B.酚能与碳酸氢钠溶液反应C.油脂水解可得到丙三醇D.烯烃能与酸性高锰酸钾溶液反应12.X、Y、Z、W、U是分别位于短周期的元素,原子序数依次增大。
2017年重庆市一诊试题
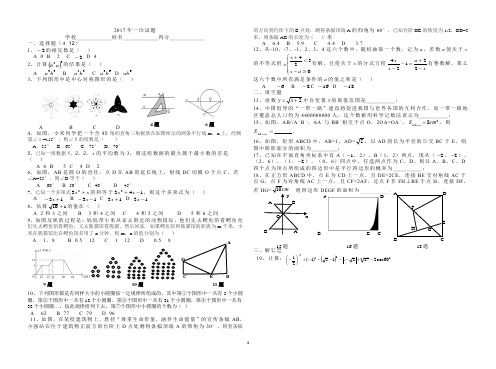
12017年一诊试题学校____________姓名____________得分____________一、选择题(4×12)1、2-的相反数是( ) A 0 B 2 C 2- D 42、计算()32a b 的结果是( )A 33b aB 35b aC 63b aD 6ab 3、下列图形中是中心对称图形的是( )A 6B 5C 4D 26、如图,AB 是圆O 的直径,点D 在AB 的延长线上,射线DC 切圆O 于点C ,若 ∠A=25°,则∠D 等于( )A 60°B 50°C 40°D 45°7、已知一个多项式x x +23的和等于1432-+x x ,则这个多项式为( ) A 13+-x B 13--x C 13+x D 13-x 8、估算110+的值在( )10、下列图形都是有同样大小的小圆圈按一定规律所组成的,其中第①个图形中一共有11、如图,在某校建筑物上,悬挂“尊重生命价值,涵养生命能量”的宣传条幅AB ,小强站在位于建筑物正前方的台阶上D 点处测得条幅顶端A 的仰角为30°,朝着条幅的方向到台阶下的E 点处,测得条幅顶端A 的仰角为60°,已知台阶DE 的坡度为1:2,DE=2米,则条幅AB 的长度为( )米A 6.4B 5.9C 4.4D 3.712、从-10、-7、-1、2、3、4这六个数中,随机抽取一个数,记为a ,若数a 使关于x的不等式组⎪⎩⎪⎨⎧≥-<+0324a x x x 有解,且使关于x 的分式方程x a x x -+=--22124有整数解,那么这六个数中所有满足条件的a 的值之和是( )A 6-B 8-C 16-D 18- 二、填空题13、函数2+=x y 中自变量x 的取值范围是__________;14、中国倡导的“一带一路”建设将促进我国与世界各国的互利合作,而一带一路地区覆盖总人口约为4400000000人,这个数据用科学记数法表示为__________; 15、如图,AB//A /B /,AA /与BB /相交于点O ,2OA=OA /,28cm S AO B =∆,则______.A OB S ∆=、、 16、如图,矩形ABCD 中,AB=1,AD=2,以AD 的长为半径的⊙交BC 于E ,则图中阴影部分的面积为_________;17、已知在平面直角坐标系中有A (1-,2)、B (1,2)两点,现从(2-,2-)、(2,6)、(1,2-)、(0,6)四点中,任选两点作为C 、D ,则以A 、B 、C 、D 四个点为顶点所组成的四边形中是平行四边形的概率为__________;18、在正方形ABCD 中,点E 为CD 上一点,且DE=2CE ,连接BE 交对角线AC 于点G ,点F 为对角线AC 上一点,且CF=2AF ,过点F 作FH ⊥BE 于点H ,连接DF , 19、计算:()()0305260cos 2272115121-+-----+⎪⎭⎫ ⎝⎛--9题 E C A220、我校学生会新闻社准备近期做一个关于“减负十条”的专刊,想知道同学们对禽流感知识的了解程度,决定随机抽取部分同学进行一次问卷调查,并根据收集到的信息进行了统计,绘制了下面两幅尚不完整的统计图.请你根据统计图中所提供的信息解答下列问题:(1)接受问卷调查的同学共有_____名,请补全折线统计图,并求出扇形统计图中“基本了解”部分所对应扇形的圆心角的大小; (2)为了让全校师生都能更好地实施减负十条,学生会准备组织一次宣讲活动,由问卷调查中“了解”的几名同学组成一个宣讲团. 已知了解的这几名同学中只有两个女生,若要在该宣讲团中任选两名同学在全校师生大会上作代表发言,请用列表或画树状图的方法,求选取的两名同学都是女生的概率.21、先化解,再求值:⎪⎭⎫ ⎝⎛+---÷-+-393399622x x x x x x ,其中x 是不等式组()⎩⎨⎧+≥+<+xx x 12201的整数解22、如图,在∆ABC 中,sin ∠B=21,AD ⊥BC 于点D ,∠DAC=45°,AC=210(所得结果保留根号)(1)求线段BD 的长 (2)求∆ABC 的面积23、某体育用品专卖店今年3月初用4000元购进了一批“中考体能测试专用绳”,上市后很快售完.该店于3月中旬又购进了和第一批数量相同的专用绳,由于第二批专用绳的进价每根比第一批提高了10元,结果进第二批专用绳共用了5000元. (1)第一批专用绳每根的进货价是多少元?(2)若第一批专用绳的售价是每根60元,为保证第二批专用绳的利润率不低于第一批的利润率,那么第二批专用绳每根售价至少是多少元?24、定义:如果M 个不同的正整数,对其中的任意两个数,这两个数的积能被这两个数的和整除,则称这组数为M 个数的祖冲之数组。
【重庆市】2017届高三上学期第一次诊断模拟语文试卷

重庆市2017届高三上学期第一次诊断模拟语文试卷第Ⅰ卷阅读题一、现代文阅读(35分)(一)论述类文本阅读(9分,每小题3分)阅读下面的文字,完成1~3题。
全球化的基点在于,突破或超越民族国家的领土边界为范围的市场体系以及法律政治和社会文化。
由此,形成了全球化与民族国家之间既对立又依存的关系。
民族国家为其领土范围内的生产资料、生产工具、劳动力和资本的有效配置和生产、交换、分配的顺利运行,提供了法律依据、社会秩序和控制机构,并“画地为牢”似地为领土范围之外的介入设立了森严的壁垒,从而为资本主义在本国范围内的孕育和发展创造了有利条件,然而,当民族国家领土范围内的经济要素不能满足机器大。
生产发展到一定程度所提出的生产资料、劳动力、市场和资本投资等需要时,以突破民族国家边界为前提的全球化,就成为不可遏止的洪流。
至20世纪初期,欧洲殖民主义将世界版图几乎瓜分完毕,而其结果却导致了两次世界大战的爆发。
其后世界各地民族主义运动的勃然兴起和创建民族国家的浪潮,最终瓦解了持续近4个世纪的西方殖民主义体系。
摆脱了殖民统治而建立起的民族国家,为了国家的富强和国民的福祉,又纷纷放弃闭关锁国的治理理念和自我结构自给自足的生计模式,转而选择市场经济体制和融入全球经济体系的策略。
否则,只有承受经济贫困、发展落后和政治边缘化的后果。
正是在这种相生相克的过程中,民族国家的含义、形式和治理逐渐转换和更新,全球化的模式不断创新,程度趋于深化。
全球化促使分布于不同国家的移民、社区、民间组织、公司及政府机构之间,进行频繁而持续性的联系和共同性的活动,从而形成跨越民族国家的地理空间、政治空间和文化空间的社会场域、社会网络和互动模式,也就是所谓“跨国主义”。
跨国主义研究一般围绕着跨国实践、跨国社会空间和跨国认同。
跨国实践指各种跨国主义的行为和活动。
跨国实践衍生出了跨国社会空间。
全球化推进所产生的频繁密切的跨国实践,摆脱了传统社会空间所依托的地理空间和国家边界的束缚。
重庆2017一诊政治参考答案

高2017届“学业质量调研抽测”(第一次)政治试题参考答案一、选择题(本大题共12小题,每小题4分,共48分。
)二、非选择题38.(26分)(1)①国家利益是国家生存与发展的权益,维护国家利益是主权国家对外活动的出发点和落脚点。
国家间的共同利益是国家合作的基础。
中、美共同批准《巴黎协,表明坚持绿色低碳发展,正是基于两国的国家利益和共同利益。
(4分)②维护国际和平与安全,促进国际合作与发展,是联合国的宗旨。
中、美同为联合国安理会常任理事国,批准《巴黎协定》是两国履行联合国宗旨的体现。
(4分)③大国有大国的义务、责任和担当。
作为全球两个最大经济体和最大碳排放国,中、美批约对推动《巴黎协定》生效起到了决定性作用,也为其他国家批约和推动可持续发展做出了表率,树立了积极的形象。
(4分)(2)①市场在资源配置中起决定作用。
启动碳市场,有利于培育为绿色低碳经济筹集资金的新渠道和新机制,是新时期社会主义市场经济的客观要求;有利于推动经济发展方式的转变,挖掘增长动能。
(6分)②政府应运用经济、法律、行政等手段,精心设计、宏观协调未来中国的碳市场;加快完备碳市场条件,扩大碳市场需求,提高碳市场供给质量,借鉴国际碳市场经验,规避碳市场高杠杆、高泡沫等风险。
(4分)企业应科学制定碳市场的投资、融资战略;诚信参与碳市场交易,预防盲目投机逐利,形成自己的竞争优势和品牌形象。
(4分)39.(26分)(1)①社会存在决定社会意识,社会意识具有相对独立性。
社会意识随着社会存在的变化发展而变化发展。
伟大长征精神铸就于长征这一伟大壮举,是中国共产党人和红军将士留下的最可宝贵的精神财富;在新的长征路上长征精神必将不断丰富发展,续写新的篇章。
(6分)②先进的社会意识对社会发展起积极的推动作用。
今天,我们这一代人的长征,就是要实现“两个一百年”奋斗目标、实现中华民族伟大复兴的中国梦。
伟大长征精神是鼓舞和激励我们在新长征中不断攻坚克难、从胜利走向胜利的强大精神动力。
2017届重庆一中高三上学期一诊模拟考试语文试题 及答案

秘密★启用前2017年重庆一中高2017级高三上期一诊模拟考试语文试题卷2017.1本试题共8页,满分150分,考试时间150分钟。
注意事项:1.答题前,务必将自己的姓名、准号证号填写在答题卡规定的位置上。
2.答选择题时,必须使用2B铅笔将答题卡上对应题目....的答案标号涂黑,如需改动,用橡皮擦擦干净后,再选涂其他答案标号。
3.答非选择题时,必须使用0.5毫米黑色签字笔,将答案书写在答题卡规定的位置上。
4.所有题目必须在答题卡上作答,在试题卷上答题概不给分。
第Ⅰ卷一、(本大题共3小题,每小题3分,共9分)1、下列词语中,字形和加点字的读音全部正确的是()A.摈.除(bìn)瞥.见(piē) 水蒸气擢发难数B.祛.暑(qū)揶.揄(yē)天然气熙熙攘攘C.诤.言(zhèng)新正.(zhēng)泊来品词不达意D.巷.战(xiàng)顷.刻(qīng)水龙头殒身不恤2、下列各句中,加点成语使用不恰当的一句是()A. 重庆市近日对全市驾校教练员进行了考试,考试的结果让人大跌眼镜....:有40%的教练员不合格。
B. 安全生产的措施落实了,人们的环保意识增强了,黄河中下流地区现在出现了天空明净、绿树葱郁、河清海晏....的喜人景象。
C. 近年来,在中国,志愿者事业不断发展壮大,即使不是所有志愿者都出类拔萃....,但绝大多数都已具备志愿服务的专业精神。
D.《中国最强音》节目一推出,就受到各方诟病。
有人认为,简单地模仿电视台同类节目并不一定会产生好的效果, 邯郸学步....只会丢掉自己的长处。
3.依此填入下面一段文字横线处的语句,衔接最恰当的一组是()在我看来,钱理群是我们这个时代的堂吉诃德。
他在人们没有发现问题的地方发现了问题,在太平之景中意识到了危机。
,。
他常常以真诚的、大胆的姿态冲向风车,。
他自觉地把生命难题与社会难题转化为一种理论的难题,,。
①他带着忧患之心面对众生,但热情之高超出常人②他热情之高超出常人,带着忧患之心面对众生③给我们留下悲壮的形影④我们看到他悲壮的形影⑤但这些难题没有给他退缩的理由,反而有着解析的冲动⑥但他有着解析的冲动,这些难题没有给他退缩的理由A.①③⑤B.②③⑥C. ①④⑤D. ②④⑤二、(本大题共3小题,共11分)阅读下文,完成4-6题。
【全国百强校】重庆市第一中学2017届高三上学期一诊模拟考试理数(解析版)

重庆市第一中学2017届高三上学期一诊模拟考试理数试题第Ⅰ卷(共60分)一、选择题:本大题共12个小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的.1.复数z 满足(1)4z i +=,则复数z 在复平面上对应的点与点(1,0)间的距离为 ( )A .2B .4 D 【答案】B2.已知集合{|2},{|1},1xA x xB x R x =<=<-为实数集,则集合()R AC B = ( ) A .R B .(,2)-∞ C .(1,2)D .[1,2)【答案】D 【解析】由11x x <-,得101x x -<-,即{}{}10,1,|1,|11R x B x x C B x x x <<∴=<=≥-,又 {}{}[)|2,|121,2R A x x A C B x x =<∴=≤<= ,故选D.3.将函数sin cos y x x =+图象上各点的横坐标缩短到原来的12倍,得到()y f x =的图象,则()y f x =的最小正周期为( )A .2πB .πC .2πD .4π 【答案】B【解析】sin cos 4y x x x π⎛⎫=+=+ ⎪⎝⎭图象上各点的横坐标缩短到原来的12倍,得到函数()24y f x x π⎛⎫==+ ⎪⎝⎭,其最小正周期为22T ππ==,故选B.4.已知双曲线2222:1(0,0)x y C a b a b-=>>,且点P 到其渐近线的距离为8,则C 的实轴长为( )A .2B .4C .8D .16【答案】C5.设13482,log 3,log 5a b c ===,则( )A .a b c >>B .a c b >>C .c a b >>D .b c a >>【答案】A【解析】由指数函数性质知1a >,c 可化为2log b 可化为2log 66,,b c a b c <∴>∴>>,故选A.6.执行如图所示的程序框图,则输出的结果是( )A .121B .129C .178D .209【答案】B【解析】执行程序框图,第一次循环13,5,13S a b ===;第二次循环18,13,18S a b ===;第三次循环31,18,31S a b ===;第四次循环49,315,49S a b ===;第五次循环80,49,80S a b ===;第六次循环12985S =>,退出循环,输出129S =,故选B.【方法点睛】本题主要考查程序框图的循环结构流程图,属于中档题. 解决程序框图问题时一定注意以下几点:(1) 不要混淆处理框和输入框;(2) 注意区分程序框图是条件分支结构还是循环结构;(3) 注意区分当型循环结构和直到型循环结构;(4) 处理循环结构的问题时一定要正确控制循环次数;(5) 要注意各个框的顺序,(6)在给出程序框图求解输出结果的试题中只要按照程序框图规定的运算方法逐次计算,直到达到输出条件即可.7.若随机变量2(,)(0)X N u σσ> ,则有如下结论( )()0.6826,(22)0.9544P u X u P u X u σσσσ-<≤+=-<≤+=(33)0.9974P u X u σσ-<≤+=,一班有60名同学,一次数学考试的成绩服从正态分布,平均分110,方差为100,理论上说在120分到130分之间的人数约为( )A .6B .7C .8D .9【答案】C8.(原创)定义在R 上的奇函数()f x 关于点(2,1)对称,则()6f =( )A .9B .7C .5D .3【答案】D【解析】()y f x = 关于()2,1对称,()()42f x f x ∴-+=,令2x =- ,则()()622f f +-= ① 又()y f x = 是奇函数()()()()()(),42,842f x f x f x f x f x f x ∴=--∴---=---=,相加()()84f x f x ---=,令()()2,624x f f =--= , ② 由① ②得()63f =,故选D.9.(原创)将4个不同的小球装入4个不同的盒子,则在至少一个盒子为空的条件下,恰好有两个盒子为空的概率是( )A .2158 B .1229 C .2164 D .727【答案】A【解析】4个不同的球装入4个不同的盒子共有44256=(种)方法,至少一个盒子为空的方法共有44256232A -=,四个球分为两组有两种方法 ,若两组每组有两个球,不同分组的方法有24223C A =种,恰有两个盒子不放球的不同方法是24336A ⨯=种,若一组为3,一组为1个球,不同的分组方法有344C =种,恰有两个盒子不放球的不同方法是 24448A ⨯=种,综合两种情况,恰有两个盒子不放球的不同方法是364884+=种,所以恰有两个盒子为空的的概率为842123258=,故选A. 10.(原创)6()(2)x y x y z -++的展开式中,232x y z 的系数为( )A .30-B .120C .240D .420【答案】B11.(原创)过x 轴下方的一动点P 作抛物线2:2C x y =的两切线,切点分别为,A B ,若直线AB 到圆221x y +=相切,则点P 的轨迹方程为( )A .221(0)y x y -=< B .22(2)1y x ++= C .221(0)4y x y +=< D .21x y =--【答案】A【解析】设()()11221,,,,',PA A x y B x y y x k x =∴= ,可得()111:PA y y x x x -=-,化为110x x y y --=,同理PB 方程为220x x y y --=,设()()000,0P x y y <,则有100120020x x y y x x y y --=⎧⎨--=⎩,说明()()1122,,,A x y B x y 都在在直线000x x y y --=上,即AB 方程000x x y y --=,又AB 与圆220x y +=相切,1=,可化为()220010,y x y P -=<∴点轨迹方程为()2210y x y -=<,故选A.【方法点晴】本题主要考查利用导数求切线方程、直线与抛物线的位置关系及轨迹方程的求法,属于难题.求曲线切线方程的一般步骤是:(1)求出()y f x =在0x x =处的导数,即()y f x =在点P 00(,())x f x 出的切线斜率(当曲线()y f x =在P 处的切线与y 轴平行时,在 处导数不存在,切线方程为0x x =);(2)由点斜式求得切线方程'00()()y y f x x x -=∙-. 12.(原创)已知函数()22cos()(1)sin(),()233x f x x a x a g x x ππ=+-+=-,若()[]0f g x ≤对[]0,1x ∈恒成立,则实数a 的取值范围是( )A .(1]-∞B .(,0]-∞C .1]-D .(,1-∞【答案】A【解析】如图所示,在同一坐标系内画出2231,2,2x y x y y x =+==+的图象,由图象可知,在[]0,1上,223122+≤<+x x x 恒成立,即23122x x ≤-<,当且仅当0x =或1x =时等号成立,()312g x ∴≤<,设()g x t =,则()(31,02≤<≤⎤⎦t f g x 等价于()0f t ≤,即()2cos1sin 033t a t a ππ+-+≤,31,,2332t t πππ⎡⎫≤≤∴∈⎪⎢⎣⎭,再设sin 13t m m π=≤<,原不等式可化为()212sin t a 1sint a 033ππ-+-+≤,即()22211210,211m m m a m n a m m +--+-+≤≤=-+1211m -≤-<,1a ∴≤-,故选A .【方法点晴】本题主要考查函数的图象与性质、三角函数的性质及不等式恒成立问题.,属于难题.不等式恒成立问题常见方法:① 分离参数()a f x ≥恒成立(()max a f x ≥可)或()a f x ≤恒成立(()min a f x ≤即可);② 数形结合(()y f x = 图象在()y g x = 上方即可);③ 讨论最值()min 0f x ≥或()max 0f x ≤恒成立;④ 讨论参数.本题是利用方法 ① 求得a 的范围的.第Ⅱ卷(共90分)二、填空题(每题5分,满分20分,将答案填在答题纸上)13.ABC ∆中,090,2,A AC D ∠==为边BC 的中点,则AD AC ⋅= .【答案】214.已知实数,x y 满足03035x y x y x y -+≥⎧⎪+-≥⎨⎪--≥⎩,则12y z x +=的最大值为 .【答案】错误!未找到引用源。
重庆市第一中学2017届高三上学期一诊模拟考试理科综合生物试题含答案

重庆市第一中学2017届高三上学期一诊模拟考试理科综合试题生物试题一、选择题:1.下列有关细胞结构与功能的描述正确的是A.蓝藻的核糖体不具膜结构,不含磷酸基团B.染色体解螺旋形成染色质时,DNA双链也随之解旋C.动物细胞内能形成囊泡的细胞结构只有内质网和高尔基体D.草履虫捕食细菌和吸收K+进入细胞的方式不同2。
如图表示人体血液中乳酸含量和氧气消耗速率与运动强度的关系(假设细胞呼吸的底物均为葡萄糖)。
下列有关叙述正确的是A.ac段主要进行有氧呼吸,cd段主要进行无氧呼吸B.bd段无氧呼吸时有机物中的大部分能量以热能的形式散失出来C.无论图中何种运动强度下,肌肉细胞CO2的产生量始终等于O2的消耗量D.若运动强度长时间超过c,乳酸大量积累会导致内环境pH持续下降3。
下列有关生物进化及基因频率的叙述正确的是A。
基因交流是指生物个体之间的相互交配,阻断基因交流意味着新物种的产生B。
基因重组产生的新性状可为生物进化提供原材料C.诱导单倍体的染色体数目加倍获得的植株即为可育良种D.通过人工诱变可提高基因的突变率和染色体的畸变率4。
下列有关描述不正确的是A.氨基酸、性激素、抗体、溶菌酶、淀粉酶等都属于人体内环境的成分B.人体饥饿时,血液流经肝脏后,血糖的含量会升高;血液流经胰岛后血糖的含量会减少C。
血浆蛋白可参与内环境渗透压的调节,而与免疫无关D.完成膝跳反射活动中,兴奋在神经纤维上的传导是双向的,在突触的传递方向是单向的5.下图是医院验血报告单的部分截图,下列分析合理的是A.甲可能是甲亢(甲状腺功能亢进)患者,乙可能是甲状腺肿大患者B。
当体内产生TSH受体的抗体时,会引起甲状腺功能亢奋C.促甲状腺激素释放激素和甲状腺激素都能调节TSH激素的分泌D。
因垂体发生病变而缺乏甲状腺激素的患者只能通过补充甲状腺激素来治疗6。
几种染色体异常果蝇的性别、育性等如下图所示,控制眼色红眼基因(R)和白眼基因(r)位于X染色体上,下列说法正确的是A.正常果蝇在减数第一次分裂中期的细胞内染色组数为2个,在减数第二次分裂后期的细胞中染色体数是4条B。
重庆市2017届高三上学期第一次诊断模拟(期末)理数试题Word版含答案

2016 年秋高三(上)期末测试卷理科数学第Ⅰ卷一、选择题:本大题共 12 个小题 ,每题 5 分 ,共 60 分 .在每题给出的四个选项中,只有一项是切合题目要求的 .a 2ii ( a, b 是实数),此中 i 是虚数单位,则ab ()1.已知 biA.-2 B. -1 C. 1 D . 32. 已知某品种的幼苗每株成活率为p ,则种植3株这类幼苗恰巧成活 2 株的概率为()A .p2 B.p21 p C.C32p2 D.C32p21 p3. 已知会合A 1,2,3,4 , B x | y 2x,y A 则A B ()A . 2 B.1,2 C.2,4 D .1,2,44.命题p :甲的数学成绩不低于 100 分,命题q :乙的数学成绩低于 100 分,则pq 表示()A .甲、乙两人数学成绩都低于100 分B.甲、乙两人起码有一人数学成绩低于100 分C.甲、乙两人数学成绩都不低于100 分D.甲、乙两人起码有一人数学成绩不低于100分5.在平面直角坐标系xOy 中,不等式组x y1x y10表示的平面地区的面积为1 x 3()A. 4B. 8D.166.我国古代数学算经十书之一的《九章算术》有一衰分问题:今有北乡八千一百人,西乡七千四百八十八人,南乡六千九百一十二人,凡三乡,发役三百人,则北乡遣()A. 104 人B.108 人 C. 112 人D.120 人7.履行以下图的程序框图,若分别输入1, 2, 3,则输出的值的会合为()A .1,2B .1, 3 C. 2,3 D.1,3,98.2y y2 上的点到直线x y 2 0的距离的最大值为a,最小值为 b ,则设曲线 xa b 的值为()A .2B . 2 C.2D. 2 2129. 函数y sin x 1)的图象大概是(xA.B.C.D.10.已知ABC 的外接圆半径为2,D为该圆上的一点,且AB AC AD ,则ABC 的面积的最大值为()A.3B.4 C.33D.4 311. 设定义在 R 上的函数 fx 的导函数 f x ,且知足 f2 xff x 0 ,若x ,1x x 1 x 2 2, x 1x 2 ,则()A . f x 1 f x 2B . fx 1f x 2C. fx 1f x 2 D . f x 1 与 f x 2 的大小不可以确立12.设 a,b, c R 且 c 0 ,x3 56 7 8914 27lg x2a b a b a c 1 b c a 2b c 3 c a 2 a bb a3 a b若上表中的对数值恰有两个是错误的,则 a 的值为()A . lg2 B . 1 lg3C. 1 lg 3D . lg6212 1427 7第Ⅱ卷二、填空题:本大题共4 小题,每题5 分,共20 分.1513.二项式 x x 的睁开式中常数项为.(用数字做答)x14.已知 tan sin cos.2 ,则cos2sin15.已知数列 a n 的前 n 项和为 S n ,且知足: a 1 1, a 2 2, S n 1a n 2an 1nN * ,若不等式S n a n 恒成立,则实数 的取值范围是.16.已知双曲线 C :x 2y 21 a0, b 0 的左、右焦点分别为 F 1、F 2 , P 为双曲线 C 上a 2b 2一点, Q 为双曲线 C 渐近线上一点, P 、Q 均位于第一象限,且 QP PF 2,QF 1 QF 2 0 ,则双曲线 C 的离心率为 .三、解答题:本大题共 6 小题,共 70 分 .解答应写出文字说明、证明过程或演算步骤.17.已知向量 asin x,cos x , b cos xsin x,cos x ,函数 f x a b .6(1)求 f x 的单一递加区间;(2)若0,且 cos 121,求 f .2318.心理学家剖析发现“喜爱空间想象”与“性别”相关,某数学兴趣小组为了考证此结论,从全体组员中按分层抽样的方法抽取50 名同学 (男生 30 人、女生 20 人),给每位同学立体几何题、代数题各一道,让各位同学自由选择一道题进行解答,选题状况统计以下表: (单位:人)立体几何题代数题 总计 男同学 22 8 30 女同学 8 12 20 总计302050(1)可否有97.5%以上的掌握以为“喜爱空间想象”与“性别”相关?(2)经统计得,选择做立体几何题的学生正答率为4 ,且答对的学生中男生人数是女生人 5数的 5 倍,现从选择做几何题的8 名女生中随意抽取两人对她们的答题状况进行研究,记抽取的两人中答对的人数为X ,求 X 的散布列及数学希望.附表及公式:P K 2kk2K 2b n ad bcb da c d a c1 a n,n 为偶数,若b n19. 已知数列a n 知足: a 1 2, a n12a 2 n 1 1 .a n为奇数1,n(1)求证:数列 b n 是等比数列;(2)若数列a n 的前 n 项和为 S n ,求 S 2n .2220. 过椭圆 C : x2y 2 1 ab 0 的右焦点 F c,0 作 x 轴的垂线,与椭圆 C 在第一象ab限内交于点 A ,过 A 作直线 xa 2 的垂线,垂足为 B , AF3, AB2 .c32(1)求椭圆 C 的方程;(2)设P 为圆E : x2 y2 4 上随意一点,过点P 作椭圆 C 的两条切线l1、l 2,设l1、 l2分别交圆 E 于点M 、 N ,证明:MN 为圆E 的直径.21. 已知函数 f x ln x ax b a,b R 有两个不一样的零点x1, x2.(1)求f x 的最值;1(2)证明:x1 x2a2 请考生在22、 23 两题中任选一题作答,假如多做,则按所做的第一题记分.22.选修 4-4:坐标系与参数方程x t( t 为参数),以原点O为极点, x 轴正半轴为在直角坐标系 xOy 中,直线 l :5 2ty极轴成立极坐标系,曲线 C 的极坐标方程为2 cos2 4 0 .(1)写出曲线 C 的直角坐标方程;(2)已知点A 0, 51 1,直线 l 与曲线 C 订交于点 M 、 N ,求的值.AM AN23.选修 4-5:不等式选讲已知函数 f x x a x b a 0,b 0 .(1)若a 1,b 2 ,解不等式 f x 5 ;(2)若f x 的最小值为3,求 a2 b2 的最小值.b a试卷答案一、选择题1-5: ADBDB 6-10: BACBB 11、12: CB 二、填空题13. -10 14. 315. 1 16. 5 1 5三、解答题17.解:( 1)f x sin x cos x6 13sin x cosx1sin2 x 13sin 2x1cos2x 32 2 4 4 41sin 2x 3 ,2 6 42k 2x6 2k2k3x k ,2 6故 f x 的增区间为k , k6 ,k Z ;3(2)f 1 sin 26 3 sin cos123 ,2 4 12 4又cos12 1 且0,2,∴sin122 2 ,3 3∴ f 2 2 3.9 450 22 12 8218.解:( 1)K2 8 50 5.024 ,30 20 30 20 9故有 97.5%以上的掌握以为“喜爱空间想象”与“性别”相关;(2)由题知选做立体几何题且答对的共24 人,此中男生20 人、女生 4 人,故 X 的全部取值分别为0, 1,2,散布列为X01 2P3 4 314 714EX 1.19.解:( 1) b n1a2 n11 1a 2 n 11a2n11 11 a2 n 111b n ,故 b n 为等2222比数列;n 11(2)由( 1)知 ba 11,n122n 1∴a2 n 111 ,又a2na2 n 11 ,∴ a 2n 1a2n13 ,2n 22n 12 1 12n1∴S 2 n3n3n 41 12 n 2.220.解:( 1)由题知b 23 , a 2 c 2 ,∴ a 3, b 1, c2 ,a3 c2∴椭圆 C 的方程为x 2y 2 1 ;3(2)设 Px 0 , y 0 ,当切线 l 1 , l 2 的斜率均存在时,分别设为 k 1, k 2 ,设过点 P 的切线方程为 yy 0 k x x 0 ,与 C 的方程联立得1 k 2x22 y 0kx 0 kxy 0 kx 021 0 ,34k 2y 02 4 k21y 0 kx 0 21 0,则 kx 03即 21 121 2221 12,k y 0 kx 0 0 ,整理得 1 x 0 k x 0 y 0k y 0 03 333 3 3∴1 y 02 1 y 02,即x 02 y 02,k 1 k 23 11l 1 l 2 , MPN 90当 l 1 或 l 2 的斜率不存在时,必是 x 2 3或y 2 1 ,又 x 2y 24,∴ P3, 1 ,此时一0 0 0条切线与 x 轴垂直,一条切线与x 轴平行,仍有 l 1 l 2 即 MPN900 ,综上,对随意点 P, MN 为圆 E 的直径.121.解:(1) f xxa , f x 有两个不一样的零点,∴ f x 在 0,内必不但一,故a 0,此时 fx0 x 1 ,∴ f x在 0,1上单增, 1 ,上单减,a aa∴ f xf 1 ln a 1b ,无最小值;maxaln x 1ax 1 b 0x 1lnx1(2)由题知,两式相减得 ln a x 1 x 2 0 ,即 ax 2 ,ln x 2ax 2 b 0x 1 x 2x 2x 1 x 2 22 x 1x 1 2x 1x 2故要证 x 1 x 21 ,即证 x x,即证 ln x 22,a2 x 1x 2x 1 x 2x 2x 121 2lnx 2不如设x 1x 2 ,令x 1t 0,1 ,则只要证 ln 2 t t2 1 ,x 2t111 2ln t t 11设 g tln 2t t 2 ,则 g t2 ln t 1tt,设 ht2ln t t, ttt 2tt2则 ht 10 ,∴ h t 在 0,1 上单减,∴ h th 1 0 ,∴ gt 在 0,1 上t 2单增,∴ gtg 10 ,即 ln 2 t t 2 1 在 t0,1 时恒成立,原不等式得证.t22.解:( 1)2cos 22sin 24 0x 2 y 2 4 0 y 2x 2 4 ;x1 t,(2)将直线 l 的参数方程化为标准形式:5( t 为参数),y5 2t5代入曲线 C 的方程得 3t 2 4t 1 0 ,5则1 1 1 1 t 1 t2 4 .AMANt 1t 2t 1t 223.解:( 1) x 1 x 2 5 ,左式可看作数轴上;点 x 到 -2 和 1 两点的距离之和,当 x 3 或2时,距离之和恰为5,故 3 x 2 ;(2)f x x a x b x a x b a b ,∴a b 3,由柯西不等式得a2 b2 b a a b 2 ,∴a2 b2 a b 3,b a b a当且仅当 a b 3时等号成立,∴a2 b2 的最小值为 3.2 b a。
2017年重庆市中考数学一模试卷(解析版)

2017年重庆市中考数学一模试卷(解析版)一.选择题1.有四个数﹣6,﹣4,﹣3,﹣1,其中比﹣2大的数是()A. ﹣6B. ﹣4C. ﹣3D. ﹣12.下列图形中,是轴对称图形的是()A. B. C. D.3.下列计算正确的是()A. a3+a3=a6B. 3a﹣a=3C. (a3)2=a5D. a•a2=a34.若一个多边形的内角和为720°,则该多边形为()边形.A. 四B. 五C. 六D. 七5.函数y= +2中,自变量x的取值范围是()A. x≥1B. x>1C. x<1D. x≤16.下列实数,介于5和6之间的是()A. B. C. D.7.已知△ABC∽△DEF,面积比为9:4,则△ABC与△DEF的对应边之比为()A. 3:4B. 2:3C. 9:16D. 3:28.如果是方程ax+(a﹣2)y=0的一组解,则a的值()A. 1B. 2C. ﹣1D. ﹣29.如图,扇形AOB的圆心角为124°,C是上一点,则∠ACB=()A. 114°B. 116°C. 118°D. 120°10.下列图形都是由同样大小的矩形按一定的规律组成,其中,第①个图形中一共有6个矩形,第②个图形中一共有11个矩形,第③个图形中一共有16个矩形,…,按此规律,第⑧个图形中矩形的个数为()A. 30B. 36C. 41D. 4511.如图,小明在大楼30米高(即PH=30米)的窗口P处进行观测,测得山坡顶A处的俯角为15°,山脚处B的俯角为60°,已知该山坡的坡度i=1:,点P、H,B,C,A在同一个平面上,点HBC在同一条直线上,且PH⊥BC,则A到BC的距离为()A.10 米B.15米C.20 米D.30米12.从﹣4,﹣3,1,3,4这五个数中,随机抽取一个数,记为m,若m使得关于x,y的二元一次方程组有解,且使关于x的分式方程﹣1= 有正数解,那么这五个数中所有满足条件的m 的值之和是()A. 1B. 2C. ﹣1D. ﹣2二.填空题13.2017年第一季度,我市在改善环境绿化方面投入资金达到4080000元,4080000用科学记数法表示为________.14.2sin60°﹣(﹣)﹣2+(π﹣)0=________.15.某数学小组进行数学速算,比赛成绩如下:得100分的有2人,96分的有4人,90分的2人,那么这个数学小组速算比赛是平均成绩为________分.16.从﹣3、﹣1、、1、3这五个数中,随机抽取一个数,记为a,则关于x的一次函数y=﹣x+a的图象经过第一象限的概率为________.17.周末小明和爸爸从家里出发到野外郊游,小明骑自行车出发0.3小时后爸爸开始骑摩托车追赶,爸爸在追上小明前停留了0.1小时与碰到的朋友聊天,聊天完毕后以原来的速度继续追赶.在整个过程中,他们离家的路程y(千米)与爸爸出发的时间x(小时)之间的关系如图所示,则爸爸出发________小时后与小明相遇.18.如图,已知在正方形ABCD中,F是CD边上一点(不和C,D重合),过点D做DG⊥BF交BF延长线于点G.连接AG,交BD于点E,连接EF,交CD于点M.若DG=6,AG=7 ,则EF的长为________.三.解答题19.如图,C,E,F,D共线,AB∥FD,BG∥FH,且AB=FD,BG=FH.求证:∠A=∠D.20.最近,“校园安全”受到全社会的广泛关注,重庆八中对部分学生就校园安全知识的了解程度,采用随机抽样调查的方式,并根据收集到的信息进行统计,绘制了如下两幅尚不完整的统计图,请你根据统计图中所提供的信息解答下列问题:(1)扇形统计图中“基本了解”部分所对应扇形的圆心角为________度;请补全条形统计图________;(2)若达到“了解”程度的人中有1名男生2名女生,达到“不了解”的程度的人中有1名男生和1名女生,若分别从达到“了解”程度和“不了解”的人中分别抽取1人参加校园安全知识竞赛,请用树状图或列表法求出恰好抽到1名男生和1名女生的概率.四.解答题21.化简:整式与分式(1)(2x+1)(2x﹣1)﹣(x+1)(3x﹣2)(2)(﹣x+1)÷ .22.一次函数y=ax+b(a≠0)的图象与反比例函数y= (k≠0)的图象相交于A,B两点,与y轴交于点C,与x轴交于点D,点D的坐标为(﹣1,0),点A的横坐标是1,tan∠CDO=2.过点B作BH⊥y轴交y轴于H,连接AH.(1)求一次函数和反比例函数的解析式;(2)求△ABH面积.23.某文具店今年1月份购进一批笔记本,共2290本,每本进价为10元,该文具店决定从2月份开始进行销售,若每本售价为11元,则可全部售出;且每本售价每增长0.5元,销量就减少15本.(1)若该种笔记本在2月份的销售量不低于2200本,则2月份售价应不高于多少元?(2)由于生产商提高造纸工艺,该笔记本的进价提高了10%,文具店为了增加笔记本的销量,进行了销售调整,售价比中2月份在(1)的条件下的最高售价减少了m%,结果3月份的销量比2月份在(1)的条件下的最低销量增加了m%,3月份的销售利润达到6600元,求m的值.24.在△ABC中,AB=AC,D为射线BA上一点,连接DC,且DC=BC.(1)如图1,若DC⊥AC,AB= ,求CD的长;(2)如图2,若E为AC上一点,且CE=AD;连接BE,BE=2CE,连接DE并延长交BC于F.求证:DF=3EF.25.一个数能否被99整除是从这个数的末位开始,两位一段,看看这些数段的和能否被99整除.像这样能够被99整除的数,我们称之为“长久数”.例如542718,因为18+27+54=99,所以542718能够被99整除;又例如25146,因为46+51+2=99,所以25146能够被99整除.(1)若这个三位数是“长久数”,求a的值;(2)在(1)中的三位数的首位和个位与十位之间加上和为9的两个数字,让其成为一个五位数,该五位数仍是“长久数”,求这个五位数.26.如图,在平面直角坐标系xOy中,拋物线y=﹣x2x与x轴交于O,A,点B在抛物线上且横坐标为2.(1)如图1,△AOB的面积是多少?(2)如图1,在线段AB上方的抛物线上有一点K,当△ABK的面积最大时,求点K的坐标及△ABK的面积;(3)在(2)的条件下,点H 在y轴上运动,点I在x轴上运动.则当四边形BHIK周长最小时,求出H、I的坐标以及四边形BHIK周长的最小值.答案解析部分一. 选择题1.【答案】D【考点】有理数大小比较【解析】【解答】解:|﹣6|>|﹣4|>|﹣3|>|﹣2|>|﹣1|,∴﹣6<﹣4<﹣3<<﹣2<﹣1,故答案为:D.【分析】可根据两负数比较大小法则:两负数相比较,绝对值大的反而小.2.【答案】B【考点】轴对称图形【解析】【解答】解:A、不是轴对称图形,故本选项不符合题意;B、是轴对称图形,故本选项不符合题意;C、不是轴对称图形,故本选项错误;D、不是轴对称图形,故本选项错误.故答案为:B.【分析】根据轴对称定义可判断:沿某一条直线对折,两边能完全重合的图形3.【答案】D【考点】同底数幂的乘法,幂的乘方与积的乘方,合并同类项法则和去括号法则【解析】【解答】解:A、a3+a3=2a3,不符合题意;B、3a﹣a=2a,不符合题意;C、(a3)2=a6,不符合题意;D、a•a2=a3,符合题意;故答案为:D.【分析】同底数幂的加法,同类项可系数相加,字母及指数不变;同底数幂的乘法底数不变,指数相加;幂的乘方,底数不变指数相乘.4.【答案】C【考点】多边形内角与外角【解析】【解答】解:设多边形为n边形,由题意,得(n﹣2)•180°=720°,解得n=6,故答案为:C.【分析】利用内角和公式构建方程(n﹣2)•180°=720°,求出n.5.【答案】A【考点】函数自变量的取值范围【解析】【解答】解:由题意得,x﹣1≥0,解得x≥1.故答案为:A.【分析】二次根式有意义的条件为被开方数大于或等于0.6.【答案】B【考点】估算无理数的大小【解析】【解答】解:A、∵4<<5,∴本选项不符合题意;B、∵5<<6,∴本选项符合题意;C、∵6<<7,∴本选项不符合题意;D、∵=4,∴本选项不符合题意;故答案为:B.【分析】被开方数n介于两个完全平方数之间,则介于两个两个完全平方数的算术平方根之间.7.【答案】D【考点】相似三角形的性质【解析】【解答】解:∵△ABC∽△DEF,面积比为9:4,∴△ABC与△DEF的对应边之比3:2.故答案为:D.【分析】利用相似三角形的性质:面积比等于相似比的平方可解决.8.【答案】C【考点】二元一次方程的解【解析】【解答】解:将代入方程ax+(a﹣2)y=0得:﹣3a+a﹣2=0.解得:a=﹣1.故答案为:C.【分析】利用方程解的定义,把解代入方程可解出待定字母a.9.【答案】C【考点】圆周角定理,圆内接四边形的性质【解析】【解答】解:如图所示,在⊙O上取点D,连接AD,BD,∵∠AOB=124°,∴∠ADB= ∠AOB= ×124°=62°.∵四边形ADBC是圆内接四边形,∴∠ACB=180°﹣62°=118°.故答案为:C.【分析】须在⊙O上取点D,连接AD,BD,构造出弧ACB所对的圆周角,再利用圆内接四边形的对角互补性质可解决.10.【答案】C【考点】探索数与式的规律【解析】【解答】解:∵图①有矩形有6个=5×1+1,图②矩形有11个=5×2+1,图③矩形有16=5×3+1,∴第n个图形矩形的个数是5n+1当n=8时,5×8+1=41个.故答案为:C.【分析】等差数列的通项公式可以第一个为基础,列出等式观察规律:图①有矩形有6个=6,图②矩形有11个=6+5×1图③矩形有16=6+5×2第n个图形矩形的个数是6+5(n-1)=5n+111.【答案】A【考点】解直角三角形的应用,解直角三角形的应用-仰角俯角问题【解析】【解答】解:如图作AM⊥BC于M,设AM=x.∵tan∠ABM= ,∴∠ABM=30°,∴AB=2AM=2x,∵∠HPB=30°,∴∠PBH=90°﹣∠HPB=60°,∴∠ABP=180°﹣∠PBH﹣∠ABM=90°,∴∠BPA=∠BAP=45°,∴AB=BP=2x,在Rt△PBH中,∵sin∠PBH= ,∴= ,∴x=10 .故答案为:A.【分析】可通过作垂线把特殊角放到直角三角形中,可设出未知数,在Rt△PBH中利用三角函数列出方程.12.【答案】D【考点】二元一次方程组的解,分式方程的解【解析】【解答】解:∵有解,∴直线y=﹣2x+2与直线y= x+ 不平行,∴≠﹣2,∴m≠﹣4,解﹣1= 得,x=4﹣m,∵x=4﹣m是正数,∴m=﹣3,1,3,当m=3时,原方式方程无意义,故m=﹣3,1,∴﹣3+1=﹣2,故答案为:D.【分析】可以数形结合,方程组的两个方程可看作两直线,方程组有解就是它们相交,比例系数k不相等,分式方程的正数解不能取1,m不能取3,可得出答案.二.<b >填空题</b>13.【答案】4.08×106【考点】科学记数法—表示绝对值较大的数【解析】【解答】解:4080000=4.08×106.故答案为:4.08×106.【分析】绝对值较大数的科学记数法可表示为a×10n ,a是只有1位整数的小数或整数,n是原整数位数减1.14.【答案】﹣3【考点】实数的运算,零指数幂,负整数指数幂,特殊角的三角函数值【解析】【解答】解:原式=2× ﹣4+1= ﹣3.故答案为﹣3.【分析】本题易错点在于=4,非零数的0次幂等于1.15.【答案】95.5【考点】加权平均数【解析】【解答】解:(100×2+96×4+90×2)÷(2+4+2)=(200+384+180)÷8=764÷8=95.5(分).答:这个数学小组速算比赛的平均成绩为95.5分.故答案为:95.5.【分析】利用加权平均数定义,即可求出结果.16.【答案】【考点】概率公式【解析】【解答】解:关于x的一次函数y=﹣x+a的图象经过第一象限,则a>0,﹣3、﹣1、、1、3这五个数中有3个大于0,则关于x的一次函数y=﹣x+a的图象经过第一象限的概率为,故答案为:.【分析】关注的结果有3个正数,3种结果,机会均等的结果为5种,因此概率为.17.【答案】0.7【考点】一次函数的应用【解析】【解答】解:爸爸的速度为36÷(1﹣0.1)=40(千米/小时),小明的速度为36÷(1.2+0.3)=24(千米/小时).设爸爸出发t小时后与小明相遇,此时,小明出发了(t+0.3)小时,根据题意得:40(t﹣0.1)=24(t+0.3),解得:t=0.7.答:爸爸出发0.7小时后与小明相遇.故答案为:0.7.【分析】由图像可求出二人速度,根据相遇时二人距离家的路程相等列出方程40(t﹣0.1)=24(t+0.3),可求出时间.18.【答案】【考点】全等三角形的判定与性质,正方形的性质【解析】【解答】解:如图作AH⊥BG于H交BC于T,AN⊥GD于N,取BD的中点O,连接OA、OG.∴∠BAD=∠BGD=90°,∴OA=OD=OB=OG,∴A、B、G、D四点共圆,∴∠AGB=∠ADB=45°,∠AGD=∠ABD=45°,∴AH=GH,AN=NG,∵∠N=∠AHG=∠HGN=90°,∴四边形ANGH是矩形,∵AH=HG,∴四边形ANGH是正方形,∵AG=7 ,∴AH=HG=GN=AN=7,易证△AND≌△AHB,∴DN=BH,∴GD+GB=GN﹣DN+GH+BH=2GN= AG,∴6+GB=14,∴GB=8,BD= =10,∴BH=1,∵△BHT∽△AHB,∴BH2=AH•HT,∴HT= ,∴AT=AH+TH= ,易证△ABT≌△BCF,∴AT=BF= ,∵△BEF∽△BGD,∴= ,∴= ,∴EF= ,故答案为.【分析】通过作垂线,即作AH⊥BG于H交BC于T,AN⊥GD于N,构造出全等三角形△AND≌△AHB,△ABT≌△BCF,利用△BEF∽△BGD对应边成比例列出关系式,求出EF.三.<b >解答题</b>19.【答案】证明:∵AB∥FD,BG∥FH,∴∠B=∠BEF,∠BEF=∠DFH,∴∠B=∠DFH,在△ABG和△DHF中,,∴△ABG≌△DHF(SAS),∴∠A=∠D.【考点】平行线的性质,全等三角形的判定与性质【解析】【分析】要证两角相等,可证两角所在的三角形全等,即须证△ABG≌△DHF(SAS),可得∠A=∠D.20.【答案】(1)120;(2)解:设了解的学生为(A男,A女,A女),不了解的为(B男,B女),则出现的所有可能性为:(A男,B男)、(A男、B女)、(A女,B男)、(A女,B女)、(A女,B 男)、(A女,B女),∴恰好抽到1名男生和1名女生的概率是:,即恰好抽到1名男生和1名女生的概率是.【考点】扇形统计图,条形统计图,列表法与树状图法【解析】【解答】解:(1)由题意可得,本次调查的学生有:15÷50%=30(人),扇形统计图中“基本了解”部分所对应扇形的圆心角为:360°× =120°,了解的有:30﹣10﹣15﹣2=3(人),【分析】(1)圆心角=360°百分比;条形统计图的补全关键是求出所缺部分的数量,部分百分比=总数,具体量=样本容量相应百分比;(2)关注的结果为3个,机会均等所谓结果有6个,代入概率公式即可得概率为0.5.四.<b >解答题</b>21.【答案】(1)解:原式=4x2﹣1﹣3x2﹣x+2=x2﹣x+1(2)解:原式= • =﹣• =﹣【考点】多项式乘多项式,平方差公式,分式的混合运算【解析】【分析】(1)利用平方差公式和多项式乘多项式法则即可;(2)分式化简的基本方法有通分、约分,分子分母出现多项式时看能否分解因式,便于约分.22.【答案】(1)解:∵点D的坐标为(﹣1,0),tan∠CDO=2,∴CO=2,即C(0,2),把C(0,2),D(﹣1,0)代入y=ax+b可得,,解得,∴一次函数解析式为y=2x+2,∵点A的横坐标是1,∴当x=1时,y=4,即A(1,4),把A(1,4)代入反比例函数y= ,可得k=4,∴反比例函数解析式为y=(2)解:解方程组,可得或,∴B(﹣2,﹣2),又∵A(1,4),BH⊥y轴,∴△ABH面积= ×2×(4+2)=6.【考点】反比例函数与一次函数的交点问题,解直角三角形【解析】【分析】(1)先由tan∠CDO=2可求出C坐标,再把D点坐标代入直线解析式,可求出一次函数解析式,再由直线解析式求出A坐标,代入双曲线解析式,可求出双曲线解析式;(2)△ABH面积可以BH为底,高=y A-y B=4-(-2)=6.23.【答案】(1)解:设售价应为x元,依题意得:2290﹣15(x﹣11)÷0.5≥2200,解得x≤14.答:2月份售价应不高于14元(2)解:[14(1﹣m%)﹣10(1+10%)]×2200(1+m%)=6600,令m%=t,原式为(3﹣2t)(1+t)=3.t1=0(不合题意,舍去),t2=0.5,∴m=50.答:m的值是50.【考点】一元二次方程的应用,一元一次不等式的应用【解析】【分析】由"笔记本在2月份的销售量不低于2200本“可翻译为不等式2290﹣15(x﹣11)÷0.5≥2200;(2)“3月份的销量比2月份在(1)的条件下的最低销量增加了m%,3月份的销售利润达到6600元”可转化为“方程[14(1﹣ 1 7 m%)﹣10(1+10%)]×2200(1+m%)=6600,解出m的值.24.【答案】(1)解:∵AB=AC,BC=DC∴∠B=∠ACB,∠B=∠D,∴∠ACB=∠D=∠B 又∵DC⊥AC,∴∠ACD=90°∴∠B+∠ACB+∠D=90°∴∠B=∠ACD=∠D=30°∵AB= ,∴AC= ,∴CD= AC= .(2)解:证明:∵AB=AC,BC=DC∴∠ABC=∠ACB,∠ABC=∠CDA∴∠BCE=∠CDA 又∵BC=DC,CE=DA,∴△BCE≌△DCA,∴CE=AD,BE=AC又∵BE=2CE,∴AE=CE,AD=AE,过A作AH⊥DF于H,则∠DAH=∠HAE,DH=EH,又∵∠DAC=∠ABC+∠ACB=2∠ACB,∴∠HAE=∠ACB,又∵∠AEH=∠CEF,AE=CE,∴△AEH≌△CEF,∴EH=EF,∴DH=EH=EF,即DF=3EF【考点】全等三角形的判定与性质【解析】【分析】(1)由AB=AC,BC=DC,可得∠B=∠ACB,∠B=∠D,又DC⊥AC,可得∠B=∠ACD=∠D=30°,再由30度角的正切可得CD= AC= 6;(2)由已知易证△BCE≌△DCA,可得AE=CE,再由AD=AE,AH⊥DF,可得,DH=EH,进而须证HE=EF,因此证出EH=EF即可.25.【答案】(1)解:∵这个三位数是“长久数”,∴4+10a+5=99,解得:a=9.(2)解:设这个五位数为,根据题意得:10(9﹣x)+5+49+x=99k(k为正整数),∴144﹣9x=99k.∵x、k均为正整数,且144<198,∴k=1,x=5.答:这个五位数为54945.【考点】一元一次方程的应用【解析】【分析】(1)利用新定法则,把这个“长久数”转换为各数的和;(2)仍利用新法则,两位一段,构建关于x的方程,求出x.26.【答案】(1)解:当y=0时,得A(10,0);当x=2时,y=4,所以B(2,4),∴;(2)解:过K作KM⊥x轴交AB于M点,设K(m,﹣m2m),(2<m<10),∵A(10,0),B(2,4),∴直线AB的解析式为y=﹣x+5,则KM=﹣m2m﹣(﹣m+5)=﹣m2+3m﹣5,∴S△ABK= •KM•|x A﹣x B|=4KM=﹣m2+12m﹣20=﹣(m﹣6)2+16,∴当m=6时,S△ABK有最大值.此时,K(6,6),S△ABK=16.(3)解:如图,作点B关于y轴的对称点B′(﹣2,4)、点K关于x轴的对称点K′(6,﹣6),连接B′K′,分别交x轴于点I,交y轴于点H,此时四边形BHIK的周长最小,∴B′K′的解析式为y=﹣x+ ,∴H(0,)、I(,0),∴四边形BHIK周长的最小值为B′K′+BK= + =2 +2 .【考点】轴对称-最短路线问题,与二次函数有关的动态几何问题【解析】【分析】(1)要求面积可求高,即y B;(2)(三边均没有水平边或竖直边的三角形可称为斜三角形)△ABK是斜三角形,须过点K做x轴的垂线,把它分割为两个有竖直边的三角形,设出自变量,构建函数,解决最值问题;(3)四边形BHIK周长可转化为多条线段的和,可利用对称法求两线段之和最小,即做出定点B、K分别关于y、x轴的对称点,当三条线段B'H,HI、IK' 在一条直线上时,周长最短..。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
2017年一诊试题
学校____________姓名____________得分____________
一、选择题(4×12)
1、2-的相反数是( ) A 0 B 2 C 2- D 4
2、计算()
3
2a b 的结果是( )
A 33b a
B 35b a
C 63b a
D 6ab 3、下列图形中是中心对称图形的是( )
A B C D
4、如图,小米同学把一个含45°角的直角三角板放在如图所示的两条平行线m ,n 上,经测量∠α=115°,则∠β的度数是( ) A .55° B .65° C .75° D .70°
5、已知一组数据1、2、2、x 的平均数为3,则这组数据的最大属于最小数的差是 ( )
A 6
B 5
C 4
D 2
6、如图,AB 是圆O 的直径,点D 在AB 的延长线上,射线DC 切圆O 于点C ,若 ∠A=25°,则∠D 等于( )
A 60°
B 50°
C 40°
D 45°
7、已知一个多项式x x +23的和等于1432-+x x ,则这个多项式为( ) A 13+-x B 13--x C 13+x D 13-x 8、估算110+的值在( )
A 2和3之间
B 3和4之间
C 4和5之间
D 5和6之间
9、如图反映的过程是:妈妈带小米从家去附近的动物园玩,他们先去鳄鱼馆看鳄鱼他们先去鳄鱼馆看鳄鱼,又去熊猫馆看熊猫,然后回家.如果鳄鱼馆和熊猫馆的距离为m 千米,小米在熊猫馆比在鳄鱼馆多用了n 分钟,则m ,n 的值分别为( ) A 1、8 B 0.5 12 C 1 12 D 0.5 8
10、下列图形都是有同样大小的小圆圈按一定规律所组成的,其中第①个图形中一共有5个小圆圈,第②个图形中一共有12个小圆圈,第③个图形中一共有21个小圆圈,第④个图形中一共有32个小圆圈…,按此规律排列下去,第⑦个图形中小圆圈的个数为( ) A 62 B 77 C 79 D 96
11、如图,在某校建筑物上,悬挂“尊重生命价值,涵养生命能量”的宣传条幅AB ,小强站在位于建筑物正前方的台阶上D 点处测得条幅顶端A 的仰角为30°,朝着条幅
的方向到台阶下的E 点处,测得条幅顶端A 的仰角为60°,已知台阶DE 的坡度为1:2,DE=2米,则条幅AB 的长度为( )米
A 6.4
B 5.9
C 4.4
D 3.7
12、从-10、-7、-1、2、3、4这六个数中,随机抽取一个数,记为a ,若数a 使关于
x 的不等式组⎪⎩⎪⎨
⎧≥-<+0
3
24
a x x x 有解,且使关于x 的分式方程x a x x -+=--22124有整数解,那么这六个数中所有满足条件的a 的值之和是( )
A 6-
B 8-
C 16-
D 18- 二、填空题
13、函数2+=x y 中自变量x 的取值范围是__________;
14、中国倡导的“一带一路”建设将促进我国与世界各国的互利合作,而一带一路地区覆盖总人口约为4400000000人,这个数据用科学记数法表示为__________;
15、如图,AB//A /B /,AA /与BB /相交于点O ,2OA=OA /
,28cm S AOB =∆,则______.A OB S ∆=、
、
16、如图,矩形ABCD 中,AB=1,AD=2,以AD 的长为半径的⊙交BC 于E ,则图中阴影部分的面积为_________;
17、已知在平面直角坐标系中有A (1-,2)、B (1,2)两点,现从(2-,2-)、(2,6)、(1,2-)、(0,6)四点中,任选两点作为C 、D ,则以A 、B 、C 、D 四个点为顶点所组成的四边形中是平行四边形的概率为__________;
18、在正方形ABCD 中,点E 为CD 上一点,且DE=2CE ,连接BE 交对角线AC 于点G ,点F 为对角线AC 上一点,且CF=2AF ,过点F 作FH ⊥BE 于点H ,连接DF ,若HG=cm 10,则四边形DEGF 的面积为__________。
三、解答题
19、计算:()()03052
60cos 2272115121-+-----+⎪⎭
⎫ ⎝
⎛--
20、我校学生会新闻社准备近期做一个关于“减负十条”的专刊,想知道同学们对禽流感知识的
4题 6题
9题 10题 11题 D C E B A y O x B / A / A B
B E
C A
D G H \ E
F B C A D 15题 16题 18题
了解程度,决定随机抽取部分同学进行一次问卷调查,并根据收集到的信息进行了统计,绘制了下面两幅尚不完整的统计图.请你根据统计图中所提供的信息解答下列问题:
(1)接受问卷调查的同学共有_____名,请补全折线统计图,并求出扇形统计图中“基本了解”部分所对应扇形的圆心角的大小; (2)为了让全校师生都能更好地实施减负十条,学生会准备组织一次宣讲活动,由问卷调查中“了解”的几名同学组成一个宣讲团. 已知了解的这几名同学中只有两个女生,若要在该宣讲团中任选两名同学在全校师生大会上作代表发言,请用列表或画树状图的方法,求选取的两名同学都是女生的概率.
21、先化解,再求值:⎪⎭
⎫ ⎝
⎛+---÷-+-39339
9622x x x x x x ,其中x 是不等式组()⎩⎨
⎧+≥+<+x
x x 12201的整数解
22、如图,在∆ABC 中,sin ∠B=2
1,AD ⊥BC 于点D ,∠DAC=45°,AC=210(所得结果
保留根号)
(1)求线段BD 的长 (2)求∆ABC 的面积
23、某体育用品专卖店今年3月初用4000元购进了一批“中考体能测试专用绳”,上市后很快售完.该店于3月中旬又购进了和第一批数量相同的专用绳,由于第二批专用绳的进价每根比第一批提高了10元,结果进第二批专用绳共用了5000元. (1)第一批专用绳每根的进货价是多少元?
(2)若第一批专用绳的售价是每根60元,为保证第二批专用绳的利润率不低于第一批的利润率,那么第二批专用绳每根售价至少是多少元?
24、定义:如果M 个不同的正整数,对其中的任意两个数,这两个数的积能被这两个数的和整除,则称这组数为M 个数的祖冲之数组。
如(3,6)为两个数的祖冲之数组,因为3×6能被(36)整除;又如(15,30,60)为三个数的祖冲之数组,因为(1530)能被(1530)整除,(1560)能被(1560)整除,(3060)能被(3060)整除…
… (1)我们发现,3和6,4和12,5和20,6和30……,都是两个数的祖冲之数组;由此猜测n 和(1)nn (2n ,n 为整数)组成的数组是两个数的祖冲之数组,请证明这一猜想。
(2)若(4,5,6)aaa 是三个数的祖冲之数组,求满足条件的所有三位正整数a
25、如图∆ABC 和∆DEC 都是等腰直角三角形,C 为它们的公共顶点,连接AD 、BE 、F 如图,△ABC 和△DEC 都是等腰直角三角形,C 为它们的公共直角顶点,连AD ,BE ,F 为线段AD 的中点,连CF ,(1)如图1,当D 点在BC 上时,BE=24,求CF 的长(2)如图2,把△DEC 绕C 点顺时针旋转∂角(
)0
090
0<∂<,其他条件不变,求证:BE=2CF,FC ⊥BER ;如图3,当∂=45°,
BE 、CD 交于点O ,若∠DCF=30°,试求2
2
OC OB 的值.
26、如图,在平面直角坐标系中,点A (2,3)为二次函数y=ax 2
+bx-2(a≠0)与反
比例函数x
k y =
(k≠0)在第一象限的交点,已知该抛物线y=ax 2
+bx-2(a≠0)交x 轴正负半轴分别于E 点、D 点,交y 轴负半轴于B 点,且tan ∠ADE=2
1
.
(1)求二次函数和反比例函数的解析式;
(2)已知点M 为抛物线上一点,且在第三象限,顺次连接点D 、M 、B 、E ,求四边形DMBE 面积的最大值;
(3)在(2)中四边形DMBE 面积最大的条件下,过点M 作MH ⊥x 轴于点H ,交EB 的延长线于点F ,Q 为线段HF 上一点,且点Q 到直线BE 的距离等于线段OQ 的长,求Q 点的坐标.。
