第二章课后习题与答案

合集下载

《基础会计学》第二章课后习题及参考答案

是指用来检查、验证全部账户借方和贷方的期末余额是否相等的一种试算平衡方法。其计算公式为：
全部账户的借方余额的合计=全部账户的贷方余额的合计。
五，
1．简述借贷复式记账法的内容和特点。
答：
借贷复式记账法是以“资产=负债+所有者权益”为记账原理，以“借、贷”为记账符号，以“有借必有贷，借贷必相等”为记账规则，以发生额平衡法和余额平衡法为检查方法的一种记账方法。
3．会计等式揭示了会计要素之间的联系，因而成为复式记账、会计报表等会计核算方法建立的
理论依据。（）
4．不论发生什么样的经济业务，会计等式的平衡关系都不会被打破。（）
5．所有账户的本期借方发生额合计与贷方发生额合计是相等的（）
6．所有经济业务的发生都会引起会计等式两边同时发生变化。（）
7．资产与所有者权益在总金额上是一种必然相等的关系。（）
（5）+500万+500万累计折旧、库存商品、产成品本期发生额合计：
+540万+540万0权益类账户：
包括负债类和所有者权益类期末余额73540万65540万8000万负债类账户（增加发生额在贷方，减少发生额在借方，期末有正常余额，一般在贷方）：
预提费所以，资产=73540万用、应付账款、预收账款、其他应付款、应交税金、短期借款、
答：
要点：
依据相同、方向一致、金额相等、同时登记。
公式：
总分类账户本期发生额=所属明细账户本期发生额合计总分类账户期末余额=所属明细账户期末余额合计
3．简述借贷记账法的试算平衡。
答：
借贷记账法的试算平衡有发生额试算平衡法和余额试算平衡法。前者是根据“有借必有贷，
2式为：
发生额试算平衡法：
一般在借方收入成果类账户：

机械振动-课后习题和答案--第二章-习题和答案

弹簧下悬挂一物体，弹簧静伸长为δ。

设将物体向下拉，使弹簧有静伸长3δ，然后无初速度地释放，求此后的运动方程。

解：设物体质量为m ，弹簧刚度为k ，则：mg k δ=，即：n ω==取系统静平衡位置为原点0x =，系统运动方程为： δ⎧+=⎪=⎨⎪=⎩00020mx kx x x （参考教材P14）解得：δω=()2cos n x t t弹簧不受力时长度为65cm ，下端挂上1kg 物体后弹簧长85cm 。

设用手托住物体使弹簧回到原长后无初速度地释放，试求物体的运动方程、振幅、周期及弹簧力的最大值。

解：由题可知：弹簧的静伸长0.850.650.2()m =-=、所以：9.87(/)0.2n g rad s ω=== 取系统的平衡位置为原点，得到：系统的运动微分方程为：20n x x ω+=其中，初始条件：(0)0.2(0)0x x =-⎧⎨=⎩ （参考教材P14）所以系统的响应为：()0.2cos ()n x t t m ω=-弹簧力为：()()cos ()k n mg F kx t x t t N ω===- 因此：振幅为、周期为2()7s π、弹簧力最大值为1N 。

重物1m 悬挂在刚度为k 的弹簧上并处于静平衡位置，另一重物2m 从高度为h 处自由落到1m 上而无弹跳，如图所示，求其后的运动。

<解：取系统的上下运动x 为坐标，向上为正，静平衡位置为原点0x =，则当m 有x 位移时，系统有： 2121()2T E m m x =+ 212U kx =由()0T d E U +=可知：12()0m m x kx ++= 即：12/()n k m m ω=+系统的初始条件为：⎧=⎪⎨=-⎪+⎩2020122m gx k m x gh m m （能量守恒得：221201()2m gh m m x =+）因此系统的响应为：01()cos sin n n x t A t A t ωω=+其中:ω⎧==⎪⎨==-⎪+⎩200021122n m g A x k x m g ghk A k m m即：ωω=-2()(cos )n n m g x t t t k "一质量为m 、转动惯量为I 的圆柱体作自由纯滚动，圆心受到一弹簧k 约束，如图所示，求系统的固有频率。

流体力学课后习题答案第二章

第二章流体静力学2-1 密闭容器测压管液面高于容器内液面h=1.8m,液体密度为850kg/m3, 求液面压强。

解：08509.8 1.814994Pa p gh ρ==⨯⨯=2-2 密闭水箱，压力表测得压强为4900Pa,压力表中心比A 点高0.4米，A 点在液面下1.5m ，液面压强。

解：0()490010009.8(0.4 1.5) 49009800 1.15880PaM B A p p g h h ρ=+-=+⨯⨯-=-⨯=-2-3 水箱形状如图，底部有4个支座。

试求底面上的总压力和四个支座的支座反力，并讨论总压力和支座反力不相等的原因。

解：底面上总压力（内力，与容器内的反作用力平衡）()10009.81333352.8KN P ghA ρ==⨯⨯+⨯⨯=支座反力支座反力（合外力）3312()10009.8(31)274.4KN G g V V ρ=+=⨯⨯+=2-4盛满水的容器顶口装有活塞A ，直径d=0.4m ，容器底直径D=1.0m ，高h=1.8m 。

如活塞上加力为2520N(包括活塞自重)。

求容器底的压强和总压力。

解：压强2252010009.8 1.837.7kPa (0.4)/4G p gh A ρπ=+=+⨯⨯= 总压力 237.71/429.6KN P p A π=⋅=⨯⋅=2-5多管水银测压计用来测水箱中的表面压强。

图中高程单位为m ，试求水面的绝对压强。

解：对1-1等压面02(3.0 1.4)(2.5 1.4)p g p g ρρ+-=+-汞对3-3等压面 2(2.5 1.2)(2.3 1.2)a p g p g ρρ+-=+-汞将两式相加后整理0(2.3 1.2)(2.5 1.4)(2.5 1.2)(3.0 1.4)264.8kPap g g g g ρρρρ=-+-----=汞汞绝对压强 0.0264.8+98=362.8kPa abs a p p p =+=2-6水管A 、B 两点高差h 1=0.2m ，U 形管压差计中水银液面高差h 2=0.2m 。

大学物理学(第三版)第二章课后答案

习题22.1选择题(1) 一质点作匀速率圆周运动时，(A)它的动量不变，对圆心的角动量也不变。

(B)它的动量不变，对圆心的角动量不断改变。

(C)它的动量不断改变，对圆心的角动量不变。

(D)它的动量不断改变，对圆心的角动量也不断改变。

[答案：C](2) 质点系的内力可以改变(A)系统的总质量。

(B)系统的总动量。

(C)系统的总动能。

(D)系统的总角动量。

[答案：C](3) 对功的概念有以下几种说法：①保守力作正功时，系统内相应的势能增加。

②质点运动经一闭合路径，保守力对质点作的功为零。

③作用力与反作用力大小相等、方向相反，所以两者所作功的代数和必为零。

在上述说法中：(A)①、②是正确的。

(B)②、③是正确的。

(C)只有②是正确的。

(D)只有③是正确的。

[答案：C]2.2填空题(1) 某质点在力（SI）的作用下沿x轴作直线运动。

在从x=0移动到x=10m的过程中，力所做功为。

[答案：290J](2) 质量为m的物体在水平面上作直线运动，当速度为v时仅在摩擦力作用下开始作匀减速运动，经过距离s后速度减为零。

则物体加速度的大小为，物体与水平面间的摩擦系数为。

[答案：](3) 在光滑的水平面内有两个物体A和B，已知m A=2m B。

（a）物体A以一定的动能E k与静止的物体B发生完全弹性碰撞，则碰撞后两物体的总动能为；（b）物体A 以一定的动能E k与静止的物体B发生完全非弹性碰撞，则碰撞后两物体的总动能为。

[答案：]2.3 在下列情况下，说明质点所受合力的特点：（1）质点作匀速直线运动；（2）质点作匀减速直线运动；（3）质点作匀速圆周运动；（4）质点作匀加速圆周运动。

解：（1）所受合力为零；（2）所受合力为大小、方向均保持不变的力，其方向与运动方向相反；（3）所受合力为大小保持不变、方向不断改变总是指向圆心的力；（4）所受合力为大小和方向均不断变化的力，其切向力的方向与运动方向相同，大小恒定；法向力方向指向圆心。

第二章课后作业答案

第二章线性表习题(答案)1.描述以下三个概念的区别：头指针，头结点，首元素结点。

首元结点是指链表中存储线性表中第一个数据元素a1的结点。

为了操作方便，通常在链表的首元结点之前附设一个结点，称为头结点，该结点的数据域中不存储线性表的数据元素，其作用是为了对链表进行操作时，可以对空表、非空表的情况以及对首元结点进行统一处理。

头指针是指向链表中第一个结点（或为头结点或为首元结点）的指针。

若链表中附设头结点，则不管线性表是否为空表，头指针均不为空。

否则表示空表的链表的头指针为空。

2.填空：（1）在顺序表中插入或删除一个元素，需要平均移动一半元素，具体移动的元素个数与插入或删除的位置有关。

（2）在顺序表中，逻辑上相邻的元素，其物理位置也相邻。

在单链表中，逻辑上相邻的元素，其物理位置不一定相邻。

（3）在带头结点的非空单链表中，头结点的存储位置由头指针指示，首元素结点的存储位置由头结点的next域指示，除首元素结点外，其它任一元素结点的存储位置由其直接前趋的next域指示。

3．已知L是无表头结点的单链表，且P结点既不是首元素结点，也不是尾元素结点。

按要求从下列语句中选择合适的语句序列。

a. 在P结点后插入S结点的语句序列是：（4）、（1）。

b. 在P结点前插入S结点的语句序列是：（7）、（11）、（8）、（4）、（1）。

c. 在表首插入S结点的语句序列是：（5）、（12）。

d. 在表尾插入S结点的语句序列是：（11）、（9）、（1）、（6）。

供选择的语句有：（1）P->next=S; （2）P->next= P->next->next; （3）P->next= S->next;（4）S->next= P->next; （5）S->next= L; （6）S->next= NULL;（7）Q= P; （8）while(P->next!=Q) P=P->next;（9）while(P->next!=NULL) P=P->next; （10）P= Q;（11）P= L; （12）L= S; （13）L= P;4.设线性表存于a[n]中且递增有序。

会计学原理课后习题及答案

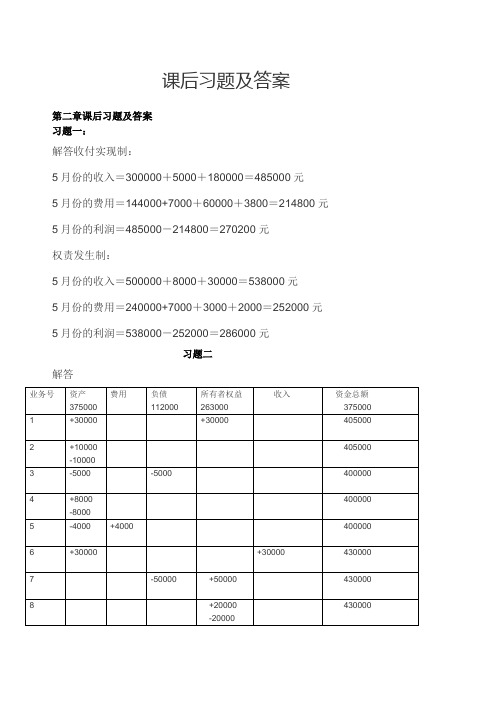
课后习题及答案第二章课后习题及答案习题一：解答收付实现制：5月份的收入＝300000＋5000＋180000＝485000元5月份的费用＝144000+7000＋60000＋3800＝214800元5月份的利润＝485000－214800＝270200元权责发生制：5月份的收入＝500000＋8000＋30000＝538000元5月份的费用＝240000+7000＋3000＋2000＝252000元5月份的利润＝538000－252000＝286000元习题二解答2016年9月末资产总额=476000 元负债总额=107000 元所有者权益=343000+30000-4000=369000 元第三章课后习题及答案习题一解答A=350000-450000+320000=220000元B=680000+4=730000元D=600000+200000-400000=400000元习题二解答1.登记期初余额贷：银行存款 100000（5）借：应付账款 13000贷：银行存款 13000（6）借：生产成本 25000贷：原材料 25000（7）借：银行存款 3000贷：应收账款 3000（8）借：短期借款 12000应付账款 4000贷：银行存款 16000（9）借：银行存款 20000贷：实收资本 20000（10）借：银行存款 14000贷：应收账款 14000（2）登记账户,计算发生额及期末余额见上述T字账（3）编制总分类账发生额和余额试算平衡表某公司总分类账发生额和余额试算平衡表单位：元解答1.编制会计分录（1）借：原材料——乙48000——丙25000贷：应付账款——红光工厂73000（2）借：应付账款——兴华工厂20000贷：银行存款20000（3）借：原材料——丙1500贷：应付账款——新飞工厂1500（4）借：生产成本179000贷：原材料——甲140000——乙36000——丙30002.用丁字账开设并登记“原材料”和“应付账款”总分类账及所属明细分类账,计算各账户的发生额和期末余额;单位：元“应付账款”总分类账户与明细分类账户发生额及余额表2016年11月30日单位：元。

有机化学课后习题答案第二章

有机化学课后习题答案第⼆章2章思考题2.1 分析共轭效应和超共轭效应的异同点，重点阐述σ-π和p-π共轭。

2.2 请举例说明同分异构体中各种异构体的定义及其异同点。

2.3解释甲烷氯化反应中观察到的现象：（1）（1）甲烷和氯⽓的混合物于室温下在⿊暗中可以长期保存⽽不起反应。

（2）（2）将氯⽓先⽤光照射，然后迅速在⿊暗中与甲烷混合，可以得到氯化产物。

（3）（3）将氯⽓⽤光照射后在⿊暗中放⼀段时期,再与甲烷混合，不发⽣氯化反应。

（4）（4）将甲烷先⽤光照射后，在⿊暗中与氯⽓混合，不发⽣氯化反应。

（5）（5）甲烷和氯⽓在光照下起反应时，每吸收⼀个光⼦产⽣许多氯化甲烷分⼦。

2.4 3-氯-1,2-⼆溴丙烷是⼀种杀根瘤线⾍的农药，试问⽤什么原料，怎样合成？2.5 写出烯烃C5H10的所有同分异构体，命名之，并指出哪些有顺反异构体。

2.6 找出下列化合物的对称中⼼.(1)⼄烷的交叉式构象(2)丁烷的反交叉式构象(3)反-1,4-⼆甲基环已烷(椅式构象)(4)写出1,2,3,4,5,6-六氯环已烷有对称中⼼的异构体的构象式(椅式)。

2.7 ⼀个化合物的氯仿溶液的旋光度为+10o, 如果把溶液稀释⼀倍, 其旋光度是多少? 如化合物的旋光度为-350o, 溶液稀释⼀倍后旋光度是多少?2.8 ⼄烯、丙烯、异丁烯在酸催化下与⽔加成，⽣成的活性中间体分别为、、，其稳定性＞＞, 所以反应速度是＞＞。

解答2.1 答：在离域体系中，键长趋于平均化，体系能量降低⽽使分⼦稳定性增加。

共轭体所表现出来的这种效应叫共轭效应。

共轭体系分为π-π共轭体系和p-π共轭体系。

超共轭效应是当C—H键与相邻的π键处于能重叠位置时，C—H键的轨道与π轨道也有⼀定程度的重叠，发⽣电⼦的离域现象，此时，键向π键提供电⼦，使体系稳定性提⾼。

它分为-p 和-π超共轭。

超共轭效应⽐共轭效应⼩。

异构现象异同点举例构造异构分了中原互相联结的⽅式和次序不同1. 碳链异构碳链不同2. 位置异构取代基在碳链或环上的位置不同3.官能团异构官能团不同⽴体异构分⼦中原⼦在空间2.3 答：（1）⽆引发剂⾃由基产⽣（2）光照射，产⽣Cl·，氯⾃由基⾮常活泼与甲烷⽴即反应。

第二章课后习题答案

第二章习题（二）判断题1．用户构建单片机应用系统，只能使用芯片提供的信号引脚。

（T）2．程序计数器（PC）不能为用户使用，因此它没有地址。

（T）3．内部RAM的位寻址区，只能提供位寻址使用而不能供字节寻址使用。

（F）4．在程序执行过程中，由PC提供数据存储器的读/写地址。

（F）5．80C51共有21个专用寄存器，它们的位都是可用软件设置的，因此是可以进行位寻址的。

（T）（三）填空题1. MCS-51单片机引脚信号中，信号名称带上划线表示该信号低电平或下跳变有效。

2. MCS-51单片机内部RAM的寄存区共有32 个单元，分为4 组寄存器，每组8 个单元，以R7~R0 作为寄存器名称。

3. 单片机系统复位后，（PSW）=00H，因此内部RAM寄存区的当前寄存器是第0 组，8个寄存器的单元地址为00H ～07H 。

4.通过堆栈操作实现子程序调用，首先要把PC 的内容入栈，以进行断点保护。

调用返回时再进行出栈操作，把保护的断点送回PC 。

5. 为寻址程序状态字的F0位，可使用的地址和符号有D5H 、F0 、PSW.5和D5H.5 。

6. MCS-51单片机的时钟电路包括两部分内容，即芯片内的高增益反相放大器和芯片外跨接的晶体震荡器,微调电容。

7. 在MCS-51中，位处理器的数据位存储空间是由专用寄存器的可寻址位和内部RAM为寻址区的128 个位。

8. MCS-51的4个I/O口中，P0是真正的双向口，而其他口则为准双向口，这一区别在口线电路结构中表现在口的输出缓冲器的不同上。

（四）选择题1．单片机芯片内提供了一定数量的工作寄存器，这样做的好处不应包括（A）提高程序运行的可靠性（B）提高程序运行速度（C）为程序设计提供方便（D）减少程序长度2．内部RAM中的位寻址区定义的位是给（A）位操作准备的（B）移位操作准备的（C）控制转移操作准备的（D）以上都对3．对程序计数器PC的操作（A）是自动进行的（B）是通过传送进行的（C）是通过加“1”指令进行的（D）是通过减“1”指令进行的4．以下运算中对溢于言表标志位OV没有影响或不受OV影响的运算是（A）逻辑运算（B）符号数加减法运算（C）乘法运算（D）除法运算5．单片机程序存储器的寻址范围是由程序计数器PC的位数决定的，MCS-51的PC为16位，因此其寻址范围是（A）4KB （B）64KB （C）8KB （D）128KB6．在算术运算中，与辅助进位位AC有关的是（A）二进制数（B）八进制数（C）十进制数（D）十六进制数7．以下有关PC和DPTR的结论中错误的是（A）DPTR是可以访问的而PC是不能访问的（B）它们都是16位的寄存器（C）它们都具有加“1”的功能（D）DPTR可以分为2个8位的寄存器使用，但PC不能8．PC的值是（A）当前指令前一条指令的地址（B）当前正在执行指令的地址（C）下一条指令的地址（D）控制器中指令寄存器的地址9．假定设置堆栈指针SP的值为37H，在进行子程序调用时把断点地址进栈保护后，SP的值为（A）36H （B）37H （C）38H （D）39H10. 80C51中，可使用的堆栈最大深度为（A）80个单元（B）32个单元（C）128个单元（D）8个单元11. 位处理器是单片机面向控制应用的重要体现，下列中不属于位处理器资源的是（A）位累加器CY （B）通用寄存器的可寻址位（C）专用寄存器的可寻址位（D）位操作指令集12. 在MCS-51单片机的运算电路中，不能为ALU提供数据的是（A）累加器A （B）暂存器（C）寄存器B （D）状态寄存器PSW13. 在MCS-51中（A）具有独立的专用的地址线（B）在P0口和P1口的口线作地址线（C）在P0口和P2口的口线作地址线（D）在P1口和P2口的口线作地址线。

机械制造技术第二章课后答案

第二章加工设备自动化（课后习题）2-1.实现加工设备自动化的意义是什么？（P30）答：加工设备生产率得到有效提高的主要途径之一是采取措施缩短其辅助时间，加工设备工作过程自动化可以缩短辅助时间，改善公认的劳动条件和减轻工人的劳动强度。

加工设备自动化是零件整个机械加工工艺过程自动化的基本问题之一，是机械制造厂实现零件加工自动化的基础。

2-2.为什么说单台加工设备的自动化是实现零件自动化加工的基础？（P30）答：单台加工设备的自动化能较好地满足零件加工过程中某个或几个工序的加工半自动化和自动化的需要，为多机床管理创造了条件，是建立自动化生产线和过渡到全盘自动化的必要前提，是机械制造业更进一步向前发展的基础。

2-3.加工设备自动化包含的主要内容与实现的途径有哪些？（P30）答：加工设备自动化主要是指实现了机床加工循环自动化和实现了辅助工作自动化的加工设备。

其主要内容如下:匚自动装卸工件实现加工设备自动化的途径主要有以下几种:（1）对半自动加工设备通过配置自动上下料装置以实现加工设备的完全自动化；（2）对通用加工设备运用电气控制技、数控技术等进行自动化改造；（3）根据家公家的特点和工艺要求设计制造专用的自动化加工设备，如组合机床等；（4）采用数控加工设备，包括数控机床、加工中心等。

2-4.试分析一下生产率与加工设备自动化的关系？（P32）答：生产率Q=K/（1+K*tf ），式中K ——理想的工艺生产率，K=1/tq ，tq —— 切削时间，tf ——空程辅助时间。

可知：tq 和tf 对机床生产的影响是相互制约相互促进的。

当生产工艺发展到一定水平，即工艺生产率K 提高到一定程度时，必须提高机床自动化程度，进一步减少空程辅助时间，促使生产率不断提高。

另一方面，在相对落后的工艺基础上实现机床自动化，生产率的提高是有限的，为了取得良好的效果，应当在先进的工艺基础上实现机床自动化。

电工与电子技术第二章课后习题参考答案

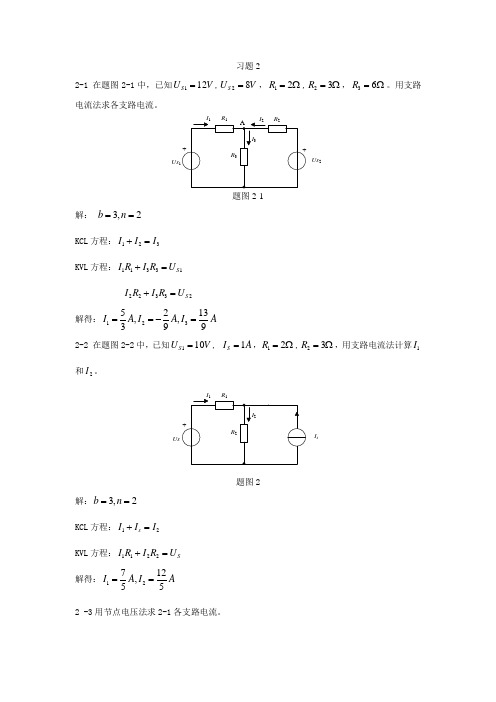
习题22-1 在题图2-1中，已知112S U V =,28S U V =，12R =Ω,23R =Ω，36R =Ω。

用支路电流法求各支路电流。

Us 2Us题图2-1解： 3,2b n == KCL 方程：123I I I += KVL 方程：11331S I R I R U += 22332S I R I R U += 解得：1235213,,399I A I A I A ==-= 2-2 在题图2-2中，已知110S U V =, 1S I A =，12R =Ω,23R =Ω，用支路电流法计算1I 和2I 。

IsUs题图2解：3,2b n == KCL 方程：12s I I I += KVL 方程：1122S I R I R U += 解得：12712,55I A I A ==2 -3用节点电压法求2-1各支路电流。

解：121212312882623611111133236s S abU U R R U V R R R ++===+=++++ 11126125323s abU U I A R --=== 2222682339S abU U I A R --===- 332613369ab U I A R ===2-4用节点电压法求2-2的电流1I 和2I 。

解：112101627.211115236sS abU I R U V R R ++====++111107.21.42s ab U U I A R --=== 227.2 2.43ab U I A R ===或211 1.41 2.4S I I I A =+=+= 2-5 在题图2-5中，已知110s U V =, 26S U V =, 2S I A =,12R =Ω,23R =Ω，36R =Ω，1S R =Ω，用节点电压法求电流1I 和2I 和3I 。

sR U题图2-5解：设上面的节点为a ，下面的节点为b 则12121231262236111111236s S S abU U I R R U V R R R +-+-===++++11112632S ab U U I A R --=== 2226603S ab U U I A R --===33616ab U I A R === 2-6在题图2-6中，已知10S U V =, 2S I A =，14R =Ω,22R =Ω，38R =Ω。

概率论与数理统计第二章课后习题及参考答案.

概率论与数理统计第二章课后习题及参考答案1．离散型随机变量X 的分布函数为⎪⎪⎩⎪⎪⎨⎧≥<≤<≤--<=≤=．4,1,42,7.0,21,2.0,1,0)()(x x x x x X P x F 求X 的分布律．解：)0()()(000--==x F x F x X P ，∴2.002.0)01()1()1(=-=----=-=F F X P ，5.02.07.0)02()2()2(=-=--==F F X P ，3.07.01)04()4()4(=-=--==F F X P ，∴X 的分布律为2．设k a k X P 32()(==， ,2,1=k ，问a 取何值时才能成为随机变量X 的分布律．解：由规范性，a a a n n k k 2321]32(1[32lim)32(11=--=⋅=+∞→∞+=∑，∴21=a ，此时，k k X P 32(21)(⋅==， ,2,1=k ．3．设离散型随机变量X 的分布律为求：(1)X 的分布函数；(2)21(>X P ；(3))31(≤≤-X P ．解：(1)1-<x 时，0)()(=≤=x X P x F ，11<≤-x 时，2.0)1()()(=-==≤=X P x X P x F ，21<≤x 时，7.0)1()1()()(==+-==≤=X P X P x X P x F ，2≥x 时，1)2()1()1()()(==+=+-==≤=X P X P X P x X P x F ，∴X 的分布函数为⎪⎪⎩⎪⎪⎨⎧≥<≤<≤--<=．2,1,21,7.0,11,2.0,1,0)(x x x x x F ．(2)方法1：8.0)2()1()21(==+==>X P X P X P ．方法2：8.02.01)21(121(1)21(=-=-=≤-=>F X P X P ．(3)方法1：1)2()1()1()31(==+=+-==≤≤-X P X P X P X P ．方法2：101)01()3()31(=-=---=≤≤-F F X P ．4．一制药厂分别独立地组织两组技术人员试制不同类型的新药．若每组成功的概率都是0.4，而当第一组成功时，每年的销售额可达40000元；当第二组成功时，每年的销售额可达60000元，若失败则分文全无．以X 记这两种新药的年销售额，求X 的分布律．解：设=i A {第i 组取得成功}，2,1=i ，由题可知，1A ，2A 相互独立，且4.0)()(21==A P A P ．两组技术人员试制不同类型的新药，共有四种可能的情况：21A A ，21A A ，21A A ，21A A ，相对应的X 的值为100000、40000、60000、0，则16.0)()()()100000(2121====A P A P A A P X P ，24.0)()()()40000(2121====A P A P A A P X P ，24.0)()()()60000(2121====A P A P A A P X P ，36.0)()()()0(2121====A P A P A A P X P ，∴X 的分布律为5．对某目标进行独立射击，每次射中的概率为p ，直到射中为止，求：(1)射击次数X 的分布律；(2)脱靶次数Y 的分布律．解：(1)由题设，X 所有可能的取值为1，2，…，k ，…，设=k A {射击时在第k 次命中目标}，则k k A A A A k X 121}{-== ，于是1)1()(--==k p p k X P ，所以X 的分布律为1)1()(--==k p p k X P ， ,2,1=k ．(2)Y 的所有可能取值为0，1，2，…，k ，…，于是Y 的分布律为1)1()(--==k p p k Y P ， ,2,1,0=k ．6．抛掷一枚不均匀的硬币，正面出现的概率为p ，10<<p ，以X 表示直至两个面都出现时的试验次数，求X 的分布律．解：X 所有可能的取值为2，3，…，设=A {k 次试验中出现1-k 次正面，1次反面}，=B {k 次试验中出现1-k 次反面，1次正面}，由题知，B A k X ==}{，=AB ∅，则)1()(1p p A P k -=-，p p B P k 1)1()(--=，p p p p B P A P B A P k X P k k 11)1()1()()()()(---+-=+=== ，于是，X 的分布律为p p p p k X P k k 11)1()1()(---+-==， ,3,2=k ．7．随机变量X 服从泊松分布，且)2()1(===X P X P ，求)4(=X P 及)1(>X P ．X 100000060000400000P0.160.240.240.36解： )2()1(===X P X P ，∴2e e2λλλλ--=，∴2=λ或0=λ(舍去)，∴224e 32e !42)4(--===X P ．)1()0(1)1(1)1(=-=-=≤-=>X P X P X P X P 222e 31e 2e 1----=--=．8．设随机变量X 的分布函数为⎩⎨⎧<≥+-=-．0,0,0,e )1(1)(x x x x F x 求：(1)X 的概率密度；(2))2(≤X P ．解：(1)⎩⎨⎧<≥='=-．0,0,0,e )()(x x x x F x f x ；(2)2e 31)2()2(--==≤F X P ．9．设随机变量X 的概率密度为xx Ax f e e )(+=-，求：(1)常数A ；(2))3ln 210(<<X P ；(3)分布函数)(x F ．解：(1)⎰⎰+∞∞--+∞∞-+==xAx x f xx d e e d )(1A A x A x x x 2|e arctan d e 21e 2π==+=∞+∞-∞+∞-⎰，∴π2=A ．(2)61|e arctan 2d e e 12)3ln 210(3ln 2103ln 210==+=<<⎰-x xx x X P ππ．(3)x xx x xx t t f x F e arctan 2d e e 12d )()(ππ=+==⎰⎰∞--∞-．10．设连续型随机变量X 的分布函数为⎪⎪⎩⎪⎪⎨⎧>≤<-+-≤=．a x a x a a x B A a x x F ,1,,arctan ,,0)(其中0>a ，试求：(1)常数A ，B ；(2)概率密度)(x f ．解：(1) 2arcsin (lim )0()(0)(π⋅-=+=+-=-=+-→B A a x B A a F a F a x ，1)(lim )0()(2==+==⋅++→x F a F a F B A a x π，∴21=A ，π1=B ．(2)⎪⎩⎪⎨⎧≥<-='=．a x a x x a x F x f ,0,,1)()(22π．11．设随机变量X 的概率密度曲线如图所示，其中0>a ．(1)写出密度函数的表达式，求出h ；(2)求分布函数)(x F ；(3)求)2(a X aP ≤<．解：(1)由题设知⎪⎩⎪⎨⎧≤≤-=其他．,0,0,)(a x x ah h x f 2d )(d )(10ahx x a h h x x f a=-==⎰⎰+∞∞-，∴ah 2=，从而⎪⎩⎪⎨⎧≤≤-=其他．,0,0,22)(2a x x a a x f ．y hO a x(2)0<x 时，0d 0d )()(===⎰⎰∞-∞-xxt t t f x F ，a x <≤0时，220202d )22(d 0d )()(a x a x t t a a t t t f x F xx-=-+==⎰⎰⎰∞-∞-，a x ≥时，1)(=x F ，∴X 的分布函数为⎪⎪⎩⎪⎪⎨⎧≥<≤-<=．a x a x axa x x x F ,1,0,2,0,0)(22．(3)41411(1)2()()2(=--=-=≤<a F a F a X a P ．12．设随机变量X 在]6,2[上服从均匀分布，现对X 进行三次独立观察，试求至少有两次观测值大于3的概率．解：由题意知⎪⎩⎪⎨⎧≤≤=其他．,0,62,41)(x x f ，记3}{>=X A ，则43d 41)3()(63==>=⎰x X P A P ，设Y 为对X 进行三次独立观测事件}3{>X 出现的次数，则Y ～43,3(B ，所求概率为)3()2()2(=+==≥Y P Y P Y P )(()(333223A P C A P A P C +=3227)43(41)43(333223=+⋅=C C ．13．设随机变量X 的概率密度为⎩⎨⎧<<=其他．,0,10,3)(2x x x f 以Y 表示对X 的三次独立重复观察中事件}21{≤X 出现的次数，求：(1)}21{≤X 至少出现一次的概率；(2)}21{≤X 恰好出现两次的概率．解：由题意知Y ～),3(p B ，其中81d 321(2102==≤=⎰x x X P p ，(1)}21{≤X 至少出现一次的概率为512169)811(1)1(1)0(1)1(33=--=--==-=≥p Y P Y P ．(2)}21{≤X 恰好出现两次的概率为51221811(81()1()2(223223=-=-==C p p C Y P ．14．在区间],0[a 上任意投掷一个质点，以X 表示这个质点的坐标．设这个质点落在],0[a 中任意小区间内的概率与这个小区间的长度成正比例．试求X 的分布函数．解：0<x 时，事件}{x X ≤表示X 落在区间],0[a 之外，是不可能事件，此时0)()(=≤=x X P x F ；a x ≤≤0时，事件}{x X ≤发生的概率等于X 落在区间],0[x 内的概率，它与],0[x 的长度x 成正比，即x k x X P x F =≤=)()(，a x =时，1)(=≤x X P ，所以a k 1=，则此时axx F =)(；a x ≥时，事件}{x X ≤是必然事件，有1)(=x F ，综上，⎪⎪⎩⎪⎪⎨⎧≥<≤<=，a x a x a x x x F ,1,0,,0,0)(．15．设X ～),2(2σN ，又3.0)42(=<<X P ，求)0(>X P ．解：)24222()42(σσσ-<-<-=<<X P X P 3.0)0(2(=Φ-Φ=σ，∴8.03.0)0()2(=+Φ=Φσ，∴8.0)2()2(1)0(1)0(=Φ=-Φ-=≤-=>σσX P X P ．16．设X ～)4,10(N ，求a ，使得9.0)10(=<-a X P ．解：)10()10(a X a P a X P <-<-=<-)22102(a X a P <-<-=)2()2(a a -Φ-Φ=9.01)2(2=-Φ=a，∴95.0)2(=Φa，查标准正态分布表知645.12=a，∴290.3=a ．17．设X ～)9,60(N ，求分点1x ，2x ，使得X 分别落在),(1x -∞，),(21x x ，),(2∞x 的概率之比为3：4：5．解：由题知5:4:3)(:)(:)(2211=><<<x X P x X x P x X P ，又1)()()(2211=>+<<+<x X P x X x P x X P ，∴25.041)(1==<x X P ，33.031)(21==<<x X x P ，125)(2=>x X P ，则5833.0127)(1)(22==>-=≤x X P x X P ．25.0)360()360360()(111=-Φ=-<-=<x x X P x X P ，查标准正态分布表知03601<-x ，∴03601>--x ，则75.0)360(1)360(11=-Φ-=--Φx x 查标准正态分布表，有7486.0)67.0(=Φ，7517.0)68.0(=Φ，75.02)68.0()67.0(=Φ+Φ，∴675.0268.067.03601=+=--x ，即975.571=x ．5833.0360()360360()(222=-Φ=-≤-=≤x x X P x X P ，查标准正态分布表知5833.0)21.0(=Φ，∴21.03602=-x ，即63.602=x ．18．某高校入学考试的数学成绩近似服从正态分布)100,65(N ，如果85分以上为“优秀”，问数学成绩为“优秀”的考生大致占总人数的百分之几？解：设X 为考生的数学成绩，则X ～)100,65(N ，于是)85(1)85(≤-=>X P X P )1065851065(1-≤--=X P 0228.09772.01)2(1=-=Φ-=，即数学成绩为“优秀”的考生大致占总人数的2.28%．19．设随机变量X 的分布律为求2X Y =的分布律．解：Y 所有可能的取值为0，1，4，9，则51)0()0(====X P Y P ，307)1()1()1(==+-===X P X P Y P ，51)2()4(=-===X P Y P ，3011)3()9(====X P Y P ，∴Y 的分布律为20．设随机变量X 在)1,0(上服从均匀分布，求：(1)X Y e =的概率密度；(2)X Y ln 2-=的概率密度．解：由题设可知⎩⎨⎧<<=其他．,0,10,1)(x x f ，(1)当0≤y 时，=≤}{y Y ∅，X 2-1-013P5161511513011X 0149P51307513011∴0)()(=≤=y Y P y F Y ，0)(=y f Y ；e 0<<y 时，)e ()()(y P y Y P y F X Y ≤=≤=)(ln )ln (y F y X P X =≤=，此时，yy f y y y F y F y f X XY X 1)(ln 1)(ln )(ln )()(=='⋅'='=；e ≥y 时，1)()(=≤=y Y P y F Y ，0)(=y f Y ；∴⎪⎩⎪⎨⎧<<=其他．,0,e 0,1)(y y y f Y ．(2)当0≤y 时，=≤}{y Y ∅，∴0)()(=≤=y Y P y F Y ，0)(=y f Y ；当0>y 时，)e ()ln 2()()(2y Y X P y X P y Y P y F -≥=≤-=≤=)e (1)e (122y X y F X P ---=<-=，此时，222e 21)e ()e ()()(yy y X Y X F y F y f ---='⋅'-='=；∴⎪⎩⎪⎨⎧≤>=-．0,0,0,e 21)(2y y y f yY ．21．设X ～)1,0(N ，求：(1)X Y e =的概率密度；(2)122+=X Y 的概率密度；(3)X Y =的概率密度．解：由题知22e 21)(x X xf -=π，+∞<<∞-x ，(1)0≤y 时，=≤=}e {y Y X ∅，∴0)()(=≤=y Y P y F Y ，0)(=y f Y ；0>y 时，)(ln )ln ()e ()()(y F y X P y P y Y P y F X X Y =≤=≤=≤=，此时，2)(ln 2e 21)(ln 1)(ln )(ln )()(y X XY X y f yy y F y F y f -=='⋅'='=π；综上，⎪⎩⎪⎨⎧≤>=-．0,0,0,e 21)(2)(ln 2y y y f y Y π．(2)1<y 时，=≤+=}12{2y X Y ∅，∴0)()(=≤=y Y P y F Y ；1≥y 时，21()12()()(22-≤=≤+=≤=y X P y X P y Y P y F Y )2121(-≤≤--=y X y P 当1=y 时，0)(=y F Y ，故1≤y 时，0)(=y F Y ，0)(=y f Y ；当1>y 时⎰⎰------==210221212d e22d e21)(22y x y y x Y x x y F ππ，此时，41e)1(21)()(---='=y Y Y y y F y f π，综上，⎪⎩⎪⎨⎧≤>-=--．1,0,1,e )1(21)(41y y y y f y Y π．(3)0<y 时，=≤=}{y X Y ∅，∴0)()()(=≤=≤=y X P y Y P y F Y ，0≥y 时，)()()()(y X y P y X P y Y P y F Y ≤≤-=≤=≤=)()(y F y F X X --=，0=y 时，0)(=y F Y ，∴0≤y 时，有0)(=y F Y ，0)(=y f Y ；0>y 时，22e 22)()()()()(y X X Y Y Y yf y f y F y F y f -=-+=-'+'=π，综上，⎪⎩⎪⎨⎧≤>=-．0,0,0,e 22)(22y y y f yY π．22．(1)设随机变量X 的概率密度为)(x f ，+∞<<∞-x ，求3X Y =的概率密度．(2)设随机变量X 的概率密度为⎩⎨⎧>=-其他．,00,e )(x x f x 求2X Y =的概率密度．解：(1)0=y 时，0)()(=≤=y Y P y F Y ，0)(=y f Y ；0≠y 时，)()()()()(333y F y X P y X P y Y P y F X Y =≤=≤=≤=，3233331())(()()(-⋅=''='=y y f y y F y F y f XY Y ；∴⎪⎩⎪⎨⎧=≠=-．0,0,0),(31)(332y y y f y y f Y ．(2)由于02≥=X Y ，故当0<y 时，}{y Y ≤是不可能事件，有0)()(=≤=y Y P y F Y ；当0≥y 时，有)()(()()()(2y F y F y X y P y X P y Y P y F X X Y --=≤≤-=≤=≤=；因为当0=y 时，0)0()0()(=--=X X Y F F y F ，所以当0≤y 时，0)(=y F Y ．将)(y F Y 关于y 求导数，即得Y 的概率密度为⎪⎩⎪⎨⎧≤>-+=．，；，000)](([21)(y y y f y f y y f X X Y ，⎪⎩⎪⎨⎧≤>+=-．0,0,0),e e (21y y yyy ．23．设随机变量X 的概率密度为⎪⎩⎪⎨⎧<<=其他．,0,0,2)(2ππx xx f 求X Y sin =的概率密度．解：由于X 在),0(π内取值，所以X Y sin =的可能取值区间为)1,0(，在Y 的可能取值区间之外，0)(=y f Y ；当10<<y 时，使}{y Y ≤的x 取值范围是),arcsin []arcsin ,0(ππy y - ，于是}arcsin {}arcsin 0{}{ππ<≤-≤<=≤X y y X y Y ．故)arcsin ()arcsin 0()()(ππ<≤-+≤<=≤=X y P y X P y Y P y F Y ⎰⎰-+=ππyX y X x x f x x f arcsin arcsin 0d )(d )(⎰⎰-+=ππππyy x xx xarcsin 2arcsin 02d 2d 2，上式两边对y 求导，得22222121)arcsin (21arcsin 2)(yyy yyy f Y -=--+-=ππππ；综上，⎪⎩⎪⎨⎧<<-=其他．,0,10,12)(2y y y f Y π．。

第二章课后习题及答案

第二章心理辅导的理论基础一、理论测试题（一）单项选择题1．（）是根据操作性条件反射原理，强调行为的改变是依据行为后果而定的。

A．强化法B．系统脱敏法C．代币法D．来访者中心疗法2．在对学生进行心理辅导时，常使用的“强化法”属于（）。

A．行为改变技术B．认知改变法C．运动改变法D．精神分析法3．在心理辅导的行为演练中，系统脱敏法是由（）首创。

A．皮亚杰B．沃尔帕C．艾利斯D．罗杰斯4．心理辅导老师帮李晓明建立焦虑等级，让他想象引起焦虑的情境，然后逐渐减少焦虑等级，直至完全放松，以缓解其考试焦虑，这种方法是（）。

A．强化法B．系统脱敏法C．理性一情绪疗法D．来访者中心疗法5．行为塑造法是根据（）的操作条件反射研究结果而设计的培育和养成新反应或行为模式的一项行为治疗技术，是操作条件作用法强化原则的有力应用之一。

A．皮亚杰B．斯金纳C．艾利斯D．奥苏贝尔6．（）就是运用代币并编制一套相应的激励系统来对符合要求的目标行为的表现进行肯定和奖励。

A．强化法B．理性一情绪疗法C．代币法D．来访者中心疗法7．李老师通过奖励小红花来表扬学生的行为，这种心理辅导方法属于（）。

A．系统脱敏法B．代币法C．行为塑造法D．来访者中心疗法8.晓红是韩老师班上的学生，她孤僻、羞涩，当她主动与同学交谈或请教老师时，韩老师就给予肯定或激励。

这种心理辅导方法是（）。

A．强化法B．系统脱敏法C．来访者中心法D．理性一情绪疗法9．（）不是行为改变的基本方法。

A．强化法B．代币法C．自我控制法D．演练法10．小伟过分害怕狗，通过让他看狗的照片，谈论狗，远看狗到近看狗、摸狗、抱狗，消除对狗的惧怕反应，这是行为训练的（）。

A．全身松弛训练B．系统脱敏法C．行为塑造法D．肯定性训练11．当一位胆小的学生敢于主动向教师提问时，教师耐心解答并给予表扬和鼓励。

教师的这种做法属于行为改变方法中的（）。

A．强化法B．示范法C．消退法D．行为塑造法12．认知疗法于20世纪六七十年代在（）产生。

微积分课后题答案第二章习题详解

解:函数在其第二类间断点处的左、右极限不一定均不存在.
例如是其的一个第二类间断点,但即在处左极限存在,而,即在处右极限不存在.
4.求下列函数的间断点，并说明间断点的类型：
(1) f(x)= ；(2) f(x)＝；
(3) f(x)= ；(4) f(x)= ；
(5) f(x)= .
解: (1)由得x=-1, x=-2
证:
,由极限的保号性知.
,使当时有,此时与同号,因为n为奇数,所以(2X)n与(-2X)n异号,于是与异号,以在上连续,由零点存在定理,至少存在一点,使,即至少有一实根.
（7）正确，见教材§2.3定理5；
（8）错误，只有非零的无穷小量的倒数才是无穷大量。零是无穷小量，但其倒数无意义。
3. 指出下列函数哪些是该极限过程中的无穷小量，哪些是该极限过程中的无穷大量.
(1) f(x)= ,x→2;(2) f(x)=lnx，x→0+，x→1,x→+∞；
(3) f(x)= ,x→0+，x→0-；(4) f(x)= -arctanx,x→+∞;
也即，所以当时，.
再证必要性：
若当时，，则，
所以＝＝.
综上所述，当x→x0时，(x)～β(x)的充要条件是
＝０.
2. 若β(x)≠0，β(x)=0且存在，证明(x)=0.
证：
即.
3. 证明：若当x→0时，f(x)=o(xa)，g(x)=o(xb)，则f(x)·g(x)＝o()，其中a,b都大于0，并由此判断当x→0时，tanx－sinx是x的几阶无穷小量.
解: ∵f(0)=a,
要f(x)在x=0处连续,必须.
即a=1.
6※.设f(x)= ，讨论f(x)的连续性.

机械振动课后习题和答案第二章习题和答案

2.1 弹簧下悬挂一物体，弹簧静伸长为δ。

设将物体向下拉，使弹簧有静伸长3δ，然后无初速度地释放，求此后的运动方程。

解：设物体质量为m ，弹簧刚度为k ，则：mg k δ=，即：n ω==取系统静平衡位置为原点0x =，系统运动方程为： δ⎧+=⎪=⎨⎪=⎩00020mx kx x x （参考教材P14）解得：δω=()2cos n x t t2.2 弹簧不受力时长度为65cm ，下端挂上1kg 物体后弹簧长85cm 。

设用手托住物体使弹簧回到原长后无初速度地释放，试求物体的运动方程、振幅、周期及弹簧力的最大值。

解：由题可知：弹簧的静伸长0.850.650.2()m =-= 所以：9.87(/)0.2n g rad s ω=== 取系统的平衡位置为原点，得到：系统的运动微分方程为：20n x x ω+=其中，初始条件：(0)0.2(0)0x x =-⎧⎨=⎩ （参考教材P14）所以系统的响应为：()0.2cos ()n x t t m ω=-弹簧力为：()()cos ()k n mg F kx t x t t N ω===-因此：振幅为0.2m 、周期为2()7s π、弹簧力最大值为1N 。

2.3 重物1m 悬挂在刚度为k 的弹簧上并处于静平衡位置，另一重物2m 从高度为h 处自由落到1m 上而无弹跳，如图所示，求其后的运动。

解：取系统的上下运动x 为坐标，向上为正，静平衡位置为原点0x =，则当m 有x 位移时，系统有： 2121()2T E m m x =+ 212U kx =由()0T d E U +=可知：12()0m m x kx ++= 即：12/()n k m m ω=+系统的初始条件为：⎧=⎪⎨=-⎪+⎩2020122m gx k m x gh m m （能量守恒得：221201()2m gh m m x =+）因此系统的响应为：01()cos sin n n x t A t A t ωω=+其中:ω⎧==⎪⎨==-⎪+⎩200021122n m g A x k x m g ghk A k m m即：ωω=-2()(cos )n n m g x t t t k2.4 一质量为m 、转动惯量为I 的圆柱体作自由纯滚动，圆心受到一弹簧k 约束，如图所示，求系统的固有频率。

生物化学教程第二章习题答案(详解)

精心整理第二章课后习题答案1.计算赖氨酸的ε-NH 3+20%被解离时的溶液PH 。

解：pH = pKa + lg20% pKa = 10.53pH = 10.53 + lg20% = 9.92. 解：3. 等电解：a4.解： pI(Ala) = 1/2（9.04+12.48）= 10.765. 向1L1mol/L 的处于等电点的甘氨酸溶液加入0.3molHCl ，问所得溶液的pH 是多少？如果加入0.3mol NaOH 以代替HCl 时，pH 将是多少？解：pH1=pKa1+lg(7/3)=2.71pH2=pKa2+lg(3/7)=9.236.计算0.25mol/L的组氨酸溶液在pH6.4时各种离子形式的浓度（mol/L）。

解：由pH=pK1+lg（His+/ His2+）=pKr+lg（His0/His+）=pK2+lg（His-/ His0）得His2+为1.87×10-6，His+为0.071，His0为0.179 His-3.0×10-47.说明用含一个结晶水的固体组氨酸盐酸盐（相对分子质量=209.6；咪唑基pKa=6.0）和1mol/L KOH配制1LpH6.5的0.2mol/L组氨酸盐缓冲液的方法1L。

8. L-。

计算解：9.为溶剂(1)利用由对于对于故利用4个分溶管组成的分溶系统中，甘氨酸和苯丙氨酸各在4管和第3管中含量最高.10.将含有天冬氨酸(pI=2.98)、甘氨酸(pI=5.97)、亮氨酸(pI=6.53)和赖氨酸(pI=5.98)的柠檬酸缓冲液，加到预先同样缓冲液平衡过的强阳离交换树脂中，随后用爱缓冲液析脱此柱，并分别收集洗出液，这5种氨基酸将按什么次序洗脱下来？、解：在pH3左右，氨基酸与阳离子交换树脂之间的静电吸引的大小次序是碱性氨基酸(A2+)>中性氨基酸(A+)>酸性氨基酸(A0)。

因此氨基酸的洗出顺序大体上是酸性氨基酸、中性氨基酸，最后是碱性氨基酸，由于氨基酸和树脂之间还存在疏水相互作用，所以其洗脱顺序为：Asp, Thr, Gly, Leu, Lys。

信息论第二章课后习题解答

这样，平均每个像素携带的信息量为：
每帧图像含有的信息量为：
按每秒传输30帧计算，每秒需要传输的比特数，即信息传输率为：
（2）需30个不同的色彩度，设每个色彩度等概率出现，则其概率空间为：
由于电平与色彩是互相独立的，因此有
这样，彩色电视系统的信息率与黑白电视系统信息率的比值为
【2.13】每帧电视图像可以认为是由3×105个像素组成，所以像素均是独立变化，且每一像素又取128个不同的亮度电平，并设亮度电平等概率出现。问每帧图像含有多少信息量？若现有一广播员在约 10000 个汉字的字汇中选 1000 个来口述此电视图像，试问广播员描述此图像所广播的信息量是多少（假设汉字是等概率分布，并且彼此无依赖）？若要恰当地描述此图像，广播员在口述中至少需用多少汉字？
解：信源为一阶马尔克夫信源，其状态转换图如下所示。
根据上述c) ，
【2.20】黑白气象传真图的消息只有黑色和白色两种，即信源, X={白黑} ，设黑色出现的概率为 P(黑) =0.3 ，白色出现的概率为P(白)=0.7。（1）假设图上黑白消息出现前后没有关联，求熵H(X) ；（2）假设消息前后有关联，其依赖关系为P(白|白)=0.9 ， P(白|黑)=0.2 ，P(黑|白)=0.1 ，P(黑|黑)=0.8 ，求此一阶马尔克夫信源的熵H2 。（3）分别求上述两种信源的冗余度，并比较H(X)和H2的大小，并说明其物理意义。
解：（1）如果出现黑白消息前后没有关联，信息熵为：
（2）当消息前后有关联时，首先画出其状态转移图，如下所示：
设黑白两个状态的极限概率为Q(黑) 和Q (白) ，
解得：
此信源的信息熵为：（3）两信源的冗余度分别为：
结果表明：当信源的消息之间有依赖时，信源输出消息的不确定性减弱。有依赖时前面已是白色消息，后面绝大多数可能是出现白色消息；前面是黑色消息，后面基本可猜测是黑色消息。这时信源的平均不确定性减弱，所以信源消息之间有依赖时信源熵小于信源消息之间无依赖时的信源熵，这表明信源熵正是反映信源的平均不确定的大小。而信源剩余度正是反映信源消息依赖关系的强弱，剩余度越大，信源消息之间的依赖关系就越大。

水力学第二章课后习题答案

2.12 密闭容器，测压管液面高于容器内液面h =1.8m ，液体的密度为850kg/m 3，求液面压强。

解：08509.807 1.8a a p p gh p ρ=+=+⨯⨯相对压强为：15.00kPa 。

绝对压强为：116.33kPa 。

答：液面相对压强为15.00kPa ，绝对压强为116.33kPa 。

2.13 密闭容器，压力表的示值为4900N/m 2，压力表中心比A 点高0.4m ，A 点在水下1.5m ，，求水面压强。

解：0 1.1a p p p g ρ=+-5.888a p =-（kPa ）相对压强为： 5.888-kPa 。

绝对压强为：95.437kPa 。

答：水面相对压强为 5.888-kPa ，绝对压强为95.437kPa 。

解：（1）总压力：433353.052Z P A p g ρ=⋅=⨯⨯=（kN ）（2）支反力：()111333R W W W W g ρ==+=+⨯⨯+⨯⨯总水箱箱980728274.596W =+⨯=箱kN W +箱不同之原因：总压力位底面水压力与面积的乘积，为压力体g ρ⨯。

而支座反力与水体重量及箱体重力相平衡，而水体重量为水的实际体积g ρ⨯。

答：水箱底面上总压力是353.052kN ，4个支座的支座反力是274.596kN 。

2.14 盛满水的容器，顶口装有活塞A ，直径d =0.4m ，容器底的直径D =1.0m ，高h =1.8m ，如活塞上加力2520N （包括活塞自重），求容器底的压强和总压力。

解：（1）容器底的压强：225209807 1.837.7064D A p p gh dρπ=+=+⨯=（kPa ）（相对压强）（2）容器底的总压力：223137.7061029.61444D D D P Ap D p ππ==⋅=⨯⨯⨯=（kN ）答：容器底的压强为37.706kPa ，总压力为29.614kN 。

2.6用多管水银测压计测压，图中标高的单位为m ，试求水面的压强0p 。

第二章课后习题

第二章课后习题2.2：假设一副充分洗乱了的扑克牌（含52张牌），（1）任一特定排列所给出的信息量是多少？（2）若从中抽取13张牌，所给出的信息量是多少？解：（1）任一特定排列所给出的信息量为事件A ；52张扑克牌的排列方式有A 5252，则牌P ()a =!521；即任一特定的信息量是I a )(=-㏒52！；（2）若从中抽取13张则其概率为P=1352134C ; 即其信息量为a I =-㏒1352134C ; 2.3：居住某地区的女孩子有25%是大学生，在女大学生中有75%是身高160CM 一上的，而女孩子中身高160cm 以上的占总数的一半。

假如我们得知“身高160cm 以上的某女生是大学生”的消息，问获得多少信息量？解：设某地区的女孩子是大学生为A 事件：则)(A P =0.25; 女孩中身高160cm 以上的为B 事件：则)(B P =0.5;且P(B/A)=0.75，则P(A/B)=)()(B P AB P =)()/()(B P A B P A P ∙=0.375; 则已知该事件获得的信息量为:I=㏒0.375= 1.415比特。

2.4：设离散无记忆信源⎪⎪⎭⎫ ⎝⎛)(X P X =⎭⎬⎫⎩⎨⎧8/14/14/18/34321a a a a ，其发出的消息为（202120130213001203210110321010021032011223210），求（1）此消息的自信息量是多少？（2）在此消息中平均每个符号携带的信息量是多少？解：信源无记忆，所以各消息之间相互独立，根据已知条件发出个消息所包含的信息量分别为:I(00=a )=㏒38=1.415比特 I(11=a )=㏒4=2比特I(22=a )=㏒4=2比特I(33=a )=㏒8=3比特得“0”共有14个，“1”有13个，“2”有12个，“3”有6个；得到的消息为I=14×1. 415+13×2+12×2+6×3≈87.81比特；（2）每个符号携带的信息量：I=4581.87=1.95比特/符号。

第二章远期合约与期货合约课后习题及答案

第二章远期合约与期货合约复习思考题2.1.简述远期合约的构成要素及其与合约损益的关系。

2.2.简述远期合约做多和做空的含义。

2.3.什么是远期汇差？阐明远期汇率与即期汇率的关系。

2.4.什么是远期外汇综合协议（SAFE）？交易者在什么情况下会买入SAFE或卖出SAFE？2.5.请说明远期外汇综合协议和远期利率协议的区别和联系。

2.6.说明远期利率协议的特点。

交易者在什么情况下选择做FRA的多头（买方）和空头（卖方）。

2.7.什么是期货合约，其基本条款包括哪些？2.8.请说明期货交易和远期交易的差异。

2.9.请说明保证金和逐日结算制度是如何使期货交易者免于违约的。

2.10.期货市场的主要功能有哪些？2.11.实物交割和现金结算有什么主要区别？哪些期货合约适宜现金结算？2.12.阐述股指期货的交易特征。

2.13.期货交易的结清方式有哪些？2.14.对比分析退出期货交易和远期交易方式的差异，并分析其背后的原因。

2.15.一家公司签订一份空头期货合约，以每蒲式耳300美分卖出5000蒲式耳小麦。

初始保证金为3000美元，维持保证金为2000美元。

价格如何变化会导致保证金催付？在什么情况下，可以从保证金账户中提取1000美元？2.16.一个投资者买入了两份冷冻橙汁期货合约。

每份合约的合约规模为15000磅。

当前期货价格为每磅170美分；每份期货合约的初始保证金都为6000美元，维持保证金都为4500美元。

价格如何变化会导致保证金催付？在什么情况下，可以从保证金账户中提取1500美元？讨论题2.1.请讨论FXA和ERA在使用中的差异。

2.2.你认为如果在期货合约中没有指明标的物的质量，会发生什么情况？2.3.结合美国次贷危机的实际，分析场外衍生工具交易的优势和劣势。

2.4.请讨论期货结算所的作用。

复习思考题答案2.1.简述远期合约的构成要素及其与合约损益的关系。

答：远期合约包括以下基本构成要素：（1）标的资产。