Maple13入门教程
Maple 入门教程
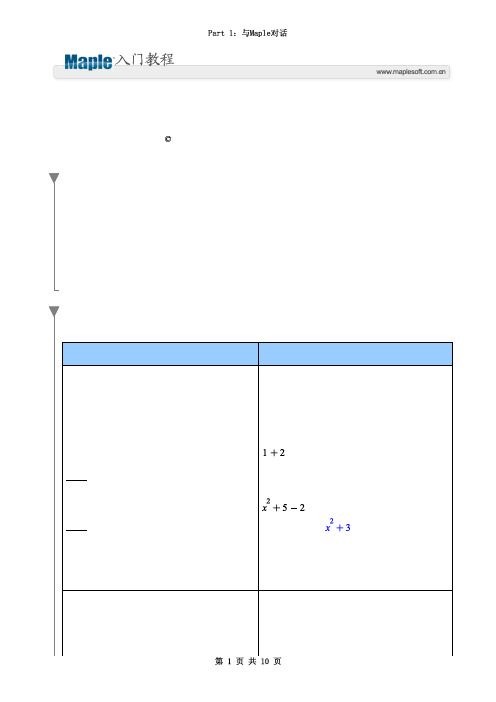
Quick Help Details
。求值多项式在 x = 10,求输出
Part 2:整合思想
西希安工程模拟软件(上海)有限公司,2008
2.0 介绍
第二部分:整合你的思想,你将学习使用一些基本工具创建出版文件,以及在文字中使用 排版数学。此外,你将使用Maple符号和数值求解方程,了解Maple中赋值语句、表达式、 函数之间的区别。
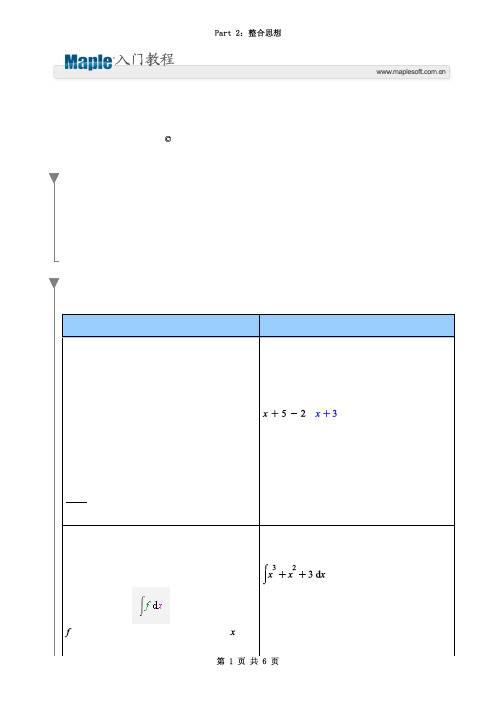
例子:键入 "x+5-2" 然后按 [Ctrl][=]。
组合文字和数学
例子: 1. 输入一个简单的计算。从表达式面板中
选择积分模板
。 用被积函数代替
。按 [Tab] 键移到下一个占位符,用 替 换。
2. 使用 [Ctrl][=] 积分计算。
3. 将光标放置在表达式的左边,切换到文
字模式
,或者按 [F5]
是一
例子:输入上面的方程(使用单引号作为 微分符号),为了验证它是一个微分方 程,从关联菜单中选择 Solve DE 求解。
标签 无论你何时使用【回车键】获得一个计算 结果,工作表将自动给出一个公式标签。 如果想引用前面的计算结果,使用 C t r l + L 并输入标签数字。
例子:将上面的结果 标签。
操作步骤
结果
求精确解和数值近似 Maple 计算精确结果,也就是说,分数计算 时保持分数形式,e 和 在整个计算过程中 保留为符号形式。这些将减少在多步计算 中由于近似产生的误差。
例子:在新的一行,输入 1/2 + 1/3。 我们注意到光标 / 自动移到分母的位置。按 回车键得到计算结果。
Maple也可以计算数值近似解。 例子:鼠标右击上面的结果表达式,选择 关联菜单的Approximate,精度位选择 5。
Maple入门教程Part2_整合思想
Part 2:整合思想
西希安工程模拟软件(上海)有限公司,2008
2.0 介绍
第二部分:整合你的思想,你将学习使用一些基本工具创建出版文件,以及在文字中使用排版数学。
此外,你将使用Maple符号和数值求解方程,了解Maple中赋值语句、表达式、函数之间的区别。
2.1 组合文字和数学
在Maple中,你可以在文件中任意组合文字和数学,创建专业的技术文件。
,重新计算。
提示:快捷键 【F5】用于切换数学/文字输入。
在数学模式下,光标显示为斜体,周围有虚线框。
在文字模式下,光标显示为垂直线。
2.2 求解方程
Maple 能够求方程和不等式中未知量的值。
用数学软件Maple做线性代数(2013.5.15)

用数学软件Maple做线性代数作者:徐小湛四川大学数学学院xuxzmail@目录前言第一章行列式行列式克拉默法则第二章矩阵及其运算矩阵的线性运算矩阵的乘法矩阵的转置逆矩阵矩阵方程第三章矩阵的初等变换与线性方程组矩阵的行最简形矩阵的秩齐次线性方程组基础解系非齐次线性方程组求通解用Solve求线性方程组的解第四章向量组的线性相关性向量的线性表示极大无关组第五章相似矩阵及二次型正交矩阵矩阵的特征值矩阵的特征向量矩阵的对角化二次型的标准化补充:向量参考文献前言Maple是著名的数学软件,具有强大的的数学运算能力和绘图功能。
本文档用Maple来进行线性代数中的各种运算。
本文档中所有的例子都是用Maple 8编程和计算的。
如有对本文档中的内容任何问题,请发邮件与作者讨论。
邮箱:xuxzmail@2012-5-11返回目录第一章 行列式行列式 det(A)例 计算三阶行列式124221342A -=---(同济5版,3页)输入:with(linalg):A:=matrix([[1,2,-4],[-2,2,1],[-3,4,-2]]);detA:=det(A);输出: := A ⎡⎣⎢⎢⎢⎢⎢⎤⎦⎥⎥⎥⎥⎥12-4-221-34-2:= detA -14例 计算四阶行列式3112513420111533A ---=---(同济5版,12页) 输入:with(linalg):A:=matrix([[3,1,-1,2],[-5,1,3,-4],[2,0,1,-1],[1,-5,3,-3]]);detA:=det(A);输出: := A ⎡⎣⎢⎢⎢⎢⎢⎢⎢⎤⎦⎥⎥⎥⎥⎥⎥⎥31-12-513-4201-11-53-3,:= d e t A 40例 求解方程211123049x x =(同济5版,3页)输入:with(linalg):A:=array([[1,1,1],[2,3,x],[4,9,x^2]]);solve(det(A)=0,x);输出:,32例 计算行列式2324323631063a b c da ab a bc a b cd a a b a b c a b c da ab a bc a b c d++++++++++++++++++(同济5版,13页)输入:with(linalg):A:=array([[a,b,c,d],[a,a+b,a+b+c,a+b+c+d],[a,2*a+b,3*a+2*b+c,4*a+3*b+2*c+d],[a,3*a+b,6*a+3*b+c,10*a+6*b+3*c+d]]); DetA:=det(A);输出: := A ⎡⎣⎢⎢⎢⎢⎢⎢⎢⎤⎦⎥⎥⎥⎥⎥⎥⎥a b c d a + a b + + a b c + + + a b c d a + 2a b + + 3a 2b c + + + 4a 3b 2c d a + 3a b + + 6a 3b c + + + 10a 6b 3c d ,,:= DetA a 4例 计算行列式000000000000000000000000a b a b a bc dc d c d (同济5版,15页)输入:with(linalg):A:=array([[a,0,0,0,0,b],[0,a,0,0,b,0],[0,0,a,b,0,0],[0,0,c,d,0,0],[0,c,0,0,d,0],[c,0,0,0,0,d]]);DetA:=det(A);输出: := A ⎡⎣⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎤⎦⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥a 0000b 0a 00b 000a b 0000c d 000c 00d 0c 0000d ,:= DetA () - d a b c 3 返回目录克拉默法则例 用克拉默法则解线性方程组:123412423412342583692254760x x x x x x x x x x x x x x +-+=⎧⎪--=⎪⎨-+=-⎪⎪+-+=⎩(同济5版,22页) 输入:with(linalg):A:=array([[2,1,-5,1],[1,-3,0,-6],[0,2,-1,2],[1,4,-7,6]]); b:=array([8,9,-5,0]);A1:=augment(b,col(A,2),col(A,3),col(A,4));A2:=augment(col(A,1),b,col(A,3),col(A,4));A3:=augment(col(A,1),col(A,2),b,col(A,4));A4:=augment(col(A,1),col(A,2),col(A,3),b);x1:=det(A1)/det(A);x2:=det(A2)/det(A);x3:=det(A3)/det(A);x4:=det(A4)/det(A);输出: := A ⎡⎣⎢⎢⎢⎢⎢⎢⎢⎤⎦⎥⎥⎥⎥⎥⎥⎥21-511-30-602-1214-76 := b [],,,89-50:= A1⎡⎣⎢⎢⎢⎢⎢⎢⎢⎤⎦⎥⎥⎥⎥⎥⎥⎥81-519-30-6-52-1204-76 := A2⎡⎣⎢⎢⎢⎢⎢⎢⎢⎤⎦⎥⎥⎥⎥⎥⎥⎥28-51190-60-5-1210-76:= A3⎡⎣⎢⎢⎢⎢⎢⎢⎢⎤⎦⎥⎥⎥⎥⎥⎥⎥21811-39-602-521406 :=A4⎡⎣⎢⎢⎢⎢⎢⎢⎢⎤⎦⎥⎥⎥⎥⎥⎥⎥21-581-30902-1-514-70方程组的解: := x13 := x2-4 := x3-1 := x41返回目录第二章 矩阵及其运算矩阵的线性运算 matadd(A,B) 或 evalm(A+B); k*B例 设352078A -⎛⎫= ⎪-⎝⎭,3912418B -⎛⎫= ⎪-⎝⎭,求A B +和43A B +输入:with(linalg):A:=array([[2,5,-2],[0,7,-8]]);B:=array([[-3,9,12],[-4,1,8]]);matadd(A,B);evalm(A+B);matadd(4*A,3*B);evalm(4*A+3*B);输出: := A ⎡⎣⎢⎢⎤⎦⎥⎥25-207-8 := B ⎡⎣⎢⎢⎤⎦⎥⎥-3912-418⎡⎣⎢⎢⎤⎦⎥⎥-11410-480 ⎡⎣⎢⎢⎤⎦⎥⎥-11410-480 ⎡⎣⎢⎢⎤⎦⎥⎥-14728-1231-8 ⎡⎣⎢⎢⎤⎦⎥⎥-14728-1231-8 返回目录矩阵的乘法 multiply(A,B) 或 evalm(A&*B)例 设10312102A -⎛⎫= ⎪⎝⎭,410113201134B ⎛⎫⎪- ⎪= ⎪ ⎪⎝⎭,求AB输入:with(linalg):A:=array([[1,0,3,-1],[2,1,0,2]]);B:=array([[4,1,0],[-1,1,3],[2,0,1],[1,3,4]]);AB:=multiply(A,B);AB:=evalm(A&*B);结果: := A ⎡⎣⎢⎢⎤⎦⎥⎥103-12102, := B ⎡⎣⎢⎢⎢⎢⎢⎢⎢⎤⎦⎥⎥⎥⎥⎥⎥⎥410-113201134,:= AB ⎡⎣⎢⎢⎤⎦⎥⎥9-2-19911 := AB ⎡⎣⎢⎢⎤⎦⎥⎥9-2-19911例 设2412A -⎛⎫= ⎪-⎝⎭,2436B ⎛⎫= ⎪--⎝⎭,求AB 和BA (同济5版,35页)输入:with(linalg):A:=array([[-2,4],[1,-2]]);B:=array([[2,4],[-3,-6]]);AB:=multiply(A,B);BA:=multiply(B,A);结果: := A ⎡⎣⎢⎢⎤⎦⎥⎥-241-2, := B ⎡⎣⎢⎢⎤⎦⎥⎥24-3-6, := AB ⎡⎣⎢⎢⎤⎦⎥⎥-16-32816, := BA ⎡⎣⎢⎢⎤⎦⎥⎥0000例 证明:cos sin cos sin sin cos sin cos n t t nt nt tt nt nt --⎛⎫⎛⎫= ⎪ ⎪⎝⎭⎝⎭(同济5版,38页) 解 取n=7输入 with(linalg):A:=array([[cos(t),-sin(t)],[sin(t),cos(t)]]);evalm(A^7);map(combine,%);结果: := A ⎡⎣⎢⎢⎤⎦⎥⎥()cos t -()sin t ()sin t ()cos t()- () - ()cos t 2()sin t 224()cos t 2()sin t 2[()- () - ()cos t 2()sin t 2()cos t 2()cos t ()sin t 24() - ()cos t 2()sin t 2()cos t ()sin t () + 2()cos t 2()sin t () - ()cos t 2()sin t 2()sin t - ,() - () - ()cos t 2()sin t 224()cos t 2()sin t 2()- - () - ()cos t 2()sin t 2()sin t 2()cos t 2()sin t 4() - ()cos t 2()sin t 2()cos t ()sin t () - () - ()cos t 2()sin t 2()cos t 2()cos t ()sin t 2 - ]4() - ()cos t 2()sin t 2()cos t ()sin t () - () - ()cos t 2()sin t 2()cos t 2()cos t ()sin t 2 + [()- () - ()cos t 2()sin t 224()cos t 2()sin t 2() + 2()cos t 2()sin t () - ()cos t 2()sin t 2()sin t ,4() - ()cos t 2()sin t 2()cos t ()sin t ()- - () - ()cos t 2()sin t 2()sin t 2()cos t 2()sin t + ()- () - ()cos t 2()sin t 224()cos t 2()sin t 2() - () - ()cos t 2()sin t 2()cos t 2()cos t ()sin t 2]化简的结果:⎡⎣⎢⎢⎤⎦⎥⎥()cos 7t -()sin 7t ()sin 7t ()cos 7t返回目录矩阵的转置 transpose(A)例 设120311A ⎛⎫= ⎪-⎝⎭,求其转置矩阵T A (同济5版,39页) 输入:with(linalg):A:=array([[1,2,0],[3,-1,1]]);B:=transpose(A);结果:原矩阵: := A ⎡⎣⎢⎢⎤⎦⎥⎥1203-11 转置矩阵: := B ⎡⎣⎢⎢⎢⎢⎢⎤⎦⎥⎥⎥⎥⎥132-101例 设201132A -⎛⎫= ⎪⎝⎭,171423201B -⎛⎫⎪= ⎪ ⎪⎝⎭,求()T AB ,并验证:()T T TAB B A= (同济5版,39页)输入with(linalg):A:=array([[2,0,-1],[1,3,2]]);B:=array([[1,7,-1],[4,2,3],[2,0,1]]); transpose(multiply(A,B));multiply(transpose(B),transpose(A)); 结果: := A ⎡⎣⎢⎢⎤⎦⎥⎥20-1132, := B ⎡⎣⎢⎢⎢⎢⎢⎤⎦⎥⎥⎥⎥⎥17-1423201⎡⎣⎢⎢⎢⎢⎢⎤⎦⎥⎥⎥⎥⎥0171413-310这是()T AB ⎡⎣⎢⎢⎢⎢⎢⎤⎦⎥⎥⎥⎥⎥0171413-310这是T TB A 可见:()T T T AB B A =返回目录逆矩阵 inverse(A) 或 evalm(A^(-1))例 设123221343A ⎛⎫⎪= ⎪ ⎪⎝⎭,求其逆矩阵1A -,并验证1AA E -=(单位矩阵) (同济5版,44页)输入:with(linalg):A:=array([[1,2,3],[2,2,1],[3,4,3]]);B:=inverse(A); C:=evalm(A^(-1)); AB:=multiply(A,B); CA:=multiply(C,A);结果: := A ⎡⎣⎢⎢⎢⎢⎢⎤⎦⎥⎥⎥⎥⎥123221343, 逆矩阵: := B ⎡⎣⎢⎢⎢⎢⎢⎢⎢⎤⎦⎥⎥⎥⎥⎥⎥⎥13-2-3-3511-1 := C ⎡⎣⎢⎢⎢⎢⎢⎢⎢⎤⎦⎥⎥⎥⎥⎥⎥⎥13-2-3-3511-1验证1AA E -=: := AB ⎡⎣⎢⎢⎢⎢⎢⎤⎦⎥⎥⎥⎥⎥10001001,:= CA ⎡⎣⎢⎢⎢⎢⎢⎤⎦⎥⎥⎥⎥⎥100010001 返回目录矩阵方程例 设123221343A ⎛⎫ ⎪= ⎪ ⎪⎝⎭,2153B ⎛⎫= ⎪⎝⎭,132031C ⎛⎫⎪= ⎪ ⎪⎝⎭,且AXB C =,求矩阵X (同济5版,45页)解 11AXB C X A CB --=⇒=输入with(linalg):A:=array([[1,2,3],[2,2,1],[3,4,3]]); B:=array([[2,1],[5,3]]);C:=array([[1,3],[2,0],[3,1]]);X:=multiply(inverse(A),C,inverse(B));结果: := A ⎡⎣⎢⎢⎢⎢⎢⎤⎦⎥⎥⎥⎥⎥123221343,:= B ⎡⎣⎢⎢⎤⎦⎥⎥2153, := C ⎡⎣⎢⎢⎢⎢⎢⎤⎦⎥⎥⎥⎥⎥132031, := X ⎡⎣⎢⎢⎢⎢⎢⎤⎦⎥⎥⎥⎥⎥-2110-4-104例 设213122132A -⎛⎫ ⎪=- ⎪ ⎪-⎝⎭,112025B -⎛⎫ ⎪= ⎪ ⎪-⎝⎭,求解矩阵方程AX B =(同济5版,65页) 解 1AX B X A B -=⇒=输入with(linalg):A:=array([[2,1,-3],[1,2,-2],[-1,3,2]]); B:=array([[1,-1],[2,0],[-2,5]]); X:=multiply(inverse(A),B);结果: := A ⎡⎣⎢⎢⎢⎢⎢⎤⎦⎥⎥⎥⎥⎥21-312-2-132, := B ⎡⎣⎢⎢⎢⎢⎢⎤⎦⎥⎥⎥⎥⎥1-120-25, := X ⎡⎣⎢⎢⎢⎢⎢⎤⎦⎥⎥⎥⎥⎥-4201-32 返回目录第三章 矩阵的初等变换与线性方程组矩阵的行最简形和标准型 阶梯形: gausselim(A)行最简形:gaussjord(A) 或 rref(A),例 设21112112144622436979B --⎛⎫⎪-⎪= ⎪--⎪-⎝⎭,求B 的阶梯形和秩(同济5版,59页) 输入:with(linalg):B:=array([[2,-1,-1,1,2],[1,1,-2,1,4],[4,-6,2,-2,4],[3,6,-9,7,9]]);GL:=gausselim(B);输出: := B ⎡⎣⎢⎢⎢⎢⎢⎢⎢⎤⎦⎥⎥⎥⎥⎥⎥⎥2-1-11211-2144-62-2436-979 阶梯形: := GL ⎡⎣⎢⎢⎢⎢⎢⎢⎢⎤⎦⎥⎥⎥⎥⎥⎥⎥2-1-1120-44-40000-1300000 阶梯形有一行全为零,矩阵的秩为3。
Maple13+入门教程

=
菜单有数百个命令,但只是跟对应表达式
相关的命令才会显示。
例:将鼠标放在最后的输出结果上,右击 鼠标右键。弹出的右键菜单将显示跟该表 达式相关的操作。为了求表达式的积分: Integrate x
=
integrate w.r.t. x
例:绘制积分结果的图形,在结果表达式 上鼠标右击,在弹出的右键菜单中选择: Plots > 2-D Plot.
(8.3)
例:输入一个几何,并赋值给变量名 .
常规操作 例:使用符号识别面板找到几何交集符
号,求
步骤
结果
定义方程
在Maple中,使用 = (等于号)定义等式。
例:求方程 "
"中x的
值,使用右键菜单 Solve > Solve for a
Variable.
求精确解
默认情况下,Maple显示方程的精确解。
例: 求方程 "
"中x的
值,使用 右键菜单Solve > Solve.
求数值解
如果您想求数值解,需要直接使用数值求
(6.6)
过程(程序) 一个函数实际上就是特殊的过程。
例: 右侧是一个简单的过程。 关于Maple 程序设计更多的内容见用户手册第八章。
提 示 :程序语句较长时,使用【S h i f t】+ 【ENTER】 在新的一行继续输入语句。
(6.7)
5
(6.8)
5 方程求解
Maple 能够求方程和不等式中未知量的值。
提示: 还有一个比较明显的提示是,当在文本(text)模式时,光标显示为竖线,而当在数 学(math)格式时,光标显示为斜线。
练习: 回到最后的练习,在多项式中添加文本说明,改变原多项式并更新计算结果。
maple入门

数的进制转换
convert 函数 binary二进制 decimal 十进制 octal 八进制 hex十六进制
小数划为分数运算
convert(x,rational) 将实数(有理数)x转换为 精确分数 convert(x,rational,n) 将实数(无理数)x转换 为分子与分母非零数码的个数和为n的分数
Maple入门 Maple入门
1.Maple概述 Maple概述
什么是Maple, 怎么学习Maple? Maple软件是加拿大Waterloo大学在1980年开始 开发,到现在最新的版本是Maple11, Maple具有强 大的数值计算能力,图形处理能力,特别是符号 计算能力. 常用的数学软件除Maple外,有Matlab等, 统计 软件: SAS,SPSS,运筹学软件:Lingo, WINQSB.
ifactor 求因子 iquo 求商 iquo(a,b,'r') irem 余数 irem(a,b,'q') isqrt 近似的平方跟整数
sqrt(x) 平方根函数 exp(x), ln(x) 指数函数和自然对数函数 log[b](x) 以b为底的对数函数 Abs(x) 绝对值函数 round(x) 最接近x的整数rand ()12位的随机数 Max(a,b,c,…),min(a,b,c,…) a, b, c, … 中的最 大(小)数 floor(x) 不大于x的最大整数 ceil(x) 不小于x的最小整数 trunc(x) x靠近0的整数部分 frac(x) x的分数部分(=x-trunc(x))signum(x)符号函数
1.5.1 fprintf
fprintf函数是用来输出到文件中,在使用该函数前,先用 fopen打开一个文件,再使用fprintf函数输出到fopen打开的文件 中,最后用fclose关闭文件. 格式:fopen(filename,mode); 其中,mode分为:WRITE和APPEND fprintf(fd,format,vars); 其中fd,为fopen打开的文件,format输出的格式,vars为变量组 fclose(fd); 演示
Maple基础教程

目录第二章MAPLE基础 (1)2.1与M APLE对话 (1)2.2使用命令和函数包 (18)2.3微积分 (23)2.4线性代数 (28)2.5微分方程 (35)2.6优化 (45)2.7动态系统 (53)2.8基础编程知识 (58)2.9M APLE使用中常犯的错误 (78)第二章Maple基础Maple是目前应用非常广泛的科学计算软件之一,具有非常强大的符号计算和数值计算功能。
Maple 提供智能界面求解复杂数学问题和创建技术文件,用户可在易于使用的智能文件环境中完成科学计算、建模仿真、可视化、程序设计、技术文件生成、报告演示等,从简单的数字计算到高度复杂的系统,满足各个层次用户的需要。
与传统工程软件不同,甚至有别于旧版本的Maple,新版本Maple为工程师提供了大量的专业计算功能,庞大的数学求解器可用于各种工程领域,如微分方程、矩阵、各种变换包括FFT、统计、小波、等等,超过5000个计算命令让用户通常只需要一个函数就可以完成复杂的分析任务。
本章主要介绍Maple的基本功能,包括:数值和符号计算计算、求解方程、微积分计算、向量及矩阵计算、微分方程求解等。
Maple是一个全面的系统,提供多种方式完成同一个任务。
在本章中,我们将通过简单、易于重复的方式求解常见的问题,但它不是唯一的操作方式。
当用户熟悉本章中的各种操作方式后,用户可以通过帮助系统了解如何使用相似的技术完成各种任务。
2.1 与Maple对话2.1.1 Maple环境Maple的用户界面是一个典型的Windows或Mac风格的操作环境。
工作环境界面如图2-1所示。
图2-1:Maple工作界面在图2-1的工作界面中,窗体的主要部分包括:●主文档,即主工作区。
事实上,用户大可以把它想象成包含有各种数学和绘图工具的Microsoft Word。
●面板区。
汇集了数学工具和特殊的数学符号,用户可以将它们直接拖拽到工作区中使用。
面板区中最重要的面板当属Expressions,Matrix,Common Symbols和Greek。
Maple13数学实验初级篇

>restart; #restart - clear internal memory > f:=int(exp(x^3),x=0..1); evalf(f); evalf(cos(1)+sin(1)I); >Product(k^3,k=1..4): value(%); #value - evaluate inert functions
SDAU
2.2.2 函数值运算
定义表达式 f:=数 或 表达式; #后赋值将替换以前的赋值, 加单引号表示符号变量 >f:=x^2; eval(f,x=3); #定义表达式并计算器在x=3处的值 右键点击输入f 后的蓝色结果 x2 可以从事多种运算! 定义函数 f:=x->x的表达式; >f:=x->x^2; f(3); #定义函数f(x)并计算其在x=3处的值 >G:=(a,b)->a^2-b^3; G(3,2); #定义多变量函数并求函数值 右键点击输入f 后的蓝色结果 x→x2 可以从事多种运算! >y:=x->piecewise(x<=1,sin(Pi*x/2),x>1,log(x)); # 定义分段函 数 y= log x (x>1), sin(x/2) (x≤1) >y:=s^2-5*s+3; z:=s^2-5*t+3; 表达式运算 >y*z+3;
常用数学常数
数学常数 I Pi False, true Catalan Infinity Fall
Gamma
意义 虚数单位 圆周率 逻辑表达式的值 Catalan常数,值为0.9159… 无穷大 表示不确定的数或操作失败
Euler 常数,值为0.577215…
MAPLE讲稿

快 速 进 入
Maple
Jan,8, 2004
毕业指导培训
M1-9
第一讲 MAPLE简介
Maple
小结:
本章仅就Maple 的基本功能作一个简短的解说, Maple的操 作界面尚有许多功能,例如,可以加入试算表,可以将文件存成 HTML格式等.限于时间的关系,本次培训不一一介绍.如果需要更 详细的说明,你可以从 Maple在线帮助系统里的Worksheet interface中查询. 当然,你也可以到 Maple 加拿大总公司的网站逛逛,收集最 新的资料,其网址为:
快 速 进 入
Maple
Jan,8, 2004
毕业指导培训
M1-10
第二讲 数值计算
2.1Maple 简介
数值运算可概括地分为精确与近似值运算.
2.1.1数值运算 一. 精确运算
通常我们把整数称为精确数,因为它不带任何小数.其它诸如3/4, sin2等数也叫精 确数.数值运算的结果为一个精确数,则称此运算为精确运算. > 1+3/7; 的结果为10/7,不是将它化为小数(1.42857142…)
Jan,8, 2004
快 速 进 入
Maple
毕业指导培训
M1-11
第二讲 数值计算
2.2 Maple 的基本运算
基本指令(一)
factorial(n)或n! irem(m,n) iquo(m,n)
基本指令(二)
计算n的阶乘 计算m/n的整数余数,其中m,n必须为整数 计算m/n的整数商,其中m,n必须为整数
快 速 进 入
Maple
Jan,8, 2004
毕业指导培训
M1-12
n e
第二讲 数值计算
Maple基础教程(修订稿).

Maple 基础一Maple 的基本运算1 数值计算问题在应用Maple 做算术运算时, 只需将Maple 当作一个“计算器”使用, 所不同的是命令结束时需加“;”或“:”.在Maple 中, 主要的算术运算符有“+”(加)、“–”(减)、“*”(乘)、“/”(除)以及“^”(乘方或幂,或记为**),值得注意的是, “^”的表达式只能有两个操作数, 换言之, c b a ^^是错误的, 而“+”或“*”的任意表达式可以有两个或者两个以上的操作数.2.1.1 有理数运算作为一个符号代数系统, Maple 可以绝对避免算术运算的舍入误差.如果要求出两个整数运算的近似值时, 只需在任意一个整数后加“.”(或“.0”), 或者利用“evalf ”命令把表达式转换成浮点形式, 默认浮点数位是10 (即: Digits:=10, 据此可任意改变浮点数位, 如Digits:=20).> 123456789/987654321;13717421109739369> evalf(%); .1249999989> big_number:=3^(3^3);:= big_number 7625597484987> length(%);13函数“length ”作用在整数上时是整数的十进制位数即数字的长度. “%”是一个非常有用的简写形式, 表示最后一次执行结果1)整数的余(irem)/商(iquo)命令格式:irem(m,n); #求m 除以n 的余数irem(m,n,'q'); #求m 除以n 的余数, 并将商赋给qiquo(m,n); #求m 除以n 的商数iquo(m,n,'r'); #求m 除以n 的商数, 并将余数赋给r其中, m, n 是整数或整数函数, 也可以是代数值, 此时, irem 保留为未求值.2)素数判别(isprime)命令格式: isprime(n);如果判定n 可分解, 则返回false, 如果返回true, 则n “很可能”是素数. > isprime(2^(2^4)+1);true3) 确定第i 个素数(ithprime)若记第1个素数为2,判断第i 个素数的命令格式: ithprime(i);4) 一组数的最大值(max)/最小值(min)命令格式: max(x1,x2,…,xn); #求x 1,x 2,…,x n 中的最大值min(x1,x2,…,xn); #求x 1,x 2,…,x n 中的最小值5)随机数生成器(rand)命令格式:rand( ); #随机返回一个12位数字的非负整数rand(a..b); #调用rand(a..b)返回一个程序, 它在调用时生成一个在范围[a, b]内的随机数> rand();427419669081> myproc:=rand(1..2002):> myproc();1916> myproc();1204注意, rand(n)是rand(0..n-1)的简写形式.2.1.2 复数运算复数是Maple中的基本数据类型. 虚数单位i在Maple中用I表示可以用Re( )、Im( )、conjugate( )和argument( )等函数分别计算实数的实部、虚部、共轭复数和幅角主值等运算. 试作如下实验:> complex_number:=(1+2*I)*(3+4*I);-510Icomplex_number +:=> Re(%);Im(%%);conjugate(%%%);argument(complex_number);-510-510I-- +arctan2π()1) 绝对值函数命令格式: abs(expr);当expr为实数时,返回其绝对值,当expr为复数时,返回复数的模.2)复数的幅角函数命令格式: argument(x); #返回复数x的幅角的主值3)共轭复数命令格式: conjugate(x); #返回x的共轭复数2.2 初等数学2.2.1 常用函数1) 确定乘积和不确定乘积命令格式: product(f,k);product(f,k=m..n);product(f,k=alpha);product(f,k=expr);其中, f—任意表达式, k—乘积指数名称, m,n—整数或任意表达式, alpha—代数数RootOf, expr—包含k的任意表达式.> product(k^2,k=1..10); #计算2k关于1..10的连乘13168189440000> product(k^2,k); #计算2k的不确定乘积()Γk 2> product(a[k],k=0..5); #计算a i (i=0..5)的连乘a 0a 1a 2a 3a 4a 5> Product(n+k,k=0..m)=product(n+k,k=0..m); #计算(n+k)的连乘, 并写出其惰性表达式= ∏ = k 0m() + n k ()Γ + + n m 1()Γn> product(k,k=RootOf(x^3-2)); #计算23-x 的三个根的乘积22)指数函数计算指数函数exp 关于x 的表达式的命令格式为: exp(x);3)确定求和与不确定求和sum命令格式: sum(f,k);sum(f,k=m..n);sum(f,k=alpha);sum(f,k=expr);其中, f —任意表达式, k —乘积指数名称, m,n —整数或任意表达式, alpha —代数数RootOf,expr —不含k 的表达式.> Sum(k^2,k=1..n)=sum(k^2,k=1..n);= ∑ = k 1nk 2 - + + 13() + n 1312() + n 1216n 16> Sum(1/k!,k=0..infinity)=sum(1/k!,k=0..infinity);= ∑ = k 0∞1!k e> sum(a[k]*x[k],k=0..n);∑ = k 0n a k xk> sum(k/(k+1),k=RootOf(x^2-3));33)三角函数/双曲函数命令格式: sin(x); cos(x); tan(x); cot(x); sec(x); csc(x);sinh(x); cosh(x); tanh(x); coth(x); sech(x); csch(x);其中, x 为任意表达式.> Sin(Pi)=sin(Pi);= ()Sin π04)反三角函数/反双曲函数命令格式: arcsin(x); arccos(x); arctan(x); arccot(x); arcsec(x); arccsc(x);arcsinh(x); arccosh(x); arctanh(x); arccoth(x); arcsech(x); arccsch(x);arctan(y,x);其中, x, y 为表达式. 反三角函数/反双曲函数的参数必须按弧度计算.> arcsinh(1);()ln + 12> cos(arcsin(x));- 1x 25)对数函数命令格式: ln(x); #自然对数log[a](x); #一般对数log10(x); #常用对数一般地, 在ln(x)中要求x>0. 但对于复数型表达式x, 有:)(argument *))(abs ln()ln(x I x x += (其中, ππ≤<-)(argument x )> log10(1000000);()ln 1000000()ln 10 > simplify(%); #化简上式62.2.2 函数的定义试看下面一个例子:> f(x):=a*x^2+b*x+c;---并不是函数,而是一个表达式:= ()f x + + a x 2b x c> f(x),f(0),f(1/a);,, + + a x 2b x c ()f 0⎛⎝ ⎫⎭⎪⎪f 1a 由上述结果可以看出, 用赋值方法定义的f(x)是一个表达式而不是一个函数在Maple 中, 要真正完成一个函数的定义, 需要用算子(也称箭头操作符):> f:=x->a*x^2+b*x+c;:= f → x + + a x 2b x c> f(x),f(0),f(1/a);,,+ + a x 2b x c c + + 1a b ac > f:=(x,y)->x^2+y^2; := f → (),x y + x 2y 2> f(1,2);5> f:=(x,y)->a*x*y*exp(x^2+y^2);:= f → (),x y a x y e() + x 2y 2另一个定义函数的命令是unapply,其作用是从一个表达式建立一个算子或函数.命令格式为: f:=unapply(expr, x);命令格式为: f:=unapply(expr, x, y, …);> f:=unapply(x^4+x^3+x^2+x+1,x);:= f → x + + + + x 4x 3x 2x 1借助函数piecewise 可以生成简单分段函数:> abs(x)=piecewise(x>0,x,x=0,0,x<0,-x); = x ⎧⎩⎪⎪⎪⎪⎪⎨x < 0x 0 = x 0-x < x 0清除函数的定义用命令unassign.> unassign(f);> f(1,1); ()f ,11定义了一个函数后, 就可以使用op 或nops 指令查看有关函数中操作数的信息. nops(expr), 函数op 的主要功能是,其命令格式为:op(expr); #获取表达式的操作数op(i, expr); #取出expr 里第i 个操作数,op(i .. j, expr); #expr 的第i 到第j 个操作数nops(expr); #返回操作数的个数> expr:=6+cos(x)+sin(x)*cos(x)^2;:= expr + + 6()cos x ()sin x ()cos x 2> op(expr);,,6()cos x ()sin x ()cos x 2> nops(expr);32.2.3 Maple 中的常量与变量名为了解决数学问题, 一些常用的数学常数是必要的. Maple 系统中已经存储了一些数学常数在表达式序列constants 中:> constants;,,,,,,false γ∞true Catalan FAIL π为了方便使用, 现将上述常数的具体含义列示如下:2.2.4 函数类型转换实现函数类型转换的命令是convert . 命令格式:convert(expr, form); #把数学式expr 转换成form 的形式convert(expr, form, x); #指定变量x, 此时form 只适于exp 、sin 、cosconvert 指令所提供的三角函数、指数与函数的转换共有exp 等7种:(1) exp : 将三角函数转换成指数(2) expln : 把数学式转换成指数与对数(3) expsincos : 分别把三角函数与双曲函数转换成sin 、cos 与指数的形式(4) ln : 将反三角函数转换成对数(5) sincos : 将三角函数转换成sin 与cos 的形式, 而把双曲函数转换成sinh 与cosh 的形式(6) tan : 将三角函数转换成tan 的形式(7) trig : 将指数函数转换成三角函数与对数函数> convert(sinh(x),exp); #将sinh(x)转换成exp 类型 - 12e x 121ex 2.2.5 函数的映射—map 指令在符号运算的世界里, 映射指令map 可以说是相当重要的一个指令, 它可以把函数或指令映射到这些结构里的元素, 而不破坏整个结构的完整性. 命令格式为:map(f, expr); #将函数f 映射到expr 的每个操作数map(f, expr, a); #将函数f 映射到expr 的每个操作数, 并取出a 为f 的第2个自变量map(f, expr, a1, a2,…, an); #将函数f 映射到expr 的每个操作数, 并取a1~an 为f 的第2~n+1个自变量map2(f, a1, expr, a2, …, an); #以a1为第1个自变量, expr 的操作数为第2个自变量, a2为第3个自变量…, an 为第n+1个自变量来映射函数f> f:=x->sqrt(x)+x^2;:= f → x + x x 2> map(f,[a,b,c]); [],, + a a 2 + b b 2 + c c 2> map(h, [a,b,c],x,y);[],,()h ,,a x y ()h ,,b x y ()h ,,c x y3 求 值3.1 赋值在Maple 中, 不需要申明变量的类型, 甚至在使用变量前不需要将它赋值, 这是Maple 与其它高级程序设计语言不同的一点, 也正是Maple 符号演算的魅力所在, 这个特性是由Maple 与众不同的赋值方法决定的. 为了理解其赋值机制, 先看下面的例子.> p:=9*x^3-37*x^2+47*x-19;:= p - + - 9x 337x 247x 19> roots(p);⎡⎣⎢⎢⎤⎦⎥⎥,[],12⎡⎣⎢⎢⎤⎦⎥⎥,1991> subs(x=19/9,p);3.2 变量代换subs ( var = repacedment , expression );调用的结果是将表达式expression 中所有变量var 出现的地方替换成 replacement.> f:=x^2+exp(x^3)-8;:= f + - x 2e()x 38> subs(x=1,f); - + 7e如果需要计算, 必须调用求值函数evalf . 如:> evalf(%);5.> subs(x=y,y=z,x^2*y); (顺序替换)z 3> subs({x=y,y=z},x^2*y); (同步替换)y 2z> subs((a=b,b=c,c=a),a+2*b+3*c); (顺序替换)6a> subs({a=b,b=c,c=a},a+2*b+3*c); (轮 换)+ + b 2c 3a> subs({p=q,q=p},f(p,q)); (互 换)()f ,q p3.3 求值规则1) 对表达式求值命令格式: eval(e, x=a); #求表达式e 在x=a 处的值eval(e, eqns); #对方程或方程组eqns 求值eval(e); #表达式e 求值到上面两层eval(x,n); #给出求值名称的第n 层求值> p:=x^5+x^4+x^3+x^2+x+73;:= p + + + + + x 5x 4x 3x 2x 73> eval(p,x=7);19680当表达式在异常点处求值时, eval 会给一个错误消息. 如下:> eval(sin(x)/x,x=0);Error, numeric exception: division by zero2) 在代数数(或者函数)域求值命令格式: evala(expr); # 对表达式或者未求值函数求值evala(expr,opts); #求值时可加选项(opts)在Maple 中, 代数数用函数RootOf ()来表示. 如3作为一个代数数, 可以表示为:> alpha:=RootOf(x^2-3,x);:= α()RootOf - _Z 23> simplify(alpha^2);3在Maple 内部, 代数数α不再表示为根式, 而在化简时, 仅仅利用到32=α这样的事实. 这里, Maple 用到一个内部变量_Z. 再看下面一个例子,其中alias 是缩写的定义函数,而参数lenstra 指lenstra 椭圆曲线方法:> alias(alpha=RootOf(x^2-2)):> evala(factor(x^2-2,alpha),lenstra); () + x α() - x α> evala(quo(x^2-x+3,x-alpha,x,'r'));- + + 1αx> r;- + 3αα2> simplify(%);- 5α3) 在复数域上符号求值操纵复数型表达式并将其分离给出expr 的实部和虚部的函数为evalc, 命令格式为:evalc(expr);evalc 假定所有变量表示数值, 且实数变量的函数是实数类型. 其输出规范形式为: expr1+I*expr2. > evalc(sin(6+8*I));+ ()sin 6()cosh 8I ()cos 6()sinh 8> evalc(f(exp(alpha+x*I)));()f + e α()cos x I e α()sin x4) 使用浮点算法求值命令格式为: evalf(expr, n);> evalf(Pi,50);3.1415926535897932384626433832795028841971693993751> evalf(sin(3+4*I)); - 3.853********.01681326I5) 对惰性函数求值把只用表达式表示而暂不求值的函数称为惰性函数,对任意代数表达式f 求值的命令格式为: value(f); > F:=Int(exp(x),x);:= F d ⎛⎠⎜e x x > value(%);e x> f:=Limit(sin(x)/x,x=0);:= f lim→ x 0()sin x x> value(%); 1另外, 将惰性函数的大写字母改为小写字母亦即可求值. 如下例:> Limit(sin(x)/x,x=0)=limit(sin(x)/x,x=0);= lim → x 0()sin x x1 4 数据结构Maple 中有许多内建的与FORTRAN 、C 或Pascal 不同的数据结构. 主要的数据结构有序列(sequence)、列表(list)、集合(set)、代数数( algebraic number)、未求值或惰性函数调用、表(table)、级数(series)、串(string)、索引名(index)、关系(relation)、过程体(process)以及整数(integer)、分数(fraction)、浮点数(float)、复数(complex number)等数据结构, 而矩阵(matrix)在Maple 中表示为阵列, 是一种特殊的表.4.1 数据类型查询在Maple 中, 用whattype 指令来查询某个变量的数据类型或特定类型, 命令格式为:whattype(expr) # 查询expr 的数据类型type(expr, t) # 查询expr 是否为t 类型, 若是则返回true, 否则返回false4.2 序列, 列表和集合4.2.1 序列所谓序列(Sequence), 就是一组用逗号隔开的表达式列. 如:> s:=1,4,9,16,25;:= s ,,,,1491625> t:=sin,com,tan,cot;:= t ,,,sin com tan cot一个序列也可以由若干个序列复合而成, 如:> s:=1,(4,9,16),25;:= s ,,,,1491625> s,s;,,,,,,,,,14916251491625而符号NULL 表示一个空序列. 序列有很多用途, 如构成列表、集合等. 事实上, 有些函数命令也是由序列构成. 例如:> max(s);25> min(s,0,s);函数seq 是最有用的生成序列的命令, 通常用于写出具有一定规律的序列的通项, 命令格式为: seq(f(i), i=m..n); # 生成序列f(m), f(m+1), …, f(n) (m,n 为任意有理数)seq(f(i), i=expr); # 生成一个f 映射expr 操作数的序列seq(f(op(i,expr)), i=1..nops(expr)); # 生成nops(expr)个元素组成的序列> seq(i^2,i=1..10);149162536496481100,,,,,,,,,> seq(i^3,i=x+y+z);x3y3z3,,获得一个序列中的特定元素选用操作符[ ], 如:> seq(ithprime(i),i=1..20);235711131719232931374143475359616771,,,,,,,,,,,,,,,,,,,> %[6],%[17];1359,4.2.2 列表列表(list), 就是把对象(元素)放在一起的一种数据结构, 一般地, 用方括号[ ]表示列表. 如下例: > l:=[x,1,1-z,x];x1 -1z x,,,:=l[]> whattype(%);list4.2.3 集合集合(set)也是把对象(元素)放在一起的数据结构,一般地, 用花括号表示集合.> s:={x,1,1-z,x};1z1x -,,s{}:=> whattype(%);set空集定义为{ }.Maple中集合的基本运算有交(intersect)、并(union)、差(minus):> A:={seq(i^3,i=1..10)};B:={seq(i^2,i=1..10)};,,,,,,,,,1827641252163435127291000A{}:=149162536496481100,,,,,,,,,B{}:=> A intersect B;,164{}4.3 数组和表在Maple中, 数组(array)由命令array产生, 其下标变量(index)可以自由指定. 下标由1开始的一维数组称为向量(vector), 二维以上的数组称为矩阵(matrix). 数组的元素按顺序排列, 任意存取一数组的元素要比列表或序列快的多. 区分一个数据结构是数组还是列表要用“type”命令.表(table)在建立时使用圆括号, 变量能对一个表赋值, 但一个在存取在算子中的未赋值变量会被自动地假定是表, 表的索引可以成为任意Maple表达式. 表中元素的次序不是固定的.5 Maple 高级输入与输出操作生成LATEXMaple 可以把它的表达式转换成LATEX, 使用latex 命令即可: > latex(x^2+y^2=z^2);{x}^{2}+{y}^{2}={z}^{2}还可以将转换结果存为一个文件(LatexFile):> latex(x^2 + y^2 = z^2, LatexFile);再如下例:> latex(Int(1/(x^2+1),x)=int(1/(x^2+1),x));\int \! \left( {x}^{2}+1 \right) ^{-1}{dx}=\arctan\left( x \right)二 微积分运算1 函数的极限和连续1.1 函数和表达式的极限)(lim x f ax →命令格式为: limit(f,x=a);求)(lim x f a x +→时的命令格式为limit(f, x=a, right); 求)(lim x f ax -→时的命令格式为limit(f, x=a, left); 请看下述例子:> Limit((1+1/x)^x,x=infinity)=limit((1+1/x)^x,x=infinity);= lim → x ∞⎛⎝ ⎫⎭⎪⎪ + 11x xe > Limit((x^n-1)/(x-1),x=1)=limit((x^n-1)/(x-1),x=1);= lim → x 1 - x n 1 - x 1n > Limit(x^x,x=0,right)=limit(x^x,x=0,right);= lim → +x 0x x 1> limit(a*x*y-b/(x*y),{x=1,y=1});- a b> limit(x^2*(1+x)-y^2*((1-y))/(x^2+y^2),{x=0,y=0});undefined下例就是化二重极限为二次极限而得正确结果:> limit((sin(x+y)/(sin(x)*sin(y)),{x=Pi/4,y=Pi/4}));⎛⎝ ⎫⎭⎪⎪limit ,()sin + x y ()sin x ()sin y {}, = x 14π = y 14π > limit(limit(sin(x+y)/(sin(x)*sin(y)),x=Pi/4),y=Pi/4);21.2 函数的连续性1.2.1 连续在Maple 中可以用函数iscont 来判断一个函数或者表达式在区间上的连续性. 命令格式为: iscont(expr, x=a..b, 'colsed '/'opened');其中, closed 表示闭区间, 而opened 表示开区间(此为系统默认状态).如果表达式在区间上连续, iscont 返回true, 否则返回false, 当iscont 无法确定连续性时返回FAIL. 另外, iscont 函数假定表达式中的所有符号都是实数型. 颇为有趣的是, 当给定区间[a,b ] (a >b )时, iscont 会自动按[b,a ]处理.> iscont(1/x,x=1..2);true> iscont(1/x,x=-1..1,closed);false> iscont(1/(x+a),x=0..1);FAIL> iscont(ln(x),x=10..1);true1.2.2 间断函数discont 可以寻找函数或表达式在实数域的间断点, 当间断点周期或成对出现时, Maple 会利用一些辅助变量予以表达, 比如, _Zn ~(任意整数)、_NZn ~(任意自然数)和Bn ~(一个二进制数, 0或者1), 其中n 是序号. 判定f(x)间断点的命令为:discont(f, x);> discont(ln(x^2-4),x);{},-22> discont(arctan(1/2*tan(2*x))/(x^2-1),x);{},,-11 + 12π_Z1~14π> discont(round(3*x-1/2),x);{} + 1313_Z1 函数round 为“四舍五入”函数,上例并非一目了然,对其进一步理解可借助于函数plot 或下面给出的fdiscont 例子。
Maple入门教程Part1_与Maple对话
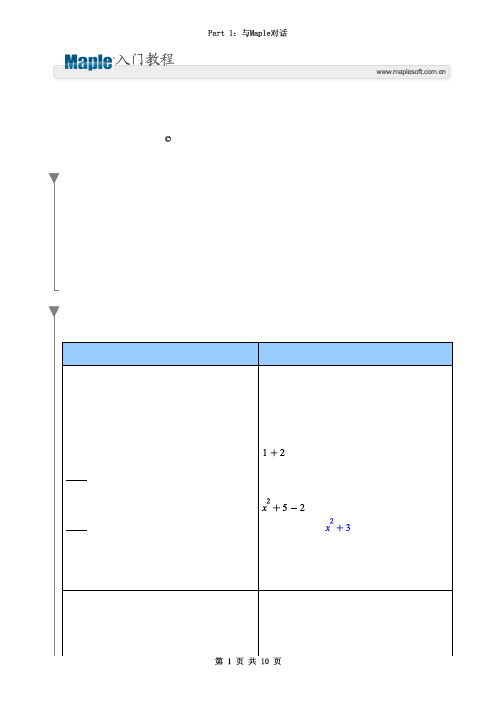
Part 1: 与Maple对话
西希安工程模拟软件(上海)有限公司,2008
1.0 介绍
第一部分:与Maple对话,熟悉Maple的环境。
你将学习如何使用关联菜单和面板完成分析,创建交互式图形,所有的操作无需你了解Maple命令。
为了获得更好的学习效果,请打开一个空白Maple文件。
按照表格左侧中的操作步骤描述,在表格右侧空白处完成操作。
1.1 如何开始
在这段落中,你将学习如何使用Maple计算一些基本问题并获得结果。
,所选的
提示: 如何找到计算机系统下的快捷键,点击菜单 帮助 > 快速帮助,并选择 切换文本/数学。
求导表达式 并画出结果的图形。
创建一个包含变量 x 和 y 的多项式,例如。
求值多项式在 x = 10,求输出结果关于变量的积分。
相关帮助
Quick Help Details。
Maple13提高教程 傅里叶变换
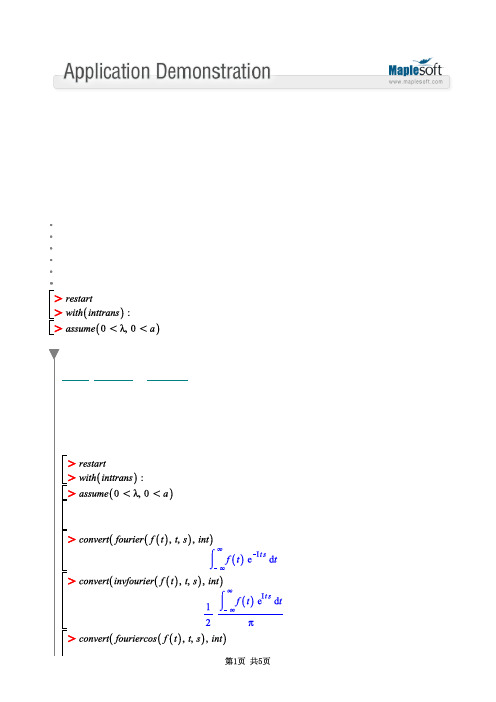
(1.1)(1.3)(1.2)傅立叶变换 (inttrans Package)西希安工程模拟软件(上海)有限公司,2009工作环境:Maple 13内容:介绍代数、指数、对数、三角、反三角、双曲函数菲涅耳正弦和余弦积分指数、正弦、余弦积分误差函数贝塞尔和修正贝塞尔函数介绍fourier , fouriersin ,和 fouriercos 变换是积分变换中特别有趣和有用的范例。
傅立叶变换有许多良好的属性,在物理学、数论、组合数学、信号处理、统计、密码学、声学、光学等工程科学中非常有用。
fouriersin 和 fouriercos 变换可以应用在实序列的频谱分析、求解某些边界值问题、以及数字信号的变换域处理。
与傅立叶对应的是傅立叶逆变换(inverse fourier transform)。
(2.8)(2.9)(2.3)(2.4)(2.6)(2.5)(1.3)(1.4)(2.2)(2.1)(2.7)代数、指数、对数、三角、反三角、双曲函数(2.14)(2.18)(2.13)(2.16)(2.11)(2.12)(2.17)(2.10)(2.15)(4.2)(4.1)(2.20)(3.1)(3.2)(2.19)菲涅耳正弦和余弦积分指数、正弦、余弦积分误差函数(6.2)(5.2)(6.3)(6.1)(5.1)贝塞尔和修正贝塞尔函数。
maple_chap13

299张量分析 第十章 本章将主要围绕Maple 的张量分析工具包,向大家介绍如何用Maple 解决数学、力学和理论物理中的张量分析问题。
将主要介绍Maple 的张量分析工具包中常用的张量运算函数。
本章具体包括以下内容:张量数据类型张量的输入输出张量的代数运算张量的导数坐标变换三自从爱因斯坦1915年发表著名的广义相对论以来,张量分析一直在理论物理领域起着无可替代的重要作用。
而张量分析在物理学中的应用,又反过来推动着张量分析本身的发展。
近几十年来,张量分析更是被广泛地应用到力学和数学的各个方面。
介于张量分析的广泛应用,Maple中也加入了张量分析软件包tensor,本章将就这个软件包,介绍应用Maple解决张量分析问题或者辅助张量分析研究的方法。
13.1 张量数据类型13.1.1张量数据类型及其建立Maple中的张量分析软件包tensor中包含张量运算的各种常用函数,它们所使用的数据类型也是一个专门的类型——tensor_type。
从一般意义的复合数据类型上讲,tensor_type是一个映射表,它包含有两个域,其一是分量域——compts,用来存储张量的各个分量;其二是指标域——index_char,用来指明对应的指标是协变指标(covariant index)或是逆变指标(contravariant index)。
举例来说,一个n阶张量,它的分量域必须是一个n维数组,而且必须是一个“方”的数组,就是说数组的每一维的分量个数必须相同。
实际上,数组每一维的分量个数就是该张量所在空间的维数。
而它的指标域则必须是一个长度为n的一维数组,数组中的元素不是1就是– 1。
如果第i个位置上是1,就表示张量的第i个指标是逆变指标;反之,则为协变指标。
例如,一个4阶张量的指标域是[-1, 1, 1, -1],这就表示张量的第2个和第3个指标是逆变指标(写成上指标),而第1个和第4个指标是协变指标(写成下指标)。
01-Maple基础和实践教程

Maple基础和实践教程Maple基础和实践教程Maple是应用最为广泛的科学计算软件之一,具有非常强大的符号计算和数值计算功能。
Maple 提供智能界面求解复杂数学问题和创建技术文件,用户可在易于使用的智能文件环境中完成科学计算、建模仿真、可视化、程序设计、技术文件生成、报告演示等,从简单的数字计算到高度复杂的系统,满足各个层次用户的需要。
与传统工程软件不同,甚至有别于旧版本的Maple,新版本Maple 为工程师提供了大量的专业计算功能,庞大的数学求解器可用于各种工程领域,如微分方程、矩阵、各种变换包括FFT、统计、小波、等等,超过5,000个计算命令让用户通常只需要一个函数就可以完成复杂的分析任务。
本章主要介绍Maple的基本功能,包括:数值和符号计算计算、求解方程、微积分计算、向量及矩阵计算、微分方程求解等。
Maple是一个全面的系统,提供多种方式完成同一个任务。
在本章中,我们将通过简单、易于重复的方式求解常见的问题,但它不是唯一的操作方式。
当用户熟悉本章中的各种操作方式后,用户可以通过帮助系统了解如何使用相似的技术完成各种任务。
Maple环境Maple的用户界面是一个典型的Windows或Mac风格的操作环境。
工作环境界面如图2-1所示。
图2-1:Maple工作界面在图2-1的工作界面中,窗体的主要部分包括:●主文档,即主工作区。
事实上,用户大可以把它想象成包含有各种数学和绘图工具的Microsoft Word。
●面板区。
汇集了数学工具和特殊的数学符号,用户可以将它们直接拖拽到工作区中使用。
面板区中最重要的面板当属Expressions,Matrix,Common Symbols和Greek。
Maple提供了总共约30个面板,用户可以在面板区空白处单击鼠标右键,并单击Arrange Palettes 来进行选择。
●工具条。
Maple提供了两个主要的工具条。
默认状态下,标准工具条含有保存、缩放等通用按钮和一些Maple特定用途的按钮。
Maple入门手册(1)

函数
7
本稿由 哈尔滨工程大学船舶工程学院 张崇伟 制作,免费学术共享,禁止用于商业目的。
定义单变量函数: 对于一个函数,给出一系列变量值,只能返回一个值。在 Maple 里,我们使用箭头符号“->”, 一个连字符跟着一个右角括号,定义函数。可通过“:=”给函数指定一个函数名,用同样的 方式,你可以定义一个表达式。在下面例子中,函数被命名为 f,并且只有一个变量 x。在 函数 f 中,f(x)=x^5+6x
怎样处理错误 如果你不小心在命令行中输入了一个错误的符号,并按了回车键,Maple 会回复“syntax error”。有两种方法改正你的错误。你可以返回这一行修改 Maple 命令,然后重新执行这行 命令;当 Maple 重新执行这行命令后,结果会随之更改。你也可以输入“restart”来清除所 有旧的信息,然后重新输入正确的 Maple 命令。
我们会得到与前面例子相同的结果。 绘制数据
9
本稿由 哈尔滨工程大学船舶工程学院 张崇伟 制作,免费学术共享,禁止用于商业目的。
Plot()函数也可被用来绘制数据系列:首先将数据定义一个数列,然后绘制数列。 在下面的例子中,我们定义一个名为 list 的数列,数列通过表达式组来定义 [3,4],[5,6],[7,8],[9,10]。表达式组中的每一项也是一个数列,对应于点的坐标。我们然后用 plot 命令绘制这列数据。如果你想指定点的形式,你也可以增加一个选项变量。Plot()函数有三 种形式:点、线、面。默认的形式是线。在这个例子中,我们制定图形的形式是点。
或者,你可以把浮点数包含在表达式中,这样它会自动是 Maple 计算得到一个近似浮点型解 。
整数计算 Maple 可以处理任意大的整数。如果一个数太大,导致它一行的长度比屏幕还要长,Maple 会在一行结束处使用一个“\”符号表示数字还要院 张崇伟 制作,免费学术共享,禁止用于商业目的。
Maple微积分计算步骤

Maple微积分计算步骤首先这个貌似要在Maple13版本以上才有。
准备工作:首先打开Maple。
再打开菜单工具栏中的工具——调用程序包。
在调用程序包中找到Student:-Calculus1。
并点击它,则Maple中出现。
当然也可以自己输入with(Student[Calculus1]):。
并按enter结束方法一:例如我想用Maple求一下三个积分的求解步骤:有了以上的准备工作后,在面板中输入。
然后鼠标右键—2-D数学—转换为—惰性形式。
转换为惰性形式之后的式子为。
(在点击右键的时候鼠标要在虚线框内。
)然后再鼠标右键—solve—Show Solution Steps。
即求解完毕。
完毕之后的内容为:这两个的方法也是同上面一样。
过程在“Maple步骤程序”中。
方法二:还是同样计算上面的三个式子。
在面板中直接输入。
然后也是鼠标右键——2-D ——转换为——惰性形式。
再按Enter就行了。
过程为:其它两个也一样。
Maple中的步骤不仅对以上三种有用。
对极限和偏导也可以。
具体的可以试试。
我在“Maple步骤程序”中也举了例子。
至于其它的,有兴趣的可以自己去研究。
但并不是每个微分里面的Maple都会有步骤显示。
而且如果你们自己试过Maple里面的步骤之后会看到,它里面的步骤是一步一步来的。
有些明明自己做起来很简单的步骤,Maple也许会很复杂。
我们自己做的时候并不需要那么多步骤。
有些还要自己省。
而且有些步骤不一定适合我们自己。
毕竟Maple不是人,它的步骤是唯一的。
但那些步骤或许会给我们点启发。
所以我们只能做参考。
maple13快速入门

Common Operations Available in Both Document and Worksheet ModesDisplay quick helpfor Quick Help . for Quick Reference Card (this guide)Refer to previous result using equation numbers then enter equation number in dialog Recompute calculations within a line on toolbar Recompute all calculations in a document on toolbarSymbol selection, e.g. εEnter leading characters (or ) e.g. eps Command completion, e.g. Lambert W function Enter leading characters (or ) e.g. Lamb Perform context operation on math expression Right-click any math expressionInsert prompt on toolbar Insert text paragraphon toolbarDrag a copy of an expression to a new locationHighlight the expression, hold , and drag to a new locationDocument Mode vs. Worksheet ModeMaple offers two primary modes of problem entry and content creation: Document mode and Worksheet mode. Both modes have respective advantages and you can easily switch from one mode to the other for maximum flexibility.Document ModeWorksheet Mode•Quick problem-solving and free-form, rich content composition •No prompt (>) displayed•Math is entered and displayed in 2-D•Solve math problems with right-click menu on input and output•Traditional Maple problem-solving environment •Enter problems at a prompt (>) •Math entered and displayed in 2-D or 1-D •Pressto evaluate expression•Solve math problems with right-click menu on math expressionsDocument mode lets you create rich content. For example, the following solves for x without any commands:The command to perform the same operation can be entered in 2-D Math:or in 1-D Maple notation:Toggle Math/Text entry modeor on toolbarToggle 2-D/1-D Math entry mode 2-D black font, 1-D red fontEvaluate math expression and display result inline Evaluate math expression and display result on new line Evaluate math expression and display result on new line Continue on next line without executingSwitch to Worksheet mode (insert prompt)on toolbar Switch to Document mode Format Create Document BlockShow hidden commandsViewExpand Document BlockHide commands. Show only results.Highlight commands to be hidden.Format Create Document Block2-D Math Editing Operations, Keyboard Shortcuts, and OperationsNavigate through expressionMove cursor to different level in expression, e.g. out of exponent Navigate through placeholders Add, remove, rearrange palettesViewPalettesArrange Palettes or right-click paletteFraction , superscript x n , subscript x n x–yx/y, x^n, x_nPrime notation for derivatives, e.g. y” + y’ = 0Square root x , n th root n x Enter leading characters sqrt , nthroot Symbol above, e.g. xxthen insert symbol, e.g.from Arrows paletteTo enter literal characters (_,^, etc.), precede character with \(backslash) e.g. foo\_bar produces foo_barGreek letter entry mode (single letter)Special characters and symbols: Enter leading characters andpi ,e ,i infinalpha ,lambda geq ,leq ,ne ,pmMathematical OperationsCommon manipulations (simplify,factor, expand,…)Right-click expression and select from menuSolve equationsRight-click equationSolveSolve numerically (floating-point)Right-click equation Numerically SolveSolve ODERight-click DE expression Solve DE Interactively Integrate, differentiate Right-click expression Integrate or Differentiate Evaluate expression at a point Right-click expression Evaluate at a Point Create a matrix or vector Matrix paletteChooseInsertInvert, transpose, solve matrix Right-click matrix Standard Operations selectInverse , Transpose , ...Evaluate as floating-point Right-click expression ApproximateVarious operations and tasksUse Task Templates: ToolsTasksBrowseExpressions vs. FunctionsOperations Expression x 2+y 2Function (operator) g (x ,y ) = x 2+y 2Definitionf := x^2 + y^2;g := (x,y) -> x^2+y^2;Evaluate at x=1, y=2eval(f, [x=1,y=2]); produces 5g(1,2); produces 53-D plot for x from 0 to 1, y from 0 to 1plot3d(f,x=0..1,y=0..1);plot3d(g(x,y),x=0..1,y=0..1);Conversion to other formf2 := unapply(f,x,y);f2(1,2);produces 5g2 := g(x,1); g2 + z;produces x 2+1+zUnits and TolerancesAdd units to value or expressionPlace cursor to right of quantity. Use Units (SI)or Units (FPS)palette or right-click Units Affix unit .Add arbitrary unitfrom Units (SI)or Units (FPS)palette and enter desired unit Simplify units in an expression Right-click expression Units Simplify Convert unitsRight-click expressionUnitsConvertEnable automatic units simplification with(Units[Standard]);Enable tolerance calculations with(Tolerances);Tolerance quantity in 2-D Math 9 pm1.1for 9 ±1.1Tolerance quantity in 1-D Math9 &+- 1.1;for 9 ±1.1Input and OutputInteractive data import assistant Tools Assistants Import Data Import audio or image file ToolsAssistantsImport DataCode generation (C, FORTRAN,Java, Visual Basic , MATLAB )Right-click expression Language Conversions .See ?CodeGeneration for help and details.Publish document in HTML, PDF ,LaTeX, or Microsoft Word-RTFFile Export As select HTML , PDF ,LaTeX , or Rich Text FormatSelect Interactive Tools and UtilitiesQuick introductory tour Help Take a Tour of Maple Show available task templatesToolsTasksBrowsePlot Builder Right-click expression Plots Plot Builder , or Tools Assistants Plot Builder ODE Analyzer Tools Assistants ODE Analyzer Data Analysis Assistant Tools Assistants Data Analysis Unit Conversion utility Tools Assistants Units Calculator Back-Solving Assistant ToolsAssistantsBackSolverApply numeric formatting Right-click expressionNumeric FormattingMaple Portal Help Manuals, Resources and more Maple Portal ManualsHelpManuals , Resources , and moreManualsGraphing Calculator InterfaceInstalls as separate program. Launch from Start Maple Maple CalculatorInteractive education tutors for topics in Calculus, Precalculus, and Linear AlgebraTools TutorsP -0648-13-EImportant Maple Syntax:=Assignment a:=2; b:=3+x; c:=a+b;produces 5 + x for c =Mathematical equation solve(2*x + a = 1,x);produces x =1-a—2=Boolean equalityif a = 0 then …Suppress display of output Terminate command with a colon, e.g. 1000! :[ ] List (ordered)z:=[c, b, a]; z[1];produces c { } Set (unordered, no duplicates){a, b, a, c};produces {a ,b,c }Display help on topic?topic |******************© Maplesoft, a division of Waterloo Maple Inc., 2009. Maplesoft and Maple are trademarks of Waterloo Maple Inc. All other trademarks are property of their respective owners.t. 519.747.2373 | f. 519.747.5284800.267.6583 (US & Canada)Plotting and AnimationPlot an existing expression - click expression PlotsPlot BuilderPlot new expressionToolsAssistantsPlot BuilderAdd new expression to existing plot Highlight and drag expression into plot Add annotations to plotsClick on plot, then on the toolbar Animation and parameter plots for functions of several variablesRight-click expression PlotsPlot Builderand select a plot type。
