lesson2(logistic模型与matlab入门)
matlab教程ppt(完整版)

矩阵的数学运算
总结词
详细描述
总结词
详细描述
掌握矩阵的数学运算,如求逆 、求行列式、求特征值等。
在MATLAB中,可以使用inv() 函数来求矩阵的逆,使用det() 函数来求矩阵的行列式,使用 eig()函数来求矩阵的特征值。 例如,A的逆可以表示为 inv(A),A的行列式可以表示 为det(A),A的特征值可以表 示为eig(A)。
• 总结词:了解特征值和特征向量的概念及其在矩阵分析中的作用。 • 详细描述:特征值和特征向量是矩阵分析中的重要概念。特征值是满足Ax=λx的标量λ和向量x,特征向量是与特征值对
应的非零向量。特征值和特征向量在许多实际问题中都有应用,如振动分析、控制系统等。
04
MATLAB图像处理
图像的读取与显示
变量定义
使用赋值语句定义变量,例如 `x = 5`。
矩阵操作
学习如何创建、访问和操作矩 阵,例如使用方括号 `[]`。
函数编写
学习如何创建自定义函数来执 行特定任务。
02
MATLAB编程
变量与数据类型
01
02
03
变量命名规则
MATLAB中的变量名以字 母开头,可以包含字母、 数字和下划线,但不应与 MATLAB保留字冲突。
了解矩阵的数学运算在实际问 题中的应用。
矩阵的数学运算在许多实际问 题中都有应用,如线性方程组 的求解、矩阵的分解、信号处 理等。通过掌握这些运算,可 以更好地理解和解决这些问题 。
矩阵的分解与特征值
• 总结词:了解矩阵的分解方法,如LU分解、QR分解等。
• 详细描述:在MATLAB中,可以使用lu()函数进行LU分解,使用qr()函数进行QR分解。这些分解方法可以将一个复杂的 矩阵分解为几个简单的部分,便于计算和分析。
用matlab绘制logistic模型图课件

用matlab绘制logistic模型图
图形的其他属性
坐标轴标注 xlabel(’text’) 或 ylabel(’text’)
例:
用matlab绘制logistic模型图
图形的其他属性
添加图例 legend(string1,string2, ...) >> legend('cos(x)');
自己动手
plot(Y): 当 Y 是矩阵时的图形是什么? >> Y=[1 2; 3 5; 6 9]; plot(Y); >> plot(Y’); 用matlab绘制logistic模型图
图形的属性
点和线的基本属性
plot(x,y,string)
其中 string 是用 单引号 括起来的字符串,用来指定图 形的属性(点、线的形状和颜色)
用matlab绘制logistic模型图
plot 举例
例:y=cos(x) 在 [0, 4*pi] 上的图像
>> x=[0:0.1:4*pi]; >> y=cos(x); >> plot(x,y);
自己动手
指出以下各个绘图命令的输出图形分别是什么,并上机验证
>> t=[0 1]; x=[1 2]; y=[x;3 4]; z=[y;5 6]; >> plot(t,x); >> plot(t,y); >> plot(t,y'); >> plot(t,z); >> plot(t,z'); 用matlab绘制logistic模型图
>> subplot(2,2,1);plot(x,sin(x)); >> subplot(2,2,2);plot(x,cos(x)); >> subplot(2,2,3);plot(x,x.^2); >> subplot(2,2,4);plot(x,exp(x));
matlab教程ppt(完整版)

可以使用`'`运算符对矩阵进行 转置。
矩阵高级运算
01
逆矩阵
可以使用`inv`函数求矩阵的逆矩阵 。
行列式
可以使用`det`函数求矩阵的行列式 。
03
02
特征值和特征向量
可以使用`eig`函数求矩阵的特征值 和特征向量。
秩
可以使用`rank`函数求矩阵的秩。
04
04
matlab绘图功能
绘图基本命令
控制设计
MATLAB提供了控制系统设计和分析 工具箱,可以方便地进行控制系统的 建模、分析和优化。
03
信号处理
MATLAB提供了丰富的信号处理工具 箱,可以进行信号的时域和频域分析 、滤波器设计等操作。
05
04
图像处理
MATLAB提供了图像处理工具箱,可 以进行图像的增强、分割、特征提取 等操作。
02
matlab程序调试技巧分享
01
调试模式
MATLAB提供了调试模式,可以 逐行执行代码,查看变量值,设 置断点等。
日志输出
02
03
错误处理
通过使用fprintf函数,可以在程 序运行过程中输出日志信息,帮 助定位问题。
MATLAB中的错误处理机制可以 帮助我们捕获和处理运行时错误 。
matlab程序优化方法探讨
显示结果
命令执行后,结果将在命令窗口中显示。
保存结果
可以使用`save`命令将结果保存到文件中。
matlab变量定义与赋值
定义变量
使用`varname = value`格式定义变 量,其中`varname`是变量名, `value`是变量的值。
赋值操作
使用`=`运算符将值赋给变量。例如 ,`a = 10`将值10赋给变量a。
matlab教程ppt(完整版)

控制流语句
使用条件语句(如if-else)和 循环语句(如for)来控制程序 流程。
变量定义
使用赋值语句定义变量,例如 `a = 5`。
矩阵运算
使用矩阵进行数学运算,如加 法、减法、乘法和除法等。
函数编写
创建自定义函数来执行特定任 务。
02
MATLAB编程语言基础
变量与数据类型
变量命名规则
数据类型转换
编辑器是一个文本编辑器 ,用于编写和编辑 MATLAB脚本和函数。
工具箱窗口提供了一系列 用于特定任务的工具和功 能,如数据可视化、信号 处理等。
工作空间窗口显示当前工 作区中的变量,可以查看 和修改变量的值。
MATLAB基本操作
数据类型
MATLAB支持多种数据类型, 如数值型、字符型和逻辑型等 。
04
MATLAB数值计算
数值计算基础
01
02
03
数值类型
介绍MATLAB中的数值类 型,包括双精度、单精度 、复数等。
变量赋值
讲解如何给变量赋值,包 括标量、向量和矩阵。
运算符
介绍基本的算术运算符、 关系运算符和逻辑运算符 及其优先级。
数值计算函数
数学函数
列举常用的数学函数,如 三角函数、指数函数、对 数函数等。
矩阵的函数运算
总结词:MATLAB提供了许多内置函 数,可以对矩阵进行各种复杂的运算
。
详细描述
矩阵求逆:使用 `inv` 函数求矩阵的 逆。
特征值和特征向量:使用 `eig` 函数 计算矩阵的特征值和特征向量。
行列式值:使用 `det` 函数计算矩阵 的行列式值。
矩阵分解:使用 `factor` 和 `expm` 等函数对矩阵进行分解和计算指数。
matlab教程ppt(完整版)

汇报人:可编辑
2023-12-24
目录
• MATLAB基础 • MATLAB编程 • MATLAB矩阵运算 • MATLAB数值计算 • MATLAB可视化 • MATLAB应用实例
01
CATALOGUE
MATLAB基础
MATLAB简介
MATLAB定义
MATLAB应用领域
菜单栏
包括文件、编辑、查看、主页 、应用程序等菜单项。
命令窗口
用于输入MATLAB命令并显示 结果。
MATLAB主界面
包括命令窗口、当前目录窗口 、工作空间窗口、历史命令窗 口等。
工具栏
包括常用工具栏和自定义工具 栏。
工作空间窗口
显示当前工作区中的变量。
MATLAB基本操作
变量定义
使用变量名和赋值符号(=)定义变 量。
详细描述
直接输入:在 MATLAB中,可以直 接通过输入矩阵的元 素来创建矩阵。例如 ,`A = [1, 2, 3; 4, 5, 6; 7, 8, 9]`。
使用函数创建: MATLAB提供了多种 函数来创建特殊类型 的矩阵,如`eye(n)`创 建n阶单位矩阵, `diag(v)`创建由向量v 的元素构成的对角矩 阵。
使用bar函数绘制柱状图 ,可以自定义柱子的宽
度、颜色和标签。
使用pie函数绘制饼图, 可以自定义饼块的比例
和颜色。
三维绘图
01
02
03
04
三维线图
使用plot3函数绘制三维线图 ,可以展示三维空间中的数据
点。
三维曲面图
使用surf函数绘制三维曲面图 ,可以展示三维空间中的曲面
。
三维等高线图
logistic在matlab中的拟合用法

logistic在matlab中的拟合用法如何在Matlab中使用logistic函数进行拟合Logistic回归是一种常见的用于分类和预测问题的统计方法。
在Matlab 中,我们可以使用logistic函数进行拟合,以从给定的数据集中学习到一个logistic模型。
在本文中,我将介绍如何使用Matlab进行logistic函数的拟合,并提供一些示例代码和解释。
第一步:准备数据集首先,我们需要准备一个包含特征和标签的数据集。
特征可以是任何我们认为与分类或预测问题相关的变量,而标签则是我们想要预测或分类的变量。
确保数据集包含足够数量的数据以获得可靠的结果。
我们可以使用readmatrix函数从CSV文件中读取数据集。
假设我们的数据集文件名为"data.csv",其中特征列是1到N-1列,标签列是N列,我们可以使用以下代码读取数据集:data = readmatrix('data.csv');第二步:拟合logistic模型一旦我们有了数据集,我们可以使用logistic函数进行模型拟合。
在Matlab中,我们可以使用fitglm函数来拟合logistic模型。
以下是使用fitglm函数进行logistic拟合的示例代码:X = data(:,1:N-1); 特征向量y = data(:,N); 标签向量model = fitglm(X,y,'Distribution','binomial','Link','logit');在上面的代码中,X是包含特征向量的矩阵,y是包含标签向量的矩阵。
我们使用fitglm函数来拟合一个logistic模型。
参数'Distribution'指定了我们的数据集的分布是二项式分布,而参数'Link'指定了logistic函数在模型中的链接。
MATLAB经典教程(全)PPT课件

THANKS FOR WATCHING
感谢您的观看
信号时域分析和频域分析
时域分析
研究信号随时间变化的规律,包括波形、幅度、频率、相位等。
频域分析
将信号转换为频域表示,研究信号的频谱结构和频率特性,包括幅 度谱、相位谱、功率谱等。
时域与频域关系
时域和频域是信号分析的两个方面,它们之间存在对应关系,可以 通过傅里叶变换相互转换。
数字信号处理基础
数字信号表示
MATLAB工作环境与界面
MATLAB工作环境
包括命令窗口、工作空间、命令历史窗口、当 前文件夹窗口等。
界面介绍
详细讲解MATLAB界面的各个组成部分,如菜 单栏、工具栏、编辑器窗口等。
基本操作
介绍如何在MATLAB环境中创建、保存、运行脚本和函数,以及如何进行基本 的文件操作。
基本数据类型与运算
数据统计描述性分析
描述性统计量
介绍均值、中位数、众数、方差、标准差等常见 描述性统计量的计算方法和意义。
数据分布形态
通过直方图、箱线图等图形展示数据的分布形态 ,帮助用户了解数据的整体特征。
数据间关系
探讨协方差、相关系数等统计量在揭示数据间关 系方面的应用。
数据可视化方法
二维图形绘制
详细讲解MATLAB中二维图形的绘制方法,包括线图、散点图、 柱状图等。
特征值与特征向量
特征值与特征向量的定义
设A为n阶方阵,若存在数λ和n维非零向量x,使得Ax=λx ,则称λ为A的特征值,x为A的对应于特征值λ的特征向量 。
特征值与特征向量的性质
包括特征值的和等于方阵对角线元素之和、特征值的积等 于方阵的行列式等性质。
MATLAB求解
使用MATLAB内置函数`eig`求解方阵的特征值和特征向量 。
Logistic模型求解怎么用matlab求解啊

Logistic模型求解怎么用matlab求解啊?已知x=0:1:12y=[43.65 109.86 187.21 312.67 496.58 707.65 960.25 1238.75 1560.00 1824.29 2199.00 2438.89 2737.71]y=L/(1+a*exp(-k*x))利用线性回归模型所得到的a和k的估计值和L=3000作为Logistic模型的拟合初值,对Logistic模型做非线性回归。
据说用lsqcurvefit求解,本人非专业人士不懂啊?只需要列出式子!!拜托了。
Logistic模型求解怎么用matlab求解啊?[此问题的推荐答案]x=0:1:12y=[43.65 109.86 187.21 312.67 496.58 707.65 960.25 1238.75 1560.00 1824.29 2199.00 2438.89 2737.71]y=L/(1+a*exp(-k*x))利用线性回归模型所得到的a和k的估计值和L=3000作为Logistic模型的拟合初值,对Logistic模型做非线性回归。
%第一步,线性回归模型得到a,k%这里假定y=a*exp(k*x),对两边取ln(Matlab中,ln用log函数表示),有%lny=lna+k*x%即logy是x的线性函数,斜率为k*loge,截距为logax=0:1:12 ;y=[43.65 109.86 187.21 312.67 496.58 707.65 960.25 1238.75 1560.00 1824.29 2199.00 2438.89 2737.71] ;line_A=polyfit(x,log(y),1);k=line_A(1);a=exp(line_A(2));plot(x,y,'*',x,a*exp(k*x))title('线性回归的参数曲线与已经点的关系')%第二步,Logistic模型%在Matlab下输入:edit,然后将下面两行百分号之间的内容,复制进去,保存function y=zhidao_liziqiangde(A,x)%其中k=A(1),a=A(2)k=A(1);a=A(2);L=3000;y=L./(1+a*exp(-k*x));%返回Matlab,输入[ABC,res]=lsqcurvefit('zhidao_liziqiangde',[k,a],x,y);kk=ABC(1)aa=ABC(2)y_logistic=zhidao_liziqiangde(ABC,x);figureplot(x,y,'*',x,y_logistic)legend('实验数据点','Logistic模型')============================================总结以上在Matlab下输入:edit,然后将下面两行百分号之间的内容,复制进去,保存%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%% %%%%%%%%%%%function y=zhidao_liziqiangde(A,x)%其中k=A(1),a=A(2)k=A(1);a=A(2);L=3000;y=L./(1+a*exp(-k*x)); %%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%% %%%%%%%%%%%返回Matlab下输入x=0:1:12 ;y=[43.65 109.86 187.21 312.67 496.58 707.65 960.25 1238.75 1560.00 1824.29 2199.00 2438.89 2737.71] ;line_A=polyfit(x,log(y),1);k=line_A(1);a=exp(line_A(2));plot(x,y,'*',x,a*exp(k*x))title('线性回归的参数曲线与已经点的关系')[ABC,res]=lsqcurvefit('zhidao_liziqiangde',[k,a],x,y);kk=ABC(1)aa=ABC(2)y_logistic=zhidao_liziqiangde(ABC,x);figureplot(x,y,'*',x,y_logistic)legend('实验数据点','Logistic模型')。
logistic模型与matlab入门

对应p的分量依次是次数从高 到底各多项式系数
用Richard模拟 水稻叶伸长生长
1
y(t) 47.1(1 98.56e 0.5398t )11.829
关于inline函数
例如: y=inline(‘sin(x)-cos(x)’,’x’) 输入y(0),可得:-1 作图: x=0:0.1:2*pi;plot(x,y(x))
(1)Logistic模型的特点: 模型具有固定的拐点,只能描述一种特定形状的S曲线 。
(2)面临的问题: 生物在一个完整的时间序列里,生物的总生长量最初比
较小,随时间的增加逐渐增长而达到一个快速生长时期,尔 后增长速度趋缓,最终达到稳定的总生长量。此生长过程的 图象描述称为是一种拉长的S形曲线。 (3)更合适的模型描述——Richards模型(1951)
什么是数学建模
把现实世界中的实际问题加以提炼,抽 象为数学模型,求出模型的解,验证模型的 合理性,并用该数学模型所提供的解答来解 释现实问题,我们把数学知识的这一应用过 程称为数学建模。
建模全过程示意图
数学建模的一般步骤
堂上思考题
如何估计一个人体内血液的总量?
示例3、人口预报
一、两个经典模型:
d=eig(A), [v,d]=eig(A): 特征值与特征向量
rand(m,n):
m行n列均匀分布随机数矩阵
randn(m,n):
m行n列正态分布随机数矩阵
Matlab使用
1、matlab使用环境 2、四则运算与一些常用函数 3、关于矩阵提取 4、图形功能 5、M-文件编写
3、关于矩阵的提取,:运算
MATLAB工作区:
可查看所有变量值
Matlab详细学习讲义

Matlab详细学习讲义《MA TLAB软件应⽤》讲义[第2 / 16次课]第1章基础准备及⼊门⼀点名⼆作业讲评三复习提问MATLAB界⾯由⼏⼤组件组成?MATLAB的搜索路径主要有什么应⽤途径?四上机练习内容启动MATLAB。
在D盘根⽬录下,以“学号_姓名”的格式创建⽂件夹,并在Matlab中将该⽬录设置为Current Folder。
(利⽤MA TLAB Toolbar 中Current Folder组合框后的按钮)。
以下为本章教学必须掌握的知识点。
在MA TLAB的Command Window中练习以下代码,并观察系统输出,并逐⾏进⾏注释。
本次课结束后将代码⽂件上传。
在MA TLAB程序界⾯中进⾏以下操作:1 上机实习内容提⽰及要求启动MATLAB后,依次练习MA TLAB的菜单项、⼯具栏和Command Window、Current Folder、Command History、Workspace等主要组件的基本功能,按指定内容在MA TLAB程序界⾯下进⾏操作练习。
2 上机实习内容在MATLAB程序界⾯中进⾏以下操作:1) Command Window指令窗⼝在集成窗体和独⽴窗体之间切换(Undock/Dock按钮)2) 在Command Window中运⾏以下指令,掌握换⾏符(...)的使⽤>> (12+2*(7-4))/3^2>> S=1-1/2+1/3-1/4+1/5-1/6+1/7-1/8>> S=1-1/2+1/3-1/4+…+1/5-1/6+1/7-1/83)在Command Window中分别输⼊以下数值,并按回车,观察MA TLAB的输出(数值如3, -99, 0.001, 9.456, 1.3e-3, 4.5e33, eps, 等)4)以下实例涉及变量的定义规则,在Command Window中分别输⼊并按回车,观察MA TLAB的输出结果.输出结果为错误提⽰时,分析出现错误的原因.>> xyz_4=32.75>> var1=3.09e-5*1028>> 4xyz=32.75>> 4*xyz=198.28>>4,xyz=198.285) 在Command Window中输⼊下列数学常数,并按回车:eps, i, j, Inf, inf, intmax, NaN, nan, pi, realmax, realmin,观察并分析系统的输出。
《Matlab教案》课件

《MATLAB教案》PPT课件第一章:MATLAB概述1.1 MATLAB简介介绍MATLAB的历史和发展解释MATLAB的含义(Matrix Laboratory)强调MATLAB在工程和科学计算中的应用1.2 MATLAB界面介绍MATLAB的工作空间解释MATLAB的菜单栏和工具栏演示如何创建、打开和关闭MATLAB文件1.3 MATLAB的基本操作介绍MATLAB的数据类型演示如何进行矩阵运算解释MATLAB中的向量和矩阵运算规则第二章:MATLAB编程基础2.1 MATLAB脚本编程解释MATLAB脚本文件的结构演示如何编写和运行MATLAB脚本强调注释和代码的可读性2.2 MATLAB函数编程介绍MATLAB函数的定义和结构演示如何创建和使用MATLAB函数强调函数的重用性和模块化编程2.3 MATLAB编程技巧介绍变量和函数的命名规则演示如何进行错误处理和调试强调代码的优化和性能提升第三章:MATLAB数值计算3.1 MATLAB数值解算介绍MATLAB中的数值解算工具演示如何解线性方程组和不等式解释MATLAB中的符号解算和数值解算的区别3.2 MATLAB数值分析介绍MATLAB中的数值分析工具演示如何进行插值、拟合和数值积分解释MATLAB中的误差估计和数值稳定性3.3 MATLAB优化工具箱介绍MATLAB优化工具箱的功能演示如何使用优化工具箱进行无约束和约束优化问题解释MATLAB中的优化算法和参数设置第四章:MATLAB绘图和可视化4.1 MATLAB绘图基础介绍MATLAB中的绘图命令和函数演示如何绘制二维和三维图形解释MATLAB中的图形属性设置和自定义4.2 MATLAB数据可视化介绍MATLAB中的数据可视化工具演示如何绘制统计图表和散点图解释MATLAB中的数据过滤和转换4.3 MATLAB动画和交互式图形介绍MATLAB中的动画和交互式图形功能演示如何创建动画和交互式图形解释MATLAB中的图形交互和数据探索第五章:MATLAB应用案例5.1 MATLAB在信号处理中的应用介绍MATLAB在信号处理中的基本概念演示如何使用MATLAB进行信号处理操作解释MATLAB在信号处理中的优势和应用场景5.2 MATLAB在控制系统中的应用介绍MATLAB在控制系统中的基本概念演示如何使用MATLAB进行控制系统分析和设计解释MATLAB在控制系统中的优势和应用场景5.3 MATLAB在图像处理中的应用介绍MATLAB在图像处理中的基本概念演示如何使用MATLAB进行图像处理操作解释MATLAB在图像处理中的优势和应用场景《MATLAB教案》PPT课件第六章:MATLAB Simulink基础6.1 Simulink简介介绍Simulink作为MATLAB的一个集成组件解释Simulink的作用:模型化、仿真和分析动态系统强调Simulink在系统级设计和多领域仿真中的优势6.2 Simulink界面介绍Simulink库浏览器和模型窗口演示如何创建、编辑和运行Simulink模型解释Simulink中的块和连接的概念6.3 Simulink仿真介绍Simulink仿真的基本过程演示如何设置仿真参数和启动仿真解释Simulink仿真结果的查看和分析第七章:MATLAB Simulink高级应用7.1 Simulink设计模式介绍Simulink的设计模式,包括连续、离散、混合和事件驱动模式演示如何根据系统特性选择合适的设计模式解释不同设计模式对系统性能的影响7.2 Simulink子系统介绍Simulink子系统的概念和用途演示如何创建和管理Simulink子系统解释子系统在模块化和层次化设计中的作用7.3 Simulink Real-Time Workshop介绍Simulink Real-Time Workshop的功能演示如何使用Real-Time Workshop进行代码解释代码对于硬件在环仿真和嵌入式系统开发的重要性第八章:MATLAB Simulink库和工具箱8.1 Simulink库介绍Simulink库的结构和分类演示如何访问和使用Simulink库中的块解释Simulink库对于模型构建和功能复用的意义8.2 Simulink工具箱介绍Simulink工具箱的概念和功能演示如何安装和使用Simulink工具箱解释Simulink工具箱在特定领域仿真和分析中的作用8.3 自定义Simulink库介绍如何创建和维护自定义Simulink库演示如何将自定义块添加到库中解释自定义库对于个人和组织级模型共享的重要性第九章:MATLAB Simulink案例分析9.1 Simulink在控制系统中的应用介绍控制系统模型在Simulink中的构建演示如何使用Simulink进行控制系统设计和分析解释Simulink在控制系统教育和研究中的应用9.2 Simulink在信号处理中的应用介绍信号处理模型在Simulink中的构建演示如何使用Simulink进行信号处理仿真解释Simulink在信号处理领域中的优势和实际应用9.3 Simulink在图像处理中的应用介绍图像处理模型在Simulink中的构建演示如何使用Simulink进行图像处理仿真解释Simulink在图像处理领域中的优势和实际应用第十章:MATLAB Simulink项目实践10.1 Simulink项目实践流程介绍从需求分析到模型验证的Simulink项目实践流程演示如何使用Simulink进行项目规划和实施解释Simulink在项目管理和协作中的作用10.2 Simulink与MATLAB的交互介绍Simulink与MATLAB之间的数据交互方式演示如何在Simulink中使用MATLAB函数和脚本解释混合仿真模式对于复杂系统仿真的优势10.3 Simulink项目案例分析具体的Simulink项目案例演示如何解决实际工程问题解释Simulink在工程教育和项目开发中的应用价值《MATLAB教案》PPT课件第十一章:MATLAB App Designer入门11.1 App Designer简介介绍App Designer作为MATLAB中的应用程序开发环境解释App Designer的作用:快速创建跨平台的MATLAB应用程序强调App Designer在简化MATLAB代码部署和用户交互中的优势11.2 App Designer界面介绍App Designer的用户界面和工作流程演示如何创建新应用和编辑应用界面解释App Designer中的组件和布局的概念11.3 App Designer编程介绍App Designer中的MATLAB编程模式演示如何使用App Designer中的MATLAB代码块解释App Designer中事件处理和应用程序生命周期管理的重要性第十二章:MATLAB App Designer高级功能12.1 App Designer用户界面设计介绍App Designer中用户界面的定制方法演示如何使用样式、颜色和主题来美化应用界面解释用户界面设计对于提升用户体验的重要性12.2 App Designer数据模型介绍App Designer中的数据模型和模型视图概念演示如何创建、使用和绑定数据模型和视图解释数据模型在应用程序中的作用和重要性12.3 App Designer部署和分发介绍App Designer应用程序的部署和分发流程演示如何打包和发布应用程序解释如何为不同平台安装和运行App Designer应用程序第十三章:MATLAB App Designer案例研究13.1 图形用户界面(GUI)应用程序设计介绍使用App Designer设计的GUI应用程序案例演示如何创建交互式GUI应用程序来简化MATLAB脚本解释GUI应用程序在数据输入和结果显示中的作用13.2 数据分析和可视化应用程序设计介绍使用App Designer进行数据分析和可视化的案例演示如何创建应用程序来处理和显示大型数据集解释App Designer在数据分析和决策支持中的优势13.3 机器学习和深度学习应用程序设计介绍使用App Designer实现机器学习和深度学习模型的案例演示如何将MATLAB中的机器学习和深度学习算法集成到应用程序中解释App Designer在机器学习和深度学习应用部署中的作用第十四章:MATLAB App Designer实战项目14.1 App Designer项目规划和管理介绍App Designer项目的规划和管理方法演示如何组织和维护大型应用程序项目解释项目管理和版本控制对于团队协作的重要性14.2 App Designer与MATLAB的集成介绍App Designer与MATLAB之间的数据和功能集成演示如何在App Designer中调用MATLAB函数和脚本解释集成MATLAB强大计算和分析能力的重要性14.3 App Designer项目案例实现分析具体的App Designer项目案例实现过程演示如何解决实际工程项目中的问题解释App Designer在工程项目实践中的应用价值第十五章:MATLAB App Designer的未来趋势15.1 App Designer的新功能和技术介绍App Designer的最新功能和技术发展演示如何利用新功能和技术提升应用程序的性能和用户体验强调持续学习和适应新技术的重要性15.2 App Designer在跨平台开发中的应用介绍App Designer在跨平台应用程序开发中的优势演示如何创建适用于不同操作系统的应用程序解释跨平台开发对于扩大应用程序市场的重要性15.3 App Designer的未来趋势和展望讨论App Designer在未来的发展趋势和潜在应用领域激发学生对于应用程序开发和创新的兴趣强调持续探索和创造新应用的重要性重点和难点解析本文档为您提供了一份详尽的《MATLAB教案》PPT课件,内容涵盖了MATLAB 的基本概念、编程基础、数值计算、绘图和可视化、应用案例、Simulink的基础知识、高级应用、库和工具箱的使用、案例分析以及项目实践、App Designer 的基础知识、高级功能、案例研究、实战项目和未来趋势等方面的内容。
(完整版)Matlab入门教程

(完整版)Matlab⼊门教程第1章MATLAB操作基础1.1 MATLAB概述1.1.2 MATLAB的主要功能1.数值计算MATLAB以矩阵作为数据操作的基本单位,还提供了⼗分丰富的数值计算函数。
2.绘图功能可以绘制⼆维、三维图形,还可以绘制特殊图形(与统计有关的图,例如:区域图、直⽅图、饼图、柱状图等)。
3.编程语⾔MATLAB具有程序结构控制、函数调⽤、数据结构、输⼊输出、⾯向对象等程序语⾔特征,⽽且简单易学、编程效率⾼。
4.MATLAB⼯具箱MATLAB包含两部分内容:基本部分和各种可选的⼯具箱。
MATLAB⼯具箱分为两⼤类:功能性⼯具箱和学科性⼯具箱。
1.1.3MATLAB语⾔的特点语⾔简洁紧凑,使⽤⽅便灵活,易学易⽤。
例如:A=[1 2 3;4 5 6;7 8 9]⼀条语句实现了对3x3矩阵的输⼊。
语句功能强⼤,⼀条语句相当于其它语⾔的⼀个⼦程序,例如fft。
语句简单,内涵丰富。
同⼀个函数有不同的输⼊变量和输出变量,分别代表不同的含义。
Matlab既具有结构化的控制语句(if、for、while)⼜⽀持⾯向对象的程序设计。
⽅便的绘图功能。
包含功能强劲的⼯具箱。
易于扩展。
1.1.4 初识MATLAB例1-1 绘制正弦曲线和余弦曲线。
x=[0:0.5:360]*pi/180;plot(x,sin(x),x,cos(x));例1-2 求⽅程3x4+7x3+9x2-23=0的全部根。
p=[3,7,9,0,-23]; %建⽴多项式系数向量x=roots(p) %求根例1-3 求积分quad('x.*log(1+x)',0,1)例1-4 求解线性⽅程组。
a=[2,-3,1;8,3,2;45,1,-9];b=[4;2;17];x=inv(a)*b1.2 MATLAB的运⾏环境与安装1.2.1 MATLAB的运⾏环境硬件环境:(1) CPU(2) 内存(3) 硬盘(4) CD-ROM驱动器和⿏标软件环境:(1) Windows 98/NT/2000 或Windows XP(2) 其他软件根据需要选⽤1.2.2 MATLAB的安装运⾏系统的安装程序setup.exe,可以按照安装提⽰依次操作。
logistic模型matlab代码

logistic模型matlab代码Logistic模型是流行的统计模型,因为它可用于分类和预测二元分类结果,比如疾病是否存在或顾客是否会购买。
在本文中,我们将介绍如何通过Matlab实现logistic模型。
我们将在以下几个部分讨论如何构建代码以获得预测结果以及如何评估模型的性能。
## 1. 数据准备首先,我们需要一些训练数据来建立模型。
通常,数据是在一个文件中存储的,其中每个行都包含一组观测值。
在我们的例子中,我们将使用从一个医疗研究中提取的数据,该研究关注高血压病患者是否患有心脏病。
为了处理数据,我们需要导入它。
我们可以使用Matlab的csvread()函数,该函数不仅可以读取CSV文件,还可以读取其他类型的文件。
下面是我们如何用Matlab导入所需数据的代码:```data = csvread('mydata.csv');```在这个例子中,我们假设我们的数据存储在一个名为“mydata.csv”的文件中。
## 2. 数据探索和准备在开始构建模型之前,我们需要对数据进行一些探索和准备。
这是一个重要的步骤,因为在数据中发现的任何模式或异常都可能影响我们的模型。
常见的探索和准备任务包括:- 数据可视化: 这有助于我们了解数据中包含的模式或异常情况。
在Matlab中,我们可以使用histogram(), boxplot()和scatter()等函数等进行数据可视化。
- 数据清洗: 在数据中,可能有缺失值、异常值或无意义的值。
在这种情况下,将其替换为中位数、平均数或其他合适的值是很有必要的。
## 3. 训练模型接下来,我们可以开始构建模型。
对于logistic模型,我们需要使用分类回归工具箱中的mnrfit()函数。
logistic模型使用了sigmoid函数来将连续值转换为二元值。
在Matlab中,该函数可以通过使用以下代码训练logistic模型来实现:```X = data(:,1:4);Y = data(:,5);B = mnrfit(X,Y)```在这个例子中,我们假设数据集中的前四列是预测变量的值,最后一列是类别变量的值。
logistic模型及其matlab算法
Logistic 曲线的三种参数估计方法作者QQ :2377389590Logistic 曲线的参数估计1844或1845年,比利时数学家Pierre François Verhulst 提出了logistic 方程,这是一个对S 型曲线进行数学描述的模型。
一百多年来,这个方程多次应用于一些特殊的领域建模与预测,例如单位面积内某种生物的数量、人口数量等社会经济指标、某种商品(例如手机)的普及率等。
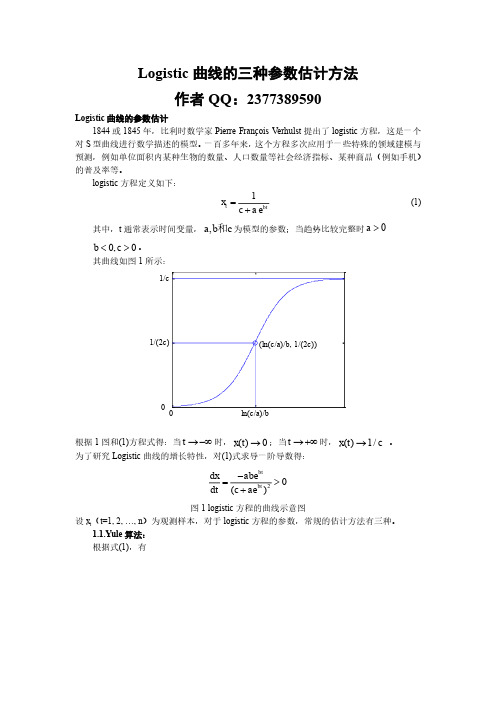
logistic 方程定义如下:1et btx c a =+ (1) 其中,t 通常表示时间变量,,a b c 和为模型的参数;当趋势比较完整时0a >0,0b c <>。
其曲线如图1所示:0 1/(2c)1/c根据1图和(1)方程式得:当t →-∞时,()0x t →;当t →+∞时,()1/x t c → 。
为了研究Logistic 曲线的增长特性,对(1)式求导一阶导数得:20()btbt dx abe dt c ae -=>+ 图1 logistic 方程的曲线示意图设x t (t =1, 2, …, n )为观测样本,对于logistic 方程的参数,常规的估计方法有三种。
1.1.Yule 算法: 根据式(1),有111(1)=11()(1)(1)(1)t t tt t b t btbt b btb b tx x xx x c ae c ae ae c c e c ae e c e x ++++--+=-++--=+=--- (2) 设11t tt t x x z x ++-=、1b e γ=-以及(1)b c e β=--,则式(2)变形为线性方程t t z x γβ=+,利用普通最小二乘(OLS )方法可以得到这个方程参数的估计值,b 和c 的估计值也可以进一步得到。
为得到a 的估计值,将式(1)变形为:1ˆˆˆln ln t c a bt x ⎛⎫-=+ ⎪⎝⎭t =1. 2.…, n (3) 左右分别对t 求和11(1)ˆˆˆln ln 2nt t n n c n a b x =⎛⎫+-=+ ⎪⎝⎭∑ (4) 因此,a 的估计值为:111(1)ˆˆˆexp ln 2n t t n n a c b n x =⎧⎫⎡⎤⎛⎫+⎪⎪=--⎨⎬⎢⎥ ⎪⎝⎭⎪⎪⎣⎦⎩⎭∑ (5)1.2.Rhodes 算法: 根据式(1),有(1)1(1)1(1)b t t b b b t bbtc ae x c ce ce ae e c e x +++=+=-++=-+(6) 设11t t z x +=、1t t s x =、(1)b c e γ=-以及b e β=,则式(6)变形为t t z s γβ=+。
matlab基础知识ppt(全)精心整理

2016/11/25
Application of Matlab Language
19
拟合曲线图
由图可见,三次拟合结果较好。
2016/11/25 Application of Matlab Language 20
2.3 数值表示、变量及表达式
数值的记述
Matlab的数只采用习惯的十进制表示,可以带小数点 和负号;其缺省的数据类型为双精度浮点型(double)。 例如:3 -10 0.001 1.3e10 1.256e-6
Matalb中指数函数exp(x), 常见的表达方式。
Application of Matlab Language
8
2.2 命令窗口 (续)
“clc”清除窗口显示内容的命令。
〘例2.2-4〙计算
y 2sin 0.3 1 5
的值。
>>y=2*sin(0.3*pi)/(1+sqrt(5)) y= 0.5000 〘例2.2-5〙计算 y 的值。 命令行编辑 “↑”键调回已 >>y=2*cos(0.3*pi)/(1+sqrt(5)) 输入过命令。 y= 修改。 0.3633
MATLAB 语言及其应用
Application of Matlab Language
第一讲 Matlab概述
前言 Matlab软件概述
Matlab的桌面环境及入门知识
2016/11/25
Application of Matlab Language
2 功Biblioteka 强大 数值运算优势 符号运算优势(Maple) 强大的2D、3D数据可视化功能 许多具有算法自适应能力的功能函数
1 5
第2章MATLAB的基本语法课件

handmard
Handmard矩 rosser 阵
hankel hilb invhilb
Hankel矩阵 toeplize Hilbert矩阵 vander
Hilbert逆矩 wilkinson 阵
魔方矩阵
Pascal矩阵
经典的对称 特征值测试 矩阵 Toeplize矩阵
Vanderm阵
此外,常用的函数还有reshape(A,m,n),它在 矩阵总元素保持不变的前提下,将矩阵A重新 排成m×n的二维矩阵。
4. 建立大矩阵 大矩阵可由方括号中的小矩阵建立起来。 例如
A=[1 2 3;4 5 6;7 8 9]; C=[A,eye(size(A)); ones(size(A)),A]
C=
3. 内存变量文件 ❖利用MAT文件(.mat)可以把当前MATLAB
工作空间中的一些有用变量长久地保留下 来。
❖MAT文件的生成和装入由save和load命令 来完成。常用格式为:
save 文件名 [变量名表] [-append][-ascii]
load 文件名 [变量名表] [-ascii]
2.3 MATLAB矩阵
• 数据输出时用户可以用format命令设置或改 变 数 据 输 出 格 式 。 format 命 令 的 格 式 为 : format 格式符
• 注意,format命令只影响数据输出格式,而 不影响数据的计算和存储。
2.2.4 预定义变量
在MATLAB工作空间中,还驻留几个由 系统本身定义的变量。它们有特定的含 义,在使用时,应尽量避免对这些变量 重新赋值。
❖ 变量的元素用圆括号“( )”中的数字 (下标)表示。一维矩阵(数组)中的
元素用一个下标表示;二维矩阵用两个 下标表示,以逗号分开
MATLAB第二章

function [egg1,egg2,chicken1]=myegg(n)
% egg1 隔1天的蛋个数 % egg2 隔2天的蛋个数 % chicken1 过n天后母鸡个数 if n==1
egg1=1; egg2=0; chicken1=1; elseif n==2 egg1=1; egg2=1; chicken1=1;
27
>> x=0:0.1:2*pi; >> y=sin(x); >> plot(x,y) >> plot(x,y,‘ro’) %默认是蓝色曲线 >> x=[0 1 2 5];y=[4 -2 1 2]; >> plot(x,y) >> fplot(‘x^2+4*x+1’,[-15 15]) %函数用字符串表示
1 -8 4 9 -4 5 7 -9 >> fun=@myfun5 %例28中的函数 fun =
@myfun5 >> y=fun(A) %直接调用 y=
1 -13 16 81 -5 25 49 -15 >> y=feval(fun,A) %利用feval y=
1 -13 16 81 -5 25 49 -15
1 4 9 16 5 10 15 20
2024/7/5
第二章 MATLAB编程与作图
24
>> k=5;
>> ff=@(x)x^2+2*x+k %可以使用空间中的变量k
ff =
@(x)x^2+2*x+k
>> ff(5)
ans =
40
>> A=[1 2 ;3 4]
数学建模竞赛培训之编程MATLAB实用教程

数学建模竞赛培训之编程MATLAB实用教程在当今的学术和工程领域,数学建模竞赛越来越受到重视,而MATLAB 作为一款强大的数学计算和编程软件,在其中发挥着至关重要的作用。
如果你正在为数学建模竞赛做准备,那么掌握 MATLAB 的编程技巧将为你在竞赛中取得优异成绩提供有力的支持。
接下来,让我们一起开启 MATLAB 编程的实用教程之旅。
一、MATLAB 基础首先,我们来了解一下 MATLAB 的基本操作界面。
当你打开MATLAB 时,会看到一个命令窗口,这是我们输入命令和查看结果的地方。
变量是编程中的重要概念,在 MATLAB 中,变量无需事先声明类型,直接赋值即可使用。
例如,我们可以输入`x = 5` ,此时`x` 就被赋值为 5 。
MATLAB 支持多种数据类型,如数值型(包括整数和浮点数)、字符型、逻辑型等。
二、矩阵操作矩阵在数学建模中经常用到,MATLAB 对矩阵的操作非常方便。
可以通过直接输入元素来创建矩阵,比如`A = 1 2 3; 4 5 6` 就创建了一个 2 行 3 列的矩阵`A` 。
矩阵的运算也十分简单,加法、减法、乘法等都有相应的运算符。
例如,两个矩阵相加可以直接使用`A + B` 。
三、函数的使用MATLAB 拥有丰富的内置函数,大大提高了编程效率。
比如求矩阵的行列式可以使用`det()`函数,求矩阵的逆可以使用`inv()`函数。
我们还可以自己定义函数,语法如下:```matlabfunction output_args = function_name(input_args)%函数体end```四、绘图功能在分析数据和展示结果时,绘图是必不可少的。
MATLAB 能够绘制各种类型的图形,如折线图、柱状图、饼图等。
以绘制简单的折线图为例,使用`plot()`函数,如`plot(x,y)`,其中`x` 和`y` 是数据向量。
五、数值计算在数学建模中,常常需要进行数值计算,如求解方程、求积分等。
2024(完整版)MATLAB自学教程

01 MATLABChapterMATLAB概述与特点发展历程及应用领域发展历程应用领域安装与界面介绍安装用户可以从MathWorks官网下载MATLAB安装程序,根据提示完成安装过程。
安装过程中需要选择安装路径、添加环境变量等步骤。
界面介绍MATLAB界面包括命令窗口、工作空间、当前目录窗口、命令历史窗口等部分。
用户可以在命令窗口中输入命令并执行,工作空间展示当前变量和函数,当前目录窗口显示当前工作路径下的文件和文件夹,命令历史窗口记录用户输入的命令历史。
01020304变量与数据类型条件语句与循环语句数组与矩阵操作函数编写与调用基本操作入门02数据类型与运算规则Chapter整数类型包括有符号和无符号整数,如int8、uint8、int16、uint16等。
浮点数类型包括单精度和双精度浮点数,如single、double。
特殊数值如Inf表示无穷大,-Inf表示负无穷大,NaN表示非数字。
字符数组01字符串操作02字符编码03逻辑型数据逻辑函数逻辑运算逻辑值(~)等逻辑运算符。
逻辑真(true)和逻辑假(false)。
数组与矩阵运算规则数组创建数组索引矩阵运算特殊矩阵03程序设计基础ChapterMATLAB 中变量名区分大小写,以字母开头,可包含字母、数字和下划线,不能是MATLAB保留字。
变量命名规则变量作用域特殊变量局部变量只在其所在的函数或脚本中有效,全局变量在整个MATLAB 工作环境中都有效。
MATLAB 提供了一些特殊变量,如ans 、pi 、i 或j (虚数单位)等,可以直接使用。
变量命名规则及作用域条件语句if-else语句用于根据条件执行不同的代码块,switch-case语句用于多分支选择。
循环语句for循环用于指定次数的重复执行,while循环用于满足条件时的重复执行。
流程控制语句break语句用于提前退出循环,continue语句用于跳过本次循环的剩余部分。
条件语句和循环语句应用函数定义MATLAB 中可以使用function 关键字定义函数,包括输入参数、输出参数和函数体。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
Matlab使用
1、matlab使用环境
2、四则运算与一些常用函数
3、关于矩阵提取
4、图形功能 5、M-文件编写
2、四则运算注意事项
(1)*与.:矩阵乘法与 数组乘法 (2)矩阵的左除运算与 右除运算
左除、右除与点除
左除:A\B =inv(A)*B 右除:A/B =A*inv(B)
常用的基本数学函数(1)
常用的基本数学函数(2)
sin(x):正弦函数 cos(x):馀弦函数 tan(x):正切函数 asin(x):反正弦函数 acos(x):反馀弦函数 atan(x):反正切函数 atan2(x,y):四象限的反正切函数 sinh(x):超越正弦函数 cosh(x):超越馀弦函数 tanh(x):超越正切函数 asinh(x):反超越正弦函数 acosh(x):反超越馀弦函数 atanh(x):反超越正切函数 min(x): 向量x的元素的最小值 max(x): 向量x的元素的最大值
什么是数学建模
把现实世界中的实际问题加以提炼,抽 象为数学模型,求出模型的解,验证模型的
合理性,并用该数学模型所提供的解答来解
释现实问题,我们把数学知识的这一应用过
程称为数学建模。
建模全过程示意图
数学建模的一般步骤
堂上思考题
如何估计一个人体内血液的总量?
示例3、人口预报
一、两个经典模型: 1、指数增长模型:
abs(x):纯量的绝对值或向量的长度 sqrt(x):开平方
round(x):四舍五入至最近整数
fix(x):无论正负,舍去小数至最近整数 floor(x):地板函数,即舍去正小数至最近整数
ceil(x):天花板函数,即加入正小数至最近整数
rat(x):将实数x化为分数表示 rats(x):将实数x化为多项分数展开 sign(x):符号函数 (Signum function)。
Matlab使用
1、matlab使用环境
2、四则运算与一些常用函数
3、关于矩阵提取
4、图形功能 5、M-文件编写
M-文件
1、关系运算符
<:小于
>:大于 ~=:不等于 2、逻辑运算符 &:与运算
<=:小于等于
>=:大于等于
|:或运算
~:非运算
3、for循环、while循环 4、break语句:跳出上述循环
开机画面:
命令编辑区:
MATLAB工作区:
可查看所有变量值
(1)一行执行一个命令 (2)表达式后面的“;”, 将不显示结果。
(ln 3 e1.2 ) 2 计算:( 1 ) 81 1 2 5 (2)设矩阵A 4 7 8 ,求A的行列式与逆矩阵 3 5 6
没有;
dis p
没有定 义变量 名
det(a) inv(a)
用Richard模型模拟
用Logistic模型模拟
5、Logistic模型的演变
(1)Logistic模型的特点:
模型具有固定的拐点,只能描述一种特定形状的S曲线 。
(2)面临的问题: 生物在一个完整的时间序列里,生物的总生长量最初比
较小,随时间的增加逐渐增长而达到一个快速生长时期,尔
后增长速度趋缓,最终达到稳定的总生长量。此生长过程的 图象描述称为是一种拉长的S形曲线。 (3)更合适的模型描述——Richards模型(1951)
d=eig(A), [v,d]=eig(A): 特征值与特征向量 rand(m,n): randn(m,n): m行n列均匀分布随机数矩阵 m行n列正态分布随机数矩阵
Matlab使用
1、matlab使用环境
2、四则运算与一些常用函数
3、关于矩阵提取
4、图形功能 5、M-文件编写
3、关于矩阵的提Байду номын сангаас,:运算
mean(x): 向量x的元素的平均值
median(x): 向量x的元素的中位数 std(x): 向量x的元素的标准差 diff(x): 向量x的相邻元素的差 sort(x): 对向量x的元素进行排序(Sorting) length(x): 向量x的元素个数 norm(x): 向量x的欧氏(Euclidean)长度 sum(x): 向量x的元素总和 prod(x): 向量x的元素总乘积 cumsum(x): 向量x的累计元素总和 cumprod(x): 向量x的累计元素总乘积 dot(x, y): 向量x和y的内 积
1、模型各项参数的意义
指数增长部分
x dx rx (1 ) xm dt
种群尚未实现 部分的比例
固有增长率:种群数 量很少时的增长率
环境容纳量
2、模型的解
方法:分离变量法
增长最快的地方
解:
x(t ) 1 (
xm xm 1)e rt x0
S形曲线
稳定生长阶段 指数增长阶段 初始生长阶段
y(t ) a(1 be )
1 kt 1 m
注:当m=2时为Logistic模型
内 容
一、Logistic模型的性质、参数估计
、应用与模型演变
二、Matlab入门
Matlab使用
1、matlab使用环境
2、一些常用函数
3、关于矩阵提取
4、图形功能 5、M-文件编写
1、Matlab使用环境
矩阵函数
det(A): inv(A): poly(A): 行列式计算 矩阵的逆 特征多项式 A/ : orth(A): rank(A): eys(n): 矩阵的转置 正交化 矩阵的秩 n阶单位矩阵
trace(A): 矩阵的迹
ones(m,n): m行n列的全1矩阵
zeros(m,n): m行n列的零矩阵
取矩阵a第三行
取矩阵a第1、2行与第2、 3列交叉点的数
将矩阵a所有元素作一列
Matlab使用
1、matlab使用环境
2、四则运算与一些常用函数
3、关于矩阵提取
4、图形功能 5、M-文件编写
二维图形功能(一)
plot: x轴和y轴均为线性刻度 注: 1、图形颜色:y(黄) k(黑) w(白) b(蓝) g(绿) r(红) 2、线条形状:-(实线) -.(点虚线) 3、图形的各种注解与处理: x轴注解 :xlabel('Input Value') y轴注解 :ylabel('Function Value'); --(虚线)
dx x rx(1 ) dt xm
dx rx dt
2、阻滞增长模型(Logistic模型)
二、两个重要名词: 固有增长率与人口容纳量 三、如何估计Logistic模型的参数
课后作业
(1)用P11表2的数据,分别确定两个模型的参数。 (2)分别对两个模型进行误差分析。 (3)将程序附上
作业编号:h01-02
更多的二维作图命令
bar 长条图 fplot 较精确的函数图形 hist 累计图 stairs 阶梯图 fill 实心图 errorbar 图形加上误差范围 polar 极座标图 rose 极座标累计图 stem 针状图 feather 羽毛图
compass 罗盘图
quiver 向量场图
x=0:0.1:2*pi; y1=sin(x);y2=cos(x);y3=log(x+1)-x.^2; subplot(1,2,1),plot(x,y1,'y',x,y2,'rd'),title('y=sin(x)与y=cos(x)') subplot(1,2,2),plot(x,y3,'b'),title('y=ln(x+1)-x^2')
3、数轴范围调整:axis([xmin,xmax,ymin,ymax])
图形标题 :title('Two Trigonometric Functions')
图形注解 :legend('y = sin(x)','y = cos(x)') 显示格线:grid on
4、画出数个小图形于同一个视窗之中: subplot
dx
dt r sx, x
r xm s
模型表达式:
x dx ) 0.5284x(1 dt 48 . 381 x(1) 0.3
程序!
关于polyfit命令
命令:p=polyfit(x,y,n) (1)x与y为模拟数据 (2)n为拟合多项式的次数 (3)当n=1时为用最小二乘法进行 直线拟合 (4)得到的向量p为长度n+1向量, 对应p的分量依次是次数从高 到底各多项式系数
5、定义函数: function y=new_fun(x)
用Logistic模拟水稻叶伸长生长
生长观测记录数据
时间 重量 时间 重量 1 0.3 8.8 23.0 1.8 0.5 9.4 25.2 2.6 0.9 10.1 30.4 3.4 1.4 10.8 33.7 4.1 2.5 11.7 38.8 4.8 3.2 12.4 41.7 5.4 4.3 13.1 43.7 6.1 7.6 14.4 44.8 6.8 10.1 15.1 45.5 7.4 14.4 15.7 45.3 8.1 18.5
3、如何对模型进行参数估计
dt r sx, x (2)如何根据数据计算 dx dt
(1)将模型变形:
dx
r xm s
以P14表4为例:
年 实际人口数 1790 3.9 1800 1810 5.3 7.2
dx dt ( xi 1 xi ) T
0.14 0.19
(3)参数估计方法:最小二乘法,用matlab实现
Richard模拟
Logistic模拟
