高频电子线路习题答案(第五版)张肃文
高频电子线路习题答案(第五版)张肃文(完整资料).doc

【最新整理,下载后即可编辑】高频电子第五版(pF)).(L C H)(.QR则L Ω取R Δf f Q (kHz)Δf MHz解:f..159101*********1159********10010100101010121010990101211362620603670036700=⨯⨯⨯⨯===⨯⨯⨯====⨯⨯===⨯-⨯==--ωμω时,产生并联谐振。
C L 或ωC L )当(时,产生串联谐振。
C L 或ωC L )当(时,产生并联谐振。
C L 或ωC L )当解:(22021101220211012202110111311211123======-ωωωR R C L R )LC ωL(j ωR )LC ωLR(j ωC L R C j ωR L j ωR )C j ωL)(R j ω(R 证明:Z =+=-+-++=+++++=-2112111133220020020000)()()()()())()()()())318010404501053514321121535100160512405354501605151431223202222μH .C C L 故采用后一个不合理舍去pF -得C C C 由pF得C C C 由解:=⨯+⨯⨯⨯⨯='+==+=⨯+=+=⨯+--ω。
L C C ’()()()()mV V Q V V mA .R V I μH ..C L ..R C 解:Q-Sm Com Lom -om om --21210121220510111210100105114321121251010010511432115330312260200126000=⨯⨯====⨯===⨯⨯⨯⨯===⨯⨯⨯⨯⨯⨯==-ωω()()()()()()Ωj ..j .C jR Z Ω.....Q LQ L R pFC pF .L C C C C .V V Q μH .C 解:L X X X X X X X S C 7967471020010143217471747100102531014321052102531014322001001025310143211100101025310100101432116312606666000626200122620-=⨯⨯⨯⨯-=-==⨯⨯⨯⨯-⨯⨯⨯⨯=-==→=⨯⨯⨯⨯==+⋅====⨯⨯⨯⨯==------ωωωωω()()()。
高频电子线路(第五版) 张素文
M
2 22
2 2 22
R X
R22
X 22
M
2 22
2 2 22
R X
X 22
R22 20
1 X 22 10 L2 6 10 C2
6
2-16:①:
Rf 1
M
R2
2
20
R总 R f 1 R1 25
6
L 100 10 Z ab 40 K 12 RC 25 100 10
②:音量位于最上端:
R R1 R2 // ri 2
R R 0.3 R R1 R2
③:不产生惰性失真:
验证是否产生负峰切割失 真,否则改变R1,R2
max RC 1.5
④:CC耦合300HZ ~ 3000HZ
C
取 : C1 C2 0.01或0.005
1 f 0 10 5 10 : V0 m 25 0.7 2 1 6 4 f 0 10 10 : V2 m 25 0.3 2
6 3
f 0 10 : V0 m 25
6
Vmax V0 m峰 V0
V0 Vmin m谷 V0
Vm 251 0.7 cos t 0.3 cos 2t
20 40 5 C Ci C1 // C2 18.3PF 20 40
C1 Ci Ri L
C'2 R'0
RP ②: Q0 100 0 L Q0 ③: QL RP RP 1 Ri R0
④:
RP 20.9K
Q0 28.1 20.9 20.9 1 10 45
高频电子线路课后习题答案第五版张肃文.doc

高频电子第五版(pF)).(L C H)(.QR则L Ω取R Δf f Q (kHz)Δf MHz解:f..159101*********11591014321010010100101010121010990101211362620603670036700=⨯⨯⨯⨯===⨯⨯⨯====⨯⨯===⨯-⨯==--ωμω时,产生并联谐振。
C L 或ωC L )当(时,产生串联谐振。
C L 或ωC L )当(时,产生并联谐振。
C L 或ωC L )当解:(22021101220211012202110111311211123======-ωωωR R C L R )LC ωL(j ωR )LC ωLR(j ωC L R C j ωR L j ωR )C j ωL)(R j ω(R 证明:Z =+=-+-++=+++++=-2112111133220020020000)()()()()())()()()())318010404501053514321121535100160512405354501605151431223202222μH .C C L 故采用后一个不合理舍去pF -得C C C 由pF得C C C 由解:=⨯+⨯⨯⨯⨯='+==+=⨯+=+=⨯+--ω。
L C C ’()()()()mV V Q V V mA .R V I μH ..C L ..R C 解:Q-Sm Com Lom -om om --21210121220510111210100105114321121251010010511432115330312260200126000=⨯⨯====⨯===⨯⨯⨯⨯===⨯⨯⨯⨯⨯⨯==-ωω()()()()()()Ωj ..j .C jR Z Ω.....Q LQ L R pF C pF .L C C C C .V V Q μH .C 解:L X X X X X X X S C 7967471020010143217471747100102531014321052102531014322001001025310143211100101025310100101432116312606666000626200122620-=⨯⨯⨯⨯-=-==⨯⨯⨯⨯-⨯⨯⨯⨯=-==→=⨯⨯⨯⨯==+⋅====⨯⨯⨯⨯==------ωωωωω()()()。
高频电子线路张肃文第五版答案

高频电子线路张肃文第五版答案【篇一:高频电子线路期末考试精华版张肃文第四版】第一章绪论一、填空题1.无线通信系统一般由信号源、__________、__________、___________、输出变换器五部分组成。
2.人耳能听到的声音的频率约在__________到__________的范围内。
(20hz、20khz )3.调制有_________、__________、_________三种方式。
(调幅、调频、调相)4.无线电波在空间的传播方式有________、_________、__________三种。
(地波、天波、直线波)二、简答或作图题1.画出无线通信调幅发射机原理框图,并说明各部分的作用,同时画出波形示意图和频谱示意图。
2. 画出超外差接收机方框图,并说明各部分的作用,同时画出波形示意图和频谱示意图。
3.在接收设备中,检波器的作用是什么?试画出检波器前后的信号波形。
4.通信系统由哪些部分组成?各组成部分的作用是什么?答:通信系统由输入、输出变换器,发送、接收设备以及信道组成。
输入变换器将要传递的声音或图像消息变换为电信号(基带信号);发送设备将基带信号经过调制等处理,并使其具有足够的发射功率,再送入信道实现信号的有效传输;信道是信号传输的通道;接收设备用来恢复原始基带信号;输出变换器将经过处理的基带信号重新恢复为原始的声音或图像。
第三章选频网络1、串联谐振和并联谐振的特征,以及失谐时表现出的特性。
如:lc回路并联谐振时,回路_阻抗___最大,且为纯__电阻__。
当所加信号频率高于并联谐振回路谐振频率时,回路失谐,此时,回路呈容性,电流超前电压。
2、由于信号源内阻或负载电阻的影响,将使谐振回路的品质因数q,选频特性,通频带。
3、课后题 3.5 4、课后题 3.6 5、课后题 3.7 6、课后题 3.9 7、课后题 3.13有一耦合回路如图,已知f?f?1mhz,????1k??,r1?r2?20?,??1010212试求:1)回路参数l1、l2、c1、c2和m;2)图中a 、b两端的等效谐振阻抗zp; 3)初级回路的等效品质因数q1’; 4)回路的通频带bw;解:由已知条件可知两个回路的参数是全同c1=c2,q1=q2 ;的,即l1=l2,1)由得:?1000l1?l2??h?159?h6?02??1011c?c??f?159pf12262?6 (2??10)?159?10?0l又由于发生临界耦合时 (?0m)2?r1r2因此???0lm?1r1r2?120?20h?3.18?h6(1000)2zab?zp?rp????25k?r1?rf140?1?1000?2540?23)初级回路的等效品质因数为q1?r1?rf14)初级回路本身的品质因数为?1000q1?1??5020因此可得出通频带为: r1f01062?f0.7?2?2?hz?28.3khzq1508.图2-18所示电路为一等效电路,其中l=0.8uh,q0=100,c=5pf,c1=20pf,c2 =20pf,r=10k?,rl =5k?,试计算回路的谐振频率、谐振电阻。
高频电子线路第五版课后习题答案

高频电子线路第五版课后习题答案高频电子线路第五版课后习题答案高频电子线路是电子工程中的一个重要分支,其研究的是高频电路的设计、分析和优化。
在学习高频电子线路的过程中,课后习题是巩固知识、提高技能的重要方式。
本文将为大家提供高频电子线路第五版课后习题的答案,希望对大家的学习有所帮助。
第一章:基础知识1. 什么是高频电子线路?高频电子线路是指工作频率在几十千赫兹(kHz)到几百千赫兹(MHz)之间的电子线路。
它主要应用于无线通信、雷达、卫星通信等领域。
2. 高频电子线路的特点有哪些?高频电子线路的特点包括信号失真小、传输损耗小、耦合效应显著、传输线效应显著、元器件参数变化大等。
3. 什么是S参数?S参数是描述高频电子线路中信号传输和反射特性的参数。
S参数包括S11、S12、S21和S22四个参数,分别表示输入端反射系数、传输系数、输出端反射系数和逆传输系数。
第二章:传输线1. 什么是传输线?传输线是一根用于传输高频信号的导线。
常见的传输线有平行线、同轴电缆和微带线等。
2. 传输线的特性阻抗有哪些?传输线的特性阻抗包括平行线的特性阻抗、同轴电缆的特性阻抗和微带线的特性阻抗等。
3. 传输线的特性阻抗如何计算?平行线的特性阻抗可以通过导线间距、导线半径和介质介电常数等参数计算得到。
同轴电缆的特性阻抗可以通过内外导体半径和介质介电常数等参数计算得到。
微带线的特性阻抗可以通过导线宽度、介质厚度和介质介电常数等参数计算得到。
第三章:射频二极管1. 什么是射频二极管?射频二极管是一种特殊的二极管,其工作频率在几十千赫兹(kHz)到几百千赫兹(MHz)之间。
射频二极管具有快速开关速度和低噪声等特点。
2. 射频二极管的工作原理是什么?射频二极管的工作原理是基于PN结的电子流动和载流子的注入与抽取。
当正向偏置时,电子从N区域流向P区域,形成电流;当反向偏置时,电子不能流动,形成电流截止。
3. 射频二极管的主要参数有哪些?射频二极管的主要参数包括最大工作频率、最大直流电流、最大反向电压、最大功率损耗和最大噪声系数等。
高频电子线路张肃文第五版Chapter4__非线性电路、时变参量电路和变频器

若能进行调幅、检波的话, 若能进行调幅、检波的话,电流 i 中必须含有
ω ± ω2 ,ω 1 1 ω 是低频信号频率。 其中 ω 为高频载波频率, 2是低频信号频率。 1 为高频载波频率, 电流 i 中却不含有 ω ± ω2 1
故不能用它进行变频,调幅与振幅检波。 故不能用它进行变频,调幅与振幅检波。
对其2次方进行分析: 对其2次方进行分析:
a2v = a2 (vs +vo ) = a v + a v + 2a2vsvo
2 2 2 2 s 2 2 o
在二次方项中出现了和的相乘项,因而可以得到 在二次方项中出现了和的相乘项, 若用带通滤波器取出所需的中 (ω0+ωs)和(ω0-ωs)。若用带通滤波器取出所需的中 频成分,可达到混频的目的。 频成分,可达到混频的目的。
2012-4-17 10
§4.3 变频电路
1 基本概念 2 晶体三极管混频器 3 二极管平衡混频器和环型混频器 4 模拟相乘器混频电路
2012-4-17
11
一、基本概念 基本概念
1. 混频器的组成
混频:对信号进行频率变换, 混频:对信号进行频率变换,将其载频变换到某一 固定频率上 而保持原信号的特征不变。 特征不变 固定频率上,而保持原信号的特征不变。
2012-4-17 15
5.混频器实现模型 5.混频器实现模型
vs(t) v 非 性 线 器 件 vo(t) i 带 通 vI(t)
⑴叠加型 图示中的非线性 器件具有如下特性: 器件具有如下特性:
叠加型混频器实现模型
2 3
i = f (v) = a0 +a1v +a2v +a3v +.......
高频电子线路张肃文第五版习题答案

高频电子线路〔用于学习之间交流,不得用于出版等商业用处!〕第2章习题答案2-1某一并联谐振回路的谐振频率f 0=1MHz ,要求对990kHz 的干扰信号有足够的衰减,问该并联回路应如何设计?解 为了有效滤除990kHz 的干扰信号,应使它位于通频带之外。
假设取BW 0.7=20kHz ,那么由通频带与回路Q 值之间的关系有502010007.00===BW f Q因此应设计Q >50的并联谐振回路。
2-2试定性分析题图2-2所示的电路在什么情况下呈现串联谐振或并联谐振状态。
解 题图2-2〔a 〕中L 1C 1或L 2C 2之一呈并联谐振状态,那么整个电路即为并联谐振状态。
假设L 1C 1与L 2C 2呈现为容抗,那么整个电路可能成为串联谐振。
题图2-2〔b 〕只可能呈现串联谐振,不可能呈现并联谐振状态。
题图2-2〔c 〕只可能呈现并联谐振,不可能呈现串联谐振状态。
2-3有一并联回路,其电感、电容支路中的电阻均为R 。
当C L R =时〔L 和C 分别为电感和电容支路的电感值和电容值〕,试证明回路阻抗Z 与频率无关。
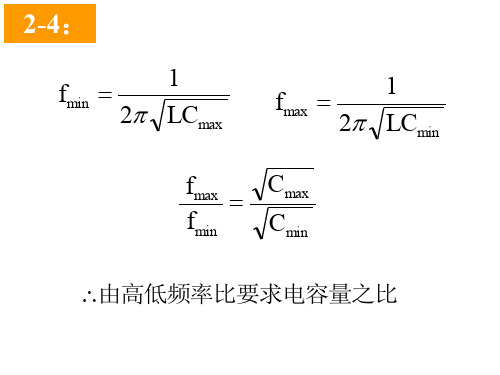
解 ()()()⎪⎭⎫ ⎝⎛-++⎪⎪⎭⎫⎝⎛-+⎪⎭⎫ ⎝⎛+=⎪⎭⎫⎝⎛-++⎪⎭⎫ ⎝⎛-+=C L j R R C R LR j C L R R C j R L j R C j R L j R Z abωωωωωωωω11121112212121 要想使Z ab 在任何频率下,都呈现纯阻性,就必须使分子与分母的相角相等,亦即必须有2121121R R C L CL R R C R LR +-==-ωωωω 上式化简得C R C L LR C L 2122222-=⎪⎪⎭⎫ ⎝⎛-ω 要使上式在任何频率下都成立,必有0222=-LR C L 或 C L R =2 0212=-C R C L 或 CL R =1 因此最后得CLR R ==212-4有一并联回路在某频段内工作,频段最低频率为535kHz ,最高频率为1605kHz 。
高频电子线路第五版课后答案张肃文

?
?45.97(mhz)
(2)rl折合到回路两端时的接入系数p为
1?c2c11p???
c1?c22?12
c1?c2
则
11?0.52??0.05?10?3?s? 3rl5?10
电感l的损耗电导g0为
p2
g0?
11
?
?0lq02??45.97?106?0.8?10?6?100
?43.30?10?6?s? 1121总电导g???g0?p??0.0433?10?3?0.05?10-3 3rrl10?10
2?l?3?
1
2
2
??100?c?535得c?-1pf?不合理舍去
。
?
1
?0?c?c??
?2?3.14
?535?10
32
?
??450?40??10
?12
?
3?5解:q
?
1
?0c0r1
2
?
1
2?3.14?1.5?10
1
?100?10
-12
?5
?212
l0?
?0c0vomr
?
?
?2?3.14
-3
?1.5?10
?0.1933?10
?3
?s?
谐振电阻rp?g??5.17?k??
========================================================================================
第四章高频小信号谐振放大器
1.高频小信号放大器的主要技术指标有、_________、________、__________。(谐振频率、增益、通频带、选择性)
高频电子线路张肃文

(pF)).(L C H)(.QR则L Ω取R Δf f Q (kHz)Δf MHz解:f..159101*********11591014321010010100101010121010990101211362620603670036700=⨯⨯⨯⨯===⨯⨯⨯====⨯⨯===⨯-⨯==--ωμω时,产生并联谐振。
C L 或ωC L )当(时,产生串联谐振。
C L 或ωC L )当(时,产生并联谐振。
C L 或ωC L )当解:(22021101220211012202110111311211123======-ωωωR R C LR )LC ωL(j ωR )LC ωLR(j ωC L R C j ωR L j ωR )C j ωL)(R j ω(R 证明:Z =+=-+-++=+++++=-21211133220020020000)()()()()())()()()())318010404501053514321121535100160512405354501605151431223202222μH .C C L 故采用后一个不合理舍去pF -得C C C 由pF得C C C 由解:=⨯+⨯⨯⨯⨯='+==+=⨯+=+=⨯+--ω。
L C C ’()()()()m V V Q V V m A .R V I μH ..C L ..R C 解:Q-Sm Com Lom -om om --21210121220510111210100105114321121251010010511432115330312260200126000=⨯⨯====⨯===⨯⨯⨯⨯===⨯⨯⨯⨯⨯⨯==-ωω()()()()()()Ωj ..j .C jR Z Ω.....Q LQ L R pF C pF .L C C C C .V V Q μH .C 解:L X X X X X X X S C 7967471020010143217471747100102531014321052102531014322001001025310143211100101025310100101432116312606666000626200122620-=⨯⨯⨯⨯-=-==⨯⨯⨯⨯-⨯⨯⨯⨯=-==→=⨯⨯⨯⨯==+⋅====⨯⨯⨯⨯==------ωωωωω()()()。
高频电子线路 习题答案(4) 张啸文

5102501050501501时,5012.1102501020501501时,20491025010501501时,154266200266200266200=⎪⎪⎭⎫⎝⎛⨯⨯⨯+=⎪⎪⎭⎫ ⎝⎛+===⎪⎪⎭⎫ ⎝⎛⨯⨯⨯+=⎪⎪⎭⎫ ⎝⎛+===⎪⎪⎭⎫ ⎝⎛⨯⨯+=⎪⎪⎭⎫ ⎝⎛+==-T T T f f ββMHz f f f ββMHz f f f ββMHz f βββ当当解:当()()()()()()()()()()()()()()()()()()()()mS j .j .j b a jb a g r C j b a jb a C j g g r C j g y mS j .j b a jb a g y mS j .j .j b a jb a C j g y mS .j ..j .j b a jb a C j g y ..r ωC b .g r a pF ..πf g C mS ..r βg mS .βI g m b b c b c b c b m b b c b ce oe m fe c b cb re e b e b ieb b e b e b b b T m eb eb m E eb 68.0049.01011.01107.377011031014321733.3327.371011.01107.37187.00187.01011.0110310143241189501011.01102410143210754.010701024101432110754070112410250143210737273710754050754015026112674223127222222322221272222127322127363300+=⎪⎭⎫ ⎝⎛+-⨯⨯⨯+⨯⨯⨯⨯≈⎪⎭⎫⎝⎛+-+≈+-+++=-=+-⨯⨯=+-=--=+-⨯⨯⨯⨯⨯-≈+-+-=+=+-⨯⨯⨯⨯⨯+⨯=+-+=≈⨯⨯⨯⨯⨯==≈⨯⨯+=+==⨯⨯⨯⨯===⨯⨯===+⨯=+=---''''''--''--''-''-''-'-''ωωωωω解:()()()()4124142701010042104010041704070121101241104221104210124212422124284--=⎪⎪⎭⎫⎝⎛-⎪⎪⎭⎫⎝⎛-==⋅⎪⎪⎭⎫ ⎝⎛-==⎪⎪⎭⎫⎝⎛+=⎪⎪⎭⎫ ⎝⎛⋅⎪⎪⎭⎫ ⎝⎛-==⎪⎪⎭⎫⎝⎛+=⎪⎪⎭⎫⎝⎛-m mm m ...r m .m.mvo v m .m.mvo v Δf Δf K Q f Δf f ΔfQ A A Qf Δf f Δf Q A A 故得令得解:令()()()()()()()()()1103101045952110830081020010286021830082501020025010237952258854tan 2tan 431100316116570316107102316104107102105228113151312312105228104525025052281028604110200411023723710410010710211250205250205943326662262621222206070666022632162626222166001345213231>>⨯⨯+⨯+⨯⨯⨯=+'++=⨯⨯+⨯=+='-=--=+==⎪⎭⎫⎝⎛-=⎪⎪⎭⎫ ⎝⎛-==⨯===⨯⨯⨯⨯⨯⨯======⨯⨯⨯⨯===⨯⨯+⨯⨯+⨯=++==⨯⨯⨯⨯⨯========-----------------∑-...y y ξg g g g S μS ....p g p g g ..ξ..Q Q K MH ...Q f Δf ..π.L ωg Q ..A A ....g y p p A μS ..g p g p g g μS ..πL Q ωg .N N p .N N p refe L oe ie s ie p L oo re fe L Z L .ΣL vo po Σfevo ie oe p p ϕϕ解:()()()()()()()()()()()()()()()()()()()()7221698266804238225025668042479479610444454782122259044546104422610441222565197445412212243822502578213445410158010410710143222782115802438303015801503008203010037010370104107101432100111104444447070707041707041704147044436260070222122222156600..-.A A ..A A ....f ΔΔf A A kHz ...Δf f ΔkHz .Δf f ΔkHz ..Δf Δf ..A A kHz ....f Lg ωΔf .....g y p p A mS .......g p g p R g g mS ...L ωQ g vovo vo vo..vo vo......vo vo .fevo ie oe p p =='-=='='=⨯='='=-=-'=-='=⨯-=⋅-=====⨯⨯⨯⨯⨯⨯⨯===+⨯⨯===⨯+⨯++=+++==⨯⨯⨯⨯⨯⨯==---∑∑∑-解:()()()()不能满足解:9.1K 522106250110511432121625011830500114r0.1122620221<=⨯⨯⨯⨯⨯===⨯+=+=--∑∑μH ....C πf L pF ..C p C C oe()74.73.05.24.364.265.2144220=⨯+==-refe S vo C y A ω解:()()()()()()()16391060104652226010491010041046527410492104057451311491001010001046521062057451349100101000104652102010044057451310001004410001205137311860731187311811810100010465211174103070612312120632112332020223612361012222236112563423612231201.K kH .Q f Δf πg C ωQ ..g y p p A μS π...Q C ωg p g μS πQ C ωg g pF ..C p C C pF C C C .L L L L μH πC ωL .r Z L.L fevo i o i o ==⨯⨯===⨯⨯⨯⨯⨯===⨯⨯⨯⨯⨯===∴=⨯⨯⨯⨯+⨯⨯⎪⎭⎫ ⎝⎛=+==⨯⨯⨯⨯+⨯=+==⨯⎪⎭⎫⎝⎛+=+==+=+==⨯+⨯+=++==⨯⨯⨯⨯==----------,则。
高频电子线路(第五版) 张肃文主编课后练习题解析
绪论 选频网络练习题一、选择题1、在调谐放大器的LC 回路两端并上一个电阻R ,可以 C 。
A .提高回路的Q 值B .提高谐振频率C .加宽通频带D .减小通频带2、在高频放大器中,多用调谐回路作为负载,其作用不包括 ( D )A .选出有用频率B .滤除谐波成分C .阻抗匹配D .产生新的频率成分3、并联谐振回路的通频带是指其输出电压下降到谐振电压的 所对应的频率范围,用7.02f ∆表示。
( D )A 、1/2B 、1/3C 、1/3D 、1/24、LC 并联谐振回路具有选频作用。
回路的品质因数越高,则 ( A )A 、回路谐振曲线越尖锐,选择性越好,但通频带越窄。
B 、回路谐振曲线越尖锐,选择性越好,通频带越宽。
C 、回路谐振曲线越尖锐,但选择性越差,通频带越窄。
D 、回路谐振曲线越尖锐,但选择性越差,通频带越宽。
5、地波传播时,传播的信号频率越高,损耗 。
( B )A 、越小B 、越大C 、不变D 、无法确定6、并联谐振回路谐振时,电纳为零,回路总导纳为 。
( B )A .最大值B .最小值C .零D .不能确定7、谐振回路与晶体管连接时,常采用部分接入方式实现阻抗匹配,控制品质因数以达到对通频带和选择性的要求,图示电路中Is 信号源的接入系数s p 为 。
( D )s iA .12L LB .21L LC .112L L L +D .212L L L +8、电路与上题同,晶体管基极与谐振回路的接入系数L p 为 。
( C )A .12C CB .21C C C .112C C C +D .212C C C +9、考虑信号源内阻和负载后,LC 选频回路的通频带变 ,选择性变 。
( D )A 、小、好B 、大、好C 、小、差D 、大、差10、LC组成并联谐振回路,谐振频率LCfoπ21=,把它串接在电路中,就能阻止频率为多少的信号通过。
( A )A.不为of B.of C.大于of D.小于of11、如图所示,将负载LR等效到ab两端LR'= 。
高频电子线路第五版课后的答案(28页)

1)如果将次级线圈短路,这时反射到初级的阻抗等于什么?
初级等效 电路 (并联型)应该怎么画?
2)如果将次级线圈开路,这时反射阻抗等于什么?
初级冬
该怎么画?
3) 如 果
,反射到初级的阻抗等于什么?
解:如2.5(a), 利用戴维南定理将互感耦合并联型回路等效 为互感耦合串联联型回路的形式。图中,
V=1z. ,
S
(1)、由等效电路图4 . 1c, 知
从而
;
::
G¹
P₂
I=P₁y V
图3.1a 图3.1b 图3.1c
4)、∴.
(5)、
例3.3.3中 频 放 大 器 设 计 ( 单 调 谐 回 路 )
步骤:(已知中心频率和通频带f、B₇ )
1、 直流偏置:(1)、直流偏置电阻R,R₂ (几千欧姆), 满足放大状态(2)、旁路电容C,C(μF), 静态工作条做 (3)、射级电阻R(几百欧姆),
解:由题知 0(t)=10⁷πt+10*πt²,
1、 当t=0时 ,o(0)=10'π
2、o (1)随t成正比例关系变化
第10章习题
· 8 . 2求 v(t)=5cos(10⁶t+sin5×10³t) 率 解 :由 题 知
θ(t)=10⁶t+sin5×10³t,
当t=0 时, o(0)=(10⁶+5×10²)rad/s
在t=0 时的瞬时频
习题
· 8.9 调制信号为正弦波,当频率为500 Hz、 振 幅 为 1V 时 , 调角波的最大频移□fi=200Hz, 若调制信号振幅仍为IV, 但调制频率增大为1kHz 时 , 要 求 将 频 偏 增 加 为f₂=20kHz 。 试问:应倍频多少次? (计算调频和调相两种情况)
高频电子线路课后答案(第五版)张肃文

高频电子第五版(张肃文)注意:3-1是2-1祝学习进步(pF)).(L C H)(.QR则L Ω取R Δf f Q (kHz)Δf MHz解:f..159101*********1159********10010100101010121010990101211362620603670036700=⨯⨯⨯⨯===⨯⨯⨯====⨯⨯===⨯-⨯==--ωμω时,产生并联谐振。
C L 或ωC L )当(时,产生串联谐振。
C L 或ωC L )当(时,产生并联谐振。
C L 或ωC L )当解:(22021101220211012202110111311211123======-ωωωR R C L R )LC ωL(j ωR )LC ωLR(j ωC L R C j ωR L j ωR )C j ωL)(R j ω(R 证明:Z =+=-+-++=+++++=-2112111133220020020000 )()()()()())()()()())318010404501053514321121535100160512405354501605151431223202222μH .C C L 故采用后一个不合理舍去pF -得C C C 由pF得C C C 由解:=⨯+⨯⨯⨯⨯='+==+=⨯+=+=⨯+--ω。
L C C ’()()()()m V V Q V V m A .R V I μH ..C L ..R C 解:Q-Sm Com Lom -om om --21210121220510111210100105114321121251010010511432115330312260200126000=⨯⨯====⨯===⨯⨯⨯⨯===⨯⨯⨯⨯⨯⨯==-ωω()()()()()()Ωj ..j .C jR Z Ω.....Q LQ L R pFC pF .L C C C C .V V Q μH .C 解:L X X X X X X X S C 7967471020010143217471747100102531014321052102531014322001001025310143211100101025310100101432116312606666000626200122620-=⨯⨯⨯⨯-=-==⨯⨯⨯⨯-⨯⨯⨯⨯=-==→=⨯⨯⨯⨯==+⋅====⨯⨯⨯⨯==------ωωωωω()()()。
高频电子线路张肃文第五版Chapter2_选频网络

1 L = 特性阻抗: r = wp L = wpC C
2013-7-29
品质因数: Q = r
R
14
谐振时的阻抗特性:
并联谐振时,回路呈纯电阻性, 且阻抗为最大值; w < wp , 呈感性 . I L C G w > wp , 呈容性 因此回路谐振时:
s
|Z|,Re,X e
Re 0 wp
|Z| w
Chapter 2 选频网络
1.选频的基本概念
所谓选频,就是选出需要的频率分量并且滤 除不需要的频率分量。
2.选频网络的分类
单谐振回路
选 振荡回路(由L、C组成) 耦合谐振回路 频 LC集中参数滤波器 网 石英晶体滤波器 络 各种滤波器 陶瓷滤波器
声表面波滤波器
2013-7-29 1
Chapter 2 选频网络
例3 设一放大器以简单并联振荡回路为负载,信号中心频率 fs=10MHz,回路电容C=50pF. ⑴ 试计算所需的线圈电感值; ⑵ 若线圈的品质因数为Q=100,试计算回路谐振电阻及回 路带宽;⑶若放大器所需带宽B=0.5MHz,则应在回路上并 联多大的电阻才能满足放大器所需带宽要求? 1 1 解:⑴ f = = 5.07μH \ L= 0 2 2 2p LC 4p f0 C ⑵ R p = Qw0 L = 2πf 0QL = 31.8k W
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
高频电子第五版(pF)).(L C H)(.QR则L Ω取R Δf f Q (kHz)Δf MHz解:f..159101*********11591014321010010100101010121010990101211362620603670036700=⨯⨯⨯⨯===⨯⨯⨯====⨯⨯===⨯-⨯==--ωμω时,产生并联谐振。
C L 或ωC L )当(时,产生串联谐振。
C L 或ωC L )当(时,产生并联谐振。
C L 或ωC L )当解:(22021101220211012202110111311211123======-ωωωR R C L R )LC ωL(j ωR )LC ωLR(j ωC L R C j ωR L j ωR )C j ωL)(R j ω(R 证明:Z =+=-+-++=+++++=-2112111133220020020000)()()()()())()()()())318010404501053514321121535100160512405354501605151431223202222μH .C C L 故采用后一个不合理舍去pF -得C C C 由pF得C C C 由解:=⨯+⨯⨯⨯⨯='+==+=⨯+=+=⨯+--ω。
L C C ’()()()()mV V Q V V mA .R V I μH ..C L ..R C 解:Q-Sm Com Lom -om om --21210121220510111210100105114321121251010010511432115330312260200126000=⨯⨯====⨯===⨯⨯⨯⨯===⨯⨯⨯⨯⨯⨯==-ωω()()()()()()Ωj ..j .C jR Z Ω.....Q LQ L R pF C pF .L C C C C .V V Q μH .C 解:L X X X X X X X S C 7967471020010143217471747100102531014321052102531014322001001025310143211100101025310100101432116312606666000626200122620-=⨯⨯⨯⨯-=-==⨯⨯⨯⨯-⨯⨯⨯⨯=-==→=⨯⨯⨯⨯==+⋅====⨯⨯⨯⨯==------ωωωωω()()()。
21k Ω0.5R ,R ,故0.5Q Q ,则f 22f 因2Δ320105105552310023100101501052220105010514321173000.70.7660036700012620电阻所以应并上='='∆⨯='=⨯⨯-⨯⨯===⨯⨯===⨯⨯⨯⨯⨯==--.f Δf Q ξΔf f Q μH ..C ω解:L . ∑===-g Q CωΔf f C πf C πΔf 证明:..070007022483()()()()()()()()MHz ...Q f Δf .....L ωR Q k Ω..R C C C C R R R k Ω..C LQ R MHz ....LC πf pF .C C C C C C C 解:C L .L P i P i 4812281064122281080106411432108858855202020209201092010202010801006411031810801432121318202020202020593607066302021102126121260102102=⨯===⨯⨯⨯⨯⨯⨯===⨯⎪⎭⎫⎝⎛++=⎪⎪⎭⎫ ⎝⎛++==⨯+⨯⨯===⨯⨯⨯⨯===++++=++++=--∑∑----)))R Z 30Z 20Z 1123f1f1f1===-解:)()()()())()()()()()()))())()()()()()()Ω.j .j ..Z M Z j ..j C L j R Z pF .L C kHz .R ρf Q f Δf .R R L Q k ΩC R R L Z Ω..R M Z μH ..ηR M pF .L C C μH .ρL L 解:f .f f f P 8437680100201018310143210020101771014321101591014322011771015910950143211522810201022224252020101591014323251015920201015920201018310143221831014322011591015910143211159101432101133266222011126662*********2322022361100706611101112611112662201160116261201216301121-=+⨯⨯⨯⨯==+=⎪⎭⎫⎝⎛⨯⨯⨯⨯-⨯⨯⨯⨯+=⎪⎪⎭⎫⎝⎛'-+==⨯⨯⨯⨯⨯='='=⨯⨯====+⨯⨯⨯⨯=+==⨯⨯+⨯=+==⨯⨯⨯⨯===⨯⨯⨯===⨯⨯⨯⨯====⨯⨯===----------ωωωωωωωωω()100101410222002010159105010159153367.00111236=⨯=∆==→=∴=Ω=⨯⨯⨯⨯==---f f Q M R R C R L R f P 解:)()()()()()()()))013.02001122211222005101001032510102402051010010205101011632207.067101671012671120126722011=⨯-⨯+=⋅-+=∆=⨯⨯===⨯==Ω=+⨯⨯=+=Ω=⨯==-----Q f f R LQ R M k R RL R R M R 解:f ab f ηηωωηωω 5.75.22303021103001010112118.111020*********.325.22115.2225.11103001010112111732332001230233200=-='-=→=⎪⎪⎭⎫⎝⎛⨯⨯+=⎪⎪⎭⎫ ⎝⎛∆+==⨯⨯⨯⨯⨯⨯==='→=⎪⎪⎭⎫⎝⎛⨯⨯'+=⎪⎪⎭⎫ ⎝⎛∆'+=--Q Q Q Q f f Q I I C Q R Q Q f f Q I I 解:ω()⎩⎨⎧==→⎪⎪⎩⎪⎪⎨⎧+==-μL μH L 并联联谐C L L ω串联联谐C L ω解:125375112183212125102501050501501时,5012.1102501020501501时,20491025010501501时,154266200266200266200=⎪⎪⎭⎫ ⎝⎛⨯⨯⨯+=⎪⎪⎭⎫ ⎝⎛+===⎪⎪⎭⎫ ⎝⎛⨯⨯⨯+=⎪⎪⎭⎫ ⎝⎛+===⎪⎪⎭⎫ ⎝⎛⨯⨯+=⎪⎪⎭⎫ ⎝⎛+==-TT T f f ββMHz f f f ββMHz f f f ββMHz f βββ当当解:当()()()()()()()()()()()()()()()()()()()()mS j .j .j b a jb a g r C j b a jb a C j g g r C j g y mS j .j b a jb a g y mS j .j .j b a jb a C j g y mS .j ..j .j b a jb a C j g y ..r ωC b .g r a pF ..πf g C mS ..r βg mS .βI g mb bc b c b c b m b b c b ce oe m fe c b cb re e b e b ieb b e b e b b b T m eb eb m E e b 68.0049.01011.01107.377011031014321733.3327.371011.01107.37187.00187.01011.0110310143241189501011.01102410143210754.010701024101432110754070112410250143210737273710754050754015026112674223127222222322221272222127322127363300+=⎪⎭⎫ ⎝⎛+-⨯⨯⨯+⨯⨯⨯⨯≈⎪⎭⎫⎝⎛+-+≈+-+++=-=+-⨯⨯=+-=--=+-⨯⨯⨯⨯⨯-≈+-+-=+=+-⨯⨯⨯⨯⨯+⨯=+-+=≈⨯⨯⨯⨯⨯==≈⨯⨯+=+==⨯⨯⨯⨯===⨯⨯===+⨯=+=---''''''--''--''-''-''-'-''ωωωωω解:()()()()4124142701010042104010041704070121101241104221104210124212422124284--=⎪⎪⎭⎫ ⎝⎛-⎪⎪⎭⎫⎝⎛-==⋅⎪⎪⎭⎫ ⎝⎛-==⎪⎪⎭⎫⎝⎛+=⎪⎪⎭⎫ ⎝⎛⋅⎪⎪⎭⎫ ⎝⎛-==⎪⎪⎭⎫⎝⎛+=⎪⎪⎭⎫⎝⎛-m mm m ...r m .m.mvo v m .m.mvo v Δf Δf K Qf Δf f ΔfQ A A Qf Δf f Δf Q A A 故得令得解:令()()()()()()()()()1103101045952110830081020010286021830082501020025010237952258854tan 2tan 431100316116570316107102316104107102105228113151********5228104525025052281028604110200411023723710410010710211250205250205943326662262621222206070666022632162626222166001345213231>>⨯⨯+⨯+⨯⨯⨯=+'++=⨯⨯+⨯=+='-=--=+==⎪⎭⎫⎝⎛-=⎪⎪⎭⎫ ⎝⎛-==⨯===⨯⨯⨯⨯⨯⨯======⨯⨯⨯⨯===⨯⨯+⨯⨯+⨯=++==⨯⨯⨯⨯⨯========-----------------∑-...y y ξg g g g S μS ....p g p g g ..ξ..Q Q K MH ...Q f Δf ..π.L ωg Q ..A A ....g y p p A μS ..g p g p g g μS ..πL Q ωg .N N p .N N p refe L oe ie s ie p L oo re fe L Z L .ΣL vo po Σfevo ie oe p p ϕϕ解:()()()()()()()()()()()()()()()()()()()()7221698266804238225025668042479479610444454782122259044546104422610441222565197445412212243822502578213445410158010410710143222782115802438303015801503008203010037010370104107101432100111104444447070707041707041704147044436260070222122222156600..-.A A ..A A ....f ΔΔf A A kHz ...Δf f ΔkHz .Δf f ΔkHz ..Δf Δf ..A A kHz ....f Lg ωΔf .....g y p p A mS .......g p g p R g g mS ...L ωQ g vovo vo vo..vo vo......vo vo .fevo ie oe p p =='-=='='=⨯='='=-=-'=-='=⨯-=⋅-=====⨯⨯⨯⨯⨯⨯⨯===+⨯⨯===⨯+⨯++=+++==⨯⨯⨯⨯⨯⨯==---∑∑∑-解:()()()()不能满足解:9.1K 522106250110511432121625011830500114r0.1122620221<=⨯⨯⨯⨯⨯===⨯+=+=--∑∑μH ....C πf L pF ..C p C C oe()74.73.05.24.364.265.2144220=⨯+==-refe S vo C y A ω解:()()()()()()()16391060104652226010491010041046527410492104057451311491001010001046521062057451349100101000104652102010044057451310001004410001205137311860731187311811810100010465211174103070612312120632112332020223612361012222236112563423612231201.K kH .Q f Δf πg C ωQ ..g y p p A μS π...Q C ωg p g μS πQ C ωg g pF ..C p C C pF C C C .L L L L μH πC ωL .r Z L.L fevo i o i o ==⨯⨯===⨯⨯⨯⨯⨯===⨯⨯⨯⨯⨯===∴=⨯⨯⨯⨯+⨯⨯⎪⎭⎫ ⎝⎛=+==⨯⨯⨯⨯+⨯=+==⨯⎪⎭⎫⎝⎛+=+==+=+==⨯+⨯+=++==⨯⨯⨯⨯==----------,则。
