二次函数压轴题解题技巧
中学数学二次函数压轴题解题技巧

中学数学二次函数压轴题解题技巧二次函数是中学数学中重要的概念之一。
在解题过程中,掌握一些解题技巧能够帮助我们更轻松地解决二次函数的压轴题。
以下是一些解题技巧的总结:1. 定义二次函数首先,我们需要清楚二次函数的定义和一般形式。
二次函数的一般形式是:$$f(x) = ax^2 + bx + c$$,其中a、b、c为常数,且$a \neq 0$。
了解二次函数的定义和形式,有助于我们在解题过程中准确理解题目和相关知识。
2. 寻找顶点二次函数的图像是一个抛物线,其中的最高点或最低点被称为顶点。
寻找顶点是解题过程中的关键步骤之一。
顶点的横坐标为$x = -\frac{b}{2a}$,纵坐标为$f\left(-\frac{b}{2a}\right)$。
通过计算这两个值,我们能够确定抛物线的位置和形状。
3. 判断开口方向通过观察二次函数的二次项系数a的正负,我们可以判断抛物线的开口方向。
当a大于0时,抛物线开口向上;当a小于0时,抛物线开口向下。
这一点在解题中很重要,因为它影响到抛物线与坐标轴的交点和极值。
4. 求解零点解题时,我们通常需要求二次函数的零点,即$f(x) = 0$的解。
求解零点的方法有两种:因式分解和配方法。
对于简单的二次函数问题,我们可以利用因式分解直接求解零点;对于复杂的问题,可以使用配方法。
5. 判断函数值的变化通过计算二次函数的值$f(x)$,我们可以判断函数在不同区间内的变化趋势。
当a大于0时,二次函数在顶点处取得最小值,且随着x增大或减小,函数值逐渐变大;当a小于0时,二次函数在顶点处取得最大值,且随着x增大或减小,函数值逐渐变小。
6. 利用对称性二次函数具有对称性,即关于顶点对称。
这一点在解题中经常用到。
通过利用对称性,我们可以快速求得函数的某些值,或者根据已知的函数值推导出其他函数值。
7. 注意特殊情况解题过程中,我们应该注意特殊情况的处理。
例如,当a等于零时,二次函数变为一次函数;当顶点坐标为整数时,我们可以在图像上快速标出顶点和其他点。
三招破解二次函数压轴题,耐心读题理清思路是关键

二次函数是一次函数的延续和发展,类似于反比例函数但又不同于反比例函数,其图像抛物线是曲线,具有对称性,当二次项系数a的绝对值越大时,其开口越小;反之,开口就越大。
特别地,当a=0时,抛物线开口大到变成一条直线(此时该函数已不是二次函数了,是一个一次函数);从数、式的角度分析,二次函数的解析式可以看作二元二次方程,二次方程显然比一次方程复杂多了,若其系数再来个字母,难度就更大了。
二次函数是个大箩筐,初中绝大多数知识点都可以往里装,代数方面数、式的计算(含幂的运算或根式的运算),因式分解、绝对值、相反数、用字母表示数(量)、列方程(组)求数值、列不等式(组)求字母的取值范围等等;几何方面线段的计算、角的计算三角形、四边形乃至圆都可以往里放,或全等或相似,或判定形状等等。
破解压轴题,是个系统工程。
不是一蹴而就的,需要一个积累和磨砺的过程。
你要有广博的知识根基,要有强大的运算能力,还必须掌握一定的数学思想方法和解题技巧,数学思想方法不是光记住两个名称,而是要掌握其本质核心的东西,比如转化思想,转化谁?怎么转化?没有谁告诉你,你得自己完成;再如分类讨论思想在什么情况下要分类讨论,分类的标准是什么?为什么要这样分而不是那样分呢?有时还涉及二次分类,即分类之后再分类,你看得出吗?你要会画草图,能从繁杂的信息里面提取有效的信息,能从复杂的图形里面抽岀基本图形,能准确理解语句的含义建立问题模型,形成简洁思路,并规范正确地表述解题过程.解题示范:边长为2的正方形OABC在平面直角坐标系中的位置如图所示,点D是边OA的中点,连接CD,点E在第一象限,且DE⊥DC,DE=DC.以直线AB为对称轴的抛物线过C,E两点.(1)求抛物线的解析式;(2)点P从点C出发,沿射线CB每秒1个单位长度的速度运动,运动时间为t秒.过点P作PF⊥CD于点F,当t为何值时,以点P,F,D为顶点的三角形与△COD相似?(3)点M为直线AB上一动点,点N为抛物线上一动点,是否存在点M,N,使得以点M,N,D,E为顶点的四边形是平行四边形?若存在,请直接写出满足条件的点的坐标;若不存在,请说明理由.破解第一招——耐心读题,瞬时记忆压轴题通常字数多,字母符号多,你得有好心态,集中思想心平气和地愉悦地读完它,第一遍读题时要在关键词语处做上记号(比如标上序号),平时要有意识地训练自己的瞬时记忆能力,即读一遍题要力求把题意90%的信息复述出来(这点非常重要)破解第二招——建立问题模型,理清解题思路第一小题求函数解析式,一看到求函数解析式的问题,应立马想到待定系数法的四个基本步骤:(见图1)—解题也有套路的;从题目中寻求可用条件,直接条件有两个:点C的坐标(0,2),对称轴AB为直线×=2;条件“抛物线经过点E",E点坐标没有直接给出,所以要先想办法求出,由“DE=DC,且∠CDE=90°”想到基本图(图2)构造三角形全等,求E点坐标,至此基本思路形成:①由全等求出E点坐标,②由C,E两点坐标及对称轴方程求函数解析式。
中考数学倒计时30:二次函数压轴的十几种问题方法思路总结

中考数学倒计时30:二次函数压轴的十几种问题方法思路总结二次函数压轴题当中,同学们会遇到各种各样的解答问题,那么最常见的那些,今天就带同学们一块总结一下,方便大家记忆解题方法。
我们只说一下方法,过程就不再详细说了,在以前的题目中都有过程。
1.首先是最简单的一种问题,给定两个固定点,然后在对称轴或者抛物线上找一点,使得该点和两个固定点组成的两个线段之和最小,即线段和最小值问题,遇到该种问题,一般直接找某个固定点关于某直线的对称点,然后寻找三点共线时的动点;2.线段和基础上延续而来的三角形或四边形周长最小值问题,同样会出现固定的点,那么就会有固定的边长,所以只需要找到另外的边长之和最小,同样使用找对称点的方法;3.垂直于x轴的一条直线,被抛物线和直线截取的两端线段之间的关系,如最大差值,或者相等、2倍关系。
最大差值问题需要找到该垂线与抛物线和直线的两个交点的纵坐标,利用纵坐标表示的线段来进行线段差的计算,将会得到另一种二次函数,那么进行配方变顶点式,得到差值的最大值;而线段倍数关系则相对更简单,只需要表示出两线段的长度,利用倍数关系建立方程即可;(注意纵坐标的正负未知,所以表示出的线段加上绝对值符号,如此就能避免遗漏一些情况)4.动点和两固定点组成的三角形面积最大值问题,该问题一般会在一段局限的图像上找一点,和其他两个固定点组成三角形,求三角形面积最大,只需要对固定点所在的直线进行平移,使平移后的直线与抛物线只要一个交点,利用判别式=0求出平移距离,从而解出交点坐标;如果要求三角形面积,一般利用面积分割法进行计算,如果有一边在轴上就会更简单;5.四边形面积最大值问题:和三角形面积类似,一般会有三个已定的点,那么就有一个固定的三角形,所以只需要动点和其中相邻的两个定点组成的三角形面积最大即可,同样使用直线平移法求出点的坐标即可;而面积同样利用面积分割法求取;6.直角三角形的存在性:一个动点和两个定点的情况,可以直接利用勾股定理求出动点的坐标;如果是两个动点,一个定点,则可利用直线垂直法,注意利用三角函数去推;同时还要注意情况讨论,三个角可能有不同情况的直角;7.等腰三角形的存在性:和直角三角形类似,包含情况讨论,如果是两个定点和一个动点,那么利用线段长相等解得动点坐标即可;如果是两个动点和一个定点,利用底边中线和底边垂直的性质,使用直线垂直法解得;8.平行四边形存在性:平行四边形对边相等,这本就是一个有利条件,所以一般利用平行且相等的两个线段来寻找;如果是菱形,只需要在平行四边形基础上加上临边相等或者对角线垂直来求解;9.正方形的存在性:一般来说正方形就比较特殊了,所以相对的有利条件也比较多,所以求解会更容易些;10.整数坐标点的存在性:该问题并不是很常见,一般在较难的压轴题中才会出现,在一个范围内寻找符合条件的动点,但前提是坐标需要是整数,所以需要找到横纵坐标的范围,在范围内去求解;11.由动点形成的整数面积问题:例如一个动点和两个定点组成的三角形面积,要求面积为整数,需要先利用平移法找到最大面积的值,然后在范围内寻找面积取整时的动点位置或者个数有多少,需要注意的是只有最大面积时的动点是一个,若无限定条件,其他整数面积时的动点则会同时出现两个,所以同学们不要忽略了;12.全等、相似三角形问题:二次函数中的全等、相似问题有时候简单有时候较难,所以要看运气如何,如果给定了对应点则还好点,如果题中只是说让两个三角形全等或相似,并未给出△∽/≌△这种形式,那么就要考虑多种情况存在了,尤其是在相似问题中,情况讨论较多,所以寻找角是很重要的,但一般又不会出现度数,所以这个时候同学们千万不要忘记三角函数;13.特殊点的存在性:类似什么共谐点、好点,遇到这类问题,一般会直接让写出答案,所以同学们在草纸上可以利用各种技巧性方法进行计算,类似一些高中的可用知识“直线垂直”“点到直线的距离”“两直线的夹角”等,没事可以先看看这些知识点的用法,反正上了高中都要学,所以不如先提前看一下,在遇到直接写答案的题目时如果用上了绝对是优势;14.至于其他的,老师一下子也想不起来,常见的就是上面这十几个种类,如果大家需要分享其他类型可以在留言中给出,方便其他人能够看到。
二次函数综合题专项讲解(经典)

第16题QP N Oyx初中二次函数综合题专项讲解引言:二次函数综合题题目难度较大,也称压轴题。
解压轴题有三个步骤:认真审题;理解题意、探究解题思路;正确解答。
审题要全面审视题目的所有条件和答题要求,在整体上把握试题的特点、结构,以利于解题方法的选择和解题步骤的设计。
二次函数一般会出现在选择题(或填空题)、解答题的倒数几个题目中。
选择题和填空题时易时难。
解答题较难,一般有2—3小题。
第1小题通常是求解析式:这一小题简单,直接找出坐标或者用线段长度而确定坐标,进而用待定系数法求出解析式即可。
第2—3小题通常是以动点为切入口,结合三角形、四边形、圆、平移、对称、解方程(组)与不等式(组)等知识呈现,知识面广,难度大;解这类题要善于运用转化、数形结合、分类讨论等数学思想,认真分析条件和结论、图形的几何特征与代数式的数量结构特征的关的关系,系,确定解题的思路和方法;同时需要心态平和,切记急躁:当思维受阻时,要及时调整思路和方法,并重新审视题意,注意挖掘隐蔽的条件和内在联系;既要防止钻牛角尖,又要防止轻易放弃。
一、重庆一中13—14学年度上期半期考试二次函数习题1212..如图,直线y kx c =+与抛物线2y ax bx c =++的图象都经过y 轴上的D 点,抛物线与x 轴交于A 、B 两点,其对称轴为直线1x =,且OA OD =直线y kx c =+与x 轴交于点C (点C 在点B 的右侧)则下列命题中正确命题的个数是(下列命题中正确命题的个数是( )). ①0abc >; ; ②②30a b +>; ; ③③10k -<<; ④k a b >+; ; ⑤⑤0ac k +>A .1 B .2 C .3 D .4 16.如右图是二次函数2y ax bx c =++的部分图象,由图象可知20ax bx c ++>时x 的取值范围是的取值范围是_______________________________________________________________________________________..1818.已知抛物线.已知抛物线2122y x x =-+的图象如左图所示,点N 为抛物线的顶点,直线ON 上有两个动点P 和Q ,且满足22PQ =,在直线x=1DCBAoyx第12题xy OEB A第25题 xyOEBA备用图备用图轴的对称图象的解析式为轴的对称图象的解析式为 ________关于关于对称图象的解析式为对称图象的解析式为 __________________,关于顶点旋转______ 对称轴为 _ ____ _ ____ x 时,时,Yy x O 22x21(轴的交点:抛物线与的图像与轴的两个交点的横坐标、轴的交点情况可以由对应的一元二次方程的①有两个交点抛物线与24b acx a-③没有交点抛物线与)直线与抛物线的交点:一次函数:一次函数与二次函数的交点, 与与212212)()(y y x x -+- 元的苹果,物价部门规定每箱元的价格调查,平均每天销售90箱,价箱)之间的函数关系式.(3分)分)开口方向0112Oxy 对称轴对称轴在对称轴在与;与轴交于正半轴;与25.已知二次函数()22a +b=0+b=0;;的横坐标分别为的横坐标分别为-1,3-1,3-1,3,,0;②20a b +=; ③⑤只有 D.5x)三点. ,)三点.x,)过点xA 72x = B(0,4) A(6,0) E F xyO 为斜边且一个角为30的直角三角形?若存,5-4-3-2-1-1 2 3 4 5 5 4 3 2 1 AEBC¢1-O2l1lx y【陈老师*专用】二次函数综合题21 轴的另一个交点为B ,过B 作⊙作⊙A A 的切线L.(1)以直线l 为对称轴的抛物线过点A 及点(及点(00,9),求此抛物线的解析式;,求此抛物线的解析式;(2)抛物线与x 轴的另一个交点为D ,过D 作⊙作⊙A A 的切线DE DE,,E 为切点,求此切线长;为切点,求此切线长;(3)点F 是切线DE 上的一个动点,当△上的一个动点,当△BFD BFD 与EAD EAD△相似时,求出△相似时,求出BF 的长的长 .。
二次函数压轴题解题口诀

二次函数压轴题解题口诀第一步:观察观察题目给出的二次函数关系式,包括一般式和顶点式。
确定二次函数的参数a、b、c的取值范围。
1.若a>0,则二次函数开口向上,最低点为最小值;若a<0,则二次函数开口向下,最高点为最大值。
2.根据顶点式形式f(x)=a(x-h)²+k,h为顶点横坐标,k为顶点纵坐标。
3. 根据一般式形式f(x)=ax²+bx+c,a为二次项系数,b为一次项系数,c为常数项。
第二步:画图根据观察结果,用适当的坐标系画出函数图像。
确定函数的顶点、对称轴、最值、切线等。
可以通过以下步骤进行画图:1.若已有顶点坐标,直接画出顶点。
2.若没有顶点坐标,可以用顶点坐标公式求得,即h=-b/2a,将h带入函数,求出k=f(h)。
3.根据顶点和对称性,确定对称轴。
对称轴方程为x=h。
4.将对称轴两边的点带入函数,得到其他点的坐标。
5.根据a的正负确定开口方向,画出函数图像。
6.根据图像确定函数的最值、相交点等。
第三步:转移对于部分二次函数题目,可能需要做坐标系的转移,以便于求解题目要求。
1.若需要移动坐标系,可通过平移或缩放来实现。
2.平移坐标系时,可以找到新坐标系原点与旧坐标系原点之间的关系,并移动坐标系。
3.缩放坐标系时,可以根据函数图像的特点来进行缩放。
第四步:求解根据题目要求,利用二次函数的相关特性进行求解。
常用的求解方法有以下几种:1.求零点:当函数值等于0时,求得函数的横坐标即为零点的横坐标。
2.求最值:如果二次函数开口向上,则最低点为最小值;如果二次函数开口向下,则最高点为最大值。
3.求交点:当两个函数相交时,求得两个函数对应的横坐标即为交点的横坐标。
通过以上四个步骤,可以有效地解决二次函数压轴题目。
在解题过程中,需要注重观察和画图,根据函数的特性来合理转移坐标系,最后通过计算求得答案。
中考压轴题-二次函数综合(八大题型+解题方法)——冲刺2024年中考数学考点押题(全国通用)(解析)

中考压轴题-二次函数综合 (八大题型+解题方法)1、求证“两线段相等”的问题:借助于函数解析式,先把动点坐标用一个字母表示出来;然后看两线段的长度是什么距离即是“点点”距离,还是“点轴距离”,还是“点线距离”,再运用两点之间的距离公式或点到x 轴y 轴的距离公式或点到直线的距离公式,分别把两条线段的长度表示出来,分别把它们进行化简,即可证得两线段相等;2、“平行于y 轴的动线段长度的最大值”的问题:由于平行于y 轴的线段上各个点的横坐标相等常设为t,借助于两个端点所在的函数图象解析式,把两个端点的纵坐标分别用含有字母t 的代数式表示出来,再由两个端点的高低情况,运用平行于y 轴的线段长度计算公式-y y 下上,把动线段的长度就表示成为一个自变量为t,且开口向下的二次函数解析式,利用二次函数的性质,即可求得动线段长度的最大值及端点坐标;3、求一个已知点关于一条已知直线的对称点的坐标问题:先用点斜式或称K ,且与已知直线垂直的直线解析式,再求出两直线的交点坐标,最后用中点坐标公式即可;4、“抛物线上是否存在一点,使之到定直线的距离最大”的问题:方法1先求出定直线的斜率,由此可设出与定直线平行且与抛物线相切的直线的解析式注意该直线与定直线的斜率相等,因为平行直线斜率k 相等,再由该直线与抛物线的解析式组成方程组,用代入法把字母y 消掉,得到一个关于x 的的一元二次方程,由题有△=2b -4ac=0因为该直线与抛物线相切,只有一个交点,所以2b -4ac=0从而就可求出该切线的解析式,再把该切线解析式与抛物线的解析式组成方程组,求出x 、y 的值,即为切点坐标,然后再利用点到直线的距离公式,计算该切点到定直线的距离,即为最大距离; 方法2该问题等价于相应动三角形的面积最大问题,从而可先求出该三角形取得最大面积时,动点的坐标,再用点到直线的距离公式,求出其最大距离;方法3先把抛物线的方程对自变量求导,运用导数的几何意义,当该导数等于定直线的斜率时,求出的点的坐标即为符合题意的点,其最大距离运用点到直线的距离公式可以轻松求出;5、常数问题:1点到直线的距离中的常数问题:“抛物线上是否存在一点,使之到定直线的距离等于一个 固定常数”的问题:先借助于抛物线的解析式,把动点坐标用一个字母表示出来,再利用点到直线的距离公式建立一个方程,解此方程,即可求出动点的横坐标,进而利用抛物线解析式,求出动点的纵坐标,从而抛物线上的动点坐标就求出来了;2三角形面积中的常数问题:“抛物线上是否存在一点,使之与定线段构成的动三角形的面积等于一个定常数”的问题:先求出定线段的长度,再表示出动点其坐标需用一个字母表示到定直线的距离,再运用三角形的面积公式建立方程,解此方程,即可求出动点的横坐标,再利用抛物线的解析式,可求出动点纵坐标,从而抛物线上的动点坐标就求出来了;3几条线段的齐次幂的商为常数的问题:用K 点法设出直线方程,求出与抛物线或其它直线的交点坐标,再运用两点间的距离公式和根与系数的关系,把问题中的所有线段表示出来,并化解即可;6、“在定直线常为抛物线的对称轴,或x 轴或y 轴或其它的定直线上是否存在一点,使之到两定点的距离之和最小”的问题:先求出两个定点中的任一个定点关于定直线的对称点的坐标,再把该对称点和另一个定点连结得到一条线段,该线段的长度〈应用两点间的距离公式计算〉即为符合题中要求的最小距离,而该线段与定直线的交点就是符合距离之和最小的点,其坐标很易求出利用求交点坐标的方法;7、三角形周长的“最值最大值或最小值”问题:① “在定直线上是否存在一点,使之和两个定点构成的三角形周长最小”的问题简称“一边固定两边动的问题:由于有两个定点,所以该三角形有一定边其长度可利用两点间距离公式计算,只需另两边的和最小即可;② “在抛物线上是否存在一点,使之到定直线的垂线,与y 轴的平行线和定直线,这三线构成的动直角三角形的周长最大”的问题简称“三边均动的问题:在图中寻找一个和动直角三角形相似的定直角三角形,在动点坐标一母示后,运用=C C 动动定定斜边斜边,把动三角形的周长转化为一个开口向下的抛物线来破解;8、三角形面积的最大值问题:① “抛物线上是否存在一点,使之和一条定线段构成的三角形面积最大”的问题简称“一边固定两边动的问题”:方法1:先利用两点间的距离公式求出定线段的长度;然后再利用上面3的方法,求出抛物线上的动点到该定直线的最大距离;最后利用三角形的面积公式= 12底×高;即可求出该三角形面积的最大值,同时在求解过程中,切点即为符合题意要求的点;方法2:过动点向y 轴作平行线找到与定线段或所在直线的交点,从而把动三角形分割成两个基本模型的三角形,动点坐标一母示后,进一步可得到)()(左(定)右(定)下(动)上(动)动三角形x x y y 21−⋅−=S ,转化为一个开口向下的二次函数问题来求出最大值;②“三边均动的动三角形面积最大”的问题简称“三边均动”的问题:先把动三角形分割成两个基本模型的三角形有一边在x 轴或y 轴上的三角形,或者有一边平行于x 轴或y 轴的三角形,称为基本模型的三角形面积之差,设出动点在x 轴或y 轴上的点的坐标,而此类题型,题中一定含有一组平行线,从而可以得出分割后的一个三角形与图中另一个三角形相似常为图中最大的那一个三角形;利用相似三角形的性质对应边的比等于对应高的比可表示出分割后的一个三角形的高;从而可以表示出动三角形的面积的一个开口向下的二次函数关系式,相应问题也就轻松解决了;9、“一抛物线上是否存在一点,使之和另外三个定点构成的四边形面积最大的问题”:由于该四边形有三个定点,,即可得到一个定三角形的面积之和,所以只需动三角形的面积最大,就会使动四边形的面积最大,而动三角形面积最大值的求法及抛物线上动点坐标求法与7相同;10、“定四边形面积的求解”问题: 有两种常见解决的方案:方案一:连接一条对角线,分成两个三角形面积之和;方案二:过不在x 轴或y 轴上的四边形的一个顶点,向x 轴或y 轴作垂线,或者把该点与原点连结起来,分割成一个梯形常为直角梯形和一些三角形的面积之和或差,或几个基本模型的三角形面积的和差11、“两个三角形相似”的问题: 两个定三角形是否相似:(1)已知有一个角相等的情形:运用两点间的距离公式求出已知角的两条夹边,看看是否成比例 若成比例,则相似;否则不相似;(2)不知道是否有一个角相等的情形:运用两点间的距离公式求出两个三角形各边的长,看看是否成比例若成比例,则相似;否则不相似;一个定三角形和动三角形相似:(1)已知有一个角相等的情形:先借助于相应的函数关系式,把动点坐标表示出来一母示,然后把两个目标三角形题中要相似的那两个三角形中相等的那个已知角作为夹角,分别计算或表示出夹角的两边,让形成相等的夹角的那两边对应成比例要注意是否有两种情况,列出方程,解此方程即可求出动点的横坐标,进而求出纵坐标,注意去掉不合题意的点;2不知道是否有一个角相等的情形:这种情形在相似性中属于高端问题,破解方法是,在定三角形中,由各个顶点坐标求出定三角形三边的长度,用观察法得出某一个角可能是特殊角,再为该角寻找一个直角三角形,用三角函数的方法得出特殊角的度数,在动点坐标“一母示”后,分析在动三角形中哪个角可以和定三角形中的那个特殊角相等,借助于特殊角,为动点寻找一个直角三角形,求出动点坐标,从而转化为已知有一个角相等的两个定三角形是否相似的问题了,只需再验证已知角的两边是否成比例若成比例,则所求动点坐标符合题意,否则这样的点不存在;简称“找特角,求动点标,再验证”;或称为“一找角,二求标,三验证”;12、“某函数图象上是否存在一点,使之与另两个定点构成等腰三角形”的问题:首先弄清题中是否规定了哪个点为等腰三角形的顶点;若某边底,则只有一种情况;若某边为腰,有两种情况;若只说该三点构成等腰三角形则有三种情况;先借助于动点所在图象的解析式,表示出动点的坐标一母示,按分类的情况,分别利用相应类别下两腰相等,使用两点间的距离公式,建立方程;解出此方程,即可求出动点的横坐标,再借助动点所在图象的函数关系式,可求出动点纵坐标,注意去掉不合题意的点就是不能构成三角形这个题意;13、“某图象上是否存在一点,使之与另外三个点构成平行四边形”问题:这类问题,在题中的四个点中,至少有两个定点,用动点坐标“一母示”分别设出余下所有动点的坐标若有两个动点,显然每个动点应各选用一个参数字母来“一母示”出动点坐标,任选一个已知点作为对角线的起点,列出所有可能的对角线显然最多有3条,此时与之对应的另一条对角线也就确定了,然后运用中点坐标公式,求出每一种情况两条对角线的中点坐标,由平行四边形的判定定理可知,两中点重合,其坐标对应相等,列出两个方程,求解即可;进一步有:①若是否存在这样的动点构成矩形呢先让动点构成平行四边形,再验证两条对角线相等否若相等,则所求动点能构成矩形,否则这样的动点不存在;②若是否存在这样的动点构成棱形呢先让动点构成平行四边形,再验证任意一组邻边相等否若相等,则所求动点能构成棱形,否则这样的动点不存在;③若是否存在这样的动点构成正方形呢先让动点构成平行四边形,再验证任意一组邻边是否相等和两条对角线是否相等若都相等,则所求动点能构成正方形,否则这样的动点不存在;14、“抛物线上是否存在一点,使两个图形的面积之间存在和差倍分关系”的问题:此为“单动问题”〈即定解析式和动图形相结合的问题〉,后面的19实为本类型的特殊情形;先用动点坐标“一母示”的方法设出直接动点坐标,分别表示如果图形是动图形就只能表示出其面积或计算如果图形是定图形就计算出它的具体面积,然后由题意建立两个图形面积关系的一个方程,解之即可;注意去掉不合题意的点,如果问题中求的是间接动点坐标,那么在求出直接动点坐标后,再往下继续求解即可;15、“某图形〈直线或抛物线〉上是否存在一点,使之与另两定点构成直角三角形”的问题:若夹直角的两边与y轴都不平行:先设出动点坐标一母示,视题目分类的情况,分别用斜率公式算出夹直角的两边的斜率,再运用两直线没有与y轴平行的直线垂直的斜率结论两直线的斜率相乘等于-1,得到一个方程,解之即可;若夹直角的两边中有一边与y 轴平行,此时不能使用斜率公式;补救措施是:过余下的那一个点没在平行于y轴的那条直线上的点直接向平行于y的直线作垂线或过直角点作平行于y轴的直线的垂线与另一相关图象相交,则相关点的坐标可轻松搞定;16、“某图象上是否存在一点,使之与另两定点构成等腰直角三角形”的问题;①若定点为直角顶点,先用k点法求出另一直角边所在直线的解析式如斜率不存在,根据定直角点,可以直接写出另一直角边所在直线的方程,利用该解析式与所求点所在的图象的解析式组成方程组,求出交点坐标,再用两点间的距离公式计算出两条直角边等否若等,该交点合题,反之不合题,舍去;②若动点为直角顶点:先利用k点法求出定线段的中垂线的解析式,再把该解析式与所求点所在图象的解析式组成方程组,求出交点坐标,再分别计算出该点与两定点所在的两条直线的斜率,把这两个斜率相乘,看其结果是否为-1 若为-1,则就说明所求交点合题;反之,舍去;17、“题中含有两角相等,求相关点的坐标或线段长度”等的问题:题中含有两角相等,则意味着应该运用三角形相似来解决,此时寻找三角形相似中的基本模型“A”或“X”是关键和突破口;18、“在相关函数的解析式已知或易求出的情况下,题中又含有某动图形常为动三角形或动四边形的面积为定常数,求相关点的坐标或线段长”的问题:此为“单动问题”〈即定解析式和动图形相结合的问题〉,本类型实际上是前面14的特殊情形;先把动图形化为一些直角梯形或基本模型的三角形有一边在x 轴或y轴上,或者有一边平行于x 轴或y 轴面积的和或差,设出相关点的坐标一母示,按化分后的图形建立一个面积关系的方程,解之即可;一句话,该问题简称“单动问题”,解题方法是“设点动点标,图形转化分割,列出面积方程”;19、“在相关函数解析式不确定系数中还含有某一个参数字母的情况下,题中又含有动图形常为动三角形或动四边形的面积为定常数,求相关点的坐标或参数的值”的问题:此为“双动问题”即动解析式和动图形相结合的问题;如果动图形不是基本模型,就先把动图形的面积进行转化或分割转化或分割后的图形须为基本模型,设出动点坐标一母示,利用转化或分割后的图形建立面积关系的方程或方程组;解此方程,求出相应点的横坐标,再利用该点所在函数图象的解析式,表示出该点的纵坐标注意,此时,一定不能把该点坐标再代入对应函数图象的解析式,这样会把所有字母消掉;再注意图中另一个点与该点的位置关系或其它关系,方法是常由已知或利用2问的结论,从几何知识的角度进行判断,表示出另一个点的坐标,最后把刚表示出来的这个点的坐标再代入相应解析式,得到仅含一个字母的方程,解之即可;如果动图形是基本模型,就无须分割或转化了,直接先设出动点坐标一母式,然后列出面积方程,往下操作方式就与不是基本模型的情况完全相同;一句话,该问题简称“双动问题”,解题方法是“转化分割,设点标,建方程,再代入,得结论”;常用公式或结论:1横线段的长 = 横标之差的绝对值 =-x x 大小=-x x 右左纵线段的长=纵标之差的绝对值=-y y 大小=-y y 下上 2点轴距离:点P 0x ,0y 到X 轴的距离为0y ,到Y 轴的距离为o x ; 3两点间的距离公式:若A 11,x y ,B 2,2x y , 则AB=目录:题型1:存在性问题 题型2:最值问题 题型3:定值问题 题型4:定点问题题型5:动点问题综合 题型6:对称问题 题型7:新定义题 题型8:二次函数与圆题型1:存在性问题1.(2024·四川广安·二模)如图,抛物线2y x bx c =−++交x 轴于()4,0A −,B 两点,交y 轴于点()0,4C .(1)求抛物线的函数解析式.(2)点D 在线段OA 上运动,过点D 作x 轴的垂线,与AC 交于点Q ,与抛物线交于点P ,连接AP 、CP ,求四边形AOCP 的面积的最大值.(3)在抛物线的对称轴上是否存在点M ,使得以点A 、C 、M 为顶点的三角形是直角三角形?若存在,请求出点M【答案】(1)234y x x =−−+;(2)四边形AOCP 的面积最大为16;(3)点M 的坐标为35,22⎛⎫−− ⎪⎝⎭或311,22⎛⎫− ⎪⎝⎭.【分析】本题主要考查了二次函数综合,熟练掌握用待定系数法求解函数解析式的方法和步骤,以及二次函数的图象和性质,是解题的关键. (1)把()4,0A −,()0,4C 代入2y x bx c =−++,求出b 和c 的值,即可得出函数解析式; (2)易得182AOCSOA OC =⋅=,设()2,34P t t t −−+,则(),4Q t t +,求出24PQ t t =−−,则()()212282ACP C A S PQ x x t =⋅−=−++,根据四边形AOCP 的面积()22216ACP AOCS St =+=−++,结合二次函数的增减性,即可解答;(3)设3,2M m ⎛⎫− ⎪⎝⎭,根据两点之间距离公式得出232AC =,22254AM m =+,229(4)4CM m =+−,然后分情况根据勾股定理列出方程求解即可.【解析】(1)解:把()4,0A −,()0,4C 代入2y x bx c =−++得:01644b c c =−−+⎧⎨=⎩,解得:34b c =−⎧⎨=⎩,∴该二次函数的解析式234y x x =−−+;(2)解:∵()4,0A −,()0,4C ,∴4,4OA OC ==,∴1144822AOC S OA OC =⋅=⨯⨯=△,设直线AC 的解析式为4y kx =+, 代入()4,0A −得,044k =−+,解得1k =,∴直线AC 的解析式为4y x =+, 设()2,34P t t t −−+,则(),4Q t t +,∴()223444PQ t t t t t=−−+−+=−−∴()()()22114422822ACPC A SPQ x x t t t =⋅−=−−⨯=−++,∴四边形AOCP 的面积()22216ACP AOCSSt =+=−++,∵20−<,∴当2t =−时,四边形AOCP 的面积最大为16; (3)解:设3,2M m ⎛⎫− ⎪⎝⎭,∵()4,0A −,()0,4C ,∴2224432AC =+=,2222325424AM m m ⎛⎫=−++=+ ⎪⎝⎭,()()2222394424CM m m ⎛⎫=−+−=+− ⎪⎝⎭,当斜边为AC 时,AM CM AC 222+=,即()2225943244m m +++−=,整理得:24150m m ++=,无解;当斜边为AM 时,222AC CM AM +=,即2292532(4)44m m ++−=+,解得:112m =;∴311,22M ⎛⎫− ⎪⎝⎭当斜边为CM 时,222AC AM CM +=,即2225932(4)44m m ++=+−, 解得:52m =−;∴35,22M ⎛⎫−− ⎪⎝⎭综上:点M 的坐标为35,22⎛⎫−− ⎪⎝⎭或311,22⎛⎫− ⎪⎝⎭.2.(2024·内蒙古乌海·模拟预测)如图(1),在平面直角坐标系中,抛物线()240y ax bx a =+−≠与x 轴交于A ,B 两点(点A 在点B 的左侧),与y 轴交于点C ,点A 的坐标为()1,0−,且OC OB =,点D 和点C 关于抛物线的对称轴对称.(1)分别求出a ,b 的值和直线AD 的解析式;(2)直线AD 下方的抛物线上有一点P ,过点P 作PH AD ⊥于点H ,作PM 平行于y 轴交直线AD 于点M ,交x 轴于点E ,求PHM 的周长的最大值;(3)在(2)的条件下,如图2,在直线EP 的右侧、x 轴下方的抛物线上是否存在点N ,过点N 作NG x ⊥轴交x 轴于点G ,使得以点E 、N 、G 为顶点的三角形与AOC 相似?如果存在,请直接写出点G 的坐标;如果不存在,请说明理由.【答案】(1)1a =,3b =−,=1y x −−(2)4+(3)存在,点G的坐标为⎫⎪⎪⎝⎭或⎫⎪⎪⎝⎭【分析】本题主要考查的是二次函数的综合应用,掌握二次函数的交点式、配方法求二次函数的最值、相似三角形的判定、等腰直角三角形的判定、一元二次方程的求根公式,列出PM 的长与a 的函数关系式是解题的关键.(1)先求得C 的坐标,从而得到点B 的坐标,设抛物线的解析式为()()14y a x x =+−,将点C 的坐标代入求解即可;先求得抛物线的对称轴,从而得到点()3,4D −,然后可求得直线AD 的解析式=1y x −−;(2)求得45BAD ∠=︒,接下来证明PMD △为等腰直角三角形,所当PM 有最大值时三角形的周长最大,设()2,34P a a a −−,()1M a −−,则223PM aa =−++,然后利用配方可求得PM 的最大值,最后根据MPH△的周长(1PM=求解即可;(3)当90EGN ∠=︒时,如果OA EG OC GN = 或OA GNOC EN =时,则AOC ∽EGN △,设点G 的坐标为(),0a ,则()2,34N a a a −−,则1EG a =−,234NG aa =−++,然后根据题意列方程求解即可.【解析】(1)点A 的坐标为()1,0−,1OA ∴=.令0x =,则4y =−,()0,4C ∴−,4OC =,OC OB =Q , 4OB ∴=,()4,0B ∴,设抛物线的解析式为()()14y a x x =+−,将0x =,4y =−代入得:44a −=−,解得1a =,∴抛物线的解析式为234y x x =−−;1a ∴=,3b =−; 抛物线的对称轴为33212x −=−=⨯,()0,4C −,点D 和点C 关于抛物线的对称轴对称,()3,4D ∴−;设直线AD 的解析式为y kx b =+.将()1,0A −、()3,4D −代入得:034k b k b −+=⎧⎨+=−⎩,解得1k =−,1b =-,∴直线AD 的解析式=1y x −−;(2)直线AD 的解析式=1y x −−,∴直线AD 的一次项系数1k =−,45BAD ∴∠=︒. PM 平行于y 轴,90AEP ∴∠=︒,45PMH AME ∴∠=∠=︒.MPH ∴的周长(122PM MH PH PM MP PM PM =++=++=. 设()2,34P a a a −−,则(),1M a a −−, 则()22213423(1)4PM a a a a a a =−−−−−=−++=−−+.∴当1a =时,PM 有最大值,最大值为4.MPH ∴的周长的最大值(414=⨯=+(3)在直线EP 的右侧、x 轴下方的抛物线上存在点N ,过点N 作NG x ⊥轴交x 轴于点G ,使得以点E 、N 、G 为顶点的三角形与AOC 相似;理由如下:设点G 的坐标为(),0a ,则()2,34N a a a −−①如图2.1,若OA EG OC GN = 时,AOC ∽EGN △. 则 211344a a a −=−++,整理得:280a a +−=.得:a =负值舍去),∴点G为⎫⎪⎪⎝⎭; ②如图2.2,若OA GN OC EN =时,AOC ∽NGE ,则21434a a a −=−++,整理得:2411170a a −−=,得:a =负值舍去),∴点G为⎫⎪⎪⎝⎭, 综上所述,点G的坐标为⎫⎪⎪⎝⎭或⎫⎪⎪⎝⎭. 3.(2024·重庆·一模)如图,在平面直角坐标系中,抛物线2y ax bx =+x 轴交于点()1,0A −,()5,0B ,与y 轴交于点C ,连接BC ,AC .(1)求抛物线的表达式;(2)P 为直线BC 上方抛物线上一点,过点P 作PD BC ⊥于点D ,过点P 作PE x 轴交抛物线于点E,求4+PD PE 的最大值及此时点P 的坐标; (3)点C 关于抛物线对称轴对称的点为Q ,将抛物线沿射线CAy ',新抛物线y '与y 轴交于点M ,新抛物线y '的对称轴与x 轴交于点N ,连接AM ,MN ,点R 在直线BC 上,连接QR .当QR 与AMN 一边平行时,直接写出点R 的坐标,并写出其中一种符合条件的解答过程.【答案】(1)2y x x =++(2)当154t =时,PE的最大值,15,416P ⎛ ⎝⎭, (3)R点的坐标为⎛ ⎝⎭或6,⎛ ⎝⎭或(.【分析】(1)利用待定系数法求抛物线解析式即可;(2)先求得2y x =2x =,过点P 作PG x ⊥轴交BC 于点F ,利用勾股定理求得BC ==DPF OBC ∽,得PF DP BC OB =即PF PD=,从而得PF =,求出设直线BC的解析式后,设2,P t ⎛+ ⎝,则,F t ⎛+ ⎝,从而2PF =+,当点P在E 点右侧时()424PE t t t =−−=−,从而得2154t ⎫=−⎪⎝⎭,利用二次函数的性质即可求解;当点P 在E 点左侧时:442PE t t t =−−=−时,同理可求.然后比较4+PE 的最大值即可得出答案. (3)先求得1OA=,OC AC =设抛物线2y =H ⎛ ⎝⎭平移后为P ,过点P 作PW ⊥直线2x =,则AOC PWH ∽,得1OA OC AC WP HW PH ====,进而得平移后的抛物线2y x +'=,从而求得()1,0N,M ⎛ ⎝⎭,然后分QR AM ∥,QR MN ∥,QR AN ∥三种情况,利用二次函数的性质及一次函数的与二元一次方程的关系求解即可得解.【解析】(1)解:∵抛物线2y ax bx =+x 轴交于点()1,0A −,()5,0B 两点,代入坐标得:02550a b a b ⎧−=⎪⎨+=⎪⎩,解得:a b ⎧=⎪⎪⎨⎪=⎪⎩,∴抛物线的函数表达式为255y x x =−++(2)解:∵)2225555y x x x =−+=−−+,∴2y x =2x=,顶点为⎛ ⎝⎭ 过点P 作PG x ⊥轴交BC 于点F ,当0x =时,200y =∴(C ∵()5,0B ∴BC ==∵PG x ⊥轴,PD BC ⊥,x 轴y ⊥轴,∴909090CBO BFG DPF PFD PDF BOC ∠∠∠∠∠∠+=︒+=︒==︒,,∵PFD BFG ∠∠=∴DPF CBO ∠∠=∴DPF OBC ∽,∴PF DP BC OB =即PF PD =,∴PF PD =∴44+PD PE =PF +PE ,设直线BC :y kx b =+,把(C ,()5,0B 代入得:05k b b =+⎧⎪=,解得5k b ⎧=−⎪⎨⎪=⎩, ∴直线BC:y =设2,P t ⎛ ⎝,则,F t ⎛+ ⎝,∴22PF ⎛⎛=−+=+ ⎝⎝,∵2y x =2x =,PE x 轴,∴24,E t ⎛−+ ⎝当点P 在E 点右侧时:()424PE t t t =−−=−,当24PE t =−时:∴+PD PE =PF +()221524545416t t ⎛⎫=−+−=−−+ ⎪⎝⎭ ∴当154t =时,的最大值∴2151544⎛⎫= ⎪⎝⎭,∴154P ⎛ ⎝⎭; 当点P 在E 点左侧时:442PE t t t =−−=−时,∴+PD PE =PF +()225424t t ⎫=−=−⎪⎝⎭, ∴当54t =时,的最大值.2,55P t ⎛−+ ⎝∴25544⎛⎫ ⎪⎝⎭∴5,416P ⎛ ⎝⎭,∵> 综上所诉,当点P 在E 点右侧时:即154t =时,的最大值,154P ⎛ ⎝⎭, (3)解:设直线AC :y mx n =+,把()1,0A −,(C , ∴1OA =,OC =∴AC ==设抛物线2y x =H ⎛ ⎝⎭平移后为P , 过点P 作PW ⊥直线2x =,则AOC PWH ∽,∴1OA OC AC WP HW PH ====∴1PW =,HW=∴21,5P ⎛−⎝即1,5P ⎛ ⎝⎭,∴平移后的抛物线)22155555y x x x =−−+=−++', ∴()1,0N令0x =,y '=,∴M ⎛ ⎝⎭ 如图,当QR AM ∥时,设直线AM 的解析式为:y px q =+,把M ⎛ ⎝⎭,()1,0A −代入得:0p q q =−+⎧=解得p q ⎧=⎪⎪⎨⎪=⎪⎩, ∴直线AM的解析式为:y =, ∴设直线QR的解析式为:y x n =∵(C ,Q 和C 关于2x =对称,∴(Q把(Q代入5y x n =+45n +,解得n =,∴直线QR的解析式为:y = 联立直线QR的解析式y =与直线BC:y x =+55y x y x ⎧=−⎪⎪⎨⎪=⎪⎩,解得3x y =⎧⎪⎨=⎪⎩,∴R ⎛ ⎝⎭ 同理可得:当QR MN ∥时,6,5R ⎛− ⎝⎭ 当QR AN ∥时,(R所有符合条件的R点的坐标为⎛ ⎝⎭或6,⎛ ⎝⎭或(. 【点睛】本题考查待定系数法求抛物线解析式,勾股定理,抛物线的性质,抛物线平移,一次函数的平移,相似三角形的判定及性质,图形与坐标,掌握待定系数法求抛物线解析式,抛物线的性质,抛物线平移,相似三角形的判定及性质,图形与坐标,利用辅助线画出准确图形是解题关键.题型2:最值问题4.(2024·安徽合肥·二模)在平面直角坐标系中,O 为坐标原点,抛物线23y ax bx =+−与x 轴交于()1,0A −,()3,0B 两点,与y 轴交于点C ,连接BC .(1)求a ,b 的值;(2)点M 为线段BC 上一动点(不与B ,C 重合),过点M 作MP x ⊥轴于点P ,交抛物线于点N . (ⅰ)如图1,当3PA PB=时,求线段MN 的长; (ⅱ)如图2,在抛物线上找一点Q ,连接AM ,QN ,QP ,使得PQN V 与APM △的面积相等,当线段NQ 的长度最小时,求点M 的横坐标m 的值.【答案】(1)1a =,2b =−(2)(ⅰ)2MN =;(ⅱ)m 的值为32或12【分析】本题考查诶粗函数的图象和性质,掌握待定系数法和利用函数性质求面积是解题的关键.(1)运用待定系数法求函数解析式即可;(2)(ⅰ)先计算BC 的解析式,然后设(),3M m m −,则3PM PB m ==−,1PA m =+,根据题意得到方程133m m +=−求出m 值,即可求出MN 的长;(ⅱ)作QR PN ⊥于点R ,由(ⅰ)可得1PA m =+,3PB PM m =−−,223PN m m =−++,然后分为点Q 在PN 的左侧和点Q 在PN 的右侧两种情况,根据勾股定理解题即可.【解析】(1)由题意得309330a b a b −−=⎧⎨+−=⎩,解得12a b =⎧⎨=−⎩;(2)(ⅰ)当0x =时,3y =−,∴()0,3C −,设直线BC 为3y kx =−,∵点()3,0B ,∴330k −=,解得1k =,∴直线BC 为3y x =−,设(),3M m m −,则3PM PB m ==−,1PA m =+, ∵3PA PB =, ∴133m m +=−,解得2m =,经检验2m =符合题意,当2m =时,222233y =−⨯−=−, ∴3PN =,31PM PB m ==−=,∴2MN =;(ⅱ)作QR PN ⊥于点R ,由(ⅰ)可得1PA m =+,3PB PM m =−−,223PN m m =−++,PQN V 的面积为()21232m m QR −++⋅,APM △的面积为()()1312m m −+,∴()()()211233122m m QR m m −++⋅=−+,解得1QR =;当点Q 在PN 的左侧时,如图1,Q 点的横坐标为1m QR m −=−,纵坐标为()()2212134m m m m −−⨯−−=−,∴R 点的坐标为()2,4m mm−,∵N 点坐标为()2,23m mm −−,∴32RN m =−,∴()22231NQ m =−+,∴当32m =时,NQ 取最小值;当点Q 在PN 的右侧时,如图2,Q 点的横坐标为1m QR m +=+,纵坐标为()()2212134m m m +−⨯+−=−,∴R 点的坐标为()2,4m m−,∵N 点的坐标为()2,23m mm −−,∴21RN m =−, ∴()222211NQ m =−+,∴当12m =时,NQ 取最小值.综上,m 的值为32或12.。
二次函数压轴题类型方法总结

二次函数压轴题总结:(凡解析几何问题,均是以几何性质探路,代数书写竣工。
) 已知、 y=322--x x (以下几种分类的函数解析式就是这个)1、和最小,差最大 在对称轴上找一点P ,使得PB+PC 的和最小,求出P 点坐标 在对称轴上找一点P ,使得PB-PC 的差最大,求出P 点坐标解决方案:识别模型,A 、若为过河问题模型,根据“异侧和最小,同侧差最大,根据问题同侧异侧相互转化”;B 、若有绝对值符号或不隶属于过河问题,可将问题形式平方,构建函数,转化为求函数最值问题(若表达式中含有根式等形式,可考虑用换元法求最值)。
2、求面积最大 连接AC,在第四象限抛物线上找一点P ,使得ACP ∆面积最大,求出P 坐标解决方案:熟悉基本图形的面积公式【或根据拼图思想,采用割补法求面积(注意不重不漏)。
】,根据问题,灵活选择面积公式,务必使表达式简单,变量的最值好求,讲变量的最值问题转化为:”定值+变量的最值“3、讨论直角三角 连接AC,在对称轴上找一点P ,使得ACP ∆为直角三角形,求出P 坐标或者在抛物线上求点P ,使△ACP 是以AC 为直角边的直角三角形.解决方案:此类问题是分类讨论思想能力的考察,由于直角三角形的”直角边“”和“斜边”不确定而展开讨论。
在不忘三角形满足三边关系的条件下,勿忘“等腰直角三角形”。
4、讨论等腰三角 连接AC,在对称轴上找一点P ,使得ACP ∆为等腰三角形,求出P 坐标 解决方案:分析同上4,在能组成△的大前提下,根据谁作为腰,谁作为底边展开讨论。
5、讨论平行四边形 1、点E 在抛物线的对称轴上,点F 在抛物线上,且以B ,A ,F ,E 四点为顶点的四 边形为平行四边形,求点F 的坐标解决方案:从平行四边形的性质入手,已知三点求另外一点,分析其位置情况(分别以3点中任一已知两点的线段为平行四边形的边或其对角线来展开所有的情况的讨论)。
6、相似三角形 问抛物线上是否存在一动点D ,使得△ABD ∽△ABC 。
二次函数压轴题基本方法和结构
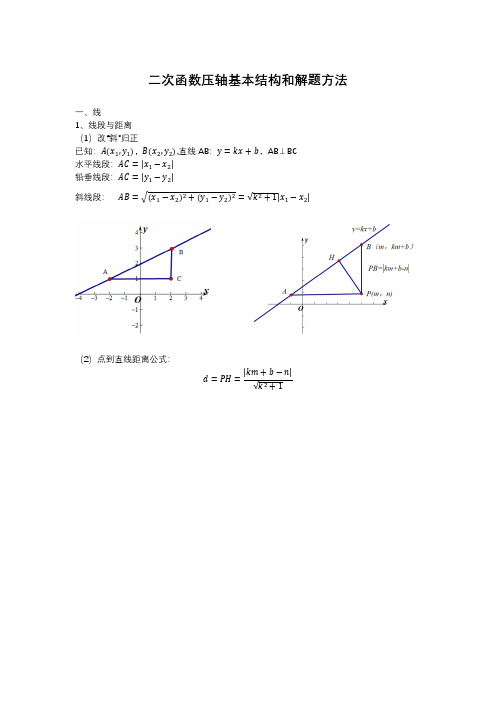
二次函数压轴基本结构和解题方法一、线1、线段与距离 (1)改“斜”归正已知:A(x 1,y 1),B(x 2,y 2),直线AB :y =kx +b ,AB ⊥BC 水平线段:AC =|x 1−x 2| 铅垂线段:AC =|y 1−y 2|斜线段: AB =√(x 1−x 2)2+(y 1−y 2)2=√k 2+1|x 1−x 2|(2)点到直线距离公式:d =PH =|km +b −n|√k 2+1(3)于涵定理 一般位置:条件:直线AB 交抛物线(二次项系数为a )于AB 两点,铅垂线PQ 交抛物线于P ,交直线AB 于P ,AE ⊥PQ ,BF ⊥PQ 结论:①PQ =|a|∙AE ∙BF ;S △PAB =12PQ ∙(AE +BF )=12|a |∙AE ∙BF ∙(AE +BF )=12|a (x A −x P )(x P −x B )(x A −x B )|特殊位置① 若AB 为水平直线: PQ =|a|∙AQ ∙BQ ② 若AB 为水平直线,且AP ⊥BP : PQ =1|a|(PQ =|a|∙AQ ∙BQ ,且PQ 2=AQ ∙BQ )③ 若AB 为水平直线,且P 为抛物线顶点(类似于圆中的垂径结构)AB =√4PQ|a|④ 若AB 为x 轴,且P 为抛物线顶点:AB =√∆|a|(4)焦点准线焦点准线的定义:将抛物线的顶点向上/下平移14|a|个单位,就得到焦点和准线的位置。
焦点:F(−b2a ,14a);准线:直线y=−14a条件:点P是抛物线上任意一点,过P点的直线(非铅垂线)与抛物线有位移公共点(“切线”),与对称轴交于S,与过顶点的水平线交于A,PM⊥准线于M;PQ过焦点F,过P、Q 的切线交于T结论:①PF=PM,DE=DF②PF=FS③FA⊥PS,PA=SA④当直线PQ绕焦点F转动时候,T点在准线上移动(阿基米德三角形特殊情况)⑤TP⊥TQ,TM=TN⑥以MN为直径的圆切PQ于F,以PQ为直径的圆切MN于T准线2、平行“弦”条件:AB//CD//l P结论:x A+x B=x C+x D=2x P变式一:若CE和DF为铅垂线,则AE=BF变式二:若将抛物线向下平移交直线AB于E、F,则AE=BF变式三:将抛物线沿着PQ方向平移,若AB//PQ,则AB=EF,AE=BF3、线段相等和比值(1)左右对称(纵向角平分线)特殊情况:条件:P为抛物线(顶点为M)对称轴上一点,过P点的直线PA交抛物线于C,过C作水平直线BC交抛物线于B点,连接AB交对称轴于Q,连接PB交抛物线于D;结论:①k PA+k PB=0;②PM=QM一般情况:条件:过抛物线内一点T作铅垂、水平直线,交抛物线于M、B、C,在铅垂线上取一点P,连接PC交抛物线于A,连接AB交铅垂线于Q结论:TBTC =QMPM(2)上下对称条件:水平直线与抛物线交于P、Q两点,直线PA、PB分别交抛物线于A、B,且∠APQ=∠BPQ,连接AB,过Q点的直线作抛物线的切线。
二次函数压轴题方法总结

二次函数压轴题方法总结一、前言二次函数压轴题是高中数学中的重要内容之一,也是考试中常见的题型。
本文将总结二次函数压轴题的解法方法,希望能够对广大学生有所帮助。
二、基础知识在开始讲解二次函数压轴题的解法方法之前,我们需要先了解一些基础知识:1. 二次函数:形如 $f(x)=ax^2+bx+c$ 的函数,其中 $a\neq 0$。
2. 抛物线:二次函数的图像称为抛物线。
当 $a>0$ 时,抛物线开口向上;当 $a<0$ 时,抛物线开口向下。
3. 平移:对于二次函数 $f(x)=ax^2+bx+c$,平移后得到的新函数为$f(x-a_1)+b_1$。
其中 $a_1$ 表示沿着 $x$ 轴平移的距离,正值表示向左平移,负值表示向右平移;$b_1$ 表示沿着 $y$ 轴平移的距离,正值表示向上平移,负值表示向下平移。
4. 压缩与拉伸:对于二次函数 $f(x)=ax^2+bx+c$,压缩后得到的新函数为 $af(\frac{x}{k})$,其中 $k>0$ 表示沿着 $x$ 轴压缩的倍数,$k<1$ 表示压缩,$k>1$ 表示拉伸;拉伸后得到的新函数为 $af(kx)$。
三、二次函数压轴题解法方法1. 压轴法压轴法是二次函数压轴题中最常用的解法方法之一。
其基本思想是通过平移和拉伸等变换将原二次函数转化为标准式$f(x)=a(x-h)^2+k$,从而求出抛物线的顶点坐标和开口方向。
具体步骤如下:(1)将原二次函数改写为 $f(x)=a(x-b)^2+c$ 的形式。
(2)确定抛物线的开口方向:当 $a>0$ 时,抛物线开口向上;当$a<0$ 时,抛物线开口向下。
(3)求出顶点坐标:由于 $(x-b)^2\geq 0$,因此当 $x=b$ 时,有$(x-b)^2=0$。
因此顶点坐标为 $(b,c)$。
(4)确定对称轴:对称轴即为顶点所在的直线。
当二次函数为标准式时,对称轴与 $y-$ 轴重合;否则需要进行平移变换。
二次函数的定义压轴题四种模型全攻略(解析版)

专题01 二次函数的定义压轴题四种模型全攻略考点一 二次函数的识别 考点二 二次函数的二次项系数、一次项系数、常数项 考点三 根据二次函数的定义求参数 考点四 列二次函数关系式考点一 二次函数的识别例题:(2022·江苏·盐城市初级中学一模)下列函数中为二次函数的是( )A .31y x =-B .231y x =-C .2y x =D .323y x x =+-【答案】B【解析】【分析】直接利用二次函数的定义进而分析得出答案.【详解】解:A 、31y x =-,是一次函数,故此选项不符合题意;B 、231y x =-,是二次函数,故此选项符合题意;C 、2y x =,不是二次函数,故此选项不符合题意;D 、323y x x =+-,未知数的最高次为3,不是二次函数,故此选项错误.故选:B .【点睛】本题考查了二次函数的定义;熟练掌握二次函数解析式的一般形式2y ax bx c =++(0a ≠),是解题的关键.【变式训练】1.(2020·陕西·西安市大明宫中学三模)观察:①26y x =;②235y x =-+;③2200400y x x =+;④32y x x =-;⑤213y x x=-+;⑥()221y x x =+-.这六个式子中二次函数有( )个. A .2B .3C .4D .5【答案】B【解析】【分析】 根据二次函数的定义判断即可.典型例题【详解】①26y x =是二次函数;②235y x =-+是二次函数;③2200400y x x =+是二次函数;④32y x x =-不是二次函数;⑤213y x x=-+不是二次函数; ⑥()22121y x x x =+-=+不是二次函数;这六个式子中二次函数有①②③故选:B .【点睛】本题考查二次函数的定义,即一般地,形如2y ax bx c =++(a ,b ,c 是常数,0a ≠)的函数,叫做二次函数.2.(2022·全国·九年级课时练习)下列函数①55y x =-;②231y x =-;③3243y x x =-;④2221y x x =-+;⑤21y x =.其中是二次函数的是____________. 【答案】②④##④②【解析】【分析】根据二次函数的定义,函数式为整式且自变量的最高次数为2,二次项系数不为0,逐一判断.【详解】解:①y =5x -5为一次函数;②y =3x 2-1为二次函数;③y =4x 3-3x 2自变量次数为3,不是二次函数;④y =2x 2-2x +1为二次函数;⑤y =21x 函数式为分式,不是二次函数. 故答案为②④.【点睛】本题考查二次函数的定义,熟记定义“函数式为整式且自变量的最高次数为2,二次项系数不为0”是解题关键.考点二 二次函数的二次项系数、一次项系数、常数项例题:(2022·福建省福州外国语学校八年级期末)二次函数223y x x =-+的一次项系数是( )A .1B .2C .2-D .3【答案】C【解析】【分析】 根据二次函数的定义:一般地,形如y =ax 2+bx +c (a 、b 、c 是常数,a ≠0)的函数,叫做二次函数.其中x 、y 是变量,a 、b 、c 是常量,a 是二次项系数,b 是一次项系数,c 是常数项作答.【详解】解:二次函数y =x 2-2x +3的一次项系数是-2;故选:C .【点睛】此题主要考查了二次函数的定义,关键是注意在找二次项系数,一次项系数和常数项时,不要漏掉符号.【变式训练】1.(2022·全国·九年级)设a ,b ,c 分别是二次函数y =﹣x 2+3的二次项系数、一次项系数、常数项,则( ) A .a =﹣1,b =3,c =0B .a =﹣1,b =0,c =3C .a =﹣1,b =3,c =3D .a =1,b =0,c =3【答案】B【解析】【分析】根据二次函数的一般形式可得答案.【详解】解:二次函数y =﹣x 2+3的二次项系数是a =﹣1,一次项系数是b =0,常数项是c =3;故选:B .【点睛】此题主要考查了二次函数的一般形式,关键是注意在找二次项系数,一次项系数和常数项时,不要漏掉符号.2.(2022·全国·九年级)已知二次函数y =1﹣5x +3x 2,则二次项系数a =___,一次项系数b =___,常数项c =___.【答案】 3 -5 1【解析】【分析】形如:()20y ax bx c a =++≠这样的函数是二次函数,其中二次项系数为,a 一次项系数为,b 常数项为,c 根据定义逐一作答即可.【详解】解:二次函数y =1﹣5x +3x 2,则二次项系数a =3,一次项系数b =﹣5,常数项c =1,故答案为:3,﹣5,1.【点睛】本题考查了二次函数的定义,熟记二次函数的定义是解题关键.考点三 根据二次函数的定义求参数例题:(2022·全国·九年级课时练习)已知y =21(1)m m x +-+2x ﹣3是二次函数式,则m 的值为 _____.【答案】-1【解析】【分析】若y =21(1)m m x +-+2x ﹣3是二次函数式,则二次项系数不等于零,可得答案;【详解】 解:由题意得:21012m m -≠⎧⎨+=⎩, 解得:m =-1,故答案为:-1.【点睛】本题考查了二次函数的定义,理解二次函数的定义是解题关键.【变式训练】1.(2021·黑龙江·塔河县第一中学校九年级期中)已知(2)21m y m x x =-+-是y 关于x 的二次函数,那么m 的值____.【答案】2-【解析】 【分析】根据二次函数的定义,(2)m m x -中,未知数x 的指数为2,系数不为0,列式计算即可. 【详解】解:∵(2)21m y m x x =-+-是y 关于x 的二次函数,∵2m =且20m -≠,∵2m =-.故答案为:2-.【点睛】本题考查的是二次函数的定义,熟练掌握形如y =ax 2+bx +c (a ,b ,c 是常数,且a ≠0)的函数,叫做二次函数是解题的关键.2.(2021·广东广州·九年级期中)关于x 的函数()21m m y m x -=+是二次函数,则m 的值为__________.【答案】2【解析】【分析】根据二次函数的定义:一般地,形如y =ax 2+bx +c (a 、b 、c 是常数,a ≠0)的函数,叫做二次函数,求出m 的值即可解决问题.【详解】解:∵()21m m y m x -=+是关于x 的二次函数,∵m 2-m =2,m +1≠0,解得:m =2.故答案为:2.【点睛】本题主要考查了二次函数的定义及解一元二次方程;牢固掌握定义和方程的解法是解题的关键.考点四 列二次函数关系式例题:(2022·上海市青浦区教育局二模)为防治新冠病毒,某医药公司一月份的产值为1亿元,若每月平均增长率为x ,第一季度的总产值为y (亿元),则y 关于x 的函数解析式为________________.【答案】233y x x =++【解析】【分析】根据题意分别求得每个月的产值,然后相加即可求解.【详解】解:∵某医药公司一月份的产值为1亿元,若每月平均增长率为x ,∵二月份的为()111x x +⨯=+三月份的为()()()2111x x x +⨯+=+第一季度的总产值为y (亿元),则()2211133y x x x x =++++=++ 故答案为:233y x x =++【点睛】本题考查了二次函数的应用,根据题意列出函数关系式是解题的关键.【变式训练】1.(2021·山东滨州·九年级期中)某商店从厂家以每件21元的价格购进一批商品,该商店可以自行定价,若每件商品的售价为x 元,则可卖出()35010x -件,那么卖出商品所赚钱y 元与售价x 元之间的函数关系为【答案】2105607350y x x =-+-【解析】【分析】由题意分析出每件商品的盈利为:()21x -元,再根据:总利润等于每件商品的利润乘以销售的数量,再化简即可.【详解】解:由题意得:每件商品的盈利为:()21x -元,所以:()()2135010y x x =--2102103507350x x x =-++-2105607350x x =-+-故答案为:2105607350y x x =-+-【点睛】本题考查的是列二次函数关系式,掌握“总利润等于每件商品的利润乘以销售的数量”是解题的关键. 2.(2022·全国·九年级课时练习)如图,在长方形ABCD 中,8cm AB =,6cm AD =,点M ,N 从A 点出发,点M 沿线段AB 运动,点N 沿线段AD 运动(其中一点停止运动,另一点也随之停止运动).若设cm AM AN x ==,阴影部分的面积为2cm y ,则y 与x 之间的关系式为______.【答案】y =-212x +48 【解析】【分析】先求出212AMN S x =,进而即可得到答案. 【详解】由题意得:21122AMN S AM AN x =⋅=, ∵阴影部分的面积=6×8-212x ,即:y =-212x +48. 故答案是:y =-212x +48.本题主要考查列二次函数解析式,解题的关键是掌握割补法求面积.一、选择题1.(2022·吉林·安图县第三中学九年级阶段练习)下列函数中是二次函数的是( )A .y =2x +1B .22y x =-C .y =-8xD .3y x = 【答案】B【分析】根据二次函数的定义进行判断.【详解】解:A 、该函数是一次函数,不是二次函数,故本选项错误;B 、该函数是二次函数,故本选项正确;C 、该函数是反比例函数,故本选项错误;D 、该函数是三次函数,故本选项错误;故选B .【点睛】本题考查二次函数的定义.熟知一般地,形如2y ax bx c =++(a 、b 、c 是常数,a ≠0)的函数,叫做二次函数是解答此题的关键.2.(2020·北京房山·九年级期中)二次函数24+3y x x =-的二次项系数、一次项系数和常数项分别是( )A .1,4,3B .0,4,3C .1,-4,3D .0,-4,3【答案】C【分析】根据二次函数的定义:一般地,形如()2,,0y ax bx c a b c a =++≠是常数,的函数,叫做二次函数.其中x ,y 是变量,,,a b c 是常量, a 是二次项系数, b 是一次项系数, c 是常数项作答.【详解】解:解:二次函数24+3y x x =-的二次项系数是1,一次项系数是4-,常数项是3.故选:C .【点睛】此题主要考查了二次函数的定义,关键是注意在找二次项系数, 一次项系数和常数项时,不要漏课后训练3.(2022·江苏·九年级专题练习)一台机器原价100万元,若每年的折旧率是x ,两年后这台机器约为y 万元,则y 与x 的函数关系式为( ) A .y =100(1﹣x )B .y =100﹣x 2C .y =100(1+x )2D .y =100(1﹣x )2【答案】D【分析】根据两年后机器价值=机器原价值×(1﹣折旧百分比)2可得函数解析式.【详解】解:根据题意知y =100(1﹣x )2,故选:D .【点睛】本题主要考查根据实际问题列二次函数关系式,根据实际问题确定二次函数关系式关键是读懂题意,建立二次函数的数学模型来解决问题.需要注意的是实例中的函数图像要根据自变量的取值范围来确定.4.(2021·河北·唐山市第九中学九年级阶段练习)若函数24(m 2)3m m y x mx +-=++-是关于x 的二次函数,则m 的取值为( )A .3-B .2C .3D .3-或2 【答案】D【分析】根据二次函数的定义,必须二次项系数不等于0,且未知数的次数等于2,据此列不等式组并求解即可. 【详解】解:由二次函数的定义可知,当22042m m m +≠⎧⎨+-=⎩时,该函数是二次函数, ∵m =-3或m =2,故选:D .【点睛】本题考查了二次函数的定义,明确二次函数的定义并正确列式,是解题的关键.5.(2022·江苏·九年级专题练习)如图所示,在Rt ABO 中,AB OB ⊥,且3AB OB ==,设直线x t =截此三角形所得的阴影部分的面积为S ,则S 与t 之间的函数关系式为( )A .S t =B .212S t =C .2S t =D .2112S t =- 【答案】B【分析】Rt ABO 中,AB OB ⊥,且3AB OB ==,可得45AOB A ∠=∠=︒;再由平行线的性质得出45OCD A ∠=∠=︒,即45COD OCD ∠=∠=︒,进而证明CD OD t ==,最后根据三角形的面积公式,求出S与t 之间的函数关系式.【详解】解:如图所示,∵Rt ABO 中,AB OB ⊥,且3AB OB ==,∵45AOB A ∠=∠=︒,∵CD OB ⊥,∵CD AB ∥,∵45OCD A ∠=∠=︒,∵45COD OCD ∠=∠=︒,∵CD OD t ==,∵12OCD S OD CD =⨯△ ()21032t t =<≤, 即:()21032S t t =<≤. 故选:B .【点睛】本题主要考查的是二次函数解析式的求法,考查了等腰直角三角形的性质,平行线的判定和性质,等腰三角形的判定,三角形的面积等知识点.解题的关键是能够找到题目中的有关面积的等量关系.二、填空题6.(2021·全国·九年级课前预习)把y =(2-3x )(6+x )变成y =ax ²+bx +c 的形式,二次项为____,一次项系数为______,常数项为______.【答案】 23x - -16 12【解析】略7.(2022·全国·九年级课时练习)如图,△ABC 中,AB =AC ,CD ∵AB 于D ,BD =1,设BC =x ,AD =y ,当x >2时,y 关于x 的函数解析式为 _____.【答案】21122y x x【分析】由BD =1,AD =y ,可得AB =AC =y +1,在Rt ∵ACD 中,CD 2=AC 2-AD 2=2y +1,在Rt ∵BCD 中,CD 2=BC 2-BD 2=x 2-1,即得2y +1=x 2-1,可得答案.【详解】解:∵BD =1,AD =y ,∵AB =y +1,∵AB =AC ,∵AC =y +1,在Rt ∵ACD 中,CD 2=AC 2-AD 2=(y +1)2-y 2=2y +1,在Rt ∵BCD 中,CD 2=BC 2-BD 2=x 2-12=x 2-1,∵2y +1=x 2-1,∵2112y x =-. 故答案为:21122yx x . 【点睛】本题考查勾股定理的应用,解题的关键是将CD 2作等量,列出y 与x 的关系式.8.(2021·重庆·垫江第八中学校九年级阶段练习)若函数y =(a +1)x |a |+1是二次函数,则a 的值是 ______ .【答案】1【分析】根据二次函数的定义,列出关于a 的方程和不等式,即可求解.【详解】根据二次函数的定义可得:1210a a ⎧+=⎨+≠⎩,解得:a =1. 故答案为:1.【点睛】本题主要考查二次函数的定义,掌握二次函数的最高次项的次数为2,二次项系数不等于零,是解题的关键.9.(2021·山东·泰安市泰山区大津口中学九年级阶段练习)已知2324m m ym x 是二次函数,则m 的值为___________.【答案】-1【分析】根据二次函数的定义,即可求解.【详解】解:∵2324m m y m x 是二次函数,∵2322m m --=且40m -≠,解得:1m =-.故答案为:-1【点睛】本题主要考查了二次函数的定义,熟练掌握二次函数()20y ax a =≠是解题的关键.10.(2021·全国·九年级专题练习)下列函数一定是二次函数的是__________.①2y ax bx c =++;②3y x=-;③2431y x x =-+;④2(1)y m x bx c =-++;⑤y =(x -3)2-x 2 【答案】③【分析】根据二次函数的定义: 一般地,把形如y =ax ²+bx +c (a ≠0)(a 、b 、c 是常数)的函数叫做二次函数,据此判断即可.【详解】解:①2y ax bx c =++,必须满足a ≠0才为二次函数,故①不一定是二次函数;②等号右边为分式,故②不是二次函数;③2431y x x =-+是二次函数,故③是二次函数;④2(1)y m x bx c =-++,1m =时,该式不是二次函数;⑤2222(3)6969y x x x x x x =--=-+-=-+,该式不是二次函数;故答案为:③.【点睛】本题考查了二次函数的识别,熟知二次函数的定义是解本题的关键.三、解答题11.(2022·全国·九年级专题练习)下列函数中,哪些是二次函数?(1)y =3x —1;(2)232y x =+ ;(3)3232y x x =+ ;(4)2221y x x =-+ ;(5)2()1y x x x =-+ ;(6)2y x x -=+【答案】(2)(4)是二次函数【分析】根据二次函数的定义,即可求解.【详解】解∵(1)不是二次函数,因为自变量的最高次数是1.(2)是二次函数,因为符合二次函数的概念.(3)不是二次函数,因为自变量的最高次数是3.(4)是二次函数,因为符合二次函数的概念.(5)不是二次函数,因为原式整理后为y =-x .(6)不是二次函数,因为x -2为分式,不是整式.故(2)(4)是二次函数.【点睛】本题主要考查了二次函数的定义,熟练掌握形如2y ax bx c =++(其中a 、b 、c 均为常数,且0a ≠)的函数关系称为二次函数是解题的关键.12.(2022·全国·九年级课时练习)已知函数y =(a +1) 21ax ++(a ﹣2)x (a 为常数),求a 的值:(1)函数为二次函数;(2)函数为一次函数.【答案】(1)a =1(2)a =0或﹣1【分析】(1)直接利用二次函数的定义得出a 2+1=2,a +1≠0得出即可;(2)利用一次函数的定义分别求出即可.(1) 当 21210a a ⎧+=⎨+≠⎩时,函数为二次函数, 解得:a =±1,a ≠-1,∵a =1;(2)当 211120a a a ⎧+=⎨++-≠⎩时,函数为一次函数, 解得:a =0,当a +1=0,即a =﹣1时,函数为一次函数,所以,当函数为二次函数时,a =1,当函数为一次函数时,a =0或﹣1.【点睛】此题主要考查了二次函数与一次函数的定义,正确把握相关定义是解题关键.13.(2022·全国·九年级课时练习)一个二次函数234(1)21kk y k x x -+=-+-.(1)求k 的值.(2)求当x =3时,y 的值?【答案】(1)k =2;(2)14【分析】(1)根据二次函数的定义列出关于k 所满足的式子,求解即可;(2)在(1)的基础上,先求出二次函数解析式,然后代入x =3求解即可. 【详解】解:(1)依题意有234210k k k ⎧-+=⎨-≠⎩, 解得:k =2,∵k 的值为2;(2)把k =2代入函数解析式中得:221y x x =+-,当x =3时,y =14,∵y 的值为14.【点睛】本题考查二次函数的定义,以及求二次函数的函数值,理解并掌握二次函数的基本定义是解题关键.14.(2022·全国·九年级专题练习)已知函数y =(k 2﹣k )x 2+kx +k +1(k 为常数).(1)若这个函数是一次函数,求k 的值;(2)若这个函数是二次函数,则k 的值满足什么条件?【答案】(1)k =1;(2)k ≠0且k ≠1【分析】(1)由一次函数的定义求解可得;(2)由二次函数的定义求解可得.【详解】解:(1)若这个函数是一次函数,则k 2﹣k =0且k ≠0,解得k =1;(2)若这个函数是二次函数,则k 2﹣k ≠0,解得k ≠0且k ≠1.【点睛】本题主要考查了一次函数的定义、二次函数的定义,准确分析判断是解题的关键.15.(2022·浙江宁波·八年级期末)荔枝是夏季的时令水果,储存不太方便.某水果店将进价为18元/千克的荔枝,以28元/千克售出时,每天能售出40千克.市场调研表明:当售价每降低1元/千克时,平均每天能多售出10千克.设降价x 元.(1)降价后平均每天可以销售荔枝 千克(用含x 的代数式表示).(2)设销售利润为y ,请写出y 关于x 的函数关系式.(3)该水果店想要使荔枝的销售利润平均每天达到480元,且尽可能地减少库存压力,应将价格定为多少元/千克?【答案】(1)()4010x +(2)21060400y x x =-++(3)24元/千克【分析】(1)根据“当售价每降低1元/千克时,平均每天能多售出10千克”可直接得出结论;(2)利用利润=(售价-成本)×销售量可得出结论;(3)令y =480,求出x 的值,再根据题意对x 的值进行取舍即可.(1)根据题意得,降价后平均每天可以销售荔枝:(40+10x )千克,故答案为:(40+10x ).(2)根据题意得,()()40102818y x x =+--整理得21060400y x x =-++(3)令480y =,代入函数得,21060400480x x -++=解方程,得14x =,22x =因为要尽可能地清空库存,所以2x =舍去取4x =此时荔枝定价为28424-=(元/千克)答:应将价格定为24元/千克.【点睛】本题考查了一元二次方程的应用,列函数关系式,列代数式,根据题意列出函数关系式是解题的关键.。
压轴题二次函数解题技巧

压轴题二次函数解题技巧
压轴题是数学考试中考察学生综合能力的一道难题,其中二次函数题目尤其考验学生的解题技巧。
以下为二次函数解题的几种技巧: 1. 求解二次函数的根,可以使用求根公式。
当方程有两个实根时,根据大小关系可以确定函数的开口方向;当有一个实根时,函数与x轴相切;当没有实根但有复根时,函数与x轴没有交点,且开口向上或向下。
2. 判断二次函数的最值,可以使用顶点公式。
当二次项系数为正数时,函数的最小值为顶点的y坐标;当二次项系数为负数时,函数的最大值为顶点的y坐标。
3. 根据函数图像确定函数表达式,可以根据函数的开口方向、顶点坐标、以及过已知点的信息来确定函数的表达式。
4. 根据函数表达式确定函数图像,可以通过分析函数的一、二阶导数来确定函数的开口方向、顶点坐标、以及拐点的位置。
掌握这些二次函数的解题技巧,可以帮助学生在考试中更加轻松地解决压轴题。
- 1 -。
(完整版)中考数学二次函数压轴题题型归纳

中考二次函数综合压轴题型归类一、常考点汇总1、两点间的距离公式:()()22B A B A x x y y AB -+-=2、中点坐标:线段AB 的中点C 的坐标为:⎪⎭⎫⎝⎛++22B A B A y y x x ,直线11b x k y +=(01≠k )与22b x k y +=(02≠k )的位置关系:(1)两直线平行⇔21k k =且21b b ≠ (2)两直线相交⇔21k k ≠ (3)两直线重合⇔21k k =且21b b = (4)两直线垂直⇔121-=k k3、一元二次方程有整数根问题,解题步骤如下:① 用∆和参数的其他要求确定参数的取值范围;② 解方程,求出方程的根;(两种形式:分式、二次根式)③ 分析求解:若是分式,分母是分子的因数;若是二次根式,被开方式是完全平方式。
例:关于x 的一元二次方程()01222=-m x m x ++有两个整数根,5<m 且m 为整数,求m 的值。
4、二次函数与x 轴的交点为整数点问题。
(方法同上)例:若抛物线()3132+++=x m mx y 与x 轴交于两个不同的整数点,且m 为正整数,试确定此抛物线的解析式。
5、方程总有固定根问题,可以通过解方程的方法求出该固定根。
举例如下:已知关于x 的方程23(1)230mx m x m --+-=(m 为实数),求证:无论m 为何值,方程总有一个固定的根。
解:当0=m 时,1=x ;当0≠m 时,()032≥-=∆m ,()m m x 213∆±-=,mx 321-=、12=x ;综上所述:无论m 为何值,方程总有一个固定的根是1。
6、函数过固定点问题,举例如下:已知抛物线22-+-=m mx x y (m 是常数),求证:不论m 为何值,该抛物线总经过一个解:把原解析式变形为关于m 的方程()x m x y -=+-122;∴ ⎩⎨⎧=-=+-01 02 2x x y ,解得:⎩⎨⎧=-=1 1 x y ;∴ 抛物线总经过一个固定的点(1,-1)。
怎样解二次函数的压轴题

怎样解二次函数的压轴题解二次函数的压轴题可以是一个相对简单的数学问题,但是需要一定的基本知识和技巧。
下面,本文将分为以下几个方面来探讨解二次函数的压轴题的方法和技巧。
一、梳理相关知识点解二次函数的压轴题需要掌握以下知识点:1.二次函数的标准式:f(x) = ax² + bx + c。
2.二次函数的图像特征:开口方向、顶点坐标、轴对称直线、零点等。
3.配方法、公式法和因式分解法。
4.顶点式:f(x) = a(x - h)² + k。
二、运用配方法如果二次函数的系数不是很好进行分解,那么就需要使用配方法了。
具体步骤如下:1.将二次函数变为标准式:f(x) = ax² + bx + c。
2.将二次项和常数项分别和一个常数项a相乘,即f(x) = a(ax² + bx +c/a)。
3.将中间项拆开,即f(x) = a(x + b/2a)² - b²/4a + c。
4.将-f(x) = -a(x + b/2a)² + b²/4a - c,即可得到顶点式,顶点坐标为(-b/2a, b²/4a - c)。
三、运用公式法当二次函数系数比较复杂,无法使用配方法进行分解时,可以考虑使用公式法。
具体步骤如下:1.将二次函数变为标准式:f(x) = ax² + bx + c。
2.将方程f(x) = 0变形为ax² + bx + c = 0。
3.求出二次函数的判别式Δ = b² - 4ac。
4.带入公式x = (-b±√Δ)/2a,求出函数的零点。
5.根据顶点公式f(h) = a(h - k)² + b,求出函数的顶点坐标。
四、运用因式分解法如果二次函数可以进行因式分解,那么就可以通过这种方法来求得函数的零点。
具体步骤如下:1.将二次函数变为标准式:f(x) = ax² + bx + c。
二次函数压轴题解题技巧

二次函数压轴题解题技巧引言:解数学压轴题一般可以分为三个步骤:认真审题,理解题意、探究解题思路、正确解答。
审题要全面审视题目的所有条件和答题要求,在整体上把握试题的特点、结构,以利于解题方法的选择和解题步骤的设计。
解数学压轴题要善于总结解数学压轴题中所隐含的重要数学思想,如转化思想、数形结合思想、分类讨论思想及方程的思想等。
认识条件和结论之间的关系、图形的几何特征与数、式的数量、结构特征的关系,确定解题的思路和方法.当思维受阻时,要及时调整思路和方法,并重新审视题意,注意挖掘隐蔽的条件和内在联系,既要防止钻牛角尖,又要防止轻易放弃。
一、动态:动点、动线1.如图,抛物线与x轴交于A(x1,0)、B(x2,0)两点,且x1>x2,与y轴交于点C(0,4),其中x1、x2是方程x2-2x-8=0的两个根.(1)求这条抛物线的解析式;(2)点P是线段AB上的动点,过点P作PE∥AC,交BC于点E,连接CP,当△CPE 的面积最大时,求点P的坐标;(3)探究:若点Q是抛物线对称轴上的点,是否存在这样的点Q,使△QBC成为等腰三角形?若存在,请直接写出所有符合条件的点Q的坐标;若不存在,请说明理由.二、圆2.如图1,在平面直角坐标系xOy,二次函数y=ax2+bx+c(a>0)的图象顶点为D,与y轴交于点C,与x轴交于点A、B,点A在原点的左侧,点B的坐标为(3,0),OB=OC,tan∠ACO= 1 3.(1)求这个二次函数的解析式;(2)若平行于x轴的直线与该抛物线交于点M、N,且以MN为直径的圆与x轴相切,求该圆的半径长度;(3)如图2,若点G(2,y)是该抛物线上一点,点P是直线AG下方的抛物线上的一动点,当点P运动到什么位置时,△AGP的面积最大?求此时点P的坐标和△AGP的最大面积.图1 图2三、比例比值取值范围3.如图是二次函数k m x y ++=2)(的图象,其顶点坐标为M(1,-4). (1)求出图象与x 轴的交点A,B 的坐标; (2)在二次函数的图象上是否存在点P ,使MAB PAB S S ∆∆=45,若存在,求出P 点的坐标;若不存在,请说明理由;(3)将二次函数的图象在x 轴下方的部分沿x 轴翻折,图象的其余部分保持不变,得到一个新的图象,请你结合这个新的图象回答:当直线)1(<+=b b x y 与此图象有两个公共点时,b 的取值范围.4. 如图,直线33+=x y 交x 轴于A 点,交y 轴于B 点,过A 、B 两点的抛物线交x 轴于另一点C (3,0).⑴ 求抛物线的解析式;⑵ 在抛物线的对称轴上是否存在点Q ,使△ABQ 是等腰三角形? 若存在,求出符合条件的Q 点坐标;若不存在,请说明理由.5.如图,在平面直角坐标系中,二次函数c bx x y ++=2的图象与x 轴交于A 、B 两点, A 点在原点的左侧,B 点的坐标为(3,0),与y 轴交于C (0,-3)点,点P 是直线BC 下方的抛物线上一动点.(1)求这个二次函数的表达式.(2)连结PO 、PC ,并把△POC 沿CO 翻折,得到四边形POP /C , 那么是否存在点P ,使四边形POP /C 为菱形?若存在,请求出此时点P 的坐标;若不存在请说明理由.(3)当点P 运动到什么位置时,四边形 ABPC 的面积最大并求出此时P 点的坐标和四边形ABPC 的最大面积.1.在平面直角坐标系中,已知A (-4,0),B (1,0),且以AB 为直径的圆交y 轴的正半轴于点C ,过点C 作圆的切线交x 轴于点D .(1)求点C 的坐标和过A ,B ,C 三点的抛物线的解析式; (2)求点D 的坐标;(3)设平行于x 轴的直线交抛物线于E ,F 两点,问:是否存在以线段EF 为直径的圆,恰好与x 轴相切?若存在,求出该圆的半径,若不存在,请说明理由.2.已知:如图,在平面直角坐标系xOy 中,矩形OABC 的边OA 在y 轴的正半轴上,OC 在x 轴的正半轴上,OA =2,OC =3.过原点O 作∠AOC 的平分线交AB 于点D ,连接DC ,过点D 作DE ⊥DC ,交OA 于点E . (1)求过点E 、D 、C 的抛物线的解析式;(2)将∠EDC 绕点D 按顺时针方向旋转后,角的一边与y 轴的正半轴交于点F ,另一边与线段OC 交于点G .如果DF 与(1)中的抛物线交于另一点M ,点M 的横坐标为56,那么EF =2GO 是否成立?若成立,请给予证明;若不成立,请说明理由;(3)对于(2)中的点G ,在位于第一象限内的该抛物线上是否存在点Q ,使得直线GQ 与AB 的交点P 与点C 、G 构成的△PCG 是等腰三角形?若存在,请求出点Q 的坐标;若不存在,请说明理由.3.如图,抛物线y =ax 2+bx +c (a ≠0)与x 轴交于A (-3,0)、B 两点,与y 轴相交于点C (0,3).当x =-4和x =2时,二次函数y =ax 2+bx +c (a ≠0)的函数值y 相等,连结AC 、BC . (1)求实数a ,b ,c 的值; (2)若点M 、N 同时从B 点出发,均以每秒1个单位长度的速度分别沿BA 、BC 边运动,其中一个点到达终点时,另一点也随之停止运动.当运动时间为t 秒时,连结MN ,将△BMN 沿MN 翻折,B 点恰好落在AC 边上的P 处,求t 的值及点P 的坐标;4. 如图,抛物线y =21x 2+bx -2与x 轴交于A 、B 两点,与y 轴交于C 点,且A (一1,0). ⑴求抛物线的解析式及顶点D 的坐标; ⑵判断△ABC 的形状,证明你的结论;⑶点M (m ,0)是x 轴上的一个动点,当CM +DM 的值最小时,求m 的值.面积最大5、如图,在平面直角坐标系中,点A 、C 的坐标分别为(-1,0)、(0,3-),点B 在x 轴上.已知某二次函数的图象经过A 、B 、C 三点,且它的对称轴为直线x =1,点P 为直线BC 下方的二次函数图象上的一个动点(点P 与B 、C 不重合),过点P 作y 轴的平行线交BC 于点F .(1)求该二次函数的解析式;(2)若设点P 的横坐标为m ,试用含m 的代数式表示线段PF 的长; (3)求△PBC 面积的最大值,并求此时点P 的坐标.6、在平面直角坐标系中,已知抛物线经过A (-4,0),B (0,-4),C (2,0)三点. (1)求抛物线的解析式;(2)若点M 为第三象限内抛物线上一动点,点M 的横坐标为m ,△AMB 的面积为S .求S 关于m 的函数关系式,并求出S 的最大值.(3)若点P 是抛物线上的动点,点Q 是直线y =-x 上的动点,判断有几个位置能够使得点P 、Q 、B 、O 为顶点的四边形为平行四边形,直接写出相应的点Q 的坐标.讨论等腰7、如图,已知抛物线y =21x2+bx +c 与y 轴相交于C ,与x 轴相交于A 、B ,点A 的坐标为(2,0),点C 的坐标为(0,-1).(1)求抛物线的解析式;(2)点E 是线段AC 上一动点,过点E 作DE ⊥x 轴于点D ,连结DC ,当△DCE 的面积最大时,求点D 的坐标; (3)在直线BC 上是否存在一点P ,使△ACP 为等腰三角形,若存在,求点P 的坐标,若不存在,说明理由.8、(武汉市中考)如图,已知抛物线y =x2+bx +3与x 轴交于点B (3,0),与y 轴交于点A ,P 是抛物线上的一个动点,点P 的横坐标为m (m >3),过点P 作y 轴的平行线PM ,交直线AB 于点M . (1)求抛物线的解析式;(2)若以AB 为直径的⊙N 与直线PM 相切,求此时点M 的坐标;(3)在点P 的运动过程中,△APM 能否为等腰三角形?若能,求出点M 的坐标;若不能,请说明理由.备用图论直角三角形9、如已知:如图一次函数y =21x +1的图象与x 轴交于点A ,与y 轴交于点B ;二次函数y =21x2+bx +c 的图象与一次函数y =21x +1的图象交于B 、C 两点,与x 轴交于D 、E 两点且D 点坐标为(1,0) (1)求二次函数的解析式;(2)求四边形BDEC 的面积S ;(3)在x 轴上是否存在点P ,使得△PBC 是以P 为直角顶点的直角三角形?若存在,求出所有的点P ,若不存在,请说明理由.10、(九市联考)如图,抛物线与x 轴交于A (-1,0)、B (3,0)两点,与y 轴交于点C (0,-3),设抛物线的顶点为D . (1)求该抛物线的解析式与顶点D 的坐标; (2)以B 、C 、D 为顶点的三角形是直角三角形吗?为什么?(3)探究坐标轴上是否存在点P ,使得以P 、A 、C 为顶点的三角形与△BCD 相似?若存在,请指出符合条件的点P 的位置,并直接写出点P 的坐标;若不存在,请说明理由.讨论四边形11、二次函数y =x2+px +q (p <0)图象与x 轴交于A 、B 两点,与y 轴交于点C (0,-1),△ABC 的面积为45.(1)求该二次函数的关系式;(2)过y 轴上的一点M (0,m )作y 轴的垂线,若该垂线与△ABC 的外接圆有公共点,求m 的取值范围;(3)在该二次函数的图象上是否存在点D ,使四边形ACBD 为直角梯形?若存在,求出点D 的坐标;若不存在,请说明理由.2018中考二次函数压轴题专题分类训练题型一:面积问题【例1】如图2,抛物线顶点坐标为点C (1,4),交x 轴于点A (3,0),交y 轴于点B . (1)求抛物线和直线AB 的解析式; (2)求△CAB 的铅垂高CD 及S △CAB ;(3)设点P 是抛物线(在第一象限内)上的一个动点,是否存在一点P ,使S △PAB =89S △CAB ,若存在,求出P 点的坐标;若不存在,请说明理由.【变式练习】1.如图,在直角坐标系中,点A 的坐标为(-2,0),连结OA ,将线段OA 绕原点O 顺时针旋转120°,得到线段OB . (1)求点B 的坐标; (2)求经过A 、O 、B 三点的抛物线的解析式;(3)在(2)中抛物线的对称轴上是否存在点C ,使△BOC 的周长最小?若存在,求出点C 的坐标;若不存在,请说明理由.(4)如果点P 是(2)中的抛物线上的动点,且在x 轴的下方,那么△PAB 是否有最大面积?若有,求出此时P 点的坐标及△PAB 的最大面积;若没有,请说明理由.2.如图,抛物线y = ax 2+ bx + 4与x 轴的两个交点分别为A (-4,0)、B (2,0),与y 轴交于点C ,顶点为D .E (1,2)为线段BC 的中点,BC 的垂直平分线与x 轴、y 轴分别交于F 、G . (1)求抛物线的函数解析式,并写出顶点D 的坐标;(2)在直线EF 上求一点H ,使△CDH 的周长最小,并求出最小周长; (3)若点K 在x 轴上方的抛物线上运动,当K 运动到什么位置时, △EFK 的面积最大?并求出最大面积.3.如图,已知:直线3+-=x y 交x 轴于点A ,交y 轴于点B ,抛物线y=ax 2+bx+c 经过A 、B 、C (1,0)三点. (1)求抛物线的解析式; (2)若点D 的坐标为(-1,0),在直线3+-=x y 上有一点P,使ΔABO 与ΔADP 相似,求出点P 的坐标;(3)在(2)的条件下,在x 轴下方的抛物线上,是否存在点E ,使ΔADE 的面积等于四边形APCE 的面积?如果存在,请求出点E 的坐标;如果不存在,请说明理由.题型二:构造直角三角形【例2】如图,已知抛物线y=ax2+bx+c(a≠0)的对称轴为x=1,且抛物线经过A(-1,0)、C(0,-3)两点,与x轴交于另一点B.(1)求这条抛物线所对应的函数关系式;(2)在抛物线的对称轴x=1上求一点M,使点M到点A的距离与到点C的距离之和最小,并求此时点M的坐标;(3)设点P为抛物线的对称轴x=1上的一动点,求使∠PCB=90º的点P的坐标.E【变式练习】1.如图,抛物线y=与x轴交于A、B两点(点A在点B的左侧),与y轴交于点C.(1)求点A、B的坐标;(2)设D为已知抛物线的对称轴上的任意一点,当△ACD的面积等于△ACB的面积时,求点D的坐标;(3)若直线l过点E(4,0),M为直线l上的动点,当以A、B、M为顶点所作的直角三角形有且只有三个时,求直线l的解析式.3.在平面直角坐标系内,反比例函数和二次函数y=k(x2+x﹣1)的图象交于点A(1,k)和点B(﹣1,﹣k).(1)当k=﹣2时,求反比例函数的解析式;(2)要使反比例函数和二次函数都是y随着x的增大而增大,求k应满足的条件以及x的取值范围;(3)设二次函数的图象的顶点为Q,当△ABQ是以AB为斜边的直角三角形时,求k的值2E的直线y x b=+与抛物线ABE与ACE的面积大小关系如何?当4>-时,上述关系还成立吗,为什么?,使得BOC是以BC为斜边的直角三角形,若存在,求出b;若不存在,说明理由.【例3】如图,已知抛物线32++=bx ax y (a ≠0)与x 轴交于点A (1,0)和点B (-3,0),与y 轴交于点C . (1)求抛物线的解析式;(2)在x 轴上是否存在一点Q 使得△ACQ 为等腰三角形?若存在,请直接写出所有符合条件的点Q 的坐标;若不存在,请说明理由;(3)设抛物线的对称轴与x 轴交于点M ,问在对称轴上是否存在点P ,使△CMP 为等腰三角形?若存在,请直接写出所有符合条件的点P 的坐标;若不存在,请说明理由.2.如图,抛物线254y ax ax =-+经过ABC △的三个顶点,已知BC x ∥轴,点A 在x 轴上,点C 在y 轴上,且AC=BC .(1)写出A,B,C 三点的坐标并求抛物线的解析式;(2)探究:若点P 是抛物线对称轴上且在x 轴下方的动点,是否存在PAB △是等腰三角形.若存在,求出所有符合条件的点P 坐标;不存在,请说明理由.【例4】如图,已知抛物线经过A(﹣2,0),B(﹣3,3)及原点O,顶点为C.(1)求抛物线的解析式;(2)若点D在抛物线上,点E在抛物线的对称轴上,且A、O、D、E为顶点的四边形是平行四边形,求点D的坐标;(3)P是抛物线上的第一象限内的动点,过点P作PM⊥x轴,垂足为M,是否存在点P,使得以P、M、A为顶点的三角形△BOC相似?若存在,求出点P的坐标;若不存在,请说明理由.【变式练习】1.如图,已知抛物线经过A(4,0),B(1,0),C(0,-2)三点.(1)求该抛物线的解析式;(2)在直线AC上方的该抛物线上是否存在一点D,使得△DCA的面积最大?若存在,求出点D的坐标及△DCA面积的最大值;若不存在,请说明理由.(3)P是直线x=1右侧的该抛物线上一动点,过P作PM⊥x轴,垂足为M,是否存在P点,使得以A、P、M为顶点的三角形与△OAC相似?若存在,请求出符合条件的点P的坐标;若不存在,请说明理由.7),且顶点C的横坐标为4,该图象在x 轴上截得的线段AB的长为6.2. 如图,二次函数的图象经过点D(0,39(1)求二次函数的解析式;(2)在该抛物线的对称轴上找一点P,使PA+PD最小,求出点P的坐标;(3)在抛物线上是否存在点Q,使△QAB与△ABC相似?如果存在,求出点Q的坐标;如果不存在,请说明理由.3.如图,二次函数y=ax2+bx+c的图象交x轴于A(﹣1,0),B(2,0),交y轴于C(0,﹣2),过A,C画直线.(1)求二次函数的解析式;(2)点P在x轴正半轴上,且P A=PC,求OP的长;(3)点M在二次函数图象上,以M为圆心的圆与直线AC相切,切点为H.①若M在y轴右侧,且△CHM∽△AOC(点C与点A对应),求点M的坐标;②若⊙M的半径为,求点M的坐标.题型六:构造平行四边形【例7】如图,在平面直角坐标系中,抛物线经过A(—1,0),B(3,0),C(0,—1)三点。
二次函数压轴题---动点问题解答方法技巧总结 (含例解答案)

07 动点个数 问题背景 两个 特殊菱形两边上移动 一个
08 两个
09
特殊直角梯形三边 上移动
抛物线中特殊直角梯形底 边上移动
考查难点
探究相似三角形
探究三角形面积函 数关系式
探究等腰三角形
考 点
①菱形性质 ②特殊角三角函数 ③求直线、抛物线解析式 ④相似三角形 ⑤不等式
①求直线解析式 ②四边形面积的表 示 ③动三角形面积函 数④矩形性质
2
(2)由(1)可计算得点 M (3 , 1),N (31) ,. 过点 N 作 NH AD ,垂足为 H . 当运动到时刻 t 时, AD 2OD 8 2t , NH 1 2t . 根据中心对称的性质 OA OD ,OM ON ,所以四边形 MDNA 是平行四边形. 所以 S 2S△ ADN . 所以,四边形 MDNA 的面积 S (8 2t )(1 2t ) 4t 14t 8 .
动点问题题型方法归纳总结
动态几何特点----问题背景是特殊图形,考查问题也是特殊图形,所以要把握好 一般与特殊的关系;分析过程中,特别要关注图形的特性(特殊角、特殊图形 的性质、图形的特殊位置。 ) 动点问题一直是中考热点,近几年考查探究运动中的特殊性:等腰三角形、直 角三角形、 相似三角形、平行四边形、梯形、特殊角或 其三角函数、线段或面积的最值。 下面就此问题的常见题型作简单介绍,解题方法、关键给以点拨。
二、
抛物线上动点
5、 (湖北十堰市)如图①, 已知抛物线 y ax 2 bx 3 (a≠0)与 x 轴交于点 A(1,0)和 点 B (-3,0),与 y 轴交于点 C. (1) 求抛物线的解析式;
(2) 设抛物线的对称轴与 x 轴交于点 M ,问在对称轴上是否存在点 P,使△CMP 为等腰三 角形?若存在,请直接写出所有符合条件的点 P 的坐标;若不存在,请说明理由. (3) 如图②,若点 E 为第二象限抛物线上一动点,连接 BE、CE,求四边形 BOCE 面积的 最大值,并求此时 E 点的坐标数的图象与 x 轴的交点坐标,需转化为一元二次方程; ⑵ 求二次函数的最大(小)值需要利用配方法将二次函数由一般式转化为顶 点式; ⑶ 根据图象的位置判断二次函数 ax²+bx+c=0 中 a,b,c 的符号, 或由二次函数 中 a,b,c 的符号判断图象的位置,要数形结合; ⑷ 二次函数的图象关于对称轴对称,可利用这一性质,求和已知一点对称的 点坐标,或已知与 x 轴的一个交点坐标,可由对称性求出另一个交点坐标. ⑸ 与二次函数有关的还有二次三项式,二次三项式 ax²+bx+c﹙a≠0﹚本身就 是所含字母 x 的二次函数;下面以 a>0 时为例,揭示二次函数、二次三项式 和一元二次方程之间的内在联系:
中考二次函数压轴题解题技巧

中考二次函数压轴题解题技巧在解题过程中,我们需要借助函数解析式来表示动点坐标。
首先,我们可以设定动点P在某条直线上,其坐标为(t,f(t))。
然后,我们可以通过计算两个线段的长度,利用代数式证明它们相等。
这种方法适用于各种类型的线段相等问题,如求证两个三角形的周长相等等。
2.求解“定三角形内一点到三边距离之和〞的问题:对于定三角形内的一个点P,我们可以利用动点的方法来求解其到三边距离之和。
具体来说,我们可以将点P的坐标表示为(x,y),然后通过计算P到三条边的距离,再将它们相加,得到定理的结论。
这种方法适用于各种类型的定三角形内点距离之和问题。
3.求解“定直线与定点之间的距离〞的问题:对于一个定点A和一条定直线L,我们可以利用点到直线的距离公式来求解它们之间的距离。
具体来说,我们可以设定一个动点P在直线L上,然后计算点P到点A的距离,即可得到定点与定直线之间的距离。
这种方法适用于各种类型的定直线与定点之间的距离问题。
4.求解“定点到定线段的最短距离〞的问题:对于一个定点A和一条定线段BC,我们可以利用点到线段的最短距离公式来求解它们之间的最短距离。
具体来说,我们可以设定一个动点P在线段BC上,然后计算点A到线段BP和线段CP的距离,取其中较小值即可得到定点到定线段的最短距离。
这种方法适用于各种类型的定点到定线段的最短距离问题。
5.求解“动三角形内一点到三边距离之和〞的问题:对于一个动三角形ABC内的一个点P,我们可以利用动点的方法来求解其到三边距离之和。
具体来说,我们可以将点P的坐标表示为(x,y),然后通过计算P到三条边的距离,再将它们相加,得到结论。
这种方法适用于各种类型的动三角形内点距离之和问题。
1.证明两线段相等的方法:首先确定两线段的距离类型(点点距离、点轴距离或点线距离),然后利用距离公式计算出两线段的长度,并进行化简,从而证明它们相等。
2.平行于y轴的动线段长度的最大值问题:对于平行于y轴的线段,可以利用端点的函数图象解析式,将两个端点的纵坐标表示为含有字母t的代数式。
数学二次函数压轴题解题技巧

数学二次函数压轴题解题技巧数学二次函数是中学数学中的一个重要内容,而在高考数学中,二次函数也是一个重要的考点。
二次函数在高考中的压轴题往往难度较大,需要学生具备扎实的数学知识和高超的解题技巧。
下面是一些解决二次函数压轴题的技巧。
1. 熟悉常见二次函数的形式和性质常见的二次函数包括:二次项系数为 1 的二次函数,即 y=x^2;二次项系数不为 1 的二次函数,即 y=ax^2+bx+c,其中 a、b、c 为常数;以及二次函数的平移变换,即 y=x^2+bx+c(x-a)。
熟悉这些函数的形式和性质,可以帮助我们更好地理解和解决问题。
2. 掌握求最值的方法在二次函数中,求最值是一个重要的问题。
常用的求最值方法包括:利用函数的导数求最值;利用二次函数的图像求最值;利用不等式求最值等。
其中,利用函数的导数求最值是最常用的方法之一,需要注意求导的方法和技巧。
3. 掌握求顶点的方法求顶点是解决二次函数压轴题的一个常用方法。
常用的求顶点的方法包括:利用函数的导数求顶点;利用二次函数的图像求顶点;利用对称轴求顶点等。
其中,利用函数的导数求顶点是最常用的方法之一,需要注意求导的方法和技巧。
4. 掌握求范围的方法在二次函数中,求范围也是一个重要的问题。
常用的求范围方法包括:利用函数的导数求范围;利用二次函数的图像求范围;利用不等式求范围等。
其中,利用函数的导数求范围是最常用的方法之一,需要注意求导的方法和技巧。
5. 利用图形结合数学方法解决问题在解决二次函数压轴题时,常常需要利用图形结合数学方法解决问题。
例如,可以利用图像的对称性质、周期性、平移变换等,帮助我们更好地理解和解决问题。
此外,还需要善于总结各种技巧和方法,熟练掌握各种解题套路,以应对各种可能出现的二次函数压轴题。
二次函数压轴题题型总结有答案

二次函数压轴题解题思路一、基本知识1会求解析式以及一些关键点的坐标如函数图像与坐标轴的交点、两函数图像的交点等;2.会利用函数性质和图像3.相关知识:如一次函数、反比例函数、点的坐标、方程;图形中的三角形、四边形、圆及平行线、垂直;一些方法:如相似、三角函数、解方程;一些转换:如轴对称、平移、旋转;二、典型例题:一、求解析式可参考一下部分试题的第一问;二、二次函数的相关应用第一类:面积问题例题. 2012莱芜如图,顶点坐标为2,﹣1的抛物线y=ax2+bx+ca≠0与y轴交于点C0,3,与x轴交于A、B两点.1求抛物线的表达式;抛物线的解析式:y=x﹣22﹣1=x2﹣4x+3.2设抛物线的对称轴与直线BC交于点D,连接AC、AD,求△ACD的面积;练习:1. 2014兰州如图,抛物线y=﹣x2+mx+n与x轴交于A、B两点,与y轴交于点C,抛物线的对称轴交x轴于点D,已知A﹣1,0,C0,2. 1求抛物线的表达式;2在抛物线的对称轴上是否存在点P,使△PCD是以CD为腰的等腰三角形如果存在,直接写出P点的坐标;如果不存在,请说明理由;3点E时线段BC上的一个动点,过点E作x轴的垂线与抛物线相交于点F,当点E运动到什么位置时,四边形CDBF的面积最大求出四边形CDBF的最大面积及此时E点的坐标.第二类:.构造问题1构造线段2014枣庄如图,在平面直角坐标系中,二次函数y=x2﹣2x﹣3的图象与x 轴交于A、B两点,与y轴交于点C,连接BC,点D为抛物线的顶点,点P是第四象限的抛物线上的一个动点不与点D重合.1求∠OBC的度数;2连接CD、BD、DP,延长DP交x轴正半轴于点E,且S△OCE =S四边形OCDB,求此时P点的坐标;3过点P作PF⊥x轴交BC于点F,求线段PF长度的最大值.2构造相似三角形2013莱芜如图,抛物线y=ax2+bx+ca≠0经过点A﹣3,0、B1,0、C﹣2,1,交y轴于点M.1求抛物线的表达式;2D为抛物线在第二象限部分上的一点,作DE垂直x轴于点E,交线段AM于点F,求线段DF长度的最大值,并求此时点D的坐标;3抛物线上是否存在一点P,作PN垂直x轴于点N,使得以点P、A、N为顶点的三角形与△MAO相似若存在,求点P的坐标;若不存在,请说明理由.3构造平行四边形2014莱芜如图,过A1,0、B3,0作x轴的垂线,分别交直线y=4﹣x 于C、D两点.抛物线y=ax2+bx+c经过O、C、D三点. 1求抛物线的表达式;2点M为直线OD上的一个动点,过M作x轴的垂线交抛物线于点N,问是否存在这样的点M,使得以A、C、M、N为顶点的四边形为平行四边形若存在,求此时点M的横坐标;若不存在,请说明理由;3若△AOC沿CD方向平移点C在线段CD上,且不与点D重合,在平移的过程中△AOC 与△OBD重叠部分的面积记为S,试求S的最大值.x2+bx+c与y轴交于点C0,-4,与x轴4构造等腰三角形2013泰安如图,抛物线y=12交于点A,B,且B点的坐标为2,0 1求该抛物线的解析式.2若点P是AB上的一动点,过点P作PE∥AC,交BC于E,连接CP,求△PCE面积的最大值.3若点D为OA的中点,点M是线段AC上一点,且△OMD为等腰三角形,求M点的坐标.5构造直角三角形2014四川内江如图,抛物线y=ax2+bx+c经过A﹣、C0,4,点B在抛物线上,CB∥x轴,且AB平分∠CAO.1求抛物线的解析式;2线段AB上有一动点P,过点P作y轴的平行线,交抛物线于点Q,求线段PQ的最大值;3抛物线的对称轴上是否存在点M,使△ABM是以AB为直角边的直角三角形如果存在,求出点M的坐标;如果不存在,说明理由.6构造角相等2014娄底如图,抛物线y=x2+mx+m﹣1与x轴交于点Ax1,0,Bx2,0,x1<x2,与y轴交于点C0,c,且满足x12+x22+x1x2=7.1求抛物线的解析式;2在抛物线上能不能找到一点P,使∠POC=∠PCO若能,请求出点P 的坐标;若不能,请说明理由.7构造菱形2013枣庄如图,在平面直角坐标系中,二次函数y=x2+bx+c的图象与x轴交于A、B两点,A点在原点的左侧,B点的坐标为3,0,与y轴交于C0,-3点,点P是直线BC下方的抛物线上一动点.1求这个二次函数的表达式.2连接PO、PC,并把△POC沿CO翻折,得到四边形POP′C,那么是否存在点P,使四边形POP′C为菱形若存在,请求出此时点P的坐标;若不存在,请说明理由.3当点P运动到什么位置时,四边形ABPC的面积最大求出此时P点的坐标和四边形ABPC的最大面积.8构造对称点11莱芜如图,在平面直角坐标系中,已知点A-2,-4,OB=2,抛物线y =ax2+bx+c经过点A、O、B三点.1求抛物线的函数表达式;2若点M是抛物线对称轴上一点,试求AM+OM的最小值;3在此抛物线上,是否存在点P ,使得以点P 与点O 、A 、B 为顶点的四边形是梯形.若存在,求点P 的坐标;若不存在,请说明理由.9构造平行线:2014山东烟台如图,在平面直角坐标系中,Rt △ABC 的顶点A ,C 分别在y 轴,x 轴上,∠ACB =90°,OA =,抛物线y =ax 2﹣ax ﹣a 经过点B 2,,与y 轴交于点D .1求抛物线的表达式;2点B 关于直线AC 的对称点是否在抛物线上请说明理由; 3延长BA 交抛物线于点E ,连接ED ,试说明ED ∥AC 的理由.10构造垂直:2014宜宾市如图,已知抛物线y = x 2+bx +c 的顶点坐标为M 0,–1,与x 轴交于A 、B 两点. 1求抛物线的解析式; 2判断△MAB 的形状,并说明理由; 3过原点的任意直线不与y 轴重合交抛物线于C 、D 两点,连结MC 、MD ,试判断MC 、MD 是否垂直,并说明理由.11构造圆2014年淄博如图,点A 与点B 的坐标分别是1,0,5,0,点P 是该直角坐标系内的一个动点.1使∠APB=30°的点P 有 个;2若点P 在y 轴上,且∠APB=30°,求满足条件的点P 的坐标;yxO MDCBA3当点P在y轴上移动时,∠APB是否有最大值若有,求点P的坐标,并说明此时∠APB 最大的理由;若没有,也请说明理由.参考答案:一、求解析式二、二次函数的相关应用第一类:面积问题2012莱芜解:1y=x﹣22﹣1=x2﹣4x+3.2S△ACD=ADCD=××2=2.32+,1﹣、2﹣,1+、1,2或4,﹣1.2014兰州解1y=﹣x2+x+2;2y=﹣x﹣2+,P 1,4,P2,,P3,﹣;3S四边形CDBF =S△BCD+S△CEF+S△BEF=﹣a﹣22+∴a=2时,S四边形CDBF的面积最大=,∴E2,19.第二类:.构造问题1构造线段2014枣庄1△OBC 为等腰直角三角形∠OBC=45°. 2P2,﹣3.3线段PF 长度=﹣x P 2+3x P =﹣x P ﹣2+,1<x P ≤3,当x P =时,线段PF 长度最大为.2构造相似三角形2013莱芜 1y=.2DF 的最大值为.此时D 的坐标为.3存在点P,使得以点P 、A 、N 为顶点的三角形与△MAO 相似.设Pm,.在Rt△MAO 中,AO=3MO,要使两个三角形相似,由题意可知,点P 不可能在第一象限.①设点P 在第二象限时,∵点P 不可能在直线MN 上,∴只能PN=3NM,故此时满足条件的点不存在.②当点P 在第三象限时,∵点P 不可能在直线MN 上,∴只能PN=3NM, P 的坐标为﹣8,﹣15. ③当点P 在第四象限时,若AN=3PN 时,此时点P 的坐标为2,﹣.若PN=3NA,此时点P 的坐标为10,﹣39.综上所述,满足条件的点P 的坐标为﹣8,﹣15、2,﹣、10,﹣39.3构造平行四边形 2014莱芜解:1y=﹣x 2+x .2存在. 或或.3∴S=S △OFQ ﹣S △OEP =OFFQ ﹣OEPG=1+t +t ﹣t t=﹣t ﹣12+当t=1时,S 有最大值为.∴S的最大值为.4构造等腰三角形PBE ABCSS=PBE S 12=x×4-1323x+835构造直角三角形2014四川内江 1y=﹣x 2+x+4.2当t=1时,PQ 取到最大值,最大值为. 3①当∠BAM=90°时,MH=11.M ,﹣11. ②当∠ABM=90°时,M ,9.综上所述:符合要求的点M 的坐标为,9和,﹣11.6构造角相等2014娄底解1依题意:x 1+x 2=﹣m,x 1x 2=m ﹣1,∵x 1+x 2+x 1x 2=7,∴x 1+x 22﹣x 1x 2=7,∴﹣m 2﹣m ﹣1=7,即m 2﹣m ﹣6=0,解得m 1=﹣2,m 2=3,∵c=m ﹣1<0,∴m=3不合题意∴m=﹣2抛物线的解析式是y=x 2﹣2x ﹣3;2能如图,设p 是抛物线上的一点,连接PO,PC,过点P 作y 轴的垂线,垂足为D .若∠POC=∠PCO 则PD 应是线段OC 的垂直平分线∵C 的坐标为0,﹣3∴D 的坐标为0,﹣∴P 的纵坐标应是﹣令x 2﹣2x ﹣3=,解得,x 1=,x 2=因此所求点P 的坐标是,﹣,,﹣7构造菱形2013枣庄 解:1.2此时P 点的坐标为,. 3 S 四边形ABPC =++==. 易知,当x=时,四边形ABPC 的面积最大.此时P 点坐标为,,四边形ABPC 的最大面积为. 8构造对称点11莱芜1212y x x =-+;2MO+MA 的最小值为42;3①若OB ∥AP P4,-4,则得梯形OAPB;②若OA ∥BP,点P 412--,,则得梯形OAPB;③若AB ∥OP,此时点P 不存在;综上所述,存在两点P4,-4或P 412--,使得以点P 与点O 、A 、B 为顶点的四边形是梯形;2=23y x x --2232-AOC S ∆POB S ∆POC S ∆239622x x -++23375()228x --+3232154-7589构造平行线:2014山东烟台解: y=x2﹣x﹣.2连接CD,过点B作BF⊥x轴于点F,则∠BCF+∠CBF=90°∵∠ACB=90°,∴∠ACO+∠BCF=90°,∴∠ACO=∠CBF,∵∠AOC=∠CFB=90°,∴△AOC∽△CFB,∴=,设OC=m,则CF=2﹣m,则有=,解得m=m=1,∴OC=OF=1,当x=0时y=﹣,∴OD=,∴BF=OD,∵∠DOC=∠BFC=90°,∴△OCD∽△FCB,∴DC=CB,∠OCD=∠FCB,∴点B、C、D在同一直线上,∴点B与点D关于直线AC对称,∴点B关于直线AC的对称点在抛物线上.3过点E作EG⊥y轴于点G,设直线AB的表达式为y=kx+b,则,解得k=﹣,∴y=﹣x+,代入抛物线的表达式﹣x+=x2﹣x﹣.解得x=2或x=﹣2,当x=﹣2时y=﹣x+=﹣×﹣2+=,∴点E的坐标为﹣2,,∵tan∠EDG===,∴∠EDG=30°∵tan∠OAC===,∴∠OAC=30°,∴∠OAC=∠EDG,∴ED∥AC.10构造垂直:2014宜宾市解:1y=x 2﹣1.2OA=OB=OC=1,∴AM=BM,∴△MAB 是等腰直角三角形.3=,即=解得m=﹣,∵==﹣n,==,∴=,∵∠CGM=∠MHD=90°,∴△CGM∽△MHD,∴∠CMG=∠MDH,∵∠MDH+∠DMH=90°∴∠CMG+∠DMH=90°,∴∠CMD=90°,即MC⊥MF. 11构造圆2014年淄博解:1∵抛物线y=﹣x 2+mx+n 经过A ﹣1,0,C0,2.解得:,∴抛物线的解析式为:y=﹣x 2+x+2;2∵y=﹣x 2+x+2,∴y=﹣x ﹣2+,∴抛物线的对称轴是x=.∴OD=.∵C0,2,∴OC=2.在Rt △OCD 中,由勾股定理,得CD=.∵△CDP 是以CD 为腰的等腰三角形, ∴CP 1=CP 2=CP 3=CD .作CH ⊥x 轴于H,∴HP 1=HD=2,∴DP 1=4.∴P 1,4,P 2,,P 3,﹣;3当y=0时,0=﹣x 2+x+2∴x 1=﹣1,x 2=4,∴B4,0.设直线BC 的解析式为y=kx+b,由图象,得,解得:,∴直线BC 的解析式为:y=﹣x+2.如图2,过点C 作CM ⊥EF 于M,设Ea,﹣a+2,Fa,﹣a 2+a+2,∴EF=﹣a 2+a+2﹣﹣a+2=﹣a 2+2a0≤x≤4.∵S 四边形CDBF =S △BCD +S △CEF +S △BEF =BDOC+EFCM+EFBN,=+a ﹣a 2+2a+4﹣a ﹣a 2+2a,=﹣a 2+4a+0≤x≤4.=﹣a ﹣22+∴a=2时,S 四边形CDBF 的面积最大=,∴E2,1.。
初中数学二次函数压轴题解题技巧

初中数学二次函数压轴题解题技巧
一、关于二次函数的基本概念
1、什么是二次函数?
二次函数是一类特殊的函数,由定义域上的每一个实数组成,关于y的方程也叫二次方程或者二次曲线,其一般形式为y=ax2+bx+c,其中a≠0。
2、什么是二次函数的图形?
二次函数的图形一般是抛物线的形状,它的顶点为抛物线函数的极值点,有3种情况:
(1)若a>0,那么抛物线为上升,顶点位于抛物线与x轴的交点,记为(x0,y0),当x变化时,y处于上升状态;
(2)若a<0,那么抛物线为下降,顶点位于抛物线与x轴的交点,记为(x0,y0),当x变化时,y处于下降状态;
(3)若a=0,那么抛物线变成一条直线,且顶点映射向无穷远,无法确定。
二、关于解题技巧
1、根据题意分析求解
判断给定的方程的类型,是一元二次方程还是方程组,是一元二次方程可以用代数法解题;是方程组则可以用代数法或者几何法求解。
2、具体的求解步骤
(1)一元二次方程
(a)将二次项系数、一次项系数、常数项分别乘以同等量的系
数,使方程左边系数统一为1;
(b)将二次项提到一边,将其他因式放到另一边,使其成一般形式;
(c)对得到的一般形式求解,它的解一定是一个双根,具体求解可利用一元二次方程的完全平方根式;
(d)将求得的解代回原方程即可得出所求解。
(2)一元二次方程组
(a)求出第一个方程的一个变量的值,代入第二个方程求解;
(b)将求出的另一个变量值代入第一个方程,得出另一个变量的值,得出全部解。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
图1图2二次函数压轴题解题技巧引言:解数学压轴题一般可以分为三个步骤:认真审题,理解题意、探究解题思路、正确解答。
审题要全面审视题目的所有条件和答题要求,在整体上把握试题的特点、结构,以利于解题方法的选择和解题步骤的设计。
解数学压轴题要善于总结解数学压轴题中所隐含的重要数学思想,如转化思想、数形结合思想、分类讨论思想及方程的思想等。
认识条件和结论之间的关系、图形的几何特征与数、式的数量、结构特征的关系,确定解题的思路和方法.当思维受阻时,要及时调整思路和方法,并重新审视题意,注意挖掘隐蔽的条件和内在联系,既要防止钻牛角尖,又要防止轻易放弃。
一、动态:动点、动线1.如图,抛物线与x 轴交于A (x 1,0)、B (x 2,0)两点,且x 1>x 2,与y 轴交于点C (0,4),其中x 1、x 2是方程x 2-2x -8=0的两个根.(1)求这条抛物线的解析式;(2)点P 是线段AB 上的动点,过点P 作PE ∥AC ,交BC 于点E ,连接CP ,当△CPE 的面积最大时,求点P 的坐标; (3)探究:若点Q 是抛物线对称轴上的点,是否存在这样的点Q ,使△QBC 成为等腰三角形?若存在,请直接写出所有符合条件的点Q二、圆2.如图1,在平面直角坐标系xOy ,二次函数y =ax 2+bx +c (a >0)的图象顶点为D ,与y 轴交于点C ,与x 轴交于点A 、B ,点A 在原点的左侧,点B 的坐标为(3,0),OB =OC , tan ∠ACO =1 3. (1)求这个二次函数的解析式;(2)若平行于x 轴的直线与该抛物线交于点M 、N ,且以MN 为直径的圆与x 轴相切,求该圆的半径长度; (3)如图2,若点G (2,y )是该抛物线上一点,点P 是直线AG 下方的抛物线上的一动点,当点P 运动到什么位置时,△AGP 的面积最大?求此时点P 的坐标和△AGP 的最大面积.三、比例比值取值范围3.如图是二次函数k m x y ++=2)(的图象,其顶点坐标为M(1,-4). (1)求出图象与x 轴的交点A,B 的坐标; (2)在二次函数的图象上是否存在点P ,使MAB PAB S S ∆∆=45,若存在,求出P 点的坐标;若不存在,请说明理由;(3)将二次函数的图象在x 轴下方的部分沿x 轴翻折,图象的其余部分保持不变,得到一个新的图象,请你结合这个新的图象回答:当直线)1(<+=b b x y 与此图象有两个公共点时,b 的取值范围.四、探究型4. 如图,直线33+=x y 交x 轴于A 点,交y 轴于B 点,过A 、B 两点的抛物线交x 轴于另一点C (3,0).⑴ 求抛物线的解析式;⑵ 在抛物线的对称轴上是否存在点Q ,使△ABQ 是等腰三角形? 若存在,求出符合条件的Q 点坐标;若不存在,请说明理由.yxO CBA五、最值类5.如图,在平面直角坐标系中,二次函数c bx x y ++=2的图象与x 轴交于A 、B 两点,A 点在原点的左侧,B 点的坐标为(3,0),与y 轴交于C (0,-3)点,点P 是直线BC 下方的抛物线上一动点.(1)求这个二次函数的表达式.(2)连结PO 、PC ,并把△POC 沿CO 翻折,得到四边形POP /C ,那么是否存在点P ,使四边形POP /C 为菱形?若存在,请求出此时点P 的坐标;若不存在请说明理由.(3)当点P 运动到什么位置时,四边形ABPC 的面积最大并求出此时P 点的坐标和四边形ABPC 的最大面积.课后作业1.在平面直角坐标系中,已知A (-4,0),B (1,0),且以AB 为直径的圆交y 轴的正半轴于点C ,过点C 作圆的切线交x 轴于点D .(1)求点C 的坐标和过A ,B ,C 三点的抛物线的解析式;(2)求点D 的坐标;(3)设平行于x 轴的直线交抛物线于E ,F 两点,问:是否存在以线段EF 为直径的圆,恰好与x 轴相切?若存在,求出该圆的半径,若不存在,请说明理由.yx OC D B A 1 -42.已知:如图,在平面直角坐标系xOy 中,矩形OABC 的边OA 在y 轴的正半轴上,OC 在x 轴的正半轴上,OA =2,OC =3.过原点O 作∠AOC 的平分线交AB 于点D ,连接DC ,过点D 作DE ⊥DC ,交OA 于点E .(1)求过点E 、D 、C 的抛物线的解析式;(2)将∠EDC 绕点D 按顺时针方向旋转后,角的一边与y 轴的正半轴交于点F ,另一边与线段OC 交于点G .如果DF 与(1)中的抛物线交于另一点M ,点M 的横坐标为56,那么EF=2GO 是否成立?若成立,请给予证明;若不成立,请说明理由;(3)对于(2)中的点G ,在位于第一象限内的该抛物线上是否存在点Q ,使得直线GQ 与AB 的交点P 与点C 、G 构成的△PCG 是等腰三角形?若存在,请求出点Q 的坐标;若不存在,请说明理由.3.如图,抛物线y =ax 2+bx +c (a ≠0)与x 轴交于A (-3,0)、B 两点,与y 轴相交于点C (0,3).当x =-4和x =2时,二次函数y =ax 2+bx +c (a ≠0)的函数值y 相等,连结AC 、BC .(1)求实数a ,b ,c 的值;(2)若点M 、N 同时从B 点出发,均以每秒1个单位长度的速度分别沿BA 、BC 边运动,其中一个点到达终点时,另一点也随之停止运动.当运动时间为t 秒时,连结MN ,将△BMN 沿MN 翻折,B 点恰好落在AC 边上的P 处,求t 的值及点P 的坐标;4. 如图,抛物线y =21x 2+bx -2与x 轴交于A 、B 两点,与y 轴交于C 点,且A (一1,0). ⑴求抛物线的解析式及顶点D 的坐标; ⑵判断△ABC 的形状,证明你的结论;⑶点M (m ,0)是x 轴上的一个动点,当CM +DM 的值最小时,求m 的值.面积最大5、如图,在平面直角坐标系中,点A 、C 的坐标分别为(-1,0)、(0,3-),点B 在x 轴上.已知某二次函数的图象经过A 、B 、C 三点,且它的对称轴为直线x =1,点P 为直线BC 下方的二次函数图象上的一个动点(点P 与B 、C 不重合),过点P 作y 轴的平行线交BC 于点F .(1)求该二次函数的解析式;(2)若设点P 的横坐标为m ,试用含m 的代数式表示线段PF 的长; (3)求△PBC 面积的最大值,并求此时点P 的坐标.yxB A FPx =1CO6、在平面直角坐标系中,已知抛物线经过A (-4,0),B (0,-4),C (2,0)三点. (1)求抛物线的解析式;(2)若点M 为第三象限内抛物线上一动点,点M 的横坐标为m ,△AMB 的面积为S .求S 关于m 的函数关系式,并求出S 的最大值.(3)若点P 是抛物线上的动点,点Q 是直线y =-x 上的动点,判断有几个位置能够使得点P 、Q 、B 、O 为顶点的四边形为平行四边形,直接写出相应的点Q讨论等腰7、如图,已知抛物线y =21x 2+bx +c 与y 轴相交于C ,与x 轴相交于A 、B ,点A 的坐标为(2,0),点C 的坐标为(0,-1). (1)求抛物线的解析式;(2)点E 是线段AC 上一动点,过点E 作DE ⊥x 轴于点D ,连结DC ,当△DCE 的面积最大时,求点D 的坐标;(3)在直线BC 上是否存在一点P ,使△ACP 为等腰三角形,若存在,求点P 的坐标,若备用图8、(武汉市中考)如图,已知抛物线y =x 2+bx +3与x 轴交于点B (3,0),与y 轴交于点A ,P 是抛物线上的一个动点,点P 的横坐标为m (m >3),过点P 作y 轴的平行线PM ,交直线AB 于点M . (1)求抛物线的解析式;(2)若以AB 为直径的⊙N 与直线PM 相切,求此时点M 的坐标;(3)在点P 的运动过程中,△APM 能否为等腰三角形?若能,求出点M 的坐标;若不能,请说明理由.论直角三角形9、如已知:如图一次函数y =21x +1的图象与x 轴交于点A ,与y 轴交于点B ;二次函数y =21x 2+bx +c 的图象与一次函数y =21x +1的图象交于B 、C 两点,与x 轴交于D 、E两点且D 点坐标为(1,0) (1)求二次函数的解析式;(2)求四边形BDEC 的面积S ; (3)在x 轴上是否存在点P ,使得△PBC 是以P 为直角顶点的直角三角形?若存在,求出所有的点P ,若不存在,请说明理由.10、(九市联考)如图,抛物线与x 轴交于A (-1,0)、B (3,0)两点,与y 轴交于点C(0,-3),设抛物线的顶点为D .(1)求该抛物线的解析式与顶点D 的坐标; (2)以B 、C 、D 为顶点的三角形是直角三角形吗?为什么?(3)探究坐标轴上是否存在点P ,使得以P 、A 、C 为顶点的三角形与△BCD 相似?若存在,请指出符合条件的点P 的位置,并直接写出点P 的坐标;若不存在,请说明理由.讨论四边形11、二次函数y =x 2+px +q (p <0)图象与x 轴交于A 、B 两点,与y 轴交于点C (0,-1),△ABC 的面积为45.(1)求该二次函数的关系式;(2)过y 轴上的一点M (0,m )作y 轴的垂线,若该垂线与△ABC 的外接圆有公共点,求m 的取值范围;(3)在该二次函数的图象上是否存在点D ,使四边形ACBD 为直角梯形?若存在,求出点D 的坐标;若不存在,请说明理由.2017中考二次函数压轴题专题分类训练题型一:面积问题【例1】如图2,抛物线顶点坐标为点C (1,4),交x 轴于点A (3,0),交y 轴于点B . (1)求抛物线和直线AB 的解析式; (2)求△CAB 的铅垂高CD 及S △CAB ;(3)设点P 是抛物线(在第一象限内)上的一个动点,是否存在一点P ,使S △PAB =89S △CAB ,若存在,求出P 点的坐标;若不存在,请说明理由.【变式练习】1.如图,在直角坐标系中,点A 的坐标为(-2,0),连结OA ,将线段OA 绕原点O 顺时针旋转120°,得到线段OB .(1)求点B 的坐标; (2)求经过A 、O 、B 三点的抛物线的解析式;(3)在(2)中抛物线的对称轴上是否存在点C ,使△BOC 的周长最小?若存在,求出点C 的坐标;若不存在,请说明理由. (4)如果点P 是(2)中的抛物线上的动点,且在x 轴的下方,那么△PAB 是否有最大面积?若有,求出此时P 点的坐标及△PAB 的最大面积;若没有,请说明理由.图22.如图,抛物线y = ax 2+ bx + 4与x 轴的两个交点分别为A (-4,0)、B (2,0),与y 轴交于点C ,顶点为D .E (1,2)为线段BC 的中点,BC 的垂直平分线与x 轴、y 轴分别交于F 、G . (1)求抛物线的函数解析式,并写出顶点D 的坐标; (2)在直线EF 上求一点H ,使△CDH 的周长最小,并求出最小周长; (3)若点K 在x 轴上方的抛物线上运动,当K 运动到什么位置时, △EFK 的面积最大?并求出最大面积.3.如图,已知:直线3+-=x y 交x 轴于点A ,交y 轴于点B ,抛物线y=ax 2+bx+c 经过A 、B 、C (1,0)三点.(1)求抛物线的解析式;(2)若点D 的坐标为(-1,0),在直线3+-=x y 上有一点P,使ΔABO 与ΔADP 相似,求出点P 的坐标;(3)在(2)的条件下,在x 轴下方的抛物线上,是否存在点E ,使ΔADE 的面积等于四边形APCE 的面积?如果存在,请求出点E 的坐标;如果不存在,请说明理由.题型二:构造直角三角形【例2】如图,已知抛物线y =ax 2+bx +c (a ≠0)的对称轴为x =1,且抛物线经过A (-1,0)、C (0,-3)两点,与x 轴交于另一点B . (1)求这条抛物线所对应的函数关系式;(2)在抛物线的对称轴x =1上求一点M ,使点M 到点A 的距离与到点C 的距离之和最小,并求此时点M 的坐标;(3)设点P 为抛物线的对称轴x =1上的一动点,求使∠PCB =90º的点P 的坐标. CEDG Axy OB FE【变式练习】1.如图,抛物线y=与x轴交于A、B两点(点A在点B的左侧),与y轴交于点C.(1)求点A、B的坐标;(2)设D为已知抛物线的对称轴上的任意一点,当△ACD 的面积等于△ACB的面积时,求点D的坐标;(3)若直线l过点E(4,0),M为直线l上的动点,当以A、B、M为顶点所作的直角三角形有且只有三个时,求直线l的解析式.3.在平面直角坐标系内,反比例函数和二次函数y=k(x2+x﹣1)的图象交于点A(1,k)和点B(﹣1,﹣k).(1)当k=﹣2时,求反比例函数的解析式;(2)要使反比例函数和二次函数都是y随着x的增大而增大,求k应满足的条件以及x的取值范围;(3)设二次函数的图象的顶点为Q,当△ABQ是以AB为斜边的直角三角形时,求k的值4.如图(1),抛物线42y x x =+-与y 轴交于点A ,E (0,b )为y 轴上一动点,过点E 的直线y x b =+与抛物线交于点B 、C .(1)求点A 的坐标;(2)当b =0时(如图(2)),ABE 与ACE 的面积大小关系如何?当4b >-时,上述关系还成立吗,为什么?(3)是否存在这样的b ,使得BOC 是以BC 为斜边的直角三角形,若存在,求出b ;若不存在,说明理由.题型三:构造等腰三角形【例3】如图,已知抛物线32++=bx ax y (a ≠0)与x 轴交于点A (1,0)和点B (-3,0),与y 轴交于点C . (1)求抛物线的解析式;(2)在x 轴上是否存在一点Q 使得△ACQ 为等腰三角形?若存在,请直接写出所有符合条件的点Q 的坐标;若不存在,请说明理由;(3)设抛物线的对称轴与x 轴交于点M ,问在对称轴上是否存在点P ,使△CMP 为等腰三角形?若存在,请直接写出所有符合条件的点P 的坐标;若不存在,请说明理由.yxCBAOE yxCBAOE 第26题图(1)图(2)2.如图,抛物线254y ax ax =-+经过ABC △的三个顶点,已知BC x ∥轴,点A 在x 轴上,点C 在y 轴上,且AC=BC .(1)写出A,B,C 三点的坐标并求抛物线的解析式;(2)探究:若点P 是抛物线对称轴上且在x 轴下方的动点,是否存在PAB △是等腰三角形.若存在,求出所有符合条件的点P 坐标;不存在,请说明理由.题型四:构造相似三角形【例4】如图,已知抛物线经过A (﹣2,0),B (﹣3,3)及原点O ,顶点为C . (1)求抛物线的解析式;(2)若点D 在抛物线上,点E 在抛物线的对称轴上,且A 、O 、D 、E 为顶点的四边形是平行四边形,求点D 的坐标;(3)P 是抛物线上的第一象限内的动点,过点P 作PM ⊥x 轴,垂足为M ,是否存在点P ,使得以P 、M 、A 为顶点的三角形△BOC 相似?若存在,求出点P 的坐标;若不存在,请说明理由.【变式练习】1.如图,已知抛物线经过A(4,0),B(1,0),C(0,-2)三点.(1)求该抛物线的解析式;(2)在直线AC上方的该抛物线上是否存在一点D,使得△DCA的面积最大?若存在,求出点D的坐标及△DCA面积的最大值;若不存在,请说明理由.(3)P是直线x=1右侧的该抛物线上一动点,过P作PM⊥x轴,垂足为M,是否存在P点,使得以A、P、M为顶点的三角形与△OAC相似?若存在,请求出符合条件的点P的坐标;若不存在,请说明理由.7),且顶点C的横坐标为4,该图象在x 轴上2. 如图,二次函数的图象经过点D(0,39截得的线段AB的长为6. (1)求二次函数的解析式;(2)在该抛物线的对称轴上找一点P,使PA+PD最小,求出点P的坐标;(3)在抛物线上是否存在点Q,使△QAB与△ABC相似?如果存在,求出点Q的坐标;如果不存在,请说明理由.3.如图,二次函数y=ax2+bx+c的图象交x轴于A(﹣1,0),B(2,0),交y轴于C(0,﹣2),过A,C画直线.(1)求二次函数的解析式;(2)点P在x轴正半轴上,且P A=PC,求OP的长;(3)点M在二次函数图象上,以M为圆心的圆与直线AC相切,切点为H.①若M在y轴右侧,且△CHM∽△AOC(点C与点A对应),求点M的坐标;②若⊙M的半径为,求点M的坐标.题型六:构造平行四边形【例7】如图,在平面直角坐标系中,抛物线经过A(—1,0),B(3,0),C(0,—1)三点。
