多面体的截面的作法
立体几何深度拔高讲义-11截面作图三步走 - 学生版

立体几何深度·拔高讲义
1.1截面作图三步走
本节学习目标
1.掌握空间几何体截面作图方法
2.会判断空间几何体截面形状
作多面体截面方法
一、理论基础
1.定义及相关要素
2.作截面的宏观思路
3.作截面的一大思维误区
4.作截面的理论依据
5.作截面具体步骤
二、典例
【典例1】如图,正方体1111ABCD A B C D 中,E 、F 、G 分别在AB 、BC 、1DD 上,求作过E 、F 、G 三点的截面.
具体步骤:
具体步骤:
【典例3】试画出过正三棱柱111ABC A B C 的底边BC 及两底中心连线1OO 中点的截面.
具体步骤:
【典例4】过正方体1111ABCD A B C D -的棱AB CB 、的中点E F 、作一个截面,使截面与底面所成的角为45︒.则此截面的形状为( )
.A 三角形或五边形
.B 三角形或六边形
.C 六边形
【解析】
(图4-1)
具体步骤:
(图4-2)具体步骤:
【典例5】已知正方体1111ABCD A B C D -的体积为1,点M 在线段BC 上(点M 异于
B C 、两点),点N 为线段1CC 的中点,若平面AMN 截正方体1111ABCD A B C D -所得的截面为四边形,则线段BM 的取值范围为_____.
具体步骤:。
多面体截面的画法

…ó压卜.r,les|
才 .口. 、牟 笋
多面体截面 的画法
合肥 二 中 魏克服
多 面体 的截 面问题 是立 体 几何 的常见 问题 之 一 , 要正 确计 算多 面 体的截面 面积 , 必 须首 先 掌握 多面 体 截 面 的作 图 。 立 体几 何教 学 的一 个很 重 要 的 目的就是 培 养学 生 具 有较 强 的 空 间 想象能 力 , 而 对 学生 进行 截面 作 图训练 正是 培 养和发展 学生 的空 间 想象力 , 正是 加 强综合运用 立 儿 各方 面 知识 的有益 课 题 。 鉴 于 目前立 体几 何教 学 中 , 截 面 作 图 问题 重 视得 不 够 , 本文 提
截面 。 解 连 E 尸 , 由题 意知 E F 是 截面 与底 面 的交线 。 两 方延 长E F 成 直线 x 叭 则 x y 土 B D , 在
平 面 B D D : B : 上 作乙 D G S = 30 。 交 D D : 于 S , 作 乙 B G H 二 30 “ 交 B 刀 , 于 H , 由三 垂 线定 理 知 刀F一 H G , E F 上 G S 。 根据 平 面 角的定 义 , 所要 求 作 的截 面 过 H G 、 S G 。
首 先定 出截 平面 与 已 知平 面的交 线 , 然后 确定截面多边 形的其 余 各顶点 的方法是 作截 面 的 一般方法 , 我们 称之 为迹 线法 。
浅谈求异面 直 线之 间 的距 离
江 苏兴化 徐 扬中学 江 西 丰城第二 中学
解正 己 邱冬根
求异 面直 线的距 离 , 是立 体几 何教 学中
挤
过棱 锥 的 P 、 Q 、 R 作截 面。
解 根 据不 在 一条直 线上 的三 点 确定一 个平 面 , 连 p Q 且延 长交 A B 的延 长线 于 E , 连 R Q 且
多面体的截面(2)
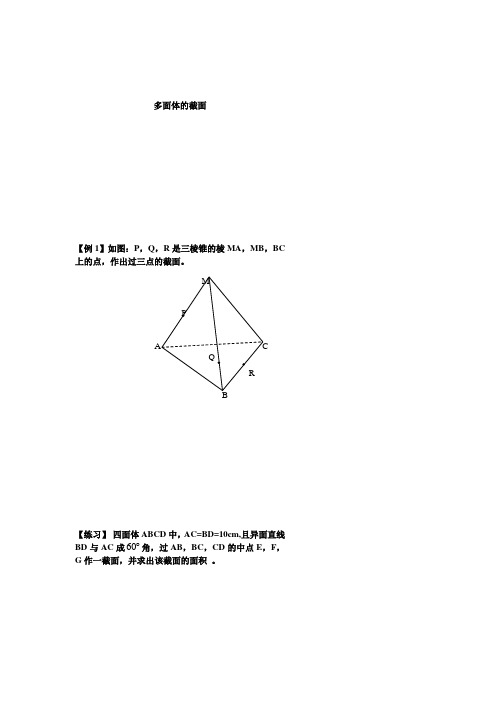
多面体的截面
【例1】如图:P,Q,R是三棱锥的棱MA,MB,BC 上的点,作出过三点的截面。
【练习】四面体ABCD中,AC=BD=10cm,且异面直线BD与AC成60 角,过AB,BC,CD的中点E,F,G作一截面,并求出该截面的面积。
【例2】已知一正三角形的边长为4cm,求这个正三角形的直观图的面积。
【练习】用一张长、宽分别为8cm和4cm的矩形硬纸折成正四棱柱的侧面,求此正四棱柱的对角线的长。
【例3】已知三棱锥P-ABC的棱PA和BC互相垂直,且它们的长分别为a,b,用平行于PA和BC的平面截三棱锥。
(1)求证:截面是一平行四边形;
(2)求截面面积的最大值。
【练习】画三棱锥的直观图,使它的底面是腰长为a的等腰直角三角形,过直角顶点的侧棱长为a,且垂直于底面。
并求出这个三角锥的表面积。
【例3】作正四棱锥的直观图,使它的高为1.5a,且底面边长为a.。
多面体截面的画法专题
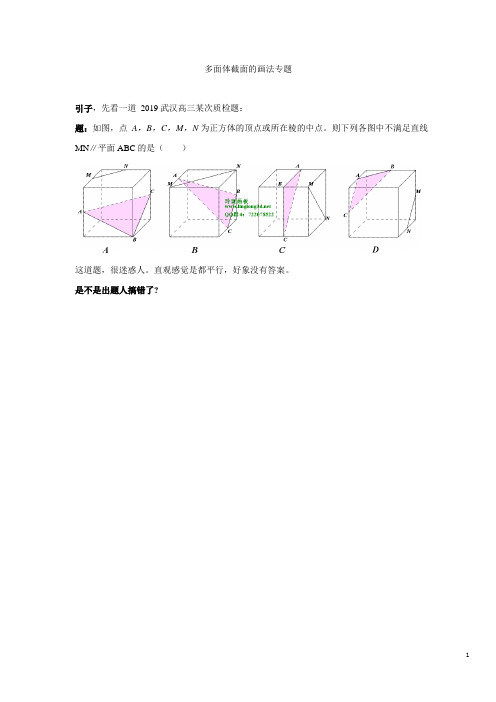
多面体截面的画法专题引子,先看一道2019 武汉高三某次质检题:题:如图,点A,B,C,M,N 为正方体的顶点或所在棱的中点。
则下列各图中不满足直线MN∥平面ABC 的是()这道题,很迷惑人。
直观感觉是都平行,好象没有答案。
是不是出题人搞错了?嘿嘿,把截面画出来,答案一下就清楚了。
所以多面体截面的画法非常重要,是基本功。
一、几何体的截面画法截面作图的题型可以分为以下几种情况:1、过某些点的截面图(见例1、2、3、4),关键:咱们的作图可分为两大类:一是作平行线,二是找交点。
★公理3:若两个不重合的平面有一个公共点,那么它们有且只有一条过该点的公共直线。
★公理2 的推论2:过两条相交直线,有且仅有一个平面。
(两条相交直线共面)★公理2 的推论3:过两条平行直线,有且仅有一个平面。
(两条平行直线共面)★平行公理:平行于同一条直线的两条直线平行。
★线面平行的性质定理:一条直线与一个平面平行,则过该直线的任一平面与此平面的交线与该直线平行。
★面面平行的性质定理:如果两个平行平面同时和第三个平面相交,那么它们的交线平行。
2、作平行于某条直线成平面的截面。
(见例5)3、作垂直于某一直线成平面的截面。
(见例6)4、作与某一直线或平面成一定角度的截面。
(见例7)★直线和平面所成角:★二面角:★三垂线定理及其逆定理:在考试中一般会考察一些较为明显的,角度易找易算的图形。
一般要求根据线面角,二面角的定义来作图。
例1:如图,点M,N,P 为正方体所在棱的中点。
作出过此三点的平面截正方体所得的截面图形。
分析点线面关系,找到突破口及思路:作平行线。
1、取棱中点A,连NA,可证NA 平行PM。
2、取棱中点B,连AB,可证AB 平行NM。
3、同利用平行关系找到棱中点C 点,然后连接各线。
总结:例1 的关键就是作平行线。
思路:延长找交点。
例2:如图,点M,N,P 为正方体所在棱的中点。
作出过此三点的平面截正方体所得的截面图形。
多面体 分割 算法

多面体分割算法多面体分割算法是一种用于将多面体划分为更小的子多面体的方法。
这个算法对于许多领域都有着广泛的应用,包括计算机图形学、计算机辅助设计和计算机模拟等。
多面体分割算法的目的是将一个复杂的多面体分解为一组简单的子多面体,以便更好地处理和分析。
这些子多面体可以是任意形状和大小的,但通常是由面、边和顶点组成的。
分割算法的关键是找到一种方法,将多面体的面切割成更小的面,同时保持多面体的整体形状和拓扑结构。
一种常见的多面体分割算法是三角剖分算法。
这个算法将多面体的面划分为一组三角形,使得每个三角形的顶点都是多面体的顶点之一,并且每个三角形的边都是多面体的边之一。
三角剖分算法可以在计算机图形学中用于三维建模和渲染,以及计算机辅助设计中的网格生成和有限元分析等。
另一种常见的多面体分割算法是四面体剖分算法。
这个算法将多面体的面划分为一组四面体,使得每个四面体的顶点都是多面体的顶点之一,并且每个四面体的边都是多面体的边之一。
四面体剖分算法常用于计算机模拟中的有限元分析和流体力学建模等。
除了三角剖分和四面体剖分算法,还有许多其他的多面体分割算法。
例如,凸包分割算法可以将多面体划分为一组凸多边形,而Voronoi图分割算法可以将多面体划分为一组以多面体的顶点为中心的泰森多边形。
多面体分割算法的选择取决于应用的具体要求和多面体的特性。
在选择算法时,需要考虑多面体的复杂度、形状和大小。
同时,还需要考虑算法的效率和精确度。
多面体分割算法是一种将复杂的多面体划分为简单的子多面体的方法。
这个算法在计算机图形学、计算机辅助设计和计算机模拟等领域有着广泛的应用。
不同的多面体分割算法适用于不同的应用场景,选择适合的算法可以提高计算效率和精确度。
多面体的截面的作法

多面体的截面用一个平面去截几何体,此平面与几何体的交集,叫做这个几何体的截面.此平面与几何体表面的交集(交线)叫做截线.此平面与几何体的棱的交集(交点)叫做截点.作多面体截面的关键在于确定截点,有了位于多面体同一表面上的两个截点即可连结成截线,从而求得截面.作截线与截点的主要根据有:(1)确定平面的条件.(2)如果两个不重合的平面有一个公共点,那么它们相交于过此点的一条直线.(3)如果一条直线上的两点在一个平面内,那么这条直线上所有的点都在这个平面内.(4)如果一条直线平行于一个平面,经过这条直线的平面与这个平面相交,那么这条直线就和交线平行.(5)如果两个平面平行,第三个平面和它们相交,那么两条交线平行.主要画法是交线法.即求出截面所在的平面与多面体某一表面所在平面的交线,再找出各有关截线(或其延长线)与此交线的交点.例1 如图,正方体1111D C B A ABCD -中,G F E 、、分别在1DD BC AB 、、上,求作过G F E 、、三点的截面.作法:(1)在底面AC 内,过F E 、作直线EF 分别与DC DA 、的延长线交于M L 、.(2)在侧面D A 1内,连结LG 交1AA 于K .(3)在侧面C D 1内,连结GM 交1CC 于H .(4)连结KE 、FH .则五边形EFHGK 即为所求的截面.有时为了便于作截面,还须引进辅助面作为作图的中介.例2 如图,正方体1111D C B A ABCD -中,F E 、在两条棱上,G 在底面11C A 内,求过G F E 、、的截面.作法:(1)在底面11C A 内,过G 作11//C B PQ ,交棱于Q P 、两点.(2)作辅助面PC ,在此面内,过F G 、作直线交BP 的延长线于M .(3)在侧面B A 1内,连结ME ,交11B A 于K .(4)在底面11C A 内,连结KG ,延长交11C B 于H .(5)连结HF . (6)在底面AC 内,作HK FL //,交AB 于L .(7)连结EL .则五边形ELFHK 为所求的截面.此外,对于面数较多的多面体,可以把其中一些表面伸展构成面数较少的多面体,使作图得解.例 3 如图,五棱锥ABCD P -中,三条侧棱上各有一已知点H G F 、、,求作过H G F 、、的截面.作法:(1)将侧面PDE PBC PAB 、、伸展得到三棱锥BST P -.(2)在侧面PBS 内,连结并延长GF ,交PS 于K .(3)在侧面PBT 内,连结并延长GH 交PT 于L .(4)在侧面PST 内,连结KL 分别交PE PD 、于N M 、.图FN、.则五边形FGHMN即为所求的截面.(5)连结MH。
多面体的截面(一)

多面体的截面(一)黄继红一、教学分析按课标,“多面体的截面”要求学生会作长方体的截面(如截面过已知不共线的、位于棱上的三点,且仅以平面的基本性质为画图依据)。
按教材,“多面体的截面”是对点、线、面的位置关系在认识上的深化和提高,又是为后继几何体的体积学习作准备。
“多面体的截面”定义在课本中仅以“小字”形式作为注意点呈现,例题的截面作法也仅用“交线法”。
我认为:我们松江二中的学生对这个内容的学习不应该仅停留在理解概念、巩固练习的层面,更应该把它上升为探究性理解水平的层次。
基于以上认识,我确立“正确理解多面体的截面概念,体会作多面体截面的基本方法——连延交”作为本课的主要目标。
在设计思路上我以“明线”和“暗线”同时进行、不断贯穿“转化”思想来组织教学,这样可以进一步体验概念学习的过程,还能在各个环节上逐步体会“连延交”的基本方法。
在问题设计上我采取“反复变式”、“层层递进”、“制造认知冲突”等手段突出本课重点、突破本课难点。
又考虑到我校学生已经较好地掌握公理4和面面平行的有关知识,所以本课我在重点突出“连延交”基本方法的同时,适当渗透“平行线法”,这样可以更好地完善学生的认知结构。
明线:形成概念理解概念巩固应用→→暗线:关于课时安排。
“多面体的截面”分为2课时完成,本课为第1课,仅以“正方体”为载体设计教学目标、重点和难点。
第2课安排以棱锥、三棱柱、长方体为例,进一步巩固多面体的截面作法,并说明截面分多面体为怎样的两个多面体、画出这两个多面体的直观图。
二、教学目标⑴通过从具体到抽象的过程,逐步形成并理解平面截多面体的截面概念。
⑵通过正方体的截面作法的探究,体会作多面体截面的基本方法——“连延交”。
⑶经历作正方体截面的过程,体会转化思想,培养空间想象力。
三、教学重点 截面的概念及作法教学难点 如何“连”四、教学过程1、形成概念引例 如图正方体ABCD A B C D ''''-,请画出由点A '、、确定的平面C 'D α与正方体表面的交线。
立体几何中一些截面图的作法
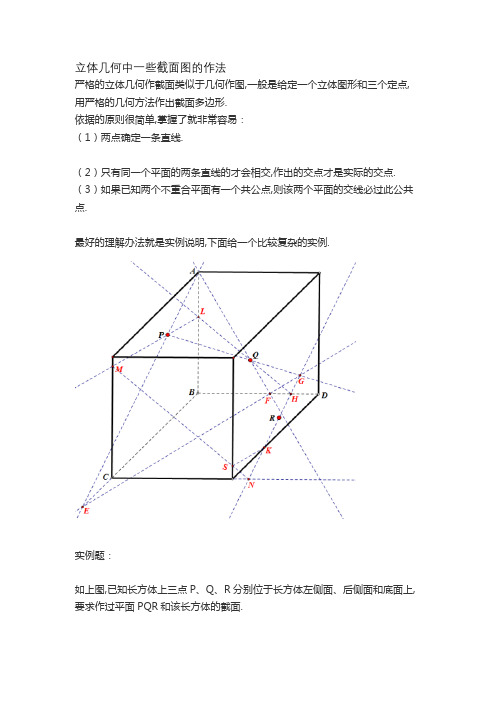
立体几何中一些截面图的作法
严格的立体几何作截面类似于几何作图,一般是给定一个立体图形和三个定点, 用严格的几何方法作出截面多边形.
依据的原则很简单,掌握了就非常容易:
(1)两点确定一条直线.
(2)只有同一个平面的两条直线的才会相交,作出的交点才是实际的交点. (3)如果已知两个不重合平面有一个共公点,则该两个平面的交线必过此公共点.
最好的理解办法就是实例说明,下面给一个比较复杂的实例.
实例题:
如上图,已知长方体上三点P、Q、R分别位于长方体左侧面、后侧面和底面上, 要求作过平面PQR和该长方体的截面.
分析:由于P、Q、R分布在不同的面上,因此无法直接连接其中两点和棱线相交来作交点,
需要借助长方体上的角点来辅助作图.
由于左侧面和后侧面有一个公共角点A,因此可以先作面APQ生成的截面.
作法:
(1)连接AP和AQ分别和棱BC(延长线)、BD交于E、F.
(原理:同平面不平行的两条直线必有交点).
此时有:PQEF共面,EF在底面上.
(2)连接PQ和EF,二者相交于G,此时得到了PQ和底面的交点Q, 于是面PQR和面PGR是同一个面,而G、R都在底面上.
(3)连接GR和底面棱线相交于H、K,此时就已经确定了截面的两个关键交点.
截面变为PQHK,剩下的步骤就简单了.
(3)连接主HQ和AB交于L,得到第三个点.
连接LP,可得到第四个点M,连接HK得到第五个点N,
连接MN,得到第六个点S.
因此最终的截面多边形是:HLMSK.。
多面体的截面(一)

多面体的截面(一)黄继红一、教学分析按课标,“多面体的截面”要求学生会作长方体的截面(如截面过已知不共线的、位于棱上的三点,且仅以平面的基本性质为画图依据)。
按教材,“多面体的截面”是对点、线、面的位置关系在认识上的深化和提高,又是为后继几何体的体积学习作准备。
“多面体的截面”定义在课本中仅以“小字”形式作为注意点呈现,例题的截面作法也仅用“交线法”。
我认为:我们松江二中的学生对这个内容的学习不应该仅停留在理解概念、巩固练习的层面,更应该把它上升为探究性理解水平的层次。
基于以上认识,我确立“正确理解多面体的截面概念,体会作多面体截面的基本方法——连延交”作为本课的主要目标。
在设计思路上我以“明线”和“暗线”同时进行、不断贯穿“转化”思想来组织教学,这样可以进一步体验概念学习的过程,还能在各个环节上逐步体会“连延交”的基本方法。
在问题设计上我采取“反复变式”、“层层递进”、“制造认知冲突”等手段突出本课重点、突破本课难点。
又考虑到我校学生已经较好地掌握公理4和面面平行的有关知识,所以本课我在重点突出“连延交”基本方法的同时,适当渗透“平行线法”,这样可以更好地完善学生的认知结构。
明线:形成概念理解概念巩固应用→→暗线:关于课时安排。
“多面体的截面”分为2课时完成,本课为第1课,仅以“正方体”为载体设计教学目标、重点和难点。
第2课安排以棱锥、三棱柱、长方体为例,进一步巩固多面体的截面作法,并说明截面分多面体为怎样的两个多面体、画出这两个多面体的直观图。
二、教学目标⑴通过从具体到抽象的过程,逐步形成并理解平面截多面体的截面概念。
⑵通过正方体的截面作法的探究,体会作多面体截面的基本方法——“连延交”。
⑶经历作正方体截面的过程,体会转化思想,培养空间想象力。
三、教学重点 截面的概念及作法教学难点 如何“连”四、教学过程1、形成概念引例 如图正方体ABCD A B C D ''''-,请画出由点A '、、确定的平面C 'D α与正方体表面的交线。
多面体截面

例1、已知:
画出过A、B、C三点的平面 与 , 的交线
l
C
l
B A
(1)
C
A
B
(2)
B C
A
(3)
例2:如图,P,Q,R分别是空间四边形ABCD的边 AB,AD,BC上的点,且PQ与BD不平行,试画出平 面PQR与平面BCD的交线 . A
P Q D
R A1 B1 A P C1 D D1
B
C
Q
D1 A1 M B1 N C1
P D C A B
例5:已知棱长为a的正方体ABCD-A1B1C1D1中,M,N,P 分别为C1D,AD,CC1的中点, (1)过M,N,P三点作正方体的截面,试画出这个截 面;(2)计算这截面的周长l.
D1 A1 M B1 P C1
N A
D C B
2 10 a 2
例6.已知正方体ABCD-A1B1C1D1直观 图,根据下列要求作出截面图形: (1)P、Q平面CDD1C1,截面A1PQ; A D 面内找两点连线
1
1
B1
C1 Q
A
B C
P
D
A1
D1
(2)M、N、K分别是 BC、AA1 、CD1的中 点,截面MNK;
B1 N
K C1
A
B M C
D
平行线确定平面
例 7.已知长方体 ABCD-A1B1C1D1, 点M 和 N 分别是矩形 ABCD 和 BB1C1C 的中 心 , 画出过点 A,M,N 的平面 截长方体 的截面. A D
1 1
B1 A B N M C
棱柱\棱锥截面多边形的作图

棱柱\棱锥截面多边形的作图用一个平面去截多面体,该平面与多面体各面的交线围成的平面图形,叫做多面体的一个截面,多面体的截面是多边形,一般的学生,对于解决有关截面的题目上,感到困难。
截面存在两个问题:①怎样作出截面;②求截面的元素及与截面有关的量。
只有正确作出截面,才能判断其形状,从而找出计算各量的途径。
要正确作出多面体的截面多边形,关键是找到截面与各棱的交点(即是截面多边形的顶点)。
本文重点介绍以“三角形奠基法”为主的两种作截面的方法,这两种方法在棱柱、棱锥等多面体中作截面是很凑效的。
1三角形奠基法这一作图法的根据是平面的三个基本性质(即三条公理,略),所谓“三角形奠基法”,即是以三点确定的三角形截平面为基础,再由平面性质确定该截平面与各棱的交点,从而完成所求作的截面多边形。
例1:在正方体ABCD——A1B1C1D1中,过AD、CD中点E、F和BB 1延长线上的H点N(B1N=BB1)作截面。
解:我们先找到确定截平面的三个点,在平面ABCD内作直线EF∩BC=N1,EF∩BA=N2。
∵EF截平面∴N1、N2截平面、于是△NN1N2为奠基三角形,其中点N、N1∈平面BB1C1C,点N、N2∈平面ABB1A1,且NN2∩AA1=P,NN2∩A1B1=Q,NN1∩B1C1=R,NN1∩CC1=S。
则多边形FEPQRS为所求作的截面,由已知条件及作图,可判定截面为正六边形。
(证明略)例2:已知四棱锥M—ABCD,其中P∈AM,E∈MD,K∈MB,作出过P、K、E的截面多边形。
解:为了作出截平面与底面的交线,必须先找出同属于截平面EPK和底平面ABCD的两个点。
在平面ABM上作PK∩AB=N1,在平面ADM上作PE∩AD=N2,则N1N2截平面EPK,且N1N2?奂底面ABCD。
于是△PN1N2为我们要找的奠基三角形,由这三角形我们来找截平面与MC的交点F,在面ABCD上作DC∩N1N2=H,则H∈面MCD,连EH∩MC=F,点F为所求另一顶点。
多面体的截面作图

能用 一 对
就名称 来 说
) 同 类的 反 三 角
,
函 数 ( 反 正 弦 函 数与 反 余 弦 函 数
反正切 函
的
。
计 算截 面的 面 积 上
,
由于 截面 的各个顶 点都在 正 六 棱柱的棱 所 以底 面 正 六 边形就 是截 面 在 底 面 上的
,
,
a 3
名,
:
.
B F 口=
=
训万
则在 截面 内 的 点或直 线
,
对应
代入
( 1 )中 0
=
,
tg
而
因此
,
1 一
着唯 一 的 一 个基 点或基 线 内的基 点或基线 线
,
,
反过 来
,
,
由基面 求 出截
。
30
F
I
“
求 出 截 面 的对应 点或对 应
,
S 截面 B c N E
I
M
=
S A BCD E F
多
面
体
的
刘
截
搔
面
作
图
多面体 的截面作 图 何知 识
,
,
要 用到许多 立 体 几 可 进 一 步巩 固直 线
, ,
例 1 已 知正 六 棱 柱 A D 的 边长 和 侧 棱 长 都 是
E F
:
.
,
底面 正 六 边形
B C 和
1 )
。
通 过 截面 作 图
,
a
求作 过 对 棱
图(
和 平面 位 置 关 系的概念 和 定理 高学 生 的 空 间 想象能力 作图 时
立体几何截面画法

例1:如图正方体ABCD-A1B1C1D1中,点M、E分别为棱C1C、
D1D上的点,且C1M=2MC1,DE=2D1E.作过A、M、E三点的截面.
D1
C1
A1
B1
E
D A
M C B
二、立体几何截面画法
方法一:平行线法
例2:如图,点A、B、C、D、M、N为正方体的顶点或所在棱上的
中点,则下列各图中,不满足直线MN∕∕平面ABC的是( )
立体几何画截面画法
教学目标:
1.会判断截面是否完整
2.会画截面
平行线法 延长线法
一、复习回顾
1.在立体几何中,什么是截面?
用一个平面去截一个几何体得到的平面图形.
2.如何判断截面是否完整?
截面轮廓均线均在几何体表面(不在几何体内部).
D1
A1 E
C1 B1
A1
D1 E B1
C1
D A
C B
D A
)
D.平面PMN截该正三棱柱,所 得截面图形为五边形
A1
B1
M
C1
N
A
P
B
C
三、课堂练习
练习2:如图,在正四棱台ABCD-A1B1C1D1中,AB=2,A1B1=1,侧
棱AA1与底面所成角为60◦.E、F、G分别为棱AD、AB、BB1中点,
则下列说法正确的是(
)
C.平面EFG截该棱台,所得截 面图形为六边形;
A N
M
A.
M
B
A
N A
B
D C
N C
B.
C.
A
B B
M
C
C
N
D
M
例谈多面体截面的作法

例谈多面体截面的作法
陈淑娟
【期刊名称】《福建中学数学》
【年(卷),期】2024()4
【摘要】在立体几何的问题解决中,经常需要用一个平面去截多面体,然后借助所得到截面的形状,求截面的周长、面积等.由于高中数学教材没有明确给出截面的定义,多数学生也就没能很好地理解截面的概念.这就导致与截面相关的问题几乎多会成为学生心目中的难题.本文拟以一些具体的案例探讨多面体截面的作法,亦能帮助学生掌握多面体截面的作法,从而为相关问题的解决奠定基础.
【总页数】3页(P29-31)
【作者】陈淑娟
【作者单位】福建省莆田市仙游县度尾中学
【正文语种】中文
【中图分类】G63
【相关文献】
1.面上寻点千百度聚焦转化见真颜——多面体截面画法的四种破解策略
2.对分课堂在高中数学学科中的应用初探——以“平面截多面体的截面”课堂教学设计为例
3.多面体截面问题的类型及求解策略
4.多面体中截面问题的探究
5.“正方体截面的探究”单元教学之课时要素设计——第2课时正方体截面的作法
因版权原因,仅展示原文概要,查看原文内容请购买。
用交线法作多面体的截面图

用交线法作多面体的截面图
陈益谦
【期刊名称】《湖北理工学院学报:人文社会科学版》
【年(卷),期】1988(000)001
【摘要】<正> 一个平面截多面体,它与多面体的表面交线所围成的封闭图形,叫做多面体的截面。
多面体截面作图的主要依据是平面的基本性质的三个公理。
多面体的截面作图。
根据多面体的形状和条件的不同,有许多不同的作图法,这里介绍一种既能通用又较简便的方法——交线
【总页数】4页(P18-20,26)
【作者】陈益谦
【作者单位】
【正文语种】中文
【中图分类】G6
【相关文献】
1.用中心投影法求作截交线作图方法初探 [J], 赵雨生
2.赋值法在作截面交线中的应用 [J], 李左杰
3.谈谈作截面图 [J], 杨文达;
4.用异心辅助球面法求作两曲面的交线 [J], 鲁建慧
5.球面与简单多面体表面交线问题探究 [J], 魏东升
因版权原因,仅展示原文概要,查看原文内容请购买。
几何体中截面问题

FE1Q1几何体中的的截面问题1.定义及相关要素用一个平面去截几何体,此平面与几何体的交集,叫做这个几何体的截面.此平面与几何体表面的交集(交线)叫做截线.此平面与几何体的棱的交集(交点)叫做截点. 2.作多面体的截面方法(交线法):该作图关键在于确定截点,有了位于多面体同一表面上的两个截点即可连结成截线,从而求得截面.题型一、截面的形状1.P 、Q 、R 三点分别在直四棱柱AC 1的棱BB 1、CC 1和DD 1上,试画出过P 、Q 、R 三点的截面.1解答:(1)连接QP 、QR 并延长,分别交CB 、CD (2)连接EF 交AB 于T,交AD 于S .(3)连接RS 、TP 。
则多边形PQRST 即为所求截面。
2.已知P 、Q 、R 分别是四棱柱ABCD ―A 1B 1C 1D 1的棱CD 、DD 1和AA 1上的点,且QR 与AD 不平行,求作过这三点的截面.2解答: (1)连接QP 并延长交DA 延长线于点I 。
(2)在平面ABCD 内连接PI 交AB 于点M 。
(3)连接QP 、RM 。
则四边形PQRM 即为所求。
注:①若已知两点在同一平面内,只要连接这两点,就可以得到截面与多面体的一个面的截线。
②若面上只有一个已知点,应设法在同一平面上再找出第二确定的点。
③若两个已知点分别在相邻的面上,应找出这两个平面的交线与截面的交点。
3.一个正方体内接于一个球,过这个球的球心作一平面,则截面图形不可能...是ACBD3答案:D解读:考虑过球心的平面在转动过中,平面在球的内接正方体上截得的截面不可能是大圆的内接正方形,故选D 。
题型二、截面面积、长度等计算4.过正方体1111D C B A ABCD -的对角线1BD 的截面面积为S ,S max 和S min 分别为S 的最大值和最小值,则m inm axS S 的值为 ( ) A .23 B .26 C .332 D .362 4答案:C解读:设M 、N 分别为AA 1、CC 1的中点.易证截面BMD 11D 15. 如图,已知球O 是棱长为1 的正方体ABCD ﹣A 1B 1C 1D 1的内切球,则平面ACD 1截球O 的截面面积为. 5答案:解读:平面ACD 1是边长为的正三角形,且球与以点D 为公共点的三个面的切点恰为三角形ACD 1三边的中点,故所求截面的面积是该正三角形的内切圆的面积,则由图得,△ACD 1内切圆的半径是×tan30°=,则所求的截面圆的面积是π××=.6.已知球的半径为2,相互垂直的两个平面分别截球面得两个圆.若两圆的公共弦长为2,则两圆的圆心距等于( )A .1BCD .26答案:C解读:1O 与2O 的公共弦为AB ,球心为O,AB 中点为C , 则四边形C OO O 21为矩形,12||||,O O OC =||2,OA = 所以||1,||AC AC OC OC =⊥∴==7.已知正四棱锥P —ABCD 的棱长都等于a ,侧棱PB 、PD 的中点分别为M 、N ,则截面AMN 与底面ABCD 所成二面角大小的正切值为. 7答案:12O2OCO2解读:过A 在平面ABCD 内作直线l BD //,连接AC,BD 交于O ,连接PO ,MN .记PO 、MN 交于O‘.因为PB 、PD 的中点分别为M 、N ,所以MN //BD ,因为l BD //,所以l MN //,A l ∈,所以l ⊂平面AMN ,l =平面AMN∩平面ABCD .易知O AO '∠即为面AMN 与底面ABCD 所成二面角的平面角.1tan 242AO PO O O a O AO ''==⇒=⇒= 8.如图,正方体1111ABCD A B C D -的棱长为1,P 为BC 的中点,Q 为线段1CC 上的动点,过点A,P,Q 的平面截该正方体所得的截面记为S 。
截面画法大全 高中数学

截面画法大全高中数学
在高中数学中,截面画法通常用于解决立体几何问题,特别是涉及到计算空间中的距离、角度等问题。
以下是一些基本的截面画法:
1. 水平截面法:这是最常见的截面画法,即在平面中通过一个水平切割来观察立体图形。
例如,如果你想要计算一个圆柱体的高度,你可以通过在底部垂直切割来得到一个水平截面,然后通过测量截面中圆形周长的一半(即圆柱体的底面直径),再根据圆周长公式计算出高度。
2. 垂直截面法:这与水平截面法类似,只是在平面中通过一个垂直切割来观察立体图形。
例如,如果你想要计算一个圆柱体的底面半径,你可以通过在顶部水平切割来得到一个垂直截面,然后通过测量截面中圆形周长的一半,再根据圆周长公式计算出底面半径。
3. 正交截面法:这是在平面中通过一个既不是水平也不是垂直的切割来观察立体图形。
例如,如果你想要计算一个圆柱体的侧面积,你可以通过
在侧面倾斜切割来得到一个正交截面,然后通过测量截面中矩形的面积(即圆柱体的侧面积)。
以上就是高中数学中常见的截面画法,希望对你有所帮助。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
多面体的截面
用一个平面去截几何体,此平面与几何体的交集,叫做这个几何体的截面.此平面与几何体表面的交集(交线)叫做截线.此平面与几何体的棱的交集(交点)叫做截点.
作多面体截面的关键在于确定截点,有了位于多面体同一表面上的两个截点即可连结成截线,从而求得截面.
作截线与截点的主要根据有:
(1)确定平面的条件.
(2)如果两个不重合的平面有一个公共点,那么它们相交于过此点的一条直线.
(3)如果一条直线上的两点在一个平面内,那么这条直线上所有的点都在这个平面内.
(4)如果一条直线平行于一个平面,经过这条直线的平面与这个平面相交,那么这条直线就和交线平行.
(5)如果两个平面平行,第三个平面和它们相交,那么两条交线平行.
主要画法是交线法.即求出截面所在的平面与多面体某一表面所在平面的交线,再找出各有关截线(或其延长线)与此交线的交点.
例1 如图,正方体1111D C B A ABCD -中,G F E 、、分别在1DD BC AB 、、上,求作过G F E 、、三点的截面.
作法:(1)在底面AC 内,过F E 、作直线EF 分别与DC DA 、的延长线
交于M L 、.
(2)在侧面D A 1内,连结LG 交1AA 于K .
(3)在侧面C D 1内,连结GM 交1CC 于H .
(4)连结KE 、FH .则五边形EFHGK 即为所求的截面.有时为了便于作截面,还须引进辅助面作为作图的中介.
例2 如图,正方体1111D C B A ABCD -中,F E 、在两条棱上,G 在底面11C A 内,求过G F E 、、的截面.
作法:(1)在底面11C A 内,过G 作11//C B PQ ,交棱于Q P 、两点.
(2)作辅助面PC ,在此面内,过F G 、作直线交BP 的延长线于M .
(3)在侧面B A 1内,连结ME ,交11B A 于K .
(4)在底面11C A 内,连结KG ,延长交11C B 于H .
(5)连结HF .
(6)在底面AC 内,作HK FL //,交AB 于L .
(7)连结EL .则五边形ELFHK 为所求的截面.此外,对于面数较多的多面体,可以把其中一些表面伸展构成面数较少的多面体,使作图得解.
例 3 如图,五棱锥ABCD P -中,三条侧棱上各有一已知点
H G F 、、,求作过H G F 、、的截面.
作法:(1)将侧面PDE PBC PAB 、、伸展得到三棱锥BST P -.
(2)在侧面PBS 内,连结并延长GF ,交PS 于K .
(3)在侧面PBT 内,连结并延长GH 交PT 于L .
(4)在侧面PST 内,连结KL 分别交PE PD 、于N M 、. 图
FN、.则五边形FGHMN即为所求的截面.(5)连结MH。
