2.1二次函数的图像与性质同步练习3

合集下载

人教版九年级数学上册二次函数的图象和性质复习同步练习题

22.1 二次函数的图象和性质1．抛物线y=－3x 2上两点A （x ，－27），B （2，y ），则x= ，y= ．2．抛物线y=－4x 2－4的开口向，当x= 时，y 有最值，y = ． 3．当m= 时，y=（m －1）xmm +2－3m 是关于x 的二次函数．4．当m= 时，抛物线y=（m ＋1）x mm +2＋9开口向下，对称轴是．在对称轴左侧，y 随x 的增大而；在对称轴右侧，y 随x 的增大而． 5．抛物线y=3x 2与直线y=kx ＋3的交点为（2，b ），则k= ，b= ．6．已知抛物线的顶点在原点，对称轴为y 轴，且经过点（－1，－2），则抛物线的表达式为．7．在同一坐标系中，图象与y=2x 2的图象关于x 轴对称的是（）A ．y=21x 2B ．y=－21x 2C ．y=－2x 2D ．y=－x 28．抛物线，y=4 x 2，y=－2x 2的图象，开口最大的是（）A ．y=41x 2B ．y=4x 2C ．y=－2x 2D ．无法确定9．对于抛物线y=31x 2和y=－31x 2在同一坐标系里的位置，下列说法错误的是（）A ．两条抛物线关于x 轴对称B ．两条抛物线关于原点对称C ．两条抛物线关于y 轴对称D ．两条抛物线的交点为原点10．二次函数y=ax 2与一次函数y=ax ＋a 在同一坐标系中的图象大致为（）错误!未找到引用源。

11．已知函数y=ax 2的图象与直线y=－x ＋4在第一象限内的交点和它与直线y=x 在第一象限内的交点相同，则a 的值为（）A ．4 B ．2 C ．21D ．4112．求符合下列条件的抛物线y=ax 2的表达式：（1）y=ax 2经过（1，2）；（2）y=ax 2与y=21x 2的开口大小相等，开口方向相反；（3）y=ax 2与直线y=21x ＋3交于点（2，m ）．13已知错误!未找到引用源。

是二次函数，且当错误!未找到引用源。

北师大版九年级数学下册《二次函数的图像与性》同步练习试题

北师大版九年级数学下册第二章二次函数（2.2二次函数的图像与性质）同步练习试题一、选择题1、已知a ≠0，在同一直角坐标系中，函数y=x 与y=x 2的图象有可能是（）A ．B ．C ．D ． 2、在同一坐标系中，抛物线y ＝4x 2,y ＝41x 2,y ＝-41 x 2的共同特点是( ) A.关于y 轴对称，抛物线开口向上; B.关于y 轴对称，y 随x 的增大而增大B.关于y 轴对称，y 随x 的增大而减小; D.关于y 轴对称，抛物线顶点在原点.3、把二次函数的图象向右平移3个单位长度，得到新的图象的函数表达式是（）A. B. C. D.4、已知二次函数的图象上有三点，则的大小关系为（）A. B. C. D.5、若二次函数的图象的顶点在轴上，则的值是（）A. B. C. D.6、对于函数，下列说法正确的是（）2x y =32+=x y 32-=x y 2)3(+=x y 2)3(-=x y 2)1(3+=x y ),2(),,2(),,1(321y C y B y A -321,,y y y 321y y y >>312y y y >>213y y y >>123y y y >>12+-=mx x y x m 22-02±2)2(3-=x yA. 当时，随的增大而减小B. 当时，随的增大而增大C. 当时，随的增大而增D. 当时，随的增大而减小7、抛物线的顶点坐标为（） A 、（-1，） B 、（1，） C 、（-1，—） D 、（1，—） 8、将抛物线向右平移一个单位长度，再向上平移3个单位长度后，所得抛物线的解析式为（）A 、B 、C 、D 、9、如图，把抛物线y=x 2沿直线y=x 平移个单位后，其顶点在直线上的A 处，则平移后的抛物线解析式是（）A 、y=（x+1）2-1B ．y=（x+1）2+1C ．y=（x-1）2+1D ．y=（x-1）2-110、若二次函数．当≤l 时，随的增大而减小，则的取值范围是（）A ．=lB ．>lC ．≥lD ．≤l11、已知二次函数y=ax 2﹣2x+2（a ＞0），那么它的图象一定不经过（）A ．第一象限B ．第二象限C ．第三象限D ．第四象限12、如图，平面直角坐标系中，点M 是直线y=2与x 轴之间的一个动点，且点M 是抛物线y=x 2+bx+c 的顶点，则方程x 2+bx+c=1的解的个数是（）0>x y x 0<x y x 2>x y x 2->x y x 21)1(22+--=x y 212121212x y =3)1(2++=x y 3)1(2+-=x y 3)1(2-+=x y 3)1(2--=x y 22()1y x m =--x y x m m m m mA ．0或2B ．0或1C ．1或2D ．0，1或2二、填空题13、如图，⊙O 的半径为2．C 1是函数y=x 2的图象，C 2是函数y=﹣x 2的图象，则阴影部分的面积是． 14、抛物线y=4x 2-1与y 轴的交点坐标是_________,与x 轴的交点坐标是_____.15、抛物线y=4x 2-3是将抛物线y=4x 2,向_____平移______个单位得到的.16、抛物线y =－3(2x 2－1)的开口方向是_____，对称轴是_____.17、抛物线的开口向，对称轴是，顶点坐标18、若抛物线的对称轴是直线，且它与函数的形状相同，开口方向相同，则，。

人教版九年级数学上册二次函数图象和性质同步练习(含答案)

人教版九年级数学上册22.1.3二次函数y=a(x-h)² +k 的图象和性质基础闯关全练1．（2019安徽合肥包河月考）在同一坐标系中，作y= 3x ²+2,y= -3x ²-1,y=的图象，则它们( )A ．都是关于y 轴对称B ．顶点都在原点C ．都是开口向上D ．以上都不对2．（2018河南许昌长葛月考）抛物线y=-2x ²-5的开口方向_______．对称轴是______，顶点坐标是_______．3．二次函数y= -2（x-1）²的图象大致是( )A.B.C.D.4．（2018广东汕尾陆丰期中）将抛物线y=-x ²向右平移一个单位，所得抛物线相应的函数解析式为_____．5．（2018江苏盐城阜宁期中）对于二次函数y=（x-1）²+2的图象，下列说法正确的是( )A ．开口向下2x31B．对称轴是x= -1C．顶点坐标是（-1，2）D．与x轴没有交点6．（2018贵州毕节中考）将抛物线y=x²向左平移2个单位，再向下平移5个单位，平移后所得新抛物线的表达式为( )A.y=(x+2)²-5B.y=(x+2)²+5C.y=(x-2)²-5D.y=(x-2)²+57．设二次函数y=（x-3）²-4图象的对称轴为直线I，若点M在直线l上，则点M的坐标可能是( )A.(1,0)B.(3,0)C.(-3,0)D.(0,-4)8．（2019湖北黄石期中）函数y=2（x+1）²+1，当x_________时，y随x的增大而减小．能力提升全练1．若抛物线y=（x-m）²+(m+1)的顶点在第一象限，则m的取值范围为( )A.m>1B.m>0C.m>-1D.-1<m<02．如图22 -1-3 -1，点A是抛物线y=a（x-3）²+k与y轴的交点，AB∥x轴交抛物线于另一点B，点C为该抛物线的顶点，若△ABC为等边三角形，则a值为( )图22 -1-3 -1A ．B ．C ．D ．13．（2018贵州贵阳模拟）如图22-1-3-2，在平面直角坐标系中，有两条位置确定的抛物线，它们的对称轴相同，表达式中的h ，k ，m ，n 都是常数，则下列关系不正确的是( )图22-1-3-2A. h<0，k>0B ．m<0，n>0B. h =mD ．k=n4．二次函数y=m （x-2m ）²+m ²，当x>m+1时，y 随x 的增大而增大，则m 的取值范围是_________.三年模拟全练212333一、选择题1．（2019湖北武汉江汉期中，3．★☆☆）关于函数y=-（x+2）²-1的图象叙述正确的是( ) A．开口向上B．顶点坐标为（2，-1）C．与y轴交点为（0，-1）D．图象都在x轴下方2．（2018甘肃平凉庄浪期中，3，★☆☆）将抛物线y=x²平移得到抛物线y=x²+5，下列叙述正确的是( )A．向上平移5个单位B．向下平移5个单位C．向左平移5个单位D．向右平移5个单位3．若二次函数y=a(x+h)²+惫的图象的对称轴是x= -2，那么h=____；若顶点坐标是（-2，-4），则k=____．五年中考全练一、选择题1．（2018四川广安中考，7，★☆☆）抛物线y=（x-2）²-1可以由抛物线y=x²平移而得到，下列平移正确的是( )A．先向左平移2个单位长度，然后向上平移1个单位长度B．先向左平移2个单位长度，然后向下平移1个单位长度C．先向右平移2个单位长度，然后向上平移1个单位长度D．先向右平移2个单位长度，然后向下平移1个单位长度2．对于二次函数y=-(x-1) ²+2的图象与性质，下列说法正确的是( )A．对称轴是直线x=1．最小值是2B．对称轴是直线x=1，最大值是2C．对称轴是直线x= -1．最小值是2D．对称轴是直线x=-1，最大值是2二、填空题3．（2018黑龙江哈尔滨中考．16．★女女）抛物线y=2（x+2）²+4的顶点坐标为_______．4．已知函数y=-（x-1）²图象上两点A(2．y₁)，B(a，y₂)，其中a>2，则y₁与y₂的大小关系是y₁____y₂（填“<”“>”或“=”）.核心素养全练1．两条抛物线与分别经过点（-2，0），(2，0)且平行于y轴的两条平行线围成的部分的面积为8，则b等于( )A．1B.-3C.4D.-1或32．如图22-1-3 -3，在平面直角坐标系中，点A在抛物线y=（x-1）²+2上运动，过点A作AB⊥x轴于点B．以AB为斜边作Rt△ABC，则AB边上的中线CD的最小值为_________．图22-1-3-3答案基础闯关全练1．A解析：观察三个二次函数解析式可知，对称轴都是y轴，故A正确：三个函数图象的顶点坐标分别为(0，2)，（0，-1），(0，0)，它们开口方向分别为向上，向下，向上，故B，C，D都错误．故选A．2．答案向下；y轴；（0，-5）解析∵y= -2x²-5，∴a=-2<0，∴抛物线开口向下，对称轴为y轴，顶点坐标为（0，-5）．3.B解析：二次函数y= -2（x-1）²的图象开口向下，对称轴是x=1，顶点坐标为(1，0)，故选B．4．答案y=-（x-1）²解析抛物线y=-x²的顶点坐标为(0，0)，把点(0，0)向右平移一个单位得到对应点的坐标为(1，0)，所以平移后，所得抛物线相应的函数解析式为y=-(x-1)²．5. D解析：∵y=（x-1）²+2，∴抛物线开口向上，对称轴为x=1，顶点坐标为(1，2)，故A、B、C均不正确．∵抛物线开口向上，顶点(1，2)在第一象限，∴抛物线与x轴没有交点，故D 正确．6. A解析：抛物线y=x²的顶点坐标为(0，0)，先向左平移2个单位，再向下平移5个单位后的抛物线的顶点坐标为（-2，-5），所以平移后的抛物线的解析式为y=(x+2)²-5.故选A．7. B解析：因为二次函数y=（x-3）²-4图象的对称轴是直线x=3，所以点M的横坐标是3．故选B．8．答案≤-1解析∵函数图象的对称轴为x=-1，且开口向上．∴在对称轴的左侧，y随x的增大而减小，即x≤-1时．y随x的增大而减小．能力推升全练1. B解析：由题意，得顶点坐标为(m，m+1)，由顶点在第一象限得解得m>0，故选B．2. C解析：过C作CD⊥AB于D，∵抛物线y=a（x-3）²+k的对称轴为x=3，△ABC为等边三角形，A 为抛物线与y 轴的交点，且AB ∥x 轴，∴AD =3，CD=，C(3，k)，∵当x=0时，y=9a+k ，∴A(0，9a+k)，∴9a+k-k=，∴．故选C ．3. D解析：根据二次函数解析式确定两抛物线的顶点坐标分别为(h ，k)，(m ，n)，对称轴都是直线x=m 或x=h ，即m=h ，由题图知h<0．k>0，m<0，n>0，因为点(h ，k)在点(m ，n)的下方，所以k=n 不正确，故选D ．4．答案0<m ≤1解析抛物线的对称轴为直线x=2m ，①m>0时,∵当x>m+1时，y 随x 的增大而增大，∴2m ≤m+1，解得m ≤1，即0<m ≤1；②m<0时，不合题意，故填0<m ≤1．三年模拟全练一、选择题1.D解析：由二次函数y=-(x+2)²-1可知a=-1<0，所以其图象开口向下，顶点坐标为（-2，-1），所以二次函数图象都在x 轴下方，令x=0，则y= -5，所以函数图象与y 轴的交点为（0，-5）．故选D ．2．A解析：将抛物线y=x ²向上平移5个单位得到抛物线y=x ²+5，故选A ．二、填空题3．答案2：-4解析 ∵二次函数y=a(x+h)²+k 的图象的对称轴是x= -2，∴h=2．∵顶点坐标是（-2，-4），∴k= -4．五年中考全练333333a一、选择题1.D解析：抛物线y=x ²的顶点坐标为(0，0)，抛物线y=（x-2）²-1的顶点坐标为（2，-1），则抛物线y =x ²向右平移2个单位长度，向下平移1个单位长度即可得到抛物线y=(x-2)² -1.故选D ．2. B解析：抛物线y=-（x-1）²+2的开口向下，顶点坐标为(1，2)，对称轴为直线x=1．∴当x=1时，y 有最大值2，故选B ．二、填空题3．答案（-2，4）解析 ∵y=2(x+2)²+4，∴该抛物线的顶点坐标是（-2，4）．4．答案>解析因为二次项系数为-1，小于0．所以在对称轴x=1的左侧，y 随x 的增大而增大；在对称轴x=1的右侧，y 随x 的增大而减小，因为a>2>1，所以y ₁>y ₂．故填“>”．核心素养全练1. A解析： ∵两解析式的二次项系数相同，∴两抛物线的形状完全相同．∴∴2bxl2-(-2)l=86=8．∴b=1．故选A ．2．答案 1解析 ∵CD 为Rt △ABC 的斜边AB 上的中线，∴CD= AB ．∵y=(x-1)²+2的顶点坐标为(1，2)，∴点A 到x 轴的最小距离为2，即垂线段AB 的最小值为2，∴中线CD 的最小值为1． 21。

人教版九年级上册 22.1 二次函数的图象和性质同步练习含答案

2020年人教版九年级上册同步练习22.1 二次函数的图象和性质一．选择题（共10小题）1．下列函数属于二次函数的是（）A．y＝x﹣B．y＝（x﹣3）2﹣x2C．y＝﹣x D．y＝2（x+1）2﹣12．当函数y＝（a﹣1）x2+bx+c是二次函数时，a的取值为（）A．a＝1B．a＝﹣1C．a≠﹣1D．a≠13．下列抛物线的图象，开口最大的是（）A．y＝x2B．y＝4x2C．y＝﹣2x2D．无法确定4．抛物线y＝（x﹣3）2﹣5的顶点坐标是（）A．（3，5）B．（﹣3，5）C．（3，﹣5）D．（﹣3，﹣5）5．抛物线y＝x2+4x+7的对称轴是（）A．直线x＝4B．直线x＝﹣4C．直线x＝2D．直线x＝﹣2 6．对于二次函数y＝2（x﹣1）2﹣8，下列说法正确的是（）A．图象开口向下B．当x＞1时，y随x的增大而减小C．当x＜1时，y随x的增大而减小D．图象的对称轴是直线x＝﹣17．下列对二次函数y＝x2﹣2x的图象的描述，正确的是（）A．开口向下B．对称轴是y轴C．经过原点D．对称轴右侧部分下降8．一次函数y＝acx+b与二次函数y＝ax2+bx+c在同一平面直角坐标系中的图象可能是（）A．B．C．D．9．二次函数y＝ax2+bx+c的图象如图所示，则下列结论正确的是（）A．abc＞0B．a+b+c＝0C．4a﹣2b+c＜0D．b2﹣4ac＜0 10．二次函数y＝﹣x2+ax+b的图象如图所示，对称轴为直线x＝2，下列结论不正确的是（）A．a＝4B．当x＞2.5时，y随x的增大而减小C．当x＝﹣1时，b＞5D．当b＝8时，函数最大值为10二．填空题（共8小题）11．若y＝（a+2）x|a|+1是以x为自变量的二次函数，则a＝．12．抛物线y＝3（x﹣1）2+8的顶点坐标为．13．二次函数y＝x2﹣16x﹣8的最小值是．14．当二次函数y＝﹣x2+4x﹣6有最大值时，x＝．15．二次函数y＝x2﹣4x+5﹣m2的图象过点（0，4），则m的值为．16．将抛物线y＝2（x+3）2+4先向右平移1个单位长度，再向下平移5个单位长度，得到的抛物线的解析式为．17．已知点P1（﹣2，y1），P2（2，y2）在二次函数y＝（x+1）2﹣2的图象上，则y1y2．（填“＞”，“＜”或“＝”）18．二次函数y＝ax2+bx+c（a≠0）的部分图象如图，图象过点（﹣1，0），对称轴为直线x ＝2，下列结论：①4a+b＝0；②9a+c＞3b；③，3a+c＞0；④当x＞﹣1时，y的值随x 值的增大而增大；⑤4a+2b≥am2﹣bm（m为任意实数）．其中正确的结论有．（填序号）三．解答题（共6小题）19．已知平面直角坐标系xOy中，抛物线y═x2﹣mx+m2+m．（1）若该抛物线经过原点，求m的值；（2）求证该抛物线的顶点在直线y＝x上；（3）若点A（﹣4，0），B（0，2），当该抛物线与线段AB只有一个公共点时，结合函数图象，直接写出m的取值范围．20．在平面直角坐标系xOy中，抛物线y＝﹣x2+2bx+b2+1的对称轴与x轴交于点A，将点A 向左平移b个单位，再向上平移3﹣b2个单位，得到点B．（1）求点B的坐标（用含b的式子表示）；（2）当抛物线经过点（0，2），且b＞0时，求抛物线的表达式；（3）若抛物线与线段AB恰有一个公共点，结合图象，直接写出b的取值范围．21．把抛物线C1：y＝x2+2x+3先向右平移4个单位长度，再向下平移5个单位长度得到抛物线C2．（1）直接写出抛物线C2的函数关系式；（2）动点P（a，﹣6）能否在抛物线C2上？请说明理由；（3）若点A（m，y1），B（n，y2）都在抛物线C2上，且m＜n＜0，比较y1，y2的大小，并说明理由．22．已知抛物线y＝ax2﹣2ax﹣3+2a2（a≠0）．（1）求这条抛物线的对称轴；（2）若该抛物线的顶点在x轴上，求其解析式；（3）设点P（m，y1），Q（3，y2）在抛物线上，若y1＜y2，求m的取值范围．23．已知二次函数y＝﹣x2+bx+c的图象与直线y＝﹣x+3相交于x轴上的点A，y轴上的点B．顶点为P．（1）求这个二次函数的解析式；（2）现将抛物线向左平移m个单位，当抛物线与△PBA有且只有一个公共点时，求m 的值．24．已知：如图，抛物线y＝ax2+4x+c经过原点O（0，0）和点A（3，3），P为抛物线上的一个动点，过点P作x轴的垂线，垂足为B（m，0），并与直线OA交于点C．（1）求抛物线的解析式；（2）当点P在直线OA上方时，求线段PC的最大值．参考答案一．选择题（共10小题）1．解：A．自变量x的次数不是2，故A错误；B．y＝（x﹣3）2﹣x2整理后得到y＝﹣6x+9，是一次函数，故B错误C．由可知，自变量x的次数不是2，故C错误；D．y＝2（x+1）2﹣1是二次函数的顶点式解析式，故D正确．故选：D．2．解：由题意得：a﹣1≠0，解得：a≠1，故选：D．3．解：∵二次函数中|a|的值越小，函数图象的开口越大，又∵||＜|﹣2|＜|4|，∴抛物线y＝x2的图象开口最大，故选：A．4．解：抛物线y＝（x﹣3）2﹣5的顶点坐标是（3，﹣5），故选：C．5．解：因为a＝1，b＝4，c＝7，所以对称轴是直线x＝﹣＝﹣＝﹣2，故选：D．6．解：A、y＝2（x﹣1）2﹣8，∵a＝2＞0，∴图象的开口向上，故本选项错误；B、当x＞1时，y随x的增大而增大；故本选项错误；C、当x＜1时，y随x的增大而减小，故本选项正确；D、图象的对称轴是直线x＝1，故本选项错误．故选：C．7．解：y＝x2﹣2x＝（x﹣1）2﹣1，A．由a＝1＞0知抛物线开口向上，此选项错误；B．此抛物线的对称轴为直线x＝1，此选项错误；C．当x＝0时，y＝0，此抛物线经过原点，此选项正确；D．由a＞0且对称轴为直线x＝1知，当x＞1，即对称轴右侧时，y随x的增大而增大，此选项错误；故选：C．8．解：A、由抛物线可知，a＞0，b＜0，c＞0，则ac＞0，由直线可知，ac＞0，b＞0，故本选项错误；B、由抛物线可知，a＞0，b＞0，c＞0，则ac＞0，由直线可知，ac＞0，b＞0，故本选项正确；C、由抛物线可知，a＜0，b＞0，c＞0，则ac＜0，由直线可知，ac＜0，b＜0，故本选项错误；D、由抛物线可知，a＜0，b＜0，c＞0，则ac＜0，由直线可知，ac＞0，b＞0，故本选项错误．故选：B．9．解：由图象可得，a＞0，b＜0，c＜0，∴abc＞0，故选项A正确；当x＝1时，y＝a+b+c＜0，故选项B错误；当x＝﹣2时，y＝4a﹣2b+c＞0，故选项C错误；该函数图象与x轴两个交点，则b2﹣4ac＞0，故选项D错误；故选：A．10．解：∵二次函数y＝﹣x2+ax+b∴对称轴为直线x＝﹣＝2∴a＝4，故结论A正确；∵对称轴为直线x＝2且图象开口向下，∴当x＞2.5时，y随x的增大而减小，故结论B正确；当x＝﹣1时，由图象知此时y＞0即﹣1﹣4+b＞0∴b＞5，故结论C正确；当b＝8时，y＝﹣x2+4x+8＝﹣（x﹣2）2+12∴函数有最大值12，故结论D不正确；故选：D．二．填空题（共8小题）11．解：由题意得：|a|＝2，且a+2≠0，解得：a＝2，故答案为：2．12．解：∵抛物线y＝3（x﹣1）2+8是顶点式，∴顶点坐标是（1，8）．故答案为：（1，8）．13．解：y＝x2﹣16x﹣8＝（x﹣8）2﹣72，由于函数开口向上，因此函数有最小值，且最小值为﹣72，故答案为：﹣72．14．解：∵y＝﹣x2+4x﹣6，＝﹣（x2﹣4x+4）+4﹣6，＝﹣（x﹣2）2﹣2，∴当x＝2时，二次函数取得最大值．故答案为：2．15．解：∵根二次函数y＝x2﹣4x+5﹣m2的图象过点（0，4），∴5﹣m2＝4，解得m＝±1．故答案为±1．16．解：将抛物线y＝2（x+3）2+4先向右平移1个单位长度，再向下平移5个单位长度可得：y＝2（x+3﹣1）2+4﹣5，即y＝2（x+2）2﹣1，故答案为y＝2（x+2）2﹣1．17．解：当x＝﹣2时，y1＝（﹣2+1）2﹣2＝﹣1；当x＝2时，y2＝（2+1）2﹣2＝7．∵﹣1＜7，∴y1＜y2．故答案为＜．18．解：抛物线过点（﹣1，0），对称轴为直线x＝2，因此可得，抛物线与x轴的另一个交点为（5，0），a﹣b+c＝0，x＝﹣＝2，即4a+b ＝0，因此①正确；当x＝﹣3时，y＝9a﹣3b+c＜0，即9a+c＜3b，因此②不正确；当x＝5时，y＝25a+5b+c＝0，又b＝﹣4a，所以5a+c＝0，而a＜0，因此有3a+c＞0，故③正确；在对称轴的左侧，即当x＜2时，y随x的增大而增大，因此④不正确；当x＝2时，y最大＝4a+2b+c，当x＝m时，y＝am2+bm+c，因此有4a+2b≥am2+bm，故⑤正确；综上所述，正确的结论有：①③⑤，故答案为：①③⑤．三．解答题（共6小题）19．解：（1）∵抛物线经过原点，∴m2+m＝0，解得m1＝0，m2＝﹣2；（2）∵y═x2﹣mx+m2+m＝（x﹣m）2+m，∴该抛物线的顶点坐标为（m，m），∴抛物线的顶点直线直线y＝x上；（3）设直线AB的解析式为y＝kx+b，把点A（﹣4，0），B（0，2）代入得，解得，∴直线AB的解析式为y＝+2，令x+2＝x2﹣mx+m2+m，整理得x2﹣（m+）x+m2+m﹣2＝0，△＝（m+）2﹣4×（m2+m﹣2）＝0，解得m＝，∵此时对称轴为x＝﹣＝＞0，故舍去；把A（﹣4，0）代入y＝x2﹣mx+m2+m得，m2+5m+8＝0，解得m＝﹣2或﹣8；把B（0，2）代入y＝x2﹣mx+m2+m得，m2+m+﹣2＝0，解得m＝﹣1，由图象可知，该抛物线与线段AB只有一个公共点时，﹣8≤m≤﹣1﹣或﹣2≤m≤﹣1+．20．解：（1）由题意得抛物线y＝﹣x2+2bx+b2+1的对称轴为，∴点A坐标为（b，0），∴点B坐标为（0，3﹣b2）（2）把（0，2）代入y＝﹣x2+2bx+b2+1中，解得b＝±1．∵b＞0，∴b＝1．∴抛物线的表达式为y＝﹣x2+2x+2；（3）当抛物线过点B时，抛物线AB有一个公共点，∴b2+1＝3﹣b2∴b＝±1，如图：当b＞1时，抛物线与线段AB无交点；当b＝1时，抛物线与线段AB有一个交点；当﹣1＜b＜1时，抛物线与线段AB有一个交点；当b＝﹣1时，抛物线与线段AB有一个交点；当b＜﹣1时，抛物线与线段AB无交点．∴若抛物线与线段AB恰有一个公共点，则﹣1≤b≤1．21．解：（1）∵y＝x2+2x+3＝（x+1）2+2，∴把抛物线C1：y＝x2+2x+3先向右平移4个单位长度，再向下平移5个单位长度得到抛物线C2：y＝（x+1﹣4）2+2﹣5，即y＝（x﹣3）2﹣3，∴抛物线C2的函数关系式为：y＝（x﹣3）2﹣3．（2）动点P（a，﹣6）不在抛物线C2上，理由如下：∵抛物线C2的函数关系式为：y＝（x﹣3）2﹣3，∴函数的最小值为﹣3，∵﹣6＜﹣3，∴动点P（a，﹣6）不在抛物线C2上；（3）∵抛物线C2的函数关系式为：y＝（x﹣3）2﹣3，∴抛物线的开口向上，对称轴为x＝3，∴当x＜3时，y随x的增大而减小，∵点A（m，y1），B（n，y2）都在抛物线C2上，且m＜n＜0＜3，22．解：（1）∵抛物线y＝ax2﹣2ax﹣3+2a2＝a（x﹣1）2+2a2﹣a﹣3．∴抛物线的对称轴为直线x＝1；（2）∵抛物线的顶点在x轴上，∴2a2﹣a﹣3＝0，解得a＝或a＝﹣1，∴抛物线为y＝x2﹣3x+或y＝﹣x2+2x﹣1；（3）∵抛物线的对称轴为x＝1，则Q（3，y2）关于x＝1对称点的坐标为（﹣1，y2），∴当a＞0，﹣1＜m＜3时，y1＜y2；当a＜0，m＜﹣1或m＞3时，y1＜y2．23．解：（1）∵直线y＝﹣x+3交于x轴上的点A，y轴上的点B，∴A（3，0），B（0，3），把A、B的坐标代入y＝﹣x2+bx+c得，解得，∴二次函数的解析式为y＝﹣x2+2x+3；（2）当抛物线经过点B时，抛物线与△PBA有且只有一个公共点，∵y＝﹣x2+2x+3＝﹣（x﹣1）2+4，∴P（1，4），将抛物线向左平移m个单位，P对应点为（1﹣m，4），∴平移后的抛物线解析式为y＝﹣（x﹣1+m）2+4，把B（0，3）代入得，3═﹣（﹣1+m）2+4，解得m1＝2，m2＝0（舍去），故m的值为2．24．解：（1）把O（0，0），A（3，3）代入得：，解得：，则抛物线解析式为y＝﹣x2+4x；（2）设直线OA解析式为y＝kx，把A（3，3）代入得：k＝1，即直线OA解析式为y＝x，∴P，C，B三点纵坐标相等，∵B（m，0），∴把x＝m代入y＝x中得：y＝m，即C（m，m），把x＝m代入y＝﹣x2+4x中得：y＝﹣m2+4m，即P（m，﹣m2+4m），∵P在直线OA上方，∴PC＝﹣m2+4m﹣m＝﹣m2+3m（0＜m＜3），当m＝﹣＝时，PC取得最大值，最大值为＝．。

人教版九年级数学上册 22.1 二次函数的图象和性质同步训练(含答案)

人教版九年级数学上册22.1 二次函数的图象和性质同步训练一、选择题1. 二次函数y＝2x2，y＝－2x2，y＝12x2的共同性质是()A．其图象开口都向上B．其图象的对称轴都是y轴C．其图象都有最高点D．y随x的增大而增大2. 若y＝ax2＋bx＋c，则由表格中的信息可知y与x之间的函数解析式是()A.y＝x2－4x＋3 B．y＝x2－3x＋4C．y＝x2－3x＋3 D．y＝x2－4x＋83. 若二次函数y＝x2＋mx的对称轴是x＝3，则关于x的方程x2＋mx＝7的解为()A. x1＝0，x2＝6B. x1＝1，x2＝7C. x1＝1，x2＝－7D. x1＝－1，x2＝74. 已知二次函数y＝－x2＋2bx＋c，当x＞1时，y的值随x值的增大而减小，则实数b的取值范围是()A．b≥－1 B．b≤－1C．b≥1 D．b≤15. 二次函数y＝2x2－3的图象是一条抛物线，下列关于该抛物线的说法，正确的是()A. 抛物线开口向下B. 抛物线经过点(2，3)C. 抛物线的对称轴是直线x＝1D. 抛物线与x轴有两个交点6. 将函数y＝x2的图象用下列方法平移后，所得的图象不经过点A(1，4)的是() A．向左平移1个单位长度B．向右平移3个单位长度C．向上平移3个单位长度D．向下平移1个单位长度7. 已知抛物线y＝2x2＋bx＋c的顶点坐标是(－1，－2)，则b与c的值分别为() A．－1，－2 B．4，－2C．－4，0 D．4，08. 已知二次函数y＝x2＋bx＋c与x轴只有一个交点，且图象过A(x1，m)、B(x1＋n，m)两点，则m、n的关系为()A. m＝12n B. m＝14n C. m＝12n2 D. m＝14n2二、填空题9. 某抛物线的形状、开口方向与抛物线y＝12x2－4x＋3相同，顶点坐标为(－2，1)，则该抛物线的函数解析式为________________．10. 已知抛物线y＝2(x－1)2上有两点(x1，y1)，(x2，y2)，且1＜x1＜x2，则y1与y2的大小关系是________．11. 抛物线y＝－8x2的开口向________，对称轴是________，顶点坐标是________；当x＞0时，y随x的增大而________，当x＜0时，y随x的增大而________．12. 已知二次函数的图象经过原点及点(－12，－14)，且图象与x轴的另一交点到原点的距离为1，则该二次函数的解析式为________________．13. 如图，抛物线y＝ax2＋bx＋c(a>0)的对称轴是过点(1，0)且平行于y轴的直线，若点P(4，0)在该抛物线上，则4a－2b＋c的值为________．14. 顶点坐标是(2，0)，且与抛物线y＝－3x2的形状、开口方向都相同的抛物线的解析式为________．15. 如图，抛物线y＝ax2＋bx＋c与x轴相交于点A，B(m＋2，0)，与y轴相交于点C，点D在该抛物线上，坐标为(m，c)，则点A的坐标是________．16. 如图，在平面直角坐标系xOy中，已知抛物线y＝ax2＋bx(a＞0)的顶点为C，与x轴的正半轴交于点A，它的对称轴与抛物线y＝ax2(a＞0)交于点B.若四边形ABOC是正方形，则b的值是________．三、解答题17. 已知抛物线y＝ax2经过点A(－2，－8)．(1)求此抛物线的解析式；(2)判断点B(－1，－4)是否在此抛物线上；(3)求出抛物线上纵坐标为－6的点的坐标．18. 在平面直角坐标系xOy中，抛物线y＝ax2＋bx＋2过B(－2，6)，C(2，2)两点．(1)试求抛物线的解析式；(2)记抛物线顶点为D，求△BCD的面积；(3)若直线y＝－12x向上平移b个单位所得的直线与抛物线段BDC(包括端点B、C)部分有两个交点，求b的取值范围．19. 如图，等腰直角三角形ABC的直角边与正方形MNPQ的边长均为10 cm，边CA与边MN在同一直线上，开始时点A与点M重合，△ABC沿MN方向以1 cm/s 的速度匀速运动，当点A与点N重合时，停止运动．设运动的时间为t s，运动过程中△ABC与正方形MNPQ重叠部分的面积为S cm2.(1)试写出S关于t的函数关系式，并指出自变量t的取值范围；(2)当MA＝2 cm时，重叠部分的面积是多少？20. 设函数y＝(x－1)[(k－1)x＋(k－3)](k是常数)．(1)当k取1和2时的函数y1和y2的图象如图所示，请你在同一直角坐标系中画出当k取0时函数的图象；(2)根据图象，写出你发现的一条结论；(3)将函数y2的图象向左平移4个单位，再向下平移2个单位，得到函数y3的图象，求函数y3的最小值．人教版九年级数学上册22.1 二次函数的图象和性质同步训练-答案一、选择题1. 【答案】B2. 【答案】A[解析] ∵x ＝1时，ax 2＝1，∴a ＝1.将(－1，8)，(0，3)分别代入y ＝x 2＋bx ＋c ，得⎩⎨⎧1－b ＋c ＝8，c ＝3，解得⎩⎨⎧b ＝－4，c ＝3.∴y 与x 之间的函数解析式是y ＝x 2－4x ＋3.故选A.3. 【答案】D【解析】∵二次函数y ＝x 2＋mx 的对称轴为x ＝－m2＝3，解得m ＝－6，则关于x 的方程为x 2－6x ＝7，解得，x 1＝－1，x 2＝7.4. 【答案】D [解析] 先根据抛物线的性质得到其对称轴为直线x ＝b ，且当x ＞b 时，y 的值随x 值的增大而减小．因为当x ＞1时，y 的值随x 值的增大而减小，所以b≤1.5. 【答案】D【解析】本题考查了二次函数的性质，由于2>0，所以抛物线的开口向上，所以A 选项错误；由于当x ＝2时，y ＝8－3＝5，所以B 选项错误；由于y ＝2x 2－3的对称轴是y 轴，所以C 选项错误；由2x 2－3＝0得b 2－4ac ＝24>0，则该抛物线与x 轴有两个交点，所以D 选项正确．6. 【答案】D [解析] A ．将函数y ＝x 2的图象向左平移1个单位长度得到函数y ＝(x ＋1)2的图象，它经过点(1，4)；B.将函数y ＝x 2的图象向右平移3个单位长度得到函数y ＝(x －3)2的图象，它经过点(1，4)；C.将函数y ＝x 2的图象向上平移3个单位长度得到函数y ＝x 2＋3的图象，它经过点(1，4)；D.将函数y ＝x 2的图象向下平移1个单位长度得到函数y ＝x 2－1的图象，它不经过点(1，4)．故选D.7. 【答案】D8. 【答案】D【解析】因为二次函数y ＝x 2＋bx ＋c 的图象与x 轴只有一个交点，∴b 2－4c ＝0，即c ＝b 24，由题意知，点A ，B 关于抛物线的对称轴对称，∴12AB＝|n|2＝－b 2－x 1，b ＝－|n|－2x 1, ∴c ＝（－|n|－2x 1）24＝|n|2＋4|n|x 1＋4x 214，∵A(x 1，m)在y ＝x 2＋bx ＋c 上，∴m ＝x 21＋bx 1＋c ，∴ m ＝x 21＋(－|n|－2x 1)· x 1＋|n|2＋4|n|x 1＋4x 214，化简整理得m ＝14n 2，故选D .二、填空题9. 【答案】y ＝12(x ＋2)2＋1 [解析] 已知抛物线的顶点坐标，可以设顶点式y ＝a(x －h)2＋k.又因为该抛物线的形状、开口方向与抛物线y ＝12x 2－4x ＋3相同，所以a ＝12，所以该抛物线的函数解析式是y ＝12(x ＋2)2＋1.10. 【答案】y 1<y 2[解析] ∵抛物线的解析式是y ＝2(x －1)2，∴其对称轴是直线x ＝1，抛物线的开口向上， ∴在对称轴右侧，y 随x 的增大而增大．又∵抛物线y ＝2(x －1)2上有两点(x 1，y 1)，(x 2，y 2)，且1＜x 1＜x 2，∴y 1<y 2.11. 【答案】下y 轴 (0，0) 减小增大12. 【答案】y ＝x 2＋x 或y ＝－13x 2＋13x 【解析】依题意，所求函数有可能经过(－1，0)，(－12，－14) 或(1，0)，(－12，－14) .设所求函数解析式为y ＝ax 2＋bx ＋c ，图象经过原点，则c ＝0，当图象经过(－1，0)，(－12，－14)时，代入可求得a ＝b ＝1，即所求解析式为y ＝x 2＋x ; 当图象经过(1，0)，(－12，－14)时，代入可求得a ＝－13，b ＝13，即所求解析式为y ＝－13x 2＋13x .综上所述，所求函数的解析式为y＝x 2＋x 或y ＝－13x 2＋13x .13. 【答案】0 【解析】设抛物线与x 轴的另一个交点是Q ，∵抛物线的对称轴是过点(1，0)的直线，与x 轴的一个交点是P(4，0)，∴与x 轴的另一个交点Q(－2，0)，把(－2，0)代入解析式得：0＝4a －2b ＋c ，∴4a －2b ＋c ＝0.14. 【答案】y ＝－3(x －2)215. 【答案】(－2，0)【解析】如解图，过D 作DM ⊥x 轴于点M ，∴M(m ，0)，又B(m ＋2，0)，∴MB ＝2，由C(0，c)，D(m ，c)知：OC ＝DM ，即点C 、D 关于对称轴对称，故点O 、M 也关于对称轴对称，∴OA ＝MB ＝2，∴A(－2，0)．16. 【答案】－2 [解析] 抛物线y ＝ax 2＋bx 的顶点C 的坐标为(－b 2a ，－b 24a)．把x ＝－b 2a 代入y ＝ax 2，得点B 的坐标为(－b 2a ，b 24a )．在y ＝ax 2＋bx 中，令y ＝0，则ax 2＋bx ＝0，解得x 1＝0，x 2＝－b a ，∴A(－ba ，0)．∵四边形ABOC 为正方形，∴BC ＝OA ，∴2·b 24a ＝－b a ，即b 2＋2b ＝0.解得b ＝－2或b ＝0(不符合题意，舍去)．三、解答题17. 【答案】解：(1)∵抛物线y ＝ax 2经过点A(－2，－8)，∴4a ＝－8，解得a ＝－2，∴此抛物线的解析式为y ＝－2x 2.(2)当x ＝－1时，y ＝－2，∴点B(－1，－4)不在此抛物线上．(3)把y ＝－6代入y ＝－2x 2，得－2x 2＝－6，解得x ＝±3，∴抛物线上纵坐标为－6的点的坐标为(3，－6)，(－3，－6)．18. 【答案】解：(1)把B(－2，6)，C(2，2)代入抛物线的解析式得： ⎩⎨⎧6＝a·（－2）2＋b·（－2）＋22＝a·22＋b·2＋2，(1分)解得⎩⎪⎨⎪⎧a ＝12b ＝－1，(2分)∴抛物线的解析式为y ＝12x 2－x ＋2.(3分)(2)抛物线解析式化为顶点式：y ＝12(x －1)2＋32，则抛物线顶点D(1，32)，(4分) 如解图①所示，过点B 、D 、C 分别向x 轴作垂线，垂足分别为点M 、N 、H ，则有：S △BCD ＝S 梯形BMHC －S 梯形BMND －S 梯形DNHC ＝12(6＋2) ×4－12(6＋32)×3－12(32＋2) ×1 ＝3.(6分)解图①解图② (3)如解图②所示，连接BC ，∵直线BC 斜率k BC ＝2－62－（－2）＝－1＜－12，∴过点C 作直线MN 与直线y ＝－12x 平行，设直线MN 的解析式为y ＝－12x ＋b 1，代入C(2，2)， ∴b 1＝3.(7分)作直线EF 与抛物线相切，且与直线y ＝－12x 平行，设直线EF 的解析式为y ＝－12x ＋b 2，联立抛物线解析式得， ⎩⎪⎨⎪⎧y ＝12x 2－x ＋2y ＝－12x ＋b 2， ∴x 2－x ＋4－2b 2＝ 0， ∵直线EF 与抛物线相切，∴b 2－4ac ＝0，即(－1)2－4(4－2b 2)＝0，(9分)∴b 2＝158，(11分) ∴158＜b ≤3.(12分)注：斜率知识为高中知识，但常渗透于中考压轴题，与二次函数相结合考查，做题时注意其性质的应用．19. 【答案】解：(1)设AB 与MQ 交于点R.∵△ABC 是等腰直角三角形，四边形MNPQ 是正方形， ∴△AMR 是等腰直角三角形．由题意知，AM ＝MR ＝t ，∴S ＝S △AMR ＝12t·t ＝12t 2(0≤t≤10)．(2)当MA ＝2 cm ，即t ＝2时，重叠部分的面积是12×2×2＝2(cm 2)．20. 【答案】解：(1)当k ＝0时，y ＝－(x －1)(x ＋3)，所画图象如解图所示．(2分)(2)①k 取0和2时的函数图象关于点(0，2)中心对称，②函数y ＝(x －1)[(k －1)x ＋(k －3)](k 是常数)的图象都经过(1，0)和(－1，4)．(5分)(3)由题意可得y 2＝(x －1)[(2－1)x ＋(2－3)]＝(x －1)2，平移后的函数y 3的表达式为y 3＝(x －1＋4)2－2＝(x ＋3)2－2，所以当x ＝－3时，函数y 3的最小值是－2.(8分)。

二次函数的图像与性质-同步练习(含解析)

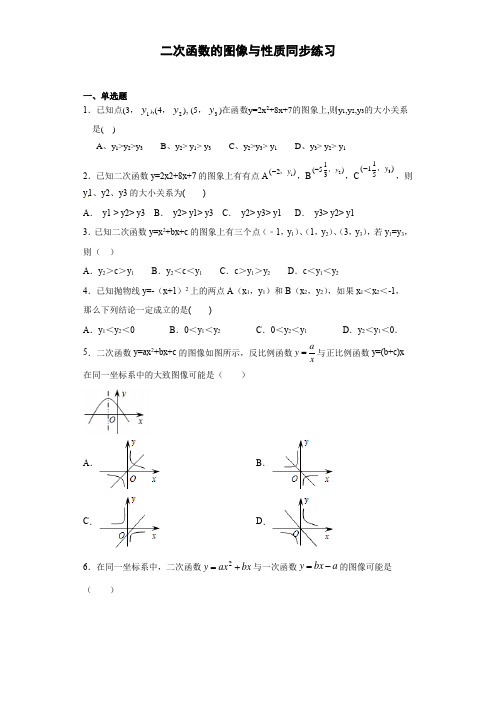
二次函数的图像与性质同步练习一、单选题1．已知点(3，1y ),(4，2y ), (5，3y )在函数y=2x 2+8x+7的图象上,则y 1,y 2,y 3的大小关系是( )A 、y 1>y 2>y 3B 、y 2> y 1> y 3C 、y 2>y 3> y 1D 、y 3> y 2> y 1 2．已知二次函数y=2x2+8x+7的图象上有有点A ，B ，C ，则y1、y2、y3的大小关系为( )A ． y1 > y2> y3B ． y2> y1> y3C ． y2> y3> y1D ． y3> y2> y13．已知二次函数y=x 2+bx+c 的图象上有三个点（﹣1，y 1）、（1，y 2）、（3，y 3），若y 1=y 3，则（）A ．y 2＞c ＞y 1B ．y 2＜c ＜y 1C ．c ＞y 1＞y 2D ．c ＜y 1＜y 24．已知抛物线y=-（x+1）2上的两点A （x 1，y 1）和B （x 2，y 2），如果x 1＜x 2＜-1，那么下列结论一定成立的是( ) A ．y 1＜y 2＜0B ．0＜y 1＜y 2C ．0＜y 2＜y 1D ．y 2＜y 1＜0．5．二次函数y=ax 2+bx+c 的图像如图所示，反比例函数ay x=与正比例函数y=(b+c)x 在同一坐标系中的大致图像可能是（）A ．B ．C ．D ．6．在同一坐标系中，二次函数2y ax bx =+与一次函数y bx a =-的图像可能是（）1(2)y -，21(5)3y -，31(1)5y -，A ．B ．C ．D ．7．反比例函数ky x=与一次函数()1y k x =-在同一坐标系中的图像可能是（） A ． B ．C ．D ．8．在同一坐标系中，函数x k y =和3+=kx y 的图像可能是（）A ．B ．C ．D ． 9．如图，坐标系中抛物线是函数y=ax 2＋bx ＋c 的图象，则下列式子能成立的是（）xxxxyyyyOOOO10．已知抛物线y=ax 2+bx+c （a≠0）在平面直角坐标系中的位置如图所示，对称轴是直线13x =．则下列结论中，正确的是（）A ．a ＜0B ．c ＜﹣1C ．a ﹣b+c ＜0D ．2a+3b=011．二次函数2y x bx c =++中（b ，c 是常数）的自变量x 与函数值y 的部分对应值如下表：下列结论正确的是：A ．当2x =时，y 有最大值1B ．当2x <时，y 随x 的增大而增大C ．点(5,9)在该函数的图像上D ．若1(,)A m y ，2(1,)B m y +两点都在该函数的图象上，则当32m >时，12y y <. 12．如图，四个二次函数的图象中，分别对应的是：①2y ax =；①2y bx =；①2y cx =；①2y dx =，则a b c d ,,,的大小关系为A ．a b c d >>>B ．a b d c >>>C ．b a c d >>>D ．b a d c >>>13．如图，抛物线的对称轴是直线x=1，且经过点P （3，0），则的值为（）A ．0B ．－1C ．1D ．214．若二次函数的x 与y 的部分对应值如下表，则当x 1=时，y 的值为( )A ．5B ．3-C ．13-D ．27-15．已知二次函数()2y ax bx c a 0=++≠，函数y 与自变量x 的部分对应值如下表所示下列说法错误的是( ) A ．图象开口向下 B ．抛物线的对称轴是直线x 2= C ．2b 4ac 0-> D ．当1x 3<<时，y 6<二、填空题16．已知抛物线2y x x =+－６５经过点1()4a -，和1()a y -，，则y 1的值是_________． 17．将抛物线()2241y x =--先向左平移4个单位长度，再向上平移2个单位长度，平移后所得抛物线的解析式为__________．18．将抛物线y ＝－2x 2向上平移2个单位长度，再向右平移3个单位长度后，得到的抛物线的解析式为_____ 19．将抛物线的解析式y=向上平移3个单位长度，在向右平移1个单位长度后，得到的抛物线的解析式是．20．如果二次函数y=（-2k+4）x 2-3x+1的图象开口向上，那么常数k 的取值范围是________三、解答题21．已知函数y=（k ﹣2）x k²﹣4k+5+2x 是关于x 的二次函数．求：（1）满足条件的k 的值；（2）当k 为何值时，抛物线有最高点？求出这个最高点，这时，x 为何值时，y 随x 的增大而增大？22．已知函数()242mm y m x +-=+是关于x 的二次函数．()1求m 的值．()2如果这个二次函数的图象经过点()18P -，求m 的值；()3对于()2中二次函数，函数有无最大值？若有，此时的x 为何值．23．求抛物线217322y x x =--+的对称轴、顶点坐标. 24．阅读下面文字:求代数式24x 7x -+的最值，我们可以这样做：()()2224x 74x 4323x x x -+=-++=-+,因为()22x -≥0，所以当x=2时，该代数式有最小值，最小值为3.仿照以上方法，求（1）28a 3a +-的最值.（2）222y y -++的最值.25．把函数y=3x 2+6x+10转化成y=a （x-h ）2+k 的形式，然后指出它的图象开口方向，对称轴，顶点坐标和最值．26．如图，已知抛物线y=2x -+mx+3与x 轴交于A ，B 两点，与y 轴交于点C ，点B 的坐标为（3，0），（1）求m 的值及抛物线的顶点坐标．（2）点P 是抛物线对称轴l 上的一个动点，当PA+PC 的值最小时，求点P 的坐标．参考答案1．D【解析】解：抛物线的对称轴为2482-=-=-=a b x ，又02φ=a ，抛物线开口向上，在对称轴的右边y 随x 的增大而增大，345φφΘ，123y y y φφ∴，故选D 。

九年级数学上册《二次函数的图像与性质》同步练习3 含答案

22.1《二次函数的图像与性质》同步练习3带答案一．选择题1.把二次函数2x y =的图象向右平移3个单位长度，得到新的图象的函数表达式是（）A. 32+=x yB. 32-=x yC. 2)3(+=x yD. 2)3(-=x y2.抛物线2)3(2--=x y 的顶点坐标和对称轴分别是（）A.3),0,3(-=-x 直线B. 3),0,3(=x 直线C. 3),3,0(-=-x 直线D. 3),3,0(-=x 直线3.已知二次函数2)1(3+=x y 的图象上有三点 ),2(),,2(),,1(321y C y B y A - ，则321,,y y y 的大小关系为（）A.321y y y >>B. 312y y y >>C. 213y y y >>D. 123y y y >>4.把抛物线2)1(6+=x y 的图象平移后得到抛物线26x y =的图象，则平移的方法可以是（）A.沿y 轴向上平移1个单位长度B.沿y 轴向下平移1个单位长度C.沿x 轴向左平移1个单位长度D.沿x 轴向右平移1个单位长度5.若二次函数12+-=mx x y 的图象的顶点在x 轴上，则m 的值是（）A. 2B. 2-C.0D. 2±6.对称轴是直线2-=x 的抛物线是（）A.22+-=x yB.22+=x yC.2)2(21+=x y D.2)2(3-=x y 7.对于函数2)2(3-=x y ，下列说法正确的是（）A. 当0>x 时，y 随x 的增大而减小B. 当0<x 时，y 随x 的增大而增大C. 当2>x 时，y 随x 的增大而增大D. 当2->x 时，y 随x 的增大而减小8.二次函数132+=x y 和2)1(3-=x y ，以下说法：①它们的图象都是开口向上；②它们的对称轴都是y 轴，顶点坐标都是原点（0,0）；③当0>x 时，它们的函数值y 都是随着x 的增大而增大；④它们的开口的大小是一样的. 其中正确的说法有（） A.1个 B.2个 C.3个 D.4个二．填空题1.抛物线2)1(3--=x y 的开口向，对称轴是，顶点坐标是。

人教版数学九年级上册《二次函数的图像和性质》综合练习(附答案)

22.1二次函数图像性质综合练习题(附答案)1、函数()2h x a y -=的图象与性质1、抛物线()2321--=x y ，顶点坐标是，当x 时，y 随x 的增大而减小，函数有最值。

2、试写出抛物线23x y =经过下列平移后得到的抛物线的解析式并写出对称轴和顶点坐标。

（1）右移2个单位；（2）左移32个单位；（3）先左移1个单位，再右移4个单位。

3、请你写出函数()21+=x y 和12+=x y 具有的共同性质（至少2个）。

4、二次函数()2h x a y -=的图象如图：已知21=a ，OA=OC ，试求该抛物线的解析式。

5、抛物线2)3(3-=x y 与x 轴交点为A ，与y 轴交点为B ，求A 、B 两点坐标及⊿AOB 的面积。

6、二次函数2)4(-=x a y ，当自变量x 由0增加到2时，函数值增加6。

求：（1）求出此函数关系式。

（2）说明函数值y 随x 值的变化情况。

7、已知抛物线9)2(2++-=x k x y 的顶点在坐标轴上，求k 的值。

2、()k h x a y +-=2的图象与性质 1、请写出一个以（2， 3）为顶点，且开口向上的二次函数：。

2、二次函数 y ＝(x －1)2＋2，当 x ＝时，y 有最小值。

3、函数 y ＝12 (x －1)2＋3，当 x 时，函数值 y 随 x 的增大而增大。

4、函数y=21(x+3)2-2的图象可由函数y=21x 2的图象向平移3个单位，再向平移2个单位得到。

5、已知抛物线的顶点坐标为()2,1，且抛物线过点()3,0，则抛物线的关系式是6、如图所示，抛物线顶点坐标是P （1，3），则函数y 随自变量x 的增大而减小的x 的取值范围是（）A 、x>3B 、x<3C 、x>1D 、x<17、已知函数()9232+--=x y 。

（1）确定下列抛物线的开口方向、对称轴和顶点坐标；（2）当x= 时，抛物线有最值，是。

人教版初中数学九年级上册《22.1二次函数图像和性质》同步练习含答案解析

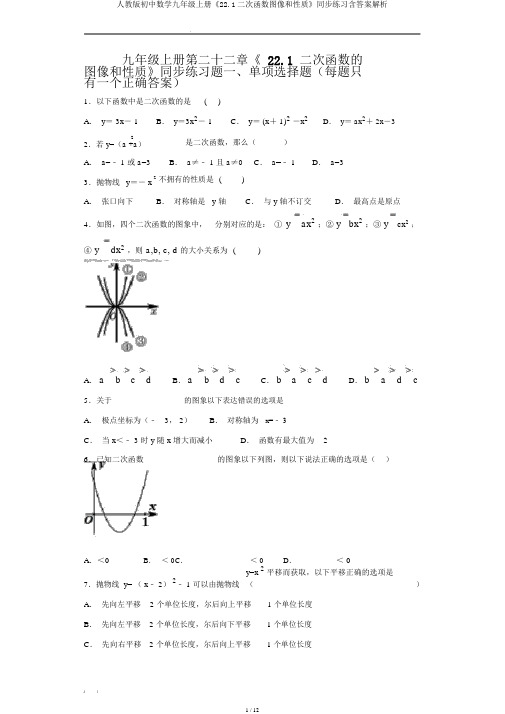
九年级上册第二十二章《 22.1 二次函数的图像和性质》同步练习题一、单项选择题（每题只有一个正确答案）1．以下函数中是二次函数的是( )A． y＝ 3x－ 1B． y＝3x2－ 1C． y＝ (x＋ 1)2－x2D． y＝ ax2＋ 2x－32 2．若 y=（a +a）A． a=﹣ 1 或 a=3 3．抛物线y＝－ x是二次函数，那么（）B． a≠﹣ 1 且 a≠0C． a=﹣ 1D． a=3 2不拥有的性质是()A．张口向下B．对称轴是y 轴C．与 y 轴不订交D．最高点是原点4．如图，四个二次函数的图象中，分别对应的是：① y ax2；② y bx2；③ y cx2；④ y dx2，则a,b, c, d的大小关系为()A．a b c d B．a b d c C．b a c d D．b a d c 5．关于的图象以下表达错误的选项是A．极点坐标为（﹣3， 2）B．对称轴为x=﹣ 3C．当 x＜﹣ 3 时 y 随 x 增大而减小D．函数有最大值为26．已知二次函数的图象以下列图，则以下说法正确的选项是（）A．＜0B．＜ 0C．＜ 0D．＜ 07．抛物线 y= （ x﹣ 2）2﹣ 1 可以由抛物线y=x 2平移而获取，以下平移正确的选项是（）A．先向左平移 2 个单位长度，尔后向上平移 1 个单位长度B．先向左平移 2 个单位长度，尔后向下平移 1 个单位长度C．先向右平移 2 个单位长度，尔后向上平移 1 个单位长度D．先向右平移 2 个单位长度，尔后向下平移 1 个单位长度8．如图，二次函数的图象张口向下，且经过第三象限的点若点P 的横坐标为，则一次函数的图象大体是A ．B ．C ．D．二、填空题9．二次函数y＝ kx2－ x－ 2 经过点 (1， 5)，则 k＝_________.10．函数 y= –的图象是抛物线，则 m= __________．11．张口向下的抛物线y＝(m 2－ 2)x2＋2mx ＋1 的对称轴经过点 (－1， 3)，则 m＝ _____．12．如图，这是小明在阅读一本关于函数的课外读物时看到的一段文字，则被墨迹污染的二次项系数是__________．13．抛物线 y=ax 2+bx+c（a≠0）的对称轴为直线x=1，与 x 轴的一个交点坐标为（﹣1，0），其部分图象以下列图，以下结论：①4ac＜ b2；②方程ax2+bx+c=0 的两个根是x1=﹣ 1，x2=3；③3a+c=0；④当 y＞ 0 时，x 的取值范围是﹣ 1≤x＜ 3；⑤当 x＜ 0 时，y 随 x 增大而增大，其中结论正确的选项是 _____（只需填序号）三、解答题14．已知函数y=- (m+2)- (m为常数),求当m为何值时:(1)y 是 x 的一次函数 ?(2)y 是 x 的二次函数 ?并求出此时纵坐标为 -8 的点的坐标 .15．某广告公司设计一幅周长为12m 的矩形广告牌，广告设计花销为1000 元 /m2.设矩形的一边长为xm，面积为ym2.(1) 求出 y 与 x 之间的函数关系式，说明y 可否是 x 的二次函数，并确定x 的取值范围；(2)若 x＝ 3 时，广告牌的面积最大，求此时的广告费应为多少？16．如图，已知二次函数 y=ax2+bx+3 的图象交 x 轴于点 A （ 1， 0）， B（ 3， 0），交 y 轴于点 C．（ 1）求这个二次函数的表达式；（ 2）点 P 是直线 BC 下方抛物线上的一动点，求△BCP面积的最大值；（3）直线 x=m 分别交直线 BC 和抛物线于点 M ， N，当△BMN 是等腰三角形时，直接写出 m 的值．参照答案1． B【解析】【解析】依照二次函数的定义:形如,则 y 是 x 的二次函数进行判断即可.【详解】A选项 ,y＝ 3x－ 1 是一次函数 ,不吻合题意 ,B选项 ,y＝3x2－ 1 是二次函数 ,吻合题意 ,C选项 , y＝ (x＋1)2－x2整理后 y=2x+1 是一次函数 ,不吻合题意 ,D选项 , y＝ ax2＋ 2x－ 3,二次项系数不确定可否等于0,不用然是二次函数 ,不吻合题意 ,应选 B.【点睛】此题主要观察二次函数的定义,解决此题的要点是要熟练掌握二次函数的定义.2． D【解析】【解析】依照二次函数定义，自变量的最高指数是二，且系数不为0，列出方程与不等式即可解答．【详解】2依照题意，得： a ﹣2a﹣ 1=22又由于 a +a≠0即 a≠0或 a≠﹣ 1应选 D．【点睛】解题要点是掌握二次函数的定义．3． C【解析】【解析】抛物线y=-x 2的二次项系数为-1，故抛物线张口向下，极点坐标（0， 0），最高点为原点，对称轴为y 轴，与 y 轴交于（ 0，0）．∵抛物线y=-x 2的二次项系数为-1，∴抛物线张口向下，极点坐标（0， 0）， A 正确；∴最高点为原点，对称轴为y 轴， B 、D 正确；与y 轴交于（ 0， 0）， C 错误，应选 C．【点睛】此题观察了基本二次函数 y=ax 2的性质：极点坐标（ 0， 0），对称轴为 y 轴，当 a＞ 0 时，张口向上，当 a＜ 0 时，张口向下．4． A【解析】由二次函数中，“当二次项系数为正时，图象张口向上，当二次项系数为负时，图象张口向下”结合“二次项系数的绝对值越大，图象的张口越大”解析可得：a b c d .应选 A.点睛：（ 1）二次函数y ax2a0的图象的张口方向由“a 的符号”确定，当a0 时，图象的张口向上，当 a 0 时，图象的张口向下；（2）二次函数y ax2a0的图象的开口大小由a的大小确定，当a越大时，图象的张口越小.5． D【解析】解析：依照二次函数的性质比较四个选项利用消除法即可得出结论.详解：依照二次函数的性质可知的极点坐标为（﹣3， 2），故 A 正确；对称轴为x=﹣ 3，故 B 正确；张口向上，在对称轴右侧y 随x 增大而减小且函数有最小值 2 ，故 C 正确 D 错误 .点睛：此题观察了二次函数的性质，在解题时可结合函数大体图象来判断. 正确理解二次函数的基本性质是解题的要点 .6． B【解析】【解析】依照抛物线的张口方向确定a，依照抛物线与y 轴的交点确定 c，依照对称轴确定b，依照抛物线与 x 轴的交点确定b2-4ac，依照 x=1 时， y＞ 0，确定 a+b+c 的符号．∵抛物线张口向上，∴a＞ 0，∵抛物线交于y 轴的正半轴，∴c＞ 0，∴ac＞ 0，A 错误；∵ - ＞ 0， a＞ 0，∴b＜ 0，∴ B 正确；∵抛物线与x 轴有两个交点，∴b2-4ac＞0，C 错误；当 x=1 时， y＞ 0，∴a+b+c＞ 0， D 错误；应选B．【点睛】此题观察的是二次函数图象与系数的关系，二次函数y=ax 2+bx+c 系数符号由抛物线张口方向、对称轴、抛物线与y 轴的交点抛物线与x 轴交点的个数确定．7． D【解析】解析：抛物线平移问题可以以平移前后两个解析式的极点坐标为基准研究．详解：抛物线y=x 2极点为（0，0），抛物线y= （x﹣ 2）2﹣ 1 的极点为（2，﹣ 1），则抛物线y=x 2向右平移 2 个单位，向下平移 1 个单位获取抛物线y= （ x﹣ 2）2﹣ 1 的图象．应选：D．点睛：此题观察二次函数图象平移问题，解答时最简单方法是确定平移前后的抛物线极点，从而确定平移方向．8． D【解析】【解析】依照二次函数的图象可以判断a、 b、的正负情况，从而可以获取一次函数经过哪几个象限，观察各选项即可得答案．【详解】由二次函数的图象可知，，，当时，，的图象经过二、三、四象限，观察可得 D 选项的图象吻合，应选 D．【点睛】此题观察二次函数的图象与性质、一次函数的图象与性质，认真识图，会用函数的思想、数形结合思想解答问题是要点.9． 8【解析】解析：把（1， 5）代入 y=kx 2-x-2 中，即可获取关于k 的一元一次方程，解这个方程即可求得k 的值．详解：∵二次函数y=kx 2-x-2 经过点（ 1，5），∴5=k-1-2 ，解得 k=8 ；故答案为 8．点睛：此题观察了二次函数图象上点的坐标特色，抛物线上的点的坐标适合解析式．10．–1【解析】依照抛物线的定义，得＝，解得： m=– 1．11．－ 1【解析】由于抛物线y= （ m2-2） x2+2mx+1 的对称轴经过点（-1， 3），b2m=-1，∴对称轴为直线 x=-1 ，x=2 m22a2解得 m1=-1 ， m2=2．由于抛物线的张口向下，所以当m=2 时， m2-2=2 ＞ 0，不合题意，应舍去，∴m=-1 ．故答案为： -1.12．－ 2【解析】由题意得,所以 a=-2.13．①②③⑤【解析】【解析】利用抛物线与x 轴的交点个数可对①进行判断;利用抛物线的对称性获取抛物线与x 轴的一个交点坐标为(3,0), 则可对②进行判断;由对称轴方程获取b=-2a,尔后依照x=-1时函数值为0可获取 3a+c=0,则可对③进行判断;依照二次函数的性质对④进行判断.【详解】①∵抛物线与x 轴有两个交点，∴△ =b2﹣ 4ac＞0，∴ 4ac＜ b2，结论①正确；②∵抛物线 y=ax2+bx+c （a≠0）的对称轴为直线x=1 ，与 x 轴的一个交点坐标为（﹣ 1， 0），∴抛物线与 x 轴的另一交点坐标为（ 3，0），∴方程 ax2+bx+c=0 的两个根是 x1=﹣ 1， x2=3 ，结论②正确；③∵抛物线 y=ax2+bx+c （a≠0）的对称轴为直线x=1，∴﹣=1，∴b= ﹣ 2a．∵当 x= ﹣1 时， y=0 ，∴a﹣ b+c=0，即 3a+c=0，结论③正确；④∵抛物线与x 轴的交点坐标为（﹣1，0）、（ 3， 0），∴当 y＞ 0 时， x 的取值范围是﹣1＜ x＜ 3，结论④错误；⑤∵抛物线张口向下，对称轴为直线x=1，∴当 x＜ 0 时， y 随 x 增大而增大，结论⑤正确．综上所述：正确的结论有①②③⑤．故答案为：①②③⑤．【点睛】二次函数图象与系数的关系：关于二次函数y=ax 2+bx+c （ a≠0），二次项系数 a 决定抛物线的张口方向和大小：当a＞ 0 时，抛物线向上张口；当a＜ 0 时，抛物线向下张口；一次项系数b 和二次项系数 a 共同决定对称轴的地址：当 a 与 b 同号时（即 ab＞ 0），对称轴在 y 轴左；当 a 与 b 异号时（即 ab＜ 0），对称轴在 y 轴右；常数项c 决定抛物线与 y 轴交点地址：抛物线与 y 轴交于（ 0， c）；抛物线与 x 轴交点个数由△决定：△=b2-4ac＞ 0 时，抛物线与 x 轴有 2 个交点；△=b2-4ac=0 时，抛物线与 x 轴有 1 个交点；△=b2-4ac＜0 时，抛物线与 x 轴没有交点．14． (1) m= ±;(2) m=2, 纵坐标为 -8 的点的坐标是 (±,-8).【解析】【解析】（ 1）依照一次函数的定义求m 的值即可；（2）依照二次函数的定义求得m 的值，从而求得二次函数的解析式，把y=-8代入解析式，求得x 的值，即可得纵坐标为-8的点的坐标.【详解】(1) 由 y=- (m+ 2)(m为常数 ),y 是 x 的一次函数,得解得m=±,当 m=±时 ,y 是 x 的一次函数.(2) 由y=- (m+ 2)(m 为常数),y是x 的二次函数,得解得m=2,m=- 2(不吻合题意的要舍去 ),当 m= 2 时 ,y 是 x 的二次函数 ,当 y=- 8 时 ,-8=- 4x2,解得 x= ±,故纵坐标为 - 8 的点的坐标是 (±,-8) .【点睛】此题观察了一次函数的定义、二次函数的定义，解题要点是掌握一次函数与二次函数的定义．15． (1)y ＝－ x2＋ 6x，是， 0＜ x＜ 6；（2） 9000 元【解析】试题解析：（ 1）矩形的一边长为 xm，依照矩形的周长是 12m，可得矩形的另一边长为（6－x） m，根据矩形的面积公式即可得出y 与 x 之间的函数表达式；（ 2）把 x＝ 3 代入函数的解析式得出y 的值即为广告牌的最大面积，再乘以1000 即为此时的广告费．试题解析：解：（ 1）由题意得出：y ＝ x(6－ x)＝－ x2＋ 6x，是二次函数，0＜ x＜ 6；（2）当 x＝ 3 时， y＝－ 32＋ 3×6＝ 9，1000×9＝ 9000 元，即此时的广告费应为9000 元．点睛：此题主要观察了依照实责问题抽象出二次函数解析式以及求二次函数值，正确得出二次函数解析式是解题要点．16．（ 1）这个二次函数的表达式是 y=x 2﹣ 4x+3 ；（ 2） S△最大 =；（ 3）当△BMN 是等腰BCP三角形时， m 的值为，﹣，1， 2．【解析】解析：（1）依照待定系数法，可得函数解析式；（ 2）依照平行于y 轴直线上两点间的距离是较大的纵坐标减较小的纵坐标，可得PE 的长，依照面积的和差，可得二次函数，依照二次函数的性质，可得答案；（ 3）依照等腰三角形的定义，可得关于m 的方程，依照解方程，可得答案．详解：（ 1）将 A （ 1， 0）， B（ 3， 0）代入函数解析式，得＝，＝解得＝，＝这个二次函数的表达式是y=x 2-4x+3 ；（ 2）当 x=0 时， y=3，即点 C（ 0，3），设 BC 的表达式为y=kx+b ，将点 B（ 3，0）点 C（ 0， 3）代入函数解析式，得＝，＝解这个方程组，得＝＝直线 BC 的解析是为y=-x+3 ，过点 P 作 PE∥ y 轴，交直线 BC 于点 E（ t， -t+3 ），22PE=-t+3-（ t -4t+3 ） =-t +3t，22，∴ S△BCP=S△BPE+S CPE= （ -t +3t）×3=- （ t- ） +∵- ＜ 0，∴当 t= 时， S△BCP最大 = .（3） M （ m， -m+3 ）， N （m， m2-4m+3 ）2MN=m -3m， BM=|m-3|，当 MN=BM时，① m2-3m=（m-3），解得m=，②m2 -3m=- （ m-3），解得 m=-当BN=MN 时，∠ NBM= ∠ BMN=45°，m2 -4m+3=0 ，解得 m=1 或 m=3（舍）当BM=BN 时，∠ BMN= ∠ BNM=45°，-（ m2-4m+3 ） =-m+3 ，解得 m=2 或 m=3（舍），当△BMN 是等腰三角形时，m 的值为，-，1，2．点睛：此题观察了二次函数综合题，解（1）的要点是待定系数法；解（2）的要点是利用面积的和差得出二次函数，又利用了二次函数的性质，解（3）的要点是利用等腰三角形的定义得出关于m 的方程，要分类谈论，以防遗漏．。

人教版九年级上册数学同步练习《二次函数的图象和性质》(习题+答案)

22.1 二次函数的图象和性质内容提要1.一般地，形如2y ax bx c =++（,,a b c 是常数，0a ≠）的函数叫做二次函数.其中，x 是自变量，a ，b ，c 分别是函数表达式的二次项系数、一次项系数和常数项.2.二次函数()20y ax bx c a =++≠的图象为抛物线，叫做抛物线2y ax bx c =++.3.二次函数()()20y a x h k a =-+≠的图象与性质：（1）二次函数()()20y a x h k a =-+≠的图象都可以由抛物线2y ax =向左（右）向上（下）平移得到，平移的方向、距离要根据h ，k 的值来决定.（2）抛物线()2y a x h k =-+的顶点为(),h k .当0a >时，开口向上；当0a <时，开口向下.对称轴为直线x h =.（3）二次函数()()20y a x h k a =-+≠的性质：①当0a >，在对称轴左侧()x h <，y 随着x 的增大而减小；在对称轴右侧()x h >，y 随着x 的增大而增大；当x h =时，y k =最小.②当0a <，在对称轴左侧()x h <，y 随着x 的增大而增大；在对称轴右侧()x h >，y 随着x 的增大而减小；当x h =时，y k =最大.4.研究二次函数()20y ax bx c a =++≠的图象特征和性质，一般都用配方法将二次函数的表达式转化为()2y a x h k =-+的形式.若问题只要求对称轴或顶点坐标，也可以直接利用顶点坐标公式计算.5.用描点法画二次函数的图象，一般采用“五点法”（顶点及抛物线上的两组对称点）；若只需画二次函数的大致图象，且抛物线与x 轴有两个交点时，可用“四点法”（顶点及抛物线与坐标轴的三个交点）.6.研究与二次函数相关的实际问题，常常需要结合图象，运用“数形结合”的方法解决.7.求二次函数的解析式，一般采用“待定系数法”. 22.1.1 二次函数基础训练1．下列函数中是二次函数的为（） A ．31y x =-B ．231y x =-C ．()221y x x =+-D ．323y x x =+-2．若函数()23y a x x a =-++是二次函数，那么a 不可以取（） A ．0B ．1C ．2D ．33．下列问题中的两个变量，能构成二次函数关系的是（） A ．在一定时间内，汽车行驶的速度与行驶路 B ．底边长度一定，三角形的面积与高 C ．正方体的体积与边长D ．计算圆的面积时，面积与半径的关系4．已知二次函数2y ax c =+，当2x =时，9y =；当3x =时，19y =，则a c +的值是（） A ．4B ．2C ．1D ．35．若二次函数2y ax =的图象经过点()2,4P -，则该图象必经过点（） A ．()2,4B ．()2,4--C ．()4,2-D ．()4,2- 6．二次函数()()31y x x =+-化为一般形式后一次项系数为.7.在半径为4的圆中，挖去一个长为a 、宽为1a -的矩形，则余下部分的面积y 与a 的函数关系式为.8.正方形对角线长为x cm ，面积为y 2cm ，则y 与x 的函数关系式是.9.张燕存入银行人民币500元，年利率为x ，一年到期后，银行将本金和利息自动按一年定期储蓄转存，那么两年后的本息和y 与x 的函数关系式是.10.已知函数()()222231y m m x m x m =--+-+.（1）当y 是x 的一次函数时，求m 的值并写出函数解析式；（2）当y 是x 的二次函数时，求m 的取值范围.22.1.2 二次函数2y ax =的图象和性质基础训练1．函数23y x =-的图象开口向，对称轴是，顶点是 .2.已知抛物线()20y ax a =≠经过点()2,8-，则a =.3.把函数22y x =-的图象沿x 轴翻折，得到的图象的解析式是 .4.函数2y x =，22y x =-图象的开口大小分别记为A ，B ，则A 与B 的大小关系为.5.若直线y ax =经过第一、三象限，则抛物线2y ax =（） A ．开口向上，且当0x <时，y 随x 的增大而增大 B ．开口向上，且当0x >时，y 随x 的增大而增大 C ．开口向下，且当0x <时，y 随x 的增大而增大 D ．开口向下，且当0x >时，y 随x 的增大而增大 6．已知二次函数2y ax =，下列说法不正确的是（） A ．对称轴为y 轴B ．当0a <，0x ≠时，y 总为负值C ．当0a >时，y 有最小值０D ．当0a <，0x <时，y 随x 的增大而减小７．已知点()11,x y ，()22,x y ，()33,x y 都在函数22y x =-的图象上，且1230x x x >>>，则（） A ．123y y y << B ．132y y y << C ．321y y y <<D ．213y y y <<８．苹果熟了，从树上落下所经过的路程s 与下落的时间t 满足212s gt =（g 是不为０的常数），则s 与t 的函数图象大致是（）9．函数()20y ax a =≠与直线y x =-交于点()1,b . （1）求a ，b 的值；（2）画出此二次函数的图象；x…2-1-0 1 2 …y……（3）结合图象，写出这个二次函数的性质.22.1.3二次函数()2=-+的图象和性质y a x h k基础训练（1）二次函数2=+的图象和性质y ax k1.抛物线2y x=-的顶点坐标为；当x时，y随x的增大而减少.212.请写出一个开口向上，并且与y轴交于点()0,1的抛物线的解析式y=.3.将抛物线23y x=+的图象向上平移1个单位，则平移后的抛物线的解析式为. 4．函数21=+的图象大致是（）y x5．已知二次函数21=-的图象开口向下，则直线1y ax=-经过的象限是（）y axA．第一、二、三象限B．第一、二、四象限C ．第一、三、四象限D ．第二、三、四象限6．抛物线21y x 2=-+的对称轴是（） A ．直线12x =B ．直线12x =-C ．y 轴D ．直线2x =7．对于抛物线231y x =-，下列说法不正确的是（） A ．向上平移一个单位可得到抛物线23y x = B ．当0x =时，函数有最小值1- C ．当0x <时，y 随x 的增大而增大 D ．与抛物线231y x =-+关于x 轴对称8．（1）在同一坐标系中，画出下列函数的图象，并写出它们共同的性质：22y x =-； 21y x 2=-+； 221y x =--.x… 2- 1- 0 1 2 … 22y x =- … … 221y x =-+ … … 221y x =--……（2）写出抛物线2y ax k =+与2y ax =的关系.基础训练（2）二次函数()2y a x h =-的图象和性质1.函数()221y x =-的图象的对称轴是，顶点坐标是 .2.函数()221y x =-+的图象可以由函数22y x =-的图象向平移1个单位得到；当x时，y 有最大值是.3.一个顶点在x 轴上的抛物线，其形状和开口方向与抛物线212y x =的相同，并且对称轴是直线2x =，这个函数的解析式是.4.将抛物线2y x =-向右平移2个单位后，得到的抛物线的解析式是（） A ．()22y x =-+ B ．22y x =-+ C ．()22y x =--D ．22y x =--5．如果y kx b =+的图象在第一、二、三象限内，那么函数()2y k x b =-的图象大致是（）6．抛物线()21y x =-与直线1y x =-在同一坐标系中交点的个数为（） A ．0个B ．1个C ．2个D ．无法确定7．（1）在同一坐标系中画出下列函数的图象：2y x =-；()22y x =-+；()22y x =--.x… 4-3-2- 1- 0 1 2 3 4 … 2y x =- …… ()22y x =-+……()22y x =--… …（2）写出抛物线()2y a x h =-与2y ax =的关系.基础训练（3）二次函数()2y a x h k =--的图象和性质1．抛物线()2534y x =+-的对称轴是，顶点坐标是 . 2.二次函数()2425y x =-++，当x =时，y 有最大值是；当x时，y 随x 的增大而增大.3.将抛物线24y x =-先向右平移2个单位，再向下平移1个单位，得到的抛物线的解析式为.4.已知抛物线()21433y x =--与x 轴的一个交点坐标为()1,0，则抛物线与x 轴的另一个交点的坐标是（） A ．()5,0B ．()6,0C ．()7,0D ．()8,05．在不同坐标系中画出下列函数的图象：（1）()2211y x =+-；（2）()21252y x =+-.6．写出抛物线()2y a x h k =-+与()2y a x h =-及2y ax =的关系.7.已知抛物线()232y a x =-+经过点()1,2-. （1）求a 的值；（2）若点()1,A m y ，()2,B n y ()3m n <<都在该抛物线上，试比较1y 与2y 的大小.8.如图是一个抛物线形拱桥的示意图，桥的跨度AB 为100米，支撑桥的是一些等距的立柱，相邻立柱间的水平距离为10米（不考虑立柱的粗细），其中距A 点10米处的立柱EF 的高度为3.6米.（1）以AB 中点O 为原点，AB 所在直线为x 轴建立直角坐标系，求抛物线顶点C 的坐标；（2）求与OC 相邻的立柱的高.22.1.4 二次函数2y ax bx c =++的图象和性质基础训练（1）二次函数2y ax bx c =++的顶点坐标与配方法1．二次函数221y x x =--+化成()2y a x h k =-+的形式是.2.抛物线2y ax bx c =++的顶点是()2,1A ，且经过点()1,0B ，则抛物线的函数关系式为.3.函数243y x x =-+，当x =时，y 有最小值是；当x时，y 随x 的增大而减小.4.如图，在平面直角坐标系中，抛物线所表示的函数解析式为()22y x h k =--+，则下列结论正确的是（） A ．0h >，0k > B ．0h <，0k > C ．0h <，0k <D ．0h >，0k <5．抛物线24y x x =-的对称轴是直线（）. A ．2x =-B ．4x =C ．2x =D ．4x =-6．抛物线2221y x ax a a =-+++的顶点在第二象限，则常数a 的取值范围是（） A ．10a -<<B ．1a >C ．12a -<<D ．1a <-或2a >7．二次函数2y ax bx c =++的图象如图所示，则一次函数y bx a =+的图象不经过（） A ．第一象限B ．第二象限C ．第三象限D ．第四象限8．用二次函数的顶点坐标公式求下列函数的顶点坐标. （1）221y x x =--；（2）2243y x x =-++.9．先将下列函数解析式化为()2y a x h k =-+形式，然后在不同坐标系内画出图象. （1）24y x x =-+；（2）2361y x x =++.基础训练（2）二次函数2y ax bx c =-+的图象和性质1．抛物线2253y x x =+-的对称轴是直线；顶点坐标是，与y 轴的交点坐标是.2.已知函数26y x x m =-+的最小值为1，那么m 的值为 .3.已知抛物线265y x x =-+的图象如图所示，当0y =时，x =.4.二次函数223=--的图象如图所示.当0y x xy<时，自变量x的取值范围是.5.二次函数2=++的图象如图所示，那么关于此二次函数的下列四个结论：y ax bx c①0a<；②0c>；③函数有最大值；④在对称轴左侧，y随x增大而增大.其中正确的结论有（）A．1个B．2个C．3个D．4个6．在同一平面直角坐标系中，函数2=+与y bx ay ax bx=+的图象可能是（）7．将抛物线2=-++先向左平移2个单位，再向上平移1个单位.y x x365（1）求平移后抛物线的解析式；（2）求平移后抛物线的对称轴和抛物线与y轴的交点坐标；（3）在（1）的条件下，求当x 取何值时，y 随x 的增大而减小？8.如图，抛物线()20y ax bx c c =++≠过点()1,0-和点()0,3-，且顶点在第四象限，设P a b c =++，求P 的取值范围.基础训练（3）用待定系数法求二次函数的解析式1.若二次函数2y x bx c =++，当2x =时，0y =；当1x =-时，3y =，则这个二次函数的解析式为.2.已知二次函数2y x bx c =++，当2x =时，0y =；当1x =-时，3y =，则这个二次函数的解析式为.3.抛物线的顶点在原点，且过点()3,27-，则这条抛物线的解析式为.4.已知二次函数的图象如图所示. （1）这个二次函数的解析式是；（2）根据图象回答：当x时，0y >.5.已知二次函数22y x bx =+-的图象与x 轴的一个交点为()1,0，则它与x 轴的另一个交点坐标是（） A ．()1,0B ．()2,0C ．()2,0-D ．()1,0-6．已知二次函数图象经过()1,0，()2,0和()0,2三点，则该函数的解析式是（ A ．222y x x =++ B ．232y x x =-+ C ．232y x x =++D ．223y x x =-+7．在下列条件下，分别求二次函数的解析式：（1）已知抛物线2y ax bx c =++与23y x =-形状相同，开口方向相反，顶点坐标为()2,4-；（2）当3x =时，最小值5y =，且过点()1,11；（3）对称轴为y 轴，且经过点()2,3，()1,6-.8.如图，抛物线()214y a x =-+与x 轴交于点A ，B ，与y 轴交于点C .过点C 作CD x ∥轴，交抛物线的对称轴于点D ，连接BD .已知点A 的坐标为()1,0-. （1）求该抛物线的解析式；（2）求梯形COBD 的面积.能力提高1．抛物线2251y ax x a =+-+过坐标原点，且开口方向向上，则a 的值是 .2.在二次函数221y x x =-++的图象中，若y 随x 的增大而增大，则x 的取值范围是.3.抛物线经过点()2,6-和()4,6，则抛物线的对称轴是（）4.已知二次函数222y x mx =++，当2x >时，y 随x 值的增大而增大，则实数m 的取值范围是.5.若抛物线22y x x c =-+与y 轴的交点为()0,3-，则下列说法不正确的是（） A ．抛物线开口向上B ．抛物线的对称轴是直线1x =C ．当1x =时，y 的最大值为4-D ．抛物线与x 轴的交点为()1,0-，()3,06．已知0b <，二次函数221y ax bx a =++-的图象为下列四个图象之一，试根据图象分析a 的值应等于（）7．二次函数()223y x =-++在43x -≤≤-范围内的最大值是 . 8.抛物线283y x x 2=-+关于x 轴对称的抛物线的解析式是.9.如图，在平面直角坐标系中，抛物线23y ax =+与y 轴交于点A ，过点A 与x 轴平行的直线交抛物线213y x =于点B ，C ，求BC 的长度.10.在关于,x y 的二元一次方程组2,21x y a x y +=⎧⎨-=⎩中，（1）若3a =，求方程组的解；（2）若()3S a x y =+，当a 为何值时，S 有最小值？是多少？11.如图，抛物线2y ax bx c =++经过原点，与x 轴相交于点()8,0E ，抛物线的顶点A 在第四象限，点A 到x 的距离4AB =，点(),0P m 在线段OB 上，连接PA ，将线段PA 绕点P 逆时针旋转90︒得到线段PC ，过点C 作y 轴的平行线交x 轴于点G ，交抛物线于点D ，连接BC 和AD .（1）求抛物线的解析式；（2）求点C 的坐标（用含m 的代数式表示）；（3）当四边形ABCD 是平行四边形时，求点P 的坐标.拓展探究1.在平面直角坐标系xOy 中，抛物线()2210y mx mx m m =-+->与x 轴的交点为A ，B . （1）求抛物线的顶点坐标.（2）横、纵坐标都是整数的点叫做整点. ①当1m =时，求线段AB 上整点的个数；②若抛物线在点A ，B 之间的部分与线段AB 所围成的区域内（包括边界）恰有6个整点，结合函数的图象，求m 的取值范围.2.已知关于x 的一元二次方程()2240x a x a +++=.（1）求证：无论a 为任何实数，此方程总有两个不相等的实数根；（2）抛物线()21:24C y x a x a =+++与x 轴的一个交点的横坐标为2a，其中0a ≠，将抛物线1C 向右平移14个单位，再向上平移18个单位，得到抛物线2C ，求抛物线2C 的解析式；（3）点(),A m n 和(),B n m 都在（2）中抛物线2C 上，且A ，B 两点不重合，求代数式m n +的值.22.1 参考答案：22.1.1 二次函数基础训练1．B 2．D 3．D 4．D 5．A 6．2 7．216y a a π=-++ 8．212y x =9．2500(1)y x =+ 10．（1）13m =，21m =-，29y x =+或21y x =-+ （2）3m ≠且1m ≠- 22.1.2 二次函数2y ax =的图象和性质1．向下 y 轴坐标原点 2．2- 3．22y x = 4．A B > 5．B 6．D 7．A 8．B 9．（1）1a =-，1b =- （2）略（3）当0x >时，y 随x 的增大而减小；当0x <时，y 随x 的增大而增大；当0x =时，函数有最大值，是0．22.1.3 二次函数2()y a x h k =-+的图象与性质基础训练（1）1．(0,1)- 0< 2．答案不唯一 3．24y x =+ 4．A 5．D 6．C 7．C8．（1）图略，共同的性质有：开口向下；对称轴都是y 轴；在对称轴左边，y 随x 的增大而增大；在对称轴右边，y 随x 的增大而减小等．（2）开口对称轴相同，抛物线2y ax k =+由2y ax =向上平称k 个单位得到基础训练（2）1．直线1x = (1,0) 2．左 1=- 0 3．21(2)2y x =- 4．C 5．D 6．C7．（1）略（2）抛物线2y ax =向右平移h 个单位得到2()y a x h =+ 基础训练（3）1．直线3x =- (3,4)-- 2．2- 5 2<- 3．24(2)1y x =--- 4．C 5．略 6．略 7．（1）1a =- （2）12y y < 8．（1）(0,10)C （2）9.6米 22.1.4 二次函数2y ax bx c =++的图象和性质基础训练（1）1．2(1)2y x =-++ 2．2(2)1y x =--+ 3．2 1- 2< 4．A 5．C 6．A 7．D 8．（1）(1,2)- （2）(1,5) 9．（1）2(2)4y x =--+ （2）23(1)2y x =+- 图略基础训练（2）1．54x =- 549,48⎛⎫-- ⎪⎝⎭ (0,3)- 2．10 3．1或5 4．13x -<< 5．D 6．C7．（1）23(1)9y x =-++ （2）对称轴为直线1x =-，与y 轴交点坐标为(0,6) （3）1x >-时，y 随x 增大而减小8．抛物线2(0)y ax bx c c =++≠过点(1,0)-和点(0,3)-，0a b c ∴=-+，3c -=，3b a ∴=-．当1x =时，2y ax bx c a b c =++=++，3326P a b c a a a ∴=++=+--=-．顶点在第四象限，0a >，30b a ∴=-<，3a ∴<，03a ∴<<，6260a ∴-<-<，即60P -<<．基础训练（3）1．3 4- 2．22y x x =- 3．23y x =- 4．（1）22y x x =- （2）2x >或0x < 5．C 6．B7．（1）23(2)4y x =++ （2）23(3)52y x =-+ （3）27y x =-+8．（1）2(1)4y x =--+ （2）8 能力提高1．1 2．1x < 3．直线1x = 4．2m ≥- 5．C 6．C 7．2 8．22(2)5y x =--+ 9．6BC = 10．（1）1,1x y =⎧⎨=⎩ （2）2(1)S a a a a =+=+，当12a =-时，S 有最小值，是14-．11．（1）2124y x x =- （2）(AAS)PCG APB ∆∆≌，4PG AB ∴==，CG PB =． (,0)P m ，4PB m ∴=-，(4,0)G m +，(4,4)C m m ∴+-．（3）当四边形ABCD 是平行四边形时，CD AB =，AB CD ∥．AB x ⊥轴，CD x ∴⊥轴，∴点C ，D 的横坐标相同．把4x m =+代入2124y x =-得2144y m =-，21(4,4)4D m m ∴+-．21(4)(4)4CD m m ∴=---．又4CD AB ==，21(4)(4)=44m m ∴---，化简得24160m m +-=，225m =-+，225m =--（舍去），(225,0)P ∴-+．拓展探究1．（1）将抛物线表达式变为顶点式2(1)1y m x =--，则抛物线顶点坐标为(1,1)-．（2）①1m =时，抛物线表达式为22y x x =-，因此A ，B 的坐标分别为(0,0)和(2,0)，则线段AB 上的整点有(0,0)，(1,0)，(2,0)共3个；②抛物线顶点为(1,1)-，则由线段AB 之间的部分及线段AB 所围成的区域的整点的纵坐标只能为1-或者0，所以即要求AB 线段上（含AB 两点）必须有5个整点；又令抛物线表达式2210y mx mx m =-+-=，得到A ，B 两点坐标分别为1,0m ⎛⎫-⎪⎝⎭，1,0m ⎛⎫+ ⎪⎝⎭，即5个整点是以(1,0)为中心向两侧分散，进而得到23m≤<，1194m ∴<≤．2．（1）22(4)4216a a a ∆=+-⨯=+，而20a ≥，2160a ∴+>，即0∆>．∴无论a 为任何实数，此方程总有两个不相等的实数根．（2）抛物线1C 与x 轴的一个交点的横坐标为2a ，∴当2a x =时，0y =，22()(4)22a aa ∴⨯++⨯+ 0a =．化简得230a a +=，即(3)0a a +=．0a ≠，3a ∴=-．∴抛物线1C 的解析式为223y x x =+-．又22125232()48y x x x =+-=+-．因此，抛物线1C 的顶点为125(,)48--．由题意得平移后抛物线2C 的顶点为(0,3)-，∴抛物线2C 的解析式223y x =-．（3）点(,)A m n 和(,)B n m 都在抛物线2C 上，223n m ∴=-，且223m n =-．222()n m m n ∴-=-．2()()n m m n m n ∴-=-+．()[2()1]0m n m n ∴-++=．A ，B 两点不重合，即m n ≠，2()10m n ∴++=．12m n ∴+=-．。

人教版九年级数学上册22.1二次函数的图像和性质同步练习附答案解析(三)

22.1二次函数的图像和性质同步练习(三)一、单项选择题（本大题共有15小题，每小题3分，共45分）1、二次函数的图象如图所示，则下列结论正确的是( )A.B.C.D.2、当取何值时，代数式的值最小（）A.B.C.D.3、已知二次函数的图像如图所示，记，.则下列选项正确的是（）.A. 的大小关系不能确定B.C.D.4、对于二次函数由下列四个结论：它的对称轴是直线；设，则当时，有它的图像与轴的两个交点是和；当时，其中正确的结论的个数是（）.A.B.C.D.5、若将抛物线的图像绕原点旋转，则旋转后的抛物线的关系式（）A.B.C.D.6、如图，在矩形中，，，点从点出发，沿边向点以的速度移动，同时点从点出发，沿以的速度移动，分别达到、两点就停止运动，则的面积最大时，所用时间为（）.A.B.C.D.7、二次函数的图象经过点，则的值是（）A.B.C.D.8、已知二次函数，当时，函数值为；当时，函数值为，若，则下列表达式正确的是（）A.B.C.D.9、在平面直角坐标系中，二次函数的图象如图所示，点，是该二次函数图象上的两点，其中，则下列结论正确的是（）A. 的最小值是B. 的最小值是C.D.10、点，，均在二次函数的图象上，则，，的大小关系是（）A.B.C.D.11、二次函数的图象如图所示，那么一次函数的图象大致是（）A.B.C.D.12、某生产不锈钢的工厂2016年上半年共生产吨不锈钢，2016年下半年的产量比2016年上半年的增产倍，2017年上半年的产量比2016年下半年的增产倍，则2017年上半年不锈钢的产量与之间的函数解析式为（）A.B.C.D.13、个球队进行单循环比赛（参加比赛的任何一只球队都与其他所有的球队各赛一场），总的比赛场数为，则有（）A.B.C.D.14、若（其中是常数）为二次函数，则（）A. 均不为B. ，且C.D. ，或15、若二次函数的与的部分对应值如下表，则当时，的值为（）A.B.C.D.二、填空题（本大题共有5小题，每小题5分，共25分）16、如图是二次函数的图象的一部分，图象过点，对称轴为直线，给出四个结论：①；②；③；④，其中正确结论的序号是．17、若抛物线与轴只有一个交点，且过点、，则 .18、如果抛物线经过点、，那么的值是 .19、图，在平面直角坐标系中，抛物线与轴交于点，过点与轴平行的直线交抛物线于点、，则的长为．20、若关于的方程有两个实数根、，则的最小值为__________．三、解答题（本大题共有3小题，每小题10分，共30分）21、求抛物线的顶点和对称轴．22、如图，在平面直角坐标系中，抛物线与轴交于两点（点在点的左侧），与轴交于点，顶点为，对称轴与轴交于点，过点的直线交抛物线于两点，点在轴的右侧．(1) 求的值及点的坐标；(2) 当直线将四边形分为面积比为的两部分时，求直线的函数表达式；23、如图，有一段长的旧围墙，现打算利用该围墙的一部分（或全部）为一边，再用长的篱笆围成一块长方形场地．(1) 怎样围成一个面积为的长方形场地？(2) 长方形场地面积能达到吗？如果能，请给出设计方案，如果不能，请说明理由．22.1二次函数同步练习(三) 答案部分一、单项选择题（本大题共有15小题，每小题3分，共45分）1、二次函数的图象如图所示，则下列结论正确的是( )A.B.C.D.【答案】C【解析】解：由图象可知：开口向上，故，对称轴，故，图象与轴的交点在轴下方，故，故正确答案为： .2、当取何值时，代数式的值最小（）A.B.C.D.【答案】C【解析】解：因为，，所以当时，取最小值．故选：．3、已知二次函数的图像如图所示，记，.则下列选项正确的是（）.A. 的大小关系不能确定B.C.D.【答案】D【解析】解：抛物线开口向下，，对称轴在轴右边，，抛物线经过原点，，；时，，，，；当对称轴时，，，，，，.当对称轴时，，，，，，，.综上，可得.故正确答案是：.4、对于二次函数由下列四个结论：它的对称轴是直线；设，则当时，有它的图像与轴的两个交点是和；当时，其中正确的结论的个数是（）.A.B.C.D.【答案】B【解析】解：故它的对称轴是直线正确，直线的两旁部分增减性不一样，设，则当时，由错误，当，则，解得:,故它的图像与轴的两个交点是和正确，，抛物线开口向下，它的图像与轴的两个交点是和，当时，正确.故正确答案是.5、若将抛物线的图像绕原点旋转，则旋转后的抛物线的关系式（）A.B.C.D.【答案】D【解析】解：对于抛物线，将其旋转后，图形关于原点对称，得到的抛物线为，即．故正确答案是．6、如图，在矩形中，，，点从点出发，沿边向点以的速度移动，同时点从点出发，沿以的速度移动，分别达到、两点就停止运动，则的面积最大时，所用时间为（）.A.B.C.D.【答案】C【解析】解：设点、运动的时间为，的面积为，那么，，.，.由矩形可得，，.当时，取最大值.即的面积最大时，所用时间为.故正确答案为.7、二次函数的图象经过点，则的值是（）A.B.C.D.【答案】A【解析】解：二次函数的图象经过点，，．8、已知二次函数，当时，函数值为；当时，函数值为，若，则下列表达式正确的是（）A.B.C.D.【答案】B【解析】解：(1)当时，二次函数图象开口向上，，，无法确定的正负情况，．(2)当时，二次函数图象开口向下，，，无法确定的正负情况，，综上，表达式正确的是．9、在平面直角坐标系中，二次函数的图象如图所示，点，是该二次函数图象上的两点，其中，则下列结论正确的是（）A. 的最小值是B. 的最小值是C.D.【答案】A【解析】解：，则二次函数与轴的两个交点横坐标分别是，．又，该抛物线的顶点坐标是，对称轴．无法确定、两点离对称轴的远近，故无法判断与的大小；正确答案为的最小值是．10、点，，均在二次函数的图象上，则，，的大小关系是（）A.B.C.D.【答案】A【解析】解：，对称轴为，，在对称轴右侧，随的增大而减小，，，根据二次函数图象的对称性可知，与关于对称轴对称，故．11、二次函数的图象如图所示，那么一次函数的图象大致是（）A.B.C.D.【答案】D【解析】解：的图象的开口向上，，对称轴在轴的左侧，，，一次函数的图象经过一，二，三象限．故正确的选项应为12、某生产不锈钢的工厂2016年上半年共生产吨不锈钢，2016年下半年的产量比2016年上半年的增产倍，2017年上半年的产量比2016年下半年的增产倍，则2017年上半年不锈钢的产量与之间的函数解析式为（）A.B.C.D.【答案】D【解析】解：由题意得，，整理得，．13、个球队进行单循环比赛（参加比赛的任何一只球队都与其他所有的球队各赛一场），总的比赛场数为，则有（）A.B.C.D.【答案】D【解析】解：根据支球队举行比赛，每个球队与其他队比赛场，由于是单循环比赛，则比赛的总场数为：．14、若（其中是常数）为二次函数，则（）A. 均不为B. ，且C.D. ，或【答案】C【解析】解：根据题意得当时，（其中是常数）为二次函数．15、若二次函数的与的部分对应值如下表，则当时，的值为（）A.B.C.D.【答案】D【解析】解：设二次函数的解析式为，当或时，，由抛物线的对称性可知，，，把代入得，，二次函数的解析式为，当时，．二、填空题（本大题共有5小题，每小题5分，共25分）16、如图是二次函数的图象的一部分，图象过点，对称轴为直线，给出四个结论：①；②；③；④，其中正确结论的序号是．【答案】①②④【解析】解：①抛物线与轴正半轴，，①正确；②抛物线与轴有两个不相等的实数根，，，②正确；③抛物线对称轴为直线，，，③错误；④抛物线对称轴为直线，且点的坐标为，抛物线与轴另一交点的坐标为，当时，，④正确．综上所述：正确结论的序号是①②④．故答案是：①②④．17、若抛物线与轴只有一个交点，且过点、，则 .【答案】9【解析】解：由抛物线与轴只有一个交点有，即，又因为、得，点、关于对称轴对称，，将点代入抛物线解析式得：正确答案是：.18、如果抛物线经过点、，那么的值是 .【答案】4【解析】解：把点代入得,把点代入得，正确答案是：.19、图，在平面直角坐标系中，抛物线与轴交于点，过点与轴平行的直线交抛物线于点、，则的长为．【答案】6【解析】解：抛物线与轴交于点，点坐标为．当时，，解得，点坐标为，点坐标为，．20、若关于的方程有两个实数根、，则的最小值为__________．【答案】【解析】由题意知，方程有两个实数根，则，，；当时，有最小值；，成立；最小值为．三、解答题（本大题共有3小题，每小题10分，共30分）21、求抛物线的顶点和对称轴．【解析】解：，抛物线的顶点坐标为，对称轴是．故答案是：，．22、如图，在平面直角坐标系中，抛物线与轴交于两点（点在点的左侧），与轴交于点，顶点为，对称轴与轴交于点，过点的直线交抛物线于两点，点在轴的右侧．(1) 求的值及点的坐标；【解析】解：抛物线与轴交于点，，解得，，当时，有，，．(2) 当直线将四边形分为面积比为的两部分时，求直线的函数表达式；【解析】解：，，四边形梯形．从面积分析知，直线只能与边或相交，所有有两种情况：①当直线边相交于点时，则，，，点，过点和的直线的解析式为．②当直线边相交于点时，同理可得点，过点和的直线的解析式为．综上所述，直线的函数表达式为或．23、如图，有一段长的旧围墙，现打算利用该围墙的一部分（或全部）为一边，再用长的篱笆围成一块长方形场地．(1) 怎样围成一个面积为的长方形场地？【解析】解：设，则，依题意得：，整理得，解得，，当时，；当时，（不合题意舍去）∴能围成一个长，宽的长方形场地．(2) 长方形场地面积能达到吗？如果能，请给出设计方案，如果不能，请说明理由．【解析】解：设，则，依题意得，整理得故方程没有实数根，长方形场地面积不能达到．。

人教版九年级数学 22.1 二次函数的图象和性质同步训练(含答案)

人教版九年级数学 22.1 二次函数的图象和性质同步训练一、选择题（本大题共10道小题）1. 对抛物线y ＝－x 2＋2x －3而言，下列结论正确的是( )A ．与x 轴有两个交点B ．开口向上C ．与y 轴的交点坐标是(0，3)D ．顶点坐标是(1，－2)2. (2019•雅安)在平面直角坐标系中，对于二次函数22()1y x =-+，下列说法中错误的是A ．y 的最小值为1B ．图象顶点坐标为(2，1)，对称轴为直线2x =C ．当2x <时，y 的值随x 值的增大而增大，当2x ≥时，y 的值随x 值的增大而减小D ．它的图象可以由2y x 的图象向右平移2个单位长度，再向上平移1个单位长度得到3.已知直线y ＝bx －c 与抛物线y ＝ax 2＋bx ＋c 在同一直角坐标系中的图象可能是( )4.如果抛物线的顶点坐标是(3，－1)，与y 轴的交点坐标是(0，－4)，那么这条抛物线的解析式是( ) A ．y ＝－13x 2－2x －4 B ．y ＝－13x 2＋2x －4 C ．y ＝－13(x ＋3)2－1 D ．y ＝－x 2＋6x －125.将抛物线y＝x2－6x＋5向上平移2个单位长度，再向右平移1个单位长度后，得到的抛物线的解析式是( )A．y＝(x－4)2－6 B．y＝(x－1)2－3C．y＝(x－2)2－2 D．y＝(x－4)2－26. 如图，抛物线y=ax2+bx+c(a≠0)与x轴交于点(-3，0)，其对称轴为直线x=-.结合图象分析下列结论:①abc>0;②3a+c>0;③当x<0时，y随x的增大而增大;④一元二次方程cx2+bx+a=0的两根分别为x1=-，x2=;⑤<0;⑥若m，n(m<n)为方程a(x+3)·(x-2)+3=0的两个根，则m<-3，n>2，其中正确的结论有()A.3个B.4个C.5个D.6个7. 二次函数y＝ax2＋bx＋c的图象如图所示，下列结论中正确的有()①abc<0；②b2－4ac<0；③2a>b；④(a＋c)2<b2.A．1个B．2个C．3个D．4个8.抛物线y＝x2＋bx＋c(其中b，c是常数)过点A(2，6)，且抛物线的对称轴与线段y ＝0(1≤x≤3)有交点，则c的值不可能是( )A. 4B. 6C. 8D. 109.如图，△ABC是等腰直角三角形，∠A＝90°，BC＝4，点P是△ABC边上一动点，沿B→A→C的路径移动．过点P作PD⊥BC于点D，设BD＝x，△BDP的面积为y，则下列能大致反映y与x函数关系的图象是( )10.如图，边长为2的等边△ABC和边长为1的等边△A′B′C′，它们的边B′C′，BC位于同一条直线l上，开始时，点C′与B重合，△ABC固定不动，然后把△A′B′C′自左向右沿直线l平移，移出△ABC外(点B′与C重合)停止，设△A′B′C′平移的距离为x ，两个三角形重合部分的面积为y，则y关于x的函数图象是( )二、填空题（本大题共7道小题）11. 已知函数y＝－x2－2x，当________时，函数值y随x的增大而增大．12. 已知二次函数y＝x2＋bx＋c中，函数值y与自变量x的部分对应值如下表：x …－1 0 1 2 3 4 …y …10 5 2 1 2 5 …则该二次函数的解析式为____________________．13. 抛物线y＝ax2＋bx＋c经过点A(－3，0)，对称轴是直线x＝－1，则a＋b＋c ＝________．14. 如图，已知抛物线过A，B，C三点，点A的坐标为(－1，0)，点B的坐标为(3，0)，且3AB＝4OC，则此抛物线的解析式为__________________．15. (2019•徐州)已知二次函数的图象经过点(2,2)P ，顶点为(0,0)O 将该图象向右平移，当它再次经过点P 时，所得抛物线的函数表达式为__________．16.如图，抛物线y ＝ax 2＋bx ＋c 与x 轴相交于点A ，B (m ＋2，0)，与y 轴相交于点C ，点D 在该抛物线上，坐标为(m ，c )，则点A 的坐标是________．17. 如图，抛物线y ＝ax 2＋bx ＋c(a ，b ，c 是常数，a≠0)与x 轴交于A ，B 两点，顶点为P(m ，n)．给出下列结论：①2a ＋c ＜0；②若(－32，y 1)，(－12，y 2)，(12，y 3)在抛物线上，则y 1＞y 2＞y 3；③若关于x 的方程ax 2＋bx ＋k ＝0有实数解，则k ＞c －n ；④当n ＝－1a 时，△ABP 为等腰直角三角形．其中正确的结论是________．(填序号)三、解答题（本大题共4道小题）18. 已知函数y ＝(m ＋3)xm 2＋m －4＋3.(1)当m 取何值时，y 是x 的二次函数？ (2)当m 取何值时，y 是x 的一次函数？19. 如图，已知二次函数y＝x2＋ax＋3的图象经过点P(－2，3)．(1)求a的值和图象的顶点坐标．(2)点Q(m，n)在该二次函数的图象上：①当m＝2时，求n的值；②若点Q到y轴的距离小于2，请根据图象直接写出n的取值范围．20. 如图，已知抛物线的顶点为A(1，4)，与y轴交于点B(0，3)，与x轴交于C，D两点，点P是x轴上的一个动点．(1)求此抛物线的解析式；(2)当PA＋PB的值最小时，求点P的坐标．21. 如图所示，抛物线y＝ax2－5x＋4a与x轴相交于点A，B，且过点C(5，4)．(1)求a的值和该抛物线顶点P的坐标；(2)若Q是横轴上方抛物线上的点，且S△QAB＝S△P AB，求点Q的坐标．人教版九年级数学 22.1 二次函数的图象和性质同步训练-答案一、选择题（本大题共10道小题） 1. 【答案】D2. 【答案】C【解析】二次函数22()1y x =-+，10a =>，∴该函数的图象开口向上，对称轴为直线2x =，顶点为(2,1)，当2x =时，y 有最小值1，当2x >时，y 的值随x 值的增大而增大，当2x <时，y 的值随x 值的增大而减小；故选项A 、B 的说法正确，C 的说法错误；根据平移的规律，2yx 的图象向右平移2个单位长度得到2(2)y x =-，再向上平移1个单位长度得到22()1y x =-+，故选项D 的说法正确，故选C ．3.【答案】C 【解析】在A 中，抛物线的对称轴在y 轴右边，∴－b 2a＞0，∵a ＞0，∴b ＜0；而从一次函数图象知b ＞0，∴选项A 错误；在B 中，抛物线对称轴－b2a＞0，∵a ＜0，∴b ＞0；而从一次函数图象知b ＜0，∴选项B 错误；在C 中，抛物线的对称轴在y 轴左边，∴－b2a＜0，∵a ＞0，∴b ＞0；抛物线与y 轴负半轴相交，∴c ＜0；而从一次函数图象知b ＞0，－c ＞0，∴c ＜0，∴选项C 正确；在D 中，抛物线与y 轴的正半轴相交，c＞0，由一次函数图象知－c＞0，即c＜0，∴选项D错误．4. 【答案】B [解析] 设这条抛物线的解析式是y＝a(x－3)2－1. ∵抛物线与y轴的交点坐标是(0，－4)，∴－4＝9a－1，解得a＝－1 3，∴y＝－13(x－3)2－1，即y＝－13x2＋2x－4.故选B.5. 【答案】 D [解析] y＝x2－6x＋5＝(x－3)2－4，将其向上平移2个单位长度，再向右平移1个单位长度后，得y＝(x－3－1)2－4＋2，即y＝(x－4)2－2.6. 【答案】C[解析]①由图象可知a<0，b<0，c>0，∴abc>0，故①正确;②由于对称轴是直线x=-，∴a=b.∵图象与x轴的一个交点是(-3，0)，∴另一个交点是(2，0)，把(2，0)代入解析式可得4a+2b+c=0，∴6a+c=0，∴3a+c=-3a，∵a<0，∴-3a>0，∴3a+c>0，故②正确;③由图象可知当-<x<0时，y随x的增大而减小，∴当x<0时，y随x的增大而增大是错误的;④一元二次方程ax2+bx+c=0的两根为x1=-3，x2=2，∴一元二次方程cx2+bx+a=0的两根分别为x1=-，x2=，正确;⑤由图象顶点的纵坐标大于0可知，>0，∴<0，正确;⑥若m，n(m<n)为方程a(x+3)(x-2)+3=0的两个根，则a(x+3)(x-2)=-3，由图象可知，当y=-3时，m<-3，n>2，⑥正确，综上，正确的结论有5个，故选C.7. 【答案】A[解析] ①由抛物线的开口方向向下知a<0，由对称轴在y轴的左侧得a ，b 同号，∴b<0.由抛物线与y 轴交于正半轴得c>0，∴abc>0，故结论①错误．②由抛物线与x 轴有两个交点得b 2－4ac>0，故结论②错误．③由图象知对称轴x ＝－b 2a >－1得b2a <1；由a<0，结合不等式的性质三可得b>2a ，即2a<b ，故结论③错误．④由图象知：当x ＝1时，y<0，即a ＋b ＋c<0；当x ＝－1时，y>0，即a －b ＋c>0， ∴(a ＋b ＋c)(a －b ＋c)<0，即(a ＋c)2－b 2<0，∴(a ＋c)2<b 2.故结论④正确．故选A.8. 【答案】A【解析】由题知，对称轴与线段y ＝0(1≤x ≤3)有交点，则有1≤－b2≤3，可得到：－6≤b ≤－2，由抛物线经过点A (2，6)，代入可得4＋2b ＋c ＝6，∴b ＝2－c 2，∴－6≤2－c2≤－2, 解得6≤c ≤14，∴c 的值不可能是4. 9. 【答案】B 【解析】∵△ABC 是等腰直角三角形，∴∠A ＝90°，∠B ＝∠C ＝45°.(1)当0≤x ≤2时，点P 在AB 边上，△BDP 是等腰直角三角形，∴PD ＝BD ＝x ，y ＝12x 2(0≤x ≤2)，其图象是抛物线的一部分；(2)当2＜x ≤4时，点P 在AC 边上，△CDP 是等腰直角三角形，∴PD ＝CD ＝4－x，∴y ＝12BD ·PD ＝12x (4－x )(2＜x ≤4)，其图象也是抛物线的一部分．综上所述，两段图象均是抛物线的一部分，因此选项B 的图象能大致反映y 与x 之间的函数关系．10. 【答案】B 【解析】由题意知：在△A ′B ′C ′移动的过程中，阴影部分总为等边三角形．当0＜x ≤1时，边长为x ，此时y ＝12x ×32x ＝34x 2；当1＜x ≤2时，重合部分为边长为1的等边三角形，此时y ＝12×1×32＝34；当2＜x ≤3时，边长为3－x ，此时y ＝12(3－x )×32(3－x )．综上，这个分段函数的图象左边为开口向上的抛物线的一部分，中间为直线的一部分，右边为开口向上抛物线的一部分，且最高点为34.故选B.二、填空题（本大题共7道小题）11. 【答案】x ≤－1 【解析】∵函数y ＝－x 2－2x ，其图象的对称轴为x ＝－b2a＝－1，且a ＝－1<0，∴在对称轴的左边y 随x 的增大而增大，∴x ≤－1.12. 【答案】y ＝x2－4x ＋5[解析] 从表格中的数据可以看出，当x ＝1和x ＝3时，函数值y ＝2，可见，抛物线的顶点坐标为(2，1)，故可设二次函数的解析式为y ＝a(x －2)2＋1，再由二次函数图象过点(1，2)，得2＝a(1－2)2＋1，解得a ＝1，故二次函数的解析式为y ＝(x －2)2＋1，即y ＝x2－4x ＋5.13. 【答案】0[解析] ∵抛物线y ＝ax 2＋bx ＋c 经过点A(－3，0)，对称轴是直线x ＝－1，∴抛物线y ＝ax 2＋bx ＋c 与x 轴的另一交点的坐标为(1，0)， ∴a ＋b ＋c ＝0.14. 【答案】y ＝－x2＋2x ＋315. 【答案】21(4)2y x =- 【解析】设原来的抛物线解析式为：2y ax =(0)a ≠，把(2,2)P 代入，得24a =，解得12a =，故原来的抛物线解析式是：212y x =，设平移后的抛物线解析式为：21()2y x b =-，把(2,2)P 代入，得212(2)2b =-，解得0b =(舍去)或4b =，所以平移后抛物线的解析式是：21(4)2y x =-，故答案为：21(4)2y x =-．16.【答案】(－2，0)【解析】如解图，过D 作DM ⊥x 轴于点M ，∴M(m ，0)，又B(m ＋2，0)，∴MB ＝2，由C(0，c)，D(m ，c)知：OC ＝DM ，即点C 、D 关于对称轴对称，故点O 、M 也关于对称轴对称，∴OA ＝MB ＝2，∴A(－2，0)．17. 【答案】②④[解析] (1)当x ＝－1时，y ＝a －b ＋c ＞0.由x ＝－b 2a ＜12和a ＞0可得－b ＜a.∴0＜a －b ＋c ＜a ＋a ＋c ＝2a ＋c ，即2a ＋c ＞0，①错误； (2)结合图象易知②正确；(3)方程ax 2＋bx ＋k ＝0有实数解，即ax 2＋bx ＋c ＝c －k 有实数解．∵y ＝ax 2＋bx ＋c≥n ，∴c －k≥n ，即k≤c －n ，③错误；(4)设抛物线的解析式为y ＝－1n (x －m)2＋n(n ＜0)．令y ＝0，得－1n (x －m)2＋n ＝0.∴n 2－(x －m)2＝0，∴(n －x ＋m)(n ＋x －m)＝0.∴x 1＝m ＋n ，x 2＝m －n.AB ＝|x 1－x 2|＝－2n.设对称轴交x 轴于点H ，则AH ＝BH ＝PH ＝－n ，∴△ABP 为等腰直角三角形，④正确．三、解答题（本大题共4道小题）18. 【答案】解：(1)由题意，得⎩⎪⎨⎪⎧m 2＋m －4＝2，m ＋3≠0，解得m ＝2.(2)由题意，得⎩⎪⎨⎪⎧m 2＋m －4＝1，m ＋3≠0，解得m ＝－1±212.19. 【答案】解：(1)把点P(－2，3)代入y ＝x 2＋ax ＋3中，得a ＝2，∴y ＝x 2＋2x ＋3＝(x ＋1)2＋2， ∴图象的顶点坐标为(－1，2)． (2)①当m ＝2时，n ＝11.②点Q 到y 轴的距离小于2，∴|m|＜2，∴－2＜m ＜2，∴2≤n ＜11.20. 【答案】解：(1)∵抛物线的顶点坐标为(1，4)，∴设此抛物线的解析式为y ＝a(x －1)2＋4.∵抛物线过点B(0，3)，∴3＝a(0－1)2＋4，解得a ＝－1，∴y ＝－(x －1)2＋4，即此抛物线的解析式为y ＝－x2＋2x ＋3.(2)作点B 关于x 轴的对称点E(0，－3)，连接AE 交x 轴于点P ，此时PA ＋PB 的值最小．设直线AE 的解析式为y ＝kx ＋b ，则⎩⎨⎧k ＋b ＝4，b ＝－3，解得⎩⎨⎧k ＝7，b ＝－3，∴直线AE 的解析式为y ＝7x －3.当y ＝0时，x ＝37，∴当PA ＋PB 的值最小时，点P 的坐标为(37，0)．21. 【答案】解：(1)把(5，4)代入y ＝ax 2－5x ＋4a ，得25a －25＋4a ＝4，解得a ＝1. ∴该抛物线的解析式为y ＝x 2－5x ＋4.∵y ＝x 2－5x ＋4＝⎝ ⎛⎭⎪⎫x －522－94， ∴顶点P 的坐标为⎝ ⎛⎭⎪⎫52，－94. (2)∵S △QAB ＝S △PAB ，∴点Q 和点P 到横轴的距离相等，即它们纵坐标的绝对值相等．由(1)可知点P 的纵坐标是－94，∴点Q 的纵坐标是94.令x 2－5x ＋4＝94，解得x ＝5±3 22.5－3 22，94)或(5＋3 22，94)．∴点Q的坐标为(。

人教版九年级数学上册：二次函数的图象和性质同步练习附加答案

22.1.2 二次函数)0()(2≠+-=a k h x a y 的图象和性质（三）知识点:1、抛物线)0()(2≠+-=a k h x a y 的对称轴为，顶点坐标为。

2、抛物线)0()(2≠+-=a k h x a y 与抛物线)0(2≠=a ax y 的形状，位置，将抛物线)0(2≠=a ax y 进行平移可得到抛物线)0()(2≠+-=a k h x a y ，平移规律为：当0,0>>k h 时，将抛物线)0(2≠=a ax y 得到抛物线)0()(2≠+-=a k h x a y ；当0,0<>k h 时，将抛物线)0(2≠=a ax y 得到抛物线)0()(2≠+-=a k h x a y ；当0,0><k h 时，将抛物线)0(2≠=a ax y 得到抛物线)0()(2≠+-=a k h x a y ；当0,0<<k h 时，将抛物线)0(2≠=a ax y 得到抛物线)0()(2≠+-=a k h x a y ；3、抛物线)0()(2≠+-=a k h x a y 的图象特点：0>a 时，抛物线开口向，左右，顶点最； 0<a 时，抛物线开口向，左右，顶点最；一、选择题：1、抛物线21)1(22+--=x y 的顶点坐标为（） A 、（-1，21） B 、（1，21） C 、（-1，—21） D 、（1，—21）2、对于2)3(22+-=x y 的图象，下列叙述正确的是（）A 、顶点坐标为（-3,2）B 、对称轴是直线3-=yC 、当3≥x 时，y 随x 的增大而增大D 、当3≥x 时，y 随x 的增大而减小 3、将抛物线2x y =向右平移一个单位长度，再向上平移3个单位长度后，所得抛物线的解析式为（）A 、3)1(2++=x yB 、3)1(2+-=x yC 、3)1(2-+=x yD 、3)1(2--=x y 4、抛物线2)1(22-+-=x y 可由抛物线22x y -=平移得到，则下列平移过程正确的是（）A 、先向右平移1个单位，再向上平移2个单位B 、先向右平移1个单位，再向下平移2个单位C 、先向左平移1个单位，再向上平移2个单位D 、先向左平移1个单位，再向下平移2个单位5、如图，把抛物线y=x 2沿直线y=x 平移2个单位后，其顶点在直线上的A 处，则平移后的抛物线解析式是（）A 、y=（x+1）2-1B ．y=（x+1）2+1C ．y=（x-1）2+1D ．y=（x-1）2-1 6、设A （-1，1y ）、B （1，2y ）、C （3，3y ）是抛物线k x y +--=2)21(21上的三个点，则1y 、2y 、3y 的大小关系是（）A 、1y <2y <3yB 、2y <1y <3yC 、3y <1y <2yD 、2y <3y <1y7、若二次函数2()1y x m =--．当x ≤l 时，y 随x 的增大而减小，则m 的取值范围是（） A ．m =l B ．m >l C ．m ≥l D ．m ≤l8、二次函数n m x a y ++=2)(的图象如图所示，则一次函数n mx y +=的图象经过（）A 、第一、二、三象限B 、第一、二、四象限C 、第二、三、四象限D 、第一、三、四象限二、填空题：1、抛物线1)3(22-+-=x y 的对称轴是，顶点坐标是；当x 时，y 随x 的增大而增大，当x 时，y 随x 的增大而减小，当x 时，y 取最值为。

二次函数的图像和性质练习(含答案)

二次函数的图像和性质一、选择题（每题3分）1．下列四个函数中，一定是二次函数的是（）A ．21y x x=+ B ．y=ax 2+bx+c C ．y=x 2﹣（x+7）2 D ．y=（x+1）（2x ﹣1）【答案】D【解析】试题分析：因为形如y=ax 2+bx+c （0a ≠）的函数叫二次函数，所以选项A 、B 、C 错误，D 正确，故选：D ．考点：二次函数的概念.2．若函数y=-2(x-1)2+(a-1)x 2为二次函数，则a 的取值范围为（） A.a≠0 B.a≠1 C.a≠2 D.a≠3【答案】D ．【解析】试题分析：根据二次函数的定义化成一般式为()2342y a x x =-+-，则30a -≠3a ≠故选D ．考点：二次函数的定义．3.下列函数中，不是二次函数的是（）A ．y ＝1－x 2B ．y ＝2（x －1）2＋4C ．y ＝（x －1）（x ＋4）D ．y ＝（x －2）2－x 2【答案】D ．【解析】试题分析：选项A ，y=1-x 2=-x 2+1，是二次函数，选项A 正确；选项B ，y=2（x-1）2+4=2x 2-4x+6，是二次函数，选项B 正确；选项C ，y=（x-1）（x+4）=x 2+x-2，是二次函数，选项C 正确；选项 D ，y=（x-2）2-x 2=-4x+4，是一次函数，选项D 错误．故答案选D ．考点：二次函数的定义．二、填空题（每题3分）4.若函数y ＝（m －3）是二次函数，则m ＝______．【答案】5．【解析】试题分析：已知函数y ＝（m －3）是二次函数，可得且m －3≠0，解得m=-5．考点：二次函数的定义．5.．一个圆柱的高等于底面半径，写出它的表面积S 与底面半径r 的函数关系式为_________．【答案】S=4π2r【解析】试题分析：根据题意可得h=2r ，则S=2πrh=4π2r ．考点：二次函数的实际应用（时间：15分钟，满分25分）班级：___________姓名：___________得分：___________一、选择题（每题3分）1.下列函数中，不属于二次函数的是（）A ．y=（x ﹣2）2B ．y=﹣2（x+1）（x ﹣1）C ．y=1﹣x ﹣x 2D ．y=211x 【答案】D【解析】试题分析：整理一般形式后根据二次函数的定义判定即可：A 、整理为y=x 2﹣4x+4，是二次函数，不合题意；B 、整理为y=﹣2x 2+2，是二次函数，不合题意；C 、整理为y=﹣x 2﹣x+1，是二次函数，不合题意；D 、不是整式方程，符合题意．故选：D ．考点：二次函数的定义2．下列函数中属于二次函数的是（）A ．12-=x yB ．12-=ax yC ．222)1(2x x y --=D ．)2)(1(π+-=x x y【答案】D ．【解析】试题分析：A ．12-=x y 是一次函数，故本选项错误；B ．当0a =时，12-=ax y 不是二次函数，故本选项错误；C ．222)1(2x x y --==42x -+是一次函数，故本选项错误；D )2)(1(π+-=x x y 是二次函数，故本选项正确．故选D ．考点：二次函数的定义．3．若函数222(1)(1)y x a x =--+-为二次函数，则a 的取值范围为（）A ．0a ≠B ．1a ≠C ．2a ≠D ．3a ≠【答案】D ．【解析】试题分析：由原函数解析式得到：222(1)(1)y x a x =--+-=2(3)42a x x -+-．∵函数 222(1)(1)y x a x =--+-为二次函数，∴30a -≠，解得3a ≠．故选D ．考点：二次函数的定义．二、填空题（每题3分）4.在边长为16cm 的正方形铁皮上剪去一个圆，则剩下的铁皮的面积S （cm 2）与圆的半径r （cm ）之间的函数表达式为（不要求写自变量的取值范围）．【答案】2256r S π-=【解析】试题分析：剩下的面积为：正方形的面积-圆的面积=162-πr 2=256-πr 2故答案为：2256r S π-=考点：函数的表达式.5.．用长为8米的铝合金制成如图所示的窗框，若设窗框的宽为x 米，窗户的透光面积为S 平方米，则S 关于x 的函数关系式．【答案】S=x x 4232+-【解析】试题分析：设窗框的宽为x 米，则长为238x -米 ∴S=x x x x 4232382+-=⨯- 考点：实际问题抽象二次函数三、计算题（每题10分）6.已知，若函数2(1)3m y m x =-+是关于x 的一次函数．（1）求m 的值，并写出解析式；（2）若函数是关于x 的二次函数，求m 的值，．【答案】（1）1m =-；（2）m =．【解析】试题分析：（1）先根据一次函数的定义求出m 的值；（2）由22m =可得出m =试题解析：（1）∵函数2(1)3m y m x =-+是一次函数，∴21m =，解得1m =或1m =-，又∵10m -≠，∴1m ≠，∴1m =-，∴函数为：23y x =-+；m=可得出m=（2）由22考点：1．一次函数的定义；2．二次函数的定义．。

2.1二次函数的图像与性质同步练习3

人教版九年级数学上册二次函数的图象和性质复习同步练习题

北师大版九年级数学下册《二次函数的图像与性》 同步练习试题

人教版九年级数学上册二次函数图象和性质 同步练习(含答案)

人教版九年级上册 22.1 二次函数的图象和性质 同步练习 含答案

人教版 九年级数学上册 22.1 二次函数的图象和性质 同步训练(含答案)