2016年中考数学专题复习:折叠题(含答案)
2016年中考数学专题复习:折叠题(含答案)

2016年中考数学专题复习:折叠题1.如图,在矩形ABCD中,点E是AD的中点,∠EBC的平分线交CD于点F,将△DEF 沿EF折叠,点D恰好落在BE上M点处,延长BC、EF交于点N.有下列四个结论:①DF=CF;②BF⊥EN;③△BEN是等边三角形;④S△BEF=3S△DEF.其中,将正确结论的序号全部选对的是()A.①②③B.①②④C.②③④D.①②③④解答:解:∵四边形ABCD是矩形,∴∠D=∠BCD=90°,DF=MF,由折叠的性质可得:∠EMF=∠D=90°,即FM⊥BE,CF⊥BC,∵BF平分∠EBC,∴CF=MF,∴DF=CF;故①正确;∵∠BFM=90°﹣∠EBF,∠BFC=90°﹣∠CBF,∴∠BFM=∠BFC,∵∠MFE=∠DFE=∠CFN,∴∠BFE=∠BFN,∵∠BFE+∠BFN=180°,∴∠BFE=90°,即BF⊥EN,故②正确;∵在△DEF和△CNF中,,∴△DEF≌△CNF(ASA),∴EF=FN,∴BE=BN,但无法求得△BEN各角的度数,∴△BEN不一定是等边三角形;故③错误;∵∠BFM=∠BFC,BM⊥FM,BC⊥CF,∴BM=BC=AD=2DE=2EM,∴BE=3EM,∴S△BEF=3S△EMF=3S△DEF;故④正确.故选B.点评:此题考查了折叠的性质、矩形的性质、角平分线的性质以及全等三角形的判定与性质.此题难度适中,注意掌握数形结合思想的应用.2.如图,将矩形ABCD的一个角翻折,使得点D恰好落在BC边上的点G处,折痕为EF,若EB为∠AEG的平分线,EF和BC的延长线交于点H.下列结论中:①∠BEF=90°;②DE=CH;③BE=EF;④△BEG和△HEG的面积相等;⑤若,则.以上命题,正确的有()A.2个B.3个C.4个D.5个解答:解:①由折叠的性质可知∠DEF=∠GEF,∵EB为∠AEG的平分线,∴∠AEB=∠GEB,∵∠AED=180°,∴∠BEF=90°,故正确;②可证△EDF∽△HCF,DF>CF,故DE≠CH,故错误;③只可证△EDF∽△BAE,无法证明BE=EF,故错误;④可证△GEB,△GEH是等腰三角形,则G是BH边的中线,∴△BEG和△HEG的面积相等,故正确;⑤过E点作EK⊥BC,垂足为K.设BK=x,AB=y,则有y2+(2y﹣2x)2=(2y﹣x)2,解得x1=y(不合题意舍去),x2=y.则,故正确.故正确的有3个.故选B.点评:本题考查了翻折变换,解答过程中涉及了矩形的性质、勾股定理,属于综合性题目,解答本题的关键是根据翻折变换的性质得出对应角、对应边分别相等,然后分别判断每个结论,难度较大,注意细心判断.3.如图,矩形ABCD中,E是AD的中点,将△ABE沿BE折叠后得到△GBE,延长BG 交CD于F点,若CF=1,FD=2,则BC的长为()A.3B.2C.2D.2解答:解:过点E作EM⊥BC于M,交BF于N,∵四边形ABCD是矩形,∴∠A=∠ABC=90°,AD=BC,∵∠EMB=90°,∴四边形ABME是矩形,∴AE=BM,由折叠的性质得:AE=GE,∠EGN=∠A=90°,∴EG=BM,∵∠ENG=∠BNM,∴△ENG≌△BNM(AAS),∴NG=NM,∴CM=DE,∵E是AD的中点,∴AE=ED=BM=CM,∵EM∥CD,∴BN:NF=BM:CM,∴BN=NF,∴NM=CF=,∴NG=,∵BG=AB=CD=CF+DF=3,∴BN=BG﹣NG=3﹣=,∴BF=2BN=5,∴BC===2.故选B.点评:此题考查了矩形的判定与性质、折叠的性质、三角形中位线的性质以及全等三角形的判定与性质.此题难度适中,注意辅助线的作法,注意数形结合思想的应用.4.如图,两个正方形ABCD和AEFG共顶点A,连BE,DG,CF,AE,BG,K,M分别为DG和CF的中点,KA的延长线交BE于H,MN⊥BE于N.则下列结论:①BG=DE 且BG⊥DE;②△ADG和△ABE的面积相等;③BN=EN,④四边形AKMN为平行四边形.其中正确的是()A.③④B.①②③C.①②④D.①②③④解答:解:由两个正方形的性质易证△AED≌△AGB,∴BG=DE,∠ADE=∠ABG,∴可得BG与DE相交的角为90°,∴BG⊥DE.①正确;如图,延长AK,使AK=KQ,连接DQ、QG,∴四边形ADQG是平行四边形;作CW⊥BE于点W,FJ⊥BE于点J,∴四边形CWJF是直角梯形;∵AB=DA,AE=DQ,∠BAE=∠ADQ,∴△ABE≌△DAQ,∴∠ABE=∠DAQ,∴∠ABE+∠BAH=∠DAQ+∠BAH=90°.∴△ABH是直角三角形.易证:△CWB≌△BHA,△EJF≌△AHE;∴WB=AH,AH=EJ,∴WB=EJ,又WN=NJ,∴WN﹣WB=NJ﹣EJ,∴BN=NE,③正确;∵MN是梯形WGFC的中位线,WB=BE=BH+HE,∴MN=(CW+FJ)=WC=(BH+HE)=BE;易证:△ABE≌△DAQ(SAS),∴AK=AQ=BE,∴MN∥AK且MN=AK;四边形AKMN为平行四边形,④正确.S△ABE=S△ADQ=S△ADG=S▱ADQG,②正确.所以,①②③④都正确;故选D.点评:当出现两个正方形时,一般应出现全等三角形.图形较复杂,选项较多时,应用排除法求解.5.如图,在△ABC中,∠C=90°,将△ABC沿直线MN翻折后,顶点C恰好落在AB边上的点D处,已知MN∥AB,MC=6,NC=,则四边形MABN的面积是()A.B.C.D.解答:解:连接CD,交MN于E,∵将△ABC沿直线MN翻折后,顶点C恰好落在AB边上的点D处,∴MN⊥CD,且CE=DE,∴CD=2CE,∵MN∥AB,∴CD⊥AB,∴△CMN∽△CAB,∴,∵在△CMN中,∠C=90°,MC=6,NC=,∴S△CMN=CM•CN=×6×2=6,∴S△CAB=4S△CMN=4×6=24,∴S四边形MABN=S△CAB﹣S△CMN=24﹣6=18.故选C.点评:此题考查了折叠的性质、相似三角形的判定与性质以及直角三角形的性质.此题难度适中,解此题的关键是注意折叠中的对应关系,注意数形结合思想的应用.6.如图,D是△ABC的AC边上一点,AB=AC,BD=BC,将△BCD沿BD折叠,顶点C 恰好落在AB边的C′处,则∠A′的大小是()A.40°B.36°C.32°D.30°解答:解:连接C'D,∵AB=AC,BD=BC,∴∠ABC=∠ACB=∠BDC,∵△BCD沿BD折叠,顶点C恰好落在AB边的C′处,∴∠BCD=∠BC'D,∴∠ABC=∠BCD=∠BDC=∠BDC'=∠BC'D,∵四边形BCDC'的内角和为360°,∴∠ABC=∠BCD=∠BDC=∠BDC'=∠BC'D==72°,∴∠A=180°﹣∠ABC﹣∠ACB=36°.故选B.点评:本题考查了折叠的性质,解答本题的关键是掌握翻折前后的对应角相等,注意本题的突破口在于得出∠ABC=∠BCD=∠BDC=∠BDC'=∠BC'D,根据四边形的内角和为360°求出每个角的度数.7.如图,已知△ABC中,∠CAB=∠B=30°,AB=2,点D在BC边上,把△ABC沿AD 翻折使AB与AC重合,得△AB′D,则△ABC与△AB′D重叠部分的面积为()A.B.C.3﹣D.解答:解:过点D作DE⊥AB′于点E,过点C作CF⊥AB,∵△ABC中,∠CAB=∠B=30°,AB=2,∴AC=BC,∴AF=AB=,∴AC===2,由折叠的性质得:AB′=AB=2,∠B′=∠B=30°,∵∠B′CD=∠CAB+∠B=60°,∴∠CDB′=90°,∵B′C=AB′﹣AC=2﹣2,∴CD=B′C=﹣1,B′D=B′C•cos∠B′=(2﹣2)×=3﹣,∴DE===,∴S阴影=AC•DE=×2×=.故选A.点评:此题考查了折叠的性质,等腰三角形的性质、直角三角形的性质以及特殊角的三角函数问题.此题难度适中,注意掌握辅助线的作法,注意数形结合思想的应用,注意掌握折叠前后图形的对应关系.8.如图,已知△ABC中,∠CAB=∠B=30°,AB=,点D在BC边上,把△ABC沿AD 翻折,使AB与AC重合,得△AED,则BD的长度为()A.B.C.D.解答:解:作CF⊥AB于点F.∵∠CA B=∠B∴AC=BC,∴BF=AB=,在直角△BCF中,BC==2,在△CD E中,∠E=∠B=30°,∠ECD=∠CAB+∠B=60°,DE=BD,∴∠CDE=90°,设BD=x,则CD=DE=2﹣x,在直角△CDE中,tanE===tan30°=,解得:x=3﹣.故选B.点评:本题考查了图形的折叠,以及三线合一定理、三角函数,正确理解折叠的性质,找出图形中相等的线段、相等的角是关键.9.如图,在Rt△ABC中,∠C=90°,AC=,BC=1,D在AC上,将△ADB沿直线BD 翻折后,点A落在点E处,如果AD⊥ED,那么△ABE的面积是()A.1 B.C.D.解答:解:∵∠C=90°,AC=,BC=1,∴AB==2,∴∠BAC=30°∵△ADB沿直线BD翻折后,点A落在点E处,∴BE=BA=2,∠BED=∠BAD=30°,DA=DE,∵AD⊥ED,∴BC∥DE,∴∠CBF=∠BED=30°,在Rt△BCF中,CF==,BF=2CF=,∴EF=2﹣,在Rt△DEF中,FD=EF=1﹣,ED=FD=﹣1,∴S△ABE=S△ABD+S△BED+S△ADE=2S△ABD+S△ADE=2×BC•AD+AD•ED=2××1×(﹣1)+×(﹣1)(﹣1)=1.故选A.点评:本题考查了折叠问题:折叠前后两图形全等,即对应线段相等;对应角相等.也考查了勾股定理和含30度的直角三角形三边的关系.。
(完整版)中考数学几何图形折叠试题典题及解答
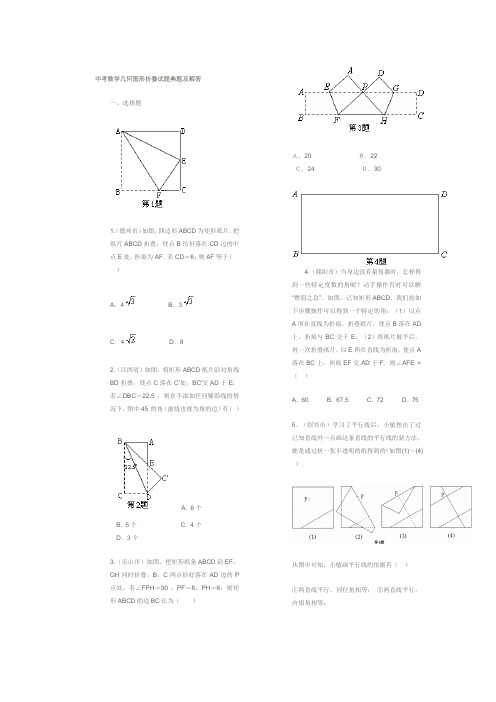
中考数学几何图形折叠试题典题及解答一、选择题1.(德州市)如图,四边形ABCD为矩形纸片.把纸片ABCD折叠,使点B恰好落在CD边的中点E处,折痕为AF.若CD=6,则AF等于()A.4B.3C.4D.82.(江西省)如图,将矩形ABCD纸片沿对角线BD折叠,使点C落在C′处,BC′交AD于E,若∠DBC=22.5°,则在不添加任何辅助线的情况下,图中45°的角(虚线也视为角的边)有()A.6个B.5个C.4个D.3个3.(乐山市)如图,把矩形纸条ABCD沿EF,GH同时折叠,B,C两点恰好落在AD边的P 点处,若∠FPH=90°,PF=8,PH=6,则矩形ABCD的边BC长为()A.20B.22C.24D.304.(绵阳市)当身边没有量角器时,怎样得到一些特定度数的角呢?动手操作有时可以解“燃眉之急”.如图,已知矩形ABCD,我们按如下步骤操作可以得到一个特定的角:(1)以点A所在直线为折痕,折叠纸片,使点B落在AD 上,折痕与BC交于E;(2)将纸片展平后,再一次折叠纸片,以E所在直线为折痕,使点A 落在BC上,折痕EF交AD于F.则∠AFE =()A.60°B.67.5°C.72°D.75°5. (绍兴市)学习了平行线后,小敏想出了过己知直线外一点画这条直线的平行线的新方法,她是通过折一张半透明的纸得到的(如图(1)~(4)).从图中可知,小敏画平行线的依据有()①两直线平行,同位角相等;②两直线平行,内错角相等;③同位角相等,两直线平行;④内错角相等,两直线平行.A.①②B.②③C.③④D.①④6.(贵阳市)如图6-1所示,将长为20cm,宽为2cm的长方形白纸条,折成图6-2所示的图形并在其一面着色,则着色部分的面积为()A.34cm2 B.36cm2C.38cm2 D.40cm2二、填空题7.(成都市)如图,把一张矩形纸片ABCD沿E F折叠后,点C,D分别落在C′,D′的位置上,EC′交AD于点G.已知∠EFG=58°,那么∠B EG°.8. (苏州市)如图,将纸片△ABC沿DE折叠,点A落在点A′处,已知∠1+∠2=100°,则∠A的大小等于____________度.三、解答题9.(荆门市)如图1,在平面直角坐标系中,有一张矩形纸片OABC,已知O(0,0),A(4,0),C(0,3),点P是OA边上的动点(与点O、A不重合).现将△PAB沿PB翻折,得到△PDB;再在OC边上选取适当的点E,将△POE沿PE翻折,得到△PFE,并使直线PD、PF重合.设P(x,0),E(0,y),求y关于x的函数关系式,并求y的最大值;如图2,若翻折后点D落在BC边上,求过点P、B、E的抛物线的函数关系式;在(2)的情况下,在该抛物线上是否存在点Q,使△P EQ是以PE为直角边的直角三角形?若不存在,说明理由;若存在,求出点Q的坐标.10. (济宁市)如图,先把一矩形ABCD纸片对折,设折痕为MN,再把B点叠在折痕线上,得到△ABE.过B点折纸片使D点叠在直线AD上,得折痕PQ.求证:△PBE∽△QAB;你认为△PBE和△BAE相似吗?如果相似给出证明,如不相似请说明理由;如果沿直线EB折叠纸片,点A是否能叠在直线EC 上?为什么?11.(威海市)如图,四边形ABCD为一梯形纸片,AB∥CD,AD=BC.翻折纸片ABCD,使点A与点C重合,折痕为EF.已知CE⊥AB.(1)求证:EF∥BD;(2)若AB=7,CD=3,求线段EF的长.12. (烟台市)生活中,有人喜欢把传送的便条折成形状,折叠过程是这样的(阴影部分表示纸条的反面):如果由信纸折成的长方形纸条(图①)长为2 6 cm,宽为xcm,分别回答下列问题:为了保证能折成图④的形状(即纸条两端均超出点P),试求x的取值范围.(2)如果不但要折成图④的形状,而且为了美观,希望纸条两端超出点P的长度相等,即最终图形是轴对称图形,试求在开始折叠时起点M与点A的距离(用x表示).13. 将平行四边形纸片ABCD按如图方式折叠,使点C与A重合,点D落到D′处,折痕为EF.(1)求证:△ABE≌△AD′F;(2)连接CF,判断四边形AECF是什么特殊四边形?证明你的结论.14.(孝感市)在我们学习过的数学教科书中,有一个数学活动,其具体操作过程是:第一步:对折矩形纸片ABCD,使AD与BC重合,得到折痕EF,把纸片展开(如图1);第二步:再一次折叠纸片,使点A落在EF上,并使折痕经过点B,得到折痕BM,同时得到线段BN(如图2).请解答以下问题:(1)如图2,若延长MN交BC于P,△BMP 是什么三角形?请证明你的结论.(2)在图2中,若AB=a,BC=b,a、b满足什么关系,才能在矩形纸片ABCD上剪出符合(1)中结论的三角形纸片BMP ?(3)设矩形ABCD的边AB=2,BC=4,并建立如图3所示的直角坐标系. 设直线BM′为y=kx,当∠M′BC=60°时,求k的值.此时,将△ABM′沿BM′折叠,点A是否落在EF上(E、F分别为AB、CD中点)?为什么?15.(邵阳市)如图①,△ABC中,∠ACB=90°,将△ABC沿着一条直线折叠后,使点A与点C 重合(图②).(1)在图①中画出折痕所在的直线l.设直线l 与AB,AC分别相交于点D,E,连结CD.(画图工具不限,不要求写画法)(2)请你找出完成问题(1)后所得到的图形中的等腰三角形.(不要求证明)16.(济宁市)如图,先把一矩形ABCD纸片对折,设折痕为MN,再把B点叠在折痕线上,得到△ABE.过B点折纸片使D点叠在直线AD上,得折痕PQ. 求证:△PBE∽△QAB;你认为△PBE和△BAE相似吗?如果相似给出证明,如补相似请说明理由;(3)如果直线EB折叠纸片,点A是否能叠在直线EC上?为什么?17.(临安市)如图,△OAB 是边长为的等边三角形,其中O是坐标原点,顶点B在y轴正方向上,将△OAB 折叠,使点A落在边OB上,记为A′,折痕为EF.(1)当A′E//x轴时,求点A′和E的坐标;(2)当A′E//x轴,且抛物线经过点A′和E时,求抛物线与x轴的交点的坐标;(3)当点A′在OB上运动,但不与点O、B重合时,能否使△A′EF成为直角三角形?若能,请求出此时点A′的坐标;若不能,请你说明理由.18.(南宁市)如图,在锐角△ABC中,BC=9,AH⊥BC于点H,且AH=6,点D为AB边上的任意一点,过点D作DE∥BC,交AC于点E.设△ADE的高AF为x(0<x<6),以DE为折线将△ADE翻折,所得的△A′DE与梯形DBCE重叠部分的面积记为y(点A关于DE的对称点A′落在AH所在的直线上).(1)分别求出当0<x≤3与3<x<6时,y与x 的函数关系式;(2)当x取何值时,y的值最大?最大值是多少?19.(宁夏回族自治区)如图,将矩形纸片ABCD沿对角线B D折叠,点C落在点E处,BE交AD于点F,连结AE.证明:(1)BF=DF;(2)AE∥BD.参考答案一、1.A 2.B 3.C 4.B 5.C 6.B二、7.648.50°三、9. 解:(1)由已知PB平分∠APD,PE平分∠OPF,且PD、PF重合,则∠OPE+∠APB= 90°.又∠APB+∠ABP=90°,∴∠OPE=∠PBA.∴Rt△POE∽Rt△BPA.∴.即.∴.且当x=2时,y 有最大值.由已知,△PAB、△POE均为等腰直角三角形,可得P(1,0),E(0,1),B(4,3).……6分设过此三点的抛物线为y=ax2+bx+c ,则∴y=.由(2)知∠EPB=90°,即点Q与点B重合时满足条件.直线PB为y=x-1,与y轴交于点(0,-1).将PB向上平移2个单位则过点E(0,1),∴该直线为y=x+1.由得∴Q(5,6).故该抛物线上存在两点Q(4,3)、(5,6)满足条件.10. 证明:(1)∵∠PBE+∠ABQ=180°-90°=90°,∠PBE+∠PEB=90°,∴∠ABQ=∠PEB.又∵∠BPE=∠AQB=90°,∴△PBE~△QAB.(2)∵△PBE~△QAB ,∴∵B Q=P B,∴.又∵∠ABE=∠BPE=90°,∴△PBE~△BAE.(3)点A能叠在直线EC上.由(2)得,∠AE B=∠CEB,∴EC和折痕AE重合.11. 解:(1)证明:过C点作CH∥BD,交AB的延长线于点H;连结AC,交EF于点K,则AK=CK.∵AB∥CD,∴BH=CD,BD=CH.∵AD=BC,∴AC=BD=CH.∵CE⊥AB,∴AE=EH.∴EK是△AHC的中位线.∴EK∥CH.∴EF∥BD.(2)解:由(1)得BH∥CD,EF∥BD,∴∠AEF=∠ABD.∵AB=7,CD=3,∴AH=10.∵AE=CE,AE=EH,∴AE=CE=EH=5.∵CE⊥AB,∴CH=5=BD.∵∠EAF=∠BAD,∠AEF=∠ABD,∴△AFE∽△ADB.∴.∴.12. 解:(1)由折纸过程知0<5x<26,,0<x <.(2)图④为轴对称图形,∴A M =.即点M与点A的距离是(13-x)cm.13. 证明:⑴由折叠可知:∠D=∠D′,CD=A D′,∠C=∠D′AE.∵四边形ABCD是平行四边形,∴∠B=∠D,AB=CD,∠C=∠BAD.∴∠B=∠D′,AB=AD′,∠D′AE=∠BAD,即∠1+∠2=∠2+∠3.∴∠1=∠3.∴△ABE ≌△AD′F.⑵四边形AECF是菱形.由折叠可知AE=EC,∠4=∠5.∵四边形ABCD是平行四边形,∴AD∥BC.∴∠5=∠6.∴∠4=∠6.∴AF=AE.∵AE=EC,∴AF=EC.又∵AF∥EC,∴四边形AECF是平行四边形.∵AF=AE,∴四边形AECF是菱形.14. 解:(1)△BMP是等边三角形.证明:连结AN.∵EF垂直平分AB,∴AN = BN.由折叠知AB = BN ,∴AN = AB = BN,∴△ABN为等边三角形.∴∠ABN =60°. ∴∠PBN =30°.又∵∠ABM =∠NBM =30°,∠BNM =∠A =9 0°.∴∠BPN =60°.∠MBP =∠MBN +∠PBN =60°.∴∠BMP =60°∴∠MBP =∠BMP =∠BPM =60°.∴△BMP为等边三角形 .(2)要在矩形纸片ABCD上剪出等边△BMP,则BC ≥BP.在Rt△BNP中,BN = BA =a,∠PBN =30°,∴BP =. ∴b≥. ∴a≤b .∴当a≤b时,在矩形上能剪出这样的等边△BMP.(3)∵∠M′BC =60°,∴∠ABM′=90°-60°= 30°.在Rt△ABM′中,tan∠ABM′ =. ∴tan3 0°=. ∴AM′ =.∴M′(,2). 代入y=kx中,得k== .设△ABM′沿BM′折叠后,点A落在矩形ABCD 内的点为A′.过A′作AH ⊥BC交BC于H.∵△A′BM′ ≌△ABM′,∴∠A′BM′=∠ABM′=3 0°, A′B = AB =2.∴∠A′BH=∠M′BH-∠A′BM′=30°.在Rt△A′BH中,A′H =A′B =1 ,BH=,∴.∴A'落在EF上.(图2)(图3)15.解:(1)如图.等腰三角形DAC.16.(1)证明:∵∠PBE+∠ABQ=180°-90°=90°,∠PBE+∠PEB=90°,∴∠ABQ=∠PEB.又∵∠BPE=∠AQB,∴△PBE∽△QAB.(2)∵△PBE∽△QAB,∴. ∵B Q=P B,∴.又∵∠ABE=∠BPE=90°,∴△PBE~△BAE.(3)点A能折叠在直线EC上.由(2)得,∠AEB=∠CEB,∴EC和折痕AE 重合.17. 解:(1)由已知可得∠A'OE=60o , A'E= AE.由A′E//x轴,得△OA'E是直角三角形.设A′的坐标为(0,b),则AE=A'E=b,OE=2b.∵b+2b=2+,∴b=1.∴A'、E的坐标分别是(0,1)与(,1).(2)因为A'、E在抛物线上,所以所以函数关系式为y =.由=0得,.与x轴的两个交点坐标分别是(-,0)与(,0).(3)不可能使△A'EF成为直角三角形.∵∠FA'E=∠FAE=60o,若△A'EF成为直角三角形,只能是∠A'EF=90o或∠A'FE=90o.若∠A'EF=90o,利用对称性,则∠AEF=90o, A'、E、A三点共线,O与A重合,与已知矛盾.同理若∠A'FE=90o也不可能.所以不能使△A′EF成为直角三角形.18. 解:(1)①当0<x≤3时,由折叠得到的△A'ED落在△ABC内部如图10(1),重叠部分为△A'ED.∵DE∥BC,∴∠ADE=∠B,∠AED=∠C.∴△ADE∽△ABC.∴.∴,即.又∵FA'=FA=x,∴y=DE·A'F=·x·x.∴(0<x≤3).②当3<x<6时,由折叠得到的△A'ED有一部分落在△ABC外,如图10(2),重叠部分为梯形EDPQ.∵FH=6-AF=6-x, A'H=A'F-FH=x-(6-x)=2x-6,又∵DE∥PQ,∴△A'PQ∽△A'DE.∴.∴∴.(2)当0<x≤3时,y的最大值;当3<x<6时,由,可知当x=4时,y的最大值y2=9.∵y1<y2,∴当x=4时,y有最大值y最大=9.19. 证明:(1)能正确说明∠ADB=∠EBD(或△ABF≌△EDF),∴BF=DF.(2)能得出∠AEB=∠DBE(或∠EAD=∠BD A),∴AE∥BD.。
中考数学折叠剪切问题(含答案)

中考数学-----折叠剪切问题折叠剪切问题是考察学生的动手操作问题,学生应充分理解操作要求方可解答出此类问题.一.折叠后求度数【1】将一张长方形纸片按如图所示的方式折叠,BC 、BD 为折痕,则∠CBD 的度数为( )A .600B .750C .900D .950答案:C【2】如图,把一个长方形纸片沿EF 折叠后,点D 、C 分别落在D ′、C ′的位置,若∠EFB=65°,则∠AED ′等于( )A .50°B .55°C .60°D .65° 答案:A【3】 用一条宽相等的足够长的纸条,打一个结,如图(1)所示,然后轻轻拉紧、压平就可以得到如图(2)所示的正五边形ABCDE,其中∠BAC= 度.答案:36°二.折叠后求面积【4】如图,有一矩形纸片ABCD,AB=10,AD=6,将纸片折叠,使AD 边落在AB 边上,折痕为AE ,再将△AED 以DE 为折痕向右折叠,AE 与BC 交于点F ,则△CEF 的面积为( ) A .4 B .6 C .8 D .10图(1)第3题图CDEBA图 (2)答案:C【5】如图,正方形硬纸片ABCD 的边长是4,点E 、F 分别是AB 、BC 的中点,若沿左图中的虚线剪开,拼成如下右图的一座“小别墅”,则图中阴影部分的面积是A .2B .4C .8 D.10答案:B【6】如图a ,ABCD 是一矩形纸片,AB =6cm ,AD =8cm ,E 是AD 上一点,且AE =6cm 。
操作:(1)将AB 向AE 折过去,使AB 与AE 重合,得折痕AF ,如图b ;(2)将△AFB 以BF 为折痕向右折过去,得图c 。
则△GFC 的面积是( )EAAABBBCCC GDDDFF F 图a图b图cA.1cm 2B.2 cm 2C.3 c m 2D.4 cm 2答案:B三.折叠后求长度【7】如图,已知边长为5的等边三角形ABC 纸片,点E 在AC 边上,点F 在AB 边上,沿着EF 折叠,使点A 落在BC 边上的点D 的位置,且E D B C ⊥,则CE 的长是( ) (A )10315- (B )1053- (C )535- (D)20103-答案:D 四.折叠后得图形【8】将一张矩形纸对折再对折(如图),然后沿着图中的虚线剪下,得到①、②两部分,将①展开后得到的平面图形是( )A .矩形B .三角形C .梯形D .菱形答案:D【9】在下列图形中,沿着虚线将长方形剪成两部分,那么由这两部分既能拼成平行四边形又能拼成三角形和梯形的是( )A. B. C. D.答案:D【10】小强拿了张正方形的纸如图(1),沿虚线对折一次如图(2),再对折一次得图(3),然后用剪刀沿图(3)中的虚线(虚线与底边平行)剪去一个角,再打开后的形状应是( )ABCDEF 第7题图第8题图第9题图答案:D【11】如图,把矩形ABCD 对折,折痕为MN (图甲),再把B 点叠在折痕MN 上的B '处。
2016届中考复习数学真题汇编20:直角三角形与勾股定理(含命题、定理和证明)(含答案) - 学生版

一、选择题1. (2015浙江台州,8,4分)如果将长为6cm,宽为5cm的长方形纸片折叠一次,那么这条折痕的长不可能...是()A.8cm B.C.5.5cm D.1cm2.(2015山东省德州市,8,3分)下列命题中,真命题的个数是①若-1<x< -12, 则-2<1x<-1;②若-1≤x≤2,则1≤x2≤4;③凸多边形的外角和为360°;④三角形中,若∠A+∠B=90°,则sin A=cos B.A. 4B. 3C. 2D.13. (2015浙江台州,10,4分)某班有20位同学参加围棋、象棋比赛.甲说:“只参加一项的人数大于14人.”乙说:“两项都参加的人数小于5人.”对于甲、乙两人的说法,有下列四个命题,其中真命题的是()A.若甲对,则乙对B.若乙对,则甲对C.若乙错,则甲错D.若甲错,则乙对4.(2015浙江省台州市,8,4)如果将长为6cm,宽为5cm的长方形纸片折叠一次,那么这条折痕的长不可能...是()A.8cm B.C.5.5cm D.1cm5.(2015浙江省台州市,10,4)某班有20位同学参加围棋、象棋比赛.甲说:“只参加一项的人数大于14人.”乙说:“两项都参加的人数小于5人.”对于甲、乙两人的说法,有下列四个命题中,其中真命题的是()A.若甲对,则乙对B.若乙对,则甲对C.若乙错,则甲错D.若甲错,则乙对6.(2015广东省广州市,8,3分)下列命题中,真命题的个数有( )①对角线互相平分的四边形是平行四边形②两组对角分别相等的四边形是平行四边形③一组对边平行,另一组对边相等的四边形是平行四边形A.3个B.2个C.1个D.0个7.(2015四川省达州市,5,3分)下列命题正确的是()A.矩形的对角线互相垂直B.两边和一角对影响等的两个三角形全等C.分式方程2 1.512112xx x-+=--可化为一元一次方程x-1+(2x-1)=-1.5D.多项式t2-16t+3t因式分解为(t+4)(t-4)+3t8.(2015山东省聊城市,7,3分)下列命题中的真命题是()A.两边和一角分别相等的两个三角形全等B.相似三角形的面积比等于相似比C.正方形不是中心对称图形D.圆内接四边形的对角互补9.(2015湖南省长沙市,5,3分)下列例题中,为真命题的是A.六边形的内角和为360度B.多边形的外角和与边数有关C.矩形的对角线互相垂直D.三角形两边的和大于第三边10. (2015贵州省安顺市,6,3分)如图,点O是矩形ABCD的中心,E是AB上的点,折叠后,点B恰好与点O重合,若BC=3。
中考数学折叠,旋转问题专题含答案

【经典例题1】如图,CD是⊙O的直径,AB是⊙O的弦,AB⊥CD,垂足为G,OG:OC=3:5,AB=8.(1)求⊙O的半径;(2)点E为圆上一点,∠ECD=15°,将沿弦CE翻折,交CD于点F,求图中阴影部分的面积.【解析】(1)连接AO,如右图1所示,∵CD为⊙O的直径,AB⊥CD,AB=8,∴AG==4,∵OG:OC=3:5,AB⊥CD,垂足为G,∴设⊙O的半径为5k,则OG=3k,∴(3k)2+42=(5k)2,解得,k=1或k=﹣1(舍去),∴5k=5,即⊙O的半径是5;(2)如图2所示,将阴影部分沿CE翻折,点F的对应点为M,∵∠ECD=15°,由对称性可知,∠DCM=30°,S阴影=S弓形CBM,连接OM,则∠MOD=60°,∴∠MOC=120°,过点M作MN⊥CD于点N,∴MN=MO•sin60°=5×,∴S阴影=S扇形OMC﹣S△OMC==,即图中阴影部分的面积是:.练习1-1如图,在⊙O中,点C在优弧上,将弧沿BC折叠后刚好经过AB 的中点D,连接AC,CD.则下列结论中错误的是()A.AC=CD B.+=C.OD⊥AB D.CD平分∠ACB 【解析】A、过D作DD'⊥BC,交⊙O于D',连接CD'、BD',由折叠得:CD=CD',∠ABC=∠CBD',∴AC=CD'=CD,故①正确;B、∵AC=CD',∴,由折叠得:,∴=,故②正确;C、∵D为AB的中点,∴OD⊥AB,故③正确;D、延长OD交⊙O于E,连接CE,∵OD⊥AB,∴∠ACE=∠BCE,∴CD不平分∠ACB,故④错误;故选:D.练习1-2如图,AB是⊙O的弦,点C在上,点D是AB的中点.将在沿AC 折叠后恰好经过点D,若⊙O的半径为2,AB=8.则AC的长是()A.6B.C.2D.4【解析】如图,延长BO交⊙O于E,连接AE,OA,OD,OC,BC,作CH⊥AB 于H.∵AD=DB,∴OD⊥AB,∴∠ADO=90°,∵OA=2,AD=DB=4,∴OD==2,∵BE是直径,∴∠BAE=90°,∵AD=DB,EO=OB,∴OD∥AE,AE=2OD=4,∴AE=AD,∴=,∴=,∴∠CAE=∠CAH=45°,∴∠BOC=2∠CAB=90°,∴BC=OC=2,∵CH⊥AB,∴∠CAH=∠ACH=45°,∴AH=CH,设AH=CH=x,则BH=8﹣x,在Rt△BCH中,∵CH2+BH2=BC2,∴x2+(8﹣x)2=(2)2,∴x=6或2(舍弃),在Rt△ACH中,∵AC=,∴AC=6.故选:A.练习1-3在扇形AOB中,∠AOB=75°,半径OA=12,点P为AO上任一点(不与A、O重合).(1)如图1,Q是OB上一点,若OP=OQ,求证:BP=AQ.(2)如图2,将扇形沿BP折叠,得到O的对称点O'.①若点O'落在上,求的长.②当BO'与扇形AOB所在的圆相切时,求折痕的长.(注:本题结果不取近似值)【解析】(1)证明:∵BO=AO,∠O=∠O,OP=OQ,∴△BOP≌△AOQ(SAS).∴BP=AQ.(2)解:①如图1,点O'落在上,连接OO',∵将扇形沿BP折叠,得到O的对称点O',∴OB=O'B,∵OB=OO',∴△BOO'是等边三角形,∴∠O'OB=60°.∵∠AOB=75°,∴∠AOO'=15°.∴的长为.②BO'与扇形AOB所在的圆相切时,如图2所示,∴∠OBO'=90°.∴∠OBP=45°.过点O作OC⊥BP于点C,∵OA=OB=12,∠COB=∠OBP=45°,∴.又∵∠AOB=75°,∠COB=45°,∴∠POC=30°,∴.∴.∴折痕的长为.旋转类【经典例题2】如图1,在锐角△ABC中,AB=5,AC=42,∠ACB=45∘. 计算:求BC的长;操作:将图1中的△ABC绕点B按逆时针方向旋转,得到△A1BC1.如图2,当点C1在线段CA的延长线上时。
中考数学中的旋转翻折类问题专项训练经典汇编(共30题)

中考数学中的旋转翻折类问题专项训练经典汇编(共30题)1.阅读下面材料.小炎遇到这个一个问题:如图1,点E、F分别在正方形ABCD的边BC、CD上,∠EAF =45°,连接EF,则EF=BE+DF,试说明理由.小炎是这样思考的:要想解决这个问题,首先应想办法将这些分散的线段相对集中,她先尝试了翻折、旋转、平移的方法,最后发现线段AB、AD是共点并且相等的,于是找到解决问题的方法.她的方法是将△ABE绕着点A逆时针旋转90°得到△ADG,再利用全等的知识解决这个问题(如图2).参考小炎同学思考问题的方法,解决下列问题:(1)写出小炎的推理过程;(2)如图3,四边形ABCD中,AB=AD,∠BAD=90°,点E、F分别在边BC、CD 上,∠EAF=45°,若∠B、∠D都不是直角,则当∠B与∠D满足于关系时,仍有EF=BE+DF;(3)如图4,在△ABC中,∠BAC=90°,AB=AC,点D、E均在边BC上,且∠DAE =45°,若BD=1,EC=2,求DE的长.2.如图1,把△ABC沿直线BC平移线段BC的长度,得到△ECD;如图2,以BC为轴,把△ABC沿BC翻折180°,可以得到△DBC;如图3,以点A为中心,把△ABC旋转180°,可以得到△AED.像这样,其中一个三角形是由另一个三角形按平移、翻折、旋转等方法得到的,这种只改变位置,不改变形状、大小的图形变换,叫做三角形的全等变换.回答下列问题:(1)在图4中,可以使△ABE通过平移、翻折、旋转中的哪一种方法得到△ADF?(2)图中线段BE与DF相等吗?为什么?3.阅读材料并解答问题:探究:小明遇到这样一个问题:如图1,在正方形ABCD,点E、F分别为BC、CD边上的点,且∠EAF=45°,求证:BE+DF=EF.小明是这样思考的:要想解决这个问题,首先应想办法将这些分散的线段集中到同一条线段上.他先后尝试了平移、翻折、旋转的方法,发现通过旋转可以解决此问题.他的方法是将△ADF绕点A顺时针旋转90°得到△ABG(如图1),此时GE即是BE+DF.请回答:在图1中,∠GAF的度数是.理解:如图2,已知Rt△ABC中,∠ACB=90°,AC=BC,点D、E在斜边AB上,且∠DCE=45°,请写出AD、DE、BE三条线段之间的数量关系,并证明.应用:如图3,正方形ABCD中,△AMN的顶点M、N分别在BC、CD边上,AH⊥MN,且AH=AB,连接BD分别交AM、AN于点E,若MH=2,NH=3,DF=2,求AH、EF的长.4.阅读下面材料:小炎遇到这样一个问题:如图1,点E、F分别在正方形ABCD的边BC,CD上,∠EAF =45°,连接EF,则EF=BE+DF,试说明理由.小炎是这样思考的:要想解决这个问题,首先应想办法将这些分散的线段相对集中.她先后尝试了翻折、旋转、平移的方法,最后发现线段AB,AD是共点并且相等的,于是找到解决问题的方法.她的方法是将△ABE绕着点A逆时针旋转90°得到△ADG,再利用全等的知识解决了这个问题(如图2).参考小炎同学思考问题的方法,解决下列问题:(1)如图3,四边形ABCD中,AB=AD,∠BAD=90°点E,F分别在边BC,CD上,∠EAF=45°.若∠B,∠D都不是直角,则当∠B与∠D满足关系时,仍有EF=BE+DF;(2)如图4,在△ABC中,∠BAC=90°,AB=AC,点D、E均在边BC上,且∠DAE =45°,若BD=1,EC=2,求DE的长.5.如图,在正方形ABCD中,E为AD的中点,F是BA延长线上一点,AF=AB.(1)图中的全等三角形是哪一对?(2)在图中,可以通过平移、翻折、旋转中哪一种方法,使△ABE变换到△ADF的位置?(3)图中线段BE与DF之间有怎样的关系?为什么?6.已知点E是△ABC内部一点.将△ABE沿BE翻折,点A落在BC上的点F′处.(1)如图1,若∠BAC﹣80°,∠C﹣40°,EF∥AC.求∠BEF的度数;(2)如图2,若∠C=2∠BAE,请说明.(3)如图3.连接AF,若AE⊥BC,∠ABC﹣70°,∠C=40°,将△BEF绕点B顺时针方向旋转一个角度α(0<α<180°)得到ΔBE1F1,则在这个旋转过程中,当E1F1与△AFC的某一边垂直时,直接写出旋转角α的度数.7.如图1,在Rt△ABC中,∠A=90°,AB=21,AC=28,点D为BC边上一点,过点作DE⊥AB于点E,作DF⊥AC于点F,且DE=DF.(1)求证:四边形AEDF为正方形;(2)如图2,将△CDF沿DF翻折,得△GDF,DG交AB于点H,求证:DH=DB;(3)将(2)中的△BDH绕点D逆时针旋转α(0°<α<180°)得△B′DH′(点B的对应点为B′,点H的对应点为H′,连接GH′,CB′,点M为线段GH′的中点,连接DM.当△B′DC为直角三角形时,直接写出线段DM的长.8.如图,在等边△ABC中,AD⊥BC于点D,E为线段AD上一动点(不与A,D重合),连接BE,CE,将CE绕点C顺时针旋转60°得到线段CF,连接AF.(1)如图1,求证:∠CBE=∠CAF;(2)如图2,连接BF交AC于点G,连接DG,EF,EF与DG所在直线交于点H,求证:EH=FH;(3)如图3,连接BF交AC于点G,连接DG,EG,将△AEG沿AG所在直线翻折至△ABC所在平面内,得到△APG,将△DEG沿DG所在直线翻折至△ABC所在平面内,得到△DQG,连接PQ,QF.若AB=4,直接写出PQ+QF的最小值.9.在Rt△ABC中,∠ABC=90°,过B点作BE⊥AC于点E,点D为线段AC的中点,连接BD.(1)如图1,AB=2,AC=6,求ED的长度;(2)如图2,将线段DB绕着点D逆时针旋转45°得到线段DG,此时DG⊥AC,连接BG,点F为BG的中点,连接EF,求证:BC=2EF;(3)如图3,∠ACB=30°,AB=3,点P是线段BD上一点,连接AP,将△APB沿AP 翻折到同一平面内得到△APB',连接CB′,将线段绕点CB′顺时针旋转60°得线段CQ,连接BQ,当BQ最小时,直接写出△BCQ的面积.10.如图,CD为△ABC的中线,以CD为直角边在其右侧作直角△CDE,CD⊥DE,BC与DE交于点F,∠E=30°.(1)如图1,若CF=EF=5,求CD的长;(2)如图2,若将BC绕点C逆时针旋转120°得CG,连接AG、AE,探究AG、AE的数量关系,并说明理由;(3)如图3,若∠ACB=90°,AC=2,.直线CE上有一点M,连接MF,将△CFM沿着MF翻折至△ABC所在的平面内得到△NFM.取NF的中点P,连接AP,当AP最小时,请直接写出△APB的面积.11.已知△ABC为等边三角形,D是边AB上一点,连接CD,点E为CD上一点,连接BE.(1)如图1,延长BE交AC于点F,若∠ABF=15°,.求AF的长;(2)如图2,将△BEC绕点C顺时针旋转60°到△AGC,延长BC至点H,使得CH=BD,连接AH交CG于点N,猜想线段CE,GN,DE之间存在的数量关系,并证明你的猜想;(3)如图3,AB=8,点H是BC上一点,且BD=2CH,连接DH,点K是AC上一点,CK=AD,连接DK,BK,将△BKD沿BK翻折到△BKQ,连接CQ,当△ADK的周长最小时,直接写出△CKQ的面积.12.在边长为8的等边三角形ABC中,D为BC的中点,E,F分别为AC、AD上任意一点,连接EF,将线段EF绕点E顺时针旋转60°得到线段EG,连接FG交AC于点N,连接AG.(1)如图1,点E与点C重合,且GF的延长线过点B,证明:四边形AFEG是菱形;(2)如图2,EF的延长线交AB于点M,当AM+MF=AE时,求∠EAG的度数;(3)如图3,E为AC的中点,连接BE,H为直线BC上一动点,连接EH,将△BEH 沿EH翻折至△ABC所在平面内,得到△B′EH,连接B′G,直接写出线段B′G长度的最小值.13.在△ABC中,∠ACB=90°,AC=BC,D是AC边上一动点,连接BD.(1)如图1,在平面内将线段DC绕点C顺时针旋转90°得到线段CK,点F为BC边上一点,连接AF交BD于M,连接AK.若∠CAF=2∠DBA,AF=8,AK=10,求CF的长;(2)如图2,在平面内将线段DB绕点B顺时针旋转一定角度得到线段BE,连接AE交BC于G,连接DE,若∠CDE=∠DBA,猜想线段AD,CG的数量关系,并证明你的猜想;(3)在(2)的条件下,将△CDB沿BD直线BD翻折至△ABC所在平面内得到△BDC1,连接AC1,若AC=2+,在点D运动过程中,当线段AC1取得最小值时,请直接写出△ABE与四边形BCDC1重叠部分的面积.14.在△ABC中,∠BAC=90°,AB=AC,点D为BC边上一动点,连接AD,将AD绕着D点逆时针方向旋转90°得到DE,连接AE.(1)如图1,AH⊥BC,点D恰好为CH中点,AE与BC交于点G,若AB=4,求AE 的长度;(2)如图2,DE与AB交于点F,连接BE,在BA延长线上有一点P,∠PCA=∠EAB,求证:AB=AP+BD;(3)如图3,DE与AB交于点F,且AB平分∠EAD,点M为线段AF上一点,点N为线段AD上一点,连接DM,MN,点K为DM延长线上一点,将△BDK沿直线BK翻折至△BDK所在平面内得到△BQK,连接DQ,在M,N运动过程中,当DM+MN取得最小值,且∠DKQ=45°时,请直接写出的值.15.在平面直角坐标系中,已知点A(4,0),点B(0,3).点P从点A出发,以每秒1个单位的速度向右平移,点Q从点B出发,以每秒2个单位的速度向右平移,又P、Q 两点同时出发.(1)连接AQ,当△ABQ是直角三角形时,则点Q的坐标为;(2)当P、Q运动到某个位置时,如果沿着直线AQ翻折,点P恰好落在线段AB上,求这时∠AQP的度数;(3)若将AP绕点A逆时针旋转,使得P落在线段BQ上,记作P',且AP'∥PQ,求此时直线PQ的解析式.16.(1)特殊发现如图1,正方形BEFG与正方形ABCD的顶点B重合,BE、BG分别在BC、BA边上,连接DF,则有:①=;②直线DF与直线AG所夹的锐角等于度;(2)理解运用将图1中的正方形BEFG绕点B逆时针旋转,连接DF、AG.①如图2,(1)中的结论是否仍然成立?请说明理由;②如图3,若D、F、G三点在同一直线上,且过AB边的中点O,BE=4,直接写出AB的长;(3)拓展延伸如图3,点P是正方形ABCD的AB边上一动点(不与A、B重合),连接PC,沿PC将△PBC翻折到△PEC位置,连接DE并延长,与CP的延长线交于点F,连接AF,若P A =3PB,则的值是否是定值?请说明理由.17.已知:如图①,在矩形ABCD中,AB=8,AD=6,连接AC,将△ABC沿AC翻折,使B点落在E点处,连接EC、AE,AE交DC于F点.(1)求DF的长.(2)若将△CEF沿着射线CA方向平移,设平移的距离为m(平移距离指点C沿CA方向所经过的线段长度).当点F平移到线段AD上时,如图②,求出相应的m的值.(3)如图③,将△CEF绕点C逆时针旋转一个角a(0°<a<∠ECB),记旋转中的△CEF为△CE'F',过E'作E'G⊥AD于G点,在旋转过程中,当△DCE'为等腰三角形时,求出线段E'G的长度.18.已知矩形ABCD中,AB=2,BC=m,点E是边BC上一点,BE=1,连接AE.(1)沿AE翻折△ABE使点B落在点F处.①连接CF,若CF∥AE,求m的值;②连接DF,若≤DF≤,求m的取值范围.(2)△ABE绕点A顺时针旋转得△AB1E1,点E1落在边AD上时旋转停止.若点B1落在矩形对角线AC上,且点B1到AD的距离小于时,求m的取值范围.19.如图,四边形OABC是一张放在平面直角坐标系中的长方形纸片,O为原点,点A在x 轴的正半轴上,点C在y轴的正半轴上,点B的坐标为(10,8),在OC边上取一点D,将纸片沿AD翻折,使点O落在BC边上的点E处.(1)求CE和OD的长;(2)求DE所在直线的解析式;(3)若直线y=kx+b与直线DE的比例系数相等,当它与矩形OABC有公共点时,请直接写出b的取值范围.20.如图1,将△ABC纸片沿中位线EH折叠,使点A对称点D落在BC边上,再将纸片分别沿等腰△BED和等腰△DHC的底边上的高线EF,HG折叠,折叠后的三个三角形拼合形成一个矩形,类似地,对多边形进行折叠,若翻折后的图形恰能拼合成一个无缝隙、无重叠的矩形,这样的矩形称为叠合矩形.(1)将▱ABCD纸片按图2的方式折叠成一个叠合矩形AEFG,则操作形成的折痕分别是线段、,S矩形AEFG:S▱ABCD=;(2)▱ABCD纸片还可以按图3的方式折叠成一个叠合矩形EFGH,若EF=9,EH=12,求AD的长;(3)如图4,四边形ABCD纸片满足AD∥BC,AD<BC,AB⊥BC,AB=12,CD=13,小明把该纸片折叠,得到叠合正方形,请你帮助画出叠合正方形的示意图,并直接写出AD、BC的长.(写出一种即可)21.如图1,在平面直角坐标系xOy中,直线y=﹣x+8分别交x轴、y轴于A、B两点,已知点C(3,0),点D是线段AB上的一个动点.(1)判断△ABO的形状;(2)OD+CD的最小值为;(3)如图2,点P为y轴正半轴上一点,连接BC、PC,若∠BCP与△ABC中的一个角相等,求点P的坐标;(4)如图3,将△ACD沿CD翻折,点A恰好落在y轴上的点A′处,求此时点D的坐标.22.在等腰△ABC中,AB=BC,高AD,BE所在的直线相交于点F,将△ACD沿直线AD 翻折,点C的对称点C′落在直线BC上,连接FC′.(1)如图1,当∠ABC=45°时,①求证:BF=AC;②求∠FC′D的度数.(2)当∠ABC=135°时,补全图2,并求证:C′F∥AB.23.如图1,在平面直角坐标系中,点A坐标为(6,3),过点A作AB⊥x轴,交x轴于点B,点P是x轴上一动点,将△ABP沿直线AP翻折,使得点B落在点B'处,点E是翻折后AB'延长后与y轴的交点.(1)若点E的坐标为(0,3),则点P坐标为;(2)如图2,若点E的坐标为(0,),直线AE与x轴交于点F.①求点F的坐标;②求直线AP的函数关系式.24.如图,在矩形ABCD中,E是BC边上的一个动点,沿着AE翻折△ABE,使点B落在点F处,AB=2,BC=AB.(1)当点E运动到点C时,求CF的长;(2)当FC∥AE时,试判断E是否为BC的中点?并说明理由;(3)当点F在矩形ABCD内部,且DF=CD时,求BE的长.25.如图,在平面直角坐标系中,四边形OABC的边OC在x轴上,OA在y轴上,O为坐标原点,AB∥OC,线段OA,AB的长分别是方程x2﹣9x+20=0的两个根(OA<AB),延长CB交y轴于点H,=.(1)求点B,C的坐标;(2)P为OA上一点,Q为OC上一点,OQ=5,将△POQ翻折,使点O落在AB上的点O'处,双曲线y=的一分支过点O′,求k的值;(3)在(2)的条件下,M为坐标轴上一点,在平面内是否存在点N,使以O',Q,M,N为顶点四边形为矩形?若存在,请直接写出点N的坐标;若不存在,请说明理由.26.如图1,在正方形ABCD中,E为边BC上一点(不与点B、C重合),垂直于AE的一条直线MN分别交AB、AE、CD于点M、P、N.(1)求证AE=MN;(2)如图2,若垂足P恰好为AE的中点,连接BD,交MN于点Q,连接EQ,并延长交边AD于点F.求∠AEF的度数;(3)如图3,若该正方形ABCD边长为10,将正方形沿着直线MN翻折,使得BC的对应边B′C′恰好经过点A,过点A作AG⊥MN,垂足分别为G,若AG=6,请直接写出AC′的长.27.如图1,矩形的边OA在x轴上,边OC在y轴上,点B的坐标为(6,8).D是AB边上一点(不与点A、B重合),将△BCD沿直线CD翻折,使点B落在点E处.(1)求直线AC所表示的函数的表达式;(2)如图2,当点E恰好落在矩形的对角线AC上时,求点D的坐标;(3)如图3,当以O、E、C三点为顶点的三角形是等腰三角形时,求△OEA的面积.28.已知在平行四边形ABCD中,AB≠BC,将△ABC沿直线AC翻折,点B落在点E处,AD与CE相交于点O,连接DE.(1)如图1,求证:AC∥DE;(2)如图2,如果∠B=90°,AB=,BC=,求△OAC的面积;(3)如果∠B=30°,AB=2,当△AED是直角三角形时,求BC的长.29.如图,矩形ABCD中,已知AB=6.BC=8,点E是射线BC上的一个动点,连接AE 并延长,交射线DC于点F.将△ABE沿直线AE翻折,点B的对应点为点B'.(1)如图1,若点E为线段BC上一点,延长AB'交CD于点M,求证:AM=FM;(2)如图2,若点B'恰好落在对角线AC上,求的值;(3)若=,求∠DAB'的正弦值.30.如图1,四边形ABCD是矩形,点O位于对角线BD上,将△ADE,△CBF分别沿DE、BF翻折,点A,点C都恰好落在点O处.(1)求证:∠EDO=∠FBO;(2)求证:四边形DEBF是菱形:(3)如图2,若AD=2,点P是线段ED上的动点,求2AP+DP的最小值.。
最新2016聚焦中考数学(辽宁省习题课件:专题二+类型三 图形折叠问题

3.(2015·鄂州)如图,在矩形 ABCD 中,AB=8,BC=12, 点 E 是 BC 的中点,连接 AE,将△ABE 沿 AE 折叠,点 B 落在点 F 处,连接 FC,则 sin∠ECF=( D )34源自 4 A.4 B.3 C.5 D.5
解析:过 E 作 EH⊥CF 于 H,由折叠的性质得:BE=EF,∠ BEA=∠FEA,∵点 E 是 BC 的中点,∴CE=BE,∴EF=CE,∴ ∠FEH=∠CEH,∴∠AEB+∠CEH=90°,又∵∠ECF+∠CEH =90°,∴∠ECF=∠AEB,在 Rt△ABE 中,AB=8,BE=12BC =6,∴AE=10,∴sin∠ECF=sin∠AEB=AAEB=45
2.找出折叠前后隐含的位置关系和数量关系; 3.一般运用三角形全等、勾股定理、相似三角形等知识及方程 思想,设出恰当的未知数,解方程求线段长; 4.求一个角的三角函数有两种方法:①直接法:找这个角所在 的直角三角形或构造一个关于这个角的直角三角形;②间接法: 找出一个与这个角相等的角,再在相应的直角三角形求出.
2016聚焦中考数学(辽宁省) 习题课件:专题二+类型三 图
形折叠问题
对于图形折叠问题,常考类型包括:求线段长,求角度大小, 求一个角的三角函数值等.解答这类问题,需掌握以下知识:
1.折叠的性质:①位于折痕两侧的图形关于折痕成轴对称;② 折叠前后的两部分图形全等,对应线段、角和面积等都相等;③ 折叠后对应点的连线被折痕垂直平分;
AB2-BH2=2 6,∴EF= 6
6.(丹东模拟)如图,正方形 ABCD 的边长是 16,点 E 在边 AB 上,AE=3,点 F 是边 BC 上不与点 B,C 重合的一个动点, 把△EBF 沿 EF 折叠,点 B 落在 B′处.若△CDB′恰为等腰三角形, 则 DB′的长为__1_6_或___4__5_.
中考数学复习《折叠问题》真题练习(含答案)

中考数学复习《折叠问题》真题练习(含答案)(2017贵州安顺第7题)如图,矩形纸片ABCD 中,AD =4cm ,把纸片沿直线AC 折叠,点B 落在E处,AE 交DC 于点O ,若AO =5cm ,则AB 的长为( )A .6cmB .7cmC .8cmD .9cm【答案】C .(2017江苏无锡第10题)如图,△ABC 中,∠BAC =90°,AB =3,AC =4,点D 是BC 的中点,将△ABD 沿AD 翻折得到△AED ,连CE ,则线段CE 的长等于( D )A .2B .54 C .53 D .75(2017新疆乌鲁木齐第9题)如图,在矩形ABCD 中,点F 在AD 上,点E 在BC 上,把这个矩形沿EF 折叠后,使点D 恰好落在BC 边上的G 点处,若矩形面积为43且60,2AFG GE BG ∠==,则折痕EF 的长为( C )A .1B .3 C. 2 D .23(2017重庆A 卷第18题)如图,正方形ABCD 中,AD =4,点E 是对角线AC 上一点,连接DE ,过点E 作EF ⊥ED ,交AB 于点F ,连接DF ,交AC 于点G ,将△EFG 沿EF 翻折,得到△EFM ,连接DM ,交EF 于点N ,若点F 是AB 的中点,则△EMN 的周长是 .(2017河南第15题)如图,在Rt ABC ∆中,90A ∠=︒,AB AC =,21BC =+,点M ,N 分别是边BC ,AB 上的动点,沿MN 所在的直线折叠B ∠,使点B 的对应点'B 始终落在边AC 上.若'MBC∆为直角三角形,则BM 的长为 .【答案】1或212+. (2017江苏苏州第18题)如图,在矩形CD AB 中,将C ∠AB 绕点A 按逆时针方向旋转一定角度后,C B 的对应边C ''B 交CD 边于点G .连接'BB 、CC ',若D 7A =,CG 4=,G ''AB =B ,则CC '='BB (结果保留根号).【答案】745. (2017海南第17题)如图,在矩形ABCD 中,AB =3,AD =5,点E 在DC 上,将矩形ABCD 沿AE 折叠,点D 恰好落在BC 边上的点F 处,那么cos ∠EFC 的值是 .【答案】35.(2016·黑龙江齐齐哈尔·3分)如图,在边长为2的菱形ABCD中,∠A=60°,点M是AD边的中点,连接MC,将菱形ABCD翻折,使点A落在线段CM上的点E处,折痕交AB于点N,则线段EC的长为﹣1.(2016·吉林·3分)在三角形纸片ABC中,∠C=90°,∠B=30°,点D(不与B,C重合)是BC上任意一点,将此三角形纸片按下列方式折叠,若EF的长度为a,则△DEF的周长为3a(用含a的式子表示).(2016河南)如图,已知AD∥BC,AB⊥BC,AB=3,点E为射线BC上一个动点,连接AE,将△ABE沿AE 折叠,点B落在点B′处,过点B′作AD的垂线,分别交AD,BC于点M,N.当点B′为线段MN的三等分点时,BE的长为或.(2017甘肃兰州第26题)如图,1,将一张矩形纸片ABCD沿着对角线BD向上折叠,顶点C落到点E处,BE交AD于点F.(1)求证:BDF△是等腰三角形;(2)如图2,过点D作DG BE∥,交BC于点G,连结FG交BD于点O.①判断四边形BFDG的形状,并说明理由;②若6AB,8AD,求FG的长.【答案】(1)证明见解析;(2) 152.【解析】试题分析: (1)根据两直线平行内错角相等及折叠特性判断;(2)①根据已知矩形性质及第一问证得邻边相等判断;②根据折叠特性设未知边,构造勾股定理列方程求解.试题解析:(1)证明:如图1,根据折叠,∠DBC=∠DBE,又AD∥BC,∴∠DBC=∠ADB,∴∠DBE=∠ADB,∴DF=BF,∴△BDF是等腰三角形;(2)①∵四边形ABCD是矩形,∴AD∥BC,∴FD∥BG,又∵FD∥BG,∴四边形BFDG是平行四边形,∵DF=BF,∴四边形BFDG是菱形;②∵AB =6,AD =8, ∴BD =10. ∴OB =12BD =5. 假设DF =BF =x ,∴AF =AD ﹣DF =8﹣x .∴在直角△ABF 中,AB 2+A 2=BF 2,即62+(8﹣x )2=x 2, 解得x =254, 即BF =254, ∴FO =222522()54BF OB -=-=154,∴FG =2FO =152.(2017浙江金华第23题)如图1,将ABC ∆纸片沿中位线EH 折叠,使点A 的对称点D 落在BC 边上,再将纸片分别沿等腰BED ∆和等腰DHC ∆的底边上的高线EF ,HG 折叠,折叠后的三个三角形拼合形成一个矩形,类似地,对多边形进行折叠,若翻折后的图形恰能拼成一个无缝隙、无重叠的矩形,这样的矩形称为叠合矩形.(1)将ABCD 纸片按图2的方式折叠成一个叠合矩形AEFG ,则操作形成的折痕分别是线段_____,_____;:ABCDAEFG S S=矩形 ______.(2)ABCD 纸片还可以按图3的方式折叠成一个叠合矩形EFGH ,若5EF =,12EH =,求AD 的长.(3)如图4,四边形ABCD 纸片满足,,,8,10AD BC AD BC AB BC AB CD <⊥==.小明把该纸片折叠,得到叠合正方形....请你帮助画出叠合正方形的示意图,并求出,AD BC 的长.【答案】(1)(1)AE ;GF ;1:2;(2)13;(3)按图1的折法,则AD =1,BC =7;按图2的折法,则AD =134 ,BC =374. 【解析】试题分析:(1)由图2观察可得出答案为AE ,GF ,由折叠的轴对称性质可得出答案为1:2;(2)由EF 和EH 的长度根据勾股定理可求出FH 的长度,再由折叠的轴对称性质易证△AEH ≌△CGF ;再根据全等三角形的性质可得出AD 的长度;(3)由折叠的图可分别求出AD 和BC 的长度.(3)解:本题有以下两种基本折法,如图1,图2所示.按图1的折法,则AD =1,BC =7. 按图2的折法,则AD =134 ,BC =374.(2015年河南3分)如图,正方形ABCD 的边长是16,点E 在边AB 上,AE =3,点F 是边BC 上不与点B 、C 重合的一个动点,把△EBF 沿EF 折叠,点B 落在B ′处,若△CDB ′恰为等腰三角形,则DB ′的长为 ▲ .【答案】16或45.(2015年江苏泰州3分)如图, 矩形ABCD 中,AB =8,BC =6,P 为AD 上一点,将△ABP 沿BP 翻折至△EBP , PE 与CD 相交于点O ,且OE =OD ,则AP 的长为 ▲ .【答案】245. (2015湖北鄂州第8题3分)如图,在矩形ABCD 中,AB =8,BC =12,点E 是BC 的中点,连接AE ,将△ABE 沿AE 折叠,点B 落在点F 处,连接FC ,则sin ∠ECF =( )A .B .C .D .【答案】D .(2015•四川自贡,第10题4分) 如图,在矩形ABCD 中,AB 4AD 6==,,E 是AB 边的中点,F 是线段BC边上的动点,将△EBF 沿EF 所在直线折叠得到△'EB F ,连接'B D ‘,则'B D ‘的最小值是 ( A )B 'EDA BCFA . 2102-B .6C .2132-D .4(2015•绵阳第12题,3分)如图,D 是等边△ABC 边AB 上的一点,且AD :DB =1:2,现将△ABC 折叠,使点C 与D 重合,折痕为EF ,点E ,F 分别在AC 和BC 上,则CE :CF =( B )A .B .C .D .(2015•四川省内江市,第14题,5分)如图,在四边形ABCD 中,AD ∥BC ,∠C =90°,E 为CD 上一点,分别以EA ,EB 为折痕将两个角(∠D ,∠C )向内折叠,点C ,D 恰好落在AB 边的点F 处.若AD =2,BC =3,则EF 的长为.(2015•浙江滨州,第17题4分)如图,在平面直角坐标系中,将矩形AOCD 沿直线AE 折叠(点E 在边DC 上),折叠后顶点D 恰好落在边OC 上的点F 处.若点D 的坐标为(10,8),则点E 的坐标为 .【答案】(10,3)。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
2016年中考数学专题复习:折叠题(含答案)2016年中考数学专题复习:折叠题1.如图,在矩形ABCD中,点E是AD的中点,∠EBC的平分线交CD于点F,将△DEF沿EF 折叠,点D恰好落在BE上M点处,延长BC、EF交于点N.有下列四个结论:①DF=CF;②BF⊥EN;③△BEN是等边三角形;④S△BEF=3S△DEF.其中,将正确结论的序号全部选对的是()A.①②③B.①②④ C.②③④D.①②③④解答:解:∵四边形ABCD是矩形,∴∠D=∠BCD=90°,DF=MF,由折叠的性质可得:∠EMF=∠D=90°,即FM⊥BE,CF⊥BC,∵BF平分∠EBC,∴CF=MF,∴DF=CF;故①正确;点评:此题考查了折叠的性质、矩形的性质、角平分线的性质以及全等三角形的判定与性质.此题难度适中,注意掌握数形结合思想的应用.2.如图,将矩形ABCD的一个角翻折,使得点D恰好落在BC边上的点G处,折痕为EF,若EB为∠AEG的平分线,EF和BC的延长线交于点H.下列结论中:①∠BEF=90°;②DE=CH;③BE=EF;④△BEG和△HEG的面积相等;⑤若,则.以上命题,正确的有()A.2个B.3个C.4个D.5个解答:解:①由折叠的性质可知∠DEF=∠GEF,∵EB为∠AEG的平分线,∴∠AEB=∠GEB,∵∠AED=180°,∴∠BEF=90°,故正确;②可证△EDF∽△HCF,DF>CF,故DE≠CH,故错误;③只可证△EDF∽△BAE,无法证明BE=EF,故错误;④可证△GEB,△GEH是等腰三角形,则G是BH边的中线,∴△BEG和△HEG的面积相等,故正确;⑤过E点作EK⊥BC,垂足为K.设BK=x,AB=y,则有y2+(2y﹣2x)2=(2y﹣x)2,解得x 1=y(不合题意舍去),x2=y.则,故正确.故正确的有3个.故选B.点评:本题考查了翻折变换,解答过程中涉及了矩形的性质、勾股定理,属于综合性题目,解答本题的关键是根据翻折变换的性质得出对应角、对应边分别相等,然后分别判断每个结论,难度较大,注意细心判断.3.如图,矩形ABCD中,E是AD的中点,将△ABE沿BE折叠后得到△GBE,延长BG交CD于F点,若CF=1,FD=2,则BC的长为()A.3B.2C.2D.2解答:解:过点E作EM⊥BC于M,交BF于N,∵四边形ABCD是矩形,∴∠A=∠ABC=90°,AD=BC,∵∠EMB=90°,∴四边形ABME是矩形,∴AE=BM,由折叠的性质得:AE=GE,∠EGN=∠A=90°,∴EG=BM,∵∠ENG=∠BNM,∴△ENG≌△BNM(AAS),∴NG=NM,∴CM=DE,∵E是AD的中点,∴AE=ED=BM=CM,∵EM∥CD,∴BN:NF=BM:CM,∴BN=NF,∴NM=CF=,∴NG=,∵BG=AB=CD=CF+DF=3,∴BN=BG﹣NG=3﹣=,∴BF=2BN=5,∴BC===2.故选B.点评:此题考查了矩形的判定与性质、折叠的性质、三角形中位线的性质以及全等三角形的判定与性质.此题难度适中,注意辅助线的作法,注意数形结合思想的应用.4.如图,两个正方形ABCD和AEFG共顶点A,连BE,DG,CF,AE,BG,K,M分别为DG 和CF的中点,KA的延长线交BE于H,MN⊥BE 于N.则下列结论:①BG=DE且BG⊥DE;②△ADG和△ABE的面积相等;③BN=EN,④四边形AKMN为平行四边形.其中正确的是()A.③④B.①②③ C.①②④D.①②③④解答:解:由两个正方形的性质易证△AED≌△AGB,∴BG=DE,∠ADE=∠ABG,∴可得BG与DE相交的角为90°,∴BG⊥DE.①正确;如图,延长AK,使AK=KQ,连接DQ、QG,∴四边形ADQG是平行四边形;作CW⊥BE于点W,FJ⊥BE于点J,∴四边形CWJF是直角梯形;∵AB=DA,AE=DQ,∠BAE=∠ADQ,∴△ABE≌△DAQ,∴∠ABE=∠DAQ,∴∠ABE+∠BAH=∠DAQ+∠BAH=90°.∴△ABH是直角三角形.易证:△CWB≌△BHA,△EJF≌△AHE;∴WB=AH,AH=EJ,∴WB=EJ,又WN=NJ,∴WN﹣WB=NJ﹣EJ,∴BN=NE,③正确;∵MN是梯形WGFC的中位线,WB=BE=BH+HE,∴MN=(CW+FJ)=WC=(BH+HE)=BE;易证:△ABE≌△DAQ(SAS),∴AK=AQ=BE,∴MN∥AK且MN=AK;四边形AKMN为平行四边形,④正确.S △ABE=S△ADQ=S△ADG=S▱ADQG,②正确.所以,①②③④都正确;故选D.点评:当出现两个正方形时,一般应出现全等三角形.图形较复杂,选项较多时,应用排除法求解.5.如图,在△ABC中,∠C=90°,将△ABC 沿直线MN翻折后,顶点C恰好落在AB边上的点D处,已知MN∥AB,MC=6,NC=,则四边形MABN的面积是()A.B.C.D.解答:解:连接CD,交MN于E,∵将△ABC沿直线MN翻折后,顶点C恰好落在AB边上的点D处,∴MN⊥CD,且CE=DE,∴CD=2CE,∵MN∥AB,∴CD⊥AB,∴△CMN∽△CAB,∴,∵在△CMN中,∠C=90°,MC=6,NC=,∴S △CMN=CM•CN=×6×2=6,∴S △CAB=4S△CMN=4×6=24,∴S 四边形MABN=S△CAB﹣S△CMN=24﹣6=18.故选C.点评:此题考查了折叠的性质、相似三角形的判定与性质以及直角三角形的性质.此题难度适中,解此题的关键是注意折叠中的对应关系,注意数形结合思想的应用.6.如图,D是△ABC的AC边上一点,AB=AC,BD=BC,将△BCD沿BD折叠,顶点C恰好落在AB边的C′处,则∠A′的大小是()A.40°B.36° C.32°D.30°解答:解:连接C'D,∵AB=AC,BD=BC,∴∠ABC=∠ACB=∠BDC,∵△BCD沿BD折叠,顶点C恰好落在AB边的C′处,∴∠BCD=∠BC'D,∴∠ABC=∠BCD=∠BDC=∠BDC'=∠BC'D,∵四边形BCDC'的内角和为360°,∴∠ABC=∠BCD=∠BDC=∠BDC'=∠BC'D= =72°,∴∠A=180°﹣∠ABC﹣∠ACB=36°.故选B.点评:本题考查了折叠的性质,解答本题的关键是掌握翻折前后的对应角相等,注意本题的突破口在于得出∠ABC=∠BCD=∠BDC=∠BDC'=∠BC'D,根据四边形的内角和为360°求出每个角的度数.7.如图,已知△ABC中,∠CAB=∠B=30°,AB=2,点D在BC边上,把△ABC沿AD翻折使AB与AC重合,得△AB′D,则△ABC 与△AB′D重叠部分的面积为()A.B.C.3﹣D.解答:解:过点D作DE⊥AB′于点E,过点C 作CF⊥AB,∵△ABC中,∠CAB=∠B=30°,AB=2,∴AC=BC,∴AF=AB=,∴AC===2,由折叠的性质得:AB′=AB=2,∠B′=∠B=30°,∵∠B′CD=∠CAB+∠B=60°,∴∠CDB′=90°,∵B′C=AB′﹣AC=2﹣2,∴CD=B′C=﹣1,B′D=B′C•cos∠B′=(2﹣2)×=3﹣,∴DE===,∴S 阴影=AC•DE=×2×=.故选A.点评:此题考查了折叠的性质,等腰三角形的性质、直角三角形的性质以及特殊角的三角函数问题.此题难度适中,注意掌握辅助线的作法,注意数形结合思想的应用,注意掌握折叠前后图形的对应关系.8.如图,已知△ABC中,∠CAB=∠B=30°,AB=,点D在BC边上,把△ABC沿AD翻折,使AB与AC重合,得△AED,则BD的长度为()A.B.C.D.解答:解:作CF⊥AB于点F.∵∠CAB=∠B∴AC=BC,∴BF=AB=,在直角△BCF中,BC==2,在△CDE中,∠E=∠B=30°,∠ECD=∠CAB+∠B=60°,DE=BD,∴∠CDE=90°,设BD=x,则CD=DE=2﹣x,在直角△CDE中,tanE===tan30°=,解得:x=3﹣.故选B.点评:本题考查了图形的折叠,以及三线合一定理、三角函数,正确理解折叠的性质,找出图形中相等的线段、相等的角是关键.9.如图,在Rt△ABC中,∠C=90°,AC=,BC=1,D在AC上,将△ADB沿直线BD翻折后,点A落在点E处,如果AD⊥ED,那么△ABE 的面积是()A.1 B. C.D.解答:解:∵∠C=90°,AC=,BC=1,∴AB==2,∴∠BAC=30°∵△ADB沿直线BD翻折后,点A落在点E处,∴BE=BA=2,∠BED=∠BAD=30°,DA=DE,∵AD⊥ED,∴BC∥DE,∴∠CBF=∠BED=30°,在Rt△BCF中,CF==,BF=2CF=,∴EF=2﹣,在Rt△DEF中,FD=EF=1﹣,ED=FD=﹣1,∴S△ABE=S△ABD+S△BED+S△ADE=2S△ABD+S△ADE=2×BC•AD+AD•ED=2××1×(﹣1)+×(﹣1)(﹣1)=1.故选A.点评:本题考查了折叠问题:折叠前后两图形全等,即对应线段相等;对应角相等.也考查了勾股定理和含30度的直角三角形三边的关系.。
