研究生考试恒定磁场复习题及答案参考
习题答案(恒定磁场)优秀文档

一、选择题 BAAAB DBCBC CDBD
二、填空题 1. I1+ I2+ I3+ I4=0 2. 所围面积, 电流, 法线(n). 3. 0. 4. 0.16T. 5. 0Qv/(8l2), z轴负向. 6. 环路L所包围的电流, 环路L上的磁感应强度, 内外. 7. 0I, 0, 20I. 8. IBR .
1. 9. 10-2, /2 2. 10. 7.96×105A/m, 2.42×102A/m.
三、计算题
稳恒磁场习题
1. R=/(2a); j1/j2= r22/r12 2. B=0NI/ (4R)
3.
4. B = By= 0dI/[2(R2-R2)] 方向沿y轴正向
5. 0J; 0
6. F=0I1I2/2 方向向右
7. 课后11-8
8. 课后11-11 9. 课后11-13
10. 课后11-15 11.课后11-20 12. 课后11-22
计算题 1
稳恒磁场习题
计算题 2
稳恒磁场习题
计算题 3
12×10-21 kg·m/s B= 0NI/ (4R)
0I, 0, 2 0I. 稳恒磁场习题 R= /(2 a); j1/j2= r22/r12 课后11-15 11. 环路L所包围的电流, 环路L上的磁感应强度, 内外. 96×105A/m, 2. 2. 所围面积, 电流, 法线(n). 课后11-11 9. B= 0NI/ (4R) R= /(2 a); j1/j2= r22/r12 12×10-21 kg·m/s 96×105A/m, 2. P=mv=ReB=1.
0Qv/(8 l2), z轴负向. 96×105A/m, 2. B= 0NI/ (4R)
恒定磁场答案-清华版-终稿(1)

恒定磁场(一)参考解答一、选择题1、D2、B3、C 二、填空题 1、大小:00(1122II R R μμπ+方向:⊗2、2cos B r πα- 3、0ln 22Iaμπ三、计算题1.(1)解:金属薄片单位弧长上的电流为I Rπ IdI Rd Rθπ=θπμπμd RIR dI dB 20022==j dB i dB j dB i dB B d y x )cos (sin θθ-+=+=00220020sin 2cos 02x x y y I IB dB d R RIB dB d Rππμμθθππμθθπ=====-=⎰⎰⎰⎰∴02I B i Rμπ=r r1.(2)解:金属薄片单位弧长上的电流为2I Rπ 2IdI Rd Rθπ=0022sin (cos )x y dI I dB d R R dB dB i dB j dB i dB j μμθππθθ===+=+-r r r r r 002220002220sin cos x x y y I IB dB d R RI IB dB d R Rππμμθθππμμθθππ=====-=-⎰⎰⎰⎰∴0022x y I I B B i B j i j R Rμμππ=+=-r r r r r2.解:(1)010212()112222I I B I I dd d μμμπππ=+=+ 方向:⊙(2)010222()I I B r d r μμππ=+- 121010*******121322()ln ln 22r r m m S S S r I I d B dS BdS ldx r d r I l I l r r r r r r μμππμμππ+⎡⎤Φ=Φ===+⋅⎢⎥-⎣⎦++=+⎰⎰⎰⎰r r g四.讨论题32003200321000000440044O I IO R RI IO R Rμμππμμππ=======⊗=====101010、(1)圆环电流的B ;两直导线的B 、B ;点总磁感应强度B (2)圆环电流的B ;两直导线的B 、B ;点总磁感应强度B (3)圆环电流的B ;两直导线的B 、B ;点总磁感应强度B e ee323232000001100O O O ======⊗=⊗=+=-⊗====101012102、(1)三角形电流的B ;两直导线的B 、B ;点总磁感应强度B (2)三角形电流的B ;两直导线的B 、 B ; 点总磁感应强度B B B (3)三角形电流的B ;两直导线的B 、B ; 点总磁感应强度B 04Ilπ⊗;恒定磁场(二)参考解答一、选择题1、C二、填空题1、环路内包围的电流代数和;环路上积分点的磁场;所有电流产生的。
恒定磁场答案解读

第7章恒定磁场一、选择题1. B2. C3. A4. B5. B6. B7. C8. C9. C10. A11. A12. D13. C14. C15. D16. B17. B18. B19. B20. D21. A22. C23. C24. B25. D26. B27. C28. A29. A30. B31. D32. D33. B34. D35. D36. B37. A 38. B 39. C 40. D 41. C 42. C 43. B 44. B 45. D 46. C 47. A 48. D 49. C 50. A 51. C 52. B 53. B 54. B 55. A 56. C 57. A 58. C 59. C 60. D 二、填空题1. (T)1045-⨯,500A2. RI80μ,⊗ 3. (T)108.83-⨯4. r I π20μ5. 1.4 A6.a 37. 动能, 动量8. (N)102.323-⨯,(m)101.75-⨯ 9. )s (m 103.6214-⋅⨯,(m)101.33-⨯10. (V)102.25-⨯11. )m (A 100.8823--⋅⨯,m)(N 0.352⋅ 12. )m (A 1026.9224--⋅⨯ 13. -0.14 J 14. 2, 1 15. 7:8 16. 减小; 2R x <区域减小,在2R x >区域增大(x 为离圆心的距离)17. 0, I 0μ- 18. bba aI+lnπ20μ 19.⎪⎭⎫ ⎝⎛+1π240R I μ 20. I 0μ, 0, I 02μ21. 向着长直导线平移22.aBI 223. r I H π2=, r IH B π2μμ==24. 2ln π20IaΦμ=25. x RIz y R I ˆ83)ˆˆ(π400μμ-+- 26. αsin π2B r -27. (Wb)24.0-, 0, (Wb)24.0 28.22IT m π三、计算题1. 解:由载流直导线磁场公式2204π2rL L rIB +=μ一段载流直线在P 点的磁场大小为22222201)(4)2(2π2x l l l xl IB +++=μ2222021π2xl xl Il++=μ正方形线圈整体在P 点的磁场大小为222220221121)π(24cos 4x l x l l I x l l B B B ++=+==μθ方向沿x 轴由B 与H的关系式得22222021)π(2xl x l l I BH ++==μ 方向沿x 轴2. 解:由毕奥—萨伐尔定律可知,两直线部分电流在其延长线上O 点产生的磁感应强度为0.半圆弧电流在O 点的磁感应强度B垂直于半圆面向上,大小为RI R I B 422100μμ==3. 解:由毕奥—萨伐尔定律和电流分布的对称性可知,半径为R 、载流I 的的圆电流在轴线上距离圆心r 处产生的磁感应强度B 沿电流I 的右旋前进方向,大小为2/32220)(2R x IRB +=μ此处设水平向右为正,则两圆电流在O 点r 处的磁感应强度为2/32222202/321221021])[(2])[(2R r l IR R r l IR B B B +-+++=+=μμ4. 解:由于细导线密绕,每匝电流都可以看作圆电流,于是宽度为r d 的圆电流(电流元)总匝数r n d 载流为r nI I d d =由圆电流在轴线上的磁场公式 x R x IRB ˆ)(22/32220+=μ 可得电流元I d 在P 点的磁场为 xr x rnIr xr x Ir B ˆ)(2d ˆ)(2d d 2/322202/32220+=+=μμA7-3-4图所有电流在P 点产生的磁场为x R x R rR x R nI x r x r r nI B B R ˆln 2ˆ)(d 2d 2222002/32220⎥⎥⎦⎤⎢⎢⎣⎡+-⎪⎪⎭⎫ ⎝⎛++=+==⎰⎰μμ5. 解:建立图所示的Oxyz 平面,将导体薄片分成许多沿z 轴的“无限长”直线电流,其中一根电流的载流量为y d II d d =.利用“无限长”直线电流产生磁场的公式r I B π20μ=可得r IB '=π2d d 0μ其中22y r r +='由对称性分析可知,导体薄片上所有电流在P 点产生的磁场将沿y 轴,其大小为⎪⎭⎫⎝⎛=+==⎰⎰-r d Iy y r d rI B B d d 2arctan π2d )(π2sin d 02/2/220μμθ讨论:当∞→d 时,如果保持j dI=为恒量,由上式可得 j I B 00212ππμμ==即无穷大载流平面产生的磁场为均匀场.6. 解:带电圆盘转动时,可看作无数圆电流的磁场在O 点的叠加. 取半径为ξ,宽为ξd 的圆环,其上电流ξσωξπωξπξσd 2d 2d =⋅=i它在中心O 产生的磁感应强度为:ξσωμξμd 212d d 00==i B正电荷部分产生的磁场为:r B r⎰==+00021d 21σωμξσωμ 负电荷部分产生的磁场为:)(21d 2100r R B R r -==⎰-σωμξσωμ 而题设-+=B B ,故得R=2r7. 解:电子运动速度⊥+=v v v// 由电子运动方程B e rm ⊥⊥=v v 2 得电子绕磁力线转一圈的时间为(s)1057.310100.1106.1101.914.32π2π22451931-----⊥⨯=⨯⨯⨯⨯⨯⨯⨯===B e m r T v 电子沿着磁场方向前进一光年所需时间为(s)1015.310301.0103606024365988//⨯=⨯⨯⨯⨯⨯⨯⨯==v 光年s t 在这段时间里电子绕磁力线转的圈数为1029108.81057.31015.3⨯=⨯⨯==-T t N8. 解:导线中通过电流I 时,上面一段通电导线所受的安培力大小为ILB F =方向向上,使得导线跳起. 由牛顿定律得 t F m d d =v 因F v 、同向,故t ILB t F m d d d ==v所以00d 0v v v m m =⎰⎰⎰==qqLBq q LB t I LB 0d d又因为gh 20=v所以,通过导线的电量为gh LBmq 2=A7-3-8图9. 解:建立如图所示的坐标系Ox ,在离“无限长”直线电流x 远处电流元l d I 受力21d d B l I F⨯=方向垂直于电流2I 向上. 于是,整个电流2I 所受的力为21d d B l I F F⨯==⎰⎰大小为2ln π2d 1π22102210I I x x I I F LLμμ==⎰10. 解:(1)在均匀磁场中,圆弧⋂CD 所受的磁力与弧线通以同样的电流所受的磁力相等由安培定律得 (N)283.05.022.022=⨯⨯⨯===⋂RIB F F CD方向与CD 弧线垂直,与OD 夹角为45度,如A7-3-10图所示.(2) 线圈的磁矩 n n n IS P 22m 10π22.0π412-⨯=⨯⨯==所受磁力矩大小为夹角为与,30)6090(=-B n 30sin m B P M =215.010π22⨯⨯⨯=-m)(N 1057.12⋅⨯=- M 的方向将驱使线圈法线n转向与B 平行.11. 解:建立如A7-3-11图所示的坐标系,轴方向,沿z j平板在yz 平面内,取宽度为y d , 长直电流y j I d d =,它在P 点产生的磁感应强度大小为:,π2d π2d d 00r yj r I B μμ==方向如A7-3-11图所示 将y x B B B d d d 和分解为,由对称性可知0d ==⎰x x B B ,θθcos π2d cos d d 0ryj u B B y ==又2222cos ,yx xr x y x r +==+=θ,代入上式并积分,则j u x y y jx u B B y 022021d π2d =+==⎰⎰∞∞-A7-3-9图1IO d A7-3-11图A7-3-10图12. 解:带电圆筒旋转相当于圆筒表面有面电流,单位长度上电流为ωσωσR R i =⋅=π2π2与长直通电螺线管内磁场分布类似.圆筒内为均匀磁场,ω的方向与B 一致(若0<σ,则相反).圆筒外0=B.作如图所示的安培环路L ,由安培环路定理i ab ab B l B L⋅=⋅=⋅⎰0d μ 得圆筒内磁感应强度大小为ωσμμR i B 00==写成矢量式:ωσμμR i B 00==13. 解:(1) 如图示在CD 上距O 点r 处取线元r d ,其上带电量r q d d λ=q d 旋转对应的电流强度为 r q I d π2d π2d λωω==它在O 点产生的磁感应强度大小为rrr I B d 42d d 00⋅==πλωμμ O 点的磁感应强度大小为 aba rrB B b a aO +===⎰⎰+lnπ4d π4d 00λωμωλμ 0>λ时的方向为⊗(2) I d 的磁矩为 r r I r P d 21d πd 22m λω== 总磁矩大小为])[(d 21d 332m m a b a b r r P P ba a-+===⎰⎰+λωλω0>λ时的方向与ω相同,即⊗(3) 若a >> b ,则)31()(,ln 33a ba b a a b a b a +≈+≈+,则有 a qa b B O π4π400ωμωλμ=⋅=,其中b q λ= q a b a b P m 22213ωλω=⋅=o B及m P 的方向同前.14. 解:(1)设上下两电流在P 点产生的磁感应强度分别为1B 和2B由安培环路定理⎰∑=⋅LI l B 0d μ 可得1B 和2B的大小分别为22001π2π2xa IrIB +==μμA7-3-12图22002π2π2xa IrIB +==μμ方向如图所示.由二者叠加,可得:x x x B B B 21+=22220π22xa ax a I +⋅+⋅=μ)π(220x a Ia +=μ 0=y Bi x a Ia x B)π()(220+=μ(2) 令0)π(2d d 2220=+-=x a Iax x Bμ,得0=x ,又得0d d 22<x B所以0=x 出B 有极大值.15. 解:由电流分布具有轴对称,可知磁场分布也应有轴对称,即与轴线距离相同的场点,其场强大小相等,其方向沿以圆筒轴线为轴的过场点的圆环的切向; 又因电流无限长,场强与场点的轴向位置无关.过场点作垂直于圆筒轴线,半径为r 的圆周,由安培环路定理,有 ∑⎰==⋅i L I r B l B 0π2d μ1R r <: 0=∑i I , 0=∴B 21R r R <<:)π(212R r j Ii-=∑rR r j B 2)(220-=μ写成矢量式为 r 21202)(e j rR r B⨯-=μ 2R r >:I R R j Ii=-=∑)π(2122rIrR R j B π22)(021220μμ=-=圆筒外部的磁场相当于全部电流集中在轴线上所产生的场.结果讨论:若R 1=0, 即电流均匀流过无限长实心圆柱,这时由上述解答易得, 圆柱内 r j B⨯=20μ;圆柱外解答不变.16. 解:由于电流分布对于平板厚度的平分面CD 对称,并且沿平面任意方向平移不变, 因此磁场亦具有平面对称性, 即在与平板距离相同的场点, 其磁感应强度相同, 且其值与场点沿板平面的位置坐标无关.磁感应强度的方向可作如下分析:沿电流方向将平板分成许多细长条,如A7-3-16图所示.取一对相对场点位置对称的细长条,由无限长直电流的场强叠加可知,合场强的方向垂直于电流方向而与板面平行.选择坐标如A7-3-16图, 由场分布的对称情况,过场点作图示矩形,使其中两对边与板面平行,由安培环路定理有∑⎰==⋅i LI Bh l B 02d μ2bx <, xh j I i 2⋅=∑, jx B 0μ= 或 x j B ⨯=0μ2b x >’j b hI i =∑, 20jbB μ=或 n 02e j b B⨯=μ 其中, n e为平板的外法线方向.17. 解:闭合曲线1L 环绕电流两圈,每一圈电流均是反向穿过,所以⎰-=⋅102d L I l B μ闭合曲线2L 可看成由2L '和2L ''两部分曲线构成,如A7-3-17图所示,加一辅助线AB ,则A L AB 2'构成一闭合回路,B L BA 2''构成另一回路,对两个回路,电流均是反向穿过,所以II I l B l B l B l B l B l B l B l B l B B L BA A L AB L BA AB L L L L 0002d d d d d d d d d 2222222μμμ-=--=⋅+⋅=⋅+⋅+⋅+⋅=⋅+⋅=⋅⎰⎰⎰⎰⎰⎰⎰⎰⎰'''''''''这样可看作电流I 反向穿过回路2L 两次,所以有上式.A7-3-16图A7-3-17图18. 解:在半圆形电流上任取电流元l I d , 该电流元所受磁力为B l I F⨯=d d , 则此半圆弧导线受力为)d (⎰⨯=baB l I F由于磁场均匀,B可移至积分符号之外,因而有 B l I F b a ⨯⎪⎭⎫ ⎝⎛=⎰d 式中⎰b ald 为半圆弧上各有向线元l d 的矢量和,它等于由半圆一端a 到另一端b 的矢量,以l 表示,则B l I B l I F b a ⨯=⨯⎪⎭⎫ ⎝⎛=⎰d上式表示,均匀磁场中半圆形载流导线所受磁力与一段连接其两端的载流直导线所受的磁力相同. 按题设, l 与B之间夹角为α, 因此磁力的大小为IRB RB I F ==αsin 2F 的方向与纸面垂直,指向纸面外.19. 解:带缺口的圆柱面电流的磁场可看作一完整均匀柱面电流的磁场和在缺口位置的密度相同、方向相反的电流的磁场的叠加.由于均匀圆柱面电流在其轴线处的磁感应强度为零, 轴线处磁感应强度由缺口的反向电流的磁场决定.而由于R b <<,缺口电流可视为无限长的载流直导线, 它在轴线处产生的磁感应强度大小RjbB π20μ=方向垂直于轴线由安培力公式, 轴线位置处的载流长直导线所受磁力大小为RIjb IB l Fπ2d d 0μ== 因为两电流平行反向,故磁力方向为垂直于导线的斥力20. 解:载流线圈在均匀磁场中所受合力为⎰⎰=⨯=⨯=0]d [d B l I B l I F所受合力矩大小为()的夹角为线圈法线与B B P B P M m mϕϕ0sin ==⨯=所以线圈处于平衡状态.但因线圈上各电流元都受到安培力作用且沿径向向外,所以线圈导线中存在张力,且各处张力相等,沿切向.T7-3-18图 bA7-3-19图如A7-3-20(a)图任取一电流元,它对圆心O 所张的角为θd ,它两端受张力T 的作用,沿径向受安培力Fd 作用,导线元处于平衡态,则 2d sin 2d θT F = 又 θd d d d IBR lB I B l I F ==⨯=因电流元足够小,θd 足够小2d 2d sinθθ≈ 于是有IBR T =本题也可通过分析一段弧的受力求解.如7-3-20(b)图,考虑半圆形载流导线受力,其所受安培力为 R IB B l I F 2d =⨯=⎰由圆线圈处于平衡态,有T F 2=故IBR T =21. 解:设小磁针的等效磁矩为m p,则小磁针在磁场中所受力矩为θθB p B p M m m -≈-=sin式中θ为m p与B 间的夹角,负号表示该磁力矩为恢复力矩,由定轴转动定律22d d tJ M θ=θθJ B p tm -=22d d J B p m =2ω, B p J T m π=2所以 =π=)2(TB J p m 2.63×10-2 A ·m 2A7-3-20(a)图⋅⋅⋅⋅⋅⋅A7-3-20(b)图⋅⋅⋅⋅⋅⋅T。
恒定磁场习题解答

第七章 恒定磁场7 -1 两根长度相同的细导线分别多层密绕在半径为R 和r 的两个长直圆筒上形成两个螺线管,两个螺线管的长度相同,R =2r ,螺线管通过的电流相同为I ,螺线管中的磁感强度大小B R 、B r 满足( )(A ) r R B B 2= (B ) r R B B = (C ) r R B B =2 (D )r R B B 4= 分析与解 在两根通过电流相同的螺线管中,磁感强度大小与螺线管线圈单位长度的匝数成正比.根据题意,用两根长度相同的细导线绕成的线圈单位长度的匝数之比21==R r n n r R 因而正确答案为(C )。
7 -2 一个半径为r 的半球面如图放在均匀磁场中,通过半球面的磁通量 为( )(A )B r 2π2 (B ) B r 2π(C )αB r cos π22 (D ) αB r cos π2分析与解 作半径为r 的圆S ′与半球面构成一闭合曲面,根据磁场的高斯定理,磁感线是闭合曲线,闭合曲面的磁通量为零,即穿进半球面S 的磁通量等于穿出圆面S ′的磁通量;S B ⋅=m Φ.因而正确答案为(D ). 7 -3 下列说法正确的是( )(A ) 闭合回路上各点磁感强度都为零时,回路内一定没有电流穿过(B ) 闭合回路上各点磁感强度都为零时,回路内穿过电流的代数和必定为零(C ) 磁感强度沿闭合回路的积分为零时,回路上各点的磁感强度必定为零(D ) 磁感强度沿闭合回路的积分不为零时,回路上任意一点的磁感强度都不可能为零分析与解 由磁场中的安培环路定律,磁感强度沿闭合回路的积分为零时,回路上各点的磁感强度不一定为零;闭合回路上各点磁感强度为零时,穿过回路的电流代数和必定为零。
因而正确答案为(B ).7 -4 在图(a)和(b)中各有一半径相同的圆形回路L1 、L2 ,圆周内有电流I1 、I2 ,其分布相同,且均在真空中,但在(b)图中L2 回路外有电流I3 ,P 1 、P 2 为两圆形回路上的对应点,则( )(A ) ⎰⎰⋅=⋅21L L d d l B l B ,21P P B B = (B ) ⎰⎰⋅≠⋅21L L d d l B l B ,21P P B B= (C ) ⎰⎰⋅=⋅21L L d d l B l B ,21P P B B≠(D ) ⎰⎰⋅≠⋅21L L d d l B l B ,21P P B B ≠分析与解 由磁场中的安培环路定律,积分回路外的电流不会影响磁感强度沿回路的积分;但同样会改变回路上各点的磁场分布.因而正确答案为(C ). *7 -5 半径为R 的圆柱形无限长载流直导体置于均匀无限大磁介质之中,若导体中流过的恒定电流为I ,磁介质的相对磁导率为μr (μr<1),则磁介质内的磁化强度为( )(A )()r I μr π2/1-- (B ) ()r I μr π2/1-(C ) r I μr π2/- (D ) r μI r π2/分析与解 利用安培环路定理可先求出磁介质中的磁场强度,再由M =(μr-1)H 求得磁介质内的磁化强度,因而正确答案为(B ). 7 -6 北京正负电子对撞机的储存环是周长为240 m 的近似圆形轨道,当环中电子流强度为8 mA 时,在整个环中有多少电子在运行? 已知电子的速率接近光速。
磁场考试题及答案

磁场考试题及答案一、单项选择题(每题2分,共20分)1. 磁场的基本性质是()。
A. 对电流有力的作用B. 对电荷有力的作用C. 对磁体有力的作用D. 对所有物体都有力的作用答案:A2. 磁场的方向规定为()。
A. 从北极指向南极B. 从南极指向北极C. 从南极指向北极,内部从北极指向南极D. 从北极指向南极,内部从南极指向北极答案:C3. 磁感应强度的单位是()。
A. 特斯拉(T)B. 高斯(Gs)C. 奥斯特(Oe)D. 韦伯(Wb)答案:A4. 磁场中某点的磁感应强度的方向与该点的磁场方向()。
A. 相同B. 相反C. 不一定D. 垂直答案:A5. 磁通量的大小等于()。
A. 磁感应强度与面积的乘积B. 磁感应强度与面积的乘积再乘以夹角的正弦值C. 磁感应强度与面积的乘积再乘以夹角的余弦值D. 磁感应强度与面积的乘积再乘以夹角的正切值答案:C6. 磁通量的方向规定为()。
A. 垂直于磁场方向B. 垂直于平面方向C. 垂直于磁感线方向D. 垂直于磁感应强度方向答案:B7. 磁感应强度的大小与()无关。
A. 磁场方向B. 磁场强度C. 磁感线密度D. 磁通量大小答案:D8. 磁感应强度的方向与()有关。
A. 磁场方向B. 磁场强度C. 磁感线密度D. 磁通量大小答案:A9. 磁通量的变化率与()有关。
A. 磁感应强度的变化率B. 面积的变化率C. 磁场方向的变化率D. 磁感应强度和面积的变化率答案:D10. 根据法拉第电磁感应定律,感应电动势的大小与()有关。
A. 磁感应强度的变化率B. 磁通量的变化率C. 磁感应强度和面积的变化率D. 磁通量和面积的变化率答案:B二、多项选择题(每题3分,共15分)11. 磁场对运动电荷的作用力称为()。
A. 洛伦兹力B. 磁力C. 洛伦兹力和磁力D. 都不是答案:A12. 磁场对电流的作用力称为()。
A. 安培力B. 磁力C. 安培力和磁力D. 都不是答案:A13. 磁场中某点的磁感应强度的方向与()有关。
第七章 恒定磁场-习题解答

解 (1)r<a B dl 0 应用安培环路定理 L i 在r<a柱体内绕轴作环形回路L,其中
于是有
I
i
r2 Ii a 2 I
πr 2 B1 2πr 0 I 2 πa
B1
0 Ir
2πa 2
第七章、稳恒磁场
0 I (2)a r b : B 2r 0 I , B 2r
霍尔电势差有多大?(铜的电子浓度n=8.41028 l/m3)。 解 (1)根据洛伦兹力
F qv B
可判断铜片内载流子(电子)在磁场中 的受力方向向右,因此右侧积聚了电子 带负电,左侧因缺少电子而带等量的正 电。所以左侧电势高
(2)霍耳电势差
1 IB 5 UH 2.2 10 V ne a
方向沿oo’竖直向下。
第七章、稳恒磁场
习题7-19 如图所示,一闭合回路由半径 为a和b的两个同心半圆连成,载有电流I。 试求(1)圆心P点处磁感应强度B的大小 和方向;(2)回路的磁矩。 解: (1)由磁场叠加原理
方向垂直纸面向里。 (2)由磁矩定义
方向垂直纸面向里。
第七章、稳恒磁场
7-20 质谱仪的构造原理如图所示。离子源S提供质量为M、 电荷为q的离子。离子初速很小,可以看作是静止的,然后经 过电压U的加速,进入磁感应强度为B的均匀磁场,沿着半圆 周运动,最后到达记录底片P上。测得离子在P上的位置到入 qB 2 x 2 。 口处A的距离为x。试证明该离子的质量为:M
S
B dS 0
三、安培环路定理——求解磁感应强度B
B dl 0 I i
L i
四、磁场对载流导线的作用——安培力
dF Idl B
恒定磁场参考答案

恒定磁场参考答案恒定磁场参考答案磁场是我们日常生活中常见的物理现象之一。
它是由电流或磁体产生的,并且可以对其他物体产生各种各样的影响。
在这篇文章中,我们将探讨恒定磁场的一些基本概念和应用。
首先,我们来了解一下什么是恒定磁场。
恒定磁场是指磁场的强度和方向在空间中保持不变的情况。
这意味着无论我们在磁场中的位置如何,磁场的性质都是一样的。
这与变化磁场不同,变化磁场的强度和方向会随着时间的推移而改变。
恒定磁场有许多重要的应用。
其中一个应用是在磁共振成像(MRI)中。
MRI是一种医学成像技术,它利用恒定磁场和无线电波来生成人体内部的图像。
MRI可以帮助医生诊断各种疾病,如肿瘤和神经系统疾病。
恒定磁场在MRI中起到了至关重要的作用,它能够使人体内的原子核在磁场中产生共振,从而产生信号被接收器捕获并转化为图像。
另一个应用是在磁力计中。
磁力计是一种测量磁场强度和方向的仪器。
它通常由一个磁针和一个刻度盘组成。
当磁针暴露在磁场中时,它会受到磁场力的作用,从而指向磁场的方向。
通过读取刻度盘上的刻度,我们可以确定磁场的强度。
磁力计在许多领域中都有广泛的应用,包括地质勘探、导航和科学研究等。
此外,恒定磁场还与电磁感应相关。
电磁感应是指当导体在恒定磁场中运动时,会在导体中产生感应电流。
这个现象是由法拉第电磁感应定律描述的。
根据这个定律,感应电流的大小与导体的速度、磁场的强度和导体的几何形状有关。
电磁感应在发电机和变压器等电力设备中起着重要的作用。
最后,让我们来看一下恒定磁场对物体运动的影响。
当一个带电粒子进入恒定磁场时,它会受到洛伦兹力的作用。
洛伦兹力是由带电粒子的速度和磁场的方向决定的。
根据洛伦兹力的方向,带电粒子可能会被弯曲成一个圆形轨道,这被称为磁场中的圆周运动。
这个现象在粒子加速器和等离子体物理学中非常常见。
总之,恒定磁场是一个重要的物理现象,它在许多领域中都有广泛的应用。
无论是在医学成像、磁力计、电磁感应还是物体运动中,恒定磁场都起着关键的作用。
《恒定磁场习题》word版

恒定磁场作业班级:_____________ 姓名:_____________ 学号:_____________ 日期:__________年_______月_______日 成绩:_____________ 一、选择题 1.边长为l 的正方形线圈,分别用图示两种方式通以电流I (其中ab 、cd 与正方形共面),在这两种情况下,线圈在其中心产生的磁感强度的大小分别为 (A) ,.(B) ,. (C) ,.(D) ,. []2. 如图,两根直导线ab 和cd 沿半径方向被接到一个截面处处相等的铁环上,稳恒电流I 从a 端流入而从d 端流出,则磁感强度沿图中闭合路径L 的积分等于(A) . (B) .(C) . (D) . [ ]3.一个动量为p 的电子,沿图示方向入射并能穿过一个宽度为D 、磁感强度为(方向垂直纸面向外)的均匀磁场区域,则该电子出射方向和入射方向间的夹角为 (A) . (B) .(C) . (D) . [ ]4.四条皆垂直于纸面的载流细长直导线,每条中的电流皆为I .这四条导线被纸面截得的断面,如图所示,它们组成了边长为2a 的正方形的四个角顶,每条导线中的电流流向亦如图所示.则在图中正方形中心点O 的磁感强度的大小为 (A) . (B) .(C) B = 0. (D) . [ ]5.无限长直导线在P 处弯成半径为R 的圆,当通以电流I 时,则在圆心O 点的磁感强度大小等于(A) . (B) . (C) 0. (D) . (E) . [ ]6. 有一半径为R 的单匝圆线圈,通以电流I ,若将该导线弯成匝数N= 2的平面圆线圈,导线长度不变,并通以同样的电流,则线圈中心的磁感强度和线圈的磁矩分别是原来的(A) 4倍和1/8. (B) 4倍和1/2.(C) 2倍和1/4. (D) 2倍和1/2. [ ]7.四条平行的无限长直导线,垂直通过边长为a =20 cm 的正方形顶点,每条导线中的电流都是I =20 A ,这四条导线在正方形中心O 点产生的磁感强度为(μ0 =4π×10-7 N ·A -2)(A) B =0. (B) B = 0.4×10-4 T .I B 1 I B 12a bc d IO RP I(C) B = 0.8×10-4 T. (D) B =1.6×10-4 T . [ ]8.一载有电流I 的细导线分别均匀密绕在半径为R 和r 的长直圆筒上形成两个螺线管,两螺线管单位长度上的匝数相等.设R = 2r ,则两螺线管中的磁感强度大小B R 和B r 应满足: (A) B R = 2 B r . (B) B R = B r .(C) 2B R = B r . (D) B R = 4 B r . [ ]9.有一无限长通电流的扁平铜片,宽度为a ,厚度不计,电流I 在铜片上均匀分布,在铜片外与铜片共面,离铜片右边缘为b 处的P 点(如图)的磁感强度的大小为 (A) . (B) . (C)bba bI+πln20μ. (D) . [ ] 10.关于稳恒电流磁场的磁场强度,下列几种说法中哪个是正确的? (A) 仅与传导电流有关. (B) 若闭合曲线内没有包围传导电流,则曲线上各点的必为零.(C) 若闭合曲线上各点均为零,则该曲线所包围传导电流的代数和为零. (D) 以闭合曲线L为边缘的任意曲面的通量均相等. [ ]二、填空题 11.图中所示的一无限长直圆筒,沿圆周方向上的面电流密度(单位垂直长度上流过的电流)为i ,则圆筒内部的磁感强度的大小为B =________,方向_______________.12.如图所示,在宽度为d 的导体薄片上有电流I 沿此导体长度方向流过,电流在导体宽度方向均匀分布.导体外在导体中线附近处P 点的磁感强度的大小为________________________.13.有一长直金属圆筒,沿长度方向有横截面上均匀分布的稳恒电流I 流通.筒内空腔各处的磁感强度为______________,筒外空间中离轴线r 处的磁感强度为______________.14.一质量为m ,电荷为q 的粒子,以0v速度垂直进入均匀的稳恒磁场中,电荷将作半径为____________________的圆周运动.15.在磁场中某点放一很小的试验线圈.若线圈的面积增大一倍,且其中电流也增大一倍,该线圈所受的最大磁力矩将是原来的______________倍.16.有一半径为a ,流过稳恒电流为I 的1/4圆弧形载流导线bc ,按图示方式置于均匀外磁场中,则该载流导线所受的安培力大小为_______________________.17.氢原子中电子质量m ,电荷e ,它沿某一圆轨道绕原子核运动,其等效圆电流的磁矩大小p m 与电子轨道运动的动量矩大小L 之比=Lp m________________. 18.一无限长载流直导线,通有电流I ,弯成如图形状.设各线段皆在纸面内,则P点磁感强度的大小为________________.19.一根无限长直导线通有电流I ,在P 点处被弯成了一个半径为R 的圆,且P 点处无交叉和接触,则圆心O 处的磁感强度大小为_______________________________________,方向为______________________________.20.图示为三种不同的磁介质的B ~H 关系曲线,其中虚线表示的是B = μ0H 的关系.说明a 、b 、c 各代表哪一类磁介质的B ~H 关系曲线:a 代表______________________________的B ~H 关系曲线.b 代表______________________________的B ~H 关系曲线.c 代表______________________________的B ~H 关系曲线.三、计算题 21.真空中有一边长为l 的正三角形导体框架.另有相互平行并与三角形的bc 边平行的长直导线1和2分别在a 点和b 点与三角形导体框架相连(如图).已知直导线中的电流为I ,三角形框的每一边长为l ,求正三角形中心点O 处的磁感强度.22.横截面为矩形的环形螺线管,圆环内外半径分别为R1和R2,芯子材料的磁导率为μ,导线总匝数为N,绕得很密,若线圈通电流I,求.(1) 芯子中的B值和芯子截面的磁通量.(2) 在r < R1和r > R2处的B值.23.在一无限长的半圆筒形的金属薄片中,沿轴向流有电流,在垂直电流方向单位长度的电流为i = k sinθ,其中k为常量,θ 如图所示.求半圆筒轴线上的磁感强度.24.在真空中有两根相互平行的无限长直导线L1和L2,相距10 cm,通有方向相反的电流,I1 =20 A,I2 =10 A,试求与两根导线在同一平面内且在导线L2两侧并与导线L2的距离均为5.0 cm的两点的磁感强度的大小.(μ0 =4π×10-7 H·m-1)参考答案1.C2.D3.B4.C5.D6.B7.C8.B9.B 10.C11.0i2分沿轴线方向朝右1分12.3分13.0 1分2分14.3分15.4 3分16.aIB3分17.3分18.3分19.2分垂直纸面向里.1分20铁磁质1分顺磁质1分抗磁质1分21.解:令、、和分别代表长直导线1、2和通电三角框的、和边在O点产生的磁感强度.则:对O点,直导线1为半无限长通电导线,有,的方向垂直纸面向里.2分:由毕奥-萨伐尔定律,有方向垂直纸面向里.2分和:由于ab和acb并联,有根据毕奥-萨伐尔定律可求得=且方向相反.2分所以1分把,代入B1、B2,则的大小为的方向:垂直纸面向里.1分22.解:(1) 在环内作半径为r的圆形回路, 由安培环路定理得,3分在r处取微小截面d S = b d r, 通过此小截面的磁通量穿过截面的磁通量5分(2)同样在环外( r < R1和r > R2 )作圆形回路, 由于∴B = 0 2分23.解:设轴线上任意点的磁感强度为B,半圆筒半径为R.先将半圆筒面分成许多平行轴线的宽度为d l的无限长直导线,其中流过的电流为2分它在轴线上产生的磁感强度为,方向如图.2分由对称性可知:在z轴向的分量为0,在y轴的分量叠加中相互抵消,只需考虑在x轴的分量d B x.2分d B x = d B sin 2分积分:2分的方向沿x轴负方向.24.解:(1) L1中电流在两导线间的a点所产生的磁感强度T 2分L2中电流在a点所产生的磁感强度T 1分由于、的方向相同,所以a点的合磁感强度的大小T 2分(2) L中电流在两导线外侧b点所产生的磁感强度T 2分L2中电流在b点所产生的磁感强度T 1分由于和和的方向相反,所以b点的合磁感强度的大小T 2分温馨提示-专业文档供参考,请仔细阅读后下载,最好找专业人士审核后使用!。
习题答案(恒定磁场)解读

三、计算题
稳恒磁场习题
1. R=/(2a); j1/j2= r22/r12
2. B=0NI/ (4R) 3. 4. B = By= 0dI/[2(R2-R2)] 方向沿y轴正向 5. 0J; 0 7. 课后11-8 10. 课后11-15 6. F=0I1I2/2 方向向右 8. 课后11-11 11.课后11-20 9. 课后11-13 12. 课后11-22
稳恒磁场习题
计算题 1
稳恒磁场习题
计算题 2
计算题 3
稳恒磁场习题
计算题 4
稳恒磁ห้องสมุดไป่ตู้习题
计算题 5
稳恒磁场习题
计算题 6
稳恒磁场习题
稳恒磁场习题
计算题 7
稳恒磁场习题
计算题 8
稳恒磁场习题
计算题 9
计 算 题 10
稳 恒 磁 场 习 题
计算题 11
稳恒磁场习题
解:根据带电粒子回旋半径与粒子运动速率的关系有
稳 恒 磁 场 习 题
一、选择题 BAAAB
DBCBC CDBD
二、填空题 1. I1+ I2+ I3+ I4=0 2. 所围面积, 电流, 法线(n). 3. 0. 4. 0.16T. 5. 0Qv/(8l2), z轴负向. 6. 环路L所包围的电流, 环路L上的磁感应强度, 内外. 7. 0I, 0, 20I. 8. IBR . 9. 10-2, /2 10. 7.96×105A/m, 2.42×102A/m.
P=mv=ReB=1.12×10-21 kg·m/s Ek=p2/(2m)=2.35 keV
稳恒磁场习题
计算题 12
稳恒磁场作业习题及参考答案

9-6 已知磁感应强度0.2=B Wb·m -2 的均匀磁场,方向沿x 轴正方向,如题9-6图所示.试求: (1)通过图中abcd 面的磁通量;(2)通过图中befc 面的磁通量;(3)通过图中aefd 面的磁通量. 解: 如题9-6图所示(1) 通过abcd 面积1S 的磁通是: 24.0)4.03.0(0.211=⨯⋅=⋅=Φi i S B(Wb )(2) 通过befc 面积2S 的磁通量: 0)3.03.0(0.222=⨯⋅=⋅=Φk i S B(3) 设aefd 面积3S 的法线正方向如图,则通过aefd 面积3S 的磁通量:24.05415.02cos )5.03.0(233=⨯⨯=⨯⨯⨯=⋅=ΦθS B (Wb )9-7 如题9-7图所示,AB 、CD 为长直导线,C B为圆心在O 点的一段圆弧形导线,其半径为R .若通以电流I ,求O 点的磁感应强度. 解:如题9-7图所示,O 点磁场由AB 、C B、CD 三部分电流产生.其中AB 段产生: 01=BC B 段产生: R IR I B 12360602002μμ=⋅=,方向⊗(即垂直纸面向里) CD 段产生:)231(2)60sin 90(sin 24003-πμ=-πμ=︒︒R I R I B ,方向⊗ 【或:)231(2)180cos 120(cos 24003-=-=︒︒R I R IB πμπμ,方向⊗】 ∴ )6231(203210ππμ+-=++=R I B B B B , 方向⊗.9-8 在真空中,有两根互相平行的无限长直导线1L 和2L ,相距0.1m ,通有方向相反的电流,1I =20A,2I =10A ,如题9-8图所示.A ,B 两点与导线在同一平面内.这两点与导线2L 的距离均为5.0cm .试求A ,B 两点处的磁感应强度,以及磁感应强度为零的点的位置.解:如题9-8图所示,A B方向垂直纸面向里,大小为:42010102.105.02)05.01.0(2-⨯=⨯+-=πμπμI I B A TB B方向垂直纸面向外,大小为:520101033.105.02)05.01.0(2-⨯≈⨯++-=πμπμI I B B T设0=B在2L 外侧距离2L 为r 处,则02)1.0(220=-+rI r Iπμπμ, 解得:1.0=r m题9-6图题9-7图题9-8图9-12 两平行长直导线相距d =40cm ,每根导线载有电流1I =2I =20A ,如题9-12图所示.求: (1) 两导线所在平面内与该两导线等距的一点A 处的磁感应强度; (2) 通过图中斜线所示面积的磁通量.(1r =3r =10cm, l =25cm). 解:(1) 52010104)2(2)2(2-⨯=+=d I dI B A πμπμ(T) 方向⊥纸面向外(2) 取面元 r l S d d =,则:Bldr S d B d =⋅=Φ6120102010102.23ln 31ln 23ln 2])(22[211-+⨯==-=-+=Φ=Φ⎰⎰πμπμπμπμπμlI l I l I ldr r d I r I d r r r S(Wb )9-13 一根很长的铜导线载有电流10A ,设电流均匀分布。
恒定磁场题解

恒定磁场题解第四章恒定磁场(注意:以下各题中凡是未标明磁媒质的空间,按真空考虑)4-1 如题4-1图所示,两条通以电流的半无穷长直导线垂直交于O 点。
在两导线所在平面,以O 点为圆心作半径为的圆。
求圆周上A 、B 、C 、D 、E 、F 各点的磁感应强度。
解参考教材71页的例4-1,可知,图4-2所示通有电流I 的直导线在P 点产生的磁感应强度为()αθθπμe B 120cos cos 4--=rI因此,可得(设参考正方向为指出纸面)R IR R I B A πμπμ422135cos 180cos 220cos 135cos 400=----= ()RIR I B B πμπμ410cos 90cos 400=--=用类似的方法可得 RI B C πμ40=,I R B C 0212μπ-=,RI B D πμ40=,R I B E πμ20=,I R B F 0212μπ+-= 4-2平面上有一正边形导线回路。
回路的中心在原点,边形顶点到原点的距离为。
导线中电流为。
1)求此载流回路在原点产生的磁感应强度;2)证明当趋近于无穷大时,所得磁感应强度与半径为的圆形载流导线回路产生的磁感应强度相同; 3)计算等于3时原点的磁感应强度。
解如图4-3中所示为正边形导线回路的一个边长,则所对应的圆心角为nπ2,各边在圆心产生的磁感应强度为()()()()()αααααααππμππμθπμθπμθπμθθπμθθπμe e e e e e e B ??=??? ??====---=--=n R I n r I r I r I rIr I r I tan 2sin 2cos 2cos 2cos 24cos cos 4cos cos 40010101011012011)n 条边在圆心产生的磁感应强度为αππμe B ??=n R I n tan 20 2)当n ∞→时,圆心处的磁感应强度为ααμππμe e B R I n R I n n 2tan 2lim 00=??=∞→3)当等于3时圆心处的磁感应强度为ααπμππμe e B R I R I 2333tan 2300=??=4-3 设矢量磁位的参考点为无穷远处,计算半径为的圆形导线回路通以电流时,在其轴线上产生的矢量磁位。
稳恒磁场习题

稳恒磁场复习题一 判断题1 一带电粒子作匀速直线运动通过某区域,所以该区域的磁场为零。
2 一闭合回路中有两条通有大小相同、方向相反电流的两条导线,则闭合回路上各点的磁感应强度为零。
3 一对相同带电量和相同质量的正、负电子同时在同一点入射一均匀磁场,已知他们的速度非别为2v 和v ,都和磁场垂直,若只考虑磁场作用,则他们同时回到出发点。
4 若闭合曲线上各点的H 为零,则该曲线所包围的传导电流的代数和为零二选择题1 如图所示电流分布,O 点的磁感应强度为 ( )(A)0022I I R R μμπ+; (B) 0024I IR Rμμπ+; (C) 004I I R R μμπ+; (D) 0I R μπ. 2 如图所示电流分布,O 点的磁感应强度为 ( )(A)0022I I R R μμπ+; (B) 002I I R R μμπ-; (C) 0022I IR Rμμπ-; (D) 0I R μπ. 3 一条无限长直导线在一处弯折为半径为R 的圆弧,如图。
已知导线电流强度为I ,圆心O 处的磁感应强度为(A)08IRμ; (B) 04I R μ; (C) 02I R μ; (D) 0.4 两根长直导线沿半径方向连接到粗细均匀的铁环上的A 、B 两点,并与很远处的电源相连,两段弧AB 的长度和电流分别为L 1、L 2和I 1、I 2,则圆环中心的磁感应强度为(A)01124I L R μπ; (B) 02224I L R μπ; (C) 022*******I L I LR Rμμππ+; (D) 0. 5、关于稳恒电流磁场的磁场强度H,下列几种说法中哪个是正确的 ( )(A) H仅与传导电流有关.(B) 若闭合曲线内没有包围传导电流,则曲线上各点的H必为零. (C) 若闭合曲线上各点H均为零,则该曲线所包围传导电流的代数和为零.(D) 以闭合曲线L为边缘的任意曲面的H通量均相等.6、在磁感强度为B的均匀磁场中作一半径为r 的半球面S ,S 边线所在平面的法线方向单位矢量n 与B 的夹角为a ,则通过半球面S 的磁通量(取弯面向外为正)为(A) SB (B) 2SB (C) -SBsina (D) -SBcosa7、六根无限长导线互相绝缘,通过电流均为I ,区域Ⅰ、Ⅱ、Ⅲ、Ⅳ均为相等的正方形,哪一个区域指向纸内的磁通量最大?(A) Ⅰ区域. (B) Ⅱ区域.(C) Ⅲ区域. (D) Ⅳ区域.8 边长为L 的一个导线方框上同有电流I ,则此框中心的磁感应强度( ) (A)与L 无关. (B) 正比于L 2.(C) 与L 成反比. (D) 与I 2有关域.9 无限长通电流扁平铜片,宽度为a ,厚度不计,电流I 在铜片上均匀分布,在铜片外与铜片共面,离铜片最近边缘为b 处的P 点的磁感应强度B 的大小为( ) (A) ()02Ia b μπ+; (B)0ln()2I a ba b μπ+; (C) 0ln()2I a b b aμπ+; (D)()02/2I a b μπ+.三 填空题1 三根直载流导线A 、B 和C 平行地放置于同一平面内,分别载有恒定电流I 、2I 和3I 。
电磁场与电磁波典型习题及答案(恒定磁场)
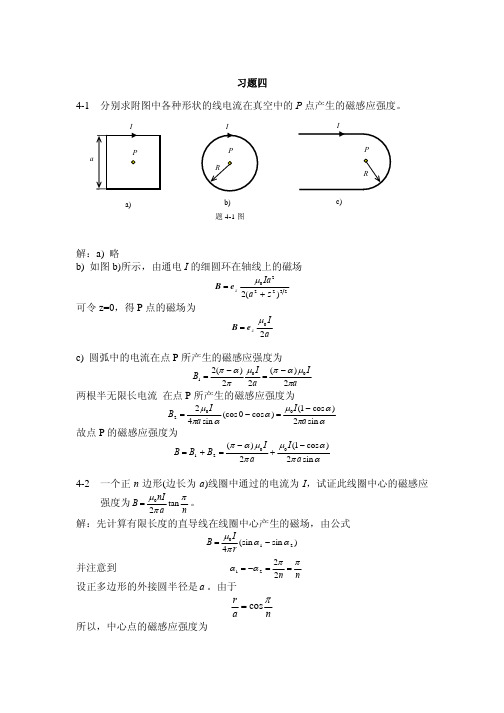
4-5 一根细的圆铁杆和一个很薄的圆铁盘样品放在磁场 B0 中,并使它们的轴与 B0 平行(铁的磁导率为 µ )。求样品内的 B 和 H;若已知 B0=1T,µ = 5000µ0 , 求两样品内的磁化强度 M。
解:对于极细的圆铁杆样品,根据边界条件有
H = H 0 = B0 / µ0
B = µH
=
µ µ0
+ π (r 2
− a12 )J 2 ] ⇒
B
=
eφ
⎜⎜⎝⎛
10 3
r
− 10−5 r
⎟⎟⎠⎞
当r
>
a2 时,有 B
= eφ
µ0I 2π r
=
eφ
2 ×10−5 r
4-8 已知在半径为 a 的圆柱区域内有沿轴向方向的电流,其电流密度为
J
= ex
J0r a
,其中 J0 为常数,求圆柱内外的磁感应强度。
解:用安培环路定律,
当计算的点位于柱内(r<a),
B
=
µ0 J 0 3a
r 2eφ
r>a
时, B
=
µ0 J 0 3r
a 2eφ
4-9 有一圆截面的环形螺线管,其圆形截面积为 S,平均半径为 l,铁环的相对 磁导率为 µr,环上绕的线圈匝数为 N,通过恒定电流 I。假设铁心内部的磁 场均匀分布且空气中没有漏磁,求:(1)铁心内磁场强度 H 和磁感应强度 B; (2)环内的总磁通;(3)计算该螺线管的电感。(4)磁场能量。
B ≈ µ0M
4-11 已知一个平面电流回路在真空中产生的磁场强度为 H0,若此平面电流回路 位于磁导率分别为 µ1 和 µ2 的两种均匀磁介质的分界平面上,试求两种磁介
稳恒磁场习题(包含答案)

练习八磁感应强度毕奥—萨伐尔定律(黄色阴影表示答案) 一、选择题如图所示,边长为l的正方形线圈中通有电流I,则此线圈在: AlIπμ220.(C)lIπμ2(D) 以上均不对.电流I由长直导线1沿对角线AC方向经A点流入一电阻均匀分布的正方形导线框,再由D点沿对角线BD方向流出,经长直导线2返回电源, 如图所示. 若载流直导线1、2和正方形框在导线框中心O点产生的磁感强度分别用B1、B2和B3表示,则O点磁感强度的大小为:A(A) B = 0. 因为B1 = B2 = B3 = 0 .(B) B = 0. 因为虽然B1 0, B2 0, B1+B2 = 0, B3=0(C) B 0. 因为虽然B3 = 0, 但B1+B2 0(D) B0. 因为虽然B1+B2 = 0, 但B3 03. 如图所示,三条平行的无限长直导线,垂直通过边长为a 的正三角形顶点,每条导线中的电流都是I,这三条导线在正三角形中心O点产生的磁感强度为:B(D) B=30I/(3a) . .如图所示,无限长直导线在P处弯成半径为R的圆,当通以电流I时,则在圆心O 点的磁感强度大小等于:C(A)RIπμ20.(B)Iμ.(D) )11(4πμ+RI.二、填空题如图所示,在真空中,电流由长直导线1沿切向经a点流入一电阻均匀分布的圆环,再由b点沿切向流出,经长直导线2返回电源.已知直导线上的电流强度为I,圆环半径为R,aob=180.则圆心O点处的磁感强度的大小B = .0图图图图图I练习九毕奥—萨伐尔定律(续)一、选择题1. 在磁感强度为B的均匀磁场中作一半径为r的半球面S,S边线所在平面的法线方向单位矢量n与B的夹角为,如图所示. 则通过半球面S的磁通量为:(A) r2B.(B) 2r2B.(C) r2B sin.(D) r2B cos.如图,载流圆线圈(半径为R)与正方形线圈(边长为a)通有相同电流I ,若两线圈中心O1与O2处的磁感应强度大小相同,R: a为(A) 1:1.(B) π2:1.三、计算题1.在无限长直载流导线的右侧有面积为S1和S2的两个矩形回路,回路旋转方向如图所示, 两个回路与长直载流导线在同一平面内, 且矩形回路的一边与长直载流导线平行. 求通过两矩形回路的磁通量及通过S1回路的磁通量与通过S2回路的磁通量之比.(此题作为悬赏题)练习十安培环路定理一、选择题2. 无限长直圆柱体,半径为R,沿轴向均匀流有电流. 设圆柱体内(r< R)的磁感强度为B1,圆柱体外(r >R)的磁感强度为B2,则有:(A) B1、B2均与r成正比.(B) B1、B2均与r成反比.(C) B1与r成正比, B2与r成反比.(D) B1与r成反比, B2与r成正比.在图(a)和(b)中各有一半径相同的圆形回路L1和L2,圆周内有电流I2和I2,其分布相同,且均在真空中,但在图(b)中,L2回路外有电流I3,P1、P2为两圆形回路上的对应点,则:(A) ⎰⋅1dLlB=⎰⋅2dLlB,21PPBB=.(B) ⎰⋅dLlB⎰⋅dLlB,21PPBB=.图图图图P1L(a)3P2(b)图(D)⎰⋅1d L l B ⎰⋅2d L l B , 21P P B B≠.如图所示,两根直导线ab 和cd 沿半径方向被接到一个截面处处相等的铁环上,恒定电流I 从a 端流入而从d 端流 出,则磁感强度B 沿图中闭合路径的积分⎰⋅Ll B d 等于:(A) 0I . (B) 0I /3. (C) 0I /4. (D) 20I /3 . 如图,在一圆形电流I 所在的平面内,选取一个同心圆形闭合回路L ,则由安培环路定理(B) 0 d =⋅⎰L l B ,且环路上任意点B =0. (C) 0 d ≠⋅⎰Ll B ,且环路上任意点B 0. (D) 0 d ≠⋅⎰Ll B,且环路上任意点B =0.二、填空题两根长直导线通有电流I ,图所示有三种环路,对于环路a ,=⋅⎰a L l B d ;对于环路b , =⋅⎰bL l B d ;对于环路c ,=⋅⎰cL l B d . 0I , 0, 20I .练习十一安培力 洛仑兹力一、选择题如图所示. 匀强磁场中有一矩形通电线圈,它的平面与磁场平行,在磁场作用下,线圈发生转动,其方向是:B(A) ab 边转入纸内,cd 边转出纸外. (B) ab 边转出纸外,cd 边转入纸内. (C) ad 边转入纸内,bc 边转出纸外. (D) ad 边转出纸外,cd 边转入纸内.5. 一电子以速度v 垂直地进入磁感强度为B 的均匀磁场中,此电子在磁场中运动的轨道所围的面积内的磁通量是(A) 正比于B ,反比于v 2. (B) 反比于B,正比于v 2.图图图(C) 正比于B ,反比于v. (D) 反比于B ,反比于v练习十三 静磁场习题课一、选择题1. 一质量为m 、电量为q 的粒子,以与均匀磁场B 垂直的速度v 射入磁场中,则粒子运动轨道所包围范围内的磁通量m 与磁场磁感强度B 的大小的关系曲线是图中的哪一条 D边长为l 的正方形线圈,分别用图所示两种方式通以电流I (其中ab 、cd 与正方形共面),在这两种情况下,线圈在其中心产生的磁感强度的大小分别为:(A) B 1 = 0 . B 2 = 0.(B) B 1 = 0 . lIB πμ0222=lπ01l Iπμ0222.如图, 质量均匀分布的导线框abcd 置于均匀磁场中(B 的方向竖直向上),线框可绕AA 轴转动,导线通电转过 角后达到稳定平衡.如果导线改用密度为原来1/2的材料做,欲保持原来的稳定平衡位置(即 角不变),可以采用哪一种办法(A) 将磁场B 减为原来的1/2或线框中电流减为原来的1/2. (B) 将导线的bc 部分长度减小为原来的1/2. (C) 将导线ab 和cd 部分长度减小为原来的1/2. (D)将磁场B 减少1/4,线框中电流强度减少1/4.图图l (1)d图(A)(D) (C)(B) (E)。
《大学物理》恒定磁场练习题及答案

《大学物理》恒定磁场练习题及答案一、简答题1、如何使一根磁针的磁性反转过来?答:磁化:比如摩擦,用一个磁体的N 极去摩擦小磁针的N 极可以让它变为S 极,另一端成N 极。
2、为什么装指南针的盒子不是用铁,而是用胶木等材料做成的? 答:铁盒子产生磁屏蔽使得指南针无法使用。
3、在垂直和水平的两个金属圆中通以相等的电流,如图所示,问圆心O 点处的磁场强度大小及方向如何?答:根据圆电流中心处磁感应强度公式,水平金属圆在O 点的磁感应强度大小为RI20μ;方向垂直向下,竖直金属圆在O 点的磁感应强度大小为RI20μ;方向垂直指向纸面内。
故O 点叠加后的磁感应强度大小为RI220μ;方向为斜下450指向纸面内。
4、长直螺旋管中从管口进去的磁力线数目是否等于管中部磁力线的数目? 为什么管中部的磁感应强度比管口处大?答:因为磁力线是闭合曲线,故磁力线数目相等。
根据载流长直螺旋管磁感应强度计算公式)cos (cos 21120θθμ-=nI B 可知,管口处21πθ→,0cos 1=θ,管口处磁感应强度为20cos 21θμnI B =;中心处212cos 2cos cos θθθ'='-',故中心处磁感应强度为20cos θμ'=nI B ,因为22θθ>',所以中心处磁感应强度比管口处大。
5、电荷在磁场中运动时,磁力是否对它做功? 为什么? 答:不作功,因为磁力和电荷位移方向成直角。
6、在均匀磁场中,怎样放置一个正方型的载流线圈才能使其各边所受到的磁力大小相等?答:磁力线垂直穿过正四方型线圈的位置。
因为线圈每边受到的安培力为B Ia F ⨯=,由于处在以上平面时,每边受到的磁力为IaB F =。
7、一个电流元Idl 放在磁场中某点,当它沿x 轴放置时不受力,如把它转向y 轴正方向时,则受到的力沿z 铀负方向,问该点磁感应强度的方向如何?答:由安培力公式B Idl dF ⨯=可知,当Idl 沿x 轴放置时不受力,即0=dF ,可知B 与Idl 的方向一致或相反,即B 的方向沿x 轴线方向。
稳恒磁场练习题及答案

稳恒磁场练习题及答案一、 选择题1、在一个平面内,有两条垂直交叉但相互绝缘的导线,流过每条导线的电流相等,方向如图所示。
问哪个区域中有些点的磁感应强度可能为零 ( D ) (A )仅在象限1 (B )仅在象限2(C )仅在象限1、3 (D )仅在象限2、42、关于洛仑兹力,下列说法错误的是:( D ) (A )带电粒子在磁场中运动,不一定受洛仑兹力 (B )洛仑兹力不做功(C )洛仑兹力只改变粒子运动方向(D )当磁场方向与粒子运动方向一致时,洛仑兹力对粒子作正功 3、一电量为q 的粒子在匀强磁场中运动,下面哪种说法是正确的:( B ) (A )只要速度大小相同,粒子所受的洛仑兹力就相同(B )在速度不变的前提下,若电荷电量q 变为-q ,则粒子受力方向相反,数值不变 (C )粒子进入磁场后,其动量和动能都不改变(D )洛仑兹力与速度方向垂直,所以带电粒子运动的轨迹一定是圆4、由磁场的高斯定理可知 (D )(A )穿入闭合曲面的磁感应线条数必然多于穿出的磁感应线条数; (B )穿入闭合曲面的磁感应线条数必然少于穿出的磁感应线条数; (C )一根磁感应线可以始于闭合曲面外,终止在闭合曲面内; (D )一根磁感应线可以完全处于闭合曲面内。
5、对于某一回路L ,安培环路积分等于零,则可以断定(D )(A) 回路L 内一定有电流。
(B) 回路L 内可能有电流,且代数和不为零。
(C) 回路L 内一定无电流。
(D) 回路L 内可能有电流,但代数和为零。
6、电流I 1穿过一回路L ,而电流I 2则在回路的外面,于是有 ( C )(A) L 上各点的磁感应强度及积分⎰⋅Ll d B都只与I 1有关。
(B) L 上各点的磁感应强度B 只与I 1有关,积分⎰⋅Ll d B与I 1、I 2有关。
(C) L 上各点的磁感应强度B 与I 1、I 2有关,积分⎰⋅L l d B只与I 1有关。
(D) L 上各点的磁感应强度B 及积分⎰⋅Ll d B都与I 1、I 2有关。
研究生考试恒定磁场复习题及答案参考

(B) Байду номын сангаас方向与 方向相同
(C) 的方向垂直于 与 组成的平面
(D) 的方向为( )方向
10. 决定长直螺线管中磁感应强度大小的因素是
[](A)通入导线中的电流强度(B)螺线管的体积
(C)螺线管的直径(D)与上述各因素均无关
11. 磁场的高斯定理 ,说明
[](A)穿入闭合曲面的磁感应线的条数必然等于穿出的磁感应线的条数
[](A)条形磁铁的磁力线是从N极到S极的
(B)条形磁铁的磁力线在磁铁内部是从S极到N极的
(C)磁力线是从N极出发终止在S极的曲线
(D)磁力线是不封闭的曲线
5. 下列叙述中不能正确反映磁力线性质的是
[](A)磁力线是闭合曲线
(B)磁力线上任一点的切线方向为运动电荷的受力方向
(C)磁力线与载流回路象环一样互相套连
[](A)圆形环路上各点的磁场强度为零
(B)圆形环路上各点的磁场强度方向垂直于环路平面
(C)圆形环路上各点的磁场强度方向指向圆心
(D)圆形环路上各点的磁场强度方向为该点的切线方向
17. 下述情况中能用安培环路定律求磁感应强度的是
[](A)一段载流直导线(B)无限长直线电流
(C)一个环形电流(D)任意形状的电流
15. 对于安培环路定律 ,在下面说法中正确的是
[](A) 只是穿过闭合环路的电流所激发,与环路外的电流无关
(B)I是环路内、外电流的代数和
(C)安培环路定律只在具有高度对称的磁场中才成立
(D)只有磁场分布具有高度对称性时,才能用它直接计算磁场强度的大小
16. 在圆形电流的平面内取一同心圆形环路,由于环路内无电流穿过,所以 ,由此可知
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
(C) 2BR=Br(D)BR=4Br
25. 两根载有相同电流的通电导线,彼此之间的斥力为F.如果它们的电流均增加一倍,相互之间的距离也加倍,则彼此之间的斥力将为变为
[](A) (B) (C) (D)
26. 两束阴极射线(电子流),以不同的速率向同一方向发射,则两束射线间
15. 对于安培环路定律 ,在下面说法中正确的是
[](A) 只是穿过闭合环路的电流所激发,与环路外的电流无关
(B)I是环路内、外电流的代数和
(C)安培环路定律只在具有高度对称的磁场中才成立
(D)只有磁场分布具有高度对称性时,才能用它直接计算磁场强度的大小
16. 在圆形电流的平面内取一同心圆形环路,由于环路内无电流穿过,所以 ,由此可知
(D)磁力线与电流的流向互相服从右手定则
6. 关于磁场之间的相互作用有下列说法,其中正确的是
[](A)同性磁极相吸,异性磁极相斥
(B)磁场中小磁针的磁力线方向只有与磁场磁力线方向一致时,才能保证稳定平稳
(C)小磁针在非均匀磁场中一定向强磁场方向运动
(D)在涡旋电场中,小磁针沿涡旋电场的电场线运动
7. 一电荷放置在行驶的列车上,相对于地面来说,电荷产生电场和磁场的情况将是
(D)B1与r成正比,B2与r成反比
21. 如T7-1-21图所示,两根载有相同电流的无限长直导线,分别通过x1=1和x2=3的点,且平行于y轴.由此可知,磁感应强度 为零的地方是
[](A)x=2的直线上(B)x>2的区域
(C)x<1的区域(D)不在xOy平面内
22. 一个半径为R的圆形电流I,其圆心处的磁场强度大小为
[](A)与L成正比(B)与L成反比
(C)与L无关(D)与L3成正比
20. 一无限长直圆柱体,半径为R,沿轴向均匀流有电流.设圆柱体内(r<R)的磁感应强度大小为B1,圆柱体外(r>R)感应强度大小为B2,则有
[](A)B1、B2均与r成正比
(B)B1、B2均与r成反比
(C)B1与r成反比,B2与r成正比
[](A)圆形环路上各点的磁场强度为零
(B)圆形环路上各点的磁场强度方向垂直于环路平面
(C)圆形环路上各点的磁场强度方向指向圆心
(D)圆形环路上各点的磁场强度方向为该点的切线方向
17. 下述情况中能用安培环路定律求磁感应强度的是
[](A)一段载流直导线(B)无限长直线电流
(C)一个环形电流(D)任意形状的电流
(B)穿入闭合曲面的磁感应线的条数不等于穿出的磁感应线的条数
(C)一根磁感应线可以终止在闭合曲面内
(D)一根磁感应线不可能完全处于闭合曲面内
12. 安培环路定律 说明了磁场的性质之一是
[](A)磁力线是闭合曲线(B)磁场力是保守力
(C)磁场是无源场(D)磁场是无势场
13. 磁场中的高斯定理 说明了磁场的性质之一是
(C)电流元在该点不受力的方向
(D)载流线圈稳定平稳时,磁矩在该点的指向
3. 下列叙述中错误的是
[](A)一根给定的磁力线上各点处的 的大小一定相等
(B)一根给定的磁力线上各点处的 的方向不一定相同
(C)均匀磁场的磁力线是一组平行直线
(D)载流长直导线周围的磁力线是一组同心圆环
4. 下列关于磁力线的描述中正确的是
18. 取一闭合积分回路L,使三根载流导线穿过L所围成的面.现改变三根导线之间的相互间隔,但不越出积分回路,则
[](A)回路L内的I不变,L上各点的B不变
(B)回路L内的I不变,L上各点的B改变
(C)回路L内的I改变,L上各点的B不变
(D)回路L内的I改变,L上各点的B改变
19. 边长为L的一个正方形线圈中通有电流I,则线圈中心的磁感应强度的大小将
[](A)条形磁铁的磁力线是从N极到S极的
(B)条形磁铁的磁力线在磁铁内部是从S极到N极的
(C)磁力线是从N极出发终止在S极的曲线
(D)磁力线是不封闭的曲线
5. 下列叙述中不能正确反映磁力线性质的是
[](A)磁力线是闭合曲线
(B)磁力线上任一点的切线方向为运动电荷的受力方向
(C)磁力线与载流回路象环一样互相套连
[](A) 的方向与 方向相同
(B) 的方向与 方向相同
(C) 的方向垂直于 与 组成的平面
(D) 的方向为( )方向
10. 决定长直螺线管中磁感应强度大小的因素是
[](A)通入导线中的电流强度(B)螺线管的体积
(C)螺线管的直径(D)与上述各因素均无关
11. 磁场的高斯定理 ,说明
[](A)穿入闭合曲面的磁感应线的条数必然等于穿出的磁感应线的条数
[](A) (B)∞(C)0(D)
23. 有一个圆形回路1及一个正方形回路2,圆的直径和正方形回路的边长相等,二者中通有大小相等的电流,它们在各自中心产生的磁感应强度的大小之比B1/B2为
[](A) 0.90(B) 1.00
(C) 1.11(D) 1.22
24. 一载有电流I的细导线分别均匀密绕在半径为R和r的长直圆筒上形成两个螺线管(R=2r),两螺线管单位长度上的匝数相等.两螺线管中的磁感应强度大小BR和Br应满足关系
第7章恒定磁场
一、选择题
1. 磁场可以用下述哪一种说法来定义?
[](A)只给电荷以作用力的物理量(B)只给运动电荷以作用力的物理量
(C)贮存有能量的空间(D)能对运动电荷作功的物理量
2. 空间某点磁感应强度的方向,在下列所述定义中错误的是
[](A)小磁针N极在该点的指向
(B)运动正电荷在该点所受最大的力与其速度的矢积的方向
[](A)磁场力是保守力(B)磁力线可能闭合
(C)磁场是无源场(D)磁场是无势场
14. 若某空间存在两无限长直载流导线,空间的磁场就不存在简单的对称性.此时该磁场的分布
[](A)可以直接用安培环路定理来计算
(B)只能用安Biblioteka 环路定理来计算(C)只能用毕奥--萨伐尔定律来计算
(D)可以用安培环路定理和磁场的叠加原理求出
[](A)只产生电场
(B)只产生磁场
(C)既产生电场,又产生磁场
(D)既不产生电场,又不产生磁场
8. 通以稳恒电流的长直导线,在其周围产生电场和磁场的情况将是
[](A)只产生电场
(B)只产生磁场
(C)既产生电场,又产生磁场
(D)既不产生电场,又不产生磁场
9. 在电流元 激发的磁场中,若在距离电流元为 处的磁感应强度为 .则下列叙述中正确的是
