一次函数之等腰直角三角形的存在性 (讲义及答案).
一次函数与特殊三角形~存在性问题

一次函数与特殊三角形~存在性问题坚持的力量,时间的证明,难忘的经历!一次函数与特殊三角形~存在性问题—【数学压轴题】盘点思考题目:一次函数与等腰三角形~存在性问题【两定一动】一次函数与直角三角形~存在性问题【两定一动】一次函数与等腰直角三角形~存在性问题【一定两动】适用范围:初二与初三学生【考点串讲,拓展思路,体味方法】解题方法:一次函数与等腰三角形~存在性问题【两定一动】一次函数与直角三角形~存在性问题【两定一动】一次函数与等腰直角三角形~存在性问题【一定两动】【考点总结】1.一次函数与等腰三角形~存在性问题:(1)类型:两定一动&一定两动。
(2)思路:代数法&几何法。
注意:遇到'一定两动'时,尽量先画图,再结合【等腰三角形性质——等边对等角&三线合一】进行思考。
另外,这里的“等腰三角形~存在性问题”与初三数学中的“菱形~存在性问题”密切相关,大家必须掌握。
2.一次函数与直角三角形~存在性问题:(1)类型:两定一动&一定两动。
(2)思路:代数法&几何法&函数法。
注意:三种方法都可以使用,'代数法'侧重—计算量;“几何法”侧重—构图及转化能力;“函数法”—侧重公式记忆的应用及特殊情况的处理。
另外,这里的“直角三角形~存在性问题”与初三数学中的“矩形~存在性问题”密切相关,大家必须掌握。
3.一次函数与等腰直角三角形~存在性问题:(1)类型:两定一动&一定两动。
(2)思路:几何法——构造“一线三垂直~全等三角形模型”。
注意:这里的“等腰直角三角形~存在性问题”与初三数学中的“正方形~存在性问题”密切相关,大家必须掌握。
综上所述,这种【数学压轴题】需要思考,敢于挑战,发挥想象,坚持总结,重在积累,走好初中的每一步,在会的基础上提升自己的做题速度,节省时间才能在考试中发挥出真实水平。
加油,我们一起同行【从不同的出发点思考,便会发现不一样的风景】。
专题11 存在性-等腰直角三角形(解析版)

中考数学压轴题--二次函数--存在性问题第11节等腰直角三角形的存在性方法点拨第一步:易证ΔBAD∽ΔECB,如果再加一个条件BD=BE,此时ΔBAD≌ΔECB (AAS)所以,AB=CE,AD=CB第二步:根据点坐标来表示线段长度,列等式求解。
例题演练1.如图所示,抛物线y=a(x+1)(x﹣5)(a≠0)的图象与x轴交于A、B两点,与y轴交于点C.(1)当a=﹣时,①求点A、B、C的坐标;②如果点P是抛物线上一点,点M是该抛物线对称轴上的点,当△OMP是以OM为斜边的等腰直角三角形时,求出点P的坐标;(2)点D是抛物线的顶点,连接BD、CD,当四边形OBDC是圆的内接四边形时,求a 的值.【解答】解:对于y=a(x+1)(x﹣5)(a≠0),令y=a(x+1)(x﹣5)=0,解得x =5或﹣1,令x=0,则y=﹣5a,故点A、B、C的坐标分别为(5,1)、(﹣1,0)、(0,﹣5a),当x=2时,y=a(x+1)(x﹣5)=﹣9a,顶点的坐标为(2,﹣9a).(1)①当a=﹣时,函数的表达式为y=﹣(x+1)(x﹣5),则点A、B、C的坐标分别为(5,1)、(﹣1,0)、(0,2);②过点P作y轴的平行线交过点M与x轴的平行线于点F,交x轴于点E,设点P的坐标为(x,﹣(x+1)(x﹣5)),∵∠MPO=90°,∴∠MPF+∠OPE=90°,∵∠OPE+∠POE=90°,∴∠POE=∠MPF,∵∠PFM=∠OEP=90°,PM=PO,∴△PFM≌△OEP(AAS),∴PE=MF,则﹣(x+1)(x﹣5)=x﹣2,解得x=﹣或4,故点P的坐标为(﹣,﹣)或(4,2);(2)点B、C的坐标分别为(﹣1,0)、(0,﹣5a),顶点D的坐标为(2,﹣9a).当四边形OBDC是圆的内接四边形时,则BC的中点为该圆的圆心,设BC的中点为点Q,由中点坐标公式得,点Q(,﹣a),则OQ=DQ,即()2+(﹣)2=(2﹣)2+(﹣9a+a)2,解得a=±.2.如图,已知抛物线y=ax2+4x+c与直线AB相交于点A(0,1)和点B(3,4).(1)求该抛物线的解析式;(2)设C为直线AB上方的抛物线上一点,当△ABC的面积最大时,求点C的坐标;(3)将该抛物线向左平移2个单位长度得到抛物线y=a1x2+b1x+c1(a1≠0),平移后的抛物线与原抛物线相交于点D,是否存在点E使得△ADE是以AD为腰的等腰直角三角形?若存在,直接写出点E的坐标;若不存在,请说明理由.【解答】解:(1)将A、B两点代入到解析式中,得,,解得,∴抛物线的解析式为:y=﹣x2+4x+1;(2)设直线AB为:y=k1x+1,代入点B,得,3k1+1=4,解得k1=1,∴直线AB为:y=x+1,设C(m,﹣m2+4m+1),过C作CM∥y轴交AB于M,如图1,则M(m,m+1),∴CM=﹣m2+4m+1﹣m﹣1=﹣m2+3m,∴S△ABC=S△ACM+S△BCM==,∵C为直线AB上方抛物线上一点,∴0<m<3,∴时,△ABC的面积最大值为,此时C();(3)∵抛物线y=﹣(x﹣2)2+5,∴将抛物线向右平移2个单位后得到的抛物线为:y=﹣x2+5,联立,解得,∴D(1,4),①如图2,当DA=DE,∠EDA=90°,E在AD右侧时,过D作x轴平行线交y轴于N,过E作y轴平行线,两线交于F点∵∠DAN+∠NDA=∠NDA+∠EDF=90°∴∠DAN=∠EDF,又∠DNA=∠EFD=90°,DA=DE,∴△DNA≌△EFD(AAS),∴DN=EF=1,AN=DF=3,∴E(4,3),②当DA=DE,∠EDA=90°,E在AD左侧,同理可得,E(﹣2,5),③当AD=AE,∠DAE=90°,E在AD左侧时,同理可得,E(﹣3,2),④当AD=AE,∠DAE=90°,E在AD右侧时,同理可得,E(3,0),综上所述,E(4,3)或(﹣2,5)或(﹣3,2)或(3,0).3.如图,已知抛物线y=﹣x2+bx+c与x轴交于A,B两点,与y轴交于点C,其中A(﹣1,0),C(0,3).(1)求该抛物线的函数表达式;(2)抛物线与直线y=﹣x﹣1交于A、E两点,P是x轴上点B左侧一动点,当以P、B、C为顶点的三角形与△ABE相似时,求点P的坐标;(3)若F是直线BC上一动点,在抛物线上是否存在动点M,使△MBF为等腰直角三角形,若存在,请直接写出点M的坐标;否则说明理由.【解答】解:(1)把A(﹣1,0),C(0,3)代入y=﹣x2+bx+c,得:,解得:,∴抛物线的函数表达式为y=﹣x2+2x+3;(2)联立直线AE和抛物线的函数关系式成方程组,得:,解得:,,∴点E的坐标为(4,﹣5),∴AE==5,在y=﹣x2+2x+3中,令y=0,得:﹣x2+2x+3=0,解得:x1=3,x2=﹣1,∴点B的坐标为(3,0),∵C(0,3),∴OB=OC=3,∵∠BOC=90°,∴∠CBO=45°,BC=3,∵直线AE的函数表达式为y=﹣x﹣1,∴∠BAE=45°=∠CBO.设点P的坐标为(m,0),则PB=3﹣m,∵以P、B、C为顶点的三角形与△ABE相似,∴=或=,∴=或=,解得:m=或m=﹣,∴点P的坐标为(,0)或(﹣,0);(3)∵∠CBO=45°,∴存在两种情况(如图2).①取点M1与点A重合,过点M1作M1F1∥y轴,交直线BC于点F1,∵∠CBM1=45°,∠BM1F1=90°,∴此时△BM1F1为等腰直角三角形,∴点M1的坐标为(﹣1,0);②取点C′(0,﹣3),连接BC′,延长BC′交抛物线于点M2,过点M2作M2F2∥y 轴,交直线BC于点F2,∵点C、C′关于x轴对称,∠OBC=45°,∴∠CBC′=90°,BC=BC′,∴△CBC′为等腰直角三角形,∵M2F2∥y轴,∴△M2BF2为等腰直角三角形.∵点B(3,0),点C′(0,﹣3),∴直线BC′的函数关系式为y=x﹣3,联立直线BC′和抛物线的函数关系式成方程组,得:,解得:,,∴点M2的坐标为(﹣2,﹣5),综上所述:点M的坐标为(﹣1,0)或(﹣2,﹣5).4.如图,抛物线y=ax2+bx﹣3(a>0)与x轴交于A、B两点,交y轴于点C,OB=3,抛物线经过点(2,5).(1)求该抛物线解析式;(2)如图1,该抛物线顶点D,连接BD、BC,点P是线段BD下方抛物线上一点,过点P作PE∥y轴,分别交线段BD、BC于点F、E,过点P作PG⊥BD于点G,求2PG+EF 的最大值,及此时点P的坐标;(3)如图2,在y轴左侧抛物线上有一动点M,在y轴上有一动点N,是否存在以AN 为直角边的等腰直角三角形AMN?若存在,请直接写出点M的坐标.【解答】解:(1)∵OB=3,∴B(﹣3,0)把C(﹣3,0)和点(2,5),代入抛物线y=ax2+bx﹣3,得,解得,∴抛物线解析式为y=x2+2x﹣3;(2)延长PE与x轴交于点M,FM⊥x轴,PG⊥BD,如图所示,∠FMB=90°,∠PGF=90°,∵∠BFM=∠PFG,∴∠MBF=∠GPF,∴B(﹣3,0),D(﹣1,﹣4),B、D两点的横坐标距离为2,纵坐标距离为4,由勾股定理得BD==2,∴cos∠MBF=cos∠GPF=,∴2PG+EF=EF+2FP,∴C(0,﹣3),设直线BC解析式为l BC:y=kx+b(b≠0),把B(﹣3,0)和C(0,﹣3)代入得,,解得,∴l BC:y=﹣x﹣3,同理,直线BD得解析式为:y=﹣2x﹣6,设E(m,﹣m﹣3),P(m,m2+2m﹣3),F(m,﹣2m﹣6),∴EF+2FP=[﹣m﹣3﹣(﹣2m﹣6)]+2[(﹣2m﹣6)﹣(m2+2m﹣3)]=﹣2(m+)2+,∴当m=﹣时,EF+2FP有最大值,∵2PG+EF=EF+2FP,∴此时,P点坐标为P(﹣,﹣);(3)存在,设N(0,y1),M(x2,+2x2﹣3),当y=0时,代入抛物线y=x2+2x+3中,解得两根为﹣3和1,A在y轴右侧,∴A(1,0),∴AN2=OA2+ON2=1+y12,AM2=(x2﹣1)2+(+2x2﹣3)2,MN2=+(+2x2﹣3﹣y1)2,①当AN⊥MN时,此时由AN=MN,等腰直角三角形各边比为1:1:,∴M点横坐标为﹣﹣1或﹣3﹣1,将M的横坐标为﹣﹣1或﹣3﹣1,代入y=x2+2x﹣3中得,∴M点坐标为(﹣﹣1,﹣2)或(﹣3﹣1,14),②由AN⊥MA得:M点横坐标为﹣2﹣2或﹣2﹣2,将M点横坐标为﹣2﹣2或﹣2﹣2代入y=x2+2x+3中,得M点坐标为(﹣2﹣2,17+8﹣4﹣4)或(﹣2﹣2,33+8﹣4﹣4),综上所述,M点坐标为(﹣﹣1,﹣2)或(﹣3﹣1,14),(﹣2﹣2,17+8﹣4﹣4)或(﹣2﹣2,33+8﹣4﹣4),5.如图,抛物线C1:y=x2+bx+c经过原点,与x轴的另一个交点为(2,0),将抛物线C1向右平移m(m>0)个单位得到物度C2,C2交x轴于A、B两点(点A在点B的左边),交y轴于点C.(1)求抛物线C1的解析式及顶点坐标;(2)以AC为斜边向上作等腰直角三角形ACD,当点D落在抛物线C2的对称轴上时,求抛物线C2的解析式及D点坐标.【解答】解:(1)∵抛物线C1经过原点,与x轴的另一个交点为(2,0),∴,解得,∴抛物线C1的解析式为y=x2﹣2x,∴抛物线C1的顶点坐标(1,﹣1).(2)如图,∵抛物线C1的向右平衡m(m>0)个单位得到抛物线C2,∴C2的解析式为y=(x﹣m﹣1)2﹣1,∴A(m,0),B(m+2,0),C(0,m2+2m),过点C作CH⊥对称轴DE,垂足为H,∵△ACD为等腰直角三角形,∴AD=CD,∠ADC=90°,∴∠CDH+∠ADE=90°,∴△HCD=△ADE,∵∠DEA=90°,∴△CHD≌△DEA,∴AE=HD=1,CH=DE=m+1,∴EH=HD+DE=1+m+1=m+2,由OC=EH得m2+2m=m+2,解得m1=1,m2=﹣2(舍去),∴抛物线C2的解析式为:y=(x﹣2)2﹣1,∴D点坐标(2,2).6.已知:如图,抛物线y=ax2+bx+6与x轴交于点B(6,0),C(﹣2,0),与y轴交于点A,点P是线段AB上方抛物线上的一个动点.(1)如图,连接P A、PB.设△P AB的面积为S,点P的横坐标为m.请说明当点P运动到什么位置时,△P AB的面积有最大值?(2)过点P作x轴的垂线,交线段AB于点D,再过点P作PE∥x轴交抛物线于点E,连接DE,请问是否存在点P使△PDE为等腰直角三角形?若存在,请直接写出点P的坐标;若不存在,请说明理由.【解答】解:(1)∵抛物线y=ax2+bx+6与x轴交于点B(6,0),C(﹣2,0),∴可设抛物线的表达式为:y=a(x+2)(x﹣6),∴﹣12a=6,解得a=﹣,∴抛物线的表达式为:y=﹣x2+2x+6,∴A(0,6)∴直线AB的表达式为:y=﹣x+6,点P的横坐标为m,则P(m,﹣m2+2m+6),过点P作x轴的垂线,交线段AB于点D,则D(m,﹣m+6),∴S=×OB×PD=×6×(﹣m2+2m+6+m﹣6)==﹣(m﹣3)2+,∴当m=3时,S的值取最大,此时P(3,);(2)存在,理由如下:由题意可知,PD⊥PE,若△PDE是等腰直角三角形,则PE=PD,由(1)可得,PD=﹣m2+2m+6+m﹣6=﹣m2+3m,∵PE∥x轴,∴E(4﹣m,﹣m2+2m+6),∴PE=|2m﹣4|,∴|2m﹣4|=﹣m2+3m,解得m1=﹣2(舍),m2=4,m3=5+(舍),m4=5﹣,∴当△PDE是等腰直角三角形时,点P的坐标为(4,6),(5﹣,3﹣5).7.如图1.二次函数y=﹣x2+6与x轴交于A,B两点(点A在点B的左侧),与y轴交于点C.(1)求出点A,B,C的坐标;(2)连接AC,求直线AC的表达式;(3)如图2,点D为线段AC上的一个动点,连接BD,以点D为直角顶点,BD为直角边,在x轴的上方作等腰直角三角形BDE,若点E在y轴上时,求点D的坐标;(4)若点D在线段AC上,点D由A到C运动的过程中,以点D为直角顶点,BD为直角边作等腰直角三角形BDE,当抛物线的顶点C在等腰直角三角形BDE的边上(包括三角形的顶点)时,请直接写出顶点E的坐标.【解答】解:(1)当x=0时,y=6.∴C点坐标为(0,6).当y=0时,.解得x1=﹣4,x2=4.∵A点在B点左侧,∴点A坐标为(﹣4,0),点B坐标为(4,0).(2)设直线AC的表达式为:y=kx+b.∵点A坐标为(﹣4,0),点C坐标为(6,0).∴.解得.∴直线AC的表达式为.(3)如答图1,过点D分别作DF⊥x轴于点F,DG⊥y轴于G. ∴四边形DGOF为矩形,∠FDG=90°.∵△BDE为等腰直角三角形,BD为直角边.∴BD=ED,∠EDB=90°.∴∠EDB﹣∠GDB=∠FDG﹣∠GDB.即∠EDG=∠BDF.在△BDF和△EDG中,.∴△BDF≌△EDG(AAS).∴DF=DG.设点D的坐标为(m,).∴.解得m=,∴点D的坐标为().(4)由(2)可得直线AC的表达式为.∵点D在直线AC上,∴设点D坐标为().设直线BC的解析式为:y=kx+b.将B(4,0),C(0,6)代入得.解得.∴直线BC的解析式为.①当C位于斜边BE上时,∵点E在直线BC上,∴设点E坐标为(b,).如答图2所示.作EM⊥x轴于点M,DQ⊥x轴于点Q,DN⊥EM于点N.易知四边形DQMN为矩形.∴∠QDN=90°.∵△BDE为等腰直角三角形,BD为直角边.∴BD=ED,∠EDB=90°.∴∠EDB﹣∠NDB=∠QDN﹣∠NDB.即∠EDN=∠BDQ.在△BDQ和△EDN中,.∴△BDQ≌△EDN(AAS).∴DN=DQ,EN=BQ.∵E坐标为(b,),D坐标为().∴DN=b﹣a,EN=.DQ=,BQ=4﹣a.∴.解得.∴=.∴点E的坐标是().②当点D在直角边DE上时,BD交y轴于点F,如答图3所示.∵∠CDF=∠BOF=90°,∠CFD=∠BFO.∴∠DCF=∠OBF.∴tan∠DCF=tan∠OBF.即.亦即.∴OF=.∴点F坐标为(0,).设直线BF解析式为y=kx+b.将B(4,0),F(0,)代入得.解得.∴直线BF解析式为y=.∵B、F、D三点共线,亦即直线BD解析式为y=.联立直线AC解析式得解得.故点D坐标为().∵BD⊥AC,BD=DE,∴BD2=DE2.∴.解得b=.∴=.∴点E的坐标为().③当点D与点C重合时,即点C为直角顶点时.如答图4所示.作EG⊥y轴于点G.∵∠BCE=90°.∴∠ECG+∠BCO=90°.又∵∠ECG+∠GEC=90°∴∠BCO=∠GEC.在△GEC和△OCB中,.∴△GEC≌△OCB(AAS).∴GE=OC=6,GC=OB=4.∴点E的坐标为(6,10).由图知点E关于点C对称的点E'亦满足题意.则由中点坐标公式可得点E'的横坐标为2×0﹣6=﹣6,纵坐标为2×6﹣10=2.故点E'坐标为(﹣6,2).综上所述,点E的坐标为()或()或(6,10)或(﹣6,2).8.如图,抛物线y=ax2+bx+5交x轴于A(﹣1,0)、B(5,0)两点,交y轴于点C.(1)求抛物线的解析式;(2)点P是对称轴上一点,当P A+PC达到最小值时,求点P的坐标;(3)M、N为线段BC上两点(N在M的右侧,且M、N不与B、C重合),MN=2,在第一象限的抛物线上是否存在这样的点R,使△MNR为等腰直角三角形?若存在,求出点R的坐标;若不存在,请说明理由.【解答】解:(1)∵抛物线y=ax2+bx+5交x轴于A(﹣1,0),B(5,0),∴,解得:,∴抛物线的解析式为:y=﹣x2+4x+5;(2)当x=0时,y=5,∴C(0,5),∵A与B关于抛物线的对称轴对称,∴直线BC与对称轴的交点就是点P,此时P A+PC达到最小值,∵y=﹣x2+4x+5=﹣(x﹣2)2+9,∴抛物线对称轴为直线x=2,设直线BC的解析式为:y=kx+b(k≠0),∵点B坐标为(5,0),则,解得:,∴直线BC的解析式为y=﹣x+5,与对称轴的交点为(2,3),∴点P的坐标(2,3);(3)分三种情况:①以点M为直角顶点,如图1,∵MN=2,∴RN=MN=4,∵C(0,5),B(5,0),∴OC=OB=5,∴∠OCB=∠OBC=45°,∵∠RNM=45°=∠BCO,∴RN∥OC,由(2)知:直线BC的解析式为y=﹣x+5,设R(m,﹣m2+4m+5),则N(m,﹣m+5),则RN=(﹣m2+4m+5)﹣(﹣m+5)=4,解得m1=4,m2=1,∵点N在点M右侧,∴m=4,∴R(4,5);②以点R为直角顶点,如图2,∵MN=2,∴RN=MN=2,设R(m,﹣m2+4m+5),则Q(m,﹣m+5),∴RN=(﹣m2+4m+5)﹣(﹣m+5)=2,解得m1=,m2=,∵点N在点M右侧,∴m=,∴R(,);③以点N为直角顶点,如图3,∵MN=2,∴RM=MN=4,∵∠RMN=∠OBC=45°,∴MR∥OB,设R(m,﹣m2+4m+5),则M(m﹣4,﹣m2+4m+5),把M(m﹣4,﹣m2+4m+5)代入y=﹣x+5,得﹣(m﹣4)+5=﹣m2+4m+5,解得m1=4,m2=1,此时点M(0,5),因为点M在线段BC上运动,且不与B、C重合,所以不存在以N为直角顶点的情况;综上所述:当R(4,5)或(,)时,△MNR为等腰直角三角形.9.抛物线y=ax2﹣6ax+4(a≠0)交y轴正半轴于点C,交x轴负半轴于点A,交x轴正半轴于点B,且AB=10.(1)如图(1),求抛物线的解析式;(2)如图(2),连接BC,点P为第一象限抛物线上一点,设点P横坐标为t,△PBC 的面积为S,求S与t之间的函数关系式(不用写出自变量t的取值范围);(3)如图(3),在(2)的条件下,连接P A交y轴于点D,过点P作x轴的垂线,交x轴于点E,交BC于点F,连接DF,当∠APE+∠CFD=90°时,在抛物线上是否存在点Q,使得点Q、PE的中点N、点C、是构成以CN为斜边的等腰直角三角形?若存在,请求出点Q的坐标,若不存在,请说明理由.【解答】解:(1)如图1中,设A(m,0),B(n,0),由题意:,解得,∴A(﹣2,0),B(8,0),把A(﹣2,0)代入y=ax2﹣6ax+4,得到a=﹣,∴抛物线的解析式为y=﹣x2+x+4.(2)如图2中,连接OP.设P(t,﹣t2+t+4),∵B(8,0),C(0,4),∴OB=8,OC=4,∴S=S△POC+S△POB﹣S△OBC=×4×t+×8×(﹣t2+t+4)﹣×4×8=﹣t2+8t(0<t<8).(3)存在.理由:如图3中,设P(t,﹣t2+t+4),∵A(﹣2,0),B(8,0),C(0,4),∴直线P A的解析式为y=﹣(t﹣8)x﹣t+4,直线BC的解析式为y=﹣x+4,∵PE⊥x轴,∴F(t,﹣t+4),∵D(0,﹣t+4),∴FD∥AB,∴∠CFD=∠CBA,∵∠APF+∠CFD=90°,∠APF+∠P AE=90°,∴∠P AB=∠CFD=∠CBO,∴tan∠CBO=tan∠P AB==,∴=,∵OA=2,∴OD=1,∴﹣t+4=1,∴t=6,∴P(6,4),E(6,0),∵PN=NE,∴N(6,2),∵C(0,4),△CNQ是等腰直角三角形,CN是斜边,当点Q在CN的上方时,如图3,过点Q作x轴的平行线交y轴于点G,交EP的延长线于点H,设点Q(s,k),易证△QGC≌△NHQ(AAS),则GC=QH,GQ=HN,即s=k﹣2,k﹣4=6﹣s,解得,∴点Q的坐标为(4,6),∵当x=4时,y=﹣×42+×4+4=6,∴点Q在抛物线y=﹣x2+x+4上,∴满足条件的点Q的坐标为(4,6).10.如图,抛物线y=ax2+bx过A(4,0),B(1,3)两点,点C、B关于抛物线的对称轴对称,过点B作直线BH⊥x轴,交x轴于点H.(1)求抛物线的表达式;(2)直接写出点C的坐标和△ABC的面积.(3)点P是抛物线对称轴上一点,且使得P A﹣PC最大,求点P的坐标.(4)若点M在直线BH上运动,点N在x轴上运动,当以点C、M、N为顶点的三角形为等腰直角三角形时,请直接写出此时△CMN的面积.【解答】解:(1)∵抛物线y=ax2+bx过A(4,0),B(1,3)两点,∴,解得,∴抛物线的解析式为y=﹣x2+4x.(2)如图1中,∵y=﹣x2+4x=﹣(x﹣2)2+4,∴对称轴x=2,∵B,C关于对称轴对称,B(1,3),∴C(3,3),∴S△ABC=×2×3=3.(3)如图1中,∵A(4,0),C(3,3),∴直线AC的解析式为y=﹣3x+12,∵P A﹣PC≤AC,∴当点P在直线AC上时,P A﹣PC的值最大,此时P(2,6).(4)如图4﹣1中,如图,当∠CNM=90°,NC=NM时,可知N(4,0),M(1,﹣1),CN=NM=,∴S△MNC=×CN×MN=5.如图4﹣2中,当∠CMN=90°,MN=MC时,M(1,﹣2),N(﹣4,0),可知MN =MC==,∴S△MNC=.如图4﹣3中,当∠CMN=90°,MC=MN时,可知M(1,2),N(2,0),MN=CM ==,∴S△MNC=××=,如图4﹣4中,当∠CNM=90°,CN=MN时,N(﹣2,0),M(1,﹣5),可得S△MNC =17.综上所述,满足条件的△MNC的面积为5或或或17.。
第4章一次函数-一次函数之等腰直角三角形的存在性(教案)

五、教学反思
今天我们在课堂上探讨了《一次函数之等腰直角三角形的存在性》,整体来看,学生的学习效果还是不错的。但在教学过程中,我也发现了一些值得思考的问题。
首先,我发现有些学生对一次函数图像与等腰直角三角形之间的关系理解不够深入。在讲解过程中,我尽量用生动的例子和形象的比喻来帮助他们理解,但显然,这部分内容对于他们来说还是有一定难度的。在今后的教学中,我需要更加关注这部分学生的需求,尽可能用简单易懂的方式讲解难点,让他们能够真正消化吸收。
(二)新课讲授(用时10分钟)
1.理论介绍:首先,我们要了解一次函数和等腰直角三角形的基本概念。一次函数是形如y=kx+b的函数,其中k是斜率,b是y轴截距。等腰直角三角形是一种特殊的三角形,它的两条腰相等且与底边成直角。在一次函数图像中,等腰直角三角形的存在性与函数的斜率有关。
2.案例分析:接下来,我们来看一个具体的案例。这个案例将展示如何在一次函数图像中找出等腰直角三角形,以及它如何帮助我们解决实际问题。
-运用逻辑推理和分析数据的能力,解决一次函数图像中等腰直角三角形的定位问题。
举例解释:
-解释斜率为1或-1时,图像上的点与原点的连线和x轴或y轴形成的特殊角度题时,指导学生如何从问题描述中提取关键信息,构建一次函数模型,并利用等腰直角三角形的性质进行解答。
其次,在实践活动环节,学生们的参与度很高,但部分小组在讨论时显得有些拘谨,可能是因为对等腰直角三角形在实际生活中的应用不够了解。在今后的教学中,我会多设计一些与实际生活紧密相关的案例,让学生在实践中更好地理解理论知识。
一次函数等腰直角

一次函数等腰直角
一次函数等腰直角,是指在一次函数图像上存在等腰直角三角形的情况。
例如,在等腰直角三角形ABC中,∠ACB=90°,CB=CA,直线ED经过点C,过A作AD⊥ED于点D,过B作BE⊥ED于点E。
在这种情况下,我们可以证明 BEC≌ CDA。
这个问题还涉及到一次函数图像上点的坐标特征、等腰直角三角形性质、用待定系数法求一次函数的解析式、相似三角形的性质和判定、勾股定理等多个知识点的综合运用。
例如,已知一次函数 y=﹣ x+6 的图象与 x 轴、y 轴分别交于点 A、点 B,与直线 y= x 相交于点 C。
过点 B 作 x 轴的平行线 l。
点 P 是直线 l 上的一个动点。
在这种情况下,我们可以通过计算和推理来找出点 P 的坐标。
一次函数等腰直角是一个相当复杂的问题,需要对多个数学知识点有深入的理解和掌握。
专题55一次函数中的构造等腰直角三角形(解析版)
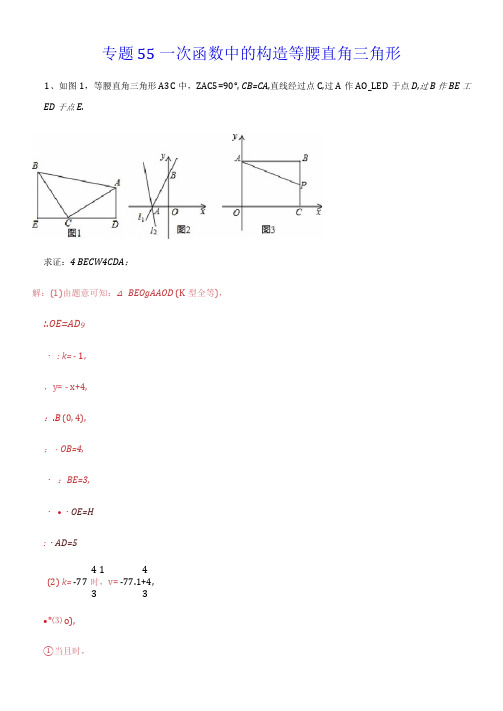
专题55 一次函数中的构造等腰直角三角形1、如图1,等腰直角三角形A3C中,ZAC5=90°, CB=CA,直线经过点C,过A作AO_LED于点D,过B作BE工ED于点E.求证:4 BECW4CDA;解:(1)由题意可知:△ BEOgAAOD (K型全等),:.OE=AD9・: k= - 1,,y= - x+4,:.B(0, 4),;・OB=4,・:BE=3,・•・OE=H:・AD=54 1 4(2) k=-77时,v= -77.1+4,3 3•"⑶ o),①当且时,过点"作加人」丫轴,:•△BMNWMBO (AAS),:・MN=OB, BN=OA,:.MN=49 BN=3,:.M (4, 7):②当且AM=A3 时,过点M作x轴垂线MK,:.^ABO^/^AMK (AAS),:.OB=AK, OA=MK t,AK=4, MK=3,:.M(7, 3):③当且AM=3M 时,过点M作轴,MG_Ly轴,:•△BMGQAAHM (AAS),;・BG=AH, GM=MH,:・GM=MH,,MH=二,7 7 综上所述:M(7, 3)或M (4, 7)或M (左彳)乙乙4 (3)当Q0 时,4?=子.k过点。
作3。
轴,:•△ABO94BQS (AAS),:・BS=OA, SQ=OB,4:.Q(4, 4-丁),k,当k=l时,。
最小值为4:4当&VO 时,Q(4, 4-丁),k,当k=l时,。
最小值为明与k<0矛盾, ,。
的最小值为4.2、己如,在平面直角坐标系中,点A的坐标为(6, 0)、点8的坐标为(0, 8),点。
在y轴上,作直线AC.点3关于直线AC的对称点方刚好在x轴上,连接。
夕.(1)写出点夕的坐标,并求出直线AC对应的函数表达式:(2)点。
在线段AC上,连接。
5、DB\ BB',当△。
89是等腰直角三角形时,求点。
坐标:(3)如图2,在(2)的条件下,点尸从点3出发以每秒2个单位长度的速度向原点。
专题55 一次函数背景下的图形存在性问题(解析版)-中考数学解题大招复习讲义

例题精讲考点一:一次函数中等腰三角形存在性问题【例1】.如果一次函数y=﹣x+6的图象与x轴、y轴分别交于A、B两点,M点在x轴上,并且使得以点A、B、M为定点的三角形是等腰三角形,则M点的坐标为(﹣8,0)或(﹣2,0)或(18,0)或(﹣,0).解:一次函数y=﹣x+6中令x=0,解得y=6;令y=0,解得x=8,∴A(8,0),B(0,6),即OA=8,OB=6,在直角三角形AOB中,根据勾股定理得:AB=10,分四种情况考虑,当BM=BA时,由BO⊥AM,根据三线合一得到O为MA的中点,此时M1(﹣8,0);当AB=AM时,由AB=10,得到OM=﹣2或18,此时M2(﹣2,0),M3(18,0);当MA=MB时,∵A(8,0),B(0,6),∴AB的中点的坐标为(4,3),设直线AB的垂直平分线的解析式为y=x+b,代入(4,3)得3=+b,解得b=﹣,∴直线AB的垂直平分线的解析式为y=x﹣,令y=0,解得x=,此时M4(,0).综上,这样的M点有4个,分别为(﹣8,0)或(﹣2,0)或(18,0)或(,0).故答案为(﹣8,0)或(﹣2,0)或(18,0)或(,0).变式训练【变1-1】.如图,在平面直角坐标系中,直线MN的函数解析式为y=﹣x+3,点A在线段MN上且满足AN=2AM,B点是x轴上一点,当△AOB是以OA为腰的等腰三角形时,则B点的坐标为(2,0)或(,0)或(,0).解:∵在y=﹣x+3中,令x=0,则y=3;令y=0,则﹣x+3=0,解得x=3,∴N(3,0),M(0,3),∴OM=ON=3,∵AN=2AM,∴A(1,2),∴OA==,当AO=OB时,则OB=,∴点B的坐标为(﹣,0)或(,0);②当AO=AB时,设点B的坐标为(m,0),则=,整理得,(1﹣m)2=1,解得m=2或m=0(舍去),∴点B的坐标为(2,0).综上所述:点B的坐标为(2,0)或(,0)或(,0).【变1-2】.如图,在平面直角坐标系中,直线y=﹣2x+12与x轴交于点A,与y轴交于点B,与直线y=x交于点C.(1)求点C的坐标.(2)若P是x轴上的一个动点,直接写出当△OPC是等腰三角形时P的坐标.解:(1)联立两直线解析式成方程组,得,解得:,∴点C的坐标为(4,4);(2)设点P(m,0),而点C(4,4),点O(0,0);PC2=(m﹣4)2+16,PO2=m2,OC2=42+42=32;当PC=PO时,(m﹣4)2+16=m2,解得:m=4;当PC=OC时,同理可得:m=0(舍去)或8;当PO=OC时,同理可得:m=±4;故点P的坐标为(4,0)或(8,0)或(4,0)或(﹣4,0).考点二:一次函数中直角三角形存在性问题【例2】.已知点A、B的坐标分别为(2,2)、(5,1),试在x轴上找一点C,使△ABC为直角三角形.解:当△ABC为直角三角形时,设点C坐标为(x,0),分三种情况:①如果A为直角顶点,则AB2+AC2=BC2,即(2﹣5)2+(2﹣1)2+(2﹣x)2+22=(5﹣x)2+1,解得:x=,②如果B为直角顶点,那么AB2BC2=AC2,即(2﹣5)2+(2﹣1)2+(5﹣x)2+1=(2﹣x)2+22,解得x=,③如果C为直角顶点,那么AB2=AC2+BC2,即(2﹣5)2+(2﹣1)2=(2﹣x)2+22+(5﹣x)2+1,解得x=3或4,综上可知,使△PAB为直角三角形的点C坐标为(,0)或(,0)或(3,0)或(4,0).变式训练【变2-1】.如图,一次函数y=kx+1的图象过点A(1,2),且与x轴相交于点B.若点P 是x轴上的一点,且满足△ABP是直角三角形,则点P的坐标是(1,0)或(3,0).解:∵一次函数y=kx+1的图象过点A(1,2),∴2=k+1,解得k=1,∴一次函数的解析式为y=x+1.∴当∠APB=90°时,P1(1,0);当∠BAP=90°时,∵一次函数的解析式为y=x+1,∴设直线AP的解析式为y=﹣x+b,∵A(1,2),∴2=﹣1+b,解得b=3,∴直线AP的解析式为y=﹣x+3,∴当y=0时,x=3,∴P2(3,0).综上所述,点P的坐标是(1,0)或(3,0).【变2-2】.如图,已知一次函数y=x﹣2的图象与y轴交于点A,一次函数y=4x+b的图象与y轴交于点B,且与x轴以及一次函数y=x﹣2的图象分别交于点C、D,点D的坐标为(﹣2,﹣4).(1)关于x、y的方程组的解为.(2)求△ABD的面积;(3)在x轴上是否存在点E,使得以点C,D,E为顶点的三角形是直角三角形?若存在,求出点E的坐标;若不存在,请说明理由.解:(1)∵一次函数y=x﹣2的图象与一次函数y=4x+b的图象交于点D,且点D的坐标为(﹣2,﹣4),∴关于x、y的方程组的解是,∴关于x、y的方程组的解是,故答案为:;(2)把点D的坐标代入一次函数y=4x+b中得:﹣8+b=﹣4,解得:b=4,∴B(0,4),∵A(0,﹣2),∴AB=4﹣(﹣2)=6,==6;∴S△ABD(3)存在,如图1,当点E为直角顶点时,过点D作DE⊥x轴于E,∵D(﹣2,﹣4),∴E(﹣2,0);当点C为直角顶点时,x轴上不存在点E;当点D为直角顶点时,过点D作DE⊥CD交x轴于点E,作DF⊥x轴于F,设E(t,0),当y=0时,4x+4=0,∴x=﹣1,∴C(﹣1,0),∵F(﹣2,0),∴CE=﹣1﹣t,EF=﹣2﹣t,∵D(﹣2,﹣4),∴DF=4,CF=﹣1﹣(﹣2)=1,在Rt△DEF中,DE2=EF2+DF2=42+(﹣2﹣t)2=t2+4t+20,在Rt△CDF中,CD2=12+42=17,在Rt△CDE中,CE2=DE2+CD2,∴(﹣1﹣t)2=t2+4t+20+17,解得t=﹣18,∴E(﹣18,0),综上,点E的坐标为:(﹣2,0)或(﹣18,0).考点三:一次函数中平行四边形存在性问题【例3】.如图,已知一次函数y=kx+b的图象经过A(1,3),B(﹣2,﹣1)两点,并且交x轴于点C,交y轴于点D.(1)求该一次函数的表达式;(2)求△AOB的面积;(3)平面内是否存在一点M,使以点M、C、O、B为顶点的四边形是平行四边形,若存在,请直接写出点M的坐标,若不存在,请说明理由.解:(1)将A(1,3)、B(﹣2,﹣1),代入y=kx+b得:,解得,∴一次函数的表达式为y=x+;(2)在y=x+中,令x=0得y=,∴OD=,=OD•|x A|=××1=,∴S△AODS△BOD=OD•|x B|=××2=,=S△BOD+S△AOD=;∴△AOB的面积S△AOB(3)存在,理由如下:在y=x+中,令y=0得y=﹣,∴C(﹣,0),设M(m,n),而B(﹣2,﹣1),O(0,0),①以OB、CM为对角线,则OB的中点即是CM的中点,如图:∴,解得,∴M(﹣,﹣1);②以BC、OM为对角线,则BC的中点即是OM的中点,如图:∴,解得,∴M(﹣,﹣1);③以BM、CO为对角线,则BM的中点即是CO的中点,如图:∴,解得,∴M(,1);综上所述,M的坐标为:(﹣,﹣1)或(﹣,﹣1);或(,1).变式训练【变3-1】.如图1,在平面直角坐标系中,直线y=﹣x+3与x轴、y轴相交于A、B两点,点C在线段OA上,将线段CB绕着点C顺时针旋转90°得到CD,此时点D恰好落在直线AB上,过点D作DE⊥x轴于点E.(1)求证:△BOC≌△CED;(2)如图2,将△BCD沿x轴正方向平移得△B'C'D',当B'C'经过点D时,求△BCD平移的距离及点D的坐标;(3)若点P在y轴上,点Q在直线AB上,是否存在以C、D、P、Q为顶点的四边形是平行四边形?若存在,直接写出所有满足条件的P点的坐标;若不存在,请说明理由.(1)证明:∵∠BOC=∠BCD=∠CED=90°,∴∠OCB+∠OBC=90°,∠OCB+∠ECD=90°,∴∠OBC=∠ECD.∵将线段CB绕着点C顺时针旋转90°得到CD,∴BC=CD.在△BOC和△CED中,,∴△BOC≌△CED(AAS).(2)解:∵直线y=﹣x+3与x轴、y轴相交于A、B两点,∴点B的坐标为(0,3),点A的坐标为(6,0).设OC=m,∵△BOC≌△CED,∴OC=ED=m,BO=CE=3,∴点D的坐标为(m+3,m).∵点D在直线y=﹣x+3上,∴m=﹣(m+3)+3,解得:m=1,∴点D的坐标为(4,1),点C的坐标为(1,0).∵点B的坐标为(0,3),点C的坐标为(1,0),∴直线BC的解析式为y=﹣3x+3.设直线B′C′的解析式为y=﹣3x+b,将D(4,1)代入y=﹣3x+b,得:1=﹣3×4+b,解得:b=13,∴直线B′C′的解析式为y=﹣3x+13,∴点C′的坐标为(,0),∴CC′=﹣1=,∴△BCD平移的距离为.(3)解:设点P的坐标为(0,m),点Q的坐标为(n,﹣n+3).分两种情况考虑,如图3所示:①若CD为边,当四边形CDQP为平行四边形时,∵C(1,0),D(4,1),P(0,m),Q(n,﹣n+3),∴,解得:,∴点P1的坐标为(0,);当四边形CDPQ为平行四边形时,∵C(1,0),D(4,1),P(0,m),Q(n,﹣n+3),∴,解得:,∴点P2的坐标为(0,);②若CD为对角线,∵C(1,0),D(4,1),P(0,m),Q(n,﹣n+3),∴,解得:,∴点P的坐标为(0,).综上所述:存在,点P的坐标为(0,)或(0,).考点四:一次函数中矩形存在性问题【例4】.Rt△AOB的两直角边OA、OB分别在x轴的负半轴和y轴的正半轴上,且OA、OB的长满足|OA﹣8|+(OB﹣6)2=0,∠ABO的平分线交x轴于点C过点C作AB的垂线,垂足为点D,交y轴于点E.(1)求线段AB的长;(2)求直线CE的解析式;(3)若M是射线BC上的一个动点,在坐标平面内是否存在点P,使以A、B、M、P为顶点的四边形是矩形?若存在,请直接写出点P的坐标;若不存在,请说明理由.解:(1)∵|OA﹣8|+(OB﹣6)2=0,∴OA=8,OB=6,在直角△AOB中,AB===10;(2)∵BC平分∠ABO,CD⊥AB,AO⊥BO,∴OC=CD,设OC=x,则AC=8﹣x,CD=x.∵△ACD和△ABO中,∠CAD=∠BAO,∠ADC=∠AOB=90°,∴△ACD相似于△ABO,∴,即,解得:x=3.即OC=3,则C的坐标是(﹣3,0).设AB的解析式是y=kx+b,根据题意得解得:则直线AB的解析式是y=x+6,设CD的解析式是y=﹣x+m,则4+m=0,则m=﹣4.则直线CE的解析式是y=﹣x﹣4;(3)①当AB为矩形的边时,如图所示矩形AM1P1B,易知BC的直线方程为y=2x+6,设M1(m,2m+6),P1(x,y),因为A(﹣8,0),B(0,6),则AM12=(m+8)2+(2m+6)2,=5m2+40m+100,BM12=m2+(2m+6﹣6)2=5m2,AB=10,根据AB2+AM12=BM12得100+5m2+40m+100=5m2,m=﹣5,∴M1(﹣5,﹣4),根据平移规律可以解得P1(3,2)②当AB为矩形的对角线时,此时有AB2=AM22+BM22,即100=5m2+40m+100+5m2,m =﹣4或m=0(舍去),∴M2(﹣4,﹣2),根据平移规律可以解得P2(﹣4,8)综上可得,满足条件的P点的坐标为P1(3,2)或P2(﹣4,8).变式训练【变4-1】.如图,四边形OABC是矩形,点A、C在坐标轴上,△ODE是△OCB绕点O顺时针旋转90°得到的,点D在x轴上,直线BD交y轴于点F,交OE于点H,线段BC、OC的长是方程x2﹣4x+3=0的两个根,且OC>BC.(1)求直线BD的解析式;(2)求点H到x轴的距离;(3)点M在坐标轴上,平面内是否存在点N,使以点D、F、M、N为顶点的四边形是矩形?若存在,请直接写出点N的坐标;若不存在,请说明理由.解:(1)x2﹣4x+3=0,解得:x=3或1,故BC=1,OC=3,即点C(0,3)、点A(﹣1,0),则点B(﹣1,3),点D(3,0),点E(3,1),将B、D点的坐标代入一次函数表达式:y=kx+b得:,解得:,故直线BD的表达式为:y=﹣x+…①;(2)同理可得:直线OE的表达式为:y=x…②,联立①②并解得:y=,即点H到x轴的距离为:;(3)直线BD的表达式为:y=﹣x+,则点F(0,),①当FD是矩形的一条边时,当点M在x轴上时,∵MF⊥BD,则直线MF的表达式为:y=x+,当y=0,x=﹣,即点M(﹣,0),点F向右平移3个单位向下平移单位得到D,则点M向右平移3个单位向下平移单位得到N,则点N(,﹣);当点M在y轴上时,同理可得:点N(﹣3,﹣);②当FD是矩形的对角线时,此时点M在原点O,则点N(3,);综上,点N的坐标为:(,﹣)或(﹣3,﹣)或(3,).考点五:一次函数中菱形存在性问题【例5】.如图1,直线y=x+6与x,y轴分别交于A,B两点,∠ABO的角平分线与x轴相交于点C.(1)求点C的坐标;(2)在直线BC上有两点M,N,△AMN是等腰直角三角形,∠MAN=90°,求点M 的坐标;(3)点P在y轴上,在平面上是否存在点Q,使以点A、B、P、Q为顶点的四边形为菱形?若存在,请直接写出点Q的坐标;若不存在,请说明理由.解:(1)对于直线y=x+6,令x=0,得到y=6,∴B(0,6),令y=0,得到x=﹣8,∴A(﹣8,0).∵A(﹣8,0),B(0,6),∴OA=8,OB=6,∵∠AOB=90°,∴AB==10,过点C作CH⊥AB于H,设OC=t,∵BC平分∠ABO,∠AOB=90°,∴CH=OC=t,=S△ABC+S△BCO,∵S△ABO∴OA•OB=AB•CH+OC•OB,∴6×8=10t+6t,∴t=3,∴OC=3,∴C(﹣3,0);(2)设线BC的表达式为:y=kx+b,∵B(0,6),C(﹣3,0),∴直线BC的表达式为:y=2x+6,设点M(m,2m+6)、N(n,2n+6),过点M作MF⊥x轴于点F,过点N作NE⊥x轴于点E,∵△AMN为等腰直角三角形,故AM=AN,∵∠NAE+∠MAF=90°,∠MAF+∠AMF=90°,∴∠NAE=∠AMF,∵∠AFM=∠NEA=90°,AM=AN,∴△FMA≌△EAN(AAS),∴EN=AF,MF=AE,即﹣2n﹣6=m+8,2m+6=8+n,解得:m=﹣2,n=﹣6,故点M的坐标为(﹣2,2)、点N(﹣6,﹣6);由于M,N的位置可能互换,故点N的坐标为(﹣2,2)、点M(﹣6,﹣6);综上所述,点M的坐标为(﹣2,2)或(﹣6,﹣6);(3)设点P(0,p),∴BP2=(p﹣6)2,AP2=82+p2,①当AB是边时,如图,∵点A、B、P、Q为顶点的四边形为菱形,∴BP=AB=10,BP′=AB=10,OB=OP″,∵B(0,6),∴P(0,16),P′(0,﹣4),P″(0,﹣6),∵A(﹣8,0),∴Q(﹣8,10),Q′(﹣8,﹣10),Q″(8,0);②当AB是对角线时,如图,∵点A、B、P、Q为顶点的四边形为菱形,∴AP=BP,∴BP2=AP2,∴(p﹣6)2=82+p2,解得p=﹣,∴P(0,﹣),∵A(﹣8,0),B(0,6),∴Q(﹣8,);综上所述,点Q的坐标为(﹣8,10)或(﹣8,﹣10)或(8,0)或(﹣8,).变式训练【变5-1】.如图,在平面直角坐标系中,直线y=x+4与x轴、y轴分别交于点D、C,直线AB与y轴交于点B(0,﹣2),与直线CD交于点A(m,2).(1)求直线AB的解析式;(2)点E是射线CD上一动点,过点E作EF∥y轴,交直线AB于点F,若以O、C、E、F为顶点的四边形是平行四边形,请求出点E的坐标;(3)设P是射线CD上一点,在平面内是否存在点Q,使以B、C、P、Q为顶点的四边形是菱形?若存在,请直接写出点Q的坐标;若不存在,请说明理由.解:(1)∵点A(m,2)在直线y=x+4上∴m+4=2解得m=﹣2∴点A的坐标为(﹣2,2)设直线AB的解析式为y=kx+b∴解得∴直线AB的解析式为y=﹣2x﹣2;(2)如图1,由题意设点E的坐标为(a,a+4),则∵EF∥y轴,点F在直线y=﹣2x﹣2上∴点F的坐标为(a,﹣2a﹣2)∴EF=|a+4﹣(﹣2a﹣2)|=|3a+6|,∵以点O、C、E、F为顶点的四边形是平行四边形,且EF∥OC∴EF=OC∵直线y=x+4与y轴交于点C∴点C的坐标为(0,4)∴OC=4,即|3a+6|=4解得:a=﹣或a=﹣∴点E的坐标为(﹣,)或(﹣,);(3)如图2,当BC为对角线时,点P,Q都是BC的垂直平分线,且点P和点Q关于BC对称,∵B(0,﹣2),C(0,4),∴点P的纵坐标为1,将y=1代入y=x+4中,得x+4=1,∴x=﹣3,∴P''(﹣3,1),∴Q''(3,1)当CP是对角线时,CP是BQ的垂直平分线,设Q(m,n),∴BQ的中点坐标为(,),代入直线y=x+4中,得+4=①,∵CQ=CB,∴m2+(n﹣4)2=36②,联立①②得,(舍)或,∴Q'(﹣6,4),当PB是对角线时,PC=BC=6,设P(c,c+4),∴c2+(c+4﹣4)2=36,∴c=3(舍)或c=﹣3,∴P(﹣3,﹣3+4),设Q(d,e)∴(﹣3+0)=(0+d),(﹣3+4﹣2)=(e+4),∴d=﹣3,e=﹣3﹣2,∴Q(﹣3,﹣3﹣2),即:点Q的坐标为(3,1),(﹣6,4)或(﹣3,﹣3﹣2).1.一次函数y=x+4分别交x轴、y轴于A、B两点,在x轴上取一点C,使△ABC为等腰三角形,则这样的点C的坐标为(﹣8,0)(3,0)(2,0)(,0).解:当x=0时,y=4,当y=0时,x=﹣3,即A(﹣3,0),B(0,4),OA=3,OB=4,由勾股定理得:AB=5,有三种情况:①以A为圆心,以AB为半径交x轴于两点,此时AC=AB=5,C的坐标是(2,0)和(﹣8,0);②以B为圆心,以AB为半径交x轴于一点(A除外),此时AB=BC,OA=OC=3,C的坐标是(3,0);③作AB的垂直平分线交x轴于C,设C的坐标是(a,0),A(﹣3,0),B(0,4),∵AC=BC,由勾股定理得:(a+3)2=a2+42,解得:a=,∴C的坐标是(,0),故答案为:(﹣8,0)(3,0)(2,0)(,0).2.如图,在平面直角坐标系中,点A坐标为(2,1),连接OA,点P是x轴上的一动点,如果△OAP是等腰三角形,请你写出符合条件的点P坐标P1(4,0),P2(,0),P3(﹣,0),P4(,0).解:设P(x,0),当OA=AP时,∵A(2,1),∴P1(4,0);当OA=OP时,∵A(2,1),∴OA==,∴P2(,0),P3(﹣,0);当AP=OP时,∵P(x,0),(2,1),∴(2﹣x)2+12=x2,解得x=,∴P4(,0).综上所述,P点坐标为:P1(4,0),P2(,0),P3(﹣,0),P4(,0).故答案为:P1(4,0),P2(,0),P3(﹣,0),P4(,0).3.如图,在平面直角坐标系中,点A的坐标为(1,0),点B的坐标为(4,0),点C在y 的正半轴上,且OB=2OC,在直角坐标平面内确定点D,使得以点D、A、B、C为顶点的四边形是平行四边形,请写出点D的坐标为(3,2)(﹣3,2)(5,﹣2).解:如图,①当BC为对角线时,易求M1(3,2);②当AC为对角线时,CM∥AB,且CM=AB.所以M2(﹣3,2);③当AB为对角线时,AC∥BM,且AC=BM.则|M y|=OC=2,|M x|=OB+OA=5,所以M3(5,﹣2).综上所述,符合条件的点D的坐标是M1(3,2),M2(﹣3,2),M3(5,﹣2).故答案为:(3,2)(﹣3,2)(5,﹣2).4.如图,一次函数y=k2x+b的图象与y轴交于点B,与正比例函数y=k1x的图象相交于点A(3,4),且OA=OB.(1)分别求出这两个函数的解析式;(2)求△AOB的面积;(3)点P在x轴上,且△POA是等腰三角形,请直接写出点P的坐标.解:(1)∵正比例函数y=k1x的图象经过点A(3,4),∴3k1=4,∴k1=,∴正比例函数解析式为y=x.如图1中,过A作AC⊥x轴于C,在Rt△AOC中,OC=3,AC=4,∴AO==5,∴OB=OA=5,∴B(0,﹣5),∴,解得,∴一次函数的解析式为y=3x﹣5.(2)如图1中,过A作AD⊥y轴于D,∵A(3,4),∴AD=3,=;∴S△AOB(3)当OP=OA时,P1(﹣5,0),P2(5,0),当AO=AP时,P3(6,0),当PA=PO时,线段OA的垂直平分线为y=﹣,∴,满足条件的点P的坐标(﹣5,0)或(5,0)或(6,0)或.5.直线l1交x轴于点A(6,),交y轴于B(0,6).(1)如图,折叠△AOB,使BA落在y轴上,折痕所在直线为l2,直线l2与x轴交于C 点,求C点坐标及l2的解析式;(2)在直线l1上找点M,使得以M、A、C为顶点的三角形是等腰三角形,求出所有满足条件的M点的坐标.解:∵点A(6,0),交y轴于B(0,6).∴OA=6,OB=6,∴tan∠OAB==,∴∠OAB=30°,∴∠OBA=60°,∵折叠△AOB,∴∠OBC=∠ABC=30°,∴BC=2OC,BO=OC=6,∴OC=2,∴点C(2,0),设直线BC解析式为:y=kx+b,解得:∴直线BC解析式为:y=﹣x+6;(2)当点M与点B重合时,由(1)可知:∠AMC=∠MAC=30°,∴CM=AC,∴△ACM是等腰三角形,∴当M为(0,6)时,△ACM是等腰三角形,∵OC=2,OA=6,∴AC=4,若AM=AC=4,如图1:过点M作MH⊥AC,∵∠MAH=30°,∴MH=AM=2,AH=2MH=6,∴OH=6﹣6或6+6,∴点M(6﹣6,2)或(6+6,﹣2)若AM=MC,如图2,过点M作MH⊥AC,∵AM=MC,MH⊥AC,∴AH=CH=2,∴OC=4,∵∠MAH=30°,∴AH=MH,∴MH=2,∴点M(4,2),综上所述:点M(6﹣6,2)或(6+6,﹣2)或(4,2)或(0,6).6.在平面直角坐标系中,直线y=kx+8k(k是常数,k≠0)与坐标轴分别交于点A,点B,且点B的坐标为(0,6).(1)求点A的坐标;(2)如图1,将直线AB绕点B逆时针旋转45°交x轴于点C,求直线BC的解析式;(3)在(2)的条件下,直线BC上有一点M,坐标平面内有一点P,若以A、B、M、P 为顶点的四边形是菱形,请直接写出点P的坐标.解:(1)令y=kx+8k=0,解得x=﹣8,故点A的坐标为(﹣8,0);(2)过点A作AD⊥AB交BC于点D,过点A作y轴的平行线交过点B与x轴的平行线于点M,交过点D与x轴的平行线于点N,∵∠ABC=45°,故△ABD为等腰直角三角形,则AD=AB,∵∠BAM+∠DAN=90°,∠DAN+∠ADN=90°,∴∠BAM=∠ADN,∵∠BMA=∠AND=90°,∴△BMA≌△AND(AAS),∴AN=BM=8,ND=AM=6,故点D的坐标为(﹣2,﹣8),设直线BC的表达式为y=kx+b,则,解得,故直线BC的表达式为y=7x+6;(3)设点M的坐标为(m,7m+6),点P(s,t),而点A、B的坐标分别为(﹣8,0)、(0,6),①当AB是边时,点A向右8个单位向上6个单位得到点B,同样,点M(P)向右8个单位向上6个单位得到点P(M),且AB=BP(AB=BM),则或,解得或或(不合题意的值已舍去);故点P的坐标为(﹣8,7)或(﹣﹣8,﹣7)或(6,﹣2);②当AB是对角线时,由中点坐标公式和AM=BM得:,解得,故点P的坐标为(﹣7,7);综上,点P的坐标为(﹣8,7)或(﹣﹣8,﹣7)或(6,﹣2)或(﹣7,7).7.如图,在平面直角坐标系中,一次函数的图象与x轴交于点A(﹣4,0),与y轴交于点B,且与正比例函数y=x的图象交于点C(m,6).(1)求一次函数的解析式;(2)求△BOC的面积;(3)在x轴上是否存在一点P,使得△ABP是等腰三角形?若存在,请直接写出符合条件的所有点P的坐标;若不存在,请说明理由.解:(1)∵将点C(m,6)代入y=x,∴6=m,∴m=4,∴C(4,6),设一次函数的解析式为y=kx+b,∴,∴,∴y=x+3;(2)在y=x+3中,令x=0得y=3,∴B(0,3),=OB•|x C|=×3×4=6;∴S△BOC(3)在x轴上存在一点P,使得△ABP是等腰三角形,理由如下:∵A(﹣4,0),B(0,3),∴AB=5,OA=4,当B为等腰三角形顶角顶点时,P点与A点关于y轴对称,∴P(4,0);当A为等腰三角形顶角顶点时,AP=AB=5,∴P(﹣9,0)或P(1,0);当P为等腰三角形顶角顶点时,设P(t,0),∵PA=PB,∴(t+4)2=t2+9,解得t=﹣,∴P(﹣,0),综上所述:P点坐标为(﹣9,0)或(1,0)或(4,0)或(﹣,0).8.如图,已知一次函数y=x+m的图象与x轴交于点A(﹣6,0),交y轴于点B.(1)求m的值与点B的坐标(2)问在x轴上是否存在点C,使得△ABC的面积为16?若存在,求出点C的坐标;若不存在,说明理由.(3)问在x轴是否存在点P,使得△ABP为等腰三角形,求出点P坐标.(4)一条经过点D(0,2)和直线AB上的一点的直线将△AOB分成面积相等的两部分,请求出这条直线的函数表达式.解:(1)把点A(﹣6,0)代入y=x+m,得m=8,∴点B坐标为(0,8).(2)存在,设点C坐标为(a,0),由题意•|a+6|•8=16,解得a=﹣2或﹣10,∴点C坐标(﹣2,0)或(﹣10,0).(3)如图1中,①当AB=AP时,AP=AB==10,可得P1(﹣16,0),P2(4,0).②当BA=BP时,OA=OP,可得P3(6,0).③当PA=PB时,∵线段AB的垂直平分线为y=﹣x+,可得P4(,0),综上所述,满足条件的点P坐标为(﹣16,0)或(4,0)或(6,0)或(,0).(4)如图2中,设过点D的直线交AB于E,设E(b,),由题意BD•(﹣b)=××6×8,∴b=﹣4,∴点E坐标(﹣4,),设直线DE的解析式为y=kx+b则有,解得,∴这条直线的函数表达式y=﹣x+2.9.在平面直角坐标系中,一次函数y=﹣x+2的图象交x轴、y轴分别于A、B两点,交直线y=kx于P(2,a).(1)求点A、B的坐标;(2)若Q为x轴上一动点,△APQ为等腰三角形,直接写出Q点坐标;(3)点C在直线AB上,过C作CE⊥x轴于E,交直线OP于D,我们规定若C,D,E 中恰好有一点是其他两点所连线段的中点,则称C,D,E三点为“和谐点”,求出C,D,E三点为“和谐点”时C点的坐标.解:(1)当x=0时,y=﹣x+2=2,∴点B的坐标为(0,2);当y=0时,有﹣x+2=0,解得:x=4,∴点A的坐标为(4,0);(2)∵一次函数y=﹣x+2的图象交直线y=kx于P(2,a).∴a=﹣×2+2=1,∴点P的坐标为(2,1),设点Q(m,0),而点A、P的坐标分别为:(4,0)、(2,1),则AP==,AQ=|4﹣m|,PQ=,当AP=AQ时,则=|4﹣m|,解得m=4±,∴点Q(4±,0);当AP=PQ时,=,解得m=0或4(舍去),∴点Q(0,0);当PQ=AQ时,即=|4﹣m|,解得:m=,∴点Q(,0);综上,点Q的坐标为(4±,0)或(0,0)或(,0);(3)∵y=kx过P(2,1).∴2k=1,解得k=,∴y=x,设点C的坐标为(n,﹣n+2),则点D的坐标为(n,n),点E的坐标为(n,0),∴CD=|﹣n+2﹣n|=|2﹣n|,DE=|n|,CE=|﹣n+2|=|n﹣2|,当D为CE的中点时,CD=DE,∴|2﹣n|=|n|,解得n=或4(舍去),∴点C的坐标为(,);当C为DE的中点时,CD=CE,∴|2﹣n|=|n﹣2|,解得n=或0(舍去),∴点C的坐标为(,);当E为CD的中点时,DE=CE,∴|n|=|n﹣2|,无解;综上,C,D,E三点为“和谐点”时C点的坐标为(,)或(,).10.如图所示,直线l:y=﹣x+2与x轴、y轴分别交于A、B两点,在y轴上有一点C(0,4).(1)求△AOB的面积;(2)动点M从A点以每秒1个单位的速度沿x轴向左移动,求△COM的面积S与M的移动时间t之间的函数关系式;(3)当动点M在x轴上移动的过程中,在平面直角坐标系中是否存在点N,使以点A,C,N,M为顶点的四边形为菱形,若存在,请直接写出点N的坐标;若不存在,请说明理由.解:(1)令y=0,,解得x=.令x=0,y=.∴A(,0),B(0,).=.∴△AOB的面积为12.(2)∵动点M从A点以每秒1个单位的速度沿x轴向左移动,∴AM=t.当0≤t≤时,OM=,OC=.∴==.当t>时,OM=t﹣.∴==.综上,△COM的面积S与M的移动时间t之间的函数关系式:S=.(3)在平面直角坐标系中存在点N,使以点A,C,N,M为顶点的四边形为菱形.①当AC,AM为菱形的边时,情况一:如图1,当点M在点A的左侧时,Rt△AOC中,=,∴NC=AC=.∵NC∥AM,∴点N(,).情况二,如图1′,当点M在点A的右侧时,由情况一同理可得点N的坐标为.②当AC为菱形的对角线时,如图2,此时M,O重合,四边形OANC为正方形,则点N(,).③如图3,当AC为菱形的边,AM为菱形的对角线时,此时点C,N关于x轴对称,∴点N(0,﹣).综上,在平面直角坐标系中存在点N,使以点A,C,N,M为顶点的四边形为菱形,此时点N的坐标为:(,),,(,),(0,﹣).11.如图,直线y=﹣x+4与x轴、y轴分别交于A、B两点,直线BC与x轴、y轴分别交于C、B两点,连接BC,且OC=OB.(1)求点A的坐标及直线BC的函数关系式;(2)点M在x轴上,连接MB,当∠MBA+∠CBO=45°时,求点M的坐标;(3)若点P在x轴上,平面内是否存在点Q,使点B、C、P、Q为顶点的四边形是菱形?若存在,请直接写出点Q的坐标;若不存在,请说明理由.解:(1)对于直线y=﹣x+4,令x=0的y=4,令y=0得x=4,∴A(4,0),B(0,4),∴OB=OA=4,∵OC=OB,∴OC=3,∴C(﹣3,0),设直线BC的解析式为y=kx+b,则有,解得,∴直线BC的解析式为y=x+4.(2)如图1中,当点M在点A的左边时,∵OB=OA=4,∠AOB=90°,∴∠ABO=45°,∴∠CBO+∠MBA=∠MBA+∠MBO=45°,∴∠CBO=∠OBM,∵∠CBO+∠BCO=90°,∠BMO+∠OBM=90°,∴∠BCO=∠BMO,∴BC=BM,OC=OM=3,∴M(3,0),作点M关于直线AB的对称点N,作直线BN交x轴于M1,则∠M1BA=∠MBA,点M1满足条件.∵N(4,1),B(0,4),∴直线BN的解析式为y=﹣x+4,令y=0,得x=,∴M1(,0),综上所述,满足条件的点M的坐标为(3,0)或(,0).(3)如图2中,∵BC==5,当BC为菱形的边时,四边形CP1Q1B,四边形CP3Q3B,四边形BCQ2P2是菱形,此时Q1(﹣5,4),Q3(5,4),Q2(0,4),当BC是菱形的对角线时,四边形CP4BQ4是菱形,可得Q4(﹣,4).综上所述,满足条件的点Q的坐标为(﹣5,4)或(5,4)或(0,﹣4)或.12.已知,一次函数y=的图象与x轴、y轴分别交于点A、点B,与直线y=相交于点C.过点B作x轴的平行线l.点P是直线l上的一个动点.(1)求点A,点B的坐标.(2)求点C到直线l的距离.=S△BCP,求点P的坐标.(3)若S△AOC(4)若点E是直线y=上的一个动点,当△APE是以AP为直角边的等腰直角三角形时,请直接写出点E的坐标.解:(1)∵一次函数y=的图象与x轴、y轴分别交于点A、点B,∴令y=0,则=0,∴x=8,令x=0,则y=6,∴点A、B的坐标分别为:(8,0)、(0,6);(2)解:得,,∴点C(3,),则C到直线l的距离为6﹣=;=×8×=15=S△BCP=×BP×(y P﹣y C)=BP×,(3)∵S△AOC解得:BP=,故点P(,6)或(﹣,6);(4)设点E(m,m)、点P(n,6);①当∠EPA=90°时,当点P在y轴右侧时,当点P在点E的左侧时,如图1,∵∠MEP+∠MPE=90°,∠MPE+∠NPA=90°,∴∠MEP=∠NPA,AP=PE,∵△EMP≌△PNA(AAS),则ME=PN=6,MP=AN,即m﹣n=6,m﹣6=8﹣n,解得:m=,当点P在点E的右侧时,如图,同理可得m=16,当∠EAP=90°时,当点P在y轴左侧时,如图2,同理可得:m﹣8=6,m=8﹣n,解得:m=14,故点E(14,);故点E(,)或(14,)或(16,20);如图3,同理可得:△AMP≌△ANE(AAS),故MP=EN,AM=AN=6,即m=n﹣8,|8﹣m|=6,解得:m=2或14(不合题意舍去),故点E(2,);综上,E(,)或(16,20)或(2,)或(14,).13.如图,在平面直角坐标系xOy中,直线y=﹣x+与y=x相交于点A,与x轴交于点B.(1)求点A,B的坐标;(2)在平面直角坐标系xOy中,是否存在一点C,使得以O,A,B,C为顶点的四边形是平行四边形?如果存在,试求出所有符合条件的点C的坐标;如果不存在,请说明理由;(3)在直线OA上,是否存在一点D,使得△DOB是等腰三角形?如果存在,试求出所有符合条件的点D的坐标,如果不存在,请说明理由.解:(1)∵直线y=﹣x+与y=x相交于点A,∴联立得,解得,∴点A(1,1),∵直线y=﹣x+与x轴交于点B,∴令y=0,得﹣x+=0,解得x=3,∴B(3,0),(2)存在一点C,使得以O,A,B,C为顶点的四边形是平行四边形.①如图1,过点A作平行于x轴的直线,过点O作平行于AB的直线,两直线交于点C,∵AC∥x轴,OC∥AB,∴四边形CABO是平行四边形,∵A(1,1),B(3,0),∴AC=OB=3,∴C(﹣2,1),②如图2,过点A作平行于x轴的直线,过点B作平行于AO的直线,两直线交于点C,∵AC∥x轴,BC∥AO,∴四边形CAOB是平行四边形,∵A(1,1),B(3,0),∴AC=OB=3,∴C(4,1),③如图3,过点O作平行于AB轴的直线,过点B作平行于AO的直线,两直线交于点C,∵OC∥AB,BC∥AO,∴四边形CBAO是平行四边形,∵A(1,1),B(3,0),∴AO=BC,OC=AB,作AE⊥OB,CF⊥OB,易得OE=EF=FB=1,∴C(2,﹣1),(3)在直线OA上,存在一点D,使得△DOB是等腰三角形,①如图4,当OB=OD时,作DE⊥x轴,交x轴于点E∵OB=3,点D在OA上,∠DOE=45°∴DE=OE=,∴D(﹣,﹣),②如图5,当OD=OB时,作DE⊥x轴,交x轴于点E∵OB=3,点D在OA上,∠DOE=45°∴DE=OE=,∴D(,),③如图6,当OB=DB时,∵∠AOB=∠ODB=45°,∴DB⊥OB,∵OB=3,∴D(3,3),④如图7,当DO=DB时,作DE⊥x轴,交x轴于点E∵∠AOB=∠OBD=45°,∴OD⊥DB,∵OB=3,∴OE=,AE=,∴D(,).综上所述,在直线OA上,存在点D(﹣,﹣),D(,),D(3,3)或D(,),使得△DOB是等腰三角形,14.如图,经过点B(0,2)的直线y=kx+b与x轴交于点C,与正比例函数y=ax的图象交于点A(﹣1,3)(1)求直线AB的函数的表达式;(2)直接写出不等式(kx+b)﹣ax<0的解集;(3)求△AOC的面积;(4)点P是直线AB上的一点,且知△OCP是等腰三角形,写出所有符合条件的点P的坐标.解:(1)依题意得:,解得,∴所求的一次函数的解析式是y=﹣x+2.(2)观察图形可知:不等式(kx+b)﹣ax<0的解集;x<﹣1.(3)对于y=﹣x+2,令y=0,得x=2∴C(1,0),∴OC=2.=×2×3=3.∴S△AOC(4)①当点P与B重合时,OP1=OC,此时P1(0,2);②当PO=PC时,此时P2在线段OC的垂直平分线上,P2(1,1);③当PC=OC=2时,设P(m.﹣m+2),∴(m﹣2)2+(﹣m+2)2=4,∴m=2±,可得P3(2﹣,),P4(2+,﹣),综上所述,满足条件的点P坐标为:(1,1)或(0,2)或P(2+,﹣)或(2﹣,).15.如图1,已知直线l1:y=kx+4交x轴于A(4,0),交y轴于B.(1)直接写出k的值为﹣1;(2)如图2,C为x轴负半轴上一点,过C点的直线l2:经过AB的中点P,点Q(t,0)为x轴上一动点,过Q作QM⊥x轴分别交直线l1、l2于M、N,且MN=2MQ,求t的值;(3)如图3,已知点M(﹣1,0),点N(5m,3m+2)为直线AB右侧一点,且满足∠OBM=∠ABN,求点N坐标.解:(1)把A(4,0)代入y=kx+4,得0=4k+4.解得k=﹣1.故答案是:﹣1;(2)∵在直线y=﹣x+4中,令x=0,得y=4,∴B(0,4),∵A(4,0),∴线段AB的中点P的坐标为(2,2),代入,得n=1,∴直线l2为,∵QM⊥x轴分别交直线l1、l2于M、N,Q(t,0),∴M(t,﹣t+4),,∴,MQ=|﹣t+4|=|t﹣4|,∵MN=2MQ,∴,分情况讨论:①当t≥4时,,解得:t=10.②当2≤t<4时,,解得:.③当t<2时,,解得:t=10>2,舍去.综上所述:或t=10.(3)在x轴上取一点P(1,0),连接BP,作PQ⊥PB交直线BN于Q,作QR⊥x轴于R,∴∠BOP=∠BPQ=∠PRQ=90°,∴∠BPO=∠PQR,∵OA=OB=4,∴∠OBA=∠OAB=45°,∵M(﹣1,0),∴OP=OM=1,∴BP=BM,∴∠OBP=∠OBM=∠ABN,∴∠PBQ=∠OBA=45°,∴PB=PQ,∴△OBP≌△RPQ(AAS),∴RQ=OP=1,PR=OB=4,∴OR=5,∴Q(5,1),∴直线BN的解析式为,将N(5m,3m+2)代入,得3m+2=﹣×5m+4解得,∴.16.如图,平面直角坐标系中,直线l分别交x轴、y轴于A、B两点(OA<OB)且OA、OB的长分别是一元二次方程x2﹣(+1)x+=0的两个根,点C在x轴负半轴上,且AB:AC=1:2(1)求A、C两点的坐标;(2)若点M从C点出发,以每秒1个单位的速度沿射线CB运动,连接AM,设△ABM 的面积为S,点M的运动时间为t,写出S关于t的函数关系式,并写出自变量的取值范围;(3)点P是y轴上的点,在坐标平面内是否存在点Q,使以A、B、P、Q为顶点的四边形是菱形?若存在,请直接写出Q点的坐标;若不存在,请说明理由.解:(1)x2﹣(+1)x+=0,(x﹣)(x﹣1)=0,解得x1=,x2=1,∵OA<OB,∴OA=1,OB=,∴A(1,0),B(0,),∴AB=2,又∵AB:AC=1:2,∴AC=4,∴C(﹣3,0);(2)∵AB=2,AC=4,BC=2,∴AB2+BC2=AC2,即∠ABC=90°,由题意得:CM=t,CB=2.①当点M在CB边上时,S=2﹣t(0≤t);②当点M在CB边的延长线上时,S=t﹣2(t>2);(3)存在.①当AB是菱形的边时,如图所示,在菱形AP1Q1B中,Q1O=AO=1,所以Q1点的坐标为(﹣1,0),在菱形ABP2Q2中,AQ2=AB=2,所以Q2点的坐标为(1,2),在菱形ABP3Q3中,AQ3=AB=2,所以Q3点的坐标为(1,﹣2),②当AB为菱形的对角线时,如图所示的菱形AP4BQ4,设菱形的边长为x,则在Rt△AP4O中,AP42=AO2+P4O2,即x2=12+(﹣x)2,解得x=,所以Q4(1,).综上可得,平面内满足条件的Q点的坐标为:Q1(﹣1,0),Q2(1,2),Q3(1,﹣2),Q4(1,).17.如图1,在平面直角坐标系中.直线与x轴、y轴相交于A、B两点,动点C 在线段OA上,将线段CB绕着点C顺时针旋转90°得到CD,此时点D恰好落在直线AB上时,过点D作DE⊥x轴于点E.(1)求证:△BOC≌△CED;(2)如图2,将△BCD沿x轴正方向平移得△B'C'D',当直线B′C′经过点D时,求点D的坐标;(3)若点P在y轴上,点Q在直线AB上.是否存在以C、D、P、Q为顶点的四边形是平行四边形?若存在,直接写出所有满足条件的Q点坐标;若不存在,请说明理由.(1)证明:∵∠BOC=∠BCD=∠CED=90°,∴∠OCB+∠DCE=90°,∠DCE+∠CDE=90°,∴∠BCO=∠CDE,在△BOC和△CED中,。
一次函数与三角形

【说明】
①若为顶角,则点在以点【说明】
①若为直角,则点在经过点18/06/12
∠A P ∠A P
【说明】
①若为直角,则点在经过点垂直于线段的直线上,且;
②若为直角,则点在经过点垂直于线段的直线上,且;
③若为直角,则点在线段的垂直平分线上,且.
【方法】
①在平面直角坐标系中需要计算线段长度时,通常作轴或轴的平行线(或垂线),目的是实现坐标与线段长度之
间的相互转换.
②等腰直角三角形中通常通过构造“一线三垂直”模型来解题.
爱
智
康
2
1
8
/
6
/
1
2
∠A P A AB AP=AB
∠B P B AB AP=AB
∠P P AB∠AP B=90∘
x y
已知点和点,点在轴上,若以,,三点为顶点的三角形是等腰直角三角形,求点
的坐标.
A(0 , 1)B(1 , 3)P y A B P
P。
一次函数中特殊三角形的存在性问题(上课)

如图,线段AB的端点A在直线l上,AB与l的夹角是30°,请在 直线l上另找一点C,使△ABC是等腰三角形。这样的点能找到几个? 请找出所有符合条件的点C。
C3 l
C1 C4 A
B C2
合作交流,探索新知
如图,直线 y 3 x 3与x轴、y轴分别交于A、B两点.
4
(1)直接写出A、B两点的坐标; (2)在x轴上是否存在点P,使以A,B,P为顶点的三角形是
y
B
O
A
x
2、本节课涉及了哪些数学思想或方法?
(1).数形结合思想
(2).分类讨论思想
(3).方程思想
课后练习,巩固提高
1、如图,在平面直角坐标系xOy中,四边形OABC的边OC,OA
分别与x轴、y轴重合,AB∥OC,∠AOC=90°,∠BCO=45°,
BC= ,点C的坐标为(-9,0).
(1)求点B的坐标.
件的点;
存(2象.在的2为)交点底在点P:,就x做轴是使已上符以知合是线A条否、段件的的垂点直.平分线,中垂线y与所要求的图
B、P为顶点的三角
形是等腰三角形?
若存在,求出点P的
B 3 4-m
坐标;若不存在, 请说明理由;
P3
P1 O m P4 4-mA
P2
x
合作解交决存流在,性问探题小索策新略:知 如图假若,设能直存导线在出合→y 理推 的理3结论x 果证3与,→就得x轴做出、出结“论y轴存。分在别”的交判于断A;、B两点. 导出矛盾,就做4出不存在的判断。
B
么问题?你能解决它吗?
O
A
x
合作交流,探索新知
如图,直线 y 3 x 3与x轴、y轴分别交于A、B两点.
一次函数与等腰三角形存在性问题

每日一题 079一次函数与等腰三角形武穴市百汇学校徐国纲解题技巧如果△ABC是等腰三角形,那么存在①AB=AC,②BA=BC,③CA=CB三种情况.已知腰长画等腰三角形用圆规画圆,已知底边画等腰三角形用刻度尺画垂直平分线.如图,已知线段AB作等腰三角形,则符合要求的点都在以A、B为圆心,AB长为半径的圆和AB的垂直平分线上,这就是传说中的“两圆一线”.解等腰三角形的存在性问题,有几何法和代数法,把几何法和代数法相结合,可以使得解题又好又快.几何法一般分三步:分类、画图、计算.代数法一般也分三步:表示三边长,分类列方程,解方程并检验.例题解析例❶ 如图1-1,在平面直角坐标系xOy中,已知点D的坐标为(3, 4),点P是x轴正半轴上的一个动点,如果△DOP是等腰三角形,求点P的坐标.图1-1【解析】分三种情况讨论等腰三角形△DOP:①DO=DP,②OD=OP,③PO=PD.①当DO=DP时,以D为圆心、DO为半径画圆,与x轴的正半轴交于点P,此时点D 在OP的垂直平分线上,所以点P的坐标为(6, 0)(如图1-2).②当OD=OP=5时,以O为圆心、OD为半径画圆,与x轴的正半轴交于点P(5, 0) (如图1-3).③当PO=PD时,画OD的垂直平分线与x轴的正半轴交于点P,设垂足为E(如图1-4).可求325:48PEl y x=-+,∴25(,0)6P.图1-2 图1-3 图1-4上面是几何法的解题过程,我们可以看到,画图可以帮助我们快速找到目标P ,其中①和②画好图就知道答案了,只需要对③进行计算.代数法先设点P 的坐标为(x , 0),其中x >0,然后表达△DOP 的三边长(的平方). DO 2=52,OP 2=x 2,PD 2=(x -3)2+42.①当DO =DP 时,52=(x -3)2+42.解得x =6,或x =0.当x =0时既不符合点P 在x 轴的正半轴上,也不存在△DOP .②当OD =OP 时,52=x 2.解得x =±5.当x =-5时等腰三角形DOP 是存在的,但是点P 此时不在x 轴的正半轴上(如图1-5).③当PO =PD 时,x 2=(x -3)2+42.这是一个一元一次方程,有唯一解,它的几何意义是两条直线(x 轴和OD 的垂直平分线)有且只有一个交点.代数法不需要画三种情况的示意图,但是计算量比较大,而且要进行检验.图1-5例❷ 如图2-1,直线3y x =+与y 、x 轴相交于点A 、C ,动点P 以1个单位/秒的速度从点A 出发,沿AC 向点C 移动,同时动点Q 以1个单位/秒的速度从点C 出发,沿CO 向点O 移动,当P 、Q 两点中其中一点到达终点时则停止运动.在P 、Q 两点移动的过程中,当△PCQ 为等腰三角形时,求t 的值.图2-1【解析】在P 、Q 两点移动的过程中,△PCQ 的6个元素(3个角和3条边)中,唯一不变的就是∠PCQ 的大小,夹∠PCQ 的两条边CQ =t ,CP =6-t .因此△PQC 符合“边角边”的解题条件,我们只需要在∠PCQ 的边上取点P 或Q 画圆.图2-2 图2-3 图2-4①如图2-2,当CP =CQ 时,t =6-t ,解得3t =(秒).②如图2-3,当QP =QC 时,过点Q 作QM ⊥AC 于M ,则CM 1622t PC -==. 在Rt △QMC 中,∵30PCQ =︒∠,∴2CQ =,62tt -=,解得3t =-(秒). ③如图2-4,当PQ =PC 时,过点P 作PN ⊥BC 于N ,则1122CN CQ t ==. 在Rt △PNC 中,∵30PCQ =︒∠,∴2CP =,62tt -=,解得9t =-秒).例❸ 如图3-1,已知正方形OABC 的边长为2,顶点A 、C 分别在x 、y 轴的正半轴上,M 是BC 的中点.P(0, m)是线段OC 上一动点(C 点除外),直线PM 交AB 的延长线于点D .当△APD 是等腰三角形时,求m 的值.图3-1【解析】点P(0, m)在运动的过程中,△APD 的三个角都在变化,因此不符合几何法“边角边”的解题条件,我们用代数法来解.因为PC//DB ,M 是BC 的中点,所以BD =CP =2-m .所以D(2, 4-m).于是我们可以表达出△APD 的三边长(的平方):22(4)AD m =-,224AP m =+,2222(42)PD m =+-.①当AP =AD 时,22(4)4m m -=+.解得32m =(如图3-2). ②当P A =PD 时,22242(42)m m +=+-. 解得43m =(如图3-3)或4m =(不合题意,舍去). ③当DA =DP 时,222(4)2(42)m m -=+-.解得23m=(如图3-4)或2m=(不合题意,舍去).综上所述,当△APD为等腰三角形时,m的值为32,43或23.图3-2 图3-3 图3-4其实①、②两种情况,可以用几何说理的方法,计算更简单:①如图3-2,当AP=AD时,AM垂直平分PD,那么△PCM∽△MBA.所以12PC MBCM BA==.因此12PC=,32m=.②如图3-3,当P A=PD时,P在AD的垂直平分线上.所以DA=2PO.因此42m m-=.解得43m=.小结:1、等腰三角形的存在性问题,又可以细分为两个定点一个动点,或一个定点一个定角,或只有一个定点,甚至三个点都是动点等几种类型;2、当条件中有定线段时,可以利用“两圆一线”来画图,再计算;在有定角时,可以借助特殊三角形三边比的特征或相似来建立方程;对于既无定线又无定角的问题,可以用代数法来解,即先表达三边,再分类列方程求解,要注意根据题目条件进行检验.对于不同类型的等腰三角形,我们可以灵活选用几何法或代数法,有时候将两种方法结合起来使用,可以使得解题又快又好;3、在进行有关等腰三角形的计算时,常用到勾股定理、三线合一、特殊角的三角函数、相似、一元二次方程等知识;在这个过程中,贯穿了分类讨论、数形结合、方程等数学思想方法.。
八年级数学一次函数之等腰三角形存在性(人教版)(专题)(含答案)

∵AE=2,
∴
∴
又∵ ,
BC=OE=1,
∴
②如图,当AB为底时,作线段AB的垂直平分线,交直线x=-1于
点 ,并记AB的中点为D.
易得直线 的表达式为:y=x
∴ .
综上,符合题意的点P的坐标为:
.
故选C.
试题难度:三颗星知识点:略
5.如图,直线 与x轴、y轴分别交于A,B两点,点P是坐标轴上一动点,若使△ABP为等腰三角形,则符合条件的点P共有( )
A.8个B.6个
C.4个D.2个
答案:B
解题思路:
特征:
A,B为定点,P为坐标轴上的动点,
定线段AB当腰当底来分类,
当腰时利用两圆来找点,当底时利用一线来找点.
操作:
①当AB为腰时,以点A为圆心,AB长为半径作圆,与x轴交于点P1,P2,与y轴交于点P3;再以点B为圆心,AB长为半径作圆,与x轴的交点与P2重合(因为△ABP2是等边三角形),与y轴交于点P4,P5;
A.
B.
C.
D.
答案:D
解题思路:
研究背景图形:
由直线y=-x+2知,B(0,2),A(2,0),∠OAB=45°,
∴∠OBA=45°,
特征:
O,B为定点,P为直线AB上的动点.
定线段OB当腰当底来分类,
当腰时利用两圆来找点,当底时利用一线来找点.
操作:
①如图,当OB为腰时,分别以点O,B为圆心,OB长为半径作圆,与直线AB分别交于点P1,P2,P3,
则有 ,
∴
∴
在等腰 中,
∴ ,
∴
②如图,当AB为底时,作线段AB的垂直平分线,与y轴交于点P4,
在等腰 中, ,
一次函数之等腰直角三角形的存在性 (习题及答案).
一次函数之等腰直角三角形的存在性(习题)
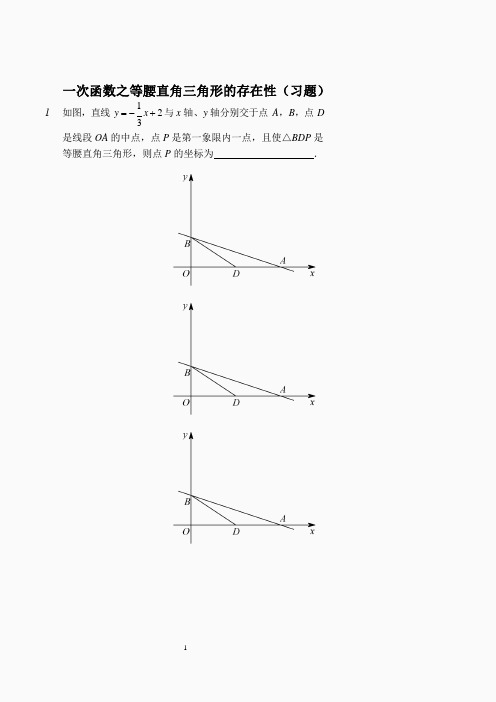
1.如图,直线y =-1
x + 2 与x 轴、y 轴分别交于点A,B,点D 3
是线段OA 的中点,点P 是第一象限内一点,且使△BDP 是等腰直角三角形,则点P 的坐标为.
2.如图,直线AB:y=-x+b 交y 轴于点A(0,4),交x 轴于点B,
直线l 垂直平分OB 交AB 于点D,交x 轴于点E,点P 是直线l 上一点,且在点D 的上方,PD=4.
(1)求点P 的坐标;
(2)以PB 为直角边作等腰直角△PBQ,直接写出所有符合条件的点Q 的坐标.
3.如图,直线y=-2x+4 与x 轴、y 轴分别交于点A,B,点P 是
直线x=5 上的一个动点,点Q 是射线AB 上的一个动点,若△APQ 为等腰直角三角形,则点Q 的坐标为.
4.如图,直线l1:y=-x+10 与y 轴交于点A,与直线l2:y 1 x 2
交于点B,点C 是线段AB 上的一动点,过点C 作y 轴的平行线交直线l2 于点D,点P 是y 轴上一动点,且满足△CDP 是等腰直角三角形,则点P 的坐标为.
【参考答案】
1. (2,5),(5,3),( 5
,
5
).
2 2
2. (1)点P 的坐标为(2,6);
(2)点Q 的坐标为(-4,4),(8,8),(-2,-2) 或(10,2).
3. ( 1
,3),(-4,12),(-1,6);
2
4. (0,6),(0,2),(0,30
).7。
初中数学课件一次函数中三角形的存在性问题

求出的值,并求此时点的坐标;若不能,请说明理由.
课堂小结
等腰三角形的存在性:两圆加一中垂线,记得去掉共线点.
知识讲解
直角三角形的存在性
关联知识点
1
尺规作图:作弧
2
直角三角形斜边上的中线等于斜边上的
一半
知识讲解
直角三角形的存在性:一圆加上两垂线,构造思想得坐标.
△ 为直角三角形 ,写出所有符合条件的点的坐标.
课堂小结
直角三角形的存在性:一圆加上两垂线,构造思想得坐标.
原题证明
一次函数 =
4
3
+ 4分别交轴、y轴于、两点,在轴上取一点C,使
△ 为等腰三角形 ,写出所有符合条件的点的坐标.
原题证明
如图,点坐标为(4,0),点在第一象限,且在直线 = − + 5上,
此时,2 = = 4 − (−3) = 7,点2 在第一象限,离轴的距离为7,离
轴的距离为4,∴ 2 (4, 7);
③当∠3 是直角时,∵∠ = 45∘
∴此情况不存在,应舍去
综上所述,当取0.5或4时,△ 是直角三角形.
应用练习
一次函数 =
4
3
+ 4分别交轴、y轴于、两点,在轴上取一点C,使
当 = 时,3 点的坐标为(2, 0),
当 = 时,4 点的坐标为(0, 0),
综上所述,点的坐标为(2 2 − 2, 0),(−2 2 − 2, 0),(2, 0),(0, 0).
应用练习
如图,在平面直角坐标系中,一次函数 = 1 + 的图象与轴交于点
(−3, 0),与 轴交于点 ,且与正比例函数 = 的图象交点为(3, 4).求:
一次函数压轴题专题突破4:一次函数与等腰直角三角形(含解析)

一次函数压轴题之等腰直角三角形1.【模型建立】如图1,等腰直角三角形ABC中,∠ACB=90°,CB=CA,直线ED经过点C,过A作AD⊥ED于点D,过B作BE⊥ED于点E.求证:△BEC≌△CDA;【模型应用】①已知直线l1:y=x+4与x轴交于点A,与y轴交于点B,将直线l1绕着点A逆时针旋转45°至直线l2,如图2,求直线l2的函数表达式;②如图3,在平面直角坐标系中,点B(8,6),作BA⊥y轴于点A,作BC⊥x轴于点C,P是线段BC上的一个动点,点Q是直线y=2x﹣6上的动点且在第一象限内.问点A、P、Q能否构成以点Q为直角顶点的等腰直角三角形,若能,请直接写出此时点Q的坐标,若不能,请说明理由.2.已知,一次函数y=﹣x+6的图象与x轴、y轴分别交于点A、点B,与直线y=x相交于点C.过点B作x轴的平行线l.点P是直线l上的一个动点.(1)求点A,点B的坐标.(2)若S△AOC=S△BCP,求点P的坐标.(3)若点E是直线y=x上的一个动点,当△APE是以AP为直角边的等腰直角三角形时,求点E的坐标.3.如图,在平面直角坐标系中,直线l1的解析式为y=x,直线l2的解析式为y=﹣x+3,与x轴、y轴分别交于点A、点B,直线l1与l2交于点C.(1)求点A、点B、点C的坐标,并求出△COB的面积;(2)若直线l2上存在点P(不与B重合),满足S△COP=S△COB,请求出点P的坐标;(3)在y轴右侧有一动直线平行于y轴,分别与l1,l2交于点M、N,且点M在点N的下方,y轴上是否存在点Q,使△MNQ为等腰直角三角形?若存在,请直接写出满足条件的点Q的坐标;若不存在,请说明理由.4.如图1,在平面直角坐标系中,直线l1:y=x+b与直线l2:y=﹣x﹣8交于点A,已知点A的横坐标为﹣5,直线l1与x轴交于点B,与y轴交于点C,直线l2与y轴交于点D.(1)求直线l1的解析式;(2)将直线l2向上平移6个单位得到直线l3,直线l3与y轴交于点E,过点E作y轴的垂线l4,若点M为垂线l4上的一个动点,点N为x轴上的一个动点,当CM+MN+NA的值最小时,求此时点M的坐标及CM+MN+NA 的最小值;(3)在(2)条件下,如图2,已知点P、Q分别是直线l1、l2上的两个动点,连接EP、EQ、PQ,是否存在点P、Q,使得△EPQ是以点P为直角顶点的等腰直角三角形,若存在,求点P的坐标,若不存在,说明理由.5.如图,在平面直角坐标系中,已知直线BD:y=x﹣2与直线CE:y=﹣x+4相交于点A.(1)求点A的坐标;(2)点P是△ABC内部一点,连接PA、PB、PC,求PB+PA+PC的最小值;(3)将点D向下平移一个单位得到点D1,连接BD1,将△OD1B绕点O旋转至△OB1D2的位置,使B1D2∥x轴,再将△OB1D2沿y轴向下平移得到△O1B2D3,在平移过程中,直线O1D3与x轴交于点K,在直线x=3上任取一点T,连接KT,O1T,△O1KT能否以O1K为直角边构成等腰直角三角形?若能,请直接写出所有符合条件的T点的坐标;若不能,请说明理由.6.如图1,直线y=﹣x+3交x轴于点B,交y轴于点C.点A在x轴负半轴上且∠CAO=30°.(1)求直线AC的解析式;(2)如图2,边长为3的正方形DEFG,G点与A点重合,现将正方形以每秒1个单位地速度向右平移,当点G与点O重合时停止运动.设正方形DEFG与△ACB重合部分的面积为S,正方形DEFG运动的时间为t,求s关于t的函数关系式;(3)如图3,已知点Q(1,0),点M为线段AC上一动点,点N为直线BC上一动点,当三角形QMN为等腰直角三角形时,求M点的坐标.7.已知直线l1:y=﹣x+b与x轴交于点A,直线l2:y=x﹣与x轴交于点B,直线l1、l2交于点C,且C点的横坐标为1.(1)如图1,过点A作x轴的垂线,若点P(x,2)为垂线上的一个点,Q是y轴上一动点,若S△CPQ=5,求此时点Q的坐标;(2)若P在过A作x轴的垂线上,点Q为y轴上的一个动点,当CP+PQ+QA的值最小时,求此时P的坐标;(3)如图2,点E的坐标为(﹣2,0),将直线l1绕点C旋转,使旋转后的直线l3刚好过点E,过点C作平行于x轴的直线l4,点M、N分别为直线l3、l4上的两个动点,是否存在点M、N,使得△BMN是以M点为直角顶点的等腰直角三角形?若存在,求出N点的坐标;若不存在,请说明理由.8.如图,在矩形ABCO中,点O为坐标原点,点B(4,3),点A、C在坐标轴上,点Q在BC边上,直线L1:y=kx+k+1交y轴于点A.对于坐标平面内的直线,先将该直线向右平移1个单位长度,再向下平移1个单位长度,这种直线运动称为直线的斜平移.现将直线L1经过2次斜平移,得到直线L2.(1)求直线L1与两坐标轴围成的面积;(2)求直线L2与AB的交点坐标;(3)在第一象限内,在直线L2上是否存在一点M,使得△AQM是等腰直角三角形?若存在,请直接写出点M 的坐标;若不存在,请说明理由.9.如图1,在平面直角坐标系中,直线l:y=与x轴交于点A,且经过点B(2,m),已知点C(3,0).(1)求直线BC的函数解析式;(2)在线段BC上找一点D,使得△ABO与△ABD的面积相等,求出点D的坐标;(3)y轴上有一动点P,直线BC上有一动点M,若△APM是以线段AM为斜边的等腰直角三角形,求出点M 的坐标;(4)如图2,E为线段AC上一点,连结BE,一动点F从点B出发,沿线段BE以每秒1个单位运动到点E 再沿线段EA以每秒个单位运动到A后停止,设点F在整个运动过程中所用时间为t,求t的最小值.10.已知直线l1:y=﹣x+b与x轴交于点A,直线l2:y=x﹣与x轴交于点B,直线l1,l2交于点C,且C点的横坐标为1.(1)求直线l1的解析式;(2)如图1,过点A作x轴的垂线,若点P为垂线上的一个动点,点Q(0,2),若S△CPQ=4,求此时点P 的坐标;(3)如图2,点E的坐标为(﹣2,0),将直线l1绕点C逆时针旋转,使旋转后的直线l3刚好过点E,过点C作平行于x轴的直线l4,点M、N分别为直线l3、l4上的两个动点,是否存在点M、N,使得△BMN是以M 点为直角顶点的等腰直角三角形,若存在,直接写出N点的坐标;若不存在,请说明理由.11.已知直线l1:y=﹣x+b与x轴交于点A,直线l2:y=x﹣与x轴交于点B,直线l1、l2交于点C,且C点的纵坐标为﹣4.(1)求△ABC的面积;(2)如图1,过点A作x轴的垂线,若点P为垂线上的一个动点,点Q(0,2),若S△CPQ=2,求此时点P 的坐标;(3)如图2,点E的坐标为(﹣2,0),将直线l1绕点C顺时针旋转,使旋转后的直线l3刚好过点E.过点C作平行于x轴的直线l4,点M、N分别为直线l3、l4上的两个动点,是否存在点M、N,使得△BMN是以M 点为直角顶点的等腰直角三角形,若存在,直接写出N点的坐标:若不存在,请说明理由.12.如图,直线y=kx+k分别交x轴、y轴于点A,C,直线BC过点C交x轴于点B,且OA=OC,∠CBA =45°,点P是直线BC上的一点.(1)求直线BC的解析式;(2)若动点P从点B出发沿射线BC方向匀速运动,速度为个单位长度/秒,连接AP,设△PAC的面积为S,点P的运动时间为t秒,求S与t之间的函数关系式,并写出t的取值范围;(3)若点Q是直线AC上且位于第三象限图象上的一个动点,点M是y轴上的一个动点,当以点B、M、Q 为顶点的三角形为等腰直角三角形时,求点Q和点M的坐标.13.如图,在平面直角坐标系中,直线AB:y=﹣x+与直线AC:y=+8交于点A,直线AB分别交x轴、y轴于B、E,直线AC分别交x轴、y轴于点C、D.(1)求点A的坐标;(2)在y轴左侧作直线FG∥y轴,分别交直线AB、直线AC于点F、G,当FG=3DE时,过点G作直线GH ⊥y轴于点H,在直线GH上找一点P,使|PF﹣PO|的值最大,求出P点的坐标及|PF﹣PO|的最大值;(3)将一个45°角的顶点Q放在x轴上,使其角的一边经过A点,另一边交直线AC于点R,当△AQR为等腰直角三角形时,请直接写出点R的坐标.14.模型建立:如图1,等腰直角三角形ABC中,∠ACB=90°,CB=CA,直线ED经过点C,过A作AD⊥ED 于D,过B作BE⊥ED于E.求证:△BEC≌△CDA.模型应用:(1)已知直线l1:y=x+4与y轴交与A点,将直线l1绕着A点顺时针旋转45°至l2,如图2,求l2的函数解析式.(2)如图3,矩形ABCO,O为坐标原点,B的坐标为(8,6),A、C分别在坐标轴上,P是线段BC上动点,设PC=m,已知点D在第一象限,且是直线y=2x﹣6上的一点,若△APD是不以A为直角顶点的等腰Rt△,请直接写出点D的坐标.15.如图,已知直线y=x+4与x轴、y轴分别相交于点A、B,点C从O点出发沿射线OA以每秒1个单位长度的速度匀速运动,同时点D从A点出发沿AB以每秒1个单位长度的速度向B点匀速运动,当点D到达B点时C、D都停止运动.点E是CD的中点,直线EF⊥CD交y轴于点F,点E′与E点关于y轴对称.点C、D的运动时间为t(秒).(1)当t=1时,AC=,点D的坐标为;(2)设四边形BDCO的面积为S,当0<t<3时,求S与t的函数关系式;(3)当直线EF与△AOB的一边垂直时,求t的值;(4)当△EFE′为等腰直角三角形时,直接写出t的值.16.如图1,在平面直角坐标系中,O为坐标原点,直线l:y=﹣x+m与x、y轴的正半轴分别相交于点A、B,过点C(﹣4,﹣4)画平行于y轴的直线交直线AB于点D,CD=10.(1)求点D的坐标和直线l的解析式;(2)求证:△ABC是等腰直角三角形;(3)如图2,将直线l沿y轴负方向平移,当平移适当的距离时,直线l与x、y轴分别相交于点A′、B′,在直线CD上存在点P,使得△A′B′P是等腰直角三角形.请直接写出所有符合条件的点P的坐标.(不必书写解题过程)17.如图,在平面直角坐标系中,直线y=﹣x+b(b>0)分别交x轴,y轴于A,B两点,以OA,OB为边作矩形OACB,D为BC的中点.以M(4,0),N(8,0)为斜边端点作等腰直角三角形PMN,点P在第一象限,设矩形OACB与△PMN重叠部分的面积为S.(1)求点P的坐标.(2)当b值由小到大变化时,求S与b的函数关系式.(3)若在直线y=﹣x+b(b>0)上存在点Q,使∠OQM等于90°,请直接写出b的取值范围.(4)在b值的变化过程中,若△PCD为等腰三角形,请直接写出所有符合条件的b值.18.如图,直线l与x轴、y轴的正半轴分别交于A、B两点,OA、OB的长分别是关于x的方程x2﹣14x+4(AB+2)=0的两个根(OB>OA),P是直线l上A、B两点之间的一动点(不与A、B重合),PQ∥OB交OA 于点Q.(1)求tan∠BAO的值;(2)若S△PAQ=S四边形OQPB时,请确定点P在AB上的位置,并求出线段PQ的长;(3)当点P在线段AB上运动时,在y轴上是否存在点M,使△MPQ为等腰直角三角形?若存在,请直接写出点M的坐标;若不存在,请说明理由.1.【解答】解:(1)证明:∵△ABC为等腰直角三角形∴CB=CA,∠ACD+∠BCE=180°﹣90°=90°又∵AD⊥CD,BE⊥EC∴∠D=∠E=90°又∵∠EBC+∠BCE=90°∴∠ACD=∠EBC在△ACD与△CBE中,∠D=∠E,∠ACD=∠EBC,CA=BC,∴△ACD≌△CBE(AAS);(2)过点B作BC⊥AB交l2于C,过C作CD⊥y轴于D,∵∠BAC=45°∴△ABC为等腰Rt△由(1)可知:△CBD≌△BAO∴BD=AO,CD=OB∵l1:,令y=0,则x=﹣3∴A(﹣3,0),令x=0,则y=4∴B(0,4)∴BD=AO=3,CD=OB=4∴OD=4+3=7.∴C(﹣4,7),设直线l2的解析式为y=kx+b,将点A(﹣3,0),C(﹣4,7)代入y=kx+b中,得解得,k=﹣7,b=﹣21,则l2的解析式:y=﹣7x﹣21;(3)如下图,设点Q(m,2m﹣6),当∠AQP=90°时,由(1)知,△AMQ≌△QNP(AAS),∴AM=QN,即|8﹣m|=6﹣(2m﹣6),解得:m=4或,故:Q(4,2),.2.【解答】解:(1)一次函数y=﹣x+6的图象与x轴、y轴分别交于点A、点B,则点A、B的坐标分别为:(8,0)、(0,6);(2)联立y=﹣x+6、y=x并解得:x=3,故点C(3,),S△AOC=8×=15=S△BCP=BP×(yP﹣yC)=BP×(6﹣),解得:BP=,故点P(,6)或(﹣,6)(3)设点E(m,m)、点P(n,6);①当∠EPA=90°时,如左图,∵∠MEP+∠MPE=90°,∠MPE+∠NPA=90°,∴∠MEP=∠NPA,AP=PE,∵△EMP≌△PNA(AAS),则ME=PN=6,MP=AN,即|m﹣n|=6,m﹣6=8﹣n,解得:m=或16,故点E(,)或(16,20);②当∠EAP=90°时,如右图,同理可得:△AMP≌△ANE(AAS),故MP=EN,AM=AN=6,即m=n﹣8,|8﹣m|=6,解得:m=2或14,故点E(2,)或(14,);综上,E(,)或(14,)或;(2,)或(16,20).3.【解答】解:(1)直线l2的解析式为y=﹣x+3,与x轴、y轴分别交于点A、点B,则点A、B的坐标分别为(6,0)、(0,3),联立式y=x,y=﹣x+3并解得:x=2,故点C(2,2);△COB的面积=×OB×x C=×3×2=3;(2)设点P(m,﹣m+3),S△COP=S△COB,则BC=PC,则(m﹣2)2+(﹣m+3﹣2)2=22+12=5,解得:m=4或0(舍去0),故点P(4,1);(3)设点M、N、Q的坐标分别为(m,m)、(m,3﹣m)、(0,n),①当∠MQN=90°时,∵∠GNQ+∠GQN=90°,∠GQN+∠HQM=90°,∴∠MQH=∠GNQ,∠NGQ=∠QHM=90°,QM=QN,∴△NGQ≌△QHM(AAS),∴GN=QH,GQ=HM,即:m=3﹣m﹣n,n﹣m=m,解得:m=,n=;②当∠QNM=90°时,则MN=QN,即:3﹣m﹣m=m,解得:m=,n=y N=3﹣=;③当∠NMQ=90°时,同理可得:n=;综上,点Q的坐标为(0,)或(0,)或(0,).4.【解答】解:(1)∵点A的横坐标为﹣5,∴A(﹣5,﹣3),将点A代入y=x+b,∴b=4,∴直线l1的解析式y=x+4;(2)l2:y=﹣x﹣8与y轴的交点D(0,﹣8),∵将直线l2向上平移6个单位得到直线l3,直线l3与y轴交于点E,∴E(0,﹣2),∵过点E作y轴的垂线l4,点D是点C关于直线l4的对称点,作点A关于x轴的对称点A′(﹣5,3),连接AD′交x轴、l4于点N、M,则此时CM+MN+NA最小,最小值为:A′D,CM+MN+NA=MD+MN+A′N=A′D,A′D==;∴CM+MN+NA的值最小为;(3)存在,理由:设点P、Q的坐标分别为:(m,m+4)、(n,﹣n﹣8),当点E在点P右边时,过点Q作x轴的平行线交y轴于点M,过点P作PN⊥QM于点N,PN交l4于点K,则△PNQ≌△EKP(AAS),∴PN=KE,QN=PK,即:m+4+n+8=﹣m,m﹣n=m+4+2,解得:m=﹣3,∴点P(﹣3,﹣)当点E在点P的左侧时,同理可得:(﹣,﹣5),故答案为:(﹣3,﹣)或(﹣,﹣5),5.【解答】解:(1)直线,则点B、D的坐标分别为:(,0)、(0,﹣2);直线,则点C、E的坐标分别为:(4,0)、(0,4);联立BD、CE的表达式并解得:x=2,故点A(2,2);(2)如图,将△APB绕点C逆时针旋转60°得到△EFC,则△BFP是等边三角形,∠ECB=90°,BC=3,AC==CE,在Rt△EBC中,BE==,∵PA+PB+PC=EF+FP+PB≥BE,∴PA+PB+PC≥,∴PA+PB+PC的最小值为;(3)存在,理由:点D1(0,﹣3),点B(,0),则∠BD1O=30°,B1D2∥x轴,则直线OD2的倾斜角为30°,设直线O1K的表达式为:y=x+m,则点O1(0,m),点K(﹣m,0),则MO1=﹣m,MK=﹣m,KN=﹣m,TN=|﹣m﹣3|,则点T(3,﹣m)△O1KT能否以O1K为直角边构成等腰直角三角形,则O1K=TK,TK⊥O1K,过点K作y轴的平行线分别交过点O1、T与x轴的平行线于点M、N,∵∠NKT+∠NTK=90°,∠NKT+∠O1KM=90°,∴∠O1KM=∠NTK,∠KNT=∠O1MK=90°,O1K=TK,∴△KNT≌△O1MK(AAS),∴TN=KM,即:|﹣m﹣3|=﹣m,解得:m=,故点T(3,)或(3,).6.【解答】解:(1)直线y=﹣x+3交x轴于点B,交y轴于点C,则点B、C的坐标为(3,0)、(0,3),∵∠CAO=30°,则AC=2OC=6,则OA=3,将点A、C的坐标代入一次函数表达式:y=kx+b并解得:直线AC的表达式为:y=x+3;(2)如图2所示:①当0≤t≤3时,(左侧图),正方形的DA边交AC于点H,点A运动到点M处,则点M(﹣3+t,0),则点H(﹣3+t,t),S=S△AHM=×AM×HM=×t×t=t2,②当3<t≤3时,(右侧图),正方形的DA边交AC于点H,点A运动到点G处,E、F交直线AC于点R、S,AG=t,则AS=t﹣3,则RS=(t﹣3),同理HG=t,同理可得:S=S梯形RSHG=×3×(t+t﹣)=t﹣;故:S=;(3)∵点M为线段AC上一动点,经画图,∠MQN分别为90°时,点M不在线段AC上,①NMQ=90°时,三角形QMN为等腰直角三角形,过点M作y轴的平行线交x轴于点G,过点N作x轴的平行线交MG于点R、交y轴于点H,设点M、N的坐标分别为(m,m+3)、(n,3﹣n),∵∠NMR+∠RNM=90°,∠MNR+∠GMQ=90°,∴∠GMQ=∠RNM,∠NRM=∠MGO=90°,MR=MQ,∴△NRM≌△MGO(AAS),则MG=RN,GQ=RM,即:n﹣m=m+3,3﹣n﹣(m+3)=1﹣m,解得:m=﹣2,故点M的坐标为(﹣2,1);②当∠MNQ=90°时,同理可得:点M(﹣,2);综上,点M的坐标为:(﹣2,1)或(﹣,2).7.【解答】解:(1)直线l2:y=x﹣,令x=1,则y=﹣4,故C(1,﹣4),把C(1,﹣4)代入直线l1:y=﹣x+b,得:b=﹣3,则l1为:y=﹣x﹣3,所以A(﹣3,0),所以点P坐标为(﹣3,2),如图,设直线AC交y轴于点M,设y PC:y=mx+t得:,解得,∴y PC=﹣1.5x﹣2.5,即M(0,﹣2.5).S△CPQ=QM×(x C﹣x P)=(y Q+2.5)×4=5,解得:y Q=0或﹣5,∴Q的坐标为(0,0)或(0,﹣5);(2)确定C关于过A垂线的对称点C′(﹣7,﹣4)、A关于y轴的对称点A′(3,0),连接A′C′交过A点的垂线与点P,交y轴于点Q,此时,CP+PQ+QA的值最小,将点A′、C′点的坐标代入一次函数表达式:y=k′x+b′得:则直线A′C′的表达式为:y=x﹣,即点P的坐标为(﹣3,﹣),(3)将E、C点坐标代入一次函数表达式,同理可得其表达式为:y=﹣x﹣①当点M在直线l4上方时,设点N(n,﹣4),点M(s,﹣s﹣),点B(4,0),过点N、B分别作y轴的平行线交过点M与x轴的平行线分别交于点R、S,∵∠RMN+∠RNM=90°,∠RMN+∠SMR=90°,∴∠SMR=∠RNM,∠MRN=∠MSB=90°,MN=MB,∴△MSB≌△NRM(AAS),∴RN=MS,RM=SB,即,解得:,故点N的坐标为(﹣16,﹣4),②当点M在l4下方时,同理可得:N(﹣,﹣4),即:点N的坐标为(﹣,﹣4)或(﹣16,﹣4).8.【解答】解:(1)将点A(0,3)代入直线L1:y=kx+k+1并解得:k=2,故L1的表达式为:y=2x+3,设:L1与x轴交点坐标为D,则其坐标为(﹣,0),直线l1与两坐标轴围成的面积=OD×AO=×3=;(2)将直线L1经过2次斜平移,得到直线L2:y=2(x﹣2)+3﹣2=2x﹣3,当y=3时,x=3,即直线L2与AB的交点坐标为(3,3);(3)①当∠QAM为直角时,点M在第四象限,舍去;②当∠AQM为直角时,对于L2,当x=4时,y=5,故点M(4,5)(舍去);③当∠AMQ为直角时,AM=MQ,过点M作x轴的平行线分别交AO、BC于点G、H,设点M(m,2m﹣3),点Q(4,n),∵∠AMG+∠GAM=90°,∠AMG+∠QMH=90°,∴∠QMH=∠GAM,∠AGM=∠MHQ=90°,AM=MQ,∴△AGM≌△MHQ(AAS),∴AG=MH,即:|3﹣2m+3|=4﹣m,解得:m=2或,故点M(,)或(2,1),故点M(,)或(2,1).9.【解答】解:(1)将点B坐标代入直线l的表达式得:m==3,点B(2,3),令y=0,则x=﹣2,即点A(﹣2,0),将点B、C的坐标代入一次函数表达式:y=kx+b得:,解得:,故:直线BC的表达式为:y=﹣3x+9;(2)过点O作OD∥AB交BC于点D,则D点为所求,直线AB表达式得k值为,则直线OD的表达式为y=x,将直线BC与OD表达式联立并解得:x=,即:点D的坐标为(,);(3)过点P作x轴的平行线分别于过点A、M与y轴的平行线于点G、H,设点P的坐标为(0,n)、点M(m,9﹣3m),∵∠GPA+∠GAP=90°,∠GPA+∠HPM=90°,∴∠HPM=∠GAP,又PA=PM,∠G=∠H=90°,∴△AGP≌△PHM(AAS),GP=HM=2,GA=PH,即:,解得:m=或,即点M的坐标为(,)或(,﹣);(4)t=+=BE+AE,过点A作倾斜角为45度的直线l2,过点E作EF⊥l2交于点F,则:EF=AE,即t=BE+EF,当B、E、F三点共线且垂直于直线l2时,t最小,即:t=BF′,同理,直线l2的表达式为:y=﹣x﹣2,直线BF表达式为:y=x+1,将上述两个表达式联立并解得:x=﹣,即:点F′(﹣,﹣),t=BF′==.10.【解答】解:(1)直线l2:y=,令x=1,则y=﹣4,故点C(1,﹣4),把点C(1,﹣4)代入直线l1:y=﹣x+b,得:b=﹣3,则直线l1的表达式为:y=﹣x﹣3,(2)对于直线y=﹣x﹣3,当y=0时,有﹣x﹣3=0,解得x=﹣3,即A(﹣3,0),如图,设直线AC交y轴于点M,设点P坐标为(﹣3,m),将点P、C的坐标代入一次函数表达式y=sx+t得:,解得,即M.S△CPQ=QM×(x C﹣x P)=•|2﹣+3|•(1+3)=4,解得:m=12或28,即点P的坐标为(﹣3,12)或(﹣3,28);(3)将E、C点坐标代入一次函数表达式,同理可得其表达式为①当点M在直线l4上方时,设点N(n,﹣4),点M(s,﹣s﹣),点B(4,0),过点N、B分别作y轴的平行线交过点M与x轴的平行线分别交于点R、S,∵∠RMN+∠RNM=90°,∠RMN+∠SMR=90°,∴∠SMR=∠RNM,∠MRN=∠MSB=90°,MN=MB,∴△MSB≌△NRM(AAS),∴RN=MS,RM=SB,即,解得.故点N的坐标为(﹣16,﹣4),②当点M在l4下方时,如图1,过点M作PQ∥x轴,与过点B作y轴的平行线交于Q,与过点N作y轴的平行线交于P,同①的方法得N(﹣,﹣4),③如图2中,当点N在y轴的右侧,△BMN是等腰直角三角形时,同法可得N(,﹣4)即:点N的坐标为(﹣,﹣4)或(﹣16,﹣4)或(,﹣4).11.【解答】解:(1)直线l2:y=x﹣,令y=4,则x=1,则点C(1,﹣4),令y=0,则x=4,即点B(4,0),把点C坐标代入直线l1:y=﹣x+b得:b=﹣3,则直线l1的表达式为:y=﹣x﹣3,令y=0,则x=﹣3,即点A(﹣3,0),S△ABC=AB×|y C|=7×4=14;(2)如下图,设直线AC交y轴于点M,设点P坐标为(﹣3,m),将点P、C的坐标代入一次函数表达式y=sx+t得:,解得:,即:点M坐标为(0,),S△CPQ=QM×(x C﹣x P)=(2﹣+3)×(1+3)=2,解得:m=16,即点P的坐标为(﹣3,16)当PC与y轴交于x轴上方时,同理可得:点P(﹣3,24),故点P(﹣3,16)或(﹣3,24);(3)将E、C点坐标代入一次函数表达式,同理可得其表达式为:y=﹣x﹣,设点N(n,﹣4),点M(s,﹣s﹣),点B(4,0),过点N、B分别作y轴的平行线交过点M与x轴的平行线分别交于点R、S,∵∠RMN+∠RNM=90°,∠RMN+∠SMR=90°,∴∠SMR=∠RNM,∠MRN=∠MSB=90°,MN=MB,∴△MSB≌△NRM(AAS),∴RN=MS,RM=SB,即:,解得:,故点N的坐标为(﹣16,﹣4).12.【解答】解:(1)直线y=kx+k分别交x轴、y轴于点A,C,则点A(﹣1,0),且OA=OC,则点C(0,3),则k=3,故直线AC的表达式为:y=3x+3,∵∠CBA=45°,∴OB=OC=3,∴点B(3,0),∵点C(0,3)、点B(3,0),则直线BC的表达式为:y=﹣x+3;(2)当点P在线段BC时,过点P作PH⊥x轴于点H,∵∠CBA=45°,PH=PBsin45°=t×=t,S=S△ABC﹣S△ABP=×BA×(OC﹣PH)=4×(3﹣t)=6﹣2t,(0≤t≤3);当点P在y轴右侧的射线BC上时,同理可得:S=S△ABP﹣S△ABC=2t﹣6,(t>3);故S=;(3)设点M(0,m),点Q(n,3n+3),①如图2(左侧图),当∠BMQ=90°时,(点M在x轴上方),分别过点Q、P作y轴的平行线QG、BH,过点M作x轴的平行线分别交GQ、BH于点G、H,∵∠GMQ+∠MQG=90°,∠GMQ+∠HMB=90°,∴∠HMB=∠GQM,∠MHB=∠QGM=90°,MB=MQ,∴△MHB≌△QGM(AAS),∴GQ=MH,BH=GM,即:m=﹣n,m﹣3n﹣3=3,解得:m=,n=﹣;故点M(0,)、点Q(﹣,﹣);同理当点M在x轴下方时,3n+3﹣m=3且﹣m=﹣n,解得:m=n=0(舍去);②当∠MQB=90°时,同理可得:﹣n=﹣3n﹣3,3n+3﹣m=3﹣n,解得:m=﹣6,n=﹣,故点M(0,﹣6)、点Q(﹣,﹣);③当∠QBM=90°时,同理可得:﹣3n﹣3=3,m=3﹣n解得:m=5,n=﹣2,点M(0,5)、点Q(﹣2,﹣3);综上,M(0,)、Q(﹣,﹣)或M(0,﹣6)、Q(﹣,﹣)或M(0,5)点Q(﹣2,﹣3).13.【解答】解:(1)联立,解得:,故点A的坐标为(﹣2,7);(2)由题意得:点E、D、B、C的坐标分别为(0,)、(0,8)、(,0)、(﹣16,0),过点A作MN∥x轴,分别交FG、DE于点M、N,则:AN=2,∵FG∥DE,∴△AFG∽△AED,∴=3,则AM=6,∴点M的横坐标为:﹣8,则点F、G的坐标分别为(﹣8,)、(﹣8,4),在y轴上找到点O关于直线GH的对称点O′(0,8),连接FO′并延长,交直线GH于点P,此时,|PF﹣PO|的值最大,最大值为PO′,直线O′F的表达式为:y=﹣x+8,当y=4时,x=,即点P坐标为(,4),|PF﹣PO|=FO′==,故:点P坐标为(,4),|PF﹣PO|=;(3)△AQR为等腰直角三角形,有如下图所示的两种情况,①当AQ⊥AC,当点R在点A下方时,∴直线AQ的表达式为:y=﹣2x+b,将点A坐标代入得:7=﹣2×(﹣2)+b,解得:b=3,故:直线AQ的表达式为:y=﹣2x+3,则点Q坐标为(,0),过点A作x轴的平行线,过点R作y轴的平行线,过点Q作y轴的平行线,围成矩形GMQH,∠GAR+∠QAH=90°,∠QAH+∠AQH=90°,∴∠AQH=∠GAR,∠AGR=∠QHA=90°,AR=AQ,∴△AGR≌△QHA(AAS),∴HQ=GA=7,GR=AH=2+=,OM=2+GA=9,∴RM=7﹣=故点R的坐标为(﹣9,),当点R在点A上方时,同理可得点R坐标为(5,);②当R′Q′⊥AC时,同理,点R′的坐标为(12,14)或(﹣,),故:点R的坐标为(﹣9,)或(5,)或(12,14)或(﹣,).14.【解答】(1)证明:∵△ABC为等腰直角三角形,∴CB=CA,又∵AD⊥CD,BE⊥EC,∴∠D=∠E=90°,∠ACD+∠BCE=180°﹣90°=90°,又∵∠EBC+∠BCE=90°,∴∠ACD=∠EBC,在△ACD与△CBE中,,∴△ACD≌△EBC(AAS);(2)解:过点B作BC⊥AB于点B,交l2于点C,过C作CD⊥x轴于D,如图1,∵∠BAC=45°,∴△ABC为等腰Rt△,由(1)可知:△CBD≌△BAO,∴BD=AO,CD=OB,∵直线l1:y=x+4,∴A(0,4),B(﹣3,0),∴BD=AO=4.CD=OB=3,∴OD=4+3=7,∴C(﹣7,3),设l2的解析式为y=kx+b(k≠0),∴,∴,∴l2的解析式:y=x+4;(3)当点D位于直线y=2x﹣6上时,分两种情况:①点D为直角顶点,分两种情况:当点D在矩形AOCB的内部时,过D作x轴的平行线EF,交直线OA于E,交直线BC于F,设D(x,2x﹣6);则OE=2x﹣6,AE=6﹣(2x﹣6)=12﹣2x,DF=EF﹣DE=8﹣x;则△ADE≌△DPF,得DF=AE,即:12﹣2x=8﹣x,x=4;∴D(4,2);当点D在矩形AOCB的外部时,设D(x,2x﹣6);则OE=2x﹣6,AE=OE﹣OA=2x﹣6﹣6=2x﹣12,DF=EF﹣DE=8﹣x;同1可知:△ADE≌△DPF,∴AE=DF,即:2x﹣12=8﹣x,x=;∴D(,);②点P为直角顶点,显然此时点D位于矩形AOCB的外部;设点D(x,2x﹣6),则CF=2x﹣6,BF=2x﹣6﹣6=2x﹣12;同(1)可得,△APB≌△PDF,∴AB=PF=8,PB=DF=x﹣8;∴BF=PF﹣PB=8﹣(x﹣8)=16﹣x;联立两个表示BF的式子可得:2x﹣12=16﹣x,即x=;∴D(,);综合上面六种情况可得:存在符合条件的等腰直角三角形;且D点的坐标为:(4,2),(,),(,).15.【解答】解:(1)如图1,过D作DH⊥AC于H,∵直线y=x+4与x轴、y轴分别相交于点A,A、B,∴A(﹣3,0),B(0,4),∴AO=3,BO=4,∴AB===5,当0≤t≤3时,如图1,∵CO=t,AD=t,∴AC=3﹣t,DH=AD•sin∠BAO=t,AH=ADcos∠BAO=t,当t=1时,AC=3﹣1=2,点D的坐标为(,);(2)∵AO=3,BO=4,AB=5∴sin∠BAO==,cos∠BAO==过D作DH⊥AC于H,当0≤t≤3时,如图1,∵CO=t,AD=t,∴AC=3﹣t,DH=AD•sin∠BAO=t,∴S=S△ABO﹣S△ADC=×3×4﹣•(3﹣t)•t,S=t2﹣t+6(0<t<3).(3)如图2,当EF⊥BO时,∵EF⊥CD,∴CD∥BO,∴∠ACD=90°,在Rt△ADC中,=cos∠BAO,∴=,t=,当EF⊥AB时,如图3,∵EF⊥CD,∴直线CD和直线AB重合,∴C点和A点重合,∴t=3.(4)①如图4,当0<t<,且且重叠部分为等腰梯形PEQM时,则∠PEQ=∠MQE,∵菱形CDMN,∴CD∥MN,∴∠MQE=∠CEQ,∵EF⊥CD,即∠CEF=90°,∴∠CEQ=45°,∴∠ACD=∠CEQ=45°,过D作DH⊥AC于H,则△DHC是等腰直角三角形,∴DH=HC,∴t=3﹣t﹣t,∴t=;②如图5,当<t<5,且重叠部分为等腰梯形EHNK时,同理可得∠CHE=45°,连接DHDH,∵EF垂直平分CD,∴CH=DH,∠DHE=∠CHE=45°,∴∠DHC=90°,∴DH=t,而CH=CO﹣HO=CO﹣(AO﹣AH)=t﹣(3﹣t),∴t﹣(3﹣t)=t,∴t=.16.【解答】解:(1)∵CD=10,点C的坐标为(﹣4,﹣4),∴点D的坐标为(﹣4,6),把点D(﹣4,6)代入得,m=4.∴直线l的解析式是;(2)∵,∴A(8,0),B(0,4),过点C画CH⊥y轴于H,则CH=OH=4,BH=8.在△AOB和△BHC中,∵AO=BH,∠AOB=∠BHC,BO=CH,∴△AOB≌△BHC,∴AB=BC,∠HBC=∠OAB,∴∠ABC=90°,∴△ABC是等腰直角三角形;(3)p(﹣4,﹣)或(﹣4,8)或(﹣4,﹣12)或(﹣4,﹣4)或(﹣4,4).17.【解答】解:(1)作PK⊥MN于K,则PK=KM=NM=2,∴KO=6,∴P(6,2);(2)①当点A落在线段OM上(可与点M重合)时,如图(一),此时0<b≤2,S=0;②当点A落在线段AK上(可与点K重合)时,如图(二),此时2<b≤3,设AC交PM于H,MA=AH=2b﹣4,∴S=(2b﹣4)2=2b2﹣8b+8,③当点A落在线段KN上(可与点N重合)时,如图(三),此时3<b≤4,设AC交PN于H,AN=AH=8﹣2b,∴S=S△PMN﹣S△ANH=4﹣2(4﹣b)2=﹣2b2+16b﹣28,④当点A落在线段MN的延长线上时,b>4,如图(四),S=4;(3)以OM为直径作圆,当直线y=﹣x+b(b>0)与圆相切时,b=+1,如图(五);当b≥4时,重合部分是△PMN,S=4设Q(x,b﹣x),因为∠OQM=90°,O(0,0),M(4,0)所以OQ2+QM2=OM2,即[x2+(b﹣x)2]+[(x﹣4)2+(b﹣x)2]=42,整理得x2﹣(2b+8)x+2b2=0,x2﹣(b+4)x+b2=0,根据题意这个方程必须有解,也就是判别式△≥0,即(b+4)2﹣5b2≥0,﹣b2+2b+4≥0,b2﹣2b﹣4≤0,可以解得 1﹣≤b≤1+,由于b>0,所以0<b≤1+.故0<b≤+1;(4)b的值为4,5,.∵点C、D的坐标分别为(2b,b),(b,b)当PC=PD时,b=4;当PC=CD时,b1=2(P、C、D三点共线,舍去),b2=5;当PD=CD时,b=8±2.18.【解答】解:(1)∵OA、OB的长分别是关于x的方程x2﹣14x+4(AB+2)=0的两个根,∴OA+OB=﹣=14,由已知可得,又∵OA2+OB2=AB2,∴(OA+OB)2﹣2OA•OB=AB2,即142﹣8(AB+2)=AB2,∴AB2+8AB﹣180=0,∴AB=10或AB=﹣18(不合题意,舍去),∴AB=10,∴x2﹣14x+48=0,解得x1=6,x2=8,∵OB>OA,∴OA=6,OB=8,∴tan∠BAO=.(2)∵S△PAQ=S四边形OQPB,∴S△PAQ=S△AOB,∵PQ∥BO,∴△PQA∽△BOA,∴,∴.∵AB=10,∴AP=5,又∵tan∠BAO=,∴sin∠BAO=,∴PQ=PA•sin∠BAO=.(3)存在,设AB的解析式是y=kx+b,则,解得:,则解析式是:y=﹣x+8,即4x+3y=24(*)①当∠PQM=90°时,由PQ∥OB且|PQ|=|MQ|此时M点与原点O重合,设Q(a,0)则P(a,a)有(a,a)代入(*)得a=.②当∠MPQ=90°,由PQ∥OB且|MP|=|PQ|设Q(a,0)则M(0,a),P(a,a)进而得a=247.③当∠PMQ=90°,由PQ∥OB,|PM|=|MQ|且|OM|=|OQ|=|PQ|设Q(a,0)则M(0,a)点P坐标为(a,2a)代入(*)得a=125.综上所述,y轴上有三个点M1(0,0),M2(0,247)和M3(0,125)满足使△PMQ为等腰直角三角形.。
初中数学等腰三角形的存在性问题(word版+详解答案)

等腰三角形的存在性问题【考题研究】近几年各地的中考数学试题中,探索等腰三角形的存在性问题频频出现,这类试题的知识覆盖面较广,综合性较强,题意构思精巧,要求学生要有较高的分析问题的能力和解决问题的能力,这类问题符合课标对学生能力提高的要求。
【解题攻略】在讨论等腰三角形的存在性问题时,一般都要先分类.如果△ABC是等腰三角形,那么存在①AB=AC,②BA=BC,③CA=CB三种情况.解等腰三角形的存在性问题,有几何法和代数法,把几何法和代数法相结合,可以使得解题又好又快.几何法一般分三步:分类、画图、计算.哪些题目适合用几何法呢?如果△ABC的∠A(的余弦值)是确定的,夹∠A的两边AB和AC可以用含x的式子表示出来,那么就用几何法.①如图1,如果AB=AC,直接列方程;②如图2,如果BA=BC,那么;③如图3,如果CA=CB,那么.代数法一般也分三步:罗列三边长,分类列方程,解方程并检验.如果三角形的三个角都是不确定的,而三个顶点的坐标可以用含x的式子表示出来,那么根据两点间的距离公式,三边长(的平方)就可以罗列出来.【解题类型及其思路】解题类型:动态类型:1.一动点类型问题;2.双动点或多动点类型问题背景类型:1.几何图形背景;2.平面直角坐标系和几何图形背景解题思路:几何法一般分三步:分类、画图、计算;代数法一般也分三步:罗列三边长,分类列方程,解方程并检验.如果△ABC是等腰三角形,那么存在①AB=AC,②BA=BC,③CA=CB三种情况.已知腰长画等腰三角形用圆规画圆,已知底边画等腰三角形用刻度尺画垂直平分线.解等腰三角形的存在性问题,有几何法和代数法,把几何法和代数法相结合,可以使得解题又好又快.【典例指引】类型一【二次函数综合题中根据条件判定三角形的形状】典例指引1.抛物线2y x bx c =++与x 轴交于点A ,点B (1,0),与y 轴交于点C (0,﹣3),点M 是其顶点. (1)求抛物线解析式;(2)第一象限抛物线上有一点D,满足∠DAB=45°,求点D 的坐标;(3)直线x t = (﹣3<t <﹣1)与x 轴相交于点H .与线段AC ,AM 和抛物线分别相交于点E ,F ,P .证明线段HE ,EF ,FP 总能组成等腰三角形.【举一反三】(2020·江西初三期中)如图①,已知抛物线y=ax 2+bx+3(a≠0)与x 轴交于点A (1,0)和点B (-3,0),与y 轴交于点C .(1)求抛物线的解析式;(2)设抛物线的对称轴与x 轴交于点M ,问在对称轴上是否存在点P ,使△CMP 为等腰三角形?若存在,请直接写出所有符合条件的点P 的坐标;若不存在,请说明理由;(3)如图②,若点E 为第二象限抛物线上一动点,连接BE 、CE ,求四边形BOCE 面积的最大值,并求此时E 点的坐标.类型二【利用二次函数的性质与等腰三角形的性质确定点的坐标】典例指引2.(2019·山东初三期末)如图1,已知抛物线2()30y ax bx a =++≠与x 轴交于点(1,0)A 和点(3,0)B -,与y 轴交于点C .(l )求抛物线的表达式;(2)如图l ,若点E 为第二象限抛物线上一动点,连接,BE CE ,求四边形BOCE 面积的最大值,并求此时E 点的坐标;(3)如图2,在x 轴上是否存在一点D 使得ACD ∆为等腰三角形?若存在,请求出所有符合条件的点D 的坐标;若不存在,请说明理由.【举一反三】(2019·广东省中山市中山纪念中学三鑫双语学校初三期中)如图,已知抛物线y =ax 2+bx +c 的图象与x 轴交于A (2,0),B (﹣8,0)两点,与y 轴交于点C (0,﹣8).(1)求抛物线的解析式;(2)点F是直线BC下方抛物线上的一点,当△BCF的面积最大时,求出点F的坐标;(3)在(2)的条件下,是否存在这样的点Q(0,m),使得△BFQ为等腰三角形?如果有,请直接写出点Q的坐标;如果没有,请说明理由.类型三【确定满足等腰三角形的动点的运动时间】典例指引3.(2018济南中考)如图1,抛物线平移后过点A(8,,0)和原点,顶点为B,对称轴与轴相交于点C,与原抛物线相交于点D.(1)求平移后抛物线的解析式并直接写出阴影部分的面积;(2)如图2,直线AB与轴相交于点P,点M为线段OA上一动点,为直角,边MN与AP相交于点N,设,试探求:①为何值时为等腰三角形;②为何值时线段PN的长度最小,最小长度是多少.【举一反三】如图所示,抛物线y=ax2+bx+c(a≠0)经过A(﹣1,0)、B(3,0)、C(0,3)三点.点D从C出发,沿线段CO以1个单位/秒的速度向终点O运动,过点D作OC的垂线交BC于点E,作EF∥OC,交抛物线于点F.(1)求此抛物线的解析式;(2)小明在探究点D运动时发现,①当点D与点C重合时,EF长度可看作O;②当点D与点O重合时,EF长度也可以看作O,于是他猜想:设点D运动到OC中点位置时,当线段EF最长,你认为他猜想是否正确,为什么?(3)连接CF、DF,请直接写出△CDF为等腰三角形时所有t的值.【新题训练】1.(2020·江西初三)如图,在平面直角坐标系中,已知点A(﹣2,﹣4),直线x=﹣2与x轴相交于点B,连接OA,抛物线y=﹣x2从点O沿OA方向平移,与直线x=﹣2交于点P,顶点M到点A时停止移动.(1)线段OA 所在直线的函数解析式是 ;(2)设平移后抛物线的顶点M 的横坐标为m ,问:当m 为何值时,线段PA 最长?并求出此时PA 的长. (3)若平移后抛物线交y 轴于点Q ,是否存在点Q 使得△OMQ 为等腰三角形?若存在,请求出点Q 的坐标;若不存在,请说明理由.2.(2018·山东中考真题)如图,在平面直角坐标系中,二次函数2y ax bx c =++交x 轴于点()4,0A -、()2,0B ,交y 轴于点()0,6C ,在y 轴上有一点()0,2E -,连接AE .(1)求二次函数的表达式;(2)若点D 为抛物线在x 轴负半轴上方的一个动点,求ADE ∆面积的最大值;(3)抛物线对称轴上是否存在点P ,使AEP ∆为等腰三角形,若存在,请直接写出所有P 点的坐标,若不存在请说明理由.3.(2016·广西中考真题)在平面直角坐标系中,抛物线223y x x =--+与x 轴交于A ,B 两点(A 在B的左侧),与y 轴交于点C ,顶点为D . (1)请直接写出点A ,C ,D 的坐标;(2)如图(1),在x 轴上找一点E ,使得△CDE 的周长最小,求点E 的坐标;(3)如图(2),F 为直线AC 上的动点,在抛物线上是否存在点P ,使得△AFP 为等腰直角三角形?若存在,求出点P的坐标,若不存在,请说明理由.4.(2019·广东广州市第二中学初三)如图(1),在平面直角坐标系中,矩形ABCO,B点坐标为(4,3),抛物线y=12-x2+bx+c经过矩形ABCO的顶点B、C,D为BC的中点,直线AD与y轴交于E点,与抛物线y=12-x2+bx+c交于第四象限的F点.(1)求该抛物线解析式与F点坐标;(2)如图,动点P从点C出发,沿线段CB以每秒1个单位长度的速度向终点B运动;同时,动点M从点A出发,沿线段AE 13个单位长度的速度向终点E运动.过点P作PH⊥OA,垂足为H,连接MP,MH.设点P的运动时间为t秒.①问EP+PH+HF是否有最小值,如果有,求出t的值;如果没有,请说明理由.②若△PMH是等腰三角形,求出此时t的值.5.(2019·湖南中考模拟)如图,关于x的二次函数y=x2+bx+c的图象与x轴交于点A(1,0)和点B与y 轴交于点C(0,3),抛物线的对称轴与x轴交于点D.(1)求二次函数的表达式;(2)在y轴上是否存在一点P,使△PBC为等腰三角形?若存在.请求出点P的坐标;(3)有一个点M从点A出发,以每秒1个单位的速度在AB上向点B运动,另一个点N从点D与点M 同时出发,以每秒2个单位的速度在抛物线的对称轴上运动,当点M到达点B时,点M、N同时停止运动,问点M、N运动到何处时,△MNB面积最大,试求出最大面积.6.(2018·山东中考模拟)如图,抛物线y=﹣x2+mx+n与x轴交于A、B两点,与y轴交于点C,抛物线的对称轴交x轴于点D,已知A(﹣1,0),C(0,2).(1)求抛物线的表达式;(2)在抛物线的对称轴上是否存在点P,使△PCD是以CD为腰的等腰三角形?如果存在,直接写出P点的坐标;如果不存在,请说明理由;(3)点E时线段BC上的一个动点,过点E作x轴的垂线与抛物线相交于点F,当点E运动到什么位置时,四边形CDBF的面积最大?求出四边形CDBF的最大面积及此时E点的坐标.7.(2019·山东中考模拟)已知:如图,抛物线y=ax2+bx+c与坐标轴分别交于点A(0,6),B(6,0),C (﹣2,0),点P是线段AB上方抛物线上的一个动点.(1)求抛物线的解析式;(2)当点P运动到什么位置时,△PAB的面积有最大值?(3)过点P作x轴的垂线,交线段AB于点D,再过点P做PE∥x轴交抛物线于点E,连结DE,请问是否存在点P 使△PDE 为等腰直角三角形?若存在,求出点P 的坐标;若不存在,说明理由.8.(2018·广东中考模拟)如图,在平面直角坐标系xOy 中,二次函数24y ax bx =+-(0a ≠)的图象与x 轴交于A (﹣2,0)、B (8,0)两点,与y 轴交于点B ,其对称轴与x 轴交于点D .(1)求该二次函数的解析式;(2)如图1,连结BC ,在线段BC 上是否存在点E ,使得△CDE 为等腰三角形?若存在,求出所有符合条件的点E 的坐标;若不存在,请说明理由;(3)如图2,若点P (m ,n )是该二次函数图象上的一个动点(其中m >0,n <0),连结PB ,PD ,BD ,求△BDP 面积的最大值及此时点P 的坐标.9.(2019·四川中考模拟)如图,已知二次函数y =﹣x 2+bx+c (c >0)的图象与x 轴交于A 、B 两点(点A 在点B 的左侧),与y 轴交于点C ,且OB =OC =3,顶点为M .(1)求二次函数的解析式;(2)点P 为线段BM 上的一个动点,过点P 作x 轴的垂线PQ ,垂足为Q ,若OQ =m ,四边形ACPQ 的面积为S ,求S 关于m 的函数解析式,并写出m 的取值范围;(3)探索:线段BM 上是否存在点N ,使△NMC 为等腰三角形?如果存在,求出点N 的坐标;如果不存在,请说明理由.10.(2019·甘肃中考模拟)如图,已知二次函数y=ax 2+bx+c 的图象与x 轴相交于A (﹣1,0),B (3,0)两点,与y 轴相交于点C (0,﹣3). (1)求这个二次函数的表达式;(2)若P 是第四象限内这个二次函数的图象上任意一点,PH ⊥x 轴于点H ,与BC 交于点M ,连接PC . ①求线段PM 的最大值;②当△PCM 是以PM 为一腰的等腰三角形时,求点P 的坐标.11.(2019·安徽中考模拟)如图,已知直线1y x =+与抛物线2y ax 2x c =++相交于点()1,0A -和点()2,B m 两点.(1)求抛物线的函数表达式;(2)若点P 是位于直线AB 上方抛物线上的一动点,当PAB ∆的面积S 最大时,求此时PAB ∆的面积S 及点P 的坐标;(3)在x 轴上是否存在点Q ,使QAB ∆是等腰三角形?若存在,直接写出Q 点的坐标(不用说理);若不存在,请说明理由.12.(2018·江苏中考模拟)(2017南宁,第26题,10分)如图,已知抛物线2239y ax ax a =--与坐标轴交于A ,B ,C 三点,其中C (0,3),∠BAC 的平分线AE 交y 轴于点D ,交BC 于点E ,过点D 的直线l 与射线AC ,AB 分别交于点M ,N .(1)直接写出a的值、点A的坐标及抛物线的对称轴;(2)点P为抛物线的对称轴上一动点,若△PAD为等腰三角形,求出点P的坐标;(3)证明:当直线l绕点D旋转时,11AM AN均为定值,并求出该定值.13.(2019·重庆中考模拟)如图,在平面直角坐标系中,一抛物线的对称轴为直线,与y轴负半轴交于C点,与x轴交于A、B两点,其中B点的坐标为(3,0),且OB=OC.(1)求此抛物线的解析式;(2)若点G(2,y)是该抛物线上一点,点P是直线AG下方的抛物线上一动点,当点P运动到什么位置时,△APG的面积最大?求出此时P点的坐标和△APG的最大面积.(3)若平行于x轴的直线与该抛物线交于M、N两点(其中点M在点N的右侧),在x轴上是否存在点Q,使△MNQ为等腰直角三角形?若存在,请求出点Q的坐标;若不存在,请说明理由.14.(2019·辽宁中考模拟)抛物线y=ax2+bx﹣3(a≠0)与直线y=kx+c(k≠0)相交于A(﹣1,0)、B(2,﹣3)两点,且抛物线与y轴交于点C.(1)求抛物线的解析式;(2)求出C、D两点的坐标(3)在第四象限抛物线上有一点P,若△PCD是以CD为底边的等腰三角形,求出点P的坐标.15.(2020·浙江初三期末)如图,抛物线y=﹣12x2+2x+6交x轴于A,B两点(点A在点B的右侧),交y轴于点C,顶点为D,对称轴分別交x轴、线段AC于点E、F.(1)求抛物线的对称轴及点A的坐标;(2)连结AD,CD,求△ACD的面积;(3)设动点P从点D出发,沿线段DE匀速向终点E运动,取△ACD一边的两端点和点P,若以这三点为顶点的三角形是等腰三角形,且P为顶角顶点,求所有满足条件的点P的坐标.16.(2020·湖北初三期末)如图,已知二次函数的图象经过点A(4,4),B(5,0)和原点O,P为二次函数图象上的一个动点,过点P作x轴的垂线,垂足为D(m,0),并与直线OA相较于点C.(1)求出二次函数的解析式;(2)当点P在直线OA的上方时,求线段PC的最大值;(3)当点P在直线OA的上方时,是否存在一点P,使射线OP平分∠AOy,若存在,请求出P点坐标;若不存在.请说明理由;(4)当m>0时,探索是否存在点P,使得△PCO为等腰三角形,若存在,求出P点的坐标;若不存在,请说明理由.17.(2019·吉林初三)如图1,抛物线与y =﹣211433x x ++与x 轴交于A 、B 两点(点A 在点B 的左侧),与y 轴交于点C ,连接AC 、BC ,点D 是线段AB 上一点,且AD =CA ,连接CD .(1)如图2,点P 是直线BC 上方抛物线上的一动点,在线段BC 上有一动点Q ,连接PC 、PD 、PQ ,当△PCD 面积最大时,求PQ +10CQ 的最小值; (2)将过点D 的直线绕点D 旋转,设旋转中的直线l 分别与直线AC 、直线CO 交于点M 、N ,当△CMN 为等腰三角形时,直接写出CM 的长.18.(2020·江苏初三期末)在平面直角坐标系xOy 中,抛物线2y x mx n =-++与x 轴交于点A,B ( A 在B的左侧)(1)如图1,若抛物线的对称轴为直线3,4x AB =-= .①点A 的坐标为( , ),点B 的坐标为( , ); ②求抛物线的函数表达式;(2)如图2,将(1)中的抛物线向右平移若干个单位,再向下平移若干个单位,使平移后的抛物线经过点O ,且与x 正半轴交于点C ,记平移后的抛物线顶点为P ,若OCP ∆是等腰直角三角形,求点P 的坐标.等腰三角形的存在性问题【考题研究】近几年各地的中考数学试题中,探索等腰三角形的存在性问题频频出现,这类试题的知识覆盖面较广,综合性较强,题意构思精巧,要求学生要有较高的分析问题的能力和解决问题的能力,这类问题符合课标对学生能力提高的要求。
一次函数之等腰三角形存在性(一)(北师版)(含答案)
学生做题前请先回答以下问题问题1:如图,AD是△ABC的外角∠CAE的平分线,∠B=35°,∠DAC=60°,则∠ACD的度数为( )问题2:如图,在△ABC中,AE平分∠BAC交BC于点E,BF平分∠ABC交AC于点F,AE,BF相交于点O.若∠BAC=50°,∠C=70°,则∠BOE的度数为( )问题3:如图,D是AC上一点,F是CE上一点,DF的延长线与AE的延长线交于点B,若∠A=45°,∠B=30°,∠C=40°,则∠BFC的度数为( )问题4:如图,在△ABC中,∠BAC=50°,∠ABC=60°,AD⊥BC,BE⊥AC,垂足分别为D,E,AD,BE相交于点H,则∠AHB的度数为( )问题5:如图,在△ABC中,E是CA延长线上一点,点D在BC上,DE交AB于点F,若∠C=90°,∠B=45°,∠E=30°,则∠BFD的度数为( )问题6:如图,EG∥AD,EG交AB于点F,交CA的延长线于点G,若∠B=20°,∠GFA=30°,则∠ADC的度数为( )问题7:已知:如图,AB∥CD,∠B=65°,∠E=20°,则∠D的度数为( )问题8:如图,已知∠B=∠ADB,∠3=55°,∠2=20°,则∠1的度数为( )一次函数之等腰三角形存在性(一)(北师版)一、单选题(共5道,每道20分)1.在平面直角坐标系中,已知两个点A(3,0),B(0,2),在y轴上是否存在点p,使△ABP 为等腰三角形,若存在,点P的坐标为( )A.B.C.D.答案:B解题思路:试题难度:三颗星知识点:等腰三角形存在性2.在平面直角坐标系内,已知一次函数y=-x+6的图象与x、y轴分别交于A、B两点,点P 是直线AB上的一个动点,当△OAP为等腰三角形时,点P的坐标为( )A.B.C.D.答案:A解题思路:试题难度:三颗星知识点:等腰三角形存在性3.如图,直线与x轴、y轴分别交于A,B两点,点P是x轴上的动点,若使△ABP为等腰三角形,则点P的坐标是( )A.B.C.D.答案:C解题思路:试题难度:三颗星知识点:等腰三角形存在性4.如图,直线与x轴、y轴分别交于A,B两点,过点O作OC⊥AB于点C,点P是线段OA上的动点,若使△PAC为等腰三角形,则点P的坐标是( )A.B.C.D.答案:A解题思路:试题难度:三颗星知识点:等腰三角形存在性5.如图,直线与x轴、y轴分别交于A,B两点,点P是线段AB上的动点,若使△OAP为等腰三角形,则点P的坐标是( )A.B.C.D.答案:A解题思路:试题难度:三颗星知识点:等腰三角形存在性学生做题后建议通过以下问题总结反思问题1:本套试题是对等腰三角形存在性问题的训练,应用的存在性问题的处理框架,我们一起来小结一下吧!一次函数背景下的存在性问题,首先第一步是:研究背景图形,即把函数信息中的_____________转化到几何图形中.问题2:第二步是:分析不变特征,确定分类标准;具体分析过程是什么?。
等腰直角三角形存在性(含答案)

学生做题前请先回答以下问题问题1:存在性问题的处理思路①分析特征:分析背景图形中的__________、__________及____________,结合图形形成因素(判定等)考虑分类.②画图求解:分析各种状态的可能性,画出符合题意的图形.通常先尝试画出其中一种情形,分析解决后,再类比解决其他情形.③结果验证:回归________________,画图或推理,验证结果.问题2:等腰直角三角形存在性根据什么分类?如何确定点的位置?等腰直角三角形存在性一、单选题(共4道,每道25分)1.如图,抛物线342+-=x x y 交x 轴于A ,C 两点(点A 在点C 的右侧),交y 轴于点B .点D 的坐标为(-1,0),若在直线AB 上存在点P ,使得以A ,D ,P 为顶点的三角形是等腰直角三角形,则点P 的坐标为( )A. B.(-1,3)或(1,2)C.(-1,4)或(1,2)D.(-1,4),(1,2)或(5,-2)答案:C解题思路:试题难度:三颗星知识点:等腰直角三角形存在性2.如图,抛物线23432-2++=x x y 与x 轴交于A ,B 两点(点A 在点B 左侧),与y 轴交于点C .P 是线段AC 上的一个动点(不与点A ,C 重合),过点P 作平行于x 轴的直线,交BC 于点Q ,若在x 轴上存在点R ,使得△PQR 是等腰直角三角形,则点R 的坐标为( )A. B. C. D.答案:C解题思路:试题难度:三颗星知识点:等腰直角三角形存在性3.如图,二次函数23-212x x y +=的图象与x 轴交于A ,B 两点(点A 在点B 的左侧),以 AB 为边在x 轴上方作正方形ABCD ,P 是x 轴上的一动点(不与点A 重合),连接DP ,过点P 作PE ⊥DP 交y 轴于点E .当△PED 是等腰直角三角形时,点P 的横坐标为( )A.-4B.-3C.-3或-4D.-4或4答案:D解题思路:试题难度:三颗星知识点:等腰直角三角形存在性4.如图,在平面直角坐标系xOy 中,直线y=x+4与x 轴、y 轴分别交于点A ,B ,D 为线段AB 上一动点,过点D 作x 轴的垂线,垂足为点C ,CD 的延长线交抛物线43-2+-=x x y 于点E ,连接BE .若△DBE 为等腰直角三角形,则点D 的坐标为( )A.(-2,2)B.(-2,6)C.(-3,4)或(-2,6)D.(-3,1)或(-2,2)答案:D解题思路:试题难度:三颗星知识点:等腰直角三角形存在性。
一次函数压轴题专题突破4:一次函数与等腰直角三角形(含解析)

一次函数压轴题之等腰直角三角形1.【模型建立】如图1,等腰直角三角形ABC中,∠ACB=90°,CB=CA,直线ED经过点C,过A作AD⊥ED于点D,过B作BE⊥ED于点E.求证:△BEC≌△CDA;【模型应用】①已知直线l1:y=x+4与x轴交于点A,与y轴交于点B,将直线l1绕着点A逆时针旋转45°至直线l2,如图2,求直线l2的函数表达式;②如图3,在平面直角坐标系中,点B(8,6),作BA⊥y轴于点A,作BC⊥x轴于点C,P是线段BC上的一个动点,点Q是直线y=2x﹣6上的动点且在第一象限内.问点A、P、Q能否构成以点Q为直角顶点的等腰直角三角形,若能,请直接写出此时点Q的坐标,若不能,请说明理由.2.已知,一次函数y=﹣x+6的图象与x轴、y轴分别交于点A、点B,与直线y=x相交于点C.过点B作x轴的平行线l.点P是直线l上的一个动点.(1)求点A,点B的坐标.(2)若S△AOC=S△BCP,求点P的坐标.(3)若点E是直线y=x上的一个动点,当△APE是以AP为直角边的等腰直角三角形时,求点E的坐标.3.如图,在平面直角坐标系中,直线l1的解析式为y=x,直线l2的解析式为y=﹣x+3,与x轴、y轴分别交于点A、点B,直线l1与l2交于点C.(1)求点A、点B、点C的坐标,并求出△COB的面积;(2)若直线l2上存在点P(不与B重合),满足S△COP=S△COB,请求出点P的坐标;(3)在y轴右侧有一动直线平行于y轴,分别与l1,l2交于点M、N,且点M在点N的下方,y轴上是否存在点Q,使△MNQ为等腰直角三角形?若存在,请直接写出满足条件的点Q的坐标;若不存在,请说明理由.4.如图1,在平面直角坐标系中,直线l1:y=x+b与直线l2:y=﹣x﹣8交于点A,已知点A的横坐标为﹣5,直线l1与x轴交于点B,与y轴交于点C,直线l2与y轴交于点D.(1)求直线l1的解析式;(2)将直线l2向上平移6个单位得到直线l3,直线l3与y轴交于点E,过点E作y轴的垂线l4,若点M为垂线l4上的一个动点,点N为x轴上的一个动点,当CM+MN+NA的值最小时,求此时点M的坐标及CM+MN+NA 的最小值;(3)在(2)条件下,如图2,已知点P、Q分别是直线l1、l2上的两个动点,连接EP、EQ、PQ,是否存在点P、Q,使得△EPQ是以点P为直角顶点的等腰直角三角形,若存在,求点P的坐标,若不存在,说明理由.5.如图,在平面直角坐标系中,已知直线BD:y=x﹣2与直线CE:y=﹣x+4相交于点A.(1)求点A的坐标;(2)点P是△ABC内部一点,连接PA、PB、PC,求PB+PA+PC的最小值;(3)将点D向下平移一个单位得到点D1,连接BD1,将△OD1B绕点O旋转至△OB1D2的位置,使B1D2∥x轴,再将△OB1D2沿y轴向下平移得到△O1B2D3,在平移过程中,直线O1D3与x轴交于点K,在直线x=3上任取一点T,连接KT,O1T,△O1KT能否以O1K为直角边构成等腰直角三角形?若能,请直接写出所有符合条件的T点的坐标;若不能,请说明理由.6.如图1,直线y=﹣x+3交x轴于点B,交y轴于点C.点A在x轴负半轴上且∠CAO=30°.(1)求直线AC的解析式;(2)如图2,边长为3的正方形DEFG,G点与A点重合,现将正方形以每秒1个单位地速度向右平移,当点G与点O重合时停止运动.设正方形DEFG与△ACB重合部分的面积为S,正方形DEFG运动的时间为t,求s关于t的函数关系式;(3)如图3,已知点Q(1,0),点M为线段AC上一动点,点N为直线BC上一动点,当三角形QMN为等腰直角三角形时,求M点的坐标.7.已知直线l1:y=﹣x+b与x轴交于点A,直线l2:y=x﹣与x轴交于点B,直线l1、l2交于点C,且C点的横坐标为1.(1)如图1,过点A作x轴的垂线,若点P(x,2)为垂线上的一个点,Q是y轴上一动点,若S△CPQ=5,求此时点Q的坐标;(2)若P在过A作x轴的垂线上,点Q为y轴上的一个动点,当CP+PQ+QA的值最小时,求此时P的坐标;(3)如图2,点E的坐标为(﹣2,0),将直线l1绕点C旋转,使旋转后的直线l3刚好过点E,过点C作平行于x轴的直线l4,点M、N分别为直线l3、l4上的两个动点,是否存在点M、N,使得△BMN是以M点为直角顶点的等腰直角三角形?若存在,求出N点的坐标;若不存在,请说明理由.8.如图,在矩形ABCO中,点O为坐标原点,点B(4,3),点A、C在坐标轴上,点Q在BC边上,直线L1:y=kx+k+1交y轴于点A.对于坐标平面内的直线,先将该直线向右平移1个单位长度,再向下平移1个单位长度,这种直线运动称为直线的斜平移.现将直线L1经过2次斜平移,得到直线L2.(1)求直线L1与两坐标轴围成的面积;(2)求直线L2与AB的交点坐标;(3)在第一象限内,在直线L2上是否存在一点M,使得△AQM是等腰直角三角形?若存在,请直接写出点M 的坐标;若不存在,请说明理由.9.如图1,在平面直角坐标系中,直线l:y=与x轴交于点A,且经过点B(2,m),已知点C(3,0).(1)求直线BC的函数解析式;(2)在线段BC上找一点D,使得△ABO与△ABD的面积相等,求出点D的坐标;(3)y轴上有一动点P,直线BC上有一动点M,若△APM是以线段AM为斜边的等腰直角三角形,求出点M 的坐标;(4)如图2,E为线段AC上一点,连结BE,一动点F从点B出发,沿线段BE以每秒1个单位运动到点E 再沿线段EA以每秒个单位运动到A后停止,设点F在整个运动过程中所用时间为t,求t的最小值.10.已知直线l1:y=﹣x+b与x轴交于点A,直线l2:y=x﹣与x轴交于点B,直线l1,l2交于点C,且C点的横坐标为1.(1)求直线l1的解析式;(2)如图1,过点A作x轴的垂线,若点P为垂线上的一个动点,点Q(0,2),若S△CPQ=4,求此时点P 的坐标;(3)如图2,点E的坐标为(﹣2,0),将直线l1绕点C逆时针旋转,使旋转后的直线l3刚好过点E,过点C作平行于x轴的直线l4,点M、N分别为直线l3、l4上的两个动点,是否存在点M、N,使得△BMN是以M 点为直角顶点的等腰直角三角形,若存在,直接写出N点的坐标;若不存在,请说明理由.11.已知直线l1:y=﹣x+b与x轴交于点A,直线l2:y=x﹣与x轴交于点B,直线l1、l2交于点C,且C点的纵坐标为﹣4.(1)求△ABC的面积;(2)如图1,过点A作x轴的垂线,若点P为垂线上的一个动点,点Q(0,2),若S△CPQ=2,求此时点P 的坐标;(3)如图2,点E的坐标为(﹣2,0),将直线l1绕点C顺时针旋转,使旋转后的直线l3刚好过点E.过点C作平行于x轴的直线l4,点M、N分别为直线l3、l4上的两个动点,是否存在点M、N,使得△BMN是以M 点为直角顶点的等腰直角三角形,若存在,直接写出N点的坐标:若不存在,请说明理由.12.如图,直线y=kx+k分别交x轴、y轴于点A,C,直线BC过点C交x轴于点B,且OA=OC,∠CBA =45°,点P是直线BC上的一点.(1)求直线BC的解析式;(2)若动点P从点B出发沿射线BC方向匀速运动,速度为个单位长度/秒,连接AP,设△PAC的面积为S,点P的运动时间为t秒,求S与t之间的函数关系式,并写出t的取值范围;(3)若点Q是直线AC上且位于第三象限图象上的一个动点,点M是y轴上的一个动点,当以点B、M、Q 为顶点的三角形为等腰直角三角形时,求点Q和点M的坐标.13.如图,在平面直角坐标系中,直线AB:y=﹣x+与直线AC:y=+8交于点A,直线AB分别交x轴、y轴于B、E,直线AC分别交x轴、y轴于点C、D.(1)求点A的坐标;(2)在y轴左侧作直线FG∥y轴,分别交直线AB、直线AC于点F、G,当FG=3DE时,过点G作直线GH ⊥y轴于点H,在直线GH上找一点P,使|PF﹣PO|的值最大,求出P点的坐标及|PF﹣PO|的最大值;(3)将一个45°角的顶点Q放在x轴上,使其角的一边经过A点,另一边交直线AC于点R,当△AQR为等腰直角三角形时,请直接写出点R的坐标.14.模型建立:如图1,等腰直角三角形ABC中,∠ACB=90°,CB=CA,直线ED经过点C,过A作AD⊥ED 于D,过B作BE⊥ED于E.求证:△BEC≌△CDA.模型应用:(1)已知直线l1:y=x+4与y轴交与A点,将直线l1绕着A点顺时针旋转45°至l2,如图2,求l2的函数解析式.(2)如图3,矩形ABCO,O为坐标原点,B的坐标为(8,6),A、C分别在坐标轴上,P是线段BC上动点,设PC=m,已知点D在第一象限,且是直线y=2x﹣6上的一点,若△APD是不以A为直角顶点的等腰Rt△,请直接写出点D的坐标.15.如图,已知直线y=x+4与x轴、y轴分别相交于点A、B,点C从O点出发沿射线OA以每秒1个单位长度的速度匀速运动,同时点D从A点出发沿AB以每秒1个单位长度的速度向B点匀速运动,当点D到达B点时C、D都停止运动.点E是CD的中点,直线EF⊥CD交y轴于点F,点E′与E点关于y轴对称.点C、D的运动时间为t(秒).(1)当t=1时,AC=,点D的坐标为;(2)设四边形BDCO的面积为S,当0<t<3时,求S与t的函数关系式;(3)当直线EF与△AOB的一边垂直时,求t的值;(4)当△EFE′为等腰直角三角形时,直接写出t的值.16.如图1,在平面直角坐标系中,O为坐标原点,直线l:y=﹣x+m与x、y轴的正半轴分别相交于点A、B,过点C(﹣4,﹣4)画平行于y轴的直线交直线AB于点D,CD=10.(1)求点D的坐标和直线l的解析式;(2)求证:△ABC是等腰直角三角形;(3)如图2,将直线l沿y轴负方向平移,当平移适当的距离时,直线l与x、y轴分别相交于点A′、B′,在直线CD上存在点P,使得△A′B′P是等腰直角三角形.请直接写出所有符合条件的点P的坐标.(不必书写解题过程)17.如图,在平面直角坐标系中,直线y=﹣x+b(b>0)分别交x轴,y轴于A,B两点,以OA,OB为边作矩形OACB,D为BC的中点.以M(4,0),N(8,0)为斜边端点作等腰直角三角形PMN,点P在第一象限,设矩形OACB与△PMN重叠部分的面积为S.(1)求点P的坐标.(2)当b值由小到大变化时,求S与b的函数关系式.(3)若在直线y=﹣x+b(b>0)上存在点Q,使∠OQM等于90°,请直接写出b的取值范围.(4)在b值的变化过程中,若△PCD为等腰三角形,请直接写出所有符合条件的b值.18.如图,直线l与x轴、y轴的正半轴分别交于A、B两点,OA、OB的长分别是关于x的方程x2﹣14x+4(AB+2)=0的两个根(OB>OA),P是直线l上A、B两点之间的一动点(不与A、B重合),PQ∥OB交OA 于点Q.(1)求tan∠BAO的值;(2)若S△PAQ=S四边形OQPB时,请确定点P在AB上的位置,并求出线段PQ的长;(3)当点P在线段AB上运动时,在y轴上是否存在点M,使△MPQ为等腰直角三角形?若存在,请直接写出点M的坐标;若不存在,请说明理由.1.【解答】解:(1)证明:∵△ABC为等腰直角三角形∴CB=CA,∠ACD+∠BCE=180°﹣90°=90°又∵AD⊥CD,BE⊥EC∴∠D=∠E=90°又∵∠EBC+∠BCE=90°∴∠ACD=∠EBC在△ACD与△CBE中,∠D=∠E,∠ACD=∠EBC,CA=BC,∴△ACD≌△CBE(AAS);(2)过点B作BC⊥AB交l2于C,过C作CD⊥y轴于D,∵∠BAC=45°∴△ABC为等腰Rt△由(1)可知:△CBD≌△BAO∴BD=AO,CD=OB∵l1:,令y=0,则x=﹣3∴A(﹣3,0),令x=0,则y=4∴B(0,4)∴BD=AO=3,CD=OB=4∴OD=4+3=7.∴C(﹣4,7),设直线l2的解析式为y=kx+b,将点A(﹣3,0),C(﹣4,7)代入y=kx+b中,得解得,k=﹣7,b=﹣21,则l2的解析式:y=﹣7x﹣21;(3)如下图,设点Q(m,2m﹣6),当∠AQP=90°时,由(1)知,△AMQ≌△QNP(AAS),∴AM=QN,即|8﹣m|=6﹣(2m﹣6),解得:m=4或,故:Q(4,2),.2.【解答】解:(1)一次函数y=﹣x+6的图象与x轴、y轴分别交于点A、点B,则点A、B的坐标分别为:(8,0)、(0,6);(2)联立y=﹣x+6、y=x并解得:x=3,故点C(3,),S△AOC=8×=15=S△BCP=BP×(yP﹣yC)=BP×(6﹣),解得:BP=,故点P(,6)或(﹣,6)(3)设点E(m,m)、点P(n,6);①当∠EPA=90°时,如左图,∵∠MEP+∠MPE=90°,∠MPE+∠NPA=90°,∴∠MEP=∠NPA,AP=PE,∵△EMP≌△PNA(AAS),则ME=PN=6,MP=AN,即|m﹣n|=6,m﹣6=8﹣n,解得:m=或16,故点E(,)或(16,20);②当∠EAP=90°时,如右图,同理可得:△AMP≌△ANE(AAS),故MP=EN,AM=AN=6,即m=n﹣8,|8﹣m|=6,解得:m=2或14,故点E(2,)或(14,);综上,E(,)或(14,)或;(2,)或(16,20).3.【解答】解:(1)直线l2的解析式为y=﹣x+3,与x轴、y轴分别交于点A、点B,则点A、B的坐标分别为(6,0)、(0,3),联立式y=x,y=﹣x+3并解得:x=2,故点C(2,2);△COB的面积=×OB×x C=×3×2=3;(2)设点P(m,﹣m+3),S△COP=S△COB,则BC=PC,则(m﹣2)2+(﹣m+3﹣2)2=22+12=5,解得:m=4或0(舍去0),故点P(4,1);(3)设点M、N、Q的坐标分别为(m,m)、(m,3﹣m)、(0,n),①当∠MQN=90°时,∵∠GNQ+∠GQN=90°,∠GQN+∠HQM=90°,∴∠MQH=∠GNQ,∠NGQ=∠QHM=90°,QM=QN,∴△NGQ≌△QHM(AAS),∴GN=QH,GQ=HM,即:m=3﹣m﹣n,n﹣m=m,解得:m=,n=;②当∠QNM=90°时,则MN=QN,即:3﹣m﹣m=m,解得:m=,n=y N=3﹣=;③当∠NMQ=90°时,同理可得:n=;综上,点Q的坐标为(0,)或(0,)或(0,).4.【解答】解:(1)∵点A的横坐标为﹣5,∴A(﹣5,﹣3),将点A代入y=x+b,∴b=4,∴直线l1的解析式y=x+4;(2)l2:y=﹣x﹣8与y轴的交点D(0,﹣8),∵将直线l2向上平移6个单位得到直线l3,直线l3与y轴交于点E,∴E(0,﹣2),∵过点E作y轴的垂线l4,点D是点C关于直线l4的对称点,作点A关于x轴的对称点A′(﹣5,3),连接AD′交x轴、l4于点N、M,则此时CM+MN+NA最小,最小值为:A′D,CM+MN+NA=MD+MN+A′N=A′D,A′D==;∴CM+MN+NA的值最小为;(3)存在,理由:设点P、Q的坐标分别为:(m,m+4)、(n,﹣n﹣8),当点E在点P右边时,过点Q作x轴的平行线交y轴于点M,过点P作PN⊥QM于点N,PN交l4于点K,则△PNQ≌△EKP(AAS),∴PN=KE,QN=PK,即:m+4+n+8=﹣m,m﹣n=m+4+2,解得:m=﹣3,∴点P(﹣3,﹣)当点E在点P的左侧时,同理可得:(﹣,﹣5),故答案为:(﹣3,﹣)或(﹣,﹣5),5.【解答】解:(1)直线,则点B、D的坐标分别为:(,0)、(0,﹣2);直线,则点C、E的坐标分别为:(4,0)、(0,4);联立BD、CE的表达式并解得:x=2,故点A(2,2);(2)如图,将△APB绕点C逆时针旋转60°得到△EFC,则△BFP是等边三角形,∠ECB=90°,BC=3,AC==CE,在Rt△EBC中,BE==,∵PA+PB+PC=EF+FP+PB≥BE,∴PA+PB+PC≥,∴PA+PB+PC的最小值为;(3)存在,理由:点D1(0,﹣3),点B(,0),则∠BD1O=30°,B1D2∥x轴,则直线OD2的倾斜角为30°,设直线O1K的表达式为:y=x+m,则点O1(0,m),点K(﹣m,0),则MO1=﹣m,MK=﹣m,KN=﹣m,TN=|﹣m﹣3|,则点T(3,﹣m)△O1KT能否以O1K为直角边构成等腰直角三角形,则O1K=TK,TK⊥O1K,过点K作y轴的平行线分别交过点O1、T与x轴的平行线于点M、N,∵∠NKT+∠NTK=90°,∠NKT+∠O1KM=90°,∴∠O1KM=∠NTK,∠KNT=∠O1MK=90°,O1K=TK,∴△KNT≌△O1MK(AAS),∴TN=KM,即:|﹣m﹣3|=﹣m,解得:m=,故点T(3,)或(3,).6.【解答】解:(1)直线y=﹣x+3交x轴于点B,交y轴于点C,则点B、C的坐标为(3,0)、(0,3),∵∠CAO=30°,则AC=2OC=6,则OA=3,将点A、C的坐标代入一次函数表达式:y=kx+b并解得:直线AC的表达式为:y=x+3;(2)如图2所示:①当0≤t≤3时,(左侧图),正方形的DA边交AC于点H,点A运动到点M处,则点M(﹣3+t,0),则点H(﹣3+t,t),S=S△AHM=×AM×HM=×t×t=t2,②当3<t≤3时,(右侧图),正方形的DA边交AC于点H,点A运动到点G处,E、F交直线AC于点R、S,AG=t,则AS=t﹣3,则RS=(t﹣3),同理HG=t,同理可得:S=S梯形RSHG=×3×(t+t﹣)=t﹣;故:S=;(3)∵点M为线段AC上一动点,经画图,∠MQN分别为90°时,点M不在线段AC上,①NMQ=90°时,三角形QMN为等腰直角三角形,过点M作y轴的平行线交x轴于点G,过点N作x轴的平行线交MG于点R、交y轴于点H,设点M、N的坐标分别为(m,m+3)、(n,3﹣n),∵∠NMR+∠RNM=90°,∠MNR+∠GMQ=90°,∴∠GMQ=∠RNM,∠NRM=∠MGO=90°,MR=MQ,∴△NRM≌△MGO(AAS),则MG=RN,GQ=RM,即:n﹣m=m+3,3﹣n﹣(m+3)=1﹣m,解得:m=﹣2,故点M的坐标为(﹣2,1);②当∠MNQ=90°时,同理可得:点M(﹣,2);综上,点M的坐标为:(﹣2,1)或(﹣,2).7.【解答】解:(1)直线l2:y=x﹣,令x=1,则y=﹣4,故C(1,﹣4),把C(1,﹣4)代入直线l1:y=﹣x+b,得:b=﹣3,则l1为:y=﹣x﹣3,所以A(﹣3,0),所以点P坐标为(﹣3,2),如图,设直线AC交y轴于点M,设y PC:y=mx+t得:,解得,∴y PC=﹣1.5x﹣2.5,即M(0,﹣2.5).S△CPQ=QM×(x C﹣x P)=(y Q+2.5)×4=5,解得:y Q=0或﹣5,∴Q的坐标为(0,0)或(0,﹣5);(2)确定C关于过A垂线的对称点C′(﹣7,﹣4)、A关于y轴的对称点A′(3,0),连接A′C′交过A点的垂线与点P,交y轴于点Q,此时,CP+PQ+QA的值最小,将点A′、C′点的坐标代入一次函数表达式:y=k′x+b′得:则直线A′C′的表达式为:y=x﹣,即点P的坐标为(﹣3,﹣),(3)将E、C点坐标代入一次函数表达式,同理可得其表达式为:y=﹣x﹣①当点M在直线l4上方时,设点N(n,﹣4),点M(s,﹣s﹣),点B(4,0),过点N、B分别作y轴的平行线交过点M与x轴的平行线分别交于点R、S,∵∠RMN+∠RNM=90°,∠RMN+∠SMR=90°,∴∠SMR=∠RNM,∠MRN=∠MSB=90°,MN=MB,∴△MSB≌△NRM(AAS),∴RN=MS,RM=SB,即,解得:,故点N的坐标为(﹣16,﹣4),②当点M在l4下方时,同理可得:N(﹣,﹣4),即:点N的坐标为(﹣,﹣4)或(﹣16,﹣4).8.【解答】解:(1)将点A(0,3)代入直线L1:y=kx+k+1并解得:k=2,故L1的表达式为:y=2x+3,设:L1与x轴交点坐标为D,则其坐标为(﹣,0),直线l1与两坐标轴围成的面积=OD×AO=×3=;(2)将直线L1经过2次斜平移,得到直线L2:y=2(x﹣2)+3﹣2=2x﹣3,当y=3时,x=3,即直线L2与AB的交点坐标为(3,3);(3)①当∠QAM为直角时,点M在第四象限,舍去;②当∠AQM为直角时,对于L2,当x=4时,y=5,故点M(4,5)(舍去);③当∠AMQ为直角时,AM=MQ,过点M作x轴的平行线分别交AO、BC于点G、H,设点M(m,2m﹣3),点Q(4,n),∵∠AMG+∠GAM=90°,∠AMG+∠QMH=90°,∴∠QMH=∠GAM,∠AGM=∠MHQ=90°,AM=MQ,∴△AGM≌△MHQ(AAS),∴AG=MH,即:|3﹣2m+3|=4﹣m,解得:m=2或,故点M(,)或(2,1),故点M(,)或(2,1).9.【解答】解:(1)将点B坐标代入直线l的表达式得:m==3,点B(2,3),令y=0,则x=﹣2,即点A(﹣2,0),将点B、C的坐标代入一次函数表达式:y=kx+b得:,解得:,故:直线BC的表达式为:y=﹣3x+9;(2)过点O作OD∥AB交BC于点D,则D点为所求,直线AB表达式得k值为,则直线OD的表达式为y=x,将直线BC与OD表达式联立并解得:x=,即:点D的坐标为(,);(3)过点P作x轴的平行线分别于过点A、M与y轴的平行线于点G、H,设点P的坐标为(0,n)、点M(m,9﹣3m),∵∠GPA+∠GAP=90°,∠GPA+∠HPM=90°,∴∠HPM=∠GAP,又PA=PM,∠G=∠H=90°,∴△AGP≌△PHM(AAS),GP=HM=2,GA=PH,即:,解得:m=或,即点M的坐标为(,)或(,﹣);(4)t=+=BE+AE,过点A作倾斜角为45度的直线l2,过点E作EF⊥l2交于点F,则:EF=AE,即t=BE+EF,当B、E、F三点共线且垂直于直线l2时,t最小,即:t=BF′,同理,直线l2的表达式为:y=﹣x﹣2,直线BF表达式为:y=x+1,将上述两个表达式联立并解得:x=﹣,即:点F′(﹣,﹣),t=BF′==.10.【解答】解:(1)直线l2:y=,令x=1,则y=﹣4,故点C(1,﹣4),把点C(1,﹣4)代入直线l1:y=﹣x+b,得:b=﹣3,则直线l1的表达式为:y=﹣x﹣3,(2)对于直线y=﹣x﹣3,当y=0时,有﹣x﹣3=0,解得x=﹣3,即A(﹣3,0),如图,设直线AC交y轴于点M,设点P坐标为(﹣3,m),将点P、C的坐标代入一次函数表达式y=sx+t得:,解得,即M.S△CPQ=QM×(x C﹣x P)=•|2﹣+3|•(1+3)=4,解得:m=12或28,即点P的坐标为(﹣3,12)或(﹣3,28);(3)将E、C点坐标代入一次函数表达式,同理可得其表达式为①当点M在直线l4上方时,设点N(n,﹣4),点M(s,﹣s﹣),点B(4,0),过点N、B分别作y轴的平行线交过点M与x轴的平行线分别交于点R、S,∵∠RMN+∠RNM=90°,∠RMN+∠SMR=90°,∴∠SMR=∠RNM,∠MRN=∠MSB=90°,MN=MB,∴△MSB≌△NRM(AAS),∴RN=MS,RM=SB,即,解得.故点N的坐标为(﹣16,﹣4),②当点M在l4下方时,如图1,过点M作PQ∥x轴,与过点B作y轴的平行线交于Q,与过点N作y轴的平行线交于P,同①的方法得N(﹣,﹣4),③如图2中,当点N在y轴的右侧,△BMN是等腰直角三角形时,同法可得N(,﹣4)即:点N的坐标为(﹣,﹣4)或(﹣16,﹣4)或(,﹣4).11.【解答】解:(1)直线l2:y=x﹣,令y=4,则x=1,则点C(1,﹣4),令y=0,则x=4,即点B(4,0),把点C坐标代入直线l1:y=﹣x+b得:b=﹣3,则直线l1的表达式为:y=﹣x﹣3,令y=0,则x=﹣3,即点A(﹣3,0),S△ABC=AB×|y C|=7×4=14;(2)如下图,设直线AC交y轴于点M,设点P坐标为(﹣3,m),将点P、C的坐标代入一次函数表达式y=sx+t得:,解得:,即:点M坐标为(0,),S△CPQ=QM×(x C﹣x P)=(2﹣+3)×(1+3)=2,解得:m=16,即点P的坐标为(﹣3,16)当PC与y轴交于x轴上方时,同理可得:点P(﹣3,24),故点P(﹣3,16)或(﹣3,24);(3)将E、C点坐标代入一次函数表达式,同理可得其表达式为:y=﹣x﹣,设点N(n,﹣4),点M(s,﹣s﹣),点B(4,0),过点N、B分别作y轴的平行线交过点M与x轴的平行线分别交于点R、S,∵∠RMN+∠RNM=90°,∠RMN+∠SMR=90°,∴∠SMR=∠RNM,∠MRN=∠MSB=90°,MN=MB,∴△MSB≌△NRM(AAS),∴RN=MS,RM=SB,即:,解得:,故点N的坐标为(﹣16,﹣4).12.【解答】解:(1)直线y=kx+k分别交x轴、y轴于点A,C,则点A(﹣1,0),且OA=OC,则点C(0,3),则k=3,故直线AC的表达式为:y=3x+3,∵∠CBA=45°,∴OB=OC=3,∴点B(3,0),∵点C(0,3)、点B(3,0),则直线BC的表达式为:y=﹣x+3;(2)当点P在线段BC时,过点P作PH⊥x轴于点H,∵∠CBA=45°,PH=PBsin45°=t×=t,S=S△ABC﹣S△ABP=×BA×(OC﹣PH)=4×(3﹣t)=6﹣2t,(0≤t≤3);当点P在y轴右侧的射线BC上时,同理可得:S=S△ABP﹣S△ABC=2t﹣6,(t>3);故S=;(3)设点M(0,m),点Q(n,3n+3),①如图2(左侧图),当∠BMQ=90°时,(点M在x轴上方),分别过点Q、P作y轴的平行线QG、BH,过点M作x轴的平行线分别交GQ、BH于点G、H,∵∠GMQ+∠MQG=90°,∠GMQ+∠HMB=90°,∴∠HMB=∠GQM,∠MHB=∠QGM=90°,MB=MQ,∴△MHB≌△QGM(AAS),∴GQ=MH,BH=GM,即:m=﹣n,m﹣3n﹣3=3,解得:m=,n=﹣;故点M(0,)、点Q(﹣,﹣);同理当点M在x轴下方时,3n+3﹣m=3且﹣m=﹣n,解得:m=n=0(舍去);②当∠MQB=90°时,同理可得:﹣n=﹣3n﹣3,3n+3﹣m=3﹣n,解得:m=﹣6,n=﹣,故点M(0,﹣6)、点Q(﹣,﹣);③当∠QBM=90°时,同理可得:﹣3n﹣3=3,m=3﹣n解得:m=5,n=﹣2,点M(0,5)、点Q(﹣2,﹣3);综上,M(0,)、Q(﹣,﹣)或M(0,﹣6)、Q(﹣,﹣)或M(0,5)点Q(﹣2,﹣3).13.【解答】解:(1)联立,解得:,故点A的坐标为(﹣2,7);(2)由题意得:点E、D、B、C的坐标分别为(0,)、(0,8)、(,0)、(﹣16,0),过点A作MN∥x轴,分别交FG、DE于点M、N,则:AN=2,∵FG∥DE,∴△AFG∽△AED,∴=3,则AM=6,∴点M的横坐标为:﹣8,则点F、G的坐标分别为(﹣8,)、(﹣8,4),在y轴上找到点O关于直线GH的对称点O′(0,8),连接FO′并延长,交直线GH于点P,此时,|PF﹣PO|的值最大,最大值为PO′,直线O′F的表达式为:y=﹣x+8,当y=4时,x=,即点P坐标为(,4),|PF﹣PO|=FO′==,故:点P坐标为(,4),|PF﹣PO|=;(3)△AQR为等腰直角三角形,有如下图所示的两种情况,①当AQ⊥AC,当点R在点A下方时,∴直线AQ的表达式为:y=﹣2x+b,将点A坐标代入得:7=﹣2×(﹣2)+b,解得:b=3,故:直线AQ的表达式为:y=﹣2x+3,则点Q坐标为(,0),过点A作x轴的平行线,过点R作y轴的平行线,过点Q作y轴的平行线,围成矩形GMQH,∠GAR+∠QAH=90°,∠QAH+∠AQH=90°,∴∠AQH=∠GAR,∠AGR=∠QHA=90°,AR=AQ,∴△AGR≌△QHA(AAS),∴HQ=GA=7,GR=AH=2+=,OM=2+GA=9,∴RM=7﹣=故点R的坐标为(﹣9,),当点R在点A上方时,同理可得点R坐标为(5,);②当R′Q′⊥AC时,同理,点R′的坐标为(12,14)或(﹣,),故:点R的坐标为(﹣9,)或(5,)或(12,14)或(﹣,).14.【解答】(1)证明:∵△ABC为等腰直角三角形,∴CB=CA,又∵AD⊥CD,BE⊥EC,∴∠D=∠E=90°,∠ACD+∠BCE=180°﹣90°=90°,又∵∠EBC+∠BCE=90°,∴∠ACD=∠EBC,在△ACD与△CBE中,,∴△ACD≌△EBC(AAS);(2)解:过点B作BC⊥AB于点B,交l2于点C,过C作CD⊥x轴于D,如图1,∵∠BAC=45°,∴△ABC为等腰Rt△,由(1)可知:△CBD≌△BAO,∴BD=AO,CD=OB,∵直线l1:y=x+4,∴A(0,4),B(﹣3,0),∴BD=AO=4.CD=OB=3,∴OD=4+3=7,∴C(﹣7,3),设l2的解析式为y=kx+b(k≠0),∴,∴,∴l2的解析式:y=x+4;(3)当点D位于直线y=2x﹣6上时,分两种情况:①点D为直角顶点,分两种情况:当点D在矩形AOCB的内部时,过D作x轴的平行线EF,交直线OA于E,交直线BC于F,设D(x,2x﹣6);则OE=2x﹣6,AE=6﹣(2x﹣6)=12﹣2x,DF=EF﹣DE=8﹣x;则△ADE≌△DPF,得DF=AE,即:12﹣2x=8﹣x,x=4;∴D(4,2);当点D在矩形AOCB的外部时,设D(x,2x﹣6);则OE=2x﹣6,AE=OE﹣OA=2x﹣6﹣6=2x﹣12,DF=EF﹣DE=8﹣x;同1可知:△ADE≌△DPF,∴AE=DF,即:2x﹣12=8﹣x,x=;∴D(,);②点P为直角顶点,显然此时点D位于矩形AOCB的外部;设点D(x,2x﹣6),则CF=2x﹣6,BF=2x﹣6﹣6=2x﹣12;同(1)可得,△APB≌△PDF,∴AB=PF=8,PB=DF=x﹣8;∴BF=PF﹣PB=8﹣(x﹣8)=16﹣x;联立两个表示BF的式子可得:2x﹣12=16﹣x,即x=;∴D(,);综合上面六种情况可得:存在符合条件的等腰直角三角形;且D点的坐标为:(4,2),(,),(,).15.【解答】解:(1)如图1,过D作DH⊥AC于H,∵直线y=x+4与x轴、y轴分别相交于点A,A、B,∴A(﹣3,0),B(0,4),∴AO=3,BO=4,∴AB===5,当0≤t≤3时,如图1,∵CO=t,AD=t,∴AC=3﹣t,DH=AD•sin∠BAO=t,AH=ADcos∠BAO=t,当t=1时,AC=3﹣1=2,点D的坐标为(,);(2)∵AO=3,BO=4,AB=5∴sin∠BAO==,cos∠BAO==过D作DH⊥AC于H,当0≤t≤3时,如图1,∵CO=t,AD=t,∴AC=3﹣t,DH=AD•sin∠BAO=t,∴S=S△ABO﹣S△ADC=×3×4﹣•(3﹣t)•t,S=t2﹣t+6(0<t<3).(3)如图2,当EF⊥BO时,∵EF⊥CD,∴CD∥BO,∴∠ACD=90°,在Rt△ADC中,=cos∠BAO,∴=,t=,当EF⊥AB时,如图3,∵EF⊥CD,∴直线CD和直线AB重合,∴C点和A点重合,∴t=3.(4)①如图4,当0<t<,且且重叠部分为等腰梯形PEQM时,则∠PEQ=∠MQE,∵菱形CDMN,∴CD∥MN,∴∠MQE=∠CEQ,∵EF⊥CD,即∠CEF=90°,∴∠CEQ=45°,∴∠ACD=∠CEQ=45°,过D作DH⊥AC于H,则△DHC是等腰直角三角形,∴DH=HC,∴t=3﹣t﹣t,∴t=;②如图5,当<t<5,且重叠部分为等腰梯形EHNK时,同理可得∠CHE=45°,连接DHDH,∵EF垂直平分CD,∴CH=DH,∠DHE=∠CHE=45°,∴∠DHC=90°,∴DH=t,而CH=CO﹣HO=CO﹣(AO﹣AH)=t﹣(3﹣t),∴t﹣(3﹣t)=t,∴t=.16.【解答】解:(1)∵CD=10,点C的坐标为(﹣4,﹣4),∴点D的坐标为(﹣4,6),把点D(﹣4,6)代入得,m=4.∴直线l的解析式是;(2)∵,∴A(8,0),B(0,4),过点C画CH⊥y轴于H,则CH=OH=4,BH=8.在△AOB和△BHC中,∵AO=BH,∠AOB=∠BHC,BO=CH,∴△AOB≌△BHC,∴AB=BC,∠HBC=∠OAB,∴∠ABC=90°,∴△ABC是等腰直角三角形;(3)p(﹣4,﹣)或(﹣4,8)或(﹣4,﹣12)或(﹣4,﹣4)或(﹣4,4).17.【解答】解:(1)作PK⊥MN于K,则PK=KM=NM=2,∴KO=6,∴P(6,2);(2)①当点A落在线段OM上(可与点M重合)时,如图(一),此时0<b≤2,S=0;②当点A落在线段AK上(可与点K重合)时,如图(二),此时2<b≤3,设AC交PM于H,MA=AH=2b﹣4,∴S=(2b﹣4)2=2b2﹣8b+8,③当点A落在线段KN上(可与点N重合)时,如图(三),此时3<b≤4,设AC交PN于H,AN=AH=8﹣2b,∴S=S△PMN﹣S△ANH=4﹣2(4﹣b)2=﹣2b2+16b﹣28,④当点A落在线段MN的延长线上时,b>4,如图(四),S=4;(3)以OM为直径作圆,当直线y=﹣x+b(b>0)与圆相切时,b=+1,如图(五);当b≥4时,重合部分是△PMN,S=4设Q(x,b﹣x),因为∠OQM=90°,O(0,0),M(4,0)所以OQ2+QM2=OM2,即[x2+(b﹣x)2]+[(x﹣4)2+(b﹣x)2]=42,整理得x2﹣(2b+8)x+2b2=0,x2﹣(b+4)x+b2=0,根据题意这个方程必须有解,也就是判别式△≥0,即(b+4)2﹣5b2≥0,﹣b2+2b+4≥0,b2﹣2b﹣4≤0,可以解得 1﹣≤b≤1+,由于b>0,所以0<b≤1+.故0<b≤+1;(4)b的值为4,5,.∵点C、D的坐标分别为(2b,b),(b,b)当PC=PD时,b=4;当PC=CD时,b1=2(P、C、D三点共线,舍去),b2=5;当PD=CD时,b=8±2.18.【解答】解:(1)∵OA、OB的长分别是关于x的方程x2﹣14x+4(AB+2)=0的两个根,∴OA+OB=﹣=14,由已知可得,又∵OA2+OB2=AB2,∴(OA+OB)2﹣2OA•OB=AB2,即142﹣8(AB+2)=AB2,∴AB2+8AB﹣180=0,∴AB=10或AB=﹣18(不合题意,舍去),∴AB=10,∴x2﹣14x+48=0,解得x1=6,x2=8,∵OB>OA,∴OA=6,OB=8,∴tan∠BAO=.(2)∵S△PAQ=S四边形OQPB,∴S△PAQ=S△AOB,∵PQ∥BO,∴△PQA∽△BOA,∴,∴.∵AB=10,∴AP=5,又∵tan∠BAO=,∴sin∠BAO=,∴PQ=PA•sin∠BAO=.(3)存在,设AB的解析式是y=kx+b,则,解得:,则解析式是:y=﹣x+8,即4x+3y=24(*)①当∠PQM=90°时,由PQ∥OB且|PQ|=|MQ|此时M点与原点O重合,设Q(a,0)则P(a,a)有(a,a)代入(*)得a=.②当∠MPQ=90°,由PQ∥OB且|MP|=|PQ|设Q(a,0)则M(0,a),P(a,a)进而得a=247.③当∠PMQ=90°,由PQ∥OB,|PM|=|MQ|且|OM|=|OQ|=|PQ|设Q(a,0)则M(0,a)点P坐标为(a,2a)代入(*)得a=125.综上所述,y轴上有三个点M1(0,0),M2(0,247)和M3(0,125)满足使△PMQ为等腰直角三角形.。
专题55 一次函数中的构造等腰直角三角形(解析版)
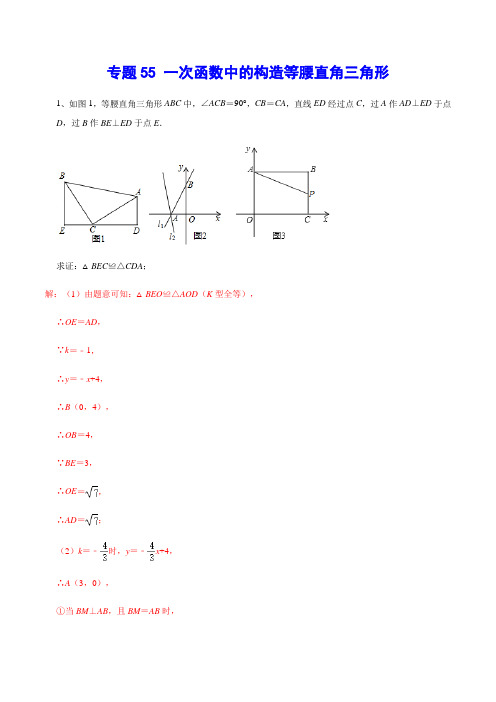
专题55 一次函数中的构造等腰直角三角形1、如图1,等腰直角三角形ABC中,∠ACB=90°,CB=CA,直线ED经过点C,过A作AD⊥ED于点D,过B作BE⊥ED于点E.求证:△BEC≌△CDA;解:(1)由题意可知:△BEO≌△AOD(K型全等),∴OE=AD,∵k=﹣1,∴y=﹣x+4,∴B(0,4),∴OB=4,∵BE=3,∴OE=,∴AD=;(2)k=﹣时,y=﹣x+4,∴A(3,0),①当BM⊥AB,且BM=AB时,过点M作MN⊥y轴,∴△BMN≌△ABO(AAS),∴MN=OB,BN=OA,∴MN=4,BN=3,∴M(4,7);②当AB⊥AM,且AM=AB时,过点M作x轴垂线MK,∴△ABO≌△AMK(AAS),∴OB=AK,OA=MK,∴AK=4,MK=3,∴M(7,3);③当AM⊥BM,且AM=BM时,过点M作MH⊥x轴,MG⊥y轴,∴△BMG≌△AHM(AAS),∴BG=AH,GM=MH,∴GM=MH,∴4﹣MH=MH﹣3,∴MH=,∴M(,);综上所述:M(7,3)或M(4,7)或M(,);(3)当k>0时,AO=,过点Q作QS⊥y轴,∴△ABO≌△BQS(AAS),∴BS=OA,SQ=OB,∴Q(4,4﹣),∴OQ=,∴当k=1时,QO最小值为4;当k<0时,Q(4,4﹣),∴OQ=,∴当k=1时,QO最小值为4,与k<0矛盾,∴OQ的最小值为4.2、已如,在平面直角坐标系中,点A的坐标为(6,0)、点B的坐标为(0,8),点C在y轴上,作直线AC.点B关于直线AC的对称点B′刚好在x轴上,连接CB′.(1)写出点B′的坐标,并求出直线AC对应的函数表达式;(2)点D在线段AC上,连接DB、DB′、BB′,当△DBB′是等腰直角三角形时,求点D坐标;(3)如图2,在(2)的条件下,点P从点B出发以每秒2个单位长度的速度向原点O运动,到达点O 时停止运动,连接PD,过D作DP的垂线,交x轴于点Q,问点P运动几秒时△ADQ是等腰三角形.解:(1)∵A的坐标为(6,0)、点B的坐标为(0,8),∴OA=6,OB=8,∵∠AOB=90°,∴AB=10,∵B与B'关于直线AC对称,∴AC垂直平分BB',∴BC=CB',AB'=AB=10,∴B'(﹣4,0),设点C(0,m),∴OC=m,∴CB'=CB=8﹣m,∵在Rt△COB'中,∠COB'=90°,∴m2+16=(8﹣m)2,∴m=3,∴C(0,3),设直线AC的解析式为y=kx+b(k≠0),把A(6,0),C(0,3)代入可得k=﹣,b=3,∴y=﹣x+3;(2)∵AC垂直平分BB',∴DB=DB',∵△BDB'是等腰直角三角形,∴∠BDB'=90°,过点D作DE⊥x轴,DF⊥y轴,∴∠DFO=∠DFB=∠DEB'=90°,∵∠EDF=360°﹣∠DFB﹣∠DEO﹣∠EOF,∠EOF=90°,∴∠EDF=90°,∴∠EDF=∠BDB',∴∠BDF=∠EDB',∴△FDB≌△EDB'(AAS),∴DF=DE,设点D(a,a)代入y=﹣x+3中,∴a=2,∴D(2,2);(3)同(2)可得∠PDF=∠QDE,∵DF=DE=2,∠PDF=∠QDE,∴△PDF≌△QDE(AAS),∴PF=QE,①当DQ=DA时,∵DE⊥x轴,∴QE=AE=4,∴PF=QE=4,∴BP=BF﹣PF=2,∴点P运动时间为1秒;②当AQ=AD时,∵A(6,0)、D(2,2),∴AD=2,∴AQ=2,∴PF=QE=2﹣4,∴BP=BF﹣PF=10﹣2,∴点P的运动时间为5﹣秒;③当QD=QA时,设QE=n,则QD=QA=4﹣n,在Rt△DEQ中,∠DEQ=90°,∴4+n2=(4﹣n)2,∴n=1.5,∴PF=QE=1.5,∴BP=BF+PF=7.5,∴点P的运动时间为3.75秒,∵0≤t≤4,∴t=3.75,综上所述:点P的运动时间为1秒或5﹣秒或3.75秒.3、定义:在平面直角坐标系中,对于任意P(x1,y1),Q(x2,y2),若点M(x,y)满足x=3(x1+x2),y=3(y1+y2),则称点M是点P,Q的“美妙点”.例如:点P(1,2),Q(﹣2,1),当点M(x,y)满足x=3×(1﹣2)=﹣3,y=3×(2+1)=9时,则点M(﹣3,9)是点P,Q的“美妙点”.(1)已知点A(﹣1,3),B(3,3),C(2,﹣2),请说明其中一点是另外两点的“美妙点”;(2)如图,已知点D是直线y=+2上的一点.点E(3,0),点M(x,y)是点D、E的“美妙点”.①求y与x的函数关系式;①若直线DM与x轴相交于点F,当①MEF为直角三角形时,求点D的坐标.解:(1)①3×(﹣1+2)=3,3×(3﹣2)=3,①点B是A、C的“美妙点”;(2)设点D(m,m+2),①①M是点D、E的“美妙点”.①x=3(3+m)=9+3m,y=3(0+m+2)=m+6,故m=x﹣3,①y=(x﹣3)+6=x+3;①由①得,点M(9+3m,m+6),如图1,当①MEF为直角时,则点M(3,4),①9+3m=3,解得:m=﹣2;①点D(﹣2,);当①MFE是直角时,如图2,则9+3m=m,解得:m=﹣,①点D(﹣,);当①EMF是直角时,不存在,综上,点D(﹣2,)或(﹣,).4、如图,过点A(1,3)的一次函数y=kx+6(k≠0)的图象分别与x轴,y轴相交于B,C两点.(1)求k的值;(2)直线l与y轴相交于点D(0,2),与线段BC相交于点E.(i)若直线l把①BOC分成面积比为1:2的两部分,求直线l的函数表达式;(①)连接AD,若①ADE是以AE为腰的等腰三角形,求满足条件的点E的坐标.解:(1)将点A的坐标代入一次函数y=kx+6并解得:k=﹣3;(2)一次函数y=﹣3x+6分别与x轴,y轴相交于B,C两点,则点B、C的坐标分别为:(2,0)、(0,6);(i)S①BCO=OB×CO=2×6=6,直线l把①BOC分成面积比为1:2的两部分,则S①CDE=2或4,而S①CDE=×CD×x E=4×x E=2或4,则x E=1或2,故点E(1,3)或(2,0),将点E的坐标代入直线l表达式并解得:直线l的表达式为:y=±x+2;(①)设点E(m,﹣3m+6),而点A、D的坐标分别为:(1,3)、(0,2),则AE2=(m﹣1)2+(3﹣3m)2,AD2=2,ED2=m2+(4﹣3m)2,当AE=AD时,(m﹣1)2+(3﹣3m)2=2,解得:m=或;当AE=ED时,同理可得:m=;综上,点E的坐标为:(,)或(,)或(,).5、建立模型:如图1,等腰Rt①ABC中,①ABC=90°,CB=BA,直线ED经过点B,过A作AD①ED于D,过C作CE①ED于E.则易证①ADB①①BEC.这个模型我们称之为“一线三垂直”.它可以把倾斜的线段AB和直角①ABC转化为横平竖直的线段和直角,所以在平面直角坐标系中被大量使用.模型应用:(1)如图2,点A(0,4),点B(3,0),①ABC是等腰直角三角形.①若①ABC=90°,且点C在第一象限,求点C的坐标;①若AB为直角边,求点C的坐标;(2)如图3,长方形MFNO,O为坐标原点,F的坐标为(8,6),M、N分别在坐标轴上,P是线段NF上动点,设PN=n,已知点G在第一象限,且是直线y=2x一6上的一点,若①MPG是以G为直角顶点的等腰直角三角形,请直接写出点G的坐标.解:(1)①过点C作CD①x轴于点D,①①BDC=90°=①AOB,①①BCD+①DCB=90°,①①ABC=90°,①①ABO+①DBC=90°,①①ABO=BCD,①AB=BC,①①AOB①①BDC(AAS),DC=OB=3,BD=OA=4,故点C(7,3);①若AB为直角边,则除了①的情况以外,另外一个点C(C′)与①中的C关于点B对称,故点C′(﹣1,﹣3);故点C的坐标为:(7,3)或(﹣1,﹣3);(2)如图2,当①MGP=90°时,MG=PG,过点P作PE①OM于E,过点G作GH①PE于H,①点E与点M重合,①GF=AB=4设G点坐标为(x,2x﹣6),6﹣(2x﹣6)=4,得x=4,易得G点坐标(4,2);如图3,当①MGP=90°时,MG=PG时,同理得G点坐标(,),综上可知,满足条件的点G的坐标分别为(4,2)或(,).6、如图1,直线l:y=x+2与x轴交于点A,与y轴交于点B.已知点C(﹣2,0).(1)求出点A,点B的坐标.(2)P是直线AB上一动点,且①BOP和①COP的面积相等,求点P坐标.(3)如图2,平移直线l,分别交x轴,y轴于交于点A1B1,过点C作平行于y轴的直线m,在直线m 上是否存在点Q,使得①A1B1Q是等腰直角三角形?若存在,请直接写出所有符合条件的点Q的坐标.解:(1)设y=0,则x+2=0,解得:x=﹣4,设x=0,则y=2,①点A的坐标为(﹣4,0),点B的坐标的坐标为(0,2);(2)①点C(﹣2,0),点B(0,2),①OC=2,OB=2,①P是直线AB上一动点,①设P(m,m+2),①①BOP和①COP的面积相等,①×2|m|=2×(|m|+2),解得:m=±4,当m=﹣4时,点P与点A重合,①点P坐标为(4,4);(3)存在;理由:如图1,①当点B1是直角顶点时,①B1Q=B1A1,①①A1B1O+①QB1H=90°,①A1B1O+①OA1B1=90°,①①OA1B1=①QB1H,在①A1OB1和①B1HQ中,,①①A1OB1①①B1HQ(AAS),①B1H=A1O,OB1=HQ=2,①B1(0,﹣2)或(0,2),当点B1(0,﹣2)时,Q(﹣2,2),当点B1(0,2)时,①B(0,2),①点B1(0,2)(不合题意舍去),①直线AB向下平移4个单位,①点Q也向上平移4个单位,①Q(﹣2,2),①当点A1是直角顶点时,A1B1=A1Q,①直线AB的解析式为y=x+2,由平移知,直线A1B1的解析式为y=x+b,①A1(﹣2b,0),B1(0,b),①A1B12=4b2+b2=5b2,①A1B1①A1Q,①直线A1Q的解析式为y=﹣2x﹣4b①Q(﹣2,4﹣4b),①A1Q2=(﹣2b+2)2+(4﹣4b)2=20b2+40b+20,①20b2﹣40b+20=5b2,①b=2或b=,①Q(﹣2,﹣4)或(﹣2,);①当Q是直角顶点时,过Q作QH①y轴于H,①A1Q=B1Q,①①QA1C1+①A1QC=90°,①A1QC+①CQB1=90°,①①QA1C=①CQB1,①m①y轴,①①CQB1=①QB1H,①①QA1C=①QB1H在①A1QC与①B1QH中,,①①A1QC①①B1QH(AAS),①CQ=QH=2,B1H=A1C,①Q(﹣2,2)或(﹣2,﹣2),即:满足条件的点Q为(﹣2,2)或(﹣2,﹣2)或(﹣2,12)或(﹣2,).7、如图1,等腰直角三角形ABC中,①ACB=90°,CB=CA,直线DE经过点C,过A作AD①DE于点D,过B作BE①DE于点E,则①BEC①①CDA,我们称这种全等模型为“K型全等”.(不需要证明)【模型应用】若一次函数y=kx+4(k≠0)的图象与x轴、y轴分别交于A、B两点.(1)如图2,当k=﹣1时,若点B到经过原点的直线l的距离BE的长为3,求点A到直线l的距离AD 的长;(2)如图3,当k=﹣时,点M在第一象限内,若①ABM是等腰直角三角形,求点M的坐标;(3)当k的取值变化时,点A随之在x轴上运动,将线段BA绕点B逆时针旋转90°得到BQ,连接OQ,求OQ长的最小值.解:(1)由题意可知:①BEO①①AOD(K型全等),①OE=AD,①k=﹣1,①y=﹣x+4,①B(0,4),①OB=4,①BE=3,①OE=,①AD=;(2)k=﹣时,y=﹣x+4,①A(3,0),①当BM①AB,且BM=AB时,过点M作MN①y轴,①①BMN①①ABO(AAS),①MN=OB,BN=OA,①MN=4,BN=3,①M(4,7);①当AB①AM,且AM=AB时,过点M作x轴垂线MK,①①ABO①①AMK(AAS),①OB=AK,OA=MK,①AK=4,MK=3,①M(7,3);①当AM①BM,且AM=BM时,过点M作MH①x轴,MG①y轴,①①BMG①①AHM(AAS),①BG=AH,GM=MH,①GM=MH,①4﹣MH=MH﹣3,①MH=,①M(,);综上所述:M(7,3)或M(4,7)或M(,);(3)当k>0时,AO=,过点Q作QS①y轴,①①ABO①①BQS(AAS),①BS=OA,SQ=OB,①Q(4,4﹣),①OQ=,①当k=1时,QO最小值为4;当k<0时,Q(4,4﹣),①OQ=,①当k=1时,QO最小值为4,与k<0矛盾,①OQ的最小值为4.8、【模型建立】(1)如图1,等腰直角三角形ABC中,∠ACB=90°,CA=CB,直线ED经过点C,过A作AD⊥ED于点D,过B作BE⊥ED于点E.求证:△CDA≌△BEC.【模型运用】(2)如图2,直线l1:y=x+4与坐标轴交于点A、B,将直线l1绕点A逆时针旋转90°至直线l2,求直线l2的函数表达式.【模型迁移】如图3,直线l经过坐标原点O,且与x轴正半轴的夹角为30°,点A在直线l上,点P为x轴上一动点,连接AP,将线段AP绕点P顺时针旋转30°得到BP,过点B的直线BC交x轴于点C,∠OCB=30°,点B到x轴的距离为2,求点P的坐标.证明:【模型建立】(1)∵AD⊥DE,BE⊥DE,∴∠D=∠E=90°∵∠ACB=90°,∴∠ACD=90°﹣∠BCE=∠CBE,且CA=BC,∠D=∠E=90°∴△CDA≌△BEC(AAS)【模型运用】(2)如图2,在l2上取D点,使AD=AB,过D点作DE⊥OA,垂足为E∵直线y=x+4与坐标轴交于点A、B,∴A(﹣3,0),B(0,4),∴OA=3,OB=4,由(1)得△BOA≌△AED,∴DE=OA=3,AE=OB=4,∴OE=7,∴D(﹣7,3)设l2的解析式为y=kx+b,得解得∴直线l2的函数表达式为:【模型迁移】(3)若点P在x轴正半轴,如图3,过点B作BE⊥OC,∵BE=2,∠BCO=30°,BE⊥OC∴BC=4,∵将线段AP绕点P顺时针旋转30°得到BP,∴AP=BP,∠APB=30°,∵∠APC=∠AOC+∠OAP=∠APB+∠BPC,∴∠OAP=∠BPC,且∠OAC=∠PCB=30°,AP=BP,∴△OAP≌△CPB(AAS)∴OP=BC=4,∴点P(4,0)若点P在x轴负半轴,如图4,过点B作BE⊥OC,∵BE=2,∠BCO=30°,BE⊥OC∴BC=4,∵将线段AP绕点P顺时针旋转30°得到BP,∴AP=BP,∠APB=30°,∵∠APE+∠BPE=30°,∠BCE=30°=∠BPE+∠PBC,∴∠APE=∠PBC,∵∠AOE=∠BCO=30°,∴∠AOP=∠BCP=150°,且∠APE=∠PBC,PA=PB∴△OAP≌△CPB(AAS)∴OP=BC=4,∴点P(﹣4,0)综上所述:点P坐标为(4,0)或(﹣4,0)9、如图1,在平面直角坐标系中,直线y=﹣x+b与x轴、y轴相交于A、B两点,动点C(m,0)在线段OA上,将线段CB绕着点C顺时针旋转90°得到CD,此时点D恰好落在直线AB上,过点D作DE⊥x 轴于点E.(1)求m和b的数量关系;(2)当m=1时,如图2,将△BCD沿x轴正方向平移得△B′C′D′,当直线B′C′经过点D时,求点B′的坐标及△BCD平移的距离;(3)在(2)的条件下,直线AB上是否存在一点P,以P、C、D为顶点的三角形是等腰直角三角形?若存在,写出满足条件的P点坐标;若不存在,请说明理由.解:(1)直线y=﹣x+b与y轴相交于B点,∴B(0,b)∴OB=b,∵点C(m,0)∴OC=m∵∠BCO+∠ECD=90°,∠BCO+∠OBC=90°,∴∠OBC=∠ECD.在△OBC和△ECD中,∴△OBC≌△ECD(AAS)∴BO=CE=b,DE=OC=m,∴点D(b+m,m)∴m=﹣(b+m)+b∴b=3m(2)∵m=1,∴b=3,点C(1,0),点D(4,1)∴直线AB解析式为:y=﹣x+3设直线BC解析式为:y=ax+3,且过(1,0)∴0=a+3∴a=﹣3∴直线BC的解析式为y=﹣3x+3,设直线B′C′的解析式为y=﹣3x+c,把D(4,1)代入得到c=13,∴直线B′C′的解析式为y=﹣3x+13,当y=3时,x=当y=0时,x=∴B′(,3),C'(,0)∴CC′=,∴△BCD平移的距离是个单位.(3)当∠PCD=90°,PC=CD时,点P与点B重合,∴点P(0,3)如图,当∠CPD=90°,PC=PD时,∵BC=CD,∠BCD=90°,∠CPD=90°∴BP=PD∴点P是BD的中点,且点B(0,3),点D(4,1)∴点P(2,2)综上所述,点P为(0,3)或(2,2)时,以P、C、D为顶点的三角形是等腰直角三角形.10、如图,已知一次函数y=﹣x+7与正比例函数y=x的图象交于点A,且与x轴交于点B.(1)求△AOB的面积:(2)在y轴上找一点C,使AC+BC最小,求最小值及C点坐标.(3)点P从O出发向B点以1个单位每秒的速度运动,点Q从B点出发向A点以同样的速度运动,两个点同时停止,当△BPQ为等腰三角形时,求Q点坐标.解:(1)∵一次函数y=﹣x+7与正比例函数y=x的图象交于点A,且与x轴交于点B.∴点B(7,0),﹣x+7=x∴x=3,∴点A(3,4)∴S△AOB=×7×4=14;(2)如图1,作点B关于y轴的对称点H(﹣7,0),连接AH,交y轴于点C,∴此时AC+BC最小值为AH,∵点A(3,4),点H(﹣7,0),∴AH==2,∴AC+BC最小值为2,设直线AH解析式为:y=kx+b,且过点A(3,4),点H(﹣7,0),∴,解得:∴直线AH解析式为:y=x+;(3)如图2,过点Q作QE⊥OB,∵以同样的速度运动,∴BQ=OP,∵一次函数y=﹣x+7与y轴交于点D,∴点D(0,7),∴OD=OB=7,且∠DOB=90°,∴∠DBO=45°,且QE⊥OB,∴∠QBE=∠EQB=45°,∴QE=BE,∴QB=QE=EB,若PB=QB,且OP=BQ,∴OP=PB==BQ,∴BE=EQ=,∴OE=7﹣,∴点Q(7﹣,),若QP=QB,且QE⊥OB,∴PE=BE,∵OB=7=OP+PE+BE,∴7=BE+2BE,∴BE==QE,∴OE=∴点Q(,),如图3,若BP=PQ,过点P作PF⊥BQ,∴BF=FQ=BQ,∵∠ABO=45°,PF⊥AB,∴∠FPB=∠ABO=45°,∴PF=BF,∴PB=BF,∴7﹣BQ=∴BQ=,∴BE=QE=,∴点Q坐标为(7﹣,).11、一边长为4正方形OACB放在平面直角坐标系中,其中O为原点,点A、B分别在x轴、y轴上,D为射线OB上任意一点.(1)如图1,若点D坐标为(0,2),连接AD交OC于点E,则△AOE的面积为;(2)如图2,将△AOD沿AD翻折得△AED,若点E在直线y=x图象上,求出E点坐标;(3)如图3,将△AOD沿AD翻折得△AED,DE和射线BC交于点F,连接AF,若∠DAO=75°,平面内是否存在点Q,使得△AFQ是以AF为直角边的等腰直角三角形,若存在,请求出所有点Q坐标;若不存在,请说明理由.解:(1)∵边长为4正方形OACB放在平面直角坐标系中,∴点A坐标(4,0),点C(4,4),∴直线OC解析式为:y=x,∵点D坐标为(0,2),点A坐标(4,0),∴直线AD解析式为:y=﹣x+2,∴解得:∴点E坐标(,)∴△AOE的面积=×4×=,故答案为:;(2)如图2,过点E作EH⊥OA,∵将△AOD沿AD翻折得△AED,∴AO=AE=4,设点E(a,a),∴OH=a,EH=a,∴AH=4﹣a,∵AE2=EH2+AH2,∴16=a2+(4﹣a)2,∴a=0(舍去),a=,∴点E(,)(3)∵将△AOD沿AD翻折得△AED,∴∠DAO=∠DAE=75°,OA=AE,∠DOA=∠DEA=90°,∴∠OAE=150°,AE=AC,∠ACF=∠AED=90°,∴∠CAE=60°,∵AE=AC,AF=AF,∴Rt△AEF≌Rt△ACF(HL)∴∠CAF=∠EAF=30°,且AC=4,∴CF=,∵△AFQ是以AF为直角边的等腰直角三角形,∴若∠AFQ=90°,AF=FQ,如图3,过点Q作QN⊥BF,∴∠NQF+∠QFN=90°,且∠QFN+∠AFC=90°,∴∠NQF=∠AFC,且∠ACF=∠QNF=90°,QF=AF,∴△QNF≌△FCA(AAS)∴QN=CF=,AC=NF=4,∴点Q(,4+)同理可求:Q'(8+,4﹣),若∠FAQ=90°,AF=AQ时,同样方法可求,Q''(0,),Q'''(8,﹣)。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
一次函数之等腰直角三角形的存在性(讲义)➢课前预习
1.如图所示的正方形网格中,网格线的交点称为格点.已知A,
B 是两个格点,若点
C 也是图中的格点,且使得△ABC 为等
腰直角三角形,则符合条件的点C 有个.
2.用铅笔做讲义第1 题,并将计算、演草保留在讲义上,先看知
识点睛,再做题,思路受阻时(某个点做了2~3 分钟)重复上述动作,若仍无法解决,课堂重点听.
➢知识点睛
1.存在性问题的处理思路
①分析不变特征
分析所求图形中的定点、定线、定角等不变特征.
②分类、画图
结合所求图形的形成因素,依据其判定、定义等确定分类,并画出符合题意的图形.
通常先尝试画出其中一种情形,分析解决后,再类比解决其他情形.
③求解、验证
围绕不变特征、画图依据来设计方案进行求解;验证时,要回归点的运动范围,画图或推理,判断是否符合题意.
注:复杂背景下的存在性问题往往需要研究背景图形,几何背景往往研究点,线,角;函数背景研究点坐标,表达式等.
2.等腰直角三角形存在性的特征分析及特征下操作要点:
三角形的三个顶点分别为直角顶点进行分类,在直角的基础上,再考虑等腰,通常借助构造弦图模型进行求解.
➢精讲精练
1.如图,直线y=-2x+6 与x 轴、y 轴分别交于点A,B,点P 是
第一象限内的一个动点,若以A,B,P 为顶点的三角形是等腰直角三角形,则点P 的坐标为.
2.如图,直线y =-1
x +b 与x 轴、y 轴分别交于点A,B,点C 3
在直线y =-1
x +b 上,且其纵坐标为1,△OAC 的面积为
3
.
3 2
(1)求直线y =-1
x +b 的表达式及点C 的坐标;3
(2)点P 是第二象限内的一个动点,若△ACP 是等腰直角三角形,则点P 的坐标为.
3.如图,在平面直角坐标系中,点A 的坐标为(2,0),点P 是y
轴正半轴上一个动点,Q是直线x=3 上的一个动点,若△APQ 为等腰直角三角形,则点P 的坐标为.
4.如图,直线y=3x+4 与y 轴交于点A,点P 是直线x=6 上的一
个动点,点Q 是直线y=3x+4 上的一个动点,且点Q 在第一象限,若△APQ 为等腰直角三角形,则点Q 的坐标为
.
5. 如图,直线 l 1:y =x +6 与 x 轴、y 轴分别交于点 A ,B ,直线 l 2:y = - 1 x - 3 与 x 轴交于点 A ,点 M 是线段 AB 上的一动点,
2
过点 M 作 y 轴的平行线交直线 l 2 于点 N ,在 y 轴上是否存在点 P ,使△MNP 为等腰直角三角形?若存在,求出点 P 的坐标;若不存在,请说明理由.
【参考答案】
➢ 课前预习
1. 6
➢ 精讲精练
1. (9,3),(6,9),( 9 , 9 )
2 2
2. (1) y = - 1 x -1,C (-6,1)
3
(2)(-2,3),(-5,4),(-4,2)
3. (0,1),(0,3),(0,4)
4. (2,10),(3,13),( 3 , 17 )
2 2 5. 存在,点 P 的坐标为(0, 12 ),(0, - 6 ),(0, 6 )
5 5 7。
