2018考研线性代数框架图公式、李永乐经典结论题型建议汇总.pdf
李永乐.线性代数

线性代数李永乐辅导笔记【例题1】B =⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡50030021a ,A 2-2AB = E ,r(AB -2BA +3A ) =( ) (A )1 (B )2 (C )3 (D )与a 有关 【解】 ∵ A (A -2B ) = E ∴ A 可逆,且A -1= A -2B⇒ A (A -2B ) = (A -2B ) A (A A-1= A -1A )⇒ AB = BA那么,AB -2BA +3A = 3A -AB = A (3E -B )又,A 可逆,知r(AB -2BA +3A ) = r(A (3E -B )) = r(3E -B )∀a 有|3E -B |=0,又3E -B 有二阶子式不得零,从而r(3E -B ) = 2.【例题2】A m ×n ,ε1,ε2,…,εt 是Ax = 0的基础解系,α是Ax = b 的一个解. (I)证明α,α+ε1,α+ε2,…,α+εt 线性无关.(II)证明Ax = b 的任意一个解都可以由α,α+ε1,α+ε2,…,α+εt 线性表出.【分析】ε1,ε2,…,εt 是Ax =0的基础解系,那么ε1,ε2,…,εt 必定线性无关,从而证明α,α+ε1,α+ε2,…,α+εt 线性无关可以用定义法。
【证】(I)(用定义,重组,同乘)设 k 0α+k 1 (α+ε1)+k 2(α+ε2)+…+ k T (α+εt )=0 (1) 即 (k 0+k 1+k 2+…+k T )α+k 1ε1+k 2ε2+…+k T εt =0(2)由A α=b , A εi =0(i =1,…,t ),用A 左乘(2),有(k 0+k 1+k 2+…+k t )A α+k 1A ε1+k 2A ε2+…+k t A εt =0即 (k 0 +k 1+k 2 +…+k t )b =0 又b ≠0,有k 0+k 1+k 2+…+k T =0(3)带入(2)有 k 1ε1+k 2ε2+…+k t εt =0,而ε1,ε2,…,εt 是Ax =0的基础解系,那么ε1,ε2,…,εt 必定线性无关, 从而k 1 =k 2 =…=k t =0,带入(3)有k 0=0.所以 k 0=k 1=k 2=…=k t =0⇒α,α+ε1,α+ε2,…,α+εt 线性无关. (或用秩)∵ε1,ε2,…,εt 线性无关,α是Ax =b 的解⇒α不能由ε1,ε2,…,εt 线性表出.⇒x 1ε1+x 2ε2+…+x t εt =α无解⇒r(ε1,ε2,…,εt )≠r(ε1,ε2,…,εt ,α)∵r(ε1,ε2,…,εt ) =t ⇒r(ε1,ε2,…,εT ,α)=t +1⇒r(α,α+ε1,α+ε2,…,α+εt )=t +1⇒α,α+ε1,α+ε2,…,α+εt 线性无关.(II)设β是Ax =b 的任意一个解,则β-α是Ax =0的解. 从而 β-α=l 1ε1+l 2ε2+…+l t εt .⇒β=α+l 1ε1+l 2ε2+…+l t εt⇒β=(1-l1-l 2 -…-l t )α+l 1ε1+l 2ε2+…+l t εt即β可由α,α+ε1,α+ε2,…,α+εt 表出.【评注】本题考查矩阵逆的概念以及矩阵的乘法.设矩阵A -n 阶,B -n 阶,若AB = BA =E ,则称矩阵A 可逆,且B 为A 的逆矩阵.由此有A A -1= A -1A .【例题3】A m ×n ,r(A )=n ,α1,α2,…,αs 是n 维列向量.证明:α1,α2,…,αs 线性无关的充分必要条件是A α1,A α2,…,A αs 线性无关.【证】必要性(用定义)设k 1A α1+k 2A α2+…+k s A αs =0,即A (k 1α1+k 2α2+… +k s αs )=0. 由A m ×n ,r(A )=n ⇒Ax =0只有零解.故k 1α1+k 2α2+…+k s αs =0,又α1,α2,…,αs 线性无关⇒k 0=k 1=k 2=…=k s =0. 从而A α1,A α2,…,A αs 线性无关. 充分性(用秩)因为A α1,A α2,…,A αs =A (α1,α2,…,αs ),所以r(A α1,A α2,…,A αs )=r(A (α1,α2,…,αs ))≤r(α1,α2,…,αs )由A α1,A α2,…,A αs 线性无关知r(A α1,A α2,…,A αs )=s.而r(α1,α2,…,αs )≤s ,从而r(α1,α2,…,αs )=s ⇒α1,α2,…,αs 线性无关.【例题4】设A =[α1,α2,α3,α4],Ax =β的通解是[1,-2,1,-1] T+k[1,3,2,0]T,B =[α3,α2,α1,β+α4],γ=α1-3α2+5α3,(I) α1能否由α2,α3线性表出? (II) α4能否由α1,α2,α3线性表出? (III) Bx =γ求的通解.【分析】由非齐次方程组解的结构知道对应的齐次方程组的解的结构.并且由于系数矩阵没有明确给出,所以要从解的结构抽象地求解方程组.用观察法得到基础解系,注意基础解系是线性无关的. 【证】(I) Ax =β解的结构知r(A )=3.由A ⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡0231=0 ⇒α1+3α2+2α3=0⇒α1能由α2,α3线性表出.(II) 设x 1α1+x 2α2+x 3α 3 =α4由(I)知r(α1,α2,α3)<3,而r(α1,α2,α3,α4)=4,知方程组无解,故α4不能由α1,α2,α3线性表出.(III)由A ⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡--1121=β⇒α 1-2α 2 +α3-α4=β,那么B =[α3,α2,α1,β+α4]=[α3,α2,α1,α1-2α2+α3-α4]⇒ r(B )=4.从而n -r(B )=2.【评注】本题考查向量小组的线性相关的证明和线性表出的证明.考查了方程组基础解系的概念:设有向量小组η1,η2,…,ηt 满足: (1) A ηi = 0(i =1,…,t ),即ηi 是Ax = 0的解. (2) Ax = 0的任意一个解都可以由η1,η2,…,ηt 表出. (3) η1,η2,…,ηt 线性无关.那么称η1,η2,…,ηt 为Ax = 0的基础解系.也就是说若η1,η2,…,ηt 是Ax = 0的基础解系,那么η1,η2,…,ηt 必满足上述3条。
2018年考研数学大纲解析:线性代数与概率论复习建议

2018年考研数学大纲解析:线性代数与概率论复习建议的更新!2018年考研数学大纲解析:线性代数与概率论复习建议2018考研大纲已公布,第一时间收录并整理了最新的考研大纲,为考生全方位解读2018考研大纲的最新变动并指导后续备考。
今年考研数学大纲并无变化,对考试并无影响。
下面老师将带领大家对大纲进行解读,并对线性代数与概率论提出一些复习上的建议。
今年大纲知识点无论数学一、数学二还是数学三都没有变化。
这样的话从知识本身来说同学们可以按照原计划进行。
成建军老师在全年复习规划时讲过,数学科目稳定,希望大家一定要稳定扎实按复习规划进行。
大家知道考研数学历来是整个考研所有学科当中最为稳定的一门,考研数学的知识经过多年考察已经达到了非常稳定的命题结构、知识,不会有巨大的变化。
尤其在考前一百多天时间里。
考研数学有三个科目构成,高等数学、线性代数与概率论与数理统计,高等数学占比很大,她是考研数学的半壁江山,因此复习周期很长,且需要将基础打牢。
许多考生在复习数学时,对高数的复习都很重视。
但不少考生却对线代与概率的复习重视不够。
事实上相比高数来看,线代与概率更容易拿分。
但从历年考试数据来看,线代与概率得分率偏低,平均分通常在十几分。
这个原因,一方面由于高数在考试中花费时间太多,后面的线代与概率大题没时间作答,而更重要在于,概率与线代复习不到位,题目不会做。
根据历年考生概率与线代复习中存在的问题,成建军老师将带领大家对线性代数与概率论的相关考点进行解读,并对线性代数与概率论提出一些复习上的建议。
我相信有许多同学在刚一开始学习线性代数和概率论与数理统计时有难处,认为看书举步维艰,对此我想谈一下我的看法,希望对那些还在这两门课上迷茫的同学能有一些启发。
首先谈一下我的看法:事实上线性代数应该是考研数学三门课中最好拿分的,但是这门课有一个特点,就是入门难,但是一旦入门就一通百通,这门课由于思维上与高数大不相同,所以一上来会很不适应,总体而言6章内容环环相扣,所以很多同学一上来看第一章发现内容涉及到第五章,看到第二章发现竟有第4章的知识点,无法形成完整的知识网络,自然无法入门,总的来说线代6章内容可分为三个部分逐个攻破,首先行列式和矩阵,这是基础,第二向量与方程组,第三特征值与特征向量,这三个内容联系得相当紧密,必须逐个攻破,这样以两章为单位,每个单位中出现的知识点定理罗列出来,找到他们彼此的关系,构建属于你的知识网络,这一部分有哪些板块,每个板块有哪些定义知识点,比如行列式的定义,矩阵的定义各是什么,你是怎么理解的,向量与方程组有什么联系与区别,这些最基础的一定要搞清。
2018年考研数学(高数、线代、概率论)最全公式手册

dy (ln x) 1 x
1 dx x ln a d (ln x) 1 dx x
特例 y ln x (5) y sin x (6) y cos x (7) y tan x (8) y cot x (9) y sec x (10) y csc x
y cos x y sin x
x x0
f ( x) f ( x0 ) x x0
(2)
2 函数 f ( x) 在 x0 处的左、右导数分别定义为: 左导数:
f ( x0 ) lim
x 0
f ( x0 x) f ( x0 ) f ( x) f ( x0 ) lim , ( x x0 x) x x0 x x x0
x 的复合函数.例如
1 , y 2 , ln y , e y 等均是 x 的复合函数. y
F ( x, y) dy ,其中, Fx( x, y) , x dx Fy( x, y )
对 x 求导应按复合函数连锁法则做. (2)公式法.由 F ( x, y) 0 知
Fy( x, y) 分别表示 F ( x, y) 对 x 和 y 的偏导数
常用的等阶无穷小:当x 0时 sin x arcsin x tan x x, arctan x ln(1 x) ex 1
1 cos x
1 2 x 2 1 1 (1 x) n 1 x n
无穷小的性质 (1) 有限个无穷小的代数和为无穷小 (2) 有限个无穷小的乘积为无穷小 (3) 无穷小乘以有界变量为无穷小 Th 在同一变化趋势下,无穷大的倒数为无穷小;非零的 无穷小的倒数为无穷大
设函数f ( x)在x x0处可导,则f ( x)在M ( x0 , y0 )处的
(word完整版)线性代数重要知识点及典型例题答案,推荐文档

线性代数知识点总结第一章 行列式二三阶行列式N 阶行列式:行列式中所有不同行、不同列的n 个元素的乘积的和n nn nj j j j j j j j j nij a a a a ...)1(21212121)..(∑-=τ(奇偶)排列、逆序数、对换行列式的性质:①行列式行列互换,其值不变。
(转置行列式TD D =) ②行列式中某两行(列)互换,行列式变号。
推论:若行列式中某两行(列)对应元素相等,则行列式等于零。
③常数k 乘以行列式的某一行(列),等于k 乘以此行列式。
推论:若行列式中两行(列)成比例,则行列式值为零; 推论:行列式中某一行(列)元素全为零,行列式为零。
④行列式具有分行(列)可加性⑤将行列式某一行(列)的k 倍加到另一行(列)上,值不变 行列式依行(列)展开:余子式ij M 、代数余子式ij j i ij M A +-=)1(定理:行列式中某一行的元素与另一行元素对应余子式乘积之和为零。
克莱姆法则:非齐次线性方程组 :当系数行列式0≠D 时,有唯一解:)21(n j DD x j j ⋯⋯==、齐次线性方程组 :当系数行列式01≠=D 时,则只有零解 逆否:若方程组存在非零解,则D 等于零 特殊行列式:①转置行列式:332313322212312111333231232221131211a a a a a a a a a a a a a a a a a a → ②对称行列式:ji ij a a =③反对称行列式:ji ij a a -= 奇数阶的反对称行列式值为零④三线性行列式:333122211312110a a a a a a a 方法:用221a k 把21a 化为零,。
化为三角形行列式 ⑤上(下)三角形行列式:行列式运算常用方法(主要)行列式定义法(二三阶或零元素多的) 化零法(比例)化三角形行列式法、降阶法、升阶法、归纳法、第二章 矩阵n (零矩阵、负矩阵、行矩阵、列矩阵、n 阶方阵、相等矩阵) ---------交换、结合律 数乘n m ij ka kA *)(=---------分配、结合律乘法nm lkj ik n l kj l m ik b a b a B A *1**)()(*)(*∑==注意什么时候有意义一般AB=BA ,不满足消去律;由AB=0,不能得A=0或B=0 转置A A T T =)( TT T B A B A +=+)( T T kA kA =)( TT T A B AB =)((反序定理) 方幂:2121k k k kA AA +=2121)(k k k k A A +=对角矩阵:若AB 都是N 阶对角阵,k 是数,则kA 、A+B 、 数量矩阵:相当于一个数(若……)单位矩阵、上(下)三角形矩阵(若……) 对称矩阵 反对称矩阵阶梯型矩阵:每一非零行左数第一个非零元素所在列的下方 注:把分出来的小块矩阵看成是元素N 阶方阵,若存在N 阶矩阵B 的AB=BA=I 则称A 是可逆的,|A|=0、伴随矩阵)2.、非零k 乘某一行(列)3、将某行(列)的K 初等变换不改变矩阵的可逆性 初等矩阵都可逆倍乘阵 倍加阵) ⎪⎪⎭⎫ ⎝⎛=O OO I D rr矩阵的秩r(A):满秩矩阵 降秩矩阵 若A 可逆,则满秩 若A 是非奇异矩阵,则r (AB )=r (B ) 初等变换不改变矩阵的秩求法:1定义2转化为标准式或阶梯形矩阵与行列式的联系与区别:都是数表;行列式行数列数一样,矩阵不一样;行列式最终是一个数,只要值相等,就相等,矩阵是一个数表,对应元素相等才相等;矩阵n ij n ij a k ka )()(=,行列式nij n n ij a k ka =逆矩阵注:①AB=BA=I 则A 与B 一定是方阵 ②BA=AB=I 则A 与B 一定互逆; ③不是所有的方阵都存在逆矩阵;④若A 可逆,则其逆矩阵是唯一的。
考研数学《线性代数》考点知识点总结
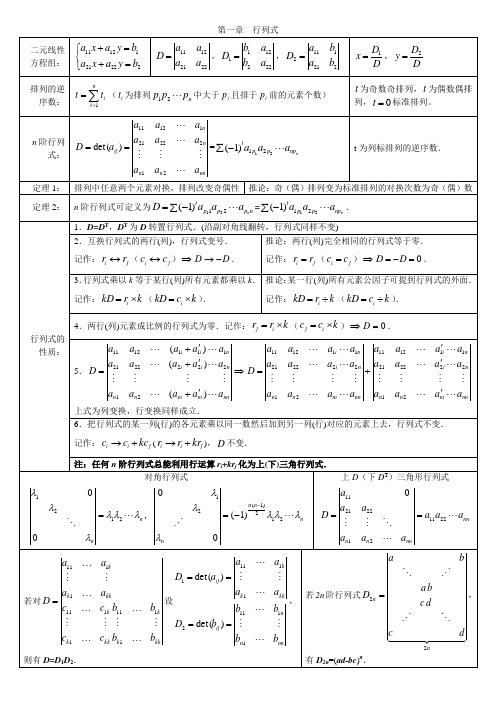
记作: ri rj ( ci cj ) D D 0 .
3.行列式乘以 k 等于某行(列)所有元素都乘以 k. 推论:某一行(列)所有元素公因子可提到行列式的外面.
记作: kD ri k ( kD ci k ).
记作: kD ri k ( kD ci k ).
行列式的 性质:
a2i a2n
a21
a22
a2i a2n
an1 an2 (ani ani ) ann
an1 an2 ani ann an1 an2 ani ann
上式为列变换,行变换同样成立.
6.把行列式的某一列(行)的各元素乘以同一数然后加到另一列(行)对应的元素上去,行列式不变.
记作: ci ci kcj ( ri ri krj ), D 不变.
n
aki Akj
k 1
Dij
D, 0,
当i 当i
j, n
j;
或
k 1
aik
Ajk
Dij
D, 0,
当i 当i
j, j; 其中ij
1, 0,
当i j, 当i j.
1 1 11
范德蒙德 行列式:
x1 Dn x12
x2 x22
x3 xn
x32 xn2 = (xi x j ) .证明用数学归纳法.
定理 2:
n 阶行列式可定义为 D (1)ta a p11 p2 2 apnn = (1)ta1p1a2 p2 anpn .
1.D=DT,DT 为 D 转置行列式.(沿副对角线翻转,行列式同样不变)
2.互换行列式的两行(列),行列式变号.
推论:两行(列)完全相同的行列式等于零.
记作: ri rj ( ci c j ) D D .
【2018最新】2018考研数学线代复习指导-范文模板 (3页)

本文部分内容来自网络整理,本司不为其真实性负责,如有异议或侵权请及时联系,本司将立即删除!== 本文为word格式,下载后可方便编辑和修改! ==2018考研数学线代复习指导在考研数学中线代既难又简单,那么在进行线代的复习时都有哪些方法呢?下面就和小编一起来看看吧。
2018考研数学线代复习指导线性代数总共分为六章。
第一章行列式本章的考试重点是行列式的计算,考查形式有两种:一是数值型行列式的计算,二是抽象型行列式的计算。
另外数值型行列式的计算不会单独的考大题,考选择填空题较多,有时出现在大题当中的一问或者是在大题的处理其他问题需要计算行列式,题目难度不是很大。
主要方法是利用行列式的性质或者展开定理即可。
而抽象型行列式的计算主要:利用行列式的性质、利用矩阵乘法、利用特征值、直接利用公式、利用单位阵进行变形、利用相似关系。
06、08、10、12年、13年的填空题均是抽象型的行列式计算问题,14年选择考了一个数值型的矩阵行列式,15、16年的数一、三的填空题考查的是一个n行列式的计算,。
今年数一、数二、数三这块都没有涉及。
第二章矩阵本章的概念和运算较多,而且结论比较多,但是主要以填空题、选择题为主,另外也会结合其他章节的知识点考大题。
本章的重点较多,有矩阵的乘法、矩阵的秩、逆矩阵、伴随矩阵、初等变换以及初等矩阵等。
其中06、09、11、12年均考查的是初等变换与矩阵乘法之间的相互转化,10年考查的是矩阵的秩,08年考的则是抽象矩阵求逆的问题,这几年考查的形式为小题,而13年的两道大题均考查到了本章的知识点,第一道题目涉及到矩阵的运算,第二道大题则用到了矩阵的秩的相关性质。
14的第一道大题的第二问延续了13年第一道大题的思路,考查的仍然是矩阵乘法与线性方程组结合的知识,但是除了这些还涉及到了矩阵的分块。
16年只有数二了矩阵等价的判断确定参数。
第三章向量本章是线代里面的重点也是难点,抽象、概念与性质结论比较多。
考研数学线性代数常用公式

考研数学线性代数常用公式数学考研考前必背常考公式集锦。
希望对考生在暑期的复习中有所帮助。
本文内容为线性代数的常考公式汇总。
1、行列式的展开定理行列式的值等于其任何一行(或列)所有元素与其对应的代数余子式乘积之和,即A= a i1 A i1+ a i2 A i2+...+ a in A in( i =1, 2,..., n)= a1j A1j+ a 2j A2j+...+ a nj A nj( j =1, 2,..., n)推论:行列式的一行(或列)所有元素与另一行(或列)对应元素的代数余子式的乘积之和为零,即n∑a ij A kj= a i1 A k1+ a i2 A k2+...+ a in A kn=0,(i≠k )j=1n∑a ji A jk= a1i A1k+ a2i A2k+...+ a ni A nk=0(i≠k )j=12、设 A =(a ij)m⨯n,B =(b ij)n⨯k(注意 A 的列数和 B 的行数相等),定义矩阵nC =(c ij)m⨯k,其中c ij=a i1b1j+a i2b2j+...+a in b nj=∑a ik b kj,称为矩阵 A 与矩阵 B 的k =1的乘积,记作 C = AB .如果矩阵A为方阵,则定义An=A⋅A...A为矩阵 A 的 n 次幂.n个A不成立的运算法则AB≠BAAB=O≠>A =O或B=O3、设 A 为n阶方阵,A*为它的伴随矩阵则有 AA *= A * A = A E .设 A 为n阶方阵,那么当 AB = E 或 BA = E 时,有 B -1 = A4、对单位矩阵实施一次初等变换得到的矩阵称之为初等矩阵.由于初等变换有三种,初等矩阵也就有三种:第一种:交换单位矩阵的第 i 行和第 j 行得到的初等矩阵记作E ij,该矩阵也⎛ 0 0 1 ⎫ 可以看做交换单位矩阵的第 i 列和第 j 列得到的.如 E 1,3 0 1 0 ⎪= ⎪ .1 0 0 ⎪⎝ ⎭第二种:将一个非零数 k 乘到单位矩阵的第 i 行得到的初等矩阵记作 E i ( k ) ;该矩 阵 也 可 以 看 做 将 单 位 矩 阵 第 i 列 乘 以 非 零 数 k 得 到 的 . 如⎛ 1 0 0 ⎫E 2 (-5) 0 -5 0 ⎪ = ⎪ .0 0 1 ⎪⎝ ⎭第三种:将单位矩阵的第 i 行的 k 倍加到第 j 行上得到的初等矩阵记作 E ij ( k ) ;该矩阵也可以看做将单位矩阵的第 j 列的 k 倍加到第 i 列上得到的.如⎛ 1 0 0 ⎫ E 3,2 (-2) 0 1 -2 ⎪= ⎪ .0 0 1 ⎪⎝ ⎭注:1)初等矩阵都只能是单位矩阵一次初等变换之后得到的.2)对每个初等矩阵,都要从行和列的两个角度来理解它,这在上面的定义中已经说明了.尤其需要注意初等矩阵 E ij ( k ) 看做列变换是将单位矩阵第 j 列的k 倍加到第 i 列,这一点考生比较容易犯错.5、矩阵 A 最高阶非零子式的阶数称之为矩阵 A 的秩,记为 r ( A ) .1) r ( A ) = r ( A T ) = r ( k A ), k ≠ 0 ;2) A ≠ O ⇔ r (A ) ≥ 1;3) r ( A ) = 1 ⇔ A ≠ O 且 A 各行元素成比例;4)设 A 为 n 阶矩阵,则 r ( A ) = n ⇔ A ≠ 0 . 6、线性表出设 α1 , α 2 ,...,αm 是 m 个 n 维 向 量 , k 1 , k 2 ,...k m 是 m 个 常 数 , 则 称k 1α1 + k 2α 2 + ... + k m αm 为向量组α1 , α 2 ,...,αm 的一个线性组合.设 α1,α2 ,...,αm 是 m 个 n 维向量, β 是一个 n 维向量,如果 β 为向量组α1 , α2 ,...,αm的一个线性组合,则称向量β可以由向量组α1 , α2 ,...,αm线性表出.线性相关设α1 , α2 ,...,αm是m个n维向量,如果存在不全为零的实数k1 , k2 ,..., k m,使得k1α1+ k 2α2+...+ k mαm=0,则称向量组α1,α2,...,αm线性相关.如果向量组α1 , α2 ,...,αm不是线性相关的,则称该向量组线性无关.与线性表出与线性相关性有关的基本定理定理1:向量组α1 , α2 ,...αm线性相关当且仅当α1 , α2 ,...αm中至少有一个是其余m-1 个向量的线性组合.定理2:若向量组α1 , α2 ,...αm线性相关,则向量组α1 , α2 ,..., αm ,αm+1也线性相关.注:本定理也可以概括为“部分相关⇒整体相关”或等价地“整体无关⇒部分无关”.定理3:若向量组α1 , α2 ,...αm线性无关,则向量组α1 , α2 ,...αm的延伸组⎛α⎫ ⎛α⎫⎛α⎫也线性无关.1⎪ , 2⎪,..., m⎪⎝β1⎭ ⎝β2 ⎭⎝βm ⎭定理4:已知向量组α1 , α2 ,...αm线性无关,则向量组α1 , α2 ,...αm , β线性相关当且仅当β可以由向量组α1,α2 ,...αm线性表出.定理 5:阶梯型向量组线性无关.定理6:若向量组α1 , α2 ,...,αs可以由向量组β1 , β2 ,..., βt线性表出,且α1 , α2 ,...,αs线性无关,则有s≤t.注:本定理在理论上有很重要的意义,是讨论秩和极大线性无关组的基础.定理内容也可以等价的描述为:若向量组α1 ,α2 ,...,αs可以由向量组β1 , β2 ,..., βt线性表出,且 s > t ,则α1,α2,...,αs线性相关.对于这种描述方式,我们可以把定理内容简单地记为:“多数被少数线性表出,则必相关.”定理7:n +1个n维向量必然线性相关.7、线性方程组解的存在性设 A =(α1,α2,...,αn),其中α1,α2,...,αn为 A 的列向量,则线性方程组 Ax = b 有解⇔向量 b 能由向量组α1,α2,...,αn线性表出;⇔r (α1,α2,...,αn)= r (α1,α2,...,αn,b );⇔r ( A )= r ( A, b)线性方程组解的唯一性当线性方程组 Ax = b 有解时, Ax = b 的解不唯一(有无穷多解)⇔线性方程组的导出组 Ax =0有非零解;⇔向量组α1 , α2 ,...,αn线性相关;⇔r (α1,α2,...,αn)< n ;⇔r ( A )< n .注:1)注意该定理成立的前提条件是线性方程组有解;也就是说,仅告知r (A )< n 是不能得到 Ax = b 有无穷多解的,也有可能无解.2)定理 2是按照 Ax = b 有无穷多解的等价条件来总结的,请考生据此自行写出 Ax = b 有唯一解的条件.8、特征值和特征向量:设 A 为 n 阶矩阵,λ是一个数,若存在一个 n 维的非零列向量α使得关系式 Aα = λα成立.则称λ是矩阵 A 的特征值,α是属于特征值λ的特征向量.称为矩阵 A 的特征多项式.设 E 为 n 阶单位矩阵,则行列式λE - A注:1)要注意:特征向量必须是非零向量;2)等式 Aα = λα也可以写成(A - λE)α =0,因此α是齐次线性方程组( A - λE ) x =0的解,由于α ≠0,可知( A - λE ) x =0是有非零解的,故A - λE =0;反之,若 A - λE =0,那么齐次线性方程组( A - λE ) x =0有非零解,可知存在α ≠ 0 使得(A-λE)α = 0,也即Aα = λα.由上述讨论过程可知:λ是矩阵 A 的特征值的充要条件是 A - λE =0(或λE- A =0),而特征值λ的特征向量都是齐次线性方程组( A - λE ) x =0的非零 解.3)由于λE - A 是 n 次多项式,可知 A - λE =0有 n 个根(包括虚根),也即 n 阶矩阵有 n 个特征值;任一特征值都有无穷多特征向量9、矩阵的相似对角化定理1: n 阶矩阵 A 可相似对角化的充要条件是矩阵 A 存在 n 个线性无关的特征向量.同时,在等式 A = P ΛP-1中,对角矩阵Λ的元素为 A 的 n 个特征值,可逆矩阵 P 的列向量为矩阵 A 的 n 个线性无关的特征向量,并且 P 中特征向量的排列顺序与Λ中特征值的排列顺序一致.推论:设矩阵 A 有 n 个互不相同的特征值,则矩阵 A 可相似对角化.定理2: n 阶矩阵 A 可相似对角化的充要条件是对任意特征值λ,λ线性无关的特征向量个数都等于λ的重数.推论: n 阶矩阵 A 可相似对角化的充要条件是对任意特征值λ,n - r (λE - A)=λ的重数.10、设 A 为实对称矩阵( A T= A ),则关于 A 的特征值与特征向量,我们有如下的结论:定理1: A 的所有特征值均为实数,且 A 的的所有特征向量均为实数.定理2: A 属于不同特征值的特征向量必正交.定理3:A 一定有 n 个线性无关的特征向量,即 A 可以对角化.且存在正交矩阵 Q ,使得 Q -1 AQ = Q T AQ = diag (λ1,λ2,...,λn),其中λ1,λ2,...,λn为矩阵 A 的特征值.我们称实对称矩阵可以正交相似于对角矩阵.n n11、如果二次型∑∑a i j x i x j中,只含有平方项,所有混合项 x i x j(i ≠ j)的系i=1j =1数全为零,也即形如 d1 x12+ d 2 x22+...+ d n x n2,则称该二次型为标准形。
2018考研线性代数真题解析_毙考题

2018考研线性代数真题解析2018年的考研线性代数一共是5道考题,两个选择题,一个填空题,两个解答题。
今年一共考了7道题,但今年数学一、二、三的选择题和解答题考得完全一样,区别仅在于填空题各不相同,下面对今年的线代考试做如下分析。
第一个选择题,即数一、三的第5题,数二的第7题,相似矩阵判定,2016,2017都以选择题考相似矩阵的判定,2014考证明矩阵相似,本题的难点在于题干所给矩阵不能对角化,所以做题时有两个思路,一个是排除法利用相似时的四相同排除掉不相似的,但这个题还要用到相似时,矩阵多项式也相似,即用到了四相似,所以有的同学可能想不到。
另一思路是利用相似的矩阵相同的特征值应该有相同个数的无关特征向量。
第二个选择题是考矩阵的秩,最简单的方法是利用向量组表示判定的三转化,考虑矩阵方程,利用矩阵方程有解马上得出系数矩阵的秩等于广义增广矩阵的秩。
填空题数一是利用向量的关系得出对应的特征值,然后求行列式;数二、数三是同一类题,利用向量组的线性表示建立相似的背景,然后求特征值。
两道大题数一、数二、数三完全一模一样,第一道大题的第一问和2000年数三的那道题极为类似,2005年数一也考过求类似方程的解,其本质是求解带参数的齐次方程组,第二问是根据参数讨论求规范形,有两种思路,配方法或者求特征值。
第二道大题的难点在于有的同学可能没懂题目说的是什么意思,其实题目就是告诉你这两个矩阵等价,即可化为已知秩求参数,第二问和2014年的一模一样,求解系数矩阵不可逆的矩阵方程。
综上所述,相对于前几年的线性代数题目来说,今年的线性代数题目难度相比去年有所提高,表现为以下特点:1.命题角度新颖。
同一个知识点从不同的角度来考,线代很大的特点之一就是知识点纵横交错,前后联系紧密,同一个点有很多不同的说法。
2.综合性提高。
实际上这次题很多都以前考过,或者干脆把以前的几个真题综合一下形成新的考题。
3.注重基础,考查全面。
基本上线代六章的内容全部都考到了,而且大部分都是考基本的计算,计算量也不算很大,但对同学们的计算能力要求较高。
考研数学线性代数知识点总结

考研数学线性代数知识点总结线性代数是考研数学中的重要组成部分,对于很多考生来说,它具有一定的难度。
但只要掌握了关键的知识点和方法,就能在考试中取得较好的成绩。
以下是对考研数学线性代数的知识点总结。
一、行列式行列式是线性代数中的基本概念之一。
1、二阶和三阶行列式的计算方法要熟练掌握,通过对角线法则可以轻松计算。
2、 n 阶行列式的定义和性质需要理解清楚。
例如,行列式的某一行(列)元素乘以同一数后,加到另一行(列)的对应元素上,行列式的值不变。
3、行列式按行(列)展开定理也是重点,它可以将高阶行列式转化为低阶行列式来计算。
二、矩阵矩阵是线性代数的核心内容。
1、矩阵的运算,包括加法、数乘、乘法以及矩阵的转置。
要特别注意矩阵乘法的规则和不满足交换律的特点。
2、逆矩阵的概念和求法至关重要。
判断矩阵是否可逆,以及通过伴随矩阵或初等变换来求逆矩阵。
3、矩阵的秩是一个关键概念,它反映了矩阵中线性无关的行(列)向量的个数。
4、分块矩阵的运算和应用也需要掌握,它可以简化一些复杂矩阵的计算。
三、向量向量是线性代数中的重要工具。
1、向量组的线性相关性是常见考点。
判断向量组是线性相关还是线性无关,以及理解相关和无关的性质。
2、向量组的秩与极大线性无关组要弄清楚它们的概念和求法。
3、向量空间的基、维数和坐标等概念也需要了解。
四、线性方程组线性方程组是线性代数的重点应用。
1、线性方程组有解的判定条件,通过系数矩阵的秩和增广矩阵的秩来判断。
2、齐次线性方程组基础解系的求法,要熟练掌握通过初等行变换将系数矩阵化为行最简形。
3、非齐次线性方程组的通解结构,由一个特解加上齐次线性方程组的通解组成。
五、矩阵的特征值和特征向量这部分内容在考研中经常出现。
1、特征值和特征向量的定义和计算方法,通过求解特征方程来得到特征值,再代入方程求解特征向量。
2、相似矩阵的概念和性质,相似矩阵具有相同的特征值。
3、矩阵可对角化的条件,以及如何将矩阵对角化。
【精品】线性代数各章知识点及脉络图(含例题)-假期预习必备

一、行列式知识结构网络图概念性质展开式计算证明0A =应用经转置行列式的值不变;某行有公因数k ,可把k 提到行列式外;某行所有元素都是两个数的和,则可写成两个行列式之和; 两行互换行列式变号;某行的k 倍加至另一行.行列式的值不变;不同行、不同列的n 个元素之积的代数和1nn ik ik k D a A ==∑(按i 行展开)1nn kj kj k D a A ==∑(按j 行展开)余子式、代数余子式给定(i ,j )元的值未给定(i ,j )元的值化三角形-加边法、爪型行列式;公式法-特殊行列式、范德蒙德行列式; 递推、数学归纳法;等用行列式性质计算; 用矩阵性质计算; 用方阵的特征值;等克拉默法则;判断方阵的可逆,利用伴随几种求逆矩阵; 线性相关性的判定;求矩阵的秩,并判断线性方程组的解存在情况; 求方阵的特征值。
()n n R n ⨯<A ;0是方阵A 的特征值;=-A A行列式行列式是线性代数中的重要工具,在求解线性方程组、求逆矩阵、判断向量组的线性相关性、求矩阵的特征值、判断二次型的正定性等方面都要用到.本章的重点是应用行列式的性质和展开定理计算行列式.行列式的计算除了利用性质及展开定理外,还有三角化法、升阶法、递推法和数学归纳法等,计算方法多,技巧性强,这是难点所在.要掌握好这些方法,首先必须具体分析所求行列式元素分布的规律,针对其特点采取适当的方法;其次是要注意总结、积累经验,不断提高运算能力.行列式的性质【例】:已知531,252,234都是9的倍数,利用行列式的性质(而不是展开),证明522353124也是9的倍数。
解答:522353124231321010r r ,r r ++522353531252234139r 5229353582726【例】:如果除最后一行外,从每一行减去后面的一行,而从最后一行减去原先的第一行,问行列式值如何变化?解答:设原行列式为⎪⎪⎪⎭⎫ ⎝⎛=n A αα 1det ,则新的行列式为⎪⎪⎪⎪⎪⎪⎭⎫ ⎝⎛----=-113221det ααααααααn n n B , ()00,,3,2det 11321113221=⎪⎪⎪⎪⎪⎪⎭⎫⎝⎛---=+⎪⎪⎪⎪⎪⎪⎭⎫ ⎝⎛----=--ααααααααααααααn n n i n n n n i r r B特殊行列式1、(主)对角行列式、上(下)三角行列式1111111111221122221111111niii nnnnnna a a a a a a a a a a a a a a a ====∏2、(次)对角行列式、上(下)三角行列式()()12111111212212121111111n n n n n nn,n,n ,n ,n iii n n,n nnn n a a a a a a a a a a aa a a a a ----=-===-∏3、分块三角行列式 形式简记为:*==⨯*A O A AB BO B,()1k n⨯*==-⨯*O A AA B BB O4、范德蒙德行列式()211112112122222221212121111111121121111111,,,11n n n n n n n n n n n n n n n n n n nn n x x x x x x x x x x f x x x x x x x x x x x x x x x x x --------------==()()121,,,n ijn i j f x x x x x ≥>≥=-∏ ()()()()()1213211212111,,,n nj n j j j n j n j j j f x x x xx xx xx x x --≥≥-≥≥≥≥≥≥=-⋅---∏∏∏∏()()()()1221n n n n n n x x x x x x x x --=----()()()()()()()12131211323121n n n n n n x x x x x x x x x x x x x x -------------认识范德蒙德行列式可以将n 阶范德蒙德行列式看成式关于n 个变量12,,,n x x x 的函数,即()12,,,n n D f x x x =。
李永乐线性代数考研复习资料。复习提纲+经典例题解答

Page 6
ABC Amber CHM Conver t er Tr i al ver si on, ht t p: / / www. pr ocesst ext . com/ abcchm. ht ml
清华大学考研辅导强化班课程 《线性代数》
同理将Dn中ak2,ak3,… ,akn分别换成c2,c3,… ,cn 则记
而中
中的
是相同的。因此通过计算行列式 解:由以上分析有:
即可求出
Pa ge 1 2
ABC Amber CHM Conver t er Tr i al ver si on, ht t p: / / www. pr ocesst ext . com/ abcchm. ht ml
思路:本行列式元素的特点:每一行与第一行只有两个元素不同,因 丝山 谝恍械模ǎ?)倍分别加到其它各行上。 小结:①对于箭头形行列式,总是用主对角线元素去化第1列(或第1 校 怪 晌 希ㄏ拢┤ 切涡辛惺健R蛭 弥鞫越窍咴 厝セ 闶 ,后边的化零过程不会破坏前面已化成的零元素(请读者思考,为什 从姓饷春玫慕峁 湓 蚴鞘裁矗浚 ②例1.6中,将D中第1列元素化为0(a 11除外)与化第1行元素为0,其难度相同,但对例1.7化第1列元素为0 比化第1行元素来得简便,读者可仔细揣摩其中的区别。
例1.11
例1.12
思路:数字较大,直接计算麻烦。观察可知其第2列与第1 列相差不大,第3列与第2列的3倍相近。 例1.13
本题行列式中没有元素1,若直接化成上(下)三角形, 突岢鱿址质 虼讼冉 ?行的(-1)倍加到第1行,得 ½a11=-1,然后再化零。 (七)、利用行列式是一个多项式,可以分解因式的性质 来计算行列式。 若f(x)是x的一个多项式,显然当f(a)=0时,f(x)应有(x -a)的因式,如f(x)=x2-5x+6,则f(2)=0,f(3)=0,故f (x)=K(x-2)(x-3),再利用x=x0可求出K, 或用某个特定的xm项对比系数定出K。 例1.14
精编考研线性代数知识框架图资料

考研线性代数知识框架图()000,nT A r A n A A Ax x Ax A Ax A A A E ββ==⇔∀≠≠≠⇔∀∈=≅可逆 的列(行)向量线性无关 的特征值全不为0 只有零解 ,0总有唯一解 是正定矩阵 R 12,s iA p p p p nB AB E AB E⎧⎪⎪⎪⎪⎪⎪⎪⎨⎪⎪⎪⎪⎪=⋅⋅⋅⎪==⎪⎩ 是初等阵存在阶矩阵使得 或 注:全体n 维实向量构成的集合nR 叫做n 维向量空间.()0A r A n A A A Ax A λ<=⇔==不可逆 0的列(行)向量线性相关 0是的特征值 有非零解,其基础解系即为关于0的⎧⎪⎪⎪⎨⎪⎪⎪⎩特征向量注:()()0a b r aE bA n aE bA aE bA x λ+<⎧⎪+=⇔+=⎨⎪⎩0有非零解=-⎫⎪≅⎪−−−→⎬⎪⎪⎭具有向量组等价矩阵等价()反身性、对称性、传递性矩阵相似()矩阵合同() √ 关于12,,,n e e e ⋅⋅⋅:①称为n的标准基,n中的自然基,单位坐标向量152p 教材;②12,,,n e e e ⋅⋅⋅线性无关; ③12,,,1n e e e ⋅⋅⋅=; ④tr =E n ;⑤任意一个n 维向量都可以用12,,,n e e e ⋅⋅⋅线性表示.1212121112121222()1212()n n nn n j j j n j j nj j j j n n nna a a a a a D a a a a a a τ==-∑1√ 行列式的计算:①行列式按行(列)展开定理:行列式等于它的任一行(列)的各元素与其对应的代数余子式的乘积之和. 推论:行列式某一行(列)的元素与另一行(列)的对应元素的代数余子式乘积之和等于零.②若A B 与都是方阵(不必同阶),则==()mn A OA A O A BO BO BBO A AA B B O B O*==**=-1③上三角、下三角、主对角行列式等于主对角线上元素的乘积.④关于副对角线:(1)211212112111()n n nnn n n n n n n a Oa a a a a a a Oa O---*==-1⑤范德蒙德行列式:()1222212111112n ij nn i j n n n nx x x xx x x x x x x ≥≥≥---=-∏111由m n ⨯个数排成的m 行n 列的表111212122212n n m m mn a a a a a a A a a a ⎛⎫⎪ ⎪= ⎪⎪⎝⎭称为m n ⨯矩阵.记作:()ij m n A a ⨯=或m nA ⨯()1121112222*12n Tn ijnnnn A A A A A A A A A A A ⎛⎫ ⎪ ⎪== ⎪ ⎪⎝⎭,ij A 为A 中各个元素的代数余子式. √ 逆矩阵的求法:① 1A A A *-= 注: 1a b d b c d c a ad bc --⎛⎫⎛⎫= ⎪ ⎪--⎝⎭⎝⎭1②1()()AE E A -−−−−→初等行变换③1231111213a a a a a a -⎛⎫⎛⎫⎪ ⎪=⎪ ⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭3211111213a a a a a a -⎛⎫⎛⎫⎪ ⎪=⎪ ⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭√ 方阵的幂的性质:m n m nA A A+= ()()m nmnA A =√ 设,,m n n s A B ⨯⨯A 的列向量为12,,,n ααα⋅⋅⋅,B 的列向量为12,,,s βββ⋅⋅⋅,则m sAB C ⨯=⇔()()1112121222121212,,,,,,s s n s n n ns b b b b b b c c c b b b ααα⎛⎫⎪ ⎪⋅⋅⋅= ⎪⎪⎝⎭⇔i iA c β= ,(,,)i s =1,2⇔iβ为iAx c =的解⇔()()()121212,,,,,,,,,s s s A A A A c c c ββββββ⋅⋅⋅=⋅⋅⋅=⇔12,,,s c c c 可由12,,,n ααα⋅⋅⋅线性表示. 同理:C 的行向量能由B 的行向量线性表示,T A 为系数矩阵.√ 用对角矩阵Λ左乘一个矩阵,相当于用Λ的对角线上的各元素依次乘此矩阵的行向量; 用对角矩阵Λ右乘一个矩阵,相当于用Λ的对角线上的各元素依次乘此矩阵的列向量. √ 两个同阶对角矩阵相乘只用把对角线上的对应元素相乘.√ 分块矩阵的转置矩阵:TTT TT A B A C C D BD ⎛⎫⎛⎫= ⎪ ⎪⎝⎭⎝⎭分块矩阵的逆矩阵:111A A B B ---⎛⎫⎛⎫=⎪ ⎪⎝⎭⎝⎭ 111A B B A---⎛⎫⎛⎫= ⎪ ⎪⎝⎭⎝⎭1111A C A A CB O B OB ----⎛⎫⎛⎫= ⎪ ⎪⎝⎭⎝⎭ 1111A O A O CB B CA B ----⎛⎫⎛⎫= ⎪ ⎪-⎝⎭⎝⎭分块对角阵相乘:11112222,A B A B A B ⎛⎫⎛⎫==⎪ ⎪⎝⎭⎝⎭11112222A B AB A B ⎛⎫= ⎪⎝⎭分块对角阵的伴随矩阵:***A BA B AB ⎛⎫⎛⎫=⎪ ⎪⎝⎭⎝⎭√ 矩阵方程的解法(0A ≠):设法化成AX B XA B ==(I) 或 (II)A B E X −−−−→初等行变换(I)的解法:构造()()T T T TA XB X X=(II)的解法:将等式两边转置化为, 用(I)的方法求出,再转置得√ 0Ax =与0Bx =同解(,A B 列向量个数相同),则:① 它们的极大无关组相对应,从而秩相等; ② 它们对应的部分组有一样的线性相关性; ③ 它们有相同的内在线性关系.√ 矩阵m n A ⨯与l n B ⨯的行向量组等价⇔齐次方程组0Ax =与0Bx =同解⇔PA B =(左乘可逆矩阵P );101p 教材 矩阵m n A ⨯与l n B ⨯的列向量组等价⇔PQ B =(右乘可逆矩阵Q ). √ 判断12,,,s ηηη是0Ax =的基础解系的条件:① 12,,,s ηηη线性无关; ② 12,,,s ηηη都是0Ax =的解;③ ()s n r A =-=每个解向量中自由未知量的个数.√ 一个齐次线性方程组的基础解系不唯一.① 零向量是任何向量的线性组合,零向量与任何同维实向量正交. ② 单个零向量线性相关;单个非零向量线性无关. ③ 部分相关,整体必相关;整体无关,部分必无关.④ 原向量组无关,接长向量组无关;接长向量组相关,原向量组相关.⑤ 两个向量线性相关⇔对应元素成比例;两两正交的非零向量组线性无关114p 教材.⑥ 向量组12,,,n ααα⋅⋅⋅中任一向量i α(1≤i ≤)n 都是此向量组的线性组合.⑦ 向量组12,,,n ααα⋅⋅⋅线性相关⇔向量组中至少有一个向量可由其余n -1个向量线性表示. 向量组12,,,n ααα⋅⋅⋅线性无关⇔向量组中每一个向量i α都不能由其余n -1个向量线性表示. ⑧ m 维列向量组12,,,n ααα⋅⋅⋅线性相关()r A n ⇔<; m 维列向量组12,,,n ααα⋅⋅⋅线性无关()r A n ⇔=. ⑨ ()r A A O =⇔=0.⑩ 若12,,,n ααα⋅⋅⋅线性无关,而12,,,,n αααβ⋅⋅⋅线性相关,则β可由12,,,n ααα⋅⋅⋅线性表示,且表示法唯一. ⑪ 矩阵的行向量组的秩=列向量组的秩=矩阵的秩. 行阶梯形矩阵的秩等于它的非零行的个数.可画出一条阶梯线,线的下方全为0;每个台阶只有一行,台阶数即是非零行的行数,阶梯线的竖线后面的第一个元素非零.当非零行的第一个非零元为1,且这些非零元所在列的其他元素都是0⑫ 矩阵的行初等变换不改变矩阵的秩,且不改变列向量间的线性关系;矩阵的列初等变换不改变矩阵的秩,且不改变行向量间的线性关系. 即:矩阵的初等变换不改变矩阵的秩. √ 矩阵的初等变换和初等矩阵的关系:对A 施行一次初等行变换得到的矩阵,等于用相应的初等矩阵左乘A ; 对A 施行一次初等列变换得到的矩阵,等于用相应的初等矩阵右乘A .如果矩阵A 存在不为零的r 阶子式,且任意r +1阶子式均为零,则称矩阵A 的秩为r .记作()r A r =向量组12,,,n ααα的极大无关组所含向量的个数,称为这个向量组的秩.记作12(,,,)n r αααA 经过有限次初等变换化为B . 记作:A B =12,,,n ααα⋅⋅⋅和12,,,n βββ⋅⋅⋅可以相互线性表示. 记作:()()1212,,,,,,n n αααβββ⋅⋅⋅=⋅⋅⋅⑬ 矩阵A 与B 等价⇔PAQ B =,,P Q 可逆⇔()(),r A r B A B =≠>作为向量组等价,即:秩相等的向量组不一定等价.矩阵A 与B 作为向量组等价⇔1212(,,,)(,,,)n n r r αααβββ⋅⋅⋅=⋅⋅⋅=1212(,,,,,,)n n r αααβββ⋅⋅⋅⋅⋅⋅⇒ 矩阵A 与B 等价.⑭ 向量组12,,,s βββ⋅⋅⋅可由向量组12,,,n ααα⋅⋅⋅线性表示⇔AX B =有解⇔12(,,,)=n r ααα⋅⋅⋅1212(,,,,,,)n s r αααβββ⋅⋅⋅⋅⋅⋅⇒12(,,,)s r βββ⋅⋅⋅≤12(,,,)n r ααα⋅⋅⋅.⑮ 向量组12,,,s βββ⋅⋅⋅可由向量组12,,,n ααα⋅⋅⋅线性表示,且s n >,则12,,,s βββ⋅⋅⋅线性相关.向量组12,,,s βββ⋅⋅⋅线性无关,且可由12,,,n ααα⋅⋅⋅线性表示,则s ≤n .⑯ 向量组12,,,s βββ⋅⋅⋅可由向量组12,,,n ααα⋅⋅⋅线性表示,且12(,,,)s r βββ⋅⋅⋅12(,,,)n r ααα=⋅⋅⋅,则两向量组等价;p 教材94,例10 ⑰ 任一向量组和它的极大无关组等价.向量组的任意两个极大无关组等价. ⑱ 向量组的极大无关组不唯一,但极大无关组所含向量个数唯一确定. ⑲ 若两个线性无关的向量组等价,则它们包含的向量个数相等.⑳ 若A 是m n ⨯矩阵,则{}()min ,r A m n ≤,若()r A m =,A 的行向量线性无关;若()r A n =,A 的列向量线性无关,即:12,,,n ααα⋅⋅⋅线性无关.√ 矩阵的秩的性质:①()A O r A ≠⇔若≥1 0≤()m n r A ⨯≤min(,)m n ②()()()TTr A r A r A A == p 教材101,例15③()()r kA r A k =≠ 若0④()r A B ±≤()()r A r B + {}max (),()r A r B ≤(,)r A B ≤()()r A r B + p 教材70⑤ ()()A O O A r r A r B O B B O ⎛⎫⎛⎫==+⎪ ⎪⎝⎭⎝⎭ ()()A C r r A r B O B ⎛⎫≠+ ⎪⎝⎭⑥()r AB ≤{}min (),()r A r B⑦ ,,()()()m n n s A B r AB r A r B ⨯⨯=⇒+若且0≤n ⑧()()A r AB r B ⇒=若可逆()()B r AB r A ⇒=若可逆⑨若0()()()m n Ax r A n r AB r B ⨯⇔=⎧=⇒⎨=⎩ 只有零解且A 在矩阵乘法中有左消去律0AB B AB AC B C =O ⇒=⎧⎨=⇒=⎩;若()()()n s r B n r AB r B ⨯=⇒= 且B 在矩阵乘法中有右消去律.√ 初等矩阵的性质:1212,,,0,,,()()A n n Ax n Ax A Ax r A r A Ax n βαααβαααβββ⇔=<⇔⇒⇔=−−−−−→=⇔=⇔=⇔==当为方阵时有无穷多解 表示法不唯一线性相关有非零解0 可由线性表示有解有唯一组解 1212,,,0()(),,,()(A n n Ax A r A r A Ax r A r αααββαααβ⎧⎪⎪⎪⎪⎨⎪⎪⇔⎪⇒⇔=−−−−−→≠⇒⎪⎩⇔≠⇔=⇔<当为方阵时表示法唯一 线性无关只有零解0克莱姆法则 不可由线性表示无解)()1()A r A r A ββ⎧⎪⎨⎪⇔+=⎩注:Ax Ax ββ⇒=<≠⇒=<≠有无穷多解其导出组有非零解有唯一解其导出组只有零解Ax β=1122n n x x x αααβ+++=1112111212222212,,n n m m mn n m a a a x b a a a x b A x a a a x b β⎛⎫⎛⎫⎛⎫⎪ ⎪ ⎪ ⎪ ⎪ ⎪=== ⎪ ⎪ ⎪⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭ 12,,2,,j j j mj j n αααα⎛⎫ ⎪ ⎪== ⎪ ⎪ ⎪⎝⎭11212(,,,)n n x x x αααβ⎛⎫ ⎪ ⎪= ⎪ ⎪⎝⎭线性方程组解的性质:1212121211221212(1),0,(2)0,,(3),,,0,,,,,(4),0,(5),,0(6k k k k Ax Ax k k Ax k Ax Ax Ax Ax Ax ηηηηηηηηηλλλληληληγβηγηβηηβηη=+⎫⎪=⎪⎬=⎪⎪++⎭==+==-= 是的解也是它的解 是的解对任意也是它的解齐次方程组 是的解对任意个常数 也是它的解 是的解是其导出组的解是的解是的两个解是其导出组的解211212112212112212),0(7),,,,100k k k k k k k Ax Ax Ax Ax Ax ηβηηηηηηβληληληβλλλληληληλλλ⎧⎪⎪⎪⎪⎪⎪⎪⎪⎨⎪⎪⎪=⇔-=⎪=⎪⎪++=⇔++=⎪⎪++=⇔++=⎩ 是的解则也是它的解是其导出组的解 是的解则也是的解 是的解 √ 设A 为m n ⨯矩阵,若()r A m =,⇒()()r A r A β=⇒Ax β=一定有解, 当m n <时,一定不是唯一解⇒<方程个数未知数的个数向量维数向量个数,则该向量组线性相关.m 是()()r A r A β和的上限.n 个n 维线性无关的向量,两两正交,每个向量长度为1.(,)0αβ=.1α==.√ 内积的性质: ① 正定性:(,)0,(,)0αααααο≥=⇔=且 ② 对称性:(,)(,)αββα=③ 双线性:1212(,)(,)(,)αββαβαβ+=+ 1212(,)(,)(,)ααβαβαβ+=+(,)(,)(,)c c c αβαβαβ==E A λ-.()E A f λλ-=.√ ()f λ是矩阵A 的特征多项式⇒()f A O =E A λ-=0. Ax x Ax x λ=→ 与线性相关√12n A λλλ= 1ni A λ=∑tr ,A tr 称为矩阵A √ 上三角阵、下三角阵、对角阵的特征值就是主对角线上的n 各元素.√ 若0A =,则λ=0为A 的特征值,且0Ax =的基础解系即为属于λ=0的线性无关的特征向量.√ ()1r A =⇔A 一定可分解为A =()1212,,,n n a a b b b a ⎛⎫ ⎪ ⎪ ⎪ ⎪⎝⎭、21122()n n A a b a b a b A =+++,从而A 的特征值为:11122n n A a b a b a b λ==+++tr ,23n λλλ====0 p 指南358.√ 若A 的全部特征值12,,,n λλλ,()f A 是多项式,则:① ()f A 的全部特征值为12(),(),,()n f f f λλλ;12()()()()n f A f f f λλλ=② 若A 满足()0f A =,则A 的任何一个特征值必满足()i f λ=0.√ 设1110()m m m m f x a x a x a x a --=++++,对n 阶矩阵A 规定:1110()m m m m f A a A a A a A a E --=++++为A 的一个多项式.√ 1231122,T A mm k kAa b aA bE A A AA A Aλλλλλλλλλλλ-*⎧⎪++⎪⎪⎨= 是的特征值则:分别有特征值 .⎪⎪⎪⎪⎪⎩ √ 1231122,A mm k kAa b aA bEAx A x A A A λλλλλλλλλλ-*⎧⎪++⎪⎪⎪⎨=⎪⎪⎪⎪⎩是关于的特征向量则也是关于的特征向量. √ 2,mA A 的特征向量不一定是A 的特征向量. √ A 与TA 有相同的特征值,但特征向量不一定相同.1B P AP -= (P 为可逆矩阵) 记为:A B1B P AP -= (P 为正交矩阵)A 与对角阵Λ相似. 记为:AΛ (称Λ是A√ A 可相似对角化⇔()i i n r E A k λ--= i k 为i λ的重数⇔A 恰有n 个线性无关的特征向量. 这时,P 为A 的特征向量拼成的矩阵,1P AP -为对角阵,主对角线上的元素为A 的特征值.设i α为对应于i λ的线性无关的特征向量,则有:121212112212(,,,)(,,,)(,,,)(,,,)n n n n n n PPA A A A λλααααααλαλαλααααλΛ⎛⎫⎪⎪=== ⎪ ⎪⎝⎭. 注:当i λ=0为A 的特征值时,A 可相似对角化⇔i λ的重数()n r A =-= 0Ax =基础解系的个数. √ 若A 可相似对角化,则其非零特征值的个数(重数重复计算)()r A =. √ 若n 阶矩阵A 有n 个互异的特征值,则A 可相似对角化.√ 若A Λ⇒k A =1k P P -Λ=,1211()()()()()n A P P P P ϕλϕλϕϕϕλ--⎛⎫⎪⎪=Λ= ⎪ ⎪⎝⎭√ 相似矩阵的性质:① A B =tr tr② A B = 从而,A B 同时可逆或不可逆 ③ ()()r A r B = ④TT AB ;11A B -- (若,A B 均可逆);**A B⑤kk AB (k 为整数);()()f A f B ,()()f A f B =⑥,A B A B CD C D ⎛⎫⎛⎫⇒ ⎪ ⎪⎝⎭⎝⎭⑦E A E B λλ-=-,从而,A B 有相同的特征值,但特征向量不一定相同.注:x 是A 关于0λ的特征向量,1P x -是B 关于0λ的特征向量.√ 数量矩阵只与自己相似.√ 对称矩阵的性质: ① 特征值全是实数,特征向量是实向量;② 不同特征值对应的特征向量必定正交;注:对于普通方阵,不同特征值对应的特征向量线性无关;③ 必可用正交矩阵相似对角化,即:任一实二次型可经正交变换化为标准形; ④ 与对角矩阵合同,即:任一实二次型可经可逆线性变换化为标准形;⑤ 一定有n 个线性无关的特征向量,A 可能有重的特征值,该特征值i λ的重数=()i n r E A λ--).TAA E =√ A 为正交矩阵⇔A 的n 个行(列)向量构成n的一组标准正交基.√ 正交矩阵的性质:① 1TA A -=;② TTAA A A E ==;③ 正交阵的行列式等于1或-1;④ A 是正交阵,则TA ,1A -也是正交阵; ⑤ 两个正交阵之积仍是正交阵;⑥ A 的行(列)向量都是单位正交向量组.1211(,,,)n nTn ij i j i j f x x x x Ax a x x ====∑∑ ij ji a a =,即A 为对称矩阵,12(,,,)T n x x x x =T B C AC =. 记作:A B (,,A B C 为对称阵为可逆阵)二次型的规范形中正项项数pr p -;2p r -. (r 为二次型的秩)√ 两个矩阵合同的充分必要条件是:它们有相同的正负惯性指数. √ 两个矩阵合同的充分条件是:AB√ 两个矩阵合同的必要条件是:()()r A r B =√ 12(,,,)Tn f x x x x Ax =经过正交变换合同变换可逆线性变换x Cy =化为21ni i f d y =∑√ 二次型的标准形不是唯一的,与所作的正交变换有关,但非零系数的个数是由()r A +正惯性指数负惯性指数唯一确定的.√ 当标准形中的系数i d 为-1或0或1时,√ 实对称矩阵的正(负)惯性指数等于它的正(负)特征值的个数.√ 惯性定理:任一实对称矩阵A 与唯一对角阵1111⎛⎫⎪ ⎪ ⎪ ⎪-⎪⎪ ⎪- ⎪ ⎪ ⎪ ⎪ ⎪⎝⎭合同. √ 用正交变换法化二次型为标准形:① 求出A 的特征值、特征向量;② 对n 个特征向量正交化、单位化;③ 构造C (正交矩阵),作变换x Cy =,则1112221()()TT T T Tn n n y d y y d y Cy A Cy y C ACY y C ACY y d y -⎛⎫⎛⎫⎛⎫ ⎪⎪⎪ ⎪⎪⎪=== ⎪ ⎪⎪ ⎪ ⎪⎪⎝⎭⎝⎭⎝⎭新的二次型为21ni if d y =∑,Λ的主对角上的元素i d 即为A 的特征值.123,,ααα线性无关,112122111313233121122()()()()()()T TT T T Tβααββαβββαβαββαββββββ=⎧⎪⎪⎪⎪=-⎨⎪⎪=--⎪⎪⎩正交化 单位化:111βηβ=222βηβ= 333βηβ= 技巧:取正交的基础解系,跳过施密特正交化。
2018李永乐线性代数冲刺班讲义

参考答案 1 -6 0 0 ù é ê ú 1 2 0 ù é ê ú êú 0 0 ú ê0 1 ê ú ( ) ( ) 1. 1 1 8, 2 2 0 2. 4. 0 0 -1ú 5. a =-1 6. a =1 -2 3. ê ú ê 5 5 2 -2 ú ê0 0 ê ú ê ú ë 0 -1 0 û ê ú ê 5 5 ú ë0 0 -2 2 û
A x =b 解的结构 : α +k k k 1 1+ 2 … + n r r. η η ηnA α =λ α, α ≠0
齐次方程组线性无关解向量的个数 : n-r(A ) .
( )λ ( ) , 或 A -λ (λ 2 E -A = 0 E =0 E -A ) x =0 i ( )若P-1 3 A P = B. 由A 由B α =λ α⇒B (P-1 α ) =λ(P-1 α) ; α =λ α⇒A (P α ) =λ(P α). ⇔ k 重特征值必有k 个线性无关的特征向量 .
1 1 1ù é ê ú ê ú 已知 A = ê0 0 0ú 和 B = 2 3. ê ú ê ú ë0 0 0û
( ( Ⅰ )求 a 的值 ; Ⅱ )求可逆矩阵 P 使P-1 A P = B.
2 -2 4ù é ê ú ê ú ê1 -1 aú 相似 . ê ú ê ú ë0 0 0û
第 8 页, 共1 0页
.
T 2 设 α, 矩阵 A = E +2 若A 则 αT 2. α A -3 E = O, +2 β 都是n 维非零列向量 , β , β=
.
0 ù é1 -1 0 ê ú ê ú 0 0 ú ê0 1 6 如A = ê 则A 3. = ú, 1 -1ú ê0 0 ê ú ê ë0 0 -1 1 ú û
线性代数公式总结大全

线性代数公式1、行列式1. n 行列式共有2n 个元素,展开后有!n 项,可分解为2n 行列式;2. 代数余子式的性质:①、ij A 和ij a 的大小无关;②、某行(列)的元素乘以其它行(列)元素的代数余子式为0; ③、某行(列)的元素乘以该行(列)元素的代数余子式为A ; 3. 代数余子式和余子式的关系:(1)(1)i j i j ij ij ij ij M A A M ++=-=-4. 设n 行列式D :将D 上、下翻转或左右翻转,所得行列式为1D ,则(1)21(1)n n D D -=-; 将D 顺时针或逆时针旋转90,所得行列式为2D ,则(1)22(1)n n D D -=-;将D 主对角线翻转后(转置),所得行列式为3D ,则3D D =;将D 主副角线翻转后,所得行列式为4D ,则4D D =; 5. 行列式的重要公式:①、主对角行列式:主对角元素的乘积;②、副对角行列式:副对角元素的乘积(1)2(1)n n -⨯ -;③、上、下三角行列式( = ◥◣):主对角元素的乘积; ④、 ◤和 ◢:副对角元素的乘积(1)2(1)n n -⨯ -;⑤、拉普拉斯展开式:A O A C ABC B O B ==、(1)m n C A O AA B B O B C==- ⑥、范德蒙行列式:大指标减小指标的连乘积; ⑦、特征值; 6.对于n 阶行列式A ,恒有:1(1)nn k n k k k E A S λλλ-=-=+-∑,其中k S 为k 阶主子式;7. 证明0A =的方法:①、A A =-; ②、反证法;③、构造齐次方程组0Ax =,证明其有非零解; ④、利用秩,证明()r A n <; ⑤、证明0是其特征值;2、矩阵8.A 是n 阶可逆矩阵:⇔0A ≠(是非奇异矩阵);⇔()r A n =(是满秩矩阵) ⇔A 的行(列)向量组线性无关; ⇔齐次方程组0Ax =有非零解; ⇔n b R ∀∈,Ax b =总有唯一解;⇔A 与E 等价;⇔A 可表示成若干个初等矩阵的乘积; ⇔A 的特征值全不为0; ⇔T A A 是正定矩阵;⇔A 的行(列)向量组是n R 的一组基; ⇔A 是n R 中某两组基的过渡矩阵;9. 对于n 阶矩阵A :**AA A A A E == 无条件恒成立; 10. 1**111**()()()()()()T T T T A A A A A A ----=== ***111()()()T T TAB B A AB B A AB B A ---===11. 矩阵是表格,推导符号为波浪号或箭头;行列式是数值,可求代数和; 12. 关于分块矩阵的重要结论,其中均A 、B 可逆:若12s A A A A ⎛⎫ ⎪⎪= ⎪ ⎪⎝⎭,则: Ⅰ、12s A A A A =;Ⅱ、111121s A A A A ----⎛⎫ ⎪⎪= ⎪ ⎪ ⎪⎝⎭; ②、111A O A O O B O B ---⎛⎫⎛⎫=⎪ ⎪⎝⎭⎝⎭;(主对角分块) ③、111O A O B B O AO ---⎛⎫⎛⎫= ⎪ ⎪⎝⎭⎝⎭;(副对角分块) ④、11111A C A A CB O B OB -----⎛⎫-⎛⎫=⎪ ⎪⎝⎭⎝⎭;(拉普拉斯) ⑤、11111A O A O C B B CAB -----⎛⎫⎛⎫= ⎪ ⎪-⎝⎭⎝⎭;(拉普拉斯)3、矩阵的初等变换与线性方程组13. 一个m n ⨯矩阵A ,总可经过初等变换化为标准形,其标准形是唯一确定的:rm nEO F OO ⨯⎛⎫= ⎪⎝⎭; 等价类:所有与A 等价的矩阵组成的一个集合,称为一个等价类;标准形为其形状最简单的矩阵;对于同型矩阵A 、B ,若()()r A r B A B = ⇔ ; 14. 行最简形矩阵:①、只能通过初等行变换获得;②、每行首个非0元素必须为1;③、每行首个非0元素所在列的其他元素必须为0;15. 初等行变换的应用:(初等列变换类似,或转置后采用初等行变换)①、若(,)(,)rA E E X ,则A 可逆,且1X A -=;②、对矩阵(,)A B 做初等行变化,当A 变为E 时,B 就变成1A B -,即:1(,)(,)cA B E A B - ~ ;③、求解线形方程组:对于n 个未知数n 个方程Ax b =,如果(,)(,)rA b E x ,则A 可逆,且1x A b -=; 16. 初等矩阵和对角矩阵的概念:①、初等矩阵是行变换还是列变换,由其位置决定:左乘为初等行矩阵、右乘为初等列矩阵;②、12n ⎛⎫⎪⎪Λ= ⎪ ⎪⎝⎭λλλ,左乘矩阵A ,i λ乘A 的各行元素;右乘,iλ乘A 的各列元素;③、对调两行或两列,符号(,)E i j ,且1(,)(,)E i j E i j -=,例如:1111111-⎛⎫⎛⎫ ⎪ ⎪= ⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭;④、倍乘某行或某列,符号(())E i k ,且11(())(())E i k E i k -=,例如:1111(0)11k k k -⎛⎫⎛⎫⎪⎪⎪=≠ ⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭; ⑤、倍加某行或某列,符号(())E ij k ,且1(())(())E ij k E ij k -=-,如:11111(0)11k k k --⎛⎫⎛⎫ ⎪ ⎪=≠ ⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭;17. 矩阵秩的基本性质:①、0()min(,)m n r A m n ⨯≤≤;②、()()T r A r A =; ③、若AB ,则()()r A r B =;④、若P 、Q 可逆,则()()()()r A r PA r AQ r PAQ ===;(可逆矩阵不影响矩阵的秩) ⑤、max((),())(,)()()r A r B r A B r A r B ≤≤+;(※) ⑥、()()()r A B r A r B +≤+;(※) ⑦、()min((),())r AB r A r B ≤;(※)⑧、如果A 是m n ⨯矩阵,B 是n s ⨯矩阵,且0AB =,则:(※) Ⅰ、B 的列向量全部是齐次方程组0AX =解(转置运算后的结论);Ⅱ、()()r A r B n +≤⑨、若A 、B 均为n 阶方阵,则()()()r AB r A r B n ≥+-;18. 三种特殊矩阵的方幂:①、秩为1的矩阵:一定可以分解为列矩阵(向量)⨯行矩阵(向量)的形式,再采用结合律;②、型如101001a c b ⎛⎫ ⎪⎪ ⎪⎝⎭的矩阵:利用二项展开式;二项展开式:01111110()nnnn m n mmn n n nm m n mnnnnnn m a b C a C a b C ab Ca bC b C a b -----=+=++++++=∑;注:Ⅰ、()n a b +展开后有1n +项;Ⅱ、0(1)(1)!1123!()!--+====-m n n n n n n n m n C C C m m n mⅢ、组合的性质:111102---+-===+==∑nmn m mm m r nr r nnn n nnn n r C C CC CCrC nC ;③、利用特征值和相似对角化: 19. 伴随矩阵:①、伴随矩阵的秩:*()()1()10()1n r A n r A r A n r A n = ⎧⎪==-⎨⎪<-⎩; ②、伴随矩阵的特征值:*1*(,)AAAX X A A A A X X λλλ- == ⇒ =;③、*1A A A -=、1*n A A-=20. 关于A 矩阵秩的描述:①、()r A n =,A 中有n 阶子式不为0,1n +阶子式全部为0;(两句话)②、()r A n <,A 中有n 阶子式全部为0; ③、()r A n ≥,A 中有n 阶子式不全为0;21. 线性方程组:Ax b =,其中A 为m n ⨯矩阵,则:①、m 与方程的个数相同,即方程组Ax b =有m 个方程;②、n 与方程组得未知数个数相同,方程组Ax b =为n 元方程; 22. 线性方程组Ax b =的求解:①、对增广矩阵B 进行初等行变换(只能使用初等行变换);②、齐次解为对应齐次方程组的解; ③、特解:自由变量赋初值后求得;23. 由n 个未知数m 个方程的方程组构成n 元线性方程:①、11112211211222221122n n n n m m nm n na x a x a xb a x a x a x b a x a x a x b +++= ⎧⎪+++= ⎪⎨⎪⎪+++=⎩;②、1112111212222212n n m m mn m m a a a x b a a a x b Ax b a a a x b ⎛⎫⎛⎫⎛⎫ ⎪⎪ ⎪ ⎪⎪ ⎪=⇔= ⎪⎪ ⎪⎪⎪ ⎪⎝⎭⎝⎭⎝⎭(向量方程,A 为m n ⨯矩阵,m 个方程,n 个未知数) ③、()1212n n x x a a a x β⎛⎫ ⎪ ⎪= ⎪ ⎪⎝⎭(全部按列分块,其中12n b b b β⎛⎫ ⎪ ⎪= ⎪ ⎪⎝⎭); ④、1122n n a x a x a x β+++=(线性表出)⑤、有解的充要条件:()(,)r A r A n β=≤(n 为未知数的个数或维数)4、向量组的线性相关性24. m 个n 维列向量所组成的向量组A :12,,,m ααα构成n m ⨯矩阵12(,,,)m A =ααα;m 个n 维行向量所组成的向量组B :12,,,T TTm βββ构成m n ⨯矩阵12T T T m B βββ⎛⎫⎪ ⎪= ⎪ ⎪ ⎪⎝⎭;含有有限个向量的有序向量组与矩阵一一对应;25. ①、向量组的线性相关、无关 0Ax ⇔=有、无非零解;(齐次线性方程组)②、向量的线性表出 Ax b ⇔=是否有解;(线性方程组) ③、向量组的相互线性表示 AX B ⇔=是否有解;(矩阵方程) 26. 矩阵m n A ⨯与l n B ⨯行向量组等价的充分必要条件是:齐次方程组0Ax =和0Bx =同解;(101P 例14)27. ()()T r A A r A =;(101P 例15) 28. n 维向量线性相关的几何意义:①、α线性相关⇔0α=; ②、,αβ线性相关⇔,αβ坐标成比例或共线(平行);③、,,αβγ线性相关 ⇔,,αβγ共面;29. 线性相关与无关的两套定理:若12,,,s ααα线性相关,则121,,,,s s αααα+必线性相关;若12,,,s ααα线性无关,则121,,,s ααα-必线性无关;(向量的个数加加减减,二者为对偶)若r 维向量组A 的每个向量上添上n r -个分量,构成n 维向量组B :若A 线性无关,则B 也线性无关;反之若B 线性相关,则A 也线性相关;(向量组的维数加加减减) 简言之:无关组延长后仍无关,反之,不确定;30. 向量组A (个数为r )能由向量组B (个数为s )线性表示,且A 线性无关,则r s ≤(二版74P 定理7);向量组A 能由向量组B 线性表示,则()()r A r B ≤;(86P 定理3) 向量组A 能由向量组B 线性表示AX B ⇔=有解; ()(,)r A r A B ⇔=(85P 定理2)向量组A 能由向量组B 等价()()(,)r A r B r A B ⇔ ==(85P 定理2推论)31. 方阵A 可逆⇔存在有限个初等矩阵12,,,l P P P ,使12l A P P P =;①、矩阵行等价:~rA B PA B ⇔=(左乘,P 可逆)0Ax ⇔=与0Bx =同解②、矩阵列等价:~cA B AQ B ⇔=(右乘,Q 可逆); ③、矩阵等价:~A B PAQ B ⇔=(P 、Q 可逆); 32.对于矩阵m n A ⨯与l n B ⨯:①、若A 与B 行等价,则A 与B 的行秩相等;②、若A 与B 行等价,则0Ax =与0Bx =同解,且A 与B 的任何对应的列向量组具有相同的线性相关性; ③、矩阵的初等变换不改变矩阵的秩; ④、矩阵A 的行秩等于列秩; 33.若m s s n m n A B C ⨯⨯⨯=,则:①、C 的列向量组能由A 的列向量组线性表示,B 为系数矩阵; ②、C 的行向量组能由B 的行向量组线性表示,T A 为系数矩阵;(转置)34.齐次方程组0Bx =的解一定是0ABx =的解,考试中可以直接作为定理使用,而无需证明; ①、0ABx = 只有零解0Bx ⇒ =只有零解;②、0Bx = 有非零解0ABx ⇒ =一定存在非零解;35. 设向量组12:,,,n r r B b b b ⨯可由向量组12:,,,n s s A a a a ⨯线性表示为:(110P 题19结论)1212(,,,)(,,,)r s b b b a a a K =(B AK =)其中K 为s r ⨯,且A 线性无关,则B 组线性无关()r K r ⇔=;(B 与K 的列向量组具有相同线性相关性) (必要性:()()(),(),()r r B r AK r K r K r r K r ==≤≤∴=;充分性:反证法)注:当r s =时,K 为方阵,可当作定理使用;36. ①、对矩阵m n A ⨯,存在n m Q ⨯,m AQ E = ()r A m ⇔=、Q 的列向量线性无关;(87P ) ②、对矩阵m n A ⨯,存在n m P ⨯,n PA E = ()r A n ⇔=、P 的行向量线性无关; 37. 12,,,s ααα线性相关⇔存在一组不全为0的数12,,,s k k k ,使得11220s s k k k ααα+++=成立;(定义)⇔1212(,,,)0s s x xx ααα⎛⎫ ⎪ ⎪= ⎪ ⎪⎝⎭有非零解,即0Ax =有非零解;⇔12(,,,)s r s ααα<,系数矩阵的秩小于未知数的个数;38. 设m n ⨯的矩阵A 的秩为r ,则n 元齐次线性方程组0Ax =的解集S 的秩为:()r S n r =-;39. 若*η为Ax b =的一个解,12,,,n r ξξξ-为0Ax =的一个基础解系,则*12,,,,n r ηξξξ-线性无关;(111P 题33结论)5、相似矩阵和二次型40. 正交矩阵T A A E ⇔=或1T A A -=(定义),性质:①、A 的列向量都是单位向量,且两两正交,即1(,1,2,)0T i j i j a a i j n i j=⎧==⎨≠⎩;②、若A 为正交矩阵,则1T A A -=也为正交阵,且1A =±; ③、若A 、B 正交阵,则AB 也是正交阵; 注意:求解正交阵,千万不要忘记施密特正交化和单位化; 41. 施密特正交化:12(,,,)r a a a11b a =;1222111[,][,]b a b a b b b =-121121112211[,][,][,][,][,][,]r r r r r r r r r b a b a b a b a b b b b b b b b b ----=----;42. 对于普通方阵,不同特征值对应的特征向量线性无关;对于实对称阵,不同特征值对应的特征向量正交; 43. ①、A 与B 等价 ⇔A 经过初等变换得到B ;⇔=PAQ B ,P 、Q 可逆; ()()⇔=r A r B ,A 、B 同型;②、A 与B 合同 ⇔=T C AC B ,其中可逆; ⇔T x Ax 与T x Bx 有相同的正、负惯性指数; ③、A 与B 相似 1-⇔=P AP B ; 44. 相似一定合同、合同未必相似;若C 为正交矩阵,则T C AC B =⇒A B ,(合同、相似的约束条件不同,相似的更严格); 45. A 为对称阵,则A 为二次型矩阵; 46. n 元二次型T x Ax 为正定:A ⇔的正惯性指数为n ;A ⇔与E 合同,即存在可逆矩阵C ,使T C AC E =; A ⇔的所有特征值均为正数; A ⇔的各阶顺序主子式均大于0;0,0ii a A ⇒>>;(必要条件)。
考研线性代数终极总结(看过就知道有多么精华了)

0是A的特征值
Ax = ο有非零解,其基础解系即为A关于λ = 0的特征向量
评注
r(aE + bA) < n
aE + bA = 0 ⇔ (aE + bA)x = 0 有非零解
λ
=
-a
,
λ为A的特征值
b
向量组等价
矩阵等价( 矩阵相似(
≅ ~
) )
具有→
反身性、对称性、传递性
矩阵合同(
~
)
1
√ 关于 e1, e2 ,⋅⋅⋅, en :
①称为 ¡n 的标准基, ¡n 中的自然基,单位坐标向量 p教材87 ;
② e1, e2,⋅⋅⋅, en 线性无关;
③ e1, e2,⋅⋅⋅, en = 1;
n
n
∑ ∑ ④ trE= aii = n ; aii (即主对角元素之和)
证明:
( ) ( )
a11x1 + a12 x2 + L + a1n xn A1 j = b1 A1 j a21x1 + a22 x2 + L + a2n xn A2 j = b2 A2
LLLLLLLLLLLL
j
( ) an1x1 + an2 x2 + L+ ann xn Anj = bn Anj
⇒
AB
=
m i =1
n j
n k =1
aik bkj
评 注: 矩阵乘法虽然不满足交换律,但仍满足结合律和分配律
矩阵乘法的几何意义:
投影:
A
=
考研数学线性代数知识点总结

考研数学线性代数知识点总结线性代数是考研数学中的重要组成部分,对于很多考生来说,它既是重点也是难点。
以下将对线性代数的主要知识点进行详细总结。
一、行列式行列式是线性代数中的一个基本概念,它是一个数值。
行列式的计算方法有很多,比如按行(列)展开、化为上三角(下三角)行列式等。
行列式的性质包括:行列式与它的转置行列式相等;行列式中某行(列)元素乘以同一数后,加到另一行(列)对应元素上,行列式的值不变等。
二、矩阵矩阵是线性代数的核心内容之一。
矩阵的运算包括加法、减法、数乘、乘法等。
矩阵乘法需要注意其运算规则,一般不满足交换律。
矩阵的逆是一个重要概念,如果矩阵 A 可逆,则存在 A 的逆矩阵 A⁻¹,使得AA⁻¹=A⁻¹A =E(单位矩阵)。
矩阵的秩也是一个关键概念,它表示矩阵中线性无关的行(列)向量的最大个数。
三、向量向量是线性代数中的重要概念,包括行向量和列向量。
向量组的线性相关性是重点,判断向量组线性相关或线性无关的方法有定义法、秩法等。
向量组的极大线性无关组和向量组的秩也是常考内容。
四、线性方程组线性方程组是线性代数中的核心问题之一。
齐次线性方程组和非齐次线性方程组的解法不同。
对于齐次线性方程组,当系数矩阵的秩等于未知数的个数时,方程组有唯一零解;当系数矩阵的秩小于未知数的个数时,方程组有非零解。
对于非齐次线性方程组,如果系数矩阵的秩等于增广矩阵的秩,则方程组有解;否则无解。
当有解时,如果秩等于未知数的个数,有唯一解;否则有无穷多解。
五、特征值与特征向量矩阵的特征值和特征向量是线性代数中的重要概念。
设 A 是 n 阶矩阵,如果存在数λ和非零向量 x,使得 Ax =λx,则称λ是 A 的特征值,x 是 A 的对应于特征值λ的特征向量。
求特征值和特征向量的方法是通过求解特征方程|λE A| = 0 得到特征值,然后代入(λE A)x = 0 求解特征向量。
六、相似矩阵相似矩阵具有相同的特征值。
考研线性代数公式必背总结汇总

行列式n 行列式共有2n 个元素,展开后有!n 项,可分解为2n 行列式;代数余子式的性质:①、ij A 和ij a 的大小无关;②、某行(列)的元素乘以其它行(列)元素的代数余子式为0; ③、某行(列)的元素乘以该行(列)元素的代数余子式为A ; 代数余子式和余子式的关系:(1)(1)i j i j ij ij ij ij M A A M ++=-=-设n 行列式D :将D 上、下翻转或左右翻转,所得行列式为1D ,则(1)21(1)n n D D -=-; 将D 顺时针或逆时针旋转90,所得行列式为2D ,则(1)22(1)n n D D -=-;将D 主对角线翻转后(转置),所得行列式为3D ,则3D D =;将D 主副角线翻转后,所得行列式为4D ,则4D D =; 行列式的重要公式:①、主对角行列式:主对角元素的乘积;②、副对角行列式:副对角元素的乘积(1)2(1)n n -⨯ -;③、上、下三角行列式( = ◥◣):主对角元素的乘积; ④、 ◤和 ◢:副对角元素的乘积(1)2(1)n n -⨯ -;⑤、拉普拉斯展开式:A O A CA B C B O B==、(1)m n C A O AA B B O B C==-⑥、范德蒙行列式:大指标减小指标的连乘积; ⑦、特征值;对于n 阶行列式A ,恒有:1(1)nn k n k k k E A S λλλ-=-=+-∑,其中k S 为k 阶主子式;证明0A =的方法:①、A A =-; ②、反证法;③、构造齐次方程组0Ax =,证明其有非零解; ④、利用秩,证明()r A n <; ⑤、证明0是其特征值;矩阵A 是n 阶可逆矩阵:⇔0A ≠(是非奇异矩阵);⇔()r A n =(是满秩矩阵) ⇔A 的行(列)向量组线性无关; ⇔齐次方程组0Ax =有非零解; ⇔n b R ∀∈,Ax b =总有唯一解; ⇔A 与E 等价;⇔A 可表示成若干个初等矩阵的乘积;⇔A 的特征值全不为0; ⇔T A A 是正定矩阵;⇔A 的行(列)向量组是n R 的一组基; ⇔A 是n R 中某两组基的过渡矩阵;对于n 阶矩阵A :**AA A A A E == 无条件恒成立;1**111**()()()()()()T T T T A A A A A A ----===***111()()()T T TAB B A AB B A AB B A ---===矩阵是表格,推导符号为波浪号或箭头;行列式是数值,可求代数和; 关于分块矩阵的重要结论,其中均A 、B 可逆:若12s A A A A ⎛⎫⎪⎪= ⎪ ⎪⎝⎭,则: Ⅰ、12s A A A A =;Ⅱ、111121s A A A A ----⎛⎫ ⎪⎪= ⎪ ⎪ ⎪⎝⎭; ②、111A O A O O B O B ---⎛⎫⎛⎫=⎪ ⎪⎝⎭⎝⎭;(主对角分块) ③、111O A O B B O AO ---⎛⎫⎛⎫= ⎪ ⎪⎝⎭⎝⎭;(副对角分块) ④、11111A C A A CB O B OB -----⎛⎫-⎛⎫=⎪ ⎪⎝⎭⎝⎭;(拉普拉斯) ⑤、11111A O A O C B B CAB -----⎛⎫⎛⎫= ⎪ ⎪-⎝⎭⎝⎭;(拉普拉斯) 矩阵的初等变换与线性方程组一个m n ⨯矩阵A ,总可经过初等变换化为标准形,其标准形是唯一确定的:rm nE OF OO ⨯⎛⎫=⎪⎝⎭; 等价类:所有与A 等价的矩阵组成的一个集合,称为一个等价类;标准形为其形状最简单的矩阵;对于同型矩阵A 、B ,若()()r A r B A B = ⇔ ; 行最简形矩阵:①、只能通过初等行变换获得;②、每行首个非0元素必须为1;③、每行首个非0元素所在列的其他元素必须为0;初等行变换的应用:(初等列变换类似,或转置后采用初等行变换)若(,)(,)rA E E X ,则A 可逆,且1X A -=;②、对矩阵(,)A B 做初等行变化,当A 变为E 时,B 就变成1AB -,即:1(,)(,)cA B E A B - ~ ;③、求解线形方程组:对于n 个未知数n 个方程Ax b =,如果(,)(,)rA b E x ,则A 可逆,且1x A b -=; 初等矩阵和对角矩阵的概念:①、初等矩阵是行变换还是列变换,由其位置决定:左乘为初等行矩阵、右乘为初等列矩阵;②、12n ⎛⎫⎪⎪Λ= ⎪ ⎪⎝⎭λλλ,左乘矩阵A ,i λ乘A 的各行元素;右乘,i λ乘A 的各列元素; ③、对调两行或两列,符号(,)E i j ,且1(,)(,)E i j E i j -=,例如:1111111-⎛⎫⎛⎫⎪ ⎪= ⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭;④、倍乘某行或某列,符号(())E i k ,且11(())(())E i k E i k -=,例如:1111(0)11k k k-⎛⎫⎛⎫⎪⎪⎪=≠ ⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭; ⑤、倍加某行或某列,符号(())E ij k ,且1(())(())E ij k E ij k -=-,如:11111(0)11k k k --⎛⎫⎛⎫ ⎪ ⎪=≠ ⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭; 矩阵秩的基本性质:①、0()min(,)m n r A m n ⨯≤≤;②、()()T r A r A =;③、若A B ,则()()r A r B =;④、若P 、Q 可逆,则()()()()r A r PA r AQ r PAQ ===;(可逆矩阵不影响矩阵的秩) ⑤、max((),())(,)()()r A r B r A B r A r B ≤≤+;(※) ⑥、()()()r A B r A r B +≤+;(※) ⑦、()min((),())r AB r A r B ≤;(※)⑧、如果A 是m n ⨯矩阵,B 是n s ⨯矩阵,且0AB =,则:(※)Ⅰ、B 的列向量全部是齐次方程组0AX =解(转置运算后的结论); Ⅱ、()()r A r B n +≤⑨、若A 、B 均为n 阶方阵,则()()()r AB r A r B n ≥+-;三种特殊矩阵的方幂:①、秩为1的矩阵:一定可以分解为列矩阵(向量)⨯行矩阵(向量)的形式,再采用结合律;②、型如101001a c b ⎛⎫⎪⎪ ⎪⎝⎭的矩阵:利用二项展开式; 二项展开式:01111110()nn n n m n m m n n n n m m n mn n n n n n m a b C a C a b C a b C a b C b C a b -----=+=++++++=∑;注:Ⅰ、()n a b +展开后有1n +项; Ⅱ、0(1)(1)!1123!()!--+====-m nn n n n n n m n C C C m m n mⅢ、组合的性质:11112---+-===+==∑nm n m m m m r nr r nnn n nnn n r C CCC CCrC nC ; ③、利用特征值和相似对角化: 伴随矩阵:①、伴随矩阵的秩:*()()1()10()1nr A n r A r A n r A n =⎧⎪==-⎨⎪<-⎩; ②、伴随矩阵的特征值:*1*(,)AAAX X A A A A X X λλλ- == ⇒ =;③、*1A A A -=、1*n A A -=关于A 矩阵秩的描述:①、()r A n =,A 中有n 阶子式不为0,1n +阶子式全部为0;(两句话)②、()r A n <,A 中有n 阶子式全部为0; ③、()r A n ≥,A 中有n 阶子式不为0;线性方程组:Ax b =,其中A 为m n ⨯矩阵,则:①、m 与方程的个数相同,即方程组Ax b =有m 个方程;②、n 与方程组得未知数个数相同,方程组Ax b =为n 元方程; 线性方程组Ax b =的求解:①、对增广矩阵B 进行初等行变换(只能使用初等行变换);②、齐次解为对应齐次方程组的解; ③、特解:自由变量赋初值后求得;由n 个未知数m 个方程的方程组构成n 元线性方程:①、11112211211222221122n n n n m m nm n n a x a x a x b a x a x a x b a x a x a x b +++= ⎧⎪+++= ⎪⎨⎪⎪+++=⎩; ②、1112111212222212n n m m mn m m a a a x b aa a xb Ax b a a a x b ⎛⎫⎛⎫⎛⎫ ⎪⎪ ⎪ ⎪⎪ ⎪=⇔= ⎪⎪ ⎪ ⎪⎪ ⎪⎝⎭⎝⎭⎝⎭(向量方程,A 为m n ⨯矩阵,m 个方程,n 个未知数) ③、()1212n n x x a a a x β⎛⎫ ⎪ ⎪= ⎪ ⎪⎝⎭(全部按列分块,其中12n b b b β⎛⎫ ⎪ ⎪= ⎪ ⎪⎝⎭); ④、1122n n a x a x a x β+++=(线性表出)⑤、有解的充要条件:()(,)r A r A n β=≤(n 为未知数的个数或维数)向量组的线性相关性m 个n 维列向量所组成的向量组A :12,,,m ααα构成n m ⨯矩阵12(,,,)m A =ααα;m 个n 维行向量所组成的向量组B :12,,,T T Tmβββ构成m n ⨯矩阵12T T T m B βββ⎛⎫⎪ ⎪= ⎪ ⎪ ⎪⎝⎭; 含有有限个向量的有序向量组与矩阵一一对应;①、向量组的线性相关、无关 0Ax ⇔=有、无非零解;(齐次线性方程组)②、向量的线性表出 Ax b ⇔=是否有解;(线性方程组) ③、向量组的相互线性表示 AX B ⇔=是否有解;(矩阵方程)矩阵m n A ⨯与l n B ⨯行向量组等价的充分必要条件是:齐次方程组0Ax =和0Bx =同解;(101P 例14)()()T r A A r A =;(101P 例15)n 维向量线性相关的几何意义:①、α线性相关⇔0α=;②、,αβ线性相关 ⇔,αβ坐标成比例或共线(平行); ③、,,αβγ线性相关 ⇔,,αβγ共面;线性相关与无关的两套定理:若12,,,s ααα线性相关,则121,,,,s s αααα+必线性相关;若12,,,s ααα线性无关,则121,,,s ααα-必线性无关;(向量的个数加加减减,二者为对偶) 若r 维向量组A 的每个向量上添上n r -个分量,构成n 维向量组B :若A 线性无关,则B 也线性无关;反之若B 线性相关,则A 也线性相关;(向量组的维数加加减减)简言之:无关组延长后仍无关,反之,不确定;向量组A (个数为r )能由向量组B (个数为s )线性表示,且A 线性无关,则r s ≤(二版74P 定理7);向量组A 能由向量组B 线性表示,则()()r A r B ≤;(86P 定理3)向量组A 能由向量组B 线性表示AX B ⇔=有解;()(,)r A r A B ⇔=(85P 定理2)向量组A 能由向量组B 等价()()(,)r A r B r A B ⇔ ==(85P 定理2推论) 方阵A 可逆⇔存在有限个初等矩阵12,,,l P P P ,使12l A P P P =;①、矩阵行等价:~rA B PA B ⇔=(左乘,P 可逆)0Ax ⇔=与0Bx =同解②、矩阵列等价:~cA B AQ B ⇔=(右乘,Q 可逆); ③、矩阵等价:~A B PAQ B ⇔=(P 、Q 可逆); 对于矩阵m n A ⨯与l n B ⨯:①、若A 与B 行等价,则A 与B 的行秩相等;②、若A 与B 行等价,则0Ax =与0Bx =同解,且A 与B 的任何对应的列向量组具有相同的线性相关性;③、矩阵的初等变换不改变矩阵的秩; ④、矩阵A 的行秩等于列秩; 若m s s n m n A B C ⨯⨯⨯=,则:①、C 的列向量组能由A 的列向量组线性表示,B 为系数矩阵;②、C 的行向量组能由B 的行向量组线性表示,T A 为系数矩阵;(转置)齐次方程组0Bx =的解一定是0ABx =的解,考试中可以直接作为定理使用,而无需证明;①、0ABx = 只有零解0Bx ⇒ =只有零解; ②、0Bx = 有非零解0ABx ⇒ =一定存在非零解;设向量组12:,,,n r r B b b b ⨯可由向量组12:,,,n s s A a a a ⨯线性表示为:(110P 题19结论)1212(,,,)(,,,)r s b b b a a a K =(B AK =)其中K 为s r ⨯,且A 线性无关,则B 组线性无关()r K r ⇔=;(B 与K 的列向量组具有相同线性相关性)(必要性:()()(),(),()r r B r AK r K r K r r K r ==≤≤∴=;充分性:反证法)注:当r s =时,K 为方阵,可当作定理使用;①、对矩阵m n A ⨯,存在n m Q ⨯,m AQ E = ()r A m ⇔=、Q 的列向量线性无关;(87P )②、对矩阵m n A ⨯,存在n m P ⨯,n PA E = ()r A n ⇔=、P 的行向量线性无关; 12,,,s ααα线性相关⇔存在一组不全为0的数12,,,s k k k ,使得11220s s k k k ααα+++=成立;(定义)⇔1212(,,,)0s s x xx ααα⎛⎫ ⎪ ⎪= ⎪ ⎪⎝⎭有非零解,即0Ax =有非零解;⇔12(,,,)s r s ααα<,系数矩阵的秩小于未知数的个数;设m n ⨯的矩阵A 的秩为r ,则n 元齐次线性方程组0Ax =的解集S 的秩为:()r S n r =-; 若*η为Ax b =的一个解,12,,,n r ξξξ-为0Ax =的一个基础解系,则*12,,,,n r ηξξξ-线性无关;(111P 题33结论)相似矩阵和二次型正交矩阵T A A E ⇔=或1T A A -=(定义),性质:①、A 的列向量都是单位向量,且两两正交,即1(,1,2,)0T i j i ja a i j n i j=⎧==⎨≠⎩;②、若A 为正交矩阵,则1T A A -=也为正交阵,且1A =±; ③、若A 、B 正交阵,则AB 也是正交阵;注意:求解正交阵,千万不要忘记施密特正交化和单位化; 施密特正交化:12(,,,)r a a a11b a =;1222111[,][,]b a b a b b b =-121121112211[,][,][,][,][,][,]r r r r r r r r r b a b a b a b a b b b b b b b b b ----=----;对于普通方阵,不同特征值对应的特征向量线性无关;对于实对称阵,不同特征值对应的特征向量正交; ①、A 与B 等价 ⇔A 经过初等变换得到B ;⇔=PAQ B ,P 、Q 可逆; ()()⇔=r A r B ,A 、B 同型;②、A 与B 合同 ⇔=T C AC B ,其中可逆;⇔T x Ax 与T x Bx 有相同的正、负惯性指数; ③、A 与B 相似 1-⇔=P AP B ; 相似一定合同、合同未必相似;若C 为正交矩阵,则T C AC B =⇒A B ,(合同、相似的约束条件不同,相似的更严格);A 为对称阵,则A 为二次型矩阵; n 元二次型T x Ax 为正定:A ⇔的正惯性指数为n ;A ⇔与E 合同,即存在可逆矩阵C ,使T C AC E =; A ⇔的所有特征值均为正数; A ⇔的各阶顺序主子式均大于0;0,0ii a A ⇒>>;(必要条件)。
李永乐线代笔记

第一章节 行列式基础知识:①算逆序的方法:从左到右一个一个看,前面有比此数大的就算一个逆序,最后加起来。
②代数余子式千万别忘记(−1)i+j③行列式两行(列)对换,行列式要变号!④克拉默法则:x n =D n D基本行列式的计算:①副对角行列式=(−1)n(n−1)2a 1n a 2,n−1···a n1②副对角拉普拉斯:|O A B ∗|=(−1)nm |A||B| ③范德蒙行列式(首行为1,每列从上往下是等比数列)=∏(x i −x j )1≤j<i≤n 即针对第二行,每个靠右的都减一次靠左的,然后乘起来。
④特征多项式(三阶):|λE −A |=λ3−(a 11+a 22+a 33)λ2+s 2λ−|A|其中s 2=|a 11a 12a 21a 22|+|a 11a 13a 31a 33|+|a 22a 23a 32a 33| ⑤零多的,直接展开算。
⑥将第一行(列)的k 倍依次加至其余各行(列)。
⑦将每一行(列)都加到第一行。
⑧逐行(列)相加。
特殊行列式的计算:①∠型行列式,从角(或边)沿第三边方向扫过去,依次把前一行(列)乘上倍数加到后一行(列)上。
②爪型行列式,↖↘头朝主对角线的,化为上(下)三角行列式;↗↙头朝副对角线的,化为副对角线三角行列式。
③对称征子型(中间斜着三道)行列式,采用逐行相加(上一行乘倍数加到下一行上)的方式化为下三角行列式。
④对角线为a ,其余都为b 的行列式,每行都减第一行,再每列都加到第一列。
第二章节 矩阵主要公式:①伴随:AA ∗=A ∗A =|A |E ; A ∗=|A|A −1 ; (A ∗)−1=(A −1)∗=A |A|(A ∗)T =(A T )∗ ; (kA)∗=k n−1A ∗ ; (A ∗)∗=|A|n−2Ar (A ∗)={n ,如果r (A )=n1,如果r (A )=n −10,如果r (A )<n −1②可逆:A−1=A∗|A|;(kA)−1=1kA−1(A n)−1=(A−1)n;(A−1)T=(A T)−1[B O O C ]−1=[B−1OO C−1];[O BC O]−1=[O C−1B−1O]③转置:(A T)T=A;(kA)T=kA T[A B C D ]T=[A T C TB T D T]④行列式:|A T|=|A|;|A−1|=|A|−1;|A∗|=|A|n−1|kA|=k n|A|;|AB|=|A|·|B|(行列式没有加减运算)⑤加与乘(A+B)T=A T+B T;(AB)T=B T A T(AB)−1=B−1A−1;(ABC)−1=C−1B−1A−1;(AB)∗=B∗A∗(求逆和伴随没有加法运算)[B O O C ]n=[Bn OO C n](副对角线分块矩阵先平方,化为主对角线,再套公式)⑥秩r(A)=r(A T);r(A T A)=r(A)(证明过程见下):设(I)A T Ax=0,(II)Ax=0,若α是(II)的解,显然也是(I)的解;若α是(I)的解,则A T Aα=0→αT A T Aα=0→(Aα)T Aα=0→|Aα|2=0→Aα=0,则α也是(II)的解,故(I)、(II)同解。
考研线性代数知识点全面总结

《线性代数》复习提纲第一章、行列式1.行列式的定义:用2n 个元素ij a 组成的记号称为n 阶行列式。
(1)它表示所有可能的取自不同行不同列的n 个元素乘积的代数和; (2)展开式共有n!项,其中符号正负各半; 2.行列式的计算一阶|α|=α行列式,二、三阶行列式有对角线法则; N 阶(n ≥3)行列式的计算:降阶法定理:n 阶行列式的值等于它的任意一行(列)的各元素与其对应的代数余子式乘积的和。
方法:选取比较简单的一行(列),保保留一个非零元素,其余元素化为0,利用定理展开降阶。
特殊情况:上、下三角形行列式、对角形行列式的值等于主对角线上元素的乘积;◊行列式值为0的几种情况:Ⅰ 行列式某行(列)元素全为0; Ⅱ 行列式某行(列)的对应元素相同; Ⅲ 行列式某行(列)的元素对应成比例; Ⅳ 奇数阶的反对称行列式。
3.概念:全排列、排列的逆序数、奇排列、偶排列、余子式ij M 、代数余子式ij j i ij M A +-=)1( 定理:一个排列中任意两个元素对换,改变排列的奇偶性。
奇排列变为标准排列的对换次数为基数,偶排列为偶数。
n 阶行列式也可定义:n q q q na a a ⋯=∑21t211-D )(,t 为n q q q ⋯21的逆序数4.行列式性质:1、行列式与其转置行列式相等。
2、互换行列式两行或两列,行列式变号。
若有两行(列)相等或成比例,则为行列式0。
3、行列式某行(列)乘数k,等于k 乘此行列式。
行列式某行(列)的公因子可提到外面。
4、行列式某行(列)的元素都是两数之和,则此行列式等于两个行列式之和。
5、行列式某行(列)乘一个数加到另一行(列)上,行列式不变。
6、行列式等于他的任一行(列)的各元素与其对应代数余子式的乘积之和。
(按行、列展开法则)7、行列式某一行(列)与另一行(列)的对应元素的代数余子式乘积之和为0. 5.克拉默法则::若线性方程组的系数行列式0D ≠,则方程有且仅有唯一解DD D Dx D D n =⋯==n 2211x ,x ,,。
2018年李永乐考研数学复习全书(高数+线性代数)

李永乐复习全书(数学一)例题(第二章矩阵)
李永乐复习全书(数学一)例题(第三章向量)
求证:
求证:
求证
李永乐复习全书(数学一)(第四章线性方程组)
证明
李永乐复习全书(数学一)例题(第五章特征值和特征向量)
李永乐复习全书(数学一)例题(第六章二次型)
求证111149112149113149114149115149116149117149118149119149120149121149122149123149124149125149李永乐复习全书数学一第四章线性方程组126149127149128149129149130149131149证明132149133149134149李永乐复习全书数学一例题第五章特征值和特征向量135149136149137149138149139149140149141149142149143149144149李永乐复习全书数学一例题第六章二次型145149146149147149148149149
