理想气体温度公式
大学物理-气体动理论必考知识点

第十章 气体动理论主要内容
一.理想气体状态方程: m PV RT M
'=; P nkT = 8.31J R k mol =;231.3810J k k -=⨯;2316.02210A N mol -=⨯;A R N k =
二. 理想气体压强公式
23kt p n ε= ε=213=22kt mv kT 分子平均平动动能
三. 理想气体温度公式
21322kt mv kT ε==
四.能均分原理
1. 自由度:确定一个物体在空间位置所需要的独立坐标数目。
2. 气体分子的自由度
单原子分子 (如氦、氖分子)3i =;刚性双原子分子5i =;刚性多原子分子6i =
3. 能均分原理:在温度为T 的平衡状态下,气体分子每一自由度上具有的平均动都相等,其值为1
2
kT
五. 理想气体的内能(所有分子热运动动能之和)
1.1mol 理想气体=⋅=22A i i E N kT RT 3. 一定量理想气体()2i m E RT M
νν'==
六.麦克斯韦速率发布函数(可能会命题计算题,各种表达式的物理含义要牢记) 1()N
f v N v =d d , 速率在v 附近,单位速率区间内分子数占总分子数的百分率。
归一化条件:0()1f v v ∞=⎰d ,
=
=≈
平均速率:v ==≈ 最概然速率
:p v =≈
七.碰撞频率:
2z d nv =
平均自由程:λ=。
理想气体压强和温度公式

理想气体压强和温度公式理想气体压强和温度公式是理想气体状态方程的重要组成部分。
理想气体状态方程描述了理想气体的状态特性,包括其压强、体积和温度之间的关系。
理想气体状态方程的公式为PV=nRT,其中P代表气体的压强,V代表气体的体积,n代表气体的物质量,R为气体常数,T代表气体的绝对温度。
理想气体状态方程可以进一步展开,得到理想气体的理想气体压强和温度公式。
理想气体的理想气体压强和温度公式可以通过两种方式得到:基于动理论和基于热力学。
基于动理论的理想气体压强和温度公式根据分子间的相互作用来推导。
在理想气体中,气体分子之间的相互作用可以被忽略不计。
基于动理论的公式为P=nmv^2/3V,其中m为气体分子的质量,v为气体分子的速度。
从公式可以看出,理想气体的压强与气体分子质量和速度的平方成正比。
基于热力学的理想气体压强和温度公式根据气体的热力学性质推导。
根据热力学第一定律,理想气体的内能变化与吸热和对外做功之间有关。
对于理想气体来说,没有分子之间的相互作用,因此其内能只与温度有关。
根据热力学方程,理想气体内能的变化为dU=CvdT,其中Cv为定容摩尔热容,dT为温度变化。
根据理想气体的状态方程PV=nRT,可得到V与T关系为V=nRT/P。
代入内能的变化公式,可以得到P=Cv(nR/P)dT。
整理可得到PdV+Cv(nR/P)dT=0,进一步整理可得到PdV/T+CvRdV/P=0。
根据微分学中的换元法,可以得到PdT/T+CvRdV/P=0。
在等温过程中,dT为0,所以PdV/T=0,进一步得到P/T=常数。
这就是理想气体的理想气体压强和温度公式。
从公式可以看出,理想气体的压强与温度成正比。
理想气体压强和温度公式在理论物理和工程领域中有着重要的应用。
例如,在热力学和热工学中,理想气体压强和温度公式可以用来计算理想气体工质在不同条件下的压强和温度变化。
在物理化学中,理想气体压强和温度公式可以用来描述理想气体的行为,例如气体反应的速率常数和平衡常数的计算。
多种气体混合温度计算公式

多种气体混合温度计算公式引言。
在工程和科学领域中,我们经常需要计算多种气体混合的温度。
这种计算对于许多领域都是至关重要的,比如在化工工业中,混合气体的温度计算可以帮助工程师设计和优化反应器和分离装置。
在本文中,我们将探讨多种气体混合温度计算的公式和方法,以便读者能够更好地理解和应用这些知识。
理想气体混合的温度计算公式。
在理想气体混合中,我们可以使用以下公式来计算混合气体的最终温度:T = (n1T1 + n2T2 + ... + nkTk) / (n1 + n2 + ... + nk)。
其中,T表示混合气体的最终温度,n表示每种气体的摩尔数,T表示每种气体的温度。
这个公式的基本原理是根据每种气体的摩尔数和温度来计算混合气体的平均温度。
这个公式适用于理想气体混合,即气体分子之间没有相互作用的情况。
实际气体混合的温度计算公式。
在实际情况下,气体分子之间会发生相互作用,因此我们需要考虑这种相互作用对混合气体温度的影响。
在这种情况下,我们可以使用以下公式来计算混合气体的最终温度:T = (n1Cp1T1 + n2Cp2T2 + ... + nkCpkTk) / (n1Cp1 + n2Cp2 + ... + nkCpk)。
其中,Cp表示每种气体的定压热容,其他符号的含义与前面的公式相同。
这个公式考虑了每种气体的热容对混合气体温度的影响,因此更适用于实际气体混合的情况。
混合气体的平均热容。
在实际气体混合中,我们还需要考虑混合气体的平均热容。
混合气体的平均热容可以通过以下公式来计算:Cp = (n1Cp1 + n2Cp2 + ... + nkCpk) / (n1 + n2 + ... + nk)。
这个公式可以帮助我们计算混合气体的平均热容,从而更准确地预测混合气体的最终温度。
混合气体的热力学性质。
除了温度计算公式之外,我们还需要考虑混合气体的热力学性质对温度的影响。
混合气体的热力学性质可以通过混合气体的组分和压力来确定。
大学物理第二十三讲 气体温度 压强 能均分 内能

(i t r )
(t 3, r 0, i 3) (t 3, r 2, i 5) (t 3, r 3, i 6)
16
5 刚性双原子分子: k kT 2 6 刚性多原子分子: k kT 2
三、理想气体的热力学能(内能)
气体内能—气体分子各种形式的动能、原子间振动 势能、分子间的相互作势能之总和。
p p p
p nkT n n
kT n kT n kT
9
p p p
例:容器内有温度27C、压强为0.01mmHg的一定量 理想气体。问容器内1cm3中有多少个气体分子?这些 分子平动动能之总和为多少? 解: p 0.010mmHg 1.33Pa, T 300K
实际气体—非刚性,还有原子间振动的自由度。
13
二、能量按自由度均分定理
1 ___ 3 2 平均平动动能 t m v kT 2 2 1 ___ v v v v2 3 ___ __ 1 ___ 1 1 1 1 2 1 2 2 2 m v x m v y m v z ( mv ) kT 2 2 2 3 2 2 1 tx ty tz kT 2
3 2 t kT , p n t 2 3
p nkT 理想气体状态方程
8
道尔顿分压定律 ◎混合气体的压强等于同一平衡态下各组分气体单 独存在时的压强之和,即 证明: 混合气体各组分处于热平衡,因而温度相同。 各分压强 p n kT , p n kT , 混合气体分子数密度 n n n
决定其空间位置需要三个独立坐标 (x, y, z),有三个自由度。
y
o z
工程热力学 温度计算公式

工程热力学温度计算公式热力学是研究热能转化和传递的科学,而工程热力学则是将热力学原理应用于工程实践中。
在工程热力学中,温度是一个非常重要的参数,它影响着物质的性质和行为。
因此,准确计算温度对于工程设计和实际操作至关重要。
在本文中,我们将介绍工程热力学中常用的温度计算公式,希望能对工程师和研究人员有所帮助。
1. 热力学基本公式。
在工程热力学中,温度通常是通过测量物体的热量和热容来计算的。
根据热力学基本公式,热量Q可以表示为:Q = mcΔT。
其中,m是物体的质量,c是物体的比热容,ΔT是物体的温度变化。
根据这个公式,我们可以通过测量物体的热量和热容来计算物体的温度变化。
2. 理想气体状态方程。
在工程热力学中,气体的温度通常是通过测量气体的压力和体积来计算的。
根据理想气体状态方程,气体的温度可以表示为:PV = nRT。
其中,P是气体的压力,V是气体的体积,n是气体的摩尔数,R是气体常数,T是气体的温度。
根据这个公式,我们可以通过测量气体的压力和体积来计算气体的温度。
3. 热传导方程。
在工程热力学中,温度还可以通过热传导方程来计算。
热传导方程描述了热量在物体中的传递过程,它可以表示为:q = -kAΔT/Δx。
其中,q是热通量,k是热导率,A是传热面积,ΔT是温度差,Δx是传热距离。
根据这个公式,我们可以通过测量热通量和传热距离来计算物体的温度差。
4. 热辐射公式。
在工程热力学中,温度还可以通过热辐射公式来计算。
热辐射公式描述了物体通过辐射传热的过程,它可以表示为:q = εσA(T^4 T0^4)。
其中,q是热通量,ε是辐射率,σ是斯特藩-玻尔兹曼常数,A是辐射面积,T是物体的温度,T0是环境的温度。
根据这个公式,我们可以通过测量热通量和环境温度来计算物体的温度。
总结。
在工程热力学中,温度是一个非常重要的参数,它影响着物质的性质和行为。
因此,准确计算温度对于工程设计和实际操作至关重要。
在本文中,我们介绍了工程热力学中常用的温度计算公式,包括热力学基本公式、理想气体状态方程、热传导方程和热辐射公式。
大学物理(12.3.2)--理想气体压强公式和温度公式

三、理想气体的压强公式推导
z
1 个分子 i 碰撞一次器壁 A1 作用冲量
为
Ii 2mvix
一次碰撞所需时间为
2l1 vix
y
o m vi l1
⊿t 时间内,分子 i 与器壁 A1 面碰撞次 数
t
vix 2l1
l2 A1
x l3
z
⊿t 时间内,分子 i 作用
在 A1 面上的冲量为:
2mvix
vix 2l1
t
m
vi2x 1
t
o m vi
y
l1
⊿t 时间内,所有分子
作用 A1 面的总冲量为:I
N i 1
m vi2x l1
t
l2 A1
x l3
按压强定义:
p
I
t l2l3
m l1l2l3
N i1
vi2x
I
N i1
m
vi2x l1
t
m V
(v12x
3 2
kT
物理意义:该公式反映产生温度的微观本质
18/4/22
8
例题:从压强公式和温度公式导出道尔顿分压公式,即 混合气体的压强等于各种气体分压之和。
混合气体单位体积的分子数为:
n n1 n2
根据温度公式:
3 2
kT
在相同温度下 , 各种气体分子的平均平动动能相等 , 即 :
1 2
m1 v12
1 2
m2 v22
1 2
mv2
3 2
kT
根据压强公式,混合气体的压强为:
理想气体的压强与温度公式

快减
快增
速率分布曲线 有单峰,不对称
两者相乘
速率
恒取正
[讨论]
① v 0, f (v ) 0 v , f (v ) 0
f (v)
线,小面积, 大面积的物 理意义?
v0 ②满足归一化条件: f (v)dv 1 o v0 v 1
dv
v 2 dv
v
③ f (v )v N 表示分布在 v v v 区间内的分子
RT
, 则 n 按指数而减小;
m ol
②分子的摩尔质量 M
RT
越大,重力
P P0 e
M m ol gh
作用越显著,n 的减小就越迅速。 ③T ,分子的无规则热运动越剧 烈,n 的减小就越缓慢。
M 2 0.1 2 P v (200) 2 3V 3 10
1.33 10 ( Pa)
5
例3:某气体在温度为T=273K时,压强为 p=1.0×10-2atm,密度 1.24 10 2 kg / m3 , 求该气体分子的方均根速率。
解:
M RT V P PV RT , P M mol M mol M
2. 平衡态理想气体分子运动的统计假设 ①分子在容器中的空间分布平均来说是均匀的,分子数
密度:
dN N n dV V N 表示容器体积V内的分子数。
②具有相同速率的分子,向各个方向运动的平均分子数 是相等的:
统 计 结 果
v v v v
2 i 2 ix 2 iy
2 iz
vx v y vz 0
8 RT v M mol
o
vp v
v2
v
v2
理想气体状态方程

理想气体状态方程理想气体状态方程是描述理想气体状态的重要公式,它揭示了气体温度、压力、体积和摩尔气体常数之间的关系。
理想气体状态方程的形式为PV = nRT,其中P代表气体的压力,V代表气体的体积,n代表气体的摩尔数,R代表摩尔气体常数,T代表气体的温度。
理想气体状态方程的推导从博得定律开始。
博得定律指出在恒定温度下,气体的压力与其体积的乘积是一个常数。
即P × V = 常数。
然而,这个式子只适用于相同温度下的气体状态。
为了将这个定律推广到不同温度下的情况,引入了摩尔气体常数和绝对温度的概念。
摩尔气体常数是一个物理常数,代表单位摩尔气体在标准状况(273.15K,1大气压)下所具有的能量。
摩尔气体常数的值为R =8.314 J·mol^-1·K^-1。
它可以用来描述不同气体在相同温度下的性质。
绝对温度是以绝对零度为零点的温度刻度,用K表示。
在绝对温度下,理想气体变体积律为V / T = 常数。
将摩尔气体常数引入这个变体积律中,得到PV / T = R,即理想气体状态方程。
理想气体状态方程的应用广泛。
首先,它用于描述理想气体在各种条件下的状态,从而推导出其他与气体性质相关的公式。
其次,它在热力学和工程学中被广泛应用,用于计算气体的体积、压力、温度等参数。
第三,它在化学反应的研究中也有重要作用,用来计算气体反应物和生成物之间的摩尔比例。
需要注意的是,理想气体状态方程是基于对理想气体的假设推导出来的,它假设气体分子之间没有相互作用,体积可忽略不计。
因此,在高压和低温条件下,理想气体状态方程可能会产生误差,需要使用修正的状态方程进行计算。
总结起来,理想气体状态方程是描述理想气体状态的重要公式,通过气体的温度、压力、体积和摩尔气体常数之间的关系来描述气体的状态。
它的推导基于博得定律和摩尔气体常数的概念,广泛应用于热力学、工程学和化学反应的研究中。
然而,需要注意理想气体状态方程的适用范围和假设条件,在特定条件下可能需要使用修正的状态方程进行计算。
大学物理6-4理想气体的温度公式

1. 温度的本质和统计意义
根据理想气体的压强公式和状态方程可导出
宏观量温度 T 与微观量的关系,从而揭示温度的
微观实质。
质量为 M 的理想气 体,分子数为 N ,分子质
PV M RT M mol
量为 m ,则有: M Nm
1 mol 气体的分子数
为N0 ,则有 Mmol N0m
(2)在高真空时,压强为1.3310-5 Pa , 在1 m3中有多少个分子?
解(1)按公式 p=nkT 可知
(1)
n
p kT
= 1.013105 1.381023 300
m3
2.451025 m3
(2)
n
p kT
= 1.33105 1.381023 300
m3
3.211015 m3
可以看到,两者相差1010倍
得到 P N R T V N0
把它们代入理想气体 状态方程:
其中 n N V
温度的本质和统计意义
NR
P
T
V N0
P nkT
k R 1.381023 J K 1 N0
由理想气体压强公式: p 2 nw 3
得: w 3 kT 2
温度的本质和统计意义
温度的统计意义 温度实质(统计概念)
3 kT=3 1.381023 123J 2.551021 101323m / s 331m / s
3
8.311273 28103 m
/
s
1.06
103
m
/
s
(2)同理在温度 t =00C 时
3 kT=3 1.381023 273J 5.651021 J
22
热力学温度与压强公式整理

热力学温度与压强公式整理热力学是研究物质内部热平衡状态及其与外界的相互作用的一门学科。
温度和压强是热力学中常用的两个重要参数。
本文将对热力学温度和压强的公式进行整理和介绍。
一、热力学温度公式热力学温度是一个物质内部热平衡状态的刻画,是物质分子运动速度和热量分布的表征。
根据理想气体状态方程,可以得到以下热力学温度公式:1.理想气体的温度公式:理想气体的温度与分子平均动能直接相关,可以用以下公式表示:T = (2/3) * (E_avg / k)其中,T为温度,E_avg为气体分子平均动能,k为玻尔兹曼常数。
2.理想气体的温标转换公式:不同的温标测量温度的单位不同,可以通过以下公式进行转换:T(℃)= T(K)- 273.15其中,T(℃)为摄氏温度,T(K)为开尔文温度。
二、热力学压强公式压强是指单位面积上受到的力的大小,在热力学中压强常用来描述气体的状态。
根据理想气体状态方程和压强定义,可以得到以下热力学压强公式:1.理想气体的压强公式:理想气体状态方程为:PV = nRT其中,P为压强,V为气体体积,n为气体的物质量,R为气体常数,T为气体的温度。
2.理想气体的分压公式:混合气体的总压强可以用各组分的分压之和表示,即:P_total = P₁ + P₂ + P₃ + ...其中,P_total为混合气体的总压强,P₁、P₂、P₃为各组分的分压。
3.理想气体的压强单位换算:不同的压强单位之间存在一定的换算关系,常用的单位换算公式如下:1 atm = 760 mmHg = 101325 Pa其中,atm为大气压,mmHg为毫米汞柱压强,Pa为帕斯卡。
综上所述,热力学温度与压强的公式整理如上。
通过这些公式,我们可以更好地理解热力学的基本概念和性质,进一步应用于相关的热力学计算和实际问题的解决中。
理想气体的温度公式

理想气体的温度公式
理想气体的温度公式是一个非常重要的物理公式,它描述了理想气体的温度与其它物理量之间的关系。
在本文中,我们将详细介绍理想气体的温度公式及其应用。
我们需要了解什么是理想气体。
理想气体是一种理论模型,它假设气体分子之间没有相互作用力,且分子体积可以忽略不计。
这种假设在实际情况中并不完全成立,但是在一定条件下,理想气体模型可以很好地描述气体的行为。
理想气体的温度公式是这样的:PV=nRT,其中P表示气体的压强,V表示气体的体积,n表示气体的摩尔数,R表示气体常数,T表示气体的温度。
这个公式可以用来计算理想气体在不同条件下的状态。
我们可以从这个公式中推导出理想气体的温度公式:T=P(V/nR)。
这个公式告诉我们,理想气体的温度与其压强、体积、摩尔数和气体常数之间有关系。
当我们知道其中任意三个量时,就可以用这个公式计算出气体的温度。
理想气体的温度公式在实际应用中非常广泛。
例如,在化学实验中,我们需要知道气体的温度、压强和体积,以便计算出气体的摩尔数。
在工程领域中,我们需要知道气体的温度和压强,以便设计和操作气体系统。
理想气体的温度公式是一个非常重要的物理公式,它描述了理想气
体的温度与其它物理量之间的关系。
在实际应用中,我们可以用这个公式计算出气体的状态,从而更好地理解和控制气体的行为。
大学物理:理想气体的温度
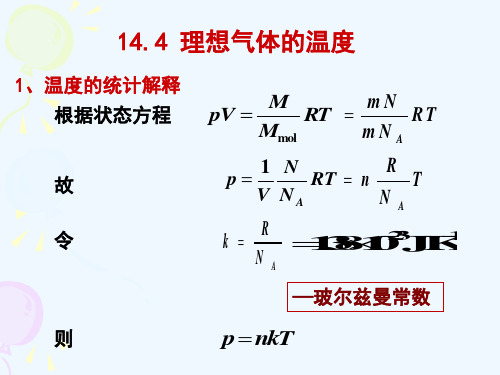
1 2 3 t m v k T 2 2
v
2
3 kT m
3RT M m ol
在相同温度下,由两种不同分子组成的混合气 体,它们的方均根速率与其质量的平方根成反比。
1 1 2 2 mv mv 1 1 2 2 2 2
v 12 v 22
m2 m1
3 t kT 2
宏观可测量量
微观量的统计平均值
理想气体分子的平均平动动能与温度成正比。 或者说: 温度 T 是分子平均平动动能的量度。 温度是大量分子集体运动的宏观表现,它反 映了大量分子集体运动的剧烈程度。
注意:
①温度公式反映了宏观量T 与微观量 t 之间的关系 T ∝ t 与气体性质无关; ②温度是大量分子无规则运动的集体表现, 单个分子的温度无意义。 ③温度平衡过程就是能量平衡过程。
例 理想气体体积为 V ,压强为 p ,温度为 T , 一个分子 的质量为 m ,k 为玻尔兹曼常量,R 为摩 尔气体常量,则该理想气体的分子数为:
(A)
pV m
(B) pV( kT ) (D)pV( m T )
(C) pV (RT )
解:
p nkT
pV N nV kT
2、方均根速率 由
讨论
一瓶氦气和一瓶氮气密度相同,分子平均平动动 能相同,而且它们都处于平衡状态,则它们 (A)温度相同、压强相同。
(B)温度、压强都不同。 (C)温度相同,但氦气的压强大于氮气的压强。 (D)温度相同,但氦气的压强小于氮气的压强。
N k 解: p nkT kT T V m p ( N ) p ( He ) m ( N ) m ( He ) 2 2
14.4 理想气体的温度
理想气体公式

理想气体公式
理想气体公式:pV=nRT。
p是指理想气体的压强;V为理想气体的体积;n表示气体物质的量;T表示理想气体的热力学温度;R为理想气体常数。
扩展资料:
理想气体是研究气体性质的一个物理模型。
从微观看,理想气体的分子有质量,无体积,是质点;每个分子在气体中的运动是独立的,与其他分子无相互作用,碰到容器器壁之前作匀速直线运动;理想气体分子只与器壁发生碰撞,碰撞过程中气体分子在单位时间里施加于器壁单位面积冲量的统计平均值,宏观上表现为气体的压强。
从宏观看,理想气体是一种无限稀薄的气体,它遵从理想气体状态方程和焦耳内能定律。
有时也将严格满足理想状态方程的气体称之为理想气体,满足公式pV=nRT的气体。
理想气体温度公式

理想气体温度公式理想气体温度公式“理想气体温度公式”是描述理想气体状态变化的公式,它被广泛应用于工程学、物理学、化学及天文学等领域。
根据所研究的气体的状态和变化,理想气体温度公式可分为以下几类:1. 压强-体积-温度关系公式作为描述气体状态的基本公式之一,压强-体积-温度关系公式亦为理想气体状态方程。
该方程描述了一定数量的气体状态随着压强、体积和温度发生变化时,它们三者之间的关系。
在理想气体的状态下,该关系可用以下公式表示:PV=nRT其中,P表示气体的压强,V表示气体的体积,T表示气体的温度,n 表示气体的物质量,R则为气体常数,其值等于8.314 J/(mol · K)。
2. 等温过程公式当一定数量的气体在温度不变的情况下改变压强和体积时,该气体状态变化称为等温过程。
根据理想气体状态方程,可得到一个描述等温过程的公式:PV=C其中C为常数,表示等温过程时气体状态的不变量。
3. 绝热过程公式在没有热量交换的情况下,一定数量的气体在改变压强和体积时发生的状态变化被称为绝热过程。
对于理想气体而言,其绝热过程的公式为:PV^γ=C其中γ为绝热指数,值与分子自由度有关。
对于单原子分子,γ=5/3,而对于双原子分子,γ=7/5。
4. 等容过程公式当一定数量的气体在体积不变的情况下改变压强和温度时,该气体状态变化称为等容过程。
对于理想气体,其等容过程公式为:P/T=C其中C为常数,表示等容过程时气体状态的不变量。
总之,“理想气体温度公式”是研究气体状态变化的基础公式,而随着不同气体的处理方式和状态参数的变化,理想气体温度公式也会有所不同。
只有通过深入理解和掌握这些公式,才能更好地理解和探究气体的状态变化规律。
理想气体公式汇总

理想气体公式汇总全文共四篇示例,供读者参考第一篇示例:理想气体是一个理想的概念,它假定气体分子之间没有相互作用,体积可以忽略,遵守玻义玻利亚定律,以及理想气体状态方程。
理想气体公式是研究气体性质时经常使用的数学表达式。
下面将详细介绍几种常见的理想气体公式,希望能对读者有所帮助。
理想气体状态方程是描述理想气体体积、压力和温度之间关系的基本方程。
它是由盖·吕萨克在19世纪初提出的,也称为理想气体定律。
理想气体状态方程的数学表达式为:PV = nRT,其中P为气体的压力,V为气体的体积,n为气体的摩尔数,R为气体常数,T为气体的温度。
根据理想气体状态方程,当温度和压力不变时,气体的体积与摩尔数成正比;当温度和摩尔数不变时,气体的体积与压力呈反比;当温度和体积不变时,气体的压力与摩尔数成正比。
理想气体状态方程可以根据波列-查理定律和理想气体状态方程推导出其他重要的理想气体公式,如分压定律和道尔顿定律。
分压定律指出,在一个封闭容器中含有两种或多种气体时,每种气体所对应的压强称为分压,而总压强等于各种气体的分压之和。
数学表达式为:P = P1 + P2 + ... + Pn。
道尔顿定律是指在一定温度下,混合气体中每种气体的分压与该气体分子在混合气体中所占的体积的比例相等。
数学表达式为:P1/P = V1/V = n1/n,其中P1为第一种气体的压力,V1为第一种气体的体积,n1为第一种气体的摩尔数。
理想气体公式还有其他一些常用的形式,如摩尔体积和密度。
摩尔体积是指单位摩尔气体所占据的体积,常用符号为V_m,数学表达式为V_m = V/n。
密度是指单位体积气体的质量,常用符号为ρ,数学表达式为ρ = m/V。
根据理想气体状态方程和摩尔体积的定义,摩尔体积和密度之间的关系可以表示为ρ = P/(RT),其中ρ为气体密度,P为气体压力,R为气体常数,T为气体温度。
除了上述几种常见的理想气体公式外,还有一些其他相关的公式和定律,如温度和摩尔数的关系、温度和体积的关系、摩尔数和压力的关系等。
大学物理-4-3 理想气体分子的平均平动动能与温度的关系

m 1 v12
1 2
m2 v22
v12 m2
v22
m1
据此可设计过滤器来分离同位素,例235U, 238U
讨论
一瓶氦气和一瓶氮气密度相同,分子平均平动动 能相同,而且它们都处于平衡状态,则它们
(A)温度相同、压强相同。
(B)温度、压强都不同。
(C)温度相同,但氦气的压强大于氮气的压强.
(D)温度相同,但氦气的压强小于氮气的压强.
V NA
在相同的体积内分
子数相等。
分子数 密度
k=R/NA=1.38×10-23J·K-1
称为玻耳斯曼常量
二、理想气体分子的平均平动动能与温度的关系
阿伏加德罗定律: p nkT
理想气体压强公式 分子平均平动动能
p 2 n 1 mv 2
3 2
k
1 mv2 2
3 kT 2
微观量的统计平均值
宏观可测量量
第三节 理想气体的温度公式
一、理想气体状态方程的分子形式
设一个分子的质量为m,质量为m’的理想气体
的分子数为N,1摩尔气体的质量为M,则m’=Nm,
M=NAm。代入理想气体的物态方程
pV m RT pV mN RT N RT
M
mN A
NA
P N
R T
p nkT
在相同温度和压强 下,各种理想气体
pV (mT )
解 p nkT
N nV pV kT
例一容器内贮有氧气压强为P=1.013×105Pa, 温度t=27℃,求(1)单位体积内的分子数; (2)氧分子的质量;(3)分子的平均平动动 解: 能。
(1)有P=nkT
(2)
n
P kT
3温度公式

5.由温度公式可计算某一温度下气体的方 均根速率。 3 1 2 k kT mv 2 2 方均根速率 3kT 3kN0T 2 v m N 0m 由
R N0k N 0m
v
2
3RT
§3.温度公式 /二、注意几点
例:求 27 C 的空气方均根速率。(空气的 摩尔质量为 29 g/mol )
P nkT 比较有
2 n k nkT 3
温度公式:
3 k kT 2
§3.温度公式 / 一、温度公式
3 k kT 二、明确几点 2 1.温度是对大量分子热运动的统计平均结 果,对个别分子温度无意义。
2. T k 分子运动得越激烈,温度越高。 •温度是分子平均平动动能的标志。
N 其中 n V
为分子数密度
k为玻尔兹曼常数 8.31 R 23 k J/k 23 1.38 10 N 0 6.022 10
P nkT
P T
§3.温度公式 / 一、温度公式
§3.温度公式 / 一、温度公式
1 2 2 再由压强公式 P nmv n k 3 3
与
解:
v
2
3RT
3 8.31 300 507.8m/s 3 29 10
3. 不同气体温度相同,平均平动动能相 同。
4.由P=nkT可知标准状况下分子数密度。
§3.温度公式 / 二、注意几点
5 P0 1 . 013 10 n0 kT0 1.38 1023 273
2.69 10
25
m
3
不同气体在标准状态下的 n 相同。
§3.温度公式 /二、注意几点
第三节
理想气体的温度和摩尔摩尔与体积的关系

理想气体的温度和摩尔摩尔与体积的关系理想气体的温度和摩尔和体积的关系理想气体是一种假设模型,它是基于一些简化的前提条件而建立的。
其中,理想气体的温度和摩尔与体积之间有一定的关系。
本文将就这一关系展开讨论。
1. 理想气体定律理想气体定律是描述理想气体性质的基本规律,它可以用来解释理想气体温度和摩尔与体积之间的关系。
根据理想气体定律,当理想气体的压强、摩尔数、绝对温度和体积之间存在关系时,可以得到以下方程:PV = nRT在这个方程中,P代表气体的压强,V代表气体的体积,n代表气体的摩尔数,R代表气体常数,T代表气体的绝对温度。
根据这个方程可以推导出理想气体温度和摩尔与体积之间的关系。
2. 温度和摩尔与体积之间的关系根据理想气体定律的PV = nRT方程,可以推导出摩尔与体积和温度的关系。
通过对该方程进行变形,可以得到以下公式:V/n = RT/P = V'在这个公式中,V/n代表单位摩尔气体的体积,R为气体常数,T为气体的绝对温度,P为气体的压强,V'代表摩尔与体积。
根据这个公式可以得知,摩尔与体积与温度成正比关系。
3. 温度和体积之间的关系理想气体定律中的PV = nRT方程中的n为摩尔数,而不是摩尔与体积。
因此,摩尔与体积和体积之间的关系与温度无关,只与摩尔数有关。
综上所述,理想气体的温度和摩尔与体积之间有一定的关系。
根据理想气体定律的PV = nRT方程,可以推导出摩尔与体积与温度成正比关系。
而温度和体积之间的关系与摩尔与体积无关,只与摩尔数有关。
这一关系在研究理想气体性质和进行气体计算时起到了重要作用。
需要注意的是,理想气体的模型是基于一些简化的假设条件建立的,因此在实际应用中可能存在一定的误差。
实际气体的行为可能会受到一些其他因素的影响,如压力高于临界点、温度较低等。
因此,在实际问题中需要综合考虑其他因素进行修正。
总之,理想气体的温度和摩尔与体积之间存在一定的关系,可以通过理想气体定律的公式进行推导和计算。
温度压强体积公式

温度压强体积公式
温度压强体积公式指的是理想气体状态方程,也称作理想气体法则,
它表示为以下公式:
PV=nRT。
其中,P表示气体的压强,V表示气体的体积,n表示气体的摩尔数,R为气体常数(也可写作k),T为气体的绝对温度。
这个公式告诉我们,在一定温度下,气体的体积和压强以及摩尔数都
是相关联的。
如果我们知道了其中三个量,就可以通过这个公式求出第四
个量。
该公式是热力学的基本公式之一,用于描述气体的物理性质,例如温度、压强和体积之间的关系。
在许多工业生产和科学实验中都有广泛应用。
气体混合后的温度计算

气体混合后的温度计算气体混合后的温度计算是一个相对复杂的计算问题,需要了解气体物理学的相关知识。
首先,我们需要明确一个概念,即理想气体状态方程:PV=nRT。
其中,P表示气体压力,V表示气体体积,n表示气体的物质量,R是气体常数,T是气体的绝对温度。
气体的物理量可以表示为标准状态或者实际状态。
标准状态指的是温度为273.15K(0度C)、压强为101.3kPa的状态;实际状态则是指任意温度和压力下的状态。
在混合过程中,我们可以通过气体混合定律来计算混合后的气体状态。
下面,我们介绍一下气体混合定律。
气体混合定律指的是:p1V1+p2V2= (n1+n2)RT。
其中,p1和p2分别是两个气体的压力,V1和V2分别是两个气体的体积,n1和n2分别是两个气体的物质量,T是气体的绝对温度。
这个公式可以用来计算不同气体混合后的物理量。
例如,假设我们有10L的氧气和20L的氮气,它们处于273.15K,1atm下的状态。
我们需要计算它们混合后的状态。
根据气体混合定律,我们可以得到:p1V1+p2V2= (n1+n2)RT1atm*10L+1atm*20L= (n1+n2)*0.0821*(273.15+0)整理一下,我们可以得到:n1+n2=3mol混合后的气体总体积为30L,平均摩尔质量为((10L*0.032g/mol+20L*0.028g/mol)/3mol)= 0.029g/mol。
这样,我们可以计算出混合后的气体温度。
T=(p1V1+p2V2)/(n1+n2)RT=(1atm*10L+1atm*20L)/(3mol*0.0821)= 300K混合后的气体温度是300K,即26.85度C。
我们可以看到,气体混合定律及理想气体状态方程可以配合使用,帮助我们计算复杂的气体混合问题。
总结一下,要计算气体混合后的温度,我们需要了解气体状态方程和气体混合定律。
通过这两个公式,我们可以计算出混合后的气体温度,以及其他的物理量,例如压力、体积、物质量等。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
单个分子对器壁碰撞特性 : 偶然性 、不连续性. 大量分子对器壁碰撞的总效果 : 恒定的、持续的
冲力的作用 (类似雨伞受到雨滴的撞击).
从气体分子运动论的观点看,气体的压强是大量分子不断 与器壁碰撞产生的冲力的结果,是一个统计平均值;
由于分子的大量性和运动的随机性,使器壁各处的压强相 等;
分子平均平动动能
1. 实验表明:1mol的任何物质所含有的分子数目相 同,且为阿伏加德罗常数:
N A 6.02 1023个 / mol
2. 根据结构,分子可分为三类: -----单原子分子:惰性气体,He、Ne、Ar、Kr、Xe -----双原子分子:H2、N2、O2、 -----多原子分子:H2O、CO2、CH4
2)、分子在永不停息地作无序热运动, 其剧烈程度和温度有关。
3)、分子间存在的相互作用力 ___ 分子力。
§2.2.1 理想气体分子模型和统计假设
理想气体:宏观上指:压强不太大,温度不太低的气体;
在常温下,压强在数个大气压以下的气体,一般都能很好地满 足理想气体。
一、理想气体的分子模型
1、分子本身尺寸比分子间距小得多而可忽略不计——质点;
k
1 mv2 2
设 边长分别为 l1,l2 及 l3 的长方体容器中有 N 个全
同的质量为 m 的气体分子,计算 A1 壁面所受压强 .
y
A2 o
z
- mmvvvxx l1
vy
A1 l2
o
l3 x vz
v vx
17
单个分子遵循力学规律
y
A2o
z
- mmvvvxx பைடு நூலகம்1
A1 l2 l3 x
第i个分子x方向动量变化:
2、除碰撞一瞬间外,分子间互作用力可忽略不计。分子重力 也忽略不计。分子间的碰撞以及分子和器壁的碰撞可看作 是完全弹性碰撞。
3、分子两次碰撞之间作自由的匀速直线运动;
统计规律的基本概念
1. 随机事件:在一定条件下可能发生也可能不发生的事情。 2. 统计规律:大量随机事件从整体上反映出来的一种规律性。
偏离统计平均值的现象称为涨落现象,即:一切与热 运动相关的宏观量的数值都是统计平均值,在某一瞬 间或局部范围内的实际数值都与统计平均值有偏差。 (扔10次硬币和扔10000次的概率可能有偏差。)
粒子数越多,涨落现象越小;
粒子数越少,涨落现象越明显。太少,统计将失去意义;
统计规律有以下几个特点: (1)只对大量偶然的随机事件才有意义。 (2)它是不同于个体规律的整体规律(量变到质变). (3)总是伴随着涨落.
3. 分子间既有引力作用, f 又有斥力作用
r ro f 0 平衡位置 o
r ro f 0 斥力起主要作用
斥力
r0
r
R
引力
v12
v12=0
r
d
d 分子有效直径 1010 m
r ro f 0 引力起主要作用
r R f 0 R—分子有效作用半径 108 m
分子力是短程力!
4. 气体分子的热运动
对少量分子,等概率假设是不成立的!
2.2.2、理想气体压强公式
压强的实质:
1.宏观上,气体压强是指容器壁单位面积上所受到 的气体的压力;
2.微观上,气体压强是大量分子对容器壁持续不断 碰撞产生的综合效果。
对于某一个分子,对器壁的碰撞是断续的,但由于分子数 目巨大,对器壁任一宏观微小面积,碰撞的分子数目非常 之巨大,它比起倾盆大雨之中雨点对雨伞的冲击要密集得 多。所以就像在大雨中撑着的伞要受到雨水的持续压力一 样,会观测到气体对器壁的一个稳恒压力.
N
ix
i
y 1 N
iy
i
z 1 N
iz
i
故,各方向运动概率均等 vx vy vz
等概率假设二:
定义:分子速率平方的统计平均值: v2 i vi2
N
v2x v2y vz2
2 vx2 vy2 vz2
各方向运动概率均等,则:
v
2 x
v
2 y
vz2
1 3
v2
等概率假设是在忽略重力的条件下,大量分子的无 规则运动的统计规律;
必然事件 必然发生。 必然不发生。
随机事件 ——在一次试验中是否发生不能事先确定,但 是,大量重复试验,遵从一定的统计规律。
9
例:抛硬币N次, NA次正面向上。 N很大时, N A 1
N2
pA
im N A N N
1 2
抛硬币的 统计规律
PA 表示正面出现的概率。
例1. 掷骰子
1 pi = 6
3、涨落现象
11
二、理想气体的统计性假设
虽然无序性是气体分子热运动的基本特性,每个分子仍满 足牛顿定律,但大量的偶然、无序的分子运动中,包含着一种 统计规律性,即:
1)分子按位置的分布是均匀的, 分子数密度均匀
n dN N dV V
2). 沿空间各个方向运动的分子数相等,平衡态下,分子在各 个方向上运动的机会是均等的,也就是说,分子的运动没 有择优方向;
《热 学》
统计物理学-----分子动理论 热力学------第一、第二定律
1
热学导论
一、热学的基本概念
热现象:物质的物理性质(P、V)随温度变化的现象.
热运动:宏观物体中的每一个分子(原子)都在作永不
停息的无规则运动,它是由大量微观粒子所组成的宏观物 体的基本运动形式。特点:偶然性和无序性;
热运动
3). 分子运动的速度不同,但分子速度的方向分布是均匀的, 即:分子速度在各个方向上的统计平均值相同。
12
等概率假设一:
分子向各个方向运动的概率均等;分子速度在各 个方向上的分量的各种统计平均值相等;
定义:分子速率的统计平均值:
i
i
N
单个分子运动速度:
vi
vixi
viy j
viz k
x 1
无序性是气体分子热运动的基本特性
系统内每个分子都在作永不停止的无规则热运动, 气体分子力很小;
分子间的碰撞极其频繁,速度瞬息万变、具有偶 然性,分子间的能量交换也是极其频繁的,从而 气体内各部分的温度、压强趋于相等。
5. 气体动理论的基本观点:
1)、宏观物体由大量粒子(分子、原子等)组成, 分子之间存在一定的空隙。
机械运动
2
热学:是研究热现象的理论,即研究物质的
热运动规律以及热运动与物质其他各种运动形 式之间相互转化规律的科学。
气体分子运动论(气体动理论): 是以气体为研究对象,从气体分子热运动的观点出发, 运用统计方法研究大量气体分子的宏观性质和统计规 律的理论,也即研究分子热运动的特征和规律;
3
§2.1 分子运动的基本概念
