曲线梁桥平面位移机理分析
浅析曲线梁桥平面位移的影响因素

浅析曲线梁桥平面位移的影响因素作者:高安林来源:《科学与财富》2015年第14期摘 ;要:随着国民经济和社会的发展,城市中需要大量兴建高架桥和立交桥,但由于城市交通功能的要求和地形条件的限制,多采用曲线桥桥梁和匝道桥。
这些桥梁线型变化多端,结构受力比较复杂,由于预加力、温度效应、车辆行驶或一些其他外力影响的作用,会产生侧向的变位。
由于曲线梁桥的结构特点、支承形式等原因,当外力等影响因素消失后,发生的变位并不能够完全恢复,会产生部分不可恢复的残余位移。
本文基于此,对曲线梁桥的平面位移的影响因素进行了初步的探讨。
关键词:曲线梁桥;平面位移;设计连续曲线梁桥在使用过程中,由于预加力、温度效应、车辆行驶或一些其他影响因素的作用,会产生侧向的变位。
由于曲线梁桥的结构特点、支承形式等原因,当外荷载等影响因素消失后,弯梁发生的侧向变位并不能够完全恢复,会产生部分不可恢复的残余位移,在长期反复作用下,侧向的残余位移就会累积,产生较大的位移,即曲线梁桥的侧向位移(或称“爬移”)。
曲线梁桥的侧向位移问题轻则导致梁段伸缩缝的剪切破坏,影响其使用寿命;严重的则会出现支承结构破坏,梁体滑移和翻转。
桥梁在使用过程中出现该类问题,不仅影响交通,而且加固起来非常困难,造成巨大的经济损失。
1 支承方式支承方式是影响曲线梁桥平面位移的内在因素,支承方式直接影响全桥的内力分布,合理的支承方式可以承受自重和活载、偏载等因素所产生的组合扭矩作用,限制结构的平面位移。
曲线梁桥可以采用多种支承布置形式。
理论上讲,连续曲线梁桥的所有支承均可采用点铰支承,但在荷载作用下梁端将产生扭转变形,从而在梁端与桥台背墙间产生上下相对变形,这会导致伸缩缝破坏。
一般在两端的桥台设置能抵抗外扭矩的抗扭支座,中间支承可以采用抗扭支承,或点铰支承,或者交替使用两种支承形式,从而限制梁端的扭转变形,以保证伸缩缝正常工作。
主梁在各种荷载作用下,除了梁端扭转变形外,在支座位置处还会产生纵桥向与横桥向的变位,为了保证结构的正常工作,总希望沿着“切线方向”移动。
浅析曲线梁桥平面位移的影响因素

浅析曲线梁桥平面位移的影响因素随着人们对桥梁建设技术的不断探索和改进,曲线梁桥已经成为现代桥梁建设中的重要形式之一,其独具特色的曲线设计在美学上能够对城市景观做出积极贡献,在技术上能够有效地分散车辆的压力,提高公路交通的流量。
曲线梁桥的平面位移是影响其安全性的重要因素之一,本文将从曲线梁桥平面位移的概念、影响因素和控制方法三个方面进行详细分析探讨。
一、曲线梁桥平面位移的概念曲线梁桥平面位移是指桥面沿曲线方向上的迎风位移,也就是桥面的偏移或摆动。
平面位移的产生原因有很多,最主要的原因是建造过程中孔洞错位、斜孔放置过程中的偏离以及落水带选择不合理等造成的。
另外还有一些外部因素,比如风荷载、温度变化、车辆经过时的地震振动等,也会对曲线梁桥平面位移产生影响,进而影响桥梁的安全性能。
二、曲线梁桥平面位移的影响因素(1)梁桥自身结构:曲线梁桥的结构形式对平面位移有一定的影响。
在桥梁设计中,如果斜向设置孔洞的位置和大小不合理,就会影响桥梁的平面位移。
此外,曲线梁桥的荷载分配方式、不规则曲线等因素也会影响平面位移的大小。
(2)风荷载:曲线梁桥比较容易受到侧风的作用,当风速较大时,会对桥梁产生强大的侧向风压力,形成横向振动,进而引起桥梁的平面位移。
风荷载是曲线梁桥平面位移的最主要外部因素之一。
(3)温度变化:桥梁的温度变化也会对平面位移产生影响。
随着外界温度的变化,桥梁构件的温度也会跟着变化,导致材料的收缩和膨胀,引起桥梁的平面位移。
尤其是在夏季或冬季,温度变化更加明显,对桥梁的平面位移影响更大。
(4)车辆荷载:车辆荷载也是影响桥梁平面位移的重要因素之一。
当车辆通过桥梁时,它产生的荷载会加速桥梁的年龄疲劳,进而导致桥梁的平面位移。
此外,车辆的速度、尺寸和数量等因素也会影响平面位移的大小。
三、曲线梁桥平面位移的控制方法(1)合理设计:受到梁桥自身结构的影响很大,因此,在桥梁设计和制造过程中,需要充分考虑平面位移因素,并在孔洞设置、梁桥结构计算、材料选用等方面进行合理设计,以控制平面位移影响。
曲线连续刚构梁桥施工过程中变形控制分析的开题报告

曲线连续刚构梁桥施工过程中变形控制分析的开题报告一、问题背景与研究意义曲线连续刚构梁桥是一种常见的大跨径桥梁结构,由于其良好的经济性和工程实用性得到了广泛的应用。
然而,在曲线连续刚构梁桥的施工过程中,由于受到各种外界因素的影响,桥梁变形不可避免地会发生。
如果这种变形不得到有效的控制,则会对整个工程产生不利的影响,进而影响到工程的安全性和稳定性。
因此,研究曲线连续刚构梁桥施工过程中的变形控制问题,对于提高桥梁工程的安全性、保证施工质量和加强桥梁结构的稳定性具有重要的研究意义。
同时,对于提高我国大跨度桥梁结构施工的技术水平和推广应用也有积极的促进作用。
二、研究目的和内容本研究的目的是通过对曲线连续刚构梁桥施工过程中变形控制的分析和研究,探讨桥梁结构在施工过程中受到各种因素影响的变形控制方法。
具体研究内容包括:1.分析曲线连续刚构梁桥的受力情况,探讨作用力的分布和传递的特点。
2.分析曲线连续刚构梁桥施工过程中受到的各种因素,包括气候、地质和施工工艺等因素的影响。
3.研究和探讨曲线连续刚构梁桥在施工过程中变形的控制方法,包括采取加固措施、调整支座高程和加强施工监管等方法。
4.进行理论分析和实际应用研究,探讨各种方法的适用范围和可行性。
三、研究方法和技术路线在本研究中,将采用理论分析和实际应用相结合的研究方法。
具体技术路线如下:1.首先,通过文献调研和实地考察,获取曲线连续刚构梁桥施工过程中受力特点、变形特点和各种影响因素的相关数据。
2.然后,建立适当的模型,对曲线连续刚构梁桥受力和变形情况进行分析和计算,得出变形控制方法的基础。
3.基于理论分析和建模结果,选择合适的现代计算机软件,进行数值模拟和仿真计算,优化控制方案。
4.最后,根据实际情况,开展桥梁施工实验,验证和评估研究结果的有效性和可行性。
四、预期成果通过本研究,预期可以得出以下成果:1.深入分析曲线连续刚构梁桥施工过程中的变形控制问题,提出具有实际意义的控制方法。
钢箱连续曲线梁横向位移原因分析

从表2可以看出:恒载对支反力和竖 向挠度影响大;活载对横移影响大。
由于钢结构是理想的弹性材料,活 载和恒载产生的横移是可以恢复的。故 对本桥而言,荷载因素不是产生梁体横 移的主要影响因素。
2.2.3温度对梁体的影响 对于桥梁结构,温度变化影响包括 日照温差和季节温差这两种情况:季节 温差产生均匀温度变化,使得连续梁结
2)该桥复位后运营近三年未出现新 问题,说明上述问题分析正确,复位措 施得当,复位成功。
铎舞镁餐
I-
王新丰.男,1 9 7 5年出生,毕业于西南
交通大学,大学本科。
图3伸缩缝处残留砼块
表2荷载效应分析
荷载名称 墩号 G19 G18 G17 Gt5 G15 G14 G13
侧移(m)
2.4 2.7 2。8 0.0 3.2 5.4 8.6
表1 自重+升温50℃工况下不同支座形式的比较分析
结构名称 墩号 G19 G18 G17 G16 竖向支反力(kg)
132
1602
100
4447
58
5180
0
6150
61
4358
91
2731
12l
1314
G13,G19约束攒桥向位移
横移(m) 竖向支反力(kN)
0
1592
由表1的分析可知,在此工况下, G13、G19墩约束横桥向位移对支反力影 响很小,但各墩横移减小到原结构的6 0 %以下,这说明支座形式对曲线梁的横 移影响很大。G13、G19墩约束横桥向位 移相当于设置一个横向限位。
图 结构平面简图
万方数据
613 G礤
615
616
曲线梁桥的受力特点和分析方法

曲线梁桥的受力特点和分析方法摘要:由于在经济和审美上的优势,曲线梁桥被广泛应用于现代公路立交系统。
曲线梁的竖曲和扭转耦合,由于结构上的特点,相对于直梁桥而言,曲线梁的分析更为复杂。
本文对弯道梁桥的受力特点进行了介绍,并总结了分析弯道梁桥的有关理论。
关键词:曲线梁桥;弯扭耦合;支承体系;有限元法引言曲线梁桥是指主梁本身为弧形的弯曲桥梁。
由于其独特的线形,曲线梁桥突破了多种地形的限制,同时在高速公路、山地公路、城市桥梁等方面,由于其优美的曲线造型而得到了更快的发展。
曲线梁桥具有现实意义,发展前景非常看好,无论从几何角度、美学角度,还是从经济角度,都是如此。
1曲线桥梁受力特性1.1弯扭耦合作用由于受弯曲率的影响,当竖向弯曲时,曲线梁截面必然会产生扭转,而这种扭转又会导致梁的挠曲变形,这种挠曲变形被称为“弯扭耦合作用”。
对于弯道梁桥的设计,相对于直线型梁桥来说,要特别注意,因为弯道扭力耦合作用所产生的附加扭力,会使梁体结构产生较不利的受力条件,从而增加结构的挠曲变形。
值得注意的是,由于自重在使用荷载下占绝大多数,对于混凝土曲线箱梁桥而言,也会导致更明显的弯扭耦合。
由于弯道梁桥沿弯梁的线形布置支承不成直线,因此由于弯道外侧较重,导致桥体恒载重心相对于形心向外偏移。
曲线梁在自重的作用下,也会产生扭转和扭曲的变形,从而使曲线桥发生翻转,出现匍匐的现象,这就是曲线梁在自重的作用下产生的变形[1]。
1.2曲线梁内外侧受力不均匀曲线桥因弯曲和扭动耦合作用,变形大于同跨径的直线桥,且曲率半径越小、桥越宽,因此其简支曲线梁外缘的挠度比内缘大,这种变化趋势是显而易见的。
曲线梁桥体具有向外扭转的较大扭力、弯曲扭力耦合和偏载作用的可能。
扭转作用会越来越明显,曲率半径越小、跨度越大的曲线梁桥甚至会引起抗扭支座内侧支座产生空心现象,这种情况在抗扭转支座的内部支座上会产生空心现象,这种情况的发生曲线桥的支点反力与直线桥相比,有一种倾向,它的外侧会变大、内侧会变小,甚至在内侧产生负反力。
某曲线梁桥上部梁体横向移位的成因分析徐景江_1

某曲线梁桥上部梁体横向移位的成因分析徐景江发布时间:2021-10-01T02:19:08.458Z 来源:《基层建设》2021年第18期作者:徐景江[导读] 某高速公路空心板桥位于半径较小的圆曲线上,桥梁按曲线梁桥进行设计,经过近10年营运,桥梁第6、7跨梁(板)出现了横向曲线内侧的移位。
文章介绍该高速公路空心板桥梁(板)移位的情况,对梁体移位的原因进行总结分析云南省交通投资建设集团有限公司普洱管理处云南普洱 665000摘要:某高速公路空心板桥位于半径较小的圆曲线上,桥梁按曲线梁桥进行设计,经过近10年营运,桥梁第6、7跨梁(板)出现了横向曲线内侧的移位。
文章介绍该高速公路空心板桥梁(板)移位的情况,对梁体移位的原因进行总结分析。
关键词:曲线梁桥;梁(板);位移;原因分析1 概况1.1 基本情况某高速公路空心板桥位于半径较小的圆曲线上,桥梁横向按左右幅分离设计,桥梁上部结构形式为25m后张法预应力简支空心板、共7跨,横桥向由7片空心板构成。
下部结构形式为门架式圆柱墩,基础为钻孔灌注桩桩基础,两岸桥台为重力式桥台。
桥梁设计荷载是汽一超20,挂-120,设计时速为80 km/h。
1.2 上部梁(板)横向移位情况该桥于2003年12月建成通车,2013年发现该桥左、右幅7#桥台伸缩缝位置处防撞护墙及路面标线均有不同程度错位,其中左幅伸缩缝位置防撞护墙及路面标线均错位4cm,中央分隔带护墙明显竖向开裂错位(见图1)。
7#桥台上方支座均严重的横向偏压变形,支座与梁板底部结合面有明显的滑移痕迹(见图2),第7跨6#墩一端少数支座也存在偏压变形现象。
经过对该桥全面的检测以及对比该桥永久性观测网历年数据可确定该桥第6、7跨梁体整体向左侧(弯道内侧)移位,于7#桥台伸缩缝位置位移4cm,位移自第7跨B端(大里程侧)向第6跨A端(小里程侧)减小为0。
图1 7#桥台伸缩缝位置防撞护墙错位4cm图2 7跨B端支座变形,支座与梁板底部结合面有明显的滑移痕迹2 位移梁体设计情况桥梁位于半径600m的圆曲线上,全桥自曲线外侧至内侧均设有超高横坡,最大超高横坡为7.1%。
曲线连续梁支座“爬移”原因分析及设计体会

随着 我 国城镇 化 的 推 进 、 城市 交 通 基 础设 施 建
计, 2 0 0 7年 4月建成 通 车 。
设速度的加快和交通快速化需求 的提升 , 城市高架 及立交桥也将在改善城市交通状况需求中发挥重要 的作用 ; 此外 , 因城市用地条件 的限制 , 曲线桥梁 和 匝道桥也被广泛采用 。但 因其结构受力复杂 , 如设
析和构造措施设置不当及施工控制不严 , 在桥梁运 营过程 中会 出现 支座限位板 损坏 、 内侧支座 脱空 、 支座 “ 爬移 ” , 甚至于整体翻转等实际问题。通过实际工程事例 , 对箱梁进行受力分析 , 阐述了曲线梁桥支座“ 爬移 ” 的原 因 , 总结 出设计体会 , 为相关 设计人员提供参考 。
1 工程概 况 1 . 1 概况
渔港路立交为半苜蓿 叶形立交 , 立交 内设一处
左转 定 向 匝道 , 平 面 线形 : 直 线 +5 0 m 缓 和 曲线 + 1 8 0 m 半径 圆 曲线 +5 0 m 缓 和 曲线 +3 5 m半 径 圆 曲
图1 渔 港 路 立 交 节点 平 面 图
2 0 1 2年 0 7月 当 地 桥 梁 管 养 部 门对 桥 梁 外 观 ( 包括 桥 面系 、 支 座、 箱梁 、 墩 台、 基础 ) 、 材质 、 线 形
线组成 , 桥梁全长 3 6 6 . 0 7 m, 桥跨组合为 ( 2 1 . 4 + 2×
2 6 . 0+ 2 1 . 0 ) m+( 2 1 . 0+ 2 6 . 0+2 1 . 0 m +( 1 6 . 8+
2 1+1 6 . 8 ) m +( 1 6 . 8+2 1 . 0+1 6 . 8 ) m +( 2 1 . 0+
考虑剪力影响的多跨曲线连续梁桥径向位移解析分析

考虑剪力影响的多跨曲线连续梁桥径向位移解析分析刘英;邬晓光;钱若霖;冯宇【摘要】考虑剪力的影响,利用经典力学方法及虚功原理,推导出同曲率两跨一次超静定曲线梁在汽车离心力及均匀变温作用下任意截面的径向位移解析公式,并推广至同曲率n等跨曲线梁,再以两跨曲线梁为算例进行公式验证.结果表明:曲线梁桥的平面内径向位移问题必须充分考虑剪力的影响,本文所得解析解与有限元解的相对误差均<10%,满足工程应用精度要求,可用于曲线梁桥初步设计阶段径向位移的估算.分析了径向位移解析公式的特点,发现引起曲线梁桥爬移病害的关键因素是曲率半径、圆心角、截面特性、支撑及支座布置形式.%Considering the influence of shear force,the radial displacement analysis formula of arbitrary cross section was deduced by using of classical mechanics method and virtual work principle under the action of centrifugal force and uniform temperature change.Taking the formula of two-span curved girder bridge with one degree of indeterminacy as an example,then extended to n-span with the same curvature.The former formula was verified.The results show that the in-plane displacement problem of the curved girder bridge must take full account of the shear force.The error of the solution and the finite element solution are less than 10%,which can meet the engineering application precision and can be used for estimating the radial displacement in the preliminary design phase.Based on the further analysis of the characteristics of the radial displacement analysis formula,it is concluded that the key factors of creeping of the curved girder bridge arethe radius of curvature,the center angle,the cross section,the support and the arrangement of the support.【期刊名称】《铁道建筑》【年(卷),期】2017(057)008【总页数】8页(P7-14)【关键词】公路曲线桥;径向位移;解析分析;汽车离心力;均匀变温【作者】刘英;邬晓光;钱若霖;冯宇【作者单位】陕西省公路桥梁与隧道重点实验室,陕西西安 710064;陕西省公路桥梁与隧道重点实验室,陕西西安 710064;陕西省公路桥梁与隧道重点实验室,陕西西安 710064;陕西省公路桥梁与隧道重点实验室,陕西西安 710064【正文语种】中文【中图分类】U448.14;TU377曲线梁桥因其占地面积小,造型美观,对地形的适应性良好等优点而被广泛应用于山区及城市桥梁,在众多桥梁结构中占有独特的地位。
曲线梁桥的受力施工特点及设计方法分析

曲线梁桥的受力施工特点及设计方法分析摘要:介绍了曲线梁桥的力学特性,结构分析及应注意的几点问题,施工特性及设计方法。
关键词:曲线梁桥,结构,施工近年来,随着公路建设事业的快速发展,涉及到曲线梁的桥梁设计已经越来越多了,以往设计者希望通过调整路线方案,尽量避开这种结构形式,或由于曲线半径较大,采用以“直”代“曲”的形式,在桥梁上部(如翼缘、护栏等)进行曲线调整,以期达到与路线线形一致。
这些严格意义上说都不是曲线桥。
由于受原有地物或地形的限制,一些城市的立交桥梁和交叉工程的桥梁曲线半径比较小,桥墩基本上要设在指定位置,这种情况下只能考虑设计曲线梁桥。
1曲线梁桥的力学特性1.1曲线梁的受力情况曲线梁桥能很好地克服地形、地物的限制,可以让设计者较自由地发挥自己的想象,通过平顺、流畅的线条给人以美的享受。
但是曲线梁桥的受力比较复杂。
与直线梁相比,曲线梁的受力性能有如下特点: (1)轴向变形与平面内弯曲的耦合; (2)竖向挠曲与扭转的耦合; (3)它们与截面畸变的耦合。
其中最主要的是挠曲变形和扭转变形的耦合。
曲梁在竖向荷载和扭距作用下,都会同时产生弯距和扭距,并相互影响。
同时弯道内外侧支座反力不等,内外侧反力差引起较大的扭距,使梁截面处于“弯-扭”耦合作用状态,其截面主拉应力比相应的直梁桥大得多。
故在曲线梁桥中,应选用抗扭刚度较大的箱型截面形式。
在曲梁中,由于存在较大的扭矩,通常会出现“外梁超载,内梁卸载”的现象,这种现象在小半径的宽桥中特别明显。
另外,由于曲梁内外侧支座反力有时相差很大,当活载偏置时,内侧支座甚至会出现负反力,如果支座不能承受拉力,就会出现梁体与支座发生脱离的现象,通常称为“支座脱空”。
1.2下部桥梁墩台的受力情况由于内外侧支座反力不相等,使各墩柱所受垂直力出现较大差距。
当扭矩很大时,如果设置了拉压支座,有些墩柱甚至会出现拉力。
曲线梁桥下部结构墩顶水平力,除了与直桥一样,有制动力、温度力、地震力等以外,还因为弯梁曲率的存在,多了离心力和预应力张拉时产生的径向力。
S型曲线桥梁纵横向爬移机理分析及纠偏设计

收稿 日期 :2018—05—08 作 者简介 :李 攀(1982一),男 ,上海人 ,工程师 ,从事桥 梁设计工 作 。
1),设计荷载标准 汽车 一超 2O级 ,挂车 120验 算 , 于 2000年建成通车 ,迄今 已有近 20 a。
摘 要 :针 对某 s型 曲线桥 梁纵 横 向出现 较大 爬移 及支 座 剪切 破坏 的情 况 ,通 过有 限元 计算 分 析并 对照 实 际情 况 ,分析 其产
生 的机理 。纠 偏设计 同时采用 PLC同步 顶升 和纵 横 向纠偏顶 推复 位两 种技术 措施 ,三个维 度 纠偏须 在一 个维 度 实施 顶升 (顶
推 )时对 另外 两个 维度 的 自由度进 行 限制 。通 过增 加水平 方 向的钢 结构 、混 凝土 结构 牛腿 ,使其 即为 提供 水平 反力 的支 撑点 又
为 纠偏 限位装 置 。
关键 词 :s型 曲线 匝道桥 ;纵横 向爬 移 ;三维 度纠偏 ;反力 和限位装置
中图分 类号 :U448.21
本 文 以某 s型 曲线 匝道 桥 发 生 的 病 害 为 研 究 对 象 ,对此类 问题 的机理进行分析 、采取 的纠偏措 施 进 行 探 讨 。本 项 目相 比于 常 见 的 曲线 桥 梁 仅 出 现横 向爬 移病害 ,本 s型曲线 匝道桥还 出现 了纵 向爬 移 的情况 。
1 工 程 概 况 1
匝道桥 支座为板式橡胶支 座 ,其 中 3#、6#双 柱 墩 的 支 座 规 格 为 西50×9,1#、2#、4#、5#、7#、8# 独 柱 墩 的 支 座 规 格 为 670×10,9#墩 过 渡 墩 的 支 座 规 格 为4)27.5×6.5。
第3讲 曲线梁桥结构力学分析方法

1. 曲线梁桥结构分析方法综述
结构力学方法是分析曲线梁的内力和变形的另一途径,具有如下 主要优点: (1)简单明了,且可以得到精确解; (2)便于计算影响线,从而可以十分方便地计算曲线梁截面内力设计 控制值(最大值和最小值); (3)分析曲线连续梁桥也有一定的优势,不过对于变截面连续曲线梁
的较为繁琐。
根据B端的变形协调条件,即
TB BB BP 0
根据虚功原理,可知计算结构变形的最为通用的公式为
0 0 0 MM P T TP0 Q QP NN P dz dz dz dz EI GI d GA EA
14
2. 单跨简支曲线梁桥结构力学求解方法
曲线梁桥一般仅考虑弯矩和扭矩对变形的贡献,则
基本结构在B端作用单位赘余力TB=1时,根据平衡条件可知
M AC 0 M OA 0
TA 1 cos 0 RB R(1 cos 0 ) 0
RB
1 sin 0 RB R sin 0 0
R A RB 0
RA
1 R
1 R
Y 0
8
2. 单跨简支曲线梁桥结构力学求解方法
2.1 一次超静定简支曲线梁定义 两端具有竖向约束,且可以发生绕横向轴自由挠曲位移;(简支特点) 两端具有抗扭支承;(超静定特点) 具备以上两个特点的曲线梁桥称为简支超静定曲线梁桥(如下图所 示)。
Fig. 2-1 简支超静定曲线梁桥
9
2. 单跨简支曲线梁桥结构力学求解方法
BB
l M l 1 T R 0 d dz X dz dz 0 GI 0 EI 0 GI GI d d d l 2 2
BP
故
曲线梁桥平面位移机理分析

主梁 在各种 荷 载 作 用下 , 了梁 端扭 转 变形 除 外, 在支 座位置 处还 会 产 生 纵 桥 向与 横桥 向 的变
发生两个 方 向的位移 分 量 : 沿 桥轴线 方 向的纵 ① 向分量 ; 沿 桥轴 线垂 直方 向的分量 ( 图 2 。 ② 见 )
图 3, ) 由此得 知 :
一 9 ( 0 1一 £ ,£一 £ p) ) ( 一 r ( 0一 ) o9
由 2 3可 知预 应力 引起 的位 移是 沿着 结构切 . 线方 向 的 , 与桥 梁 支 座 与 伸 缩 缝 的设 置 是 不矛 盾
的 。但 预 应 力 产 生 的 总 扭 矩 是 向 曲线 外 侧 翻转
伸缩缝破 坏 。一 般在两 端 的桥 台设 置能抵 抗外扭
2o ri (—) 等 t S n
式 中: 为混凝 土的收 缩应 变 。 s
矩的抗扭 支座 , 中间支 承可 以采用 抗扭支 承 , 点 或
因此温度 变 化 和混 凝 土 收缩 时 , 曲线 梁桥 会
铰支承 , 或者交替 使用两 种 支承形 式 , 而限制 梁 从
( 1。 见 图 )
一
1 1 支承 方式 . 支承方 式是影 响 曲线梁 桥平面 位移 的 内在 因 素, 支承方 式直接 影响全 桥 的 内力 分布 , 理 的支 合 承方式可 以承受 自重 和 活载 、 载 等 因 素所 产 生 偏
的组合扭矩 作用 , 限制结 构 的平面 位移 。
/ ,Leabharlann a )无 约 束 的 情 况
图 2 曲 线 梁 变 形 示 意 图
1 3 徐变 影 响[ . 1 ]
\ ! \ 、竺
第5章 曲线梁桥的理论分析
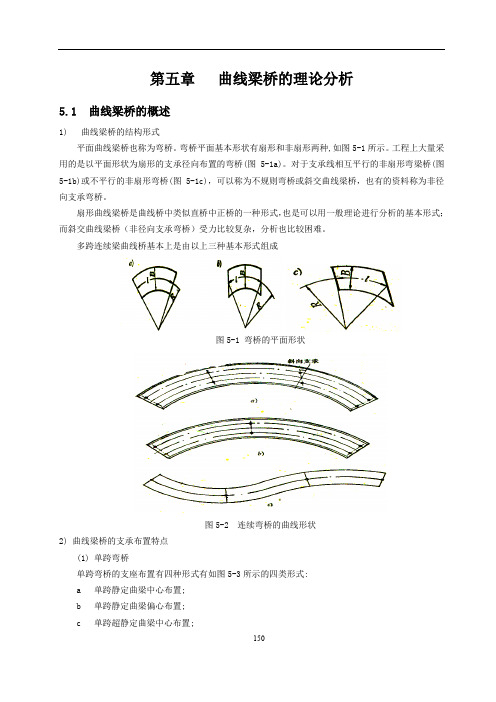
A'ch B ' sh C ' cos D ' z cos E ' sin F ' z sin
1 r2 1 mx r 3 qy EI x GI d EI x EI m , A' , B ' , 为由单跨弯梁两端边界条件确定的常数。 其中, a GI d
qz r
−
∂2 m y ∂z2
−
my r2
(5-8)
+ r ∂ z = −q y − −
Mx r
∂m x ∂z
5-9)
(5-10)
= −mz
有了力的平衡方程后, 下面需要建立变形状态的几何关系。 描述弯梁的独立位移分量为:轴向位移 u、径向位移 v、竖向 位移 w、截面扭角 φ ,它们均是坐标 z 的函数。 用弯梁的几何方程来描述截面变形与位移分量之间的几 何关系。以下讨论的截面变形包括:轴向应变εz , 饶 z 轴的扭 率k z , 饶 x、y 轴的变形曲率k z 、k y 。首先讨论轴向应变εz 。 在图 5-13 中, 将微段 AB 的 B 端轴向位移 u+du、 径向位移 v+dv 投影到 A 端的切向方向并与 A 端轴向位移 u 相减,并除以弧长 dz,略去高阶项,就得到轴向应变 图 5-13 弯梁轴向应变计算简图
(1)对于单跨弯梁,必须是等截面、等半径、荷载是沿全跨的分布函数、无集中荷载,并且需要 六个边界条件; (2)对于有集中荷载的单跨曲梁或多跨连续曲梁,应以集中力作用点或中间支座点为分段点,在 每一段分别建立方程,每一段需要六个边界条件,相邻边界条件应满足连续条件,按此方式进行方程 求解。 (3)对单跨弯梁沿全跨作用竖向均布荷载及均布扭矩时,其解为:
曲线连续梁桥变形因素分析
曲线连续梁桥变形因素分析发布时间:2022-08-21T02:45:28.646Z 来源:《城镇建设》2022年第4月7期作者:邹广林[导读] 本文对一座连续梁桥进行数值模拟分析,利用通用有限元软件MIDAS/Civil建立有限元模型,邹广林广州市城市规划勘测设计研究院广东省广州市 510060摘要:本文对一座连续梁桥进行数值模拟分析,利用通用有限元软件MIDAS/Civil建立有限元模型,从收缩、徐变、温度、离心力四个因素分析曲线梁桥的变形变化规律,并得出重要结论,分析得出温度是引起轴向位移变化重要因素,而离心力是引起横向位移变化的重要因素。
本文的分析方法和部分结论对同类桥梁的设计和施工有一定的指导意义。
关键词:曲线梁桥;结构分析;变形;MIDAS/Civil1.工程概况某座长联大跨曲线梁桥主桥为48+7×80+48m预应力混凝土变截面连续梁。
箱梁端支座处及边跨直线段和跨中处梁高为3.8m,中支点处梁高6.6m,箱梁横截面为单箱单室直腹板,顶板厚0.35m,腹板厚分别为:0.45m、0.65m、0.85m,底板厚由跨中的0.42m变化至中支点梁根部的0.758m。
中支点处加厚到1.3m。
梁高按圆曲线变化,圆曲线半径R=252.516m。
箱梁采用C55三向预应力钢筋混凝土,纵、横向预应力均采用低松弛高强钢绞线。
主桥上部结构施工方法:托架施工0号块,支架施工边跨现浇段,其余梁段采用挂篮对称悬臂施工,悬臂施工前做好临时锚固。
3 曲线梁变形分析曲线梁桥的平面变形包括:(1)轴向方向的纵向变形;(2)轴向垂直方向的横向变形。
引起梁体平面变形的荷载主要包括:温度变化、混凝土收缩、混凝土徐变、预应力、离心力等。
设计时通常在梁端设置纵向活动支座,容许梁端发生切向位移,在各支点上设置横向活动和固定支座,限制梁端整体横向位移又容许梁部自身结构局部横向变形。
但梁体的位移无论那种荷载作用下均与下部结构刚度密切相关。
第8章梁的位移分析与刚度设计ppt课件

大连大学
25
8.2.2 例题8-1 承受集中载荷的简支梁挠度和转角
▪ 已知:简支梁受力如图示。FP、 EI、l均为已知。
▪ 求:加力点B的挠度和支承A、
C处的转角。
大连大学
26
8.2.2 例题8-1 承受集中载荷的简支梁挠度和转角
▪ 解:1. 确定梁约束力
大连大学
17
8.2 小挠度微分方程及其积分
大连大学
18
8.2 小挠度微分方程及其积分
▪ 8.2.1 小挠度曲线微分方程 ▪ 8.2.2 积分常数的确定 约束条件与连续条件
大连大学
19
8.2 小挠度微分方程及其积分—— 8.2.1 小挠度曲线微分方程
大连大学
20
8.2.1 小挠度曲线微分方程
力学中的曲率公式
第8章 梁的位移分析与刚度设计
▪ 在数学上,确定杆件横截面位移的过程主要是积分运算,积分限或积 分常数则与约束条件和连续条件有关。
▪ 若材料的应力一应变关系满足胡克定律,又在弹性范围内加载,则位 移与力(均为广义的)之间均存在线性关系。因此,不同的力在同一 处引起的同一种位移可以相互叠加。
▪ 本章将在分析变形与位移关系的基础上,建立确定梁位移的小挠度微 分方程及其积分的概念,重点介绍工程上应用的叠加法以及梁的刚度 设计准则。
33
8.2.2 积分常数的确定 约束条件与连续条件
✓确定约束力,判断是否需要分段以及分几段; ✓分段写出弯矩方程; ✓分段建立挠度微分方程; ✓微分方程的积分; ✓利用约束条件和连续条件确定积分常数; ✓确定挠度与转角方程以及指定截面的挠度与转角。
大连大学
梁的位移分析

qa 3 θ A( q ) 3 EI
叠加
yC ( q )
5qL4 24 EI
=
P A B
A
q B
θ A θ A( P ) θ A( q ) a2 (3P4qa) 12 EI 4 3 5qa Pa yC 24 EI 6 EI
22
+
第五节 梁的刚度条件· 提高粱刚度的措施
y max [ y ]
23
例题
机床主轴的支承和受力可以简化为如图所示之外伸梁。其中
P1为由于切削而施加于卡盘上的力,P2为齿轮间的相互作用
力(主动力)。主轴为空心圆截面,外径D=80mm,内径 d=40mm,l=400mm,a=100mm, P1=2kN,P2=1kN。材料 的弹性模量E=200GPa。规定主轴的许用挠度和许用转角为: 卡盘C处的挠度不超过两轴承间距的1/104,轴承B处的转角不
PL yP 48EI
3
5qL4 PL3 y 384EI 48EI
19
例:求图示梁的最大转角和最大挠度。
EIz l
θmax
ymax
y max
x
Pl 3 () 3EI z Pl 2 2 EI z
P
y
θmax
20
例:按叠加原理求 A点转角 和 C点挠度。
P A q B a
解:载荷分解如图 查梁的简单载荷变形表,
2、正确理解和应用变形连续的概念,即在弹性范围
内梁的挠曲线是一条连续光滑的曲线。
18
例:图( a)所示简支梁,承受均布载荷 q和集中力 P的作用,试求梁中点C的挠度(EI为常数)。
P A L/2 C L (a) L (b)
4
曲线匝道桥梁体横向滑移的成因分析与处治

中阉科技信息 2 0 1 5年第 0 2期
C H I N A S C I F : N C E A N D T E CI 一 { N 0 L O G Y I N F O R M A T I ON J a r 1 2 0 1 5
郑
超
曲线匝道桥一般 平面半径较小 ,横 向滑移 现象较为突 出。本文通 过工程实例 ,结合空 间计算软件 mi d a s c i v i l 对支座稳 向受力进行了检算并与实测数据进行了比对 ,通过分析总结出横 向梯度温度和 离心 力是梁体产生横向滑移的主要原因 ,并争 对性地提出了合理有效的治理措施。
近年来随着国内经济的快速发展 、公路路网及城市道 路交通量的不断增大 , 为了解决交叉道路间交通 / ) l b 的转换 , 互通式 立体 交叉 的数 量也 在不 断增 多 。曲线 匝道 桥作 为 互
通 式 立体交 叉 的重要 组成 部分 ,作 为小 半径 弯桥 的代 表桥 型 ,其典型的支座脱空 、梁体横向滑移 、翘 曲、横向失稳
2 1 . 4 8
5 8 . O 6 1 1 6 . 3 6 4. 91 6 6 . 3 7 1 2 5 - 2 6
4 2 " - 2 5
6 4 . 0 1 5 O . 4 7 1 . 4 8 5 . O 1 9 2 3
1 O 6 . 8
6 8 8 8 8
6
6 0 0 8 0 0 8 0 0 8 0 0 8 0 0
6 0 0
( 注 :7 、8 、1 0 、1 1 号墩右侧支座水平力均为 0 ,表中未示出。 )
表2 第3 联 各桥 墩支座 横 向力计算 一览 表 ( 计入 横 向梯度 温度 及离 心力 )
曲线梁桥梁体偏位分析

曲线梁桥梁体偏位分析摘要:曲线梁桥能很好地适用地形、地物的限制,而且其结构线条平顺、流畅、明快,给人以美的享受。
在公路建设中,除特大桥梁外,一般要求桥梁地平面布置服从公路线形,在进行平、纵、断三方面综合设计时,应做到平面流畅、纵坡均衡、横断面合理,并避免长直线设计。
此时,曲线梁桥往往成为最优方案。
预应力混凝土连续曲线梁桥在使用过程中。
甚至在其施工的过程当中,会由于设计的不合理以及周围环境的影响,曲线梁桥的梁体可能会出现沿着径向的位移和向梁体外侧的翻转即曲线梁桥的偏位问题。
它具体表现在梁体的应力重分布,支座的竖向与横向支反力以及对桥墩应力的改变。
本文运用有限元软件对曲线梁桥进行了梁体偏位分析,探讨了曲线梁桥荷载横向分布系数的计算方法,采用有限元计算方法。
关键词:曲线梁桥;梁体偏位;荷载横向分布系数;有限元分析1.研究背景1.1.曲线梁桥梁体偏位原因连续曲线梁桥在使用过程中,由于曲率半径、自身恒载、预应力、温度效应、车辆离心力、混凝土收缩徐变以及一些其他影响因素的作用,会产生侧向的偏位。
由于曲线梁桥的结构特点、支承形式等原因,当外荷载等影响因素消失后,曲线梁桥发生的侧向偏位并不能够完全恢复,会产生部分不可恢复的残余位移,并且在长期的反复作用下,侧向的残余位移就会累积,产生较大的位移,即曲线梁桥的侧向偏位。
曲线梁桥的侧向偏位问题轻则导致梁端伸缩缝的剪切破坏,影响其使用寿命;严重的则会使支承结构产生破坏,梁体发生滑移或翻转。
曲线梁桥在使用过程中出现该类问题,不仅影响交通,并且加固起来也非常不方便,造成巨大的经济损失。
2.曲线梁桥梁体偏位原因分析2.1.曲线梁桥的曲率半径曲线梁桥的曲率半径是影响曲线梁桥侧向位移的主要因素,不同的曲率半径,对混凝土连续曲线梁桥的影响是不一样的R。
如某桥引桥为3跨单箱3室预应力混凝土连续曲线箱梁桥,箱梁顶板宽23m,梁高1.5m,翼宽2.5m,在恒载作用下,不同曲率半径情况下曲线梁桥竖向支反力如表3.1所示。
第5讲曲线梁桥结构力学分析方法

2侖大孕土木工《学兜局工《*4卜研死中心.楝*工《糸第5讲曲线梁桥结构力学分析方法内容简介1 •概述2.用结构力学方法求解一次超静定 简支曲线梁大孕土木工兜风工《世恥研3^中心・楝*工《余1.概述曲钱累基本微分方程企 Qv ■ 匹凹土汕・十创0/V - GW+=心 r r K d+马V ■许,J+:gk 捫-f 旦+«\ d r" ) r*r \ r j dz采用曲线梁的一般微分方程来求解曲线梁的内力和变形, 个四阶的联立微分方程,在此情况下,需要确定8个任意积分常数.需要解 一系列由边界条件确定的线性方程组:即便对于S 为简单的情况也十分复 杂,裾要通过边界条件来确定积分常数-纠(>+三严+2」=坐_坐_ V 厂 /• J dz r dz^ r(2-18)(276)(2-17) 需要求解两4结构力学方法:1)该方法原理简单; 2)概念明确・分类(依据;是否考虑曲线梁桥横截面在受荷后的截面翘曲变形):横截面各项尺寸与跨长相比很小(UB>=3-4 ).可以将 实际结构作为集中在剪切中心的弹性杆件来处理: 曲线梁的横截面变形后仍保持为平面; 曲线梁变形后横截面的周边形状保持不变,即无畸变: 截面的剪切中心与形心相重合。
2)翘曲扭转理论当曲线梁桥截面为开口薄壁或闭口薄壁截面时,翘曲扭矩在总扭矩 中占的比重相当大,此时必须考虑翘曲扭转的影响。
曲线梁桥的翘曲 扭转理论是在直线梁桥的薄壁直杆理论基础上提出的。
参见黄剑源 《薄壁曲线梁桥》一书相关章节或《薄壁杆件》。
实验和理论证实:钢筋混凝土和预应力混凝土曲线梁桥,由于裁 面翘曲反应引起的正应力与剪应力,与基本弯曲和扭转的应力值相比 较小,因此一般可以采用单纯扭转理论来分析:但対于薄壁截面构成 的钢结构来说,鉴于薄壁效应明显,因此宜采用翘曲扭转理论来进行 分析(如曲线钢箱梁、壁库较薄的预应力混凝土曲线梁桥)。
侖大学土*工《学兜局工《畑^研死中心.林*工《糸单纯扭转理论A1) 侖大学土*工《学兜局工《畑^研死中心.林*工《糸6M 侖大学土木工《睜兜风工厘拔恥研丸中心・楝*工2,用结构力学方法求解一次超静定简支曲线梁2. 1 一次超If 定简支曲线梁定义>两端具有竖向约束•且可以发生绕横向轴自由挠曲位移;(简支特点〉 >两端具有抗扭支承:(超静定特点)具备以上两个特点的曲线梁桥称为简支超静定曲线桀桥(如下图所示)-Fig, 2-1简支超静定曲线梁桥zT^、\M 侖大学土木工《睜兜风工厘拔恥研丸中心・楝*工2? 2 一次超静定简支曲线桀在集中荷栽作用下的内力求解W2-12基本结构体甬«誓B 点押加变影为*的协就辜件求福费余扭矩 &,从而分析曲线 畢桥的全部内力和交形•(2・8>I-在静定棊本体系作用荷ftpot ,并反力与内力计算如下, i ■图2-13所亦C2-9)8E2“4集屮衙《Pfr 用鸽徇内力计»B 氏 根》胖力衡方程可緡任意《間4处的内力为.3in &o必® w 2 g 2皿空写空•心B,3irt %WJ 由 ^A/-=0 及 »寸 Qs分别可得图:M3集•新«卩作用納式僞-&J]+ 心脚・3琨)二0P 叫吧 RsinQ"心沁-P M O故趾5-气評」am%彳・二P 血(兔"丿 Qsm%Ar ;p= -丹底十讹外-阳-1 + cox% -0』aCa0.tkDT.・ 1 CQ1&.J - Ji.■】(2-13)s R. •Rge* +】・Mn0尊=0(2-12)⑺⑷iO出矩・扃05 務./vr 他假?"丿(1-8・0」Fpsin %snCtfj -0 ) + coB (% -&J«in0p ■- ■■ P—■ ■ — 1J<2-10)I®翳」*侖大学土木工《学兜局工《认检研耙中心.楝*工《糸匚*•1・<X»0. +R. Ra-CO50u)= 0 生YLM SJA O,则I ,心仇+1/ •</?血酩»1n £r ・Q ・«?瓦+石"故S 记A 寺,}i. U 一■^工 “ 于媳可埠劉使》«的6,的内力为*剪力"』= -p 9g_&丿C ” jXffl2-n 1»«作ffiT.r 转构计算ffl 式2. «螺件用贰位赞金扭矩T. 1 时的反力与内力如S 2-15 所不,由= 0可待(0仏“丿幽侖大学土木工《睜兜风工《拔恥研丸中心,楝*工《糸3.庄一次趙静&閒支曲域集桥上作用P 荷裁时的反力芍内力根常B 端的交形协调协条件有:<2-15)式中,S.——单拉養余豹知?;=】作用下静定基本结构在B 划的扛角<A.—荷载P 作履下»定着本绪恂衣B 錢引起的扭* -式中* 外荷tt 左X®构上引起的各项内力,M,r^—a 位爸tt 在荃丈您构上引fe 的各项内力.对于曲绘集桥P 只计入弯矩和村矩对变拉的妙响,而不计»力与^^力 的形喑.幽侖大学土木工《睜兜风工《拔恥研丸中心,楝*工《糸技变位厶刖计算如“r 厂為> PR ・ 鸟 Gff G/d L 血©檢"瓷E 先評一叫智于是可和《趙»定ftA 曲tt«桥在集中荷ttP 件阳卩的rt 力为. Wf<2-18>由皮功s«可知计算喪位的一般公式为"y 警"哦山11^2rl7)NN^ib ■>■ C* ib C2・16〉*幽侖大孕土木工《睜兜风工厘世恥研^^中心,楝*工《余扭矩前(兔"丿 q 外,気口r-i0 3UJI 令"曲恆-石© w%) 分别令耳二04二%时・町得离支点反力及仪力按毎:(2-21>\ji ◎易i *侖大学土木工《学兜局工《**研丸中心.林*工《糸(2・23)R”=PQrjaj同理,可求^9左简支聽»定曲线聚上作用酬的内力馬反力。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
总第222期交 通 科 技Ser ial No.222 2007年第3期T r anspor tation Science&T echno log y N o.3June.2007收稿日期:2007 01 23曲线梁桥平面位移机理分析刘柱国(河北省交通厅公路管理局 石家庄 050051)摘 要 分析了曲线梁桥平面位移的机理,探讨了影响平面位移的主要因素,并结合工程实例对影响因素进行了验证。
关键词 曲线梁桥 平面位移 温度效应 收缩 徐变连续曲线梁桥在使用过程中,由于预加力、温度效应、车辆行驶或一些其他影响因素的作用,会产生侧向的变位。
由于曲线梁桥的结构特点、支承形式等原因,当外荷载等影响因素消失后,弯梁发生的侧向变位并不能够完全恢复,会产生部分不可恢复的残余位移,在长期反复作用下,侧向的残余位移就会累积,产生较大的位移,即曲线梁桥的侧向位移(或称 爬移)。
曲线梁桥的侧向位移问题轻则导致梁段伸缩缝的剪切破坏,影响其使用寿命;严重的则会出现支承结构破坏,梁体滑移和翻转。
桥梁在使用过程中出现该类问题,不仅影响交通,而且加固起来非常困难,造成巨大的经济损失。
1 影响曲线梁桥平面位移的因素1.1 支承方式支承方式是影响曲线梁桥平面位移的内在因素,支承方式直接影响全桥的内力分布,合理的支承方式可以承受自重和活载、偏载等因素所产生的组合扭矩作用,限制结构的平面位移。
曲线梁桥可以采用多种支承布置形式。
理论上讲,连续曲线梁桥的所有支承均可采用点铰支承,但在荷载作用下梁端将产生扭转变形,从而在梁端与桥台背墙间产生上下相对变形,这会导致伸缩缝破坏。
一般在两端的桥台设置能抵抗外扭矩的抗扭支座,中间支承可以采用抗扭支承,或点铰支承,或者交替使用两种支承形式,从而限制梁端的扭转变形,以保证伸缩缝正常工作[1 2]。
主梁在各种荷载作用下,除了梁端扭转变形外,在支座位置处还会产生纵桥向与横桥向的变位,为了保证结构的正常工作,总希望沿着 切线方向移动。
为此,除了在桥台处设置抗扭支座外,还必须采取一些 限制措施,一般可以在活动端的定向切线支座上安置 限制位移方向的措施,以保证桥头的位移能符合 切线方向的运动要求,但在设计计算时,必须计及这个 强制力的影响。
根据具体桥型,充分考虑各种因素,设置合理的支承方式,就可以使曲线梁桥的平面变形顺着目标方向进行,阻止非正常变位的发生。
1.2 温度和混凝土收缩的影响温度变化和混凝土收缩引起在平面内的位移属于弧段膨胀或收缩性质的位移[1],涉及到弧段的半径变化但圆心角不变,即r0!r,而 0= (见图1)。
图1 曲线梁桥平面内变形在此情况下:r=r0(1- ), =∀!t+ cs∀3=2(r0-r)sin 02式中: cs为混凝土的收缩应变。
因此温度变化和混凝土收缩时,曲线梁桥会发生两个方向的位移分量:#沿桥轴线方向的纵向分量;∃沿桥轴线垂直方向的分量(见图2)。
温度变化和收缩在各种活动支座处将引起纵桥向与横桥向的变形,横桥向的变形不仅给伸缩缝的活动带来困难,而且产生了曲线梁桥的支座受力、布置以及一些侧向问题。
a)无约束的情况 b)有约束的情况图2 曲线梁变形示意图1.3 徐变影响[1]混凝土徐变与预应力引起的位移只涉及到力作用方向(切向)的位移,即r 0=r ,而 0! (见图3),由此得知:= 0(1- ), = (p )∀3=r 0( 0- )式中: (p )为预应力和混凝土徐变引起的应变。
混凝土徐变引起的位移是沿着结构切线方向的,与桥梁支座与伸缩缝的设置是不矛盾的。
图3 曲线梁桥平面内变形1.4 预应力影响曲线梁桥的预应力钢束不仅有平面弯曲同时还有沿梁高度方向的竖向弯曲,这样预应力钢束径向力的作用点总是沿梁高度方向在变化。
当其作用点位于主梁截面剪切中心以上或以下时,钢束径向力就会对主梁产生扭转作用(见图4),位于截面剪切中心以上的钢束径向力产生的扭矩方向与位于截面剪切中心以下的钢束径向力产生的扭矩方向是相反的。
两者的扭矩之和构成了预应力钢束对曲线梁的整体扭转作用。
当M T 上大于M T 下时,主梁就产生向圆心方向的扭转,反之主梁则产生背离圆心方向的扭转。
这样预应力钢束就会引起曲线梁向内偏转或向外偏转的情况。
预应力混凝土曲线梁往往产生向外偏转的情况,这是其结构特点造成的。
任何桥梁的主梁都是以受弯为主的构件,所以预应力钢束应首先满足纵向弯矩的受力要求。
对于连续梁,正弯矩区段的长度远大于负弯矩区段的长度,所以相应的预应力钢束重心位于主梁底部的长度远大于位于主梁顶部的长度。
这使得预应力径向力产生的M T 上大于M T 下,所以预应力产生的总扭矩是向曲线外侧翻转的,相应地弯箱梁内侧支座将会产生拉反力,外侧支座成压反力状态[3]。
图4 预应力钢束径向力对混凝土的作用力由2.3可知预应力引起的位移是沿着结构切线方向的,与桥梁支座与伸缩缝的设置是不矛盾的。
但预应力产生的总扭矩是向曲线外侧翻转的,相应地弯箱梁内侧支座将会产生拉反力,外侧支座成压反力状态。
这对曲线梁桥的平面变位是不利的,在与其他荷载共同作用时,将加速桥梁的横向变位。
1.5 车辆荷载曲线梁桥在汽车活载的离心力和制动力长期反复作用下容易产生主梁向曲线外侧及汽车制动力方向的水平错位(见图5),一般匝道桥都是单向行驶,所以这种作用力总是朝着固定方向。
当主梁设置纵坡时,主梁易产生向下的滑动,这种滑动与汽车制动力一致时就更加剧了主梁的水平错位。
车辆荷载是影响曲线梁桥平面变位的又一主要因素[4]。
图5 活载对曲线梁平面滑移的影响2 工程实例2.1 工程概况旧城胜利大桥位于津保公路,由31%20m 普通钢筋混凝土现浇箱梁和1%14.1m 钢筋混凝土空心简支板构成,其中31%20m 普通混凝土现浇箱梁分为三联,第一联为11%20m,第二、三联为10%20m,本桥平面线形为R =1000m 曲线+缓和曲线+直线(见图6),该桥设计荷载为汽车 20级,挂车 100。
上部结构由现浇单室普通混凝土连续箱梁和钢筋混凝土空心简支板构成,桥面横坡由混凝土铺装层调整。
改桥第一联位于R =1000m 的圆曲线上,在运营过程中,第一联主梁发生严重变位,从第7212007年第3期 刘柱国:曲线梁桥平面位移机理分析号墩(固结墩)开始主梁都有不同程度变位,变位趋势为统一向圆曲线外侧平移,其中第11号墩(过渡墩)处主梁变位最大,达18cm,封闭交通后,变位有所恢复,现在变位为12cm 。
图6 第一联结构示意图(单位:cm)2.2 结构变位计算2.2.1 计算模型对该桥采用空间有限元程序进行计算,建立板单元模型,板单元模型中共2545个节点,2512个单元。
计算过程中考虑以下荷载,按规范要求进行组合:#自重;∃二期恒载;&收缩徐变;∋车辆偏心荷载:汽车 20级,挂车 100级;(温度影响:整体升温30),降温20),上、下缘温差10);∗离心力作用。
2.2.2 计算结果分析经过计算,在温度荷载、离心力等荷载作用下,桥梁发生扭转爬移。
其中8~11号墩(双向活动支座)变位计算结果见表1所列。
表1 各荷载及荷载组合下主梁变位数值对比表cm 项目8号墩9号墩10号墩11号墩自重与二期恒载0.000.000.000.030.07汽车偏载效应0.240.370.510.640.64升温荷载 1.56 3.08 4.71 6.23 6.35温度梯度 0.240.440.720.910.90徐变 0.80 1.67 2.53 3.20 2.80收缩 -0.30-0.60-1.00-1.00-2.10离心力 0.160.320.500.680.68最不利荷载组合 2.36 4.677.109.509.61 (1)由表1可以看出,在最不利荷载组合下,主梁在8~11号桥墩处横向变位分别为2.36、4.67、7.10、9.50、9.61cm,其中11号桥墩处主梁最大变位为9.61cm,这与实际情况中梁体自8号桥墩开始统一向曲线外侧爬移一致。
(2)在所有荷载中,温度荷载、车辆荷载、收缩徐变构成了影响主梁变位的主要因素,其中温度荷载对主梁变位影响最大。
3 结论(1)曲线梁桥会在平面内出现横桥向位移,这种位移是由于在荷载的反复作用下,主梁的横向变位不能够完全、及时地恢复,随着时间的延长而发生累积。
(2)梁体在外界因素的影响下,发生横向向外侧的扭转变形,梁体的扭转变形又使得梁体的部分支座出现脱空,一旦支座脱空,梁体会失去抗扭约束,继而扭转变形加剧。
设置合理的支承方式是限制梁体平面位移的内在因素,也是最关键的因素。
(3)温度荷载、预应力、收缩徐变、汽车荷载(离心力和制动力)等是影响曲线梁桥平面位移的外在因素,在设计时必须充分考虑。
参考文献[1] 邵容光,夏 淦.混凝土弯梁桥[M] 北京:人民交通出版社,1994[2] 姚林森.曲线梁桥[M].北京:人民交通出版社,1989[3] 刘 华.预应力混凝土连续弯箱梁的侧向位移研究[D].南京:东南大学,2004.[4] 何维利.独柱支承的曲线梁桥设计[J].北京建筑工程学院学报,2001(10):23 28Plane Displacement Mechanism Analysis of Curve Beam BridgeL iu zhuguo(Ro ads M anagement Bureau of H ebei Pr ovincial Communicat ions Depar tment,H ebei shijiazhuang,050051,China)Abstract:T his article analyzes the plane displacement mechanism of curv e beam bridge.T he prim ary facto r w hich affects the plane displacem ent is analyzed,and takes an example of a real project to con firm the influence factor.T he conclusion can pr ovide reference for later eng ineering design.Key words:curv e beam bridge;plane displacement;temperatur e effects;contraction;creep22刘柱国:曲线梁桥平面位移机理分析 2007年第3期。
