八年级第二次月考试题及答案

合集下载

部编人教版八年级数学上册第二次月考试卷及答案【完美版】

部编人教版八年级数学上册第二次月考试卷及答案【完美版】班级：姓名：一、选择题（本大题共10小题，每题3分，共30分）1．若分式211xx-+的值为0，则x的值为（）A．0 B．1 C．﹣1 D．±1 2．（-9）2的平方根是x，64的立方根是y，则x+y的值为（）A．3 B．7 C．3或7 D．1或7 3．若﹣2a m b4与5a n+2b2m+n可以合并成一项，则m-n的值是（）A．2 B．0 C．-1 D．14．已知关于x的分式方程21mx-+=1的解是负数，则m的取值范围是（）A．m≤3 B．m≤3且m≠2 C．m＜3 D．m＜3且m≠2 5．已知a与b互为相反数且都不为零，n为正整数，则下列两数互为相反数的是（）A．a2n－1与－b2n－1 B．a2n－1与b2n－1 C．a2n与b2n D．a n与b n6．已知关于x的不等式组320x ax->⎧⎨->⎩的整数解共有5个，则a的取值范围是（）A．﹣4＜a＜﹣3 B．﹣4≤a＜﹣3 C．a＜﹣3 D．﹣4＜a＜3 27．如图，在数轴上表示实数15的点可能是（）A．点P B．点Q C．点M D．点N8．如图，每个小正方形的边长为1，A、B、C是小正方形的顶点，则∠ABC的度数为（）A．90°B．60°C．45°D．30°9．如图所示，下列推理及括号中所注明的推理依据错误的是（）A．∵∠1＝∠3，∴AB∥CD（内错角相等，两直线平行）B．∵AB∥CD，∴∠1＝∠3（两直线平行，内错角相等）C．∵AD∥BC，∴∠BAD+∠ABC＝180°（两直线平行，同旁内角互补）D．∵∠DAM＝∠CBM，∴AB∥CD（两直线平行，同位角相等）10．如图，已知∠ABC=∠DCB，下列所给条件不能证明△ABC≌△DCB的是（）A．∠A=∠D B．AB=DC C．∠ACB=∠DBC D．AC=BD二、填空题（本大题共6小题，每小题3分，共18分）1．已知1＜x＜5，化简2(1)x-+|x-5|=________．2．分解因式：22a4a2-+=__________．3．将“对顶角相等”改写为“如果．．．那么．．．”的形式，可写为__________．4．如图，一次函数y=﹣x﹣2与y=2x+m的图象相交于点P（n，﹣4），则关于x的不等式组22{20x m xx+----＜＜的解集为________．5．如图，OP平分∠MON，PE⊥OM于点E，PF⊥ON于点F，OA＝OB，则图中有__________对全等三角形．6．如图，在平行四边形ABCD中，连接BD，且BD＝CD，过点A作AM⊥BD于点M，过点D作DN⊥AB于点N，且DN＝32，在DB的延长线上取一点P，满足∠ABD＝∠MAP＋∠PAB，则AP＝________.三、解答题（本大题共6小题，共72分）1．解下列方程组：（1）257320x yx y-=⎧⎨-=⎩（2）134342x yx y⎧-=⎪⎨⎪-=⎩2．先化简，再求值：2282442xxx x x⎛⎫÷--⎪-+-⎝⎭，其中2x=.3．已知，a、b互为倒数，c、d互为相反数，求31ab c d+的值.4．如图，在Rt△ABC中，∠ACB=90°，∠A=40°，△ABC的外角∠CBD的平分线BE交AC的延长线于点E．（1）求∠CBE的度数；（2）过点D作DF∥BE，交AC的延长线于点F，求∠F的度数．5．我们给出如下定义：顺次连接任意一个四边形各边中点所得的四边形叫中点四边形．（1）如图1，四边形ABCD中，点E，F，G，H分别为边AB，BC，CD，DA的中点．求证：中点四边形EFGH是平行四边形；（2）如图2，点P是四边形ABCD内一点，且满足PA=PB，PC=PD，∠APB=∠CPD，点E，F，G，H分别为边AB，BC，CD，DA的中点，猜想中点四边形EFGH 的形状，并证明你的猜想；（3）若改变（2）中的条件，使∠APB=∠CPD=90°，其他条件不变，直接写出中点四边形EFGH的形状．（不必证明）6．为加强中小学生安全和禁毒教育，某校组织了“防溺水、交通安全、禁毒”知识竞赛，为奖励在竞赛中表现优异的班级，学校准备从体育用品商场一次性购买若干个足球和篮球（每个足球的价格相同，每个篮球的价格相同），购买1个足球和1个篮球共需159元；足球单价是篮球单价的2倍少9元．（1）求足球和篮球的单价各是多少元？（2）根据学校实际情况，需一次性购买足球和篮球共20个，但要求购买足球和篮球的总费用不超过1550元，学校最多可以购买多少个足球？参考答案一、选择题（本大题共10小题，每题3分，共30分）1、B2、D3、A4、D5、B6、B7、C8、C9、D10、D二、填空题（本大题共6小题，每小题3分，共18分）1、42、()2 2a1-3、如果两个角互为对顶角，那么这两个角相等4、﹣2＜x＜25、36、6三、解答题（本大题共6小题，共72分）1、（1）55xy=⎧⎨=⎩；（2）64xy=⎧⎨=⎩．2、22x-，12-.3、0.4、(1) 65°；(2) 25°．5、（1）略；（2）四边形EFGH是菱形，略；（3）四边形EFGH是正方形.6、（1）一个足球的单价103元、一个篮球的单价56元；（2）学校最多可以买9个足球．。

新人教版八年级语文上册第二次月考试题及答案(全面)

新人教版八年级语文上册第二次月考试题及答案（全面）满分：120分考试时间：120分钟一、语言的积累与运用。

（35分）1、下列词语中加点字注音完全正确的一项是（）A．诘．责（jié）燥．热（zào）翘．首（qiào）锐不可当．（dǎng）B．炽．热（zhì）佃．农（diàn）黝．黑（yǒu）意趣盎．然（áng）C．桅．杆（wěi）窒．息（zhì）镌．刻（juàn）坦荡如砥．（dǐ）D．悄．然（qiǎo ）滞．留（zhì）锃．亮（zèng）殚．精竭虑（dān）3、下列句子中加点成语使．用．恰．当．的一项是（）A．也许是物质生活丰富让味觉麻木了吧，面对美味大餐，我们常有味同嚼蜡．．．．的感觉。

B．总决赛现场，面对歌手的突然退场，主持人看风使舵．．．．，冷静救场。

C．这伙人伪装成政府机关人员，到处招摇撞骗，其手段之卑劣已达到了叹为观．．．止．的地步。

D．春节期间，越来越多的人忙于抢红包并乐此不疲．．．．。

4、下列句子中没有语病的一项是（）A．有关部门最近发出通知，要求各地在中考期间严防安全不出问题。

B．我反对将儿子送到贵族幼儿园去，希望儿子不毁在优裕的生活环境里，让他从小就具有刚毅、诚实、吃苦耐劳。

C．保障儿童权利是设置儿童节的初衷，这一要义在今天丝毫没有过时，所以仍需要成人时时反思。

D．虽然人生的幕布徐徐拉开，但在少年的眼里，世界和未来都是崭新的充满吸引力的。

5、下列句子没有运用比喻修辞手法的一项是( )A．一些薄云掠过月亮时,就像丽江古城中,一个银匠,正在擦拭一只硕大的银盘。

B．活动时只能以极轻极慢动作进行,犹如霹雳舞的“太空步”。

C．洁白轻薄的云朵,微光闪烁,仿佛身披霓裳羽衣的纯洁天使。

D．当河水正这般畅畅快快地驰骋着时,突然脚下出现一条四十多米宽的深沟,它们还来不及想一下,便一齐跌了进去,更闹,更挤,更急。

八年级数学第二次月考试题含答案

密封线学校班级姓名座号八年级上期段考试题一、选择题（每小题3分，共30分） 1、16的算术平方根是（）A ．4B ． ±4C ．2D ．±2 2、下列四组数据中，不能．．作为直角三角形的三边长是（） A ．3，4，6 B ．7，24，25 C ．6，8，10 D ．9，12，153、已知下列各式：①x 1＋y ＝2，②2x －3y ＝5，③21x ＋xy ＝2，④x ＋y ＝z －1，⑤21+x ＝312-x ，其中二元一次方程的个数有( )A ．1个B ．2个C ．3个D ．4个4、点P （-1，2）关于x 轴对称点的坐标为（）A ．（1，-2）B ．（-1，2）C ．（1，2）D ．（-1，-2） 5、二元一次方程组⎩⎨⎧=-=+ky x k y x 7252的解满足方程31x －2y ＝5，那么k 的值为 ( )A ．53B ．35 C ．－5 D ．16、一次函数b kx y +=的图象如图(1)所示，则b k ,的值为（） A ．0,0<<b k B ．0,0><b k C ．0,0<>b k D ．0,0>>b k7、32-的绝对值是（）A ．23+B ．23- C． D ．32-8、点P )1,3(++m m 在直角坐标系的x 轴上，则点P 的坐标为（）A ．（0，2）B ．（2，0）C ．（4，0）D ．（0，-2）9、点P 1（x 1，y 1），点P 2（x 2，y 2）是一次函数y ＝－4x + 3 图象上的两个点，且 x 1＜x 2，则y 1与y 2的大小关系是（）．A 、y 1＞y 2B 、y 1＞y 2 ＞0C 、y 1＜y 2D 、y 1＝y 210、点A 的坐标是（2，2），若点P 在X 轴上，三角形AOP 是等腰三角形，则点P 的坐标可能有（）个 A ．1个 B ．2个 C ．3个 D ．4个二、填空题（每空3分，共30分） 11、下列实数：21，16-，3π-，︱－1︱，722，39 ，0.1010010001……中无理数的个数有个。

新人教版八年级语文上册第二次月考试卷(附参考答案)

新人教版八年级语文上册第二次月考试卷（附参考答案）满分：120分考试时间：120分钟一、语言的积累与运用。

（35分）1、下列加点字的读音全部正确的一项是（）A．歼．灭（jiān）炽．热（zhì）要塞．（sài）坠．毁（zhuì）B．仲．裁（zhòng）匿．名（nì）滞．留（zhì）沿溯．（sù）C．悄．然（qiǎo）畸．形（jī）鬈．发（juǎn）篡．改（cuàn）D．颔．首（hàn）窒．息（zhì）禁锢．（gù）殷．红（yīn）3、下列句子中加着重号的成语使用不当的一项是（）A．他是个音乐才子，这是无可置疑．．．．的。

B．每次我向老师请教时，他都和颜悦色．．．．地给我解答。

C．跑完了5 000米，同学们个个筋疲力尽．．．．。

D．在上学的路上，他把昨天看到的故事惟妙惟肖．．．．地讲给我听。

4、下列句子中没有语病、句意明确的一项是（）A．“一带一路”这一合作倡议不仅迅速得到国际社会关注，并且业已形成大量的合作机会。

B．通过观看央视播放的《记住乡愁》节目，使我对中国乡村及民俗文化有了更多的了解。

C．本月首飞的C919大飞机是我国按照适航审定要求和主流市场标准自主研发的首款干线客机。

D．能否切实减轻学生课业负担，让他们快乐成长，是我国中小学教学工作的当务之急。

5、下列各项判断与分析中，不正确的一项是（）A．咝溜溜的南风吹动了高粱叶子。

（这个句子的谓语是“吹动”。

）B．那树有一点佝偻，露出老态，但是坚固稳定，树顶像刚炸开的焰火一样繁密。

（这句话运用拟人和比喻的修辞手法，写出那树虽老但枝繁叶茂的状态。

）C．“狂澜”“沉湎”“鞠躬尽瘁”“呕心沥血”（这四个词感情色彩相同。

）D．防止校园欺凌事件不再发生，不让戾气弥漫整个校园，是一个系统工程，需要多方面、多领域齐心协力。

（这个句子是个病句，否定不当。

）6、给下列句子排序，最合理的一项是( )①但是自卑的人永远会失去本来就属于他的机会。

八年级下第二次月考试题--语文(含解析).(含答案)

八年级语文下学期第二次月考试题一、积累与运用1.古诗文名句默写。

（1）读书破万卷，__________。

（2）独学而无友，__________。

（3）__________，不知其可。

（4）《桃花源记》中描绘桃花林草美花繁的语句是：__________，__________。

【答案】 (1). （1）下笔如有神 (2). （2）则孤陋而寡闻 (3). （3）人而无信 (4). （4）芳草鲜美 (5). 落英缤纷【解析】【详解】试题分析：默写题作答时，一是要透彻理解诗文的内容；二是要认真审题，找出符合题意的诗文句子；三是答题内容要准确，做到不添字、不漏字、不写错字。

本题中的“孤陋、寡、缤纷”等字词容易写错。

2.阅读下面的文字，按要求答题。

田野里，冬季的冰冷刚刚过去，春季就来了。

花儿草儿们用色彩xuàn染着土地，那迎春绽放的花蕊，吐纳着香甜的空气，那翠绿欲滴的桃浪，拥顶着希望的甜蜜；那冰雪消溶的小河，流淌着生命的脉动。

阳光灿烂的春季拔弄着大地，把地上的生灵变得生机盎然，每个角落都充满了春天的气息。

（1）根据拼音写出相应的汉字，给加点的字注音。

xuàn染（）脉．动（）（2）语段中有两个错别字，找出并改正____改为____ ____改为____【答案】 (1). （1）渲 (2). mài (3). （2）溶 (4). 融 (5). 拔 (6). 拨【解析】【详解】试题分析：（1）作答时，注意易错音的积累，掌握汉语拼写规则，规范拼音书写，不要写成英语字母；根据拼音写汉字，除了根据具体的语境，还要注意同音字、形似字的辨析，避免混淆。

注意“渲”的字形和多音字“脉”字的读音。

（2）错别字的产生原因主要是音同或形似，掌握这个易错点，根据汉字的特点，结合句意和词义辨析判断。

消溶－消融；拔弄－拨弄。

3.下列句子中加点词语使用不正确的一项是（）A. 出了三峡，江面宽阔，眼前豁然开朗．．．．。

2023～2024学年度第二学期第二次月考试题八年级物理(下)

2023～2024学年度第二学期第二次月考试题八年级物理（下）一、单选题(共40 分)1. 下列物体重约为1N的是（）A.一支铅笔B.一根香蕉C.一瓶矿泉水D.一桶食用油2. 在下列说法中，正确的是（）A.船桨是费力杠杆B.物体运动速度越大其惯性越大C.运输机起落架装有宽大的轮子是为了减小对地面的压力D.运动的物体不受力时，运动的速度会减小，最终会停下来3. 目前，我国“天宫”空间站已实现航天员长期驻留，航天员在空间站中可以实施的是（）A.用托盘天平测物体质量B.用哑铃锻炼手臂肌肉C.用弹簧测力计测量物体重力D.用弹簧拉力器健身4. 如图所示，一个装有水的平底密闭矿泉水瓶，先正立放置在水平桌面上，再倒立放置。

两次放置时，瓶对桌面的压力分别为F甲和F乙，瓶对桌面的压强分别为p甲和p乙，则（）A.F甲＞F乙B.p甲＞p乙C.F甲＜F乙D.p甲＜p乙5. 如图所示，O为轻质杠杆AB的支点，B点挂一重物G，若在B点施加F1、或在A点分别施加F2、F3、F4四个力后，杠杆均保持水平位置平衡，则这四个力中最小的力是（）A.F1B.F2C.F3D.F46. 把体积相同、质量不同的三个小球A、B、C放入同种液体中，静止后的位置如图所示，它们所受的浮力分别为F A、F B、F C，则这三力大小关系正确的是（）A.F A＞F B＞F CB.F A=F B=F CC.F A＜F B＜F CD.F A＜F B=F C7. 关于下面四幅图的说法中错误的是（）A.图甲所示托里拆利实验中，将竖直玻璃管倾斜，水银柱的高度不变B.图乙所示排水管U形“反水弯”是一个连通器C.图丙所示在B管吹气，A管中水而上升，是因为流体中流速越大的位置压强越大D.图丁所示把这自制气压计从山下移到山顶，细管内的水柱上升8. 下列说法中正确的是（）A.做功越多的机械，功率一定越大B.功率越大的机械，机械效率越大C.功率越大的机械，所用时间越少D.功率越大的机械，做功一定越快9. 如图所示，小黄家里悬挂着的吊灯处于静止状态，以下说法正确的是（）A.天花板对绳子的拉力与绳子对灯的拉力是一对平衡力B.绳子对灯的拉力与灯受到的重力是一对平衡力C.天花板对绳子的拉力与灯受到的重力是一对平衡力D.吊灯对绳子的拉力与绳子对吊灯的拉力是一对平衡力10. 如图所示，细线上端固定，下端拉着小球在竖直平面内摆动，A、B是球摆动过程中的最高点，C是最低点，当小球到达C点时，所受的力全部消失，则小球将（）A.一定处于静止状态B.一定做匀速直线运动C.可能处于静止状态可能做匀速直线运动D.可能加速运动二、填空题(共32 分)11. 如图甲所示，工人师傅实际上是因陋就简制成了一个简单的工具，这是利用了重力的方向总是___________的知识；如图乙所示，在A、B、C三点用扳手拧螺母，更省力的是___________点，这说明力的作用效果跟它的___________有关。

人教版八年级第二学期第二次月考检测数学试卷含答案

一、选择题1．如图，正方形ABCD 的对角线AC ，BD 相交于点O ，E 是AC 上的一点，且AB=AE ，过点A 作AF ⊥BE ，垂足为F ，交BD 于点G ，点H 在AD 上，且EH ∥AF.若正方形ABCD 的边长为2，下列结论：①OE=OG ；②EH=BE ；③AH=222-，其中正确的有（）A ．0个B ．1个C ．2个D ．3个2．如图，已知△ABC 中，∠ACB =90°，AC =BC =2，将直角边AC 绕A 点逆时针旋转至AC ′，连接BC ′，E 为BC ′的中点，连接CE ,则CE 的最大值为( ).A ．5B ．21+C ．21+D ．51+ 3．如图，是由两个正方形组成的长方形花坛ABCD ，小明从顶点A 沿着花坛间小路直到走到长边中点O ，再从中点O 走到正方形OCDF 的中心1O ，再从中心1O 走到正方形1O GFH 的中点2O ，又从中心2O 走到正方形2O IHJ 的中心3O ，再从中心3O 走到正方形3O KJP 的中心4O ，一共走了312m ，则长方形花坛ABCD 的周长是（）A ．36mB ．48mC ．96mD ．60m4．如图，在平行四边形ABCD 中，120C ∠=︒，28AD AB ==，点H 、G 分别是边AD 、BC 上的动点．连接AH 、HG ，点E 为AH 的中点，点F 为GH 的中点，连接EF ．则EF 的最大值与最小值的差为（）A ．2B ．232-C ．3D ．43-5．如图，正方形ABCD 的边长为1，顺次连接正方形ABCD 四边的中点得到第一个正方形1111D C B A ，又顺次连接正方形1111D C B A 四边中点得到第二个正方形2222A B C D ，……，以此类推，则第六个正方形6666A B C D 的面积是（）A ．164B ．116C ．132D ．186．如图，△ABC 的周长为19，点D ，E 在边BC 上，∠ABC 的平分线垂直于AE ，垂足为N ，∠ACB 的平分线垂直于AD ，垂足为M ，若BC=7，则MN 的长度为（）A ．32B ．2C ．52D ．3 7．如图，90MON ∠=︒，矩形ABCD 在MON ∠的内部，顶点A ，B 分别在射线OM ，ON 上，4AB =，2BC =，则点D 到点O 的最大距离是（）A ．22B ．222C ．252D 22+8．如图，正方形ABCD 中，在AD 的延长线上取点E ，F ，使DE ＝AD ，DF ＝BD ，连接BF 分别交CD ，CE 于H ，G 下列结论：①EC≠2HG ；②∠GDH ＝∠GHD ；③图中有8个等腰三角形；④CDG DHF S S △△＝．其中正确的结论有（）个A ．1B ．2C ．3D ．4 9．如图，正方形ABCD 的边长为10，AG=CH=8，BG=DH=6，连接GH ，则线段GH 的长为（）A ．2.8B ．22C ．2.4D ．3.510．如图，矩形ABCD 中，,AC BD 相交于点O ，过点B 作BF AC ⊥交CD 于点F ，交AC 于点M ，过点D 作//DE BF 交AB 于点E ，交AC 于点N ，连接,FN EM ．则下列结论：①DN BM =；②//EM FN ；③AE FC =；④当AO AD =时，四边形DEBF 是菱形．其中，正确结论的个数是（）A ．1个B ．2个C ．3个D ．4个二、填空题11．如图，正方形ABCD 中，AB=4，E 是BC 的中点，点P 是对角线AC 上一动点，则PE+PB 的最小值为．12．如图，正方形ABCD 的对角线相交于点O ，对角线长为1cm ，过点O 任作一条直线分别交AD ，BC 于E ，F ，则阴影部分的面积是_____．13．如图，在矩形ABCD 中，∠BAD 的平分线交BC 于点E ，交DC 的延长线于点F ，点G 是EF 的中点，连接CG ，BG ，BD ，DG ，下列结论：①BC=DF ；②135DGF ︒∠=；③BG DG ⊥；④34AB AD =，则254BDG FDG S S =，正确的有__________________．14．如图，动点E F 、分别在正方形ABCD 的边AD BC 、上，AE CF =，过点C 作CG EF ⊥，垂足为G ，连接BG ，若4AB =，则线段BG 长的最小值为_________．15．如图所示，菱形ABCD ，在边AB 上有一动点E ，过菱形对角线交点O 作射线EO 与CD 边交于点F ，线段EF 的垂直平分线分别交BC 、AD 边于点G 、H ，得到四边形EGFH ，点E 在运动过程中，有如下结论：①可以得到无数个平行四边形EGFH ；②可以得到无数个矩形EGFH ；③可以得到无数个菱形EGFH ；④至少得到一个正方形EGFH ．所有正确结论的序号是__．16．如图，Rt ABE ∆中，90,B AB BE ︒∠==, 将ABE ∆绕点A 逆时针旋转45︒，得到,AHD ∆过D 作DC BE ⊥交BE 的延长线于点C ，连接BH 并延长交DC 于点F ，连接DE 交BF 于点O ．下列结论：①DE 平分HDC ∠；②DO OE =； ③CD HF =； ④2BC CF CE -=； ⑤H 是BF 的中点，其中正确的是___________17．如图，在正方形ABCD 中，AC=62，点E 在AC 上，以AD 为对角线的所有平行四边形AEDF 中，EF 最小的值是_________．18．如图，矩形ABCD 中，CE CB BE ==，延长BE 交AD 于点M ，延长CE 交AD 于点F ，过点E 作EN BE ⊥，交BA 的延长线于点N ，23FE AN ==，，则BC =_________．19．如图，在Rt △ABC 中，∠ACB ＝90°，AC ＝8，BC ＝6，点D 为平面内动点，且满足AD ＝4，连接BD ，取BD 的中点E ，连接CE ，则CE 的最大值为_____．20．如图所示，已知AB ＝ 6，点C ，D 在线段AB 上，AC ＝DB ＝ 1，P 是线段CD 上的动点，分别以AP ，PB 为边在线段AB 的同侧作等边△AEP 和等边△PFB ，连接EF ，设EF 的中点为G ，当点P 从点C 运动到点D 时，则点G 移动路径的长是_________．三、解答题21．如图正方形ABCD ，DE 与HG 相交于点O （O 不与D 、E 重合）．（1）如图（1），当90GOD ∠=︒，①求证：DE GH =； ②求证：2GD EH DE +>；（2）如图（2），当45GOD ∠=︒，边长4AB =，5HG =，求DE 的长．22．如下图1，在平面直角坐标系中xoy 中，将一个含30的直角三角板如图放置，直角顶点与原点重合，若点A 的坐标为()1,0-，30ABO ∠=︒．（1）旋转操作：如下图2，将此直角三角板绕点O 顺时针旋转30时，则点B 的坐标为．（2）问题探究：在图2的基础上继续将直角三角板绕点O 顺时针60︒，如图3，在AB 边上的上方以AB 为边作等边ABC ，问：是否存在这样的点D ，使得以点A 、B 、C 、D 四点为顶点的四边形构成为菱形，若存在，请直接写出点D 所有可能的坐标；若不存在，请说明理由．（3）动点分析：在图3的基础上，过点O 作OP AB ⊥于点P ，如图4，若点F 是边OB 的中点，点M 是射线PF 上的一个动点，当OMB △为直角三角形时，求OM 的长．23．如图1，AC 是平行四边形ABCD 的对角线，E 、H 分别为边BA 和边BC 延长线上的点，连接EH 交AD 、CD 于点F 、G ，且//EH AC .（1）求证：AEF CGH ∆≅∆（2）若ACD ∆是等腰直角三角形，90ACD ∠=，F 是AD 的中点，8AD =，求BE 的长：（3）在（2）的条件下，连接BD ，如图2，求证：22222()AC BD AB BC +=+24．如图，在矩形ABCD 中，∠BAD 的平分线交BC 于点E ，AE =AD ，作DF ⊥AE 于点F ．（1）求证：AB ＝AF ；（2）连BF 并延长交DE 于G ．①EG ＝DG ；②若EG ＝1，求矩形ABCD 的面积．25．如图，在Rt ABC ∆中，90,40,60B AC cm A ∠=︒=∠=︒，点D 从点C 出发沿CA 方向以4/cm 秒的速度向点A 匀速运动，同时点E 从点A 出发沿AB 方向以2/cm 秒的速度向点B 匀速运动，当其中一个点到达终点时，另一个地点也随之停止运动.设点,D E 运动的时间是t 秒（010t <≤）.过点D 作DF BC ⊥于点F ，连接,DE EF .（1）试问四边形AEFD 能够成为菱形吗？如果能，求出相应的t 值；如果不能，请说明理由；（2）当t 为何值时，90FDE ∠=︒？请说明理由.26．直线1234,,,,l l l l 是同一平面内的一组平行线．(1)如图1．正方形ABCD 的4个顶点都在这些平行线上，若四条直线中相邻两条之间的距离都是1，其中点A ，点C 分别在直线1l 和4l 上，求正方形的面积；(2)如图2，正方形ABCD 的4个顶点分别在四条平行线上，若四条直线中相邻两条之间的距离依次为123h h h ，，．①求证：13h h =；②设正方形ABCD 的面积为S ，求证222211 2 2 S h h h h =++．27．如图，锐角ABC ∆，AB AC =，点D 是边BC 上的一点，以AD 为边作ADE ∆，使AE AD =，EAD BAC ∠=∠．（1）过点E 作//EF DC 交AB 于点F ，连接CF （如图①）①请直接写出EAB ∠与DAC ∠的数量关系；②试判断四边形CDEF 的形状，并证明；（2）若60BAC ∠=，过点C 作//CF DE 交AB 于点F ，连接EF （如图②），那么（1）②中的结论是否任然成立？若成立，请给出证明，若不成立，请说明理由．28．已知：在矩形ABCD 中，点F 为AD 中点,点E 为AB 边上一点，连接CE 、EF 、CF ，EF平分∠AEC ．(1)如图1，求证：CF ⊥EF;(2)如图2，延长CE 、DA 交于点K, 过点F 作FG ∥AB 交CE 于点G 若，点H 为FG 上一点，连接CH,若∠CHG=∠BCE, 求证：CH=FK;(3)如图3, 过点H 作HN ⊥CH 交AB 于点N,若EN=11,FH-GH=1,求GK 长.29．如图，在正方形ABCD 中，点E 、F 是正方形内两点，BE DF ∥，EF BE ⊥，为探索这个图形的特殊性质，某数学兴趣小组经历了如下过程：（1）在图1中，连接BD ，且BE DF =①求证：EF 与BD 互相平分；②求证：222()2BE DF EF AB ++=；（2）在图2中，当BE DF ≠，其它条件不变时，222()2BE DF EF AB ++=是否成立？若成立，请证明：若不成立，请说明理由.（3）在图3中，当4AB =，135DPB ∠=︒2246B BP PD +=时，求PD 之长.∆是边长为3的等边三角形，点D是射线BC上的一个动点（点D不与30．如图，ABC∆是以AD为边的等边三角形，过点E作BC的平行线，交直线点B、C重合），ADEAC于点F，连接BE．（1）判断四边形BCFE的形状，并说明理由；（2）当DE AB⊥时，求四边形BCFE的周长；（3）四边形BCFE能否是菱形？若可为菱形，请求出BD的长，若不可能为菱形，请说明理由．【参考答案】***试卷处理标记，请不要删除一、选择题1．D解析：D【分析】根据正方形的性质及全等三角形的判定与性质即可分别求证判断.【详解】在正方形ABCD中，AO=BO，∠AOG=∠BOE，AC⊥BD∵AF⊥BE，∴∠EAF+∠BEO=∠BEO+∠OBE=90°，∴∠OAG=∠OBE，∴△OAG≌△OBE，故OE=OG，①正确；∵AB=AE,∴∠ABE=∠AEB，∵EH∥AF∴HE⊥BE，∴∠AEF+∠AEH=∠ABE+∠CBE,∴∠AEH=∠CBE又∵AE=AB=CB,∠HAE=∠ECB=45°，∴△AEH≌△CBE，∴EH=BE，②正确；∵△AEH≌△22+=222∴AH=CE=AC-AE=22-2，③正确. 故选D【点睛】此题主要考查正方形的性质与线段的证明，解题的关键是熟知正方形的性质定理及全等三角形的判定与性质.2．B解析：B【分析】取AB 的中点M ，连接CM ，EM ，当CE ＝CM +EM 时，CE 的值最大，根据旋转的性质得到AC ′＝AC ＝2，由三角形的中位线的性质得到EM 12=AC ′＝1，根据勾股定理得到AB ＝22，即可得到结论．【详解】取AB 的中点M ，连接CM ，EM ，∴当CE ＝CM +EM 时，CE 的值最大．∵将直角边AC 绕A 点逆时针旋转至AC ′，∴AC ′＝AC ＝2．∵E 为BC ′的中点，∴EM 12=AC ′＝1． ∵∠ACB ＝90°，AC ＝BC ＝2，∴AB ＝22，∴CM 12=AB 2=，∴CE ＝CM +EM 21=+．故选B ．【点睛】本题考查了旋转的性质，直角三角形的性质，三角形的中位线的性质，正确的作出辅助线是解题的关键．3．C解析：C【解析】设正方形O 3KJP 的边长为a ，根据正方形的性质知：O 3O 4=22a ，正方形O 2IHJ 的边长为2a ，O 2O 32a ，正方形O 1GFH 的边长为4a ，O 1O 22a ，正方形OCDF 的边长为8a ，OO 1=42a ， ∵AO=2OO 1=82am ，∴22a+2a+22a+42a+82a=312，解得：a=2m ，∴FD=8a=16m ， ∴长方形花坛ABCD 的周长是2×（2FD+CD ）=6FD=96m ，故选C ．【点睛】本题考查了正方形的性质，主要利用了正方形的对角线与边长的关系，正方形的中心到顶点的距离等于到边的距离的2倍，熟记性质是解题的关键．4．C解析：C【分析】如图，取AD 的中点M ，连接CM 、AG 、AC ，作AN ⊥BC 于N ．首先证明∠ACD ＝90°，求出AC ，AN ，利用三角形中位线定理，可知EF ＝12AG ，求出AG 的最大值以及最小值即可解决问题．【详解】解：如图，取AD 的中点M ，连接CM 、AG 、AC ，作AN ⊥BC 于N ．∵四边形ABCD 是平行四边形，∠BCD ＝120°，28AD AB ==∴∠D ＝180°−∠BCD ＝60°，AB ＝CD ＝4，∵AM ＝DM ＝DC ＝4，∴△CDM 是等边三角形，∴∠DMC ＝∠MCD ＝60°，AM ＝MC ，∴∠MAC ＝∠MCA ＝30°，∴∠ACD ＝90°，∴AC ＝43在Rt △ACN 中，∵AC ＝3ACN ＝∠DAC ＝30°，∴AN ＝12AC ＝3∵AE ＝EH ，GF ＝FH ，∴EF ＝12AG ，∵点G 在BC 上，∴AG 的最大值为AC 的长，最小值为AN 的长，∴AG 的最大值为∴EF 的最大值为∴EF 故选：C【点睛】本题考查平行四边形的性质、三角形的中位线定理、等边三角形的判定和性质、直角三角形30度角性质、垂线段最短等知识，解题的关键是学会添加常用辅助线，本题的突破点是证明∠ACD ＝90°，属于中考选择题中的压轴题．5．A解析：A【分析】计算前三个正方形的面积从而得出一般规律求解.【详解】顺次连接正方形ABCD 四边的中点得到第一个正方形1111D C B A则正方形1111D C B A 的面积为11122⨯= 正方形2222A B C D 的面积为111224⨯= 正方形3333A B C D 的面积为11112228⨯⨯= 正方形n n n n A B C D 的面积为11()22n n= 根据规律可得，第六个正方形6666A B C D 的面积为66111()2264== 【点睛】本题考查了特殊正方形中的面积计算，解题的关键在于找出规律，根据规律求解.6．C解析：C【分析】证明△BNA ≌△BNE ，得到BA=BE ，即△BAE 是等腰三角形，同理△CAD 是等腰三角形，根据题意求出DE ，根据三角形中位线定理计算即可．【详解】解：∵BN 平分∠ABC ，BN ⊥AE ，∴∠NBA=∠NBE ，∠BNA=∠BNE ，在△BNA 和△BNE 中，ABN EBN BN BNANB ENB ∠∠⎧⎪⎨⎪∠∠⎩＝＝＝， ∴△BNA ≌△BNE ，∴BA=BE ，∴△BAE 是等腰三角形，同理△CAD 是等腰三角形，∴点N 是AE 中点，点M 是AD 中点（三线合一），∴MN 是△ADE 的中位线，∵BE+CD=AB+AC=19-BC=19-7=12，∴DE=BE+CD-BC=5，∴MN=12DE=52．故选C ．【点睛】本题考查的是三角形中位线定理、等腰三角形的性质，掌握三角形的中位线平行于第三边，并且等于第三边的一半是解题的关键．7．B解析：B【分析】取DC 的中点E ，连接OE 、DE 、OD ，根据三角形的任意两边之和大于第三边可知当O 、E 、D 三点共线时，点D 到点O 的距离最大，再根据勾股定理求出DE 的长，根据直角三角形斜边上的中线等于斜边的一半求出OE 的长，两者相加即可得解．【详解】取AB 中点E ，连接OE 、DE 、OD ，90MON ∠=︒，122OE AB ∴==．在Rt DAE ∆中，利用勾股定理可得22DE =．在ODE ∆中，根据三角形三边关系可知DE OE OD +>，∴当O 、E 、D 三点共线时，OD 最大为222OE DE +=+．故选B ．【点睛】本题考查了直角三角形斜边上的中线等于斜边的一半得到性质，三角形的三边关系，矩形的性质，勾股定理，根据三角形的三边关系判断出点O、E、D三点共线时，点D到点O 的距离最大是解题的关键．8．B解析：B【分析】关键结合图形证明△CHG≌△EGD，即可逐项判断求解【详解】解：∵DF=BD，∴∠DFB=∠DBF，∵AD∥BC，DE=BC，∴四边形DBCE是平行四边形，∠DFB=∠GBC，∴∠DEC=∠DBC=45°，∴∠DEC=2∠EFB，∴∠EFB=22.5°，∠CGB=∠CBG=22.5°，∴CG=BC=DE，∵DE=DC，∴∠DEG=∠DCE，∵∠GHC=∠CDF+∠DFB=90°+22.5°=112.5°，∠DGE=180°-（∠BGD+∠EGF），=180°-（∠BGD+∠BGC），=180°-（180°-∠DCG）÷2，=180°-（180°-45°）÷2，=112.5°，∴∠GHC=∠DGE，∴△CHG≌△EGD，∴∠EDG=∠CGB=∠CBF，∴∠GDH=90°-∠EDG，∠GHD=∠BHC=90°-∠CGB，∴∠GDH=∠GHD故②正确；∴∠GDH=∠GHD又∠EFB=22.5°,∴∠DHG=∠GDH=67.5°∴∠GDF=90°-∠GDH=22.5°=∠EFB,∴DG=GF,∴HG=DG=GF∴HF=2HG,显然CE≠HF=2HG,故①正确；∵△CHG ≌△EGD ，∴CHG EGD S S ∆∆=∴CHG DHG EGD DHG S S S S ∆∆∆∆+=+，即CDG DHGE S S △四边形＝而=EFG DHGE DHF S S S ∆+四边形△，故CDG DHF S S ≠△△故④不正确；结合前面条件易知等腰三角形有△ABD ，△CDB ，△BDF ，△CDE ，△BCG ，△DGH ，△EGF ，△CDG ，△DGF 共9个，∴③错误；故正确的有①②，有2个，故选：B【点睛】本题主要考查对三角形的内角和定理，全等三角形的判定和性质，等腰三角形的性质和判定，正方形的性质，等知识点的理解和掌握，综合运用这些性质进行推理是解此题的关键．9．B解析：B【分析】延长BG 交CH 于点E ，根据正方形的性质证明△ABG ≌△CDH ≌△BCE ，可得GE=BE-BG=2，HE=CH-CE=2，∠HEG=90°，从而由勾股定理可得GH 的长．【详解】解：如图，延长BG 交CH 于点E ，∵四边形ABCD 是正方形，∴∠ABC=90°，AB=CD=10，∵AG=8，BG=6，∴AG 2+BG 2=AB 2，∴∠AGB=90°，∴∠1+∠2=90°，又∵∠2+∠3=90°，∴∠1=∠3，同理：∠4=∠6，在△ABG和△CDH中，AB＝CD＝10AG＝CH＝8BG＝DH＝6∴△ABG≌△CDH（SSS），∴∠1=∠5，∠2=∠6，∴∠2=∠4，在△ABG和△BCE中，∵∠1＝∠3，AB＝BC，∠2＝∠4，∴△ABG≌△BCE（ASA），∴BE=AG=8，CE=BG=6，∠BEC=∠AGB=90°，∴GE=BE－BG=8－6=2，同理可得HE=2，在Rt△GHE中，GH===故选：B．【点睛】本题主要考查正方形的性质、全等三角形的判定与性质、勾股定理及其逆定理的综合运用，通过证三角形全等得出△GHE为直角三角形且能够求出两条直角边的长是解题的关键．10．D解析：D【分析】通过判断△AND≌△CMB即可证明①，再判断出△ANE≌△CMF证明出③，再证明出△NFM≌△MEN，得到∠FNM=∠EMN，进而判断出②，通过 DF与EB先证明出四边形为平行四边形，再通过三线合一以及内角和定理得到∠NDO=∠ABD=30°，进而得到DE=BE，即可知四边形为菱形．【详解】∵BF⊥AC∴∠BMC=90°DE BF又∵//∴∠EDO=∠MBO，DE⊥AC∴∠DNA=∠BMC=90°∵四边形ABCD为矩形∴AD=BC，AD∥BC，DC∥AB∴∠ADB=∠CBD∴∠ADB-∠EDO=∠CBD-∠MBO即∠AND=∠CBM在△AND与△CMB∵90DNA BMC AND CBM AD BC ∠=∠=︒⎧⎪∠=∠⎨⎪=⎩∴△AND ≌△CMB(AAS)∴AN=CM ，DN=BM ，故①正确．∵AB ∥CD∴∠NAE=∠MCF又∵∠DNA=∠BMC=90°∴∠ANE=∠CMF=90°在△ANE 与△CMF 中∵90ANE CMF AN CM NAE MCF ∠=∠=⎧⎪=⎨⎪∠=∠⎩∴△ANE ≌△CMF （ASA ）∴NE=FM ，AE=CF ，故③正确．在△NFM 与△MEN 中∵90FM NE FMN ENM MN MN =⎧⎪∠=∠=︒⎨⎪=⎩∴△NFM ≌△MEN （SAS ）∴∠FNM=∠EMN∴NF ∥EM ，故②正确．∵AE=CF∴DC-FC=AB-AE ，即DF=EB又根据矩形性质可知DF ∥EB∴四边形DEBF 为平行四边根据矩形性质可知OD=AO ，当AO=AD 时，即三角形DAO 为等边三角形∴∠ADO=60°又∵DN ⊥AC根据三线合一可知∠NDO=30°又根据三角形内角和可知∠ABD=180°-∠DAB-∠ADB=30°故DE=EB∴四边形DEBF 为菱形，故④正确．故①②③④正确故选D ．【点睛】本题矩形性质、全等三角形的性质与证明、菱形的判定，能够找对相对应的全等三角形是解题关键．二、填空题11．25 【详解】由于点B 与点D 关于AC 对称，所以如果连接DE ，交AC 于点P ，那PE+PB 的值最小．在Rt △CDE 中，由勾股定理先计算出DE 的长度，即为PE+PB 的最小值．连接DE ，交AC 于点P ，连接BD ．∵点B 与点D 关于AC 对称，∴DE 的长即为PE+PB 的最小值，∵AB=4，E 是BC 的中点，∴CE=2，在Rt △CDE 中， DE=25．考点：(1)、轴对称-最短路线问题；(3)、正方形的性质．12．218cm 【分析】根据正方形的性质可以证明△AEO ≌CFO ，就可以得出S △AEO =S △CFO ，就可以求出△AOD 面积等于正方形面积的14，根据正方形的面积就可以求出结论．【详解】解：如图：∵正方形ABCD 的对角线相交于点O ，∴△AEO 与△CFO 关于O 点成中心对称，∴△AEO ≌CFO ，∴S △AEO ＝S △CFO ，∴S △AOD ＝S △DEO +S △CFO ，∵对角线长为1cm ，∴S 正方形ABCD ＝1112⨯⨯＝12cm 2， ∴S △AOD ＝18cm 2， ∴阴影部分的面积为18cm 2．故答案为：18cm 2．【点睛】本题考查了正方形的性质的运用，全等三角形的判定及性质的运用正方形的面积及三角形的面积公式的运用，在解答时证明△AEO ≌CFO 是关键．13．①③④【分析】由矩形的性质可得AB=CD ，AD=BC ，∠BAD=∠ABC=∠BCD=∠ADC=90°，AC=BD ，由角平分线的性质和余角的性质可得∠F=∠FAD=45°，可得AD=DF=BC ，可判断①；通过证明△DCG ≌△BEG ，可得∠BGE=∠DGC ，BG=DG ，即可判断②③；过点G 作GH ⊥CD 于H ，设AD=4x=DF ，AB=3x ，由勾股定理可求BD=5x ，由等腰直角三角形的性质可得HG=CH=FH=12x ，DG=GB=2x ，由三角形面积公式可求解，可判断④．【详解】解：∵四边形ABCD 是矩形，∴AB=CD ，AD=BC ，∠BAD=∠ABC=∠BCD=∠ADC=90°，AC=BD ，∵AE 平分∠BAD ，∴∠BAE=∠DAE=45°，∴∠F=∠FAD ，∴AD=DF ，∴BC=DF ，故①正确；∵∠EAB=∠BEA=45°，∴AB=BE=CD ，∵∠CEF=∠AEB=45°，∠ECF=90°，∴△CEF 是等腰直角三角形，∵点G 为EF 的中点，∴CG=EG ，∠FCG=45°，CG ⊥AG ，∴∠BEG=∠DCG=135°，在△DCG 和△BEG 中， ===BE CD BEG DCG CG EG ⎧⎪∠∠⎨⎪⎩，∴△DCG≌△BEG（SAS）．∴∠BGE=∠DGC，BG=DG，∵∠BGE＜∠AEB，∴∠DGC=∠BGE＜45°，∵∠CGF=90°，∴∠DGF＜135°，故②错误；∵∠BGE=∠DGC，∴∠BGE+∠DGA=∠DGC+∠DGA，∴∠CGA=∠DGB=90°，∴BG⊥DG，故③正确；过点G作GH⊥CD于H，∵34AB AD=，∴设AD=4x=DF，AB=3x，∴CF=CE=x，22AB AD x+，∵△CFG，△GBD是等腰直角三角形，∴HG=CH=FH=12x，DG=GB=522x，∴S△DGF=12×DF×HG=x2，S△BDG=12DG×GB=254x2，∴254BDG FDGS S=，故④正确；故答案为：①③④．【点睛】本题考查了矩形的性质、全等三角形的判定与性质、等腰直角三角形的判定与性质；熟练掌握矩形的性质，证明三角形全等和等腰直角三角形是解决问题的关键．14102【分析】连结AC，取OC中点M，连结 MB，MG，则MB，MG为定长，利用两点之间线段最短解决问题即可．【详解】连接AC，交EF于O，∵AD∥BC，∴∠EAO＝∠FCO，∠AEO＝∠CFO，∵AE＝CF，∴△AEO≌△CFO（ASA），∴OA＝OC，∴O是正方形的中心，∵AB＝BC＝4，∴AC＝2OC＝2，取OC中点M，连结 MB，MG，过点M作MH⊥BC于H，∵MC＝12OC2，∴MH＝CH＝1，∴BH＝4−1＝3，由勾股定理可得MB223110在Rt△GOC中，M是OC的中点，则MG＝12OC2∵BG≥BM−MG102，当B，M，G三点共线时，BG102，102．【点睛】本题主要考查了正方形的性质，根据正方形的性质得出当E，F运动到AD，BC的中点时，MG最小是解决本题的关键．15．①③④【分析】由“AAS”可证△AOE≌△COF，△AHO≌△CGO，可得OE=OF，HO=GO，可证四边形EGFH 是平行四边形，由EF⊥GH，可得四边形EGFH是菱形，可判断①③正确，若四边形ABCD 是正方形，由“ASA”可证△BOG≌△COF，可得OG=OF，可证四边形EGFH是正方形，可判断④正确，即可求解．【详解】解：如图，∵四边形ABCD是菱形，∴AO＝CO，AD∥BC，AB∥CD，∴∠BAO＝∠DCO，∠AEO＝∠CFO，∴△AOE≌△COF（AAS），∴OE＝OF，∵线段EF的垂直平分线分别交BC、AD边于点G、H，∴GH过点O，GH⊥EF，∵AD∥BC，∴∠DAO＝∠BCO，∠AHO＝∠CGO，∴△AHO≌△CGO（AAS），∴HO＝GO，∴四边形EGFH是平行四边形，∵EF⊥GH，∴四边形EGFH是菱形，∵点E是AB上的一个动点，∴随着点E的移动可以得到无数个平行四边形EGFH，随着点E的移动可以得到无数个菱形EGFH，故①③正确；若四边形ABCD是正方形，∴∠BOC＝90°，∠GBO＝∠FCO＝45°，OB＝OC；∵EF⊥GH，∴∠GOF＝90°；∠BOG+∠BOF＝∠COF+∠BOF＝90°，∴∠BOG＝∠COF；在△BOG和△COF中，∵BOG COF BO COGBO FCO ∠=∠⎧⎪=⎨⎪∠=∠⎩，∴△BOG≌△COF（ASA）；∴OG＝OF，同理可得：EO＝OH，∴GH＝EF；∴四边形EGFH是正方形，∵点E是AB上的一个动点，∴至少得到一个正方形EGFH，故④正确，故答案为：①③④．【点睛】本题考查了菱形的判定和性质，平行四边形的判定，正方形的判定，全等三角形的判定和性质等知识，灵活运用这些性质进行推理是关键．16．①②④⑤【分析】根据∠B=90°，AB=BE，△ABE绕点A逆时针旋转45°，得到△AHD，可得△ABE≅△AHD，并且△ABE和△AHD都是等腰直角三角形，可证AD//BC，根据DC⊥BC，可得∠HDE=∠CDE，根据三角形的内角和可得∠HDE=∠CDE，即DE平分∠HDC，所以①正确；利用∠DAB=∠ABC=∠BCD=90°，得到四边形ABCD是矩形，有∠ADC=90°，∠HDC=45°，由①有DE平分∠HDC，得∠HDO=22.5°，可得∠AHB=67.5°，∠DHO=22.5°，可证OD=OH，利用 AE=AD易证∠OHE=∠HEO=67.5°，则有OE=OH，OD=OE，所以②正确；利用AAS证明ΔDHE≅ΔDCE，则有DH=DC，∠HDE=∠CDE=22.5°，易的∠DHF=22.5°，∠DFH=112.5°，则△DHF不是直角三角形，并DH≠HF，即有：CD≠HF，所以③错误；根据△ABE是等腰直角三角形，JH⊥JE，∵J是BC的中点，H是BF的中点，得到2JH=CF，2JC=BC，JC=JE+CE，易证BC−CF=2CE，所以④正确；过H作HJ⊥BC于J，并延长HJ交AD于点I，得IJ⊥AD，I是AD的中点，J是BC的中点，H是BF的中点，所以⑤正确；【详解】∵Rt△ABE中，∠B=90°，AB=BE，∴∠BAE=∠BEA=45°，又∵将△ABE绕点A逆时针旋转45°，得到△AHD，∴△ABE≅△AHD，并且△ABE和△AHD都是等腰直角三角形，∴∠EAD=45°，AE=AD ，∠AHD=90°，∴∠ADE=∠AED，∴∠BAD=∠BAE+∠EAD=45°+45°=90°，∴AD//BC，∴∠ADE=∠DEC，∴∠AED=∠DEC，又∵DC⊥BC，∴∠DCE=∠DHE=90°∴由三角形的内角和可得∠HDE=∠CDE，即：DE平分∠HDC，所以①正确；∵∠DAB=∠ABC=∠BCD=90°，∴四边形ABCD是矩形，∴∠ADC=90°，∴∠HDC=45°，由①有DE平分∠HDC，∴∠HDO=12∠HDC=12×45°=22.5°，∵∠BAE=45°，AB=AH，∴∠OHE=∠AHB=12(180°−∠BAE)=12×(180°−45°)=67.5°，∴∠DHO=∠DHE−∠FHE=∠DHE−∠AHB=90°−67.5°=22.5°，∴OD=OH，在△AED中，AE=AD，∴∠AED=12(180°−∠EAD)=12×(180°−45°)=67.5°，∴∠OHE=∠HEO=67.5°，∴OE=OH，∴OD=OE，所以②正确；在△DHE和△DCE中，DHE DCEHDE CDEDE DE∠=∠⎧⎪∠=∠⎨⎪=⎩，∴ΔDHE≅ΔDCE(AAS)，∴DH=DC，∠HDE=∠CDE=12×45°=22.5°，∵OD=OH，∴∠DHF=22.5°，∴∠DFH=180°−∠HDF−∠DHF=180°−45°−22.5°=112.5°，∴△DHF不是直角三角形，并DH≠HF，即有：CD≠HF，所以③不正确；如图，过H作HJ⊥BC于J，并延长HJ交AD于点I，∵△ABE是等腰直角三角形，JH⊥JE，∴JH=JE ，又∵J 是BC 的中点，H 是BF 的中点，∴2JH=CF ，2JC=BC ，JC=JE+CE ，∴2JC=2JE+2CE=2JH+2CE=CF+2CE=BC ，即有：BC−CF=2CE ，所以④正确；∵AD//BC ，∴IJ ⊥AD ，又∵△AHD 是等腰直角三角形，∴I 是AD 的中点，∵四边形ABCD 是矩形，HJ ⊥BC ，∴J 是BC 的中点，∴H 是BF 的中点，所以⑤正确；综上所述，正确的有①②④⑤，故答案为：①②④⑤．【点睛】本题考查了全等三角形的判定与性质、旋转的性质、矩形的性质、角平分线的性质以及等腰直角三角形的判定与性质；证明三角形全等和等腰直角三角形是解决问题的关键．17．【详解】解析：∵在正方形ABCD 中，AC=∴AB=AD=BC=DC=6，∠EAD=45°设EF 与AD 交点为O ，O 是AD 的中点,∴AO=3以AD 为对角线的所有▱AEDF 中，当EF ⊥AC 时，EF 最小，即△AOE 是直角三角形，∵∠AEO=90°，∠EAD=45°，OE=2OA=2，∴EF=2OE=18．663【分析】通过四边形ABCD 是矩形以及CE CB BE ==，得到△FEM 是等边三角形，根据含30°直角三角形的性质以及勾股定理得到KM ，NK ，KE 的值，进而得到NE 的值，再利用30°直角三角形的性质及勾股定理得到BN ，BE 即可．【详解】解：如图，设NE 交AD 于点K ，∵四边形ABCD 是矩形，∴AD ∥BC ，∠ABC=90°，∴∠MFE=∠FCB ，∠FME=∠EBC∵CE CB BE ==，∴△BCE 为等边三角形，∴∠BEC=∠ECB=∠EBC=60°，∵∠FEM=∠BEC ，∴∠FEM=∠MFE=∠FME=60°，∴△FEM 是等边三角形，FM=FE=EM=2，∵EN ⊥BE ，∴∠NEM=∠NEB=90°，∴∠NKA=∠MKE=30°，∴KM=2EM=4，NK=2AN=6，∴在Rt △KME 中，KE=2223KM EM -=，∴NE=NK+KE=6+23，∵∠ABC=90°，∴∠ABE=30°，∴BN=2NE=12+43，∴BE=22663BN NE -=+，∴BC=BE=663，故答案为：663【点睛】本题考查了矩形，等边三角形的性质，以及含30°直角三角形的性质与勾股定理的应用，解题的关键是灵活运用30°直角三角形的性质．19．【分析】作AB 的中点E ，连接EM 、CE ，根据直角三角形斜边上的中线等于斜边的一半以及三角形的中位线定理求得CE 和EM 的长，然后确定CM 的范围．【详解】解：作AB 的中点M ，连接EM 、CM ．在Rt △ABC 中，AB 22AC BC +2286+10，∵M 是直角△ABC 斜边AB 上的中点，∴CM ＝12AB ＝5． ∵E 是BD 的中点，M 是AB 的中点，∴ME＝12AD＝2．∴5﹣2≤CE≤5+2，即3≤CE≤7．∴最大值为7，故答案为：7．【点睛】本题考查了三角形的中位线定理，勾股定理，直角三角形斜边中线的性质等知识，掌握基本性质定理是解题的关键．20．2【分析】分别延长AE，BF交于点H，易证四边形EPFH为平行四边形，得出点G为PH的中点，则G的运动轨迹为△HCD的中位线MN，再求出CD的长度，运用中位线的性质求出MN的长度即可．【详解】解：如图，分别延长AE，BF交于点H，∵∠A=∠FPB=60°，∴AH∥PF，∵∠B=∠EPA=60°，∴BH∥PE∴四边形EPFH为平行四边形，∴EF与HP互相平分，∵点G为EF的中点，∴点G为PH的中点，即在P运动的过程中，G始终为PH的中点，∴G的运动轨迹为△HCD的中位线MN，∵CD=6-1-1=4，∴MN=12CD=2，∴点G移动路径的长是2，故答案为：2．【点睛】本题考查了等边三角形及中位线的性质，以及动点的问题，是中考热点，解题的关键是得出G 的运动轨迹为△HCD 的中位线MN ．三、解答题21．（1）①证明见解析；②证明见解析；（2）103DE =．【分析】（1）过点D 作//DM GH 交BC 延长线于点M ，连接EH ，①由正方形的性质可得//AD BC ，AD CD =，90A ADC DCM ∠=∠=∠=︒，即可证明四边形DGHM 是平行四边形，可得DM=GH ，由90GOD ∠=︒可得∠EDM=90°，根据直角三角形两锐角互余的性质可得12∠=∠，利用ASA 可证明△ADE≌△CDM，可得DE=DM ，即可证明DE=GH ；②由①得DM=DE ，根据勾股定理可得2，利用三角形三边关系即可得结论；（2）过点D 作DN//GH 交BC 于点N ，作ADM CDN ∠=∠，DM 交BA 延长线于点M ，可证明四边形GHND 为平行四边形，可得DN HG =，GD HN =，根据勾股定理可求出CN 的长，利用AAS 可证明ADM CDN ∆∆≌，可得AM NC =，DM DN =，根据平行线的性质∠EDN=45°，根据角的和差故选可得∠MDE=∠EDN ，利用SAS 可证明MDE NDE ∆∆≌，即可证明AE CN EN +=，设AE x =，利用勾股定理可求出x 的值，进而利用勾股定理求出DE 的值即可得答案．【详解】（1）如图（1），过点D 作//DM GH 交BC 延长线于点M ，连接EH ，EM ， ①∵四边形ABCD 为正方形，∴//AD BC ，AD CD =，90A ADC DCM ∠=∠=∠=︒∴四边形DGHM 为平行四边形，∴DM=GH ，GD HM =，∵90GOD ∠=︒，∴90EDM EOH ∠=∠=︒，∴290EDC ∠+∠=︒，∵90ADC ∠=︒，∴190EDC ∠+∠=︒，∴12∠=∠，在ADE ∆和CDM ∆中12A DCM AD DC ∠=∠⎧⎪=⎨⎪∠=∠⎩，∴ADE CDM ∆∆≌，∴DE DM =，∴DE GH =．②在DEM ∆中，∠EDM=90°，∴222DE DM EM +=，∵DE DM =，∴222DE EM =， ∴2EM DE =，在EHM ∆中，HM EH EM +>，∵GD HM =， ∴2GD EH GH +≥．（2）如图（2），过点D 作DN//GH 交BC 于点N ，则四边形GHND 为平行四边形， ∴DN HG =，GD HN =，∵90C ∠=︒，4CD AB ==，25HG DN == ∴222CN DN DC =-=，∴422BN BC CN =-=-=，作ADM CDN ∠=∠，DM 交BA 延长线于点M ，在ADM ∆和CDN ∆中90C MAD CDN ADM DC AD ∠=∠=︒⎧⎪∠=∠⎨⎪=⎩，∴ADM CDN ∆∆≌，∴AM NC =，DM DN =，∵45GOD EOH ∠=∠=︒，∴45EDN ∠=︒，∴45ADE CDN ∠+∠=︒，∴45ADE ADN MDE ∠+∠=︒=∠，在MDE ∆和NDE ∆中MD ND MDE EDN DE DE =⎧⎪∠=∠⎨⎪=⎩，∴MDE NDE ∆∆≌，∴EM EN =，即AE AM AE CN EN +=+=，设AE x =，则BE=4-x ，在Rt BEN ∆中，2222(2)x x +=+，解得：43x =， ∴2222441043DE AD AE ⎛⎫=+=+= ⎪⎝⎭．【点睛】本题考查正方形的性质、平行四边形的判定与性质、全等三角形的判定与性质、三角形的三边关系及勾股定理，熟练掌握相关性质及判定定理，并正确作出辅助线是解题关键．22．（1）（32，32）；（2）存在，点D 的坐标为（0，3）或（231）或（0，-1）；（3）OM=32或212 【分析】（1）过点B 作BD ⊥y 轴于D ，利用30°所对的直角边是斜边的一半和勾股定理求出OB ，再利用30°所对的直角边是斜边的一半和勾股定理求出BD 和OD 即可得出结论；（2）根据题意和等边三角形的性质分别求出点A 、B 、C 的坐标，然后根据菱形的顶点顺序分类讨论，分别画出对应的图形，根据菱形的对角线互相平分即可分别求出结论；（3）利用30°所对的直角边是斜边的一半和勾股定理求出OP 和BP ，然后根据直角三角形的直角顶点分类讨论，分别画出对应的图形，利用直角三角形斜边上的中线等于斜边的一半、平行四边形的判定及性质、等腰三角形的判定及性质求解即可．【详解】解：（1）如图2，过点B 作BD ⊥y 轴于D由图1中，点A 的坐标为()1,0-，30ABO ∠=︒，∠AOB=90°∴OA=1，AB=2OA=2由勾股定理可得223AB OA -=∵将此直角三角板绕点O 顺时针旋转30∴∠BOD=30°∴BD=1322OB =∴2232OB BD -=∴点B 332） 332）；（2）在图2的基础上继续将直角三角板绕点O 顺时针60︒，此时点A 落在y 轴上，点B 落在x 轴上∴点A 的坐标为（0,1），点B 30）∵△ABC 为等边三角形∴∠ABC=60°，AB=BC=AC=2∴∠OBC=90°∴点C 32）设点D 的坐标为（a ，b ）如图所示，若四边形ABCD 为菱形，连接BD ，与AC 交于点O∴点O既是AC的中点，也是BD的中点∴03322 12022ab⎧++=⎪⎪⎨++⎪=⎪⎩解得：3ab=⎧⎨=⎩∴此时点D的坐标为（0，3）；当四边形ABDC为菱形时，连接AD，与BC交于点O∴点O既是AD的中点，也是BC的中点∴0332212022ab⎧++=⎪⎪⎨++⎪=⎪⎩解得：231ab⎧=⎪⎨=⎪⎩∴此时点D的坐标为（23，1）；当四边形ADBC为菱形时，连接CD，与AB交于点O∴点O既是AB的中点，也是CD的中点∴03322 10222ab⎧++=⎪⎪⎨++⎪=⎪⎩解得：1ab=⎧⎨=-⎩∴此时点D的坐标为（0，-1）；综上：点D的坐标为（0，3）或（23，1）或（0，-1）；（3）∵OB=3，∠ABO=30°∴OP=12OB=32∴BP=2232OB OP-=当∠OMB=90°时，如下图所示，连接BM∵F为OB的中点∴PF=12OB，MF=12OB，OF=BF∴PF=MF∴四边形OPBM为平行四边形∴OM=BP=32；当∠OBM=90°时，如下图所示，连接OM，∴∠PBM=∠PBO＋∠OBM=120°∵点F为OB的中点。

八年级第二次月考参考答案(配套试卷)

八年级思品第二次月考参考答案一、单项选择题（每小题3分，共60分）题号 1 2 3 4 5 6 7 8 9 10 答案 B C D C A B C D B B 题号11 12 13 14 15 16 17 18 19 20 答案 C D C B C D C A A B21、（1）不对。

（1分）继续这样的话，他的成绩会越来越差，而且会造成师生感情的隔阂，影响师生之间的正常交流与和沟通。

（2分）【ps：由于不适应老师的教学方式或者听不懂老师的话而讽刺老师，自己也不愿意去与老师沟通，这样造成的后果可以用成绩下降，师生关系不和谐，师生感情受到伤害来阐述。

】（2）①老师是人类文明的传播者，是老师，教给我们做人的道理，帮助我们掌握科学文化知识和技能。

老师被誉为人类灵魂的工程师。

（2分）②即使是因为老师的原因，学生不适应，学生也不能因此而诋毁老师，不尊重老师。

我们应当主动与老师沟通，反映自己的困难和问题，并适时提供意见和建议，做到礼貌待师、注意场合、勿失分寸。

（2分）③因此，如果我是他，我会及时找老师沟通，把自己学习上的困难和想法告诉老师，请老师给予帮助。

（1分）22、（1）该观点是错误的。

网络是一把双刃剑，它有利又有弊。

（1分）（2）①网络具有积极作用。

网络交往超越了空间，扩大了我们交往的领域、对象，改变了以往的交往方式，丰富了我们的人生经验。

网络为我们了解时事、学习知识、与人沟通、休闲娱乐等提供了便捷的条件。

可以通过网络可以开阔眼界、放松心情、学习新知、结交新友等。

（2分）②网络也有消极作用。

网络交往对象具有虚拟性、间接性和隐蔽性，可能对部分网络使用者造成伤害。

网络信息良莠不齐，个别不法分子利用网络实施违法犯罪活动。

过分沉迷网络会给我们生活带来负面影响：影响学习成绩，影响身心健康，还可能诱发犯罪，影响家庭和谐与社会稳定。

（2分）（3）因此，我们上网，要发挥网络的积极作用，避免“网毒”的伤害。

（1分）23、（1）这位同学在与他人的交往中封闭自己，不能与同学正常来往。

人教版八年级第二学期第二次月考数学试题含答案

一、选择题1．如图，E 、F 、G 、H 分别是BD 、BC 、AC 、AD 的中点，且AB ＝CD ．结论：①EG ⊥FH ；②四边形EFGH 是矩形；③HF 平分∠EHG ；④EG 12=BC ；⑤四边形EFGH 的周长等于2AB ．其中正确的个数是( )A ．1B ．2C ．3D ．42．在边长为2的正方形ABCD 中，P 为AB 上的一动点，E 为AD 中点，PE 交CD 延长线于Q ，过E 作EF PQ ⊥交BC 的延长线于F ，则下列结论：①APE DQE ∆≅∆；②PQ EF =；③当P 为AB 中点时，2CF =；④若H 为QC 的中点，当P 从A 移动到B 时，线段EH 扫过的面积为12，其中正确的是（）A ．①②B ．①②④C ．②③④D ．①②③3．如图，在矩形ABCD 中，AB=2，BC=4，P 为边AD 上一动点，连接BP ，把△ABP 沿BP 折叠，使A 落在A′处，当△A′DC 为等腰三角形时，AP 的长为（）A ．2B ．233C ．2或33D ．2或334．如图，已知正方形ABCD 的边长为2，点,E F 在正方形ABCD 内， ,EAB FDC ∆∆都是等边三角形，则EF 的长为（）A ．23-B ．232-C ．31-D ．35．如图，边长为8的正方形ABCD 的对角线交于点O ，点,E F 分别在边,CD DA 上（CE DE <），且90,,EOF OE BC ︒∠=的延长线交于点 ,,G OF CD 的延长线交于点,H E 恰为OG 的中点．下列结论：①OCE ODF ∆∆≌；②OG OH =；③210GH =．其中，正确结论的个数是（）A ．0个B ．1个C ．2个D ．3个6．正方形ABCD ，CEFG 按如图放置，点B ，C ，E 在同一条直线上，点P 在BC 边上，PA PF =，且APF 90∠=︒，连接AF 交CD 于点M ，有下列结论：EC BP =①；BAP GFP ∠∠=②；2221AB CE AF 2+=③；APF ABCD CEFG S S 2S +=正方形正方形④．其中正确的是（）A ．①②③B ．①③④C ．①②④D ．①②③④7．如图，直角梯形ABCD 中AD ∥BC ，∠D ＝90°．∠A 的平分线交DC 于E ，EF ⊥AB 于F ．已知AD ＝3.5cm ，DC ＝4cm ，BC ＝6.5cm ．那么四边形BCEF 的周长是（）A ．10cmB ．11cmC ．11.5cmD ．12cm8．如图，在等腰Rt ABC △中，908C AC ∠==°，，F 是AB 边上的中点，点D 、E 分别在AC 、BC 边上运动，且保持AD CE =．连接DE 、DF 、EF ．在此运动变化的过程中，下列结论：①DFE △是等腰直角三角形； ②四边形CDFE 不可能为正方形，③DE 长度的最小值为4； ④四边形CDFE 的面积保持不变；⑤△CDE 面积的最大值为8．其中正确的结论是（）A ．①②③B ．①④⑤C ．①③④D ．③④⑤9．已知菱形ABCD 的面积为83，对角线AC 的长为43，∠BCD=60°，M 为BC 的中点，若P 为对角线AC 上一动点，则PB+PM 的最小值为（）A ．3B ．2C ．23D ．410．如图，已知一个矩形纸片OACB ，将该纸片放置在平面直角坐标系中，点A （10，0），点B （0，6），点P 为BC 边上的动点，将△OBP 沿OP 折叠得到△OPD ，连接CD 、AD ．则下列结论中：①当∠BOP ＝45°时，四边形OBPD 为正方形；②当∠BOP ＝30°时，△OAD 的面积为15；③当P 在运动过程中，CD 的最小值为234﹣6；④当OD ⊥AD 时，BP ＝2．其中结论正确的有（）A ．1个B ．2个C ．3个D ．4个二、填空题11．如图，四边形ABCD ，四边形EBFG ，四边形HMPN 均是正方形，点E 、F 、P 、N 分别在边AB 、BC 、CD 、AD 上，点H 、G 、M 在AC 上，阴影部分的面积依次记为1S ，2S ，则12:S S 等于__________．12．如图，在平行四边形ABCD ，AD ＝2AB ，F 是AD 的中点，作CE ⊥AB ，垂足E 在线段AB 上，连接EF 、CF ，则下列结论：①∠BCD ＝2∠DCF ；②EF ＝CF ；③S △CDF ＝S △CEF ；④∠DFE ＝3∠AEF ，－定成立的是_________．(把所有正确结论的序号都填在横线上)13．在锐角三角形ABC 中，AH 是边BC 的高，分别以AB ，AC 为边向外作正方形ABDE 和正方形ACFG ，连接CE ，BG 和EG ，EG 与HA 的延长线交于点M ，下列结论：①BG=CE ；②BG ⊥CE ；③AM 是△AEG 的中线；④∠EAM=∠ABC ．其中正确的是_________．14．在ABC 中，AB=12，AC=10，BC=9，AD 是BC 边上的高．将ABC 按如图所示的方式折叠，使点A 与点D 重合，折痕为EF ，则DEF 的周长为______．15．如图，在菱形ABCD 中，AC 交BD 于P ，E 为BC 上一点，AE 交BD 于F ，若AB=AE ，EAD 2BAE ∠∠=，则下列结论：①AF=AP ；②AE=FD ；③BE=AF ．正确的是______（填序号）．16．如图，已知在△ABC 中，AB=AC=13，BC=10，点M 是AC 边上任意一点，连接MB ，以MB 、MC 为邻边作平行四边形MCNB ，连接MN ，则MN 的最小值是______17．如图，在正方形ABCD 中，点F 为CD 上一点，BF 与AC 交于点E ，若∠CBF=20°，则∠AED 等于__度．18．已知：如图，在长方形ABCD 中，4AB =，6AD =．延长BC 到点E ，使2CE =，连接DE ，动点P 从点B 出发，以每秒2个单位的速度沿BC CD DA --向终点A 运动，设点P 的运动时间为t 秒，当t 的值为_____秒时，ABP ∆和DCE ∆全等．19．如图，正方形ABCD 的边长为4，点E 为AD 的延长线上一点，且DE ＝DC ，点P 为边AD 上一动点，且PC ⊥PG ，PG ＝PC ，点F 为EG 的中点．当点P 从D 点运动到A 点时，则CF 的最小值为___________20．如图，点E 、F 分别在平行四边形ABCD 边BC 和AD 上（E 、F 都不与两端点重合），连结AE 、DE 、BF 、CF ，其中AE 和BF 交于点G ，DE 和CF 交于点H ．令AF n BC=，EC m BC=．若m n =，则图中有_______个平行四边形（不添加别的辅助线）；若1m n +=，且四边形ABCD 的面积为28，则四边形FGEH 的面积为_______．三、解答题21．在数学的学习中，有很多典型的基本图形．（1）如图①，ABC 中，90BAC ∠=︒，AB AC =，直线l 经过点A ，BD ⊥直线l ，CE ⊥直线l ，垂足分别为D 、E ．试说明ABD CAE ≌；（2）如图②，ABC 中，90BAC ∠=︒，AB AC =，点D 、A 、F 在同一条直线上，BD DF ⊥，3AD =，4BD =．则菱形AEFC 面积为______．（3）如图③，分别以Rt ABC 的直角边AC 、AB 向外作正方形ACDE 和正方形ABFG ，连接EG ，AH 是ABC 的高，延长HA 交EG 于点I ，若6AB =，8AC =，求AI 的长度．22．已知，在△ABC 中，∠BAC =90°，∠ABC =45°，D 为直线BC 上一动点（不与点B ，C 重合），以AD 为边作正方形ADEF ，连接CF ．（1）如图1，当点D 在线段BC 上时，BC 与CF 的位置关系是，BC 、CF 、CD 三条线段之间的数量关系为；（2）如图2，当点D 在线段BC 的延长线上时，其他条件不变，请猜想BC 与CF 的位置关系BC ，CD ，CF 三条线段之间的数量关系并证明；（3）如图3，当点D 在线段BC 的反向延长线上时，点A ，F 分别在直线BC 的两侧，其他条件不变．若正方形ADEF 的对角线AE ，DF 相交于点O ，OC =132，DB =5，则△ABC 的面积为．（直接写出答案）23．如图，在平行四边形ABCD 中，AB ⊥AC ，对角线AC ，BD 相交于点O ，将直线AC 绕点O 顺时针旋转一个角度α（0°＜α≤90°），分别交线段BC ，AD 于点E ，F ，连接BF ．（1）如图1，在旋转的过程中，求证：OE ＝OF ；（2）如图2，当旋转至90°时，判断四边形ABEF 的形状，并证明你的结论；（3）若AB ＝1，BC ＝5，且BF ＝DF ，求旋转角度α的大小．24．如图，在边长为1的正方形ABCD 中，E 是边CD 的中点，点P 是边AD 上一点（与点A D 、不重合），射线PE 与BC 的延长线交于点Q ．（1）求证：PDE QCE ∆≅∆；（2）若PB PQ =，点F 是BP 的中点，连结EF AF 、，①求证：四边形AFEP 是平行四边形；②求PE 的长．25．已知四边形ABCD 是正方形，将线段CD 绕点C 逆时针旋转α（090α︒<<︒），得到线段CE ，联结BE 、CE 、DE . 过点B 作BF ⊥DE 交线段DE 的延长线于F ．（1）如图，当BE =CE 时，求旋转角α的度数；（2）当旋转角α的大小发生变化时，BEF ∠的度数是否发生变化?如果变化，请用含α的代数式表示；如果不变，请求出BEF ∠的度数；（3）联结AF ，求证：2DE =．26．定义：只有一组对角是直角的四边形叫做损矩形，连结它的两个非直角顶点的线段叫做这个损矩形的直径。

八年级第一学期语文第二次月考试卷(含答案)

八年级第一学期语文第二次月考试卷（含答案）考生注意：1.本试卷满分120分，考试时间120分钟。

2.所有答案必须写在答题纸上，写在试卷上无效。

一、积累与运用（25分）1.下列词语中加点字的读音完全正确的一项是（）（3分）A. 要塞．（sài）翘．首（qiáo）镌．刻（juān）锐不可当．（dāng）B. 悄．然（qiǎo）绯．红（fēi）畸．形（jī）杳．无消息（yǎo）C. 仲．裁（zhòng）粗糙．（cāo）炽．热（zhì）深恶．痛疾（wù）D. 琐屑．（xiè）胆怯．（què）蹒．跚（pán）殚．精竭虑（dān）2.下列词语中没有错别字的一项是（）（3分）A. 狼藉秀颀长途跋涉眼花潦乱B. 燥热荧光因地制宜诚惶诚恐C. 喧嚣蔓延自出新裁为富不仁D. 推崇嶙峋重峦叠障张目结舌3.下列句子中加点成语使用恰当的一项是（）（3分）A. 他在演讲比赛中夸夸其谈．．．．，赢得了观众的阵阵掌声。

B. 他的绘画作品栩栩如生．．．．，让人叹为观止。

C. 他对这个问题的分析浅尝辄止．．．．，不够深入。

D. 他总是自吹自擂．．．．，觉得自己比别人优秀，缺乏谦虚的态度。

4.下列句子没有语病的一项是（）（3分）A. 通过这次活动，使我们开阔了眼界，增长了知识。

B. 为了防止这类事故不再发生，我们必须采取有效措施。

C. 他的写作水平明显提高了，这主要是因为他注重阅读和积累的结果。

D. 一个人是否拥有健康的心态，关键在于他能否正确对待困难和挫折。

5.默写填空。

（8分）（1）树树皆秋色，____________________。

（王绩《野望》）（2）____________________，长河落日圆。

（王维《使至塞上》）（3）晴川历历汉阳树，____________________。

（崔颢《黄鹤楼》）（4）____________________，谁家新燕啄春泥。

八年级上第二次月考语文试卷(带解析).doc

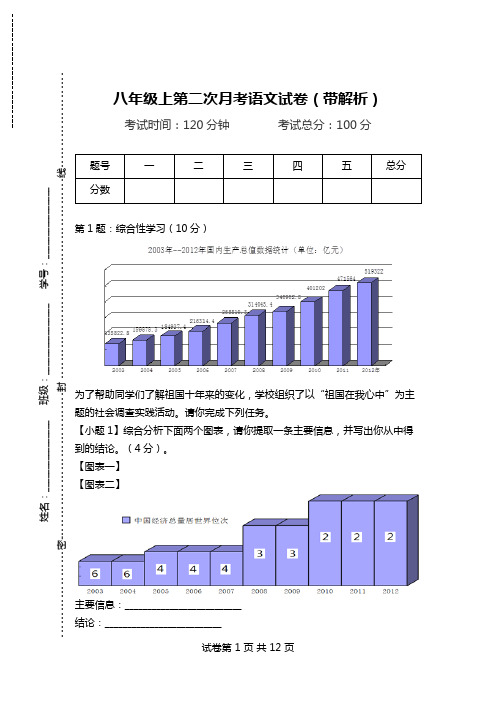
八年级上第二次月考语文试卷（带解析）考试时间：120分钟考试总分：100分题号一二三四五总分分数第1题：综合性学习（10分）为了帮助同学们了解祖国十年来的变化，学校组织了以“祖国在我心中”为主题的社会调查实践活动。

请你完成下列任务。

【小题1】综合分析下面两个图表，请你提取一条主要信息，并写出你从中得到的结论。

（4分）。

【图表一】【图表二】主要信息：__________________________ 结论：__________________________姓名：________________ 班级：________________ 学号：________________ --------------------密----------------------------------封 ----------------------------------------------线----------------------【小题2】小明准备通过走访社区居民了解祖国变化。

下面是他拟写的访谈提纲，⑴⑵两处提问有不妥之处，请你帮忙改正过来。

（4分）采访对象：社区居民访谈主题：改善居住环境，提升生活水平访谈提纲：⑴你现在的住房情况是不是还很差？⑵在这个社区生活的十年间，你对周围环境有过哪些不满？⑶十年间搬过几次家？每次搬家体现了什么？【修改】⑴ __________________________ ⑵ __________________________ 【小题3】活动结束后，学校就这次主题活动收集“感言”。

下面是某同学写下的一句话。

请你再续写一句。

（2分）世上最美丽的画卷，描绘的是祖国的大好河山；__________________________【答案】：【小题1】主要信息：十年来，国内生产总值及中国经济总量居世界位次稳步提升。

结论：中国经济快速发展。

【小题2】示例：⑴您现在与十年前的住房情况有什么不同？⑵十年间周围环境发生了什么变化？【小题3】示例：世上最动人的诗篇，歌颂的是祖国永恒的春天。

八年级数学第二学期第二次月考测试卷含解析

一、选择题1．如图，▱ABCD中，对角线AC，BD相交于O，BD=2AD，E，F，G分别是OC，OD，AB 的中点，下列结论①BE⊥AC②四边形BEFG是平行四边形③EG=GF④EA平分∠GEF其中正确的是（）A．①②③B．①②④C．①③④D．②③④2．如图，菱形ABCD中，∠BAD＝60°，AC与BD交于点O，E为CD延长线上的一点，且CD＝DE，连接BE，分别交AC、AD于点F、G，连接OG，则下列结论：①OG＝12AB；②图中与△EGD 全等的三角形共有5个；③以点A、B、D、E为项点的四边形是菱形；④ S四边形ODGF＝ S△ABF．其中正确的结论是（）A．①③B．①③④C．①②③D．②②④3．如图，菱形ABCD中，∠A是锐角，E为边AD上一点，△ABE沿着BE折叠，使点A的对应点F恰好落在边CD上，连接EF，BF，给出下列结论：①若∠A=70°，则∠ABE=35°；②若点F是CD的中点，则S△ABE13S菱形ABCD下列判断正确的是（）A．①，②都对B．①，②都错C．①对，②错D．①错，②对4．如图，把正方形ABCD 沿对边中点所在的直线对折后展开，折痕为,MN 再过点B 折叠纸片，使点A 格在MN 上的点F 处，折痕为,BE 若AB 长为2,则EN 的长为(（）A ．233-B ．322-C ．22D ．235．如图，在平行四边形ABCD 中，对角线AC 、BD 相交于O ，2BD AD =，E 、F 、G 分别是OC 、OD 、AB 的中点，下列结论：①BE AC ⊥；②EG GF =；③EFG GBE ∆∆≌；④EA 平分GEF ∠；⑤四边形BEFG 是菱形．其中正确的是( )A ．①②③B ．①③④C ．①②⑤D ．②③⑤6．如图，四边形ABCD 是平行四边形，点E 是边CD 上一点，且BC ＝EC ，CF ⊥BE 交AB 于点F ，P 是EB 延长线上一点，下列结论：①BE 平分∠CBF ；②CF 平分∠DCB ；③BC ＝FB ；④PF ＝PC ．其中正确结论的个数为（）A ．1B ．2C ．3D ．4 7．如图，在ABCD 中，AD=2AB ，CE AB ⊥，垂足E 在线段AB 上，F 、G 分别是AD 、CE 的中点，连接FG ，EF 、CD 的延长线交于点H ，则下列结论：①12DCF BCD ∠=∠；②EF CF =：③2BEC CEF S S =；④3DFE AEF ∠=∠.其中，正确结论的个数是（）A ．1个B ．2个C ．3个D ．4个8．如图，在ABC 中，AB =AC =6，∠B =45°，D 是BC 上一个动点，连接AD ，以AD 为边向右侧作等腰ADE ，其中AD =AE ，∠ADE =45°，连接CE ．在点D 从点B 向点C 运动过程中，CDE △周长的最小值是（）A ．62B ．626+C ．92D ．926+9．如图，△ABC 的周长为19，点D ，E 在边BC 上，∠ABC 的平分线垂直于AE ，垂足为N ，∠ACB 的平分线垂直于AD ，垂足为M ，若BC=7，则MN 的长度为（）A ．32B ．2C ．52D ．310．如图，在正方形ABCD 中，点E ，F 分别在BC ，CD 上，AE AF =，AC 与EF 相交于点G ．下列结论：①AC 垂直平分EF ；②BE DF EF +=；③当15DAF ∠=︒时，AEF 为等边三角形；④当60EAF ∠=︒时，AEB AEF ∠=∠．其中正确的结论是（）A ．①③B ．②④C ．①③④D ．②③④二、填空题11．如图，在平面直角坐标系中，矩形ABCO 的边CO 、OA 分别在x 轴、y 轴上，点E 在边BC 上，将该矩形沿AE 折叠，点B 恰好落在边OC 上的F 处．若OA ＝8，CF ＝4，则点E 的坐标是_____．12．如图，以Rt ABC的斜边AB为一边，在AB的右侧作正方形ABED，正方形对角线交于点O，连接CO，如果AC=4，CO=62，那么BC=______．13．如图，正方形ABCD的边长为6，点E、F分别在边AD、BC上．将该纸片沿EF折叠，使点A的对应点G落在边DC上，折痕EF与AG交于点Q，点K为GH的中点，则随着折痕EF位置的变化，△GQK周长的最小值为____．14．在锐角三角形ABC中，AH是边BC的高，分别以AB，AC为边向外作正方形ABDE和正方形ACFG，连接CE，BG和EG，EG与HA的延长线交于点M，下列结论：①BG=CE；②BG⊥CE；③AM是△AEG的中线；④∠EAM=∠ABC．其中正确的是_________．15．如图，在正方形ABCD中，点F为CD上一点，BF与AC交于点E，若∠CBF=20°，则∠AED等于__度．16．在平面直角坐标系xOy 中，点A 、B 分别在x 轴、y 轴的正半轴上运动，点M 为线段AB 的中点．点D 、E 分别在x 轴、y 轴的负半轴上运动，且DE ＝AB ＝10．以DE 为边在第三象限内作正方形DGFE ，则线段MG 长度的最大值为_____．17．如图，在ABC 中，D 是AB 上任意一点，E 是BC 的中点，过C 作//CF AB ,交DE 的延长线于F ，连BF ,CD ，若30FDB ∠=︒，45ABC ∠=︒，22BC =，则DF =_________．18．在菱形ABCD 中，M 是AD 的中点，AB ＝4，N 是对角线AC 上一动点，△DMN 的周长最小是2+23，则BD 的长为___________．19．如图，在四边形ABCD 中， //,5,18,AD BC AD BC E ==是BC 的中点．点P 以每秒1个单位长度的速度从点A 出发，沿AD 向点D 运动;点Q 同时以每秒3个单位长度的速度从点C 出发，沿CB 向点B 运动．点P 停止运动时，点Q 也随之停止运动，当运动时间为t 秒时，以点,,,P Q E D 为顶点的四边形是平行四边形，则t 的值等于_______．20．如图所示，在四边形ABCD 中，顺次连接四边中点E 、F 、G 、H ，构成一个新的四边形，请你对四边形ABCD 添加一个条件，使四边形EFGH 成一个菱形，这个条件是__________．三、解答题21．如图，在Rt ABC ∆中，090BAC ∠=，D 是BC 的中点，E 是AD 的中点，过点A 作//BC AF 交BE 的延长线于点F（1）求证：四边形ADCF 是菱形（2）若4,5AC AB ==，求菱形ADCF 的面积22．在ABCD 中，以AD 为边在ABCD 内作等边ADE ∆，连接BE ．（1）如图1，若点E 在对角线BD 上，过点A 作AH BD ⊥于点H ，且75DAB ∠=︒，AB 6=，求AH 的长度；（2）如图2，若点F 是BE 的中点，且CF BE ⊥，过点E 作MNCF ，分别交AB ，CD 于点,M N ，在DC 上取DG CN =，连接CE ，EG ．求证：①CEN DEG ∆∆≌；②ENG ∆是等边三角形．23．如图，在平行四边形ABCD 中，BAD ∠的平分线交BC 于点E ，交DC 的延长线于F ，以EC 、CF 为邻边作平行四边形ECFG ．（1）求证：四边形ECFG 是菱形；（2）连结BD 、CG ，若120ABC ∠=︒，则BDG ∆是等边三角形吗？为什么？（3）若90ABC ∠=︒，10AB =，24AD =，M 是EF 的中点，求DM 的长．24．如图，在矩形ABCD 中，∠BAD 的平分线交BC 于点E ，AE =AD ，作DF ⊥AE 于点F ．（1）求证：AB ＝AF ；（2）连BF 并延长交DE 于G ．①EG ＝DG ；②若EG ＝1，求矩形ABCD 的面积．25．在平面直角坐标中，四边形OCNM 为矩形，如图1，M 点坐标为（m ，0），C 点坐标为（0，n ），已知m ，n 满足550n m -+-=．（1）求m ，n 的值；（2）①如图1，P ，Q 分别为OM ，MN 上一点，若∠PCQ ＝45°，求证：PQ ＝OP+NQ ； ②如图2，S ，G ，R ，H 分别为OC ，OM ，MN ，NC 上一点，SR ，HG 交于点D ．若∠SDG ＝135°，55HG 2=，则RS ＝______；（3）如图3，在矩形OABC 中，OA ＝5，OC ＝3，点F 在边BC 上且OF ＝OA ，连接AF ，动点P 在线段OF 是（动点P 与O ，F 不重合），动点Q 在线段OA 的延长线上，且AQ ＝FP ，连接PQ 交AF 于点N ，作PM ⊥AF 于M ．试问：当P ，Q 在移动过程中，线段MN 的长度是否发生变化？若不变求出线段MN 的长度；若变化，请说明理由．26．（解决问题）如图1，在ABC ∆中，10AB AC ==，CG AB ⊥于点G ．点P 是BC 边上任意一点，过点P 作PE AB ⊥，PF AC ⊥，垂足分别为点E ，点F ．（1）若3PE =，5PF =，则ABP ∆的面积是______，CG =______．（2）猜想线段PE ，PF ，CG 的数量关系，并说明理由．（3）（变式探究）如图2，在ABC ∆中，若10AB AC BC ===，点P 是ABC ∆内任意一点，且PE BC ⊥，PF AC ⊥，PG AB ⊥，垂足分别为点E ，点F ，点G ，求PE PF PG ++的值．（4）（拓展延伸）如图3，将长方形ABCD 沿EF 折叠，使点D 落在点B 上，点C 落在点C '处，点P 为折痕EF 上的任意一点，过点P 作PG BE ⊥，PH BC ⊥，垂足分别为点G ，点H ．若8AD =，3CF =，直接写出PG PH +的值．27．如图，点A 的坐标为(6,6)-，AB x ⊥轴，垂足为B ，AC y ⊥轴，垂足为C ，点,D E 分别是射线BO 、OC 上的动点，且点D 不与点B 、O 重合，45DAE ︒∠=.（1）如图1，当点D 在线段BO 上时，求DOE ∆的周长；（2）如图2，当点D 在线段BO 的延长线上时，设ADE ∆的面积为1S ，DOE ∆的面积为2S ，请猜想1S 与2S 之间的等量关系，并证明你的猜想.28．阅读下列材料，并解决问题：如图1，在Rt ABC ∆中，90C ∠=︒，8AC =，6BC =，点D 为AC 边上的动点（不与A 、C 重合），以AD ，BD 为边构造ADBE ，求对角线DE 的最小值及此时AD AC的值是多少．在解决这个问题时，小红画出了一个以AD ，BD 为边的ADBE （如图2），设平行四边形对角线的交点为O ，则有AO BO =．于是得出当OD AC ⊥时，OD 最短，此时DE 取最小值，得出DE 的最小值为6．参考小红的做法，解决以下问题：（1）继续完成阅读材料中的问题：当DE 的长度最小时，AD AC=_______；（2）如图3，延长DA 到点F ，使AF DA =．以DF ，DB 为边作FDBE ，求对角线DE 的最小值及此时AD AC的值．29．已知三角形纸片ABC 的面积为48，BC 的长为8．按下列步骤将三角形纸片ABC 进行裁剪和拼图：第一步：如图1，沿三角形ABC 的中位线DE 将纸片剪成两部分．在线段DE 上任意．．取一点F ，在线段BC 上任意．．取一点H ，沿FH 将四边形纸片DBCE 剪成两部分；第二步：如图2，将FH 左侧纸片绕点D 旋转180°，使线段DB 与DA 重合；将FH 右侧纸片绕点E 旋转180°，使线段EC 与EA 重合，再与三角形纸片ADE 拼成一个与三角形纸片ABC 面积相等的四边形纸片．图1 图2（1）当点F ，H 在如图2所示的位置时，请按照第二步的要求，在图2中补全拼接成的四边形；（2）在按以上步骤拼成的所有四边形纸片中，其周长的最小值为_________．30．如图，ABCD 的对角线,AC BD 相交于点,,6,10O AB AC AB cm BC cm ⊥==，点P 从点A 出发，沿AD 方向以每秒1cm 的速度向终点D 运动，连接PO ，并延长交BC 于点Q ．设点P 的运动时间为t 秒．（1）求BQ 的长（用含t 的代数式表示）；（2）当四边形ABQP 是平行四边形时，求t 的值；（3）当325t =时，点O 是否在线段AP 的垂直平分线上？请说明理由．【参考答案】***试卷处理标记，请不要删除一、选择题1．B解析：B【解析】【分析】由平行四边形的性质可得OB=BC，由等腰三角形的性质可判断①正确，由直角三角形的性质和三角形中位线定理可判断③错误，由BG=EF，BG∥EF∥CD可证四边形BEFG是平行四边形，可得②正确．由平行线的性质和等腰三角形的性质可判断④正确．【详解】∵四边形ABCD是平行四边形，∴BO=DO=1BD，AD=BC，AB=CD，AB∥BC，2又∵BD=2AD，∴OB=BC=OD=DA，且点E 是OC中点，∴BE⊥AC，故①正确，∵E、F分别是OC、OD的中点，∴EF∥CD，EF=1CD，2∵点G是Rt△ABE斜边AB上的中点，∴GE=1AB=AG=BG，2∴EG=EF=AG=BG，无法证明GE=GF，故③错误，∵BG=EF，BG∥EF∥CD，∴四边形BEFG是平行四边形，故②正确，∵EF∥CD∥AB，∴∠BAC=∠ACD=∠AEF，∵AG=GE，∴∠GAE=∠AEG，∴∠AEG=∠AEF，∴AE平分∠GEF，故④正确，故选B．【点睛】本题考查了菱形的判定，平行四边形的性质，全等三角形的判定和性质，三角形中位线定理等知识，灵活运用相关的性质定理、综合运用知识是解题的关键．2．A解析：A【解析】【分析】由AAS 证明△ABG ≌△DEG ，得出AG=DG ，证出OG 是△ACD 的中位线，得出OG=12 CD=12AB ，①正确；先证明四边形ABDE 是平行四边形，证出△ABD 、△BCD 是等边三角形，得出AB=BD=AD ，因此OD=AG ，得出四边形ABDE 是菱形，③正确；由菱形的性质得得出△ABG ≌△BDG ≌△DEG ，由SAS 证明△ABG ≌△DCO ，得出△ABO ≌△BCO ≌△CDO ≌△AOD ≌△ABG ≌△BDG ≌△DEG ，得出②不正确；证出OG 是△ABD 的中位线，得出OG//AB ，OG=12AB ，得出△GOD ∽△ABD ，△ABF ∽△OGF ，由相似三角形的性质和面积关系得出S 四边形ODGF =S △ABF ；④不正确；即可得出结果.【详解】解：四边形ABCD 是菱形，,//,,,,AB BC CD DA AB CD OA OC OB OD AC BDBAG EDG ABO BCO CDO AOD CD DEAB DE∴=====⊥∴∠=∠∆≅∆≅∆=∴= 在△ABG 和△DEG 中，BAG EDG AGB DGE AB DE ∠=∠⎧⎪∠=∠⎨⎪=⎩∴△ABG ≌△DEG （AAS ），∴.AG=DG ，∴OG 是△ACD 的中位线，∴OG=12CD=12AB ，①正确； ∵AB//CE ，AB=DE ，∴四边形ABDE 是平行四边形，∴∠BCD=∠BAD=60°， ∴△ABD 、△BCD 是等边三角形，∴AB=BD=AD ，∠ODC=60°，∴OD=AG ，四边形ABDE 是菱形，③正确；∴AD ⊥BE ，由菱形的性质得：△ABG ≌△BDG ≌△DEG ，在△ABG 和△DCO 中，60OD AG ODC BAG AB DC ︒=⎧⎪∠=∠=⎨⎪=⎩∴△ABG ≌△DCO∴△ABO ≌△BCO ≌△CDO ≌△AOD ≌△ABG ≌△BDG ≌△DEG ，则②不正确。

八年级第二次月考答案

一、单项选择题（本题包括12个小题，每小题3分，共36分）
二、填空题
13、物体位置随时间的变化；参照物、参照物；地面14、静止15、1号和3号16、(1) m/s (2) 5m/s （3）10 m/s （4）5x10-2 （5）1.5、1秒钟内通过的距离是1.5米17、2.5m/s 18、相等、远近、相等、长短； 19、乙 20、4 m/s 21、2.5 22、14.5 23、距西直门桥还有8千米；过桥的速度不能超过40千米/时；过桥的载重量不能超过20吨；
三、实验题
25、3s ；0.17；0.9；0.18
26、设计方案如下：
器材：秒表或电子表，自行车，皮尺，一面小旗。

步骤：（1）在操场上选定出发点，用皮尺量出10m，40m，70m，80m，在各点分别作出标记S1、S2、S3和S4。

（2）一位同学准备骑自行车，另一位同学担任发令员站在出发点。

（3）请甲、乙、丙、丁四位同学手中各拿一块秒表或电子表，分别站在S1、S2、S3、和S4标记处，准备记录自行车从出发到自己所站位置的时间T1、T2、T3和T4。

（4）发令员在出发出口的同时，用小旗示意，同时甲、乙、丙、丁四位同学开始计时，骑自行车的同学也出发，速度均匀些，一直骑过80m终点。

（5）自行车骑到S1、S2、S3、和S4各标记处时，甲、乙、丙、丁四位同学分别记录时间。

(6)分析结果
四、简答题：
27. 甲图：三种可能：（1）轿车不动，公共汽车向左行驶；（2）公共汽车不动，轿车向左行驶；（3）轿车和公共汽车同时向左行驶；乙图：轿车不动，公共汽车向左行驶；
28. 地面；火车；火车；
五、计算题
30、3000m
31、30分；24km/h。

1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

八年级第二次月考
语文试卷
一、积累与运用（25分） 1、漂亮的书写能给人以美的享受。

请把下面这句话正确、规范、美观地抄写在方格内。

（3分）
感人心者莫先乎情。

——（唐代）白居易 2、下列加点的字注音有误的一组是（）（3分） A 、穹庐qióng 局促jú 狐裘qiú 羌笛qiāng B 、敕勒chì 前瞻 zhān 锦衾q īn 迁徙xǐ C 、前眺tiào 俯首fǔ 阑干lán 羞涩sè D 、瞭望liáo 渺小miǎo 风掣chè 逶迤wēi 3、下列成语中有四个错别字，划出来并在方格中改正。

（3分）敏而好学摇尾乞怜丑态必露虚怀若谷不耻下问心无旁鹜略施小计一丝不苟捉襟见肘发自肺腑怨天尤人
前仰后和
轻而易举近在指尺野心勃勃一筹莫展
4. 下列书写无误的一项是（）（3分）
班级
；
姓名：学号：
密
封
线
内
不
准
答
题
A.肤浅迄今触目惊心按步就班
B.醒豁余暇倒行逆施煞有介事
C.缥渺繁衍如法炮制不径而走
D.企及分量理屈词穷当人不让
5、对加点词语的解释不妥的一组是（）（3分）
A、而人竟然如此渺小与微不足道。

微不足道：小得不值一提。

B、敏而好学，不耻下问。

耻：羞耻。

C、风吹草低见牛羊。

见：通“现”，显现、出现。

D、将军角弓不得控。

控：拉弓
6、下列句子中，表意明确、没有语病的一项是（）（3分）
A. 据说，秦始皇每天批阅写在竹简和木片上的文字，有600公斤重。

B. 这本书已经出版好几年了，所以作者最近作了较大的修改。

C. 到目前为止，全国有百分之八十的锅炉使用了有效的消烟除尘装置和其他简易措施。

D. 正在研究课程改革的复旦大学生命科学院梅其春教授认为，随着生命科学的飞速发展，生物学作为大学必修课是一种趋势。

7、下面的文字优美深刻，富有哲理，读一读，完成题目要求。

珍惜阅读，便是珍惜便是珍惜历史，珍惜至今残留的石鼓文陶埙（xūn）（古代吹奏乐器）石磬发出的的音响以及青铜瓦当上的装饰画。

珍惜阅读，便是珍惜传统，珍惜乐山大佛永乐大钟以及太极八卦武当飒爽英姿猎猎雄风。

珍惜阅读，便是珍惜文学，珍惜楚韵风骚唐诗宋词，乃至①的
西游，②的三国，③的红楼。

⑴将下列词语填入第三段横线①②③处，顺序依次是。

（只填序号）（1分）
A.情诗千载
B.摄魂夺魄
C.剑戈惊天
（2）第三段中的“西游”指中国古典小说《三国演义》。

这部小说家喻户晓、妇孺皆知，其故事情节曲折、扣人心弦，你喜欢的两个故事是，。

（2分）
8、仿写下列句子：（4）
我梦想，来到塞外辽阔的大漠，在夕阳的金黄中，感受“长河落日圆”的雄浑；我梦想，置身于江南秀丽的小镇，在绵绵的细雨中，体味“水村山郭酒旗风”的情调；
；。

二、默写（20分）
(1)岑参在《白雪歌送武判官归京》中，以春花喻冬雪的千古名句是：，。

(2) ，春风不度玉门关。

（3），不破楼兰终不还。

（4）王维的《使至塞上》中描写大漠壮观景象的句子
是，。

（5）天苍苍，野茫茫，。

八年级第二次月考试题及答案

最新人教版八年级语文上册第二次月考试卷(附参考答案)

部编人教版八年级数学上册第二次月考试卷及答案【完美版】

新人教版八年级语文上册第二次月考试题及答案(全面)

八年级数学第二次月考试题含答案

新人教版八年级语文上册第二次月考试卷(附参考答案)

八年级下第二次月考试题--语文(含解析).(含答案)

2023～2024学年度第二学期第二次月考试题八年级物理(下)

人教版八年级第二学期第二次月考检测数学试卷含答案

八年级第二次月考参考答案(配套试卷)

最新新版人教八年级数学下册第二次月考试卷及答案

人教版八年级第二学期第二次月考数学试题含答案

八年级第一学期语文第二次月考试卷(含答案)

八年级上第二次月考语文试卷(带解析).doc

八年级数学第二学期第二次月考测试卷含解析

八年级第二次月考答案

八年级第二次月考试题及答案

最新人教版八年级语文上册第二次月考试卷(附参考答案)

部编人教版八年级数学上册第二次月考试卷及答案【完美版】

新人教版八年级语文上册第二次月考试题及答案(全面)

八年级数学第二次月考试题含答案

新人教版八年级语文上册第二次月考试卷(附参考答案)

八年级下第二次月考试题--语文(含解析).(含答案)

2023～2024学年度第二学期第二次月考试题八年级物理(下)

人教版八年级第二学期 第二次月考检测数学试卷含答案

八年级第二次月考参考答案(配套试卷)

最新新版人教八年级数学下册第二次月考试卷及答案

人教版八年级第二学期 第二次月考数学试题含答案

八年级第一学期语文第二次月考试卷(含答案)

八年级上第二次月考语文试卷(带解析).doc

八年级数学第二学期第二次月考测试卷含解析

八年级第二次月考答案

人教版八年级第二学期第二次月考检测数学试卷含答案

人教版八年级第二学期第二次月考数学试题含答案