计算机在化工中的应用-习题集
计算机在化学中的应用

计算机在化学中的应用复习题一、选择题1、下列软件中 ____一定是系统软件.A、自编的一个C程序,功能是求解一个一元二次方程B、WINDOWS操作系统C、用汇编语言编写的一个练习程序D、存储有计算机基本输入输出系统的ROM芯片2、计算机病毒是指——。
A.带细菌的磁盘 B.已损坏的磁盘C.具有破坏性的特制程序D.被破坏的程序3、目前普遍使用的微型计算机,所采用的逻辑元件是______。
A、电子管B、大规模和超大规模集成电路C、晶体管D、小规模集成电路4、计算机辅助设计的英文缩写是____。
A、CAIB、CAMC、CADD、CAT5、在Word中,______用于控制文档在屏幕上的显示大小。
A、全屏显示B、显示比例C、缩放显示D、页面显示6.PowerPoint中,要切换到幻灯片的黑白视图,请选择________。
A、视图菜单的“幻灯片浏览”B、视图菜单的“幻灯片放映”C、视图菜单的“颜色/灰度”下的“纯黑白”D、视图菜单的“幻灯片缩图”7.PowerPoint中,在浏览视图下,按住CTRL并拖动某幻灯片,可以完成________操作。
A、移动幻灯片B、复制幻灯片C、删除幻灯片D、选定幻灯片8.Windows 默认的启动方式是______。
A、安全方式B、通常方式C、具有网络支持的安全方式D、MS-DOS方式9.在Excel中,在打印学生成绩单时,对不及格的成绩用醒目的方式表示(如用红色表示等),当要处理大量的学生成绩时,利用________命令最为方便。
A、查找 B、条件格式C、数据筛选 D、定位10.在Excel中,A1单元格设定其数字格式为整数,当输入“33.51”时,显示为______ 。
A、33.51B、33C、34D、ERROR11.如要关闭工作簿,但不想退出Excel,可以单击________。
A、“文件”下拉菜单中的“关闭”命令B、“文件”下拉菜单中的“退出”命令C、关闭Excel窗口的按钮×D、“窗口”下拉菜单中的“隐藏”命令12.Excel中,让某单元格里数值保留二位小数,下列_______不可实现。
计算机在化工中的应用 结课作业
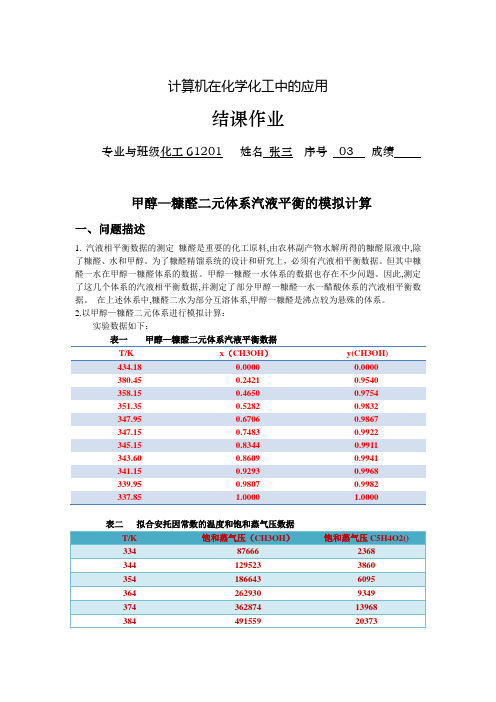
计算机在化学化工中的应用结课作业专业与班级化工61201 姓名张三序号03 成绩甲醇—糠醛二元体系汽液平衡的模拟计算一、问题描述1. 汽液相平衡数据的测定糠醛是重要的化工原料,由农林副产物水解所得的糠醛原液中,除了糠醛、水和甲醇。
为了糠醛精馏系统的设计和研究上,必须有汽液相平衡数据。
但其中糠醛一水在甲醇一糠醛体系的数据。
甲醇一糠醛一水体系的数据也存在不少问题。
因此,测定了这几个体系的汽液相平衡数据,并测定了部分甲醇一糠醛一水一醋酸休系的汽液相平衡数据。
在上述休系中,糠醛二水为部分互溶体系,甲醇一糠醛是沸点较为悬殊的体系。
2.以甲醇—糠醛二元体系进行模拟计算:实验数据如下:表一甲醇—糠醛二元体系汽液平衡数据T/K x(CH3OH)y(CH3OH)434.18 0.0000 0.0000380.45 0.2421 0.9540358.15 0.4650 0.9754351.35 0.5282 0.9832347.95 0.6706 0.9867347.15 0.7483 0.9922345.15 0.8344 0.9911343.60 0.8609 0.9941341.15 0.9293 0.9968339.95 0.9807 0.9982337.85 1.0000 1.0000表二拟合安托因常数的温度和饱和蒸气压数据T/K 饱和蒸气压(CH3OH)饱和蒸气压C5H4O2()334 87666 2368344 129523 3860354 186643 6095364 262930 9349374 362874 13968384 491559 20373394 654682 29066 404 858571 40639 414 1110200 55774 424 1417218 75245 434178797599925二、解决思路1.在进行安托因常数的拟合时,调用格式为:beta = lsqnonlin (X,y,fun,beta0)的lsqnonlin 函数,用最小二乘法拟合安托因方程:ln sat i i B p A T C=-+ (1)2.在计算对应的气相组成时,先要计算出对应的活度系数参数Λ12,Λ21。
《计算机在化学中的应用》试卷及答案

2012级应用化学、化学专业《计算机在化学中的应用》试题答题内容要求截图所做答案均为亲手制作,但是不保证答案正确性一、数据处理:(每小题15分,共30分)1、已知水在不同温度下的电导率数据如下:T/℃0 10 20 25 30 40 50 κ×106/(S•m-1) 1.2 2.3 4.2 5.5 7.1 11.3 17.1 利用Excel软件中的功能,求出5,15,28,35,45℃时的电导率κ值答题要点:①做散点图②添加趋势线方程③选择合适的拟合形式④输出拟合方程⑤进行插值计算2、在20℃,钢线中碳含量对电阻效应研究中,观测得数据如下:碳含量x% 0.10 0.30 0.40 0.55 0.70 0.80 0.95电阻y (10-5Ω)15 18 19 21 22.6 23.8 26利用Excel 软件中的功能,拟合为2321x a x a a y ++=的多项式。
答题要点:①做散点图 ②数据分析-多项式-二次③获得拟合参数或输出拟合方程二、office 软件的应用技巧(每小题5分,共20分)1、描述如何使用自动更正功能快速输入分子式 Fe 2(SO 4)3 答题要点:①使用自动更正的操作过程②选择带格式文本Fe 2(SO 4)32 函数LINEST 的使用方法? 自己百度 答题要点:描述函数的使用方法及适用范围3、描述反应加热符号的制作,与输入法的链接及输出过程 答题要点:正确描述制作及链接过程加热4、描述获取下面图片中的文本信息的方法答题要点:①转换图片格式为tiff ②使用OCR识别软件识别③粘贴文本作者注所用软件office组件中Document Imaging (WPS中没有)因为没有软件必备组件本题没有做完三、化学软件的应用技巧(共10分)1、利用Chemsketch软件调用环己烷的椅式构象及立方烷的结构式。
(2分)答题要点:①正确描述调用过程②输出调用结果模板------ 模板窗口2、利用Chemsketch软件绘制下列化学结构式,并用软件中的命名功能命名。
计算机在化工中的应用 题型集合

选择题:1.工程索引(EI)是一个主要收录工程技术期刊文献和会议文献的大型国际权威检索系统,与哪几个搜索系统并称为世界著名的四大科技文献搜索系统( ABC )。
A.SCI B.ISTP C. Scopus D. ACS KI2. 在Google搜索中,当要求搜索两个或者两个以上的关键词时,需要用到逻辑符号。
表示逻辑为“与”的操作是( C )。
A.OR B. 减号 C.空格键 D.加号3 按照最优化问题的目标来分类,可以把化工最优化问题分为( C )A、结构优化问题和无约束优化问题B、参数优化问题和目标函数优化问题C、结构优化问题和参数优化问题D、参数优化问题和无约束优化问题4 在使用Visio2007中,用于绘制标准图形时,要先单击工具栏中的(A)A 绘图工具B 缩放工具C 绘图区域D 格式5 调整图形大小时,应首先单击选中图形,在图形的四周会出现(B)个绿色的方形“调整手柄”。
A 7B 8C 9D 66 当文献作者多于(A )人时,通常只列出前三个作者并在后面加“etal.”或“等.”A、3B、4C、5D、67 在EndNote库文献用手工录入,输入作者字段时,如果输入的作者名已经存在于当前数据库中,将显示(A )色。
A、黑B、红C、黄D、蓝8EndNote数据库中由一个名为“*.enl”(这里的*代表库文件名)的库文件和一个同名的(B)的库文件夹组成。
A、“*.doc”B、“*.Data”C、“*.jpg”D、“*.bin”9从网页sciencedirect中下载的文献,在EndNote录入时,每次最多可录入(B)篇文献。
A、10B、20C、30D、4010Origin提供了多种图形模板用于快速绘制各种常用的多层图形,有(B)垂直两栏、水平两栏、四栏、九栏等。
A、双X轴B、双Y轴C、双X轴D、斜交两栏11 ACD/CHEMSKETCH的主要功能有(单选D )A 绘制各种化学结构 B.文本和图形处理C.估算分子性质D.以上三种12 以下属于文献管理软件的是(多选ABCD)全选A ENDNOTE B.BIBLIOSCAPEC .PROCITE D.NOTEEXPRESS填空题1、正交试验设计它根据正交性从全面试验中挑选出部分有代表性的点进行试验,由于这些选出的点具备均匀分散、齐整可比的特点,因而可高效、快速、经济地获得有价值的实验信息。
【免费下载】计算机在化学中应用 期末习题 答案

计算机在化学中的应用-习题社外秘一、正交实验设计软件应用题1、为了提高某种产品的质量,研究A(温度,℃),B(压力,kg),C(配比,%),D(时间,h)四个因素对质量指标的影响。
每个因素各取3个水平(见表1.1)进行实验。
请根据实验方案选择合适的正交表安排实验,并用直观分析方法寻找最优实验方案。
表1.1因素水平A(温度,℃)B(压力,kg)C(配比,%)D(时间,h)143010312450205234703073注:按L9(34)设计实验,其实验质量指标分别为54,52,63,58,61,70,55,70,64。
级差越大,影响越大。
平均值越大,条件越优越。
效应曲线分析,压力越大转化越高,二、用Origin软件制作实验曲线…1、用Origin软件画出某电池的放电电压和极化电流随时间的变化曲线(双y轴)(数据见表1)。
t /min0306080100120140150i / mA109.519.118.457.80 6.00 4.50 3.00V / V 1.711 1.290 1.256 1.201 1.141 1.101 1.030 1.000复制数据Origin表格单击,右键Paste Transpose 选中数据Plot→Multi-Curve(Origin7.0在Special Line)→Double-Y,双击线打开Plot Details对话框Connect改连接方式2、现有某活性炭吸附甲醇的实验数据见表2。
用Origin软件画图。
以压力为横坐标(x 轴),以吸附量为纵坐标(y轴),考察三个不同温度下,压力与吸附量的变化曲线(并且标示温度)。
Plot Details对话框Connect改连接方式,标示温度3、测试某材料的断裂韧度K(单位MPa·m1/2)结果见表3。
用Origin软件画图。
以温度为横坐标(x轴),以平均断裂韧度K为纵坐标(y轴),并作出每个数据点的误差线。
计算机在化学化工中的用应 习题及答案
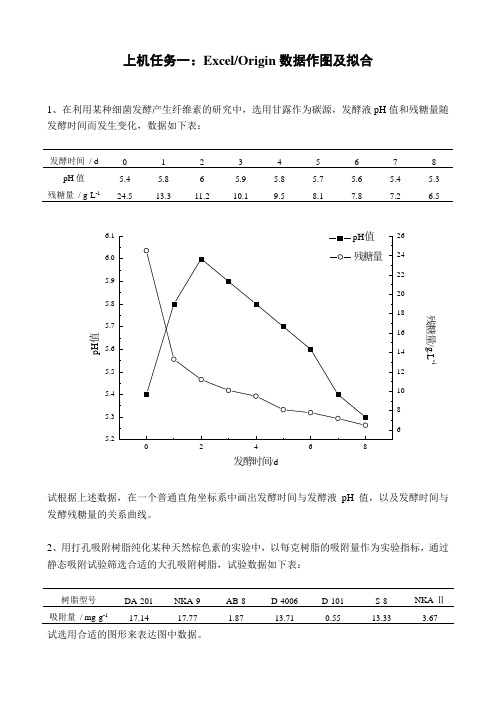
上机任务一:Excel/Origin 数据作图及拟合1、在利用某种细菌发酵产生纤维素的研究中,选用甘露作为碳源,发酵液pH 值和残糖量随发酵时间而发生变化,数据如下表:发酵时间 / d0 1 2 3 4 5 6 7 8 pH 值 5.4 5.8 6 5.9 5.8 5.7 5.6 5.4 5.3 残糖量 / g·L -124.513.311.210.19.58.17.87.26.5残糖量/g.L -1p H 值发酵时间/d试根据上述数据,在一个普通直角坐标系中画出发酵时间与发酵液pH 值,以及发酵时间与发酵残糖量的关系曲线。
2、用打孔吸附树脂纯化某种天然棕色素的实验中,以每克树脂的吸附量作为实验指标,通过静态吸附试验筛选合适的大孔吸附树脂,试验数据如下表:树脂型号 DA-201 NKA-9 AB-8 D-4006 D-101 S-8 NKA-Ⅱ -117.1417.771.8713.710.5513.333.67试选用合适的图形来表达图中数据。
NKA-9D-4006S-861218吸附量/m g .g -1树脂型号吸附量3、脂肪酸是一种重要的工业原料,下表列出了某国脂肪酸的应用领域,试根据这些数据的应用领域,试根据这些数据画出饼形图。
应用领域 橡胶工业 合成表面活性剂润滑油 肥皂及洗涤剂金属皂 其他 比例 / % 181152321224、在一定温度、压力下,测得苯(A),乙醇(B),水(C)三元物系的平衡数据如下表所示,试在三角形坐标图中绘出三元相图。
苯(A)% 乙醇(B)% 水(C)%0.1 19.9 800.4 29.6 701.3 38.7 604.4 45.6 509.2 50.8 4012.8 52.2 3517.5 52.5 3020 52.3 27.730 49.5 20.540 44.8 15.250 39 1153 37.2 9.860 32.5 7.570 25.4 4.680 17.7 2.390 9.2 0.895 4.8 0.25、由试验得到某物质的溶解度与绝对温度之间的关系可用模型C = aT b表示,试验数据如下表:T / K 273 283 293 313 333 353C / % 20 25 31 34 46 58试建立回归方程。
计算机化工应用习题与解答

>> Q1=QCal(3,50) Q1 = 0.8171
5. 采用 plot 命令一次画出两条函数曲线 sin t 和 e −t cos t , t ∈ [0,3π ] 。其中,第一条曲线采 用红色实线,第二条曲线采用蓝色虚线。给图形加上图题,图例和坐标轴名。 解:
t=[0:0.1*pi:3*pi]; y1=sin(t); y2=exp(-t).*cos(t); plot(t,y1,'-r',t,y2,'.b') title('The plots of sin(t) and exp(-t)*cos(t)') legend('sin(t)','exp(-t)*cos(t)') xlabel('t'),ylabel('function value')
0.5 x 10
4
0
-0.5
-1
-1.5
-2
-2.5 -50
-40
-30
-20
-10
0
10
>> fzero(@(x) sin(x)-4*x-exp(x), 10)
ans = -0.2569 4. function Chap2xiti4 x0 = [0 0]; x = fsolve(@fun, x0) function y = fun(x) y(1) = x(1) - 0.7*sin(x(1)) - 0.2*cos(x(2)); y(2) = x(2) - 0.7*cos(x(1)) - 0.2*sin(x(2));
Q=
23/ 2 Dc5/ 2 g (θ − 0.5sin(2θ ))3/ 2 8 sin θ (1 − cos θ )5/ 2
计算机化工运用复习题+答案

第一、二章 matlab 向量与矩阵 1、变量名由字母、数字和下划线组成。
2、利用冒号生成向量:x =x0:step:xn 3、向量的数乘、数组乘和向量乘。
4、Matlab 的流程控制语句。
5、矩阵的生成方式(直接输入、M 文件、冒号表达式),矩阵拆分。
6、矩阵的运算包括基本算术运算:+(加)、-(减)、*(乘)、/(右除)、\(左除)、^(乘方)和点运算.*、./、.\和.^。
(两矩阵进行点运算是指它们的对应元素进行相关运算,要求两矩阵的维参数相同)7. 矩阵分析(a.矩阵的转置;b.矩阵的逆inv(A)与伪逆pinv(A);c.方阵的行列式det(A);d.矩阵的秩rank(A))。
1、标点符号 ( )可以使命令行不显示运算结果,( ) 用来表示该行为注释行。
2、下列变量名中 ( ) 是合法的。
(A) char_1 ; (B) x*y ; (C) x\y ; (D) _end例1. 已知0.30.30.3sin(0.3)ln 22a a e e ay a --+=++,当a 取1和2时,求各点的函数值。
>> y1=(exp(0.3*1)-exp(-0.3*1))*sin(1+0.3)+log((0.3+1)/2) y1= 0.1561>> y2=(exp(0.3*2)-exp(-0.3*2))*sin(2+0.3)+log((0.3+2)/2) y2= 1.0893例2.当a=[1:1:3]; b=[2:2:6]时,以下命令的运行结果是什么?1)>>a1=2*a 2) >> a2=a.*b 3) >>a3=a*b>> a=[1:1:3]; b=[2:2:6];>> a1=2*a, a2=a.*b, a3=a*ba1 = 2 4 6a2 = 2 8 18Error using例3.已知12345678910111213141516A⎛⎫⎪⎪=⎪⎪⎪⎝⎭,求(1)A(3,4);(2)A(7);(3)取A矩阵第1~3行内,并在第2~4列中的所有元素组成B矩阵。
计算机在化学化工中的应用考试题库1
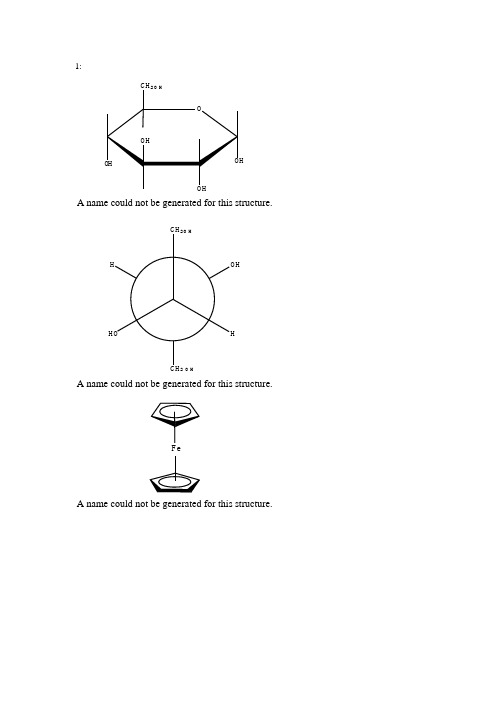
1:HA name could not be generated for this structure.HH A name could not be generated for this structure.A name could not be generated for this structure.H OH O O H3,4',4''-(2,4,6-trimethylbenzene-1,3,5-triyl)tris(methylene)tris(2,6-di-tert -butylphenol)2:NOONHH ONNH(CH 2)4SO 3KC 2H 5SO 3KS O 3-3:CH3C 2H 5-3OCH 3C H CHCOCH 3O 95%4:o-xyleneCalculation startedPi System: 4 3 2 1 5 6Warning: Some parameters are guessed (Quality = 1).Iteration 28: Minimization terminated normally because the gradient norm is less than the minimum gradient normStretch: 0.3185Bend: 0.3492Stretch-Bend: -0.0100Torsion: -7.1200Non-1,4 VDW: -0.58801,4 VDW: 4.4919Dipole/Dipole: 0.1049Total: -2.4535Calculation completedm-xyleneCalculation startedPi System: 4 3 2 1 5 6Warning: Some parameters are guessed (Quality = 1).Iteration 24: Minimization terminated normally because the gradient norm is less than the minimum gradient normStretch: 0.2042Bend: 0.2801Stretch-Bend: -0.0063Torsion: -7.0200Non-1,4 VDW: -0.83561,4 VDW: 4.3116Dipole/Dipole: 0.0286Total: -3.0373Calculation completedp-xyleneCalculation startedPi System: 1 2 3 4 6 5Warning: Some parameters are guessed (Quality = 1).Iteration 26: Minimization terminated normally because the gradient norm is less than the minimum gradient normStretch: 0.1915Bend: 0.2636Stretch-Bend: -0.0052Torsion: -7.0200Non-1,4 VDW: -0.81521,4 VDW: 4.3131Dipole/Dipole: 0.0211Total: -3.0510Calculation completed5NNHNONH 22-amino-3H -pyrrolo[3,2-d ]pyrimidin-4(7H )-oneChemical Formula: C 6H6N 4OExact Mass: 150.05Molecular Weight: 150.14m/z: 150.05 (100.0%), 151.06 (6.6%), 151.05 (1.5%)Elemental Analysis: C, 48.00; H, 4.03; N, 37.32; O, 10.66Boiling Point: 713.18 [K]Melting Point: 639.11 [K]Critical Temp: 997.6 [K]Critical Pres: 78.18 [Bar]Critical Vol: 443.5 [cm3/mol]Gibbs Energy: 442.08 [kJ/mol]Log P: -2.56MR: 38.86 [cm3/mol]Henry's Law: 0Heat of Form: 223.79 [kJ/mol]tPSA: 80.6CLogP: -2.21025CMR: 3.7897ChemNMR 1H Estimation11.242.07.506.63NNHNONH 2Estimation quality: blue = good, magenta = medium, red = rough24681012PPMProtocol of the H-1 NMR Prediction:Node Shift Base + Inc. Comment (ppm rel. to TMS)NH2 6.63 2.00 amine4.63 general corrections CH 7.50 7.50 aldimine CH2 2.0 1.37 methylene0.63 1 alpha -C=C? 1 unknown alpha substituent(s) -> 1 increment(s) not found NH 11.24 8.00 sec. amide3.24 general correctionsOH2,6-di-tert-butylphenolChemical Formula: C14H22OExact Mass: 206.17Molecular Weight: 206.32m/z: 206.17 (100.0%), 207.17 (15.4%), 208.17 (1.3%) Elemental Analysis: C, 81.50; H, 10.75; O, 7.75Boiling Point: 625.74 [K]Melting Point: 402.54 [K]Critical Temp: 758.35 [K]Critical Pres: 23.59 [Bar]Critical Vol: 705.5 [cm3/mol]Gibbs Energy: 20.84 [kJ/mol]Log P: 5.05MR: 66.44 [cm3/mol]Henry's Law: 3.82Heat of Form: -302.04 [kJ/mol]tPSA: 23.8CLogP: 4.927CMR: 6.5521ChemNMR 1H Estimation6.926.666.929.831.341.341.341.341.341.34OHEstimation quality: blue = good, magenta = medium, red = rough246810PPMProtocol of the H-1 NMR Prediction:Node Shift Base + Inc. Comment (ppm rel. to TMS) CH3 1.34 0.86 methyl0.38 1 beta -1:C*C*C*C*C*C*1 0.10 2 beta -C CH3 1.34 0.86 methyl0.38 1 beta -1:C*C*C*C*C*C*1 0.10 2 beta -C CH3 1.34 0.86 methyl0.38 1 beta -1:C*C*C*C*C*C*1 0.10 2 beta -C CH3 1.34 0.86 methyl0.38 1 beta -1:C*C*C*C*C*C*1 0.10 2 beta -C CH3 1.34 0.86 methyl0.38 1 beta -1:C*C*C*C*C*C*1 0.10 2 beta -C CH3 1.34 0.86 methyl0.38 1 beta -1:C*C*C*C*C*C*1 0.10 2 beta -C OH 9.83 5.00 aromatic C-OH4.83 general corrections CH 6.92 7.26 1-benzene -0.17 1 -O0.03 1 -C(C)(C)C -0.20 1 -C(C)(C)C CH 6.66 7.26 1-benzene -0.44 1 -O-0.08 1 -C(C)(C)C -0.08 1 -C(C)(C)C CH 6.92 7.26 1-benzene -0.17 1 -O-0.20 1 -C(C)(C)C 0.03 1 -C(C)(C)CChemNMR 13C Estimation137.6123.3120.6123.3137.6146.434.831.631.631.634.831.631.631.6OHEstimation quality: blue = good, magenta = medium, red = rough20406080100120140160PPMProtocol of the C-13 NMR Prediction:Node Shift Base + Inc. Comment (ppm rel. to TMS) CH3 31.6 -2.3 aliphatic9.1 1 alpha -C9.3 1 beta -1:C*C*C*C*C*C*1 18.8 2 beta -C 0.3 1 delta -O-3.6 general corrections CH3 31.6 -2.3 aliphatic9.1 1 alpha -C9.3 1 beta -1:C*C*C*C*C*C*1 18.8 2 beta -C 0.3 1 delta -O-3.6 general corrections CH3 31.6 -2.3 aliphatic9.1 1 alpha -C9.3 1 beta -1:C*C*C*C*C*C*1 18.8 2 beta -C 0.3 1 delta -O-3.6 general corrections C 34.8 -2.3 aliphatic24.3 1 alpha -1:C*C*C*C*C*C*1 27.3 3 alpha -C -6.2 1 gamma -O 0.3 1 delta -C-8.6 general corrections CH3 31.6 -2.3 aliphatic9.1 1 alpha -C9.3 1 beta -1:C*C*C*C*C*C*1 18.8 2 beta -C 0.3 1 delta -O-3.6 general corrections CH3 31.6 -2.3 aliphatic9.1 1 alpha -C9.3 1 beta -1:C*C*C*C*C*C*1 18.8 2 beta -C 0.3 1 delta -O-3.6 general corrections CH3 31.6 -2.3 aliphatic9.1 1 alpha -C9.3 1 beta -1:C*C*C*C*C*C*1 18.8 2 beta -C 0.3 1 delta -O-3.6 general corrections C 34.8 -2.3 aliphatic24.3 1 alpha -1:C*C*C*C*C*C*1 27.3 3 alpha -C -6.2 1 gamma -O 0.3 1 delta -C-8.6 general corrections C 146.4 128.5 1-benzene 28.8 1 -O-3.3 1 -C(C)(C)C -3.3 1 -C(C)(C)C-4.3 general corrections C 137.6 128.5 1-benzene -12.8 1 -O18.6 1 -C(C)(C)C -0.4 1 -C(C)(C)C3.7 general corrections CH 123.3 128.5 1-benzene 1.4 1 -O-3.3 1 -C(C)(C)C -3.1 1 -C(C)(C)C-0.2 general corrections CH 120.6 128.5 1-benzene -7.4 1 -O-0.4 1 -C(C)(C)C -0.4 1 -C(C)(C)C0.3 general corrections CH 123.3 128.5 1-benzene 1.4 1 -O-3.1 1 -C(C)(C)C -3.3 1 -C(C)(C)C-0.2 general corrections C 137.6 128.5 1-benzene -12.8 1 -O-0.4 1 -C(C)(C)C 18.6 1 -C(C)(C)C3.7 general corrections6:C(1)-C(2 Length:1.5253C(1)-C(2)-C(3)键角:105.9oC(1)-C(2)-C(3)-C(4)二面角:180o 7:。
计算机在化学化工中的用应 习题及答案资料
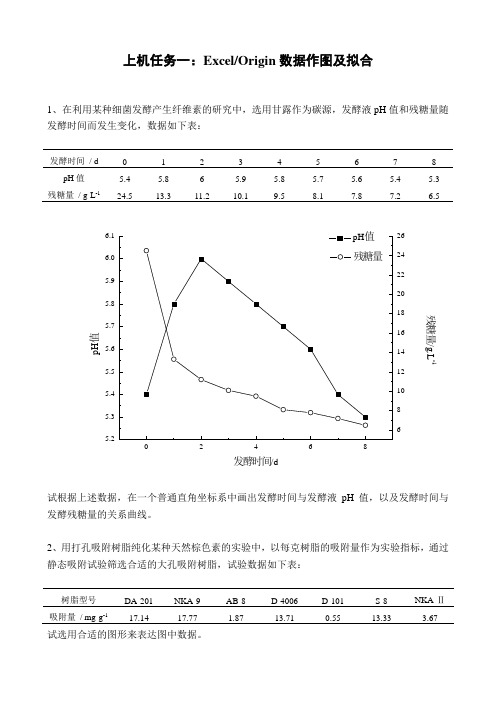
上机任务一:Excel/Origin 数据作图及拟合1、在利用某种细菌发酵产生纤维素的研究中,选用甘露作为碳源,发酵液pH 值和残糖量随发酵时间而发生变化,数据如下表:发酵时间 / d0 1 2 3 4 5 6 7 8 pH 值 5.4 5.8 6 5.9 5.8 5.7 5.6 5.4 5.3 残糖量 / g·L -124.513.311.210.19.58.17.87.26.5残糖量/g.L -1p H 值发酵时间/d试根据上述数据,在一个普通直角坐标系中画出发酵时间与发酵液pH 值,以及发酵时间与发酵残糖量的关系曲线。
2、用打孔吸附树脂纯化某种天然棕色素的实验中,以每克树脂的吸附量作为实验指标,通过静态吸附试验筛选合适的大孔吸附树脂,试验数据如下表:树脂型号 DA-201 NKA-9 AB-8 D-4006 D-101 S-8 NKA-Ⅱ -117.1417.771.8713.710.5513.333.67试选用合适的图形来表达图中数据。
NKA-9D-4006S-861218吸附量/m g .g -1树脂型号吸附量3、脂肪酸是一种重要的工业原料,下表列出了某国脂肪酸的应用领域,试根据这些数据的应用领域,试根据这些数据画出饼形图。
应用领域 橡胶工业 合成表面活性剂润滑油 肥皂及洗涤剂金属皂 其他 比例 / % 181152321224、在一定温度、压力下,测得苯(A),乙醇(B),水(C)三元物系的平衡数据如下表所示,试在三角形坐标图中绘出三元相图。
苯(A)% 乙醇(B)% 水(C)%0.1 19.9 800.4 29.6 701.3 38.7 604.4 45.6 509.2 50.8 4012.8 52.2 3517.5 52.5 3020 52.3 27.730 49.5 20.540 44.8 15.250 39 1153 37.2 9.860 32.5 7.570 25.4 4.680 17.7 2.390 9.2 0.895 4.8 0.25、由试验得到某物质的溶解度与绝对温度之间的关系可用模型C = aT b表示,试验数据如下表:T / K 273 283 293 313 333 353C / % 20 25 31 34 46 58试建立回归方程。
计算机在化学化工中的应用2011-2012-2试题

一、Origin:1-1设置工作表并绘图采用用户自定义函数作图,三个函数是F1(x)=5*EXP(-x/3),F2(x)=F1(x)*sin(2*x),F3(x)=-F1(x),请用平滑的曲线作图。
1-4设置工作表格数值(i=1~91),绘制图形。
Col(A)=(i-1)*360/90Col(B)=sin(col(A)*2*pi/360)Col(C)=cos(col(A)*2*pi/360)Col(D)=sin((col(A)-30)*2*pi/360)1-3尿中胆色素经处理后,在550nm处有很强的吸光性,现测得配置好的不同的胆色素浓度的标准溶液的吸光率数据如表所示,假定标准曲线可以用y=a+bx+cx2来表示,试计算出1-7 绘图并拟合化工原理多效蒸发系统优化设计中,要用到不同温度下饱和水蒸气的焓值,且认为焓H与温度T可用多项式H=c0+c1T+c2T2来表示。
已知0~100℃下焓与温度的关系如下表所示,求多项式的拟合系数,并在H~T图上绘出拟合曲线,用“★”号标出实验数据点。
1-8 某化学反应的速率(k)对温度(T)的关系符合Arrhenius方程k=Ae-Ea/RT(A为指前因子,Ea为反应活化能,R为气体常数),用origin绘制下表所列实验数据的图形,并用线性拟合计算活化能。
提示:将Arrhenius方程改写成lnk=lnA-Ea/RT。
P801-14 应用“Samples\Curve Fitting\Linear Fit.dat”文件中的数据进行线性拟合。
P751-2对离心泵性能进行测试的实验中,得到流量qv、压头H和效率η的数据如表1-2所示,绘制离心泵特性曲线。
m/z 14 15 19 26 27 28 29 30 相对强度 1.4 3.4 2.3 4.9 17.7 4.2 12 5 m/z 31 32 41 42 43 44 45 46 相对强度100 1.4 1 3.4 9.9 1 57.3 24.61-10m/z 14 15 28 29 30 43 44 相对强度0.7 33 0.56 0.65 0.11 100 2.2m/z 45 46 47 60 61 62相对强度26 0.31 0.1 62 1.48 0.26P741-11 使用“Samples\Curve Fitting\Linear Fit.dat” 做多层图形。
2014计算机化工应用课后作业答案(全)-隋志军

计算机化工应用课后习题答案特别鸣谢章奇明材料支持1. 已知某化工管道的真实长度为1000m,某次测量结果为1001m,其测量的绝对误差,相对误差为多少?答:绝对误差为1m,相对误差为0.1%。
2. 已知e 的真实值为2.718281828459046···,取2.71828 作为e 的替代值时,具有几位有效数字。
取2.71827 作为e 的替代值时,有几位有效数字。
答:2.71828 具有 6 位有效数字。
e − 2.71828 < 0.000001828 < 0.5×10−5,m-p=-5,m=1,所以p=6。
2.71827具有5位有效数字,e −2.71827 < 0.000011828 < 0.5×10−4,m-p=-4,m=1,所以p=5。
3. 假定使用一台十进制计算机,它表示的浮点数具有7 位尾数和1 位指数,超过计算机存储位数的数字均被舍去,试分别计算以下表达式的值,写出运算过程。
1) 123456.7+101.32542) 3563.212/12.53221答:1) 123456.7+101.3254 =0.1234567*106+0.1013254*103 =0.1234567*106+0.0001013*106=0.1235580*1062) 3563.212/12.53221=0.3563212*104/0.1253221*102=0.2843243*1034. 以下浮点数运算采用IEEE 双精度格式,eps 表示从1 到一个较大浮点数的距离;试写出其计算结果并简要说明计算过程。
1) 2+eps-2 2) 2-2+eps3) 2.0e308-1.1e308 4)1.5*(1.8e308+0.5e308)5) 0/((1+1e-16)-1) 6) 1.8e308-1.8e3087) (1 + 3e-16) – 1答:1) 0;eps 被舍掉2) eps,3) Inf 无穷减有限实数,因此结果为无穷4) Inf 有限实数乘以无穷也为无穷5) NaN 0/0 结果为非数6) NaN 无穷减无穷结果为非数7) eps 或2.22e-16 距离1 最近的实数是1+eps,下个不小于1+2eps,因此1+3e-16实际被认为是1+epsWork03Work04Work05Work06Work07Work08Work09Work10Work111.求解以下高阶常微分方程1)输出y, y’和y”与x 的关系图;2)输出x=1.2 时y, y’和y”的值。
计算机在化工中的应用-习题集

J =62.3 lbm / ft 3
1 ft=0.3048m T(o R)=1.8T(K) 1Btu=1055J 1 lbm=0.4536kg
1.8 计算双组分简单精馏塔的理论板数 氯仿-苯双组分精馏系统的气液相平衡数据如下表所示。对氯仿而言,规定:
x f 0.4, xd 0.9, xw 0.15
化率。 提示:等温管式反应器模型为: VR FA0 因此,反应器管长为: L
xA 0 x A dx dx y A0 F0 0 (r ) (rA ) A
x A dx VR 4 y A0 F0 2 2 0 (r ) ( d / 4) d A
然后得到 pA 和 ps 的表达式带入上式中的反应动力学表达式即可。 1.10 等温管式反应器的空时计算 某气相二聚反应 A→3R 在等温恒压管式反应器内进行,反应条件为 T=2150C,
Matlab 在化工中的应用习题集
第一章 化工中的数值分析与求解
1.1. 简单精馏计算(fzero) 简单精馏时,某时刻釜液残液量 F 与低沸点组成 x 之间的关系式为:
ln F0 1 x0 1 x ln ln F 1 x 1 x0
对于苯-甲苯物系,相对挥发度 a=2.5,开始时物系中含苯 60%。试求当蒸馏 至残液量为原加料量的一半时残液中的苯含量。 1.2. 气体状态方程的求解(fzero 或 roots)
6.264×108 111528
B
k3
D k5
k k0 exp( Ea / RT ) 。已知:
k0i Eai 5.7805×1010 124670 3.9232×1012 150386 1.6425×104 77954
C
计算机在化学化工中的用应 习题及答案

上机任务一:Excel/Origin 数据作图及拟合1、在利用某种细菌发酵产生纤维素的研究中,选用甘露作为碳源,发酵液pH 值和残糖量随发酵时间而发生变化,数据如下表:发酵时间 / d0 1 2 3 4 5 6 7 8 pH 值 5.4 5.8 6 5.9 5.8 5.7 5.6 5.4 5.3 残糖量 / g·L -124.513.311.210.19.58.17.87.26.5残糖量/g.L -1p H 值发酵时间/d试根据上述数据,在一个普通直角坐标系中画出发酵时间与发酵液pH 值,以及发酵时间与发酵残糖量的关系曲线。
2、用打孔吸附树脂纯化某种天然棕色素的实验中,以每克树脂的吸附量作为实验指标,通过静态吸附试验筛选合适的大孔吸附树脂,试验数据如下表:树脂型号 DA-201 NKA-9 AB-8 D-4006 D-101 S-8 NKA-Ⅱ -117.1417.771.8713.710.5513.333.67试选用合适的图形来表达图中数据。
NKA-9D-4006S-861218吸附量/m g .g -1树脂型号吸附量3、脂肪酸是一种重要的工业原料,下表列出了某国脂肪酸的应用领域,试根据这些数据的应用领域,试根据这些数据画出饼形图。
应用领域 橡胶工业 合成表面活性剂润滑油 肥皂及洗涤剂金属皂 其他 比例 / % 181152321224、在一定温度、压力下,测得苯(A),乙醇(B),水(C)三元物系的平衡数据如下表所示,试在三角形坐标图中绘出三元相图。
苯(A)% 乙醇(B)% 水(C)%0.1 19.9 800.4 29.6 701.3 38.7 604.4 45.6 509.2 50.8 4012.8 52.2 3517.5 52.5 3020 52.3 27.730 49.5 20.540 44.8 15.250 39 1153 37.2 9.860 32.5 7.570 25.4 4.680 17.7 2.390 9.2 0.895 4.8 0.25、由试验得到某物质的溶解度与绝对温度之间的关系可用模型C = aT b表示,试验数据如下表:T / K 273 283 293 313 333 353C / % 20 25 31 34 46 58试建立回归方程。
计算机在化学中的应用复习总结题

计算机在化学中的应用复习题一、选择题1、下列软件中____一定是系统软件。
A、自编的一个C程序,功能是求解一个一元二次方程WINDOWS操作系统C、用汇编语言编写的一个练习程序D ROM芯片2、计算机病毒是指。
B)已损坏的磁盘D)被破坏的程序______。
A、电子管C、晶体管D、小规模集成电路4____。
A、CAIB、CAM CAD D、CAT5、在WordA、全屏显示C、缩放显示D、页面显示2.PowerPoint________。
B、视图菜单的“幻灯片放映”/灰度”下的“纯黑白”D、视图菜单的“幻灯片缩图”PowerPoint CTRL并拖动某幻灯片,可以完成________操作。
A、移动幻灯片C、删除幻灯片D、选定幻灯片5.Windows ______。
A、安全方式C、具有网络支持的安全方式D、MS-DOS方式6.在Excel,________命令最为方便。
A、查找B、条件格式D、定位7.在Excel中,A133.51”时,显示为______ 。
A、33.51B、33 34 D、ERRORExcel,可以单击________。
“文件”下拉菜单中的“关闭”命令B、“文件”下拉菜单中的“退出”命令Excel窗口的按钮×D、“窗口”下拉菜单中的“隐藏”命令Excel中,让某单元格里数值保留二位小数,下列_______不可实现。
“数据”菜单下的“有效数据”B、选择单元格单击右键,选择“设置单元格C、选择工具条上的按钮“增加小数位数”或“减少小数位数”D、选择菜单“格式”,再选择“单元格...”Excel中按文件名查找时,可用________代替任意单个字符。
? B、* C、! D、%。
A、计算器B、记事本D、画笔7______ 。
A、“开始”菜单的内容是固定不变的“开始”菜单和“程序”里面都可以添加应用程序8、为了避免系统意外崩溃应采用的启动方式为_____。
A、通常模式B、登录模式D、命令提示模式9、______。
计算机在化工中的应用-练习题

湖北工程学院1、利用Chemdraw 绘制下列分子结构或反应式(1)、(2)、(3)、2、利用Chemdraw 绘制一套简单蒸馏装置图。
(5分)3、用Chemdraw 和Chem3D 绘制顺1-特丁基-4-硝基-环己烷优势立体构象。
(5分)三、Chemoffice 软件应用题………………(25分)1、利用word 插入对象中公式编辑器或mathtype 软件输入下列公式:012/*sp ()[2(ln )] []=r B kTc Br p pK K q e H c T C ενηηη-∆Θ==-∂⎛⎫= ⎪∂⎝⎭∏2、画出如下流程图(利用文本框操作,请用图形的组合与取消组合命令)表2 各种因素对产率的影响序号 单体与引发剂比[M]/[I](℃) (h ) 产率 (%) 1 10:1 120 16 90.22 2 20:1 120 16 96.45 330:11201695.99利用Gaussian03进行甲醛单点能,并查看分子轨道。
输入文件为: %chk=学号.chk# RHF/6-31G(d) Pop=Full Test Formaldehyde Single Point 0,1C 0. 0. 0. O 0. 1.22 0. H 0.94 -0.54 0. H -0.94 -0.54 0.采用GaussView 打开Scratch 目录中的学号.chk 文件,打开菜单的“Results”—— “Surfaces”,算出单点能,并查看HOMO 以及LUMO 轨道形状。
四、word 软件应用 五、Gaussian 软件应用题六、Aspentech软件应用题使用Aspentech软件模拟甲醇与二甲醚-水混合物精馏分离二甲醚过程。
模块选Radfrac,设定三个物流A (为输入物流)、B(为塔板顶流出物流)、C(塔板底流出物流);设定单位、名称和账号;组分分别设为1(为水)、2(为甲醇)、3(为二甲醚);设定物流估算方法为PENG-ROB;设定输入物流总流量(8kmol/hr)、温度(30℃)、压力(8kg/sqcm)和组成(摩尔分率1:2:3=0.4:0.27:0.33);设定塔板数(7)、回流比(2)、精馏流出流量(2.5kmol/hr)、输入物流输入塔板位置(中间塔板进入)、塔压(Top/Bottom=7atm)等,计算结果,显示每个塔板组分、塔热容量、二甲醚纯度。
[VIP专享]计算机在化工中的应用-上机实验五-Gaussian
![[VIP专享]计算机在化工中的应用-上机实验五-Gaussian](https://img.taocdn.com/s3/m/187bb6dfa0116c175f0e48f6.png)
3. 在 Gaussview 中把分子投入到 G03 中进行单点能计算。 计算方法与基组为:PM3, HF/STO-3G, HF/6-31G(d), MP2/6-31G(d), B3LYP/6-31G(d) 4. 练习用 Gaussview 观看结果。
X,1,1.,2,A3
O,1,R2
C
1) B2Ak+22+12=+15+c51mc+=5m=2c111++m+12+21+++2=12=2+1+2+1+2+2+22+32k+1+2
88.8918÷.12990.÷1=4214÷3922=.0034=1÷15251371=8.535.78208÷.0232173c0*0÷1=m920.30392.2c=1÷203m=2÷1202.52=3535=42314)c*5232m40341*.31252=3.*1.153.5*03134.2*920522..104455=+21*3*50202.2.0285.4850.13*50+5c8*125*12m0.2+050.+0*014.852*0051000+0+/038.T+0÷+=55*+1011+010+91÷0145405*00010200+5+0+080+40*04+***115.103910*-%*C%6(+÷*M==5M÷5)0*3*0(31÷3110**5*+*÷414.m2371e=%7)8n08%.=s8.5=77.93cc60.mc*m4*m13,101w9.9o.k24mc-.cem5nm2csp2665m*9..03-4.50c60*5.pc3m85,9cm0.5g.i50mr0l-.p.s85p/6c50bc.0om7m.yp.cs6pc5m+;c0m..m7.ckm; 1+1k+12+1+k2234=1c+m1++4+4+2
计算机在化学化工中的应用B1答案

第 1页,共 3页计算机在化学化工中的应用考试A 卷适用专业: 考试日期:试卷所需时间:120分钟 闭卷 试卷总分100分一、单项选择题(25道小题,共50分)1、第一台电子计算机是1946年在美国研制的,该机的英文缩写名是( A )。
A 、ENIAC B 、EDVAC C 、EDSAC D 、MARK-Ⅱ2、计算机辅助制造的英文缩写是( B )。
A 、CAI B 、CAM C 、CAD D 、CAT3、最大的10位无符号二进制整数转换成十进数是( C )。
A 、511 B 、512 C 、1023 D 、10244、二进制数00111101转换成十进制数为( )。
A 、57 B 、59 C 、61 D 、635、计算机的存储单元中存储的内容( C )。
A 、只能是数据 B 、只能是程序 C 、可以是数据和指令 D 、只能是指令6、计算机软件系统包括( B )。
A 、操作系统、网络软件B 、系统软件、应用软件C 、客户端应用软件、服务器端系统软件D 、操作系统、应用软件和网络软件 7、一个完整的计算机系统包括( D )。
A 、计算机及外部设备 B 、系统软件和应用软件 C 、主机、键盘和显示器 D 、硬件系统和软件系统 8、通常所说的I /O 设备指的是( A )。
A 、输入输出设备 B 、通信设备 C 、网络设备 D 、控制设备9、下列叙述中,正确的是( D )。
A 、激光打印机属于击打式打印机B 、CAI 软件属于系统软件C 、软磁盘驱动器是存储介质D 、计算机运算速度可以用MIPS 来表示 10、微型机使用Pentium Ⅲ 800的芯片,其中的800是指( B )。
A 、显示器的类型 B 、CPU 的主频 C 、内存容量 D 、磁盘空间11、CPU 主要由运算器与控制器组成,下列说法中正确的是( D )。
A 、运算器主要负责分析指令,并根据指令要求作相应的运算B 、控制器主要完成对数据的运算,包括算术运算和逻辑运算C 、控制器主要负责分析指令,并根据指令要求作相应的运算D 、控制器直接控制计算机系统的输入与输出操作12、在窗口中关于当前窗口的有关信息显示在( C )中。
《计算机在化学中的应用》试卷及答案

2012级应用化学、化学专业《计算机在化学中的应用》试题答题内容要求截图所做答案均为亲手制作,但是不保证答案正确性一、数据处理:(每小题15分,共30分)1、已知水在不同温度下的电导率数据如下:T/℃0 10 20 25 30 40 50 κ×106/(S•m-1) 1.2 2.3 4.2 5.5 7.1 11.3 17.1 利用Excel软件中的功能,求出5,15,28,35,45℃时的电导率κ值答题要点:①做散点图②添加趋势线方程③选择合适的拟合形式④输出拟合方程⑤进行插值计算2、在20℃,钢线中碳含量对电阻效应研究中,观测得数据如下:碳含量x% 0.10 0.30 0.40 0.55 0.70 0.80 0.95电阻y (10-5Ω)15 18 19 21 22.6 23.8 26利用Excel 软件中的功能,拟合为2321x a x a a y ++=的多项式。
答题要点:①做散点图 ②数据分析-多项式-二次③获得拟合参数或输出拟合方程二、office 软件的应用技巧(每小题5分,共20分)1、描述如何使用自动更正功能快速输入分子式 Fe 2(SO 4)3 答题要点:①使用自动更正的操作过程②选择带格式文本Fe 2(SO 4)32 函数LINEST 的使用方法? 自己百度 答题要点:描述函数的使用方法及适用范围3、描述反应加热符号的制作,与输入法的链接及输出过程 答题要点:正确描述制作及链接过程加热4、描述获取下面图片中的文本信息的方法答题要点:①转换图片格式为tiff ②使用OCR识别软件识别③粘贴文本作者注所用软件office组件中Document Imaging (WPS中没有)因为没有软件必备组件本题没有做完三、化学软件的应用技巧(共10分)1、利用Chemsketch软件调用环己烷的椅式构象及立方烷的结构式。
(2分)答题要点:①正确描述调用过程②输出调用结果模板------ 模板窗口2、利用Chemsketch软件绘制下列化学结构式,并用软件中的命名功能命名。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
z ?1 dp 计算其逸度系数。 p
反应物 A 在一等温间歇反应器中发生反应 A→产物,实验测得反应器中不同 时间下反应物 A 的浓度 CA 如下表所示。试根据表中数据确定其反应速率方程,并 确定 50min 时组分 A 的浓度和反应速率。假设反应速率方程表达式为:
n (? rA ) ? kC A mol/L/s
0 ? 0
Ctdt Cdt
,方差: ?
2
Ct dt ? t ? ? Cdt
0 ? 0
2 m
2 ?D ? ? 扩散特征数: ? L ? ? 2 ? uL ? 2tm
1.13 逸度系数的求取 化工热力学实验测得关于氧气的压缩因子数据如下:
时间 CA(mol/L) 0 0 20 0 40 0 60 0
80 0.4
100 5.5
120 16.2
140 11.1
2
160 1.7
180 0.1
200 0
提示:平均停留时间: tm
? ?
p=1atm, 反应器内径 d=10cm。已知反应速率为: (? rA ) ? 116 ? p A ? ps /1.27 ?
为了控制反应, 向反应物 A 中加入一定惰性气体 I, 两者的摩尔比为 A:I=1:0.5。 进气速率 F0 为 10kmol/h。
(1) 试计算转化率为 0.1,0.2,0.3,0.4 和 0.5 时所需的反应器管长和平衡转化
pi0 b ? ai ? i mmHg T /K
系数 a 和 b 列于下表: i 1 2 3 组分 苯 甲苯 乙苯 ai 7.84135 8.08840 8.11404 bi 1750 1985 2129
1.4. 等温闪蒸的计算(fzero) 如图所示,进料组成如下表所示的四组分烷烃混合物在 1380kPa 下加入闪蒸 器(pL=pV)进行等温闪蒸(TL=TV),若气化率为 40%,试问混合物能预热到多高的温 度?假设仅形成一个液相, 且具有理想溶液的性质, 即气液平衡常数 K 只与温度 T 和压力 p 有关,其函数关系为: ln ? Kp ? ? a ? b / T ? cT 序号 1 2 3 4 组分 C2 C8 n-C4 n-C5 zf 0.08 0.22 0.53 0.17
精馏段和提馏段的回流比分别为 R=5 和 R’=4。试计算所需的理论板数。
x y 0.178 0.243 0.275 0.382 0.372 0.518 0.456 0.616 0.650 0.795 0.844 0.931
2
Matlab 在化工中的应用习题集 提示:精馏段理论板数 N ? ?
率。
(2) 假设现有一长度为 5m 的管式反应器, 试计算相同条件下该反应器的出口转
化率。 提示:等温管式反应器模型为: VR ? FA0 ? 因此,反应器管长为: L ?
xA 0 x A dx dx ? y A0 F0 ? 0 (?r ) (?rA ) A
x A dx VR 4 y A0 F0 ? ? 2 2 0 (?r ) (? d / 4) ? d A
x Af
0
dx (? rA )
1.11 计算填料吸收塔的总传质单元数 逆流操作的填料吸收塔,在温度 200C,压力 1atm 下,用水洗涤含有 5.5%SO2 的空气,使 SO2 下降到 0.5%。当气液比(L/G)为 40 时,求取以气相浓度为基准的 总传质单元数。 若以气相浓度为基准的总传质单元高度 HOG=0.69m, 进而求填料塔 高度。进水塔中不含 SO2,200C 时水对 SO2 的溶解度数据列于下表。
C A0 ? 0.55 lbmol/ft 3 F0 ? F ? 40 ft 3 /h V ? 48 ft 3 T0 ? 530 o R FJ ? 49.9 ft 3 /h VJ ? 12 ft 3
TJ VJ
TJ 0 ? 530 o R AH ? 250 ft 2 Ea ? 30000 Btu/lbmol
a ? 4.17 atm ? L2 / mol2 b ? 0.0371 L/mol
思考:Van de waals 方程应有三个根,三个根各有什么物理意义? 1.3. 计算混合液体的泡点及平衡蒸汽组成(fzero) 计算 101.325kPa 下苯 50%(摩尔百分数,下同)、甲苯 30%和乙苯 20%的混合 物的泡点及平衡蒸汽组成。 已知每一纯组分 i 的饱和蒸汽压与绝对温度的关系满足 Antoine 方程: lg
k
K1 ? 0.064 K 2 ? 0.076 K 3 ? 0.00012
后续分离过程要求反应产物中丙醛的含量不大于 0.05mol%。问在所述的反应
F, cA0 ,T0 V T CA FJ TJ TJ VJ F, cA ,T
假设流量和溶液体积 V 不变,夹套冷却水流量 FJ 和冷却夹套中持液量恒定、 混合完全。 系统原先处于 FJ 稳态过程(t=0 时刻前),试确定多稳态解。已知参数 TJ0 值如下:
c pJ ? 1.0 Btu/(lbm ?o R) c p ? 0.75 Btu/(lbm ?o R) ?H ? ?30000 Btu/lbmol ? =50 lbm / ft 3 1 lbmol ? 453.6mol
U ? 150 Btu/(h ? ft 2 ?o R) R ? 1.9872 Btu/(lbmol ?o R) k0 ? 7.08 ?1010 h -1
1000x 1000y 1.96 51.3 1.40 34.2 0.846 18.6 0.562 11.2
3
0.422 7.63
0.281 4.21
0.141 1.58
0.056 0.658
湖南大学化学化工学院化工系试用讲义 提示:以气相浓度为基准的总传质单元数为: N OG ? ?
ln F0 1 ? x0 1? x ? ? ? ln ? ? ln ? F ? ?1 ? x 1 ? x0 ?
对于苯-甲苯物系,相对挥发度 a=2.5,开始时物系中含苯 60%。试求当蒸馏 至残液量为原加料量的一半时残液中的苯含量。 1.2. 气体状态方程的求解(fzero 或 roots)
时间(min)
0 10
20 8
40 6
60 5
120 3
180 2
300 1
CA(mol/L)
提示:将反应动力学方程变形为 ln(?rA ) ? n ln C A ? ln k
4
Matlab 在化工中的应用习题集
本文由铃儿响叮当MT贡献
pdf文档可能在WAP端浏览体验不佳。建议您优先选择TXT,或下载源文件到本机查看。
Matlab 在化工中ቤተ መጻሕፍቲ ባይዱ应用习题集
第一章 化工中的数值分析与求解
1.1. 简单精馏计算(fzero) 简单精馏时,某时刻釜液残液量 F 与低沸点组成 x 之间的关系式为:
p/atm z
0
20.0
40.0
60.0
80.0
100.0
120.0
1.0 0.98654 0.97420 0.96297 0.95286 0.94387 0.93599
试按逸度系数计算的定义式 ln ? ? ? 1.14 动力学数据分析
1
ai 15.57 17.14 17.83 17.91
bi -1793.4 -2843.0 -3007.2 -3412.9
ci -4.93×10-3 -6.27×10-3 -6.67×10-3 -6.12×10-3
湖南大学化学化工学院化工系试用讲义 1.5. 求绝热连续搅拌槽反应器的转化率(fzero) 如图所示,进料组成如下表所示的四组分烷烃混合物在 1380kPa 下加入闪蒸 器(pL=pV)进行等温闪蒸(TL=TV),若气化率为 40%,试问混合物能预热到多高的温 度?假设仅形成一个液相,且具有理想溶液的性质,即气液平衡常数 K 只与温度 T 和压力 p 有关,其函数关系为: 1.6 化学平衡计算(fsolve) 异丙醇于 4000C,1atm 下在 Ag 催化剂上进行脱氢反应生成丙酮,主副反应及 其在反应温度下的平衡常数如下: i ? C3 H 7 OH(IP) ? n ? C3 H 7 OH(NP) i ? C3 H 7 OH(IP) ? (CH 3 ) 2 CO(AC) ? H 2 i ? C3 H 7 OH(IP) ? C2 H 5CHO(PR) ? H 2 条件下,产物组成能否满足此要求。 1.7 非等温 CSTR 反应器模拟与多稳态解的求取(fsolve) 如图所示,在一个非等温的 CSTR 反应器中进 行反应: A ?? B ?
y1 y2
dy y ? y*
x ? y x ? y ? 填料吸收塔的操作线方程为: L ? ? 2 ? ? G? ? 2 ? ? 1 ? x 1 ? x2 ? ? 1 ? y 1 ? y2 ?
气液平衡关系:由表中的离散数据确定 1.12 反应器停留时间分布的混合特性 在 t=0 时刻,在一容器入口处突然向流进容器的流体脉冲注入一定量的示踪 剂,同时在容器出口处测量流出物料中示踪剂浓度随时间的变化,实验数据如下 表。试计算流体在容器中的平均停留时间以及扩散准数。
第二章 化工中的常微分方程与求解
2.1 微分方程的求解 求解如下的 ODEs-IVP 问题(a)和 ODEs-BVP 问题(b),并将计算结果与如下准
确进行比较:
然后得到 pA 和 ps 的表达式带入上式中的反应动力学表达式即可。 1.10 等温管式反应器的空时计算 某气相二聚反应 A→3R 在等温恒压管式反应器内进行,反应条件为 T=2150C,
p=5atm。已知反应速率为: (? rA ) ? kC 1/ 2 A
