Matrix软件操作说明
IP Matrix VJD-8000 软件手册说明书

4.5
Basic keyboard settings
5
Operation
5.1
Keyboard basics
5.2
Keyboard print template
5.3
Keyboard layout
6
Troubleshooting
Table of contents | en 3
4 4 4 4 5 5 5 6 7 8 8 8 9 12 14 15 15 18 19 20
Requirements
For configuration purposes:
Hardware
Personal Computer
CPU
Dual Core, 3.0 GHz or faster
RAM
Minimum 2 GB
Operating system
Windows Server 2008 R2 (64 bit) Windows 7 SP1 (64 bit) Windows 8.1 (64 bit) Windows 10 (64 bit)
Bosch Security Systems B.V.
Software manual
2019.04 | V2 | DOC
4 en | Introduction
IP Matrix
MATRIX-E使用手册

4.1 简介 . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 15 4.2 前视图 . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 16 4.3 侧视图 – 右侧 . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 17 4.4 侧视图 – 左侧 . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 18 4.5 后视图 . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 19
6 维护 . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .31
python中matrix用法

python中matrix用法在Python中,我们可以使用多种库来处理矩阵,包括NumPy、SciPy和SymPy等。
其中,NumPy是最常用的库之一,它提供了丰富的矩阵操作函数和方法。
首先,我们需要安装NumPy库,可以使用以下命令来安装:python.pip install numpy.接下来,我们可以使用NumPy来创建矩阵,进行矩阵运算和其他操作。
下面是一些常见的矩阵操作用法:1. 创建矩阵。
python.import numpy as np.# 创建一个2x3的矩阵。
matrix = np.array([[1, 2, 3], [4, 5, 6]])。
print(matrix)。
2. 矩阵运算。
python.# 矩阵加法。
matrix1 = np.array([[1, 2], [3, 4]])。
matrix2 = np.array([[5, 6], [7, 8]])。
result = matrix1 + matrix2。
print(result)。
# 矩阵乘法。
result = np.dot(matrix1, matrix2)。
print(result)。
3. 矩阵转置。
python.# 矩阵转置。
matrix = np.array([[1, 2], [3, 4]])。
result = matrix.T.print(result)。
4. 矩阵求逆。
python.# 矩阵求逆。
matrix = np.array([[1, 2], [3, 4]])。
result = np.linalg.inv(matrix)。
print(result)。
除了上述操作外,NumPy还提供了很多其他矩阵操作的函数和方法,如求特征值、特征向量、行列式等。
通过使用NumPy库,我们可以方便地进行矩阵运算和操作,为数据分析和科学计算提供了很大的便利。
总之,Python中的NumPy库为我们提供了丰富的矩阵操作功能,使得我们可以方便地进行矩阵的创建、运算和其他操作,为数据分析和科学计算提供了很大的便利。
蓝眼 Matrix 矩阵控制软件使用手册说明书

在使用本产品之前,请务必先仔细阅读本使用说明书。
请务必妥善保管好本书,以便日后能随时查阅。
请在充分理解内容的基础上,正确使用。
【爱护地球,蓝眼用心】本手册采用环保打印,如需电子文件请向代理商或蓝眼科技客服中心免费索取。
矩阵控制软件使用手册Version 1.5.11.52015/11/11使用手册本手册适用于以下产品蓝眼Matrix矩阵控制软件感谢您使用蓝眼科技的产品。
本手册将介绍蓝眼科技产品。
在您开始使用产品前,建议您先阅读过本手册。
手册里的信息在出版前虽已被详细确认,实际产品规格仍将以出货时为准。
蓝眼科技对本手册中的内容无任何担保、宣告或暗示,以及其他特殊目的。
除此之外,对本手册中所提到的产品规格及信息仅供参考,内容亦可能会随时更新,恕不另行通知。
本手册中所提的信息,包括软件、韧体及硬件,若有任何错误,蓝眼科技没有义务为其担负任何责任。
任何产品规格或相关信息更新请您直接到蓝眼科技官方网站查询,本公司将不另行通知。
若您想获得蓝眼科技最新产品讯息、使用手册、韧体,或对蓝眼科技产品有任何疑问,请您联络当地供货商或到蓝眼科技官方网站取得相关讯息。
本手册的内容非经蓝眼科技以书面方式同意,不得擅自拷贝或使用本手册中的内容,或以其他方式改变本手册的数据及发行。
本手册相关产品内容归蓝眼科技版权所有蓝眼科技地址:404台湾台中市北区文心路四段200号7楼之3电话:+886 4 2297-0977 / +886 982 842-977传真:+886 4 2297-0957E-mail:********************.tw网站:目录1. 準備 (3)1.1 硬體與架構圖............................................................................................ 錯誤! 尚未定義書籤。
1.2 相容表........................................................................................................ 錯誤! 尚未定義書籤。
LABEL MATRI7.0使用说明
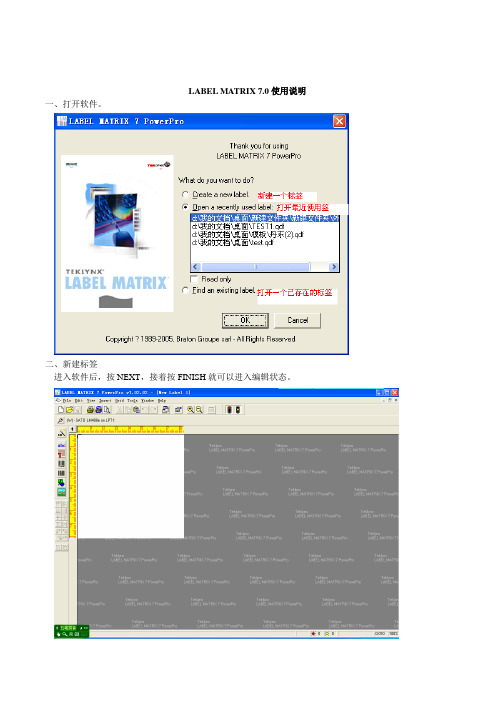
LABEL MATRIX 7.0使用说明一、打开软件。
二、新建标签进入软件后,按NEXT,接着按FINISH就可以进入编辑状态。
三、界面介绍1、常用工具栏介绍新建 打开保存 打印 快速打印 打印预览选择打印机 放大 缩小 数据库列表2、编辑工具栏介绍(左侧)四、设置标签1.设置界面介绍在空白处双击鼠标左键,出现页面属性对话框。
图1图2图3图4图1:设置标签页面大小图2:设置边距图3:设置标签排数图4:设置数据库连接。
2.页面设置(Page size Marginit)如图1所示,WIDTH(宽度)HEIGHT(高度),宽度最大10.4,高度以实际情况定,但不要超过实际一张标签的大小,否则会跳张即打印一张出来一张空白。
连续纸除外。
设置完标签大小后设置标签边距,即标签左右两边标签纸与底纸的距离。
左右根据实际情况设置,一般以0.2 0.3居多,上下设置为0.3.多排设置(Multiple)ACROSS列数WIDTH、HEIGHT一个小标签的宽度和高度4.连接数据库(Database)ADD添加数据库,NEXT (下一步),FILE(打开数据库文件),自动扫描数据库后,选择工作表(EXCEL 文件里Sheet1,2,3),NEXT(下一步),FINISH(完成)。
五、编辑内容1.文本点击左边abc按钮,然后在DATA选项卡的TEXT后面输入相应文本内容。
如果是连接数据库,则ORIGIN需要选择为DA TABASE,会在下面出现表格字段,选择相应字段。
Database数据库、文本输入选择数据库输入完成后点击数据库按钮查看数据表Constant 固定值、Counter 增量如果需要使用增量,则将Origin选择为Counter。
START BY是增量的起始值,STEP 是增量大小。
如图所示,即打印出来的增量为001 003 005 007.。
2.条码点击左边的一维条码、二维条码按钮,然后在DA TA选项卡的TEXT后面输入相应文本。
Matrix软件包说明书

2nd Introduction to the Matrix packageMartin Maechler and Douglas BatesR Core Development Team******************.ethz.ch,*******************September2006(typeset on August11,2023)AbstractLinear algebra is at the core of many areas of statistical computing and from its inception the S lan-guage has supported numerical linear algebra via a matrix data type and several functions and operators,such as%*%,qr,chol,and solve.However,these data types and functions do not provide direct accessto all of the facilities for efficient manipulation of dense matrices,as provided by the Lapack subroutines,and they do not provide for manipulation of sparse matrices.The Matrix package provides a set of S4classes for dense and sparse matrices that extend the basic matrix data type.Methods for a wide variety of functions and operators applied to objects from theseclasses provide efficient access to BLAS(Basic Linear Algebra Subroutines),Lapack(dense matrix),CHOLMOD including AMD and COLAMD and Csparse(sparse matrix)routines.One notable char-acteristic of the package is that whenever a matrix is factored,the factorization is stored as part of theoriginal matrix so that further operations on the matrix can reuse this factorization.1IntroductionThe most automatic way to use the Matrix package is via the Matrix()function which is very similar to the standard R function matrix(),>library(Matrix)>M<-Matrix(10+1:28,4,7)>M4x7Matrix of class"dgeMatrix"[,1][,2][,3][,4][,5][,6][,7][1,]11151923273135[2,]12162024283236[3,]13172125293337[4,]14182226303438>tM<-t(M)Such a matrix can be appended to(using cbind()or rbind())or indexed,>(M2<-cbind(-1,M))4x8Matrix of class"dgeMatrix"[,1][,2][,3][,4][,5][,6][,7][,8][1,]-111151923273135[2,]-112162024283236[3,]-113172125293337[4,]-1141822263034381>M[2,1][1]12>M[4,][1]14182226303438where the last two statements show customary matrix indexing,returning a simple numeric vector each1. We assign0to some columns and rows to“sparsify”it,and some NA s(typically“missing values”in data analysis)in order to demonstrate how they are dealt with;note how we can“subassign”as usual,for classical R matrices(i.e.,single entries or whole slices at once),>M2[,c(2,4:6)]<-0>M2[2,]<-0>M2<-rbind(0,M2,0)>M2[1:2,2]<-M2[3,4:5]<-NAand then coerce it to a sparse matrix,>sM<-as(M2,"sparseMatrix")>10*sM6x8sparse Matrix of class"dgCMatrix"[1,].NA......[2,]-10NA150 (310350)[3,]...NA NA...[4,]-10.170 (330370)[5,]-10.180 (340380)[6,]........>identical(sM*2,sM+sM)[1]TRUE>is(sM/10+M2%/%2,"sparseMatrix")[1]TRUEwhere the last three calls show that multiplication by a scalar keeps sparcity,as does other arithmetic, but addition to a“dense”object does not,as you might have expected after some thought about“sensible”behavior:>sM+106x8Matrix of class"dgeMatrix"[,1][,2][,3][,4][,5][,6][,7][,8][1,]10NA101010101010[2,]9NA251010104145[3,]101010NA NA101010[4,]910271010104347[5,]910281010104448[6,]10101010101010101because there’s an additional default argument to indexing,drop=TRUE.If you add“,drop=FALSE”you will get submatrices instead of simple vectors.2Operations on our classed matrices include(componentwise)arithmetic(+,−,∗,/,etc)as partly seen above,comparison(>,≤,etc),e.g.,>Mg2<-(sM>2)>Mg26x8sparse Matrix of class"lgCMatrix"[1,].N......[2,]:N|...||[3,]...N N...[4,]:.|...||[5,]:.|...||[6,]........returning a logical sparse matrix.When interested in the internal str ucture,str()comes handy,and we have been using it ourselves more regulary than print()ing(or show()ing as it happens)our matrices; alternatively,summary()gives output similar to Matlab’s printing of sparse matrices.>str(Mg2)Formal class'lgCMatrix'[package"Matrix"]with6slots..@i:int[1:16]1340113422.....@p:int[1:9]0358910101316..@Dim:int[1:2]68..@Dimnames:List of2....$:NULL....$:NULL..@x:logi[1:16]FALSE FALSE FALSE NA NA TRUE.....@factors:list()>summary(Mg2)6x8sparse Matrix of class"lgCMatrix",with16entriesi j x121FALSE241FALSE351FALSE412NA522NA623TRUE743TRUE853TRUE934NA1035NA1127TRUE1247TRUE1357TRUE1428TRUE1548TRUE1658TRUEAs you see from both of these,Mg2contains“extra zero”(here FALSE)entries;such sparse matrices may be created for different reasons,and you can use drop0()to remove(“drop”)these extra zeros.This should never matter for functionality,and does not even show differently for logical sparse matrices,but the internal structure is more compact:3>Mg2<-drop0(Mg2)>str(Mg2@x)#length 13,was 16logi [1:13]NA NA TRUE TRUE TRUE NA ...For large sparse matrices,visualization (of the sparsity pattern)is important,and we provide image()methods for that,e.g.,>data(CAex,package ="Matrix")>print(image(CAex,main ="image(CAex)"))#print(.)needed for Sweaveimage(CAex)Dimensions: 72 x 72Column R o w204060204060−0.4−0.20.00.20.40.60.81.0Further,i.e.,in addition to the above implicitly mentioned "Ops"operators (+,*,...,<=,>,...,&which all work with our matrices,notably in conjunction with scalars and traditional matrices),the "Math"-operations (such as exp(),sin()or gamma())and "Math2"(round()etc)and the "Summary"group of functions,min(),range(),sum(),all work on our matrices as they should.Note that all these are implemented via so called group methods ,see e.g.,?Arith in R .The intention is that sparse matrices remain sparse whenever sensible,given the matrix classes and operators involved,but not content specifically. E.g.,<sparse>+<dense>gives <dense>even for the rare cases where it would be advantageous to get a <sparse>result.These classed matrices can be “indexed”(more technically “subset”)as traditional S language (and hence R )matrices,as partly seen above.This also includes the idiom M [M op num ]which returns simple vectors,>sM[sM >2][1]NA NA 151718NA NA 313334353738>sml <-sM[sM <=2]>sml [1]0-10-1-10NA NA 000000000NA[24]NA 0000000and “subassign”ment similarly works in the same generality as for traditional S language matrices.41.1Matrix package for numerical linear algebraLinear algebra is at the core of many statistical computing techniques and,from its inception,the S language has supported numerical linear algebra via a matrix data type and several functions and operators,such as %*%,qr,chol,and solve.Initially the numerical linear algebra functions in R called underlying Fortran routines from the Linpack(Dongarra et al.,1979)and Eispack(Smith et al.,1976)libraries but over the years most of these functions have been switched to use routines from the Lapack(Anderson et al.,1999) library which is the state-of-the-art implementation of numerical dense linear algebra.Furthermore,R can be configured to use accelerated BLAS(Basic Linear Algebra Subroutines),such as those from the Atlas(Whaley et al.,2001)project or other ones,see the R manual“Installation and Administration”.Lapack provides routines for operating on several special forms of matrices,such as triangular matrices and symmetric matrices.Furthermore,matrix decompositions like the QR decompositions produce multiple output components that should be regarded as parts of a single object.There is some support in R for operations on special forms of matrices(e.g.the backsolve,forwardsolve and chol2inv functions)and for special structures(e.g.a QR structure is implicitly defined as a list by the qr,qr.qy,qr.qty,and related functions)but it is not as fully developed as it could be.Also there is no direct support for sparse matrices in R although Koenker and Ng(2003)have developed the SparseM package for sparse matrices based on SparseKit.The Matrix package provides S4classes and methods for dense and sparse matrices.The methods for dense matrices use Lapack and BLAS.The sparse matrix methods use CHOLMOD(Davis,2005a), CSparse(Davis,2005b)and other parts(AMD,COLAMD)of Tim Davis’“SuiteSparse”collection of sparse matrix libraries,many of which also use BLAS.Todo:triu(),tril(),diag(),...and as(.,.),but of course only when they’ve seen a few different ones.Todo:matrix operators include%*%,crossprod(),tcrossprod(),solve()Todo:expm()is the matrix exponential......Todo:symmpart()and skewpart()compute the symmetric part,(x+t(x))/2and the skew-symmetric part,(x-t(x))/2of a matrix x.Todo:factorizations include Cholesky()(or chol()),lu(),qr()(not yet for dense)Todo:Although generally the result of an operation on dense matrices is a dgeMatrix,certain operations return matrices of special types.Todo: E.g.show the distinction between t(mm)%*%mm and crossprod(mm).2Matrix ClassesThe Matrix package provides classes for real(stored as double precision),logical and so-called“pattern”(binary)dense and sparse matrices.There are provisions to also provide integer and complex(stored as double precision complex)matrices.Note that in R,logical means entries TRUE,FALSE,or NA.To store just the non-zero pattern for typical sparse matrix algorithms,the pattern matrices are binary,i.e.,conceptually just TRUE or FALSE.In Matrix, the pattern matrices all have class names starting with"n"(patter n).2.1Classes for dense matricesFor the sake of brevity,we restrict ourselves to the real(d ouble)classes,but they are paralleled by l ogical and patter n matrices for all but the positive definite ones.dgeMatrix Real matrices in general storage modedsyMatrix Symmetric real matrices in non-packed storagedspMatrix Symmetric real matrices in packed storage(one triangle only)5dtrMatrix Triangular real matrices in non-packed storagedtpMatrix Triangular real matrices in packed storage(triangle only)dpoMatrix Positive semi-definite symmetric real matrices in non-packed storagedppMatrix ditto in packed storageMethods for these classes include coercion between these classes,when appropriate,and coercion to the matrix class;methods for matrix multiplication(%*%);cross products(crossprod),matrix norm(norm); reciprocal condition number(rcond);LU factorization(lu)or,for the poMatrix class,the Cholesky decom-position(chol);and solutions of linear systems of equations(solve).Whenever a factorization or a decomposition is calculated it is preserved as a(list)element in the factors slot of the original object.In this way a sequence of operations,such as determining the condition number of a matrix then solving a linear system based on the matrix,do not require multiple factorizations of the same matrix nor do they require the user to store the intermediate results.2.2Classes for sparse matricesUsed for large matrices in which most of the elements are known to be zero(or FALSE for logical and binary (“pattern”)matrices).Sparse matrices are automatically built from Matrix()whenever the majority of entries is zero(or FALSE respectively).Alternatively,sparseMatrix()builds sparse matrices from their non-zero entries and is typically recommended to construct large sparse matrices,rather than direct calls of new().Todo: E.g.model matrices created from factors with a large number of levelsTodo:or from spline basis functions(e.g.COBS,package cobs),etc.Todo:Other uses include representations of graphs.indeed;good you mentioned it!particularly since we still have the interface to the graph package.I think I’d like to draw one graph in that article—maybe the undirected graph corresponding to a crossprod()result of dimension ca.502Todo:Specialized algorithms can give substantial savings in amount of storage used and execution time of operations.Todo:Our implementation is based on the CHOLMOD and CSparse libraries by Tim Davis.2.3Representations of sparse matrices2.3.1Triplet representation(TsparseMatrix)Conceptually,the simplest representation of a sparse matrix is as a triplet of an integer vector i giving the row numbers,an integer vector j giving the column numbers,and a numeric vector x giving the non-zero values in the matrix.2In Matrix,the TsparseMatrix class is the virtual class of all sparse matrices in triplet representation.Its main use is for easy input or transfer to other classes.As for the dense matrices,the class of the x slot may vary,and the subclasses may be triangular, symmetric or unspecified(“general”),such that the TsparseMatrix class has several3‘actual”subclasses,the most typical(numeric,general)is dgTMatrix:>getClass("TsparseMatrix")#(i,j,Dim,Dimnames)slots are common to allVirtual Class"TsparseMatrix"[package"Matrix"]Slots:2For efficiency reasons,we use“zero-based”indexing in the Matrix package,i.e.,the row indices i are in0:(nrow(.)-1)and the column indices j accordingly.3the3×3actual subclasses of TsparseMatrix are the three structural kinds,namely t riangular,s ymmetric and g eneral, times three entry classes,d ouble,l ogical,and patter n.6Name:i j Dim DimnamesClass:integer integer integer listExtends:Class"sparseMatrix",directlyClass"Matrix",by class"sparseMatrix",distance2Class"mMatrix",by class"Matrix",distance3Class"replValueSp",by class"Matrix",distance3Known Subclasses:"ngTMatrix","ntTMatrix","nsTMatrix","lgTMatrix","ltTMatrix", "lsTMatrix","dgTMatrix","dtTMatrix","dsTMatrix">getClass("dgTMatrix")Class"dgTMatrix"[package"Matrix"]Slots:Name:i j Dim Dimnames x factorsClass:integer integer integer list numeric listExtends:Class"TsparseMatrix",directlyClass"dsparseMatrix",directlyClass"generalMatrix",directlyClass"dMatrix",by class"dsparseMatrix",distance2Class"sparseMatrix",by class"dsparseMatrix",distance2Class"compMatrix",by class"generalMatrix",distance2Class"Matrix",by class"TsparseMatrix",distance3Class"xMatrix",by class"dMatrix",distance3Class"mMatrix",by class"Matrix",distance4Class"replValueSp",by class"Matrix",distance4Note that the order of the entries in the(i,j,x)vectors does not matter;consequently,such matrices are not unique in their representation.42.3.2Compressed representations:CsparseMatrix and RsparseMatrixFor most sparse operations we use the compressed column-oriented representation(virtual class CsparseMatrix) (also known as“csc”,“compressed sparse column”).Here,instead of storing all column indices j,only the start index of every column is stored.Analogously,there is also a compressed sparse row(csr)representation,which e.g.is used in in the SparseM package,and we provide the RsparseMatrix for compatibility and completeness purposes,in ad-dition to basic coercion((as(.,<cl>)between the classes.These compressed representations remove the redundant row(column)indices and provide faster access to a given location in the matrix because you only need to check one row(column).There are certain advantages5to csc in systems like R,Octave and Matlab where dense matrices are stored in column-major order,therefore it is used in sparse matrix libraries such as CHOLMOD or CSparse 4Furthermore,there can be repeated(i,j)entries with the customary convention that the corresponding x entries are addedto form the matrix element m ij.5routines can make use of high-level(“level-3”)BLAS in certain sparse matrix computations7of which we make use.For this reason,the CsparseMatrix class and subclasses are the principal classes for sparse matrices in the Matrix package.The Matrix package provides the following classes for sparse matrices ...FIXME many more —maybe ex plain naming scheme?...dgTMatrix general,numeric,sparse matrices in (a possibly redundant)triplet form.This can be a conve-nient form in which to construct sparse matrices.dgCMatrix general,numeric,sparse matrices in the (sorted)compressed sparse column format.dsCMatrix symmetric,real,sparse matrices in the (sorted)compressed sparse column format.Only theupper or the lower triangle is stored.Although there is provision for both forms,the lower triangle form works best with TAUCS.dtCMatrix triangular,real,sparse matrices in the (sorted)compressed sparse column format.Todo:Can also read and write the Matrix Market and read the Harwell-Boeing representations.Todo:Can convert from a dense matrix to a sparse matrix (or use the Matrix function)but going through an intermediate dense matrix may cause problems with the amount of memory required.Todo:similar range of operations as for the dense matrix classes.3More detailed examples of “Matrix”operationsHave seen drop0()above,showe a nice double example (where you see “.”and “0”).Show the use of dim<-for resizing a (sparse)matrix.Maybe mention nearPD().Todo:Solve a sparse least squares problem and demonstrate memory /speed gain Todo:mention lme4and lmer(),maybe use one example to show the matrix sizes.4Notes about S4classes and methods implementationMaybe we could give some glimpses of implementations at least on the R level ones?Todo:The class hierarchy:a non-trivial tree where only the leaves are “actual”classes.Todo:The main advantage of the multi-level hierarchy is that methods can often be defined on a higher (virtual class)level which ensures consistency [and saves from “cut &paste”and forgetting things]Todo:Using Group Methods5Session Info>toLatex(sessionInfo())•R version 4.3.1Patched (2023-08-09r84931),x86_64-pc-linux-gnu•Locale:LC_CTYPE=de_CH.UTF-8,LC_NUMERIC=C ,LC_TIME=en_US.UTF-8,LC_COLLATE=C ,LC_MONETARY=en_US.UTF-8,LC_MESSAGES=de_CH.UTF-8,LC_PAPER=de_CH.UTF-8,LC_NAME=C ,LC_ADDRESS=C ,LC_TELEPHONE=C ,LC_MEASUREMENT=de_CH.UTF-8,LC_IDENTIFICATION=C •Time zone:Europe/Zurich •TZcode source:system (glibc)•Running under:Fedora Linux 36(Thirty Six)•Matrix products:default8•BLAS:/u/maechler/R/D/r-patched/F36-64-inst/lib/libRblas.so•LAPACK:/usr/lib64/liblapack.so.3.10.1•Base packages:base,datasets,grDevices,graphics,methods,stats,utils•Other packages:Matrix1.6-1•Loaded via a namespace(and not attached):compiler4.3.1,grid4.3.1,lattice0.21-8,tools4.3.1 ReferencesE.Anderson,Z.Bai,C.Bischof,S.Blackford,J.Demmel,J.Dongarra,J.Du Croz,A.Greenbaum,S.Ham-marling,A.McKenney,and PACK Users’Guide.SIAM,Philadelphia,PA,3rd edition, 1999.Tim Davis.CHOLMOD:sparse supernodal Cholesky factorization and update/downdate. http://www.cise.ufl.edu/research/sparse/cholmod,2005a.Tim Davis.CSparse:a concise sparse matrix package.http://www.cise.ufl.edu/research/sparse/CSparse, 2005b.Jack Dongarra,Cleve Moler,Bunch,and G.W.Stewart.Linpack Users’Guide.SIAM,1979.Roger Koenker and Pin Ng.SparseM:A sparse matrix package for R.J.of Statistical Software,8(6),2003.B.T.Smith,J.M.Boyle,J.J.Dongarra,B.S.Garbow,Y.Ikebe,V.C.Klema,and C.B.Moler.Matrix Eigensystem Routines.EISPACK Guide,volume6of Lecture Notes in Computer Science.Springer-Verlag, New York,1976.R.Clint Whaley,Antoine Petitet,and Jack J.Dongarra.Automated empirical optimization of software and the ATLAS project.Parallel Computing,27(1–2):3–35,2001.Also available as University of Tennessee LAPACK Working Note#147,UT-CS-00-448,2000(/lapack/lawns/lawn147.ps).9。
PLATO软件操作手册-Matrix模块

目录一、Matrix简介 (1)1.1 打开程序 (1)1.2 菜单栏介绍 (1)二、创建Matrix过程 (3)2.1 创建一个新项目和新的系统元素 (3)2.2 开始创建系统Matrix (4)2.3 创建组件Matrix (8)2.4 创建元件Matrix (9)2.5 规格编辑器(specification edit) (10)三、使用优先级对功能或结构进行分析 (11)四、其它操作技巧 (12)4.1 删除系统元素 (12)4.2 使用已有系统元素 (13)4.3 功能重用 (14)4.4 查找系统元素 (15)一、Matrix模块简介SCIO-Matrix模块可以对产品进行系统的结构功能分析,为后两个模块Net-Builder和FMEA提供基础。
本手册将以Iphone4s为例对Matrix模块操作步骤进行讲解。
注:在软件中进行任何操作后无需手动保存,所有数据变动都会自动保存到数据库。
1.1 打开程序从开始菜单中找到SCIO-Matrix程序()并打开,会出现以下登录界面:默认数据库是本地,输入用户名及密码(默认用户名和密码皆为plato)即可进入Matrix 模块。
1.2 菜单栏介绍1.2.1 The Application bar ()点击此图标可以在最右侧看到三个部分:Documents,SCIO,Plug-ins。
其中documents栏下面,可以显示最近打开过的系统元素或者创建新的系统元素;SCIO 栏下面,有SCIO软件的各个模块图标,点击即可切换到该模块;Plug-ins栏下则是一些插件程序。
如若想隐藏最右侧栏,再次点击The Application bar ()图标即可。
1.2.2 Structure tree(结构树)和function tree(功能树)点击图标,则会打开结构树,如上图(左)所示,会显示所有项目及系统元素;点击图标,则会打开功能树,如上图(右)所示,会显示元素的所有功能。
Matrix 中文手册

重要的安全指导!请阅读这本手册!它提供了很重要的安全、安装和操作指导,使您的设备发挥最高的性能,并且能够延长设备的使用寿命。
请保存这本手册!它包含了安全使用UPS 的重要指导,而且还告诉您,如何在需要时获得厂家提供的服务。
在以后对UPS的维修和存放中,以及遇到问题时,都需要参看这本手册以获得正确的指导。
射频干扰重要的安全指导!警告:我们只对遵守规则的用户负责,千万不要自行更改或拆卸,否则用户将失去使用这个设备的权力。
注意:此设备被检测通过,并且符合FCC第15部分A规则,由于该设备会产生和发出射频干扰,这些限制使得设备在商用环境下运行时产生的有害干扰保持在一定限度内,使其它通讯设备得到有效的保护。
如果没有根据指导安装或使用,可能会对无线电通讯产生有害的干扰。
总而言之,我们并不保证在特殊情况下安装时不会出现干扰。
如果该设备的关闭和打开对无线电设备产生干扰和影响,我们建议用户用以下方法中的一种或几种去尝试消除干扰。
■重置天线的方向。
■加大设备和接收器的距离。
■使设备连接在与接收器不在同一电路的插座上。
■向销售商、经验丰富的无线电调试人员咨询求助。
■该产品必须使用屏蔽通讯电缆接口。
目录1.0简介(1)2.0安全(3)3.0外观(4)隔离模块(4)电子模块(6)电池组(8)4.0安装(10)开箱检查,保护措施,移动UPS,放置(10)输入电压要求(11)安装步骤(12)输入线安装(13)输入电压插头选择(15)输出线安装过程(16)模块连接(18)紧急断电接口(Emergency Power Off Interface)(20)5.0操作(21)显示与控制操作(22)6.0UPS监控(29)计算机接口(29)7.0问题(30)故障查找(31)故障信息(33)重装电子模块(33)重装或增加了电池组(35)获得服务(36)8.0UPS存放(37)9.0指标(38)1.0简介1.1概述Matrix-UPS是一种高性能在线互动式的不间断电源。
Mares Matrix 潜水电脑 中文说明书

Matrix 潜水电脑
MATRIX 潜水电脑
目录
1. 简介 1.1 词汇表 1.2 运行模式 1.3 充电电池 1.3.1 电池充电 1.3.2 将 MATRIX 与电脑连接 1.4 按钮操作 1.4.1 数字手表显示 1.4.2 指针式电子表显示 1.4.3 数字式罗盘 1.4.3.1 设定方位 1.5 紧急情况
MATRIX 潜水电脑
1.2 运行模式 Matrix 电脑的功能可分成两大类,每种功能 对应特定的运行模式: z 手表:Matrix 处于水面位置,保持干燥
状态。在此模式下,您可将其作为普通 手表使用。您还可以更改设置,查阅潜 水日志,使用潜水规划功能,在潜水后 查看剩余减饱和时间和下载数据至电 脑等。 z 潜水:Matrix 用于监视深度、时间、温 度,并进行减压计算;潜水模式可细分 为四小类: -潜水前[Matrix 位于水面位置,但已开始对 环境压力进行监控,从到达 1.2 米/4 英尺以 下位置的那一刻起即开始对潜水进行计算]; -潜水 -水面时间[Matrix 在潜水结束后位于水面位 置;潜水时间计算暂停,但如果潜水员在三 分钟内下潜,则将恢复计算潜水时间,其中 也包含了水面时间。这一功能便于潜水员短 暂地停留水面,设定船只的方向,然后再次 下潜并游向船只]; -潜水后[设置为水面模式三分钟后,Matrix 将关闭日志并恢复显示减饱和时间,不宜飞 行时间和两次上升至水面的间隔时间;该状 态将持续至减饱和与不宜飞行时间均减为 零]。
3. 佩戴 Matrix 进行潜水 3.1 关于高氧气体的说明 3.2 警报 3.2.1 上升速度 3.2.2 MOD/PPO2 3.2.3 CNS=100% 3.2.4 错过的减压停留 3.2.4.1 错过的减压停留模式 3.2.5 电池电量不足 3.3 显示信息 3.3.1 交替显示 3.3.1.1 图表 3.3.1.2 罗盘 3.4 潜水后 3.5 采用一种以上气体混合物进行潜水 3.5.1 设置一种以上气体 3.5.2 气体切换 3.5.3 特殊情况 3.5.3.1 切回较低氧浓度的气体混合物 3.5.3.2 在切换气体后潜入 MOD 以下位置 3.6 水底时间定时器模式 3.6.1 违规潜水对水底时间定时器模式的影响
Matrix中文手册

学习使人进步MATRIX手册1、特性和优点发送端电源来自交换机的STP CAT 5e/6线缆32口交换机支持双电源USB2.0支持发送端支持分离的线缆连接目标视频、USB、声音2、安全交换机支持SSL、AES,提供访问控制,可以对每个用户、发送、接收器设置允许的USB类型使用先进的Dambrackas视频压缩算法,6个USB2.0接口,提供板载OBWImatrix交换机有20、32端口2种32口支持600W冗余电源,20口支持350W单电源支持级联,双网卡故障自动切换3、设备3.1 MATRIX SWITCH3.2 MATRIX RECEIVER3.3 MATRIX TRANSMITTER4、安装和配置4.1 配置选项交换机的DHCP默认开启,当交换机获取到IP地址,会显示在LCD上。
SETUP端口连接默认用户名Admin,密码为空,第一次登录会要求修改密码。
9600,8,1,无,无。
4.1.1 单交换机4.1.2 多交换机多个交换机可以互连以创建更大的交换系统支持多个接收器和发射器。
这被称为级联系统。
当级联矩阵交换机,您可以无缝连接到任何目标设备从屏幕显示(OSD)接口一个单独的列表,仿佛一切目标设备被连接到一台交换机。
使用无缝级联,您将需要配置级联交换机作为一个主站和从站(次)。
只能有一个主的交换机。
4.1.3 级联设置1、选择一个主交换机;2、用STP线缆分别连接主、从交换机的RJ-45口;3、连接发送和接收到主、从交换机;4、配置交换机的主从模式。
4.2 用户名、密码更改设置端口密码选项允许用户启用或更改设置端口密码。
这将启用或禁用进入启动菜单,允许用户选择当前或以前的版本固件引导。
当从设置端口连接到交换机,管理员还可以选择引导图像。
当新的固件加载到交换机,允许管理员选择使用哪个启动映像。
开机1-5秒按任意键进入引导菜单。
4.3 交换机OBWI第一次访问OBWI必须设置管理员密码,管理员帐号Admin,密码为空。
Datalogic Matrix 210(200)条码扫描器设置软件Visiset中文说明书

1、启动Visiset软件。
2、Visiset软件启动后的画面。
通讯设置 日志设置选项 所有选择 保存 退出 日志 运行界面 默认打开状态 删除旧的日志日志打印等级仅错误 仅编码关 开关 开日志文件名【log 】菜单激活时通讯设置 字体&背景改变背景改变字体 文本举例恢复出厂设置保存 退出日志 运行界面 【Environment 】菜单激活时通讯设置 自动连接端口 网口串口通讯方式 波特率 端口停止位校检位自动搜索端口配置 保存 退出日志 运行界面 USB 口 【Communication 】菜单激活时4、菜单栏【File】下拉菜单子项开始日志文件重设日志文件查看统计重设统计退出5、菜单栏【Edit】下拉菜单子项清除屏幕显示从文件获取配置读码器程序升级参数设置帮助关于VisiSet9、点击菜单栏【connect】按钮后跳出下面的功能配置窗口。
安装向导校准工具符号验证运行模式捕获图像解码最后一张图像查看最后一张图像下载最后一张图像上传Bmp图像图像效果按钮功能菜单左上方右下方图像采集信息采集设置解码结果符号代码数据代码中心选定的代码停止图像采集关闭在没有解码时在解码时在捕获之后屏幕模式已解码图像代码位置相机模式强制触发查看图像下载图像图像明暗质量关闭输入输出状态统计最后的样品信息解码率文件模式下载发送发送默认值临时/永久即时生效发送生效设备二维码一维码邮政码图像处理杂项数据收集代码匹配代码验证通讯设置读码系统布置接线盒网关显示诊断运行模式IO输入输出读码特性校准LED灯和按键10、点击【Calibration Tool】按钮后跳出下面两个窗口,左侧为【校准工具】窗口,右侧为【参数设置】窗口。
11、关闭左侧【校准窗口】后,右侧【参数设置窗口】功能按钮变黑激活。
12、【参数设置】窗口菜单栏【File】子菜单内容。
文件加载配置信息文件保存配置信息文件把配置信息文件保存为text文本格式把配置信息文件保存为html网页格式退出永久生效 临时生效获取配置信息发送配置信息 》 发送配置信息及选项发送默认配置信息发送默认配置信息及选项选择下一个参数 选择前一个参数驱动设置12、【参数设置】窗口菜单栏【Device 】子菜单内容。
Matrix系统说明书

Production of precision parts – the Matrix systemRequired air pressure, pneumatic chucks: 6±1 barRepetition accuracy – within 0.002 mmAll references hardened and groundTHE MATRIX SYSTEMMeasures to reduce the downtime of your machines are significantly more worth while than chasing seconds in the actual machining process. What matters is to keep the machines running. And that’s when you need an interface that gives fast setting-up.The Matrix system is just that kind of interface. Setting-up in parallel away from the machine while it is working and then setting up in a matter of seconds in the stationary machine. Important for long runs, but crucial for the profitability of short runs or one-piece production.The design has been optimised for metal-cutting machining and is ideal for work involving high machining forces. The generous diameter of the drawbar means short distances between the references and the applied locking force, giving maximum stability and accuracy. The inherentproperties of the Matrix system truly come into their own in tough machining applications.As well as extreme accuracy, Matrix features low construction height, ultra-precise indexing, a drawbar with through hole, and a broad range of pallets.Locking force –16 000 NFixed index positions 4x90°MATRIX...… reduces setting-up times… ensures precision and quality… has automatic air-blast cleaning of the references … is sealed against dirt and swarf – withstands severe work environments … has enhanced clamping force – turbo locking … is suitable for automatic changing with System 3R’s automation programüüüüüOVERVIEW OF TABLE CHUCKSArticle number RequiredDrawbar FeatureEUROPESystem 3R Europe GmbH Wasserweg 19DE-64521, GROSS-GERAU tel +49 61 52 80 02 0fax +49 61 52 80 02 35e-mail:********************Chech Republic & SlovakiaSystem 3R Czech Tiskarska 10/257CZ-108 28 PRAHA 10tel +420 234 054 224fax +420 234 054 225e-mail:****************France & PortugalSystem 3R France56 Boulevard de Courcerin Les Espaces Multiservices 15F-77183 CROISSY BEAUBURG tel +33-01 60 95 90 80fax +33-01 60 37 88 16e-mail:********************Germany & BeNeLuxSystem 3R Deutschland Wasserweg 19DE-64521, GROSS-GERAU tel +49 61 52 80 02 0fax +49 61 52 80 02 35e-mail:********************Italy & SpainSystem 3R Italia Via Ponchielli, 2/4IT-20063 CERNUSCO SUL NAVIGLIO (MI)tel +39 02 92 38 821fax +39 02 92 11 23 19e-mail:********************ScandinaviaSystem 3R Nordic Sorterargatan 1SE-162 50 VÄLLINGBY tel +46-08 620 20 00fax +46-08 38 81 84e-mail:********************Järfälla Härdverkstad Elektronikhöjden 8SE-175 43 JÄRFÄLLA tel +46-08 580 125 50fax +46-08 580 126 55e-mail:***********Switzerland & AustriaSystem 3R Schweiz AG Wilerstrasse 98CH-9230 FLAWIL tel +41-071 394 13 50fax +41-071 394 13 60e-mail:********************TurkeySystem 3R TürkiyeAbdi Ipekci Cad. Ozel Idare Is Merk 150/209Bayrampasa 34030 ISTANBUL tel +90-212 613 8062-8063fax +90-212 613 8069e-mail:********************United KingdomSystem 3R UK Paradise WayWalsgrave TriangleCoventry, West Midlands CV2 2ST, United Kingdom tel +44-02476 538653fax +44-02476 538695T -2250-E 09.08 S u b j e c t t o m o d i fi c a t i o n s • S y s t e m 3R , a m e m b e r o f t h e G e o r g F i s c h e r G r o u p .ASIAFar East, China & IndiaSystem 3R Far East Pte.Ltd.6 Harper RoadLeong Huat Building, 01-01SINGAPORE SG-369 674tel +65-6289 4811fax +65-6289 3011**************************Shanghai Contact Office tel +86-21 6432 7927fax +86-21 6432 7928**************************Beijing Contact Office tel +86-10 8225 1632fax +86-10 8225 1635Guangdong Contact Office tel +86-769 8162 0628fax +86-769 8162 0638Malaysia Contact Office tel +60-03 7877 4785fax +60-03 7877 5948Taiwan Re gional Office tel +886-02 2278 3126fax +886-02 2278 3108Thailand Contact Office tel / fax +66-2 6422 764Japan & KoreaSystem 3R Japan CO., Ltd.Kaki Building2-5-22, Suido, Bunkyo-ku TOKYO JP-112-0005tel +81-03 5840-7383fax +81-03 5840-8723**************************Nagoya Regional Office tel +81-052 774 6250fax +81-052 774 6285Osaka Regional Office tel +81-06 6396 1500fax +81-06 6396 2855System 3R International ABSorterargatan 1, SE-162 50 VÄLLINGBYtel+46-086202000,fax+46-087595234,e-mail:*****************,Combi, Delphin, Dynafix, Locx, LX, Macro, One Minute Set-Up, One System Partner, R2R, System 3R, VDP , WorkMaster, WorkPal, WorkPartner, WorkShopManager, 3HP , 3R, 3Ready-To-Run and 3Refix are registered trademarks of System 3R.AMERICASSystem 3R USA Inc.Headquarters & Technical Center 915 Busse RoadELK GROVE VILLAGE, US-IL 60007tel +1 847 439 4888fax +1 847 439 5099e-mail:********************Canada & Eastern MItel +1 847 439 4888fax +1 847 439 5099e-mail:*********************AZ, CA, CO, ID, MT, NM, NV, OR, UT, WA, WY & Mexicotel +1 847 439 4888fax +1 847 439 5099e-mail:*********************IA, MN, ND, NE, SD & WItel +1 847 439 4888fax +1 847 439 5099e-mail:*********************AR, IN, KY, OH & TNtel +1 847 439 4888fax +1 847 439 5099e-mail:*********************AL, FL, GA, LA, MS, NC, SC & TXtel +1 847 439 4888fax +1 847 439 5099e-mail:*********************IL, KS, MO, OK & Western MItel +1 847 439 4888fax +1 847 439 5099e-mail:*********************NJ, NY & PAtel +1 847 439 4888fax +1 847 439 5099e-mail:*********************CT, DC, DE, MA, MD, ME, NH, RI, VA, VT & WVtel +1 847 439 4888fax +1 847 439 5099e-mail:*********************Eastern WItel +1 847 439 4888fax +1 847 439 5099e-mail:*********************For further information, see 。
Matrix软件操作说明

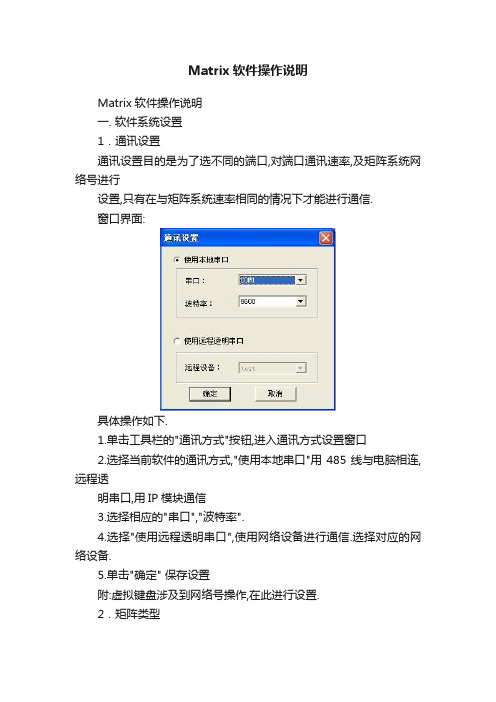
Matrix软件操作说明一. 软件系统设置1.通讯设置通讯设置目的是为了选不同的端口,对端口通讯速率,及矩阵系统网络号进行设置,只有在与矩阵系统速率相同的情况下才能进行通信.窗口界面:具体操作如下.1.单击工具栏的"通讯方式"按钮,进入通讯方式设置窗口2.选择当前软件的通讯方式,"使用本地串口"用485线与电脑相连,远程透明串口,用IP模块通信3.选择相应的"串口","波特率".4.选择"使用远程透明串口",使用网络设备进行通信.选择对应的网络设备.5.单击"确定" 保存设置附:虚拟键盘涉及到网络号操作,在此进行设置.2.矩阵类型窗口界面具体操作1.单击"软件系统设置"->"矩阵类型",进入矩阵类型界面2.选择"矩阵类型"(此类型关系到当前所读取矩阵数据的正确性,请务必选择对应的矩阵型号).3.单击"确定" 保存设置3.修改密码窗口界面具体操作1.单击"软件系统设置"->"修改密码",进入修改密码界面2.输入"旧密码",并确认输入新密码3.单击"确定" 保存设置4.登陆/登出为防止他人任意更改系统设置,系统提供此功能,在拥有管理员权限的情况下方可操作系统.其界面如下:二. 矩阵系统设置1.时间设置设置矩阵系统时间.窗口界面具体操作:1.单击"矩阵系统设置"->"时间设置",2.进入"时间设置"界面3.可单击"同步系统时间"按钮,与计算机系统同步时间4.也可手工设置矩阵时间.5.单击"确定",保存设置2.云台协议设置云台协议窗口界面具体操作:1.单击"矩阵系统设置"->"云台协议",2.进入"云台协议"设置界面3.选择"云台协议",和对应的通信速率.4.单击"确定",保存设置3.网络编号设置矩阵系统网络号窗口界面具体操作:1.单击"矩阵系统设置"->"网络编号",2.进入"网络编号"界面3.选择"网络编号4.单击"确定",保存设置4. 键盘数量设置矩阵系统键盘数量窗口界面具体操作:1.单击"矩阵系统设置"->"键盘数量",2.进入"键盘数量"界面3.选择"键盘数量"4.单击"确定",保存设置三. 标题与显示1. 摄像机标题设置窗口界面具体操作1.单击"标题与显示"->"摄像机标题" 或工具栏上的"摄像机标题"按钮,进入摄像机标题设置界面;2.单击"读矩阵"按钮,系统从矩阵主机读取数据并显示;3.单击"写矩阵"按钮,系统将当前页数据写入矩阵主机;4.单击"读数据库",系统从数据库中读取数据,同时也可将数据库中设置的数据,写入矩阵,也可将数据写回矩阵主机;5.单击"写数据库",将当前页数据写回数据库,以备日后查看,维护.2. 监示器标题窗口界面具体操作1.单击"标题与显示"->"监示器标题" 或工具栏上的"监示器标题"按钮,进入"监示器标题"设置界面;2.单击"读矩阵"按钮,系统从矩阵主机读取数据并显示;3.单击"写矩阵"按钮,系统将当前页数据写入矩阵主机;4.单击"读数据库",系统从数据库中读取数据,同时也可将数据库中设置的数据,写入矩阵,也可将数据写回矩阵主机;5.单击"写数据库",将当前页数据写回数据库,以备日后查看,维护.3. 屏幕位置设置监示器标题/时间显示位置窗口界面具体操作:1.单击"标题与显示"->屏幕位置" ;2.进入"屏幕位置"界面;3.拖动"屏幕位置"按钮到适当位置;4.单击"确定"保存设置;5.重启矩阵系统,使设置生效.4. 标题位置设置监示器标题/时间显示位置窗口界面具体操作:1.单击"标题与显示"->标题位置"2.进入"标题位置"界面.3.拖动"标题位置"按钮到适当位置4.单击"确定"保存设置5.重启矩阵系统,使设置生效5. 时间位置设置监示器标题/时间显示位置窗口界面具体操作:1.单击"标题与显示"->时间位置" ;2.进入"时间位置"界面;3.拖动"时间位置"按钮到适当位置;4.单击"确定"保存设置;5.重启矩阵系统,使设置生效.四. 切换1. 程序切换窗口界面具体操作1.单击"切换"->"程序切换" 或工具栏上的"程序切换"按钮,进入程序切换设置界面,2.单击"读矩阵"按钮,系统从矩阵主机读取数据并显示,3.单击"写矩阵"按钮,系统将当前页数据写入矩阵主机.4.单击"读数据库",系统从数据库中读取数据,同时也可将数据库中设置的数据,写入矩阵,也可将数据写回矩阵主机.5.单击"写数据库",将当前页数据写回数据库,以备日后查看,维护.6.单击"上一页","下一页",可查看不同的切换设置2. 同步切换窗口界面具体操作1.单击"切换"->"同步切换" 或工具栏上的"同步切换"按钮,进入同步切换设置界面,2.单击"读矩阵"按钮,系统从矩阵主机读取数据并显示,3.单击"写矩阵"按钮,系统将当前页数据写入矩阵主机.4.单击"读数据库",系统从数据库中读取数据,同时也可将数据库中设置的数据,写入矩阵,也可将数据写回矩阵主机.5.单击"写数据库",将当前页数据写回数据库,以备日后查看,维护.6.单击"上一页","下一页",可查看不同的切换设置3. 群组切换窗口界面具体操作1.单击"切换"->"群组切换" 或工具栏上的"群组切换"按钮,进入群组切换设置界面,2.单击"读矩阵"按钮,系统从矩阵主机读取数据并显示,3.单击"写矩阵"按钮,系统将当前页数据写入矩阵主机.4.单击"读数据库",系统从数据库中读取数据,同时也可将数据库中设置的数据,写入矩阵,也可将数据写回矩阵主机.5.单击"写数据库",将当前页数据写回数据库,以备日后查看,维护.6.单击"上一页","下一页",可查看不同的切换设置五. 权限1. 键盘/监示器窗口界面具体操作1.单击"权限"->"键盘/监示器" ,进入"键盘/监示器"设置界面;2.单击"读矩阵"按钮,系统从矩阵主机读取数据并显示;3.单击"写矩阵"按钮,系统将当前页数据写入矩阵主机;4.单击"读数据库",系统从数据库中读取数据,同时也可将数据库中设置的数据,写入矩阵,也可将数据写回矩阵主机;5.单击"写数据库",将当前页数据写回数据库,以备日后查看,维护.2. 键盘/摄像机窗口界面具体操作1.单击"权限"->"键盘/摄像机" 进入"键盘/摄像机"设置界面;2.单击"读矩阵"按钮,系统从矩阵主机读取数据并显示;3.单击"写矩阵"按钮,系统将当前页数据写入矩阵主机;4.单击"读数据库",系统从数据库中读取数据,同时也可将数据库中设置的数据,写入矩阵,也可将数据写回矩阵主机;5.单击"写数据库",将当前页数据写回数据库,以备日后查看,维护.3. 监示器/摄像机窗口界面具体操作1.单击"权限"->"监示器/摄像机" ,进入"监示器/摄像机"设置界面;2.单击"读矩阵"按钮,系统从矩阵主机读取数据并显示;3.单击"写矩阵"按钮,系统将当前页数据写入矩阵主机;4.单击"读数据库",系统从数据库中读取数据,同时也可将数据库中设置的数据,写入矩阵,也可将数据写回矩阵主机;5.单击"写数据库",将当前页数据写回数据库,以备日后查看,维护.4. 键盘/报警窗口界面具体操作1.单击"权限"->"键盘/报警" ,进入"键盘/摄像机"设置界面;2.单击"读矩阵"按钮,系统从矩阵主机读取数据并显示;3.单击"写矩阵"按钮,系统将当前页数据写入矩阵主机;4.单击"读数据库",系统从数据库中读取数据,同时也可将数据库中设置的数据,写入矩阵,也可将数据写回矩阵主机;5.单击"写数据库",将当前页数据写回数据库,以备日后查看,维护.5. 网络/键盘窗口界面具体操作1.单击"权限"->"网络/键盘" ,进入"网络/键盘"设置界面;2.单击"读矩阵"按钮,系统从矩阵主机读取数据并显示;3.单击"写矩阵"按钮,系统将当前页数据写入矩阵主机;4.单击"读数据库",系统从数据库中读取数据,同时也可将数据库中设置的数据,写入矩阵,也可将数据写回矩阵主机;5.单击"写数据库",将当前页数据写回数据库,以备日后查看,维护.六. 报警1报警联动窗口界面具体操作1.单击"报警"->"报警联动" ,进入"报警联动"设置界面;2.单击"读矩阵"按钮,系统从矩阵主机读取数据并显示;3.单击"写矩阵"按钮,系统将当前页数据写入矩阵主机;4.单击"读数据库",系统从数据库中读取数据,同时也可将数据库中设置的数据,写入矩阵,也可将数据写回矩阵主机;5.单击"写数据库",将当前页数据写回数据库,以备日后查看,维护.2. 自动设防窗口界面具体操作1.单击"报警"->"自动设防" ,进入"自动设防"设置界面;2.单击"读矩阵"按钮,系统从矩阵主机读取数据并显示;3.单击"写矩阵"按钮,系统将当前页数据写入矩阵主机;4.单击"读数据库",系统从数据库中读取数据,同时也可将数据库中设置的数据,写入矩阵,也可将数据写回矩阵主机;5.单击"写数据库",将当前页数据写回数据库,以备日后查看,维护.3. 历史报警窗口界面具体操作1.单击"报警"->"历史报警" ,进入"历史报警"界面;2.系统自动读取矩阵系统历史报警记录;3.可单击"刷新"按钮重新读取矩阵系统数据.4. 报警端口设置窗口界面具体操作:1.单击"报警"->"报警端口设置" ;2.进入"报警端口设置"界面 ;3.选择"报警端口" ;4.单击"确定",保存设置.5. 设防/撤防状态窗口界面具体操作1.单击"报警"->"设防/撤防状态" ,进入"设防/撤防状态"界面;2.系统自动读取矩阵系统历史报警记录;3.可单击"刷新"按钮重新读取矩阵系统数据;七. 键盘设置1. 虚拟键盘虚拟键盘是为了方便用户在计算机系统操纵矩阵设计的.功能与矩阵键盘类似.可通过虚拟键盘对矩阵进行,摄像机切换等操作. 窗口界面八. 常见问题下位机无响应:可能存在以下几种情况:1.连接线路太长或线路质量存在问题.数据无法接收.2.系统波特率与矩阵主机波特率不一至.系统波特率可通过"通讯方式"进行设置;3.矩阵主机系统软件被破坏,可与厂商联系,进行系统升级.可读矩阵数据,但无法写入矩阵:1.线路或转接器存在问题.请更换好一点的通信设备.虚拟键盘无法操作:1.网络号或波特率与矩阵系统不相符;解决方法参看“通讯设置”2.线路质量问题。
Matrix中文手册

MATRIX手册1、特性和优点发送端电源来自交换机的STP CAT 5e/6线缆32口交换机支持双电源USB2.0支持发送端支持分离的线缆连接目标视频、USB、声音2、安全交换机支持SSL、AES,提供访问控制,可以对每个用户、发送、接收器设置允许的USB类型使用先进的Dambrackas视频压缩算法,6个USB2.0接口,提供板载OBWImatrix交换机有20、32端口2种32口支持600W冗余电源,20口支持350W单电源支持级联,双网卡故障自动切换3、设备3.1 MATRIX SWITCH3.2 MATRIX RECEIVER3.3 MATRIX TRANSMITTER4、安装和配置4.1 配置选项交换机的DHCP默认开启,当交换机获取到IP地址,会显示在LCD上。
SETUP端口连接默认用户名Admin,密码为空,第一次登录会要求修改密码。
9600,8,1,无,无。
4.1.1 单交换机4.1.2 多交换机多个交换机可以互连以创建更大的交换系统支持多个接收器和发射器。
这被称为级联系统。
当级联矩阵交换机,您可以无缝连接到任何目标设备从屏幕显示(OSD)接口一个单独的列表,仿佛一切目标设备被连接到一台交换机。
使用无缝级联,您将需要配置级联交换机作为一个主站和从站(次)。
只能有一个主的交换机。
4.1.3 级联设置1、选择一个主交换机;2、用STP线缆分别连接主、从交换机的RJ-45口;3、连接发送和接收到主、从交换机;4、配置交换机的主从模式。
4.2 用户名、密码更改设置端口密码选项允许用户启用或更改设置端口密码。
这将启用或禁用进入启动菜单,允许用户选择当前或以前的版本固件引导。
当从设置端口连接到交换机,管理员还可以选择引导图像。
当新的固件加载到交换机,允许管理员选择使用哪个启动映像。
开机1-5秒按任意键进入引导菜单。
4.3 交换机OBWI第一次访问OBWI必须设置管理员密码,管理员帐号Admin,密码为空。
Matrix软件操作说明
Matrix软件操作说明Matrix软件操作说明一. 软件系统设置1.通讯设置通讯设置目的是为了选不同的端口,对端口通讯速率,及矩阵系统网络号进行设置,只有在与矩阵系统速率相同的情况下才能进行通信.窗口界面:具体操作如下.1.单击工具栏的"通讯方式"按钮,进入通讯方式设置窗口2.选择当前软件的通讯方式,"使用本地串口"用485线与电脑相连,远程透明串口,用IP模块通信3.选择相应的"串口","波特率".4.选择"使用远程透明串口",使用网络设备进行通信.选择对应的网络设备.5.单击"确定" 保存设置附:虚拟键盘涉及到网络号操作,在此进行设置.2.矩阵类型窗口界面具体操作1.单击"软件系统设置"->"矩阵类型",进入矩阵类型界面2.选择"矩阵类型"(此类型关系到当前所读取矩阵数据的正确性,请务必选择对应的矩阵型号).3.单击"确定" 保存设置3.修改密码窗口界面具体操作1.单击"软件系统设置"->"修改密码",进入修改密码界面2.输入"旧密码",并确认输入新密码3.单击"确定" 保存设置4.登陆/登出为防止他人任意更改系统设置,系统提供此功能,在拥有管理员权限的情况下方可操作系统.其界面如下:二. 矩阵系统设置1.时间设置设置矩阵系统时间.窗口界面具体操作:1.单击"矩阵系统设置"->"时间设置",2.进入"时间设置"界面3.可单击"同步系统时间"按钮,与计算机系统同步时间4.也可手工设置矩阵时间.5.单击"确定",保存设置2.云台协议设置云台协议窗口界面具体操作:1.单击"矩阵系统设置"->"云台协议",2.进入"云台协议"设置界面3.选择"云台协议",和对应的通信速率.4.单击"确定",保存设置3.网络编号设置矩阵系统网络号窗口界面具体操作:1.单击"矩阵系统设置"->"网络编号",2.进入"网络编号"界面3.选择"网络编号4.单击"确定",保存设置4. 键盘数量设置矩阵系统键盘数量窗口界面具体操作:1.单击"矩阵系统设置"->"键盘数量",2.进入"键盘数量"界面3.选择"键盘数量"4.单击"确定",保存设置三. 标题与显示1. 摄像机标题设置窗口界面具体操作1.单击"标题与显示"->"摄像机标题" 或工具栏上的"摄像机标题"按钮,进入摄像机标题设置界面;2.单击"读矩阵"按钮,系统从矩阵主机读取数据并显示;3.单击"写矩阵"按钮,系统将当前页数据写入矩阵主机;4.单击"读数据库",系统从数据库中读取数据,同时也可将数据库中设置的数据,写入矩阵,也可将数据写回矩阵主机;5.单击"写数据库",将当前页数据写回数据库,以备日后查看,维护.2. 监示器标题窗口界面具体操作1.单击"标题与显示"->"监示器标题" 或工具栏上的"监示器标题"按钮,进入"监示器标题"设置界面;2.单击"读矩阵"按钮,系统从矩阵主机读取数据并显示;3.单击"写矩阵"按钮,系统将当前页数据写入矩阵主机;4.单击"读数据库",系统从数据库中读取数据,同时也可将数据库中设置的数据,写入矩阵,也可将数据写回矩阵主机;5.单击"写数据库",将当前页数据写回数据库,以备日后查看,维护.3. 屏幕位置设置监示器标题/时间显示位置窗口界面具体操作:1.单击"标题与显示"->屏幕位置" ;2.进入"屏幕位置"界面;3.拖动"屏幕位置"按钮到适当位置;4.单击"确定"保存设置;5.重启矩阵系统,使设置生效.4. 标题位置设置监示器标题/时间显示位置窗口界面具体操作:1.单击"标题与显示"->标题位置"2.进入"标题位置"界面.3.拖动"标题位置"按钮到适当位置4.单击"确定"保存设置5.重启矩阵系统,使设置生效5. 时间位置设置监示器标题/时间显示位置窗口界面具体操作:1.单击"标题与显示"->时间位置" ;2.进入"时间位置"界面;3.拖动"时间位置"按钮到适当位置;4.单击"确定"保存设置;5.重启矩阵系统,使设置生效.四. 切换1. 程序切换窗口界面具体操作1.单击"切换"->"程序切换" 或工具栏上的"程序切换"按钮,进入程序切换设置界面,2.单击"读矩阵"按钮,系统从矩阵主机读取数据并显示,3.单击"写矩阵"按钮,系统将当前页数据写入矩阵主机.4.单击"读数据库",系统从数据库中读取数据,同时也可将数据库中设置的数据,写入矩阵,也可将数据写回矩阵主机.5.单击"写数据库",将当前页数据写回数据库,以备日后查看,维护.6.单击"上一页","下一页",可查看不同的切换设置2. 同步切换窗口界面具体操作1.单击"切换"->"同步切换" 或工具栏上的"同步切换"按钮,进入同步切换设置界面,2.单击"读矩阵"按钮,系统从矩阵主机读取数据并显示,3.单击"写矩阵"按钮,系统将当前页数据写入矩阵主机.4.单击"读数据库",系统从数据库中读取数据,同时也可将数据库中设置的数据,写入矩阵,也可将数据写回矩阵主机.5.单击"写数据库",将当前页数据写回数据库,以备日后查看,维护.6.单击"上一页","下一页",可查看不同的切换设置3. 群组切换窗口界面具体操作1.单击"切换"->"群组切换" 或工具栏上的"群组切换"按钮,进入群组切换设置界面,2.单击"读矩阵"按钮,系统从矩阵主机读取数据并显示,3.单击"写矩阵"按钮,系统将当前页数据写入矩阵主机.4.单击"读数据库",系统从数据库中读取数据,同时也可将数据库中设置的数据,写入矩阵,也可将数据写回矩阵主机.5.单击"写数据库",将当前页数据写回数据库,以备日后查看,维护.6.单击"上一页","下一页",可查看不同的切换设置五. 权限1. 键盘/监示器窗口界面具体操作1.单击"权限"->"键盘/监示器" ,进入"键盘/监示器"设置界面;2.单击"读矩阵"按钮,系统从矩阵主机读取数据并显示;3.单击"写矩阵"按钮,系统将当前页数据写入矩阵主机;4.单击"读数据库",系统从数据库中读取数据,同时也可将数据库中设置的数据,写入矩阵,也可将数据写回矩阵主机;5.单击"写数据库",将当前页数据写回数据库,以备日后查看,维护.2. 键盘/摄像机窗口界面具体操作1.单击"权限"->"键盘/摄像机" 进入"键盘/摄像机"设置界面;2.单击"读矩阵"按钮,系统从矩阵主机读取数据并显示;3.单击"写矩阵"按钮,系统将当前页数据写入矩阵主机;4.单击"读数据库",系统从数据库中读取数据,同时也可将数据库中设置的数据,写入矩阵,也可将数据写回矩阵主机;5.单击"写数据库",将当前页数据写回数据库,以备日后查看,维护.3. 监示器/摄像机窗口界面具体操作1.单击"权限"->"监示器/摄像机" ,进入"监示器/摄像机"设置界面;2.单击"读矩阵"按钮,系统从矩阵主机读取数据并显示;3.单击"写矩阵"按钮,系统将当前页数据写入矩阵主机;4.单击"读数据库",系统从数据库中读取数据,同时也可将数据库中设置的数据,写入矩阵,也可将数据写回矩阵主机;5.单击"写数据库",将当前页数据写回数据库,以备日后查看,维护.4. 键盘/报警窗口界面具体操作1.单击"权限"->"键盘/报警" ,进入"键盘/摄像机"设置界面;2.单击"读矩阵"按钮,系统从矩阵主机读取数据并显示;3.单击"写矩阵"按钮,系统将当前页数据写入矩阵主机;4.单击"读数据库",系统从数据库中读取数据,同时也可将数据库中设置的数据,写入矩阵,也可将数据写回矩阵主机;5.单击"写数据库",将当前页数据写回数据库,以备日后查看,维护.5. 网络/键盘窗口界面。
【软件技术】sympy之Matrix的构造以及操作示例

【软件技术】sympy之Matrix的构造以及操作⽰例sympy中矩阵的构造⽅法很多,下⾯⽰例⼀些构造⽅法以及矩阵的操作⽅法,有助于编程时提⾼技巧:import sympyfrom sympy import Matrix,Array,init_printinginit_printing()#最基本的构造,元素可是是数值,符号表达式A = Matrix([[1,2,3],[4,5,6],[7,8,9]])B = Matrix(((1,2,3),(4,5,6),(7,8,9)))A,B#⽤已知矩阵构造新矩阵,按⾏排列C=Matrix([A,B,A,B]);C#还是按⾏排列C=Matrix([[A],[B],[A],[B]]);C#按列排列C=Matrix([[A,B,A,B]]);Cs1=Matrix.zeros(1)s2=Matrix.zeros(2)s3=Matrix.zeros(3)#不能将维数不同的矩阵混排,混排要⽤列表#C=Matrix([s1],[s2],[s3])#C#可以⽤字符串构造,必须是表达式A = Matrix([["1+1","1+2","1+3"],["2+1","2+2","2+3"],["3+1","3+2","3+3"]])/2;A#输出Latex格式print( latex(A))#列表构造P1 = [1,2,3]P2 = (4,5,6)P1,P2#输出类型print(type(P1))print(type(P2))#⽤lambda构造,不能带条件,要带条件写函数A = Matrix(3, 3, lambda row, col: row+col)A#带条件的构造构造def S(i,j):if i > j :return lambda row, col: row + colelse:return lambda row, col: row - colA = Matrix(3, 3, S(1,2))display(A)A = Matrix(3, 3, S(2,1))display(A)#⽤列表构造C1 = Matrix([P1,P1,P1]) #P1是列表C2 = Matrix([P2,P1,P2]) #P2是元组C1,C2#构造列表V = Array([1,2,3])V#转换为python的原⽣列表V.tolist()#转换为matrix,作⽤不明M = V.tomatrixM#⽤python原⽣列表构造N = Matrix(V.tolist());N#向量求和V+V#构造0向量V1 = Array.zeros(4);V1#取第0个元素V[0]#V = Matrix(V.tolist());V#⽤原⽣列表构造矩阵V11 = Matrix([V.tolist(),V.tolist()]);V11#向量点乘V.dot(V)#向量叉乘V.cross(V)#A.C#A.H#⽤⼀列表达式构造矩阵A = Matrix(3, 3, [1, 2, 0, 0, 3, 0, 2, -4, 2]);A#⽤range构造A = Matrix(3, 3, range(9));A#⽤匿名函数函数x,y = sympy.symbols("x,y")A = Matrix(2, 2, lambda i, j: i*2+j)A,A.applyfunc(lambda i: 2*i*(x+y))#构造符号函数矩阵,未定义函数的具体表达式,只定义了函数形参from sympy import symbols, Function, MatrixF = symbols('F', cls=Function)x,y = sympy.symbols("x,y")A = Matrix(2, 2, lambda i, j: F( i * (x+y)**4 , j * sin(y+x) )) ; A#将函数名称替换G = symbols('G', cls=Function)N = A.replace(F,G);N#F函数暂时没有显式表达式,但是可以求导A.diff(x).diff(y)#定义了函数的具体表达式G = mbdify((x, y), x+y )#G = x+y#⽤函数具体的表达式来构造矩阵,要点为:函数的具体表达式,矩阵的⾏、列索引号A = Matrix(3, 3, lambda i, j: G( 2*i * (2*x+3*y)**4 , 3*j * sin(4*y+5*x) ))A#矩阵函数有了显式表达式,可以求导A.diff(x)#求定积分A.integrate((x,0,1),(y,0,1))#计算定积分的值A.integrate((x,0,1),(y,0,1)).evalf()#矩阵的LDL分解A = Matrix(((10, 2,3), (4,5,6), (7,8,90)))L, D = (A+A.T).LDLdecomposition()A+A.T,L,D#矩阵的乔基斯分解A = Matrix(((10, 2,3), (4,5,6), (7,8,90)))A = A+A.TA.cholesky()A.cholesky() * A.cholesky().TA,A.cholesky()#矩阵的QR分解A = Matrix([[0,2,3], [4,5,6], [7,8,9]])Q, R = A.QRdecomposition()A,Q,R,Q*R#矩阵的LU分解A = Matrix([[1,2,3], [4,5,6], [7,8,9]])L, U,_ = A.LUdecomposition()A,L,U#矩阵求和A,A.add(A)#Conjugate transpose or Hermitian conjugationA,A.adjoint()#Returns the adjugate, or classical adjoint, of a matrix.#That is, the transpose of the matrix of cofactors.A.adjugate()#矩阵的特征多项式A.charpoly()#A,A.cofactor#A,A.cofactorMatrix#矩阵的第0列A.col(0)#矩阵的第2列A.col(2)#拷贝矩阵B = A.copy()B.col_del(0) #删除第0列BM = A.copy()V = Matrix.ones(3, 1)#向已知矩阵,按列插⼊⼀个矩阵(M.col_insert(0, V),M.col_insert(1, V),M.col_insert(3, V),M.col_insert(40, V)) #col_insert有问题M = A.copy()V = Matrix.ones(1, 3)M.col_join(V) #只能接在最后M.col_join(M)#矩阵列数A.cols#矩阵的列空间向量A.columnspace(0)#拷贝矩阵A = Matrix([[1,2,3], [4,5,6], [7,8,9]])BB = A.copy();BB#矩阵的⾏列式A,A.det()#对⾓矩阵A,A.diag()#点乘A.dot(A)#⽤数值1填充矩阵的元素A.fill(1)A#矩阵的逆A = Matrix([[0,2,3], [4,5,6], [7,8,9]])A.inv()#矩阵乘A.multiply(A)#矩阵范数A.norm()#矩阵的秩A.rank()#矩阵的迹A.trace()#转换为tableA.table#转换为列表A.tolist()#将矩阵拉直(A.vec(),A.T.vec())#矩阵的⾏A.row(0),A.row(1),A.row(2)#A.row_del()M = A.copy()V = Matrix.ones(1, 3)#向已知矩阵按⾏插⼊矩阵M.row_insert(1, V)M = A.copy()V = Matrix.ones(3, 1)M.row_join(V)#转为列表L = M.tolist()L,L[1:2]#列表索引L[:2]#列表索引L[0:]#sympy.Matrix中封装的矩阵接续不太好,可以:#将B矩阵插⼊到A矩阵的i⾏def AppendRow(A,B,row):if A.cols == B.cols:LA = A.vec()LB = B.vec()index = 0#if row == 0:# index = A.rows*A.cols#else:index = row*A.colsfirstA = LA[:index]secondA = LA[index:]firstA.extend(LB[:])firstA.extend(secondA)return Matrix(firstA).reshape(A.rows+B.rows,A.cols) #将B矩阵插⼊到A矩阵的后边def AppendRow2(A,B):return AppendRow(A,B,A.rows)#将B矩阵插⼊到A矩阵的i列def AppendCol(A,B,col):return AppendRow(A.T,B.T,col).T#将B矩阵插⼊到A矩阵的右⾯def AppendCol2(A,B):return AppendRow(A.T,B.T,A.cols).TA = Matrix([[1,2,3], [4,5,6], [7,8,9]])B = Matrix([[10,20,30], [40,50,60],[70,80,80]])#测试上⾯的插⼊函数A1 = AppendRow(A,B,0);A1A2 = AppendRow(A,B,1);A2A3 = AppendRow(A,B,2);A3A4 = AppendRow(A,B,A.rows);A4A5 = AppendRow2(A,B);A5A6 = AppendCol(A,B,0);A6A7 = AppendCol(A,B,1);A7A8 = AppendCol(A,B,2);A8A9 = AppendCol(A,B,3);A9A10 = AppendCol2(A,B);A10#如果Matrix输出的格式不能满⾜⾃⼰的要求,可以⾃⼰构造输出格式from sympy import Matrixfrom sympy.printing.str import StrPrinterM = Matrix([[1, 2], [-33, 4]])printer = StrPrinter()M.table(printer)print(M.table(printer))print(M.table(printer, rowsep=',\n'))print('[%s]' % M.table(printer, rowsep=',\n'))print(M.table(printer, colsep='\t\t\t'))print(M.table(printer, colsep=' '))print(M.table(printer, align='center'))print(M.table(printer, rowstart='{', rowend='}'))#下⾯⽰例了⼀些应⽤lambdify构造矩阵的⽅法#符号矩阵转numpyimport numpy as npx,y = sympy.symbols("x,y")X = np.arange(6).reshape(2,3)Y = np.arange(1,7).reshape(2,3)X,YMatrix(X.tolist())Matrix(Y.tolist())#定义函数,⽬的是将这个函数应⽤在矩阵的每⼀个元素上形成新矩阵,函数⾃变量的值取⾃原矩阵元素z = (x+y)**2f = mbdify((x,y),z,'numpy')Matrix(f(X,1))Matrix(f(X,Y))#直接形成矩阵import numpyarray2mat = [{'ImmutableDenseMatrix': numpy.matrix}, 'numpy']f = mbdify((x, y), ( Matrix([x, y]) ) , modules=array2mat)#⼜⼀个⽰例f = mbdify((x, y), ( Matrix([x, y-1]) + Matrix([y, x-1]) ) , modules=array2mat) Matrix(f(x, y))#⼜⼀个⽰例f = mbdify((x, y), x+y )T = [[f(x,y),f(y+1,x)] for x in range(5,10) for y in range(5,10) if x > y]T#⼜⼀个⽰例f = mbdify((x, y), x*y )T = [ str(x)+"*"+str(y)+"="+str(f(x,y)) for x in range(1,10) for y in range(1,10) ]Tfrom sympy import sin, tan, gammafrom mbdify import lambdastrfrom sympy.abc import x, yf = mbdify((x),sin(x), "math")f(1)f = mbdify(x, x**2)f(1),f(x)f = mbdify((x), [x, x**2, x**3])f(2)from sympy import sin, tan, gammafrom mbdify import lambdastrfrom sympy.abc import x, yf = mbdify((x,y), sin(x*y), "math")f(1,1)f = mbdify((x,y), sin(x*y), "numpy")f(1,1)f = mbdify(x, sin(x)*gamma(x), ("math", "mpmath", "sympy"))f(1)x,y,z = sympy.symbols("x,y,z")f = mbdify((x, (y, z)), x + y)f(1, (2, 4))from sympy.utilities.iterables import flattenw = sympy.symbols("w")args = w, (x, (y, z))vals = 1, (2, (3, 4))f = mbdify(flatten(args), w + x + y + z)f(*flatten(vals))row = mbdify((x, y), Matrix((x, x + y)).T, modules='sympy')row(1, 2)f = mbdify((x, y, z), [z, y, x])f(1,2,3)#定义⽅法来构造函数表达式def func(x,y,z,op):if op == 1:return [z, y, x]return [z*z, y*y, x*x]if op == 3:return [x*y*z]if op == 4:return Matrix([x,y,z])func1 = func(x,y,z,1)f = mbdify((x, y, z), func1 )f(1,2,3)func2 = func(x,y,z,2)f = mbdify((x, y, z), func2 )f(1,2,3)func3 = func(x,y,z,3)f = mbdify((x, y, z), func3 )f(1,2,3)func4 = func(x,y,z,4)f = mbdify((x, y, z), func4 )Matrix(f(1,2,3))f = mbdify((x, y, z), (func1,func2,func3,func4) ) v = f(1,2,3)for i in v:display(Matrix(i))a,b,c = sympy.symbols("a,b,c")v = f(a,b,c)for i in v:display(Matrix(i))f = mbdify((x, y, z), (func2) )M = Matrix(f(a,b,c));M#矩阵求导M,M.diff(a)M,M.diff(a,2)#矩阵积分M,M.integrate((a))M,M.integrate((a,0,1))M,M.integrate((a,0,1),(b,0,1))M,M.integrate((a,b,c))M,M.integrate((b,c,a))M,M.integrate((b,c))M,M.integrate((a,1),(b,2),(c,3))。
matrix meta说明书

Matrix Meta说明书一、产品概述Matrix Meta是一款高效、稳定、易用的矩阵计算库。
它提供了丰富的矩阵操作功能,包括矩阵乘法、转置、求逆、特征值、特征向量等,适用于科学计算、机器学习、图像处理等多个领域。
二、功能特点1. 高效性能:Matrix Meta采用先进的算法和优化技术,确保在各种硬件平台上都能提供高效的计算性能。
2. 稳定可靠:经过严格的质量控制和大量测试,Matrix Meta具有高度的稳定性和可靠性,适用于各种应用场景。
3. 易用性:Matrix Meta提供简洁明了的API接口和丰富的文档,方便用户快速上手并高效使用。
4. 支持多平台:Matrix Meta支持多种操作系统和硬件平台,满足不同用户的需求。
三、使用方法1. 安装与配置:用户可以通过下载安装包或使用包管理器安装Matrix Meta 库。
安装完成后,用户需要在项目中配置相关的链接器和包含目录。
2. 创建矩阵:Matrix Meta提供多种创建矩阵的方式,包括直接定义矩阵大小和数据、从文件加载矩阵等。
3. 矩阵操作:Matrix Meta提供了丰富的矩阵操作函数,如矩阵乘法、转置、求逆等。
用户可以通过调用这些函数对矩阵进行操作。
4. 结果输出:Matrix Meta支持将计算结果输出到各种格式的文件中,如文本文件、二进制文件等。
四、注意事项1. 内存管理:在使用Matrix Meta进行大规模矩阵计算时,需要注意内存管理。
避免一次性加载过大的矩阵导致内存溢出。
2. 错误处理:Matrix Meta在运行过程中可能会遇到各种错误,如内存不足、矩阵维度不匹配等。
用户需要正确处理这些错误,确保程序的稳定运行。
3. 版本兼容性:随着技术的不断进步,Matrix Meta可能会更新版本。
新版本可能引入新的功能或改进性能,但也可能引入不兼容的变更。
用户需要关注Matrix Meta的更新信息,确保正确使用新版本。
五、总结Matrix Meta是一款功能强大、高效稳定的矩阵计算库。
Matri 中文操作说明书

目录一、安装1、确定安装高度――――――――――――――――――――――――――――――――32、确定倾斜角度――――――――――――――――――――――――――――――――3二、接线―――――――――――――――――――――――――――――――――――41、电源连线――――――――――――――――――――――――――――――――――42、通讯连线――――――――――――――――――――――――――――――――――4三、调试―――――――――――――――――――――――――――――――――――51、打开VisiSet调试软件――――――――――――――――――――――――――――52、连接VisiSet与读码器――――――――――――――――――――――――――――53、调试读码器―――――――――――――――――――――――――――――――――7<1> 进入Continuous模式――――――――――――――――――――――――――――9<2> 确定条码位置――――――――――――――――――――――――――――― 10<3> 设置条码类型―――――――――――――――――――――――――――――10<4> 确定调试标准――――――――――――――――――――――――――――――11<5> 调整读码特性――――――――――――――――――――――――――――――11<6> 改回Phase Mode―――――――――――――――――――――――――――――13<7> 下载参数到读码器――――――――――――――――――――――――――――13<8> 上传和下载参数―――――――――――――――――――――――――――――141、确定安装高度Matrix 200 有四种型号,不同的型号根据其焦距安装高度也有所不同。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
Matrix软件操作说明一. 软件系统设置1.通讯设置通讯设置目的是为了选不同的端口,对端口通讯速率,及矩阵系统网络号进行设置,只有在与矩阵系统速率相同的情况下才能进行通信.窗口界面:具体操作如下.1.单击工具栏的"通讯方式"按钮,进入通讯方式设置窗口2.选择当前软件的通讯方式,"使用本地串口"用485线与电脑相连,远程透明串口,用IP模块通信3.选择相应的"串口","波特率".4.选择"使用远程透明串口",使用网络设备进行通信.选择对应的网络设备.5.单击"确定" 保存设置附:虚拟键盘涉及到网络号操作,在此进行设置.2.矩阵类型窗口界面具体操作1.单击"软件系统设置"->"矩阵类型",进入矩阵类型界面2.选择"矩阵类型"(此类型关系到当前所读取矩阵数据的正确性,请务必选择对应的矩阵型号).3.单击"确定" 保存设置3.修改密码窗口界面具体操作1.单击"软件系统设置"->"修改密码",进入修改密码界面2.输入"旧密码",并确认输入新密码3.单击"确定" 保存设置4.登陆/登出为防止他人任意更改系统设置,系统提供此功能,在拥有管理员权限的情况下方可操作系统.其界面如下:二. 矩阵系统设置1.时间设置设置矩阵系统时间.窗口界面具体操作:1.单击"矩阵系统设置"->"时间设置",2.进入"时间设置"界面3.可单击"同步系统时间"按钮,与计算机系统同步时间4.也可手工设置矩阵时间.5.单击"确定",保存设置2.云台协议设置云台协议窗口界面具体操作:1.单击"矩阵系统设置"->"云台协议",2.进入"云台协议"设置界面3.选择"云台协议",和对应的通信速率.4.单击"确定",保存设置3.网络编号设置矩阵系统网络号窗口界面具体操作:1.单击"矩阵系统设置"->"网络编号",2.进入"网络编号"界面3.选择"网络编号4.单击"确定",保存设置4. 键盘数量设置矩阵系统键盘数量窗口界面具体操作:1.单击"矩阵系统设置"->"键盘数量",2.进入"键盘数量"界面3.选择"键盘数量"4.单击"确定",保存设置三. 标题与显示1. 摄像机标题设置窗口界面具体操作1.单击"标题与显示"->"摄像机标题" 或工具栏上的"摄像机标题"按钮,进入摄像机标题设置界面;2.单击"读矩阵"按钮,系统从矩阵主机读取数据并显示;3.单击"写矩阵"按钮,系统将当前页数据写入矩阵主机;4.单击"读数据库",系统从数据库中读取数据,同时也可将数据库中设置的数据,写入矩阵,也可将数据写回矩阵主机;5.单击"写数据库",将当前页数据写回数据库,以备日后查看,维护.2. 监示器标题窗口界面具体操作1.单击"标题与显示"->"监示器标题" 或工具栏上的"监示器标题"按钮,进入"监示器标题"设置界面;2.单击"读矩阵"按钮,系统从矩阵主机读取数据并显示;3.单击"写矩阵"按钮,系统将当前页数据写入矩阵主机;4.单击"读数据库",系统从数据库中读取数据,同时也可将数据库中设置的数据,写入矩阵,也可将数据写回矩阵主机;5.单击"写数据库",将当前页数据写回数据库,以备日后查看,维护.3. 屏幕位置设置监示器标题/时间显示位置窗口界面具体操作:1.单击"标题与显示"->屏幕位置" ;2.进入"屏幕位置"界面;3.拖动"屏幕位置"按钮到适当位置;4.单击"确定"保存设置;5.重启矩阵系统,使设置生效.4. 标题位置设置监示器标题/时间显示位置窗口界面具体操作:1.单击"标题与显示"->标题位置"2.进入"标题位置"界面.3.拖动"标题位置"按钮到适当位置4.单击"确定"保存设置5.重启矩阵系统,使设置生效5. 时间位置设置监示器标题/时间显示位置窗口界面具体操作:1.单击"标题与显示"->时间位置" ;2.进入"时间位置"界面;3.拖动"时间位置"按钮到适当位置;4.单击"确定"保存设置;5.重启矩阵系统,使设置生效.四. 切换1. 程序切换窗口界面具体操作1.单击"切换"->"程序切换" 或工具栏上的"程序切换"按钮,进入程序切换设置界面,2.单击"读矩阵"按钮,系统从矩阵主机读取数据并显示,3.单击"写矩阵"按钮,系统将当前页数据写入矩阵主机.4.单击"读数据库",系统从数据库中读取数据,同时也可将数据库中设置的数据,写入矩阵,也可将数据写回矩阵主机.5.单击"写数据库",将当前页数据写回数据库,以备日后查看,维护.6.单击"上一页","下一页",可查看不同的切换设置2. 同步切换窗口界面具体操作1.单击"切换"->"同步切换" 或工具栏上的"同步切换"按钮,进入同步切换设置界面,2.单击"读矩阵"按钮,系统从矩阵主机读取数据并显示,3.单击"写矩阵"按钮,系统将当前页数据写入矩阵主机.4.单击"读数据库",系统从数据库中读取数据,同时也可将数据库中设置的数据,写入矩阵,也可将数据写回矩阵主机.5.单击"写数据库",将当前页数据写回数据库,以备日后查看,维护.6.单击"上一页","下一页",可查看不同的切换设置3. 群组切换窗口界面具体操作1.单击"切换"->"群组切换" 或工具栏上的"群组切换"按钮,进入群组切换设置界面,2.单击"读矩阵"按钮,系统从矩阵主机读取数据并显示,3.单击"写矩阵"按钮,系统将当前页数据写入矩阵主机.4.单击"读数据库",系统从数据库中读取数据,同时也可将数据库中设置的数据,写入矩阵,也可将数据写回矩阵主机.5.单击"写数据库",将当前页数据写回数据库,以备日后查看,维护.6.单击"上一页","下一页",可查看不同的切换设置五. 权限1. 键盘/监示器窗口界面具体操作1.单击"权限"->"键盘/监示器" ,进入"键盘/监示器"设置界面;2.单击"读矩阵"按钮,系统从矩阵主机读取数据并显示;3.单击"写矩阵"按钮,系统将当前页数据写入矩阵主机;4.单击"读数据库",系统从数据库中读取数据,同时也可将数据库中设置的数据,写入矩阵,也可将数据写回矩阵主机;5.单击"写数据库",将当前页数据写回数据库,以备日后查看,维护.2. 键盘/摄像机窗口界面具体操作1.单击"权限"->"键盘/摄像机" 进入"键盘/摄像机"设置界面;2.单击"读矩阵"按钮,系统从矩阵主机读取数据并显示;3.单击"写矩阵"按钮,系统将当前页数据写入矩阵主机;4.单击"读数据库",系统从数据库中读取数据,同时也可将数据库中设置的数据,写入矩阵,也可将数据写回矩阵主机;5.单击"写数据库",将当前页数据写回数据库,以备日后查看,维护.3. 监示器/摄像机窗口界面具体操作1.单击"权限"->"监示器/摄像机" ,进入"监示器/摄像机"设置界面;2.单击"读矩阵"按钮,系统从矩阵主机读取数据并显示;3.单击"写矩阵"按钮,系统将当前页数据写入矩阵主机;4.单击"读数据库",系统从数据库中读取数据,同时也可将数据库中设置的数据,写入矩阵,也可将数据写回矩阵主机;5.单击"写数据库",将当前页数据写回数据库,以备日后查看,维护.4. 键盘/报警窗口界面具体操作1.单击"权限"->"键盘/报警" ,进入"键盘/摄像机"设置界面;2.单击"读矩阵"按钮,系统从矩阵主机读取数据并显示;3.单击"写矩阵"按钮,系统将当前页数据写入矩阵主机;4.单击"读数据库",系统从数据库中读取数据,同时也可将数据库中设置的数据,写入矩阵,也可将数据写回矩阵主机;5.单击"写数据库",将当前页数据写回数据库,以备日后查看,维护.5. 网络/键盘窗口界面具体操作1.单击"权限"->"网络/键盘" ,进入"网络/键盘"设置界面;2.单击"读矩阵"按钮,系统从矩阵主机读取数据并显示;3.单击"写矩阵"按钮,系统将当前页数据写入矩阵主机;4.单击"读数据库",系统从数据库中读取数据,同时也可将数据库中设置的数据,写入矩阵,也可将数据写回矩阵主机;5.单击"写数据库",将当前页数据写回数据库,以备日后查看,维护.六. 报警1报警联动窗口界面具体操作1.单击"报警"->"报警联动" ,进入"报警联动"设置界面;2.单击"读矩阵"按钮,系统从矩阵主机读取数据并显示;3.单击"写矩阵"按钮,系统将当前页数据写入矩阵主机;4.单击"读数据库",系统从数据库中读取数据,同时也可将数据库中设置的数据,写入矩阵,也可将数据写回矩阵主机;5.单击"写数据库",将当前页数据写回数据库,以备日后查看,维护.2. 自动设防窗口界面具体操作1.单击"报警"->"自动设防" ,进入"自动设防"设置界面;2.单击"读矩阵"按钮,系统从矩阵主机读取数据并显示;3.单击"写矩阵"按钮,系统将当前页数据写入矩阵主机;4.单击"读数据库",系统从数据库中读取数据,同时也可将数据库中设置的数据,写入矩阵,也可将数据写回矩阵主机;5.单击"写数据库",将当前页数据写回数据库,以备日后查看,维护.3. 历史报警窗口界面具体操作1.单击"报警"->"历史报警" ,进入"历史报警"界面;2.系统自动读取矩阵系统历史报警记录;3.可单击"刷新"按钮重新读取矩阵系统数据.4. 报警端口设置窗口界面具体操作:1.单击"报警"->"报警端口设置" ;2.进入"报警端口设置"界面 ;3.选择"报警端口" ;4.单击"确定",保存设置.5. 设防/撤防状态窗口界面具体操作1.单击"报警"->"设防/撤防状态" ,进入"设防/撤防状态"界面;2.系统自动读取矩阵系统历史报警记录;3.可单击"刷新"按钮重新读取矩阵系统数据;七. 键盘设置1. 虚拟键盘虚拟键盘是为了方便用户在计算机系统操纵矩阵设计的.功能与矩阵键盘类似.可通过虚拟键盘对矩阵进行,摄像机切换等操作. 窗口界面八. 常见问题下位机无响应:可能存在以下几种情况:1.连接线路太长或线路质量存在问题.数据无法接收.2.系统波特率与矩阵主机波特率不一至.系统波特率可通过"通讯方式"进行设置;3.矩阵主机系统软件被破坏,可与厂商联系,进行系统升级.可读矩阵数据,但无法写入矩阵:1.线路或转接器存在问题.请更换好一点的通信设备.虚拟键盘无法操作:1.网络号或波特率与矩阵系统不相符;解决方法参看“通讯设置”2.线路质量问题。
