数据结构(严蔚敏)第7章
严蔚敏《数据结构(c语言版)习题集》答案第七章 图

严蔚敏《数据结构(c语言版)习题集》答案第七章图第七章图7.14Status Build_AdjList(ALGraph &G)//输入有向图的顶点数,边数,顶点信息和边的信息建立邻接表{InitALGraph(G);scanf("%d",&v);if(v<0) return ERROR; //顶点数不能为负G.vexnum=v;scanf("%d",&a);if(a<0) return ERROR; //边数不能为负G.arcnum=a;for(m=0;m<v;m++)G.vertices[m].data=getchar(); //输入各顶点的符号for(m=1;m<=a;m++){t=getchar();h=getchar(); //t为弧尾,h为弧头if((i=LocateVex(G,t))<0) return ERROR;if((j=LocateVex(G,h))<0) return ERROR; //顶点未找到p=(ArcNode*)malloc(sizeof(ArcNode));if(!G.vertices.[i].firstarc) G.vertices[i].firstarc=p;else{for(q=G.vertices[i].firstarc;q->nextarc;q=q->nextarc);q->nextarc=p;}p->adjvex=j;p->nextarc=NULL;}//whilereturn OK;}//Build_AdjList7.15//本题中的图G均为有向无权图,其余情况容易由此写出Status Insert_Vex(MGraph &G, char v)//在邻接矩阵表示的图G上插入顶点v {if(G.vexnum+1)>MAX_VERTEX_NUM return INFEASIBLE;G.vexs[++G.vexnum]=v;return OK;}//Insert_VexStatus Insert_Arc(MGraph &G,char v,char w)//在邻接矩阵表示的图G上插入边(v,w) {if((i=LocateVex(G,v))<0) return ERROR;if((j=LocateVex(G,w))<0) return ERROR;if(i==j) return ERROR;if(!G.arcs[i][j].adj){G.arcs[i][j].adj=1;G.arcnum++;}return OK;}//Insert_ArcStatus Delete_Vex(MGraph &G,char v)//在邻接矩阵表示的图G上删除顶点v{n=G.vexnum;if((m=LocateVex(G,v))<0) return ERROR;G.vexs[m]<->G.vexs[n]; //将待删除顶点交换到最后一个顶点for(i=0;i<n;i++){G.arcs[i][m]=G.arcs[i][n];G.arcs[m][i]=G.arcs[n][i]; //将边的关系随之交换}G.arcs[m][m].adj=0;G.vexnum--;return OK;}//Delete_Vex分析:如果不把待删除顶点交换到最后一个顶点的话,算法将会比较复杂,而伴随着大量元素的移动,时间复杂度也会大大增加.Status Delete_Arc(MGraph &G,char v,char w)//在邻接矩阵表示的图G上删除边(v,w) {if((i=LocateVex(G,v))<0) return ERROR;if((j=LocateVex(G,w))<0) return ERROR;if(G.arcs[i][j].adj){G.arcs[i][j].adj=0;G.arcnum--;}return OK;}//Delete_Arc7.16//为节省篇幅,本题只给出Insert_Arc算法.其余算法请自行写出.Status Insert_Arc(ALGraph &G,char v,char w)//在邻接表表示的图G上插入边(v,w) {if((i=LocateVex(G,v))<0) return ERROR;if((j=LocateVex(G,w))<0) return ERROR;p=(ArcNode*)malloc(sizeof(ArcNode));p->adjvex=j;p->nextarc=NULL;if(!G.vertices[i].firstarc) G.vertices[i].firstarc=p;else{for(q=G.vertices[i].firstarc;q->q->nextarc;q=q->nextarc)if(q->adjvex==j) return ERROR; //边已经存在q->nextarc=p;}G.arcnum++;return OK;}//Insert_Arc7.17//为节省篇幅,本题只给出较为复杂的Delete_Vex算法.其余算法请自行写出. Status Delete_Vex(OLGraph &G,char v)//在十字链表表示的图G上删除顶点v { if((m=LocateVex(G,v))<0) return ERROR;n=G.vexnum;for(i=0;i<n;i++) //删除所有以v为头的边{if(G.xlist[i].firstin->tailvex==m) //如果待删除的边是头链上的第一个结点{q=G.xlist[i].firstin;G.xlist[i].firstin=q->hlink;free(q);G.arcnum--;}else //否则{for(p=G.xlist[i].firstin;p&&p->hlink->tailvex!=m;p=p->hlink);if(p){q=p->hlink;p->hlink=q->hlink;free(q);G.arcnum--;}}//else}//forfor(i=0;i<n;i++) //删除所有以v为尾的边{if(G.xlist[i].firstout->headvex==m) //如果待删除的边是尾链上的第一个结点{q=G.xlist[i].firstout;G.xlist[i].firstout=q->tlink;free(q);G.arcnum--;}else //否则{for(p=G.xlist[i].firstout;p&&p->tlink->headvex!=m;p=p->tlink);if(p){q=p->tlink;p->tlink=q->tlink;free(q);G.arcnum--;}}//else}//forfor(i=m;i<n;i++) //顺次用结点m之后的顶点取代前一个顶点{G.xlist[i]=G.xlist[i+1]; //修改表头向量for(p=G.xlist[i].firstin;p;p=p->hlink)p->headvex--;for(p=G.xlist[i].firstout;p;p=p->tlink)p->tailvex--; //修改各链中的顶点序号}G.vexnum--;return OK;}//Delete_Vex7.18//为节省篇幅,本题只给出Delete_Arc算法.其余算法请自行写出.Status Delete_Arc(AMLGraph &G,char v,char w)////在邻接多重表表示的图G上删除边(v,w){if((i=LocateVex(G,v))<0) return ERROR;if((j=LocateVex(G,w))<0) return ERROR;if(G.adjmulist[i].firstedge->jvex==j)G.adjmulist[i].firstedge=G.adjmulist[i].firstedge->ilink;else{for(p=G.adjmulist[i].firstedge;p&&p->ilink->jvex!=j;p=p->ilink);if (!p) return ERROR; //未找到p->ilink=p->ilink->ilink;} //在i链表中删除该边if(G.adjmulist[j].firstedge->ivex==i)G.adjmulist[j].firstedge=G.adjmulist[j].firstedge->jlink;else{for(p=G.adjmulist[j].firstedge;p&&p->jlink->ivex!=i;p=p->jlink);if (!p) return ERROR; //未找到q=p->jlink;p->jlink=q->jlink;free(q);} //在i链表中删除该边G.arcnum--;return OK;}//Delete_Arc7.19Status Build_AdjMulist(AMLGraph &G)//输入有向图的顶点数,边数,顶点信息和边的信息建立邻接多重表{InitAMLGraph(G);scanf("%d",&v);if(v<0) return ERROR; //顶点数不能为负G.vexnum=v;scanf(%d",&a);if(a<0) return ERROR; //边数不能为负G.arcnum=a;for(m=0;m<v;m++)G.adjmulist[m].data=getchar(); //输入各顶点的符号for(m=1;m<=a;m++){t=getchar();h=getchar(); //t为弧尾,h为弧头if((i=LocateVex(G,t))<0) return ERROR;if((j=LocateVex(G,h))<0) return ERROR; //顶点未找到p=(EBox*)malloc(sizeof(EBox));p->ivex=i;p->jvex=j;p->ilink=NULL;p->jlink=NULL; //边结点赋初值if(!G.adjmulist[i].firstedge) G.adjmulist[i].firstedge=p;else{q=G.adjmulist[i].firstedge;while(q){r=q;if(q->ivex==i) q=q->ilink;else q=q->jlink;}if(r->ivex==i) r->ilink=p;//注意i值既可能出现在边结点的ivex域中, else r->jlink=p; //又可能出现在边结点的jvex域中}//else //插入i链表尾部if(!G.adjmulist[j].firstedge) G.adjmulist[j].firstedge=p;else{q=G.adjmulist[i].firstedge;while(q){r=q;if(q->jvex==j) q=q->jlink;else q=q->ilnk;}if(r->jvex==j) r->jlink=p;else r->ilink=p;}//else //插入j链表尾部}//forreturn OK;}//Build_AdjList7.20int Pass_MGraph(MGraph G)//判断一个邻接矩阵存储的有向图是不是可传递的,是则返回1,否则返回0{for(x=0;x<G.vexnum;x++)for(y=0;y<G.vexnum;y++)if(G.arcs[x][y]){for(z=0;z<G.vexnum;z++)if(z!=x&&G.arcs[y][z]&&!G.arcs[x][z]) return 0;//图不可传递的条件}//ifreturn 1;}//Pass_MGraph分析:本算法的时间复杂度大概是O(n^2*d).7.21int Pass_ALGraph(ALGraph G)//判断一个邻接表存储的有向图是不是可传递的,是则返回1,否则返回0{for(x=0;x<G.vexnum;x++)for(p=G.vertices[x].firstarc;p;p=p->nextarc){y=p->adjvex;for(q=G.vertices[y].firstarc;q;q=q->nextarc){z=q->adjvex;if(z!=x&&!is_adj(G,x,z)) return 0;}//for}//for}//Pass_ALGraphint is_adj(ALGraph G,int m,int n)//判断有向图G中是否存在边(m,n),是则返回1,否则返回0{for(p=G.vertices[m].firstarc;p;p=p->nextarc)if(p->adjvex==n) return 1;return 0;}//is_adj7.22int visited[MAXSIZE]; //指示顶点是否在当前路径上int exist_path_DFS(ALGraph G,int i,int j)//深度优先判断有向图G中顶点i到顶点j是否有路径,是则返回1,否则返回0{if(i==j) return 1; //i就是jelse{visited[i]=1;for(p=G.vertices[i].firstarc;p;p=p->nextarc){k=p->adjvex;if(!visited[k]&&exist_path(k,j)) return 1;//i下游的顶点到j有路径}//for}//else}//exist_path_DFS7.23int exist_path_BFS(ALGraph G,int i,int j)//广度优先判断有向图G中顶点i到顶点j是否有是则返回1,否则返回0 路径,{int visited[MAXSIZE];InitQueue(Q);EnQueue(Q,i);while(!QueueEmpty(Q)){DeQueue(Q,u);visited[u]=1;for(p=G.vertices[i].firstarc;p;p=p->nextarc){k=p->adjvex;if(k==j) return 1;if(!visited[k]) EnQueue(Q,k);}//for}//whilereturn 0;}//exist_path_BFS7.24void STraverse_Nonrecursive(Graph G)//非递归遍历强连通图G { int visited[MAXSIZE];InitStack(S);Push(S,GetVex(S,1)); //将第一个顶点入栈visit(1);visited =1;while(!StackEmpty(S)){while(Gettop(S,i)&&i){j=FirstAdjVex(G,i);if(j&&!visited[j]){visit(j);visited[j]=1;Push(S,j); //向左走到尽头}}//whileif(!StackEmpty(S)){Pop(S,j);Gettop(S,i);k=NextAdjVex(G,i,j); //向右走一步if(k&&!visited[k]){visit(k);visited[k]=1;Push(S,k);}}//if}//while}//Straverse_Nonrecursive 分析:本算法的基本思想与二叉树的先序遍历非递归算法相同,请参考6.37.由于是强连通图,所以从第一个结点出发一定能够访问到所有结点. 7.25见书后解答.7.26Status TopoNo(ALGraph G)//按照题目要求顺序重排有向图中的顶点 { int new[MAXSIZE],indegree[MAXSIZE]; //储存结点的新序号n=G.vexnum;FindInDegree(G,indegree);InitStack(S);for(i=1;i<G.vexnum;i++)if(!indegree[i]) Push(S,i); //零入度结点入栈count=0;while(!StackEmpty(S)){Pop(S,i);new[i]=n--; //记录结点的拓扑逆序序号count++;for(p=G.vertices[i].firstarc;p;p=p->nextarc){k=p->adjvex;if(!(--indegree[k])) Push(S,k);}//for}//whileif(count<G.vexnum) return ERROR; //图中存在环for(i=1;i<=n;i++) printf("Old No:%d New No:%d\n",i,new[i])return OK;}//TopoNo分析:只要按拓扑逆序对顶点编号,就可以使邻接矩阵成为下三角矩阵. 7.27 int visited[MAXSIZE];int exist_path_len(ALGraph G,int i,int j,int k)//判断邻接表方式存储的有向图G的顶点i到j是否存在长度为k的简单路径{if(i==j&&k==0) return 1; //找到了一条路径,且长度符合要求else if(k>0){visited[i]=1;for(p=G.vertices[i].firstarc;p;p=p->nextarc){l=p->adjvex;if(!visited[l])if(exist_path_len(G,l,j,k-1)) return 1; //剩余路径长度减一}//forvisited[i]=0; //本题允许曾经被访问过的结点出现在另一条路径中}//elsereturn 0; //没找到}//exist_path_len7.28int path[MAXSIZE],visited[MAXSIZE]; //暂存遍历过程中的路径 intFind_All_Path(ALGraph G,int u,int v,int k)//求有向图G中顶点u到v之间的所有简单路径,k表示当前路径长度{path[k]=u; //加入当前路径中visited[u]=1;if(u==v) //找到了一条简单路径{printf("Found one path!\n");for(i=0;path[i];i++) printf("%d",path[i]); //打印输出}elsefor(p=G.vertices[u].firstarc;p;p=p->nextarc){l=p->adjvex;if(!visited[l]) Find_All_Path(G,l,v,k+1); //继续寻找}visited[u]=0;path[k]=0; //回溯}//Find_All_Pathmain(){...Find_All_Path(G,u,v,0); //在主函数中初次调用,k值应为0...}//main7.29int GetPathNum_Len(ALGraph G,int i,int j,int len)//求邻接表方式存储的有向图G的顶点i到j之间长度为len的简单路径条数{if(i==j&&len==0) return 1; //找到了一条路径,且长度符合要求else if(len>0){sum=0; //sum表示通过本结点的路径数visited[i]=1;for(p=G.vertices[i].firstarc;p;p=p->nextarc){l=p->adjvex;if(!visited[l])sum+=GetPathNum_Len(G,l,j,len-1)//剩余路径长度减一}//forvisited[i]=0; //本题允许曾经被访问过的结点出现在另一条路径中}//elsereturn sum;}//GetPathNum_Len7.30int visited[MAXSIZE];int path[MAXSIZE]; //暂存当前路径int cycles[MAXSIZE][MAXSIZE]; //储存发现的回路所包含的结点 int thiscycle[MAXSIZE]; //储存当前发现的一个回路 int cycount=0; //已发现的回路个数void GetAllCycle(ALGraph G)//求有向图中所有的简单回路 {for(v=0;v<G.vexnum;v++) visited[v]=0;for(v=0;v<G.vexnum;v++)if(!visited[v]) DFS(G,v,0); //深度优先遍历}//DFSTraversevoid DFS(ALGraph G,int v,int k)//k表示当前结点在路径上的序号 {visited[v]=1;path[k]=v; //记录当前路径for(p=G.vertices[v].firstarc;p;p=p->nextarc){w=p->adjvex;if(!visited[w]) DFS(G,w,k+1);else //发现了一条回路{for(i=0;path[i]!=w;i++); //找到回路的起点for(j=0;path[i+j];i++) thiscycle[j]=path[i+j];//把回路复制下来if(!exist_cycle()) cycles[cycount++]=thiscycle;//如果该回路尚未被记录过,就添加到记录中for(i=0;i<G.vexnum;i++) thiscycle[i]=0; //清空目前回路数组}//else}//forpath[k]=0;visited[k]=0; //注意只有当前路径上的结点visited为真.因此一旦遍历中发现当前结点visited为真,即表示发现了一条回路}//DFSint exist_cycle()//判断thiscycle数组中记录的回路在cycles的记录中是否已经存在 {int temp[MAXSIZE];for(i=0;i<cycount;i++) //判断已有的回路与thiscycle是否相同{ //也就是,所有结点和它们的顺序都相同j=0;c=thiscycle�; //例如,142857和857142是相同的回路for(k=0;cycles[i][k]!=c&&cycles[i][k]!=0;k++);//在cycles的一个行向量中寻找等于thiscycle第一个结点的元素if(cycles[i][k]) //有与之相同的一个元素{for(m=0;cycles[i][k+m];m++)temp[m]=cycles[i][k+m];for(n=0;n<k;n++,m++)temp[m]=cycles[i][n]; //调整cycles中的当前记录的循环相位并放入temp 数组中if(!StrCompare(temp,thiscycle)) //与thiscycle比较return 1; //完全相等for(m=0;m<G.vexnum;m++) temp[m]=0; //清空这个数组}}//forreturn 0; //所有现存回路都不与thiscycle完全相等}//exist_cycle分析:这个算法的思想是,在遍历中暂存当前路径,当遇到一个结点已经在路径之中时就表明存在一条回路;扫描路径向量path可以获得这条回路上的所有结点.把结点序列(例如,142857)存入thiscycle中;由于这种算法中,一条回路会被发现好几次,所以必须先判断该回路是否已经在cycles中被记录过,如果没有才能存入cycles的一个行向量中.把cycles的每一个行向量取出来与之比较.由于一条回路可能有多种存储顺序,比如142857等同于285714和571428,所以还要调整行向量的次序,并存入temp数组,例如,thiscycle为142857第一个结点为1,cycles的当前向量为857142,则找到后者中的1,把1后部分提到1前部分前面,最终在temp中得到142857,与thiscycle比较,发现相同,因此142857和857142是同一条回路,不予存储.这个算法太复杂,很难保证细节的准确性,大家理解思路便可.希望有人给出更加简捷的算法.7.31int visited[MAXSIZE];int finished[MAXSIZE];int count; //count在第一次深度优先遍历中用于指示finished数组的填充位置 void Get_SGraph(OLGraph G)//求十字链表结构储存的有向图G的强连通分量 {count=0;for(v=0;v<G.vexnum;v++) visited[v]=0;for(v=0;v<G.vexnum;v++) //第一次深度优先遍历建立finished数组if(!visited[v]) DFS1(G,v);for(v=0;v<G.vexnum;v++) visited[v]=0; //清空visited数组for(i=G.vexnum-1;i>=0;i--) //第二次逆向的深度优先遍历{v=finished(i);if(!visited[v]){printf("\n"); //不同的强连通分量在不同的行输出DFS2(G,v);}}//for}//Get_SGraphvoid DFS1(OLGraph G,int v)//第一次深度优先遍历的算法{visited[v]=1;for(p=G.xlist[v].firstout;p;p=p->tlink){w=p->headvex;if(!visited[w]) DFS1(G,w);}//forfinished[++count]=v; //在第一次遍历中建立finished数组}//DFS1void DFS2(OLGraph G,int v)//第二次逆向的深度优先遍历的算法 {visited[v]=1;printf("%d",v); //在第二次遍历中输出结点序号for(p=G.xlist[v].firstin;p;p=p->hlink){w=p->tailvex;if(!visited[w]) DFS2(G,w);}//for}//DFS2分析:求有向图的强连通分量的算法的时间复杂度和深度优先遍历相同,也为O(n+e). 7.32void Forest_Prim(ALGraph G,int k,CSTree &T)//从顶点k出发,构造邻接表结构的有向图G的最小生成森林T,用孩子兄弟链表存储{for(j=0;j<G.vexnum;j++) //以下在Prim算法基础上稍作改动if(j!=k){closedge[j]={k,Max_int};for(p=G.vertices[j].firstarc;p;p=p->nextarc)if(p->adjvex==k) closedge[j].lowcost=p->cost;}//ifclosedge[k].lowcost=0;for(i=1;i<G.vexnum;i++){k=minimum(closedge);if(closedge[k].lowcost<Max_int){Addto_Forest(T,closedge[k].adjvex,k); //把这条边加入生成森林中closedge[k].lowcost=0;for(p=G.vertices[k].firstarc;p;p=p->nextarc)if(p->cost<closedge[p->adjvex].lowcost)closedge[p->adjvex]={k,p->cost};}//ifelse Forest_Prim(G,k); //对另外一个连通分量执行算法}//for}//Forest_Primvoid Addto_Forest(CSTree &T,int i,int j)//把边(i,j)添加到孩子兄弟链表表示的树T中 {p=Locate(T,i); //找到结点i对应的指针p,过程略q=(CSTNode*)malloc(sizeof(CSTNode));q->data=j;if(!p) //起始顶点不属于森林中已有的任何一棵树{p=(CSTNode*)malloc(sizeof(CSTNode));p->data=i;for(r=T;r->nextsib;r=r->nextsib);r->nextsib=p;p->firstchild=q;} //作为新树插入到最右侧else if(!p->firstchild) //双亲还没有孩子p->firstchild=q; //作为双亲的第一个孩子else //双亲已经有了孩子{for(r=p->firstchild;r->nextsib;r=r->nextsib);r->nextsib=q; //作为双亲最后一个孩子的兄弟}}//Addto_Forestmain(){...T=(CSTNode*)malloc(sizeof(CSTNode)); //建立树根T->data=1;Forest_Prim(G,1,T);...}//main分析:这个算法是在Prim算法的基础上添加了非连通图支持和孩子兄弟链表构建模块而得到的,其时间复杂度为O(n^2).7.33typedef struct {int vex; //结点序号int ecno; //结点所属的连通分量号} VexInfo; VexInfo vexs[MAXSIZE]; //记录结点所属连通分量号的数组void Init_VexInfo(VexInfo &vexs[ ],int vexnum)//初始化 { for(i=0;i<vexnum;i++)vexs[i]={i,i}; //初始状态:每一个结点都属于不同的连通分量 }//Init_VexInfoint is_ec(VexInfo vexs[ ],int i,int j)//判断顶点i和顶点j是否属于同一个连通分量{if(vexs[i].ecno==vexs[j].ecno) return 1;else return 0;}//is_ecvoid merge_ec(VexInfo &vexs[ ],int ec1,int ec2)//合并连通分量ec1和ec2{for(i=0;vexs[i].vex;i++)if(vexs[i].ecno==ec2) vexs[i].ecno==ec1;}//merge_ecvoid MinSpanTree_Kruscal(Graph G,EdgeSetType &EdgeSet,CSTree &T)//求图的最小生成树的克鲁斯卡尔算法{Init_VexInfo(vexs,G.vexnum);ecnum=G.vexnum; //连通分量个数while(ecnum>1){GetMinEdge(EdgeSet,u,v); //选出最短边if(!is_ec(vexs,u,v)) //u和v属于不同连通分量{Addto_CSTree(T,u,v); //加入到生成树中merge_ec(vexs,vexs[u].ecno,vexs[v].ecno); //合并连通分量ecnum--;}DelMinEdge(EdgeSet,u,v); //从边集中删除}//while}//MinSpanTree_Kruscalvoid Addto_CSTree(CSTree &T,int i,int j)//把边(i,j)添加到孩子兄弟链表表示的树T中 {p=Locate(T,i); //找到结点i对应的指针p,过程略q=(CSTNode*)malloc(sizeof(CSTNode));q->data=j;if(!p->firstchild) //双亲还没有孩子p->firstchild=q; //作为双亲的第一个孩子else //双亲已经有了孩子{for(r=p->firstchild;r->nextsib;r=r->nextsib);r->nextsib=q; //作为双亲最后一个孩子的兄弟}}//Addto_CSTree分析:本算法使用一维结构体变量数组来表示等价类,每个连通分量所包含的所有结点属于一个等价类.在这个结构上实现了初始化,判断元素是否等价(两个结点是否属于同一个连通分量),合并等价类(连通分量)的操作.7.34Status TopoSeq(ALGraph G,int new[ ])//按照题目要求给有向无环图的结点重新编号,并存入数组new中{int indegree[MAXSIZE]; //本算法就是拓扑排序FindIndegree(G,indegree);Initstack(S);for(i=0;i<G.vexnum;i++)if(!indegree[i]) Push(S,i);count=0;while(!stackempty(S)){Pop(S,i);new[i]=++count; //把拓扑顺序存入数组的对应分量中for(p=G.vertices[i].firstarc;p;p=p->nextarc){k=p->adjvex;if(!(--indegree[k])) Push(S,k);}}//whileif(count<G.vexnum) return ERROR;return OK;}//TopoSeq7.35int visited[MAXSIZE];void Get_Root(ALGraph G)//求有向无环图的根,如果有的话{for(v=0;v<G.vexnum;v++){for(w=0;w<G.vexnum;w++) visited[w]=0;//每次都要将访问数组清零DFS(G,v); //从顶点v出发进行深度优先遍历for(flag=1,w=0;w<G.vexnum;w++)if(!visited[w]) flag=0; //如果v是根,则深度优先遍历可以访问到所有结点if(flag) printf("Found a root vertex:%d\n",v);}//for}//Get_Root,这个算法要求图中不能有环,否则会发生误判void DFS(ALGraph G,int v){visited[v]=1;for(p=G.vertices[v].firstarc;p;p=p->nextarc){w=p->adjvex;if(!visited[w]) DFS(G,w);}}//DFS7.36void Fill_MPL(ALGraph &G)//为有向无环图G添加MPL域 {FindIndegree(G,indegree);for(i=0;i<G.vexnum;i++)if(!indegree[i]) Get_MPL(G,i);//从每一个零入度顶点出发构建MPL域 }//Fill_MPLint Get_MPL(ALGraph &G,int i)//从一个顶点出发构建MPL域并返回其MPL 值 {if(!G.vertices[i].firstarc){G.vertices[i].MPL=0;return 0; //零出度顶点}else{max=0;for(p=G.vertices[i].firstarc;p;p=p->nextarc){j=p->adjvex;if(G.vertices[j].MPL==0) k=Get_MPL(G,j);if(k>max) max=k; //求其直接后继顶点MPL的最大者}G.vertices[i]=max+1;//再加一,就是当前顶点的MPLreturn max+1;}//else}//Get_MPL7.37int maxlen,path[MAXSIZE]; //数组path用于存储当前路径 intmlp[MAXSIZE]; //数组mlp用于存储已发现的最长路径 voidGet_Longest_Path(ALGraph G)//求一个有向无环图中最长的路径 { maxlen=0;FindIndegree(G,indegree);for(i=0;i<G.vexnum;i++){for(j=0;j<G.vexnum;j++) visited[j]=0;if(!indegree[i]) DFS(G,i,0);//从每一个零入度结点开始深度优先遍历}printf("Longest Path:");for(i=0;mlp[i];i++) printf("%d",mlp[i]); //输出最长路径 }//Get_Longest_Pathvoid DFS(ALGraph G,int i,int len) {visited[i]=1;path[len]=i;if(len>maxlen&&!G.vertices[i].firstarc) //新的最长路径{for(j=0;j<=len;j++) mlp[j]=path[j]; //保存下来maxlen=len;}else{for(p=G.vertices[i].firstarc;p;p=p->nextarc){j=p->adjvex;if(!visited[j]) DFS(G,j,len+1);}}//elsepath[i]=0;visited[i]=0;}//DFS7.38void NiBoLan_DAG(ALGraph G)//输出有向无环图形式表示的表达式的逆波兰式 {FindIndegree(G,indegree);for(i=0;i<G.vexnum;i++)if(!indegree[i]) r=i; //找到有向无环图的根PrintNiBoLan_DAG(G,i);}//NiBoLan_DAGvoid PrintNiBoLan_DAG(ALGraph G,int i)//打印输出以顶点i为根的表达式的逆波兰式 {c=G.vertices[i].data;if(!G.vertices[i].firstarc) //c是原子printf("%c",c);else //子表达式{p=G.vertices[i].firstarc;PrintNiBoLan_DAG(G,p->adjvex);PrintNiBoLan_DAG(G,p->nexarc->adjvex);printf("%c",c);}}//PrintNiBoLan_DAG7.39void PrintNiBoLan_Bitree(Bitree T)//在二叉链表存储结构上重做上一题 { if(T->lchild) PrintNiBoLan_Bitree(T->lchild);if(T->rchild) PrintNiBoLan_Bitree(T->rchild);printf("%c",T->data);}//PrintNiBoLan_Bitree7.40int Evaluate_DAG(ALGraph G)//给有向无环图表示的表达式求值 { FindIndegree(G,indegree);for(i=0;i<G.vexnum;i++)if(!indegree[i]) r=i; //找到有向无环图的根return Evaluate_imp(G,i); }//NiBoLan_DAGint Evaluate_imp(ALGraph G,int i)//求子表达式的值{if(G.vertices[i].tag=NUM) return G.vertices[i].value;else{p=G.vertices[i].firstarc;v1=Evaluate_imp(G,p->adjvex);v2=Evaluate_imp(G,p->nextarc->adjvex);return calculate(v1,G.vertices[i].optr,v2);}}//Evaluate_imp分析:本题中,邻接表的vertices向量的元素类型修改如下: struct { enum tag{NUM,OPTR};union {int value;char optr;};ArcNode * firstarc;} Elemtype;7.41void Critical_Path(ALGraph G)//利用深度优先遍历求网的关键路径 { FindIndegree(G,indegree);for(i=0;i<G.vexnum;i++)if(!indegree[i]) DFS1(G,i); //第一次深度优先遍历:建立vefor(i=0;i<G.vexnum;i++)if(!indegree[i]) DFS2(G,i); //第二次深度优先遍历:建立vlfor(i=0;i<=G.vexnum;i++)if(vl[i]==ve[i]) printf("%d",i); //打印输出关键路径}//Critical_Pathvoid DFS1(ALGraph G,int i) {if(!indegree[i]) ve[i]=0;for(p=G.vertices[i].firstarc;p;p=p->nextarc) {dut=*p->info;if(ve[i]+dut>ve[p->adjvex])ve[p->adjvex]=ve[i]+dut;DFS1(G,p->adjvex);}}//DFS1void DFS2(ALGraph G,int i) {if(!G.vertices[i].firstarc) vl[i]=ve[i]; else{for(p=G.vertices[i].firstarc;p;p=p->nextarc) {DFS2(G,p->adjvex);dut=*p->info;if(vl[p->adjvex]-dut<vl[i])vl[i]=vl[p->adjvex]-dut;}}//else}//DFS27.42void ALGraph_DIJ(ALGraph G,int v0,Pathmatrix &P,ShortestPathTable &D)//在邻接表存储结构上实现迪杰斯特拉算法{for(v=0;v<G.vexnum;v++)D[v]=INFINITY;for(p=G.vertices[v0].firstarc;p;p=p->nextarc)D[p->adjvex]=*p->info; //给D数组赋初值for(v=0;v<G.vexnum;v++){final[v]=0;for(w=0;w<G.vexnum;w++) P[v][w]=0; //设空路径if(D[v]<INFINITY){P[v][v0]=1;P[v][v]=1;}}//forD[v0]=0;final[v0]=1; //初始化for(i=1;i<G.vexnum;i++){min=INFINITY;for(w=0;w<G.vexnum;w++)if(!final[w])if(D[w]<min) //尚未求出到该顶点的最短路径{v=w;min=D[w];}final[v]=1;for(p=G.vertices[v].firstarc;p;p=p->nextarc){w=p->adjvex;if(!final[w]&&(min+(*p->info)<D[w])) //符合迪杰斯特拉条件{D[w]=min+edgelen(G,v,w);P[w]=P[v];P[w][w]=1; //构造最短路径}}//for}//for}//ALGraph_DIJ分析:本算法对迪杰斯特拉算法中直接取任意边长度的语句作了修改.由于在原算法中,每次循环都是对尾相同的边进行处理,所以可以用遍历邻接表中的一条链来代替.。
严蔚敏数据结构 (7)

2.1 线性表的逻辑结构 2.2 线性表的顺序表示和实现 2.3 线性表的链式表示和实现 2.4 应用举例
P31例 前面已讲) 例1:两个链表的归并(教材P31例,前面已讲) 两个链表的归并(教材P31 教材P39 43,前面已讲) P39–43 例2:一元多项式的计算 (教材P39 43,前面已讲) 例3:试用C或类C语言编写一个高效算法,将一循 试用C或类C语言编写一个高效算法, 高效算法 环单链表就地逆置. 环单链表就地逆置. 操作前:( 操作前:(a1, a2, … ai-1,ai, ai+1 ,…, an) :( , 操作后:( 操作后:( an, … ai+1 ,ai, ai-1 ,…, a2, a1 )
head a2 a1 ^
实际上是链 栈的概念
替换法的核心语句: 替换法的核心语句: q=head; p=head->next; //有头结点 有头结点 while(p!=head) //循环单链表 循环单链表 { r=p->next; p->next=q; //前驱变后继 前驱变后继 q=p; p=r; } //准备处理下一结点 准备处理下一结点 head->next=q; // 以an为首
静态单链表的类型定义如下: 静态单链表的类型定义如下:
#define MAXSIZE 1000 //预分配最大的元素个数(连续空间 //预分配最大的元素个数 预分配最大的元素个数( typedef struct { ElemType data ; //数据域 //数据域 int cur ; //指示域 //指示域 }component , SLinkList[MAXSIZE] ; //这是一维结构型数组 //这是一维结构型数组
双向链表的插入操作: 双向链表的插入操作:
数据结构C语言版(第2版)严蔚敏人民邮电出版社课后习题答案

数据结构(C语言版)(第2版)课后习题答案李冬梅2015.3目录第 1 章绪论 (1)第 2 章线性表 (5)第 3 章栈和队列 (13)第 4 章串、数组和广义表 (26)第 5 章树和二叉树 (33)第 6 章图 (43)第7 章查找 (54)第8 章排序 (65)第1章绪论1 •简述下列概念:数据、数据元素、数据项、数据对象、数据结构、逻辑结构、存储结构、抽象数据类型。
答案:数据:是客观事物的符号表示,指所有能输入到计算机中并被计算机程序处理的符号的总称。
如数学计算中用到的整数和实数,文本编辑所用到的字符串,多媒体程序处理的图形、图像、声音、动画等通过特殊编码定义后的数据。
数据元素:是数据的基本单位,在计算机中通常作为一个整体进行考虑和处理。
在有些情况下,数据元素也称为元素、结点、记录等。
数据元素用于完整地描述一个对象,如一个学生记录,树中棋盘的一个格局(状态)、图中的一个顶点等。
数据项:是组成数据元素的、有独立含义的、不可分割的最小单位。
例如,学生基本信息表中的学号、姓名、性别等都是数据项。
数据对象:是性质相同的数据元素的集合,是数据的一个子集。
例如:整数数据对象是集合N={0,± 1,± 2,, },字母字符数据对象是集合C={ ‘ A',' B',,,‘ Z',‘ a','b',,,' z ' },学生基本信息表也可是一个数据对象。
数据结构:是相互之间存在一种或多种特定关系的数据元素的集合。
换句话说,数据结构是带“结构”的数据元素的集合,“结构”就是指数据元素之间存在的关系。
逻辑结构:从逻辑关系上描述数据,它与数据的存储无关,是独立于计算机的。
因此,数据的逻辑结构可以看作是从具体问题抽象出来的数学模型。
存储结构:数据对象在计算机中的存储表示,也称为物理结构。
抽象数据类型:由用户定义的,表示应用问题的数学模型,以及定义在这个模型上的一组操作的总称。
《数据结构》第二版严蔚敏课后习题作业参考答案(1-7章)

第1章4.答案:(1)顺序存储结构顺序存储结构是借助元素在存储器中的相对位置来表示数据元素之间的逻辑关系,通常借助程序设计语言的数组类型来描述。
(2)链式存储结构顺序存储结构要求所有的元素依次存放在一片连续的存储空间中,而链式存储结构,无需占用一整块存储空间。
但为了表示结点之间的关系,需要给每个结点附加指针字段,用于存放后继元素的存储地址。
所以链式存储结构通常借助于程序设计语言的指针类型来描述。
5. 选择题(1)~(6):CCBDDA6.(1)O(1) (2)O(m*n) (3)O(n2)(4)O(log3n) (5)O(n2) (6)O(n)第2章1.选择题(1)~(5):BABAD (6)~(10):BCABD (11)~(15):CDDAC 2.算法设计题(1)将两个递增的有序链表合并为一个递增的有序链表。
要求结果链表仍使用原来两个链表的存储空间, 不另外占用其它的存储空间。
表中不允许有重复的数据。
[题目分析]合并后的新表使用头指针Lc指向,pa和pb分别是链表La和Lb的工作指针,初始化为相应链表的第一个结点,从第一个结点开始进行比较,当两个链表La和Lb均为到达表尾结点时,依次摘取其中较小者重新链接在Lc表的最后。
如果两个表中的元素相等,只摘取La表中的元素,删除Lb表中的元素,这样确保合并后表中无重复的元素。
当一个表到达表尾结点,为空时,将非空表的剩余元素直接链接在Lc表的最后。
void MergeList(LinkList &La,LinkList &Lb,LinkList &Lc){//合并链表La和Lb,合并后的新表使用头指针Lc指向pa=La->next; pb=Lb->next;//pa和pb分别是链表La和Lb的工作指针,初始化为相应链表的第一个结点Lc=pc=La; //用La的头结点作为Lc的头结点while(pa && pb){ if(pa->data<pb->data){pc->next=pa; pc=pa; pa=pa->next;}//取较小者La中的元素,将pa链接在pc的后面,pa指针后移else if(pa->data>pb->data) {pc->next=pb; pc=pb; pb=pb->next;}//取较小者Lb中的元素,将pb链接在pc的后面,pb指针后移else //相等时取La中的元素,删除Lb中的元素{pc->next=pa;pc=pa;pa=pa->next;q=pb->next; delete pb ; pb =q;}}pc->next=pa?pa:pb; //插入剩余段delete Lb; //释放Lb的头结点}(5)设计算法将一个带头结点的单链表A分解为两个具有相同结构的链表B、C,其中B表的结点为A表中值小于零的结点,而C表的结点为A表中值大于零的结点(链表A中的元素为非零整数,要求B、C表利用A表的结点)。
《数据结构(C语言版 第2版)》(严蔚敏 著)第七章练习题答案

《数据结构(C语言版第2版)》(严蔚敏著)第七章练习题答案第7章查找1.选择题(1)对n个元素的表做顺序查找时,若查找每个元素的概率相同,则平均查找长度为()。
A.(n-1)/2B.n/2C.(n+1)/2D.n答案:C解释:总查找次数N=1+2+3+…+n=n(n+1)/2,则平均查找长度为N/n=(n+1)/2。
(2)适用于折半查找的表的存储方式及元素排列要求为()。
A.链接方式存储,元素无序B.链接方式存储,元素有序C.顺序方式存储,元素无序D.顺序方式存储,元素有序答案:D解释:折半查找要求线性表必须采用顺序存储结构,而且表中元素按关键字有序排列。
(3)如果要求一个线性表既能较快的查找,又能适应动态变化的要求,最好采用()查找法。
A.顺序查找B.折半查找C.分块查找D.哈希查找答案:C解释:分块查找的优点是:在表中插入和删除数据元素时,只要找到该元素对应的块,就可以在该块内进行插入和删除运算。
由于块内是无序的,故插入和删除比较容易,无需进行大量移动。
如果线性表既要快速查找又经常动态变化,则可采用分块查找。
(4)折半查找有序表(4,6,10,12,20,30,50,70,88,100)。
若查找表中元素58,则它将依次与表中()比较大小,查找结果是失败。
A.20,70,30,50B.30,88,70,50C.20,50D.30,88,50答案:A解释:表中共10个元素,第一次取⎣(1+10)/2⎦=5,与第五个元素20比较,58大于20,再取⎣(6+10)/2⎦=8,与第八个元素70比较,依次类推再与30、50比较,最终查找失败。
(5)对22个记录的有序表作折半查找,当查找失败时,至少需要比较()次关键字。
A.3B.4C.5D.6答案:B解释:22个记录的有序表,其折半查找的判定树深度为⎣log222⎦+1=5,且该判定树不是满二叉树,即查找失败时至多比较5次,至少比较4次。
(6)折半搜索与二叉排序树的时间性能()。
《数据结构》第二版严蔚敏课后习题作业参考答案(1-7章)

《数据结构》第二版严蔚敏课后习题作业参考答案(1-7章)【第一章绪论】1. 数据结构是计算机科学中的重要基础知识,它研究的是如何组织和存储数据,以及如何通过高效的算法进行数据的操作和处理。
本章主要介绍了数据结构的基本概念和发展历程。
【第二章线性表】1. 线性表是由一组数据元素组成的数据结构,它的特点是元素之间存在着一对一的线性关系。
本章主要介绍了线性表的顺序存储结构和链式存储结构,以及它们的操作和应用。
【第三章栈与队列】1. 栈是一种特殊的线性表,它的特点是只能在表的一端进行插入和删除操作。
本章主要介绍了栈的顺序存储结构和链式存储结构,以及栈的应用场景。
2. 队列也是一种特殊的线性表,它的特点是只能在表的一端进行插入操作,而在另一端进行删除操作。
本章主要介绍了队列的顺序存储结构和链式存储结构,以及队列的应用场景。
【第四章串】1. 串是由零个或多个字符组成的有限序列,它是一种线性表的特例。
本章主要介绍了串的存储结构和基本操作,以及串的模式匹配算法。
【第五章数组与广义表】1. 数组是一种线性表的顺序存储结构,它的特点是所有元素都具有相同数据类型。
本章主要介绍了一维数组和多维数组的存储结构和基本操作,以及广义表的概念和表示方法。
【第六章树与二叉树】1. 树是一种非线性的数据结构,它的特点是一个节点可以有多个子节点。
本章主要介绍了树的基本概念和属性,以及树的存储结构和遍历算法。
2. 二叉树是一种特殊的树,它的每个节点最多只有两个子节点。
本章主要介绍了二叉树的存储结构和遍历算法,以及一些特殊的二叉树。
【第七章图】1. 图是一种非线性的数据结构,它由顶点集合和边集合组成。
本章主要介绍了图的基本概念和属性,以及图的存储结构和遍历算法。
【总结】1. 数据结构是计算机科学中非常重要的一门基础课程,它关注的是如何高效地组织和存储数据,以及如何通过算法进行数据的操作和处理。
本文对《数据结构》第二版严蔚敏的课后习题作业提供了参考答案,涵盖了第1-7章的内容。
数据结构_(严蔚敏C语言版)_学习、复习提纲.
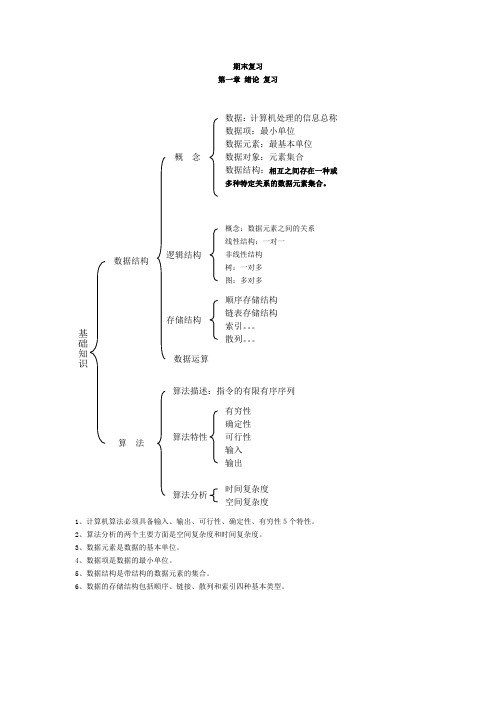
期末复习 第一章 绪论 复习1、计算机算法必须具备输入、输出、可行性、确定性、有穷性5个特性。
2、算法分析的两个主要方面是空间复杂度和时间复杂度。
3、数据元素是数据的基本单位。
4、数据项是数据的最小单位。
5、数据结构是带结构的数据元素的集合。
6、数据的存储结构包括顺序、链接、散列和索引四种基本类型。
基础知识数据结构算 法概 念逻辑结构 存储结构数据运算数据:计算机处理的信息总称 数据项:最小单位 数据元素:最基本单位数据对象:元素集合数据结构:相互之间存在一种或多种特定关系的数据元素集合。
概念:数据元素之间的关系 线性结构:一对一非线性结构 树:一对多 图:多对多顺序存储结构 链表存储结构 索引。
散列。
算法描述:指令的有限有序序列算法特性 有穷性 确定性 可行性 输入 输出 算法分析时间复杂度 空间复杂度第二章 线性表 复习1、在双链表中,每个结点有两个指针域,包括一个指向前驱结点的指针 、一个指向后继结点的指针2、线性表采用顺序存储,必须占用一片连续的存储单元3、线性表采用链式存储,便于进行插入和删除操作4、线性表采用顺序存储和链式存储优缺点比较。
5、简单算法第三章 栈和队列 复习线性表顺序存储结构链表存储结构概 念基本特点基本运算定义逻辑关系:前趋 后继节省空间 随机存取 插、删效率低 插入 删除单链表双向 链表 特点一个指针域+一个数据域 多占空间 查找费时 插、删效率高 无法查找前趋结点运算特点:单链表+前趋指针域运算插入删除循环 链表特点:单链表的尾结点指针指向附加头结点。
运算:联接1、 栈和队列的异同点。
2、 栈和队列的基本运算3、 出栈和出队4、 基本运算第四章 串 复习栈存储结构栈的概念:在一端操作的线性表 运算算法栈的特点:先进后出 LIFO初始化 进栈push 出栈pop队列顺序队列 循环队列队列概念:在两端操作的线性表 假溢出链队列队列特点:先进先出 FIFO基本运算顺序:链队:队空:front=rear队满:front=(rear+1)%MAXSIZE队空:frontrear ∧初始化 判空 进队 出队取队首元素第五章 数组和广义表 复习串存储结构运 算概 念顺序串链表串定义:由n(≥1)个字符组成的有限序列 S=”c 1c 2c 3 ……cn ”串长度、空白串、空串。
数据结构[严蔚敏]7
![数据结构[严蔚敏]7](https://img.taocdn.com/s3/m/e789ae7ff5335a8102d220ba.png)
完全有向图:对于有向图,若图中顶点数为n ,用
e表示弧的数目,则e[0,n(n-1)] 。具有n(n-1)条边的有 向图称为完全有向图。
完全有向图另外的定义是:
对于有向图G=(V,E),若vi,vjV ,当vi ≠vj时,有 <vi ,vj>E∧<vj , vi >E ,即图中任意两个不同的顶点间都有一 条弧,这样的有向图称为完全有向图。 有很少边或弧的图(e<n㏒n)的图称为稀疏图,反之称为 稠密图。
连通图、图的连通分量:对无向图G=(V,E),若vi ,
vj V,vi和vj都是连通的,则称图G是连通图,否则称为非连 通图。若G是非连通图,则极大的连通子图称为G的连通分 量。 对有向图G=(V,E),若vi ,vj V,都有以vi为起点, vj 为终点以及以vj为起点,vi为终点的有向路径,称图G是强连 通图,否则称为非强连通图。若G是非强连通图,则极大的 强连通子图称为G的强连通分量。 “极大”的含义:指的是对子图再增加图G中的其它顶 点,子图就不再连通。
a c b e d c b e a d a
6 3
b
3
2
c
4
d
1
5
e
(a) 有向图
(b) 生成森林
图7-3 有向图及其生成森林
图7-4 带权有向图
7.1.2 图的抽象数据类型定义
图是一种数据结构,加上一组基本操作就构成了图 的抽象数据类型。 图的抽象数据类型定义如下: ADT Graph{
数据对象V:具有相同特性的数据元素的集合,称为 顶点集。
(c) 邻接矩阵
图7-8 带权有向图的数组存储
⑶ 有向图邻接矩阵的特性
数据结构严蔚敏7章图ppt课件

InfoType *info;
}VNode,AdjList[MAX_V];
}ArcNode;
typedef struct //图的邻接表类型
{ AdjList vertices; //存储图中所有顶点的数组
int vexnum,arcnum; //存储图的顶点数目和边(弧)的数目
int kind; //图的种类标志
返回
表结点
adjvex nextarc info
表头结点
data firstarc
typedef struct ArcNode typedef struct
{ int adjvex;
{ VertexType data;
struct ArcNode *nextarc; ArcNode *firstarc;
}ArcCell,AdjMatrix[MAX_V][MAX_V];
typedef struct
{ VertexType vex[MAX_V]; //顶点信息数组(如顶点编号等)
AdjMatrix arcs;
//图的邻接矩阵
int vexnum,arcnum; //图的顶点数和边(弧)的数目
GraphKind kind;//图的种类标志
A CB F DE G (a) 有向图G1
A BC D EF (b) 无向图G2
返回
2 几个常用术语 可以证明,对于具有n个顶点的无向图的边和具有n个
顶点的有向图的弧的最大数目分别为n(n-1)/2和n(n-1)。 称具有n(n-1)/2条边的无向图为完全图(completed
grahp)。 称具有n(n-1)条弧的有向图为完全有向图 称边或弧的数目e<nlogn的图为稀疏图(sparse
数据结构教材 出版社: 清华大学出版社 作者: 严蔚敏吴伟民 ISBN ...

数据结构教材出版社:清华大学出版社作者:严蔚敏吴伟民ISBN :978-7-302-02368-5目录第1章绪论1.1 什么是数据结构1.2 基本概念和术语1.3 抽象数据类型的表现与实现1.4 算法和算法分析第2章线性表2.1 线性表的类型定义2.2 线性表的顺序表示和实现2.3 线性表的链式表示和实现2.4 一元多项式的表示及相加第3章栈和队列3.1 栈3.2 栈的应有和举例3.3 栈与递归的实现3.4 队列3.5 离散事件模拟第4章串4.1 串类型的定义4.2 串的表示和实现4.3 串的模式匹配算法4.4 串操作应用举例第5章数组和广义表5.1 数组的定义5.2 数组的顺序表现和实现5.3 矩阵的压缩存储5.4 广义表的定义5.5 广义表的储存结构5.6 m元多项式的表示5.7 广义表的递归算法第6章树和二叉树6.1 树的定义和基本术语6.2 二叉树6.2.1 二叉树的定义6.2.2 二叉树的性质6.2.3 二叉树的存储结构6.3 遍历二叉树和线索二叉树6.3.1 遍历二叉树6.3.2 线索二叉树6.4 树和森林6.4.1 树的存储结构6.4.2 森林与二叉树的转换6.4.3 树和森林的遍历6.5 树与等价问题6.6 赫夫曼树及其应用6.6.1 最优二叉树(赫夫曼树)6.6.2 赫夫曼编码6.7 回溯法与树的遍历6.8 树的计数第7章图7.1 图的定义和术语7.2 图的存储结构7.2.1 数组表示法7.2.2 邻接表7.2.3 十字链表7.2.4 邻接多重表7.3 图的遍历7.3.1 深度优先搜索7.3.2 广度优先搜索7.4 图的连通性问题7.4.1 无向图的连通分量和生成树7.4.2 有向图的强连通分量7.4.3 最小生成树7.4.4 关节点和重连通分量7.5 有向无环图及其应用7.5.1 拓扑排序7.5.2 关键路径7.6 最短路径7.6.1 从某个源点到其余各顶点的最短路径7.6.2 每一对顶点之间的最短路径第8章动态存储管理8.1 概述8.2 可利用空间表及分配方法8.3 边界标识法8.3.1 可利用空间表的结构8.3.2 分配算法8.3.3 回收算法8.4 伙伴系统8.4.1 可利用空间表的结构8.4.2 分配算法8.4.3 回收算法8.5 无用单元收集8.6 存储紧缩第9章查找9.1 静态查找表9.1.1 顺序表的查找9.1.2 有序表的查找9.1.3 静态树表的查找9.1.4 索引顺序表的查找9.2 动态查找表9.2.1 二叉排序树和平衡二叉树9.2.2 B树和B+树9.2.3 键树9.3 哈希表9.3.1 什么是哈希表9.3.2 哈希函数的构造方法9.3.3 处理冲突的方法9.3.4 哈希表的查找及其分析第10章内部排序10.1 概述10.2 插入排序10.2.1 直接插入排序10.2.2 其他插入排序10.2.3 希尔排序10.3 快速排序10.4 选择排序10.4.1 简单选择排序10.4.2 树形选择排序10.4.3 堆排序10.5 归并排序10.6 基数排序10.6.1 多关键字的排序10.6.2 链式基数排序10.7 各种内部排序方法的比较讨论第11章外部排序11.1 外存信息的存取11.2 外部排序的方法11.3 多路平衡归并的实现11.4 置换一选择排序11.5 最佳归并树第12章文件12.1 有关文件的基本概念12.2 顺序文件12.3 索引文件12.4 ISAM文件和VSAM文件12.4.1 ISAM文件12.4.2 VSAM文件12.5 直接存取文件(散列文件)12.6 多关键字文件12.6.1 多重表文件12.6.2 倒排文件附录A 名词索引附录B 函数索引参考书目。
数据结构c语言版严蔚敏课后习题答案

数据结构c语言版严蔚敏课后习题答案数据结构是计算机科学中的一个重要领域,它涉及到数据的组织、管理和存储方式,以便可以高效地访问和修改数据。
C语言作为一种广泛使用的编程语言,提供了丰富的数据结构实现方法。
严蔚敏教授编写的《数据结构(C语言版)》是许多计算机专业学生的必读教材。
以下是对该书课后习题的一些参考答案,供学习者参考。
第一章:绪论1. 数据结构的定义:数据结构是计算机中存储、组织数据的方式,它不仅包括数据元素的类型和关系,还包括数据操作的函数。
2. 数据结构的重要性:数据结构对于提高程序的效率至关重要。
合理的数据结构可以减少算法的时间复杂度和空间复杂度。
第二章:线性表1. 线性表的定义:线性表是由n个元素组成的有限序列,其中n称为线性表的长度。
2. 线性表的顺序存储结构:使用数组来存储线性表的元素,元素的存储关系是连续的。
3. 线性表的链式存储结构:使用链表来存储线性表的元素,每个元素包含数据部分和指向下一个元素的指针。
第三章:栈和队列1. 栈的定义:栈是一种特殊的线性表,只能在一端(栈顶)进行插入和删除操作。
2. 队列的定义:队列是一种特殊的线性表,允许在一端(队尾)进行插入操作,在另一端(队首)进行删除操作。
第四章:串1. 串的定义:串是由零个或多个字符组成的有限序列。
2. 串的存储结构:串可以采用顺序存储结构或链式存储结构。
第五章:数组和广义表1. 数组的定义:数组是由具有相同类型的多个元素组成的集合,这些元素按照索引顺序排列。
2. 广义表的定义:广义表是线性表的推广,其中的元素可以是数据也可以是子表。
第六章:树和二叉树1. 树的定义:树是由节点组成的,其中有一个特定的节点称为根,其余每个节点有且仅有一个父节点。
2. 二叉树的定义:二叉树是每个节点最多有两个子节点的树。
第七章:图1. 图的定义:图是由顶点和边组成的数据结构,可以表示复杂的关系。
2. 图的存储结构:图可以用邻接矩阵或邻接表来存储。
《数据结构(C语言版 第2版)》(严蔚敏 著)第七章练习题答案

《数据结构(C语言版第2版)》(严蔚敏著)第七章练习题答案第7章查找1.选择题(1)对n个元素的表做顺序查找时,若查找每个元素的概率相同,则平均查找长度为()。
A.(n-1)/2B.n/2C.(n+1)/2D.n答案:C解释:总查找次数N=1+2+3+…+n=n(n+1)/2,则平均查找长度为N/n=(n+1)/2。
(2)适用于折半查找的表的存储方式及元素排列要求为()。
A.链接方式存储,元素无序B.链接方式存储,元素有序C.顺序方式存储,元素无序D.顺序方式存储,元素有序答案:D解释:折半查找要求线性表必须采用顺序存储结构,而且表中元素按关键字有序排列。
(3)如果要求一个线性表既能较快的查找,又能适应动态变化的要求,最好采用()查找法。
A.顺序查找B.折半查找C.分块查找D.哈希查找答案:C解释:分块查找的优点是:在表中插入和删除数据元素时,只要找到该元素对应的块,就可以在该块内进行插入和删除运算。
由于块内是无序的,故插入和删除比较容易,无需进行大量移动。
如果线性表既要快速查找又经常动态变化,则可采用分块查找。
(4)折半查找有序表(4,6,10,12,20,30,50,70,88,100)。
若查找表中元素58,则它将依次与表中()比较大小,查找结果是失败。
A.20,70,30,50B.30,88,70,50C.20,50D.30,88,50答案:A解释:表中共10个元素,第一次取⎣(1+10)/2⎦=5,与第五个元素20比较,58大于20,再取⎣(6+10)/2⎦=8,与第八个元素70比较,依次类推再与30、50比较,最终查找失败。
(5)对22个记录的有序表作折半查找,当查找失败时,至少需要比较()次关键字。
A.3B.4C.5D.6答案:B解释:22个记录的有序表,其折半查找的判定树深度为⎣log222⎦+1=5,且该判定树不是满二叉树,即查找失败时至多比较5次,至少比较4次。
(6)折半搜索与二叉排序树的时间性能()。
数据结构严蔚敏7章

最新数据结构(严蔚敏)课件第7章

【学习目标】
1.领会图的类型定义。 2.熟悉图的各种存储结构及其构造算法, 了解各种存储结构的特点及其选用原则。 3.熟练掌握图的两种遍历算法。 4.理解各种图的应用问题的算法。
2020/12/4
第2页
【重点和难点】
图的应用极为广泛,而且图的各种应用问题的 算法都比较经典,因此本章重点在于理解各种图的 算法及其应用场合。
顶点的度(TD)= 出度(OD)+入度(ID)
第13页
设图G=(V,{VR})中的一个顶点序列
{ u=vi,0,vi,1, …, vi,m=w}中,(vi,j-1,vi,j)VR 1≤j≤m, 则称从顶点u 到顶点w 之间存在一条路径。
路径上边(或弧)的数目称作路径长度。
如:长度为3的路径 简单路径:序列中顶点
由顶点集和边 集构成的图称
作无向图。
例如: G2=(V2,VR2)
V2={A, B, C, D, (A,E),
(B,E),(C,D),(D,F),
A
(B,F),(C,F)}
2020/12/4
F
第8页
C D
E
名词和术语
网、子图 完全图、稀疏图、稠密图
邻接点、度、入度、出度 路径、路径长度、简单路径、简单回路
Graph = (V , VR ) 其中,VR={<v,w>| v,w∈V 且 P(v,w)}
<v,w>表示从 v 到 w 的一条弧,并称 v 为 弧头,w 为弧尾。 谓词 P(v,w) 定义了弧第6页<v,w>的意义或信息
2020/12/4
由于“弧”是有方向的,因此称由顶点集 和弧集构成的图为有向图。
数据结构第七章--图(严蔚敏版)
8个顶点的无向图最多有 条边且该图为连通图 个顶点的无向图最多有28条边且该图为连通图 个顶点的无向图最多有 连通无向图构成条件:边 顶点数 顶点数-1)/2 顶点数*(顶点数 连通无向图构成条件 边=顶点数 顶点数 顶点数>=1,所以该函数存在单调递增的单值反 顶点数 所以该函数存在单调递增的单值反 函数,所以边与顶点为增函数关系 所以28个条边 函数 所以边与顶点为增函数关系 所以 个条边 的连通无向图顶点数最少为8个 所以28条边的 的连通无向图顶点数最少为 个 所以 条边的 非连通无向图为9个 加入一个孤立点 加入一个孤立点) 非连通无向图为 个(加入一个孤立点
28
无向图的邻接矩阵为对称矩阵
2011-10-13
7.2
图的存储结构
Wij 若< vi,vj > 或<vj,v i > ∈E(G)
若G是网(有权图),邻接矩阵定义为 是网(有权图), ),邻接矩阵定义为
A [ i,j ] = , 0或 ∞
如图: 如图:
V1
若其它
V2
3 4
2
V3
2011-10-13
C
A
B
D 2011-10-13 (a )
3
Königsberg七桥问题
• Königsberg七桥问题就是说,能否从某点出发 通过每桥恰好一次回到原地?
C
C
A B
.
A D
B
D (a)
2011-10-13
(b)
4
第七章 图
7.1 图的定义 7.2 图的存储结构 7.3 图的遍历 7.4 图的连通性问题 7.5 有向无环图及其应用 7.6 最短路径
2011-10-13
数据结构c语言版严蔚敏课后习题答案

数据结构c语言版严蔚敏课后习题答案数据结构是计算机科学中非常重要的一门学科,它研究的是数据的组织、存储和管理方式。
而C语言作为一种广泛应用于系统编程和嵌入式开发的高级编程语言,与数据结构的学习息息相关。
本文将针对《数据结构(C语言版)》严蔚敏教材的课后习题提供一些答案,希望能够帮助读者更好地理解和掌握数据结构。
第一章:绪论在第一章中,主要介绍了数据结构的基本概念和基本术语。
课后习题主要是一些概念性的问题,例如数据结构与算法的关系、数据的逻辑结构和物理结构等。
这些问题的答案可以通过仔细阅读教材中的相关内容来得到。
第二章:线性表线性表是数据结构中最基本、最常用的一种结构。
课后习题主要涉及线性表的基本操作,如插入、删除、查找等。
这些问题的答案可以通过编写相应的C语言代码来实现。
第三章:栈和队列栈和队列是线性表的特殊形式,具有后进先出(LIFO)和先进先出(FIFO)的特点。
课后习题主要涉及栈和队列的基本操作,如进栈、出栈、入队、出队等。
这些问题的答案同样可以通过编写相应的C语言代码来实现。
第四章:串串是由零个或多个字符组成的有限序列,是一种特殊的线性表。
课后习题主要涉及串的模式匹配、串的替换等操作。
这些问题的答案可以通过使用C语言的字符串处理函数来实现。
第五章:数组和广义表数组是一种线性表的顺序存储结构,广义表是线性表的扩展。
课后习题主要涉及数组和广义表的创建、访问和操作等。
这些问题的答案可以通过编写相应的C语言代码来实现。
第六章:树树是一种非线性的数据结构,具有层次关系。
课后习题主要涉及树的遍历、节点的插入和删除等操作。
这些问题的答案可以通过使用C语言的指针和递归来实现。
第七章:图图是一种非线性的数据结构,由节点和边组成。
课后习题主要涉及图的遍历、最短路径、最小生成树等操作。
这些问题的答案可以通过使用C语言的图算法来实现。
通过以上的简要介绍,读者可以了解到《数据结构(C语言版)》严蔚敏教材的课后习题主要涵盖了线性表、栈和队列、串、数组和广义表、树、图等各个方面。
数据结构 C语言版(严蔚敏版)第7章 图

1
2
4
1
e6 2 4
2016/11/7
29
7.3 图的遍历
从已给的连通图中某一顶点出发,沿着一 些边访遍图中所有的顶点,且使每个顶点 仅被访问一次,就叫做图的遍历 ( Graph Traversal )。 图中可能存在回路,且图的任一顶点都可 能与其它顶点相通,在访问完某个顶点之 后可能会沿着某些边又回到了曾经访问过 的顶点。 为了避免重复访问,可设置一个标志顶点 是否被访问过的辅助数组 visited [ ]。
2
1 2
V2
V4
17
结论:
无向图的邻接矩阵是对称的; 有向图的邻接矩阵可能是不对称的。 在有向图中, 统计第 i 行 1 的个数可得顶点 i 的出度,统计第 j 行 1 的个数可得顶点 j 的入度。 在无向图中, 统计第 i 行 (列) 1 的个数可得 顶点i 的度。
2016/11/7
18
2
邻接表 (出度表)
adjvex nextarc
data firstarc
0 A 1 B 2 C
2016/11/7
1 0 1
逆邻接表 (入度表)
21
网络 (带权图) 的邻接表
6 9 0 2 1 C 2 8 3 D
data firstarc Adjvex info nextarc
2016/11/7
9
路径长度 非带权图的路径长度是指此路径 上边的条数。带权图的路径长度是指路径 上各边的权之和。 简单路径 若路径上各顶点 v1,v2,...,vm 均不 互相重复, 则称这样的路径为简单路径。 回路 若路径上第一个顶点 v1 与最后一个 顶点vm 重合, 则称这样的路径为回路或环。
数据结构C语言版(第2版)严蔚敏人民邮电出版社课后习题答案

数据结构( C语言版)(第 2版)课后习题答案李冬梅2015.3目录第 1 章绪论 (1)第 2 章线性表 (5)第 3 章栈和队列 (13)第 4 章串、数组和广义表 (26)第 5 章树和二叉树 (33)第 6 章图 (43)第 7 章查找 (54)第 8 章排序 (65)第1章绪论1.简述下列概念:数据、数据元素、数据项、数据对象、数据结构、逻辑结构、存储结构、抽象数据类型。
答案:数据:是客观事物的符号表示,指所有能输入到计算机中并被计算机程序处理的符号的总称。
如数学计算中用到的整数和实数,文本编辑所用到的字符串,多媒体程序处理的图形、图像、声音、动画等通过特殊编码定义后的数据。
数据元素:是数据的基本单位,在计算机中通常作为一个整体进行考虑和处理。
在有些情况下,数据元素也称为元素、结点、记录等。
数据元素用于完整地描述一个对象,如一个学生记录,树中棋盘的一个格局(状态)、图中的一个顶点等。
数据项:是组成数据元素的、有独立含义的、不可分割的最小单位。
例如,学生基本信息表中的学号、姓名、性别等都是数据项。
数据对象:是性质相同的数据元素的集合,是数据的一个子集。
例如:整数数据对象是集合N={0 ,± 1,± 2,, } ,字母字符数据对象是集合C={‘A’,‘B’, , ,‘Z’,‘ a’,‘ b’, , ,‘z ’} ,学生基本信息表也可是一个数据对象。
数据结构:是相互之间存在一种或多种特定关系的数据元素的集合。
换句话说,数据结构是带“结构”的数据元素的集合,“结构”就是指数据元素之间存在的关系。
逻辑结构:从逻辑关系上描述数据,它与数据的存储无关,是独立于计算机的。
因此,数据的逻辑结构可以看作是从具体问题抽象出来的数学模型。
存储结构:数据对象在计算机中的存储表示,也称为物理结构。
抽象数据类型:由用户定义的,表示应用问题的数学模型,以及定义在这个模型上的一组操作的总称。
具体包括三部分:数据对象、数据对象上关系的集合和对数据对象的基本操作的集合。
《数据结构》第二版严蔚敏课后习题作业参考答案(1-7章)

第1章4.答案:(1)顺序存储结构顺序存储结构是借助元素在存储器中的相对位置来表示数据元素之间的逻辑关系,通常借助程序设计语言的数组类型来描述。
(2)链式存储结构顺序存储结构要求所有的元素依次存放在一片连续的存储空间中,而链式存储结构,无需占用一整块存储空间。
但为了表示结点之间的关系,需要给每个结点附加指针字段,用于存放后继元素的存储地址。
所以链式存储结构通常借助于程序设计语言的指针类型来描述。
5. 选择题(1)~(6):CCBDDA\6.(1)O(1) (2)O(m*n) (3)O(n2)(4)O(log3n) (5)O(n2) (6)O(n)(第2章1.选择题(1)~(5):BABAD (6)~(10): BCABD (11)~(15):CDDAC\2.算法设计题(1)将两个递增的有序链表合并为一个递增的有序链表。
要求结果链表仍使用原来两个链表的存储空间, 不另外占用其它的存储空间。
表中不允许有重复的数据。
[题目分析]合并后的新表使用头指针Lc指向,pa和pb分别是链表La和Lb的工作指针,初始化为相应链表的第一个结点,从第一个结点开始进行比较,当两个链表La和Lb均为到达表尾结点时,依次摘取其中较小者重新链接在Lc表的最后。
如果两个表中的元素相等,只摘取La表中的元素,删除Lb表中的元素,这样确保合并后表中无重复的元素。
当一个表到达表尾结点,为空时,将非空表的剩余元素直接链接在Lc表的最后。
void MergeList(LinkList &La,LinkList &Lb,LinkList &Lc){法设计题(1)将编号为0和1的两个栈存放于一个数组空间V[m]中,栈底分别处于数组的两端。
当第0号栈的栈顶指针top[0]等于-1时该栈为空,当第1号栈的栈顶指针top[1]等于m时该栈为空。
两个栈均从两端向中间增长。
试编写双栈初始化,判断栈空、栈满、进栈和出栈等算法的函数。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
B A,则
含有 e=n(n-1)/2 条边的无向图称作完 全图;
含有 e=n(n-1) 条弧的有向图称作 有 向完全图;
若边或弧的个数 e<nlogn,则称作 稀疏图,否则称作稠密图。
.页 08.06.2020
假若顶点v 和顶点w 之间存在一条边, 则称顶点v 和w 互为邻接点, 边(v,w) 和顶点v 和w 相关联。
图的结构定义:
图是由一个顶点集 V 和一个弧集 R构成 的数据结构。
Graph = (V , VR ) 其中,VR={<v,w>| v,w∈V 且 P(v,w)}
<v,w>表示从 v 到 w 的一条弧,并称 v 为 弧头,w 为弧尾。 谓词 P(v,w) 定义了弧.页<v,w>的意义或信息
08.06.2020
7.7,7.9,7.10,7.12,7.14,7.15.,页7.22
08.06.2020
7.1 图的定义与术语
7.2 图的存储表示
7.3 图的遍历
7.4 最小生成树
7.5 重(双)连通图和关节点
7.6 两点之间的最短路径问题
7.7 拓扑排序
08.06.2020
7.8 关键路径 .页
7.1 图的定义与术语
和顶点v 关联的边的数目定义为顶点v的度。
例如:
B
C
ID(B) = 3 ID(A) = 2
08.06.2020
A F
.页
D E
对有向图来说,
A
B
E
CF 例如:
OD(B) = 1
顶点的出度: 以顶点v 为弧尾的弧的数目;
顶点的入度: 以顶点v 为弧头的弧的数目。
ID(B) = 2
TD(B) = 3
08.06.2020
顶点的度(TD)=
出度(OD)+入度(ID)
.页
设图G=(V,{VR})中的一个顶点序列
{ u=vi,0,vi,1, …, vi,m=w}中,(vi,j-1,vi,j)VR 1≤j≤m, 则称从顶点u 到顶点w 之间存在一条路径。
路径上边(或弧)的数目称作路径长度。
如:长度为3的路径 简单路径:序列中顶点
由顶点集和边 集构成的图称
作无向图。
例如: G2=(V2,VR2)
V2={A, B, C, D, E, F}
B
VR2={(A,B),(A,E),
(B,E),(C,D),(D,F),
A
(B,F),(C,F)}
08.06.2020
F
.页
C D
E
名词和术语
网、子图 完全图、稀疏图、稠密图
邻接点、度、入度、出度 路径、路径长度、简单路径、简单回路
2. 如果每次让三条路同时通行,那么从图看出哪些路可以同时通行? 同时可通行的路为: (AB,BC,CA),(AB,BC,BA),(AB,AC,CA),(CB,CA,BC)
.页 08.06.2020
【学习目标】
1.领会图的类型定义。 2.熟悉图的各种存储结构及其构造算法, 了解各种存储结构的特点及其选用原则。 3.熟练掌握图的两种遍历算法。 4.理解各种图的应用问题的算法。
B
A F
08.06.2020
C
D
E
.页
对非连通图,则 称由各个连通分 量的生成树的集 合为此非连通图 的生成森林。
基本操作
结构的建立和销毁 对顶点的访问操作
连通图、连通分量、 强连通图、强连通分量
生成树、生成森林
.页 08.06.2020
15 A 9
11
B 7 21
E
3
C2 F
弧或边带权的图 分别称作有向网或 无向网。
设图G=(V,{VR}) 和 图 G=(V,{VR}), 且 VV, VRVR, 则称 G 为 G 的子图。
.页 08.06.2020
【学习指南】
离散数学中的图论是专门研究图性质的一个数学分 支,但图论注重研究图的纯数学性质,而数据结构中对 图的讨论则侧重于在计算机中如何表示图以及如何实现 图的操作和应用等。图是较线性表和树更为复杂的数据 结构,因此和线性表、树不同,虽然在遍历图的同时可 以对顶点或弧进行各种操作,但更多图的应用问题如求 最小生成树和最短路径等在图论的研究中都早已有了特 定算法,在本章中主要是介绍它们在计算机中的具体实 现。这些算法乍一看都比较难,应多对照具体图例的存 储结构进行学习。而图遍历的两种搜索路径和树遍历的 两种搜索路径极为相似,应将两者的算法对照学习以便 提高学习的效果。本章必须完成的算法设计题为 :
由于“弧”是有方向的,因此称由顶点集 和弧集构成的图为有向图。
例如: G1 = (V1, VR1)
A
B
E
CD
其中
V1={A, B, C, D, E} VR1={<A,B>, <A,E>,
<B,C>, <C,D>, <D,B>, <D,A>, <E,C> }
.页 08.06.2020
若<v, w>VR 必有<w, v>VR, 则称 (v,w) 为顶点v 和顶点 w 之间存在一条边。
第七章 图
.页 08.06.2020
【课前思考】
1. 同学们有没有发现现在的十字路口的交通灯已从过去的一对改为三对, 即每个方向的直行、左拐和右拐能否通行都有相应的交通灯指明。你能否 对某个丁字路口的6条通路画出和第一章绪论中介绍的"五叉路口交通管理 示意图"相类似的图?
同学们一定可以画出如下所示类似的图形。
{A,B,C,F}
不重复出现的路径。
A
简单回路:序列中第一
B
E 个顶点和最后一个顶
点相同的路径而其余
C
08.06.2020
F
.页顶点不重复。
若图G中任意两个顶
B
点之间都有路径相通,
则称此图为连通图; A
C D
B A
F
08.06.2020
C
F
E
D 若无向图为非连通图, 则图中各个极大连通
E
子图称作此图的连通
分量。
.页
对有向图,若任意两个顶点之间都存在
一条有向路径,则称此有向图为强连通图。
否则,其各个强连通子图称作它的 强连通分量。
A
A
B
EB
E
CF
CF
.页 08.06.2020
假设一个连通图有 n 个顶点和 e 条边, 其中 n-1 条边和 n 个顶点构成一个极小连 通子图,称该极小连通子图为此连通图的 生成树。
.页 08.06.2020
【重点和难点】
图的应用极为广泛,而且图的各种应用问题的 算法都比较经典,因此本章重点在于理解各种图的 算法及其应用场合。
【知识点】
图的类型定义、图的存储表示、图的深度优先搜 索遍历和图的广度优先搜索遍历、无向网的最小生成 树、最短路径、拓扑排序、关键路径。
.页 08.06.2020
