2018年985核心密卷文科数学(答案)
2018届全国统一招生高考押题卷文科数学(二)试卷(含答案)

绝密 ★ 启用前2018年普通高等学校招生全国统一考试文 科 数 学(二)注意事项:1、答题前,考生务必将自己的姓名、准考证号填写在答题卡上。
2、回答选择题时,选出每小题答案后,用铅笔把答题卡上对应题目的答案标号涂黑。
如需改动,用橡皮擦干净后,再选涂其它答案标号。
回答非选择题时,将答案写在答题卡上,写在本试卷上无效。
3、考试结束后,请将本试题卷和答题卡一并上交。
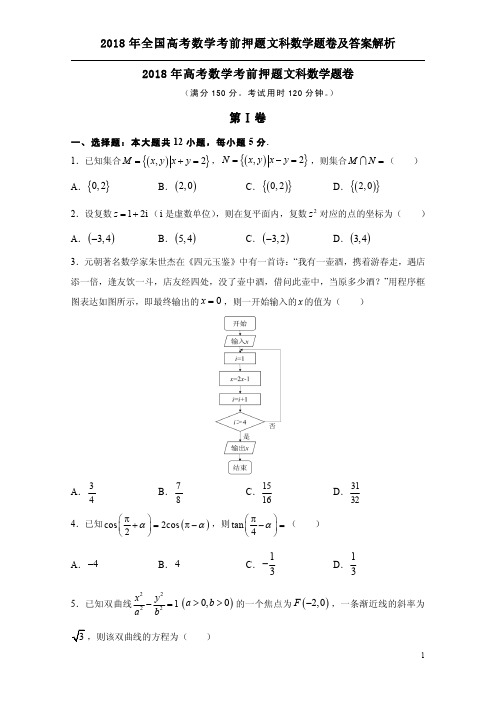
第Ⅰ卷一、选择题:共12小题,每小题5分,共60分.在每个小题给出的四个选项中,只有一项是符合题目要求的.1.已知集合,,则(){}2340A x x x =∈--≤Z {}0ln 2B x x =<<A B = A .B .C .D .{}1,2,3,4{}3,4{}2,3,4{}1,0,1,2,3,4-【答案】C【解析】,{}{}{}2340141,0,1,2,3,4A x x x x x =∈--≤=∈-≤≤=-Z Z ,所以.{}{}20ln 21e B x x x x =<<=<<{}2,3,4A B = 2.设复数(是虚数单位),则的值为()1z=i z z+A .B .C.D .21【答案】B【解析】,.2z z +=2z z +=3.“为假”是“为假”的( )条件.p q ∧p q ∨A .充分不必要B .必要不充分C .充要D .既不充分也不必要【答案】B【解析】由“为假”得出,中至少一个为假.当,为一假一真时,为真,故不充分;p q ∧p q p q p q ∨当“为假”时,,同时为假,所以为假,所以是必要的,所以选B .p q ∨p q p q ∧4.已知实数,满足约束条件,则的最大值为( )x y 222020x x y x y ≤⎧⎪-+≥⎨⎪++≥⎩3x z y =-+A .B .C .D .143-2-434【答案】C【解析】作出的可行域为三角形(包括边界),把改写为,当且仅当动直线3x z y =-+3xy z =+过点时,取得最大值为.3x y z =+()2,2z 435.据有关文献记载:我国古代一座9层塔共挂了126盏灯,且相邻两层中的下一层灯数比上一层灯数都多(为常数)盏,底层的灯数是顶层的13倍,则塔的底层共有灯( )盏.n n A .2B .3C .26D .27【答案】C【解析】设顶层有灯盏,底层共有盏,由已知得,则,1a 9a ()91991132691262a a a a a =⎧⎪⇒=⎨+=⎪⎩所以选C .6.如图是一个算法流程图,若输入的值是13,输出的值是46,则的值可以是( )n S a A .8B .9C .10D .11【答案】C【解析】依次运行流程图,结果如下:,;,;,;,,此时退出循环,所以的值可13S =12n =25S =11n =36S =10n =46S =9n =a 以取10.故选C .7.设双曲线的两条渐近线互相垂直,顶点到一条渐近线的距离为1,则双曲()2222:10,0x y C a b a b-=>>线的一个焦点到一条渐近线的距离为()A .2BC .D .4【答案】B【解析】因为双曲线的两条渐近线互相垂直,所以渐近线方程为,所以.因2222:1x yC a b -=y x =±a b =为顶点到一条渐近线的距离为1,所以,双曲线的方程为,所1=a b ==C 22122x y -=以双曲线的一个焦点到一条渐近线的距离为.b =8.已知数据,,,,的平均值为2,方差为1,则数据,,,相对于原数据( )1x 2x 10x 21x 2x 10x A .一样稳定B .变得比较稳定C .变得比较不稳定D .稳定性不可以判断【答案】C【解析】因为数据,,,,的平均值为2,所以数据,,,的平均值也为2,因为数据,1x 2x 10x 21x 2x 10x 1x ,,,的方差为1,所以,所以,所以数据,2x 10x 2()()102211222111i i x =⎡⎤-+-=⎢⎥⎣⎦∑()10212=11i i x =-∑1x ,,的方差为,因为,所以数据,,,相对于原数据变得比较不2x 10x ()102112=1.110ii x =-∑ 1.11>1x 2x 10x 稳定.9.设表示正整数的所有因数中最大的奇数与最小的奇数的等差中项,数列的前n 项和为,那n a n {}n a n S 么( )21n S -=A .B .C .D .122n n +--11222433n n --+⋅-2nn -22nn +-【答案】B【解析】由已知得,当为偶数时,,当为奇数时,.n 2n n a a =n 12n na +=因为,12342121n n S a a a a a --=+++++ 所以1112342121n n S a a a a a ++--=+++++ ()()111352462122+n n a a a a a a a a ++--=++++++++ ()1123211113151212222n n a a a a +-⎛⎫++++-=+++++++++ ⎪⎝⎭ ,()()123211232n na a a a -=+++++++++ ()211222n nnS -+=+()211242n nn S -=++即,()121211242n n nn S S +--=++所以.()()()1112211112121111224242422422233n n n n n n n S S --------=+++++++=+⋅- 10.过抛物线的焦点作直线交抛物线于,两点,若线段中点的横坐标为3,2y mx =()0m >P Q PQ ,则( )54PQ m =m =A .4B .6C .8D .10【答案】C【解析】因为,所以焦点到准线的距离,设,的横坐标分别是,,则2y mx =2mp =P Q 1x 2x ,,因为,所以,即,解得.1232x x +=126x x +=54PQ m =125+4x x p m +=5624m m +=8m =11.已知一个三棱锥的三视图如图所示,其中三视图的长、宽、高分别为2,1,,则此三棱锥外接球的12表面积为()A .B .C .D .174π214π4π5π【答案】B【解析】由已知条件及三视图得,此三棱锥的四个顶点位于长方体的四个顶点,即为三1111ABCD A B C D -棱锥,且长方体的长、宽、高分别为2,1,,11A CB D -1111ABCD A B C D-12所以此三棱锥的外接球即为长方体的外接球,半径,所以1111ABCD A B C D -R ==三棱锥外接球的表面积为.2221444S R π=π=π=12.已知点是曲线上任意一点,记直线(为坐标系原点)的斜率为,则下列一定P sin ln y x x =+OP O k 成立的为( )A .B .C .D .1k <-0k <1k <1k ≥【答案】C【解析】任意取为一正实数,一方面,另一方面容易证成立,所以x sin ln ln 1y x x x =+≤+ln 1x x +≤,因为与中两个等号成立条件不一样,所以sin ln y x x x =+≤sin ln ln 1y x x x =+≤+ln 1x x +≤恒成立,所以,所以排除D ;当时,,所以,所以sin ln y x x x =+<1k <2x π≤<πsin ln 0y x x =+>0k >排除A ,B .所以选C .第Ⅱ卷本卷包括必考题和选考题两部分。
2018全国I卷高考压轴卷 文科数学 Word版含答案

2018全国卷Ⅰ高考压轴卷文科数学本试卷共23题(含选考题)。
全卷满分150分。
考试用时120分钟。
一、选择题:本大题共12小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的. 1. 若集合{}1,2lg<=⎭⎬⎫⎩⎨⎧-==x x N x x y x M ,则=⋂N C M R (A ))2,0( (B )(]2,0 (C )[)2,1 (D )()+∞,0 2. 若a R ∈,则“1=a ”是“()10a a -=”的A .充分而不必要条件B .必要而不充分条件C .充要条件D .既不充分又不必要条件3. 若复数z 满足(1﹣i )z=2+3i (i 为虚数单位),则复数z 对应点在( ) A .第一象限B .第二象限C .第三象限D .第四象限4. 已知数列{}n a 的前n 项和22n S n n =+,则数列11{}n n a a +⋅的前6项和为( )A .215 B .415 C.511D .1011 5. 在区间[-1,1]上任选两个数x y 和,则221x y +≥的概率为( ) A .14π-B .128π- C. 18π- D .124π- 6. 过直线23y x =+上的点作圆2246120x y x y +-++=的切线,则切线长的最小值为( )A.[] 7. 已知1x ,2x (12x x <)是函数x x x f ln 11)(--=的两个零点, 若()1,1a x ∈,()21,b x ∈,则A .()0f a <,()0f b <B .()0f a <,()0f b >C .()0f a >,()0f b >D .()0f a >,()0f b <8. F 1,F 2分别是双曲线)0,0(12222>>=-b a by a x 的左、右焦点,过F 1的直线l 与双曲线的左、右两支分别交于A 、B 两点.若△ABF 2是等边三角形,则该双曲线的离心率为 (A )2 (B )3 (C )5 (D )79. 若程序框图如图所示,则该程序运行后输出k 的值是( )A .5B .6 C.7 D .810. 在ABC △中,60A ∠=,3AB AC ==,D 是ABC △所在平面上的一点. 若3BC DC =,则DB AD ⋅=A. 1-B. 2-C. 5D.9211. 有人发现,多看手机容易使人变冷漠,下表是一个调查机构对此现象的调查结果:附:K 2=附表:P(K 2≥k 0) 0.050 0.010 k 03.841 6.635则认为多看手机与人冷漠有关系的把握大约为A. %99B. %5.97C. %95D. %9012. 已知函数2||33()()(3)(3)3x x f x g x b f x x x -≤⎧⎪==--⎨-->⎪⎩,,函数,,其中b R ∈,若函数()()y f x g x =-恰有4个零点,则实数b 的取值范围是( )A. 11(,)4-+∞ B. 11(3,)4--C. 11(,)4-∞-D. (3,0)-二、填空题:本题共4小题,每小题5分,共20分。
2018年全国高考数学考前押题文科数学题卷及答案解析
1 2
D. ,
1 2
第Ⅱ卷
本 卷 包 括 必 考 题 和 选 考 题 两 部 分 。 第 (13)~(21) 题 为 必 考 题 , 每 个 试 题 考 生 都 必须作答。第 (22)~(23) 题为选考题,考生根据要求作答。 二、填空题:本大题共 4 小题,每小题 5 分。
… , x10 ,
是抛物线 C 的焦点,若 x1 x2 x10 10 ,则
x y 2≥0 y 15.若 x , y 满足约束条件 x y 4≤0 ,则 的取值范围为__________. x 1 y≥2
16 .在三棱椎 P ABC 中,底面 ABC 是等边三角形,侧面 PAB 是直角三角形,且
F F 2 PF2 ,设 C1 与 C2 的 的焦点 F 1, F 2 ,若点 P 是 C1 与 C2 在第一象限内的交点,且 1 2
离心率分别为 e1 , e2 ,则 e2 e1 的取值范围是( A. , )
1 3
B. ,
1 3
C. ,
B. n 2017 i
C. n 2018 i )
D. n 2017 i
π 2 ,则“ cosx x ”是“ cos x<x ”的( 2
A.充分而不必要条件 C.充分必要条件
B.必要而不充分条件 D.既不充分也不必要条件
9.如图为正方体 ABCD A1B1C1D1 ,动点 M 从 B1 点出发,在正方体表面上沿逆时针方
PA PB 2 , PA AC ,则该三棱椎外接球的表面积为________.
三、解答题:解答应写出文字说明、证明过程或演算步骤。
(完整word版)2018年文科数学(全国卷3-含答案),推荐文档

2018年数学试题文(全国卷3)、选择题(本题共12小题,每小题5分,共60分•在每小题给的四个选项中,只有一项符 合题目要求的.)1.已知集合 A x|x 1> 0 ,B0 , 1, 2,则 AI B ( )A.0 B. 1C. 1 , 2D. 0 , 1 , 22. 1 i 2i( )A. 3 iB. 3 iC. 3 iD. 3 i3.中国古建筑借助榫卯将木构件连接起来, 构件的凸出部分叫棒头, 凹进部分叫卯眼,图中木构件右边的小长方体是棒头.若如图摆放的木构件与某一带卯眼的木构件咬合成长方体, 则咬合时带卯眼的木构件的俯视图可以: ■是( )5.若某群体中的成员只用现金支付的概率为0.45,既用现金支付也用非现金支付的概率为0.15,则不用现金支付的概率为(6.函数 f xta=L 的最小正周期为( 1 tan x4.右 sin1,则 cos2 300 - 9A00 - 9D7 - 9A. 0.3B. 0.4C. 0.6D. 0.7HI -- .冋AA.-4 B. C.7.下列函数中,其图像与函数In x的图像关于直线1对称的是(A. y In 1 xB. y In 2 xC. y In 1 xD. 2)D. y In 2 x20310•已知双曲线 c :笃 為 1 ( a 0, b 0 )的离心率为 2,则点4, 0到C 的渐近线的 a b 距离为( )A .2B. 2C. 42D.2422 ‘ 2211. ABC 的内角 A , B , C 的对边分别为a , b , c . 若 ABC 的面积为ab c ,则C4( )A.—B.—C.D.2 34612.设A , B , C , D 是同一个半径为 4的球的球面上四点,ABC 为等边三角形且其面积为9、3,则三棱锥D ABC 体积的最大值为( )8直线x y 2 0分别与x 轴,y 轴交于A , B 两点,点P 在圆x 22y 2上,贝U ABP面积的取值范围是()A . 2,6B . 4, 8C.2 ,3 .2D. 2 .2 ,3 .29.函数y x 4 x 22的图像大致为()二、填空题(本题共4小题,每小题5分,共20分)13.已知向量a= 1,2 , b= 2, 2 , c= 1,入.若c // 2a + b,贝U _________________ . 14•某公司有大量客户,且不同年龄段客户对其服务的评价有较大差异•为了解客户的评价, 该公司准备进行抽样调查,可供选择的抽样方法有简单随机抽样、分层抽样和系统抽样, 则最合适的抽样方法是__________15 .若变量x, y满足约束条件2x yx 2yx 2 w3 > 0,4 > 0 ,则z x - y的最大值是30.16.已知函数f x ln .1 x2x1,f a4,则f a三、解答题(共70分,解答应写出文字说明、证明过程或演算步骤,第17~31题为必考题,每个试题考生都必须作答,第22、23题为选考题,考生根据要求作答.)(一)必考题:共60分。
2018年985核心密卷文科数学(试卷)

6.在三棱锥 D ABC 中, DC 底面 ABC , AD 6, AB BC ,且三棱锥 D ABC 的每个顶
点都在球 O 的表面上,则球 O 的表面积为( )
A.144π
B.100π
C. 64π
x 2y 19 0,
7.若关于
x
,
y
的混合组:
x
y
8
0,
2x y 14
Hale Waihona Puke ,1 2e
C.
2 e3
,
1 2e
D.
2 e2
,
1 e
第Ⅱ卷
二、填空题(本题共 4 小题,每小题 5 分,共 20 分)
13. x 3y 2x y 5 的展开式中,含 x2 y4 项的系数为_____________.(用数字作答)
14.若圆 : x2 y 2 4x 8y 0 ,直线 l1过点 (1,0) 且与直线 l2 : 2x y 0 垂直,则直线 l1 截
10.若非零向量 a, b 的夹角为锐角
,且
a
cos
,则称
a
被
b
“同余”.已知
b
被
a
“同余”,则
a
b
在
a
b
上的投影是(
2 2
a
A.
b
a
)
a
2
b
2
B.
2
a
2 2
C.
b
2018届全国统一招生高考押题卷文科数学(一)试卷(含答案)

绝密 ★ 启用前2018年普通高等学校招生全国统一考试文 科 数 学(一)注意事项:1、答题前,考生务必将自己的姓名、准考证号填写在答题卡上。
2、回答选择题时,选出每小题答案后,用铅笔把答题卡上对应题目的答案标号涂黑。
如需改动,用橡皮擦干净后,再选涂其它答案标号。
回答非选择题时,将答案写在答题卡上,写在本试卷上无效。
3、考试结束后,请将本试题卷和答题卡一并上交。
第Ⅰ卷一、选择题:共12小题,每小题5分,共60分.在每个小题给出的四个选项中,只有一项是符合题目要求的.1.复数132i z =+,121i z z +=+,则复数12z z ⋅=( ) A .47i -- B .2i --C .1+iD .14+5i【答案】A【解析】根据题意可得,21i 32i 2i z =+--=--,所以()()1232i 2i 47i z z ⋅=+⋅--=--. 2.集合{}|A x x a =<,{}3log 1B x x =<,若{}3A B x x =<U ,则a 的取值范围是( )A .[]0,3B .(]0,3C .(],3-∞D .(),3-∞【答案】B【解析】根据题意可得{}{}3log 103x B x x x <=<<=,因为{}3A B x x =<U ,所以03a <≤. 3.汉代数学家赵爽在注解《周髀算经》时给出的“赵爽弦图”(如下图),四个全等的直角三角形(朱实),可以围成一个大的正方形,中空部分为一个小正方形(黄实).若直角三角形中一条较长的直角边为8,直角三角形的面积为24,若在上面扔一颗玻璃小球,则小球落在“黄实”区域的概率为( )A .14B .13C .125D .2573【答案】C【解析】根据题意可得,另外一条直角边长为6,所以“黄实”区域的面积为()286=4-,大正方形的面积是228+6=100,所以小球落在“黄实”区域的概率是4110025=. 4.若双曲线C :()222210,0x y a b a b-=>>的焦点到渐近线的距离等于其实轴长,则双曲线C 的离心率为( ) A .2 B .3C .5D .22【答案】C【解析】由题意可知:2b a =,224ba =,2224c a a -=,5e =.5.将函数215log cos π262x y ⎛⎫⎛⎫- ⎪⎪⎝⎭⎝⎭=对应的曲线沿着x 轴水平方向向左平移2π3个单位,得到曲线为( )A .1πcos 26y x ⎛⎫ ⎪⎝⎭=- B .1πsin 26y x ⎛⎫ ⎪⎝⎭=- C .1sin 2y x =-D .1sin2y x = 【答案】D【解析】因为215log cos π26152cos π26x y x ⎛⎫⎛⎫- ⎪⎪⎝⎭⎝⎭⎛⎫ ⎪⎝⎭==-,所以沿着x 轴水平方向向左平移2π3个单位,得到曲线为1251151π1cos ππcos ππcos sin 236236222y x x x x ⎛⎫⎛⎫⎛⎫⎛⎫=+-=+-=-= ⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭⎝⎭.6.如图的程序框图,则输出y 的最大值是( ) A .3B .0C .15D .8此卷只装订不密封班级 姓名 准考证号 考场号 座位号【答案】C【解析】当3x =-时,3y =;当2x =-时,0y =;当1x =-时,1y =-;当0x =时,0y =;当1x =时,3y=;当2x =时,8y =;当3x =时,15y =,所以y 的最大值为15.7.一个几何体的三视图如图所示,则该几何体的体积为( )正视图侧视图A .2π+B .1+πC .2+2πD .12π+【答案】A【解析】根据三视图可得该几何体为一个长方体和半个圆柱组合所成,21112π122π2V =⨯⨯+⨯⨯⨯=+.8.已知某函数图象如图所示,则图象所对应的函数可能是( )A .2x x y =B .22xy =-C .e xy x =-D .|2|2x y x =﹣【答案】D【解析】对于A ,函数()2x x xf =,当0x >时,0y >,0x <时,0y <,不满足题意;对于B ,当0x ≥时,()f x 递增,不满足题意;对于C ,当0x ≥时,()0f x >,不满足题意.故选D .9.在平面直角坐标系中,已知直线l的方程为:20x y -=,圆C 的方程为()222423100x y ax y a a +--++=>,动点P 在圆C 上运动,且动点P 到直线l 的最大距离为2,则圆C 的面积为( ) A .π或(201π- B .πC.(201π+D .π或(201π+【答案】B【解析】因为()()2222224231210x y ax y a x a y a +--++=-+--=,所以()()22221x a y a -+-=,圆C 的圆心为(2,1)a ,半径为a .因为点P 在圆C 上的动点,所以P 到直线l的最大距离为2a +=,当a ≥时,解得11a =-2112-当0a <<1a =,符合题意,所以1a =,2S a =π=π圆. 10.已知函数()y f x =为定义域R 上的奇函数,且在R 上是单调函数,函数()()5g x f x =-;数列{}n a 为等差数列,且公差不为0,若()()190g a g a +=,则129a a a +++=L ( )A .45B .15C .10D .0【答案】A【解析】由函数()y f x =为定义域R 上的奇函数,且在R 上是单调函数,可知()()5g x f x =-关于()5,0对称,且在R 上是单调函数, 由()()190g a g a +=,所以1910a a +=,即55a =, 根据等差数列的性质,1295945a a a a +++==L .11.若x =()()22e x f x x ax =-的极值点,则函数()y f x =的最小值为( )A.(2e +B .0C.(2-D .e -【答案】C【解析】()()22e x f x x ax =-,∴()()()()2222e 2e 212e x x xf x x a x ax x a x a '⎡⎤=-+=+--⎣⎦-,由已知得,0f '=,∴220a +-=,解得1a =.∴()()22e x f x x x =-,∴()()22e x f x x '-=,所以函数的极值点为,当(x ∈时,()0f x '<,所以函数()y f x =是减函数,当(,x ∈-∞或)x ∈+∞时,()0f x '>,函数()y f x =是增函数.又当()(),02,+x ∈-∞∞U 时,220x x ->,()0f x >,当()0,2x ∈时,220x x -<,()0f x <,∴()min f x 在()0,2x ∈上,又当(x ∈时,函数()y f x =递减,当)x ∈时,函数()y f x =递增,∴()(min 2f x f==-.12.已知0b a >>,函数()2log 21log 2xf x x ⎛⎫=- ⎪⎝⎭在[],a b 上的值域为132⎡⎤-⎢⎥⎣⎦,,则ab =( ) A .14B .12C .2D【答案】D【解析】()2log 2211log log 2xf x x x x ⎛⎫=-=- ⎪⎝⎭()a x b ≤≤,又()2110ln2f x x x '=--<,所以()y f x =在[],a b 上递减,∴()()312f a f b ⎧=⎪⎨=-⎪⎩,即2213log 11log 2a a b b ⎧-=⎪⎪⎨⎪+=⎪⎩①,由1y t x =+与2log y x =的图象只有唯一交点可知方程21log t x x +=只有唯一解,经检验122a b ⎧=⎪⎨⎪=⎩是方程组①的唯一解,所以ab =第Ⅱ卷本卷包括必考题和选考题两部分。
2018年三好网985核心密卷理科数学(试卷)

2.已知实数 m, n 满足 m 2i n(2 i) ,则在复平面内,复数 z m ni 所对应的点位于( )
A.第一象限
B.第二象限
C.第三象限
D.第四象限
3.已知向量 m (1,1) , n (1, ) ,若 m n ,则 m n 与 m 之间的夹角为( )
A. 4
B. 3
5.如图是一个算法流程图,若输入 n 的值是 13,输出 S 的值是 46,则 a 的取值范围是( ) A. 9 a 10 B. 9 a 10 C. 10 a 11 D. 8 a 9
注意事项:
(考试时间:120 分钟 试卷满分:150 分)
1.本试卷分第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分.答卷前,考生务必将自己的姓 名、准考证号填写在答题卡上. 2.回答第Ⅰ卷时,选出每小题答案后,用 2B 铅笔把答题卡上对应题目的答案标号涂黑. 如需改动,用橡皮擦干净后,再选涂其他答案标号,写在本试卷上无效. 3.回答第Ⅱ卷时,将答案写在答题卡上.写在本试卷上无效. 4.考试结束后,将本试卷和答题卡一并交回.
(1)先将曲线 C 的参数方程化成直角坐标方程,再将直线 l 的极坐标方程化成参数方程(使 得参数具有几何意义);
(2)求直线 l 与曲线 C 相交所得的弦 AB 的长.
…
三好网“985”核心密卷
理科数学试题 第 5页(共 8页)
公众号:2020押题
三好网“985”核心密卷
理科数学试题 第 6页(共 8页)
………………○………………内………………○………………装………………○………………订………………○………………线………………○………………
学 校 : ______________姓 名 : _____________班 级 : _______________考 号 : ______________________
2018年三好网985核心密卷文科数学(试卷)

(1)下表是所得红包的频数分布表,求实数 m , a , b , c 的值;
区间
[0,100) [100, 200) [200,300) [300, 400) [400,500]
人数
50
250
a
b
c
(2)现在要从第 3,4,5 组中用分层抽样的方法抽取 7 人,则在第 3,4,5 组中抽取的学
A.144π
B.100π
C. 64π
x 2y 19 0,
7.若关于
x
,
y
的混合组:
x
y
8
0,
2x y 14
0,
有解,则 a 的取值范围是(
)
y ax a 0,a 1
A.[1,3]
B.[2, 10]
C.[2,9]
D.[ 10,9]
D. 36π
8.如图所示,网格纸上小正方形的边长为 1,下图画出的是某几何体的三视图,则该几何体 的体积为( )
9.若函数 f x ln x 2 a (a 是与 x 无关的实数)在区间 1, e 上存在零点,则实数 a 的取值范围为
x
()
A. 0 a 2 B. 2 a 2 C. 2 1 a 2
e
e
D. 2 +1 a 2 e
三好网“985”核心密卷
文科数学试题 第 1页(共 6页)
公众号:2020押题
2.已知实数 m, n 满足 m 2i n(2 i) ,则在复平面内,复数 z m ni 所对应的点位于( )
A.第一象限
B.第二象限
C.第三象限
D.第四象限
3.已知向量 m (1,1) , n (1, ) ,若 m n ,则 m n 与 m 之间的夹角为( )
文科数学2018高考985核心密卷五月版(一)(试卷)-1

2 ,高为 3 的正四棱柱 ABCD A1B1C1D1 中, BC 与平面
1 5
B.
3 7
C.
7 3
D. 3
AB1C 所成角的余弦值为( )
A.
x2 y 2 5.过点 (2, 4 2) 的抛物线与双曲线 C : 2 2 1 ( a 0, b 0) 有一个共同的焦点,若双曲线 C 的渐 a b
封
区间 人数
[0,100) [100, 200) [200, 300) [300, 400) [400, 500]
10 . (2)求证: f ( x) f ( )≥
1 x
50
250
a
b
c
(2)现在要从第 3,4,5 组中用分层抽样的方法抽取 7 人,则在第 3,4,5 组中抽取的学生的人数分别
C 相交于 M , N 两点. (1)求直线 l 的普通方程和圆 C 的直角坐标方程;
(2)求弦长 | MN | . 23. (本小题满分 10 分)选修 4-5:不等式选讲 已知函数 f ( x) | a 4 x | | 2a x | . (1)若 a 1 ,解不等式 f ( x) 3 ;
第Ⅱ卷 二、填空题:(本大题共 4 小题,每小题 5 分,共 20 分.)
x2 3 x 2 , 13.函数 f x 若 f a 1 ,则实数 a _________. 2 log x 1 x ≥ 2 , 3
是多少? (3)在(2)的前提下,从这 7 人中随机抽取 2 人参加社区宣传交流活动,求 2 人都来自第 3 组的概率. (本小题满分 12 分) 已知圆 A : ( x 1) 2 y 2 4 20. 且离心率等于 , 中心在坐标原点的椭圆 C 的一个焦点为圆心 A ,
2018全国II卷高考压轴卷 文科数学 Word版含解析

2018全国卷II 高考压轴卷文科数学本试卷共23题(含选考题)。
全卷满分150分。
考试用时120分钟。
一、选择题:本大题共12小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的.1. 设集合{}0,1,2,3,4A =---,{}210B x x =<,则A B =( )A .{}4B .{}1,2,3--C .{}0,1,2,3--D .{}3,2,1,0,1,2,3---2. 已知复数()z a i a R =+∈,若4z z +=,则复数z 的共轭复数z = A .2i + B .2i - C .2i -+ D .2i --3. 设等差数列{}n a 的前n 项和为n S ,若81126a a =+,则9S =( ) A .27 B .36 C.45 D .544. 已知命题p :“a b >”是“22ab>”的充要条件;q :x R ∃∈,ln x e x <,则A .¬p ∨q 为真命题B .p ∧¬q 为假命题C .p ∧q 为真命题D .p ∨q 为真命题5. 若命题:0,,sin 2p x x x p π⎛⎫∀∈<⌝ ⎪⎝⎭,则为 A .0,,sin 2x x x π⎛⎫∀∈≥ ⎪⎝⎭B .0,,sin 2x x x π⎛⎫∀∉≥ ⎪⎝⎭C .0000,,sin 2x x x π⎛⎫∃∈≥ ⎪⎝⎭D .0000,,sin 2x x x π⎛⎫∃∈≤ ⎪⎝⎭6. 将函数cos 2y x =的图象向左平移2π个单位,得到函数()y f x =的图象,则下列说法正确的是( )A .()y f x =是奇函数B .()y f x =的周期为2πC .()y f x =的图象关于直线2x π=对称 D .()y f x =的图象关于点(,0)2π-的对称7. 执行如图的程序框图,则输出的S 值为A.1B.23 C.12-D.0 8. 函数2()(3)ln f x x x =-⋅的大致图象为( )A B C D9. 多面体MN ABCD -的底面ABCD 为矩形,其正(主)视图和侧(左)视图如图,其中正(主)视图为等腰梯形,侧(左)视图为等腰三角形,则AM 的长为( )A 3B 5C 6D .210. 已知向量()()2,1,1,1m n =-=.若()()2m n am n -⊥+,则实数a =( )A .57-B .57C .12-D .1211. 已知P 为抛物线y 2=4x 上一个动点,Q 为圆x 2+(y ﹣4)2=1上一个动点,那么点P 到点Q 的距离与点P 到抛物线的准线距离之和的最小值是( ) A .B .C .D .12. 已知()f x 是定义在R 上的偶函数,且x R ∈时,均有()()32f x f x +=-,()28f x ≤≤,则满足条件的()f x 可以是( )A .()263cos5x f x π=+ B .()53cos 5xf x π=+ C .()2,8,R x Q f x x C Q ∈⎧=⎨∈⎩ D .()2,08,0x f x x ≤⎧=⎨>⎩二、填空题:本题共4小题,每小题5分,共20分。
2018年高等学校招生全国统一考试押题卷文科数学试卷(三)含解析

【答案】 C
【解析】 函数 f x asin x b cosx( x R ),若 x x0 是函数 f x 的一条对称轴,
则 x x0 是 函 数 f x 的 一 个 极 值 点 , f x a cos x bsin x , 根 据 题 意 有
f x0 a cosx0 b sin x0 0 ,又 tan x0 2 ,故 a b tan x 0 2b ,结合选项,点 a, b
2
2 m 3 18≤18 ,当且仅当 m 3 , n 6 等号
成立,故选 B.
8.已知函数 f x a sin x bcosx ( x R ),若 x x0 是函数 f x 的一条对称轴,
且 tan x0 2 ,则 a,b 所在的直线为(
)
A. 2x y 0
B. x 2y 0
C. x 2 y 0
D. 2x y 0
4、选考题的作答:先把所选题目的题号在答题卡上指定的位置用
2B 铅笔涂黑。答案
写在答题卡上对应的答题区域内,写在试题卷、草稿纸和答题卡上的非答题区域均无
效。
5、考试结束后,请将本试题卷和答题卡一并上交。
第Ⅰ卷
一、选择题:本大题共 12 小题,每小题 5 分,在每小题给出的四个选项中, 只有一项是符合题目要求的。 1.已知全集 U 1,2,3, 4 ,若 A 1,3 , B 3 ,则 痧U A U B 等于( )
号 位
封座
密
号
不
场 考
订
装号 证 考 准
只
卷
名 姓 此
级 班
绝密 ★ 启用前
2018 年普通高等学校招生全国统一考试押题卷
文科数学(三)
本试题卷共 2 页, 23 题(含选考题) 。全卷满分 150 分。考试用时 120 分钟。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
更多押题入群 提分热线:4000—176—333
或入听课网下载
系列资料 BY 三好网汇编
当曲线 y=ax 过 A(1,9)时,a 取最大值,此时 a=9; 当曲线 y=ax 过 C(3,8)时,a 取最小值,此时 a=2,∴2≤a≤9. 8.【答案】B 【解析】通过三视图可知该几何体是正方体的一部分,在正方体中作出该几何体的直观图如图中三棱锥
因为 CF∥AE , CF 1 AE ,所以 CF∥AN ,且 CF AN .(2 分) 2
所以四边形 ANFC 为平行四边形,所以 NF∥AC . 因为 FN 平面 ABCD , AC 平面 ABCD ,所以 NF∥平面 ABCD , 又 M 为 DE 的中点,所以 MN∥AD .(4 分) 因为 MN 平面 ABCD , AD 平面 ABCD ,所以 MN∥平面 ABCD , 因为 MN NF N ,所以平面 MNF∥平面 ABCD . 因为 FM 平面 MNF ,所以 FM ∥平面 ABCD .(6 分)
因为 OC OA 1 OB ,
系列资料 BY 三好网汇编
所以 DC
DO OC
OA
1 2
OB
.
所以 DC OC
OA
1 2
OB
故 m n (1,1) (1,1) (0, 2) ,则 m n 与 m 之间夹角的余弦值为 cos 2 2 ,故 ,故
22 2
4
选 A.
4.【答案】 B
【解析】由命题的否定和否命题的构成法则得, p 的否定为“ x , 0, 2x2 3x 1 0 ”,q 的否命题
系列资料 BY 三好网汇编
2018 届三好网 985 核心密卷
文科数学参考答案及解析
1.【答案】C
【解析】依题意, A {x | 6 x 3} , B {x | x 2}, ðR B {x | x 2},
故 A ðRB x 6 x 2 ,故选 C.
为“若 x 0 ,则 2x2 3x 1 0 ”.故选 B.
5.【答案】B 【解析】第一次到第五次循环结果依次如下:S=13,n=12;S=25,n=11;S=36,n=10;S=46,n=9;S=55,
n=8,所以 a 的取值范围是 9 a 10 .
6.【答案】D
【解析】结合题意,可以将三棱锥 D ABC 补成一个长方体,且此长方体的体对角线长为 6, 则球 O 的半
A BCD ,以
A 为顶点, △BCD 为底面,可以求出该几何体的体积V
1 3
6
1 2
3
6
18 ,故选
B. 9.【答案】C
【解析】因为 f x ln x 2 a (a 是与 x 无关的实数)在 1, e 单调增,在区间 1, e 上存在零点,所
cos C cos B
cos C
cos B
即 (2sin A sin C) cos B sin B cos C ,所以 2sin Acos B sin(B C) sin A .
因为 sin A 0 ,所以 cos B 1 ,因为 B (0, ) ,所以 B .
32
322
所以 AE 3 .(12 分)
19.【解析】(1)由频率分布直方图知 (m 0.0005 0.001 0.0025 0.004) 100 1,解得 m 0.002 ,
a 0.0041001000 400 , b 0.0021001000 200 , c 0.0011001000 100 .(2 分) (2)由(1)知第 3,4,5 组的总人数为 700 ,按分层抽样抽取 7 人,则第 3,4,5 组中抽取的人数分别
2.【答案】C
【解析】依题意,得 m 2i 2n ni ,解得 m 4, n 2 ,故 z 4 2i ,则在复平面内,复数 z 所对
应的点为 (4, 2) ,位于第三象限,故选 C.
3.【答案】A
【解析】设 m n 与 m 之间的夹角为 ,依题意得,m n (1,1) (1, ) 0 ,即 1 0 ,解得 1,
g ( x)
1
2 ln x3
x
,可得
g
x
在
1 e
,
e
上递增,
在 ( e, e2 ]上递减,则 g x 在 x
e
处取得最大值
1 2e
,由 g(1) e
e2, g(e2 )
2 e4
,可得当
2 e4
k
1 2e
时,直线
y
k
和函数
g x 的图象有两个交点,即有函数
2
7
7
18.【解析】(1)解法一:如图①,取 AD 的中点 N ,连接 MN , CN ,
因为
M
为
DE
的中点,所以
MN∥AE
,
MN
1 2
AE
.(2
分)
领 2018 高考冲刺 985 押题密卷 专家揭秘,深度解析,紧抓最后提分机会
4/8
更多押题入群 提分热线:4000—176—333
或入听课网下载
又平面 ACFE 平面 ABCD AC ,所以 BD 平面 ACFE .(9 分)
系列资料 BY 三好网汇编
因为 ABC 60 ,所以 BD 4 3 , AC 4 .(10 分)
所以几何体 ABCDEF 的体积为
1 1 (AE CF) AC BD 1 1 3 AE 4 4 3 12 3 ,
a
11.【答案】C
【解析】选项 A 对应的是 a 2 ,选项 B 对应的是 a 4 ,选项 D 对应的是 a 1 .在选项 C 的图象中,由
f (x) sin ax(a R) 的图象可知, a 1 ,故 g(x) 2x2 x ,则 g(x) (a 1)x2 ax 的图象的对称
为 4, 2,1.(6 分)
(3)把第 3 组的 4 人分别记作 a1, a2 , a3, a4 ,第 4 组的 2 人分别记作 b1, b2 ,第 5 组的 1 人记作 c .
则从这 7 人中抽取 2 人的所有情况有:
a
a
b
sin
.
又a
ab
a
2 a b
a
2
a
b
cos
a
2
2 b,
所以
a
2
2 b
a
a
b
sin
.
领 2018 高考冲刺 985 押题密卷 专家揭秘,深度解析,紧抓最后提分机会
或入听课网下载
系列资料 BY 三好网汇编
又 CF∥AE , CF 1 AE ,所以 MN∥CF ,且 MN CF , 2
所以四边形 CFMN 为平行四边形,所以 FM ∥CN .(4 分) 又因为 CN 平面 ABCD , FM 平面 ABCD ,所以 FM ∥平面 ABCD .(6 分) 解法二:如图②,取 AE 的中点 N ,连接 MN , FN , AC ,
f
x 在区间
1 e
,
e
上有两个零点,所以
2 e4
k
1
.
2e
13.【答案】 110
【解析】依题意可知,所求系数为1 C15 2 3C52 22 110 .
14.【答案】 2 15
【 解 析 】 依 题 意 , 由 : x2 y 2 4x 8 y 0 , 得 圆 心 坐 标 为 (2, 4) , 半 径 为 2 5 , 设 直 线
x
以函数
f
x
ln
x
2 x
a
在区间
1,
e
上存在唯一零点,所以
f f
1 0, e 0, 解之,得,
2 e
1
a
2
.
10.【答案】A
【解析】令 a, b 的夹角为锐角 ,因为 b 被 a 同余,所以
b
cos ,所以
b
a
cos
,
a
l1 : x 2 y m 0 ,将点 (1, 0) 的坐标代入,解得 m 1,故直线 l1 : x 2 y 1 0 .圆心到直线 l1 的距离
d 5 ,故弦长为 2 20 5 = 2 15 .
9
15.【答案】
16
【解析】选取 OA,OB 为基向量.
2/8
更多押题入群 提分热线:4000—176—333
或入听课网下载
系列资料 BY 三好网汇编
∴ab在a
上的投影
a
b
cos
2
a
b
sin
2 2 a b ,故选 A.
轴在 y 轴右侧,而图中的的对称轴在 y 轴左侧,故选 C.
12.【答案】A
【解析】由
f
x 0 ,可得 kx
ln x x
,则
k
ln x x2
