网络规划3-最小树问题
最小树问题

6.3.1 狄克斯特拉算法 (Dijkstra algorithm, 1959) 计算两节点之间或一个节点到所有节点之间的最短路 令 dij 表示 vi vj 的直接距离(两点之间有边),若两点之间 没有边,则令 dij = ,若两点之间是有向边,则 dji = ; 令 dii = 0,s 表示始点,t 表示终点 • 对每个节点,用两种标号:T和P,表示从始点到该节点的距 离,P是最短距离(权),为永久标号,T是目前路径的距离,是 临时标号。 • 通过不断改进T值,当其最小时,将其改为P标号。 • 开始时,令始点有P=0的P标号,其它节点为T=+ .
•(3)Kruskal 算法:将图中所有边 v1 按权值从小到大排列,依次选 1 所剩最小的边加入边集 T,只 v8 要不和前面加入的边构成回路, 5 直到 T 中有 n1 条边,则 T 是最小生成树
v7
4
v2
1
v3
2
4 5
1
3
4
1
v4 5 v5
v0 2 3 v6 2 4
图的矩阵表示
将图的几何形状转化为代数矩阵形式,可大 大方便计算机对图的处理与运算。 1、无权图的矩阵表示:
6.2.3 最小生成树
v5 9 v6 17 10 8 7 11 v4 16 v3 9.5 v2 v1 10
12 7 19.5
10 16 11 10 17 10 9.5 19.5 16 9.5 7 12 7 8 7 11 10 8 9 17 19.5 12 7 9
寻找连通图支撑树的方法有“破圈法”。就是从图中 任取一个圈,去掉一条边。再对剩下的图重复以上步 骤,直到不含圈时为止,这样就得到一个支撑树。 例4 用破圈法求出下图的一个支撑树。 v2 e1 v1 e2 v3 e3 e4 e7 e8 e6 v5
最小树

∑
),W 弧e =(i,j)上的权常记为 (e), e 或w(e),wij等 , )上的权常记为W( ), ( ) 如果T*是 的一棵生成树 且对G的任何一棵生成树 的一棵生成树, 的任何一棵生成树T都有 如果 是G的一棵生成树,且对 的任何一棵生成树 都有 W( T* )≤W(T),则T*称为网络 的最小支撑树或者最小生 ),则 称为网络 称为网络G的最小支撑树或者最小生 ( ( ), 成树( ),或者简称最小树 成树(MST:minimum spanning tree),或者简称最小树 : ),或者简称最小树. 图的最小树一般不唯一
{
}
11
SOLLIN 算法 (1961) 基本思想:前面介绍的两种算法的综合。每次迭代同 基本思想:前面介绍的两种算法的综合。 时扩展多棵子树, 时扩展多棵子树,直到得到最小树 T.
STEP0 中任意一个顶点i, STEP0. 对N中任意一个顶点 ,定义 i={i}. 令T= 。 中任意一个顶点 定义N STEP1 如果T 中已有n-1条弧 条弧, 的最小树; STEP1. 如果 中已有 条弧,则T为G的最小树;否则,对T 中的所有子树 为 的最小树 否则, * 节点集合N 中的最小弧, 节点集合 k,计算边割 [ N k , N k ] 中的最小弧,即计算 w(ek ) = min w(e), 其中 e
该图正好含有一个圈.
5
最小树
定义2 为权函数, 定义 G=(N,E,W)为一个无向网络,W为权函数 即W: ( , , )为一个无向网络, 为权函数 E→R (这里 表示实数集合). G中权最小(大)的弧称为最小 这里R表示实数集合 表示实数集合) 中权最小 中权最小( (大)弧. 如果H=( 的一个子图, 的权定义为H所包含 如果 (N1,E1)为G的一个子图,子图 的权定义为 所包含 的一个子图 子图H的权定义为 的所有弧的权之和,记为W(H),即W(H)= 的所有弧的权之和,记为 , ( ) W ( e) .
教学课件:第五章-最小树问题

最小树问题在现实生活中具有广泛的应用,如电路设计、网络路由、物流配送等。通过解 决最小树问题,可以优化网络结构、降低成本、提高效率,为实际问题的解决提供重要的 理论支持和实践指导。
最小树问题的未来研究方向
算法优化与改进
尽管已经存在许多有效的算 法用于解决最小树问题,但 随着问题规模的扩大和复杂 度的增加,需要进一步优化 和改进现有算法,以提高求 解速度和精度。
04 最小小生成树问题是在最小生成树问题的基础上,给 每条边赋予一个权重值,目标是寻找一棵权值最小的生成树 。
详细描述
在带权重的最小生成树问题中,每条边都有一个关联的权重 ,表示该边的长度或代价。算法需要选择一组边,这些边能 够连接所有节点并且总权值最小。常见的带权重的最小生成 树算法有普里姆算法和克鲁斯卡尔算法。
理论分析与证明
对于最小树问题的求解算法 ,需要深入的理论分析和证 明,以揭示算法的内在机制 和性能。未来可以进一步研 究算法的理论基础和数学证 明,为算法的设计和分析提 供更严格的依据。
THANKS FOR WATCHING
感谢您的观看
05 总结与展望
最小树问题的研究现状与成果
最小树问题的定义和性质
最小树问题是一类组合优化问题,旨在寻找一棵具有最小权值的树,该树连接给定的顶点 集。最小树问题在计算机科学、运筹学和图论等领域具有广泛的应用。
最小树问题的研究进展
近年来,最小树问题的研究取得了重要的进展。研究者们提出了许多有效的算法和近似算 法,用于解决最小树问题及其变种。这些算法在理论和实践方面都取得了重要的突破,为 解决实际问题提供了有效的工具。
教学课件:第五章-最小树问
目录
• 引言 • 最小树问题的算法 • 最小树问题的实例分析 • 最小树问题的扩展问题 • 总结与展望
最小生成树实际城市建设例题

最小生成树实际城市建设例题在实际的城市规划和建设中,经常需要考虑如何在城市中建立高效的交通网络,以便居民可以便捷地出行,最小生成树实际城市建设例题:1. 最小生成树算法可以通过计算城市道路网络的最短路径来确定交通系统的建设方案。
这意味着,我们可以通过最小生成树来找到连接城市不同区域的最佳道路,确保居民可以高效地到达目的地。
2. 在城市建设中,最小生成树算法可以帮助决策者选择相对最优的交通线路布局。
通过计算不同道路之间的权重(如距离、交通流量等),最小生成树可以找到连接城市不同区域的最短路径,并在最佳位置建设道路。
3. 最小生成树算法还可以帮助决策者优化城市交通网络的设计。
通过分析城市道路的拓扑结构,最小生成树可以帮助找到一个连接城市各个地区的最小的道路集合,从而提高交通系统的效率和可持续性。
4. 最小生成树算法在城市建设中可以被用来规划公共交通系统。
通过将公交线路视作图中的节点,道路视作图中的边,可以利用最小生成树算法来确定最佳的公交线路布局,以满足居民的出行需求。
5. 最小生成树算法还可以应用于城市供水系统的规划。
通过将供水管道网络看作图中的边,不同供水站点看作图中的节点,可以使用最小生成树算法来确定供水系统的建设方案,确保每个区域都能获得足够的水源。
6. 在城市绿化方面,最小生成树算法可以用来规划公园和绿地的布局。
通过将不同公园和绿地看作图中的节点,道路连接的路径看作图中的边,最小生成树算法可以帮助确定最佳的公园布局,使得每个居民都能够方便地享受自然环境。
7. 最小生成树算法在城市建设中还可以被用来规划电力系统的布局。
通过将不同电源点和用电点看作图中的节点,电力线路看作图中的边,可以使用最小生成树算法来确定最佳的电力线路布局,以确保电力供应的连通性和稳定性。
8. 最小生成树算法还可以应用于城市安防系统的规划。
通过将不同监控点看作图中的节点,监控设备之间的连接路径看作图中的边,使用最小生成树算法可以确定最佳的监控点布局,提高城市的安全性和治安。
最小生成树题目

最小生成树题目 最小生成树是图论中的一个重要概念,被广泛应用于路由算法、网络设计、电力传输等领域。
最小生成树问题可以简单描述为:给定一个连通图,选择一些边使得图中所有节点都能够连接,并且总边权之和最小。
最小生成树题目是在解决最小生成树问题时所遇到的具体情境。
以下通过分析两个不同的最小生成树题目,来理解最小生成树算法的应用。
题目1:某城市的道路规划 假设一个城市有多个地区,每个地区之间需要建立道路来连接。
已知每条道路的长度,在保证每个地区都能连通的情况下,设计一个道路规划方案,使得总道路长度最小。
解题思路: 1、首先,根据题目中给出的道路长度,建立一个无向带权图。
其中,每个地区对应图的节点,道路对应图的边,道路长度对应边的权值。
2、通过使用Kruskal或Prim算法,从这个带权图中构建最小生成树,即选取一些道路使得所有地区连通,并且这些道路的权值之和最小。
3、最小生成树即为最优的道路规划方案,输出最小生成树的边集合即可。
题目2:电力传输网络设计 某地区有多个居民点,需要建立电力传输网络来确保每个居民点都能接收到电力供应。
已知每个居民点之间建立电力线路的成本,在保证每个居民点都能接收到电力供应的情况下,设计一个电力传输网络,使得总成本最小。
解题思路: 1、根据题目给出的电力线路成本,建立一个带权完全图。
其中,每个居民点对应图的节点,电力线路对应图的边,电力线路成本对应边的权值。
2、通过使用Kruskal或Prim算法,从这个带权图中构建最小生成树,即选取一些电力线路使得所有居民点都能接收到电力供应,并且这些电力线路的成本之和最小。
3、最小生成树即为最优的电力传输网络设计方案,输出最小生成树的边集合即可。
最小生成树问题是一个经典的优化问题,通过构建最小生成树,我们可以找到图中连接所有节点的最优边集合。
在实际应用中,最小生成树算法可以帮助我们进行有效的资源分配、网络规划等决策。
总体来说,最小生成树题目涉及到图的建模和优化算法的运用。
最小树问题.

W T ' W T w e w e '
证明:(1)→(2) 由于T是树,由定义知T连通且无圈。只须证明m=n-1。 归纳法:当n=2时,由于T是树,所以两点间显然有且 仅有一条边,满足m=n-1。 假设 n=k-1时命题成立,即有k-1个顶点时,T有 k-2条边。 当n=k时,因为T连通无圈,k个顶点中至少有一 个点次为1。设此点为u,即u为悬挂点,设连接点u的 悬挂边为[v,u],从T中去掉[v,u]边及点u ,不会影 响T的连通性,得图T’,T’为有k-1个顶点的树,所以 T’有k-2条边,再把( v,u)、点u加上去,可知当T 有k个顶点时有k-1条边。
第2步:在Xi 确定的割集(Xi)中选一条最小权边ek, ek=[v’,vk], v’∈Xi ,vk ∈ Xi , Ei-1= Ei∪ek
Xi+1= Xi ∪﹛vk﹜,Xi+1= Xi \ ﹛vk﹜
第3步:若Xi+1=V,结束,(V,Ei+1)是所求的最 小树。否则,把i换成i+1,返回第2步。
例:
定理3:图T是树的充分必要条件是任意两个顶点之间恰 有一条链。
证明:必要性 因T是连通的,故任两个点之 间至少有一条链。但如果某两个点之间有两条链 的话,那么图T中含有圈,这与树的定义矛盾, 从而任两个点之间恰有一条链。
充分性 设图T中任两个点之间恰有一条链, 那么易见T是连通的,如果T中含有圈,那么这个 圈上的两个顶点之间有两条链,这与假设矛盾, 故T不含圈,于是T是树。
最小树问题

V1
V4
V5
0Байду номын сангаас
0
1
1
0
1
0
1
1
0
两顶点间有边连接的记为 1 ,无边连接的记为 0。 得到的矩阵一定是对称矩阵。
2、赋权无向图的矩阵表示: 两顶点间有边 连接的记为该边的权数。无边相连的记为 , 对角线上的数是 0 。得到的矩阵也是对称矩阵。 例如:
5
v7
5
4
最小树,权为13
2.最小树的求法
(2)破圈法: ① 在网络图中寻找 一个圈。若不存在圈, 则已经得到最短树或网 络不存在最短树; ② 去掉该圈中权数 最大的边; 反复重复 ① ② 两 步,直到最小树。
v1 1 v8 4
4 2
v2 1
1 3 4
v3
1 v4 5 v5
5
v7
5
v0 2 3 v6 2 4
2.最小树的求法
求最小树的两种方法,是避圈法与破圈法
(1)避圈法: 从网络图中 任意节点开始寻 找与该节点关联 的权数最小的边, 使之与已选边不 构成为圈,直到 选够n-1条边为 止。
例
v1 1 v8 4 4 2 v2 1 1 3 4 v0 2 3 v6 2
从网络中 任选一点
v3 1 v4 5 v5
•(3)Kruskal 算法:将图中所有边 v1 按权值从小到大排列,依次选 1 所剩最小的边加入边集 T,只 v8 要不和前面加入的边构成回路, 5 直到 T 中有 n1 条边,则 T 是最小生成树
v7
4
最小树问题

6.3 图与网络规划问题图与网络规划问题归纳起来主要有最小树问题、最短路问题、最大流问题、最小费用最大流问题、指派问题、货郎担问题(TSP)、选址问题等,本节将基于图与网络给出描述这些问题的最优化模型,介绍问题求解的常用算法,给出实现算法的程序和应用它们解决实际问题的实例. 6.3.1 最小树问题最小树问题就是如何求一个网络),,(W E V G 的最小树. 在交通网、电力网、管道网等的设计中常涉及最小树问题, 如“已知n 个城市间的交通线建造费用, 如何建造一个联结这n 个城市的交通网, 使总的建造费用最小.”就是一个最小树问题.[Ⅰ] 最小树问题模型设连通网络)3)(,,( V n W E V G 的邻接矩阵为n n ij a A )(, 权矩阵为n n ij w W )(, 求(0, 1)矩阵n n ij t T )(, 使得11111min (),..0,0(,1,2,,),1,.n nij ij i jij ij n n ij i j i n i i W T w t s t t a i j n t n T当时不含非零元 (6.4) 邻接矩阵为n n ij t T )(的图T 即为网络G 的最小树, )(T W 为最小树T 的权.[Ⅱ] 求最小树的算法 i) Kruskal 算法[4]Kruskal 算法是Joseph Kruskal 于1956年首次提出的求最小树算法, 属贪心算法, 依据是定理6.7, 其基本思路是从连通网络),,(W E V G (记E m V n ,)的m 条边中选取1 n 条权尽量小的边, 并使所选边的导出子图没有回路, 从而构成G 的最小树T . 算法步骤可描述如下:Step1: 把网络),,(W E V G (记E m V n ,)的m 条边从小到大排序,即.,,,21m a a a置1,0, j i S .Step2: 若1 n i S 则停止, 这时T S G ][即为所求;否则转到Step3. Step3: 若][j a S G 不构成回路, 则置j i a e 1,}{1 i e S S , 1 i i ,1 j j , 转到Step2;否则置1 j j , 转到Step2.Step3中要判断][j a S G 是否构成回路, 需确定j a 的两个端点是否在][S G 的不同连通分支中, 这可用标号法实现, 即每一步都给G 的顶点标号, 当且仅当两个点有相同的标号时, 它们才属于][S G 中的同一连通分支中.标号方法: 开始时, 将点l v 赋以标号)1(n l l , 以后取边j a , 若j a 的两个端点标号不同, 则置j i a e 1, 并用两个标号的较小者对较大标号的端点及与之有相同标号的端点标号;否则就抛弃j a , 再取边1 j a 检查.例6.6 在图6.22的网络中求一个最小树, 首先对每个点标号, 如图6.23(a), 然后再取边和修改点的标号, 直至取出4条边为止, 如图6.23(b)~(d)的实线边.按Kruskal 算法, 用Matlab 语言编程求解模型(6.4)的程序见本书配套光盘中Textbook_programs 目录的子目录Chapter06下的M 文件:KRmintree.m .Kruskal 算法属避圈法之一, 计算量为)log (22n n O , 算法的效率不太高, 特42 3 44 221v 3v 2 v 4 v 1v 5图6.22别是当问题规模比较大时, 效率更低.(a) (b)(c) (d)图6.23ii) Prim 算法Prim 算法也称Dijkstra 算法[5], 其基本思路是从G 的1 n 个独立割集中的每一个都选取一条权最小的边, 所选取边的导出子图即是所求的最小树. 算法步骤可描述如下:Step1: 置),,2,1(1n j w u j j , S , }{1v P , },,{2n v v T . Step2: 取ik j Tj k w u u }{min , 置}{ik e S S (ik e 为权值ik w 对应的边),}{k v P P ,}{\k v T T .Step3: 若 T , 则停止;否则置},{min kj j Tv j w u u j , 返回Step2.按Prim 算法, 用标号方式求图6.22的网络的最小树过程如图6.24(a)~(d). 首先给第1个点1v 以0标号, 点T v j 以j u 标号, 如图6.24(a). 点2v 的标号最小, 取边],[21v v 加入S , 检查修改与2v 相邻点的标号, 如图6.24(b). 如此直到42 3 44 221(v 3, 1) (v 2, 1) (v 4, 4) (v 1, 1)(v 5, 4) 42 3 44 221(v 3, 1)(v 2, 1)(v 4, 1) (v 1, 1)(v 5, 1)42 3 44 2 21(v 3, 3) (v 2, 1)(v 4, 4) (v 1, 1)(v 5, 5)42 3 44 221(v 3, 3) (v 2, 2) (v 4, 4) (v 1, 1)(v 5, 5)图6.24(d), 剩最后一个点4v , 它标号为2, 为边],[45v v 的权值, 取它加入S 后,][S G 即为所小的最小树.(a) (b)(c) (d)图6.24(v 3, 2) (v 2, 1)(v 4, 4) (v 1, 0)(v 5, 3)42 3 44 2 21(v 3, 2) (v 2, 1) (v 4, ∞) (v 1, 0)(v 5, ∞) 423 44 221(v 3, 2)(v 2, 1)(v 4, 2) (v 1, 0)(v 5, 3)42 3 44 22 1(v 3, 2) (v 2, 1) (v 4, 4) (v 1, 0)(v 5, 3) 42 3 44 221。
最小生成树与最短路径问题的解法

最小生成树与最短路径问题的解法在计算机科学中,图论是一门重要的研究领域,用于研究图、网络等数学结构和算法。
图论中两个重要的问题是最小生成树和最短路径问题,它们在各个领域都有广泛的应用,比如网络设计、路线规划、优化问题等。
本文将介绍最小生成树和最短路径问题及其解法。
一、最小生成树最小生成树是指一个无向连通图的一个生成树,使得树上所有边的权值之和最小。
最小生成树问题是一个经典的图论问题,也是一个基础的优化问题,有很多经典的算法,包括Prim算法、Kruskal算法等等。
1. Prim算法Prim算法是一种贪心算法,它从一个任意点开始,依次加入新的点和它们之间的最小边,直到所有点都被加入为止。
具体步骤如下:- 选取任意一个顶点作为起点,将其加入集合U中;- 在集合V-U中选择权值最小的边(u,v),将顶点v加入U中,并将边(u,v)加入最小生成树的集合E中;- 重复步骤2,直到所有顶点都被加入为止。
Prim算法的时间复杂度为O(ElogV),其中E表示边的数目,V 表示顶点数目。
Prim算法的缺点是比较容易陷入局部最优情况,在有些情况下可能并不能得出全局最优解。
2. Kruskal算法Kruskal算法也是一种贪心算法,与Prim算法不同的是,它是以边为基础,而不是以点为基础,依次加入最小的边,直到所有点都被加入为止。
具体步骤如下:- 对所有边按照权值从小到大排序;- 依次加入最小的边,如果新加入的边不会形成环,则将其加入最小生成树集合E中;- 重复步骤2,直到所有顶点都被加入为止。
Kruskal算法的时间复杂度为O(ElogE),其中E表示边的数目。
Kruskal算法比Prim算法更加简单易懂,也更容易推广到带有权重的多种数据结构中。
二、最短路径最短路径是指在一个加权图中,从一个顶点到另一个顶点间的权值和最小的路径。
最短路径问题是一个基本的图论问题,也是很多实际应用问题中的一个基本问题,有很多经典的算法,包括Dijkstra算法、Bellman-Ford算法等等。
最小生成树题目

最小生成树题目(最新版)目录1.最小生成树概念介绍2.最小生成树的性质3.最小生成树的算法4.最小生成树的应用正文【最小生成树概念介绍】最小生成树(Minimum Spanning Tree,简称 MST)是一种图论中的算法,用于在一个加权连通图中找到一棵包含所有顶点且边权值之和最小的生成树。
生成树是指一个连通图的生成树是指保留图中所有的节点,但只保留足以保持这些节点连通的边的集合。
最小生成树是一种生成树,其中所有边的权值之和最小。
【最小生成树的性质】最小生成树有以下性质:1.一棵生成树包含图中所有的节点。
2.一棵生成树中的每一条边都是必要的,即如果删除这条边,生成树将不再连通。
3.在最小生成树中,所有边的权值之和最小。
【最小生成树的算法】常见的最小生成树算法有 Kruskal 算法和 Prim 算法。
1.Kruskal 算法:Kruskal 算法是一种基于边的算法。
它从所有边中选择权值最小的边,如果这条边连接的两个节点不在同一个连通分量中,则将这条边加入生成树中。
重复这个过程,直到所有节点都被包含在生成树中。
2.Prim 算法:Prim 算法是一种基于节点的算法。
它从一个节点开始,逐步扩展生成树。
每次选择一个未被包含在生成树中的节点,如果这个节点连接的边权值最小,则将这条边加入生成树中。
重复这个过程,直到所有节点都被包含在生成树中。
【最小生成树的应用】最小生成树在实际应用中有广泛的应用,包括网络设计、图像处理、数据压缩等。
在网络设计中,最小生成树可以用于设计最短路径网络,从而减少网络成本。
在图像处理中,最小生成树可以用于图像分割和特征提取。
最小生成树(Minimal Spanning Tree,MST)问题

例7.6 最小生成树(Minimal Spanning Tree,MST)问题求解最小生成树的方法虽然很多,但是利用LINGO建立相应的整数规划模型是一种新的尝试。
这对于处理非标准的MST问题非常方便。
我们主要参考了文[7]。
在图论中,称无圈的连通图为树。
在一个连通图G中,称包含图G全部顶点的树为图G 的生成树。
生成树上各边的权之和称为该生成树的权。
连通图G的权最小的生成树称为图G 的最小生成树。
许多实际问题都可以归结为最小生成树。
例如,如何修筑一些公路把若干个城镇连接起来;如何架设通讯网络将若干个地区连接起来;如何修筑水渠将水源和若干块待灌溉的土地连接起来等等。
为了说明问题,以下面的问题作为范例。
范例:假设某电话公司计划在六个村庄架设电话线,各村庄之间的距离如图所示。
试求出使电话线总长度最小的架线方案。
为了便于计算机求解,特作如下规定:(1)节点V1表示树根;(2)当两个节点之间没有线路时,规定两个节点之间的距离为M(较大的值)。
MST的整数规划模型如下:Array运用WinSQB软件:Network Modeling1——3——4——2,,,,4——6——5 最短距离为8Solution for Minimal Spanning Tree Problem road07-25-2000 From Node Connect To Distance/Cost From Node Connect To Distance/Cost1 Node4 Node2 2 4 Node6 Node5 22 Node1 Node3 1 5 Node4 Node6 13 Node3 Node4 2Total Minimal Connected Distance or Cost = 8直接用人脑算:避圈法:把图中所以的点分为V 与_V 两个部分。
其步骤为:(1) 从图中任选一点i v 为树根, 让i v V ∈,图中其余的点均包含在_V 中。
图论经典问题
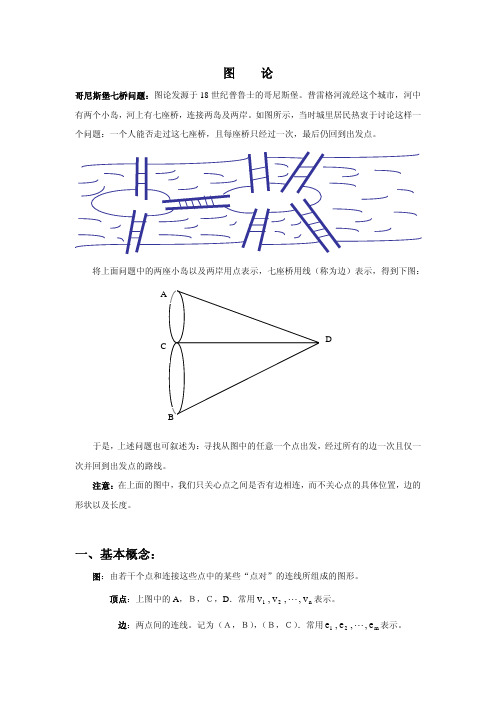
图 论哥尼斯堡七桥问题:图论发源于18世纪普鲁士的哥尼斯堡。
普雷格河流经这个城市,河中有两个小岛,河上有七座桥,连接两岛及两岸。
如图所示,当时城里居民热衷于讨论这样一个问题:一个人能否走过这七座桥,且每座桥只经过一次,最后仍回到出发点。
将上面问题中的两座小岛以及两岸用点表示,七座桥用线(称为边)表示,得到下图:于是,上述问题也可叙述为:寻找从图中的任意一个点出发,经过所有的边一次且仅一次并回到出发点的路线。
注意:在上面的图中,我们只关心点之间是否有边相连,而不关心点的具体位置,边的形状以及长度。
一、基本概念:图:由若干个点和连接这些点中的某些“点对”的连线所组成的图形。
顶点:上图中的A ,B,C,D .常用表示。
n 21 v , , v , v 边:两点间的连线。
记为(A,B),(B,C).常用表示。
m 21e , , e , e次:一个点所连的边数。
定点v的次记为d(v).图的常用记号:G=(V,E),其中,}{v V i =,}{e E i =子图:图G的部分点和部分边构成的图,成为其子图。
路:图G中的点边交错序列,若每条边都是其前后两点的关联边,则称该点边序列为图G的一条链。
圈(回路):一条路中所含边点均不相同,且起点和终点是同一点,则称该路为圈(回路)。
有向图:,其中(,)G N A =12{,,,}k N n n n = 称为的顶点集合,A a 称为G 的弧集合。
G {(,)ij i j }n n ==若,则称为的前驱, 为n 的后继。
(,)ij i j a n n =i n j n j n i 赋权图(网络):设是一个图,若对G 的每一条边(弧)都赋予一个实数,称为边的权,。
记为。
G (,,)G N E W =两个结论:1、图中所有顶点度数之和等于边数的二倍; 2、图中奇点个数必为偶数。
二、图的计算机存储:1. 关联矩阵简单图:,对应(,)G N E =N E ×阶矩阵()ik B b =10ik i k b ⎧=⎨⎩点与边关联否则简单有向图:,对应(,)G N A =N A ×阶矩阵()ik B b =110ik ik ik a i b a i ⎧⎪=−⎨⎪⎩弧以点为尾弧以点为头否则2. 邻接矩阵简单图:,对应(,)G N E =N N ×阶矩阵()ij A a =10ij i j a ⎧=⎨⎩点与点邻接否则简单有向图:,对应(,)G N A =N N ×阶矩阵()ij A a =10ij i ja ⎧=⎨⎩有弧从连向否则5v 34v01010110100101011110101000110111101065432166654321⎥⎥⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎢⎢⎣⎡=×v v v v v v A v v v v v v3. 权矩阵:简单图:,对应(,)G N E =N N ×阶矩阵()ij A a =ij ij i j a ω⎧=⎨∞⎩点与点邻接否则123456781234567802130654.5061002907250473080 v v v v v v v v v v v v v v v v 48∞∞∞∞⎡⎤⎢⎥∞∞∞∞∞⎢⎥⎢⎥∞∞∞∞∞⎢⎥∞∞∞∞∞⎢⎥⎢⎥∞∞∞∞⎢⎥∞∞∞∞⎢⎥⎢⎥∞∞∞∞⎢⎥∞∞∞∞∞∞⎢⎥⎣⎦三、图的应用:例:如图,用点代表7个村庄,边上的权代表村庄之间的路长,现在要在这7个村庄中布电话线,如何布线,使材料最省?分析:需要将图中的边进行删减,使得最终留下的图仍然连通,并且使总的权值最小。
图论:最小树、最短路、最大流问题

(3,3)
(2)可增值链(增广链)
:中的正向弧集 D中由v 至v 的链,记 , :中的反向弧集 中弧皆未饱 若 ,则称为D中关于可行流f 的 中弧皆非零 一条可增值链。
v2 (3,3)
(4,3)
v4
(5,3) (1,1) (3,0) vs vt (1,1) (2,1) (5,1) v1 v3 (2,2)
例 2 求如图网络的最小部分树。
v2 2 v1 3 5 1 v4 5 v3 2 7 5 3 v5 v6 1 7 5 v7
2017/10/16
避圈法是一种选边的过程,其步骤如下:
1. 从网络D中任选一点vi,找出与vi相关联的 权最小的边[vi,vj],得第二个顶点vj; 2. 把顶点集V分为互补的两部分V1, V1 ,其中 V, 与已选边相关联的点集, V, 不与已选边相关联的点集;
8
9 7 6
5
9
E 2 D 3 F
3
2017/10/16
4
二. 最短路问题
1. 问题:求网络D中一定点v1到其它点的最短路。 例3 求如图网络中v1至v7的最短路,图中数字 为两点间距离。
v2
2
v1 3 5 1
v3
2
7 5 3
v6 1 7
5
v7
v5 5 2. 方法:标号法(Dijkstra,1959)
1 1
挑选其中与v 距最短(mind c )的v 进行标号。
1
1
1
4. 重复3,直至终点(本例即v )标上号[d ,v ],则
7 7
d 即最短距,反向追踪可求出最短路。
7
2017/10/16
用标号法解例3
最小树问题

(2)破圈法:
① 在网络图中寻找 一个圈。若不存在圈, 则已经得到最短树或网 络不存在最短树;
② 去掉该圈中权数 最大的边;
反复重复 ① ② 两 步,直到最小树。
v1
4
v2
1
v3
1
2 13
1
v8
4
55
4
v4
v0
2
4
5
v7
3
v6
2
v5
•(3)Kruskal 算法:将图中所有边 v1
按权值从小到大排列,依次选
V1 0 1 1 0 0
V1 V3
V2
V3 V5
V4
1 0011 1 0001 0 10 0 1
V5 0 1 1 1 0
两顶点间有边连接的记为 1 ,无边连接的记为 0。 得到的矩阵一定是对称矩阵。
2、赋权无向图的矩阵表示: 两顶点间有边
连接的记为该边的权数。无边相连的记为 ,
对角线上的数是 0 。得到的矩阵也是对称矩阵。
些边
v2
v5
v6
v3
二、最小生成树及其算法
1.最小生成树
一个网络图可以有多个生成树.记N的所有生成 树的集合为:T={ Tk | k=1,2,…,L }
设Tk =(V, Ek )是网络图N=(G,w)的一棵生成树, 则边集Ek中所有边的权数之和称为树Tk 的权数,记为
w Tk w e
e Ek
1、根据网路写出边权矩阵,两点间若没有边,则用表示;
2、从 v1 开始标记,在第一行打 ,划去第一列; 3、从所有打 的行中找出尚未划掉的最小元素,对该元素
画圈,划掉该元素所在列,与该列数对应的行打 ;
4、若所有列都划掉,则已找到最小生成树(所有画圈元素所 对应的边);否则,返回第 3 步。
最小生成树问题

2020/4/1
赋权连通图的最小支撑树
边的权:G=(V,E)对每边ei∈E规定一个非负的实数w(ei)叫“权”; 带权图:每边都有权的图叫赋权图或带权图; 树:其特点之一是边数比顶点数少一; 图G的支撑树T:E(T)E(G),V(T)=V(G),即由G找T,顶点一个不能少,
边可能删去几条,但T必须是树[当然如G不是连通图,则没有支撑树]。 最小树:赋权的连通图G的众多支撑树中必至少有一,其各边权之和为
2020/4/1
用Kruskal算法求最小树
用Kruskal算法(避圈法)求赋权连通图G的最小树
V2
5
V6
4
2
9
12
V1
3
8
V3
6
4
5
6
V5
V7
10 7
7
11
2020/4/1
V4
∴最小树的权为24,最小树为 T={v1v2,v1v3,v2v5,v5v6,v6v7,v6v4}
避圈法求最小树的分析
Kruskal算法的“主要”工作如认为是[S1:] 对m条边的边长排序,m个元素排序较好的算法是基于分治 策略的快速排序(Quick Sorting),其时间复杂性是O(m㏒ m)。
2020/4/1
求最小树的Kruskal算法
赋权的连通图G=(V,E)中 m=|E|,n=|V|,
S1:对E中各边的权排序,设 w1≤w2≤…≤wm,wi=w(ei)
S2:初始化:
w←0,T←φ,k←1,t←0
S3:若t=n-1则转S6,否则转S4 S4:若T∪{ek}有圈则k←k+1转S4,
否则转S5 S5: T←T∪{ek},w←w+wk,
最小支撑树问题

Minimum Spanning Tree Problem
Ch6 Graph and Network
2012年4月20日星期五 Page 1 of 5
定义:设G=[V,E]是一个无向图,对每一条边ei∈E有一个长 度C(ei) ≥0,G的任意支撑树T各条边的长度之和称为树T的长度, 记为C(T)。长度最小的支撑树称为最小树。 求最小树是在一个无向连通图G中求一棵最小支撑树。 求最小树问题的应用: 求最小树问题的应用: • 电信网络(计算机网络、电话专用线网络、有线电视网络等等) 的设计 • 低负荷运输网络的设计,使得网络中提供链接的部分(如铁路、 公路等 等)的总成本最小 • 高压输电线路网络的设计 电器设备线路网络(如数字计算机系统)的设计,使得线路总长 度最短 • 连接多个场所的管道网络设计
§6.2 最小支撑树问题
Minimum Spanning Tree Problem
Ch6 Graph and Network
2012年4月20日星期五 Page 5 of 5
作业: 作业:P283 10.4 10.5
最短路问题
Exit
§6.2 小支撑树问题
Minimum Spanning Tree Problem
Ch6 Graph and Network
2012年4月20日星期五 Page 2 of 5
求最小树的方法:破圈法和避圈法 破圈法:任取一圈,去掉圈中最长边,直到无圈。 v1 v3 7 v5 8 5 4 5 8 1 2 v2 v1 4 2 v2 3 v4 v6 3 v4 v3 6 5 1 v6 v5
§6.2 最小支撑树问题
Minimum Spanning Tree Problem
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
第三节 最小树问题
一、最小树问题
1、什么是树? 无圈连通图。 2、什么是最小树? 权重之和最小的树。 3、最小树问题: 例6.3.1:电话线架设问题 某地7个村镇之间的现有交通道路如下图6.3-1所示, 边旁数字为各村镇之间道路的长度。现要沿交通道路架设 电话线,使各村之间均能通话。应如何架线使总长最短?
单位:海里
2 8
3 13 10
4 9 7 18
5 16 12 11 9
6 20 15 6 17 19
1 2 3 4 5
§6.3 最小树问题
二、最小树的求解方法
1、破圈法:1)适用于网络图已存在的问题;2)基本思 路;对网络图中每一个圈都破掉其最长边,直至网络图中 不存在圈为止。3)例:以例6.3-1为例,步骤如下图6.3-2
§6.3 最小树问题
6
1
4
8
3
2 9 7
1
2
9
2
7
5
9
7
4
5
例6.3.2:
3
图6.3-1
6
某公司拟铺设海上油管,要求将海上六口油井连通,仅
1号油井与海岸相连,距离为5海里。已知,海上六口油井
Hale Waihona Puke §6.3 最小树问题间的距离如下表6.3-1。试问,应如何铺设油管使铺设油 管的总长最短? 表6.3-1
到 从
§6.3 最小树问题
表6.3-2
从
1 2 3 4 5
单位:海里
2 3 4 5 6
到
8
13 10
9 7 18
16 12 11 9
20 15 6 17 19
3
海岸
5
6 10
6
5
9 7
1
8
2
4
图6.3-3
§6.3 最小树问题
THE END
6
1
4
8
2
1
2
9
2
7
3
5 9
5
7
9
4
7
3
最短距离为:17海里
图6.2-2
6
§6.3 最小树问题
2、避圈法: 1)适用于网络图不存在的问题; 2)基本思路: 对网络图中在不构成圈的条件下,每次连接距离最短 的边,直至网络图中各点连通为止。 3)例:以例6.3-2为例, 具体步骤如下表6.3-2和图6.3-3。 最短距离为:45海里
