组成原理课程设计报告(浮点数加法器
计算机组成原理实验报告

重庆理工大学《计算机组成原理》实验报告学号 __***********____姓名 __张致远_________专业 __软件工程_______学院 _计算机科学与工程二0一六年四月二十三实验一基本运算器实验报告一、实验名称基本运算器实验二、完成学生:张致远班级115030801 学号11503080109三、实验目的1.了解运算器的组成结构。
2.掌握运算器的工作原理。
四、实验原理:两片74LS181 芯片以并/串形式构成的8位字长的运算器。
右方为低4位运算芯片,左方为高4位运算芯片。
低位芯片的进位输出端Cn+4与高位芯片的进位输入端Cn相连,使低4位运算产生的进位送进高4位。
低位芯片的进位输入端Cn可与外来进位相连,高位芯片的进位输出到外部。
两个芯片的控制端S0~S3 和M 各自相连,其控制电平按表2.6-1。
为进行双操作数运算,运算器的两个数据输入端分别由两个数据暂存器DR1、DR2(用锁存器74LS273 实现)来锁存数据。
要将内总线上的数据锁存到DR1 或DR2 中,则锁存器74LS273 的控制端LDDR1 或LDDR2 须为高电平。
当T4 脉冲来到的时候,总线上的数据就被锁存进DR1 或DR2 中了。
为控制运算器向内总线上输出运算结果,在其输出端连接了一个三态门(用74LS245 实现)。
若要将运算结果输出到总线上,则要将三态门74LS245 的控制端ALU-B 置低电平。
否则输出高阻态。
数据输入单元(实验板上印有INPUT DEVICE)用以给出参与运算的数据。
其中,输入开关经过一个三态门(74LS245)和内总线相连,该三态门的控制信号为SW-B,取低电平时,开关上的数据则通过三态门而送入内总线中。
总线数据显示灯(在BUS UNIT 单元中)已与内总线相连,用来显示内总线上的数据。
控制信号中除T4 为脉冲信号,其它均为电平信号。
由于实验电路中的时序信号均已连至“W/R UNIT”单元中的相应时序信号引出端,因此,需要将“W/R UNIT”单元中的T4 接至“STATE UNIT”单元中的微动开关KK2 的输出端。
组成原理课程设计报告(浮点数加法器

组成原理课程设计报告(浮点数加法器LT第1章总体设计方案1.1 设计原理本次课程设计的题目为浮点数加法器的设计,使用Xilinx Foundation F3.1可编程器件开发工具软件,以及伟福COP2000试验箱实现目的设计。
具体要求为必须用基本逻辑门实现,浮点数的长度固定。
根据所学可知,浮点数共由两部分组成。
第一部分是阶码,第二部分是数据。
这两部分又分别分为两部分。
阶码由阶符和数值组成,数据由数符和数字组成。
由于在计算机的存储和运算中,数据由补码表示。
故首先应将输入的原码转化为补码。
在此过程中,正数保持不变,负数则对除符号位以外的各位按位取反,再进行加1操作。
然后对两数的阶码进行运算,决定移位的次数和结果的阶码。
在移位时,对正数进行补0操作,对负数则进行补1操作。
再对移位后的数据视为定点数进行相加运算。
进而实现浮点数相加的功能。
最后再将得到的结果转化为原码,进行输出。
1.2设计思路按照课设题目要求及原理图,先设计出电路的具体模块图,浮点数加法器的设计共包含如下五个模块:①原补转换模块②阶码选择模块③数值选择模块④数据移位模块⑤超前进位加法模块在五个部分中分别设计实现相应功能的器件,包括二选一数据选择器等。
在连接具体电路时配合门电路以达到预期效果。
浮点数加法器的底层、顶层的设计都采用原理图设计输入方式,经编译、调试后形成zyks.bit文件并下载到XCV200可编程逻辑芯片中,经硬件测试验证设计的正确性。
1.3设计环境1.3.1 硬件环境•伟福COP2000型计算机组成原理实验仪COP2000计算机组成原理实验系统由实验平台、开关电源、软件三大部分组成实验平台上有寄存器组R0-R3、运算单元、累加器A、暂存器B、直通/左移/右移单元、地址寄存器、程序计数器、堆栈、中断源、输入/输出单元、存储器单元、微地址寄存器、指令寄存器、微程序控制器、组合逻辑控制器、扩展座、总线插孔区、微动开关/指示灯、逻辑笔、脉冲源、20个按键、字符式LCD、RS232口。
32位浮点加法器设计

32位浮点加法器设计32位浮点加法器是一种用于计算机中的算术逻辑单元(ALU),用于执行浮点数的加法运算。
它可以将两个32位浮点数相加,并输出一个32位的结果。
设计一个高效的32位浮点加法器需要考虑多个方面,包括浮点数的表示形式、运算精度、舍入方式、运算逻辑等。
下面将详细介绍32位浮点加法器的设计。
1.浮点数的表示形式:浮点数通常采用IEEE754标准进行表示,其中32位浮点数由三个部分组成:符号位、阶码和尾数。
符号位用来表示浮点数的正负,阶码用来表示浮点数的指数,尾数用来表示浮点数的小数部分。
2.运算精度:在浮点数加法运算中,精度是一个重要的考虑因素。
通常,浮点数加法器采用单精度(32位)进行设计,可以处理较为广泛的应用需求。
如果需要更高的精度,可以考虑使用双精度(64位)浮点加法器。
3.舍入方式:浮点数加法运算中,结果通常需要进行舍入处理。
常见的舍入方式有以下几种:舍入到最近的偶数、舍入向上、舍入向下、舍入到零。
具体的舍入方式可以根据应用需求来确定。
4.运算逻辑:浮点数加法运算涉及到符号位、阶码和尾数的加法。
首先,需要判断两个浮点数的阶码大小,将较小的阶码移到较大的阶码对齐,并相应调整尾数。
然后,将尾数进行相加并进行规格化处理。
最后,根据求和结果的大小,进行溢出处理和舍入操作。
在32位浮点加法器的设计中,还需要考虑到性能和效率。
可以采用流水线技术来提高运算速度,将加法运算划分为多个阶段,并在每个阶段使用并行处理来加速运算。
此外,还可以使用硬件加速器和快速逻辑电路来优化运算过程。
总结起来,设计一个高效的32位浮点加法器需要考虑浮点数的表示形式、运算精度、舍入方式、运算逻辑以及性能和效率。
在实际设计中,还需要根据具体应用需求进行功能扩展和优化。
通过合理的设计和调优,可以实现高性能的浮点加法器,满足不同应用场景的需求。
32位浮点数加法设计仿真实验报告

32位浮点数加法设计仿真实验报告名字:李磊学号:10045116 班级:1004221132位浮点数的IEEE-754格式单精度格式IEEE.754标准规定了单精度浮点数共32位,由三部分组成:23位尾数f,8位偏置指数e,1位符号位s。
将这三部分由低到高连续存放在一个32位的字里,对其进行编码。
其中[22:0]位包含23位的尾数f;[30:23]位包含8位指数e;第31位包含符号s{s[31],e[30:23],f[22:0]}其中偏置指数为实际指数+偏置量,单精度浮点数的偏置量为128,双精度浮点数的偏置量为1024。
规格化的数:由符号位,偏置指数,尾数组成,实际值为1.f乘2的E-128次方非规格化的数:由符号位,非偏置指数,尾数组成,实际值为0.f乘2的E次方特殊的数:0(全为零),+无穷大(指数全为1,尾数为0,符号位为0),-无穷大(指数全为1,尾数为0,符号位为1),NAN(指数全为1,尾数为不全为0)浮点数加法器设计设计思路:1.前端处理,还原尾数2.指数处理,尾数移位,使指数相等3.尾数相加4.尾数规格化处理5.后端处理,输出浮点数具体设计:设计全文:module flowadd(ix, iy, clk, a_en, ost,oz);input ix, iy, clk, a_en;output oz, ost;wire[31:0] ix,iy;reg[31:0] oz;wire clk,ost,a_en;reg[25:0] xm, ym, zm;reg[7:0] xe, ye, ze;reg[2:0] state;parameter start = 3'b000, //设置状态机zerock = 3'b001,exequal = 3'b010,addm = 3'b011,infifl = 3'b100,over = 3'b110;assign ost = (state == over) ? 1 : 0; /*后端处理,输出浮点数*/always@(posedge ost)beginif(a_en)oz <= {zm[25],ze[7:0],zm[22:0]};endalways@(posedge clk) //状态机begincase(state)start: //前端处理,分离尾数和指数,同时还原尾数beginxe <= ix[30:23];xm <= {ix[31],1'b0,1'b1,ix[22:0]};ye <= iy[30:23];ym <= {iy[31],1'b0,1'b1,iy[22:0]};state <= zerock;endzerock:beginif(ix == 0)begin{ze, zm} <= {ye, ym};state <= over;endelseif(iy == 0)begin{ze, zm} <= {xe, xm};state <= over;endelsestate <= exequal;endexequal: //指数处理,使得指数相等beginif(xe == ye)state <= addm;elseif(xe > ye)beginye <= ye + 1;ym[24:0] <= {1'b0, ym[24:1]};if(ym == 0)beginzm <= xm;ze <= xe;state <= over;endelsestate <= exequal;endelsebeginxe <= xe + 1;xm[24:0] <= {1'b0,xm[24:1]};if(xm == 0)beginzm <= ym;ze <= ye;state <= over;endelsestate <= exequal;endendaddm: //带符号位和保留进位的尾数相加beginif ((xm[25]^ym[25])==0)beginzm[25] <= xm[25];zm[24:0] <= xm[24:0]+ym[24:0];endelseif(xm[24:0]>ym[24:0])beginzm[25] <= xm[25];zm[24:0] <=xm[24:0]-ym[24:0];endelsebeginzm[25] <= ym[25];zm[24:0] <=ym[24:0]-xm[24:0];endze <= xe;state <= infifl;endinfifl: //尾数规格化处理beginif(zm[24]==1)beginzm[24:0] <= {1'b0,zm[24:1]};ze <= ze + 1;state <= over;endelseif(zm[23]==0)beginzm[24:0] <= {zm[23:0],1'b0};ze <= ze - 1;state <= infifl;endelsestate <= over;endover:beginstate<= start;enddefault:beginstate<= start;endendcaseendendmodule设计结果仿真仿真结果为41A00000H+41080000H=41E40000H41A00000H=10D,41080000H=4.25D,41E40000H=14.25D,验证成功。
浮点数加法运算

浮点数加法运算浮点数加法是一种常见的数学运算,用于对两个浮点数进行求和操作。
在计算机中,浮点数采用科学计数法来表示,主要由两部分组成:尾数和指数。
尾数表示实际的数值部分,而指数表示小数点的位置。
浮点数加法是一种基本的算术运算,可用于处理诸如物理模拟、图形渲染、金融计算等领域的问题。
在这些应用中,对数字的精度要求较高,因此浮点数加法的正确性和精度是非常重要的。
浮点数加法的过程可以简单描述为以下几个步骤:1.对两个浮点数进行对齐,即使它们的小数点位置相同。
2.将尾数相加,得到新的尾数。
3.对新的尾数进行规格化,以保持其精度。
4.对指数进行调整,使结果尽可能接近原始数值。
5.如果结果超过浮点数的表示范围,则进行上溢或下溢处理。
在进行浮点数加法运算时,需要考虑以下一些问题:1.浮点数的表示范围有限:由于计算机内存和处理器的限制,浮点数的表示范围是有限的。
当两个浮点数相加的结果超过表示范围时,就会发生上溢或下溢。
2.精度损失:由于浮点数使用有限的二进制位数来表示实数,因此在进行加法运算时会有一定程度的精度损失。
这是由于浮点数的规格化和舍入操作引起的。
3.舍入错误:在浮点数加法中,舍入操作是必要的,因为结果小数位数的表示是有限的。
不同的舍入方法会导致不同的舍入误差,从而影响计算结果的精度。
为了解决这些问题,计算机科学家和数学家们提出了一些技术和算法来提高浮点数加法的精度和正确性。
其中一种方法是使用更高精度的浮点数表示,例如双精度浮点数(Double)和扩展精度浮点数(Extended)。
这些浮点数使用更多比特位来表示尾数和指数,从而提供更高的精度。
另一种方法是使用更精确的计算算法,例如Kahan算法和四舍五入算法。
这些算法通过降低舍入误差和提高计算结果的精度来改善浮点数加法运算。
还可以使用符号位来表示浮点数的正负,通过特殊的编码方式来表示无穷大和NaN(非数值)等特殊情况。
这些机制能够处理浮点数加法中可能出现的异常情况。
计算机组成原理加法器实验实训报告

计算机组成原理加法器实验实训报告一、实验目的本次实验旨在通过实际操作加法器电路,加深对计算机组成原理中加法器的理解,掌握加法器的工作原理和实验操作技能。
二、实验内容1. 搭建基本加法器电路2. 进行加法器实验3. 分析实验结果并撰写实验报告三、实验器材和工具1. 电路实验箱2. 电源3. 电路连接线4. 示波器5. 多用途数字实验仪6. 逻辑门集成电路四、实验步骤1. 搭建基本加法器电路1) 将逻辑门集成电路插入电路实验箱中2) 连接逻辑门的输入端和输出端3) 接入电源并进行必要的调试2. 进行加法器实验1) 输入两个二进制数,并将其连接到逻辑门输入端2) 观察输出端的变化3) 调节输入信号,验证加法器的正确性和稳定性3. 分析实验结果1) 记录实验数据2) 分析实验结果,对比理论值和实际值的差异3) 总结实验中的经验和问题,并提出改进建议五、实验数据1. 输入数据:A = 1010B = 11012. 输出数据:Sum = xxxCarryout = 1六、实验结果分析通过实验,我们成功搭建了基本加法器电路,并进行了加法器实验。
实验结果表明,加法器能够正确地对两个二进制数进行加法运算,并输出正确的结果。
通过比对理论值和实际值,我们发现存在一定的偏差,可能是由于电路连接不良或逻辑门延迟等因素导致。
在今后的实验中,我们需要注意电路连接质量和信号延迟,以提高实验结果的准确性和稳定性。
七、实验总结通过本次加法器实验,我们加深了对计算机组成原理中加法器的理解,掌握了基本的加法器实验操作技能。
我们也发现了一些问题并提出了改进建议。
在今后的学习和实验中,我们将继续加强对计算机组成原理的学习,不断提升实验操作能力,为今后的科研工作和实际应用打下坚实的基础。
八、参考资料1. 《计算机组成原理》(第五版),唐朔飞,张善民,电子工业出版社2. 《数字逻辑与计算机设计》(第三版),David M. Harris,Sarah L. Harris,清华大学出版社以上是本次计算机组成原理加法器实验实训报告的全部内容,谢谢阅读。
32位浮点加法器设计

32位浮点加法器设计一、基本原理浮点数加法运算是在指数和尾数两个部分进行的。
浮点数一般采用IEEE754标准表示,其中尾数部分采用规格化表示。
浮点加法的基本原理是将两个浮点数的尾数对齐并进行加法运算,再进行规格化处理。
在加法运算过程中,还需考虑符号位、指数溢出、尾数对齐等特殊情况。
二、设计方案1. 硬件实现方案:采用组合逻辑电路实现浮点加法器,以保证运算速度和实时性。
采用Kogge-Stone并行加法器、冒泡排序等技术,提高运算效率。
2.数据输入:设计32位浮点加法器,需要提供两个浮点数的输入端口,包括符号位、指数位和尾数位。
3.数据输出:设计32位浮点加法器的输出端口,输出相加后的结果,包括符号位、指数位和尾数位。
4.控制信号:设计合适的控制信号,用于实现指数对齐、尾数对齐、规格化等操作。
5.流程控制:设计合理的流程控制,对各个部分进行并行和串行处理,提高加法器的效率。
三、关键技术1. Kogge-Stone并行加法器:采用Kogge-Stone并行加法器可以实现多位数的并行加法运算,提高运算效率。
2.浮点数尾数对齐:设计浮点加法器需要考虑浮点数尾数的对齐问题,根据指数大小进行右移或左移操作。
3.溢出判断和处理:浮点加法器需要判断浮点数的指数是否溢出,若溢出需要进行调整和规格化。
4.符号位处理:设计浮点加法器需要考虑符号位的处理,确定加法结果的符号。
四、性能评价性能评价是衡量浮点加法器设计好坏的重要指标。
主要从以下几个方面进行评价:1.精度:通过与软件仿真结果进行比较,评估加法器的运算精度,误差较小的加法器意味着更高的性能。
2.速度:评估加法器的运行速度,主要考虑延迟和吞吐量。
延迟越低,意味着加法器能够更快地输出结果;吞吐量越高,意味着加法器能够更快地处理多个浮点加法运算。
3.功耗:评估加法器的功耗情况,低功耗设计有助于提高整个系统的能效。
4.面积:评估加法器的硬件资源占用情况,面积越小意味着设计更紧凑,可用于片上集成、嵌入式系统等场景。
计算机组成原理第12-浮点数的运算2

CK=TL/TK=(n·k)/(k+(n-1)) 当 n>>k 时, Ck->k 。这就是说,理论上k级线性流水线处理几乎 可以提高k倍速度。但实际上由于存储器冲突、数据相关,这个理想的加速比不一定能 达到。
[解:] (1)加法器的流水线时钟周期至少为 τ=90ns+10ns=100ns
如果采用同样的逻辑电路,但不是流水线方式,则浮点加法所需的时间为 τ1+τ2+τ3+τ4 =300ns
因此,4级流水线加法器的加速比为 Ck=300/100=3
(2) 当每个过程段的时间都是75ns时,加速比为 Ck=300/75=4
[例30] 已知计算一维向量x,y的求和表达式如下:
x
y
z
56
65
20.5
14.6
0
336
121 35.1 336
114.3 + 7.2 = 121.5
69.6
72.8
142.4
3.14
1.41
4.55
试用4段的浮点加法流水线来实现一维向量的求和运算,这4段流水线是阶码比较、 对阶操作、尾数相加、规格化。只要求画出向量加法计算流水时空图。
2.CPU之内的浮点运算器
奔腾CPU将浮点运算器包含在芯片内。浮点运算部件采用流水线设计。
指令执行过程分为8段流水线。前4 段为指令预取(DF)、指令译码(D1)、地址生 成(D2)、取操作数(EX),在U、V流水线中完成;后4段为执行1(X1)、执行2(X2) 、结果写回寄存器堆(WF)、错误报告(ER),在浮点运算器中完成。一般情况下 ,由U流水线完成一条浮点数操作指令。
浮点数运算与加法器

2020/9/23
3.4 加法器和ALU
2.进位链电路
并行加法器中的每一个全加器都有一个 从低位送来的进位和一个传送给较高位的 进位。我们将各位之间传递进位信号的逻 辑线路连接起来构成的进位网络称为进位 链。
2020/9/23
3.4 加法器和ALU
单级先行进位
这种进位方式就是将n位全加器分成若干个小组 ,小组内的进位同时产生,实行并行进位,小组 与小组之间采用串行进位,这种进位又称为组内 并行、组间串行。
以16位加法器为例,可分为4组,每组4位。第1 组组内的进位逻辑函数C0 、C1 、C2、、C3的 表达式与前述相同,C0-C3信号是同时产生的, 实现上述进位逻辑函数的电路称之为四位先行进 位电路CLA(Carry Look Ahead),其延迟时间 是2ty。
2020/9/23
3.4 加法器和ALU
C4=G4+P4C3 C5=G5+P5C4= G5+ P5G4+ P5P4C3 C6=G6+P6C5= G6+ P6G5+ P6P5G4+ P6 P5P4C3 C7=G7+P7C6= G7+ P7G6+ P7P6G5+ P7P6 P5 G4+ P7P6 P5P4C3
2020/9/23
3.4 加法器与ALU
S16~S13
S12~S9
S8~S5
S4~S1
4位CLA
4位CLA
4位CLA
计算机组成原理第11-浮点数的运算1

x±y=(Mx2Ex-Ey±My)2Ey, Ex<=Ey
12/31/2023
信 息 科 学 与 工 程 学 院1
两数首先均为规格化数,进行规格化浮点数的加减运 算需经过5步完成: (1)对阶操作:低阶向高阶补齐,使阶码相等。 (2)尾数运算:阶码对齐后直接对尾数运算。 (3)结果规格化:对运算结果进行规格化处理(使补码尾 数的最高位和尾数符号相反)。如溢出则需右规;如不是 规格化时应左规。 (4)舍入操作:丢失位进行0舍1入或恒置1处理。 (5)判断溢出:判断阶码是否溢出,下溢则将运算结果置 0(机器0),上溢则中断。
14 12/31/2023
信 息 科 学 与 工 程 学 1院4
第二章 运算方法和运算器
2、乘、除法运算步骤 浮点数的乘除运算大体分为以下几个步骤:
1> 0 操作数检查。 2> 阶码加/减操作。 3> 尾数乘/除操作。 4> 结果规格化 5> 舍入处理。
15 12/31/2023
信 息 科 学 与 工 程 学 1院5
18 12/31/2023
信 息 科 学 与 工 程 学 1院8
第二章 运算方法和运算器
当尾数用原码表示时,舍入规则比较简单。最简便的方法,是只要尾数的最低位 为1,或移出的几位中有为1的数值位,就是最低位的值为1。 另一种是0舍1入法,即当丢失的最高位的值为1时,把这个1加到最低数值位上进 行修正,否则舍去丢失的的各位的值。 当尾数是用补码表示时,所用的舍入规则,应该与用原码表示时产生相同的处理 效果。 具体规则是:
(4) 右规
当 尾数溢出( >1)时,需 右规 即尾数出现 01. ×× …×或 10. ×× …×时
尾数 1,阶码加 1
12/31/2023
计算机组成原理实验报告

计算机组成原理实验报告计算机组成原理实验报告引言:计算机组成原理是计算机科学与技术专业的重要课程之一,通过实验可以更好地理解和掌握计算机的组成原理。
本篇实验报告将介绍我们在计算机组成原理实验中所进行的实验内容和实验结果。
实验一:逻辑门电路设计在这个实验中,我们学习了逻辑门电路的设计和实现。
通过使用门电路,我们可以实现与门、或门、非门等基本逻辑运算。
我们首先学习了逻辑门电路的真值表和逻辑代数的基本运算规则,然后根据实验要求,使用逻辑门电路设计了一个简单的加法器电路,并通过仿真软件进行了验证。
实验结果表明,我们设计的加法器电路能够正确地进行二进制数的加法运算。
实验二:数字逻辑电路实现在这个实验中,我们进一步学习了数字逻辑电路的实现。
通过使用多路选择器、触发器等数字逻辑元件,我们可以实现更复杂的逻辑功能。
我们首先学习了多路选择器的原理和使用方法,然后根据实验要求,设计了一个4位二进制加法器电路,并通过数字逻辑实验板进行了搭建和测试。
实验结果表明,我们设计的4位二进制加法器能够正确地进行二进制数的加法运算。
实验三:存储器设计与实现在这个实验中,我们学习了存储器的设计和实现。
存储器是计算机中用于存储和读取数据的重要组成部分。
我们首先学习了存储器的基本原理和组成结构,然后根据实验要求,设计了一个简单的8位存储器电路,并通过实验板进行了搭建和测试。
实验结果表明,我们设计的8位存储器能够正确地存储和读取数据。
实验四:计算机硬件系统设计与实现在这个实验中,我们学习了计算机硬件系统的设计和实现。
计算机硬件系统是计算机的核心部分,包括中央处理器、存储器、输入输出设备等。
我们首先学习了计算机硬件系统的基本原理和组成结构,然后根据实验要求,设计了一个简单的计算机硬件系统,并通过实验板进行了搭建和测试。
实验结果表明,我们设计的计算机硬件系统能够正确地进行指令的执行和数据的处理。
结论:通过这些实验,我们深入学习了计算机组成原理的相关知识,并通过实践掌握了计算机组成原理的基本原理和实现方法。
计算机组成原理加法器实验
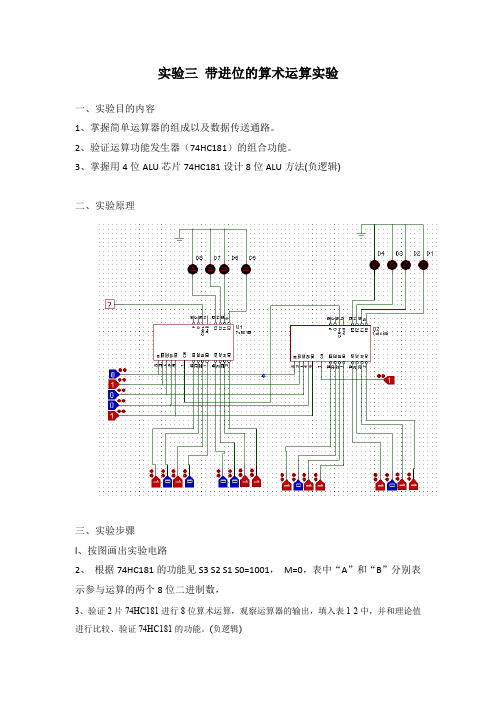
实验三带进位的算术运算实验
一、实验目的内容
1、掌握简单运算器的组成以及数据传送通路。
2、验证运算功能发生器(74HC181)的组合功能。
3、掌握用4位ALU芯片74HC181设计8位ALU方法(负逻辑)
二、实验原理
三、实验步骤
l、按图画出实验电路
2、根据74HC181的功能见S3 S2 S1 S0=1001,M=0,表中“A”和“B”分别表示参与运算的两个8位二进制数,
3、验证2片74HC181进行8位算术运算,观察运算器的输出,填入表1-2中,并和理论值进行比较、验证74HC181的功能。
(负逻辑)
四、实验结果
完成实验步骤,完成实表1-2,在显示结果后将指示灯显示的值与输入的数据进行比较;比较理论分析值与实验结果值;并对结果进行分析。
五、实验过程中出现的问题
六、实验收获和体会
七、实验思考题
1、实验电路中,如果将低4位的ALU芯片的输出脚CN+4与高4位ALU芯片的输入脚CN之间的连线去掉,将高4位ALU芯片的输入脚CN接地,表2-1中的输出F有变化吗?为什么?
2、如何用4位ALU芯片74LS181设计16位ALU?。
计算机组成原理实验报告说明

实验一运算器组成实验一、实验目的1、掌握运算器的组成及工作原理;2、了解4位函数运算器74LS181的组合功能,熟悉运算器执行算术和逻辑操作的具体实现过程;3、验证带进位控制的运算器功能。
二、实验设备1、EL-JY系列计算机组成及系统结构实验系统一套2、排线若干。
三、工作原理:算术逻辑单元ALU是运算器的核心。
集成电路74LS181是4位运算器,四片74LS181以并/串形式构成16位运算器。
它可以对两个16位二进制数进行多种算术或逻辑运算,74LS181 有高电平和低电平两种工作方式,高电平方式采用原码输入输出,低电平方式采用反码输入输出,这里采用高电平方式。
三态门74LS244作为输出缓冲器由ALU-G信号控制,ALU-G 为“0”时,三态门开通,此时其输出等于其输入;ALU-G 为“1”时,三态门关闭,此时其输出呈高阻。
四片74LS273作为两个16数据暂存器,其控制信号分别为LDR1和LDR2,当LDR1和LDR2 为高电平有效时,在T4脉冲的前沿,总线上的数据被送入暂存器保存。
四、实验内容:验证74LS181运算器的逻辑运算功能和算术运算功能。
五、实验步骤1、按照实验指导说明书连接硬件系统;2、启动实验软件,打开实验课题菜单,选中实验课题打开实验课题参数对话窗口:1)、在数据总线上输入有效数据,按"Ldr1",数据送入暂存器1;2)、在数据总线上输入有效数据,按"Ldr2",数据送入暂存器2;3)、在S3...Ar上输入有效数据组合,按"ALU功能选择端",运算器按规定进行运算,运算结果送入数据缓冲器;4)、按"ALU_G",运算结果送入数据总线。
5)、执行完后,按"回放",可对已执行的过程回看。
6)、回放结束后,按"继续"(继续按钮在点击回放后出现),进行下次数据输入。
计算机组成原理实验报告

当x≥0时,[x]原=x;当x≤0时,[x]原=2^(n-1)-x或2^(n-Hale Waihona Puke )+|x|,“^”表示指数。
B反码
1.如果真值是正数,反码的最高位为“0”,其余各位与真值的对应位相同;
2.如果真值是负数,反码的最高位为“1”,其余各位将真值的各位取反;
2.按等于号即可得到计算结果。
3.由于本例采用四位二进制数表示的补码,可表示的整数范围为-8~+7,如果
操作数或运算结果超出该范围,运算将出错。
4.如果加数为负数,就相当于被加数减去该数的绝对值,因此相当于做减法。反过来说,做减法,实际上就是被减数的补码加上减数的相反数的补码。而求一个数的相反数的补码的规则是将该数的补码连同符号位按位取反,末位加1。
3.如果真值是“0”,反码有两种表示法,即000…0或111…1,分别表示+0或-0;
4.综上所述,如果把反码看成无符号整数,则真值到反码的转换规则是:
当x≥0时,[x]反=x;当x≤0时,[x]反=2^(n)+x-1(模2^n),“^”表示指数。
C补码
1.如果真值是正数,补码的最高位为“0”,其余各位与真值的对应位相同;
⑶ 给存储器的 00地址单元中写入数据 11,具体操作步骤如下:
如果要对其它地址单元写入内容,方法同上,只是输入的地址和内容不同。
⑷ 读出刚才写入 00地址单元的内容,观察内容是否与写入的一致。具体操作步骤如下
3、调试过程
三.结果
完成实验内容,按照要求验证了实验数据
四.总结
在这次的实验中我们首次用到了试验箱,这要求我们学会连线,在众多接口中找到需要的接口就要求我们有足够的耐心,也更要细心。实验的内容虽然不多,但是在过程中我加深了对静态存储的理解。
运算器组成原理实验报告

运算器组成原理实验报告运算器组成原理实验报告一、引言运算器作为计算机中的重要组成部分,承担着数据处理和运算任务。
本实验旨在通过实际操作,深入了解运算器的组成原理和工作机制。
二、实验目的1. 理解运算器的基本概念和功能。
2. 掌握运算器的组成原理及其实际应用。
3. 学会使用逻辑门电路构建简单的运算器。
三、实验器材与步骤1. 实验器材:- 逻辑门电路芯片(如AND、OR、NOT等);- 运算器实验板;- 连接线等。
2. 实验步骤:1) 连接逻辑门电路芯片到运算器实验板上的相应位置。
2) 根据实验要求,设置逻辑门的输入信号。
3) 运行实验板,观察输出结果。
4) 记录实验数据,并进行分析。
四、实验原理运算器由多个逻辑门电路组成,主要包括加法器、减法器、乘法器和除法器等。
这些逻辑门电路通过接收输入信号并进行逻辑运算,最终输出结果。
1. 加法器加法器是运算器的基本组成部分,用于实现数字的加法运算。
它由多个逻辑门电路组成,其中包括半加器和全加器。
半加器用于实现两个数字的个位相加,全加器则用于实现多位数的相加。
2. 减法器减法器是运算器的另一个重要组成部分,用于实现数字的减法运算。
它通过将减法转化为加法运算来实现。
减法器的输入包括被减数、减数和借位,输出为差值。
3. 乘法器乘法器用于实现数字的乘法运算。
它通过多次的加法运算来实现乘法。
乘法器的输入包括被乘数和乘数,输出为积。
4. 除法器除法器用于实现数字的除法运算。
它通过多次的减法运算来实现除法。
除法器的输入包括被除数和除数,输出为商和余数。
五、实验结果与分析根据实验步骤进行操作后,我们观察到运算器实验板上的LED显示屏显示出了正确的运算结果。
通过分析实验数据,我们得出了以下结论:1. 运算器能够正确地进行加法、减法、乘法和除法运算,验证了其组成原理的正确性。
2. 运算器的性能受到逻辑门电路的质量和连接线的稳定性等因素的影响。
在实际应用中,需要保证这些因素的稳定性和可靠性,以确保运算器的正常工作。
32位浮点加法器设计[整理版]
![32位浮点加法器设计[整理版]](https://img.taocdn.com/s3/m/c6464a9e2af90242a895e5f9.png)
32位浮点加法器设计
苦行僧宫城
摘要:运算器的浮点数能够提供较大的表示精度和较大的动态表示范围,浮点 运算已成为现代计算程序中
不可缺少的部分。浮点加法运算是浮点运算中使用频率最高的运算。因此,浮 点加法器的性能影响着整个
CPU勺浮点处理能力。文中基于浮点加法的原理,采用Verilog硬件描述语言
设计32位单精度浮点数加法
f)规格化移位:对尾数加减结果进行移位,消除尾数的非有效位,使其最高位为
1。Байду номын сангаас
g)舍入:有限精度浮点表示需要将规格化后的尾数舍入到固定结果。 由以上 基本算法可见,它包含2个全长的移位即对阶移位和规格化移位,还要包括3个全 长的有效加法,即步骤c、d、g。由此可见,基本算法将会有很大的时延。
2 32位浮点加法器设计与实现
器,并用modelsim对浮点加法器进行仿真分析,从而验证设计的正确性和可 行性。
关键词:浮点运算 浮点加法器Verilog硬件描述语言
Studying on Relation of Technology and Civilization苦行僧宫城
(School of Mechatronic Engineering and Automation, Shanghai
University, Shanghai,China)
Abstract: The floating-point arithmetic provides greater precision and greater dynamic representation indication range, with floating point calculations have become an indispensable part of the program.Floatingpoint adder is the most frequently used floating point arithmetic. Therefore, the performance of floating point adder affecting the entire CPU floating point processing capabilities. In this paper the principlebased floating-point addition, Verilog hardware description language
计算机浮点运算详解深入学习计算机组成原理

深入剖析浮点运算性能优化
04
策略
减少不必要的数据转换和传输延迟
数据重用
避免不必要的数据类型转换
尽量保持数据在运算过程中的类型一致,避免频繁 进行数据类型转换,以减少转换带来的性能开销。
通过缓存最近使用过的数据,减少从主存中 加载数据的次数,从而降低数据传输延迟。
优化数据布局
合理安排数据在内存中的布局,使得访问局 部性更好,减少缓存失效和页面换入换出的 次数。
性能问题
浮点运算通常比整数运算更复杂,需要更多的CPU周期和内存带宽。这可能导致性能瓶颈,特别是在需要大量浮点运 算的应用中。
兼容性问题
不同的计算机系统和编程语言可能采用不同的浮点表示方法和运算规则,这可能导致兼容性问题。例如, 一个系统上的计算结果可能在另一个系统上无法重现。
未来发展趋势预测及建议
• 精度提升:随着计算机硬件和算法的不断进步,未来浮点运算的精度将得到进 一步提升。例如,采用更高精度的浮点数表示方法和更精确的运算算法。
• 性能优化:为了提高浮点运算的性能,未来可能会采用更高效的硬件设计、并 行计算技术和优化算法。例如,利用GPU和TPU等专用硬件加速浮点运算, 以及采用分布式计算等技术提高大规模浮点运算的效率。
进行实验和编程实践
通过编写程序和使用相关工具 进行实验,加深对浮点数运算 的理解和掌握程度。
THANKS
感谢观看
数值积分与微分
利用浮点运算进行数值积分和微 分,可以求解函数的定积分、不 定积分、导数等。
图形图像处理领域应用
01
3D图形变换
02
03
图像滤波与处理
计算机视觉
在3D图形处理中,浮点运算用于 实现各种复杂的图形变换,如旋 转、缩放、平移等。
32位浮点加法器设计

32位浮点加法器设计苦行僧宫城摘要:运算器的浮点数能够提供较大的表示精度和较大的动态表示范围,浮点运算已成为现代计算程序中不可缺少的部分。
浮点加法运算是浮点运算中使用频率最高的运算。
因此,浮点加法器的性能影响着整个CPU的浮点处理能力。
文中基于浮点加法的原理,采用Verilog硬件描述语言设计32位单精度浮点数加法器,并用modelsim对浮点加法器进行仿真分析,从而验证设计的正确性和可行性。
关键词:浮点运算浮点加法器 Verilog硬件描述语言Studying on Relation of Technology and Civilization苦行僧宫城(School of Mechatronic Engineering and Automation, Shanghai University, Shanghai , China) Abstract: The floating-point arithmetic provides greater precision and greater dynamic representation indication range, with floating point calculations have become an indispensable part of the program. Floating-point adder is the most frequently used floating point arithmetic. Therefore, the performance of floating point adder affecting the entire CPU floating point processing capabilities. In this paper the principle-based floating-point addition, Verilog hardware description language design 32-bit single-precision floating-point adder and floating-point adder using modelsim simulation analysis in order to verify the correctness and feasibility of the desig小组成员及任务分配:1浮点数和浮点运算1.1浮点数浮点数是属于有理数中某特定子集的数的数字表示,在计算机中用以近似表示任意某个实数。
浮点数的加法减法运算

2.6.1 浮点加法、减法运算
•浮点数的加法、减法运算
设有两个浮点数的分别为X=Mx*2Ex,Y=My*2Ey, 实现浮点加减法算的基本步骤分为四步完成:
0操作数检查:用来判断两个操作数中是否有一 个为0.
对阶操作:即比较两个浮点数的阶码值的大小 ,求E=Ex-Ey,然后将小阶对大阶。
阶码大的数对齐;
若△E=0,表示两数阶码相等,即Ex=Ey; 若△E>0,表示Ex>Ey; 若△E<0,表示Ex>Ey。 当Ex≠Ey 时,要通过尾数的移动以改变Ex或Ey
,使之相等。
解:浮点表示为: [X]浮= 00 010,0. 11011011 [Y]浮= 00 100,1. 01010100
规则:尾数右移1位,阶码加1
(2)结果是00.0..01.....或11.1...10...时,则向左规 格化
规则:尾数左移1位,阶码减1,直到规格化
右规,阶码加1,左规,阶码减1
例子中左规为11.00010101(10),阶码减1为00011
练习:01.1101
10.0001
2.6 浮点运算方法和浮点运算器
2.6.1 浮点加法、减法运算 2.6.2 浮点乘法、除法运算 2.6.3 浮点运算流水线 2.6.4 浮点运算器实例
2.6.1 浮点加法、减法运算
1、浮点加减运算
设有两个浮点数x和y,它们分别为 x=2Ex·Mx y=2Ey·My
其中Ex和Ey分别为数x和y的阶码,Mx和My为 数x和y的尾数。两浮点数进行加法和减法的运算规 则是
0操作数检查 阶码加减操作 尾数乘除操作 结果规格化和舍入处理
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
沈阳航空航天大学课程设计报告课程设计名称:计算机组成原理课程设计课程设计题目:浮点数加法器院(系):计算机学院专业:计算机科学和技术班级:学号:姓名:指导教师:完成日期:目录第1章总体设计方案 (1)1.1设计原理 (1)1.2设计思路 (1)1.3设计环境 (2)1.3.1 硬件环境 (2)1.3.2 EDA环境 (2)第2章详细设计方案 (3)2.1总体方案的设计和实现 (3)2.2功能模块的设计和实现 (4)2.2.1 原补转换模块的设计和实现 (4)2.2.2 阶码选择模块的设计和实现 (6)2.2.3 数值选择模块的设计和实现 (8)2.2.4 数据移位模块的设计和实现 (10)2.2.5 加法模块的设计和实现 (13)2.3总电路仿真测试 (15)第3章编程下载和硬件测试 (18)3.1编程下载 (18)3.2硬件测试及结果分析 (18)参考文献 (20)附录 (21)第1章总体设计方案1.1 设计原理本次课程设计的题目为浮点数加法器的设计,使用Xilinx Foundation F3.1可编程器件开发工具软件,以及伟福COP2000试验箱实现目的设计。
具体要求为必须用基本逻辑门实现,浮点数的长度固定。
根据所学可知,浮点数共由两部分组成。
第一部分是阶码,第二部分是数据。
这两部分又分别分为两部分。
阶码由阶符和数值组成,数据由数符和数字组成。
由于在计算机的存储和运算中,数据由补码表示。
故首先应将输入的原码转化为补码。
在此过程中,正数保持不变,负数则对除符号位以外的各位按位取反,再进行加1操作。
然后对两数的阶码进行运算,决定移位的次数和结果的阶码。
在移位时,对正数进行补0操作,对负数则进行补1操作。
再对移位后的数据视为定点数进行相加运算。
进而实现浮点数相加的功能。
最后再将得到的结果转化为原码,进行输出。
1.2设计思路按照课设题目要求及原理图,先设计出电路的具体模块图,浮点数加法器的设计共包含如下五个模块:①原补转换模块②阶码选择模块③数值选择模块④数据移位模块⑤超前进位加法模块在五个部分中分别设计实现相应功能的器件,包括二选一数据选择器等。
在连接具体电路时配合门电路以达到预期效果。
浮点数加法器的底层、顶层的设计都采用原理图设计输入方式,经编译、调试后形成zyks.bit文件并下载到XCV200可编程逻辑芯片中,经硬件测试验证设计的正确性。
1.3设计环境1.3.1 硬件环境•伟福COP2000型计算机组成原理实验仪COP2000计算机组成原理实验系统由实验平台、开关电源、软件三大部分组成实验平台上有寄存器组R0-R3、运算单元、累加器A、暂存器B、直通/左移/右移单元、地址寄存器、程序计数器、堆栈、中断源、输入/输出单元、存储器单元、微地址寄存器、指令寄存器、微程序控制器、组合逻辑控制器、扩展座、总线插孔区、微动开关/指示灯、逻辑笔、脉冲源、20个按键、字符式LCD、RS232口。
系统在实验时即使不借助PC 机,也可实时监控数据流状态及正确和否, 实验系统的软硬件对用户的实验设计具有完全的开放特性,系统提供了微程序控制器和组合逻辑控制器两种控制器方式,系统还支持手动方式、联机方式、模拟方式三种工作方式,系统具备完善的寻址方式、指令系统和强大的模拟调试功能。
1.3.2 EDA环境•Xilinx foundation f3.1设计软件Xilinx foundation f3.1是Xilinx公司的可编程期间开发工具,该平台功能强大,主要用于百万逻辑门设计。
该系统由设计入口工具、设计实现工具、设计验证工具三大部分组成。
设计入口工具用于接收各种图形或文字的设计输入,并最终生成网络表文件。
设计实现工具用于将网络表转化为配置比特流,并下载到器件。
设计验证工具用来对设计中的逻辑关系及输出结果进行检验,并分析各个时序限制的满足情况。
•COP2000集成调试软件COP2000集成开发环境是为COP2000实验仪和PC机相连进行高层次实验的配套软件,它通过实验仪的串行接口和PC机的串行接口相连,提供汇编、反汇编、编辑、修改指令、文件传送、调试FPGA实验等功能,该软件在Windows 下运行。
第2章详细设计方案2.1 总体方案的设计和实现本课设要求控制信号可以采用外部开关输入或用VHDL语言编写的控制器输出的控制信号,其他部分可以调用系统资源库中的器件;必须用基本的逻辑门实现,然后封装。
通过设计和分析,将本次设计分为五个模块来实现。
原补转换模块用于整个过程中的原补转换。
如将输入的原码转换为补码。
阶码选择模块用于选择结果的阶码。
数值选择模块用于选择需要移位的数据并将其传送给移位器。
数据移位模块用于将需要移位的数据进行移位并将其传送给加法器进行相加运算。
超前进位加法模块用于过程的各种计算。
例如补码的相减和数据的相加。
本次实验逻辑层次分明,共分为六个层次,分别完成输入的原补转换,移位次数的计算,数据选择,数据移位,数据相加计算及最后结果的输出。
其总体设计框图如图2.1所示。
补码转为原码并输出数据相加数据移位数据选择两阶码相减决定移位次数及结果阶码原码输入并求补码图2.1 浮点数加法器整体设计框图2.2功能模块的设计和实现2.2.1 原补转换模块的设计和实现2.2.1.1功能描述由于在计算机内部数据的存储以及运算是以补码的方式进行,因此首先我们应将输入的原码转换为补码。
对于正数(带符号位)来说,其原码、补码一致。
对于负数(带符号位)来说,其反码为符号位不变,其余各位按位取反(即反码)后末位加1。
故对原补转换模块来说,其功能为将输入的原码转化为补码。
其输入为原始数据的原码,输出为供以后继运算的补码。
2.2.1.2电路图正数的符号位为0,负数的符号位为1,故如将符号位和数据位进行异或运算,即可获得反码。
而对于正数原码、反码、补码相同。
而负数的补码则为反码加1,加1操作可由数据位的末位和上符号位产生,经由和门逐级传递进位。
并且由于正数的符号位为0,该逻辑对正数无影响。
其电路图如图2.2所示。
图2.2 原补转换电路封装图如图2.3所示。
图2.3 原补转换芯片封装外观图2.2.1.3功能仿真输入数据输出数据1,10010111010 1,0,10010111010 0,100101110101, 1,100101101010, 0,测试数据如表2.1所示。
图2.4 原补转换电路测试图仿真图说明:图2.4中,红线所示数据输入为1,10010111010,其真实输出为1,。
蓝线所示数据输入为0,,其真实输出为0,。
从仿真结果分析,对于给定的例子,其输出和预想的输出完全一致,说明电路的实现符合设计要求。
2.2.2 阶码选择模块的设计和实现2.2.2.1功能描述对于浮点数来说,在运算时需要进行对阶操作,然后选择较大的阶码作为输出结果的阶码,并且对阶码较小的数字的补码进行移位操作。
故阶码选择模块的输入和输出均为阶码的补码。
其功能为对阶码进行选择。
2.2.2.2电路图在阶码选择电路中,我们采用了二选一数据选择器。
它包括一个控制端S0,两个数据输入端D0,D1及一个数据输出端O。
其真值表如表2.2:表2.2 二选一数据选择器真值表控制端S0 输入端D0 输入端D1 输出端O0 0 X 00 1 X 11 X 0 01 X 1 1由真值表可看出。
当S0为0时,输出为D0,S0为1时,输出为D1。
故可将两阶码相减之后产生的符号位作为S0的输入信号,被减数的阶码和D0相连,件数的阶码和D1相连,这样就可以实现选择输出。
其电路图如图2.5所示。
图2.5 补码选择电路封装图如图2.6所示。
图2.6 补码选择电路封装效果图2.2.2.3功能仿真表2.3 补码选择电路测试数据COIN(相减符号位)输入阶码1 输入阶码2 输出阶码0 0110 0011 01101 1010 1100 1100测试数据如表2.3所示。
图2.7 补码选择电路测试图仿真图说明:图2.7中,红线所示数据输入C0IN为1,阶码1为1010,阶码2为1100,其真实输出1100。
蓝线所示数据输入COIN为0,阶码1为0110,阶码2为0011,其真实输出为0110。
从仿真结果分析,对于给定的例子,其输出和预想的输出完全一致,说明电路的实现符合设计要求。
2.2.3 数值选择模块的设计和实现2.2.3.1功能描述在对阶过程结束后,需要对阶码较小的数字的补码进行移位操作。
这时便需要对输入的两个数据进行选择,然后再进行移位和相加等操作。
故数值选择模块的输入和输出均为数值的补码。
其功能为对数值进行选择和分流输出。
2.2.3.2电路图在数值选择电路中,我们同样采用了二选一数据选择器。
但此时,输出由原来的4位更改为了8位,即输入的两组数值均要进行输出。
其中,高四位为需要进行移位的数据,低四位为不需要进行移位的数据。
此时的COIN(和数据选择器的控制端S0相连)仍为两阶码相减之后产生的符号位。
被减数连至A23-A20,减数连至A13-A10。
其电路图如图2.8所示。
图2.8 数值选择器电路图封装图如图2.9所示。
图2.9 数值选择电路封装效果图2.2.3.3功能仿真COIN(相减符号位)输入数值1 输入数值2 输出数值0 0110 0011 0110,00111 1010 1100 1100,1010测试数据如表2.4所示。
图2.10 数值选择电路测试图仿真图说明:图2.10中,红线所示数据输入C0IN为1,数值1为1010,数值2为1100,其真实输出11001010。
蓝线所示数据输入COIN为0,数值1为0110,数值2为0011,其真实输出为01100011。
从仿真结果分析,对于给定的例子,其输出和预想的输出完全一致,说明电路的实现符合设计要求。
2.2.4 数据移位模块的设计和实现2.2.4.1功能描述经过对阶过程和数据选择过程后,我们得到了移位的次数和待移位的数据,接下来则需要用数据移位模块对数据进行移位操作。
故数据移位模块的输入为待移位的数据(补码)和移位次数(原码),输出为移位后的数据(补码)。
其功能为对数据进行移位和输出。
2.2.4.2电路图根据计算机中数据存储的特点可知S2,S1,S0的位权分别为4,2,1。
即若S2为1,数据需右移四位,S1为1,数据需右移两位,S0为1,数据需右移一位。
另根据数据补位的原则可知,如原数据为正数则补0,为负数则补1。
故当S0为控制信号时,可在相邻两位间用二选一数据选择器相连,当S0为1时输出高位,S0为0时输出低位。
本级的输出用以作为当S1为控制信号时的输入。
当S1为控制信号时,每隔一位进行选择。
同理S2为控制信号时,每隔三位进行选择。
而对于补位来说,则由符号位和数据位进行数据选择得到。
S0为控制信号时符号位仅和最高位相和,S1为控制信号时符号位和最高两位相和,S3时则为最高四位。
